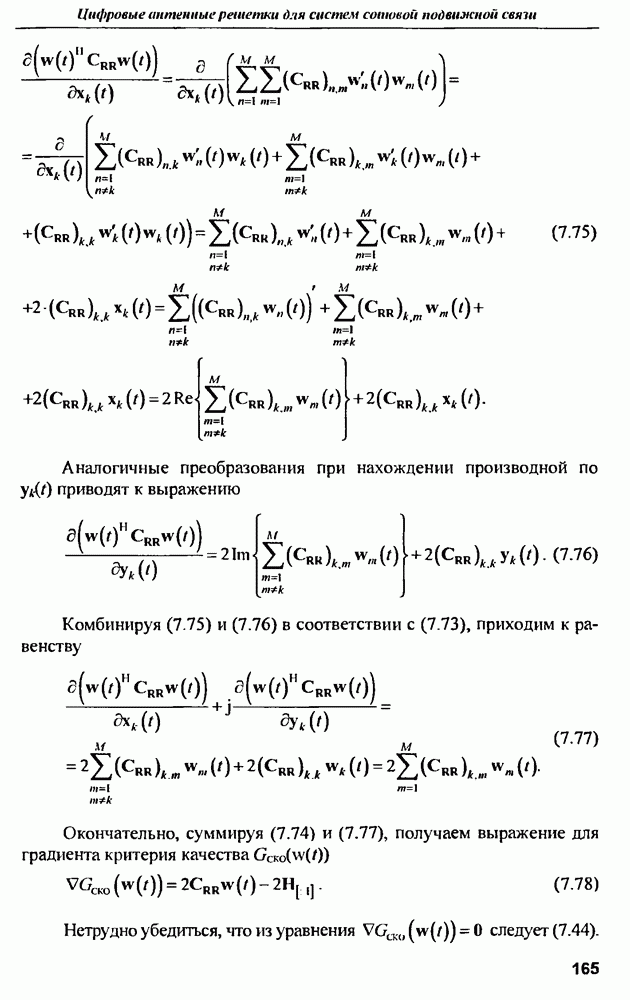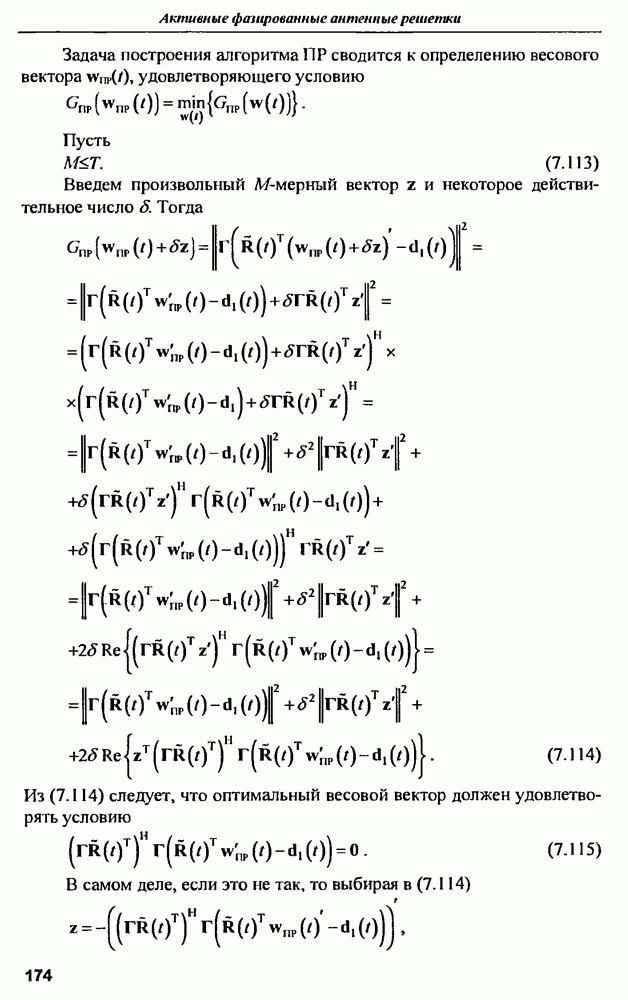| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.2.3. Алгоритмы адаптации ИА
Классификация алгоритмов. В реальных условиях работы  передаточная матрица канала
передаточная матрица канала  следовательно, корреляционная матрица
следовательно, корреляционная матрица  а также вектор взаимной корреляции
а также вектор взаимной корреляции  непрерывно изменяются. Как следствиие,
непрерывно изменяются. Как следствиие,  вынуждена постоянно адаптировать значение оптимального весового вектора (7.44) к новым условиям распространения сигнала и помех. Алгоритмы, позволяющие отслеживать изменения в условиях функционирования
вынуждена постоянно адаптировать значение оптимального весового вектора (7.44) к новым условиям распространения сигнала и помех. Алгоритмы, позволяющие отслеживать изменения в условиях функционирования  и согласовывать с ними значение весового вектора называются алгоритмами адаптации.
и согласовывать с ними значение весового вектора называются алгоритмами адаптации.
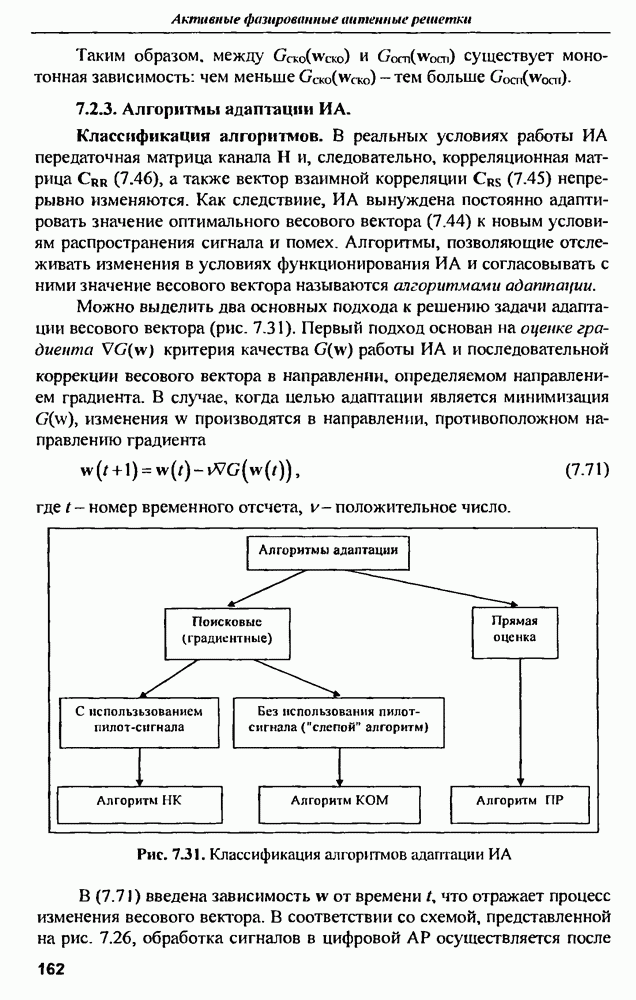
Можно выделить два основных подхода к решению задачи адаптации весового вектора (рис. 7.31) Первый подход основан на оценке градиента  критерия качества
критерия качества  работы
работы  и последовательной коррекции весового вектора в направлении, определяемом направлением градиента. В случае, когда целью адаптации является минимизация
и последовательной коррекции весового вектора в направлении, определяемом направлением градиента. В случае, когда целью адаптации является минимизация  изменения
изменения  производятся в направлении, противоположном направлению градиента
производятся в направлении, противоположном направлению градиента

где  номер временного отсчета,
номер временного отсчета,  положительное число.
положительное число.

Рис. 7.31. Классификация алгоритмов адаптации 
В (7.71) введена зависимость  от времени
от времени  что отражает процесс изменения весового вектора. В соответствии со схемой, представленной на рис. 7.26, обработка сигналов в цифровой
что отражает процесс изменения весового вектора. В соответствии со схемой, представленной на рис. 7.26, обработка сигналов в цифровой  осуществляется после
осуществляется после
АЦП, поэтому входными данными алгоритма адаптации служат отсчеты сигналов, взятые в дискретные моменты времени. При анализе алгоритмов адаптации частота дискретизации не играет принципиальной роли и может быть принята равной единице [6].
К градиентным алгоритмам адаптации относится алгоритм наименьших квадратов  основанный на применении критерия
основанный на применении критерия  так называемые, «слепые» алгоритмы адаптации, среди которых наиболее распространенным является алгоритм адаптации, построенный на базе критерия квадрата отклонения модуля
так называемые, «слепые» алгоритмы адаптации, среди которых наиболее распространенным является алгоритм адаптации, построенный на базе критерия квадрата отклонения модуля  [4]:
[4]:

В отличие от критерия СКО, критерий  позволяет оценивать градиент без использования пилот-сигнала, т.е. «вслепую».
позволяет оценивать градиент без использования пилот-сигнала, т.е. «вслепую».
Второй тип алгоритмов адаптации основан на прямой оценке корреляционной матрицы  и непосредственном вычислении оптимального весового вектора с помощью (7.44). Наиболее известным алгоритмом прямой оценки является алгоритм последовательной регрессии
и непосредственном вычислении оптимального весового вектора с помощью (7.44). Наиболее известным алгоритмом прямой оценки является алгоритм последовательной регрессии  [6]
[6]
При использовании алгоритмов адаптации, подразумевающих применение обучающих последовательностей или пилот-сигналов, необходима временная синхронизация по задержке генератора копии пилот-сигнала в  с пилот-сигналом, передаваемым
с пилот-сигналом, передаваемым  Работа схемы синхронизации основана на вычислении корреляции сигнала
Работа схемы синхронизации основана на вычислении корреляции сигнала  генератора
генератора  с временной задержкой
с временной задержкой  и выходного сигнала И А
и выходного сигнала И А

Учитывая, что выходной сигнал  содержит пилот-сигнал, принятый от
содержит пилот-сигнал, принятый от  значение
значение  при котором
при котором  достигает максимума, считается моментом прихода пилот-сигнала на
достигает максимума, считается моментом прихода пилот-сигнала на  и определяет временную задержку генератора копии пилот-сигнала.
и определяет временную задержку генератора копии пилот-сигнала.
Алгоритмы градиентного поиска.
Алгоритм наименьших квадратов. Алгоритм  относится к типу градиентных алгоритмов адаптации и основан на применении критерия
относится к типу градиентных алгоритмов адаптации и основан на применении критерия  Его реализация требует вычисления градиента
Его реализация требует вычисления градиента  [6]
[6]
Пусть векторы х и у представляют, соответственно, действительную и мнимую части весового вектора

 является действительной функцией комплексного аргумента. Следуя [4], для такой функцни можно определить градиент в виде комплексного вектора
является действительной функцией комплексного аргумента. Следуя [4], для такой функцни можно определить градиент в виде комплексного вектора

Частные производные действительной функции  по
по  в (7.73) являются действительными числами. Использование комплексной единицы
в (7.73) являются действительными числами. Использование комплексной единицы  в (7.73) позволяет их разделить так, что только одновременное обращение в ноль как производных по
в (7.73) позволяет их разделить так, что только одновременное обращение в ноль как производных по  так и по
так и по  соответствует нулю
соответствует нулю 
Очевидно, что частные производные первого слагаемого в (7.53) равны нулю. Для частных производных второго слагаемого получаем выражения

В соответствии с (7.73),

Частные производные последнего слагаемого в (7.53) по  определяются следующим образом:
определяются следующим образом:
(см. скан)
В соответствии с (7.78), для вычисления градиента целевой функции требуются значения  (7.43) и
(7.43) и  которые, в общем случае, оцениваются усреднением величин
которые, в общем случае, оцениваются усреднением величин  по большому числу принимаемых реализаций. В то же время, если выбрать в (7.71) значение
по большому числу принимаемых реализаций. В то же время, если выбрать в (7.71) значение  достаточно маленьким, то усреднение можно производить непосредственно в процессе адаптации весового вектора.
достаточно маленьким, то усреднение можно производить непосредственно в процессе адаптации весового вектора.
Примем в качестве грубых приближений к  и
и  величины, получаемые из текущих реализаций сигнала
величины, получаемые из текущих реализаций сигнала

где  пилот сигнал, соответствующий
пилот сигнал, соответствующий 
Подстановка (7.79) и (7.80) в (7.78), с учетом (7.33), дает

Использование (7.81) в (7.71) приводит к уравнентпо адаптации весового вектора в соответствии с алгоритмом 

схема  использующая алгоритм
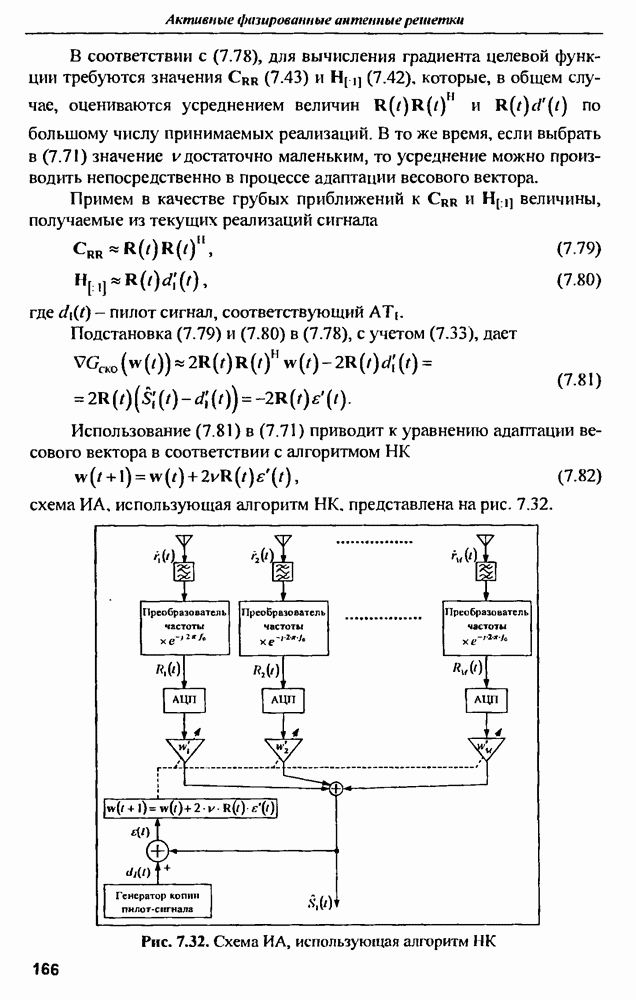
использующая алгоритм  представлена на рис. 7.32.
представлена на рис. 7.32.

Рис. 7.32. Схема  использующая алгоритм
использующая алгоритм 
Коэффициент  в (7.82) существенным образом влияет на характеристики алгоритма адаптации. Слишком маленькое значение
в (7.82) существенным образом влияет на характеристики алгоритма адаптации. Слишком маленькое значение  приводит к низкой скорости адаптации, тогда как большое значение сможет повлечь неустойчивую работу алгоритма, при которой не обеспечивается сходимость к оптимальному значению
приводит к низкой скорости адаптации, тогда как большое значение сможет повлечь неустойчивую работу алгоритма, при которой не обеспечивается сходимость к оптимальному значению 
При анализе влияния величины у на поведение алгоритма адаптации понадобятся некоторые сведения из теории матриц. Пусть  матрица, столбцы которой представлены нормированными собственными векторами корреляционной матрицы
матрица, столбцы которой представлены нормированными собственными векторами корреляционной матрицы  диагональная матрица, составленная из соответствующих собственных
диагональная матрица, составленная из соответствующих собственных  что
что

Верны следующие равенства [11]:

Собственные значения корреляционной матрицы являются действительными неотрицательными числами [6,11], т.е.

Кроме того след  матрицы
матрицы 

равен следу корреляционной матрицы  т.е.
т.е. 

которое показывает, что сумма собственных значений матрицы  равна суммарной мощности реализаций
равна суммарной мощности реализаций  принимаемых элементами
принимаемых элементами 
Определим диапазон значений  при которых процедура адаптации весового вектора сходится. Взятие математического ожидания обоих частей равенства (7.82), с учетом (7.33), дает
при которых процедура адаптации весового вектора сходится. Взятие математического ожидания обоих частей равенства (7.82), с учетом (7.33), дает

а осуществив преобразование последнего выражения, при условии независимости векторов 

(см. скан)
Неравенство (7.97) предоставляет практический способ получения оценки и по измерению мощности принимаемой реализации.
«Слепой» алгоритм адаптации. Функционирование «слепого» алгоритма адаптации основано на использовании свойства принимаемого сигнала, которое известно  и может быть оценено без применения пилот-сигнала. Одним из таких свойств обладают сигналы с постоянной амплитудой. В случае их применения «слепой» алгоритм оценивает модуль принимаемого сигнала и производит адаптацию весового вектора, основываясь на критерии КОМ.
и может быть оценено без применения пилот-сигнала. Одним из таких свойств обладают сигналы с постоянной амплитудой. В случае их применения «слепой» алгоритм оценивает модуль принимаемого сигнала и производит адаптацию весового вектора, основываясь на критерии КОМ.
В общем случае, суперпозицпия полезного сигнала и помех имеет случайную, быстроменяющуюся амплитуду. Если  удается осуществить пространственную режекцию помех, то модуль принимаемого сигнала будет определяться только амплитудой полезного сигнала, т.е. окажется постоянным. Именно к такому результату стремится "слепой" алгоритм адаптации.
удается осуществить пространственную режекцию помех, то модуль принимаемого сигнала будет определяться только амплитудой полезного сигнала, т.е. окажется постоянным. Именно к такому результату стремится "слепой" алгоритм адаптации.
Критерий качества (7.72) функционирования "слепого" алгоритма адаптации можно записать в виде

в этом случае ошибкой при приеме сигнала служит величина

Используя другое представление модуля

из (7.98) получаем:

Результаты вычисления градиента квадратичной функции  отраженные в (7.77), позволяют определить
отраженные в (7.77), позволяют определить

Применяя обозначение

можно записать (7.101) в более компактной форме

Подстановка (7.103) в (7.71) приводит к уравнению адаптации весового вектора при использовании алгоритма 

Как следует из (7.104), алгоритм  относится к типу блочных алгоритмов. Изменение весового вектора происходит с периодом
относится к типу блочных алгоритмов. Изменение весового вектора происходит с периодом  который, в общем случае, больше единицы.
который, в общем случае, больше единицы.
Определим диапазон значений коэффициента  при котором процесс адаптации сходится. Пусть
при котором процесс адаптации сходится. Пусть  матрица собственных векторов
матрица собственных векторов  диагональная матрица соответствующих собственных значений
диагональная матрица соответствующих собственных значений  Изменим систему координат представления вектора
Изменим систему координат представления вектора  введя в рассмотрение векторы
введя в рассмотрение векторы 

Тогда уравнение (7.104) запишется в виде

Умножение обеих частей (7.105) слева на  дает
дает

В случае, если процесс адаптации расходится, вектор  а значит и модуль принимаемого сигнала
а значит и модуль принимаемого сигнала  неконтролируемо растут. В какой-то момент окажется
неконтролируемо растут. В какой-то момент окажется

Нормально функционирующий алгоритм адаптациии должен в этом случае произвести уменьшение компонент весового вектора. При условии (7.107), в соответствии с (7.102)

Матрица (7.108) является эрмитовой с действительными неотрицательными собственными значениями. Поэтому, как следует из (7.106), условием уменьшения компонент весового вектора является неравенство  или ему эквивалентное
или ему эквивалентное 

Учитывая (7.108), условие (7.109) можно записать в форме

Как следует из (7.110), верхняя оценка допустимых значений  изменяется во времени. Таким образом, само значение
изменяется во времени. Таким образом, само значение  также может изменяться с течением времени, от блока к блоку.
также может изменяться с течением времени, от блока к блоку.
Для случая 

уравнение адаптации (7.104) принимает вид

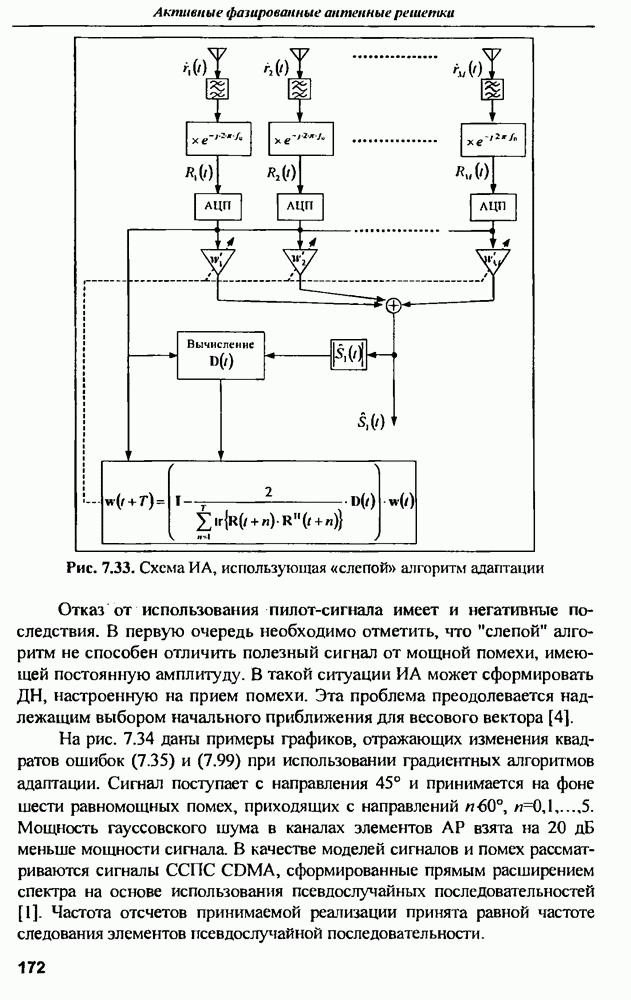
Схема  использующая "слепой" алгоритм адаптации представлена на рис. 7.33.
использующая "слепой" алгоритм адаптации представлена на рис. 7.33.
Рис. 7.33. (см. скан) Схема ИА, использующая «слепой» алгоритм адаптации
Отказ от использования пилот-сигнала имеет и негативные последствия. В первую очередь необходимо отметить, что "слепой" алгоритм не способен отличить полезный сигнал от мощной помехи, имеющей постоянную амплитуду. В такой ситуации  может сформировать
может сформировать  настроенную на прием помехи. Эта проблема преодолевается надлежащим выбором начального приближения для весового вектора [4].
настроенную на прием помехи. Эта проблема преодолевается надлежащим выбором начального приближения для весового вектора [4].
На рис. 7.34 даны примеры графиков, отражающих изменения квадратов ошибок (7.35) и (7 99) при использовании градиентных алгоритмов адаптации. Сигнал поступает с направления 45° и принимается на фоне шести равномощных помех, приходящих с направлений  Мощность гауссовского шума в каналах элементов
Мощность гауссовского шума в каналах элементов  взята на
взята на  меньше мощности сигнала. В качестве моделей сигналов и помех рассматриваются сигналы ССПС CDMA, сформированные прямым расширением спектра на основе использования псевдослучайных последовательностей [1]. Частота отсчетов принимаемой реализации принята равной частоте следования элементов псевдослучайной последовательности.
меньше мощности сигнала. В качестве моделей сигналов и помех рассматриваются сигналы ССПС CDMA, сформированные прямым расширением спектра на основе использования псевдослучайных последовательностей [1]. Частота отсчетов принимаемой реализации принята равной частоте следования элементов псевдослучайной последовательности.
Рис. 7.34. (см. скан) Зависимость квадрата ошибки приема сигнала от времени адаптации для: а - алгоритма НК; б - «слепого» алгоритма
Графики на рис. 7.34 показывают, что время сходимости алгоритма  на порядок меньше времени сходимости «слепого» алгоритма.
на порядок меньше времени сходимости «слепого» алгоритма.
Алгоритм последовательной регрессии. Вывод уравнений регрессии. Работа алгоритма последовательной регрессии  основана на вычислении оптимального весового вектора непосредственно по результатам оценки корреляционной матрицы принимаемой реализации. Вместо критерия СКО, алгоритм
основана на вычислении оптимального весового вектора непосредственно по результатам оценки корреляционной матрицы принимаемой реализации. Вместо критерия СКО, алгоритм  использует критерий качества функционирования, описываемый выражением [12]
использует критерий качества функционирования, описываемый выражением [12] 

где  Критерий (7.111) лучше, чем СКО, подходит для работы
Критерий (7.111) лучше, чем СКО, подходит для работы  в условиях меняющейся передаточной матрицы канала связи. Применение коэффициента
в условиях меняющейся передаточной матрицы канала связи. Применение коэффициента  позволяет управлять «памятью»
позволяет управлять «памятью»  варьируя степень влияния на весовой вектор реализаций, в зависимости от давности их приема.
варьируя степень влияния на весовой вектор реализаций, в зависимости от давности их приема.
Введя обозначения  для матрицы размером
для матрицы размером  со столбцами
со столбцами  а также
а также  для
для  -мерного вектора, составленного из значений пилот-сигнала
-мерного вектора, составленного из значений пилот-сигнала  можно представить в виде
можно представить в виде

где

(см. скан)
получим

и при достаточно малых доказывается

что противоречит предположению об оптимальности вектора  Преобразования (7.115) дают
Преобразования (7.115) дают

Если  имеет полный столбцовый ранг (это верно для случайных сигналов при выполнении (7.113)), то оптимальный весовой вектор может быть найден из выражения
имеет полный столбцовый ранг (это верно для случайных сигналов при выполнении (7.113)), то оптимальный весовой вектор может быть найден из выражения

Выражения в (7.116)

и

представляют собой оценки корреляционной матрицы  и вектора взаимной корреляции
и вектора взаимной корреляции  соответственно.
соответственно.
Таким образом, (7.116) можно записать в виде

Сравнение уравнений (7.119) и (7.44) подчеркивает единство принципов построения алгоритмов  и
и 
При работе алгоритма  в каждый новый временной отсчет изменяется только один столбец матрицы
в каждый новый временной отсчет изменяется только один столбец матрицы  Это наводит на мысль, что вычисление весового вектора
Это наводит на мысль, что вычисление весового вектора  может осуществляться рекурентно, с учетом его предыдущего значения
может осуществляться рекурентно, с учетом его предыдущего значения  .
.
Действительно, (7.117) и (7.118) можно представить в виде
(см. скан)
Применение к (7.129) формулы Шермана-Моррисона-Вудбери [10]:

дает

Начальным приближением для  может служить единичная матрица.
может служить единичная матрица.
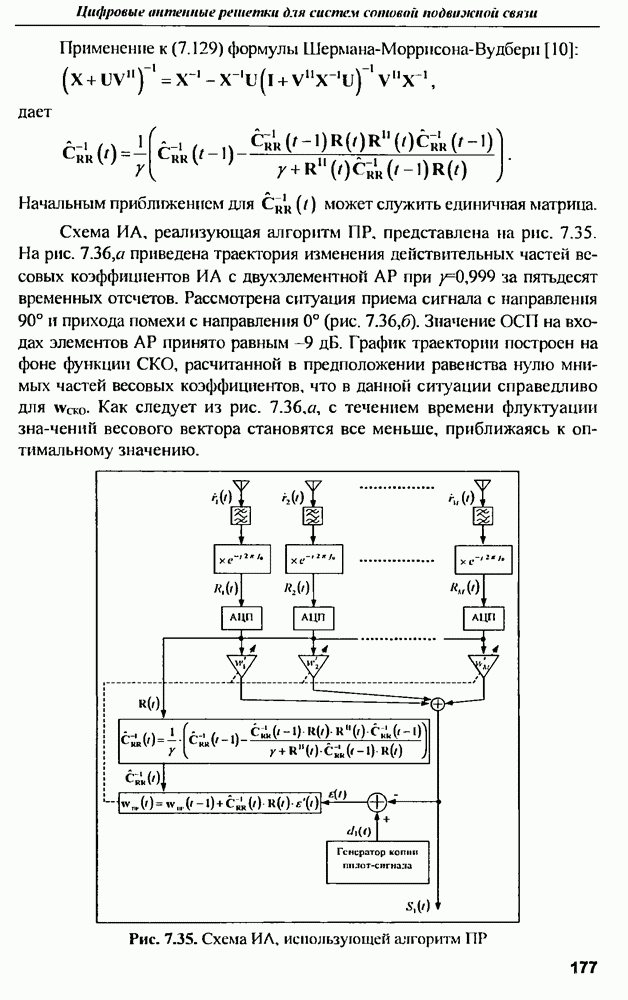
Схема ИА, реализующая алгоритм  представлена на рис. 7.35. На рис. 7.36,а приведена траектория изменения действительных частей весовых коэффициентов
представлена на рис. 7.35. На рис. 7.36,а приведена траектория изменения действительных частей весовых коэффициентов  с двухэлементной
с двухэлементной  при
при  за пятьдесят временных отсчетов. Рассмотрена ситуация приема сигнала с направления 90° и прихода помехи с направления 0° (рис. 7.36,б). Значение ОСП на входах элементов
за пятьдесят временных отсчетов. Рассмотрена ситуация приема сигнала с направления 90° и прихода помехи с направления 0° (рис. 7.36,б). Значение ОСП на входах элементов  принято равным
принято равным  График траектории построен на фоне функции СКО, расчитанной в предположении равенства нулю мнимых частей весовых коэффициентов, что в данной ситуации справедливо для
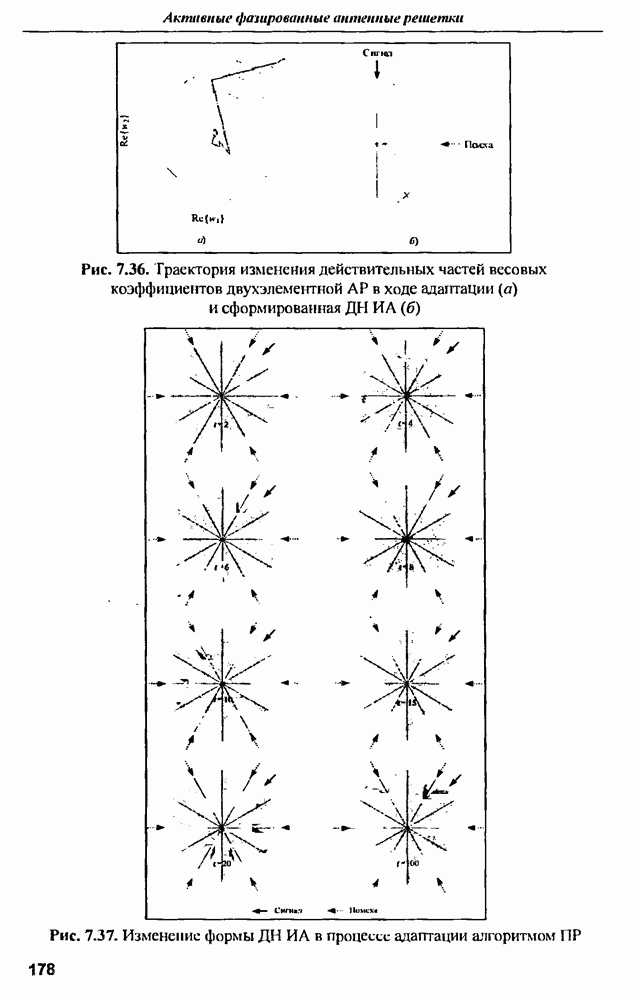
График траектории построен на фоне функции СКО, расчитанной в предположении равенства нулю мнимых частей весовых коэффициентов, что в данной ситуации справедливо для  Как следует из рис. 7.36,а, с течением времени флуктуации значений весового вектора становятся все меньше, приближаясь к оптимальному значению.
Как следует из рис. 7.36,а, с течением времени флуктуации значений весового вектора становятся все меньше, приближаясь к оптимальному значению.

Рис. 7.35. Схема  использующей алгоритм
использующей алгоритм 

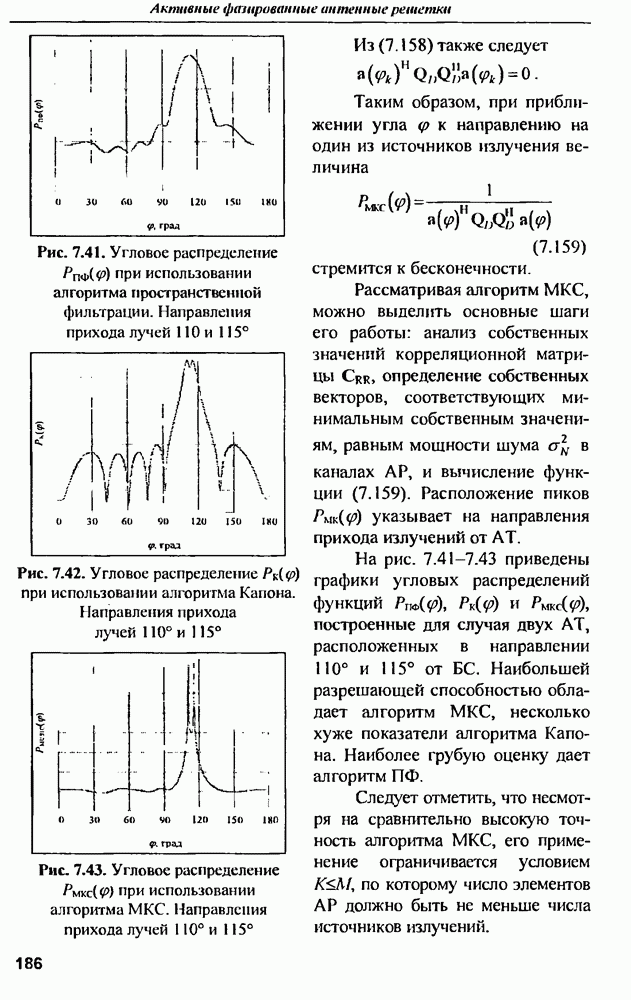
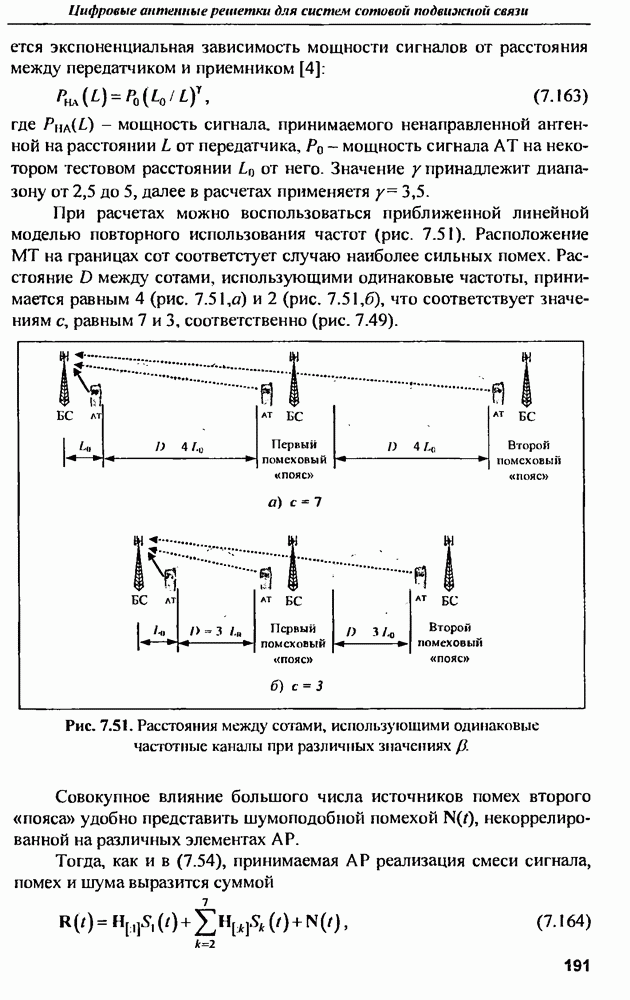
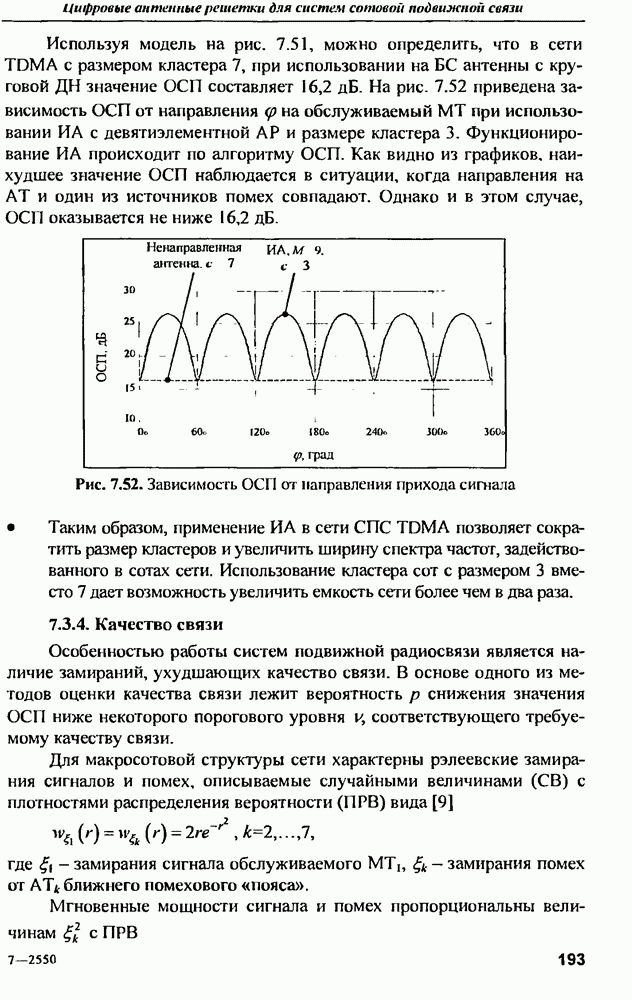
(кликните для просмотра скана)
На рис. 7.37 представлена последовательность  отражающая процесс адаптации с помощью алгоритма
отражающая процесс адаптации с помощью алгоритма  Рассматривается случай семи равномощных излучений, одно из которых, приходящее с направления 45°, соответствует полезному сигналу.
Рассматривается случай семи равномощных излучений, одно из которых, приходящее с направления 45°, соответствует полезному сигналу.
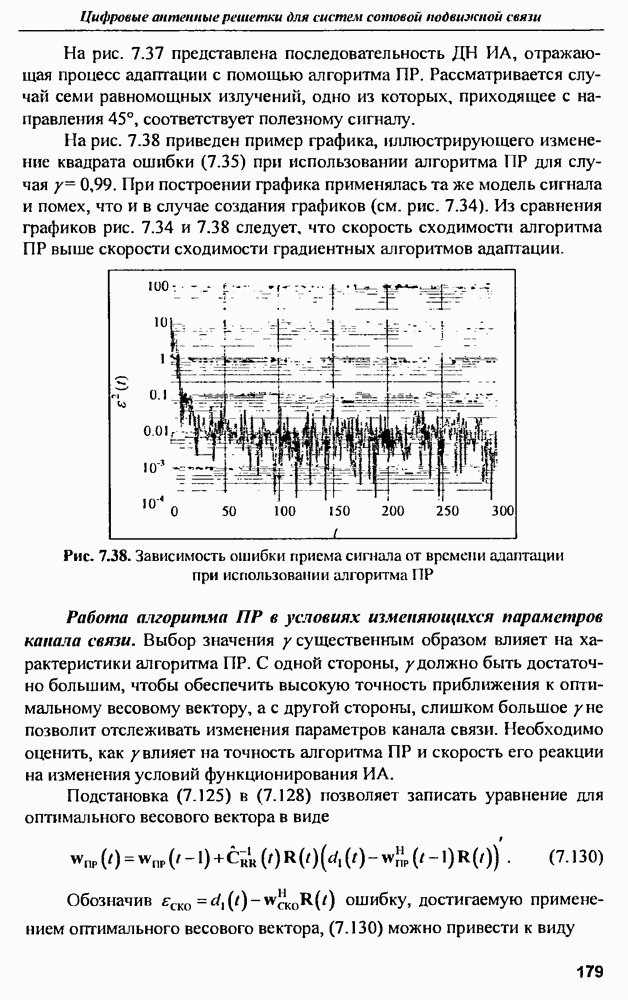
На рис. 7.38 приведен пример графика, иллюстрирующего изменение квадрата ошибки (7.35) при использовании алгоритма  для случая
для случая  При построении графика применялась та же модель сигнала и помех, что и в случае создания графиков (см. рис. 7.34). Из сравнения графиков рис. 7.34 и 7.38 следует, что скорость сходимости алгоритма
При построении графика применялась та же модель сигнала и помех, что и в случае создания графиков (см. рис. 7.34). Из сравнения графиков рис. 7.34 и 7.38 следует, что скорость сходимости алгоритма  выше скорости сходимости градиентных алгоритмов адаптации.
выше скорости сходимости градиентных алгоритмов адаптации.

Рис. 7.38. Зависимость ошибки приема сигнала от времени адаптации при использовании алгоритма 
Работа алгоритма  в условиях изменяющихся параметров канала связи. Выбор значения у существенным образом влияет на характеристики алгоритма ПР. С одной стороны, должно быть достаточно большим, чтобы обеспечить высокую точность приближения к оптимальному весовому вектору, а с другой стороны, слишком большое
в условиях изменяющихся параметров канала связи. Выбор значения у существенным образом влияет на характеристики алгоритма ПР. С одной стороны, должно быть достаточно большим, чтобы обеспечить высокую точность приближения к оптимальному весовому вектору, а с другой стороны, слишком большое  не позволит отслеживать изменения параметров канала связи. Необходимо оценить, как
не позволит отслеживать изменения параметров канала связи. Необходимо оценить, как  влияет на точность алгоритма
влияет на точность алгоритма  и скорость его реакции на изменения условий функционирования
и скорость его реакции на изменения условий функционирования 
Подстановка (7.125) в (7.128) позволяет записать уравнение для оптимального весового вектора в виде

Обозначив  ошибку, достигаемую применением оптимального весового вектора, (7.130) можно привести к виду
ошибку, достигаемую применением оптимального весового вектора, (7.130) можно привести к виду

Правомерно считать, что входные реализации не коррелированны с весовым вектором. Тогда вычитание из левой и правой частей последнего равенства вектора  а также взятие математического ожидания от обеих частей равенства с использованием обозначения
а также взятие математического ожидания от обеих частей равенства с использованием обозначения  дают
дают

При значениях у, близких к единице, величина  статистически не зависит ни от реализации
статистически не зависит ни от реализации  ни от ошибки
ни от ошибки  Кроме того,
Кроме того,  некоррелированны (п.п. 7.2.2.2). Отсюда следует, что второе слагаемое в правой части (7.131) равно нулю и
некоррелированны (п.п. 7.2.2.2). Отсюда следует, что второе слагаемое в правой части (7.131) равно нулю и

Принимая во внимание, что  выражение (7.120) можно представить суммой
выражение (7.120) можно представить суммой

где  некоторая Эрмитова матрица, с достаточно малыми по модулю элементами, математическое ожидание которой равно нулю
некоторая Эрмитова матрица, с достаточно малыми по модулю элементами, математическое ожидание которой равно нулю

Для обратной матрицы (7.133) верно приближенное равенство [13]

Вычисление математического ожидания (7.135) с учетом (7.134) приводит к соотношению

Подстановка (7.133) в (7.132), с учетом (7.136), позволяет получить рекурентное уравнение

решением которого служит

Как следует из (7.138), в процессе адаптации с помощью алгоритма  среднее отклонение весового вектора от оптимального по критерию СКО-вектора стремится к нулю.
среднее отклонение весового вектора от оптимального по критерию СКО-вектора стремится к нулю.
Число итераций  , необходимое для уменьшения
, необходимое для уменьшения  раз, называется временем сходимости процесса адаптации и вычисляется по формуле
раз, называется временем сходимости процесса адаптации и вычисляется по формуле

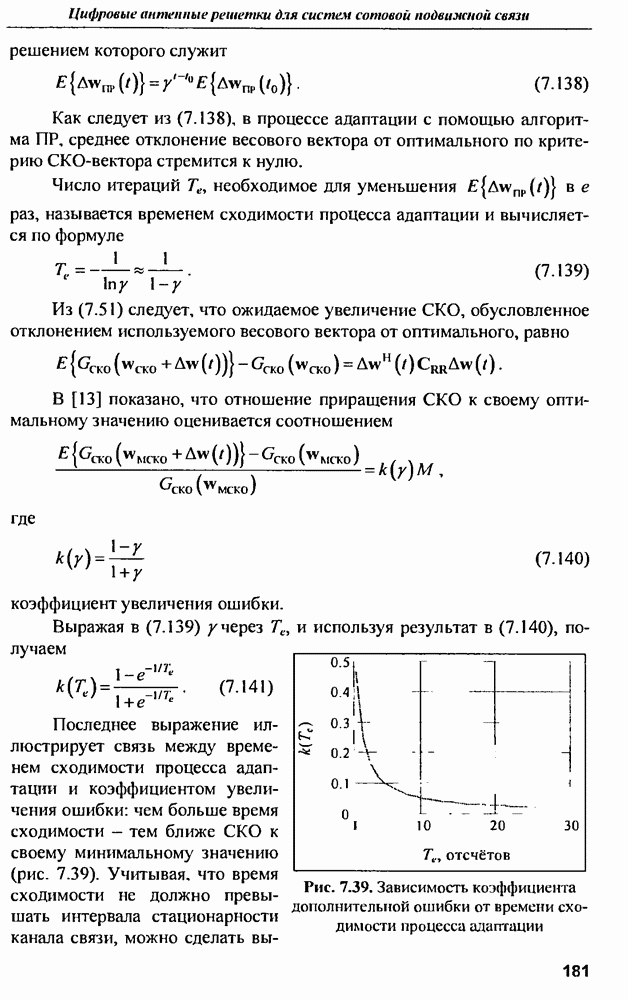
Из (7.51) следует, что ожидаемое увеличение СКО, обусловленное отклонением используемого весового вектора от оптимального, равно

В [13] показано, что отношение приращения СКО к своему оптимальному значению оценивается соотношением

где

коэффициент увеличения ошибки.
Выражая в (7.139)  через
через  , и используя результат в (7.140), получаем
, и используя результат в (7.140), получаем


Рис. 7.39. Зависимость коэффициента дополнительной ошибки от времени сходимости процесса адаптации
Последнее выражение иллюстрирует связь между временем сходимости процесса адаптации и коэффициентом увеличения ошибки: чем больше время сходимости — тем ближе СКО к своему минимальному значению (рис. 7.39). Учитывая, что время сходимости не должно превышать интервала стационарности канала связи, можно сделать вывод
об ухудшении характеристик алгоритма адаптации в реальных условиях работы ИА по сравнению с оптимальным алгоритмом.
Пусть отсчеты принимаемой реализации берутся с периодом  где
где  ширина спектра сигнала. Тогда число отсчетов за интервал стационарности канала
ширина спектра сигнала. Тогда число отсчетов за интервал стационарности канала  равно
равно

В соответствии с [14],  может быть найдено из соотношения
может быть найдено из соотношения

где  доплеровский спектр сигнала [14]
доплеровский спектр сигнала [14]

 скорость перемещения
скорость перемещения  длина волны несущей,
длина волны несущей,  частота несущей, с - скорость распространения ЭМВ.
частота несущей, с - скорость распространения ЭМВ.
Подстановка (7.144) в (7.143) и далее в (7.142) приводит к равенству

из которого следует, что число отсчетов принимаемой реализации, взятых за интервал стационарности канала, обратно пропорционально скорости перемещения  Учитывая (7.141), можно сделать вывод, что чем выше скорость перемещения
Учитывая (7.141), можно сделать вывод, что чем выше скорость перемещения  тем больше коэффициент дополнительной ошибки при работе
тем больше коэффициент дополнительной ошибки при работе 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. Особенности построения активной фазированной антенной решетки для радиоэлектронных комплексов
- 1.2. Особенности расчета характеристик АФАР
- 1.3. Приемопередающий модуль АФАР
- 1.4. Активные приборы, используемые в модулях современных АФАР
- 1.5. Состояние и перспективы развития ППМ
- 1.5.2. Параметры и конструкции типичных модулей АФАР
- ГЛАВА 2. Активная передающая ФАР современной твердотельной РЛС
- 2.2. Особенности энергетики АФАР
- 2.3. Расчет прямых потерь мощности в АФАР
- 2.4. Расчет потерь мощности в АФАР за счет ошибок распределения
- 2.5. АФАР твердотельной РЛС 67Н6Е
- ГЛАВА 3. Антенные комплексы для РЛС дальнего обнаружения и контроля космического пространства
- 3.2. Антенные комплексы РЛС «Дунай-3» и «Дунай-3У»
- 3.3. Приемопередающая ФАР для РЛС наблюдения за космическими объектами
- 3.4. Антенный комплекс РЛС дальнего обнаружения «Волга»
- 3.5. Приемопередающее антенно-фидерное устройство РЛС сантиметрового диапазона
- 3.6. Антенные комплексы для перспективных РЛС дальнего обнаружения «Воронеж-ДМ»
- ГЛАВА 4. Цифровая интеллектуальная ФАР — перспективная технология для радиолокационных и радиоинформационных комплексов XXI века
- 4.1. Преимущества адаптивной цифровой ФАР
- 4.2. Структура ЦИФАР и ее основные алгоритмы обработки сигналов
- 4.3. Требования к частоте дискретизации и уровням квантования сигналов в ЦИФАР
- 4.4. Требования к производительности цифровых вычислителен ЦИФАР
- 4.5. Пример реализации ЦИФАР для перспективной крупноапертурной крупномодульной широкополосной РЛС в диапазонах 10—20 см
- 4.6. Пример построения ЦИФАР для бортового ретранслятора в диапазоне частот 8 ГГц перспективной спутниковой телекоммуникационной системы высокоскоростной мобильной связи «Ростелесат»
- ГЛАВА 5. Многофункциональная бортовая активная фазированная антенная решетка для РЛС
- 5.2. Формулировка задач
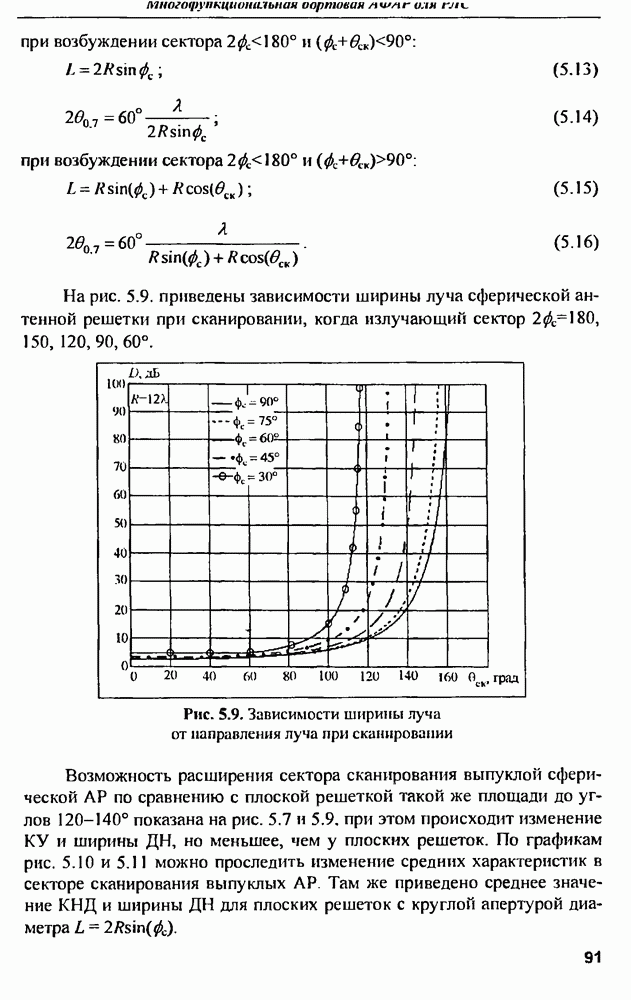
- 5.3. Решение внешней задачи для сферической решетки
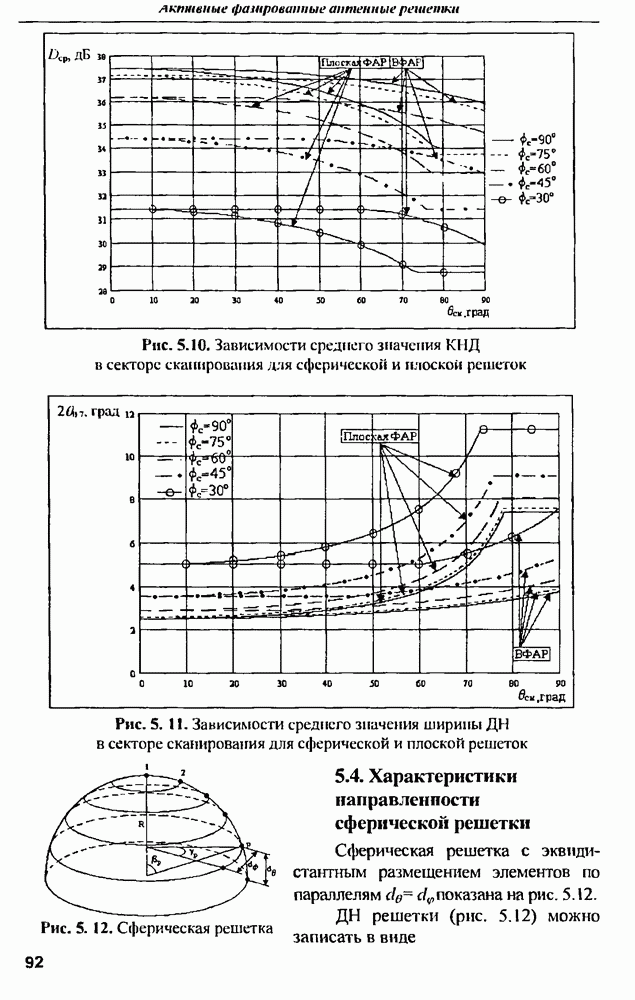
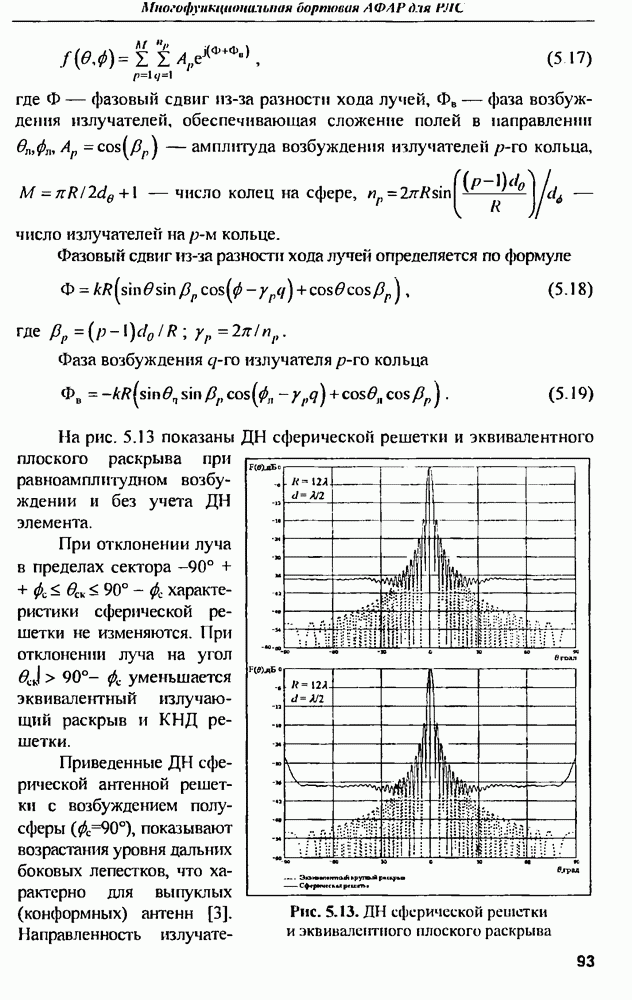
- 5.4. Характеристики направленности сферической решетки
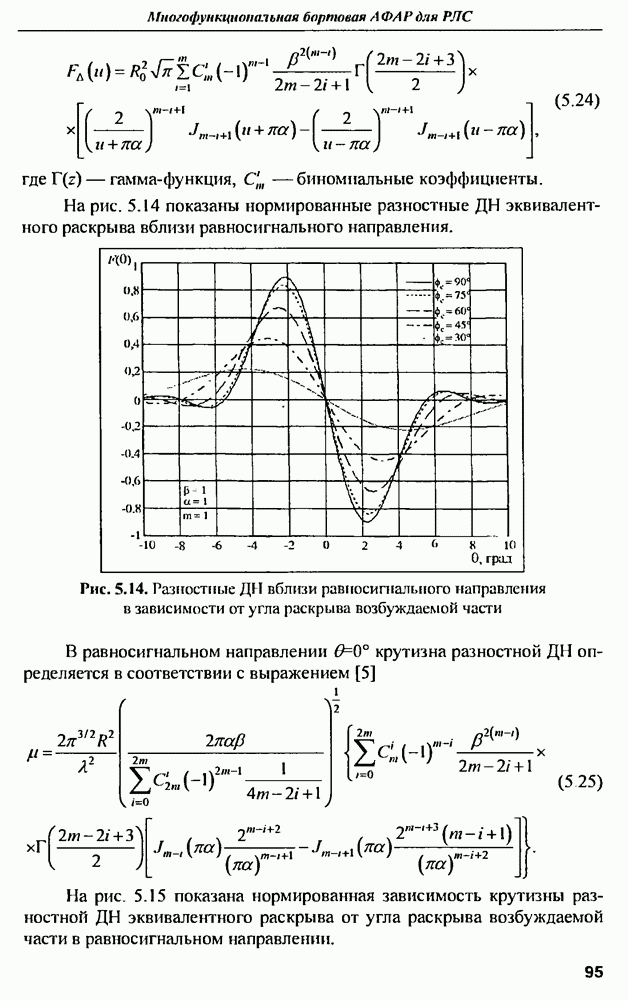
- 5.5. Пеленгационные характеристики сферической решетки
- 5.6. Сектор обзора сферической решетки и других вариантов выпуклой ФАР
- 5.7. Решение внутренней задачи
- 5.8. Система возбуждения модулей
- ГЛАВА 6. Адаптивная цифровая приемная ФАР
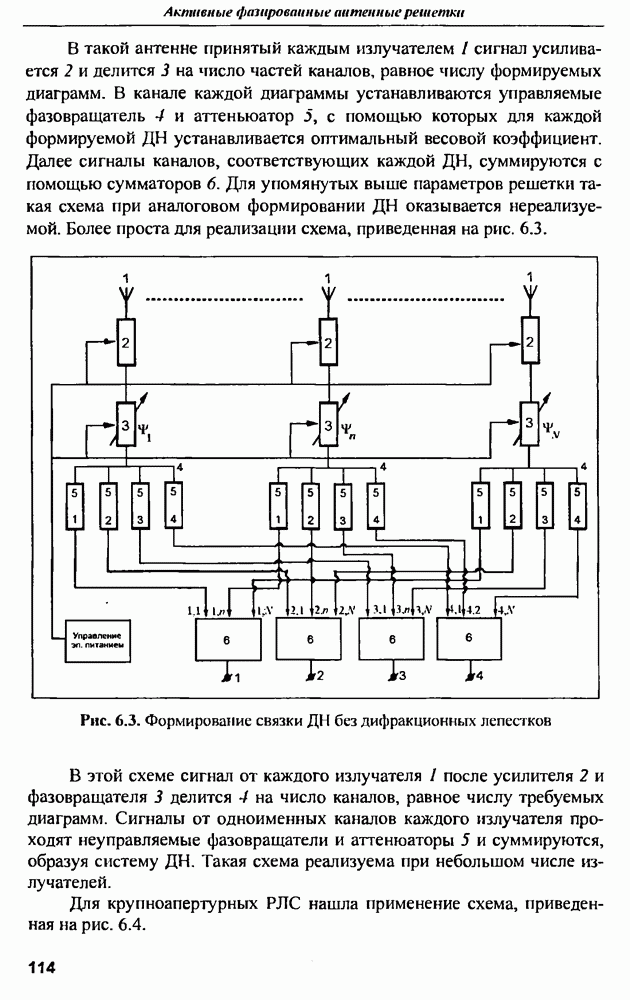
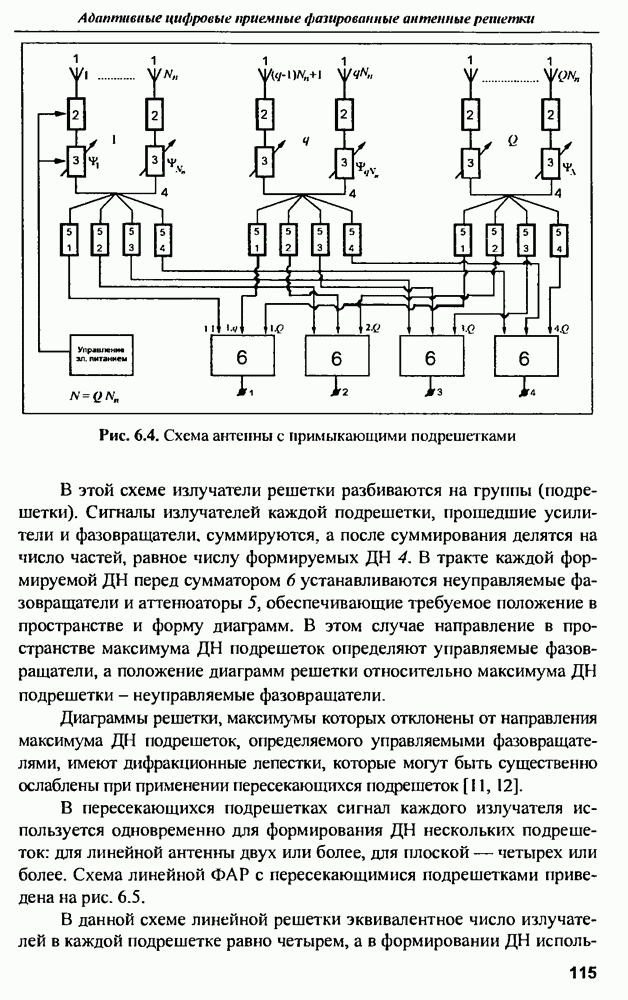
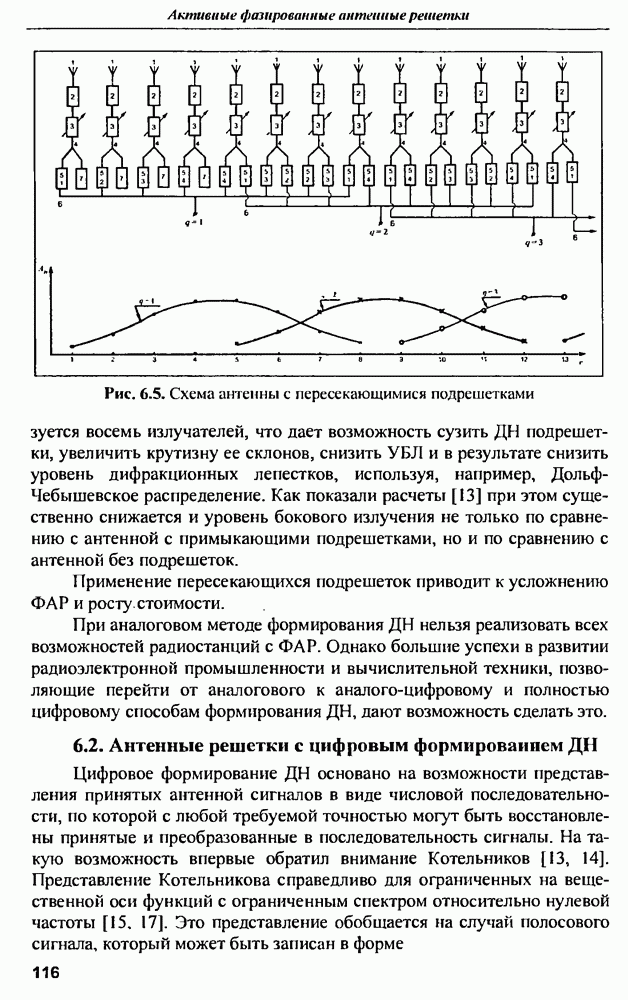
- 6.1. Антенные решетки с аналоговым формированием диаграмм направленности
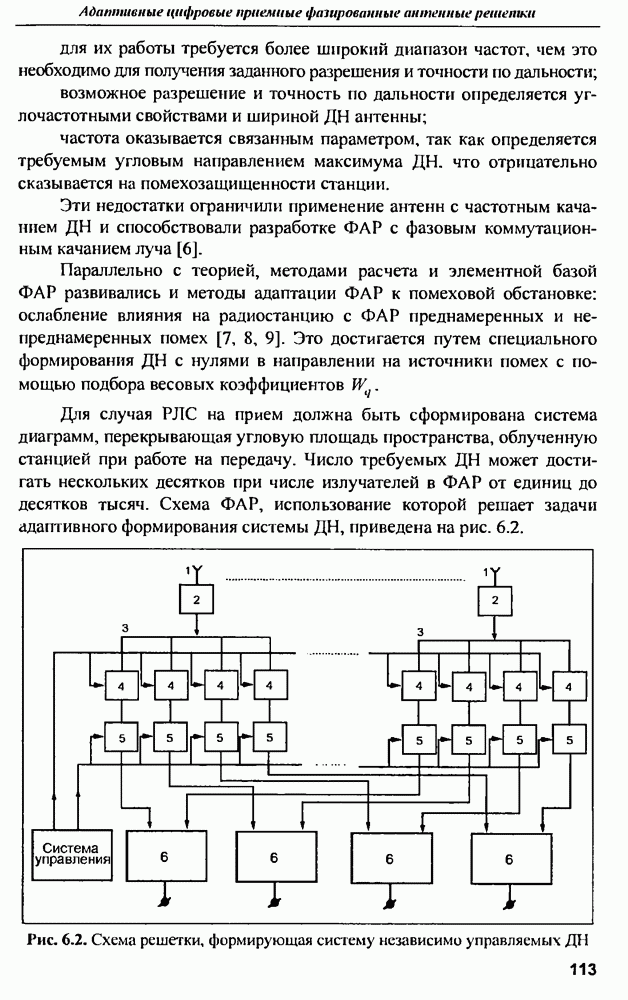
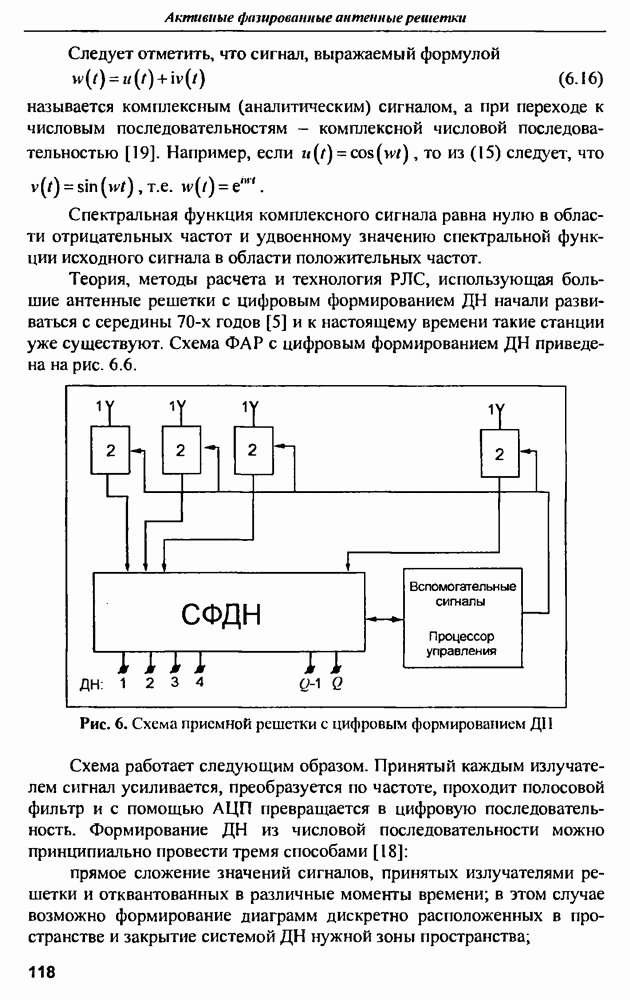
- 6.2. Антенные решетки с цифровым формированием ДН
- 6.3. Элементы и характеристики АЦПФАР
- 6.3.2. Полоса пропускания приемного канала и частота квантования
- 6.3.3. Аналого-цифровое преобразование
- 6.3.4. Спектры шумов и сигналов после квантования
- 6.3.5. Температура шумов приемного тракта
- 6.3.6. Динамическим диапазон
- 6.4. Применение, особенности и элементная база АЦПФАР
- ГЛАВА 7. Цифровые антенные решетки для систем сотовой подвижной связи
- 7.1. Влияние антенных технологий на развитие систем сотовой подвижной связи (ССПС)
- 7.2. Интеллектуальные антенны на основе цифровых АР
- 7.2.1. Принципы работы: модель адаптивного линейного сумматора
- 7.2.2. Пространственная обработка при приеме сигналов в обратном канале ССПС
- 7.2.3. Алгоритмы адаптации ИА
- 7.2.4. Применение ИА для передачи сигналов в прямом канале ССПС
- 7.3. Влияние ИА на характеристики ССПС
- 7.3.2. Расчетные модели
- 7.3.3. Абонентская емкость ССПС
- 7.3.4. Качество связи
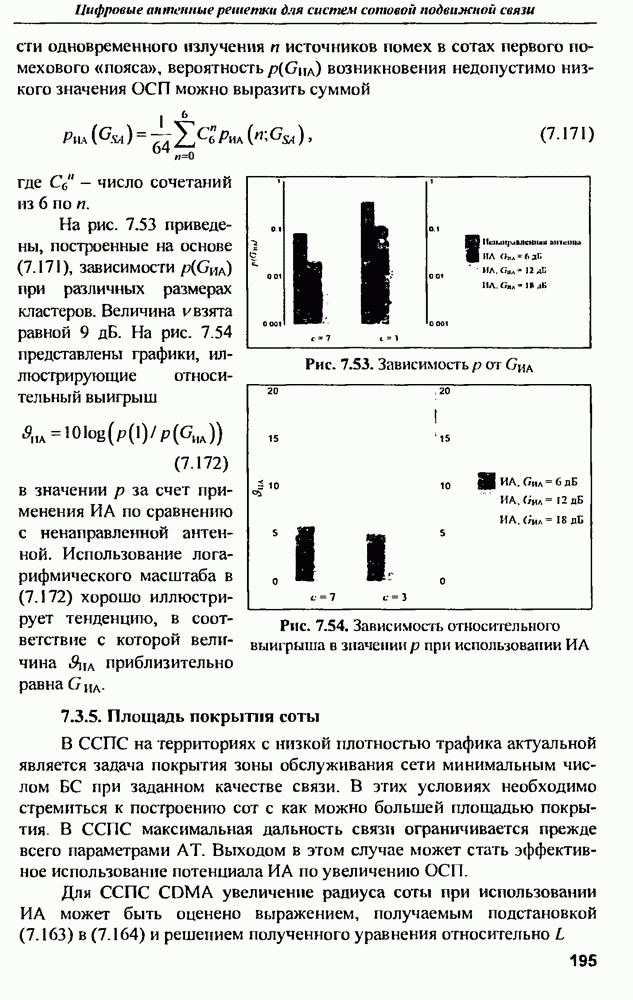
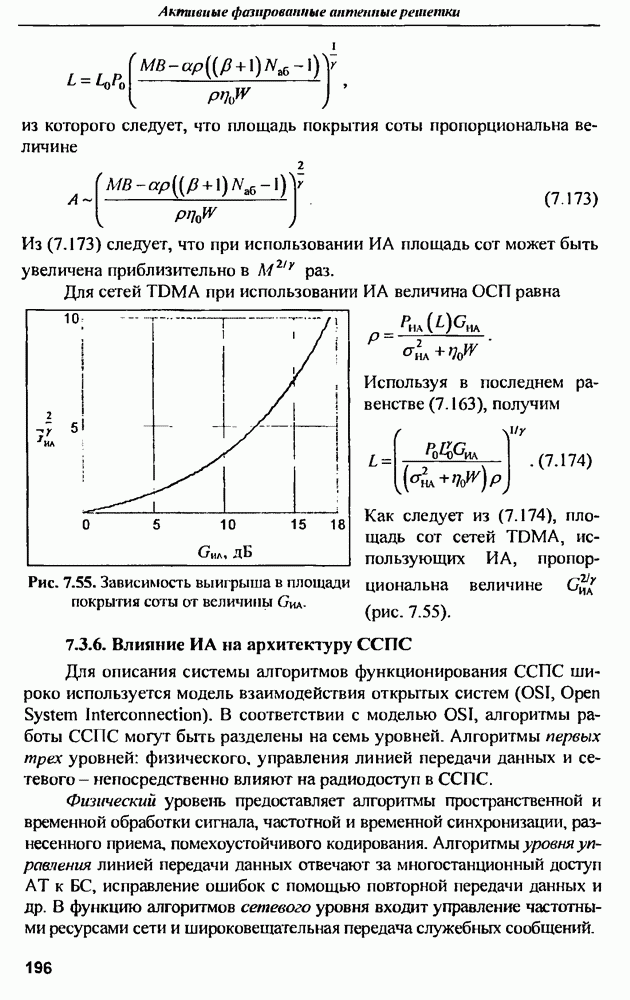
- 7.3.5. Площадь покрытия соты
- 7.3.6. Влияние ИА на архитектуру ССПС
- 7.4. Пространственные каналы с МВМВ на основе цифровых АР
- 7.4.1. Теоретико-информационные аспекты передачи данных в пространственных каналах МВМВ
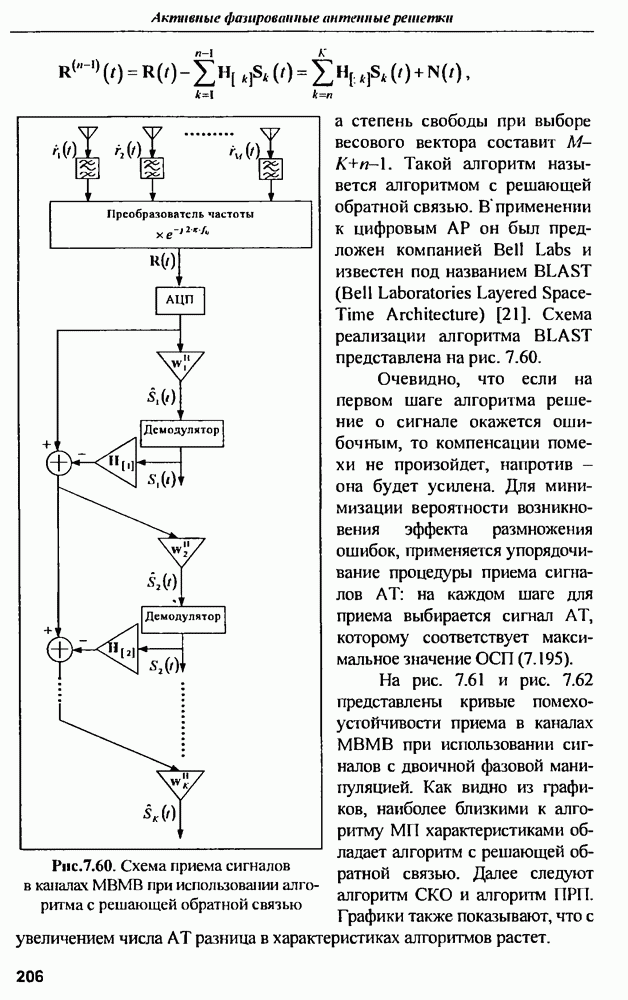
- 7.4.2. Алгоритмы приема сигналов
- 7.4.3. Передача сигналов в каналах с МВМВ
- 7.4.4. Пространственно-временное кодирование и разнесенная передача
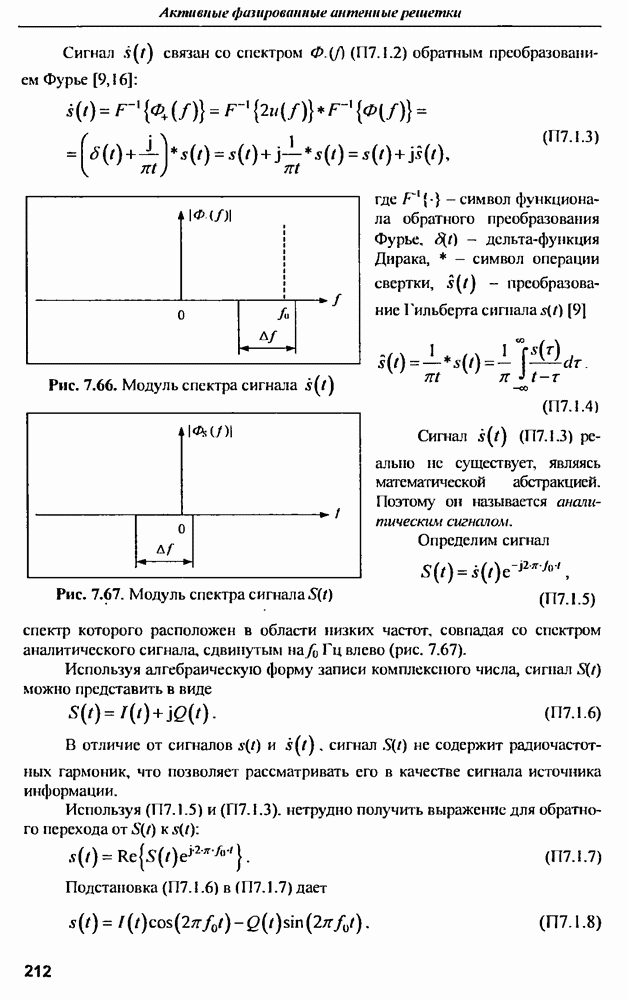
- Приложение 7.1. Комплексная огибающая сигнала и квадрату рная обработка в системах радиосвязи
- Приложение 7.2. Многолучевые ИА
- ГЛАВА 8. Оценка отношения сигнал/шум на выходе приемной АФАР с пространственным возбуждением
- 8.2. Определение мощности шума на выходе приемной АФАР
- 8.3. Отношение сигнал/шум на выходе приемной АФАР
- 8.4. Задача формирования расширенного луча АФАР
- 8.4.2. Использование метода статистического фазового синтеза для расширения луча
- 8.4.3. Оценка возможностей метода оптимального фазового синтеза расширенного луча, минимизирующего потери принимаемой мощности
- 8.4.4. Сравнение характеристик АФАР при различных методах формирования расширенного луча
- ГЛАВА 9. Распознавание целей в сверхширокополосной радиолокации
- 9.1.1. Методы теоретического расчета ЭПР
- 9.1.2. Тела простой геометрической формы
- 9.1.3. Характеристики рассеянна антенн
- 9.2. Резонансная модель рассеяния целей в сверхширокополосной радиолокации
- 9.2.2. Резонансная модель рассеяння электромагнитного поля радиолокационных объектов
- 9.3. Методы оценки характеристик сигналов
- 9.3.1. Метод Прони
- 9.3.2. Метод матричных пучков
- 9.4. Обработка сигналов с использованием статистик высокого порядка
- 9.4.2. Статистики высокого порядка детерминированных импульсных и периодических сигналов
- 9.4.3. СВП резонансной модели объектов в СШП радиолокации
- 9.5. Оценка параметров резонансных моделей целей в СШП радиолокации
- 9.5.1. Статистики высокого порядка резонансной модели объектов
- 9.5.2. Сравнительный анализ методов оценки параметров резонансных моделей с использованием статистик высокого порядка
- 9.6. Распознавание радиолокационных объектов
- 9.6.1. Сигнатурное распознавание целей по результатам оценки параметров резонансной модели
- 9.6.2. Распознавание радиолокационных объектов с помощью метода Е-импульса
- 9.7. Заключение
- ГЛАВА 10. Обеспечение инвариантности оптимальных пространственно-многоканальных РЛС с АФАР к коррелированным помехам
- 10.2. Обнаружение цели с известными координатами
- 10.3. Обнаружение цели и определение ее угловых координат
- 10.4. Обнаружение цели и измерение ее скорости сближения с РЛС
- 10.5. Условия инвариантности оптимальных РЛС к помехам
- 10.6. Потенциальные возможности оптимальных антенно-приемных трактов РЛС, соответствующих алгоритмам (10.39), (10.43)
- ГЛАВА 11. Характеристики активных ФАР при отказах активных модулей
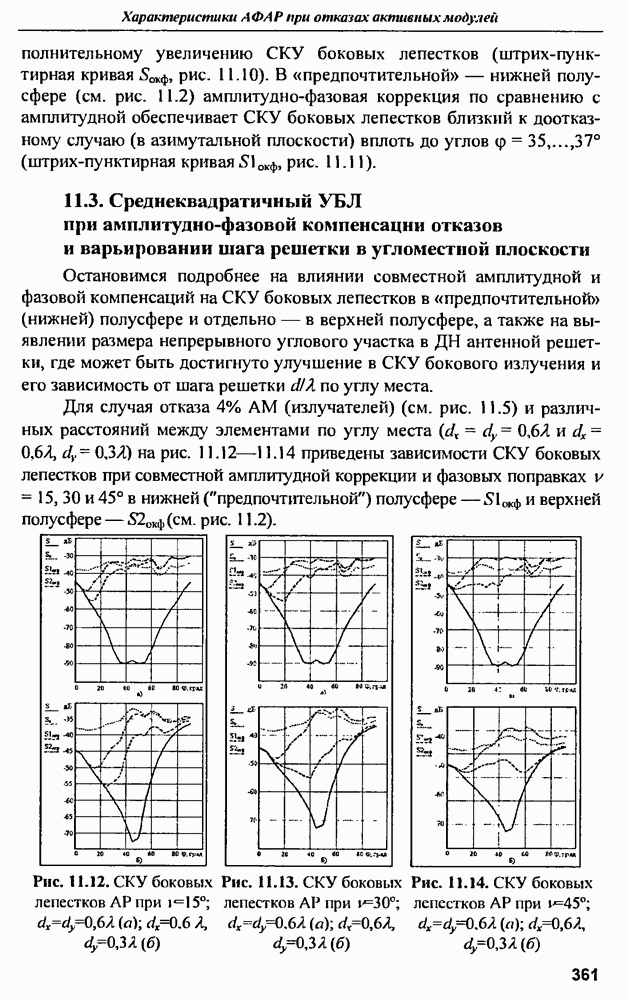
- 11.2. Диаграммы направленности и СКУ боковых лепестков при амплитудной и амплитудно-фазовой компенсании множественных отказов
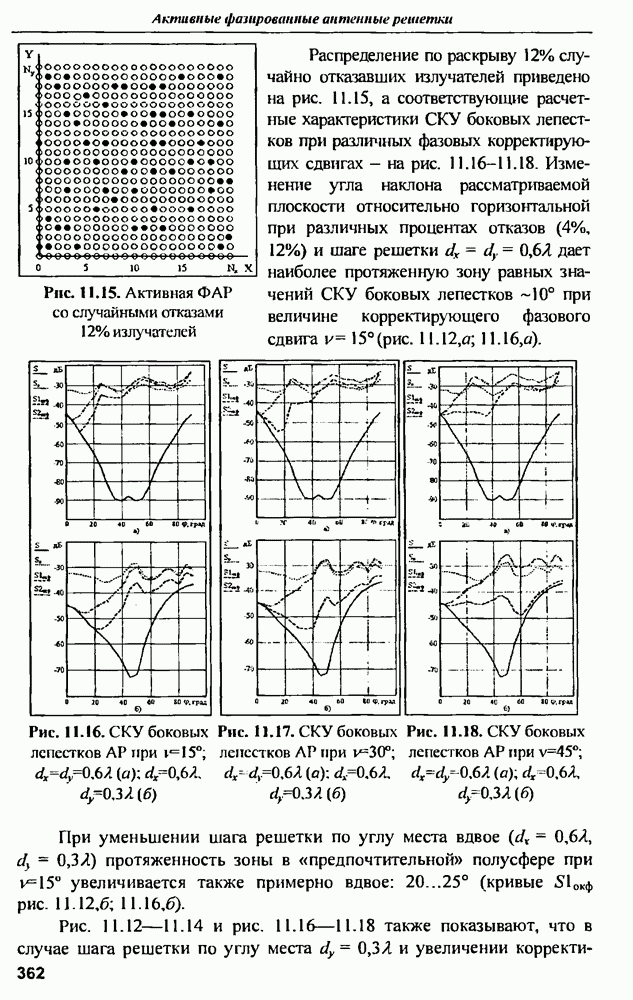
- 11.3. Среднеквадратичный УБЛ при амплитудно-фазовой компенсации отказов и варьировании шага решетки в угломестной плоскости
- 11.4. Влияние закона амплитудного распределения на характеристики АФАР при отказах АМ
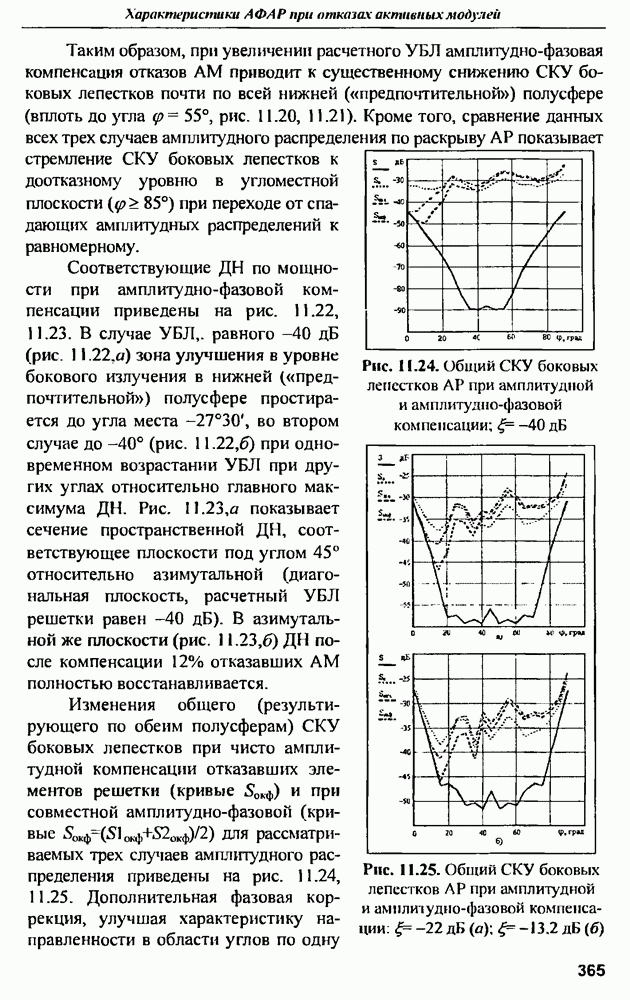
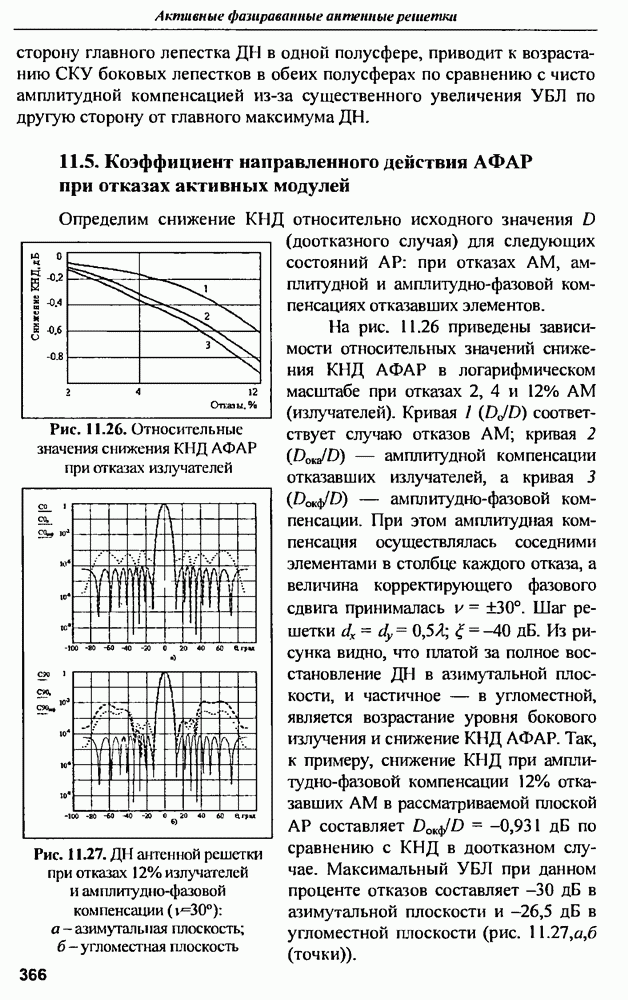
- 11.5. Коэффициент направленного действия АФАР при отказах активных модулей
- 11.6. Особенности восстановления характеристик направленности АФАР при немонохроматическом сигнале
- ГЛАВА 12. Вопросы расчета линейных антенных решеток бегущей волны
- 12.1. Общие свойства линейных антенных решеток бегущей волны
- 12.2. Расчет на заданное амплитудное распределение и энергетические характеристики антенны
- ГЛАВА 13. Диагностика антенных решеток
- 13.2. Ближнезонные фазовые методы диагностики ФАР
- 13.2.2. Метод реконструктивной диагностики (МРД) ФАР
- 13.2.4. Селективная диагностика ФАР
- 13.2.5. Цифровая реализация МРД
- 13.2.6. Возможности МРД
- 13.2.7. МРД на основе дискретного преобразования Фурье (ДПФ)
- 13.2.8. Комбинированный МРД на основе БПУА и БПФ
- 13.2.9. Сопоставление МРД с другими методами
- 13.3. Бесфазовые методы диагностики ФАР
- 13.3.1. Метод, использующий ДПФ в базисе экспоненциальных функций
- 13.3.2 Метод, использующий ДПФ в базисе функций Уолша (метод ДПУ)
- 13.3.3. Адаптивный алгоритм диагностики ФАР
- 13.3.4. Сравнение метода ДПУ и адаптивного метода диагностики ФАР
- Приложение 13.П1. Алгоритм диагностики ФАР методом ДПФ в базисе функций Уолша (метод ДПУ)
- Приложение 13.П2. Адаптивный алгоритм диагностики ФАР, основанный на измерении комплексных амплитуд сигналов
- Приложение 13.П3. Адаптивный алгоритм диагностики ФАР, основанный на измерении мощности сигналов
- Дополнения к приложениям 13.П1, 13.П2,13.П3
- ГЛАВА 14. Мощные импульсы сверхширокополосного излучения для радиолокации
- 14.2. Синтез сверхширокополосных антенн
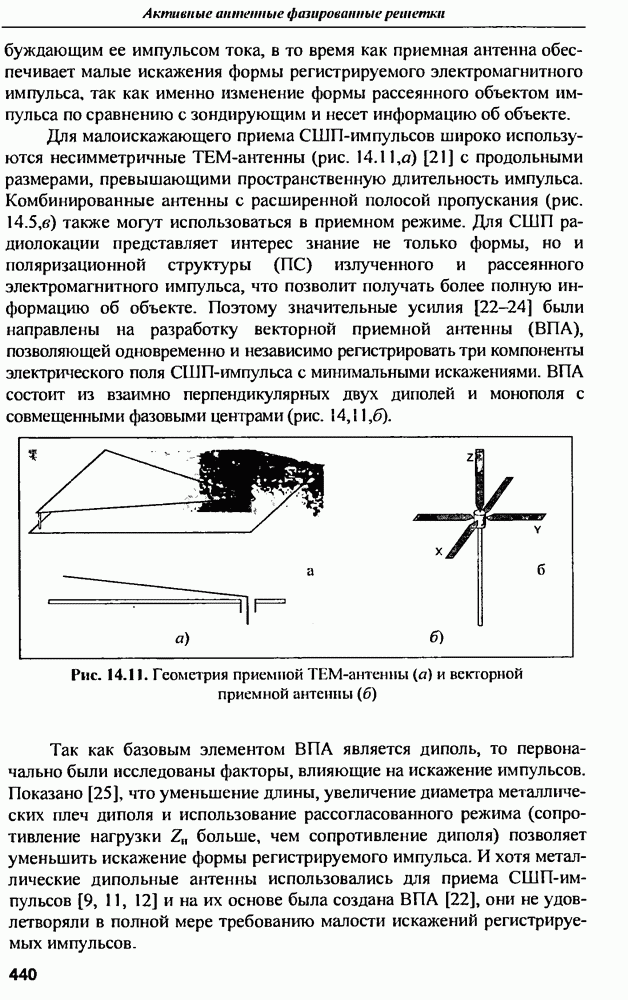
- 14.3. Комбинированные антенны
- 14.4. Антенные решетки
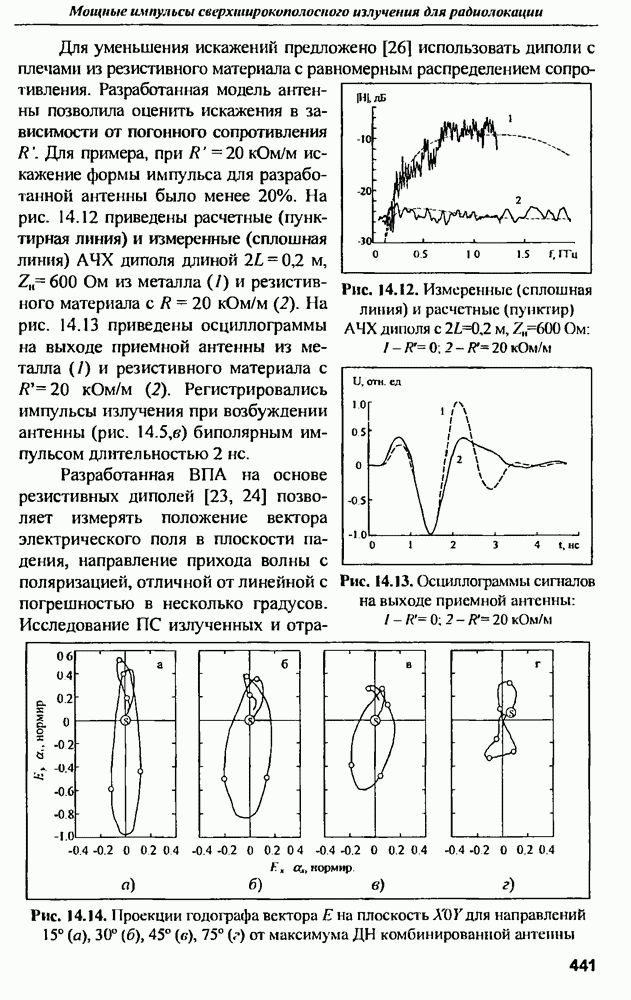
- 14.5. Приемные антенны
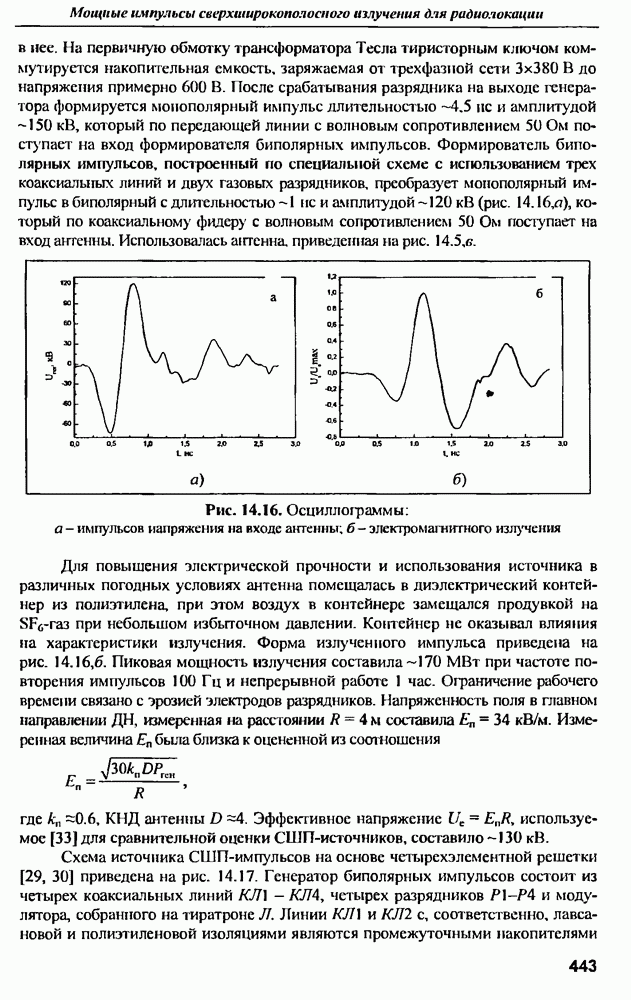
- 14.6. Мощные источники СШП-излучения
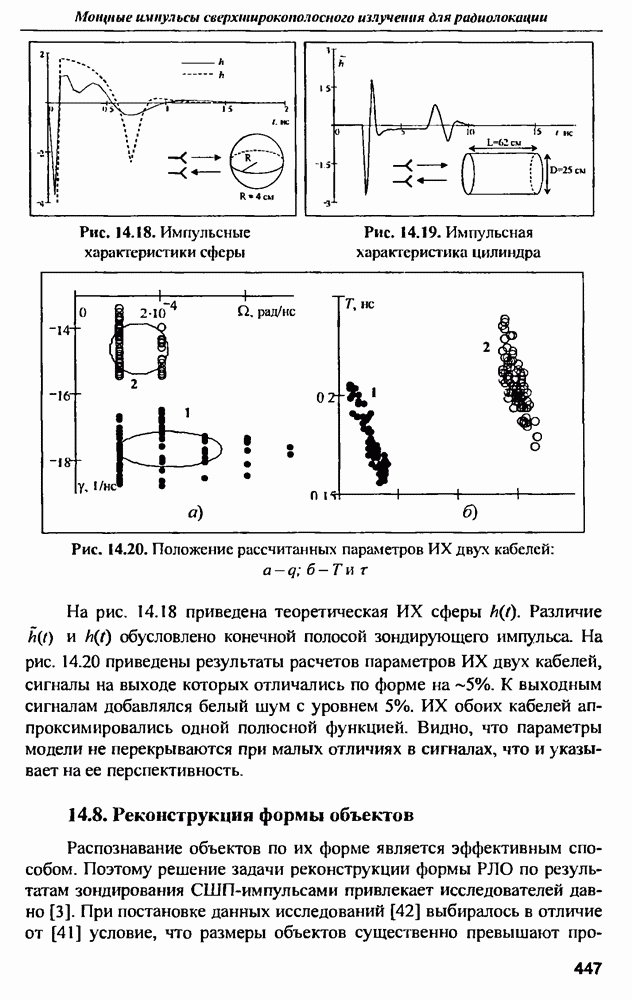
- 14.7. Методы оценивания импульсных характеристик
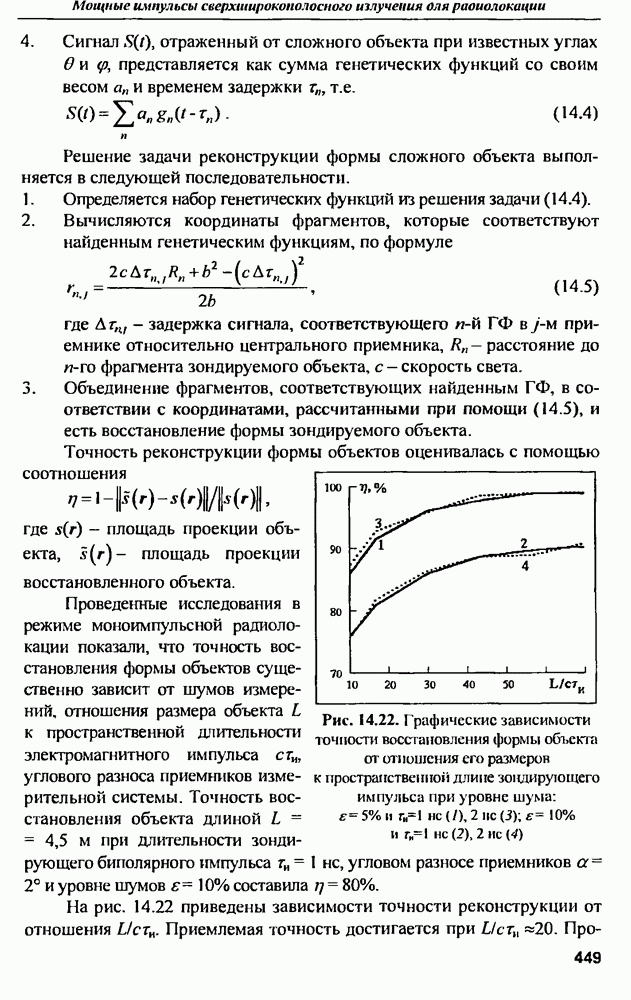
- 14.8. Реконструкция формы объектов
- ГЛАВА 15. Волоконно-оптическое распределение сигналов по модулям АФАР
- 15.1. Проблема распределения сигналов АФАР и основные подходы к ее решению с использовнием волоконных систем
- 15.2. Краткий анализ и классификация сигналов активного модуля ФАР
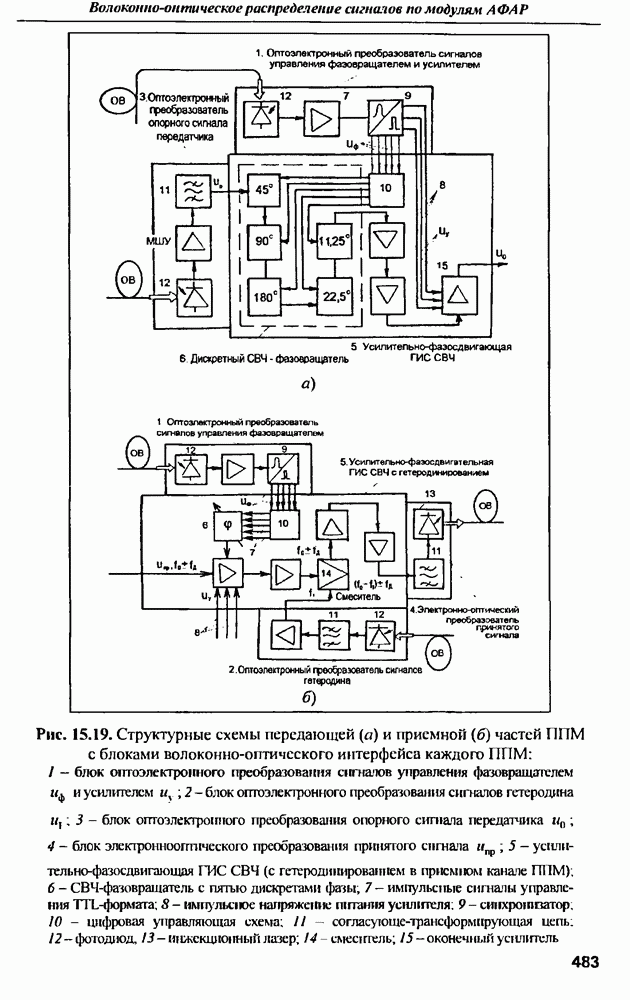
- 15.3. Структурная схема волоконного канала передачи сигналов в ППМ АФАР
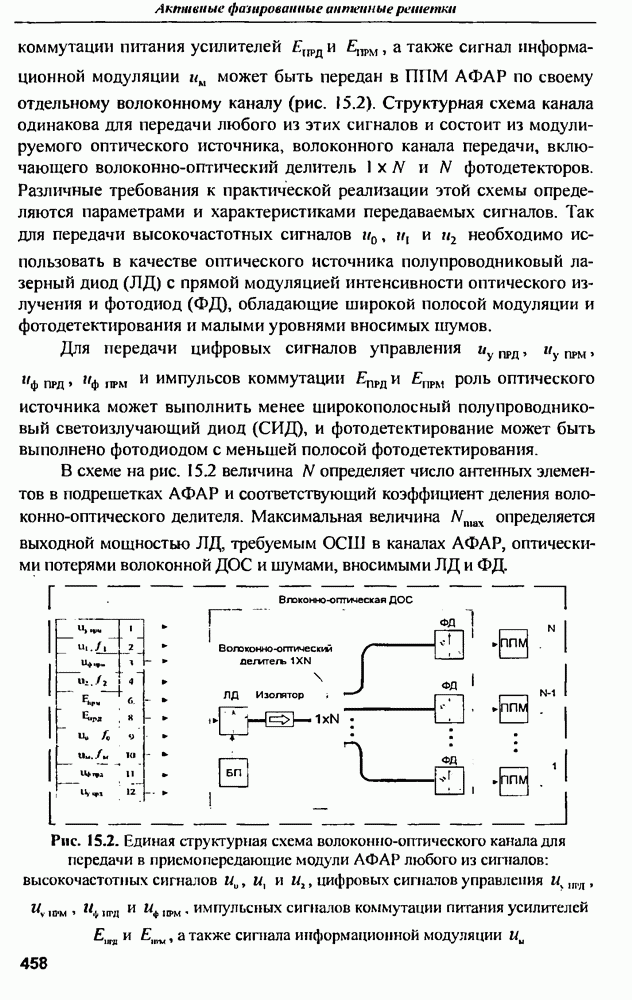
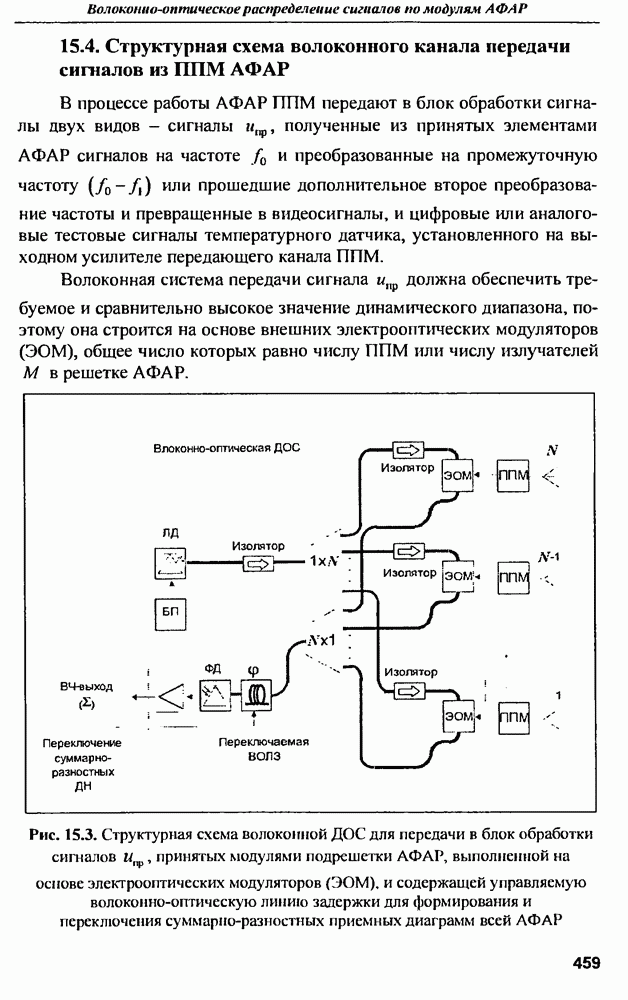
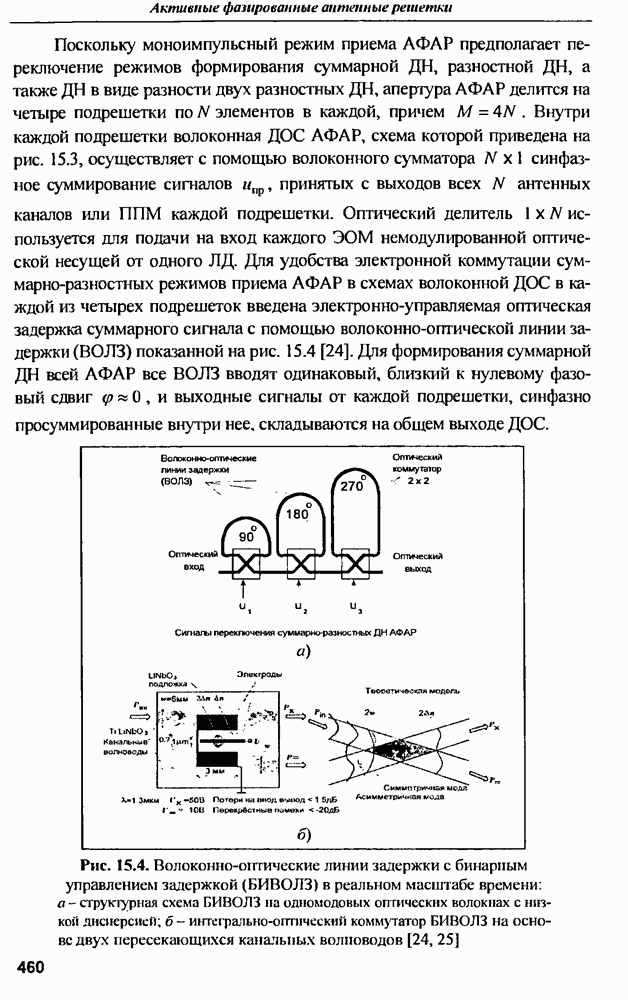
- 15.4. Структурная схема волоконного канала передачи сигналов из ППМ АФАР
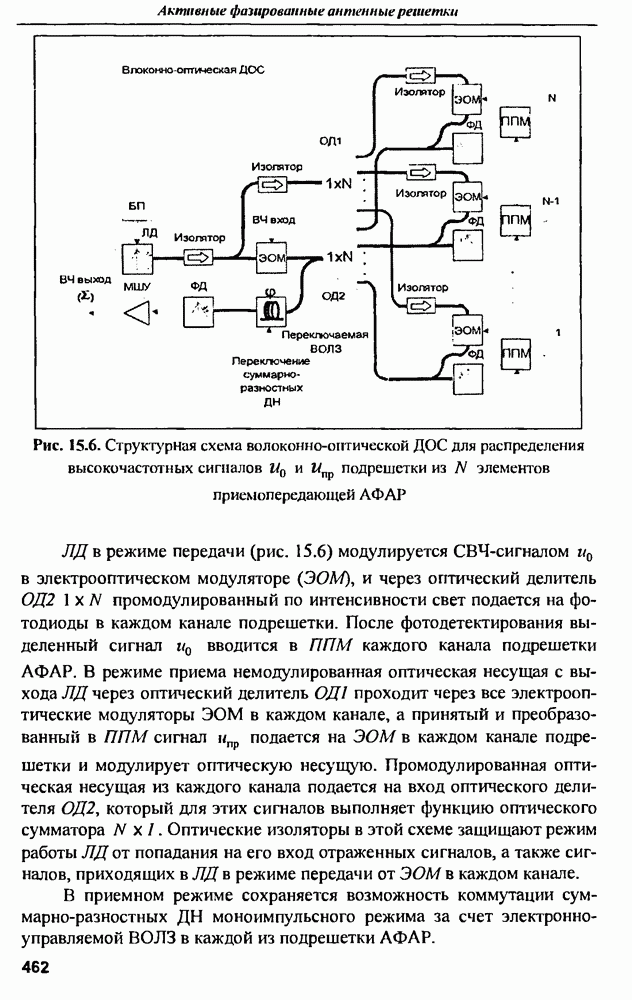
- 15.5. Структурные схемы волоконных систем распределения высокочастотных сигналов по модулям приемопередающей АФАР
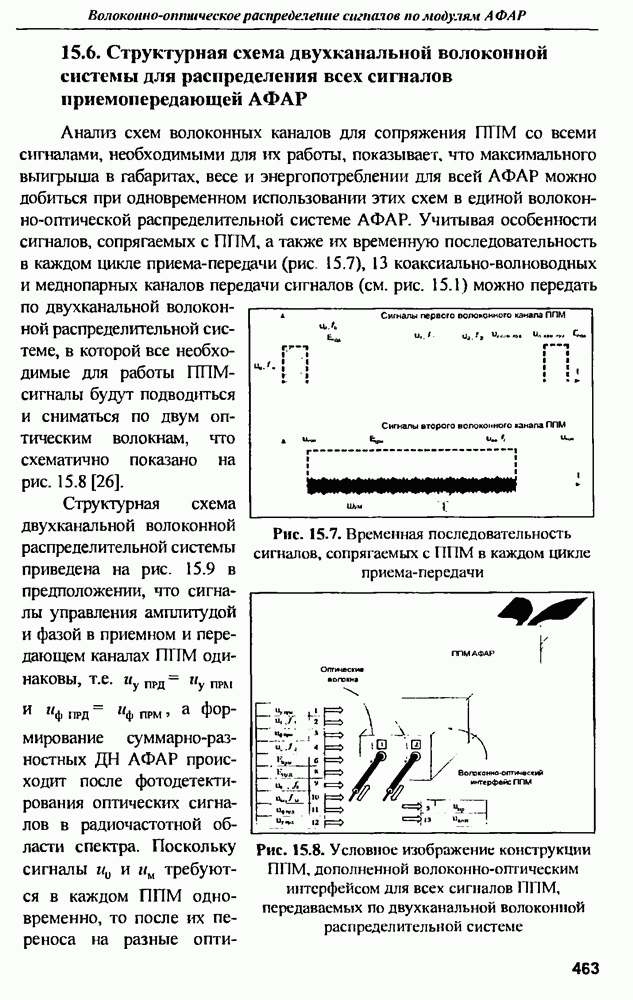
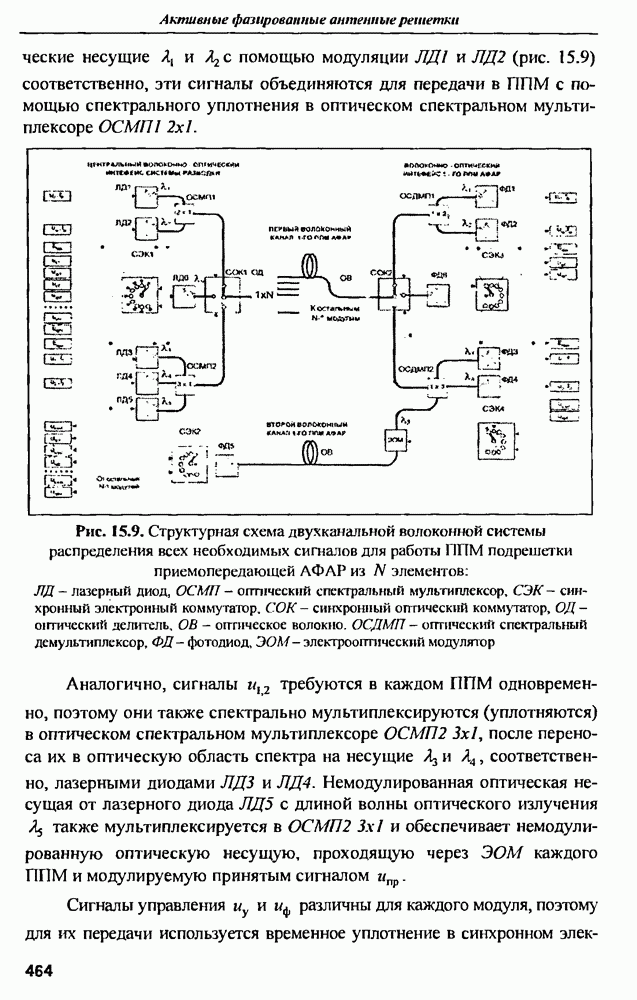
- 15.6. Структурная схема двухканальной волоконной системы для распределения всех сигналов приемопередающей АФАР
- 15.7. Основные типы волоконных каналов, используемых для построения волоконных распределительных систем.
- 15.7.1. Волоконный канал с МИПД-ПМ
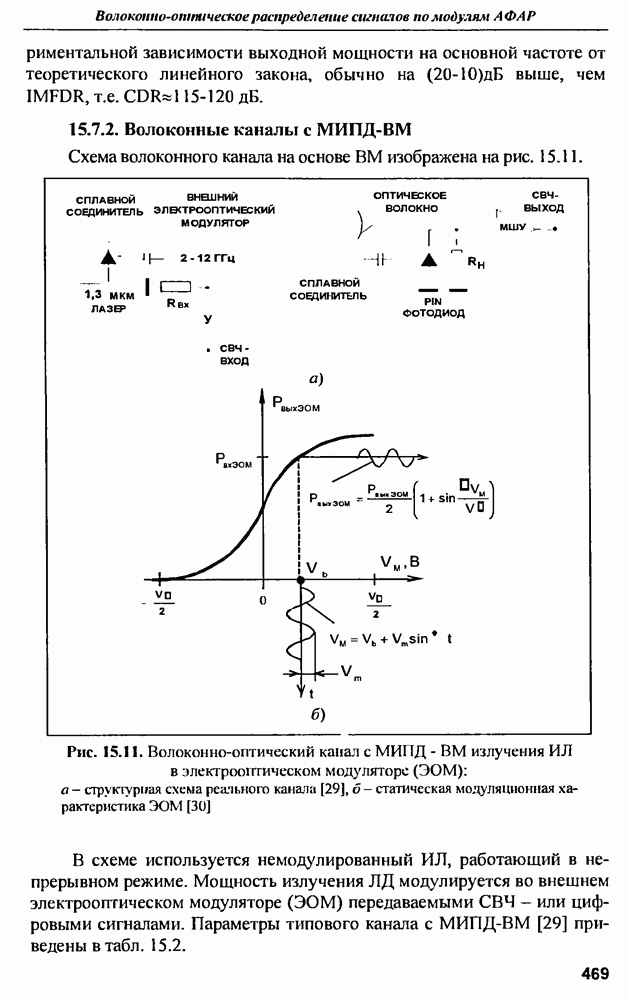
- 15.7.2. Волоконные каналы с МИПД-ВМ
- 15.7.3. Сравнение характеристик волоконных каналов с прямой и внешней модуляцией оптической несущей
- 15.8. Элементная база волоконной распределительной системы АФАР
- 15.8.1. Источники оптического излучения
- 15.8.2. Фотодетекторы
- 15.8.3. Оптическое волокно
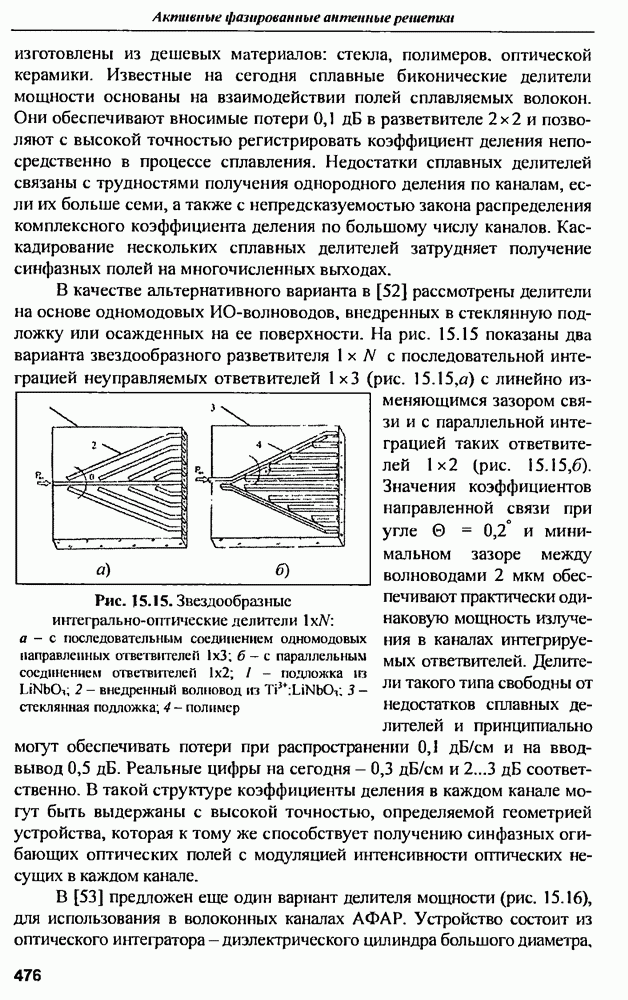
- 15.8.4. Оптические делители
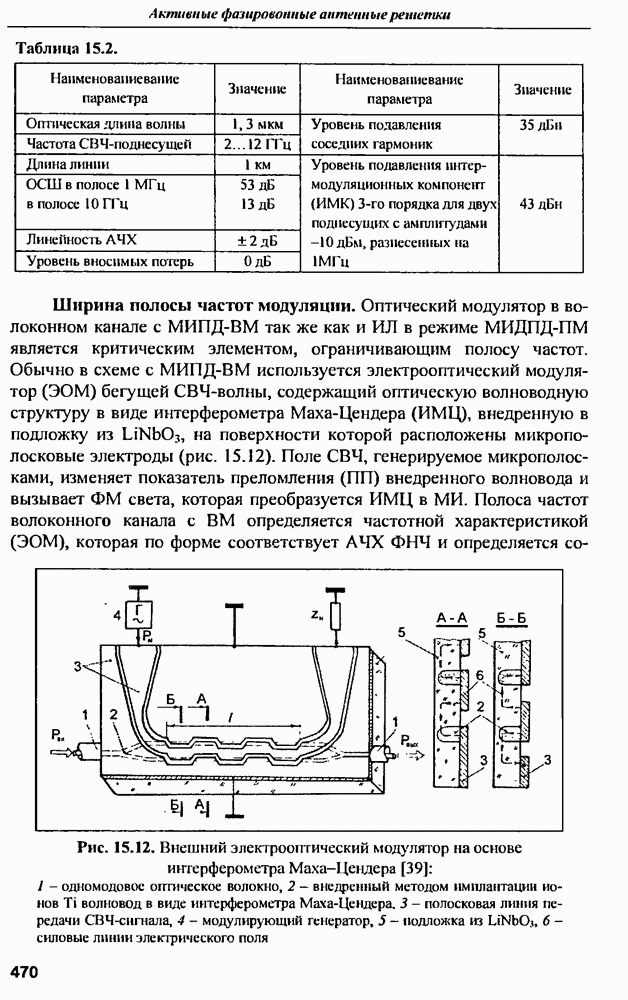
- 15.8.5. Внешние модуляторы
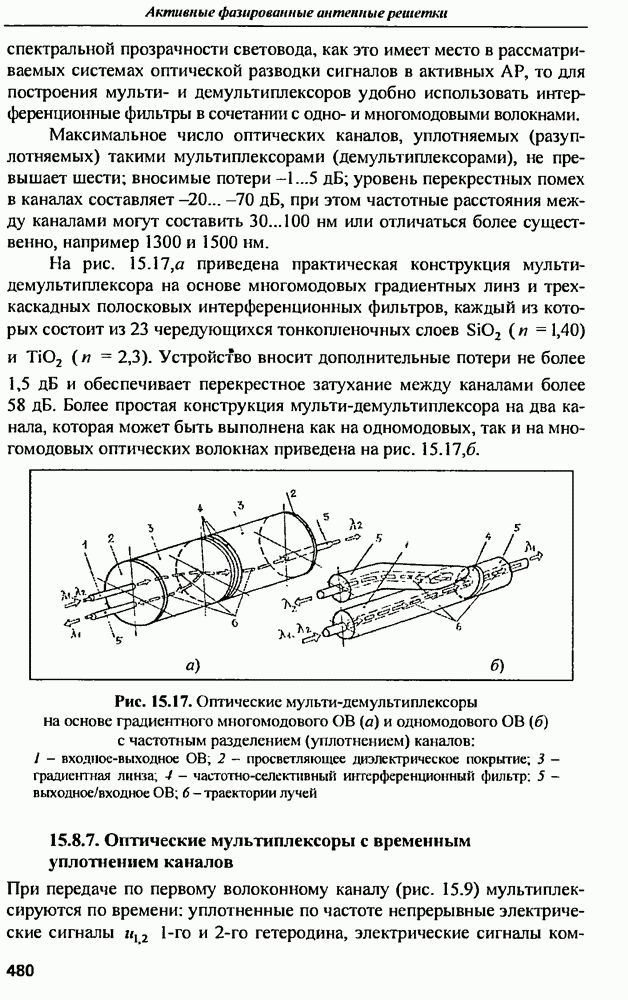
- 15.8.6. Оптические мультиплексоры с частотным уплотнением каналов
- 15.8.7. Оптические мультиплексоры с временным уплотнением каналов
- 15.9. Примеры практической реализации волоконных каналов для передачи отдельных сигналов АФАР