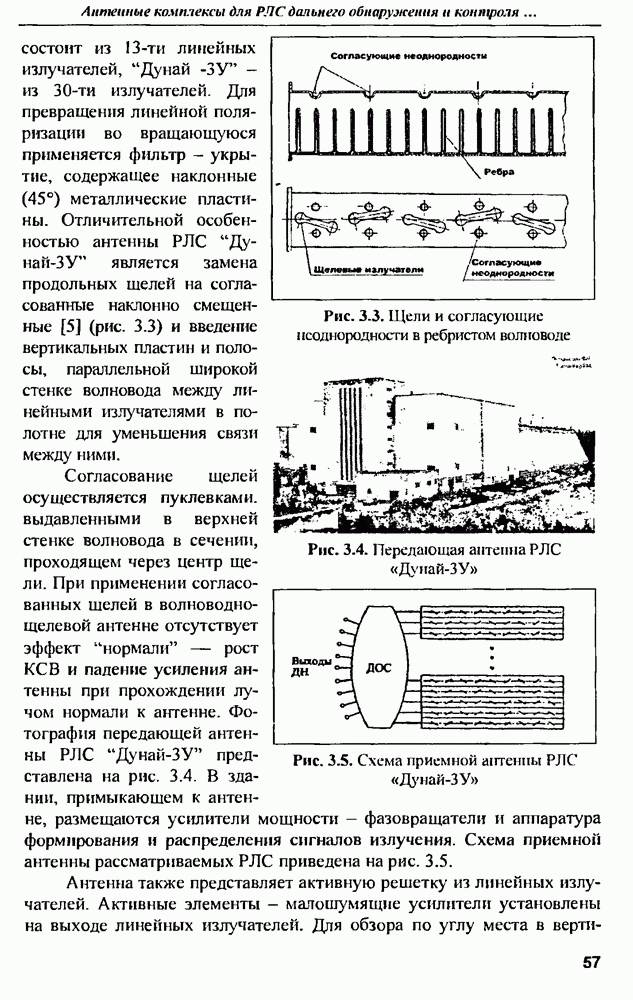
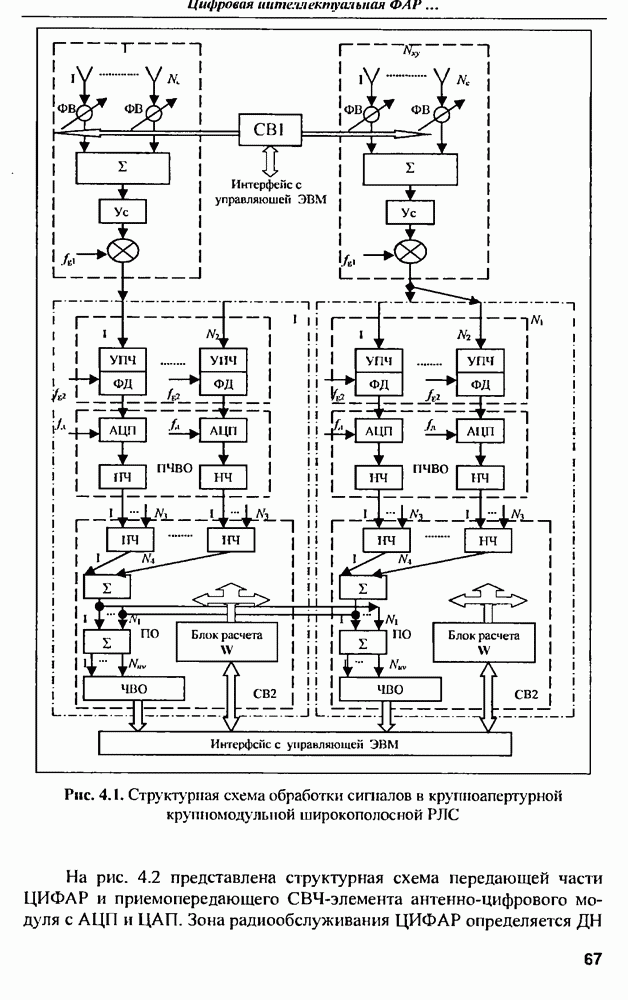
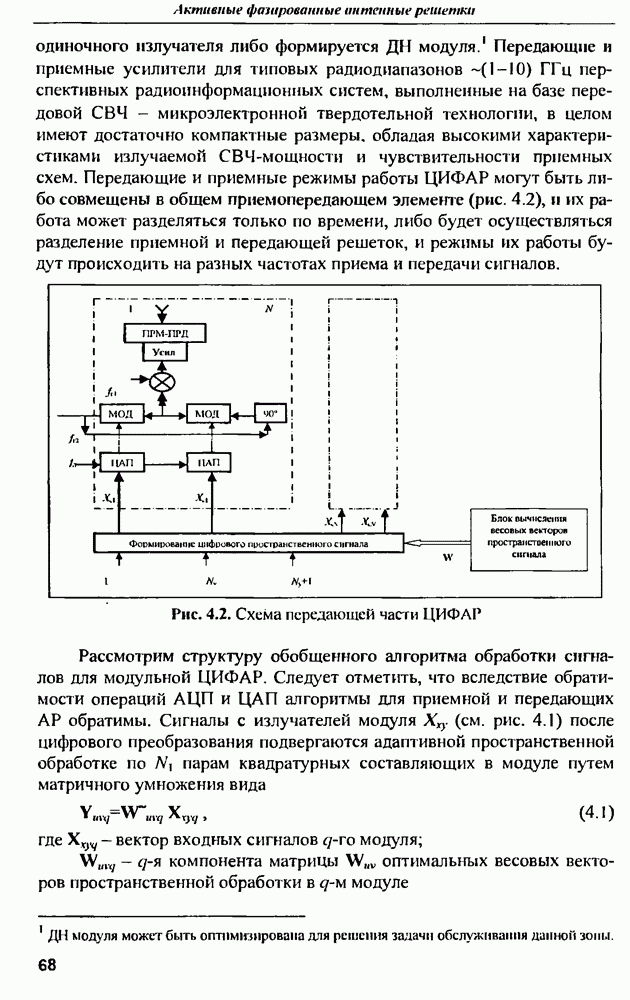
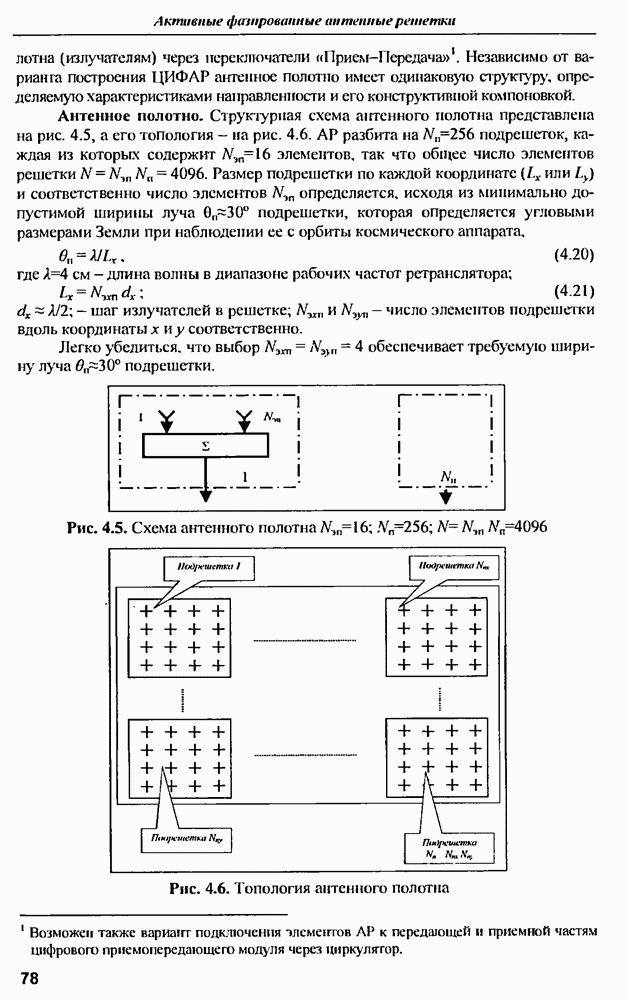
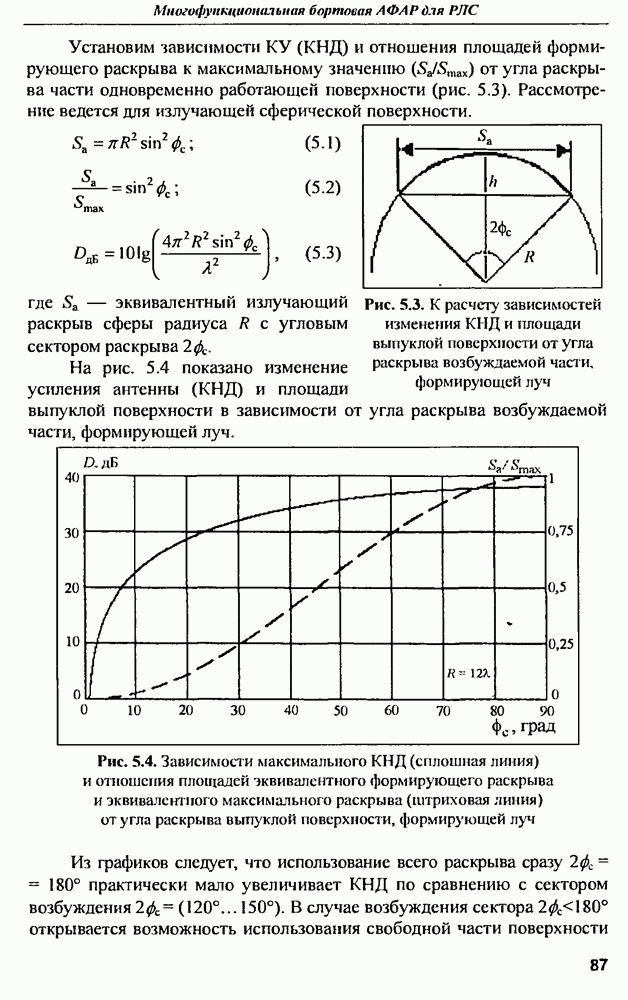
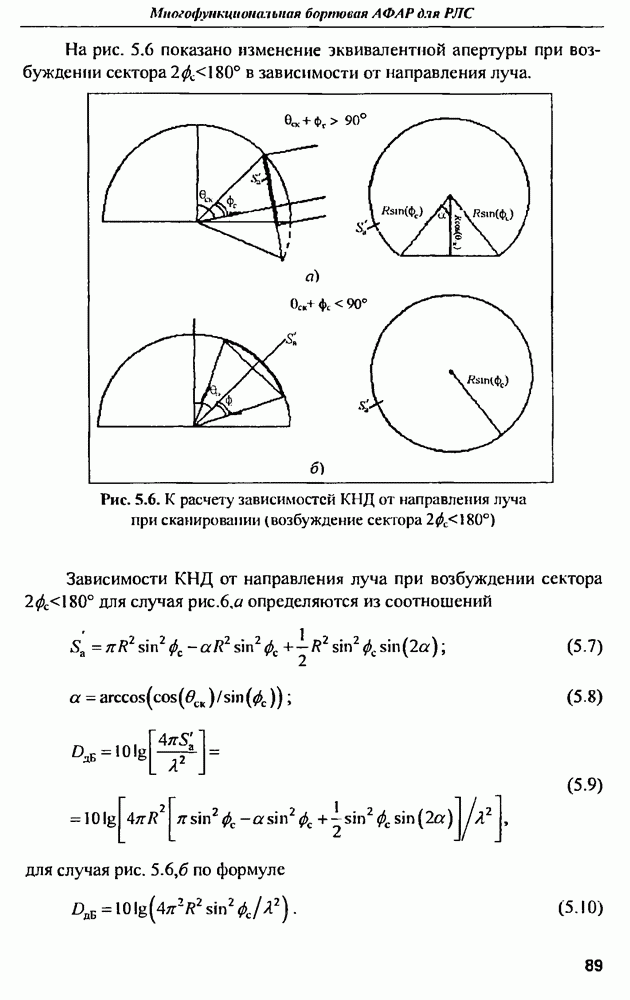
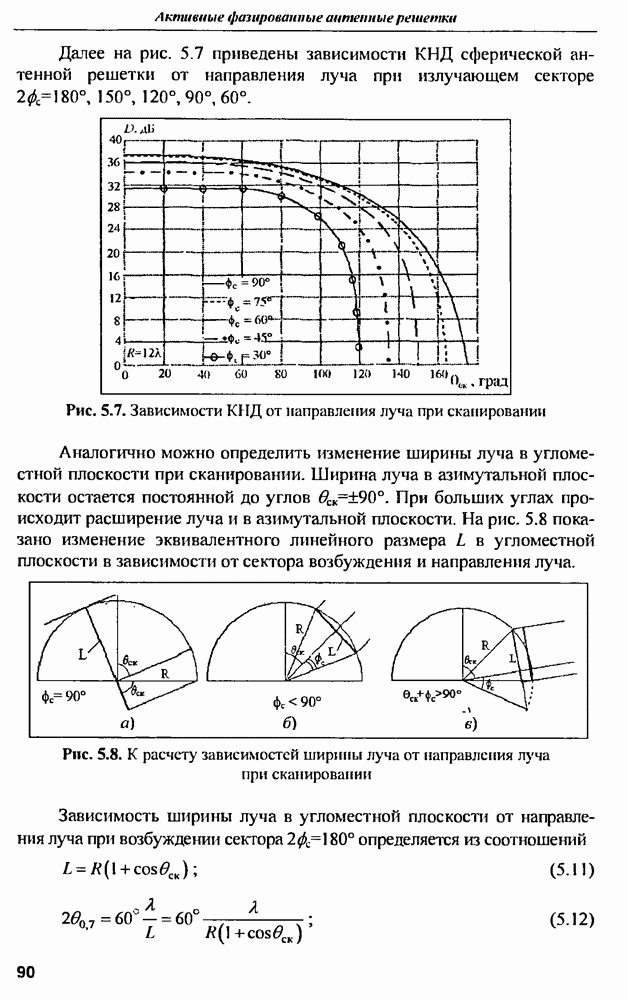
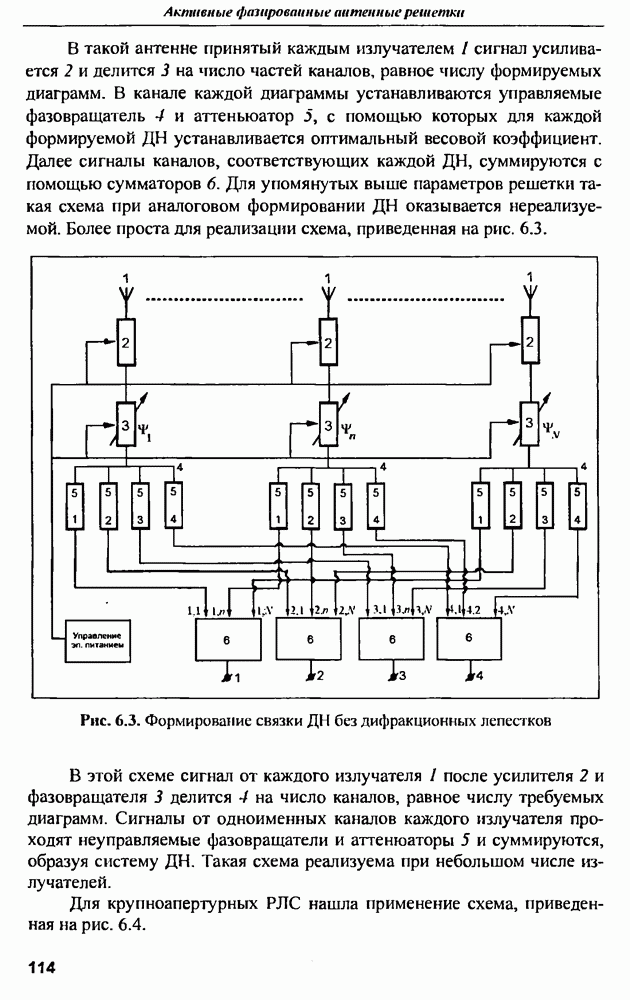
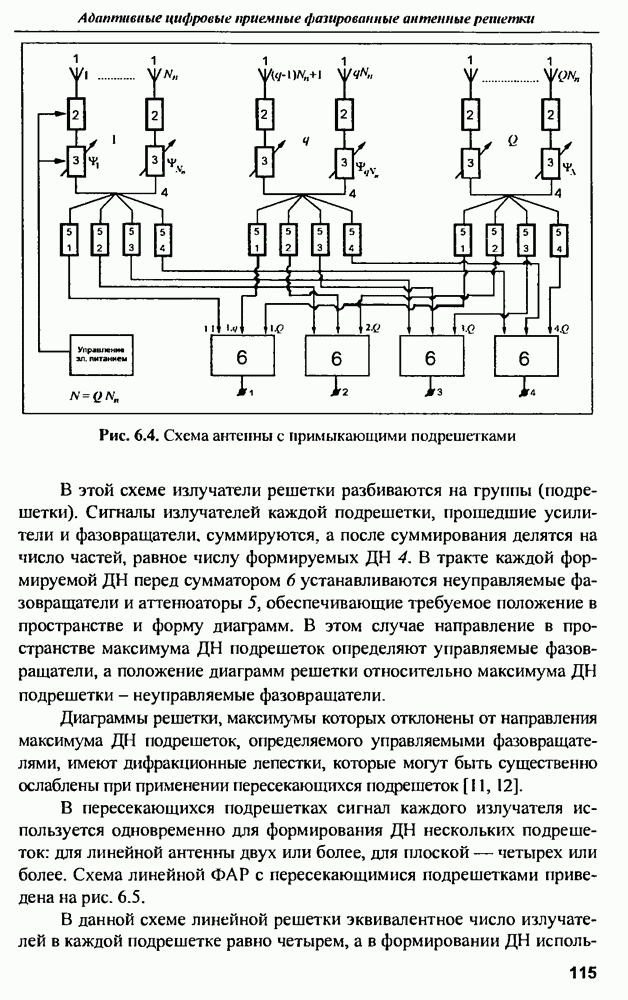
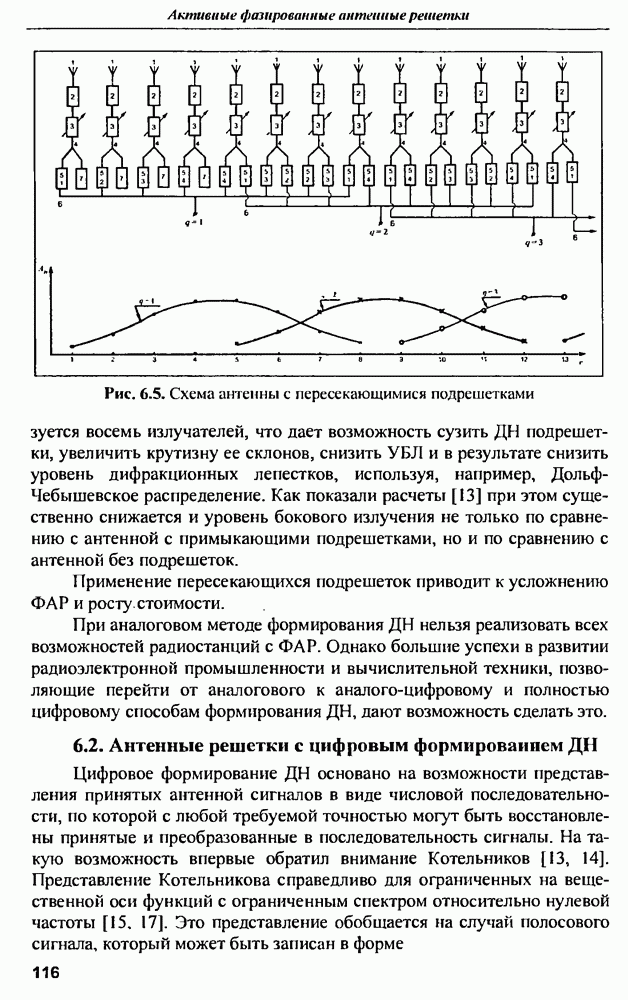
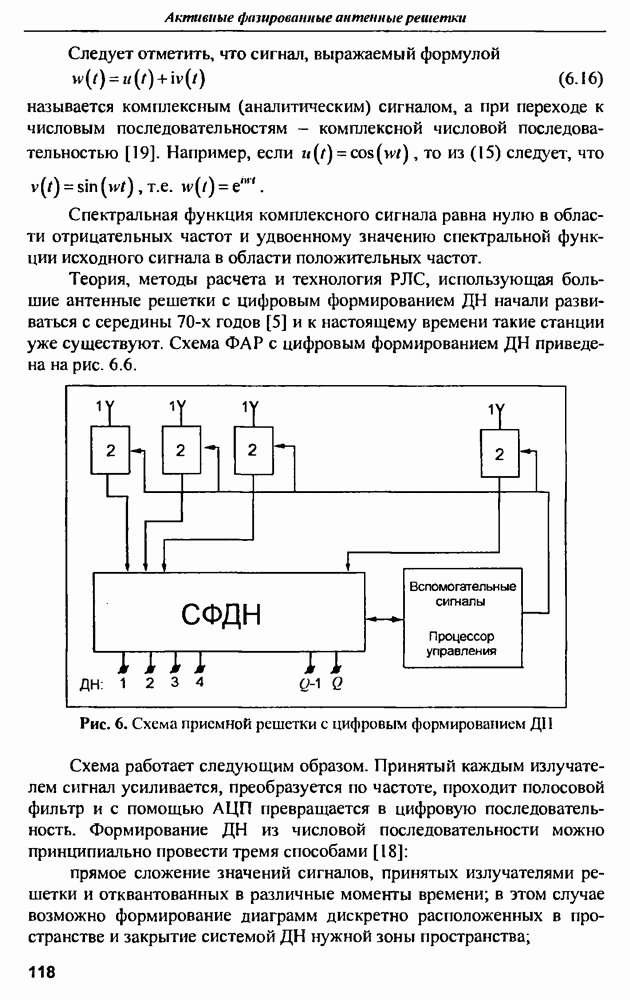
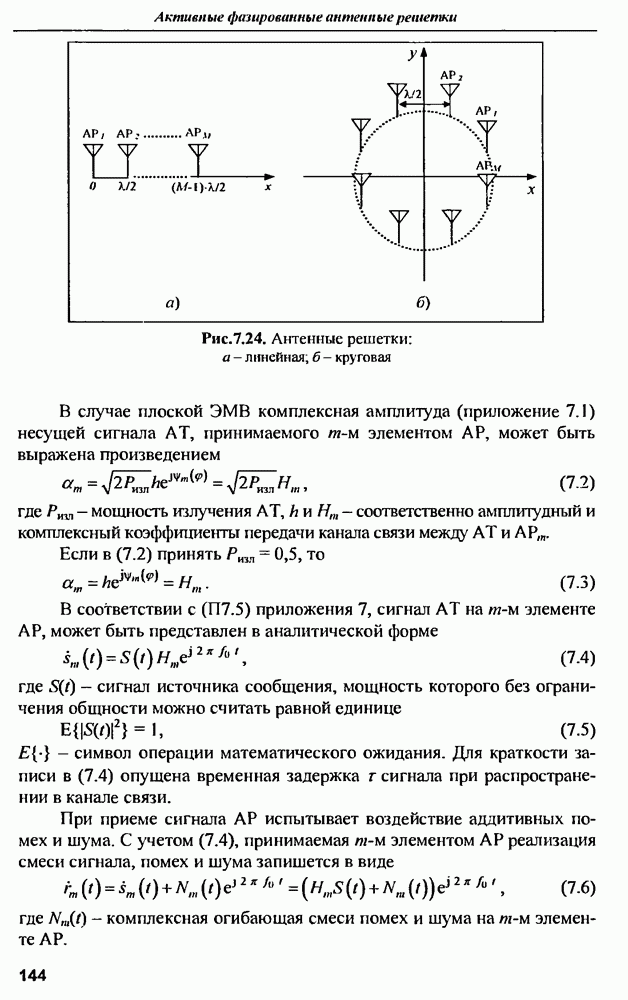
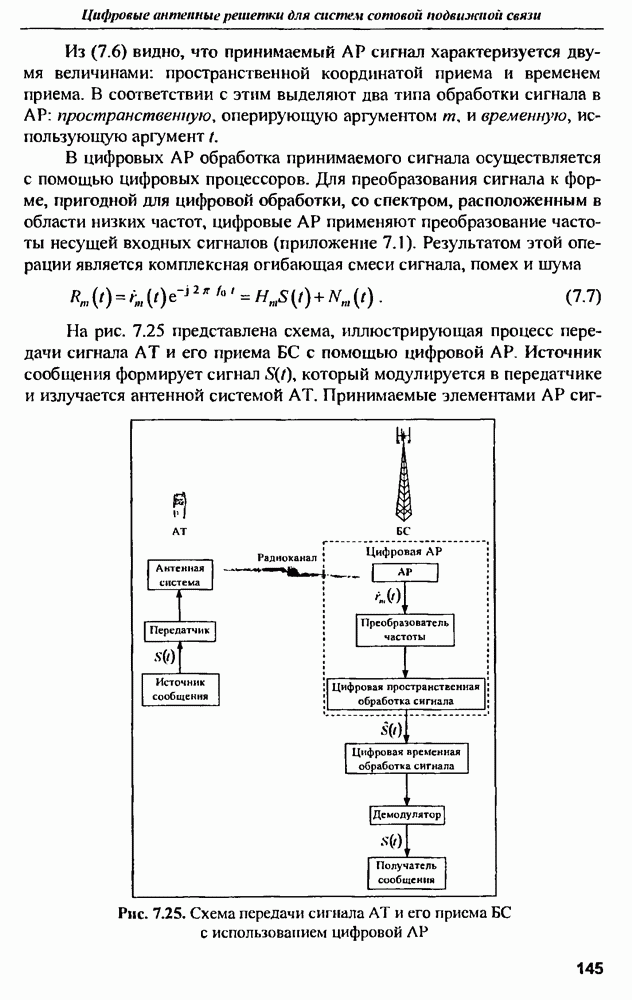
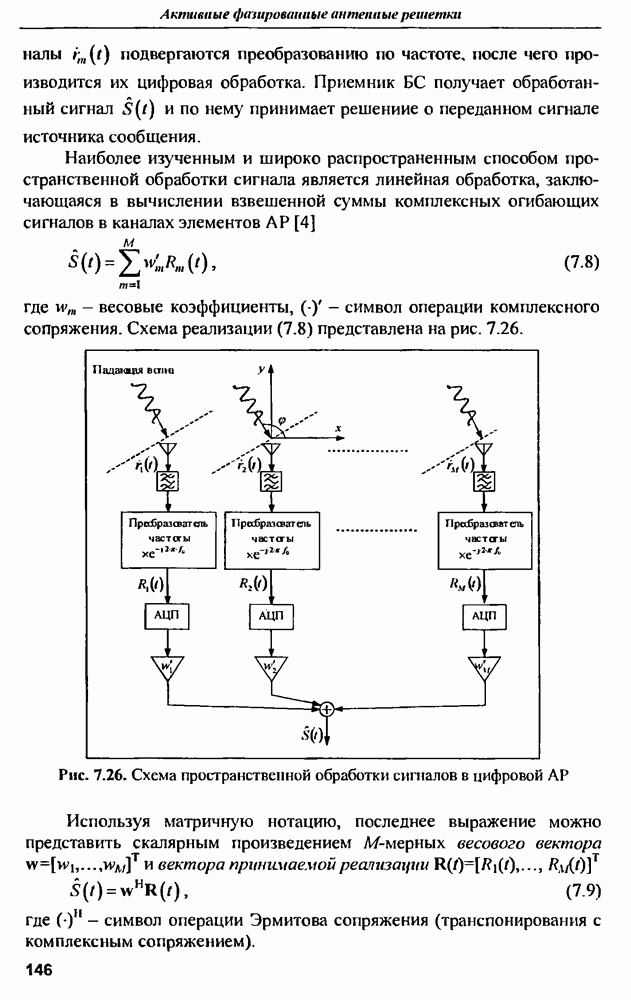
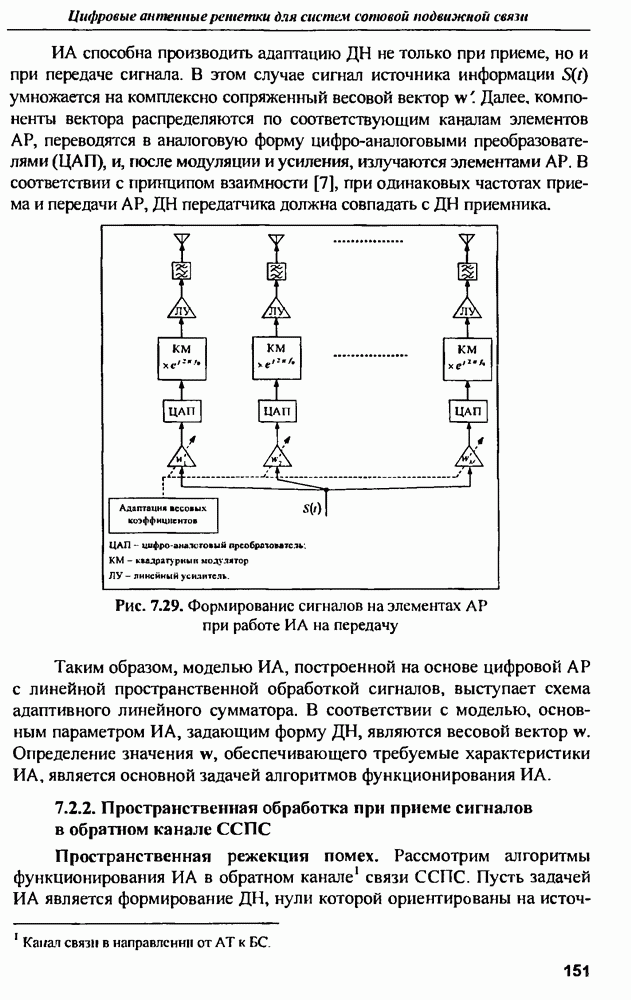
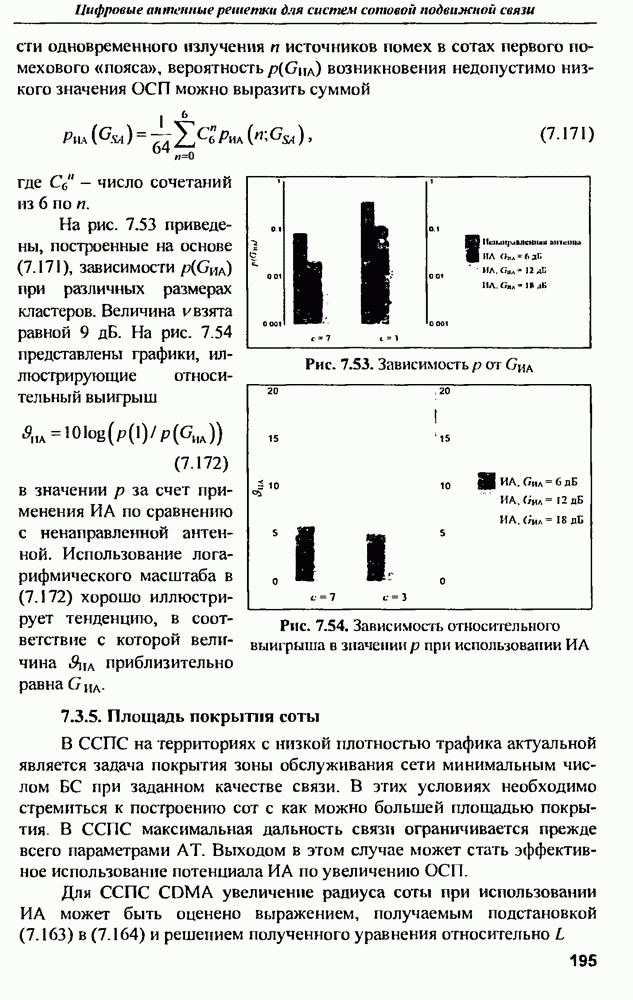
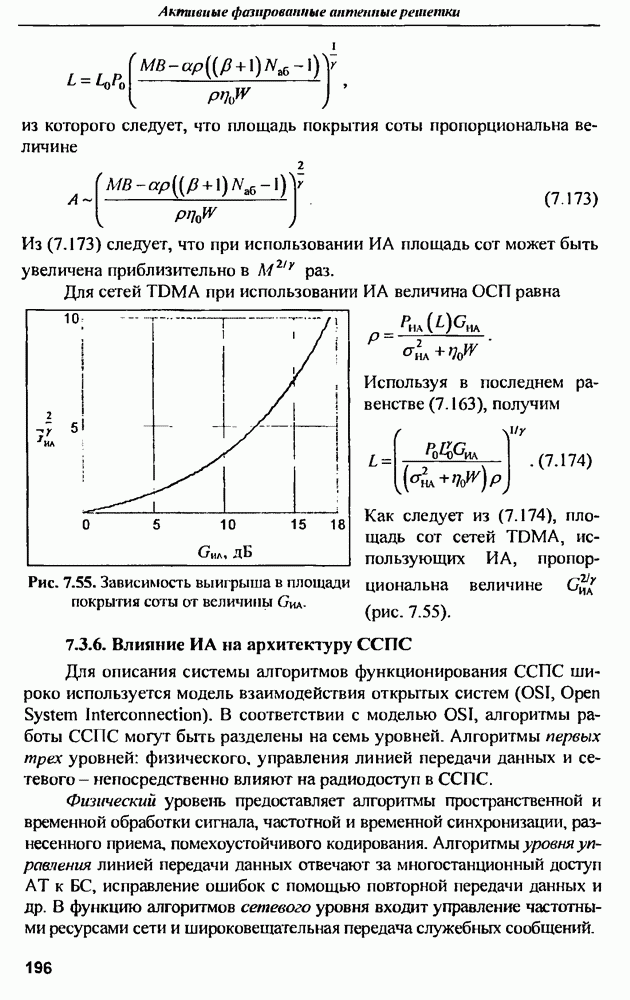
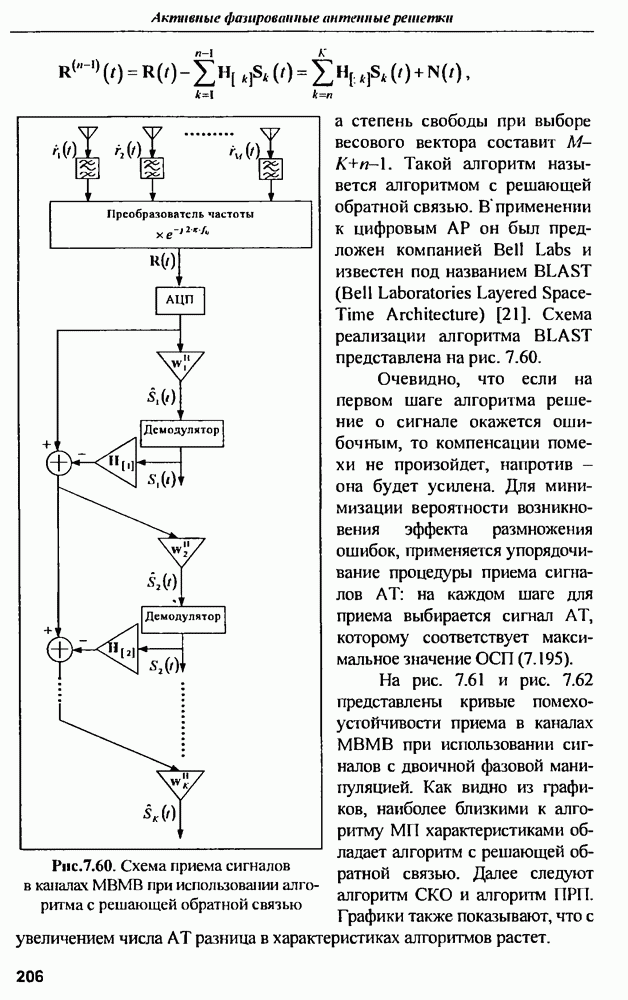
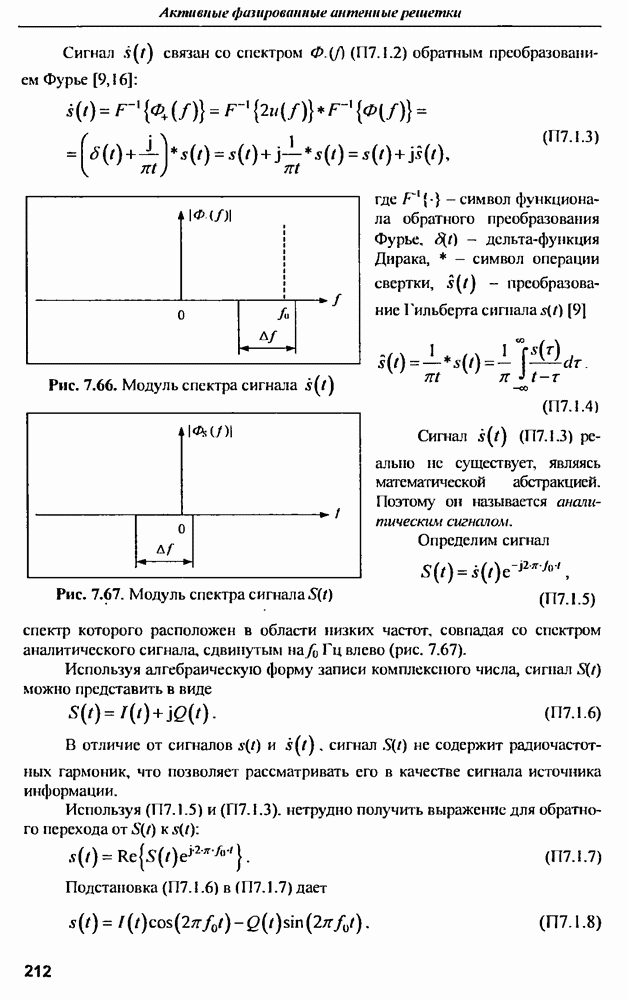
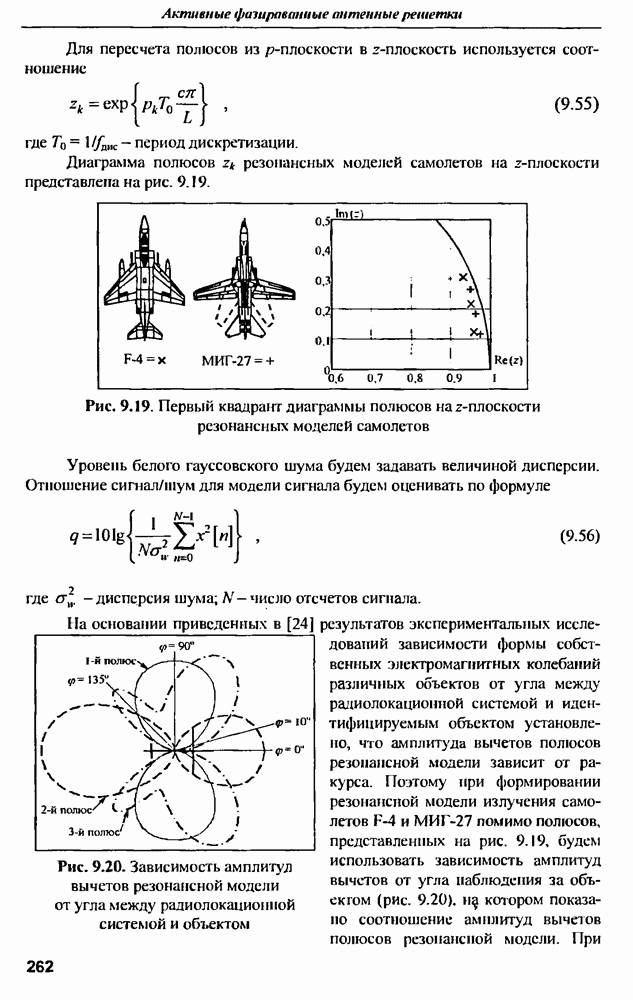
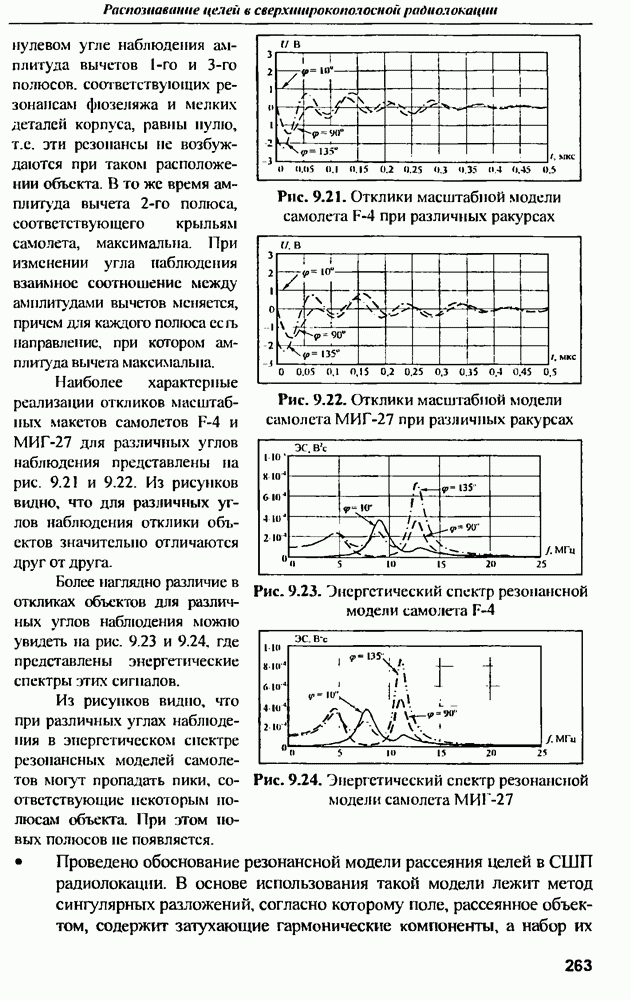
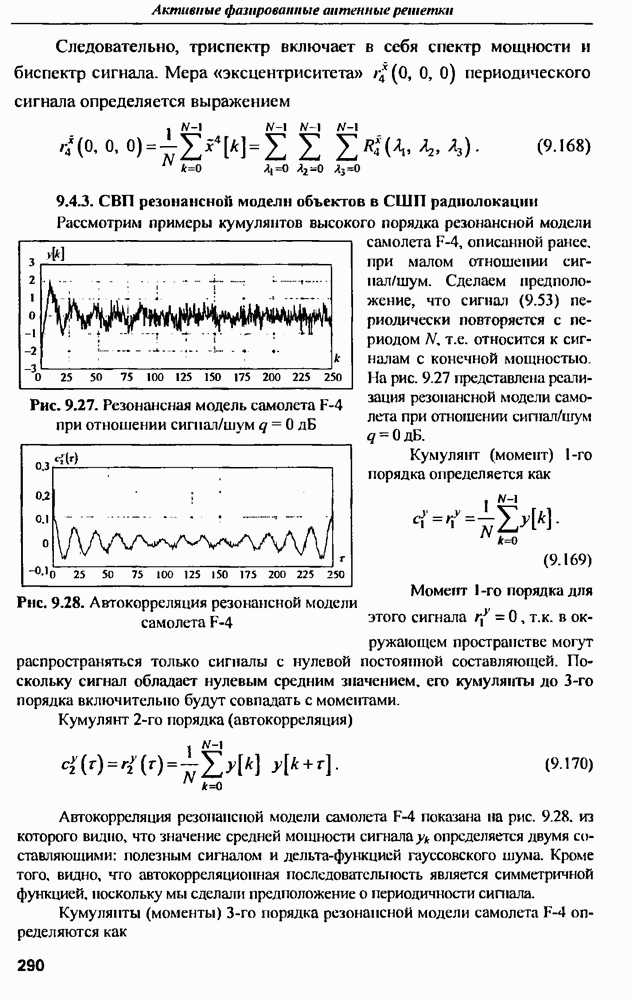
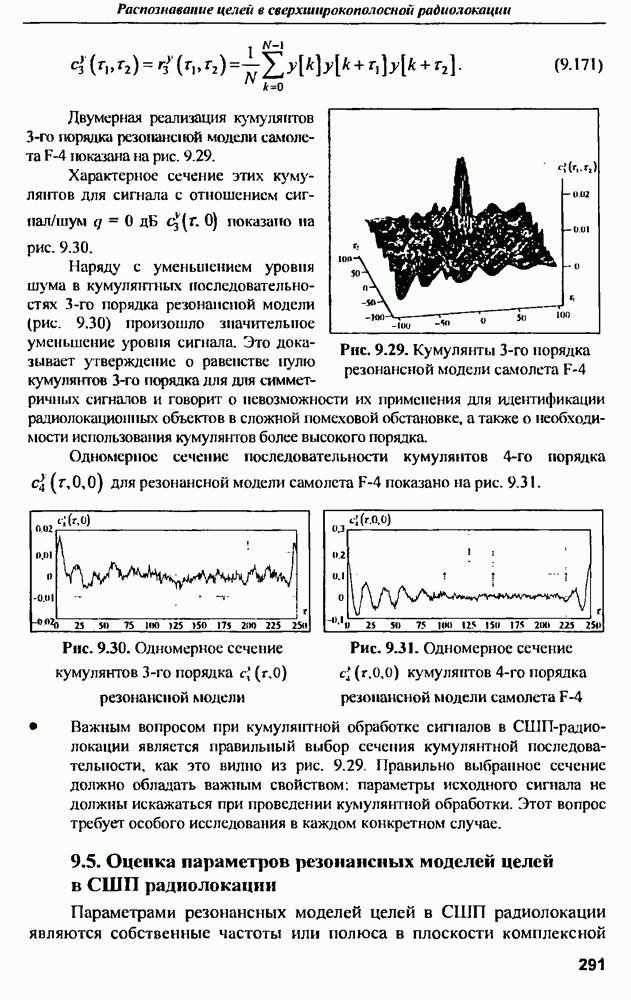
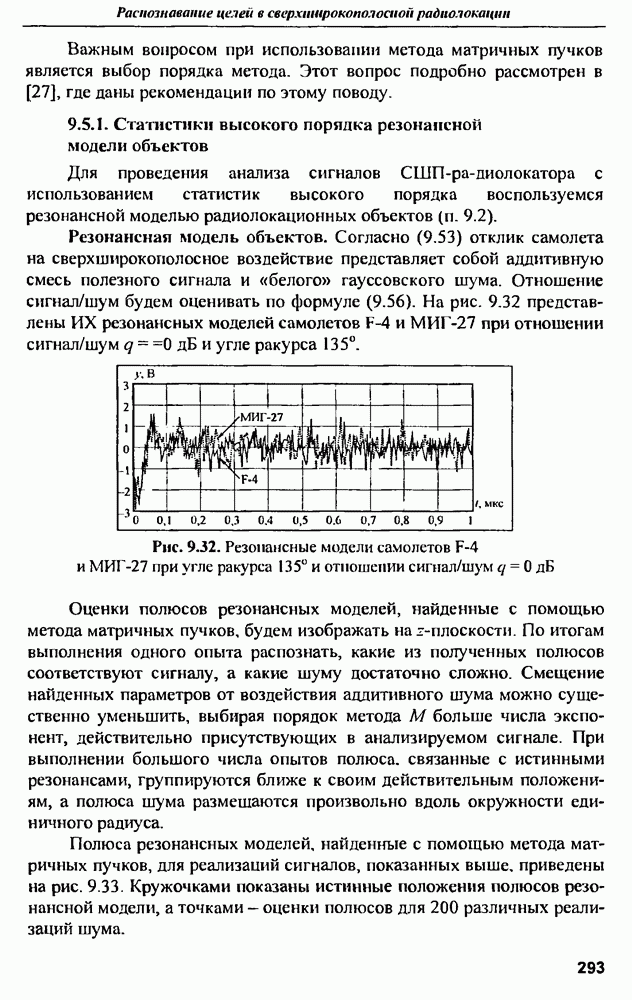
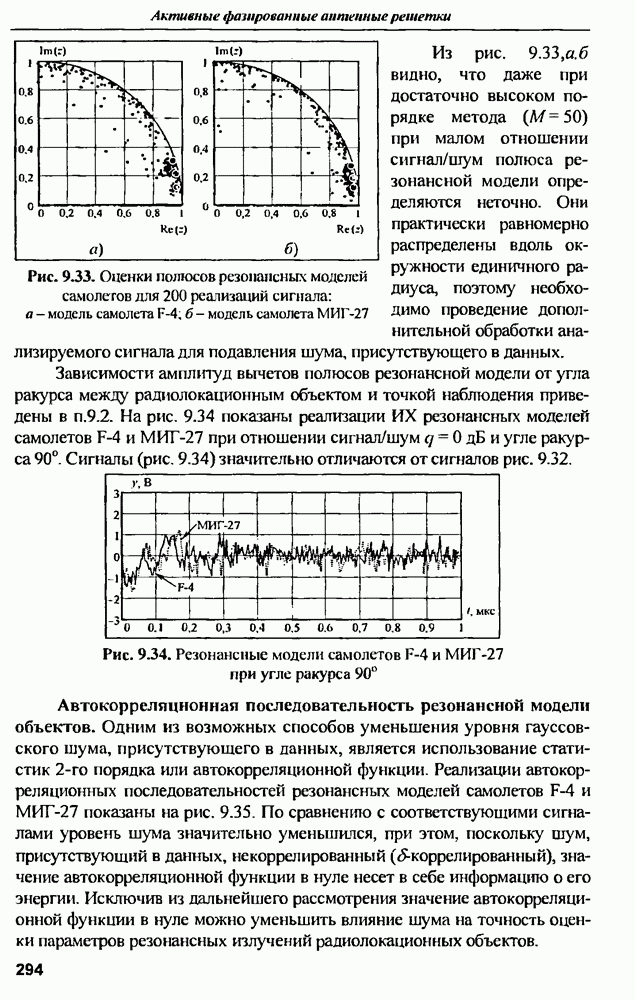
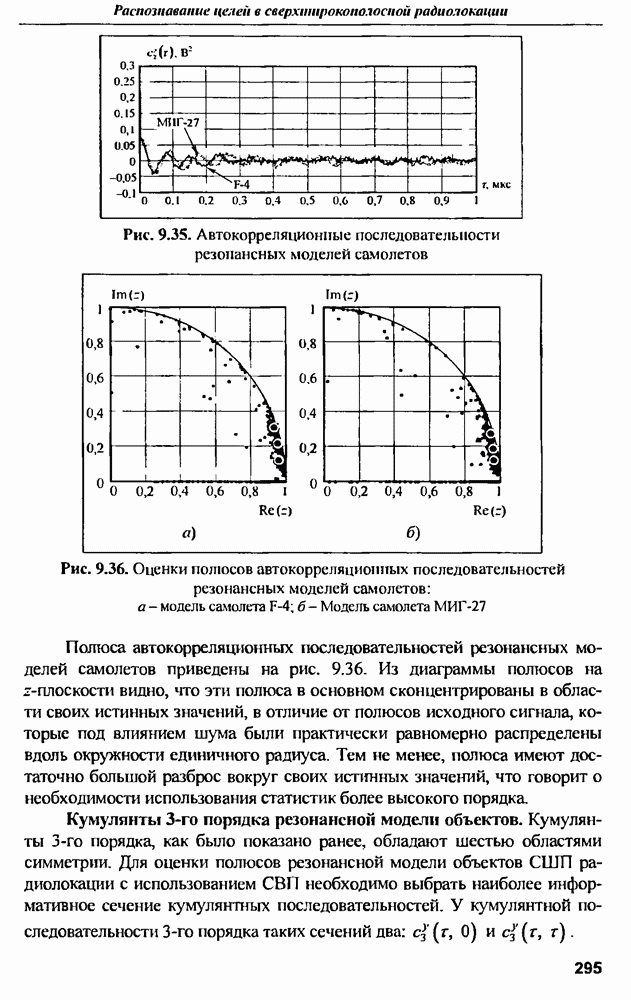
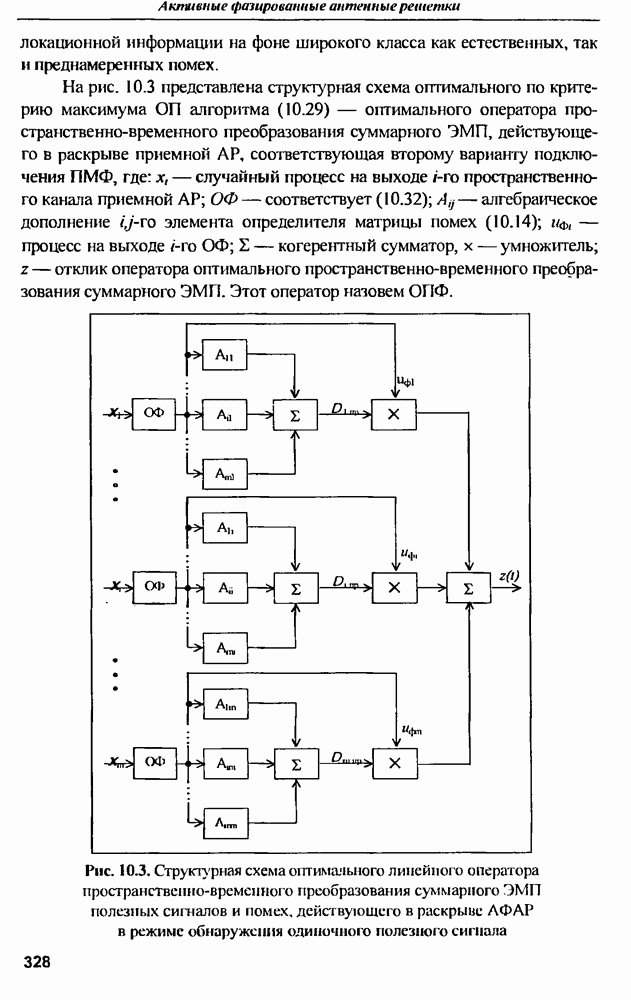
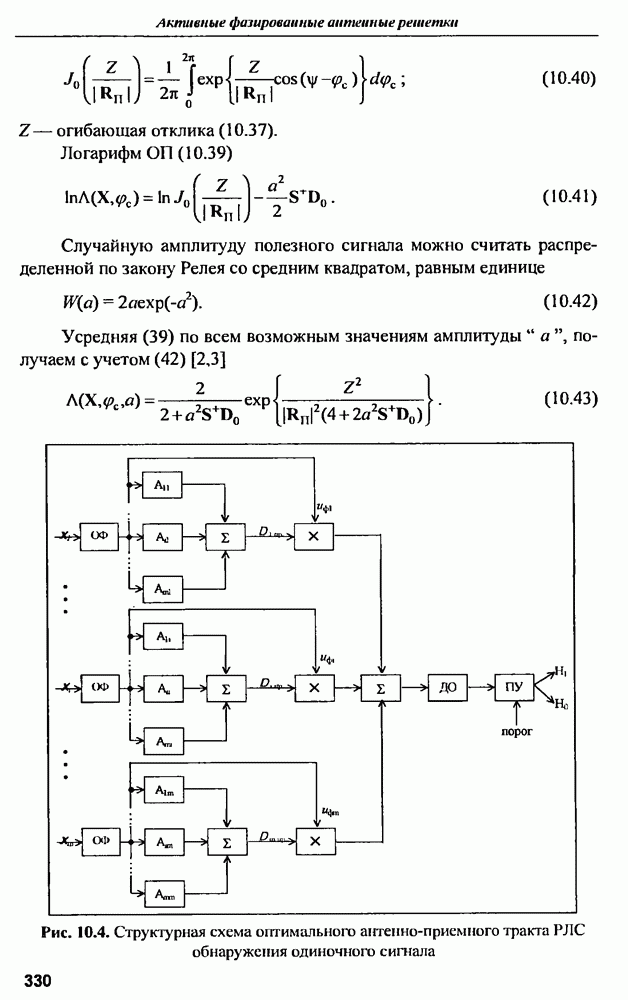
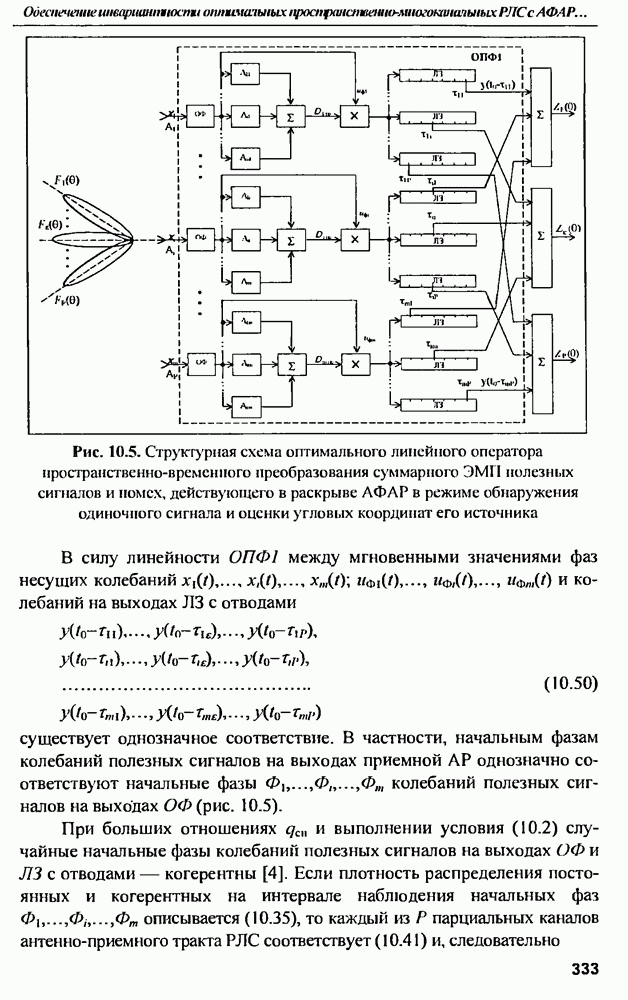
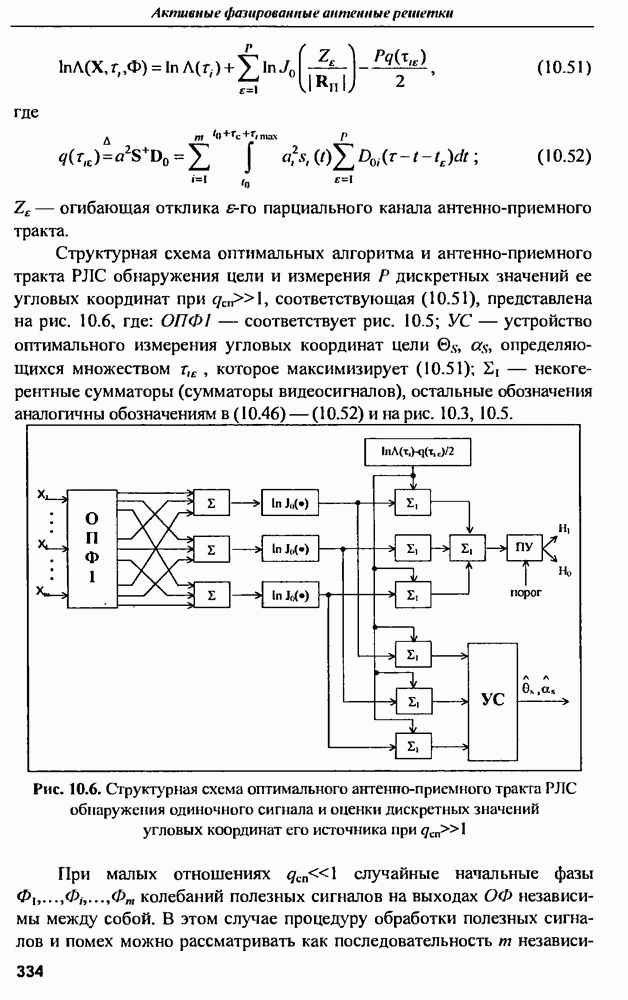
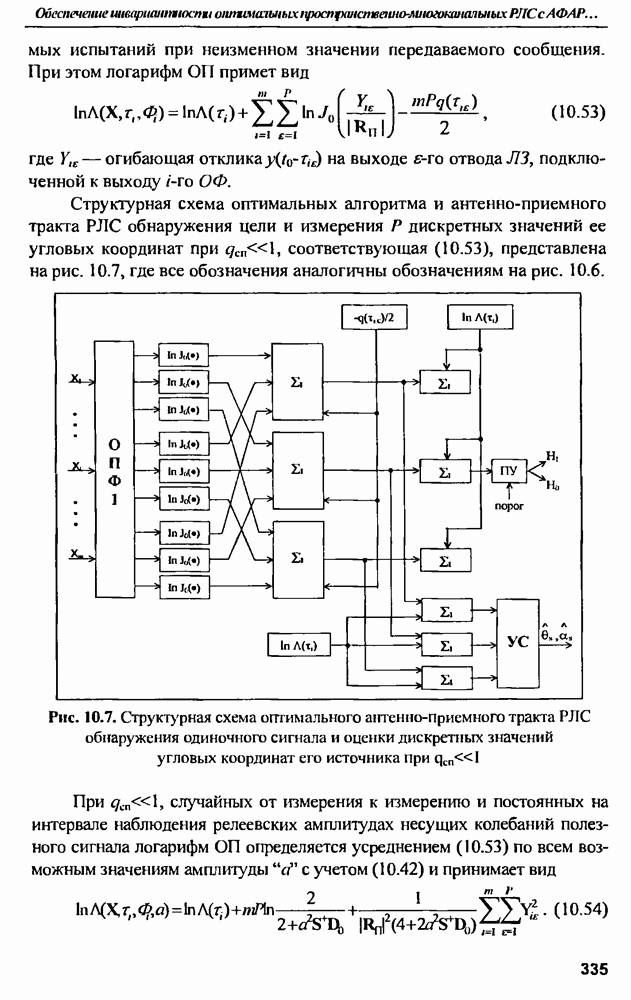
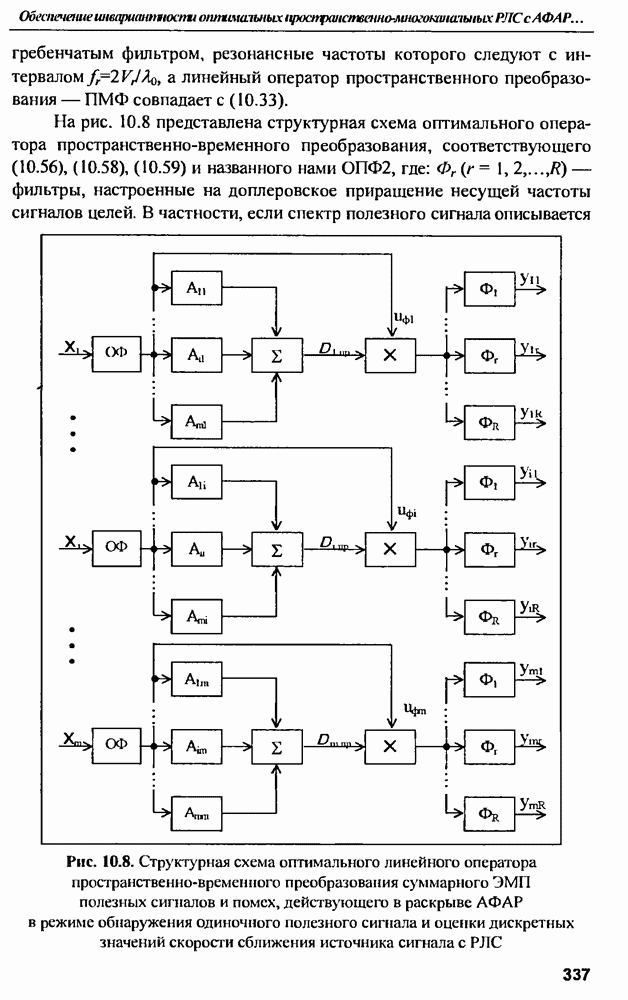
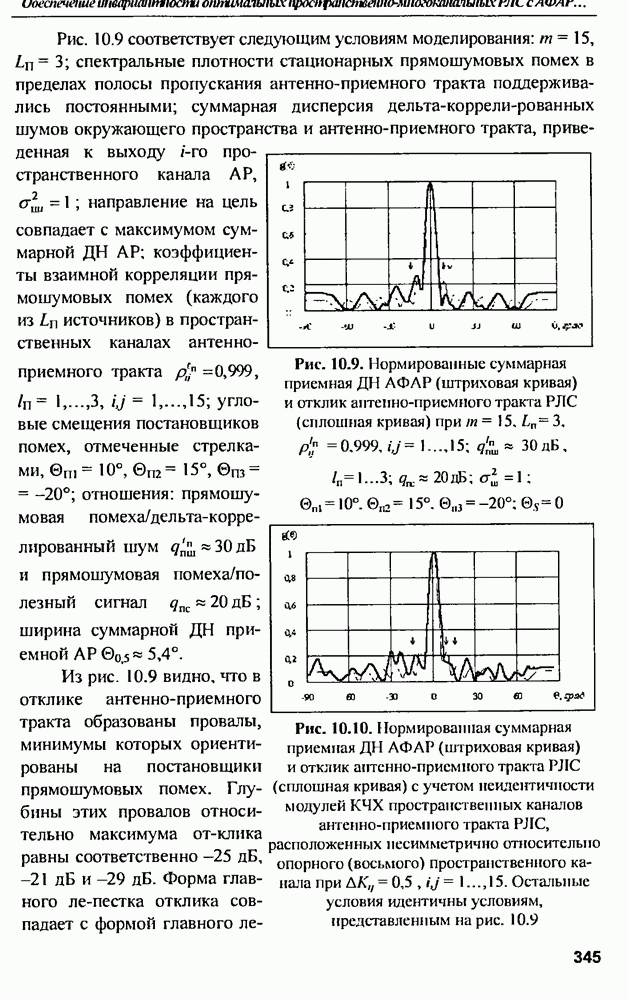
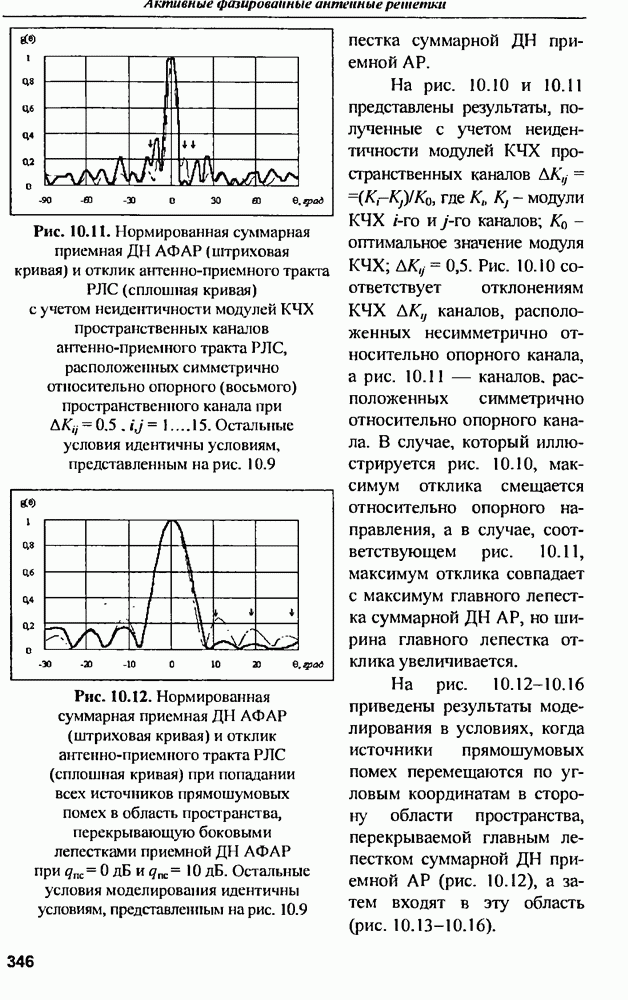
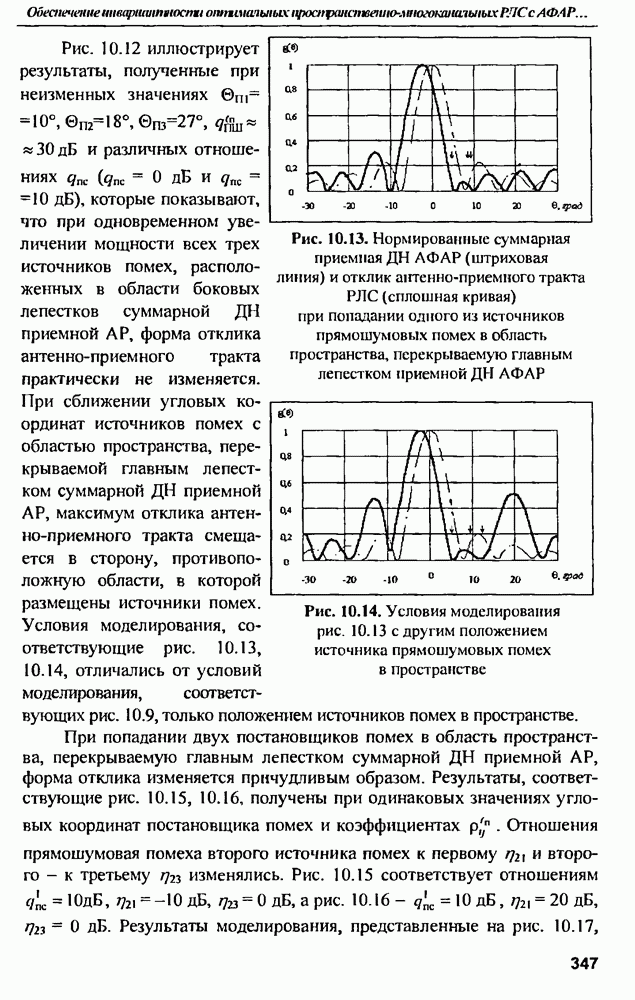
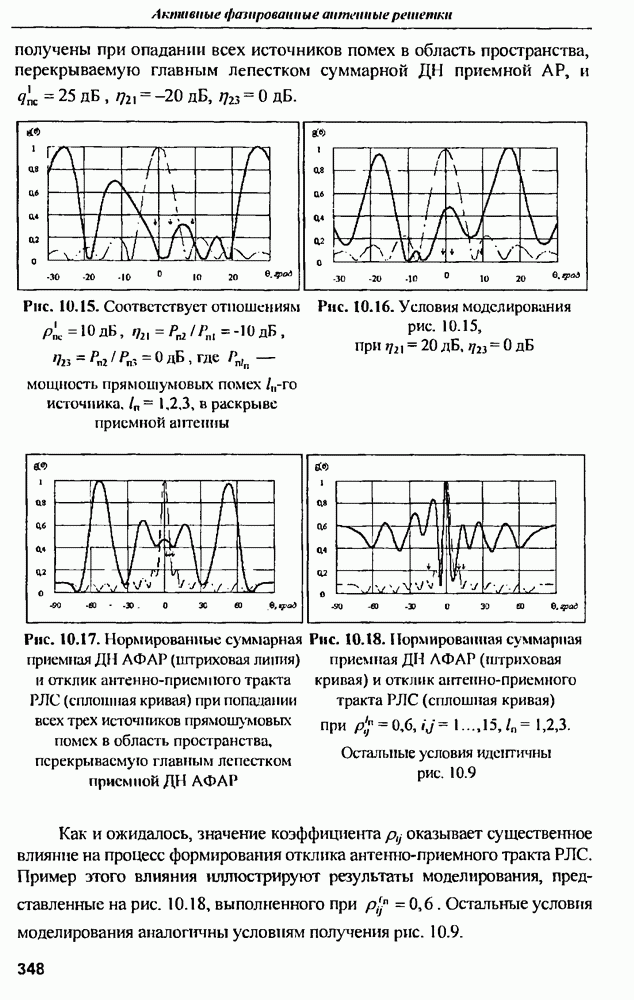
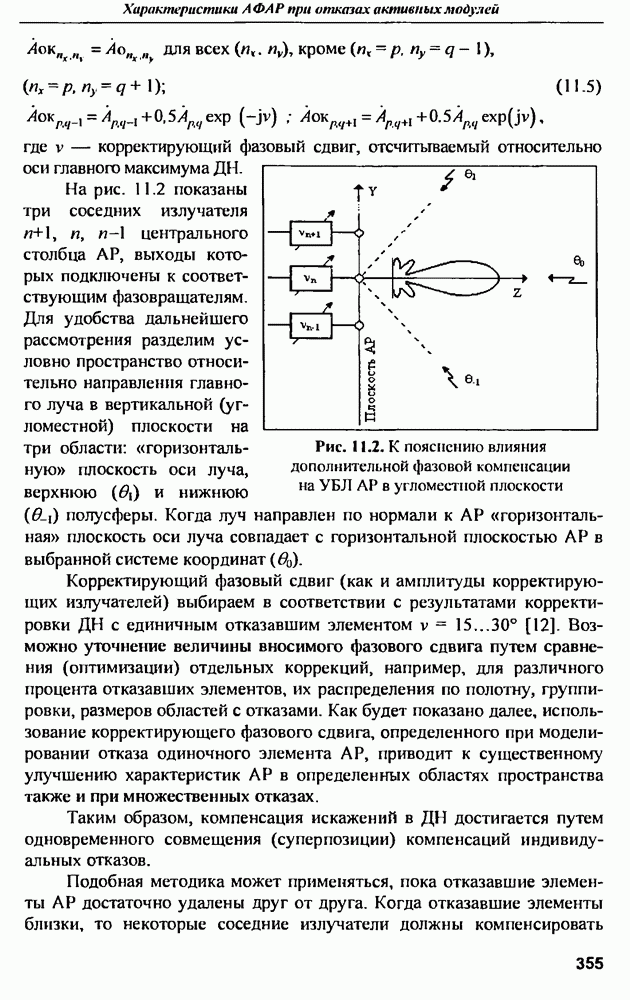
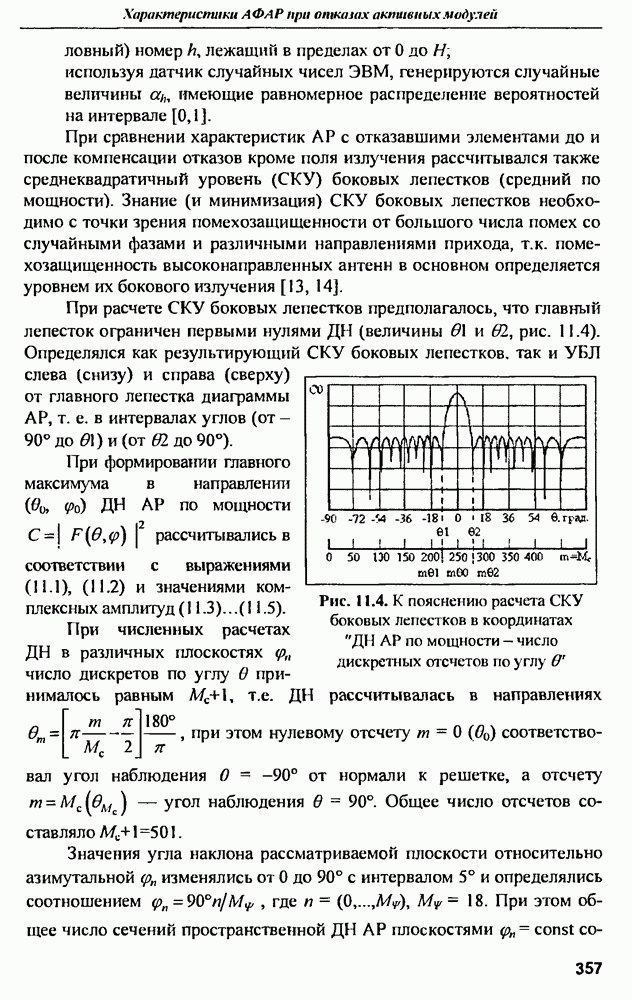
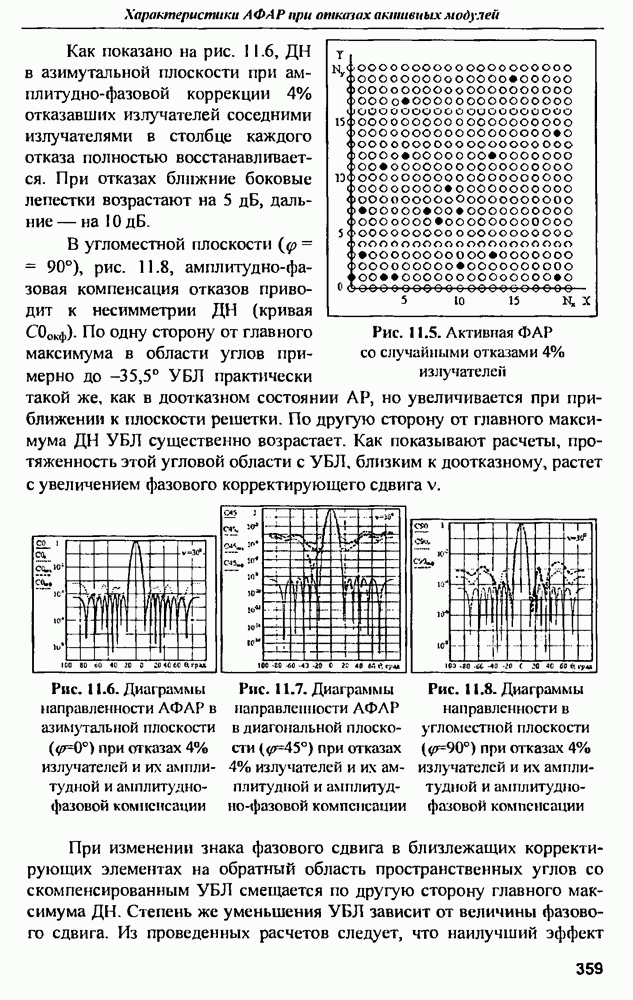
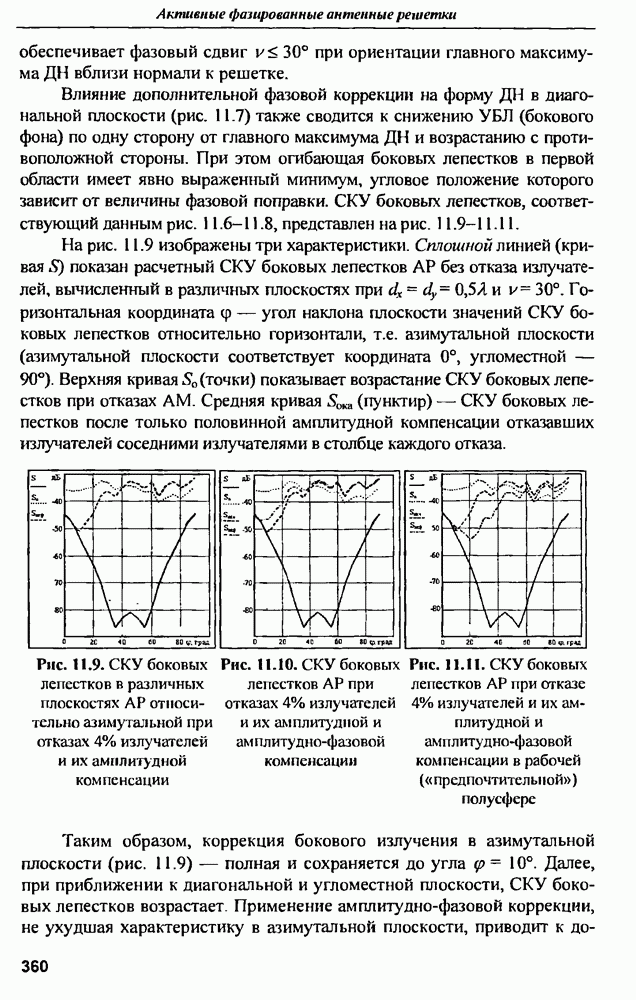
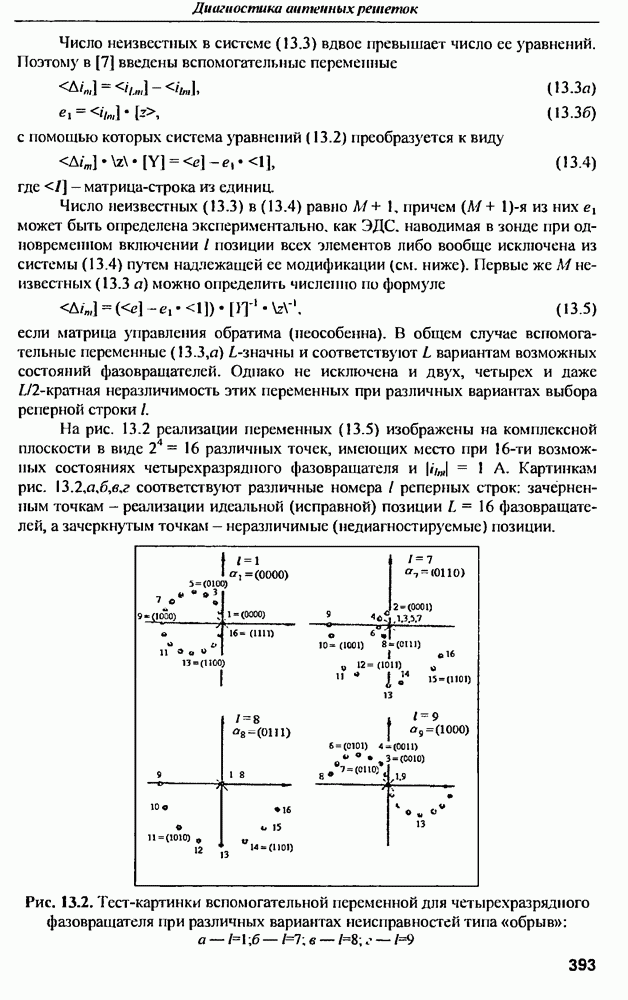
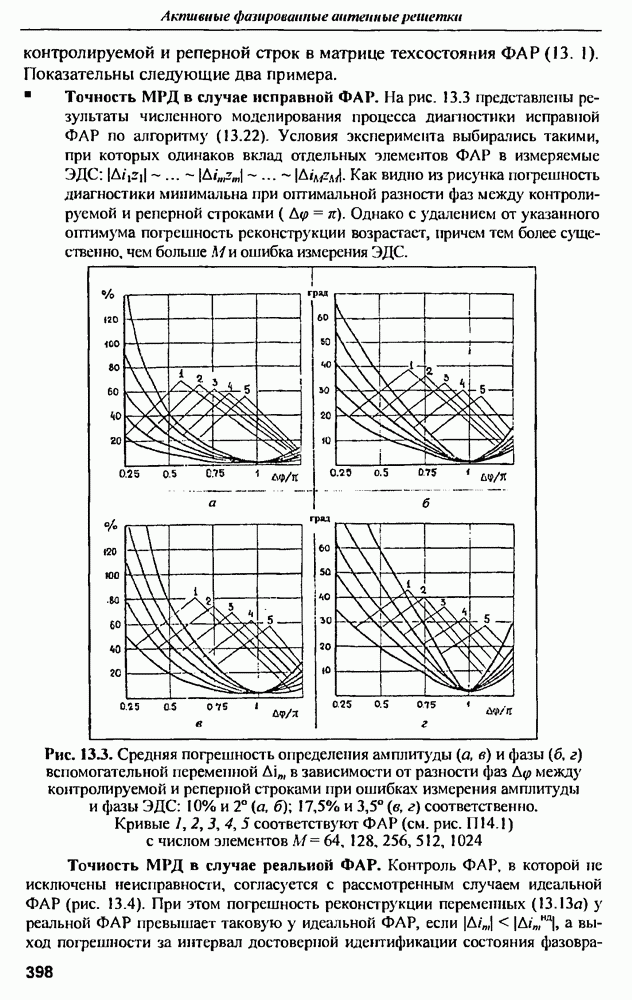
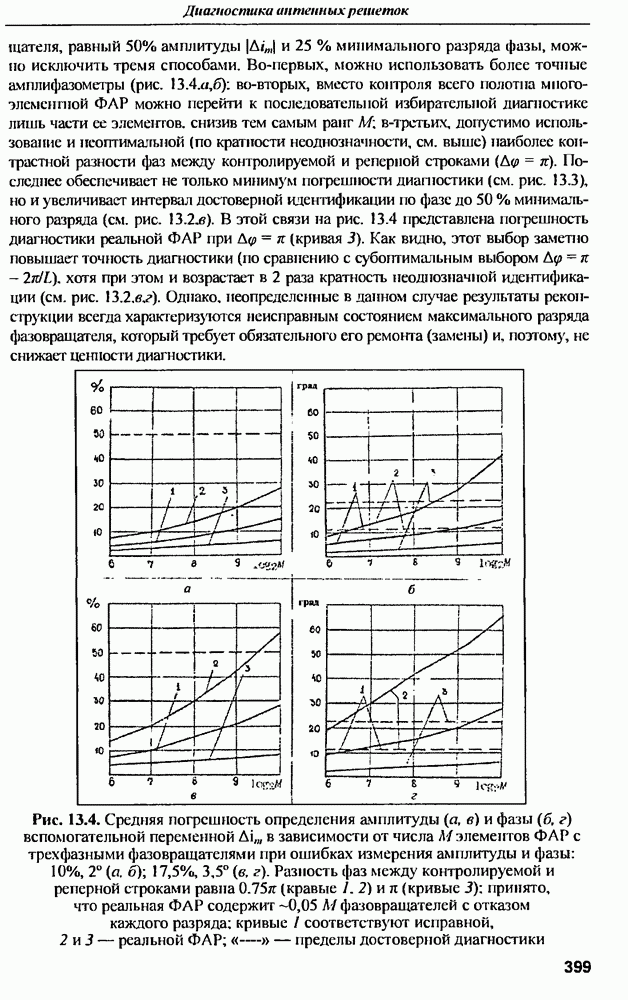
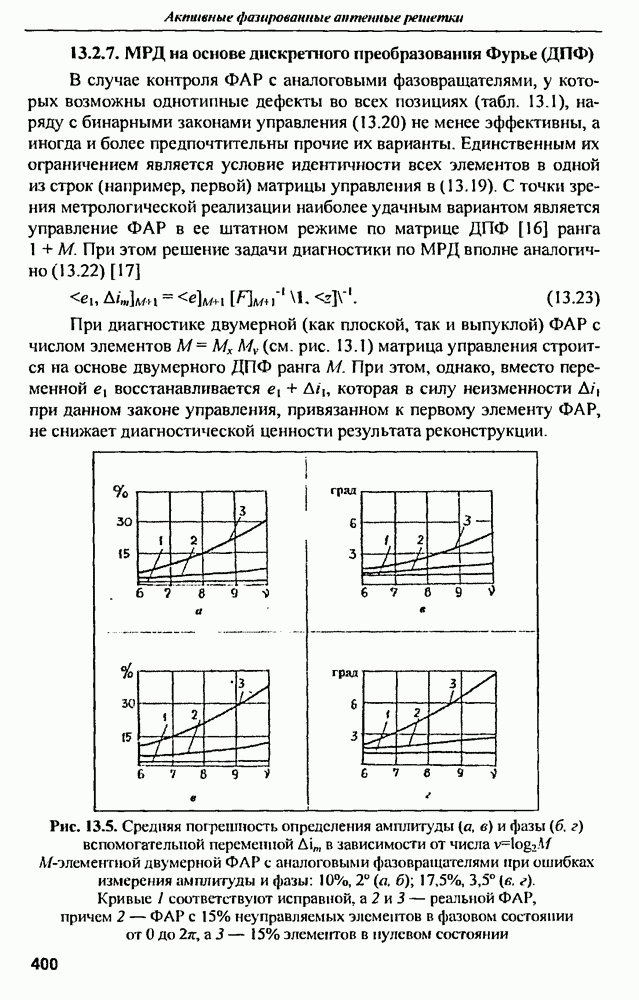
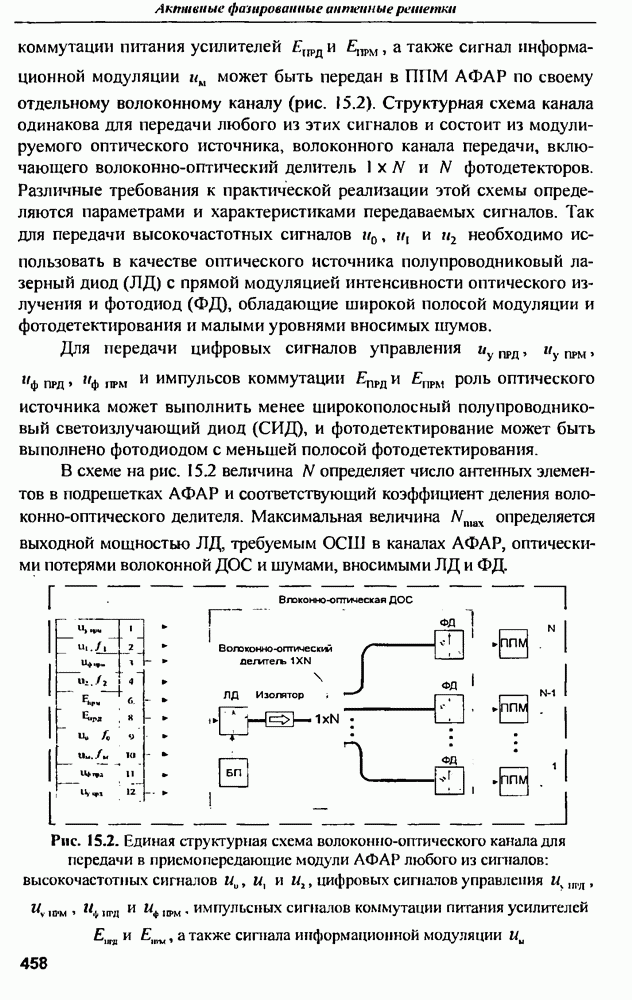
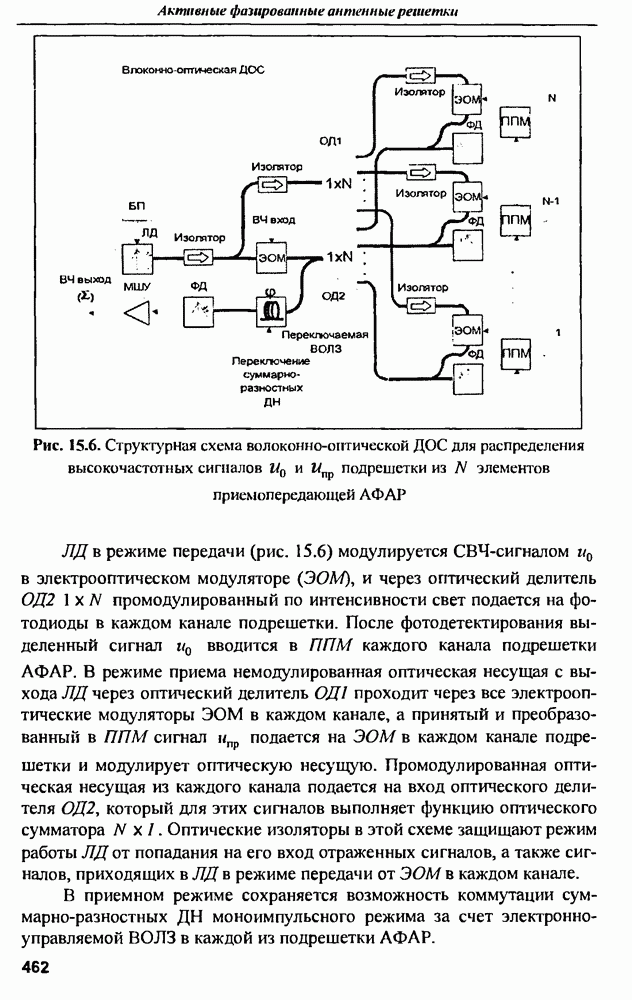
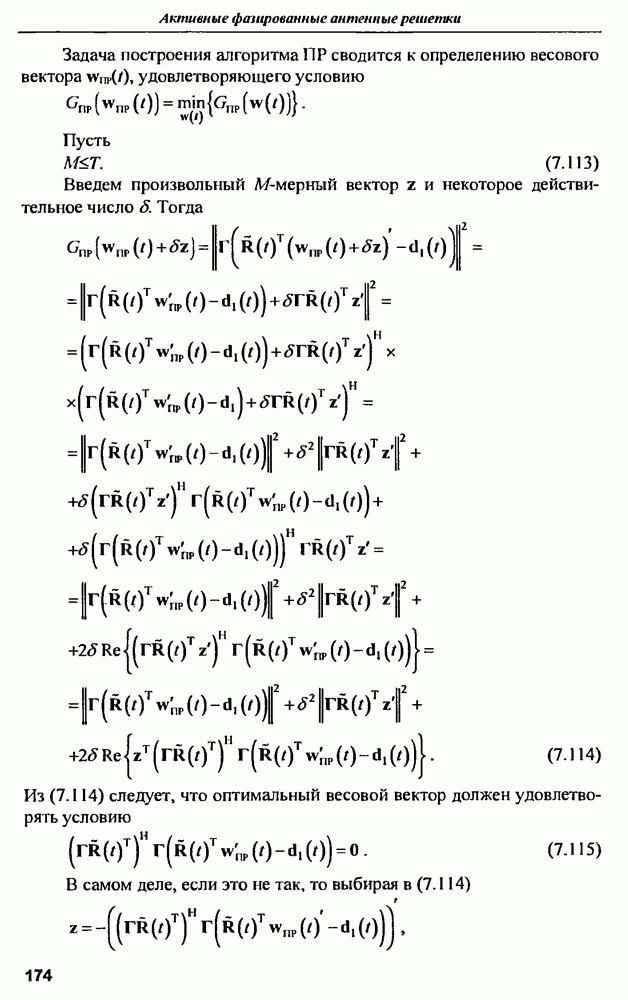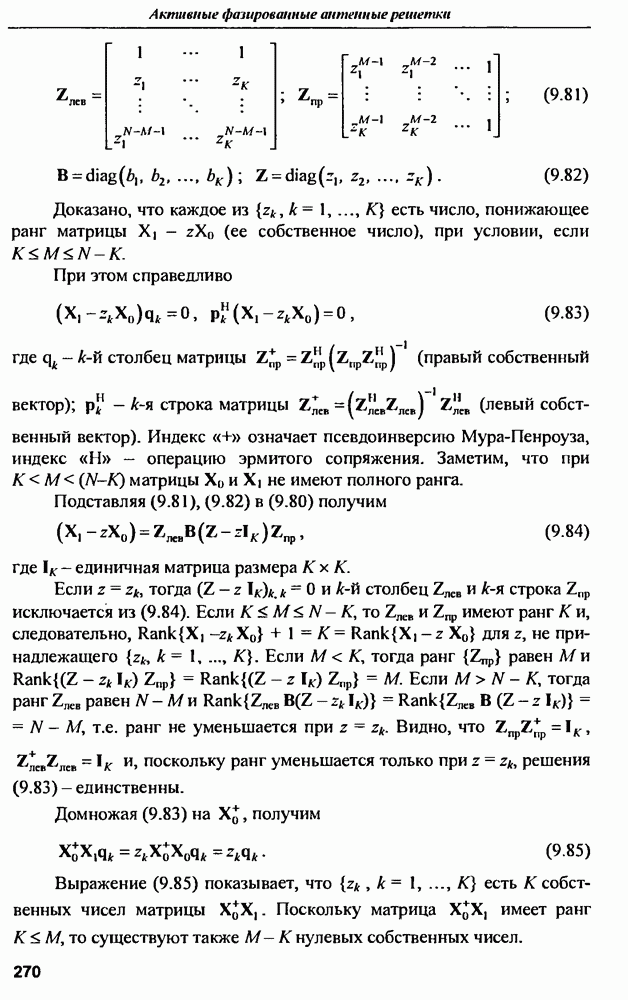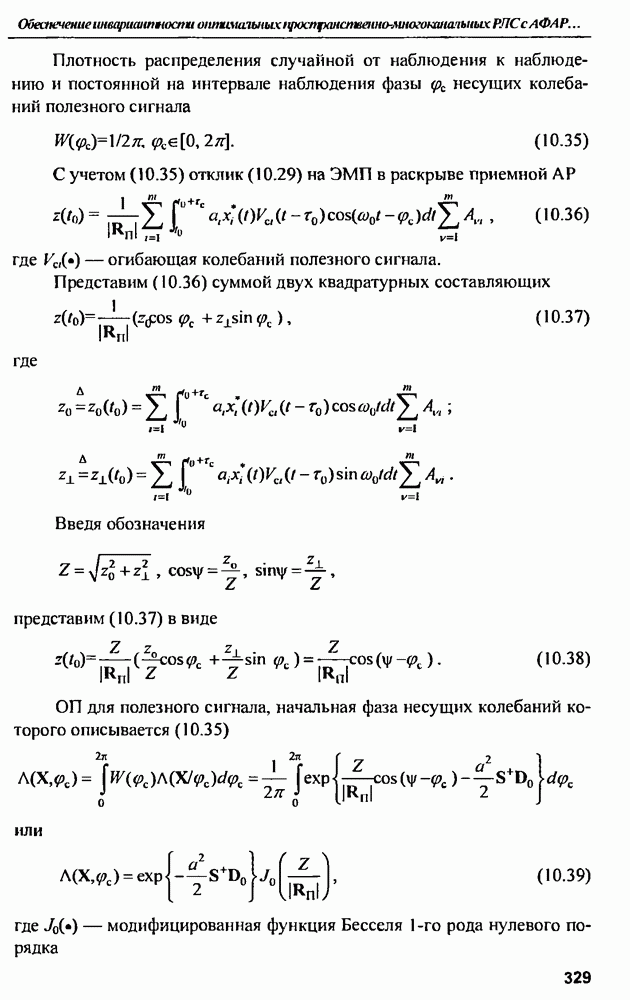| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
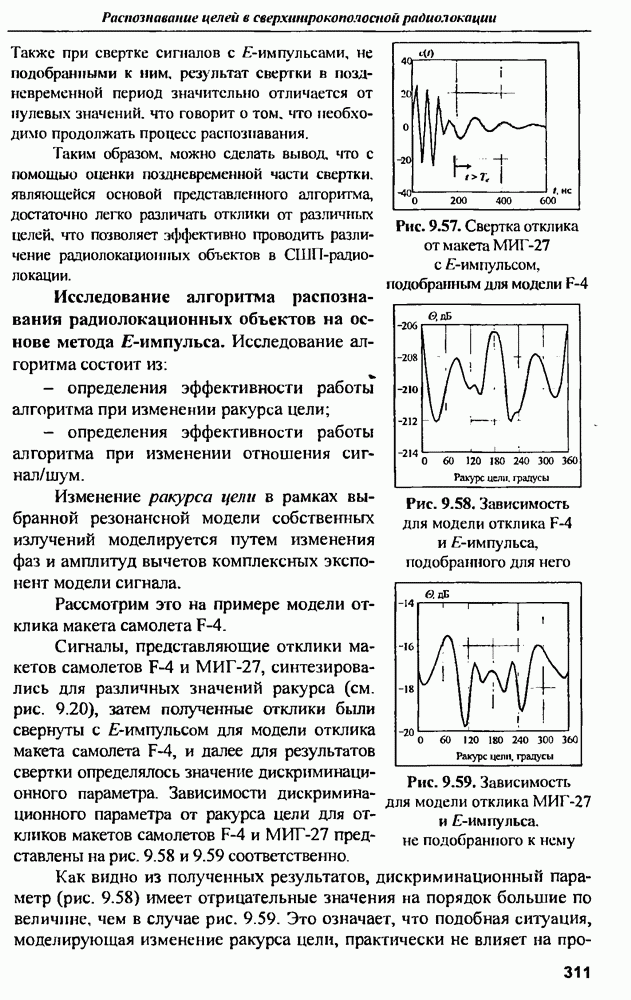
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
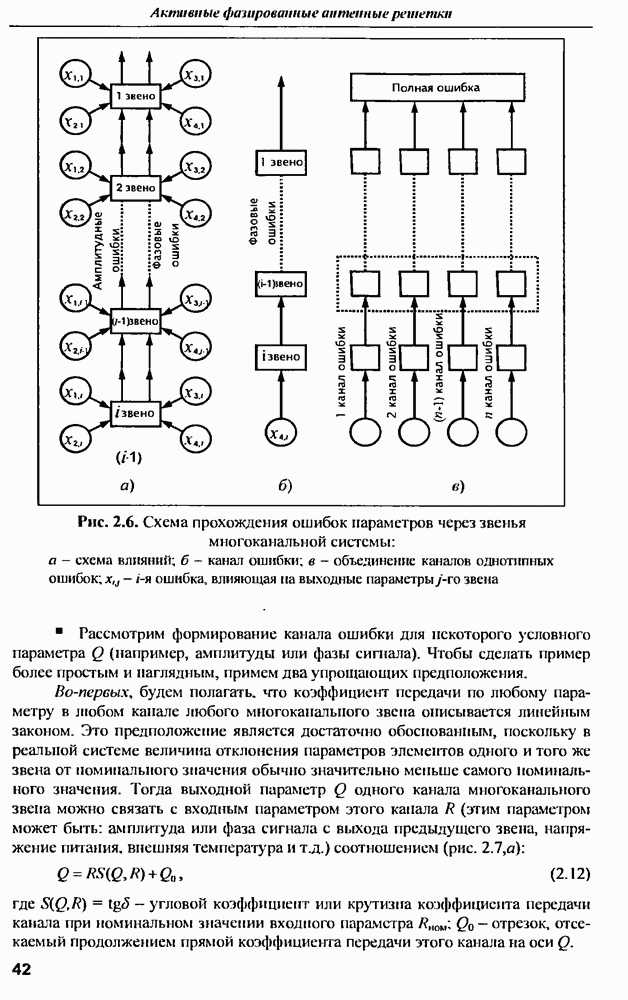
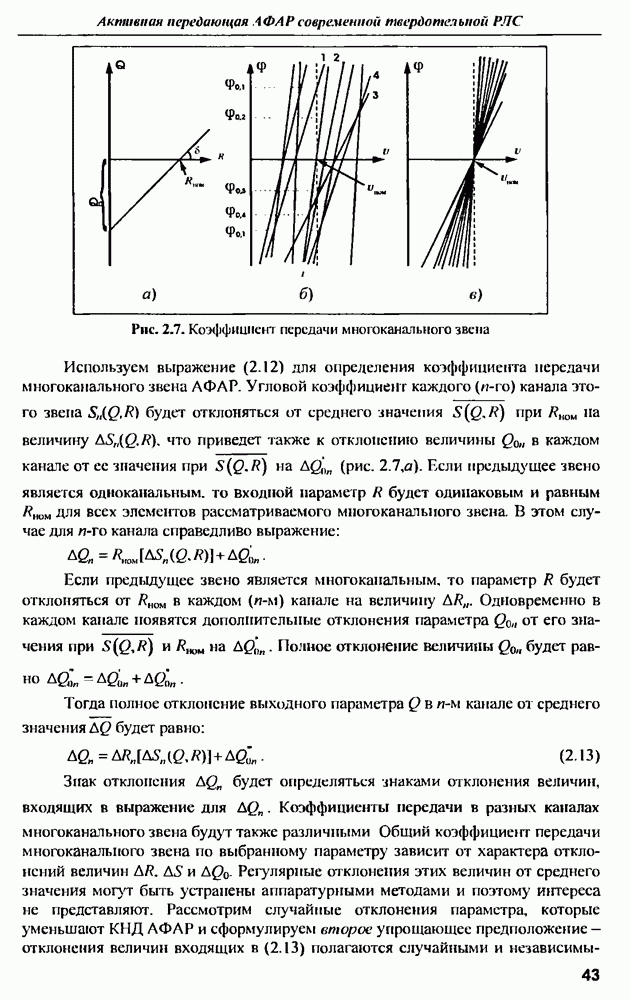
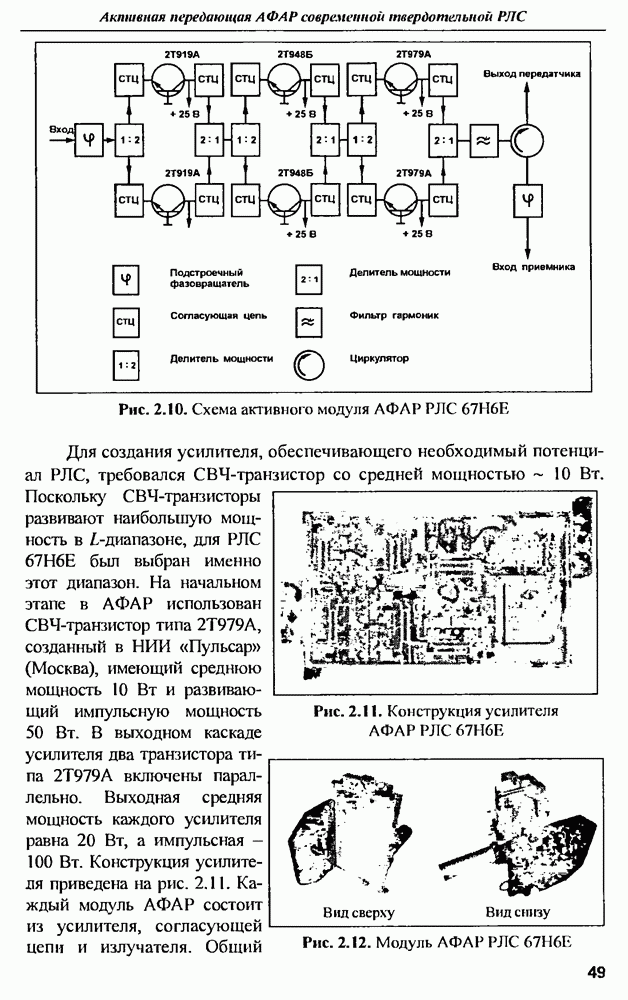
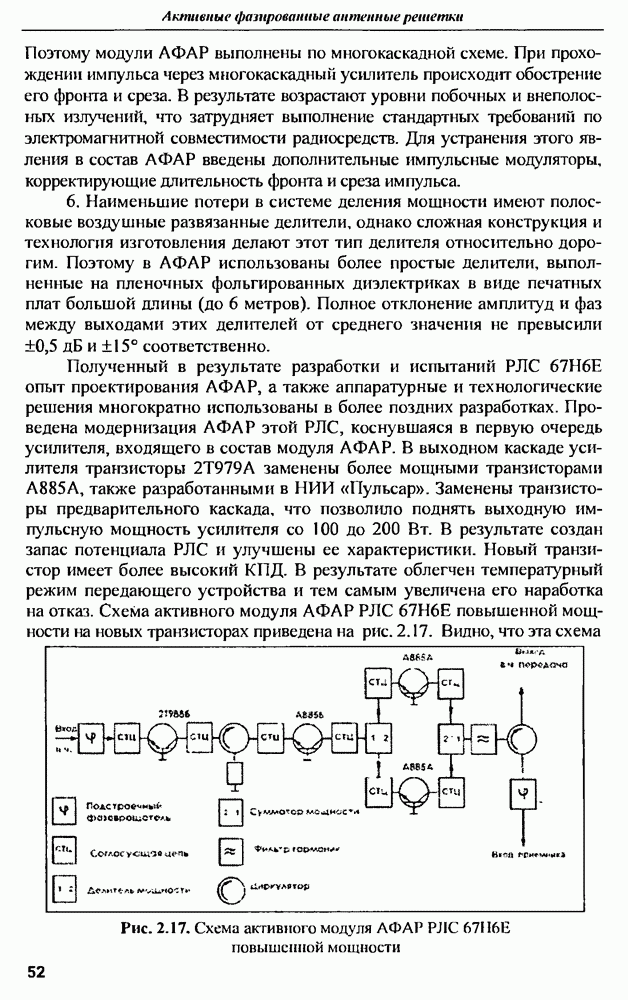
9.1.2. Тела простой геометрической формы
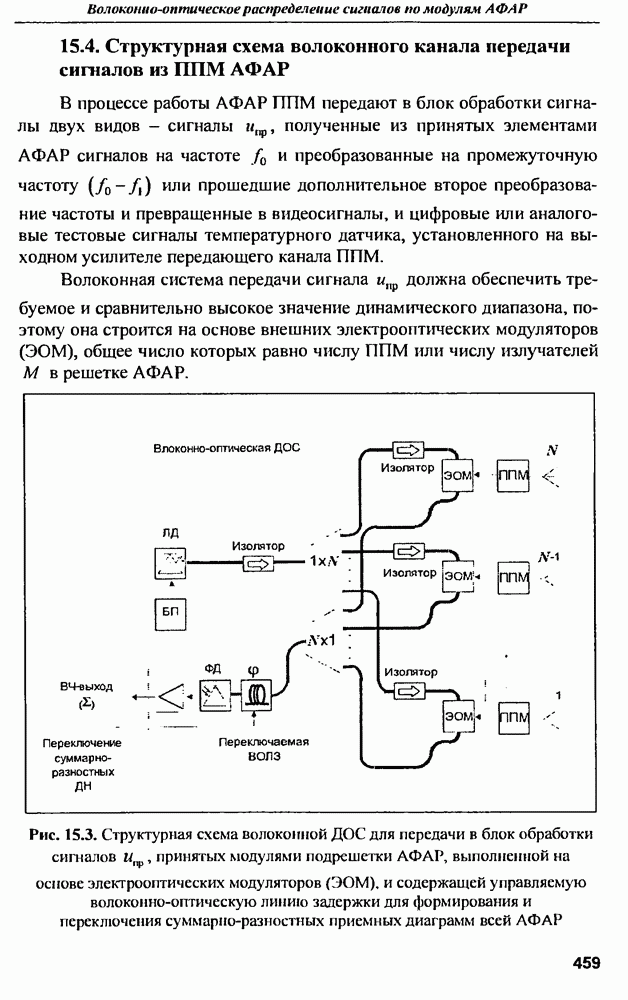
Реальные радиолокационные цели имеют довольно сложную форму поверхности и выполняются из самых различных материалов. Поэтому приближенные численные методы расчета характеристик рассеяния радиоволн объектами сложной геометрической формы в широком диапазоне частот при воздействии короткого по длительности импульса дают результаты, которые довольно сложно интерпретировать физически. Это приводит к тому, что оценить степень близости результатов к истинным значениям, а также обоснованно выбрать параметры приближенных методов, например, интервалы дискретизации по времени и пространству, не всегда просто. Одним из возможных путей решения этой проблемы является проведение расчетов на тестовых задачах, точный результат решения которых известен.
Точные аналитические решения задач дифракции электромагнитных волн получены для некоторых тел, имеющих правильную геометрическую форму: сфера (шар), цилиндр, часть плоской поверхности и т.д. [10]. Наиболее простые результаты получаются для тел с идеально проводящими поверхностями при стационарном воздействии гармонических колебаний, когда поле рассматривается в дальней зоне. Анализ этих известных зависимостей позволяет выявить некоторые общие закономерности, которые целесообразно было бы использовать в сверхширокополосной радиолокации.
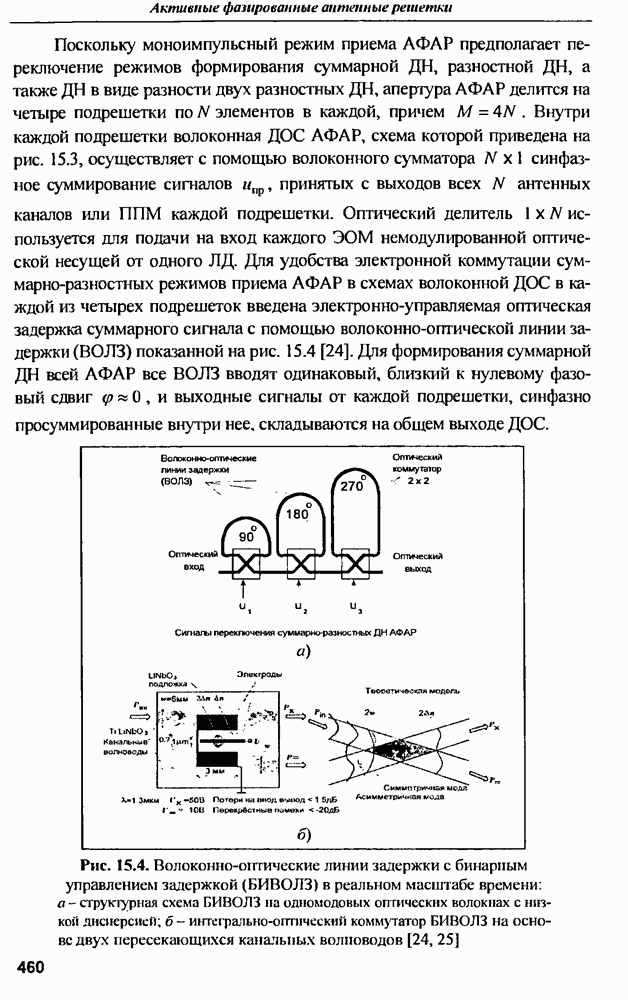
Характеристики рассеяния шара. Самым простым и хорошо изученным объектом с точки зрения рассеяния электромагнитной волны является идеально проводящая сфера. Для нее проведен точный расчет методом криволинейных координат в сферических координатах. Впервые анализ рассеяния сферы был проведен в 1908 г. ученой  поэтому некоторые формулы и зависимости для сферы носят ее имя.
поэтому некоторые формулы и зависимости для сферы носят ее имя.
Применительно к СШП радиолокации наибольший интерес представляет обратное рассеяние электромагнитной волны, т.е. в направлении на источник падающего поля, причем на большом расстоянии от шара достаточно определить только одну из компонент вектора напряженности рассеянного электромагнитного поля.
Она имеет вид

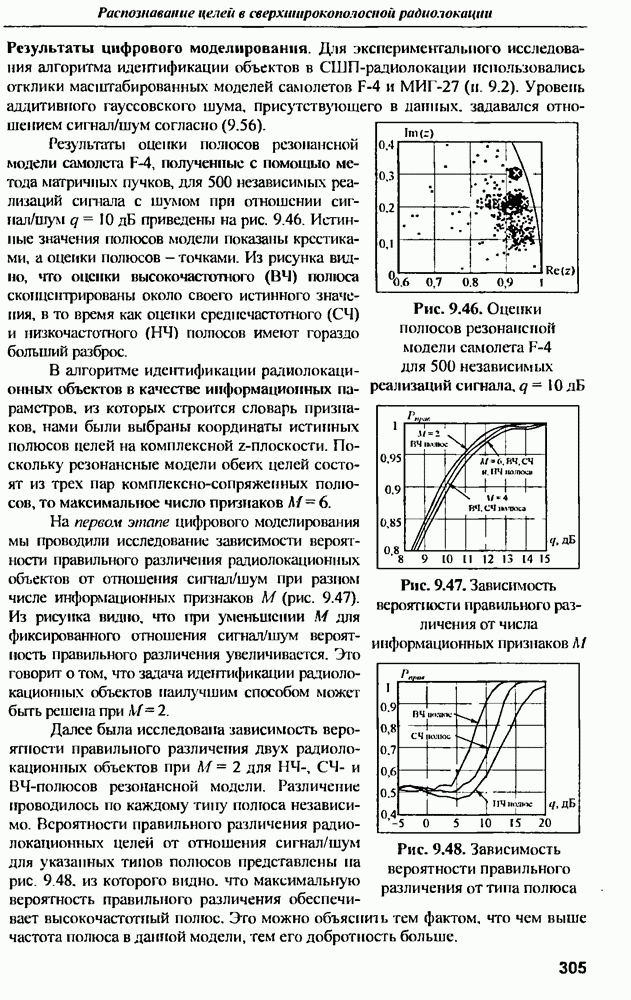
где  комплексные амплитуды рассеянного в обратном направлении и падающего электрического полей соответственно;
комплексные амплитуды рассеянного в обратном направлении и падающего электрического полей соответственно;  волновое число;
волновое число;  длина волны падающего поля для среды, в которой находится сфера;
длина волны падающего поля для среды, в которой находится сфера;  расстояние от шара до точки наблюдения; а - радиус шара.
расстояние от шара до точки наблюдения; а - радиус шара.
Функции, входящие в соотношение (9.20), выражаются следующим образом:

где  функция Бесселя 1-го рода;
функция Бесселя 1-го рода;  первые функции Ханкеля, или функции Бесселя 3-го рода.
первые функции Ханкеля, или функции Бесселя 3-го рода.
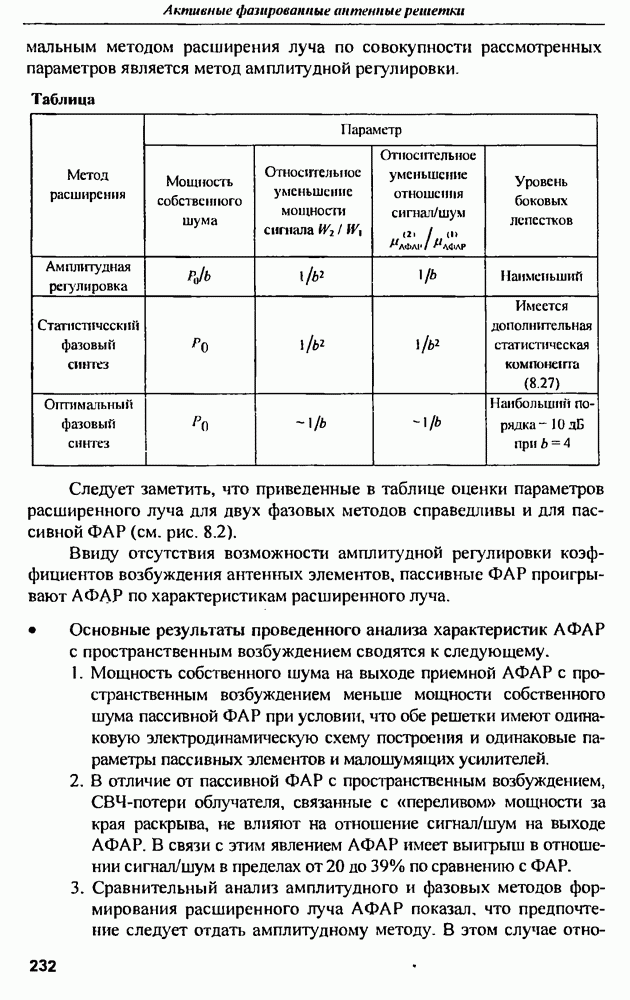
Определив модуль комплексной амплитуды рассеянного поля, возведя его в квадрат и подставив в формулу (9.1), получим выражение для эффективной поверхности рассеяния (ЭПР) сферы в зависимости от соотношения между радиусом сферы а и длиной волны в среде распространения  где
где  скорость света в среде; f - частота гармонического электромагнитного поля в Гц. Если ЭПР сферы отнести к площади ее поперечного сечения, равной
скорость света в среде; f - частота гармонического электромагнитного поля в Гц. Если ЭПР сферы отнести к площади ее поперечного сечения, равной  получим нормированную ЭПР, изображенную на рис. 9.3 [1].
получим нормированную ЭПР, изображенную на рис. 9.3 [1].
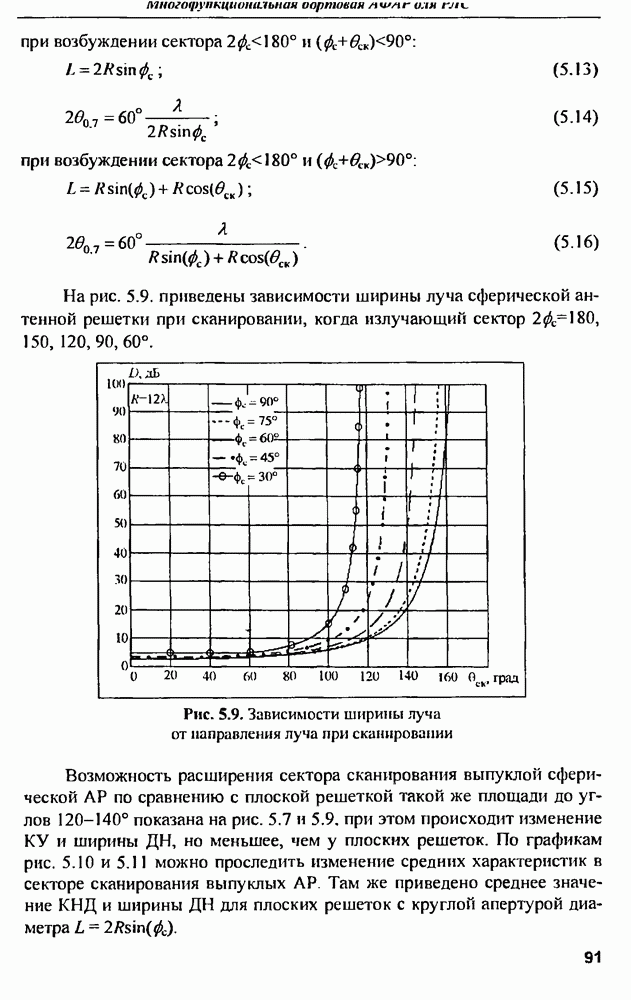
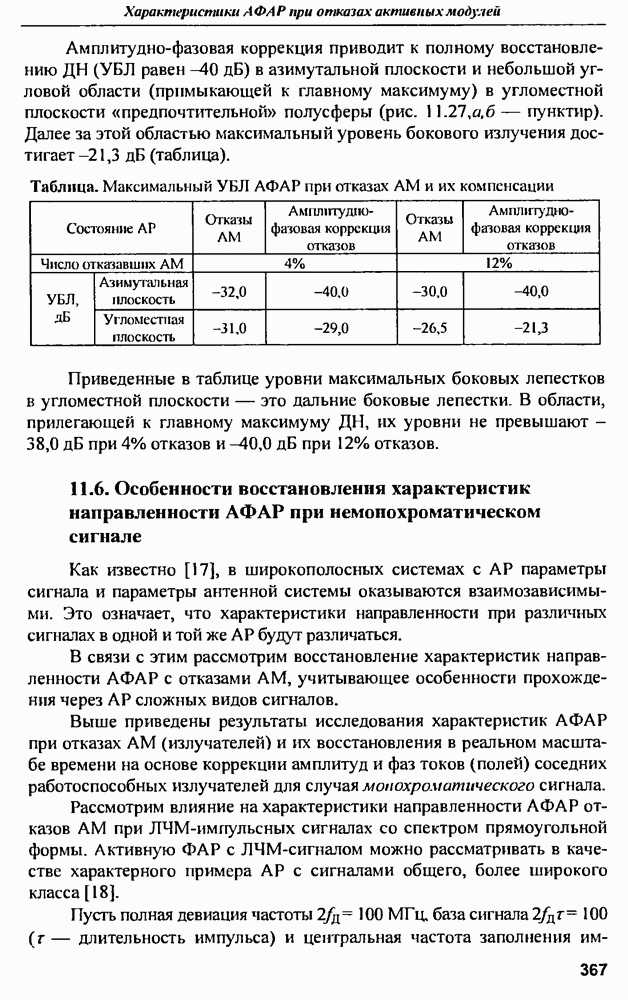
Из рис. 9.3 можно довольно четко выделить три области для величины отношения длины окружности сферы  к длине волны А.
к длине волны А.
Релеевская область (область низких частот), - длина окружности меньше одной длины волны, а ЭПР изменяется пропорционально четвертой степени частоты облучающего сферу поля. Эта зависимость в релеевской области характерна для любого объекта, наибольший размер которого меньше длины волны.

Рис. 9.3. ЭПР сферы
Следующая область нормированных длин волн, располагающаяся приближенно от  до
до  называется резонансной областью. Здесь ярко выражена зависимость ЭПР от частоты колебания, представляющая
называется резонансной областью. Здесь ярко выражена зависимость ЭПР от частоты колебания, представляющая
собой осциллирующую зависимость с ярко выраженным первым резонансным горбом и довольно большим числом более тупых резонансных пиков. Физически это объясняется тем, что сфера, являющаяся линейной колебательной системой с распределенными параметрами, может быть возбуждена кроме основной частоты еще и гармониками, приближенно кратными этой основной частоте, причем добротности резонансов, определяемых отношением резонансной частоты к ширине полосы по уровню половинной мощности, уменьшаются при удалении от основного резонанса. Колебательный характер в этой области также объясняется интерференцией между зеркальным отражением от облучаемой (освещенной) части сферы и волной, сформированной за счет огибания обратной (теневой) поверхности сферы с последующим излучением в направлении обратного зеркального рассеяния.
Высокочастотная область также называется оптической,  и ЭПР приближенно равно площади проекции сферы на плоскость, перпендикулярную направлению распространения облучающей волны, и не зависит от частоты электромагнитного поля.
и ЭПР приближенно равно площади проекции сферы на плоскость, перпендикулярную направлению распространения облучающей волны, и не зависит от частоты электромагнитного поля.
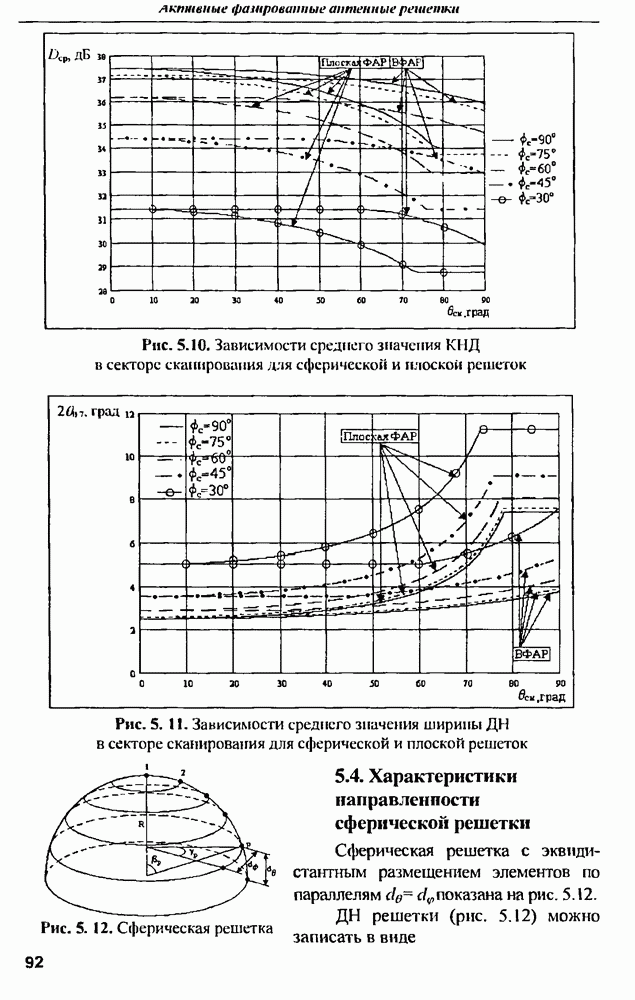
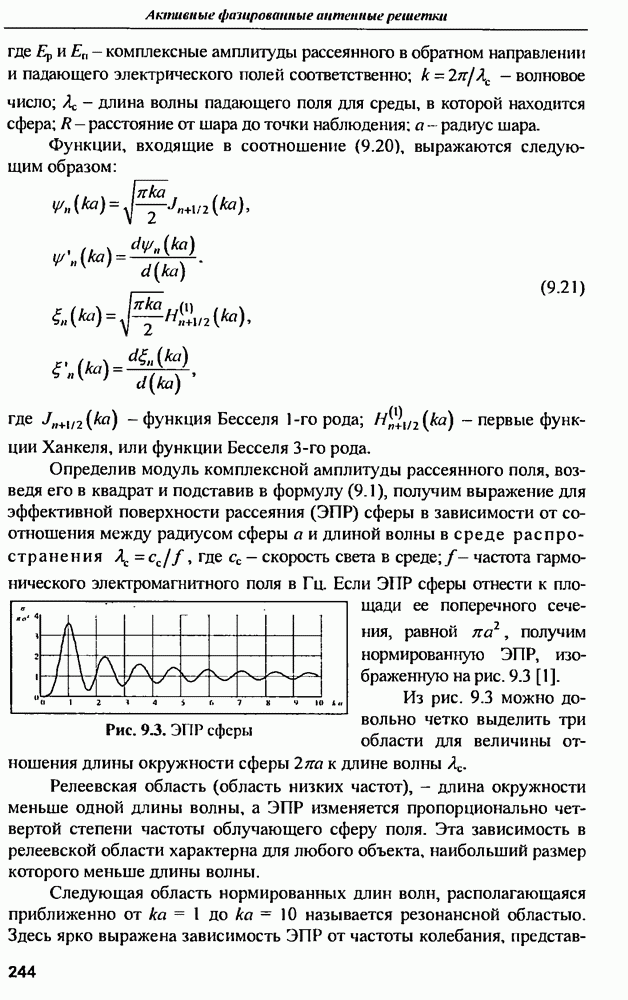
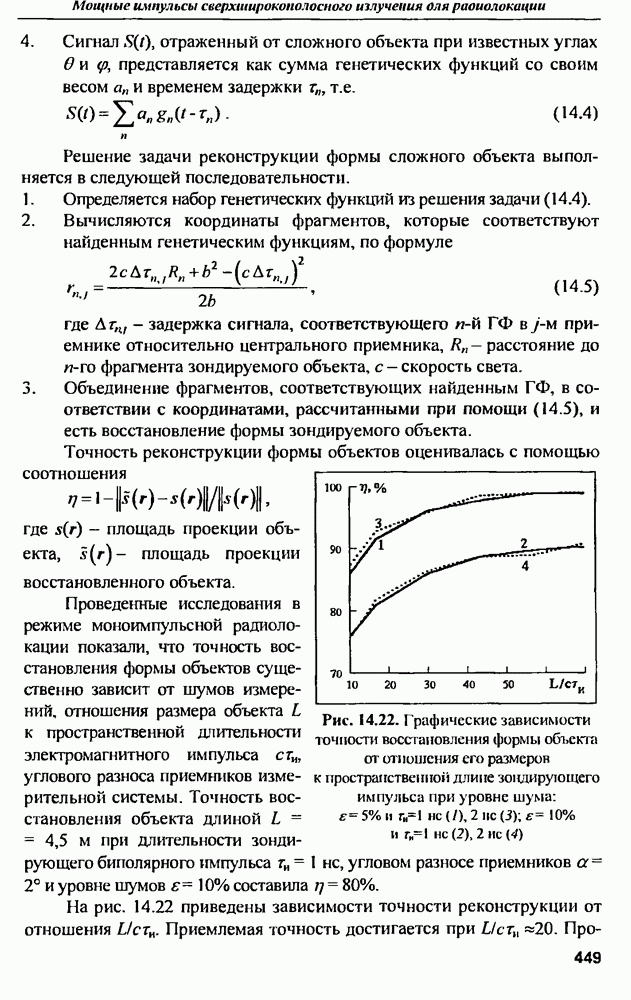
Рассмотрение приведенной зависимости ЭПР от длины волны позволяет сделать вывод о том, что по измеренной частотной характеристике рассеяния сферы можно довольно точно определить радиус сферы а, для чего нужно определить частоту первого резонанса. Например, для сферы радиусом в  частота первого резонанса составляет примерно 50 МГц, а добротность этого резонанса достигает величины порядка 1,5 (рис. 9.4).
частота первого резонанса составляет примерно 50 МГц, а добротность этого резонанса достигает величины порядка 1,5 (рис. 9.4).
Для определения резонансной частоты можно воспользоваться формулой

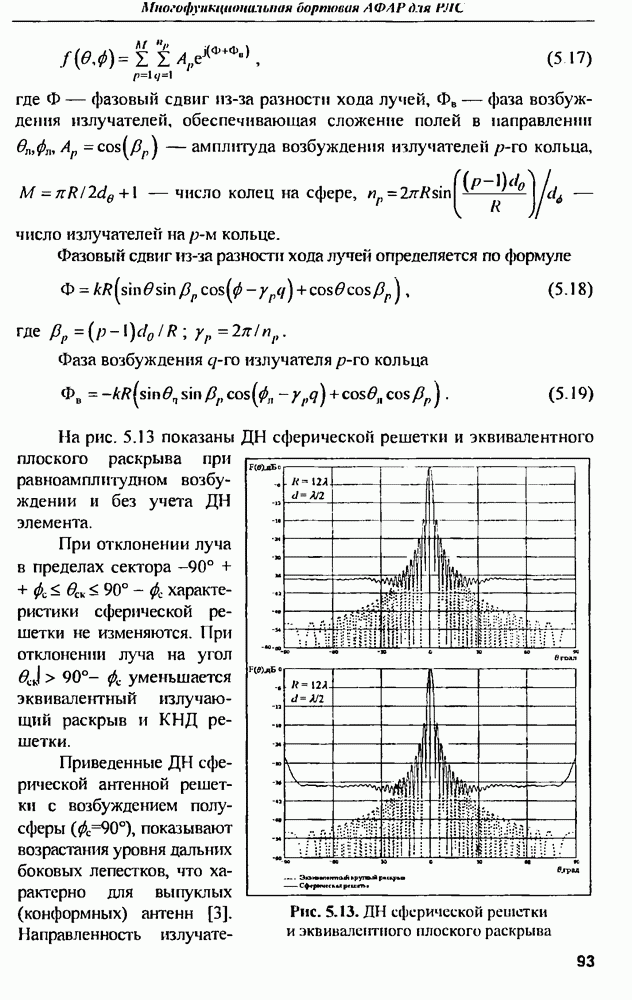
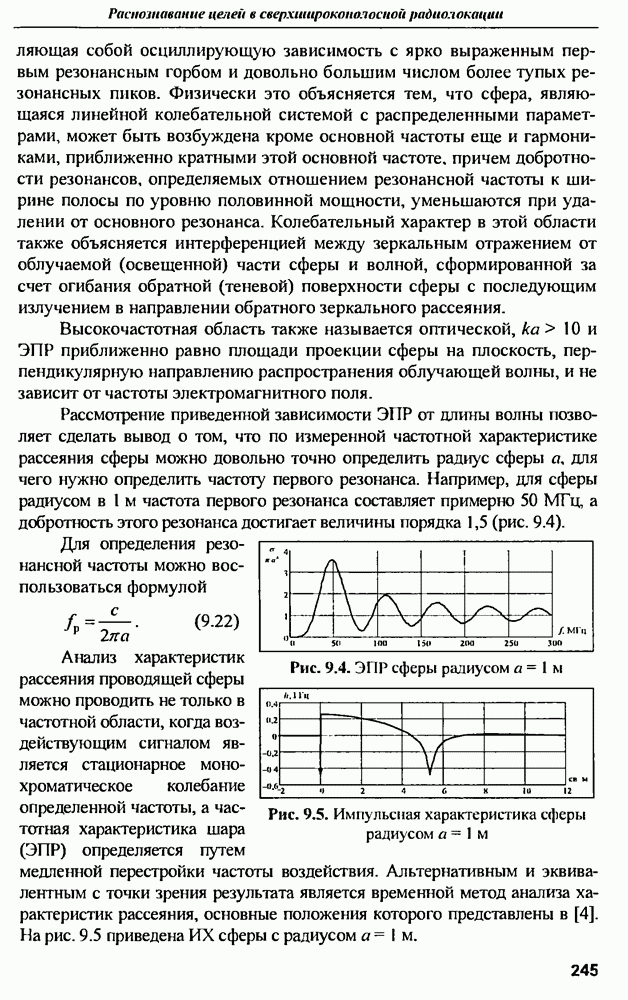
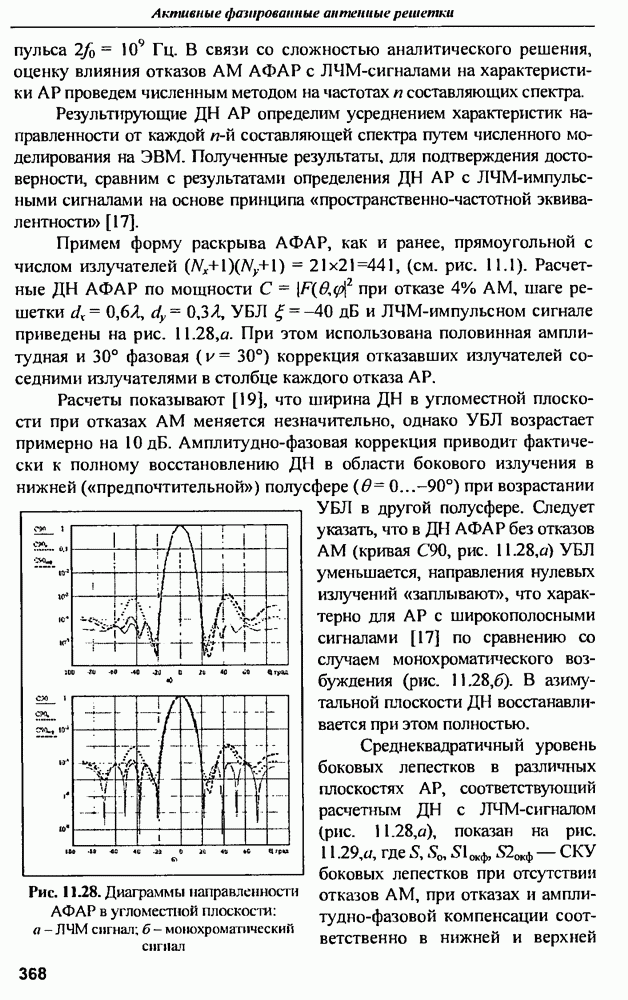
Анализ характеристик рассеяния проводящей сферы можно проводить не только в частотной области, когда воздействующим сигналом является стационарное монохроматическое колебание определенной частоты, а частотная характеристика шара (ЭПР) определяется путем медленной перестройки частоты воздействия. Альтернативным и эквивалентным с точки зрения результата является временной метод анализа характеристик рассеяния, основные положения которого представлены в [4]. На рис. 9.5 приведена  сферы с радиусом
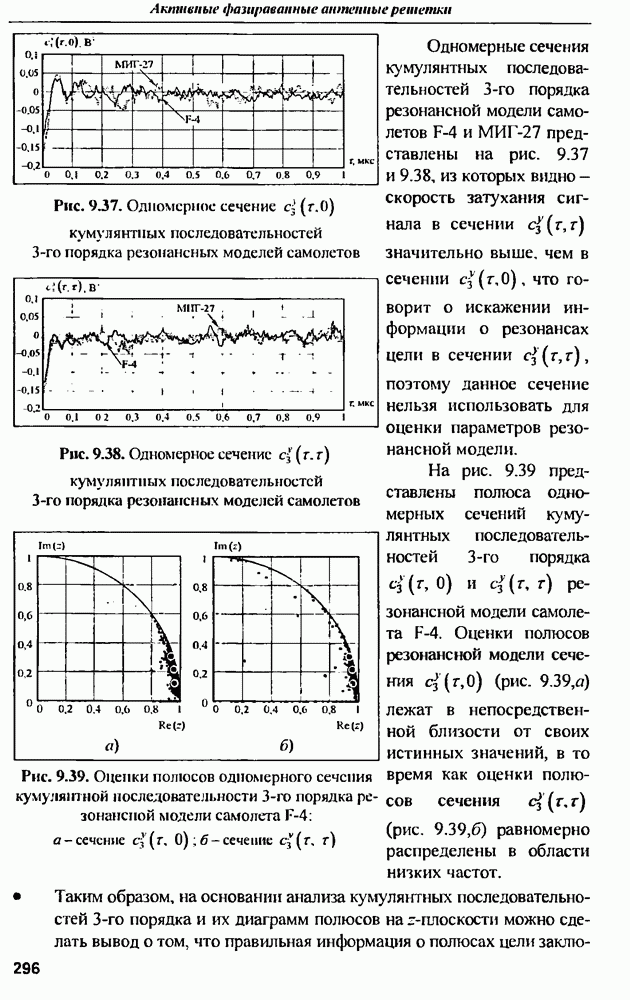
сферы с радиусом 

Рис. 9.4. ЭПР сферы радиусом 

Рис. 9.5. Импульсная характеристика сферы радиусом 
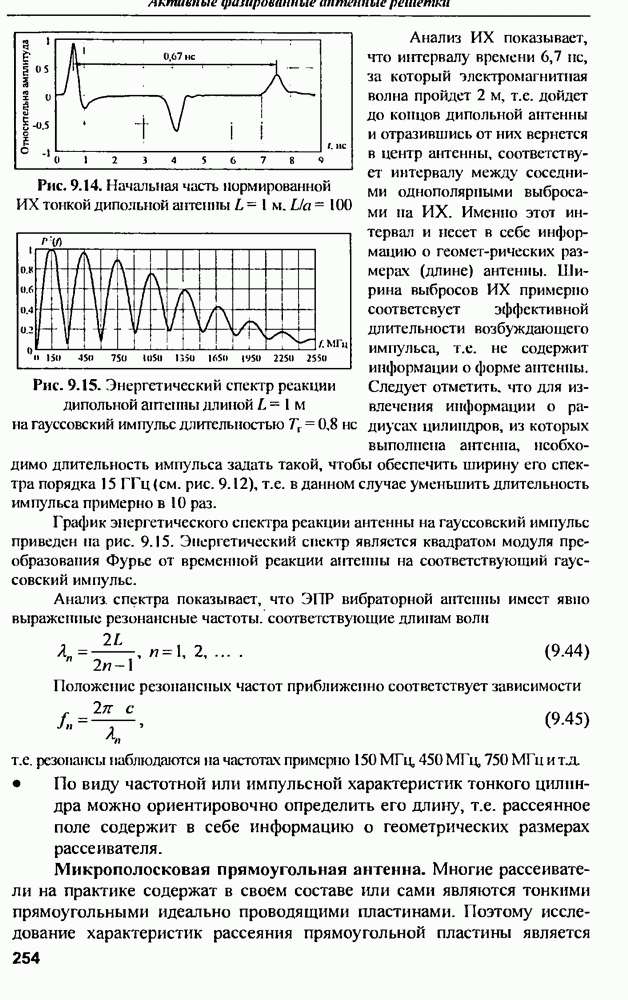
Анализ формы  сферы показывает, что она начинается с импульса, имеющего относительную амплитуду 0,5. Этот импульс обусловлен прямым отражением облучающего импульса по нормали от сферы в обратном направлении. Далее следует ступенчатый скачок с амплитудой 0,25 противоположной полярности, обусловленный отражением волны от окрестностей зеркальной точки на поверхности сферы, что согласуется с теорией дифракции волны на сфере в приближении физической оптики. Второй импульс той же полярности, что и зеркально отраженный, обусловлен так называемой ползущей волной, обтекающей оборотную сторону сферы и излучающей в сторону обратного рассеяния. Задержка этого импульса для сферы радиусом
сферы показывает, что она начинается с импульса, имеющего относительную амплитуду 0,5. Этот импульс обусловлен прямым отражением облучающего импульса по нормали от сферы в обратном направлении. Далее следует ступенчатый скачок с амплитудой 0,25 противоположной полярности, обусловленный отражением волны от окрестностей зеркальной точки на поверхности сферы, что согласуется с теорией дифракции волны на сфере в приближении физической оптики. Второй импульс той же полярности, что и зеркально отраженный, обусловлен так называемой ползущей волной, обтекающей оборотную сторону сферы и излучающей в сторону обратного рассеяния. Задержка этого импульса для сферы радиусом  составляет порядка 18 нс.
составляет порядка 18 нс.
Она определяется скоростью света в среде, радиусом сферы и может быть оценена по формуле 

причем форма  на участке между первым и вторым импульсом определяется радиусом кривизны объекта вблизи зеркальной точки обратного рассеяния.
на участке между первым и вторым импульсом определяется радиусом кривизны объекта вблизи зеркальной точки обратного рассеяния.
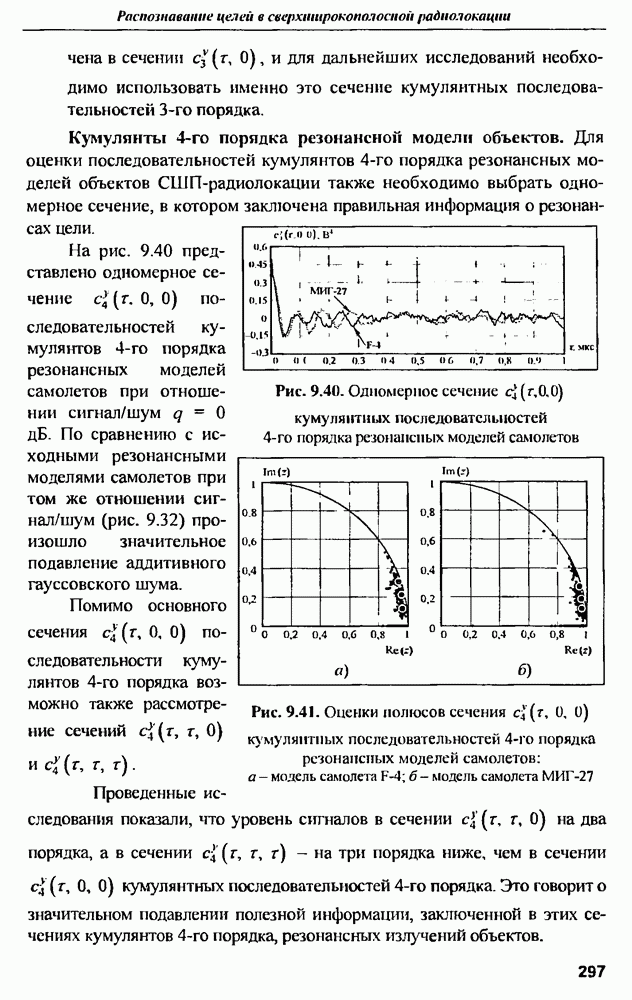
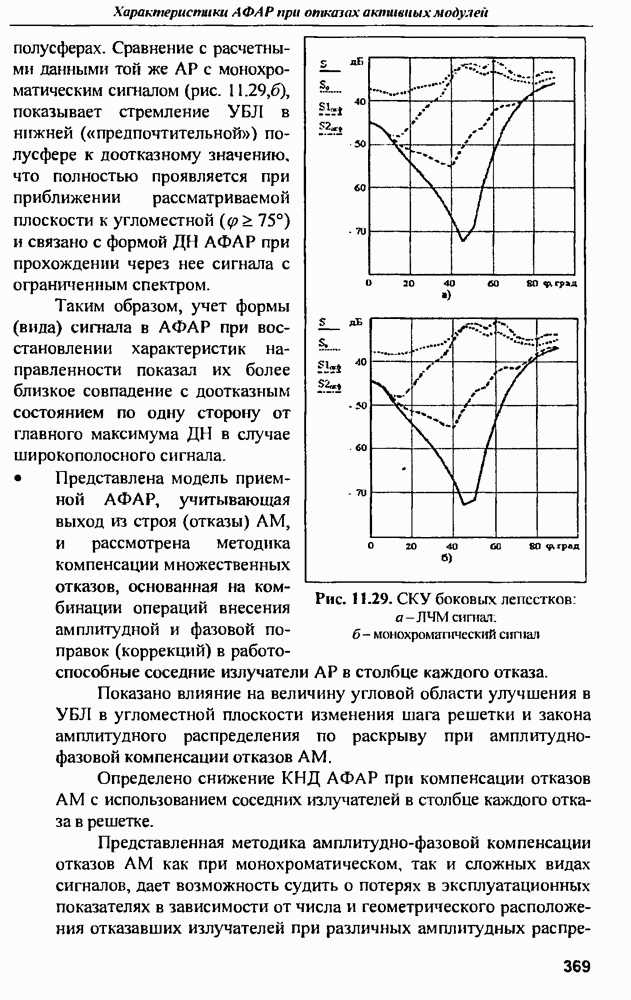
Большой практический интерес представляет проверка того факта, что временные и частотные характеристики рассеяния связаны преобразованием Фурье. Результат нахождения энергетического спектра  для
для  сферы, изображенной на рис. 9.5, являющейся преобразованием Фурье от автокорреляционной функции
сферы, изображенной на рис. 9.5, являющейся преобразованием Фурье от автокорреляционной функции  показан на рис. 9.6. Сравнение
показан на рис. 9.6. Сравнение  сферы с теоретической ЭПР сферы (см. рис. 9.4) показывает очень хорошую согласованность этих результатов. Степень рассогласования теоретической и расчетной характеристик не превышает нигде 10%, что подтверждает возможность использования соотношений (9.4) и (9.5), т.е. переход при необходимости от частотного к временному методам анализа и обратно без потери информации о рассеивающем волну объекте.
сферы с теоретической ЭПР сферы (см. рис. 9.4) показывает очень хорошую согласованность этих результатов. Степень рассогласования теоретической и расчетной характеристик не превышает нигде 10%, что подтверждает возможность использования соотношений (9.4) и (9.5), т.е. переход при необходимости от частотного к временному методам анализа и обратно без потери информации о рассеивающем волну объекте.

Рис. 9.6. Энергетический спектр сферы радиусом 
Импульсная характеристика является, конечно, наиболее информативной функцией, так как описывает рассеяние на всех частотах и сохраняет фазовые соотношения интерферирующих электромагнитных волн. Однако ее получение при компьютерном моделировании процессов рассеяния весьма затруднительно, поскольку возбуждающий импульс должен приближаться по форме  -функции, проведение дискретизации которой, а также операции дифференцирования по времени в
-функции, проведение дискретизации которой, а также операции дифференцирования по времени в
цифровой форме, невозможны. Как уже указывалось ранее, наиболее удобным в этом случае является выбор гауссовской формы возбуждающего импульса (9 15) Это объясняется тем, что гауссовский импульс имеет гладкую форму и высокую степень концентрации энергии вблизи середины импульса и в полосе частот, т.е. быстро затухающие «хвосты» по времени и частоте.
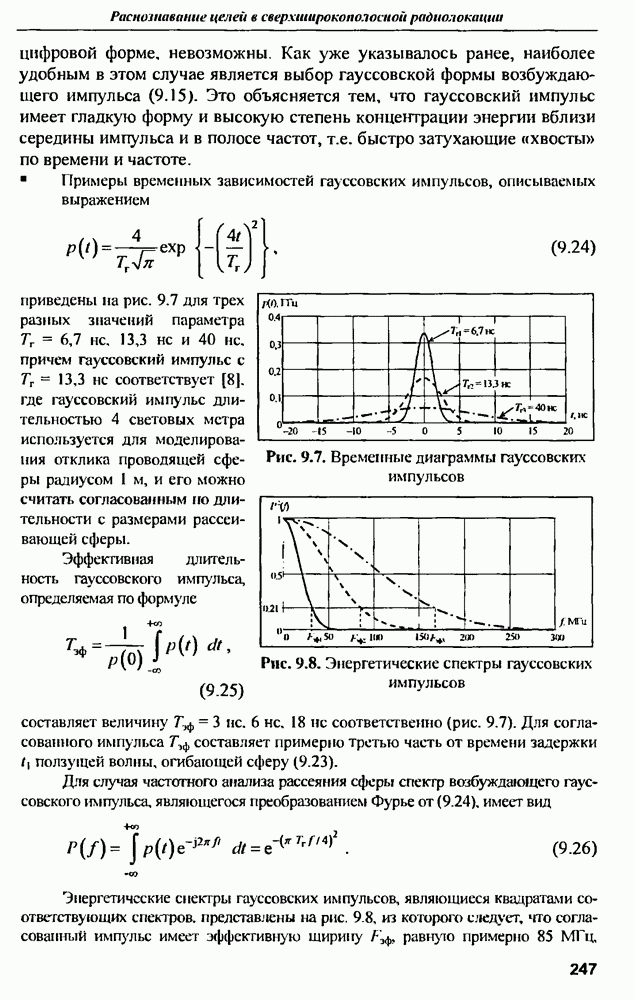
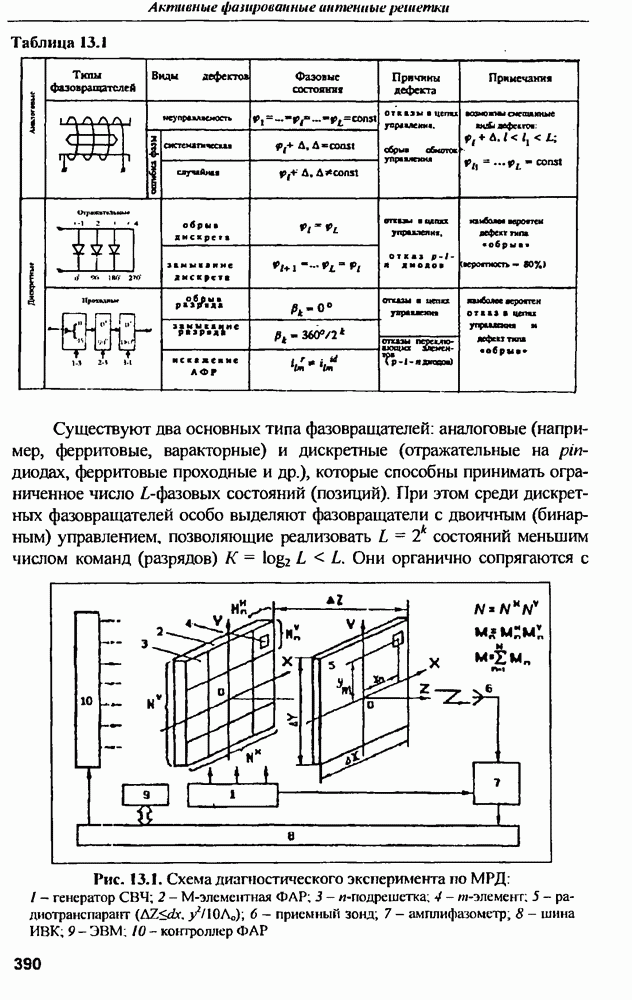
Примеры временных зависимостей гауссовских импульсов, описываемых выражением

приведены на рис. 9.7 для трех разных значений параметра  , причем гауссовский импульс с
, причем гауссовский импульс с  не соответствует [8]. где гауссовский импульс длительностью 4 световых метра используется для моделирования отклика проводящей сферы радиусом
не соответствует [8]. где гауссовский импульс длительностью 4 световых метра используется для моделирования отклика проводящей сферы радиусом  и его можно считать согласованным по длительности с размерами рассеивающей сферы.
и его можно считать согласованным по длительности с размерами рассеивающей сферы.
Эффективная длительность гауссовского импульса, определяемая по формуле

составляет величину  соответственно (рис. 9.7). Для согласованного импульса
соответственно (рис. 9.7). Для согласованного импульса  составляет примерно третью часть от времени задержки 11 ползущей волны, огибающей сферу (9.23)
составляет примерно третью часть от времени задержки 11 ползущей волны, огибающей сферу (9.23)
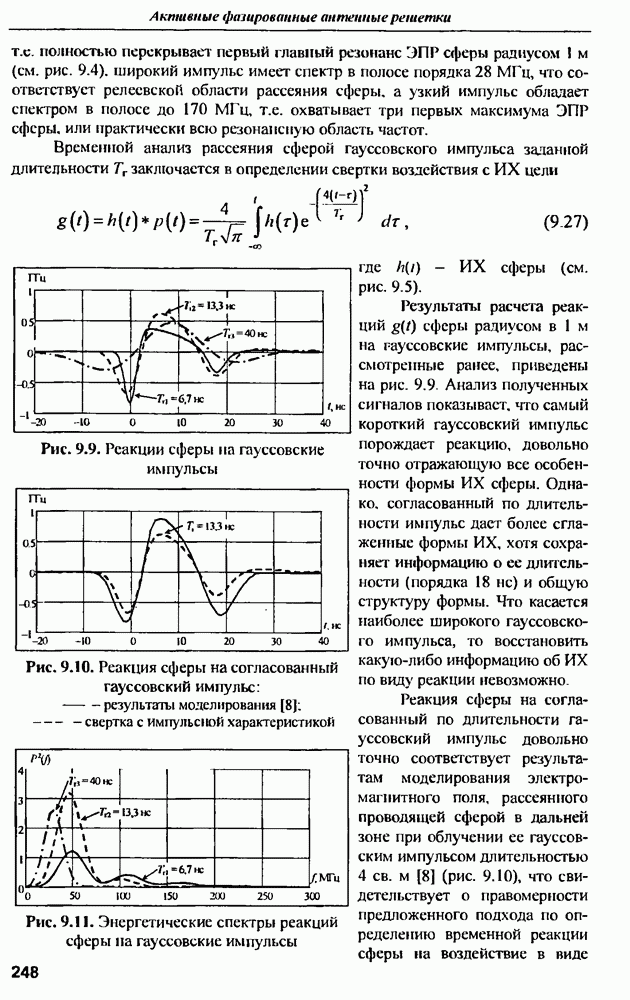
Для случая частотного анализа рассеяния сферы спектр возбуждающего гауссовского импульса, являющегося преобразованием Фурье от (9.24), имеет вид


Рис. 9.7. Временные диаграммы гауссовских импульсов

Рис. 9.8. Энергетические спектры гауссовских импульсов
Энергетические спектры гауссовских импульсов, являющиеся квадратами соответствующих спектров, представлены на рис. 9.8, из которого следует, что согласованный импульс имеет эффективную ширину  равную примерно 85 МГц,
равную примерно 85 МГц,
т.е. полностью перекрывает первый главный резонанс ЭПР сферы радиусом 1 м (см. рис. 9.4). широкий импульс имеет спектр в полосе порядка 28 МГц, что соответствует релеевской области рассеяния сферы, а узкий импульс обладает спектром в полосе до 170 МГц, те охватывает три первых максимума ЭПР сферы, или практически всю резонансную область частот.
Временной анализ рассеяния сферой гауссовского импульса заданной длительности  заключается в определении свертки воздействия с
заключается в определении свертки воздействия с  цели
цели

где  сферы (см. рис. 9.5).
сферы (см. рис. 9.5).
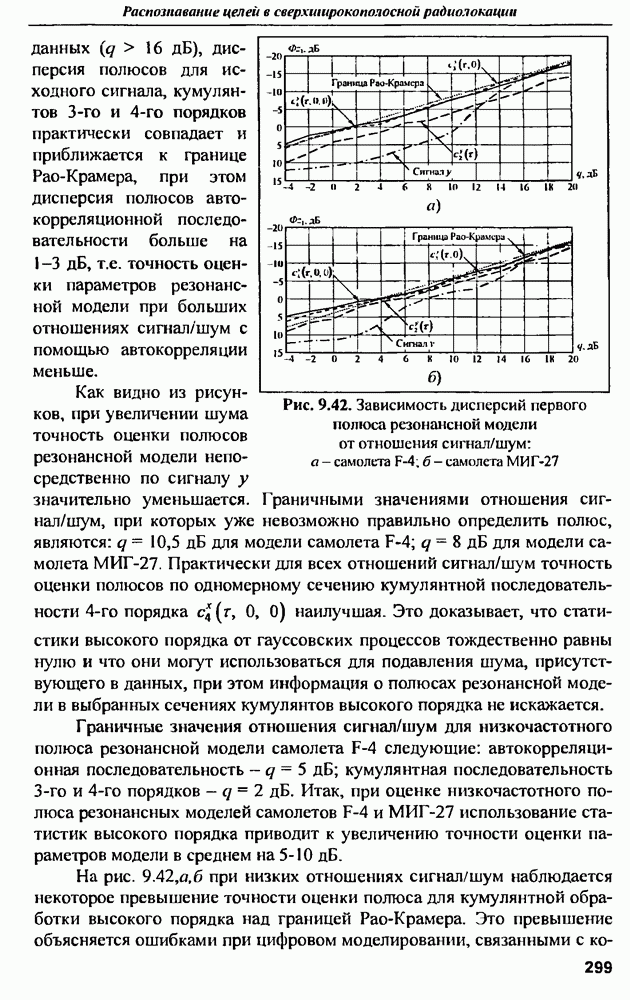
Результаты расчета реакций  сферы радиусом в
сферы радиусом в  на гауссовские импульсы, рассмотренные ранее, приведены на рис. 9.9. Анализ полученных сигналов показывает, что самый короткий гауссовский импульс порождает реакцию, довольно точно отражающую все особенности формы
на гауссовские импульсы, рассмотренные ранее, приведены на рис. 9.9. Анализ полученных сигналов показывает, что самый короткий гауссовский импульс порождает реакцию, довольно точно отражающую все особенности формы  сферы. Однако согласованный по длительности импульс даст более сглаженные формы
сферы. Однако согласованный по длительности импульс даст более сглаженные формы  хотя сохраняет информацию о ее длительности (порядка 18 не) и общую структуру формы. Что касается наиболее широкого гауссовского импульса, то восстановить какую-либо информацию об
хотя сохраняет информацию о ее длительности (порядка 18 не) и общую структуру формы. Что касается наиболее широкого гауссовского импульса, то восстановить какую-либо информацию об  по виду реакции невозможно.
по виду реакции невозможно.

Рис. 9.9. Реакции сферы на гауссовские импульсы

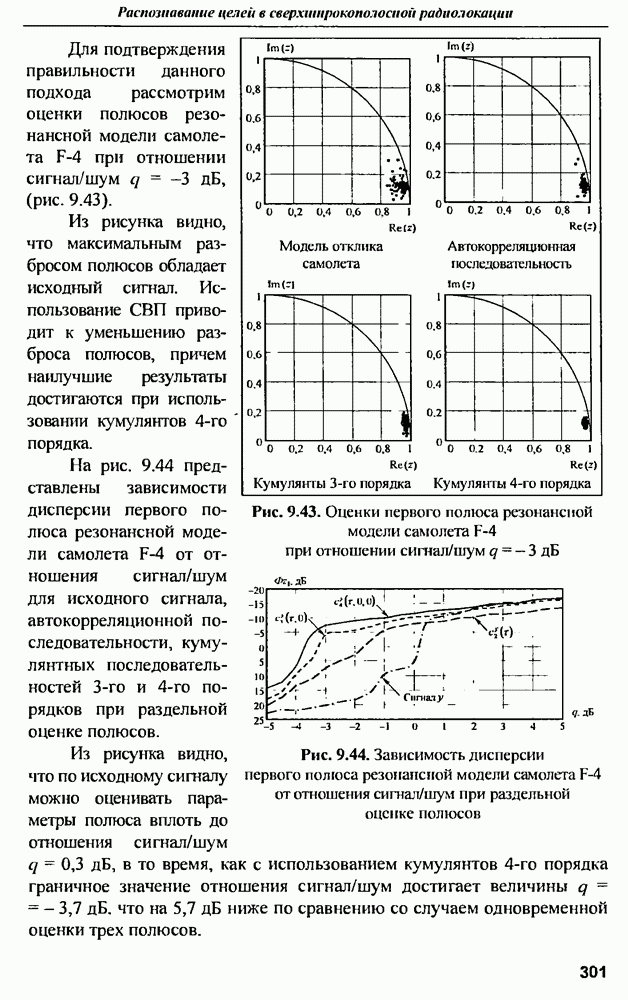
Рис. 9.10. Реакция сферы на согласованный гауссовский импульс

Рис. 9.11. Энергетические спектры реакций сферы на гауссовские импульсы
Реакция сферы на согласованный по длительности гауссовский импульс довольно точно соответствует результатам моделирования электромагнитного поля, рассеянного проводящей сферой в дальней зоне при облучении ее гауссовским импульсом длительностью 4 св м [8] (рис. 9 10), что свидетельствует о правомерности предложенного подхода по определению временной реакции сферы на воздействие в виде
гауссовского импульса с помощью свертки  сферы и возбуждающего импульса.
сферы и возбуждающего импульса.
При энергетическом взаимодействии сферы с облучающим ее импульсом, энергетический спектр реакции сферы на гаусеовский импульс можно пайти как произведение ЭПР сферы на  импульса
импульса

Соответствующие  реакций сферы радиусом
реакций сферы радиусом  на гауссовские импульсы с параметрами
на гауссовские импульсы с параметрами  приведены на рис. 9.11. Сопоставительный анализ спектров показывает, что при воздействии согласованного гауссовского импульса с
приведены на рис. 9.11. Сопоставительный анализ спектров показывает, что при воздействии согласованного гауссовского импульса с  не в реакции полностью сохраняется первый максимум резонансной области ЭПР сферы, т.е. в отраженном сигнале имеется информация о размерах сферы. Более короткий импульс с
не в реакции полностью сохраняется первый максимум резонансной области ЭПР сферы, т.е. в отраженном сигнале имеется информация о размерах сферы. Более короткий импульс с  не вызывает реакцию с более широким спектром, захватывающим первые три резонанса ЭПР сферы, при этом первый главный резонанс практически не изменился по положению на полосе частот и по форме - следовательно, соответствующая информация о размерах сферы также не изменились. С этой точки зрения импульс длительностью 6,7 не можно считать избыточно коротким для сферы радиусом
не вызывает реакцию с более широким спектром, захватывающим первые три резонанса ЭПР сферы, при этом первый главный резонанс практически не изменился по положению на полосе частот и по форме - следовательно, соответствующая информация о размерах сферы также не изменились. С этой точки зрения импульс длительностью 6,7 не можно считать избыточно коротким для сферы радиусом 
Что касается импульса длительностью  , то
, то  реакции сферы на него существенно отличается от ЭПР сферы и практически не содержит информации о ее размерах, поэтому такой импульс является недостаточно коротким для данной сферы.
реакции сферы на него существенно отличается от ЭПР сферы и практически не содержит информации о ее размерах, поэтому такой импульс является недостаточно коротким для данной сферы.
В целом полученные результаты частотного анализа рассеяния сферой электромагнитной волны полностью согласуются с результатами временного анализа этого рассеяния.
Электромагннтное поле, вызванное рассеянием достаточно короткого импульса сферой с проводящей поверхностью, имеет в себе информацию о геометрических размерах цели и может быть использовано для идентификации шара.
Характеристики рассеяния кругового цилиндра. Строгое решение задачи о дифракции на круговом цилиндре методом криволинейных координат приведено в [10], при этом полагалось, что цилиндр имеет идеально проводящую поверхность, радиус а и неограниченную длину. Рассмотрено два случая ориентации вектора падающего электрического поля  относительно оси цилиндра: перпендикулярно и параллельно ей. Любую другую ориентацию вектора электрического поля можно представить с помощью суперпозиции этих парциальных полей
относительно оси цилиндра: перпендикулярно и параллельно ей. Любую другую ориентацию вектора электрического поля можно представить с помощью суперпозиции этих парциальных полей
Для параллельного падения электрического поля рассеянное поле также имеет только одну компоненту, совпадающую по ориентации с полем падающей волны и выражается бесконечным рядом

где  угол наблюдения рассеянного поля относительно направления падающего поля, для обратного рассеяния
угол наблюдения рассеянного поля относительно направления падающего поля, для обратного рассеяния  остальные символы имеют тот же смысл, что и в формулах для сферы (см. (9 20), (9 21)).
остальные символы имеют тот же смысл, что и в формулах для сферы (см. (9 20), (9 21)).
Магнитная компонента поля в этом случае имеет две составляющие в цилиндрической системе координат

где  и
и  комплексные амплитуды компонент рассеянного и падающего магнитного полей соответственно. Амплитуды электрического и магнитного полей связаны через электрическое сопротивление среды, окружающей рассеиватель
комплексные амплитуды компонент рассеянного и падающего магнитного полей соответственно. Амплитуды электрического и магнитного полей связаны через электрическое сопротивление среды, окружающей рассеиватель 
Если точка наблюдения рассеянного поля находится в дальней зоне  можно применить асимптотические формулы для функций Ханкеля
можно применить асимптотические формулы для функций Ханкеля

Пренебрегая радиальными компонентами поля на большом расстоянии от рассеивателя, получим упрощенные выражения для рассеянного электрического и магнитного полей в дальней зоне для случая падения электрического поля параллельно оси цилиндра

где через  обозначена функция, определяемая суммой (9.30)
обозначена функция, определяемая суммой (9.30)

Выражения для электрического и магнитного полей одинаковы, что является характерным для электромагнитного поля на большом расстоянии
от источника. Поэтому в дальнейшем можно рассматривать одну из этих компонент.
Для нахождения удельной ЭПР цилиндра на единицу длины воспользуемся выражением

Учитывая, что квадрат модуля напряженности рассеянного электрического поля

и переходя к энергетическому спектру рассеянного поля, получим частотную зависимость удельной ЭПР цилиндра

Проводя аналогичные выкладки для случая падения электрического поля перпендикулярно оси цилиндра, получим выражение для удельной ЭПР цилиндра в зависимости от частоты облучающей волны

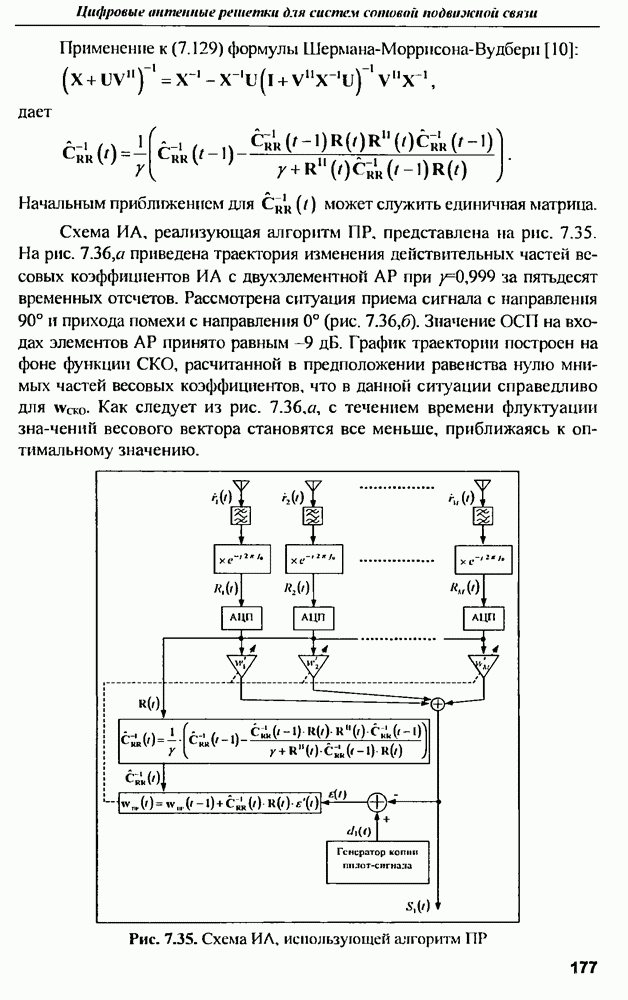
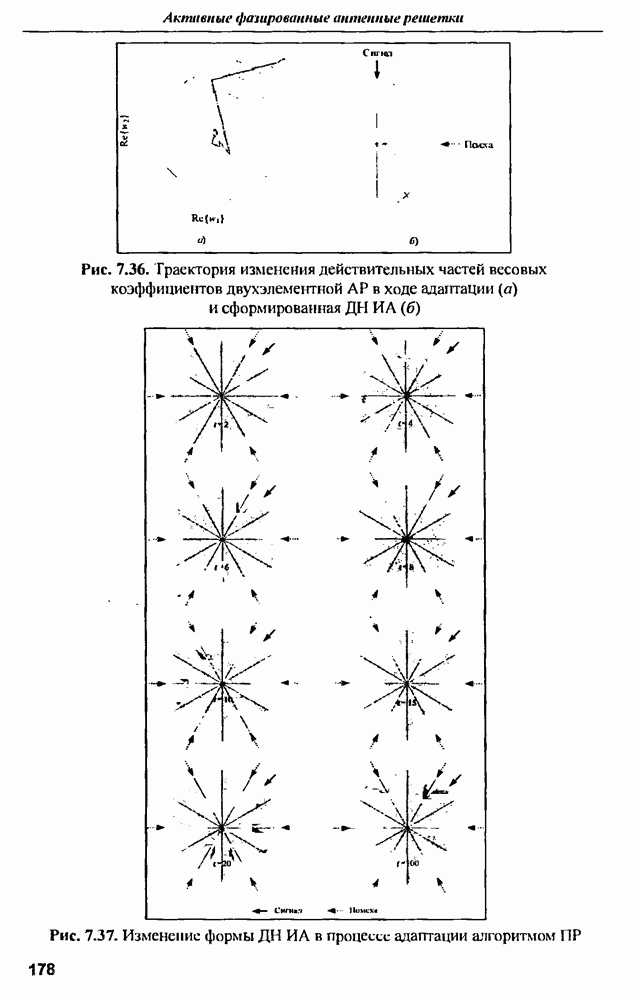
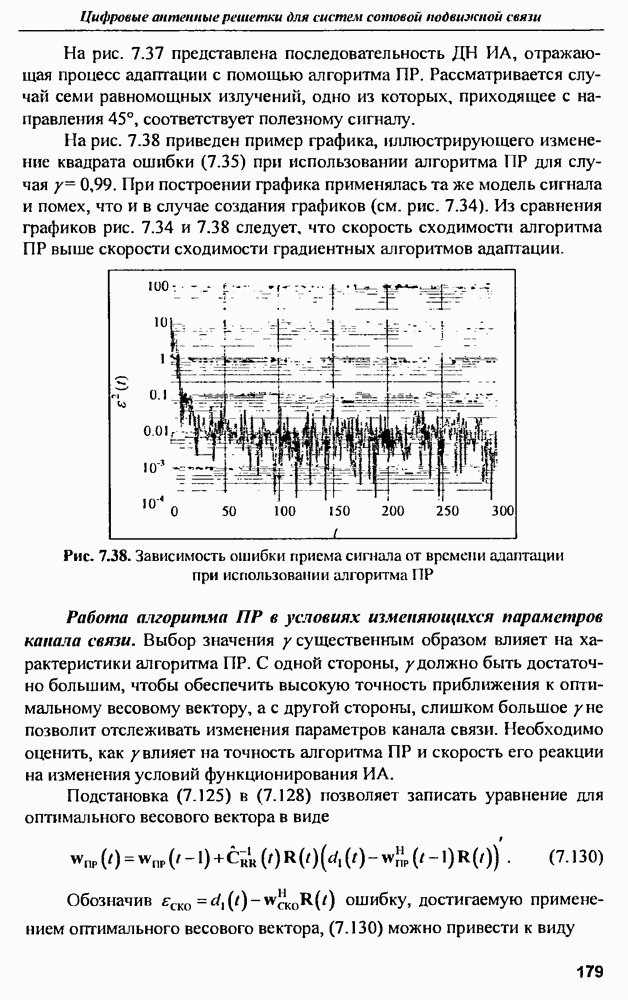
где функция  определена в [10] через соответствующие цилиндрические функции:
определена в [10] через соответствующие цилиндрические функции:

где  - производные функций Бесселя и Ханкеля по переменной
- производные функций Бесселя и Ханкеля по переменной  .
.

Рис. 9.12. Удельная ЭПР бесконечного цилиндра радиусом 
Зависимости удельных ЭПР цилиндра от частоты для параллельного и перпендикулярного падения волны на цилиндр радиусом  приведены на рис. 9.12
приведены на рис. 9.12
Графики  рассчитаны для направления обратного рассеяния электромагнитной волны, т.е. для
рассчитаны для направления обратного рассеяния электромагнитной волны, т.е. для  . Анализ полученных зависимостей показывает, что на высоких частотах в оптической области удельная ЭПР при любой ориентации вектора электрического поля относительно оси цилиндра стремится к величине,
. Анализ полученных зависимостей показывает, что на высоких частотах в оптической области удельная ЭПР при любой ориентации вектора электрического поля относительно оси цилиндра стремится к величине,
равной  что совпадает с известным результатом анализа рассеяния цилиндра методом геометрической оптики.
что совпадает с известным результатом анализа рассеяния цилиндра методом геометрической оптики.
При параллельном облучении цилиндра удельная ЭПР монотонно растет с уменьшением частоты, что можно объяснить увеличением длины волны, а, значит, и линейной длины синфазно засвечиваемой поверхности цилиндра, при этом кривая ЭПР уходит в бесконечность, но это не означает. что дифрагированное поле возрастает неограниченно при  поскольку это ведет к уменьшению относительного расстояния от точки наблюдения до цилиндра, а значит приближение дальней зоны, использованное при выводе формулы (9.34), выполняться не будет.
поскольку это ведет к уменьшению относительного расстояния от точки наблюдения до цилиндра, а значит приближение дальней зоны, использованное при выводе формулы (9.34), выполняться не будет.
Возвращаясь к точному выражению (9.29) для рассеянного электрического поля и переходя к пределу  получим
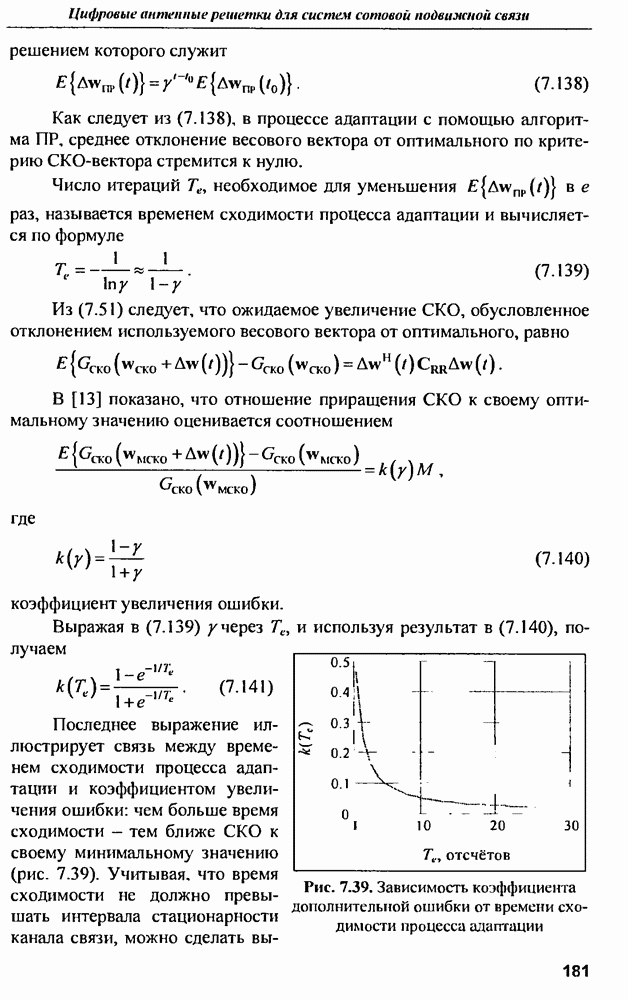
получим

откуда согласно выражению 
Таким образом, приведенные кривые справедливы только для дальней зоны точки наблюдения относительно цилиндра. При параллельном облучении цилиндра резонансных явлений не наблюдается, а на частотах свыше  цилиндр радиусом
цилиндр радиусом  имеет практически одинаковую удельную ЭПР, близкую к геометрическому пределу. Рассмотрим теперь график
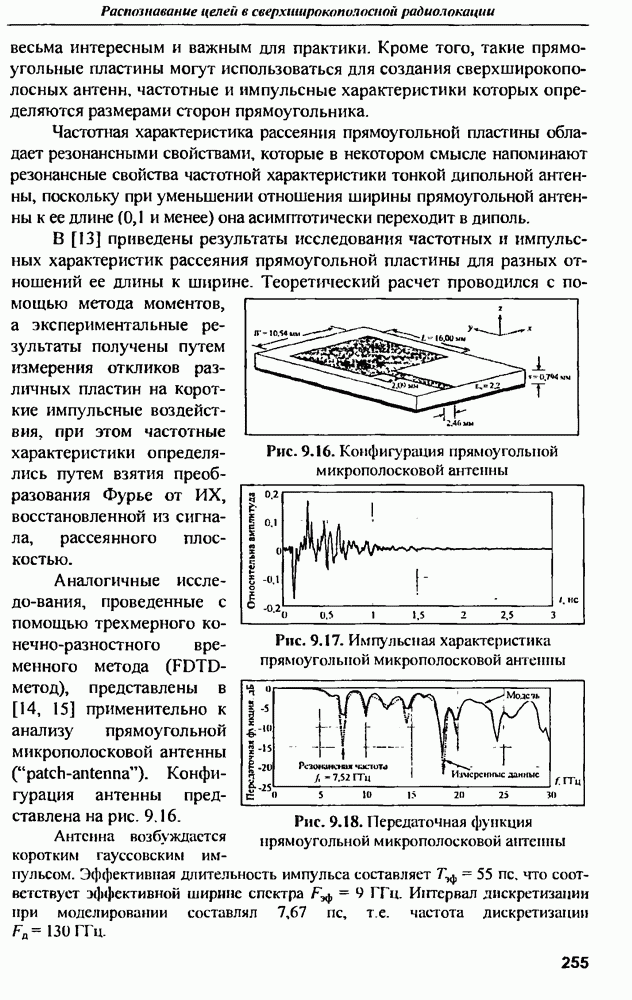
имеет практически одинаковую удельную ЭПР, близкую к геометрическому пределу. Рассмотрим теперь график  соответствующий перпендикулярному к оси направлению вектора напряженности электрического поля. Эта зависимость во многом напоминает поведение ЭПР сферы при изменении частоты (см. рис. 9.4). Хорошо видны релеевская и резонансная области частот. Резонанс повторяется, когда число полуволн, укладывающихся на половине окружности цилиндра, увеличивается на единицу. Первый наиболее резкий резонанс проявляется на частоте примерно
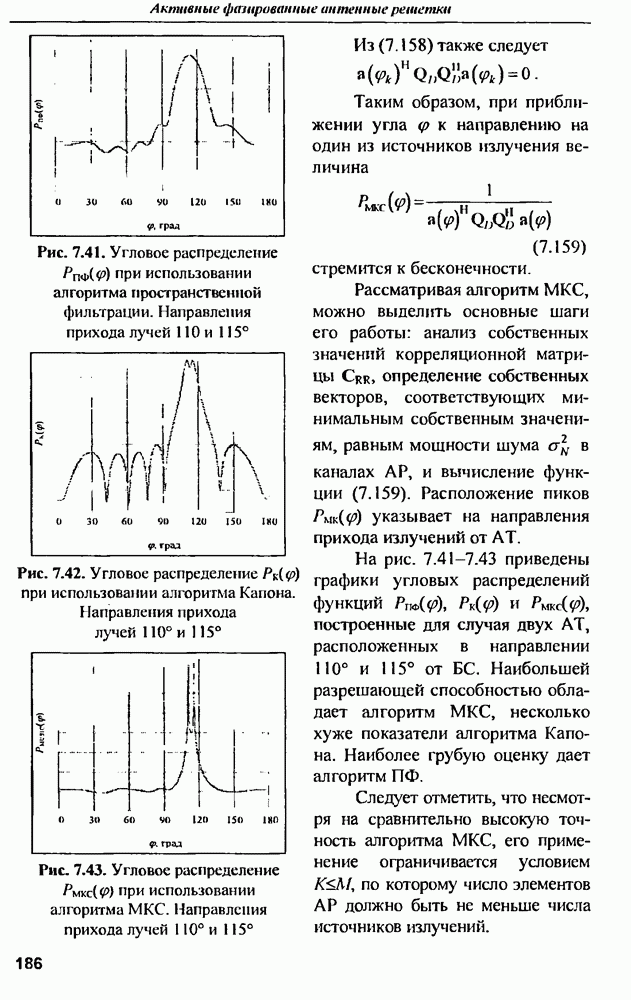
соответствующий перпендикулярному к оси направлению вектора напряженности электрического поля. Эта зависимость во многом напоминает поведение ЭПР сферы при изменении частоты (см. рис. 9.4). Хорошо видны релеевская и резонансная области частот. Резонанс повторяется, когда число полуволн, укладывающихся на половине окружности цилиндра, увеличивается на единицу. Первый наиболее резкий резонанс проявляется на частоте примерно  и имеет добротность порядка единиц. Последующие резонансы постепенно сглаживаются.
и имеет добротность порядка единиц. Последующие резонансы постепенно сглаживаются.
Что касается  всего цилиндра, то она определяется умножением удельной ЭПР на длину
всего цилиндра, то она определяется умножением удельной ЭПР на длину  облучаемого участка цилиндра
облучаемого участка цилиндра

Эта длина определяется либо по фактической ширине луча антенны, либо по эффективной ширине луча, определяемой длительностью облучающего импульса  [11]. Диаграмма, иллюстрирующая определение длины облучаемого участка, показана на рис. 9.13.
[11]. Диаграмма, иллюстрирующая определение длины облучаемого участка, показана на рис. 9.13.

Рис. 9.13. Определение длины облучаемого участка цилиндра
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. Особенности построения активной фазированной антенной решетки для радиоэлектронных комплексов
- 1.2. Особенности расчета характеристик АФАР
- 1.3. Приемопередающий модуль АФАР
- 1.4. Активные приборы, используемые в модулях современных АФАР
- 1.5. Состояние и перспективы развития ППМ
- 1.5.2. Параметры и конструкции типичных модулей АФАР
- ГЛАВА 2. Активная передающая ФАР современной твердотельной РЛС
- 2.2. Особенности энергетики АФАР
- 2.3. Расчет прямых потерь мощности в АФАР
- 2.4. Расчет потерь мощности в АФАР за счет ошибок распределения
- 2.5. АФАР твердотельной РЛС 67Н6Е
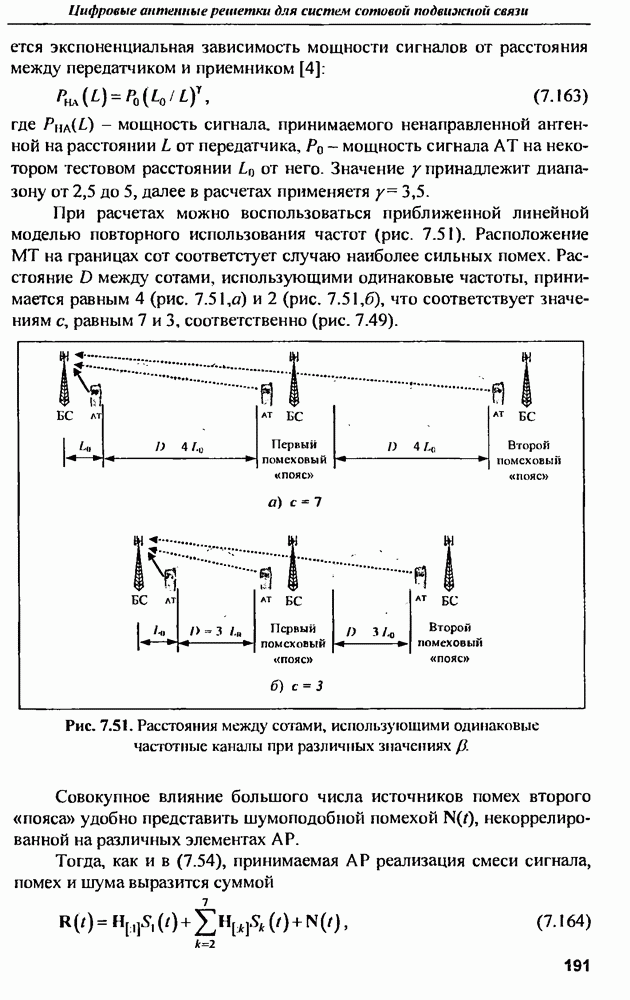
- ГЛАВА 3. Антенные комплексы для РЛС дальнего обнаружения и контроля космического пространства
- 3.2. Антенные комплексы РЛС «Дунай-3» и «Дунай-3У»
- 3.3. Приемопередающая ФАР для РЛС наблюдения за космическими объектами
- 3.4. Антенный комплекс РЛС дальнего обнаружения «Волга»
- 3.5. Приемопередающее антенно-фидерное устройство РЛС сантиметрового диапазона
- 3.6. Антенные комплексы для перспективных РЛС дальнего обнаружения «Воронеж-ДМ»
- ГЛАВА 4. Цифровая интеллектуальная ФАР — перспективная технология для радиолокационных и радиоинформационных комплексов XXI века
- 4.1. Преимущества адаптивной цифровой ФАР
- 4.2. Структура ЦИФАР и ее основные алгоритмы обработки сигналов
- 4.3. Требования к частоте дискретизации и уровням квантования сигналов в ЦИФАР
- 4.4. Требования к производительности цифровых вычислителен ЦИФАР
- 4.5. Пример реализации ЦИФАР для перспективной крупноапертурной крупномодульной широкополосной РЛС в диапазонах 10—20 см
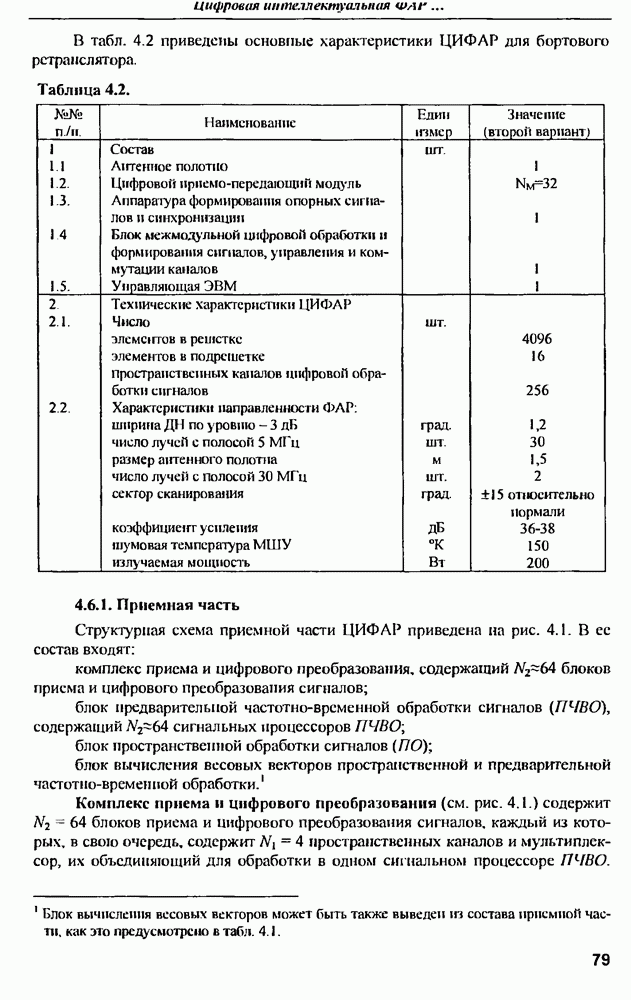
- 4.6. Пример построения ЦИФАР для бортового ретранслятора в диапазоне частот 8 ГГц перспективной спутниковой телекоммуникационной системы высокоскоростной мобильной связи «Ростелесат»
- ГЛАВА 5. Многофункциональная бортовая активная фазированная антенная решетка для РЛС
- 5.2. Формулировка задач
- 5.3. Решение внешней задачи для сферической решетки
- 5.4. Характеристики направленности сферической решетки
- 5.5. Пеленгационные характеристики сферической решетки
- 5.6. Сектор обзора сферической решетки и других вариантов выпуклой ФАР
- 5.7. Решение внутренней задачи
- 5.8. Система возбуждения модулей
- ГЛАВА 6. Адаптивная цифровая приемная ФАР
- 6.1. Антенные решетки с аналоговым формированием диаграмм направленности
- 6.2. Антенные решетки с цифровым формированием ДН
- 6.3. Элементы и характеристики АЦПФАР
- 6.3.2. Полоса пропускания приемного канала и частота квантования
- 6.3.3. Аналого-цифровое преобразование
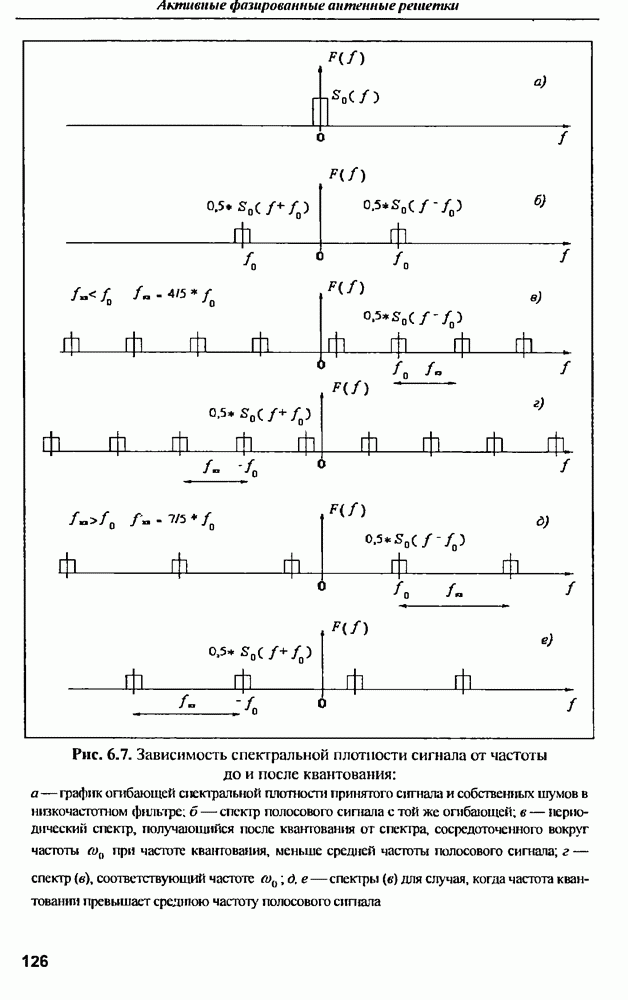
- 6.3.4. Спектры шумов и сигналов после квантования
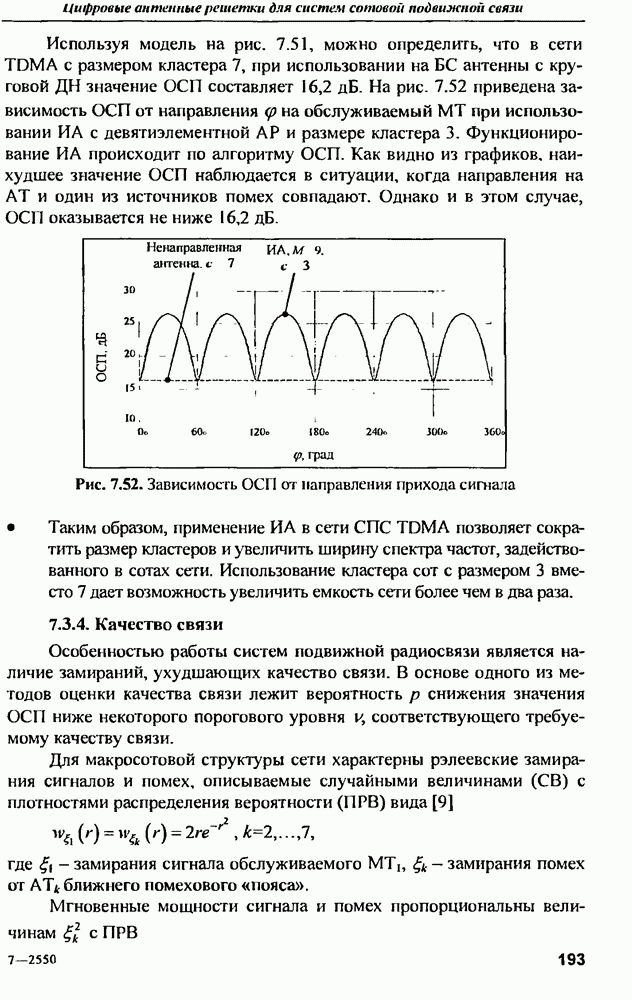
- 6.3.5. Температура шумов приемного тракта
- 6.3.6. Динамическим диапазон
- 6.4. Применение, особенности и элементная база АЦПФАР
- ГЛАВА 7. Цифровые антенные решетки для систем сотовой подвижной связи
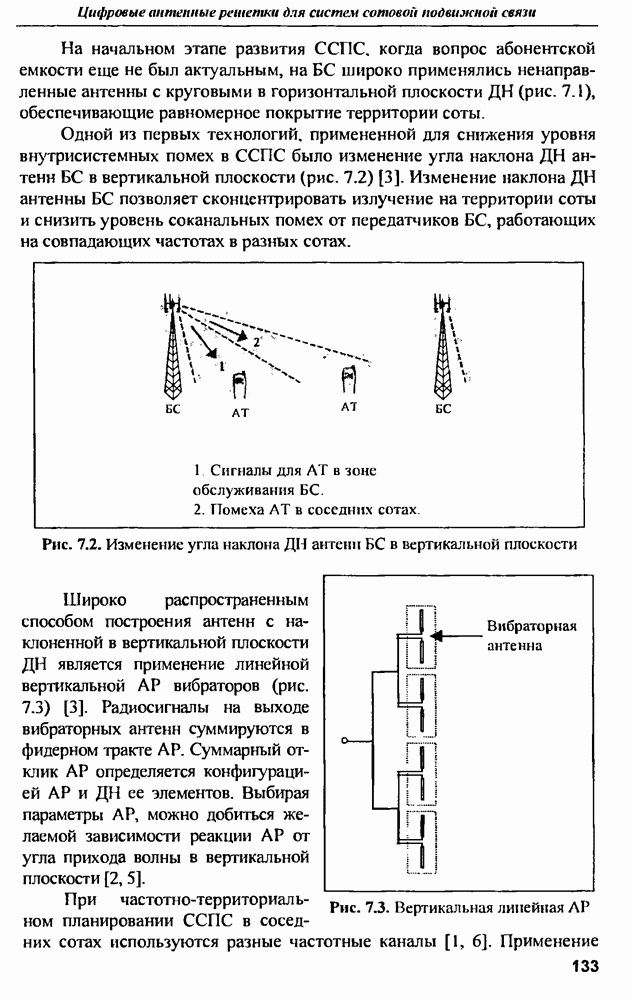
- 7.1. Влияние антенных технологий на развитие систем сотовой подвижной связи (ССПС)
- 7.2. Интеллектуальные антенны на основе цифровых АР
- 7.2.1. Принципы работы: модель адаптивного линейного сумматора
- 7.2.2. Пространственная обработка при приеме сигналов в обратном канале ССПС
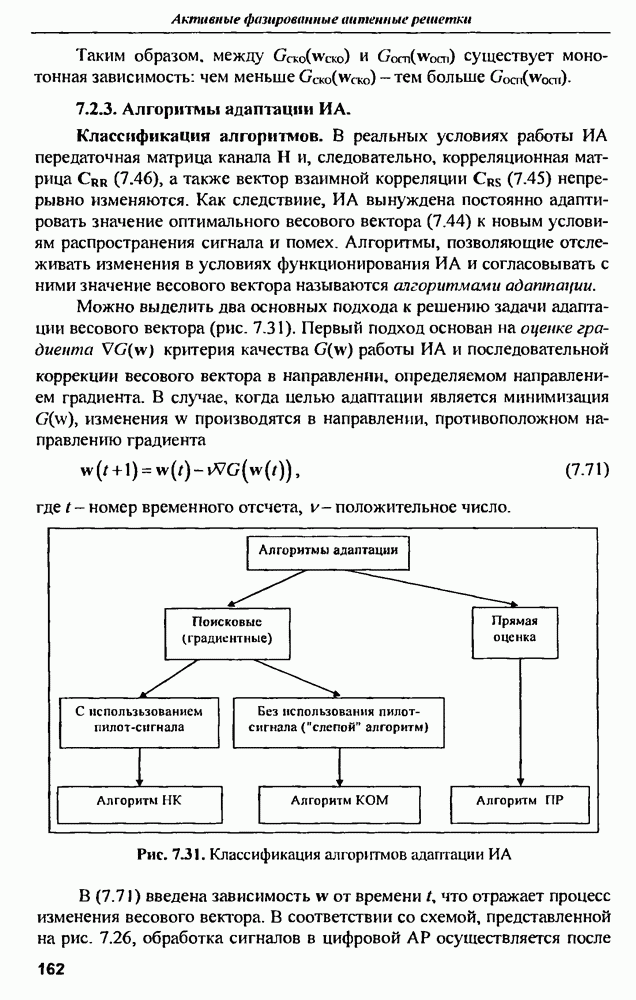
- 7.2.3. Алгоритмы адаптации ИА
- 7.2.4. Применение ИА для передачи сигналов в прямом канале ССПС
- 7.3. Влияние ИА на характеристики ССПС
- 7.3.2. Расчетные модели
- 7.3.3. Абонентская емкость ССПС
- 7.3.4. Качество связи
- 7.3.5. Площадь покрытия соты
- 7.3.6. Влияние ИА на архитектуру ССПС
- 7.4. Пространственные каналы с МВМВ на основе цифровых АР
- 7.4.1. Теоретико-информационные аспекты передачи данных в пространственных каналах МВМВ
- 7.4.2. Алгоритмы приема сигналов
- 7.4.3. Передача сигналов в каналах с МВМВ
- 7.4.4. Пространственно-временное кодирование и разнесенная передача
- Приложение 7.1. Комплексная огибающая сигнала и квадрату рная обработка в системах радиосвязи
- Приложение 7.2. Многолучевые ИА
- ГЛАВА 8. Оценка отношения сигнал/шум на выходе приемной АФАР с пространственным возбуждением
- 8.2. Определение мощности шума на выходе приемной АФАР
- 8.3. Отношение сигнал/шум на выходе приемной АФАР
- 8.4. Задача формирования расширенного луча АФАР
- 8.4.2. Использование метода статистического фазового синтеза для расширения луча
- 8.4.3. Оценка возможностей метода оптимального фазового синтеза расширенного луча, минимизирующего потери принимаемой мощности
- 8.4.4. Сравнение характеристик АФАР при различных методах формирования расширенного луча
- ГЛАВА 9. Распознавание целей в сверхширокополосной радиолокации
- 9.1.1. Методы теоретического расчета ЭПР
- 9.1.2. Тела простой геометрической формы
- 9.1.3. Характеристики рассеянна антенн
- 9.2. Резонансная модель рассеяния целей в сверхширокополосной радиолокации
- 9.2.2. Резонансная модель рассеяння электромагнитного поля радиолокационных объектов
- 9.3. Методы оценки характеристик сигналов
- 9.3.1. Метод Прони
- 9.3.2. Метод матричных пучков
- 9.4. Обработка сигналов с использованием статистик высокого порядка
- 9.4.2. Статистики высокого порядка детерминированных импульсных и периодических сигналов
- 9.4.3. СВП резонансной модели объектов в СШП радиолокации
- 9.5. Оценка параметров резонансных моделей целей в СШП радиолокации
- 9.5.1. Статистики высокого порядка резонансной модели объектов
- 9.5.2. Сравнительный анализ методов оценки параметров резонансных моделей с использованием статистик высокого порядка
- 9.6. Распознавание радиолокационных объектов
- 9.6.1. Сигнатурное распознавание целей по результатам оценки параметров резонансной модели
- 9.6.2. Распознавание радиолокационных объектов с помощью метода Е-импульса
- 9.7. Заключение
- ГЛАВА 10. Обеспечение инвариантности оптимальных пространственно-многоканальных РЛС с АФАР к коррелированным помехам
- 10.2. Обнаружение цели с известными координатами
- 10.3. Обнаружение цели и определение ее угловых координат
- 10.4. Обнаружение цели и измерение ее скорости сближения с РЛС
- 10.5. Условия инвариантности оптимальных РЛС к помехам
- 10.6. Потенциальные возможности оптимальных антенно-приемных трактов РЛС, соответствующих алгоритмам (10.39), (10.43)
- ГЛАВА 11. Характеристики активных ФАР при отказах активных модулей
- 11.2. Диаграммы направленности и СКУ боковых лепестков при амплитудной и амплитудно-фазовой компенсании множественных отказов
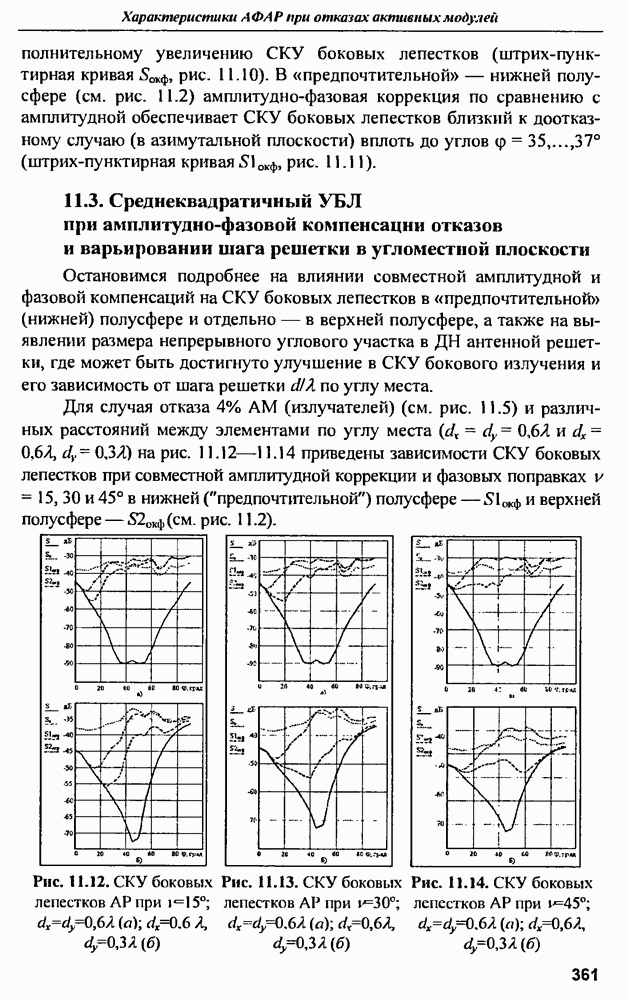
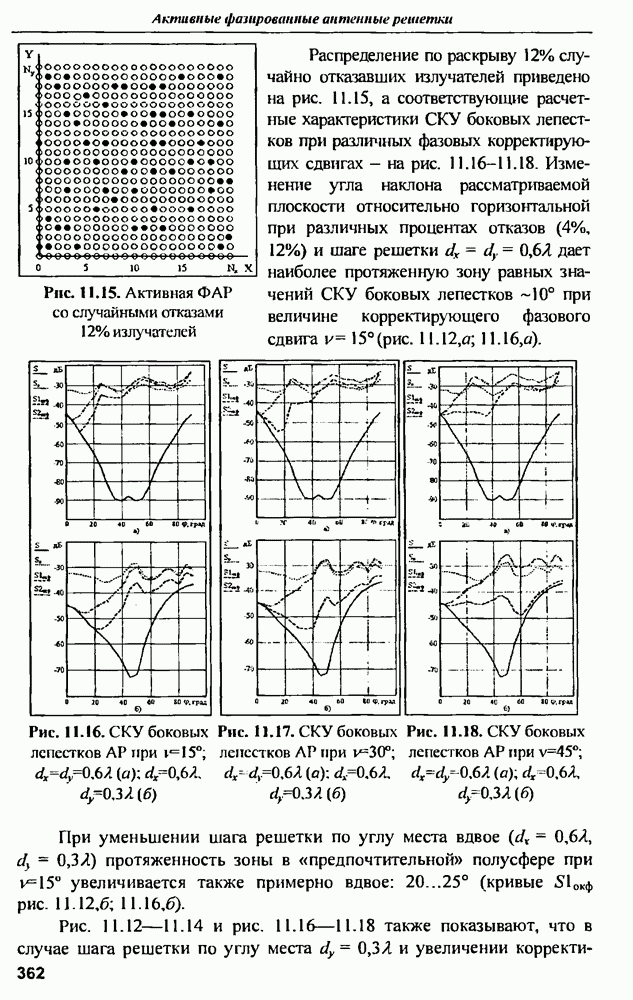
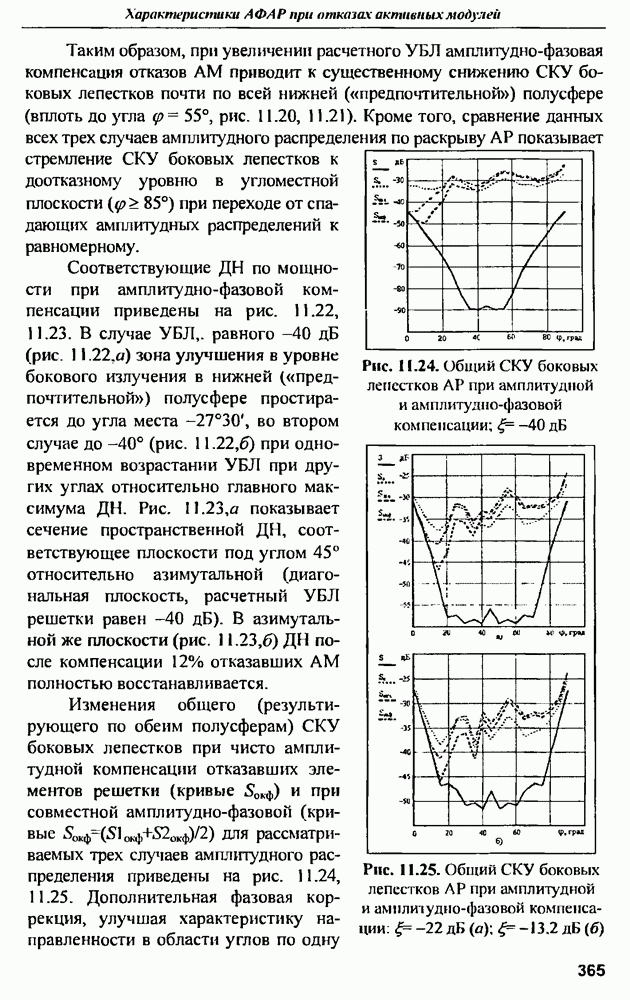
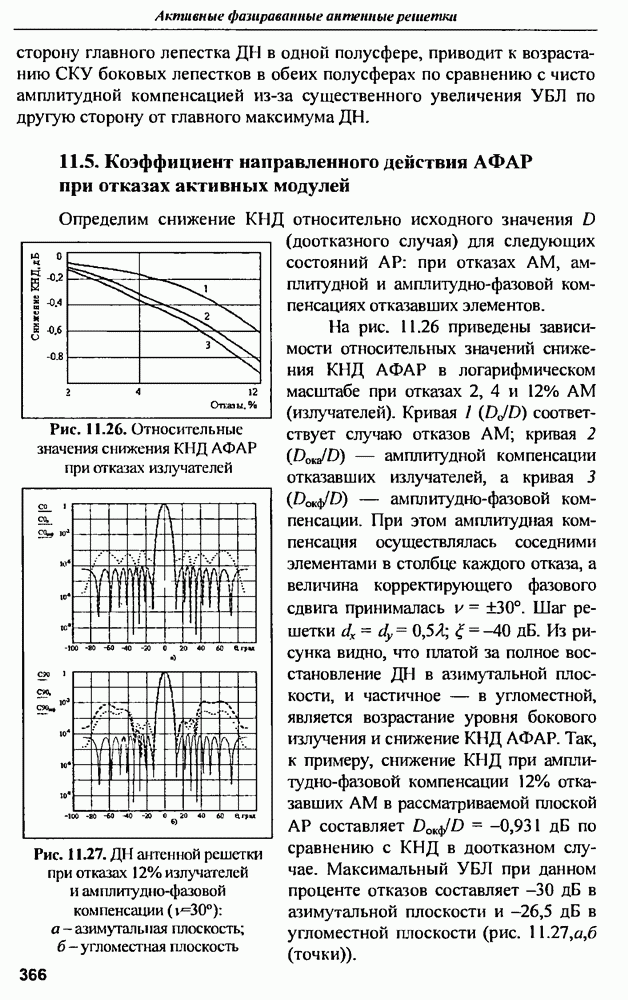
- 11.3. Среднеквадратичный УБЛ при амплитудно-фазовой компенсации отказов и варьировании шага решетки в угломестной плоскости
- 11.4. Влияние закона амплитудного распределения на характеристики АФАР при отказах АМ
- 11.5. Коэффициент направленного действия АФАР при отказах активных модулей
- 11.6. Особенности восстановления характеристик направленности АФАР при немонохроматическом сигнале
- ГЛАВА 12. Вопросы расчета линейных антенных решеток бегущей волны
- 12.1. Общие свойства линейных антенных решеток бегущей волны
- 12.2. Расчет на заданное амплитудное распределение и энергетические характеристики антенны
- ГЛАВА 13. Диагностика антенных решеток
- 13.2. Ближнезонные фазовые методы диагностики ФАР
- 13.2.2. Метод реконструктивной диагностики (МРД) ФАР
- 13.2.4. Селективная диагностика ФАР
- 13.2.5. Цифровая реализация МРД
- 13.2.6. Возможности МРД
- 13.2.7. МРД на основе дискретного преобразования Фурье (ДПФ)
- 13.2.8. Комбинированный МРД на основе БПУА и БПФ
- 13.2.9. Сопоставление МРД с другими методами
- 13.3. Бесфазовые методы диагностики ФАР
- 13.3.1. Метод, использующий ДПФ в базисе экспоненциальных функций
- 13.3.2 Метод, использующий ДПФ в базисе функций Уолша (метод ДПУ)
- 13.3.3. Адаптивный алгоритм диагностики ФАР
- 13.3.4. Сравнение метода ДПУ и адаптивного метода диагностики ФАР
- Приложение 13.П1. Алгоритм диагностики ФАР методом ДПФ в базисе функций Уолша (метод ДПУ)
- Приложение 13.П2. Адаптивный алгоритм диагностики ФАР, основанный на измерении комплексных амплитуд сигналов
- Приложение 13.П3. Адаптивный алгоритм диагностики ФАР, основанный на измерении мощности сигналов
- Дополнения к приложениям 13.П1, 13.П2,13.П3
- ГЛАВА 14. Мощные импульсы сверхширокополосного излучения для радиолокации
- 14.2. Синтез сверхширокополосных антенн
- 14.3. Комбинированные антенны
- 14.4. Антенные решетки
- 14.5. Приемные антенны
- 14.6. Мощные источники СШП-излучения
- 14.7. Методы оценивания импульсных характеристик
- 14.8. Реконструкция формы объектов
- ГЛАВА 15. Волоконно-оптическое распределение сигналов по модулям АФАР
- 15.1. Проблема распределения сигналов АФАР и основные подходы к ее решению с использовнием волоконных систем
- 15.2. Краткий анализ и классификация сигналов активного модуля ФАР
- 15.3. Структурная схема волоконного канала передачи сигналов в ППМ АФАР
- 15.4. Структурная схема волоконного канала передачи сигналов из ППМ АФАР
- 15.5. Структурные схемы волоконных систем распределения высокочастотных сигналов по модулям приемопередающей АФАР
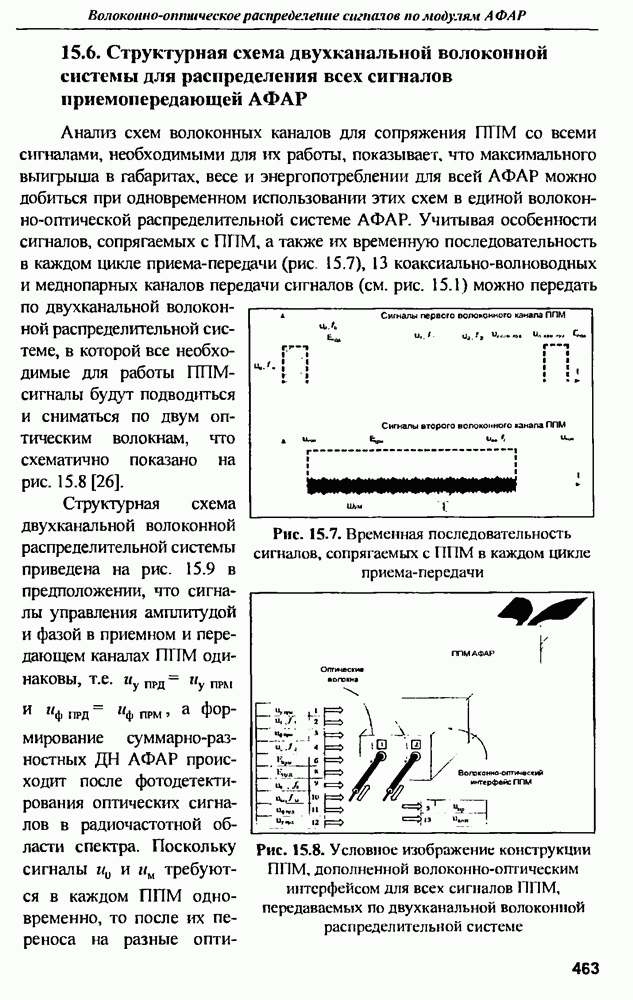
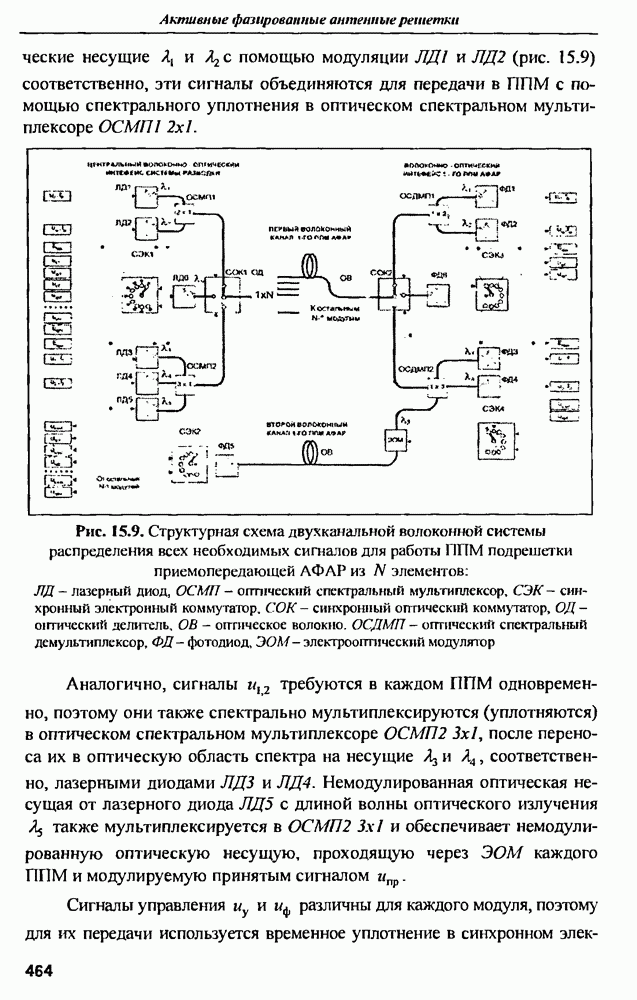
- 15.6. Структурная схема двухканальной волоконной системы для распределения всех сигналов приемопередающей АФАР
- 15.7. Основные типы волоконных каналов, используемых для построения волоконных распределительных систем.
- 15.7.1. Волоконный канал с МИПД-ПМ
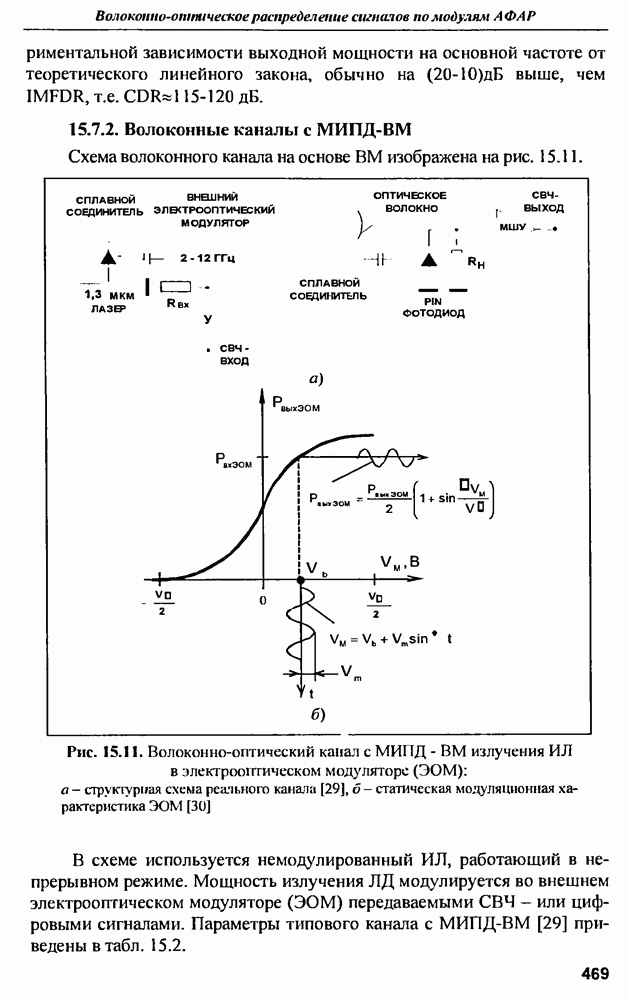
- 15.7.2. Волоконные каналы с МИПД-ВМ
- 15.7.3. Сравнение характеристик волоконных каналов с прямой и внешней модуляцией оптической несущей
- 15.8. Элементная база волоконной распределительной системы АФАР
- 15.8.1. Источники оптического излучения
- 15.8.2. Фотодетекторы
- 15.8.3. Оптическое волокно
- 15.8.4. Оптические делители
- 15.8.5. Внешние модуляторы
- 15.8.6. Оптические мультиплексоры с частотным уплотнением каналов
- 15.8.7. Оптические мультиплексоры с временным уплотнением каналов
- 15.9. Примеры практической реализации волоконных каналов для передачи отдельных сигналов АФАР