| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.9. Трехуровневая система
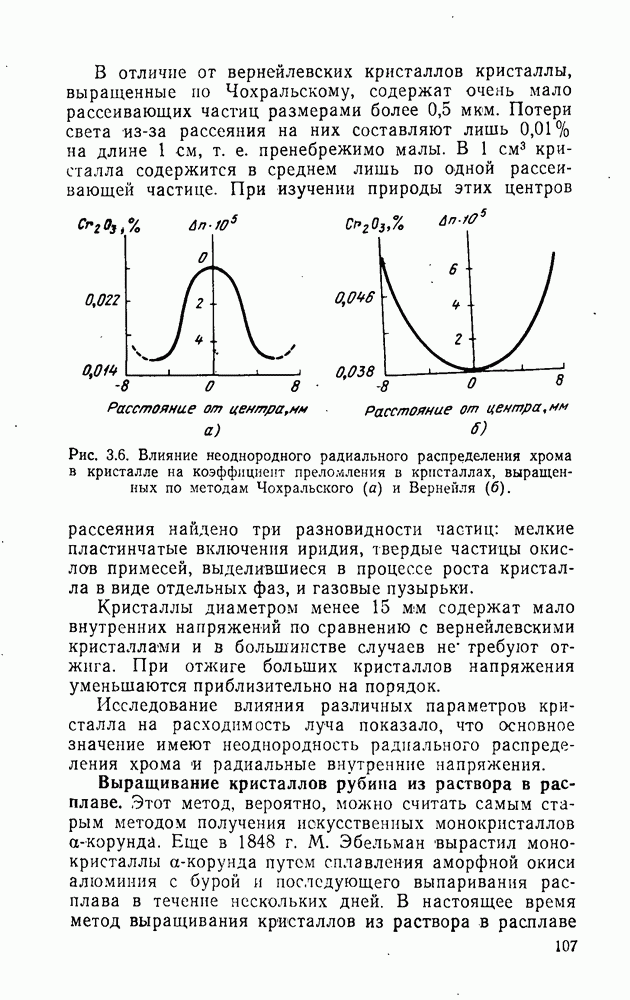
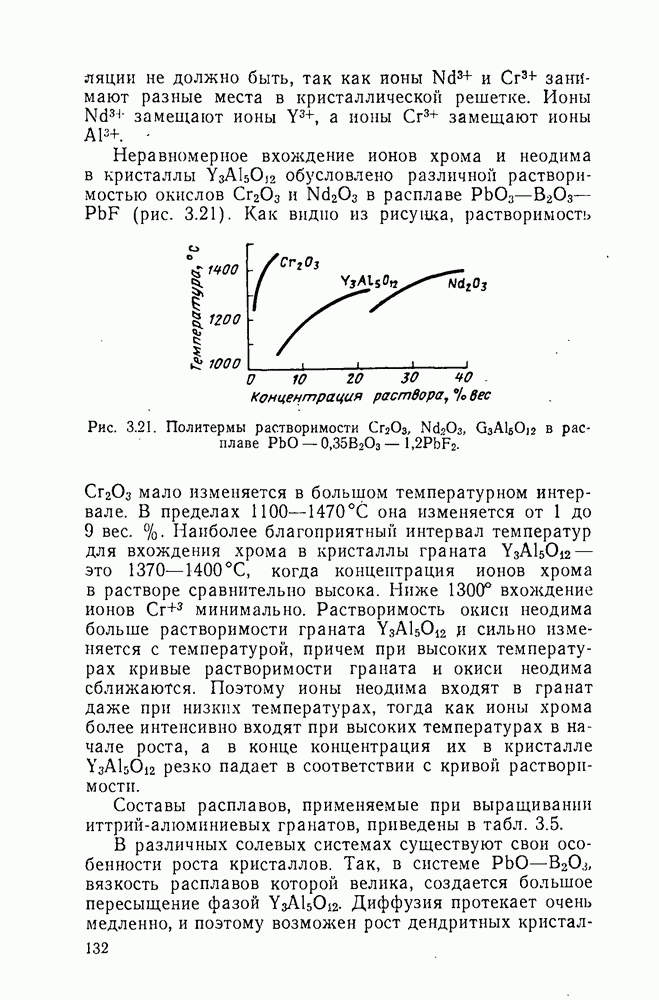
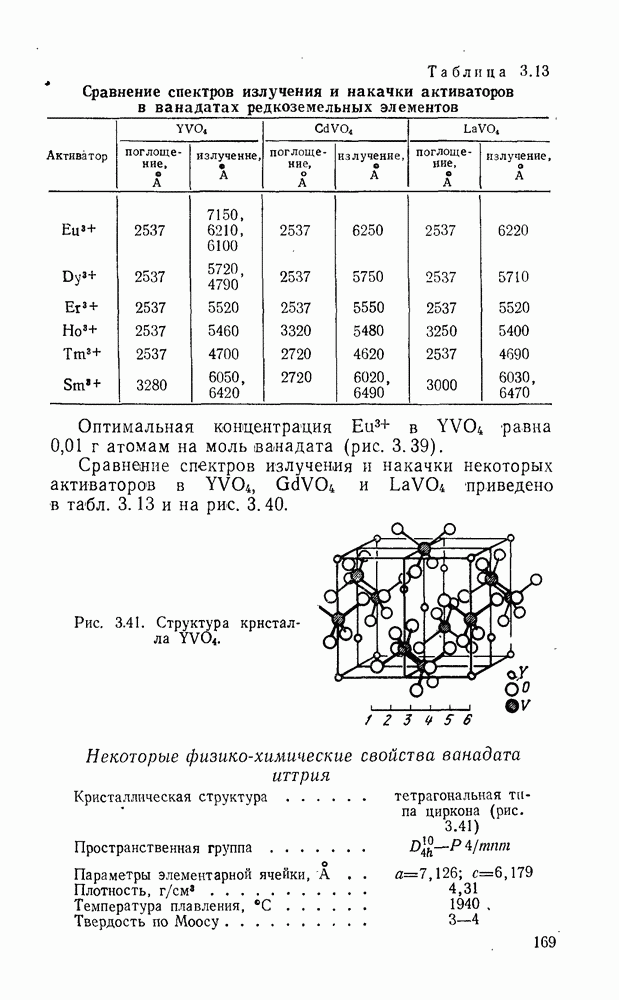
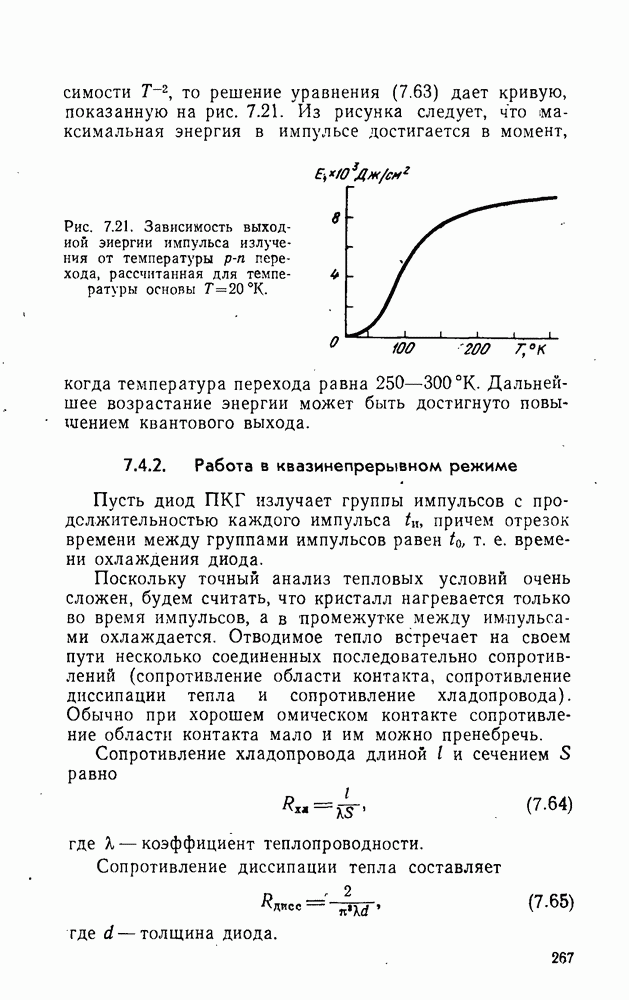
В оптйческих квантовых генераторах, работающих на твердых кристаллических телах, перевод системы в возбужденное состояние можно осуществить с помощью внешнего электромагнитного поля. При таком способе достижения инверсной населенности использование только двух уровней невозможно, так как вероятности переходов равны. Поэтому при облучении можно только уменьшить разность  по сравнению с равновесной, но не сделать ее отрицательной и. следовательно, нельзя получить отрицательный коэффициент поглощения.
по сравнению с равновесной, но не сделать ее отрицательной и. следовательно, нельзя получить отрицательный коэффициент поглощения.

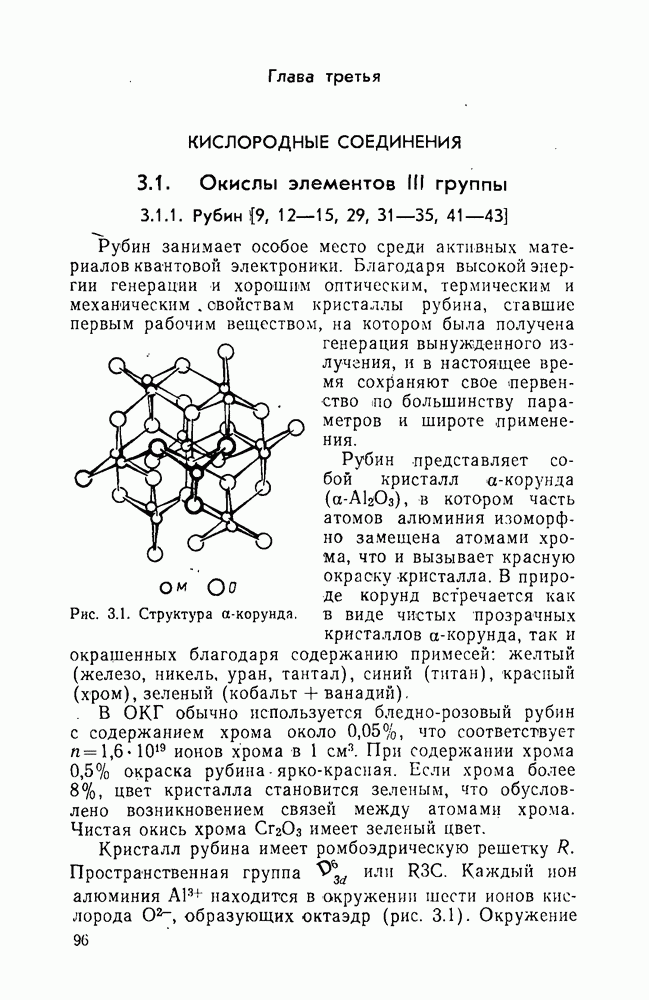
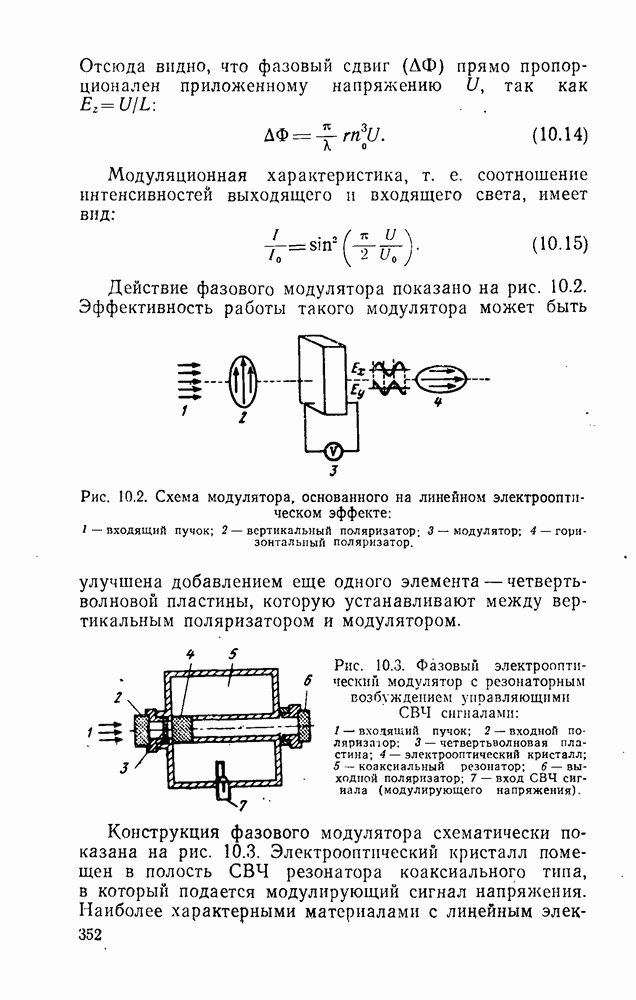
Рис. 1.9. Переходы в трехуровневой системе.
Исходя из этих соображений, Н. Г. Басовым и А. М. Прохоровым была предложена система с гремя уровнями. Рассмотрим такую систему с темя энергетическими уровнями  и
и  причем
причем  и с населенностями
и с населенностями  о и
о и  соответственно (рис. 1.9). В равновесном состоянии в кристалле почти все атомы находятся на нижнем основном энергетическом уровне, т. е.
соответственно (рис. 1.9). В равновесном состоянии в кристалле почти все атомы находятся на нижнем основном энергетическом уровне, т. е. 
Под действием излучения от внешнего источника системой поглощается энергия, соответствующая частоте широкой полосы уровня 3. Полосу поглощения уровня 3 стараются подобрать по возможности более широкой. Это увеличивает к. п. д. квантового генератора. Газоразрядные лампы или другие источники энергии, как правило, имеют широкий спектр излучения. Поэтому чем шире уровень 3, тем большая доля энергии накачки используется на возбуждение квантовой системы. Обычно излучение, вызывающее переход атомов на возбужденные уровни, называют излучением накачки, а сам процесс создания инверсной населенности с помощью внешнего электромагнитного излучения называется накачкой.
При выборе системы с тремя уровнями обычно стремятся выполнить следующие условия.
Вероятность безызлучательного перехода  должна быть значительно больше, чем
должна быть значительно больше, чем  т. е.
т. е.

При этом условии через время  большая часть возбужденных атомов перейдет на уровень 2.
большая часть возбужденных атомов перейдет на уровень 2.
Вероятность спонтанного перехода  должна быть значительно меньше вероятности
должна быть значительно меньше вероятности  т. е.
т. е.

Это означает, что уровень 2 должен быть значительно более устойчивым (метастабильным) по сравнению с уровнем 3, что обеспечивает накопление возбужденных атомов на уровне 2. При достаточно высокой мощности накачки может быть достигнута инверсия населенностей между уровнем 2 и основным уровнем, но поскольку время жизни уровня 3 мало, то возбужденные атомы не задерживаются на нем и безызлучательно переходят на более долгоживущий
уровень 2, создавая инверсную населенность этого уровня по отношению к уровню 1. Время жизни уровня 2 должно быть достаточно большим, чтобы накопить на нем энергию, - необходимую для генерации. Например, для рубина  , т. е. время жизни уровня 2 в рубине в
, т. е. время жизни уровня 2 в рубине в  раз больше времени жизни уровня 3.
раз больше времени жизни уровня 3.
Учитывая изменения населенностей всех трех уровней вследствие различных переходов, кинетические уравнения переходов в квантовой трехуровневой системе можно записать в следующем виде:

Эти уравнения записаны в упрощенной форме, так как в них не учтено вырождение уровней. Если энергетические уровни характеризуются некоторыми степенями вырождения  то
то  необходимо заменить на
необходимо заменить на  и согласно первому соотношению Эйнштейна
и согласно первому соотношению Эйнштейна  , а не
, а не  . Учитывая особенности конкретной системы, эти уравнения можно упростить. Одно из них можно исключить, заменив более простым соотношением
. Учитывая особенности конкретной системы, эти уравнения можно упростить. Одно из них можно исключить, заменив более простым соотношением

где  — общее количество атомов активатора в
— общее количество атомов активатора в 
Если далее предположить, что накопление на уровне 3 не происходит, как в случае рубинового ОКГ, т. е.

то уравнение (1.65) примет вид

а сама система превратится в двухуровневую, так как

Учитывая эти допущения, преобразуем уравнения (1.63) и (1.65) к следующему виду:

Так как в рубине скорость перехода с уровня 3 на метастабильный уровень 2 значительно больше скорости перехода с уровня 3 на уровень 1, т. е.  то уравнение (1.69) принимает вид
то уравнение (1.69) принимает вид

В стационарном режиме, т. е. при  имеем
имеем

Из этого уравнения видно, что необходимое условие генерации  может быть выполнено только при таких мощностях накачки, когда
может быть выполнено только при таких мощностях накачки, когда  т. е.
т. е.

Величина вероятностей переходов атомов с уровня  на уровень 3 в результате накачки определяется из выражения
на уровень 3 в результате накачки определяется из выражения

где  — число фотонов, падающих нормально поверхности кристалла
— число фотонов, падающих нормально поверхности кристалла  в единицу времени;
в единицу времени;  — эффективное сечеиие поглощения для перехода атома с уровня 1 на уровень 3 при воздействии квантов
— эффективное сечеиие поглощения для перехода атома с уровня 1 на уровень 3 при воздействии квантов  ; Р — мощность накачки в полосе частот поглощения активного вещества.
; Р — мощность накачки в полосе частот поглощения активного вещества.
С учетом значения  и порогового условия накачки (1.72) можно получить выражение для порогового значения мощности излучения накачки;
и порогового условия накачки (1.72) можно получить выражение для порогового значения мощности излучения накачки;

Для рубина, например, при значениях  пороговая мощность накачки должна составлять
пороговая мощность накачки должна составлять  . В действительности пороговая мощность накачки значительно больше этой величины вследствие различных потерь в оптическом резонаторе.
. В действительности пороговая мощность накачки значительно больше этой величины вследствие различных потерь в оптическом резонаторе.
Согласно выражениям (1.71), (1.72) и (1.74) вероятность генерации и пороговая мощность накачки существенно зависят от вероятности спонтанного перехода  с метастабильного уровня на основной уровень 1.
с метастабильного уровня на основной уровень 1.
Этот переход обусловливает флюоресценцию возбужденного кристалла рубина, т. е. потери на некогерентное излучение. Доля
флюоресценции в излучении рубинового ОКГ довольно велика. Это приводит к тому, что энергия, необходимая для возбуждения половины всех атомов из основного состояния, не переходит в когерентное излучение.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава первая. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ И ПРИНЦИП ДЕЙСТВИЯ КВАНТОВЫХ ГЕНЕРАТОРОВ
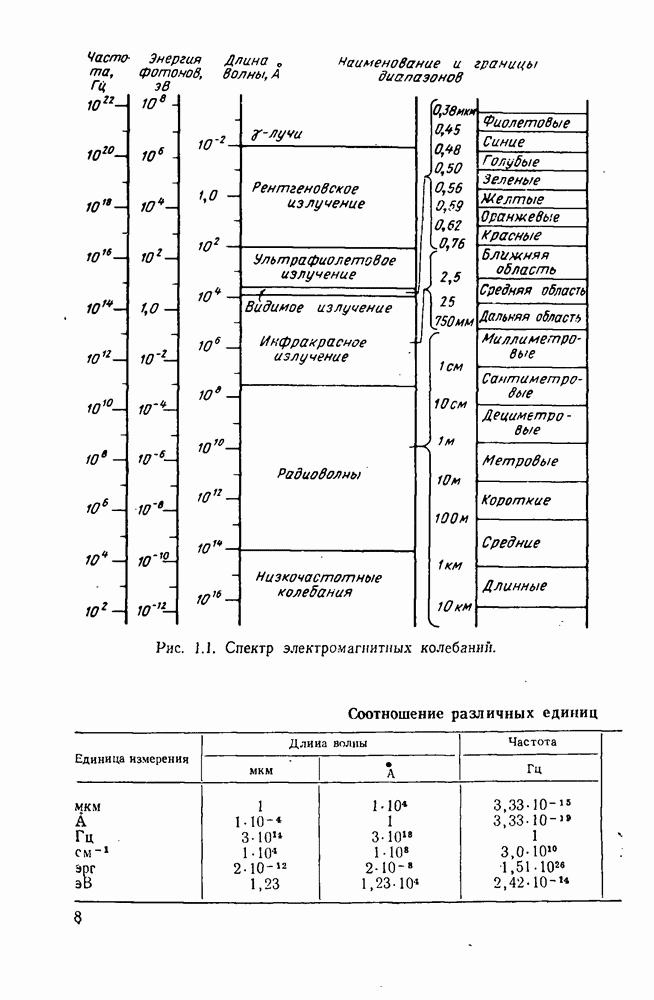
- 1.1. Спектр электромагнитных колебаний
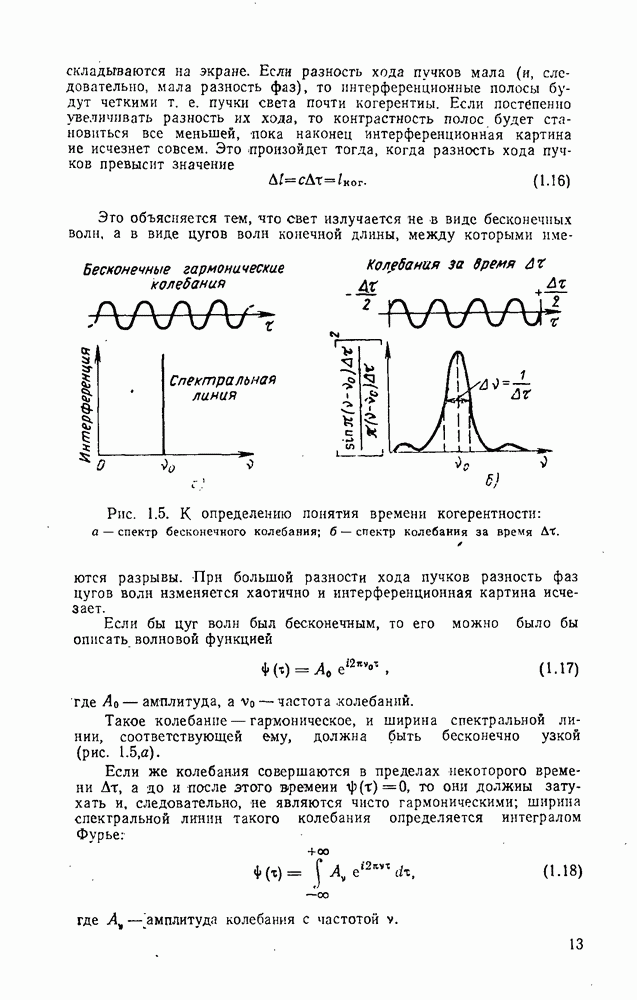
- 1.2. Когерентность
- 1.3. Направленность излучения
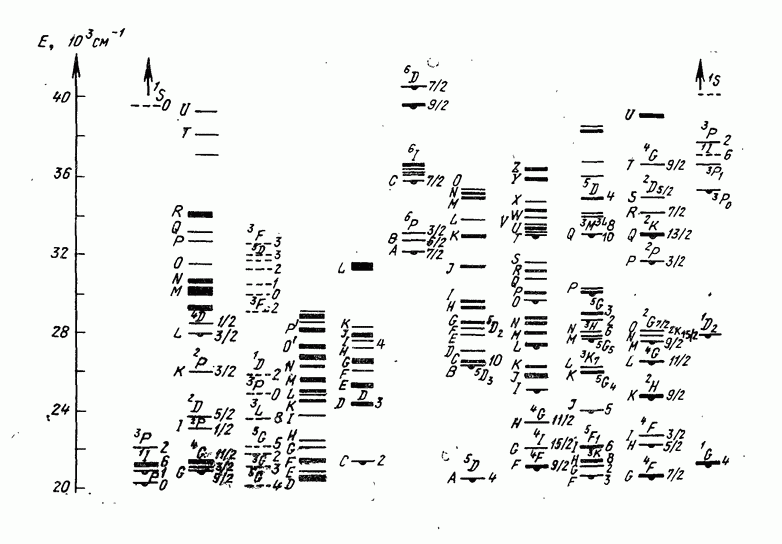
- 1.4. Символика энергетических уровней атомов и ионов
- 1.5. Инверсная населенность
- 1.6. Вероятности спонтанных и вынужденных переходов
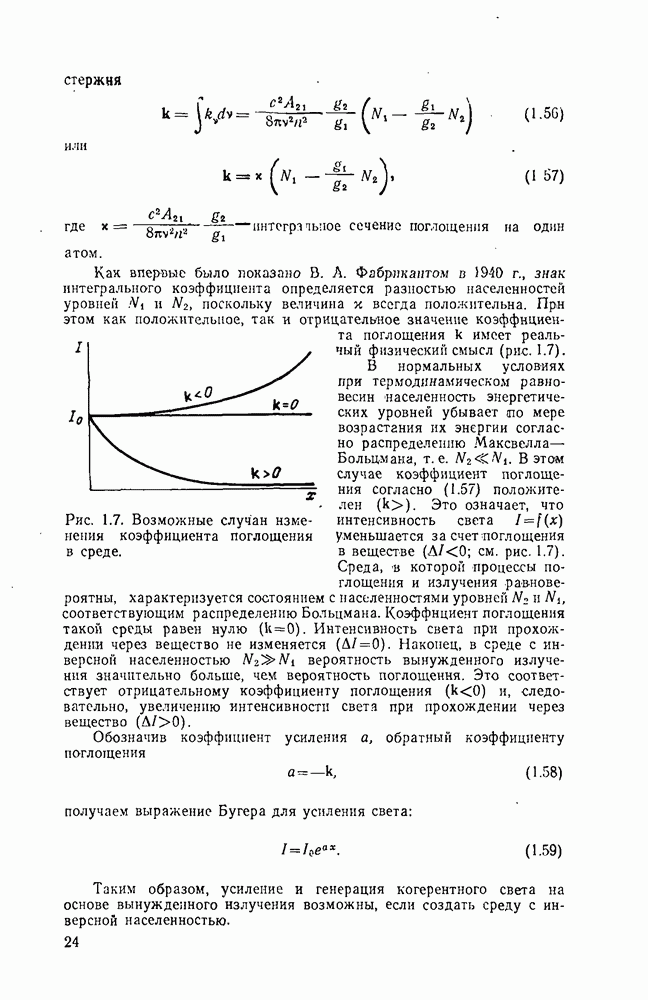
- 1.7. Усиление света при прохождении через вещество
- 1.8. Двухуровневая система
- 1.9. Трехуровневая система
- 1.10. Четырехуровневая система
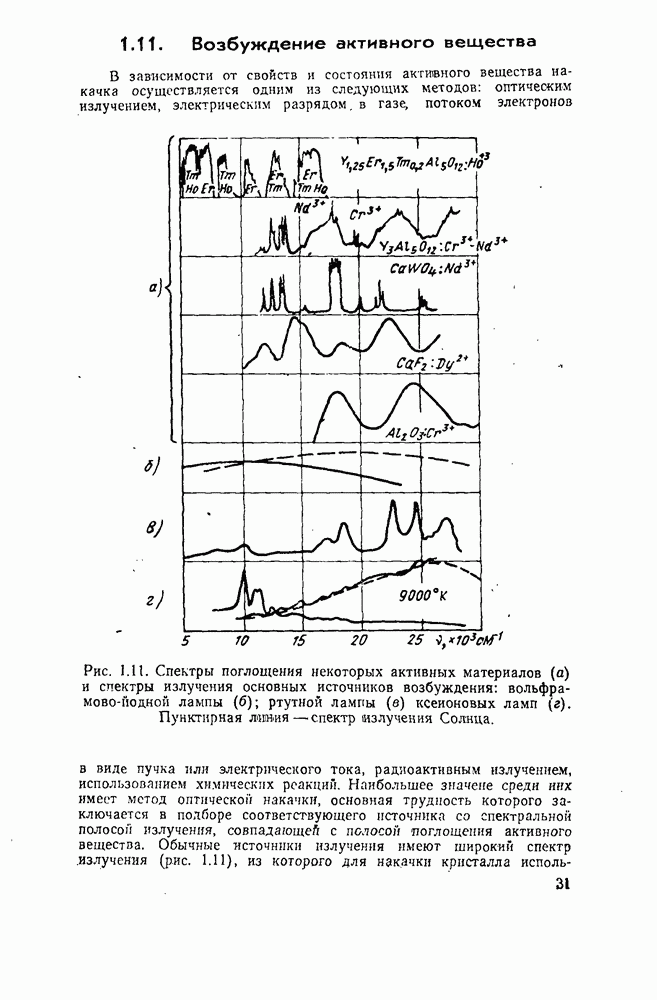
- 1.11. Возбуждение активного вещества
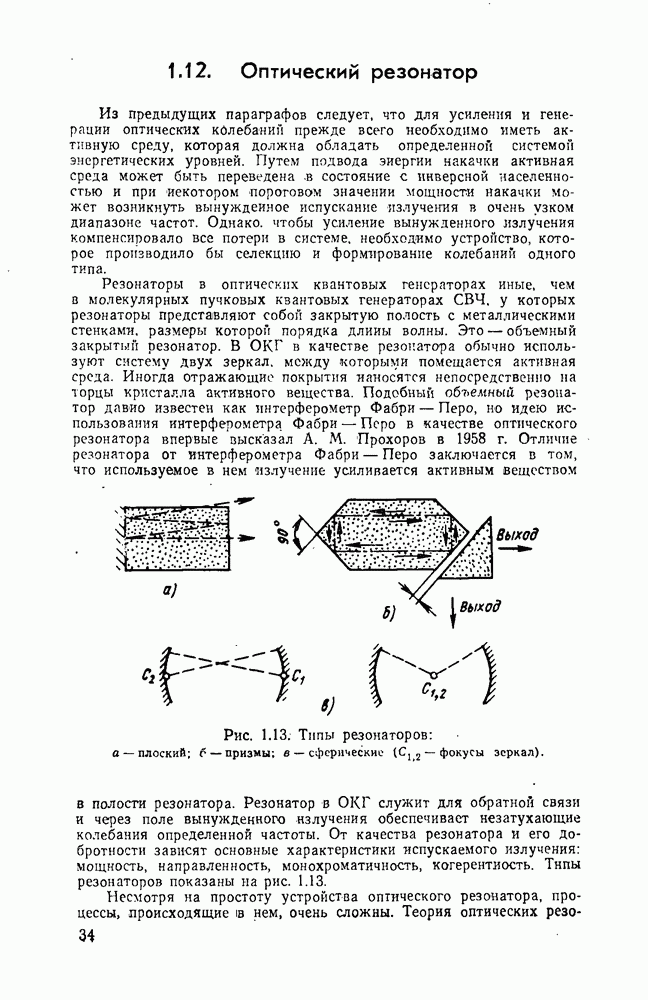
- 1.12. Оптический резонатор
- 1.13 Условие генерации
- 1.14. Потери энергии в квантовом генераторе
- 1.15. Устройство ОКГ на твердом теле
- Глава вторая. ОБЩИЕ ВОПРОСЫ ТЕХНОЛОГИИ МАТЕРИАЛОВ ТВЕРДОТЕЛЬНЫХ ОКГ
- 2.1. Особенности активного вещества ионных квантовых систем
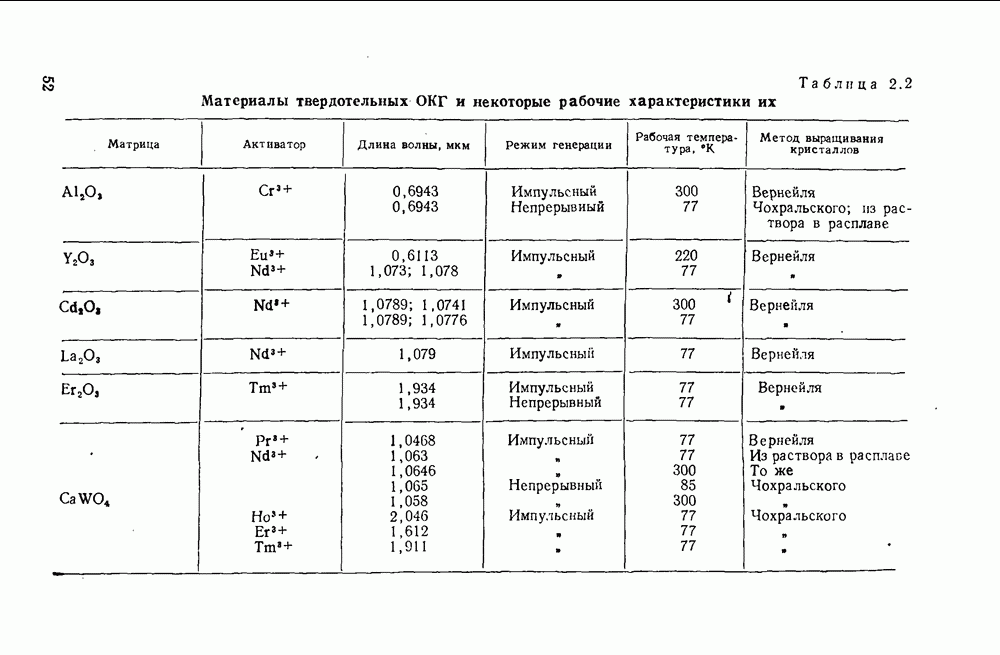
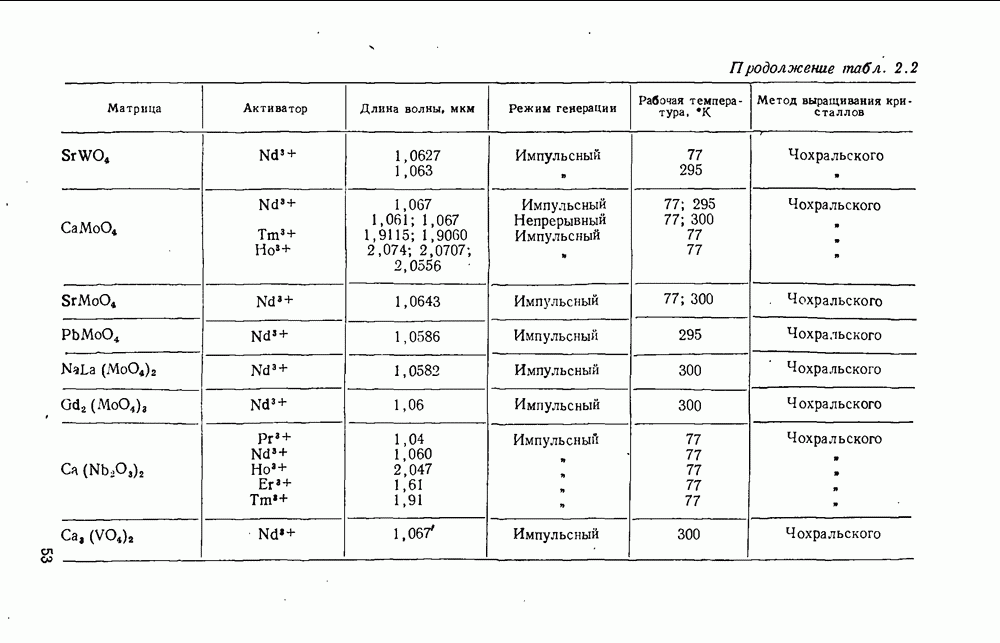
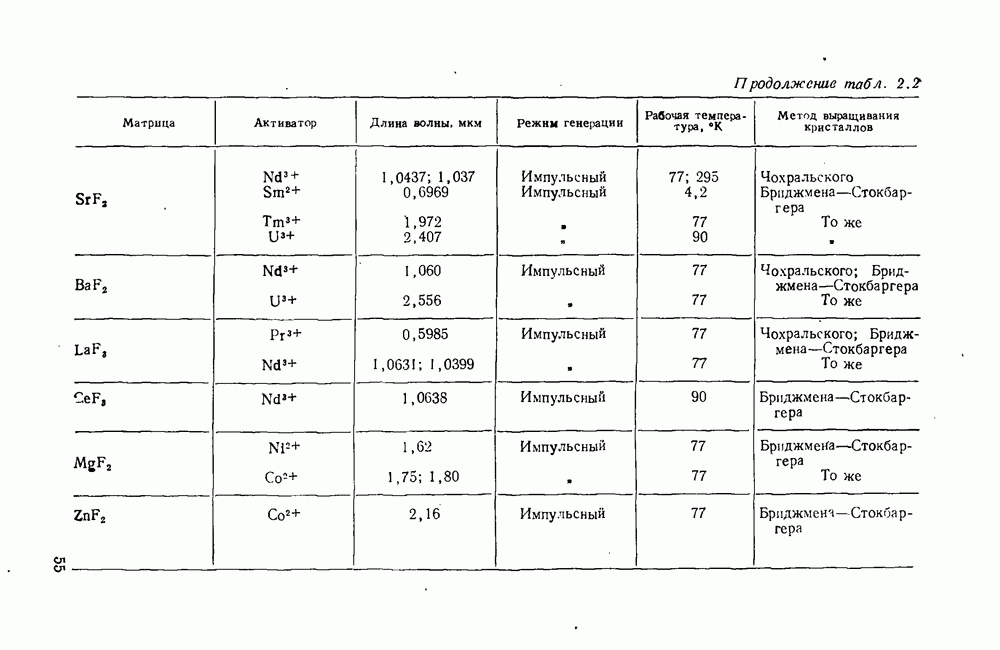
- 2.2. Особенности технологии твердотельных материалов квантовых генераторов
- 2.3. Физико-химические основы кристаллизации
- 2.3.2. Гетерогенное зародышеобразование
- 2.3.3. Скорость зарождения новой фазы
- 2.3.4. Рост кристаллов
- 2.3.5. Общее кинетическое уравнение кристаллизации
- 2.3.6. Распределение примеси в процессе роста кристалла
- 2.4. Основные методы синтеза и выращивания кристаллов
- 2.4.2. Выращивание из стехиометрических расплавов
- 2.4.3. Методы выращивания кристаллов из растворов
- 2.4.4. Гидротермальный синтез и рост кристаллов
- 2.4.5. Выращивание кристаллов из газовой фазы
- 2.5. Кристалло-химическая классификация материалов твердотельных квантовых генераторов
- Глава третья. КИСЛОРОДНЫЕ СОЕДИНЕНИЯ
- 3.1. Окислы элементов III группы
- 3.1.2. Окислы редкоземельных элементов и иттрия
- 3.3.1. Гранаты
- 3.2. Материалы на основе кислородных соединений элементов VI группы
- 3.2.2. Молибдаты
- 3.3. Материалы на основе кислородных соединений элементов V группы
- 3.3.2. Ниобаты
- 3.3.3. Фосфаты
- Выращивание кристаллов фторфосфата кальция [47]
- Глава четвертая. ФТОРИСТЫЕ СОЕДИНЕНИЯ
- 4.1. Фториды элементов II группы
- 4.2. Фториды редкоземельных элементов
- 4.3. Смешанные фториды
- 4.4. Фториды элементов VII группы
- Глава пятая. СТЕКЛО
- 5.1. Особенности стекла как активного материала ОКГ
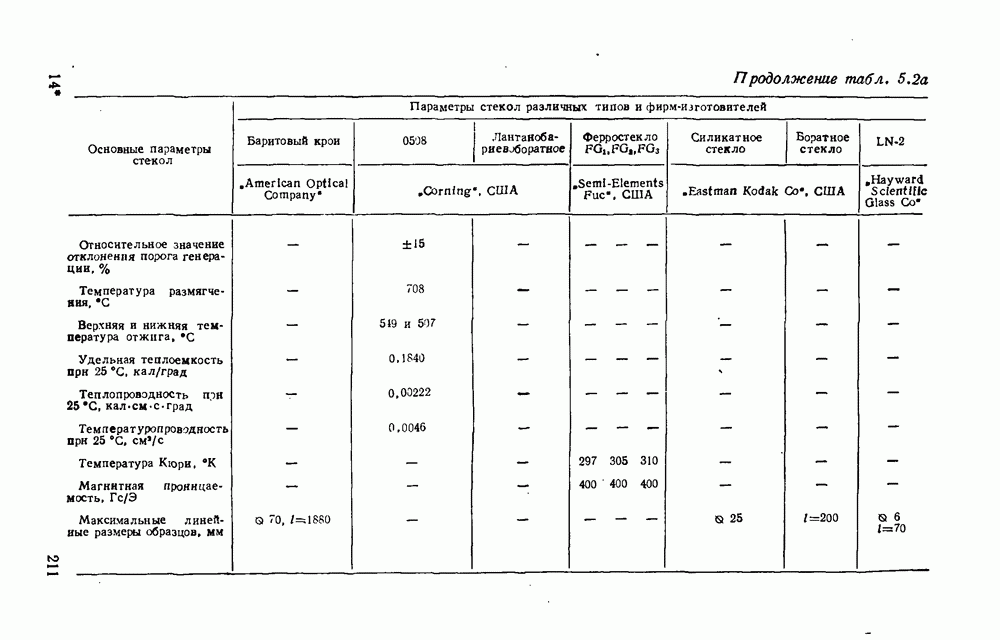
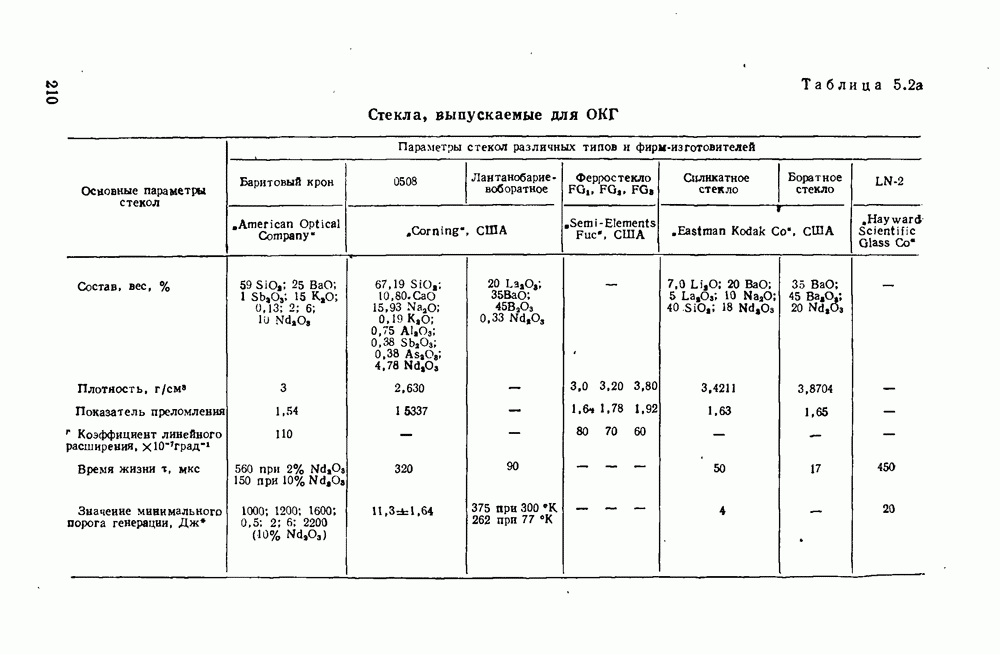
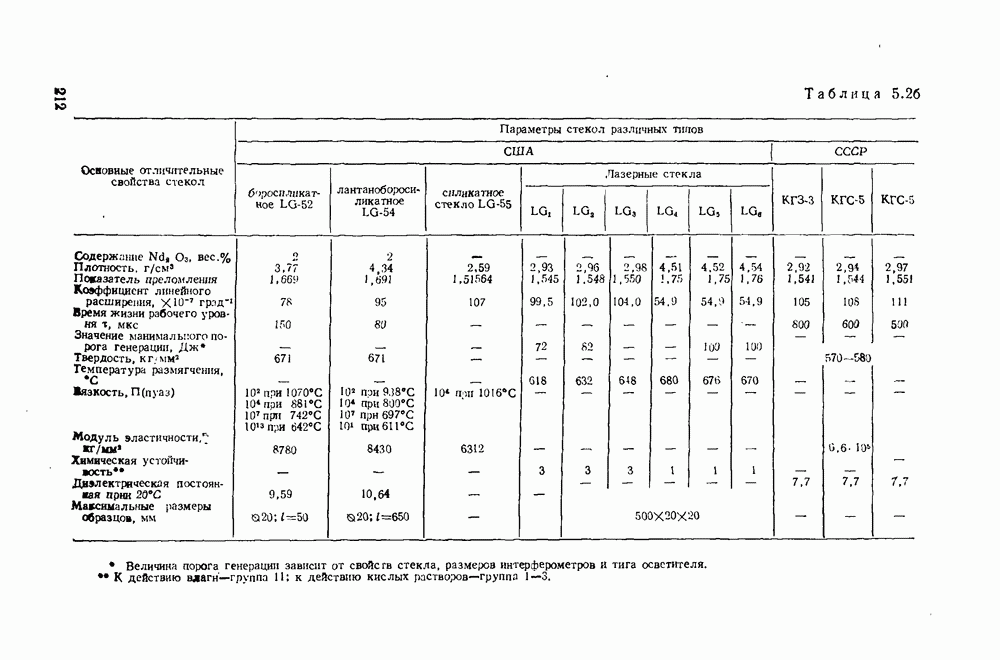
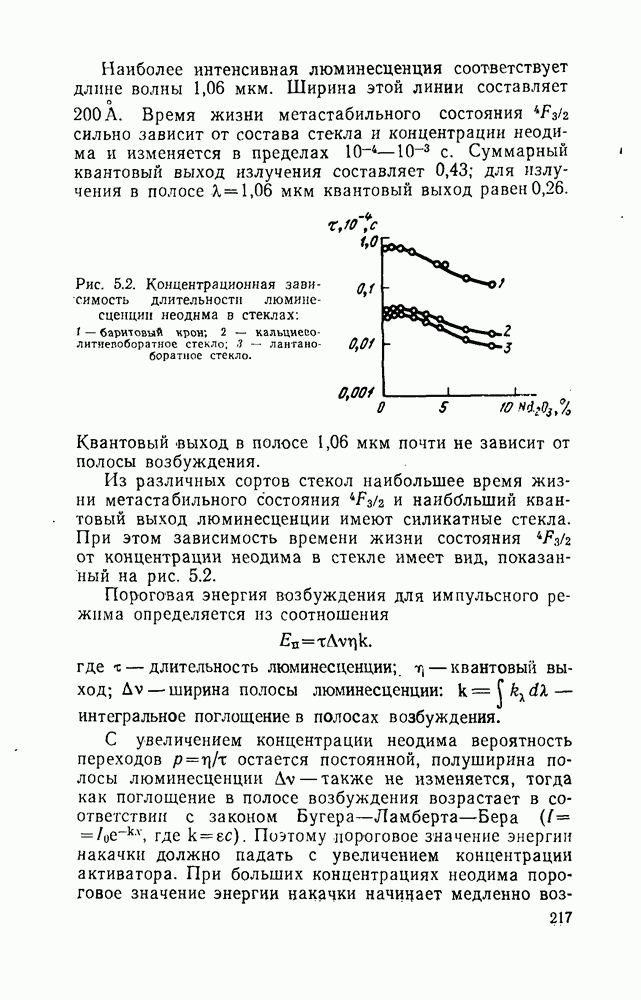
- 5.2. Общая характеристика стекол для ОКГ
- 5.3. Особенности положения атомов активатора в стекле
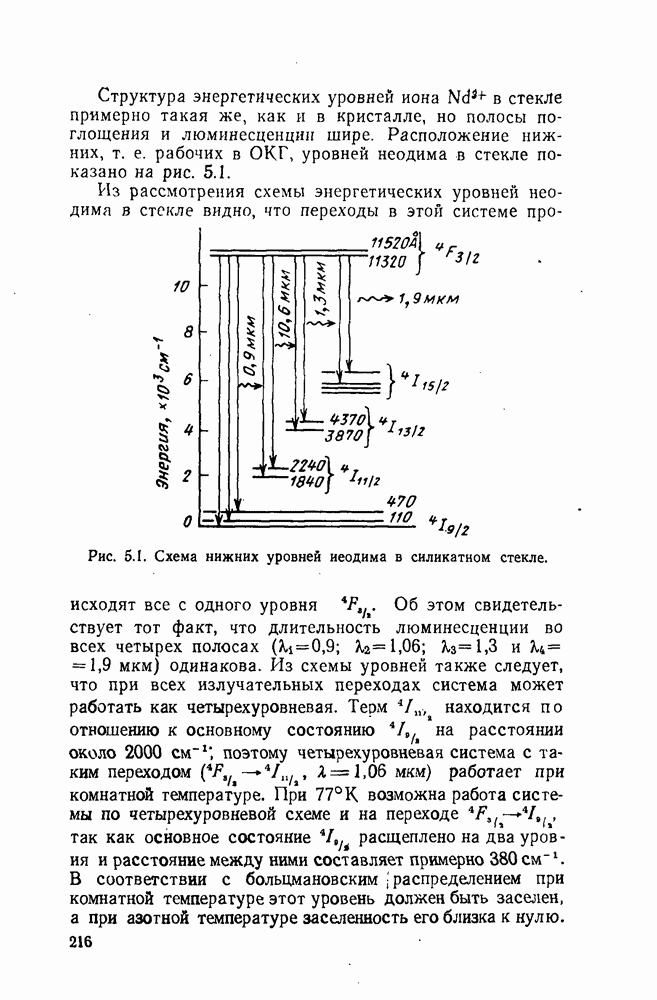
- 5.4. Стекло с неодимом
- Глава шестая. МАТЕРИАЛЫ ЖИДКОСТНЫХ ОКГ
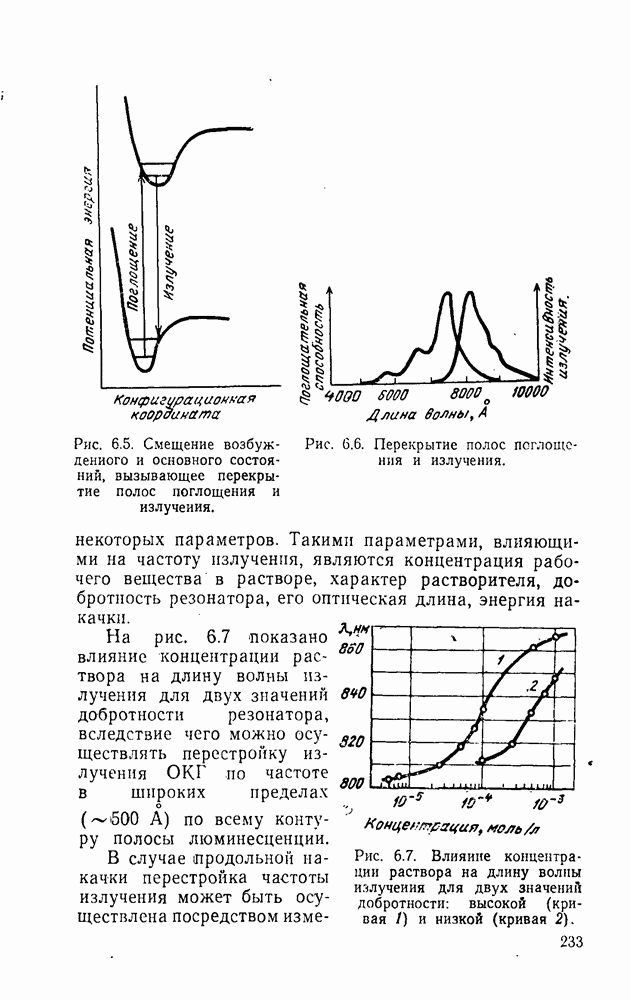
- 6.2. Механизм излучения в органических растворах
- 6.3. Растворы металлоорганических соединений
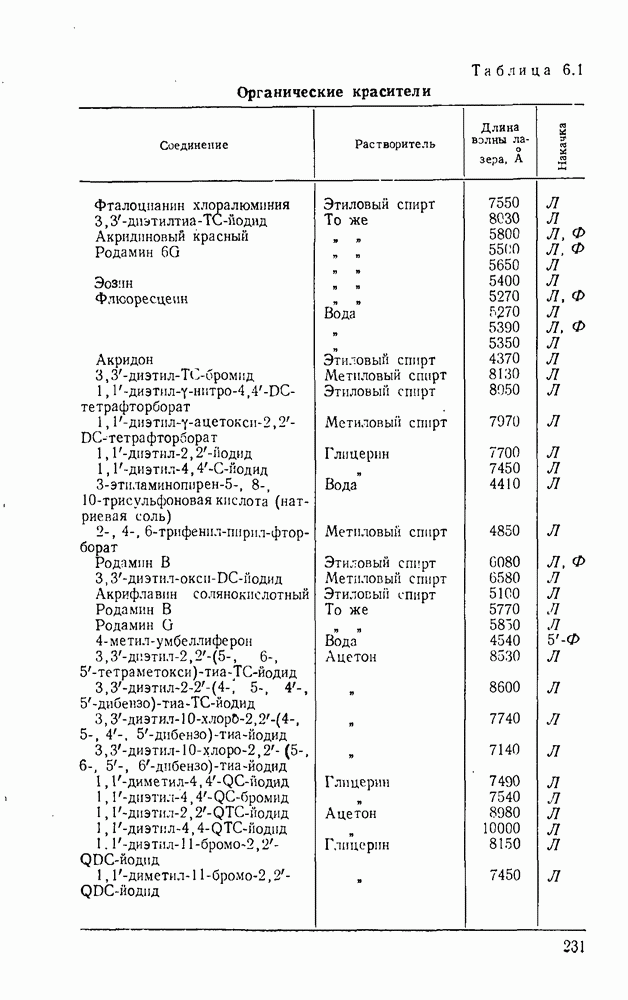
- 6.4. Растворы органических красителей
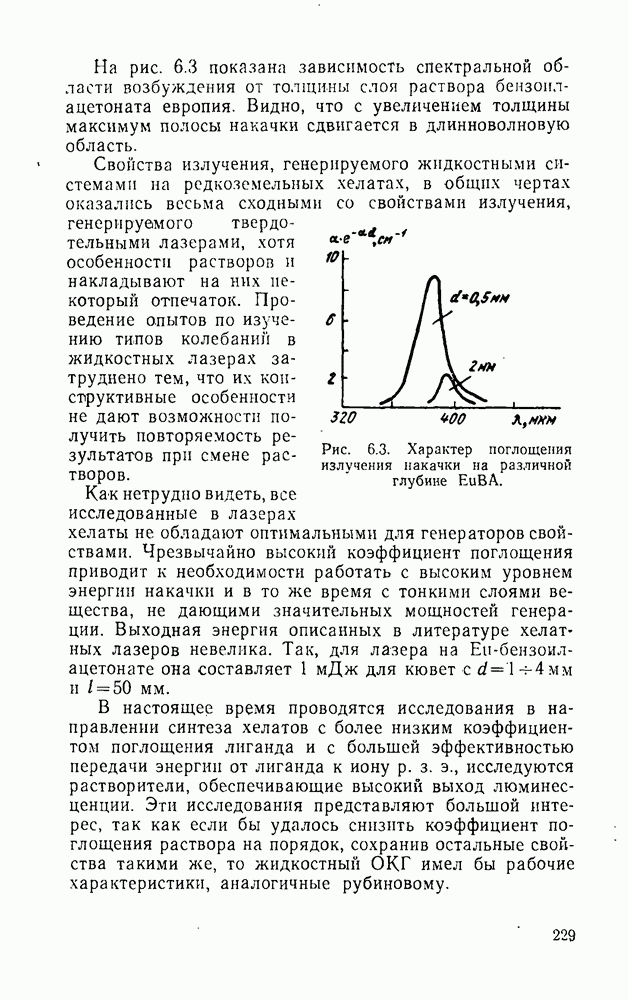
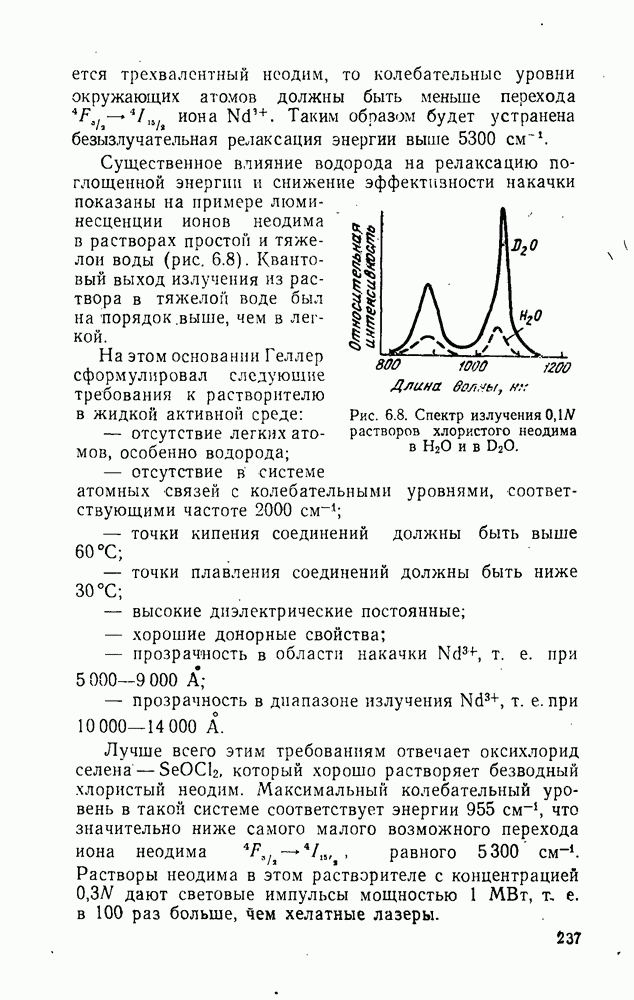
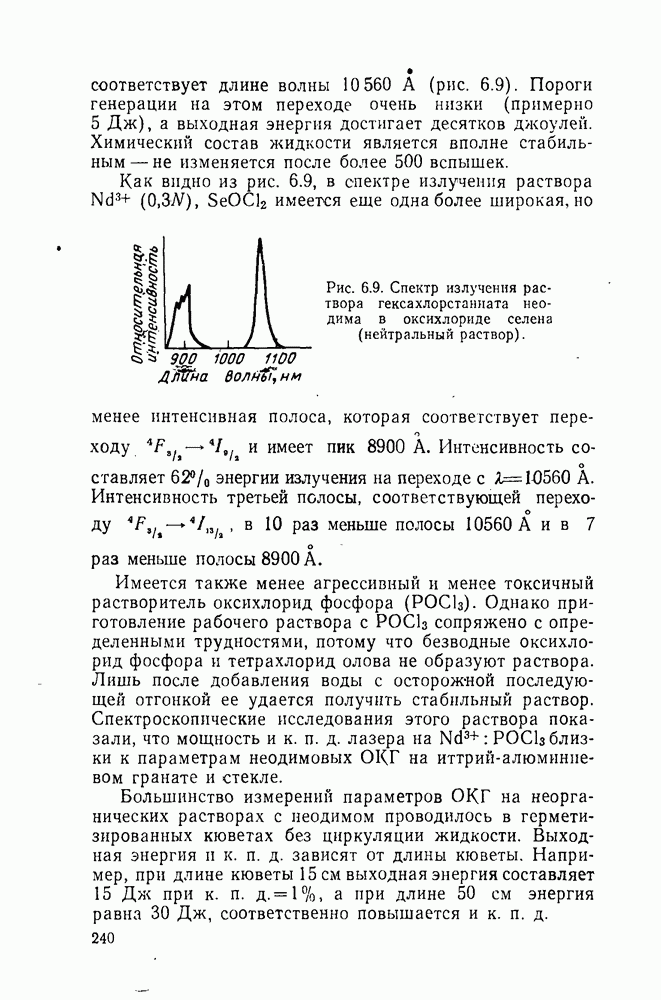
- 6.5. Растворы неорганических соединений редкоземельных элементов
- Глава седьмая. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВЫХ КВАНТОВЫХ ГЕНЕРАТОРОВ (ПКГ)
- 7.2. Основные сведения из теории люминесценции инжекционных ПКГ
- 7.3. Рабочие характеристики инжекционных ПКГ
- 7.3.2. Пространственные свойства
- 7.3.3. Пороговый ток
- 7.3.4. Квантовый выход
- 7.4. Тепловые условия работы лазерного диода
- 7.4.2. Работа в квазинепрерывном режиме
- 7.5. Другие типы ПКГ
- 7.5.1. ПКГ с электронным возбуждением
- 7.5.2. ПКГ с оптической накачкой
- 7.5.3. ПКГ с прямым электрическим возбуждением
- Глава восьмая. АРСЕНИД ГАЛЛИЯ И ТЕХНОЛОГИЯ ИЗГОТОВЛЕНИЯ ДИОДОВ ПКГ
- 8.1. Физические свойства арсенида галлия
- 8.2. Методы выращивания монокристаллов арсенида галлия
- 8.3. Методы изготовления р-n-переходов
- 8.3.2. Эпитаксия из жидкой фазы
- 8.3.3. Эпитаксия из газовой фазы
- 8.4. Изготовление невыпрямляющих низкоомных контактов к арсениду галлия
- 8.5. Изготовление резонатора
- 8.6. Общая технологическая схема изготовления диодов ПКГ
- 8.7. Конструкция ПКГ
- 8.8. Гетероструктуры на основе арсенида галлия
- 8.9. Другие материалы с прямыми переходами
- Глава девятая. МАТЕРИАЛЫ ГАЗОВЫХ ОКГ
- 9.1. Особенности газового активного вещества ОКГ и методы создания инверсной населенности
- 9.2. Газоразрядные ОКГ
- 9.2.2. Ионные газоразрядные ОКГ
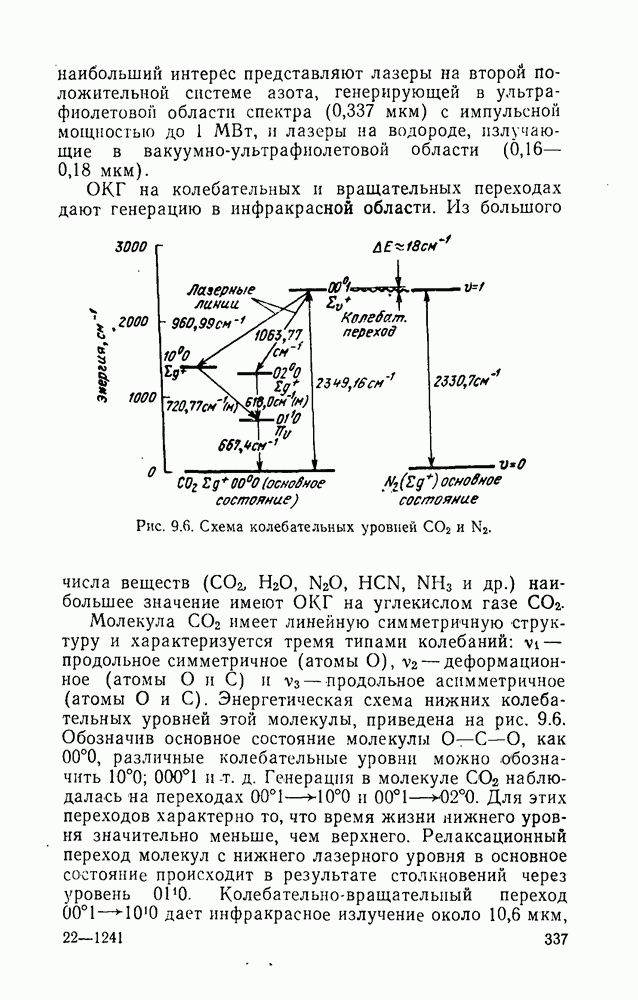
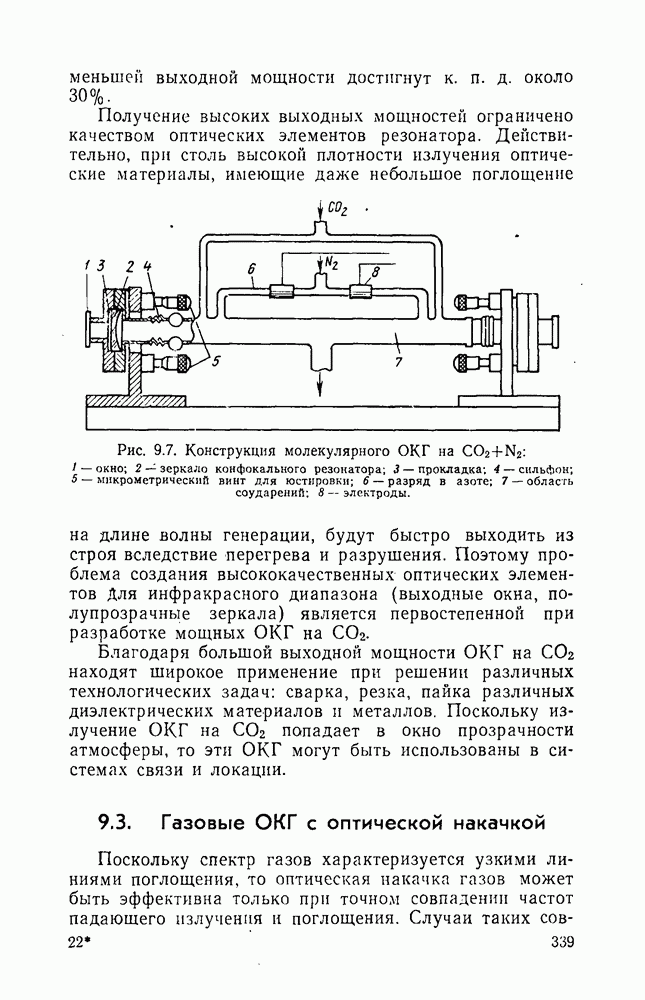
- 9.2.3. Молекулярные газоразрядные ОКГ
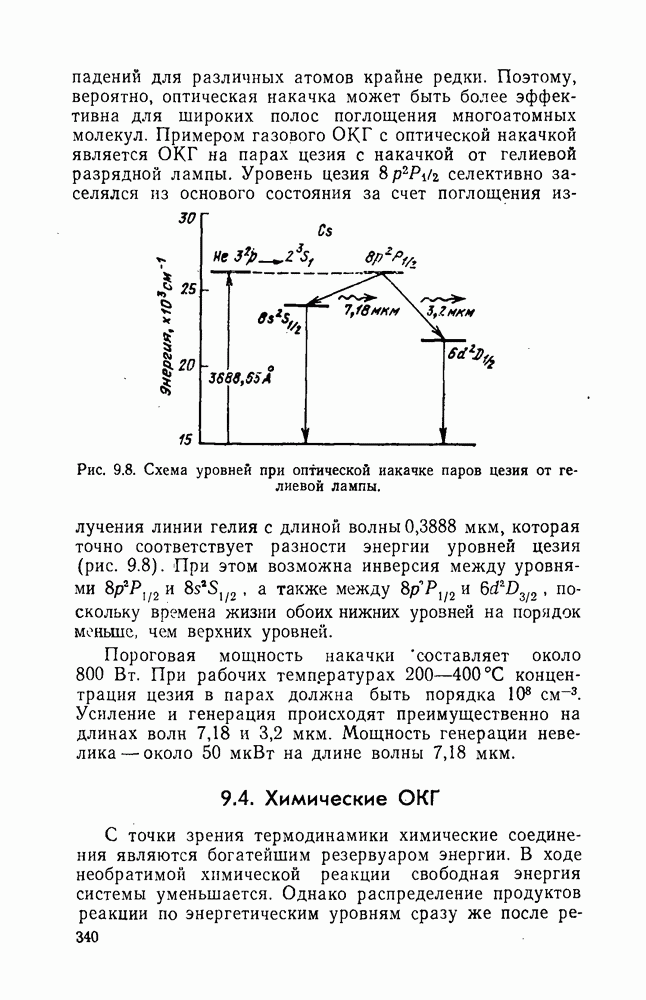
- 9.3. Газовые ОКГ с оптической накачкой
- 9.4. Химические ОКГ
- Глава десятая. МАТЕРИАЛЫ МОДУЛЯТОРОВ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ
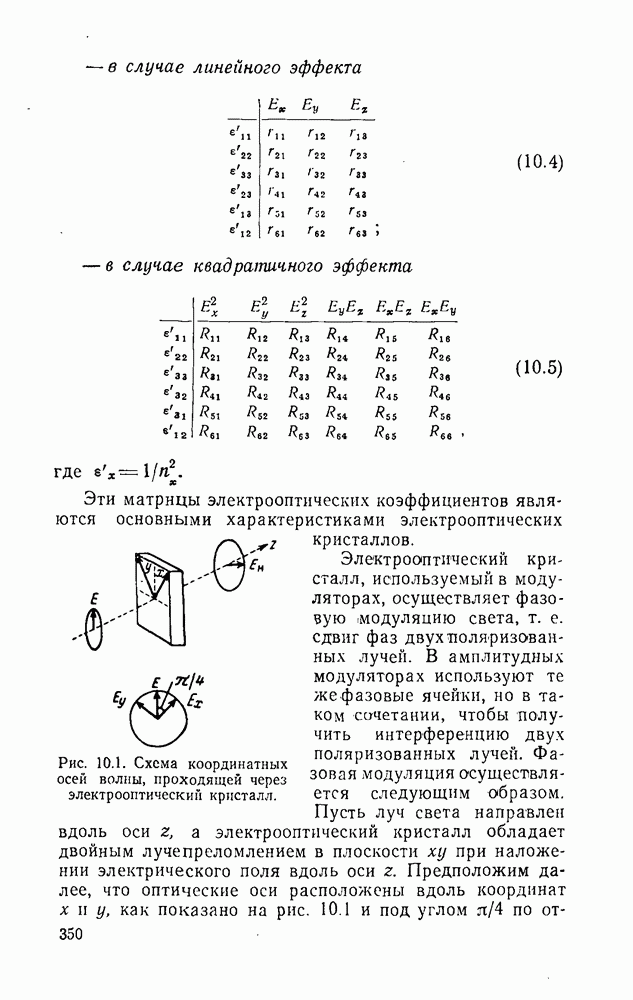
- 10.1. Некоторые физические основы модуляции оптического излучения
- 10.2. Требования к материалам модуляторов излучения ОКГ
- 10.3. Материалы с линейным электрооптическим эффектом
- 10.3.1. Тетрагональные кристаллы типа KDP
- 10.3.2. Ромбические кристаллы
- 10.3.3. Тригональные кристаллы
- 10.3.4. Кубические кристаллы
- 10.4. Кристаллы с квадратичным электрооптическим эффектом
- Литература