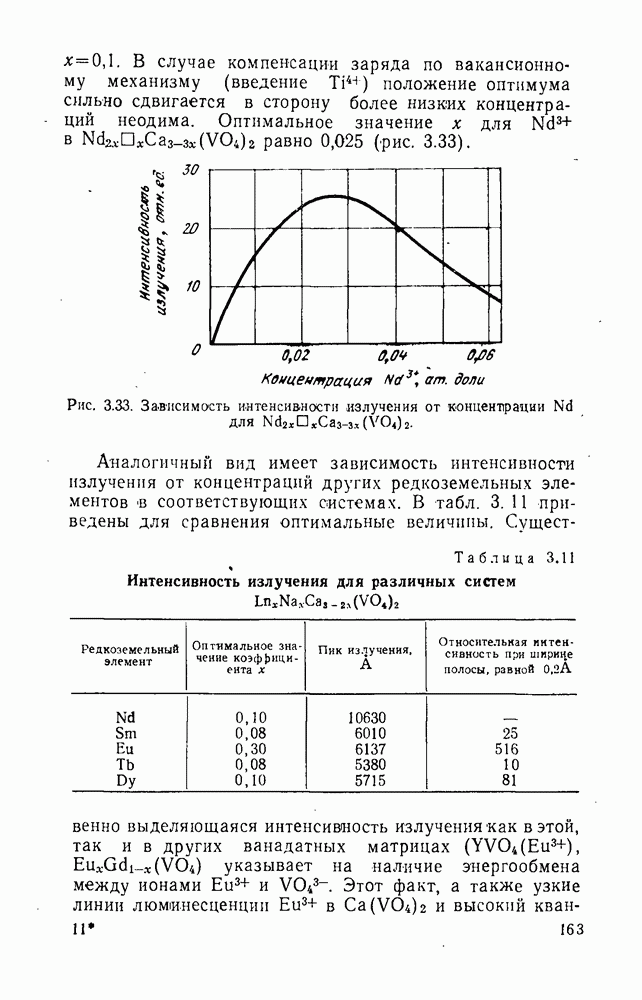
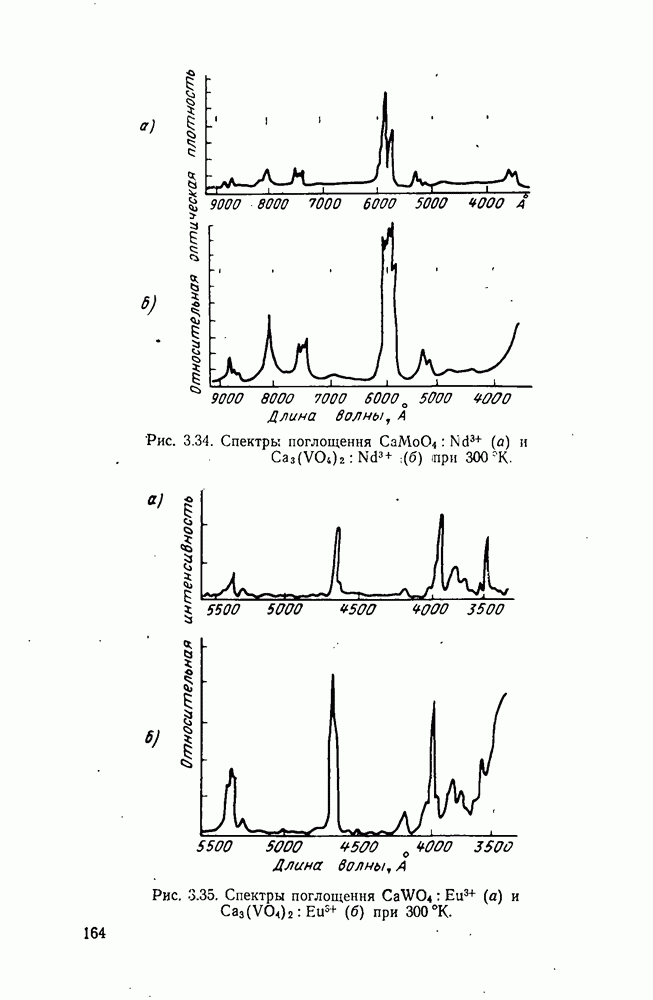
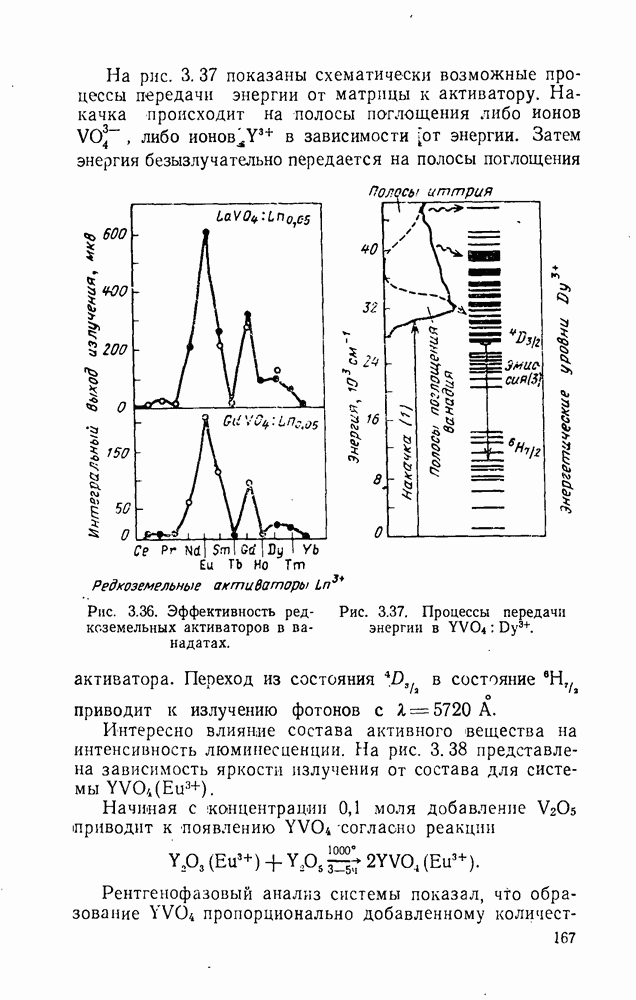
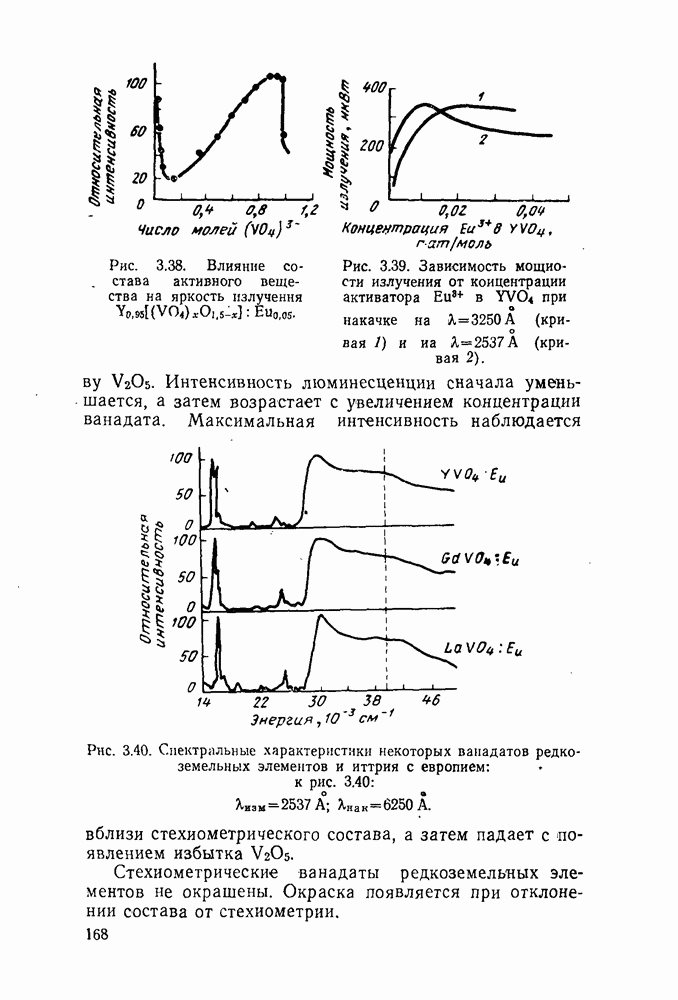
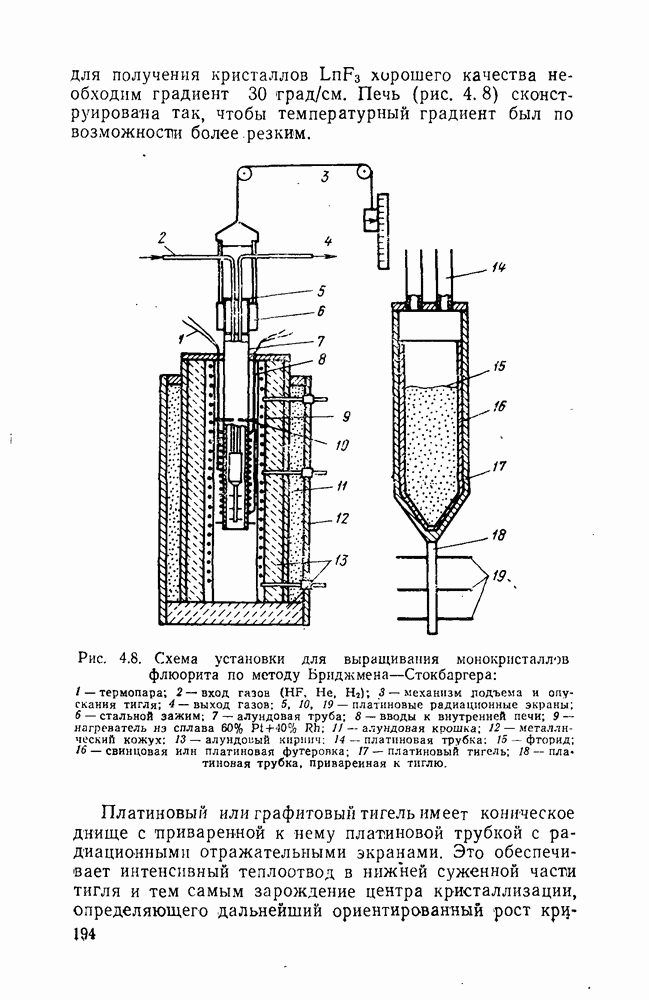
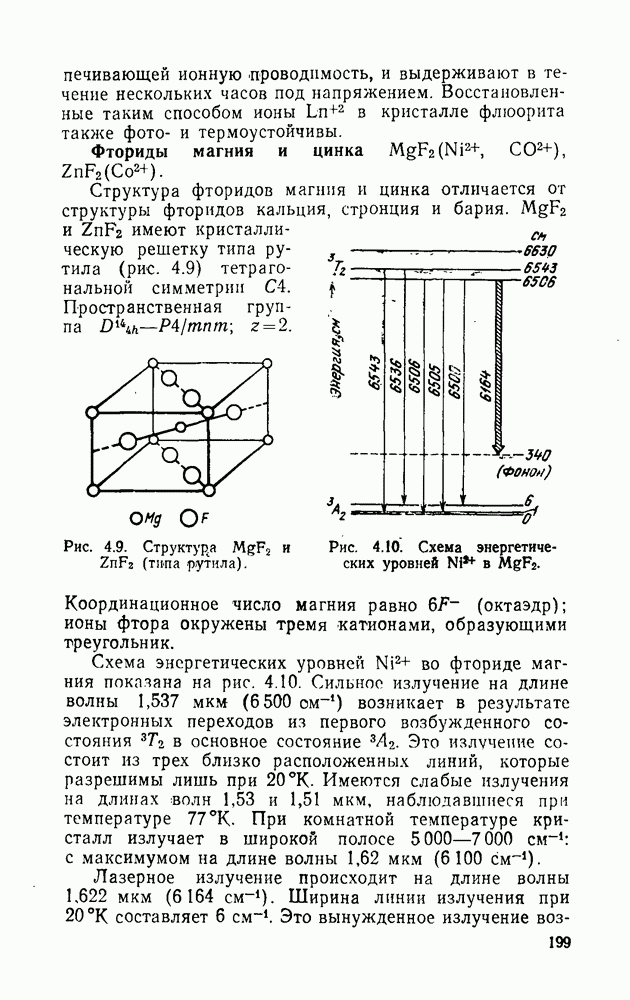
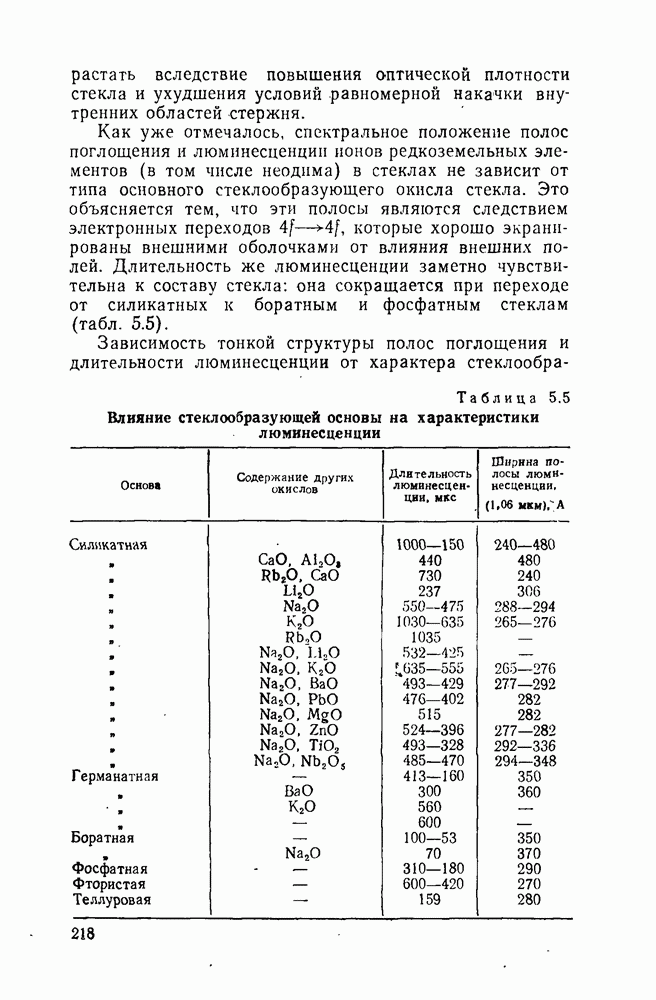
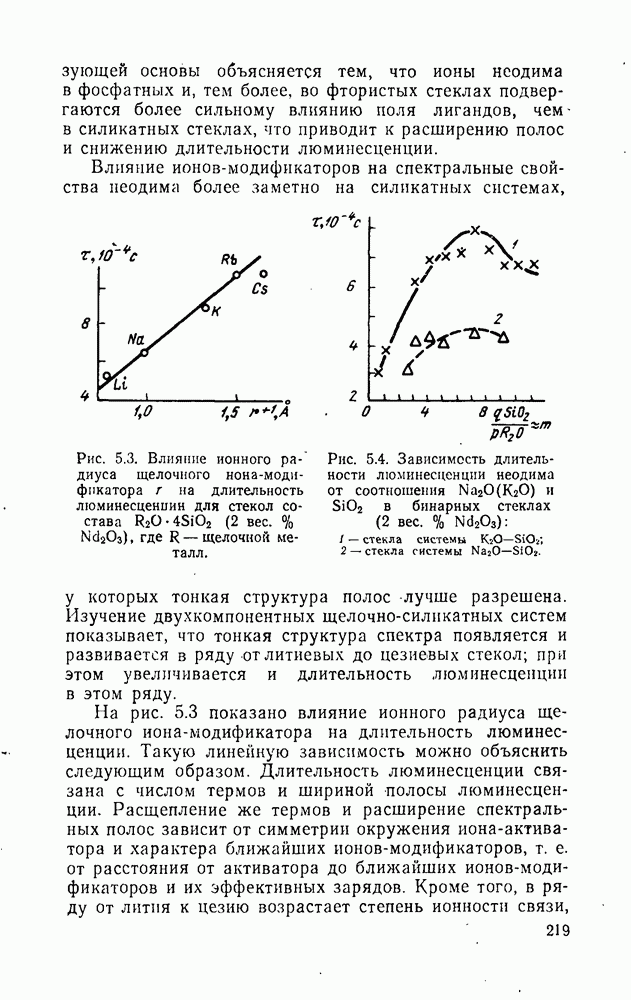
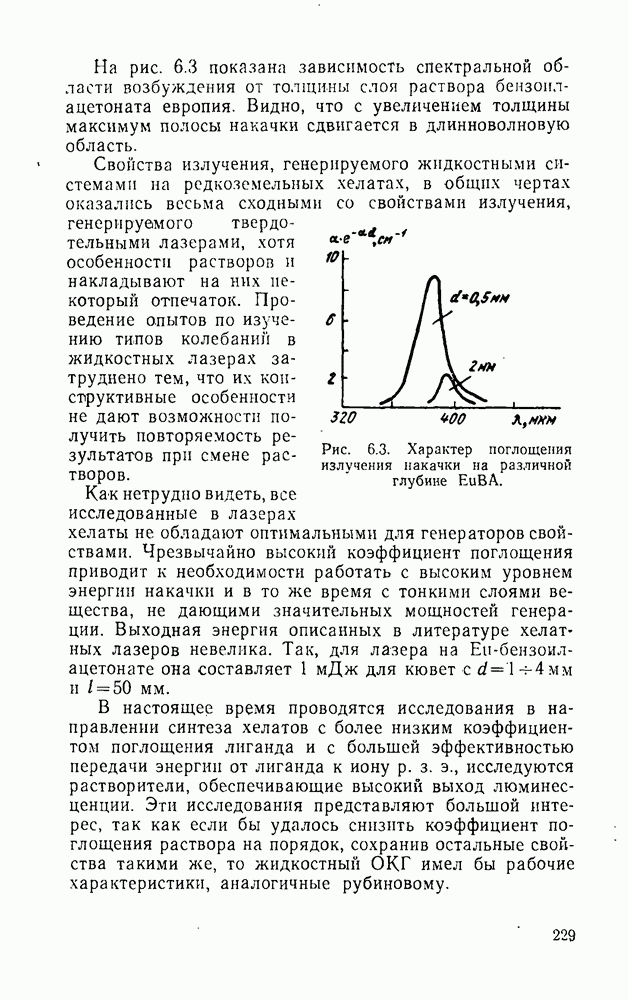
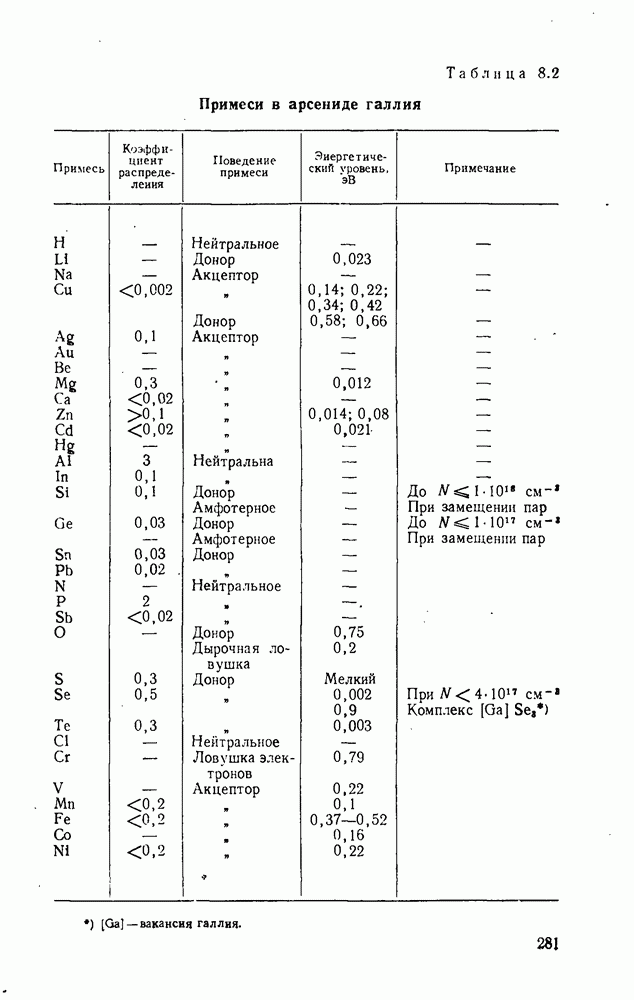
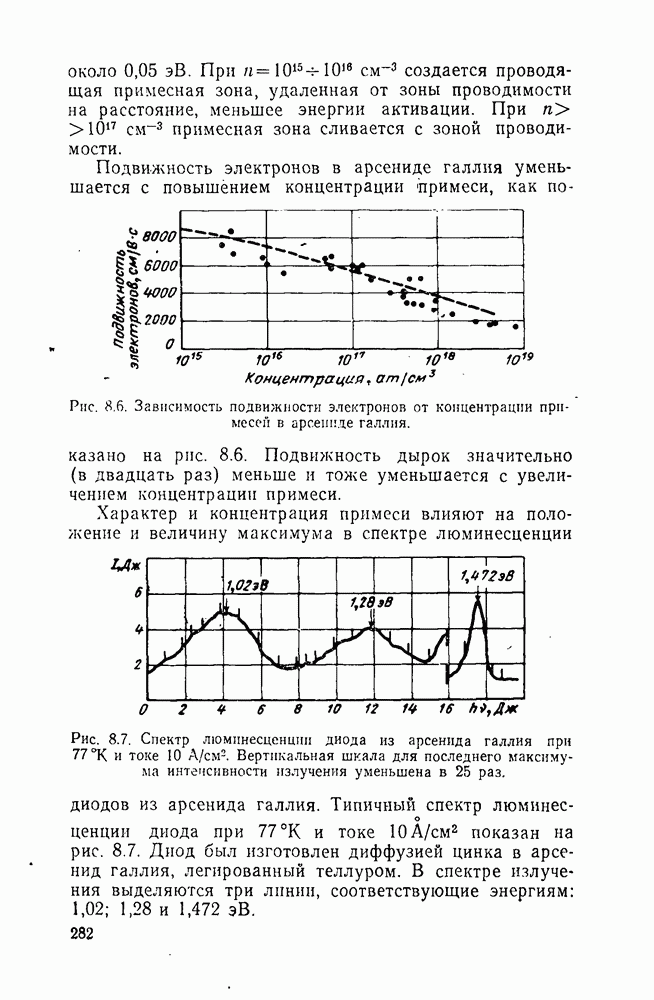
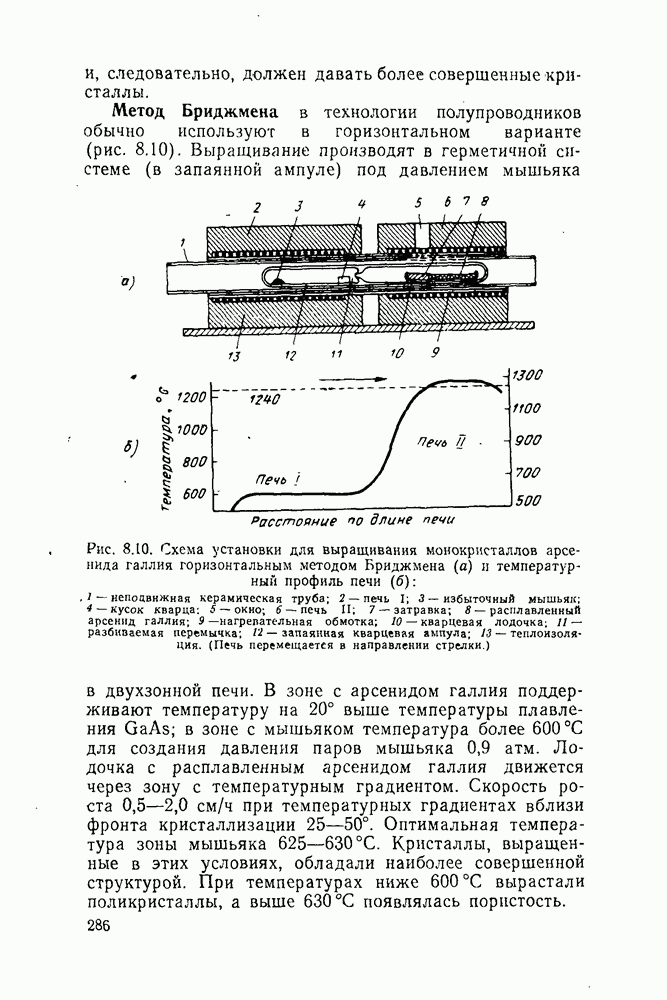
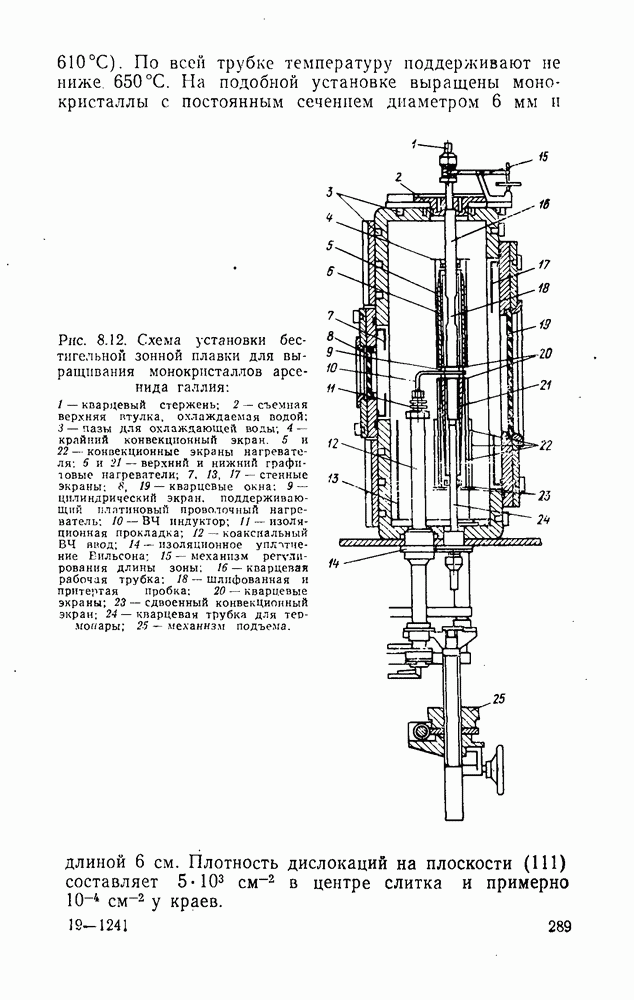
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
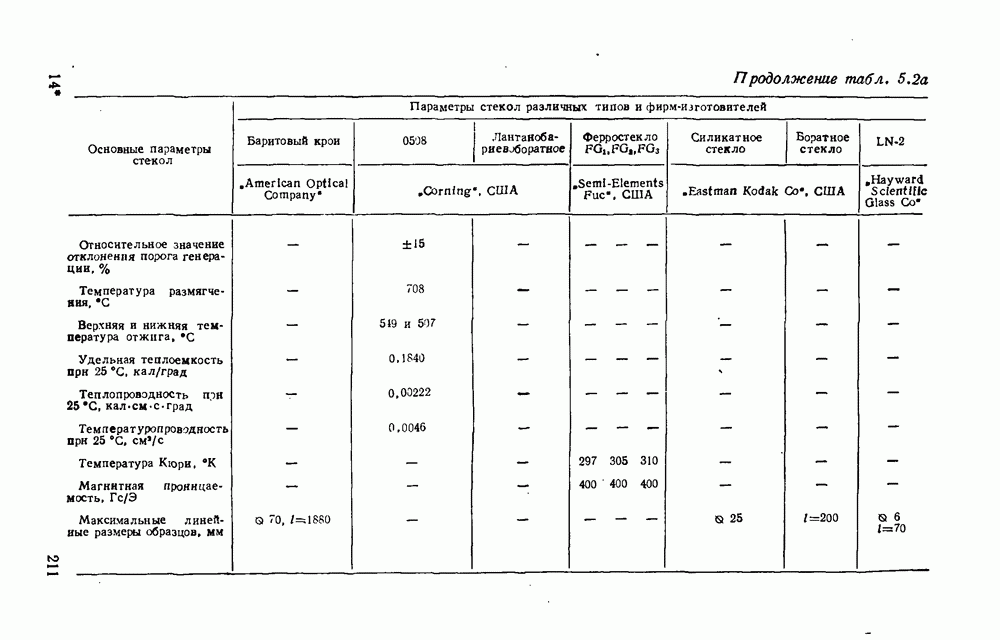
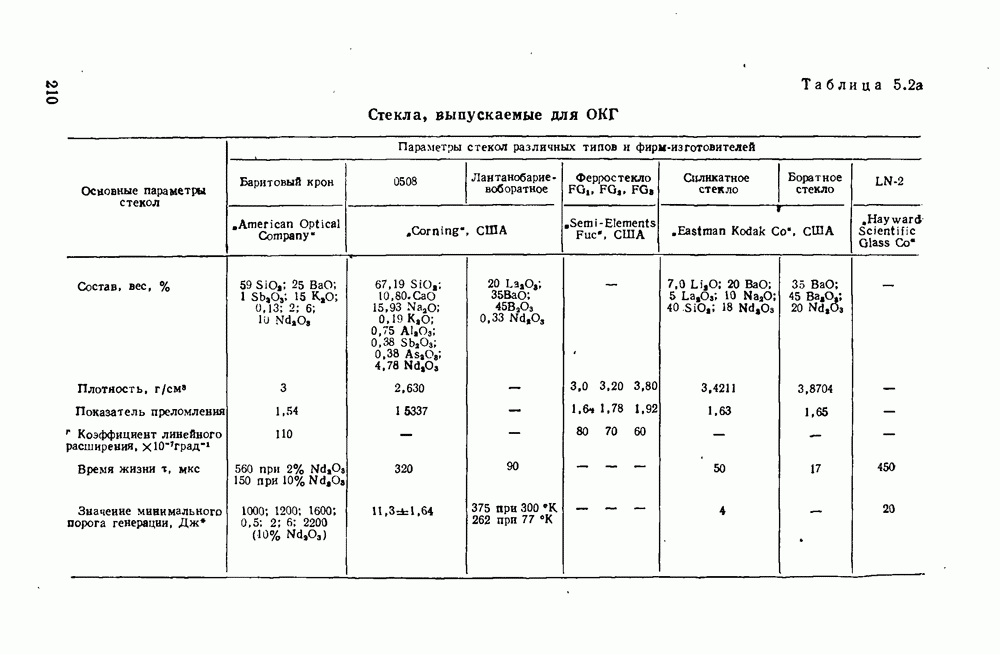
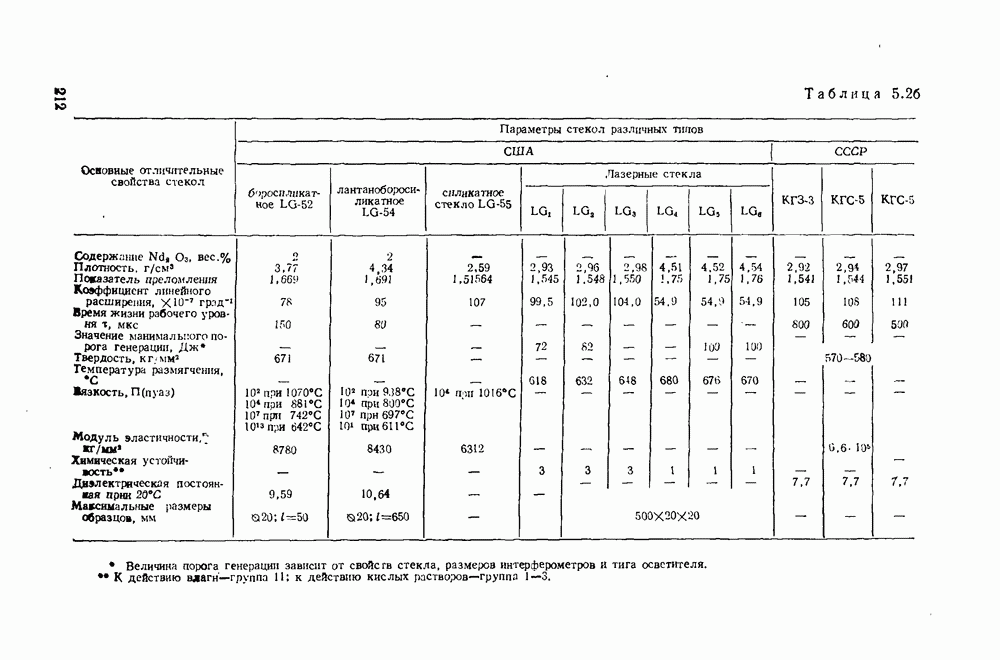
2.3.5. Общее кинетическое уравнение кристаллизации
В наиболее общей форме суммарный процесс кристаллизации может быть описан уравнением, которое впервые было получено А. Н. Колмогоровым при решении статистической задачи кристаллизации единицы объема исходной фазы:

где  — доля превращенного объема
— доля превращенного объема  — исходный объем
— исходный объем  исходная масса X плотность);
исходная масса X плотность);  — коэффициент;
— коэффициент;  — время;
— время;  — показатель степени.
— показатель степени.
Коэффициент  и показатель степени
и показатель степени  и в этом уравнении имеют важный физический смысл. Так, показатель
и в этом уравнении имеют важный физический смысл. Так, показатель  определяется механизмом роста кристаллов и характером процесса зарождения и поэтому выражается суммой числа измерений
определяется механизмом роста кристаллов и характером процесса зарождения и поэтому выражается суммой числа измерений  в которых происходит
в которых происходит
рост, и порядка временной зависимости возникновення центров кристаллизации  т. е.
т. е.

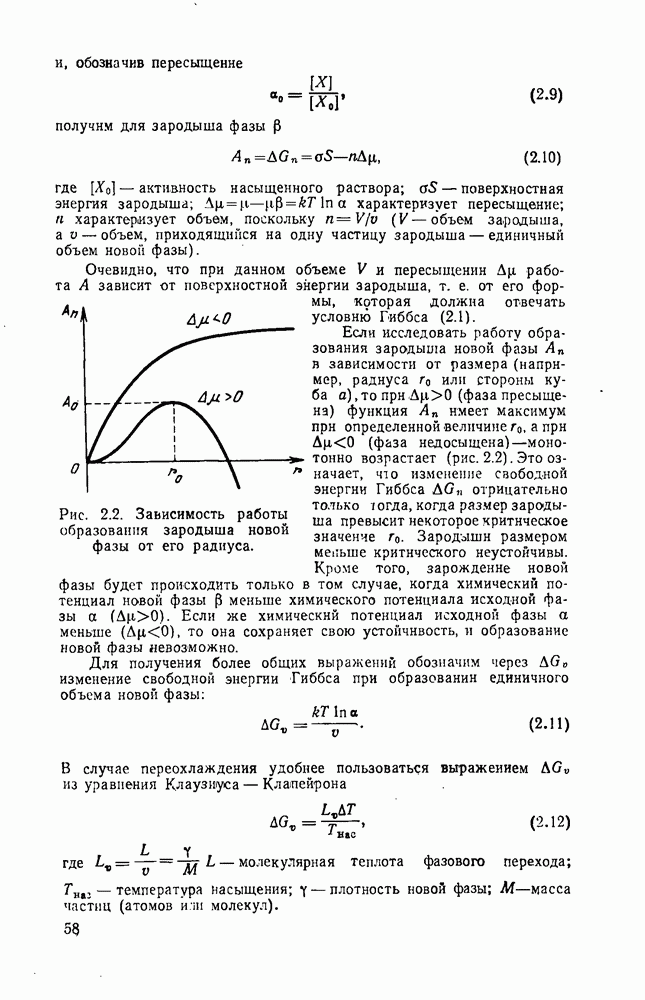
Если в процессе кристаллизации по механизму нормального роста  новые центры кристаллизации не возникают
новые центры кристаллизации не возникают  то
то  и уравнение (2.57) превращается в обычное кинетическое уравнение мопомолекулярной реакции, для которой скорость реакции пропорциональна доле непревращенной фазы. При
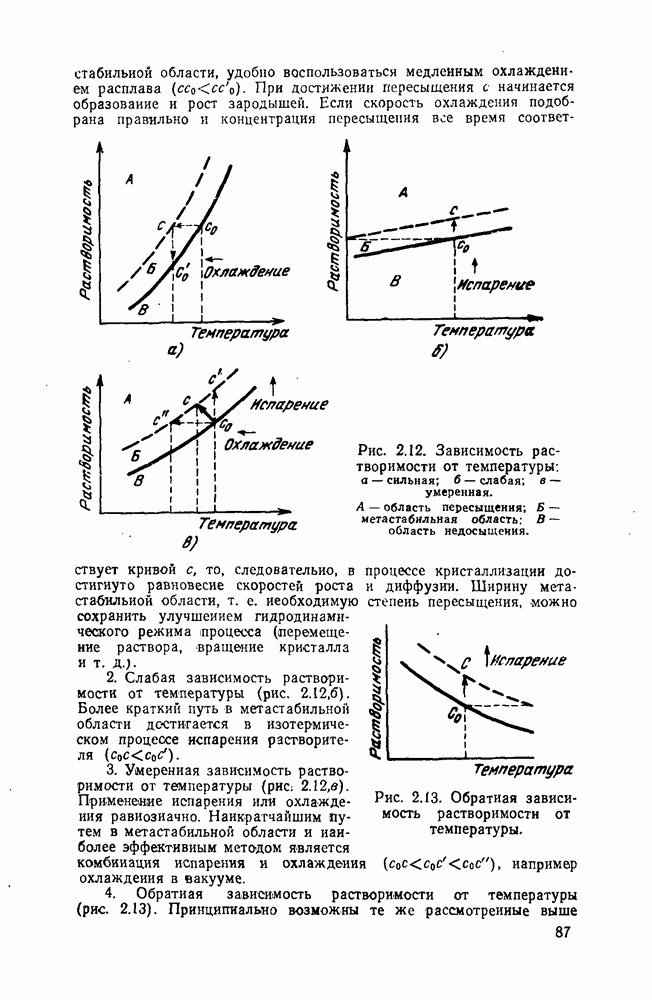
и уравнение (2.57) превращается в обычное кинетическое уравнение мопомолекулярной реакции, для которой скорость реакции пропорциональна доле непревращенной фазы. При  скорость реакции лимитируется гидродинамическими факторами, т. с. скоростью диффузии. Поэтому говорят, что процесс находится в диффузионной области.
скорость реакции лимитируется гидродинамическими факторами, т. с. скоростью диффузии. Поэтому говорят, что процесс находится в диффузионной области.

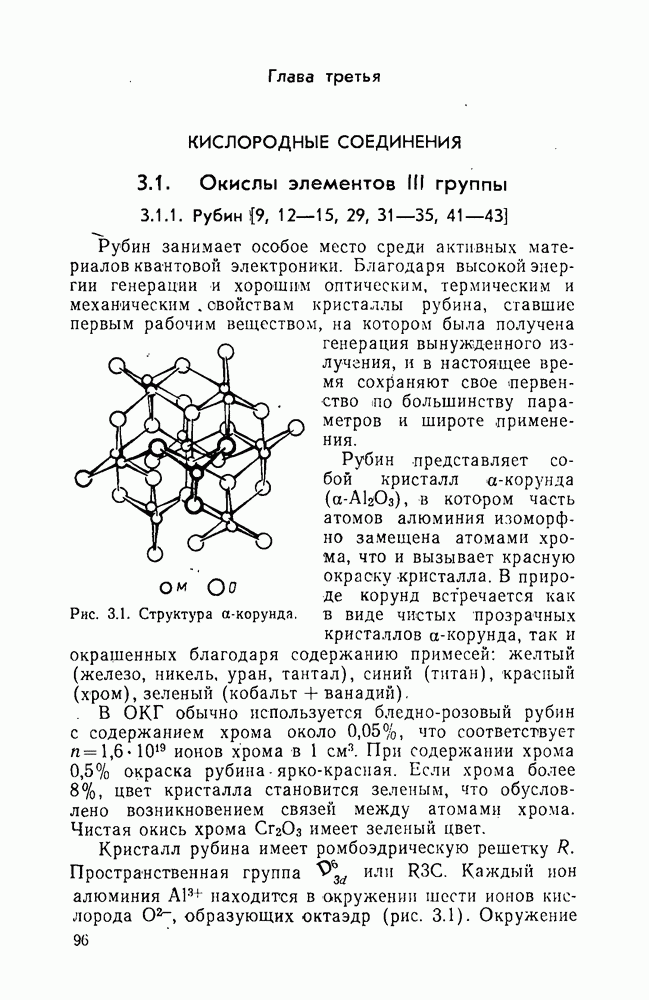
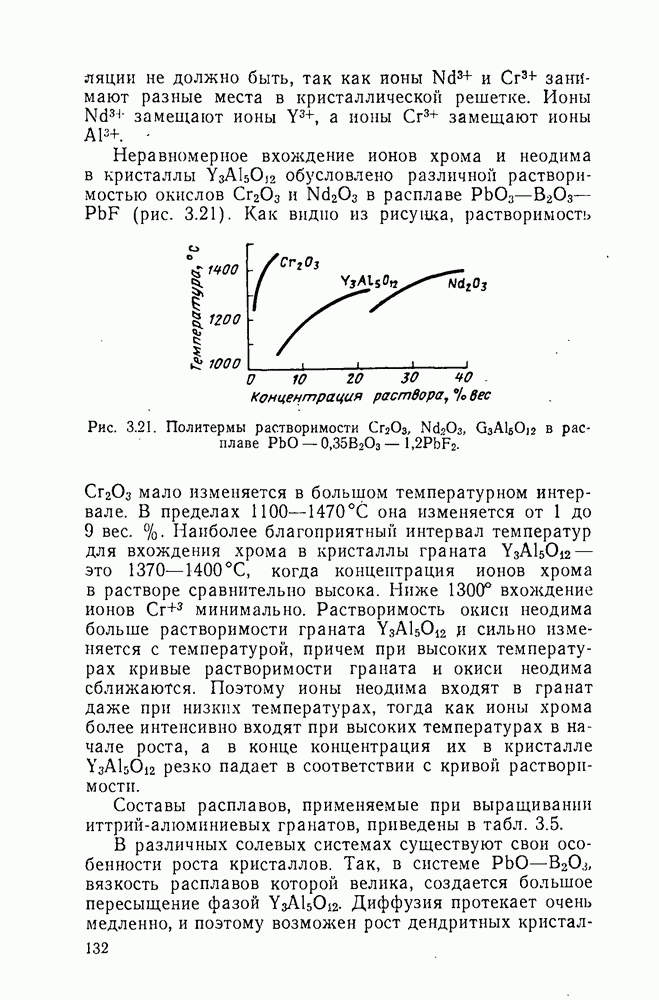
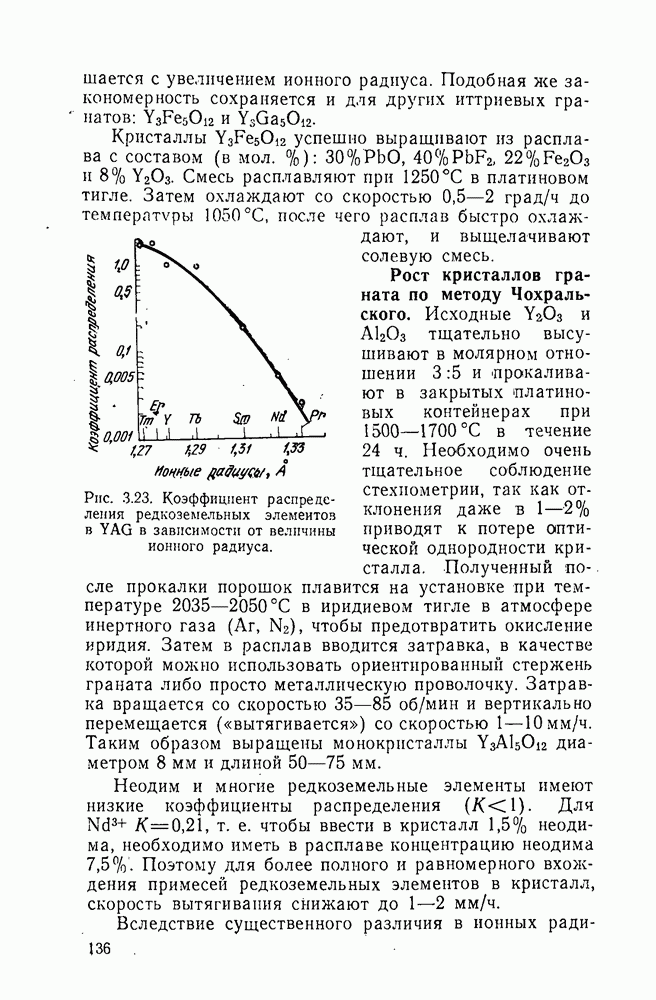
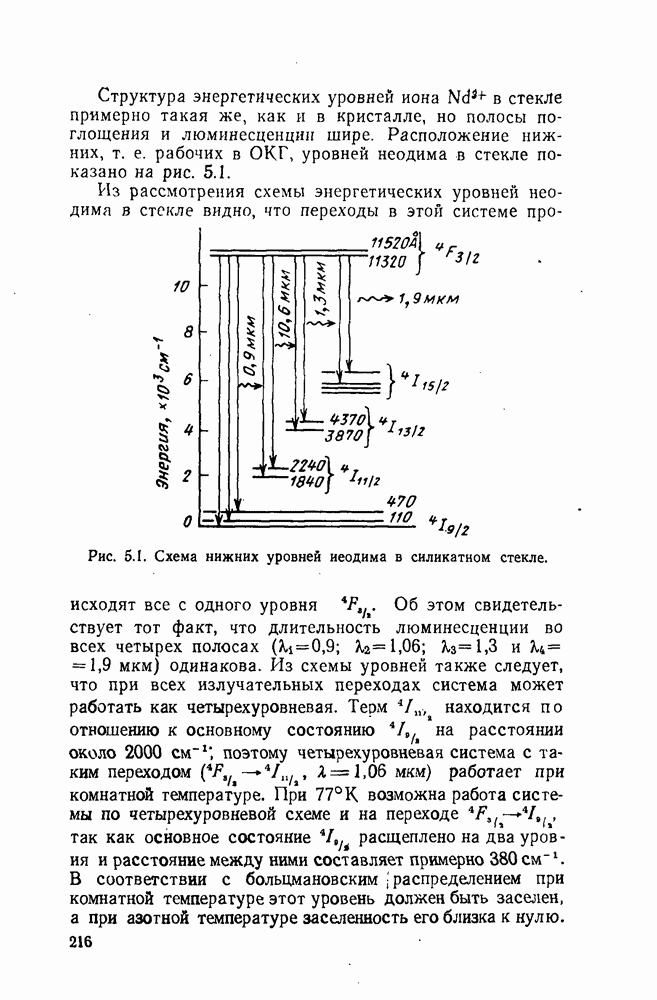
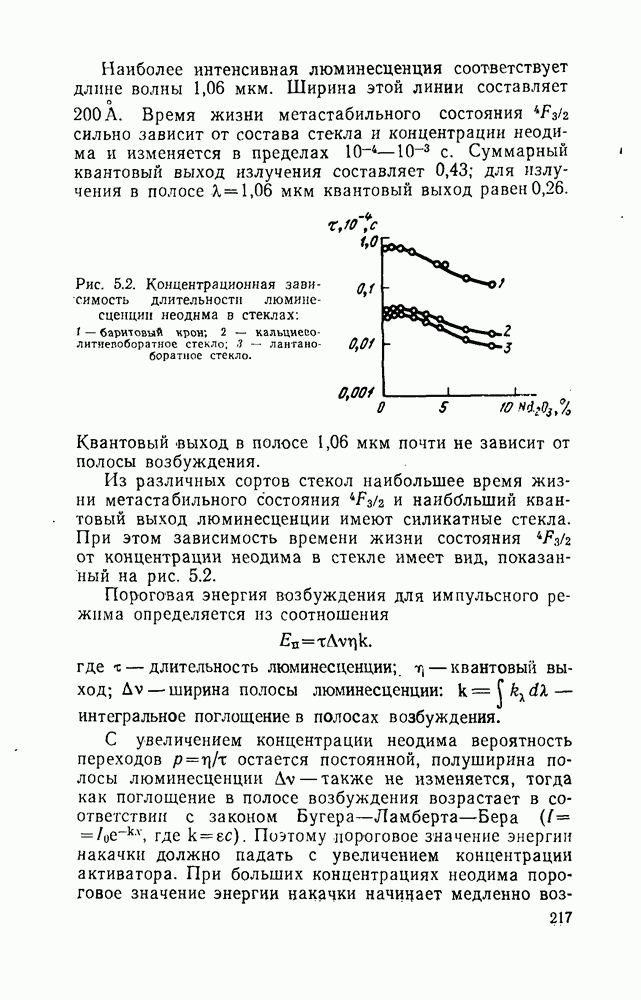
Рис.. 2.6. Типичный график кинетики кристаллизации.
Во всех случаях, когда  процесс находится в кинетической области и это позволяет исследовать его кинетические характеристики. Однако и в кинетической области величина показателя
процесс находится в кинетической области и это позволяет исследовать его кинетические характеристики. Однако и в кинетической области величина показателя  сильно зависит от механизма кристаллизации.
сильно зависит от механизма кристаллизации.
Так, если в процессе кристаллизации по механизму нормального роста  скорость возникновения новых зародышей постоянна во времени
скорость возникновения новых зародышей постоянна во времени  то
то 
При кристаллизации по механизму двумерного зарождения и при дислокационном росте показатель  может иметь значения
может иметь значения  так как
так как  Если скорость зарождения возрастает во времени
Если скорость зарождения возрастает во времени  то
то  но развитие такого процесса может привести к образованию трехмерных зародышей, т. е. к изменению механизма кристаллизации. Кристаллизация по механизму трехмерного зарождения описывается уравнением, в котором
но развитие такого процесса может привести к образованию трехмерных зародышей, т. е. к изменению механизма кристаллизации. Кристаллизация по механизму трехмерного зарождения описывается уравнением, в котором  так как
так как 
Величина коэффициента  в уравнении (2.57) находится из выражения
в уравнении (2.57) находится из выражения

где  — коэффициент формы поверхности зародыша
— коэффициент формы поверхности зародыша  для круговой поверхности и
для круговой поверхности и  для квадратной);
для квадратной);  — линейная скорость роста зародыша; показатель степени
— линейная скорость роста зародыша; показатель степени  соответствует числу линейных направлений роста в соответствии с (2.58);
соответствует числу линейных направлений роста в соответствии с (2.58);  — скорость зародышеобразования. Например, для механизмов двумерного зарождения и дислокационного роста
— скорость зародышеобразования. Например, для механизмов двумерного зарождения и дислокационного роста

а для нормального роста  дислокационного роста игл и усов
дислокационного роста игл и усов

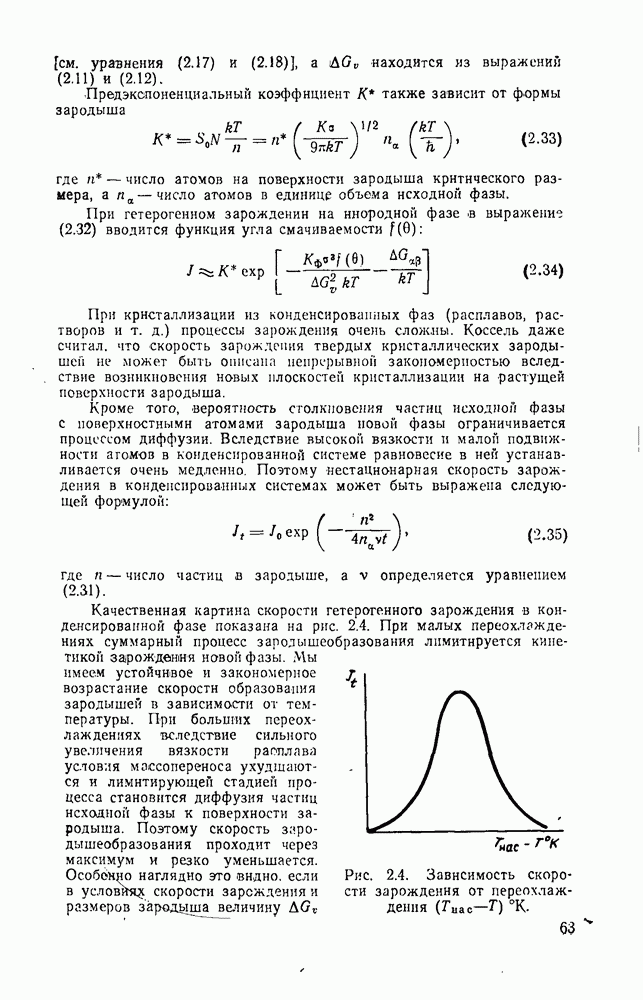
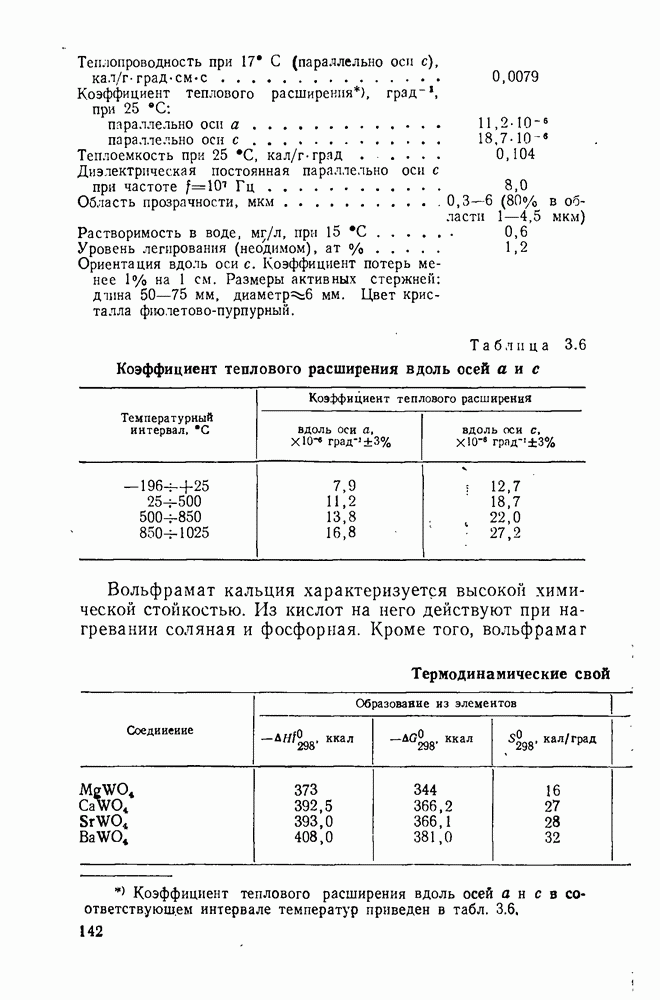
Анализ экспериментальных данных по уравнению А Н. Колмогорова обычно проводят путем построения графиков зависимости  от
от  Если уравнение А. Н. Колмогорова справедливо для рассматриваемой системы, то график имеет вид прямой линии с тангенсом угла наклона, равным
Если уравнение А. Н. Колмогорова справедливо для рассматриваемой системы, то график имеет вид прямой линии с тангенсом угла наклона, равным  . Кан [19] показал, что наиболее характерным должен быть график, состоящий из двух линейных участков с разными наклонами, соединенных переходным криволинейным участком (рис. 2.6). Переходный участок соответствует исчерпанию мест зарождения, после чего скорость зарождения
. Кан [19] показал, что наиболее характерным должен быть график, состоящий из двух линейных участков с разными наклонами, соединенных переходным криволинейным участком (рис. 2.6). Переходный участок соответствует исчерпанию мест зарождения, после чего скорость зарождения  практически падает до нуля.
практически падает до нуля.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
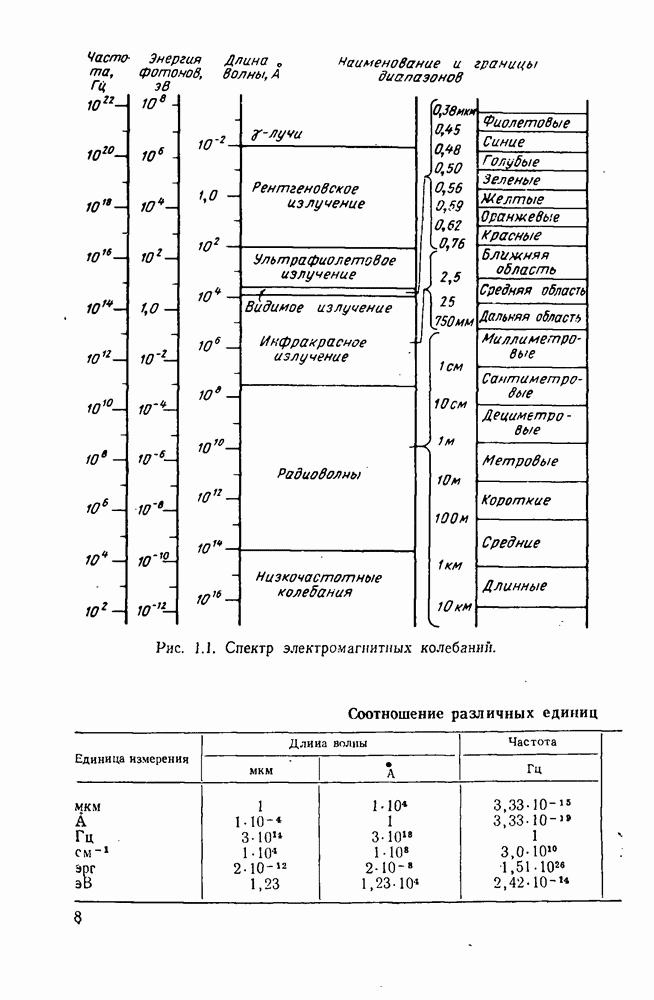
- Глава первая. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ И ПРИНЦИП ДЕЙСТВИЯ КВАНТОВЫХ ГЕНЕРАТОРОВ
- 1.1. Спектр электромагнитных колебаний
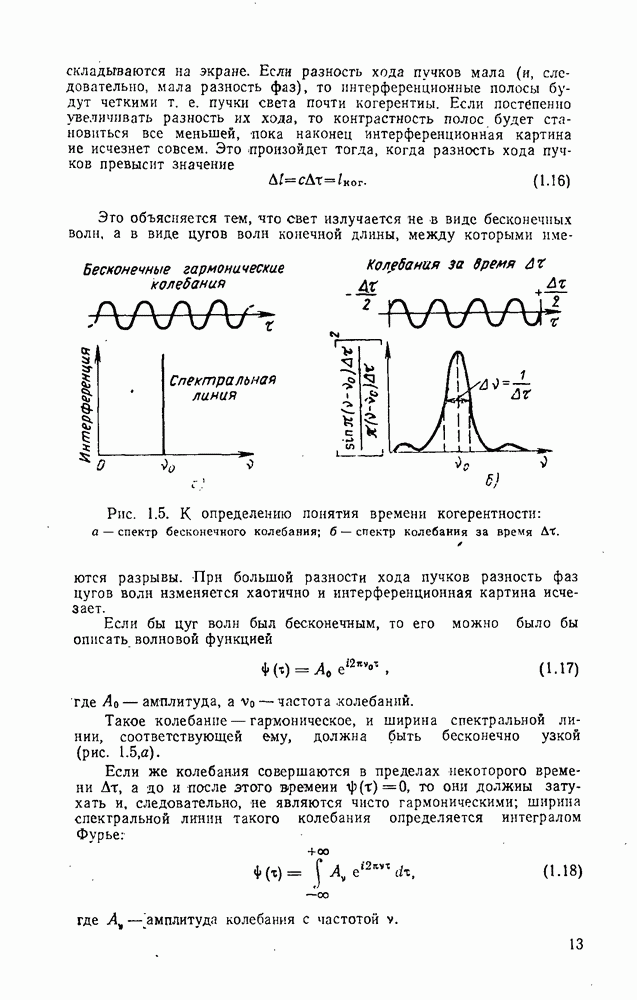
- 1.2. Когерентность
- 1.3. Направленность излучения
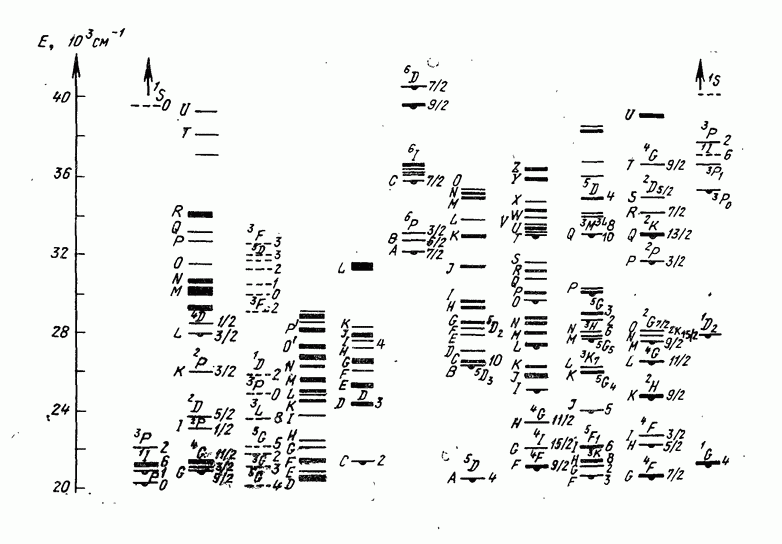
- 1.4. Символика энергетических уровней атомов и ионов
- 1.5. Инверсная населенность
- 1.6. Вероятности спонтанных и вынужденных переходов
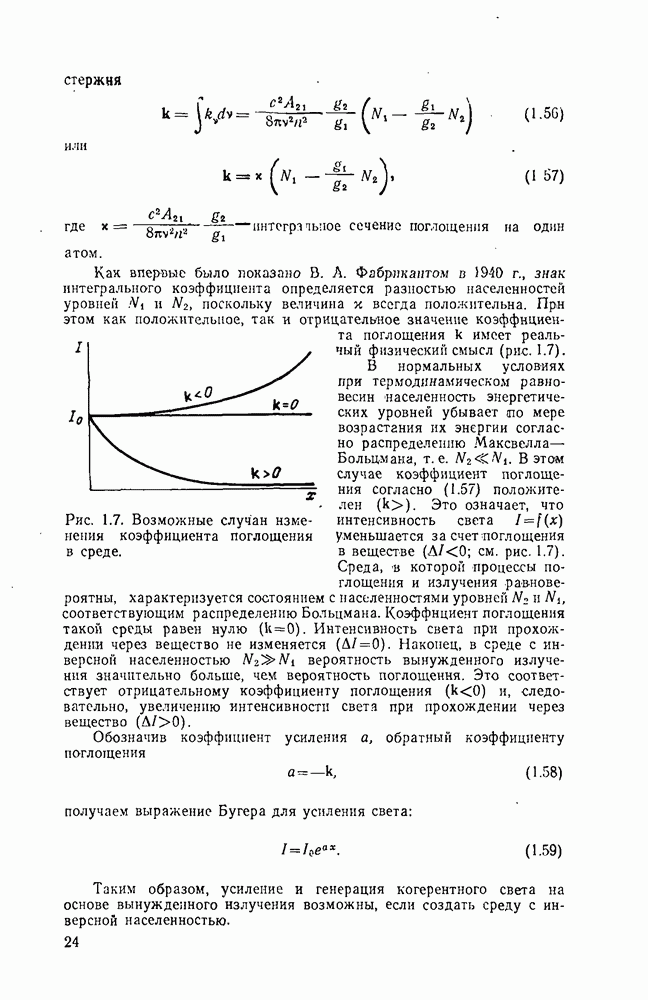
- 1.7. Усиление света при прохождении через вещество
- 1.8. Двухуровневая система
- 1.9. Трехуровневая система
- 1.10. Четырехуровневая система
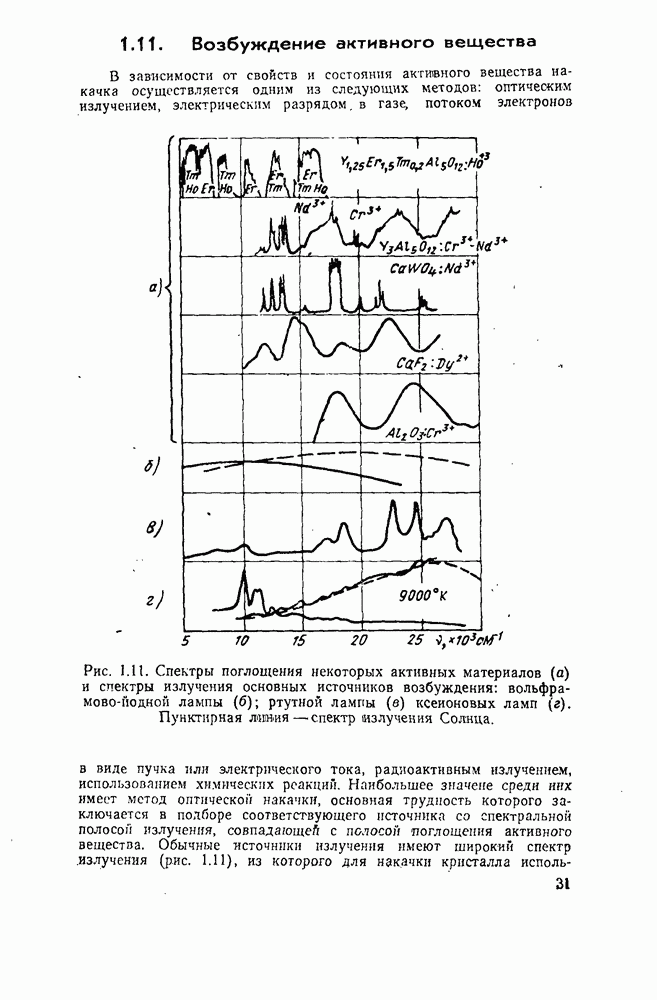
- 1.11. Возбуждение активного вещества
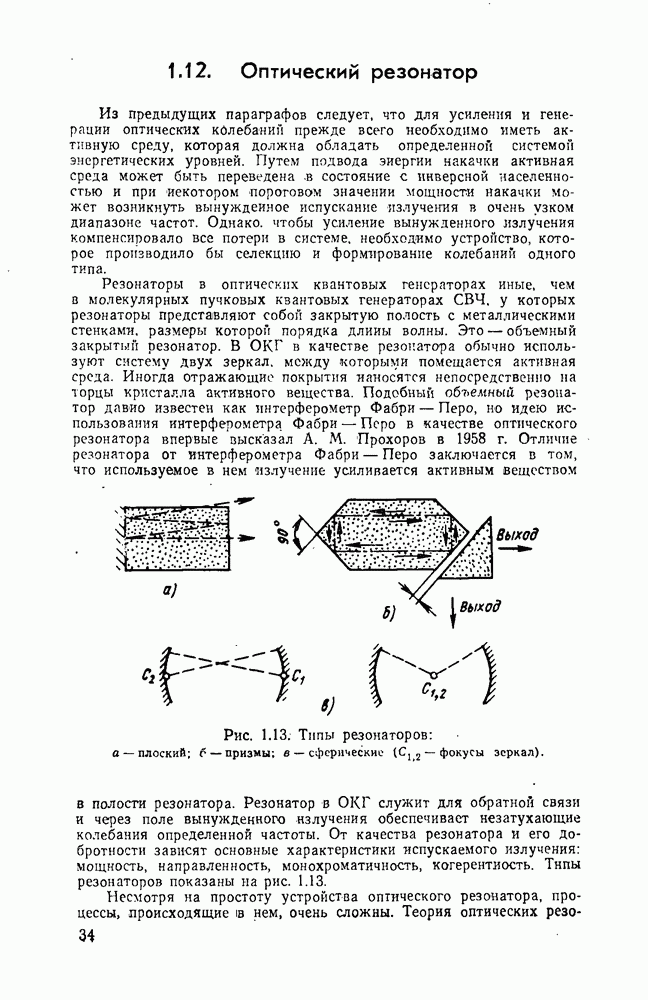
- 1.12. Оптический резонатор
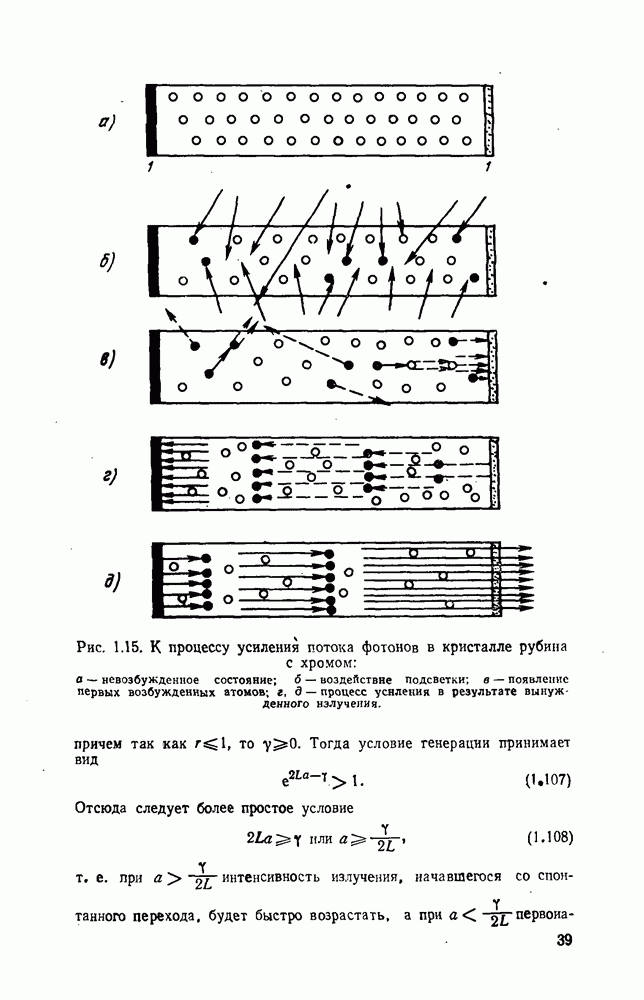
- 1.13 Условие генерации
- 1.14. Потери энергии в квантовом генераторе
- 1.15. Устройство ОКГ на твердом теле
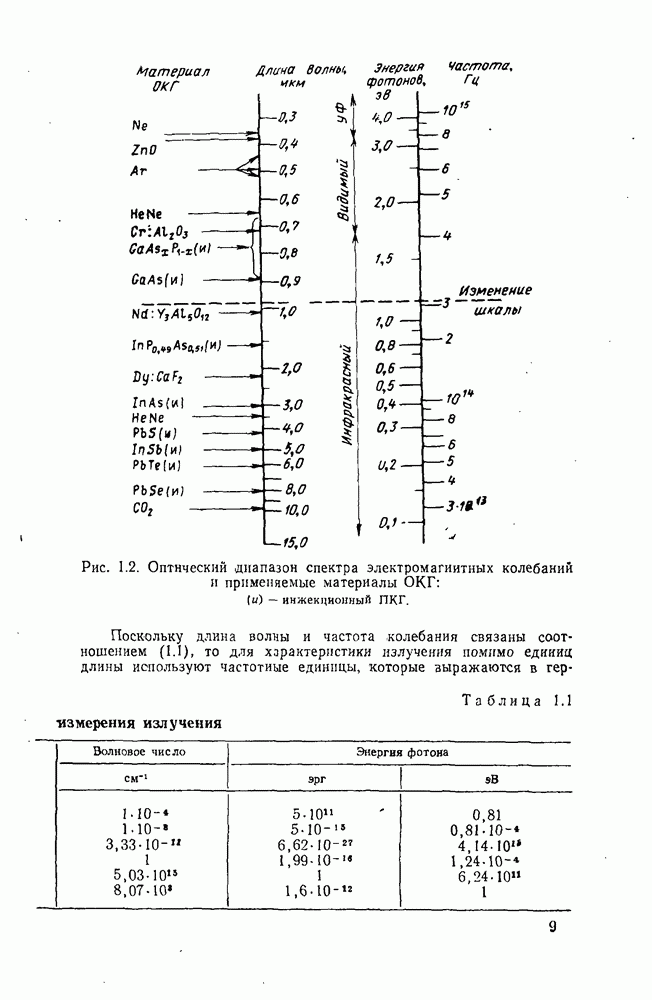
- Глава вторая. ОБЩИЕ ВОПРОСЫ ТЕХНОЛОГИИ МАТЕРИАЛОВ ТВЕРДОТЕЛЬНЫХ ОКГ
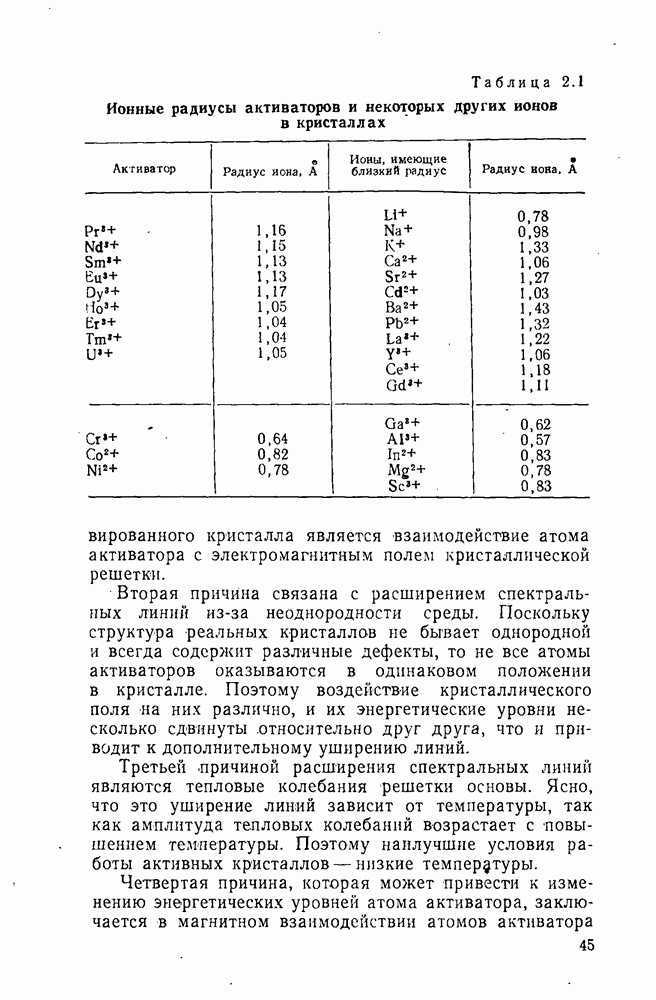
- 2.1. Особенности активного вещества ионных квантовых систем
- 2.2. Особенности технологии твердотельных материалов квантовых генераторов
- 2.3. Физико-химические основы кристаллизации
- 2.3.2. Гетерогенное зародышеобразование
- 2.3.3. Скорость зарождения новой фазы
- 2.3.4. Рост кристаллов
- 2.3.5. Общее кинетическое уравнение кристаллизации
- 2.3.6. Распределение примеси в процессе роста кристалла
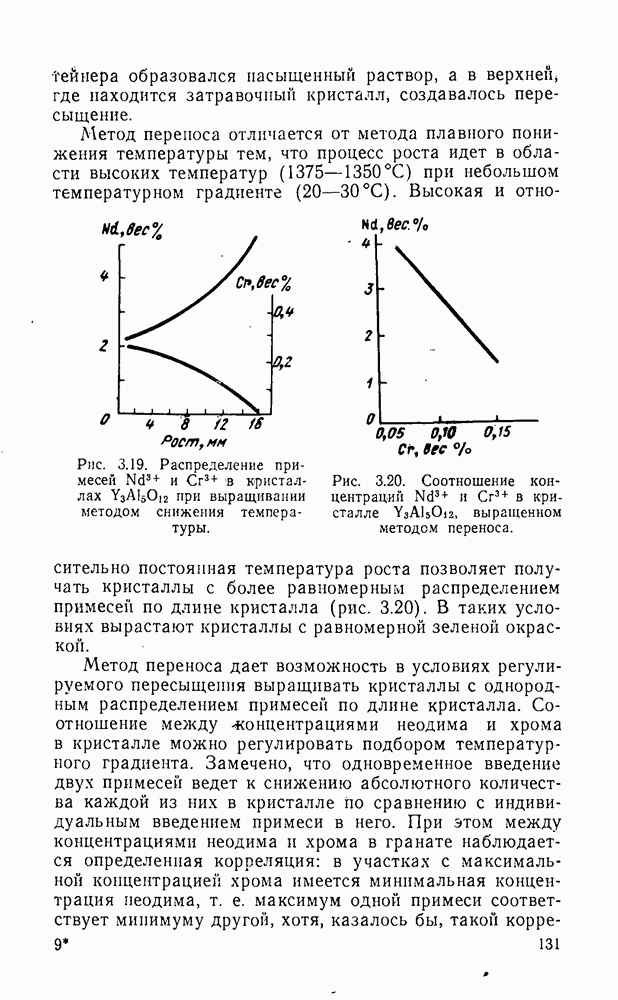
- 2.4. Основные методы синтеза и выращивания кристаллов
- 2.4.2. Выращивание из стехиометрических расплавов
- 2.4.3. Методы выращивания кристаллов из растворов
- 2.4.4. Гидротермальный синтез и рост кристаллов
- 2.4.5. Выращивание кристаллов из газовой фазы
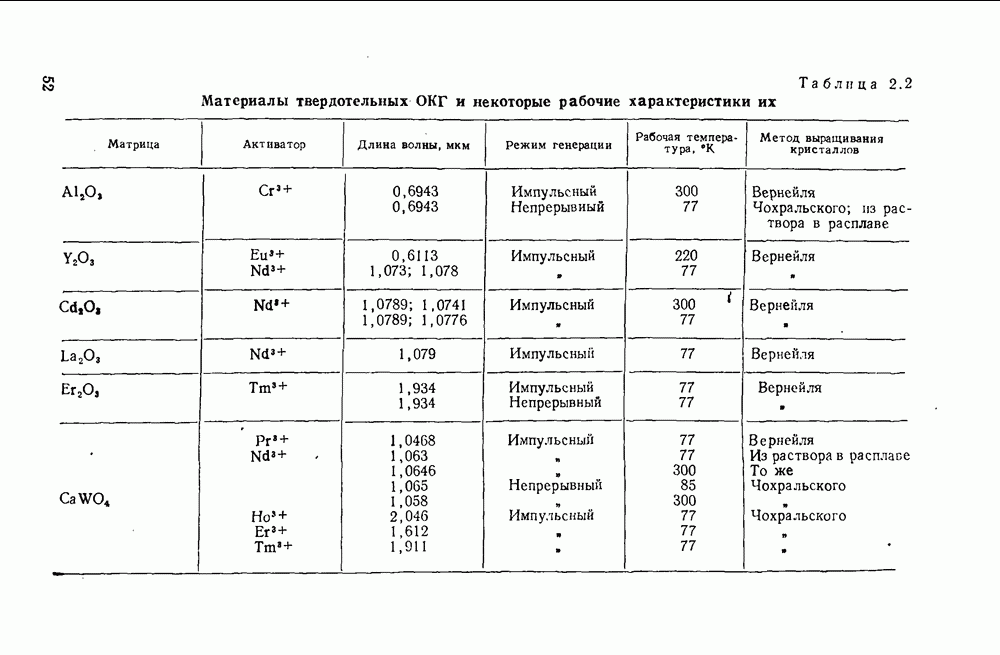
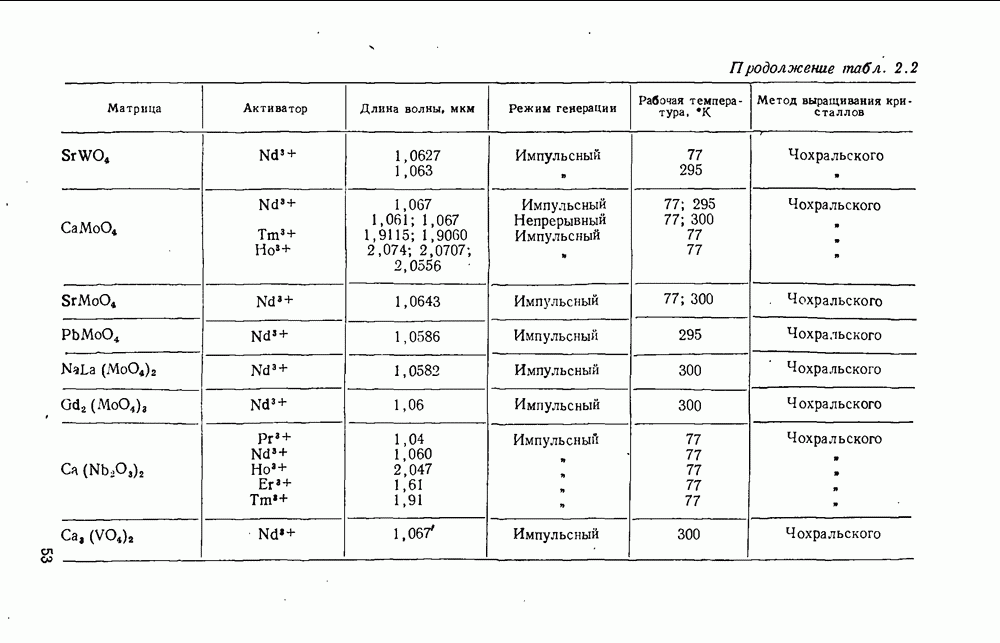
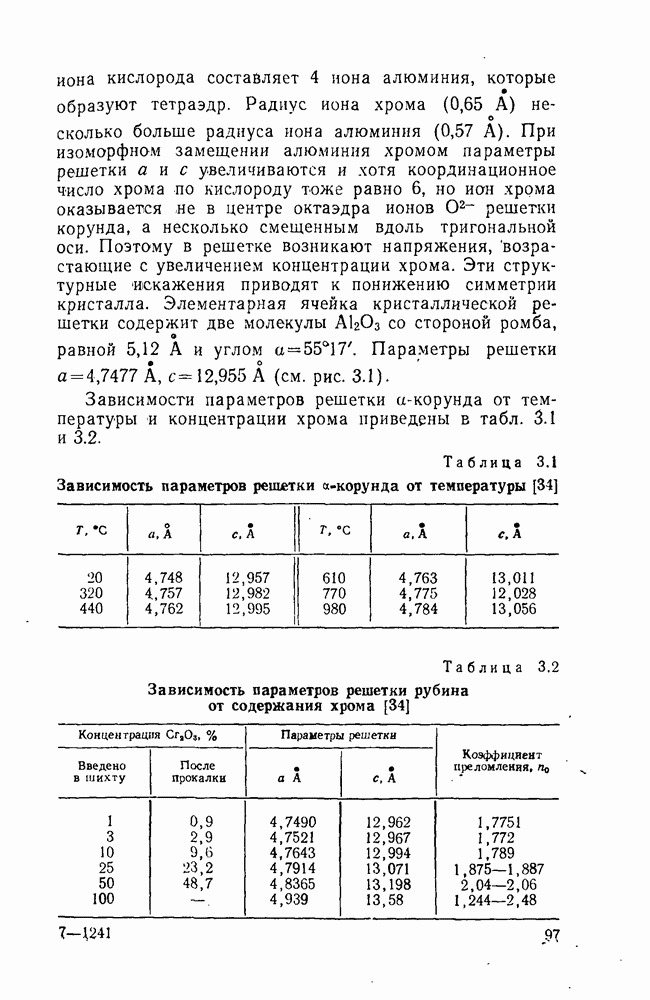
- 2.5. Кристалло-химическая классификация материалов твердотельных квантовых генераторов
- Глава третья. КИСЛОРОДНЫЕ СОЕДИНЕНИЯ
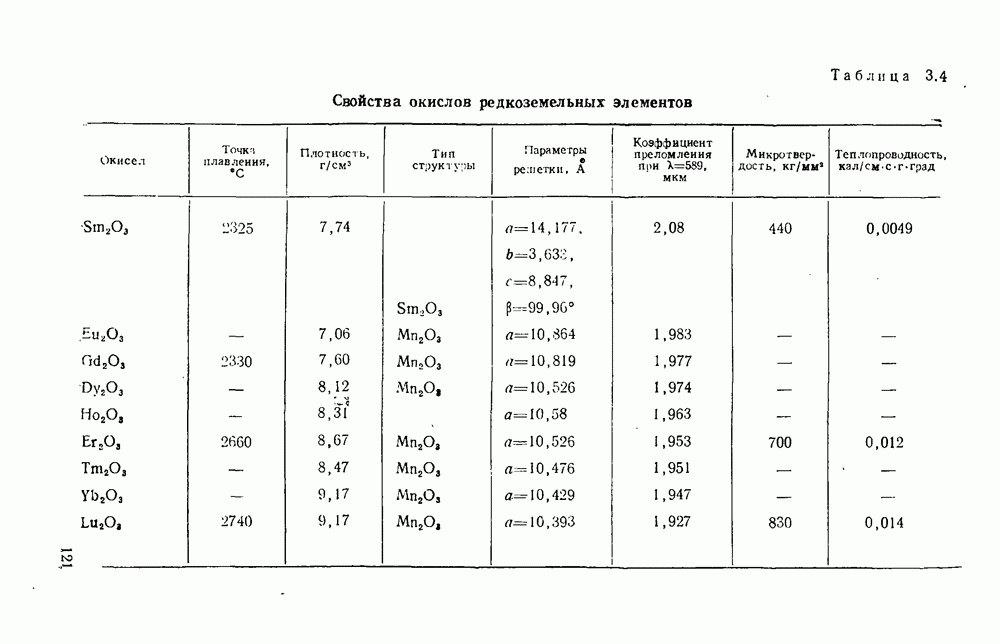
- 3.1. Окислы элементов III группы
- 3.1.2. Окислы редкоземельных элементов и иттрия
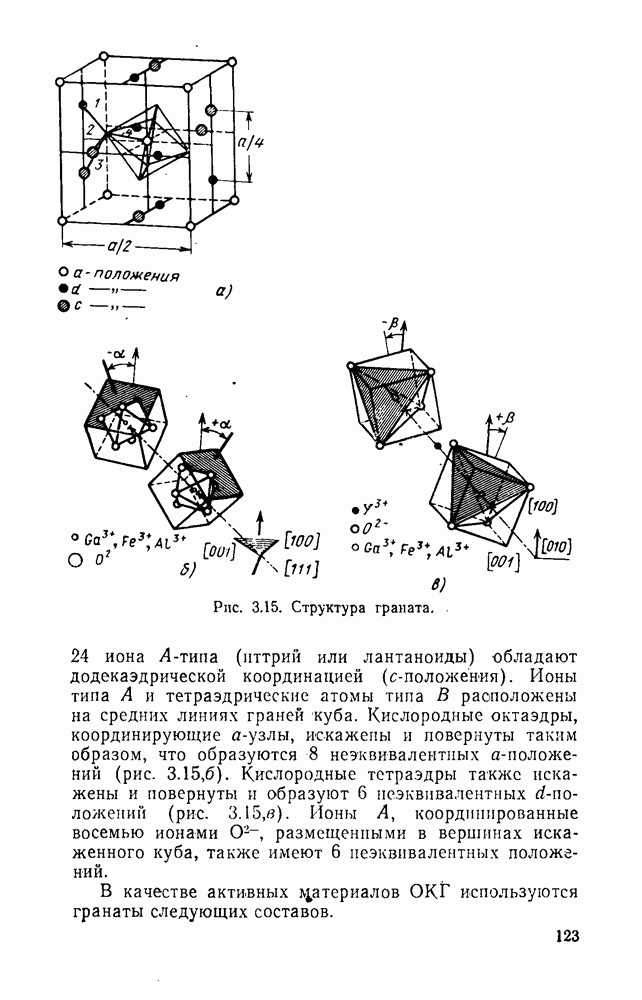
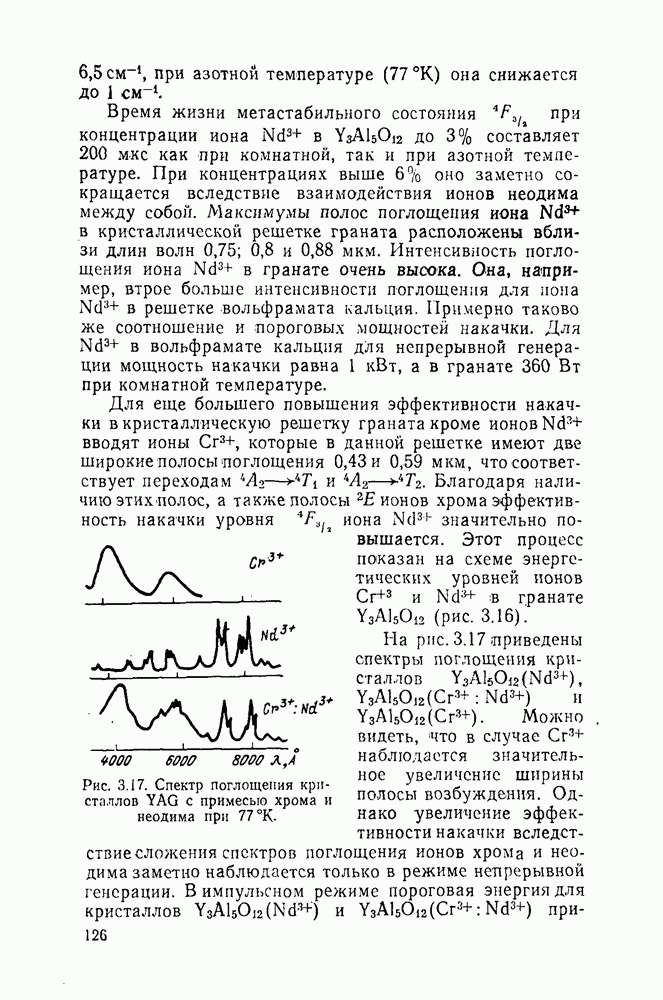
- 3.3.1. Гранаты
- 3.2. Материалы на основе кислородных соединений элементов VI группы
- 3.2.2. Молибдаты
- 3.3. Материалы на основе кислородных соединений элементов V группы
- 3.3.2. Ниобаты
- 3.3.3. Фосфаты
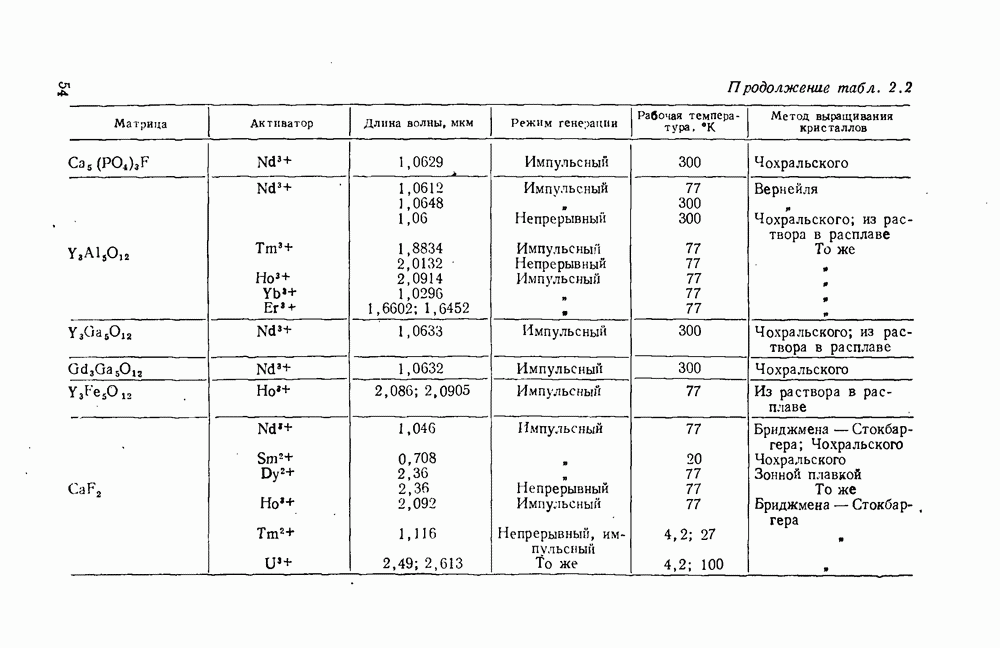
- Выращивание кристаллов фторфосфата кальция [47]
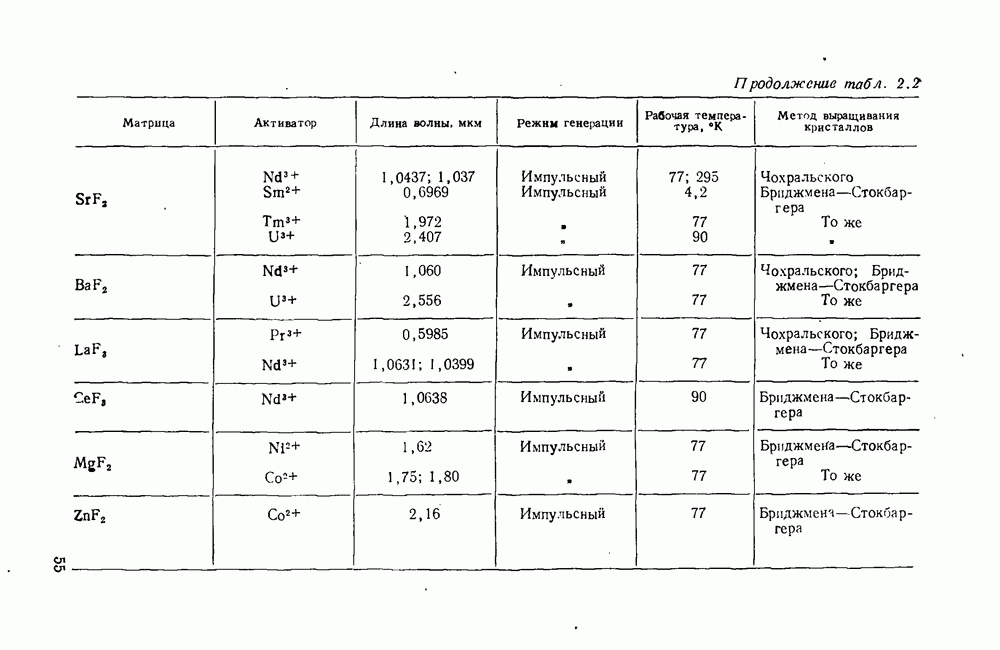
- Глава четвертая. ФТОРИСТЫЕ СОЕДИНЕНИЯ
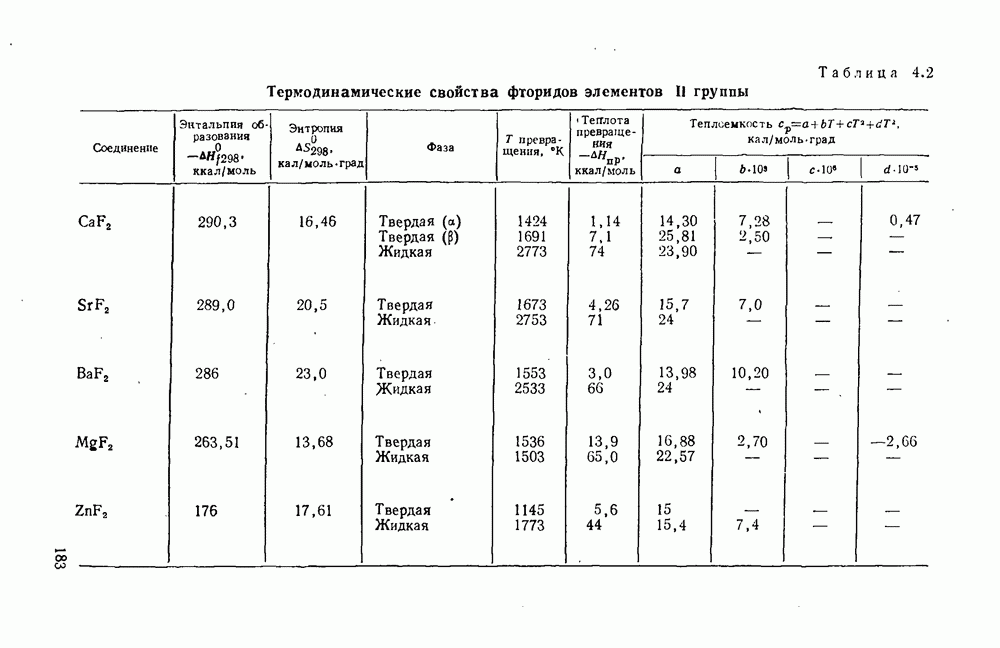
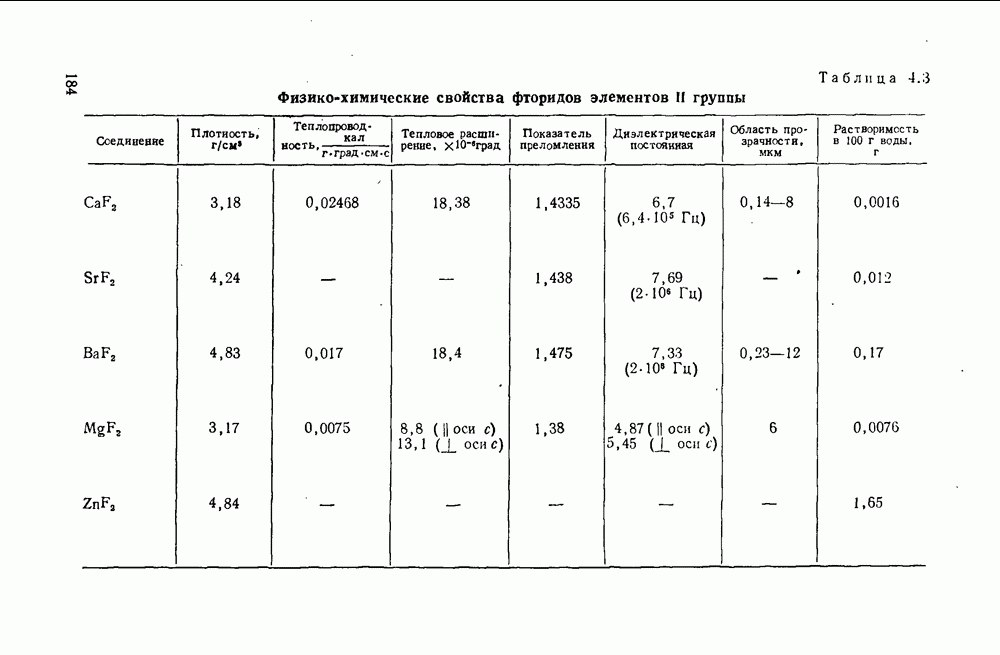
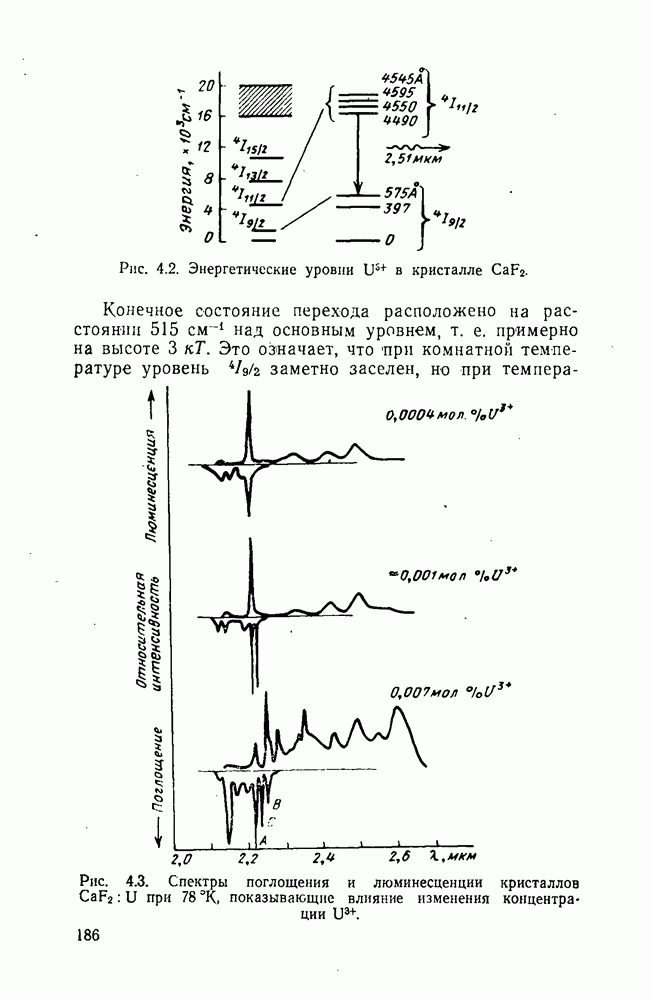
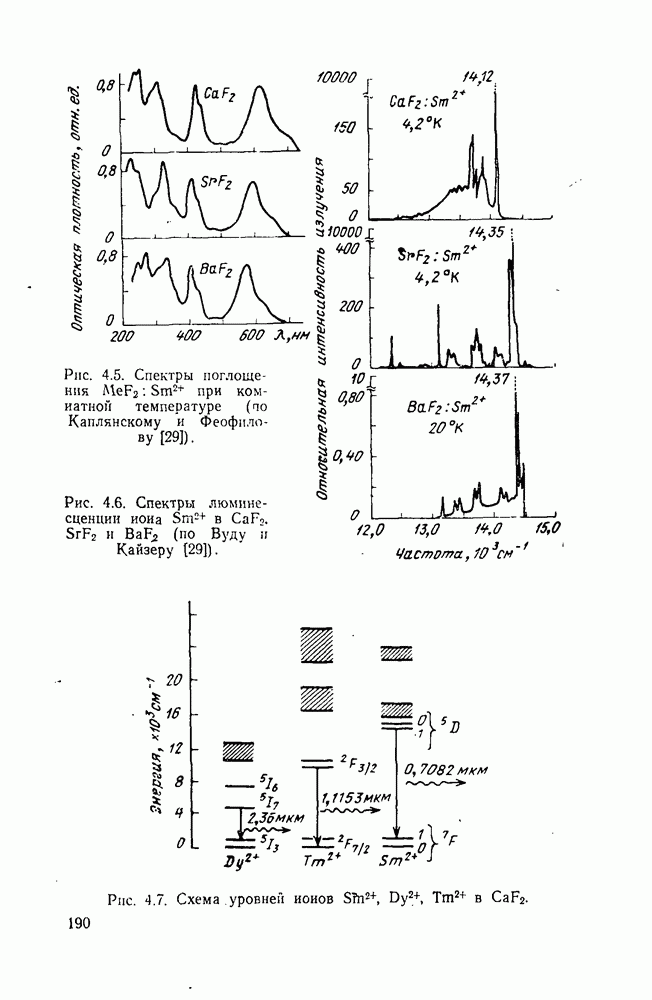
- 4.1. Фториды элементов II группы
- 4.2. Фториды редкоземельных элементов
- 4.3. Смешанные фториды
- 4.4. Фториды элементов VII группы
- Глава пятая. СТЕКЛО
- 5.1. Особенности стекла как активного материала ОКГ
- 5.2. Общая характеристика стекол для ОКГ
- 5.3. Особенности положения атомов активатора в стекле
- 5.4. Стекло с неодимом
- Глава шестая. МАТЕРИАЛЫ ЖИДКОСТНЫХ ОКГ
- 6.2. Механизм излучения в органических растворах
- 6.3. Растворы металлоорганических соединений
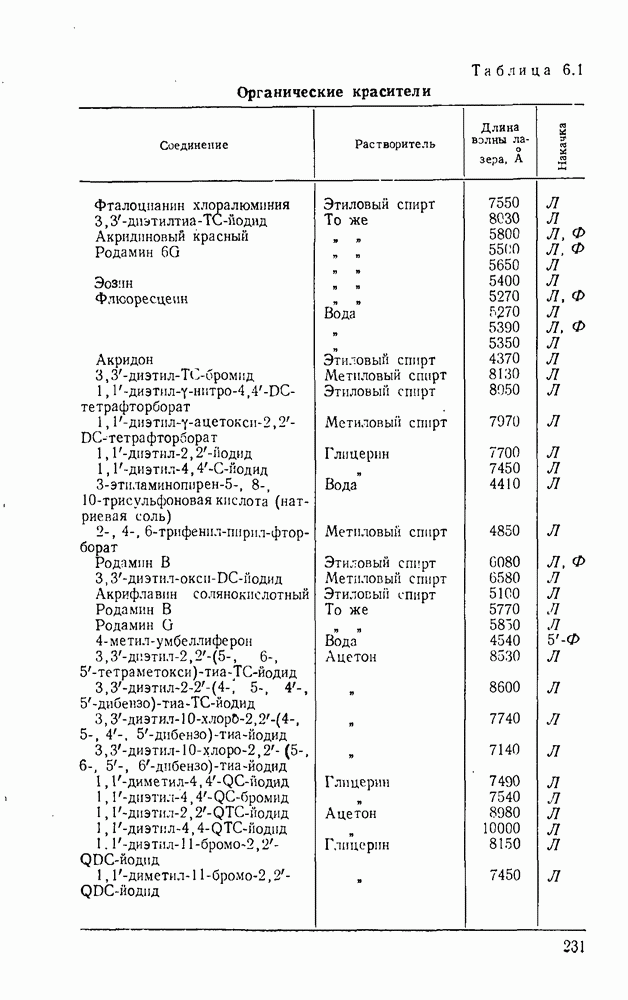
- 6.4. Растворы органических красителей
- 6.5. Растворы неорганических соединений редкоземельных элементов
- Глава седьмая. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВЫХ КВАНТОВЫХ ГЕНЕРАТОРОВ (ПКГ)
- 7.2. Основные сведения из теории люминесценции инжекционных ПКГ
- 7.3. Рабочие характеристики инжекционных ПКГ
- 7.3.2. Пространственные свойства
- 7.3.3. Пороговый ток
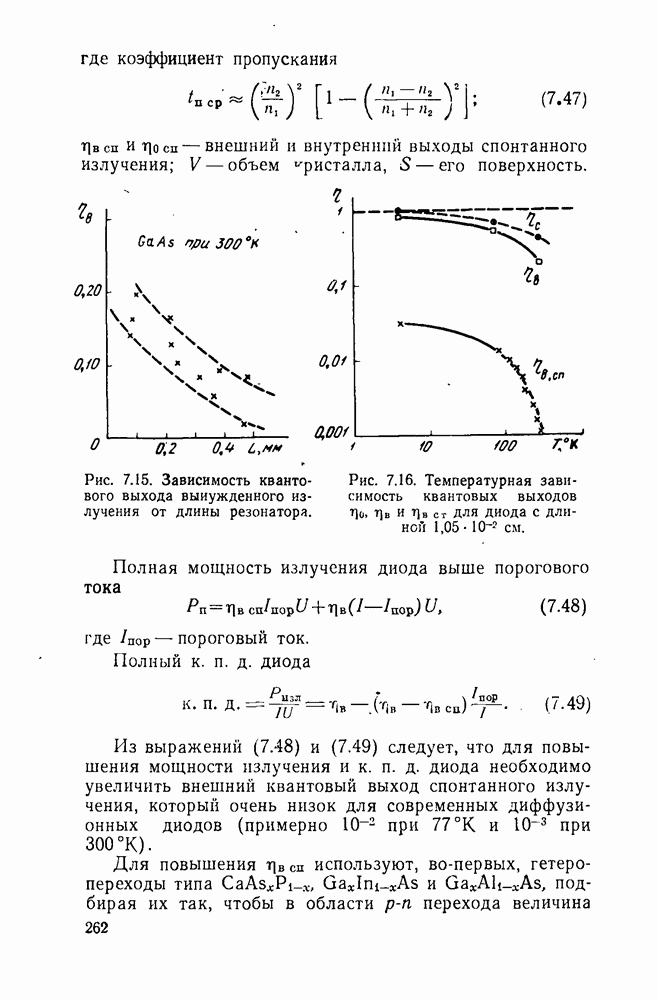
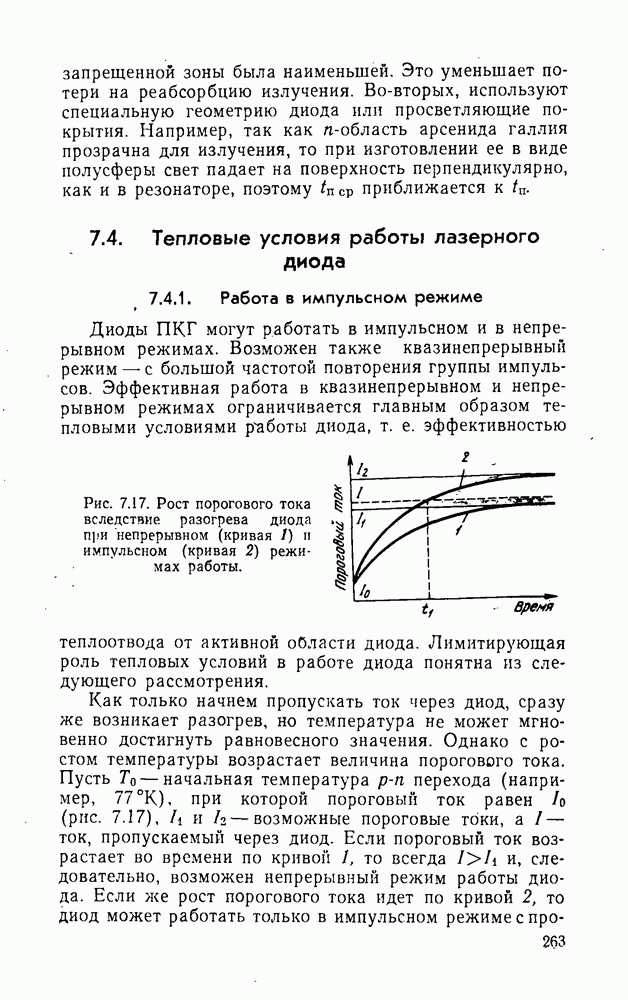
- 7.3.4. Квантовый выход
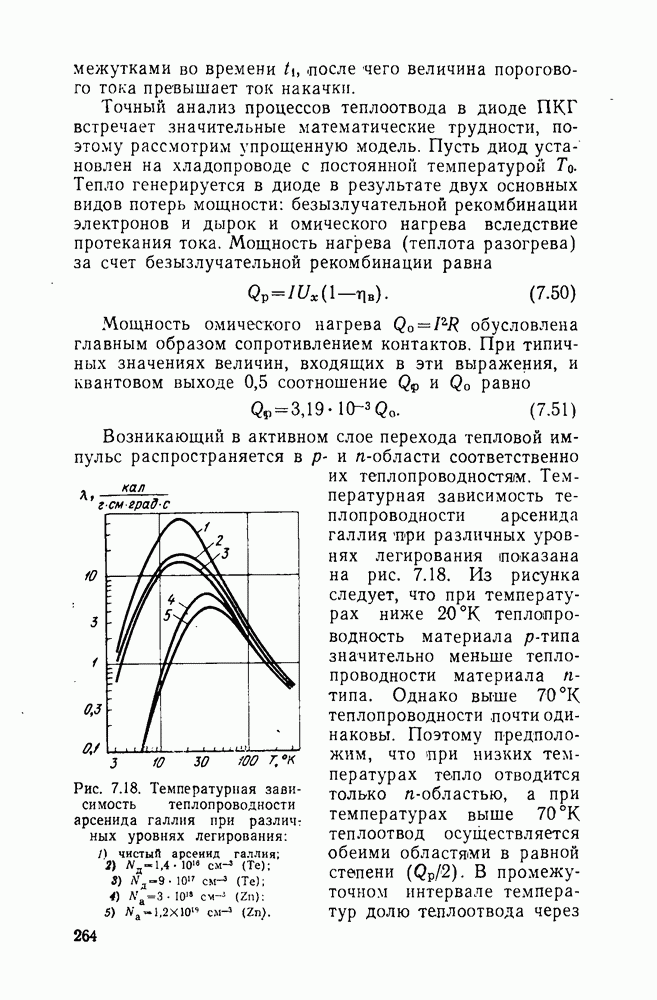
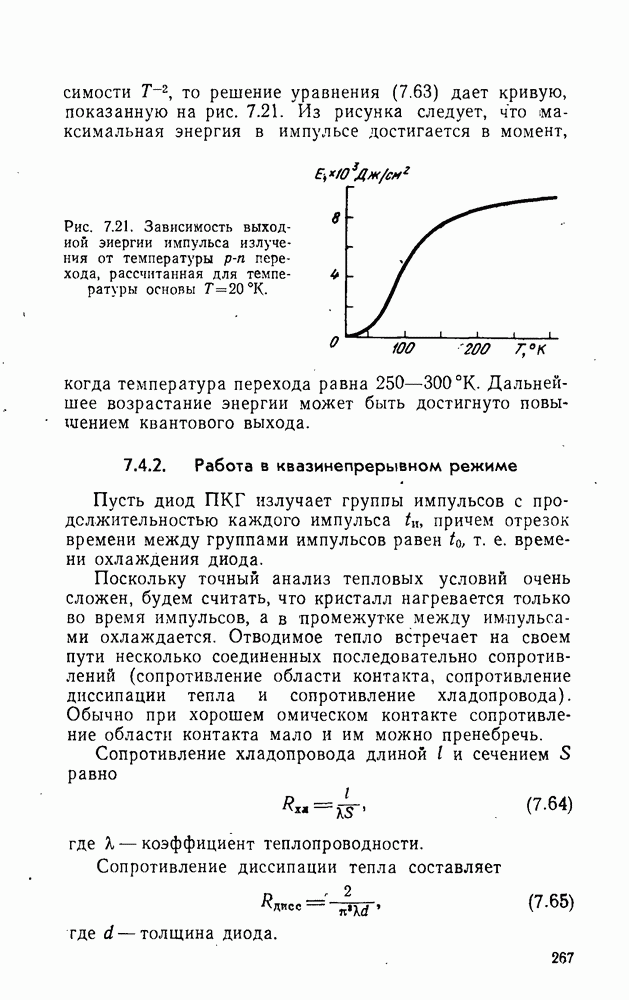
- 7.4. Тепловые условия работы лазерного диода
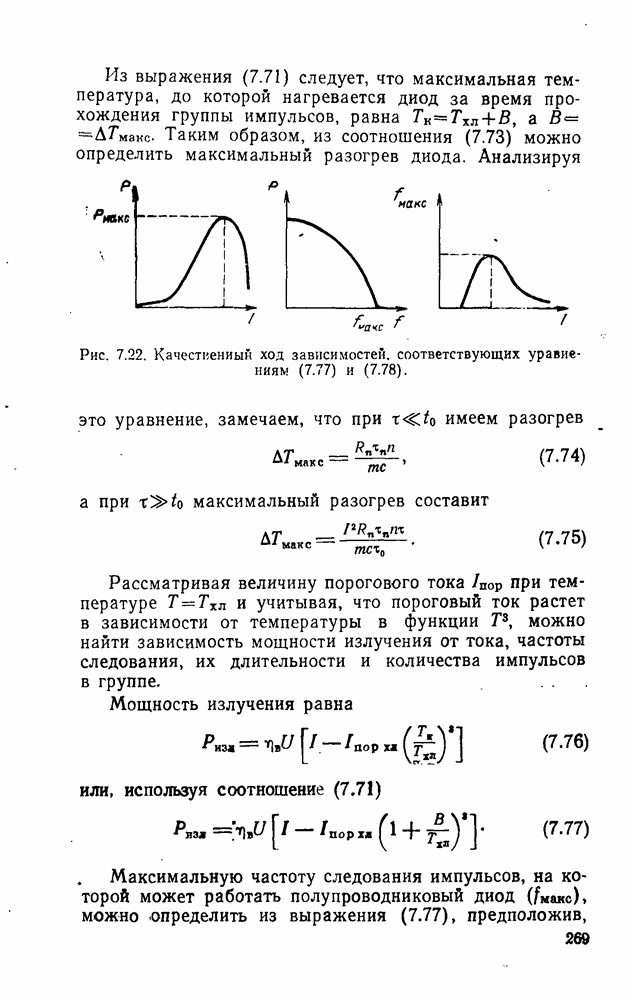
- 7.4.2. Работа в квазинепрерывном режиме
- 7.5. Другие типы ПКГ
- 7.5.1. ПКГ с электронным возбуждением
- 7.5.2. ПКГ с оптической накачкой
- 7.5.3. ПКГ с прямым электрическим возбуждением
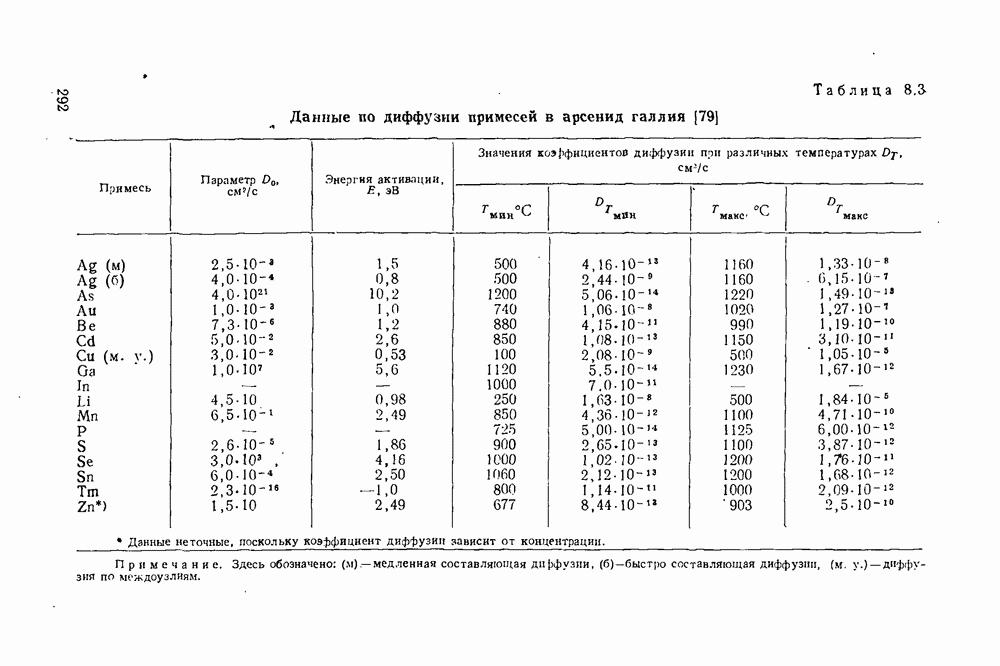
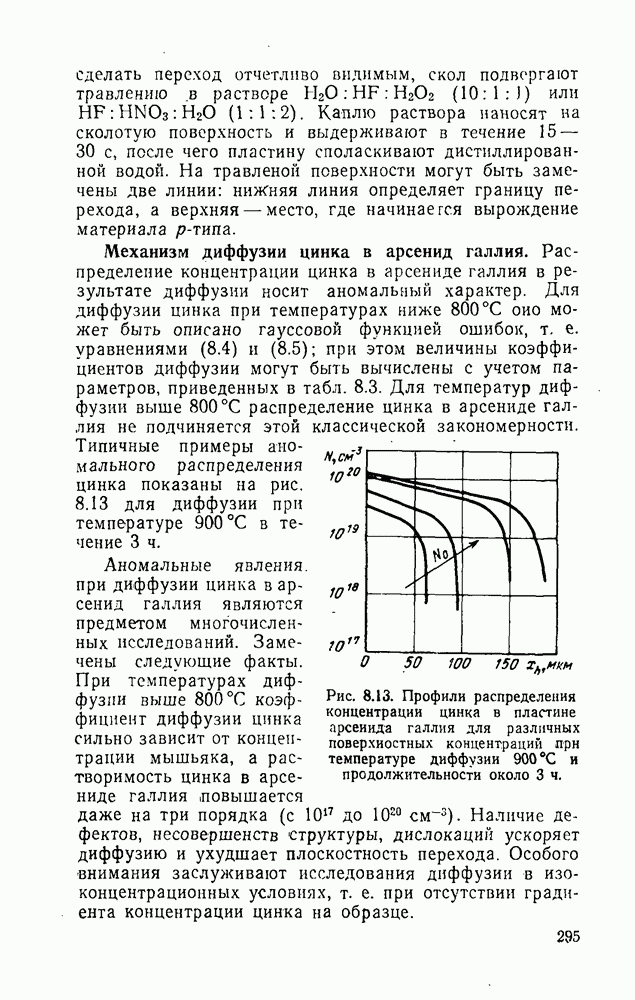
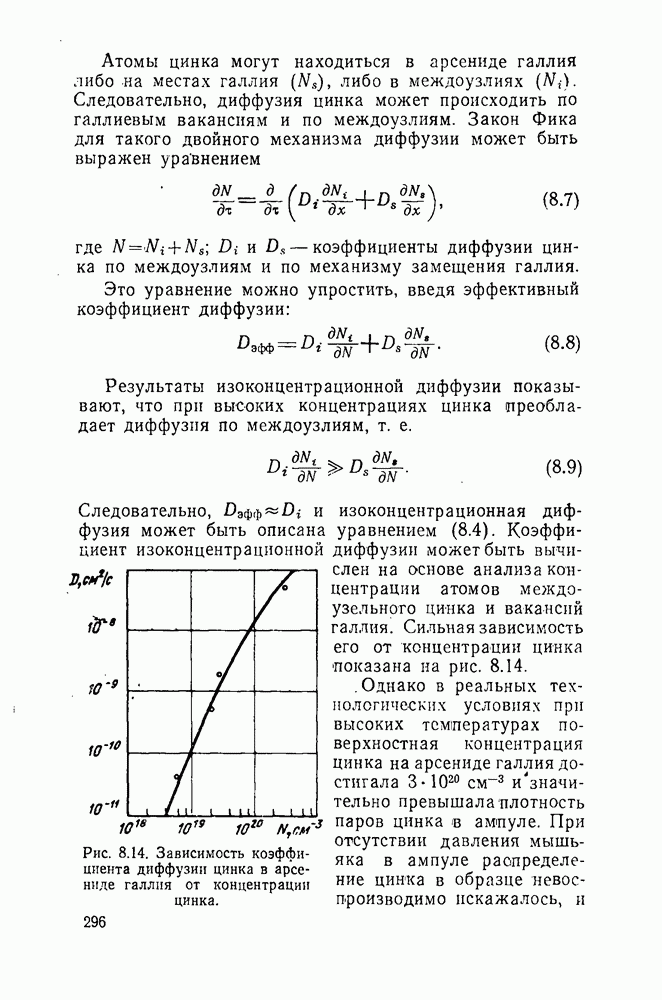
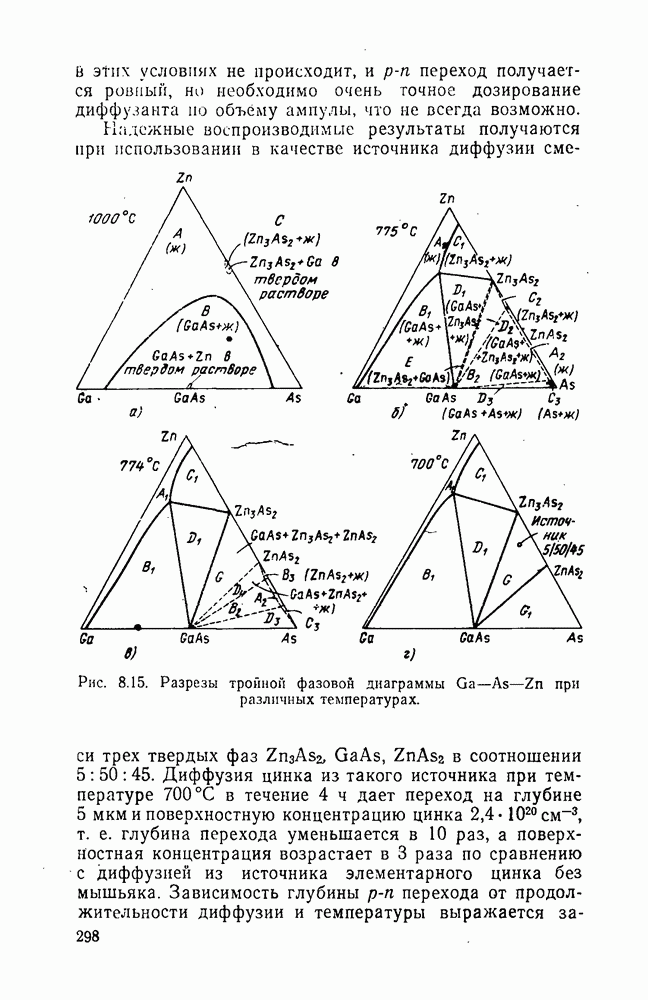
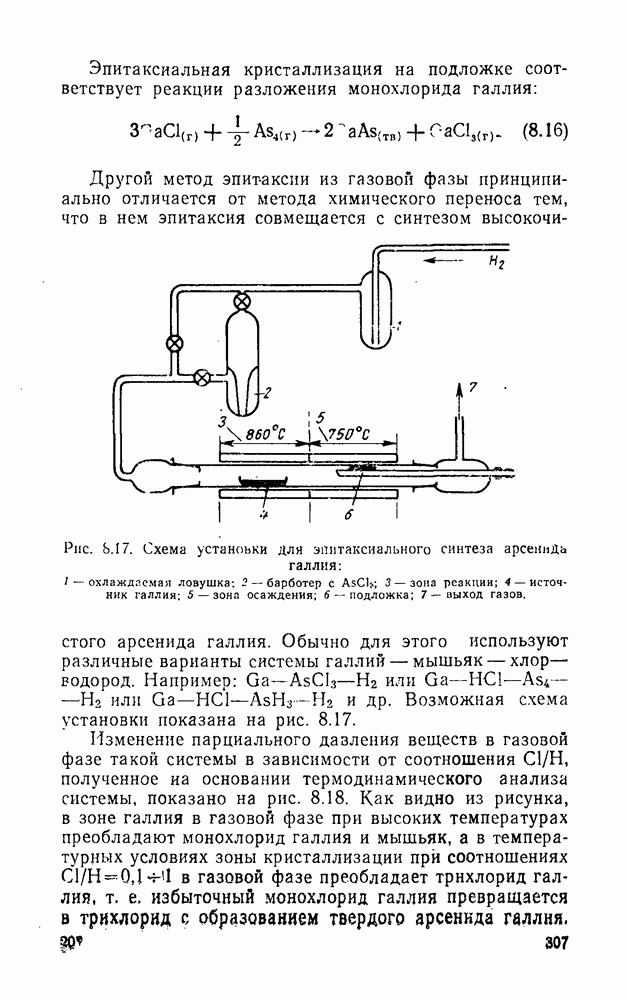
- Глава восьмая. АРСЕНИД ГАЛЛИЯ И ТЕХНОЛОГИЯ ИЗГОТОВЛЕНИЯ ДИОДОВ ПКГ
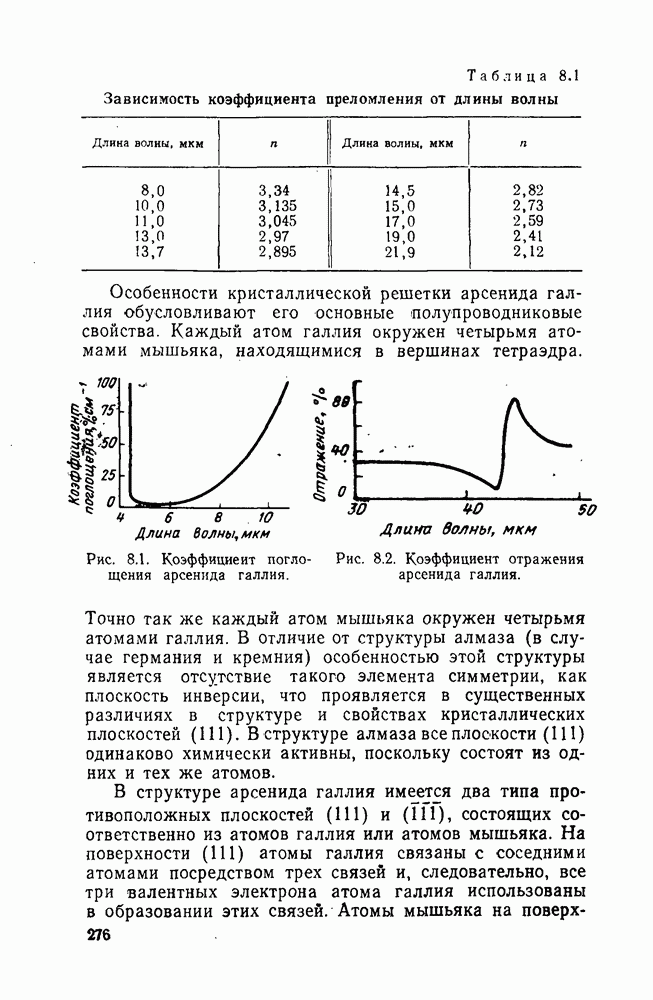
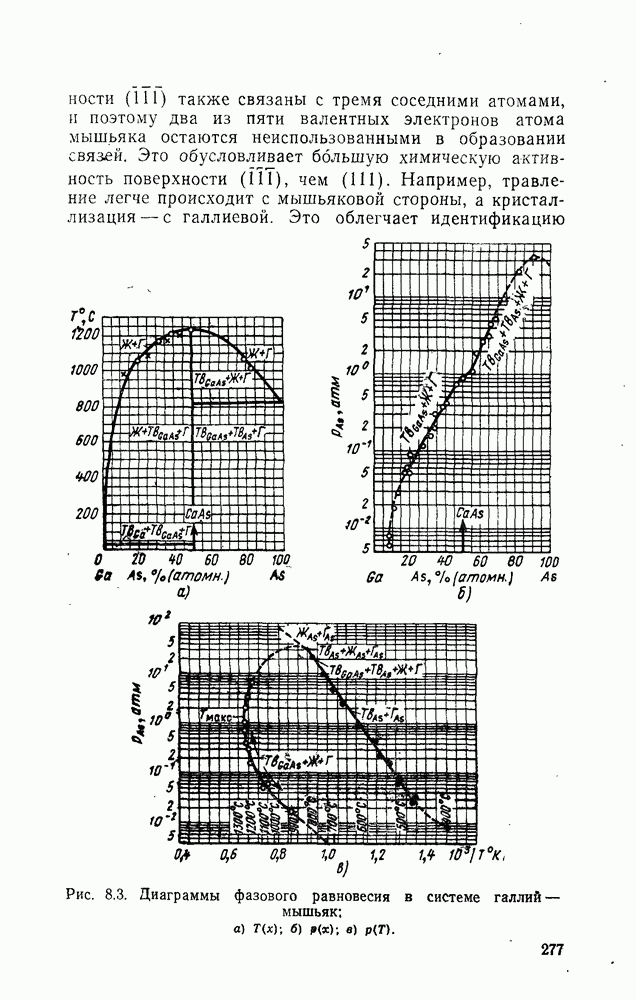
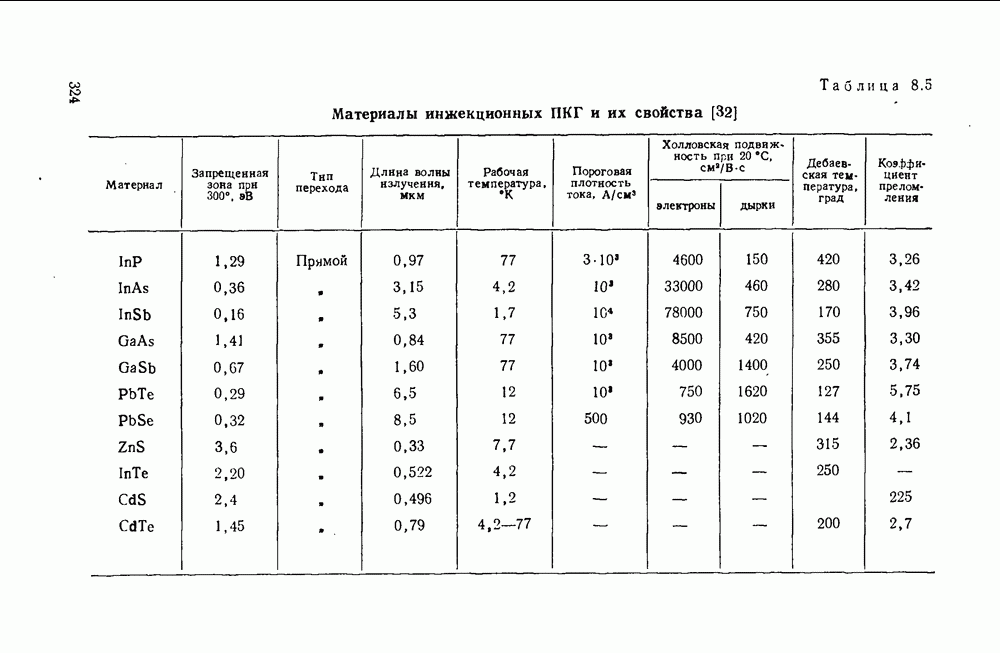
- 8.1. Физические свойства арсенида галлия
- 8.2. Методы выращивания монокристаллов арсенида галлия
- 8.3. Методы изготовления р-n-переходов
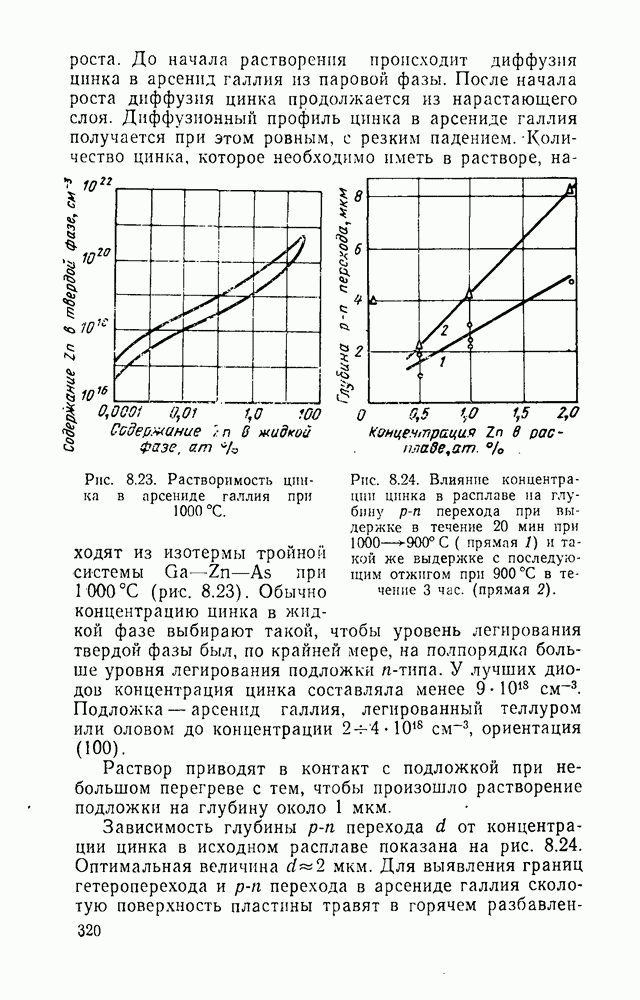
- 8.3.2. Эпитаксия из жидкой фазы
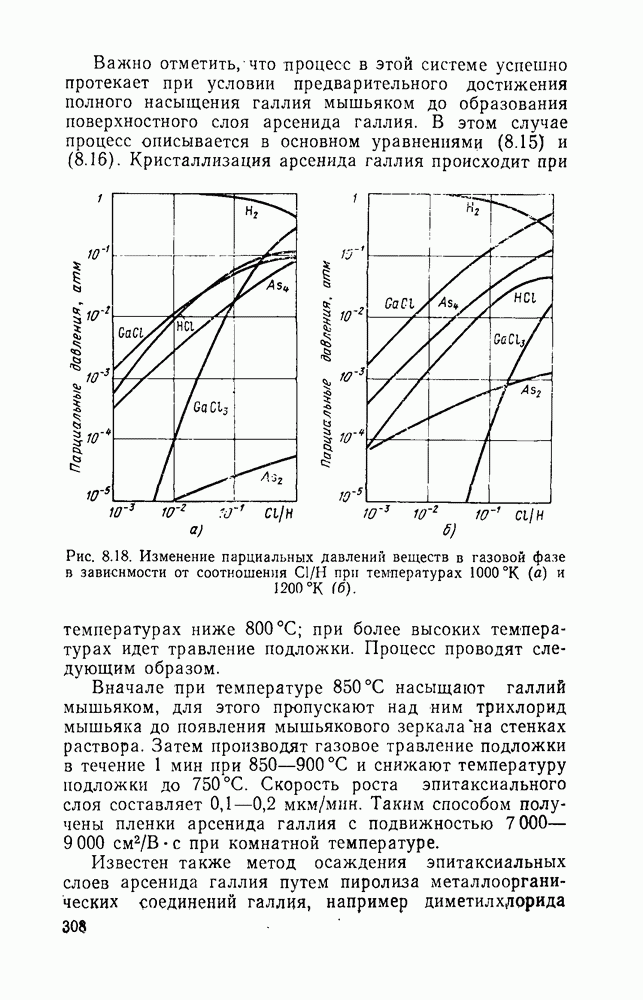
- 8.3.3. Эпитаксия из газовой фазы
- 8.4. Изготовление невыпрямляющих низкоомных контактов к арсениду галлия
- 8.5. Изготовление резонатора
- 8.6. Общая технологическая схема изготовления диодов ПКГ
- 8.7. Конструкция ПКГ
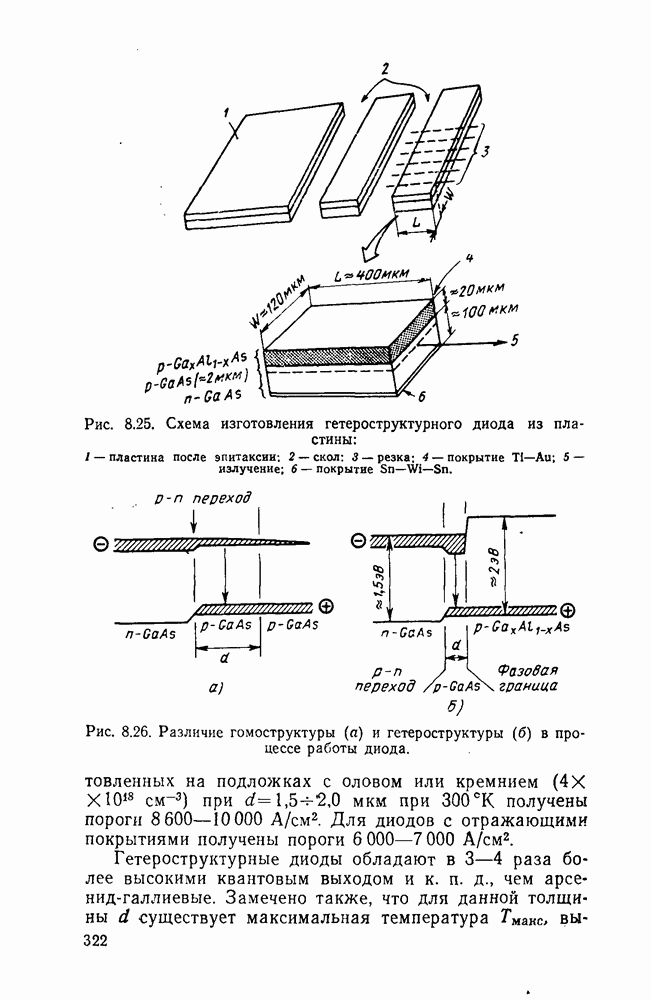
- 8.8. Гетероструктуры на основе арсенида галлия
- 8.9. Другие материалы с прямыми переходами
- Глава девятая. МАТЕРИАЛЫ ГАЗОВЫХ ОКГ
- 9.1. Особенности газового активного вещества ОКГ и методы создания инверсной населенности
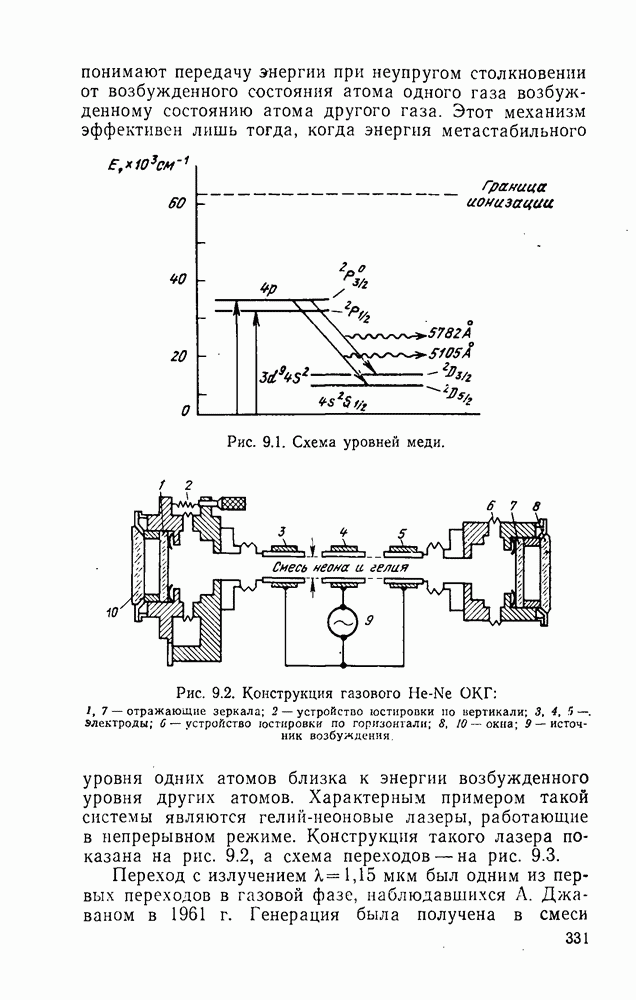
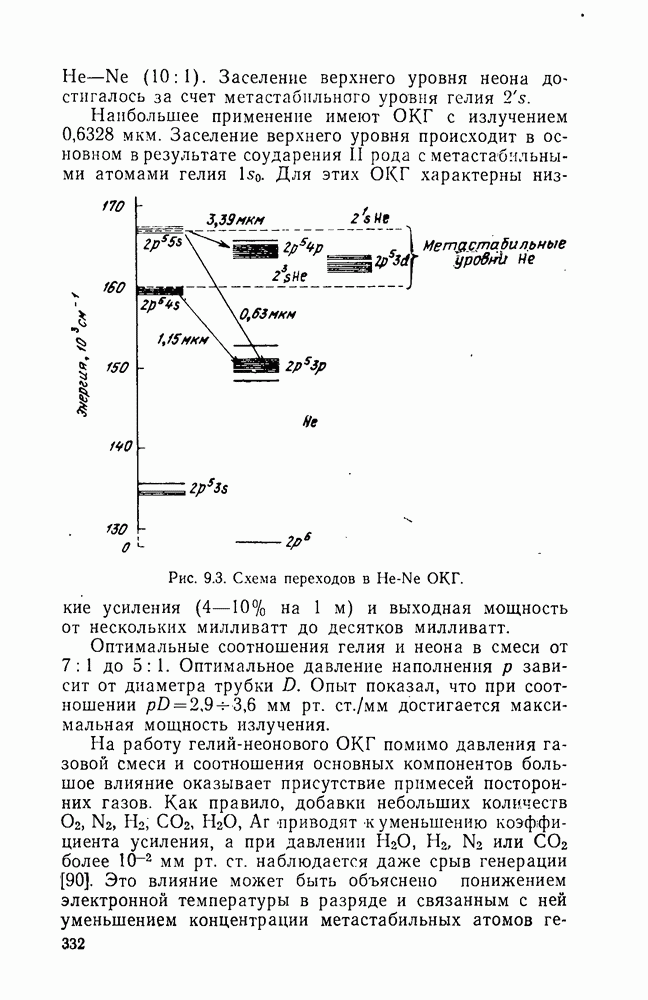
- 9.2. Газоразрядные ОКГ
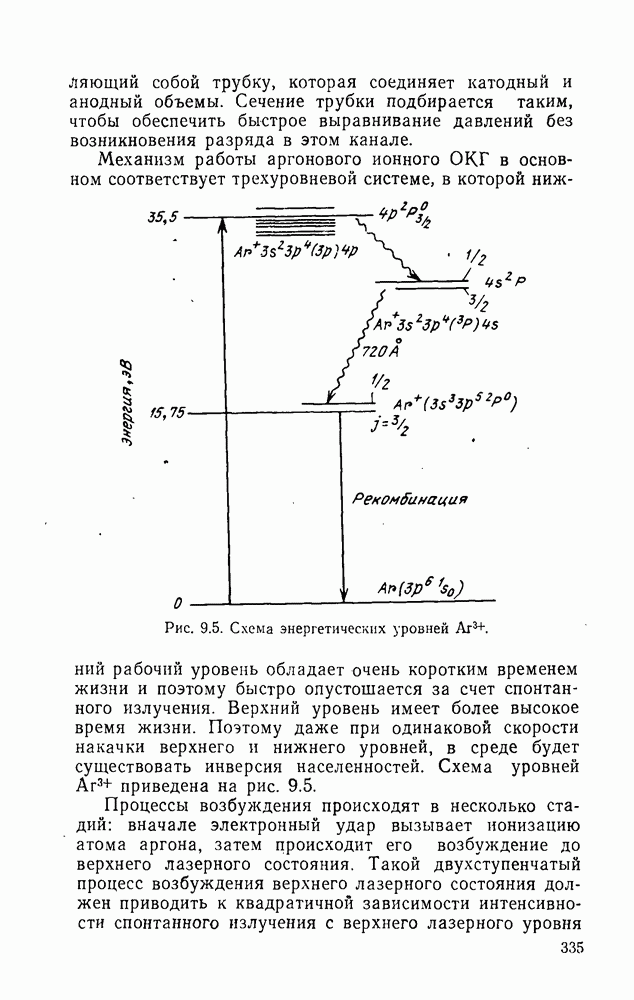
- 9.2.2. Ионные газоразрядные ОКГ
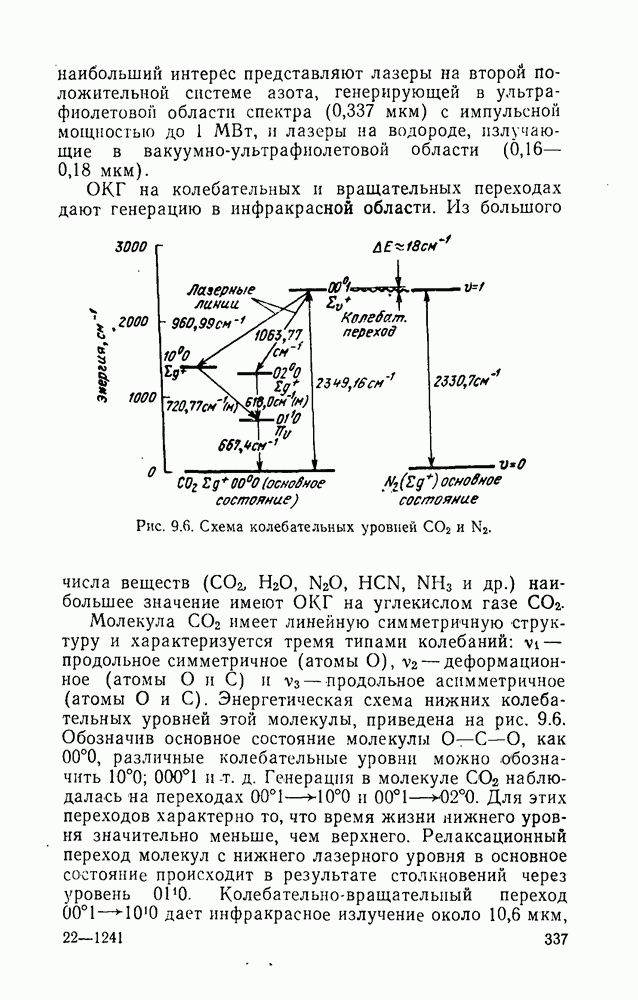
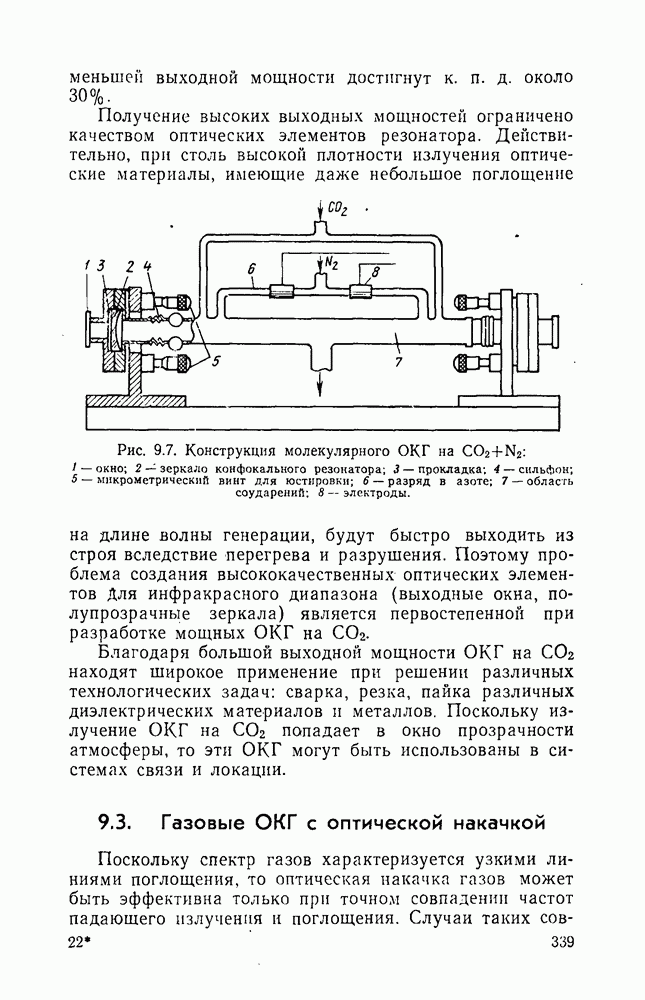
- 9.2.3. Молекулярные газоразрядные ОКГ
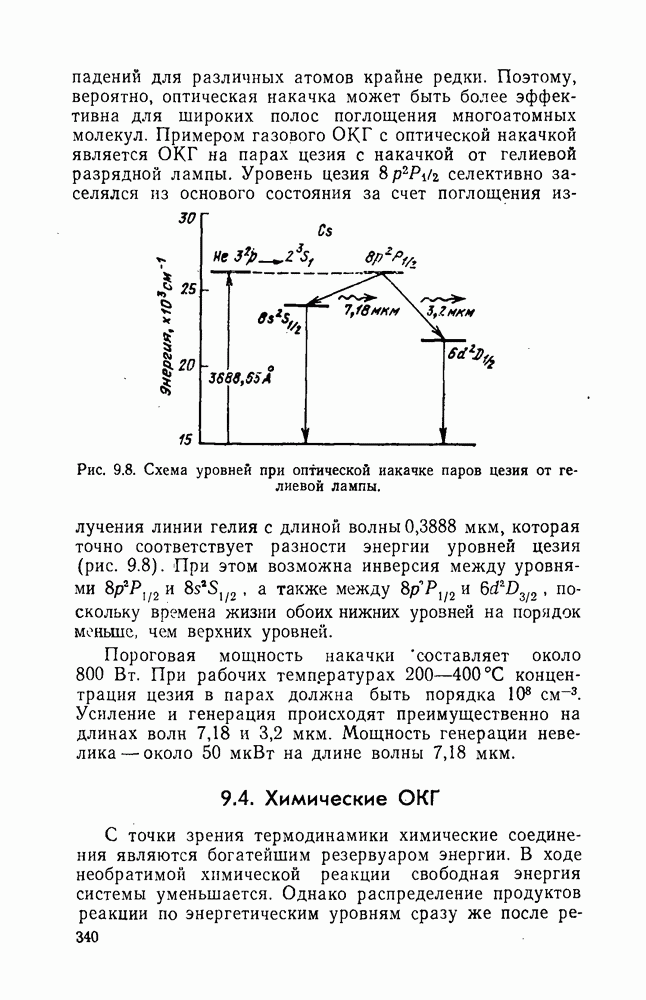
- 9.3. Газовые ОКГ с оптической накачкой
- 9.4. Химические ОКГ
- Глава десятая. МАТЕРИАЛЫ МОДУЛЯТОРОВ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ
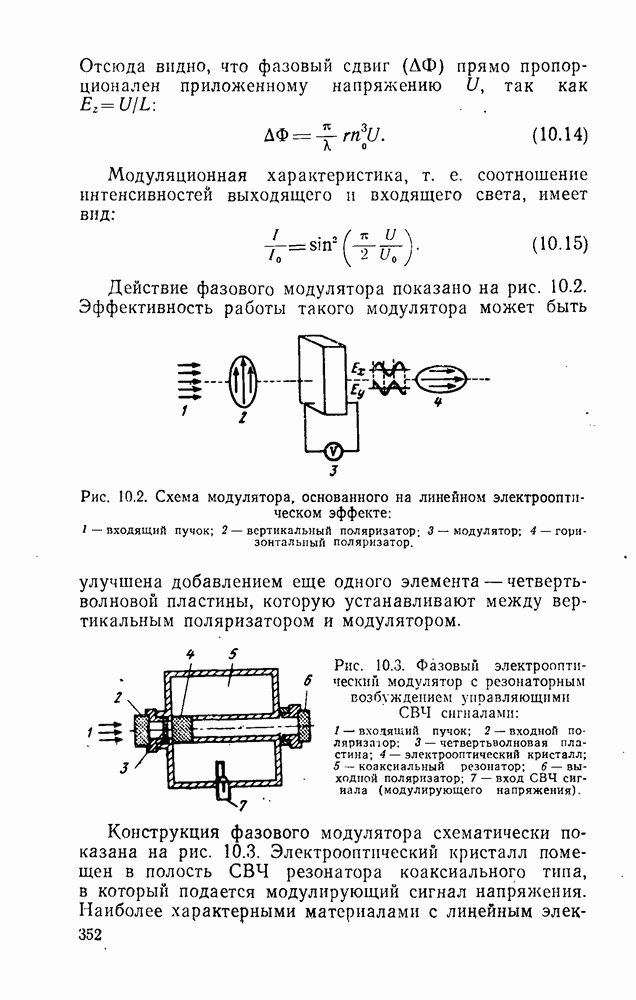
- 10.1. Некоторые физические основы модуляции оптического излучения
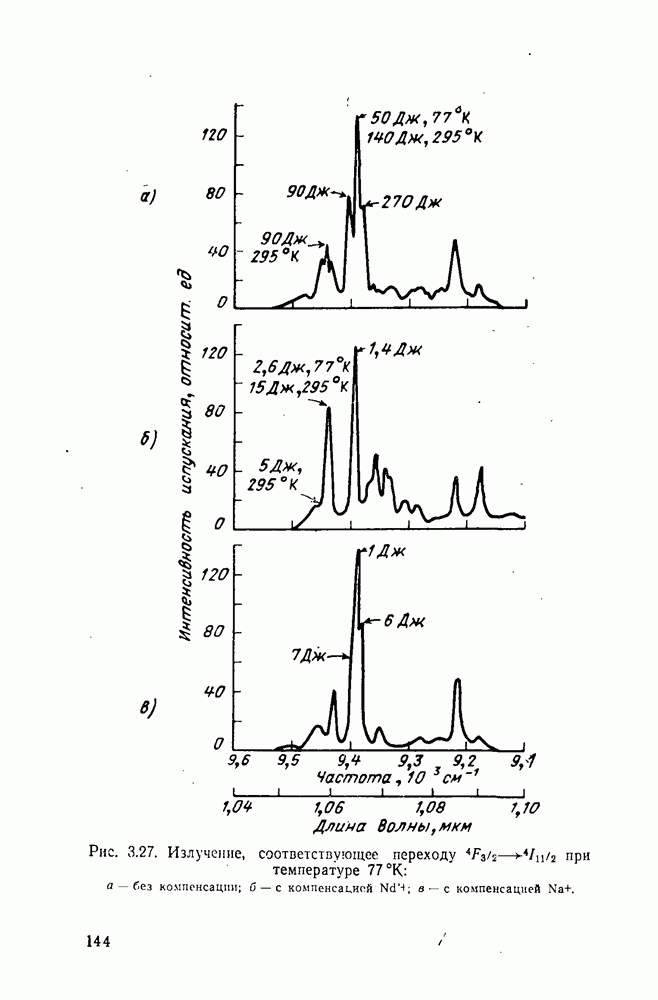
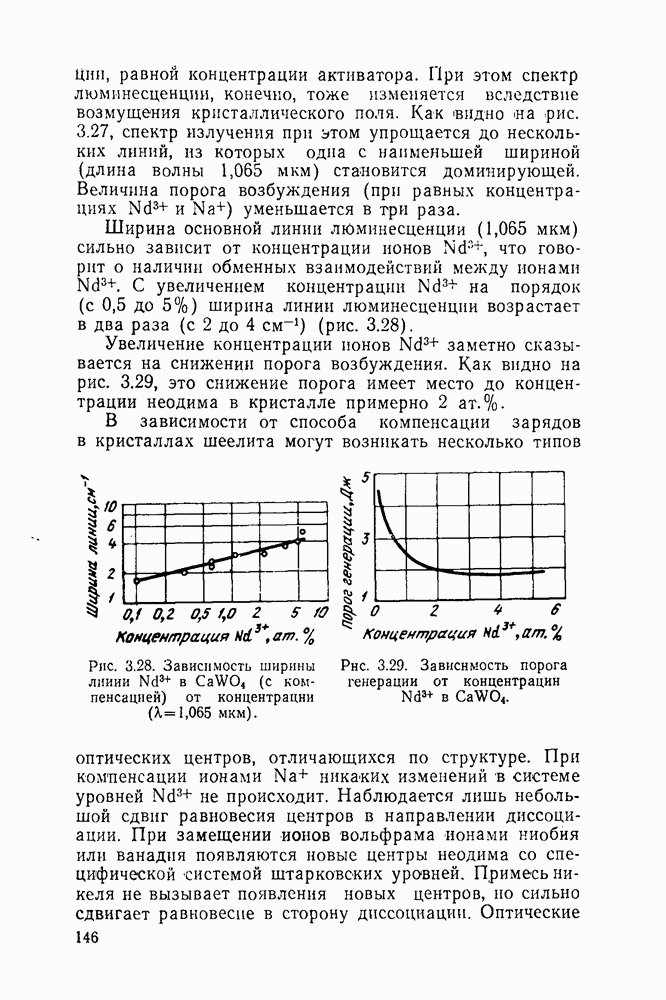
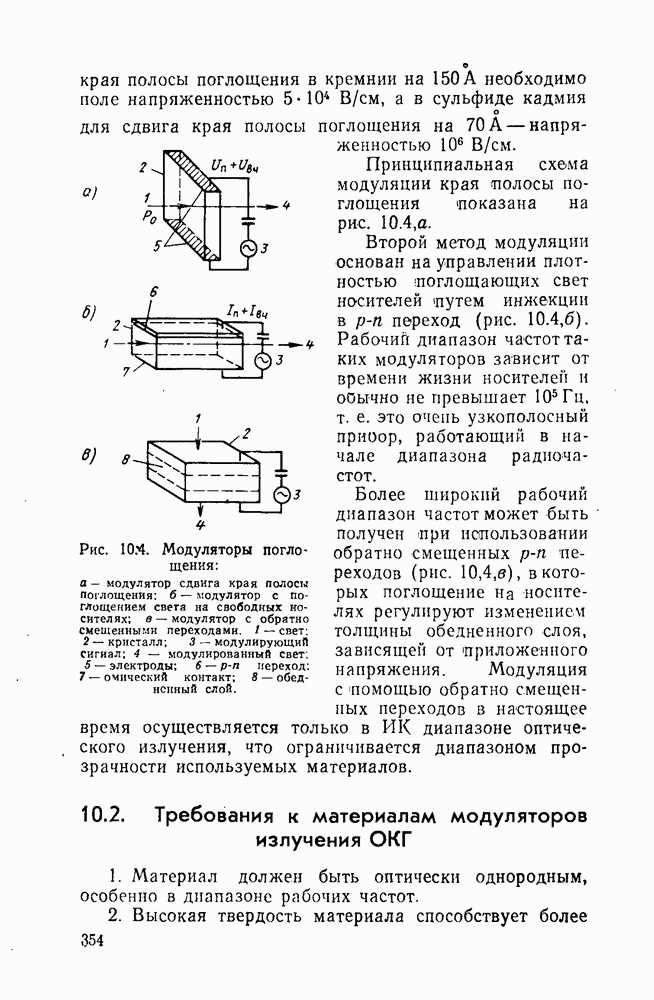
- 10.2. Требования к материалам модуляторов излучения ОКГ
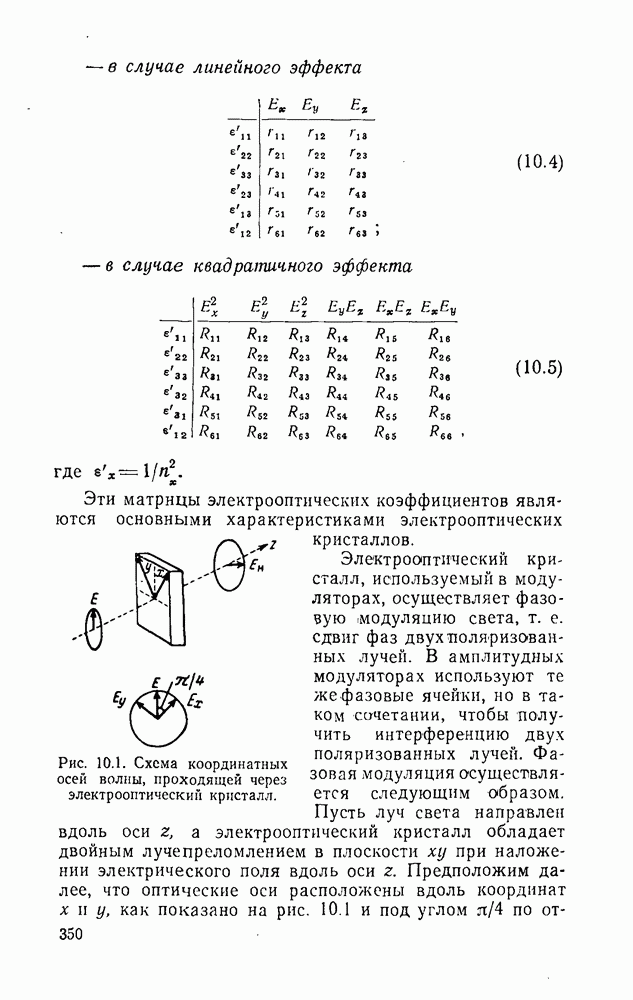
- 10.3. Материалы с линейным электрооптическим эффектом
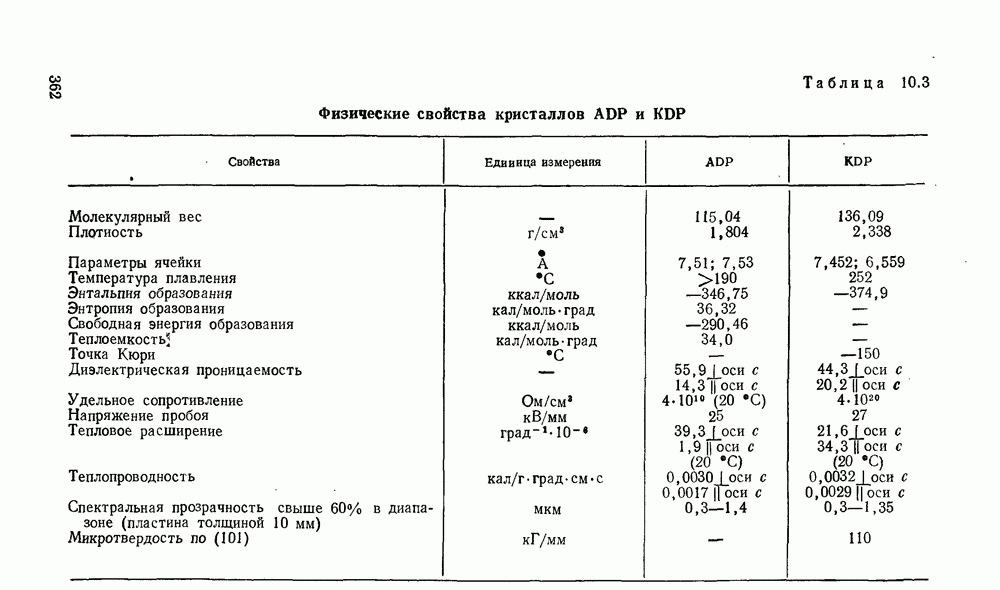
- 10.3.1. Тетрагональные кристаллы типа KDP
- 10.3.2. Ромбические кристаллы
- 10.3.3. Тригональные кристаллы
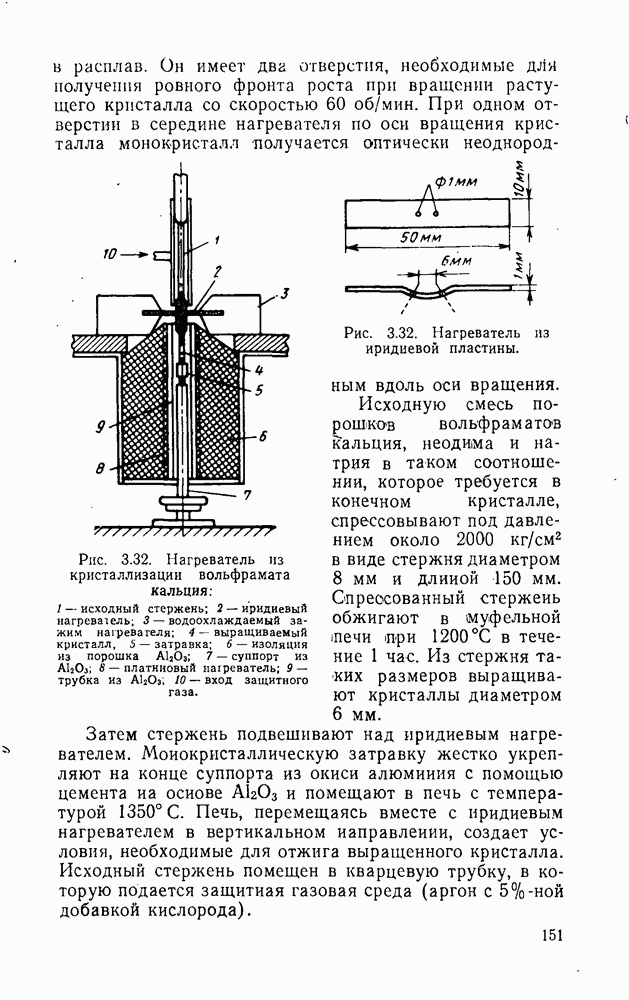
- 10.3.4. Кубические кристаллы
- 10.4. Кристаллы с квадратичным электрооптическим эффектом
- Литература