| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3.4. Рост кристаллов
Рост зародыша новой фазы (кристалла) происходит либо путем присоединения к его поверхности отдельных атомов, лнбо путем упорядоченного встраивания их комплексов.
Впервые Гиббс ввел понятие о послойном росте кристалла. Он показал, что рост совершенного кристалла должен происходить путем возникновения двумерных зародышей на поверхности кристалла и роста этого мононуклеарного двумерного слоя с образованием кристаллической грани. Энергетически это обеспечивается критическим пересыщением, ниже которого кристалл расти не может. Однако Фольмер обнаружил ряд систем, в которых рост кристаллов происходил при пересыщениях ниже критического, что противоречило теории Гиббса.
Фольмер предположил, что непосредственно около поверхности кристалла существует подвижный адсорбционный слой частиц, находящийся в термодинамическом равновесии с поверхностью кристалла и окружающей средой. При неровной поверхности рост кристалла может происходить и путем присоединения отдельных атомов без образования критических поверхностных зародышей. Для описания перехода атома из окружающей среды к поверхности кристалла согласно Фольмеру необходимо учитывать диффузионные характеристики в общем кинетическом уравнении, которое имеет вид (2.34).
Скорость роста кристалла определяется скоростью перехода атомов из адсорбционного слоя в кристаллическую решетку. Миграция атомов по поверхности, что Фольмеру удалось доказать экспериментально. приводит к образованию двумерных зародышей и разрастанию их до завершения нового кристаллического слоя. Предполагается, что рост двумерного зародыша происходит достаточно быстро, поэтому рост кристалла лимитируется процессом зародышеобразования. Образование двумерного зародыша описывается уравнением, аналогичным рассмотренным в § 2.3.2 и 2.3.3 для объемного (трехмерного) зародыша. Работа образования двумерного зародыша равна

где  линейный размер;
линейный размер;  — удельная линейная поверхностная энергия;
— удельная линейная поверхностная энергия;  — изменение химического потенциала.
— изменение химического потенциала.
Тогда энергия активации образования двумерного зародыша критического размера составит

а критический размер двумерного зародыша

Линейная скорость роста кристалла, т. е. скорость движения границу кристалла перпендикулярно самой себе, равна

где  — толщина монослоя;
— толщина монослоя;  — средний конечный размер зародышей к моменту их срастания.
— средний конечный размер зародышей к моменту их срастания.
Поэтому скорость роста больших монокристаллов, поверхность граней которых практически постоянна, зависит только от пересыщения, а скорость роста малых кристаллов быстро меняется вследствие увеличения поверхности граней.
Основываясь на термодинамической теории Гиббса — Фольмера, Коссель, а затем Странский и Каишев рассмотрели молекулярно-кинетический механизм встраивания частиц в кристаллическую решетку.

Рис. 2.5. Варианты встраивания частиц на поверхности кристалла.
Пусть совершенный кристалл находится в слабопересмщенной среде в состоянии, близком к равновесию. Взаимодействие частиц с поверхностью кристалла осуществляется посредством либо кулоновых  (ионные кристаллы), либо ван-дер-ваальсовых сил (гомополярные кристаллы). И те и другие силы являются функцией расстояния, а энергия присоединения частицы к кристаллу равна сумме энергий взаимодействия этой частицы с соседними. Для решетки ионного кристалла типа
(ионные кристаллы), либо ван-дер-ваальсовых сил (гомополярные кристаллы). И те и другие силы являются функцией расстояния, а энергия присоединения частицы к кристаллу равна сумме энергий взаимодействия этой частицы с соседними. Для решетки ионного кристалла типа  и поверхности
и поверхности  возможны следующие основные варианты встраивания частиц (рис. 2.5):
возможны следующие основные варианты встраивания частиц (рис. 2.5):
1) при закреплении частицы на гладкой грани кристалла действуют только вертикальные составляющие энергии прнсоеднения 
2) образовании нового ряда, расположенного вплотную с уже завершенным рядом, действуют краевые силы завершенного ряда и исходной грани с выделением энергии 
3) при образовании нового ряда  края грани кристалла выделяется энергия
края грани кристалла выделяется энергия 
4) при встраивании частицы в достраивающийся ряд выделяется энергия 
Начало застраивания новой плоскости также может произойти с различных мест (рис. 2.5):
а) с гладкой поверхности 
б) с края плоскости 
в) с угла 
Вероятность присоединения частицы к кристаллу пропорциональна выделяющейся энергии присоединения в этом месте. Поскольку для начала застраивания в ионном кристалле  то наиболее вероятно начало застраивания плоскости с угла. Почти также относительную вероятность присоединения частиц в разных местах можно выразить рядом
то наиболее вероятно начало застраивания плоскости с угла. Почти также относительную вероятность присоединения частиц в разных местах можно выразить рядом 
В случае ковалентных кристаллов действующие силы (ван-дер-ваальсовы силы) слабы и быстро уменьшаются с расстоянием. Энергия присоединения частицы к кристаллу распределяется по числу ближайших соседних частиц (атомов) в вертикальном направлении. Например, при присоединении частиц к гладкой поверхности  с ребра
с ребра  и с угла
и с угла  , так. что
, так. что  т. е. совершенно противоположная закономерность по сравнению с ионными кристаллами.
т. е. совершенно противоположная закономерность по сравнению с ионными кристаллами.
Молекулярно-кинетическая, теория дает возможность не только количественно оценить механизм роста кристалла, но и предсказать его морфологию.
Согласно упомянутым теориям рост совершеннного. кристалла может происходить только при больших пересыщениях. Однако реальные кристаллы растут при пересыщениях, меиыинх критических, и быстрее совершенных. Франк объяснил этот факт наличием на гранях реальных кристаллов ненечезающих ступеней роста, начинающихся на выходе винтовых дислокаций.
По мере роста дислокация закручивается в спираль, образуя последовательные витки ступеней. На поверхности кристаллов образуются пирамиды роста: Так как вероятность присоединения частиц к ступеням дислокационного роста одинакова во всех местах, то
фронт роста будет продвигаться поступательно с одинаковой скоростью:

где  — коэффициент, учитывающий активность дислокаций роста;
— коэффициент, учитывающий активность дислокаций роста;  — коэффициент диффузии;
— коэффициент диффузии;  — радиус двумерного зародыша;
— радиус двумерного зародыша;  — радиус кривизны террасы роста;
— радиус кривизны террасы роста;  расстояние по вертикали. Подставив значение
расстояние по вертикали. Подставив значение

в (2.47) получим

Коэффициент Кл необходимо учитывать вследствие взаимодействия дислокаций роста. Плотность дислокаций в кристаллах составляет до  Однако на поверхности грани в процессе роста работает всего несколько, а иногда и один центр роста. Если изменить пересыщение, то на поверхности появляется множество мелких центров. Затем постепенно в результате отбора остается несколько, по уже новых центров роста. При восстановлении прежнего пересыщения восстанавливаются и старые центры роста. Возникновение дислокаций возможно вследствие напряжений, включений посторонних агомов или частиц и
Однако на поверхности грани в процессе роста работает всего несколько, а иногда и один центр роста. Если изменить пересыщение, то на поверхности появляется множество мелких центров. Затем постепенно в результате отбора остается несколько, по уже новых центров роста. При восстановлении прежнего пересыщения восстанавливаются и старые центры роста. Возникновение дислокаций возможно вследствие напряжений, включений посторонних агомов или частиц и 
Дислокационный рост кристалла состоит из трех последовательных процессов: маесообмен между исходной средой и адсорбционными слоями; диффузия адсорбированных частиц к ступеням роста и обмен между ступенью и адсорбционным слоем; диффузия адсорбированных частиц на самих ступенях и обмен с изломами.
Следует упомянуть еще об одном механизме роста кристаллов, известном под названием нормальный рост кристаллов. Он характерен для роста кристаллов из чистых слабоперсохлажденных жидких фаз (особенно металлов и неполярных веществ). Скорость процесса взаимодействия фаз при малом отклонении от состояния равновесия пропорциональна градиенту химического потенциала:

где  — коэффициент диффузии для переноса вещества через границу раздела;
— коэффициент диффузии для переноса вещества через границу раздела;  — длина скачка частицы по нормали к поверхности раздела,
— длина скачка частицы по нормали к поверхности раздела,  — молярная энтропия плавления.
— молярная энтропия плавления.
Таким образом, рост кристаллов может осуществляться тремя различными механизмами:
1) путем образования двумерных зародышей и их разрастания;
2) путем дислокационного роста граней, т. е. присоединением частиц к неисчезающим ступеням, образованным выходом винтовых дислокаций;
3) путем нормального послойного роста, т. е. путем беспорядочного присоединения частиц к поверхности раздела; при этом фронг кристаллизации перемещается однородно, нормально плоскости кристалла.
Каждый механизм характеризуется своей функциональной зависимостью скорости роста  от переохлаждения на границе раздела фаз
от переохлаждения на границе раздела фаз  При росте кристаллов по механизму двумерного зарождения эта зависимость (2.46) имеет вид
При росте кристаллов по механизму двумерного зарождения эта зависимость (2.46) имеет вид

при дислокационном механизме роста (2.48) — вид

а в случае нормального роста (2.49) — вид

Величины  в малом интервале переохлаждений могут быть приняты константами. Преобладание того или иного механизма роста кристалла определяется структурой поверхности раздела кристалл — расплав. Механизм двумерного зарождения характерен для атомно-гладких, низкоиндексных поверхностей раздела, дислокационный рост — для поверхностей, содержащих неисчезающие ступени роста, образованные выходом винтовых дислокаций, а нормальный рост для атомно-шероховатых и высокоиндексных плоскостей.
в малом интервале переохлаждений могут быть приняты константами. Преобладание того или иного механизма роста кристалла определяется структурой поверхности раздела кристалл — расплав. Механизм двумерного зарождения характерен для атомно-гладких, низкоиндексных поверхностей раздела, дислокационный рост — для поверхностей, содержащих неисчезающие ступени роста, образованные выходом винтовых дислокаций, а нормальный рост для атомно-шероховатых и высокоиндексных плоскостей.
Предполагается также, что нормальный рост возможен при значительно меньших переохлаждениях, чем дислокационный. Наибольшее переохлаждение требуется при реализации механизма образования и роста двумерных зародышей. При очень больших переохлаждениях рост кристалла может идти не только за счет двумерного зарождения на поверхности раздела фаз, по и путем присоединения уже имеющихся в среде трехмерных частиц. С увеличением пересыщения вклад этого механизма должен возрастать. Качество кристалла при этом резко ухудшается, так как ориентация трехмерных частиц не будет строго совпадать, и поэтому образуется поликристалличеокий блочный материал.
Помимо рассмотренных трех основных механизмов роста кристаллов возможны несколько режимов, определяемых гидродинамическими условиями процесса. Гидродинамика массообмспа растущего кристалла с окружающей средой илрает очень важную роль в процессе роста. Движущей силой в процессе роста кристалла является градиент химического потенциала между поверхностью кристалла и окружающей средой, возникающий вследствие пересыщения или переохлаждения слоя среды, непосредственно контактирующего с кристаллом.
Стремясь возвратиться  состояние равновесия согласно второму закону термодинамики, система уменьшает этот градиент посредством днффузлн. Однако в процессе роста участвует не вся среда, а лишь тонкий слой, находящийся непосредственно у поверхности кристалла. Интенсификация массообмена между кристаллом и средой может привести к ускоренному росту совершенного кристалла и к более полному использованию ресурсов среды как источника вещества.
состояние равновесия согласно второму закону термодинамики, система уменьшает этот градиент посредством днффузлн. Однако в процессе роста участвует не вся среда, а лишь тонкий слой, находящийся непосредственно у поверхности кристалла. Интенсификация массообмена между кристаллом и средой может привести к ускоренному росту совершенного кристалла и к более полному использованию ресурсов среды как источника вещества.
В применяемых в настоящее время методах выращивания кристаллов возможны три типа гидродинамических режимов:
1) режим молекулярной диффузии;
2) режим естественной конвекции;
3) вынужденный гидродинамический режим (или режим «вынужденной конвекции»).
Молекулярная диффузия лимитирует процесс при кристаллизации из неподвижной вязкой среды с малым пересыщением. Скорость такого процесса согласно первому закону Фика равна

или при постоянной поверхности раздела фаз (сечение диффузионного потока)  и толщине диффузионного пограничного слоя
и толщине диффузионного пограничного слоя 

где Р — коэффициент массообмена.
Поскольку в ходе процесса толщина диффузионного слоя возрастает, а градиент концентрации уменьшается, то скорость роста кристалла в режиме молекулярной диффузия уменьшается со временем. Так как условия диффузии к вершинам и ребрам кристалла лучше, чем к плоским граням, то помимо градиента концентрации по нормали возникает градиент концентрации вдоль поверхности грани. Вследствие этого происходит преимущественный дендритный рост у вершины кристалла и поликрпсталлические или слоистые отложения с включениями раствора у середины граней. Только при сохранении очень малых пересыщений можно устранить эти эффекты и получить сравнительно качественный кристалл. Это частично достигается в режиме естественной конвекции.
Естественная конвекция вызывается градиентом плотности маловязкой среды вблизи кристалла и в объеме расплава. Градиент плотности возникает либо за счет температурного градиента в результате выделения или отвода тепла, либо за счет концентрационного градиента в результате кристаллизации. Конвекционный поток обеспечивает замену истощенной среды в пограничном слое и помогает сохранять меньшую степень пересыщения и меньшую толщину диффузионного слоя, чем в чисто диффузионном процессе. При этом выравниваются и градиенты концентраций вдоль поверхности грани. Это увеличивает скорость роста кристалла и позволяет получать более однородные и более качественные кристаллы при больших пересыщениях, чем в режиме диффузии. Скорость процесса, контролируемого конвекцией, может быть найдена из выражения

где  коэффициент массообмена;
коэффициент массообмена;  — гравитационная постоянная;
— гравитационная постоянная;  градиент плотности;
градиент плотности;  вязкость среды.
вязкость среды.
Еще лучшие условия роста могут быть получены в вынужденном гидродинамическом режиме, который достигается путем принудительного движения раствора вблизи кристалла или кристалла в растворе. При увеличении скорости относительного движения улучшается снабжение межфазовой границы веществом и уменьшаются, а иногда исчезают, градиенты концентрации вдоль поверхности грани. Это позволяет выращивать крупные однородные кристаллы с высокой скоростью. Однако скорость движения для данных веществ, температурных градиентов и пересыщений в каждом случае имеет оптимальное значение, выше которого скорость роста кристалла уменьшается, а качество его становится хуже. Это обусловлено тем, что слишком быстрый поток может ограничивать межфазовый массообмен и вызовет эррозию поверхности кристалла.
Скорость процесса доставки вещества к данному месту гладкой поверхности грани в вынужденном гидродинамическом режиме определяется выражением

где  — скорость движения раствора относительно грани кристалла; х — расстояние вдоль поверхности грани от переднего ребра кристалла.
— скорость движения раствора относительно грани кристалла; х — расстояние вдоль поверхности грани от переднего ребра кристалла.
Отсюда можно вычислить, на каком расстоянии от переднего ребра на поверхности грани при данном пересыщении и данной скорости движения раствор истощается, и рост грани прекратится. Если же скорость роста известна, можно рассчитать оптимальную скорость движения.
Правильно организованный вынужденный гидродинамический режим позволяет выращивать однородные совершенные кристаллы при больших пересыщениях и повышенных температурах, т. е. в условиях, обеспечивающих высокую скорость роста кристалла.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава первая. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ И ПРИНЦИП ДЕЙСТВИЯ КВАНТОВЫХ ГЕНЕРАТОРОВ
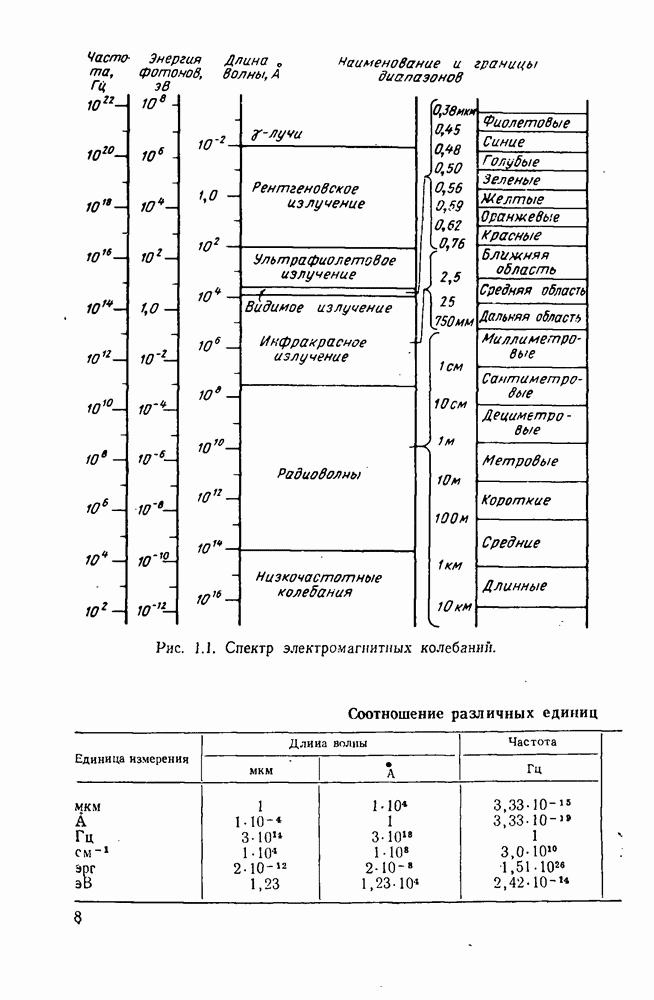
- 1.1. Спектр электромагнитных колебаний
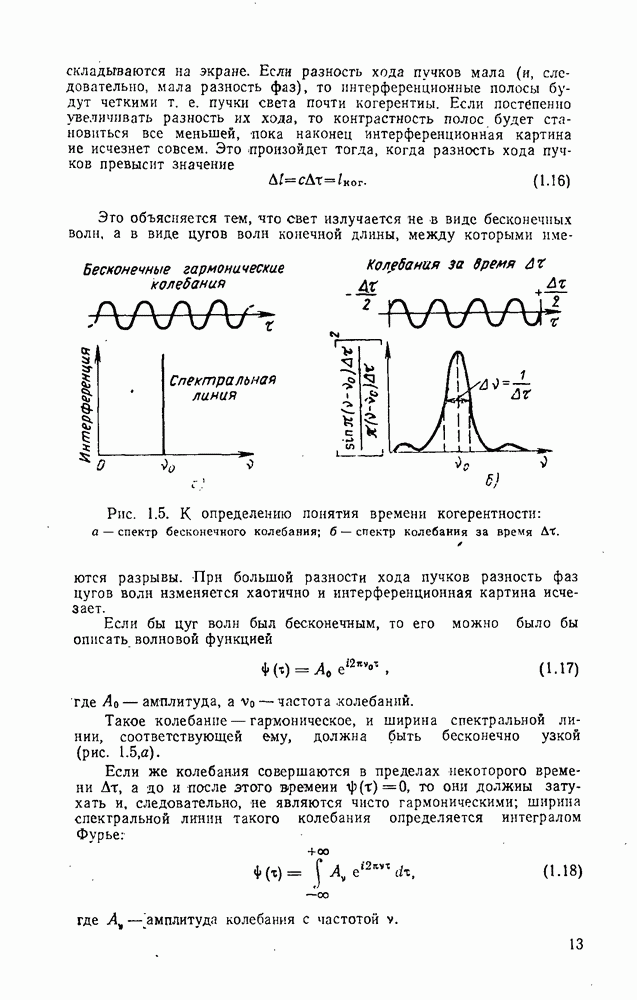
- 1.2. Когерентность
- 1.3. Направленность излучения
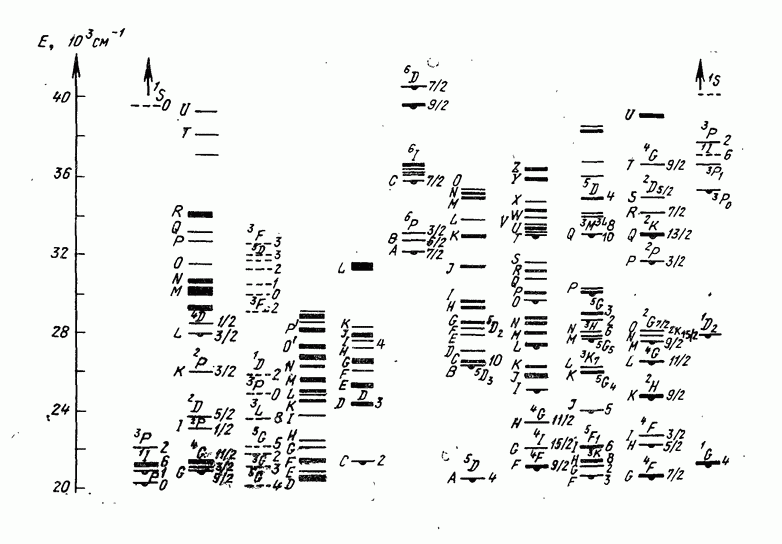
- 1.4. Символика энергетических уровней атомов и ионов
- 1.5. Инверсная населенность
- 1.6. Вероятности спонтанных и вынужденных переходов
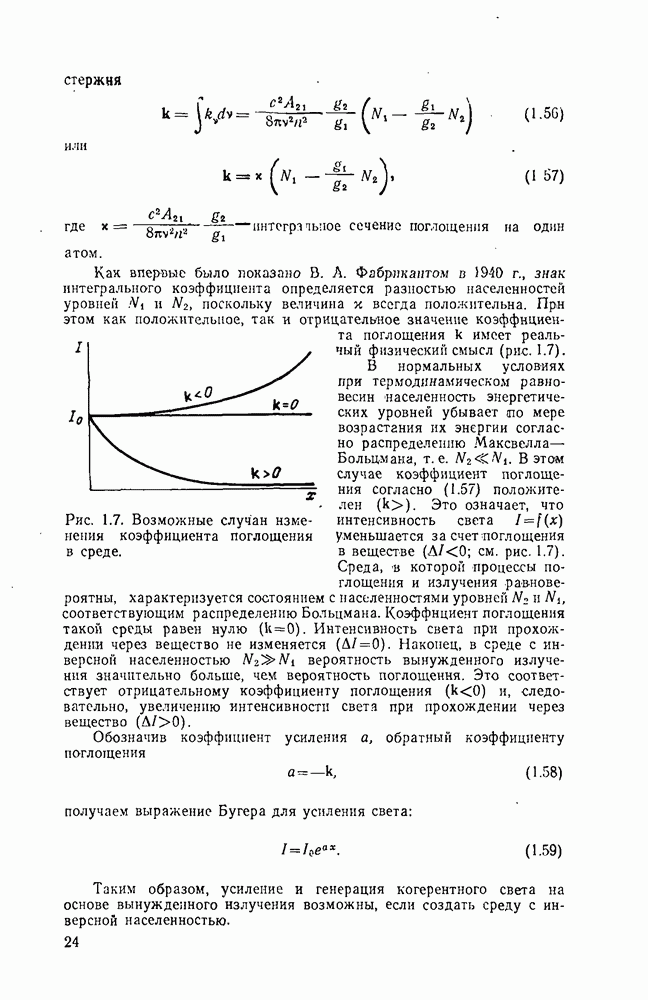
- 1.7. Усиление света при прохождении через вещество
- 1.8. Двухуровневая система
- 1.9. Трехуровневая система
- 1.10. Четырехуровневая система
- 1.11. Возбуждение активного вещества
- 1.12. Оптический резонатор
- 1.13 Условие генерации
- 1.14. Потери энергии в квантовом генераторе
- 1.15. Устройство ОКГ на твердом теле
- Глава вторая. ОБЩИЕ ВОПРОСЫ ТЕХНОЛОГИИ МАТЕРИАЛОВ ТВЕРДОТЕЛЬНЫХ ОКГ
- 2.1. Особенности активного вещества ионных квантовых систем
- 2.2. Особенности технологии твердотельных материалов квантовых генераторов
- 2.3. Физико-химические основы кристаллизации
- 2.3.2. Гетерогенное зародышеобразование
- 2.3.3. Скорость зарождения новой фазы
- 2.3.4. Рост кристаллов
- 2.3.5. Общее кинетическое уравнение кристаллизации
- 2.3.6. Распределение примеси в процессе роста кристалла
- 2.4. Основные методы синтеза и выращивания кристаллов
- 2.4.2. Выращивание из стехиометрических расплавов
- 2.4.3. Методы выращивания кристаллов из растворов
- 2.4.4. Гидротермальный синтез и рост кристаллов
- 2.4.5. Выращивание кристаллов из газовой фазы
- 2.5. Кристалло-химическая классификация материалов твердотельных квантовых генераторов
- Глава третья. КИСЛОРОДНЫЕ СОЕДИНЕНИЯ
- 3.1. Окислы элементов III группы
- 3.1.2. Окислы редкоземельных элементов и иттрия
- 3.3.1. Гранаты
- 3.2. Материалы на основе кислородных соединений элементов VI группы
- 3.2.2. Молибдаты
- 3.3. Материалы на основе кислородных соединений элементов V группы
- 3.3.2. Ниобаты
- 3.3.3. Фосфаты
- Выращивание кристаллов фторфосфата кальция [47]
- Глава четвертая. ФТОРИСТЫЕ СОЕДИНЕНИЯ
- 4.1. Фториды элементов II группы
- 4.2. Фториды редкоземельных элементов
- 4.3. Смешанные фториды
- 4.4. Фториды элементов VII группы
- Глава пятая. СТЕКЛО
- 5.1. Особенности стекла как активного материала ОКГ
- 5.2. Общая характеристика стекол для ОКГ
- 5.3. Особенности положения атомов активатора в стекле
- 5.4. Стекло с неодимом
- Глава шестая. МАТЕРИАЛЫ ЖИДКОСТНЫХ ОКГ
- 6.2. Механизм излучения в органических растворах
- 6.3. Растворы металлоорганических соединений
- 6.4. Растворы органических красителей
- 6.5. Растворы неорганических соединений редкоземельных элементов
- Глава седьмая. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВЫХ КВАНТОВЫХ ГЕНЕРАТОРОВ (ПКГ)
- 7.2. Основные сведения из теории люминесценции инжекционных ПКГ
- 7.3. Рабочие характеристики инжекционных ПКГ
- 7.3.2. Пространственные свойства
- 7.3.3. Пороговый ток
- 7.3.4. Квантовый выход
- 7.4. Тепловые условия работы лазерного диода
- 7.4.2. Работа в квазинепрерывном режиме
- 7.5. Другие типы ПКГ
- 7.5.1. ПКГ с электронным возбуждением
- 7.5.2. ПКГ с оптической накачкой
- 7.5.3. ПКГ с прямым электрическим возбуждением
- Глава восьмая. АРСЕНИД ГАЛЛИЯ И ТЕХНОЛОГИЯ ИЗГОТОВЛЕНИЯ ДИОДОВ ПКГ
- 8.1. Физические свойства арсенида галлия
- 8.2. Методы выращивания монокристаллов арсенида галлия
- 8.3. Методы изготовления р-n-переходов
- 8.3.2. Эпитаксия из жидкой фазы
- 8.3.3. Эпитаксия из газовой фазы
- 8.4. Изготовление невыпрямляющих низкоомных контактов к арсениду галлия
- 8.5. Изготовление резонатора
- 8.6. Общая технологическая схема изготовления диодов ПКГ
- 8.7. Конструкция ПКГ
- 8.8. Гетероструктуры на основе арсенида галлия
- 8.9. Другие материалы с прямыми переходами
- Глава девятая. МАТЕРИАЛЫ ГАЗОВЫХ ОКГ
- 9.1. Особенности газового активного вещества ОКГ и методы создания инверсной населенности
- 9.2. Газоразрядные ОКГ
- 9.2.2. Ионные газоразрядные ОКГ
- 9.2.3. Молекулярные газоразрядные ОКГ
- 9.3. Газовые ОКГ с оптической накачкой
- 9.4. Химические ОКГ
- Глава десятая. МАТЕРИАЛЫ МОДУЛЯТОРОВ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ
- 10.1. Некоторые физические основы модуляции оптического излучения
- 10.2. Требования к материалам модуляторов излучения ОКГ
- 10.3. Материалы с линейным электрооптическим эффектом
- 10.3.1. Тетрагональные кристаллы типа KDP
- 10.3.2. Ромбические кристаллы
- 10.3.3. Тригональные кристаллы
- 10.3.4. Кубические кристаллы
- 10.4. Кристаллы с квадратичным электрооптическим эффектом
- Литература