| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
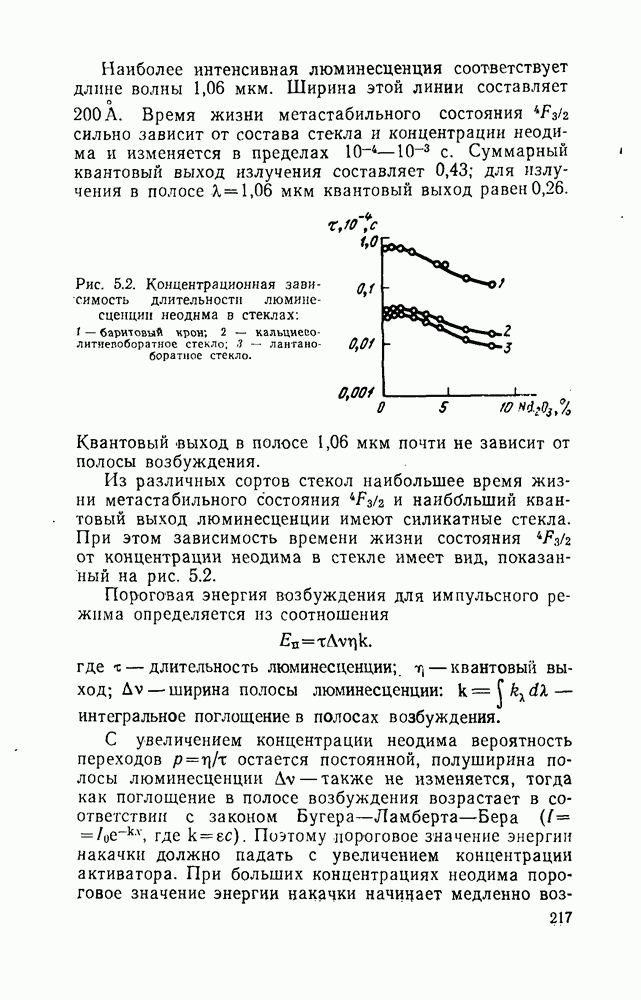
1.5. Инверсная населенность
Если система находится в состоянии термодинамического равновесия с внешней средой, то вероятность того, что какой-либо атом находится на энергетическом уровне  характеризуется множителями
характеризуется множителями  или
или  Если общее число атомов
Если общее число атомов  составляющих систему, то число атомов, населяющих энергетические уровни
составляющих систему, то число атомов, населяющих энергетические уровни  т. е. населенности этих уровней, равно
т. е. населенности этих уровней, равно

Здесь  — статистические веса данных уровней (степени вырождения), т. е. число различных состояний или наборов квантовых чисел для данного энергетического уровня.
— статистические веса данных уровней (степени вырождения), т. е. число различных состояний или наборов квантовых чисел для данного энергетического уровня.
Следовательно, соотношение населенностей этих энергетических уровней определяется выражением

В случае невырожденных состояний, т. е. когда  имеем
имеем

Если  то при термодинамическом равновесии населенность
то при термодинамическом равновесии населенность  и температура, выраженная через отношение населенностей уровней, будет равна
и температура, выраженная через отношение населенностей уровней, будет равна

Согласно второму закону термодинамики система всегда стремится к равновесию, и если какое-либо внешнее воздействие выведет
ее из состояния термодинамического равновесия (например, состояния атомов активатора в рубине после оптической накачки), тогда система путем перераспределения энергии сама перейдет в новое термодинамическое равновесие. Обычно такие процессы, возвращающие систему в состояние равновесия, называются релаксационными. Проанализируем выражение температуры системы через населенности энергетических уровней.
1.  , если
, если  т. е. все атомы находятся в основном в устойчивом состоянии.
т. е. все атомы находятся в основном в устойчивом состоянии.
2.  , если населенность
, если населенность  т. е. низкие энергетические уровни имеют большую населенность, чем высокие. Эти состояния системы приближаются к равновесному состоянию.
т. е. низкие энергетические уровни имеют большую населенность, чем высокие. Эти состояния системы приближаются к равновесному состоянию.
3. Если в результате внешнего воздействия нам удалось перераспределить частицы в системе так, что населенность высоких энергетических уровней стала больше, чем низких, т. е.  то легко убедиться, что этому состоянию отвечает отрицательное значение температуры
то легко убедиться, что этому состоянию отвечает отрицательное значение температуры  Такое состояние системы называется состоянием с инверсной населенностью. Правда, следует учитывать, что при инверсной населенности распределение Больцмана не имеет места, поэтому определение отрицательной температуры можно рассматривать лишь как определение неравновесного состояния.
Такое состояние системы называется состоянием с инверсной населенностью. Правда, следует учитывать, что при инверсной населенности распределение Больцмана не имеет места, поэтому определение отрицательной температуры можно рассматривать лишь как определение неравновесного состояния.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- Глава первая. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ И ПРИНЦИП ДЕЙСТВИЯ КВАНТОВЫХ ГЕНЕРАТОРОВ
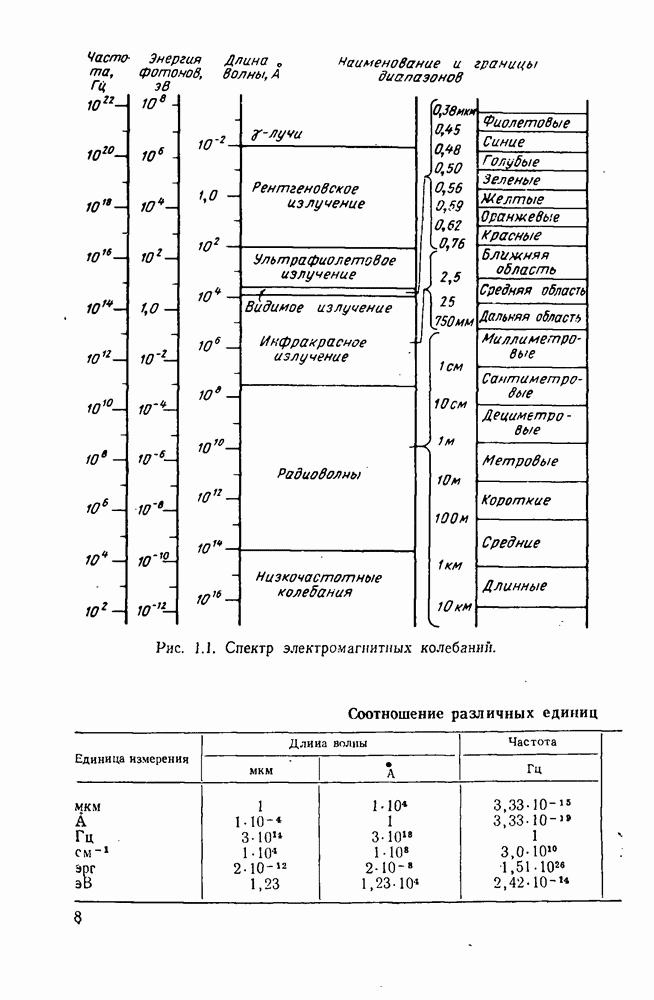
- 1.1. Спектр электромагнитных колебаний
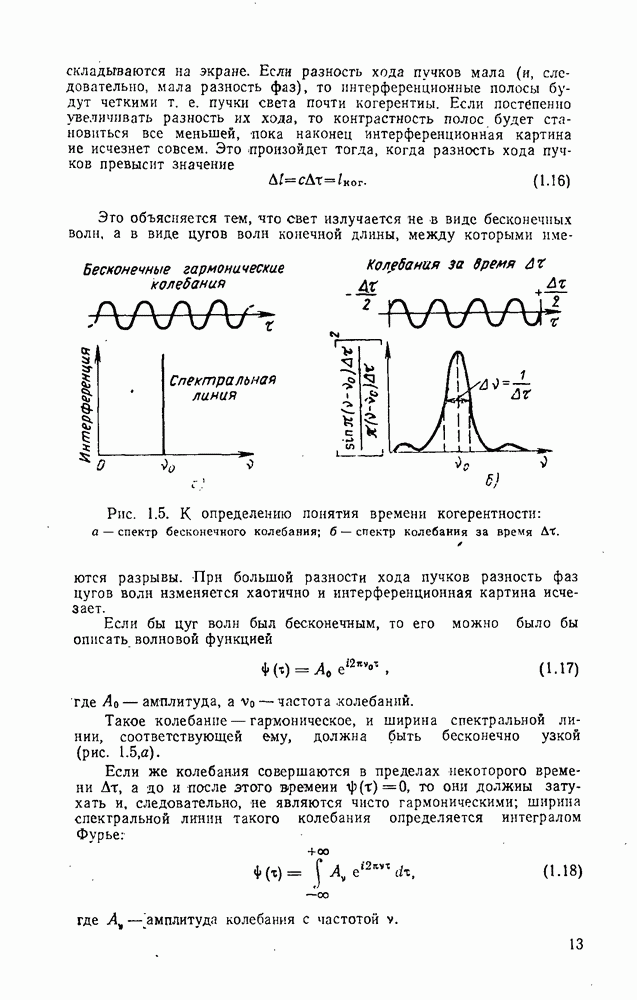
- 1.2. Когерентность
- 1.3. Направленность излучения
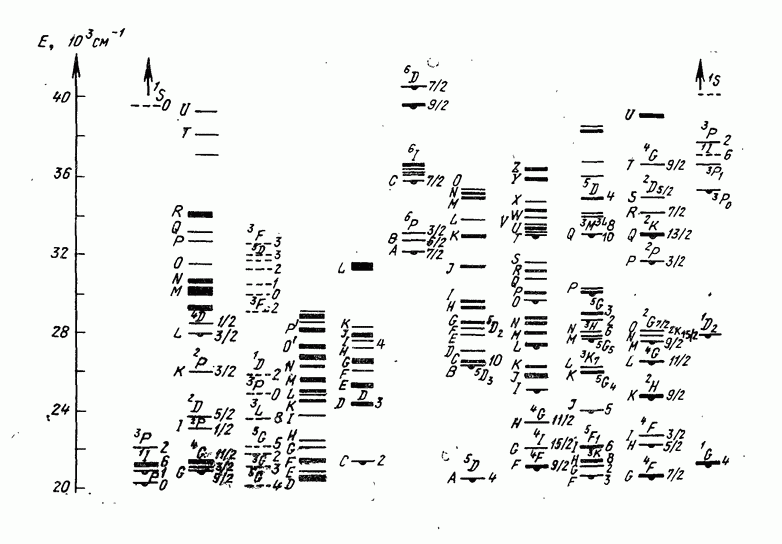
- 1.4. Символика энергетических уровней атомов и ионов
- 1.5. Инверсная населенность
- 1.6. Вероятности спонтанных и вынужденных переходов
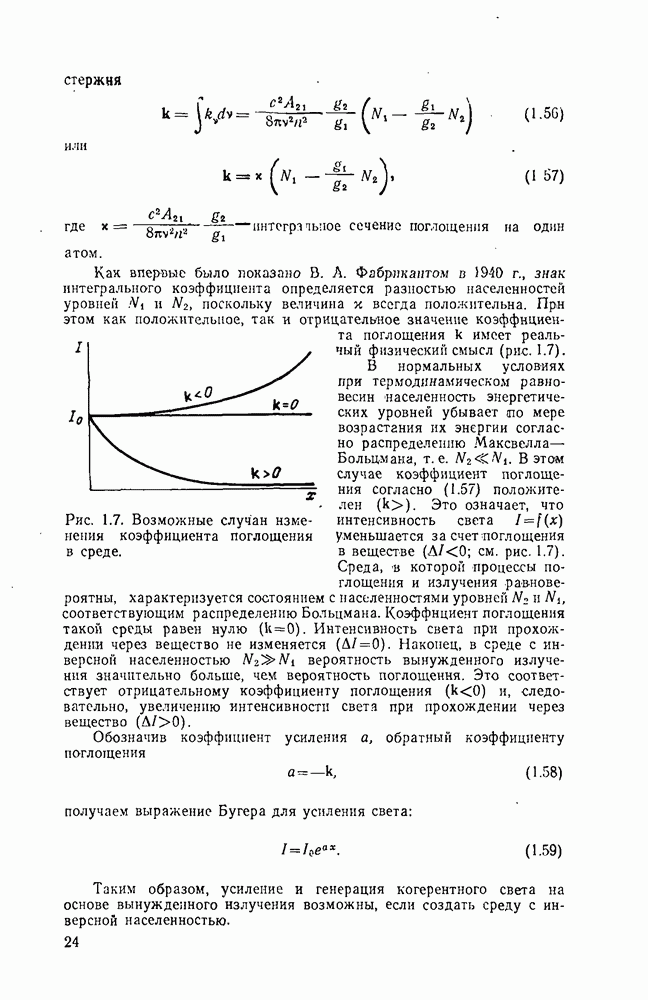
- 1.7. Усиление света при прохождении через вещество
- 1.8. Двухуровневая система
- 1.9. Трехуровневая система
- 1.10. Четырехуровневая система
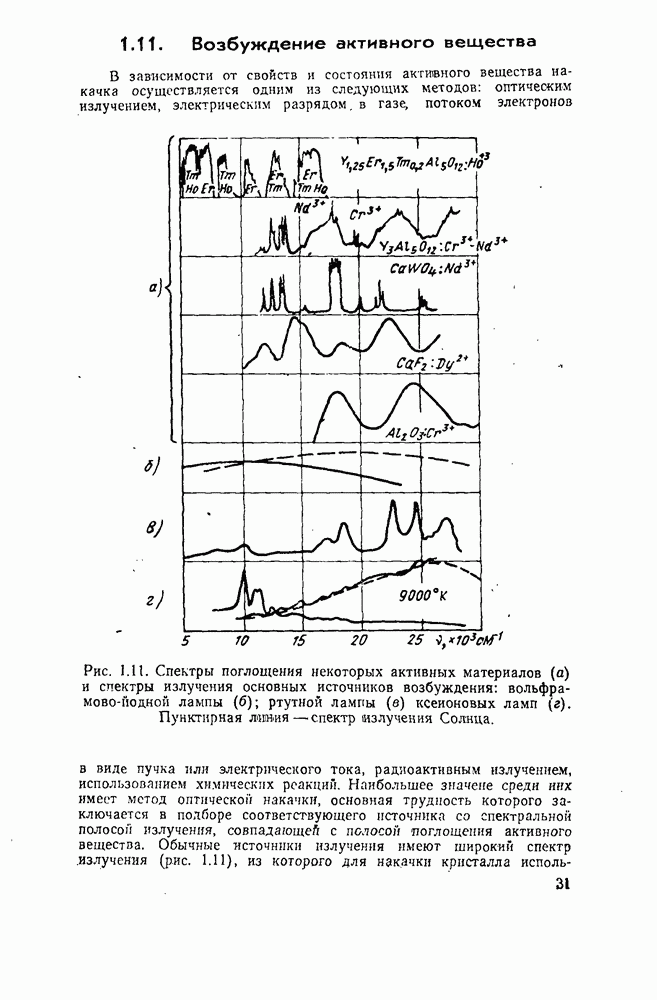
- 1.11. Возбуждение активного вещества
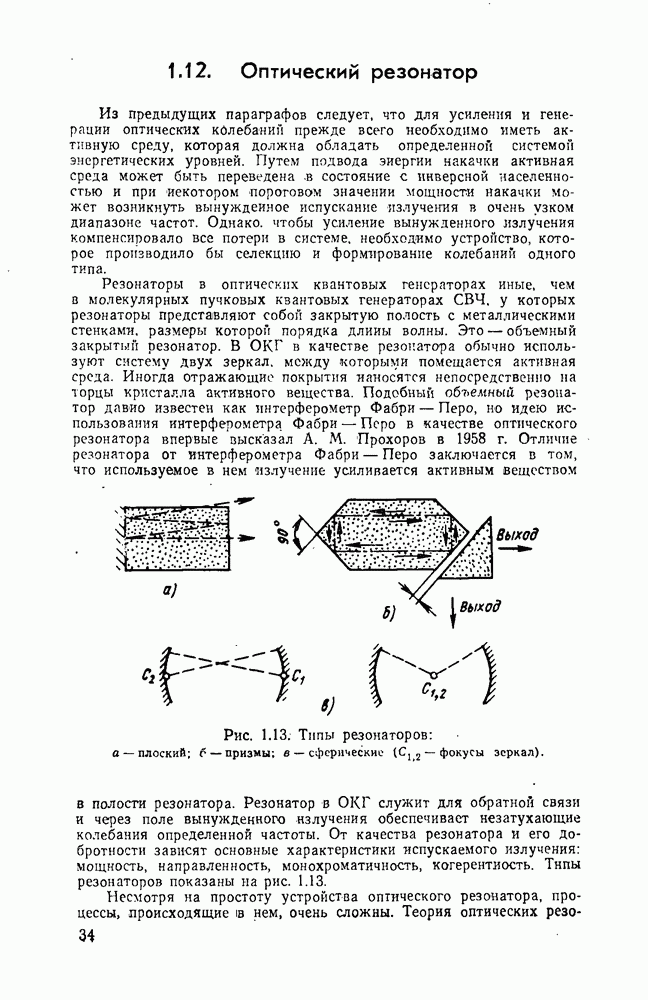
- 1.12. Оптический резонатор
- 1.13 Условие генерации
- 1.14. Потери энергии в квантовом генераторе
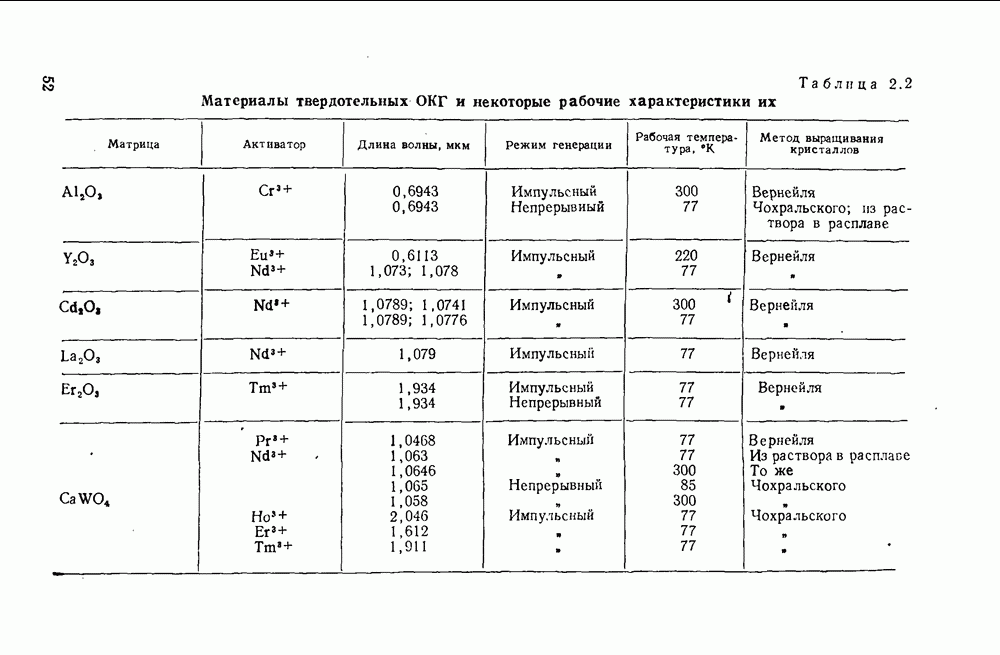
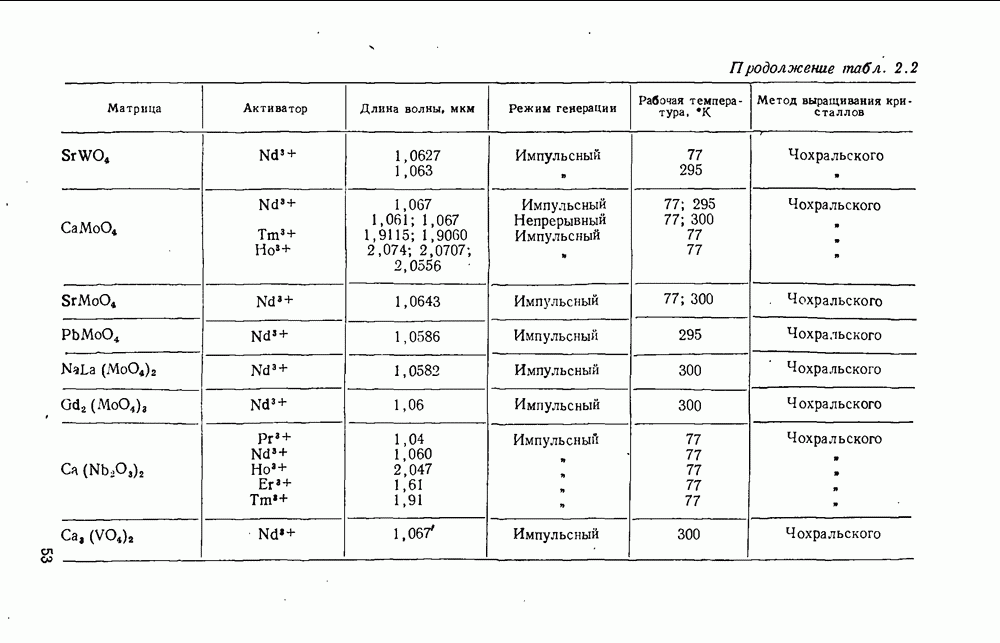
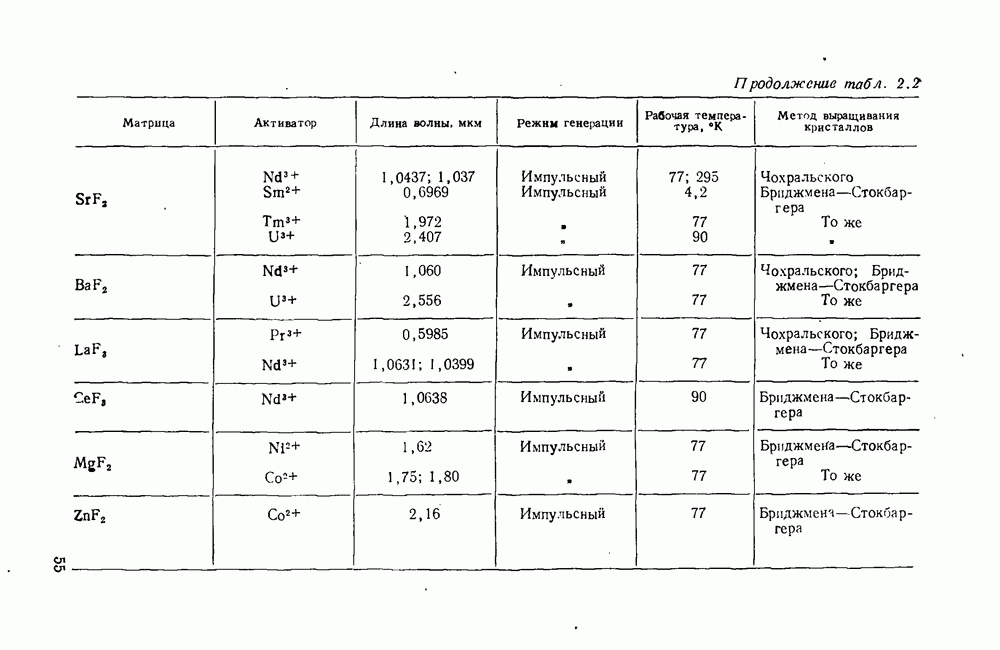
- 1.15. Устройство ОКГ на твердом теле
- Глава вторая. ОБЩИЕ ВОПРОСЫ ТЕХНОЛОГИИ МАТЕРИАЛОВ ТВЕРДОТЕЛЬНЫХ ОКГ
- 2.1. Особенности активного вещества ионных квантовых систем
- 2.2. Особенности технологии твердотельных материалов квантовых генераторов
- 2.3. Физико-химические основы кристаллизации
- 2.3.2. Гетерогенное зародышеобразование
- 2.3.3. Скорость зарождения новой фазы
- 2.3.4. Рост кристаллов
- 2.3.5. Общее кинетическое уравнение кристаллизации
- 2.3.6. Распределение примеси в процессе роста кристалла
- 2.4. Основные методы синтеза и выращивания кристаллов
- 2.4.2. Выращивание из стехиометрических расплавов
- 2.4.3. Методы выращивания кристаллов из растворов
- 2.4.4. Гидротермальный синтез и рост кристаллов
- 2.4.5. Выращивание кристаллов из газовой фазы
- 2.5. Кристалло-химическая классификация материалов твердотельных квантовых генераторов
- Глава третья. КИСЛОРОДНЫЕ СОЕДИНЕНИЯ
- 3.1. Окислы элементов III группы
- 3.1.2. Окислы редкоземельных элементов и иттрия
- 3.3.1. Гранаты
- 3.2. Материалы на основе кислородных соединений элементов VI группы
- 3.2.2. Молибдаты
- 3.3. Материалы на основе кислородных соединений элементов V группы
- 3.3.2. Ниобаты
- 3.3.3. Фосфаты
- Выращивание кристаллов фторфосфата кальция [47]
- Глава четвертая. ФТОРИСТЫЕ СОЕДИНЕНИЯ
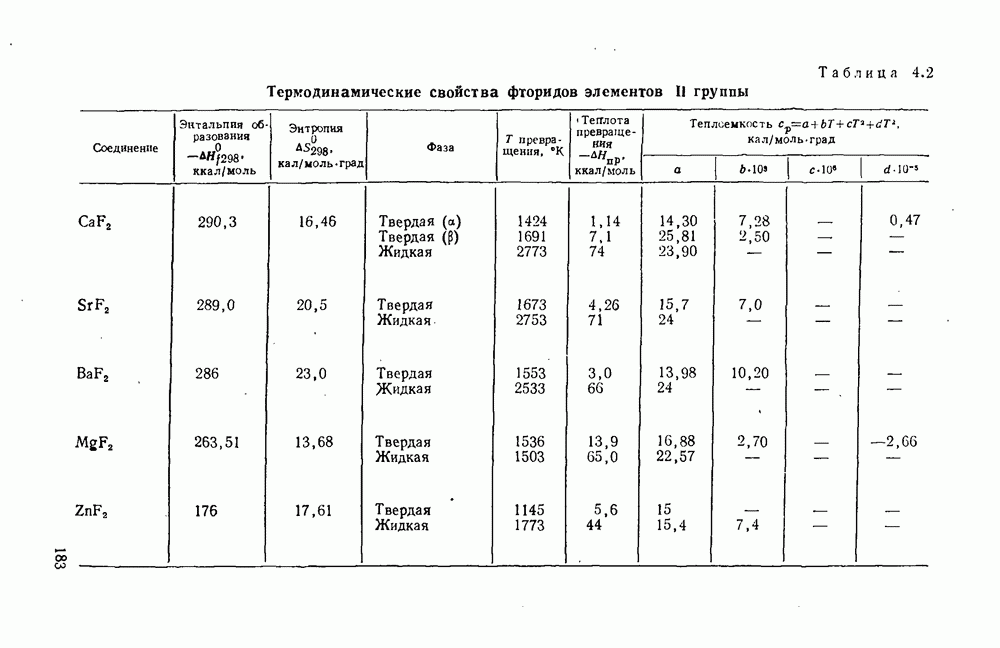
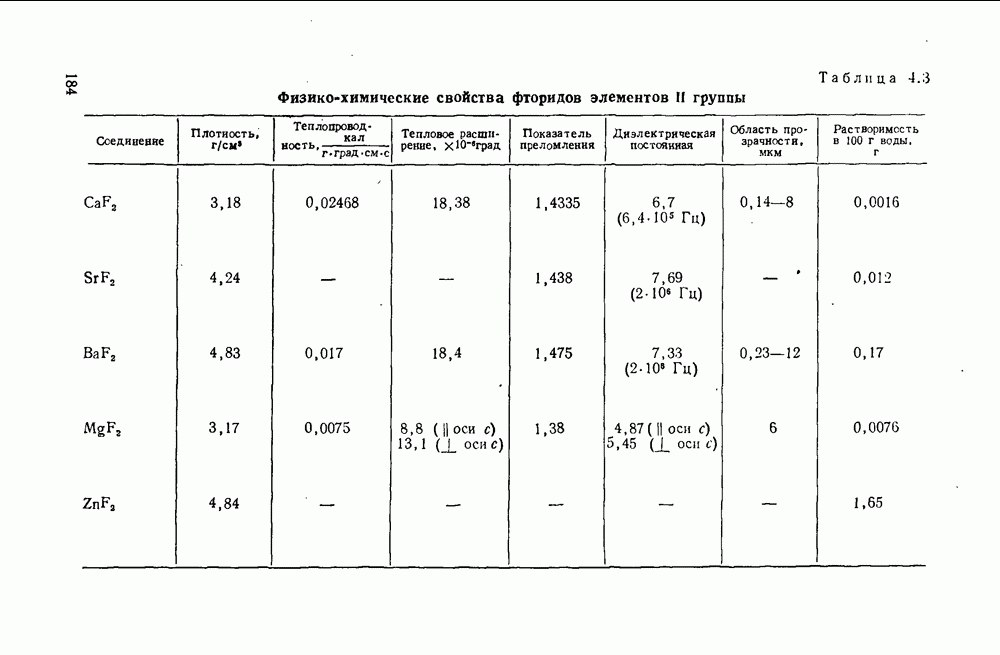
- 4.1. Фториды элементов II группы
- 4.2. Фториды редкоземельных элементов
- 4.3. Смешанные фториды
- 4.4. Фториды элементов VII группы
- Глава пятая. СТЕКЛО
- 5.1. Особенности стекла как активного материала ОКГ
- 5.2. Общая характеристика стекол для ОКГ
- 5.3. Особенности положения атомов активатора в стекле
- 5.4. Стекло с неодимом
- Глава шестая. МАТЕРИАЛЫ ЖИДКОСТНЫХ ОКГ
- 6.2. Механизм излучения в органических растворах
- 6.3. Растворы металлоорганических соединений
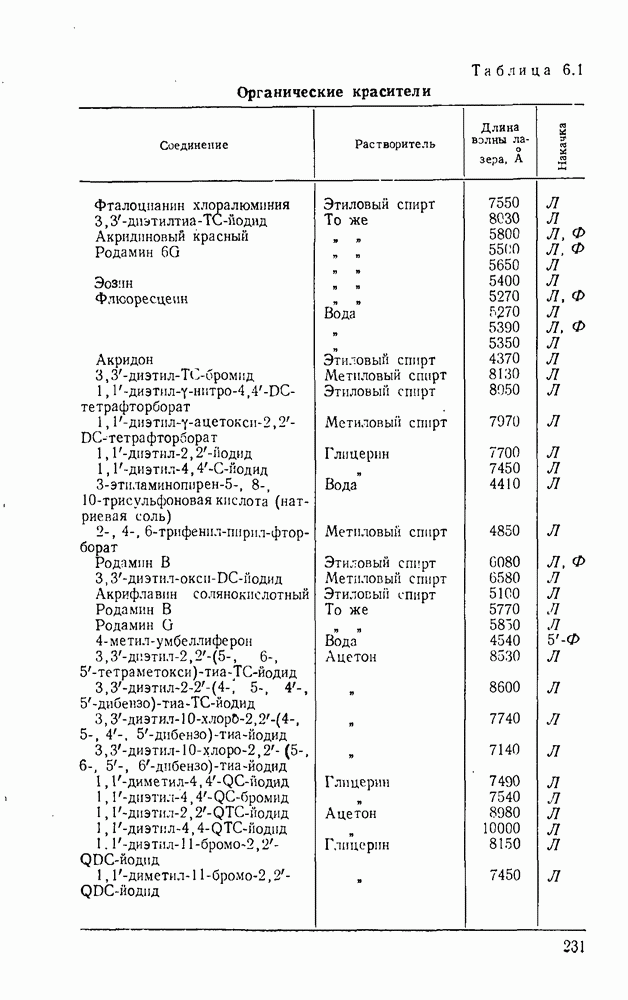
- 6.4. Растворы органических красителей
- 6.5. Растворы неорганических соединений редкоземельных элементов
- Глава седьмая. ОБЩАЯ ХАРАКТЕРИСТИКА ПОЛУПРОВОДНИКОВЫХ КВАНТОВЫХ ГЕНЕРАТОРОВ (ПКГ)
- 7.2. Основные сведения из теории люминесценции инжекционных ПКГ
- 7.3. Рабочие характеристики инжекционных ПКГ
- 7.3.2. Пространственные свойства
- 7.3.3. Пороговый ток
- 7.3.4. Квантовый выход
- 7.4. Тепловые условия работы лазерного диода
- 7.4.2. Работа в квазинепрерывном режиме
- 7.5. Другие типы ПКГ
- 7.5.1. ПКГ с электронным возбуждением
- 7.5.2. ПКГ с оптической накачкой
- 7.5.3. ПКГ с прямым электрическим возбуждением
- Глава восьмая. АРСЕНИД ГАЛЛИЯ И ТЕХНОЛОГИЯ ИЗГОТОВЛЕНИЯ ДИОДОВ ПКГ
- 8.1. Физические свойства арсенида галлия
- 8.2. Методы выращивания монокристаллов арсенида галлия
- 8.3. Методы изготовления р-n-переходов
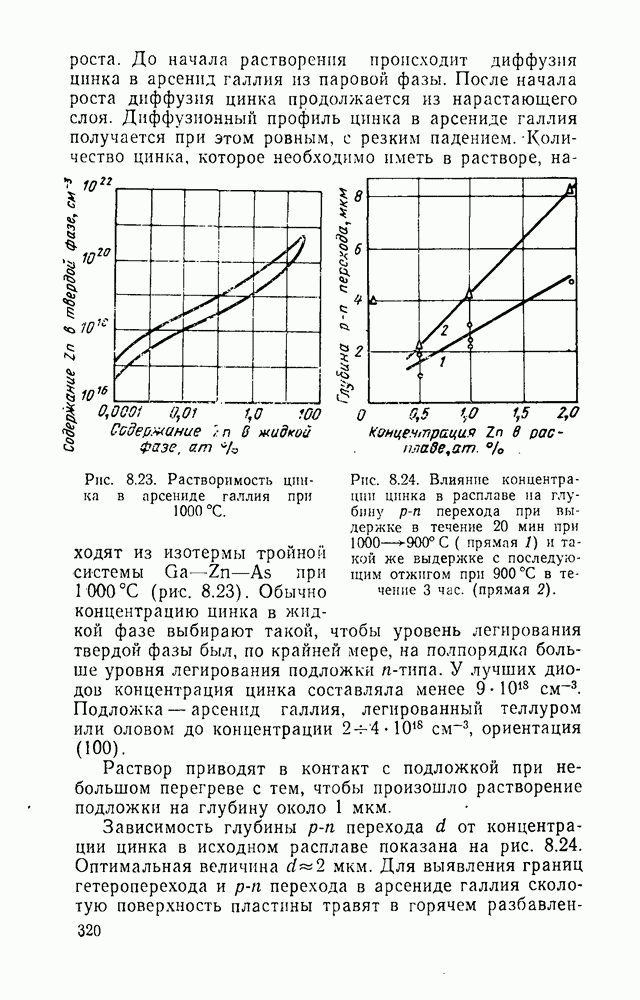
- 8.3.2. Эпитаксия из жидкой фазы
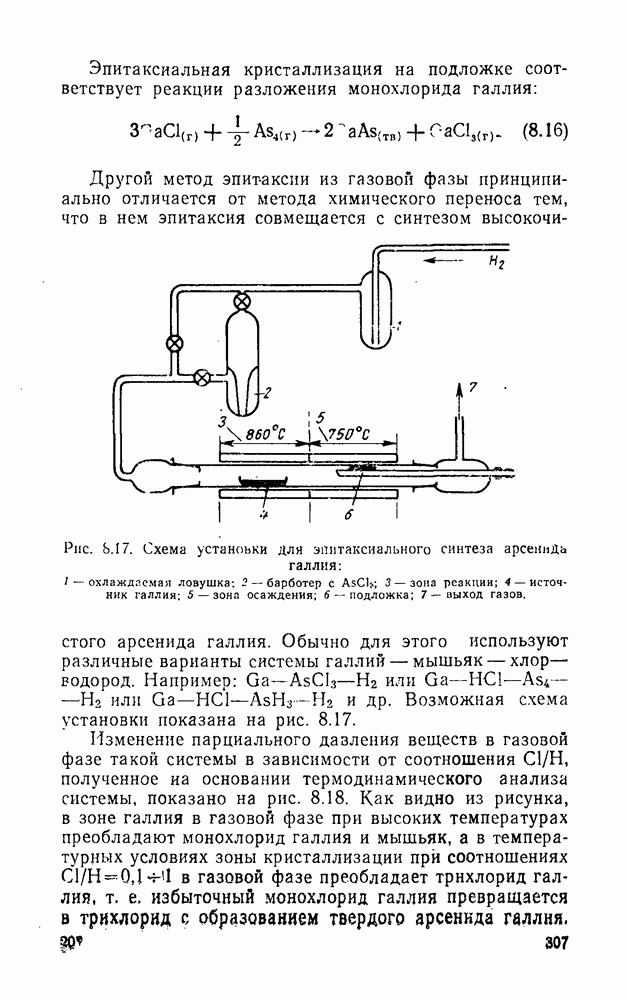
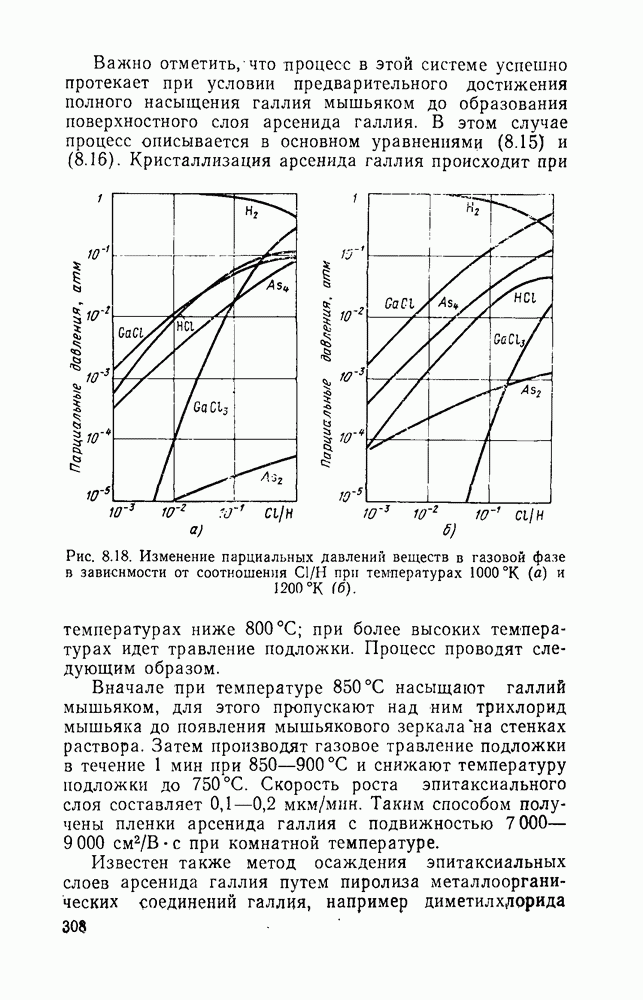
- 8.3.3. Эпитаксия из газовой фазы
- 8.4. Изготовление невыпрямляющих низкоомных контактов к арсениду галлия
- 8.5. Изготовление резонатора
- 8.6. Общая технологическая схема изготовления диодов ПКГ
- 8.7. Конструкция ПКГ
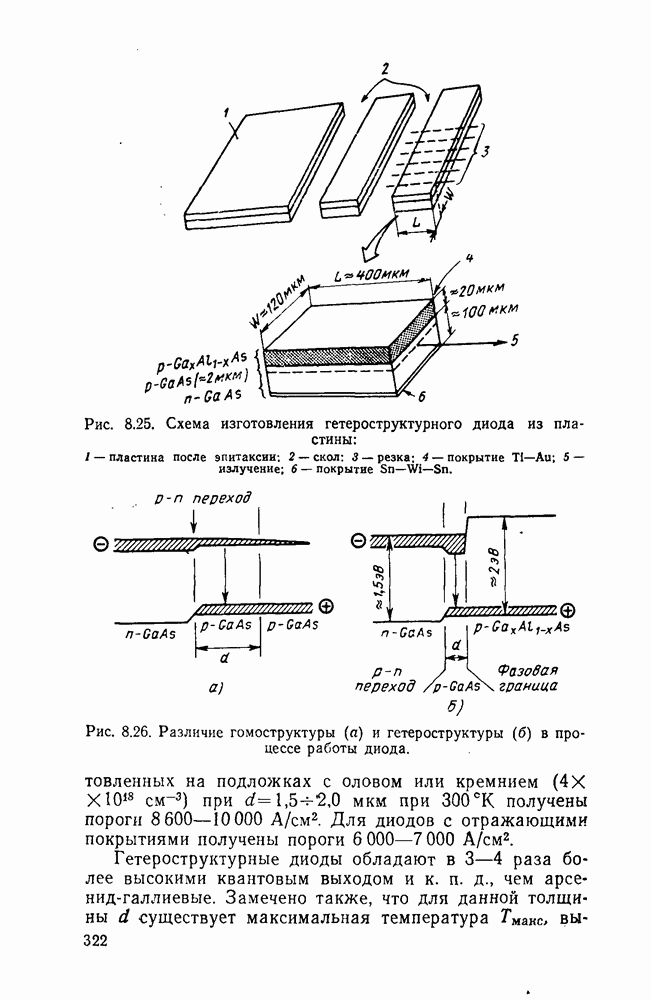
- 8.8. Гетероструктуры на основе арсенида галлия
- 8.9. Другие материалы с прямыми переходами
- Глава девятая. МАТЕРИАЛЫ ГАЗОВЫХ ОКГ
- 9.1. Особенности газового активного вещества ОКГ и методы создания инверсной населенности
- 9.2. Газоразрядные ОКГ
- 9.2.2. Ионные газоразрядные ОКГ
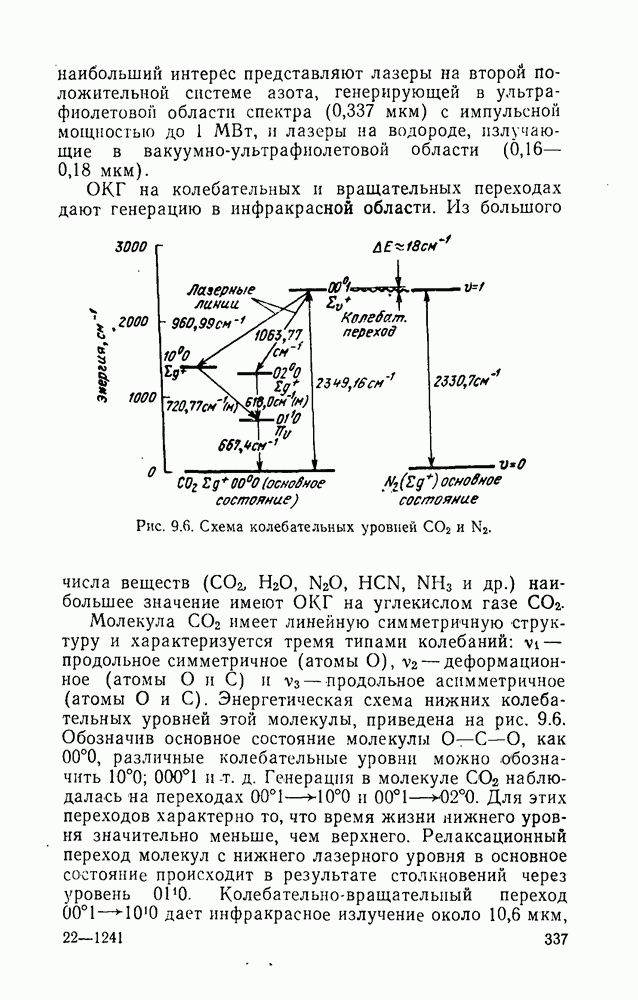
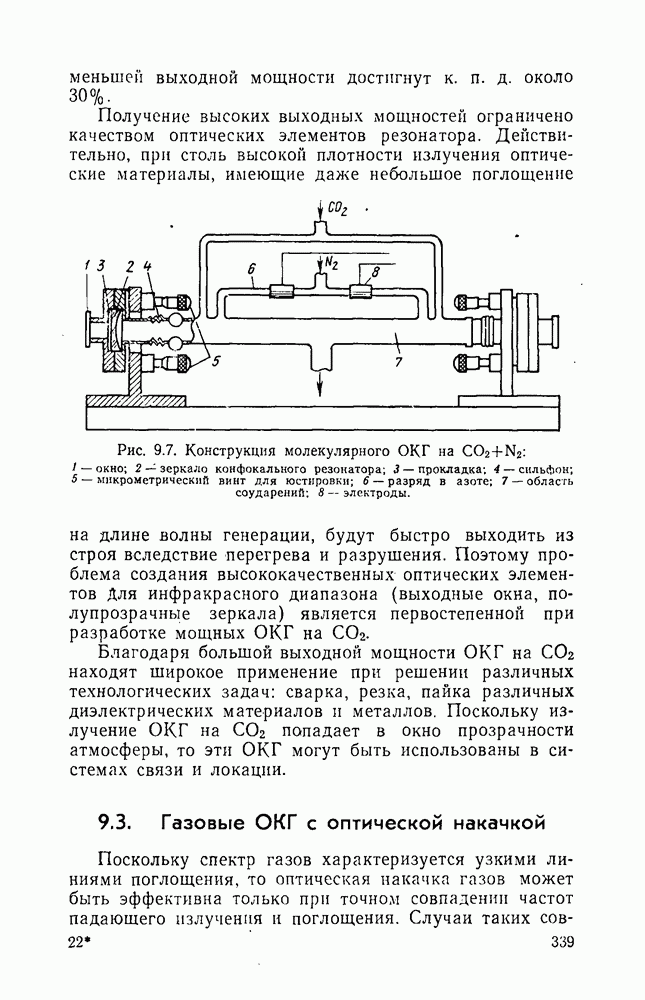
- 9.2.3. Молекулярные газоразрядные ОКГ
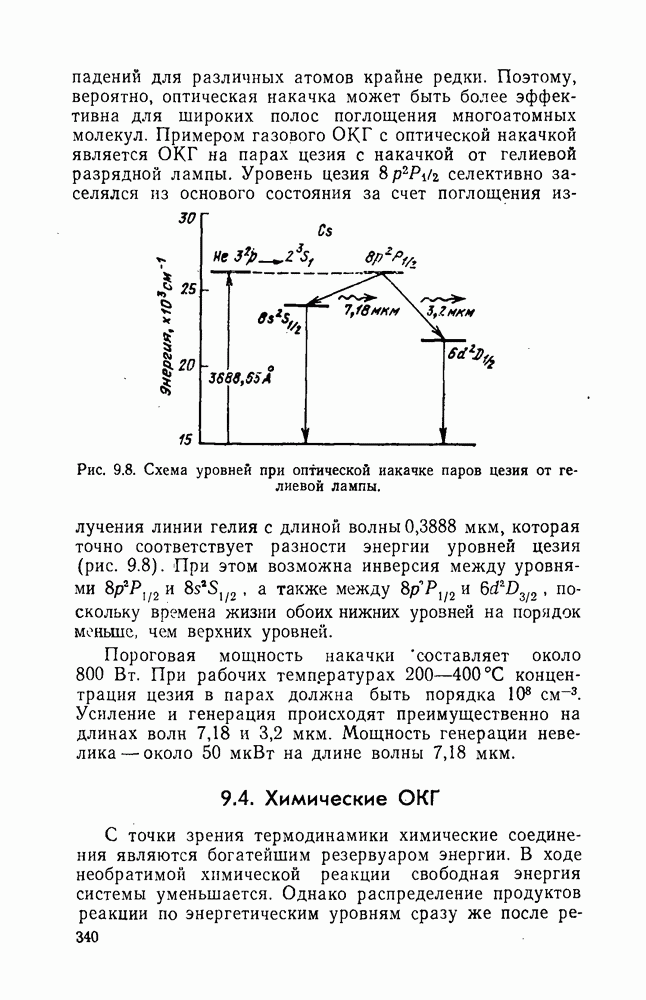
- 9.3. Газовые ОКГ с оптической накачкой
- 9.4. Химические ОКГ
- Глава десятая. МАТЕРИАЛЫ МОДУЛЯТОРОВ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ
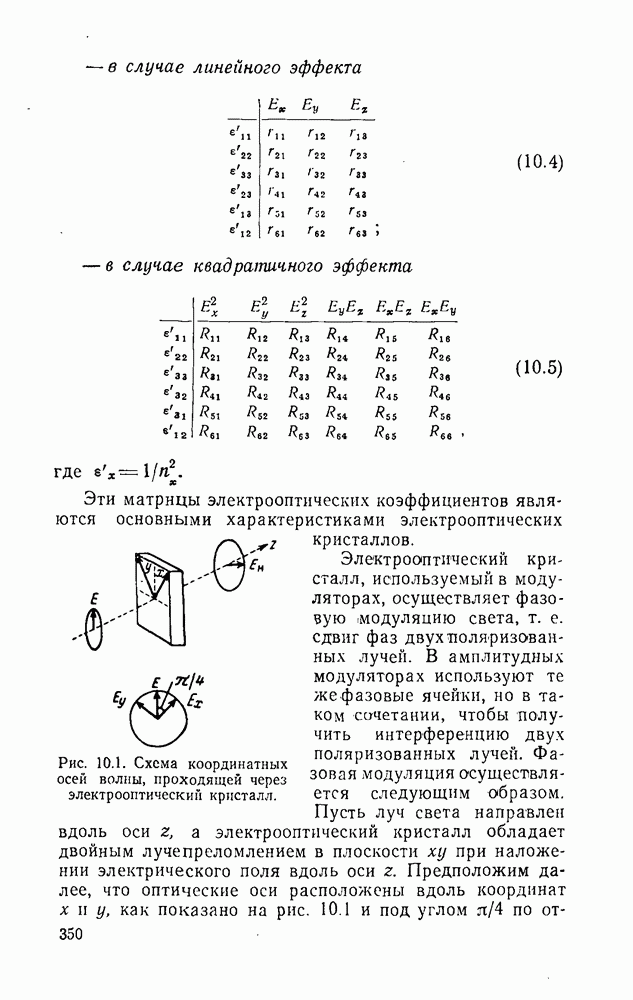
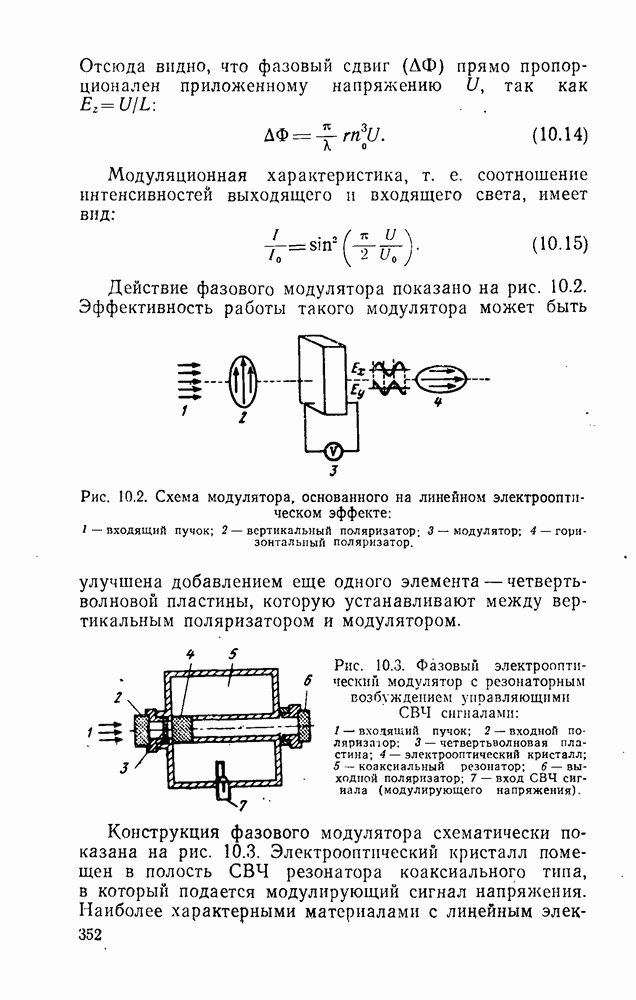
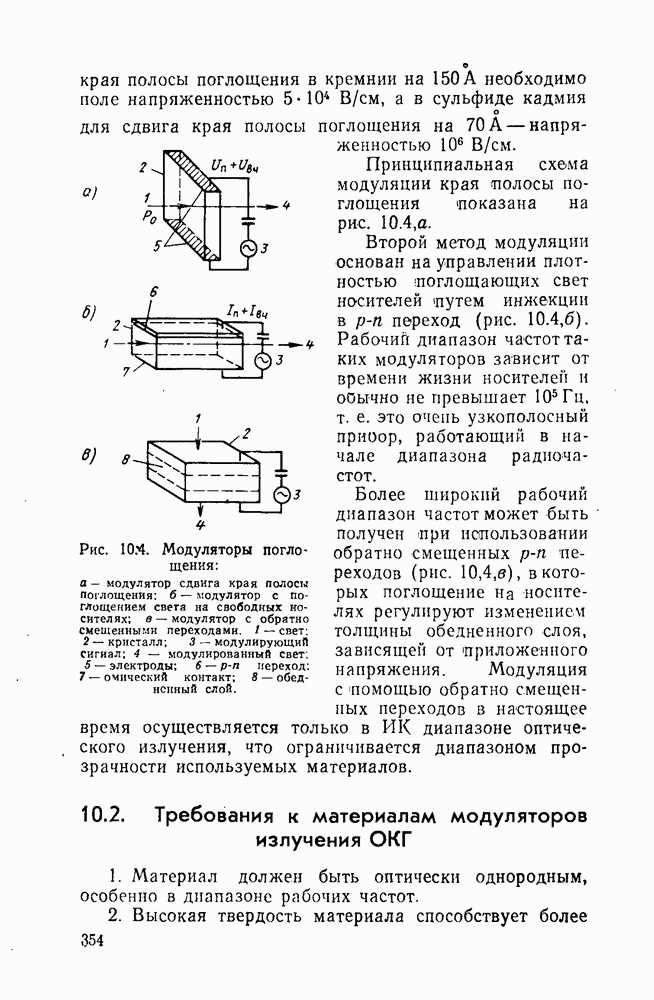
- 10.1. Некоторые физические основы модуляции оптического излучения
- 10.2. Требования к материалам модуляторов излучения ОКГ
- 10.3. Материалы с линейным электрооптическим эффектом
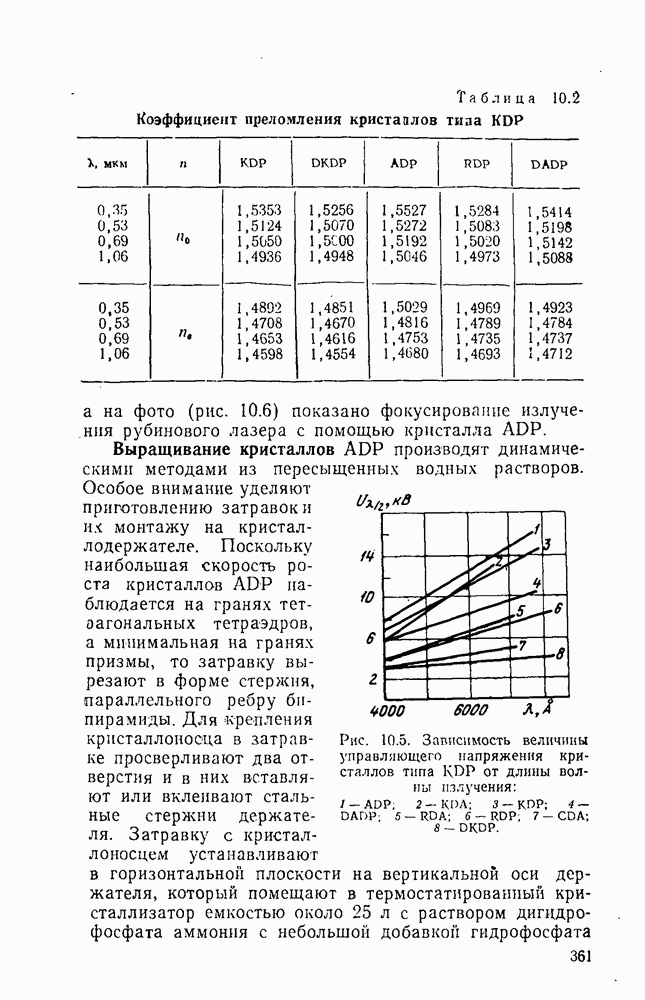
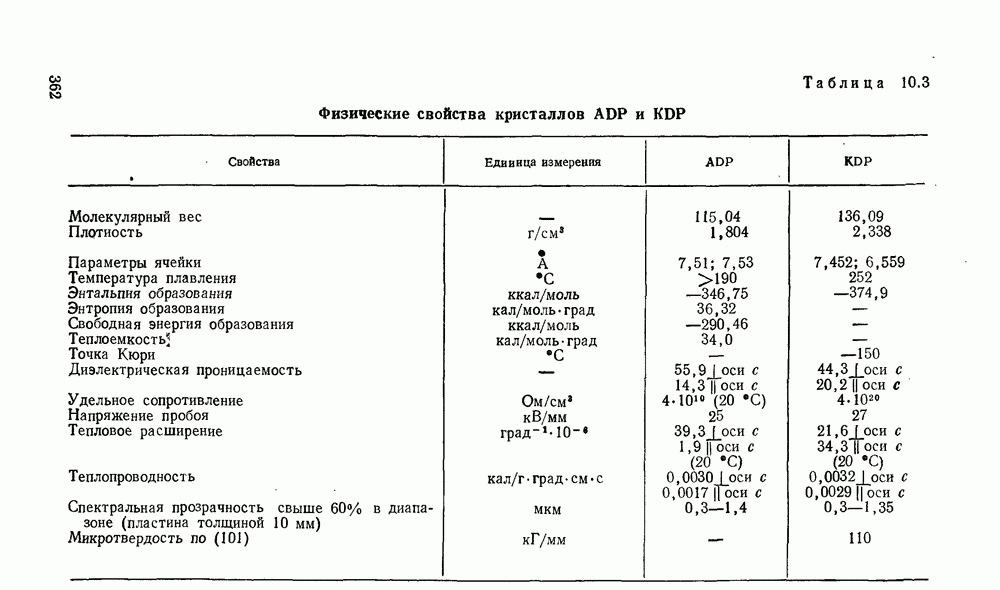
- 10.3.1. Тетрагональные кристаллы типа KDP
- 10.3.2. Ромбические кристаллы
- 10.3.3. Тригональные кристаллы
- 10.3.4. Кубические кристаллы
- 10.4. Кристаллы с квадратичным электрооптическим эффектом
- Литература