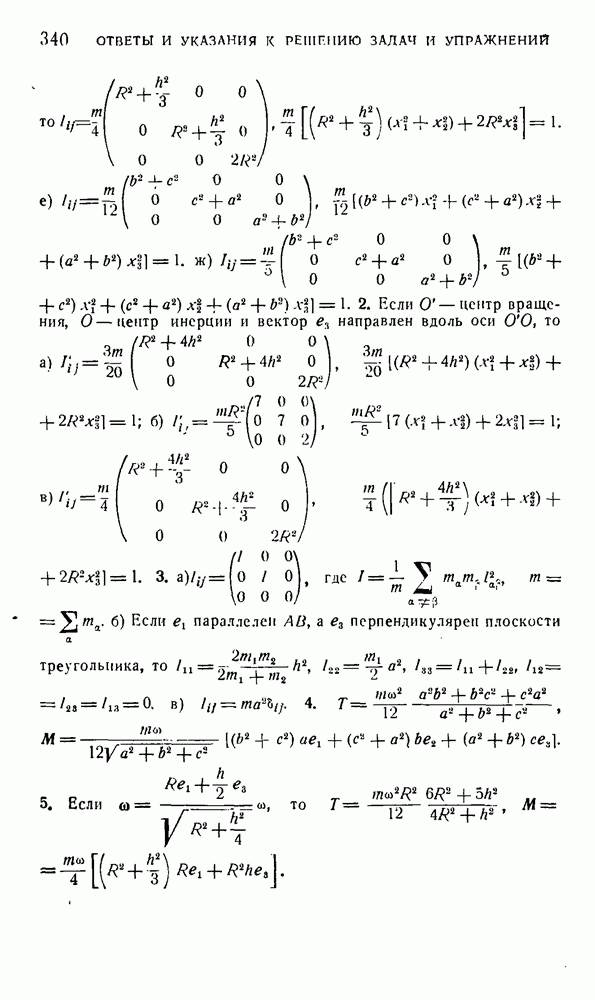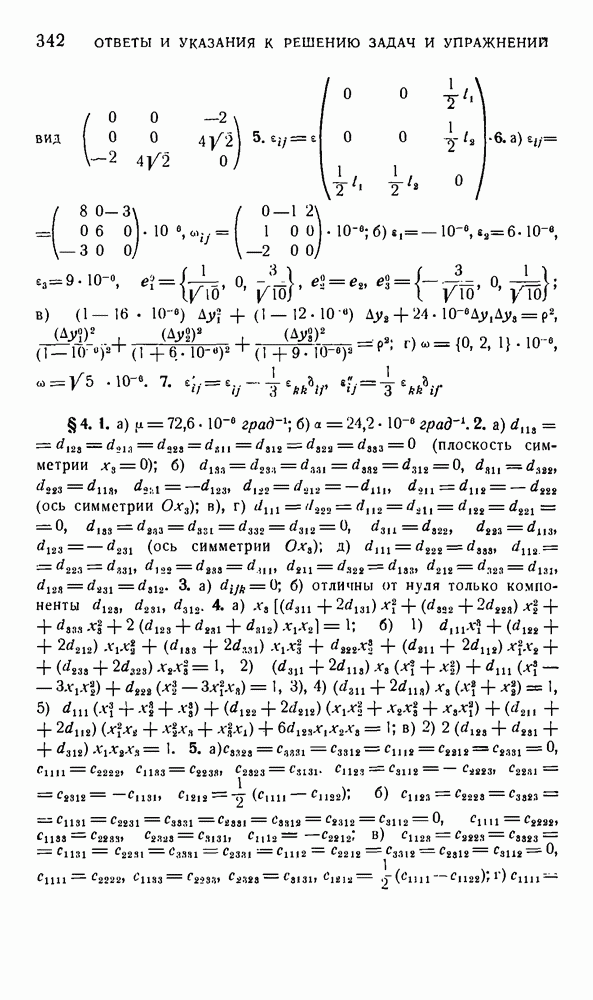| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Линейные преобразования и билинейные формы
1. Пусть х и у — два произвольных вектора линейного пространства  и А — линейное преобразование этого пространства. Пусть
и А — линейное преобразование этого пространства. Пусть  — вектор, получающийся в результате применения преобразования А к вектору у. Образуем скалярное произведение векторов х и u. Тогда выражение
— вектор, получающийся в результате применения преобразования А к вектору у. Образуем скалярное произведение векторов х и u. Тогда выражение

будет скалярной функцией векторных аргументов х и у. Эта скалярная функция, как легко видеть, является билинейной формой. В самом деле,

Докажем теперь, что компоненты тензора второй валентности, определяемого билинейной формой  совпадают, с элементами матрицы лииейного преобразования А. Действительно, если в пространстве
совпадают, с элементами матрицы лииейного преобразования А. Действительно, если в пространстве  задан ортонормировапный базис
задан ортонормировапный базис  то
то

и так как  то
то

где  - матрица линейного преобразования А. Билинейная форма
- матрица линейного преобразования А. Билинейная форма  записывается теперь в виде
записывается теперь в виде

Это выражение показывает, что матрица коэффициентов билинейной формы  совпадает с матрицей
совпадает с матрицей  линейного преобразования А. Но матрица коэффициентов билинейной формы
линейного преобразования А. Но матрица коэффициентов билинейной формы  образует, как мы знаем, тензор валентности два. Следовательно, матрица линейного преобразования А также представляет собой тензор валентности два.
образует, как мы знаем, тензор валентности два. Следовательно, матрица линейного преобразования А также представляет собой тензор валентности два.
Но легко видеть, что и, обратно, всякий тензор валентности два определяет в линейном пространстве  линейное преобразование. В самом деле, пусть
линейное преобразование. В самом деле, пусть  такой тензор и X; — координаты произвольного вектора х пространства. Свернув тензор
такой тензор и X; — координаты произвольного вектора х пространства. Свернув тензор  с вектором х, получим координаты нового вектора и:
с вектором х, получим координаты нового вектора и:

Определенная таким образом вектор-функция, как легко доказать, будет линейной. Следовательно, тензор  определяет в пространстве
определяет в пространстве  линейное преобразование А, матрица которого совпадает с матрицей
линейное преобразование А, матрица которого совпадает с матрицей  составленной из компонент этого тензора.
составленной из компонент этого тензора.
2. В § 4 гл. II (стр. 66) было доказано, что тензоры любой фиксированной валентности  образуют линейное пространство размерности
образуют линейное пространство размерности  . В частности, это относится и к тензорам второй валентности. Поставим в соответствие сумме тензоров
. В частности, это относится и к тензорам второй валентности. Поставим в соответствие сумме тензоров  линейное преобразование С, матрицей которого является тензор
линейное преобразование С, матрицей которого является тензор  . Это преобразование С называется суммой преобразований А к В, матрицами которых служат тензоры
. Это преобразование С называется суммой преобразований А к В, матрицами которых служат тензоры 

Точно так же произведению тензора  на действительное число X поставим в соответствие линейное преобразование
на действительное число X поставим в соответствие линейное преобразование  матрица которого есть тензор
матрица которого есть тензор  Это преобразование называется произведением преобразования А на число X:
Это преобразование называется произведением преобразования А на число X:

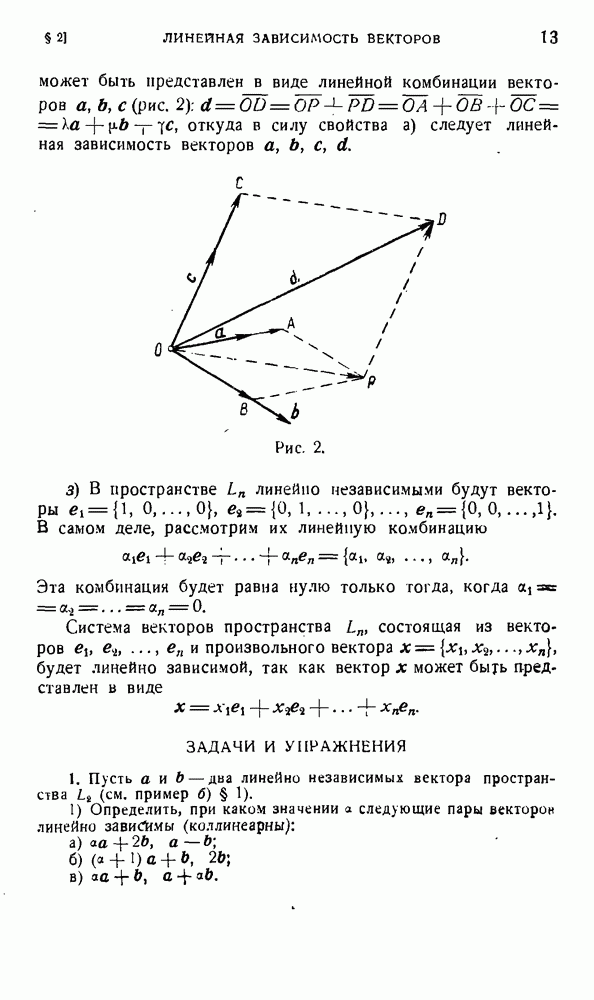
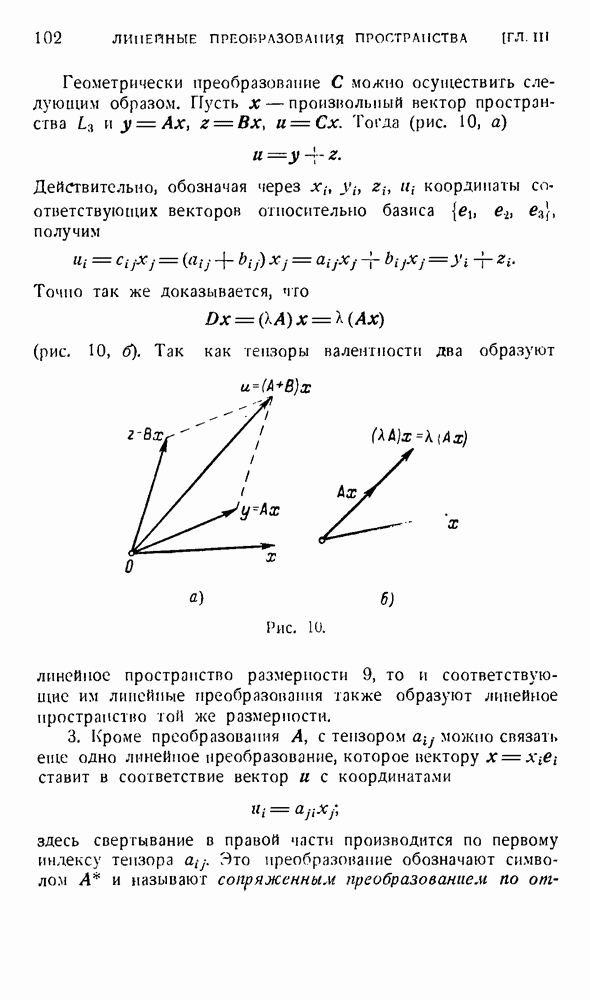
Геометрически преобразование С можно осуществить следующим образом. Пусть  произвольный вектор пространства и
произвольный вектор пространства и  Тогда (рис. 10, а)
Тогда (рис. 10, а)

Действительно, обозначая через  ; координаты соответствующих векторов относительно базиса
; координаты соответствующих векторов относительно базиса  , получим
, получим

Точно так же доказывается, что

(рис. 10, б). Так как тензоры валентности два образуют линейное пространство размерности 9, то и соответствующие им линейные преобразования также образуют линейное пространство той же размерности.

Рис. 10.
3. Кроме преобразования А, с тензором  можно связать еще одно линейное преобразование, которое вектору
можно связать еще одно линейное преобразование, которое вектору  ставит в соответствие вектор и с координатами
ставит в соответствие вектор и с координатами

здесь свертывание в правой части производится по первому индексу тензора  Это преобразование обозначают символом А и называют сопряженным преобразованием по
Это преобразование обозначают символом А и называют сопряженным преобразованием по
отношению к преобразованию А. Если положить  то линейное преобразование А запишется в виде
то линейное преобразование А запишется в виде

Следовательно, матрицей преобразования А служит матрица  получающаяся из матрицы А путем замены ее строк столбцами; такая операция называется операцией транспонирования матрицы А.
получающаяся из матрицы А путем замены ее строк столбцами; такая операция называется операцией транспонирования матрицы А.
Рассмотрим теперь произвольную билинейную форму  . В ортонормированном базисе
. В ортонормированном базисе  эта форма записывается в виде
эта форма записывается в виде

Пусть А — линейное преобразование, матрица которого совпадает с матрицей  этой билинейной формы. Тогда форма
этой билинейной формы. Тогда форма  может быть записана в виде
может быть записана в виде

По можно провести другую группировку членов в билинейной форме  и записать ее так:
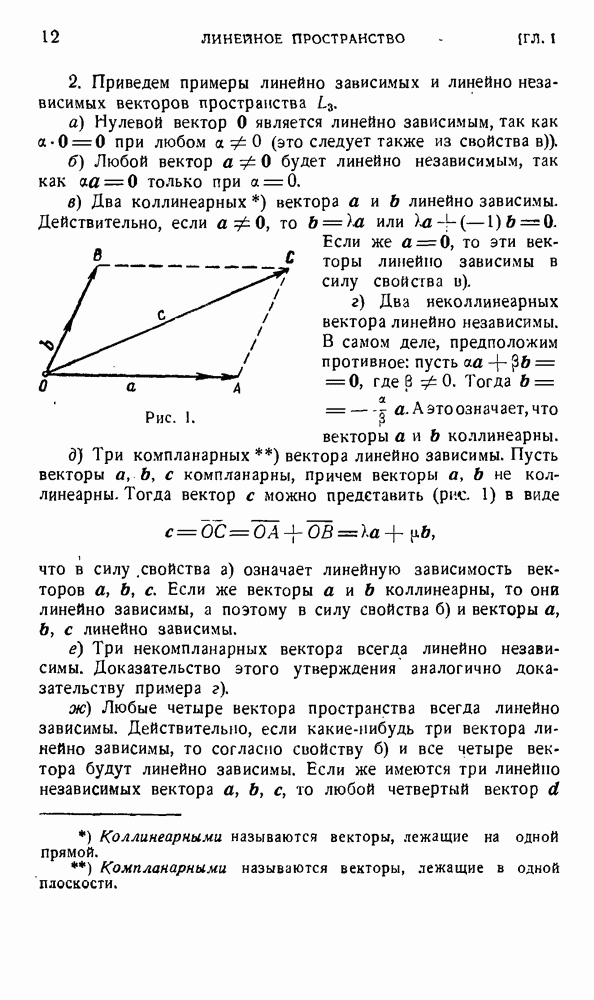
и записать ее так:

Вектор и с координатами  получается из вектора
получается из вектора  при помощи преобразования А. Поэтому билинейная форма с может быть записана и так:
при помощи преобразования А. Поэтому билинейная форма с может быть записана и так:

Сравнивая два полученных выше выражения для формы  находим, что
находим, что

4. Лииейное преобразование А называется симметричным, если оно совпадает с преобразованием А, сопряженным по отношению к А.
Докажем, что для того, чтобы линейное преобразование А было симметричным, необходимо и достаточно, чтобы связанная с ним билинейная форма  была симметричной.
была симметричной.
Пусть  Тогда
Тогда

что и означает симметрию формы 
Пусть, обратно, форма  симметрична. Это означает, что
симметрична. Это означает, что  т. е.
т. е.

Сравнивая полученное равенство с соотношением (1), найдем, что

Так как это равенство должно выполняться для любого вектора у, то

А так как последнее равенство должно выполняться для любого вектора х, то  .
.
Из доказанного предложения следует, что матрица симметричного преобразования является симметричной, т. е. удовлетворяет условию  . В самом деле, ведь этим свойством обладает тензор, определяемый симметричной билинейной формой.
. В самом деле, ведь этим свойством обладает тензор, определяемый симметричной билинейной формой.
Далее, из того же предложения следует также, что между симметричными линейными преобразованиями и квадратичными формами существует взаимно однозначное соответствие, а именно: симметричному линейному преобразованию А с матрицей  соответствует квадратичная форма
соответствует квадратичная форма

которая теперь может быть записана в виде

Обратно, квадратичной форме  соответствует симметричное линейное преобразование с матрицей
соответствует симметричное линейное преобразование с матрицей 
Рассмотрим характеристическую поверхность тензора, соответствующую симметричному линейному преобразованию А. Уравнение этой поверхности, записанное раньше (гл. II, стр. 79) в виде

может быть переписано так:

Эту поверхность называют также характеристической поверхностью симметричного линейного преобразования А.
Докажем теперь, что вектор и  имеет направление нормали к характеристической поверхности симметричного линейного преобразования А, проведенной в той ее точке М, для которой ее к тор
имеет направление нормали к характеристической поверхности симметричного линейного преобразования А, проведенной в той ее точке М, для которой ее к тор  коллинеарен ректору х (рис. 11). В самом деле, вектор нормали к поверхности, заданной в декартовой прямоугольной системе координат уравнением
коллинеарен ректору х (рис. 11). В самом деле, вектор нормали к поверхности, заданной в декартовой прямоугольной системе координат уравнением  имеет своими координатами величины
имеет своими координатами величины  так что
так что  Но
Но 

и

что и доказывает наше утверждение.

Рис. 11.
5. Линейное преобразование А называется антисимметричным, если

Аналогично тому, как это было сделано для симметричного преобразования, можно доказать, что билинейная форма, соответствующая антисимметричному преобразованию, будет антисимметричной, и обратно. Отсюда непосредственно следует, что матрица антисимметричного линейного преобразования антисимметрична, т. е. удовлетворяет условию

и, в частности, 
Рассмотрим теперь вектор  где
где

Подставляя сюда значения компонент дискриминантного тензора (стр. 26), получим, что

где нелпчмна  равна
равна  в правой и
в правой и  в левой системе координат. Поэтому матрица антисимметричного преобразования может быть записана так:
в левой системе координат. Поэтому матрица антисимметричного преобразования может быть записана так:

Докажем теперь, что антисимметричное линейное преобразование А может быть представлено в виде

В самом деле, если  то
то

Но выражения, стоящие в правой части этих формул, в точности совпадают с координатами векторного произведения векторов  (гл. I, стр. 27).
(гл. I, стр. 27).
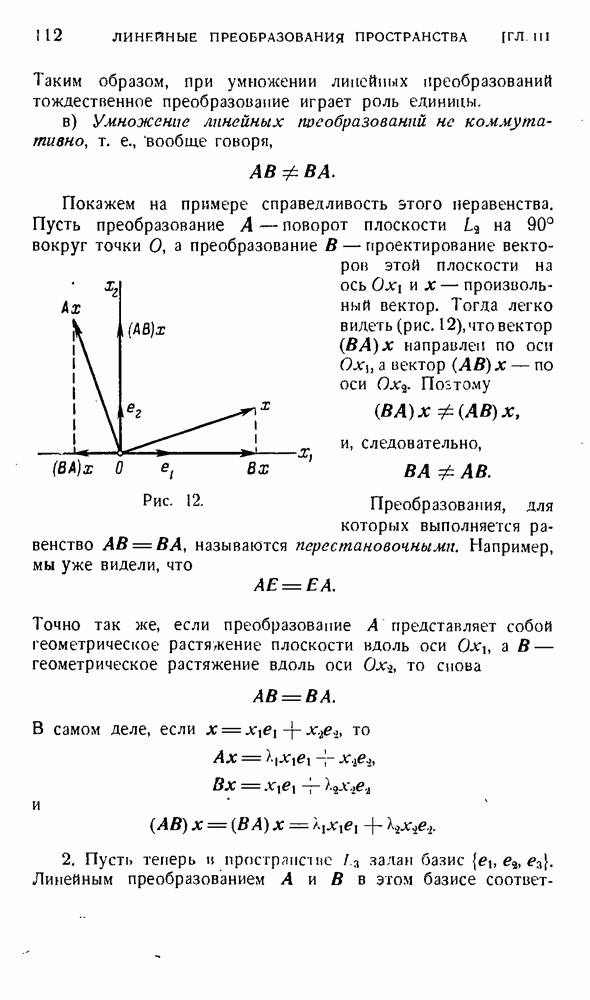
6. Найдем билинейные формы, соответствующие некоторым из линейных преобразований рассмотренных в предыдущих параграфах этой главы.
а) Тождественному преобразованию  будет соответствовать билинейная форма
будет соответствовать билинейная форма

совпадающая со скалярным произведением векторов х и у. Так как эта форма симметрична, то Е — симметричное линейное преобразование. Соответствующая ему квадратичная форма имеет вид

Поэтому его характеристической поверхностью будет единичная сфера 
б) Преобразованию гомотетии  соответсгнует билинейная форма
соответсгнует билинейная форма

только множителем X отличающаяся от предыдущей. Эта форма симметрична, так же как и преобразование гомотетии. Матрица билинейной формы  и соответствующего ей преобразования гомотетии имеет вид
и соответствующего ей преобразования гомотетии имеет вид  . Определяемый этой матрицей тензор иногда называют шаровым. Квадратичная форма, соответствующая преобразованию гомотетии, записывается в виде
. Определяемый этой матрицей тензор иногда называют шаровым. Квадратичная форма, соответствующая преобразованию гомотетии, записывается в виде

Его характеристической поверхностью будет сфера  радиуса
радиуса  Заметим, что коэффициент гомотетии X может быть и отрицательным. В этом случае характеристической поверхностью будет сфера «мнимого» радиуса.
Заметим, что коэффициент гомотетии X может быть и отрицательным. В этом случае характеристической поверхностью будет сфера «мнимого» радиуса.
в) Преобразованию А, которое ставит в соответствие вектору  вектор и
вектор и  , соответствует билинейная форма
, соответствует билинейная форма  Эта форма является симметричной. Таким же будет и преобразование А. Его матрицей является диагональная матрица (пример и) § 2), которая, конечно, симметрична. Квадратичная форма, соответствующая этому преобразованию, записывается в виде
Эта форма является симметричной. Таким же будет и преобразование А. Его матрицей является диагональная матрица (пример и) § 2), которая, конечно, симметрична. Квадратичная форма, соответствующая этому преобразованию, записывается в виде

а ее характеристическая поверхность имеет уравнение

Полученное уравнение определяет центральную поверхность второго порядка, для которой координатные оси являются осями симметрии, Если  коэффициенты растяжения
коэффициенты растяжения  положительны, то эта поверхность будет эллипсоидом. Если два из чисел
положительны, то эта поверхность будет эллипсоидом. Если два из чисел  положительны, а одно отрицательно, то характеристической поверхностью будет однополостныи гиперболоид. Если одно из чисел
положительны, а одно отрицательно, то характеристической поверхностью будет однополостныи гиперболоид. Если одно из чисел  положительно, а два отрицательны, то характеристическая поверхность является двуполостным гиперболоидом. И, наконец, если все числа Х? отрицательны, то характеристическая поверхность будет мнимым эллипсоидом, Если два какие-либо значения
положительно, а два отрицательны, то характеристическая поверхность является двуполостным гиперболоидом. И, наконец, если все числа Х? отрицательны, то характеристическая поверхность будет мнимым эллипсоидом, Если два какие-либо значения  одинаковы, то характеристическая поверхность становится
одинаковы, то характеристическая поверхность становится
поверхностью вращения. Если  то характеристическая поверхность становится сферой.
то характеристическая поверхность становится сферой.
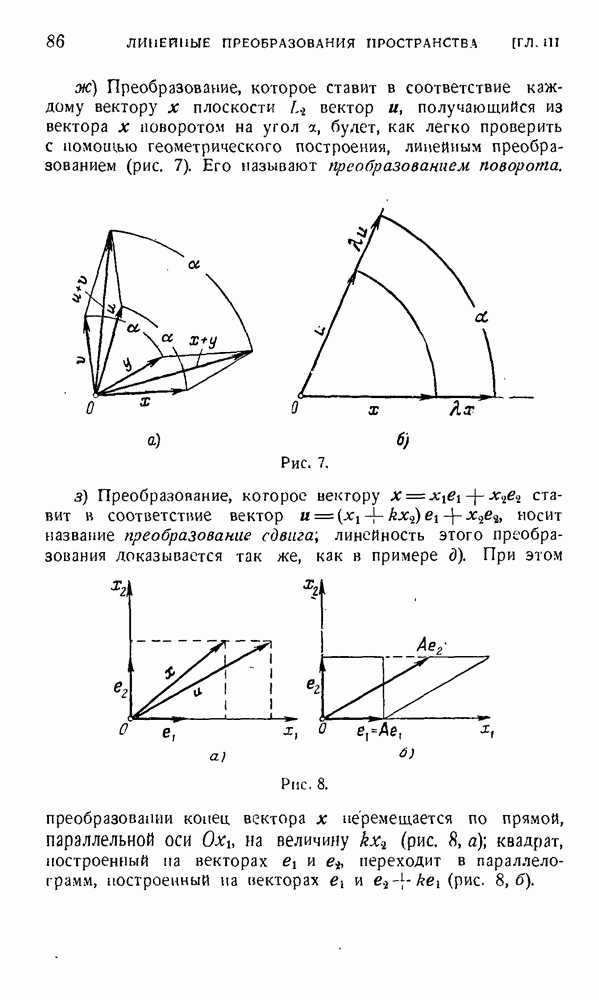
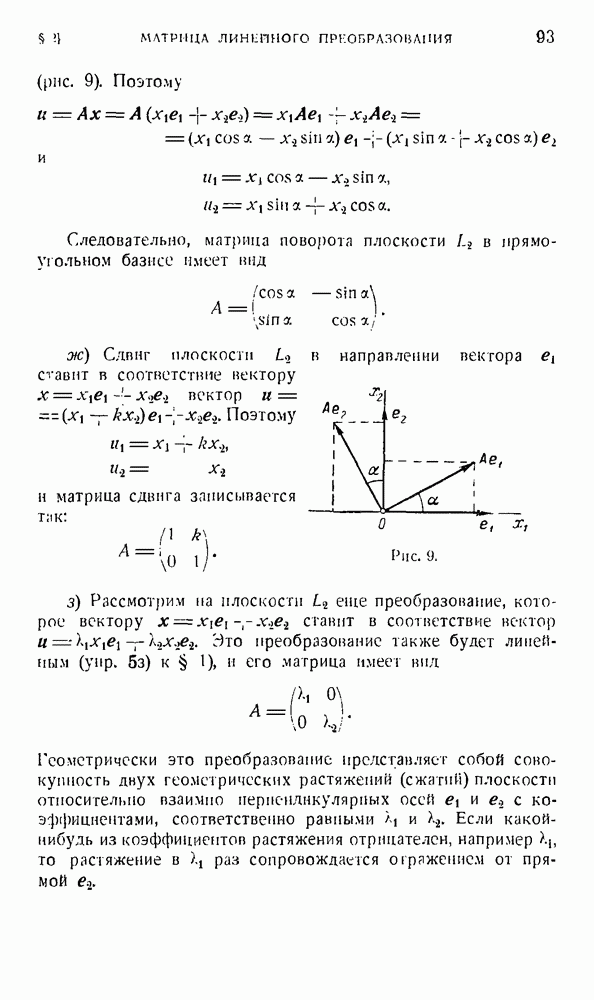
г) Преобразование поворота плоскости  вокруг точки О на угол а определяется тензором, матрица которого, как мы видели на стр. 93, имеет вид
вокруг точки О на угол а определяется тензором, матрица которого, как мы видели на стр. 93, имеет вид

Билинейная форма, соответствующая этому преобразованию, запишется так:

или

Эта билииейная форма уже не является симметричной. Поэтому преобразование А, сопряженное преобразованию А, не совпадает с А. Его матрица имеет вид

Геометрически преобразование А означает поворот вокруг точки О на угол —а,
б) Преобразование сдвига плоскости  в направлении вектора
в направлении вектора  определяется тензором, матрица которого имеет вид (§ 2, пример
определяется тензором, матрица которого имеет вид (§ 2, пример 

Это преобразование не является симметричным, как и соответствующая ему билинейная форма

Преобразование А, сопряженное преобразованию А, будет  иметь матрицу
иметь матрицу

Геометрически преобразование А также представляет собой сдвиг, но теперь уже в направлении вектора 
Так как преобразования, рассмотренные в двух последних примерах, не являются симметричными, то для них не имеет смысла строить характеристические поверхности.
ЗАДАЧИ И УПРАЖНЕНИЯ
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ЛИНЕЙНОЕ ПРОСТРАНСТВО
- § 1. Понятие линейного пространства
- § 2. Линейная зависимость векторов
- § 3. Размерность и базис линейного пространства
- § 4. Прямоугольный базис в трехмерном пространстве. Скалярное произведение векторов
- § 5. Векторное и смешанное произведения векторов
- § 6. Преобразования ортонормированного базиса. Основная задача тензорного исчисления
- § 7. Некоторые вопросы аналитической геометрии в пространстве
- ГЛАВА II. ПОЛИЛИНЕЙНЫЕ ФОРМЫ И ТЕНЗОРЫ
- § 2. Билинейные формы
- § 3. Полилинейные формы. Общее определение тензора
- § 4. Алгебраические операции над тензорами
- § 5. Симметричные и антисимметричные тензоры
- ГЛАВА III. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ ВЕКТОРНОГО ПРОСТРАНСТВА И ТЕНЗОРЫ ВТОРОЙ ВАЛЕНТНОСТИ
- § 2. Матрица линейного преобразования
- § 3. Определитель матрицы линейного преобразования. Ранг матрицы
- § 4. Линейные преобразования и билинейные формы
- § 5. Умножение линейных преобразований и умножение матриц
- § 6. Обратное линейное преобразование и обратная матрица
- § 7. Группа линейных преобразований и ее подгруппы
- ГЛАВА XIV. ПРИВЕДЕНИЕ К ПРОСТЕЙШЕМУ ВИДУ МАТРИЦЫ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- § 1. Собственные векторы и собственные значения линейного преобразования
- § 2. Приведение к простейшему виду матрицы линейного преобразования в случае различных собственных значений
- § 3. Многочлены от матриц и теорема Гамильтона—Кэли
- § 4. Свойства собственных векторов и собственных значений симметричного линейного прейбразования
- § 5. Приведение к диагональному виду матрицы симметричного линейного преобразования
- § 6. Приведение квадратичной формы к каноническому виду
- § 7. Представление невырожденного линейного преобразования в виде произведения симметричного и ортогонального преобразований
- ГЛАВА V. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Общее уравнение поверхности второго порядка. Его инварианты
- § 2. Приведение к простейшему виду общего уравнения поверхности второго порядка
- § 3. Определение типа поверхности второго порядка при помощи инвариантов
- § 4. Классификация поверхностей второго порядка
- § 5. Приложение теории инвариантов к классификации поверхностей второго порядка
- § 6. Центральные и нецентральные поверхности второго порядка
- § 7. Примеры
- ГЛАВА VI. ПРИЛОЖЕНИЕ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ К НЕКОТОРЫМ ВОПРОСАМ МЕХАНИКИ И ФИЗИКИ
- § 2. Некоторые свойства кристаллов, связанные с тензорами второй валентности
- § 3. Тензоры напряжений и деформации
- § 4. Дальнейшие свойства кристаллов
- ГЛАВА VII. ОСНОВЫ ТЕНЗОРНОГО АНАЛИЗА
- § 1. Тензорное поле и его дифференцирование
- § 2. Механика деформируемой среды
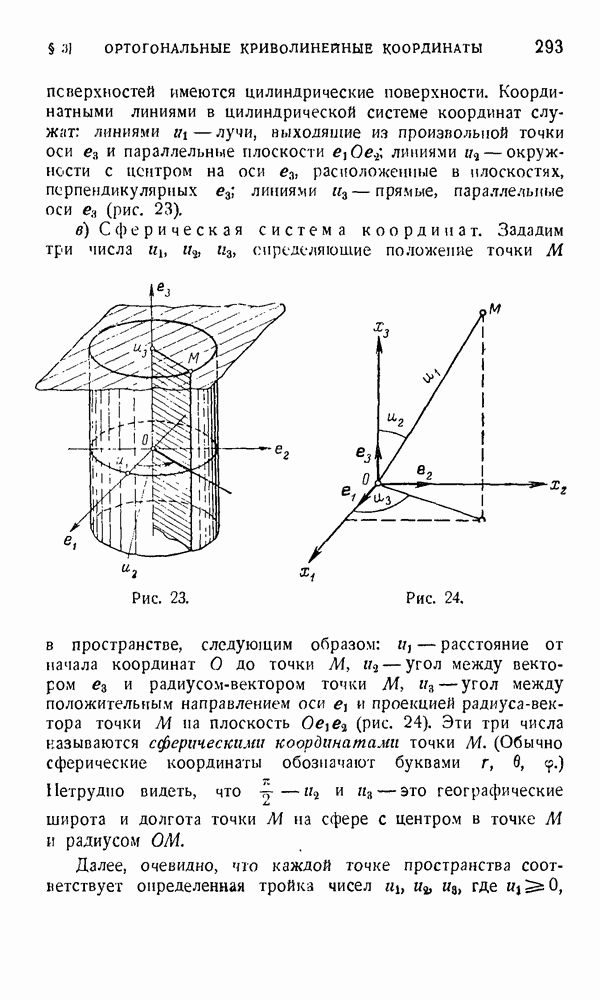
- § 3. Ортогоналыше криволинейные системы координат
- § 4. Подвижной репер ортогональной криволинейной системы координат и тензорные поля
- § 5. Дифференцирование тензорного поля в криволинейных координатах
- ОТВЕТЫ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ И УПРАЖНЕНИЙ
- ЛИТЕРАТУРА