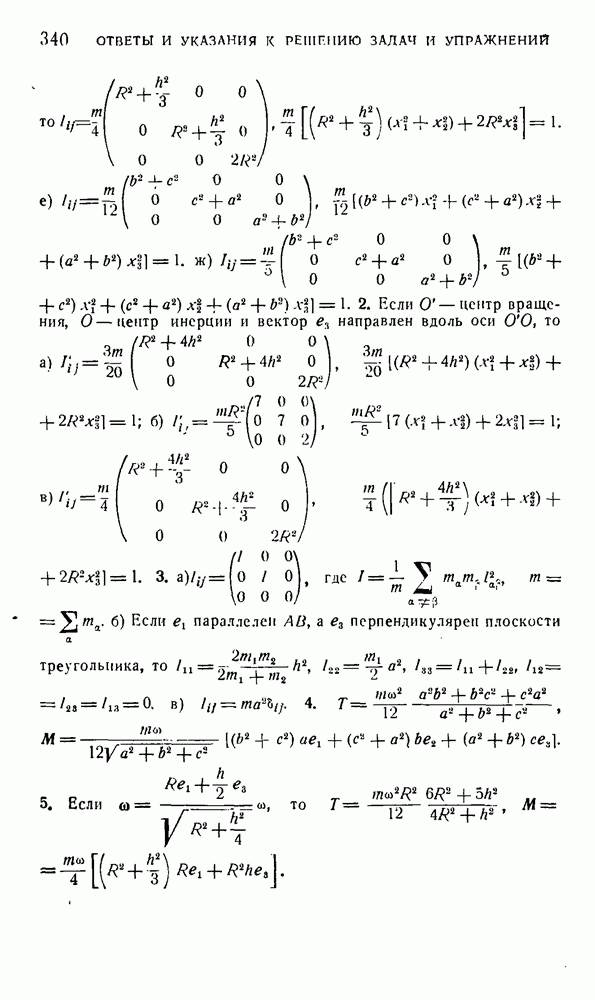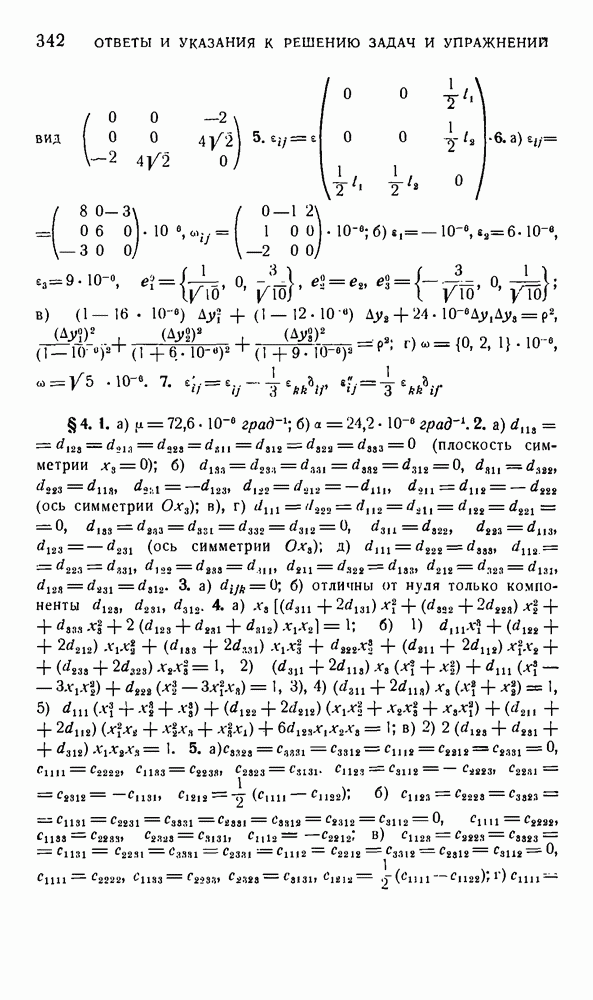§ 5. Дифференцирование тензорного поля в криволинейных координатах

1. Перейдем теперь к рассмотрению операции дифференцирования тензорного поля в криволинейных координатах.

Займемся сначала вопросом о дифференцировании скаляр но поля. Пусть в некоторой ортогональной криволинейной системе координат определенной в некоторой области пространства задано скалярное поле

Дифференциал его определяется равенством

(здесь мы воспользовались формулами (2) § 4). Далее, обозначая коэффициент при через

будем иметь

Совокупность величин назовем ковариантной (абсолютной) производной скалярного поля.

Поскольку как и образует некоторое скалярное поле, а тензорное поле первой валентности (стр. 307), то коэффициенты в равенстве (2) также образуют тензорное поле первой валентности. Вектор с координатами япляется инвариантным вектором, не зависящим от выбора системы координат в рассматриваемой области пространства Докажем, что этот вектор является градиентом скалярного поля , т. е.

В самом деле, если мы перейдем к декартовой прямоугольной системе координат, то получим

и

в соответствии с определением градиента скалярного поля, которое было дано в § 1 этой главы. Но последнее равенство не зависит от выбора системы координат и области Поэтому оно остается верным для любой криволинейной системы координат.

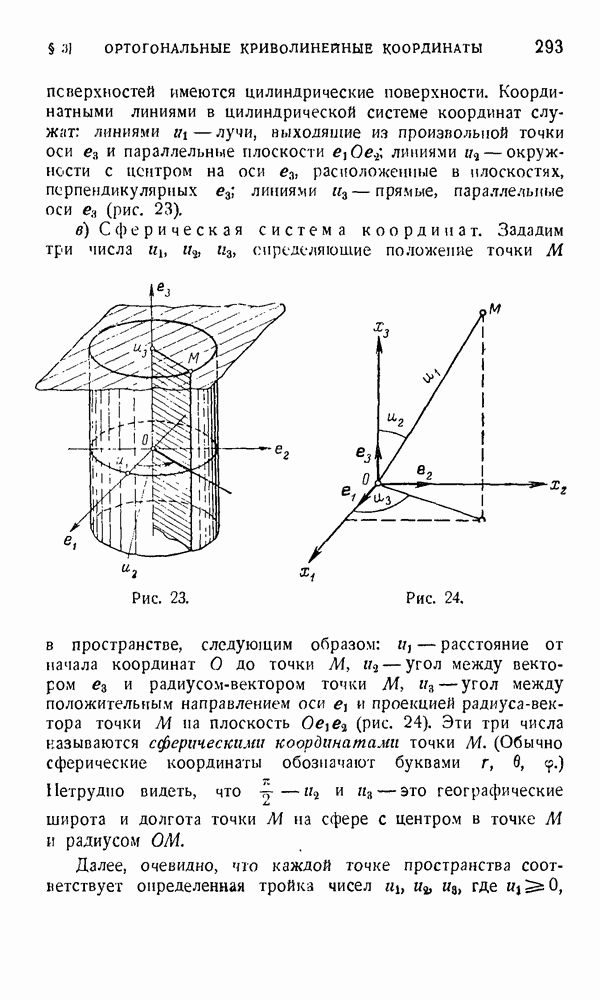
Найдем еще выражение градиента скалярного поля в цилиндрической и сферической системах координат.

а) В цилиндрической системе координат мы имели (см. пример б) на стр. 304)

поэтому по формуле (1) получаем

откуда в силу формулы (3)

б) В сферической системе координат коэффициенты Ламе определялись формулами (см. пример а) на стр. 305)

отсюда в силу формулы (1)

и по формуле (3)

2. Перейдем теперь к дифферепциронанию векторного поля.

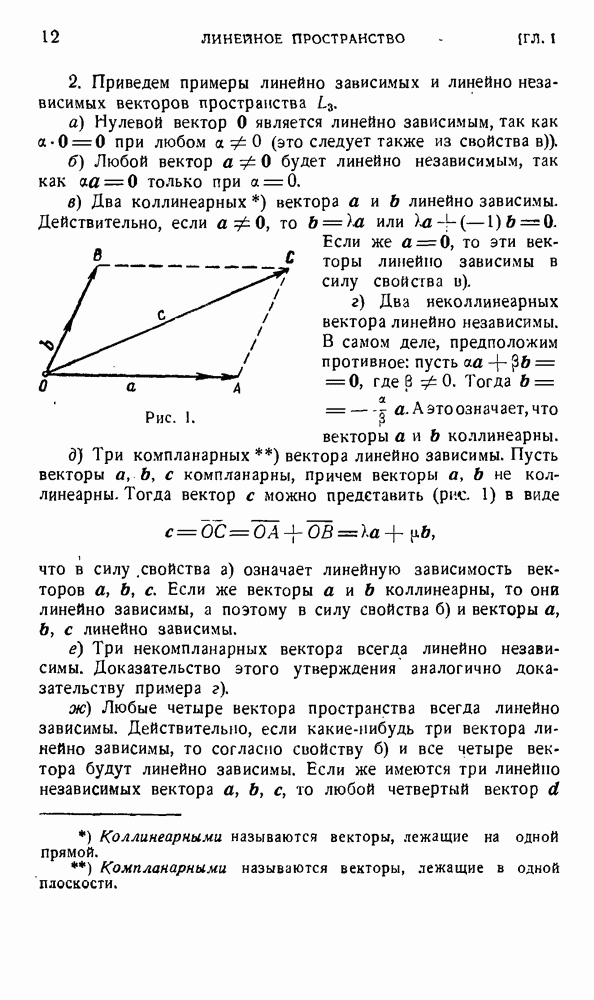
Пусть дано векторное поле

Найдем его дифференциал. Пользуясь формулами (5) § 4, получим

или, меняя индекс суммирования в первом слагаемом на и пользуясь кососимметричностью форм будем иметь

Полагая

найдем

Так как — вектор, то из равенства (5) следует, что — координаты тензора первой валентности. Этот тензор называется абсолютным дифференциалом тензора

Отметим, что обычные дифференциалы координат векторного поля в криволинейной системе координат уже не образуют тензора первой валентности. Так как в прямоугольной декартовой системе координат (и только в такой системе координат) то в ней и только в ней абсолютные дифференциалы координат вектора совпадают с его обычными дифференциалами. Заметим еще, что для того, чтобы некторное поле заданное в криволинейной системе координат, было однородным полем (т. е. чтобы все векторы поля были

равны между собой), необходимо и достаточно, чтобы выполнялось условие

Далее, если воспользоваться тем, что

и

то формулу (4) можно записать в виде

Обозначив выражение в скобках через

получим

Поскольку - тензорное ноле первой валентности и — координаты произнольного вектора (стр. 307), то на основании обратного тензорного признака можно утверждать, что величины к образуют тензорное поле второй валентности. Это поле называется абсолютной производной векторного поля Легко видеть, что абсолютная производная тензорного поля совпадает с его обыкновенной производной тогда и только тогда, когда криволинейная система координат станонится декартовой прямоугольной.

Таким образом, мы ввели понятия абсолютного дифференциала и абсолютной производной векторного поля. Они вычисляются по формулам (4) и (6) и представляют собой тензорные поля соответственно первой и второй валентности.

Если абсолютную производную к векторного поля свернуть по индексам и то получим инвариант, совпадающий с дивергенцией векторного поля

В самом деле, инвариант не зависит от выбора системы координат, но в прямоугольной декартовой системе координат

Используя формулу (11) § 4, приведем выражение для дивергенции к виду

или, собирая члены с к виду

Если же абсолютную производную свернуть с дискриминантным тензором то получим ротор векторного поля

В самом деле, так как в прямоугольной декартовой системе координат то эта формула совпадает с формулой (9) § 1 (стр. 273) и в правой системе координат может быть записана в виде

С помощью соотношений (11) §4 формула для проекции ротора на ось преобразуется следующим образом:

Аналогично можно преобразовать формулы для проекций ротора на оси Окончательно формула для вычисления ротора в криволинейных ортогональных координатах принимает вид

Найдем еще выражение оператора Лапласа в общей ортогональной криволинейной системе координат. Так как

то, пользуясь формулами (1), (3), (8), получим

Запишем теперь абсолютную производную, дивергенцию и ротор векторного ноля, а также оператор Лапласа в цилиндрической и сферической системах координат, которые при выбранном нами порядке координат все были правыми.

а) В цилиндрической системе координат, если использовать результаты примера § 4 (стр. 304), по формуле (3) получим

Поэтому из (8) имеем

или

(последний результат можно получить также непосредственно из формулы (8)),

По формуле (9) получаем следующее выражение ротора в цилиндрических координатах:

и, наконец, пользуясь (10), найдем выражение для оператора Лапласа:

б) В сферической системе координат, используя результаты примера в) § 4 (стр. 305), получим

Далее по формулам (8) и (9) имеем

или

Наконец, по формуле (10) найдем следующее выражение оператора Лапласа в сферических координатах:

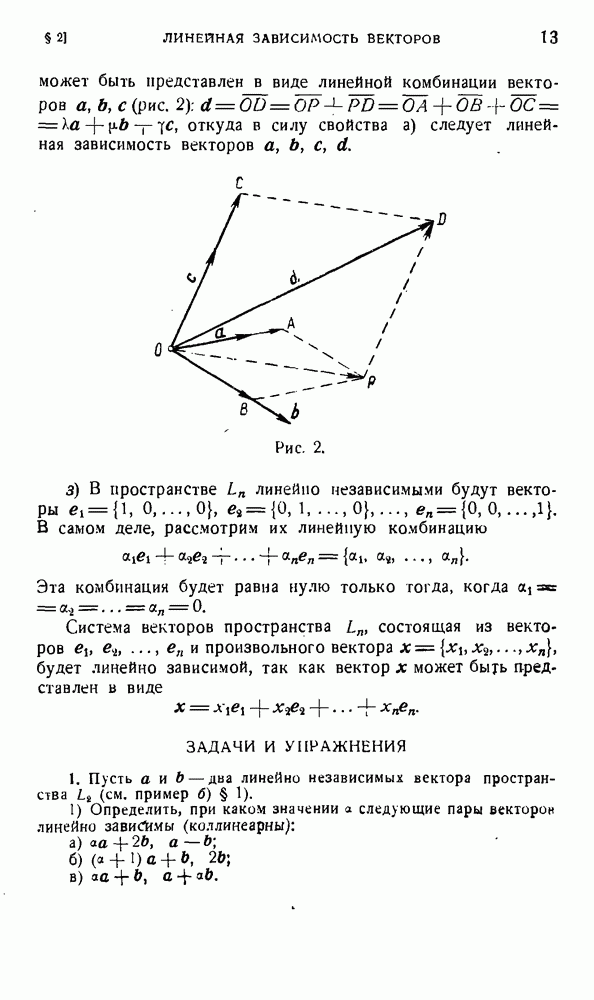
3. Рассмотрим далее операцию абсолютного дифференцирования поля тензора второй валентности, которое задано в некоторой криволинейной ортогональной системе координат

В каждой точке компоненты этого тензора можно рассматривать как коэффициент билинейной формы

где х и у — произвольные векторные поля, имеющие относительно подвижного репера, присоединенного к криволинейной системе координат, соответственно координаты и У] !. 2. 3).

Пользуясь формулами (4) для абсолютного дифференциала векторного поля, находим дифференциал формы

(в последнем переходе мы дважды поменяли индексы суммирования: в одном слагаемом на и обратно, в другом на А и обратно).

Второе и третье слагаемые здесь показывают, как меняется билинейная форма в зависимости от изменения векторов нолей х и у при переходе из точки М в бесконечно близкую точку. Первое из слагаемых отражает изменение этой формы за счет приращения коэффициентов Поскольку — инвариант, тоже инварианты, как результаты свертывания тензора соответственно с векторами то первое слагаемое также представляет собой инвариант — некоторую билинейную форму относительно векторов х и у. Коэффициенты этой последней билинейной формы образуют тензор второй валентности,

называемый абсолютным дифференциалом тензора и обозначаемый

Далее, если воспользоваться формулами

то соотношение (11) можно записать в виде

Обозначив выражение, стоящее в скобках, через

получим

Отсюда ясно, что величины образуют тензорное поле валентности три, называемое абсолютной производной тензорного поля

Таким образом, абсолютный дифференциал и абсолютная производная тензорного поля второй валентности образуют тензорные ноля соответственно второй и третьей валентности и вычисляются по формулам (11) и (13).

Совершенно аналогично тому, как введены абсолютный дифференциал и абсолютная производная тензорного ноля второй валентности, можно внести абсолютный дифференциал и абсолютную производную тензорного ноля валентности (для этого придется использовать уже не билинейные, а полилинейные формы). Аналогично окажется, что абсолютный дифференциал такого ноля образует тензор той же валентности, а абсолютная производная — тензор на единицу большей валентности.

Формулы для их вычисления будут иметь вид, аналогичный формулам (4), (11) и (6), (12). Например, для тензора четвертой валентности абсолютный дифференциал и абсолютная

производная находятся по формулам

4. Установим теперь правила абсолютного дифференцирования, т. е. определим, как находятся абсолютные дифференциалы и абсолютные производные от суммы тензоров, от произведения тензоров, от свернутого тензора и от свернутого произведения тензоров. Для простоты мы выведем эти правила на примерах тензоров небольших валентностей — вывод в общем случае будет точно таким же.

а) Абсолютное дифференцирование суммы. Пусть дано тензорное поле второй валентности которое является суммой двух тензорных полей той же валентности:

Продифференцируем это равенство обычный способом:

Отсюда, пользуясь формулой (11), получим

или, используя, что найдем

Таким образом, абсолютный дифференциал суммы тензоров равен сумме абсолютных дифференциалов слагаемых.

б) Абсолютное дифференцирование произведения тензоров. Пусть теперь

Дифференцируем это равенство:

отсюда, пользуясь формулами для абсолютных дифференциалов будем иметь

откуда, используя равенство получаем

Таким образом, абсолютный дифференциал произведения тензоров равен абсолютному дифференциалу первого множителя, умноженному на второй множитель, плюс произведение первого множителя на абсолютный дифференциал второго.

а) Абсолютное дифференциронание свернутого тензора. Пусть тензор свернут по первым двум индексам:

Продифференцируем это равенство:

отсюда, пользуясь выражениями для найдем

Последние слагаемые в левой и правой частях этого соотношения равны, так как Кроме того

Поэтому

Это равенство можно записать еще таким образом:

т. e. операции абсолютного дифференцирования и свертывания тензоров перестановочны.

г) Абсолютное дифференцирование свернутого произведения тензоров. Пусть, наконец,

Тогда, пользуясь правилом абсолютного дифференцирования свернутого тензора и произведения тензоров, найдем

т. е. правило дифференцирования произведения тензоров сохраняется и при наличии свертывания перемножаемых тензоров.

Полученные здесь правила абсолютного дифференцирования автоматически переносятся и на абсолютные производные:

Доказательство всех этих формул протекает аналогично. Докажем какую-нибудь одну из них, например вторую. В формуле

заменим абсолютные дифференциалы по формулам (13), (7) и аналогичной формуле для абсолютного дифференциала трехвалентного тензора тогда получим

Так как формы линейно независимы, то коэффициенты при и правой и левой частях последнего соотношения будут равны, что приведет нас к доказываемой формуле:

Таким образом, мы видим, что операция абсолютного дифференцирования тензоров обладает всеми свойствами обычного дифференцирования. Этого, конечно, и следовало ожидать, так как абсолютное дифференцирование — инвариантная операция, не зависящая от выбора криволинейной ортогональной системы координат. А в прямоугольных декартовых координатах абсолютное дифференцирование совпадает с обычным дифференцированием тензоров.

5. Как уже отмечалось выше, абсолютные производные скалярного и векторного полей при переходе к прямоугольной декартовой системе координат совпадают с обычными производными этих полей. Это утверждение остается верным и для абсолютных производных тензорного поля любой валентности, что сразу следует из формул типа (14), если учесть, что в прямоугольных координатах Именно поэтому для обыкновенных производных тензорного ноля, заданного в прямоугольной декартовой системе координат, в § 1 использовались те же самые обозначения, что и в этом параграфе для абсолютных производных тензорного поля, заданного в произвольной криволинейной ортогональной системе координат.

Теперь ясно, что все тензорные уравнения, записанные в прямоугольной декартовой системе координат и содержащие обычные производные тензорного поля, при переходе к ортогональным криволинейным координатам перейдут в точно такие же уравнения, и которых вместо обычных производных будут стоять абсолютные производные.

В частности, полученные в § 2 уравнения механики сплошных сред будут справедливыми не только в прямоугольной системе координат, в которой они были выведены, но также и в произвольной ортогональной криволинейной системе координат. При этом входящие в них обыкновенные производные надо заменить абсолютными производными.

ЗАДАЧИ И УПРАЖНЕНИЯ

(см. скан)

(см. скан)