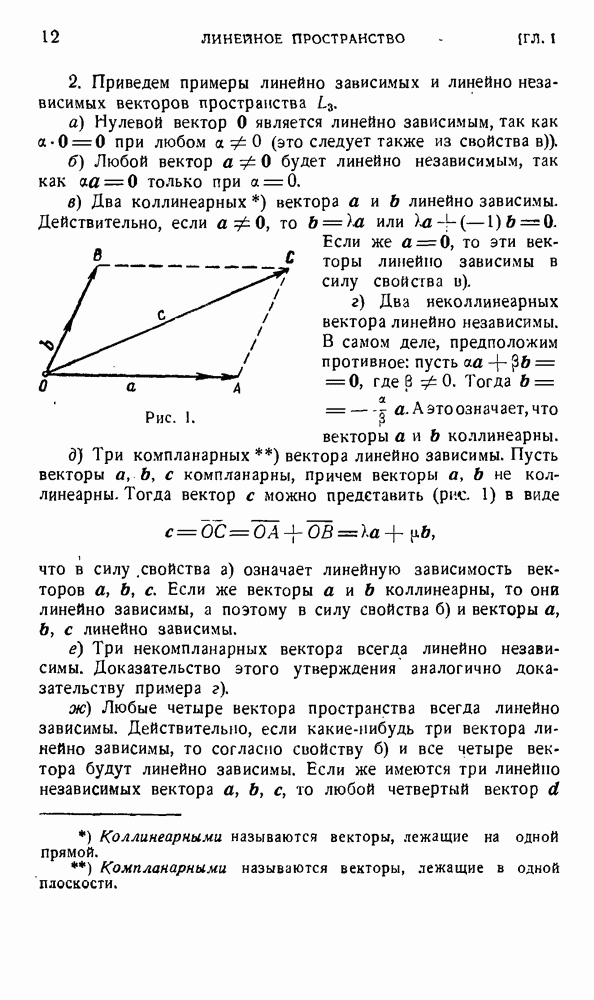
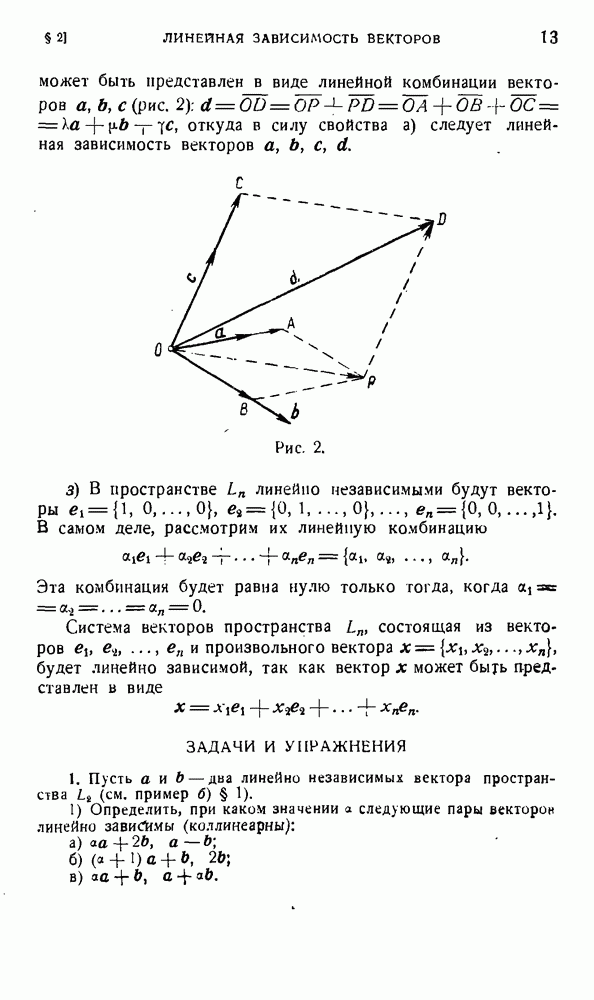
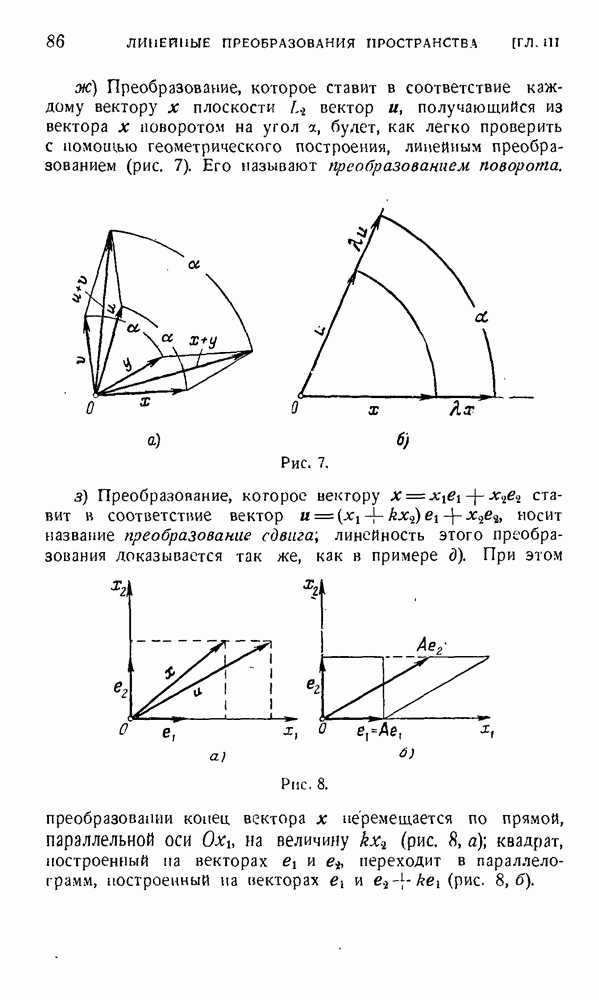
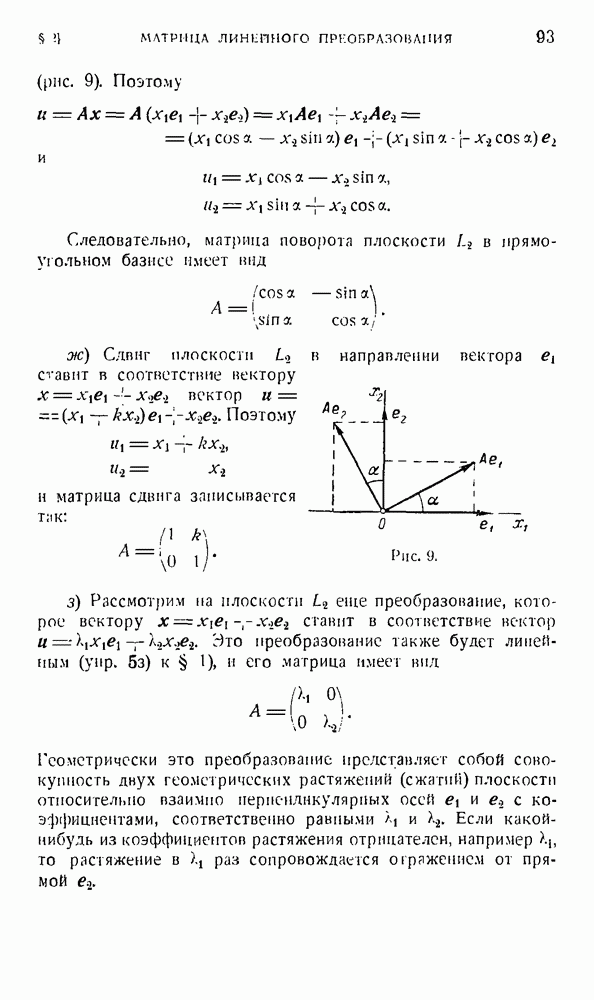
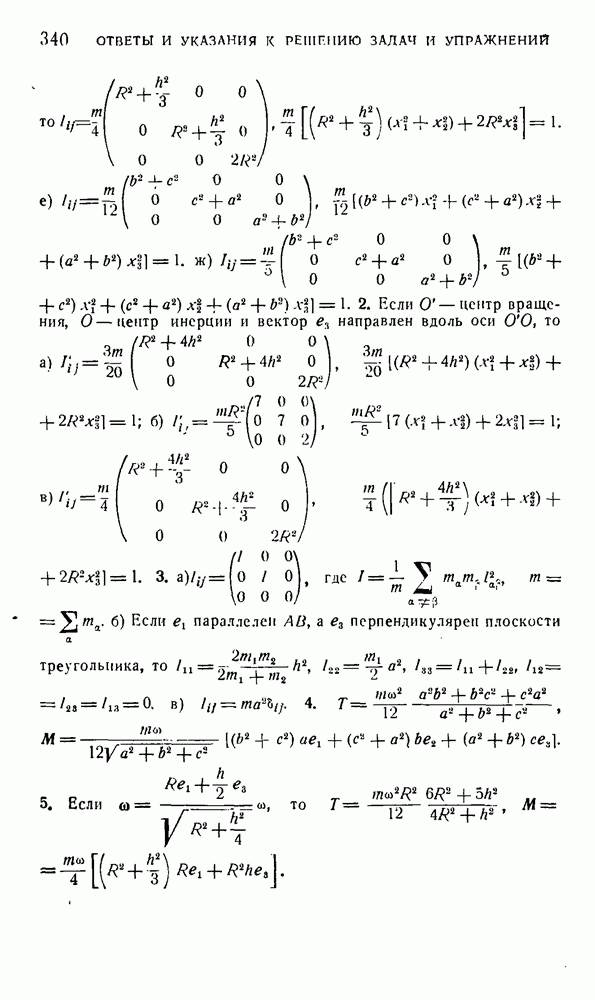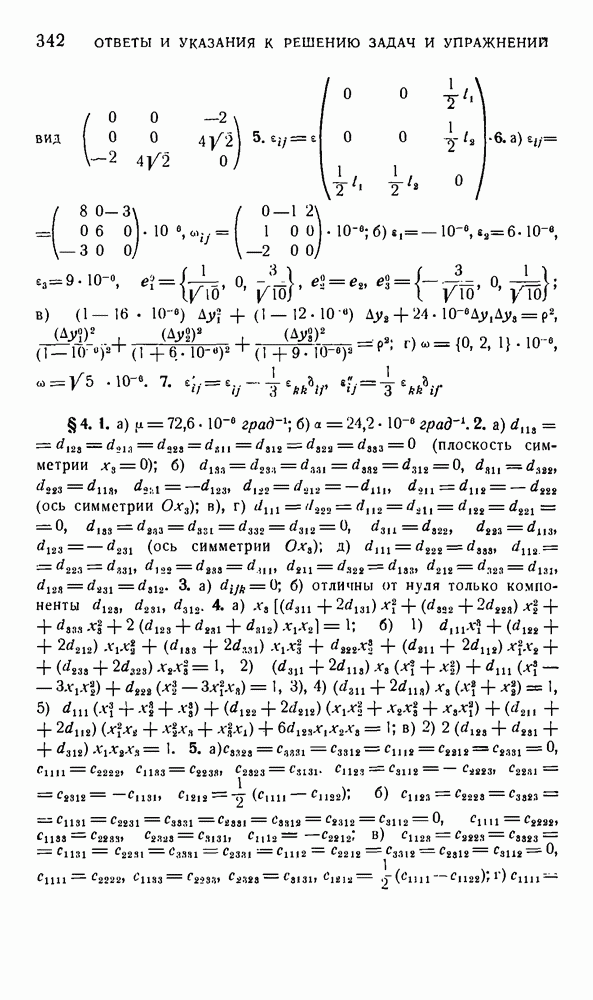| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА VII. ОСНОВЫ ТЕНЗОРНОГО АНАЛИЗА
§ 1. Тензорное поле и его дифференцирование
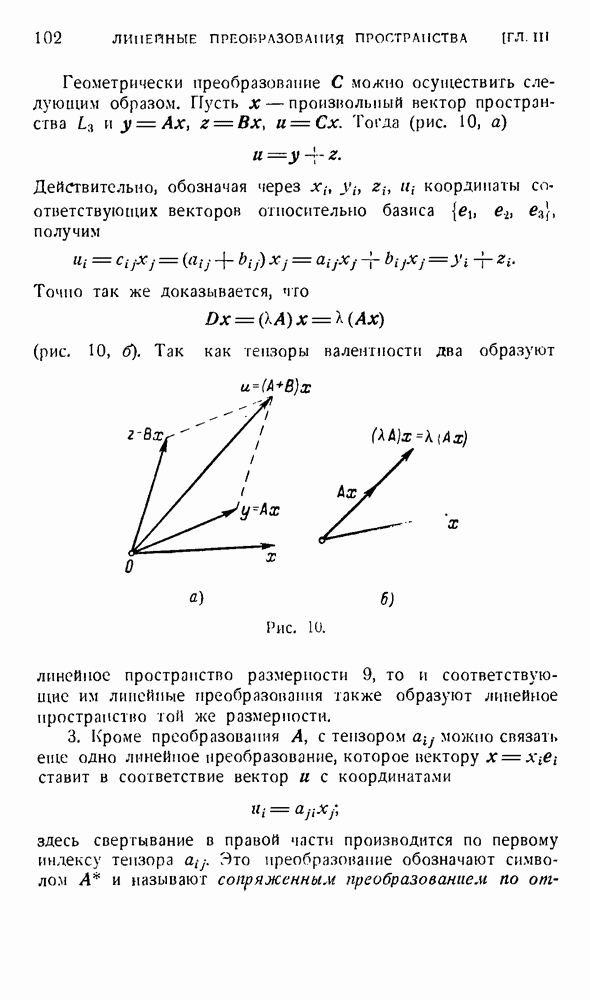
1. До сих пор при рассмотрении тензоров в евклидовом пространстве  мы не задумывались над тем, в какой точке заданы тензоры. Можно считать, что
мы не задумывались над тем, в какой точке заданы тензоры. Можно считать, что  введенные нами операции над тензорами осуществлялись в одной точке, по можно считать также, что
введенные нами операции над тензорами осуществлялись в одной точке, по можно считать также, что  эти операции осуществлялись в некоторой области
эти операции осуществлялись в некоторой области  пространства Ел (или даже во всем
пространства Ел (или даже во всем  если считать, что изучаемые тензоры одинаковы во всех точках области
если считать, что изучаемые тензоры одинаковы во всех точках области
В настоящей главе мы перейдем от тензорной алгебры к тензорному анализу. В связи с этим будем рассматривать тензорные поля, для которых, кроме изученных выше алгебраических операций, будет определена еще одна операция — дифференцирование.
В § 1 мы построим тензорный анализ в трехмерном евклидовом пространстве  в прямоугольной декартовой системе координат и в § 2 рассмотрим некоторые его приложения. Затем, в §§ 3, 4, 5, мы введем криволинейные координаты в
в прямоугольной декартовой системе координат и в § 2 рассмотрим некоторые его приложения. Затем, в §§ 3, 4, 5, мы введем криволинейные координаты в  и построим тензорный анализ в криволинейных, по по-прежнему ортогональных системах координат.
и построим тензорный анализ в криволинейных, по по-прежнему ортогональных системах координат.
2. Перейдем теперь к определению тензорного поля. Будем говорить, что в области  (запись
(запись  означает, что область
означает, что область  принадлежит пространству
принадлежит пространству  задано тензорное поле, если каждой точке
задано тензорное поле, если каждой точке  поставлен в соответствие тензор одной и той же валентности. Этот тензор называется тензором поля. Он, вообще говоря, меняется от точки к точке. Пусть, например, валентность заданного тензорного поля равна трем, тогда тензор
поставлен в соответствие тензор одной и той же валентности. Этот тензор называется тензором поля. Он, вообще говоря, меняется от точки к точке. Пусть, например, валентность заданного тензорного поля равна трем, тогда тензор  будет
будет
функцией точки М (или радиуса-вектора этой точки):

или

где  — координаты точки М относительно некоторого прямоугольного базиса
— координаты точки М относительно некоторого прямоугольного базиса 
Будем считать в дальнейшем, что функции, задающие тензорное поле, непрерывны и имеют непрерывные частные производные любого нужного нам порядка по нсем аргументам.
Теперь можно сказать, что  предыдущих главах мы рассматривали однородные тензорные поля, т. е. такие поля, тензор которых не меняется от точки к точке.
предыдущих главах мы рассматривали однородные тензорные поля, т. е. такие поля, тензор которых не меняется от точки к точке.
Приведем несколько примеров тензорных полей.
а) Скалярное поле. Так называется поле тензора пулевой валентности. Мы знаем, что такой тензор является инвариантом. Поэтому для задания скалярного поля надо в каждой точке  задать инвариант
задать инвариант 

или

т. е. скалярное поле задается некоторой функцией трех переменных.
Укажем некоторые конкретные скалярные поля: ноле температур неравномерно нагретого тела, поле плотностей неоднородного тела, поле давлений газа и т. д.
б) Векторное поле. Так называют ноле тензора первой валентности:

поскольку, как мы знаем (гл. 11, стр. 53), компоненты тензора первой валентности являются координатами вектора

Равенства (1) показывают, что векторное поле задается уже тремя функциями от трех аргументов.
Укажем несколько примером векторных полей: поле вектора скорости (или ускорения) движущейся жидкости пли газа, поле вектора плотности электрического тока в некотором
проводнике большого сечения, поле сил тяготения, создаваемых каким-нибудь массивным телом, и т. д.
в) Поле двухвалентного тензора:

Здесь поле задается уже девятью функциями от трех аргументов. Конкретными примерами таких полей могут служить поле напряжений и поле деформаций твердого тела (ср. гл. VI, § 3, где рассмотрены однородные поля напряжений и деформаций).
Отметим, что в приложениях обычно встречаются именно тензорные поля, а не отдельные тензоры.
Алгебраические операции над тензорами, построенные в § 4 гл. И для тензором, определенных в одной точке, естественным образом переносятся и на тензорные поля: надо считать, что эти операции производятся над тензором поля в каждой точке 
Например, если в области даны тензорные поля

то, складывая компоненты тензоров первых двух полей в каждой точке  мы получим в
мы получим в  новое тензорное поле
новое тензорное поле

являющееся суммой двух первых полей, а перемножая в каждой точке  компоненты первого и третьего тензорных полей, получим новое тензорное поле
компоненты первого и третьего тензорных полей, получим новое тензорное поле

— произведение первого и третьего тензорных полей.
Аналогично можно рассмотреть операции свертывания тензорных полей и перестановки индексов в данном тензорном ноле, производя эти операции над тензорами заданных нолей в каждой точке М
3. В тензорном поле кроме алгебраических операций можно определить еще операцию дифференцирования — основную операцию тензорного анализа. Эту операцию можно ввести следующим образом.
Пусть, например, в области  дано поле тензора третьей валентности
дано поле тензора третьей валентности

Выясним, как меняется этот тензор при переходе из точки  бесконечно близкую к М точку М. Положение точки М относительно точки М определяется вектором
бесконечно близкую к М точку М. Положение точки М относительно точки М определяется вектором  разложение которого по базисным векторам записывается
разложение которого по базисным векторам записывается  виде
виде

При переходе к новому ортопормировапному базису  координаты вектора
координаты вектора  преобразуются по формулам
преобразуются по формулам

Так как  то компоненты
то компоненты  точки М теперь выразятся так:
точки М теперь выразятся так:

Обозначим через  прирашения, которые получают компоненты тензора
прирашения, которые получают компоненты тензора  при переходе из точки М в точку М. Если предположить, что эти компоненты являются дифференцируемыми функциями от координат точки
при переходе из точки М в точку М. Если предположить, что эти компоненты являются дифференцируемыми функциями от координат точки  то главные части приращений могут быть записаны так:
то главные части приращений могут быть записаны так:

Докажем, что совокупность величин  образует тензор третьей валентности. Действительно, при переходе к базису
образует тензор третьей валентности. Действительно, при переходе к базису  компоненты тензора
компоненты тензора  преобразуются по формулам
преобразуются по формулам

Дифференцируя их почленно и учитывая, что величины  постоянны (они не зависят от положения точки М, так как являются косинусами углов между векторами старого и нового базисов), мы получим
постоянны (они не зависят от положения точки М, так как являются косинусами углов между векторами старого и нового базисов), мы получим

Эти равенства показывают, что величины  при замене базиса преобразуются по тензорному закону. Тензор с
при замене базиса преобразуются по тензорному закону. Тензор с
координатами  назовем абсолютным дифференциалом тензора поля
назовем абсолютным дифференциалом тензора поля 
Теперь формулы (3) показывают, что при свертывании величин  с координатами произвольного вектора
с координатами произвольного вектора  получается тензор
получается тензор  . В силу обратного тензорного признака (стр. 69) отсюда следует, что величины образуют тензор четвертой валентности
. В силу обратного тензорного признака (стр. 69) отсюда следует, что величины образуют тензор четвертой валентности  точке М.
точке М.
Поскольку наши построения можно провести в любой точке  мы получаем
мы получаем  новое тензорное поле, называемое абсолютной производной тензорного поля
новое тензорное поле, называемое абсолютной производной тензорного поля  Для абсолютной производной тензора поля
Для абсолютной производной тензора поля  применяется обозначение
применяется обозначение

к котором  качестве добавочного индекса I на последнем месте ставится индекс той координаты
качестве добавочного индекса I на последнем месте ставится индекс той координаты  точки
точки  по которой производится дифференцирование, причем этот индекс от остальных отделяется запятой.
по которой производится дифференцирование, причем этот индекс от остальных отделяется запятой.
Перепишем формулы (3) в новых обозначениях:

Эти формулы показывают, что абсолютный дифференциал тензора  есть резуль
есть резуль  свертывания тензора
свертывания тензора  и абсолютной производной
и абсолютной производной  этого тензора.
этого тензора.
Аналогичные рассуждения могут быть проведены для тензорного поля любой валентности. Совокупность всех частных производных первого порядка от компонент данного тензорного поля по координатам  той точки, в которой рассматривается тензорное поле, образует тензор, валентность которого на единицу больше валентности исходного тензорного поля, — абсолютную производную данного поля. Результат свертывания этой абсолютной производной по индексу, который возникает при дифференцировании, с координатами вектора
той точки, в которой рассматривается тензорное поле, образует тензор, валентность которого на единицу больше валентности исходного тензорного поля, — абсолютную производную данного поля. Результат свертывания этой абсолютной производной по индексу, который возникает при дифференцировании, с координатами вектора  представляет собой абсолютный дифференциал заданного векторного поля.
представляет собой абсолютный дифференциал заданного векторного поля.
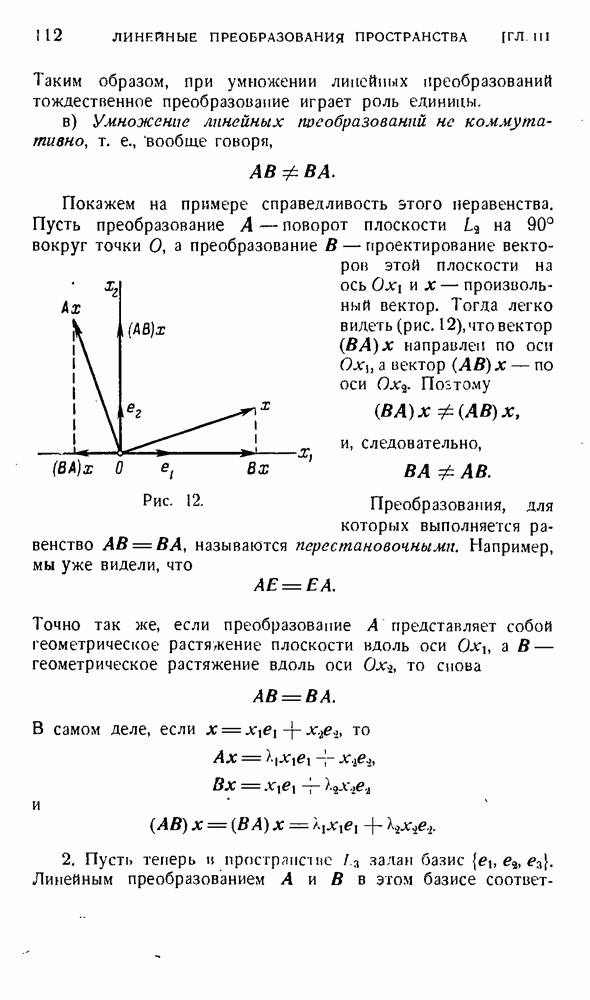
Сделаем еще три замечания.
Замечание 1. Поскольку в прямоугольной декартовой системе координат координаты абсолютного дифференциала и
абсолютной производной тензорного поля совпадают с обычными дифференциалами и частными производными компонент исходного поля, правила абсолютного дифференцирования будут точно такими же, как иранпла обычного дифференцирования.
Замечание 2. Точно так же, как были построены абсолютный дифференциал и абсолютная производная первого порядка для произвольного тензорного поля, можно построить абсолютный дифференциал и абсолютную производную второго порядка, а затем и высших порядков для этого поля. Панример, для тензорного поля  частные производные
частные производные

образуют нторую абсолютную производную тензора  которая является тензором пятой валентности. Результат свертывания этого тензора с дифференциалами
которая является тензором пятой валентности. Результат свертывания этого тензора с дифференциалами  приведет к выражению для второго абсолютного дифференциала тензора
приведет к выражению для второго абсолютного дифференциала тензора 

Вообще, абсолютный дифференциал порядка  от произвольного, не менее чем
от произвольного, не менее чем  раз дифференцируемого тензорного поля представляет собой тензорное поле той же валентности, что и исходное поле, а его абсолютная производная порядка
раз дифференцируемого тензорного поля представляет собой тензорное поле той же валентности, что и исходное поле, а его абсолютная производная порядка  — тензорное поле, валентность которого на
— тензорное поле, валентность которого на  единиц больше валентности исходного поля.
единиц больше валентности исходного поля.
Замечание 3. Предположим, что функции, определяющие тензорное поле, имеют непрерывные частные производные  порядка в точке
порядка в точке  ее окрестности. Тогда в окрестности точки М эти функции могут быть разложены по формуле Тейлора. Полученное разложение будем называть разложением тензора по формуле Тейлора. Для тензорного поля
ее окрестности. Тогда в окрестности точки М эти функции могут быть разложены по формуле Тейлора. Полученное разложение будем называть разложением тензора по формуле Тейлора. Для тензорного поля  это разложение запишется так:
это разложение запишется так:

или, в развернутом виде,

Здесь  причем
причем  вообще говоря, различны для разных наборов
вообще говоря, различны для разных наборов  Важно заметить, что коэффициенты в каждой группе членов этой формулы ян-ляются тензорами: это компоненты тензоров
Важно заметить, что коэффициенты в каждой группе членов этой формулы ян-ляются тензорами: это компоненты тензоров  вычисленные в точке М.
вычисленные в точке М.
4. Рассмотрим дифференцирование скалярного поля — поля тензора нулевой валентности:

Согласно общему правилу абсолютная производная этого поля

является тензором первой валентности, который, как известно, определяет векторное поле. Это поле называется градиентом скалярного поля и обозначается 

Поскольку новое поле есть поле одновалентного тензора, его инвариантный смысл не вызывает сомнения. Из курса высшей математики (см., например, [2], стр. 427) известно, что градиент скалярного поля в данной точке М — это вектор, в направлении которого скалярное поле возрастает с наибольшей скоростью и модуль которого равен этой наибольшей скорости.
Приведем некоторые примеры скалярных полей и их градиентов.
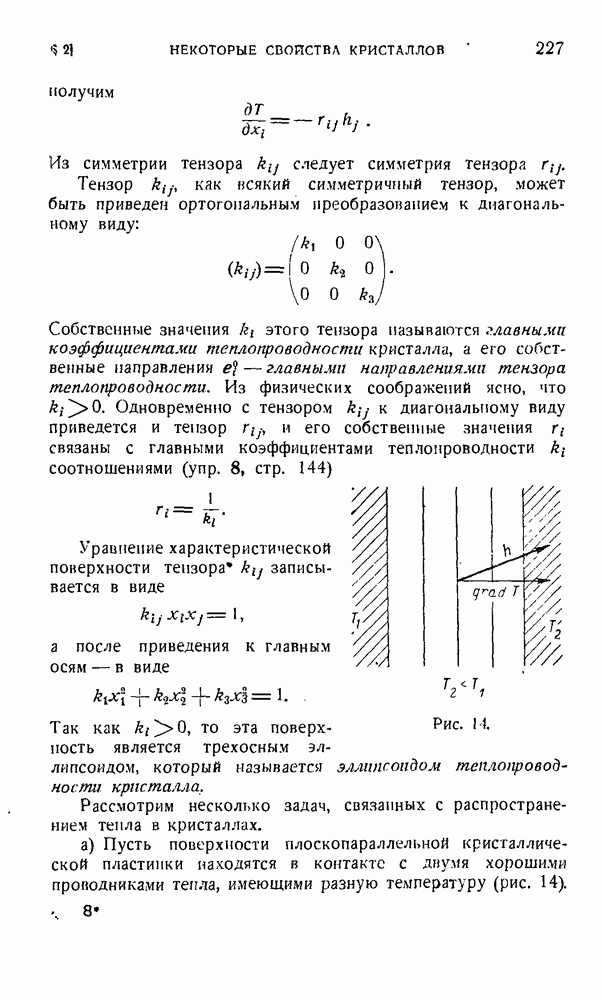
а) Если имеется скалярное поле температуры

неравномерно нагретого изотропного тела, то вектор

выражает плотность теплового потока, идущего от более нагретых частей тела к менее нагретым его частям; здесь  — постоянный множитель, называемый коэффициентом теплопроводности (ср. стр. 226). Тепловой поток в каждой точке гела идет по направлению вектора
— постоянный множитель, называемый коэффициентом теплопроводности (ср. стр. 226). Тепловой поток в каждой точке гела идет по направлению вектора  причем через ортогональную
причем через ортогональную  площадку
площадку  за одну секунду проходит
за одну секунду проходит  единиц тепла.
единиц тепла.
б) Если имеется скалярное поле давлений

в различных точках идеальной жидкости, заполняющей некоторый объем V, то вектор

дает равнодействующую сил давления, приложенных к элементу объема  .
.
в) В электростатике напряженность Е электрического поля, т. е. сила, действующая на единицу заряда положительного электричества, как установлено опытом, равна

 — потенциал электрического поля. Если ноле порождается положительным зарядом
— потенциал электрического поля. Если ноле порождается положительным зарядом  помещенным в начало координат, то по закону Кулона
помещенным в начало координат, то по закону Кулона

где  — радиус-вектор данной точки. Отсюда следует, что
— радиус-вектор данной точки. Отсюда следует, что

5. Применим теперь полученные в этом параграфе результаты и условия Сильвестра положительной и отрицательной определенности квадратичной формы (гл. IV, стр. 167, 169) для вывода достаточных условий экстремума функции двух и трех переменных. Заметим, что в курсе высшей математики для технических вузов эти условия обычно сообщаются без доказательства и  только для случая функции двух переменных (см., например, [2], стр. 413).
только для случая функции двух переменных (см., например, [2], стр. 413).
Пусть функция

определена, непрерывна и имеет непрерывные частные производные первого и второго порядков в окрестности некоторой точки  и пусть эта точка является стационарной, т. е. в пей
и пусть эта точка является стационарной, т. е. в пей

Тогда, чтобы выяснить, достигается ли в стационарной точке экстремум, воспользуемся формулой Тейлорп (4), записал ее для тензорного ноля  нулевой валентности. Обозначим
нулевой валентности. Обозначим

Если учесть условие стационарности (5), то, пользуясь формулой Тейлора, приращение функции  можно записать в виде
можно записать в виде

здесь  а через [3] обозначены члены не менее третьего порядка малости.
а через [3] обозначены члены не менее третьего порядка малости.
Так как при малых  члены третьего порядка значительно меньше членов второго порядка, то знак всей правой части определяется знаком квадратичной формы
члены третьего порядка значительно меньше членов второго порядка, то знак всей правой части определяется знаком квадратичной формы

Если эта форма будет положительно определенной, то 

и в точке  функция
функция  имеет минимум. Если же эта форма отрицательно определена, то
имеет минимум. Если же эта форма отрицательно определена, то 

и в точке  будет максимум.
будет максимум.
Что касается необходимых и достаточных условий положительной и отрицательной определенности формы  то они нам известны — это условия Сильвестра (гл. IV, сгр. 167, 169). Таким образом, достаточными условиями того, чтобы в стационарной точке
то они нам известны — это условия Сильвестра (гл. IV, сгр. 167, 169). Таким образом, достаточными условиями того, чтобы в стационарной точке  функции
функции  достигался минимум или максимум, будут соответственно условия
достигался минимум или максимум, будут соответственно условия

Если ни условие а), ни условие 3) не выполнены, то возможны два случая: или форма  — неопределенная, т. е. принимает и окрестиостг стационарной точки значения разных знаков,
— неопределенная, т. е. принимает и окрестиостг стационарной точки значения разных знаков,  же она является полу определенной, т. е. принимает значения одного знака, но обращается в пуль не только при
же она является полу определенной, т. е. принимает значения одного знака, но обращается в пуль не только при  (и частности, она может быть тождественно равна нулю).
(и частности, она может быть тождественно равна нулю).
В первом случае в стационарной точке экстремума не будет, а во втором — экстремум может быть, а может и не быть: в этом случае надо исследовать аналогичным образом члены третьего порядка формулы Тейлора при тех значениях  при которых члены пторсго порядка обращаются и нуль (и частности, при любых
при которых члены пторсго порядка обращаются и нуль (и частности, при любых  когда
когда  частные производные второго порядка и стационарной точке равны 0).
частные производные второго порядка и стационарной точке равны 0).
Замечание. Для функции  одного переменного кпадратичпая форма
одного переменного кпадратичпая форма  сводится к одному члену
сводится к одному члену

 — стационарная точка. Эта форма будет положительно определенной при
— стационарная точка. Эта форма будет положительно определенной при  и отрицательно определенной при
и отрицательно определенной при  . В первом случае функция
. В первом случае функция  точке
точке  будет иметь минимум, а во втором — максимум.
будет иметь минимум, а во втором — максимум.
Для функции  двух переменных исследование ее поведения в окрестности стационарной точки
двух переменных исследование ее поведения в окрестности стационарной точки  сводится к исследованию квадратичной формы от двух
сводится к исследованию квадратичной формы от двух
переменных и 

где снова  Критерий Сильвестра показывает, что исследуемая функция имеет в точке
Критерий Сильвестра показывает, что исследуемая функция имеет в точке  минимум, если
минимум, если

и максимум, если

Если  то квадратичная форма
то квадратичная форма  является неопределенной и функция
является неопределенной и функция  имеет экстремума в точке М (Если же
имеет экстремума в точке М (Если же  то форма
то форма  полуопределенная и для выяснения вопроса о наличии экстремума в точке
полуопределенная и для выяснения вопроса о наличии экстремума в точке  необходимо дальнейшее исследование.
необходимо дальнейшее исследование.
6. Рассмотрим теперь дифференцирование векторного поля — тензорного поля первой валентности:

Абсолютная производная этого поля равна

Полученный тензор второй валентности  иногда называют градиентом векторного поля.
иногда называют градиентом векторного поля.
Напишем теперь формулу, связывающую абсолютный дифференциал  и абсолютную производную
и абсолютную производную 

где  — координаты вектора
— координаты вектора  Тензор второй валентности
Тензор второй валентности  как мы зпаем (гл. III, стр. 101), порождает линейное преобразование
как мы зпаем (гл. III, стр. 101), порождает линейное преобразование

или, в координатной форме,

Поэтому формулу (6) можно переписать в виде

Поскольку  то с точностью до бесконечно малых высшего порядка линейное преобразование
то с точностью до бесконечно малых высшего порядка линейное преобразование  действуя на нектор бесконечно малого смещения
действуя на нектор бесконечно малого смещения  дает соответствующее приращение векторного поля
дает соответствующее приращение векторного поля 

Последнее соотношение показывает, что линейное преобразование  определяет главную линейную част
определяет главную линейную част  приращения векторного поля а в точке М.
приращения векторного поля а в точке М.
Рассмотрим след линейного преобразования 

Так как производная  векторного поля есть тензор второй валентности, то этот след представляет собой инвариант, который называют дивергенцией векторного поля а:
векторного поля есть тензор второй валентности, то этот след представляет собой инвариант, который называют дивергенцией векторного поля а:

Поле этого инварианта будет скалярным полем, определенным в той же области в которой определено исходное векторное поле а. Так как инвариант  получается из векторного поля
получается из векторного поля  в результате дифференцирования, то его называют дифференциальным инвариантом поля а
в результате дифференцирования, то его называют дифференциальным инвариантом поля а 
Рассмотрим еще вектор  координаты которого получаются в результате свертывания тензора
координаты которого получаются в результате свертывания тензора  с дискриминантным тензором
с дискриминантным тензором  а именно положим
а именно положим

Этот вектор  называется ротором векторного поля а:
называется ротором векторного поля а:

Расписывая подробно формулы (9) для координат вектора  найдем
найдем

где величина  равна
равна  в правой
в правой  в левой системах координат. Мы видим отсюда, что компоненты вектора
в левой системах координат. Мы видим отсюда, что компоненты вектора  а с точностью до множителя
а с точностью до множителя  совпадают с компонентами удвоенного альтернированного тензора а;
совпадают с компонентами удвоенного альтернированного тензора а;  Таким образом, с векторным полем
Таким образом, с векторным полем  определенным в области
определенным в области  инвариантно связывается повое векторное поле — поле вектора
инвариантно связывается повое векторное поле — поле вектора  , определенное в той же области
, определенное в той же области 
Дивергенция и ротор векторного поля являются основными понятиями векторного анализа. При обычном изложении векторного анализа (см., например, [2], стр. 519) необходимо доказательство инвариантности этих полей.  данном же случае инвариантность непосредственно вытекает из тензорной природы этих понятий.
данном же случае инвариантность непосредственно вытекает из тензорной природы этих понятий.
Напомним еще, что векторное поле  называется соленопдальным и области если в этой области
называется соленопдальным и области если в этой области  векторное поле называется безвихревым в если в ней
векторное поле называется безвихревым в если в ней 
Найдем, наконец, дивергенцию векторного поля, являющегося градиентом некоторого скалярного поля 

Для определения дпнергепции векторного поля  как мы знаем, надо взять производную этого векторного поля
как мы знаем, надо взять производную этого векторного поля  и свернуть его но индексам
и свернуть его но индексам  и
и  Но
Но  поэтому
поэтому

Оператор

называется оператором Лапласа (или «лапласианом»). С помощью этого оператора дивергенция векторного поля  может быть записана и виде
может быть записана и виде

Если скалярное поле  удовлетворяет условию
удовлетворяет условию

то оно называется гармоническим (или лапласовым) полем. Уравнение

которому удовлетворяет определяющая такое поле функция  называется уравнением Лапласа. Функция
называется уравнением Лапласа. Функция  удовлетворяющая этому уравнению, называется гармонической.
удовлетворяющая этому уравнению, называется гармонической.
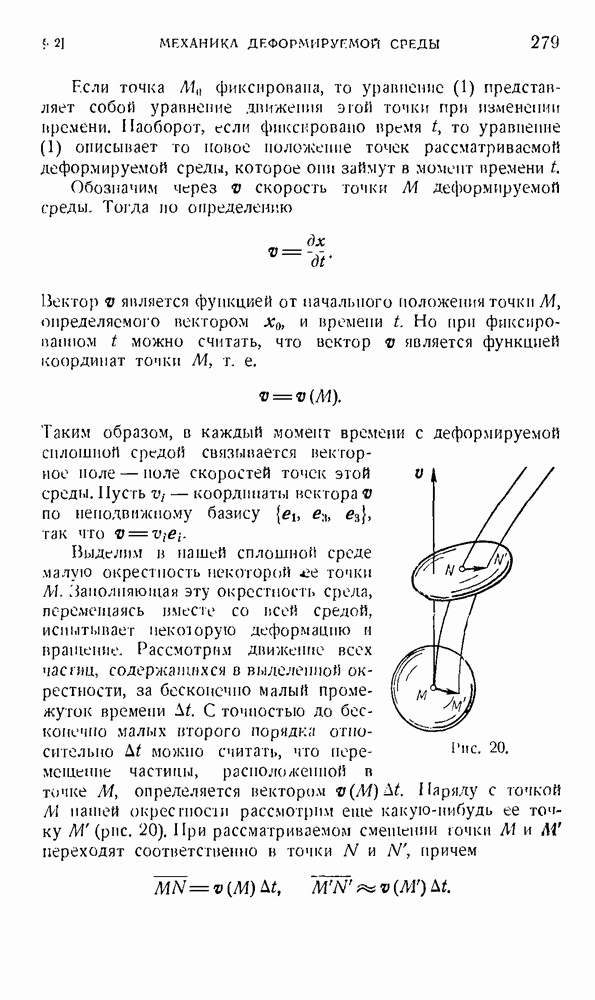
7. До сих пор мы изучали тензорные поля, тензоры которых зависят  положения точки в пространстве, но не зависят от момента времени, в который рассматривается это поле. Такие тензорные ноля называются стационарными. Если же тензор поля зависит не только
положения точки в пространстве, но не зависят от момента времени, в который рассматривается это поле. Такие тензорные ноля называются стационарными. Если же тензор поля зависит не только  положения точки в пространстве, но и от времени, то поле называется нестационарным. Компоненты нестационарного тензорного поля будут функциями координат
положения точки в пространстве, но и от времени, то поле называется нестационарным. Компоненты нестационарного тензорного поля будут функциями координат  точки М и времени
точки М и времени  Например, для трехвалечтпого тензорного поля эта зависимость запишется так:
Например, для трехвалечтпого тензорного поля эта зависимость запишется так:

Скорость изменения тензорного поля во времени в некоторой неподвижной точке М будет описываться частными производными  которые, как легко видеть, снопа образуют тензорное поле той же валентности, что и исходное поле. Предположим теперь, что нестационарное тензорное поле
которые, как легко видеть, снопа образуют тензорное поле той же валентности, что и исходное поле. Предположим теперь, что нестационарное тензорное поле  описывает некоторое свойство материальной среды, частицы которой находятся в движении. Определим, как изменятся компоненты тензора
описывает некоторое свойство материальной среды, частицы которой находятся в движении. Определим, как изменятся компоненты тензора  связанные с некоторой фиксированной частицей, при ее движении. Пусть траектория движения этой частицы описывается уравнениями
связанные с некоторой фиксированной частицей, при ее движении. Пусть траектория движения этой частицы описывается уравнениями

Тогда скорость изменения компонент тензора  связанных с частицей, будет равна
связанных с частицей, будет равна

 компоненты скорости частицы движущейся материальной среды, которые мы обозначим через
компоненты скорости частицы движущейся материальной среды, которые мы обозначим через  Тогда предыдущая формула перепишется так:
Тогда предыдущая формула перепишется так:

Первый член правой части этого соотношения описывает изменение компонент тензора  в неподвижной точке М, а второй член связан с движением частицы в пространстве. Он называется переносным членом.
в неподвижной точке М, а второй член связан с движением частицы в пространстве. Он называется переносным членом.
Очевидно, что формулы вида (10) будут иметь место для нестационарных тензорных полей любой паленпюсти. Для скалярного поля  эта формула примет вид
эта формула примет вид

Если обозначить вектор скорости частицы через то

Для нестационарного векторного поля  формула, аналогичная формуле (10), выглядит так:
формула, аналогичная формуле (10), выглядит так:

Последняя формула равносильна соотношению

где  — линейное преобразование, определяемое тензором
— линейное преобразование, определяемое тензором 
ЗАДАЧИ И УПРАЖНЕНИЯ
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ЛИНЕЙНОЕ ПРОСТРАНСТВО
- § 1. Понятие линейного пространства
- § 2. Линейная зависимость векторов
- § 3. Размерность и базис линейного пространства
- § 4. Прямоугольный базис в трехмерном пространстве. Скалярное произведение векторов
- § 5. Векторное и смешанное произведения векторов
- § 6. Преобразования ортонормированного базиса. Основная задача тензорного исчисления
- § 7. Некоторые вопросы аналитической геометрии в пространстве
- ГЛАВА II. ПОЛИЛИНЕЙНЫЕ ФОРМЫ И ТЕНЗОРЫ
- § 2. Билинейные формы
- § 3. Полилинейные формы. Общее определение тензора
- § 4. Алгебраические операции над тензорами
- § 5. Симметричные и антисимметричные тензоры
- ГЛАВА III. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ ВЕКТОРНОГО ПРОСТРАНСТВА И ТЕНЗОРЫ ВТОРОЙ ВАЛЕНТНОСТИ
- § 2. Матрица линейного преобразования
- § 3. Определитель матрицы линейного преобразования. Ранг матрицы
- § 4. Линейные преобразования и билинейные формы
- § 5. Умножение линейных преобразований и умножение матриц
- § 6. Обратное линейное преобразование и обратная матрица
- § 7. Группа линейных преобразований и ее подгруппы
- ГЛАВА XIV. ПРИВЕДЕНИЕ К ПРОСТЕЙШЕМУ ВИДУ МАТРИЦЫ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- § 1. Собственные векторы и собственные значения линейного преобразования
- § 2. Приведение к простейшему виду матрицы линейного преобразования в случае различных собственных значений
- § 3. Многочлены от матриц и теорема Гамильтона—Кэли
- § 4. Свойства собственных векторов и собственных значений симметричного линейного прейбразования
- § 5. Приведение к диагональному виду матрицы симметричного линейного преобразования
- § 6. Приведение квадратичной формы к каноническому виду
- § 7. Представление невырожденного линейного преобразования в виде произведения симметричного и ортогонального преобразований
- ГЛАВА V. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Общее уравнение поверхности второго порядка. Его инварианты
- § 2. Приведение к простейшему виду общего уравнения поверхности второго порядка
- § 3. Определение типа поверхности второго порядка при помощи инвариантов
- § 4. Классификация поверхностей второго порядка
- § 5. Приложение теории инвариантов к классификации поверхностей второго порядка
- § 6. Центральные и нецентральные поверхности второго порядка
- § 7. Примеры
- ГЛАВА VI. ПРИЛОЖЕНИЕ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ К НЕКОТОРЫМ ВОПРОСАМ МЕХАНИКИ И ФИЗИКИ
- § 2. Некоторые свойства кристаллов, связанные с тензорами второй валентности
- § 3. Тензоры напряжений и деформации
- § 4. Дальнейшие свойства кристаллов
- ГЛАВА VII. ОСНОВЫ ТЕНЗОРНОГО АНАЛИЗА
- § 1. Тензорное поле и его дифференцирование
- § 2. Механика деформируемой среды
- § 3. Ортогоналыше криволинейные системы координат
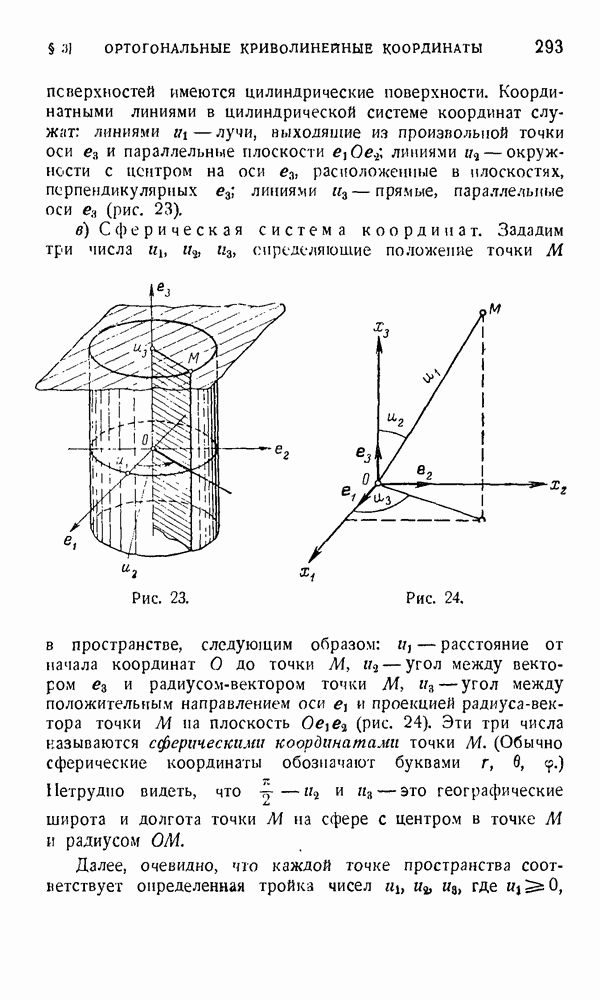
- § 4. Подвижной репер ортогональной криволинейной системы координат и тензорные поля
- § 5. Дифференцирование тензорного поля в криволинейных координатах
- ОТВЕТЫ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ И УПРАЖНЕНИЙ
- ЛИТЕРАТУРА