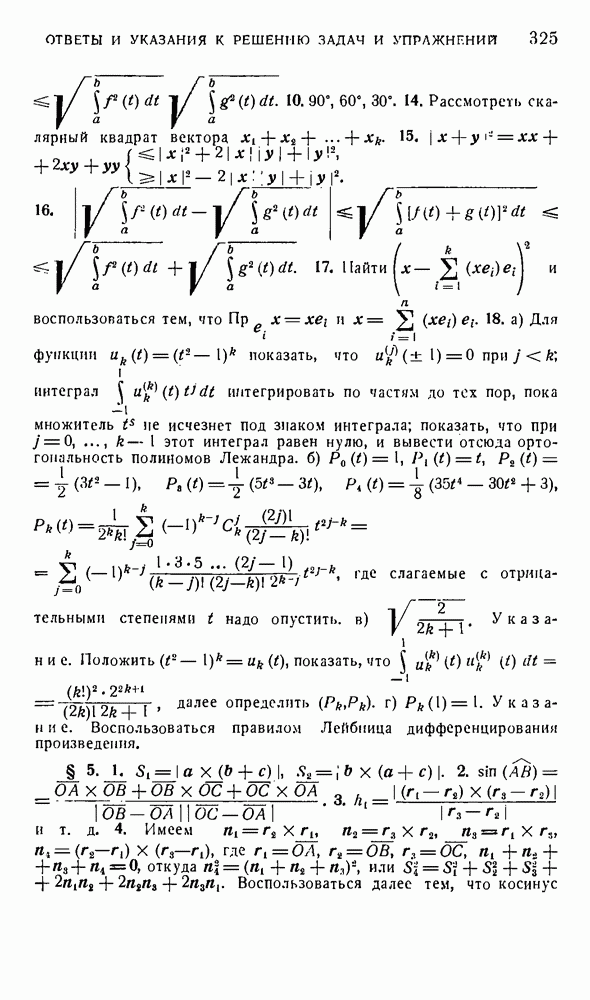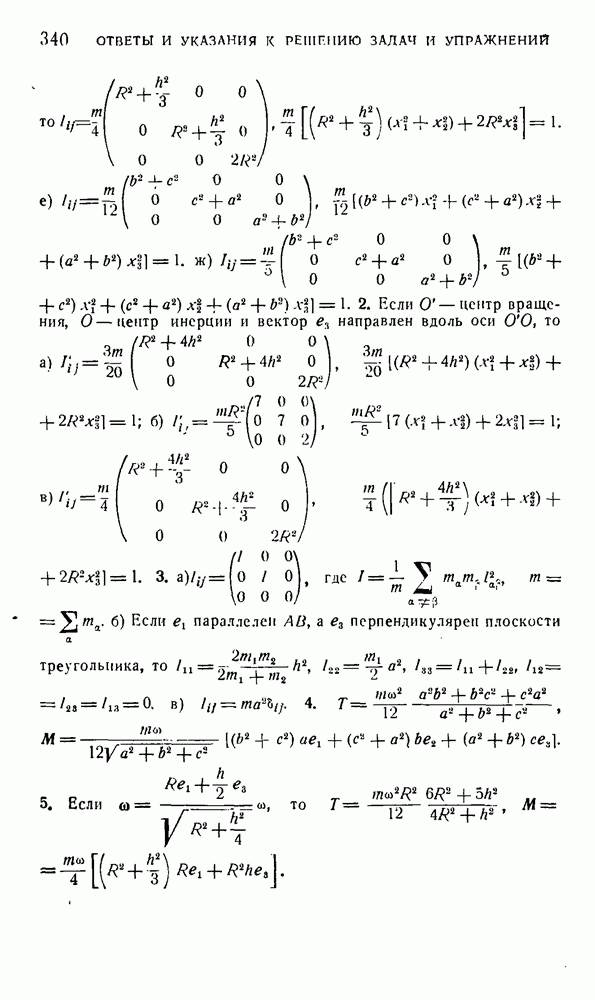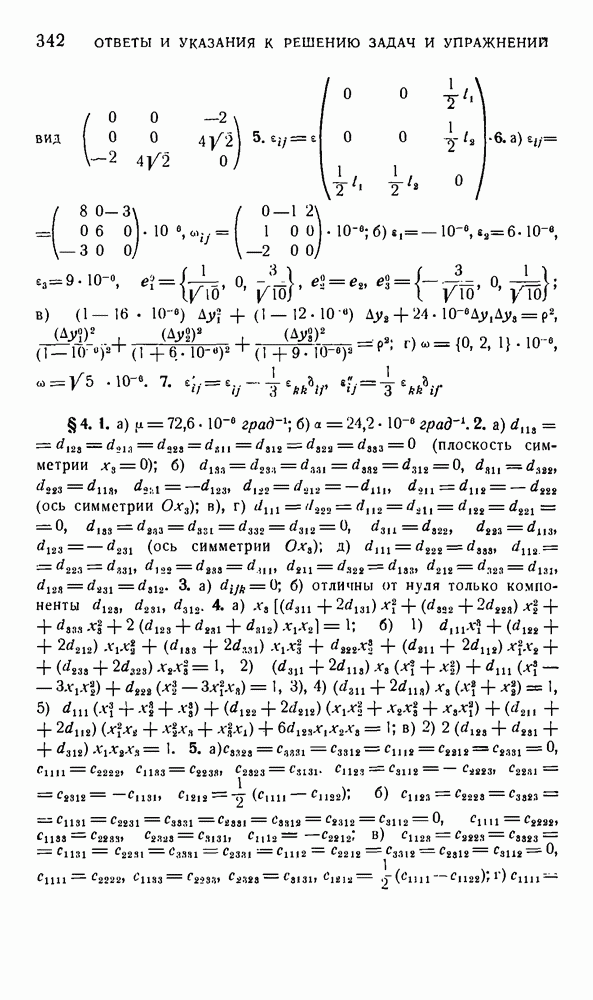| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. Группа линейных преобразований и ее подгруппы
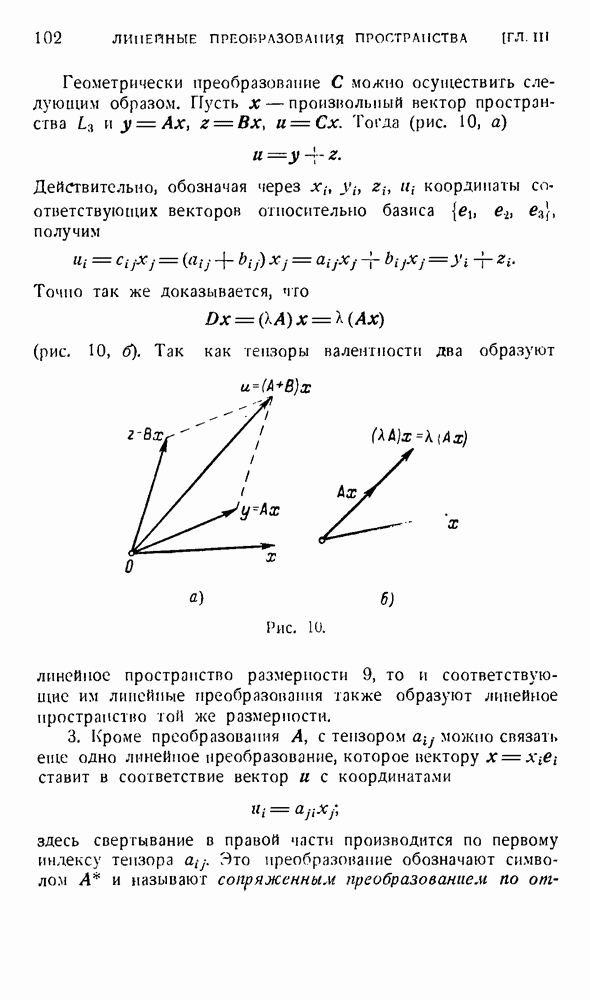
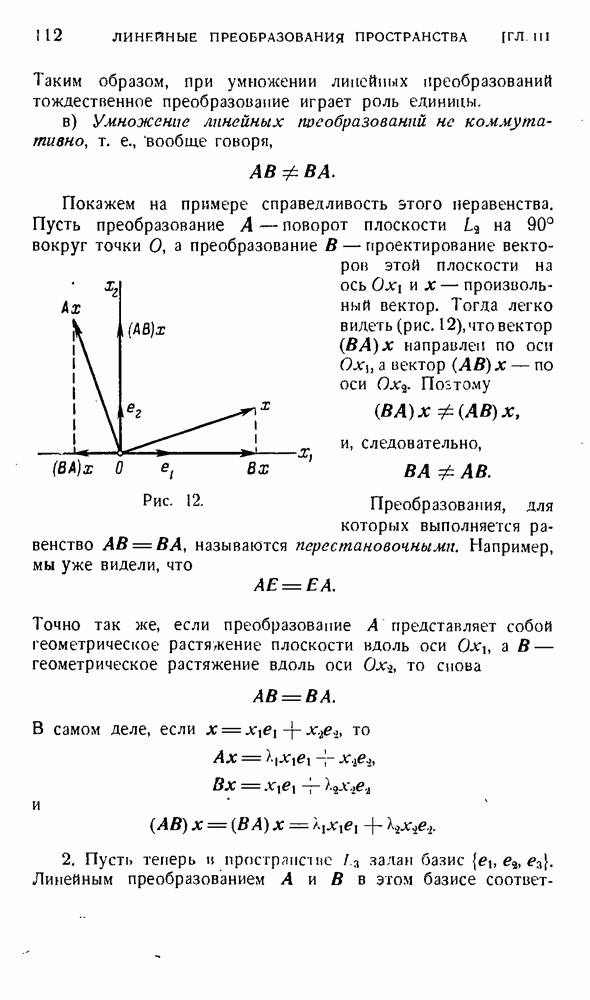
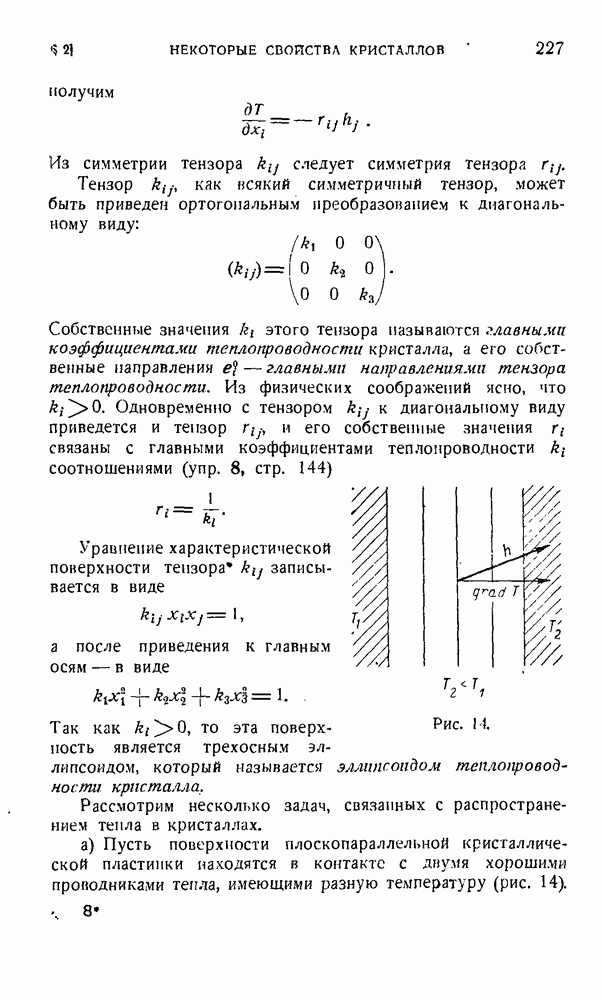
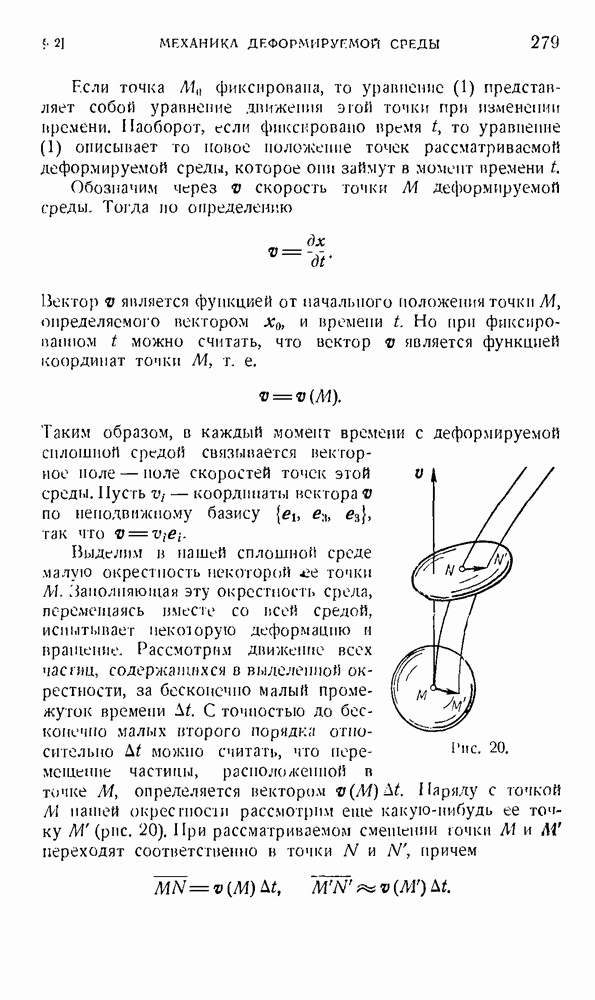
1. Рассмотрим совокупность невырожденных линейных преобразований трехмерного линейного пространства. В эгой совокупности определена операция умножения преобразований, обладающая следующими свойствами:
а) Совокупность невырожденных преобразований замкнута относительно умножения, так как  — невырожденное преобразование, если А и В не вырождены.
— невырожденное преобразование, если А и В не вырождены.
б) Операция умножения преобразований подчиняется сочетательному закону. 
в) Совокупности невырожденных преобразований принадлежит тождественное преобразование Е такое, что 
г) Для каждого невырожденного преобразования А существует единственное обратное преобразование  такое, что
такое, что 
Этими свойствами обладает умножение не только линейных преобразований. Например, для совокупности всех положительных рациональных чисел обычное умножение также обладает перечисленными выше четырьмя свойствами, то же самое можно сказать и об умножении во множестве отличных от нуля комплексных чисел. Число таких примеров легко увеличить. Любое множество элементов, в котором определена операция умножения, обладающая перечисленными выше свойствами, называется группой.
Таким образом, совокупность невырожденных линейных преобразований трехмерного линейного пространства образует группу. Эту группу называют полной линейной группой третьего порядка и обозначают через 
Так как каждому невырожденному линейному преобразованию пространства  при заданном базисе соответствует квадратная матрица третьего порядка с определителем, отличным от нуля, и умножению преобразований соогисктвует
при заданном базисе соответствует квадратная матрица третьего порядка с определителем, отличным от нуля, и умножению преобразований соогисктвует
умножение матриц, то эти матрицы также образуют группу. По существу, эта группа ничем не отличается от группы линейных преобразований, и ее мы тоже будем называть полной линейной группой и обозначать через 
Точно так же совокупность невырожденных линейных преобразований векторов плоскости образует группу — полную линейную группу второго порядка, обозначаемую через  Матрицы второго порядка с определителями, отличными от пуля, образуют такую же группу. Вообще, совокупность невырожденных линейных преобразований пространства так же как и совокупность квадратных матриц
Матрицы второго порядка с определителями, отличными от пуля, образуют такую же группу. Вообще, совокупность невырожденных линейных преобразований пространства так же как и совокупность квадратных матриц  порядка с определителями, отличными от нуля, образует группу
порядка с определителями, отличными от нуля, образует группу  — полную линейную группу порядка
— полную линейную группу порядка 
2. Но не только вся совокупность невырожденных лпнейных преобразований трехмерного пространства образует группу. 13 этой совокупности имеются подмножества, которые также замкнуты относительно умножения и вместе с каждым своим элементом содержат обратный ему элемент, а значит, образуют группу (что касается свойств б) и в), то они для подмножества выполняются автоматически: свойство сочетательности, справедливое для всего множества, выполняется и для подмножества, а тождественное преобразование принадлежит подмножеству, поскольку последнее вместе с каждым преобразованием А содержит обратное к нему преобразование  ,з также их произведение
,з также их произведение  Такие группы называются подгруппами полной линейной группы. Рассмотрим несколько примеров таких подгрупп.
Такие группы называются подгруппами полной линейной группы. Рассмотрим несколько примеров таких подгрупп.
а) Пусть преобразование А пространства  не меняет ориентацию некомпланарных троек векторов. Определитель матрицы А такого преобразования будет положителен,
не меняет ориентацию некомпланарных троек векторов. Определитель матрицы А такого преобразования будет положителен,  Произведение двух преобразований, не меняющих ориентации тройки векторов, очевидно, также не меняет их ориентации. Таким же свойством обладает и преобразование
Произведение двух преобразований, не меняющих ориентации тройки векторов, очевидно, также не меняет их ориентации. Таким же свойством обладает и преобразование  , обратное преобразованию А. Поэтому совокупность таких преобразований образует группу, которая является подгруппой группы
, обратное преобразованию А. Поэтому совокупность таких преобразований образует группу, которая является подгруппой группы  Этой группе соответствует группа матриц третьего порядка с положительными определителями. Заметим, что совокупность матриц с отрицательными определителями группы не образует, так как произведением днух матриц с отрицательными определителями будет матрица с положительным определителем.
Этой группе соответствует группа матриц третьего порядка с положительными определителями. Заметим, что совокупность матриц с отрицательными определителями группы не образует, так как произведением днух матриц с отрицательными определителями будет матрица с положительным определителем.
б) Пусть преобразование А не меняет абсолютной величины объема параллелепипеда, натянутого на любые три вектора. Тогда абсолютная величина определи гели матрицы этого преобразования равна единице, преобрззопапия, обладающие этим свойством, как и их матрицы, очевидно, образуют группу. Эта группа называется унимодулярной группой. Подгруппу упимодулярпой группы образуют преобразования, сохраняющие и объем, и ориентацию тройки векторов. Для таких преобразований 
в) Рассмотрим совокупность поворотов плоскости  вокруг начала координат. Эта совокупность является группой, так как произведение двух поворотов, очевидно, также является поворотом, как
вокруг начала координат. Эта совокупность является группой, так как произведение двух поворотов, очевидно, также является поворотом, как  преобразование, обратное к повороту. Подтвердим это формальной выкладкой. Н самом деле, если
преобразование, обратное к повороту. Подтвердим это формальной выкладкой. Н самом деле, если

— матрицы поворота на угол  угол
угол 

— матрица поворота на угол  и
и

— матрица поворота на угол 
3. Рассмотрим  одну важную подгруппу полной линейной группы
одну важную подгруппу полной линейной группы  - подгруппу ортогональных преобразований. Линейное преобразование А называется ортогональным, если оно
- подгруппу ортогональных преобразований. Линейное преобразование А называется ортогональным, если оно  меняет величину скалярного произведения векторов. Это значит, что если А — ортогональное преобразование,
меняет величину скалярного произведения векторов. Это значит, что если А — ортогональное преобразование,  и у — два произвольных вектора и
и у — два произвольных вектора и  то
то

Докажем прежде всего, что ортогональные преобразования сохраняют длины векторов и углы между ними. В самом деле, если А — ортогональное преобразование и  то
то
— огкуда следует, что  Пусть, далее,
Пусть, далее, 
 - угол между векторами
- угол между векторами  и
и  — угол между векторами и и
— угол между векторами и и  Так как
Так как

то  и так как угол между векторами изменяется в пределах от 0 до
и так как угол между векторами изменяется в пределах от 0 до  Поэтому ортогональные преобразования пространства
Поэтому ортогональные преобразования пространства  называют также вращениями.
называют также вращениями.
Заметим, что если потребовать от преобразования А только сохранения длин векторов, то уже этого достаточно для того, чтобы оно было ортогональным. В самом деле, пусть преобразование А оставляет неизменными длины векторов и  Тогда и
Тогда и  откуда
откуда

Так как 

что и требовалось доказать.
Докажем следующую теорему.
Теорема.  того чтобы линейное преобразование А было ортогональным, необходимо и достаточно, чтобы оно удовлетворяло соотношению
того чтобы линейное преобразование А было ортогональным, необходимо и достаточно, чтобы оно удовлетворяло соотношению

В самом деле, пусть  Тогда, пользуясь свойствами билинейной формы, доказанными в § 5 (см. также упр. 8 на стр. 118), получим
Тогда, пользуясь свойствами билинейной формы, доказанными в § 5 (см. также упр. 8 на стр. 118), получим

Если  то
то  и А — ортогональное преобразование. Обратно, если А—ортогональное преобразование, то
и А — ортогональное преобразование. Обратно, если А—ортогональное преобразование, то 
Соотношение (1), которому удовлетворяет ортогональное преобразование, может быть записано в виде

Докажем теперь, что ортогональные преобразования образуют группу. Пусть  ортогональные преобразования, тогда
ортогональные преобразования, тогда

Если  то
то

Следовательно, С — ортогональное преобразование. А это означает, что совокупность ортогональных преобразований замкнута по отношению к операции умножения. Далее, если А — ортогональное преобразование, то этим же свойством обладает и преобразование  . В самом деле, из того, что
. В самом деле, из того, что  следует, что
следует, что

А это означает ортогональность преобразования  Следовательно, ортогональные преобразования образуют группу. Эту группу обозначают через
Следовательно, ортогональные преобразования образуют группу. Эту группу обозначают через  Она, конечно, является подгруппой полной линейной группы
Она, конечно, является подгруппой полной линейной группы 
Заметим, что доказать групповой характер совокупности ортогональных преобразований можно чисто геометрически. Действительно, если преобразования А и В не меняют длин векторов и углов между ними, то и их произведение  обладает этим свойством, так же как и преобразования
обладает этим свойством, так же как и преобразования 
Рассмотрим теперь матрицы ортогональных преобразований — так называемые ортогональные матрицы. С такими матрицами мы уже встречались, когда рассматривали преобразования ортогонального базиса (гл. 1, § 6). В силу соотношения (1) матрица  ортогонального преобразования А удовлетворяет условию
ортогонального преобразования А удовлетворяет условию

и ранносильному условию

Если обозначить через  элемент матрицы А, то
элемент матрицы А, то  Поэтому написанные выше условия в координантной форме запишутся гак:
Поэтому написанные выше условия в координантной форме запишутся гак:

Первое из этих соотношений означает, что сумма квадратов элементов какого-либо столбца ортогональной матрицы равна единице (случай  а сумма произведений соответствующих элементов различных ее столбцов равна
а сумма произведений соответствующих элементов различных ее столбцов равна
нулю (случай  ). Второе соотношение означает то же самое Для строк ортогональной матрицы. Заметим, что соотношения (2) только обозначениями отличаются от формул (6) из § 6 гл. I.
). Второе соотношение означает то же самое Для строк ортогональной матрицы. Заметим, что соотношения (2) только обозначениями отличаются от формул (6) из § 6 гл. I.
Ранее (гл. I, стр. 34) было доказано геометрически, что определитель ортогональной матрицы равен  Теперь можно дать простое аналитическое доказательство этого утверждения. Из соотношения
Теперь можно дать простое аналитическое доказательство этого утверждения. Из соотношения  и теоремы об умножении определителей следует, что
и теоремы об умножении определителей следует, что

так как  Отсюда непосредственно следует, что
Отсюда непосредственно следует, что 
Ортогональные преобразования, определитель матрицы которых равен  сохраняют ориентацию троек векторов и называются собственными вращениями. Собственные вращения, как легко видеть, образуют группу, являющуюся подгруппой группы
сохраняют ориентацию троек векторов и называются собственными вращениями. Собственные вращения, как легко видеть, образуют группу, являющуюся подгруппой группы  Ее обозначают через и называют подгруппой собственных вращений.
Ее обозначают через и называют подгруппой собственных вращений.
Ортогональные преобразования, определитель матрицы которых равен — 1, меняют ориентацию троек векторов и называются несобственными вращениями. Несобственные вращения, конечно, группы не образуют (почему?). К несобственным вращениям относятся, например, преобразования, состоящие в отражении пространства относительно некоторой плоскости т., проходящей через начало координат О. В самом деле, при отражении пространства относительно плоскости  длины векторов и углы между ними сохраняются, а ориентация троек векторов меняется на противоположную. Легко доказать, что любое несобственное вращение можно представить в виде произиедепии собственного вращения и отражения относительно некоторой плоскости.
длины векторов и углы между ними сохраняются, а ориентация троек векторов меняется на противоположную. Легко доказать, что любое несобственное вращение можно представить в виде произиедепии собственного вращения и отражения относительно некоторой плоскости.
4. Все рассмотренные до сих пор подгруппы полпой линейной группы, как и сама эта группа, состоят из бесконечного числа элементов. Но существуют такие подгруппы этой группы, которые состоят из конечного числа элементов, — так называемые конечные подгруппы. Особенно интересны конечные подгруппы ортогональной группы, которые называют группами симметрии. Эги группы имеют важное значение для кристаллографии и других разделов физики.
Рассмотрим некоторые примеры групп симметрии на плоскости и в пространстве
а) Пусть Е — тождественное преобразование и  — преобразование, состоящее в отражении всех векторов пространства от начала координат. Для этих преобразований мы имеем
— преобразование, состоящее в отражении всех векторов пространства от начала координат. Для этих преобразований мы имеем

Следовательно, совокупность преобразований, состоящая из двух элементов Е и А, замкнута относительно операции умножения и операции обращения, а значит, она представляет собой группу. Таблица умножения элементов этой группы может быть записана в виде

Произведение любых двух сомножителей этой группы не зависит от их порядка. Такие группы называются коммутативными. Преобразования этой группы переводят в себя любую фигуру, для которой точка О является центром симметрии.
б) Пусть Е — тождественное преобразование плоскости и А—поворот плоскости на угол Тогда преобразование А представляет собой поворот плоскости на угол  в частности,
в частности,  Преобразования
Преобразования  образуют группу, так как
образуют группу, так как

где  — остаток от деления числа
— остаток от деления числа  на
на  Эта группа тоже будет коммутативной. Она называется циклической группой
Эта группа тоже будет коммутативной. Она называется циклической группой  порядка.
порядка.
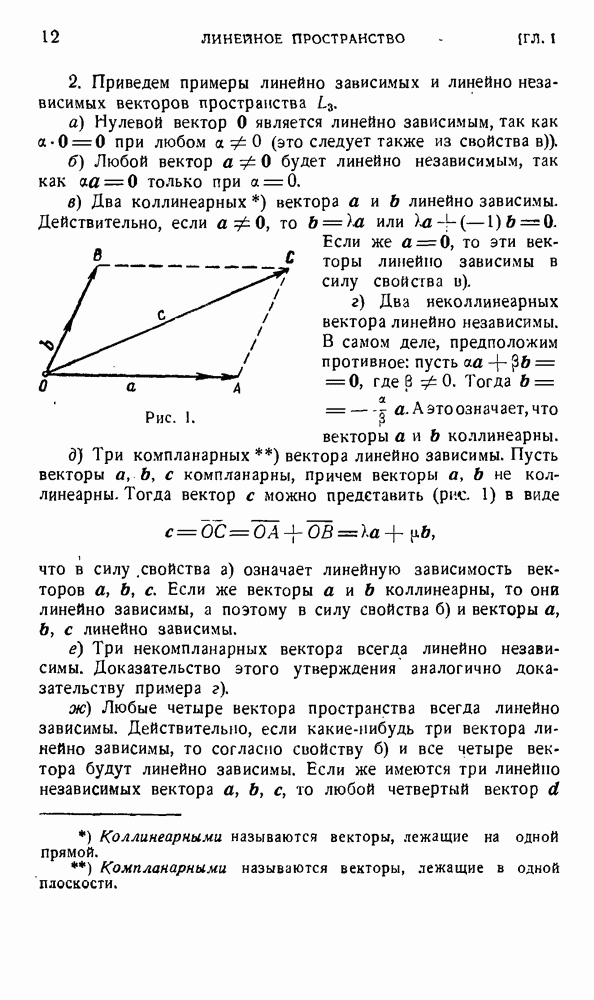
б) Пусть  с — три взаимно перпендикулярные оси пространства
с — три взаимно перпендикулярные оси пространства  проходящие через точку О, и А, В, С
проходящие через точку О, и А, В, С
преобразования, представляющие собой поворот на угол  вокруг соответствующей осн. Четыре преобразования Е, А, В, С образуют группу с таблицей умножения
вокруг соответствующей осн. Четыре преобразования Е, А, В, С образуют группу с таблицей умножения

Так как произведение любых элементов этой группы не зависит от порядка сомножителей, то эта группа будет коммутативной. Преобразования этой группы переводят в себя любую фигуру, для которой оси  являются осями симметрии.
являются осями симметрии.
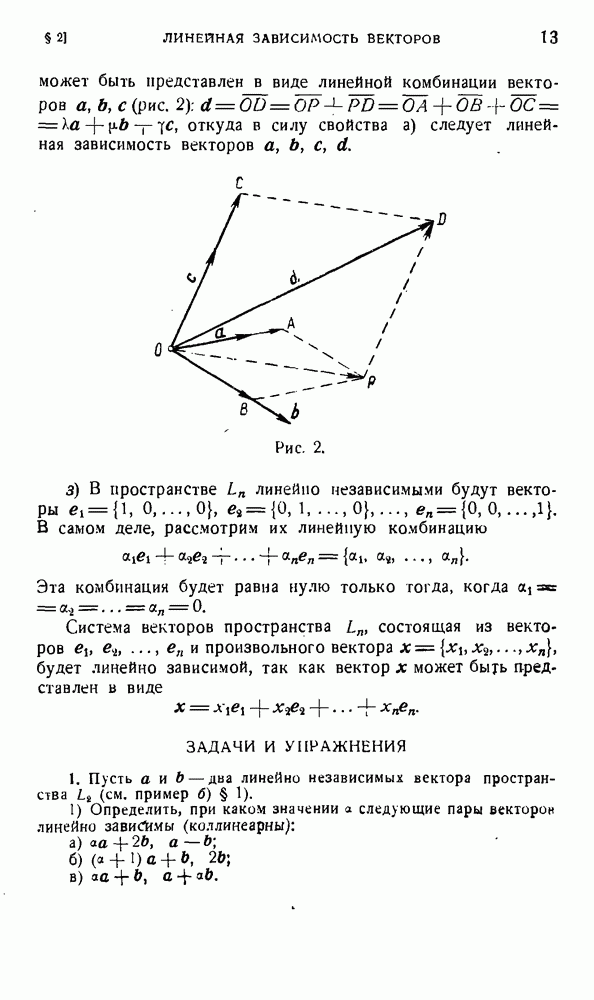
г) Пусть  дне взаимно перпендикулярные оси, проходящие через точку О и А — поворот на угол
дне взаимно перпендикулярные оси, проходящие через точку О и А — поворот на угол  вокруг оси
вокруг оси  поворот на угол - вокруг оси
поворот на угол - вокруг оси  Рассмотрим преобразования
Рассмотрим преобразования

Докажем, что эти преобразования образуют группу. Заметим, что преобразование  представляет собой поворот на угол
представляет собой поворот на угол  вокруг оси
вокруг оси  получающейся из оси
получающейся из оси  при преобразовании
при преобразовании  Точно так же преобразование
Точно так же преобразование  есть поворот на угол
есть поворот на угол  вокруг оси
вокруг оси  получающейся из оси
получающейся из оси  при преобразовании А. Поэтому
при преобразовании А. Поэтому

Кроме того, пользуясь тем, что  найдем
найдем

Теперь таблица умножения этих преобразований может быть записана в виде

В этой таблице слева стоит первый сомножитель произведения, а сверху — второй. Так как таблица не является симметричной, то рассматриваемая группа не будет коммутативной.
ЗАДАЧИ И УПРАЖНЕНИЯ
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ЛИНЕЙНОЕ ПРОСТРАНСТВО
- § 1. Понятие линейного пространства
- § 2. Линейная зависимость векторов
- § 3. Размерность и базис линейного пространства
- § 4. Прямоугольный базис в трехмерном пространстве. Скалярное произведение векторов
- § 5. Векторное и смешанное произведения векторов
- § 6. Преобразования ортонормированного базиса. Основная задача тензорного исчисления
- § 7. Некоторые вопросы аналитической геометрии в пространстве
- ГЛАВА II. ПОЛИЛИНЕЙНЫЕ ФОРМЫ И ТЕНЗОРЫ
- § 2. Билинейные формы
- § 3. Полилинейные формы. Общее определение тензора
- § 4. Алгебраические операции над тензорами
- § 5. Симметричные и антисимметричные тензоры
- ГЛАВА III. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ ВЕКТОРНОГО ПРОСТРАНСТВА И ТЕНЗОРЫ ВТОРОЙ ВАЛЕНТНОСТИ
- § 2. Матрица линейного преобразования
- § 3. Определитель матрицы линейного преобразования. Ранг матрицы
- § 4. Линейные преобразования и билинейные формы
- § 5. Умножение линейных преобразований и умножение матриц
- § 6. Обратное линейное преобразование и обратная матрица
- § 7. Группа линейных преобразований и ее подгруппы
- ГЛАВА XIV. ПРИВЕДЕНИЕ К ПРОСТЕЙШЕМУ ВИДУ МАТРИЦЫ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- § 1. Собственные векторы и собственные значения линейного преобразования
- § 2. Приведение к простейшему виду матрицы линейного преобразования в случае различных собственных значений
- § 3. Многочлены от матриц и теорема Гамильтона—Кэли
- § 4. Свойства собственных векторов и собственных значений симметричного линейного прейбразования
- § 5. Приведение к диагональному виду матрицы симметричного линейного преобразования
- § 6. Приведение квадратичной формы к каноническому виду
- § 7. Представление невырожденного линейного преобразования в виде произведения симметричного и ортогонального преобразований
- ГЛАВА V. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Общее уравнение поверхности второго порядка. Его инварианты
- § 2. Приведение к простейшему виду общего уравнения поверхности второго порядка
- § 3. Определение типа поверхности второго порядка при помощи инвариантов
- § 4. Классификация поверхностей второго порядка
- § 5. Приложение теории инвариантов к классификации поверхностей второго порядка
- § 6. Центральные и нецентральные поверхности второго порядка
- § 7. Примеры
- ГЛАВА VI. ПРИЛОЖЕНИЕ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ К НЕКОТОРЫМ ВОПРОСАМ МЕХАНИКИ И ФИЗИКИ
- § 2. Некоторые свойства кристаллов, связанные с тензорами второй валентности
- § 3. Тензоры напряжений и деформации
- § 4. Дальнейшие свойства кристаллов
- ГЛАВА VII. ОСНОВЫ ТЕНЗОРНОГО АНАЛИЗА
- § 1. Тензорное поле и его дифференцирование
- § 2. Механика деформируемой среды
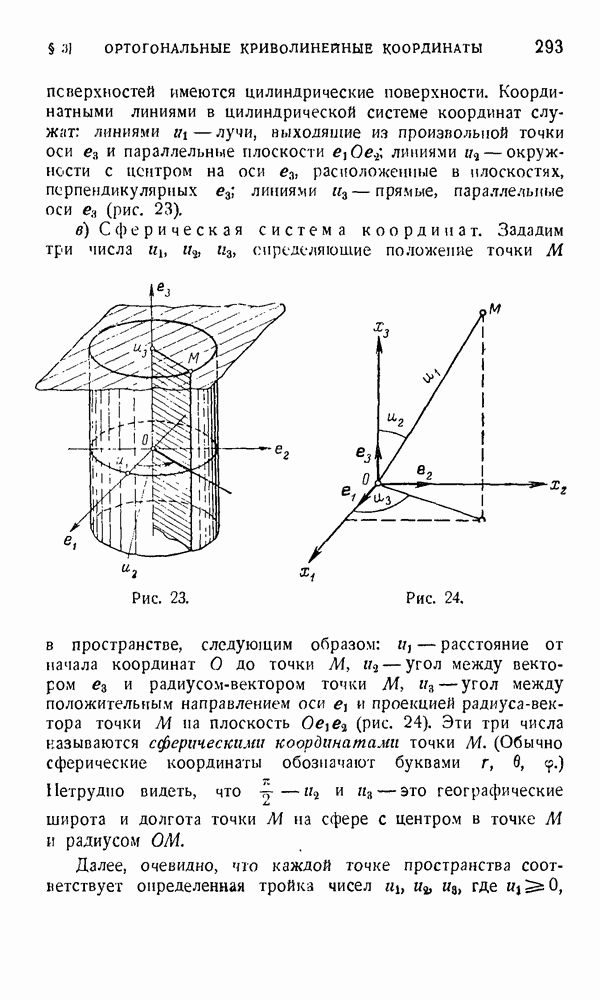
- § 3. Ортогоналыше криволинейные системы координат
- § 4. Подвижной репер ортогональной криволинейной системы координат и тензорные поля
- § 5. Дифференцирование тензорного поля в криволинейных координатах
- ОТВЕТЫ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ И УПРАЖНЕНИЙ
- ЛИТЕРАТУРА