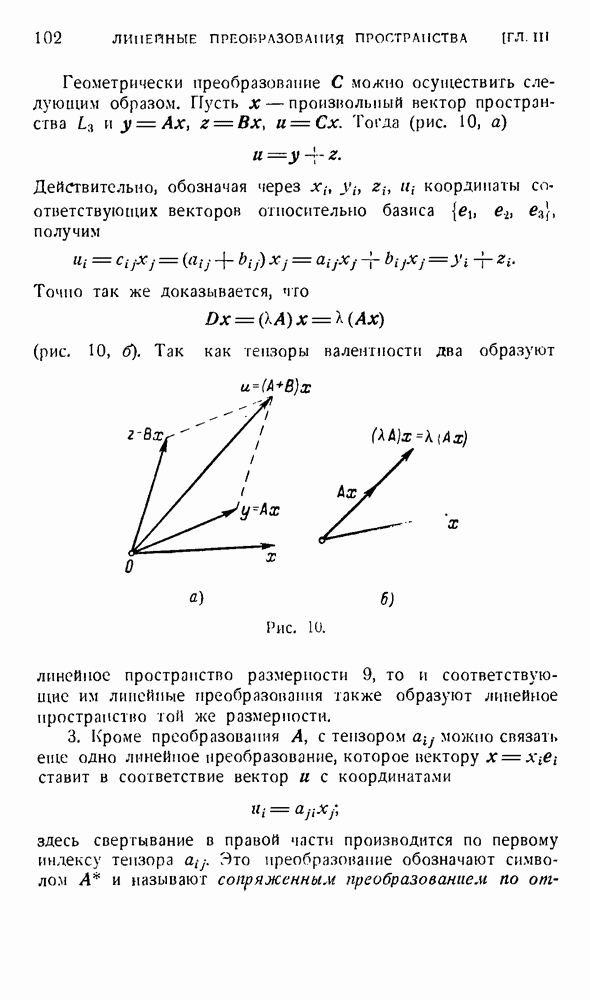
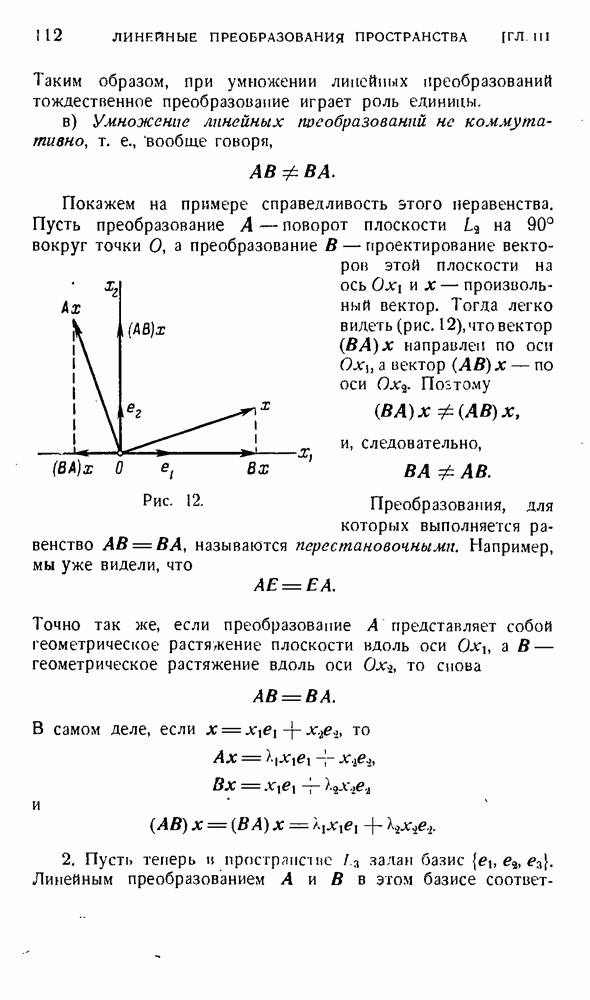
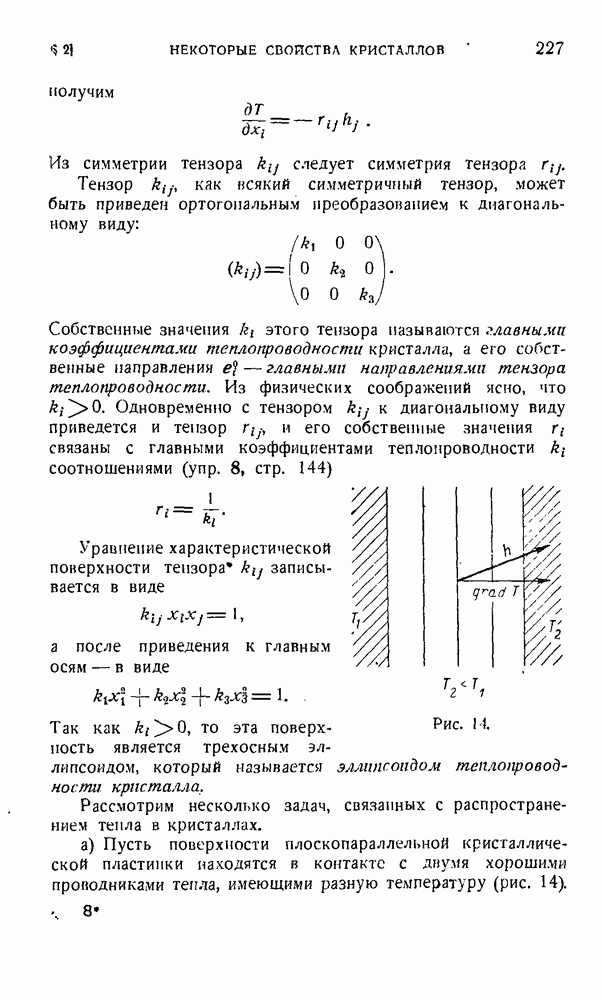
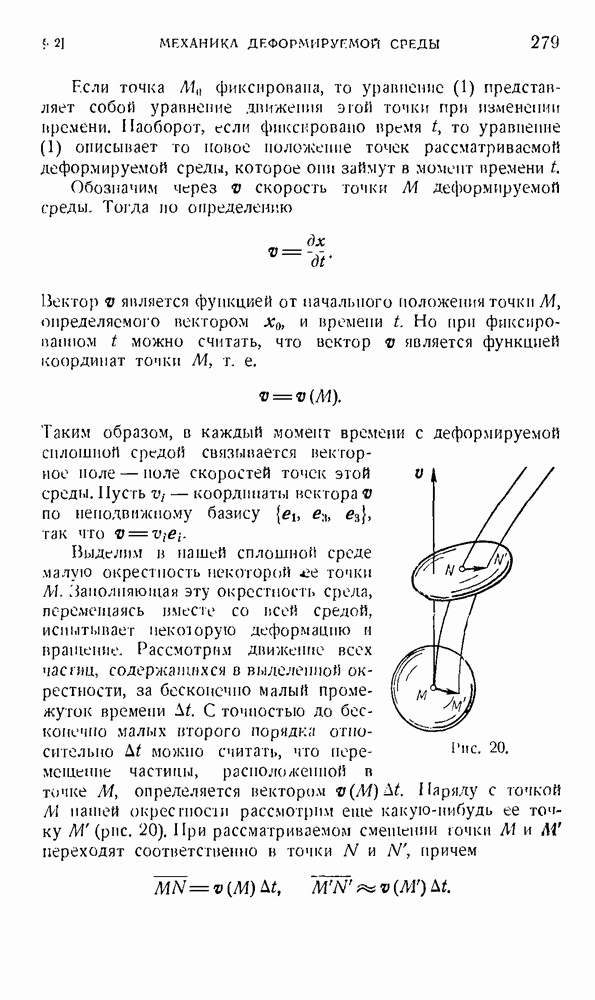
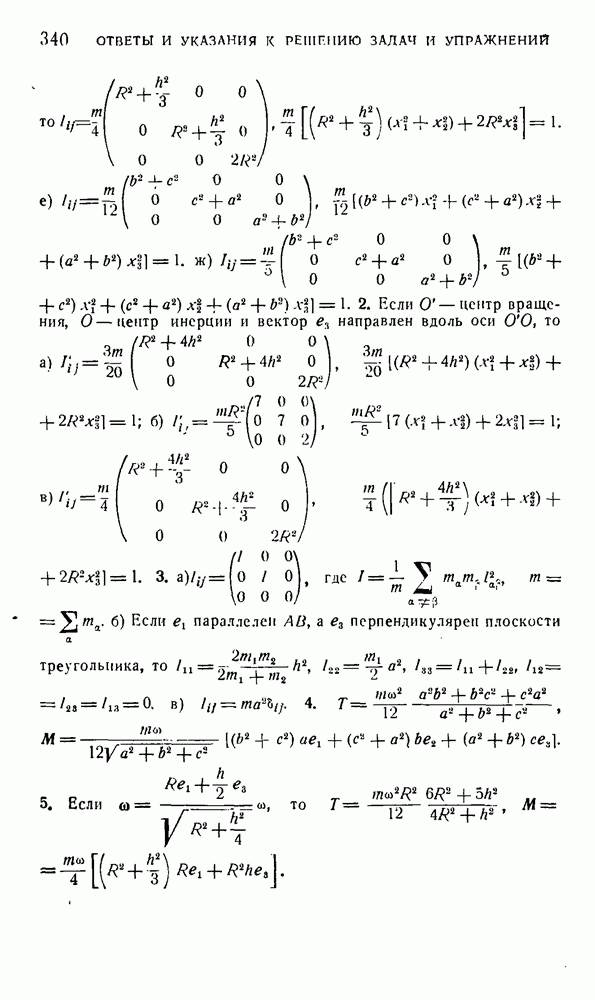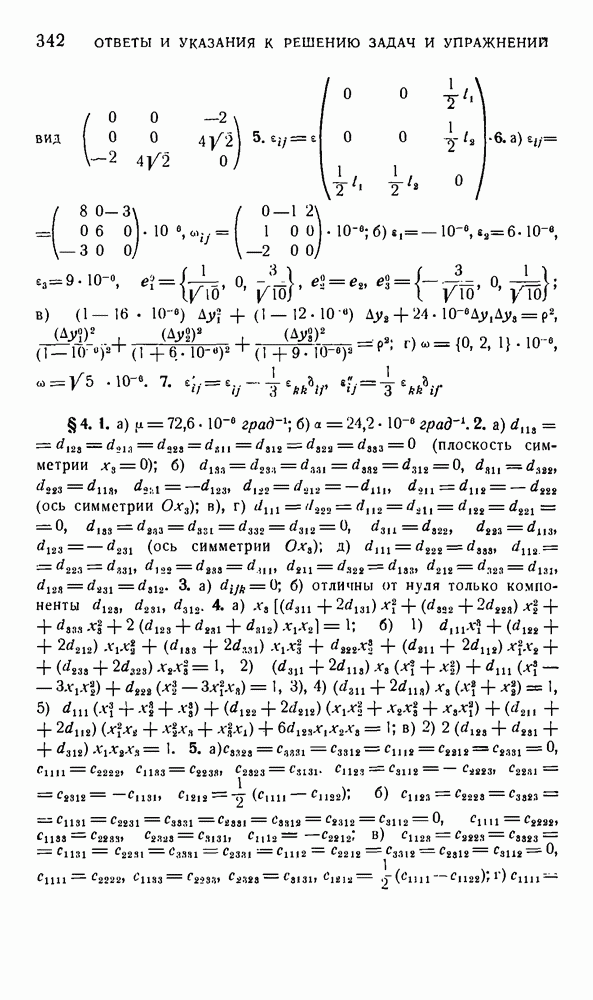| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
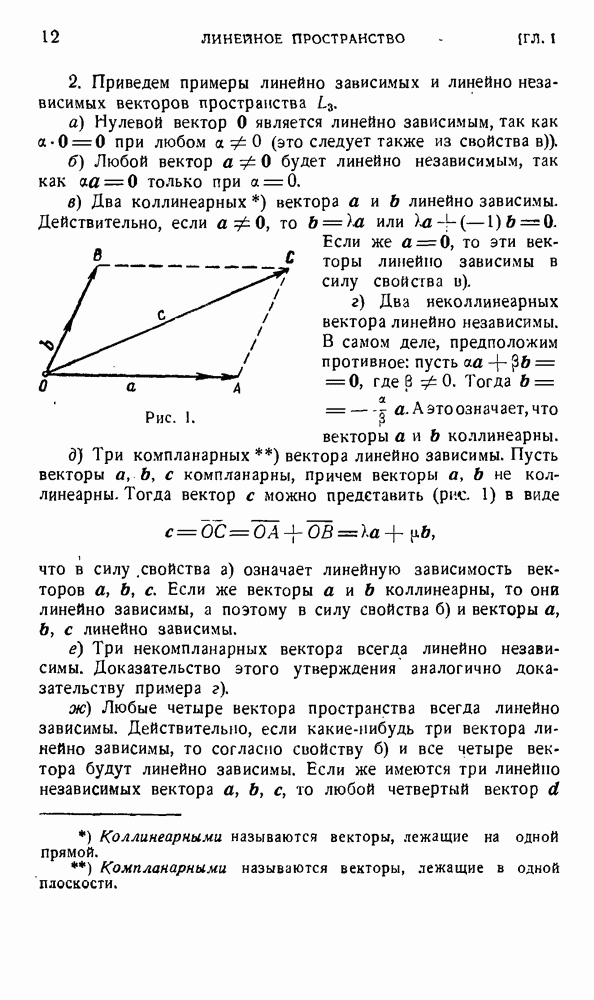
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6. Преобразования ортонормированного базиса. Основная задача тензорного исчисления
1. Пусть в пространстве  наряду с ортонормированным базисом
наряду с ортонормированным базисом  с началом в О, задан другой ортонормированный базис
с началом в О, задан другой ортонормированный базис  тем же началом О (рис. 3). Векторы нового базиса есами могут быть разложены по векторам старого базиса. Будем обозначать через
тем же началом О (рис. 3). Векторы нового базиса есами могут быть разложены по векторам старого базиса. Будем обозначать через  коэффициент при в; в разложении вектора
коэффициент при в; в разложении вектора  по векторам старого базиса. Тогда разложения векторов будут иметь вид
по векторам старого базиса. Тогда разложения векторов будут иметь вид


Рис. 3.
Короче эти три равенства можно записать так:

Умножим скалярно каждое из равенств (1) на каждый из векторов  Тогда, учитывая, что
Тогда, учитывая, что  получим
получим

Но так как векторы  и единичные, то
и единичные, то

где через  обозначен угол между векторами и
обозначен угол между векторами и  Поэтому
Поэтому

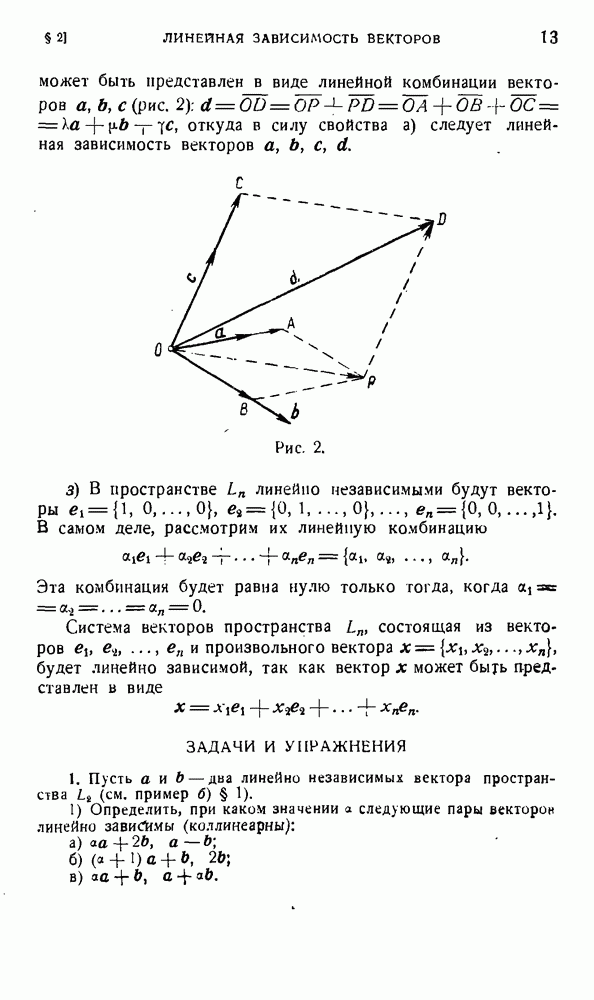
С другой стороны, мы можем записать разложение векторов старого базиса по векторам нового. Если обозначить
через  коэффициент при
коэффициент при  разложении векторов
разложении векторов  по векторам нового базиса, то эти разложения будут иметь вид
по векторам нового базиса, то эти разложения будут иметь вид

 Тззез или, в сокращенной записи,
Тззез или, в сокращенной записи,

Теперь, если каждое из равенств (3) скалярно умножить на каждый из векторов  то получим
то получим

Равенства (2) и (4) означают, что

Числа  можно записать в виде таблицы
можно записать в виде таблицы

Таблица с одинаковым количеством строк и столбцов называется квадратной матрицей. Число строк (столбцов) называется порядком матрицы. Таким образом, таблица Г представляет собой квадратную матрицу третьего порядка и называется матрицей перехода от старого базиса к новому. Аналогично числа  образуют матрицу
образуют матрицу

— матрицу перехода от нового базиса к старому (обозначение  показывает, что эта матрица обратного перехода). Более коротко матрицы Г и
показывает, что эта матрица обратного перехода). Более коротко матрицы Г и  будем записывать в виде
будем записывать в виде

Равенство (5) означает, что матрица  получается из матрицы Г, если в последней строки заменить столбцами.
получается из матрицы Г, если в последней строки заменить столбцами.
Кроме того, для элементов этих двух матриц имеем

Действительно,

Второе равенство доказывается аналогично.
Равенства (6) означают, что для матриц Г и  сумма произведений элементов какой-нибудь строка (столбца) на соответствующие элементы другой строки (другого столбца) равна нулю, а сумма квадратов элементов любой строки (столбца) равна единице.
сумма произведений элементов какой-нибудь строка (столбца) на соответствующие элементы другой строки (другого столбца) равна нулю, а сумма квадратов элементов любой строки (столбца) равна единице.
Матрицы, элементы которых обладают указанным свойством, называются ортогональными.
Мы доказали тем самым, что переход от одного ортонормированного базиса к другому в  задается ортогональной матрицей.
задается ортогональной матрицей.
Пусть теперь нам дана произвольная ортогональная матрица  Векторы
Векторы  определяемые формулами (1), будут тогда, в силу свойств (6) ортогональной матрицы, попарно ортогональными и единичными. Поэтому всякая ортогональная матрица служит матрицей перехода от одного ортонормированного базиса к другому.
определяемые формулами (1), будут тогда, в силу свойств (6) ортогональной матрицы, попарно ортогональными и единичными. Поэтому всякая ортогональная матрица служит матрицей перехода от одного ортонормированного базиса к другому.
Рассмотрим определитель ортогональной матрицы Г:

Поскольку строки определителя  составлены из координат векторов
составлены из координат векторов  относительно базиса
относительно базиса  то
то  равен смешанному произведению векторов
равен смешанному произведению векторов  (см. формулу в конце § 5):
(см. формулу в конце § 5):

Абсолютная величина этого смешанного произведения равна единице, гак как она равна объему куба, построенного на векторах 
Следовательно, определитель любой ортогональной матрицы равен  причем из рассмотрений § 5 (см. стр. 25)
причем из рассмотрений § 5 (см. стр. 25)
следует, что знак плюс или минус будет в зависимости от того, имеют ли базисы  одинаковую или противоположную ориентацию. В первом случае базис
одинаковую или противоположную ориентацию. В первом случае базис  может быть совмещен с базисом
может быть совмещен с базисом  путем поворота вокруг точки О, во втором случае одного поворота оказывается недостаточно — к нему следует добавить еще отражение базиса
путем поворота вокруг точки О, во втором случае одного поворота оказывается недостаточно — к нему следует добавить еще отражение базиса  относительно некоторой плоскости, проходящей через точку О.
относительно некоторой плоскости, проходящей через точку О.
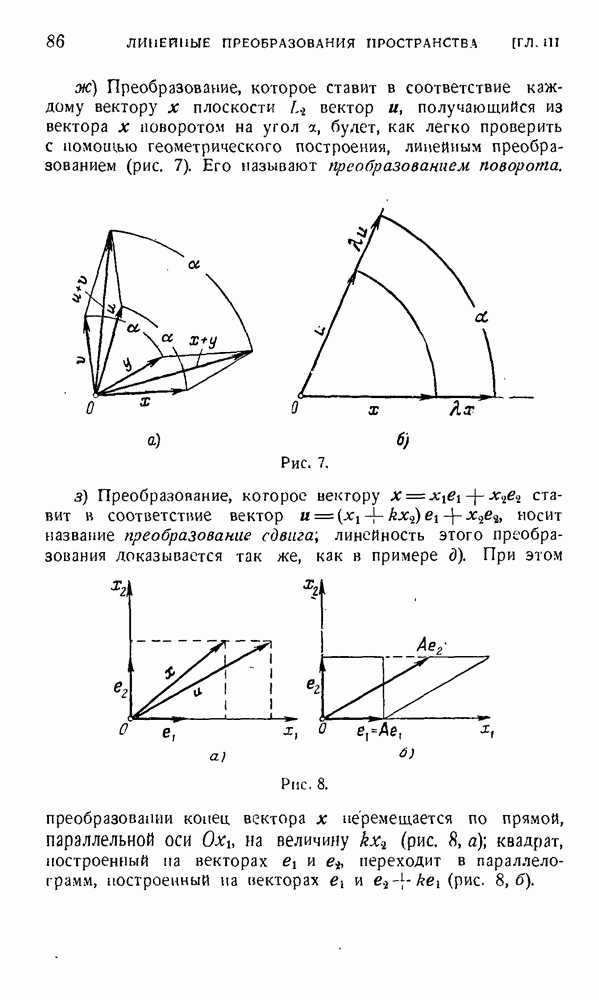
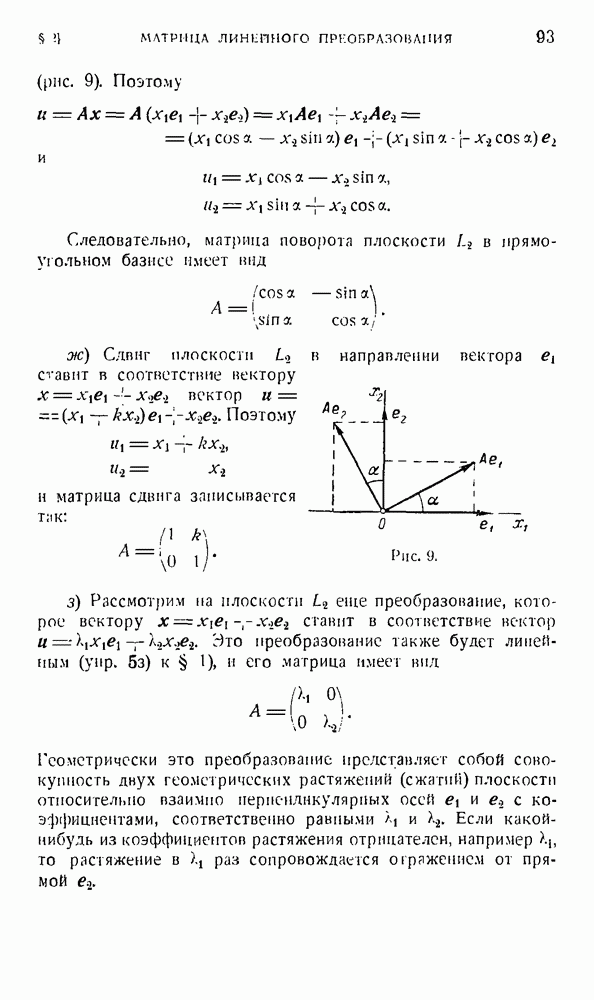
Запишем еще формулы преобразования оронормированного базиса для плоскости. Это преобразование представляет собой либо чистый поворот на некоторый угол а вокруг начала координат О, либо поворот на угол а с последующим отражением относительно некоторой прямой, проходящей через начало координат. В первом случае формулы преобразования базиса запишутся в виде

и матрица Г запишется так:

Определитель этой матрицы будет равен единице. Во втором случае формулы преобразования базиса будут выглядеть так:

и определитель матрицы

будет равен —1.
2. Пусть теперь в пространстве задан вектор х. Он представляет собой некоторый геометрический или физический обьект, заданный как по величине, так и по направлению (например, силу, скорость, ускорение, напряженность электрического поля и т. п.). Этот реально существующий объект не зависит от того, в какой системе координат мы его рассматриваем. Любые действия или вычисления, проводимые
непосредственно над векторами, можно, таким образом, всегда физически истолковать,
Наряду с исчислением, связанным непосредственно с векторами, большую роль в геометрии и ее приложениях играет координатный метод, применение которого позволяет изучать геометрические образы не непосредственно, а достаточно хорошо развитыми методами алгебры (в аналитической геометрии) и анализа (в дифференциальной геометрии). На этом пути удается довольно легко получить много результатов, непосредственное доказательство которых иногда вообще невозможно, а иногда очень громоздко.
Однако при применении координатного метода мы с каждым вектором х связываем его координаты  которые зависят уже не только от самого вектора X, но и от рассматриваемой координатной системы (ортонормированного базиса). Такие ортонормированные базисы можно выбирать различными способами: например, выбрав один базис и поворачивая его вокруг начала, можно получить из него другие. Тем самым при применении координатного метода мы получаем данные, отражающие не только геометрическую картину, но и произвол выбора координатной системы. Например, сами координаты вектора, конечно, зависят от координатной системы, но сумма их квадратов (которая, как мы знаем, дает квадрат длины нектора) уже не должна зависеть от выбора координатной системы. (Немного ниже мы увидим, что эта величина оказывается одинаковой во всех ортонормированных базисах.)
которые зависят уже не только от самого вектора X, но и от рассматриваемой координатной системы (ортонормированного базиса). Такие ортонормированные базисы можно выбирать различными способами: например, выбрав один базис и поворачивая его вокруг начала, можно получить из него другие. Тем самым при применении координатного метода мы получаем данные, отражающие не только геометрическую картину, но и произвол выбора координатной системы. Например, сами координаты вектора, конечно, зависят от координатной системы, но сумма их квадратов (которая, как мы знаем, дает квадрат длины нектора) уже не должна зависеть от выбора координатной системы. (Немного ниже мы увидим, что эта величина оказывается одинаковой во всех ортонормированных базисах.)
Свойства геометрических или физических объектов, не зависящие  выбора системы координат, в которой эти объекты рассматриваются, называются их инвариантными свойствами. Только такие свойства и представляют интерес для изучения.
выбора системы координат, в которой эти объекты рассматриваются, называются их инвариантными свойствами. Только такие свойства и представляют интерес для изучения.
Основная задача тензорного исчисления как раз и заключается в том, чтобы научиться отделять результаты, относящиеся к самим геометрическим объектам, от того, что привнесено случайным выбором координатной системы.
Для этой цели прежде всего выясним, как преобразуются координаты вектора х при переходе от ортонормированного базиса  с началом в О к другому оргонормированному базису
с началом в О к другому оргонормированному базису  с тем же началом О. Запишем
с тем же началом О. Запишем
разложения вектора х в каждом  этих двух базисов:
этих двух базисов:

Поскольку это — разложения одного и того же вектора, мы можем приравнять правые части этих равенств:

Заменяя векторы  по формулам (3), получим
по формулам (3), получим

откуда, в силу линейной независимости векторов  следует, что
следует, что

учитывая, что  запишем полученное равенство в виде
запишем полученное равенство в виде

Эти формулы дают выражение новых координат вектора х через старые.
Если бы в равенстве  мы заменяли векторы
мы заменяли векторы  по формулам (1), то получили бы выражение старых координат вектора х через новые:
по формулам (1), то получили бы выражение старых координат вектора х через новые:

Отметим, что формулы (8) можно получить из формул (7), если умножить обе части (7) на просуммировать по  и воспользоваться равенствами (6).
и воспользоваться равенствами (6).
Теперь мы можем выяснить, какие из проведенных нами в этой главе рассмотрений имеют инвариантный характер, т. е. не зависят от выбора системы координат.
Начнем со скалярного произведения векторов. В пространстве  оно было определено геометрически (стр. 19), и поэтому инвариантность его не вызывает сомнений. Убедимся в этом еще раз, показав, что полученное в § 4 выражение скалярного произведения через координаты перемножаемых векторов в некотором ортонормированном базисе обладает свойством инвариантности. Это важно потому, что и
оно было определено геометрически (стр. 19), и поэтому инвариантность его не вызывает сомнений. Убедимся в этом еще раз, показав, что полученное в § 4 выражение скалярного произведения через координаты перемножаемых векторов в некотором ортонормированном базисе обладает свойством инвариантности. Это важно потому, что и  скалярное произведение векторов в ортонормированном базисе определяется как сумма произведений одноименных координат (см. упражнения § 4) и там доказательство его инвариантности уже не может носить геометрического
скалярное произведение векторов в ортонормированном базисе определяется как сумма произведений одноименных координат (см. упражнения § 4) и там доказательство его инвариантности уже не может носить геометрического
характера и должно быть обязательно проведено аналитически, например так, как мы сейчас будем это делать в 
В § 4 доказано, что скалярное произведение векторов х и у, имеющих в базисе  координаты
координаты  а в базисе
а в базисе  -координаты
-координаты  можно записать в виде
можно записать в виде  в первом базисе и
в первом базисе и  — во втором.
— во втором.
Покажем тождественность этих выражений. Действительно, пользуясь формулами (7) и (6), получим

Из инвариантности формулы для вычисления скалярного произведения немедленно следует инвариантность формул для вычисления длины вектора и косинуса угла между двумя векторами, так как эти величины выражаются через скалярное произведение векторов.
Прежде чем доказывать инвариантность формул, по которым вычисляются векторное и смешанное произведения векторов через координаты сомножителей, посмотрим, как изменяются компоненты кососимметричного символа Кронекера при переходе к новому базису. В новом базисе мы получим

и так как

то

В частности,

Но в этой сумме отличными от нуля будут только шесть членов, которые можно переписать так:

Стоящее в скобках выражение представляет собой определитель матрицы Г, так что

или, если обозначить через  значение величины
значение величины  в новом базисе,
в новом базисе,

Эта формула показывает, что если ориентация базиса не меняется, то не меняется и величина  если же ориентация базиса меняется на противоположную, то величина
если же ориентация базиса меняется на противоположную, то величина  меняет знак, т. е. эта формула согласуется с определением величины
меняет знак, т. е. эта формула согласуется с определением величины 
Пусть теперь  Тогда в старом базисе
Тогда в старом базисе

а в новом базисе

Покажем инвариантность этой формулы, т. е. покажем, что формула (9) переходит в (9) при преобразовании базиса. В самом деле, подставляя выражения

в первую формулу, получим

Умножим эти соотношения на и просуммируем по индексу  Так как
Так как

то

а поскольку

полученная формула совпадает с формулой (9).
Аналогично можно доказать, что вычислительная формула для смешанного произведения, полученная в § 5, также остается инвариантной при преобразовании базиса, т. е.

Заметим, что инвариантность формулы для смешанного произведения следует из того, что

а векторное и скалярное произведения векторов, как мы только что доказали, выражаются инвариантными формулами.
ЗАДАЧИ И УПРАЖНЕНИЯ
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ЛИНЕЙНОЕ ПРОСТРАНСТВО
- § 1. Понятие линейного пространства
- § 2. Линейная зависимость векторов
- § 3. Размерность и базис линейного пространства
- § 4. Прямоугольный базис в трехмерном пространстве. Скалярное произведение векторов
- § 5. Векторное и смешанное произведения векторов
- § 6. Преобразования ортонормированного базиса. Основная задача тензорного исчисления
- § 7. Некоторые вопросы аналитической геометрии в пространстве
- ГЛАВА II. ПОЛИЛИНЕЙНЫЕ ФОРМЫ И ТЕНЗОРЫ
- § 2. Билинейные формы
- § 3. Полилинейные формы. Общее определение тензора
- § 4. Алгебраические операции над тензорами
- § 5. Симметричные и антисимметричные тензоры
- ГЛАВА III. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ ВЕКТОРНОГО ПРОСТРАНСТВА И ТЕНЗОРЫ ВТОРОЙ ВАЛЕНТНОСТИ
- § 2. Матрица линейного преобразования
- § 3. Определитель матрицы линейного преобразования. Ранг матрицы
- § 4. Линейные преобразования и билинейные формы
- § 5. Умножение линейных преобразований и умножение матриц
- § 6. Обратное линейное преобразование и обратная матрица
- § 7. Группа линейных преобразований и ее подгруппы
- ГЛАВА XIV. ПРИВЕДЕНИЕ К ПРОСТЕЙШЕМУ ВИДУ МАТРИЦЫ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- § 1. Собственные векторы и собственные значения линейного преобразования
- § 2. Приведение к простейшему виду матрицы линейного преобразования в случае различных собственных значений
- § 3. Многочлены от матриц и теорема Гамильтона—Кэли
- § 4. Свойства собственных векторов и собственных значений симметричного линейного прейбразования
- § 5. Приведение к диагональному виду матрицы симметричного линейного преобразования
- § 6. Приведение квадратичной формы к каноническому виду
- § 7. Представление невырожденного линейного преобразования в виде произведения симметричного и ортогонального преобразований
- ГЛАВА V. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Общее уравнение поверхности второго порядка. Его инварианты
- § 2. Приведение к простейшему виду общего уравнения поверхности второго порядка
- § 3. Определение типа поверхности второго порядка при помощи инвариантов
- § 4. Классификация поверхностей второго порядка
- § 5. Приложение теории инвариантов к классификации поверхностей второго порядка
- § 6. Центральные и нецентральные поверхности второго порядка
- § 7. Примеры
- ГЛАВА VI. ПРИЛОЖЕНИЕ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ К НЕКОТОРЫМ ВОПРОСАМ МЕХАНИКИ И ФИЗИКИ
- § 2. Некоторые свойства кристаллов, связанные с тензорами второй валентности
- § 3. Тензоры напряжений и деформации
- § 4. Дальнейшие свойства кристаллов
- ГЛАВА VII. ОСНОВЫ ТЕНЗОРНОГО АНАЛИЗА
- § 1. Тензорное поле и его дифференцирование
- § 2. Механика деформируемой среды
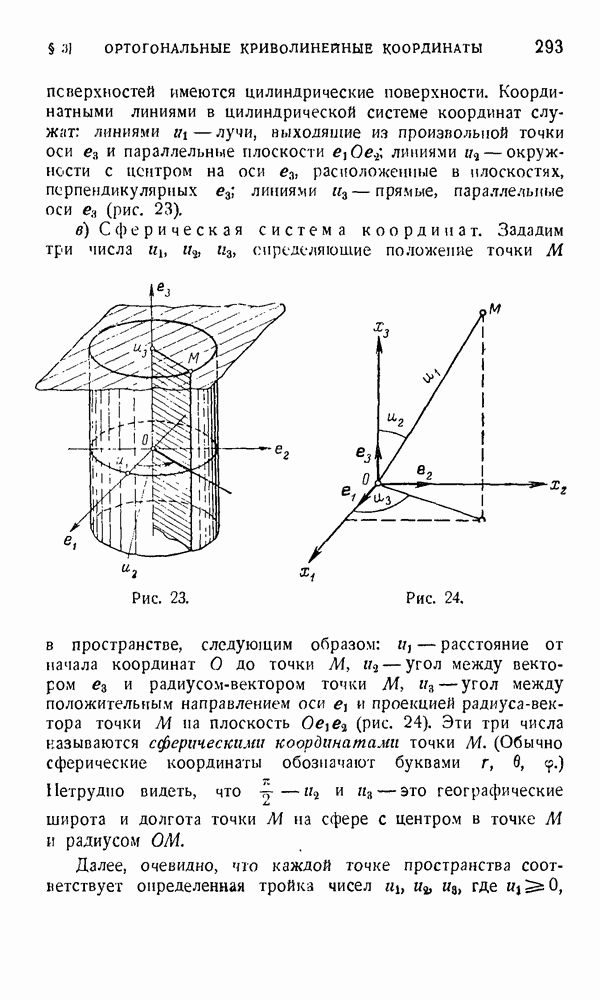
- § 3. Ортогоналыше криволинейные системы координат
- § 4. Подвижной репер ортогональной криволинейной системы координат и тензорные поля
- § 5. Дифференцирование тензорного поля в криволинейных координатах
- ОТВЕТЫ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ И УПРАЖНЕНИЙ
- ЛИТЕРАТУРА