| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Однородные линейные дифференциальные уравнения с частными производными и свойства их решений.
Если в уравнении (7) правая часть равна нулю, то уравнение называется однородным. Оно имеет вид

Вообще в теории дифференциальных уравнений уравнение называется однородным, если функция, тождественно равная нулю  является его решением. Решения линейных однородных уравнений вида (8) обладают следующим свойством:
является его решением. Решения линейных однородных уравнений вида (8) обладают следующим свойством:
Если каждая из функций  является решением уравнения (8), то и их линейная комбинация
является решением уравнения (8), то и их линейная комбинация

где  — произвольные постоянные, также является решением этого уравнения. Для доказательства достаточно заметить, что если и есть линейная комбинация частных решений:
— произвольные постоянные, также является решением этого уравнения. Для доказательства достаточно заметить, что если и есть линейная комбинация частных решений:

(для краткости аргументы функций не пишутся), то любая производная функции и будет такой же линейной комбинацией соответствующих производных функций 

Разумеется, так же будут выглядеть и производные второго порядка. Еспу подставить выражения для производных функций в левую часть уравнения (8) и перегруппировать слагаемые, то получим

Поскольку по условию функции  являются решениями уравнения (8), то каждая из скобок обратится в нуль, а вместе с ними и вся левая часть уравнения; это в означает, что функция и является его решением.
являются решениями уравнения (8), то каждая из скобок обратится в нуль, а вместе с ними и вся левая часть уравнения; это в означает, что функция и является его решением.
Точно такое же свойство, как известно, имеет место и для обыкновенных линейных дифференциальных уравнений. Однако надо иметь в виду, что обыкновенное линейное  ференциальное уравнение
ференциальное уравнение  порядка имеет в точности я линейно независимых частных решений, линейная комбинация которых и дает общее решение.
порядка имеет в точности я линейно независимых частных решений, линейная комбинация которых и дает общее решение.
Уравнение же в частных производных может иметь, как мы убедимся в дальнейшем, бесконечное множество линейно независимых частных решений, т. е. такое множество решений, любое конечное число которых является функциями линейно независимыми. (Система функций  называется линейно независимой, если ни одна из этих функций не является линейной комбинацией остальных.)
называется линейно независимой, если ни одна из этих функций не является линейной комбинацией остальных.)
В соответствии с этим нам придется иметь дело не только с линейными комбинациями конечного числа решений, но и с рядами, членами которых служат произведения произвольных постоянных на частные решения:

Мы дадим здесь необходимые определения и укажем некоторые свойства рядов, членами которых являются функции нескольких переменных. Этими свойствами мы будем пользоваться в дальнейшем.
Будем считать, что члены ряда — функции двух переменных; все определения легко переносятся на случай функций трех переменных.
Рассмотрим функциональный ряд

Этот ряд называется сходящимся в точке  , если числовой ряд
, если числовой ряд  сходится. Совокупность всех точек, в которых ряд сходится, называется областью сходимости ряда. Все члены ряда считаются непрерывными и дифференцируемыми функциями переменных х и у во всей области сходимости ряда.
сходится. Совокупность всех точек, в которых ряд сходится, называется областью сходимости ряда. Все члены ряда считаются непрерывными и дифференцируемыми функциями переменных х и у во всей области сходимости ряда.
Мы будем в дальнейшем рассматривать только такие ряды, суммы которых есть непрерывные функции от х и у,

Кроме того, будем предполагать, что все встречающиеся ряды можно дважды почленно дифференцировать, т. е. что

Очень часто нам придется интегрировать ряд (12) либо по некоторой области D, либо по одной из переменных. Последнее означает,  мы полагаем, например,
мы полагаем, например,  и интегрируем по
и интегрируем по  в некоторых пределах от
в некоторых пределах от  до
до  . Возможность почленного интегрирования ряда заключается в том, что
. Возможность почленного интегрирования ряда заключается в том, что

(Разумеется, предполагается, что рассматриваемые значения  принадлежат области сходимости ряда.)
принадлежат области сходимости ряда.)
Обозначим сумму ряда (10) через  и будем считать, что выполняются все введенные предположения. Тогда
и будем считать, что выполняются все введенные предположения. Тогда

Отсюда ясно, что функция  — сумма ряда (10), так же как и члены ряда, является решением уравнения (8).
— сумма ряда (10), так же как и члены ряда, является решением уравнения (8).
Можно указать сравнительно простые признаки, при соблюдении которых все высказанные предположения о рядах будут справедливы. Введем для этого следующее определение.
Функциональный ряд

называется правильно сходящимся в области D, принадлежащей области сходимости ряда, если все члены его по абсолютной величине не превосходят соответствующих членов некоторого сходящегося знакоположительного числового ряда, т. е.

причем неравенство соблюдается во всех точках области D, а  — член сходящегося числового ряда.
— член сходящегося числового ряда.
Для правильно сходящихся рядов имеют место следующие теоремы, которые мы приводим без доказательства.
1. Сумма правильно сходящегося ряда из непрерывных функций есть функция непрерывная.
2. Правильно сходящийся ряд можно почленно интегрировать.
3. Если ряды, составленные из производных сходящегося ряда, сходятся правильно, то ряд можно почленно дифференцировать.
Определение правильно сходящегося ряда без всяких изменений переносится как на функции одной переменной, так и на функции трех и большею числа переменных.
Напомним, что все три сформулированные свойства имели место для степенных рядов апхп в интервале их сходимости. Нетрудно показать, что степенной ряд является правильно сходящимся в любом интервале, целиком заключенном в интервале сходимости ряда (см. [1], п. 190).
В дальнейшем нам встретятся и такие случаи, когда функция  при всех значениях параметра
при всех значениях параметра  заключенных в некотором интервале
заключенных в некотором интервале  , является решением уравнения (8). Тогда говорят, что частные решения зависят от непрерывно изменяющегося параметра. Обычно интервал изменения параметра
, является решением уравнения (8). Тогда говорят, что частные решения зависят от непрерывно изменяющегося параметра. Обычно интервал изменения параметра  составляет или всю числовую ось, или положительную полуось.
составляет или всю числовую ось, или положительную полуось.
Мы будем в дальнейшем функцию  записывать в виде
записывать в виде  . Этой формой записи подчеркивается аналогия между случаями, когда решения зависят от параметра, принимающего только целые значения
. Этой формой записи подчеркивается аналогия между случаями, когда решения зависят от параметра, принимающего только целые значения  и когда решения зависят от параметра, принимающего любые значения
и когда решения зависят от параметра, принимающего любые значения 
Покажем, что если мы умножим функцию  на произвольную функцию
на произвольную функцию  и проинтегрируем в пределах изменения параметра X:
и проинтегрируем в пределах изменения параметра X:

то вновь получим решение уравнения (8). Ясно, что интеграл (15) есть некоторая функция переменных х и у.
Предварительно познакомимся с некоторыми свойствами интегралов типа (15). Пусть дан интеграл

где  — конечные пределы. Имеет место следующая теорема, которую мы приводим без доказательства
— конечные пределы. Имеет место следующая теорема, которую мы приводим без доказательства
Если подынтегральная функция  , а также ее частные производные по
, а также ее частные производные по  и по у непрерывны при всех рассматриваемых значениях аргументов х, у и
и по у непрерывны при всех рассматриваемых значениях аргументов х, у и  , то и функция
, то и функция  непрерывна вместе со аоими частными производными, причем
непрерывна вместе со аоими частными производными, причем

В случае, когда хотя бы один из пределов интегрирования обращается в бесконечность, интеграл (16) становится несобственным и указанные свойства функции  соблюдаются лишь при некоторых дополнительных условиях, о которых мы скажем ниже.
соблюдаются лишь при некоторых дополнительных условиях, о которых мы скажем ниже.
Возвращаясь к интегралу (15), обозначим его через  и предположим, что для него справедливы формулы (17). При этом пределы интегрирования
и предположим, что для него справедливы формулы (17). При этом пределы интегрирования  могут быть как конечными, так и бесконечными. Тогда
могут быть как конечными, так и бесконечными. Тогда

Подставляя выражения для функции  и ее производных в уравнение (8) и заменяя сумму интегралов интегралом от суммы функций, получим в левой части
и ее производных в уравнение (8) и заменяя сумму интегралов интегралом от суммы функций, получим в левой части

Так как по предположению выражение в квадратных скобках при любом  равно нулю (ведь функция их
равно нулю (ведь функция их  при любом
при любом  является решением уравнения (8)), то и весь интеграл равен нулю. Следовательно, функция
является решением уравнения (8)), то и весь интеграл равен нулю. Следовательно, функция  действительно является решением уравнения.
действительно является решением уравнения.
Сформулируем простой признак, аналогичный соответствующему признаку для рядов, при соблюдении которого выполняются все приведенные свойства для несобственных интегралов вида  , где один или оба предела интегрирования обращаются в бесконечность.
, где один или оба предела интегрирования обращаются в бесконечность.
Если можно указать такую положительную функцию  , что для всех рассматриваемых значений
, что для всех рассматриваемых значений  соблюдается неравенство
соблюдается неравенство  и несобственный интеграл от функции
и несобственный интеграл от функции  сходится, то функция
сходится, то функция  непрерывна. Такую сходимость несобственного интеграла от функции
непрерывна. Такую сходимость несобственного интеграла от функции  будем называть правильной.
будем называть правильной.
Если аналогичное свойство имеет место и для интегралов от частных производных функции  , то функция
, то функция  дифференцируема и ее производные находятся по формулам (17). Например, если
дифференцируема и ее производные находятся по формулам (17). Например, если  и интеграл от
и интеграл от  сходится, то
сходится, то 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- 1. Дифференциальные уравнения с частными производными.
- 2. Однородные линейные дифференциальные уравнения с частными производными и свойства их решений.
- 3. Оператор Лапласа в полярных, цилиндрических и сферических координатах.
- ГЛАВА 1. УРАВНЕНИЯ КОЛЕБАНИЙ
- § 1. Уравнение колебаний струны
- 5. Постановка начальных и краевых условий.
- § 2. Колебания бесконечной и полубесконечной струны. Метод Даламбера
- 7. Распространение волн отклонения.
- 8. Распространение волн импульса.
- 9. Полубесконечная струна.
- § 3. Метод Фурье
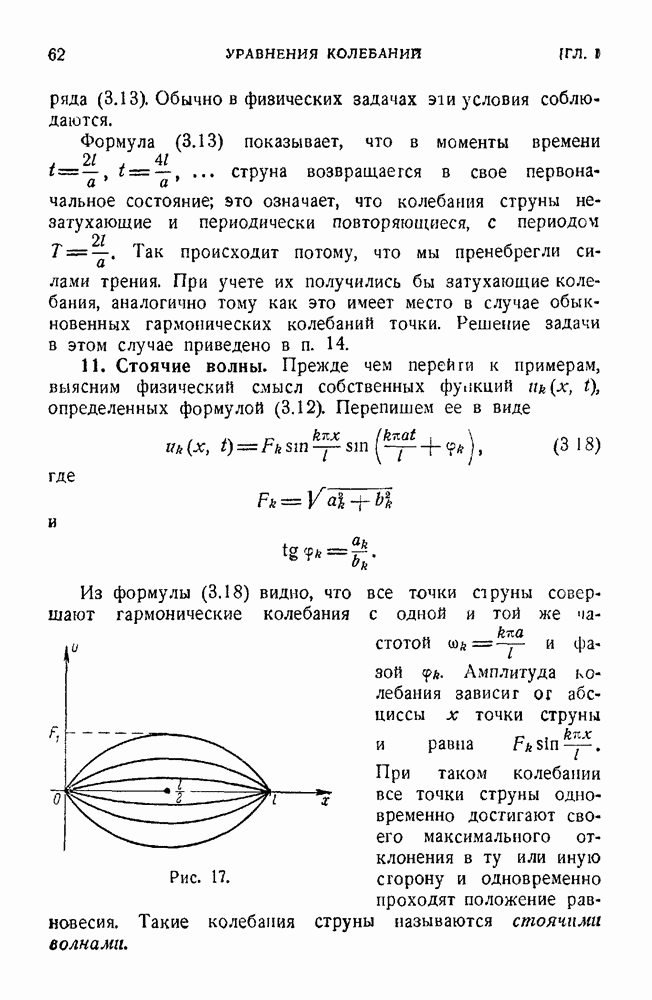
- 11. Стоячие волны.
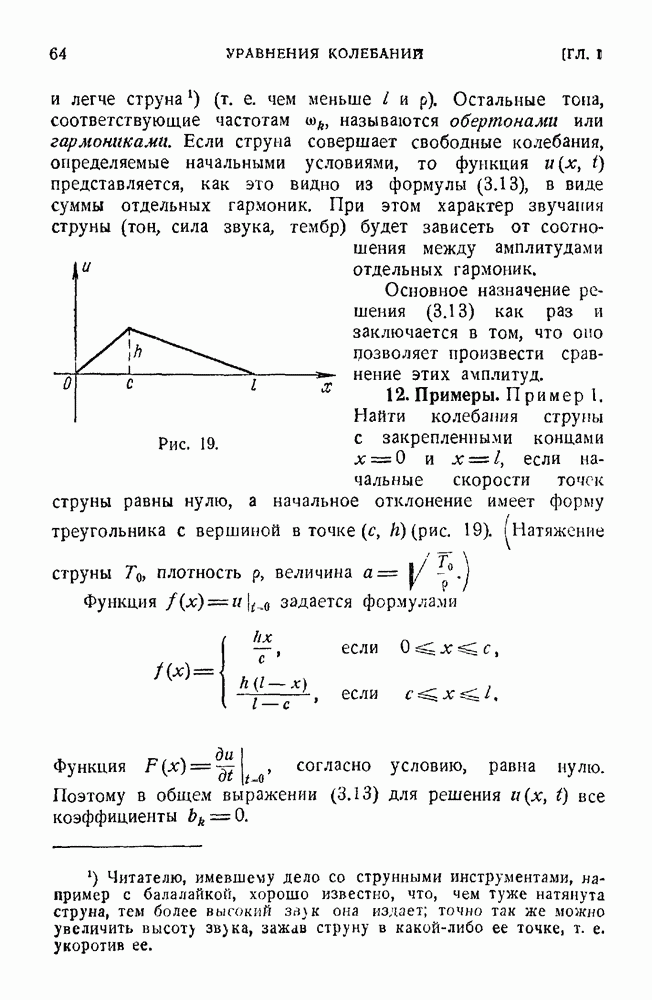
- 12. Примеры.
- § 4. Вынужденные колебания и колебания струны в среде с сопротивлением
- 14. Колебания струны в среде с сопротивлением.
- § 5. Продольные колебания стержня
- 16. Примеры.
- § 6. Крутильные колебания вала
- 18. Крутильные колебания вала с диском на одном конце.
- § 7. Электрические колебания в длинных однородных линиях
- 20. Линия без потерь.
- 21. Линия без искажения.
- 22. Линии конечной длины.
- § 8. Уравнение колебаний мембраны
- 24. Уачальные и краевые условия.
- § 9. Колебания прямоугольной мембраны
- 26. Стоячие волны прямоугольной мембраны.
- 27. Вторая часть метода Фурье.
- 28. Стоячие волны с одинаковой частотой.
- § 10. Уравнение и функции Бесселя
- 30. Условие ортогональности функций Бесселя нулевого порядка.
- 31. Функции Бесселя первого порядка.
- § 11. Колебания круглой мембраны
- 33. Стоячие волны круглой мембраны.
- ГЛАВА II. УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ
- § 12. Уравнение линейной теплопроводности
- 35. Начальное и краевые условия.
- 36. Теплопроводность в стержне при наличии теплообмена через боковую поверхность.
- § 13. Теплопроводность в бесконечном стержне
- 38. Преобразование решения уравнения теплопроводности.
- 39. Фундаментальное решение уравнения теплопроводности и его физический смысл.
- 40. Примеры.
- § 14. Теплопроводность в конечном стержне
- 42. Распространение тепла в стержне в случаях постоянной температуры на концах или теплоизоляции концов.
- 43. Общий случай краевых условий.
- 44. Примеры.
- § 15. Теплопроводность в полубесконечном стержне
- 46. Примеры.
- § 16. Некоторые пространственные задачи теплопроводности
- 48. Начальное и краевые условия.
- 49. Распространение тепла в однородном цилиндре
- 50. Распространение тепла в однородном шаре.
- § 17. Задачи диффузии
- 52. Уравнения теплопроводности и диффузии с краевым условием, зависящим от времени.
- 53. Примеры.
- ГЛАВА III. УРАВНЕНИЕ ЛАПЛАСА
- § 18. Краевые задачи для уравнения Лапласа. Метод функции Грина
- 55. Метод функции Грина для задачи Дирихле (трехмерный случай).
- 56. Метод функции Грина для задачи Дирихле (двумерный случай).
- 57. Задача Неймана.
- § 19. Решение задачи Дирихле для шара и полупространства
- 59. Задача Дирихле для шара.
- 60. Задача Дирихле для внешности шара.
- 61. Задача Дирихле для полупространства.
- § 20. Решение задачи Дирихле для круга и полуплоскости
- 63. Задача Дирихле для внешности круга.
- 64. Задача Дирихле для полуплоскости.
- § 21. Метод Фурье для уравнения Лапласа
- 66. Разделение переменных в трехмерном уравнении Лапласа в сферических координатах. Многочлены Лежандра.
- 67. Решение задачи Дирихле для шара в осесимметричном случае разложением по многочленам Лежандра.
- Заключение
- 69. Корректность постановки задач математической физики.
- ЛИТЕРАТУРА