| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10.3.2. Соотношения совпадающих систем первого и второго порядков
Незапаздывающая система первого порядка: В-представление. Непрерывная система, удовлетворяющая уравнению
![]() ,
(10.3.3)
,
(10.3.3)
для скачкообразного входа является дискретно-совпадающей с дискретной системой
![]() ,
(10.3.4)
,
(10.3.4)
где
![]() ,
(10.3.5)
,
(10.3.5)
выражено через параметры ![]() -представления. Можно
записать разностное уравнение иначе:
-представления. Можно
записать разностное уравнение иначе:![]() , (10.3.6)
, (10.3.6)
где
![]() ,
(10.3.7)
,
(10.3.7)
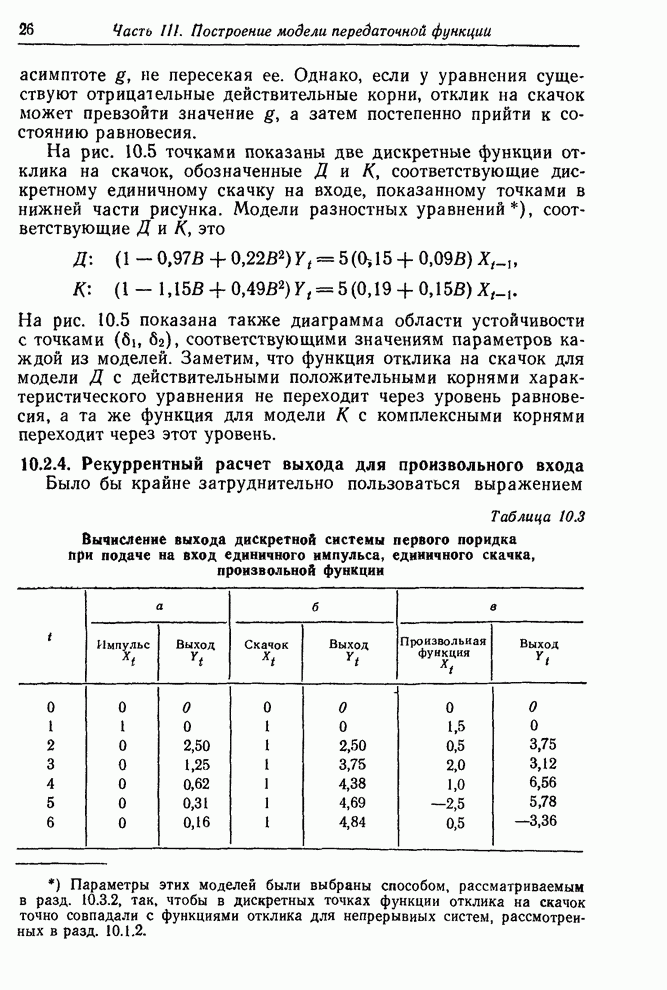
В качестве иллюстрации рассмотрим опять пример разд. 10.2.4 в случае «произвольного» входа. Выход для этого случая рассчитан в табл. 10.3 (в) и представлен на рис. 10.7, в. Предположим, что в действительности мы имеем непрерывную систему
![]() .
.
Тогда она будет дискретно-совпадающей с дискретной моделью (10.2.14), рассмотренной ранее, а именно с
![]() .
.

Рис. 10.10. Непрерывный отклик
системы ![]() на
скачкообразный вход.
на
скачкообразный вход.
Если вход и выход были непрерывны, а вход был скачкообразным, истинный ход отклика был бы таким, как показано непрерывными линиями на рис. 10.10. Выход представлял собой последовательность экспонент. Каждая пунктирная линия показывает дальнейший ход отклика при отсутствии дальнейших изменений входа. Кривые точно совпадают в дискретные моменты отсчета с дискретным выходом, рассчитанным в табл. 10.3 (в) и приведенным на рис. 10.7, в.
Запаздывающая система первого порядка: В-представление. Непрерывная система, удовлетворяющая уравнению
![]() , (10.3.8)
, (10.3.8)
для скачкообразного входа, дискретно совпадает с системой, удовлетворяющей разностному уравнению
![]() , (10.3.9)
, (10.3.9)
где
![]() ,
(10.3.10)
,
(10.3.10)
выражено
через параметры ![]() -представления. Разностное
уравнение можно записать иначе:
-представления. Разностное
уравнение можно записать иначе:
![]() ,
(10.3.11)
,
(10.3.11)
где
![]() ,
(10.3.12)
,
(10.3.12)
Заметим, что
![]() (10.3.13)
(10.3.13)
может
рассматриваться как интерполяция приращения ![]() между
между ![]() и
и ![]() . По табл. 10.4 могут быть определены соответствующие
параметры
. По табл. 10.4 могут быть определены соответствующие
параметры ![]() и
и
![]() дискретных
и непрерывных моделей для ряда случаев.
дискретных
и непрерывных моделей для ряда случаев.
Таблица
10.4. Значения ![]() при различных
при различных ![]() и
и ![]() для системы первого
порядка с запаздыванием. Показаны также соответствующие значения
для системы первого
порядка с запаздыванием. Показаны также соответствующие значения ![]() и
и ![]()
|
|
|
|
|
|
|
|
|
|
0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 |
9,00 4,00 2,33 1,50 1,00 0,67 0,43 0,25 0,11 |
9,49 4,48 2,80 1,95 1,44 1,09 0,83 0,62 0,43 |
0,90 0,89 0,88 0,88 0,87 0,85 0,84 0,82 0,77 |
0,69 0,68 0,66 0,64 0,62 0,60 0,57 0,52 0,45 |
0,49 0,47 0,46 0,44 0,41 0,39 0,35 0,31 0,24 |
0,29 0,28 0,26 0,25 0,23 0,21 0,19 0,15 0,11 |
0,10 0,09 0,09 0,08 0,07 0,06 0,05 0,04 0,03 |
Система второго порядка без запаздывания. В-представление. Непрерывная система, удовлетворяющая уравнению
![]() ,
(10.3.14)
,
(10.3.14)
для скачкообразного входа дискретно совпадает с системой
![]() ,
(10.3.15)
,
(10.3.15)
или, что эквивалентно, с системой
![]() ,
(10.3.16)
,
(10.3.16)
где
 (10.3.17)
(10.3.17)
выражено
через параметры ![]() -представления.
Разностное уравнение можно записать также в виде
-представления.
Разностное уравнение можно записать также в виде
![]() ,
(10.3.18)
,
(10.3.18)
где
![]() ,
(10.3.19)
,
(10.3.19)
может
рассматриваться как приращение интерполяции между ![]() и
и ![]() . Значения
. Значения ![]() и
и ![]() , выраженные через
, выраженные через ![]() , можно получить
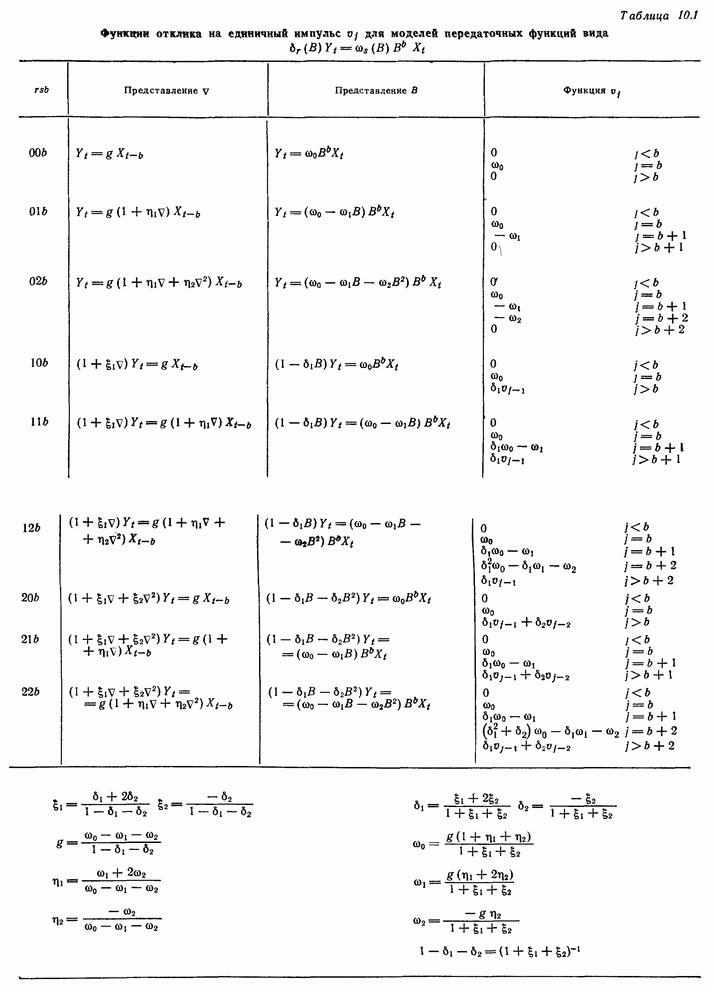
непосредственно из данных табл. 10.1.
, можно получить
непосредственно из данных табл. 10.1.
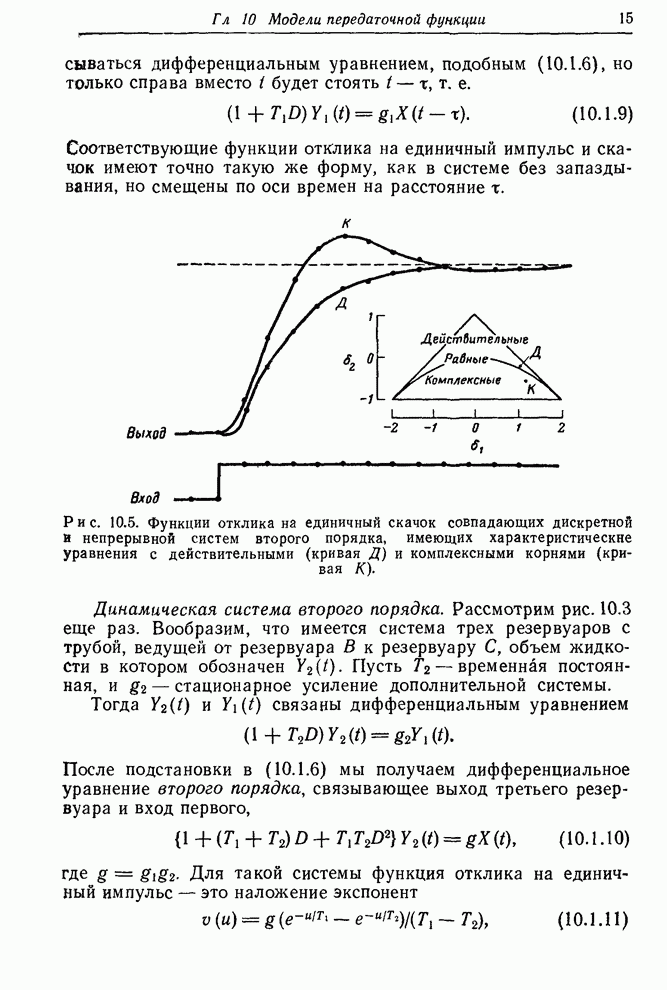
В качестве конкретного примера на рис. 10.5 показаны функции отклика на скачок двух дискретных систем, рассмотренных прежде, там же приведены соответствующие непрерывные отклики для дискретно-совпадающих систем. Эти пары моделей таковы:
непрерывная модель: ![]()
Кривая К
дискретная модель: ![]()
непрерывная модель: ![]()
Кривая Д
дискретная модель: ![]()
Непрерывные кривые были построены согласно (10.1.18)4 и (10.1.12). Эти формулы определяют непрерывные функции отклика на скачок для систем второго порядка, характеристические уравнения которых имеют соответственно комплексные и действительные корни.
Дискретное представление запаздывающей непрерывной системы второго порядка для скачкообразного входа приведено в приложении П10.1.
| << Предыдущий параграф | Следующий параграф >> |
- Часть III. ПОСТРОЕНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- Глава 10. Модели передаточной функции
- 10.1. ЛИНЕЙНЫЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 10.1.1. Дискретная передаточная функция
- 10.1.2. Непрерывные динамические модели, описываемые дифференциальными уравнениями
- 10.2. ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ МОДЕЛИ, ОПИСЫВАЕМЫЕ РАЗНОСТНЫМИ УРАВНЕНИЯМИ
- 10.2.1. Общая форма разностного уравнения
- 10.2.2. Природа передаточной функции
- 10.2.3. Дискретные модели передаточных функций первого и второго порядков
- 10.2.4. Рекуррентный расчет выхода для произвольного входа
- 10.3. СООТНОШЕНИЕ МЕЖДУ ДИСКРЕТНОЙ И НЕПРЕРЫВНОЙ МОДЕЛЯМИ
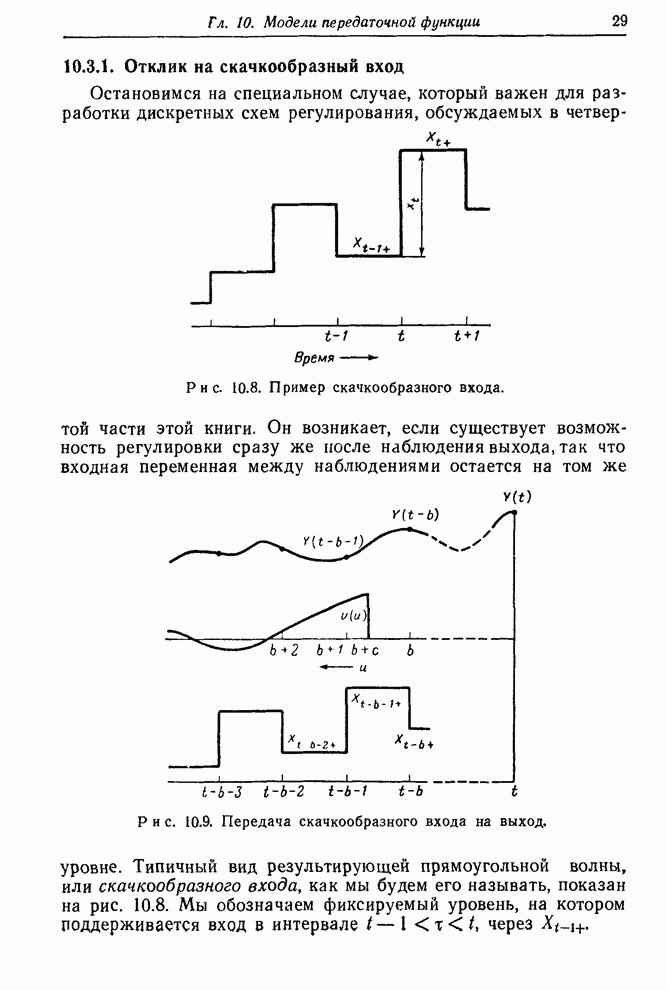
- 10.3.1. Отклик на скачкообразный вход
- 10.3.2. Соотношения совпадающих систем первого и второго порядков
- 10.3.3. Аппроксимация общих непрерывных моделей дискретными моделями
- 10.3.4. Модели передаточных функций с добавленным шумом
- ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
- ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
- Глава 11. Идентификация, подгонка и проверка моделей передаточных функций
- 11.1. Взаимная корреляционная функция
- 11.1.1. Свойства взаимных ковариационной и корреляционной функций
- 11.1.2. Оценивание взаимных ковариационных и корреляционных функций
- 11.1.3. Приближенные стандартные ошибки выборочных оценок взаимных корреляций
- 11.2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.2.1. Идентификация моделей передаточной функции с предварительным выравниванием спектра входа
- 11.2.2. Пример идентификации модели передаточной функции
- 11.2.3. Идентификация модели шума
- 11.2.4. Некоторые общие соображения об идентификации моделей передаточных функций
- 11.3. ПОДГОНКА И ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.3.1. Условная сумма квадратов
- 11.3.2. Нелинейное оценивание
- 11.3.3. Использование остаточных ошибок для диагностической проверки
- 11.3.4. Конкретные способы проверки остаточных ошибок
- 11.4. Некоторые примеры подгонок и проверок моделей передаточных функций
- 11.4.1. Подгонка и проверка модели газовой печи
- 11.4.2. Искусственный пример с двумя входами
- 11.5. ПРОГНОЗИРОВАНИЕ ПРИ ПОМОЩИ УПРЕЖДАЮЩИХ ИНДИКАТОРОВ
- 11.5.1. Прогноз с минимальной среднеквадратичной ошибкой
- 11.5.2. Прогнозы выхода СO2 из газовой печи
- 11.5.3. Прогноз нестационарных данных сбыта при помощи упреждающего индикатора
- 11.6. НЕКОТОРЫЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОЦЕНИВАНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ П11.1. ИСПОЛЬЗОВАНИЕ ВЗАИМНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
- Заключение
- Часть IV. Проектирование дискретных схем регулирования
- Глава 12. Проектирование схем регулирования с прямой и обратной связями
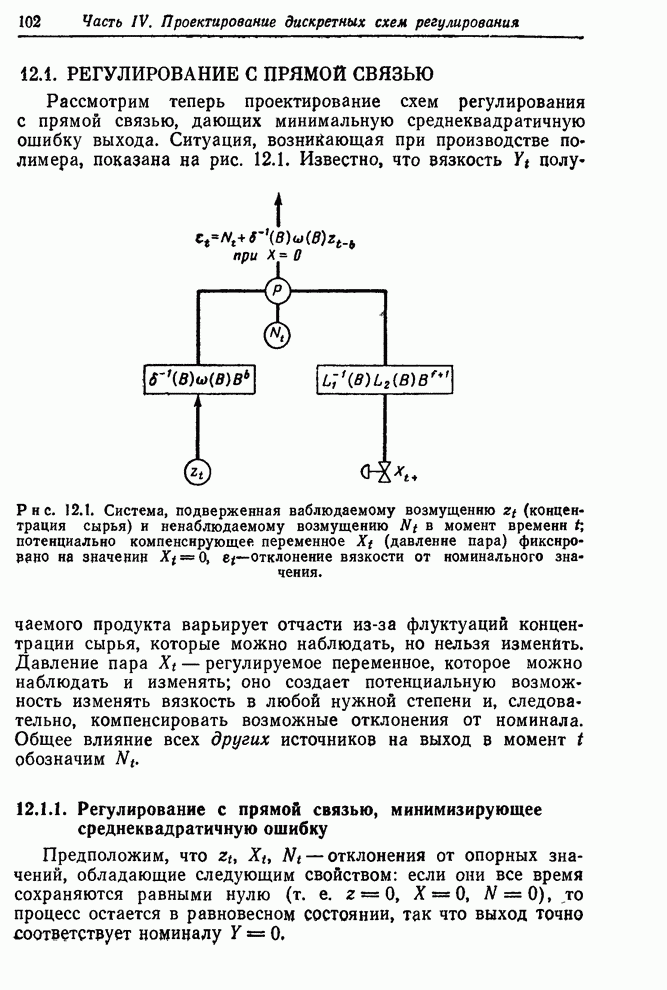
- 12.1. РЕГУЛИРОВАНИЕ С ПРЯМОЙ СВЯЗЬЮ
- 12.1.1. Регулирование с прямой связью, минимизирующее среднеквадратичную ошибку
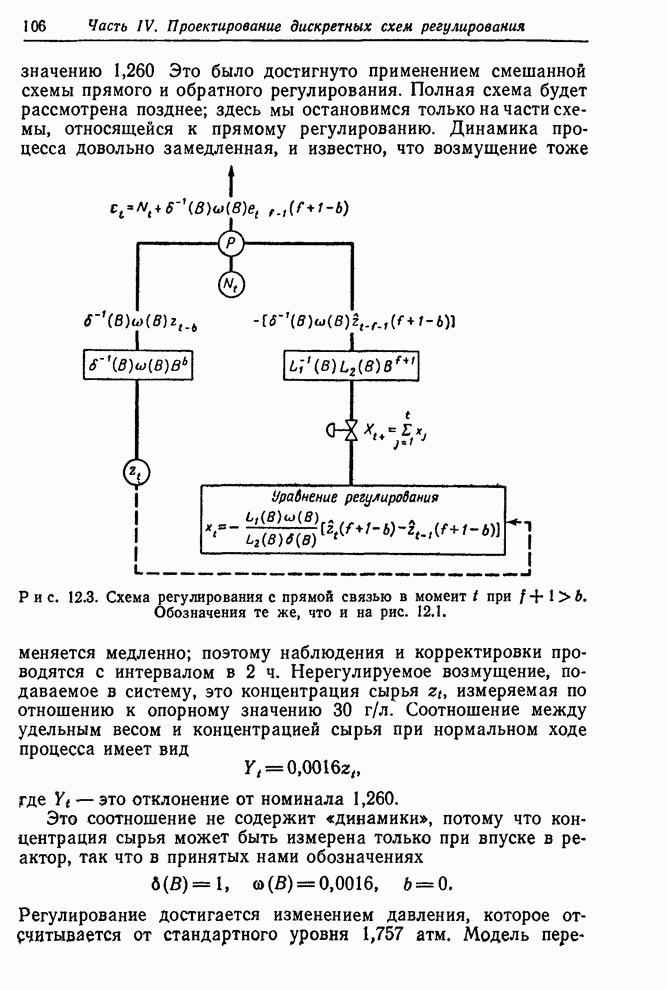
- 12.1.2. Пример — регулирование удельного веса промежуточного продукта
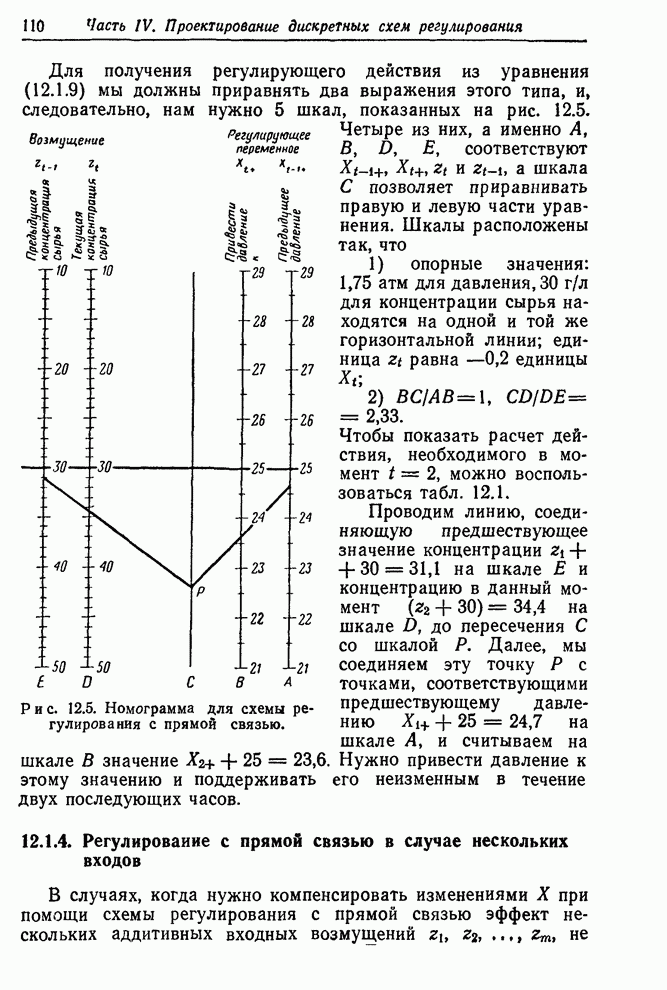
- 12.1.3. Номограмма для регулирования с прямой связью
- 12.1.4. Регулирование с прямой связью в случае нескольких входов
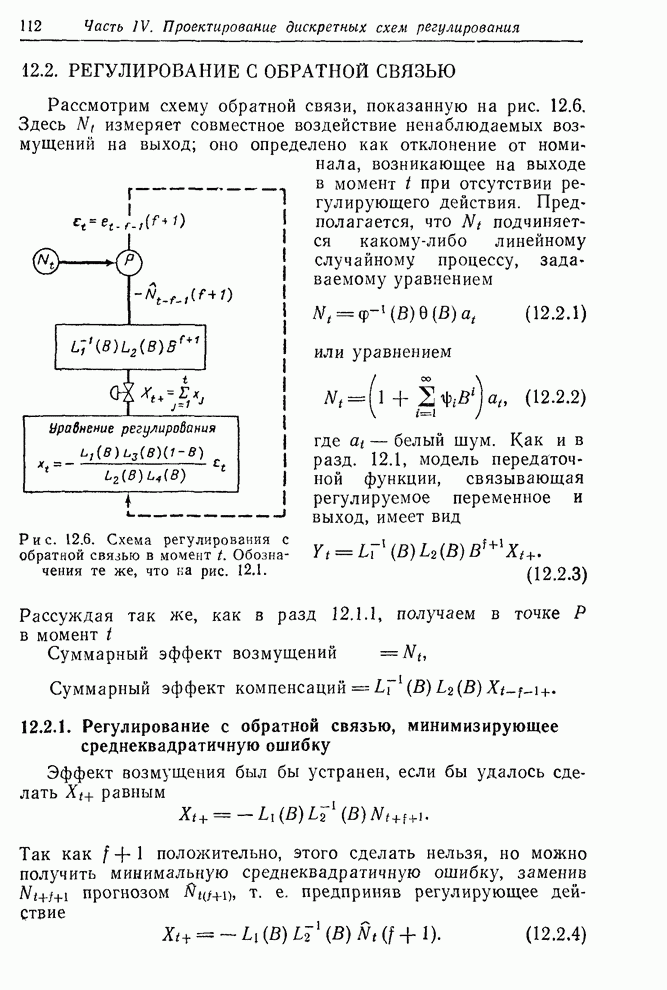
- 12.2. РЕГУЛИРОВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ
- 12.2.1. Регулирование с обратной связью, минимизирующее среднеквадратичную ошибку
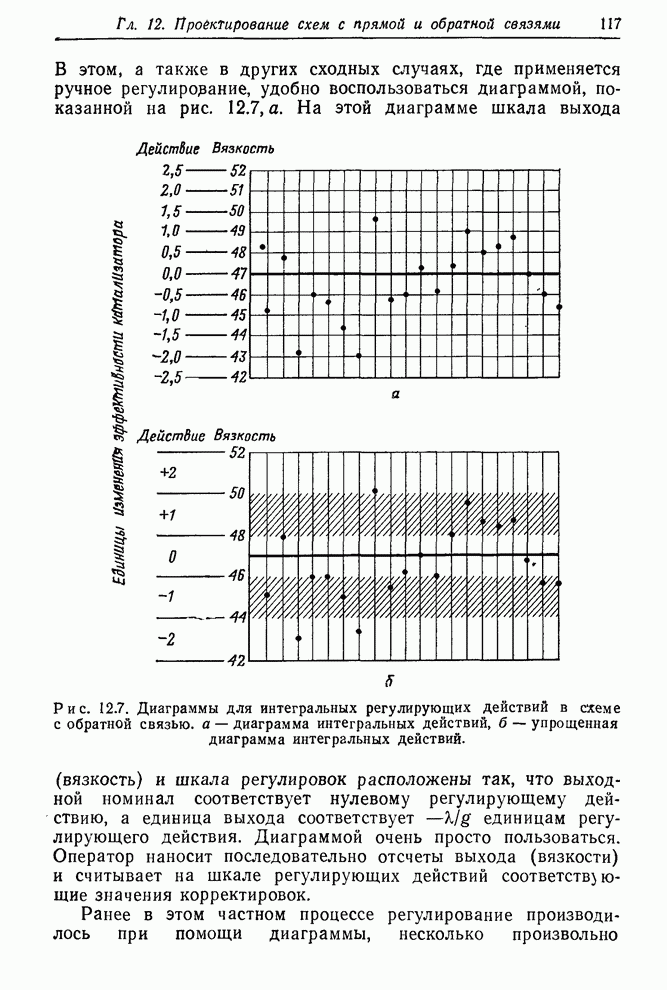
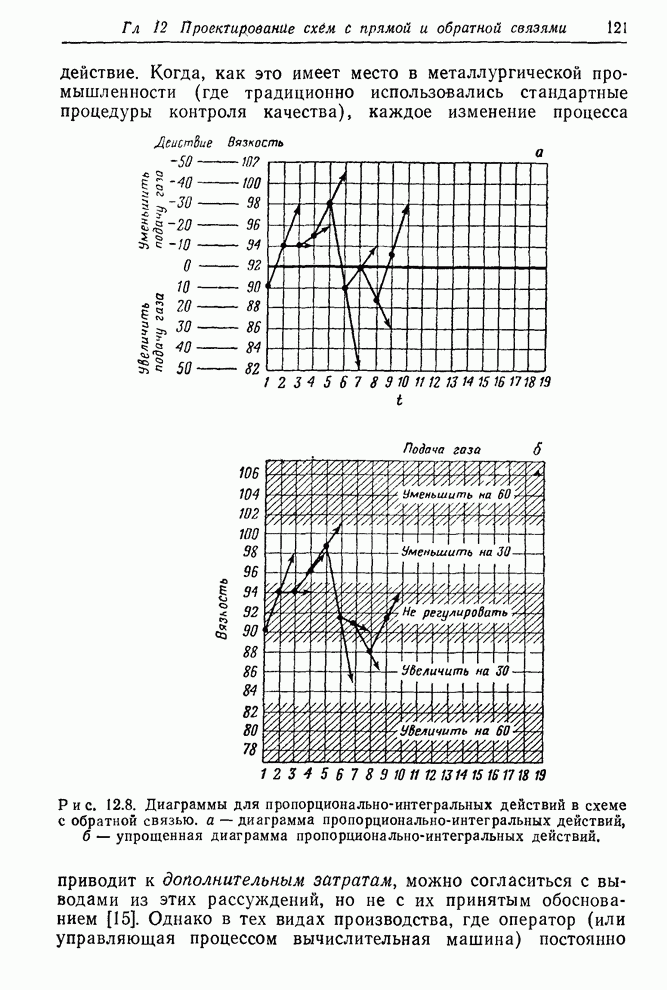
- 12.2.2. Применение уравнения регулирования: ПИД-регулятор
- 12.2.3. Примеры дискретного регулирования с обратной связью
- 12.3. РЕГУЛИРОВАНИЕ С ПРЯМОЙ И ОБРАТНОЙ СВЯЗЯМИ
- 12.3.1. Регулирование с прямой и обратной связями, минимизирующее выходную среднеквадратичную ошибку
- 12.3.2. Пример регулирования с прямой и обратной связями
- 12.3.3. Преимущества и недостатки регулирования с прямой и обратной связями
- 12.4. Подгонка моделей передаточных функций шума по оперативным данным
- 12.4.1. Итеративный способ построения моделей
- 12.4.2. Оценивание по оперативным данным
- 12.4.3. Пример
- Глава 13. Некоторые дальнейшие проблемы регулирования
- 13.1. ЭФФЕКТ ДОБАВОЧНОГО ШУМА В СХЕМАХ РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ
- 13.1.1. Эффект пренебрежения добавочным шумом; упрощенные схемы
- 13.1.2. Оптимальное действие в случаях, когда корректировки содержат ошибки наблюдения
- 13.1.3. Перенос источника шума
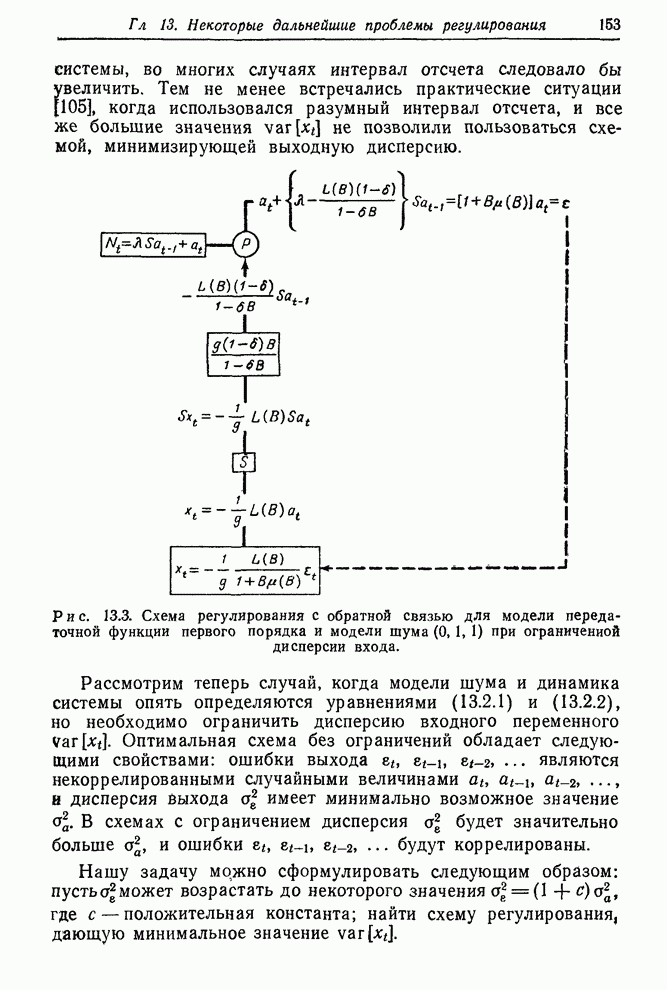
- 13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
- 13.2.1. Вывод выражения для оптимальной корректировки
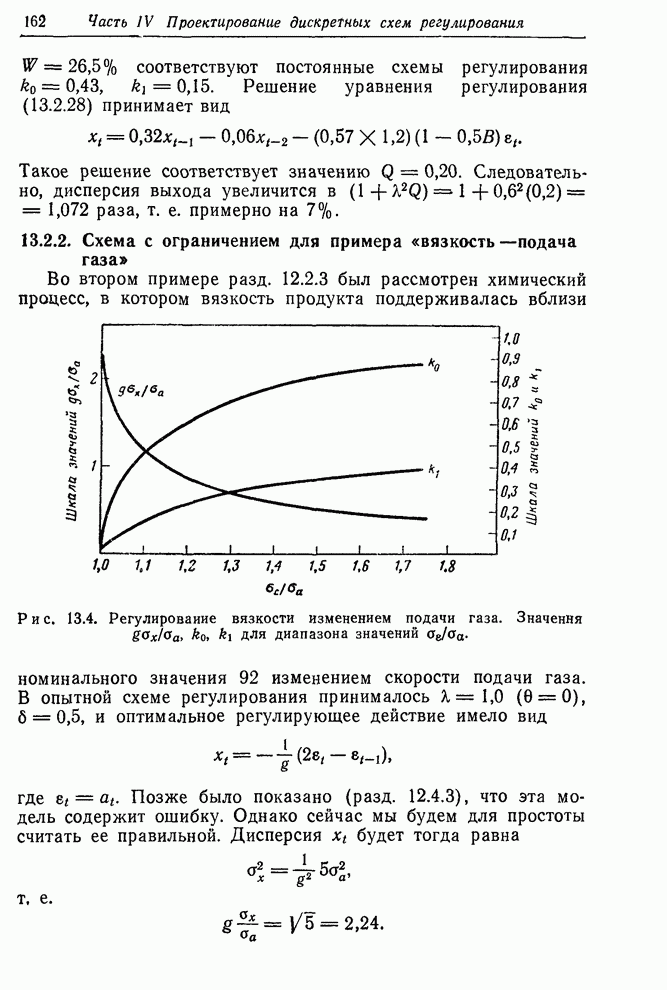
- 13.2.2. Схема с ограничением для примера «вязкость–подача газа»
- 13.3. ВЫБОР ИНТЕРВАЛА ОТСЧЕТА
- 13.3.1. Пример эффекта уменьшения частоты отсчетов
- 13.3.2. Влияние интервала отсчета на процесс ПСС(0,1,1)
- ПРОГРАММА 5. ИДЕНТИФИКАЦИЯ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 6. ПРЕДВАРИТЕЛЬНОЕ ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 7. ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
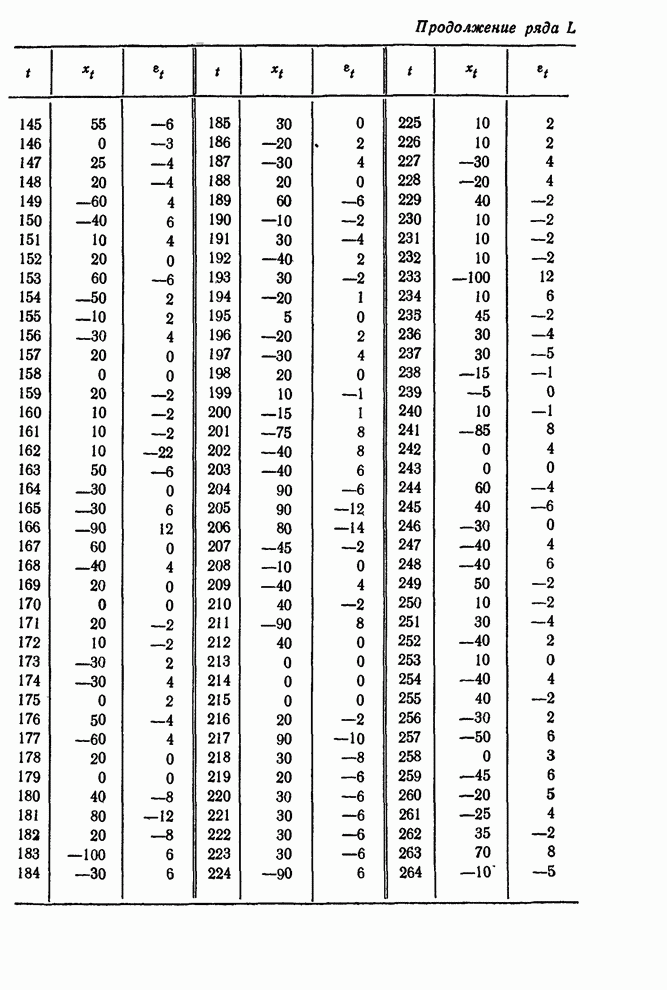
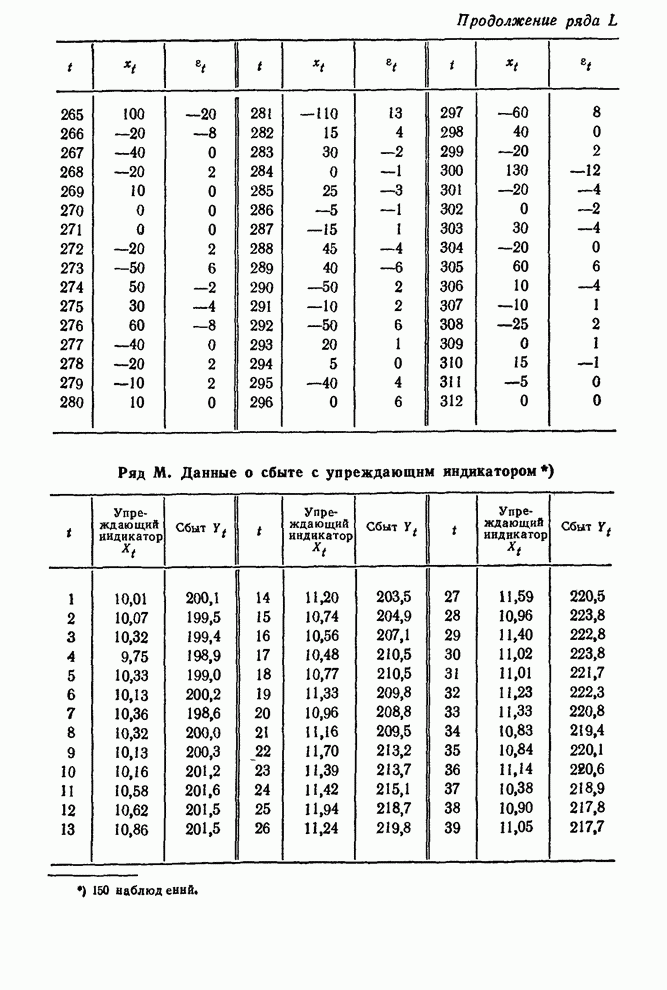
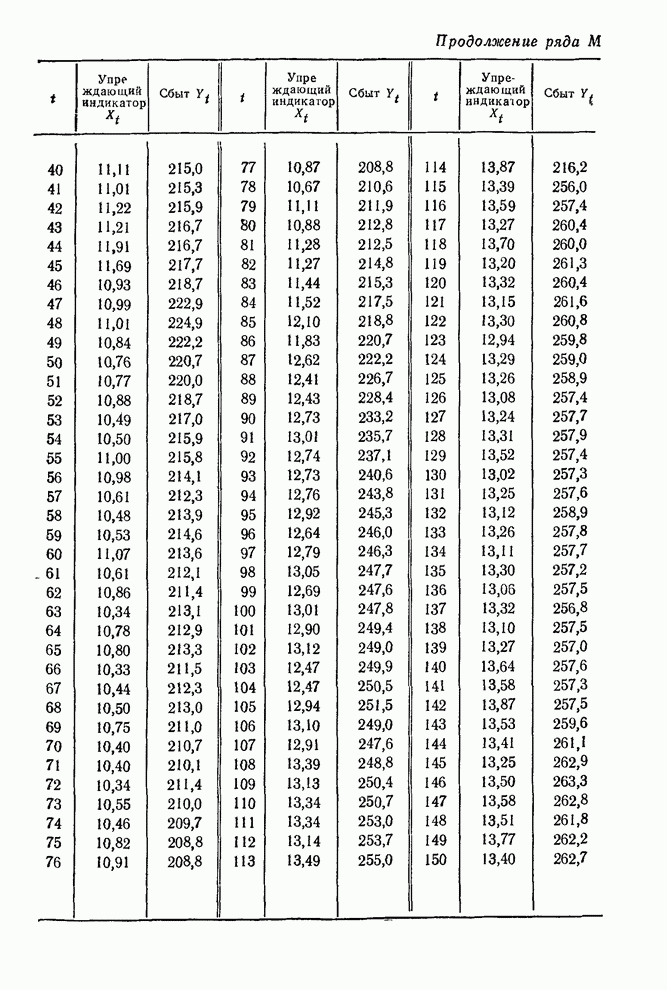
- ТАБЛИЦЫ ВРЕМЕННЫХ РЯДОВ