| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
13.1.2. Оптимальное действие в случаях, когда корректировки  содержат ошибки наблюдения
содержат ошибки наблюдения
Уравнение
(13.1.11) позволяет вычислить эффект добавочного шума в ![]() в тех случаях, когда
оптимальная схема такой шум не учитывает. Интересно получить также оптимальную
схему для конкретного добавочного шума и увидеть, насколько она отличается от
схемы, где такой шум не учтен. Рассмотрим опять пример из разд. 13.1.1.
в тех случаях, когда
оптимальная схема такой шум не учитывает. Интересно получить также оптимальную
схему для конкретного добавочного шума и увидеть, насколько она отличается от
схемы, где такой шум не учтен. Рассмотрим опять пример из разд. 13.1.1.
Пусть фактически выполненное регулирующее действие равно
![]() ,
,
где
![]() , как и
ранее, некоррелированы и имеют дисперсию
, как и
ранее, некоррелированы и имеют дисперсию ![]() , а шум
, а шум ![]() представим процессом
представим процессом ![]() . Необходимо выбрать
. Необходимо выбрать ![]() так, чтобы
минимизировать
так, чтобы
минимизировать ![]() .
.
Рассмотрим,
как и ранее, точку ![]() в
петле обратной связи. Здесь
в
петле обратной связи. Здесь
![]()
или
![]() ,
,
и, следовательно,
![]() . (13.1.14)
. (13.1.14)
Правая часть уравнения (13.1.14) описывает процесс скользящего среднего второго порядка с добавочным белым шумом и, следовательно, может (разд. П4.4.1) быть представлена другим процессом скользящего среднего второго порядка:
![]() ,
,
где
![]() – белый
шум. Следовательно, задача сводится к выбору такого оператора
– белый
шум. Следовательно, задача сводится к выбору такого оператора ![]() , чтобы
минимизировалась
, чтобы
минимизировалась ![]() ,
где
,
где
![]() .
.
Можно записать это равенство в виде
![]() ,
,
так что
![]() ,
,
и
![]() минимально,
только если
минимально,
только если ![]() ;
это приводит к
;
это приводит к
![]() , (13.1.15)
, (13.1.15)
или к
![]() .
.
Следовательно, оптимальная корректировка равна
 . (13.1.16)
. (13.1.16)
Подставляя (13.1.15) в (13.1.14), получаем
![]() ,
,
откуда
![]() и
и ![]() находятся
приравниванием ковариации при задержках 0, 1, 2.
находятся
приравниванием ковариации при задержках 0, 1, 2.
Обозначив
![]() , получаем
, получаем
 (13.1.17)
(13.1.17)
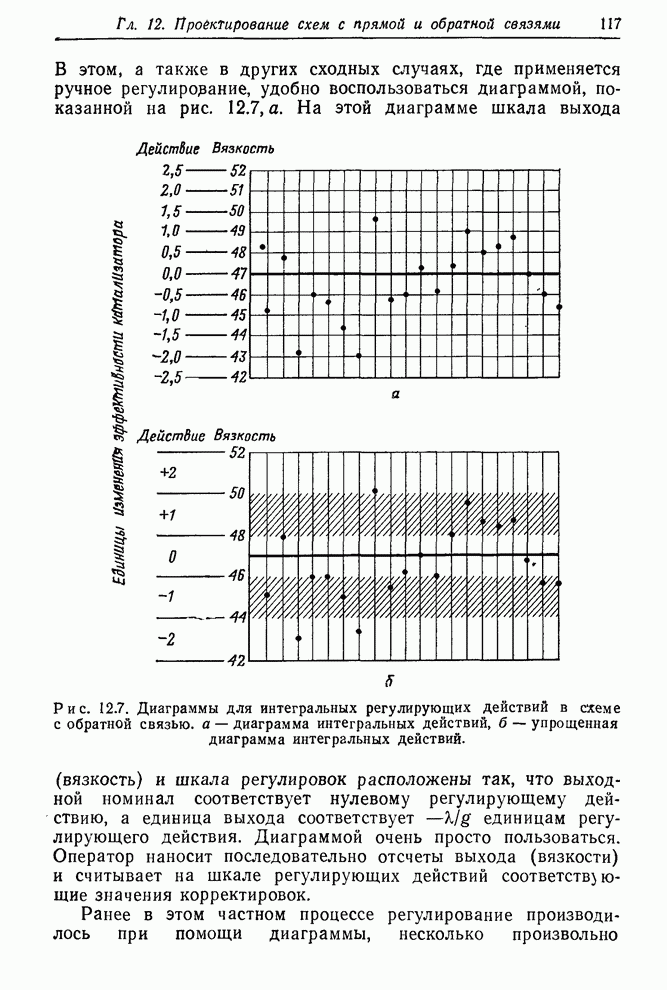
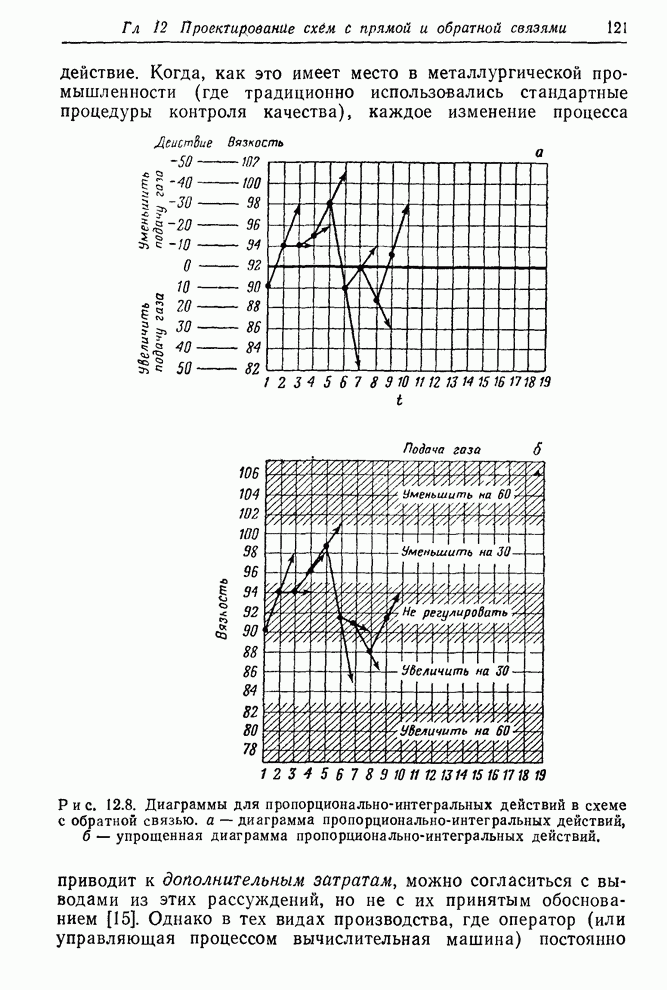
Оптимальная упрощенная схема регулирования. Рассмотрим опять в качестве примера упрощенную диаграмму на рис. 12.8,б. Делая те же приближения, что и ранее, рассмотрим, что дала бы такая схема, если учесть дополнительные ошибки округления.
Пусть,
как и в предшествующем обсуждении в конце разд. 13.1.1, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и, следовательно,
и, следовательно,
 .
.
Тогда, пользуясь (13.1.17), получаем
![]() ,
,
![]() ,
,
![]() .
.
Отсюда
![]() ,
,
![]() ,
, ![]() .
.
Подставляя эти значения в (13.1.16), находим оптимальную корректировку
![]()
с
![]() . Можно
сравнить эту схему с фактически использованной схемой
. Можно
сравнить эту схему с фактически использованной схемой
![]()
и
![]() , которая
является оптимальной в предположении об отсутствии дополнительных ошибок. Ясно,
что в этом случае добавочный шум незначительно повлиял на выбор оптимального
уравнения регулирования.
, которая
является оптимальной в предположении об отсутствии дополнительных ошибок. Ясно,
что в этом случае добавочный шум незначительно повлиял на выбор оптимального
уравнения регулирования.
Изменения оптимальной корректировки, вызванные шумом на входе. Если, как и ранее, принять
 ,
,
то из уравнения (13.1.17) получаем
![]() , (13.1.18а)
, (13.1.18а)
![]() , (13.1.18б)
, (13.1.18б)
 , (13.1.18в)
, (13.1.18в)
где,
как и прежде, ![]() .
На практике, чтобы связать
.
На практике, чтобы связать ![]() с
с ![]() , проще всего выразить решение
(13.1.18в) через
, проще всего выразить решение
(13.1.18в) через ![]() для
ряда нужным образом заданных
для
ряда нужным образом заданных ![]() и затем найти соответствующие значения
и затем найти соответствующие значения ![]() и
и ![]() , подставив
результаты в (13.1.18а) и (13.1.18б).
, подставив
результаты в (13.1.18а) и (13.1.18б).
В
этом примере умеренный добавочный шум, вызванный сильным округлением, не привел
к значительному увеличению ![]() , и оптимальная схема, учитывающая этот
шум, не привела к заметным улучшениям по сравнению со схемой, игнорирующей шум.
Такое заключение справедливо (при умеренном шуме) для широкого диапазона
параметров. Однако оно становится неверным, когда
, и оптимальная схема, учитывающая этот
шум, не привела к заметным улучшениям по сравнению со схемой, игнорирующей шум.
Такое заключение справедливо (при умеренном шуме) для широкого диапазона
параметров. Однако оно становится неверным, когда ![]() приближается к 1 (система имеет постоянную
времени, существенно превышающую интервал выборки) и при наличии в петле
обратной связи очень сильной компоненты добавочного шума. Чтобы получить
представление об этих случаях, рассмотрим несколько примеров. В каждом случае
примем
приближается к 1 (система имеет постоянную
времени, существенно превышающую интервал выборки) и при наличии в петле
обратной связи очень сильной компоненты добавочного шума. Чтобы получить
представление об этих случаях, рассмотрим несколько примеров. В каждом случае
примем ![]() ,
, ![]() , так что
, так что ![]() . Это соответствует
добавочному шуму
. Это соответствует
добавочному шуму ![]() со
стандартным отклонением
со
стандартным отклонением ![]() , таким же, как у ошибок округления, в
случае, когда интервал округления равен
, таким же, как у ошибок округления, в
случае, когда интервал округления равен ![]() . Здесь
. Здесь ![]() – стандартное отклонение
– стандартное отклонение ![]() , когда шум
отсутствует.
, когда шум
отсутствует.
Рассмотрим два случая.
Случай
1: ![]() ,
, ![]() ,
, ![]() .
.
Случай
2: ![]() ,
, ![]() ,
, ![]() .
.
Оптимальные схемы регулирования, соответствующие этим параметрам, приведены в табл. 13.1.
Таблица 13.1. Поведение конкретных схем регулирования в случае добавочного шума на входе
|
Случай 1: |
||
|
|
Уравнение регулирования для
корректировки |
Дисперсия на выходе |
|
Оптимальная схема без учета добавочного шума |
|
|
|
Действие схемы, не учитывающей шум,
при наличии на входе шума с |
Как и ранее |
|
|
Оптимальная схема с учетом добавочного шума |
|
|
|
Случай 2: |
||
|
|
Уравнение регулирования для
корректировки |
Дисперсия на выходе |
|
Оптимальная схема без учета добавочного шума |
|
|
|
Действие схемы, не учитывающей шум,
при наличии шума на входе с |
Как и ранее |
|
|
Оптимальная схема с учетом добавочного шума |
|
|
Чтобы
лучше понять табл. 13.1, заметим, что если записать уравнение регулирования не
для корректировки ![]() ,
а для уровня
,
а для уровня ![]() ,
на котором поддерживается регулируемая переменная между моментами времени
,
на котором поддерживается регулируемая переменная между моментами времени ![]() и
и ![]() , то все схемы табл. 13.1
примут вид
, то все схемы табл. 13.1
примут вид
![]() ,
,
что означает необходимость пропорционально-интегрального регулирования.
Корректирующее действие будет иметь вид
 . (13.1.19)
. (13.1.19)
Из
таблицы видно, что при ![]() (постоянная времени системы не слишком
велика по сравнению с интервалом отсчета) отношение пропорционального
регулирования к интегральному
(постоянная времени системы не слишком
велика по сравнению с интервалом отсчета) отношение пропорционального
регулирования к интегральному ![]() , и введение шума не изменяет характера
оптимального регулирования. Однако при
, и введение шума не изменяет характера
оптимального регулирования. Однако при ![]() (постоянная времени системы очень
велика по сравнению с интервалом отсчета) отношение пропорционального
регулирования к интегральному велико
(постоянная времени системы очень
велика по сравнению с интервалом отсчета) отношение пропорционального
регулирования к интегральному велико ![]() . Оптимальная схема реагирует на
добавочный шум увеличением
. Оптимальная схема реагирует на
добавочный шум увеличением ![]() и резким уменьшением отношения
и резким уменьшением отношения ![]() . Чтобы измерить
эффективность оптимальной схемы, не учитывающей шум, в ситуации, когда шум имеется,
можно использовать отношение
. Чтобы измерить
эффективность оптимальной схемы, не учитывающей шум, в ситуации, когда шум имеется,
можно использовать отношение
![]() .
.
Для рассмотренных выше схем
![]() для
для
![]() ,
,
![]() для
для
![]() .
.
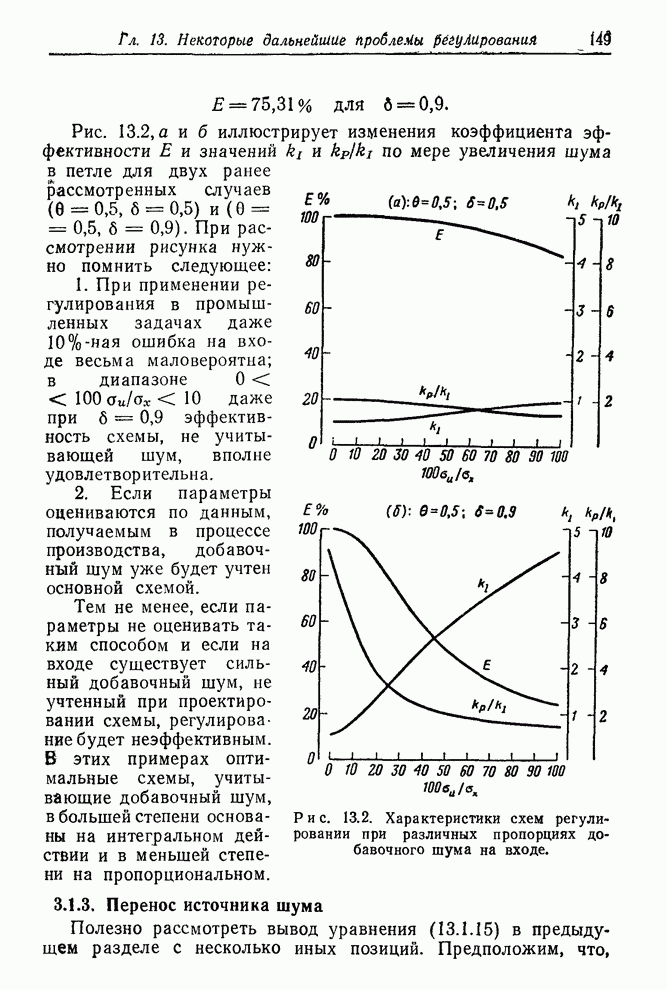
Рис.
13.2,а и б иллюстрирует изменения коэффициента эффективности ![]() и значений
и значений ![]() и
и ![]() по мере увеличения
шума в петле для двух ранее рассмотренных случаев
по мере увеличения
шума в петле для двух ранее рассмотренных случаев ![]() и
и ![]() . При рассмотрении рисунка
нужно помнить следующее:
. При рассмотрении рисунка
нужно помнить следующее:
1.
При применении регулирования в промышленных задачах даже 10%-ная ошибка на
входе весьма маловероятна; в диапазоне ![]() даже при
даже при ![]() эффективность схемы, не учитывающей
шум, вполне удовлетворительна.
эффективность схемы, не учитывающей
шум, вполне удовлетворительна.
2. Если параметры оцениваются по данным, получаемым в процессе производства, добавочный шум уже будет учтен основной схемой.

Рис. 13.2. Характеристики схем регулирования при различных пропорциях добавочного шума на входе.
Тем не менее, если параметры не оценивать таким способом и если на входе существует сильный добавочный шум, не учтенный при проектировании схемы, регулирование будет неэффективным.
В этих примерах оптимальные схемы, учитывающие добавочный шум, в большей степени основаны на интегральном действии и в меньшей степени на пропорциональном.
| << Предыдущий параграф | Следующий параграф >> |
- Часть III. ПОСТРОЕНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- Глава 10. Модели передаточной функции
- 10.1. ЛИНЕЙНЫЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 10.1.1. Дискретная передаточная функция
- 10.1.2. Непрерывные динамические модели, описываемые дифференциальными уравнениями
- 10.2. ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ МОДЕЛИ, ОПИСЫВАЕМЫЕ РАЗНОСТНЫМИ УРАВНЕНИЯМИ
- 10.2.1. Общая форма разностного уравнения
- 10.2.2. Природа передаточной функции
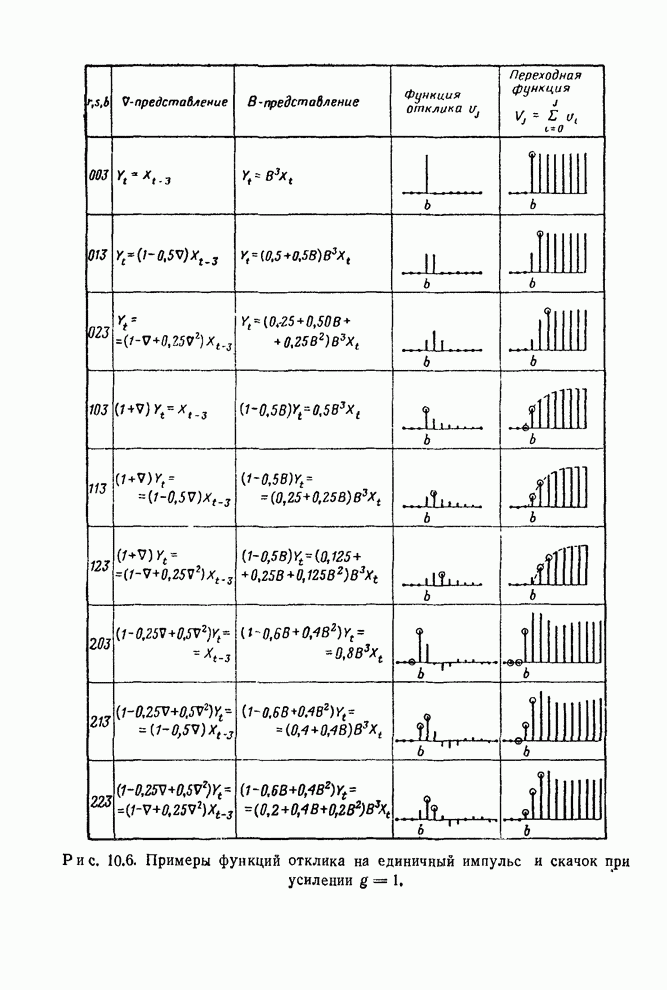
- 10.2.3. Дискретные модели передаточных функций первого и второго порядков
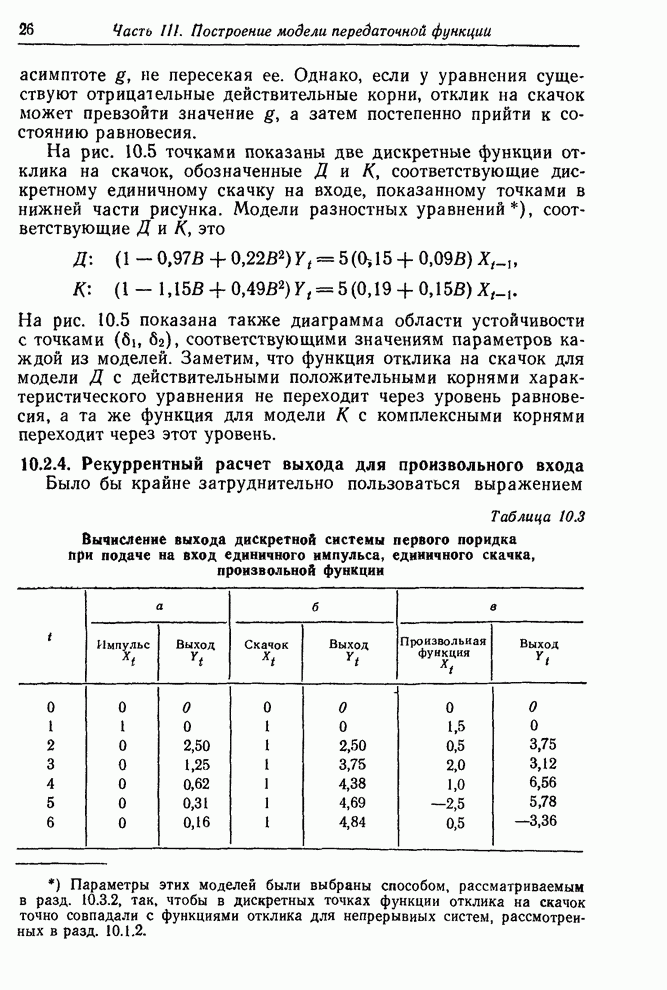
- 10.2.4. Рекуррентный расчет выхода для произвольного входа
- 10.3. СООТНОШЕНИЕ МЕЖДУ ДИСКРЕТНОЙ И НЕПРЕРЫВНОЙ МОДЕЛЯМИ
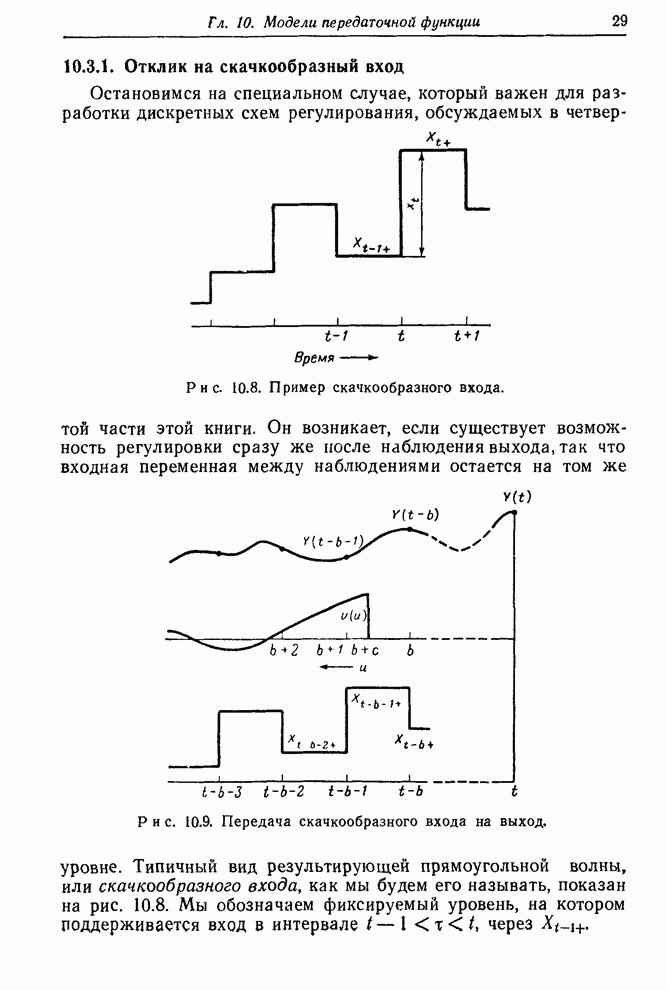
- 10.3.1. Отклик на скачкообразный вход
- 10.3.2. Соотношения совпадающих систем первого и второго порядков
- 10.3.3. Аппроксимация общих непрерывных моделей дискретными моделями
- 10.3.4. Модели передаточных функций с добавленным шумом
- ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
- ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
- Глава 11. Идентификация, подгонка и проверка моделей передаточных функций
- 11.1. Взаимная корреляционная функция
- 11.1.1. Свойства взаимных ковариационной и корреляционной функций
- 11.1.2. Оценивание взаимных ковариационных и корреляционных функций
- 11.1.3. Приближенные стандартные ошибки выборочных оценок взаимных корреляций
- 11.2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.2.1. Идентификация моделей передаточной функции с предварительным выравниванием спектра входа
- 11.2.2. Пример идентификации модели передаточной функции
- 11.2.3. Идентификация модели шума
- 11.2.4. Некоторые общие соображения об идентификации моделей передаточных функций
- 11.3. ПОДГОНКА И ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.3.1. Условная сумма квадратов
- 11.3.2. Нелинейное оценивание
- 11.3.3. Использование остаточных ошибок для диагностической проверки
- 11.3.4. Конкретные способы проверки остаточных ошибок
- 11.4. Некоторые примеры подгонок и проверок моделей передаточных функций
- 11.4.1. Подгонка и проверка модели газовой печи
- 11.4.2. Искусственный пример с двумя входами
- 11.5. ПРОГНОЗИРОВАНИЕ ПРИ ПОМОЩИ УПРЕЖДАЮЩИХ ИНДИКАТОРОВ
- 11.5.1. Прогноз с минимальной среднеквадратичной ошибкой
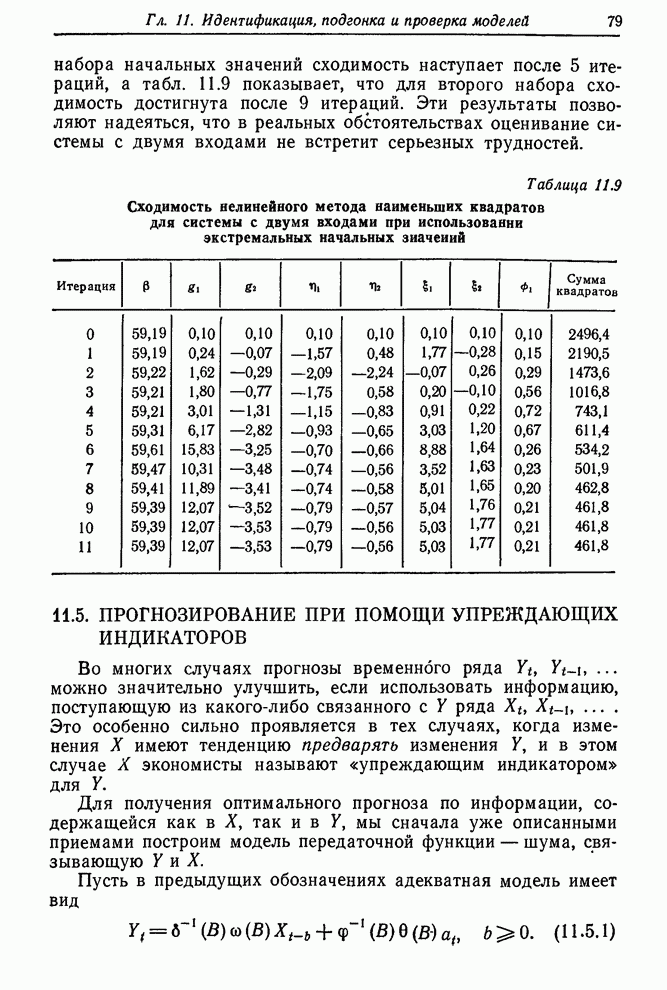
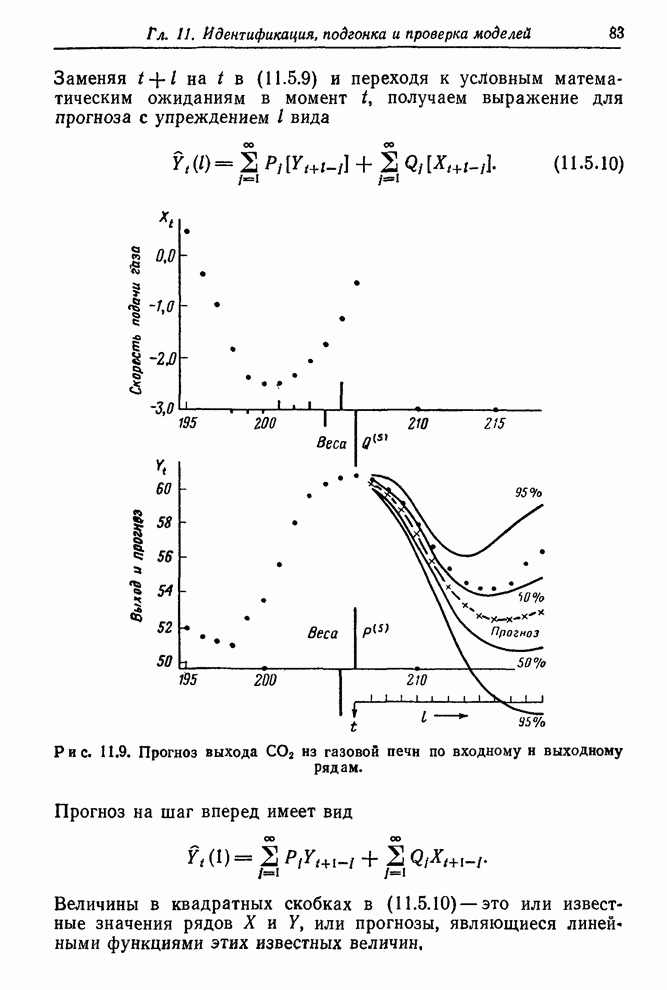
- 11.5.2. Прогнозы выхода СO2 из газовой печи
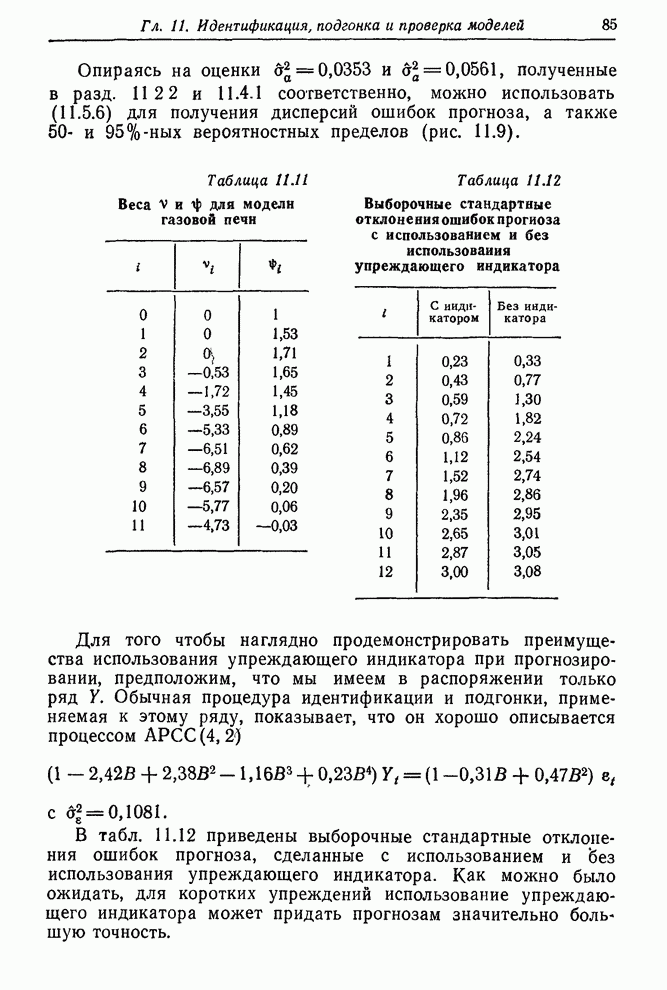
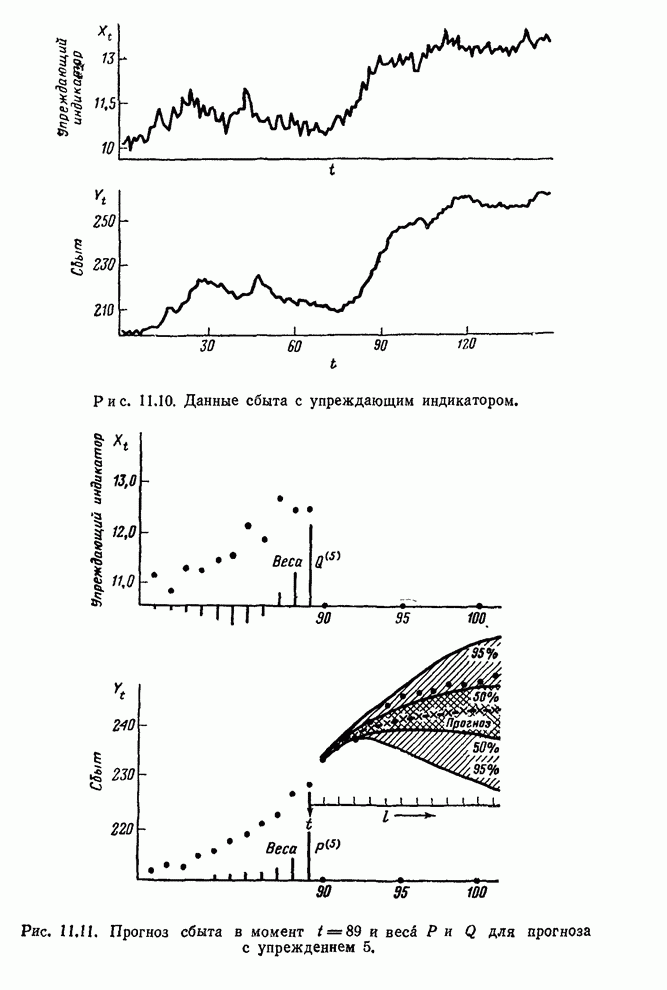
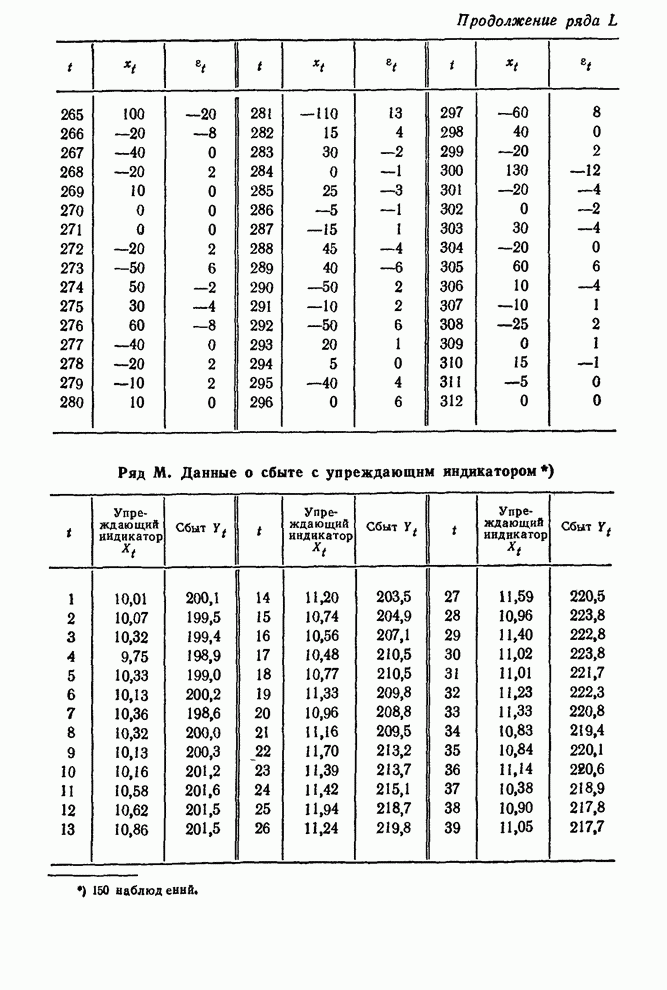
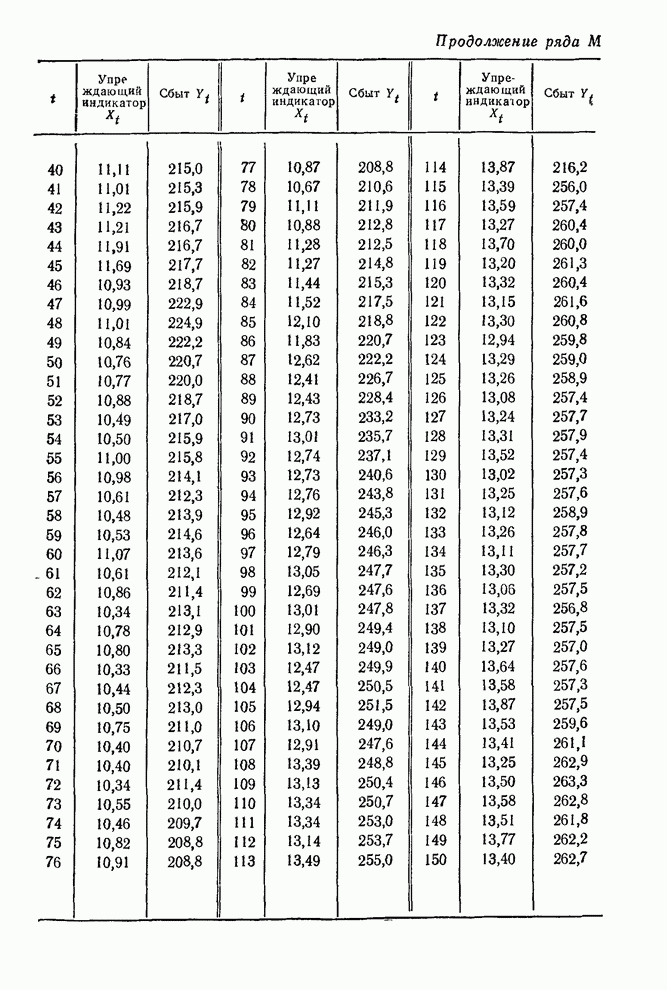
- 11.5.3. Прогноз нестационарных данных сбыта при помощи упреждающего индикатора
- 11.6. НЕКОТОРЫЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОЦЕНИВАНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ П11.1. ИСПОЛЬЗОВАНИЕ ВЗАИМНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
- Заключение
- Часть IV. Проектирование дискретных схем регулирования
- Глава 12. Проектирование схем регулирования с прямой и обратной связями
- 12.1. РЕГУЛИРОВАНИЕ С ПРЯМОЙ СВЯЗЬЮ
- 12.1.1. Регулирование с прямой связью, минимизирующее среднеквадратичную ошибку
- 12.1.2. Пример — регулирование удельного веса промежуточного продукта
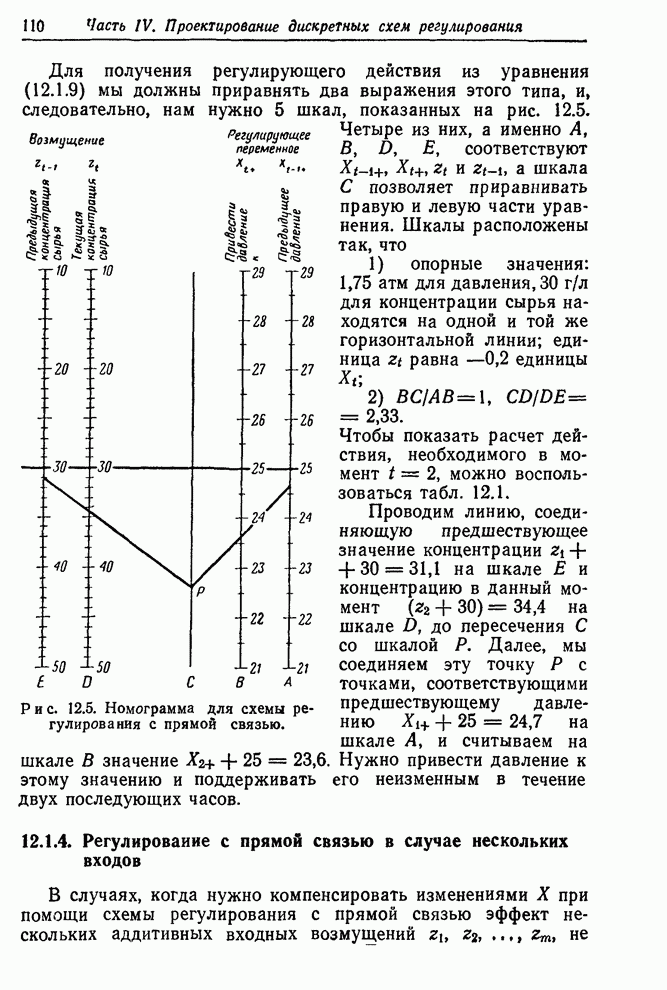
- 12.1.3. Номограмма для регулирования с прямой связью
- 12.1.4. Регулирование с прямой связью в случае нескольких входов
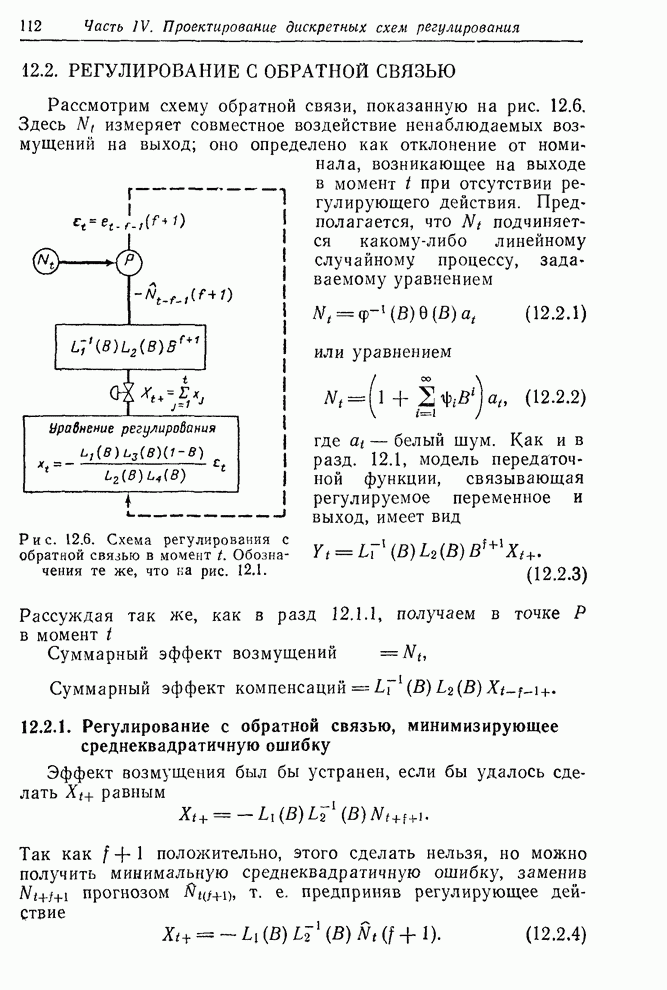
- 12.2. РЕГУЛИРОВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ
- 12.2.1. Регулирование с обратной связью, минимизирующее среднеквадратичную ошибку
- 12.2.2. Применение уравнения регулирования: ПИД-регулятор
- 12.2.3. Примеры дискретного регулирования с обратной связью
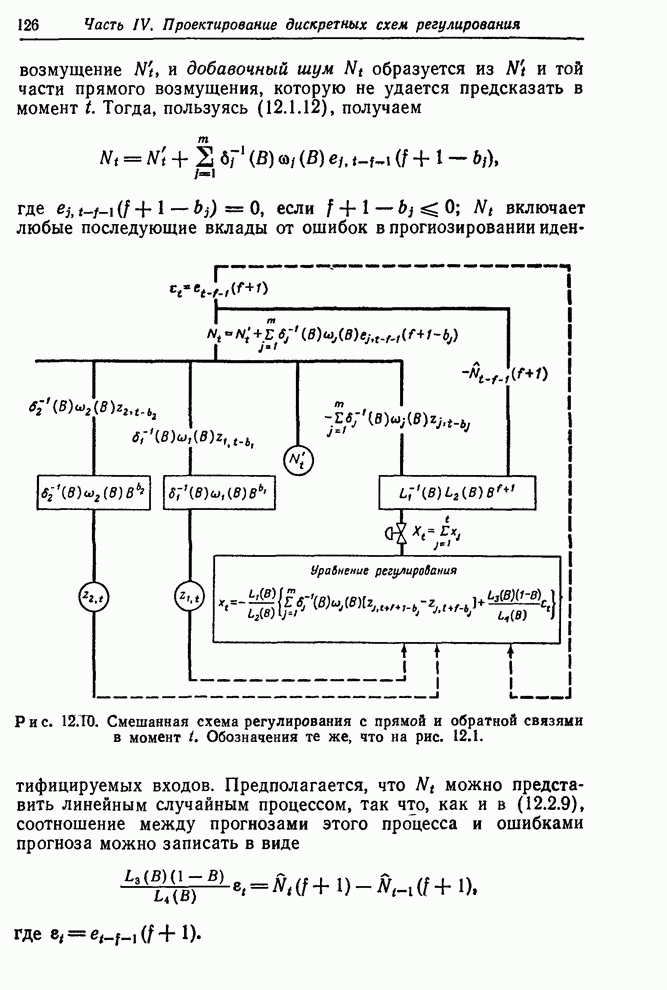
- 12.3. РЕГУЛИРОВАНИЕ С ПРЯМОЙ И ОБРАТНОЙ СВЯЗЯМИ
- 12.3.1. Регулирование с прямой и обратной связями, минимизирующее выходную среднеквадратичную ошибку
- 12.3.2. Пример регулирования с прямой и обратной связями
- 12.3.3. Преимущества и недостатки регулирования с прямой и обратной связями
- 12.4. Подгонка моделей передаточных функций шума по оперативным данным
- 12.4.1. Итеративный способ построения моделей
- 12.4.2. Оценивание по оперативным данным
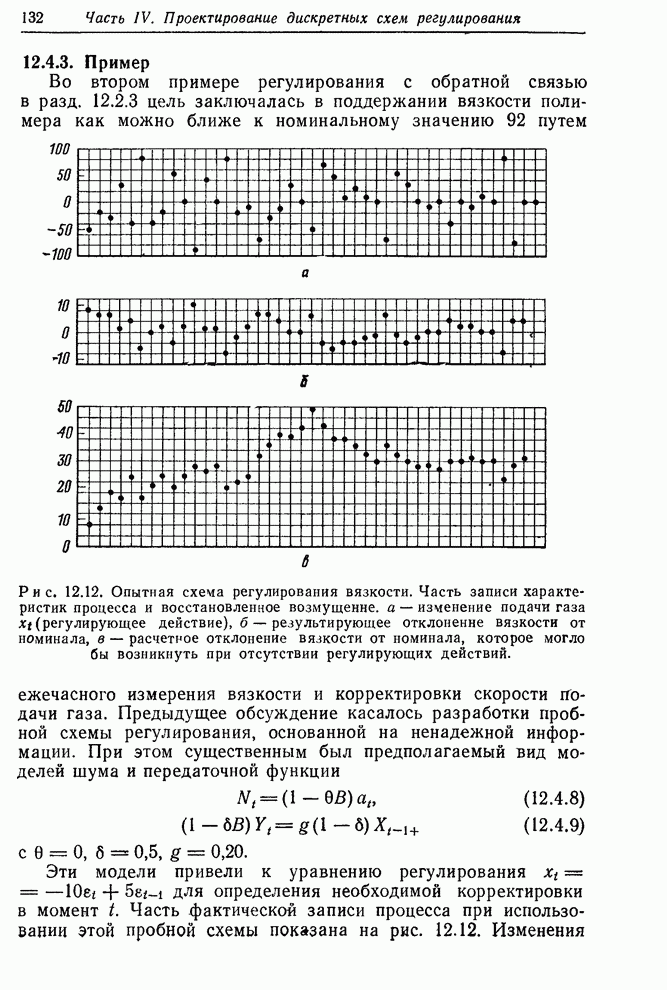
- 12.4.3. Пример
- Глава 13. Некоторые дальнейшие проблемы регулирования
- 13.1. ЭФФЕКТ ДОБАВОЧНОГО ШУМА В СХЕМАХ РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ
- 13.1.1. Эффект пренебрежения добавочным шумом; упрощенные схемы
- 13.1.2. Оптимальное действие в случаях, когда корректировки содержат ошибки наблюдения
- 13.1.3. Перенос источника шума
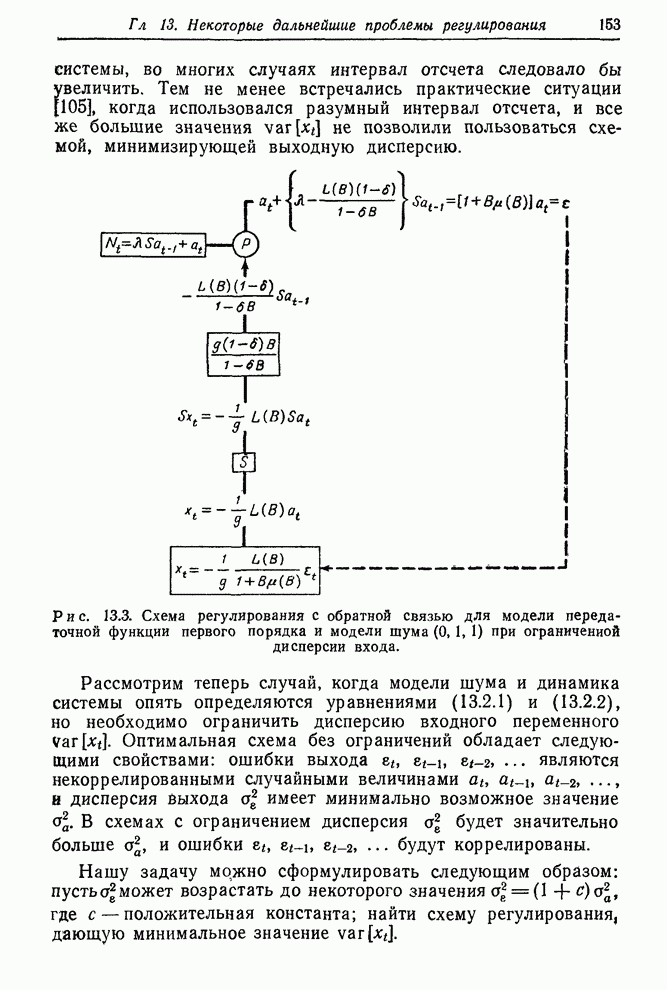
- 13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
- 13.2.1. Вывод выражения для оптимальной корректировки
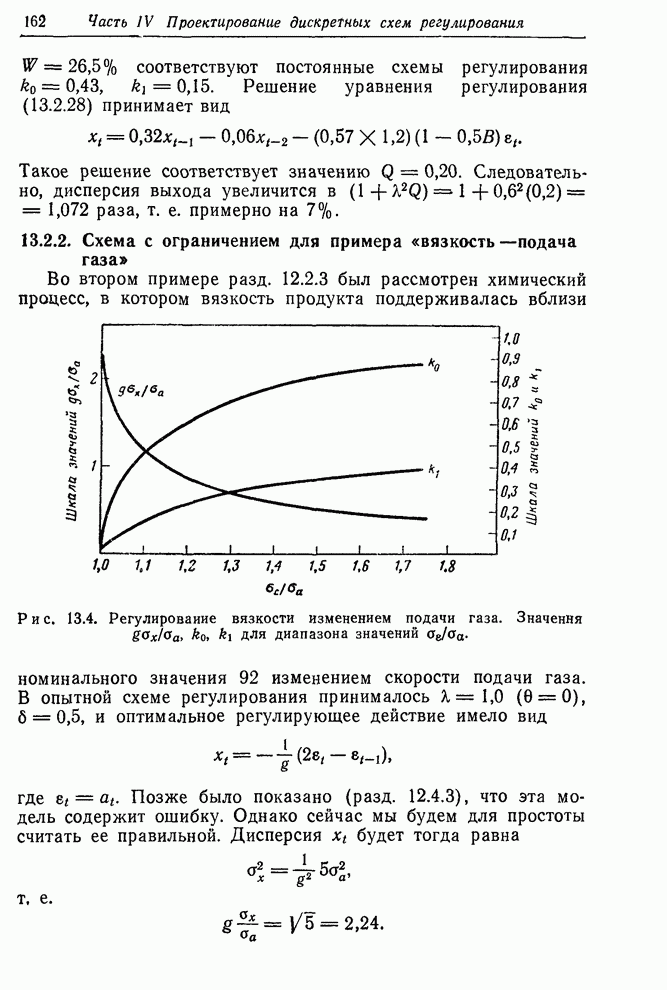
- 13.2.2. Схема с ограничением для примера «вязкость–подача газа»
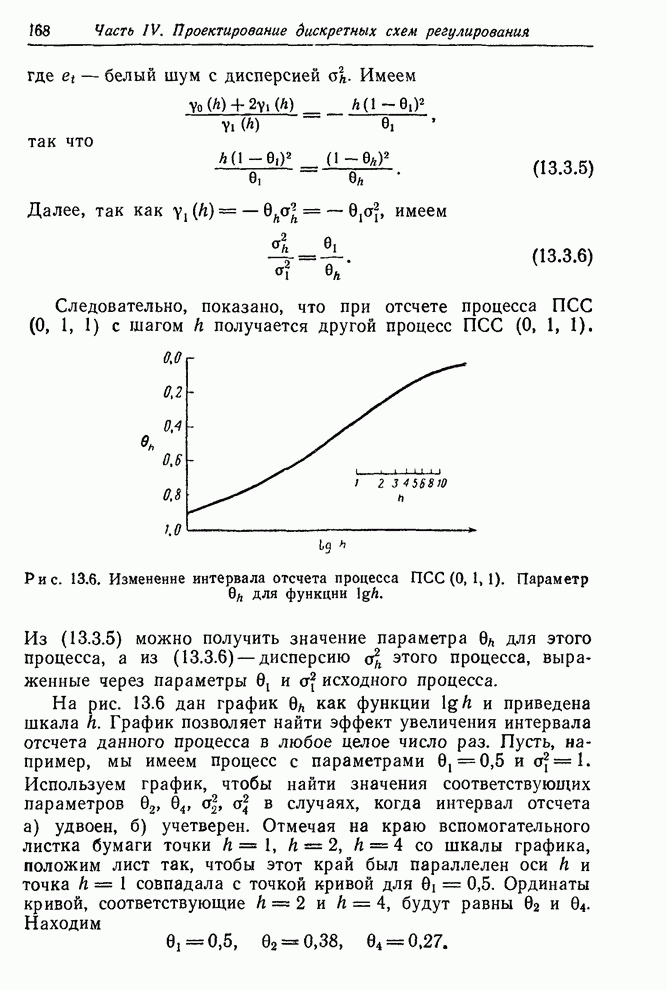
- 13.3. ВЫБОР ИНТЕРВАЛА ОТСЧЕТА
- 13.3.1. Пример эффекта уменьшения частоты отсчетов
- 13.3.2. Влияние интервала отсчета на процесс ПСС(0,1,1)
- ПРОГРАММА 5. ИДЕНТИФИКАЦИЯ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 6. ПРЕДВАРИТЕЛЬНОЕ ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 7. ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
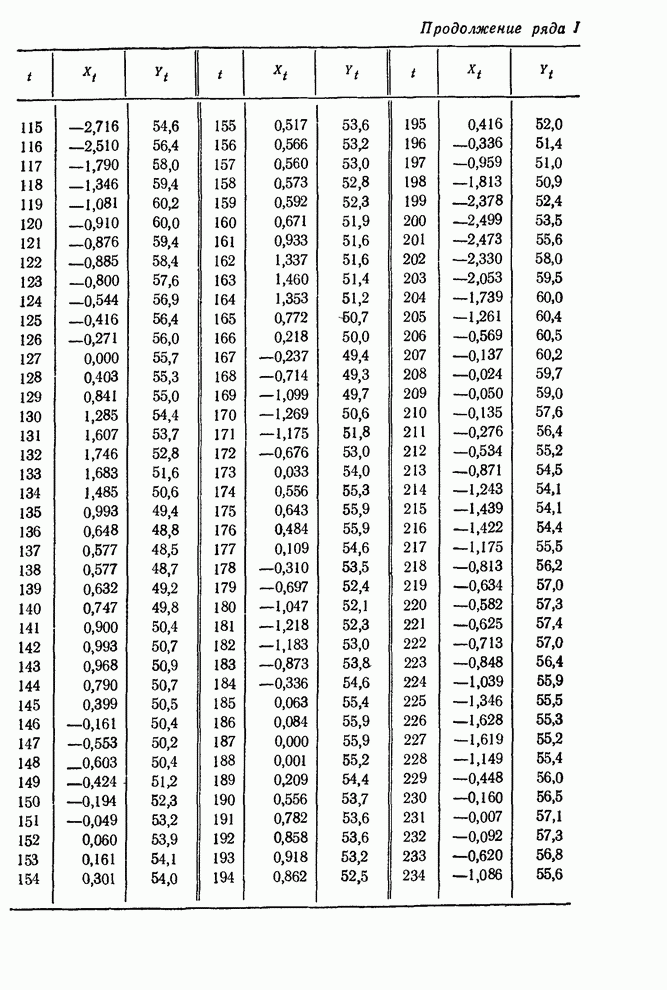
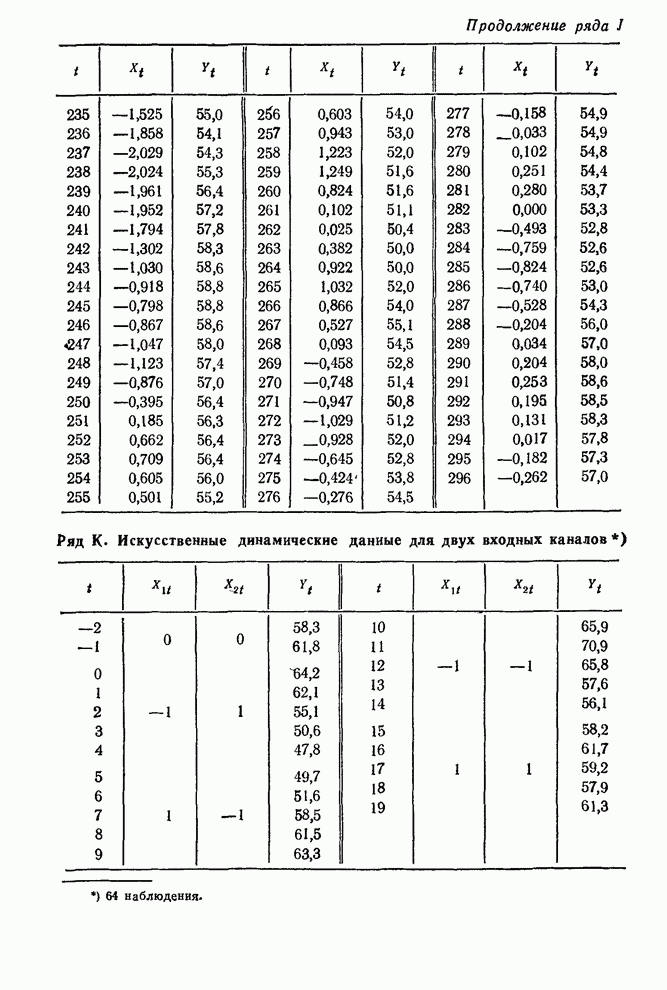
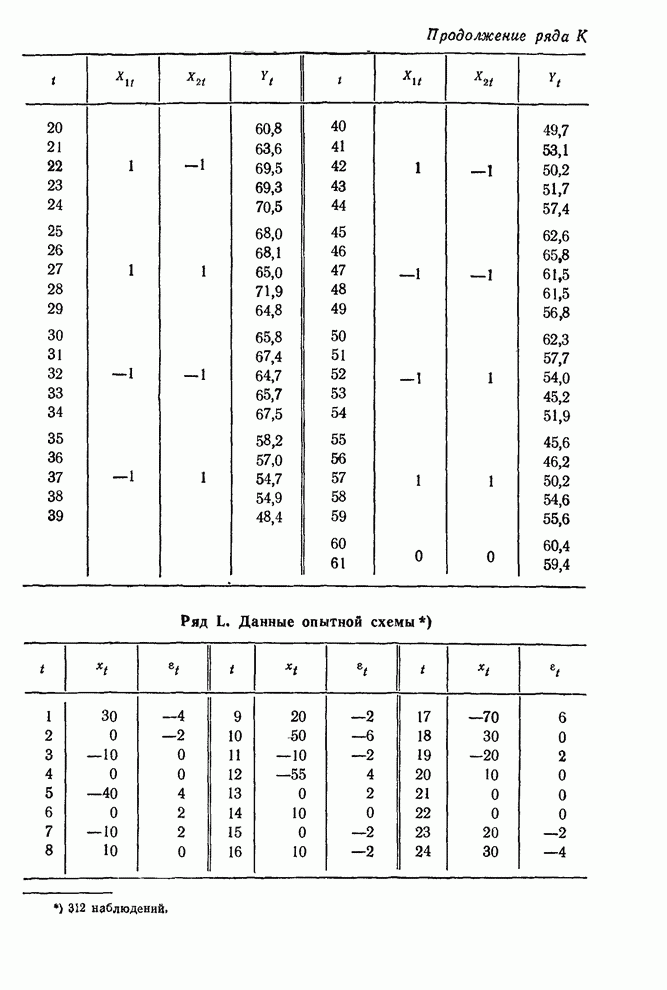
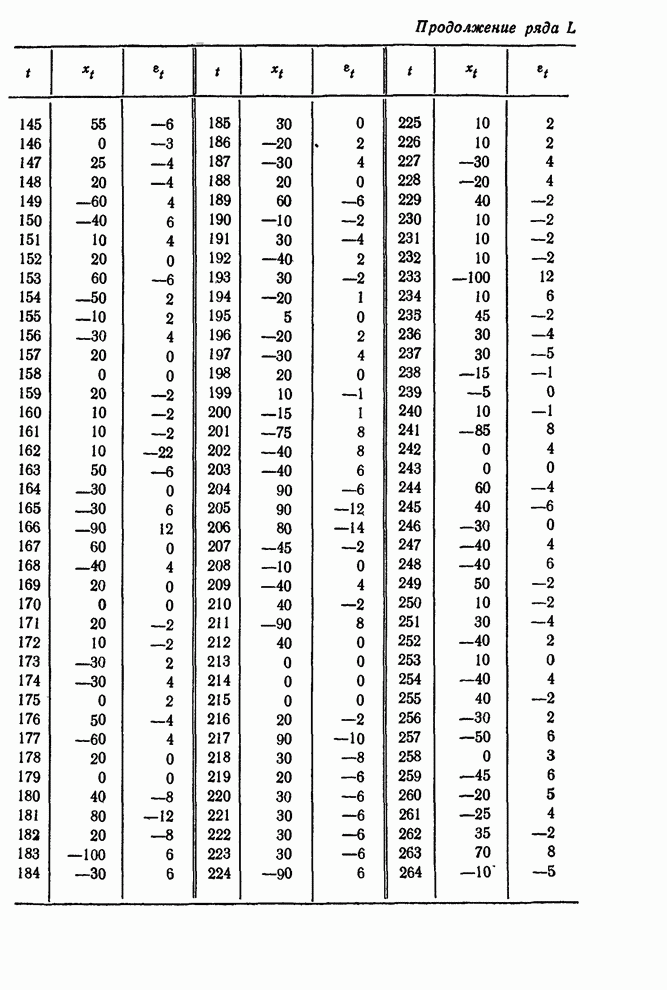
- ТАБЛИЦЫ ВРЕМЕННЫХ РЯДОВ