| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
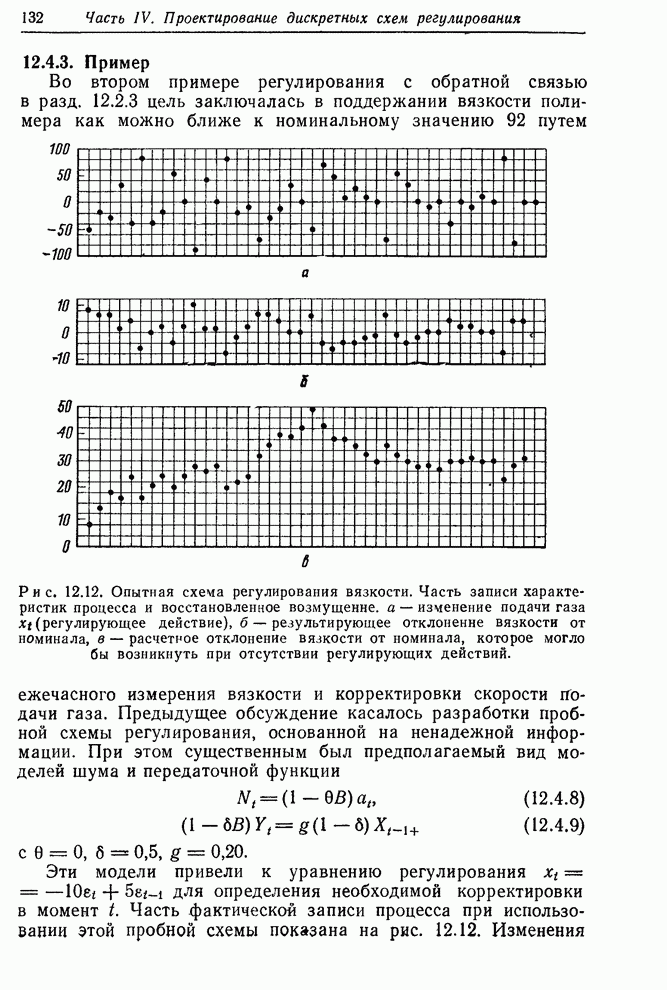
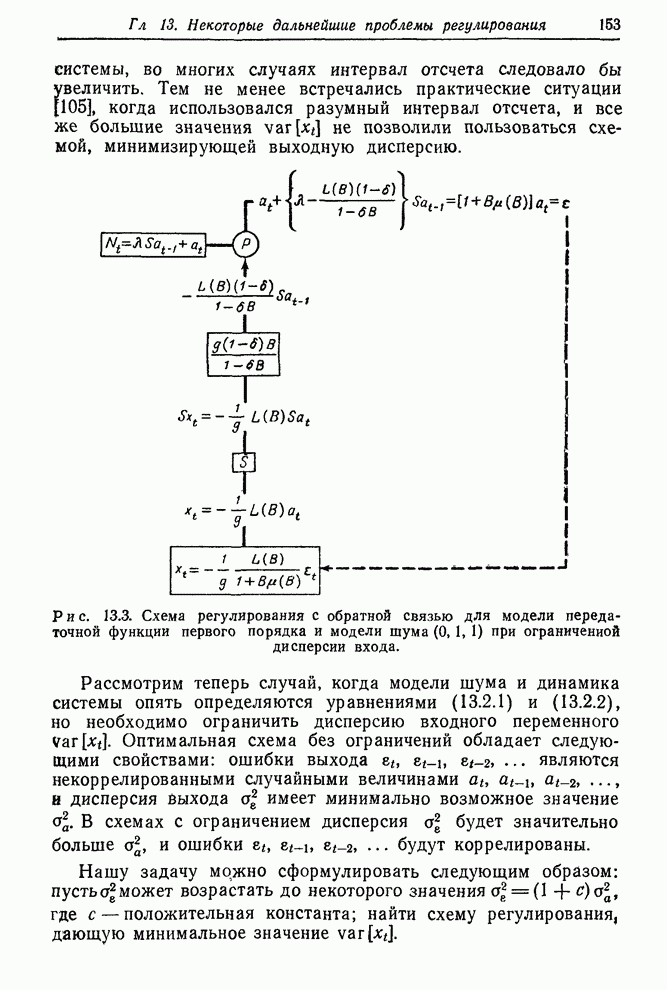
13.2.2. Схема с ограничением для примера «вязкость–подача газа»
Во
втором примере разд. 12.2.3 был рассмотрен химический процесс, в котором
вязкость продукта поддерживалась вблизи номинального значения 92 изменением
скорости подачи газа. В опытной схеме регулирования принималось ![]()
![]() ,
, ![]() , и оптимальное регулирующее
действие имело вид
, и оптимальное регулирующее
действие имело вид
![]() ,
,
где
![]() . Позже
было показано (разд. 12.4.3), что эта модель содержит ошибку. Однако сейчас мы
будем для простоты считать ее правильной. Дисперсия
. Позже
было показано (разд. 12.4.3), что эта модель содержит ошибку. Однако сейчас мы
будем для простоты считать ее правильной. Дисперсия ![]() будет тогда равна
будет тогда равна
![]() ,
,
т, е.
![]() .
.
На
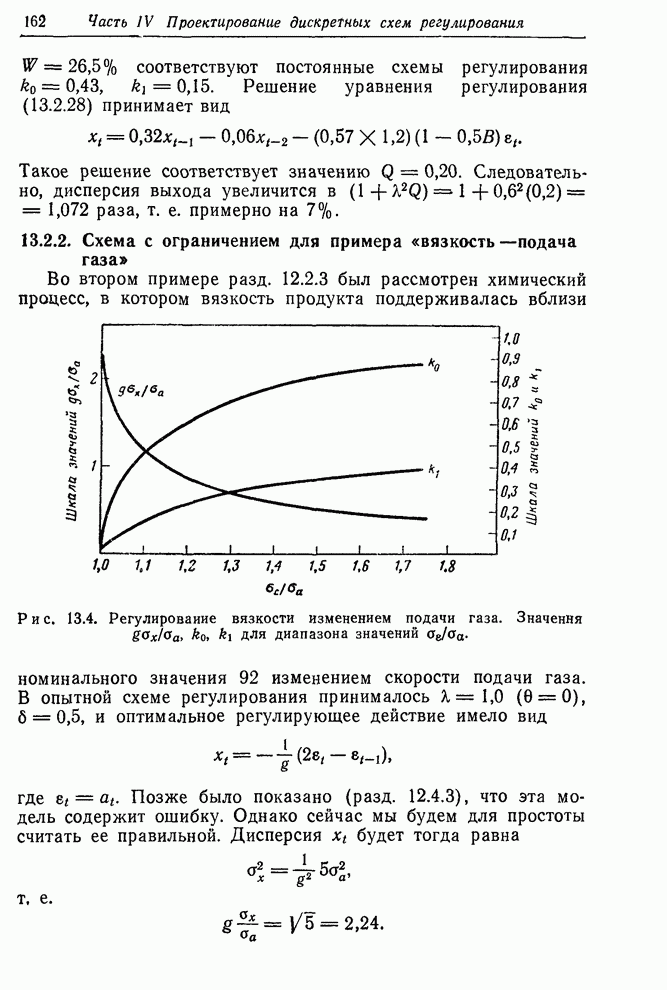
рис. 13.4 показано возможное уменьшение ![]() для различных значений
для различных значений ![]() , а также другие
параметры оптимального регулирования. В частности, видно, что уменьшение в 2
раза стандартного отклонения входа приводит к увеличению стандартного
отклонения выхода лишь на 10%.
, а также другие
параметры оптимального регулирования. В частности, видно, что уменьшение в 2
раза стандартного отклонения входа приводит к увеличению стандартного
отклонения выхода лишь на 10%.

Рис. 13.4. Регулирование вязкости
изменением подачи газа. Значения ![]() ,
, ![]() ,
, ![]() для диапазона значений
для диапазона значений ![]() .
.
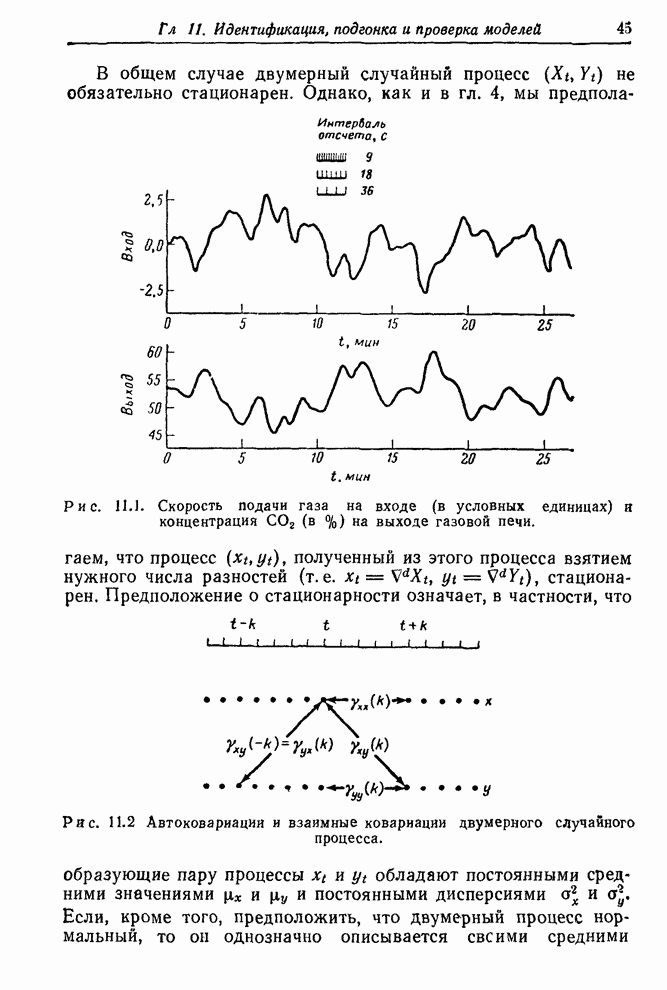
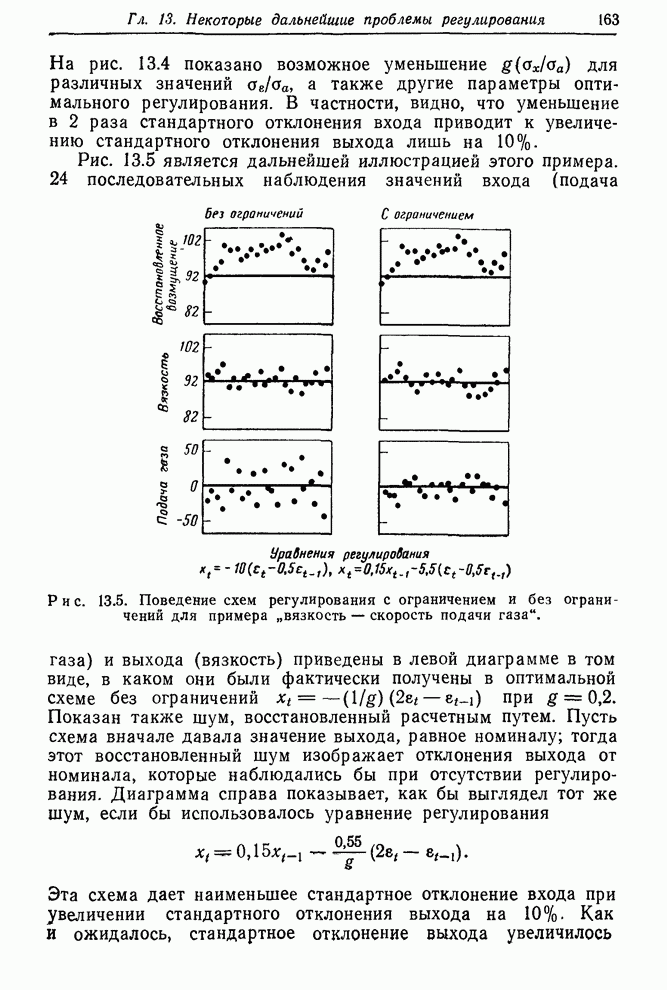
Рис.
13.5 является дальнейшей иллюстрацией этого примера. 24 последовательных
наблюдения значений входа (подача газа) и выхода (вязкость) приведены в левой
диаграмме в том виде, в каком они были фактически получены в оптимальной схеме
без ограничений ![]() при
при
![]() . Показан
также шум, восстановленный расчетным путем. Пусть схема вначале давала значение
выхода, равное номиналу; тогда этот восстановленный шум изображает отклонения
выхода от номинала, которые наблюдались бы при отсутствии регулирования.
Диаграмма справа показывает, как бы выглядел тот же шум, если бы использовалось
уравнение регулирования
. Показан
также шум, восстановленный расчетным путем. Пусть схема вначале давала значение
выхода, равное номиналу; тогда этот восстановленный шум изображает отклонения
выхода от номинала, которые наблюдались бы при отсутствии регулирования.
Диаграмма справа показывает, как бы выглядел тот же шум, если бы использовалось
уравнение регулирования
![]() .
.

Уравнения регулирования ![]() ,
, ![]()
Рис. 13.5. Поведение схем регулирования с ограничением и без ограничений для примера «вязкость – скорость подачи газа».
Эта
схема дает наименьшее стандартное отклонение входа при увеличении стандартного
отклонения выхода на 10%. Как и ожидалось, стандартное отклонение выхода
увеличилось незначительно, зато стандартное отклонение входа ![]() уменьшилось вдвое.
уменьшилось вдвое.
Схемы с ограничением для систем с запаздыванием. Общий анализ для схем с ограничением рассмотренного типа был недавно проведен Вилсоном [107]; он базировался на теории Винера-Хопфа [106], изложенной Уиттлом [49]. Пользуясь результатами Вилсона, Макгрегор провел предварительное исследование интересной ситуации, когда в петле обратной связи имеется запаздывание (холостое время). Ниже мы частично воспроизведем его результаты. Проиллюстрируем их на важном случае, для которого решение без ограничений приведено в разд. 12.2.3 (пример 3).
Предполагается,
что динамика системы описывается моделью первого порядка с запаздыванием выхода
![]() относительно
входа
относительно
входа ![]() и
что возмущение
и
что возмущение ![]() может
быть представлено процессом
может
быть представлено процессом ![]() . Тогда
. Тогда
![]() ,
,
![]() .
.
Оптимальный
регулятор с ограничением при ![]() имеет вид
имеет вид
![]() ,
,
частным случаем которого является оптимальный регулятор без ограничений (12.2.13).
Предположим,
в частности, что ![]() .
Динамическая модель будет тогда иметь аналогом непрерывную систему, у которой
холостое время равно целому периоду плюс его дробная часть. Тогда оптимальный
регулятор с ограничением – это
.
Динамическая модель будет тогда иметь аналогом непрерывную систему, у которой
холостое время равно целому периоду плюс его дробная часть. Тогда оптимальный
регулятор с ограничением – это
![]() ,
,
где
![]() ,
,
![]() ,
,
![]()
и
![]() ,
,
![]() ,
,
![]() ,
,
где
![]() –
некоторая неизвестная константа.
–
некоторая неизвестная константа.
Дисперсии
![]() и
и ![]() имеют вид
имеют вид
 ,
,
 .
.
Случай
системы с запаздыванием представляет собой интерес, поскольку схемы без
ограничений, дающие минимальную среднеквадратичную ошибку, часто требуют
практически нереализуемых больших корректировок переменного знака. Чтобы
показать, насколько сильно уменьшается дисперсия корректировок ![]() при использовании
таких схем, был проведен расчет для случая
при использовании
таких схем, был проведен расчет для случая ![]() ,
, ![]() ,
, ![]() ,
, ![]() при
при ![]() и
и ![]() .
.
Характеристики
схемы без ограничения таковы: при ![]()
![]() ,
,
 ,
, 
и
при ![]()
![]() ,
,
 ,
,  .
.
Различные оптимальные схемы с ограничением приведены в табл. 13.4.
Таблица 13.4. Сравнение схем регулирования с обратной связью с ограничением и без ограничений
|
|
Увеличение |
Уменьшение |
Параметры регулятора |
||
|
|
|
|
|||
|
0,5 |
0 |
0 |
схема без ограничений |
||
|
1,07 |
0,27 |
1,33 |
|||
|
0,2 |
49,1 |
0,88 |
0,24 |
1,19 |
|
|
0,7 |
69,8 |
0,69 |
0,23 |
1,06 |
|
|
2,8 |
90,0 |
0,24 |
0,20 |
0,74 |
|
|
0,9 |
0 |
0 |
схема без ограничений |
||
|
1,07 |
0,27 |
1,33 |
|||
|
0,1 |
40,5 |
0,93 |
0,25 |
1,23 |
|
|
0,7 |
71,7 |
0,68 |
0,23 |
1,05 |
|
|
2,4 |
89,4 |
0,29 |
0,21 |
0,78 |
|
| << Предыдущий параграф | Следующий параграф >> |
- Часть III. ПОСТРОЕНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- Глава 10. Модели передаточной функции
- 10.1. ЛИНЕЙНЫЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 10.1.1. Дискретная передаточная функция
- 10.1.2. Непрерывные динамические модели, описываемые дифференциальными уравнениями
- 10.2. ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ МОДЕЛИ, ОПИСЫВАЕМЫЕ РАЗНОСТНЫМИ УРАВНЕНИЯМИ
- 10.2.1. Общая форма разностного уравнения
- 10.2.2. Природа передаточной функции
- 10.2.3. Дискретные модели передаточных функций первого и второго порядков
- 10.2.4. Рекуррентный расчет выхода для произвольного входа
- 10.3. СООТНОШЕНИЕ МЕЖДУ ДИСКРЕТНОЙ И НЕПРЕРЫВНОЙ МОДЕЛЯМИ
- 10.3.1. Отклик на скачкообразный вход
- 10.3.2. Соотношения совпадающих систем первого и второго порядков
- 10.3.3. Аппроксимация общих непрерывных моделей дискретными моделями
- 10.3.4. Модели передаточных функций с добавленным шумом
- ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
- ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
- Глава 11. Идентификация, подгонка и проверка моделей передаточных функций
- 11.1. Взаимная корреляционная функция
- 11.1.1. Свойства взаимных ковариационной и корреляционной функций
- 11.1.2. Оценивание взаимных ковариационных и корреляционных функций
- 11.1.3. Приближенные стандартные ошибки выборочных оценок взаимных корреляций
- 11.2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.2.1. Идентификация моделей передаточной функции с предварительным выравниванием спектра входа
- 11.2.2. Пример идентификации модели передаточной функции
- 11.2.3. Идентификация модели шума
- 11.2.4. Некоторые общие соображения об идентификации моделей передаточных функций
- 11.3. ПОДГОНКА И ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.3.1. Условная сумма квадратов
- 11.3.2. Нелинейное оценивание
- 11.3.3. Использование остаточных ошибок для диагностической проверки
- 11.3.4. Конкретные способы проверки остаточных ошибок
- 11.4. Некоторые примеры подгонок и проверок моделей передаточных функций
- 11.4.1. Подгонка и проверка модели газовой печи
- 11.4.2. Искусственный пример с двумя входами
- 11.5. ПРОГНОЗИРОВАНИЕ ПРИ ПОМОЩИ УПРЕЖДАЮЩИХ ИНДИКАТОРОВ
- 11.5.1. Прогноз с минимальной среднеквадратичной ошибкой
- 11.5.2. Прогнозы выхода СO2 из газовой печи
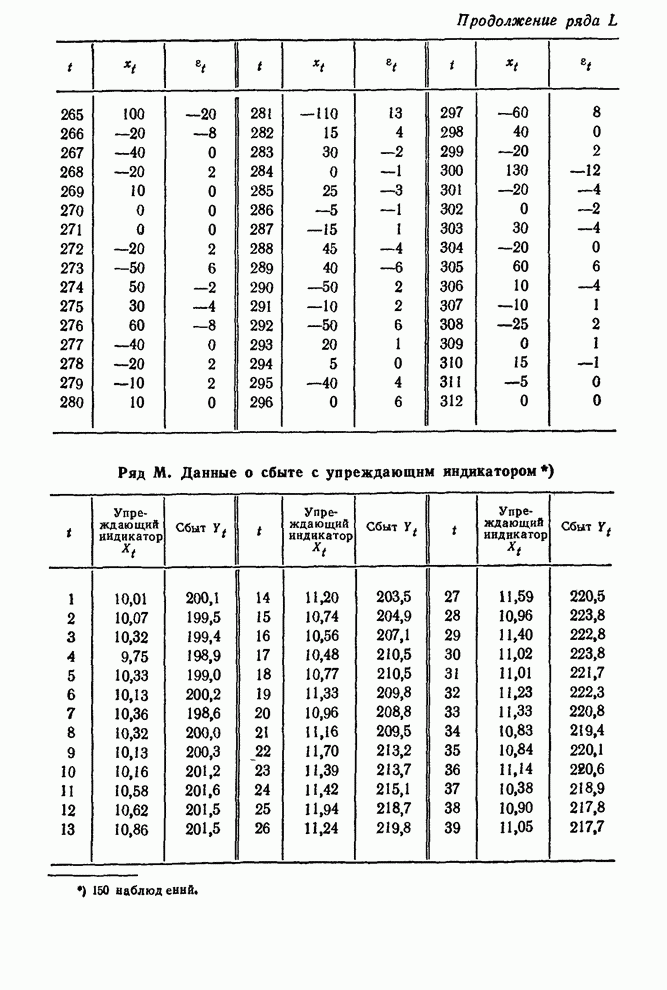
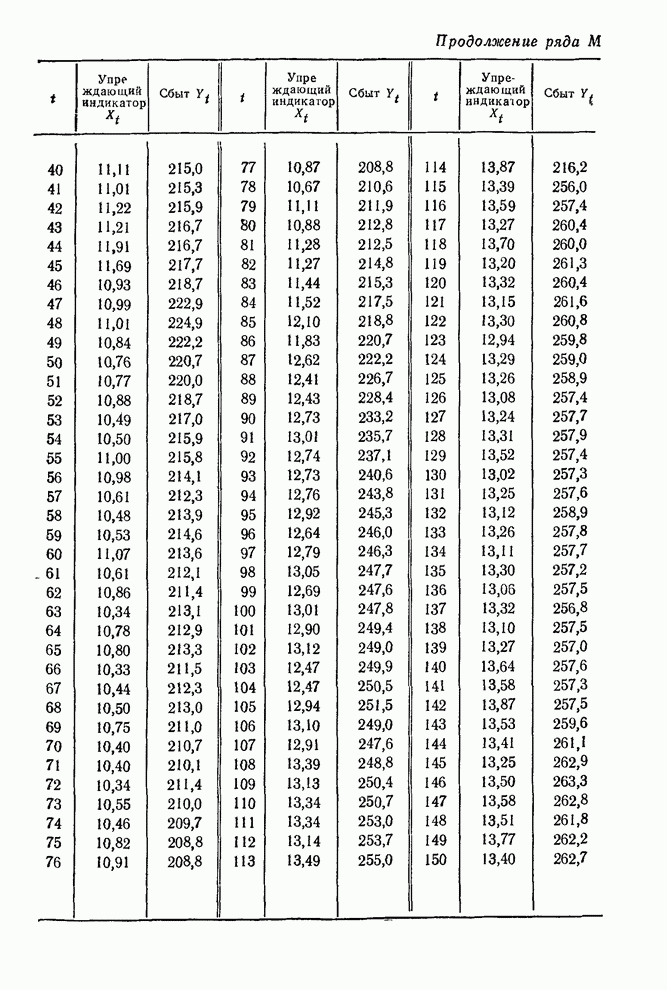
- 11.5.3. Прогноз нестационарных данных сбыта при помощи упреждающего индикатора
- 11.6. НЕКОТОРЫЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОЦЕНИВАНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ П11.1. ИСПОЛЬЗОВАНИЕ ВЗАИМНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
- Заключение
- Часть IV. Проектирование дискретных схем регулирования
- Глава 12. Проектирование схем регулирования с прямой и обратной связями
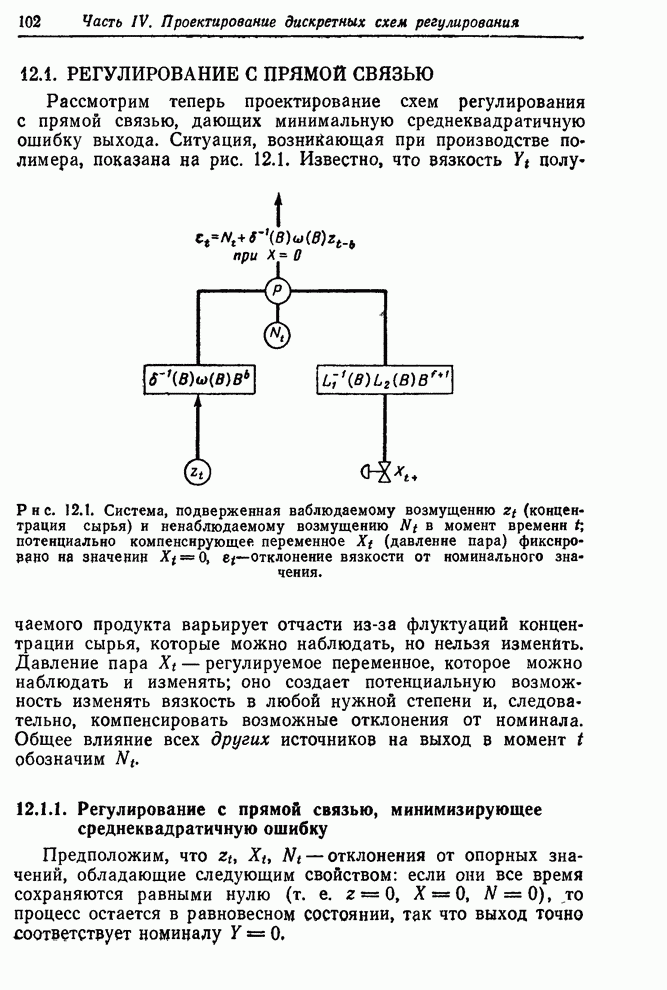
- 12.1. РЕГУЛИРОВАНИЕ С ПРЯМОЙ СВЯЗЬЮ
- 12.1.1. Регулирование с прямой связью, минимизирующее среднеквадратичную ошибку
- 12.1.2. Пример — регулирование удельного веса промежуточного продукта
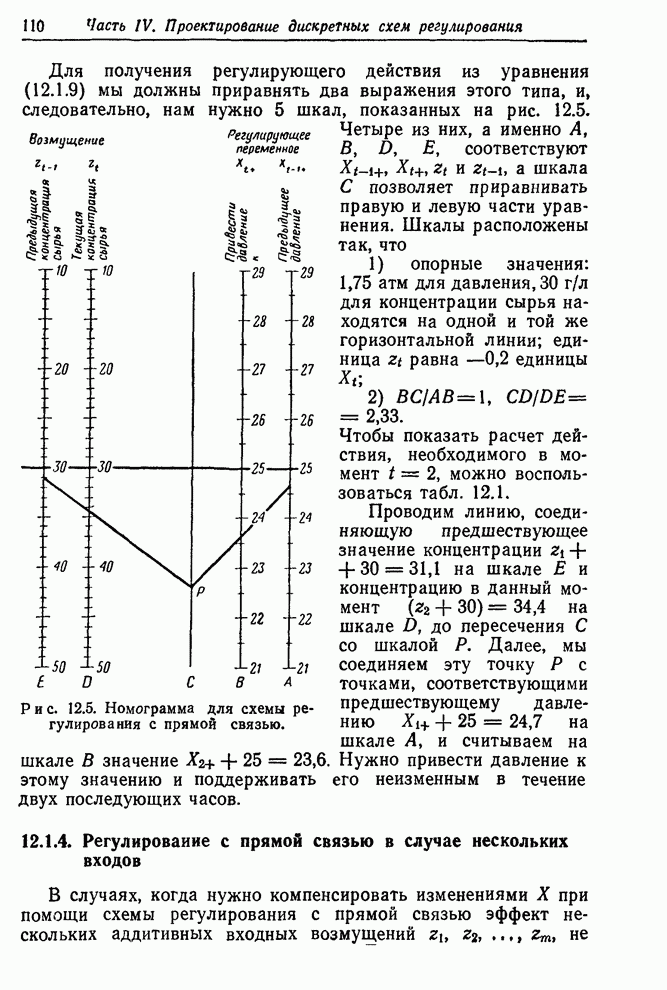
- 12.1.3. Номограмма для регулирования с прямой связью
- 12.1.4. Регулирование с прямой связью в случае нескольких входов
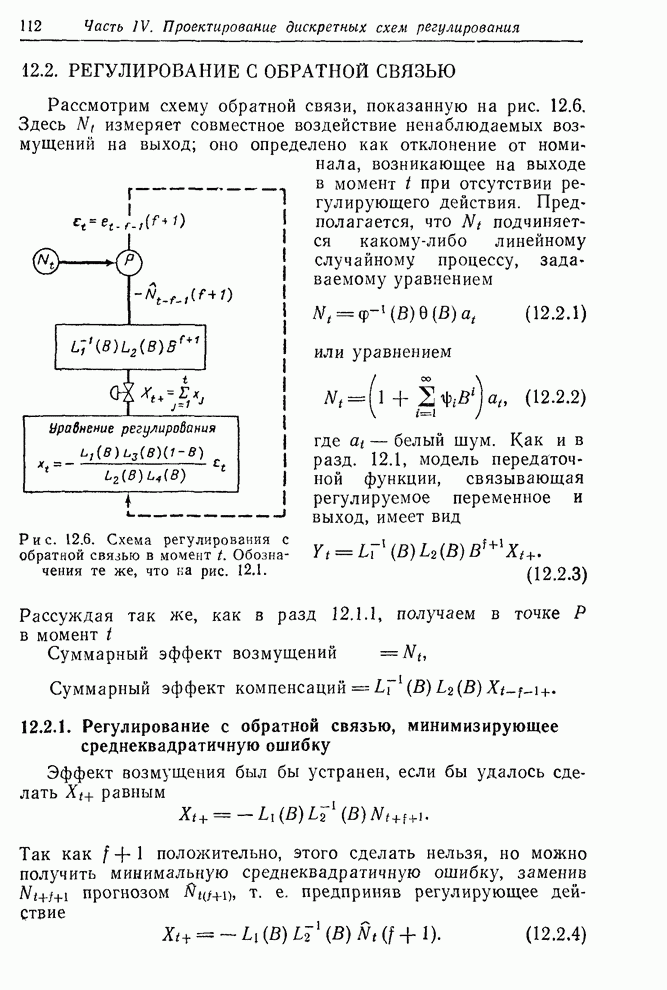
- 12.2. РЕГУЛИРОВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ
- 12.2.1. Регулирование с обратной связью, минимизирующее среднеквадратичную ошибку
- 12.2.2. Применение уравнения регулирования: ПИД-регулятор
- 12.2.3. Примеры дискретного регулирования с обратной связью
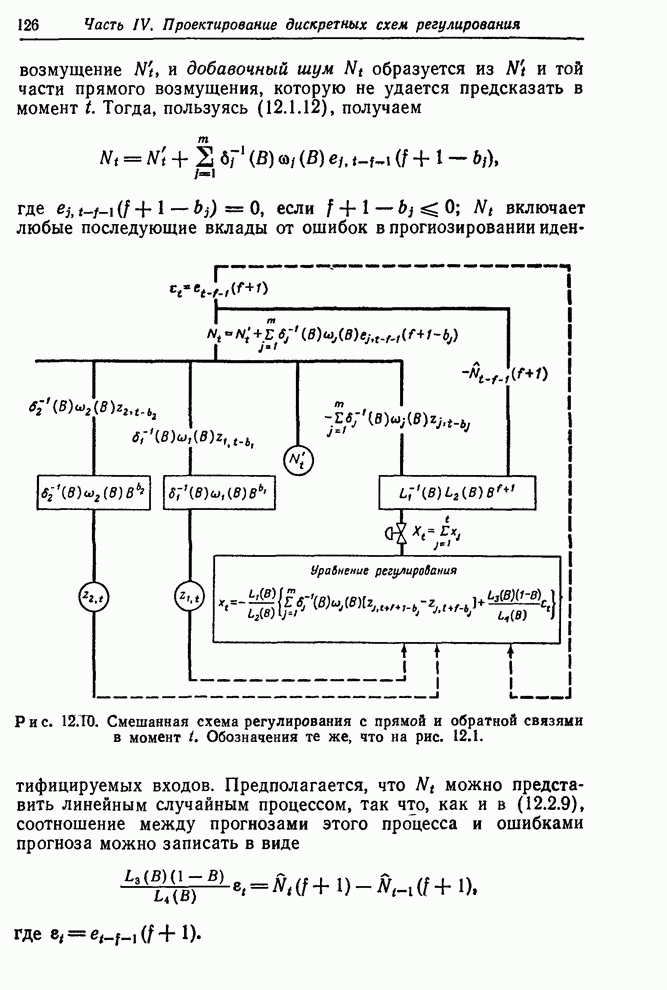
- 12.3. РЕГУЛИРОВАНИЕ С ПРЯМОЙ И ОБРАТНОЙ СВЯЗЯМИ
- 12.3.1. Регулирование с прямой и обратной связями, минимизирующее выходную среднеквадратичную ошибку
- 12.3.2. Пример регулирования с прямой и обратной связями
- 12.3.3. Преимущества и недостатки регулирования с прямой и обратной связями
- 12.4. Подгонка моделей передаточных функций шума по оперативным данным
- 12.4.1. Итеративный способ построения моделей
- 12.4.2. Оценивание по оперативным данным
- 12.4.3. Пример
- Глава 13. Некоторые дальнейшие проблемы регулирования
- 13.1. ЭФФЕКТ ДОБАВОЧНОГО ШУМА В СХЕМАХ РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ
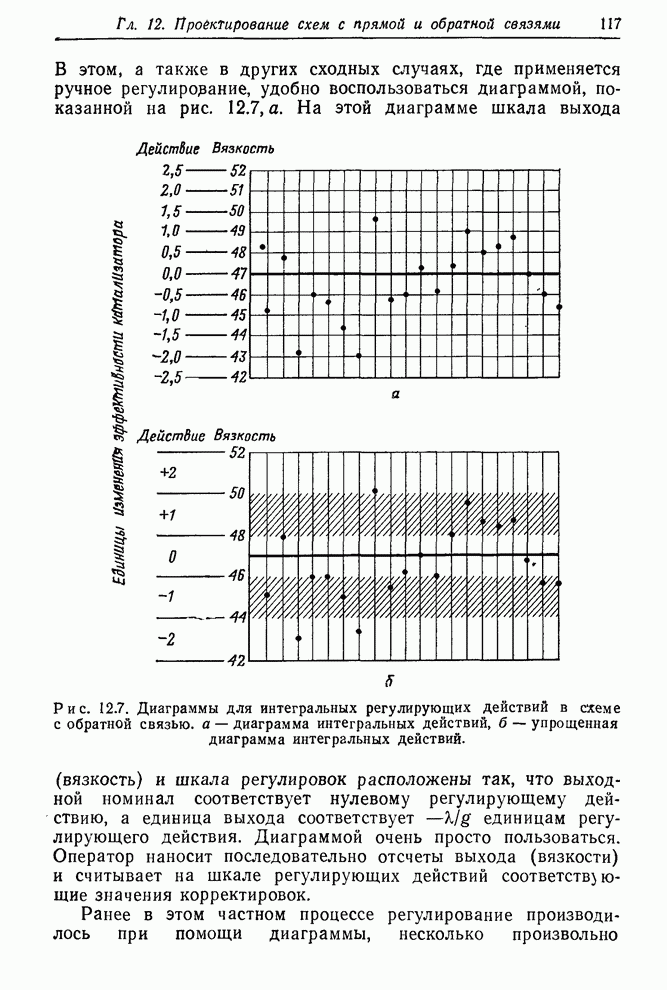
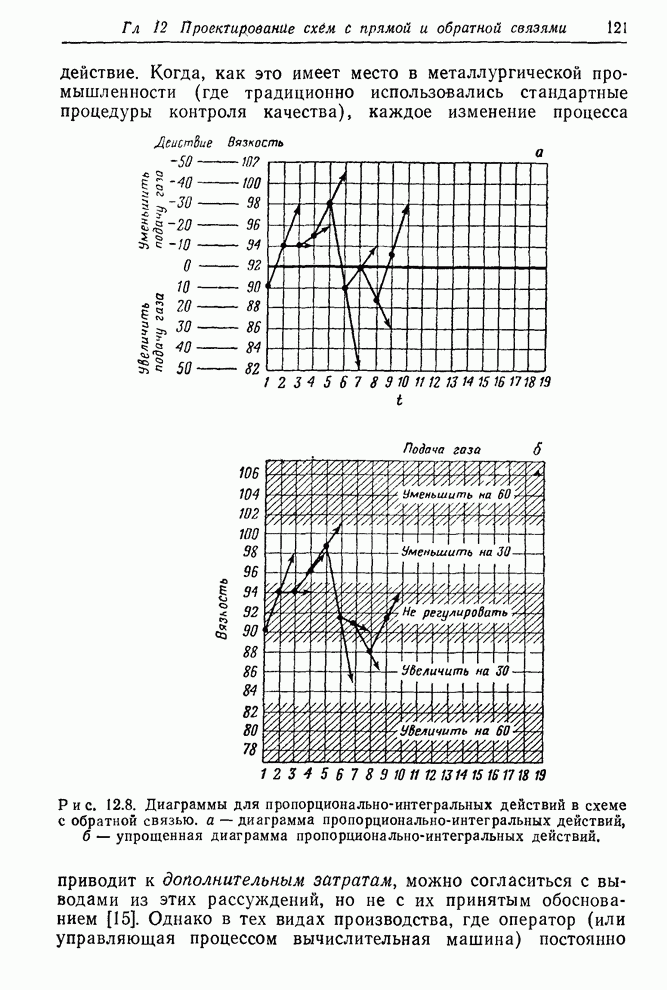
- 13.1.1. Эффект пренебрежения добавочным шумом; упрощенные схемы
- 13.1.2. Оптимальное действие в случаях, когда корректировки содержат ошибки наблюдения
- 13.1.3. Перенос источника шума
- 13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
- 13.2.1. Вывод выражения для оптимальной корректировки
- 13.2.2. Схема с ограничением для примера «вязкость–подача газа»
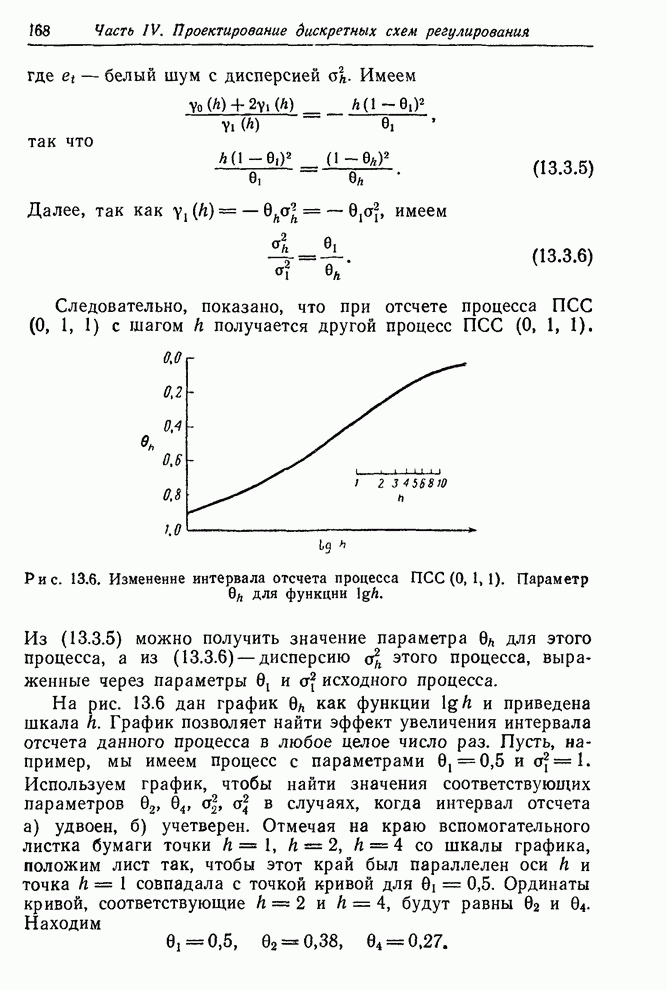
- 13.3. ВЫБОР ИНТЕРВАЛА ОТСЧЕТА
- 13.3.1. Пример эффекта уменьшения частоты отсчетов
- 13.3.2. Влияние интервала отсчета на процесс ПСС(0,1,1)
- ПРОГРАММА 5. ИДЕНТИФИКАЦИЯ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 6. ПРЕДВАРИТЕЛЬНОЕ ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 7. ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
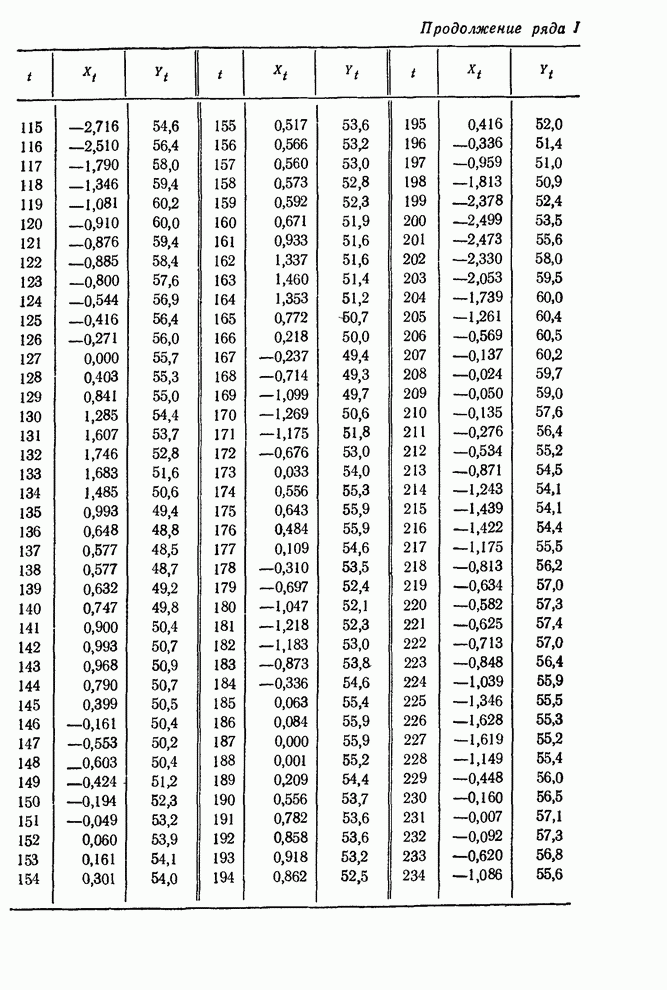
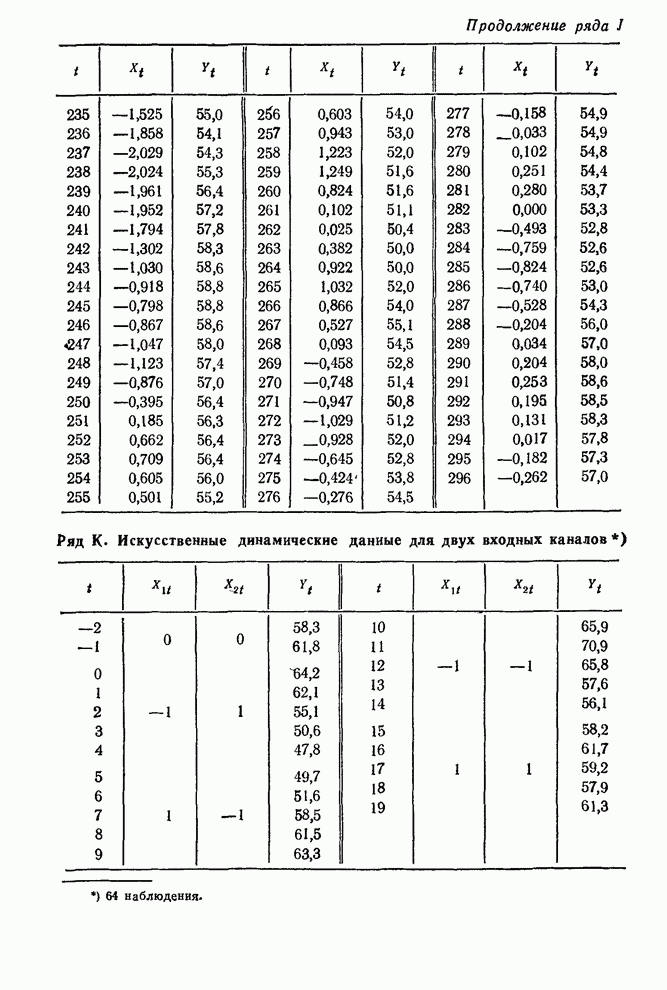
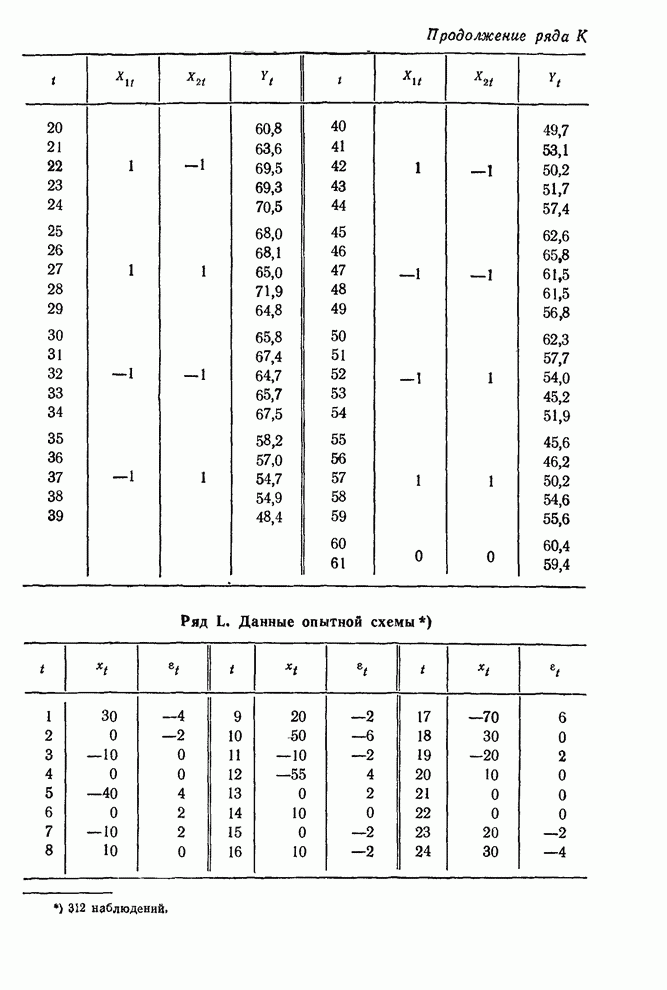
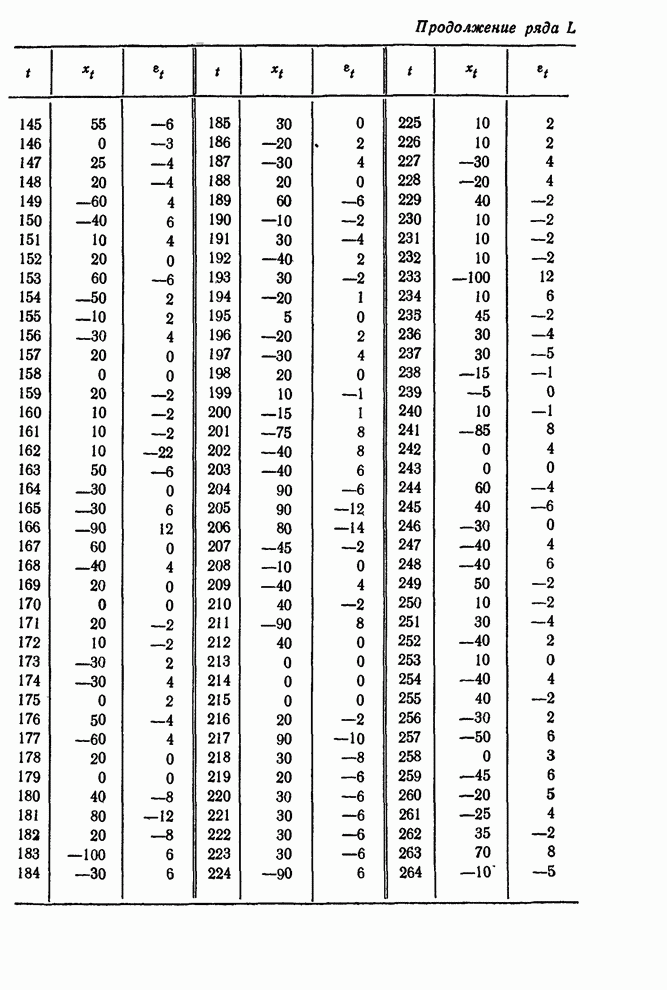
- ТАБЛИЦЫ ВРЕМЕННЫХ РЯДОВ