| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
Рассмотренные
выше дискретные схемы регулирования с обратной связью предназначались для
минимизации среднеквадратичной ошибки выхода. При этом неявно предполагалось,
что не существует ограничения величины корректировки, которую можно выполнить
для достижения этой цели. Иногда случается, что эти схемы нельзя применить, так
как по практическим причинам допустимые вариации ![]() ограничены. Поэтому нужно представлять,
как изменится конкретный класс схем регулирования с обратной связью при наложении
ограничения на
ограничены. Поэтому нужно представлять,
как изменится конкретный класс схем регулирования с обратной связью при наложении
ограничения на ![]() ;
предполагается, что
;
предполагается, что ![]() – стационарный процесс.
– стационарный процесс.
Рассмотрим
опять важный случай, когда возмущение выхода ![]() представимо моделью порядка
представимо моделью порядка ![]() :
:
![]() ,
, ![]() , (13.2.1)
, (13.2.1)
а выход и вход связаны передаточной функцией первого порядка, т. е.
![]() , (13.2.2)
, (13.2.2)
где
![]() . Напомним,
что
. Напомним,
что ![]() можно
трактовать как долю общей реакции на единичный входной скачок, происходящую в
первом временном интервале. Как мы видели в разд. 12.2.3, уравнение
регулирования, дающее минимальную дисперсию выхода, имеет вид
можно
трактовать как долю общей реакции на единичный входной скачок, происходящую в
первом временном интервале. Как мы видели в разд. 12.2.3, уравнение
регулирования, дающее минимальную дисперсию выхода, имеет вид
![]() , (13.2.3)
, (13.2.3)
Где
![]() и
и ![]() .
.
Если
![]() пренебрежимо
мало, оптимальное регулирование достигается, согласно формуле, при
пренебрежимо
мало, оптимальное регулирование достигается, согласно формуле, при ![]() ; в этом случае будем
иметь
; в этом случае будем
иметь ![]() .
Отсюда следует, что когда
.
Отсюда следует, что когда ![]() пренебречь нельзя,
пренебречь нельзя, ![]() . Если
. Если ![]() близко к своему верхнему
пределу – единице, то
близко к своему верхнему
пределу – единице, то ![]() может стать очень большой. Например,
если
может стать очень большой. Например,
если ![]() (т.
е. только 0,1 возможного изменения, вызванного единичным скачком на входе,
проявилось в первом временном интервале), то
(т.
е. только 0,1 возможного изменения, вызванного единичным скачком на входе,
проявилось в первом временном интервале), то ![]() . Действительно, когда
. Действительно, когда ![]() приближается к
единице, регулирующее действие
приближается к
единице, регулирующее действие
![]()
принимает
все более «знакопеременный» характер; корректировка в момент ![]() устраняет существенную часть
корректировки, проделанной в момент
устраняет существенную часть
корректировки, проделанной в момент ![]() . Значение
. Значение ![]() соответствует постоянной времени
системы, превышающей девять интервалов отсчета (см., например, табл. 10.4).
Появление такого значения говорит о том, что интервал отсчета мал, а инерция
процесса велика, так что менее частые наблюдения не приведут к потерям.
соответствует постоянной времени
системы, превышающей девять интервалов отсчета (см., например, табл. 10.4).
Появление такого значения говорит о том, что интервал отсчета мал, а инерция
процесса велика, так что менее частые наблюдения не приведут к потерям.
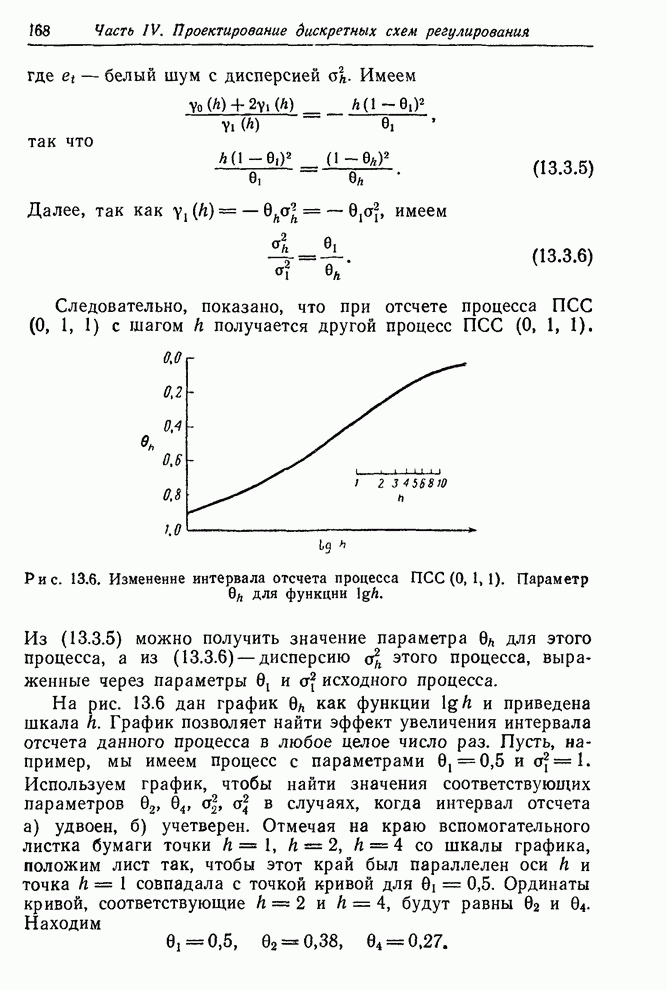
В
разд. 13.3 будет показано, что выбор интервала отсчета должен зависеть от
природы шума, существующего в системе. Поскольку свойства шума обычно хорошо
отражают инерцию системы, во многих случаях интервал отсчета следовало бы
увеличить. Тем не менее встречались практические ситуации [105], когда
использовался разумный интервал отсчета, и все же большие значения ![]() не позволили
пользоваться схемой, минимизирующей выходную дисперсию.
не позволили
пользоваться схемой, минимизирующей выходную дисперсию.

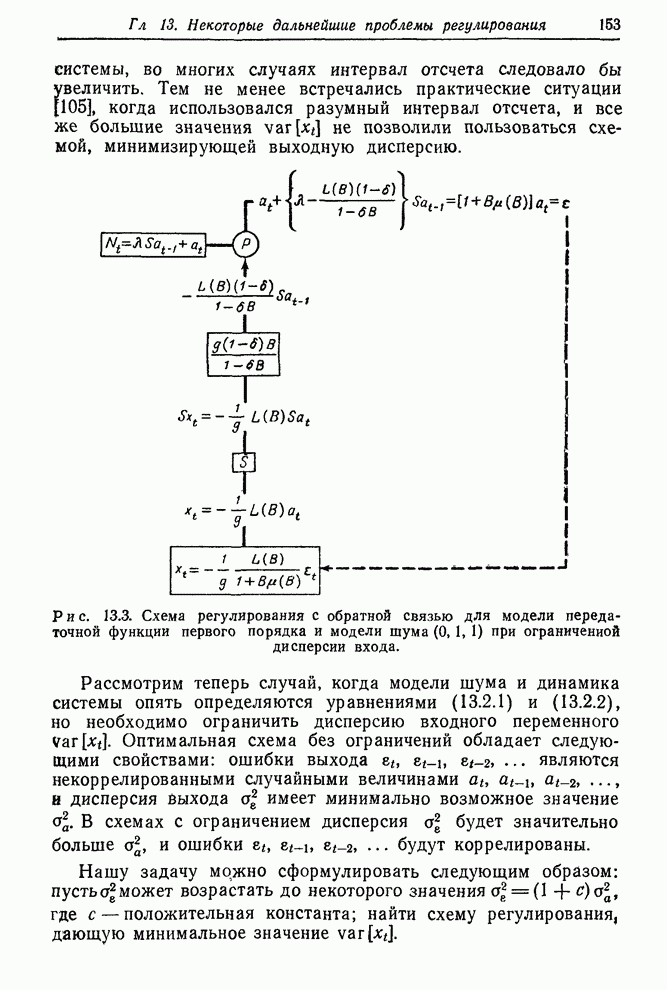
Рис. 13.3. Схема регулирования с
обратной связью для модели передаточной функции первого порядка и модели шума ![]() при ограниченной дисперсии
входа.
при ограниченной дисперсии
входа.
Рассмотрим
теперь случай, когда модели шума и динамика системы опять определяются
уравнениями (13.2.1) и (13.2.2), но необходимо ограничить дисперсию входного
переменного ![]() .
Оптимальная схема без ограничений обладает следующими свойствами: ошибки выхода
.
Оптимальная схема без ограничений обладает следующими свойствами: ошибки выхода
![]() являются
некоррелированными случайными величинами
являются
некоррелированными случайными величинами ![]() , и дисперсия выхода
, и дисперсия выхода ![]() имеет минимально возможное
значение
имеет минимально возможное
значение ![]() .
В схемах с ограничением дисперсия
.
В схемах с ограничением дисперсия ![]() будет значительно больше
будет значительно больше ![]() , и ошибки
, и ошибки ![]() будут коррелированы.
будут коррелированы.
Нашу
задачу можно сформулировать следующим образом: пусть ![]() может возрастать до
некоторого значения
может возрастать до
некоторого значения ![]() , где
, где ![]() – положительная константа; найти схему
регулирования, дающую минимальное значение
– положительная константа; найти схему
регулирования, дающую минимальное значение ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Часть III. ПОСТРОЕНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- Глава 10. Модели передаточной функции
- 10.1. ЛИНЕЙНЫЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 10.1.1. Дискретная передаточная функция
- 10.1.2. Непрерывные динамические модели, описываемые дифференциальными уравнениями
- 10.2. ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ МОДЕЛИ, ОПИСЫВАЕМЫЕ РАЗНОСТНЫМИ УРАВНЕНИЯМИ
- 10.2.1. Общая форма разностного уравнения
- 10.2.2. Природа передаточной функции
- 10.2.3. Дискретные модели передаточных функций первого и второго порядков
- 10.2.4. Рекуррентный расчет выхода для произвольного входа
- 10.3. СООТНОШЕНИЕ МЕЖДУ ДИСКРЕТНОЙ И НЕПРЕРЫВНОЙ МОДЕЛЯМИ
- 10.3.1. Отклик на скачкообразный вход
- 10.3.2. Соотношения совпадающих систем первого и второго порядков
- 10.3.3. Аппроксимация общих непрерывных моделей дискретными моделями
- 10.3.4. Модели передаточных функций с добавленным шумом
- ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
- ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
- Глава 11. Идентификация, подгонка и проверка моделей передаточных функций
- 11.1. Взаимная корреляционная функция
- 11.1.1. Свойства взаимных ковариационной и корреляционной функций
- 11.1.2. Оценивание взаимных ковариационных и корреляционных функций
- 11.1.3. Приближенные стандартные ошибки выборочных оценок взаимных корреляций
- 11.2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.2.1. Идентификация моделей передаточной функции с предварительным выравниванием спектра входа
- 11.2.2. Пример идентификации модели передаточной функции
- 11.2.3. Идентификация модели шума
- 11.2.4. Некоторые общие соображения об идентификации моделей передаточных функций
- 11.3. ПОДГОНКА И ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.3.1. Условная сумма квадратов
- 11.3.2. Нелинейное оценивание
- 11.3.3. Использование остаточных ошибок для диагностической проверки
- 11.3.4. Конкретные способы проверки остаточных ошибок
- 11.4. Некоторые примеры подгонок и проверок моделей передаточных функций
- 11.4.1. Подгонка и проверка модели газовой печи
- 11.4.2. Искусственный пример с двумя входами
- 11.5. ПРОГНОЗИРОВАНИЕ ПРИ ПОМОЩИ УПРЕЖДАЮЩИХ ИНДИКАТОРОВ
- 11.5.1. Прогноз с минимальной среднеквадратичной ошибкой
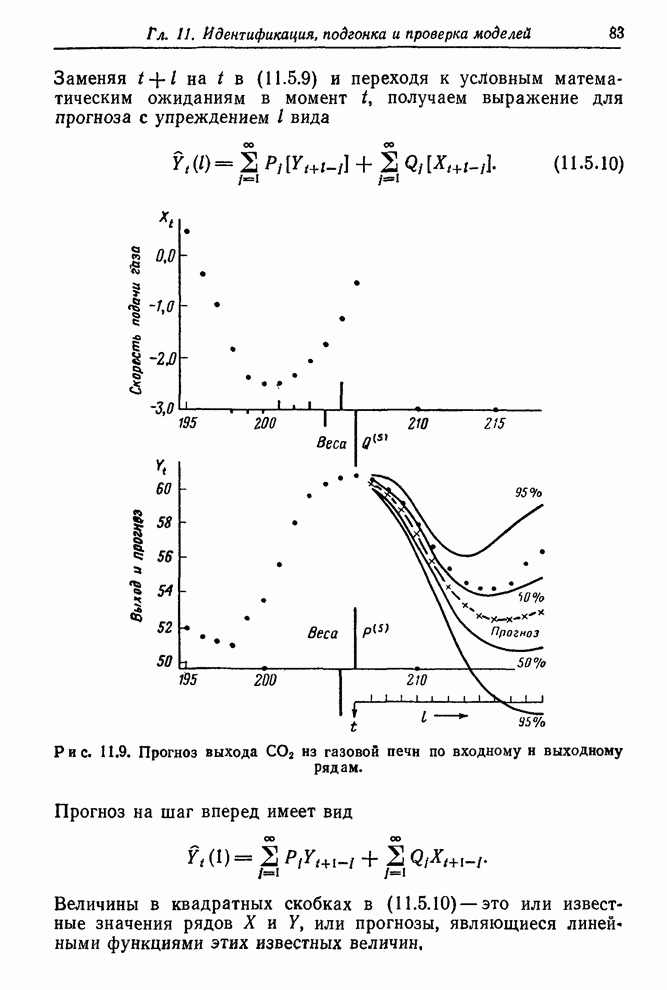
- 11.5.2. Прогнозы выхода СO2 из газовой печи
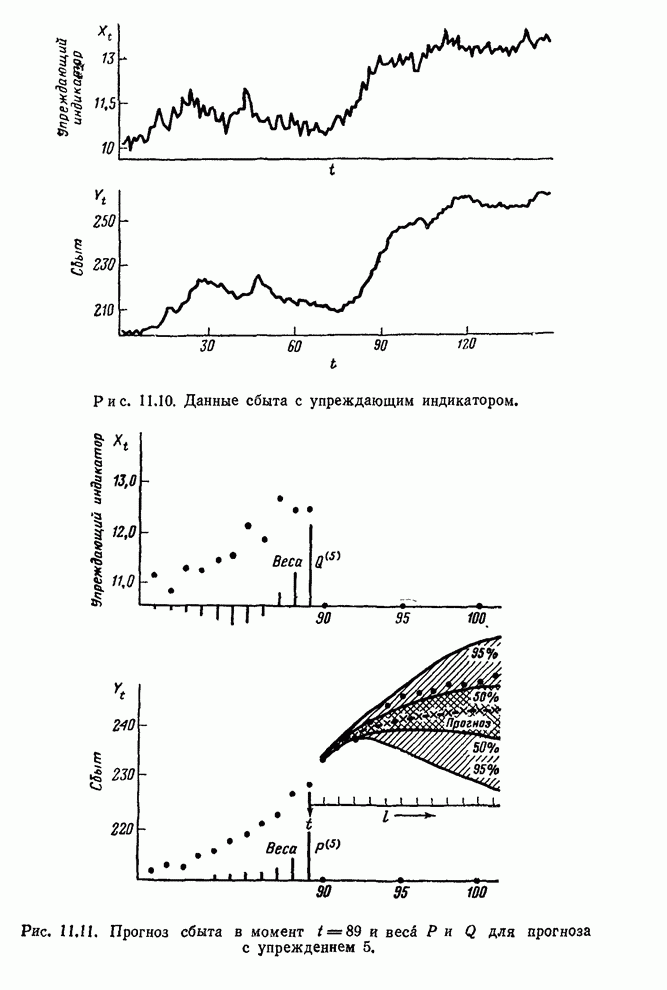
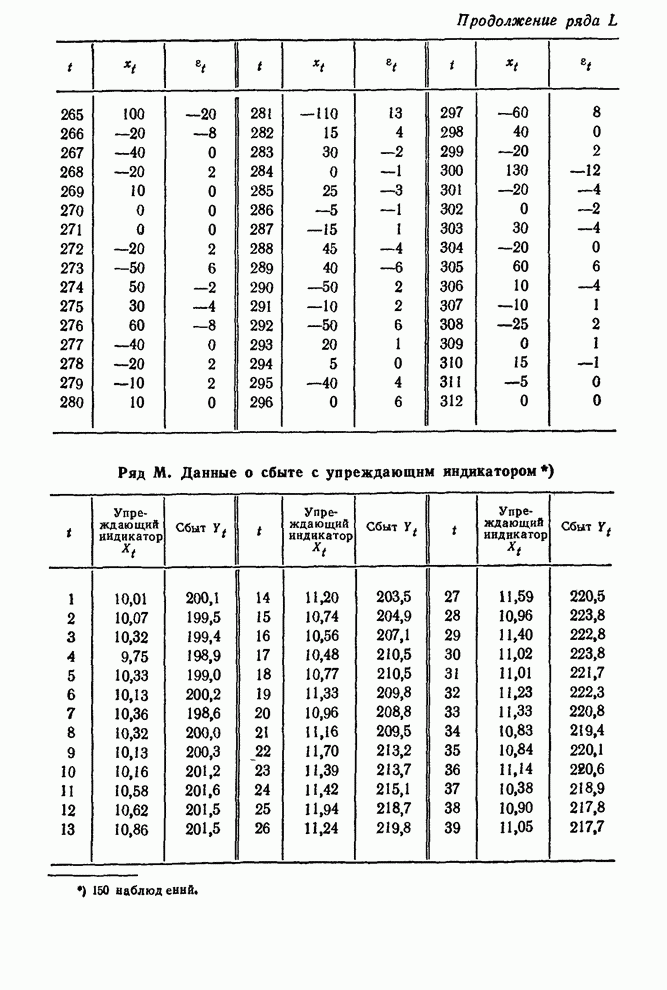
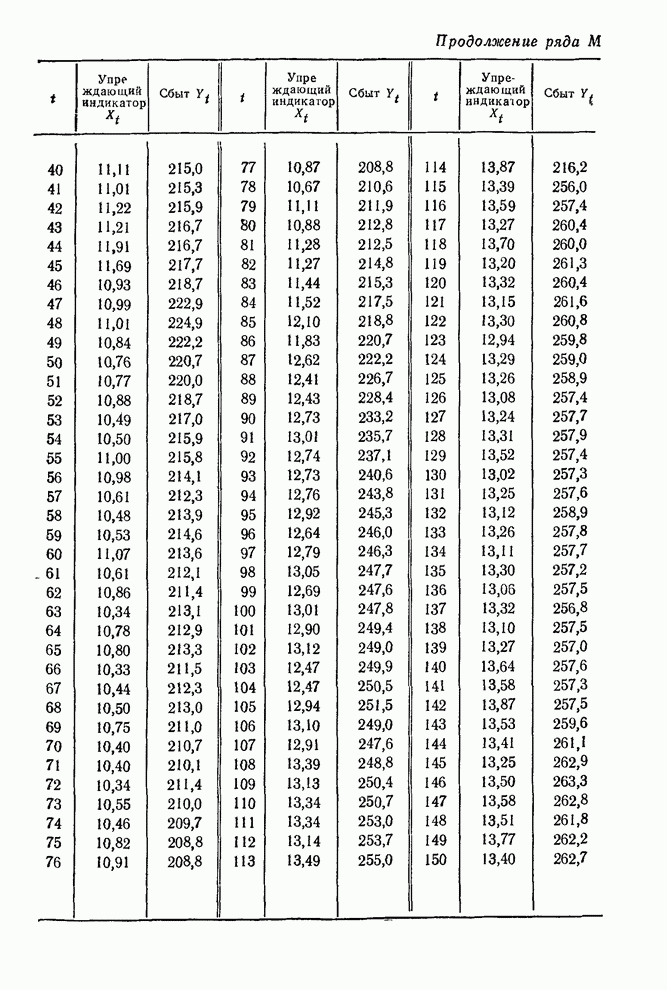
- 11.5.3. Прогноз нестационарных данных сбыта при помощи упреждающего индикатора
- 11.6. НЕКОТОРЫЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОЦЕНИВАНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ П11.1. ИСПОЛЬЗОВАНИЕ ВЗАИМНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
- Заключение
- Часть IV. Проектирование дискретных схем регулирования
- Глава 12. Проектирование схем регулирования с прямой и обратной связями
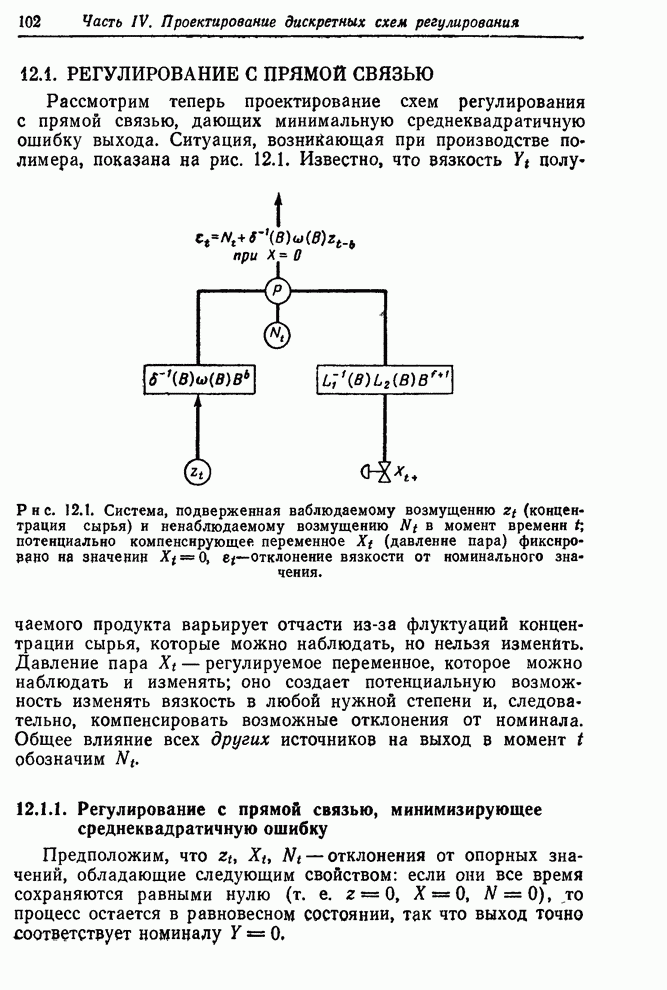
- 12.1. РЕГУЛИРОВАНИЕ С ПРЯМОЙ СВЯЗЬЮ
- 12.1.1. Регулирование с прямой связью, минимизирующее среднеквадратичную ошибку
- 12.1.2. Пример — регулирование удельного веса промежуточного продукта
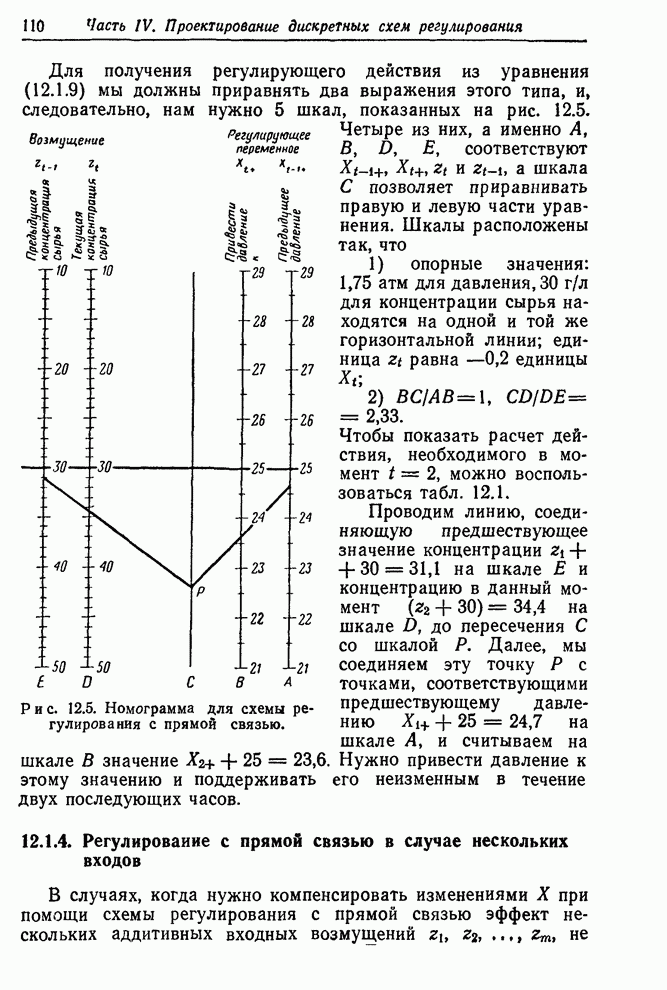
- 12.1.3. Номограмма для регулирования с прямой связью
- 12.1.4. Регулирование с прямой связью в случае нескольких входов
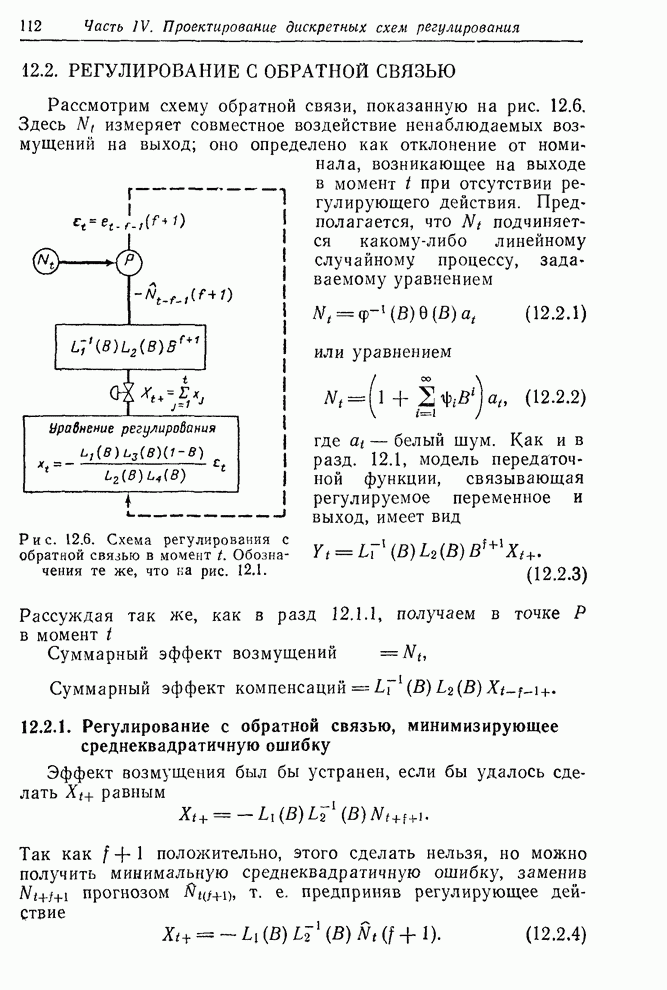
- 12.2. РЕГУЛИРОВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ
- 12.2.1. Регулирование с обратной связью, минимизирующее среднеквадратичную ошибку
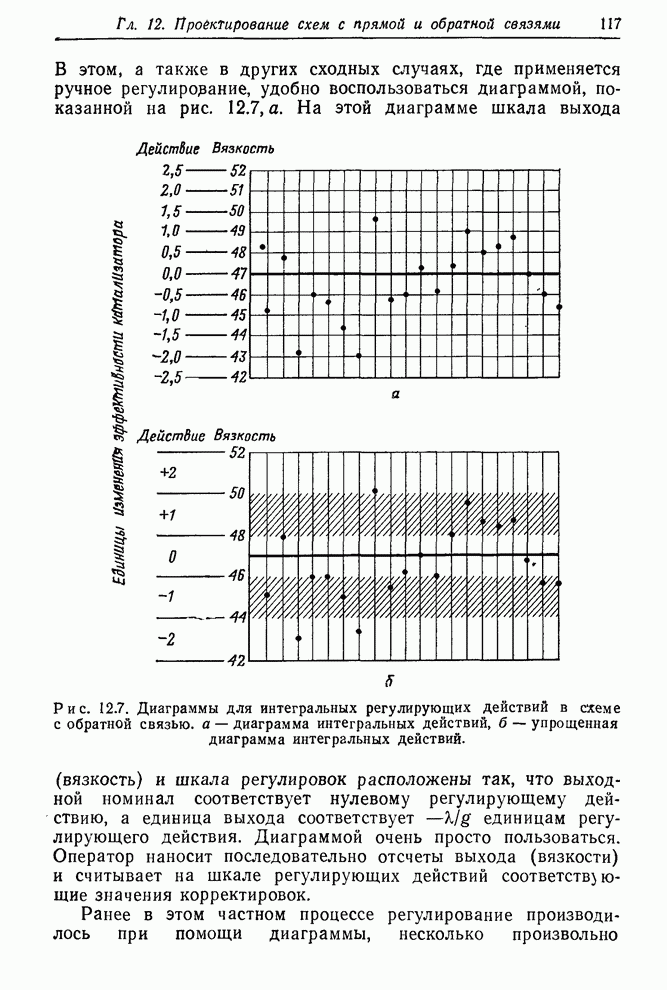
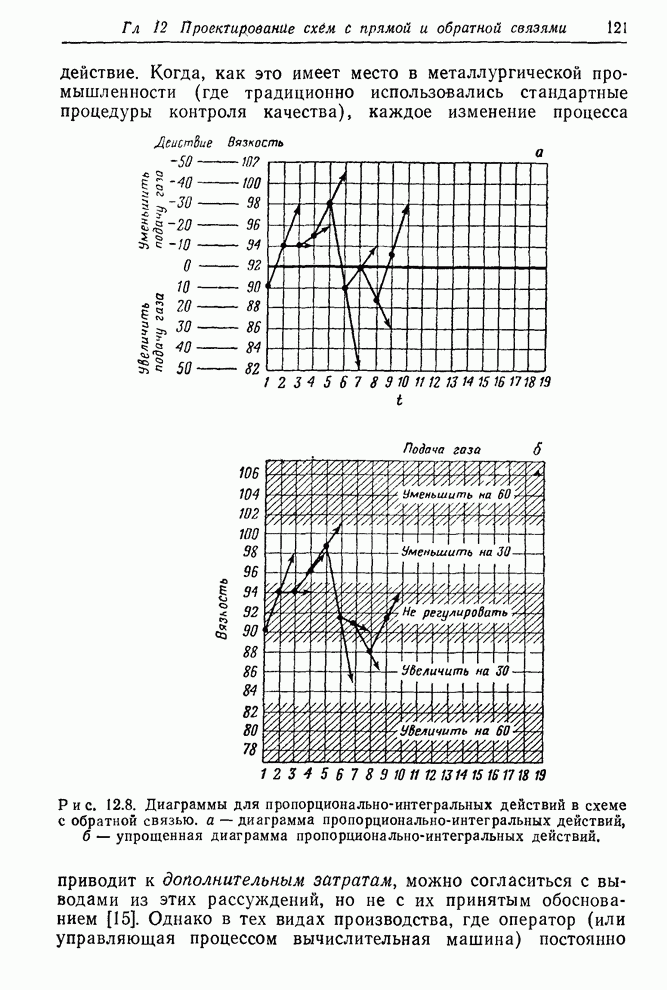
- 12.2.2. Применение уравнения регулирования: ПИД-регулятор
- 12.2.3. Примеры дискретного регулирования с обратной связью
- 12.3. РЕГУЛИРОВАНИЕ С ПРЯМОЙ И ОБРАТНОЙ СВЯЗЯМИ
- 12.3.1. Регулирование с прямой и обратной связями, минимизирующее выходную среднеквадратичную ошибку
- 12.3.2. Пример регулирования с прямой и обратной связями
- 12.3.3. Преимущества и недостатки регулирования с прямой и обратной связями
- 12.4. Подгонка моделей передаточных функций шума по оперативным данным
- 12.4.1. Итеративный способ построения моделей
- 12.4.2. Оценивание по оперативным данным
- 12.4.3. Пример
- Глава 13. Некоторые дальнейшие проблемы регулирования
- 13.1. ЭФФЕКТ ДОБАВОЧНОГО ШУМА В СХЕМАХ РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ
- 13.1.1. Эффект пренебрежения добавочным шумом; упрощенные схемы
- 13.1.2. Оптимальное действие в случаях, когда корректировки содержат ошибки наблюдения
- 13.1.3. Перенос источника шума
- 13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
- 13.2.1. Вывод выражения для оптимальной корректировки
- 13.2.2. Схема с ограничением для примера «вязкость–подача газа»
- 13.3. ВЫБОР ИНТЕРВАЛА ОТСЧЕТА
- 13.3.1. Пример эффекта уменьшения частоты отсчетов
- 13.3.2. Влияние интервала отсчета на процесс ПСС(0,1,1)
- ПРОГРАММА 5. ИДЕНТИФИКАЦИЯ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 6. ПРЕДВАРИТЕЛЬНОЕ ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 7. ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
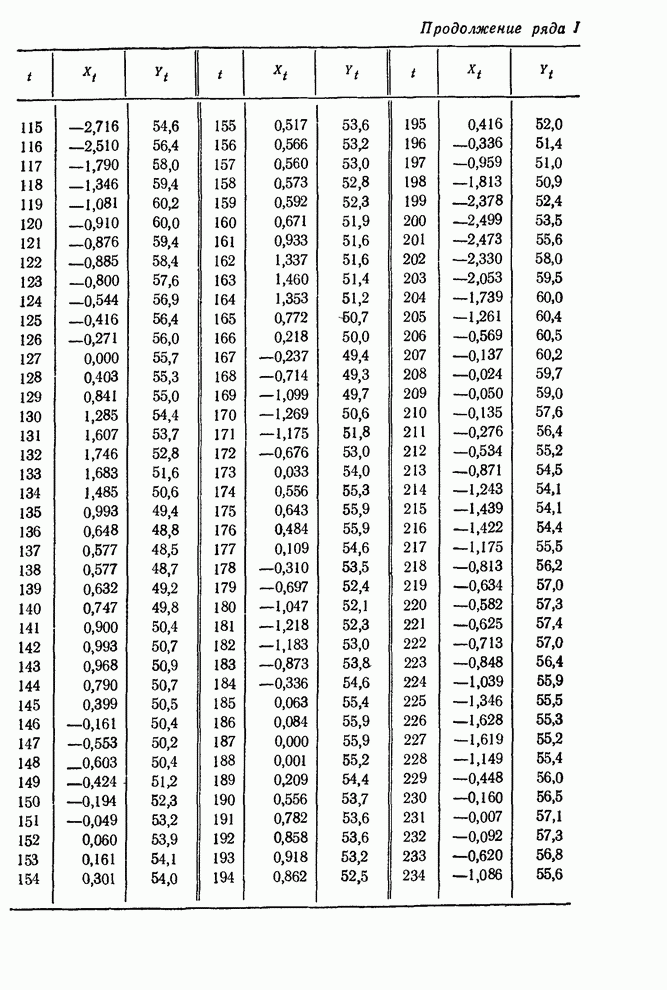
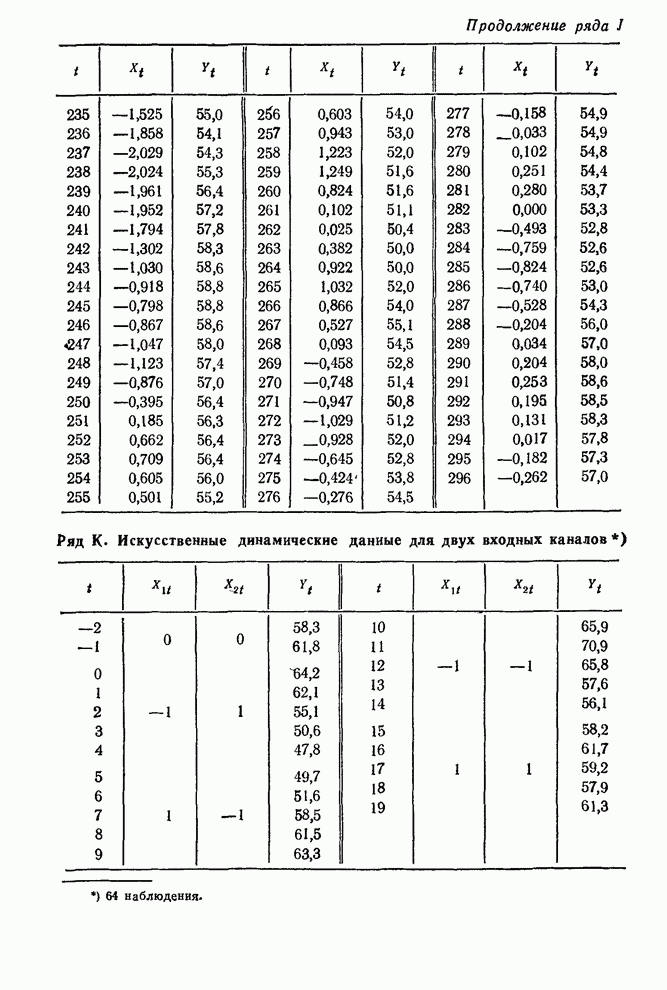
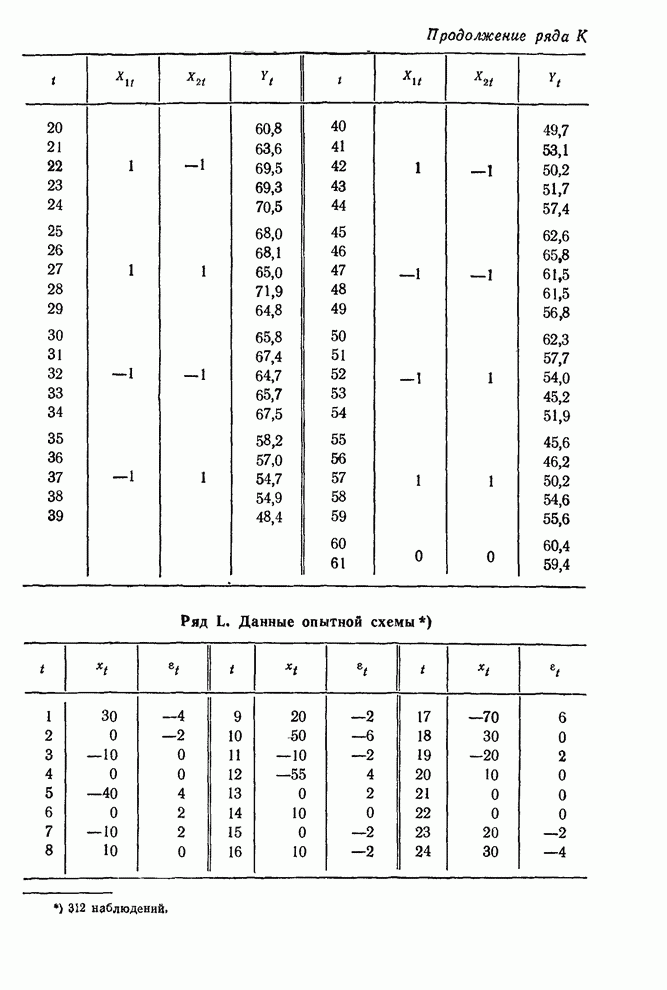
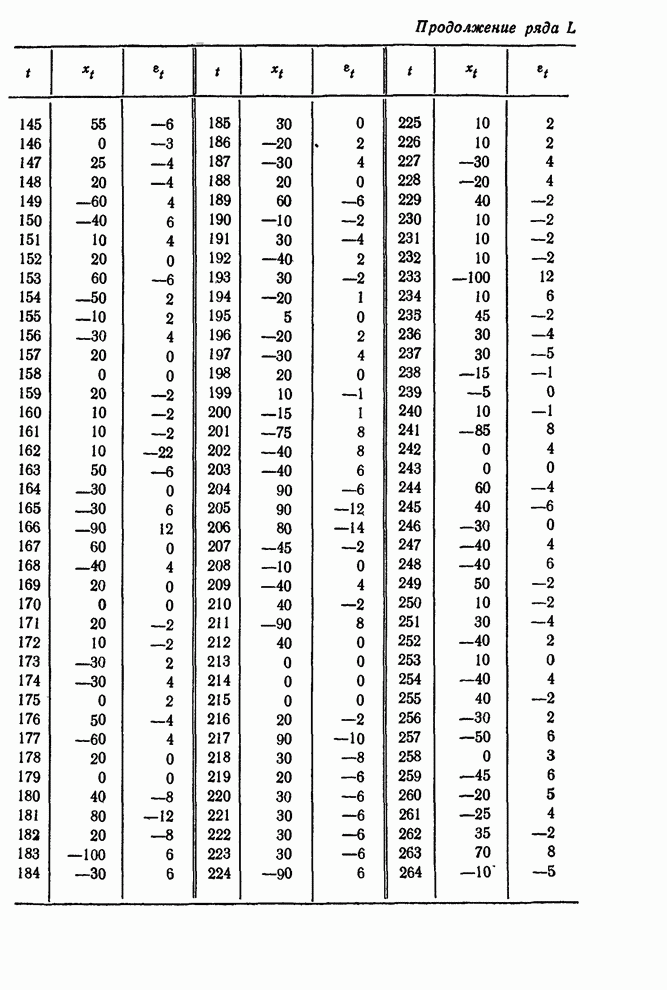
- ТАБЛИЦЫ ВРЕМЕННЫХ РЯДОВ