| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
12.2.2. Применение уравнения регулирования: ПИД-регулятор
В этой книге мы интересуемся в основном выводом уравнения для оптимального регулирования, указывающего, как нужно изменять регулирующее переменное, чтобы поддерживать регулируемое переменное близким к некоторому номиналу. На практике фактические измерения, расчет и выполнение требуемых регулирующих действий могут осуществляться различными способами. В наиболее сложной форме это может выполняться при помощи электроизмерительной аппаратуры, данные с которой поступают в вычислительную машину, рассчитывающую необходимое регулирующее действие и непосредственно управляющую датчиками, выполняющими это действие. В простейшей форме регулирование может осуществляться оператором, который периодически делает замеры, определяет по простой диаграмме или номограмме требуемое регулирующее действие и сам вручную его выполняет. Описанная выше теория успешно применялась в обеих ситуациях. Мы приводим здесь, казалось бы, с излишней детальностью некоторые приложения к ручному регулированию, так как считаем, что в прошлом нередко пренебрегали элементарными идеями регулирования, помогающими оператору успешно выполнять свою работу. Хотя, бесспорно, использование схем автоматического регулирования становится все более обыденным делом, все еще очень много процессов регулируется вручную, и такое положение сохранится еще надолго.
ПИД-регулятор.
Уже много лет известен тип автоматического регулирующего устройства, получивший
название ПИД-регулятор (пропорциональный, интегральный и дифференциальный
регулятор). Такие регуляторы реализуются на механической, пневматической,
гидравлической или электрической основе; измерения и коррекция осуществляются с
их помощью чаще в непрерывном, а не в дискретном режиме. Если ![]() – ошибка на выходе в
момент
– ошибка на выходе в
момент ![]() регулирующее
действие может быть сделано пропорциональным самому
регулирующее
действие может быть сделано пропорциональным самому ![]() , его интегралу или
производной по времени. ПИД-регулятор использует линейную комбинацию этих
элементарных действий, так что если
, его интегралу или
производной по времени. ПИД-регулятор использует линейную комбинацию этих
элементарных действий, так что если ![]() – уровень регулирующего переменного,
уравнение регулирования имеет вид
– уровень регулирующего переменного,
уравнение регулирования имеет вид
![]() ,
,
где
![]() ,
, ![]() и
и ![]() – константы.
– константы.
В
некоторых случаях в правой части используются только один или два члена. Так,
известны примеры простого пропорционального ![]() , простого интегрального
, простого интегрального ![]() ,
пропорционально-интегрального
,
пропорционально-интегрального ![]() и пропорционально-дифференциального
и пропорционально-дифференциального ![]() регулирования.
регулирования.
Дискретным аналогом этого непрерывного уравнения регулирования является уравнение
![]()
или, если выразить все через необходимые корректировки,
![]() .
.
Мы
покажем, что многие простые ситуации, которые будут рассмотрены, приводят к
уравнениям регулирования, содержащим члены такого типа. Например, если шум
можно представить как процесс порядка ![]()
![]() , а динамика описывается системой
первого порядка
, а динамика описывается системой
первого порядка ![]() уравнение
(12.2.7) сводится к
уравнение
(12.2.7) сводится к
![]() .
.
Таким образом, нужное действие – дискретный аналог пропорционально-интегрального регулирования.
Однако ясно, что не все регулирующие действия, описываемые (12.2.7), могут быть осуществлены ПИД-регулятором; можно привести сравнительно элементарные случаи, в которых необходим другой способ регулирования. Рассмотрим теперь ряд конкретных примеров.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Часть III. ПОСТРОЕНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- Глава 10. Модели передаточной функции
- 10.1. ЛИНЕЙНЫЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 10.1.1. Дискретная передаточная функция
- 10.1.2. Непрерывные динамические модели, описываемые дифференциальными уравнениями
- 10.2. ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ МОДЕЛИ, ОПИСЫВАЕМЫЕ РАЗНОСТНЫМИ УРАВНЕНИЯМИ
- 10.2.1. Общая форма разностного уравнения
- 10.2.2. Природа передаточной функции
- 10.2.3. Дискретные модели передаточных функций первого и второго порядков
- 10.2.4. Рекуррентный расчет выхода для произвольного входа
- 10.3. СООТНОШЕНИЕ МЕЖДУ ДИСКРЕТНОЙ И НЕПРЕРЫВНОЙ МОДЕЛЯМИ
- 10.3.1. Отклик на скачкообразный вход
- 10.3.2. Соотношения совпадающих систем первого и второго порядков
- 10.3.3. Аппроксимация общих непрерывных моделей дискретными моделями
- 10.3.4. Модели передаточных функций с добавленным шумом
- ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
- ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
- Глава 11. Идентификация, подгонка и проверка моделей передаточных функций
- 11.1. Взаимная корреляционная функция
- 11.1.1. Свойства взаимных ковариационной и корреляционной функций
- 11.1.2. Оценивание взаимных ковариационных и корреляционных функций
- 11.1.3. Приближенные стандартные ошибки выборочных оценок взаимных корреляций
- 11.2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.2.1. Идентификация моделей передаточной функции с предварительным выравниванием спектра входа
- 11.2.2. Пример идентификации модели передаточной функции
- 11.2.3. Идентификация модели шума
- 11.2.4. Некоторые общие соображения об идентификации моделей передаточных функций
- 11.3. ПОДГОНКА И ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.3.1. Условная сумма квадратов
- 11.3.2. Нелинейное оценивание
- 11.3.3. Использование остаточных ошибок для диагностической проверки
- 11.3.4. Конкретные способы проверки остаточных ошибок
- 11.4. Некоторые примеры подгонок и проверок моделей передаточных функций
- 11.4.1. Подгонка и проверка модели газовой печи
- 11.4.2. Искусственный пример с двумя входами
- 11.5. ПРОГНОЗИРОВАНИЕ ПРИ ПОМОЩИ УПРЕЖДАЮЩИХ ИНДИКАТОРОВ
- 11.5.1. Прогноз с минимальной среднеквадратичной ошибкой
- 11.5.2. Прогнозы выхода СO2 из газовой печи
- 11.5.3. Прогноз нестационарных данных сбыта при помощи упреждающего индикатора
- 11.6. НЕКОТОРЫЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОЦЕНИВАНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ П11.1. ИСПОЛЬЗОВАНИЕ ВЗАИМНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
- Заключение
- Часть IV. Проектирование дискретных схем регулирования
- Глава 12. Проектирование схем регулирования с прямой и обратной связями
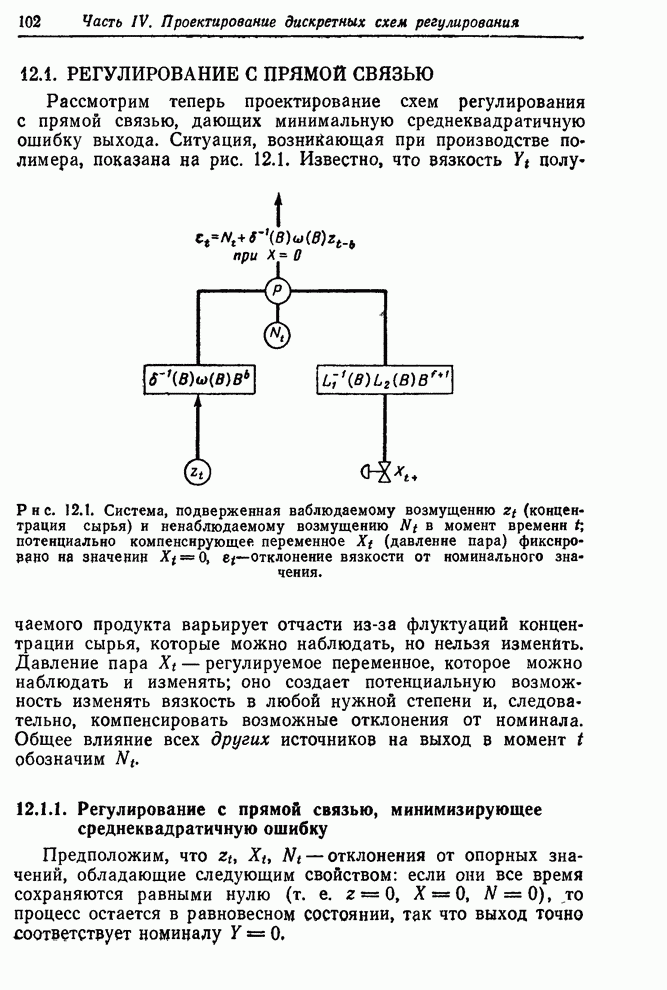
- 12.1. РЕГУЛИРОВАНИЕ С ПРЯМОЙ СВЯЗЬЮ
- 12.1.1. Регулирование с прямой связью, минимизирующее среднеквадратичную ошибку
- 12.1.2. Пример — регулирование удельного веса промежуточного продукта
- 12.1.3. Номограмма для регулирования с прямой связью
- 12.1.4. Регулирование с прямой связью в случае нескольких входов
- 12.2. РЕГУЛИРОВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ
- 12.2.1. Регулирование с обратной связью, минимизирующее среднеквадратичную ошибку
- 12.2.2. Применение уравнения регулирования: ПИД-регулятор
- 12.2.3. Примеры дискретного регулирования с обратной связью
- 12.3. РЕГУЛИРОВАНИЕ С ПРЯМОЙ И ОБРАТНОЙ СВЯЗЯМИ
- 12.3.1. Регулирование с прямой и обратной связями, минимизирующее выходную среднеквадратичную ошибку
- 12.3.2. Пример регулирования с прямой и обратной связями
- 12.3.3. Преимущества и недостатки регулирования с прямой и обратной связями
- 12.4. Подгонка моделей передаточных функций шума по оперативным данным
- 12.4.1. Итеративный способ построения моделей
- 12.4.2. Оценивание по оперативным данным
- 12.4.3. Пример
- Глава 13. Некоторые дальнейшие проблемы регулирования
- 13.1. ЭФФЕКТ ДОБАВОЧНОГО ШУМА В СХЕМАХ РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ
- 13.1.1. Эффект пренебрежения добавочным шумом; упрощенные схемы
- 13.1.2. Оптимальное действие в случаях, когда корректировки содержат ошибки наблюдения
- 13.1.3. Перенос источника шума
- 13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
- 13.2.1. Вывод выражения для оптимальной корректировки
- 13.2.2. Схема с ограничением для примера «вязкость–подача газа»
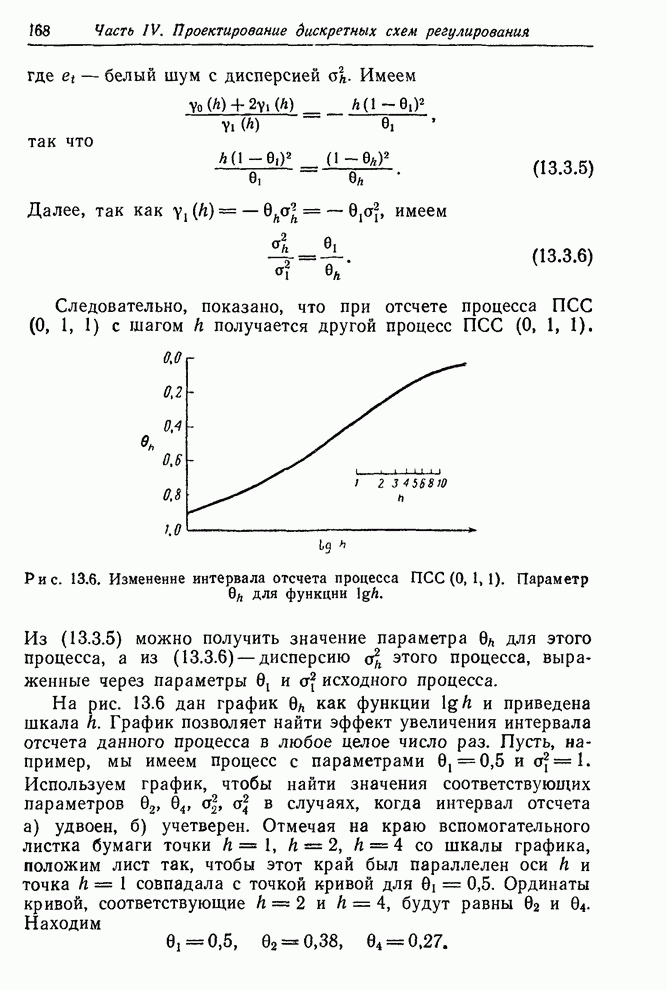
- 13.3. ВЫБОР ИНТЕРВАЛА ОТСЧЕТА
- 13.3.1. Пример эффекта уменьшения частоты отсчетов
- 13.3.2. Влияние интервала отсчета на процесс ПСС(0,1,1)
- ПРОГРАММА 5. ИДЕНТИФИКАЦИЯ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 6. ПРЕДВАРИТЕЛЬНОЕ ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 7. ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
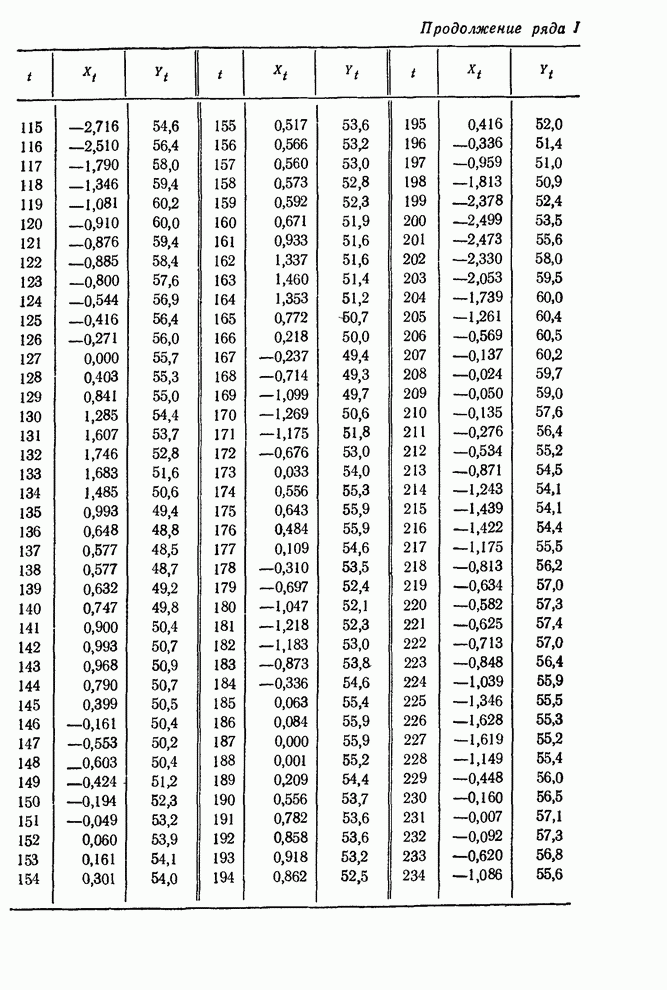
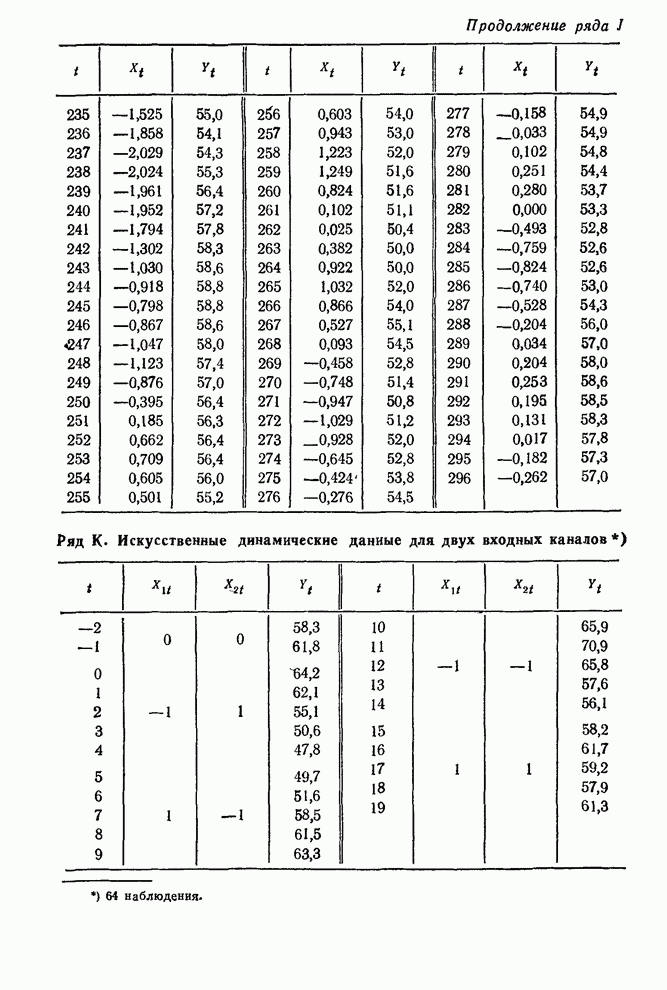
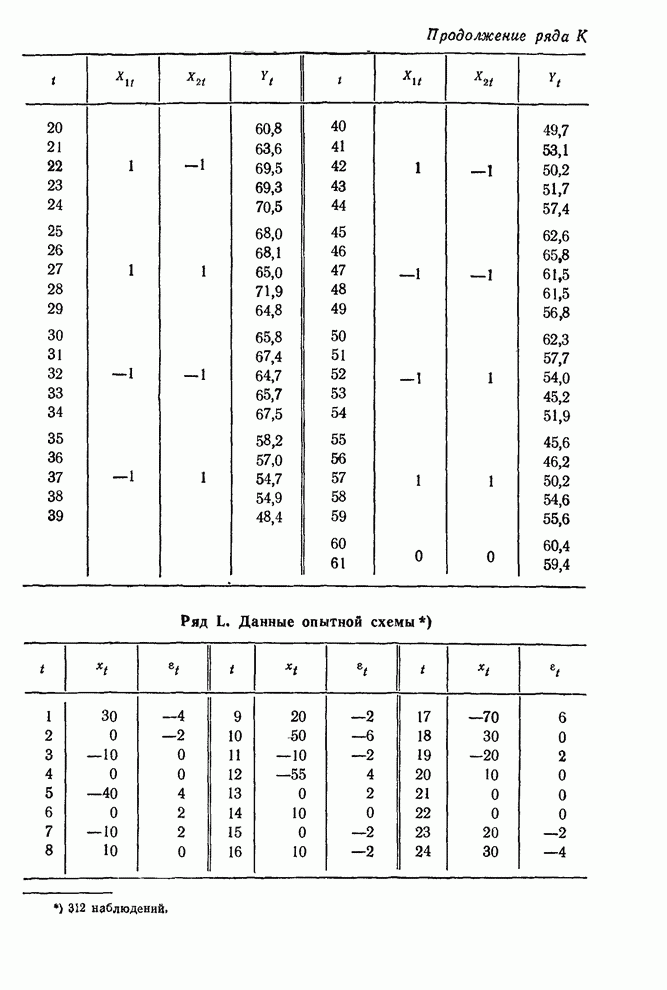
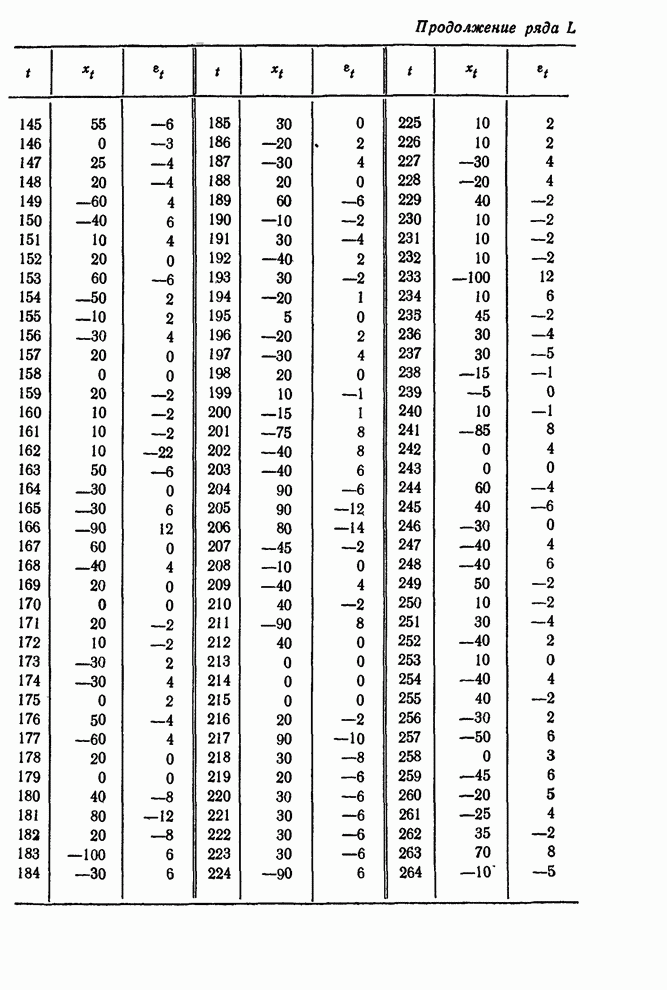
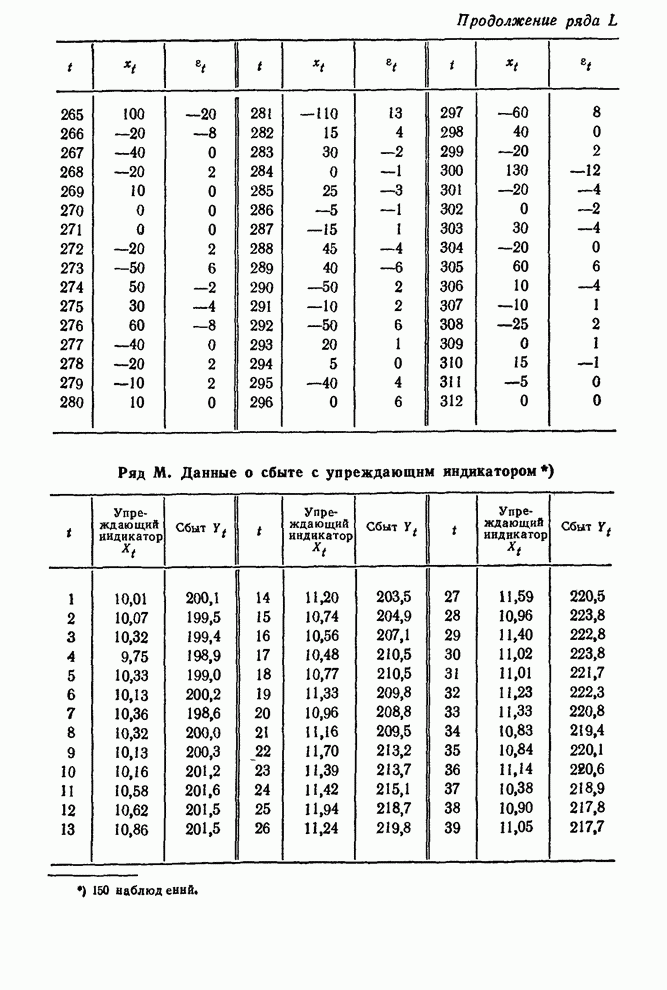
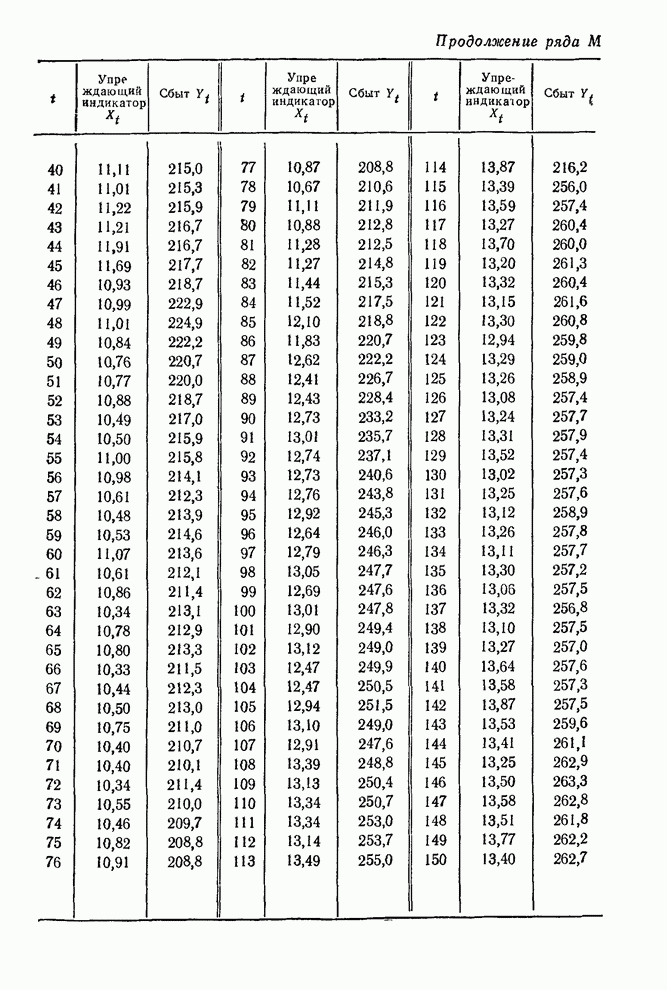
- ТАБЛИЦЫ ВРЕМЕННЫХ РЯДОВ