| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
11.4. НЕКОТОРЫЕ ПРИМЕРЫ ПОДГОНОК И ПРОВЕРОК МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
11.4.1. Подгонка и проверка модели газовой печи
Проиллюстрируем теперь подход, описанный в разд. 11.3, на подгонке модели
 ,
,
идентифицированной для данных газовой печи в разд. 11.2.2 и 11.2.3.
Нелинейное оценивание. Использовались начальные
оценки ![]() ,
полученные в разд. 11.2.2 и 11.2.3. При помощи алгоритма условных наименьших
квадратов, описанного в разд. 11.3.2, значения наименьших квадратов с точностью
в два десятичных знака были получены за четыре итерации. Чтобы показать
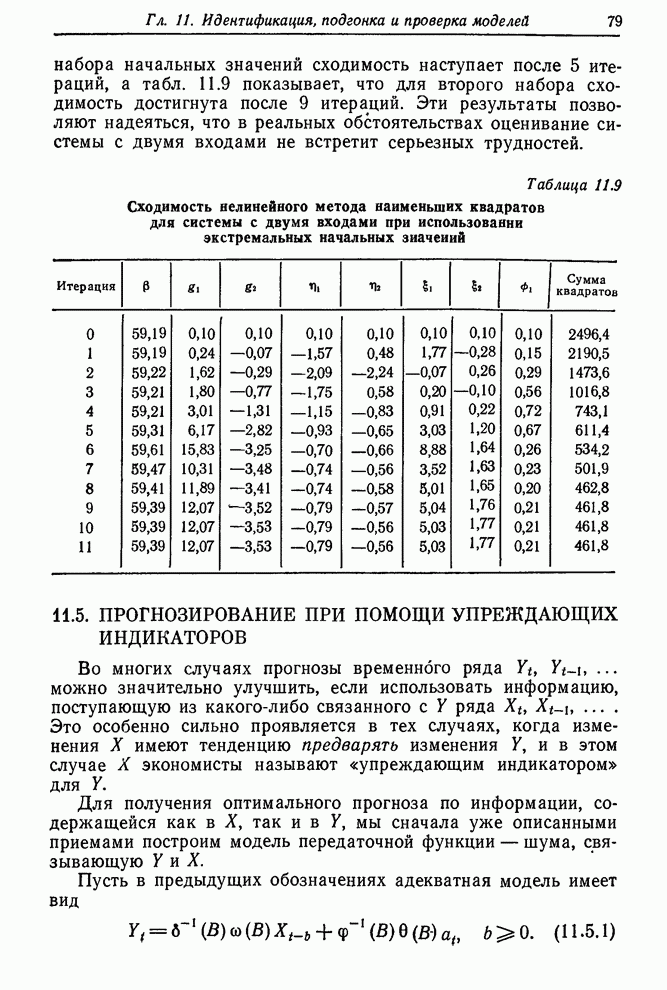
сходимость итерационного процесса в неблагоприятных обстоятельствах, в табл.
11.4 приведены последовательности итераций с начальными значениями, равными
+0,1 или -0,1. Тот факт, что даже в этих условиях сходимость для модели с
таким большим числом параметров, как 7, была достигнута за 10 итераций, весьма
ободряет.
,
полученные в разд. 11.2.2 и 11.2.3. При помощи алгоритма условных наименьших
квадратов, описанного в разд. 11.3.2, значения наименьших квадратов с точностью
в два десятичных знака были получены за четыре итерации. Чтобы показать
сходимость итерационного процесса в неблагоприятных обстоятельствах, в табл.
11.4 приведены последовательности итераций с начальными значениями, равными
+0,1 или -0,1. Тот факт, что даже в этих условиях сходимость для модели с
таким большим числом параметров, как 7, была достигнута за 10 итераций, весьма
ободряет.
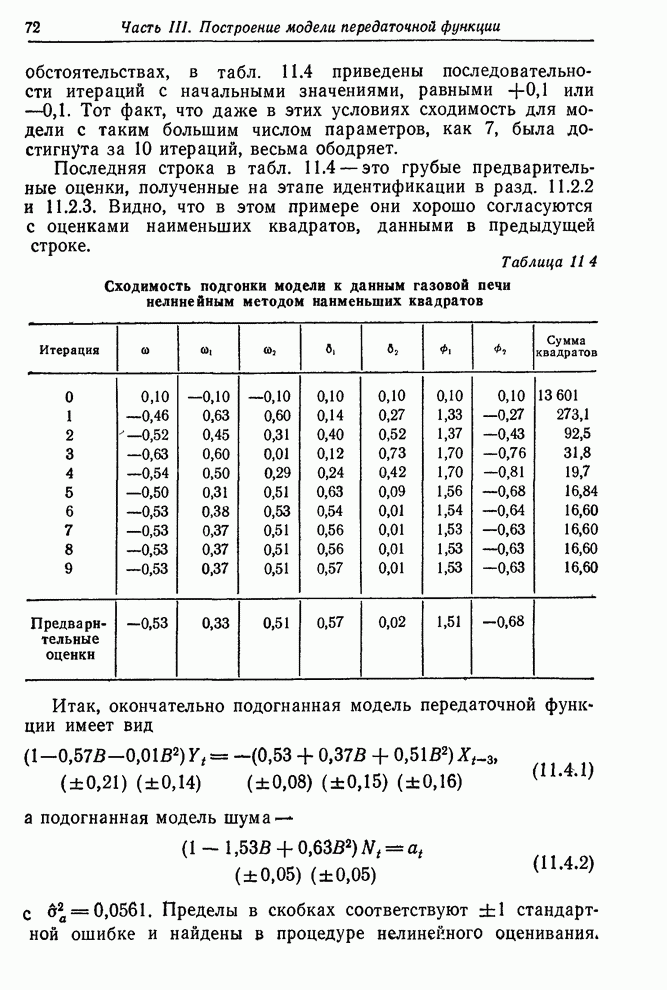
Последняя строка в табл. 11.4 — это грубые предварительные оценки, полученные на этапе идентификации в разд. 11.2.2 и 11.2.3. Видно, что в этом примере они хорошо согласуются с оценками наименьших квадратов, данными в предыдущей строке.
Таблица 11.4. Сходимость подгонки модели к данным газовой печи нелинейным методом наименьших квадратов
|
Интерация |
|
|
|
|
|
|
|
Сумма квадратов |
|
0 1 2 3 4 5 6 7 8 9 |
0,10 -0,46 -0,52 -0,63 -0,54 -0,50 -0,53 -0,53 -0,53 -0,53 |
-0,10 0,63 0,45 0,60 0,50 0,31 0,38 0,37 0,37 0,37 |
-0,10 0,60 0,31 0,01 0,29 0,51 0,53 0,51 0,51 0,51 |
0,10 0,14 0,40 0,12 0,24 0,63 0,54 0,56 0,56 0,57 |
0,10 0,27 0,52 0,73 0,42 0,09 0,01 0,01 0,01 0,01 |
0,10 1,33 1,37 1,70 1,70 1,56 1,54 1,53 1,53 1,53 |
0,10 -0,27 -0,43 -0,76 -0,81 -0,68 -0,64 -0,63 -0,63 -0,63 |
13 601 273,1 92,5 31,8 19,7 16,84 16,60 16,60 16,60 16,60 |
|
Предварительные оценки |
-0,53 |
0,33 |
0,51 |
0,57 |
0,02 |
1,51 |
-0,68 |
|
Итак, окончательно подогнанная модель передаточной функции имеет вид
![]() , (11.4.1)
, (11.4.1)
![]()
![]() ,
,
а подогнанная модель шума —
![]() , (11.4.2)
, (11.4.2)
![]()
с ![]() . Пределы в скобках
соответствуют ±1 стандартной ошибке и найдены в процедуре нелинейного
оценивания.
. Пределы в скобках
соответствуют ±1 стандартной ошибке и найдены в процедуре нелинейного
оценивания.
Диагностическая проверка. Прежде чем принять эту
модель как адекватное представление системы, следует проделать проверки
автокорреляций и взаимных корреляций способами, описанными в разд. 11.34
Выборочные автокорреляции для первых 36 задержек приведены в табл. 11.5 вместе
с верхней гранью их стандартных ошибок ![]() в предположении об адекватности модели.
Поведение отдельных выборочных автокорреляций не дает указаний на
неадекватность модели. Это подтверждается вычислением критерия
в предположении об адекватности модели.
Поведение отдельных выборочных автокорреляций не дает указаний на
неадекватность модели. Это подтверждается вычислением критерия ![]() (11.3.18):
(11.3.18):
 .
.
Таблица 11.5. Выборочная автокорреляционная функция ![]() остаточных ошибок
для подогнанной модели газовой печи
остаточных ошибок
для подогнанной модели газовой печи
|
Задержка
|
|
Крайние Границы Стандартной ошибки |
|||||||||||
|
1-12 13-24 25-36 |
0,02 -0,04 0,04 |
0,06 0,05 -0,02 |
-0,07 -0,09 0,02 |
-0,05 -0,01 0,09 |
-0,05 -0,08 -0,12 |
0,12 0,00 0,06 |
0,03 -0,12 -0,03 |
0,03 0,00 -0,06 |
-0,08 -0,01 -0,11 |
0,05 0,08 0,02 |
0,02 0,02 0,03 |
0,10 -0,10 0,06 |
±0,08 ±0,06 ±0,08 |
Сравнение
![]() с таблицей
с таблицей
![]() для
для ![]() степеней свободы не
дает основания оспаривать адекватность модели.
степеней свободы не
дает основания оспаривать адекватность модели.
В
табл. 11.6а приведены значения выборочной взаимной корреляционной функции ![]() для первых 36
задержек, а также верхняя граница
для первых 36
задержек, а также верхняя граница ![]() их стандартных ошибок. Видно, что
хотя выборочные взаимные корреляции не слишком велики по сравнению с их
стандартными ошибками, они сильно коррелированы. Этого следовало ожидать, так
как, согласно (11.3.19), выборочные взаимные корреляции подчиняются тому же
стохастическому процессу, что и вход
их стандартных ошибок. Видно, что
хотя выборочные взаимные корреляции не слишком велики по сравнению с их
стандартными ошибками, они сильно коррелированы. Этого следовало ожидать, так
как, согласно (11.3.19), выборочные взаимные корреляции подчиняются тому же
стохастическому процессу, что и вход ![]() , а как мы уже видели, вход в этом
примере сильно автокоррелирован.
, а как мы уже видели, вход в этом
примере сильно автокоррелирован.
Соответствующие
выборочные взаимные корреляции между ![]() и предварительно выравненным входом
и предварительно выравненным входом ![]() приведены в табл.
11.66. Критерий (11.3.20) дает
приведены в табл.
11.66. Критерий (11.3.20) дает
 .
.
Таблица
11.6а. Выборочная
взаимная корреляционная функция ![]() остаточных ошибок входа и выхода для
данных газовой печи
остаточных ошибок входа и выхода для
данных газовой печи
|
Задержка
|
|
Крайние Границы Стандартной ошибки |
|||||||||||
|
0-11 12-23 24-35 |
0,00 -0,03 -0,03 |
0,00 -0,03 -0,04 |
0,00 -0,03 -0,04 |
0,00 -0,07 -0,02 |
0,00 -0,10 -0,01 |
0,00 -0,12 0,02 |
-0,01 -0,12 0,04 |
-0,02 -0,10 0,05 |
-0,03 -0,04 0,06 |
-0,05 -0,01 0,07 |
-0,06 -0,01 0,07 |
-0,05 -0,02 0,06 |
±0,06 ±0,06 ±0,06 |
Таблица
11.6б. Выборочная
взаимная корреляционная функция ![]() остаточных ошибок предварительно
выравнеииого входа и выхода для данных газовой печи
остаточных ошибок предварительно
выравнеииого входа и выхода для данных газовой печи
|
Задержка
|
|
Крайние Границы Стандартной ошибки |
|||||||||||
|
0-11 12-23 24-35 |
-0,06 -0,03 -0,01 |
0,03 -0,11 -0,02 |
-0,01 0,02 0,05 |
0,00 0,04 -0,07 |
0,01 0,04 0,00 |
0,01 0,01 0,04 |
0,01 0,01 0,15 |
-0,04 -0,15 0,04 |
0,02 -0,03 0,03 |
0,07 -0,07 -0,02 |
-0,03 -0,08 0,00 |
-0,02 0,02 0,03 |
±0,06 ±0,06 ±0,06 |
Сравнение
![]() с таблицей
с таблицей
![]() для
для ![]() степеней свободы
также не дает указания на неадекватность модели.
степеней свободы
также не дает указания на неадекватность модели.
Импульсный отклик и отклик на единичный скачок. Выборочная оценка ![]() в (11.4.1) очень
мала по сравнению с ее стандартной ошибкой ±0,14, и параметр модели
в (11.4.1) очень
мала по сравнению с ее стандартной ошибкой ±0,14, и параметр модели ![]() может быть опущен
практически без влияния на точность оценок других рассматриваемых параметров.
Окончательный вид комбинированной модели передаточной функции — шума для данных
газовой печи есть
может быть опущен
практически без влияния на точность оценок других рассматриваемых параметров.
Окончательный вид комбинированной модели передаточной функции — шума для данных
газовой печи есть
 .
.
Функции отклика на единичный скачок и единичный импульс, соответствующие модели передаточной функции
![]() ,
,
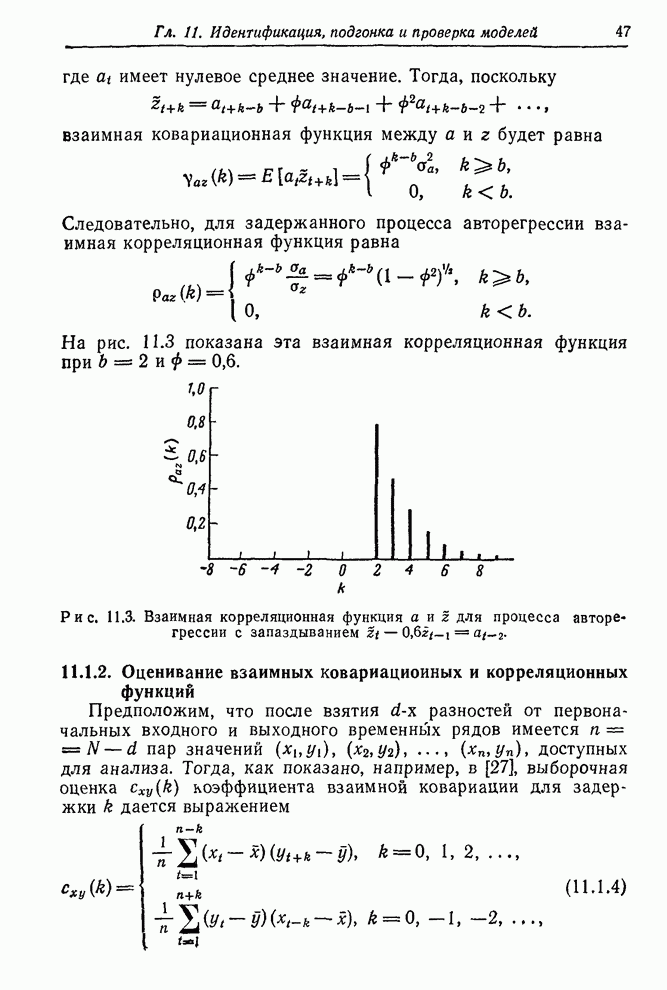
приведены на рис. 11.6. Согласно (10.2.5), установившееся усиление кодированных данных равно
![]() .
.
Результаты хорошо согласуются с полученными взаимным спектральным анализом [27].
|
|
|
|
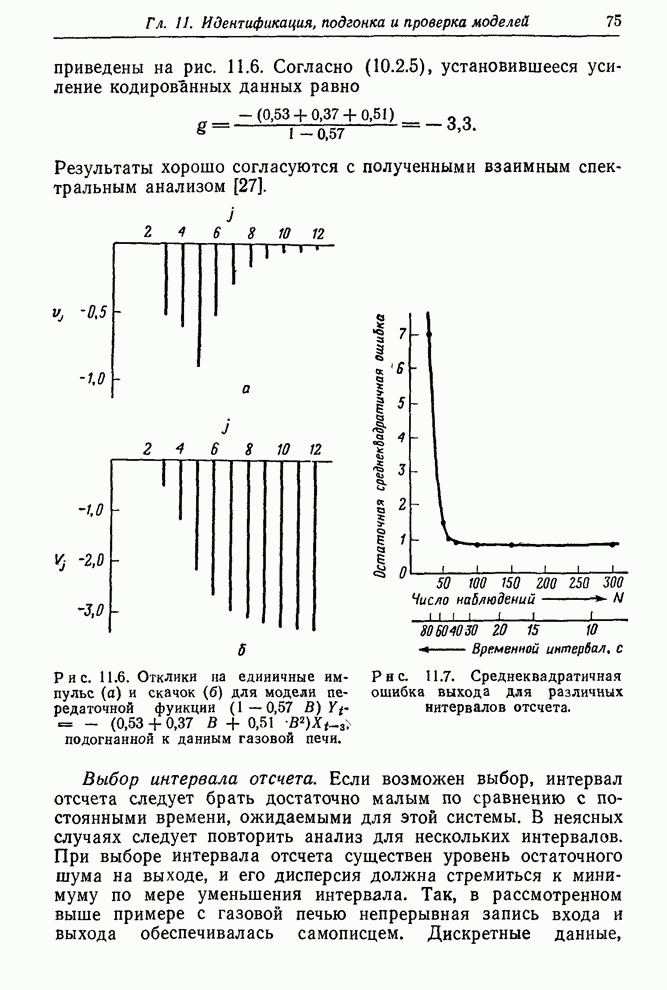
Рис. 11.6. Отклики на единичные импульс
(а) и скачок (б) для модели передаточной функции |
Рис. 11.7. Среднеквадратичная ошибка выхода для различных интервалов отсчета. |
Выбор интервала отсчета. Если возможен выбор, интервал
отсчета следует брать достаточно малым по сравнению с постоянными времени,
ожидаемыми для этой системы. В неясных случаях следует повторить анализ для
нескольких интервалов. При выборе интервала отсчета существен уровень
остаточного шума на выходе, и его дисперсия должна стремиться к минимуму по
мере уменьшения интервала. Так, в рассмотренном выше примере с газовой печью
непрерывная запись входа и выхода обеспечивалась самописцем. Дискретные данные,
использованные в нашем анализе, были получены считыванием значений в точках
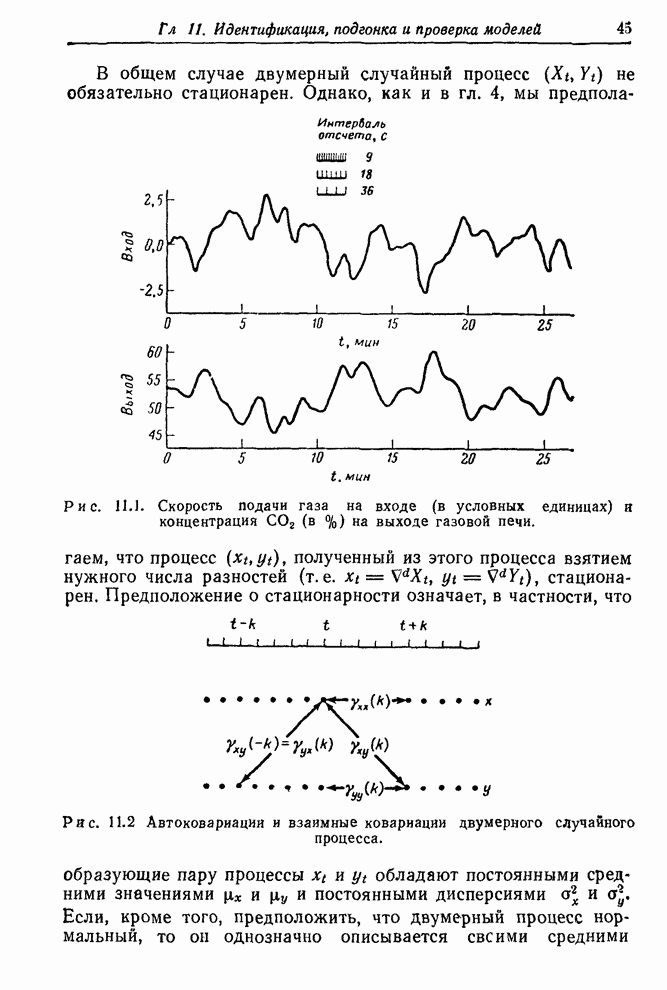
этой непрерывной записи с интервалом 9 с. Этот интервал был выбран после
рассмотрения записей, показанных на рис. 11.1; он показался достаточным для
описания всех вариаций (кроме легкого дрожания пера) входа и выхода. Такого
рода разумные практические предположения обычно достаточно надежны при выборе
интервала. Выборочная среднеквадратичная ошибка для данных о газовой печи
(полученная делением ![]() на соответствующее число степеней
свободы, где
на соответствующее число степеней
свободы, где ![]() —
значения подогнанной модели выхода) при различных временных интервалах
приведена в табл. 11.7. Эти значения показаны также на рис. 11.7. До тех пор
пока интервал меньше 40 с, среднеквадратичная ошибка изменяется незначительно,
а затем она резко возрастает. Для 9-, 18-и 27-секундных интервалов различия в
среднеквадратичной ошибке невелики, а при интервале 36 с происходит
значительное изменение. Видно, что интервал 9 с, использованный в этом примере,
даже излишне безопасен.
—
значения подогнанной модели выхода) при различных временных интервалах
приведена в табл. 11.7. Эти значения показаны также на рис. 11.7. До тех пор
пока интервал меньше 40 с, среднеквадратичная ошибка изменяется незначительно,
а затем она резко возрастает. Для 9-, 18-и 27-секундных интервалов различия в
среднеквадратичной ошибке невелики, а при интервале 36 с происходит
значительное изменение. Видно, что интервал 9 с, использованный в этом примере,
даже излишне безопасен.
Таблица 11.7. Среднеквадратичная ошибка выхода для различных интервалов отсчета
|
Длина интервала, с Число наблюдений, Среднеквадратичная ошибка |
9 296 0,71 |
18 148 0,78 |
27 98 0,74 |
36 74 0,95 |
45 59 0,97 |
54 49 1,56 |
72 37 7,11 |
| << Предыдущий параграф | Следующий параграф >> |
- Часть III. ПОСТРОЕНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- Глава 10. Модели передаточной функции
- 10.1. ЛИНЕЙНЫЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 10.1.1. Дискретная передаточная функция
- 10.1.2. Непрерывные динамические модели, описываемые дифференциальными уравнениями
- 10.2. ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ МОДЕЛИ, ОПИСЫВАЕМЫЕ РАЗНОСТНЫМИ УРАВНЕНИЯМИ
- 10.2.1. Общая форма разностного уравнения
- 10.2.2. Природа передаточной функции
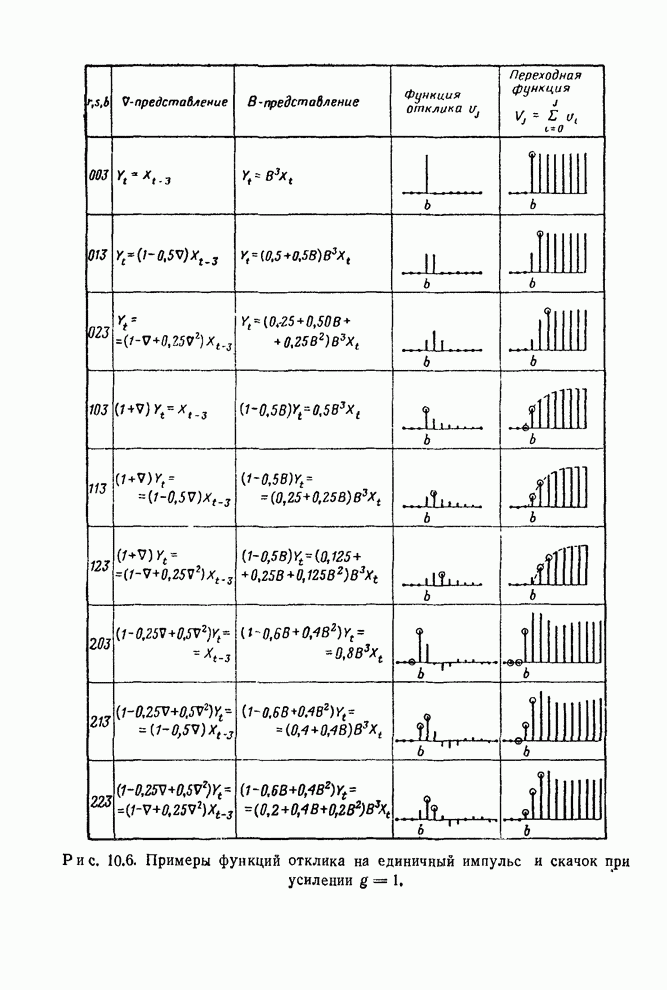
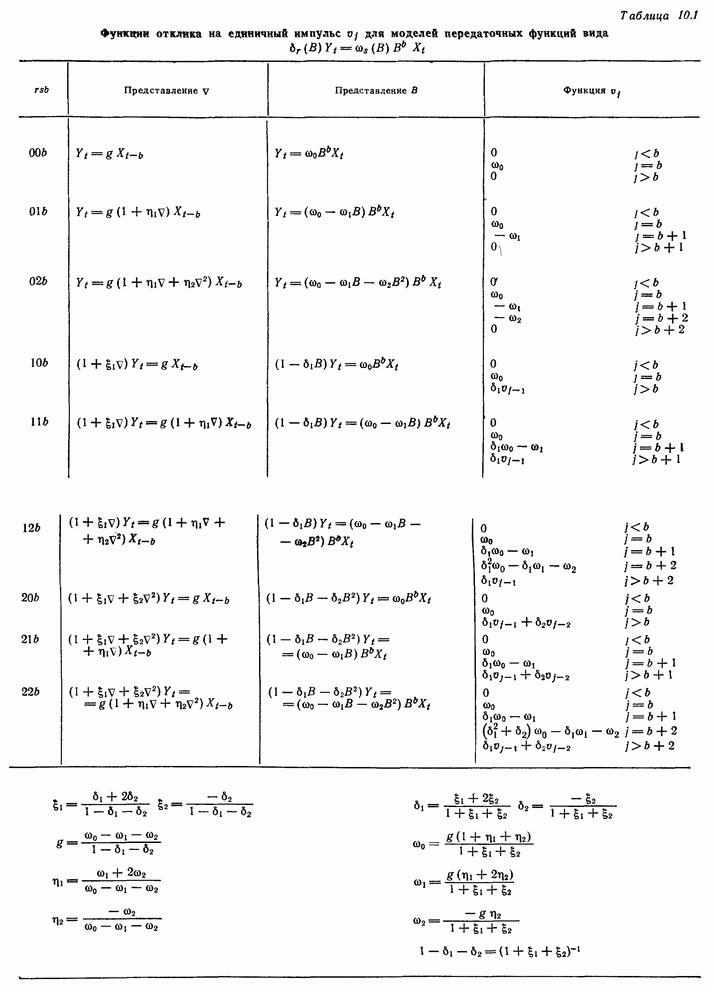
- 10.2.3. Дискретные модели передаточных функций первого и второго порядков
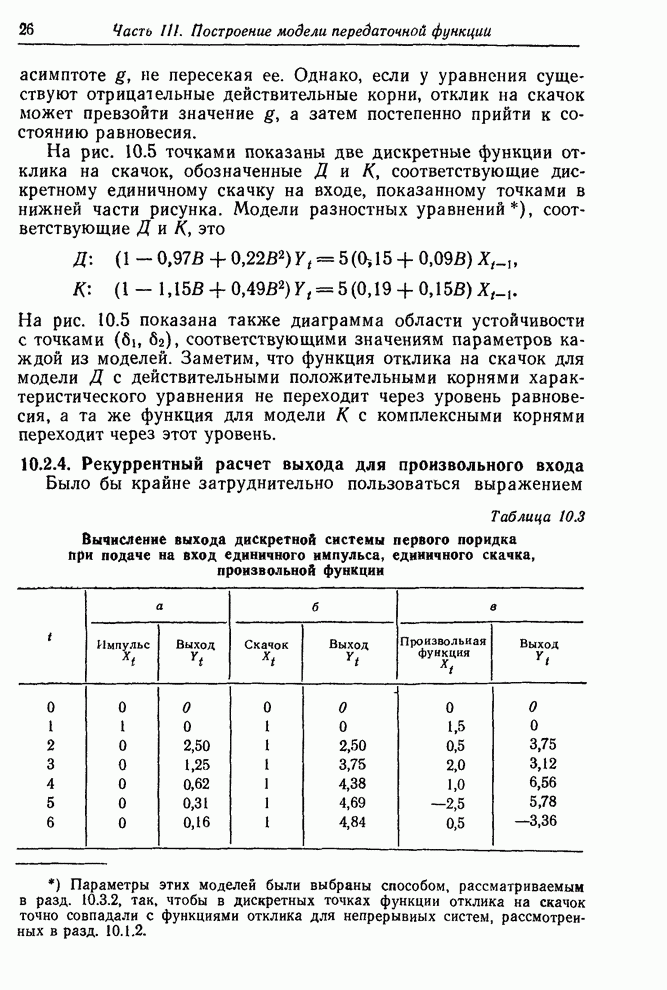
- 10.2.4. Рекуррентный расчет выхода для произвольного входа
- 10.3. СООТНОШЕНИЕ МЕЖДУ ДИСКРЕТНОЙ И НЕПРЕРЫВНОЙ МОДЕЛЯМИ
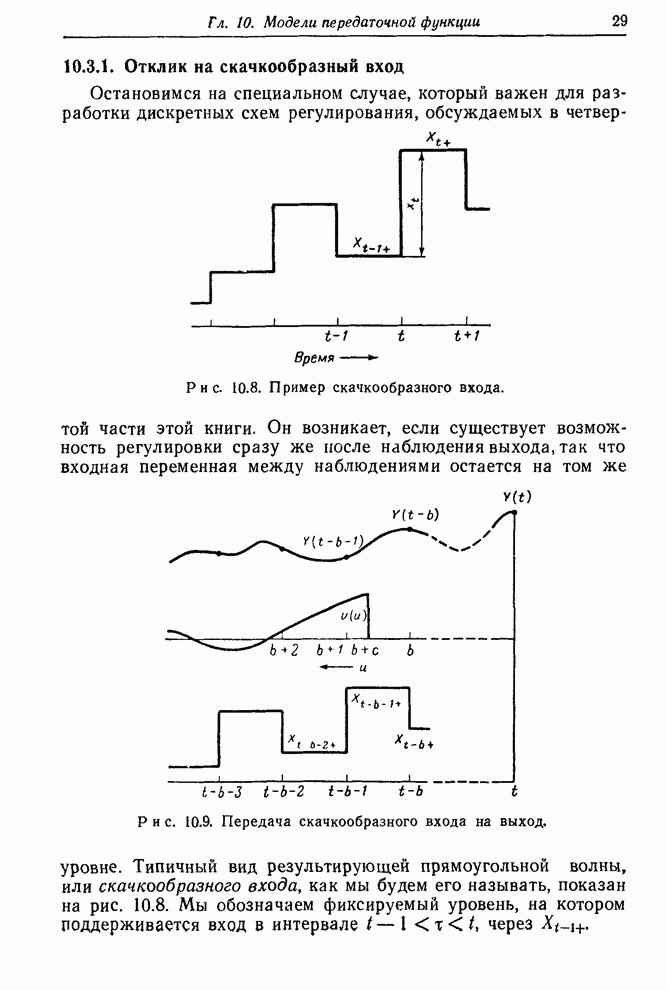
- 10.3.1. Отклик на скачкообразный вход
- 10.3.2. Соотношения совпадающих систем первого и второго порядков
- 10.3.3. Аппроксимация общих непрерывных моделей дискретными моделями
- 10.3.4. Модели передаточных функций с добавленным шумом
- ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
- ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
- Глава 11. Идентификация, подгонка и проверка моделей передаточных функций
- 11.1. Взаимная корреляционная функция
- 11.1.1. Свойства взаимных ковариационной и корреляционной функций
- 11.1.2. Оценивание взаимных ковариационных и корреляционных функций
- 11.1.3. Приближенные стандартные ошибки выборочных оценок взаимных корреляций
- 11.2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.2.1. Идентификация моделей передаточной функции с предварительным выравниванием спектра входа
- 11.2.2. Пример идентификации модели передаточной функции
- 11.2.3. Идентификация модели шума
- 11.2.4. Некоторые общие соображения об идентификации моделей передаточных функций
- 11.3. ПОДГОНКА И ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.3.1. Условная сумма квадратов
- 11.3.2. Нелинейное оценивание
- 11.3.3. Использование остаточных ошибок для диагностической проверки
- 11.3.4. Конкретные способы проверки остаточных ошибок
- 11.4. Некоторые примеры подгонок и проверок моделей передаточных функций
- 11.4.1. Подгонка и проверка модели газовой печи
- 11.4.2. Искусственный пример с двумя входами
- 11.5. ПРОГНОЗИРОВАНИЕ ПРИ ПОМОЩИ УПРЕЖДАЮЩИХ ИНДИКАТОРОВ
- 11.5.1. Прогноз с минимальной среднеквадратичной ошибкой
- 11.5.2. Прогнозы выхода СO2 из газовой печи
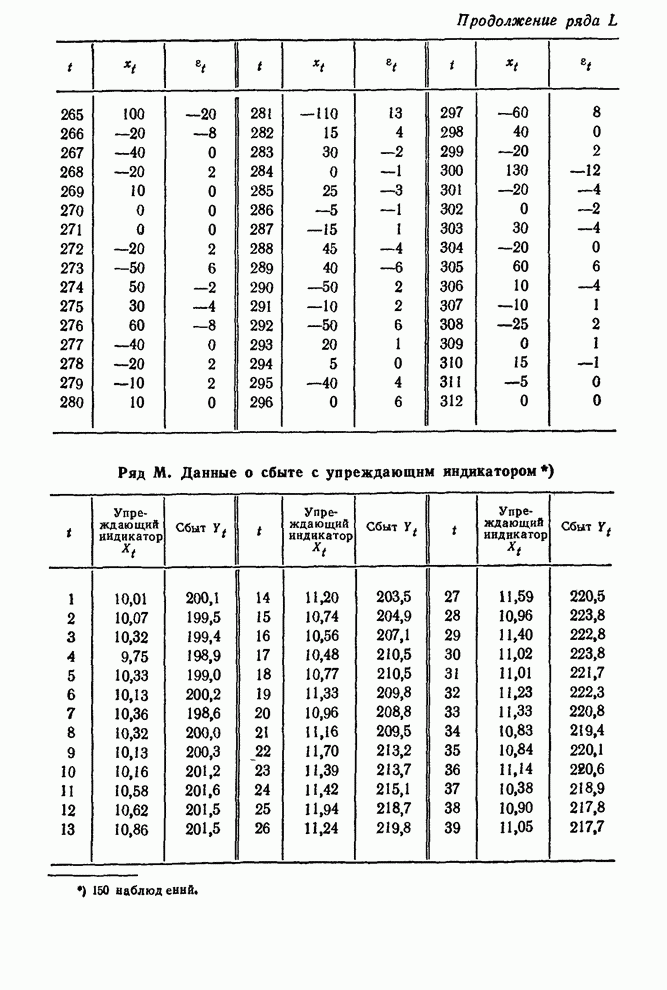
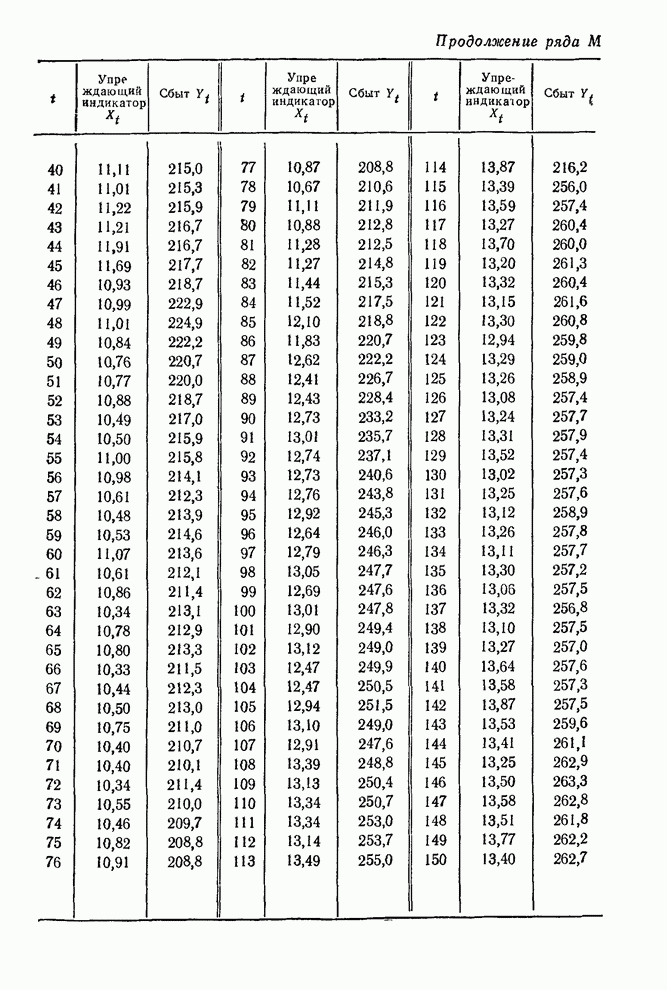
- 11.5.3. Прогноз нестационарных данных сбыта при помощи упреждающего индикатора
- 11.6. НЕКОТОРЫЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОЦЕНИВАНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ П11.1. ИСПОЛЬЗОВАНИЕ ВЗАИМНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
- Заключение
- Часть IV. Проектирование дискретных схем регулирования
- Глава 12. Проектирование схем регулирования с прямой и обратной связями
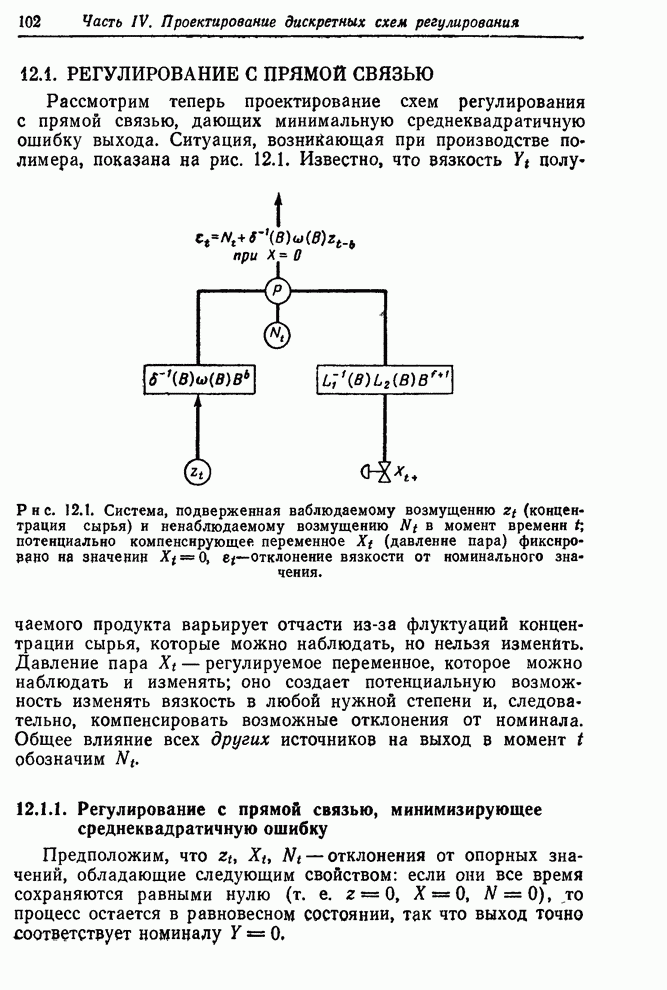
- 12.1. РЕГУЛИРОВАНИЕ С ПРЯМОЙ СВЯЗЬЮ
- 12.1.1. Регулирование с прямой связью, минимизирующее среднеквадратичную ошибку
- 12.1.2. Пример — регулирование удельного веса промежуточного продукта
- 12.1.3. Номограмма для регулирования с прямой связью
- 12.1.4. Регулирование с прямой связью в случае нескольких входов
- 12.2. РЕГУЛИРОВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ
- 12.2.1. Регулирование с обратной связью, минимизирующее среднеквадратичную ошибку
- 12.2.2. Применение уравнения регулирования: ПИД-регулятор
- 12.2.3. Примеры дискретного регулирования с обратной связью
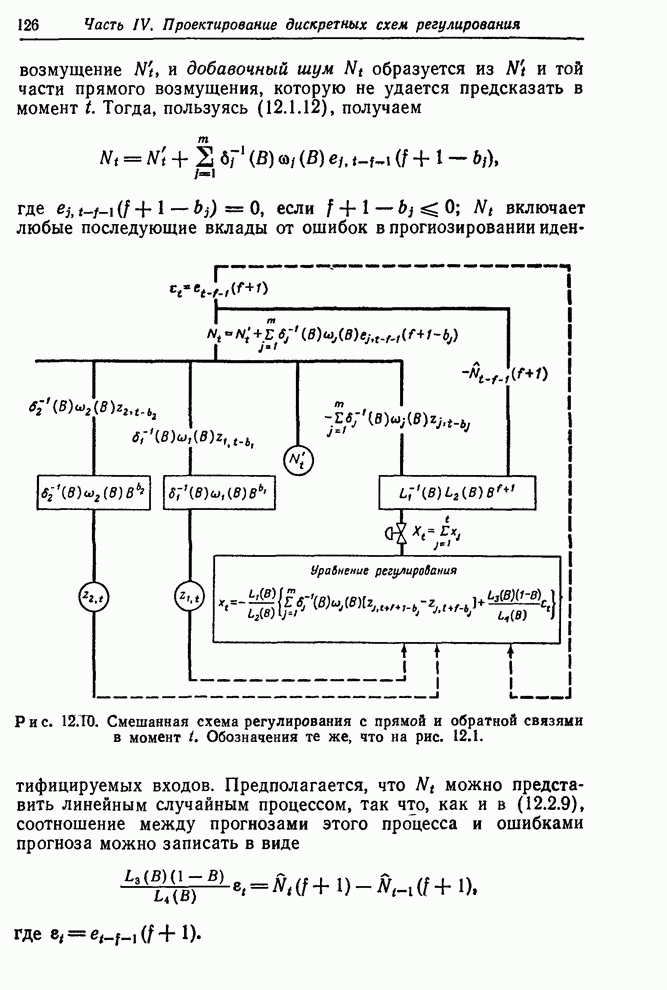
- 12.3. РЕГУЛИРОВАНИЕ С ПРЯМОЙ И ОБРАТНОЙ СВЯЗЯМИ
- 12.3.1. Регулирование с прямой и обратной связями, минимизирующее выходную среднеквадратичную ошибку
- 12.3.2. Пример регулирования с прямой и обратной связями
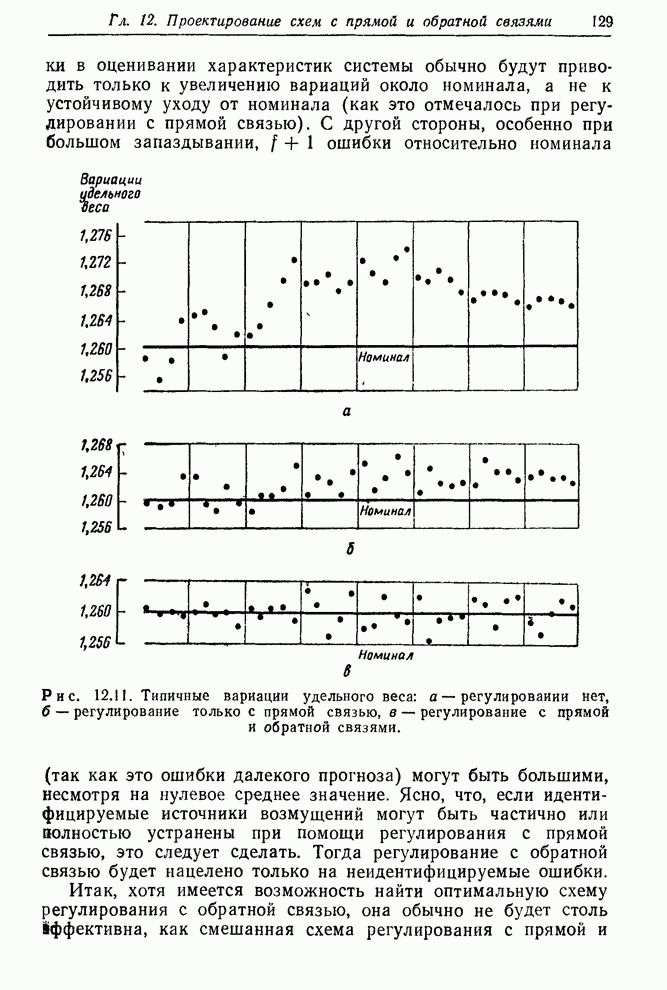
- 12.3.3. Преимущества и недостатки регулирования с прямой и обратной связями
- 12.4. Подгонка моделей передаточных функций шума по оперативным данным
- 12.4.1. Итеративный способ построения моделей
- 12.4.2. Оценивание по оперативным данным
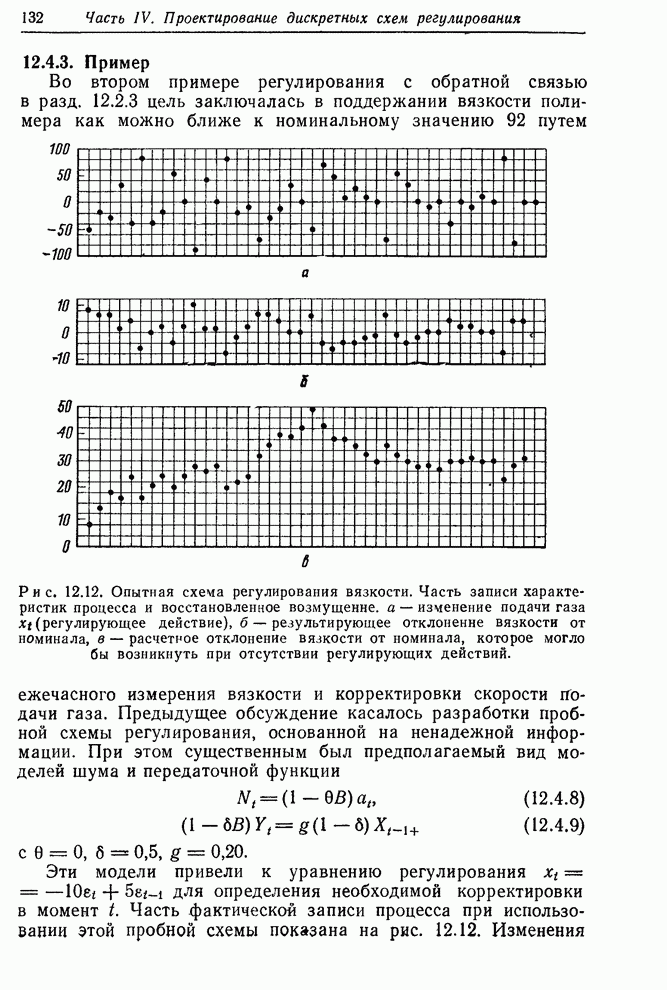
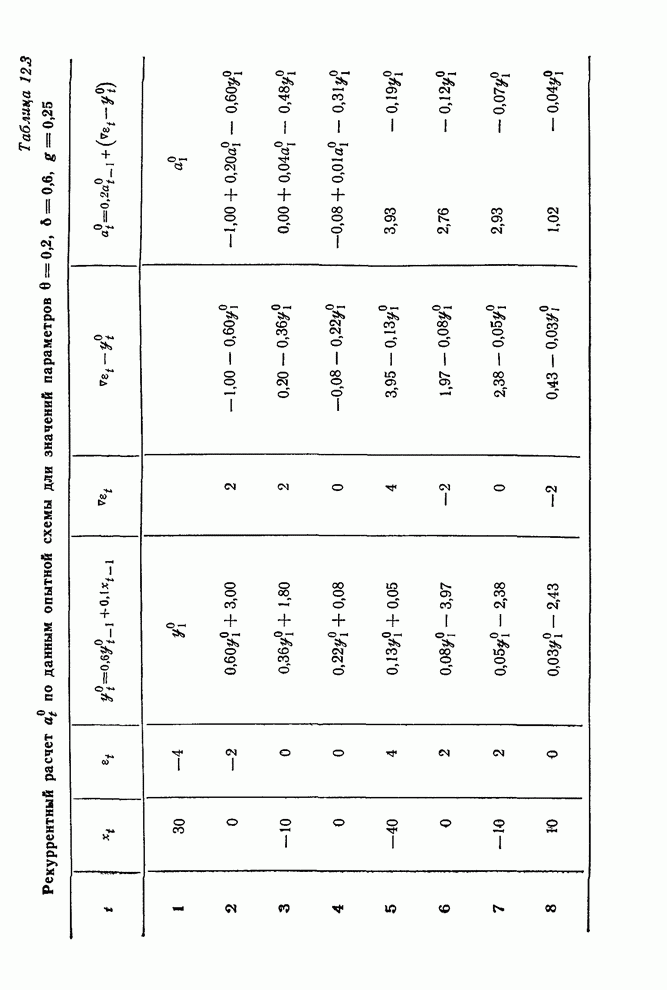
- 12.4.3. Пример
- Глава 13. Некоторые дальнейшие проблемы регулирования
- 13.1. ЭФФЕКТ ДОБАВОЧНОГО ШУМА В СХЕМАХ РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ
- 13.1.1. Эффект пренебрежения добавочным шумом; упрощенные схемы
- 13.1.2. Оптимальное действие в случаях, когда корректировки содержат ошибки наблюдения
- 13.1.3. Перенос источника шума
- 13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
- 13.2.1. Вывод выражения для оптимальной корректировки
- 13.2.2. Схема с ограничением для примера «вязкость–подача газа»
- 13.3. ВЫБОР ИНТЕРВАЛА ОТСЧЕТА
- 13.3.1. Пример эффекта уменьшения частоты отсчетов
- 13.3.2. Влияние интервала отсчета на процесс ПСС(0,1,1)
- ПРОГРАММА 5. ИДЕНТИФИКАЦИЯ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 6. ПРЕДВАРИТЕЛЬНОЕ ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 7. ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
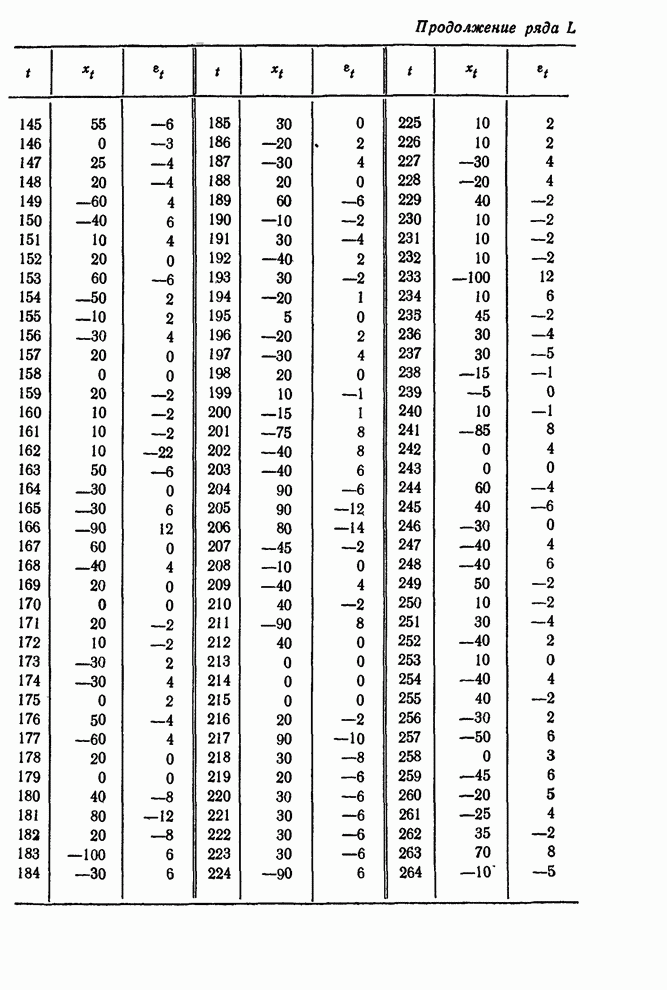
- ТАБЛИЦЫ ВРЕМЕННЫХ РЯДОВ