| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
Пусть в качестве входа динамической системы можно выбрать по нашему усмотрению некоторый случайный процесс. Например, это может быть процесс авторегрессии, скользящего среднего или белый шум. Для того чтобы иллюстрировать проблемы, связанные с оптимальным выбором этого случайного процесса, достаточно рассмотреть элементарный пример.
П11.2.1. Конструирование оптимальных входов для простой системы
Пусть исследуется система с моделью передаточной функции — шума вида
![]() ,
, ![]() , (П11.2.1)
, (П11.2.1)
где
![]() — белый
шум. Предположим также, что процессы на входе и выходе стационарны, a
— белый
шум. Предположим также, что процессы на входе и выходе стационарны, a ![]() обозначают отклонения
этих процессов от соответствующих средних значений. Для больших выборок и
любого фиксированного значения вероятности приближенное значение площади
байесовской области высоких значений плотности вероятности для
обозначают отклонения
этих процессов от соответствующих средних значений. Для больших выборок и
любого фиксированного значения вероятности приближенное значение площади
байесовской области высоких значений плотности вероятности для ![]() и
и ![]() также
соответствующей доверительной области пропорционально
также
соответствующей доверительной области пропорционально ![]() , где
, где ![]() — следующий определитель:
— следующий определитель:
 .
.
Мы
попытаемся разработать способ минимизации этой площади и, следовательно,
максимизации ![]() .
Имеем
.
Имеем
 (П11.2.2)
(П11.2.2)
где
 ,
, ![]() .
.
Значение
определителя можно выразить через ![]() , а именно
, а именно
 . (П11.2.3)
. (П11.2.3)
Тогда,
как и следовало ожидать, уменьшить площадь области можно, увеличивая ![]() (т. е. изменяя
переменное на входе в широких пределах). На практике могут существовать пределы
допустимых изменений
(т. е. изменяя
переменное на входе в широких пределах). На практике могут существовать пределы
допустимых изменений ![]() . Поэтому рассмотрим сначала случай,
когда
. Поэтому рассмотрим сначала случай,
когда ![]() фиксировано.
фиксировано.
Решение для фиксированного ![]() . Поскольку
. Поскольку ![]() , из (П11.2.3) следует, что для любого
фиксированного
, из (П11.2.3) следует, что для любого
фиксированного ![]() значение
значение
![]() будет
максимально, если
будет
максимально, если
 ,
,
т. е.
![]() .
.
Существует бесчисленное множество способов обеспечения этого равенства при заданном
![]() . Одно из возможных
решений получается при
. Одно из возможных
решений получается при
![]()
Следовательно,
один из способов максимизировать ![]() при фиксированном
при фиксированном ![]() — это заставить вход быть
процессом авторегрессии
— это заставить вход быть
процессом авторегрессии
![]() ,
,
где
![]() — белый
шум с дисперсией
— белый
шум с дисперсией ![]() .
.
Решение для фиксированного ![]() . До этого момента мы предполагали, что
. До этого момента мы предполагали, что ![]() не ограничено. В
некоторых случаях мы, возможно, захотим избежать слишком больших изменений выхода,
а не входа. Пусть
не ограничено. В
некоторых случаях мы, возможно, захотим избежать слишком больших изменений выхода,
а не входа. Пусть ![]() зафиксировано
на некотором приемлемом уровне, а
зафиксировано
на некотором приемлемом уровне, а ![]() не ограничено. Тогда можно выразить
не ограничено. Тогда можно выразить ![]() через
через ![]() :
:
 , (П11.2.4)
, (П11.2.4)
где
 , (П11.2.5)
, (П11.2.5)
и
 , (П11.2.6)
, (П11.2.6)
Максимум
![]() достигается
при
достигается
при
![]() , (П11.2.7)
, (П11.2.7)
т. е.
![]() .
.
Опять существует бесконечное множество способов выполнить это равенство. В частности, мы можем получить
![]() , (П11.2.8)
, (П11.2.8)
если вход будет следовать процессу авторегрессии
![]() , (П11.2.9)
, (П11.2.9)
где
![]() — белый
шум с дисперсией
— белый
шум с дисперсией ![]() .
Так как
.
Так как ![]() положительно,
знак параметра
положительно,
знак параметра ![]() этого
процесса авторегрессии обратен найденному для оптимального входа в случае,
когда фиксировано
этого
процесса авторегрессии обратен найденному для оптимального входа в случае,
когда фиксировано ![]() .
.
Решение при фиксированном ![]() . На практике могут встретиться случаи, когда
желательно обойтись без излишне сильных изменений как на входе, так и на
выходе. Если при этом заданное относительное уменьшение дисперсии
. На практике могут встретиться случаи, когда
желательно обойтись без излишне сильных изменений как на входе, так и на
выходе. Если при этом заданное относительное уменьшение дисперсии ![]() столь же важно, как
такое же относительное уменьшение дисперсии
столь же важно, как
такое же относительное уменьшение дисперсии ![]() , то целесообразно
максимизировать
, то целесообразно
максимизировать ![]() в
предположении о постоянстве произведения
в
предположении о постоянстве произведения ![]() . Определитель равен
. Определитель равен
![]() (П11.2.10)
(П11.2.10)
и
при заданном ![]() достигает
максимума при
достигает
максимума при ![]() .
Опять-таки существует бесчисленное множество способов достичь этого равенства.
Однако если пользоваться в качестве входного процесса белым шумом, максимум
.
Опять-таки существует бесчисленное множество способов достичь этого равенства.
Однако если пользоваться в качестве входного процесса белым шумом, максимум ![]() может быть достигнут
при любом значении
может быть достигнут
при любом значении ![]() . При таком входе в соответствии с
(П11.2.2)
. При таком входе в соответствии с
(П11.2.2) ![]() —
это положительный корень уравнения
—
это положительный корень уравнения
![]() , (П11.2.11)
, (П11.2.11)
где
![]()
П11.2.2. Численный пример
Пусть
мы исследуем динамическую систему первого порядка (П11.2.1) с ![]() ,
, ![]() , так что
, так что
![]() ,
,
где
![]() .
.
![]() фиксировано,
фиксировано, ![]() не ограничено. Пусть сначала необходимо
максимизировать
не ограничено. Пусть сначала необходимо
максимизировать ![]() при
при
![]() . Тогда
оптимальным входом
. Тогда
оптимальным входом ![]() будет, в частности, процесс
авторегрессии
будет, в частности, процесс
авторегрессии
![]() ,
,
где
![]() — белый
шум с дисперсией
— белый
шум с дисперсией ![]() .
Как следует из (П11.2.2), дисперсия
.
Как следует из (П11.2.2), дисперсия ![]() выхода будет равна 2,49, и площадь
байесовской области для
выхода будет равна 2,49, и площадь
байесовской области для ![]() и
и ![]() . Для этого режима на входе будет
пропорциональна
. Для этого режима на входе будет
пропорциональна ![]() .
.
![]() фиксировано,
фиксировано, ![]() не ограничено. Полученный ранее режим
оптимален в предположении, что дисперсия входа
не ограничено. Полученный ранее режим
оптимален в предположении, что дисперсия входа ![]() и дисперсия выхода
и дисперсия выхода ![]() не ограничена. Она
оказывается при этом равной 2,49. Если бы, наоборот, была неограниченной
дисперсия входа, то при заданной дисперсии выхода 2,49 мы могли бы,
конечно, достичь лучших результатов. Действительно, пользуясь (П11.2.6),
находим
не ограничена. Она
оказывается при этом равной 2,49. Если бы, наоборот, была неограниченной
дисперсия входа, то при заданной дисперсии выхода 2,49 мы могли бы,
конечно, достичь лучших результатов. Действительно, пользуясь (П11.2.6),
находим ![]() ,
так что, согласно (П11.2.9), одним из возможных оптимальных процессов на входе
при отсутствии ограничений, наложенных на дисперсию, был бы процесс
авторегрессии
,
так что, согласно (П11.2.9), одним из возможных оптимальных процессов на входе
при отсутствии ограничений, наложенных на дисперсию, был бы процесс
авторегрессии
![]() ,
,
где
![]() — белый
шум с дисперсией
— белый
шум с дисперсией ![]() .
Дисперсия входа
.
Дисперсия входа ![]() увеличилась
бы при этом до 2,91, а
увеличилась
бы при этом до 2,91, а ![]() которому пропорциональна площадь
байесовской области, уменьшилось бы до
которому пропорциональна площадь
байесовской области, уменьшилось бы до ![]() .
.
Произведение ![]() фиксировано. Рассмотрим наконец случай
оптимизации режима на входе при фиксированном произведении
фиксировано. Рассмотрим наконец случай
оптимизации режима на входе при фиксированном произведении ![]() . В предыдущем примере с
фиксированным
. В предыдущем примере с
фиксированным ![]() мы
нашли, что
мы
нашли, что ![]() при
при
![]() и
и ![]() , так что их
произведение
, так что их
произведение ![]() .
Если бы нашей целью было минимизировать
.
Если бы нашей целью было минимизировать ![]() при постоянстве этого произведения на
уровне 7,25, мы могли бы выбрать оптимальный режим на входе, не зная
при постоянстве этого произведения на
уровне 7,25, мы могли бы выбрать оптимальный режим на входе, не зная ![]() и задав вход в виде
белого шума
и задав вход в виде
белого шума ![]() .
Согласно (П11.2.11),
.
Согласно (П11.2.11), ![]() ,
, ![]() ; в этом случае
; в этом случае ![]() , т. е., как и следовало
ожидать, слегка меньше, чем в предыдущем примере.
, т. е., как и следовало
ожидать, слегка меньше, чем в предыдущем примере.
Стоит
рассмотреть этот пример в свете спектральных представлений. Чтобы
оптимизировать режим при фиксированном ![]() , мы подавали на вход процесс
авторегрессии с положительным
, мы подавали на вход процесс
авторегрессии с положительным ![]() , имеющий большую мощность в области
низких частот. Так как усиление системы на низких частотах велико, передача от
, имеющий большую мощность в области
низких частот. Так как усиление системы на низких частотах велико, передача от ![]() к
к ![]() наиболее эффективна,
и мы приходим к большим изменениям в
наиболее эффективна,
и мы приходим к большим изменениям в ![]() . При фиксированном
. При фиксированном ![]() мы подаем на вход процесс
авторегрессии с отрицательным
мы подаем на вход процесс
авторегрессии с отрицательным ![]() , мощность которого сосредоточена на
высоких частотах. Так как передачу высоких частот от
, мощность которого сосредоточена на
высоких частотах. Так как передачу высоких частот от ![]() к
к ![]() система осуществляет
неэффективно, необходимо ввести сильные возмущения в
система осуществляет
неэффективно, необходимо ввести сильные возмущения в ![]() . При фиксированном
. При фиксированном ![]() приемлем
«компромиссный» вход в виде белого шума и знание
приемлем
«компромиссный» вход в виде белого шума и знание ![]() не обязательно. Этот способ
максимизации эквивалентен минимизации корреляции между выборочными оценками
не обязательно. Этот способ
максимизации эквивалентен минимизации корреляции между выборочными оценками ![]() и
и ![]() ; действительно, если
на вход подается белый шум, корреляция между этими оценками равна нулю.
; действительно, если
на вход подается белый шум, корреляция между этими оценками равна нулю.
| << Предыдущий параграф | Следующий параграф >> |
- Часть III. ПОСТРОЕНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- Глава 10. Модели передаточной функции
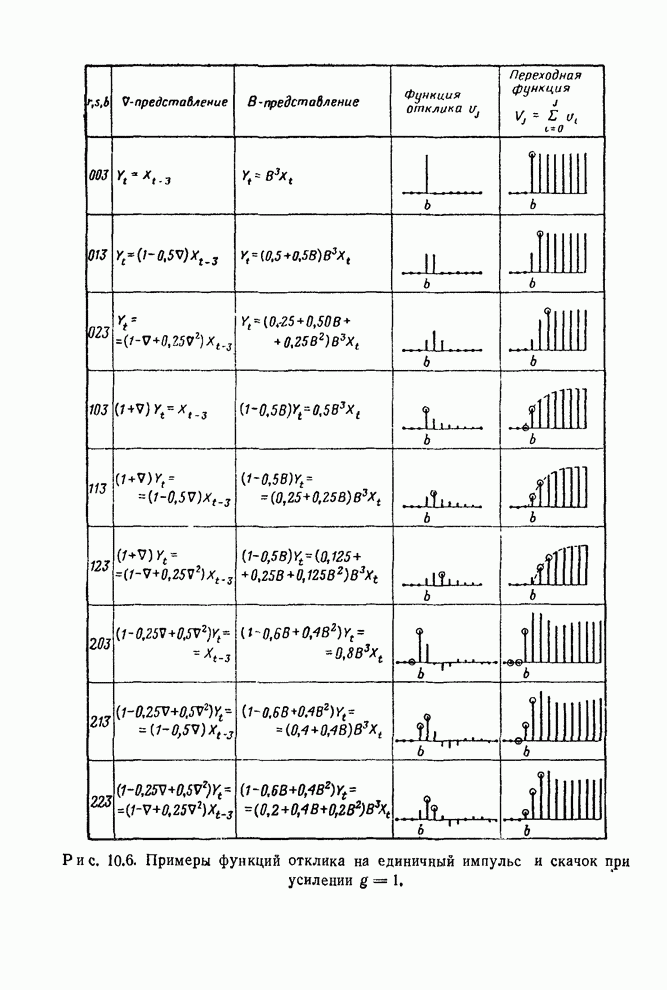
- 10.1. ЛИНЕЙНЫЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 10.1.1. Дискретная передаточная функция
- 10.1.2. Непрерывные динамические модели, описываемые дифференциальными уравнениями
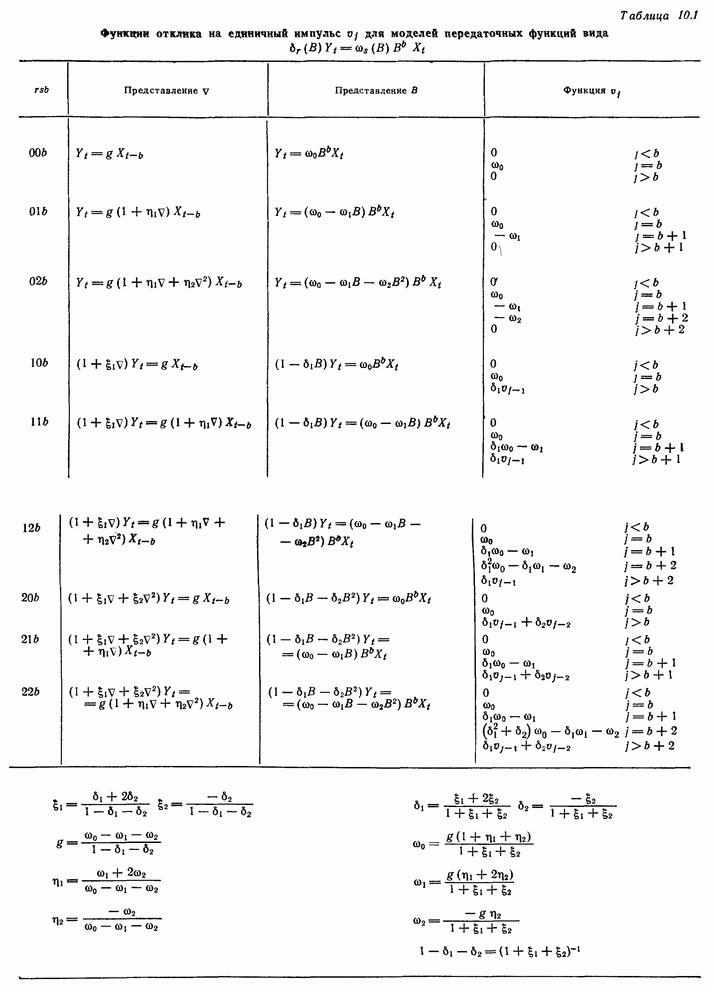
- 10.2. ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ МОДЕЛИ, ОПИСЫВАЕМЫЕ РАЗНОСТНЫМИ УРАВНЕНИЯМИ
- 10.2.1. Общая форма разностного уравнения
- 10.2.2. Природа передаточной функции
- 10.2.3. Дискретные модели передаточных функций первого и второго порядков
- 10.2.4. Рекуррентный расчет выхода для произвольного входа
- 10.3. СООТНОШЕНИЕ МЕЖДУ ДИСКРЕТНОЙ И НЕПРЕРЫВНОЙ МОДЕЛЯМИ
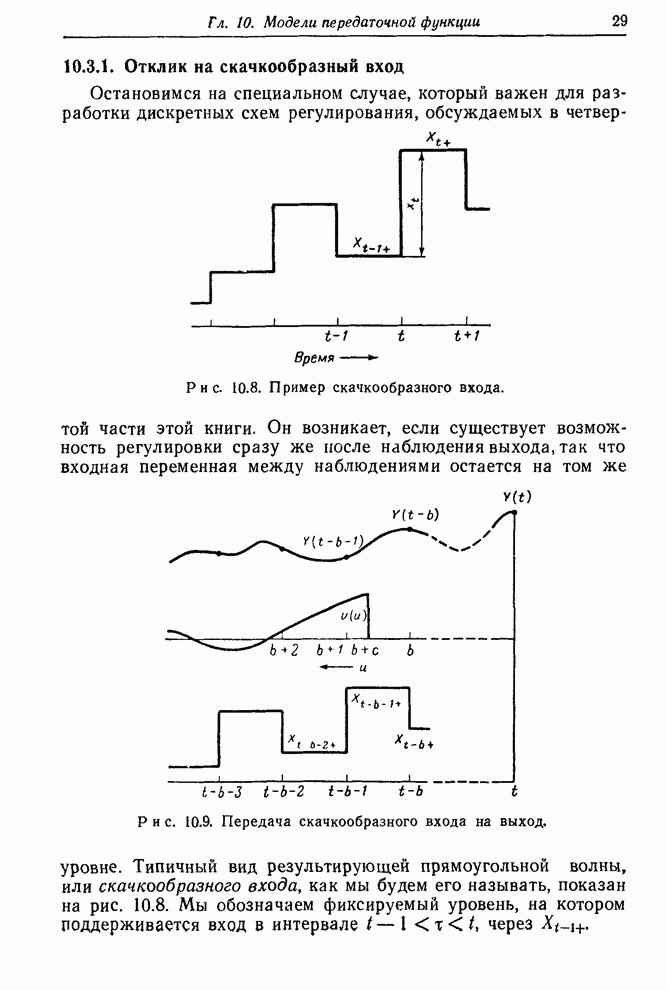
- 10.3.1. Отклик на скачкообразный вход
- 10.3.2. Соотношения совпадающих систем первого и второго порядков
- 10.3.3. Аппроксимация общих непрерывных моделей дискретными моделями
- 10.3.4. Модели передаточных функций с добавленным шумом
- ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
- ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
- Глава 11. Идентификация, подгонка и проверка моделей передаточных функций
- 11.1. Взаимная корреляционная функция
- 11.1.1. Свойства взаимных ковариационной и корреляционной функций
- 11.1.2. Оценивание взаимных ковариационных и корреляционных функций
- 11.1.3. Приближенные стандартные ошибки выборочных оценок взаимных корреляций
- 11.2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.2.1. Идентификация моделей передаточной функции с предварительным выравниванием спектра входа
- 11.2.2. Пример идентификации модели передаточной функции
- 11.2.3. Идентификация модели шума
- 11.2.4. Некоторые общие соображения об идентификации моделей передаточных функций
- 11.3. ПОДГОНКА И ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.3.1. Условная сумма квадратов
- 11.3.2. Нелинейное оценивание
- 11.3.3. Использование остаточных ошибок для диагностической проверки
- 11.3.4. Конкретные способы проверки остаточных ошибок
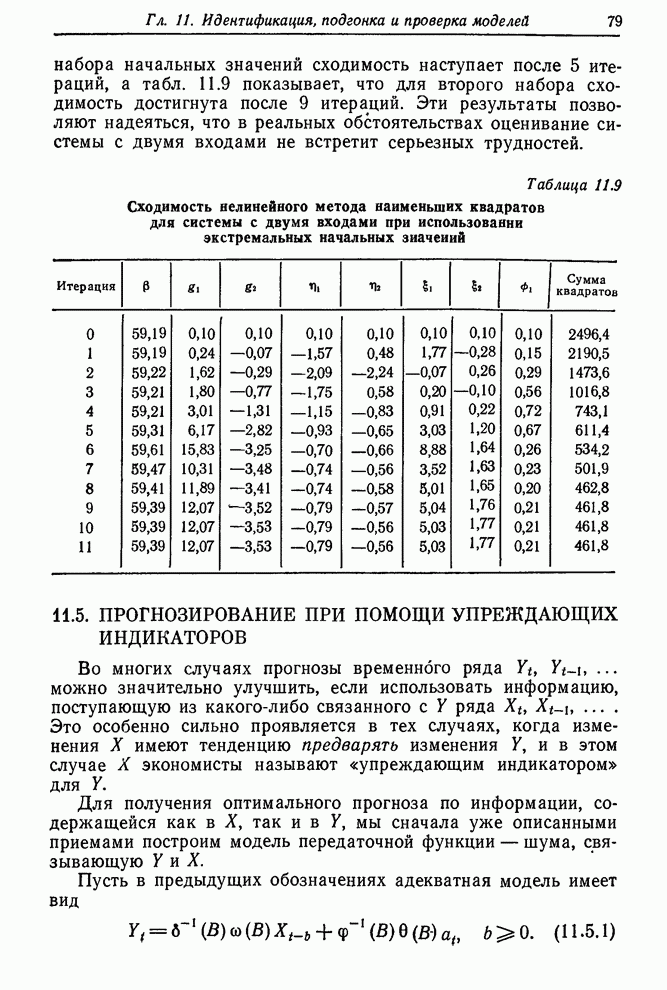
- 11.4. Некоторые примеры подгонок и проверок моделей передаточных функций
- 11.4.1. Подгонка и проверка модели газовой печи
- 11.4.2. Искусственный пример с двумя входами
- 11.5. ПРОГНОЗИРОВАНИЕ ПРИ ПОМОЩИ УПРЕЖДАЮЩИХ ИНДИКАТОРОВ
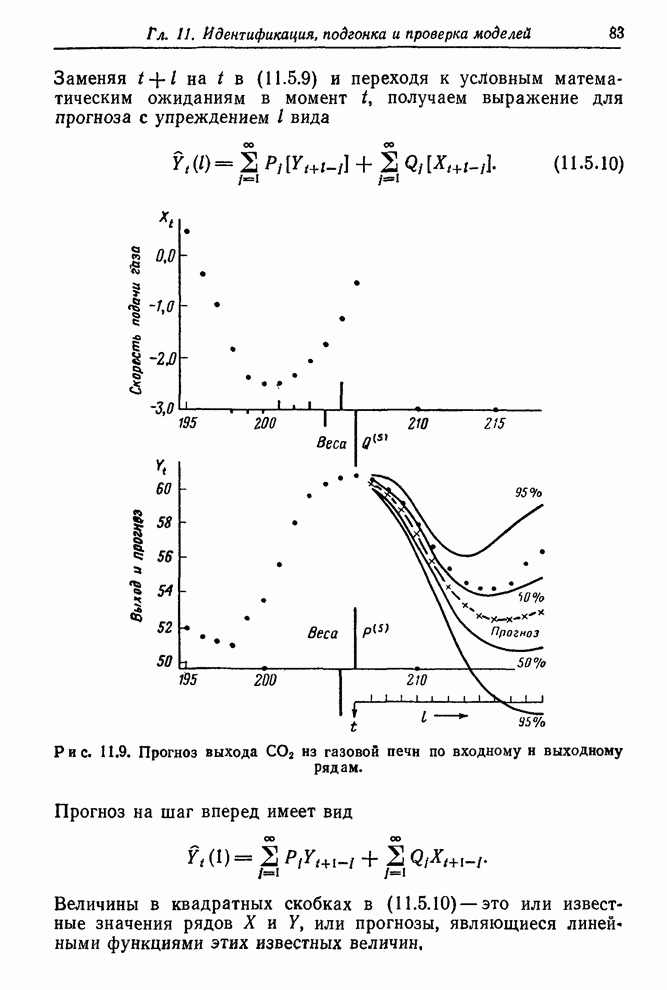
- 11.5.1. Прогноз с минимальной среднеквадратичной ошибкой
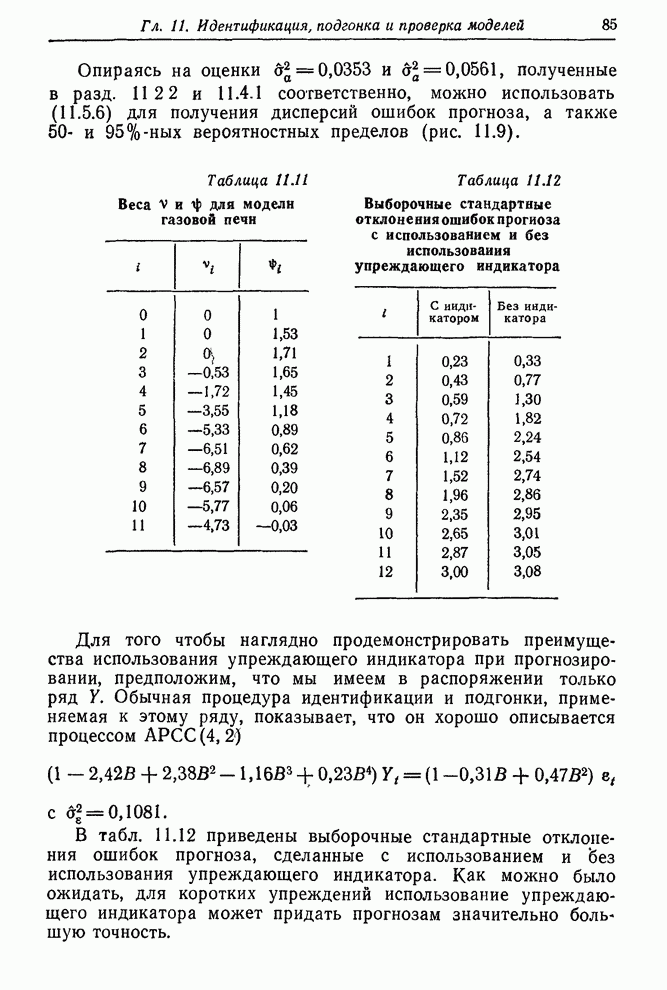
- 11.5.2. Прогнозы выхода СO2 из газовой печи
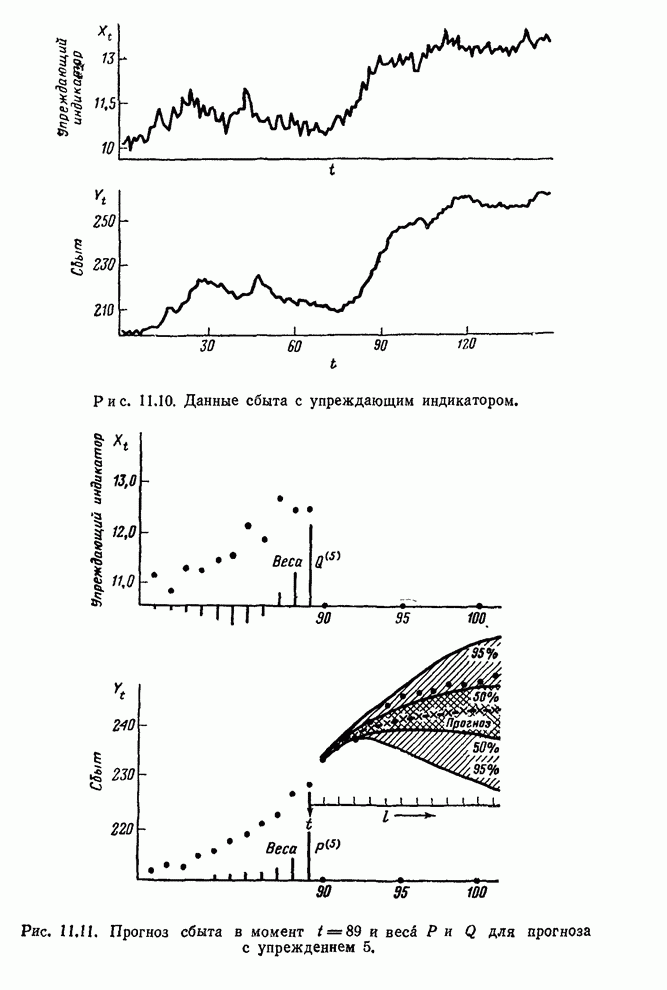
- 11.5.3. Прогноз нестационарных данных сбыта при помощи упреждающего индикатора
- 11.6. НЕКОТОРЫЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОЦЕНИВАНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ П11.1. ИСПОЛЬЗОВАНИЕ ВЗАИМНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
- Заключение
- Часть IV. Проектирование дискретных схем регулирования
- Глава 12. Проектирование схем регулирования с прямой и обратной связями
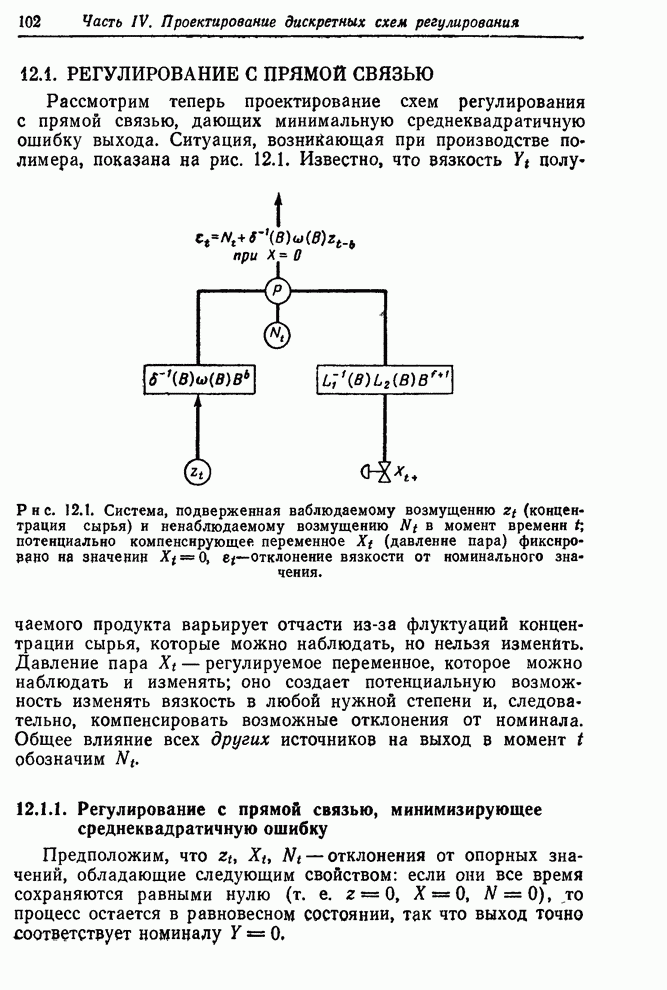
- 12.1. РЕГУЛИРОВАНИЕ С ПРЯМОЙ СВЯЗЬЮ
- 12.1.1. Регулирование с прямой связью, минимизирующее среднеквадратичную ошибку
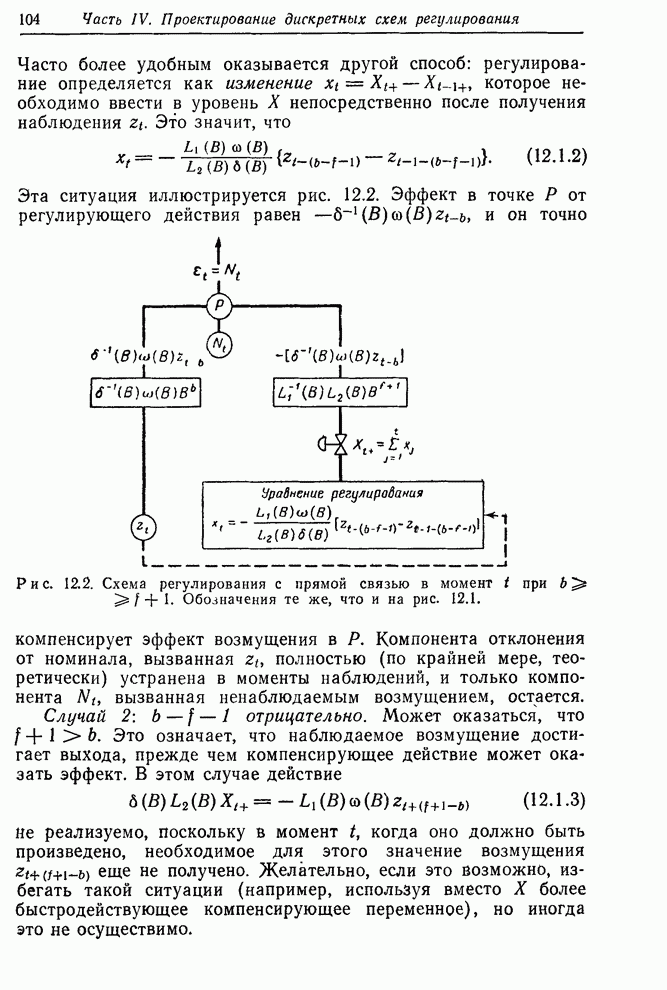
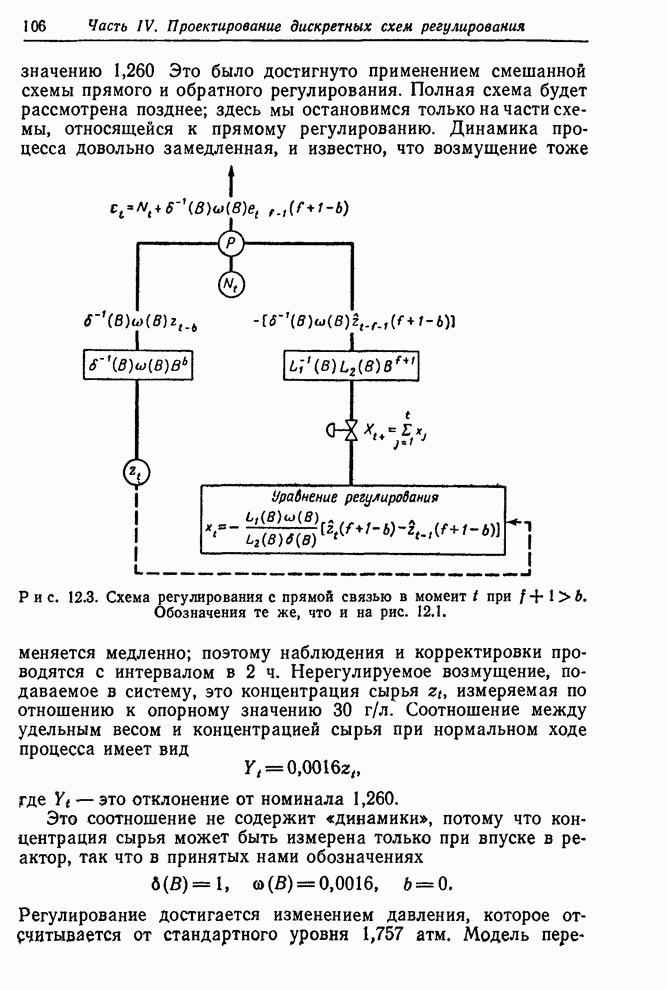
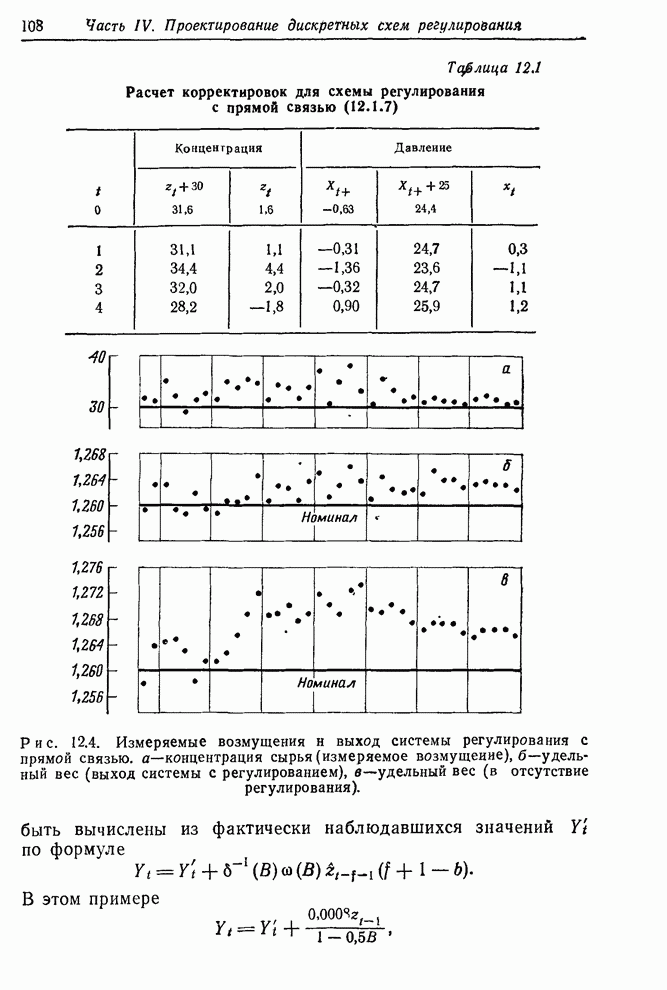
- 12.1.2. Пример — регулирование удельного веса промежуточного продукта
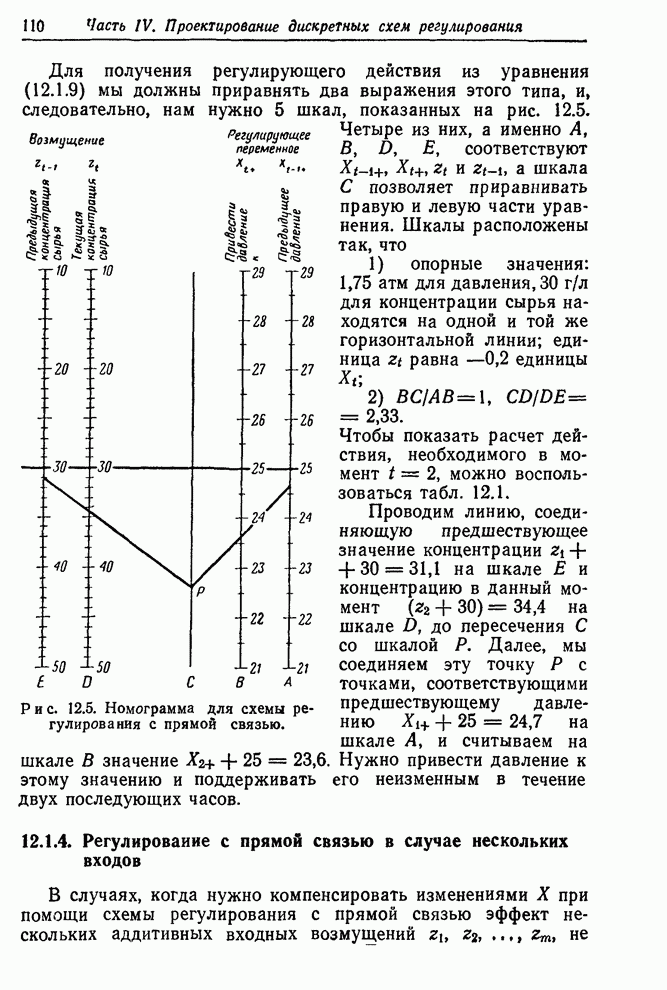
- 12.1.3. Номограмма для регулирования с прямой связью
- 12.1.4. Регулирование с прямой связью в случае нескольких входов
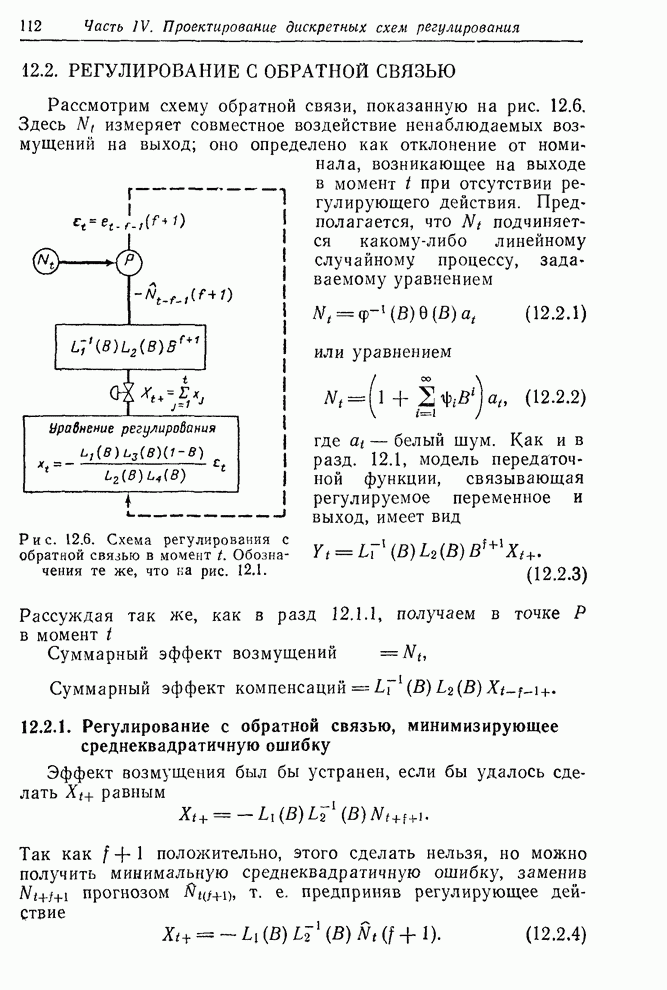
- 12.2. РЕГУЛИРОВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ
- 12.2.1. Регулирование с обратной связью, минимизирующее среднеквадратичную ошибку
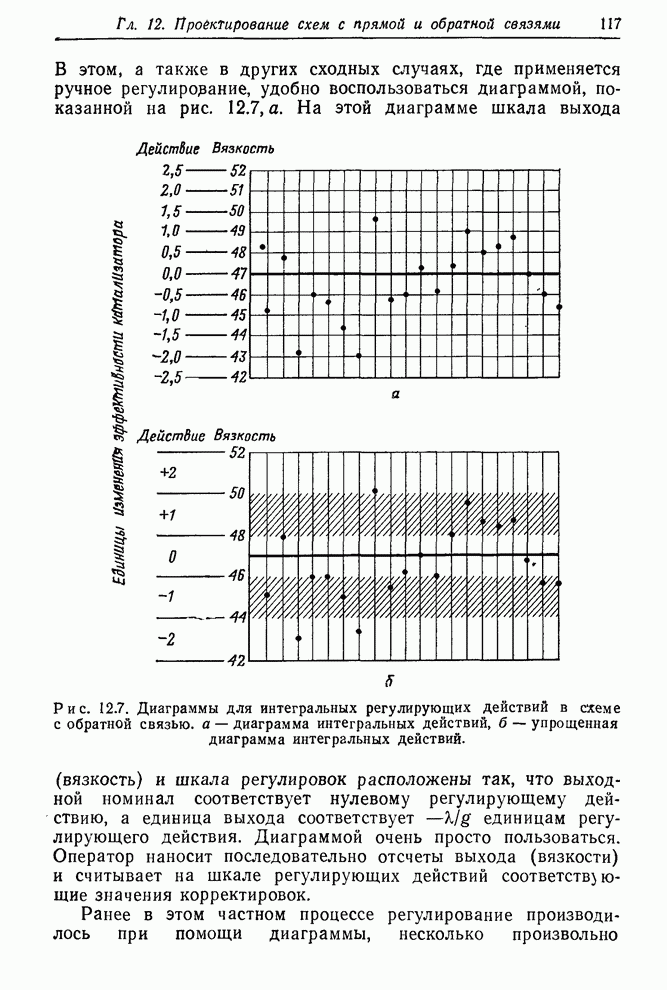
- 12.2.2. Применение уравнения регулирования: ПИД-регулятор
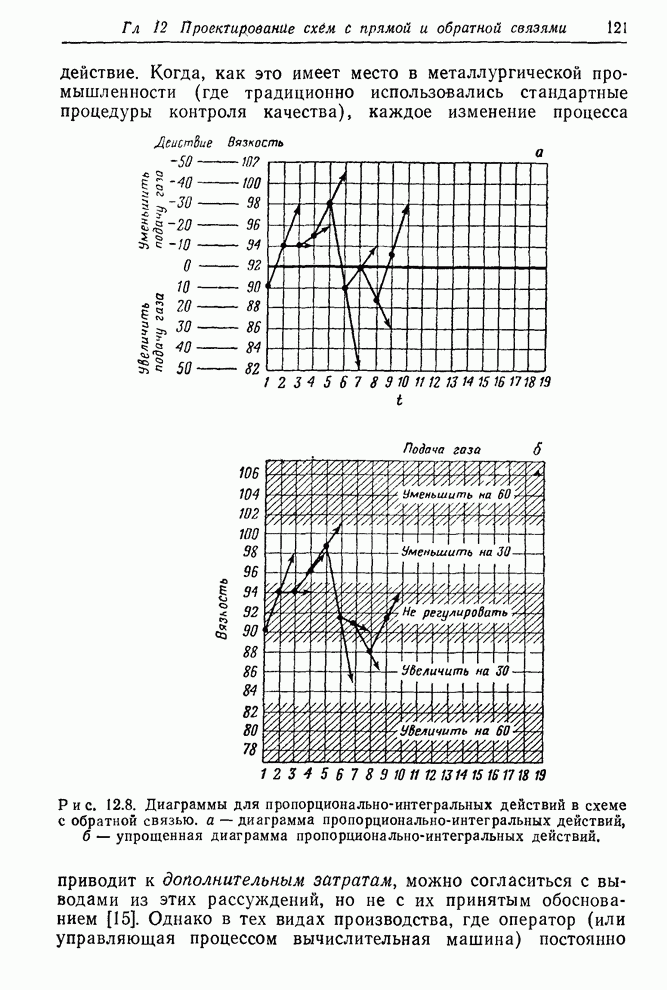
- 12.2.3. Примеры дискретного регулирования с обратной связью
- 12.3. РЕГУЛИРОВАНИЕ С ПРЯМОЙ И ОБРАТНОЙ СВЯЗЯМИ
- 12.3.1. Регулирование с прямой и обратной связями, минимизирующее выходную среднеквадратичную ошибку
- 12.3.2. Пример регулирования с прямой и обратной связями
- 12.3.3. Преимущества и недостатки регулирования с прямой и обратной связями
- 12.4. Подгонка моделей передаточных функций шума по оперативным данным
- 12.4.1. Итеративный способ построения моделей
- 12.4.2. Оценивание по оперативным данным
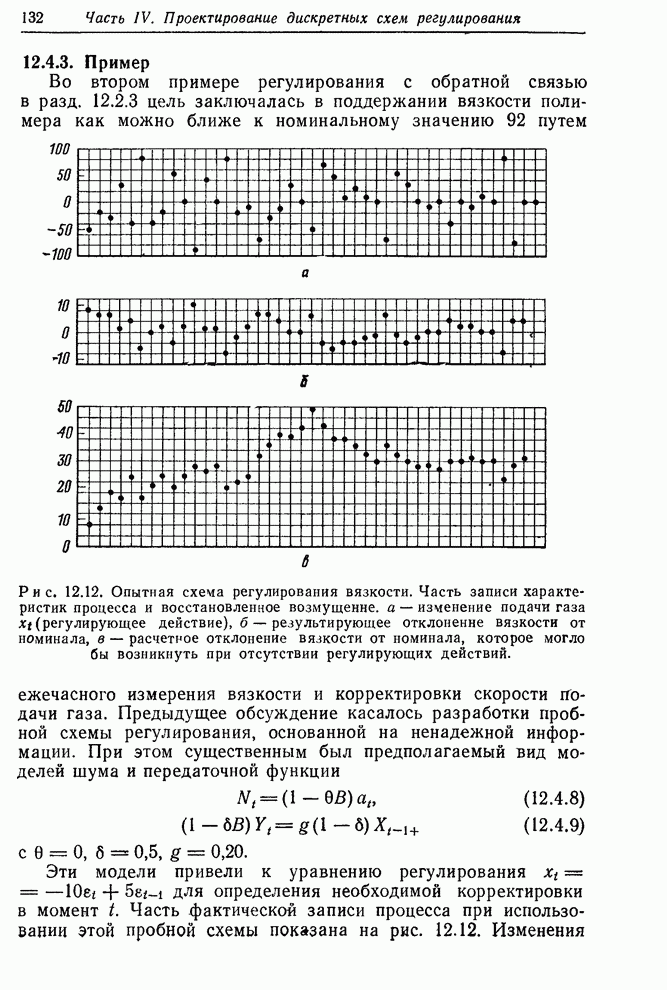
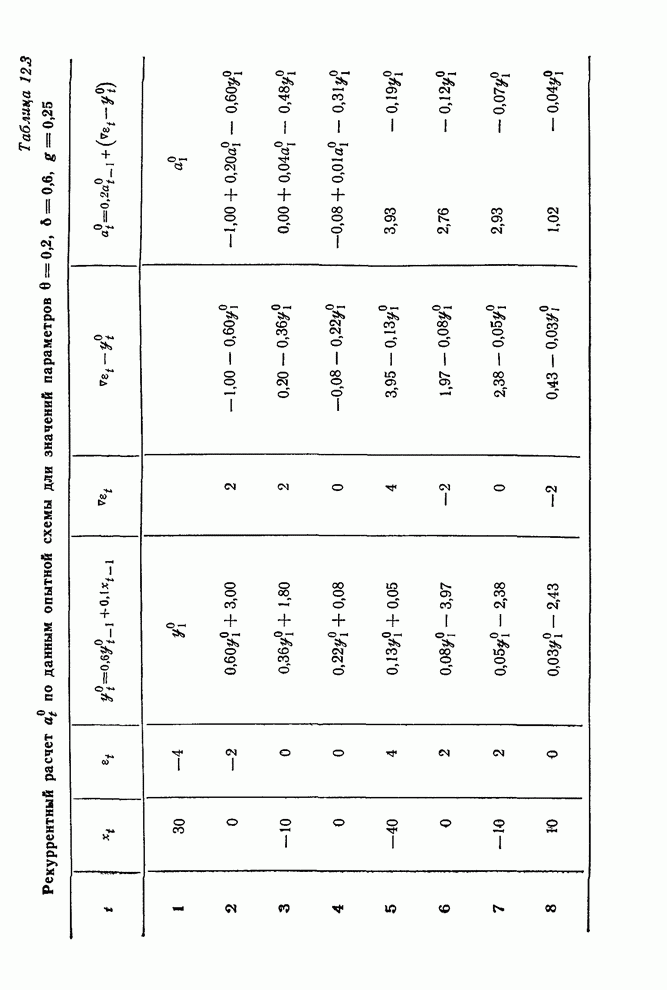
- 12.4.3. Пример
- Глава 13. Некоторые дальнейшие проблемы регулирования
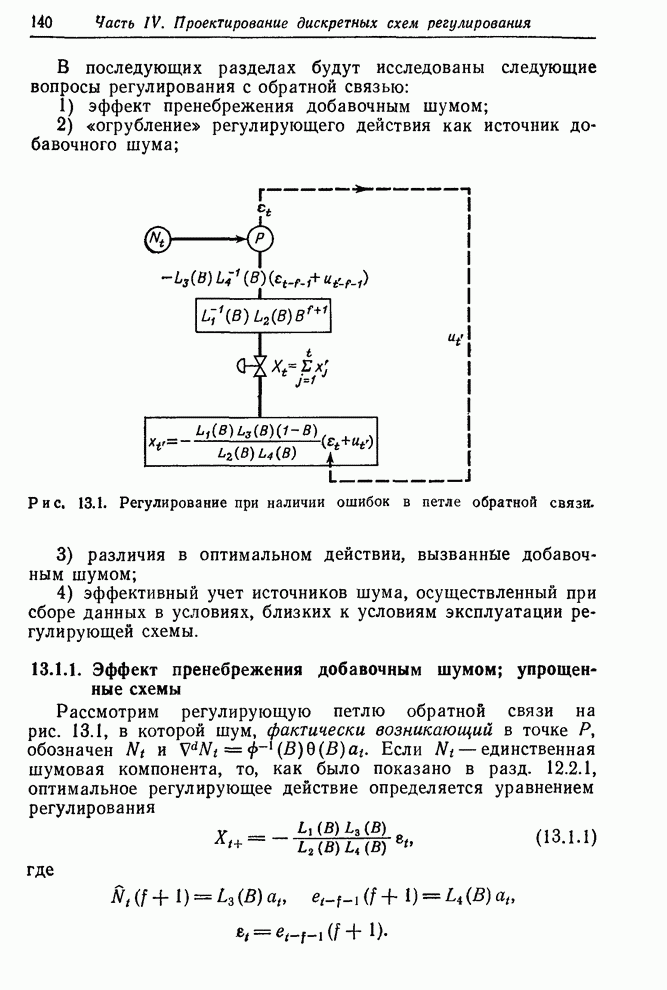
- 13.1. ЭФФЕКТ ДОБАВОЧНОГО ШУМА В СХЕМАХ РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ
- 13.1.1. Эффект пренебрежения добавочным шумом; упрощенные схемы
- 13.1.2. Оптимальное действие в случаях, когда корректировки содержат ошибки наблюдения
- 13.1.3. Перенос источника шума
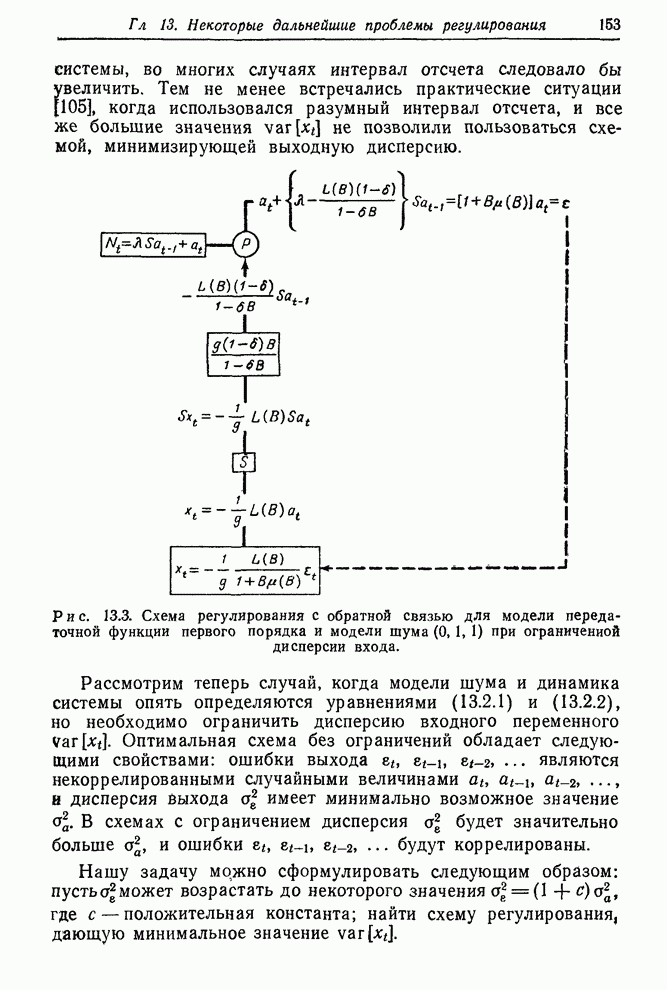
- 13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
- 13.2.1. Вывод выражения для оптимальной корректировки
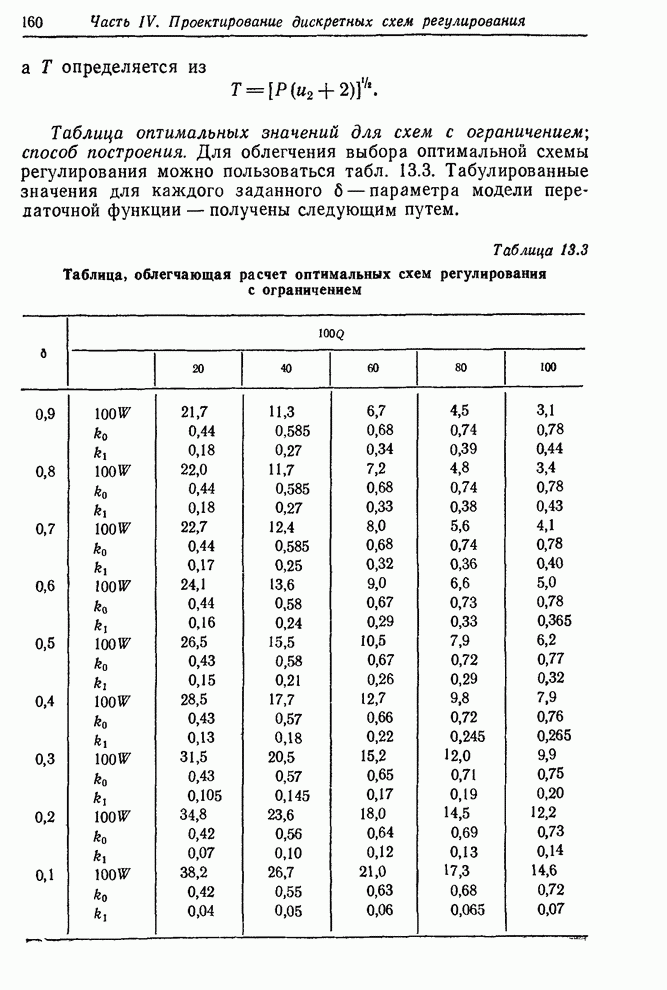
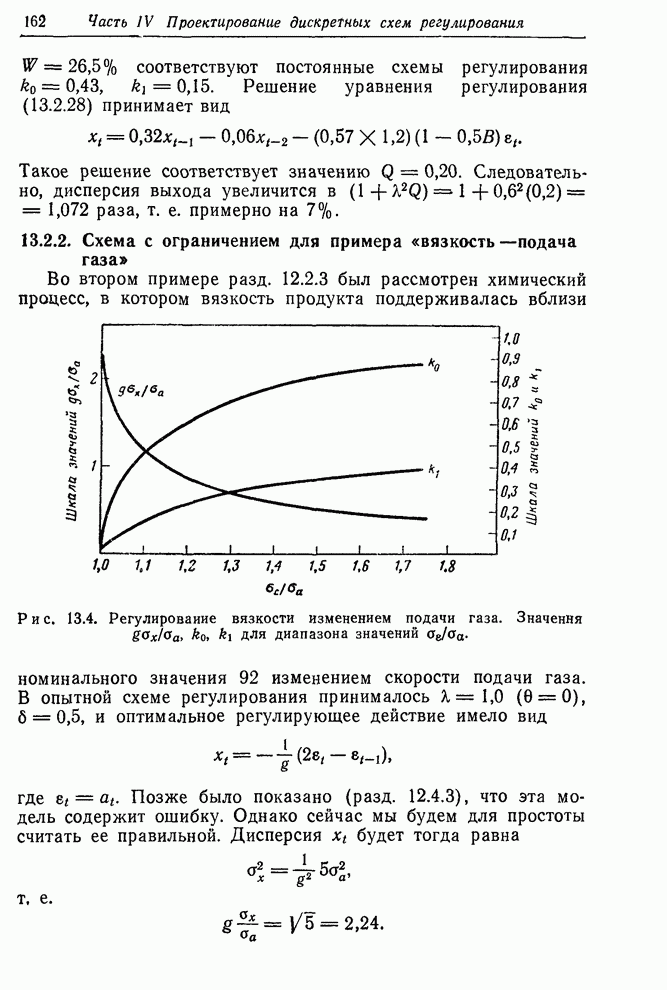
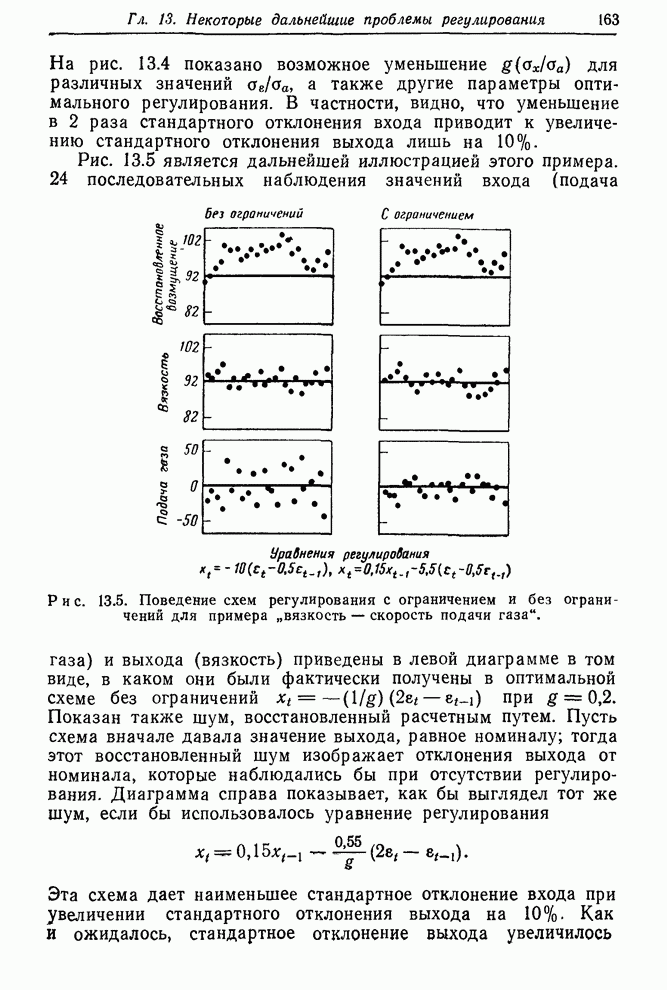
- 13.2.2. Схема с ограничением для примера «вязкость–подача газа»
- 13.3. ВЫБОР ИНТЕРВАЛА ОТСЧЕТА
- 13.3.1. Пример эффекта уменьшения частоты отсчетов
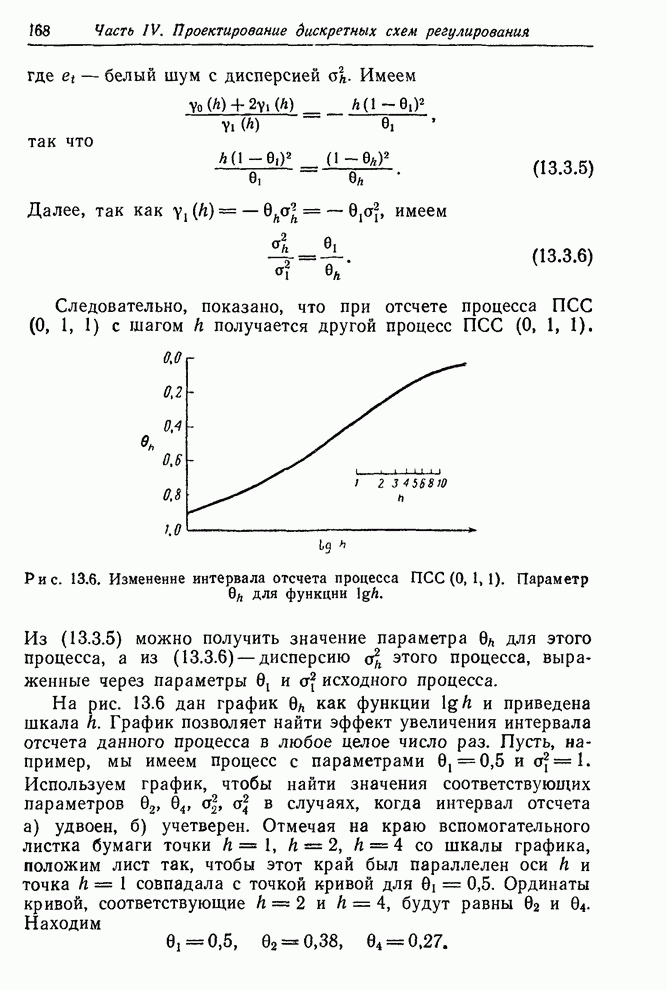
- 13.3.2. Влияние интервала отсчета на процесс ПСС(0,1,1)
- ПРОГРАММА 5. ИДЕНТИФИКАЦИЯ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 6. ПРЕДВАРИТЕЛЬНОЕ ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 7. ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
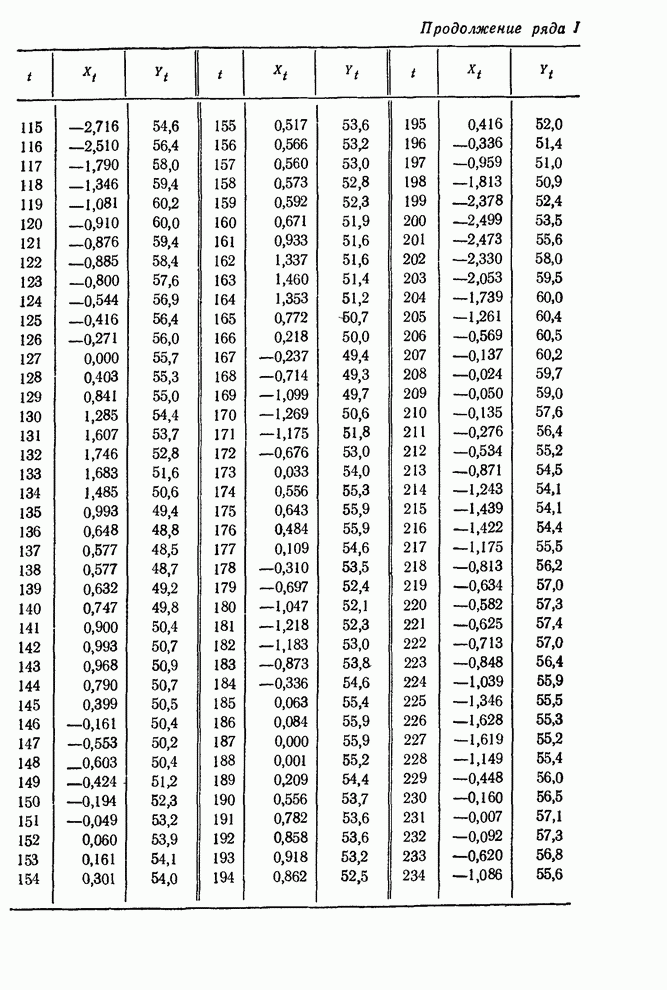
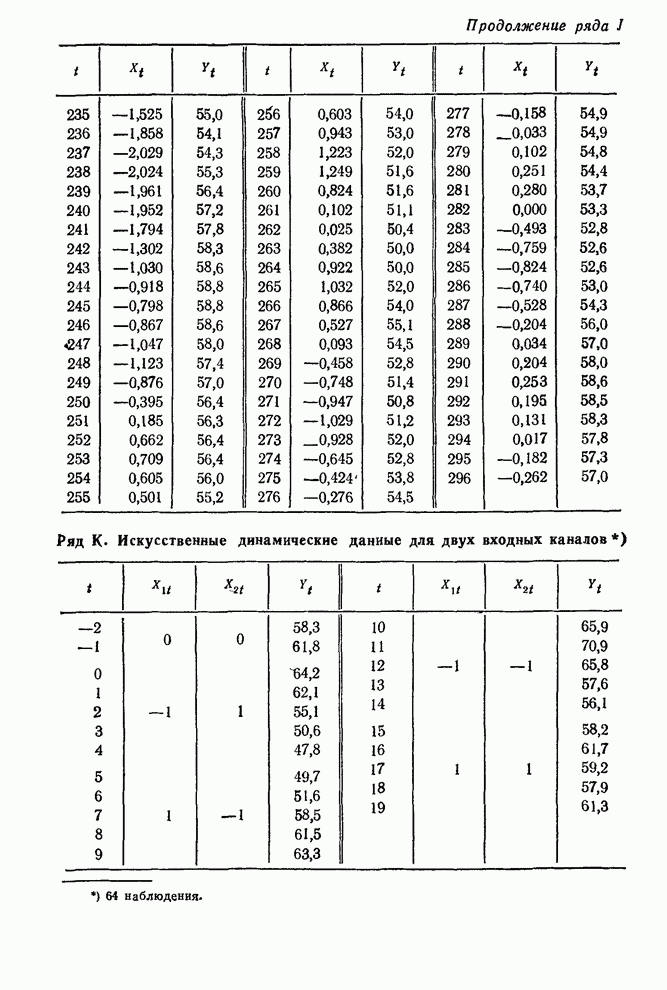
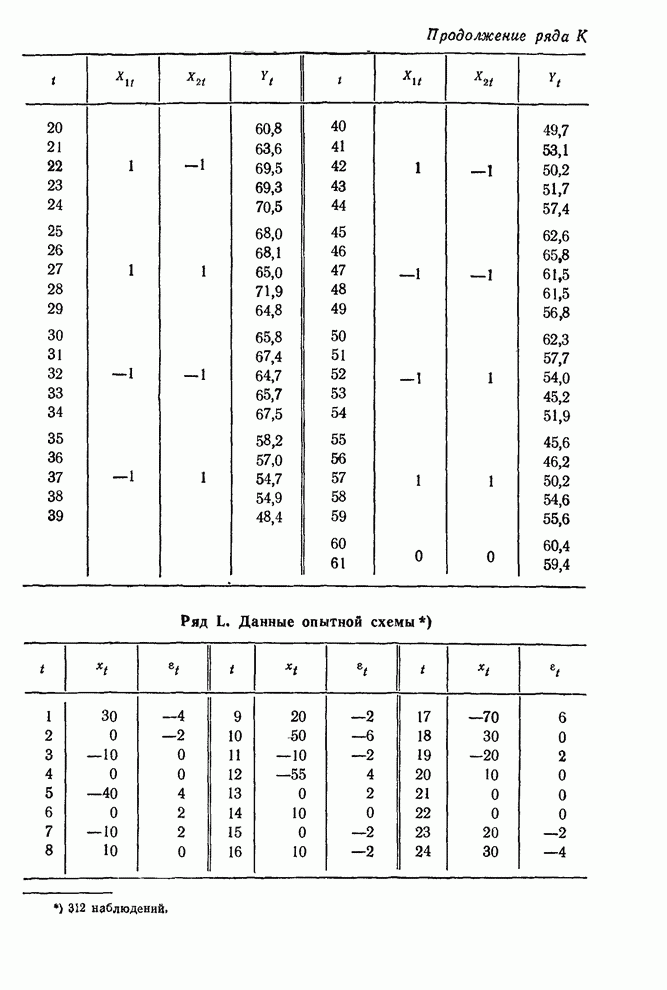
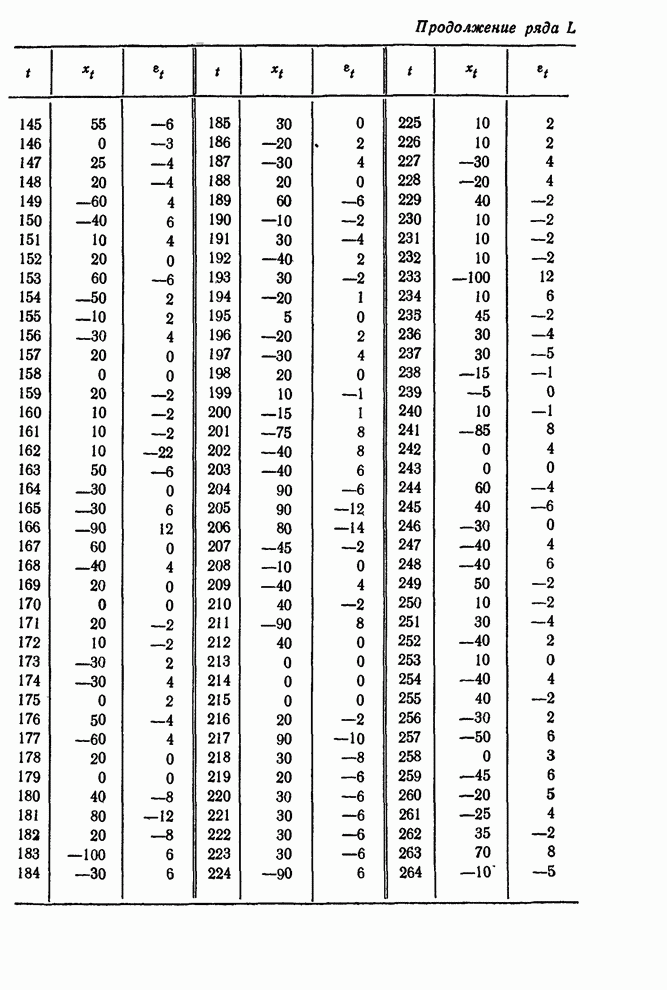
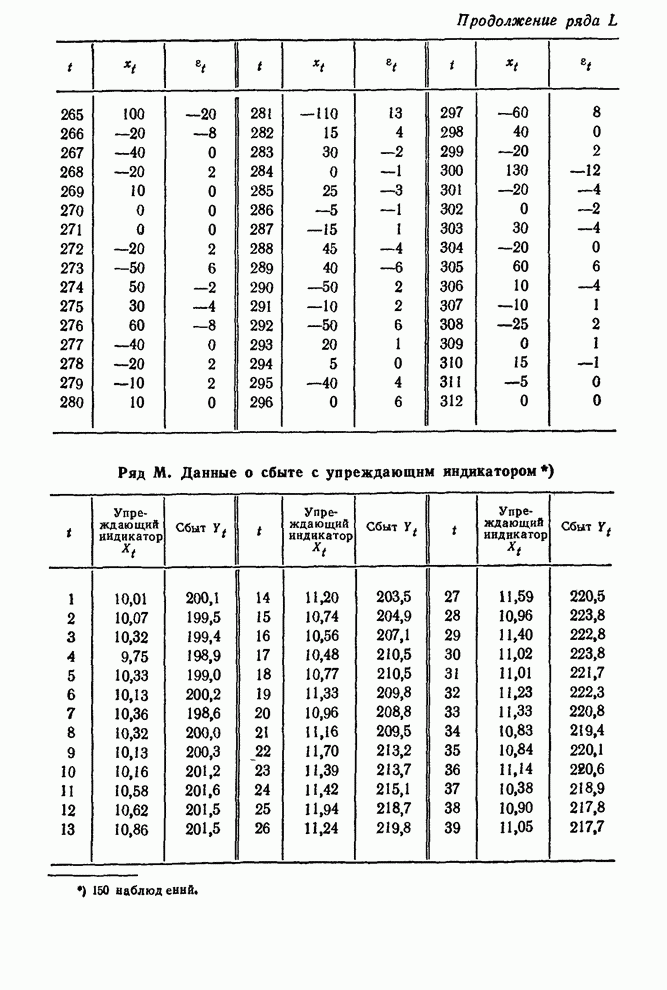
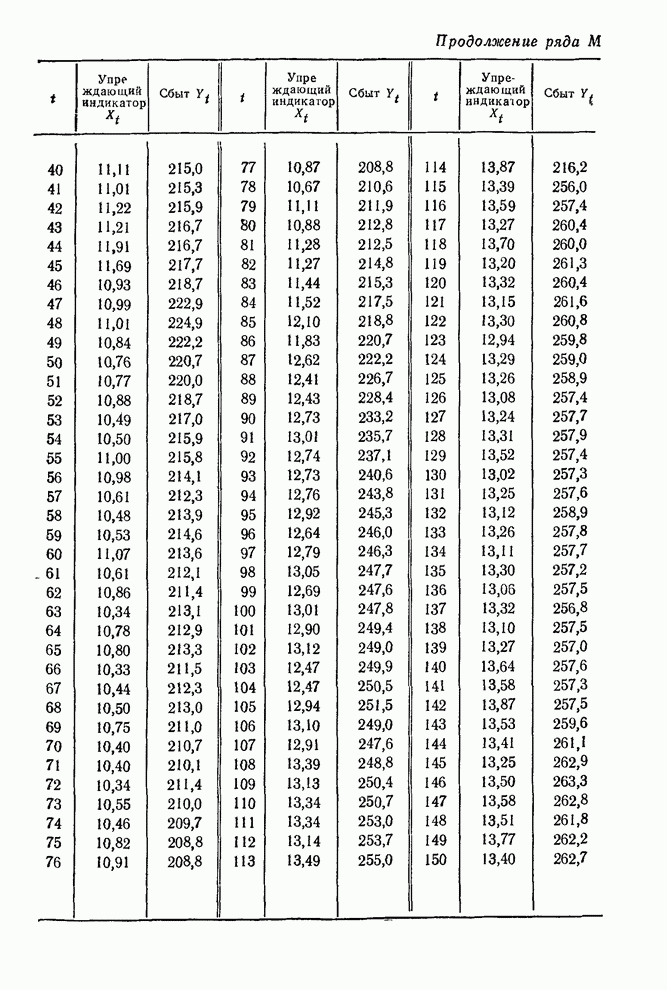
- ТАБЛИЦЫ ВРЕМЕННЫХ РЯДОВ