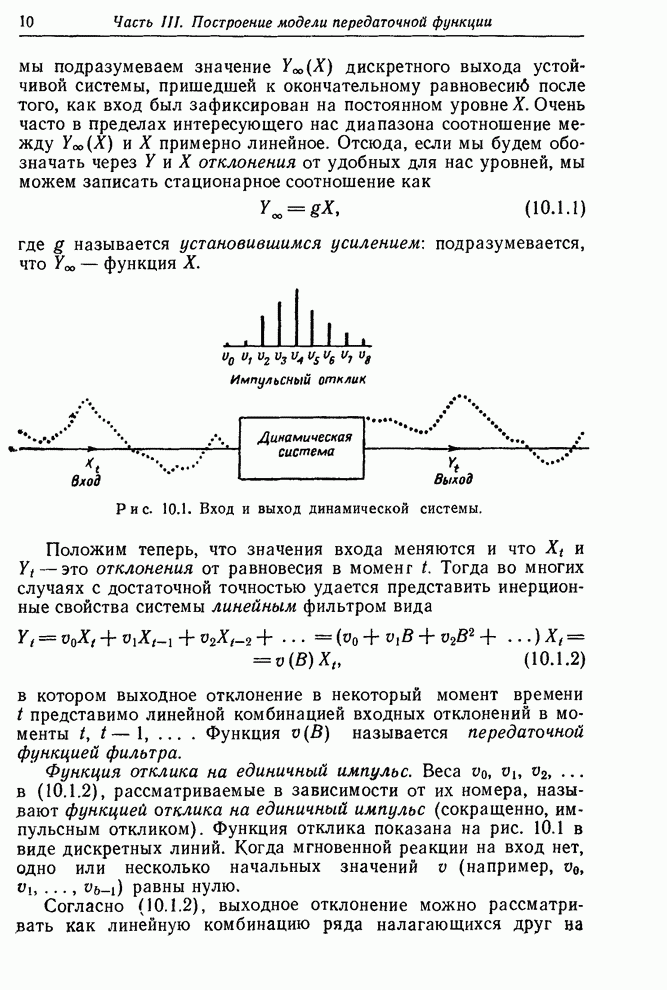
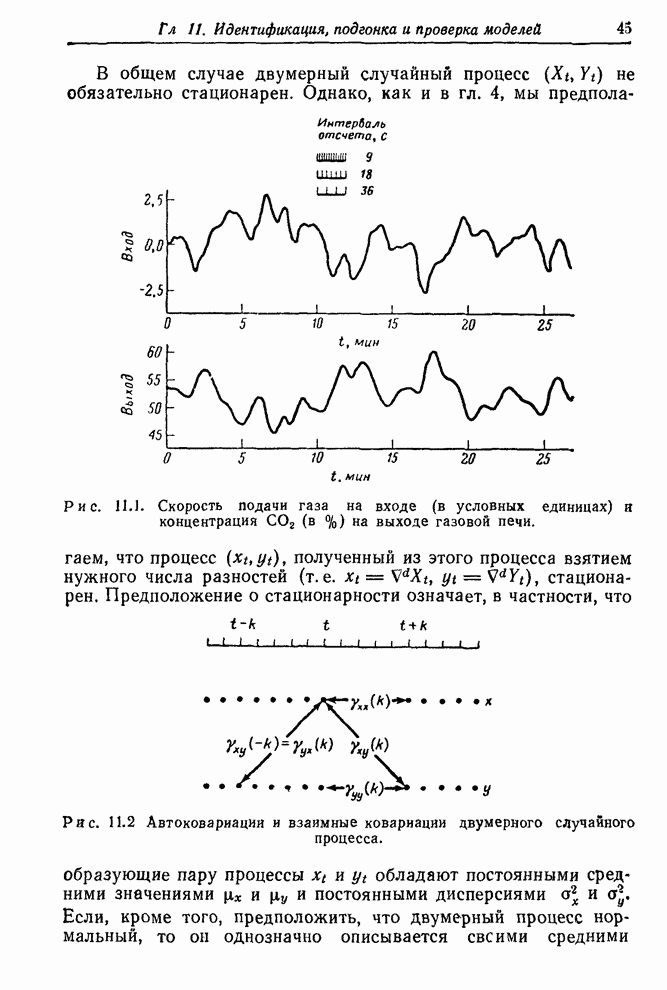
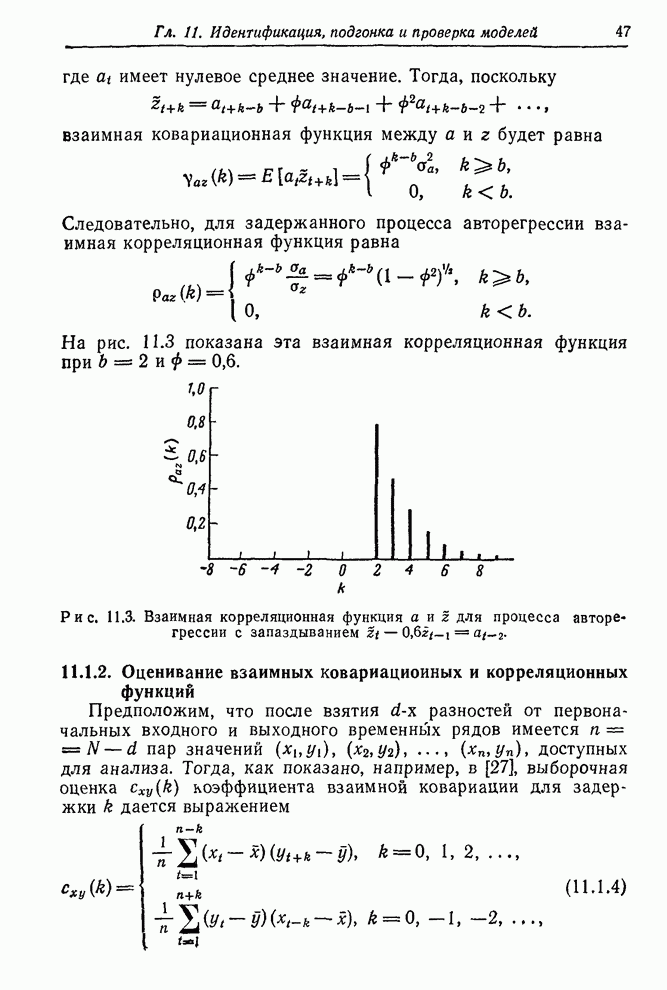
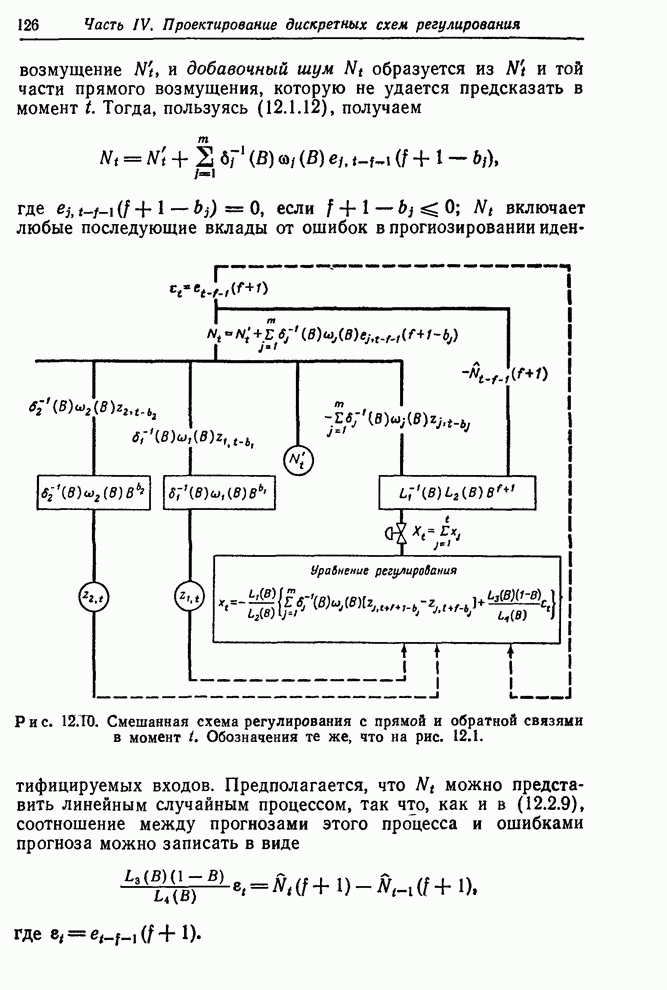
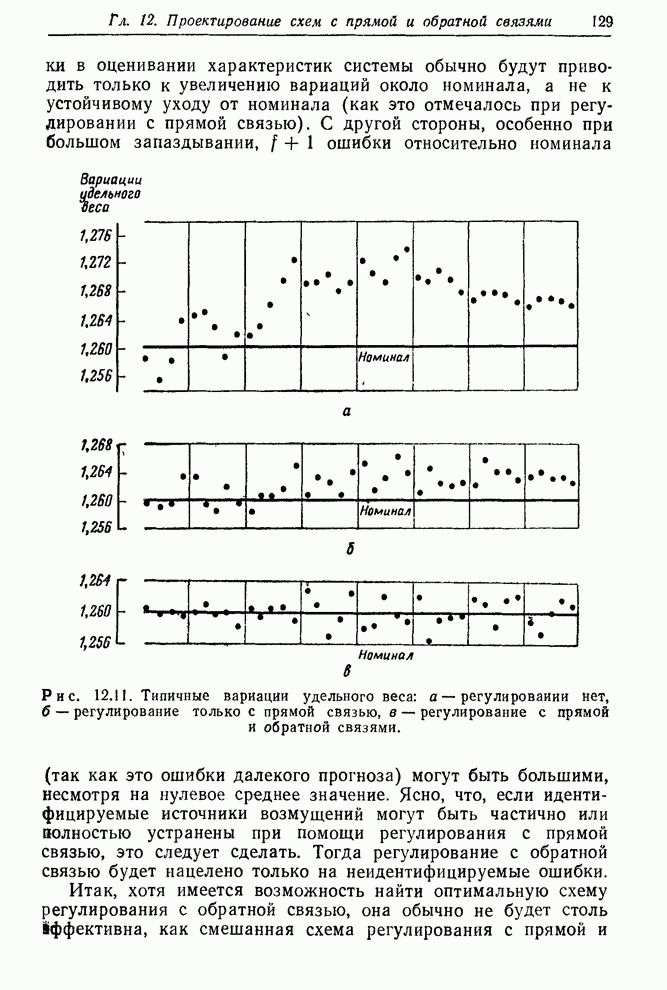
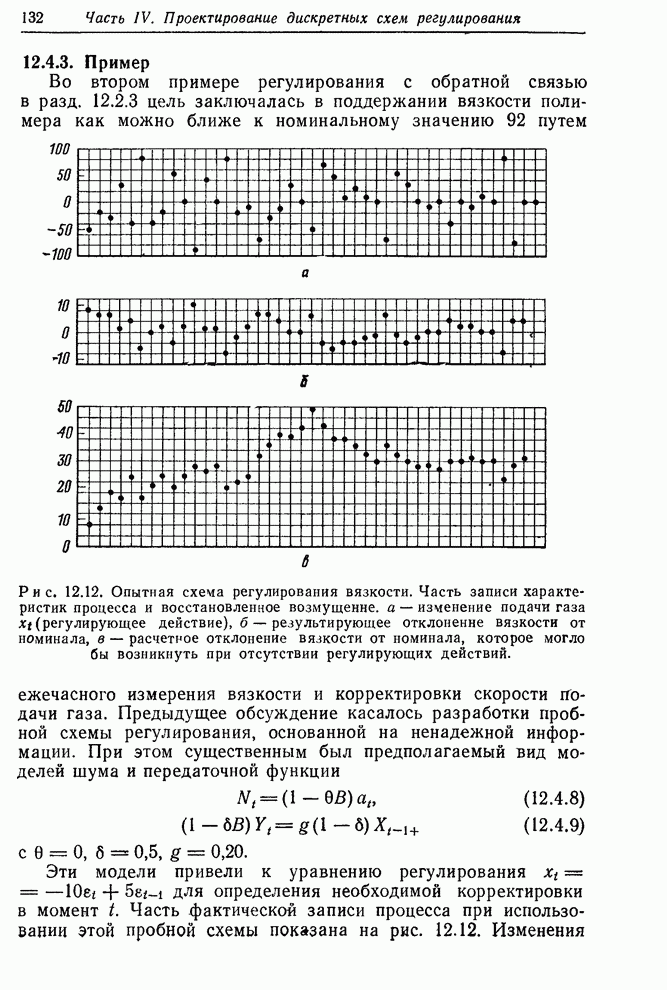
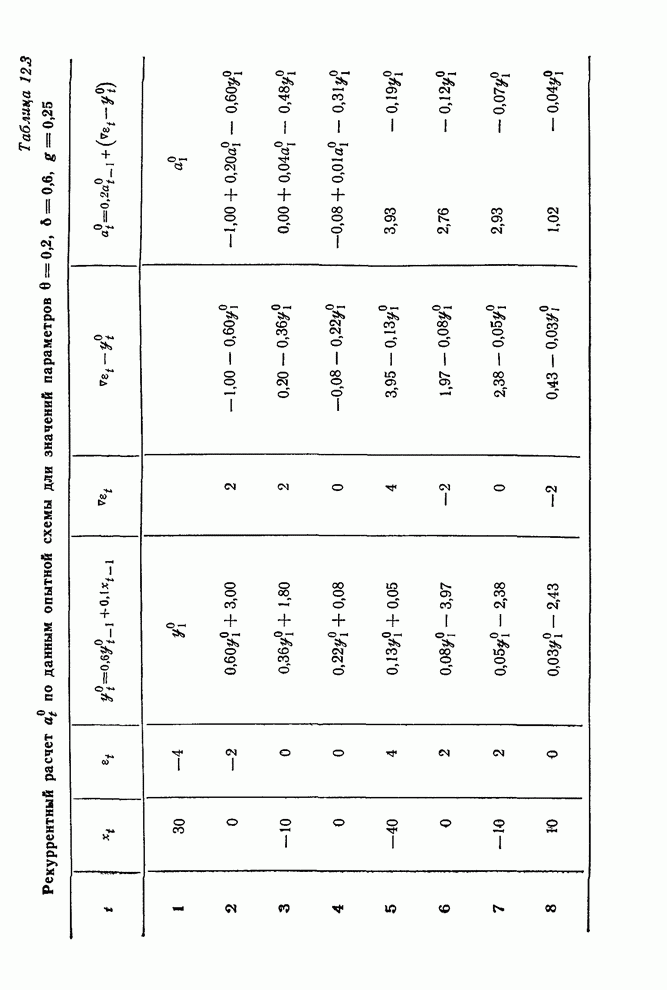
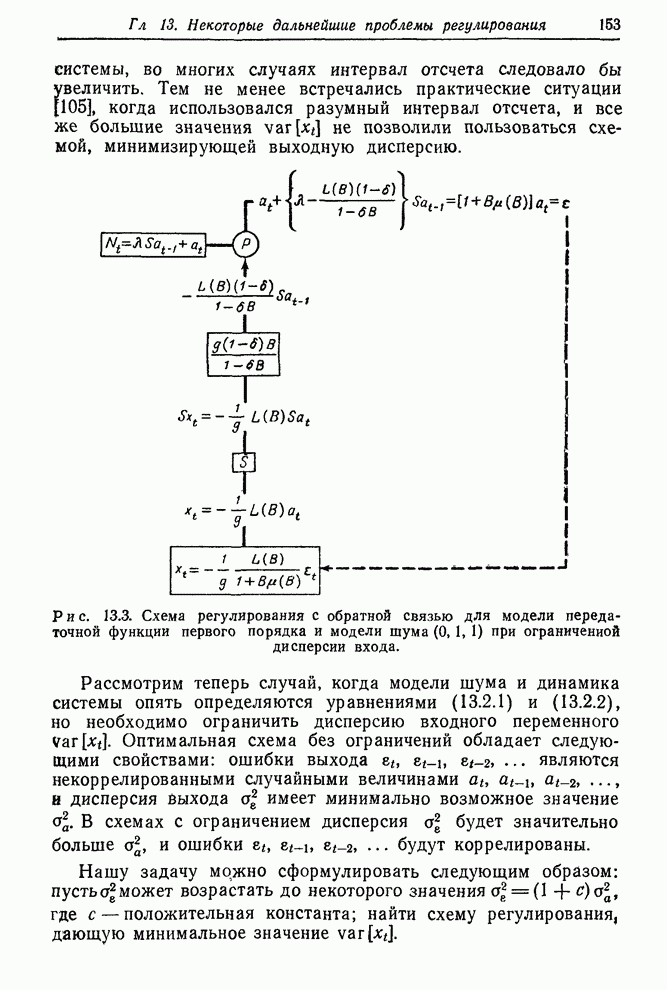
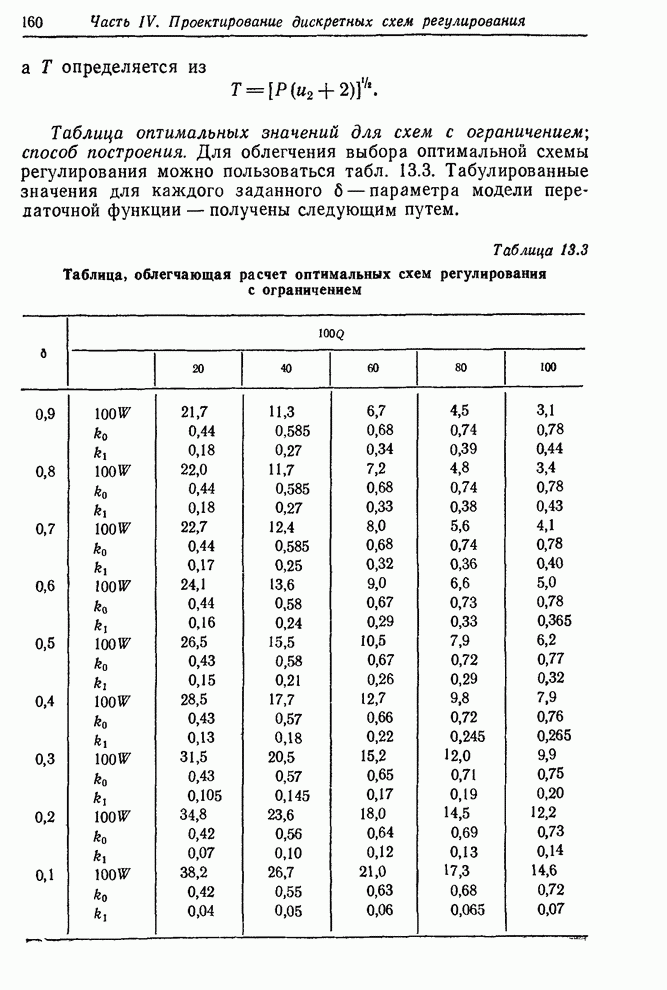
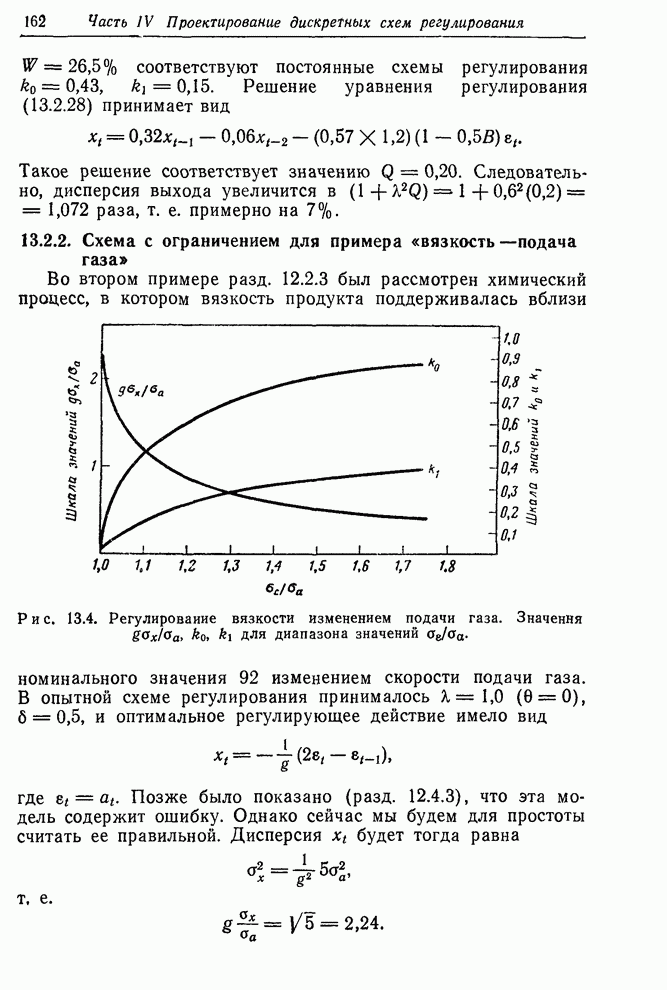
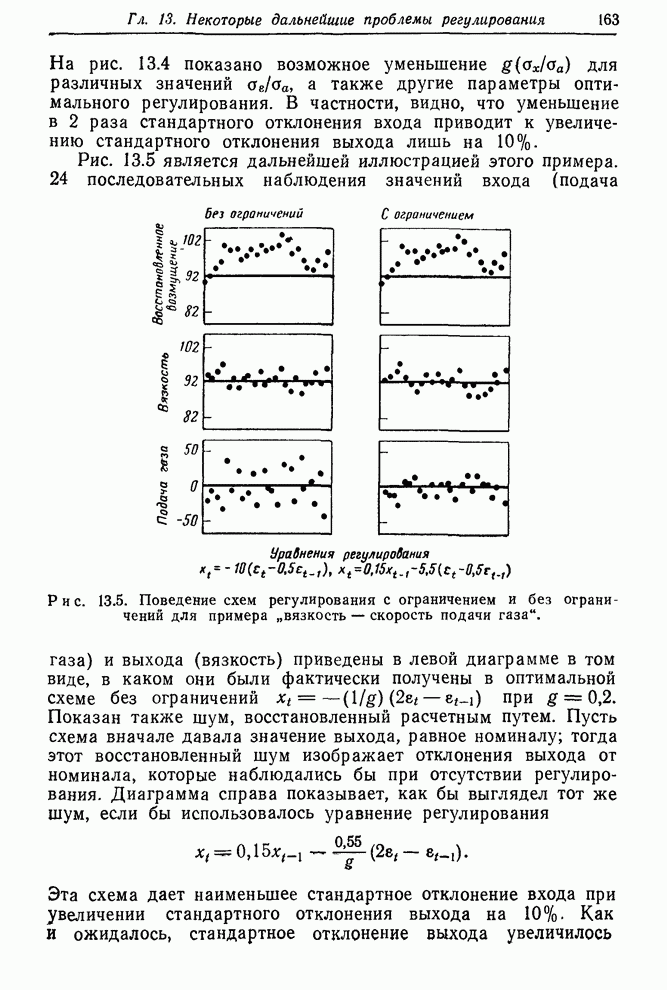
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
11.4.2. Искусственный пример с двумя входами
Подгонка моделей более чем с одним входным рядом не вызывает принципиальных трудностей, если не считать увеличения числа анализируемых параметров.
Например, в случае двух входов можно записать модель как
![]()
с
![]() ,
,
где
![]() ,
, ![]() ,
, ![]() и
и ![]() — стационарные процессы. Для
вычисления
— стационарные процессы. Для
вычисления ![]() мы
вначале вычислим при конкретных значениях параметров
мы
вначале вычислим при конкретных значениях параметров ![]()
![]() , (11.4.3)
, (11.4.3)
и
при конкретных значениях параметров ![]()
![]() . (11.4.4)
. (11.4.4)
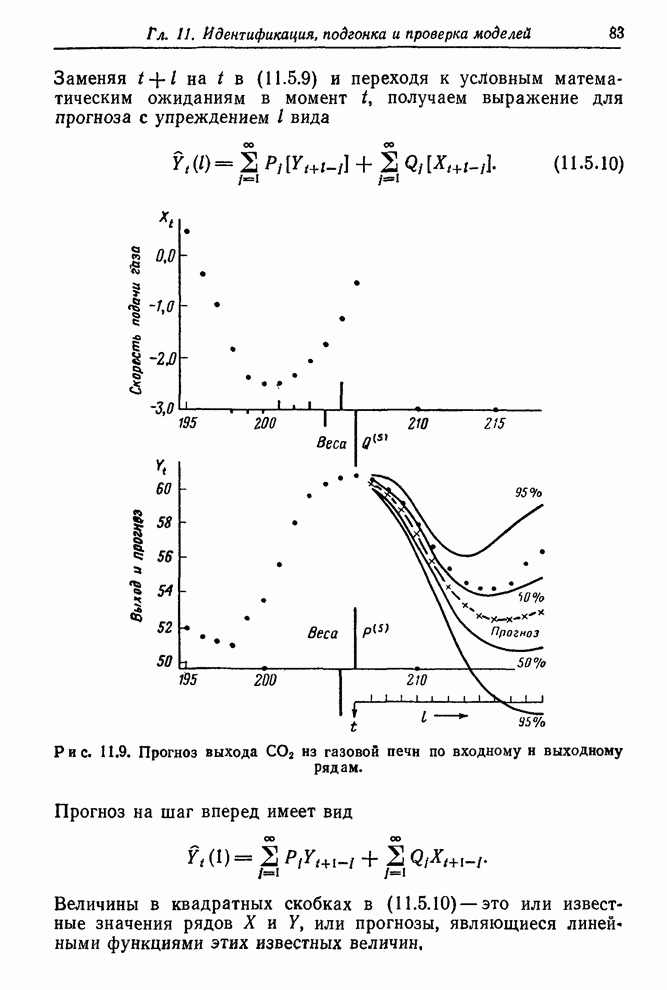
Тогда
шум ![]() можно
вычислить по формуле
можно
вычислить по формуле
![]() , (11.4.5)
, (11.4.5)
и,
наконец, ![]() по
формуле
по
формуле
![]() . (11.4.6)
. (11.4.6)
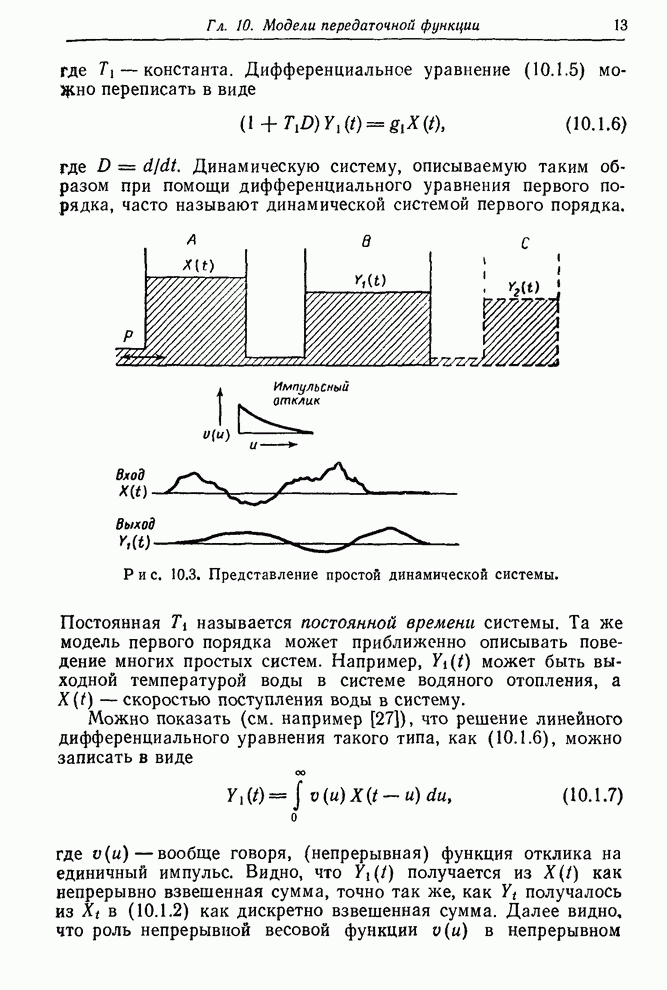
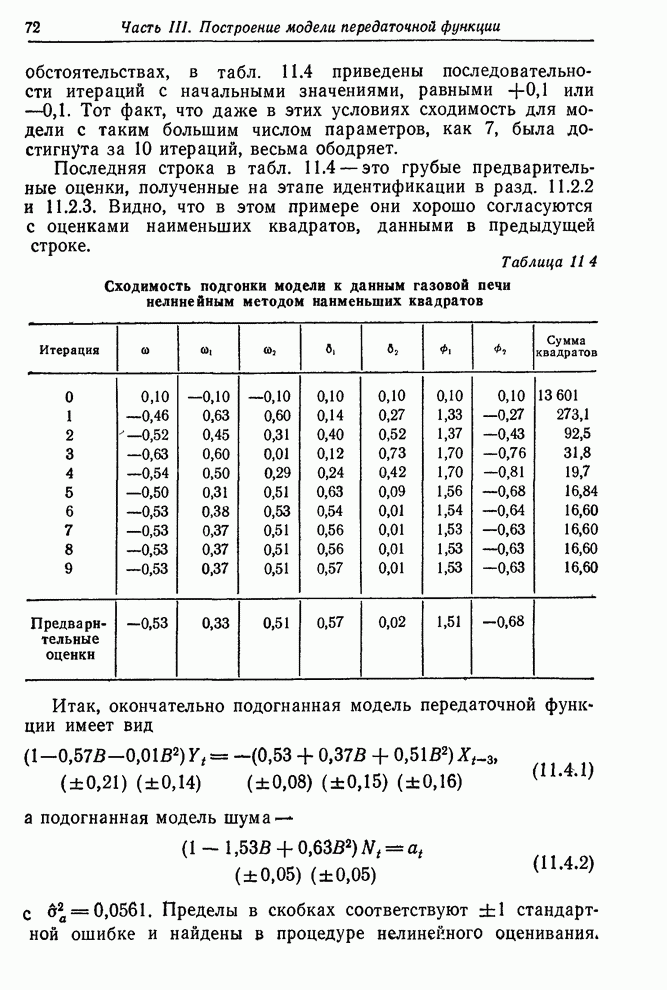
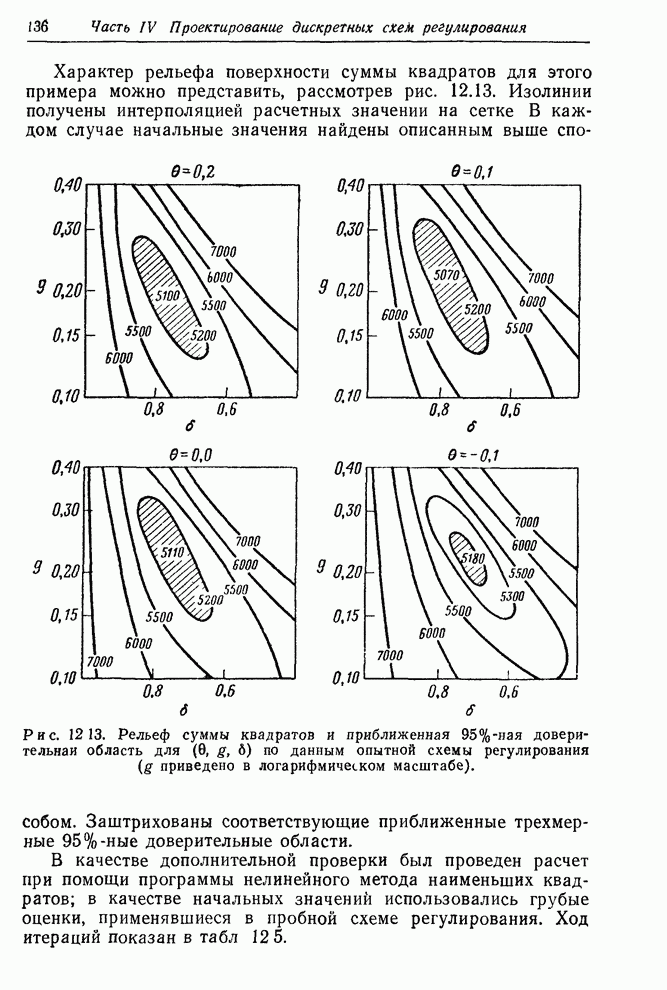
Искусственный пример. Ясно, что даже простая ситуация может привести к оцениванию большого числа параметров. В нижеследующем примере с двумя входными переменными и моделями первого порядка с запаздыванием имеется восемь неизвестных параметров. Для того чтобы определить, применима ли для оценок параметров в таких моделях нелинейная процедура наименьших квадратов, описанная в разд. 11.3.2, был проведен эксперимент с искусственными данными.

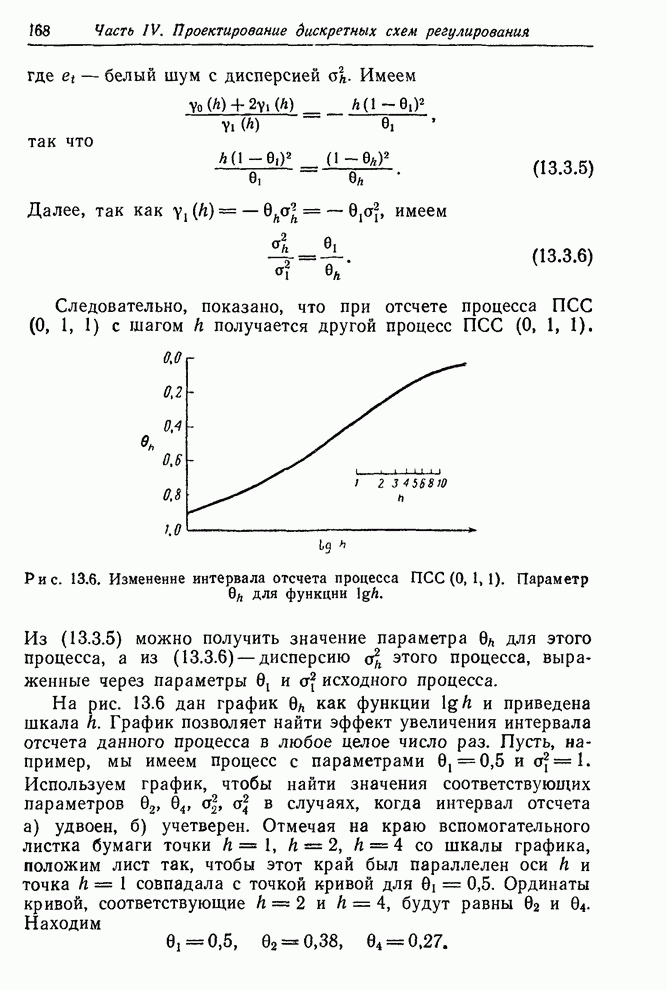
Рис. 11.8. Данные искусственного
примера с двумя входами (ряд ![]() ).
).
Подробности
эксперимента описаны в [85]. Данные генерировались моделью, ![]() -представление
которой имело вид
-представление
которой имело вид
![]() (11.4.5)
(11.4.5)
с
![]() и
и ![]() . Входные переменные
. Входные переменные ![]() ,
, ![]() изменялись в соответствии с
рандомизированным
изменялись в соответствии с
рандомизированным ![]() -факториальным
планом с тремя репликами. Предполагалось, что каждое значение на входе
поддерживалось постоянным в течение 5 мин, а наблюдения на выходе делались
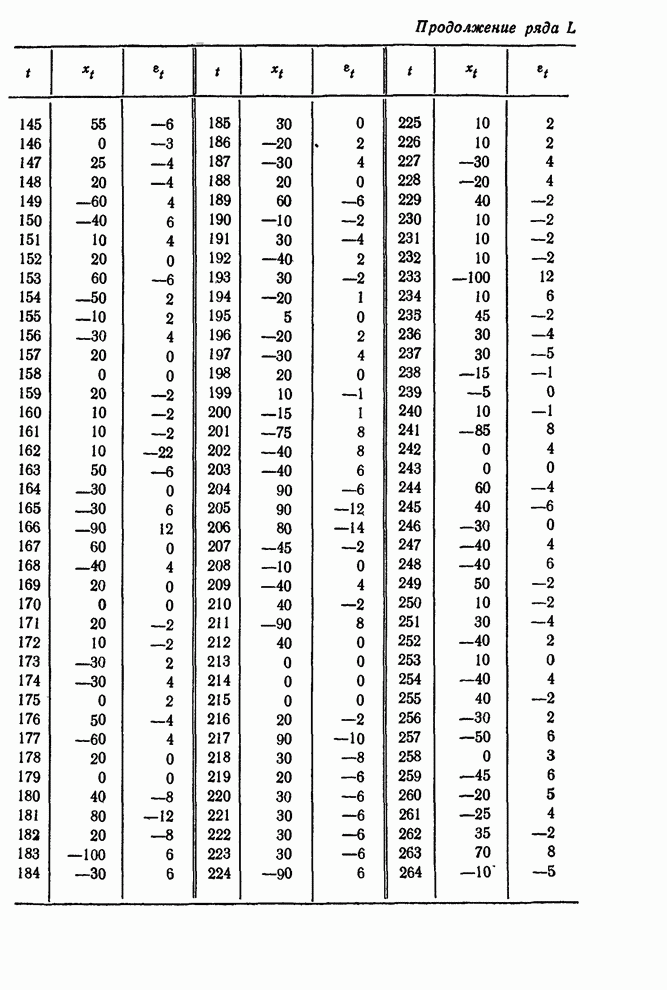
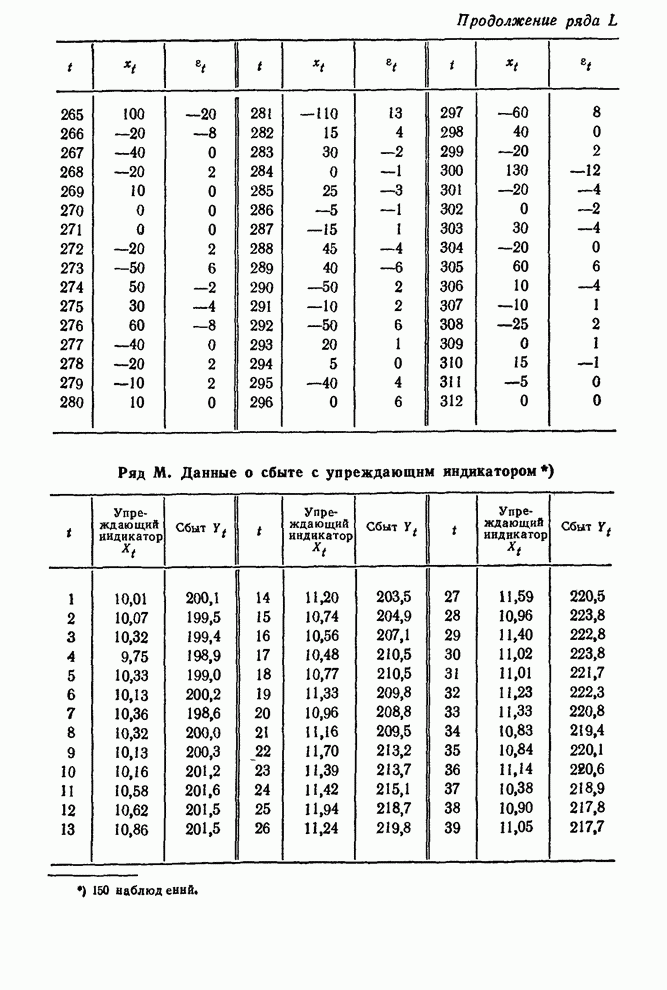
каждую минуту. Данные представлены на рис. 11.8 и содержатся в виде ряда
-факториальным
планом с тремя репликами. Предполагалось, что каждое значение на входе
поддерживалось постоянным в течение 5 мин, а наблюдения на выходе делались
каждую минуту. Данные представлены на рис. 11.8 и содержатся в виде ряда ![]() в сводке временных
рядов в конце книги.
в сводке временных
рядов в конце книги.
Для
получения оценок наименьших квадратов использовалась итеративная нелинейная
процедура с ограничениями, описанная в гл. 7. Необходимо было только вычислять
![]() . Так, для
заданных значений параметров
. Так, для
заданных значений параметров ![]() значения
значения ![]() и
и ![]() можно было получить из
можно было получить из
![]() ,
,
![]() .
.
Они
использовались для расчета ![]() :
:
![]() .
.
Наконец,
при заданных ![]() значения
значения
![]() можно было
вычислить по формуле
можно было
вычислить по формуле
![]() .
.
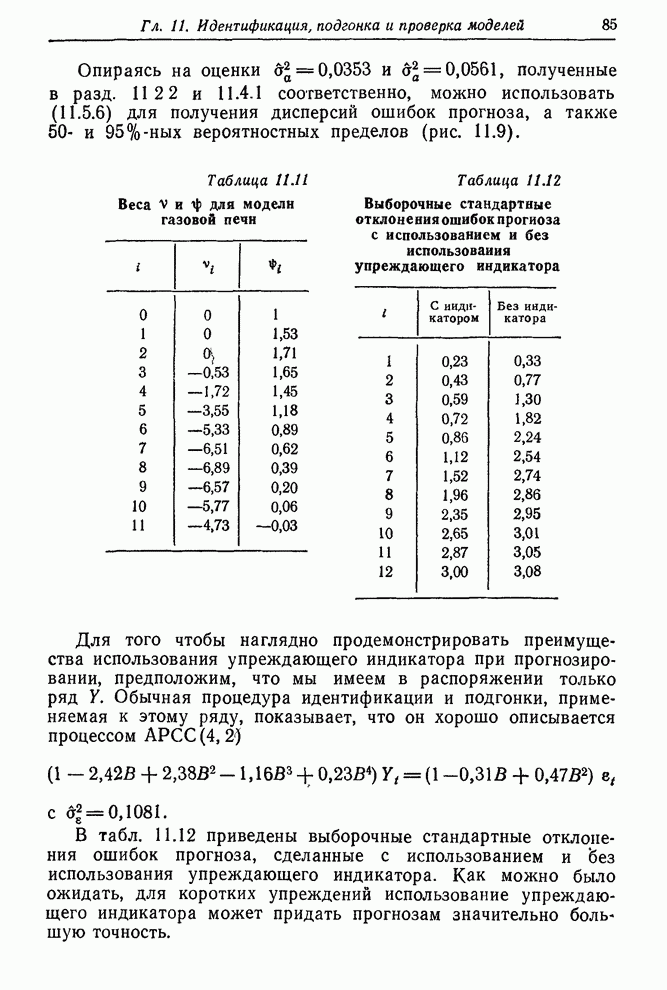
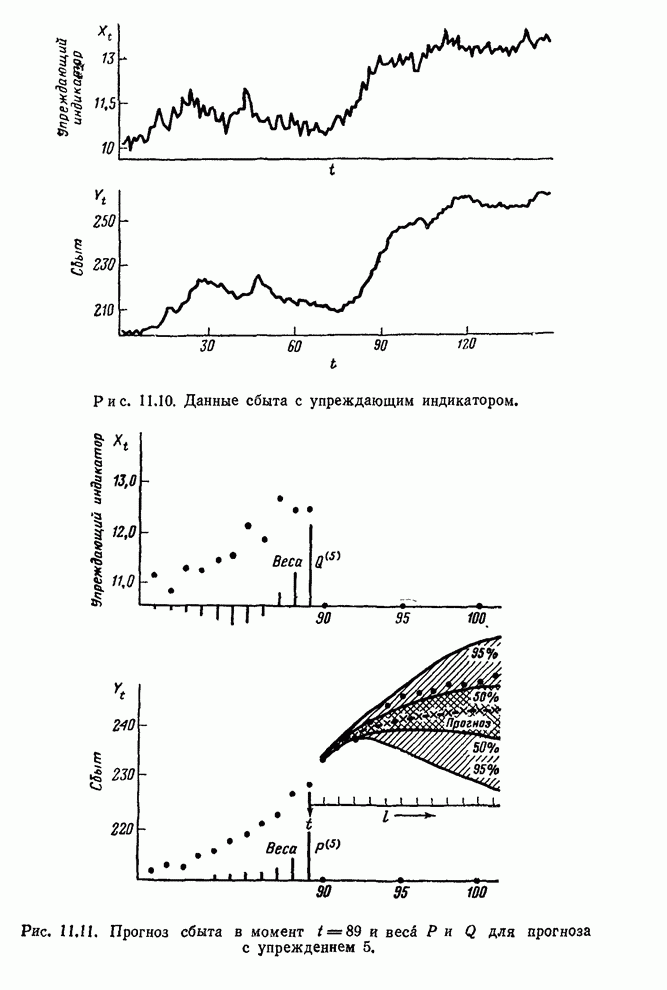
Предполагалось,
что входы процесса поддерживаются в типичных условиях некоторое время до
начала эксперимента, так что ![]() и
и ![]() и, следовательно,
и, следовательно, ![]() можно вычислять вперед с
можно вычислять вперед с ![]() , а
, а ![]() с
с ![]() .
.
Процедура
опробовалась дважды, с разными наборами начальных значений. В первом расчете
был взят набор параметров, который мог бы предложить человек, знакомый с
изучаемым процессом. Во втором в качестве начального значения ![]() было взято среднее
значение
было взято среднее
значение ![]() всех
наблюдений, а остальные начальные значения были приравнены 0,1. Поэтому вторая
попытка описывает значительно худшую ситуацию, чем обычно бывает на практике.
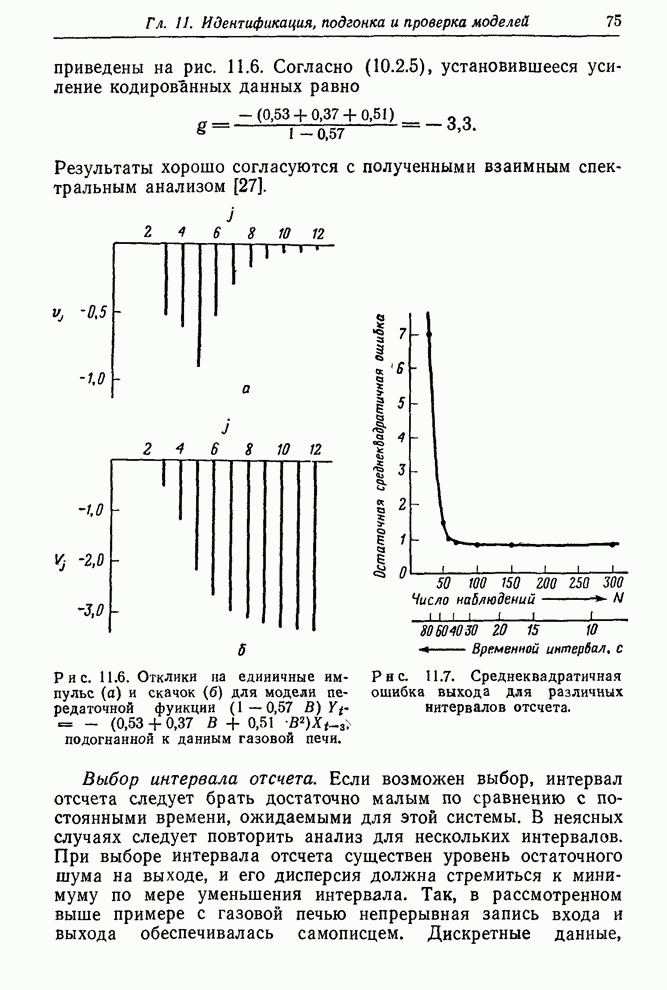
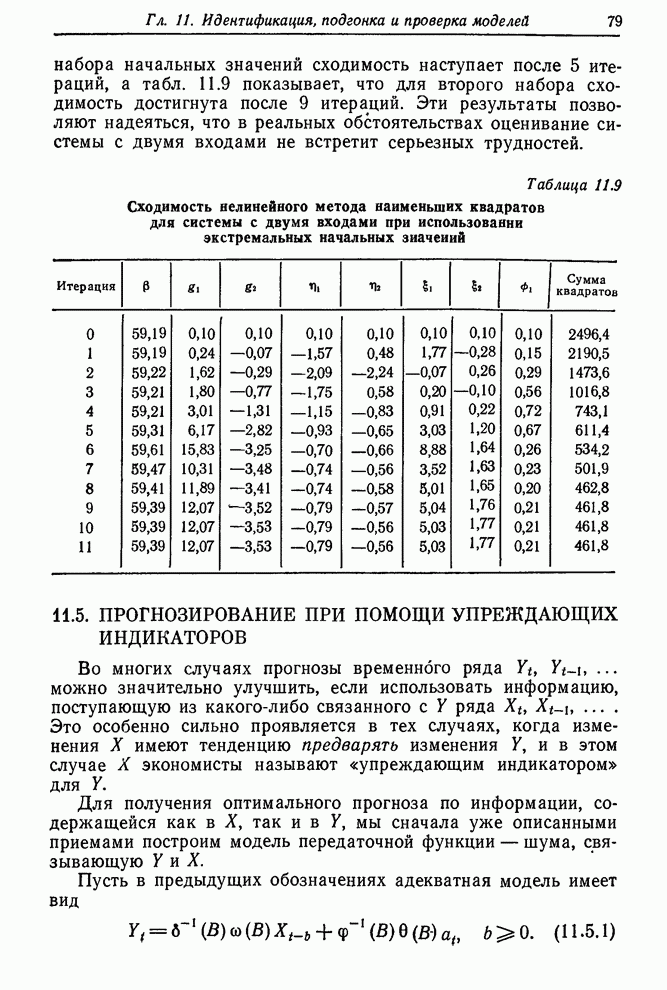
В табл. 11.8 показано, что для первого набора начальных значений сходимость
наступает после 5 итераций, а табл. 11.9 показывает, что для второго набора
сходимость достигнута после 9 итераций. Эти результаты позволяют надеяться,
что в реальных обстоятельствах оценивание системы с двумя входами не встретит
серьезных трудностей.
всех
наблюдений, а остальные начальные значения были приравнены 0,1. Поэтому вторая
попытка описывает значительно худшую ситуацию, чем обычно бывает на практике.
В табл. 11.8 показано, что для первого набора начальных значений сходимость
наступает после 5 итераций, а табл. 11.9 показывает, что для второго набора
сходимость достигнута после 9 итераций. Эти результаты позволяют надеяться,
что в реальных обстоятельствах оценивание системы с двумя входами не встретит
серьезных трудностей.
Таблица 11.8. Сходимость нелинейного метода наименьших квадратов для системы с двумя входами при использовании предположительных начальных значений
|
Интерация |
|
|
|
|
|
|
|
|
Сумма квадратов |
|
0 1 2 3 4 5 6 7 8 |
59,19 59,20 59,24 59,35 59,41 59,39 59,39 59,39 59,39 |
10,00 9,07 8,38 9,24 11,90 12,03 12,08 12,07 12,07 |
-7,00 -6,37 -5,35 -3,98 -3,40 -3,52 -3,53 -3,53 -3,53 |
-0,50 -0,58 -0,70 -0,75 -0,75 -0,80 -0,79 -0,79 -0,79 |
-0,50 -0,56 -0,59 -0,55 -0,56 -0,57 -0,56 -0,56 -0,56 |
1,00 1,33 2,03 3,45 5,21 4,99 5,03 5,03 5,03 |
1,00 1,31 1,75 1,95 1,66 1,76 1,77 1,77 1,77 |
0,10 0,24 0,39 0,36 0,22 0,21 0,21 0,21 0,21 |
2046,8 1085,4 621,5 503,5 463,7 461,8 461,8 461,8 461,8 |
Таблица 11.9. Сходимость нелинейного метода наименьших квадратов для системы с двумя входами при использовании экстремальных начальных значений
|
Интерация |
|
|
|
|
|
|
|
|
Сумма квадратов |
|
0 1 2 3 4 5 6 7 8 9 10 11 |
59,19 59,19 59,22 59,21 59,21 59,31 59,61 59,47 59,41 59,39 59,39 59,39 |
0,10 0,24 1,62 1,80 3,01 6,17 15,83 10,31 11,89 12,07 12,07 12,07 |
0,10 -0,07 -0,29 -0,77 -1,31 -2,82 -3,25 -3,48 -3,41 -3,52 -3,53 -3,53 |
0,10 -1,51 -2,09 -1,75 -1,15 -0,93 -0,70 -0,74 -0,74 -0,79 -0,79 -0,79 |
0,10 1,77 -0,07 0,20 0,91 3,03 8,88 3,52 5,01 5,04 5,03 5,03 |
0,10 1,77 -0,07 0,20 0,91 3,03 8,88 3,52 5,01 5,04 5,03 5,03 |
0,10 -0,28 0,26 -0,10 0,22 1,20 1,64 1,63 1,65 1,76 1,77 1,77 |
0,10 0,15 0,29 0,56 0,72 0,67 0,26 0,23 0,20 0,21 0,21 0,21 |
2496,4 2190,5 1473,6 1016,8 743,1 611,4 534,2 501,9 462,8 461,8 461,8 461,8 |
| << Предыдущий параграф | Следующий параграф >> |
- Часть III. ПОСТРОЕНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- Глава 10. Модели передаточной функции
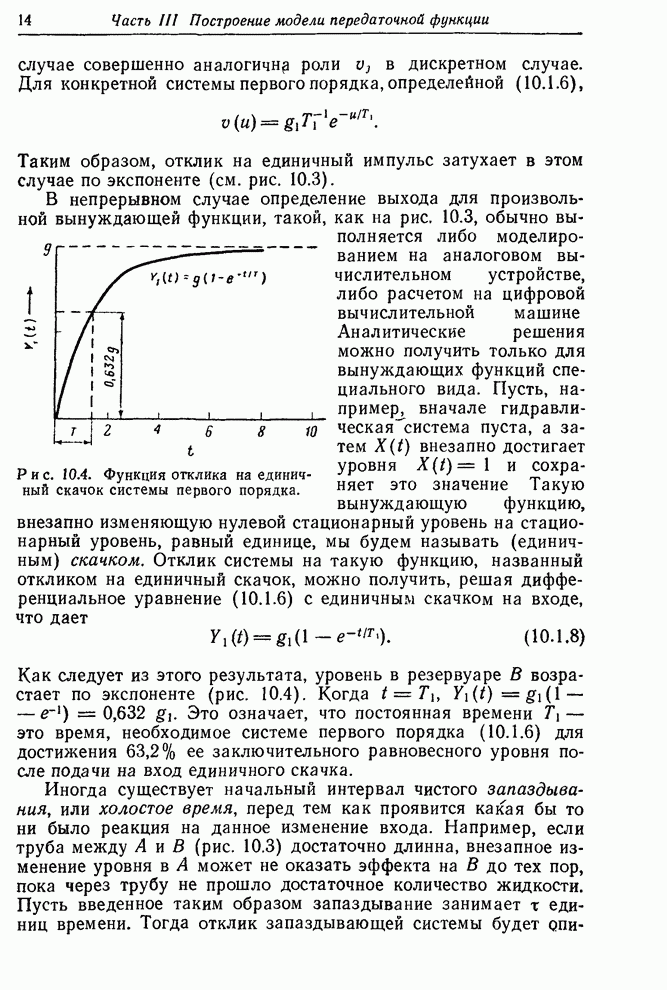
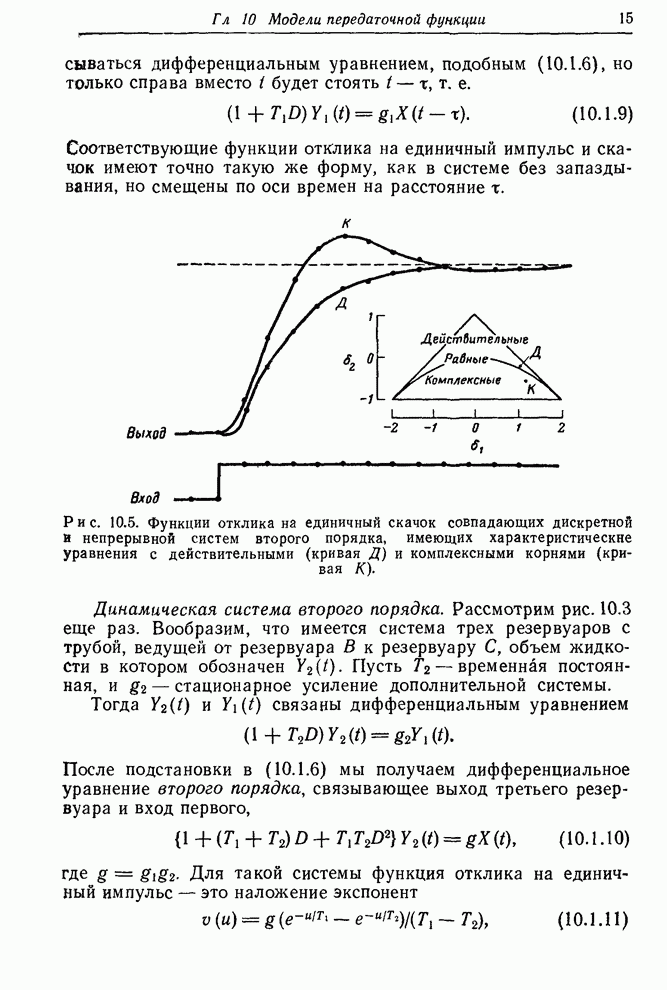
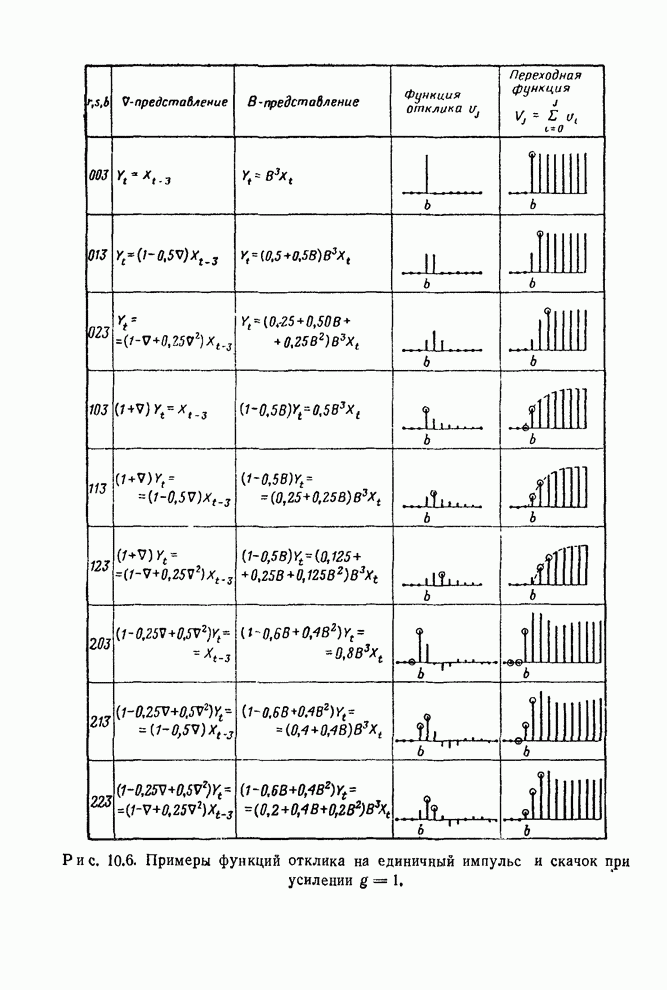
- 10.1. ЛИНЕЙНЫЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 10.1.1. Дискретная передаточная функция
- 10.1.2. Непрерывные динамические модели, описываемые дифференциальными уравнениями
- 10.2. ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ МОДЕЛИ, ОПИСЫВАЕМЫЕ РАЗНОСТНЫМИ УРАВНЕНИЯМИ
- 10.2.1. Общая форма разностного уравнения
- 10.2.2. Природа передаточной функции
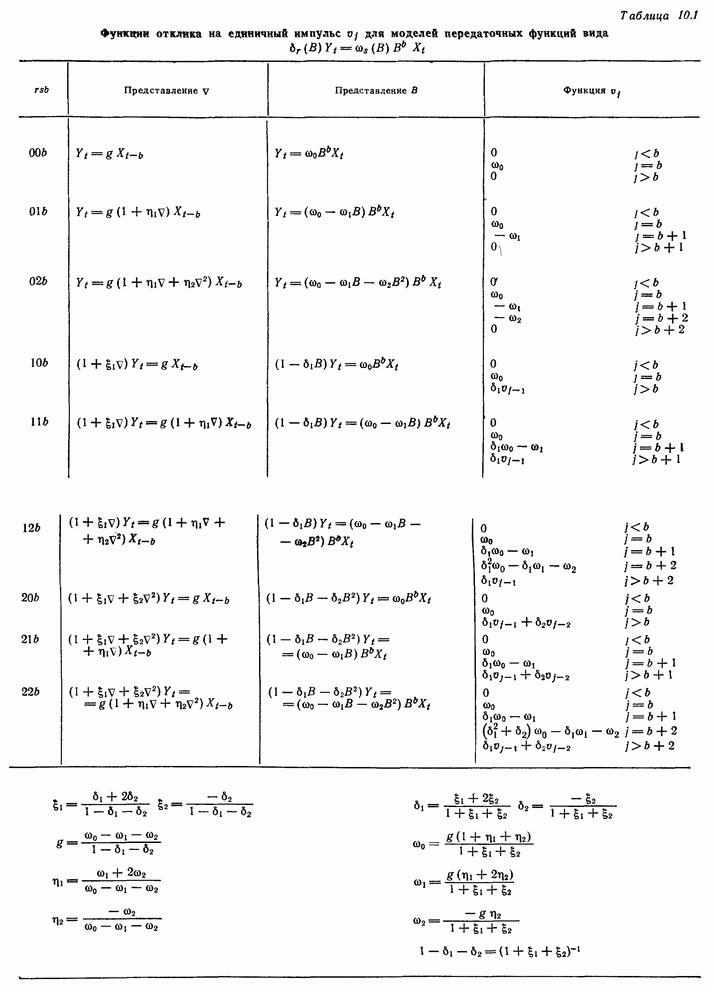
- 10.2.3. Дискретные модели передаточных функций первого и второго порядков
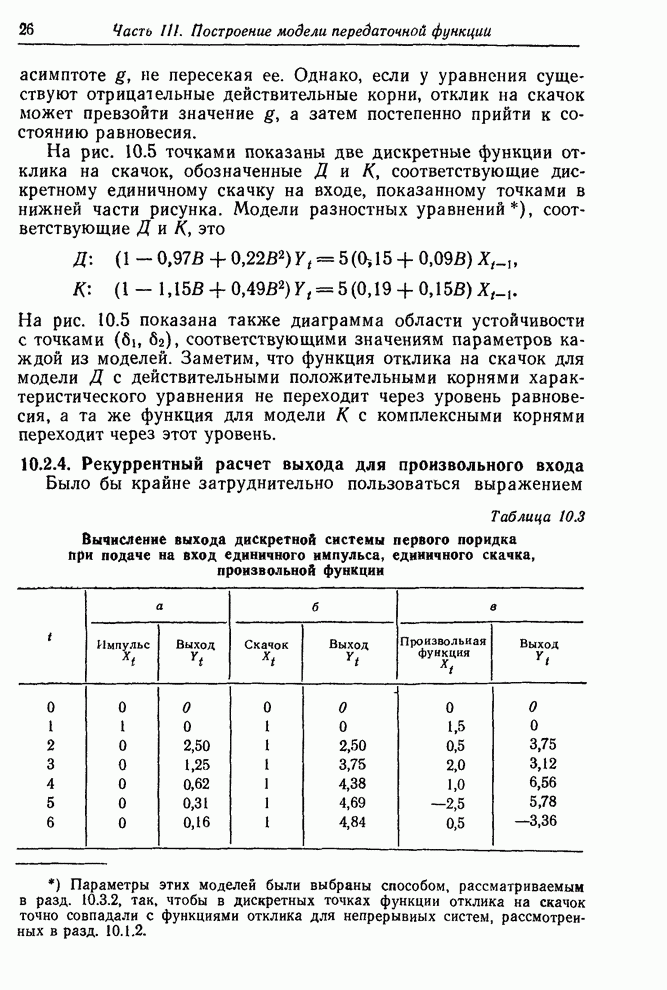
- 10.2.4. Рекуррентный расчет выхода для произвольного входа
- 10.3. СООТНОШЕНИЕ МЕЖДУ ДИСКРЕТНОЙ И НЕПРЕРЫВНОЙ МОДЕЛЯМИ
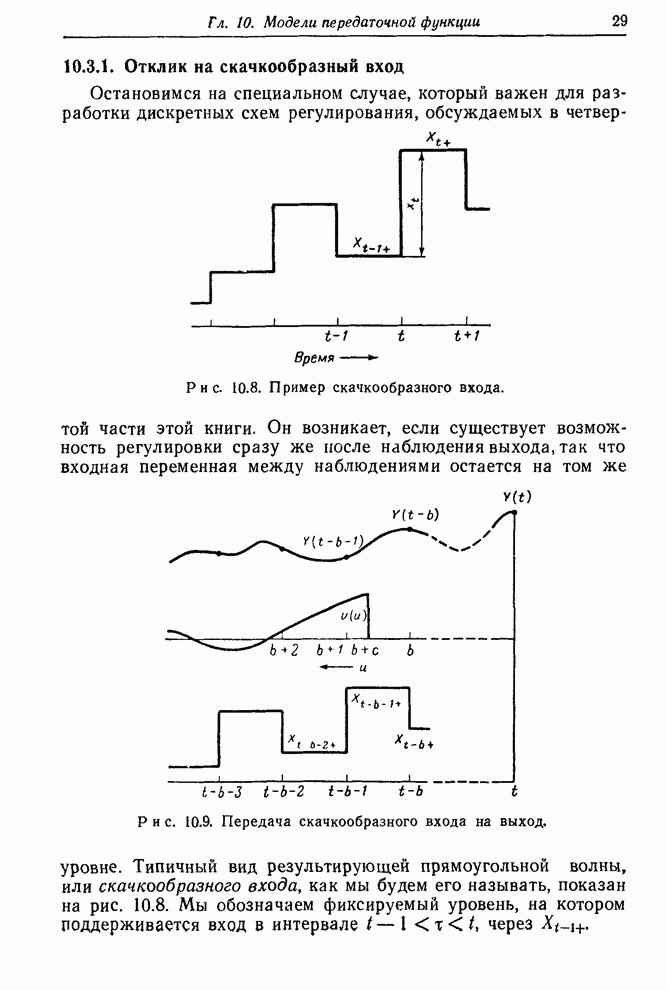
- 10.3.1. Отклик на скачкообразный вход
- 10.3.2. Соотношения совпадающих систем первого и второго порядков
- 10.3.3. Аппроксимация общих непрерывных моделей дискретными моделями
- 10.3.4. Модели передаточных функций с добавленным шумом
- ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
- ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
- Глава 11. Идентификация, подгонка и проверка моделей передаточных функций
- 11.1. Взаимная корреляционная функция
- 11.1.1. Свойства взаимных ковариационной и корреляционной функций
- 11.1.2. Оценивание взаимных ковариационных и корреляционных функций
- 11.1.3. Приближенные стандартные ошибки выборочных оценок взаимных корреляций
- 11.2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.2.1. Идентификация моделей передаточной функции с предварительным выравниванием спектра входа
- 11.2.2. Пример идентификации модели передаточной функции
- 11.2.3. Идентификация модели шума
- 11.2.4. Некоторые общие соображения об идентификации моделей передаточных функций
- 11.3. ПОДГОНКА И ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.3.1. Условная сумма квадратов
- 11.3.2. Нелинейное оценивание
- 11.3.3. Использование остаточных ошибок для диагностической проверки
- 11.3.4. Конкретные способы проверки остаточных ошибок
- 11.4. Некоторые примеры подгонок и проверок моделей передаточных функций
- 11.4.1. Подгонка и проверка модели газовой печи
- 11.4.2. Искусственный пример с двумя входами
- 11.5. ПРОГНОЗИРОВАНИЕ ПРИ ПОМОЩИ УПРЕЖДАЮЩИХ ИНДИКАТОРОВ
- 11.5.1. Прогноз с минимальной среднеквадратичной ошибкой
- 11.5.2. Прогнозы выхода СO2 из газовой печи
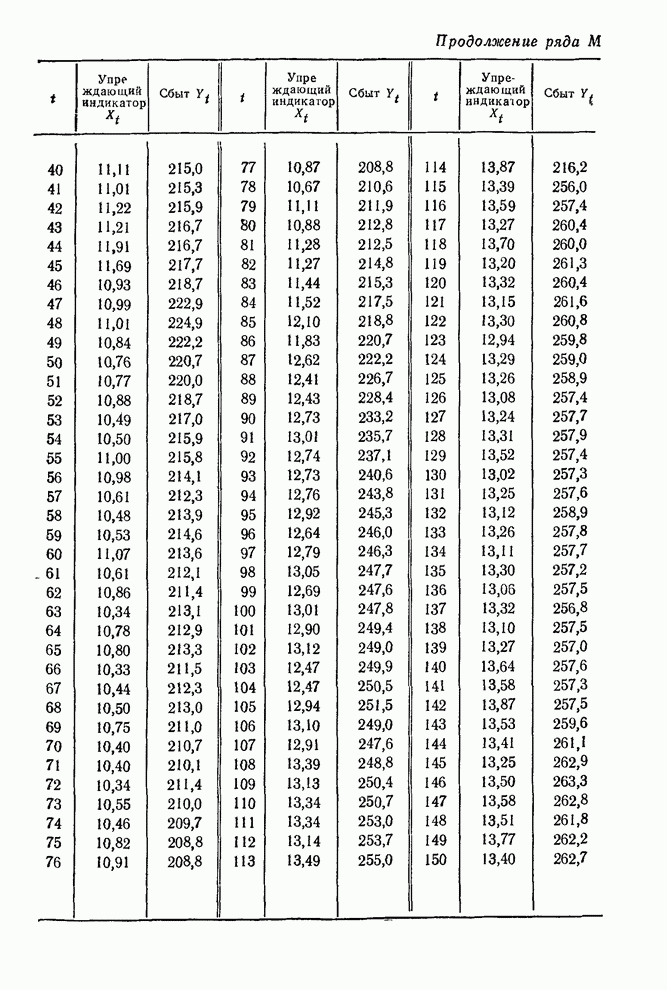
- 11.5.3. Прогноз нестационарных данных сбыта при помощи упреждающего индикатора
- 11.6. НЕКОТОРЫЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОЦЕНИВАНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ П11.1. ИСПОЛЬЗОВАНИЕ ВЗАИМНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
- Заключение
- Часть IV. Проектирование дискретных схем регулирования
- Глава 12. Проектирование схем регулирования с прямой и обратной связями
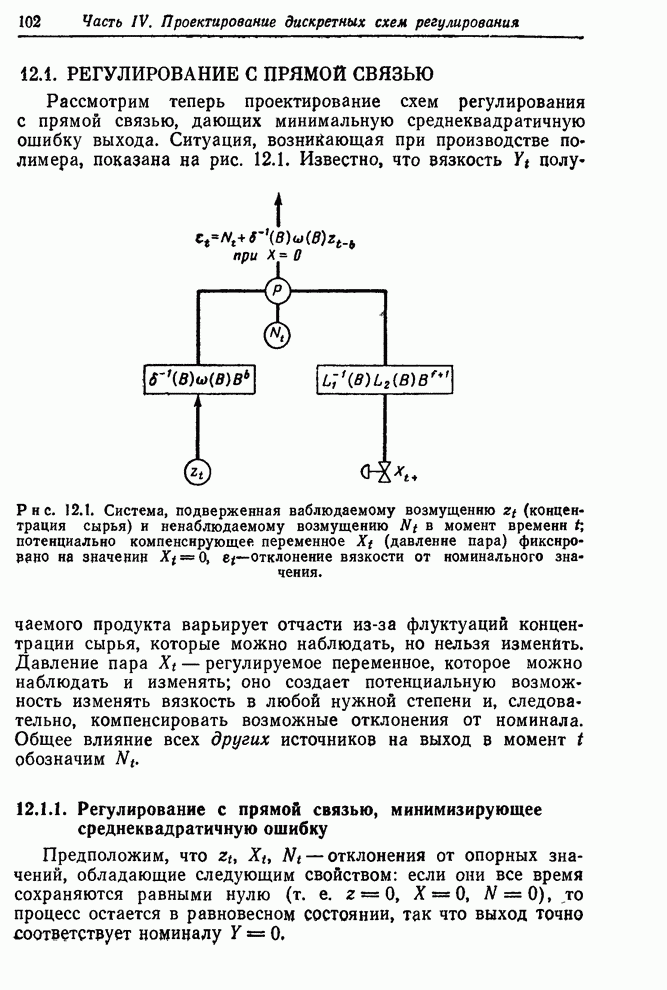
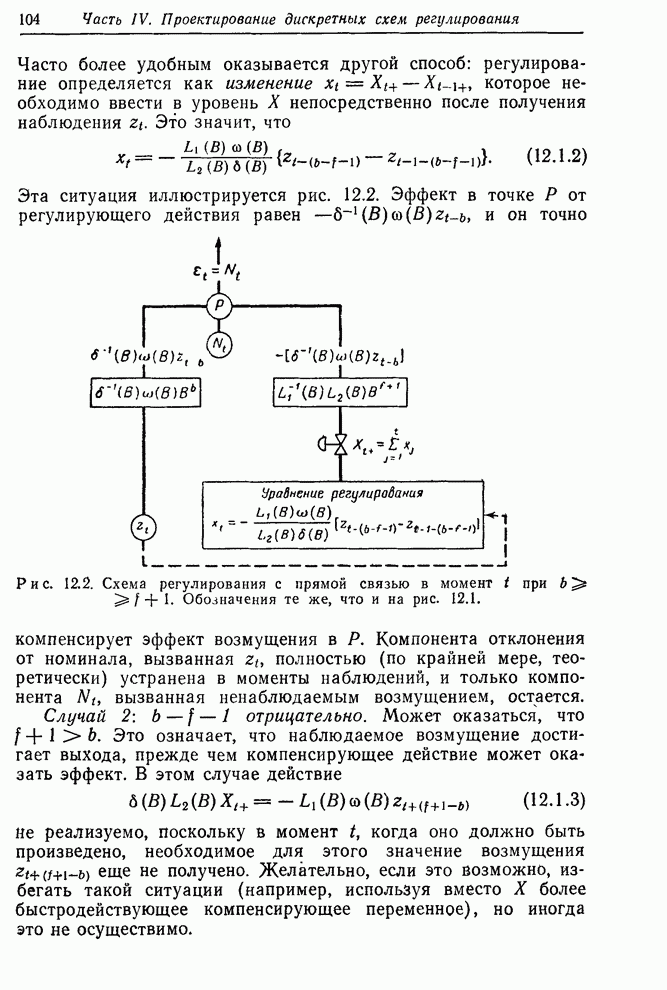
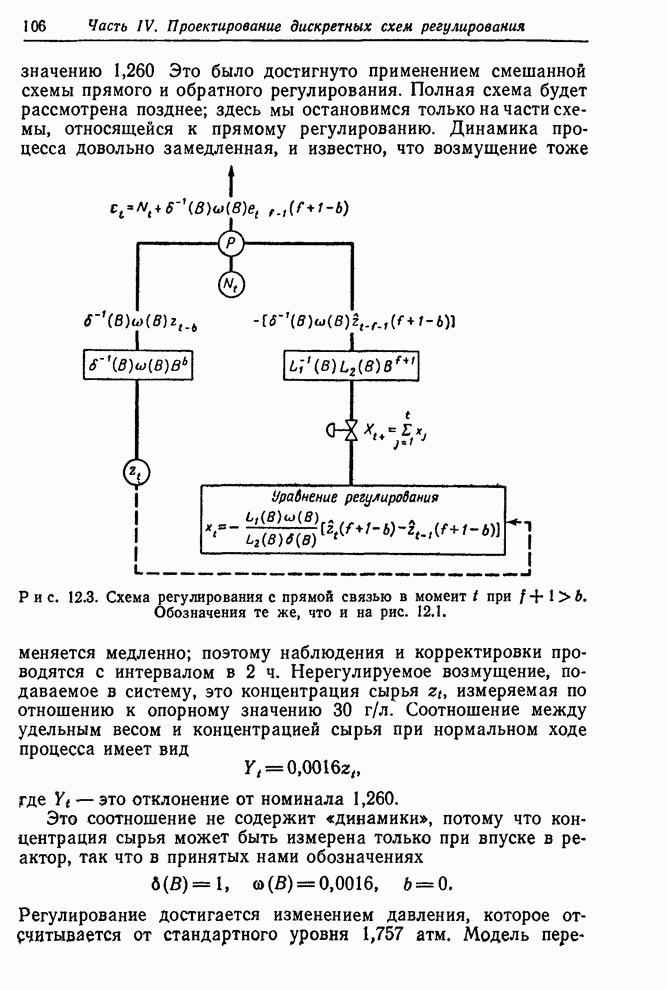
- 12.1. РЕГУЛИРОВАНИЕ С ПРЯМОЙ СВЯЗЬЮ
- 12.1.1. Регулирование с прямой связью, минимизирующее среднеквадратичную ошибку
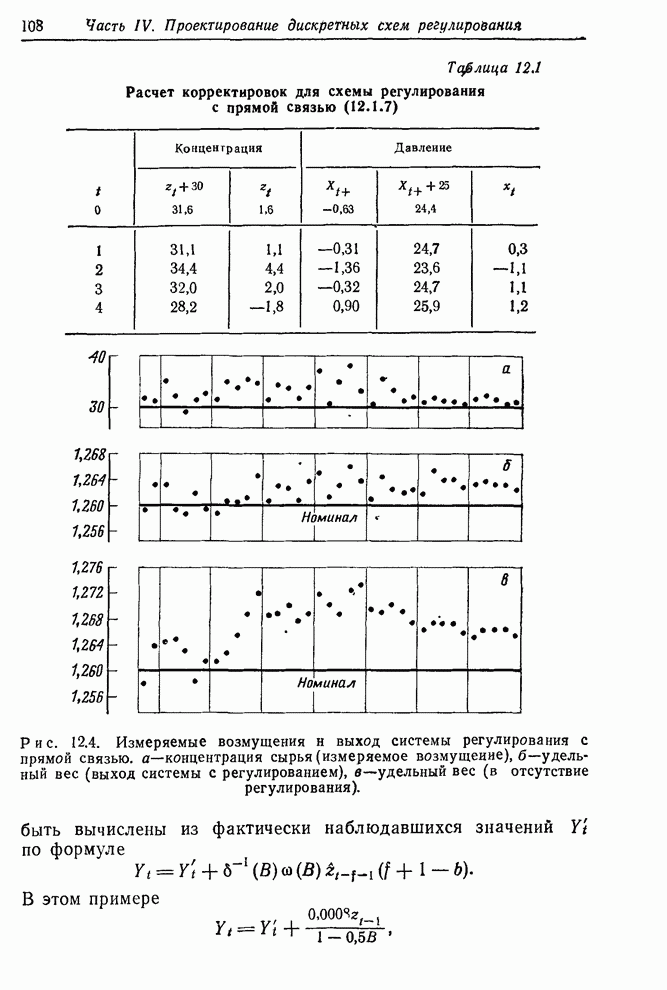
- 12.1.2. Пример — регулирование удельного веса промежуточного продукта
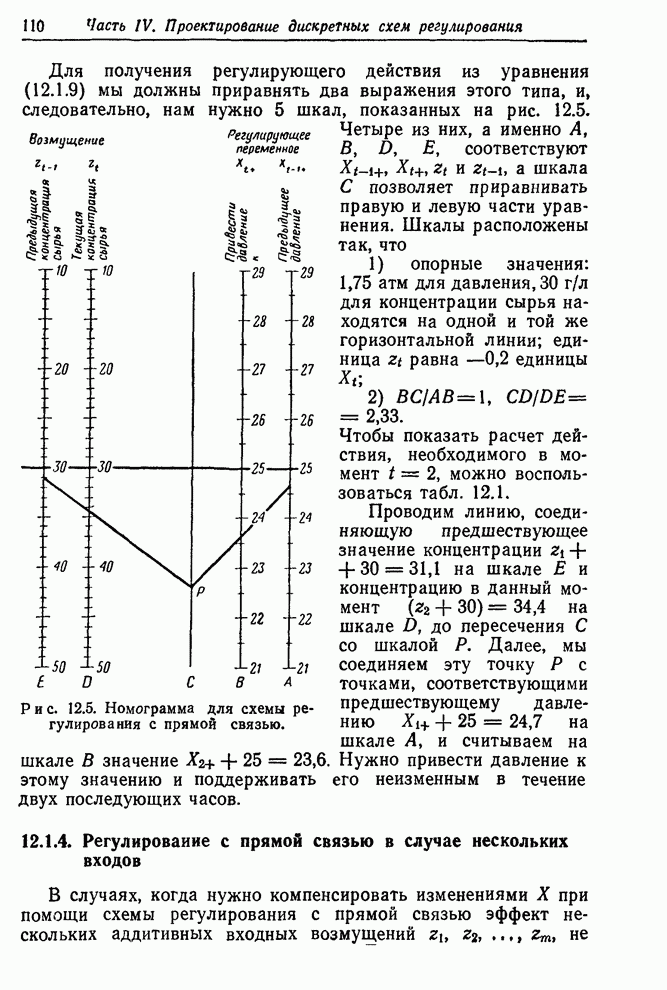
- 12.1.3. Номограмма для регулирования с прямой связью
- 12.1.4. Регулирование с прямой связью в случае нескольких входов
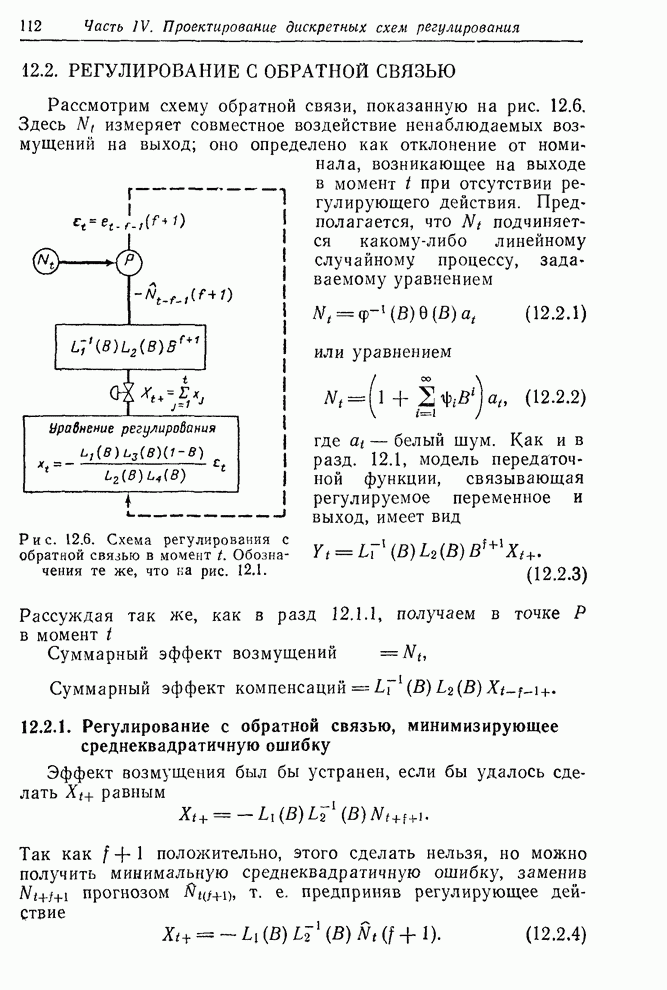
- 12.2. РЕГУЛИРОВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ
- 12.2.1. Регулирование с обратной связью, минимизирующее среднеквадратичную ошибку
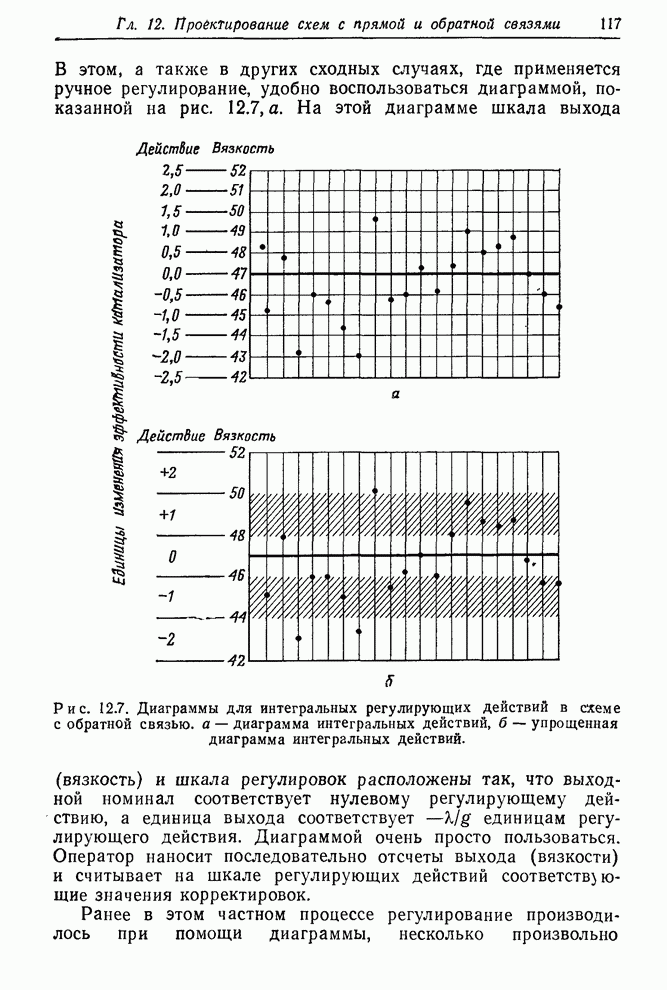
- 12.2.2. Применение уравнения регулирования: ПИД-регулятор
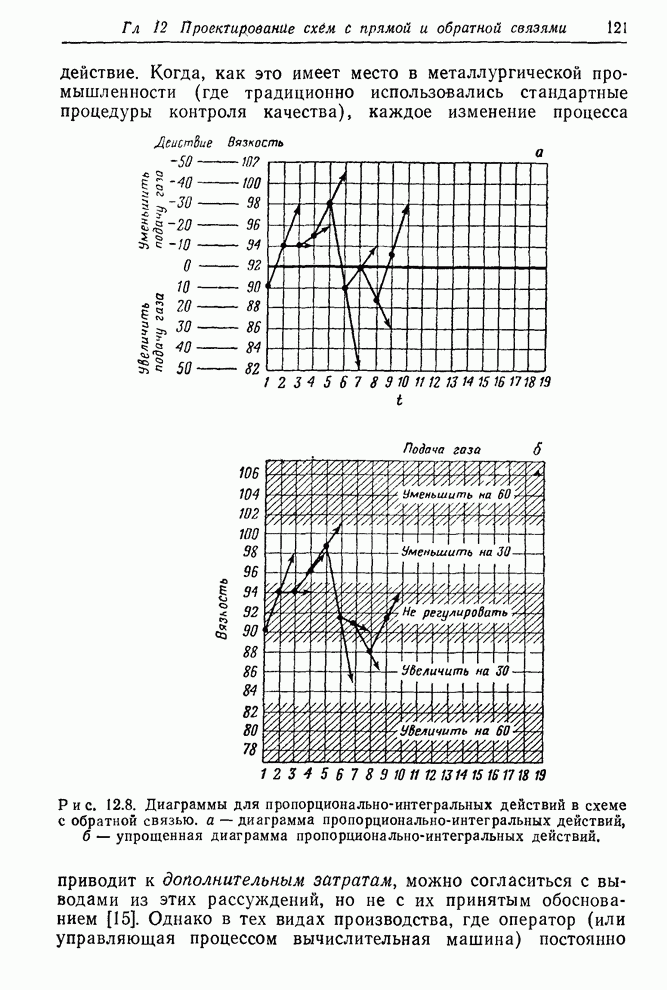
- 12.2.3. Примеры дискретного регулирования с обратной связью
- 12.3. РЕГУЛИРОВАНИЕ С ПРЯМОЙ И ОБРАТНОЙ СВЯЗЯМИ
- 12.3.1. Регулирование с прямой и обратной связями, минимизирующее выходную среднеквадратичную ошибку
- 12.3.2. Пример регулирования с прямой и обратной связями
- 12.3.3. Преимущества и недостатки регулирования с прямой и обратной связями
- 12.4. Подгонка моделей передаточных функций шума по оперативным данным
- 12.4.1. Итеративный способ построения моделей
- 12.4.2. Оценивание по оперативным данным
- 12.4.3. Пример
- Глава 13. Некоторые дальнейшие проблемы регулирования
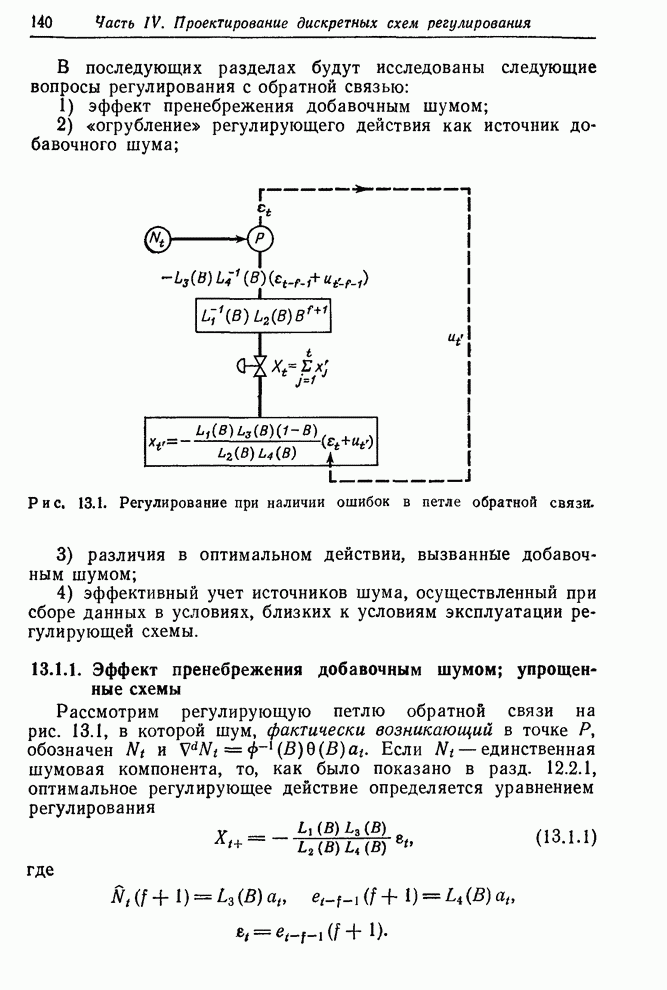
- 13.1. ЭФФЕКТ ДОБАВОЧНОГО ШУМА В СХЕМАХ РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ
- 13.1.1. Эффект пренебрежения добавочным шумом; упрощенные схемы
- 13.1.2. Оптимальное действие в случаях, когда корректировки содержат ошибки наблюдения
- 13.1.3. Перенос источника шума
- 13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
- 13.2.1. Вывод выражения для оптимальной корректировки
- 13.2.2. Схема с ограничением для примера «вязкость–подача газа»
- 13.3. ВЫБОР ИНТЕРВАЛА ОТСЧЕТА
- 13.3.1. Пример эффекта уменьшения частоты отсчетов
- 13.3.2. Влияние интервала отсчета на процесс ПСС(0,1,1)
- ПРОГРАММА 5. ИДЕНТИФИКАЦИЯ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 6. ПРЕДВАРИТЕЛЬНОЕ ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 7. ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ТАБЛИЦЫ ВРЕМЕННЫХ РЯДОВ