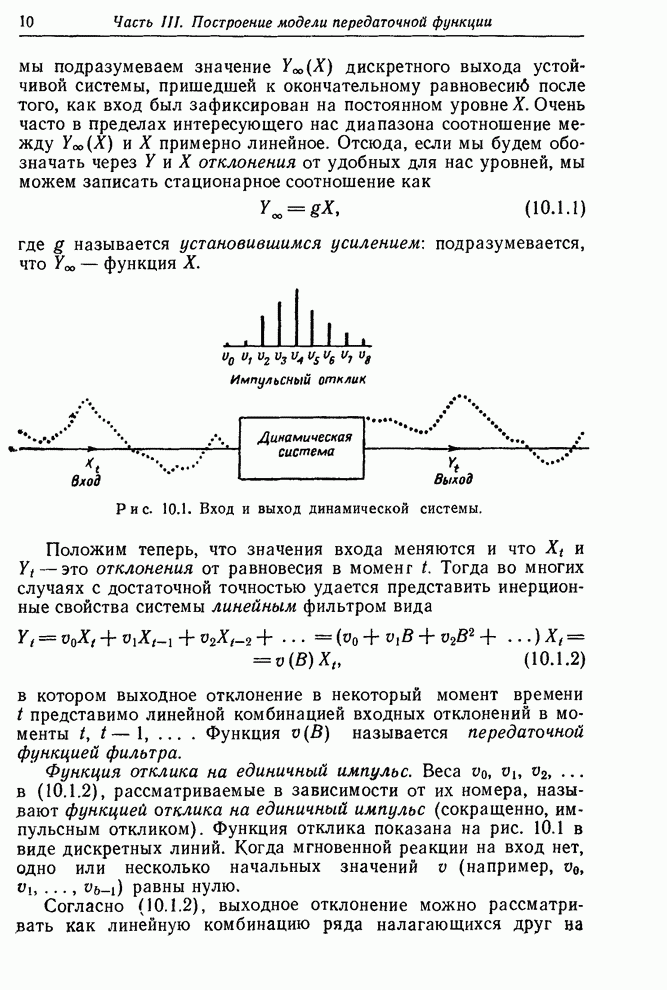
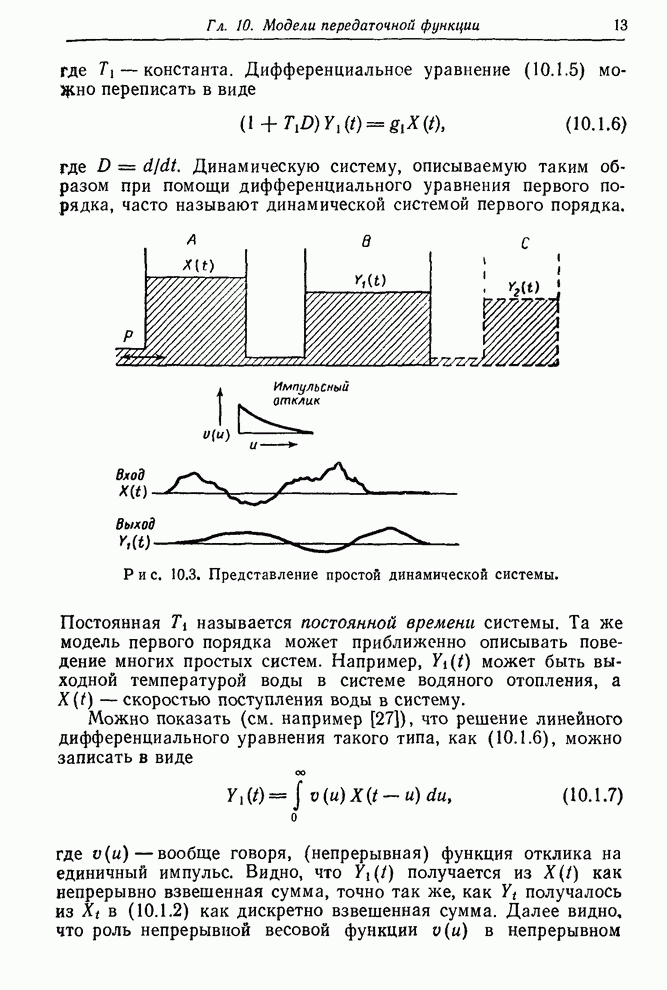
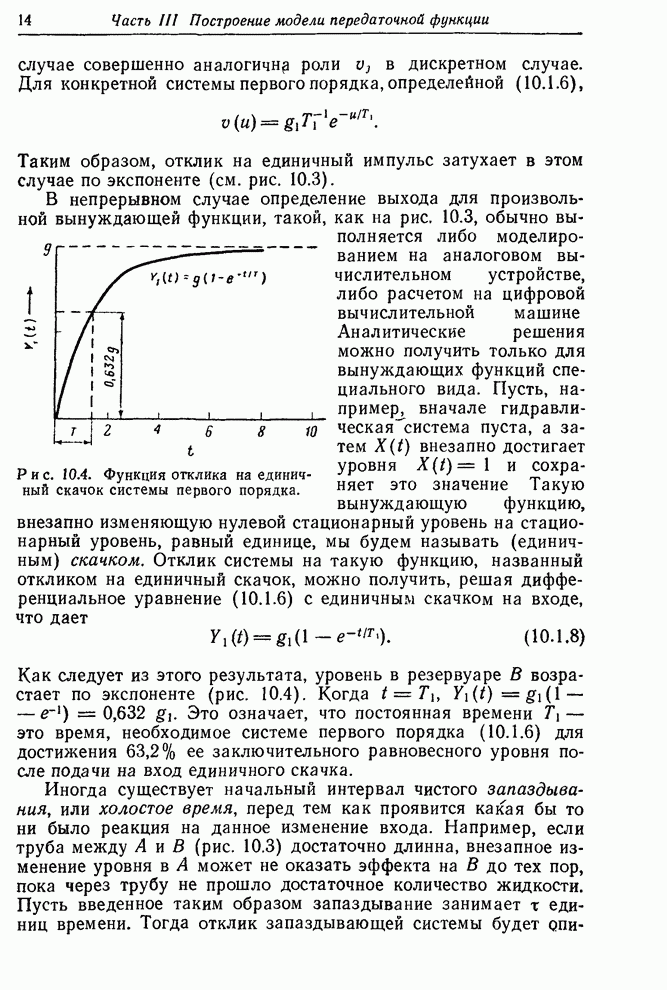
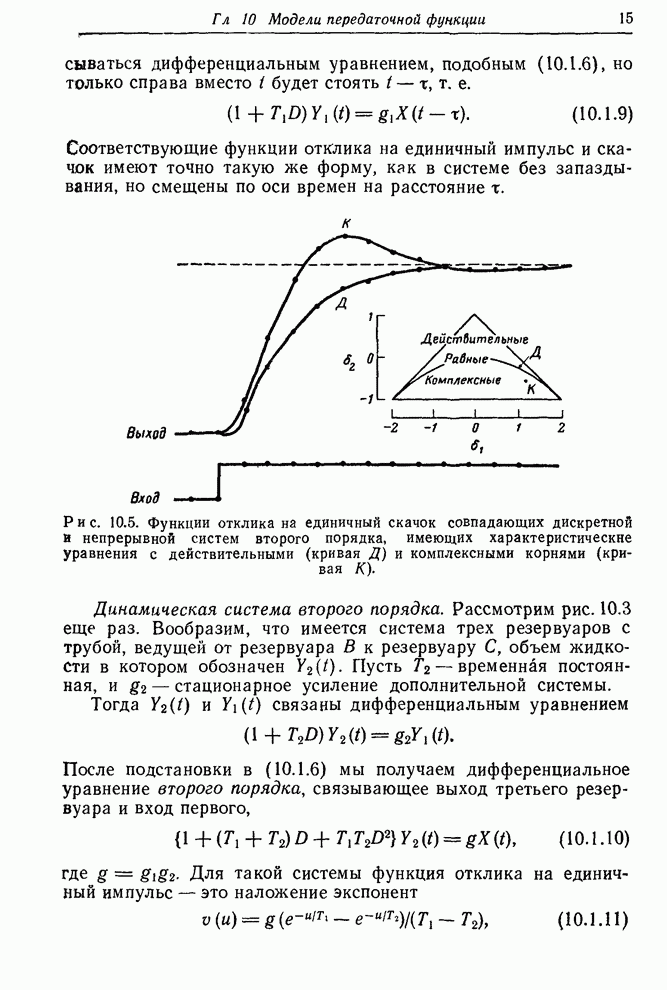
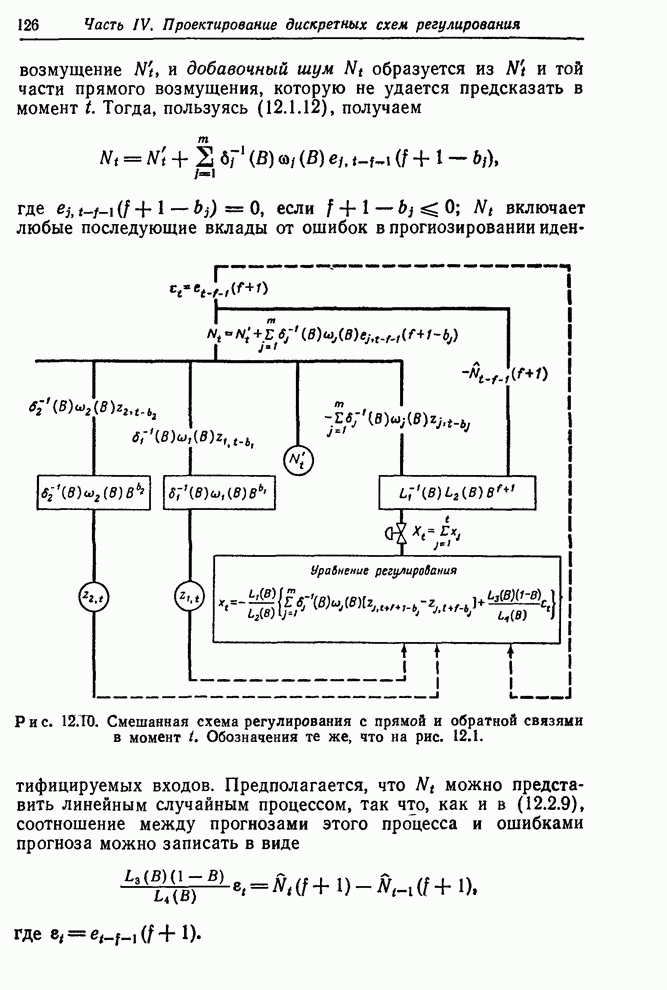
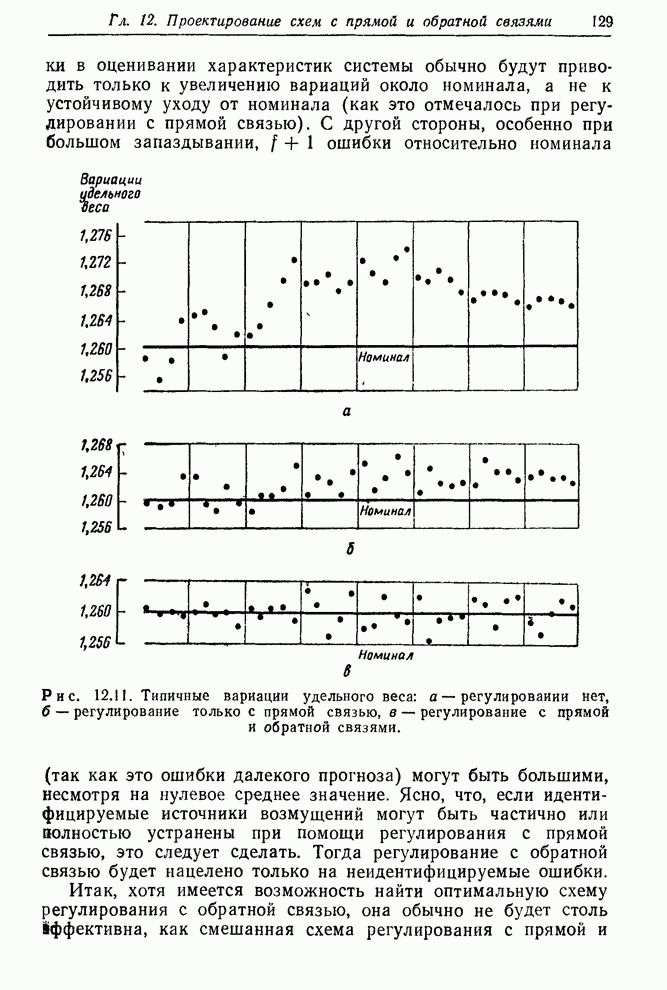
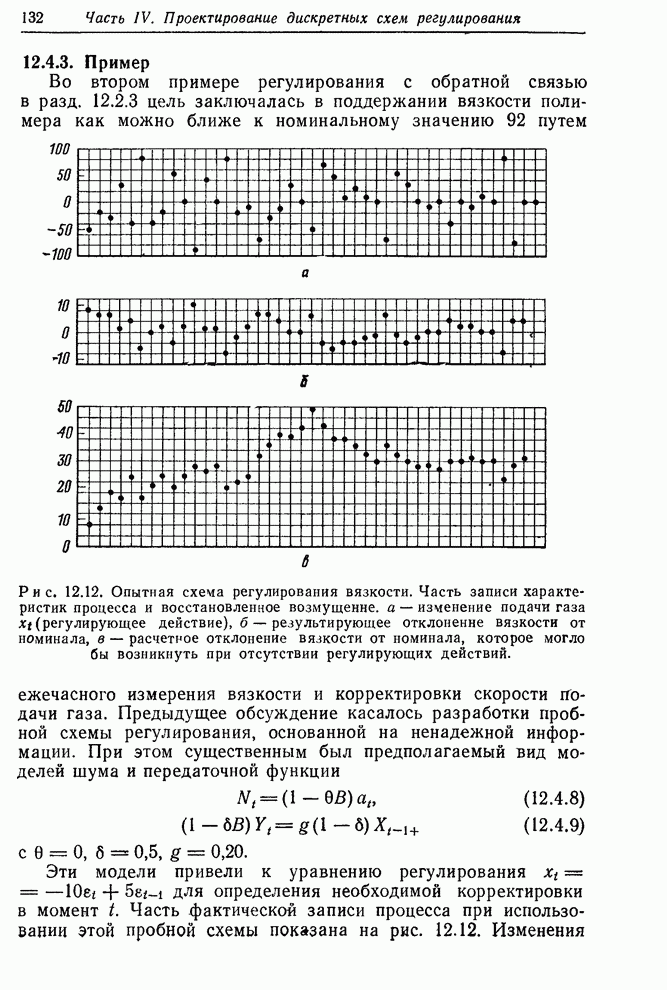
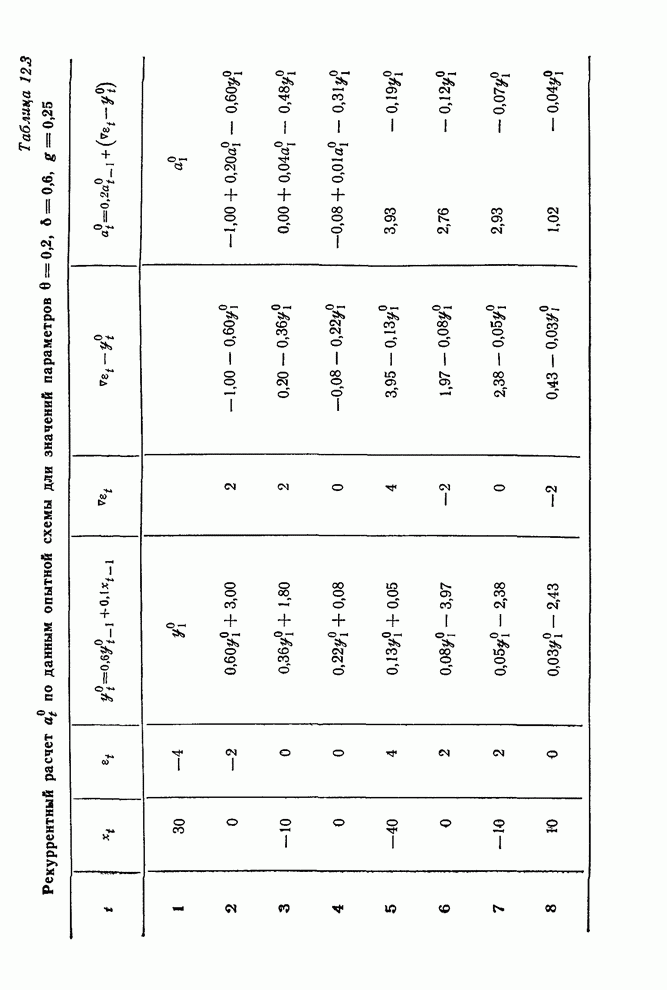
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
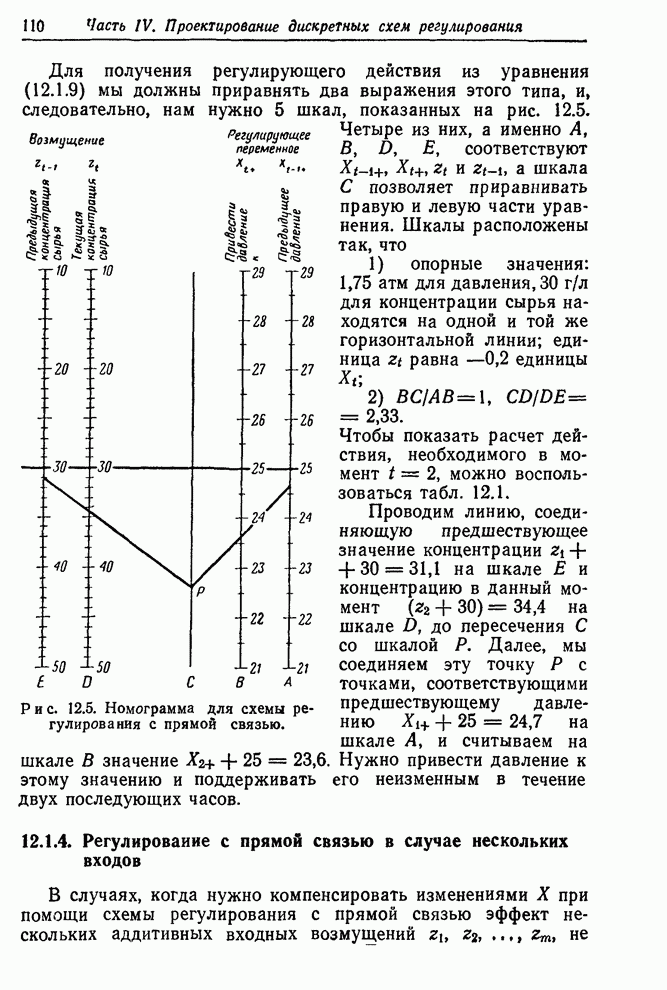
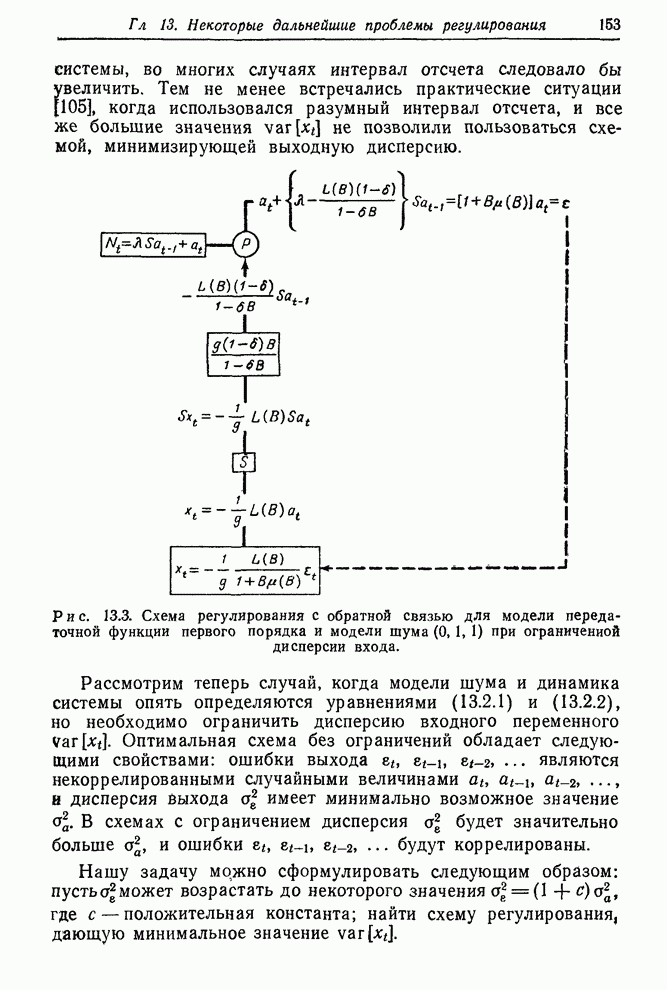
12.2.3. Примеры дискретного регулирования с обратной связью
Пример
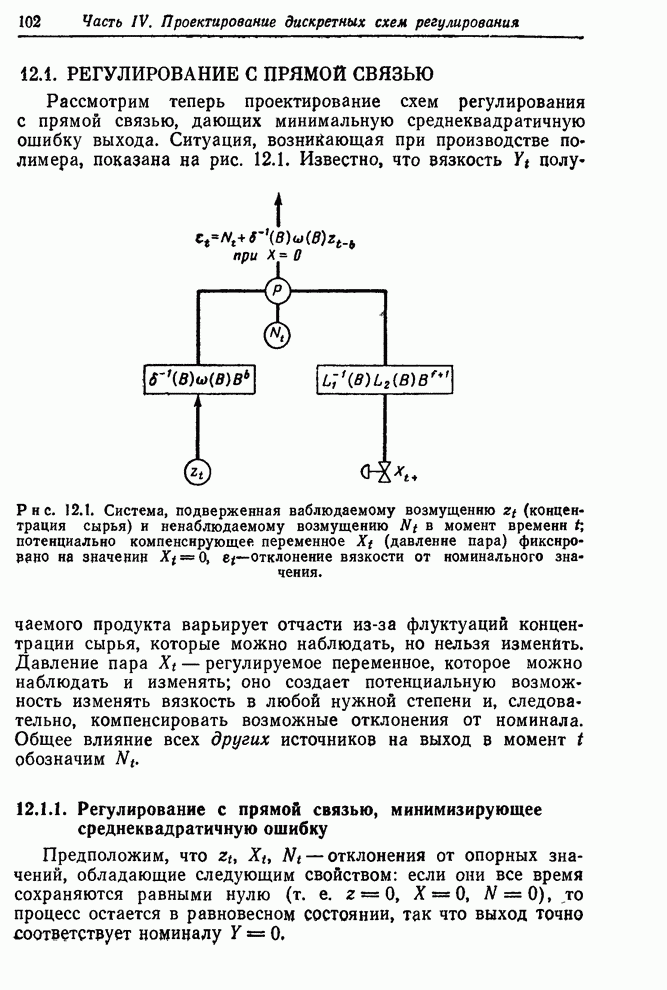
1. В схеме, предназначенной для регулирования вязкости ![]() полимера, используемого в
производстве искусственного волокна, регулируемое переменное – вязкость –
контролировалось каждый час; коррекции производились изменением эффективности
катализатора
полимера, используемого в
производстве искусственного волокна, регулируемое переменное – вязкость –
контролировалось каждый час; коррекции производились изменением эффективности
катализатора ![]() .
Нужное номинальное значение вязкости равнялось 47 единицам. Модель передаточной
функции между
.
Нужное номинальное значение вязкости равнялось 47 единицам. Модель передаточной
функции между ![]() и
и
![]() достаточно
точно описывалась простой системой первого порядка
достаточно
точно описывалась простой системой первого порядка
![]() .
.
Далее,
временная постоянная системы была мала по сравнению с интервалом отсчета.
Конкретно, ![]() ,
так что примерно 96% возможных изменений происходило в пределах интервала
отсчета в один час. Следовательно, с достаточной точностью можно принять
,
так что примерно 96% возможных изменений происходило в пределах интервала
отсчета в один час. Следовательно, с достаточной точностью можно принять ![]() . Далее, изменения
эффективности катализатора, как принято, измерялись в единицах эффекта, который
вносился ими в процесс. Так, увеличение эффективности катализатора на единицу
уменьшало вязкость на единицу. Отсюда
. Далее, изменения
эффективности катализатора, как принято, измерялись в единицах эффекта, который
вносился ими в процесс. Так, увеличение эффективности катализатора на единицу
уменьшало вязкость на единицу. Отсюда ![]() , и модель передаточной функции
принималась в виде
, и модель передаточной функции
принималась в виде
![]()
![]() ,
или, в терминах общей модели (12.2.3),
,
или, в терминах общей модели (12.2.3),
![]() ,
, ![]() ,
, ![]() .
.
Возмущение
![]() на выходе,
которое определено нами ранее как вариация вязкости при отсутствии
регулирования, адекватно описывалось случайным процессом порядка
на выходе,
которое определено нами ранее как вариация вязкости при отсутствии
регулирования, адекватно описывалось случайным процессом порядка ![]()
![]()
с
![]() ;
; ![]() , так что
, так что
![]() .
.
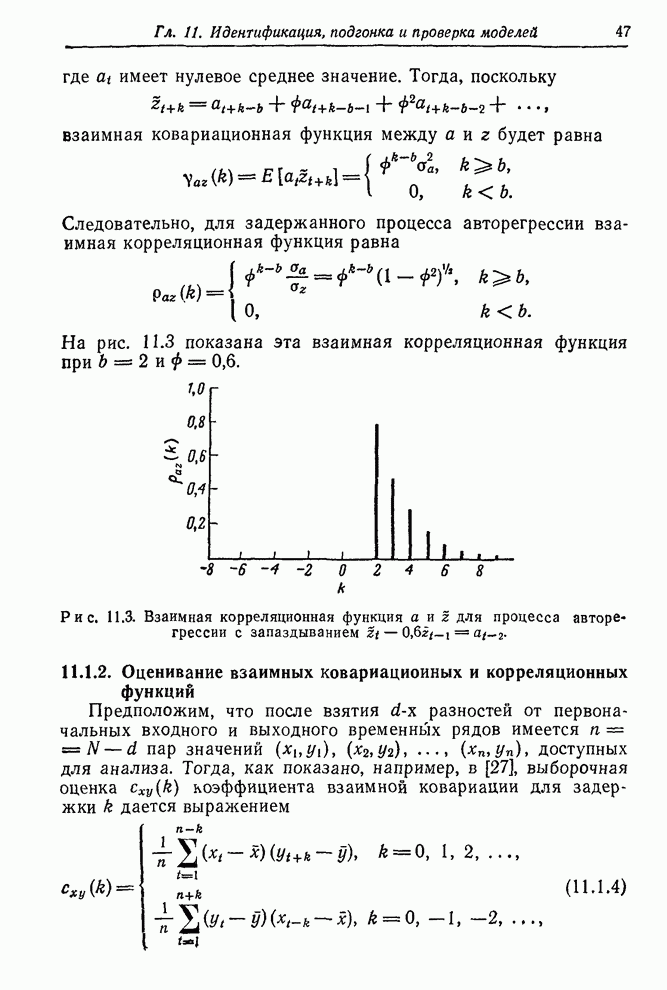
Отсюда,
пользуясь (12.2.9), получаем ![]() . Далее, так как
. Далее, так как ![]() , то, пользуясь (12.2.6),
получаем
, то, пользуясь (12.2.6),
получаем
![]() .
.
Наконец,
корректировка, необходимая в момент ![]() , равна
, равна
![]() ,
,
т. е.
![]() ,
или
,
или ![]() .
.
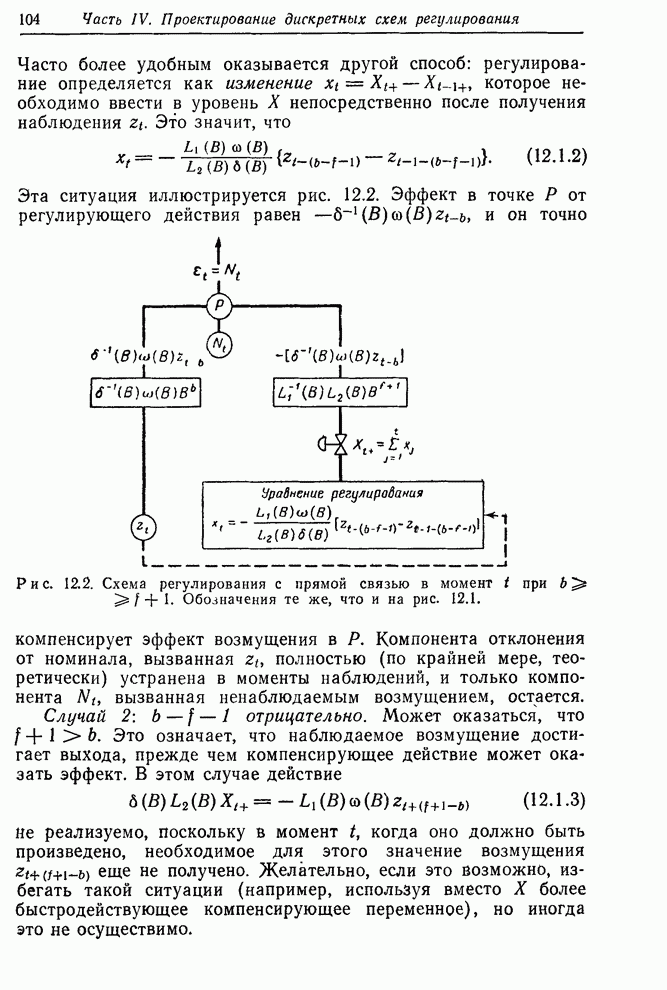
В такой ситуации, когда временная постоянная системы мала по сравнению с интервалом отсчета, оптимальное регулирование является дискретным аналогом непрерывного интегрального регулирующего действия. Можно получить выражение для необходимого регулирующего действия в этом случае более прямым способом:
Предсказываемое
изменение выхода ![]() ,
,
Эффект
корректировки ![]() .
.
Следовательно,
корректировка, необходимая для компенсации изменений выхода, такова, что ![]() . При такой
корректировке ошибка на выходе
. При такой
корректировке ошибка на выходе ![]() . Тогда уравнение оптимального
регулирования с обратной связью будет
. Тогда уравнение оптимального
регулирования с обратной связью будет ![]() .
.
Эффективность регулирования такого типа не чувствительна к умеренным изменениям значений параметров, и с достаточной точностью можно принять
![]() .
.
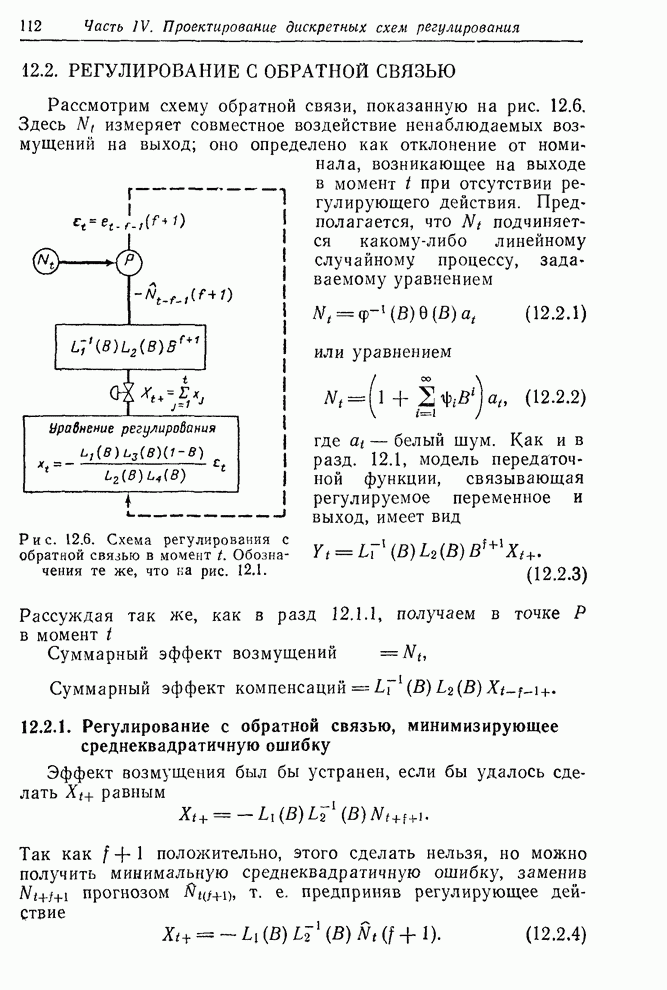
В
этом, а также в других сходных случаях, где применяется ручное регулирование,
удобно воспользоваться диаграммой, показанной на рис. 12.7,а. На этой диаграмме
шкала выхода (вязкость) и шкала регулировок расположены так, что выходной
номинал соответствует нулевому регулирующему действию, а единица выхода
соответствует ![]() единицам
регулирующего действия. Диаграммой очень просто пользоваться. Оператор наносит
последовательно отсчеты выхода (вязкости) и считывает на шкале регулирующих
действий соответствующие значения корректировок.
единицам
регулирующего действия. Диаграммой очень просто пользоваться. Оператор наносит
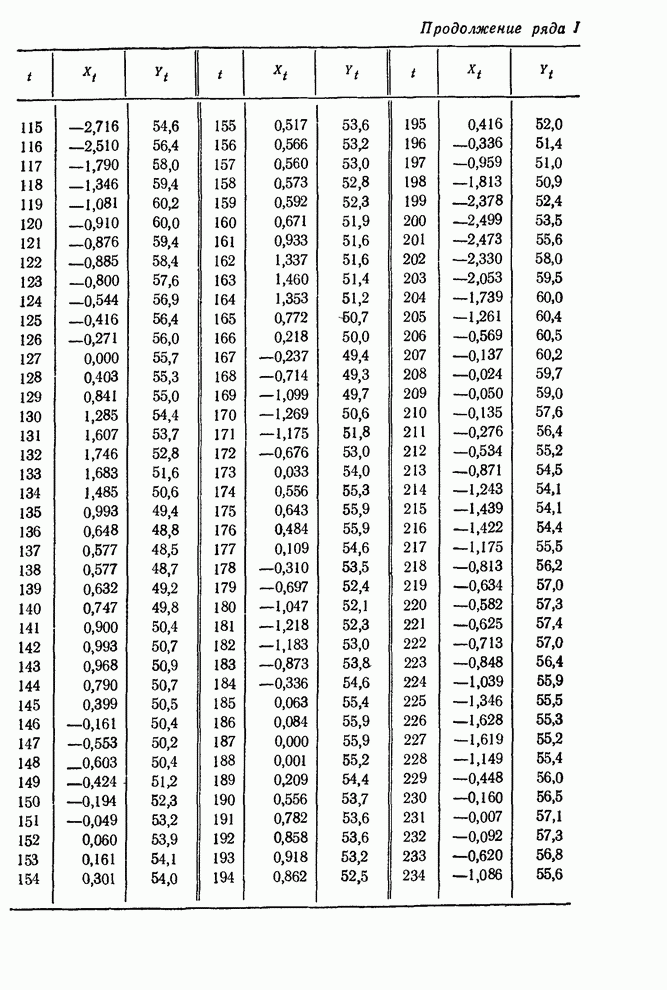
последовательно отсчеты выхода (вязкости) и считывает на шкале регулирующих
действий соответствующие значения корректировок.

Рис. 12.7. Диаграммы для интегральных регулирующих действий в схеме с обратной связью: а – диаграмма интегральных действий, б – упрощенная диаграмма интегральных действий.
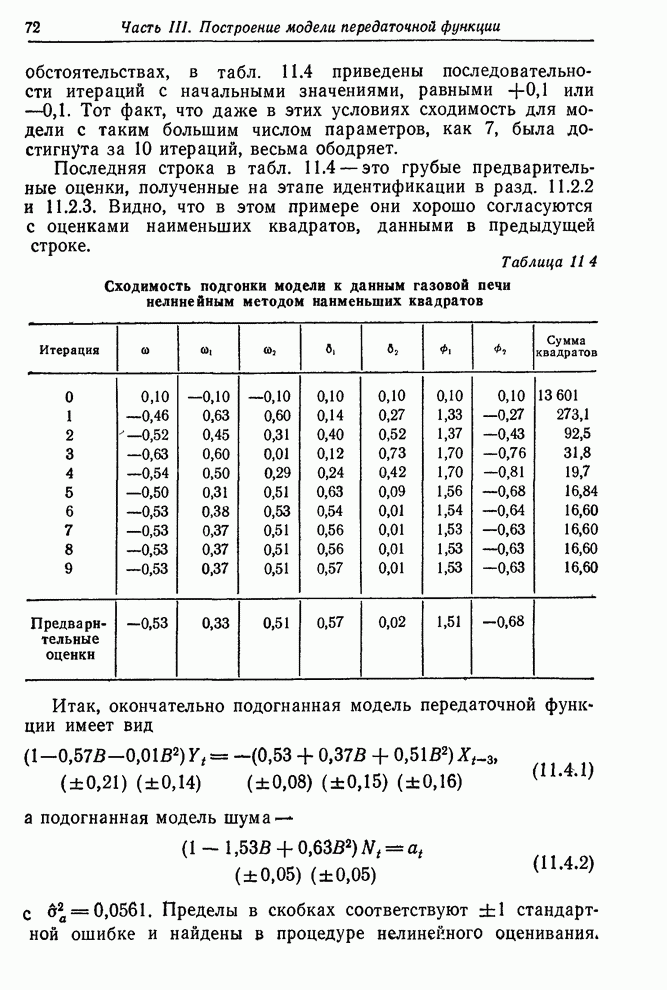
Ранее в этом частном процессе регулирование производилось при помощи диаграммы, несколько произвольно базирующейся на схеме с последовательным критерием значимости. Оказалось, что удобно изменять эффективность катализатора определенными ступенями. Возможными действиями в этом случае были: отсутствие действия; ± одна единица эффекта; ± две единицы эффекта.
Критерии значимости почти не применялись в рассматриваемой задаче. Все же использовавшаяся схема обладала рядом достоинств: 1) не нужно было вносить изменения после каждого отсчета; 2) когда нужно было вносить изменения, то они были одного из пяти заданных типов, что весьма упрощало их выполнение и контроль за ними. Однако эти достоинства легко сохранить и в предлагаемой нами схеме регулирования, используя «округленные» диаграммы регулирования, что приводит лишь к незначительному увеличению ошибок.
«Округленные»
диаграммы. Такая диаграмма легко строится по исходной диаграмме разбиением
шкалы регулирующих действий на интервалы. Корректировка, которую нужно
выполнить, если наблюденное значение попало в данный интервал, соответствует
средней точке интервала. На рис. 12.7,б показана «округленная» диаграмма, в
которой возможные регулирующие действия ограничены изменениями катализатора на –2,
–1, 0, 1 или 2 единицы. Рис. 12.7,а и б были рассчитаны путем вычислений назад
значений ![]() по
множеству оперативных данных о процессе и восстановления диаграмм, которые
получились бы от использования округленной и неокругленной схем. Увеличение
среднеквадратичной ошибки (для этого случая оно меньше, чем 5%), вызванное
применением округленной схемы, часто оправдывается удобством работы с малым
числом стандартных корректировок. Более подробно эффект округления рассмотрен в
разд. 13.1.1.
по
множеству оперативных данных о процессе и восстановления диаграмм, которые
получились бы от использования округленной и неокругленной схем. Увеличение
среднеквадратичной ошибки (для этого случая оно меньше, чем 5%), вызванное
применением округленной схемы, часто оправдывается удобством работы с малым
числом стандартных корректировок. Более подробно эффект округления рассмотрен в
разд. 13.1.1.
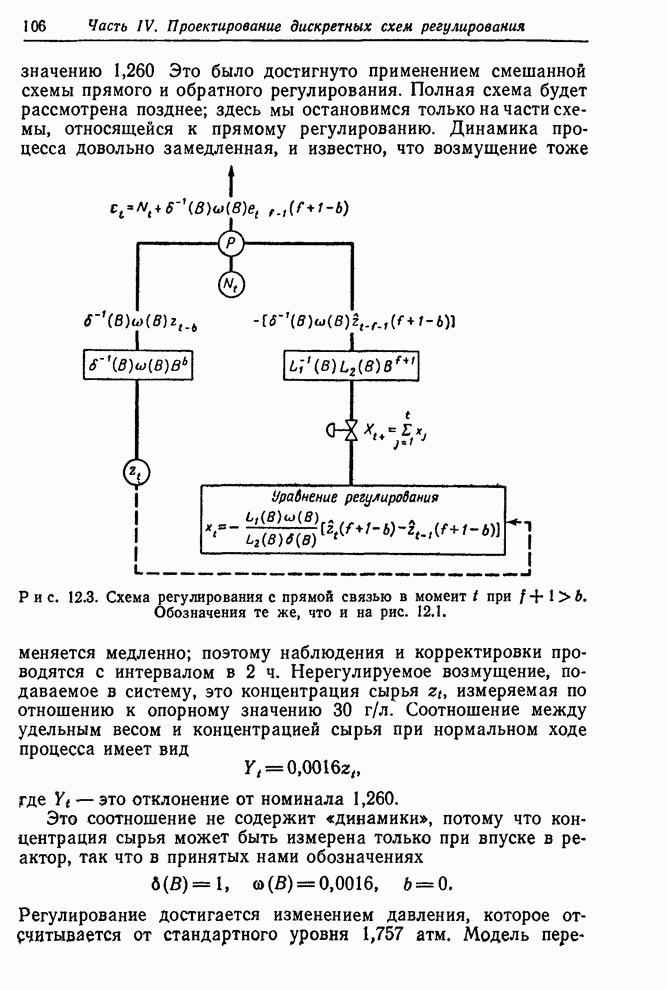
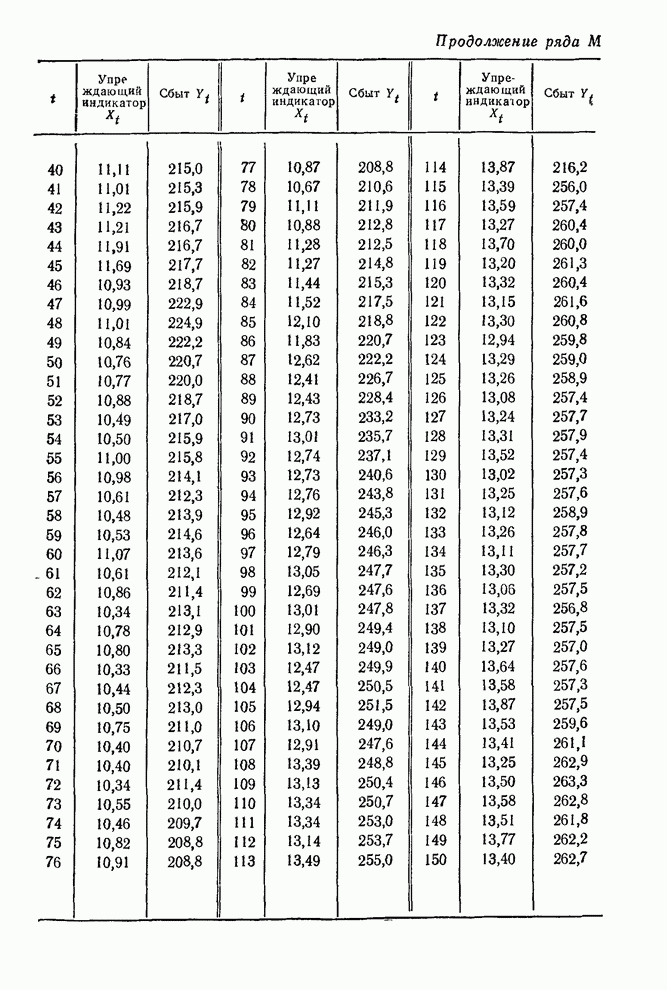
Пример
2. На более поздней стадии изготовления полимера задача заключалась в
поддержании выходной вязкости ![]() как можно более близкой к номинальному
значению 92 путем регулировок подачи газа. Вязкость измерялась каждый час; с
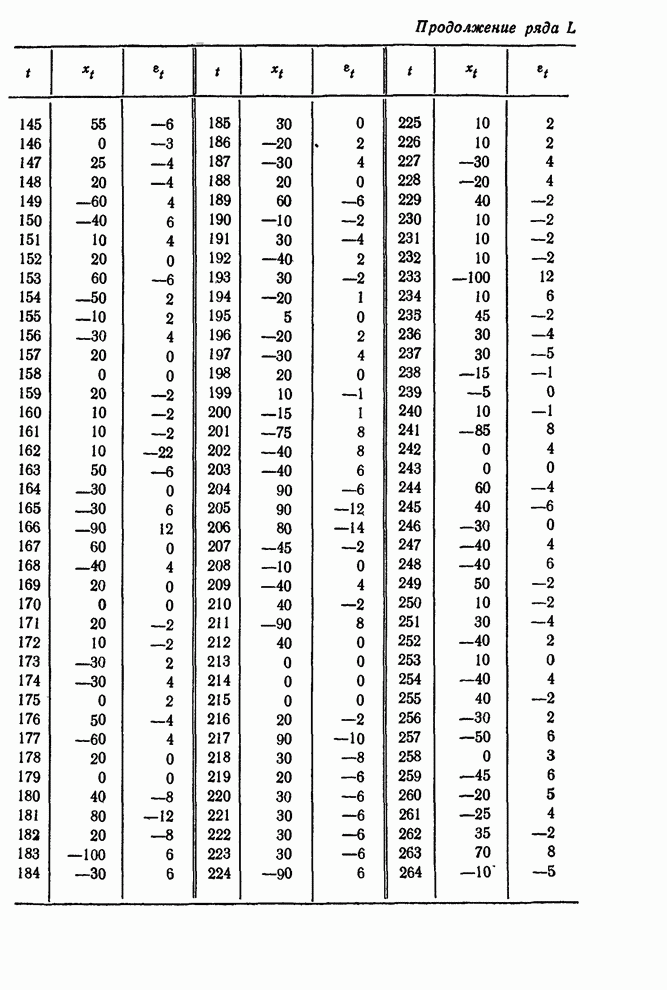
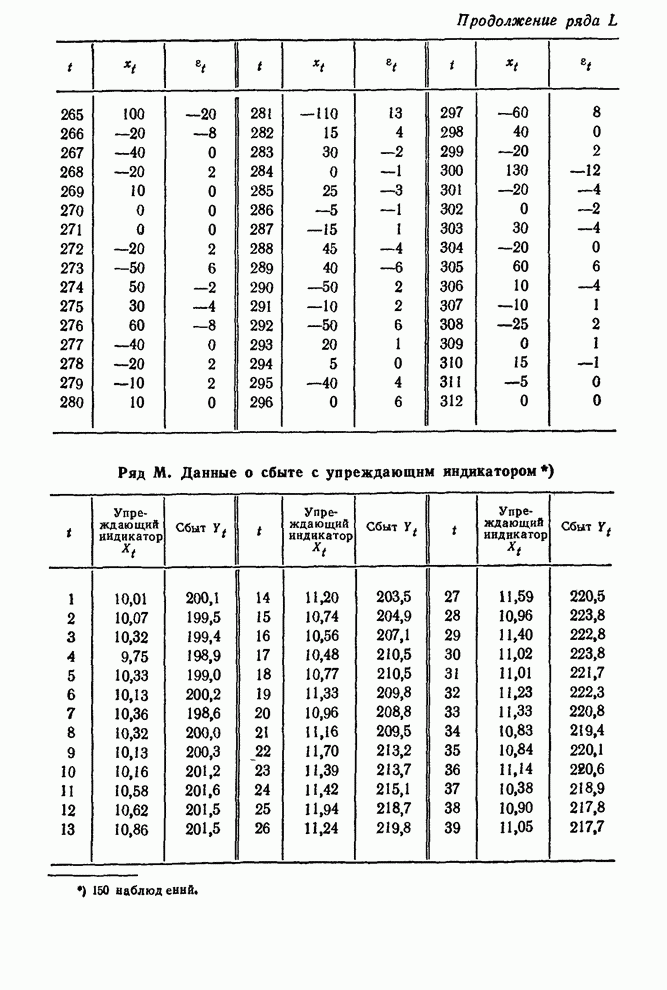
таким же интервалом делались регулярные корректировки подачи газа. Мы обсудим
здесь разработку пробной схемы регулирования этого процесса. Позднее будет
описано, как данные, собранные в процессе испытания этой схемы, использовались
для переоценок параметров и создания улучшенной схемы регулирования.
как можно более близкой к номинальному
значению 92 путем регулировок подачи газа. Вязкость измерялась каждый час; с
таким же интервалом делались регулярные корректировки подачи газа. Мы обсудим
здесь разработку пробной схемы регулирования этого процесса. Позднее будет
описано, как данные, собранные в процессе испытания этой схемы, использовались
для переоценок параметров и создания улучшенной схемы регулирования.
На
этом этапе исследования имелись данные о том, как варьировала вязкость при
отсутствии регулирования (т. е. при постоянной скорости подачи газа). Эти
данные были получены в предшествующий период, во время которого компенсации
вариаций вязкости производились существенно позднее, чем измерения. Данные
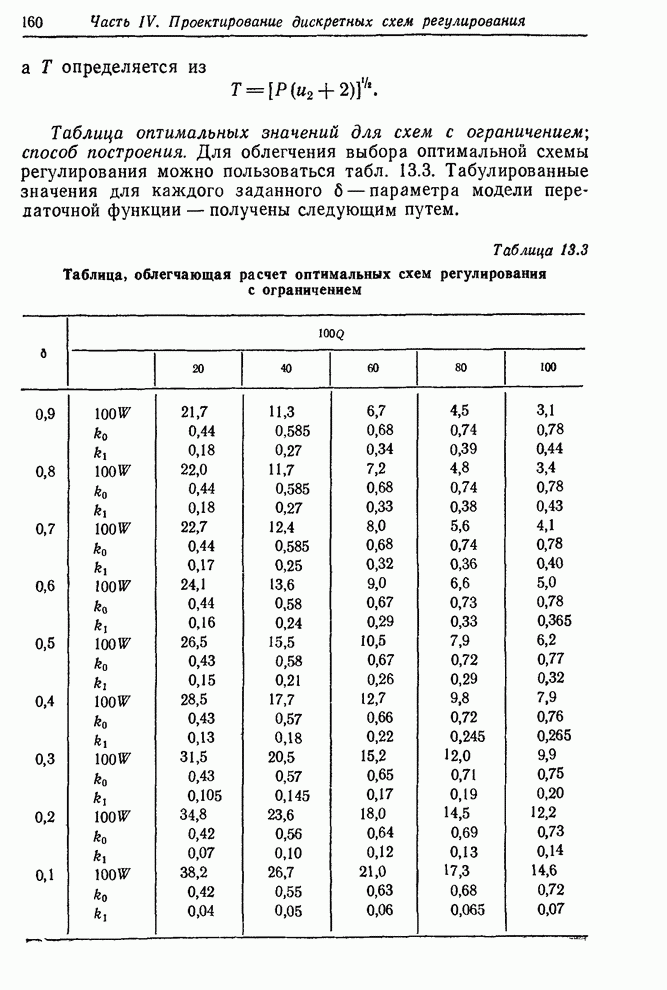
образуют ряд ![]() ,
приведенный в сборнике рядов из 1-го выпуска этой книги. В гл. 6 и 7 было
показано, что этот ряд можно хорошо описать процессом
,
приведенный в сборнике рядов из 1-го выпуска этой книги. В гл. 6 и 7 было
показано, что этот ряд можно хорошо описать процессом ![]()
![]() с
с ![]() , близким к нулю (и,
следовательно, с
, близким к нулю (и,
следовательно, с ![]() ,
близким к единице). Имелись явные свидетельства того, что в рабочем диапазоне
стационарное соотношение между скоростью подачи газа и вязкостью было линейным
и что единичное изменение скорости подачи газа вызвало изменение в вязкости на
0,2 единицы, что соответствовало установившемуся усилению
,
близким к единице). Имелись явные свидетельства того, что в рабочем диапазоне
стационарное соотношение между скоростью подачи газа и вязкостью было линейным
и что единичное изменение скорости подачи газа вызвало изменение в вязкости на
0,2 единицы, что соответствовало установившемуся усилению ![]() . Экспериментальные (не очень
надежные) данные свидетельствовали о простой экспоненциальной динамической
картине с отсутствием запаздывания – примерно половина возможного изменения
происходила в течение одного часа.
. Экспериментальные (не очень
надежные) данные свидетельствовали о простой экспоненциальной динамической
картине с отсутствием запаздывания – примерно половина возможного изменения
происходила в течение одного часа.
Отсюда
мы получили пробную модель передаточной функции, связывающей вязкость ![]() и скорость подачи
газа
и скорость подачи
газа ![]()
![]() ,
,
так
что ![]() ,
, ![]() ,
, ![]() . Используя модель возмущения
. Используя модель возмущения
![]() ,
,
получаем
![]() ,
, ![]() , и соответствующее
уравнение регулирования с обратной связью имеет вид
, и соответствующее
уравнение регулирования с обратной связью имеет вид
![]() ,
,
или
![]() ,
,
где
![]() – выходное
отклонение от номинала в момент
– выходное
отклонение от номинала в момент ![]() .
.
Если
выразить регулирующее действие при помощи разностного оператора ![]() , имеем
, имеем
![]()
или
![]() ,
,
т. е. комбинацию интегрального и пропорционального регулирования.
Проективная
диаграмма. Ситуация, в которой возмущение ![]() может быть представлено линейной
моделью порядка
может быть представлено линейной
моделью порядка ![]()
![]() ,
,
а передаточная функция – моделью первого порядка
![]() ,
,
встречается достаточно часто и заслуживает специального упоминания. В этом случае регулирующая корректировка (12.2.8) будет иметь вид
![]() , (12.2.10)
, (12.2.10)
и нужное значение регулируемого переменного будет
 .
.
При
ручном регулировании это пропорционально-интегральное действие удобно
определить при помощи специальной «проективной» диаграммы. Такая диаграмма
приведена на рис. 12.8,а, она использовалась для определения регулирующего
действия в рассмотренном примере, ее применение объясняет общий способ
конструирования диаграмм. Отклонение от центральной линии (линии номинала),
отсчитываемое по шкале вязкости, соответствует отклонению ![]() от номинала. Вторая шкала,
имеющаяся на рисунке, указывает, какое регулирующее действие
от номинала. Вторая шкала,
имеющаяся на рисунке, указывает, какое регулирующее действие ![]() следует предпринять,
причем нулевое действие
следует предпринять,
причем нулевое действие ![]() расположено на уровне номинального
значения. Шкалы построены так, что единице выхода на шкале вязкости
соответствует
расположено на уровне номинального
значения. Шкалы построены так, что единице выхода на шкале вязкости
соответствует ![]() единиц
на шкале регулирующего действия.
единиц
на шкале регулирующего действия.

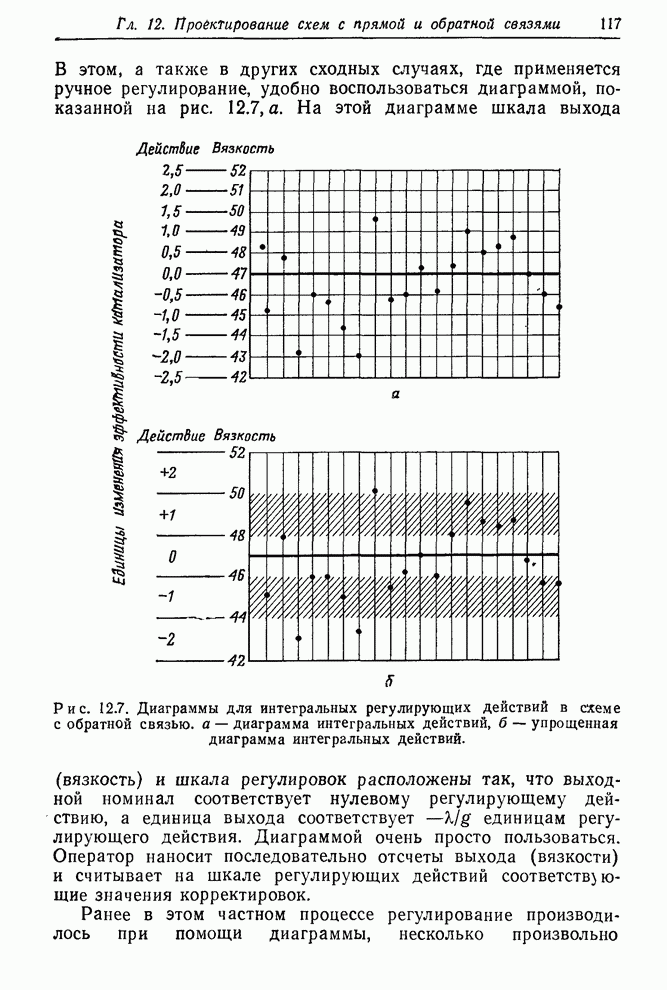
Рис. 12.8. Диаграммы для пропорционально-интегральных действий в схеме с обратной связью: а – диаграмма пропорционально-интегральных действий, б – упрощенная диаграмма пропорционально-интегральных действий.
Действие,
которое нужно выполнить в момент ![]() можно найти, продолжая на
можно найти, продолжая на ![]() временных единиц
вперед линию, проходящую через
временных единиц
вперед линию, проходящую через ![]() и
и ![]() (или, что то же самое, через два
последних измерения вязкости). Для рассматриваемой пробной схемы
(или, что то же самое, через два
последних измерения вязкости). Для рассматриваемой пробной схемы ![]() , так что нужно
продолжать прямую на единицу времени вперед. Так, например, регулирующее
действие в момент
, так что нужно
продолжать прямую на единицу времени вперед. Так, например, регулирующее
действие в момент ![]() находим,
соединяя значения вязкости в моменты
находим,
соединяя значения вязкости в моменты ![]() и
и ![]() прямой, продолжая прямую на один шаг
вперед и считывая значение –30 на шкале регулирующих действий. Это означает,
что скорость подачи газа нужно уменьшить на 30 единиц и удерживать на новом
значении до поступления новой информации в момент
прямой, продолжая прямую на один шаг
вперед и считывая значение –30 на шкале регулирующих действий. Это означает,
что скорость подачи газа нужно уменьшить на 30 единиц и удерживать на новом
значении до поступления новой информации в момент ![]() .
.
«Округленная» диаграмма. Как уже упоминалось в этом разделе, схемы регулирования, основанные на диаграммах приведенного выше типа, иногда рассматриваются как неприемлемые, поскольку они требуют, чтобы действие предпринималось после каждого наблюдения. Возможно, удобнее предпринимать корректировки, только «если они необходимы». Имеются два оправдания такого подхода, одно из которых более основательно, чем второе.
1) Практик, знакомый со статистическими критериями значимости и стандартными диаграммами контроля качества, может считать, что он должен иметь реальные свидетельства «ухода процесса от номинала», прежде чем предпринять любое действие. Когда, как это имеет место в металлургической промышленности (где традиционно использовались стандартные процедуры контроля качества), каждое изменение процесса приводит к дополнительным затратам, можно согласиться с выводами из этих рассуждений, но не с их принятым обоснованием [15]. Однако в тех видах производства, где оператор (или управляющая процессом вычислительная машина) постоянно находится в действии для периодического контроля процесса, введение изменений не приводит к дополнительным затратам. В этом случае достаточно просто минимизировать некоторую меру отклонения от номинала (например, среднеквадратичную ошибку); именно это мы здесь и предлагаем.
2) Второй, более серьезный аргумент заключается в том, что в производственных процессах всегда целесообразно как можно более упрощать действия, выполняемые оператором. Если можно разработать диаграмму, позволяющую без существенных потерь выбрать одно из немногих различных действий, это существенно поможет ее использованию.
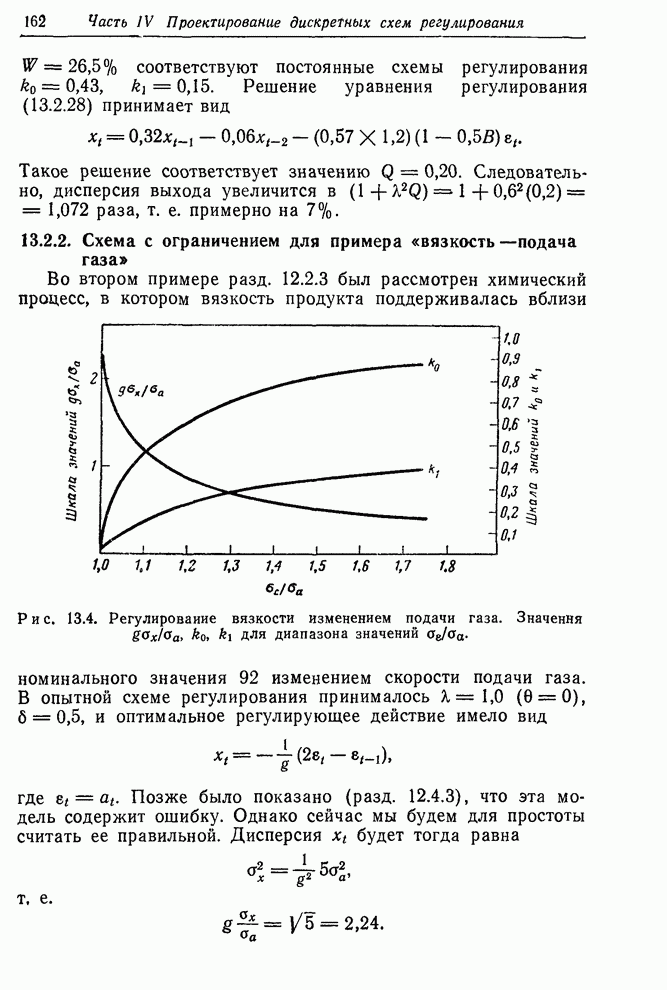
Как уже было показано, эта цель легко достижима при помощи «округленной» диаграммы. Подходящая «округленная» диаграмма для рассматриваемого примера показана на рис. 12.8,б. На этой диаграмме шкала действий разделена на 5 интервалов, каждый шириной в 30 единиц скорости подачи газа. Эти интервалы соответствуют 5 действиям: уменьшить скорость подачи газа на 60 единиц, на 30 единиц, не изменять подачу газа, увеличить скорость подачи на 30 единиц, на 60 единиц. Значение вязкости наносится на график, и точки проектируются на шкалу действий так же, как и ранее, но действия «округляются» так, что становятся равными центральным значениям интервала, в который попали спроектированные точки наблюдений. Вероятность, что точки попадут вне крайних интервалов, невелика, и такие точки рассматриваются как лежащие внутри существующих крайних интервалов. Другими словами, крайние интервалы рассматриваются как полубесконечные.
Конечно,
результатом округления диаграммы является некоторое увеличение дисперсии
вязкости на выходе относительно номинала. Однако даже при таком существенном
округлении, как показанное здесь, это увеличение обычно не столь уж
значительно. В разд. 13.1.1 мы обсудим общий вопрос о влиянии добавочного шума
на входе процесса. Пользуясь полученным там выводом, можно утверждать, что
увеличение стандартного отклонения вязкости от номинала, вызванное округлением
такого вида, как на рис. 12.8,б, равно примерно 7%. Точки, которые в
иллюстративных целях были размещены на рис. 12.8,б, фактически были найдены
обратным расчетом в предположении, что присутствует то же возмущение, что и на
неокругленной диаграмме на рис. 12.8,а. В гл. 13 показано, что, если ![]() не слишком близко к
1 (т. е. что временная постоянная системы не слишком велика по сравнению с
интервалом отсчета), можно воспользоваться интервалом округления шириной в одно
стандартное отклонение
не слишком близко к
1 (т. е. что временная постоянная системы не слишком велика по сравнению с
интервалом отсчета), можно воспользоваться интервалом округления шириной в одно
стандартное отклонение ![]() , не увеличивая заметно дисперсию
выхода. Рассмотрим теперь приближенный эффект такого округления в уравнении
регулирования (12.2.10).
, не увеличивая заметно дисперсию
выхода. Рассмотрим теперь приближенный эффект такого округления в уравнении
регулирования (12.2.10).
Обозначим
интервал округления ![]() . Тогда при частном значении
. Тогда при частном значении ![]() в предположении о
нормальном распределении имелось бы следующее распределение действий для
диаграммы типа 12.8,б.
в предположении о
нормальном распределении имелось бы следующее распределение действий для
диаграммы типа 12.8,б.
|
Зона |
|
|
|
|
|
|
Центральное значение зоны |
|
|
0 |
|
|
|
Вероятность попадания в зону, % |
6,7 |
24,2 |
38,3 |
24,2 |
6,7 |
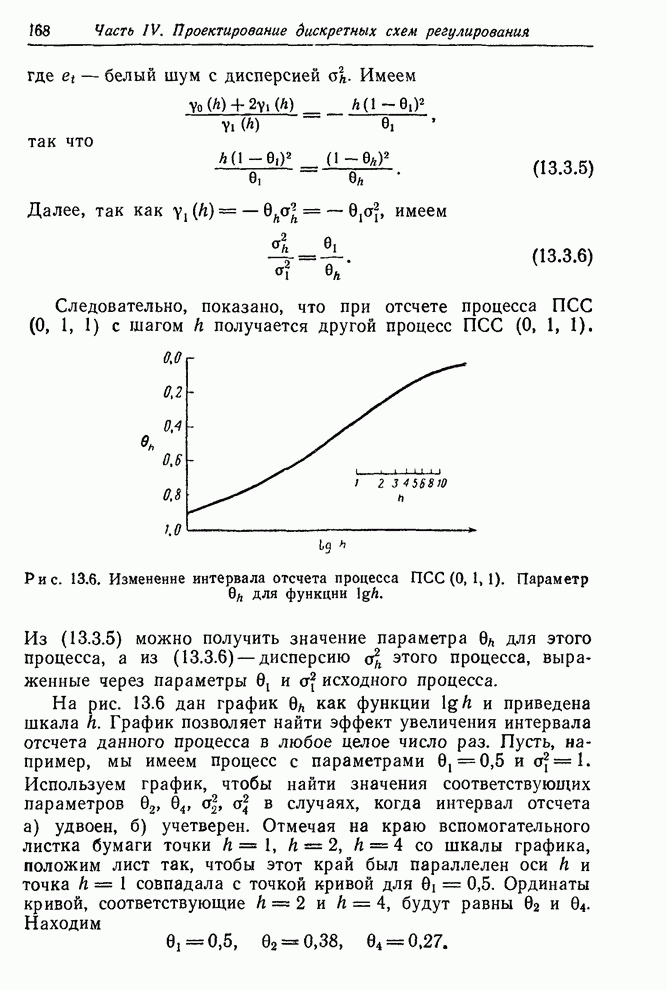
Строго
говоря, теоретические результаты разд. 13.1.1, относящиеся к увеличению
дисперсии выхода из-за округления, используют предположение о существовании зон
с центрами в ![]() ,
,
![]() ,
, ![]() ,
, ![]() и т. д. Однако вероятность
попадания в эти внешние зоны равна 1,24%, и эффект объединения их всех в зоны
и т. д. Однако вероятность
попадания в эти внешние зоны равна 1,24%, и эффект объединения их всех в зоны ![]() считается малым.
считается малым.
Конкретно
можно показать, что при всех этих предположениях стандартное отклонение выхода
возрастает в ![]() раз,
где
раз,
где
 . (12.2.11)
. (12.2.11)
Для
диаграммы на рис. 12.8,б ![]() ,
, ![]() ,
, ![]() , так что
, так что ![]() .
.
Пример 3. В качестве следующего примера рассмотрим несколько более сложную ситуацию, возникающую в случаях, когда модель передаточной функции может быть представлена системой первого порядка с холостым временем (запаздыванием). Тогда при
![]() ,
,
пользуясь выражением для общей модели (12.2.3), получаем
![]() .
.
Если
возмущение ![]() ,
как и прежде, – процесс порядка
,
как и прежде, – процесс порядка ![]()
![]() ,
,
![]() ,
,
то
![]() ,
,
так что
![]() ,
,
![]() .
.
Отсюда,
используя (12.2.8), получаем, что оптимальное действие заключается в
корректировке ![]() ,
определяемой уравнением
,
определяемой уравнением
![]() , (12.2.12)
, (12.2.12)
т. е.
![]() . (12.2.13)
. (12.2.13)
Видно,
что введение запаздывания в модель передаточной функции приводит к способу
регулирования, при котором текущая корректировка зависит от прошлых
корректировок в течение периода запаздывания, а также от настоящих и прошлых
ошибок ![]() . В
частности, в обычной ситуации, когда
. В
частности, в обычной ситуации, когда ![]() , получаем
, получаем
![]() .
.
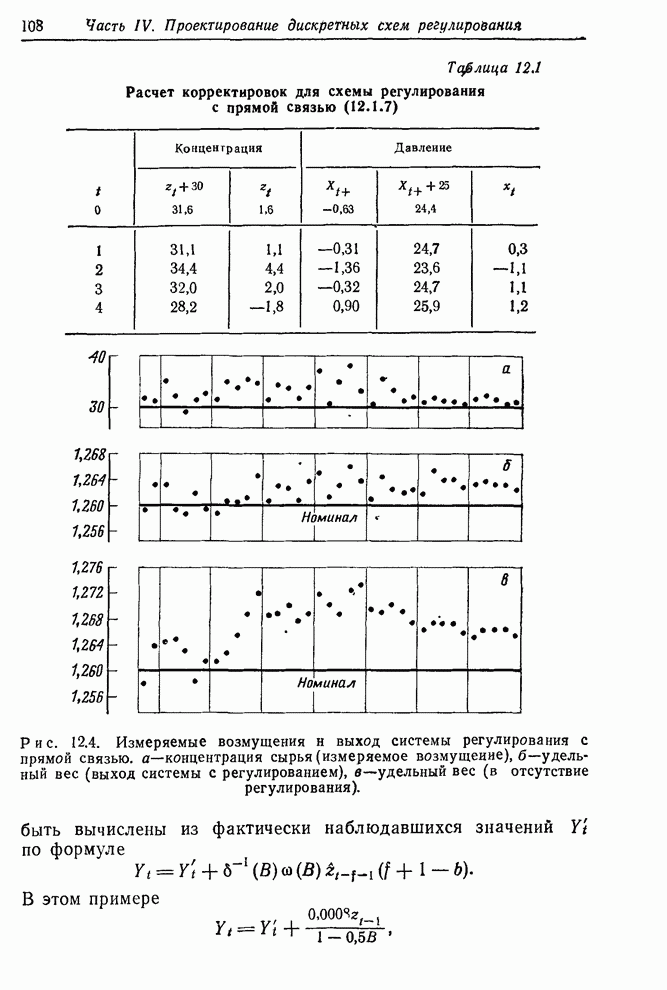
Номограмма запаздывания. Рассуждая так же, как в разд. 12.1.3, легко разработать номограмму для вычисления необходимых действий
![]() , (12.2.14)
, (12.2.14)
подходящую
к частному случаю ![]() .
Пусть мы встретились с ситуацией, сходной с рассмотренной в примере 2, когда
необходимо было поддерживать вязкость как можно ближе к значению 92. Положим, однако,
что в этом случае
.
Пусть мы встретились с ситуацией, сходной с рассмотренной в примере 2, когда
необходимо было поддерживать вязкость как можно ближе к значению 92. Положим, однако,
что в этом случае
![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
Тогда, подставляя эти значения в (12.2.14), находим, что необходимая корректировка имеет вид
![]() ,
,
т. е.
![]() .
.
Это
действие вычислено при помощи номограммы на рис. 12.9 со шкалами ![]() для
для ![]() и шкалой
и шкалой ![]() для приравнивания
обеих частей уравнения регулирования. Шкалы устроены так, что
для приравнивания
обеих частей уравнения регулирования. Шкалы устроены так, что
1) нулевое действие и номинальное значение выхода располагаются на одной линии;
2)
единица шкалы вязкости равна ![]() единицы шкалы скорости подачи газа;
единицы шкалы скорости подачи газа;
3)
расстояние между шкалами таково, что ![]() ,
, ![]() .
.

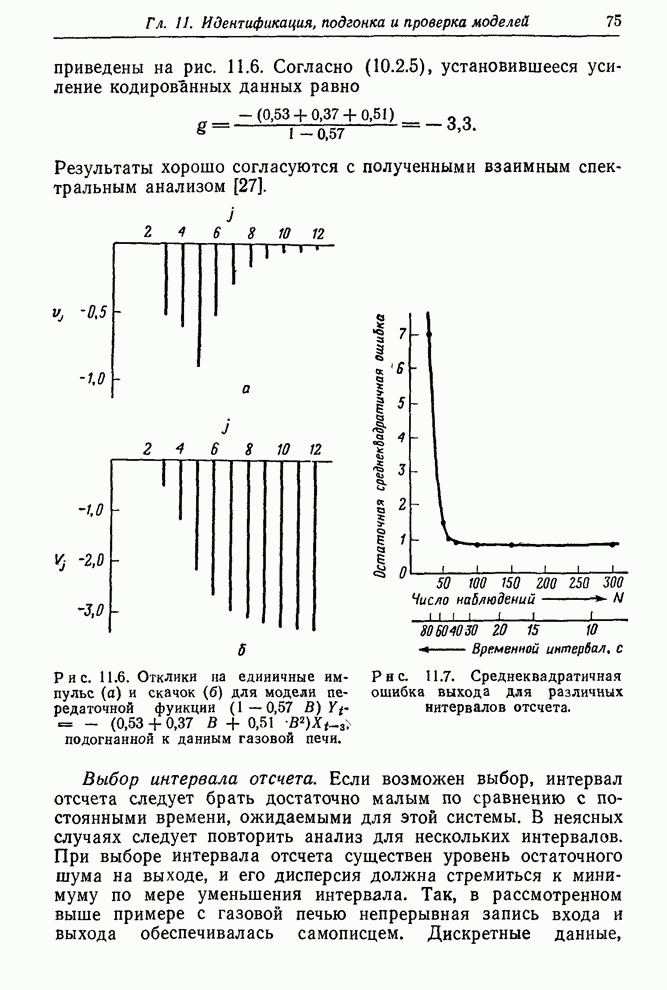
Рис. 12.9. Номограмма регулирования для простой системы с запаздыванием
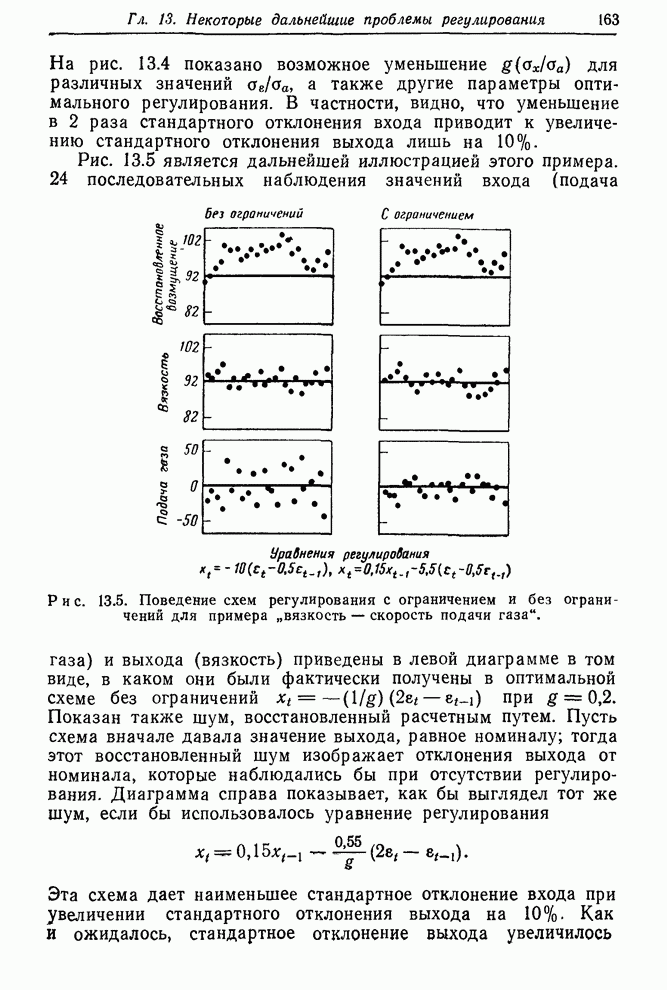
На
номограмме, показанной на рис. 12.9, только что измерено значение вязкости 92.
Прямая линия, соединяющая это значение с предыдущим значением 96, пересекает
шкалу ![]() в
точке
в
точке ![]() .
Прямая, проведенная через
.
Прямая, проведенная через ![]() и предыдущую корректировку –32,
пересекает шкалу действий на значении 20. Поэтому оптимальным действием в
настоящий момент является увеличение скорости подачи газа на 20 единиц.
и предыдущую корректировку –32,
пересекает шкалу действий на значении 20. Поэтому оптимальным действием в
настоящий момент является увеличение скорости подачи газа на 20 единиц.
Отметим, что в этом конкретном примере текущее значение вязкости равно номиналу. Тем не менее предшествующий ход процесса и его динамически-стохастические характеристики указывают на необходимость корректирующего действия. Если задача оператора процесса – минимизировать среднеквадратичное отклонение вязкости от номинала, он должен увеличить скорость подачи газа на 20 единиц.
Как и ранее, если существует необходимость упростить регулирующее действие, можно воспользоваться «округленной» номограммой со шкалой действия, разбитой на удобное число зон.
| << Предыдущий параграф | Следующий параграф >> |
- Часть III. ПОСТРОЕНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- Глава 10. Модели передаточной функции
- 10.1. ЛИНЕЙНЫЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 10.1.1. Дискретная передаточная функция
- 10.1.2. Непрерывные динамические модели, описываемые дифференциальными уравнениями
- 10.2. ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ МОДЕЛИ, ОПИСЫВАЕМЫЕ РАЗНОСТНЫМИ УРАВНЕНИЯМИ
- 10.2.1. Общая форма разностного уравнения
- 10.2.2. Природа передаточной функции
- 10.2.3. Дискретные модели передаточных функций первого и второго порядков
- 10.2.4. Рекуррентный расчет выхода для произвольного входа
- 10.3. СООТНОШЕНИЕ МЕЖДУ ДИСКРЕТНОЙ И НЕПРЕРЫВНОЙ МОДЕЛЯМИ
- 10.3.1. Отклик на скачкообразный вход
- 10.3.2. Соотношения совпадающих систем первого и второго порядков
- 10.3.3. Аппроксимация общих непрерывных моделей дискретными моделями
- 10.3.4. Модели передаточных функций с добавленным шумом
- ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
- ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
- Глава 11. Идентификация, подгонка и проверка моделей передаточных функций
- 11.1. Взаимная корреляционная функция
- 11.1.1. Свойства взаимных ковариационной и корреляционной функций
- 11.1.2. Оценивание взаимных ковариационных и корреляционных функций
- 11.1.3. Приближенные стандартные ошибки выборочных оценок взаимных корреляций
- 11.2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.2.1. Идентификация моделей передаточной функции с предварительным выравниванием спектра входа
- 11.2.2. Пример идентификации модели передаточной функции
- 11.2.3. Идентификация модели шума
- 11.2.4. Некоторые общие соображения об идентификации моделей передаточных функций
- 11.3. ПОДГОНКА И ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.3.1. Условная сумма квадратов
- 11.3.2. Нелинейное оценивание
- 11.3.3. Использование остаточных ошибок для диагностической проверки
- 11.3.4. Конкретные способы проверки остаточных ошибок
- 11.4. Некоторые примеры подгонок и проверок моделей передаточных функций
- 11.4.1. Подгонка и проверка модели газовой печи
- 11.4.2. Искусственный пример с двумя входами
- 11.5. ПРОГНОЗИРОВАНИЕ ПРИ ПОМОЩИ УПРЕЖДАЮЩИХ ИНДИКАТОРОВ
- 11.5.1. Прогноз с минимальной среднеквадратичной ошибкой
- 11.5.2. Прогнозы выхода СO2 из газовой печи
- 11.5.3. Прогноз нестационарных данных сбыта при помощи упреждающего индикатора
- 11.6. НЕКОТОРЫЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОЦЕНИВАНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ П11.1. ИСПОЛЬЗОВАНИЕ ВЗАИМНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
- Заключение
- Часть IV. Проектирование дискретных схем регулирования
- Глава 12. Проектирование схем регулирования с прямой и обратной связями
- 12.1. РЕГУЛИРОВАНИЕ С ПРЯМОЙ СВЯЗЬЮ
- 12.1.1. Регулирование с прямой связью, минимизирующее среднеквадратичную ошибку
- 12.1.2. Пример — регулирование удельного веса промежуточного продукта
- 12.1.3. Номограмма для регулирования с прямой связью
- 12.1.4. Регулирование с прямой связью в случае нескольких входов
- 12.2. РЕГУЛИРОВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ
- 12.2.1. Регулирование с обратной связью, минимизирующее среднеквадратичную ошибку
- 12.2.2. Применение уравнения регулирования: ПИД-регулятор
- 12.2.3. Примеры дискретного регулирования с обратной связью
- 12.3. РЕГУЛИРОВАНИЕ С ПРЯМОЙ И ОБРАТНОЙ СВЯЗЯМИ
- 12.3.1. Регулирование с прямой и обратной связями, минимизирующее выходную среднеквадратичную ошибку
- 12.3.2. Пример регулирования с прямой и обратной связями
- 12.3.3. Преимущества и недостатки регулирования с прямой и обратной связями
- 12.4. Подгонка моделей передаточных функций шума по оперативным данным
- 12.4.1. Итеративный способ построения моделей
- 12.4.2. Оценивание по оперативным данным
- 12.4.3. Пример
- Глава 13. Некоторые дальнейшие проблемы регулирования
- 13.1. ЭФФЕКТ ДОБАВОЧНОГО ШУМА В СХЕМАХ РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ
- 13.1.1. Эффект пренебрежения добавочным шумом; упрощенные схемы
- 13.1.2. Оптимальное действие в случаях, когда корректировки содержат ошибки наблюдения
- 13.1.3. Перенос источника шума
- 13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
- 13.2.1. Вывод выражения для оптимальной корректировки
- 13.2.2. Схема с ограничением для примера «вязкость–подача газа»
- 13.3. ВЫБОР ИНТЕРВАЛА ОТСЧЕТА
- 13.3.1. Пример эффекта уменьшения частоты отсчетов
- 13.3.2. Влияние интервала отсчета на процесс ПСС(0,1,1)
- ПРОГРАММА 5. ИДЕНТИФИКАЦИЯ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 6. ПРЕДВАРИТЕЛЬНОЕ ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 7. ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ТАБЛИЦЫ ВРЕМЕННЫХ РЯДОВ