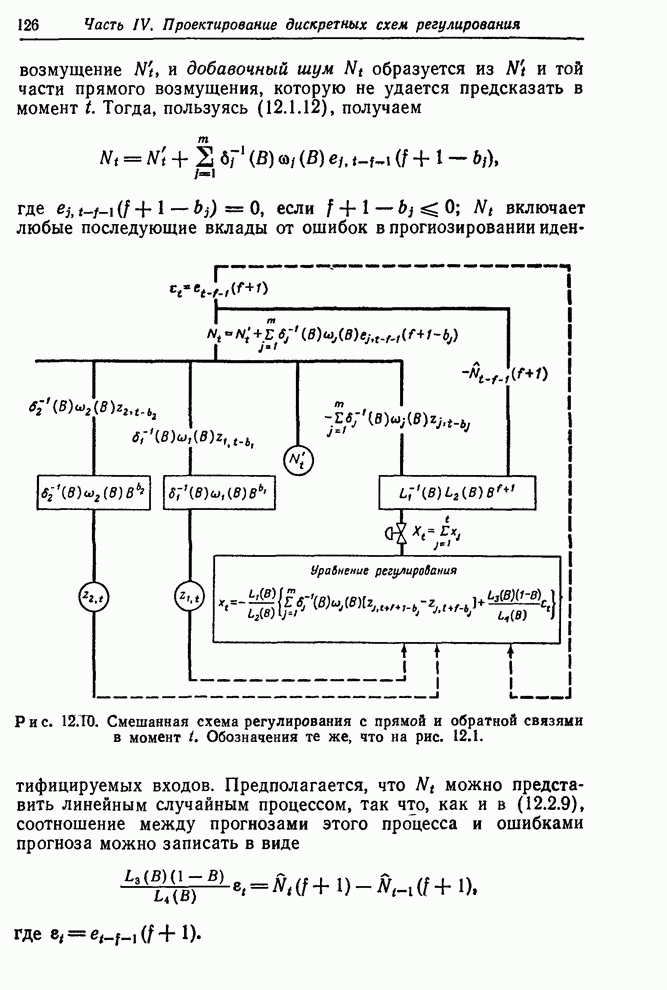
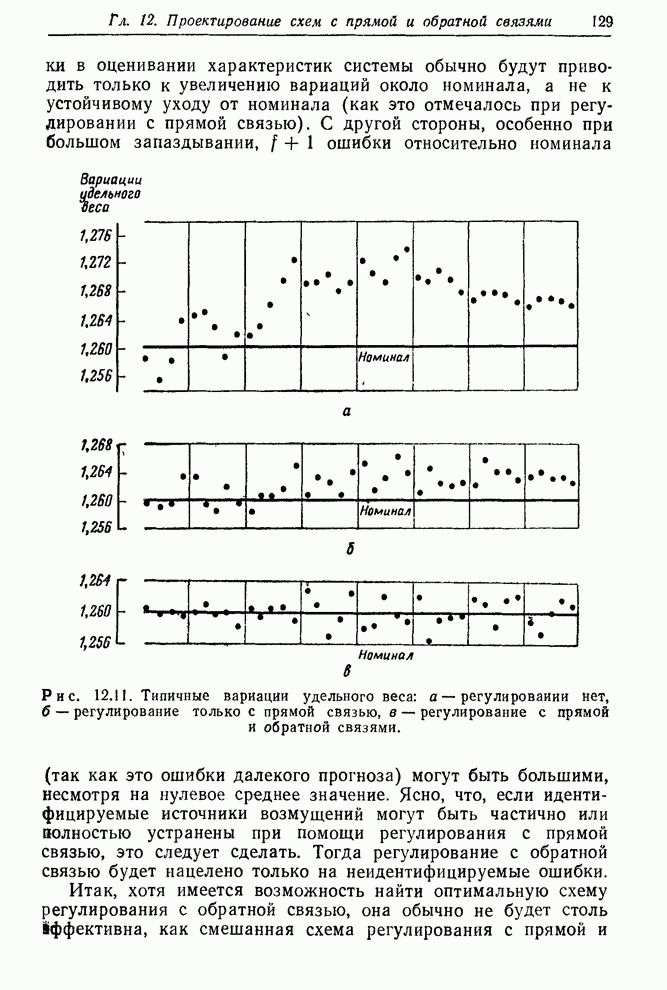
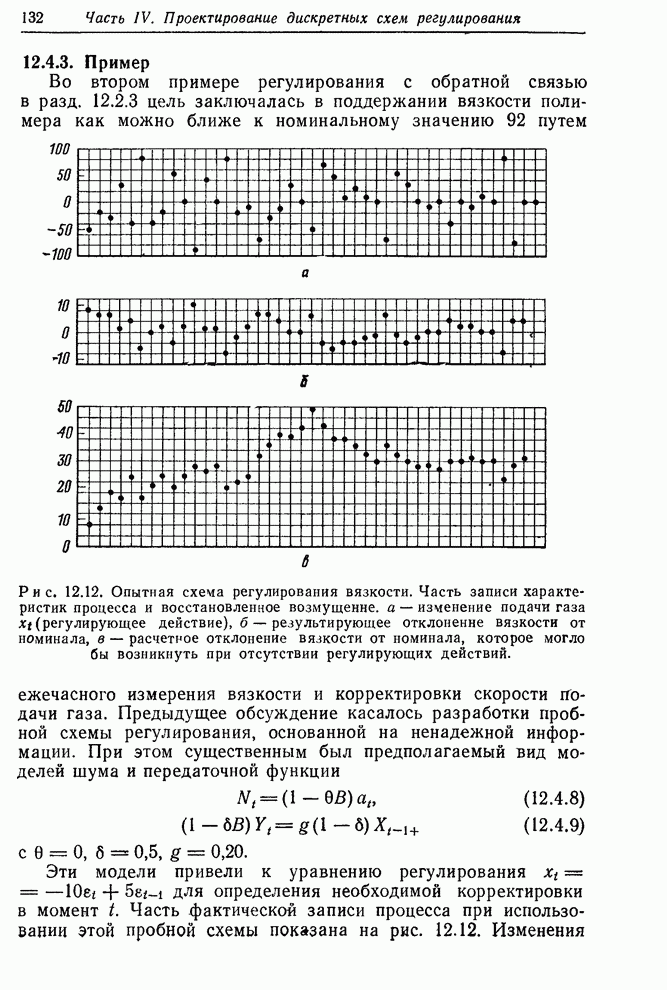
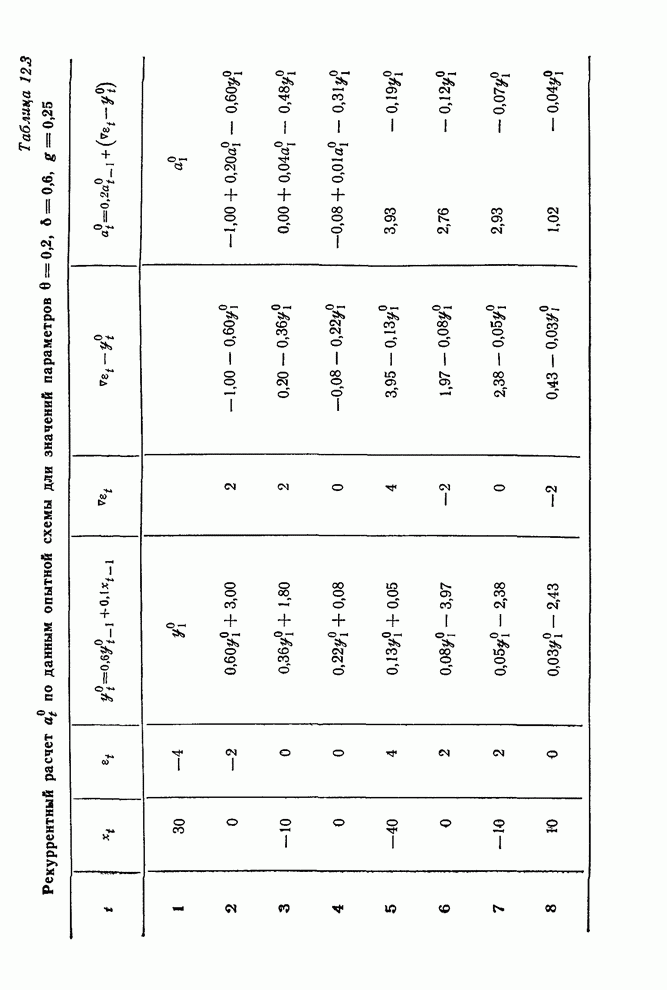
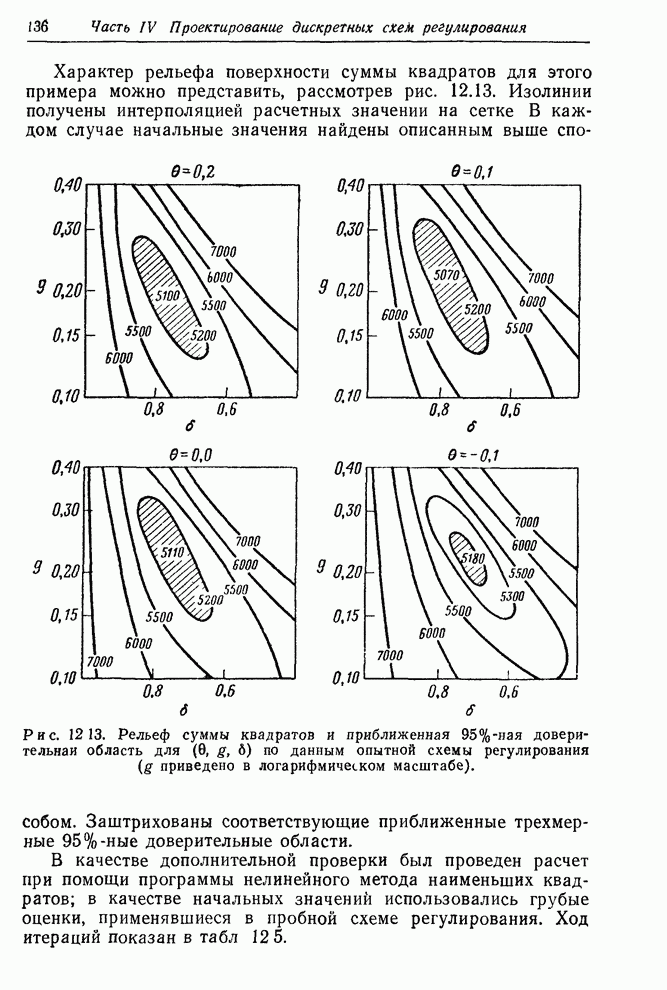
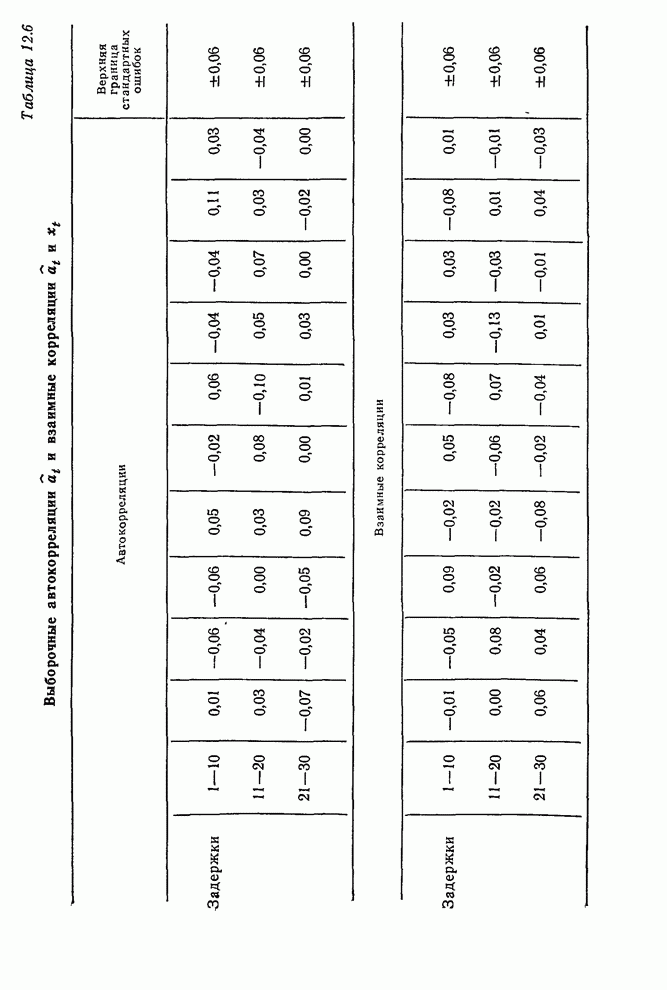
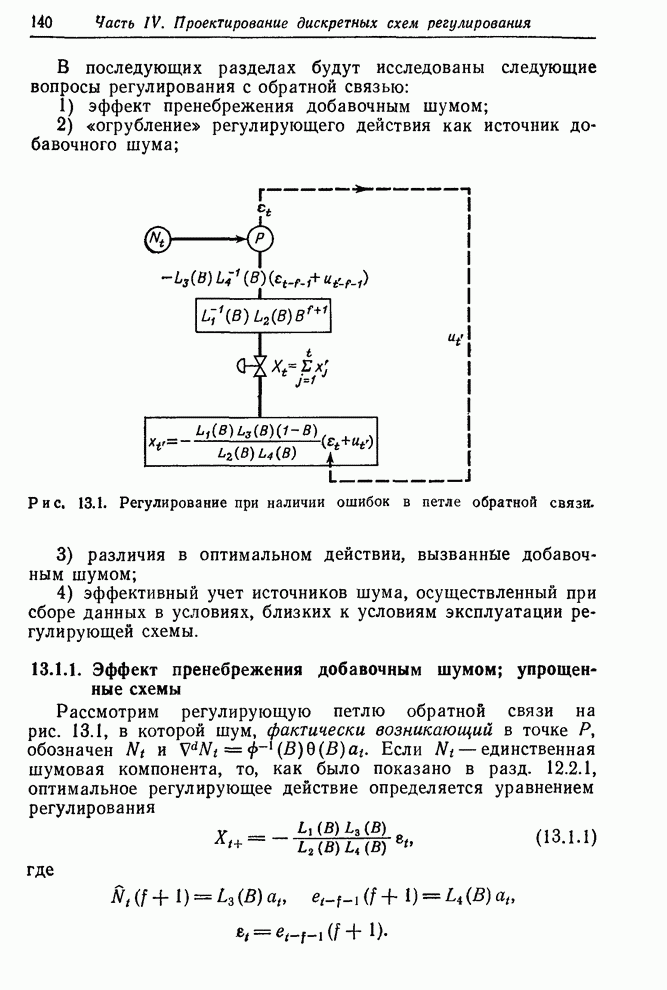
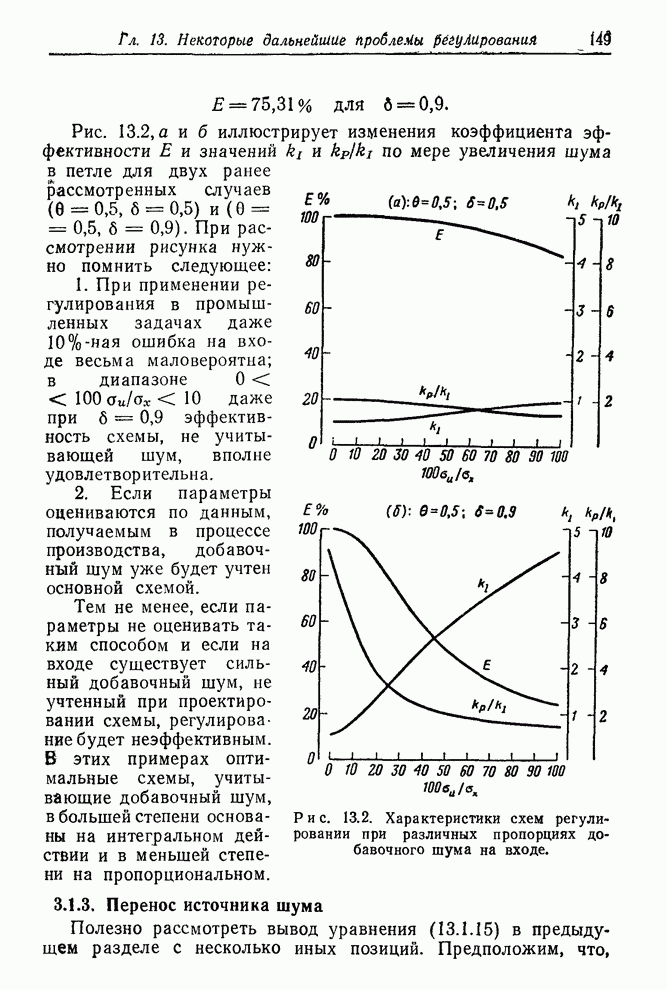
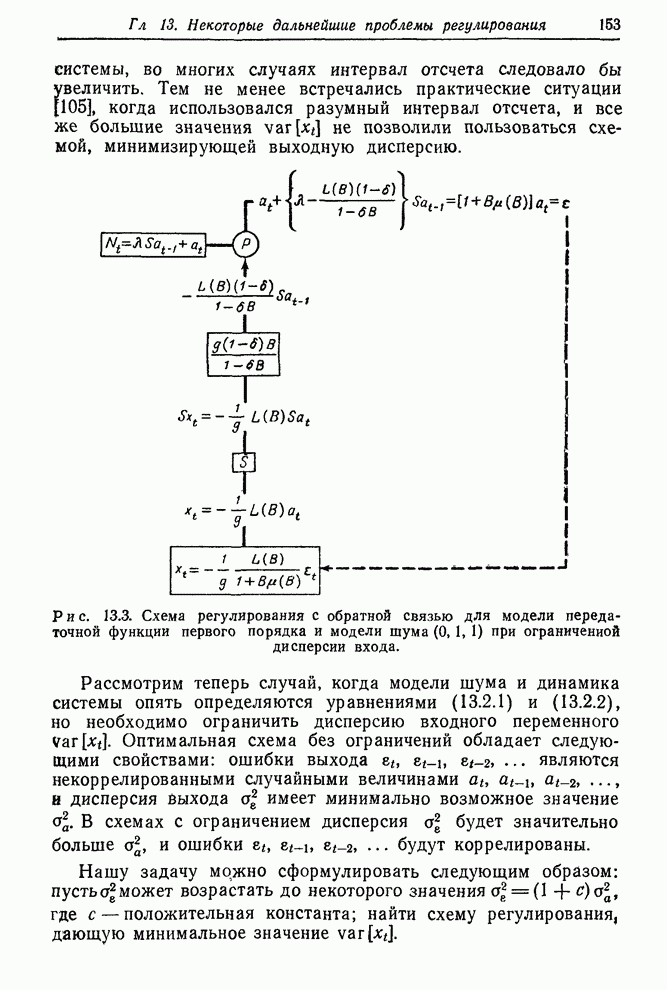
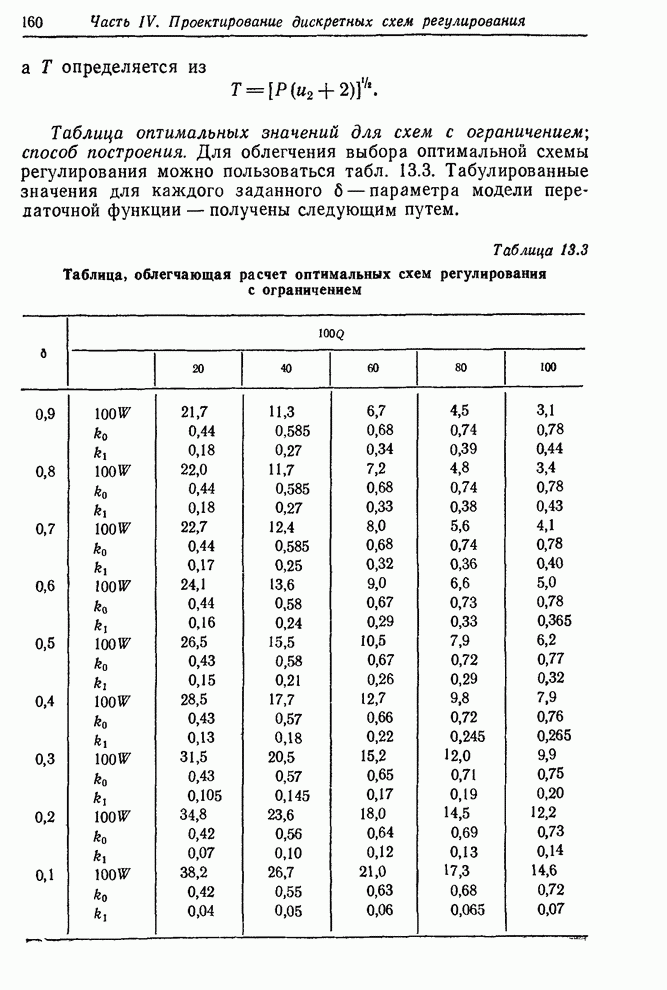
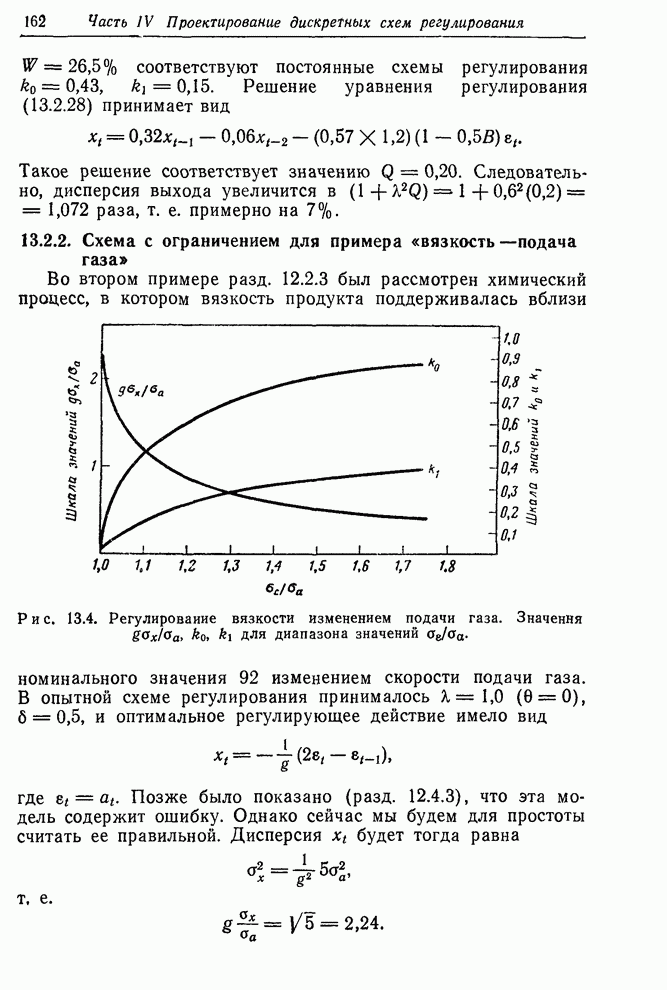
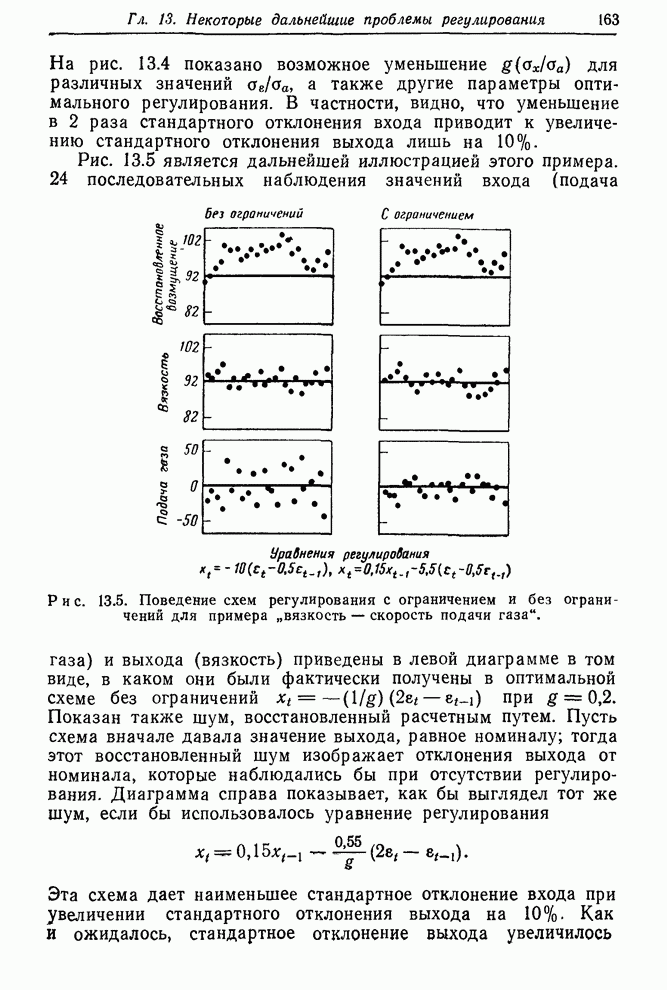
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
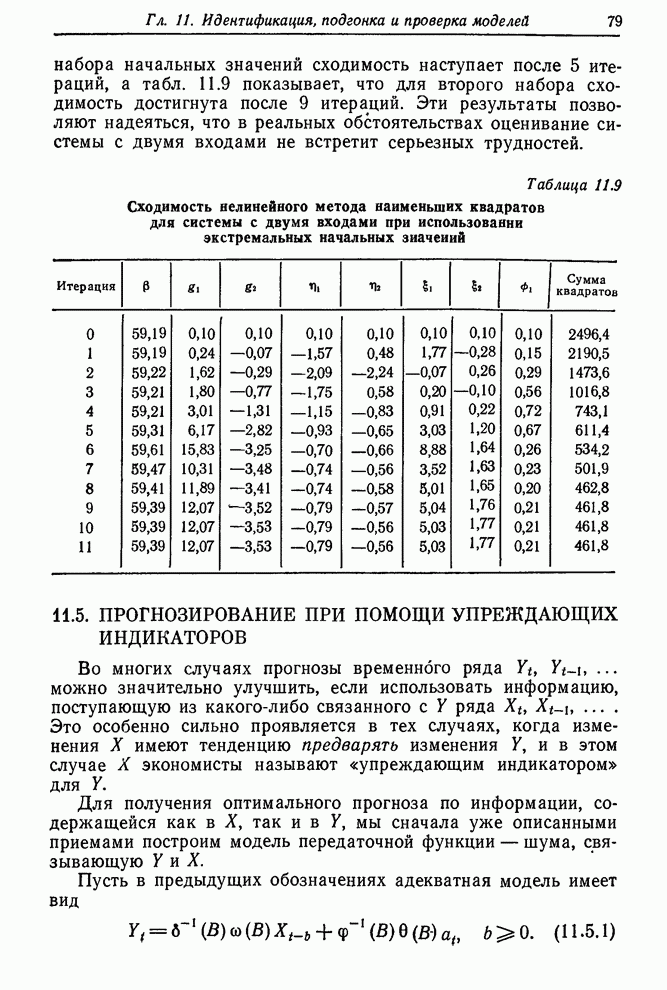
11.3.4. Конкретные способы проверки остаточных ошибок
На практике мы не знаем точно
параметров процесса и должны делать проверки по остаточным ошибкам, вычисленным
после подгонки методом наименьших квадратов. Даже если функциональная форма
подгоняемой модели адекватна, выборочные оценки параметров отличаются от
истинных значений, и распределение корреляций остаточных ошибок ![]() несколько отличается
от распределения автокорреляций
несколько отличается
от распределения автокорреляций ![]() . Поэтому следует быть осторожным при
использовании результатов предыдущего раздела для анализа корреляций
остаточных ошибок. Краткое последующее рассмотрение основывается на более
полном исследовании, приведенном в [84].
. Поэтому следует быть осторожным при
использовании результатов предыдущего раздела для анализа корреляций
остаточных ошибок. Краткое последующее рассмотрение основывается на более
полном исследовании, приведенном в [84].
Проверка выборочных
автокорреляций. Пусть после подгонки модели
передаточной функций — шума методом наименьших квадратов и вычисления
остаточных ошибок ![]() с
заменой параметров их оценками наименьших квадратов найдена выборочная
автокорреляционная функция этих ошибок
с
заменой параметров их оценками наименьших квадратов найдена выборочная
автокорреляционная функция этих ошибок ![]() . Тогда, как мы уже видели,
. Тогда, как мы уже видели,
а) заметные а регулярно
меняющиеся значения функции ![]() свидетельствуют о неадекватности
модели;
свидетельствуют о неадекватности
модели;
б) если проверка
автокорреляций не приводит к выявлению неадекватности модели передаточной
функции, то эта неадекватность, вероятно, вызвана подогнанной моделью шума ![]() .
.
В последнем случае идентификация вспомогательной модели
![]()
для описания корреляции остаточных ошибок от первичной модели может в соответствии с (11.3.15) дать весьма приближенное представление
![]()
о виде модели шума, которую следует выбрать. Однако при вынесении суждений о том, указывает ли кажущееся отклонение выборочной взаимной корреляции от нуля на ненулевое теоретическое значение, нужно учитывать некоторые факты, аналогичные рассмотренным в разд. 8.2.1.
Положим, что после
использования части ряда в качестве начальных значений ![]() значений
значений ![]() можно включить в расчет.
Тогда, если функциональный вид модели выбран правильно и в соответствующее
уравнение подставлены истинные значения параметров, остаточные ошибки
будут белым шумом и выборочные корреляции будут распределены взаимно
независимо с нулевым средним значением и дисперсией
можно включить в расчет.
Тогда, если функциональный вид модели выбран правильно и в соответствующее
уравнение подставлены истинные значения параметров, остаточные ошибки
будут белым шумом и выборочные корреляции будут распределены взаимно
независимо с нулевым средним значением и дисперсией ![]() . Когда вместо значений
параметров подставляются их выборочные оценки, распределение корреляций с
малыми задержками искажается. В частности, дисперсия выборочных корреляций с
малыми задержками может быть значительно меньше
. Когда вместо значений
параметров подставляются их выборочные оценки, распределение корреляций с
малыми задержками искажается. В частности, дисперсия выборочных корреляций с
малыми задержками может быть значительно меньше ![]() , а их значения сильно коррелированы.
Поэтому сравнение выборочной автокорреляции
, а их значения сильно коррелированы.
Поэтому сравнение выборочной автокорреляции ![]() при малых
при малых ![]() со «стандартной ошибкой»
со «стандартной ошибкой» ![]() может создавать
ложное впечатление о малости первой. Кроме того, всплески выборочной
автокорреляционной функции при малых задержках могут происходить просто из-за
высокой корреляции между выборочными оценками. Если амплитуда таких всплесков
мала по сравнению с
может создавать
ложное впечатление о малости первой. Кроме того, всплески выборочной
автокорреляционной функции при малых задержках могут происходить просто из-за
высокой корреляции между выборочными оценками. Если амплитуда таких всплесков
мала по сравнению с ![]() они могут быть чисто случайными и не
свидетельствовать о каком-либо реальном поведении теоретических автокорреляций.
они могут быть чисто случайными и не
свидетельствовать о каком-либо реальном поведении теоретических автокорреляций.
Существует следующий способ
проверки, учитывающий эти эффекты искажения распределения, вызываемые
подгонкой. Рассмотрим первые ![]() выборочных автокорреляций,
выборочных автокорреляций, ![]() и пусть
и пусть ![]() будет достаточно
велико, так что если записать модель в виде
будет достаточно
велико, так что если записать модель в виде
![]() ,
,
то можно ожидать, что веса ![]() при
при ![]() окажутся пренебрежимо
малыми. Тогда при адекватности функциональной формы модели величина
окажутся пренебрежимо
малыми. Тогда при адекватности функциональной формы модели величина
 (11.3.18)
(11.3.18)
распределена примерно как ![]() с
с ![]() степенями свободы.
Заметим, что число степеней свободы
степенями свободы.
Заметим, что число степеней свободы ![]() зависит от числа параметров в модели
шума, но не зависит от числа параметров в модели передаточной функции. Сравнив
значение
зависит от числа параметров в модели
шума, но не зависит от числа параметров в модели передаточной функции. Сравнив
значение ![]() с
таблицей уровней значимости
с
таблицей уровней значимости ![]() , мы можем приближенно проверить
гипотезу об адекватности модели.
, мы можем приближенно проверить
гипотезу об адекватности модели.
Проверка выборочных взаимных корреляций. Как мы показали в предыдущем разделе,
1) появление
регулярных заметно отличающихся от нуля выборочных взаимных корреляций ![]() свидетельствует о неадекватности
модели передаточной функции;
свидетельствует о неадекватности
модели передаточной функции;
2) по другим
свойствам взаимной корреляции можно выявить тип необходимых изменений.
Конкретно, если подгоняемая передаточная функция ![]() и мы рассматриваем взаимные корреляции
между величинами
и мы рассматриваем взаимные корреляции
между величинами ![]() и
и
![]() то весьма
приближенные оценки расхождений
то весьма
приближенные оценки расхождений ![]() можно найти по формуле
можно найти по формуле
![]() .
.
Пусть предполагаемая
функциональная форма модели верна и в уравнение подставляются истинные
значения параметров. Остаточные ошибки будут белым шумом, не коррелированным с ![]() и, согласно
(11.1.11), дисперсия
и, согласно
(11.1.11), дисперсия ![]() для ряда с эффективной длиной
для ряда с эффективной длиной ![]() будет близка к
будет близка к ![]() . Однако в отличие от
выборочных автокорреляций
. Однако в отличие от
выборочных автокорреляций ![]() эти взаимные корреляции будут
приближенно не коррелированы. В общем случае, если
эти взаимные корреляции будут
приближенно не коррелированы. В общем случае, если ![]() автокоррелированы, то и
выборочные взаимные корреляции
автокоррелированы, то и
выборочные взаимные корреляции ![]() также коррелированы. Как следует из (11.1.12),
в предположении, что
также коррелированы. Как следует из (11.1.12),
в предположении, что ![]() и
и ![]() взаимно некоррелированы, коэффициент
корреляции между
взаимно некоррелированы, коэффициент
корреляции между ![]() и
и
![]() равен
равен
![]() , (11.3.19)
, (11.3.19)
Это означает, что приближенно
выборочные взаимные корреляции имеют ту же автокорреляционную функцию,
что и первоначальный входной ряд ![]() . Поэтому, если
. Поэтому, если ![]() автокоррелированы, абсолютно
адекватная модель переходной функции будет приводить к выборочным взаимным
корреляциям
автокоррелированы, абсолютно
адекватная модель переходной функции будет приводить к выборочным взаимным
корреляциям ![]() ,
хотя и малым по величине, но с заметной регулярностью поведения. Этот
эффект будет устранен, если проводить проверку путем
,
хотя и малым по величине, но с заметной регулярностью поведения. Этот
эффект будет устранен, если проводить проверку путем
вычисления выборочных
взаимных корреляций ![]() с предварительно выравненным входом
с предварительно выравненным входом
![]() .
.
Как и в случае
автокорреляций, при подстановке выборочных оценок вместо истинных значений
параметров, распределение выборочных взаимных корреляций искажается. Однако,
исходя из амплитуд взаимных корреляций, можно выполнить грубую проверку
гипотезы об адекватности модели. Для этого нужно оценить взаимные корреляции ![]()
![]() между выравненным
входом
между выравненным
входом ![]() и
остаточными ошибками
и
остаточными ошибками ![]() .
. ![]() должно быть достаточно большим, чтобы
веса
должно быть достаточно большим, чтобы
веса ![]() и
и ![]() в (11.3 13) можно
было бы принять пренебрежимо малыми при
в (11.3 13) можно
было бы принять пренебрежимо малыми при ![]() . Эффекты, вызванные использованием выборочных
параметров при вычислении остаточных ошибок, как и ранее, ограничены в основном
корреляциями при малых задержках, чьи дисперсии значительно меньше
. Эффекты, вызванные использованием выборочных
параметров при вычислении остаточных ошибок, как и ранее, ограничены в основном
корреляциями при малых задержках, чьи дисперсии значительно меньше ![]() . Эти выборочные
корреляции могут быть сильно зависимыми, даже если вход — белый шум.
. Эти выборочные
корреляции могут быть сильно зависимыми, даже если вход — белый шум.
Однако справедливо [84], что
 (11.3.20)
(11.3.20)
приближенно распределено как ![]() с
с ![]() степенями свободы, где
степенями свободы, где ![]() — число параметров в
подгоняемой модели передаточной функции. Заметим, что число степеней свободы
не зависит от числа параметров в подгоняемой модели шума.
— число параметров в
подгоняемой модели передаточной функции. Заметим, что число степеней свободы
не зависит от числа параметров в подгоняемой модели шума.
| << Предыдущий параграф | Следующий параграф >> |
- Часть III. ПОСТРОЕНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- Глава 10. Модели передаточной функции
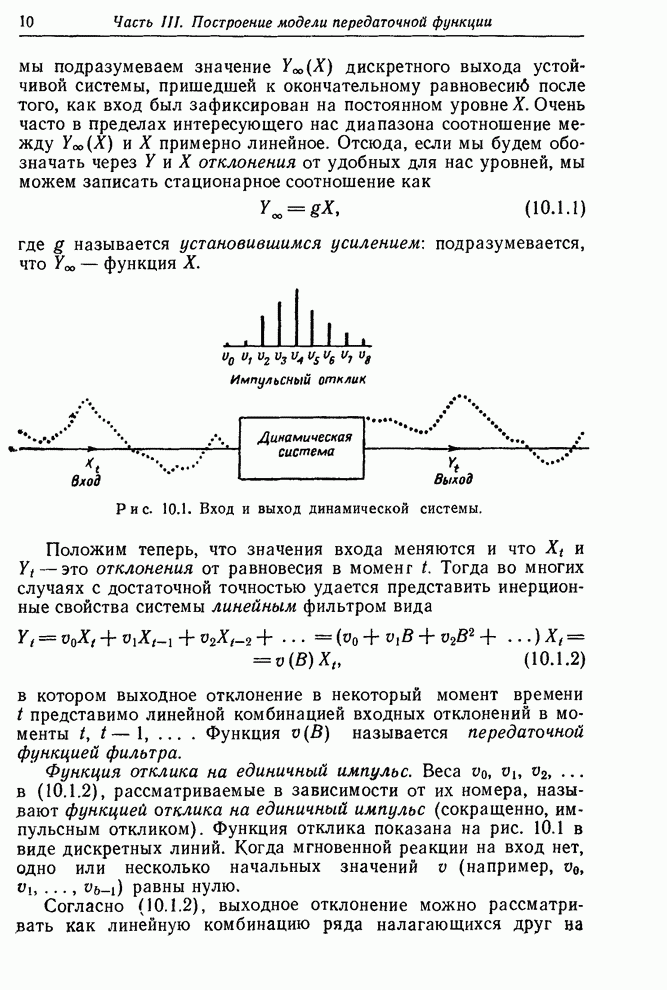
- 10.1. ЛИНЕЙНЫЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 10.1.1. Дискретная передаточная функция
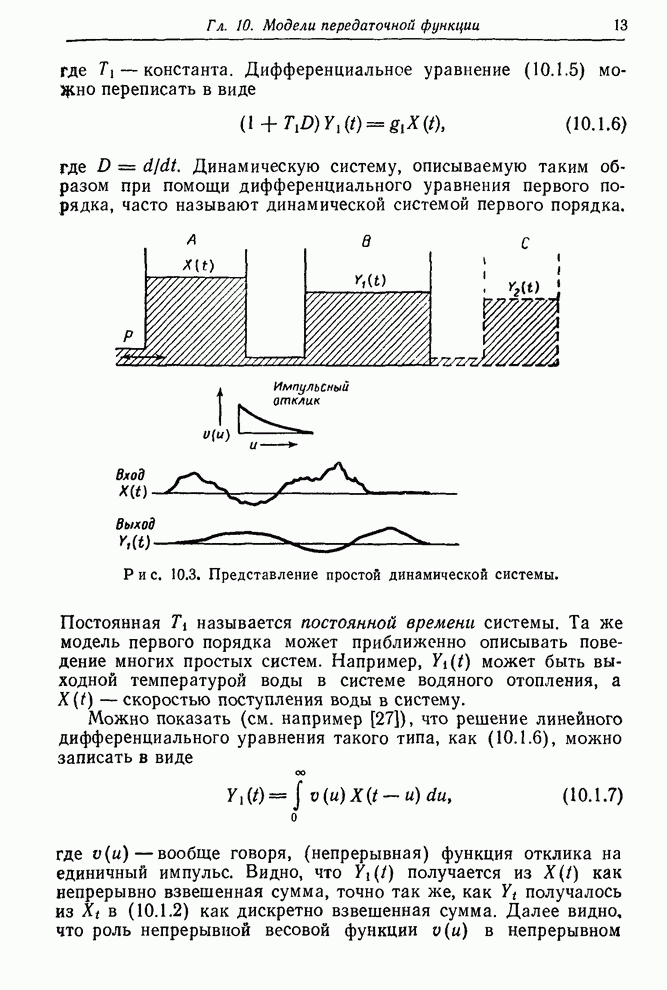
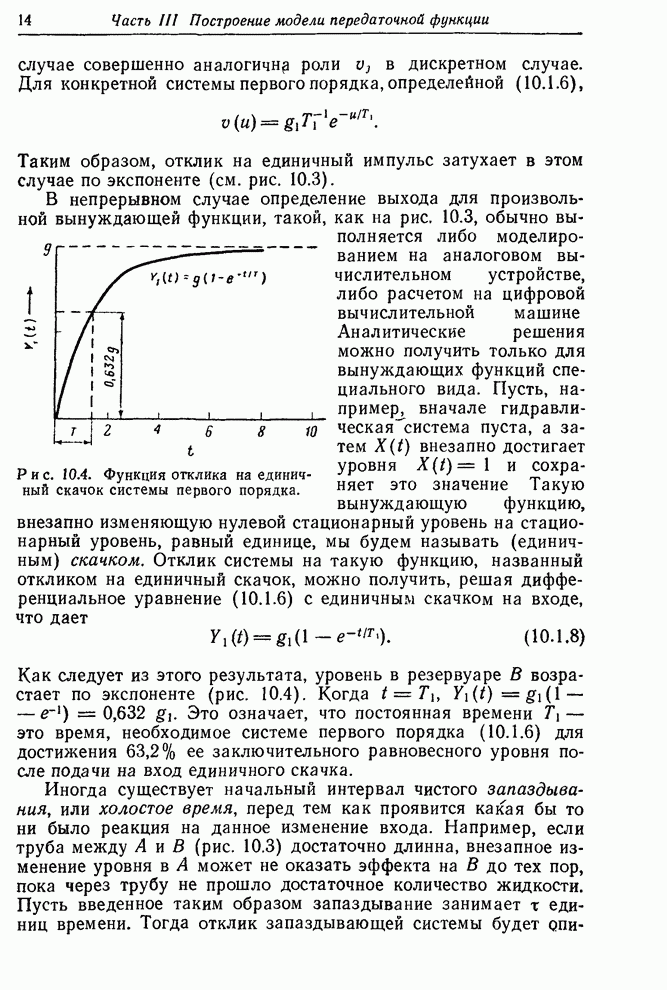
- 10.1.2. Непрерывные динамические модели, описываемые дифференциальными уравнениями
- 10.2. ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ МОДЕЛИ, ОПИСЫВАЕМЫЕ РАЗНОСТНЫМИ УРАВНЕНИЯМИ
- 10.2.1. Общая форма разностного уравнения
- 10.2.2. Природа передаточной функции
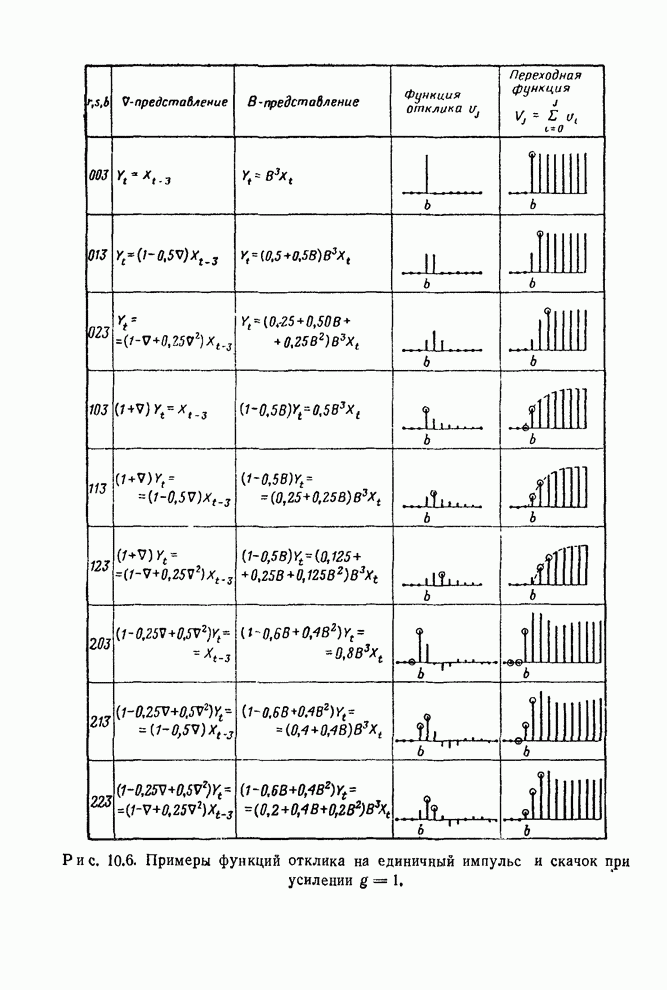
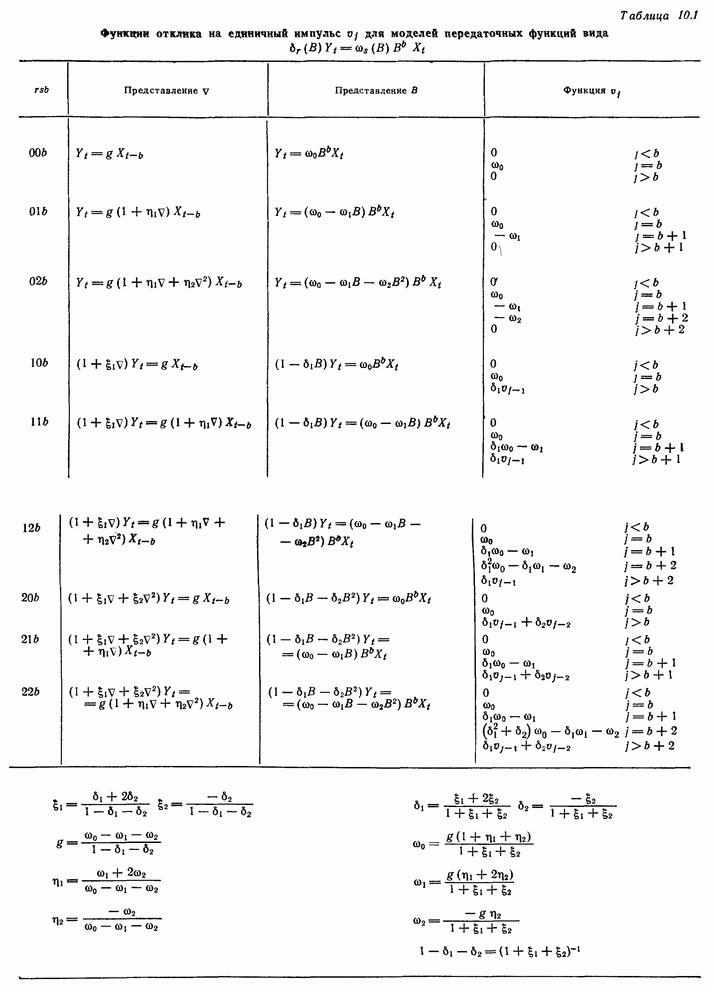
- 10.2.3. Дискретные модели передаточных функций первого и второго порядков
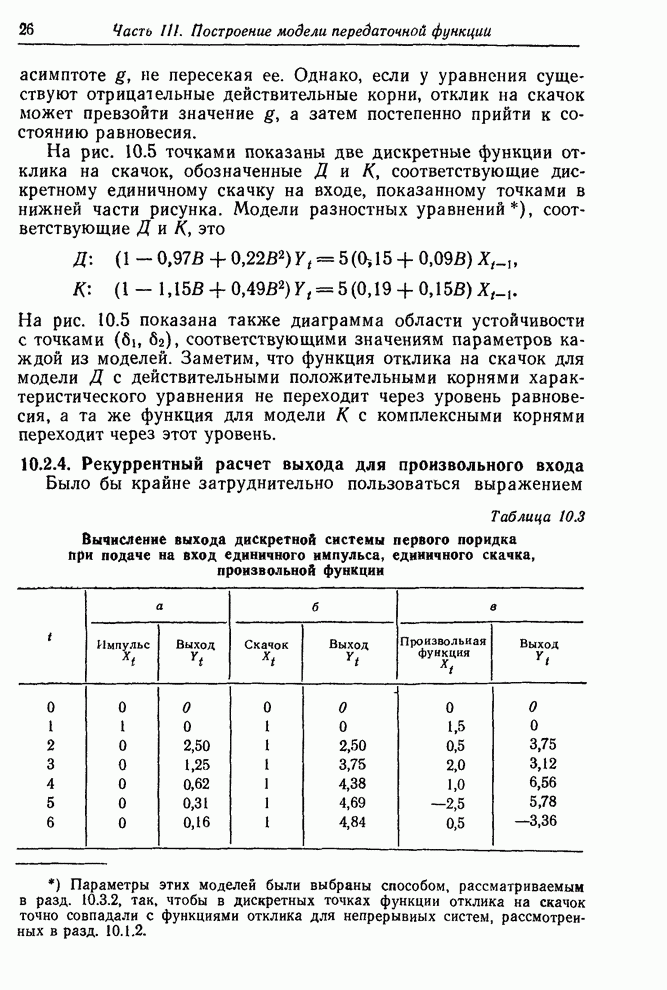
- 10.2.4. Рекуррентный расчет выхода для произвольного входа
- 10.3. СООТНОШЕНИЕ МЕЖДУ ДИСКРЕТНОЙ И НЕПРЕРЫВНОЙ МОДЕЛЯМИ
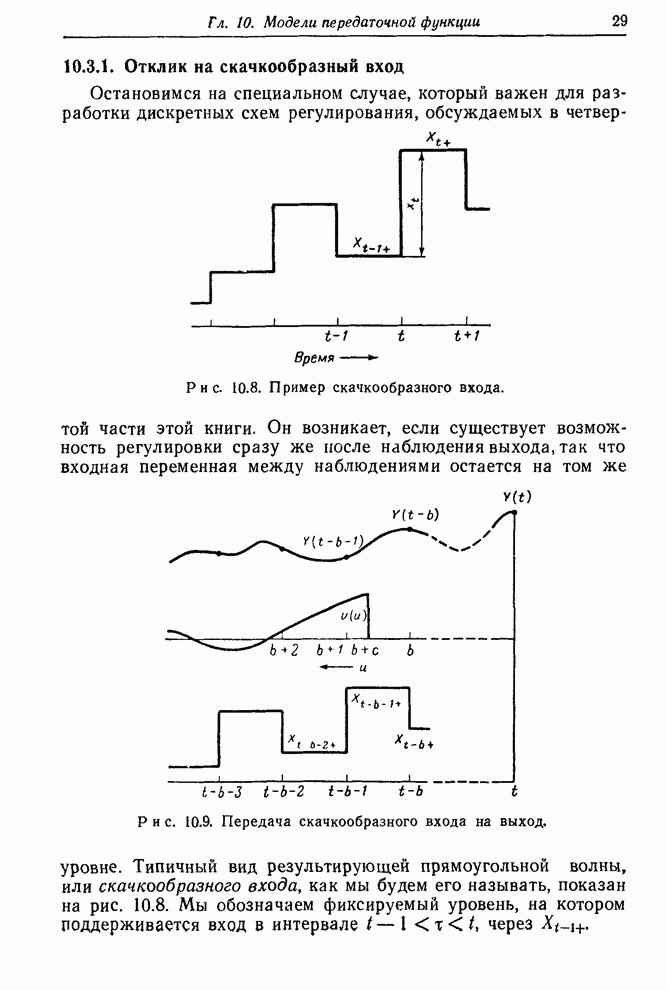
- 10.3.1. Отклик на скачкообразный вход
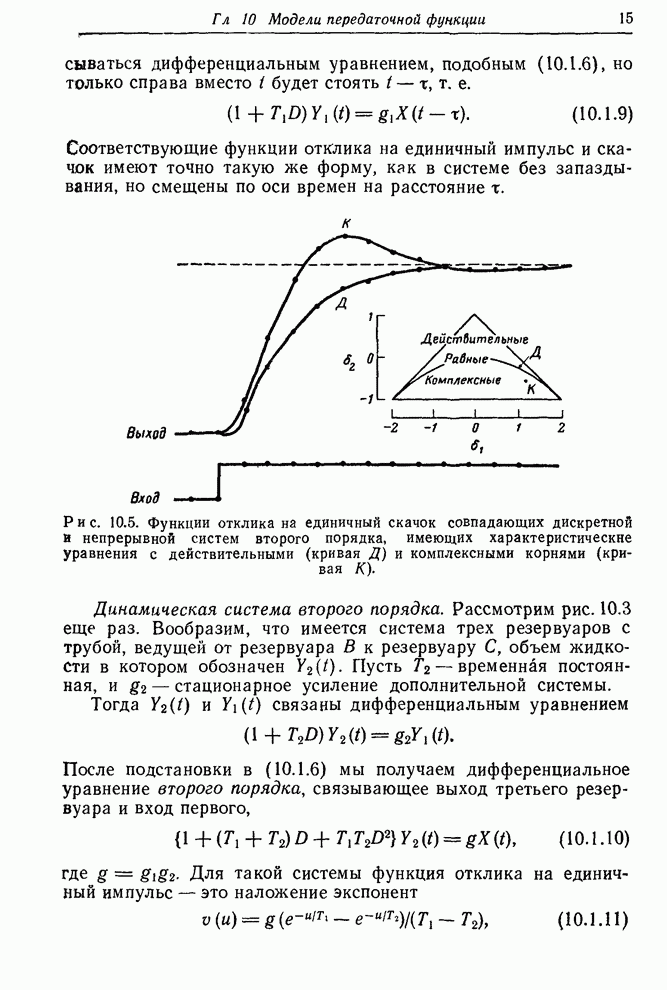
- 10.3.2. Соотношения совпадающих систем первого и второго порядков
- 10.3.3. Аппроксимация общих непрерывных моделей дискретными моделями
- 10.3.4. Модели передаточных функций с добавленным шумом
- ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
- ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
- Глава 11. Идентификация, подгонка и проверка моделей передаточных функций
- 11.1. Взаимная корреляционная функция
- 11.1.1. Свойства взаимных ковариационной и корреляционной функций
- 11.1.2. Оценивание взаимных ковариационных и корреляционных функций
- 11.1.3. Приближенные стандартные ошибки выборочных оценок взаимных корреляций
- 11.2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.2.1. Идентификация моделей передаточной функции с предварительным выравниванием спектра входа
- 11.2.2. Пример идентификации модели передаточной функции
- 11.2.3. Идентификация модели шума
- 11.2.4. Некоторые общие соображения об идентификации моделей передаточных функций
- 11.3. ПОДГОНКА И ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.3.1. Условная сумма квадратов
- 11.3.2. Нелинейное оценивание
- 11.3.3. Использование остаточных ошибок для диагностической проверки
- 11.3.4. Конкретные способы проверки остаточных ошибок
- 11.4. Некоторые примеры подгонок и проверок моделей передаточных функций
- 11.4.1. Подгонка и проверка модели газовой печи
- 11.4.2. Искусственный пример с двумя входами
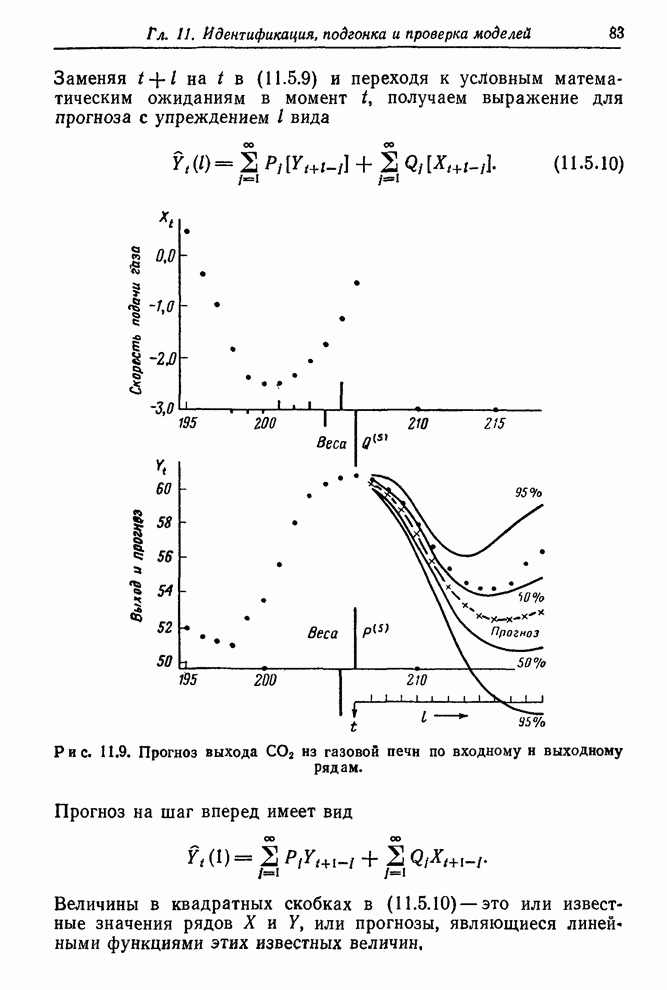
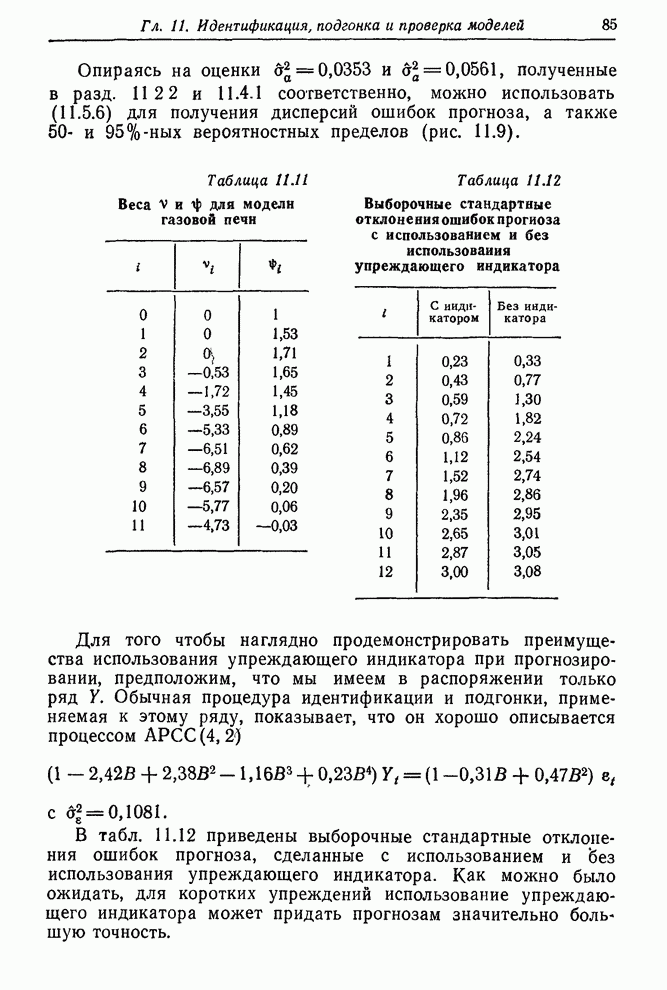
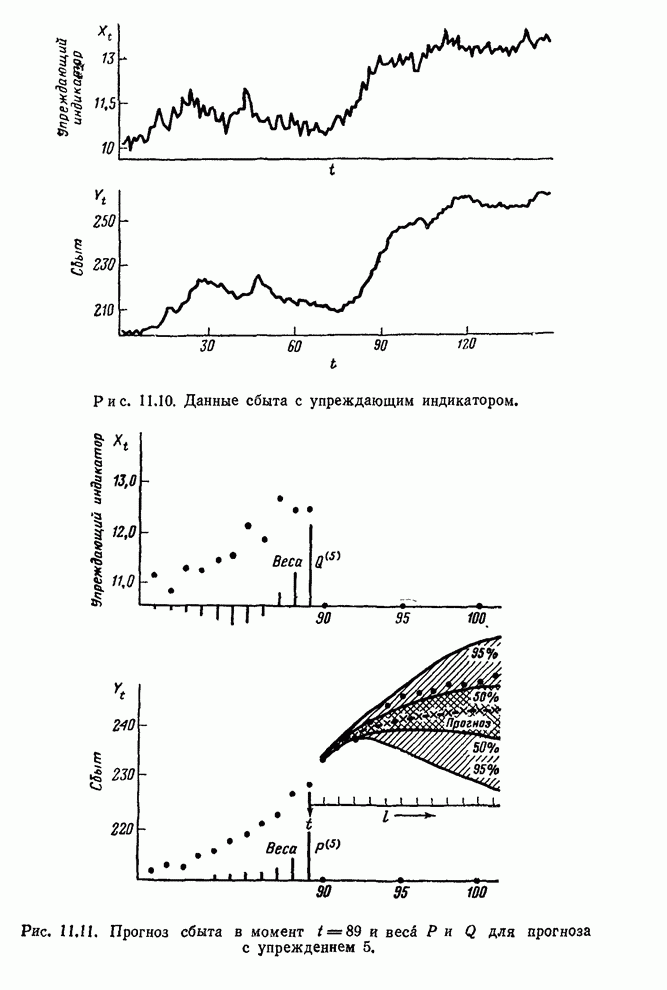
- 11.5. ПРОГНОЗИРОВАНИЕ ПРИ ПОМОЩИ УПРЕЖДАЮЩИХ ИНДИКАТОРОВ
- 11.5.1. Прогноз с минимальной среднеквадратичной ошибкой
- 11.5.2. Прогнозы выхода СO2 из газовой печи
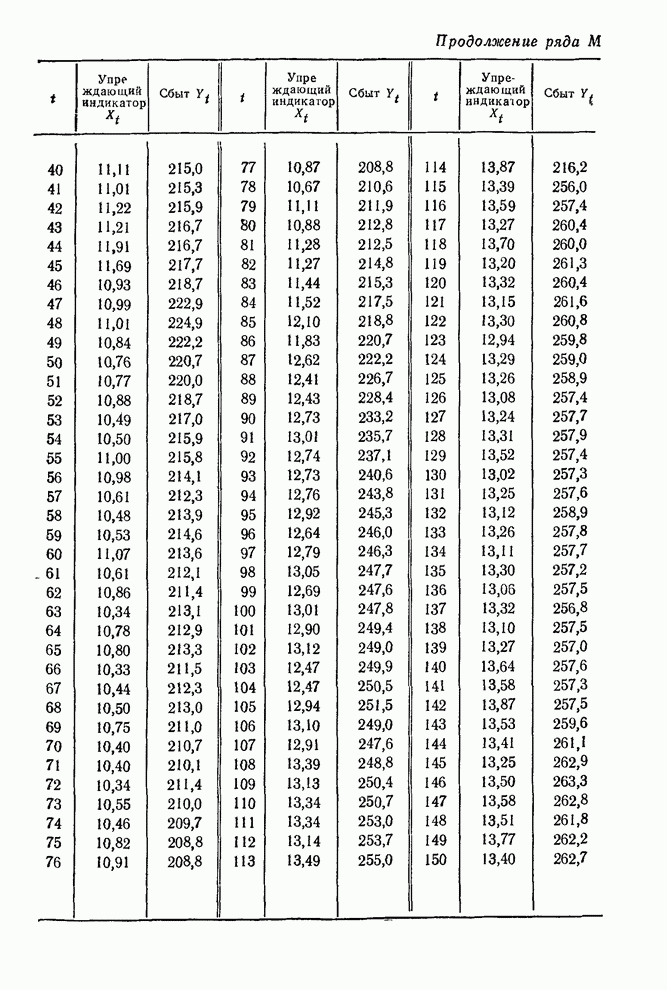
- 11.5.3. Прогноз нестационарных данных сбыта при помощи упреждающего индикатора
- 11.6. НЕКОТОРЫЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОЦЕНИВАНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ П11.1. ИСПОЛЬЗОВАНИЕ ВЗАИМНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
- Заключение
- Часть IV. Проектирование дискретных схем регулирования
- Глава 12. Проектирование схем регулирования с прямой и обратной связями
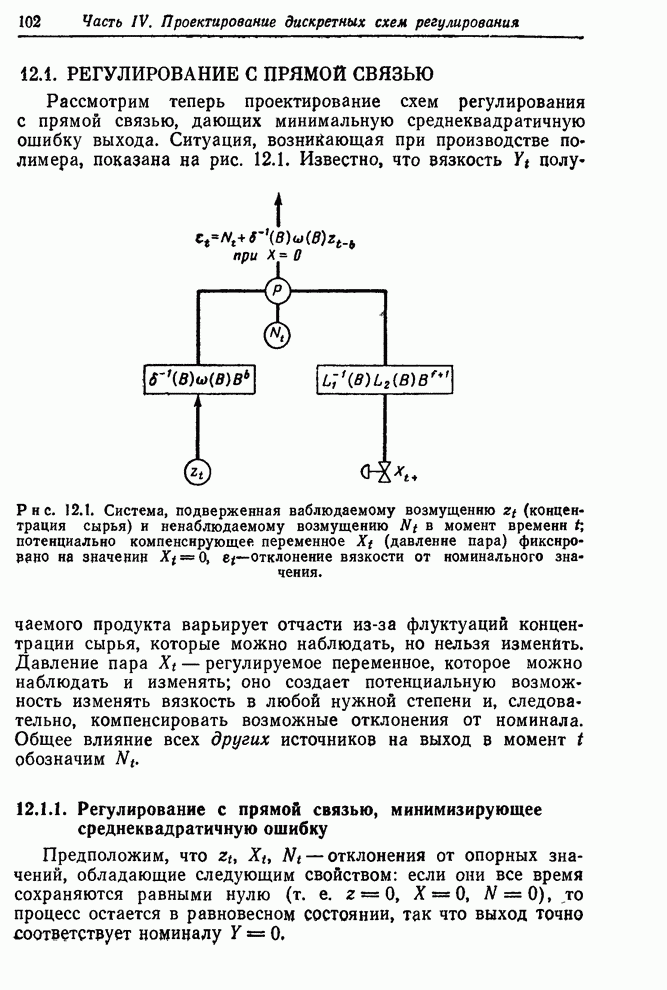
- 12.1. РЕГУЛИРОВАНИЕ С ПРЯМОЙ СВЯЗЬЮ
- 12.1.1. Регулирование с прямой связью, минимизирующее среднеквадратичную ошибку
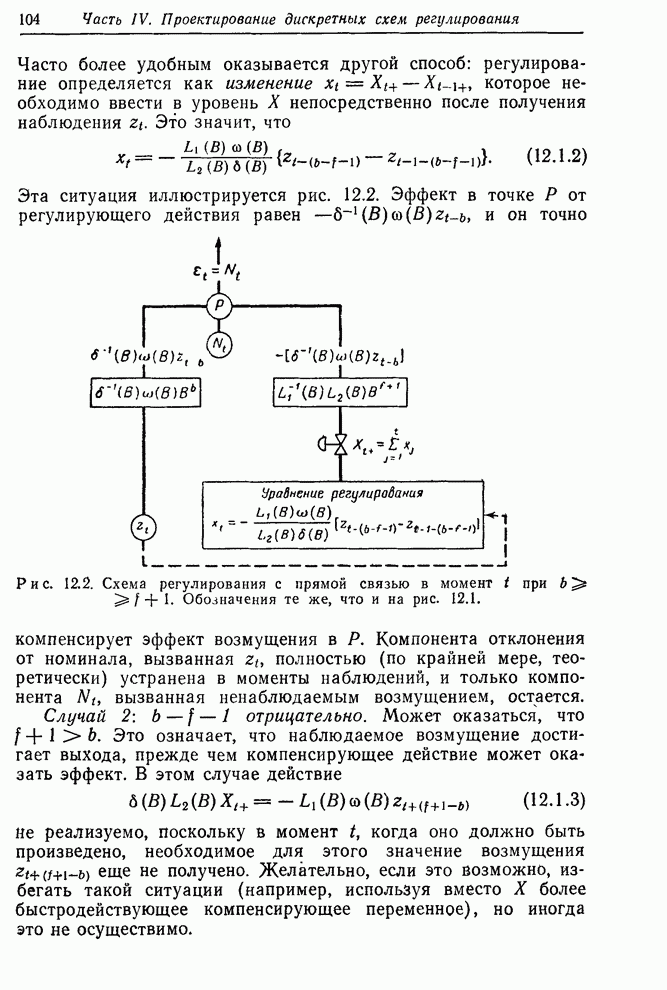
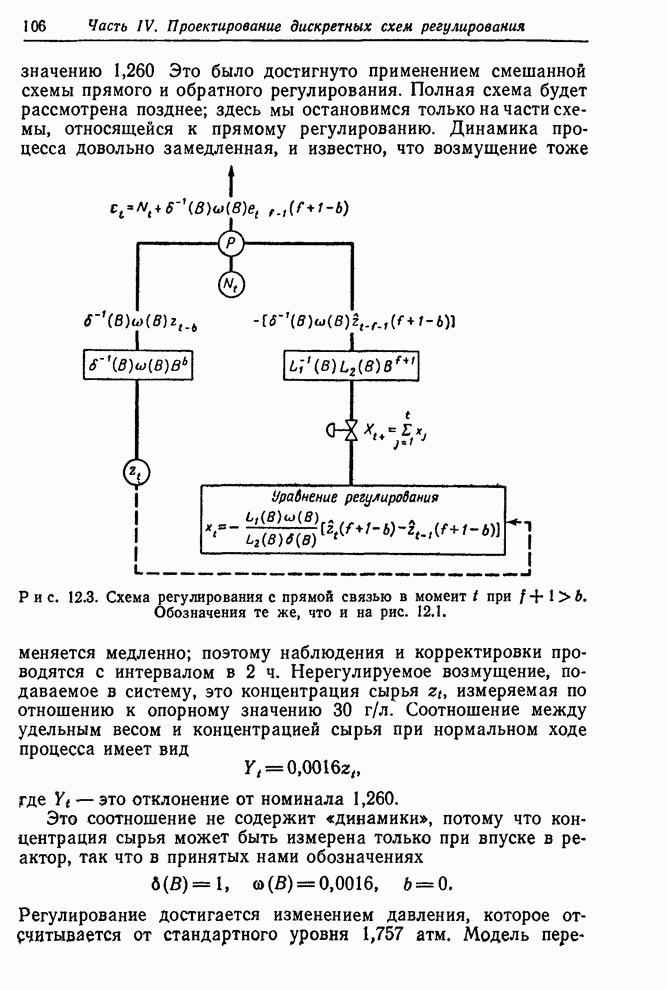
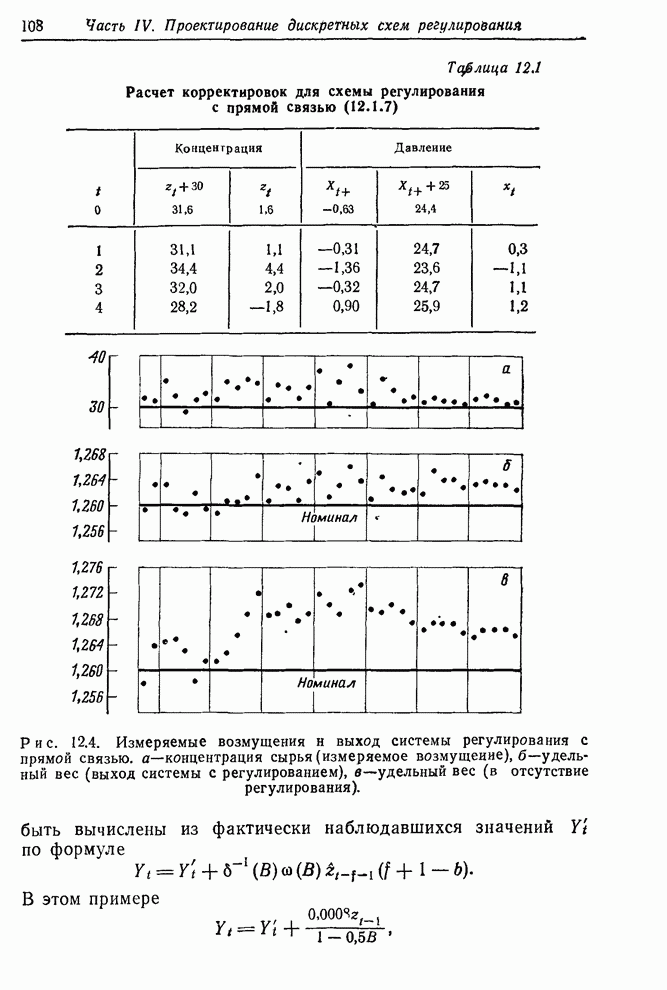
- 12.1.2. Пример — регулирование удельного веса промежуточного продукта
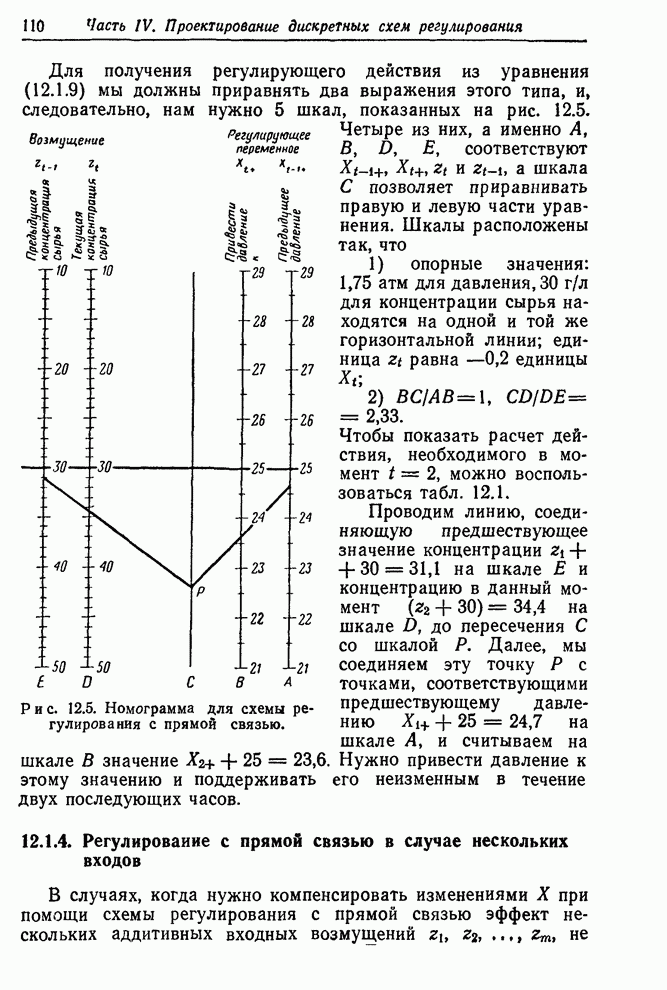
- 12.1.3. Номограмма для регулирования с прямой связью
- 12.1.4. Регулирование с прямой связью в случае нескольких входов
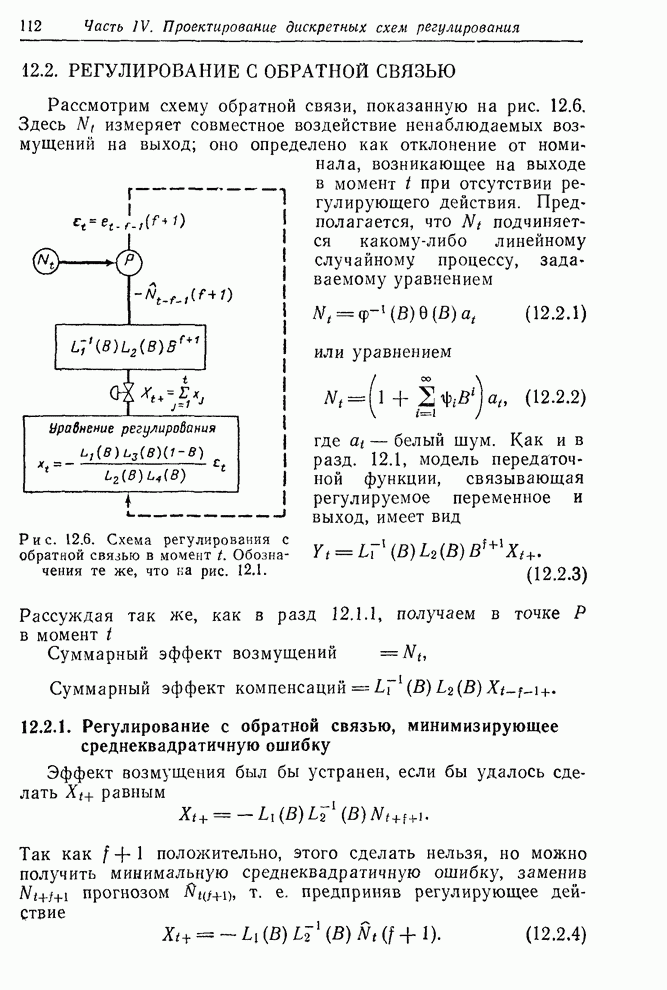
- 12.2. РЕГУЛИРОВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ
- 12.2.1. Регулирование с обратной связью, минимизирующее среднеквадратичную ошибку
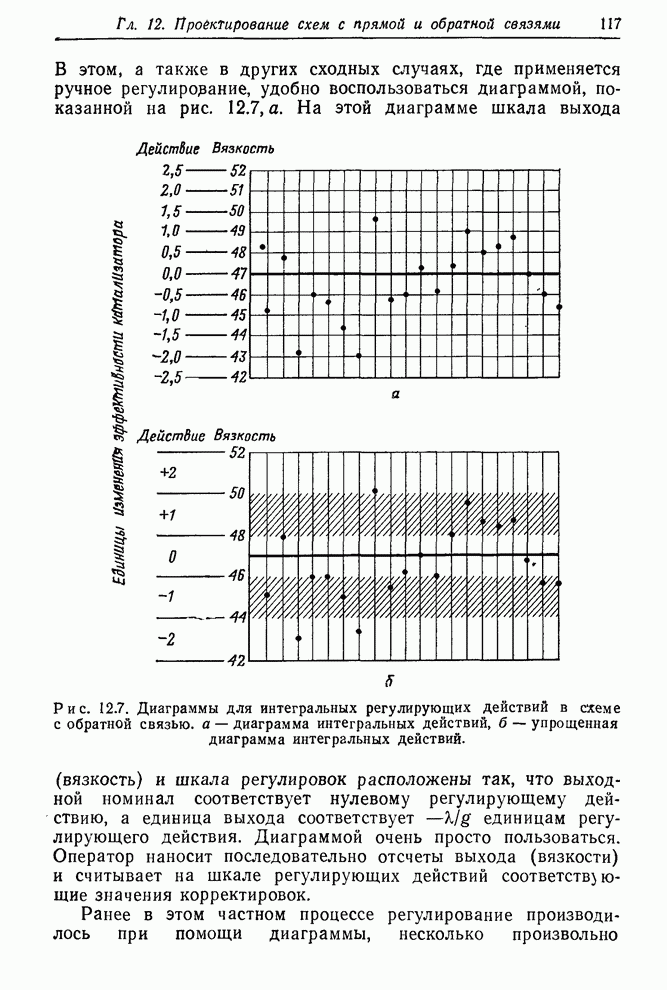
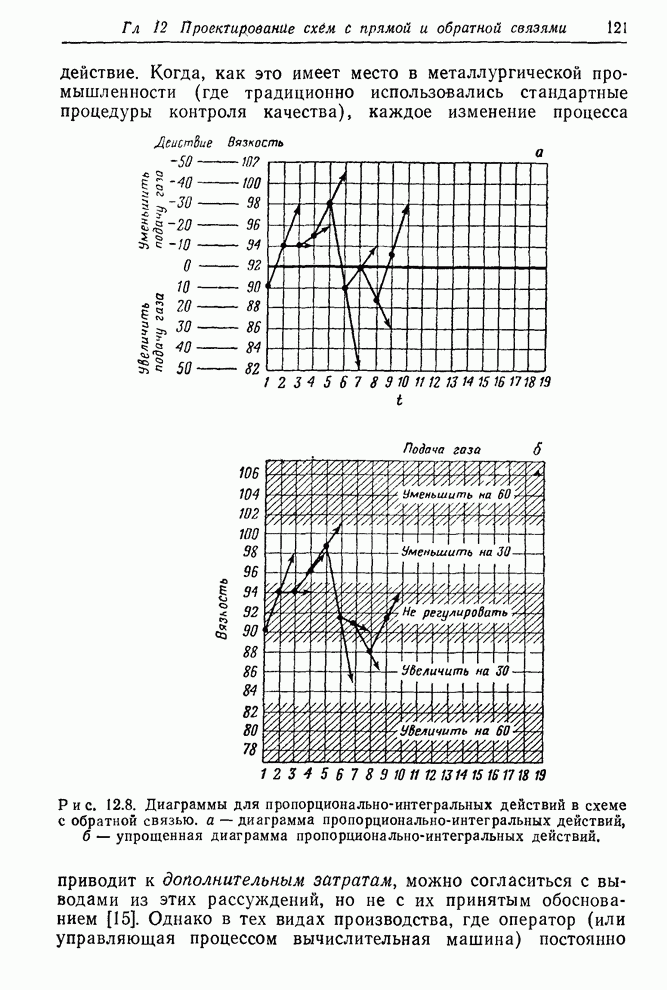
- 12.2.2. Применение уравнения регулирования: ПИД-регулятор
- 12.2.3. Примеры дискретного регулирования с обратной связью
- 12.3. РЕГУЛИРОВАНИЕ С ПРЯМОЙ И ОБРАТНОЙ СВЯЗЯМИ
- 12.3.1. Регулирование с прямой и обратной связями, минимизирующее выходную среднеквадратичную ошибку
- 12.3.2. Пример регулирования с прямой и обратной связями
- 12.3.3. Преимущества и недостатки регулирования с прямой и обратной связями
- 12.4. Подгонка моделей передаточных функций шума по оперативным данным
- 12.4.1. Итеративный способ построения моделей
- 12.4.2. Оценивание по оперативным данным
- 12.4.3. Пример
- Глава 13. Некоторые дальнейшие проблемы регулирования
- 13.1. ЭФФЕКТ ДОБАВОЧНОГО ШУМА В СХЕМАХ РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ
- 13.1.1. Эффект пренебрежения добавочным шумом; упрощенные схемы
- 13.1.2. Оптимальное действие в случаях, когда корректировки содержат ошибки наблюдения
- 13.1.3. Перенос источника шума
- 13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
- 13.2.1. Вывод выражения для оптимальной корректировки
- 13.2.2. Схема с ограничением для примера «вязкость–подача газа»
- 13.3. ВЫБОР ИНТЕРВАЛА ОТСЧЕТА
- 13.3.1. Пример эффекта уменьшения частоты отсчетов
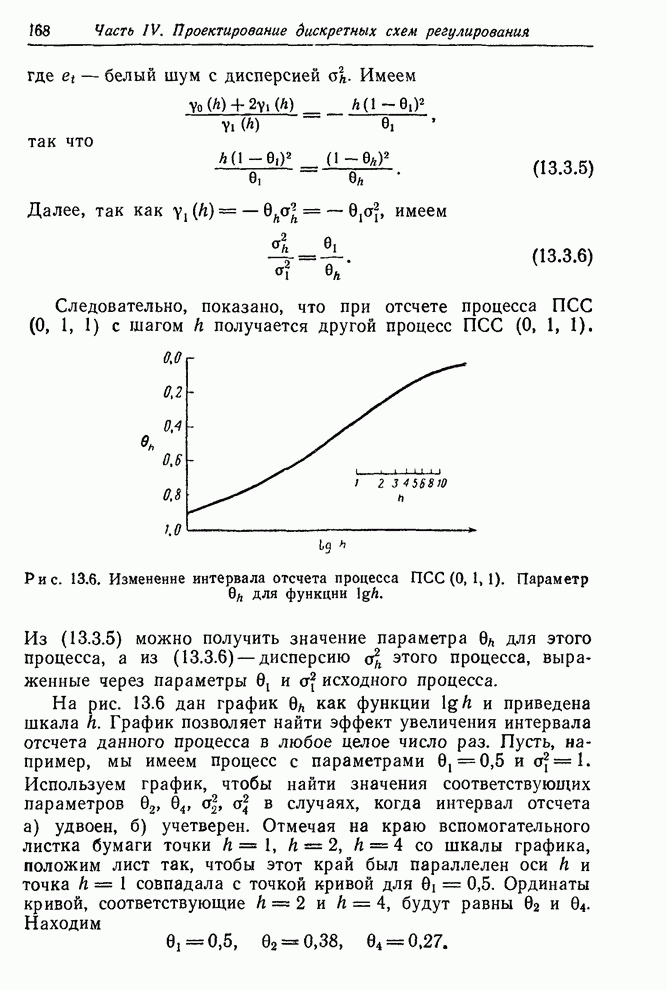
- 13.3.2. Влияние интервала отсчета на процесс ПСС(0,1,1)
- ПРОГРАММА 5. ИДЕНТИФИКАЦИЯ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 6. ПРЕДВАРИТЕЛЬНОЕ ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 7. ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
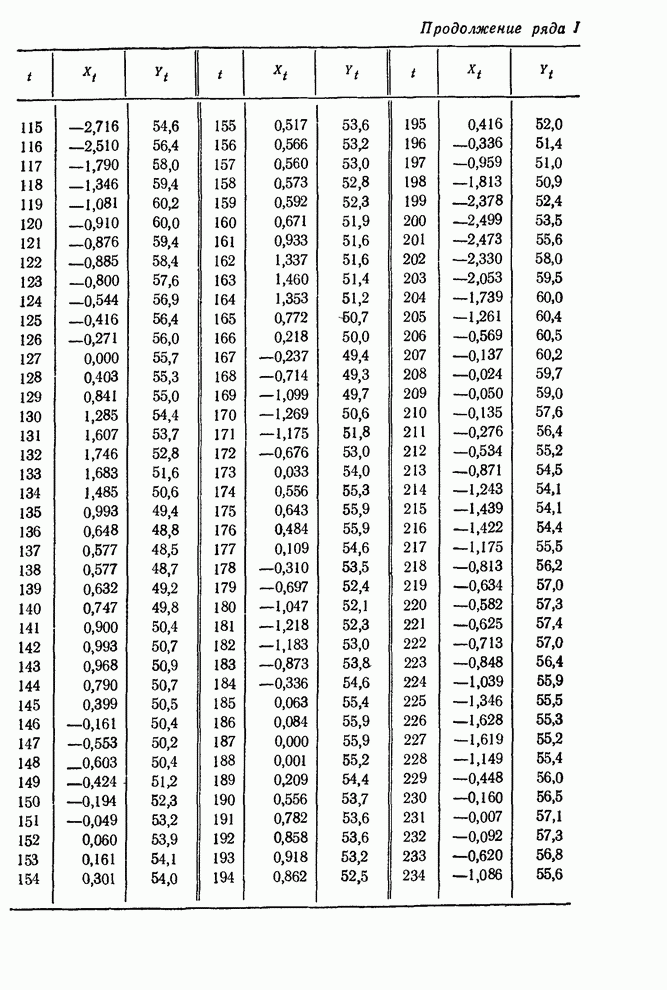
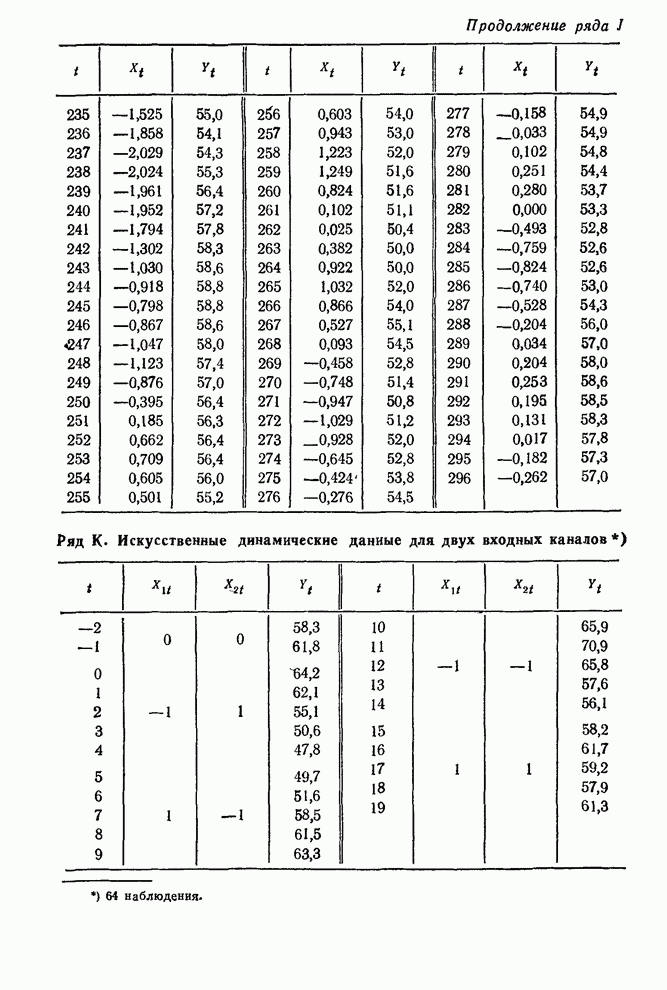
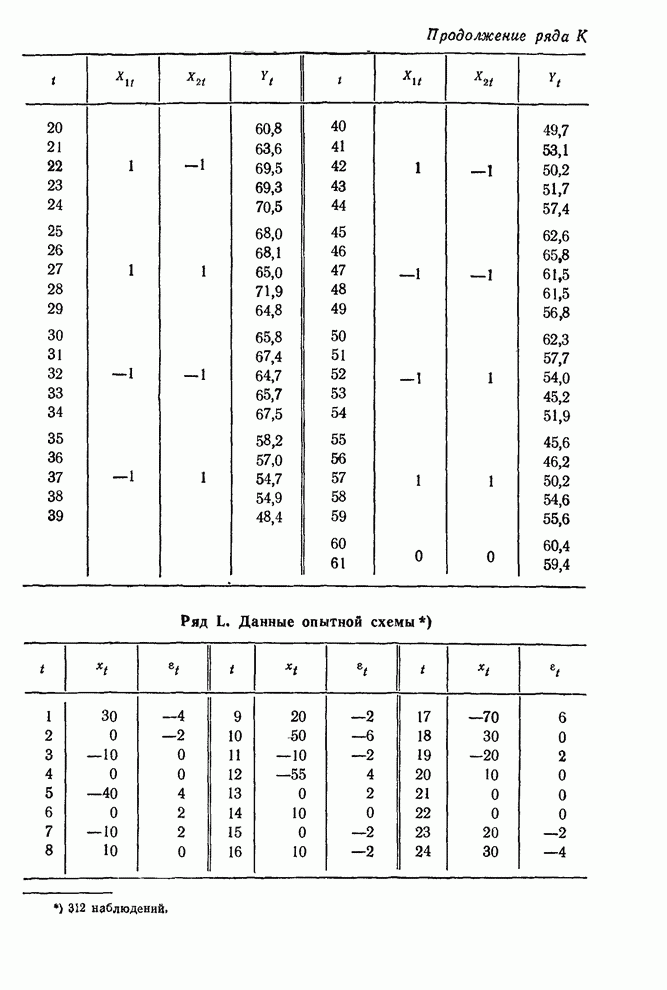
- ТАБЛИЦЫ ВРЕМЕННЫХ РЯДОВ