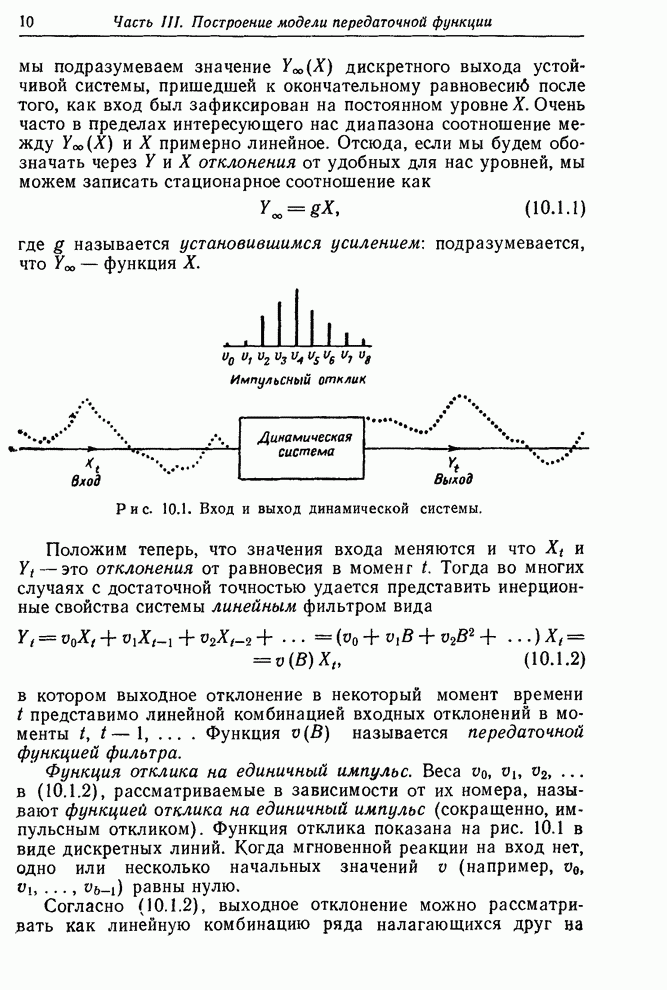
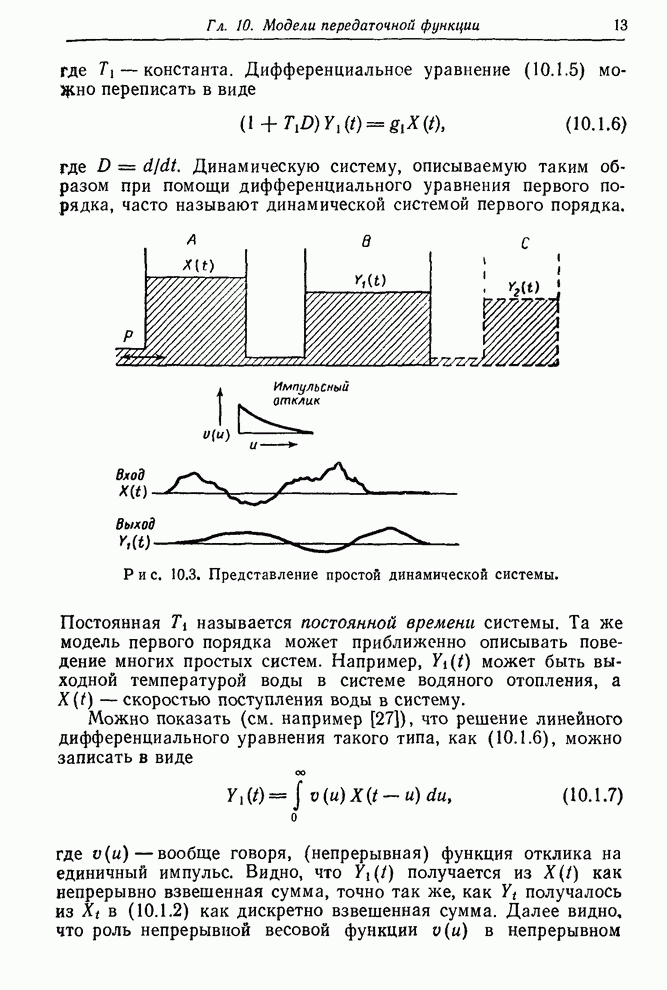
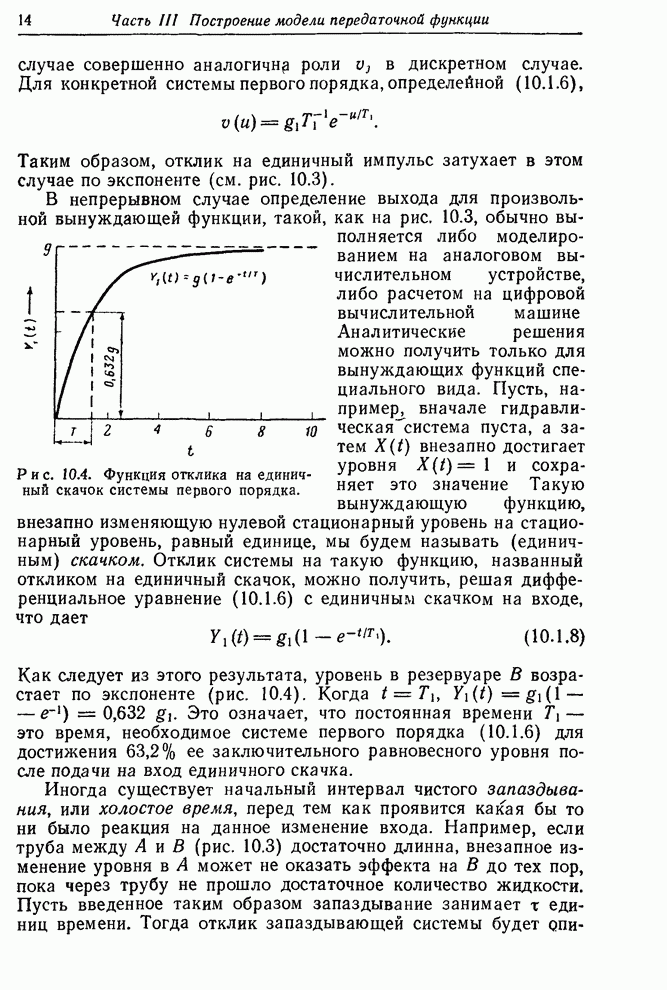
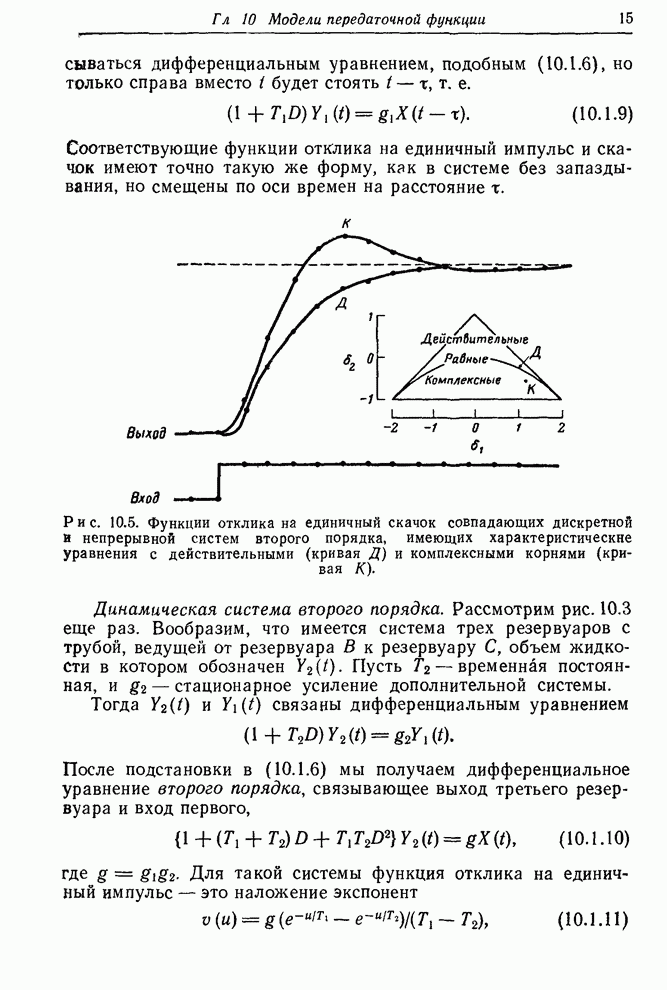
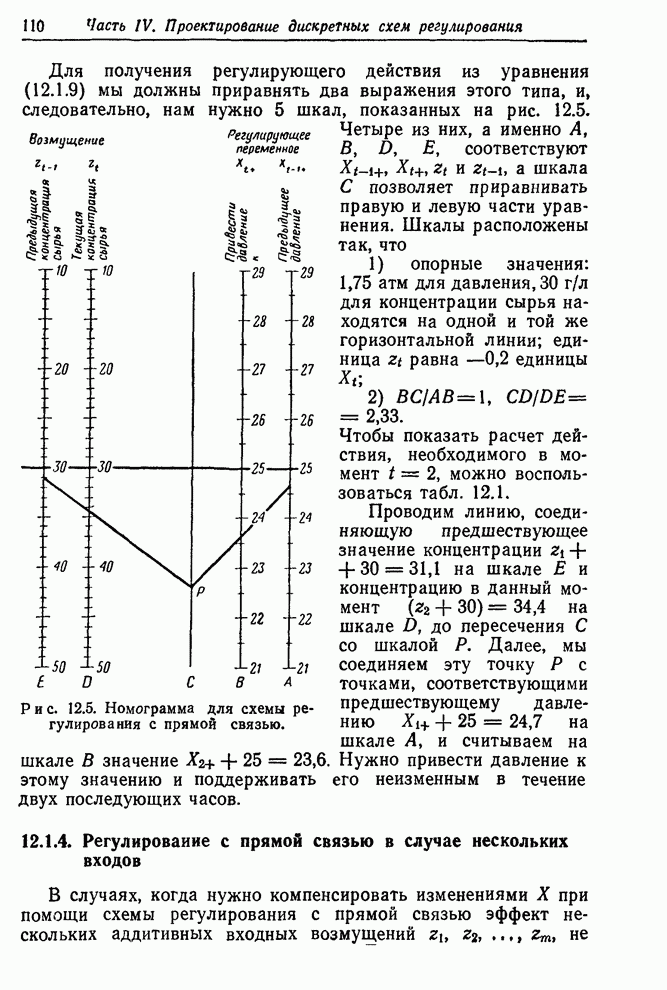
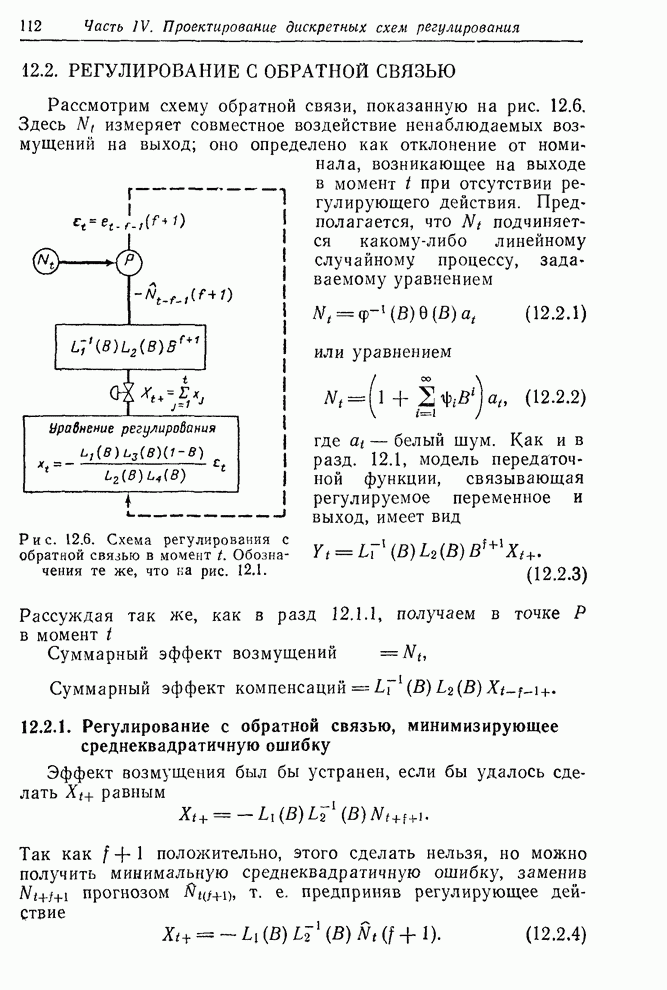
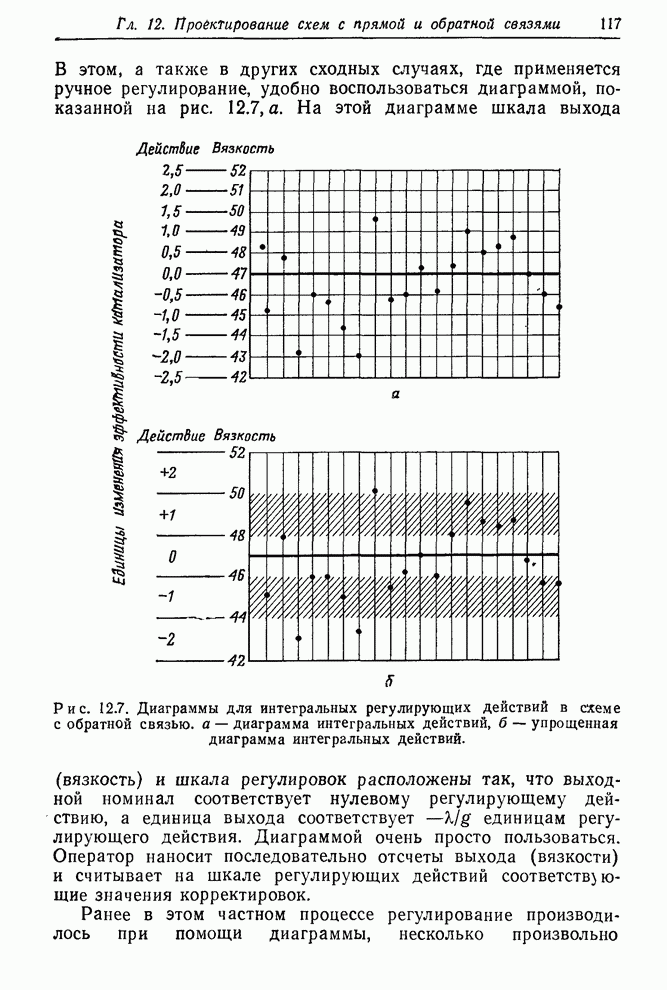
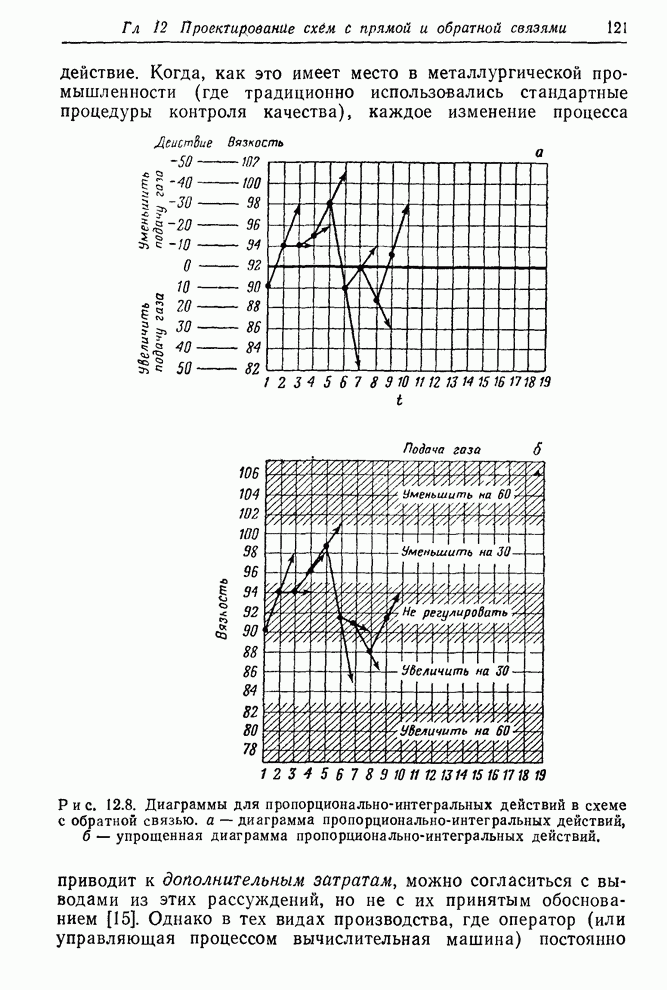
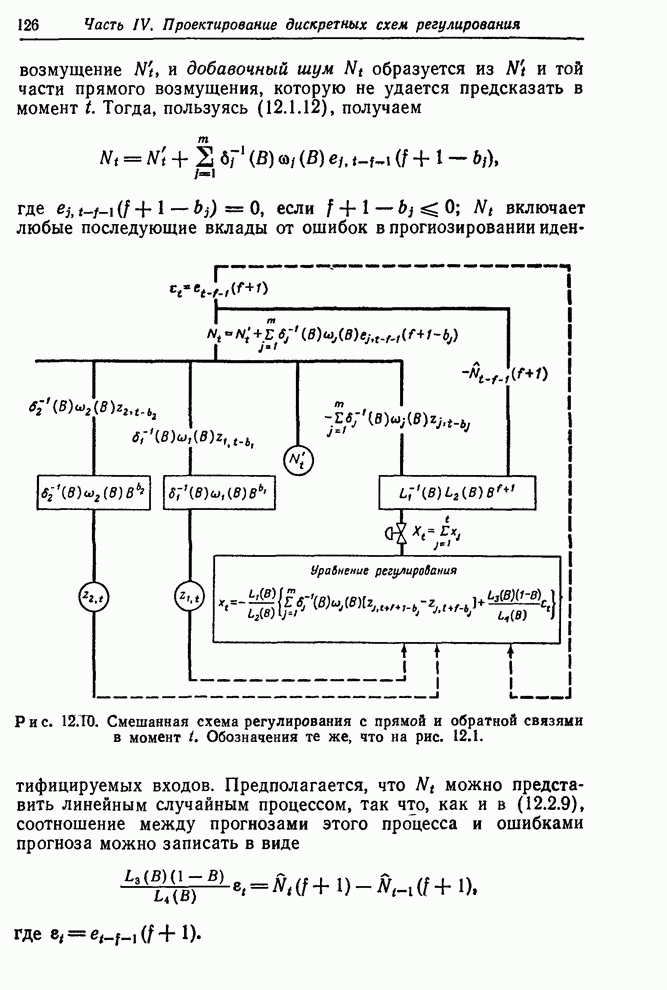
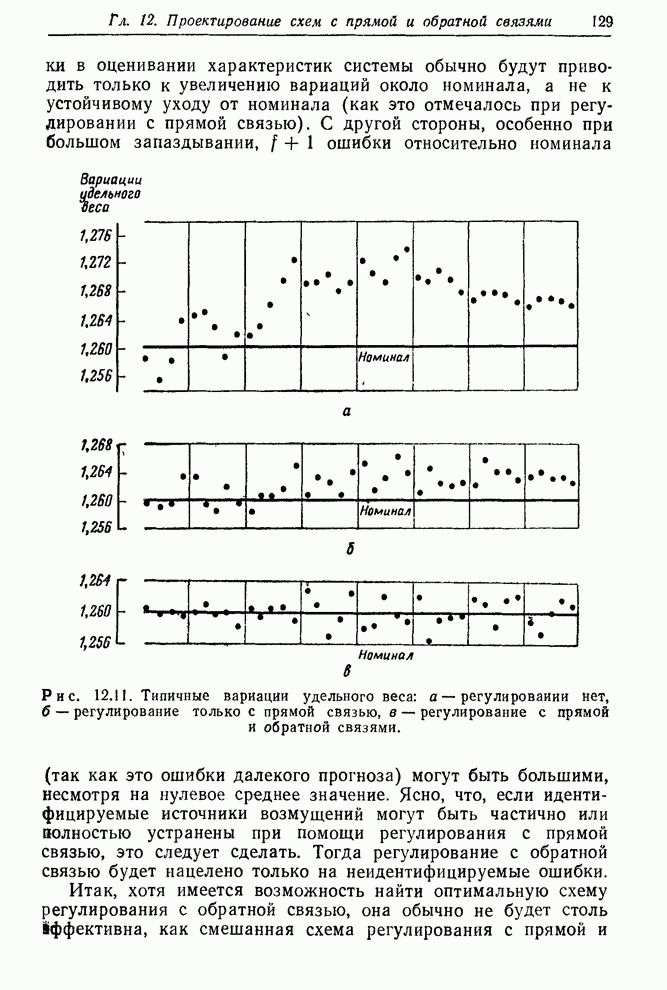
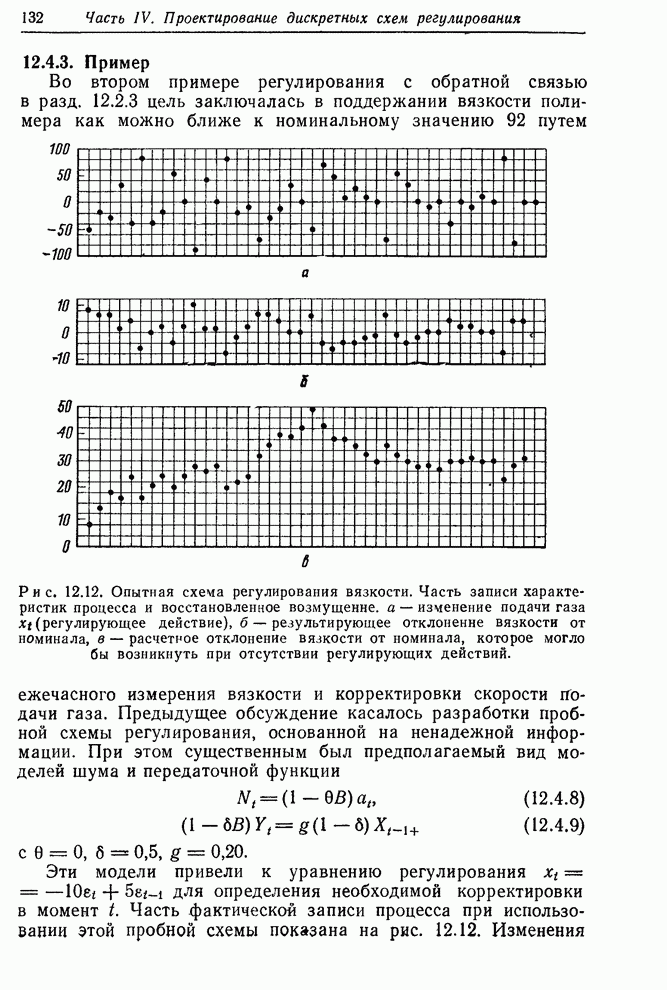
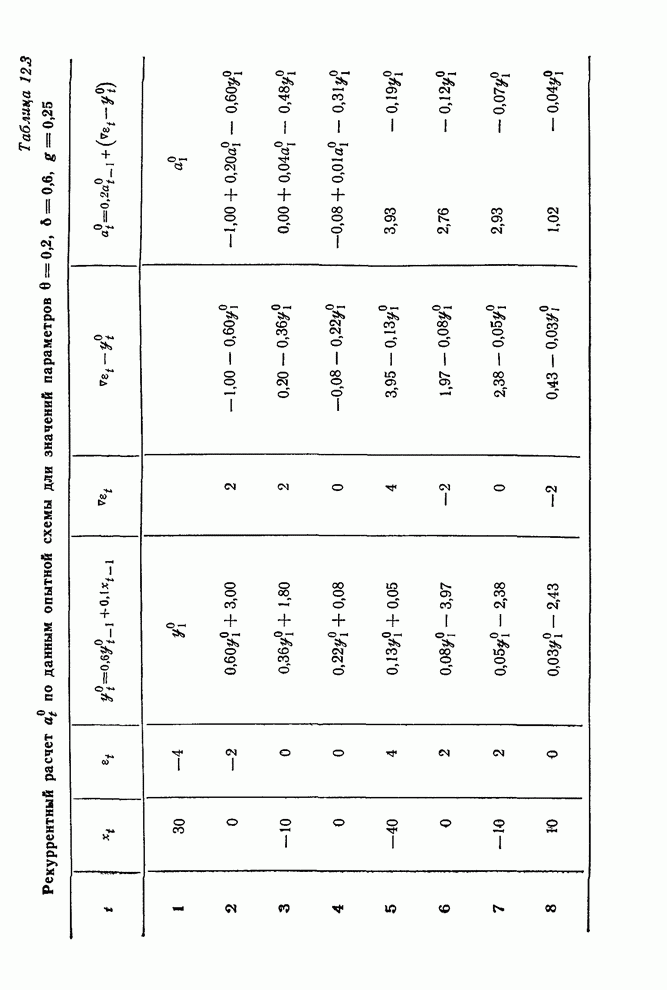
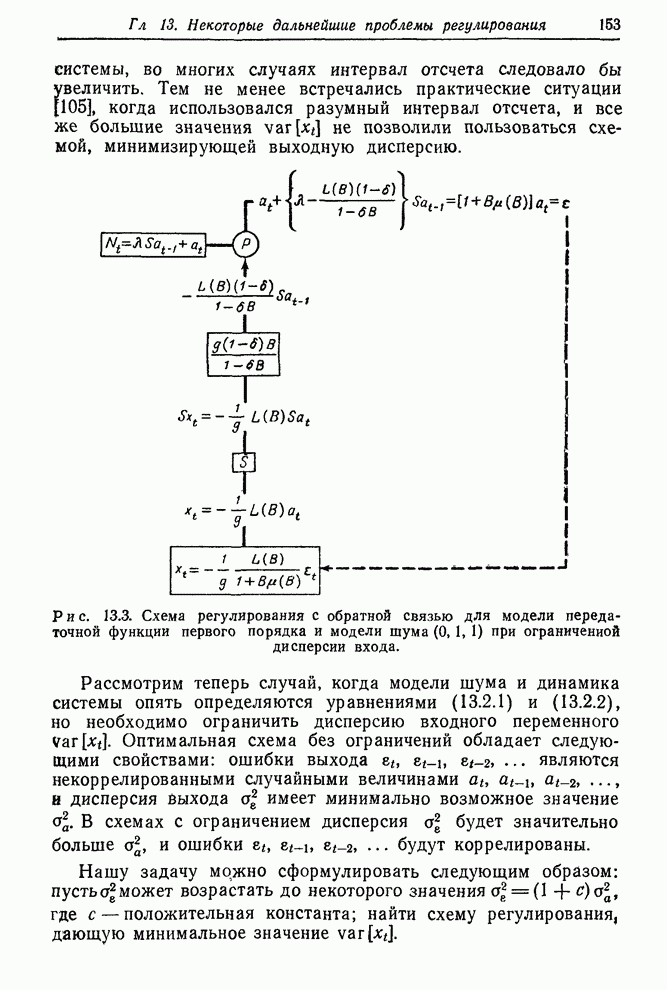
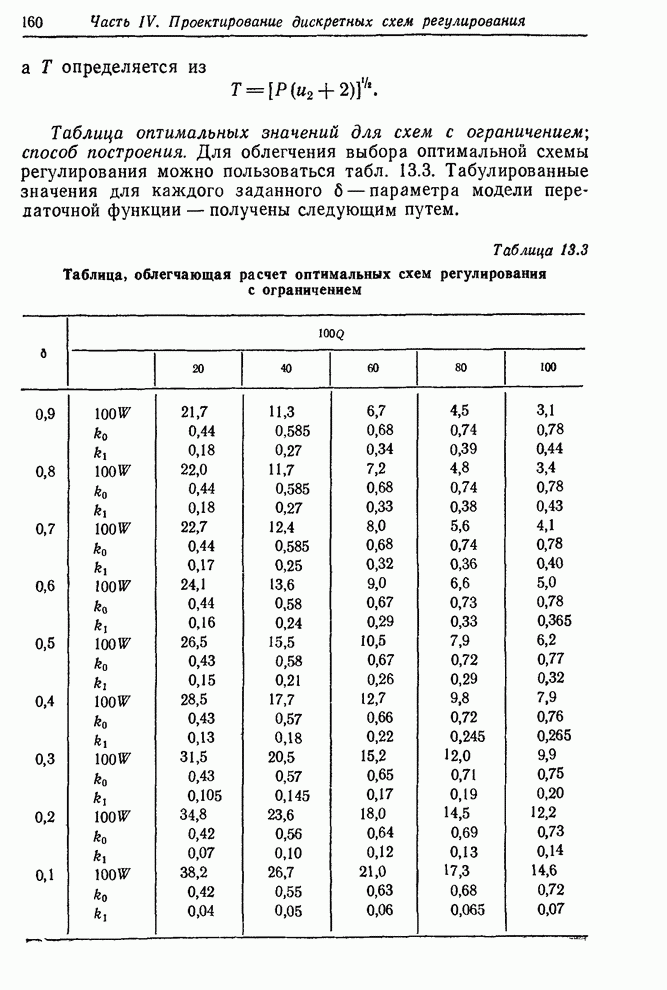
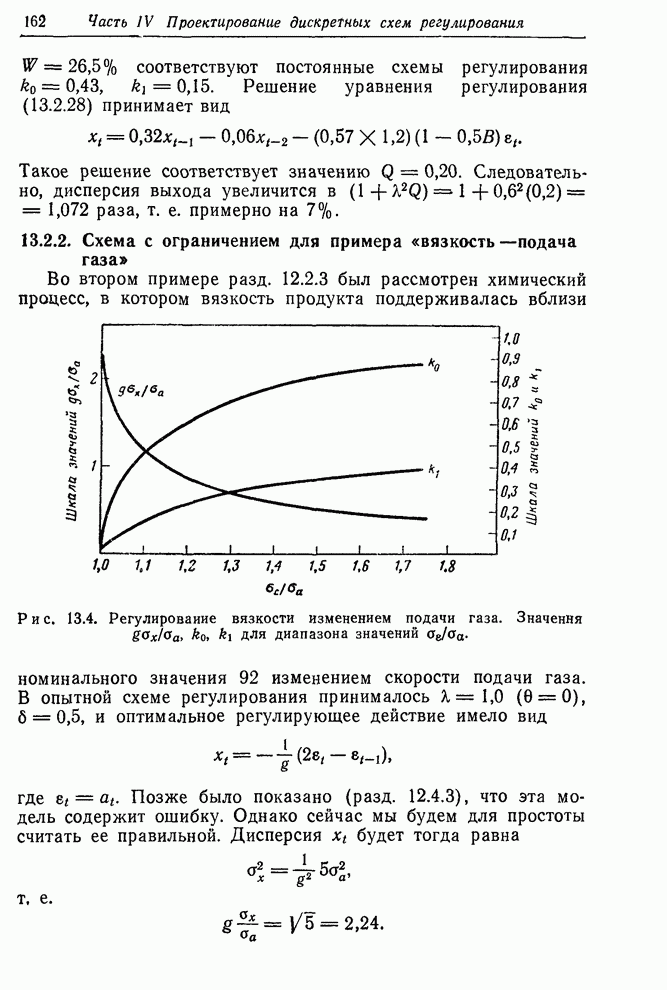
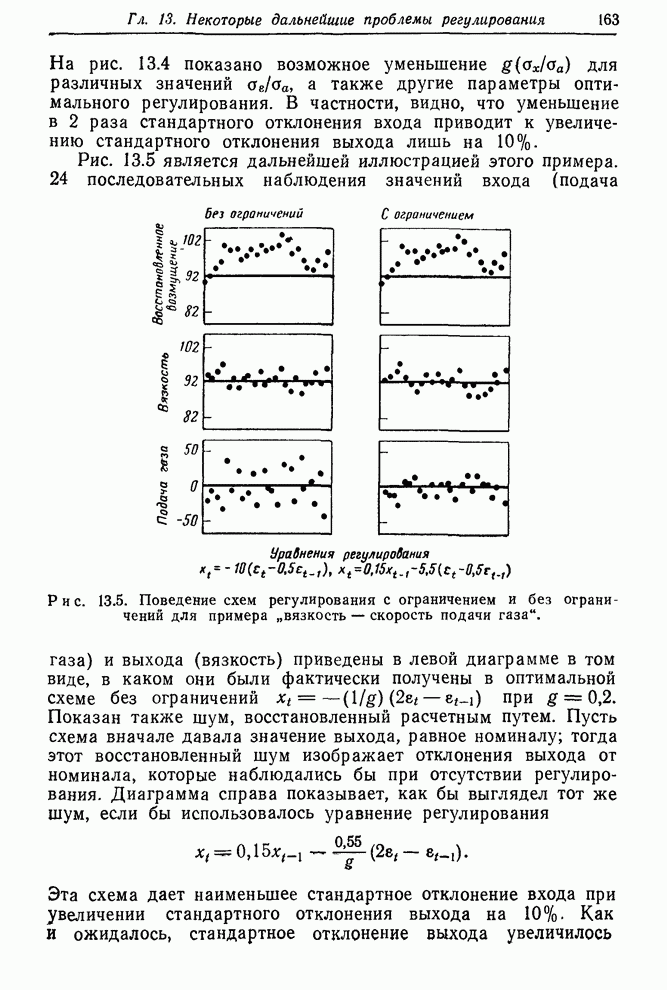
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
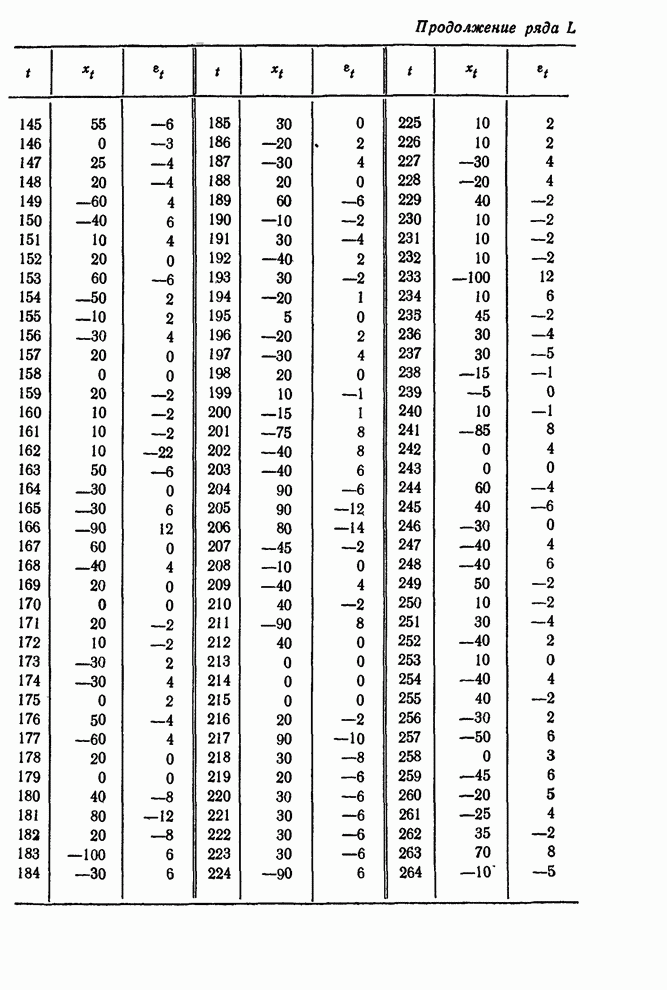
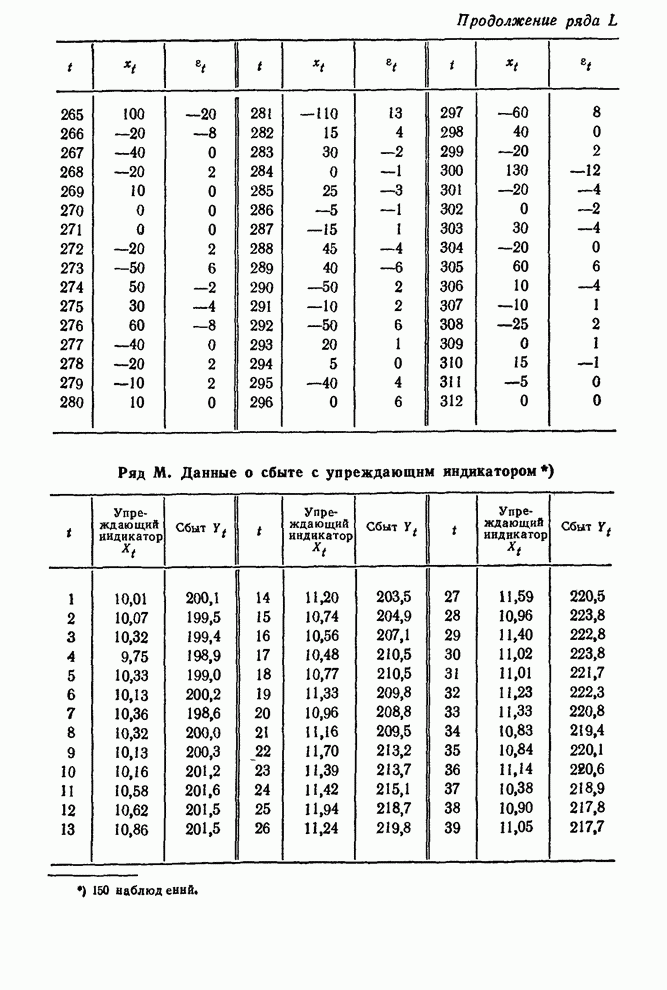
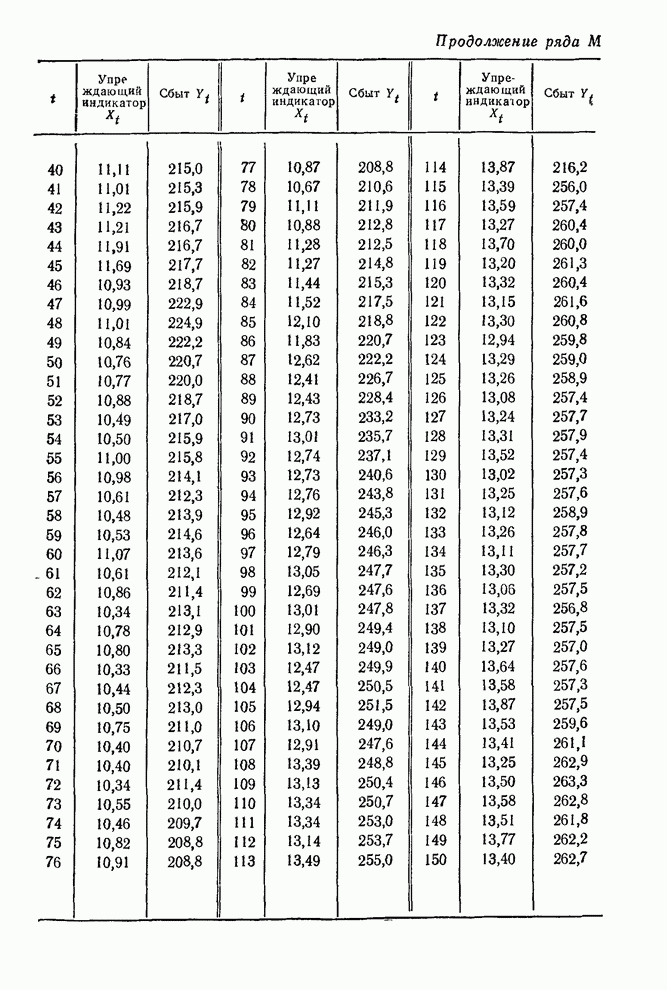
ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
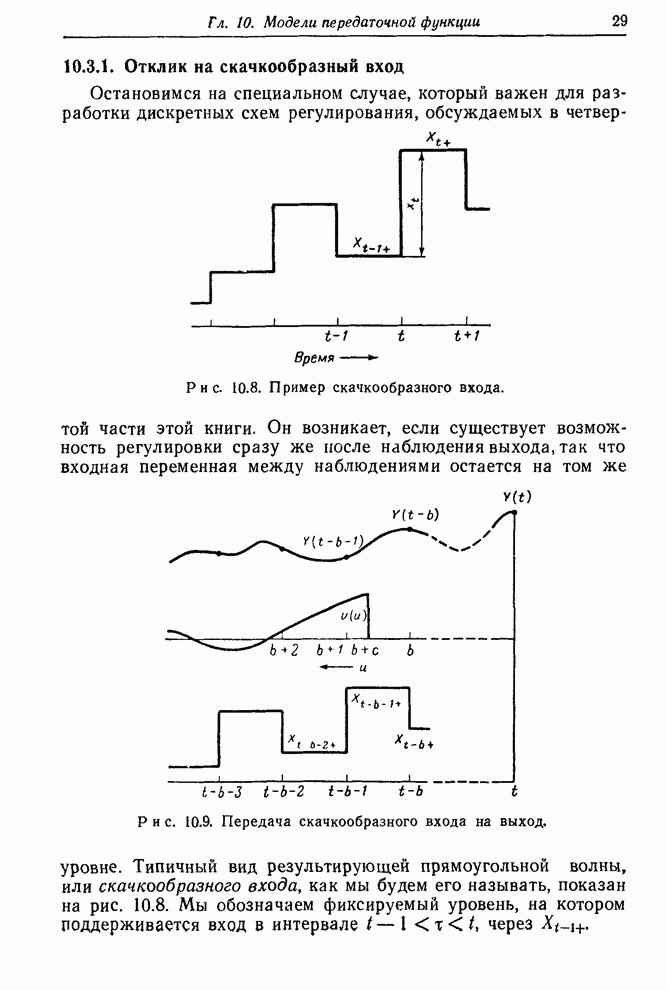
В разд. 10.3.1 (см. также рис. 10.9) было показано, что для скачкообразного входа выход любой запаздывающей непрерывной линейной системы
 ,
,
где
![]() для
для ![]() , может быть выдан в
дискретные времена
, может быть выдан в
дискретные времена ![]() дискретным
линейным фильтром
дискретным
линейным фильтром
![]() ,
,
где
веса ![]() все
равны нулю, а веса
все
равны нулю, а веса ![]() определены
как
определены
как
 ,
(П10.1.1)
,
(П10.1.1)
 ,
,
![]() , (П10.1.2)
, (П10.1.2)
Пусть
теперь динамика непрерывной системы описывается линейным дифференциальным
уравнением ![]() -го
порядка
-го
порядка
![]() , (П10.1.3)
, (П10.1.3)
которое можно представить в виде
 ,
,
где
![]() могут быть
действительными или комплексными. Покажем теперь, что для скачкообразного входа
выход этой непрерывной системы дискретно совпадает с выходом дискретной модели
разностного уравнения порядка
могут быть
действительными или комплексными. Покажем теперь, что для скачкообразного входа
выход этой непрерывной системы дискретно совпадает с выходом дискретной модели
разностного уравнения порядка ![]() или порядка
или порядка ![]() при
при ![]() . При
. При ![]()
![]() , а для
, а для ![]() в общем случае
в общем случае ![]() не равно нулю и удовлетворяет
дифференциальному уравнению
не равно нулю и удовлетворяет
дифференциальному уравнению

![]()
Отсюда
![]()
![]()
![]() ,
, ![]() ,
,
откуда при помощи (П10.1.1) и (П10.1.2) получаем
 , (П10.1.4)
, (П10.1.4)
 ,
(П10.1.5)
,
(П10.1.5)
Нужно
заметить, что в частном случае, когда ![]() , веса
, веса ![]() определены по (П10.1.2) для всех
определены по (П10.1.2) для всех ![]() . Рассмотрим теперь
модель разностного уравнения порядка
. Рассмотрим теперь
модель разностного уравнения порядка ![]()
![]() .
(П10.1.6)
.
(П10.1.6)
Если записать
![]() ,
,
то дискретная передаточная функция для этой модели удовлетворяет уравнению
![]() .
(П10.1.7)
.
(П10.1.7)
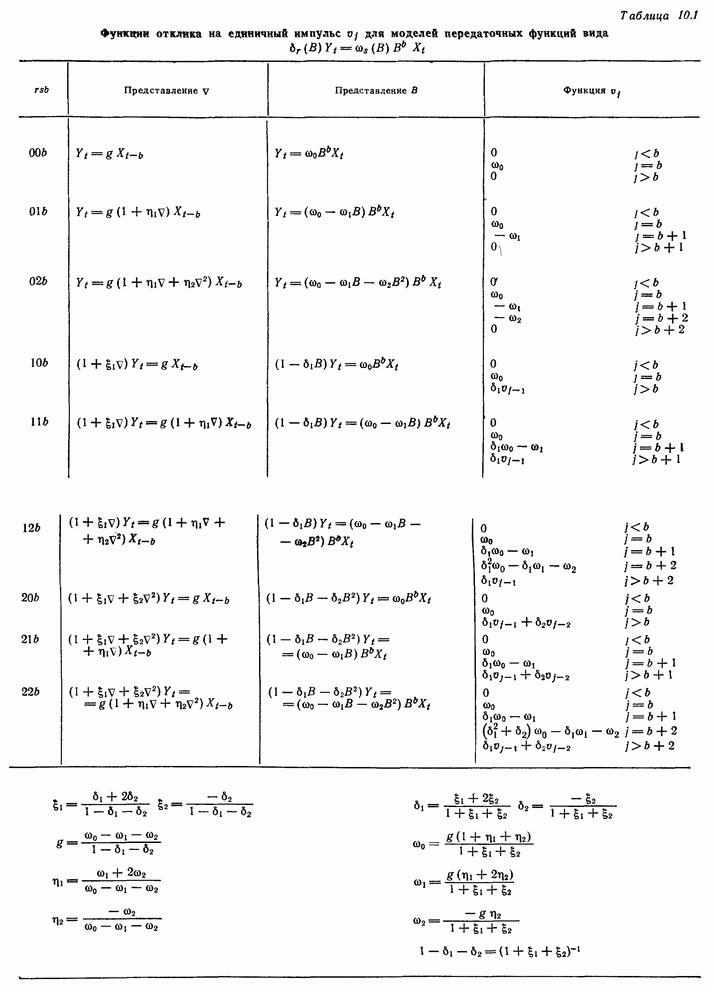
Как
было замечено в (10.2.8), приравнивая коэффициенты в (П10.1.7), мы получаем ![]() нулевых весов
нулевых весов ![]() и, если
и, если ![]() , последующие
, последующие ![]() значений
значений ![]() не подчиняются
общему ходу. Веса
не подчиняются
общему ходу. Веса ![]() будут
при достаточно больших
будут
при достаточно больших ![]() удовлетворять уравнению
удовлетворять уравнению
![]() ,
,
![]() , (П10.1.8)
, (П10.1.8)
для
которого ![]() дают
дают
![]() требуемых
начальных значений. Запишем теперь
требуемых
начальных значений. Запишем теперь
 ,
,
где
![]() — корни
уравнения
— корни
уравнения ![]() .
Тогда решение (П10.1.8) имеет вид
.
Тогда решение (П10.1.8) имеет вид
![]() ,
(П10.1.9)
,
(П10.1.9)
![]() ,
,
где
коэффициенты ![]() выбраны
так, что решения (П10.1.9) для
выбраны
так, что решения (П10.1.9) для ![]() дают начальные значения
дают начальные значения ![]() . Обозначение
. Обозначение ![]() напоминает о том,
что А — функции
напоминает о том,
что А — функции ![]() . Тогда, если принять
. Тогда, если принять ![]() , то для данных
параметров
, то для данных
параметров ![]() в
(П10.1.6) и, следовательно, для данных параметров
в
(П10.1.6) и, следовательно, для данных параметров ![]() существует соответствующий набор
значений
существует соответствующий набор
значений ![]()
![]() , дающий
соответствующие
, дающий
соответствующие ![]() начальных
значений
начальных
значений ![]() .
Далее нам известно, что
.
Далее нам известно, что ![]() . Отсюда
. Отсюда
![]() ,
(П10.1.10)
,
(П10.1.10)
 ,
(П10.1.11)
,
(П10.1.11)
и мы можем приравнять значения весов в (П10.1.4) и (П10.1.5), полученных из дифференциального уравнения, и весов в (П10.1.10) и (П10.1.11), полученных из разностного уравнения. Для этого мы должны принять
![]() ,
,
![]() ,
,
тогда
остающиеся ![]() уравнений
уравнений

определяют
![]() через
через ![]() и
и ![]() .
.
При
![]() мы
полагаем
мы
полагаем ![]() ,
и для данных параметров
,
и для данных параметров ![]() разностного уравнения существует набор
значений
разностного уравнения существует набор
значений ![]() —
функций
—
функций ![]() ,
производящих
,
производящих ![]() начальных
значений
начальных
значений ![]() .
Их можно приравнять значениям (П10.1.5) для
.
Их можно приравнять значениям (П10.1.5) для ![]() . Для этого полагаем
. Для этого полагаем
![]() ,
, ![]() ,
,
и
остальные ![]() уравнений
уравнений
![]()
определяют
![]() через
через ![]() и
и ![]() .
.
В
общем для скачкообразного входа выход непрерывной динамической системы ![]() -го порядка,
задаваемой уравнением
-го порядка,
задаваемой уравнением
![]() ,
(П10.1.12)
,
(П10.1.12)
в
моменты времени ![]() равен
выходу дискретной модели
равен
выходу дискретной модели
![]() , (П10.1.1З)
, (П10.1.1З)
порядка
![]() с
соответственно выбранными параметрами. Далее, если
с
соответственно выбранными параметрами. Далее, если ![]() , выход непрерывной модели
(П10.1.12) равен в дискретные моменты времени выходу модели (П10.1.13) порядка
, выход непрерывной модели
(П10.1.12) равен в дискретные моменты времени выходу модели (П10.1.13) порядка
![]() .
.
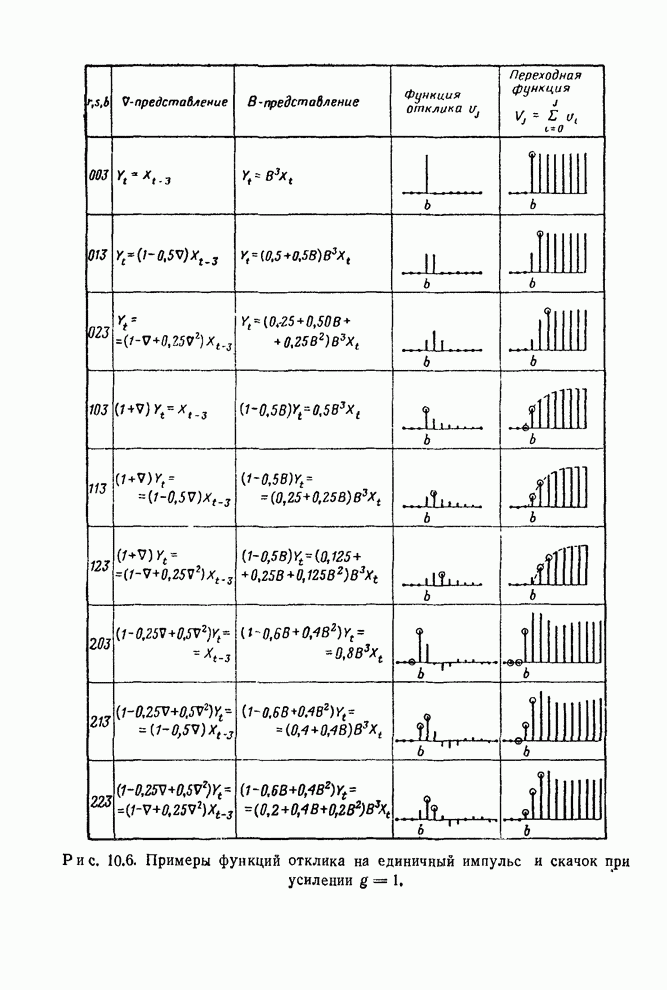
Введем теперь дискретную модель, соответствующую системе второго порядка с запаздыванием, для которой результаты разд. 10 3 2 можно получить как частные случаи.
Система второго порядка с запаздыванием. Пусть дифференциальное уравнение, связывающее вход и выход непрерывной системы, имеет вид
![]() ,
(П10.1.14)
,
(П10.1.14)
Тогда непрерывный импульсный отклик равен
![]() , (П10.1.15)
, (П10.1.15)
![]() .
.
Для
скачкообразного входа выход в дискретные моменты времени ![]() связан с входом разностным
уравнением
связан с входом разностным
уравнением
![]() , (П10.1.16)
, (П10.1.16)
с соответственно подобранными параметрами Разностное уравнение можно также записать как
![]()
или как
![]() .
(П10.1.17)
.
(П10.1.17)
Воспользовавшись (П10.1.1) и (П10.1.2) и подставив
![]() ,
,
получаем
 ,
,
 .
.
Отсюда
![]() . Но из
(П10.1.17) следует
. Но из
(П10.1.17) следует
 ,
,
откуда получаем
 (П10.1.18)
(П10.1.18)
и
 (П10.1.19)
(П10.1.19)
Комплексные корни. Если ![]() и
и ![]() — комплексные величины, то с
помощью подстановки
— комплексные величины, то с
помощью подстановки
![]()
получим соответствующие выражения
 (П10.1.20)
(П10.1.20)
где
 (П10.1.21)
(П10.1.21)
| << Предыдущий параграф | Следующий параграф >> |
- Часть III. ПОСТРОЕНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- Глава 10. Модели передаточной функции
- 10.1. ЛИНЕЙНЫЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 10.1.1. Дискретная передаточная функция
- 10.1.2. Непрерывные динамические модели, описываемые дифференциальными уравнениями
- 10.2. ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ МОДЕЛИ, ОПИСЫВАЕМЫЕ РАЗНОСТНЫМИ УРАВНЕНИЯМИ
- 10.2.1. Общая форма разностного уравнения
- 10.2.2. Природа передаточной функции
- 10.2.3. Дискретные модели передаточных функций первого и второго порядков
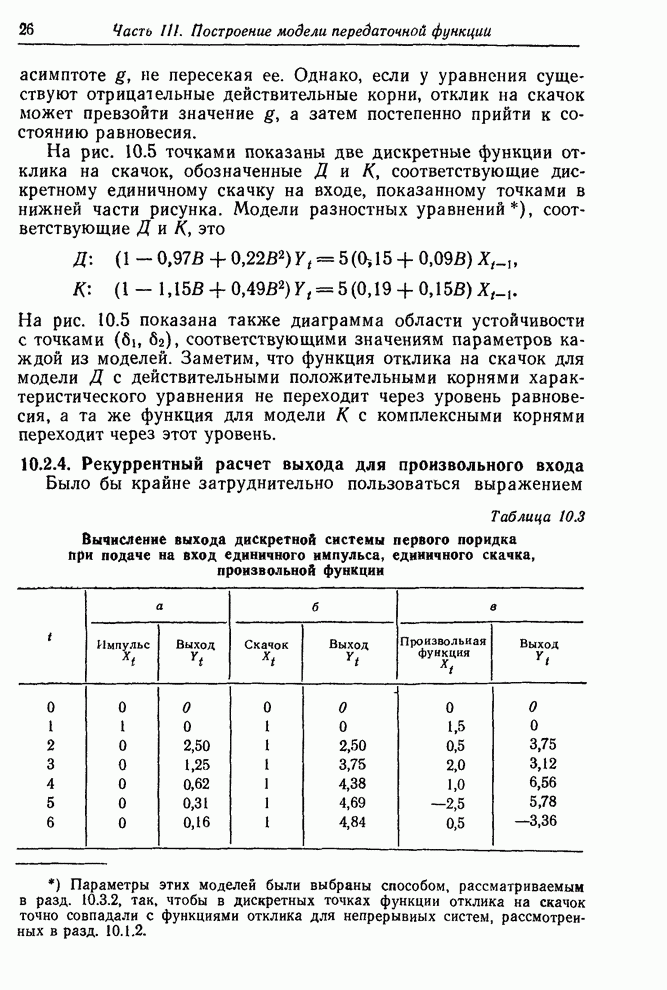
- 10.2.4. Рекуррентный расчет выхода для произвольного входа
- 10.3. СООТНОШЕНИЕ МЕЖДУ ДИСКРЕТНОЙ И НЕПРЕРЫВНОЙ МОДЕЛЯМИ
- 10.3.1. Отклик на скачкообразный вход
- 10.3.2. Соотношения совпадающих систем первого и второго порядков
- 10.3.3. Аппроксимация общих непрерывных моделей дискретными моделями
- 10.3.4. Модели передаточных функций с добавленным шумом
- ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
- ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
- Глава 11. Идентификация, подгонка и проверка моделей передаточных функций
- 11.1. Взаимная корреляционная функция
- 11.1.1. Свойства взаимных ковариационной и корреляционной функций
- 11.1.2. Оценивание взаимных ковариационных и корреляционных функций
- 11.1.3. Приближенные стандартные ошибки выборочных оценок взаимных корреляций
- 11.2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.2.1. Идентификация моделей передаточной функции с предварительным выравниванием спектра входа
- 11.2.2. Пример идентификации модели передаточной функции
- 11.2.3. Идентификация модели шума
- 11.2.4. Некоторые общие соображения об идентификации моделей передаточных функций
- 11.3. ПОДГОНКА И ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.3.1. Условная сумма квадратов
- 11.3.2. Нелинейное оценивание
- 11.3.3. Использование остаточных ошибок для диагностической проверки
- 11.3.4. Конкретные способы проверки остаточных ошибок
- 11.4. Некоторые примеры подгонок и проверок моделей передаточных функций
- 11.4.1. Подгонка и проверка модели газовой печи
- 11.4.2. Искусственный пример с двумя входами
- 11.5. ПРОГНОЗИРОВАНИЕ ПРИ ПОМОЩИ УПРЕЖДАЮЩИХ ИНДИКАТОРОВ
- 11.5.1. Прогноз с минимальной среднеквадратичной ошибкой
- 11.5.2. Прогнозы выхода СO2 из газовой печи
- 11.5.3. Прогноз нестационарных данных сбыта при помощи упреждающего индикатора
- 11.6. НЕКОТОРЫЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОЦЕНИВАНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ П11.1. ИСПОЛЬЗОВАНИЕ ВЗАИМНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
- Заключение
- Часть IV. Проектирование дискретных схем регулирования
- Глава 12. Проектирование схем регулирования с прямой и обратной связями
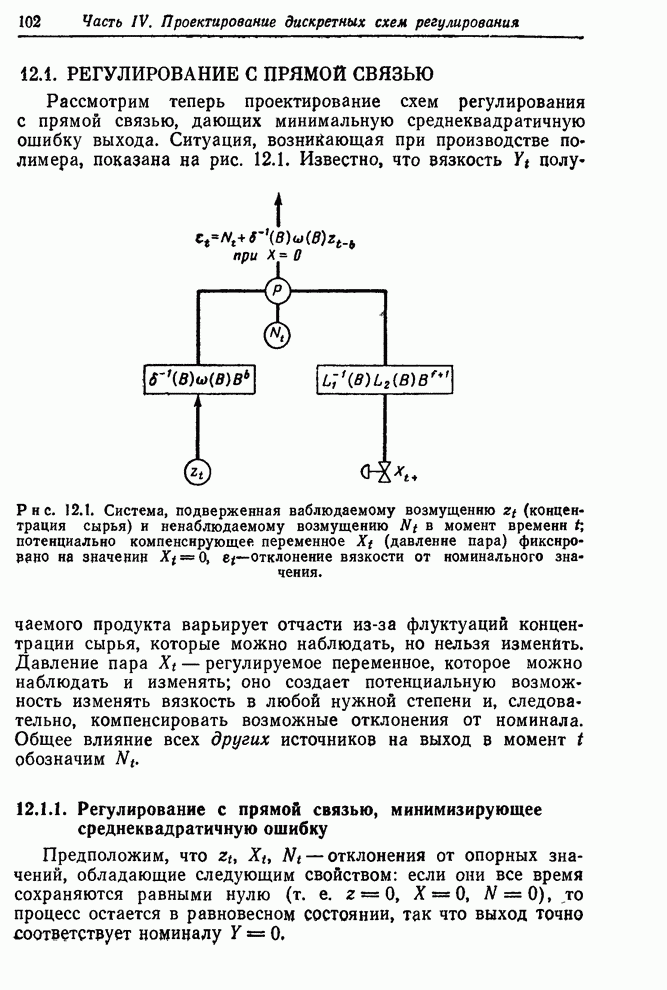
- 12.1. РЕГУЛИРОВАНИЕ С ПРЯМОЙ СВЯЗЬЮ
- 12.1.1. Регулирование с прямой связью, минимизирующее среднеквадратичную ошибку
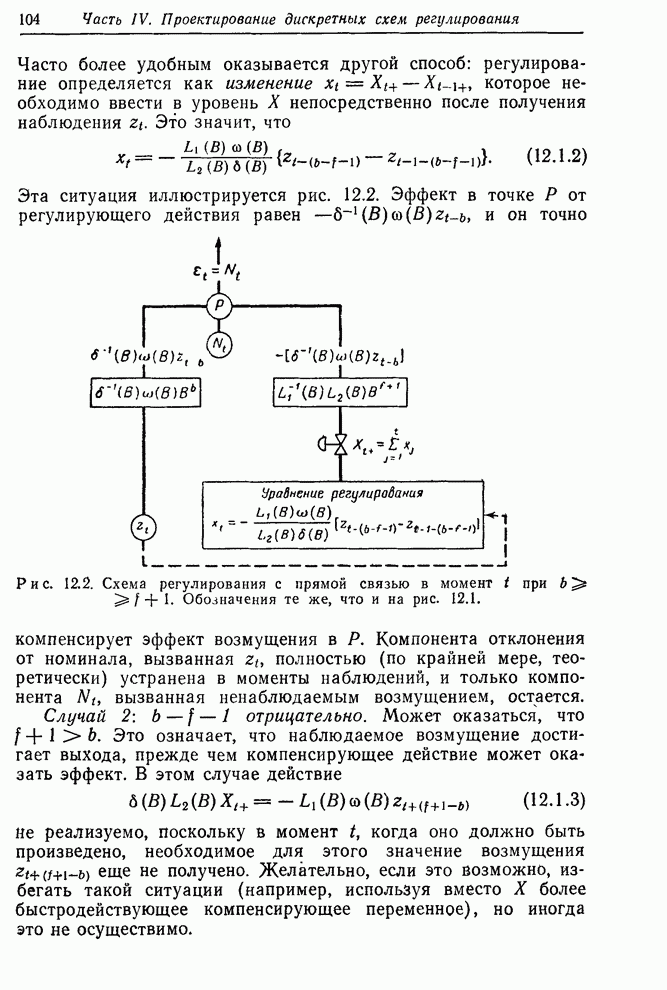
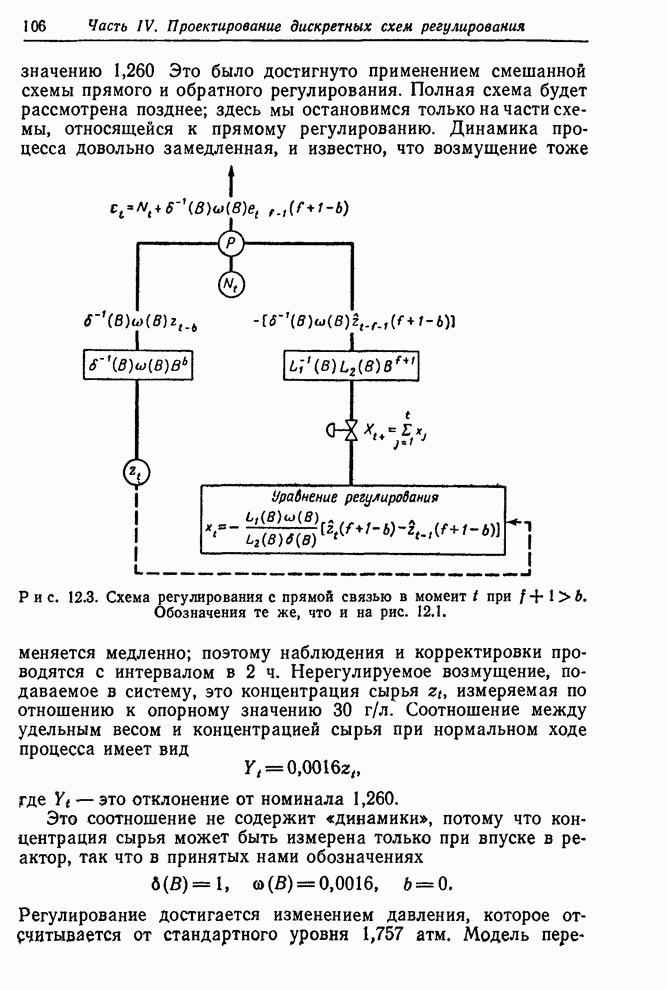
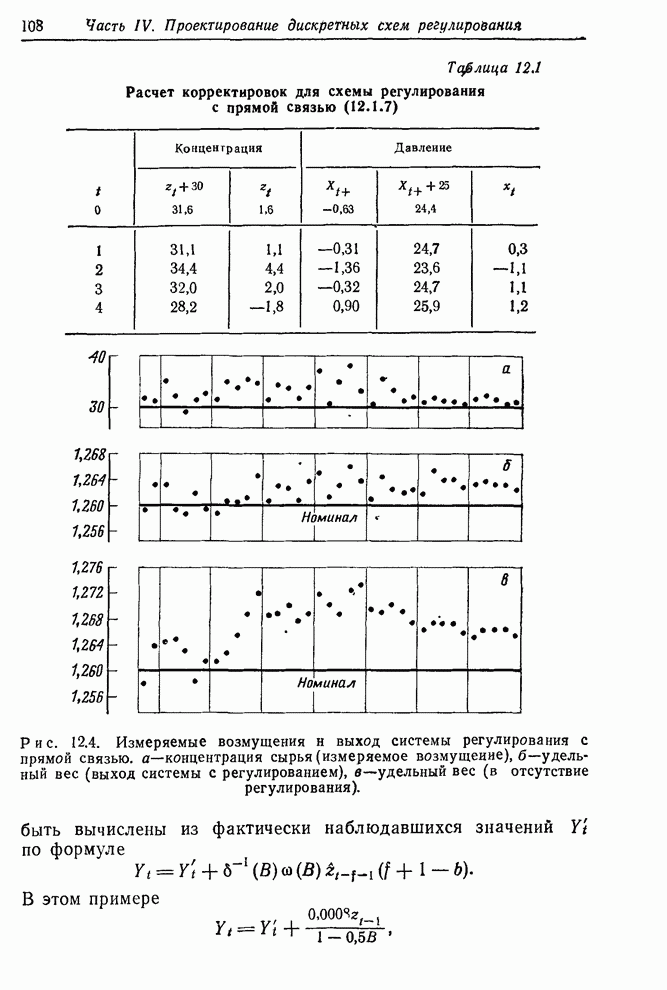
- 12.1.2. Пример — регулирование удельного веса промежуточного продукта
- 12.1.3. Номограмма для регулирования с прямой связью
- 12.1.4. Регулирование с прямой связью в случае нескольких входов
- 12.2. РЕГУЛИРОВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ
- 12.2.1. Регулирование с обратной связью, минимизирующее среднеквадратичную ошибку
- 12.2.2. Применение уравнения регулирования: ПИД-регулятор
- 12.2.3. Примеры дискретного регулирования с обратной связью
- 12.3. РЕГУЛИРОВАНИЕ С ПРЯМОЙ И ОБРАТНОЙ СВЯЗЯМИ
- 12.3.1. Регулирование с прямой и обратной связями, минимизирующее выходную среднеквадратичную ошибку
- 12.3.2. Пример регулирования с прямой и обратной связями
- 12.3.3. Преимущества и недостатки регулирования с прямой и обратной связями
- 12.4. Подгонка моделей передаточных функций шума по оперативным данным
- 12.4.1. Итеративный способ построения моделей
- 12.4.2. Оценивание по оперативным данным
- 12.4.3. Пример
- Глава 13. Некоторые дальнейшие проблемы регулирования
- 13.1. ЭФФЕКТ ДОБАВОЧНОГО ШУМА В СХЕМАХ РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ
- 13.1.1. Эффект пренебрежения добавочным шумом; упрощенные схемы
- 13.1.2. Оптимальное действие в случаях, когда корректировки содержат ошибки наблюдения
- 13.1.3. Перенос источника шума
- 13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
- 13.2.1. Вывод выражения для оптимальной корректировки
- 13.2.2. Схема с ограничением для примера «вязкость–подача газа»
- 13.3. ВЫБОР ИНТЕРВАЛА ОТСЧЕТА
- 13.3.1. Пример эффекта уменьшения частоты отсчетов
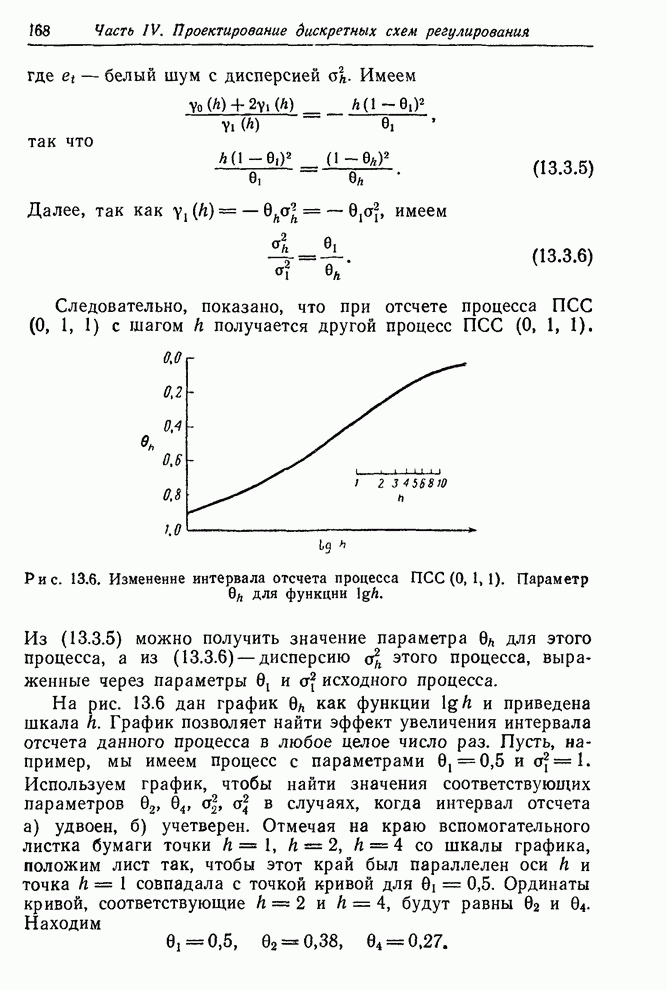
- 13.3.2. Влияние интервала отсчета на процесс ПСС(0,1,1)
- ПРОГРАММА 5. ИДЕНТИФИКАЦИЯ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 6. ПРЕДВАРИТЕЛЬНОЕ ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 7. ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
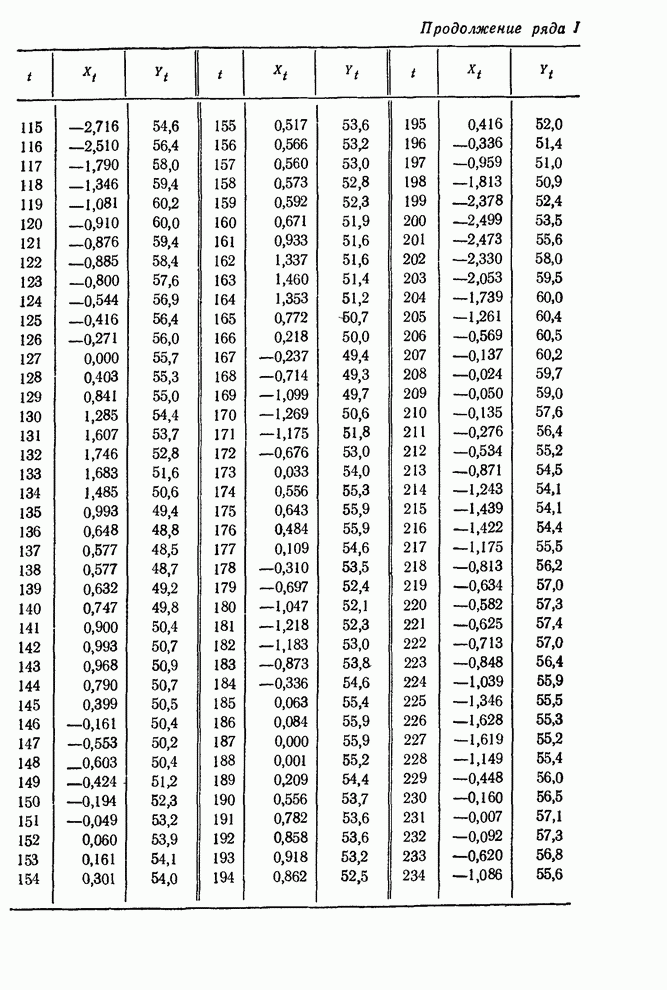
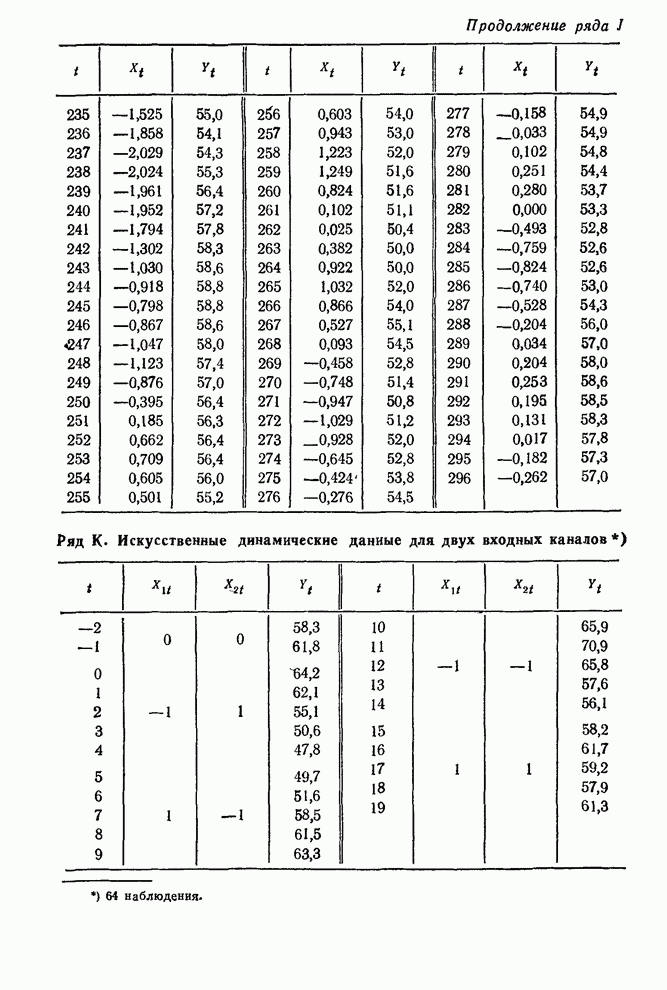
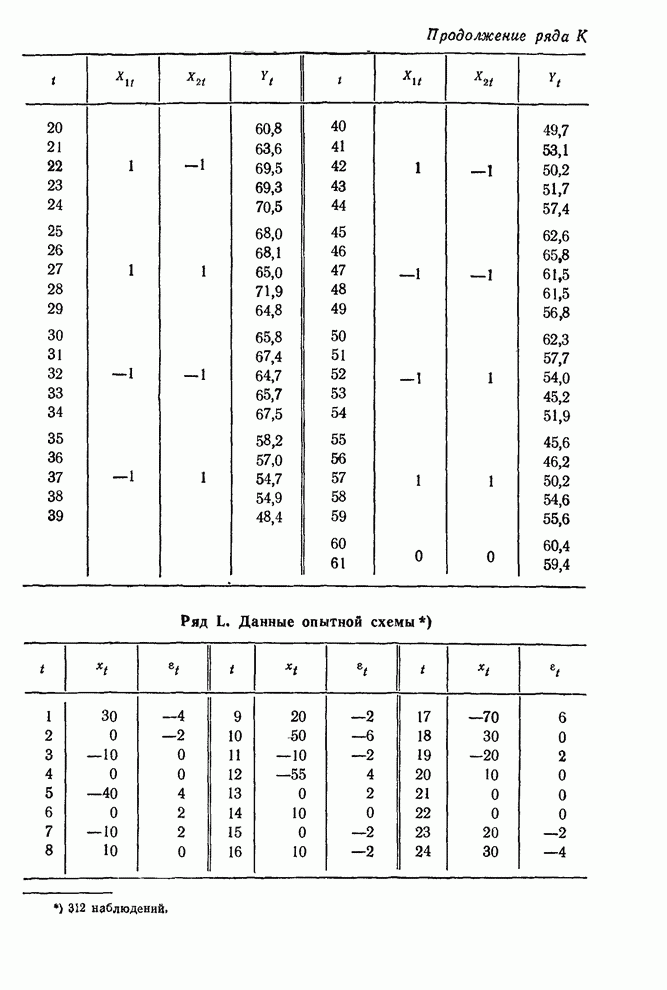
- ТАБЛИЦЫ ВРЕМЕННЫХ РЯДОВ