| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
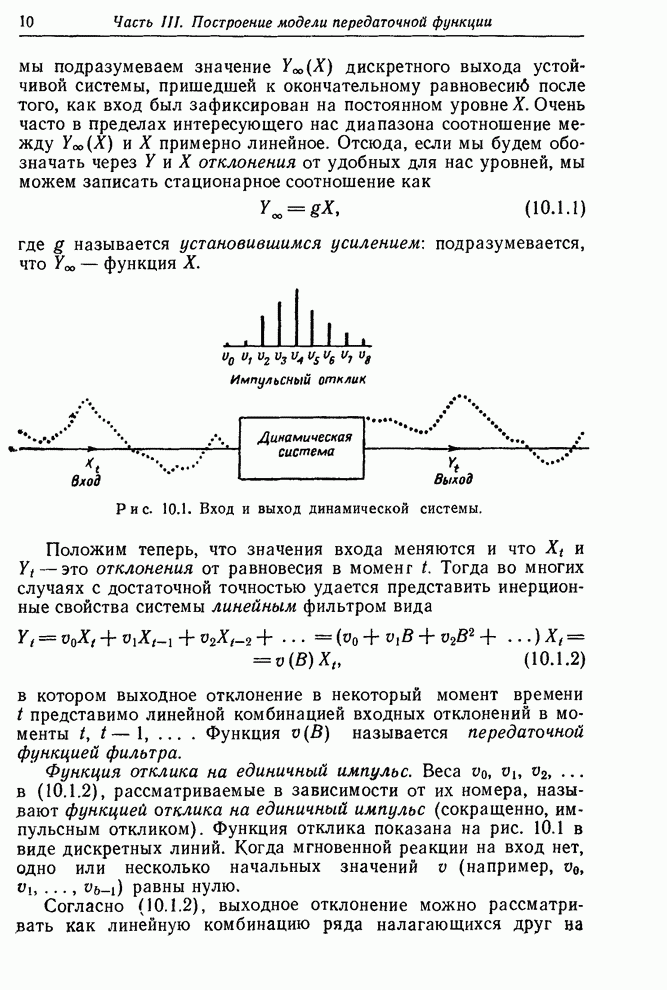
10.2.3. Дискретные модели передаточных функций первого и второго порядков
Модели
передаточных функций первого и второго порядков для всех комбинаций ![]() и
и ![]() подробно описаны в табл. 10.1.
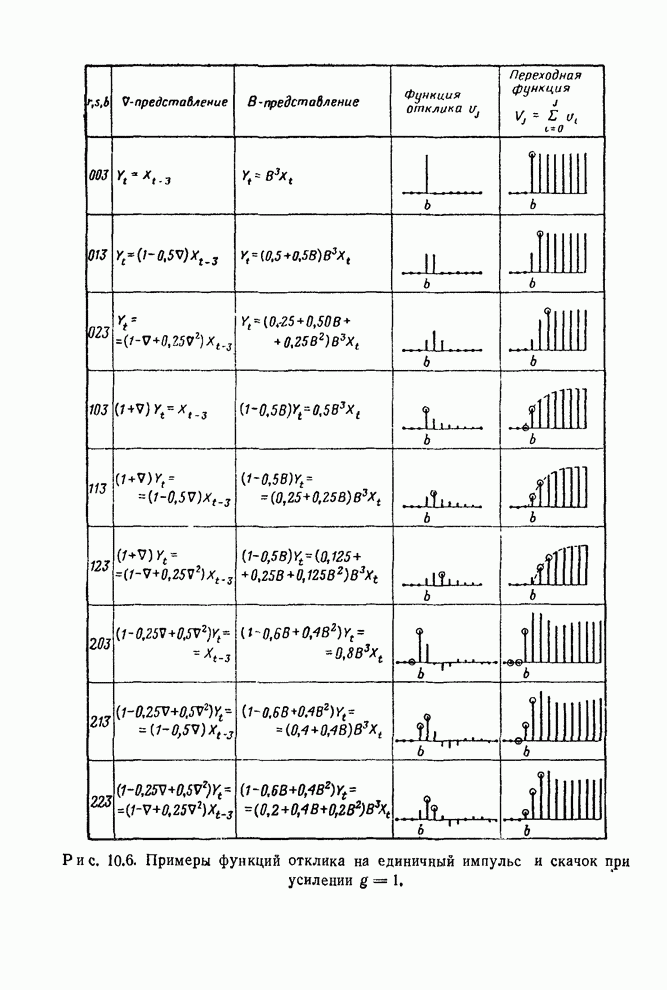
Примеры некоторых моделей с дискретными диаграммами откликов на единичные
скачок и импульс приведены на рис. 10.6.
подробно описаны в табл. 10.1.
Примеры некоторых моделей с дискретными диаграммами откликов на единичные
скачок и импульс приведены на рис. 10.6.
Уравнения
в конце табл. 10.1 выражают параметры ![]() разностной
разностной ![]() -формы модели через параметры
-формы модели через параметры ![]() представления модели
через оператор
представления модели
через оператор ![]() .
Эти уравнения соответствуют самой общей модели с
.
Эти уравнения соответствуют самой общей модели с ![]() . Все остальные модели — это частные
случаи общей модели, и соответствующие им уравнения можно получить
приравниванием нулю соответствующих коэффициентов. Например, если
. Все остальные модели — это частные
случаи общей модели, и соответствующие им уравнения можно получить
приравниванием нулю соответствующих коэффициентов. Например, если ![]() и
и ![]() ,
, ![]() , то
, то
![]() ,
, ![]() ,
, ![]() .
.
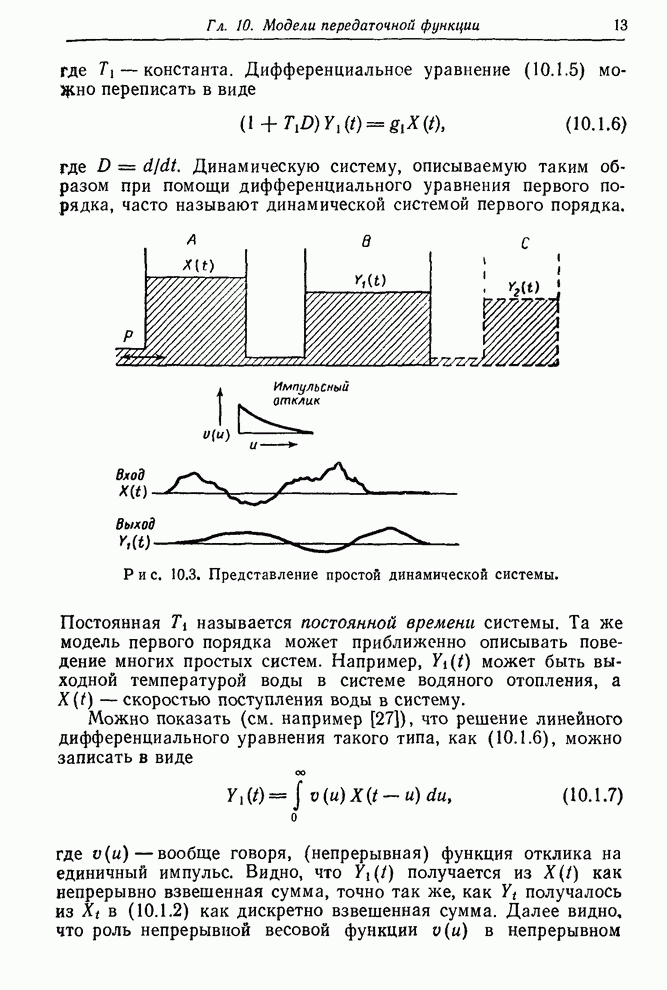
На рис. 10.6 начальные значения для дифференциальных уравнений, соответствующие откликам на единичные импульс и скачок, показаны кружками.
Обсуждение моделей, приведенных в таблице. Модели, свойства которых
рассмотрены в табл. 10.1 и на рис. 10.6, заслуживают очень внимательного
изучения, так как они полезны для описания многих часто встречающихся на
практике динамических систем. Во всех этих моделях оператор ![]() в правой части
показывает, что первый ненулевой член в функции отклика на единичный импульс
равен
в правой части
показывает, что первый ненулевой член в функции отклика на единичный импульс
равен ![]() . В
примерах, приведенных на рис. 10.6, g предполагается равным единице, a
. В
примерах, приведенных на рис. 10.6, g предполагается равным единице, a ![]() .
.
Модели с ![]() . Когда
. Когда ![]() и
и ![]() равны нулю, функция отклика на единичный
импульс содержит только один член
равны нулю, функция отклика на единичный
импульс содержит только один член ![]() . Выход пропорционален входу, но смещен
на
. Выход пропорционален входу, но смещен
на ![]() временных
интервалов. В более общем случае, если оператор справа имеет порядок
временных
интервалов. В более общем случае, если оператор справа имеет порядок ![]() , выходной отклик
будет задержан на
, выходной отклик
будет задержан на ![]() временных
интервалов относительно импульсного входа и будет занимать
временных
интервалов относительно импульсного входа и будет занимать ![]() значение с
амплитудами
значение с
амплитудами ![]() .
Отклик на скачок получается суммированием весов отклика на единичный импульс и
удовлетворяет уравнению
.
Отклик на скачок получается суммированием весов отклика на единичный импульс и
удовлетворяет уравнению ![]() с начальными значениями
с начальными значениями ![]() .
.
|
|
|
|
|
|
|
003 |
|
|
|
|
|
013 |
|
|
|
|
|
023 |
|
|
|
|
|
103 |
|
|
|
|
|
113 |
|
|
|
|
|
123 |
|
|
|
|
|
203 |
|
|
|
|
|
213 |
|
|
|
|
|
223 |
|
|
|
|
Рис.
10.6. Примеры функций отклика на единичный импульс и скачок при усилении ![]() .
.
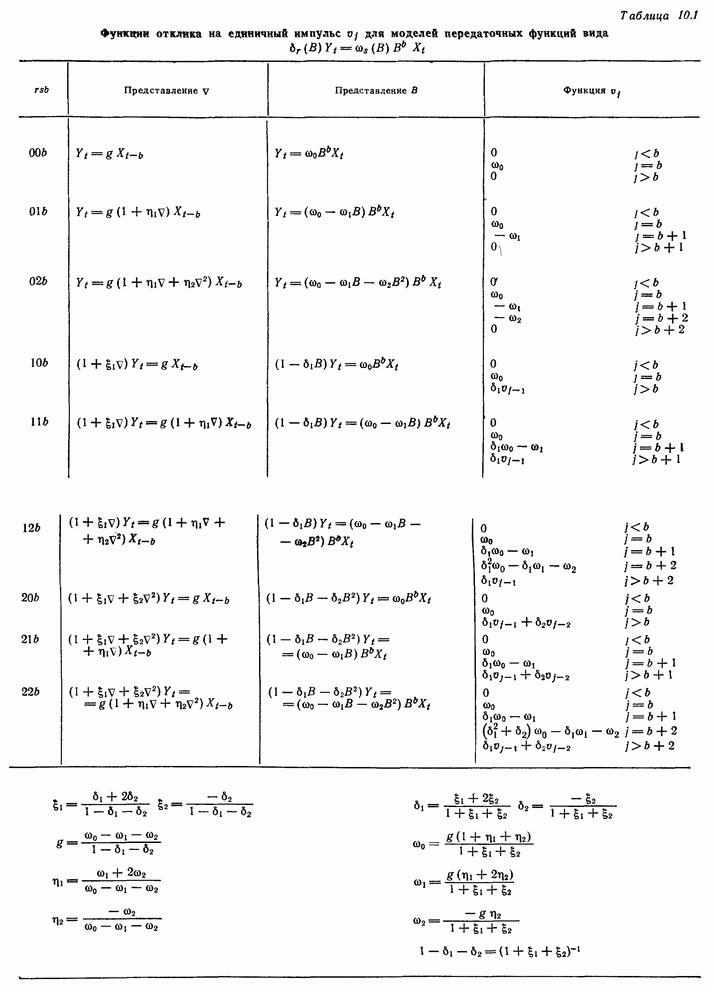
Таблица
10.1. Функции
отклика на единичный импульс ![]() для моделей передаточных функций вида
для моделей передаточных функций вида ![]()
|
|
Представление |
Представление |
Функция |
|
|
|
|
0 j<b
0 j>b
0 j<b
- 0 j>b+1
0 j<b
- - 0 j>b+2
0 j<b
0 j<b
0 j<b
0 j<b
0 j<b
0 j<b
|
|
|
|
||
Модели
с ![]() . При
. При ![]() отклик на единичный импульс
экспоненциально затухает от начального значения
отклик на единичный импульс
экспоненциально затухает от начального значения ![]() . Отклик на единичный скачок экспоненциально
затухает, пока не достигнет значения
. Отклик на единичный скачок экспоненциально
затухает, пока не достигнет значения ![]() . Если экспоненциальную функцию отклика
на скачок проэкстраполировать назад (как показано точками), она пересечет ось
времен в момент
. Если экспоненциальную функцию отклика
на скачок проэкстраполировать назад (как показано точками), она пересечет ось
времен в момент ![]() .
Это соответствует тому факту, что и
.
Это соответствует тому факту, что и ![]() , и
, и ![]() являются начальными значениями соответствующего
разностного уравнения
являются начальными значениями соответствующего
разностного уравнения ![]() .
.
При
![]() существует
начальное значение отклика на единичный импульс
существует
начальное значение отклика на единичный импульс ![]() , которое не соответствует общему ходу.
Экспоненциальная кривая, определяемая разностным уравнением
, которое не соответствует общему ходу.
Экспоненциальная кривая, определяемая разностным уравнением ![]() , соответствующим оператору в
левой части, начинается со значения
, соответствующим оператору в
левой части, начинается со значения ![]() .
.
Отклик
на скачок ведет себя как экспонента, удовлетворяющая разностному уравнению ![]() ; его начальные
значения
; его начальные
значения ![]() и
и ![]() ; с ростом
; с ростом ![]() отклик асимптотически
приближается к
отклик асимптотически
приближается к ![]() .
Экстраполяция этой экспоненциальной кривой назад показана точечной линией. В
общем случае она пересекает ось времен в некоторой промежуточной точке между
отсчетами. В разд. 10.3 будет показано, что некоторые дискретные модели,
аппроксимирующие непрерывные системы первого порядка с дробным временем
запаздывания, могут быть описаны разностным уравнением первого порядка с оператором
в правой части, у которого
.
Экстраполяция этой экспоненциальной кривой назад показана точечной линией. В
общем случае она пересекает ось времен в некоторой промежуточной точке между
отсчетами. В разд. 10.3 будет показано, что некоторые дискретные модели,
аппроксимирующие непрерывные системы первого порядка с дробным временем
запаздывания, могут быть описаны разностным уравнением первого порядка с оператором
в правой части, у которого ![]() .
.
При
![]() имеются два
значения
имеются два
значения ![]() и
и ![]() отклика на единичный
импульс, не следующие общему ходу: за ними с
отклика на единичный
импульс, не следующие общему ходу: за ними с ![]() начинается экспоненциальный спад.
Соответственно у отклика на единичный скачок имеется единственное значение
начинается экспоненциальный спад.
Соответственно у отклика на единичный скачок имеется единственное значение ![]() , не согласующееся с
общим экспоненциальным поведением, выраженным проэкстраполированной назад
точечной линией. Эта кривая, как и ранее, определена разностным уравнением
, не согласующееся с
общим экспоненциальным поведением, выраженным проэкстраполированной назад
точечной линией. Эта кривая, как и ранее, определена разностным уравнением ![]() , но с начальными
значениями
, но с начальными
значениями ![]() и
и
![]() .
.
Модели с ![]() . Гибкость моделей с
. Гибкость моделей с ![]() весьма ограниченна, потому что первое
начальное значение функции отклика на единичный импульс должно равняться нулю.
Более полезными являются модели с
весьма ограниченна, потому что первое
начальное значение функции отклика на единичный импульс должно равняться нулю.
Более полезными являются модели с ![]() и
и ![]() . Использование этих моделей для
аппроксимации непрерывных систем второго порядка обсуждается в разд. 10.3 и
приложении П10.1.
. Использование этих моделей для
аппроксимации непрерывных систем второго порядка обсуждается в разд. 10.3 и
приложении П10.1.
Поведение
динамических весовых значений ![]() которые при достаточно больших
которые при достаточно больших ![]() удовлетворяют
уравнению
удовлетворяют
уравнению
![]() (10.2.13)
(10.2.13)
зависит
от природы корней ![]() и
и
![]() характеристического
уравнения
характеристического
уравнения
![]() .
.
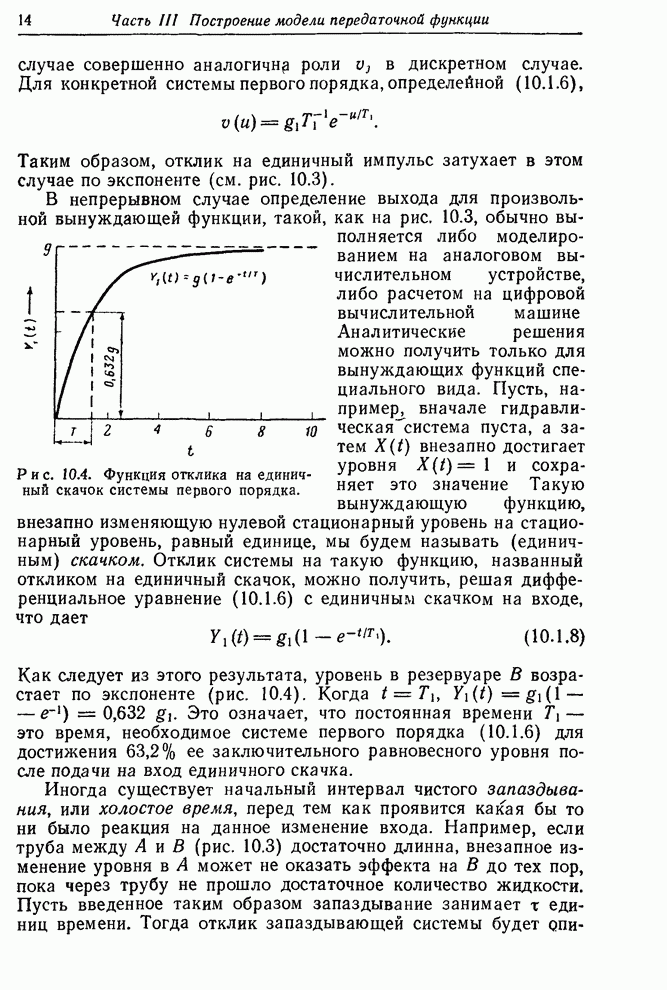
Эта зависимость показана в табл. 10.2. Как и в непрерывном случае, модель может быть перезатушена, критически затушена или недозатушена в зависимости от природы корней характеристического уравнения.
Таблица
10.2. Зависимость
свойств системы второго порядка от корней уравнения ![]()
|
Корни |
Условия |
Затухание |
|
Действительные Действительные и равные Комплексные |
|
Перезатушенная Критически затушенная Недозатушенная |
Когда
корни уравнения комплексные, решение (10.2.13) будет затухающей синусоидой,
как в примерах систем второго порядка на рис. 10.6. Когда корни уравнения
действительны, решение будет суммой двух экспонент. Как и в непрерывном случае,
рассмотренном в разд. 10.1.2, можно трактовать эту систему как эквивалентную
двум последовательно соединенным системам первого порядка с параметрами ![]() и
и ![]() .
.
Веса
![]() функции
отклика на единичный скачок при достаточно больших
функции
отклика на единичный скачок при достаточно больших ![]() подчиняются разностному
уравнению
подчиняются разностному
уравнению
![]() ,
,
имеющему
ту же форму, что и (10.2.13). Следовательно, характер изменения функции
отклика на скачок ![]() относительно
его асимптотического значения
относительно
его асимптотического значения ![]() такой же, как и у отклика на единичный
импульс относительно оси времен. В случаях, когда у характеристического
уравнения существуют комплексные корни, функция отклика на скачок достигает
значений, больших
такой же, как и у отклика на единичный
импульс относительно оси времен. В случаях, когда у характеристического
уравнения существуют комплексные корни, функция отклика на скачок достигает
значений, больших ![]() ,
а затем осциллирует относительно этого значения, пока не достигнет равновесия.
Когда корни уравнения действительны и положительны, функция отклика на скачок,
являющаяся суммой двух экспоненциальных членов, приближается к своей асимптоте
,
а затем осциллирует относительно этого значения, пока не достигнет равновесия.
Когда корни уравнения действительны и положительны, функция отклика на скачок,
являющаяся суммой двух экспоненциальных членов, приближается к своей асимптоте ![]() , не пересекая ее.
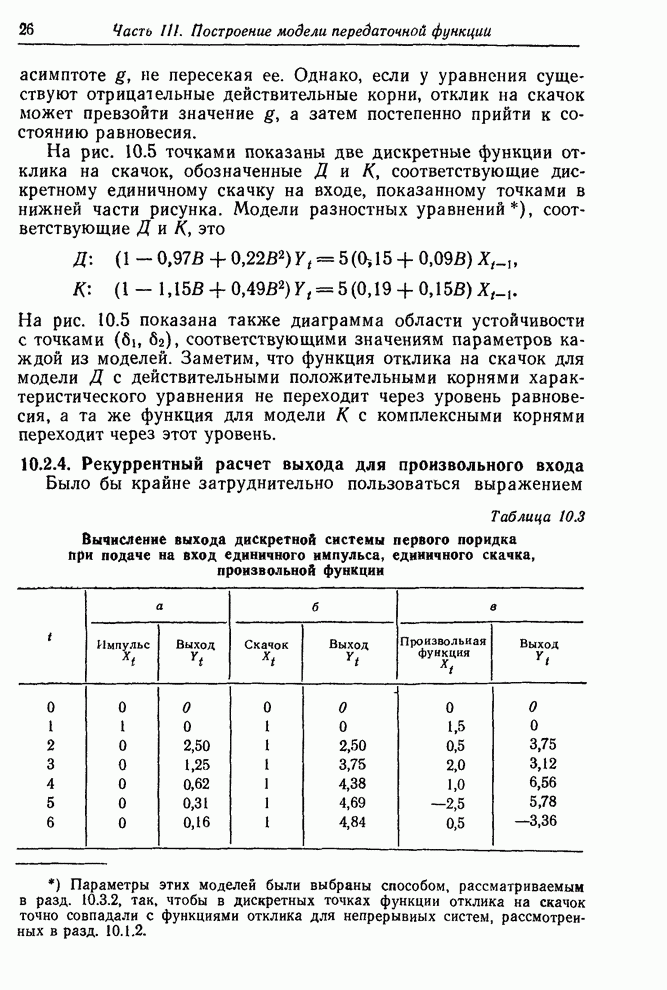
Однако, если у уравнения существуют отрицательные действительные корни, отклик
на скачок может превзойти значение
, не пересекая ее.
Однако, если у уравнения существуют отрицательные действительные корни, отклик
на скачок может превзойти значение ![]() , а затем постепенно прийти к состоянию
равновесия.
, а затем постепенно прийти к состоянию
равновесия.
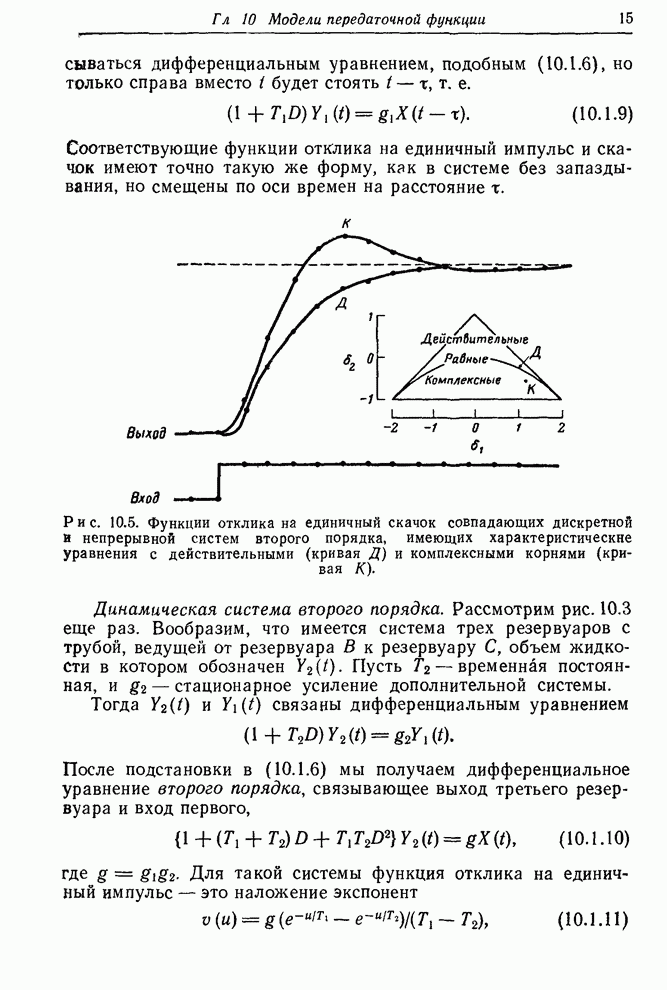
На
рис. 10.5 точками показаны две дискретные функции отклика на скачок,
обозначенные ![]() и
и
![]() ,
соответствующие дискретному единичному скачку на входе, показанному точками в
нижней части рисунка. Модели разностных уравнений, соответствующие
,
соответствующие дискретному единичному скачку на входе, показанному точками в
нижней части рисунка. Модели разностных уравнений, соответствующие ![]() и
и ![]() , это
, это
![]()
![]() ,
,
![]()
![]() .
.
На
рис. 10.5 показана также диаграмма области устойчивости с точками ![]() , соответствующими
значениям параметров каждой из моделей. Заметим, что функция отклика на скачок
для модели
, соответствующими
значениям параметров каждой из моделей. Заметим, что функция отклика на скачок
для модели ![]() с
действительными положительными корнями характеристического уравнения не
переходит через уровень равновесия, а та же функция для модели
с
действительными положительными корнями характеристического уравнения не
переходит через уровень равновесия, а та же функция для модели ![]() с комплексными
корнями переходит через этот уровень.
с комплексными
корнями переходит через этот уровень.
| << Предыдущий параграф | Следующий параграф >> |
- Часть III. ПОСТРОЕНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- Глава 10. Модели передаточной функции
- 10.1. ЛИНЕЙНЫЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 10.1.1. Дискретная передаточная функция
- 10.1.2. Непрерывные динамические модели, описываемые дифференциальными уравнениями
- 10.2. ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ МОДЕЛИ, ОПИСЫВАЕМЫЕ РАЗНОСТНЫМИ УРАВНЕНИЯМИ
- 10.2.1. Общая форма разностного уравнения
- 10.2.2. Природа передаточной функции
- 10.2.3. Дискретные модели передаточных функций первого и второго порядков
- 10.2.4. Рекуррентный расчет выхода для произвольного входа
- 10.3. СООТНОШЕНИЕ МЕЖДУ ДИСКРЕТНОЙ И НЕПРЕРЫВНОЙ МОДЕЛЯМИ
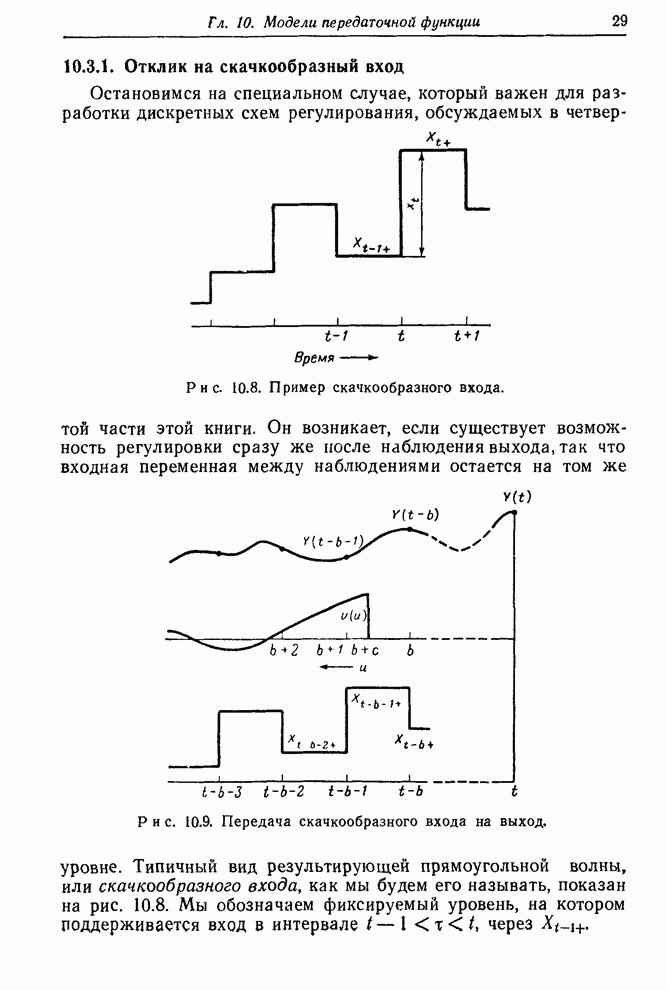
- 10.3.1. Отклик на скачкообразный вход
- 10.3.2. Соотношения совпадающих систем первого и второго порядков
- 10.3.3. Аппроксимация общих непрерывных моделей дискретными моделями
- 10.3.4. Модели передаточных функций с добавленным шумом
- ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
- ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
- Глава 11. Идентификация, подгонка и проверка моделей передаточных функций
- 11.1. Взаимная корреляционная функция
- 11.1.1. Свойства взаимных ковариационной и корреляционной функций
- 11.1.2. Оценивание взаимных ковариационных и корреляционных функций
- 11.1.3. Приближенные стандартные ошибки выборочных оценок взаимных корреляций
- 11.2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.2.1. Идентификация моделей передаточной функции с предварительным выравниванием спектра входа
- 11.2.2. Пример идентификации модели передаточной функции
- 11.2.3. Идентификация модели шума
- 11.2.4. Некоторые общие соображения об идентификации моделей передаточных функций
- 11.3. ПОДГОНКА И ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.3.1. Условная сумма квадратов
- 11.3.2. Нелинейное оценивание
- 11.3.3. Использование остаточных ошибок для диагностической проверки
- 11.3.4. Конкретные способы проверки остаточных ошибок
- 11.4. Некоторые примеры подгонок и проверок моделей передаточных функций
- 11.4.1. Подгонка и проверка модели газовой печи
- 11.4.2. Искусственный пример с двумя входами
- 11.5. ПРОГНОЗИРОВАНИЕ ПРИ ПОМОЩИ УПРЕЖДАЮЩИХ ИНДИКАТОРОВ
- 11.5.1. Прогноз с минимальной среднеквадратичной ошибкой
- 11.5.2. Прогнозы выхода СO2 из газовой печи
- 11.5.3. Прогноз нестационарных данных сбыта при помощи упреждающего индикатора
- 11.6. НЕКОТОРЫЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОЦЕНИВАНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ П11.1. ИСПОЛЬЗОВАНИЕ ВЗАИМНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
- Заключение
- Часть IV. Проектирование дискретных схем регулирования
- Глава 12. Проектирование схем регулирования с прямой и обратной связями
- 12.1. РЕГУЛИРОВАНИЕ С ПРЯМОЙ СВЯЗЬЮ
- 12.1.1. Регулирование с прямой связью, минимизирующее среднеквадратичную ошибку
- 12.1.2. Пример — регулирование удельного веса промежуточного продукта
- 12.1.3. Номограмма для регулирования с прямой связью
- 12.1.4. Регулирование с прямой связью в случае нескольких входов
- 12.2. РЕГУЛИРОВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ
- 12.2.1. Регулирование с обратной связью, минимизирующее среднеквадратичную ошибку
- 12.2.2. Применение уравнения регулирования: ПИД-регулятор
- 12.2.3. Примеры дискретного регулирования с обратной связью
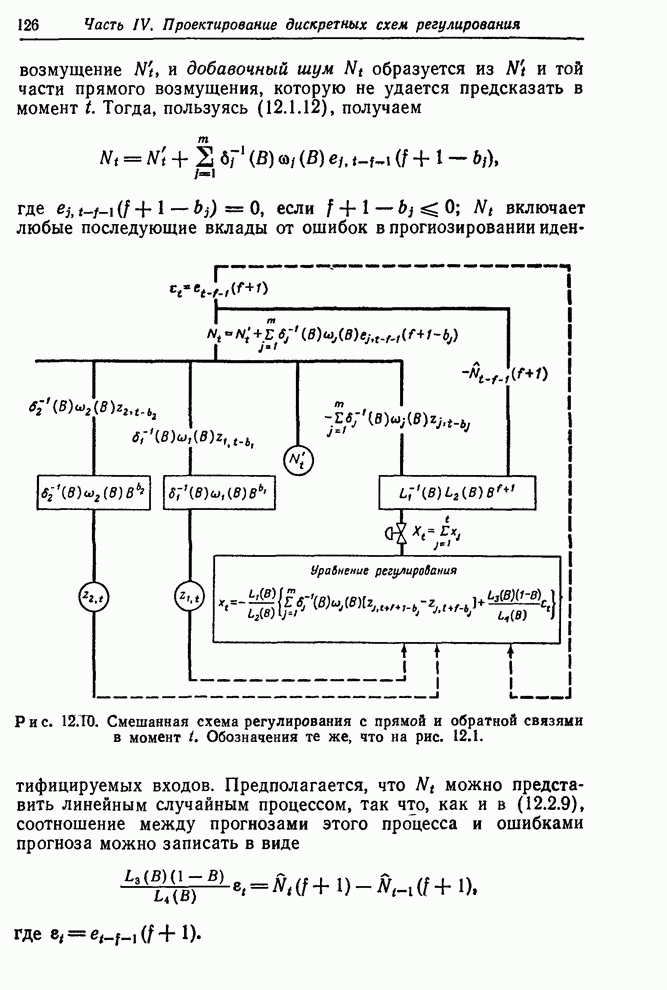
- 12.3. РЕГУЛИРОВАНИЕ С ПРЯМОЙ И ОБРАТНОЙ СВЯЗЯМИ
- 12.3.1. Регулирование с прямой и обратной связями, минимизирующее выходную среднеквадратичную ошибку
- 12.3.2. Пример регулирования с прямой и обратной связями
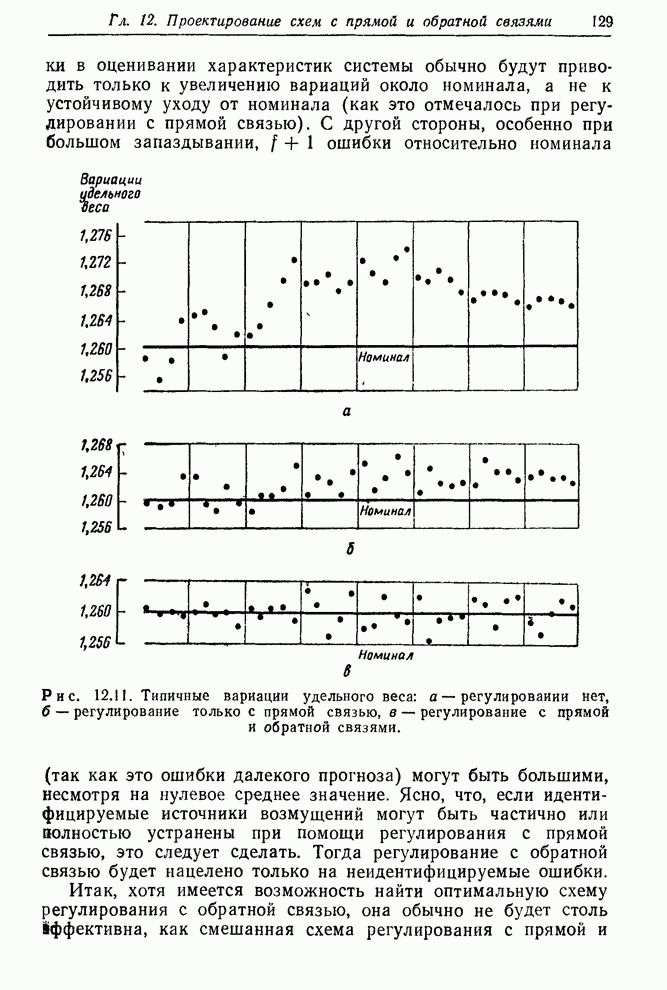
- 12.3.3. Преимущества и недостатки регулирования с прямой и обратной связями
- 12.4. Подгонка моделей передаточных функций шума по оперативным данным
- 12.4.1. Итеративный способ построения моделей
- 12.4.2. Оценивание по оперативным данным
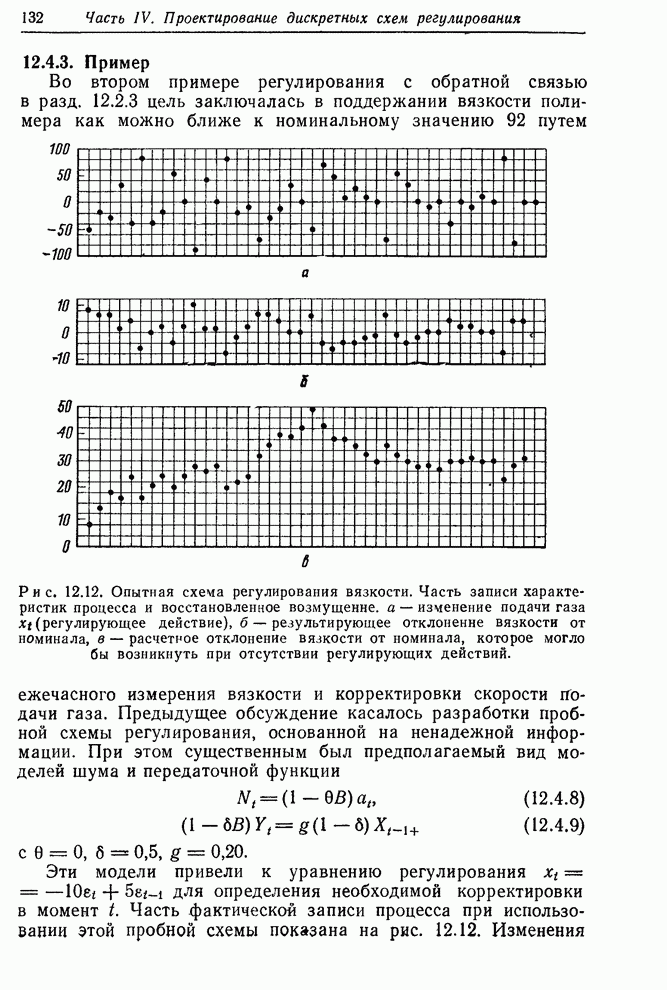
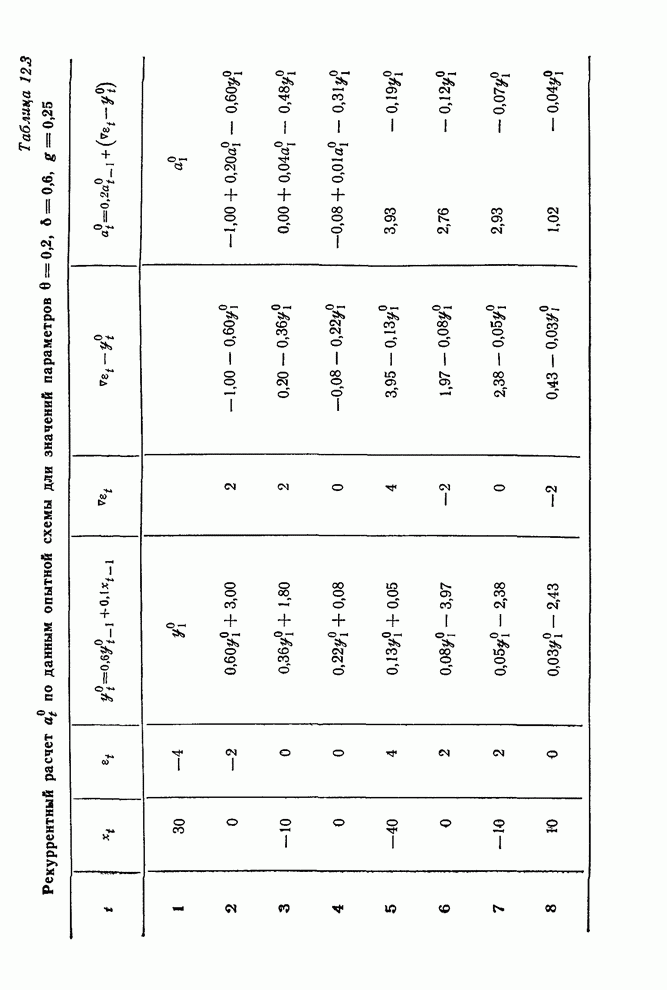
- 12.4.3. Пример
- Глава 13. Некоторые дальнейшие проблемы регулирования
- 13.1. ЭФФЕКТ ДОБАВОЧНОГО ШУМА В СХЕМАХ РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ
- 13.1.1. Эффект пренебрежения добавочным шумом; упрощенные схемы
- 13.1.2. Оптимальное действие в случаях, когда корректировки содержат ошибки наблюдения
- 13.1.3. Перенос источника шума
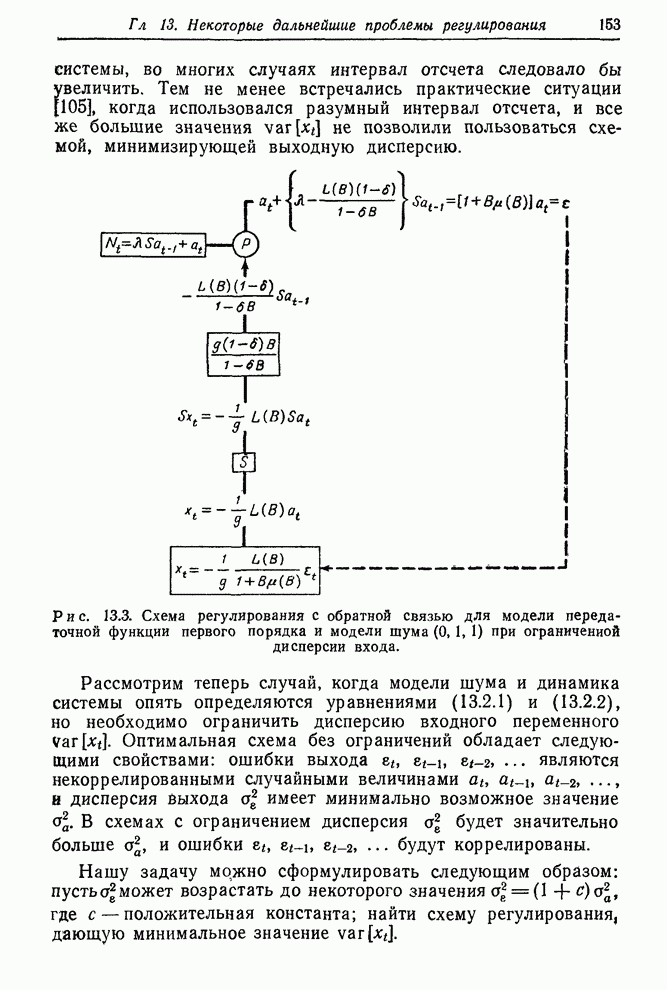
- 13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
- 13.2.1. Вывод выражения для оптимальной корректировки
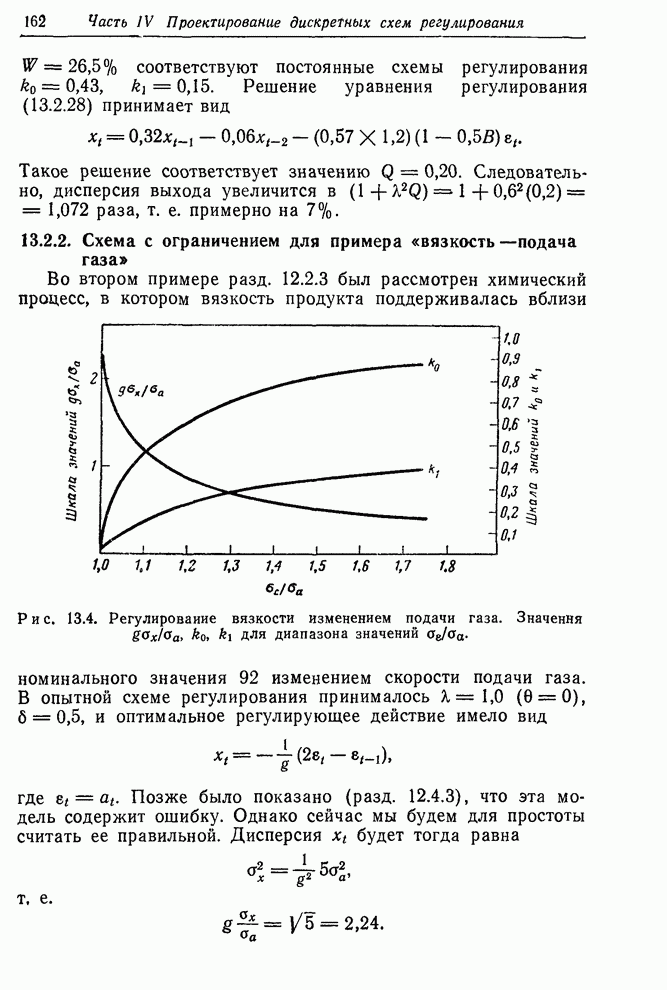
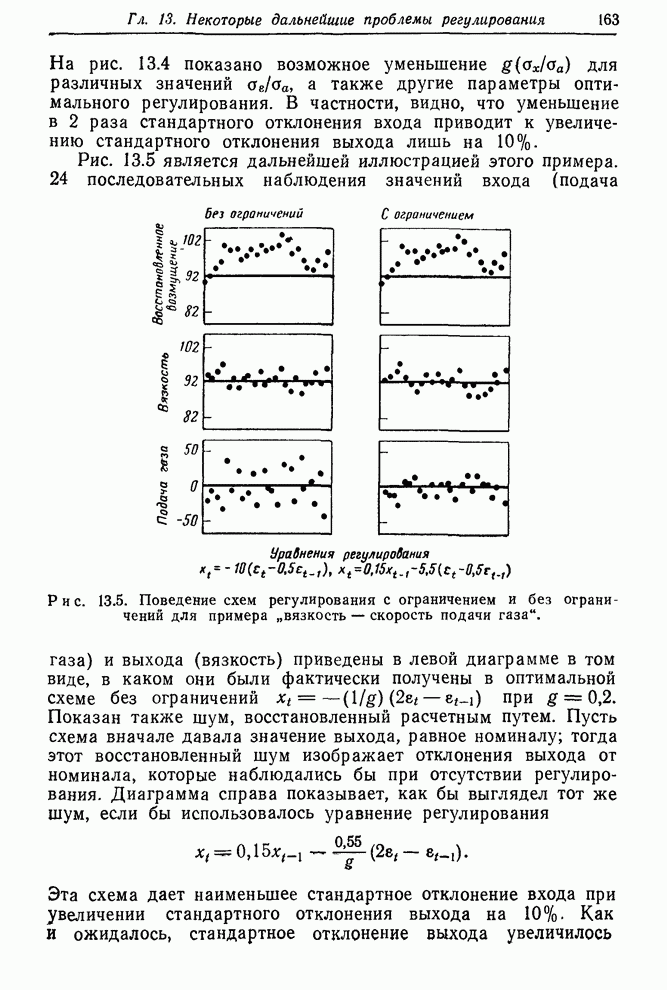
- 13.2.2. Схема с ограничением для примера «вязкость–подача газа»
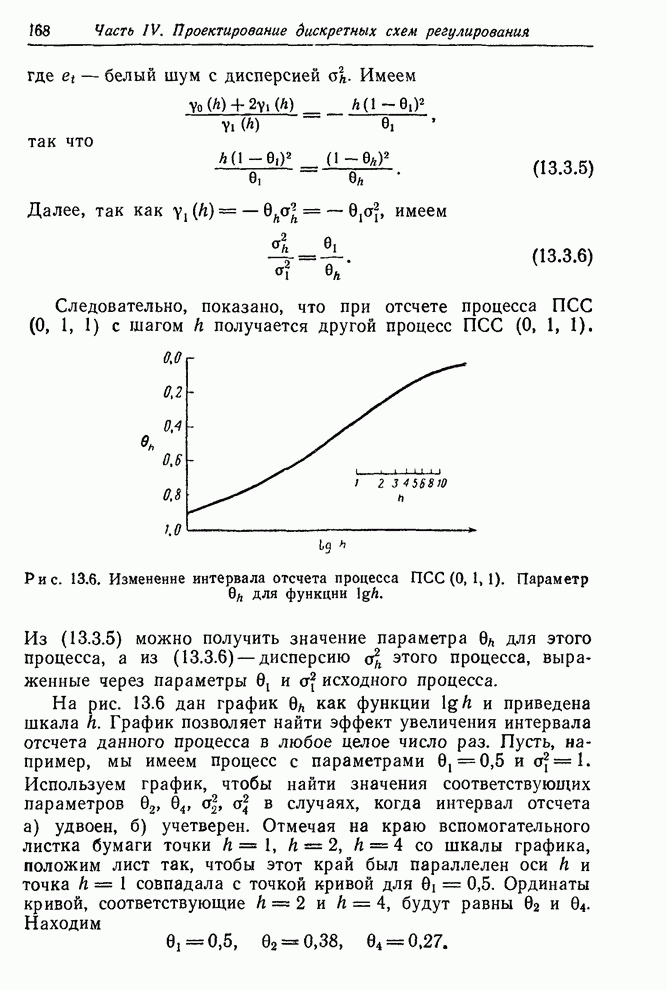
- 13.3. ВЫБОР ИНТЕРВАЛА ОТСЧЕТА
- 13.3.1. Пример эффекта уменьшения частоты отсчетов
- 13.3.2. Влияние интервала отсчета на процесс ПСС(0,1,1)
- ПРОГРАММА 5. ИДЕНТИФИКАЦИЯ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 6. ПРЕДВАРИТЕЛЬНОЕ ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 7. ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
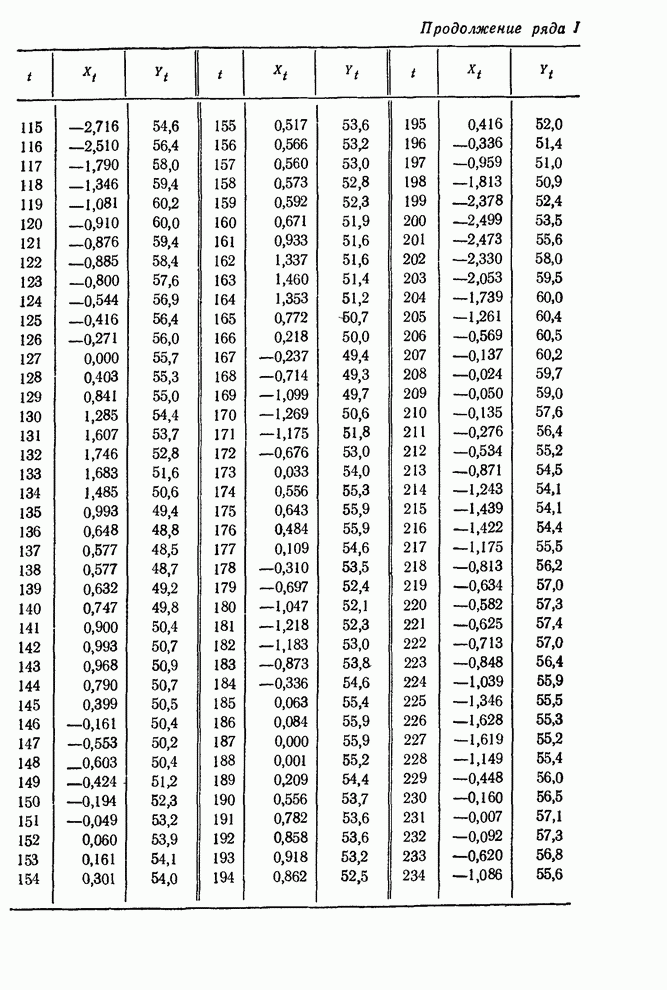
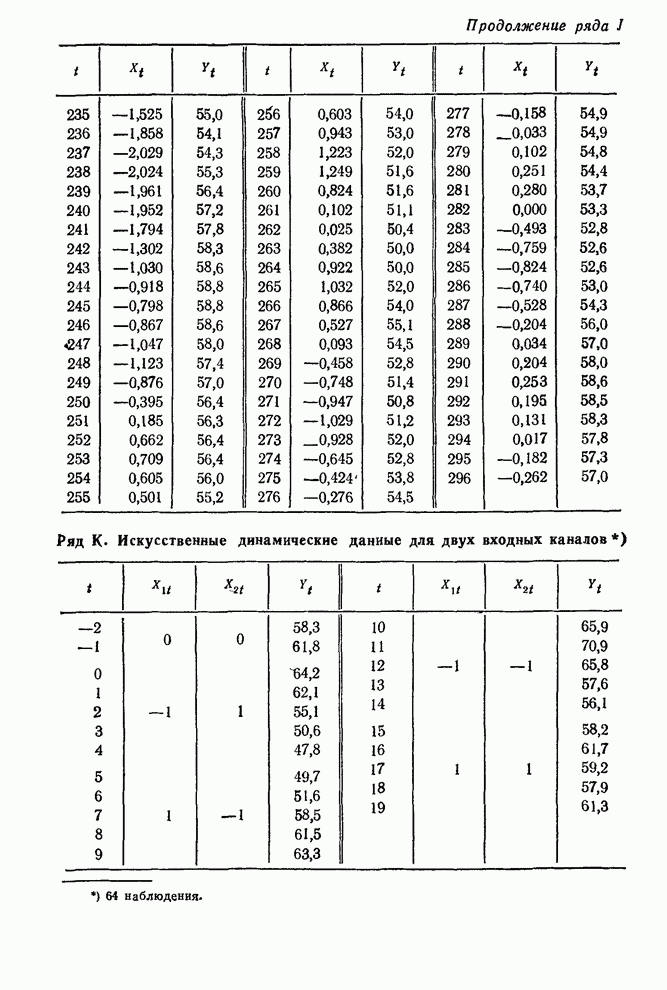
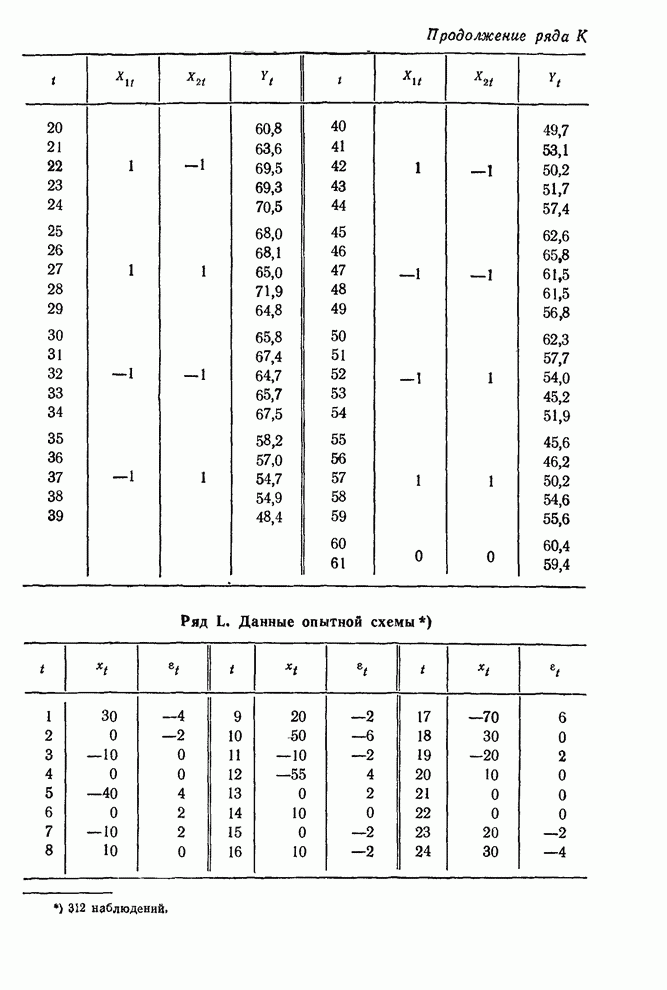
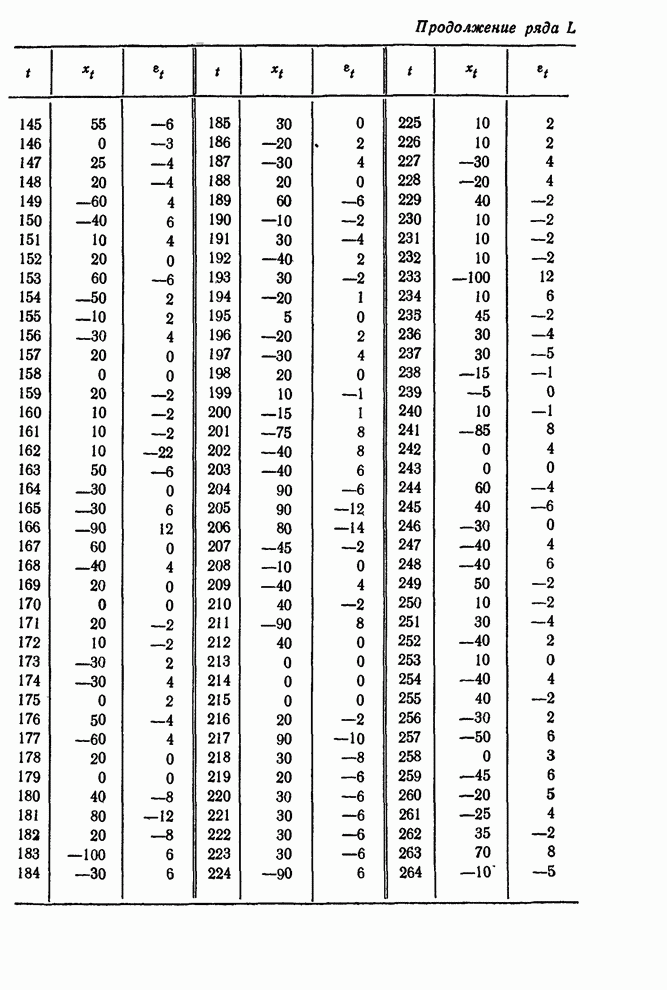
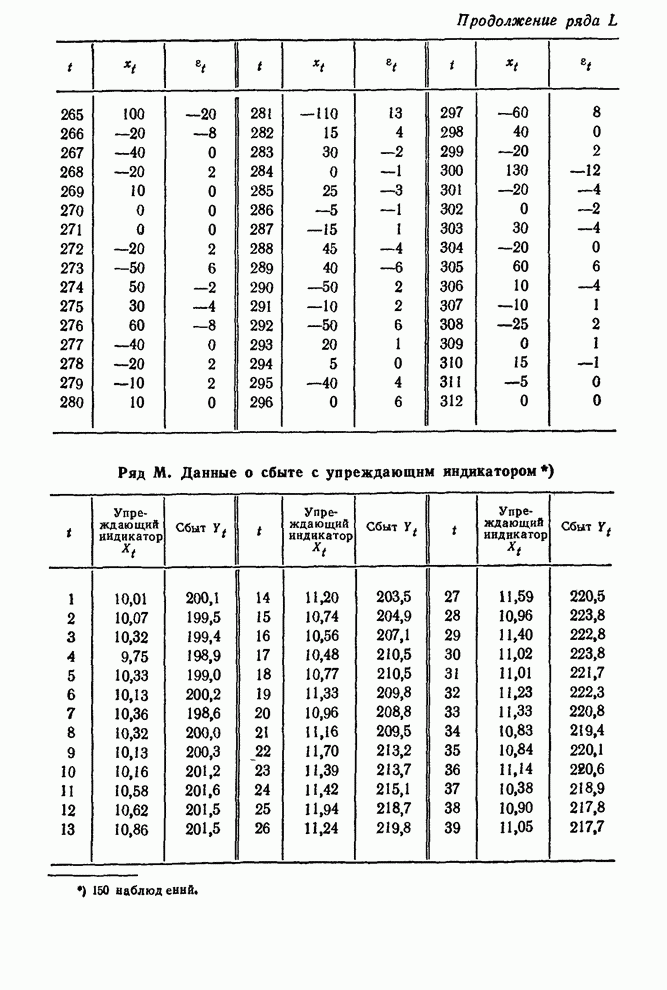
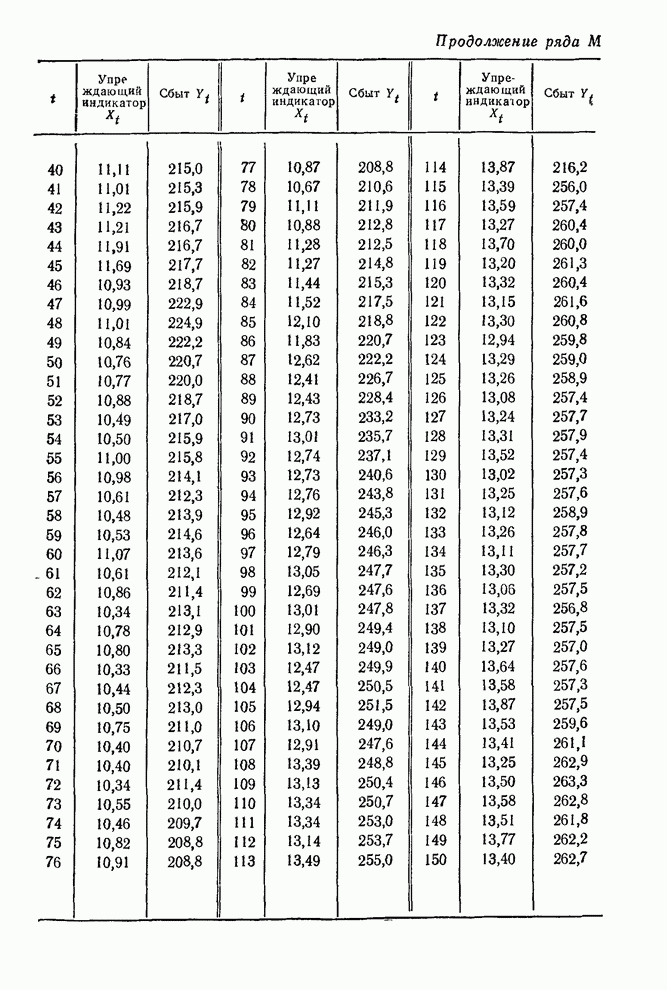
- ТАБЛИЦЫ ВРЕМЕННЫХ РЯДОВ





































































































































































 j=b+2
j=b+2
