| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
13.2.1. Вывод выражения для оптимальной корректировки
Пусть
оптимальная корректировка, выраженная через ![]() , будет равна
, будет равна
![]() , (13.2.4)
, (13.2.4)
где
![]() .
.
Тогда,
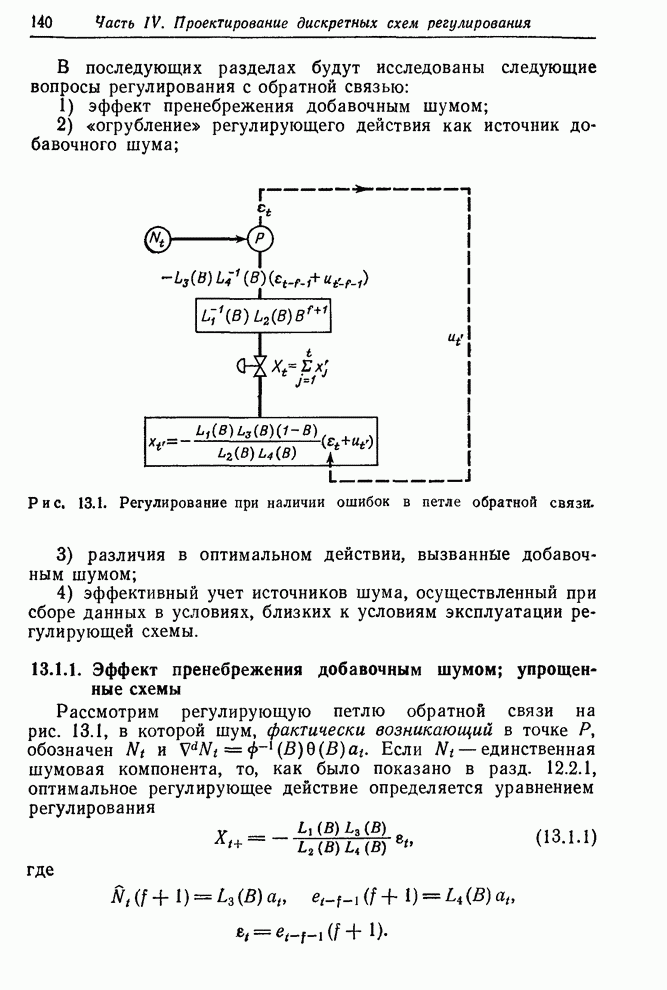
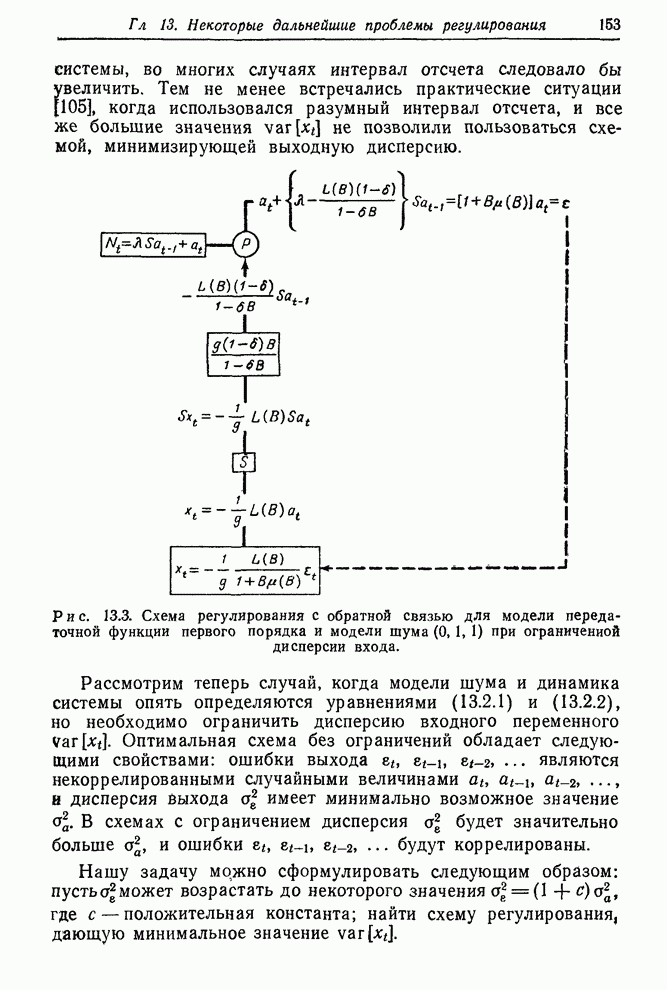
обращаясь к рис. 13.3, мы видим, что ошибка выхода ![]() определяется выражением
определяется выражением
 . (13.2.5)
. (13.2.5)
Коэффициент
при ![]() в этом
выражении равен единице, так что можно записать
в этом
выражении равен единице, так что можно записать
![]() , (13.2.6)
, (13.2.6)
где
![]() .
.
Далее,
практически регулирование нужно выразить через наблюдаемые ошибки выхода ![]() , а не через
, а не через ![]() , так чтобы
регулирующее действие имело вид
, так чтобы
регулирующее действие имело вид
![]() . (13.2.7)
. (13.2.7)
Приравнивая (13.2.5) и (13.2.6), получаем
![]() . (13.2.8)
. (13.2.8)
Так
как ![]() ,
, ![]() и
и ![]() – константы, можно
стандартным образом найти безусловный минимум выражения
– константы, можно
стандартным образом найти безусловный минимум выражения
 ; (13.2.9)
; (13.2.9)
здесь
![]() и т. п.
Точно так же, пользуясь производящими функциями, мы будем искать (безусловный)
минимум коэффициента при
и т. п.
Точно так же, пользуясь производящими функциями, мы будем искать (безусловный)
минимум коэффициента при ![]() в выражении
в выражении
![]() ,
,
или, в несколько ином виде, в
 (13.2.10)
(13.2.10)
где
![]() . Этот
минимум мы можем найти, дифференцируя
. Этот
минимум мы можем найти, дифференцируя ![]() по каждому
по каждому ![]()
![]() , выбирая коэффициенты при
, выбирая коэффициенты при ![]() в результирующем
выражении, приравнивая их нулю и решая получившиеся уравнения. Имеем
в результирующем
выражении, приравнивая их нулю и решая получившиеся уравнения. Имеем
 (13.2.11)
(13.2.11)
Найдя
коэффициенты при ![]() для
для
![]() и
приравнивая их нулю, получаем уравнения
и
приравнивая их нулю, получаем уравнения
![]() (13.2.12)
(13.2.12)
![]() (13.2.13)
(13.2.13)
![]() . (13.2.14)
. (13.2.14)
Случай
пренебрежимо малого ![]() . Рассмотрим сначала простейший случай,
когда
. Рассмотрим сначала простейший случай,
когда ![]() пренебрежимо
мало и может считаться нулем. Тогда приведенные выше уравнения принимают вид
пренебрежимо
мало и может считаться нулем. Тогда приведенные выше уравнения принимают вид
![]() , (13.2.15)
, (13.2.15)
![]() . (13.2.16)
. (13.2.16)
Эти разностные уравнения имеют решения вида
![]() ,
,
где
![]() и
и ![]() – корни
характеристического уравнения
– корни
характеристического уравнения
![]() , (13.2.17)
, (13.2.17)
т. е.
![]() .
.
Очевидно,
если ![]() –
корень этого уравнения, то и
–
корень этого уравнения, то и ![]() – тоже корень. Поэтому решение имеет
вид
– тоже корень. Поэтому решение имеет
вид ![]() . Если
. Если
![]() по модулю
меньше или равно 1, то
по модулю
меньше или равно 1, то ![]() по модулю больше или равно 1, и так как
по модулю больше или равно 1, и так как
![]() должно
иметь конечную дисперсию,
должно
иметь конечную дисперсию, ![]() должно быть равно нулю, а
должно быть равно нулю, а ![]() . Подставляя решение
. Подставляя решение ![]() в (13.2.15),
находим, что
в (13.2.15),
находим, что ![]() .
.
Наконец,
так как ![]() и
и ![]() и
и ![]() должны быть
действительными числами, корень уравнения
должны быть
действительными числами, корень уравнения ![]() тоже действителен. Отсюда
тоже действителен. Отсюда
![]() ,
, ![]() , (13.2.18)
, (13.2.18)
![]() , (13.2.19)
, (13.2.19)
где
![]() . Тогда
. Тогда
![]() ,
,
так что
 . (13.2.20)
. (13.2.20)
Из
(13.2.8) при ![]() получаем
получаем
![]() . (13.2.21)
. (13.2.21)
Отсюда
![]()
и
 . (13.2.22)
. (13.2.22)
Из
(13.2.7), (13.2.19) и (13.2.21) находим, что оптимальное регулирующее действие,
выраженное через наблюденные ошибки на выходе ![]() , равно
, равно
![]() ,
,
т. е.
![]() . (13.2.23)
. (13.2.23)
Отметим, что уравнение регулирования с ограничением отличается от уравнения без ограничения в двух отношениях.
1.
Вводится новый множитель ![]() , в результате чего текущее действие
частично зависит от предыдущего.
, в результате чего текущее действие
частично зависит от предыдущего.
2.
Постоянная, определяющая долю интегрального регулирования, уменьшается в ![]() раз.
раз.
Мы
предполагали, что допускается увеличение дисперсии выхода до значения ![]() . Из (13.2.20)
следует, что
. Из (13.2.20)
следует, что
 ,
,
т. е.
![]() ,
,
где
берется положительное значение корня. Удобно ввести обозначение ![]() . Тогда
. Тогда ![]() и
и ![]() , а дисперсия выхода
имеет вид
, а дисперсия выхода
имеет вид ![]() .
.
Допустим,
что мы согласны на увеличение дисперсии выхода до значения ![]() . Тогда
. Тогда
1) вычисляем
![]() ,
,
2) оптимальное регулирование достигается при помощи действия
![]() ,
,
3) дисперсия входа может быть уменьшена до
 ,
,
т.
е. уменьшится до ![]() от
дисперсии схемы без ограничения, где
от
дисперсии схемы без ограничения, где
![]() .
.
В
табл. 13.2 приведены значения ![]() и
и ![]() для
для ![]() , заключенного между 0,1 и 1,0.
, заключенного между 0,1 и 1,0.
Таблица 13.2. Значения параметров для простой схемы регулирования с ограничением
|
|
0,10 |
0,20 |
0,30 |
0,40 |
0,50 |
0,60 |
0,70 |
0,80 |
0,90 |
1,00 |
|
|
0,302 |
0,408 |
0,480 |
0,535 |
0,577 |
0,612 |
0,641 |
0,667 |
0,688 |
0,707 |
|
|
53,7 |
42,0 |
35,1 |
30,3 |
26,8 |
24,0 |
21,9 |
20,0 |
18,5 |
17,2 |
Пусть,
например, ![]() .
Тогда оптимальная схема без ограничений будет требовать регулирующего действия
.
Тогда оптимальная схема без ограничений будет требовать регулирующего действия
![]()
с
![]() . Дисперсия
. Дисперсия
![]() равна
равна ![]() . Пусть
потребовалось понизить ее в 4 раза, т. е. до значения
. Пусть
потребовалось понизить ее в 4 раза, т. е. до значения ![]()
![]() . Из табл. 13.2 вытекает, что уменьшение
дисперсии входа до 24% от его значения при отсутствии ограничений возможно при
. Из табл. 13.2 вытекает, что уменьшение
дисперсии входа до 24% от его значения при отсутствии ограничений возможно при ![]() и
и ![]() . Если мы используем
схему с этими значениями, дисперсия выхода будет равна
. Если мы используем
схему с этими значениями, дисперсия выхода будет равна
![]() .
.
Итак, применив регулирующее действие
![]()
вместо
![]() ,
,
мы уменьшаем дисперсию входа до четверти ее предыдущего значения, а дисперсия выхода увеличивается на 10%.
Случай,
когда нельзя пренебречь ![]() . Рассмотрим теперь более общий случай,
когда
. Рассмотрим теперь более общий случай,
когда ![]() непренебрежимо
мало и необходимо учитывать динамику системы. Разностное уравнение (13.2.14)
имеет вид
непренебрежимо
мало и необходимо учитывать динамику системы. Разностное уравнение (13.2.14)
имеет вид
![]() ,
,
и
если ![]() –
корень характеристического уравнения, то и
–
корень характеристического уравнения, то и ![]() – корень того же уравнения. Пусть корни
уравнения равны
– корень того же уравнения. Пусть корни
уравнения равны ![]() ,
причем
,
причем ![]() и
и ![]() по модулю меньше
единицы. Тогда в решении
по модулю меньше
единицы. Тогда в решении
![]()
![]() и
и
![]() должны
быть равны нулю, так как дисперсия
должны
быть равны нулю, так как дисперсия ![]() конечна.
конечна.
Итак, решение имеет вид
![]() ,
, ![]() ,
, ![]() .
.
Пользуясь
начальными условиями (13.2.12) и (13.2.13), находим коэффициенты ![]() :
:
![]() ,
, ![]() .
.
Если
обозначить ![]() ,
,
![]() , то
, то
 (13.2.24)
(13.2.24)
и
 . (13.2.25)
. (13.2.25)
Подставляя (13.2.24) в (13.2.8), получаем
 (13.2.26)
(13.2.26)
и
 .
.
Тогда
из (13.2.7) вытекает, что оптимальное регулирующее действие, выраженное через
ошибку ![]() ,
имеет вид
,
имеет вид
 (13.2.27)
(13.2.27)
или
 . (13.2.28)
. (13.2.28)
Итак,
в модифицированной схеме регулирования ![]() зависит как от
зависит как от ![]() , так и от
, так и от ![]() (только от
(только от ![]() , если
, если ![]() ); эта схема
уменьшает стандартное интегральное и пропорциональное действие в
); эта схема
уменьшает стандартное интегральное и пропорциональное действие в ![]() раз.
раз.
Дисперсии на выходе и входе. Легко найти фактические дисперсии на выходе и входе. Имеем
![]() .
.
Второй
член в правой части – смешанный процесс авторегрессии – скользящего среднего
порядка ![]() ,
дисперсия которого без труда определяется как
,
дисперсия которого без труда определяется как
 . (13.2.29)
. (13.2.29)
Далее,
 . (13.2.30)
. (13.2.30)
Вычисление
![]() и
и ![]() . Для разностного
уравнения (13.2.14) характеристическое уравнение имеет вид
. Для разностного
уравнения (13.2.14) характеристическое уравнение имеет вид
![]() ,
,
где
![]() и
и ![]() . Его можно также
представить в виде
. Его можно также
представить в виде
![]() ,
,
где
![]() и
и
![]() .
.
Приравнивая
коэффициенты при одинаковых степенях ![]() , находим
, находим
![]() ,
т. е.
,
т. е. ![]() ,
,
![]() .
.
Отсюда
![]() , т. е.
, т. е.
![]() ,
,
![]() .
.
При
подходящих значениях ![]() это квадратное уравнение имеет два
действительных корня:
это квадратное уравнение имеет два
действительных корня:
![]() ,
, ![]()
![]() .
Искомая величина
.
Искомая величина ![]() –
это меньший из корней квадратного уравнения
–
это меньший из корней квадратного уравнения
![]() ,
,
а
![]() определяется
из
определяется
из
![]() .
.
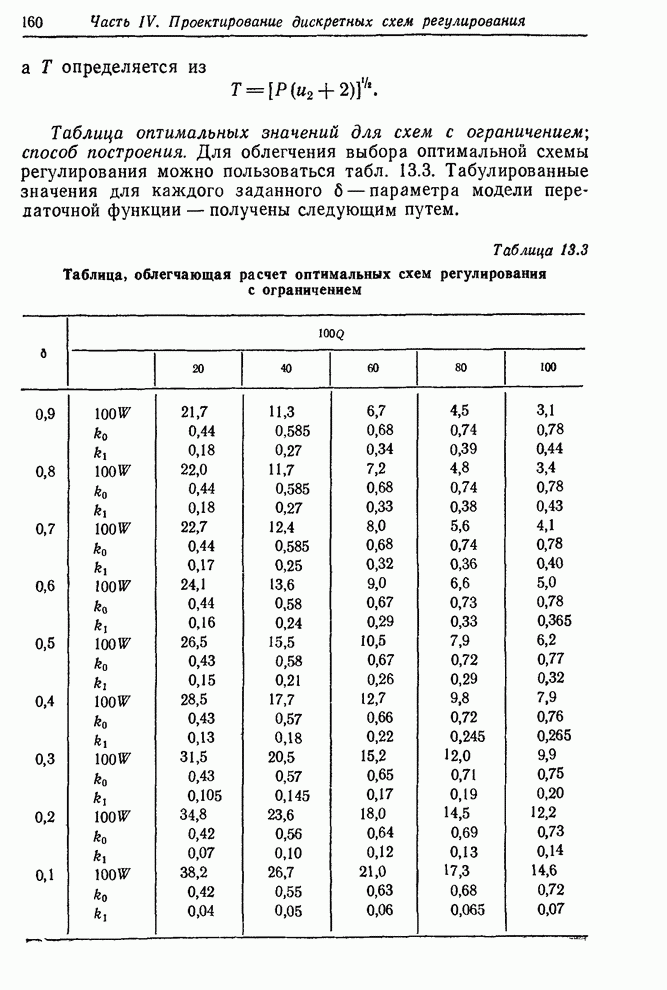
Таблица
оптимальных значений для схем с ограничением; способ построения. Для облегчения
выбора оптимальной схемы регулирования можно пользоваться табл. 13.3.
Табулированные значения для каждого заданного ![]() – параметра модели передаточной функции
– получены следующим путем.
– параметра модели передаточной функции
– получены следующим путем.
Таблица 13.3. Таблица, облегчающая расчет оптимальных схем регулирования с ограничением
|
|
|
|||||
|
|
20 |
40 |
60 |
80 |
10 |
|
|
0,9 |
|
21,7 |
11,3 |
6,7 |
4,5 |
3,1 |
|
|
0,44 |
0,585 |
0,68 |
0,74 |
0,78 |
|
|
|
0,18 |
0,27 |
0,34 |
0,39 |
0,44 |
|
|
0,8 |
|
22,0 |
11,7 |
7,2 |
4,8 |
3,4 |
|
|
0,44 |
0,585 |
0,68 |
0,74 |
0,78 |
|
|
|
0,18 |
0,27 |
0,33 |
0,38 |
0,43 |
|
|
0,7 |
|
22,7 |
12,4 |
8,0 |
5,6 |
4,1 |
|
|
0,44 |
0,585 |
0,68 |
0,74 |
0,78 |
|
|
|
0,17 |
0,25 |
0,32 |
0,36 |
0,40 |
|
|
0,6 |
|
24,1 |
13,6 |
9,0 |
6,6 |
5,0 |
|
|
0,44 |
0,58 |
0,67 |
0,73 |
0,78 |
|
|
|
0,16 |
0,24 |
0,29 |
0,33 |
0,365 |
|
|
0,5 |
|
26,5 |
15,5 |
10,5 |
7,9 |
6,2 |
|
|
0,43 |
0,58 |
0,67 |
0,72 |
0,77 |
|
|
|
0,15 |
0,21 |
0,26 |
0,29 |
0,32 |
|
|
0,4 |
|
28,5 |
17,7 |
12,7 |
9,8 |
7,9 |
|
|
0,43 |
0,57 |
0,66 |
0,72 |
0,76 |
|
|
|
0,13 |
0,18 |
0,22 |
0,245 |
0,265 |
|
|
0,3 |
|
31,5 |
20,5 |
15,2 |
12,0 |
9,9 |
|
|
0,43 |
0,57 |
0,65 |
0,71 |
0,75 |
|
|
|
0,105 |
0,145 |
0,17 |
0,19 |
0,20 |
|
|
0,2 |
|
34,8 |
23,6 |
18,0 |
14,5 |
12,2 |
|
|
0,42 |
0,56 |
0,64 |
0,69 |
0,73 |
|
|
|
0,07 |
0,10 |
0,12 |
0,13 |
0,14 |
|
|
0,1 |
|
38,2 |
26,7 |
21,0 |
17,3 |
14,6 |
|
|
0,42 |
0,55 |
0,63 |
0,68 |
0,72 |
|
|
|
0,04 |
0,05 |
0,06 |
0,065 |
0,07 |
|
1) Вычисляем
![]() и
и

для
ряда значений ![]() ,
выбранных так, чтобы обеспечить нужный диапазон
,
выбранных так, чтобы обеспечить нужный диапазон ![]() .
.
2) Вычисляем

и
 .
.
3) Вычисляем

и
![]() .
.
4) Вычисляем
 .
.
5) Вычисляем
 .
.
6)
Значения ![]() ,
, ![]() ,
, ![]() для подходящих значений
для подходящих значений ![]() находим
интерполяцией.
находим
интерполяцией.
Пользование
таблицей. Табл. 13.3 нужно пользоваться следующим образом. В левом столбце
находим нужное значение ![]() . Пользуясь тем, что
. Пользуясь тем, что ![]() , находим, что
увеличение дисперсии выхода (в %) будет равно
, находим, что
увеличение дисперсии выхода (в %) будет равно ![]() . Подходящее значение
. Подходящее значение ![]() находим в верхней
строке. Итак, входными данными таблицы будут
находим в верхней
строке. Итак, входными данными таблицы будут
а)
![]() ,
процентное уменьшение дисперсии
,
процентное уменьшение дисперсии ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
Примем,
например, ![]() ,
,
![]() ,
, ![]() . Уравнение
оптимального регулирования без ограничений имеет вид
. Уравнение
оптимального регулирования без ограничений имеет вид
![]()
и
![]() .
Предположим, что такая дисперсия входной переменной создает трудности при
осуществлении производственного процесса, и желательно уменьшить
.
Предположим, что такая дисперсия входной переменной создает трудности при
осуществлении производственного процесса, и желательно уменьшить ![]() до
до ![]() , т. е. до 28% от
значения дисперсии в схеме без ограничений. По табл. 13.3 находим, что
значениям
, т. е. до 28% от
значения дисперсии в схеме без ограничений. По табл. 13.3 находим, что
значениям ![]() и
и
![]() соответствуют
постоянные схемы регулирования
соответствуют
постоянные схемы регулирования ![]() ,
, ![]() . Решение уравнения регулирования
(13.2.28) принимает вид
. Решение уравнения регулирования
(13.2.28) принимает вид
![]() .
.
Такое
решение соответствует значению ![]() . Следовательно, дисперсия выхода
увеличится в
. Следовательно, дисперсия выхода
увеличится в ![]() раза,
т. е. примерно на 7%.
раза,
т. е. примерно на 7%.
| << Предыдущий параграф | Следующий параграф >> |
- Часть III. ПОСТРОЕНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- Глава 10. Модели передаточной функции
- 10.1. ЛИНЕЙНЫЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 10.1.1. Дискретная передаточная функция
- 10.1.2. Непрерывные динамические модели, описываемые дифференциальными уравнениями
- 10.2. ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ МОДЕЛИ, ОПИСЫВАЕМЫЕ РАЗНОСТНЫМИ УРАВНЕНИЯМИ
- 10.2.1. Общая форма разностного уравнения
- 10.2.2. Природа передаточной функции
- 10.2.3. Дискретные модели передаточных функций первого и второго порядков
- 10.2.4. Рекуррентный расчет выхода для произвольного входа
- 10.3. СООТНОШЕНИЕ МЕЖДУ ДИСКРЕТНОЙ И НЕПРЕРЫВНОЙ МОДЕЛЯМИ
- 10.3.1. Отклик на скачкообразный вход
- 10.3.2. Соотношения совпадающих систем первого и второго порядков
- 10.3.3. Аппроксимация общих непрерывных моделей дискретными моделями
- 10.3.4. Модели передаточных функций с добавленным шумом
- ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
- ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
- Глава 11. Идентификация, подгонка и проверка моделей передаточных функций
- 11.1. Взаимная корреляционная функция
- 11.1.1. Свойства взаимных ковариационной и корреляционной функций
- 11.1.2. Оценивание взаимных ковариационных и корреляционных функций
- 11.1.3. Приближенные стандартные ошибки выборочных оценок взаимных корреляций
- 11.2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.2.1. Идентификация моделей передаточной функции с предварительным выравниванием спектра входа
- 11.2.2. Пример идентификации модели передаточной функции
- 11.2.3. Идентификация модели шума
- 11.2.4. Некоторые общие соображения об идентификации моделей передаточных функций
- 11.3. ПОДГОНКА И ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.3.1. Условная сумма квадратов
- 11.3.2. Нелинейное оценивание
- 11.3.3. Использование остаточных ошибок для диагностической проверки
- 11.3.4. Конкретные способы проверки остаточных ошибок
- 11.4. Некоторые примеры подгонок и проверок моделей передаточных функций
- 11.4.1. Подгонка и проверка модели газовой печи
- 11.4.2. Искусственный пример с двумя входами
- 11.5. ПРОГНОЗИРОВАНИЕ ПРИ ПОМОЩИ УПРЕЖДАЮЩИХ ИНДИКАТОРОВ
- 11.5.1. Прогноз с минимальной среднеквадратичной ошибкой
- 11.5.2. Прогнозы выхода СO2 из газовой печи
- 11.5.3. Прогноз нестационарных данных сбыта при помощи упреждающего индикатора
- 11.6. НЕКОТОРЫЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОЦЕНИВАНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ П11.1. ИСПОЛЬЗОВАНИЕ ВЗАИМНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
- Заключение
- Часть IV. Проектирование дискретных схем регулирования
- Глава 12. Проектирование схем регулирования с прямой и обратной связями
- 12.1. РЕГУЛИРОВАНИЕ С ПРЯМОЙ СВЯЗЬЮ
- 12.1.1. Регулирование с прямой связью, минимизирующее среднеквадратичную ошибку
- 12.1.2. Пример — регулирование удельного веса промежуточного продукта
- 12.1.3. Номограмма для регулирования с прямой связью
- 12.1.4. Регулирование с прямой связью в случае нескольких входов
- 12.2. РЕГУЛИРОВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ
- 12.2.1. Регулирование с обратной связью, минимизирующее среднеквадратичную ошибку
- 12.2.2. Применение уравнения регулирования: ПИД-регулятор
- 12.2.3. Примеры дискретного регулирования с обратной связью
- 12.3. РЕГУЛИРОВАНИЕ С ПРЯМОЙ И ОБРАТНОЙ СВЯЗЯМИ
- 12.3.1. Регулирование с прямой и обратной связями, минимизирующее выходную среднеквадратичную ошибку
- 12.3.2. Пример регулирования с прямой и обратной связями
- 12.3.3. Преимущества и недостатки регулирования с прямой и обратной связями
- 12.4. Подгонка моделей передаточных функций шума по оперативным данным
- 12.4.1. Итеративный способ построения моделей
- 12.4.2. Оценивание по оперативным данным
- 12.4.3. Пример
- Глава 13. Некоторые дальнейшие проблемы регулирования
- 13.1. ЭФФЕКТ ДОБАВОЧНОГО ШУМА В СХЕМАХ РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ
- 13.1.1. Эффект пренебрежения добавочным шумом; упрощенные схемы
- 13.1.2. Оптимальное действие в случаях, когда корректировки содержат ошибки наблюдения
- 13.1.3. Перенос источника шума
- 13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
- 13.2.1. Вывод выражения для оптимальной корректировки
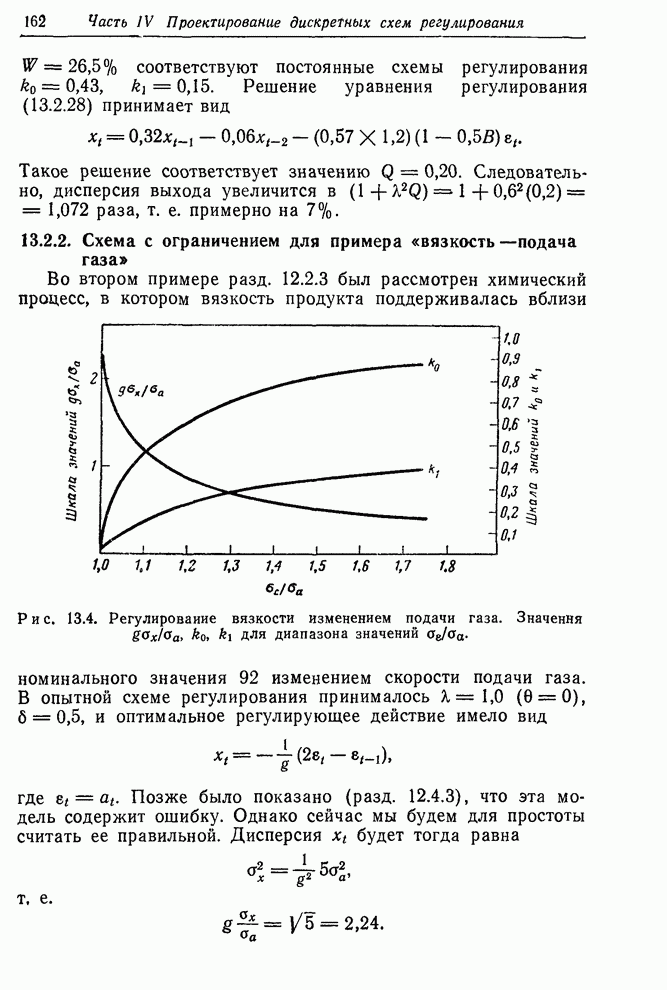
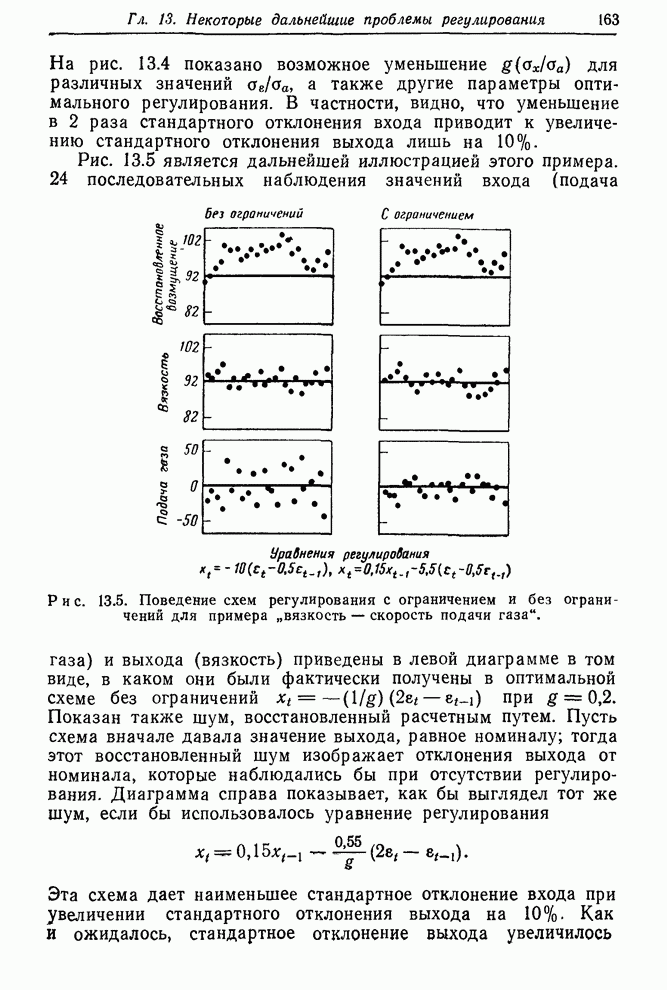
- 13.2.2. Схема с ограничением для примера «вязкость–подача газа»
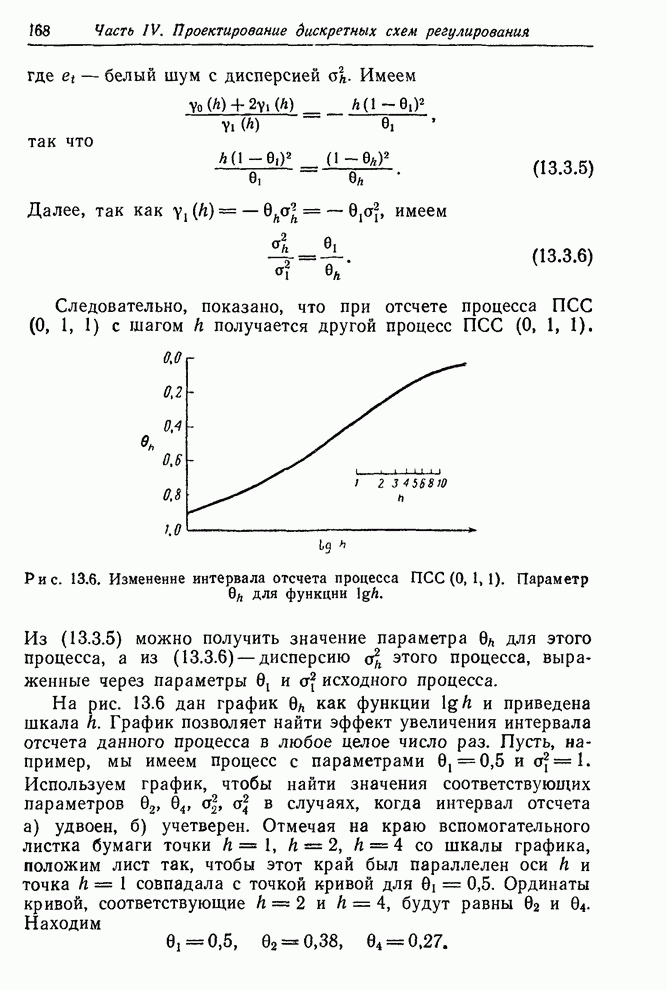
- 13.3. ВЫБОР ИНТЕРВАЛА ОТСЧЕТА
- 13.3.1. Пример эффекта уменьшения частоты отсчетов
- 13.3.2. Влияние интервала отсчета на процесс ПСС(0,1,1)
- ПРОГРАММА 5. ИДЕНТИФИКАЦИЯ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 6. ПРЕДВАРИТЕЛЬНОЕ ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 7. ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
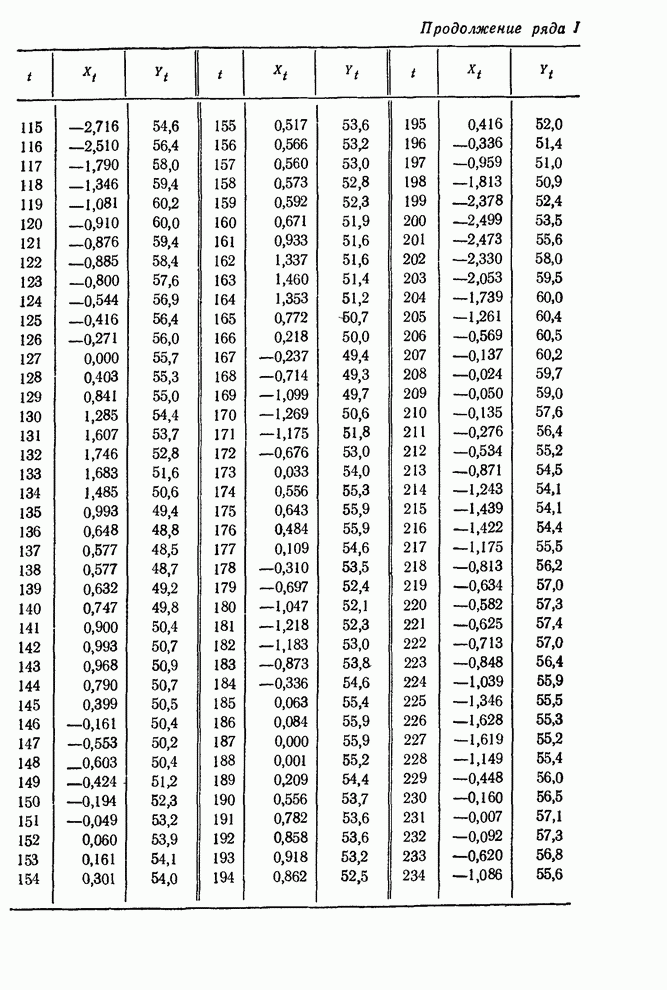
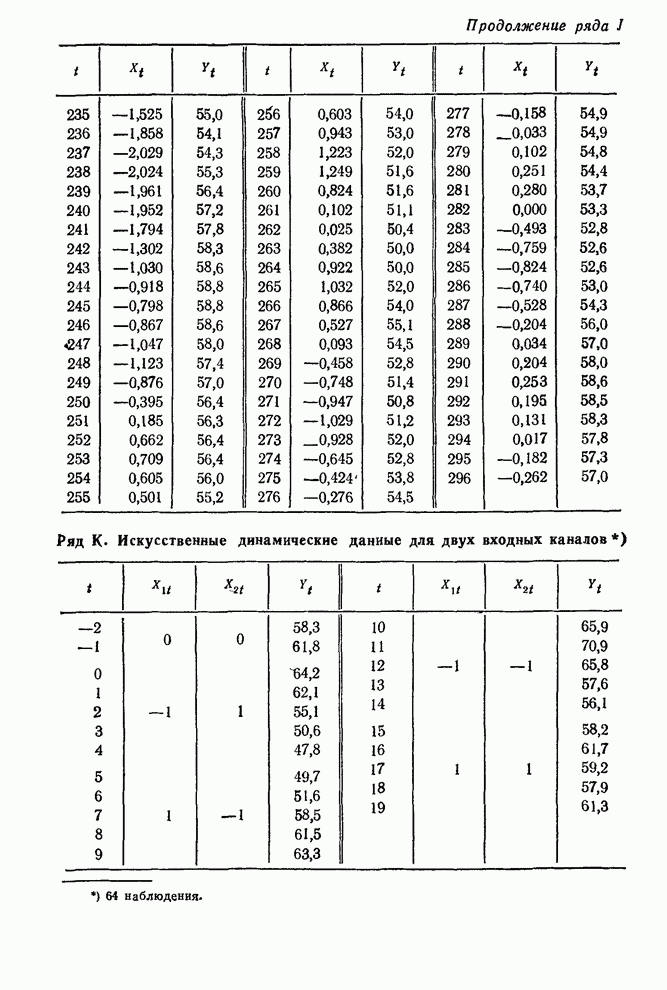
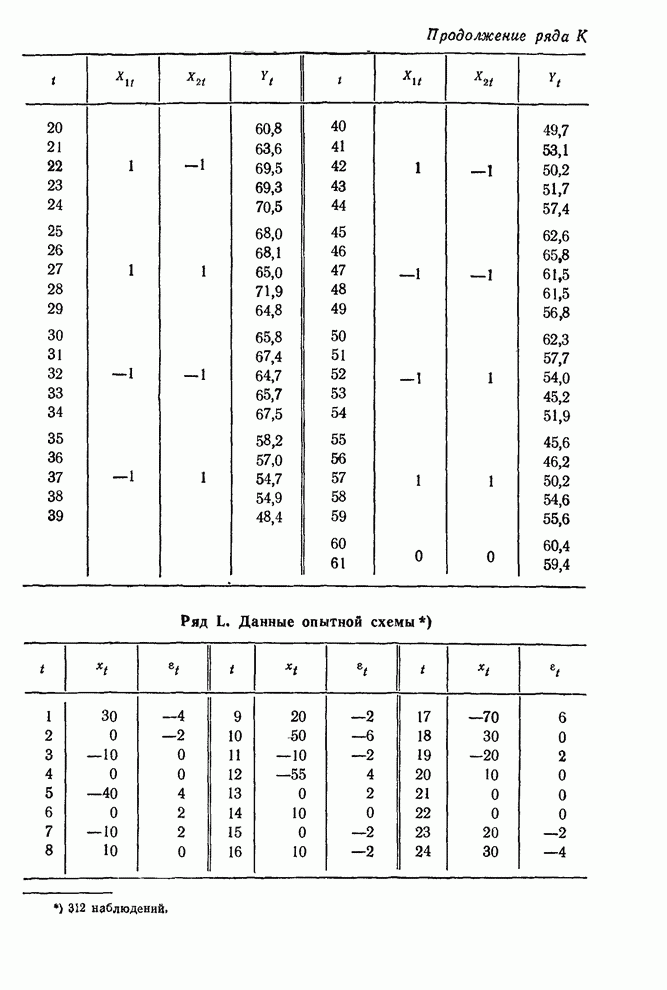
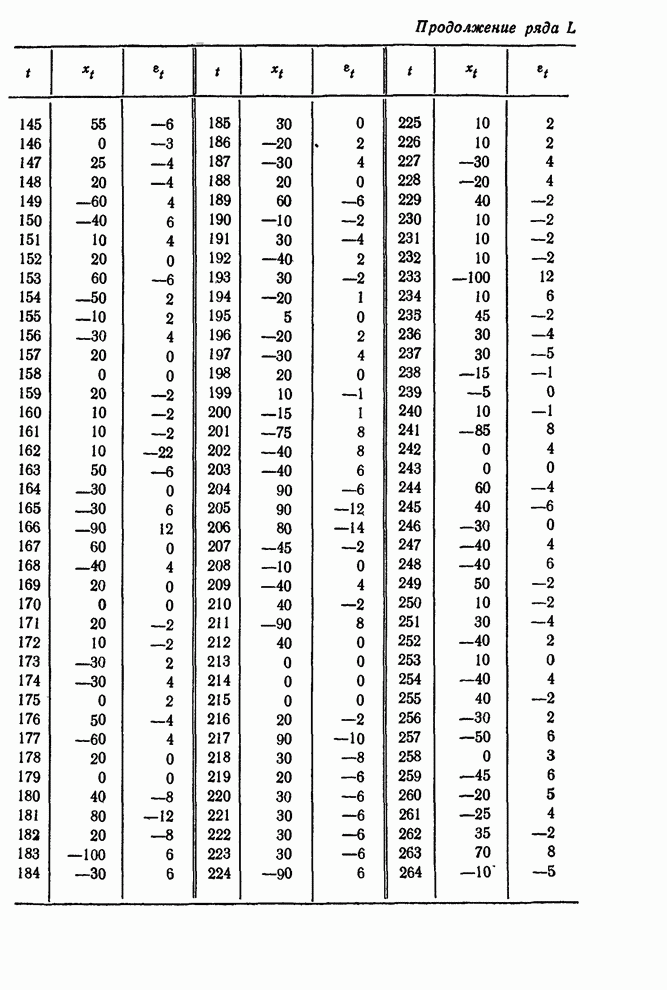
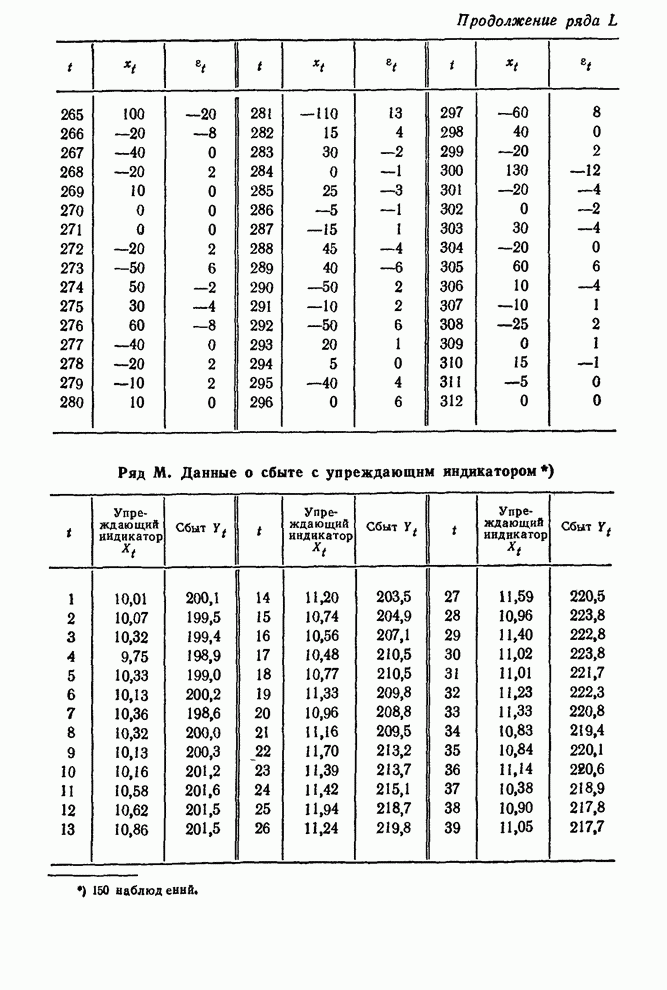
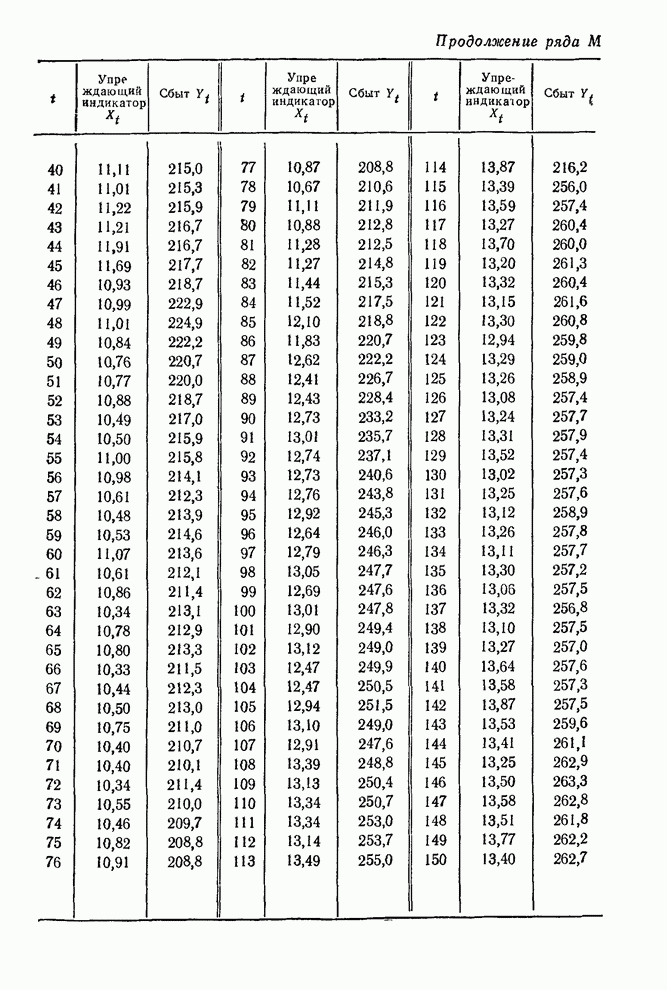
- ТАБЛИЦЫ ВРЕМЕННЫХ РЯДОВ