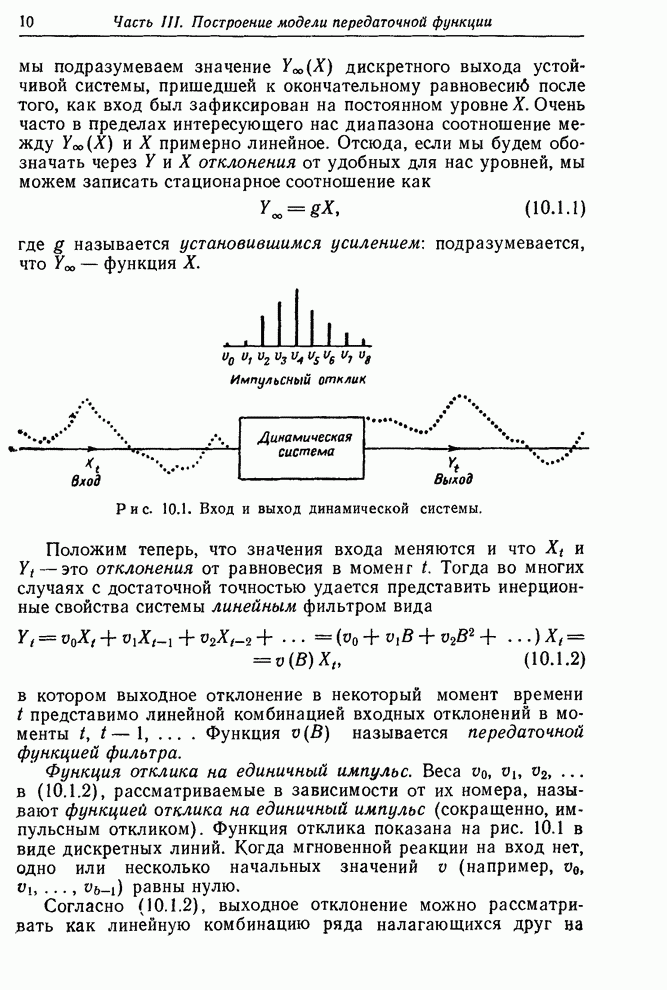
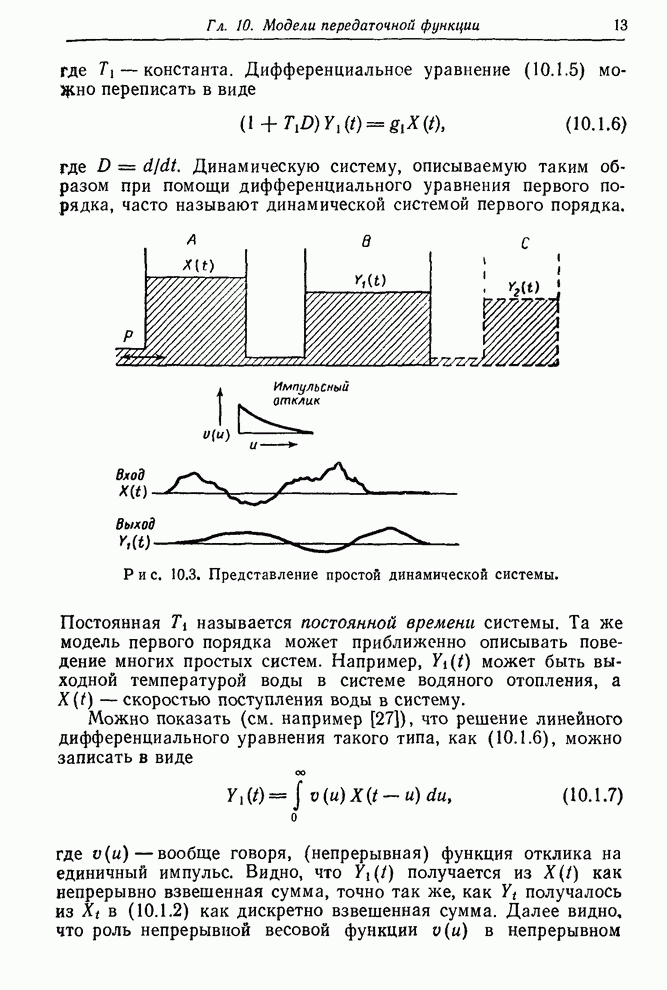
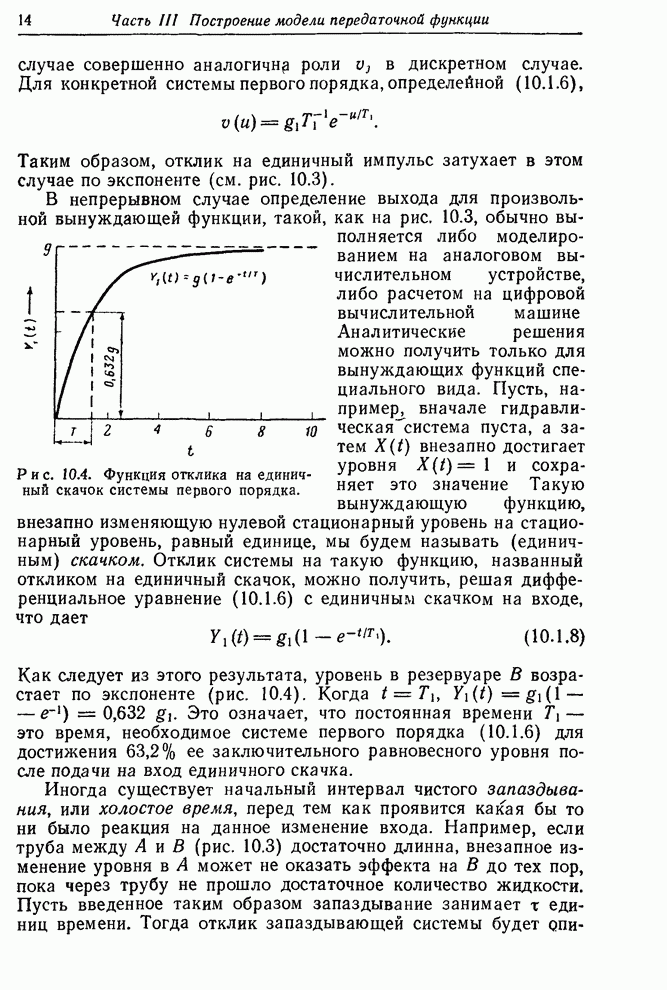
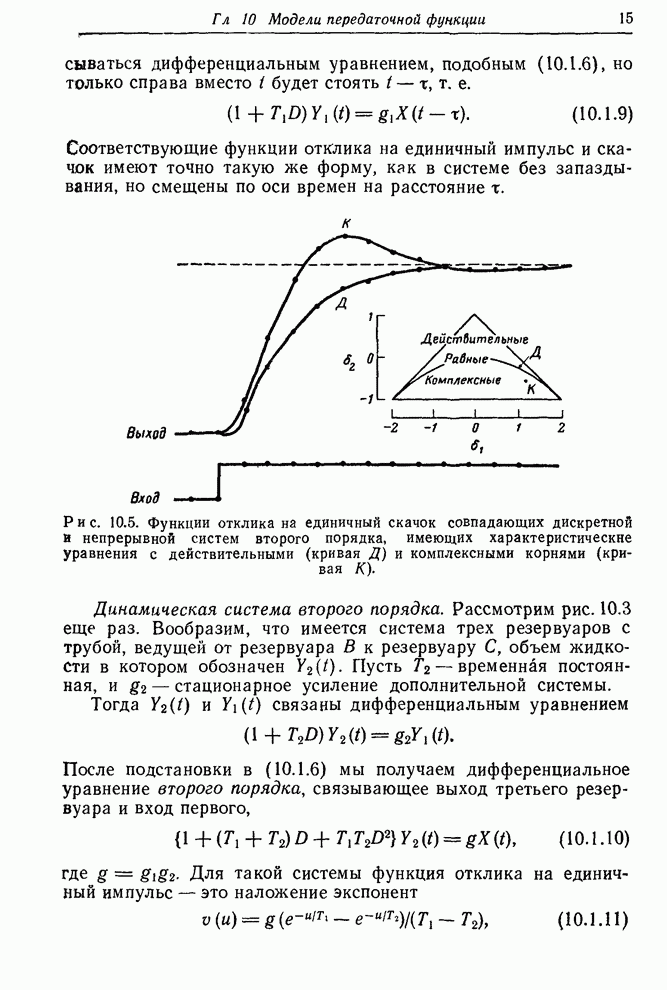
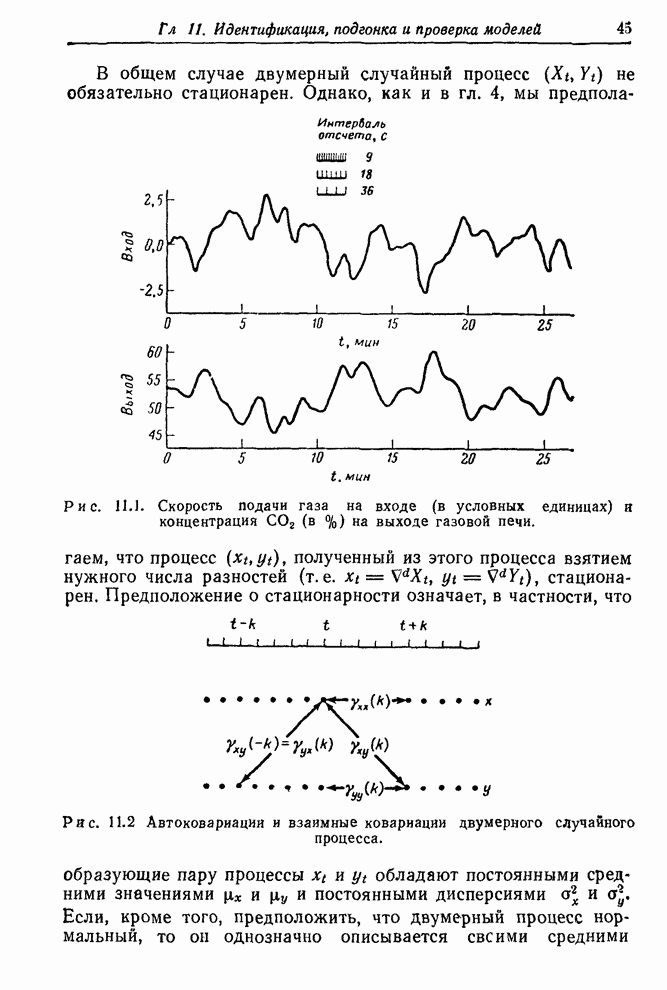
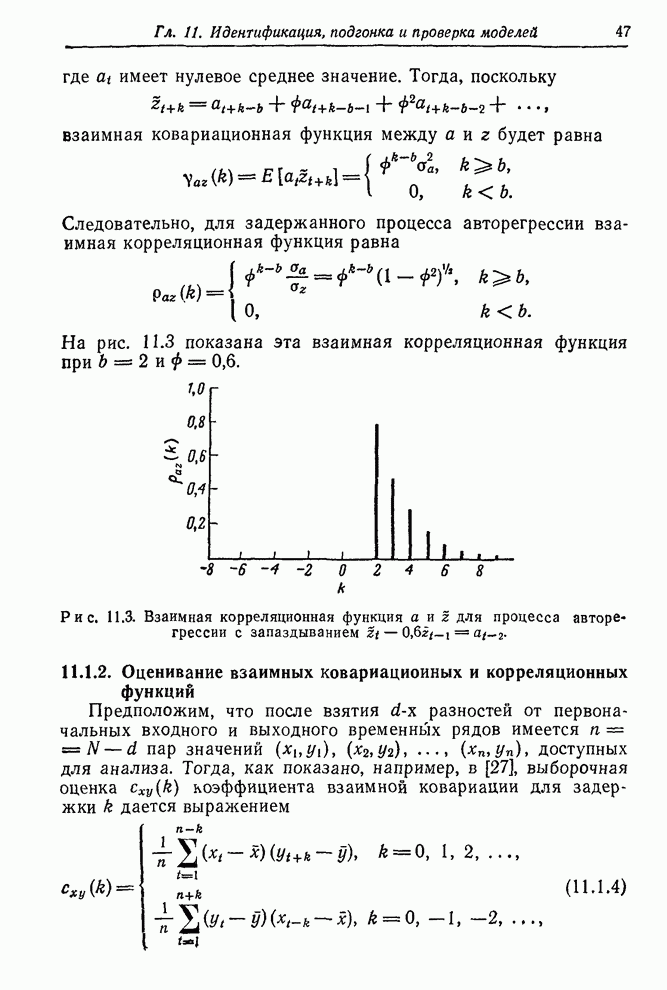
| << Предыдущий параграф | Следующий параграф >> |
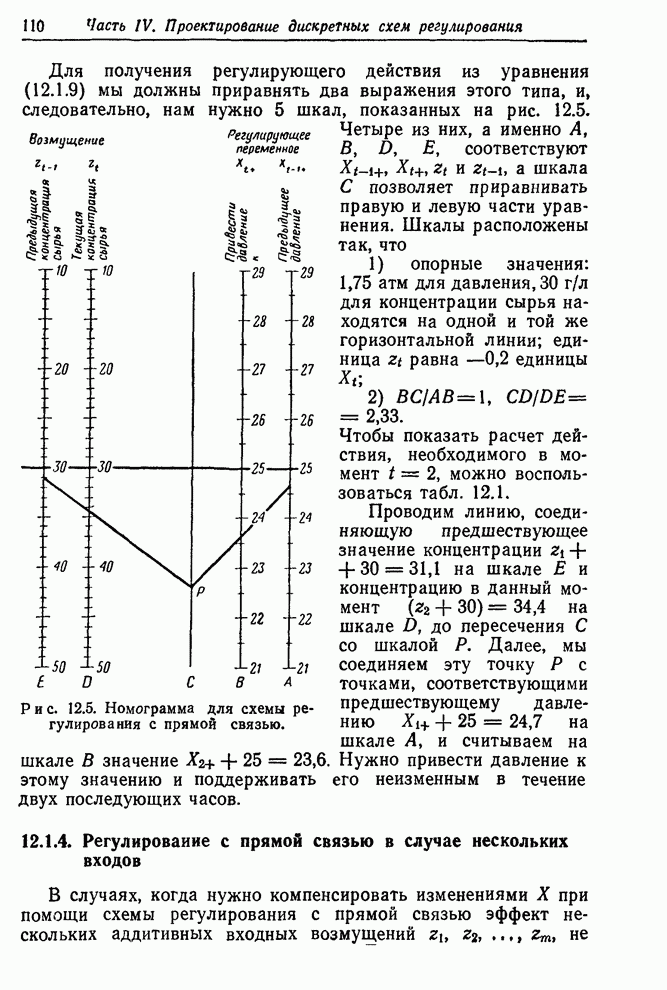
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
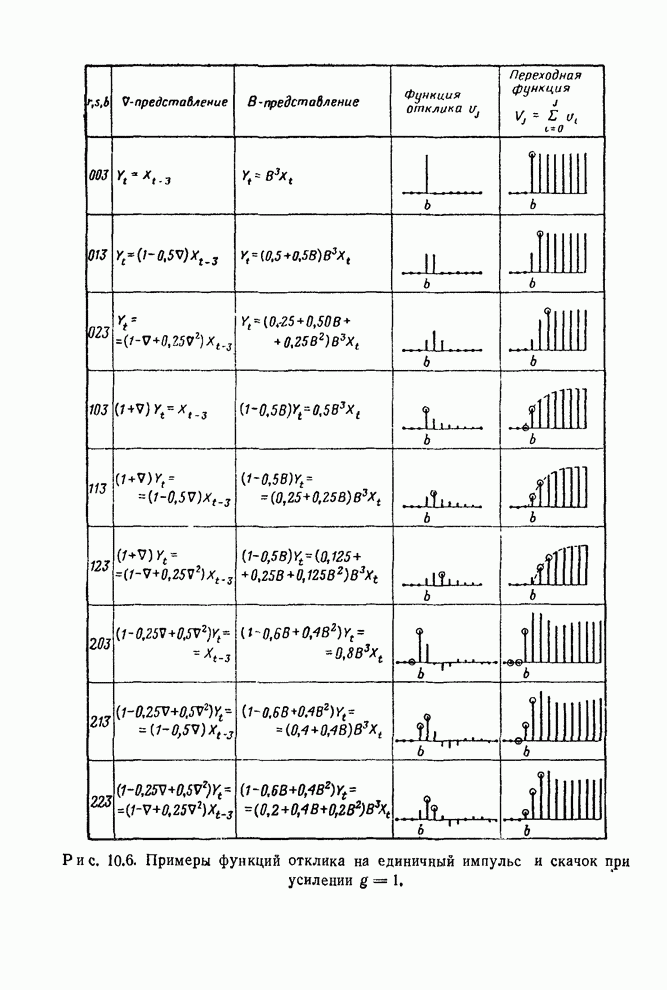
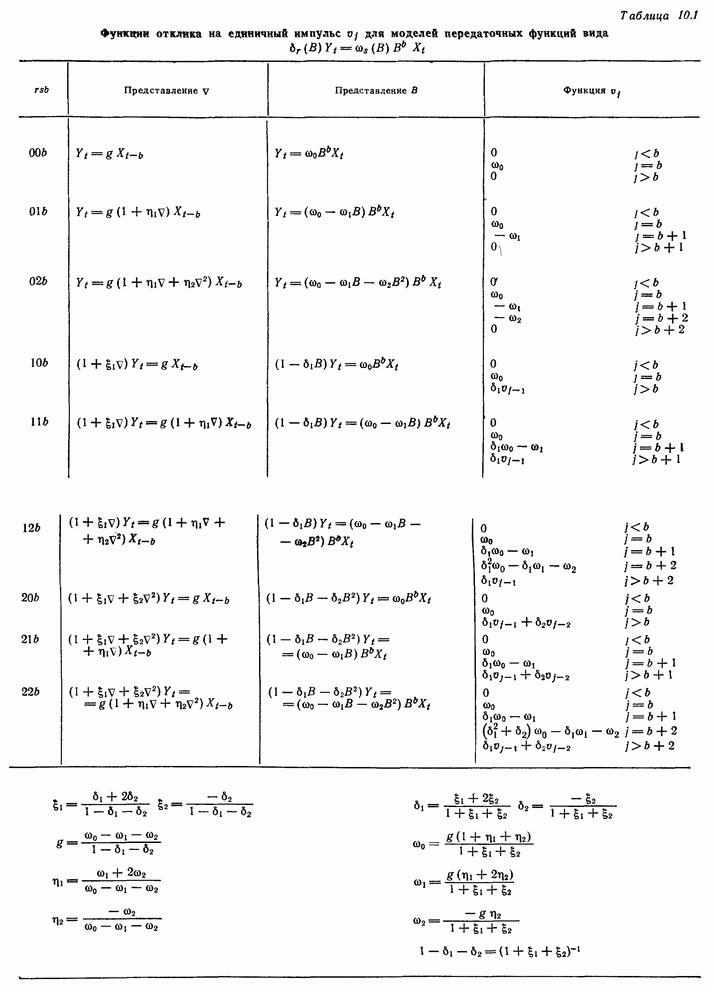
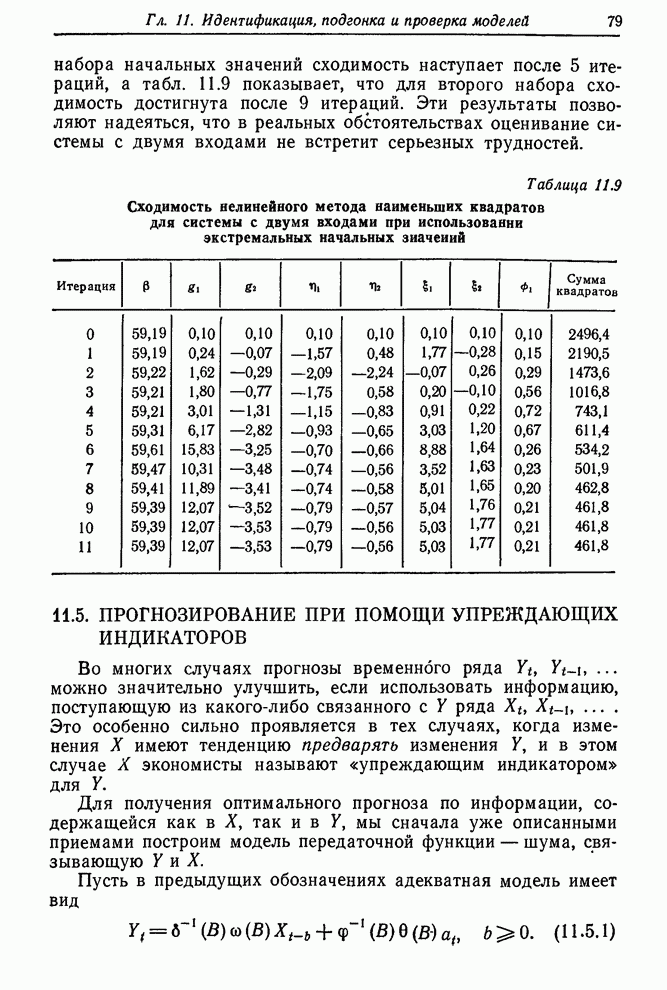
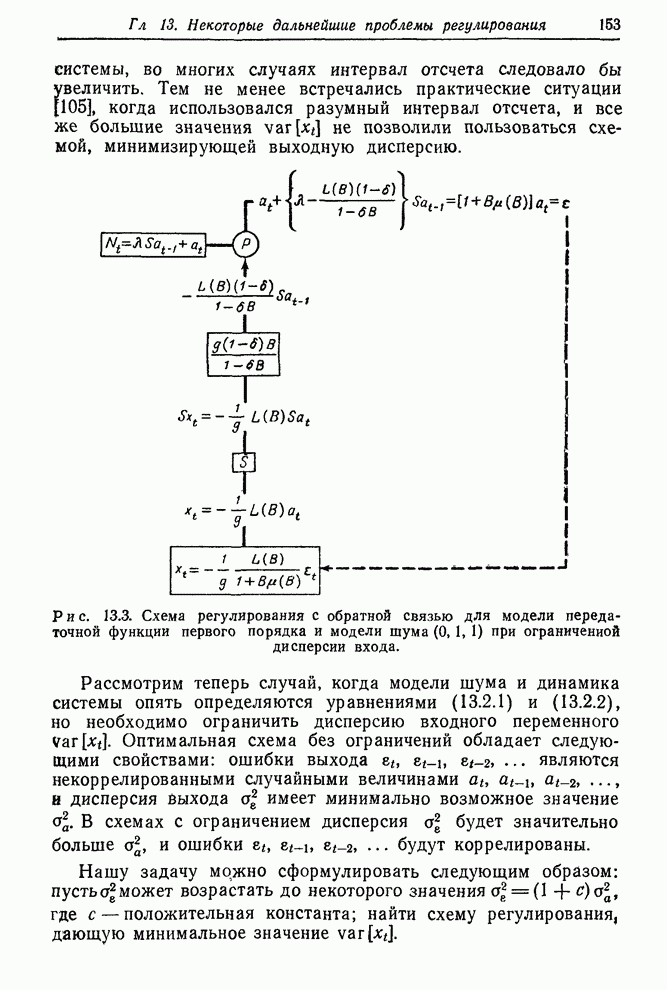
12.4.3. Пример
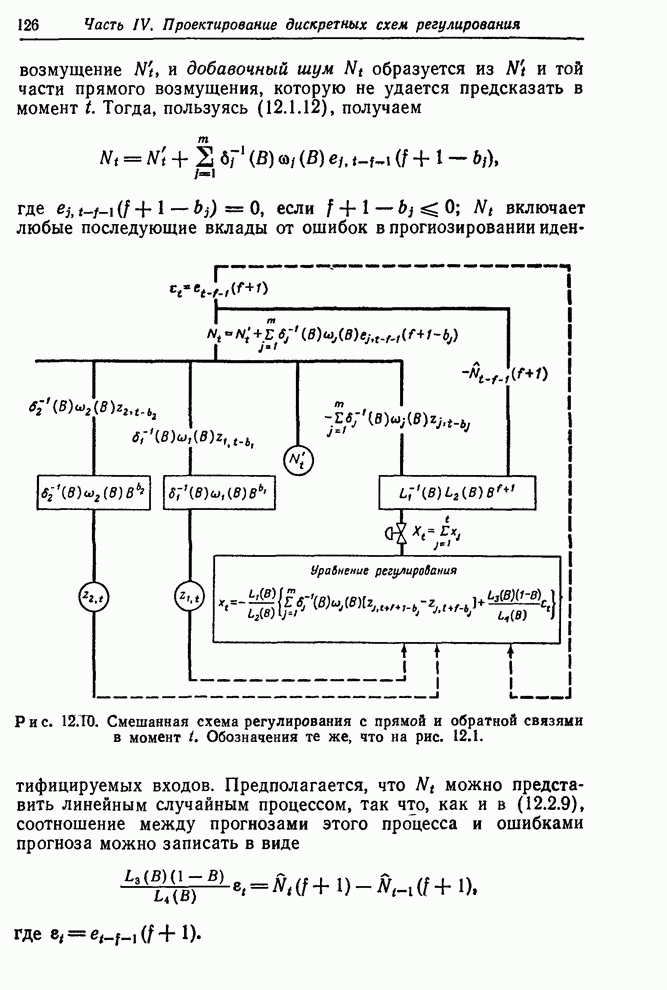
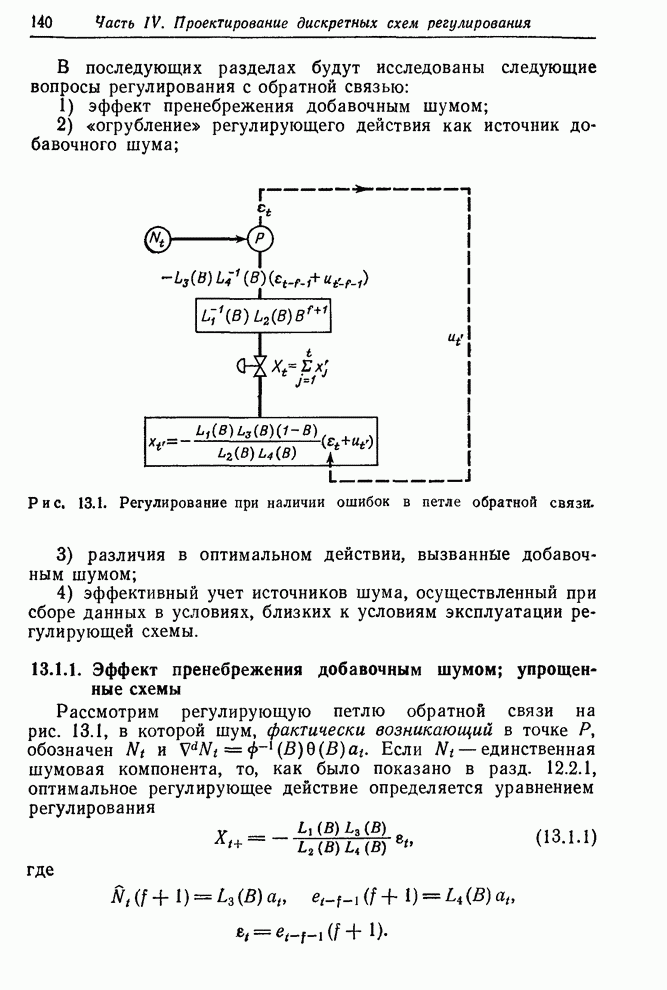
Во втором примере регулирования с обратной связью в разд. 12.2.3 цель заключалась в поддержании вязкости полимера как можно ближе к номинальному значению 92 путем ежечасного измерения вязкости и корректировки скорости подачи газа. Предыдущее обсуждение касалось разработки пробной схемы регулирования, основанной на ненадежной информации. При этом существенным был предполагаемый вид моделей шума и передаточной функции
![]() , (12.4.8)
, (12.4.8)
![]() (12.4.9)
(12.4.9)
с
![]() ,
, ![]() ,
, ![]() .
.

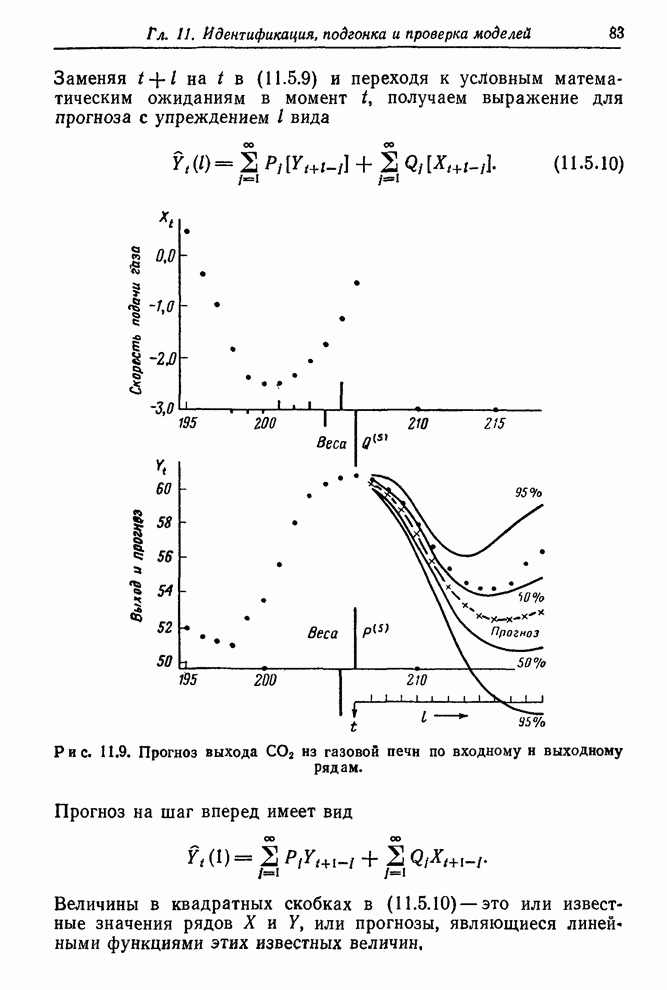
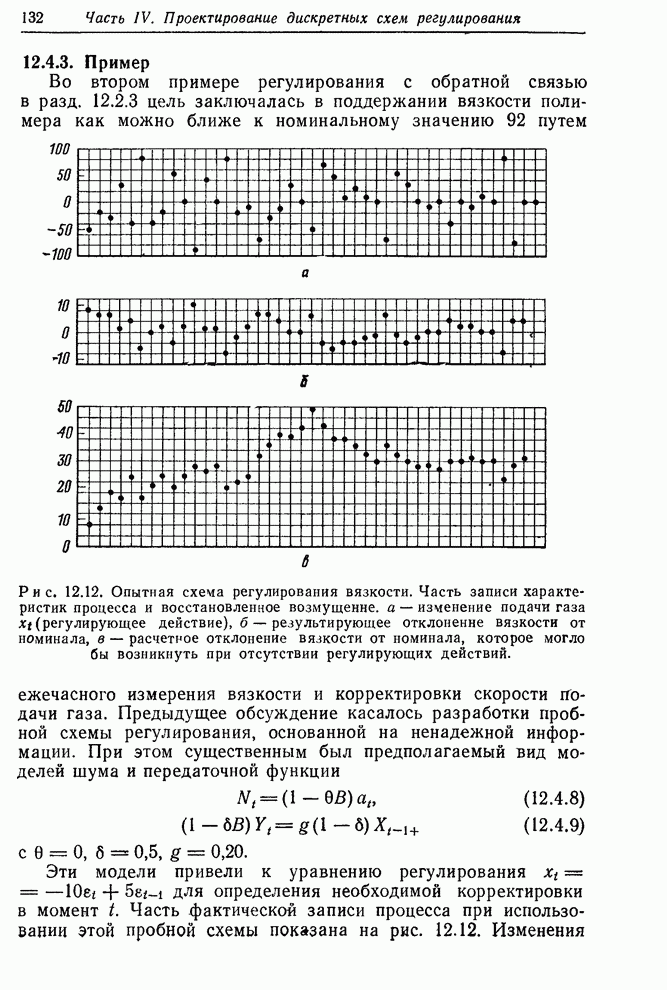
Рис. 12.12. Опытная схема
регулирования вязкости. Часть записи характеристик процесса и восстановленное
возмущение. а – изменение подачи газа ![]() (регулирующее действие), б –
результирующее отклонение вязкости от номинала, в – расчетное отклонение
вязкости от номинала, которое могло бы возникнуть при отсутствии регулирующих
действий.
(регулирующее действие), б –
результирующее отклонение вязкости от номинала, в – расчетное отклонение
вязкости от номинала, которое могло бы возникнуть при отсутствии регулирующих
действий.
Эти
модели привели к уравнению регулирования ![]() для определения необходимой
корректировки в момент
для определения необходимой
корректировки в момент ![]() . Часть фактической записи процесса при
использовании этой пробной схемы показана на рис. 12.12. Изменения скорости
подачи газа
. Часть фактической записи процесса при
использовании этой пробной схемы показана на рис. 12.12. Изменения скорости
подачи газа ![]() и
соответствующие отклонения от номинала
и
соответствующие отклонения от номинала ![]() образуют новые данные, по которым можно
получить новые оценки. Мы будем действовать в предположении, что форма модели
адекватна, но что оценки параметров
образуют новые данные, по которым можно
получить новые оценки. Мы будем действовать в предположении, что форма модели
адекватна, но что оценки параметров ![]() ,
, ![]() и
и ![]() могут быть ошибочными. В этом случае
уравнения (12.4.4), (12.4.6) и (12.4.7) принимают вид
могут быть ошибочными. В этом случае
уравнения (12.4.4), (12.4.6) и (12.4.7) принимают вид
![]() , (12.4.10)
, (12.4.10)
где
![]() ,
,
![]() ,
,
![]() . (12.4.11)
. (12.4.11)
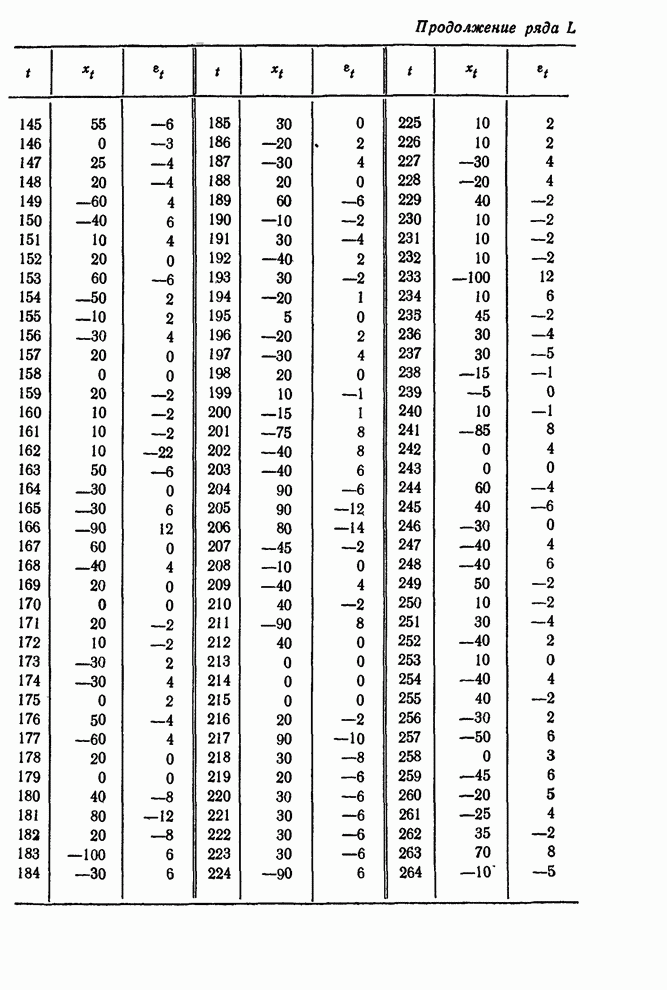
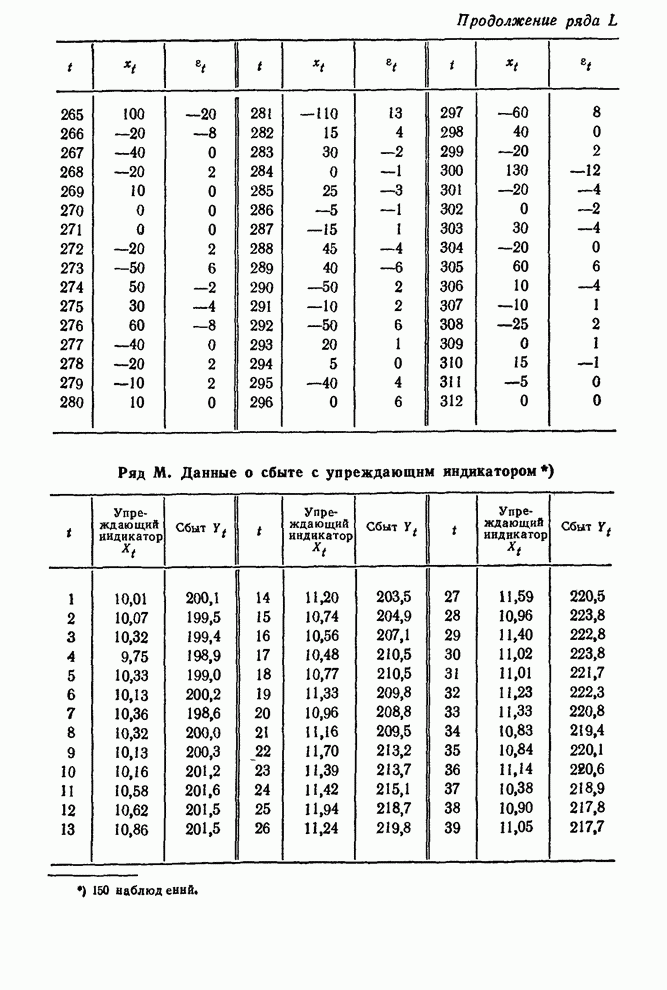
В
качестве примера в табл. 12.2 приведен набор из 8 пар значений ![]() и
и ![]() . Они являются
начальными значениями рядов из 312 наблюдений, полученных в течение 13 дней
эксплуатации обычной схемы; все наблюдения приведены под заголовком «Ряд
. Они являются
начальными значениями рядов из 312 наблюдений, полученных в течение 13 дней
эксплуатации обычной схемы; все наблюдения приведены под заголовком «Ряд ![]() , данные опытной
схемы» в сводке рядов и данных в конце книги.
, данные опытной
схемы» в сводке рядов и данных в конце книги.
Таблица
12.2. Восемь пар значений ряда ![]() для опытной схемы
для опытной схемы
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
30 |
0 |
-10 |
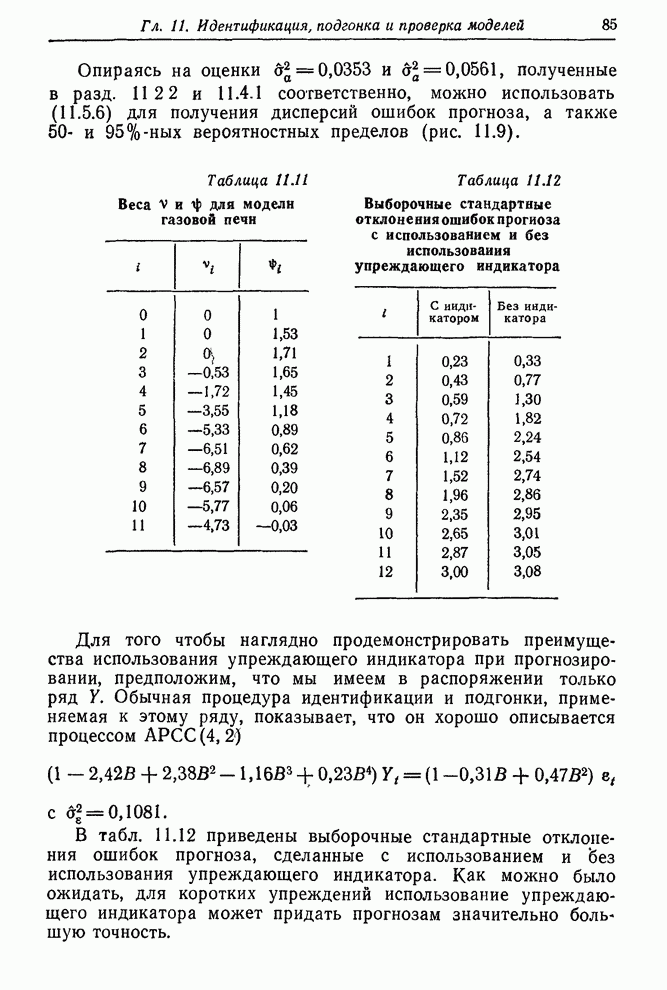
0 |
-40 |
0 |
-10 |
10 |
|
|
-4 |
-2 |
0 |
0 |
4 |
2 |
2 |
0 |
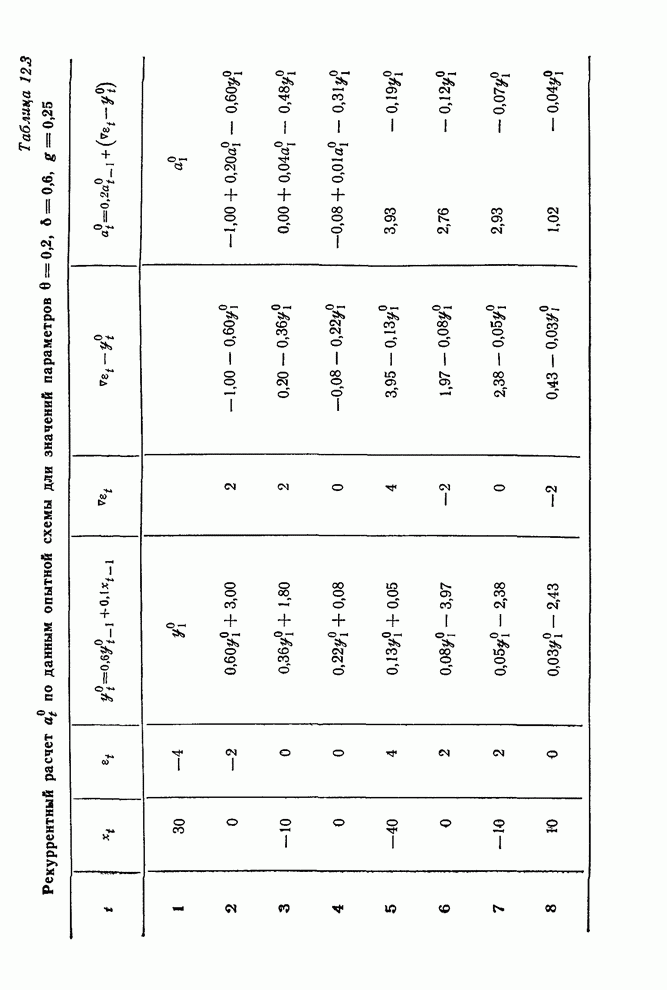
В
табл. 12.3 показано начало рекуррентного расчета ![]() для значений параметров
для значений параметров ![]() ,
, ![]() ,
, ![]() . При этих значениях уравнения
(12.4.11) и (12.4.10) приобретают вид
. При этих значениях уравнения
(12.4.11) и (12.4.10) приобретают вид
![]() , (12.4.12)
, (12.4.12)
![]() . (12.4.13)
. (12.4.13)
Данные
приведены в первых трех столбцах табл. 12.3. Величины в четвертом столбце
получены при помощи (12.4.13) и представляют собой изменения выхода, вызываемые
изменениями ![]() .
Пятый и шестой столбцы получены очевидными арифметическими действиями, а
седьмой столбец – согласно (12.4.12). В этой таблице вместо неизвестных
начальных значений были использованы
.
Пятый и шестой столбцы получены очевидными арифметическими действиями, а
седьмой столбец – согласно (12.4.12). В этой таблице вместо неизвестных
начальных значений были использованы ![]() и
и ![]() . Последовательные строки таблицы
показывают, как выбор этих величин влияет на последующие вычисления.
. Последовательные строки таблицы
показывают, как выбор этих величин влияет на последующие вычисления.
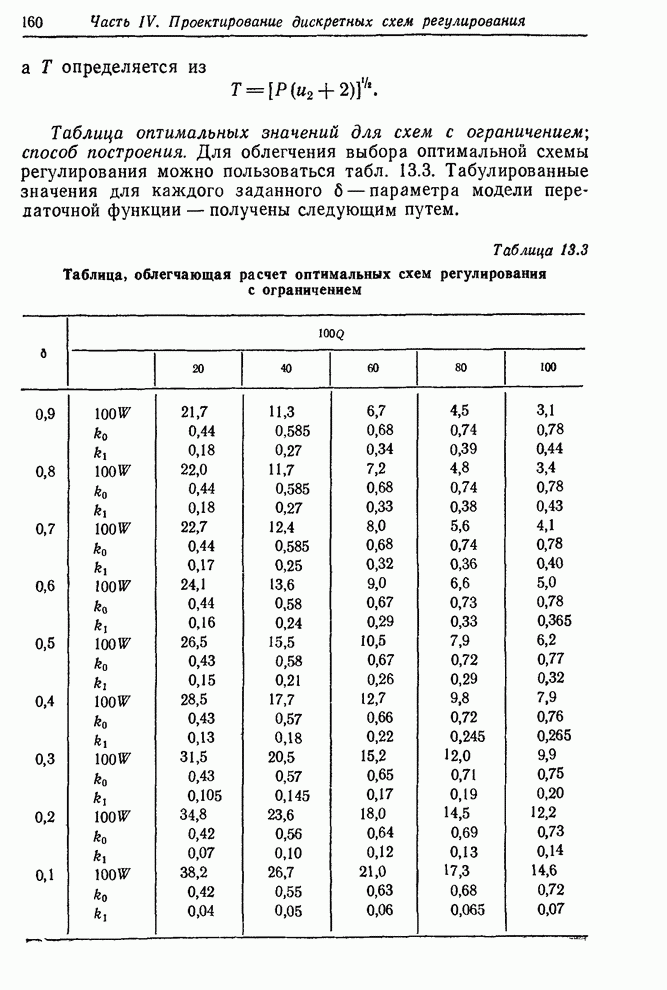
Таблица позволяет выяснить ряд вопросов.
Таблица
12.3. Рекуррентный расчет ![]() по данным опытной схемы дли значений
параметров
по данным опытной схемы дли значений
параметров ![]() ,
,
![]() ,
, ![]()
|
|
|
|
|
|
|
|
|
1 |
30 |
-4 |
|
|
|
|
|
2 |
0 |
-2 |
|
2 |
|
|
|
3 |
-10 |
0 |
|
2 |
|
|
|
4 |
0 |
0 |
|
0 |
|
|
|
5 |
-40 |
4 |
|
4 |
|
|
|
6 |
0 |
2 |
|
-2 |
|
|
|
7 |
-10 |
2 |
|
0 |
|
|
|
8 |
10 |
0 |
|
-2 |
|
|
1)
Мы замечаем, что выбор ![]() и
и ![]() влияет только на первые несколько
значений
влияет только на первые несколько
значений ![]() .
Этот факт справедлив и в более общем случае, если не считать диапазона значений
параметров, в котором весовые функции для модели шума или передаточной функции
очень медленно затухают. Для принятого здесь подхода маловероятно, чтобы
истинные значения параметров оказались в этом критическом диапазоне.
.
Этот факт справедлив и в более общем случае, если не считать диапазона значений
параметров, в котором весовые функции для модели шума или передаточной функции
очень медленно затухают. Для принятого здесь подхода маловероятно, чтобы
истинные значения параметров оказались в этом критическом диапазоне.
2)
Можно воспользоваться крайне неточными значениями ![]() и
и ![]() , и если, как в этом примере, данные
доступны, отбросить несколько первых значений
, и если, как в этом примере, данные
доступны, отбросить несколько первых значений ![]() , позволяя затухнуть переходным
явлениям, вызванным неудачным выбором
, позволяя затухнуть переходным
явлениям, вызванным неудачным выбором ![]() и
и ![]() .
.
3)
Можно вычислить и использовать в дальнейших расчетах по методу наименьших
квадратов значения ![]() ,
полученные с начальными значениями
,
полученные с начальными значениями ![]() и
и ![]() , минимизирующими условную сумму
квадратов при фиксированном выборе «главных параметров». Возможны и некоторые
дальнейшие уточнения такого типа, как описаны в разд. 7.1; мы не будем их здесь
обсуждать.
, минимизирующими условную сумму
квадратов при фиксированном выборе «главных параметров». Возможны и некоторые
дальнейшие уточнения такого типа, как описаны в разд. 7.1; мы не будем их здесь
обсуждать.
Последний
пункт мы проиллюстрируем анализом данных в табл. 12.3, по которым особенно
легко провести вычисления. Значения ![]() и
и ![]() , минимизирующие
, минимизирующие ![]() для конкретных значений
параметров
для конкретных значений
параметров ![]() ;
;
![]() ;
; ![]() , находятся
«регрессией» столбца (а) на столбцы (b)
и (с) табл. 12.4.
, находятся
«регрессией» столбца (а) на столбцы (b)
и (с) табл. 12.4.
Таблица 12.4. Расчет оценок максимального правдоподобия для начальных значений
|
|
|
|
|
0,00 |
-1,00 |
0,00 |
|
-1,00 |
-0,20 |
0,60 |
|
0,00 |
-0,04 |
0,48 |
|
-0,08 |
-0,01 |
0,31 |
|
3,93 |
0,00 |
0,19 |
|
2,76 |
0,00 |
0,12 |
|
2,93 |
0,00 |
0,07 |
|
1,02 |
0,00 |
0,04 |
Все
элементы этой таблицы получены из крайнего правого столбца табл. 12.3. Элементы
столбца (а) – это члены, не зависящие от ![]() и
и ![]() элементы столбцов (b) и (с) – это коэффициенты при
элементы столбцов (b) и (с) – это коэффициенты при ![]() и
и ![]() соответственно.
Поскольку эти коэффициенты быстро спадают до нуля, для вычисления
соответственно.
Поскольку эти коэффициенты быстро спадают до нуля, для вычисления ![]() и
и ![]() важны только первые
члены рядов. Фактически для рассматриваемого случая нам достаточно ограничиться
первыми восемью членами. Нормальные уравнения имеют вид
важны только первые
члены рядов. Фактически для рассматриваемого случая нам достаточно ограничиться
первыми восемью членами. Нормальные уравнения имеют вид
![]() ,
,
![]()
и
приводят к решениям для начальных значений ![]() ,
, ![]() .
.
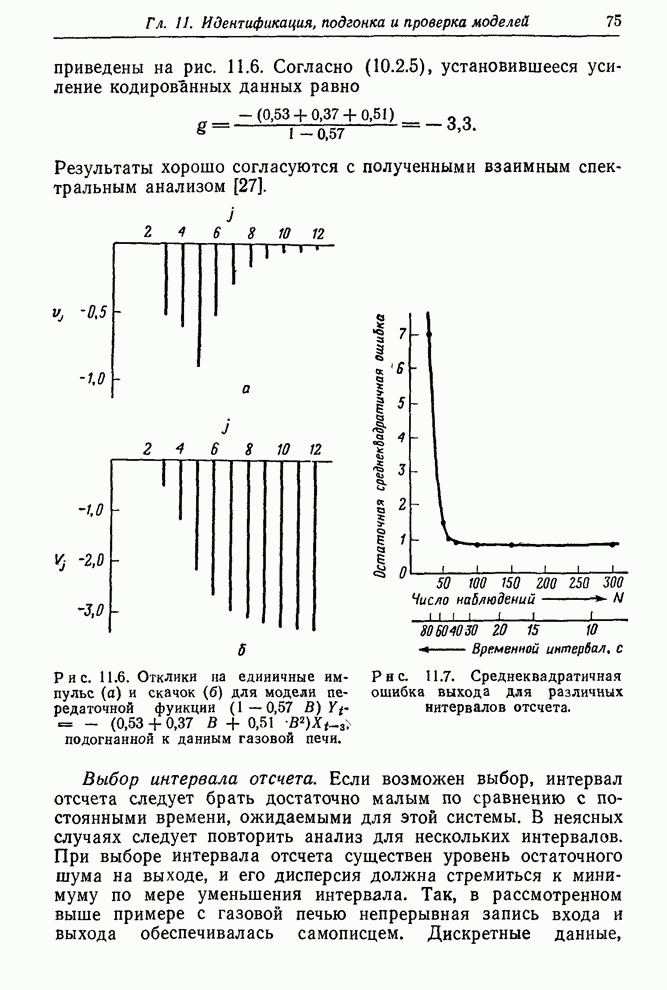
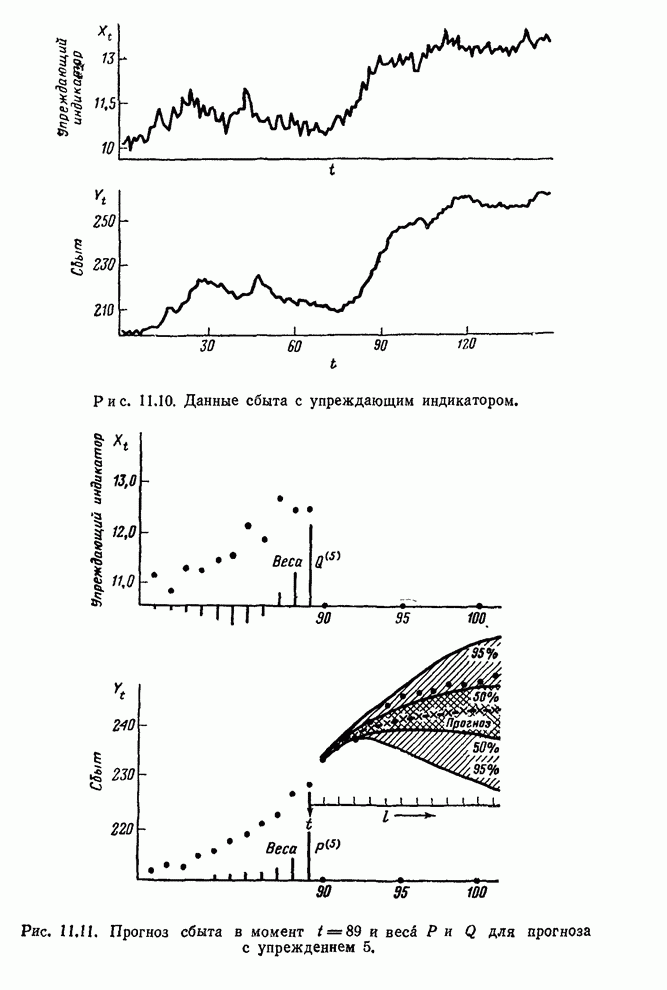
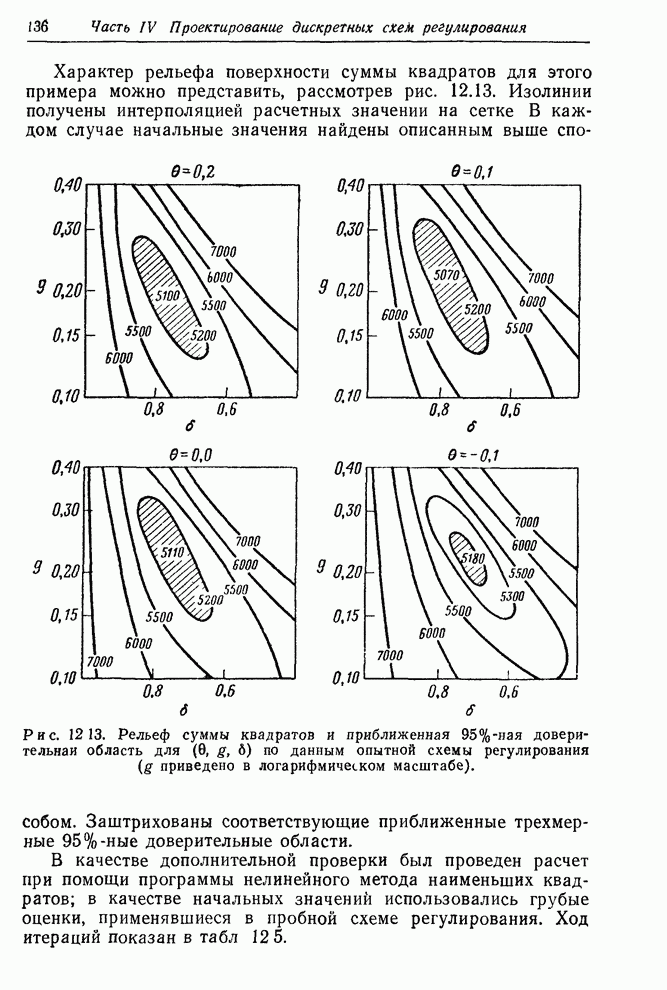
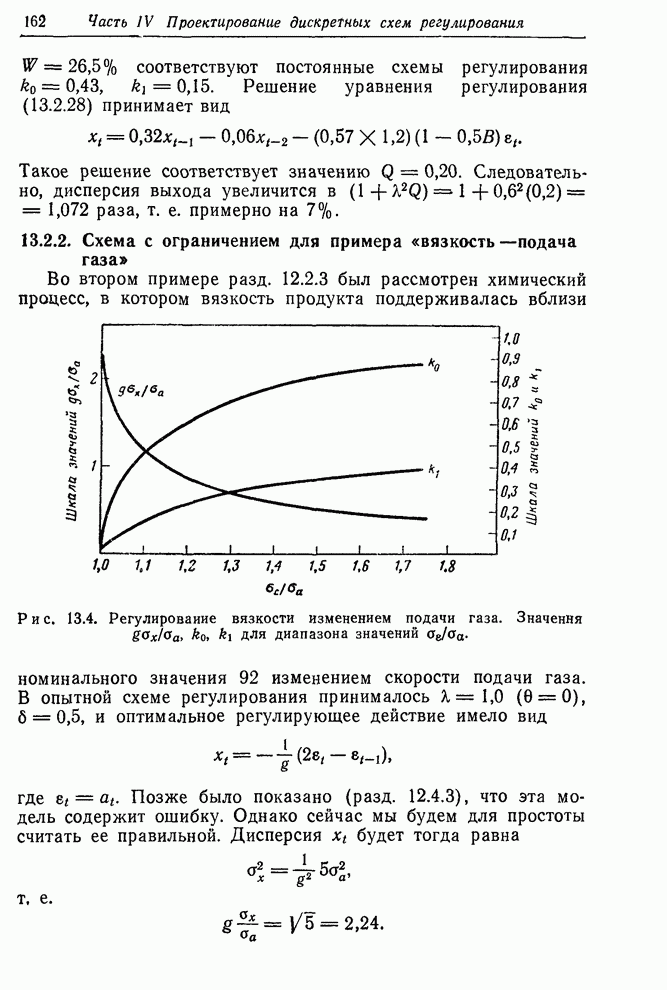
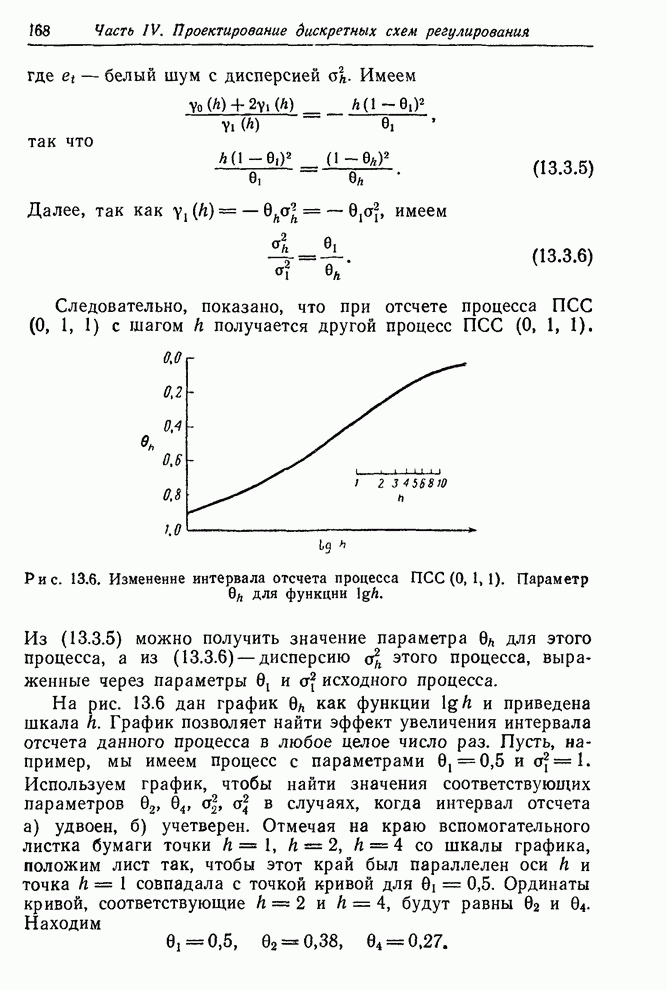
Характер рельефа поверхности суммы квадратов для этого примера можно представить, рассмотрев рис. 12.13. Изолинии получены интерполяцией расчетных значении на сетке. В каждом случае начальные значения найдены описанным выше способом. Заштрихованы соответствующие приближенные трехмерные 95%-ные доверительные области.

Рис. 12 13. Рельеф суммы
квадратов и приближенная 95%-ная доверительная область для ![]() по данным опытной схемы
регулирования (
по данным опытной схемы
регулирования (![]() приведено в логарифмическом масштабе).
приведено в логарифмическом масштабе).
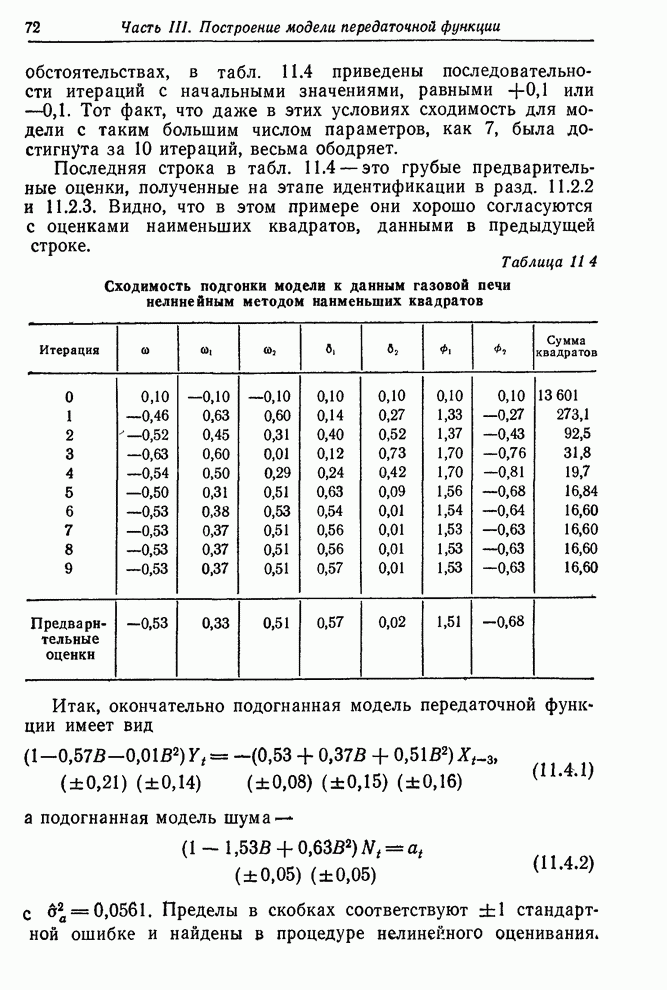
В качестве дополнительной проверки был проведен расчет при помощи программы нелинейного метода наименьших квадратов; в качестве начальных значений использовались грубые оценки, применявшиеся в пробной схеме регулирования. Ход итераций показан в табл. 12.5.
Таблица 12.5. Сходимость оценок параметров при одновременной подгонке моделей передаточной функции и шума
|
Итерация |
|
|
|
Сумма квадратов |
|
0 |
0,01 |
0,10 |
0,50 |
6247,6 |
|
1 |
-0,06 |
0,09 |
0,53 |
5661,3 |
|
2 |
-0,11 |
0,08 |
0,61 |
5275,9 |
|
3 |
-0,02 |
0,06 |
0,71 |
5115,9 |
|
4 |
0,08 |
0,05 |
0,77 |
5067,6 |
|
5 |
0,10 |
0,05 |
0,77 |
5065,2 |
|
6 |
0,11 |
0,05 |
0,77 |
5065,1 |
|
7 |
0,11 |
0,05 |
0,77 |
5065,1 |
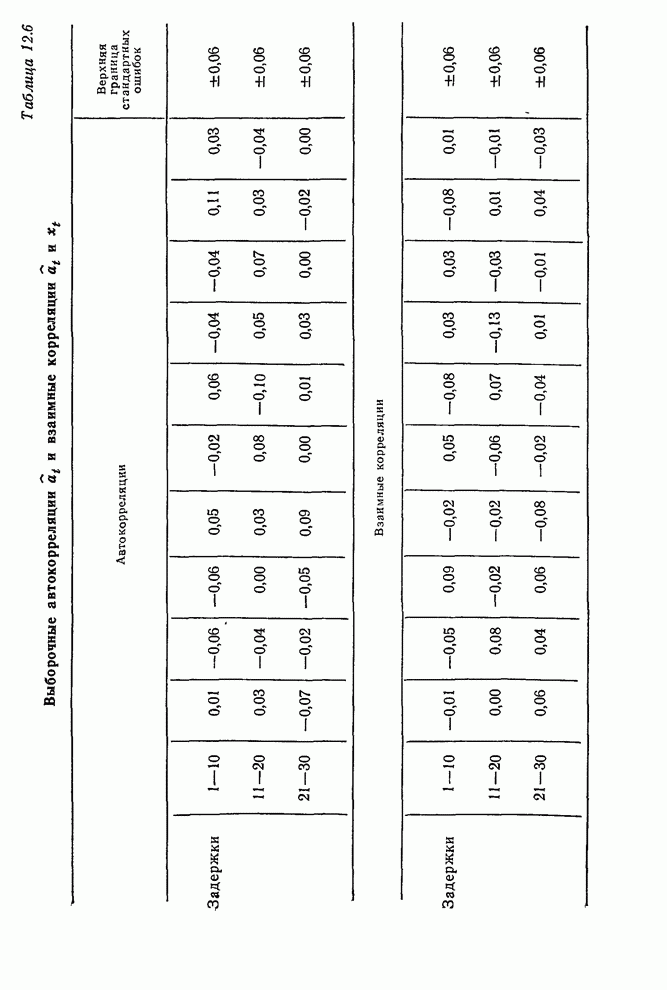
Выборочная
автокорреляционная функция остаточных ошибок ![]() показана в табл. 12.6 на следующей
странице вместе с выборочной взаимной корреляционной функцией
показана в табл. 12.6 на следующей
странице вместе с выборочной взаимной корреляционной функцией ![]() и
и ![]() Сравнение с верхними
границами стандартной ошибки не обнаруживает неадекватности модели.
Сравнение с верхними
границами стандартной ошибки не обнаруживает неадекватности модели.
Из
этого примера видно, что оценки ![]() ,
, ![]() , использованные в опытной схеме, почти
правильны, но значение
, использованные в опытной схеме, почти
правильны, но значение ![]() динамического параметра слишком мало;
следует использовать значение
динамического параметра слишком мало;
следует использовать значение ![]() . После изменения оценок параметров
оптимальная схема регулирования имеет вид
. После изменения оценок параметров
оптимальная схема регулирования имеет вид
![]() ,
,
ее следует сравнить с опытной схемой
![]() .
.
Таблица
12.6. Выборочные автокорреляции ![]() и взаимные корреляции
и взаимные корреляции ![]() и
и ![]()
|
Автокорреляция |
Верхняя граница стандартных ошибок |
|||||||||||
|
Задержки |
1-10 |
0,01 |
-0,06 |
-0,06 |
0,05 |
-0,02 |
0,06 |
-0,04 |
-0,04 |
0,11 |
0,03 |
±0,06 |
|
11-20 |
0,03 |
-0,04 |
0,00 |
0,03 |
0,08 |
-0,10 |
0,05 |
0,07 |
0,03 |
-0,04 |
±0,06 |
|
|
21-30 |
-0,07 |
-0,02 |
-0,05 |
0,09 |
0,00 |
0,01 |
0,03 |
0,00 |
-0,02 |
0,00 |
±0,06 |
|
|
Взаимные корреляции |
||||||||||||
|
Задержки |
1-10 |
-0,01 |
-0,05 |
0,09 |
-0,02 |
0,05 |
-0,08 |
0,03 |
0,03 |
-0,08 |
0,01 |
±0,06 |
|
11-20 |
0,00 |
0,08 |
-0,02 |
-0,02 |
-0,06 |
0,07 |
-0,13 |
-0,03 |
0,01 |
-0,01 |
±0,06 |
|
|
21-30 |
0,06 |
0,04 |
0,06 |
-0,08 |
-0,02 |
-0,04 |
0,01 |
-0,01 |
0,04 |
-0,03 |
±0,06 |
|
| << Предыдущий параграф | Следующий параграф >> |
- Часть III. ПОСТРОЕНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- Глава 10. Модели передаточной функции
- 10.1. ЛИНЕЙНЫЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 10.1.1. Дискретная передаточная функция
- 10.1.2. Непрерывные динамические модели, описываемые дифференциальными уравнениями
- 10.2. ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ МОДЕЛИ, ОПИСЫВАЕМЫЕ РАЗНОСТНЫМИ УРАВНЕНИЯМИ
- 10.2.1. Общая форма разностного уравнения
- 10.2.2. Природа передаточной функции
- 10.2.3. Дискретные модели передаточных функций первого и второго порядков
- 10.2.4. Рекуррентный расчет выхода для произвольного входа
- 10.3. СООТНОШЕНИЕ МЕЖДУ ДИСКРЕТНОЙ И НЕПРЕРЫВНОЙ МОДЕЛЯМИ
- 10.3.1. Отклик на скачкообразный вход
- 10.3.2. Соотношения совпадающих систем первого и второго порядков
- 10.3.3. Аппроксимация общих непрерывных моделей дискретными моделями
- 10.3.4. Модели передаточных функций с добавленным шумом
- ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
- ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
- Глава 11. Идентификация, подгонка и проверка моделей передаточных функций
- 11.1. Взаимная корреляционная функция
- 11.1.1. Свойства взаимных ковариационной и корреляционной функций
- 11.1.2. Оценивание взаимных ковариационных и корреляционных функций
- 11.1.3. Приближенные стандартные ошибки выборочных оценок взаимных корреляций
- 11.2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.2.1. Идентификация моделей передаточной функции с предварительным выравниванием спектра входа
- 11.2.2. Пример идентификации модели передаточной функции
- 11.2.3. Идентификация модели шума
- 11.2.4. Некоторые общие соображения об идентификации моделей передаточных функций
- 11.3. ПОДГОНКА И ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.3.1. Условная сумма квадратов
- 11.3.2. Нелинейное оценивание
- 11.3.3. Использование остаточных ошибок для диагностической проверки
- 11.3.4. Конкретные способы проверки остаточных ошибок
- 11.4. Некоторые примеры подгонок и проверок моделей передаточных функций
- 11.4.1. Подгонка и проверка модели газовой печи
- 11.4.2. Искусственный пример с двумя входами
- 11.5. ПРОГНОЗИРОВАНИЕ ПРИ ПОМОЩИ УПРЕЖДАЮЩИХ ИНДИКАТОРОВ
- 11.5.1. Прогноз с минимальной среднеквадратичной ошибкой
- 11.5.2. Прогнозы выхода СO2 из газовой печи
- 11.5.3. Прогноз нестационарных данных сбыта при помощи упреждающего индикатора
- 11.6. НЕКОТОРЫЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОЦЕНИВАНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ П11.1. ИСПОЛЬЗОВАНИЕ ВЗАИМНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
- Заключение
- Часть IV. Проектирование дискретных схем регулирования
- Глава 12. Проектирование схем регулирования с прямой и обратной связями
- 12.1. РЕГУЛИРОВАНИЕ С ПРЯМОЙ СВЯЗЬЮ
- 12.1.1. Регулирование с прямой связью, минимизирующее среднеквадратичную ошибку
- 12.1.2. Пример — регулирование удельного веса промежуточного продукта
- 12.1.3. Номограмма для регулирования с прямой связью
- 12.1.4. Регулирование с прямой связью в случае нескольких входов
- 12.2. РЕГУЛИРОВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ
- 12.2.1. Регулирование с обратной связью, минимизирующее среднеквадратичную ошибку
- 12.2.2. Применение уравнения регулирования: ПИД-регулятор
- 12.2.3. Примеры дискретного регулирования с обратной связью
- 12.3. РЕГУЛИРОВАНИЕ С ПРЯМОЙ И ОБРАТНОЙ СВЯЗЯМИ
- 12.3.1. Регулирование с прямой и обратной связями, минимизирующее выходную среднеквадратичную ошибку
- 12.3.2. Пример регулирования с прямой и обратной связями
- 12.3.3. Преимущества и недостатки регулирования с прямой и обратной связями
- 12.4. Подгонка моделей передаточных функций шума по оперативным данным
- 12.4.1. Итеративный способ построения моделей
- 12.4.2. Оценивание по оперативным данным
- 12.4.3. Пример
- Глава 13. Некоторые дальнейшие проблемы регулирования
- 13.1. ЭФФЕКТ ДОБАВОЧНОГО ШУМА В СХЕМАХ РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ
- 13.1.1. Эффект пренебрежения добавочным шумом; упрощенные схемы
- 13.1.2. Оптимальное действие в случаях, когда корректировки содержат ошибки наблюдения
- 13.1.3. Перенос источника шума
- 13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
- 13.2.1. Вывод выражения для оптимальной корректировки
- 13.2.2. Схема с ограничением для примера «вязкость–подача газа»
- 13.3. ВЫБОР ИНТЕРВАЛА ОТСЧЕТА
- 13.3.1. Пример эффекта уменьшения частоты отсчетов
- 13.3.2. Влияние интервала отсчета на процесс ПСС(0,1,1)
- ПРОГРАММА 5. ИДЕНТИФИКАЦИЯ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 6. ПРЕДВАРИТЕЛЬНОЕ ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 7. ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ТАБЛИЦЫ ВРЕМЕННЫХ РЯДОВ