| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
Линейность
(аддитивность) рассмотренных моделей передаточной функции означает, что
результирующий отклик на сумму отдельных входных функций равен сумме откликов
на каждую из этих входных функций. Конкретнее, если ![]() — это отклик в момент
— это отклик в момент ![]() на вход
на вход ![]() и
и ![]() — отклик в момент
— отклик в момент ![]() на вход
на вход ![]() , то отклик в момент
, то отклик в момент ![]() на вход
на вход ![]() будет равен
будет равен ![]() . Аналогичный эффект
имеем для непрерывных входов и выходов. В частности, если входное значение
умножено на некоторую константу, выходное значение умножается на ту же
константу. На практике это предположение никогда не бывает совершенно точным,
но во многих практических ситуациях оказывается достаточно хорошим
приближением.
. Аналогичный эффект
имеем для непрерывных входов и выходов. В частности, если входное значение
умножено на некоторую константу, выходное значение умножается на ту же
константу. На практике это предположение никогда не бывает совершенно точным,
но во многих практических ситуациях оказывается достаточно хорошим
приближением.
Модель
нелинейных систем можно иногда получить, если допустить, что параметры системы
в некоторых заданных пределах зависят от уровня входа. Положим, например, что
система исследовалась в диапазоне, где ![]() имеет максимум
имеет максимум ![]() , и для любого
, и для любого ![]() соотношение
установившихся значений можно аппроксимировать квадратичным выражением
соотношение
установившихся значений можно аппроксимировать квадратичным выражением
![]() ,
,
где
![]() и
и ![]() , как и ранее, —
отклонения от удобных начальных уровней.
, как и ранее, —
отклонения от удобных начальных уровней.
Тогда
![]() ,
,
и
динамическое поведение системы может быть описано разностным уравнением
первого порядка (10.3.4) с переменным усилением, пропорциональным ![]() . Тогда
. Тогда
![]() . (П10.2.1)
. (П10.2.1)
Динамика простого химического реактора. Иногда оказывается возможным провести теоретический анализ реальной Проблемы в форме, удобной для использования передаточных функций. В частности, это позволяет очень детально исследовать эффекты, связанные с линейной аппроксимацией.
Например,
положим, что чистый химический продукт ![]() непрерывно подается в управляемый
реакторный резервуар и в присутствии катализатора определенная его часть
превращается в продукт
непрерывно подается в управляемый
реакторный резервуар и в присутствии катализатора определенная его часть
превращается в продукт ![]() без изменения общего объема; продукт,
непрерывно выходящий из реактора, будет смесью
без изменения общего объема; продукт,
непрерывно выходящий из реактора, будет смесью ![]() и неизмененного
и неизмененного ![]() .
.
Пусть система вначале находится в равновесии, измеряются (в соответствующих единицах) следующие величины:
1)
![]() —скорость
подачи
—скорость
подачи ![]() в
реактор и, следовательно, скорость выхода смеси
в
реактор и, следовательно, скорость выхода смеси ![]() и
и ![]() из реактора;
из реактора;
2)
![]() — доля
неизмененного
— доля
неизмененного ![]() в
выходном продукте;
в
выходном продукте; ![]() — доля
— доля ![]() в выходном продукте;
в выходном продукте;
3)
![]() — объем
реактора;
— объем
реактора;
4)
![]() —
константа, определяющая скорость образования продукта
—
константа, определяющая скорость образования продукта ![]() .
.
Пусть
реакция имеет «первый порядок» по отношению к ![]() , это означает, что скорость образования
, это означает, что скорость образования
![]() и
использования
и
использования ![]() пропорциональна
количеству присутствующего
пропорциональна
количеству присутствующего ![]() . Скорость образования
. Скорость образования ![]() будет тогда
будет тогда ![]() , скорость выхода
, скорость выхода ![]() равна
равна ![]() , и, так как система
в равновесии,
, и, так как система
в равновесии,
![]() , (П10.2.2)
, (П10.2.2)
Пусть
теперь равновесие системы нарушено; скорость подачи ![]() в реактор в момент
в реактор в момент ![]() равна
равна ![]() ; соответствующая концентрация
; соответствующая концентрация
![]() в выходе
равна
в выходе
равна ![]() . Теперь
скорость химического образования
. Теперь
скорость химического образования ![]() , равная
, равная ![]() , вообще говоря, не будет уже равна
скорости, с которой
, вообще говоря, не будет уже равна
скорости, с которой ![]() выходит из системы (для последней имеем
выражение
выходит из системы (для последней имеем
выражение ![]() ).
Разность этих двух величин — это скорость увеличения
).
Разность этих двух величин — это скорость увеличения ![]() в реакторе, равная
в реакторе, равная ![]() . Тогда
. Тогда
![]() . (П10.2.3)
. (П10.2.3)
Пользуясь (П10.2.2) и перегруппировав члены в (П10.2.3), получаем
![]() ,
,
или
![]() , (П10.2.4)
, (П10.2.4)
где
![]() ,
, ![]() , (П10.2.5)
, (П10.2.5)
Поскольку
(П10.2.4) содержит произведение ![]() , это дифференциальное уравнение
нелинейно. Однако, как мы покажем, в некоторых практических ситуациях его можно
с достаточной точностью аппроксимировать линейным дифференциальным уравнением.
, это дифференциальное уравнение
нелинейно. Однако, как мы покажем, в некоторых практических ситуациях его можно
с достаточной точностью аппроксимировать линейным дифференциальным уравнением.
Процессы
такого рода протекают при разнообразных условиях, но вполне правдоподобной
является ситуация, при которой доля продукта ![]() , превращающаяся в
, превращающаяся в ![]() , равна
, равна ![]() % и близка к 80%, а флуктуация
% и близка к 80%, а флуктуация
![]() близка к
4%. В этом случае множитель
близка к
4%. В этом случае множитель ![]() изменяется от 0,95 до 1,05 и с хорошей
точностью равен единице. Нелинейное дифференциальное уравнение (П10.2.4) можно
заменить тогда линейным дифференциальным уравнением первого порядка
изменяется от 0,95 до 1,05 и с хорошей
точностью равен единице. Нелинейное дифференциальное уравнение (П10.2.4) можно
заменить тогда линейным дифференциальным уравнением первого порядка
![]() ,
,
где
![]() и
и ![]() определены в разд.
10.1.2. Если система наблюдалась бы в дискретные интервалы времени, это
уравнение можно было бы аппроксимировать линейным разностным уравнением.
определены в разд.
10.1.2. Если система наблюдалась бы в дискретные интервалы времени, это
уравнение можно было бы аппроксимировать линейным разностным уравнением.
Конечно,
могут встретиться ситуации, где нелинейность существенна. Это в особенности
верно при исследованиях оптимизации, где диапазон вариаций переменных может
быть велик. В условиях неадекватности линейной гипотезы иногда полезно представить
динамику системы совокупностью линейных моделей, применимых в разных диапазонах
значений входных переменных. Однако для дискретных систем часто более удобно
работать непосредственно с нелинейным разностным уравнением, которое можно
решить итерациями, а не аналитически. Например, мы можем заменить нелинейное
дифференциальное уравнение (П10.2.4) нелинейным разностным уравнением
![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- Часть III. ПОСТРОЕНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- Глава 10. Модели передаточной функции
- 10.1. ЛИНЕЙНЫЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- 10.1.1. Дискретная передаточная функция
- 10.1.2. Непрерывные динамические модели, описываемые дифференциальными уравнениями
- 10.2. ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ МОДЕЛИ, ОПИСЫВАЕМЫЕ РАЗНОСТНЫМИ УРАВНЕНИЯМИ
- 10.2.1. Общая форма разностного уравнения
- 10.2.2. Природа передаточной функции
- 10.2.3. Дискретные модели передаточных функций первого и второго порядков
- 10.2.4. Рекуррентный расчет выхода для произвольного входа
- 10.3. СООТНОШЕНИЕ МЕЖДУ ДИСКРЕТНОЙ И НЕПРЕРЫВНОЙ МОДЕЛЯМИ
- 10.3.1. Отклик на скачкообразный вход
- 10.3.2. Соотношения совпадающих систем первого и второго порядков
- 10.3.3. Аппроксимация общих непрерывных моделей дискретными моделями
- 10.3.4. Модели передаточных функций с добавленным шумом
- ПРИЛОЖЕНИЕ П10.1. НЕПРЕРЫВНЫЕ МОДЕЛИ СО СКАЧКООБРАЗНЫМИ ВХОДАМИ
- ПРИЛОЖЕНИЕ П10.2. НЕЛИНЕЙНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЛИНЕАРИЗАЦИЯ
- Глава 11. Идентификация, подгонка и проверка моделей передаточных функций
- 11.1. Взаимная корреляционная функция
- 11.1.1. Свойства взаимных ковариационной и корреляционной функций
- 11.1.2. Оценивание взаимных ковариационных и корреляционных функций
- 11.1.3. Приближенные стандартные ошибки выборочных оценок взаимных корреляций
- 11.2. ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.2.1. Идентификация моделей передаточной функции с предварительным выравниванием спектра входа
- 11.2.2. Пример идентификации модели передаточной функции
- 11.2.3. Идентификация модели шума
- 11.2.4. Некоторые общие соображения об идентификации моделей передаточных функций
- 11.3. ПОДГОНКА И ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА МОДЕЛЕЙ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 11.3.1. Условная сумма квадратов
- 11.3.2. Нелинейное оценивание
- 11.3.3. Использование остаточных ошибок для диагностической проверки
- 11.3.4. Конкретные способы проверки остаточных ошибок
- 11.4. Некоторые примеры подгонок и проверок моделей передаточных функций
- 11.4.1. Подгонка и проверка модели газовой печи
- 11.4.2. Искусственный пример с двумя входами
- 11.5. ПРОГНОЗИРОВАНИЕ ПРИ ПОМОЩИ УПРЕЖДАЮЩИХ ИНДИКАТОРОВ
- 11.5.1. Прогноз с минимальной среднеквадратичной ошибкой
- 11.5.2. Прогнозы выхода СO2 из газовой печи
- 11.5.3. Прогноз нестационарных данных сбыта при помощи упреждающего индикатора
- 11.6. НЕКОТОРЫЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОЦЕНИВАНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ П11.1. ИСПОЛЬЗОВАНИЕ ВЗАИМНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ П11.2. ВЫБОР ВХОДА ДЛЯ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ
- Заключение
- Часть IV. Проектирование дискретных схем регулирования
- Глава 12. Проектирование схем регулирования с прямой и обратной связями
- 12.1. РЕГУЛИРОВАНИЕ С ПРЯМОЙ СВЯЗЬЮ
- 12.1.1. Регулирование с прямой связью, минимизирующее среднеквадратичную ошибку
- 12.1.2. Пример — регулирование удельного веса промежуточного продукта
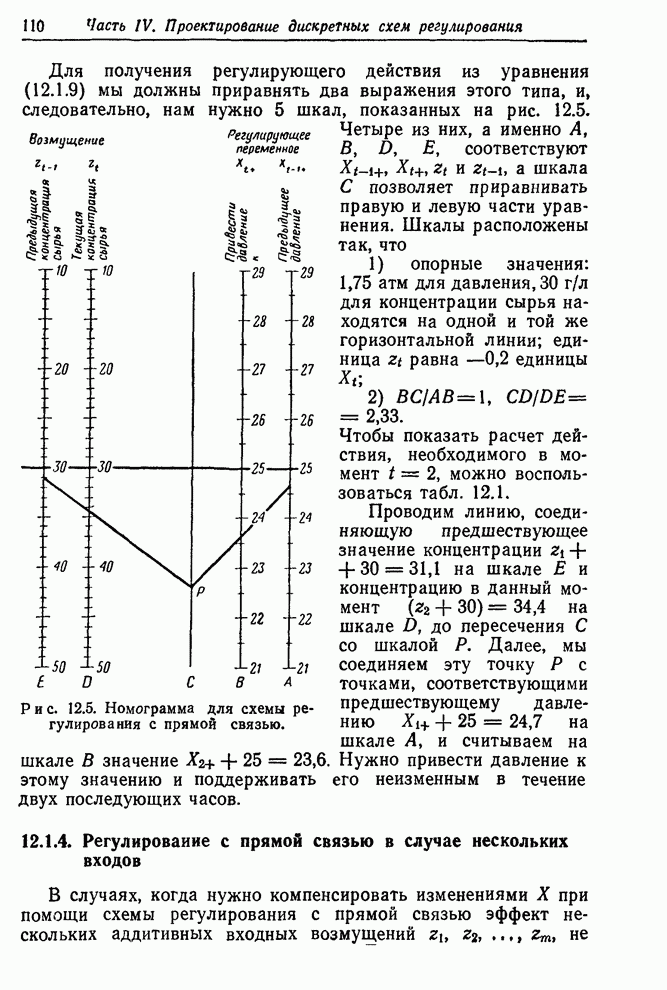
- 12.1.3. Номограмма для регулирования с прямой связью
- 12.1.4. Регулирование с прямой связью в случае нескольких входов
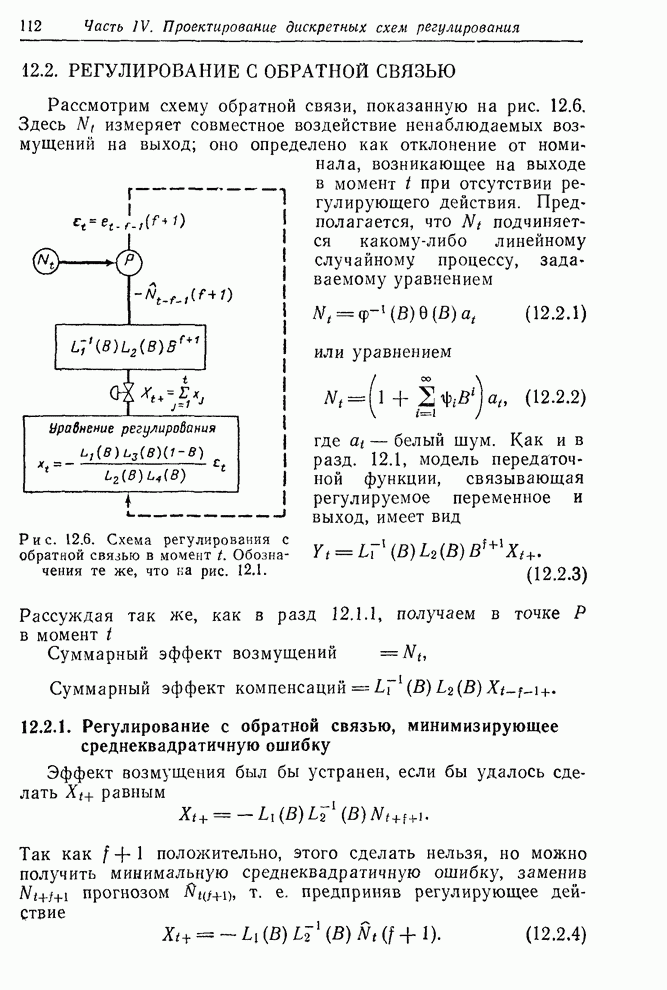
- 12.2. РЕГУЛИРОВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ
- 12.2.1. Регулирование с обратной связью, минимизирующее среднеквадратичную ошибку
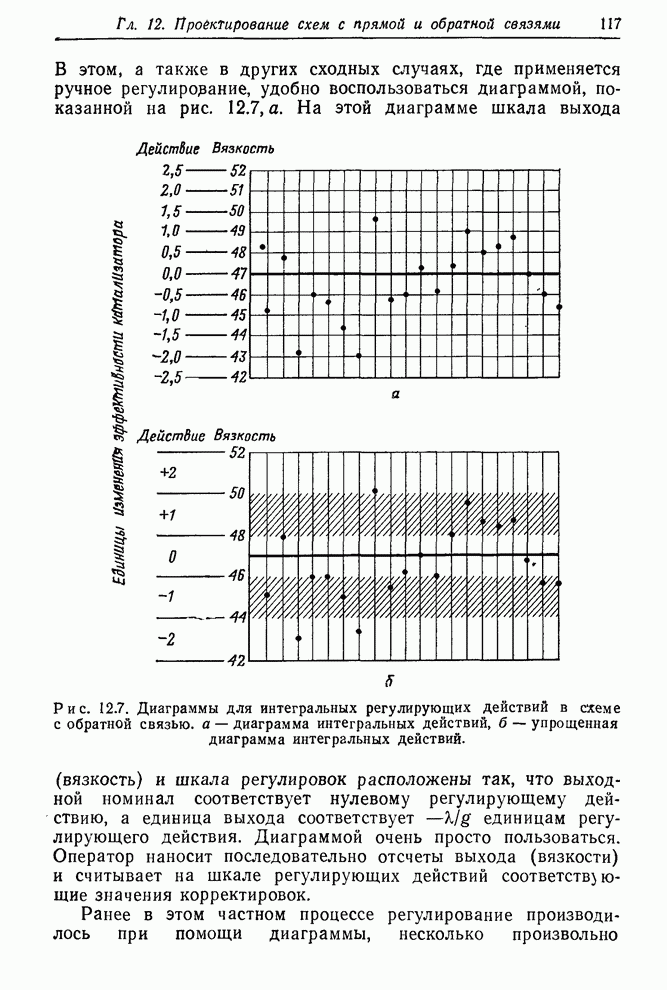
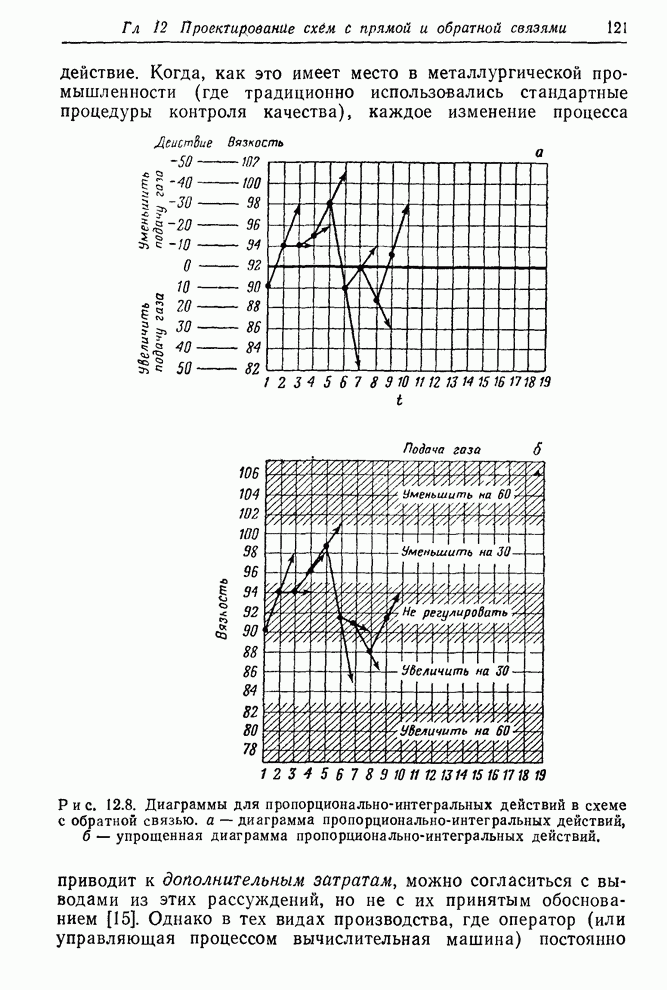
- 12.2.2. Применение уравнения регулирования: ПИД-регулятор
- 12.2.3. Примеры дискретного регулирования с обратной связью
- 12.3. РЕГУЛИРОВАНИЕ С ПРЯМОЙ И ОБРАТНОЙ СВЯЗЯМИ
- 12.3.1. Регулирование с прямой и обратной связями, минимизирующее выходную среднеквадратичную ошибку
- 12.3.2. Пример регулирования с прямой и обратной связями
- 12.3.3. Преимущества и недостатки регулирования с прямой и обратной связями
- 12.4. Подгонка моделей передаточных функций шума по оперативным данным
- 12.4.1. Итеративный способ построения моделей
- 12.4.2. Оценивание по оперативным данным
- 12.4.3. Пример
- Глава 13. Некоторые дальнейшие проблемы регулирования
- 13.1. ЭФФЕКТ ДОБАВОЧНОГО ШУМА В СХЕМАХ РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ
- 13.1.1. Эффект пренебрежения добавочным шумом; упрощенные схемы
- 13.1.2. Оптимальное действие в случаях, когда корректировки содержат ошибки наблюдения
- 13.1.3. Перенос источника шума
- 13.2. СХЕМА РЕГУЛИРОВАНИЯ С ОБРАТНОЙ СВЯЗЬЮ, ПРИ ОГРАНИЧЕНИИ, НАЛОЖЕННОМ НА ДИСПЕРСИЮ КОРРЕКТИРОВКИ
- 13.2.1. Вывод выражения для оптимальной корректировки
- 13.2.2. Схема с ограничением для примера «вязкость–подача газа»
- 13.3. ВЫБОР ИНТЕРВАЛА ОТСЧЕТА
- 13.3.1. Пример эффекта уменьшения частоты отсчетов
- 13.3.2. Влияние интервала отсчета на процесс ПСС(0,1,1)
- ПРОГРАММА 5. ИДЕНТИФИКАЦИЯ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 6. ПРЕДВАРИТЕЛЬНОЕ ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
- ПРОГРАММА 7. ОЦЕНИВАНИЕ МОДЕЛИ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
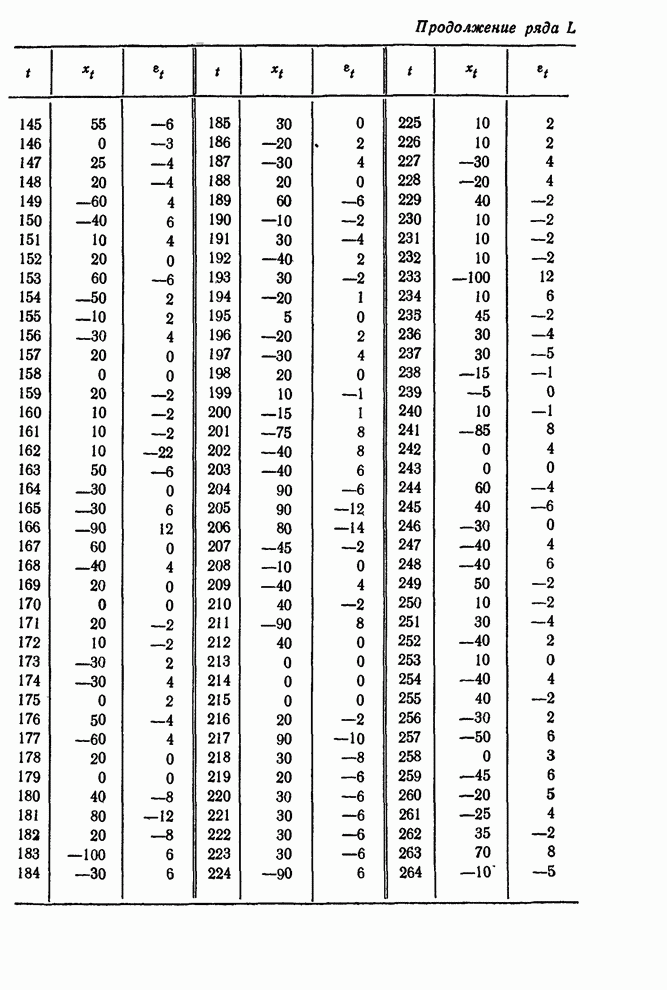
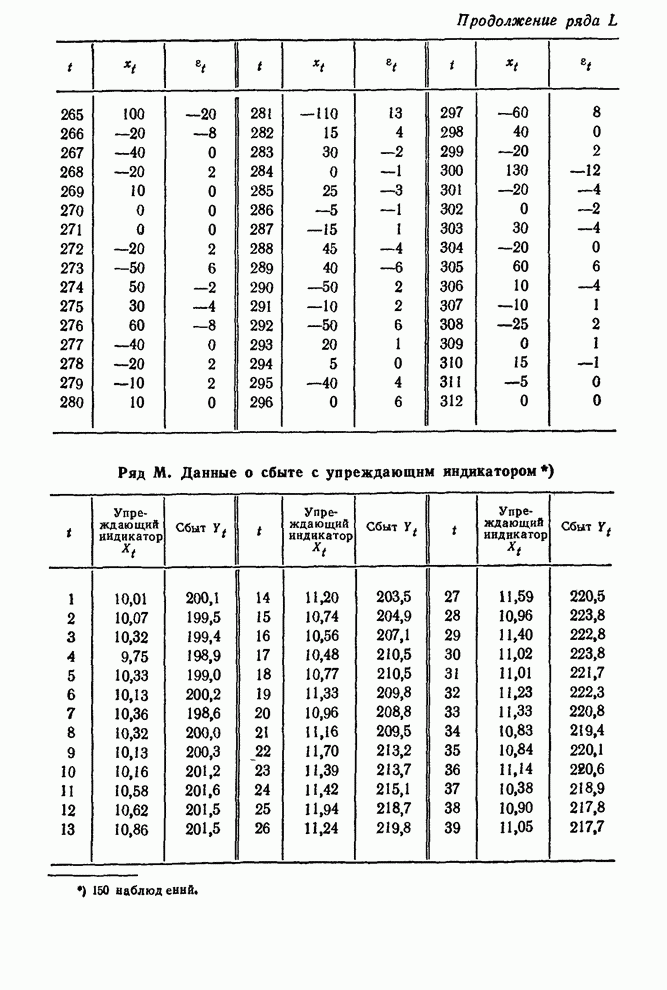
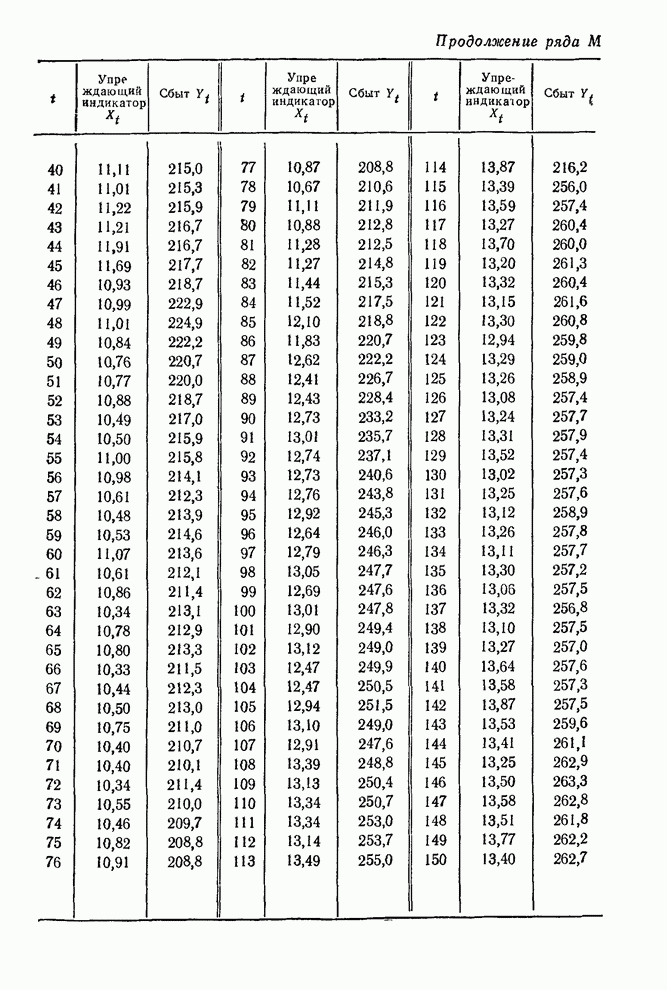
- ТАБЛИЦЫ ВРЕМЕННЫХ РЯДОВ