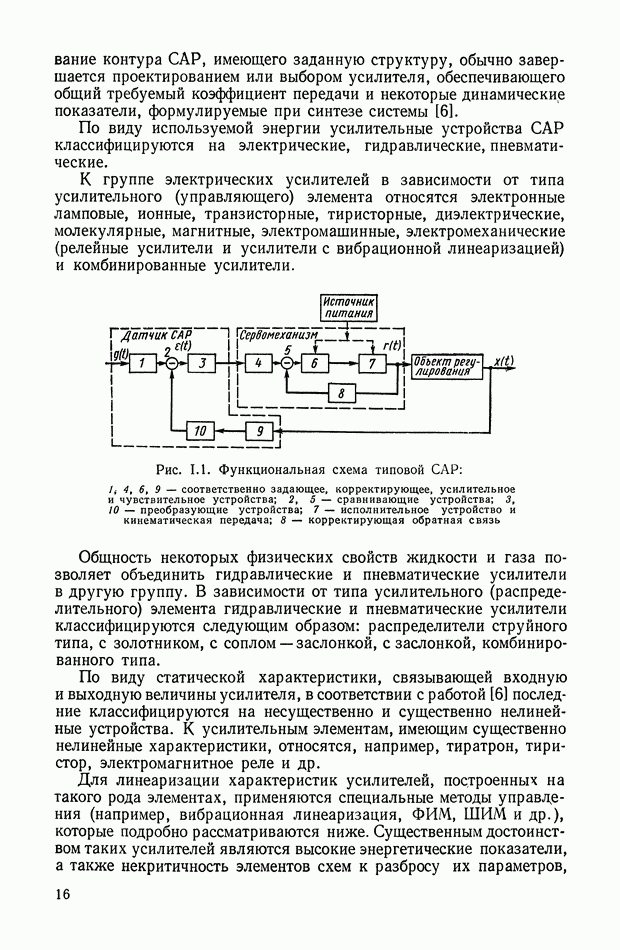
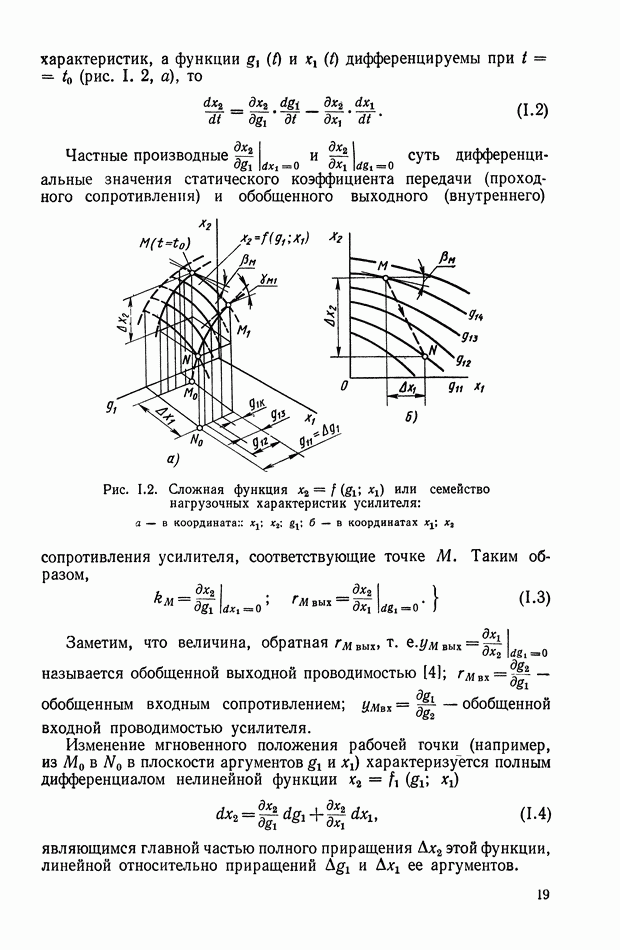
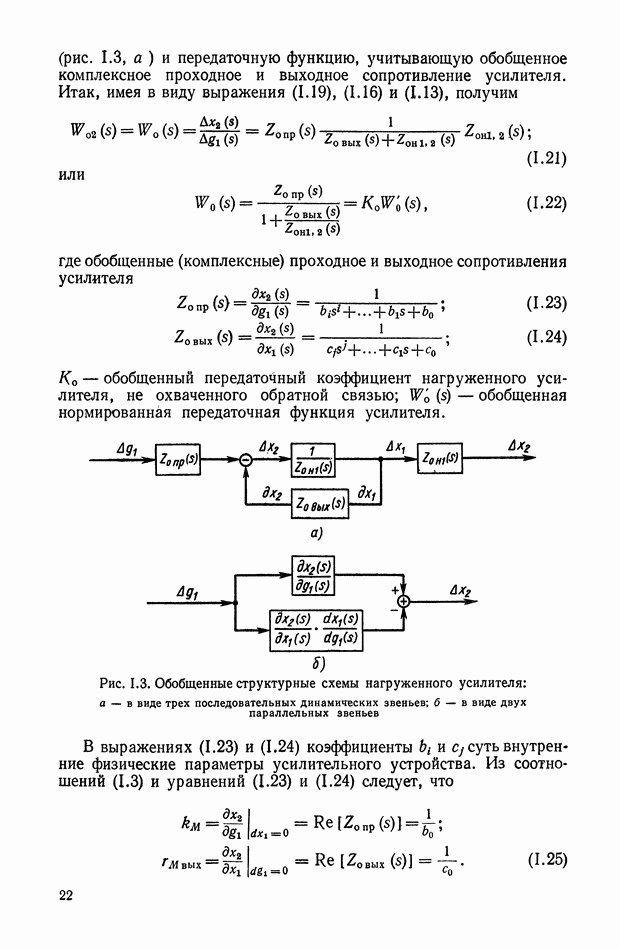
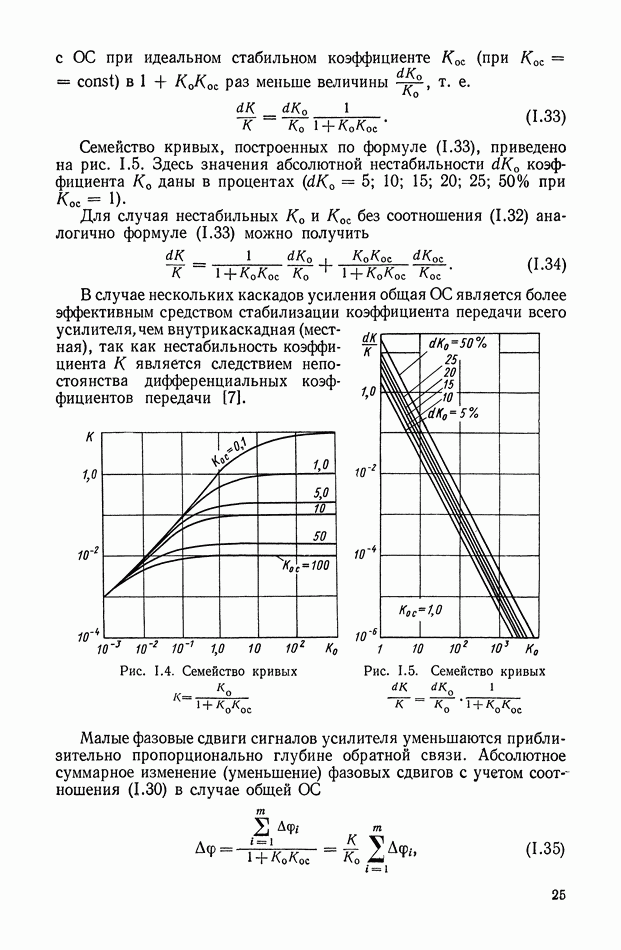
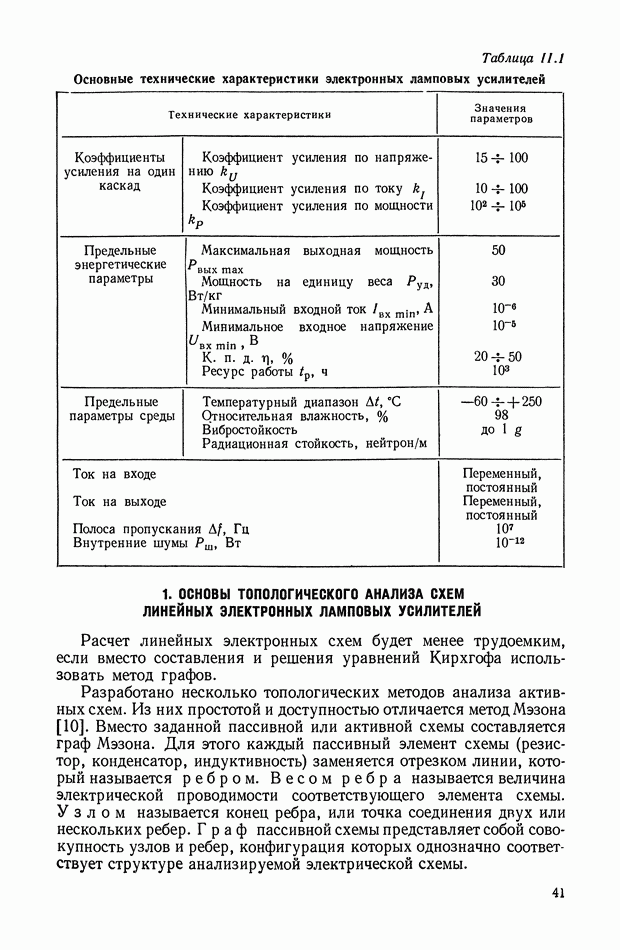
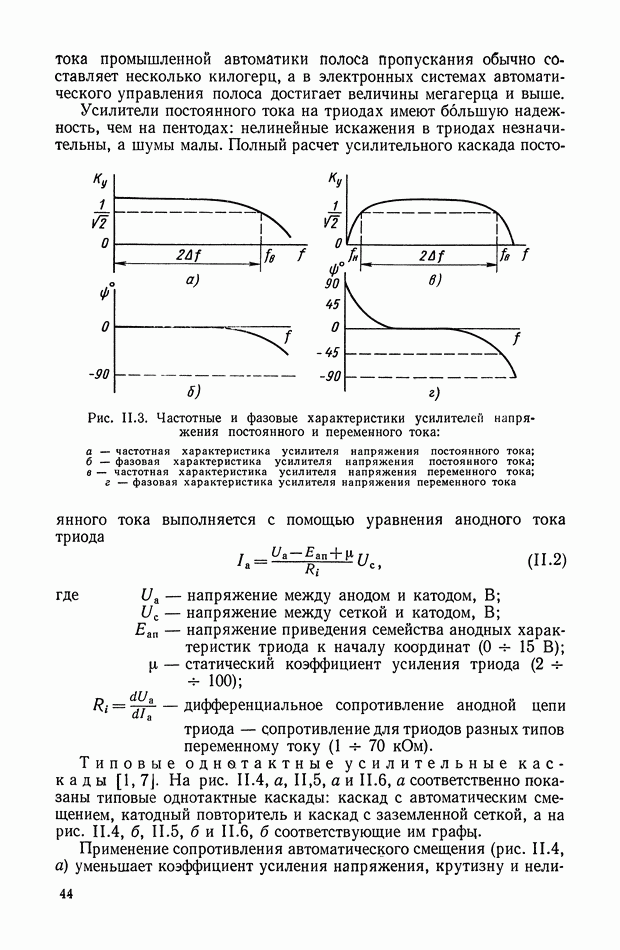
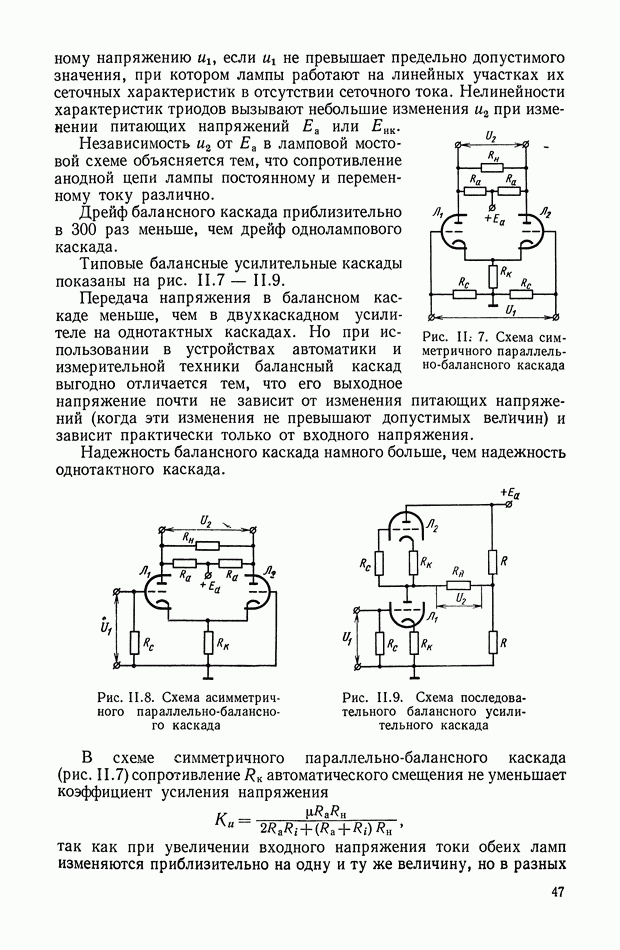
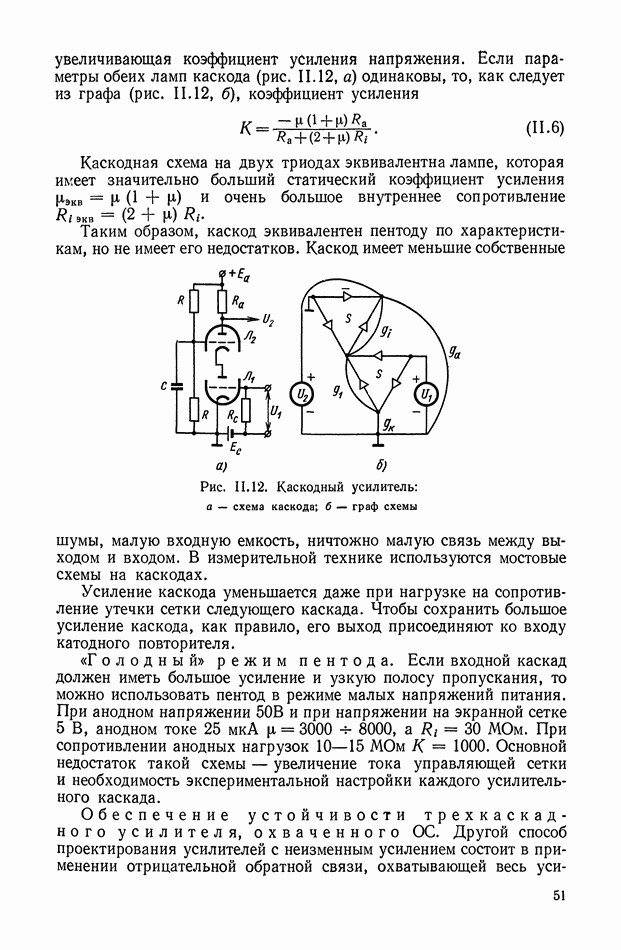
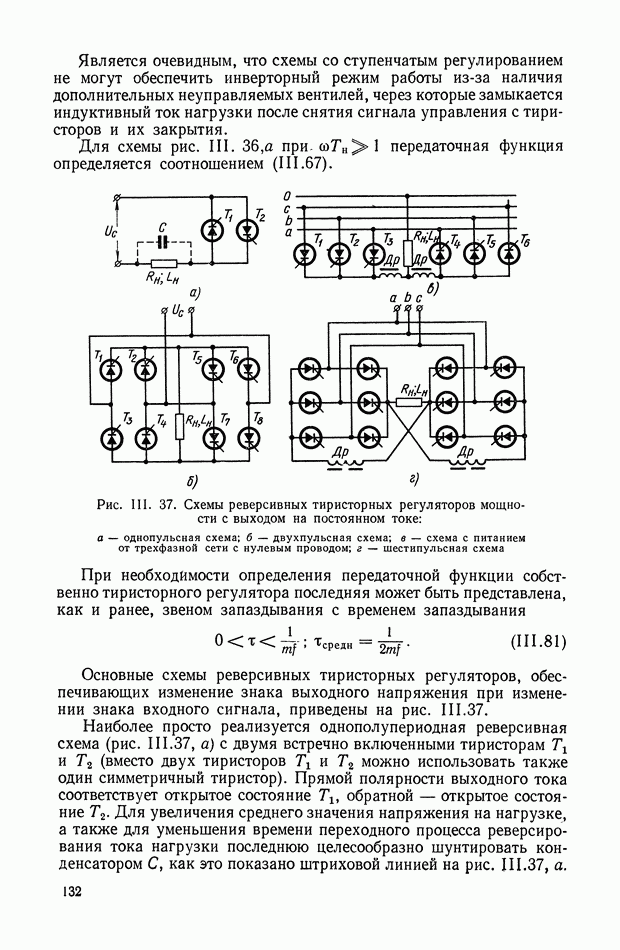
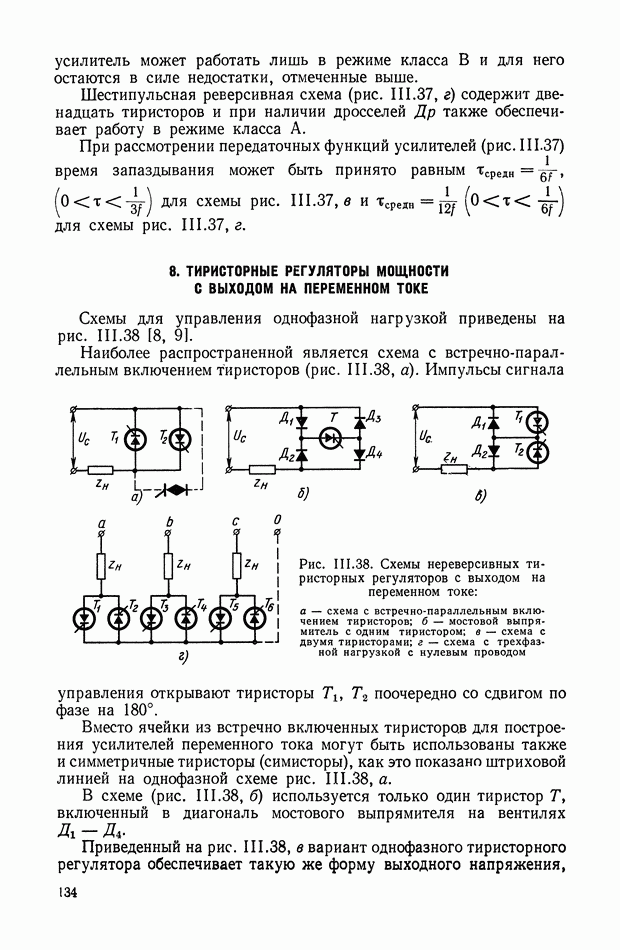
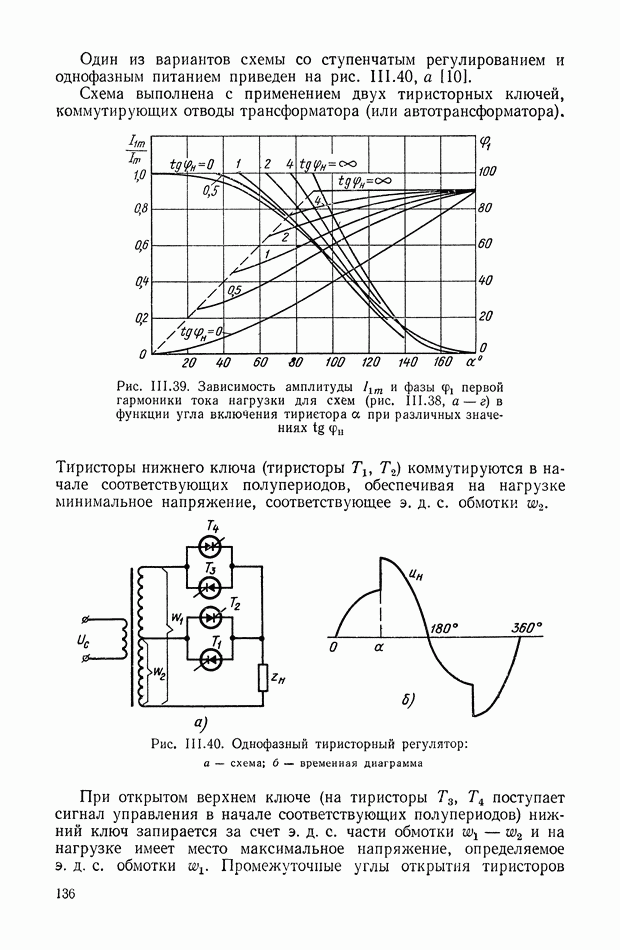
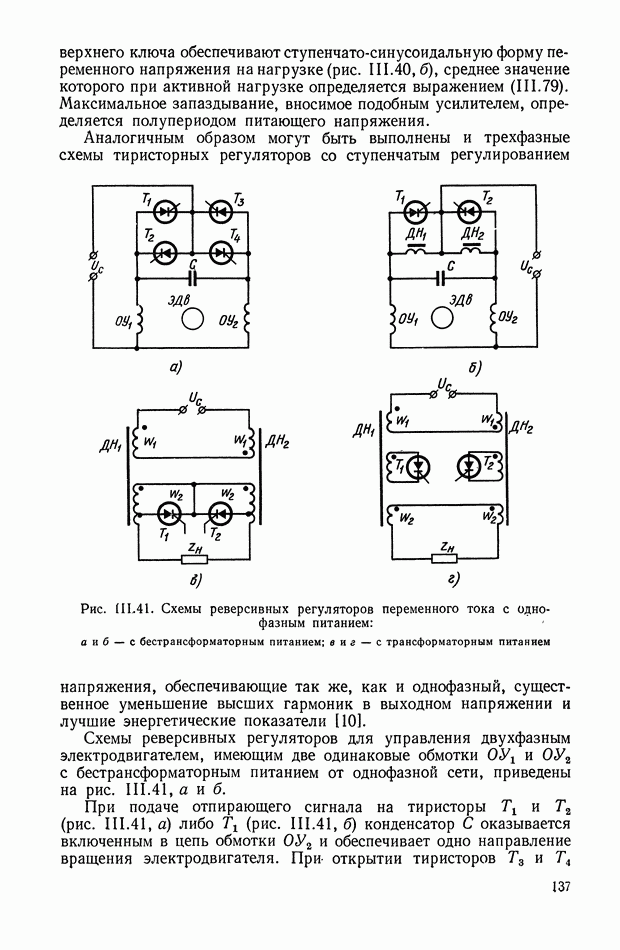
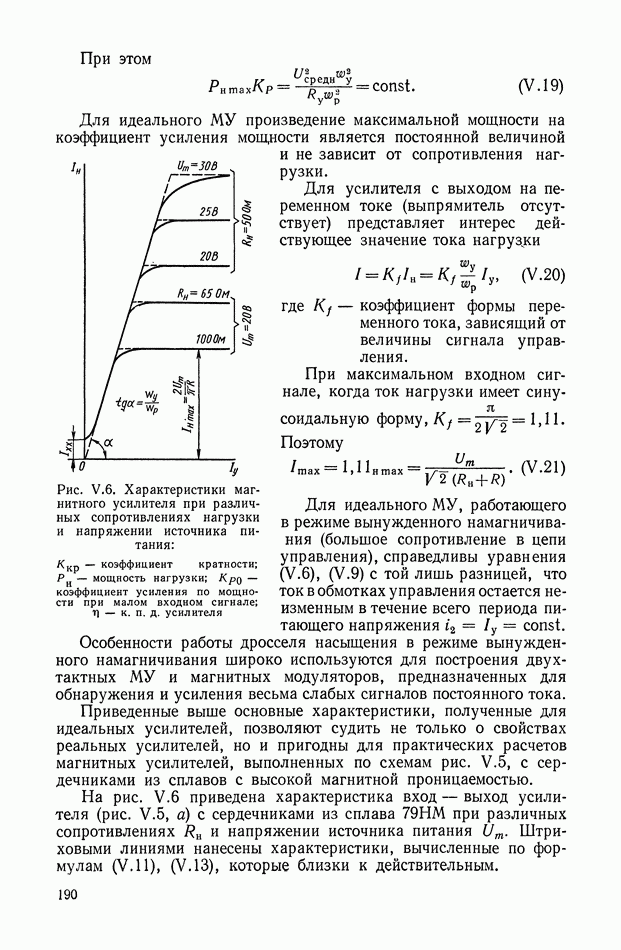
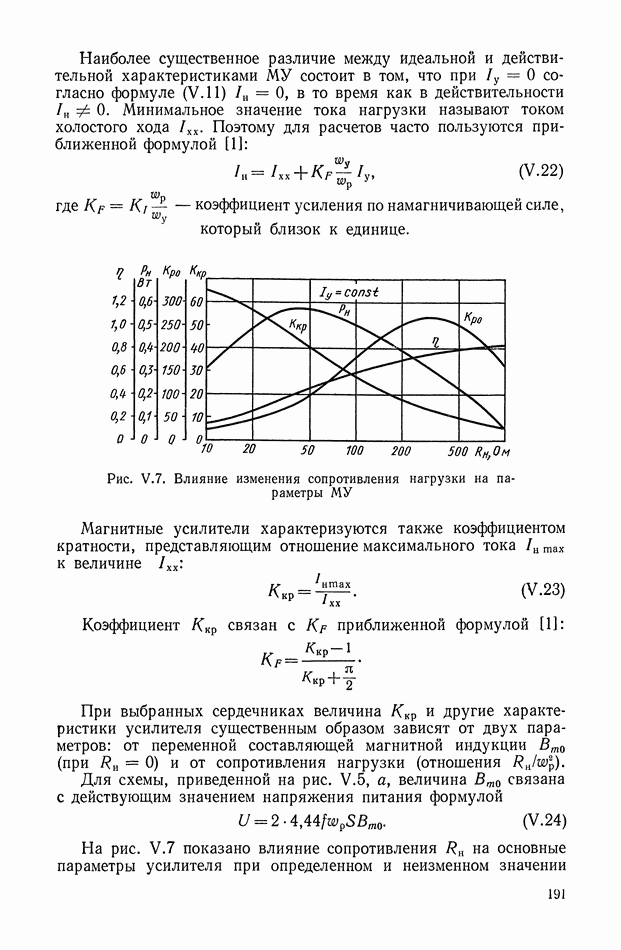
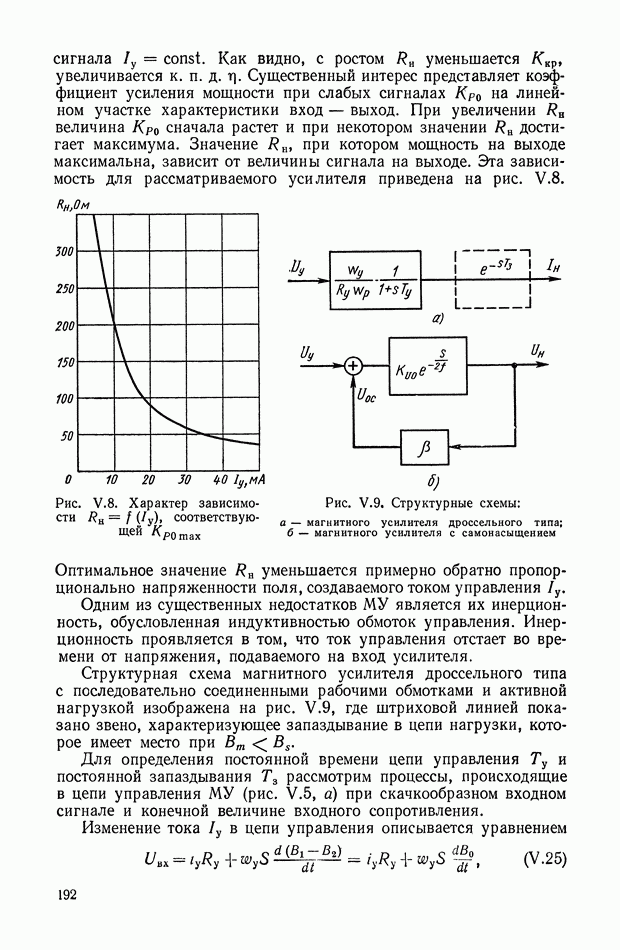
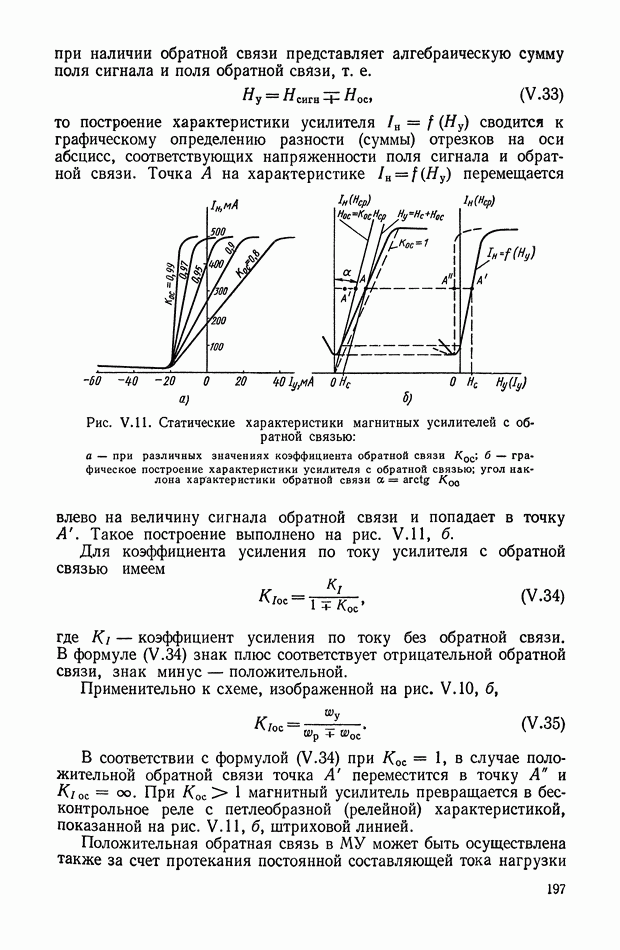
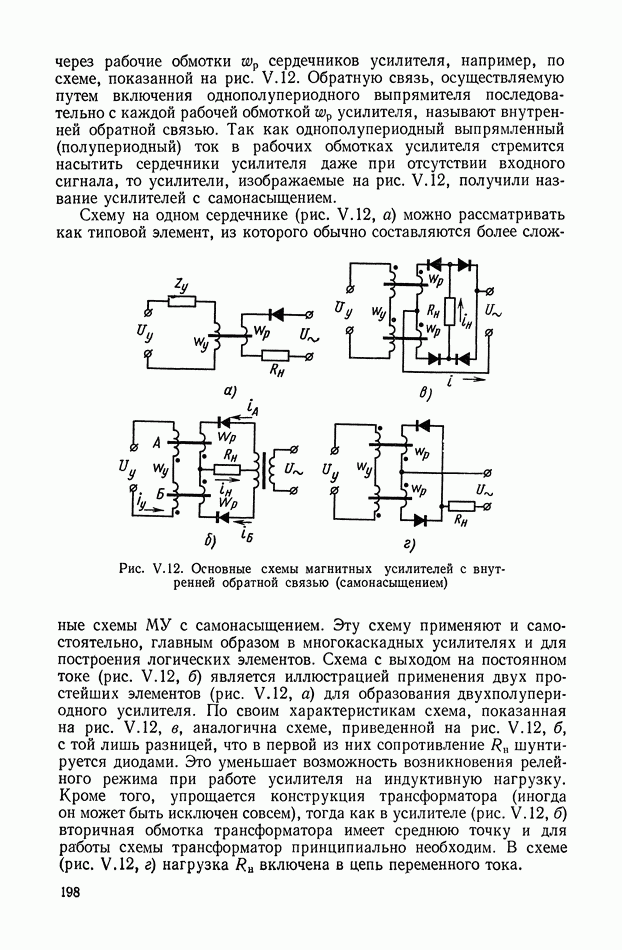
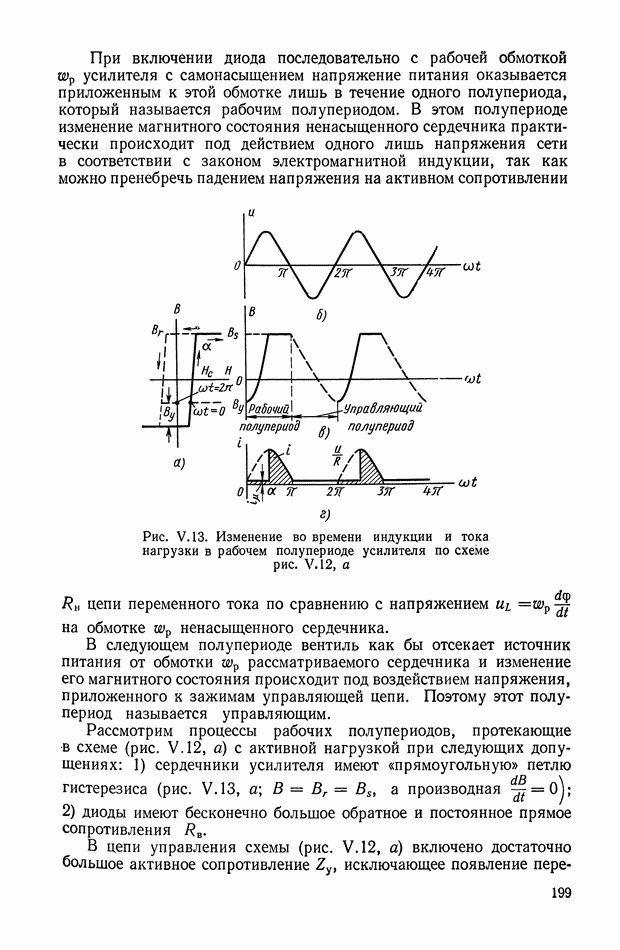
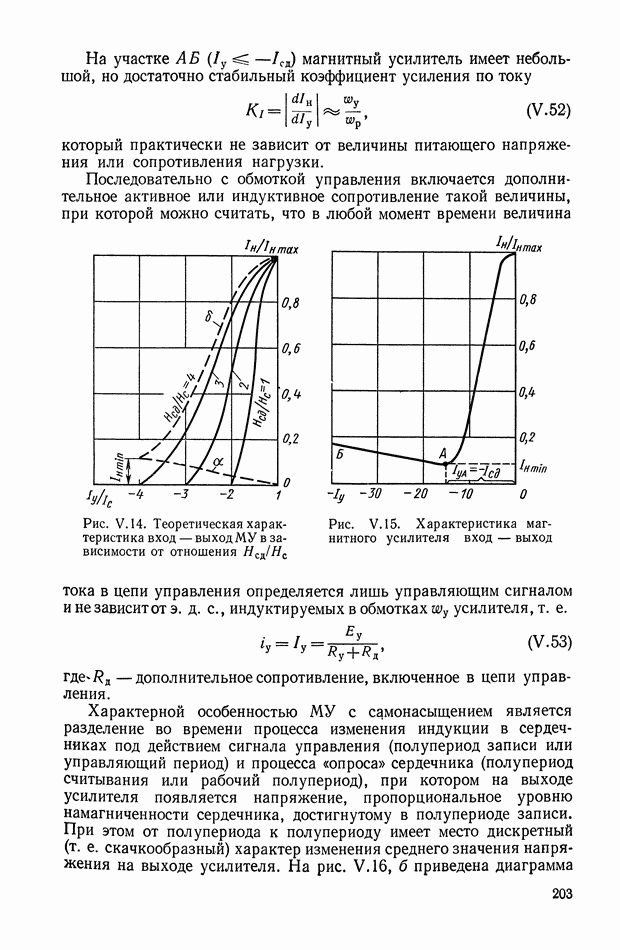
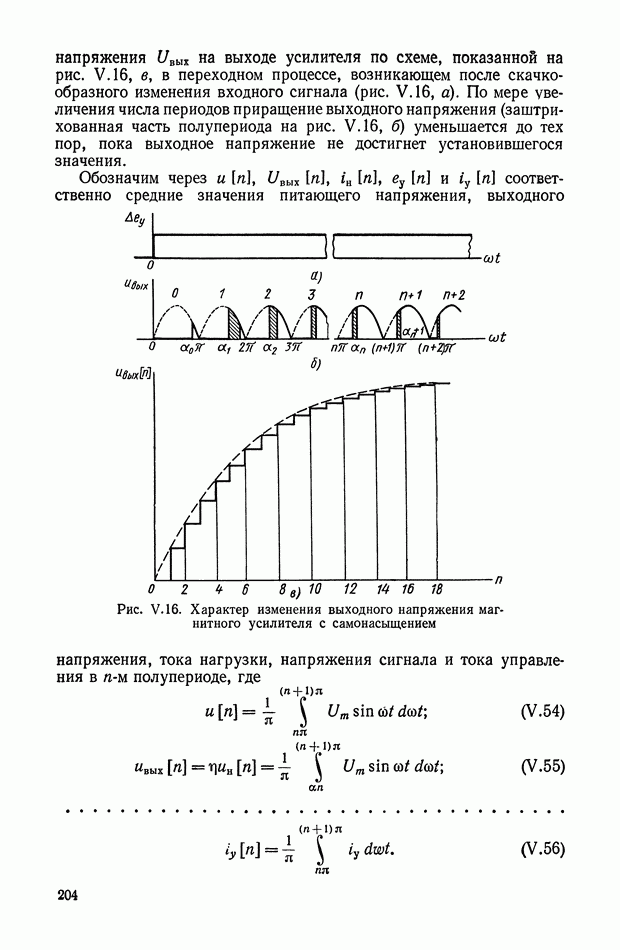
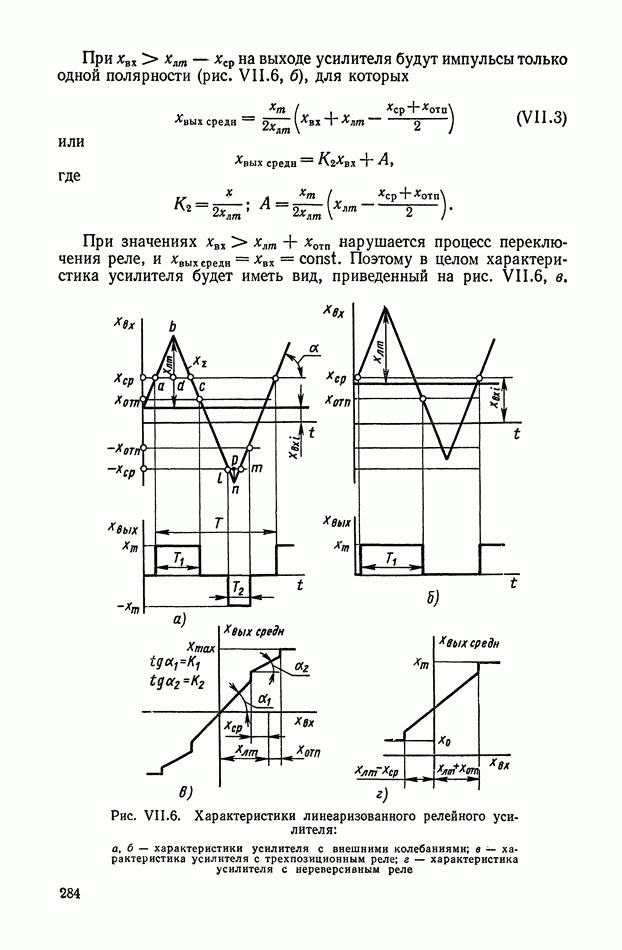
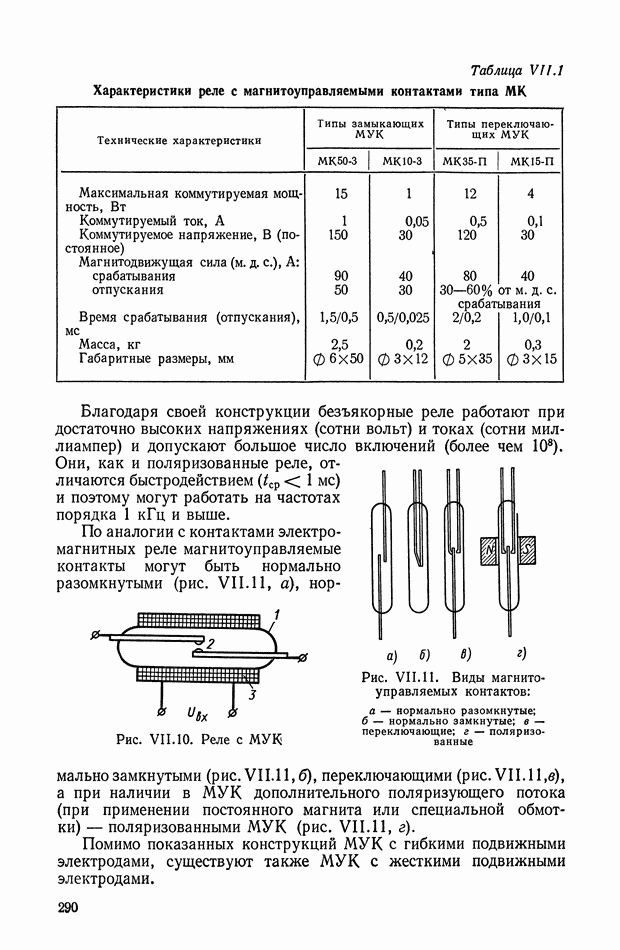
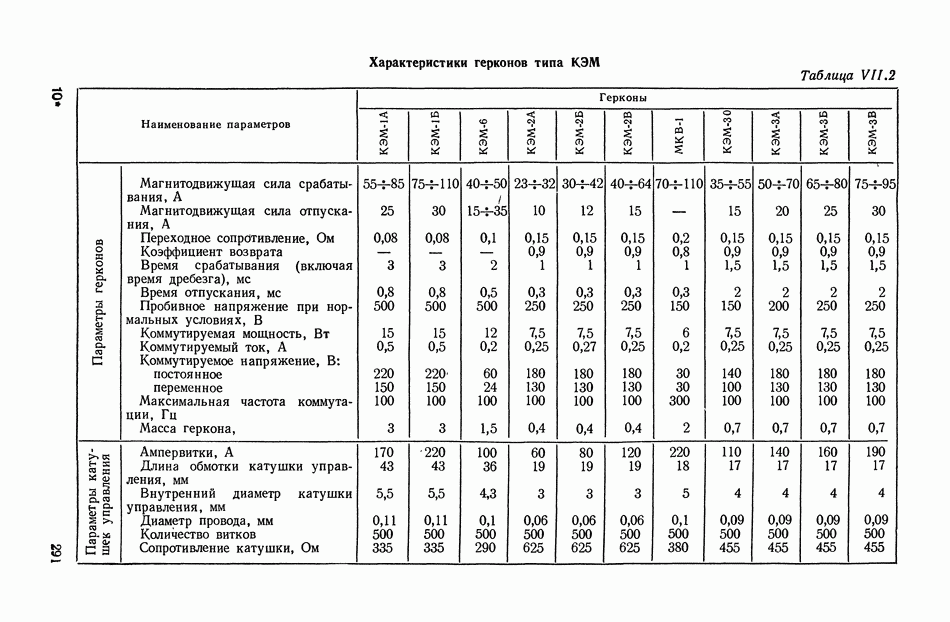
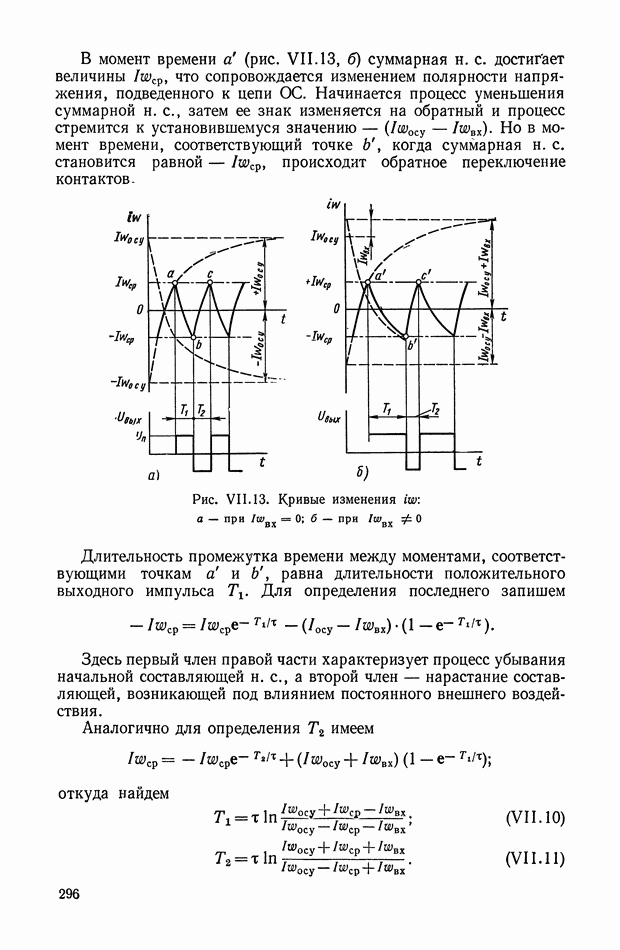
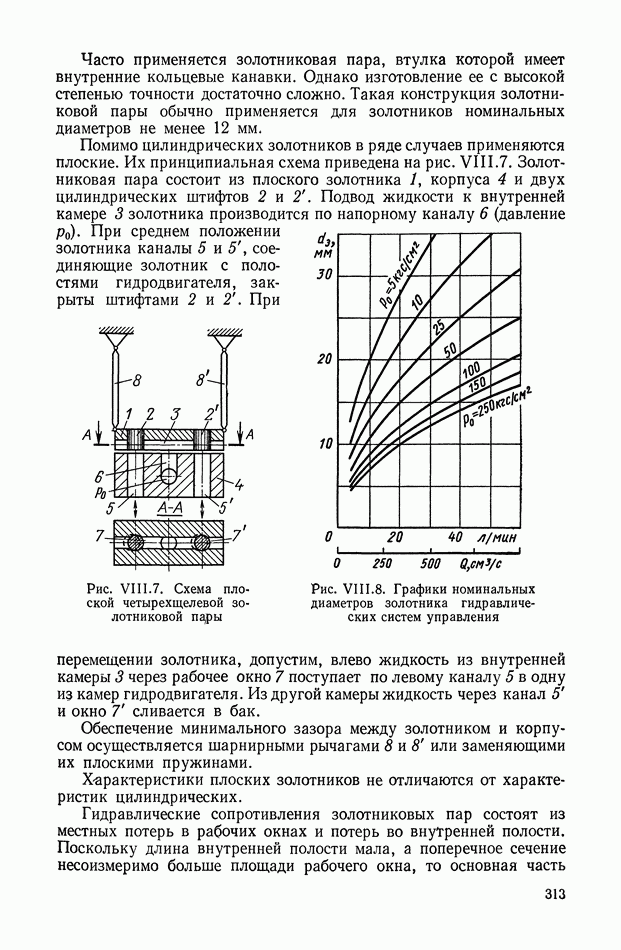
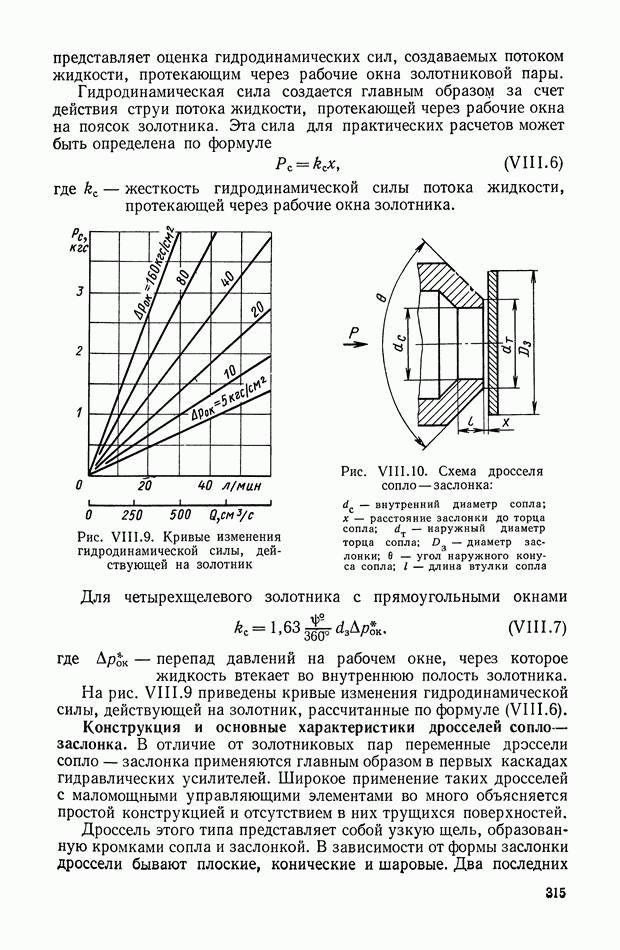
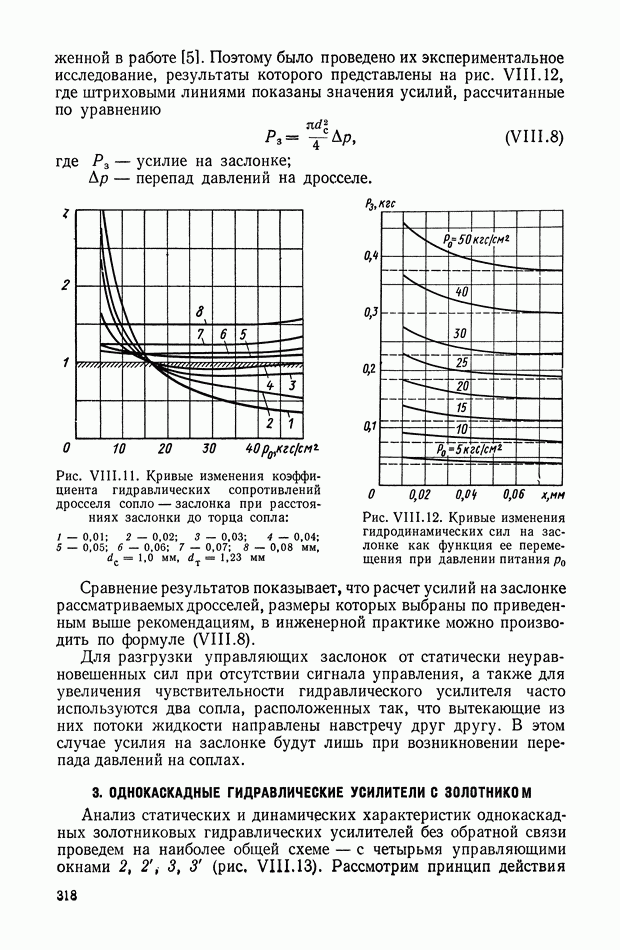
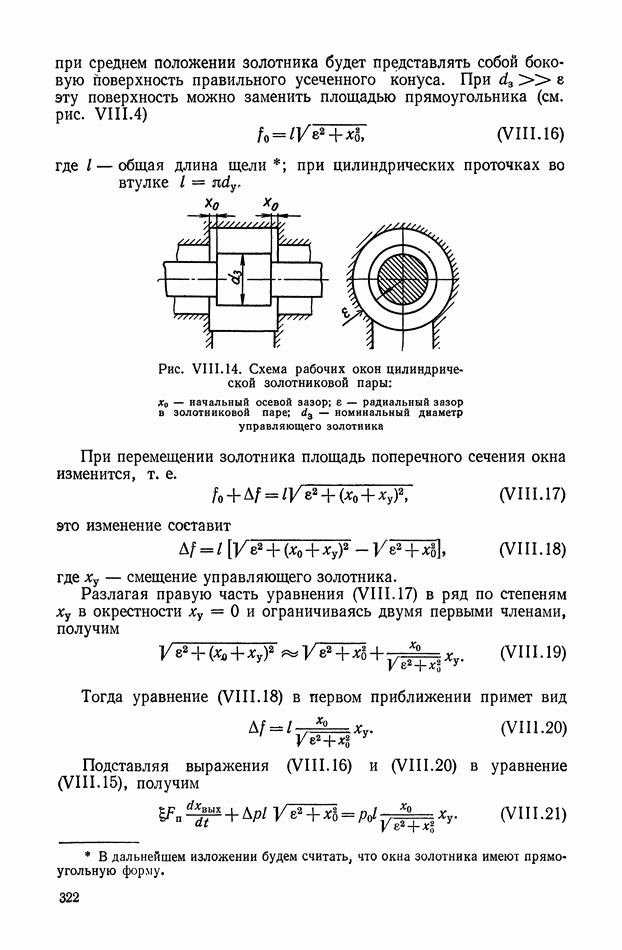
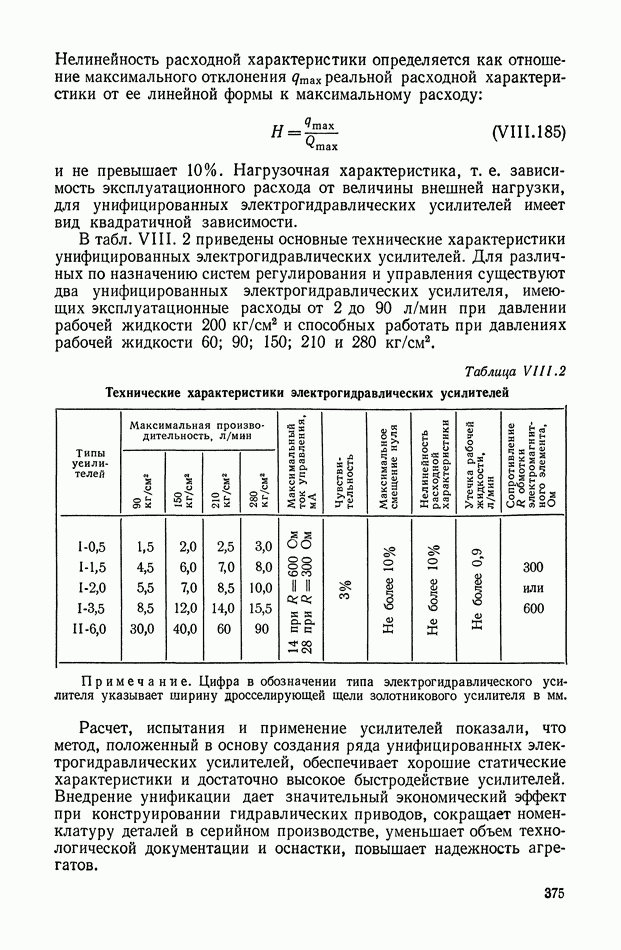
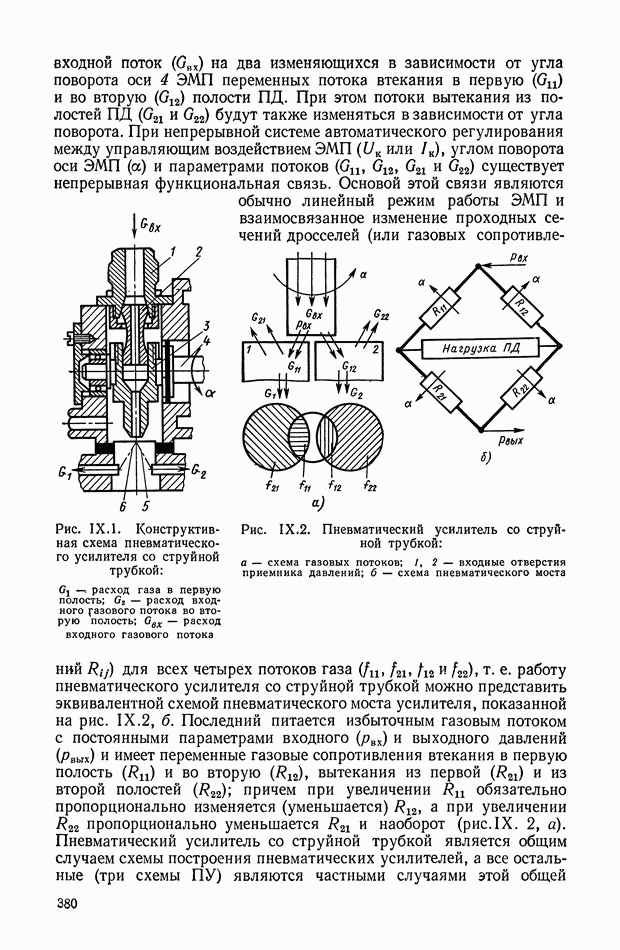
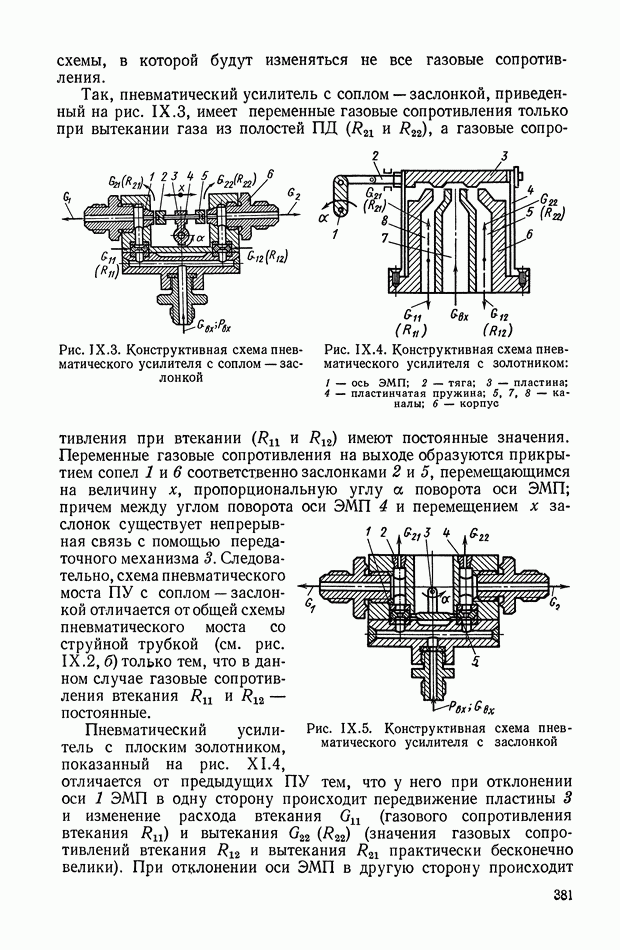
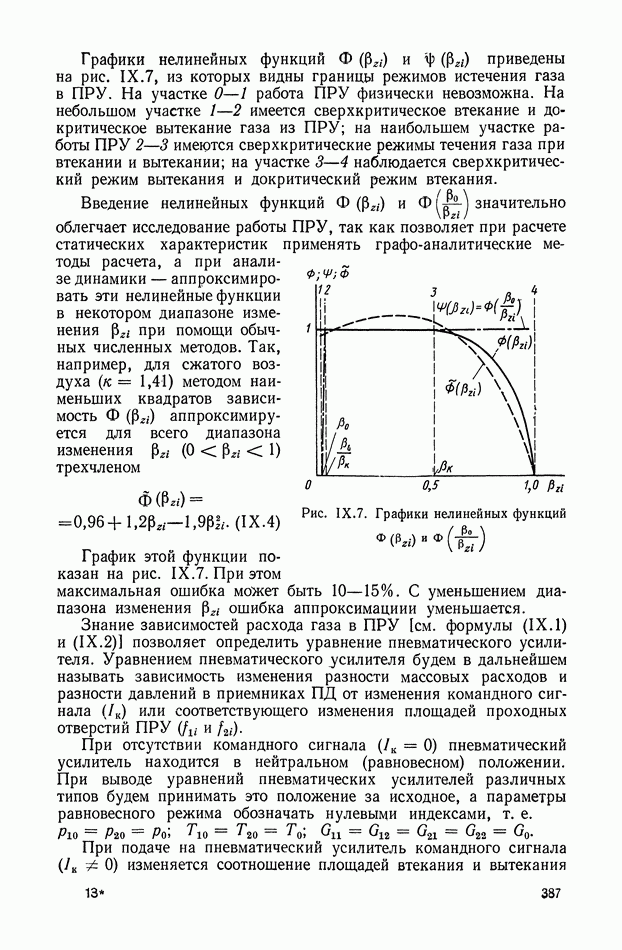
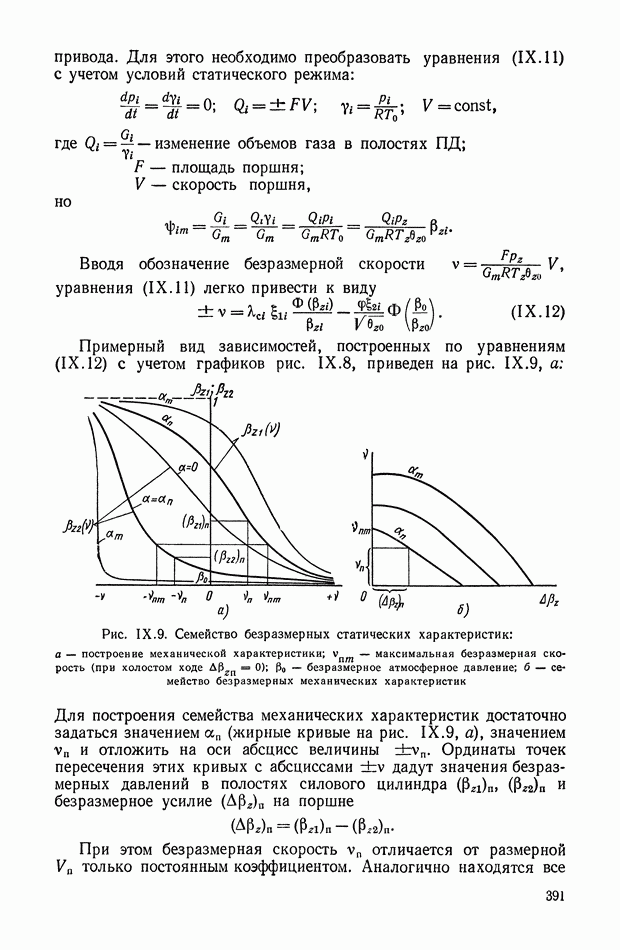
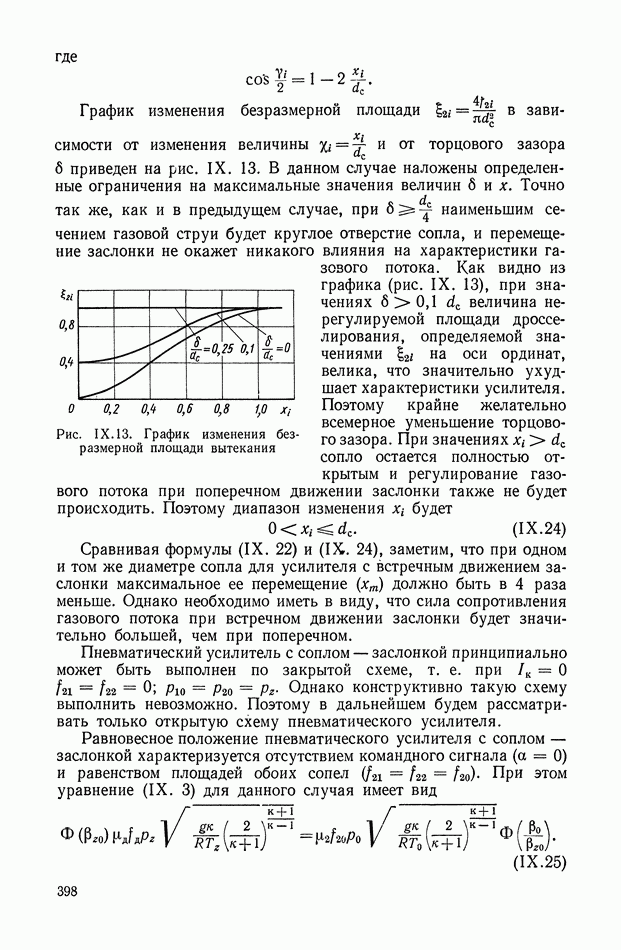
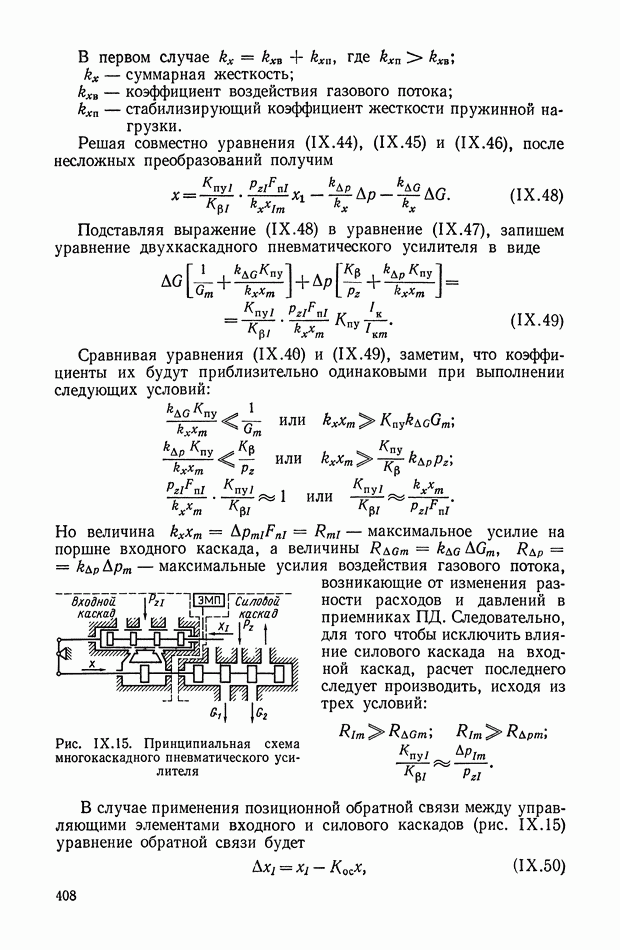
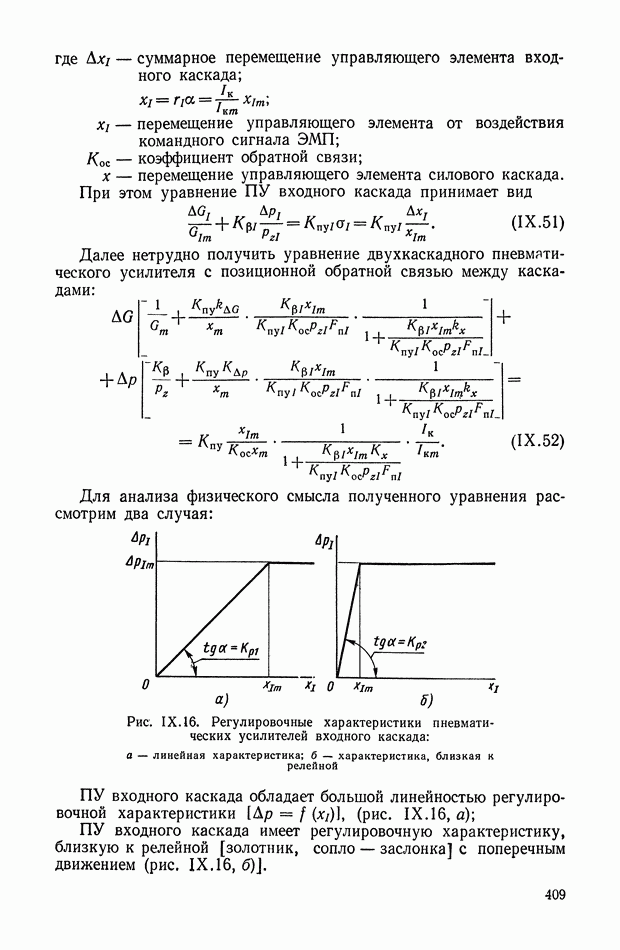
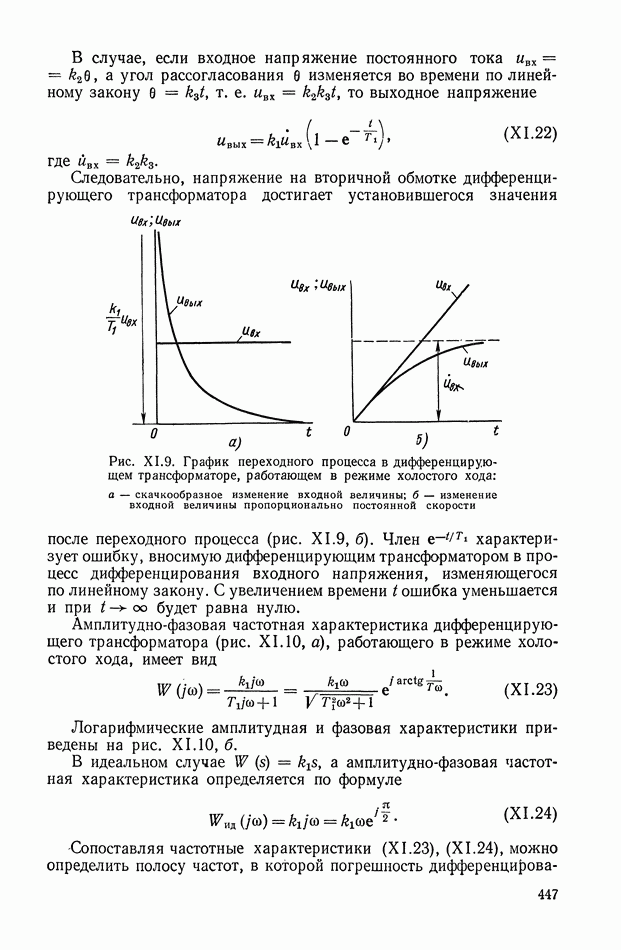
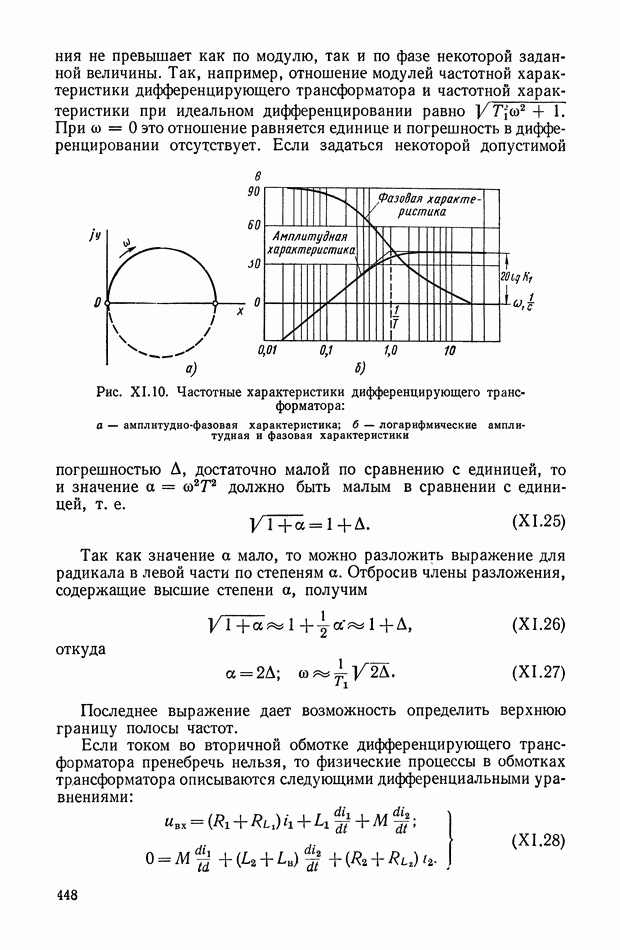
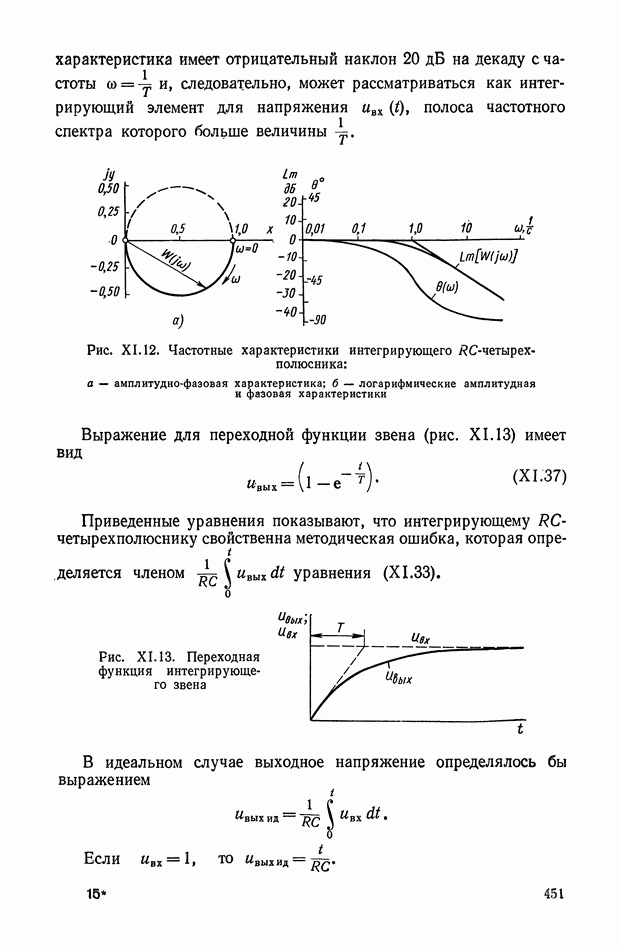
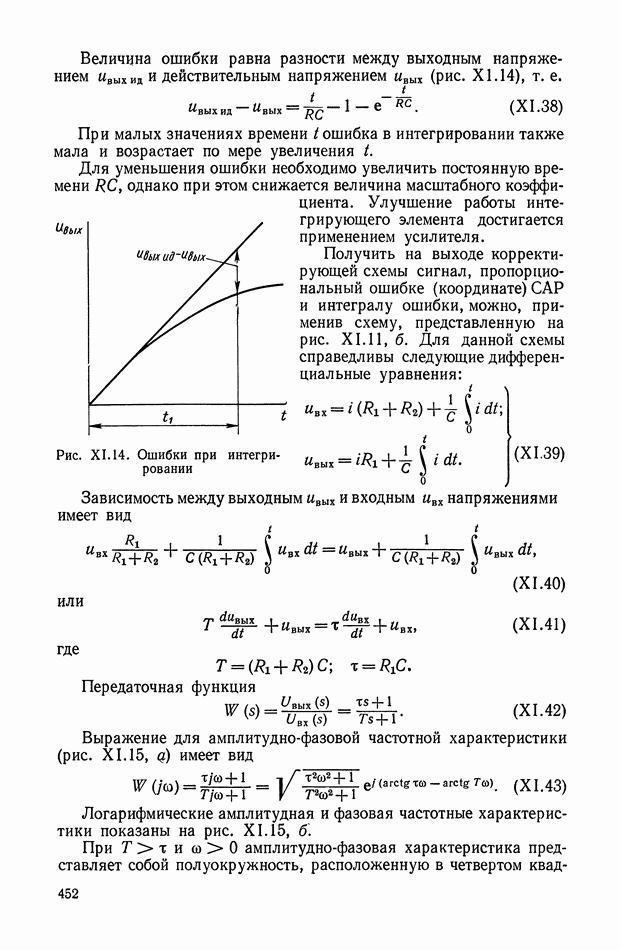
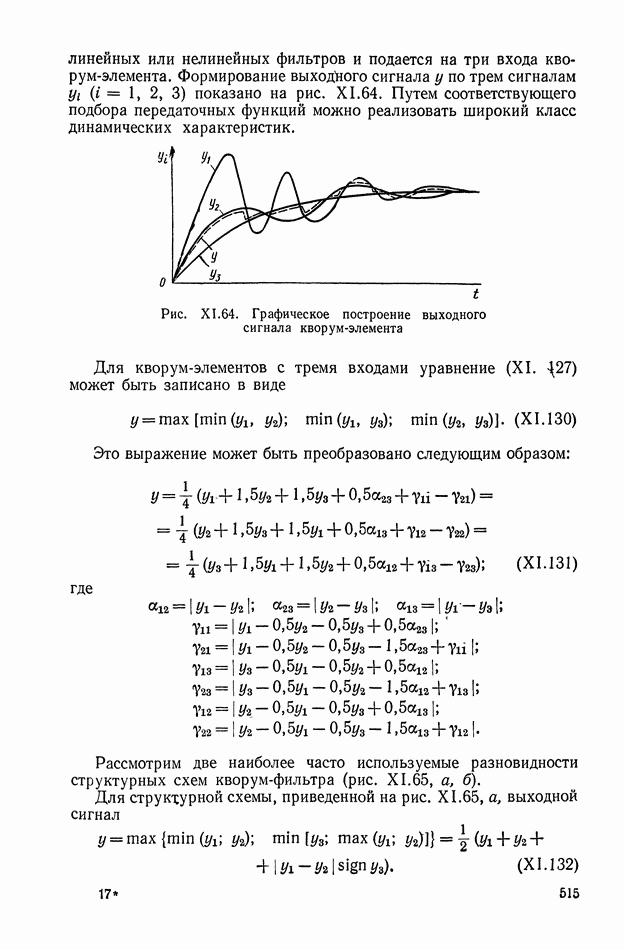
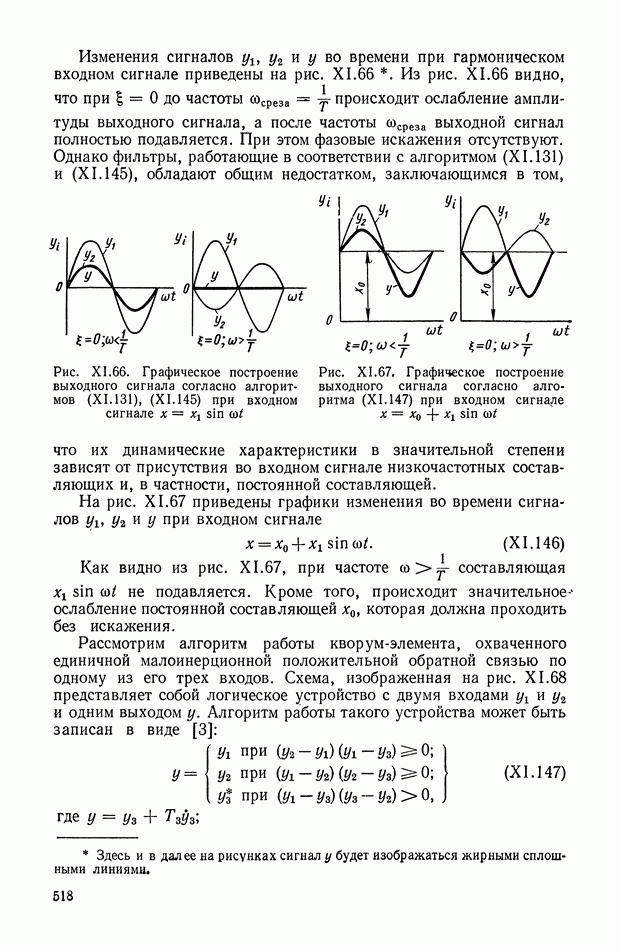
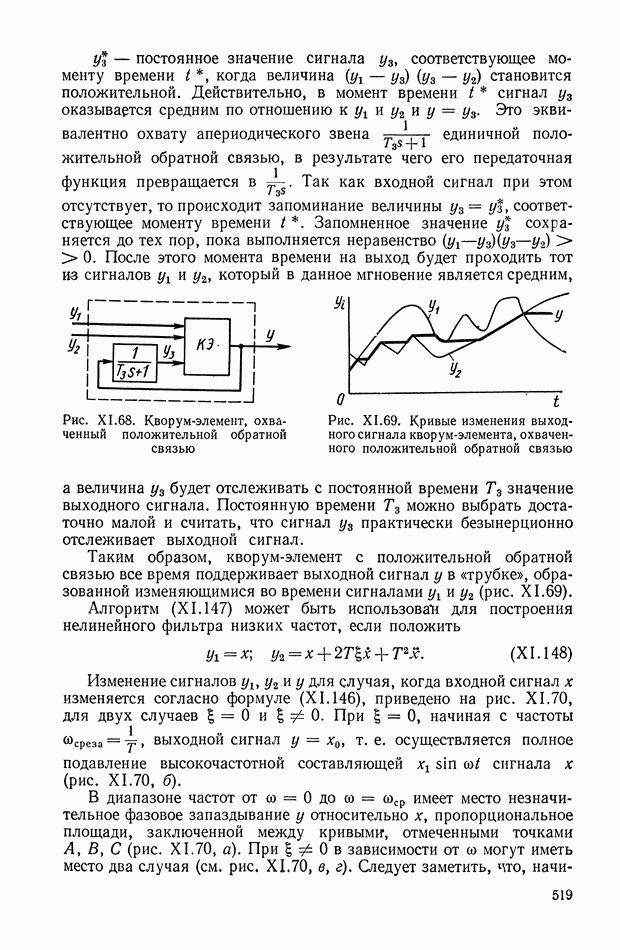
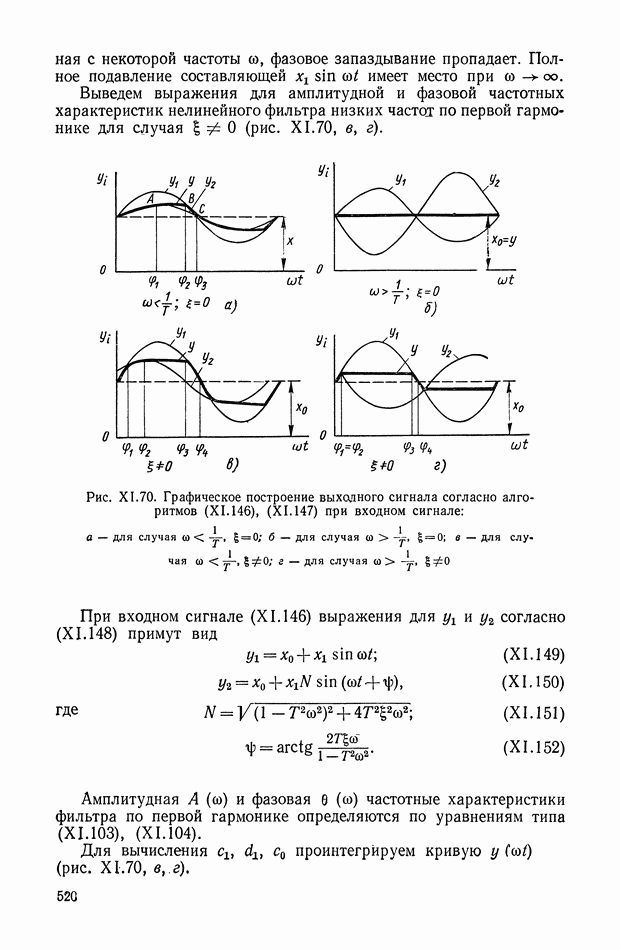
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С НЕЗАВИСИМЫМ ВОЗБУЖДЕНИЕМ И С САМОВОЗБУЖДЕНИЕМ
ЭМУ с независимым возбуждением. Простейшим типом ЭМУ является ЭМУ с независимым возбуждением, в качестве которого может быть использован генератор постоянного тока обычного исполнения.
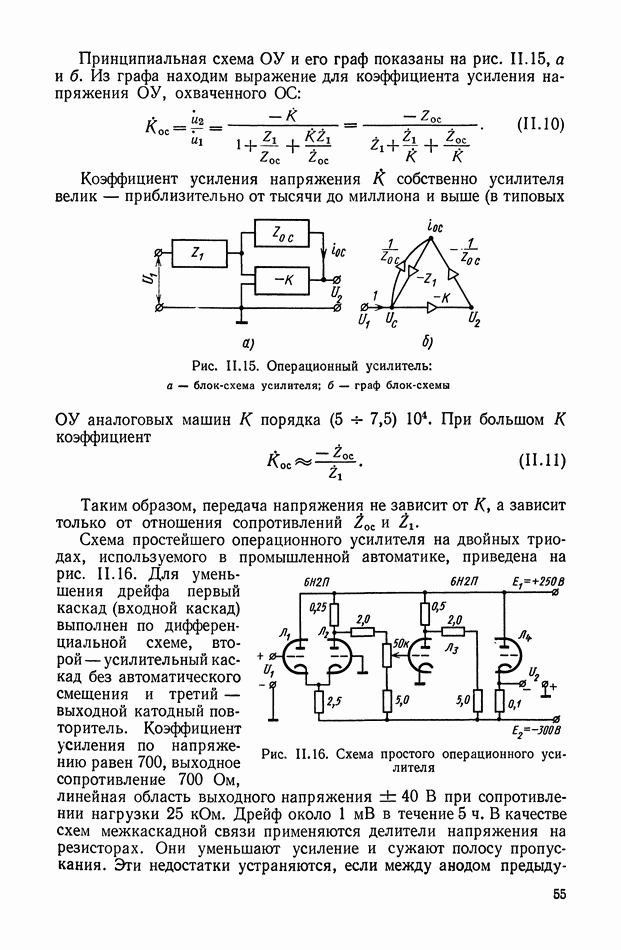
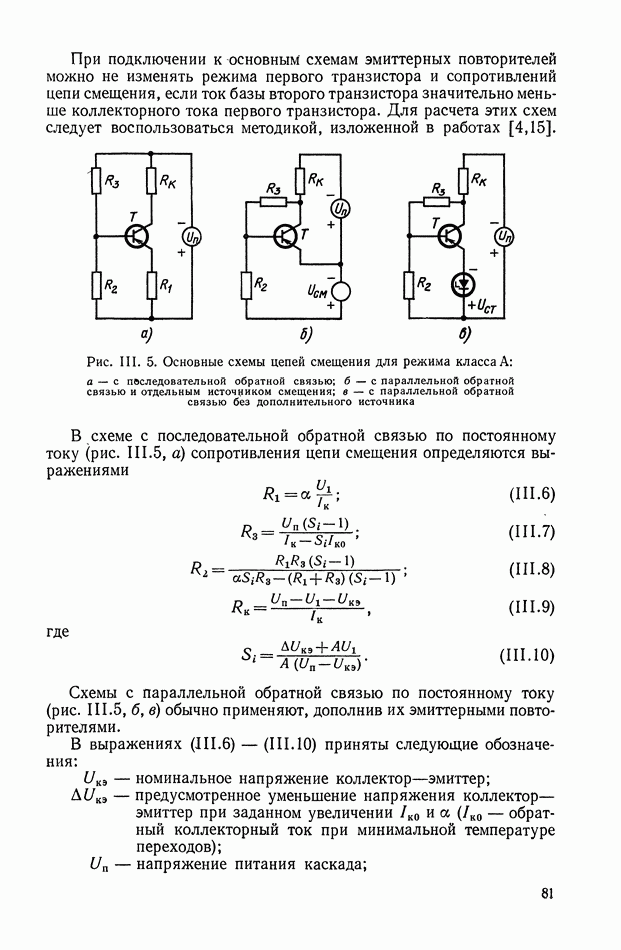
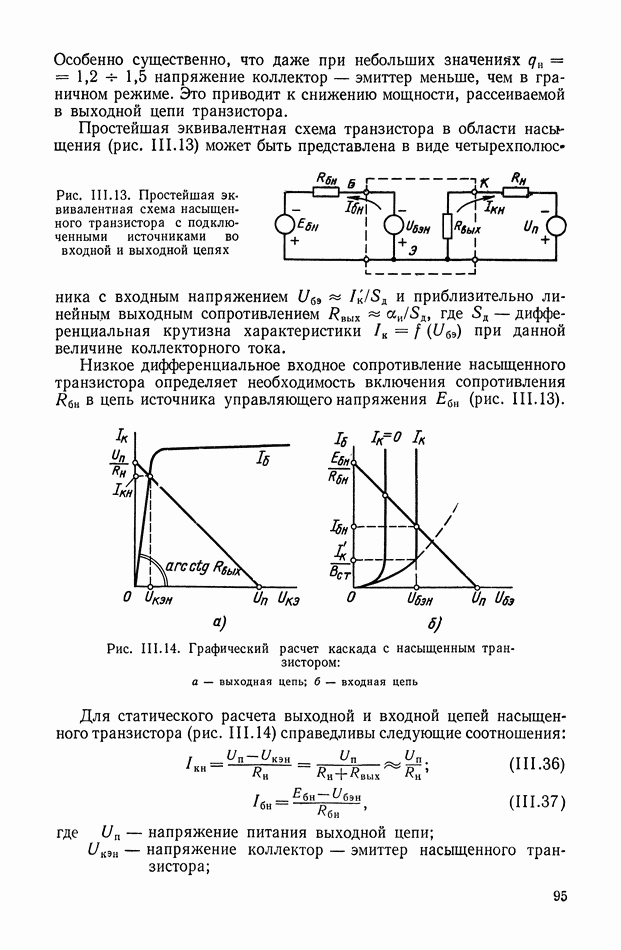
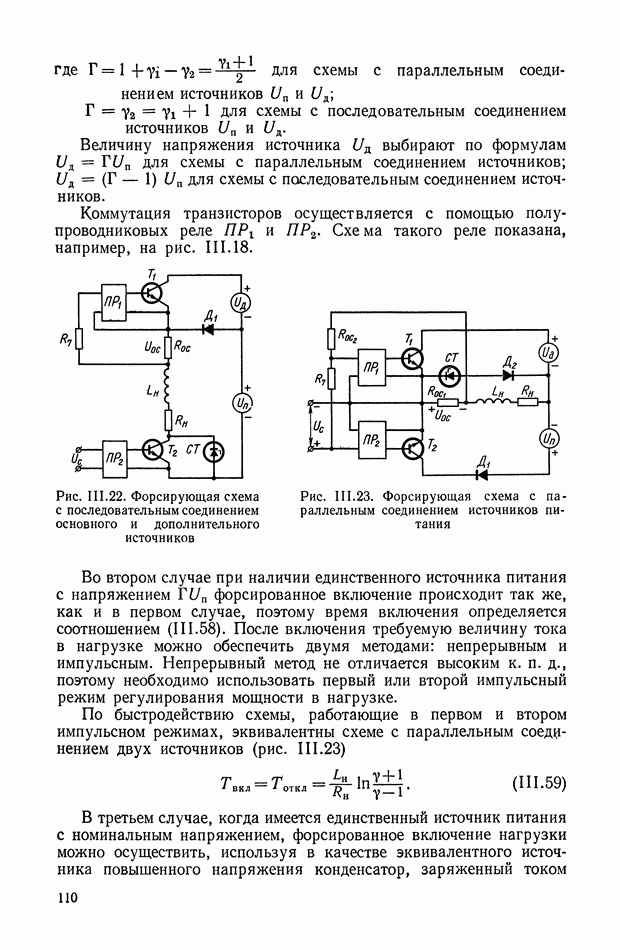
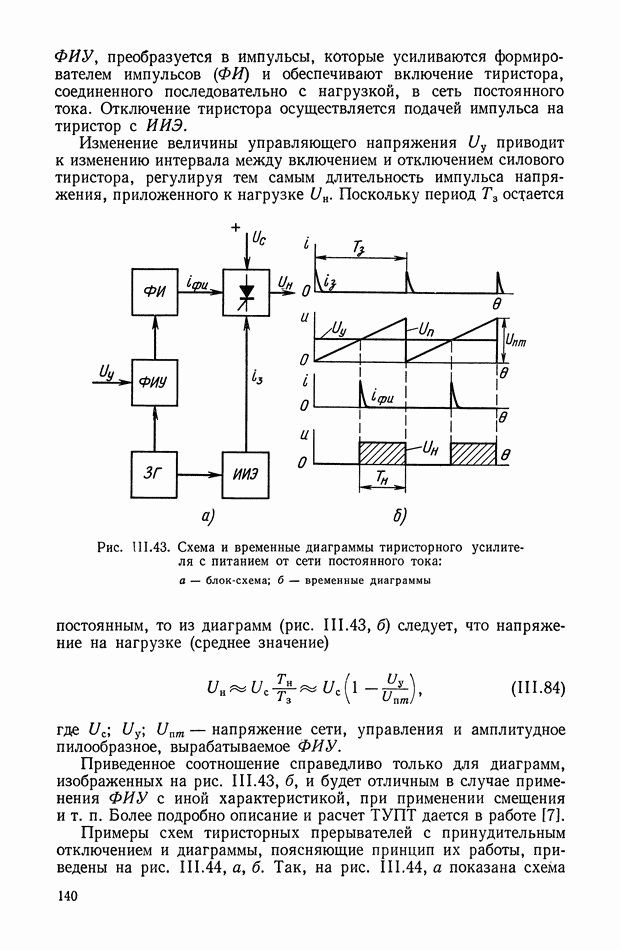
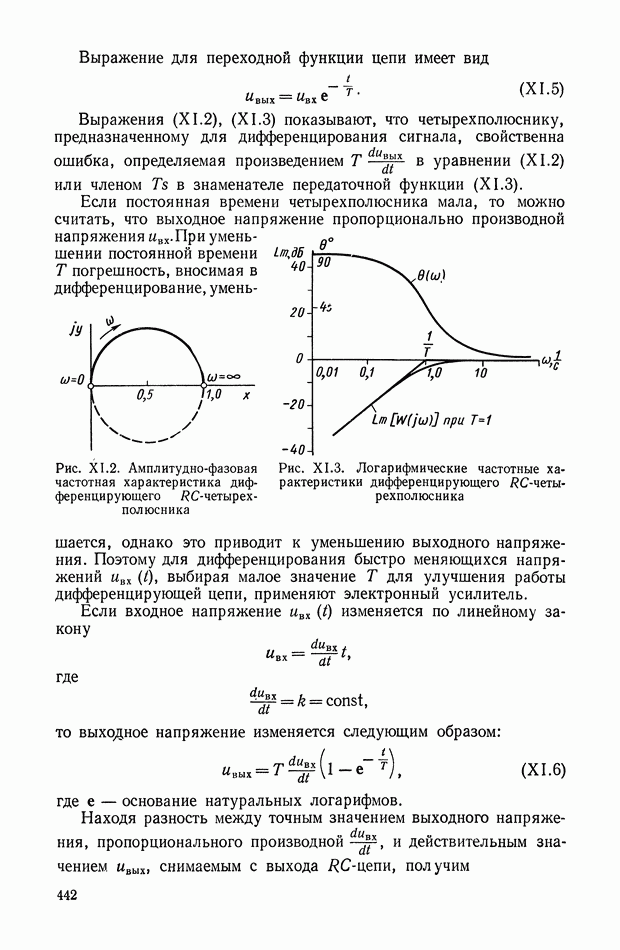
Принципиальная схема ЭМУ с независимым возбуждением приведена на рис. VI. 1. Это двухполюсная машина постоянного тока, статорная обмотка которой используется в качестве обмотки управления, а ротор вращается от приводного электродвигателя с постоянной скоростью  При подаче на обмотку управления
При подаче на обмотку управления  напряжения
напряжения  по обмотке протекает ток
по обмотке протекает ток  . В генераторе создается магнитный поток
. В генераторе создается магнитный поток  . В обмотках ротора наводится э. д. с., максимум которой евых снимается со щеток, расположенных по поперечной оси. Э. д. с.
. В обмотках ротора наводится э. д. с., максимум которой евых снимается со щеток, расположенных по поперечной оси. Э. д. с.  является выходной величиной ЭМУ.
является выходной величиной ЭМУ.
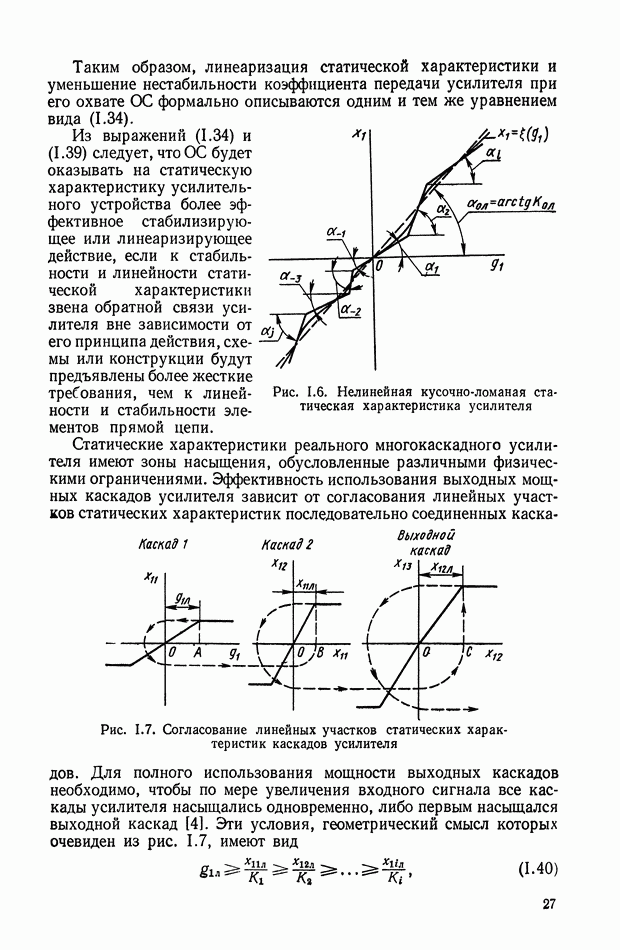
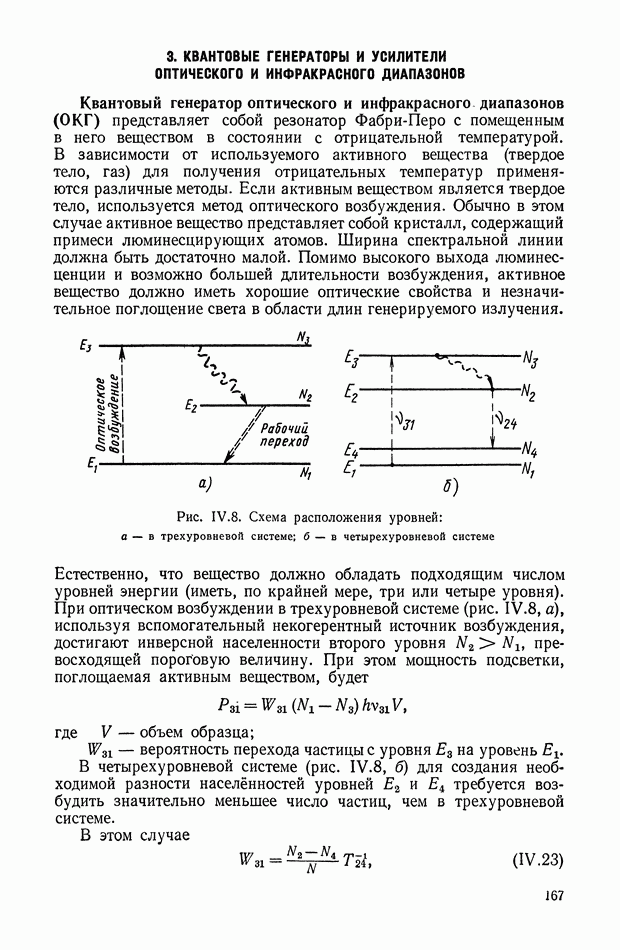
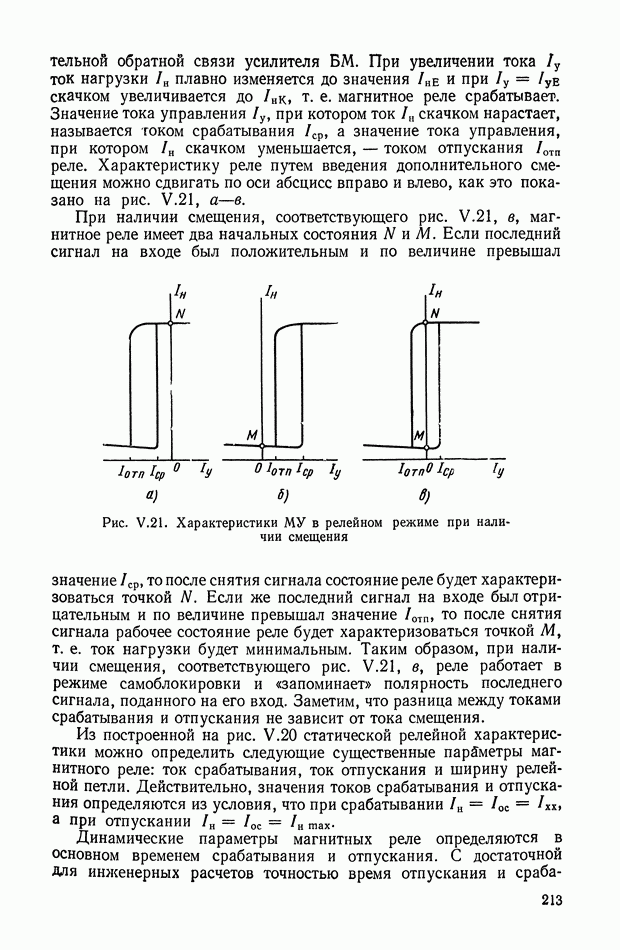
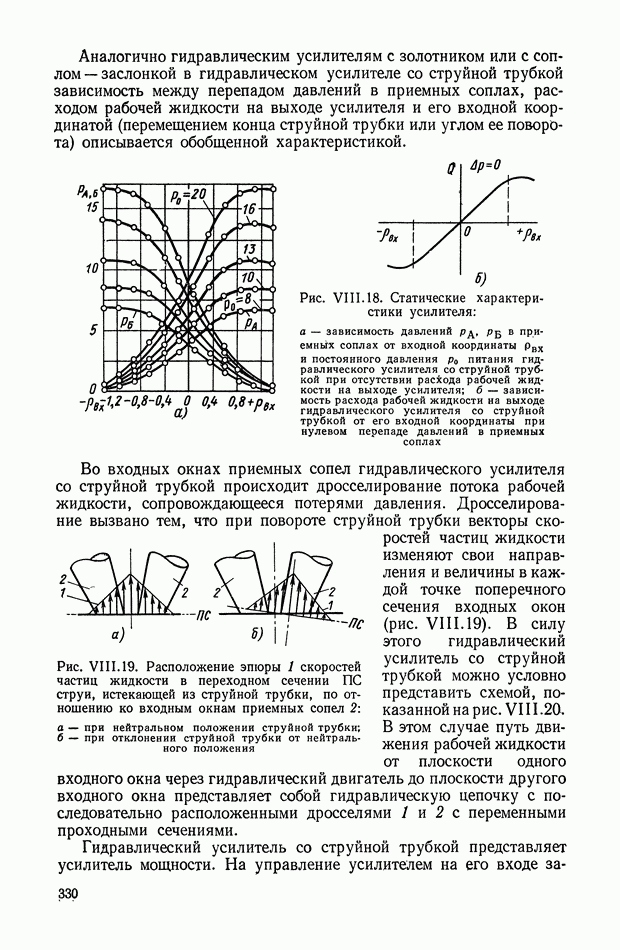
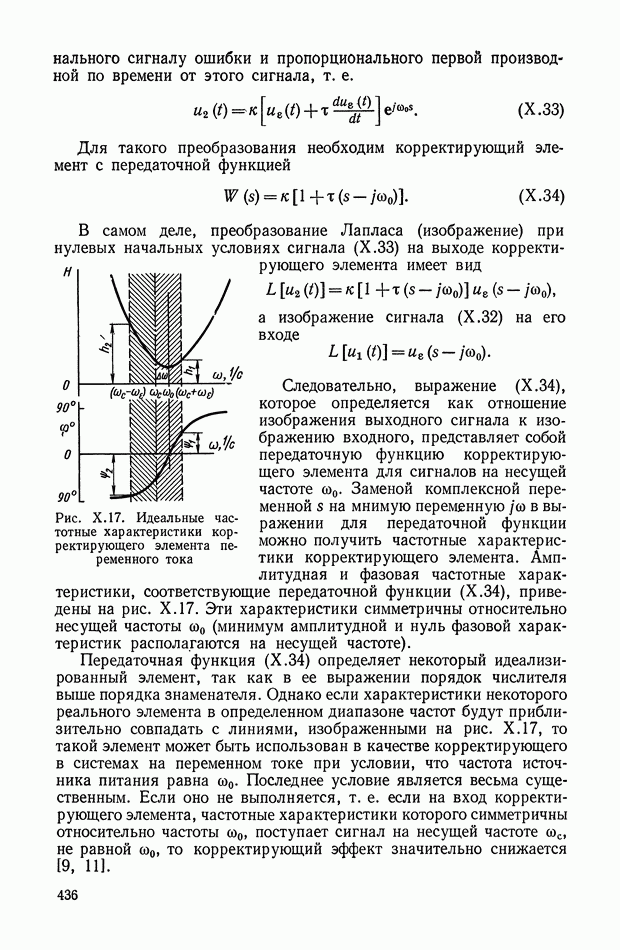
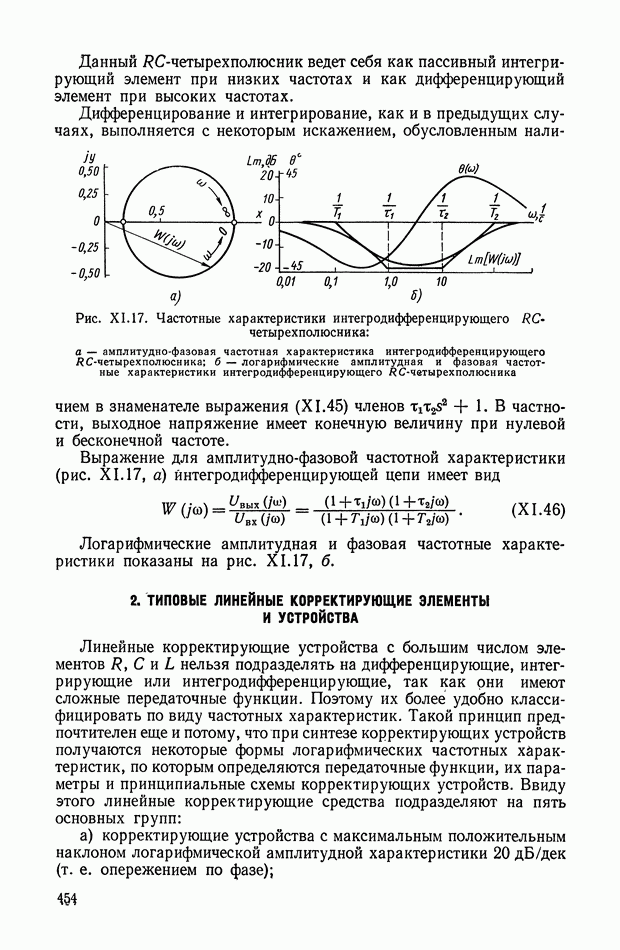
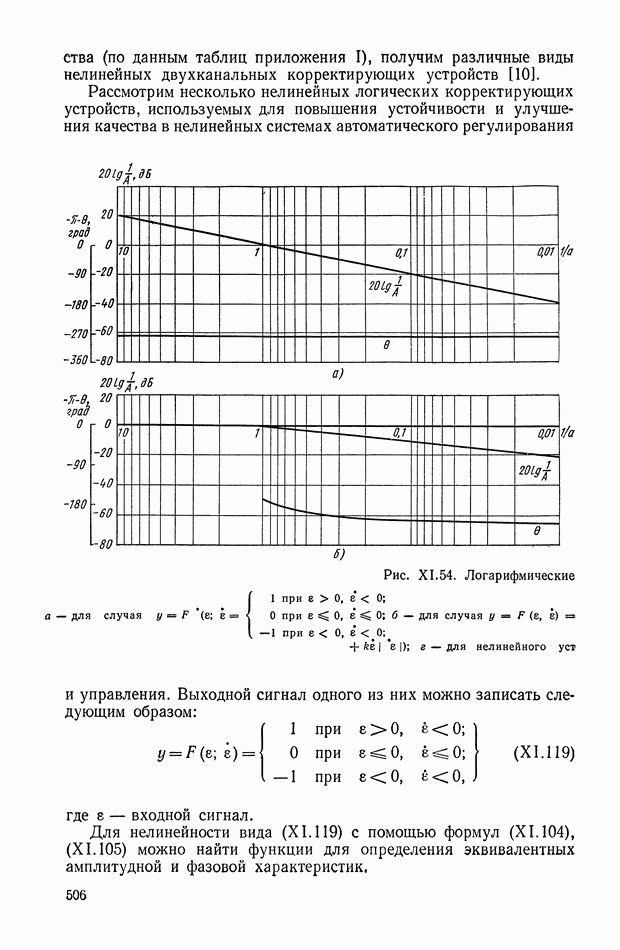
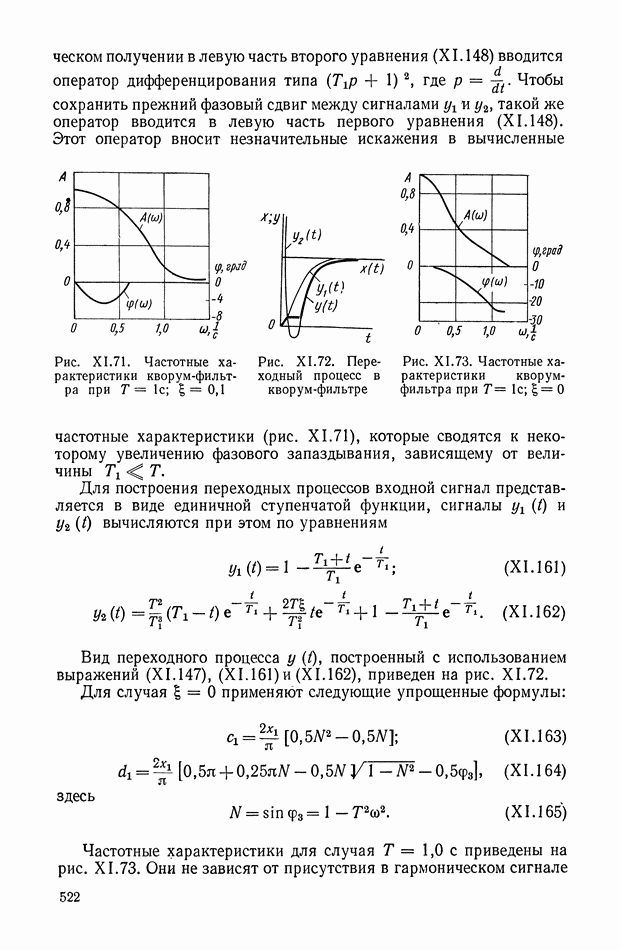
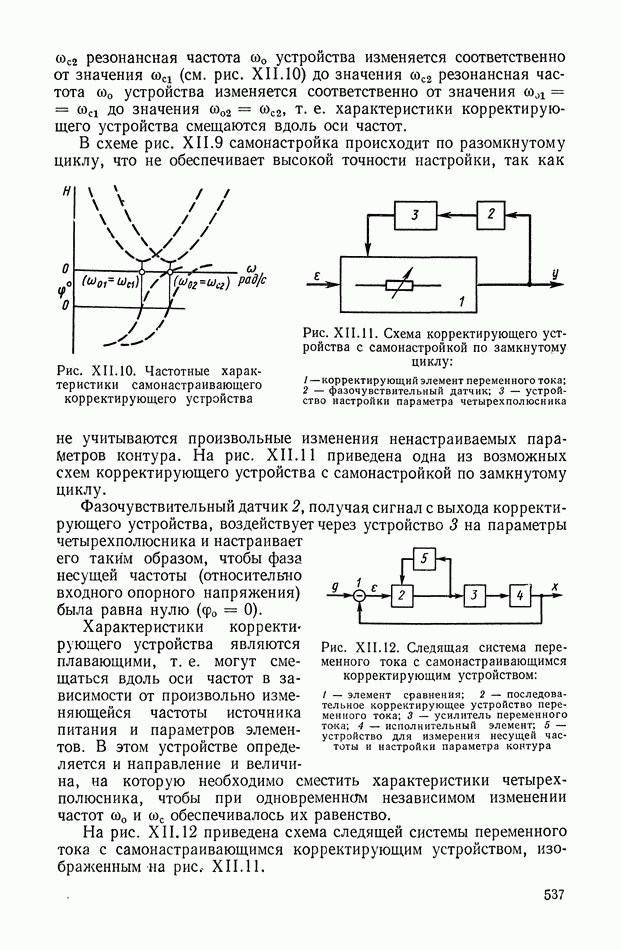
На рис. VI.2. приведена характеристика холостого хода ЭМУ с независимым возбуждением, представляющая собой зависимость э. д. с. на выходе Евых от напряжения  на управляющей обмотке в установившемся состоянии. При этом гистерезисная петля характеристики холостого хода ЭМУ заменена кривой средних значений э. д. с. при прямом и обратном намагничивании и не учтена также нелинейность характеристики холостого хода при малых значениях
на управляющей обмотке в установившемся состоянии. При этом гистерезисная петля характеристики холостого хода ЭМУ заменена кривой средних значений э. д. с. при прямом и обратном намагничивании и не учтена также нелинейность характеристики холостого хода при малых значениях 

Рис. VI. 1. Принципиальная схема ЭМУ с независимым возбуждением

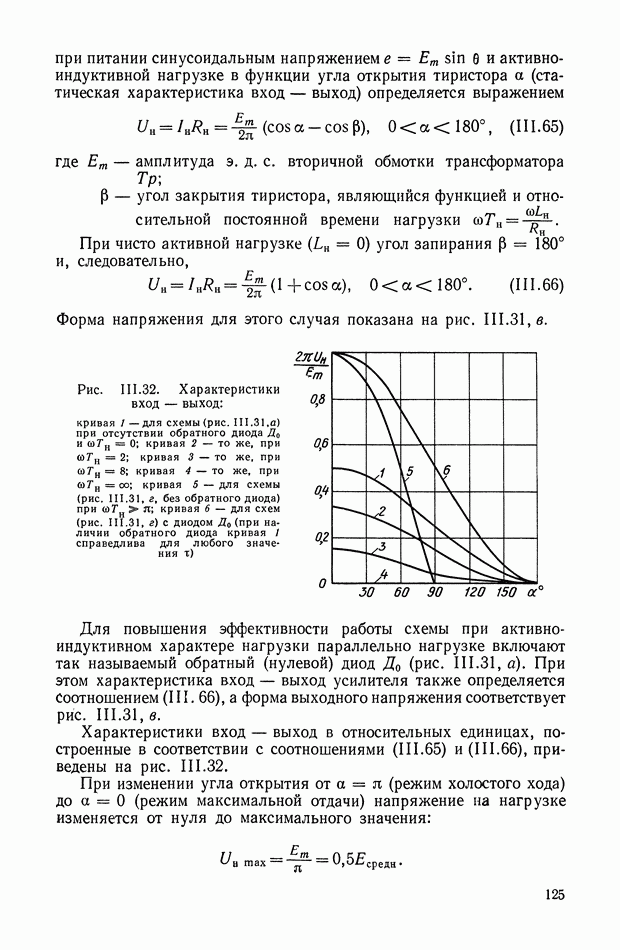
Рис. VI.2. Характеристика холостого хода ЭМУ с независимым возбуждением
При принятых упрощениях характеристика холостого хода на некотором интервале  является линейной. Номинальная величина напряжения
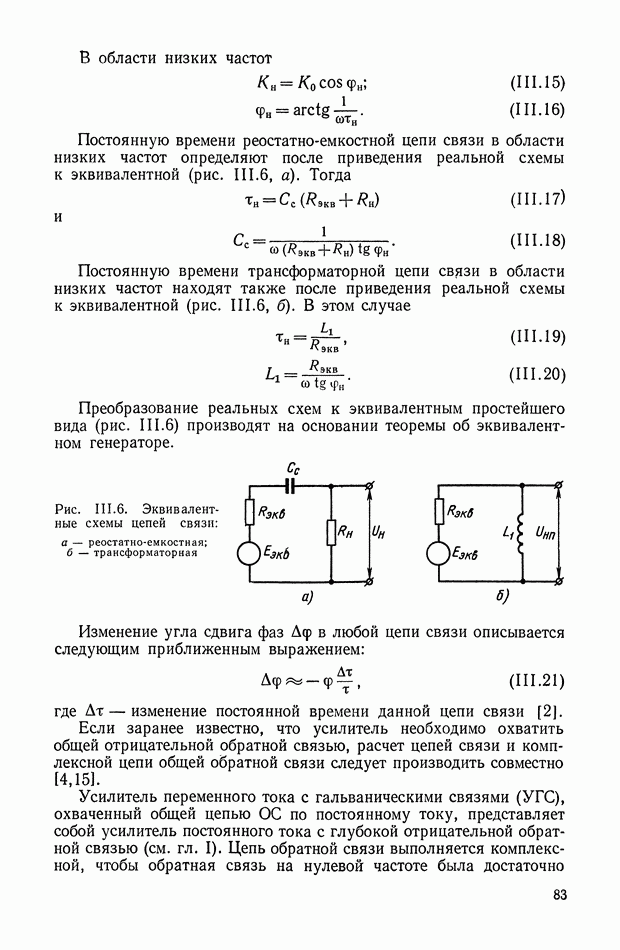
является линейной. Номинальная величина напряжения  устанавливается так, что
устанавливается так, что

и в этом случае можно принять

где  — установившееся значение напряжения на выходе ЭМУ (э. д. с. на щетках ЭМУ);
— установившееся значение напряжения на выходе ЭМУ (э. д. с. на щетках ЭМУ);
 — ток в цепи управления;
— ток в цепи управления;
 — скорость вращения якоря;
— скорость вращения якоря;
 — коэффициент взаимной индукции между обмоткой управления и цепью якоря;
— коэффициент взаимной индукции между обмоткой управления и цепью якоря;  — активное сопротивление цепи управления.
— активное сопротивление цепи управления.
Величина передаточного коэффициента усилителя, как это следует из формулы (VI.2),

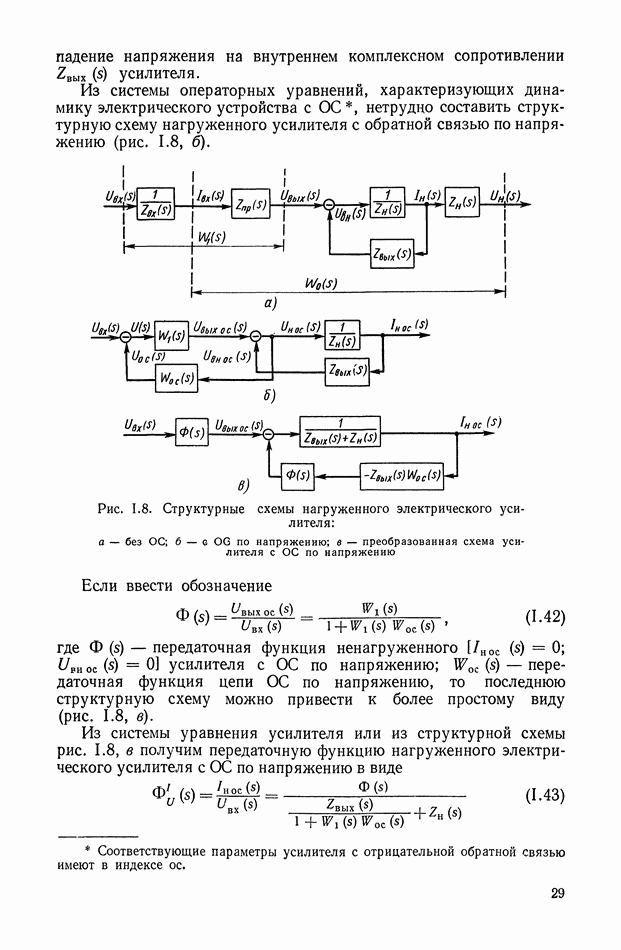
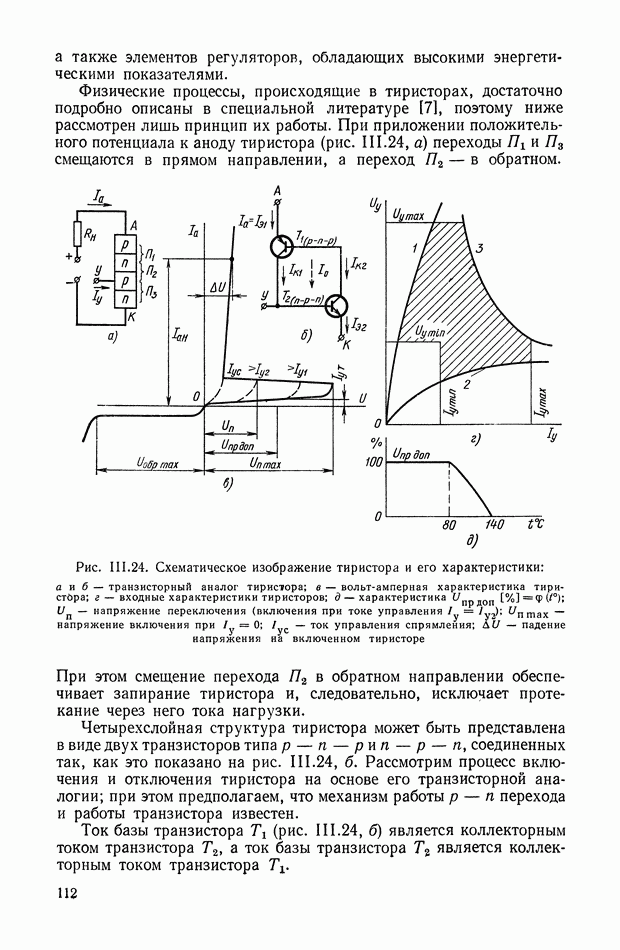
Передаточную функцию ЭМУ с независимым возбуждением можно определить, записав уравнения, устанавливающие зависимость выходной величины усилителя от входной величины. В этой зависимости должно найти свое отражение явление гистерезиса,
вихревые токи в железных частях машины, реакция якоря, коммутационные токи и сдвиг щеток с магнитной нейтрали. Существенное влияние будет оказывать также и то, какую нагрузку имеет ЭМУ, т. е. чисто активную, индуктивную, емкостную или их определенные комбинации.
Рассмотрим динамические характеристики ЭМУ с независимым возбуждением. При этом будет рассматривать так называемый идеальный ЭМУ, у которого отсутствуют вихревые и коммутационные токи и явление гистерезиса, а магнитная система настолько ненасыщена, что зависимость между магнитными потоками и наводимыми ими э. д. с. линейна.
Для случая холостого хода, т. е. когда нагрузка ЭМУ отключена (рис. VI. 1), справедливы следующие уравнения:

где  — соответственно напряжение, ток, активное сопротивление и коэффициент индуктивности обмотки управления ЭМУ.
— соответственно напряжение, ток, активное сопротивление и коэффициент индуктивности обмотки управления ЭМУ.

Рис. VI.3. Схема соединения ЭМУ и исполнительного электродвигателя постоянного тока при управлении со стороны якоря
Передаточная функция идеального ЭМУ при холостом ходе имеет вид

где

В случае нагруженного ЭМУ справедливы как уравнения (VI.4), так и уравнение

где  — соответственно ток и напряжение нагрузки;
— соответственно ток и напряжение нагрузки;
 — соответственно активное сопротивление и коэффициент индуктивности якорной цепи ЭМУ.
— соответственно активное сопротивление и коэффициент индуктивности якорной цепи ЭМУ.
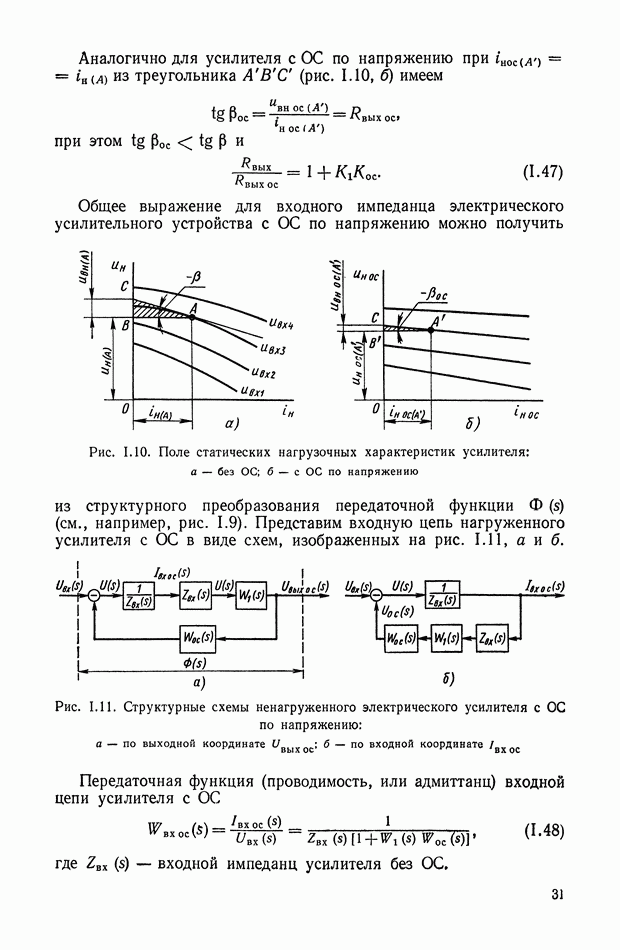
В частном случае, когда нагрузкой ЭМУ является электродвигатель постоянного тока (рис. VI.3), справедливы уравнения

где  соответственно активное сопротивление, коэффициент индуктивности и угол поворота вала исполнительного электродвигателя;
соответственно активное сопротивление, коэффициент индуктивности и угол поворота вала исполнительного электродвигателя;
 — коэффициент противо-э. д. с. электродвигателя;
— коэффициент противо-э. д. с. электродвигателя;
 — коэффициент пропорциональности между током
— коэффициент пропорциональности между током  и моментом, развиваемым электродвигателем;
и моментом, развиваемым электродвигателем;
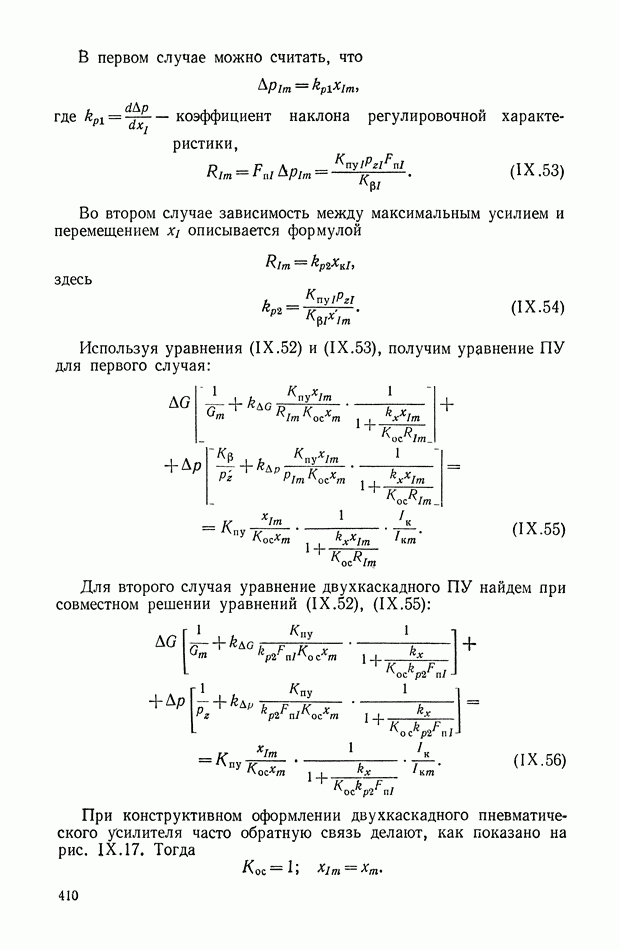
 — момент инерции вращающихся масс электродвигателя (нагрузка предполагается чисто инерционной).
— момент инерции вращающихся масс электродвигателя (нагрузка предполагается чисто инерционной).
Передаточная функция нагруженного идеального ЭМУ с независимым возбуждением имеет вид

где  — соответственно электрическая и электромеханическая постоянные времени цепи якоря
— соответственно электрическая и электромеханическая постоянные времени цепи якоря

 — передаточный коэффициент ЭМУ — электродвигатель,
— передаточный коэффициент ЭМУ — электродвигатель,

Для увеличения передаточного коэффициента и уменьшения постоянной времени ЭМУ с независимым возбуждением производят следующее:
1) магнитные системы ЭМУ выполняют шихтованными из листовой стали;
2) снижают число витков в секциях якоря (увеличивают число коллекторных пластин);
3) уменьшают отношение длины якоря к его диаметру.
Перечисленные мероприятия ослабляют демпфирующее действие вихревых токов и уменьшают э. д. с. в коммутирующих секциях якоря ЭМУ. Помимо этого, ЭМУ с независимым возбуждением имеет еще дополнительные полюса и обмотки, улучшающие коммутацию. И, наконец, ЭМУ работает обычно в таком режиме, что магнитная система является ненасыщенной.
Но даже с учетом всех этих мероприятий передаточный коэффициент по мощности такого ЭМУ равен лишь 20—100, а постоянная времени все так же велика.
ЭМУ с самовозбуждением. Усилители с самовозбуждением позволяют получить значительно большие коэффициенты усиления, нежели это возможно в случае ЭМУ с независимым возбуждением.
По принципу устройства и работы ЭМУ с самовозбуждением аналогичен генератору постоянного тока с самовозбуждением обычного исполнения. Отличается он от него по тем же самым признакам, по каким отличается ЭМУ с независимым возбуждением от генератора постоянного тока обычного исполнения,
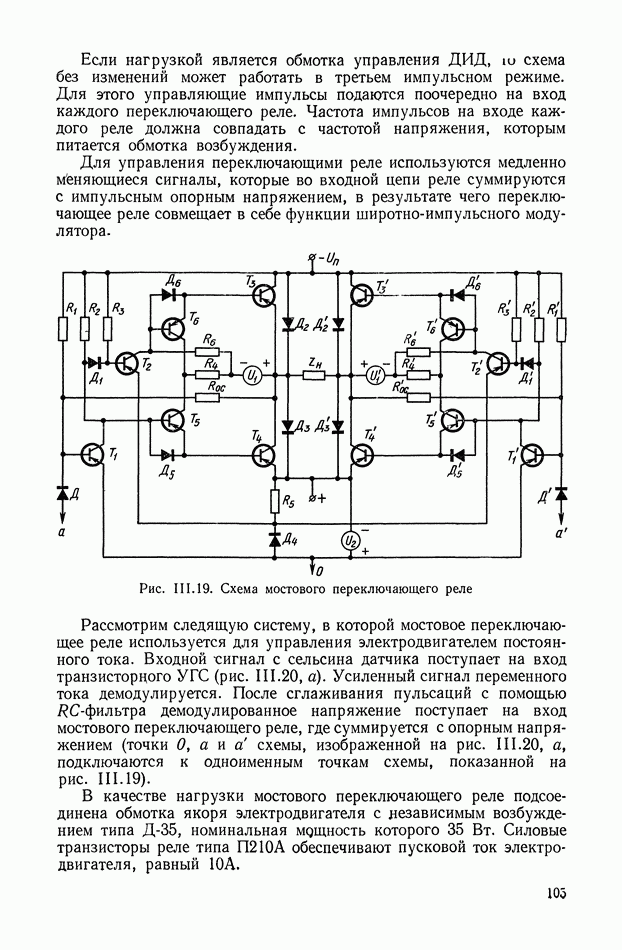
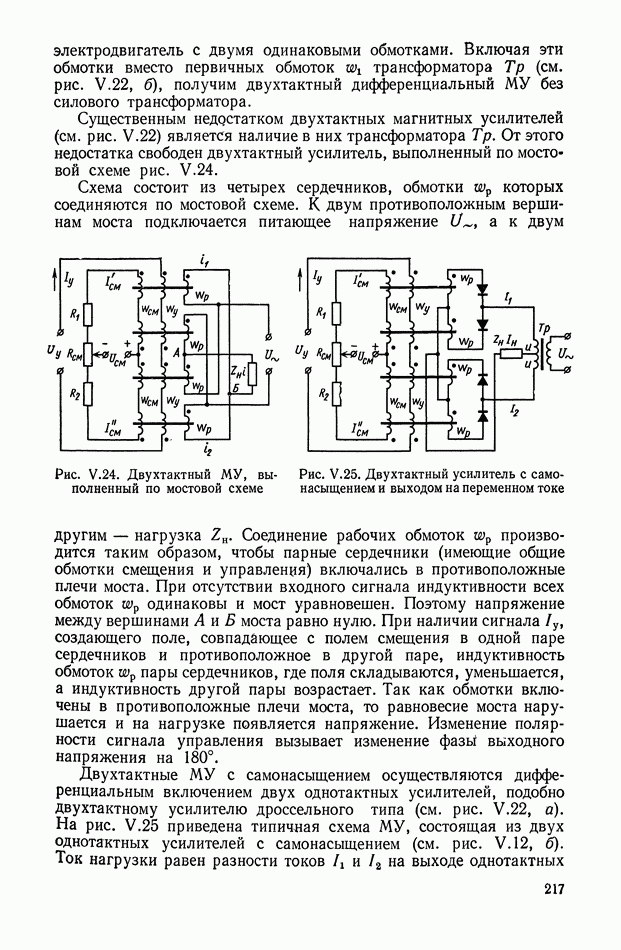
В ЭМУ с самовозбуждением обмотка самовозбуждения по отношению к нагрузке ЭМУ может быть включена параллельно, последовательно и иметь смешанное включение.
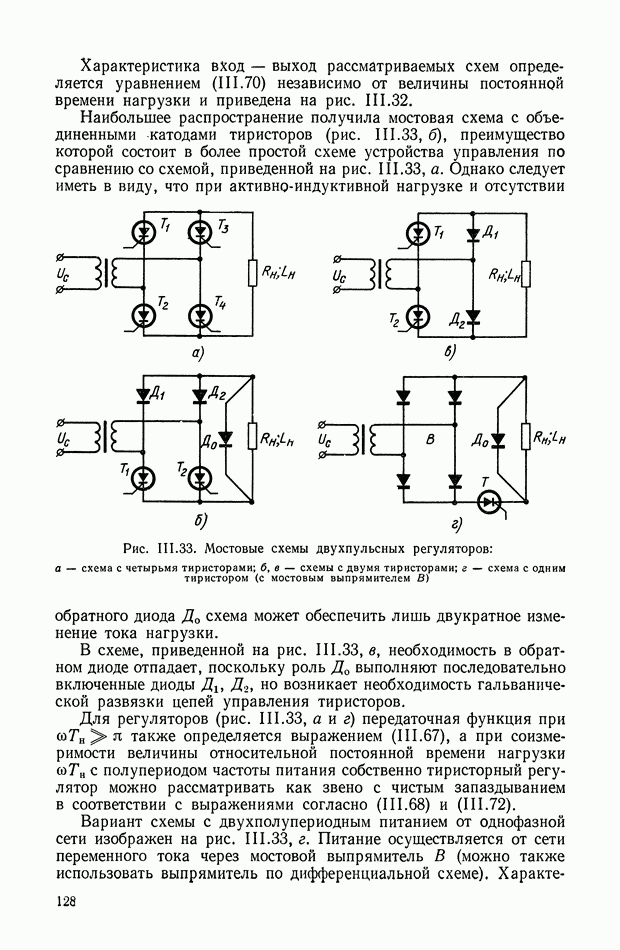
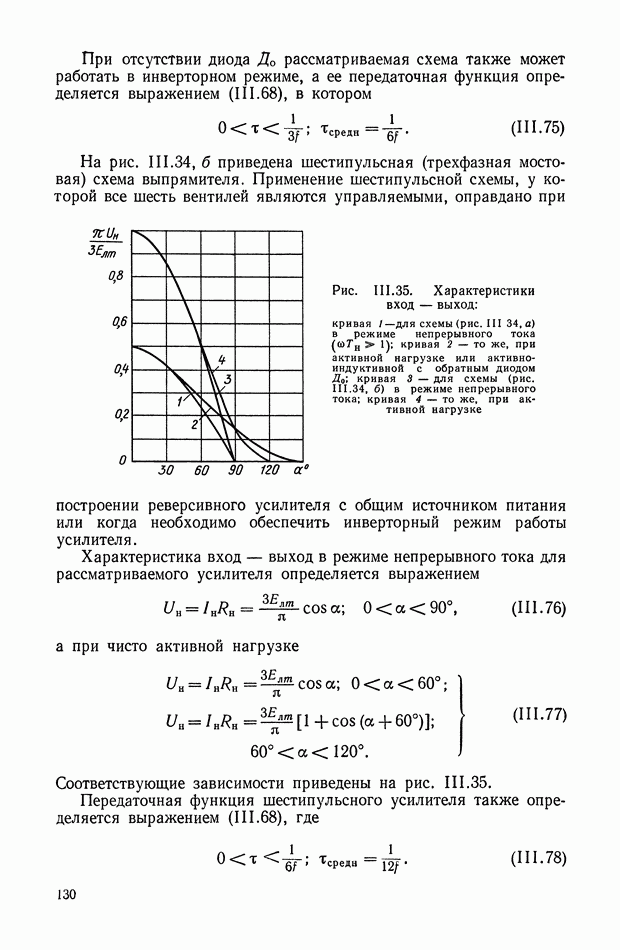
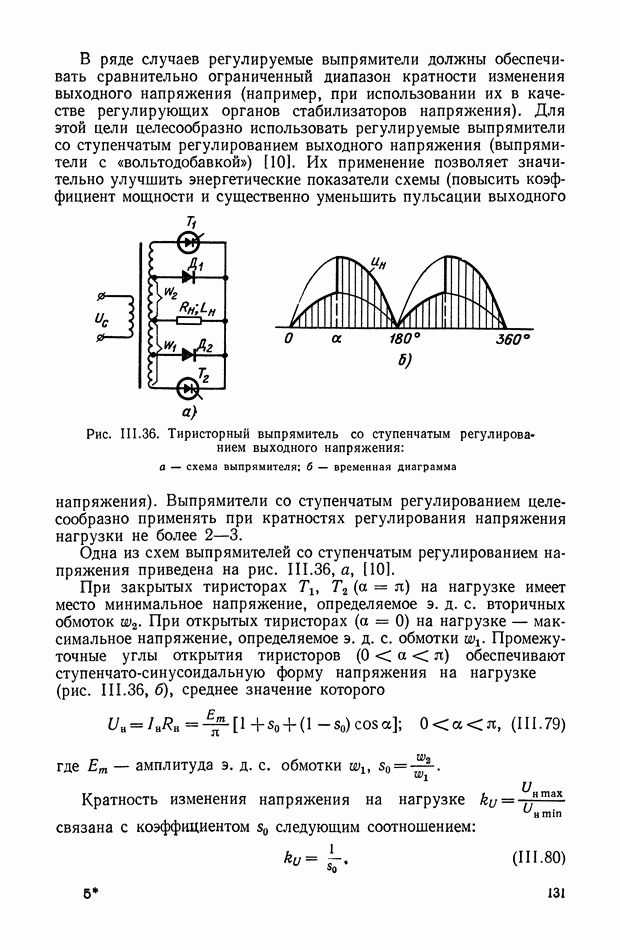
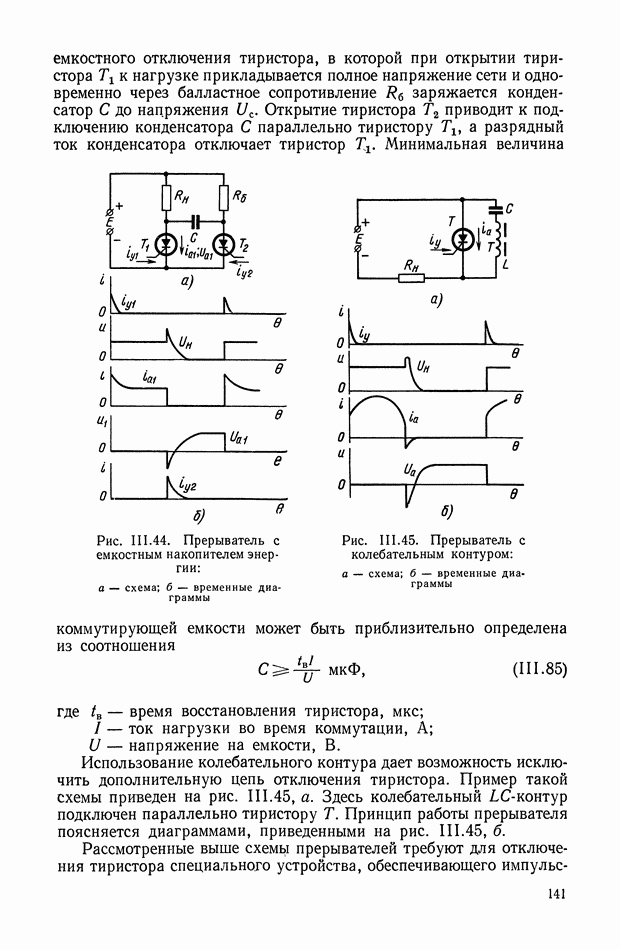
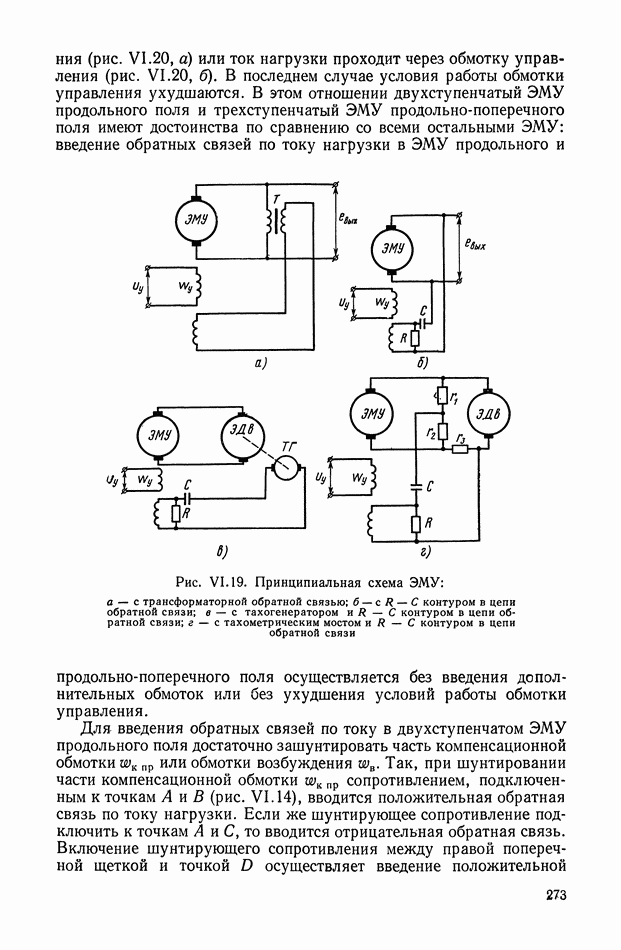
На рис. VI.4, VI.5, VI.6 приведены принципиальные схемы ЭМУ с параллельным, последовательным и смешанным включением обмоток самовозбуждения ЭМУ. По принципу работы все три ЭМУ с самовозбуждением одинаковы. Каждый из усилителей имеет цепь положительной обратной связи, за счет чего и удается получить сравнительно высокие коэффициенты усиления.

Рис. VI.4. Схема ЭМУ с параллельным включением обмотки самовозбуждения

Рис. VI. 5. Схема ЭМУ с последовательным включением обмотки самовозбуждения

Рис. VI.6. Схема ЭМУ со смешанным включением обмоток самовозбуждения
Рассмотрим режим холостого хода. Вполне очевидно, что ЭМУ с последовательным самовозбуждением в режиме холостого хода идентичен ЭМУ с независимым возбуждением. Поэтому передаточная функция, величина передаточного коэффициента и постоянная времени ЭМУ с последовательным самовозбуждением будет определяться согласно уравнениям, полученным ранее для ЭМУ с независимым возбуждением.
В режиме холостого хода ЭМУ с параллельным самовозбуждением и ЭМУ со смешанным самовозбуждением идентичны. Для них справедлива следующая система уравнений (рассматривается идеальный ЭМУ):

где  — соответственно активное сопротивление и постоянная времени цепи якоря
— соответственно активное сопротивление и постоянная времени цепи якоря 
 — индуктивность обмотки самовозбуждения;
— индуктивность обмотки самовозбуждения;
 — э. д. с., наводимая в цепи якоря;
— э. д. с., наводимая в цепи якоря;
 — коэффициенты взаимной индукции между обмотками: управления и самовозбуждения, управления и якоря, самовозбуждения и якоря соответственно.
— коэффициенты взаимной индукции между обмотками: управления и самовозбуждения, управления и якоря, самовозбуждения и якоря соответственно.
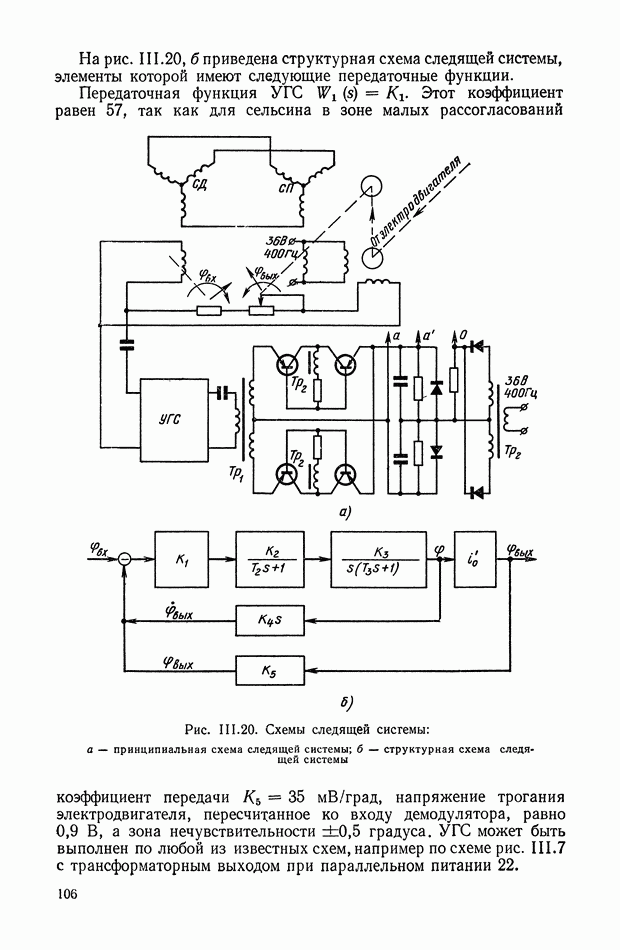
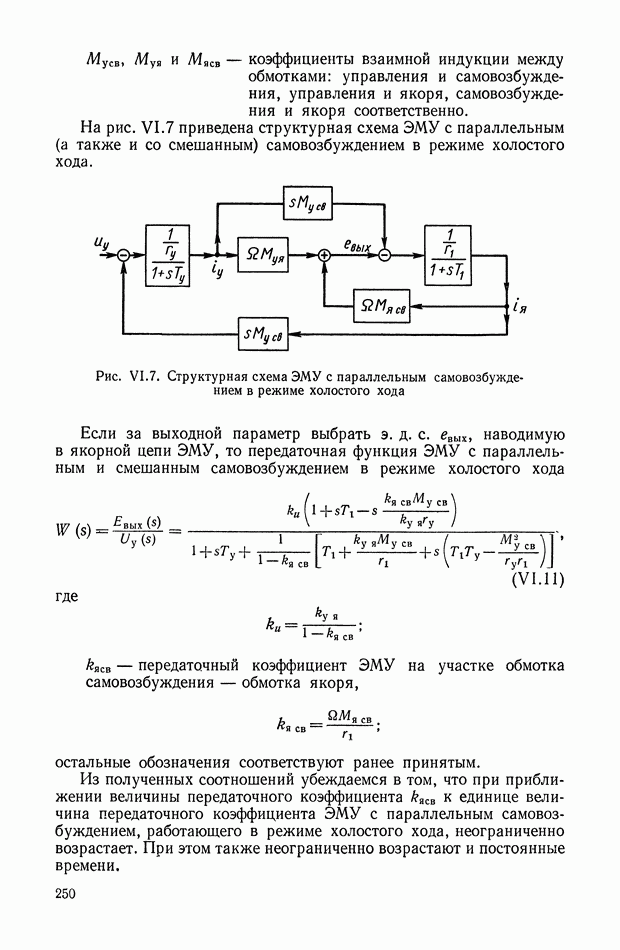
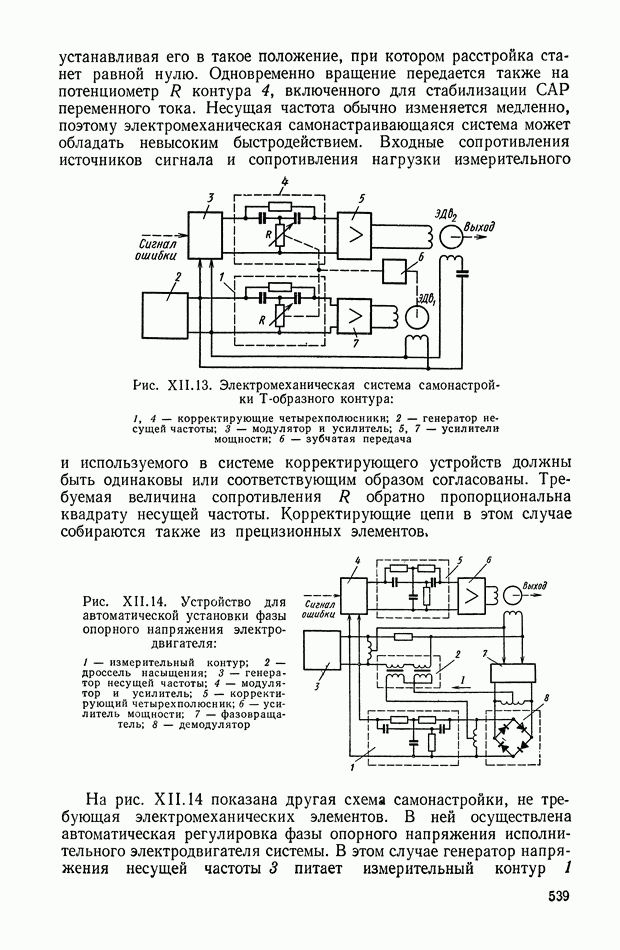
На рис. VI.7 приведена структурная схема ЭМУ с параллельным (а также и со смешанным) самовозбуждением в режиме холостого хода.

Рис. VI.7. Структурная схема ЭМУ с параллельным самовозбуждением в режиме холостого хода
Если за выходной параметр выбрать э. д. с. евых, наводимую в якорной цепи ЭМУ, то передаточная функция ЭМУ с параллельным и смешанным самовозбуждением в режиме холостого хода

где

 — передаточный коэффициент ЭМУ на участке обмотка самовозбуждения — обмотка якоря,
— передаточный коэффициент ЭМУ на участке обмотка самовозбуждения — обмотка якоря,

остальные обозначения соответствуют ранее принятым.
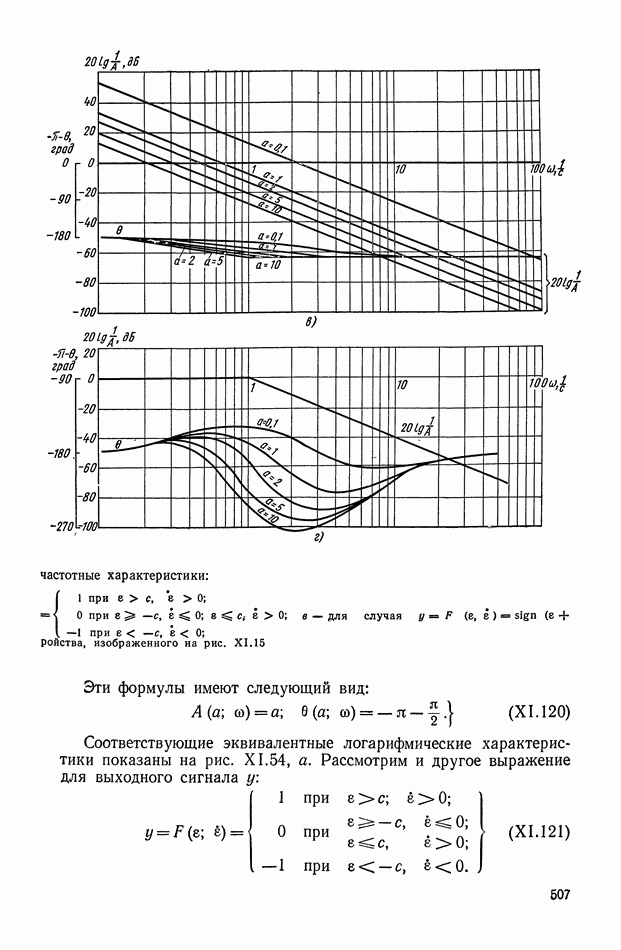
Из полученных соотношений убеждаемся в том, что при приближении величины передаточного коэффициента  к единице величина передаточного коэффициента ЭМУ с параллельным самовозбуждением, работающего в режиме холостого хода, неограниченно возрастает. При этом также неограниченно возрастают и постоянные времени.
к единице величина передаточного коэффициента ЭМУ с параллельным самовозбуждением, работающего в режиме холостого хода, неограниченно возрастает. При этом также неограниченно возрастают и постоянные времени.
При наличии нагрузки (электродвигатель постоянного тока с независимым возбуждением) процессы, имеющие место в системе идеальной ЭМУ с параллельным самовозбуждением — электродвигатель, можно исследовать, решив следующую систему уравнений (рис. VI.4):

где

 — соответственно коэффициент индуктивности и активное сопротивление обмотки самовозбуждения; остальные обозначения соответствуют ранее принятым.
— соответственно коэффициент индуктивности и активное сопротивление обмотки самовозбуждения; остальные обозначения соответствуют ранее принятым.
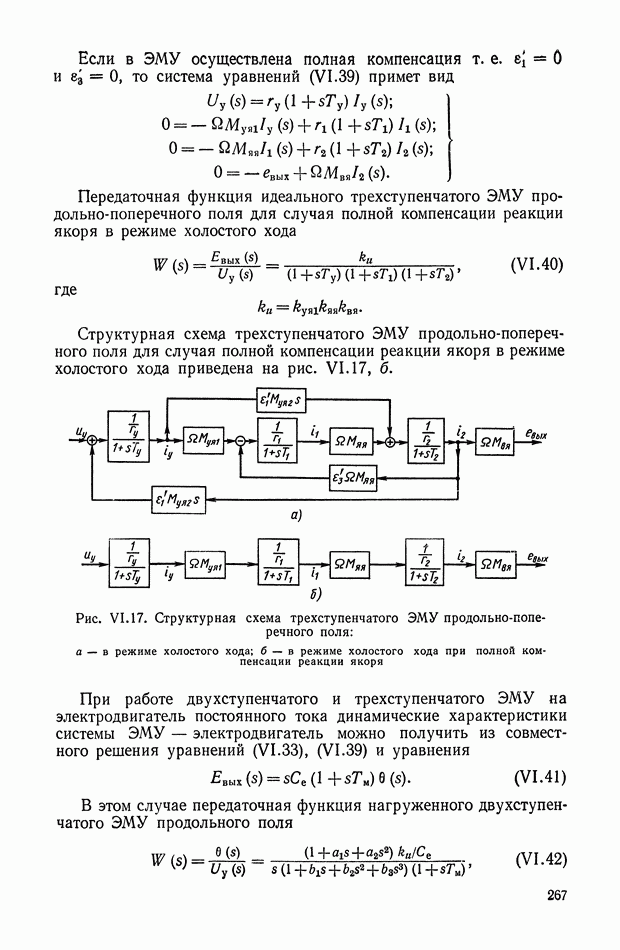
Выражение для передаточной функции нагруженного идеального ЭМУ с параллельным самовозбуждением несколько громоздко, поэтому целесообразно его представить в виде

Коэффициенты  определяются на основании уравнений (VI. 12). Здесь лишь отметим следующее:
определяются на основании уравнений (VI. 12). Здесь лишь отметим следующее:
1) величина передаточного коэффициента нагруженного идеального ЭМУ с параллельным самовозбуждением

2) величина коэффициента

где

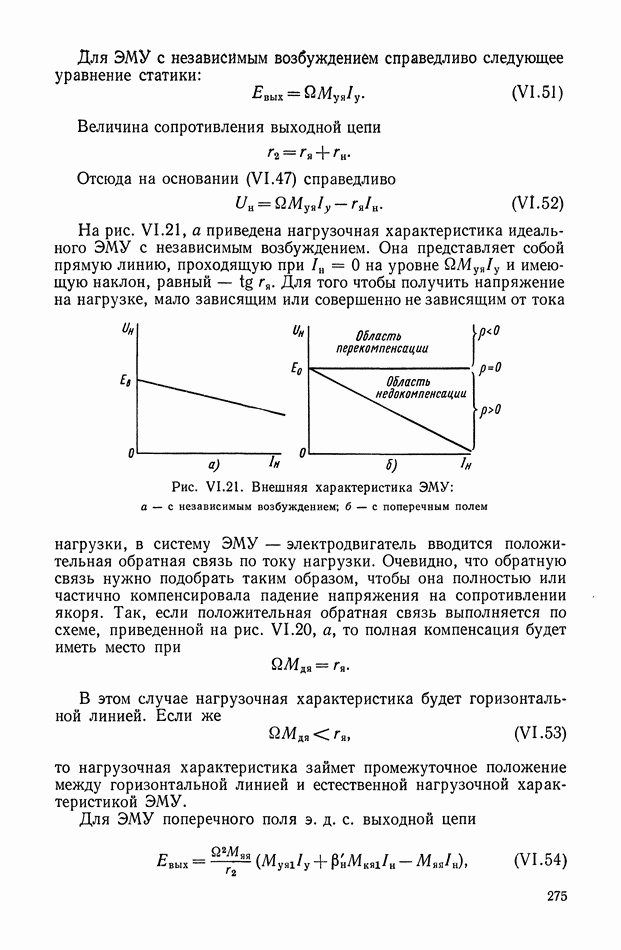
На основании выражений (VI. 14) и (VI. 15) можно сделать вывод, что при стремлении  к единице величина передаточного коэффициента нагруженного идеального ЭМУ с параллельным самовозбуждением безгранично возрастает, но при этом безгранично возрастает и инерционность ЭМУ. Наиболее широкое практическое применение нашли ЭМУ с параллельным самовозбуждением; ЭМУ с последовательным самовозбуждением применяется
к единице величина передаточного коэффициента нагруженного идеального ЭМУ с параллельным самовозбуждением безгранично возрастает, но при этом безгранично возрастает и инерционность ЭМУ. Наиболее широкое практическое применение нашли ЭМУ с параллельным самовозбуждением; ЭМУ с последовательным самовозбуждением применяется
весьма редко. Это объясняется тем, что в ЭМУ с последовательным самовозбуждением положительная обратная связь, создаваемая обмоткой самовозбуждения, зависит от нагрузки. Этот тип ЭМУ может применяться, если ЭМУ работает на постоянную нагрузку.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА САР
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ЛИНЕЙНЫХ УСИЛИТЕЛЬНЫХ УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ УСИЛИТЕЛЬНОГО УСТРОЙСТВА БЕЗ ОБРАТНОЙ СВЯЗИ
- 3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ, СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ОСОБЕННОСТИ УСИЛИТЕЛЬНОГО УСТРОЙСТВА С ОБРАТНОЙ СВЯЗЬЮ
- 4. КЛАССИФИКАЦИЯ И СВОЙСТВА УСИЛИТЕЛЬНЫХ УСТРОЙСТВ С ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 5. ВЫБОР И РАСЧЕТ УСИЛИТЕЛЬНОГО УСТРОЙСТВА
- ГЛАВА II. ЭЛЕКТРОННЫЕ ЛАМПОВЫЕ И ИОННЫЕ УСИЛИТЕЛИ
- 1. ОСНОВЫ ТОПОЛОГИЧЕСКОГО АНАЛИЗА СХЕМ ЛИНЕЙНЫХ ЭЛЕКТРОННЫХ ЛАМПОВЫХ УСИЛИТЕЛЕЙ
- 2. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПОСТОЯННОГО ТОКА
- 3. БАЛАНСНЫЕ МОСТОВЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- 4. СТАБИЛИЗАЦИЯ КОЭФФИЦИЕНТА УСИЛЕНИЯ
- 5. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- 6. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- 7. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
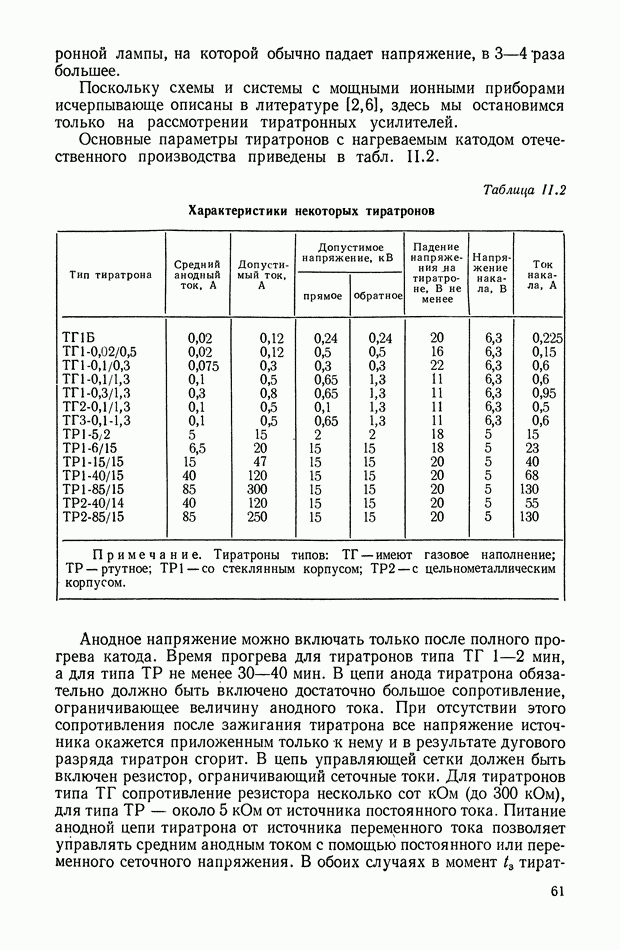
- 8. ОБЩИЕ СВОЙСТВА ИОННОГО (ТИРАТРОННОГО) УСИЛИТЕЛЯ МЕТОДЫ УПРАВЛЕНИЯ ТИРАТРОНОМ
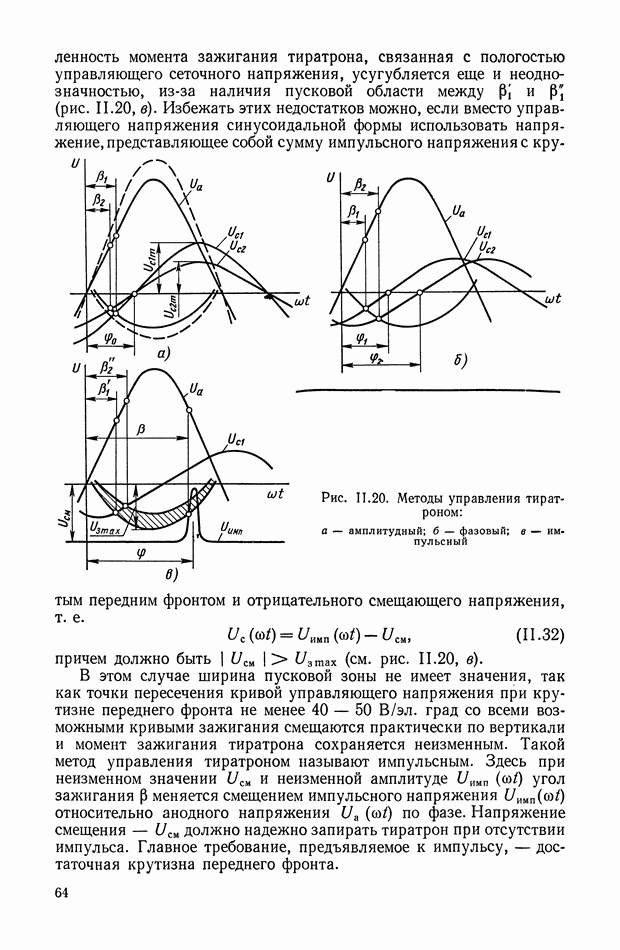
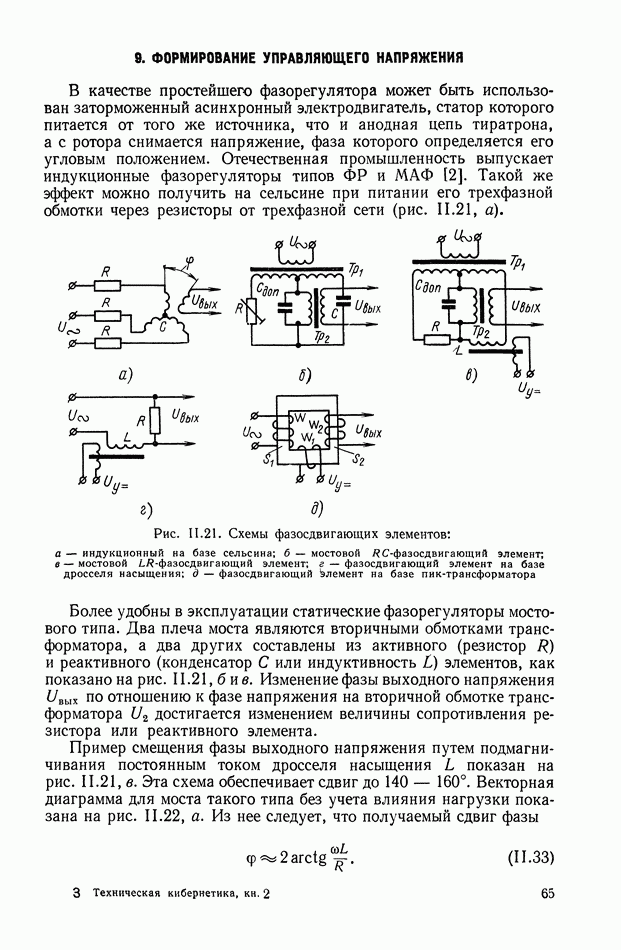
- 9. ФОРМИРОВАНИЕ УПРАВЛЯЮЩЕГО НАПРЯЖЕНИЯ
- 10. РАСЧЕТ ЭЛЕМЕНТОВ СХЕМ ТИРАТРОННОГО УСИЛИТЕЛЯ
- ГЛАВА III. ПОЛУПРОВОДНИКОВЫЕ И ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
- Цепи смещения.
- Цепи связи.
- 2. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ СРЕДНЕГО ЗНАЧЕНИЯ ТОКА
- Полупроводниковые демодуляторы.
- 3. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ В РЕЖИМЕ ПЕРЕКЛЮЧЕНИЯ
- Режимы импульсного регулирования мощности.
- Управление силовыми транзисторами.
- 4. ТРАНЗИСТОРНЫЕ УСТРОЙСТВА УПРАВЛЕНИЯ ЭЛЕКТРОДВИГАТЕЛЯМИ И ЭЛЕКТРОМАГНИТНЫМИ МЕХАНИЗМАМИ
- 5. ТИРИСТОРЫ. ХАРАКТЕРИСТИКИ, ПАРАМЕТРЫ И СВОЙСТВА
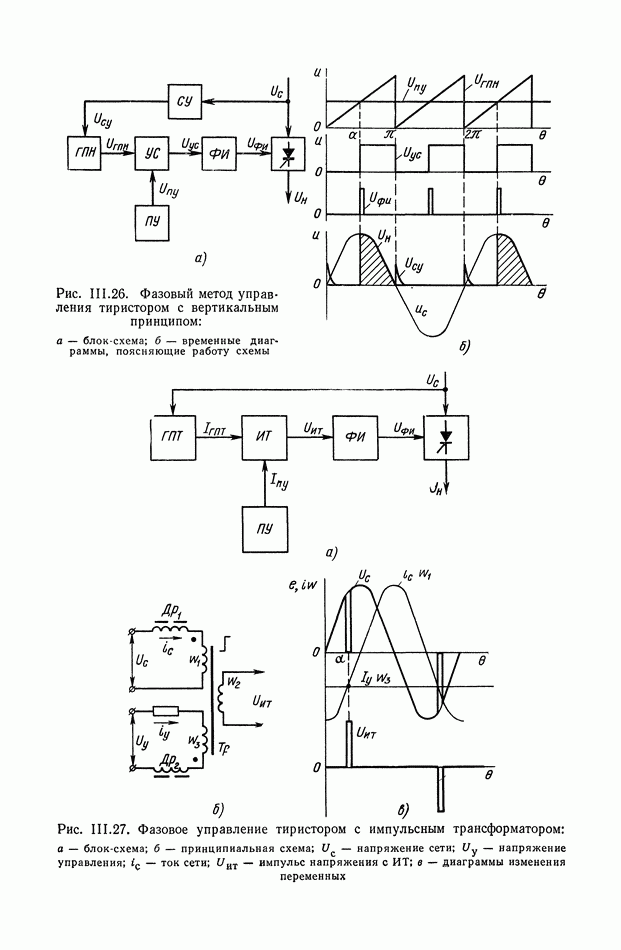
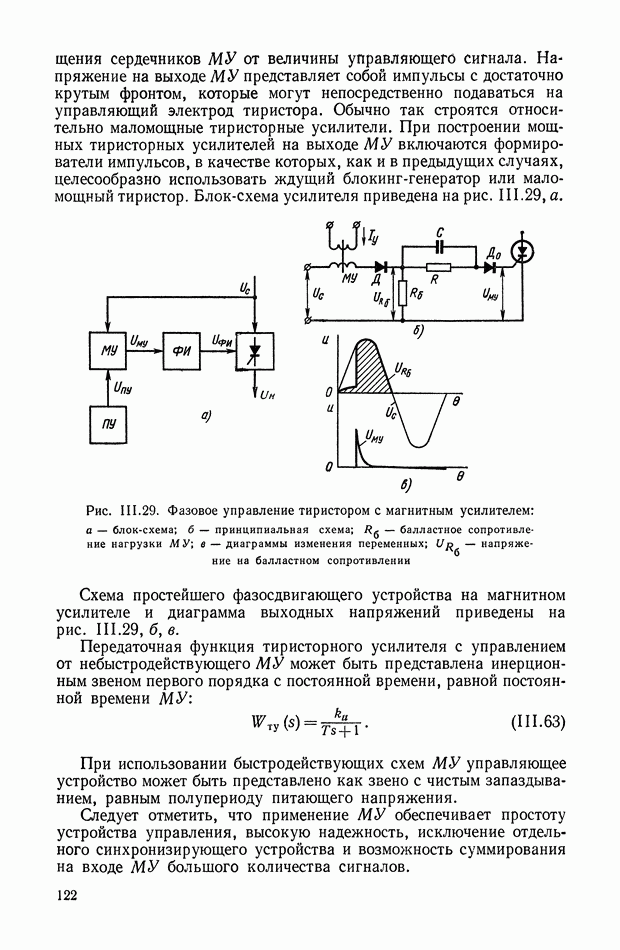
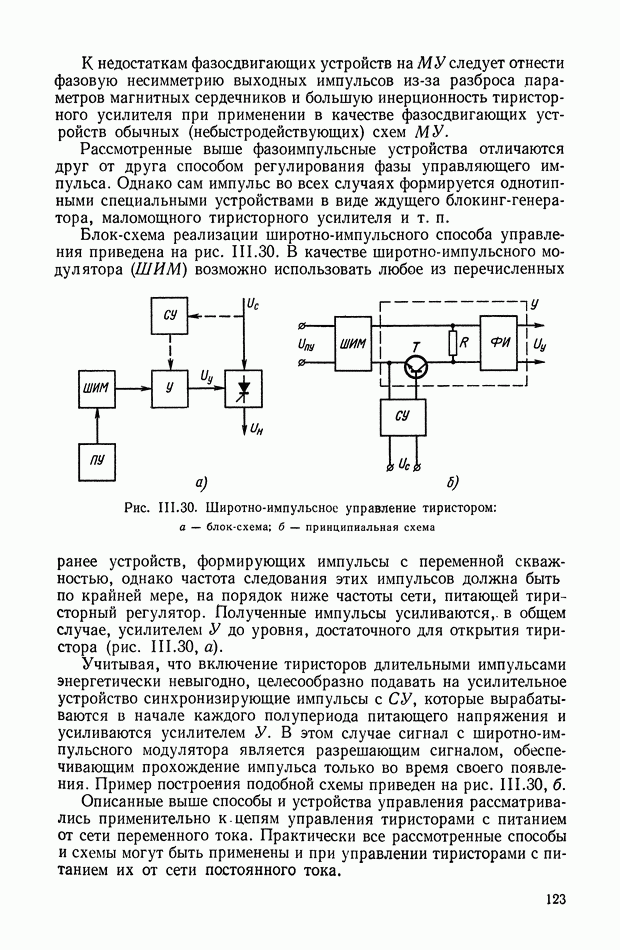
- 6. СПОСОБЫ И УСТРОЙСТВА УПРАВЛЕНИЯ ТИРИСТОРАМИ
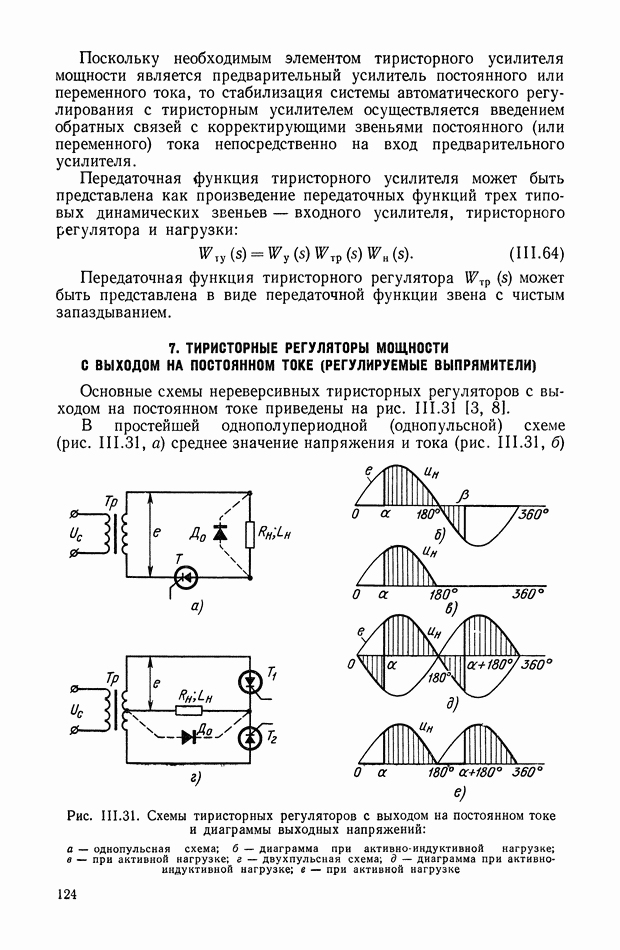
- 7. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ (РЕГУЛИРУЕМЫЕ ВЫПРЯМИТЕЛИ)
- 8. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 9. ТИРИСТОРНЫЕ УСИЛИТЕЛИ С ПИТАНИЕМ ОТ СЕТИ ПОСТОЯННОГО ТОКА
- 10. ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 11. ОСНОВЫ РАСЧЕТА ДИЭЛЕКТРИЧЕСКИХ УСИЛИТЕЛЕЙ
- ГЛАВА IV. КВАНТОВЫЕ УСИЛИТЕЛИ И ГЕНЕРАТОРЫ
- 2. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ РАДИОДИАПАЗОНА
- Квантовые усилители радиодиапазона.
- 3. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- Оптический квантовый усилитель
- 4. ПРИМЕНЕНИЕ В САР КВАНТОВЫХ УСИЛИТЕЛЕЙ И ГЕНЕРАТОРОВ РАДИОДИАПАЗОНА, ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- ГЛАВА V. МАГНИТНЫЕ И МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- 2. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ МАГНИТНЫХ УСИЛИТЕЛЕЙ
- 3. ОДНОТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ БЕЗ ОБРАТНОЙ СВЯЗИ (УПРАВЛЯЕМЫЕ ДРОССЕЛИ И ТРАНСФОРМАТОРЫ)
- 4. МАГНИТНЫЕ УСИЛИТЕЛИ С САМОНАСЫЩЕНИЕМ
- Релейный режим работы усилителей с самонасыщением.
- 5. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 6. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ
- 7. МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- ГЛАВА VI. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 2. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С НЕЗАВИСИМЫМ ВОЗБУЖДЕНИЕМ И С САМОВОЗБУЖДЕНИЕМ
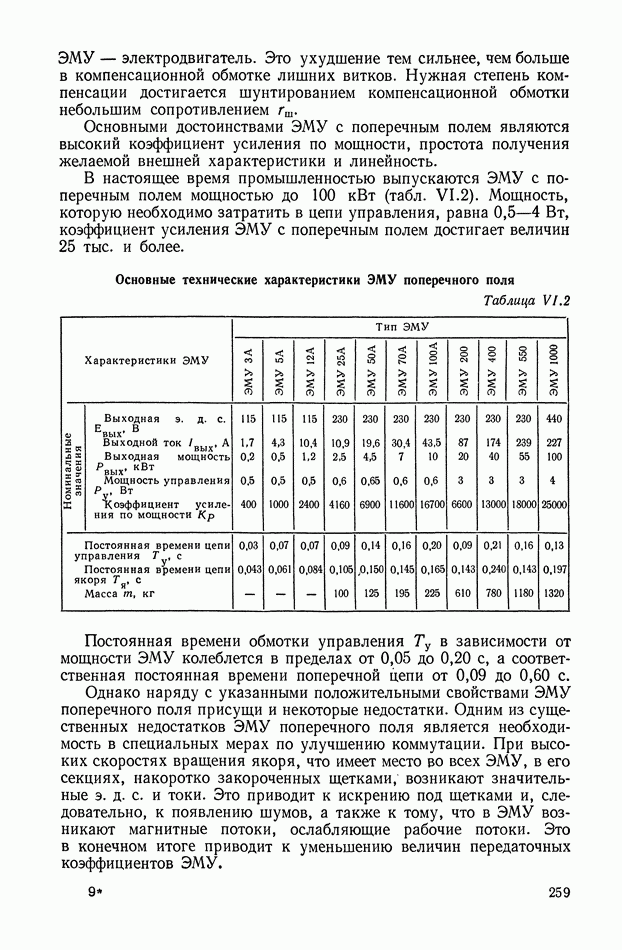
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С ПОПЕРЕЧНЫМ ПОЛЕМ
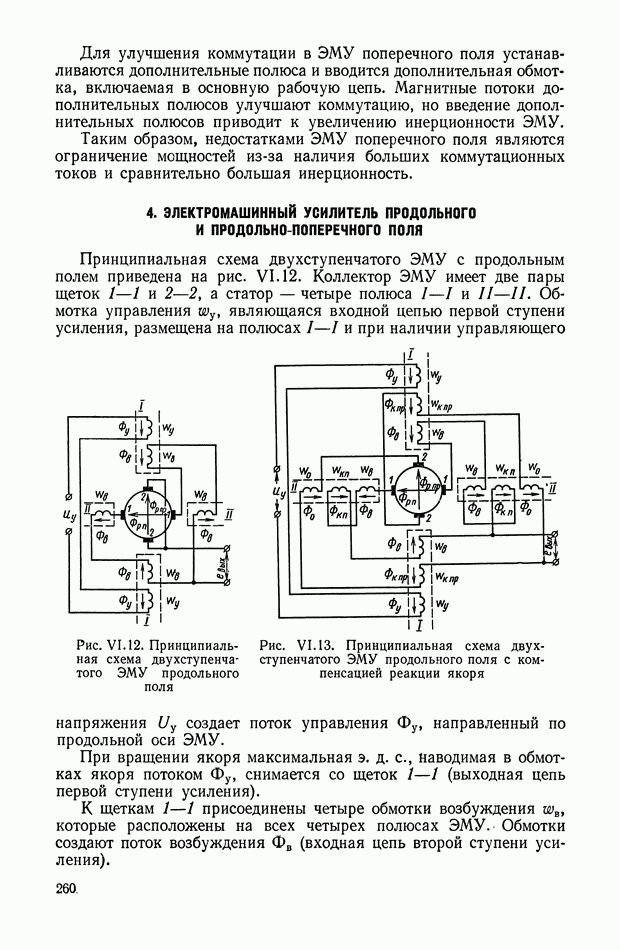
- 4. ЭЛЕКТРОМАШИННЫЙ УСИЛИТЕЛЬ ПРОДОЛЬНОГО И ПРОДОЛЬНО-ПОПЕРЕЧНОГО ПОЛЯ
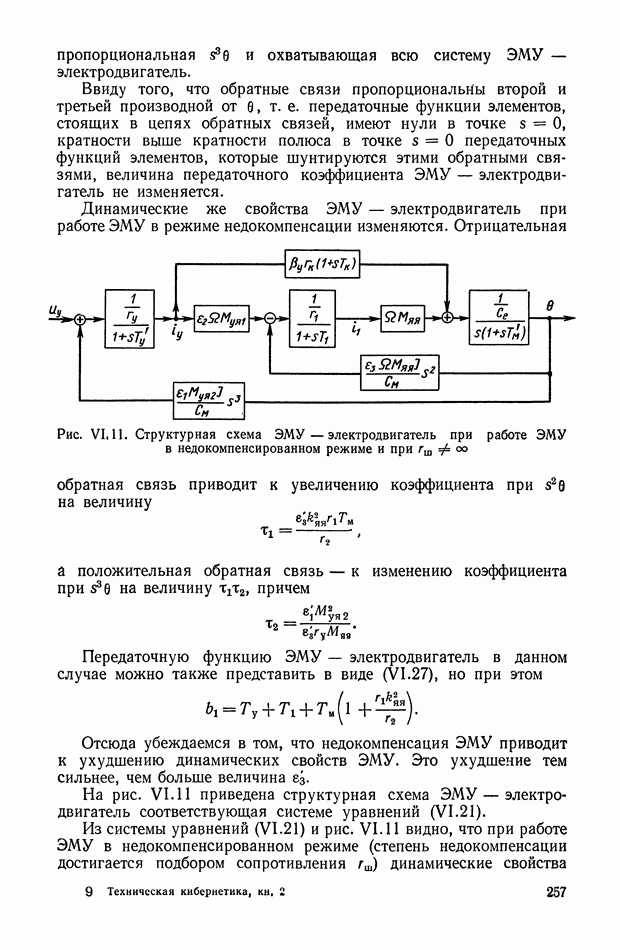
- 5. ВЛИЯНИЕ НА ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭМУ ВИХРЕВЫХ И КОММУТАЦИОННЫХ ТОКОВ, ГИСТЕРЕЗИСА И СДВИГА ЩЕТОК С НЕЙТРАЛИ
- 6. МЕТОДЫ УЛУЧШЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕКТРОМАШИННЫХ УСИЛИТЕЛЕЙ
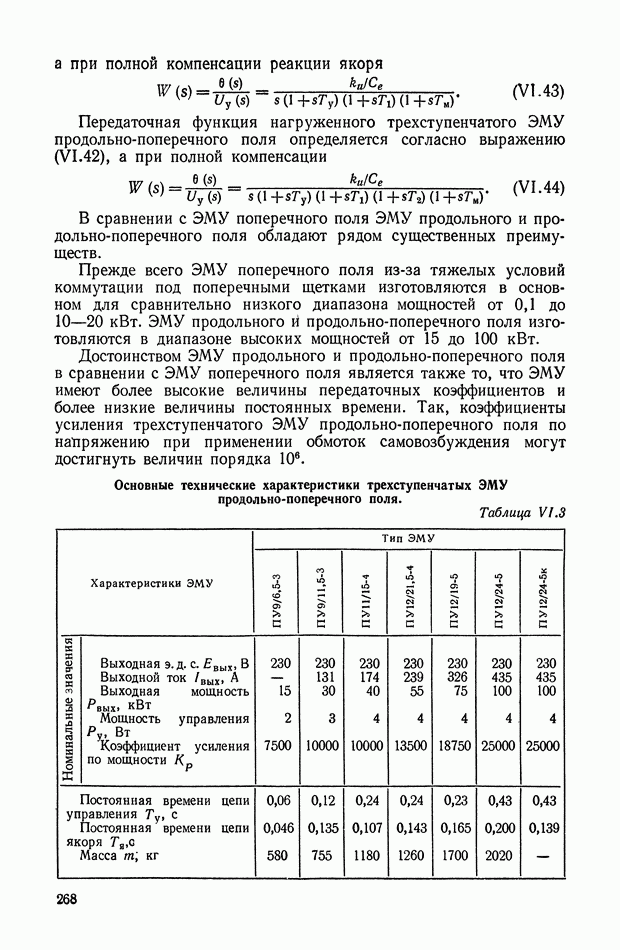
- 7. НАГРУЗОЧНАЯ ХАРАКТЕРИСТИКА ЭЛЕКТРОМАШИННОГО УСИЛИТЕЛЯ
- ГЛАВА VII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ УСИЛИТЕЛИ
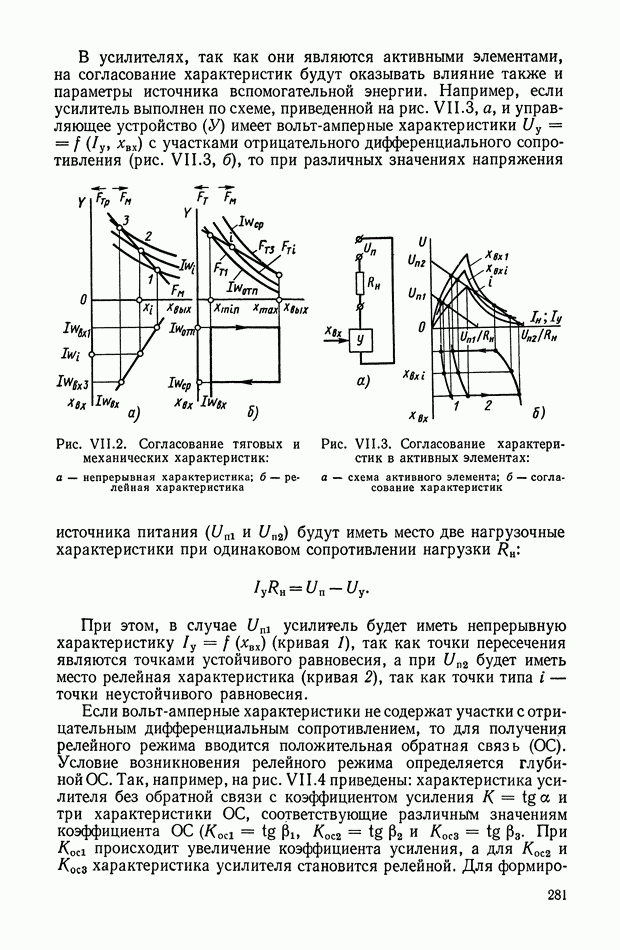
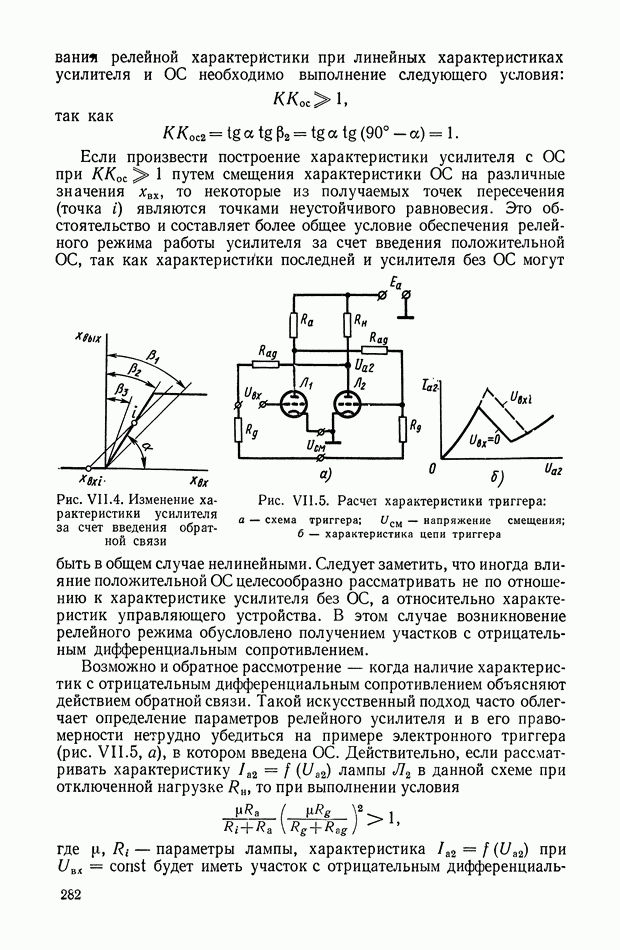
- 1. ХАРАКТЕРИСТИКИ УСИЛИТЕЛЕЙ И СПОСОБЫ ИХ ФОРМИРОВАНИЯ
- 2. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
- 3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ЛИНЕАРИЗОВАННЫЕ УСИЛИТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ РЕЛЕ
- 4. БЕСКОНТАКТНЫЕ ЛИНЕАРИЗОВАННЫЕ РЕЛЕЙНЫЕ УСИЛИТЕЛИ
- ГЛАВА VIII. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 2. ОСНОВНЫЕ ЭЛЕМЕНТЫ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ И ИХ ХАРАКТЕРИСТИКИ
- 3. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ С ЗОЛОТНИКОМ
- 4. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ СО СТРУЙНОЙ ТРУБКОЙ
- 5. СХЕМЫ И ПРИНЦИПЫ ДЕЙСТВИЯ ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 6. СТАТИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 7. ДИНАМИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
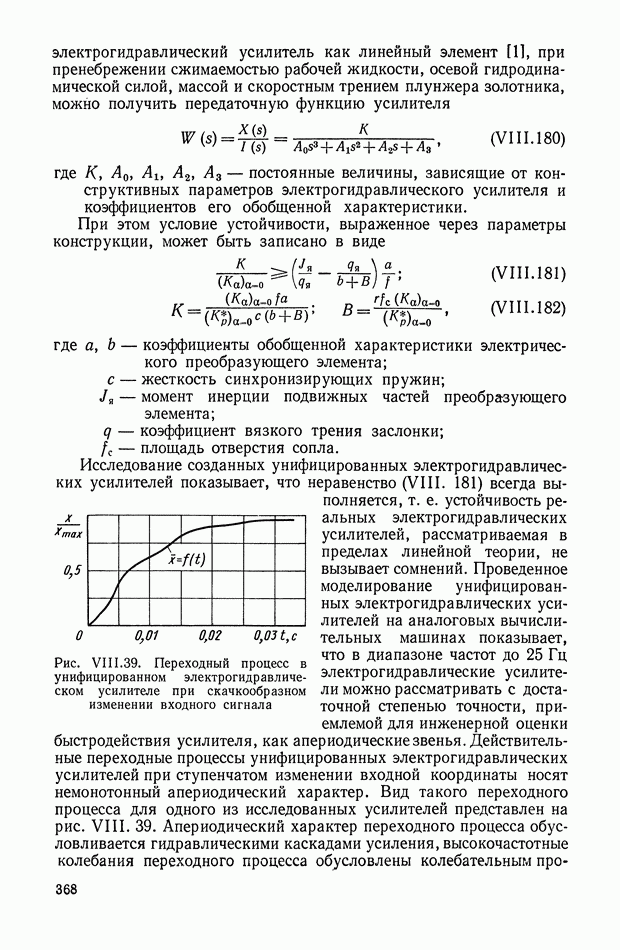
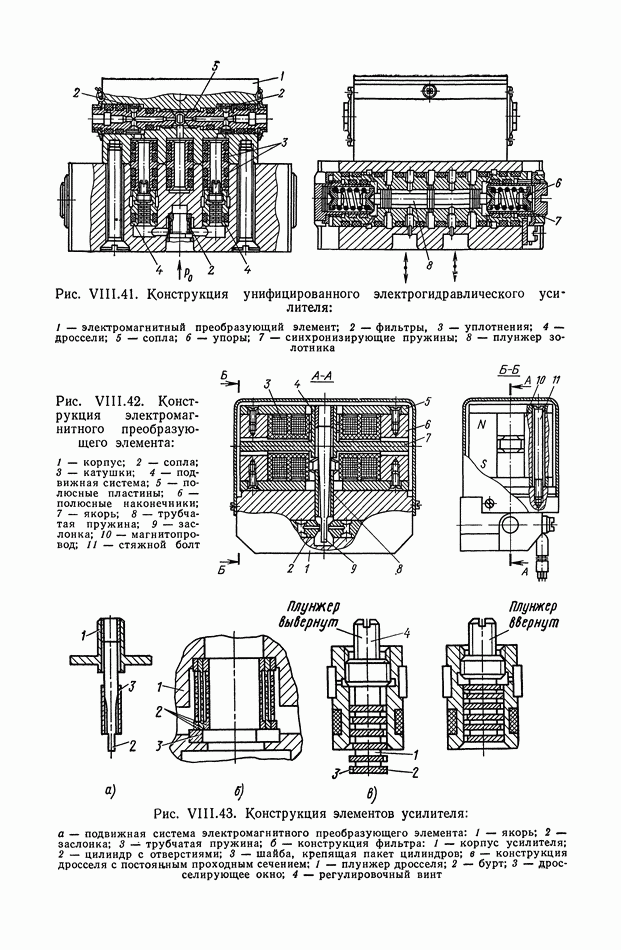
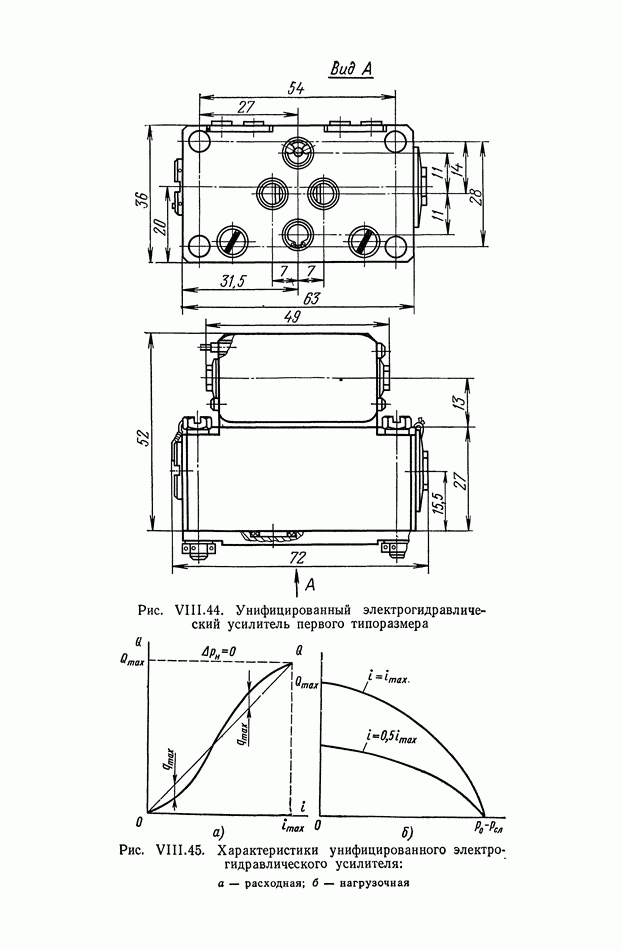
- 8. УНИФИКАЦИЯ ЭЛЕКТРОГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ ДЛЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
- ГЛАВА IX. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ И ИХ КЛАССИФИКАЦИЯ
- 2. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ СО СТРУЙНОЙ ТРУБКОЙ
- 3. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗОЛОТНИКОМ
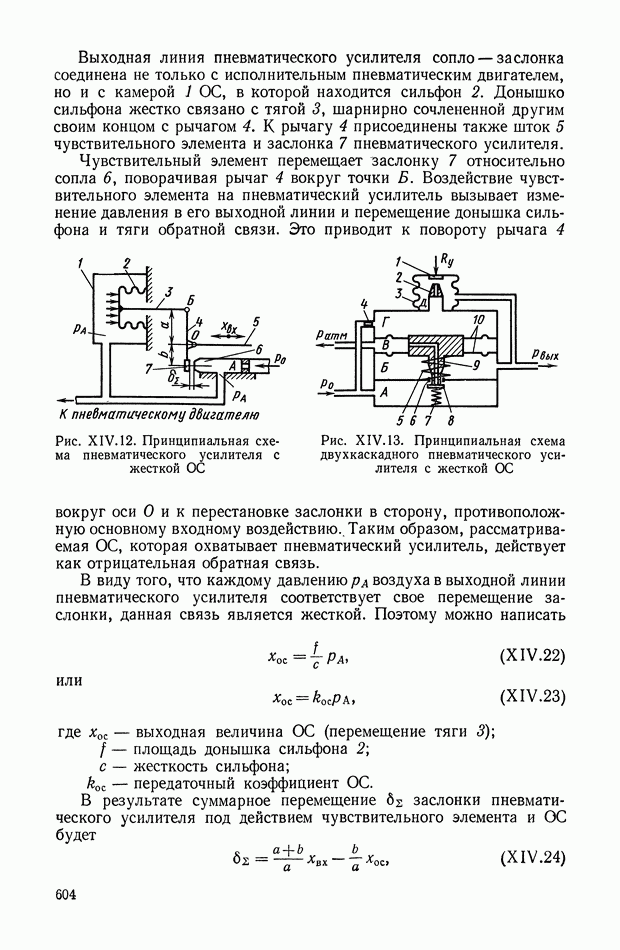
- 4. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С СОПЛОМ — ЗАСЛОНКОЙ
- 5. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗАСЛОНКОЙ
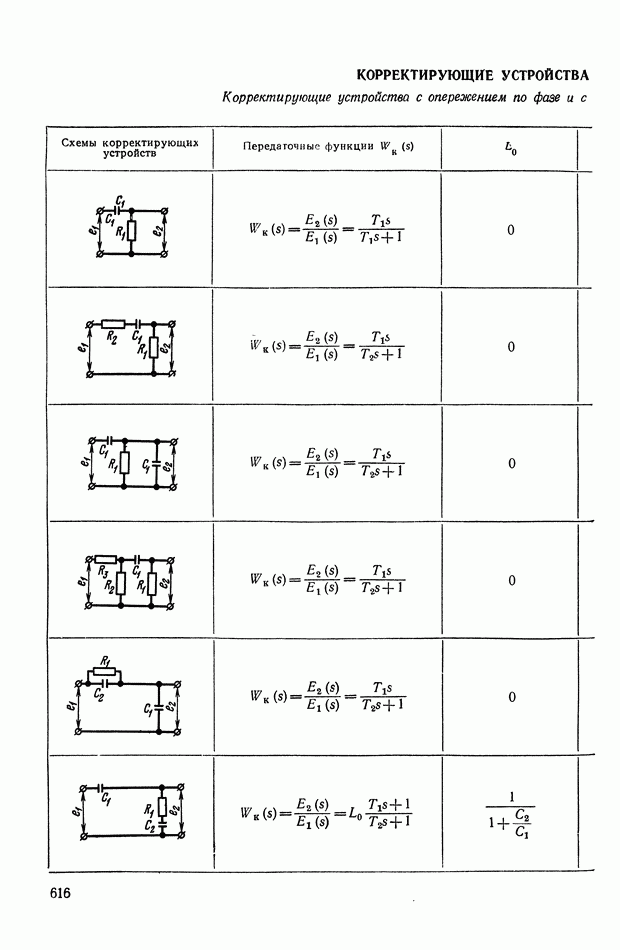
- 6. МНОГОКАСКАДНЫЕ ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- РАЗДЕЛ II. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ И УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ЛИНЕЙНЫХ ПАССИВНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
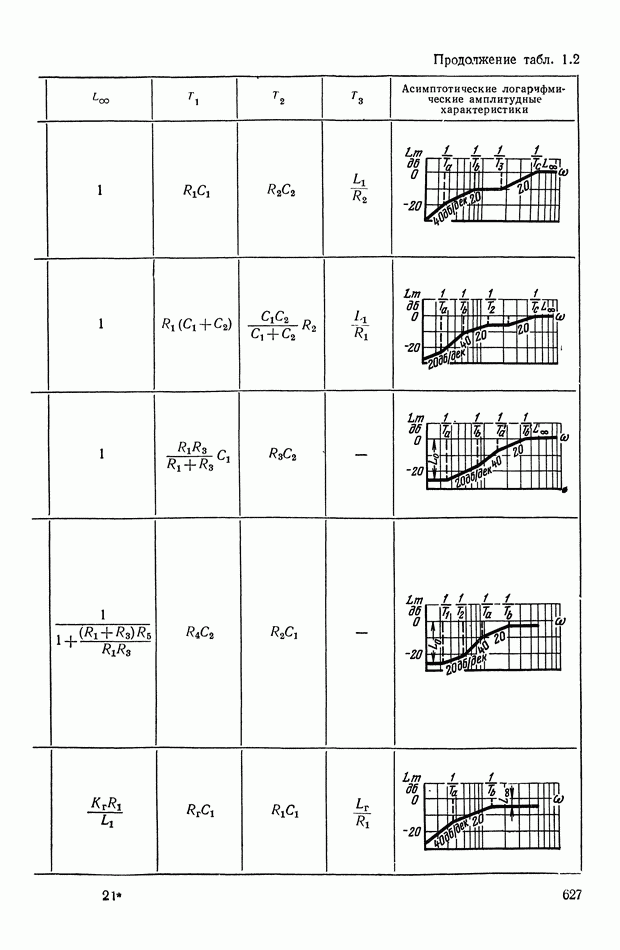
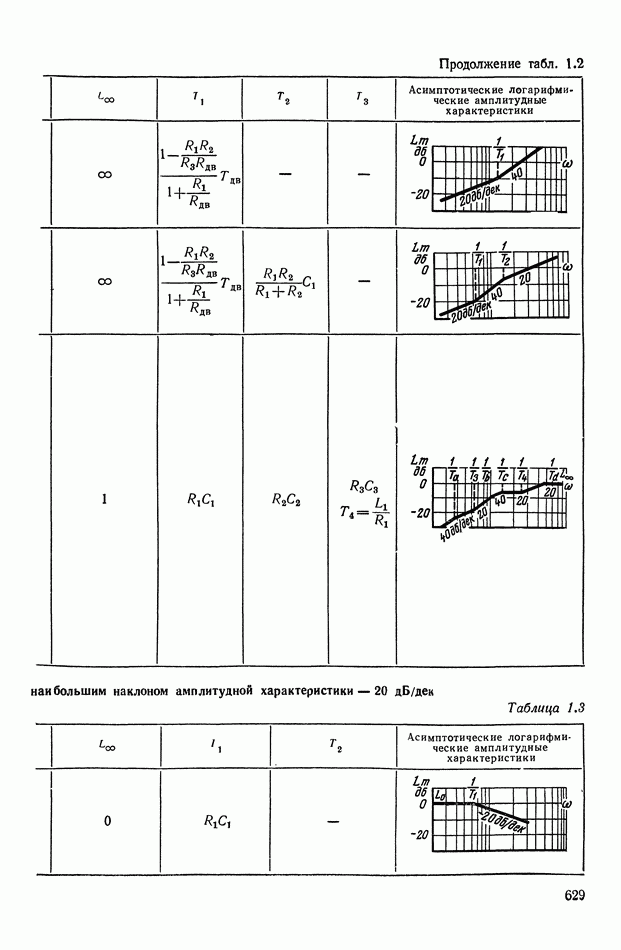
- Основные соотношения для синтеза пассивного RC-четырехполюсника.
- 3. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Активные четырехполюсники, получаемые с помощью конверторов отрицательного сопротивления.
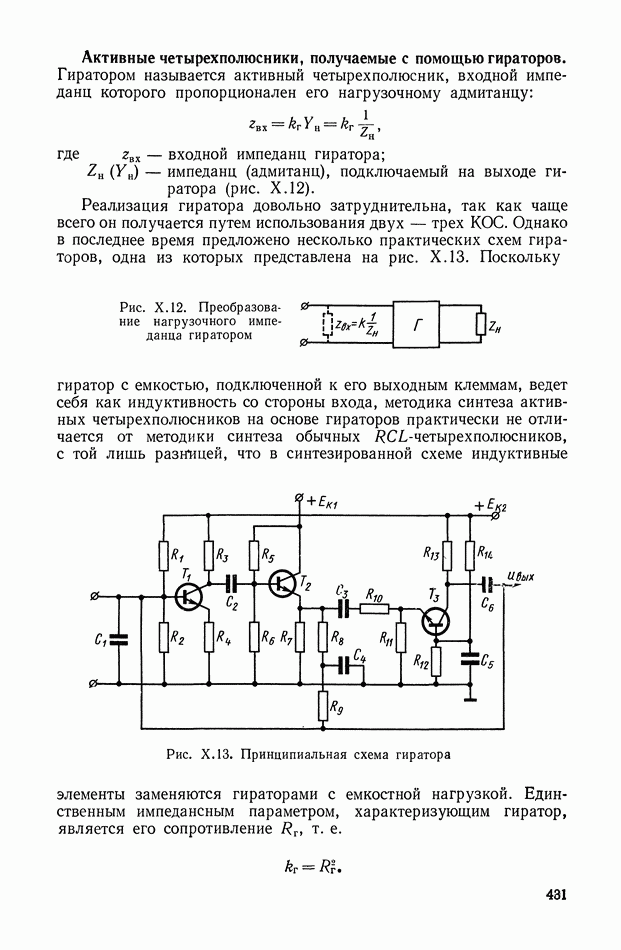
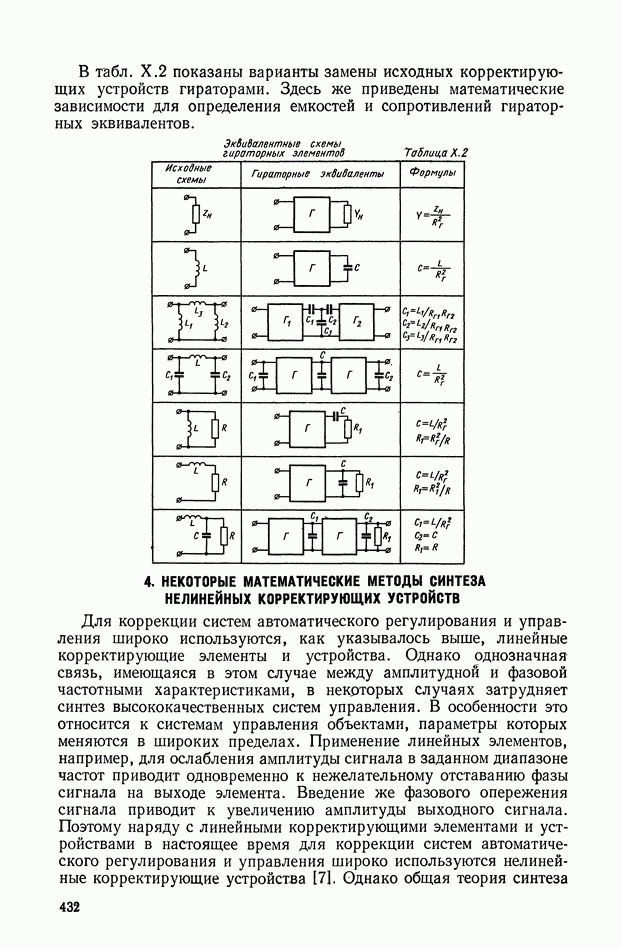
- Активные четырехполюсники, получаемые с помощью гираторов.
- 4. НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА НЕЛИНЕЙНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. ОСОБЕННОСТИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XI. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА ПОСТОЯННОГО ТОКА
- Дифференцирующий трансформатор.
- Электрические интегрирующие элементы.
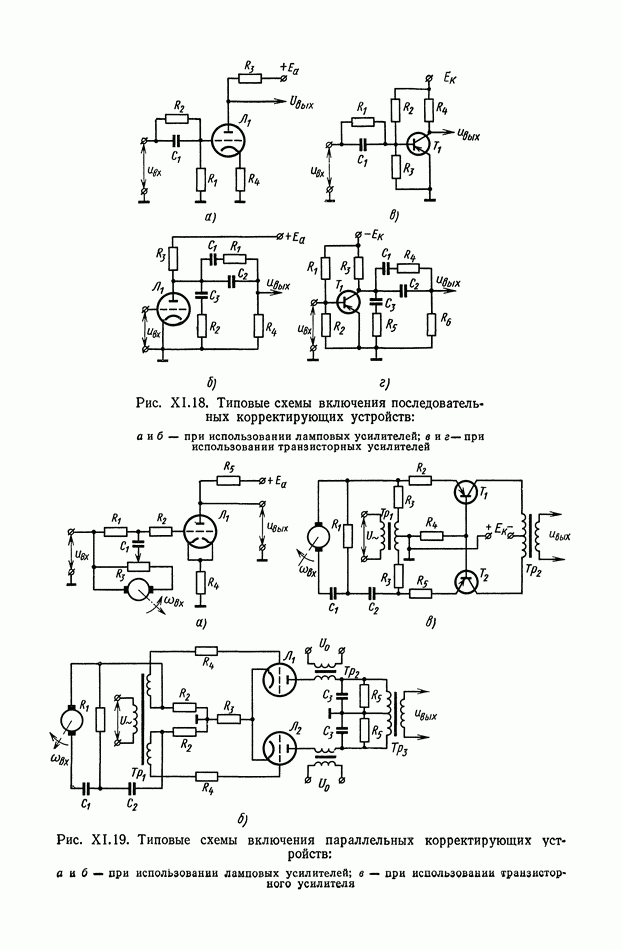
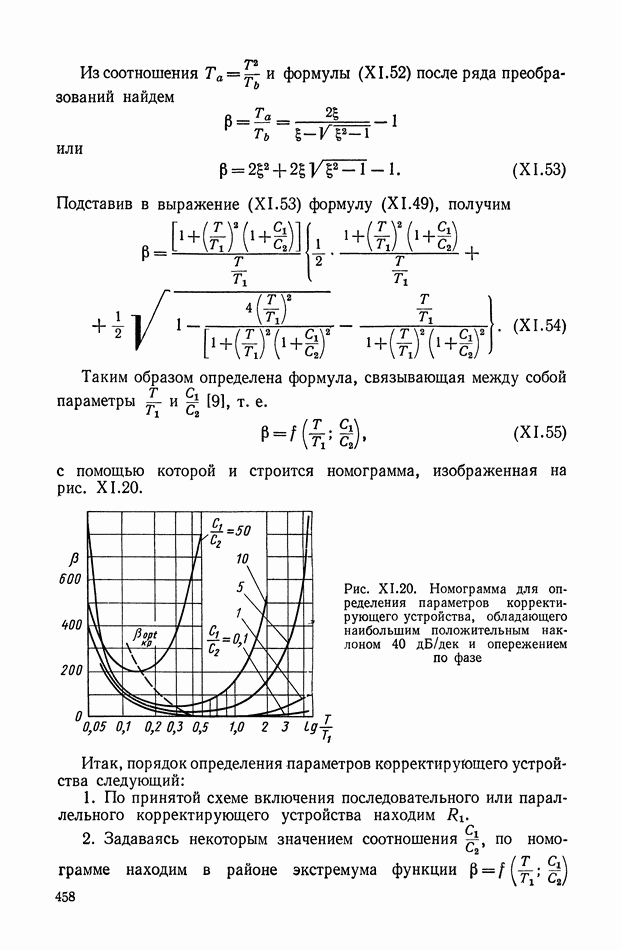
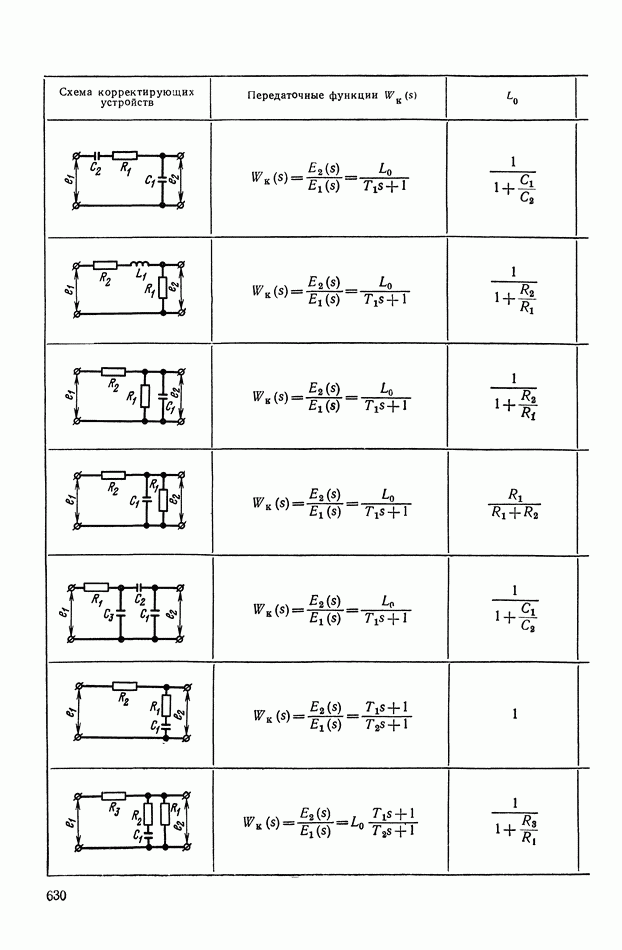
- 2. ТИПОВЫЕ ЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
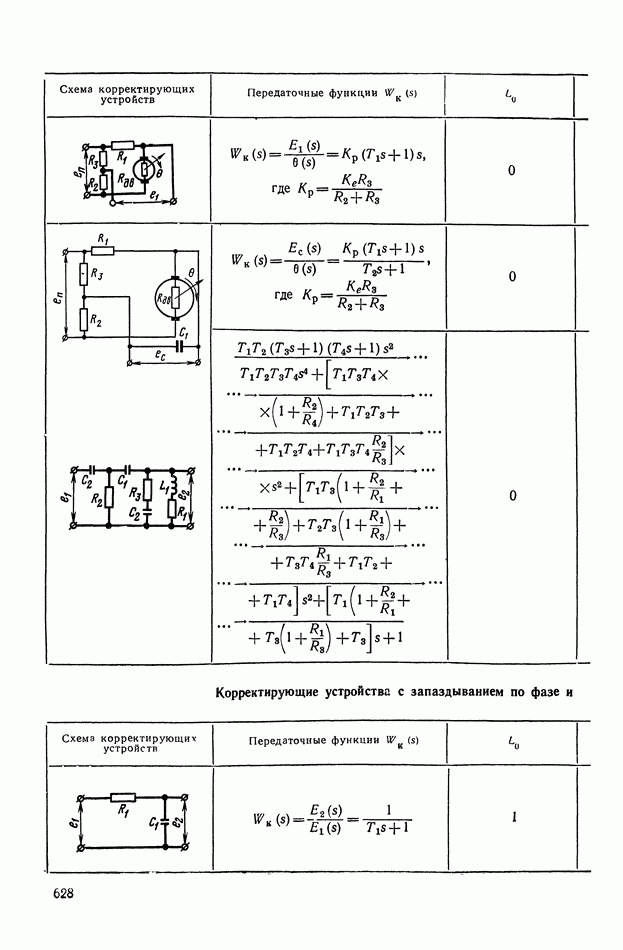
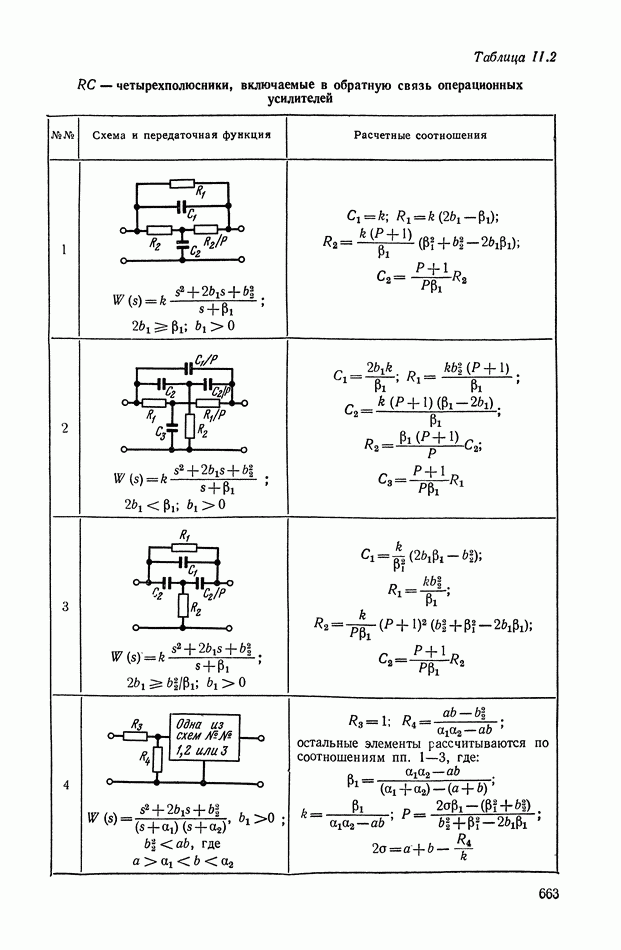
- 3. КОРРЕКТИРУЮЩИЕ ЧЕТЫРЕХПОЛЮСНИКИ С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Четырехполюсники с активными элементами на основе операционных усилителей (ОУ) и конверторов отрицательного сопротивления (КОС).
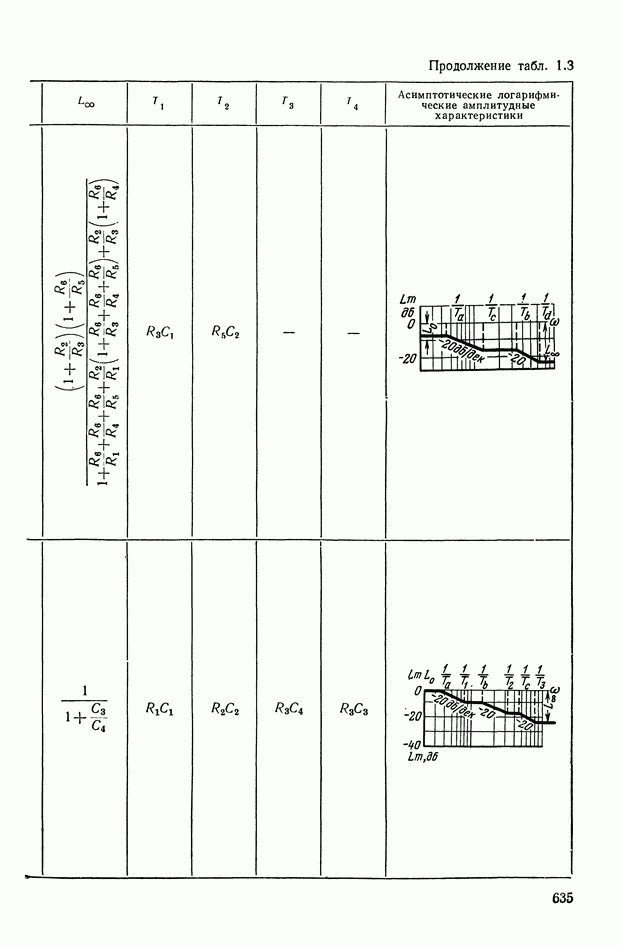
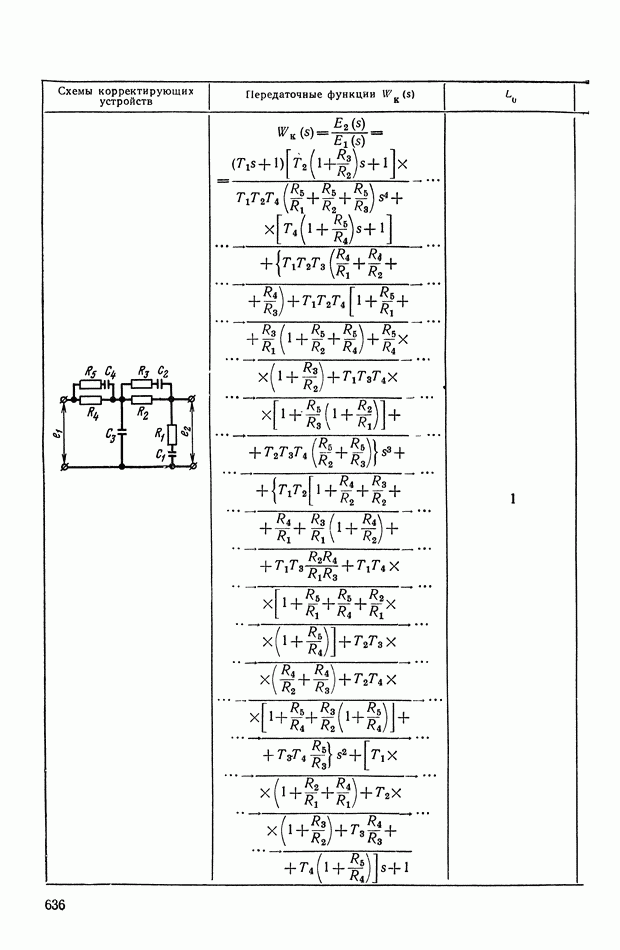
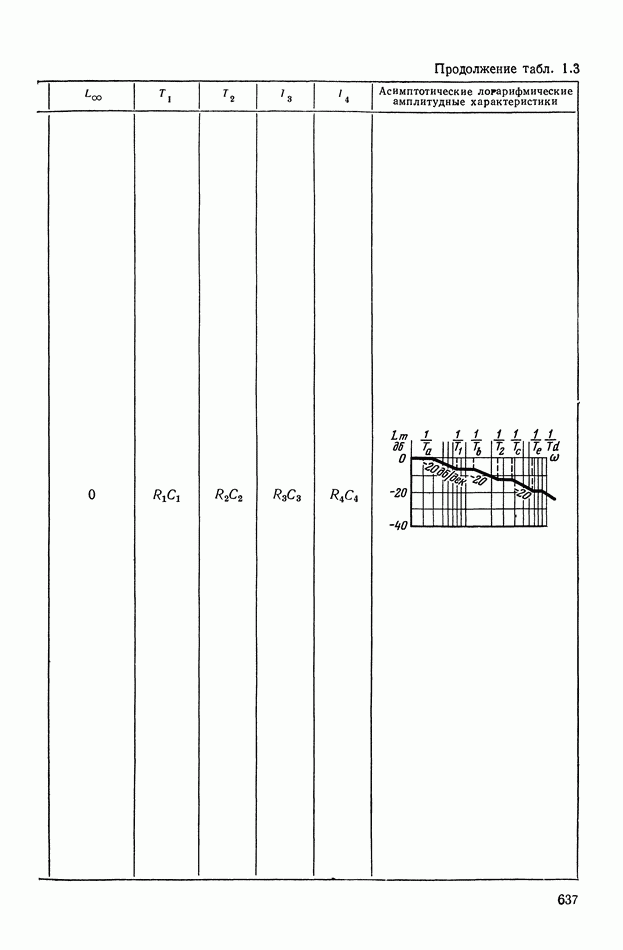
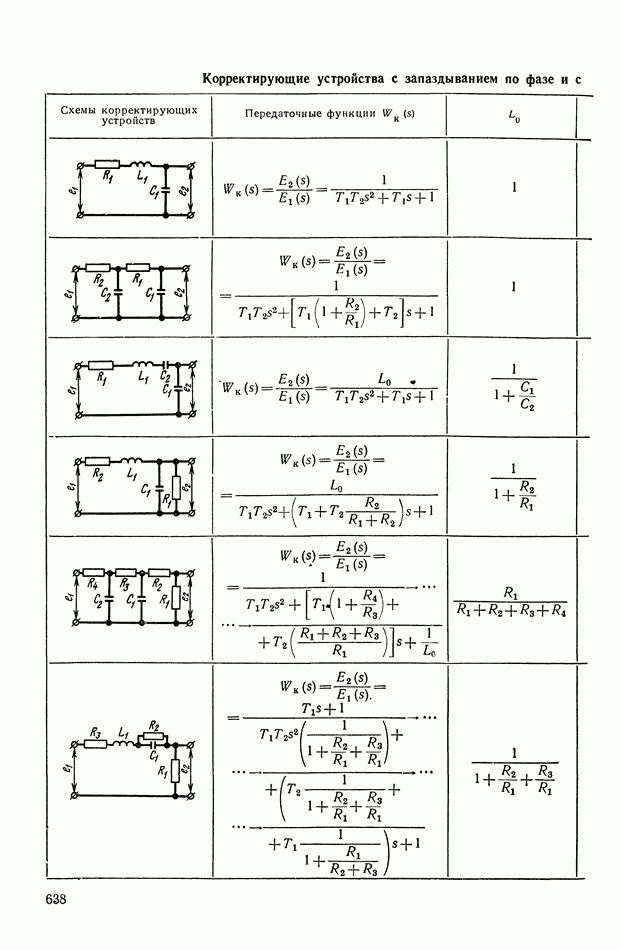
- 4. РЕАЛИЗАЦИЯ ЗАДАННОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В ВИДЕ СХЕМЫ ПАССИВНОГО ЛИНЕЙНОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА
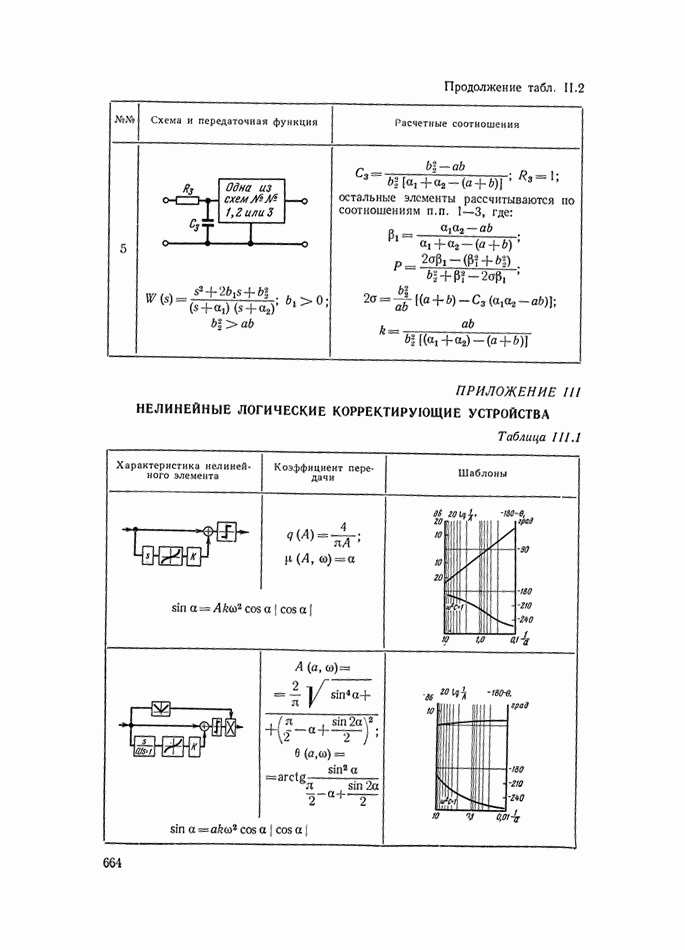
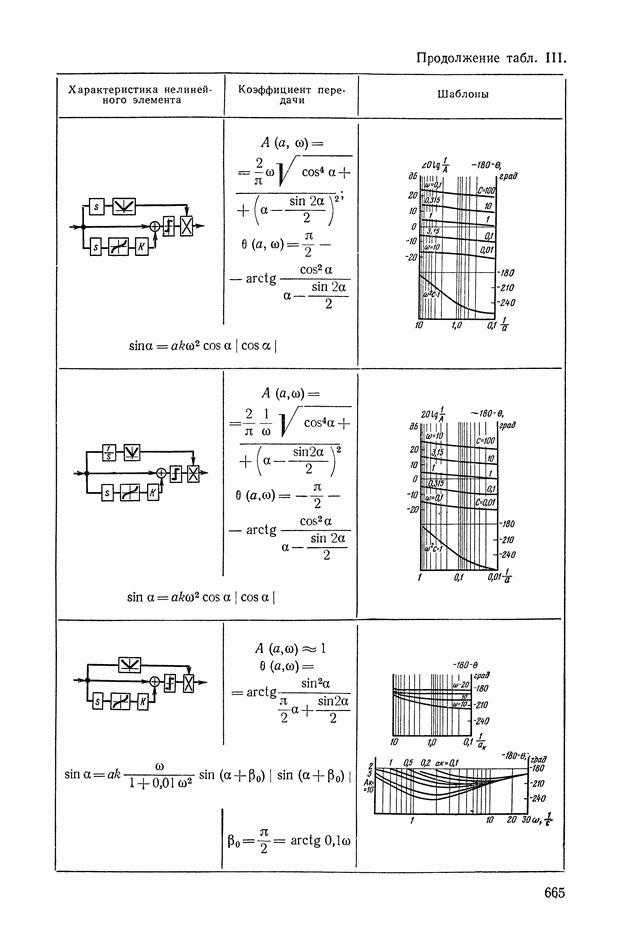
- 5. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
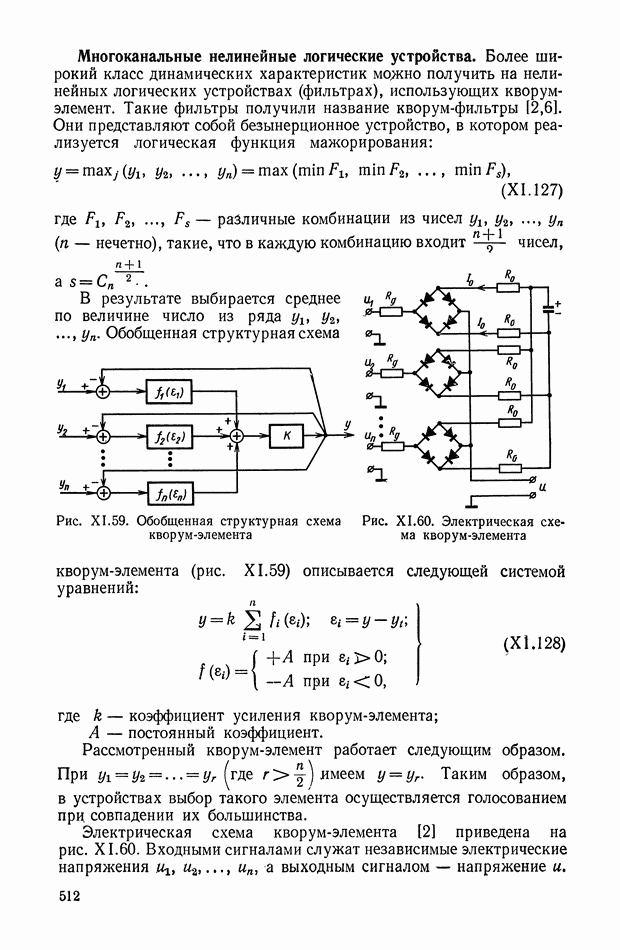
- 8. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- Многоканальные нелинейные логические устройства.
- ГЛАВА XII. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
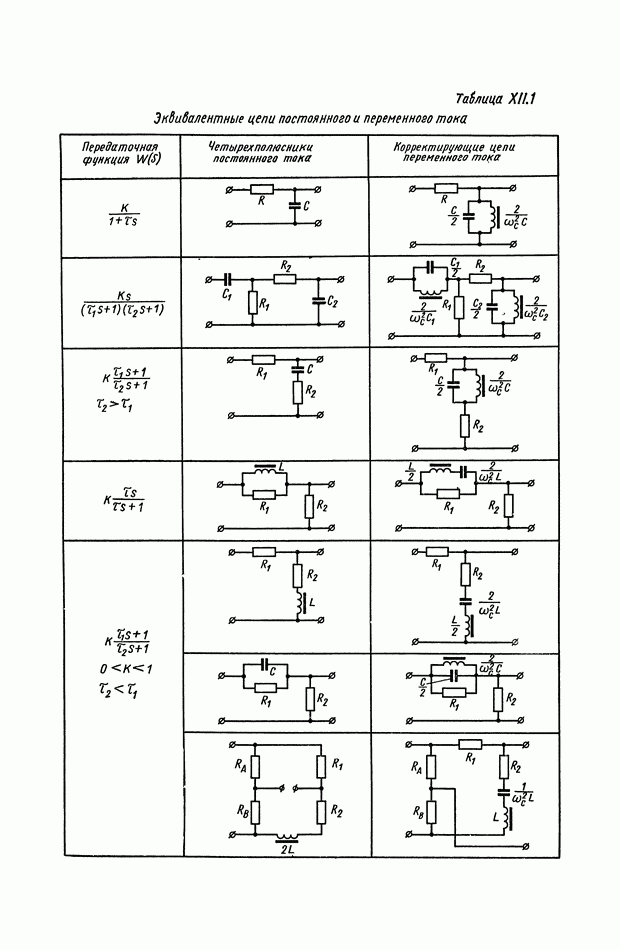
- 1. КОРРЕКТИРУЮЩИЕ RLC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 2. КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
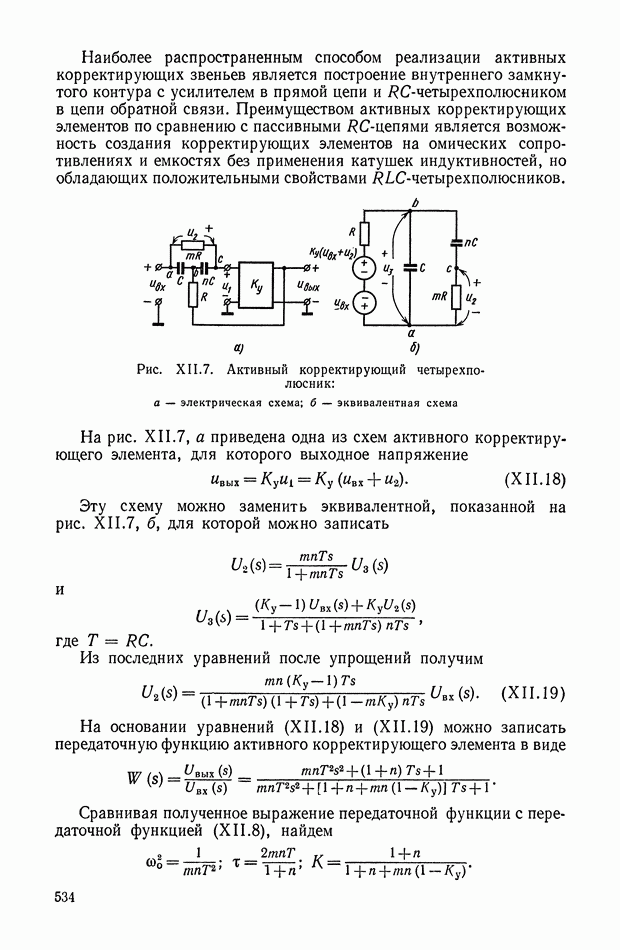
- 3. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
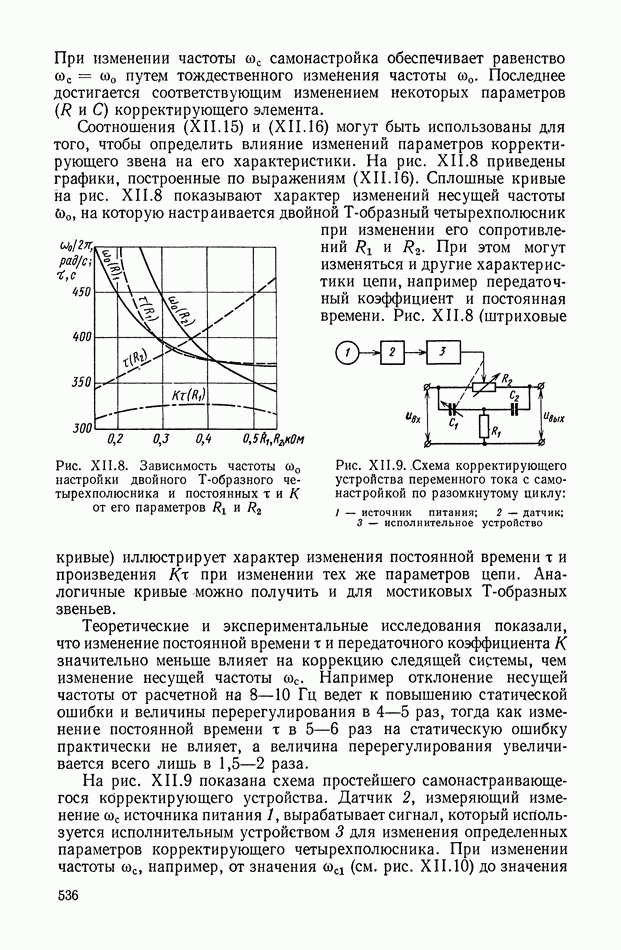
- 4. САМОНАСТРАИВАЮЩИЕСЯ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА
- 5. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА С ПРОМЕЖУТОЧНОЙ ДЕМОДУЛЯЦИЕЙ
- 6. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА С ПЕРЕКЛЮЧАТЕЛЯМИ
- 7. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XIII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ТАХОГЕНЕРАТОРЫ ПОСТОЯННОГО ТОКА
- Погрешности тахогенератора постоянного тока.
- 2. НЕКОТОРЫЕ СХЕМЫ ПРИМЕНЕНИЯ ТАХОГЕНЕРАТОРОВ
- 3. АСИНХРОННЫЕ ТАХОГЕНЕРАТОРЫ
- 4. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ ИЗМЕРЕНИЯ СКОРОСТИ ЭЛЕКТРОДВИГАТЕЛЕЙ
- Пассивный тахометрический мост переменного тока.
- Активные тахометрические мосты.
- ГЛАВА XIV. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ГИДРАВЛИЧЕСКИХ СИСТЕМАХ
- 3. ЭЛЕКТРИЧЕСКИЕ ОБРАТНЫЕ СВЯЗИ
- 4. ЖЕСТКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
- 5. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ СИСТЕМАХ
- 6. СЛОЖНЫЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
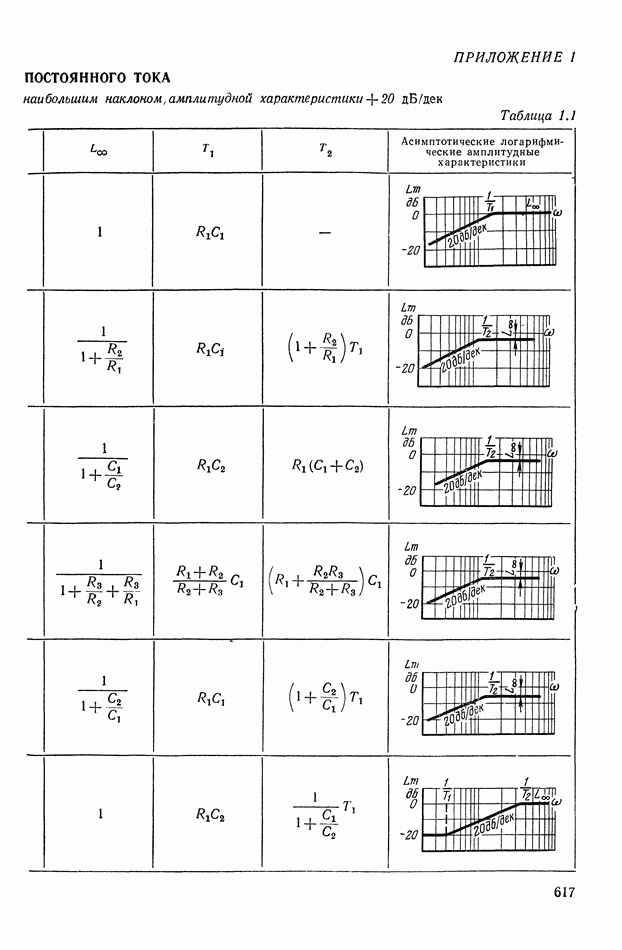
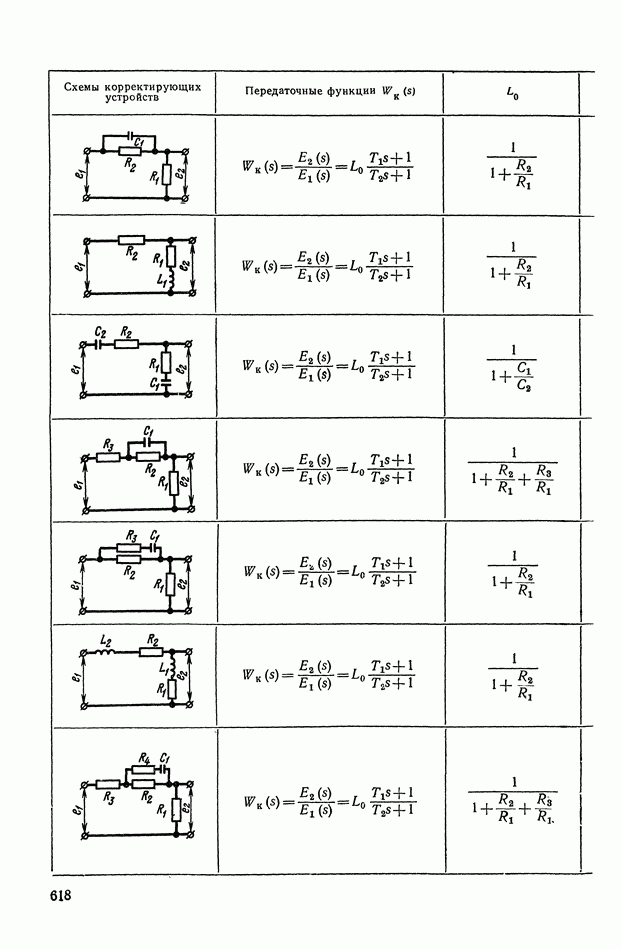
- ПРИЛОЖЕНИЕ 1. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПОСТОЯННОГО ТОКА
- ПРИЛОЖЕНИЕ II. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ОСНОВЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- ПРИЛОЖЕНИЕ III. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ