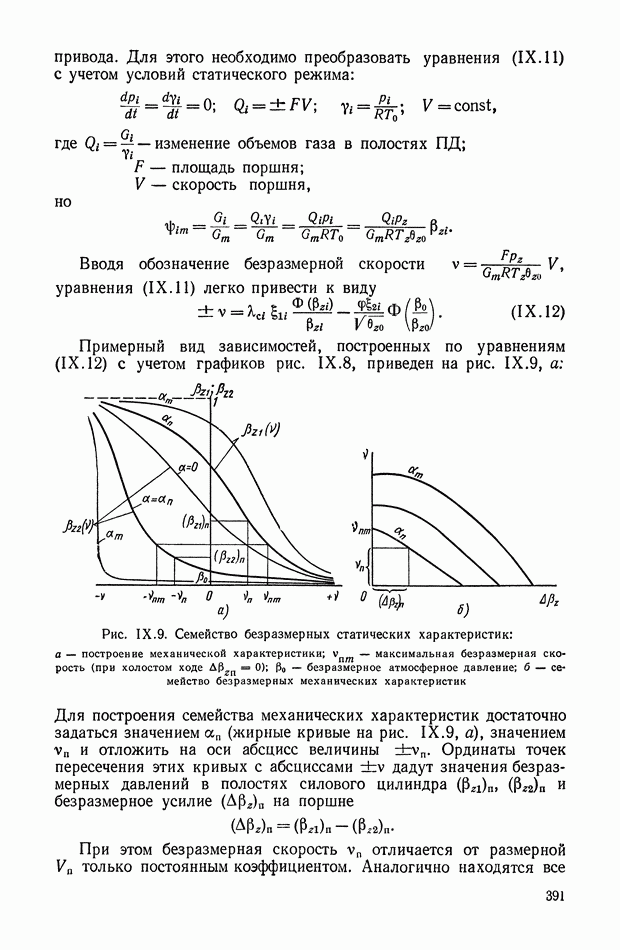
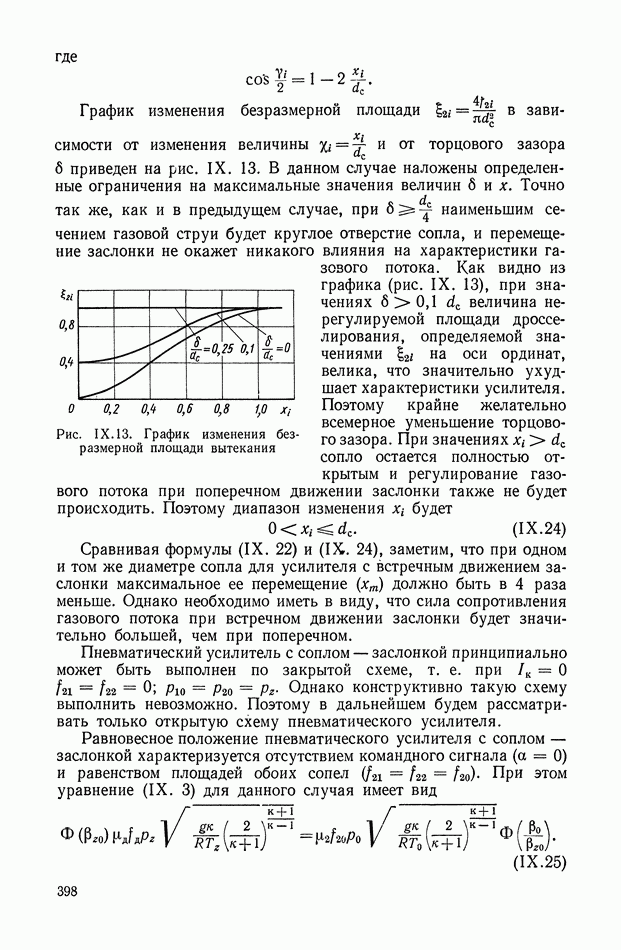
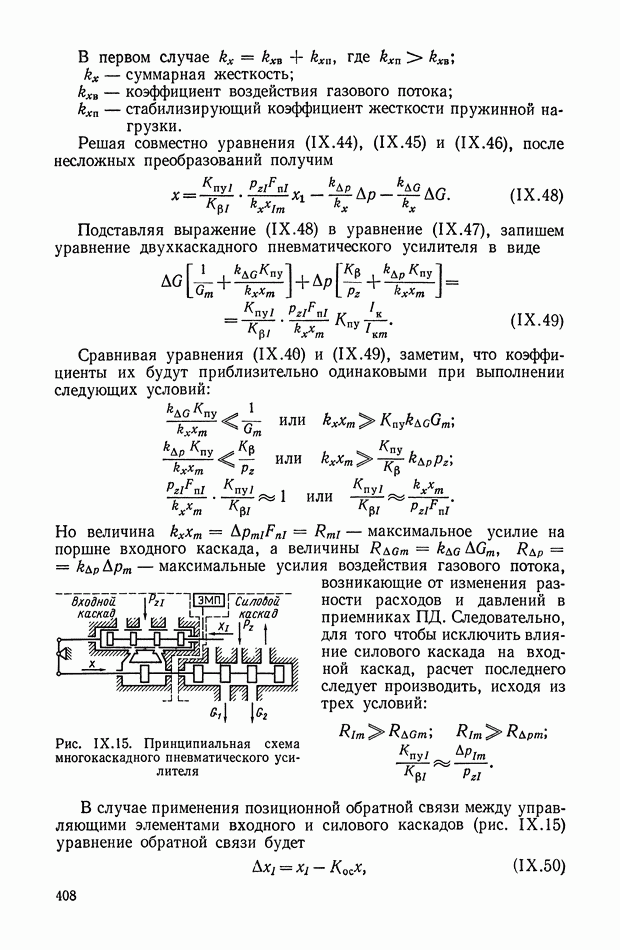
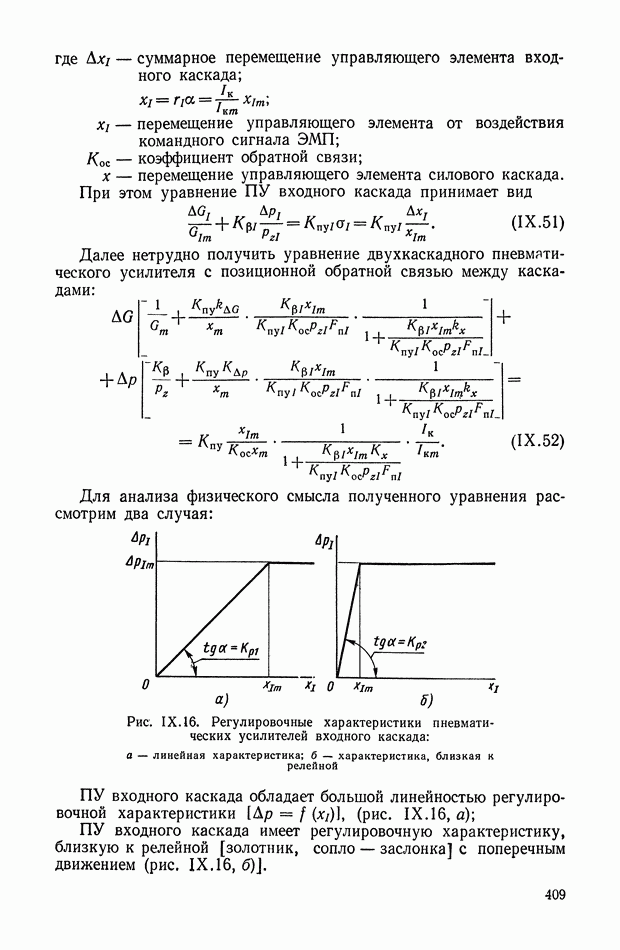
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
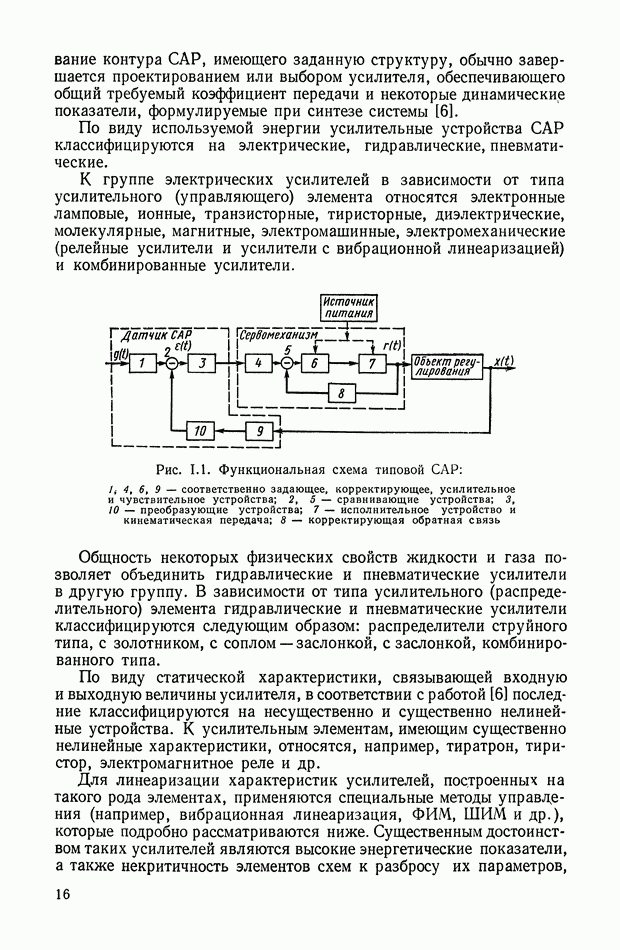
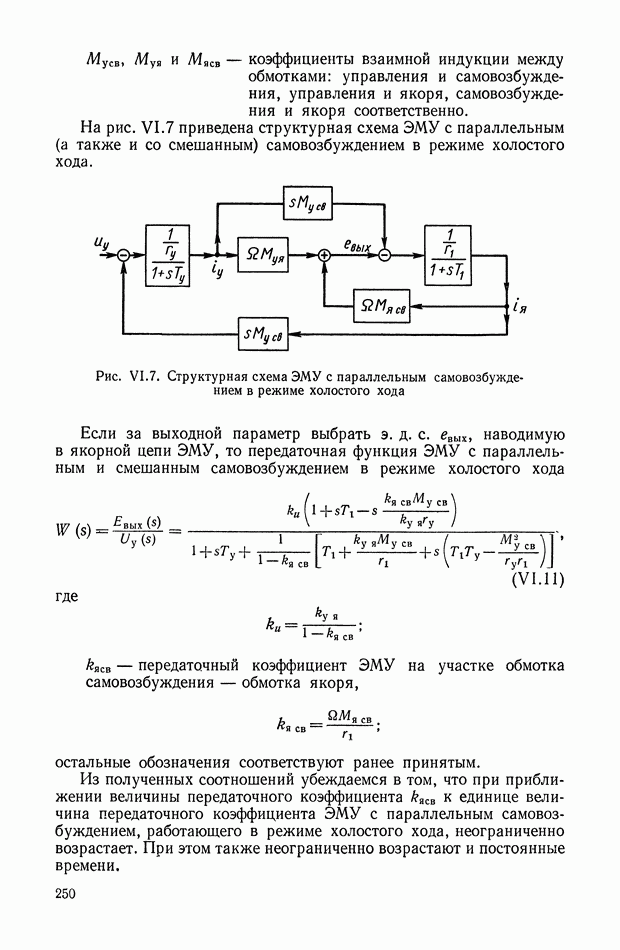
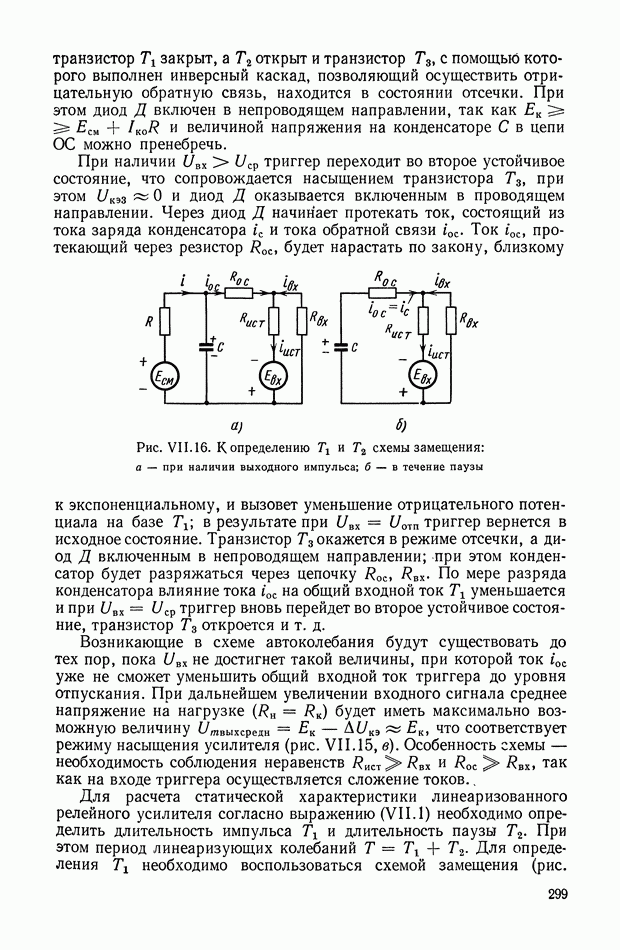
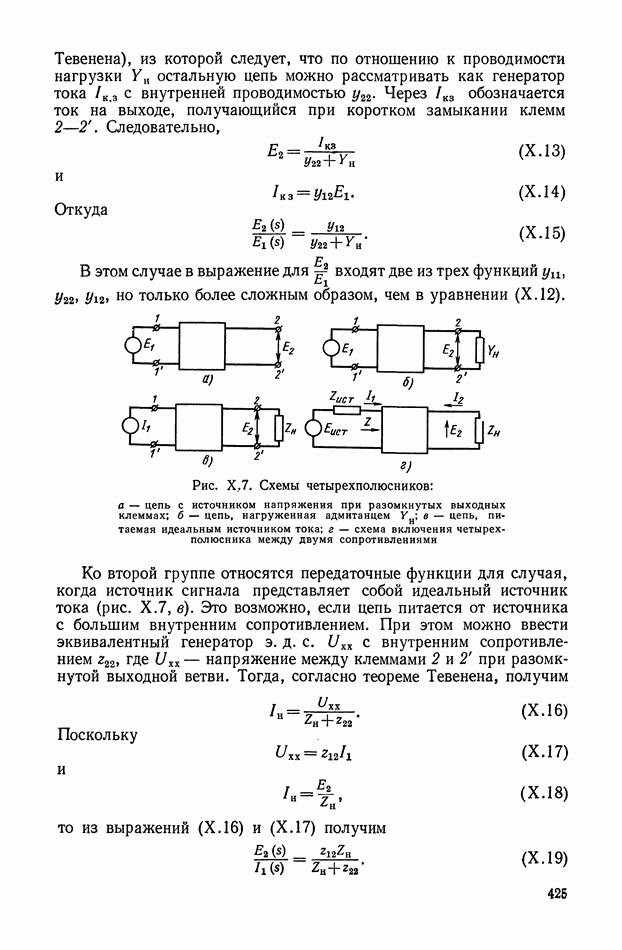
ГЛАВА XI. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА ПОСТОЯННОГО ТОКА
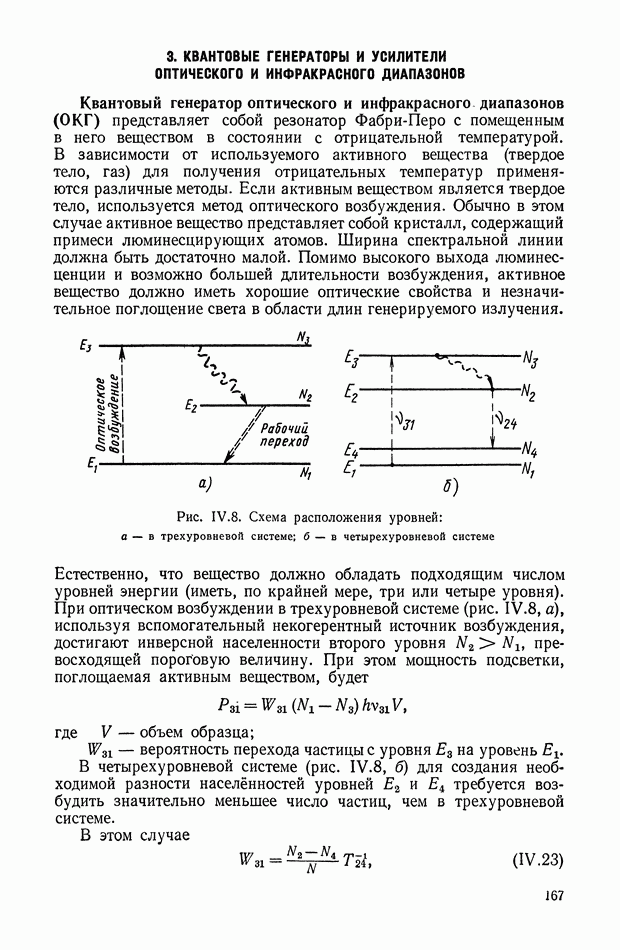
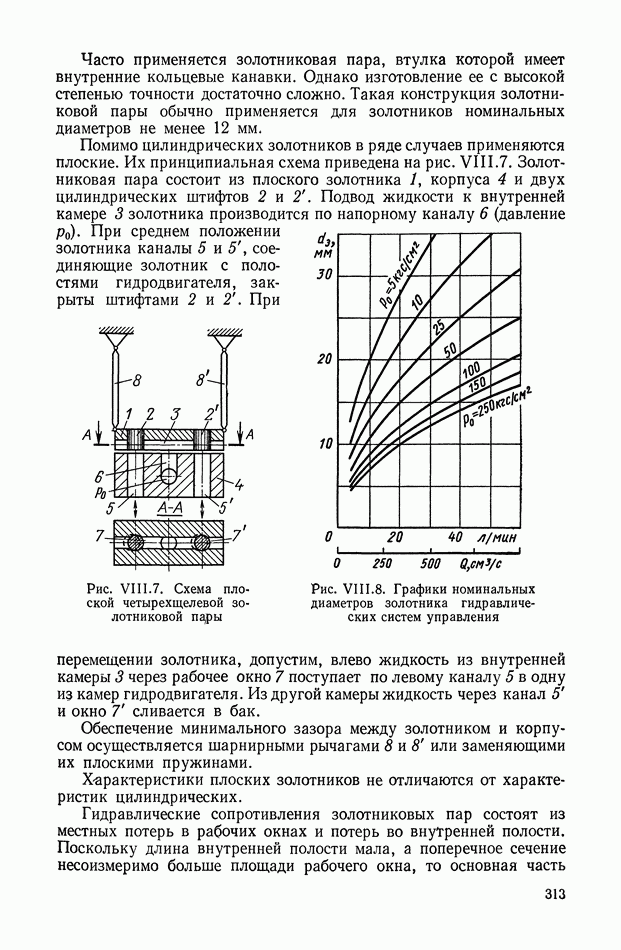
Электрические пассивные корректирующие элементы представляют собой четырехполюсники, не содержащие источников энергии. Обычно входной и выходной величинами в таких элементах являются электрические напряжения. Электрические пассивные корректирующие элементы собираются из простых стандартных деталей, не имеющих подвижных частей. Число типов таких элементов по существу не ограничено. Благодаря этому они широко применяются в системах автоматического регулирования и управления. К недостаткам пассивных элементов следует отнести невозможность получения достаточной мощности сигнала на выходе.
Наиболее широко применяемые в настоящее время электрические корректирующие элементы (четырехполюсники или цепи) подразделяются на дифференцирующие, интегрирующие и интегро-дифференцирующие. Их можно классифицировать также в зависимости от максимального наклона логарифмической амплитудной характеристики.
При решении задач синтеза сложных корректирующих устройств большие возможности открываются перед устройствами с активными элементами.
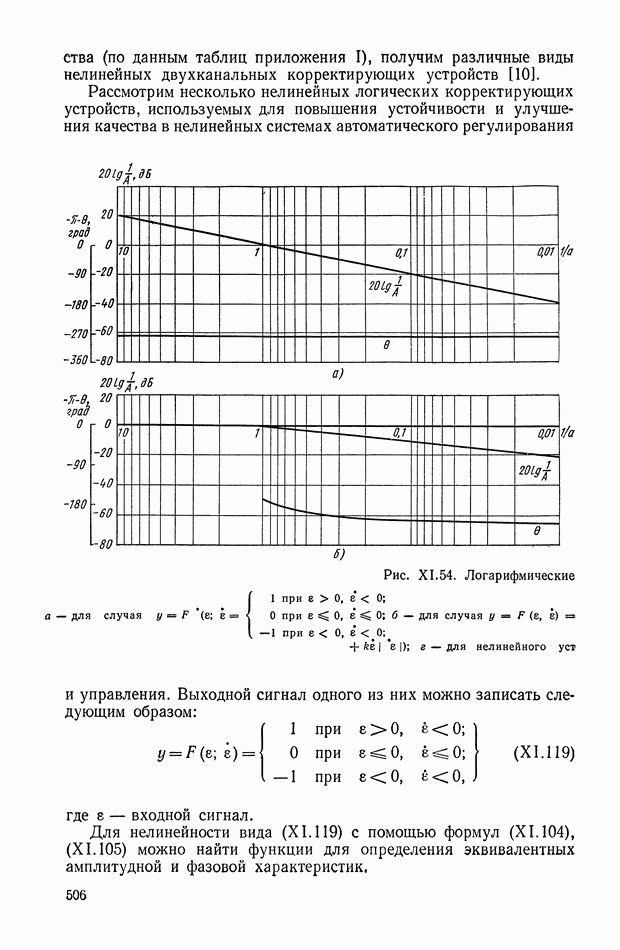
Применение линейных пассивных и активных корректирующих устройств в целом ряде случаев не позволяет достичь желаемых динамических характеристик. Это связано с тем, что их амплитудно-частотная и фазочастотная характеристики однозначно связаны между собой. Поэтому в последние годы повышенный интерес проявляется к вопросам построения нелинейных фильтров (в том числе нелинейно-логических), у которых амплитудно-частотная и фазочастотная характеристики по первой гармонике могут синтезироваться независимо друг от друга.
В этой главе рассматривается еще один класс нелинейных фильтров, который обеспечивает достижение в системе некоторых критериев оптимальности, и в частности, максимального быстродействия переходного процесса.
1. ПРОСТЕЙШИЕ ДИФФЕРЕНЦИРУЮЩИЕ И ИНТЕГРИРУЮЩИЕ ЭЛЕМЕНТЫ
Электрические дифференцирующие  -элементы. Рассмотрим схему, состоящую из резистора
-элементы. Рассмотрим схему, состоящую из резистора  и емкости С, соединенных последовательно (рис. XI.1, а).
и емкости С, соединенных последовательно (рис. XI.1, а).

Рис. XI. 1. Электрические дифференцирующие элементы: а — простейший дифференцирующий RС-четырехполюсник; б — дифференцирующий  -четырехполюсник для получения напряжения, пропорционального координате и ее производной; в — двойной дифференцирующий четырехполюсник
-четырехполюсник для получения напряжения, пропорционального координате и ее производной; в — двойной дифференцирующий четырехполюсник
Для такого электрического четырехполюсника в режиме холостого хода могут быть написаны следующие уравнения:

где  — ток в цепи.
— ток в цепи.
Из уравнений (XI.1) видно, что связь между  будет описываться дифференциальным уравнением:
будет описываться дифференциальным уравнением:

где  — постоянная времени.
— постоянная времени.
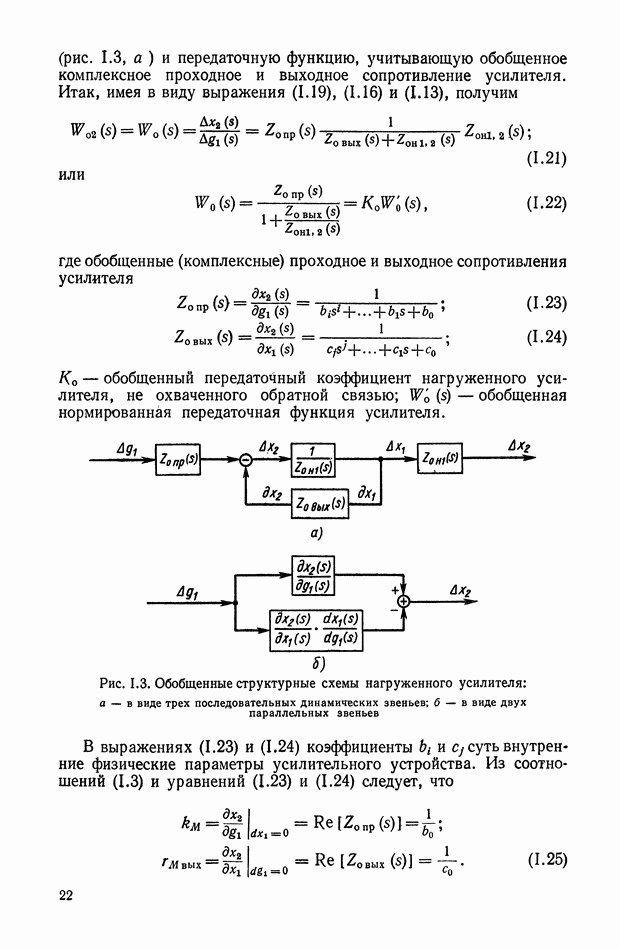
Передаточная функция четырехполюсника определяется выражением

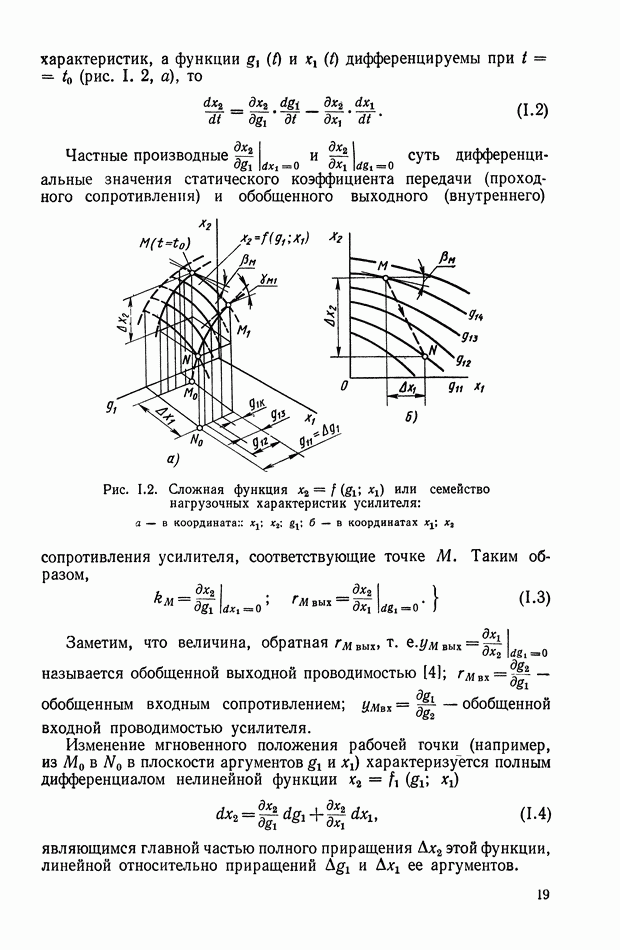
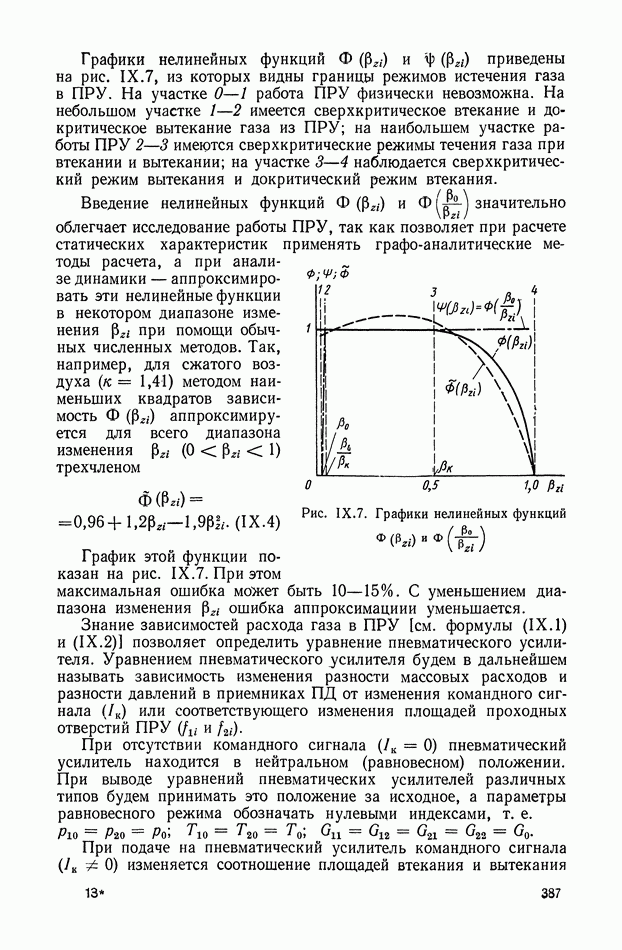
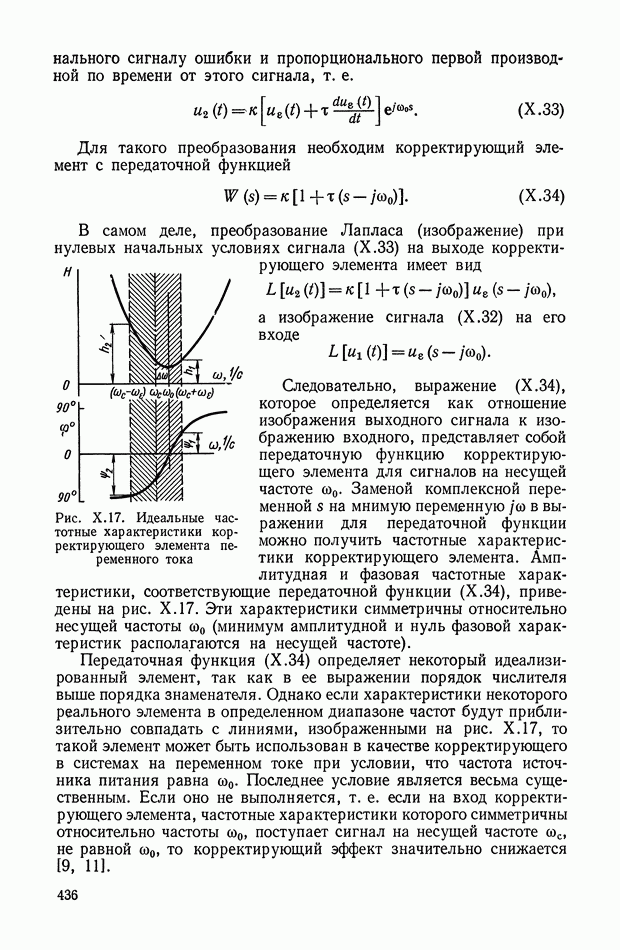
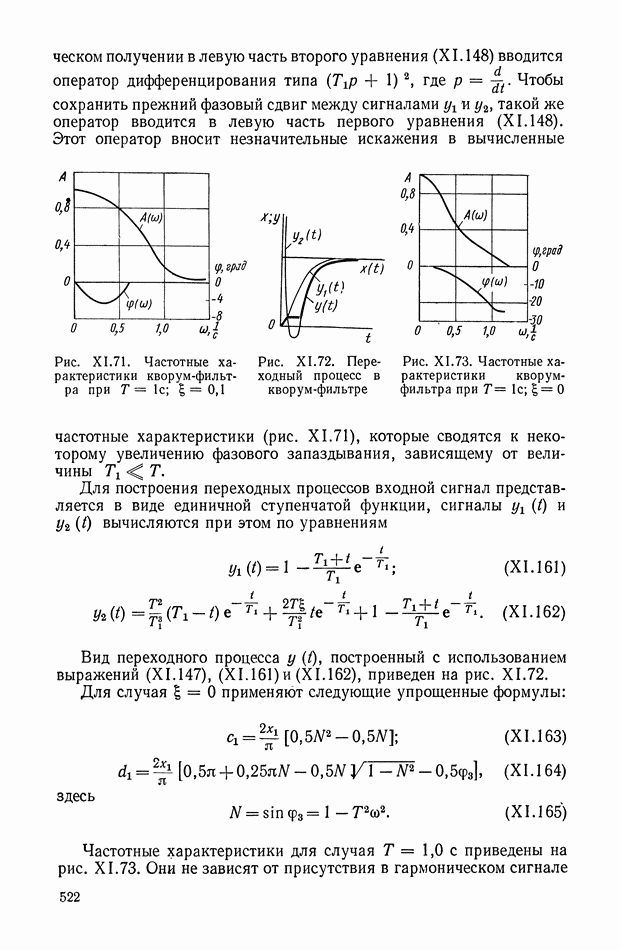
Амплитудно-фазовая частотная характеристика (рис. XI.2) описывается следующим выражением:

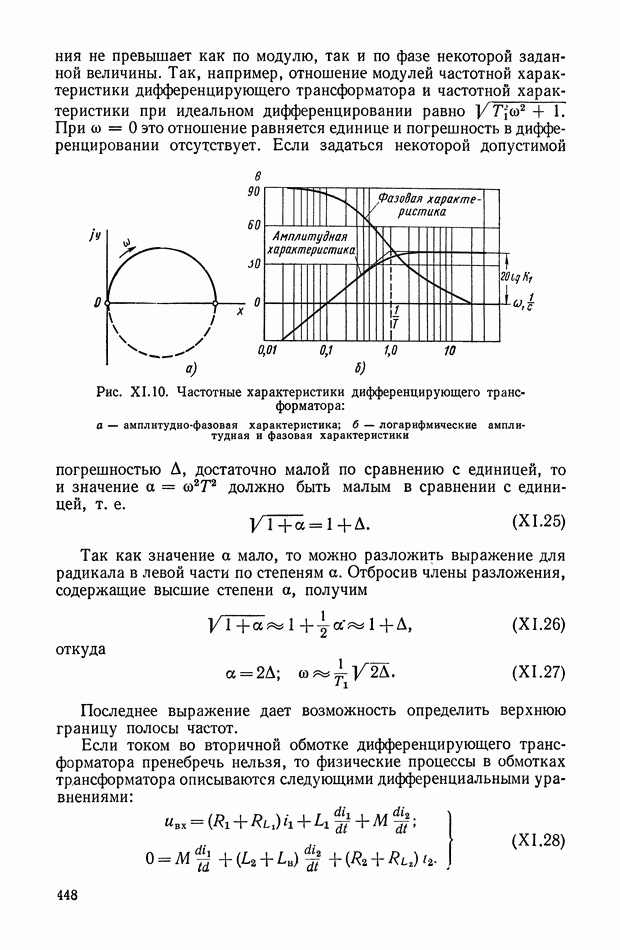
Логарифмические амплитудная и фазовая частотные характеристики показаны на рис. XI.3. При этом логарифмическая амплитудная характеристика имеет положительный наклон в 20 дБ на декаду до частоты  следовательно, четырехполюсник может рассматриваться как дифференцирующий элемент для напряжения
следовательно, четырехполюсник может рассматриваться как дифференцирующий элемент для напряжения  полоса частотного спектра которого не превышает величины 1/T.
полоса частотного спектра которого не превышает величины 1/T.
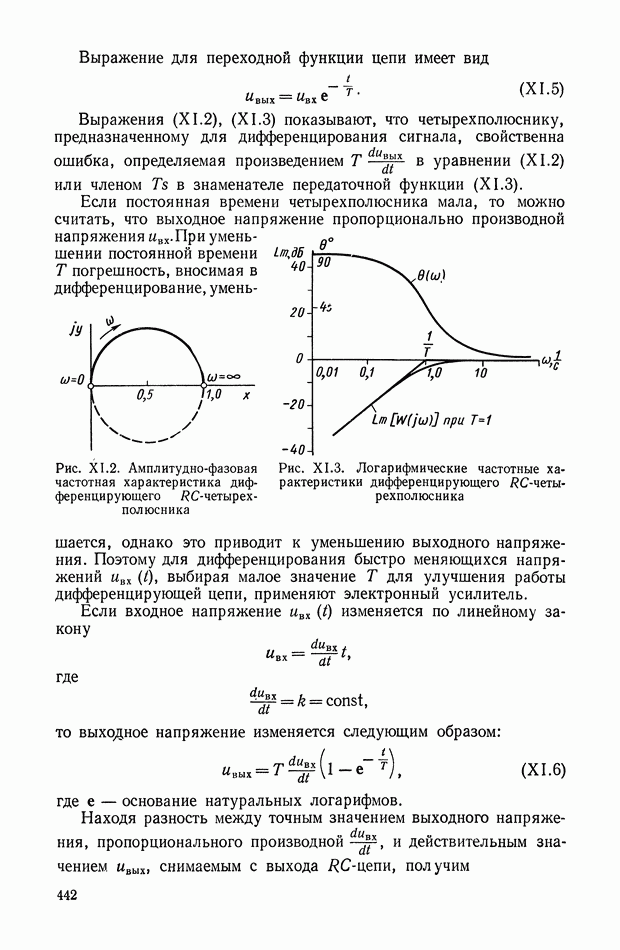
Выражение для переходной функции цепи имеет вид

Выражения (XI.2), (XI.3) показывают, что четырехполюснику, предназначенному для дифференцирования сигнала, свойственна ошибка, определяемая произведением  в уравнении (XI.2) или членом
в уравнении (XI.2) или членом  в знаменателе передаточной функции (XI.3).
в знаменателе передаточной функции (XI.3).
Если постоянная времени четырехполюсника мала, то можно считать, что выходное напряжение пропорционально производной напряжения  уменьшении постоянной времени Т погрешность, вносимая в дифференцирование, уменьшается, однако это приводит к уменьшению выходного напряжения.
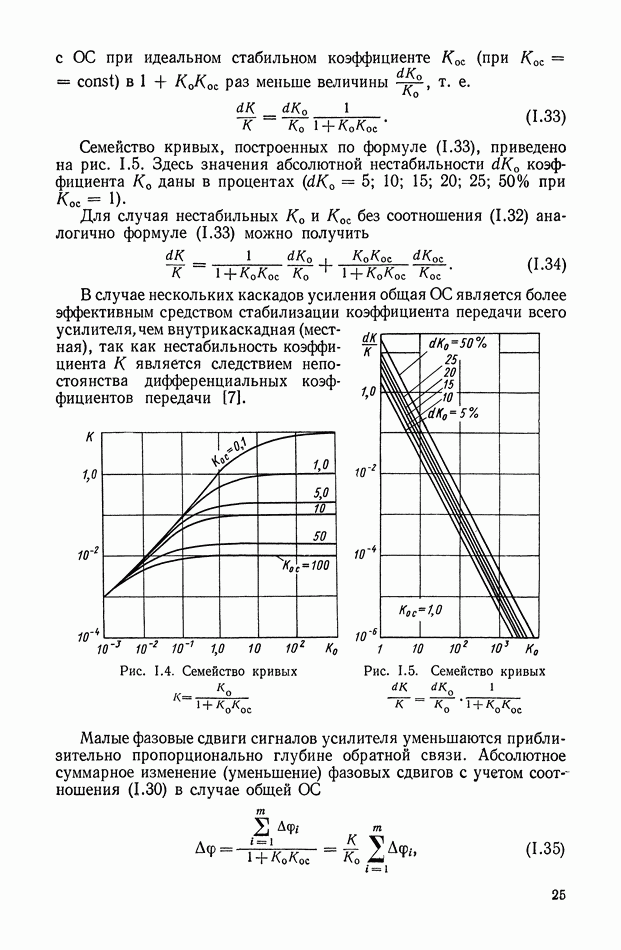
уменьшении постоянной времени Т погрешность, вносимая в дифференцирование, уменьшается, однако это приводит к уменьшению выходного напряжения.

Рис. XI.2. Амплитудно-фазовая частотная характеристика дифференцирующего RC-четырехполюсника

Рис. XI.3. Логарифмические частотные характеристики дифференцирующего RC-четырехполюсника
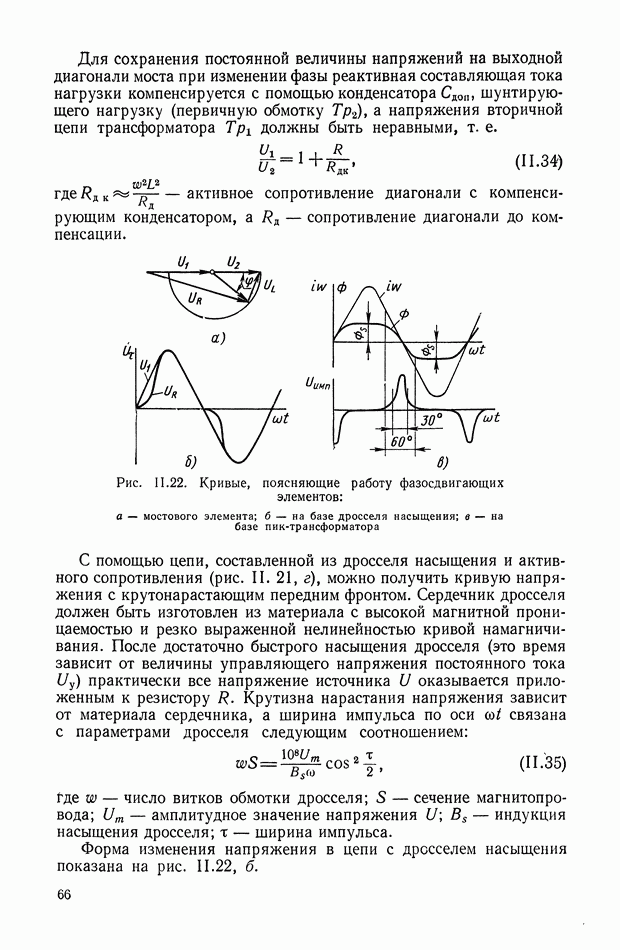
Поэтому для дифференцирования быстро меняющихся напряжений  выбирая малое значение Т для улучшения работы дифференцирующей цепи, применяют электронный усилитель.
выбирая малое значение Т для улучшения работы дифференцирующей цепи, применяют электронный усилитель.
Если входное напряжение  изменяется по линейному закону
изменяется по линейному закону

где

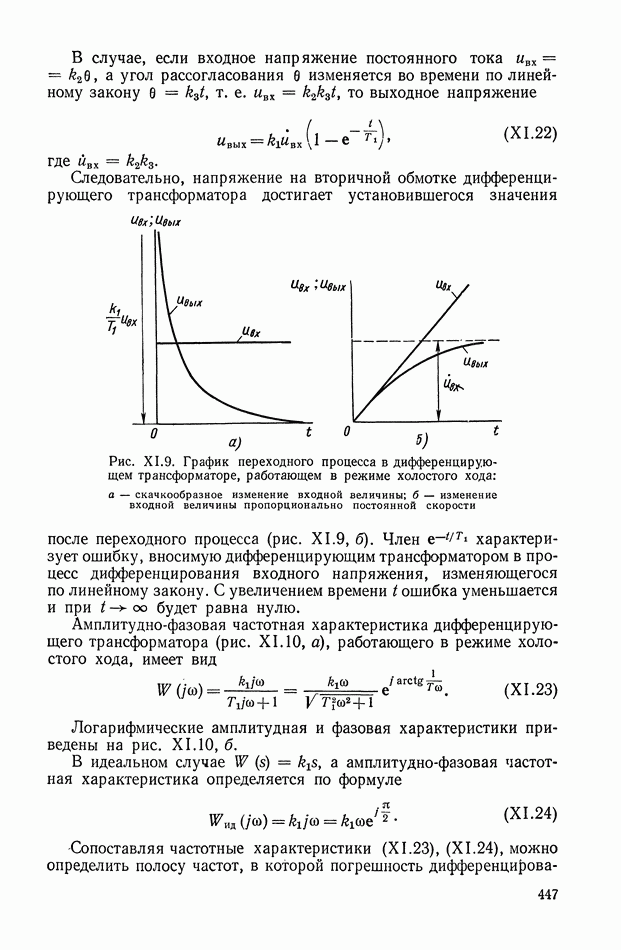
то выходное напряжение изменяется следующим образом:

где  — основание натуральных логарифмов.
— основание натуральных логарифмов.
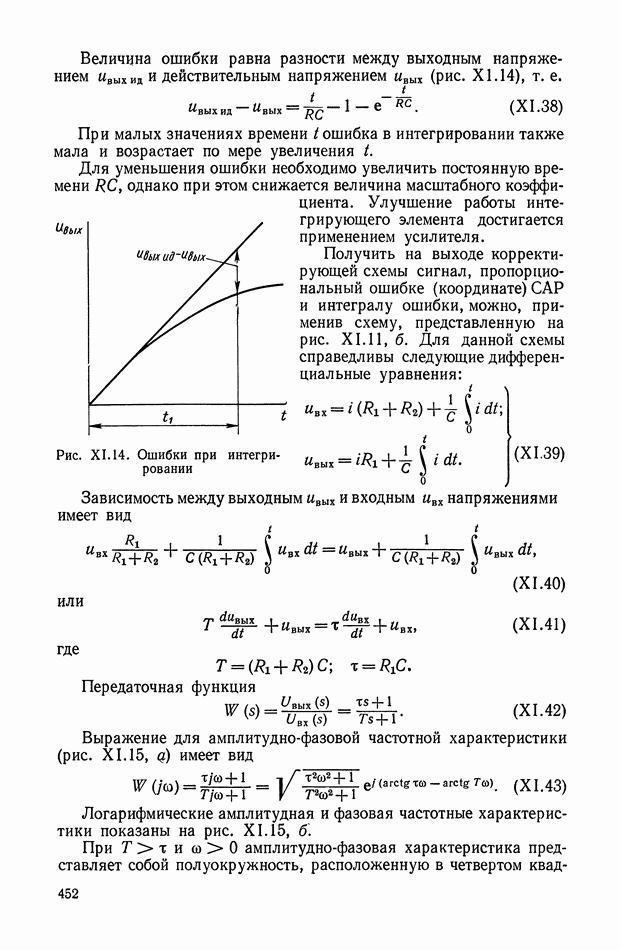
Находя разность между точным значением выходного напряжения, пропорционального производной  и действительным значением
и действительным значением  снимаемым с выхода RC-цепи, получим
снимаемым с выхода RC-цепи, получим

Затем определим величину относительной ошибки  т. Таким образом, с увеличением времени ошибка
т. Таким образом, с увеличением времени ошибка  уменьшается и через достаточно большой промежуток времени становится равной нулю. На выходе другого дифференцирующего четырехполюсника, состоящего из резисторов
уменьшается и через достаточно большой промежуток времени становится равной нулю. На выходе другого дифференцирующего четырехполюсника, состоящего из резисторов  и емкости С (рис. XI.1, б), формируется напряжение, зависящее от координаты и ее первой производной (очевидно, что в цепи, показанной на рис. XI.1, а, такое суммирование невозможно).
и емкости С (рис. XI.1, б), формируется напряжение, зависящее от координаты и ее первой производной (очевидно, что в цепи, показанной на рис. XI.1, а, такое суммирование невозможно).

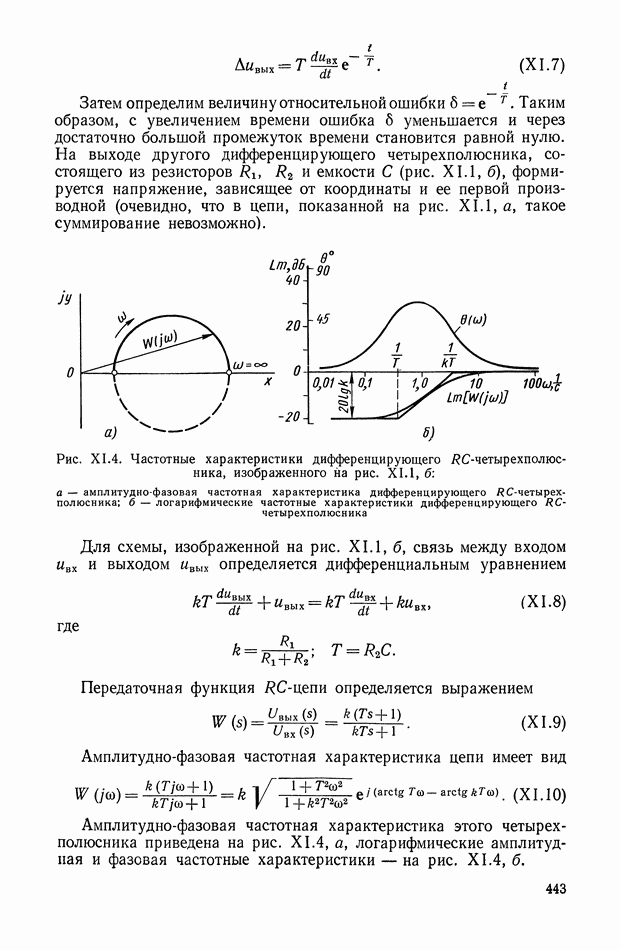
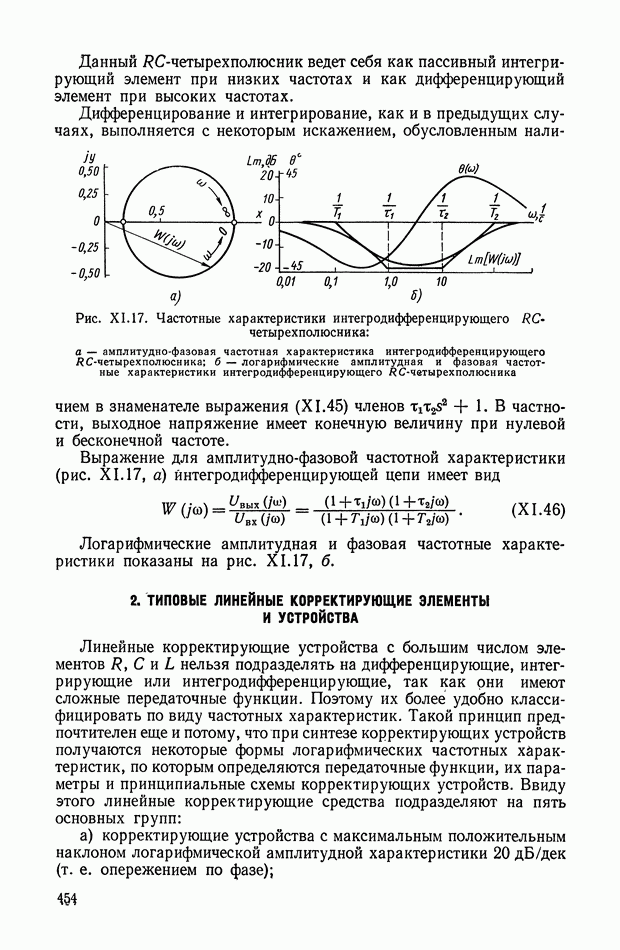
Рис. XI.4. Частотные характеристики дифференцирующего RC-четырехполюсника, изображенного на рис. XI. 1, б: а — амплитудно-фазовая частотная характеристика дифференцирующего RС-четырехполюсника; б — логарифмические частотные характеристики дифференцирующего RC-четырехполюсника
Для схемы, изображенной на рис. XI.1, б, связь между входом  и выходом
и выходом  определяется дифференциальным уравнением
определяется дифференциальным уравнением

где

Передаточная функция RC-цепи определяется выражением

Амплитудно-фазовая частотная характеристика цепи имеет вид

Амплитудно-фазовая частотная характеристика этого четырехполюсника приведена на рис. XI.4, а, логарифмические амплитудная и фазовая частотные характеристики — на рис. XI.4, б.
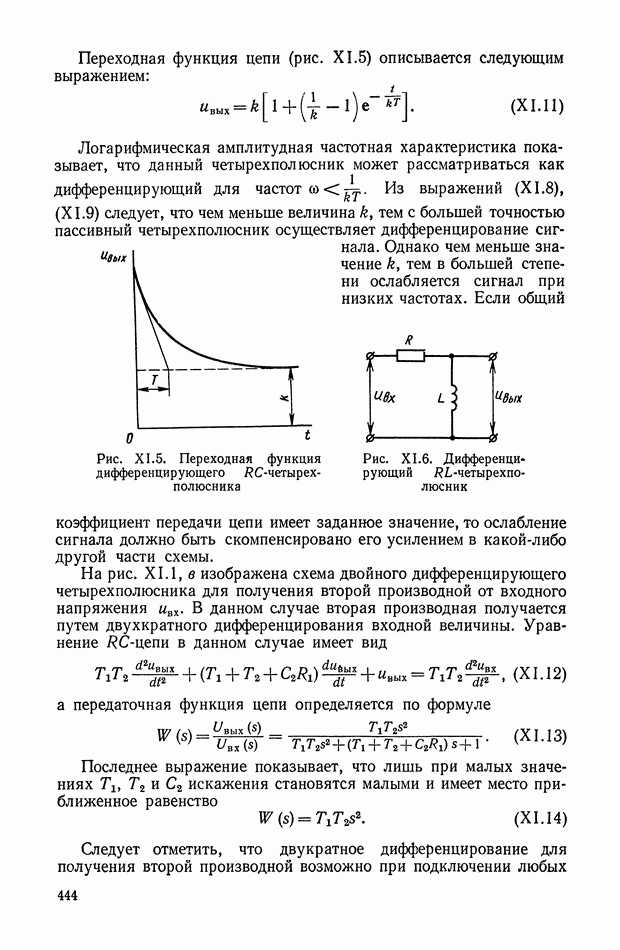
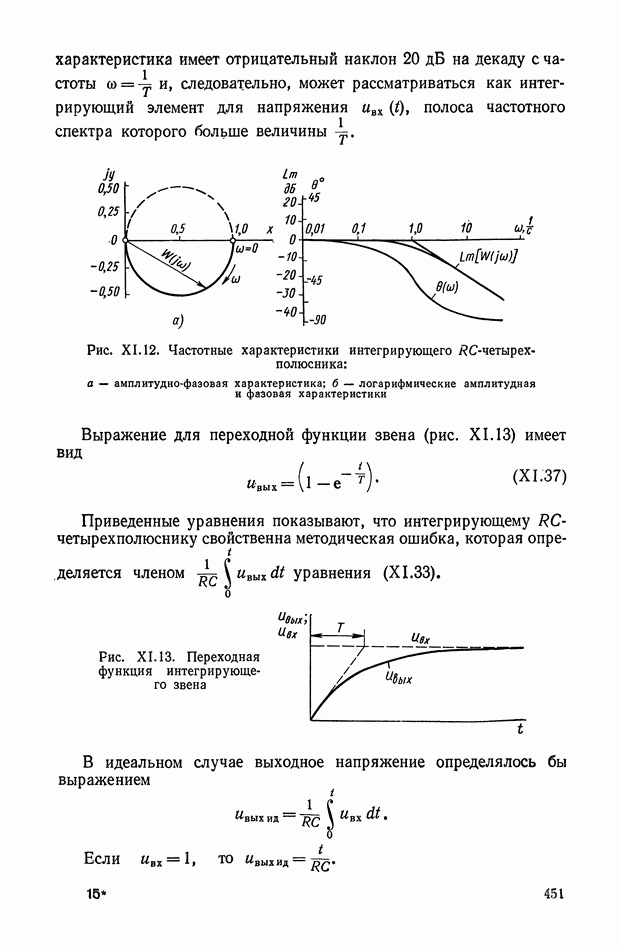
Переходная функция цепи (рис. XI.5) описывается следующим выражением:

Логарифмическая амплитудная частотная характеристика показывает, что данный четырехполюсник может рассматриваться как дифференцирующий для частот  Из выражений (XI.8), (XI.9) следует, что чем меньше величина
Из выражений (XI.8), (XI.9) следует, что чем меньше величина  тем с большей точностью пассивный четырехполюсник осуществляет дифференцирование сигнала. Однако чем меньше значение
тем с большей точностью пассивный четырехполюсник осуществляет дифференцирование сигнала. Однако чем меньше значение  тем в большей степени ослабляется сигнал при низких частотах.
тем в большей степени ослабляется сигнал при низких частотах.

Рис. XI.5. Переходная функция дифференцирующего С-четырехполюсника

Рис. XI.6. Дифференцирующий RL-четырехполюсник
Если общий коэффициент передачи цепи имеет заданное значение, то ослабление сигнала должно быть скомпенсировано его усилением в какой-либо другой части схемы.
На рис. XI. 1, б изображена схема двойного дифференцирующего четырехполюсника для получения второй производной от входного напряжения  . В данном случае вторая производная получается путем двухкратного дифференцирования входной величины. Уравнение RС-цепи в данном случае имеет вид
. В данном случае вторая производная получается путем двухкратного дифференцирования входной величины. Уравнение RС-цепи в данном случае имеет вид

а передаточная функция цепи определяется по формуле

Последнее выражение показывает, что лишь при малых значениях  искажения становятся малыми и имеет место приближенное равенство
искажения становятся малыми и имеет место приближенное равенство

Следует отметить, что двукратное дифференцирование для получения второй производной возможно при подключении любых
дифференцирующих четырехполюсников, однако погрешность дифференцирования при добавлении каждого нового элемента быстро возрастает, что ограничивает их применение.
На рис. XI.6 изображена схема дифференцирующего RL-четырехполюсника. Связь выходного напряжения с входным может быть установлена с помощью следующих уравнений:

Решая их совместно при  получим следующее дифференциальное уравнение:
получим следующее дифференциальное уравнение:

Передаточная функция данной RL-цепи имеет вид

Сравнивая уравнения (XI.16) и (XI.17) с формулами (XI.2), (XI.3), видим, что амплитудно-фазовые, логарифмические амплитудные и фазовые частотные характеристики, а также переходные функции четырехполюсников, показанных на рис. XI.6 и XI. 1, аналогичны. Следовательно, дифференцирующий RC-четырехполюсник, так же как и RC-четырехполюсник, вносит ошибку в операцию дифференцирования. Это искажение определяется членом  в уравнении (XI.16) и Т в знаменателе передаточной функции (XI.17). Для уменьшения искажения следует уменьшить постоянную времени Т, однако при этом уменьшается также величина выходного напряжения
в уравнении (XI.16) и Т в знаменателе передаточной функции (XI.17). Для уменьшения искажения следует уменьшить постоянную времени Т, однако при этом уменьшается также величина выходного напряжения  .
.
Следует отметить, что RL-цепь применяется значительно реже по сравнению с RC-цепью из-за трудности практического осуществления катушки индуктивности с большим коэффициентом самоиндукции  и малым активным сопротивлением.
и малым активным сопротивлением.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА САР
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ЛИНЕЙНЫХ УСИЛИТЕЛЬНЫХ УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ УСИЛИТЕЛЬНОГО УСТРОЙСТВА БЕЗ ОБРАТНОЙ СВЯЗИ
- 3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ, СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ОСОБЕННОСТИ УСИЛИТЕЛЬНОГО УСТРОЙСТВА С ОБРАТНОЙ СВЯЗЬЮ
- 4. КЛАССИФИКАЦИЯ И СВОЙСТВА УСИЛИТЕЛЬНЫХ УСТРОЙСТВ С ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 5. ВЫБОР И РАСЧЕТ УСИЛИТЕЛЬНОГО УСТРОЙСТВА
- ГЛАВА II. ЭЛЕКТРОННЫЕ ЛАМПОВЫЕ И ИОННЫЕ УСИЛИТЕЛИ
- 1. ОСНОВЫ ТОПОЛОГИЧЕСКОГО АНАЛИЗА СХЕМ ЛИНЕЙНЫХ ЭЛЕКТРОННЫХ ЛАМПОВЫХ УСИЛИТЕЛЕЙ
- 2. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПОСТОЯННОГО ТОКА
- 3. БАЛАНСНЫЕ МОСТОВЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- 4. СТАБИЛИЗАЦИЯ КОЭФФИЦИЕНТА УСИЛЕНИЯ
- 5. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
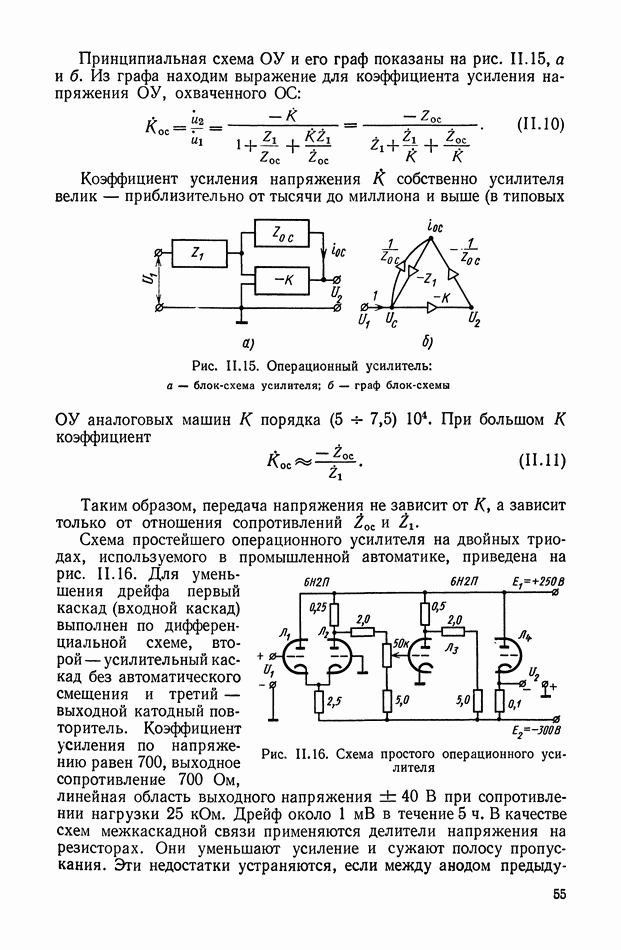
- 6. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- 7. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
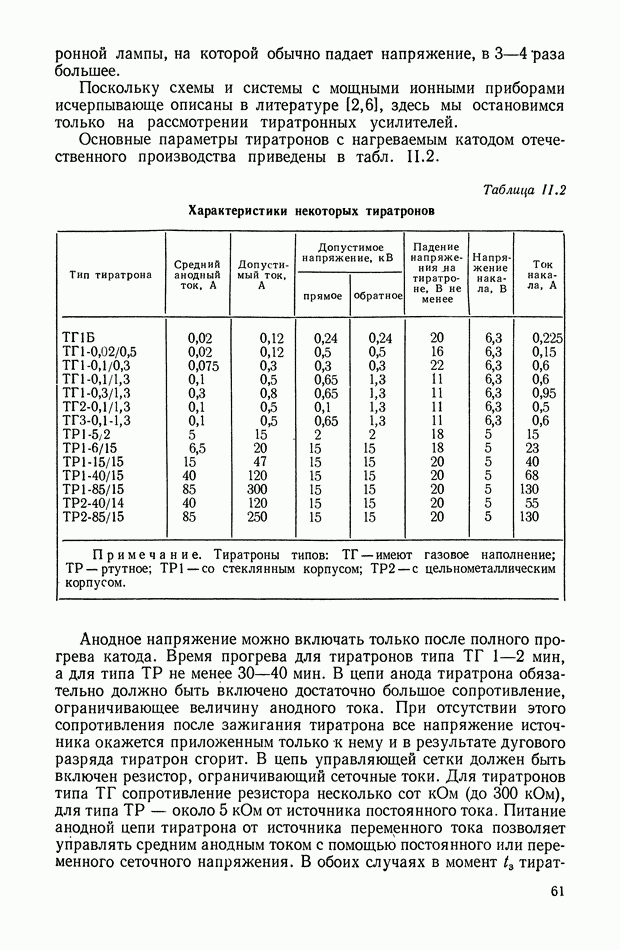
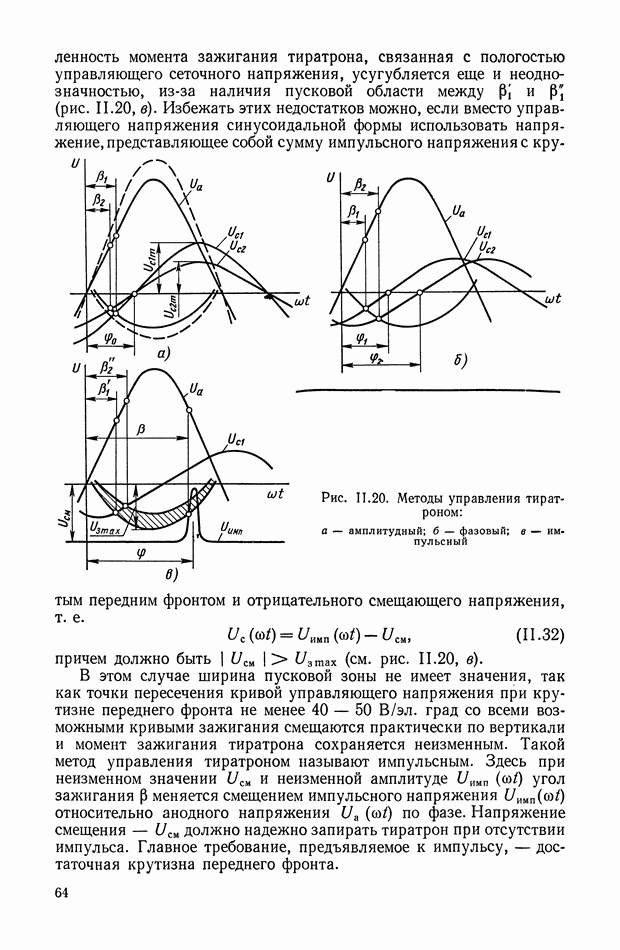
- 8. ОБЩИЕ СВОЙСТВА ИОННОГО (ТИРАТРОННОГО) УСИЛИТЕЛЯ МЕТОДЫ УПРАВЛЕНИЯ ТИРАТРОНОМ
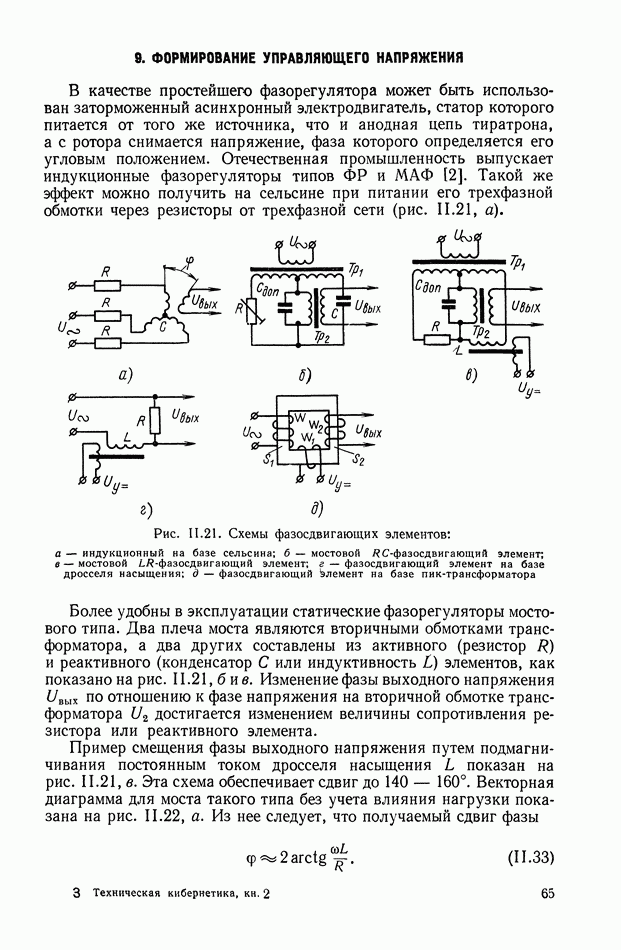
- 9. ФОРМИРОВАНИЕ УПРАВЛЯЮЩЕГО НАПРЯЖЕНИЯ
- 10. РАСЧЕТ ЭЛЕМЕНТОВ СХЕМ ТИРАТРОННОГО УСИЛИТЕЛЯ
- ГЛАВА III. ПОЛУПРОВОДНИКОВЫЕ И ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
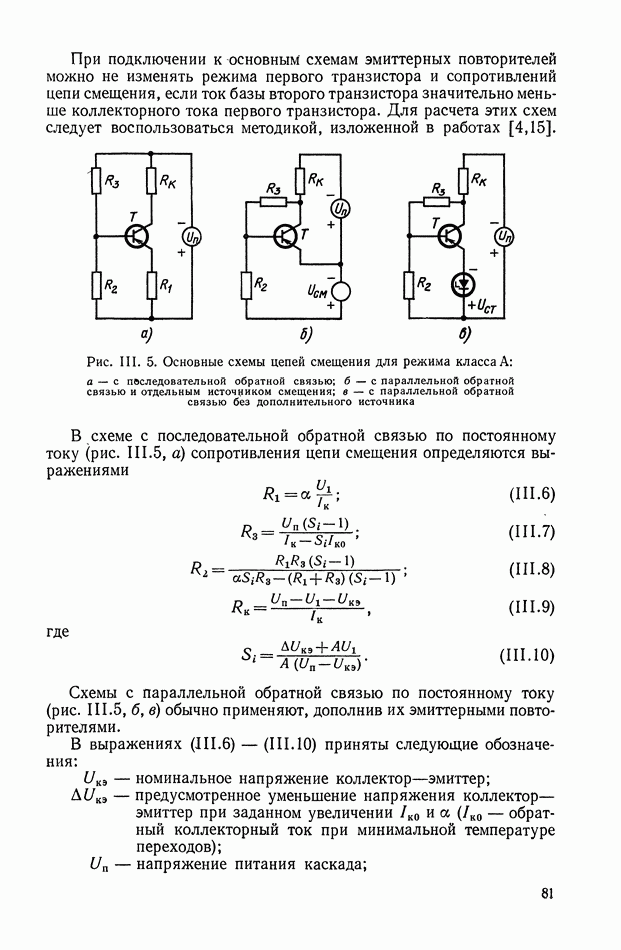
- Цепи смещения.
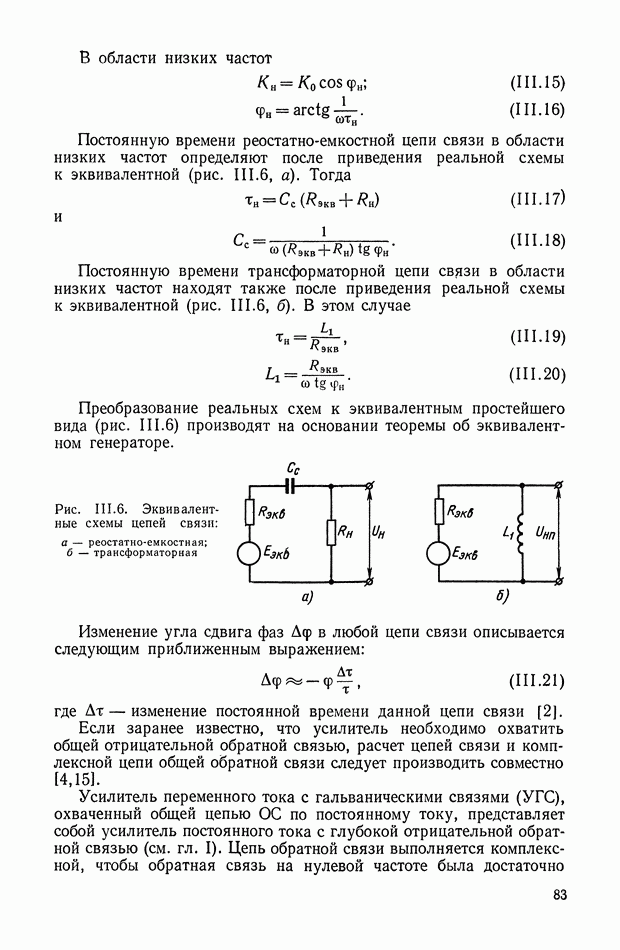
- Цепи связи.
- 2. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ СРЕДНЕГО ЗНАЧЕНИЯ ТОКА
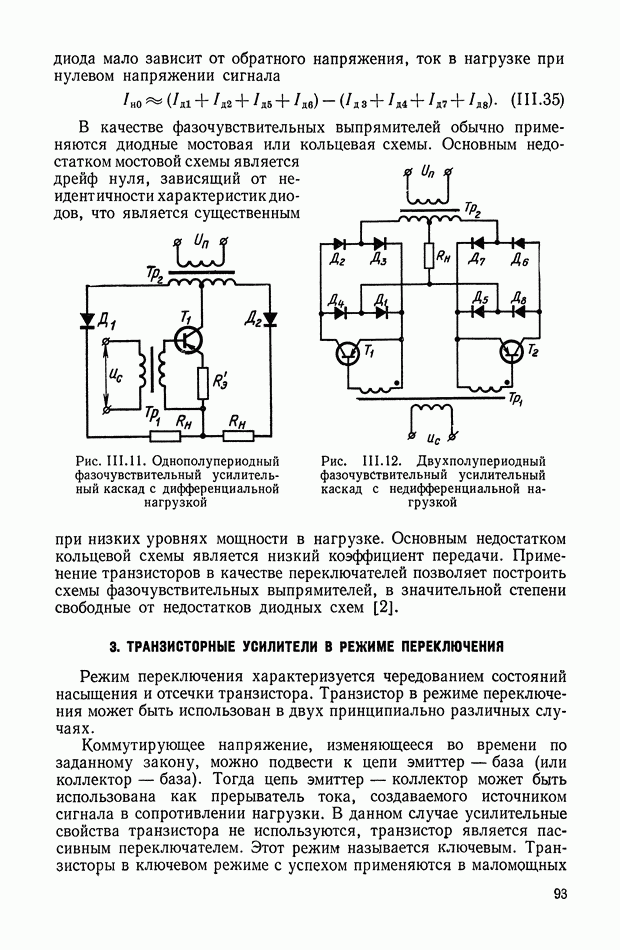
- Полупроводниковые демодуляторы.
- 3. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ В РЕЖИМЕ ПЕРЕКЛЮЧЕНИЯ
- Режимы импульсного регулирования мощности.
- Управление силовыми транзисторами.
- 4. ТРАНЗИСТОРНЫЕ УСТРОЙСТВА УПРАВЛЕНИЯ ЭЛЕКТРОДВИГАТЕЛЯМИ И ЭЛЕКТРОМАГНИТНЫМИ МЕХАНИЗМАМИ
- 5. ТИРИСТОРЫ. ХАРАКТЕРИСТИКИ, ПАРАМЕТРЫ И СВОЙСТВА
- 6. СПОСОБЫ И УСТРОЙСТВА УПРАВЛЕНИЯ ТИРИСТОРАМИ
- 7. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ (РЕГУЛИРУЕМЫЕ ВЫПРЯМИТЕЛИ)
- 8. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 9. ТИРИСТОРНЫЕ УСИЛИТЕЛИ С ПИТАНИЕМ ОТ СЕТИ ПОСТОЯННОГО ТОКА
- 10. ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 11. ОСНОВЫ РАСЧЕТА ДИЭЛЕКТРИЧЕСКИХ УСИЛИТЕЛЕЙ
- ГЛАВА IV. КВАНТОВЫЕ УСИЛИТЕЛИ И ГЕНЕРАТОРЫ
- 2. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ РАДИОДИАПАЗОНА
- Квантовые усилители радиодиапазона.
- 3. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- Оптический квантовый усилитель
- 4. ПРИМЕНЕНИЕ В САР КВАНТОВЫХ УСИЛИТЕЛЕЙ И ГЕНЕРАТОРОВ РАДИОДИАПАЗОНА, ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- ГЛАВА V. МАГНИТНЫЕ И МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- 2. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ МАГНИТНЫХ УСИЛИТЕЛЕЙ
- 3. ОДНОТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ БЕЗ ОБРАТНОЙ СВЯЗИ (УПРАВЛЯЕМЫЕ ДРОССЕЛИ И ТРАНСФОРМАТОРЫ)
- 4. МАГНИТНЫЕ УСИЛИТЕЛИ С САМОНАСЫЩЕНИЕМ
- Релейный режим работы усилителей с самонасыщением.
- 5. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 6. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ
- 7. МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- ГЛАВА VI. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 2. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С НЕЗАВИСИМЫМ ВОЗБУЖДЕНИЕМ И С САМОВОЗБУЖДЕНИЕМ
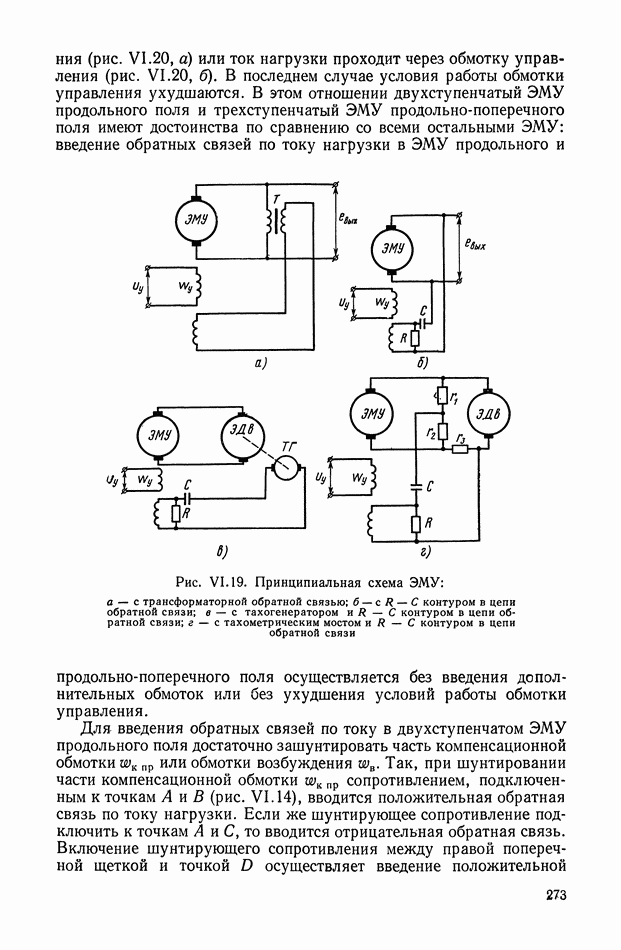
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С ПОПЕРЕЧНЫМ ПОЛЕМ
- 4. ЭЛЕКТРОМАШИННЫЙ УСИЛИТЕЛЬ ПРОДОЛЬНОГО И ПРОДОЛЬНО-ПОПЕРЕЧНОГО ПОЛЯ
- 5. ВЛИЯНИЕ НА ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭМУ ВИХРЕВЫХ И КОММУТАЦИОННЫХ ТОКОВ, ГИСТЕРЕЗИСА И СДВИГА ЩЕТОК С НЕЙТРАЛИ
- 6. МЕТОДЫ УЛУЧШЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕКТРОМАШИННЫХ УСИЛИТЕЛЕЙ
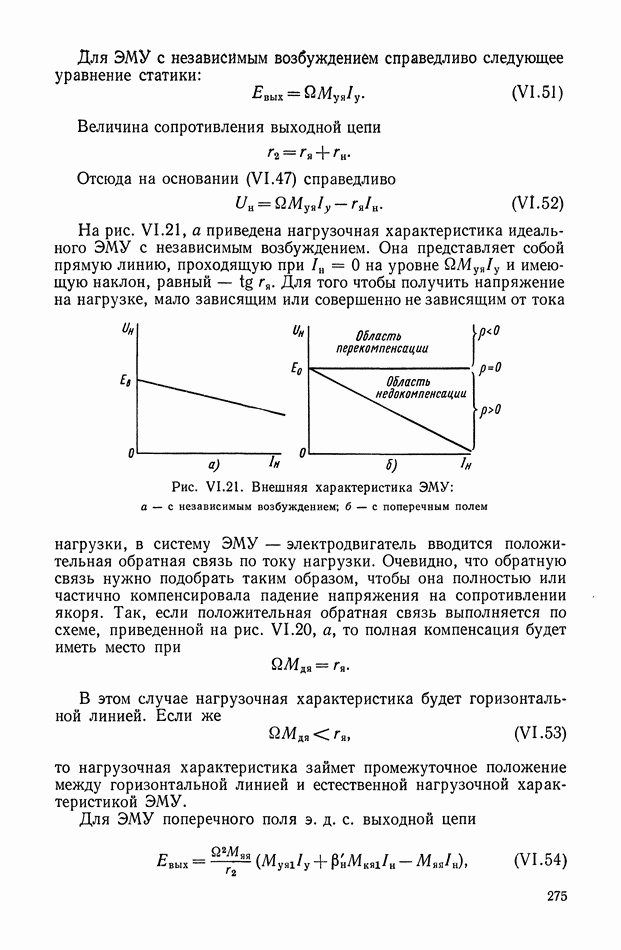
- 7. НАГРУЗОЧНАЯ ХАРАКТЕРИСТИКА ЭЛЕКТРОМАШИННОГО УСИЛИТЕЛЯ
- ГЛАВА VII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ УСИЛИТЕЛИ
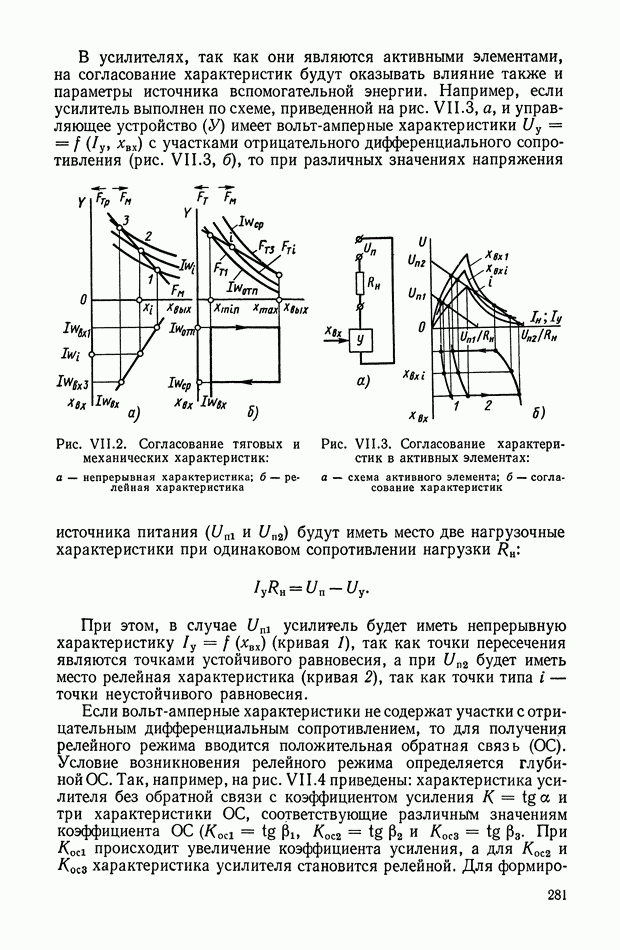
- 1. ХАРАКТЕРИСТИКИ УСИЛИТЕЛЕЙ И СПОСОБЫ ИХ ФОРМИРОВАНИЯ
- 2. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
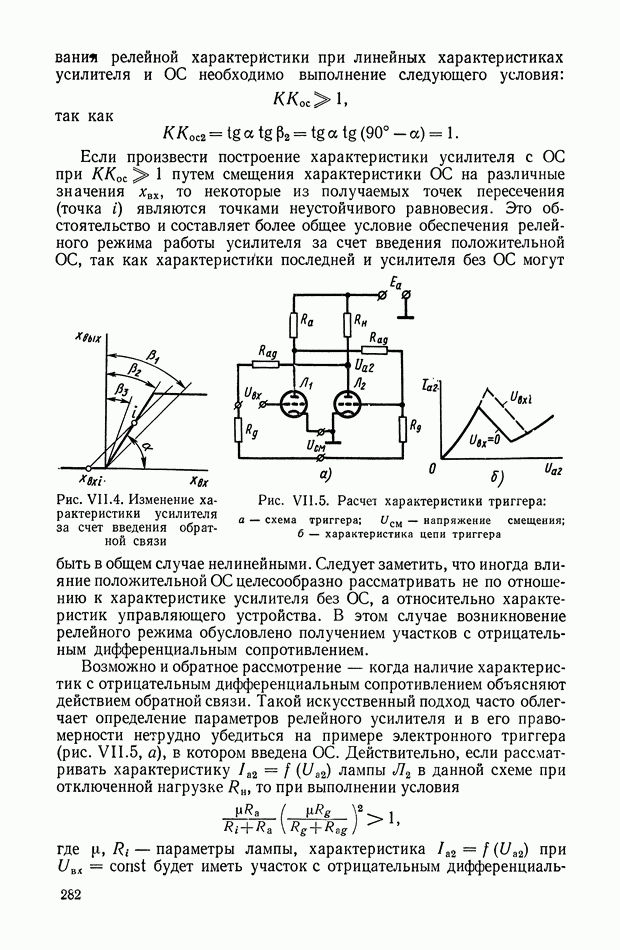
- 3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ЛИНЕАРИЗОВАННЫЕ УСИЛИТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ РЕЛЕ
- 4. БЕСКОНТАКТНЫЕ ЛИНЕАРИЗОВАННЫЕ РЕЛЕЙНЫЕ УСИЛИТЕЛИ
- ГЛАВА VIII. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 2. ОСНОВНЫЕ ЭЛЕМЕНТЫ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ И ИХ ХАРАКТЕРИСТИКИ
- 3. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ С ЗОЛОТНИКОМ
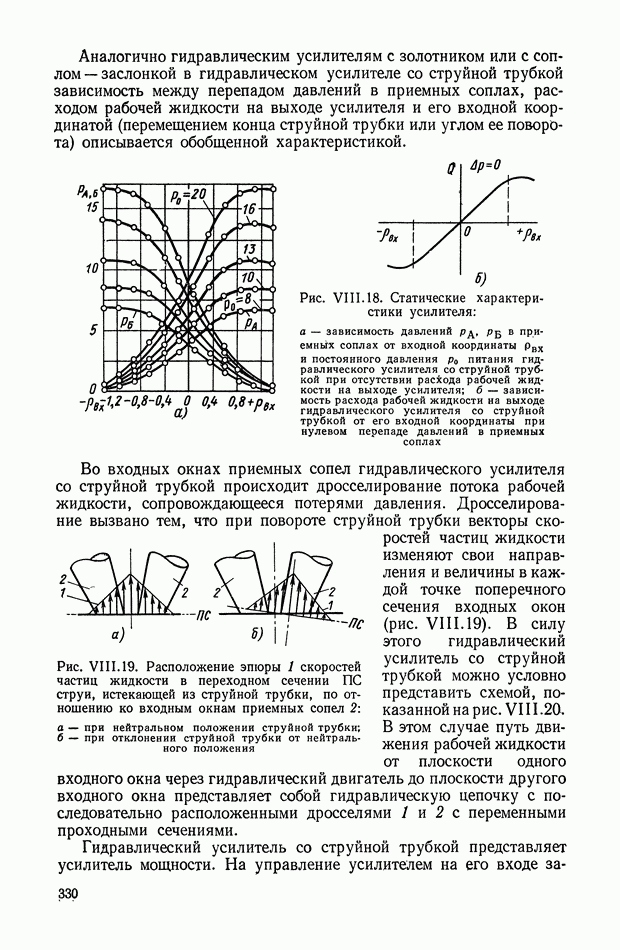
- 4. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ СО СТРУЙНОЙ ТРУБКОЙ
- 5. СХЕМЫ И ПРИНЦИПЫ ДЕЙСТВИЯ ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 6. СТАТИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 7. ДИНАМИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
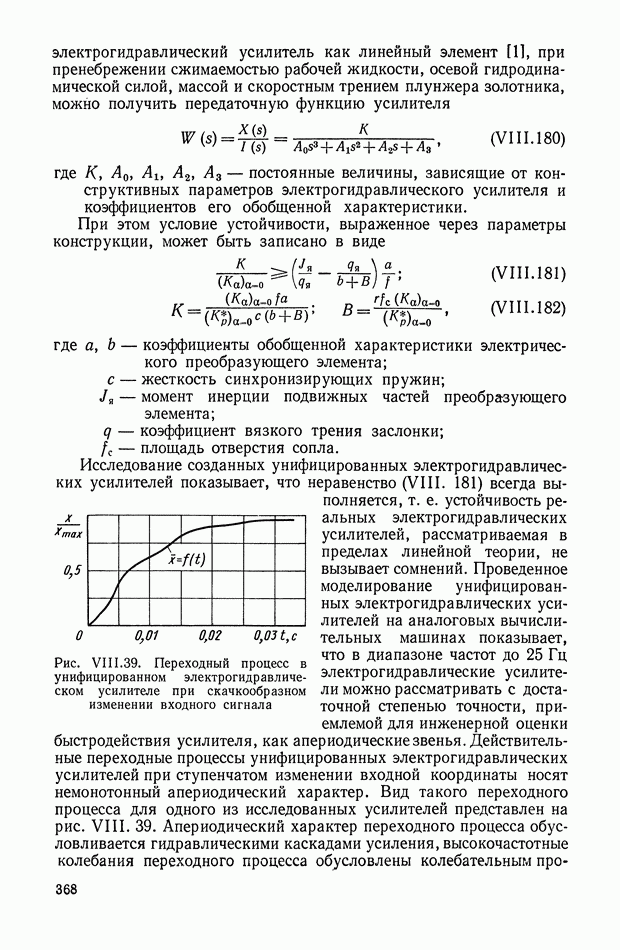
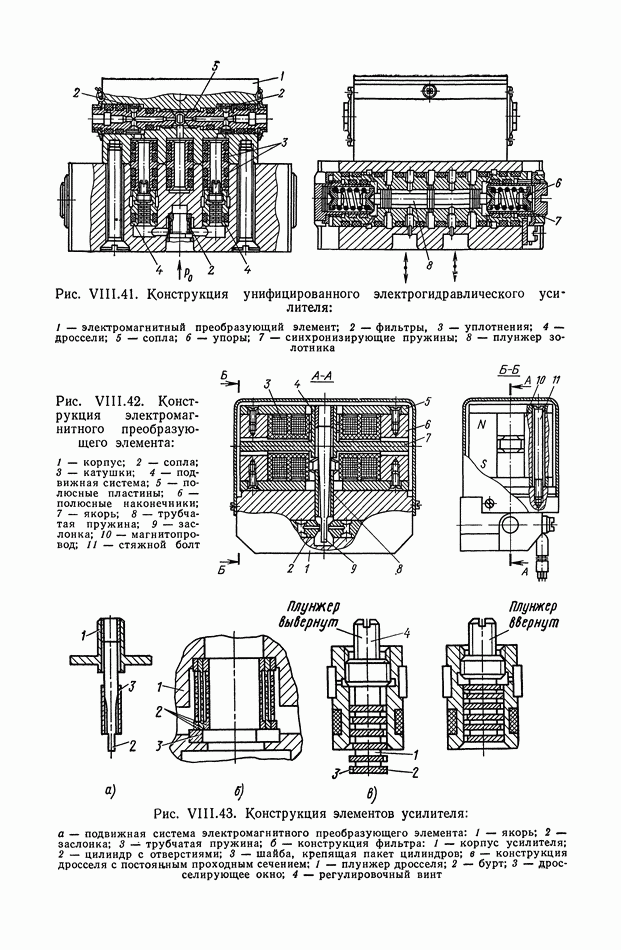
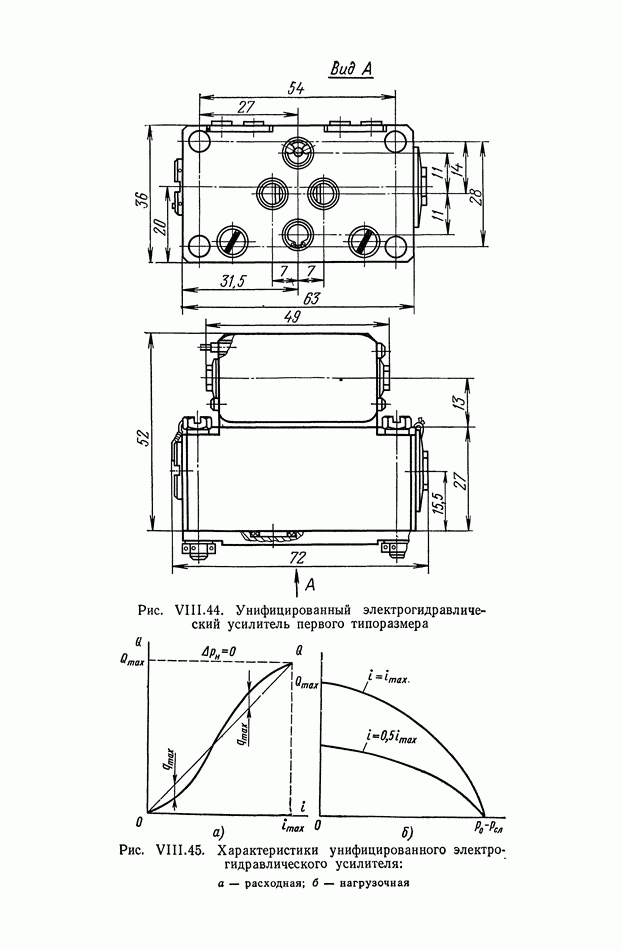
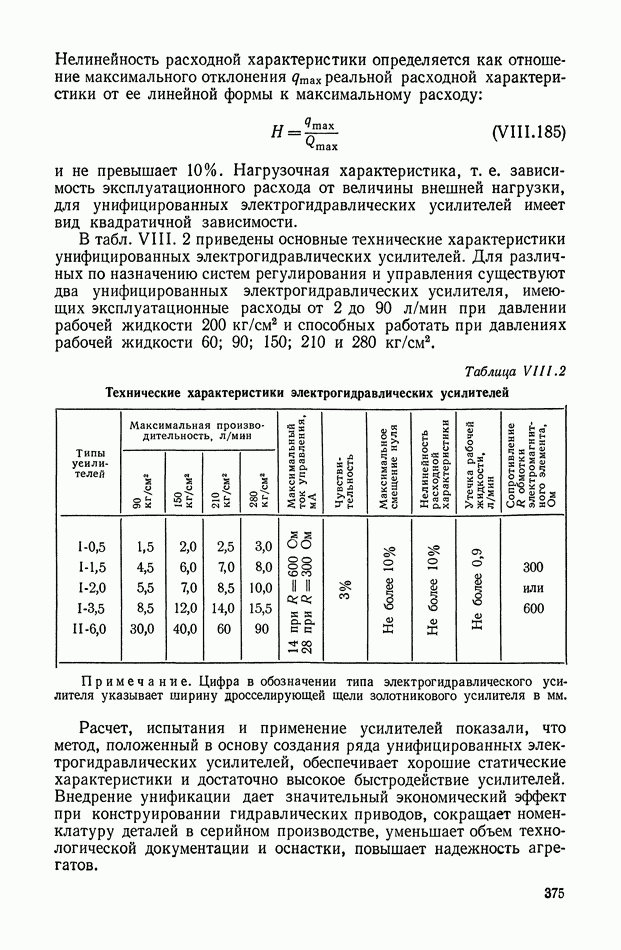
- 8. УНИФИКАЦИЯ ЭЛЕКТРОГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ ДЛЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
- ГЛАВА IX. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ И ИХ КЛАССИФИКАЦИЯ
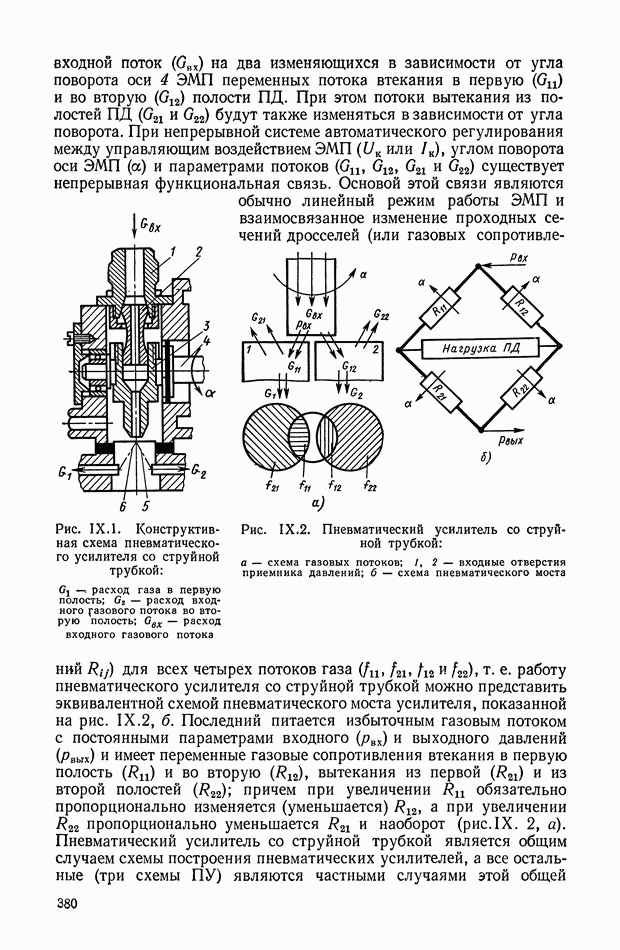
- 2. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ СО СТРУЙНОЙ ТРУБКОЙ
- 3. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗОЛОТНИКОМ
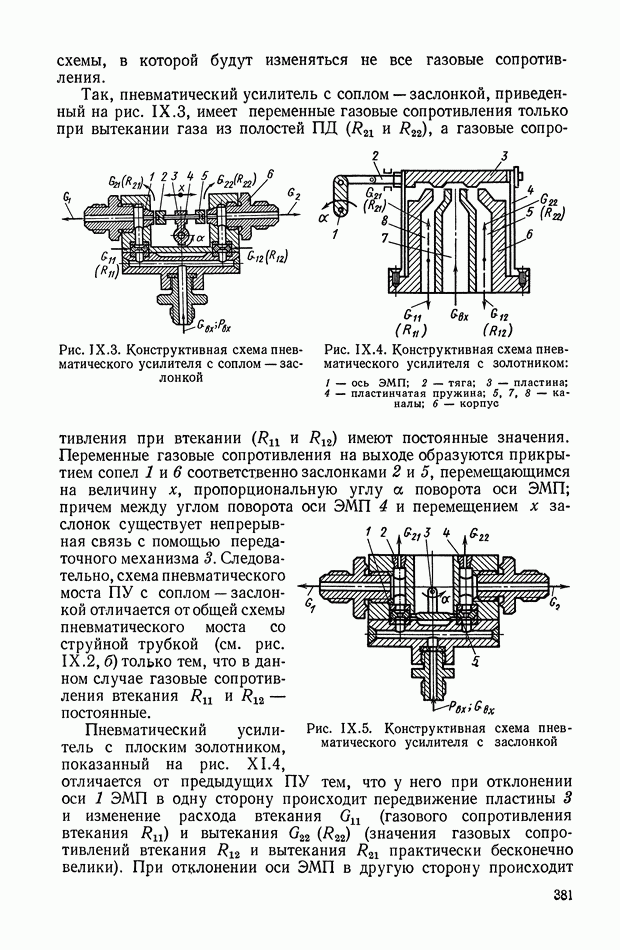
- 4. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С СОПЛОМ — ЗАСЛОНКОЙ
- 5. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗАСЛОНКОЙ
- 6. МНОГОКАСКАДНЫЕ ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- РАЗДЕЛ II. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ И УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ЛИНЕЙНЫХ ПАССИВНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Основные соотношения для синтеза пассивного RC-четырехполюсника.
- 3. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Активные четырехполюсники, получаемые с помощью конверторов отрицательного сопротивления.
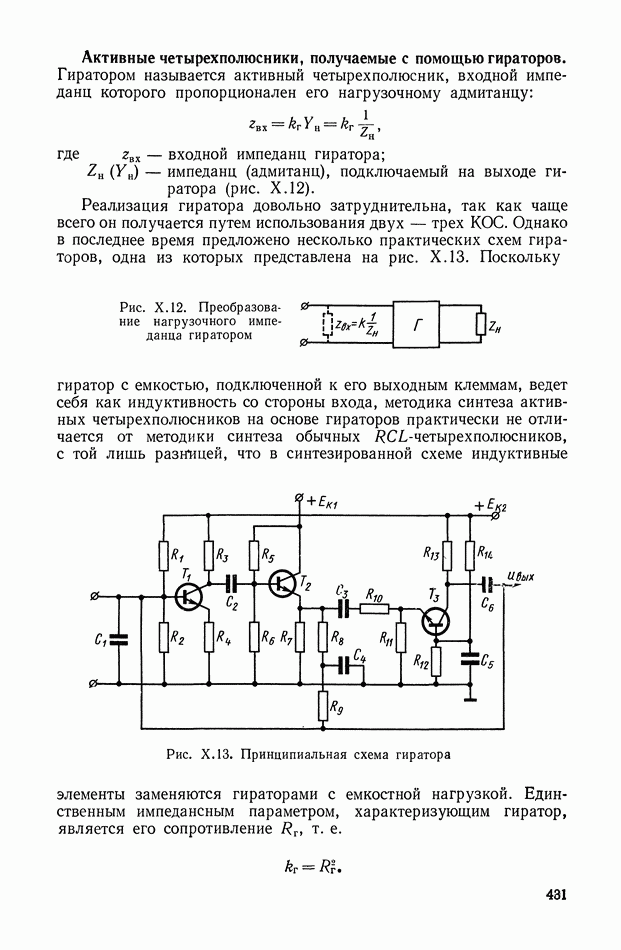
- Активные четырехполюсники, получаемые с помощью гираторов.
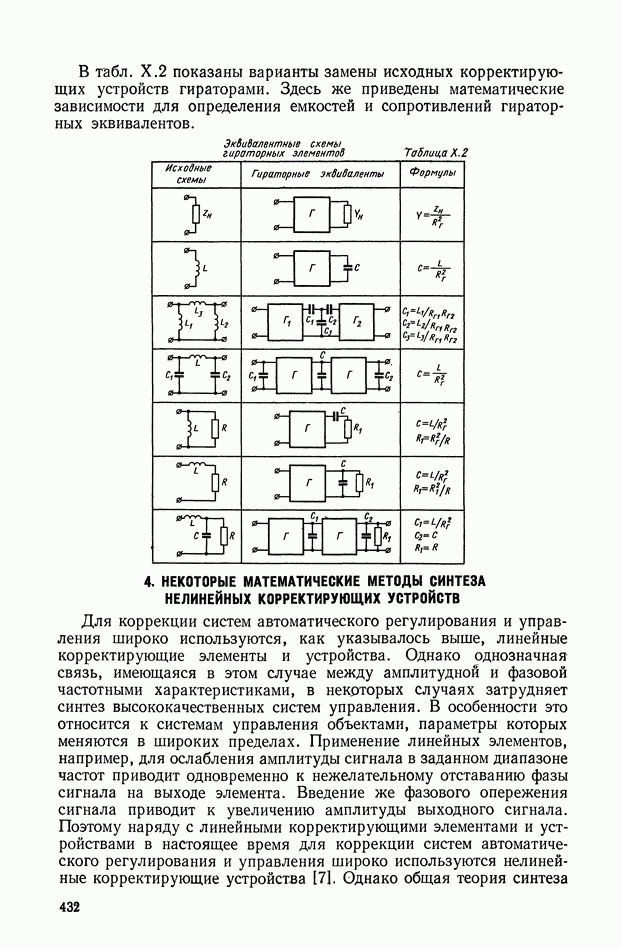
- 4. НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА НЕЛИНЕЙНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
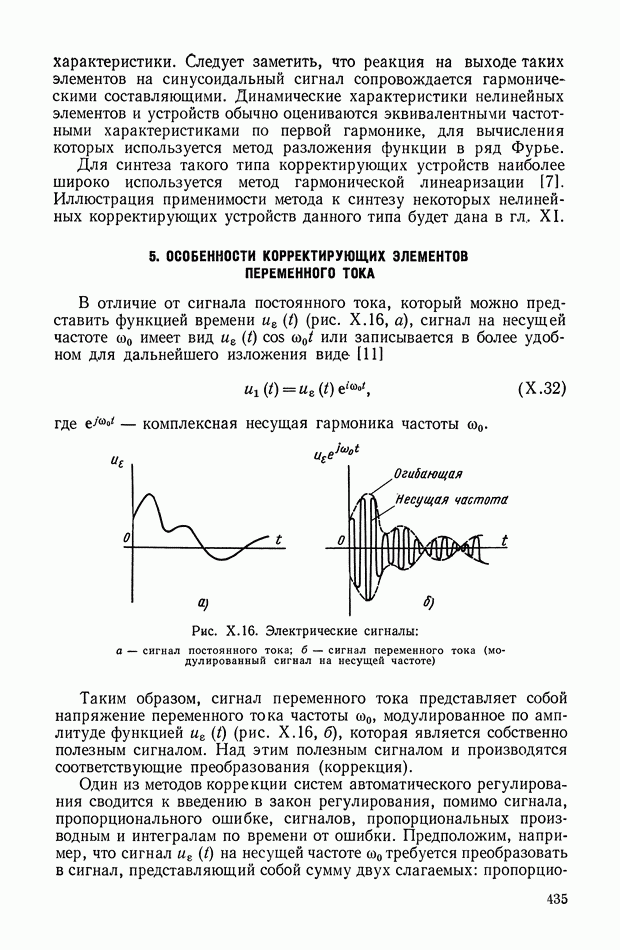
- 5. ОСОБЕННОСТИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XI. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА ПОСТОЯННОГО ТОКА
- Дифференцирующий трансформатор.
- Электрические интегрирующие элементы.
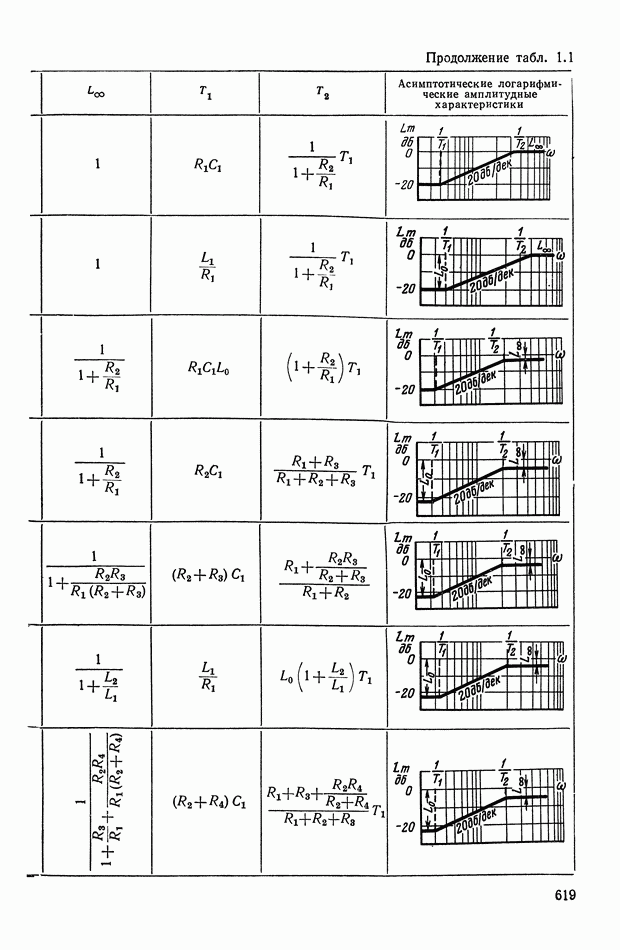
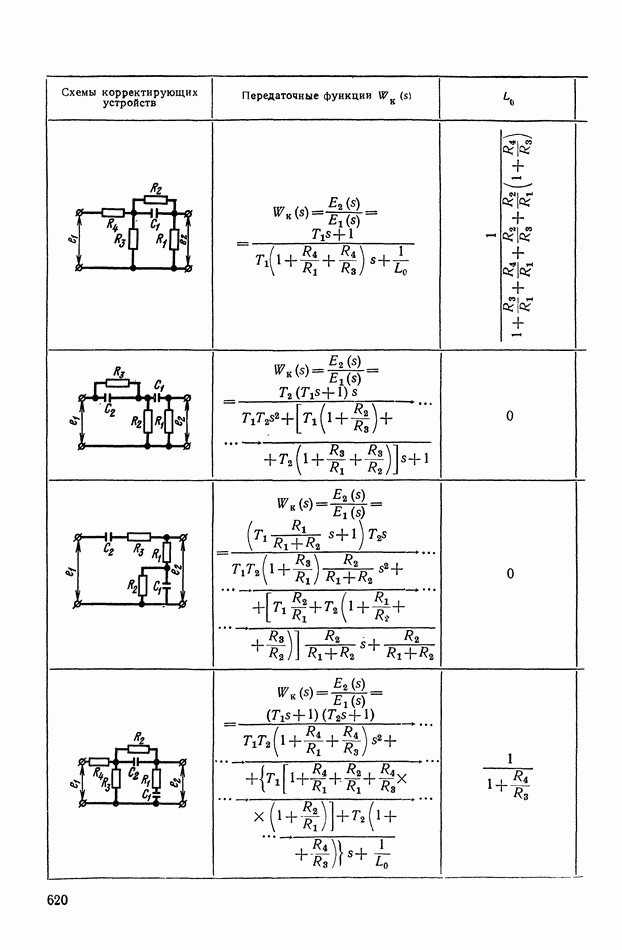
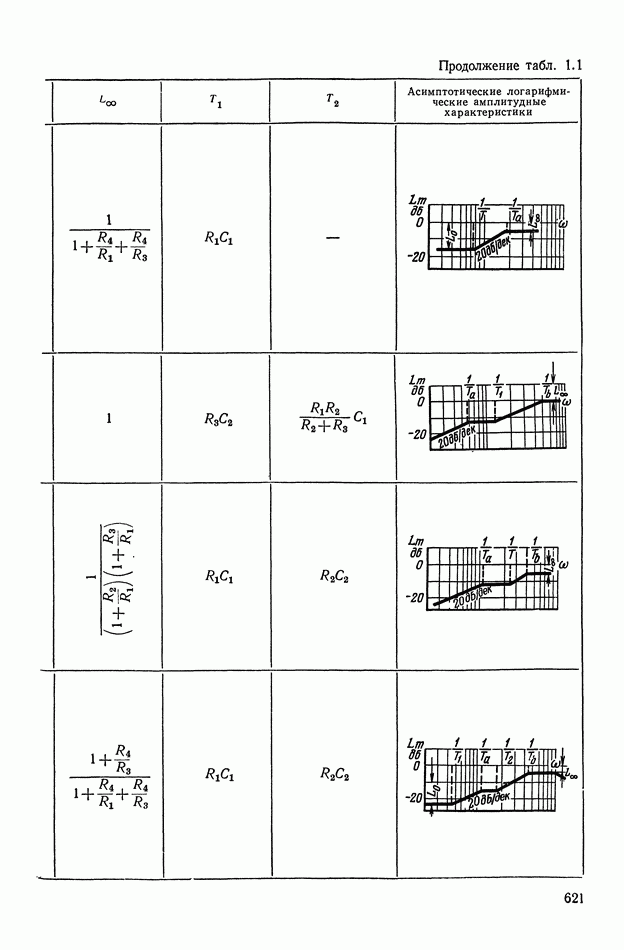
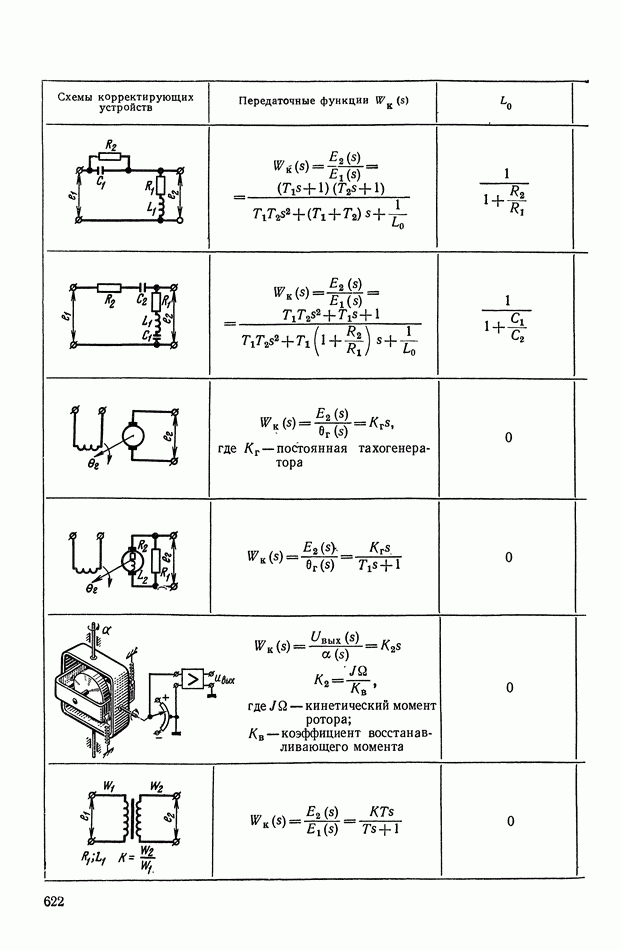
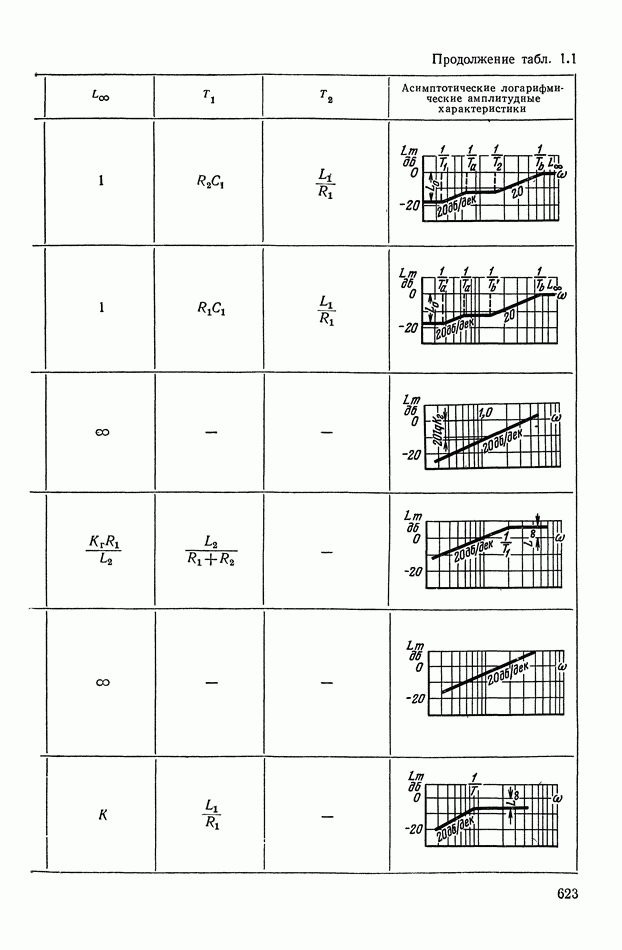
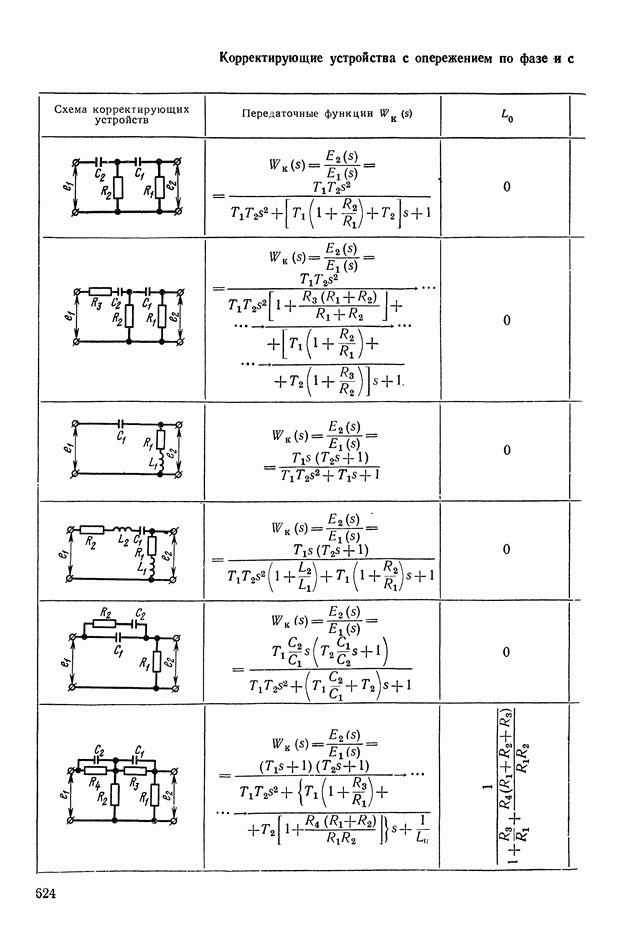
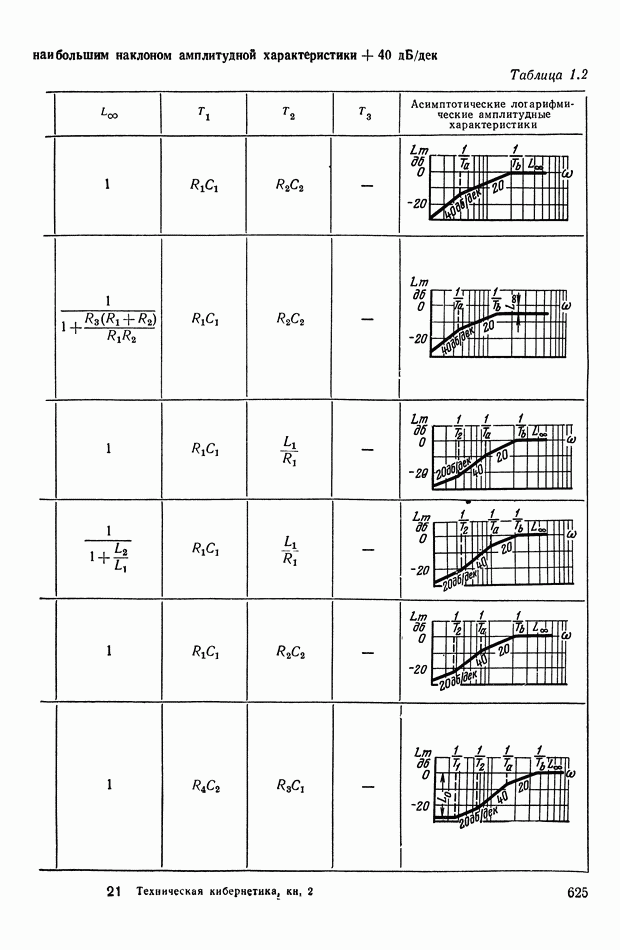
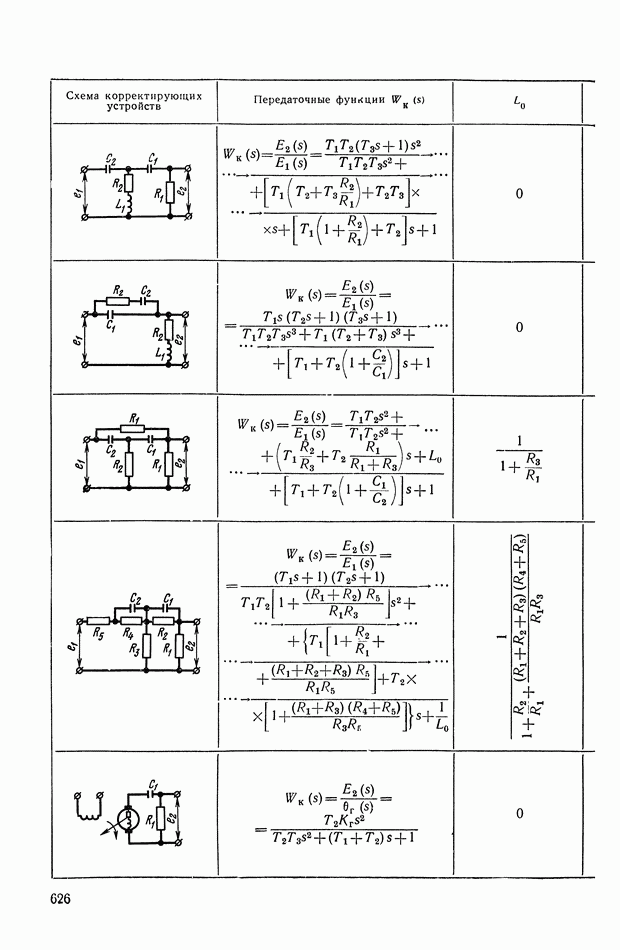
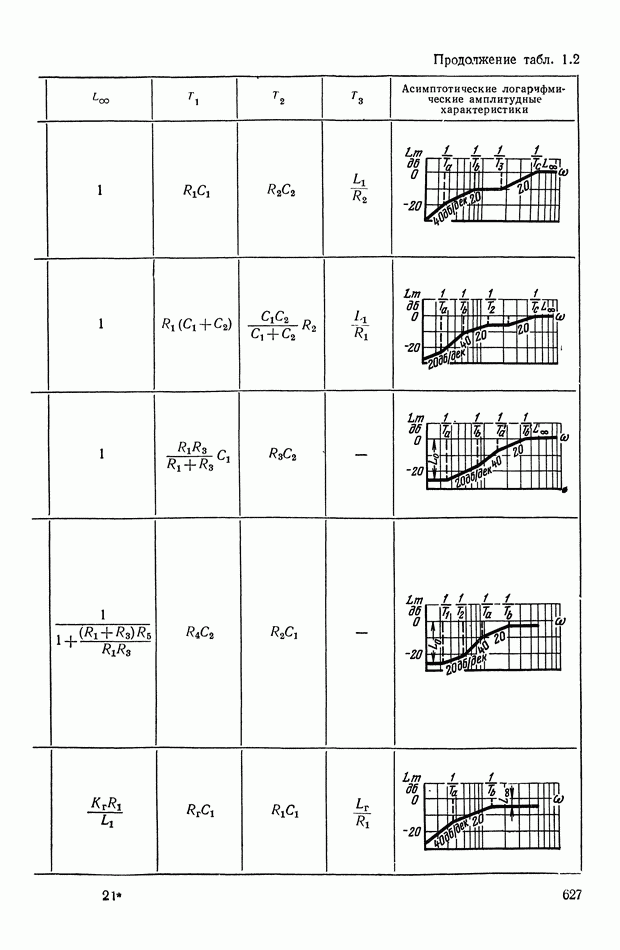
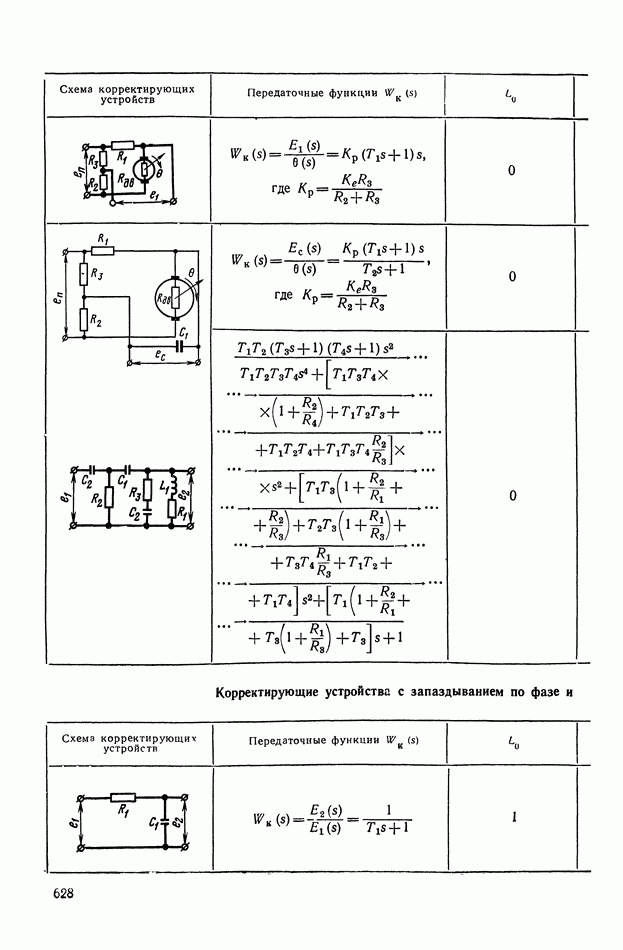
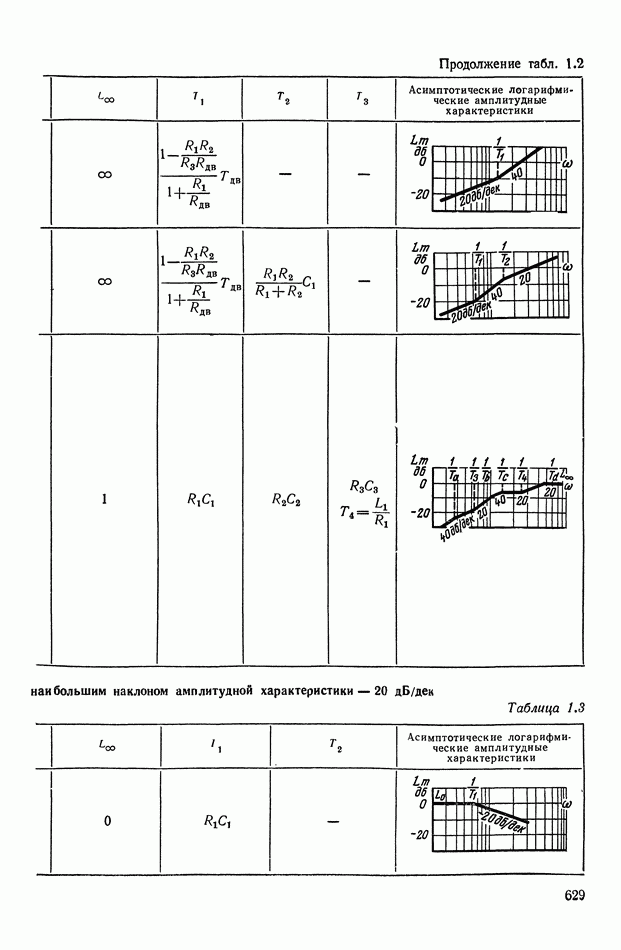
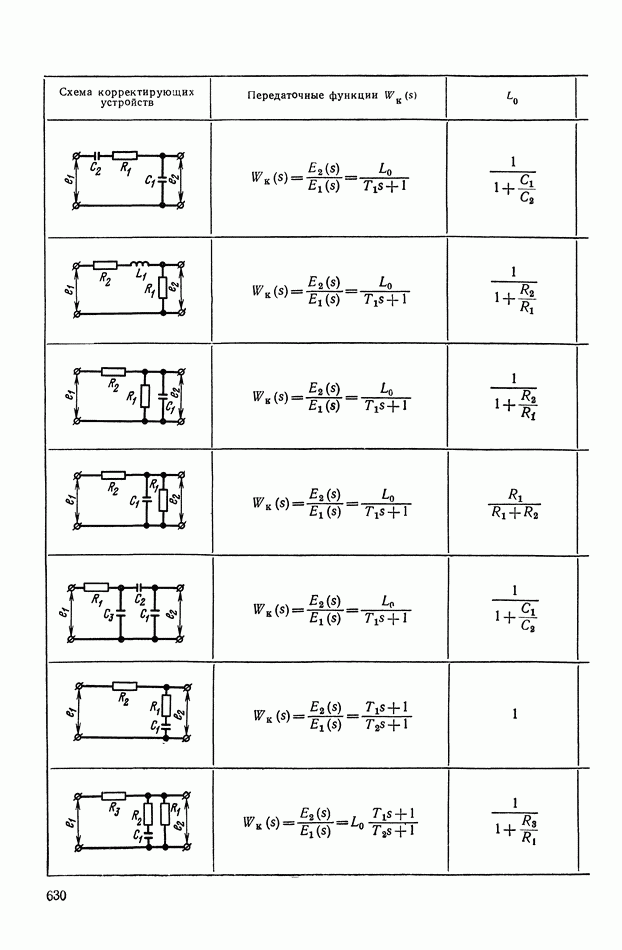
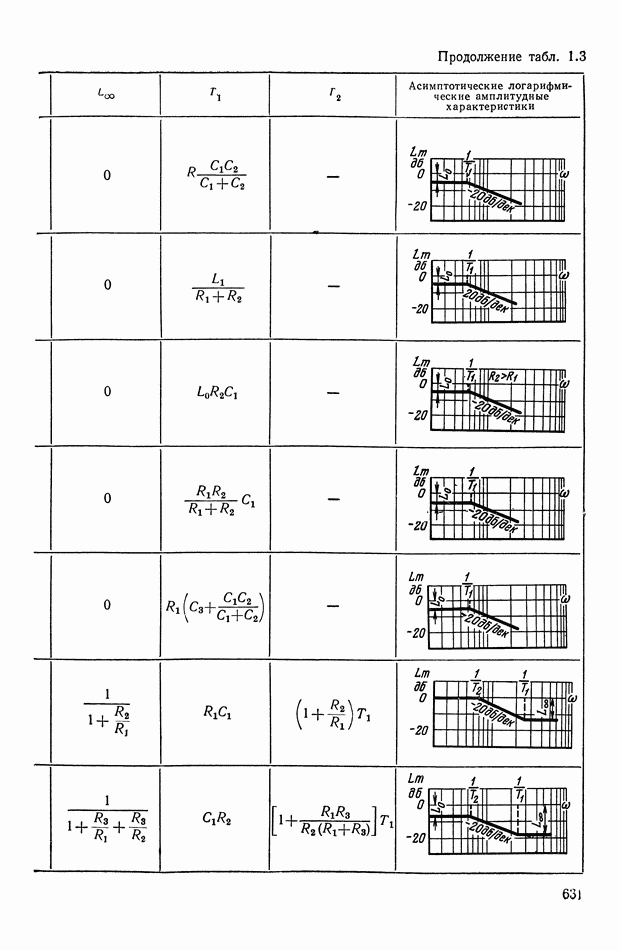
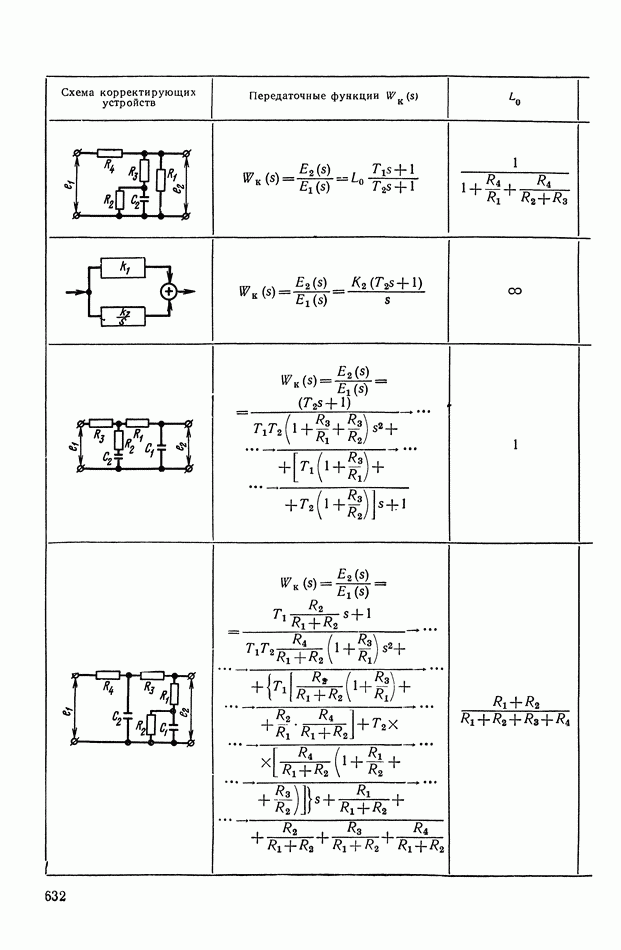
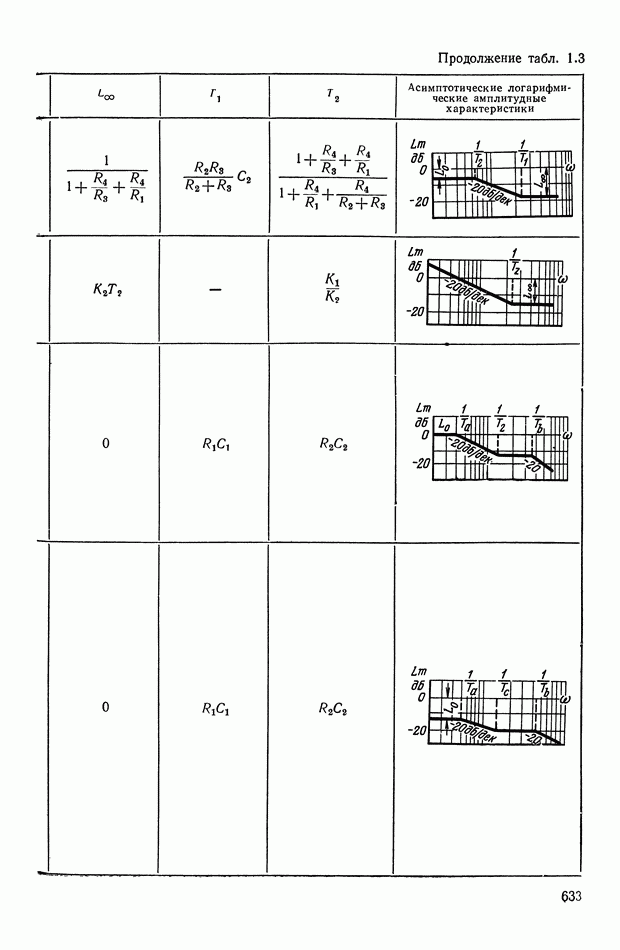
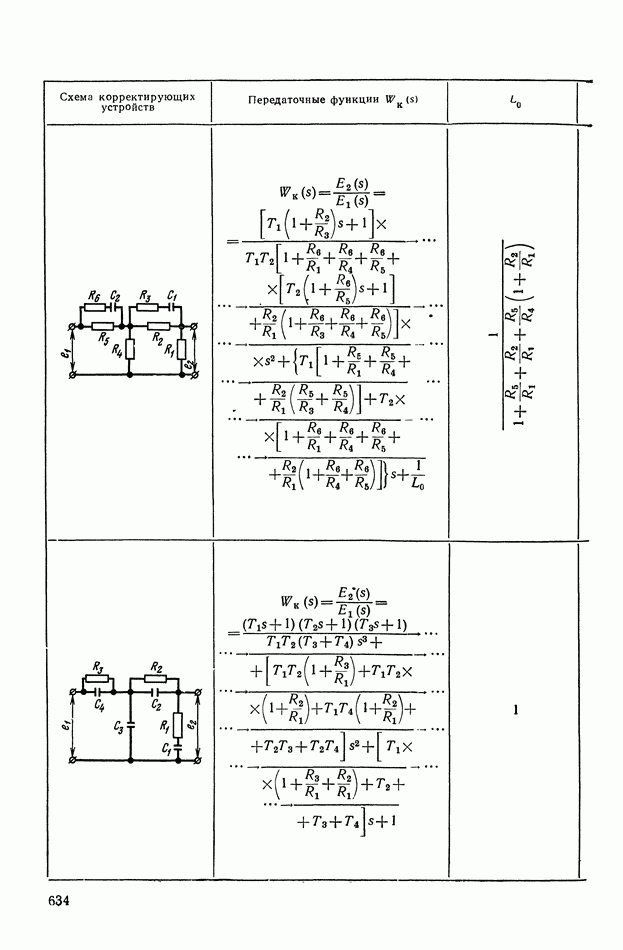
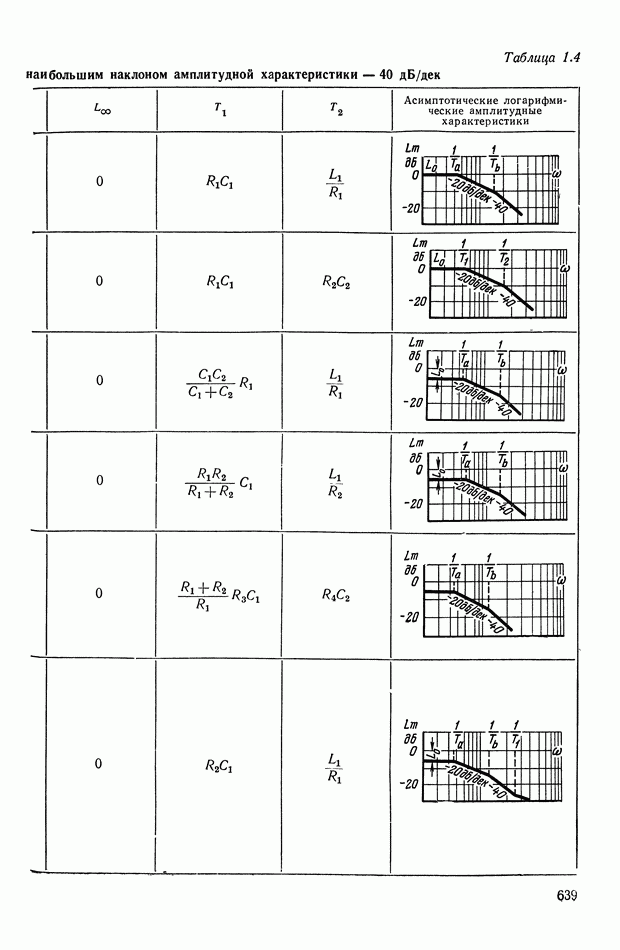
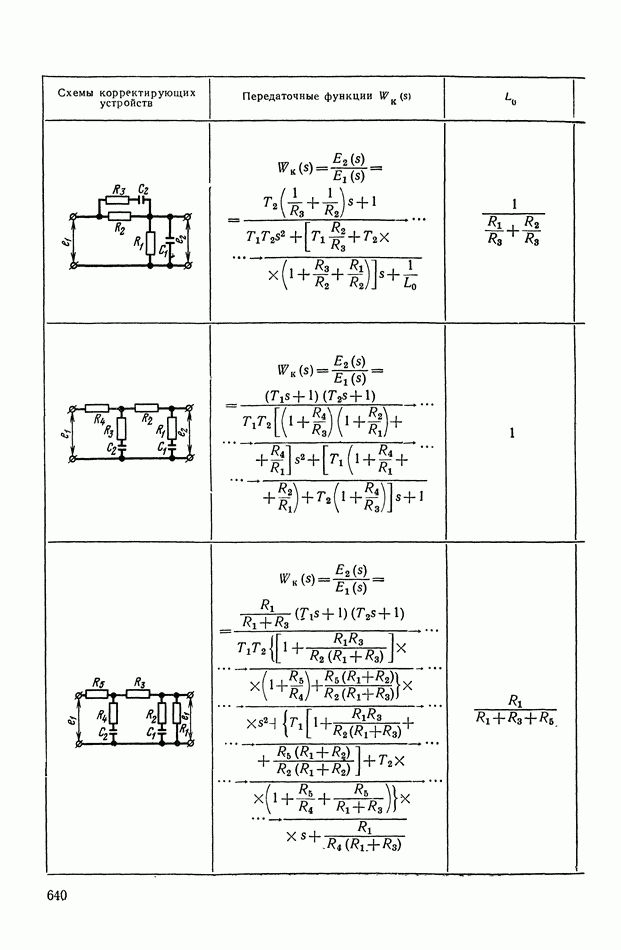
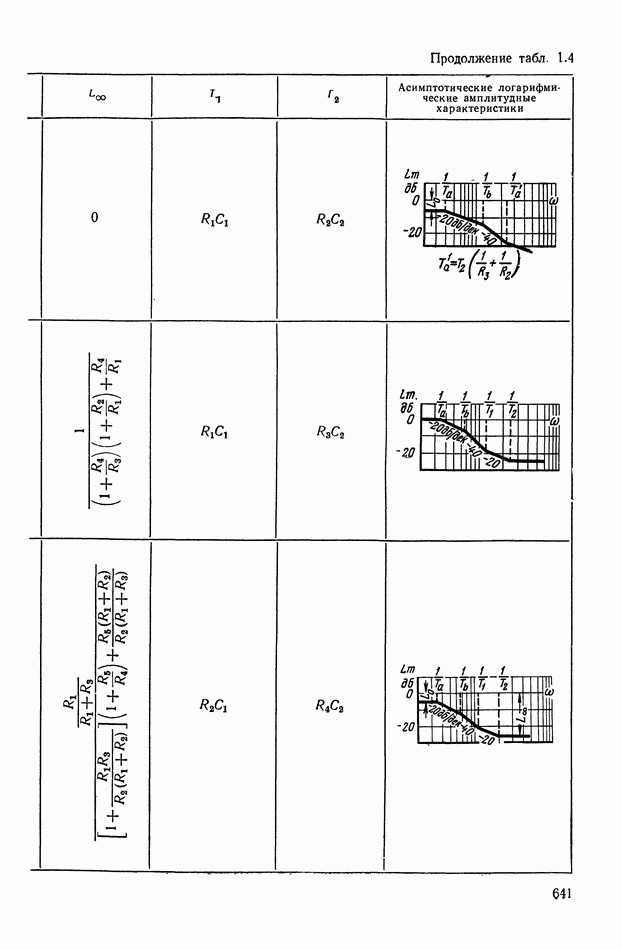
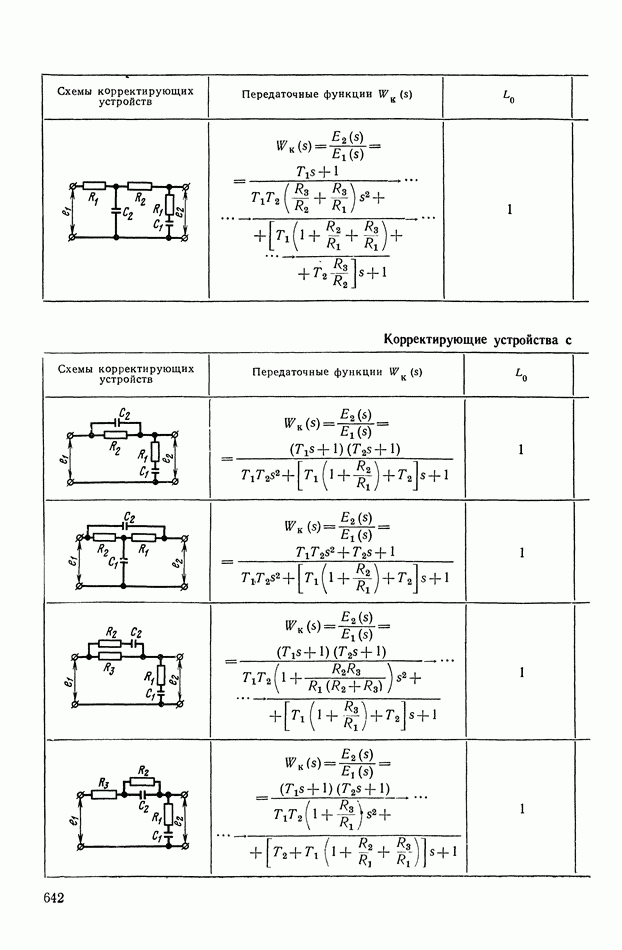
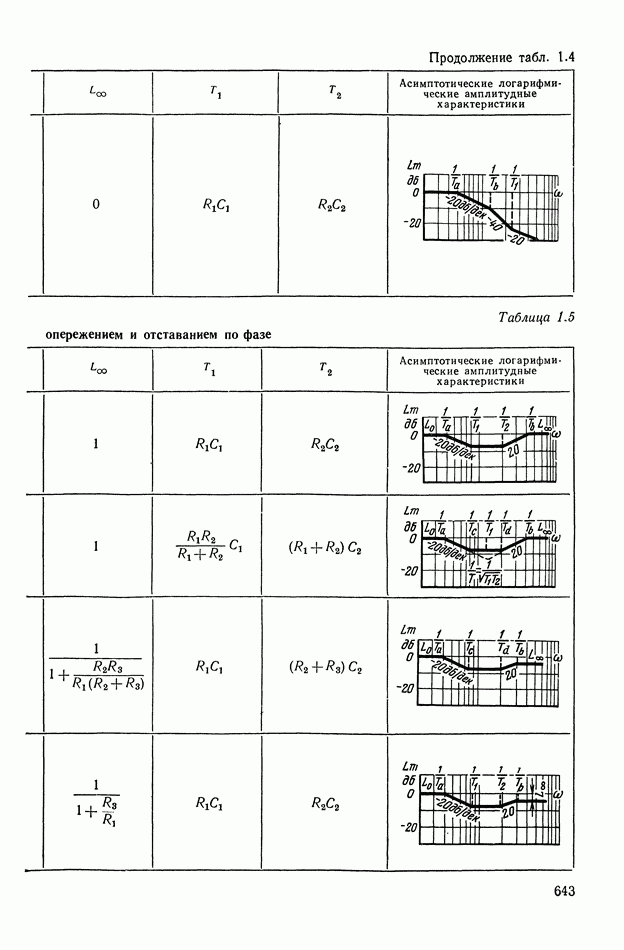
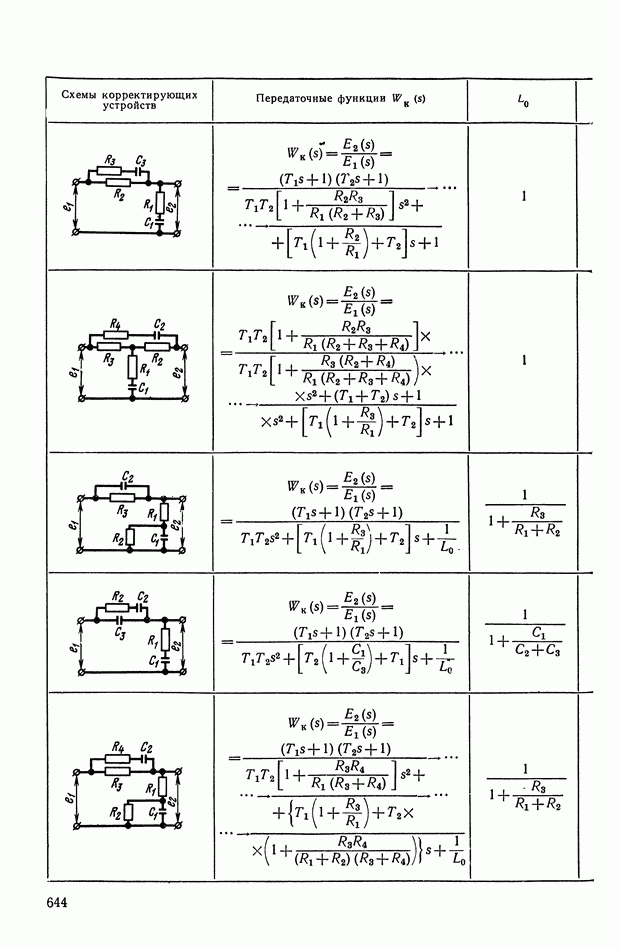
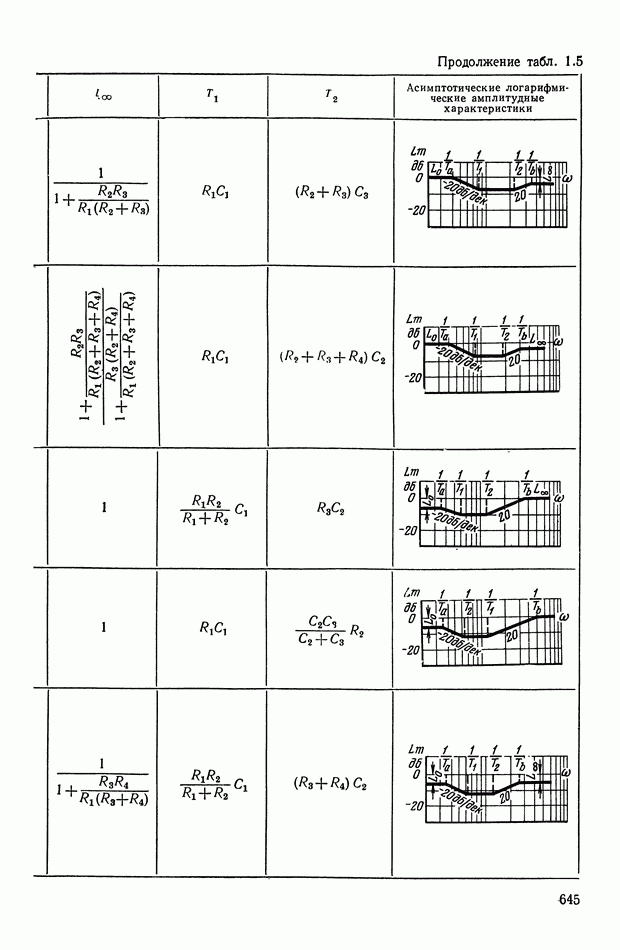
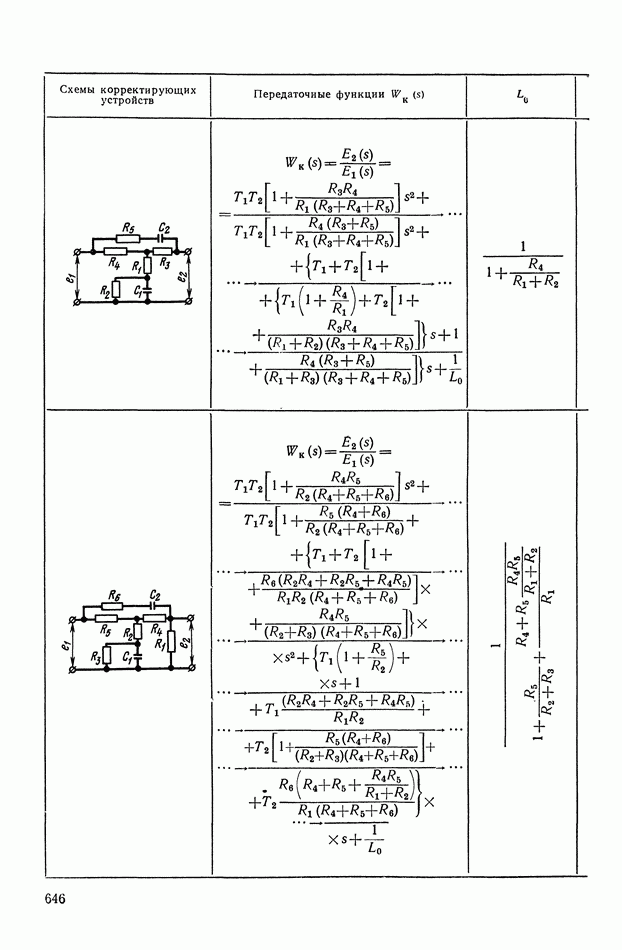
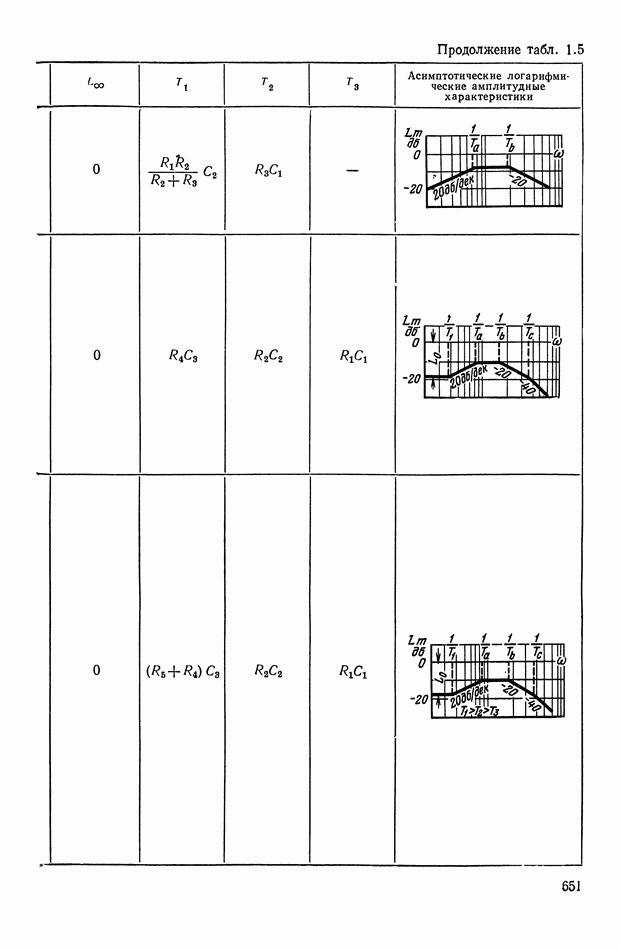
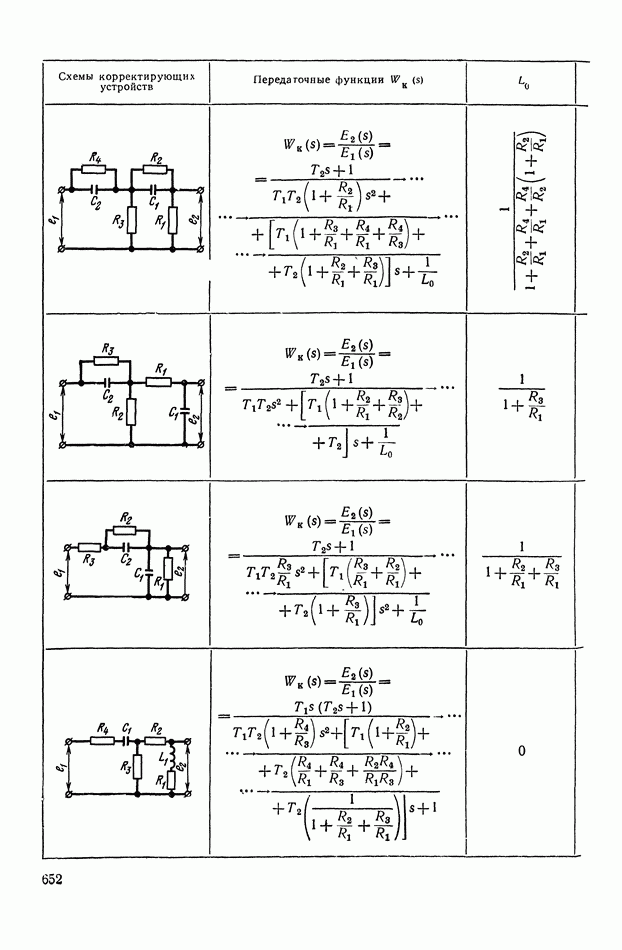
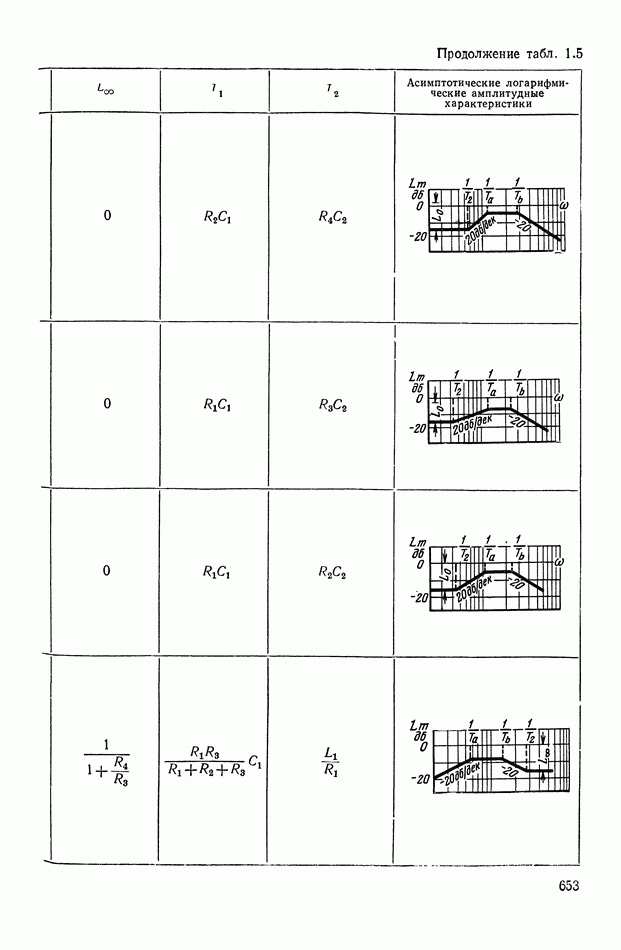
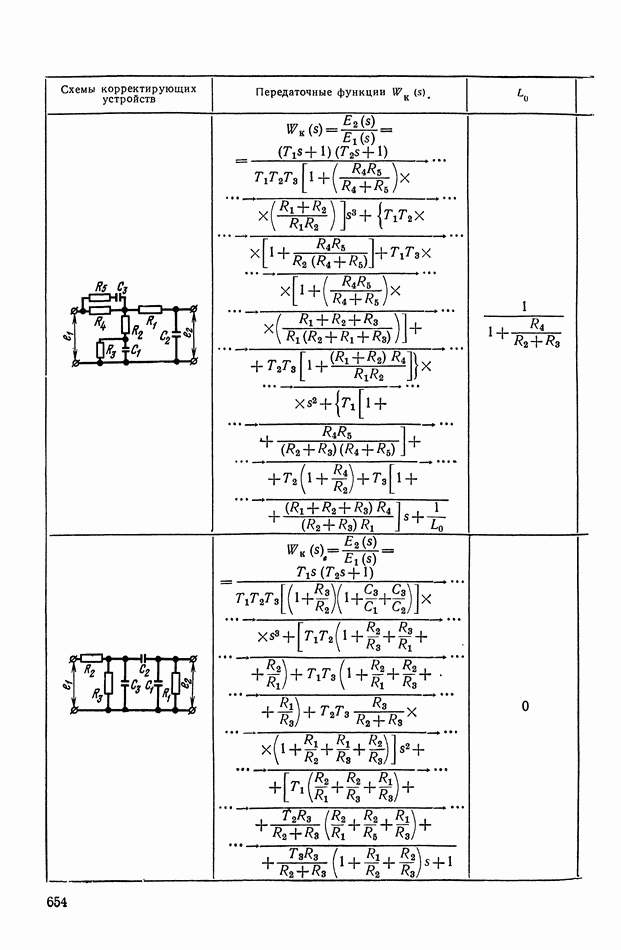
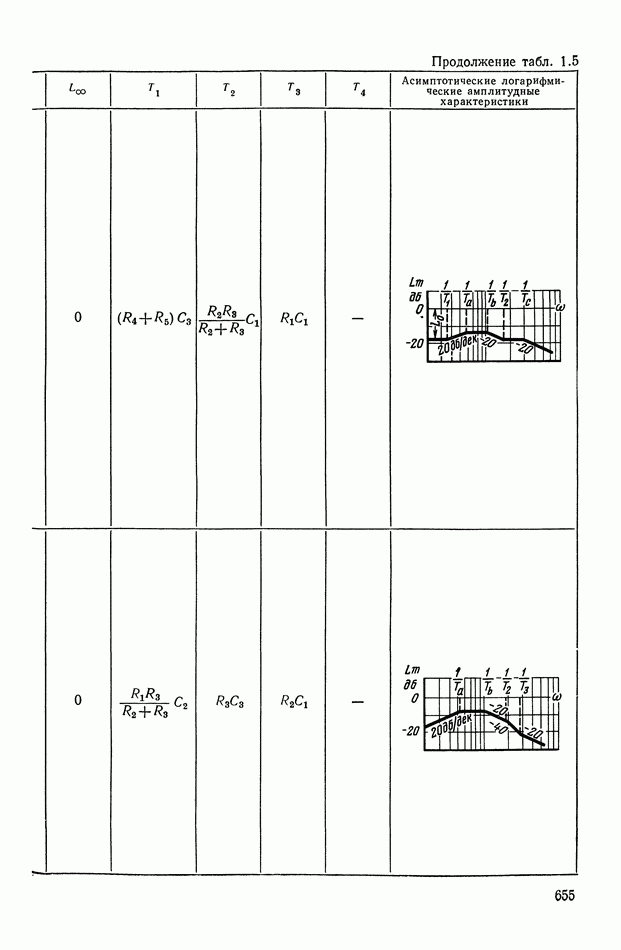
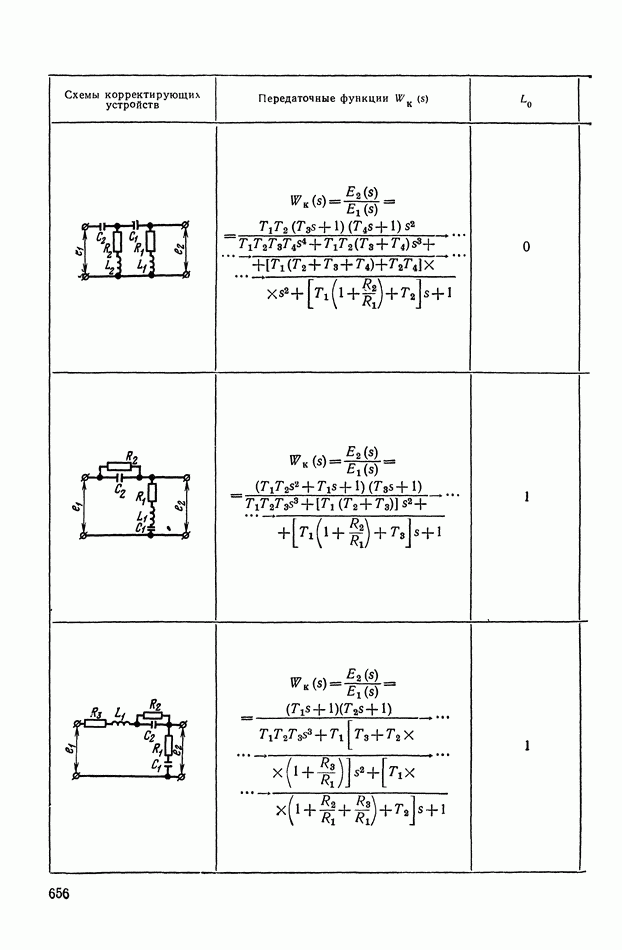
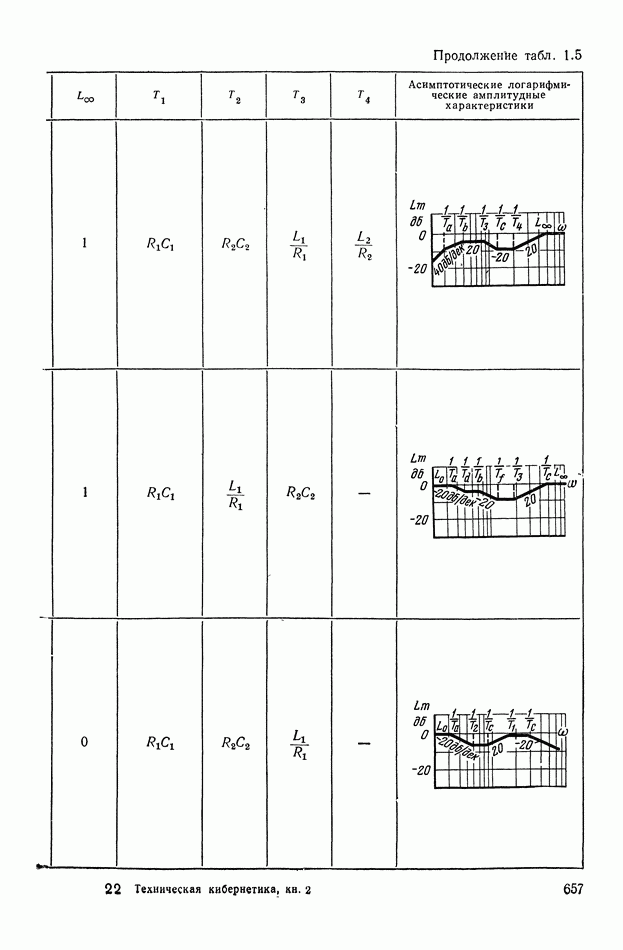
- 2. ТИПОВЫЕ ЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- 3. КОРРЕКТИРУЮЩИЕ ЧЕТЫРЕХПОЛЮСНИКИ С АКТИВНЫМИ ЭЛЕМЕНТАМИ
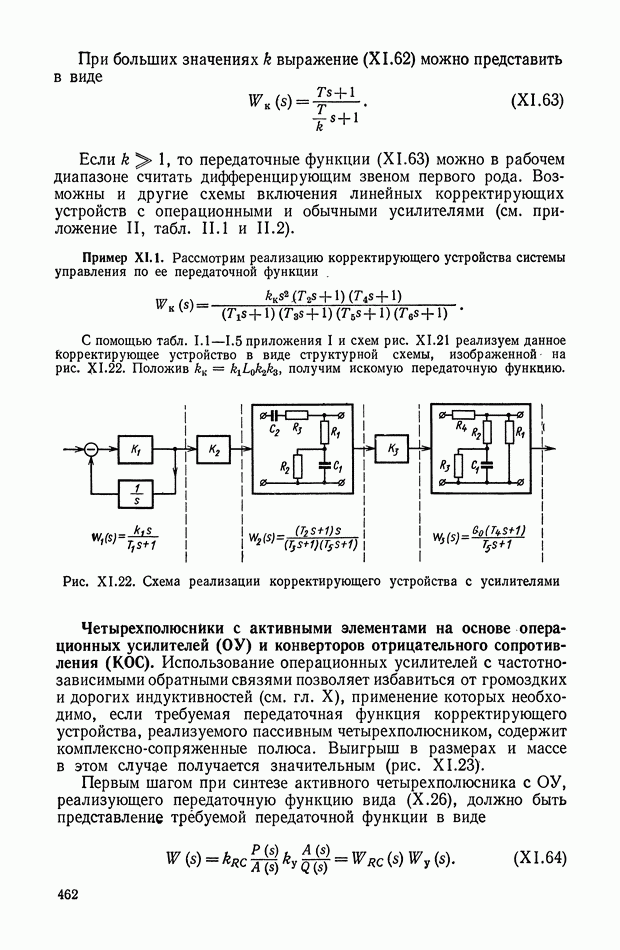
- Четырехполюсники с активными элементами на основе операционных усилителей (ОУ) и конверторов отрицательного сопротивления (КОС).
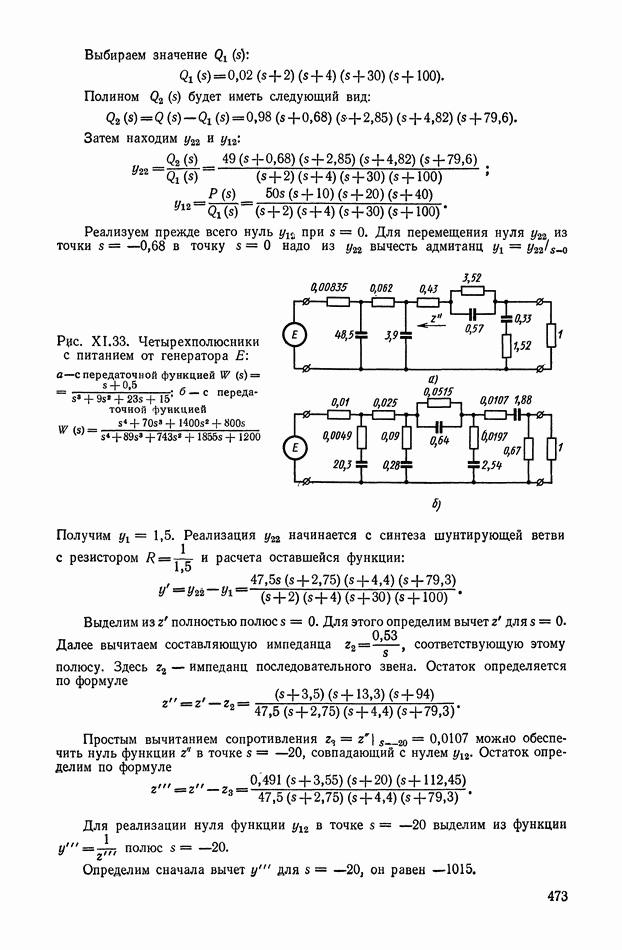
- 4. РЕАЛИЗАЦИЯ ЗАДАННОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В ВИДЕ СХЕМЫ ПАССИВНОГО ЛИНЕЙНОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА
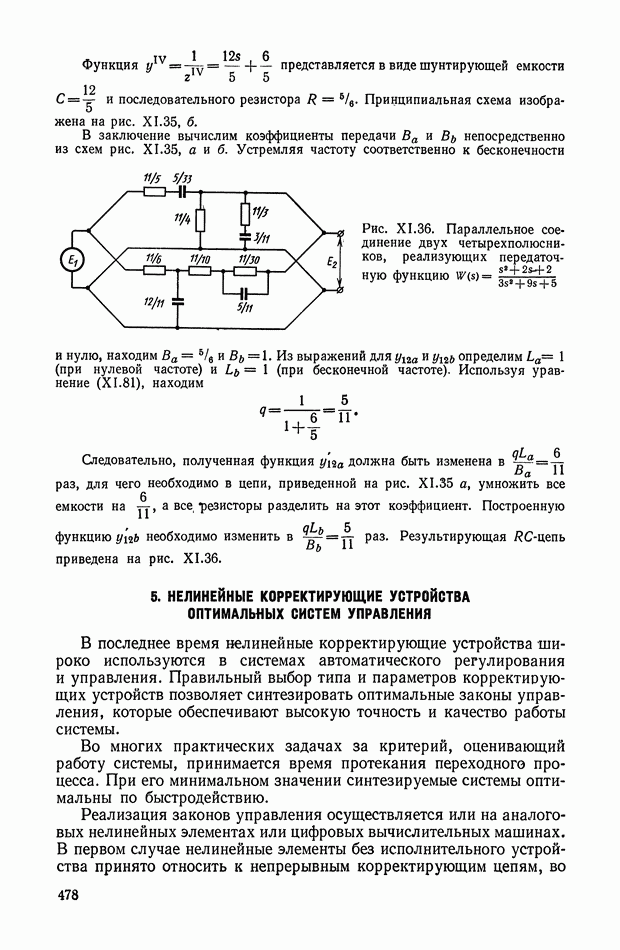
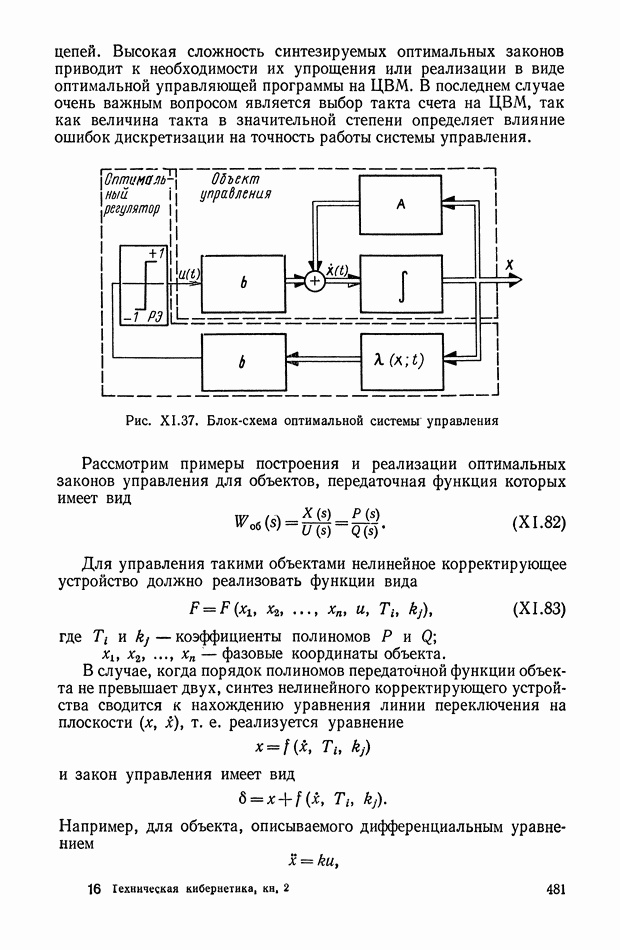
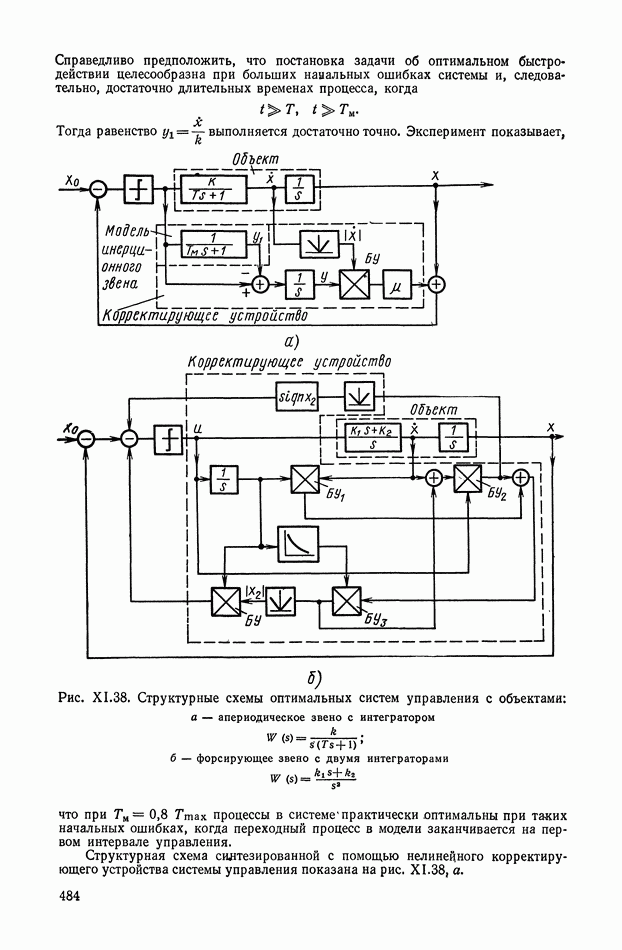
- 5. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
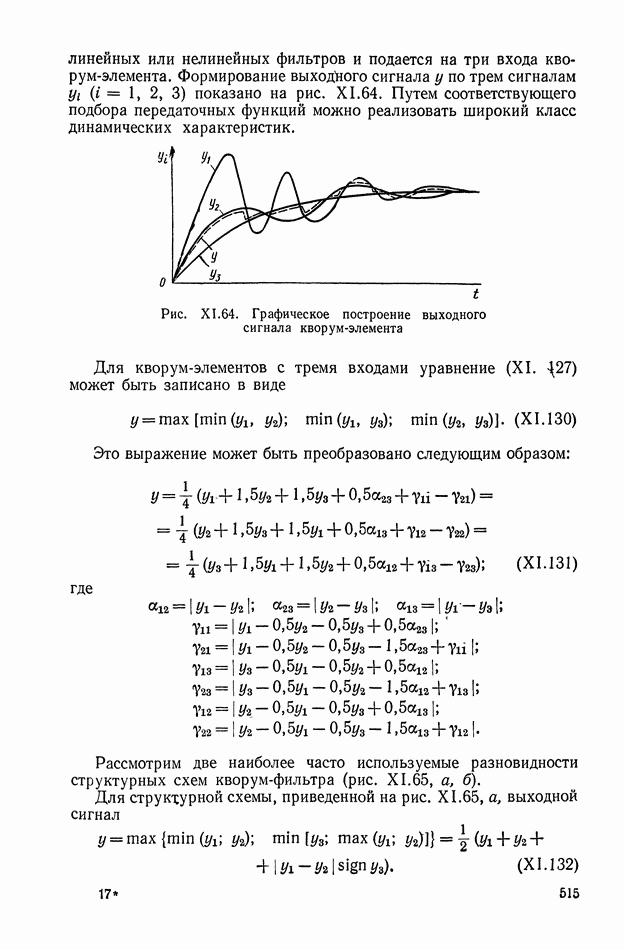
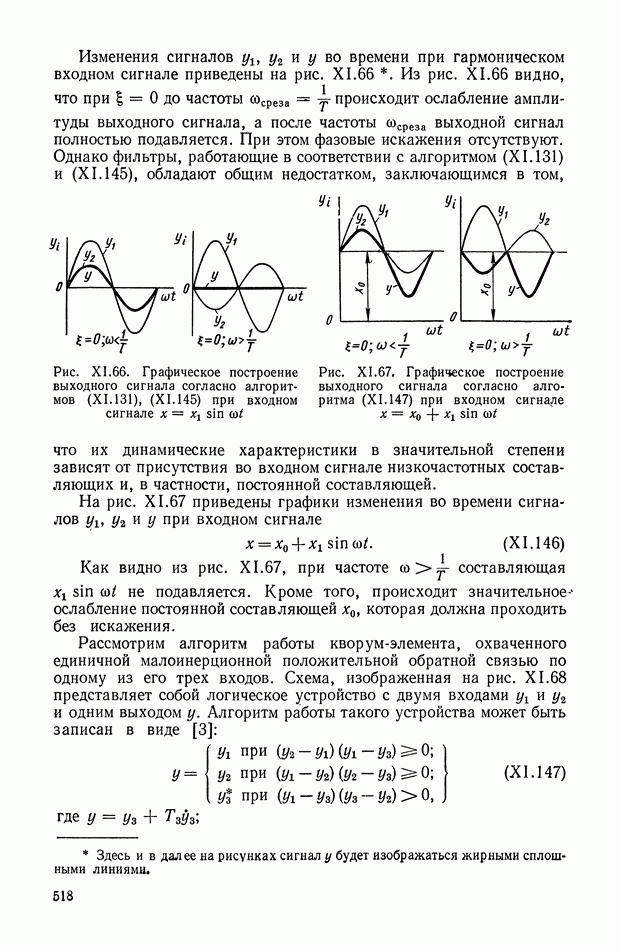
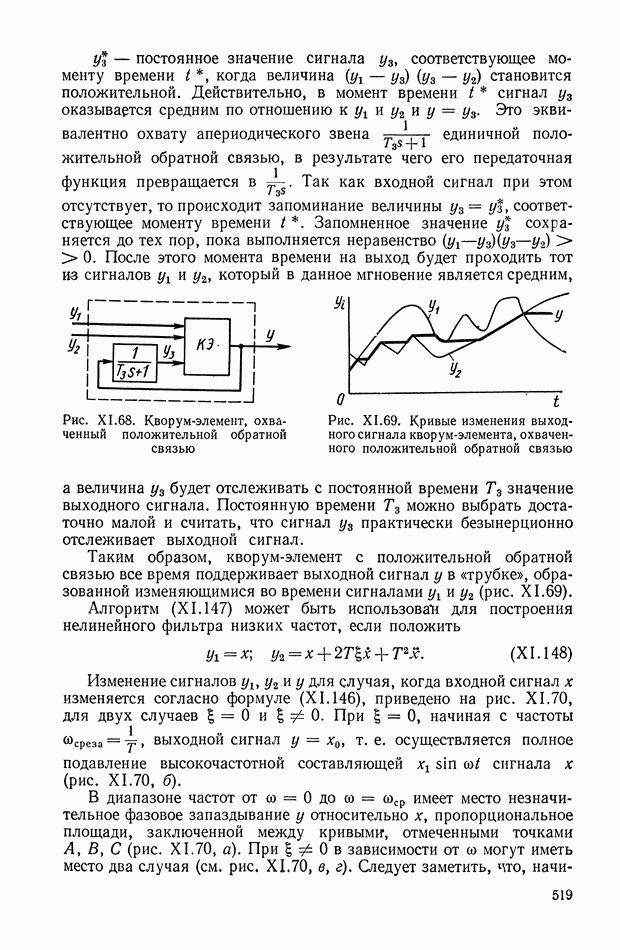
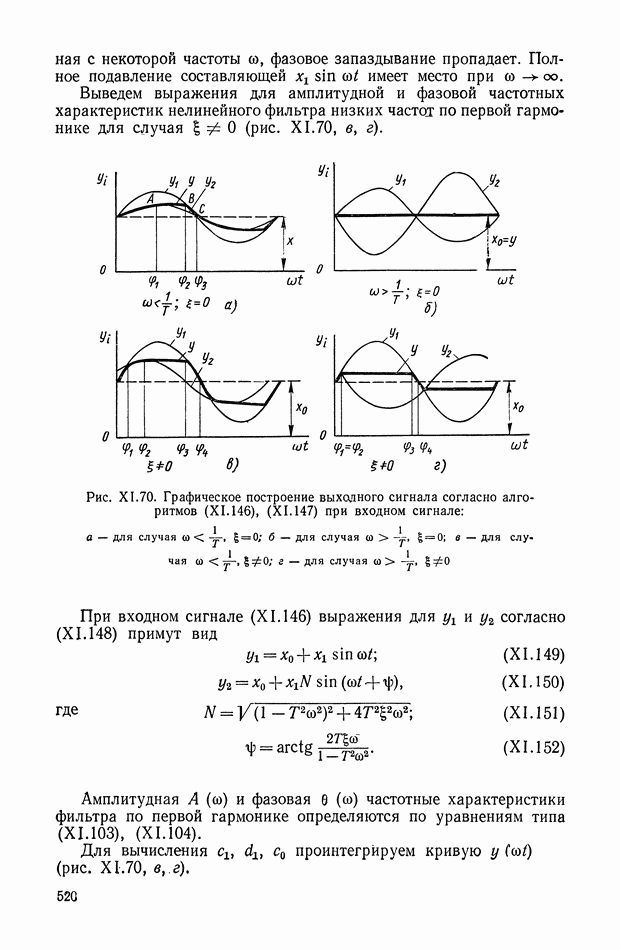
- 8. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
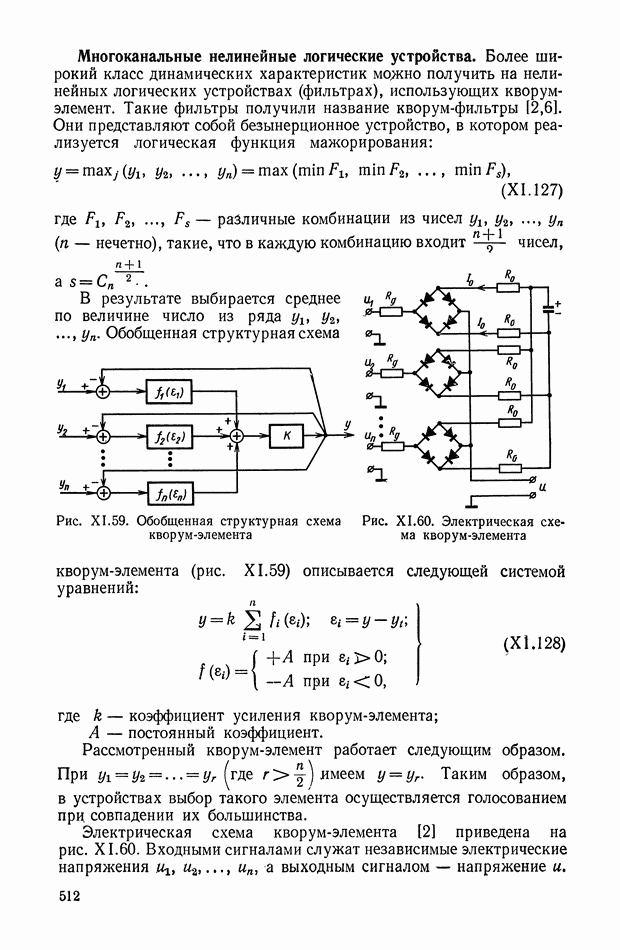
- Многоканальные нелинейные логические устройства.
- ГЛАВА XII. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- 1. КОРРЕКТИРУЮЩИЕ RLC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 2. КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 3. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 4. САМОНАСТРАИВАЮЩИЕСЯ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА
- 5. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА С ПРОМЕЖУТОЧНОЙ ДЕМОДУЛЯЦИЕЙ
- 6. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА С ПЕРЕКЛЮЧАТЕЛЯМИ
- 7. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XIII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ТАХОГЕНЕРАТОРЫ ПОСТОЯННОГО ТОКА
- Погрешности тахогенератора постоянного тока.
- 2. НЕКОТОРЫЕ СХЕМЫ ПРИМЕНЕНИЯ ТАХОГЕНЕРАТОРОВ
- 3. АСИНХРОННЫЕ ТАХОГЕНЕРАТОРЫ
- 4. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ ИЗМЕРЕНИЯ СКОРОСТИ ЭЛЕКТРОДВИГАТЕЛЕЙ
- Пассивный тахометрический мост переменного тока.
- Активные тахометрические мосты.
- ГЛАВА XIV. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ГИДРАВЛИЧЕСКИХ СИСТЕМАХ
- 3. ЭЛЕКТРИЧЕСКИЕ ОБРАТНЫЕ СВЯЗИ
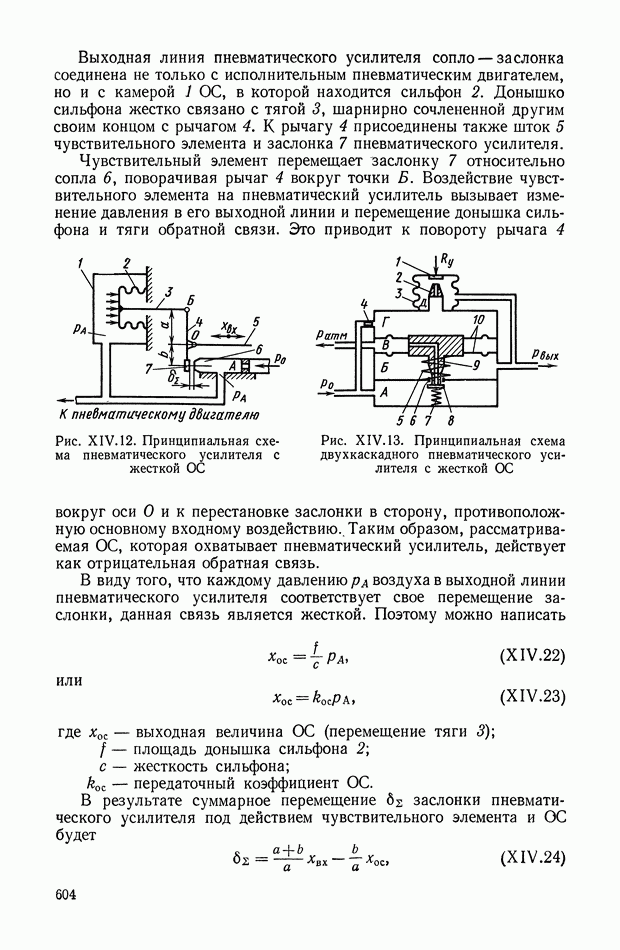
- 4. ЖЕСТКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
- 5. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ СИСТЕМАХ
- 6. СЛОЖНЫЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
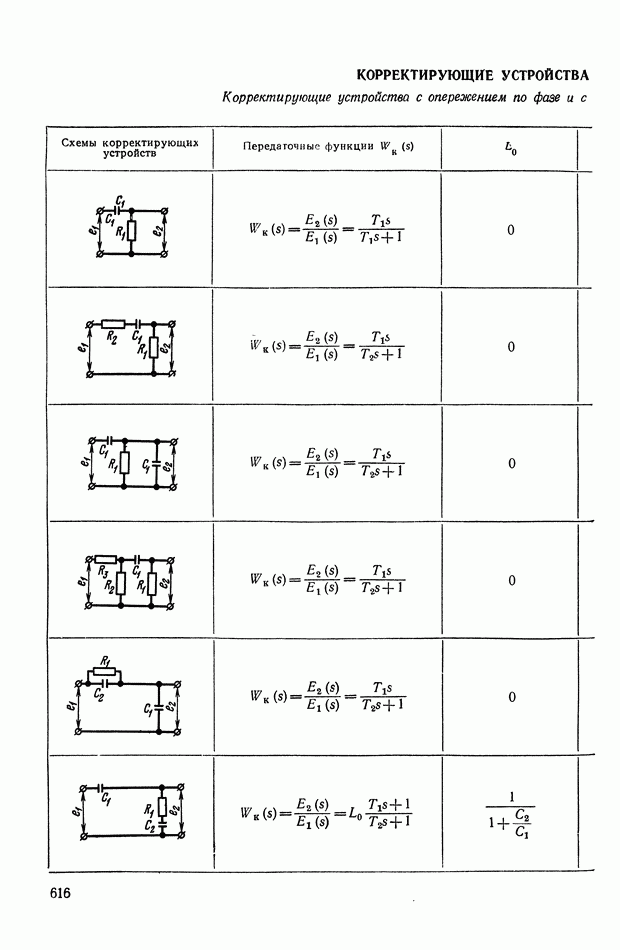
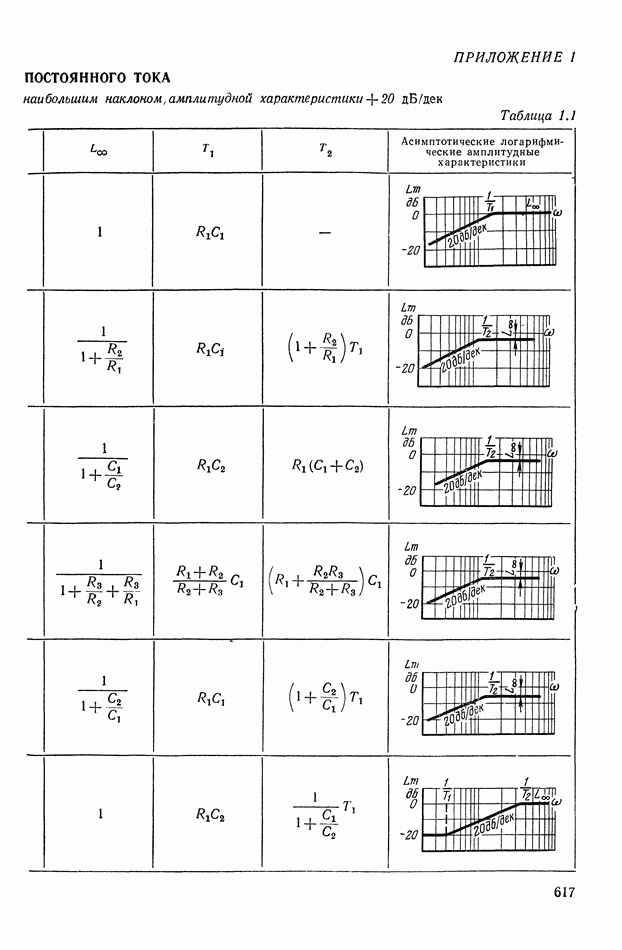
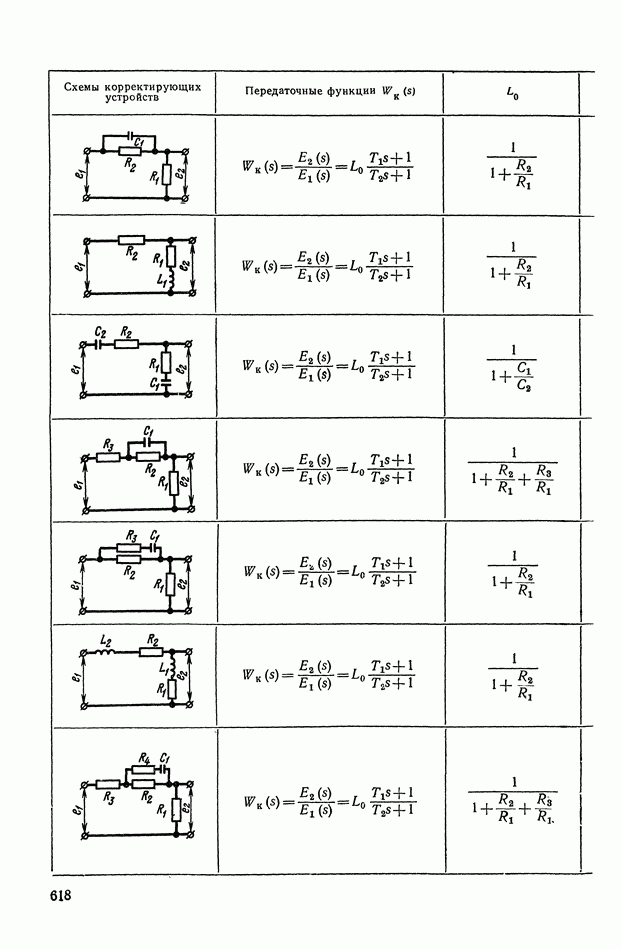
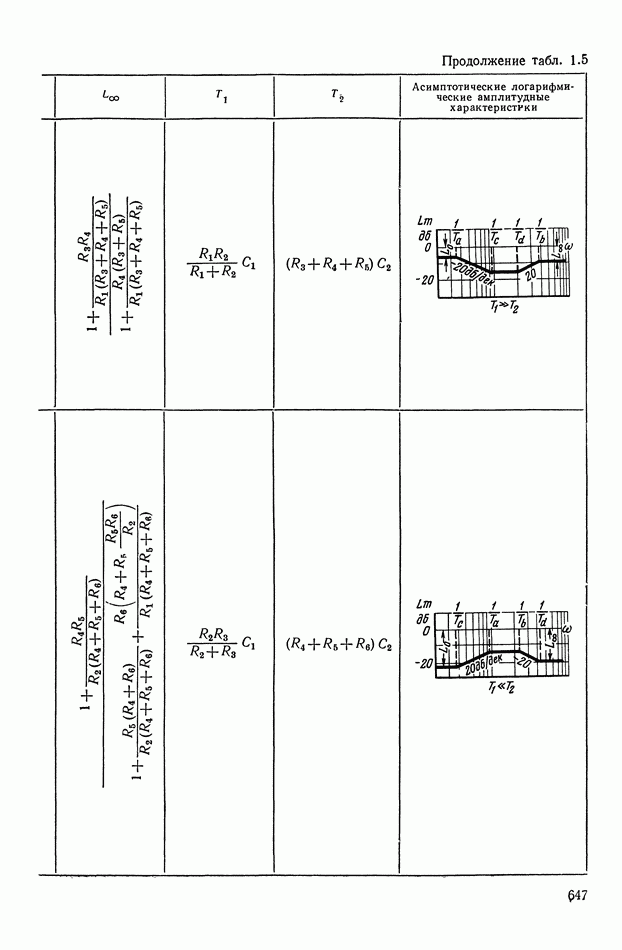
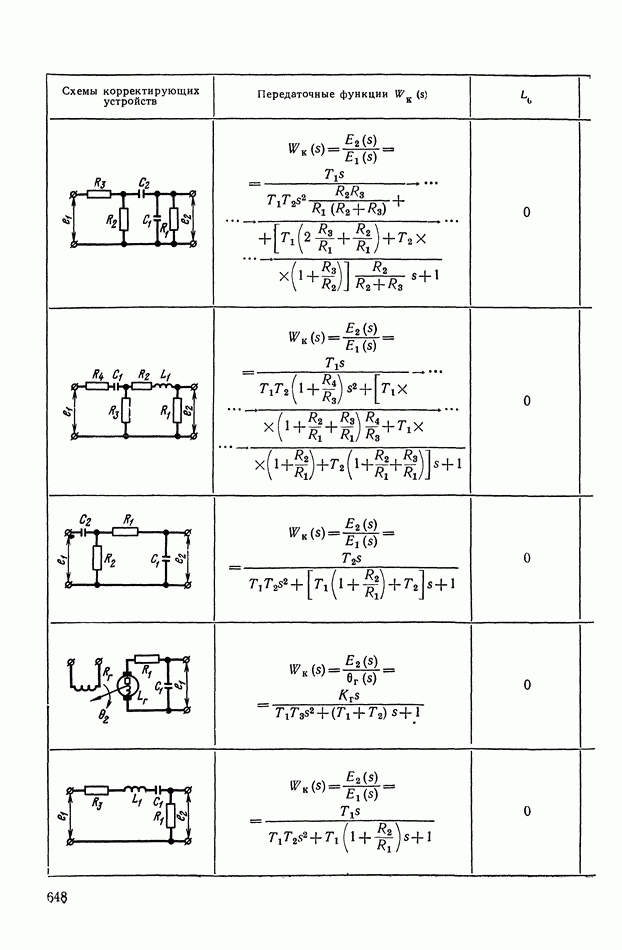
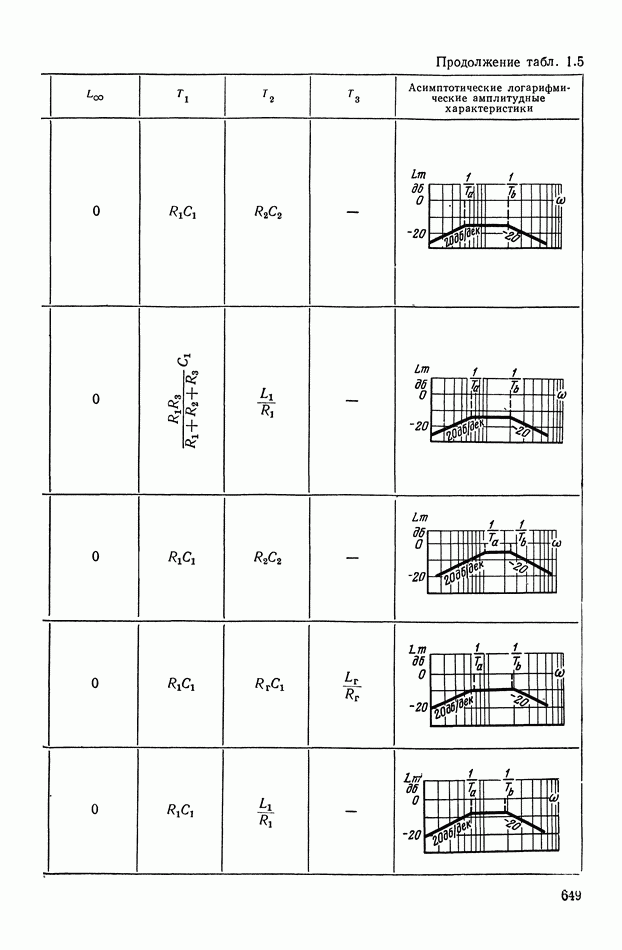
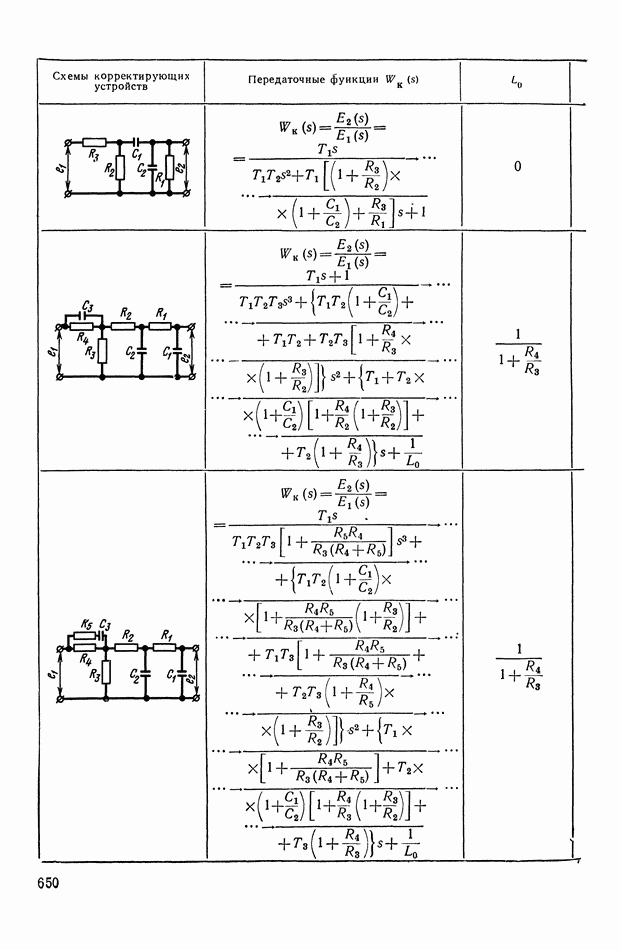
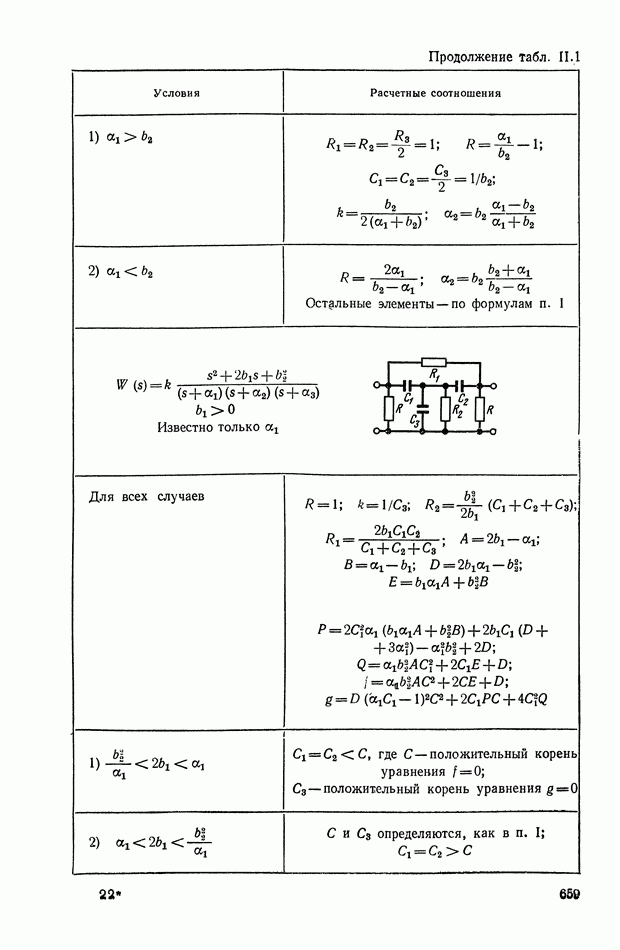
- ПРИЛОЖЕНИЕ 1. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПОСТОЯННОГО ТОКА
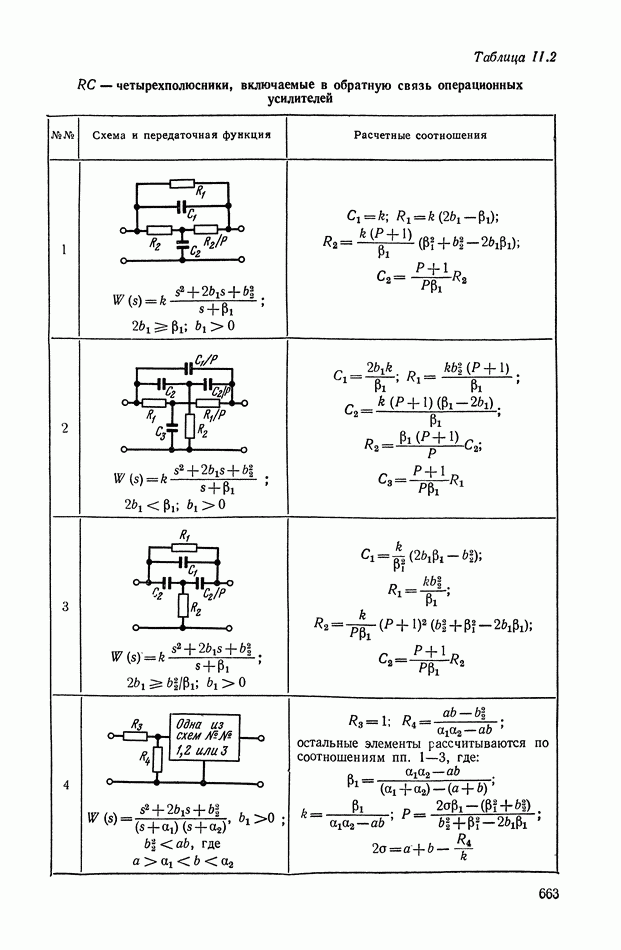
- ПРИЛОЖЕНИЕ II. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ОСНОВЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
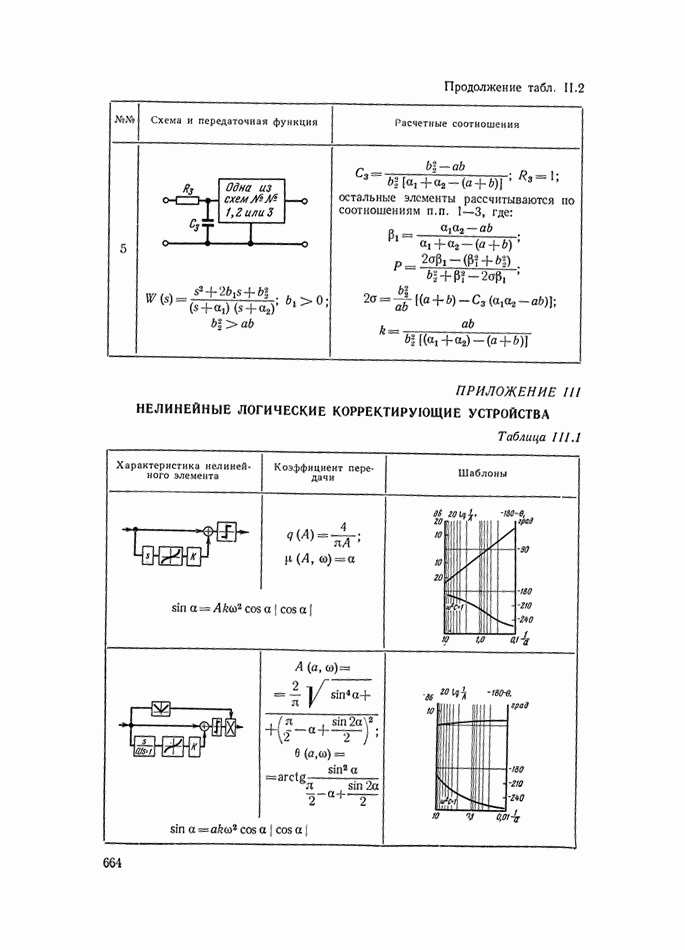
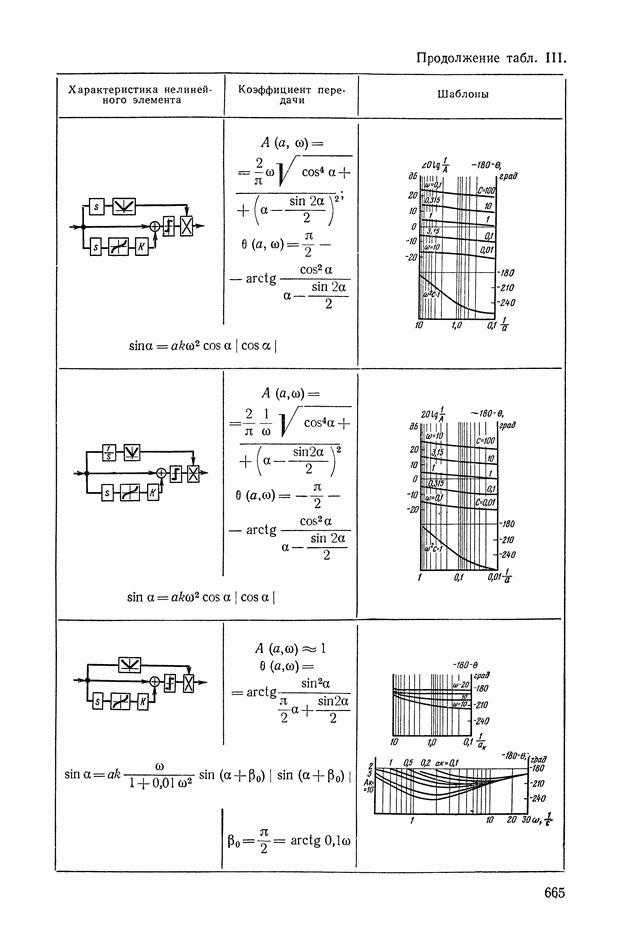
- ПРИЛОЖЕНИЕ III. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ