| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
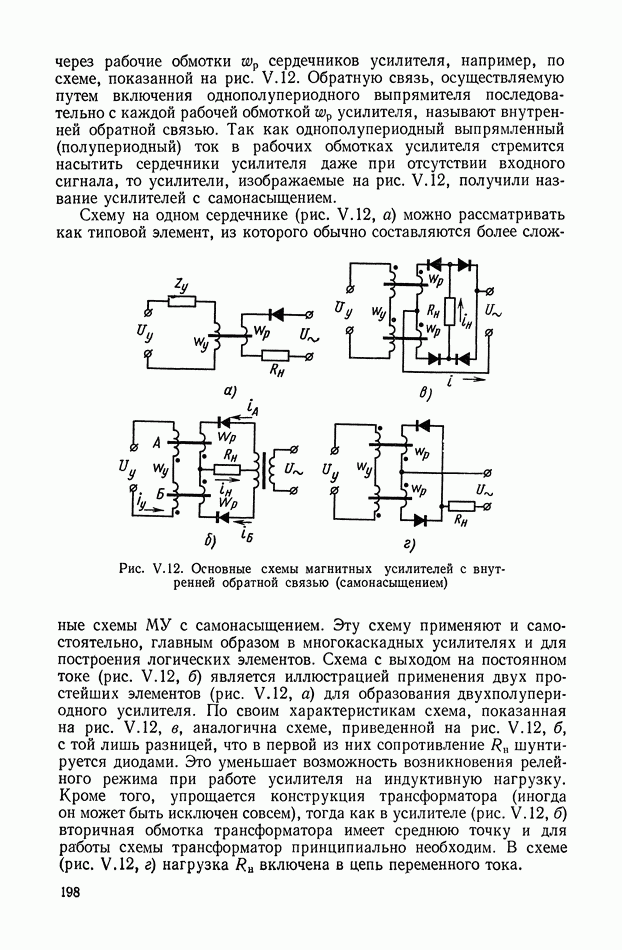
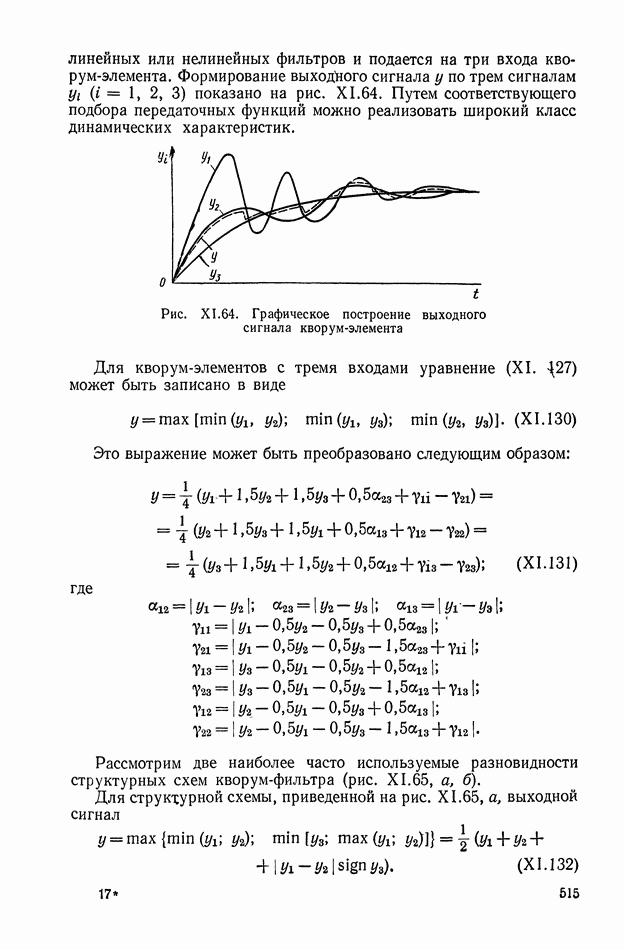
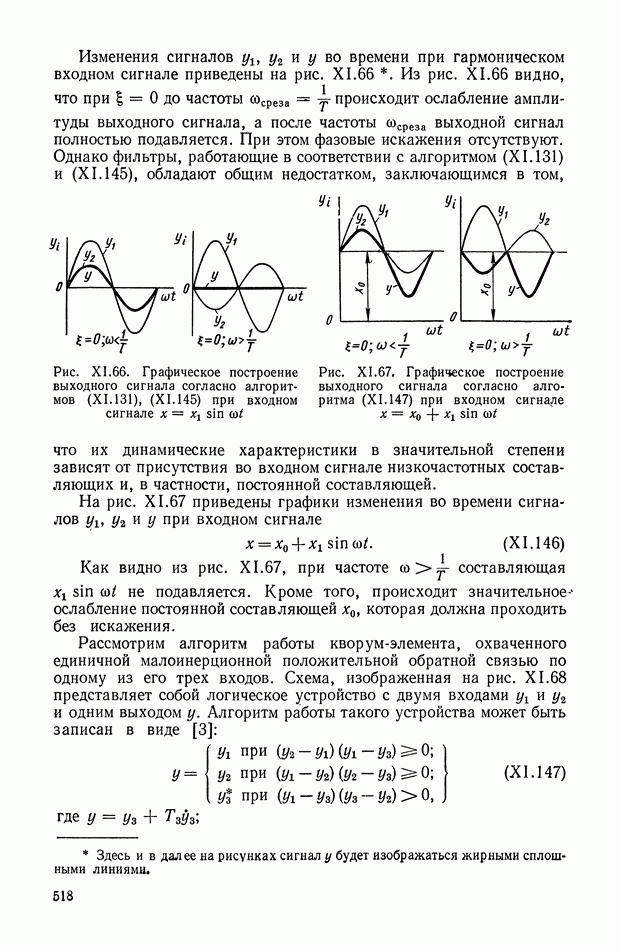
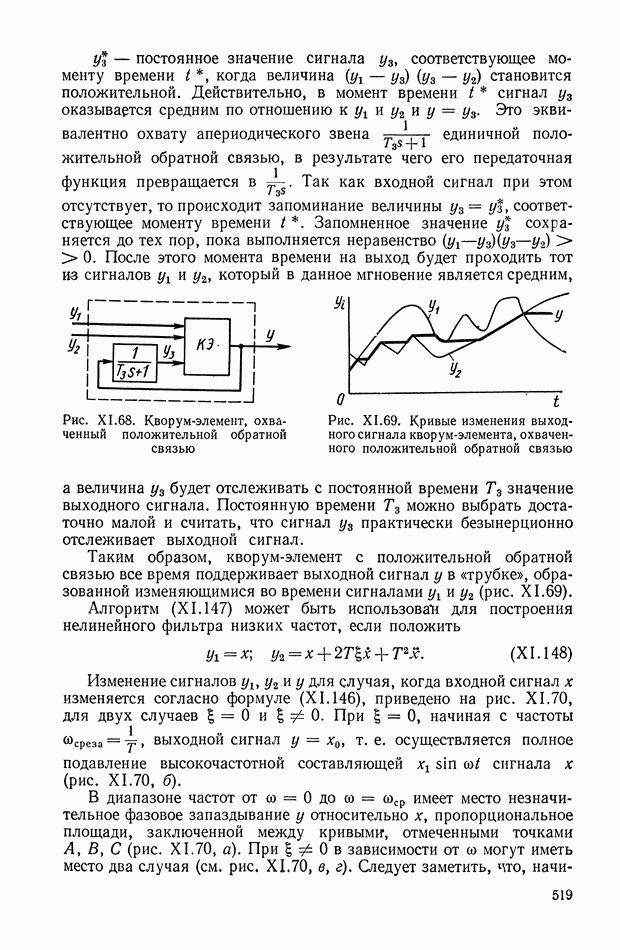
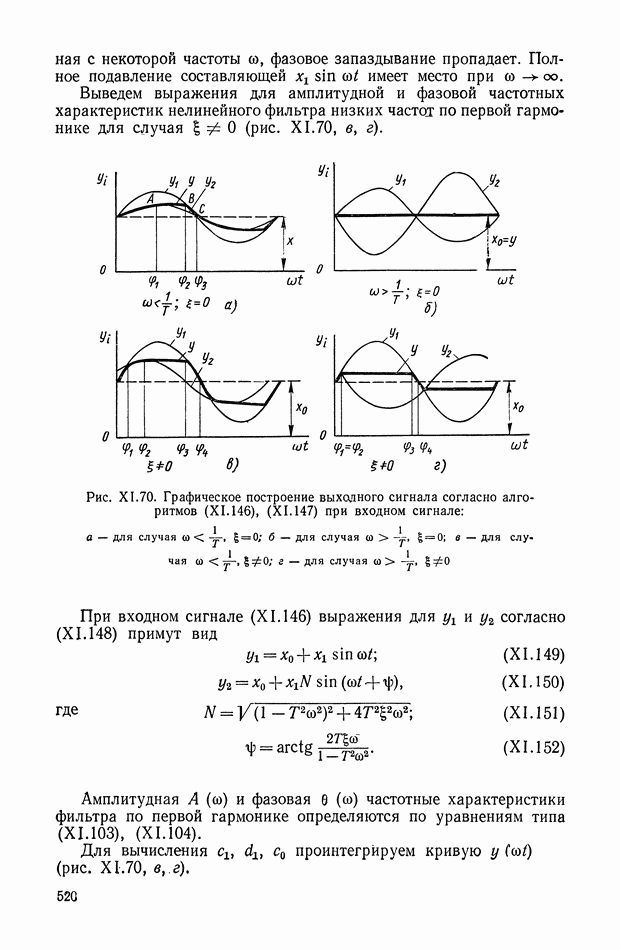
2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ УСИЛИТЕЛЬНОГО УСТРОЙСТВА БЕЗ ОБРАТНОЙ СВЯЗИ
Динамика работы непрерывного усилительного устройства [6] может быть описана при помощи нелинейных функций двух аргументов

где аргументы  или
или  являются функциями независимой переменной
являются функциями независимой переменной 
В выражении (1.1) в качестве входного сигнала усилителя может быть принята функция  или
или  соответствующая, например, функции тока или напряжения (расхода рабочего тела или давления).
соответствующая, например, функции тока или напряжения (расхода рабочего тела или давления).
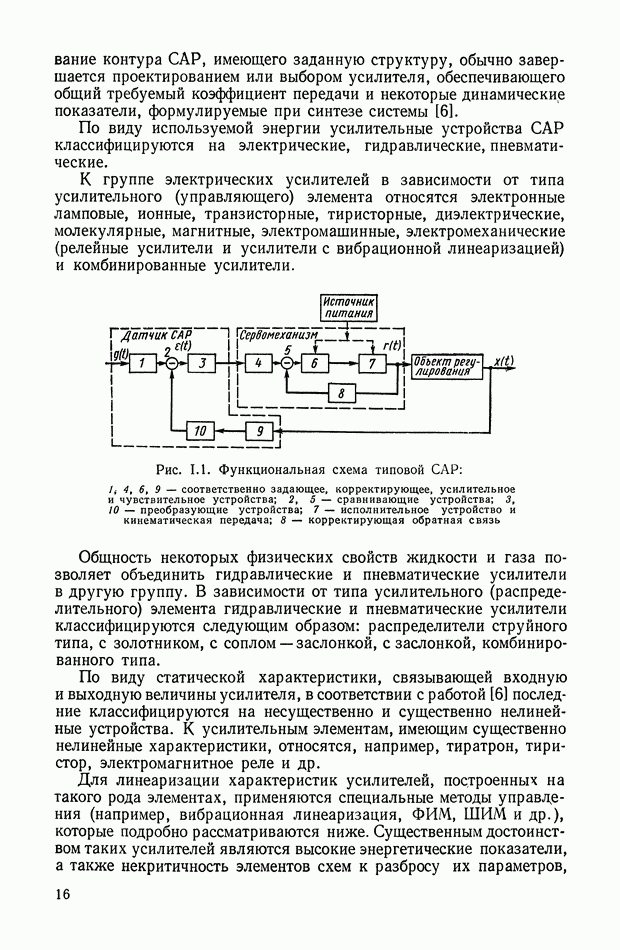
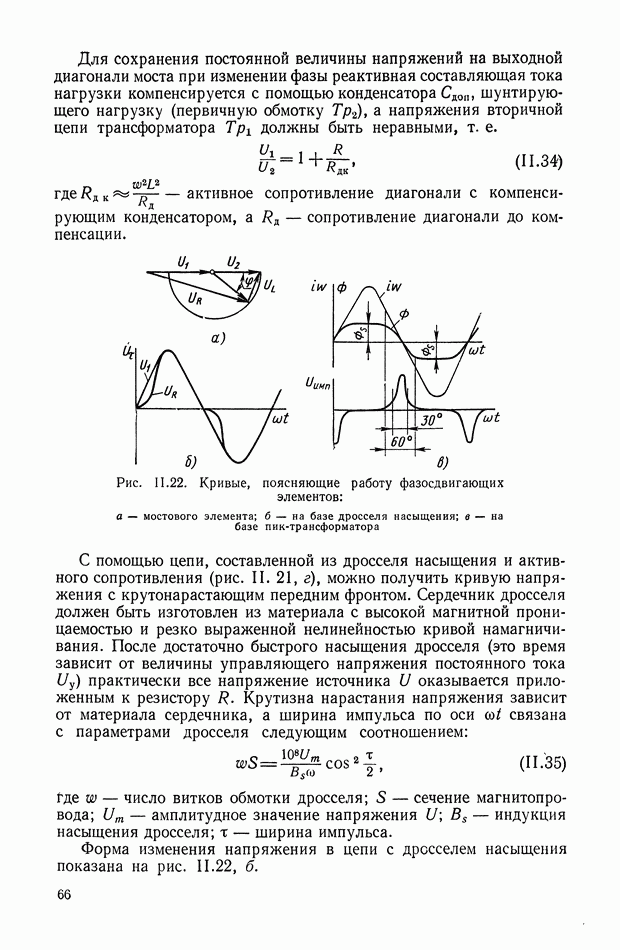
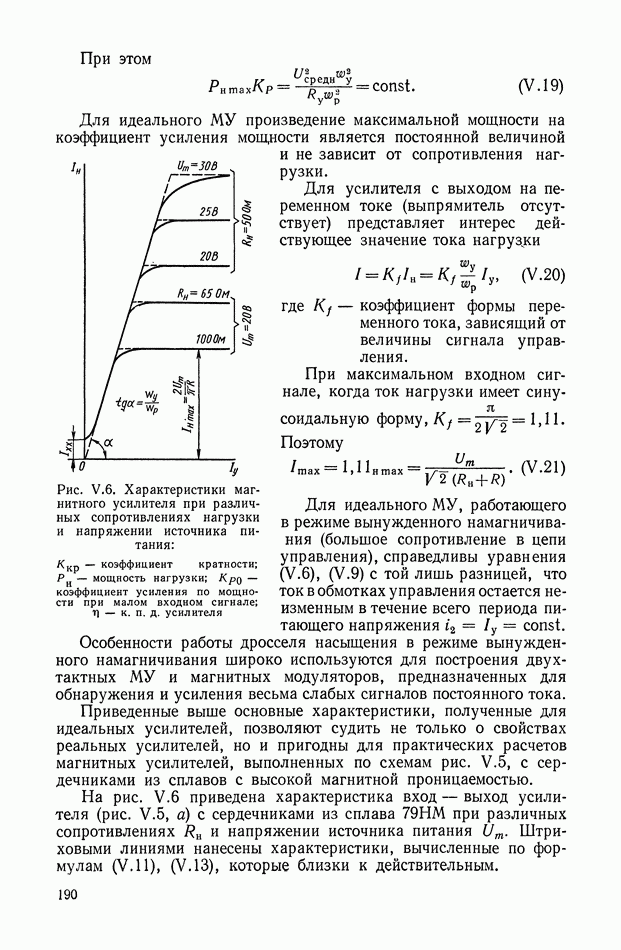
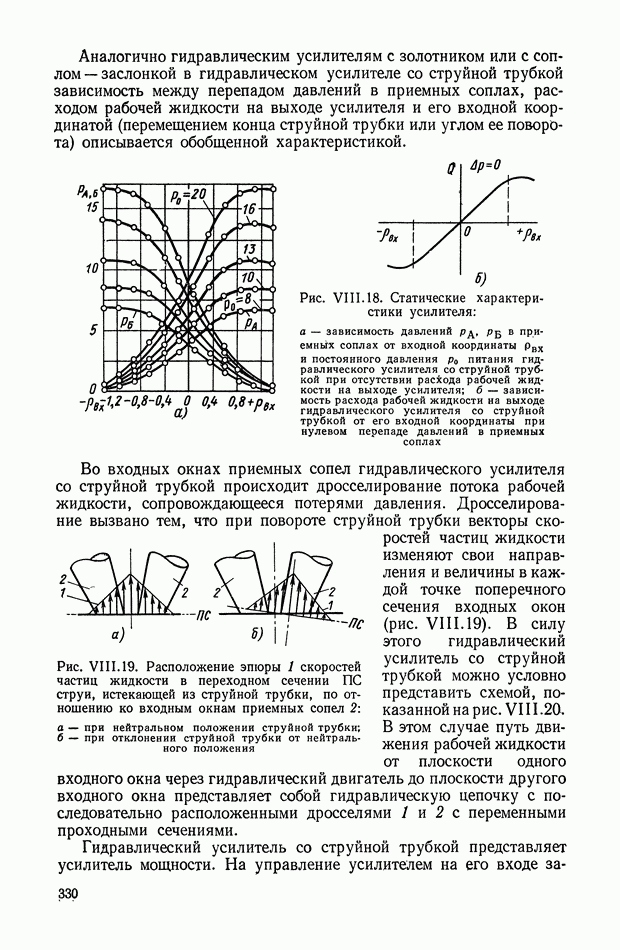
Связь между установившимися значениями входа  и выхода
и выхода  усилителя может быть представлена графически, как показано на рис. 1.2, а и б. Кривые
усилителя может быть представлена графически, как показано на рис. 1.2, а и б. Кривые  имеющие в качестве параметра фиксированные значения
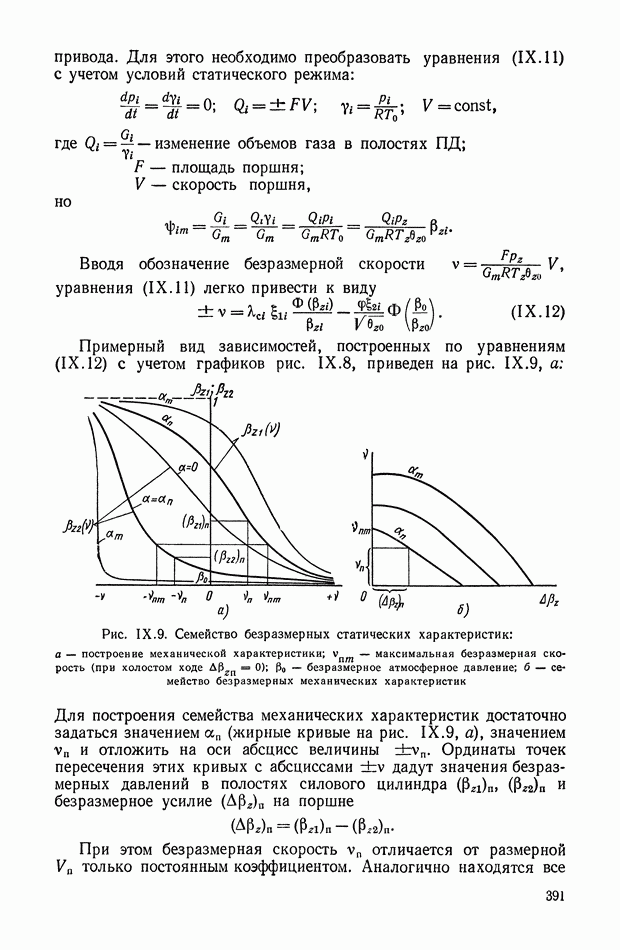
имеющие в качестве параметра фиксированные значения  и изображенные на рис. 1.2, б, называются обобщенными нагрузочными характеристиками усилительного устройства. Эти статические нагрузочные характеристики получают обычно экспериментальным путем; при этом задаются некоторыми величинами параметра и нагрузки
и изображенные на рис. 1.2, б, называются обобщенными нагрузочными характеристиками усилительного устройства. Эти статические нагрузочные характеристики получают обычно экспериментальным путем; при этом задаются некоторыми величинами параметра и нагрузки  и фиксируют соответствующие значения
и фиксируют соответствующие значения  на выходе усилителя. Нагрузочные характеристики
на выходе усилителя. Нагрузочные характеристики  или
или  используются в качестве исходных при анализе динамики усилителя.
используются в качестве исходных при анализе динамики усилителя.
Если сложная функция  имеет непрерывные частные производные и в рабочей точке М на поле нагрузочных
имеет непрерывные частные производные и в рабочей точке М на поле нагрузочных
характеристик, а функции  дифференцируемы при
дифференцируемы при  , то
, то


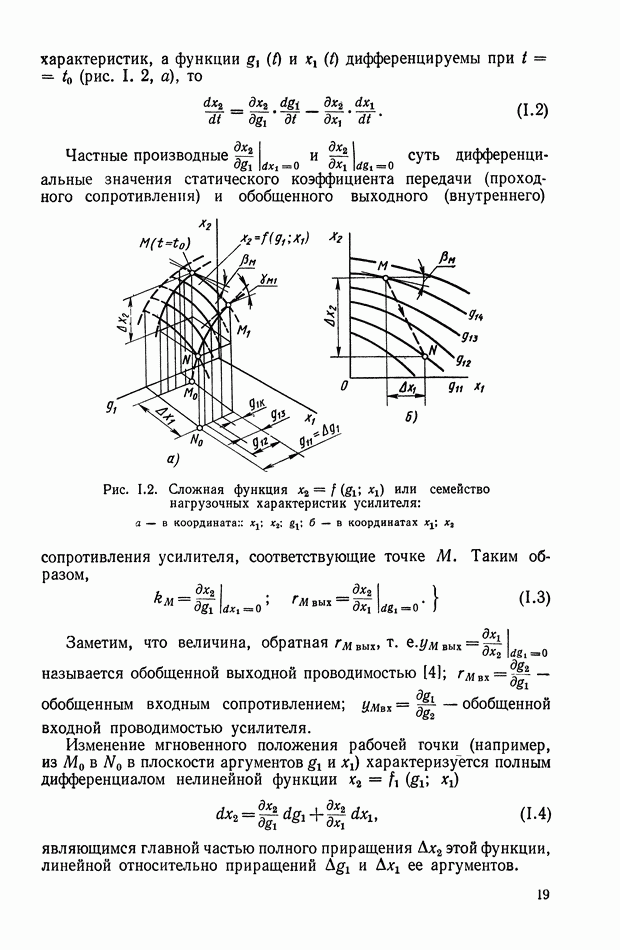
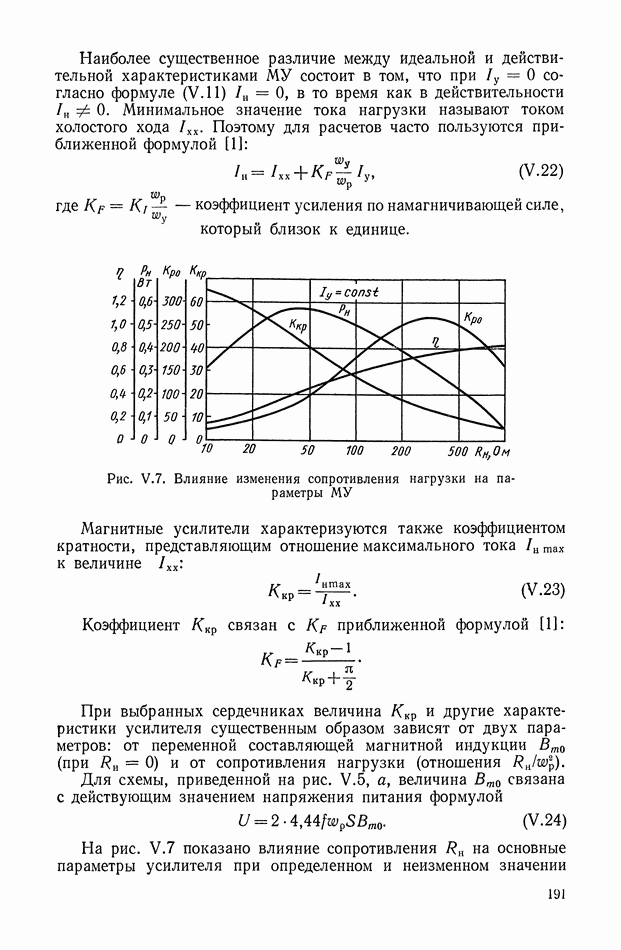
Рис. 1.2. Сложная функция  или семейство нагрузочных характеристик усилителя: а - в координатах
или семейство нагрузочных характеристик усилителя: а - в координатах  б — в координатах
б — в координатах 
Частные производные  суть дифференциальные значения статического коэффициента передачи (проходного сопротивления) и обобщенного выходного (внутреннего) сопротивления усилителя, соответствующие точке М. Таким образом,
суть дифференциальные значения статического коэффициента передачи (проходного сопротивления) и обобщенного выходного (внутреннего) сопротивления усилителя, соответствующие точке М. Таким образом,

Заметим, что величина, обратная  , т. е.
, т. е.  называется обобщенной выходной проводимостью [4];
называется обобщенной выходной проводимостью [4];  обобщенным входным сопротивлением;
обобщенным входным сопротивлением;  обобщенной входной проводимостью усилителя.
обобщенной входной проводимостью усилителя.
Изменение мгновенного положения рабочей точки (например, из  в плоскости аргументов
в плоскости аргументов  характеризуется полным дифференциалом нелинейной функции
характеризуется полным дифференциалом нелинейной функции 

являющимся главной частью полного приращения  этой функции, линейной относительно приращений и
этой функции, линейной относительно приращений и  ее аргументов.
ее аргументов.
Имея в виду линеаризацию нелинейной функции нескольких переменных по степеням малых приращений этих переменных, взятых в окрестности их значений (например, точки М), соответствующих квазиустановившемуся режиму работы усилителя, вместо выражения (1.4) можно записать (см. рис. 1.1, а)

Пусть уравнение нагрузки, связывающее функции  является линейным дифференциальным уравнением
является линейным дифференциальным уравнением  порядка с постоянными коэффициентами
порядка с постоянными коэффициентами  характеризующими физические параметры обобщенного сопротивления нагрузки:
характеризующими физические параметры обобщенного сопротивления нагрузки:

Уравнение (1.6), записанное в операторной форме относительно приращений, имеет вид

Заметим, что уравнение (1.7) соответствует нагрузке усилителя, имеющей инерционный (индуктивный) характер.
Исключая из выражения (1.5) приращение  связанное с
связанное с  соотношением (1.7), получим дифференциальное уравнение нагруженного усилителя
соотношением (1.7), получим дифференциальное уравнение нагруженного усилителя

или

Аналогично можно получить

Если выражение будет иметь вид

что соответствует нагрузке, имеющей упругий (емкостной) характер, то уравнения нагруженного усилительного устройства записываются следующим образом:

Переходя в уравнениях (1.7) и (1.10) к изображениям при нулевых начальных условиях, получим соответствующие обобщенные передаточные функции нагрузки

Наконец, из выражений (1.8), (1.9), (1.11)-(1.14) с учетом соотношений (1.3) получим передаточные функции усилительного устройства без обратной связи:

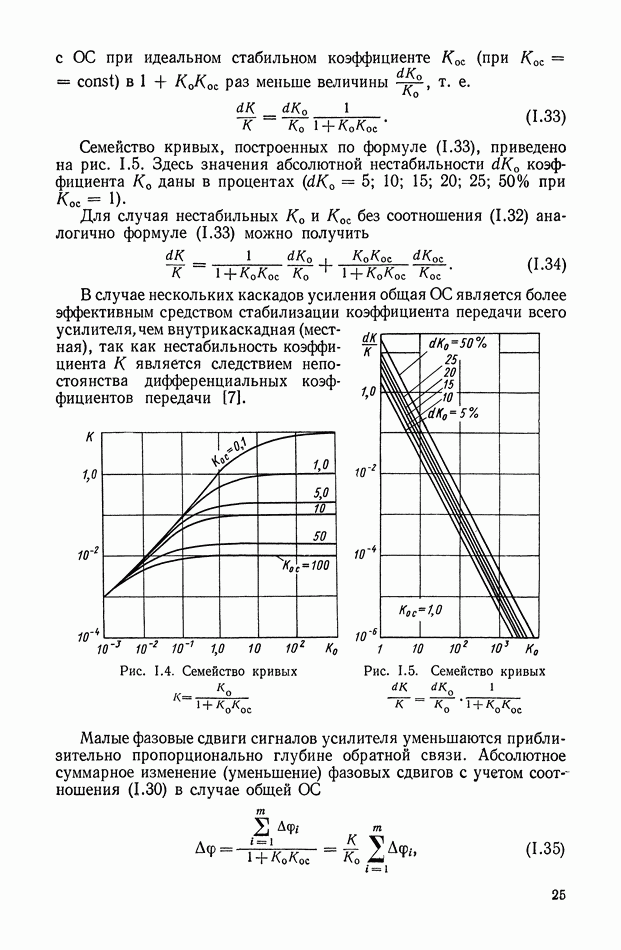
Передаточными функциями (1.15)-(1.18) следует пользоваться, если реактивными составляющими проходного и выходного сопротивлений усилительного устройства можно пренебречь.
Передаточные коэффициенты усилителя в режиме холостого хода (т. е. при  ), соответствующие передаточным функциям (1.16) и (1.18), имеют вид
), соответствующие передаточным функциям (1.16) и (1.18), имеют вид

Пра дальнейшем рассмотрении работы усилительного устройства в основном ограничимся анализом передаточной функции (1.16).
Из соотношений (1.9), (1.7) и (1.5) имеем 

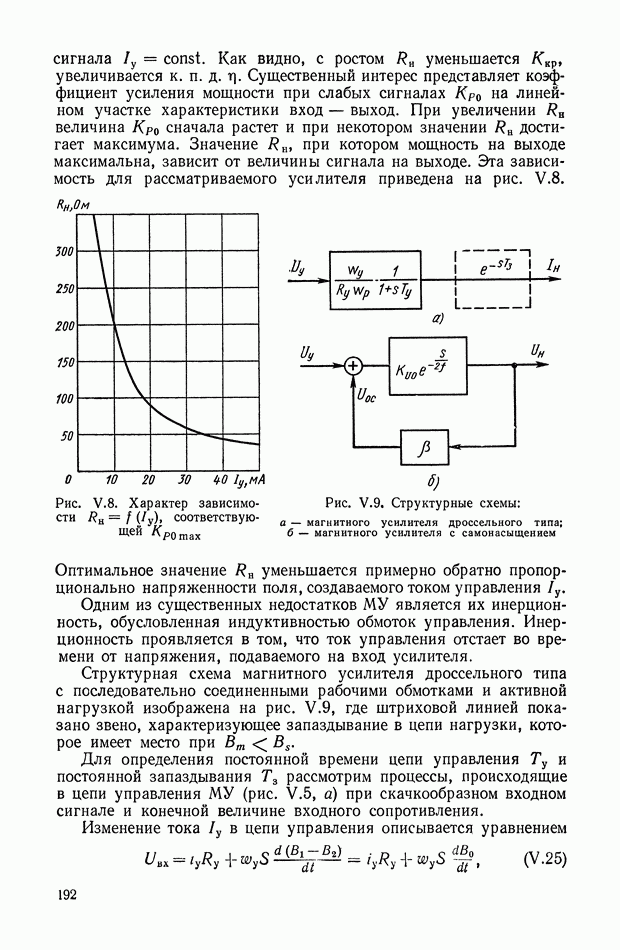
Правой части выражения (1.19) можно поставить в соответствие, например, обобщенную структурную схему нагруженного усилителя
(рис. 1.3, а) и передаточную функцию, учитывающую обобщенное комплексное проходное и выходное сопротивление усилителя. Итак, имея в виду выражения (1.19), (1.16) и (1.13), получим

или

где обобщенные (комплексные) проходное и выходное сопротивления усилителя

К — обобщенный передаточный коэффициент нагруженного усилителя, не охваченного обратной связью;  — обобщенная нормированная передаточная функция усилителя.
— обобщенная нормированная передаточная функция усилителя.

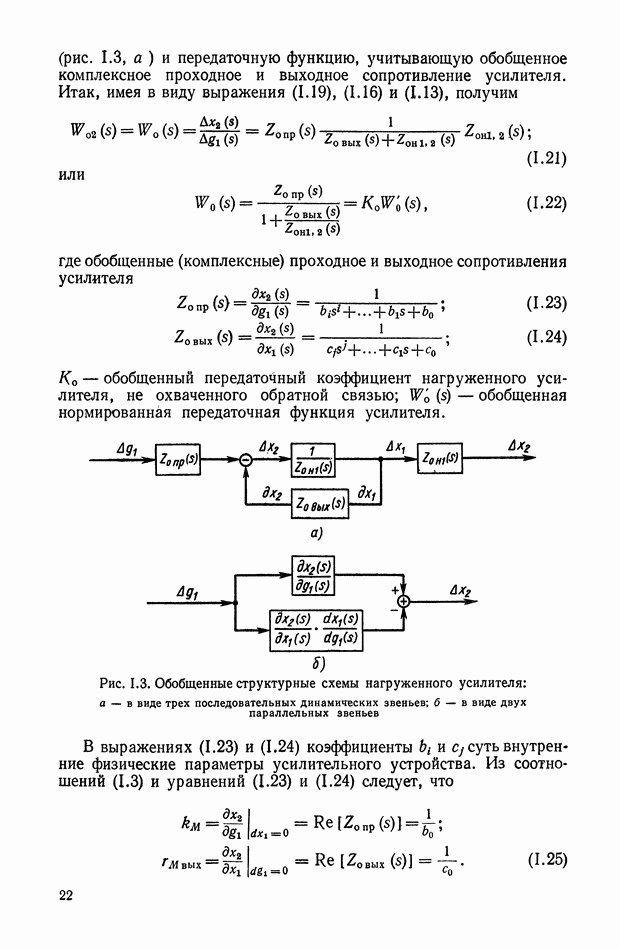
Рис. 1.3. Обобщенные структурные схемы нагруженного усилителя: а — в виде трех последовательных динамических звеньев; б — в виде двух параллельных звеньев
В выражениях (1.23) и (1.24) коэффициенты  и сусуть внутренние физические параметры усилительного устройства. Из соотношений (1.3) и уравнений (1.23) и (1.24) следует, что
и сусуть внутренние физические параметры усилительного устройства. Из соотношений (1.3) и уравнений (1.23) и (1.24) следует, что

Таким образом, по аналогии с выражением (1.21) можно записать систему обобщенных передаточных функций от параметра  к параметрам
к параметрам  учитывающих комплексное выходное и проходное сопротивления усилителя и комплексное сопротивление нагрузки:
учитывающих комплексное выходное и проходное сопротивления усилителя и комплексное сопротивление нагрузки:

Аналогично системе (1.26) можно получить обобщенные передаточные функции от параметра  к параметрам
к параметрам 

при индуктивной нагрузке  и
и

при емкостной нагрузке 
Как видно из выражения (1.21) и рис. 1.3, а, обобщенная структурная схема нагруженного усилительного устройства, имеющего передаточную функцию  представляет собой последовательное соединение трех динамических звеньев: двух звеньев однонаправленного действия
представляет собой последовательное соединение трех динамических звеньев: двух звеньев однонаправленного действия  и одного звена двухнаправленного действия.
и одного звена двухнаправленного действия.
Звено двухнаправленного действия является звеном с естественной обратной связью  характеризующей эффект уменьшения выходного параметра усилителя за счет его комплексного внутреннего сопротивления
характеризующей эффект уменьшения выходного параметра усилителя за счет его комплексного внутреннего сопротивления 
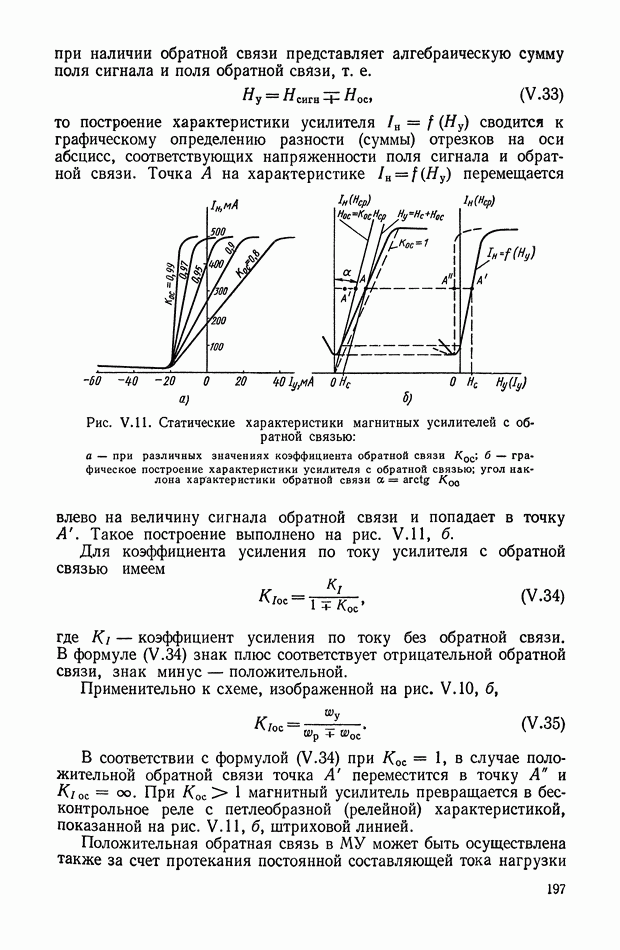
Обобщенная структурная схема усилительного устройства, соответствующая выражению (1.20), представляет собой два параллельных звена, как показано на рис. 1.3. б. Передаточная функция в этом случае имеет вид

где  — обобщенная передаточная функция усилителя от параметра
— обобщенная передаточная функция усилителя от параметра  к параметру
к параметру 
Нетрудно заметить, что

т. е. структурные схемы, представленные на рис. 1.3, а и б, эквивалентны между собой.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА САР
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ЛИНЕЙНЫХ УСИЛИТЕЛЬНЫХ УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ УСИЛИТЕЛЬНОГО УСТРОЙСТВА БЕЗ ОБРАТНОЙ СВЯЗИ
- 3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ, СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ОСОБЕННОСТИ УСИЛИТЕЛЬНОГО УСТРОЙСТВА С ОБРАТНОЙ СВЯЗЬЮ
- 4. КЛАССИФИКАЦИЯ И СВОЙСТВА УСИЛИТЕЛЬНЫХ УСТРОЙСТВ С ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 5. ВЫБОР И РАСЧЕТ УСИЛИТЕЛЬНОГО УСТРОЙСТВА
- ГЛАВА II. ЭЛЕКТРОННЫЕ ЛАМПОВЫЕ И ИОННЫЕ УСИЛИТЕЛИ
- 1. ОСНОВЫ ТОПОЛОГИЧЕСКОГО АНАЛИЗА СХЕМ ЛИНЕЙНЫХ ЭЛЕКТРОННЫХ ЛАМПОВЫХ УСИЛИТЕЛЕЙ
- 2. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПОСТОЯННОГО ТОКА
- 3. БАЛАНСНЫЕ МОСТОВЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- 4. СТАБИЛИЗАЦИЯ КОЭФФИЦИЕНТА УСИЛЕНИЯ
- 5. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
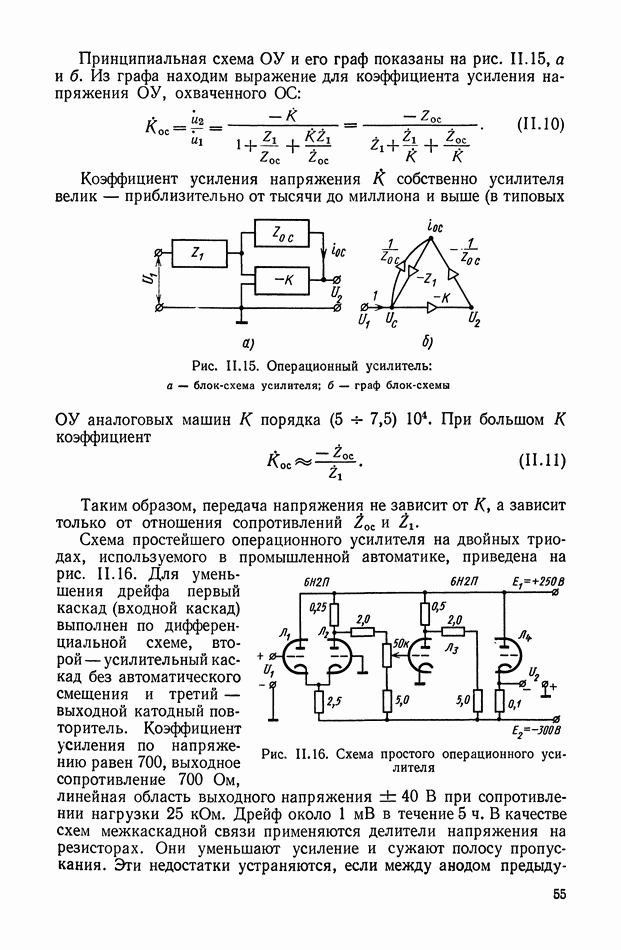
- 6. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- 7. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
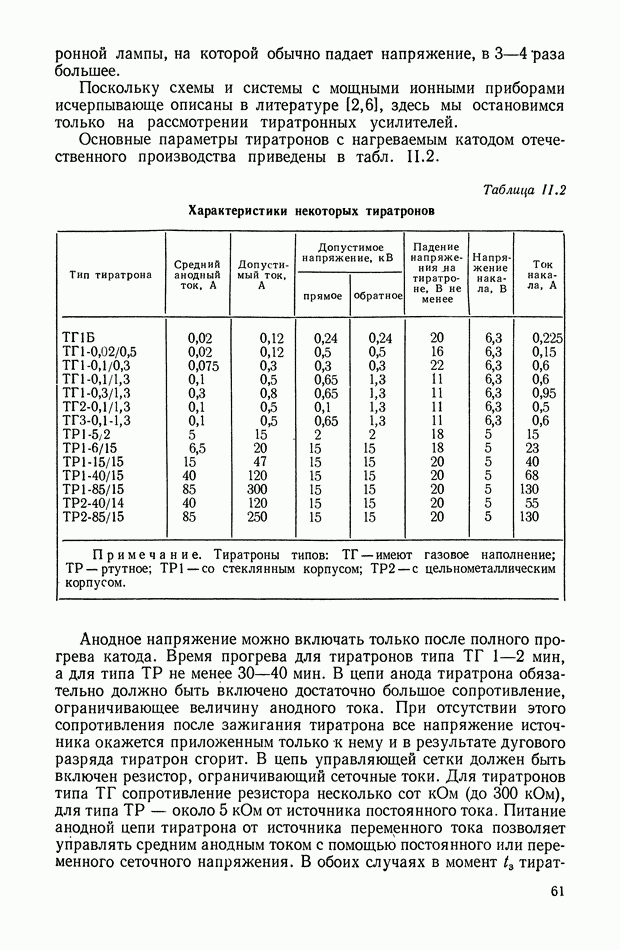
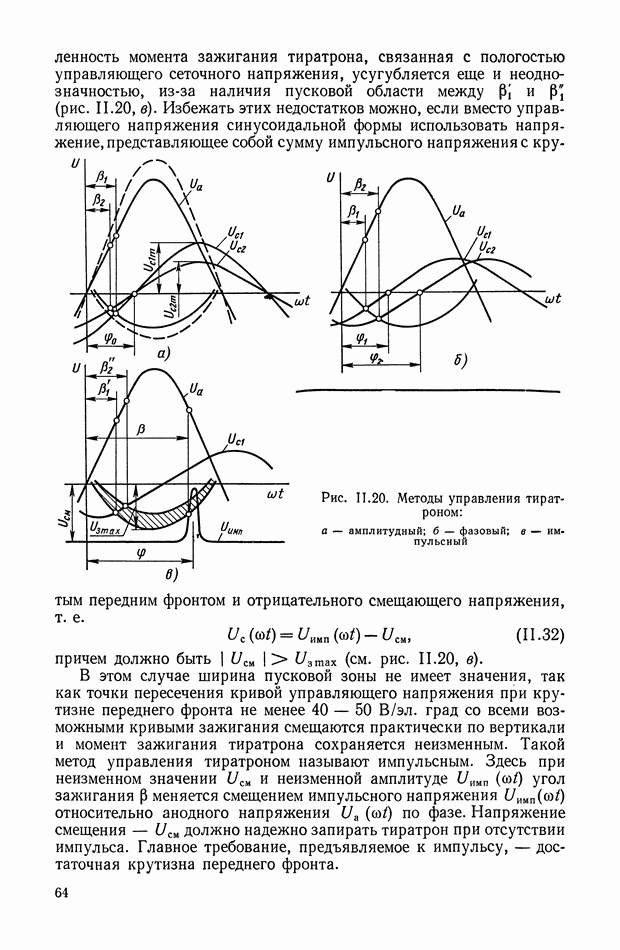
- 8. ОБЩИЕ СВОЙСТВА ИОННОГО (ТИРАТРОННОГО) УСИЛИТЕЛЯ МЕТОДЫ УПРАВЛЕНИЯ ТИРАТРОНОМ
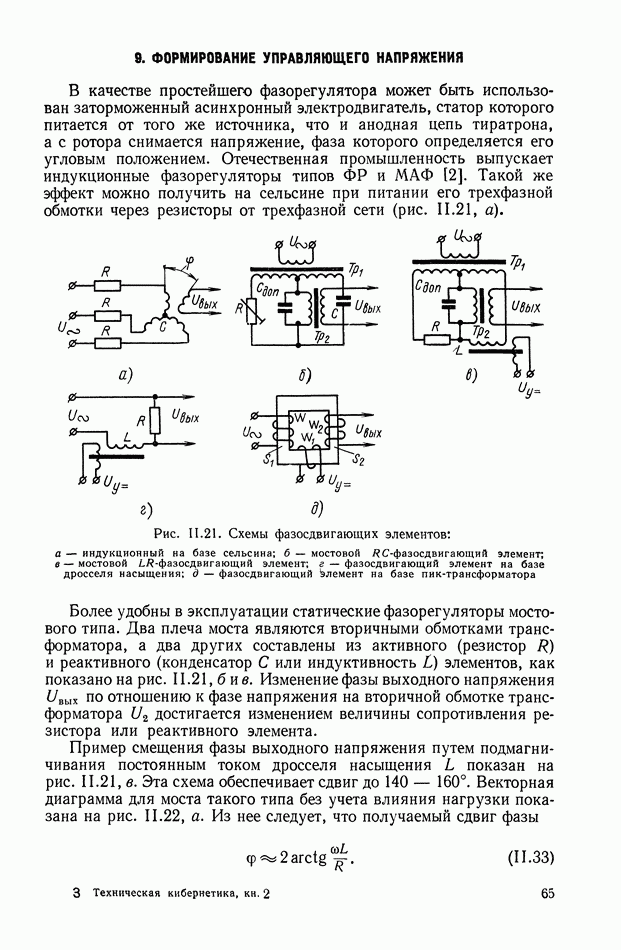
- 9. ФОРМИРОВАНИЕ УПРАВЛЯЮЩЕГО НАПРЯЖЕНИЯ
- 10. РАСЧЕТ ЭЛЕМЕНТОВ СХЕМ ТИРАТРОННОГО УСИЛИТЕЛЯ
- ГЛАВА III. ПОЛУПРОВОДНИКОВЫЕ И ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
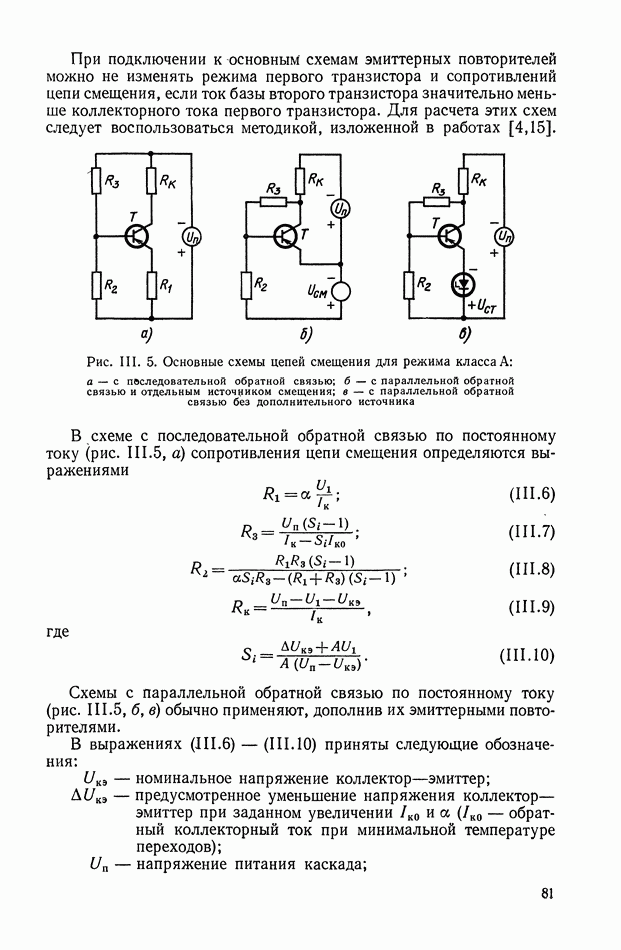
- Цепи смещения.
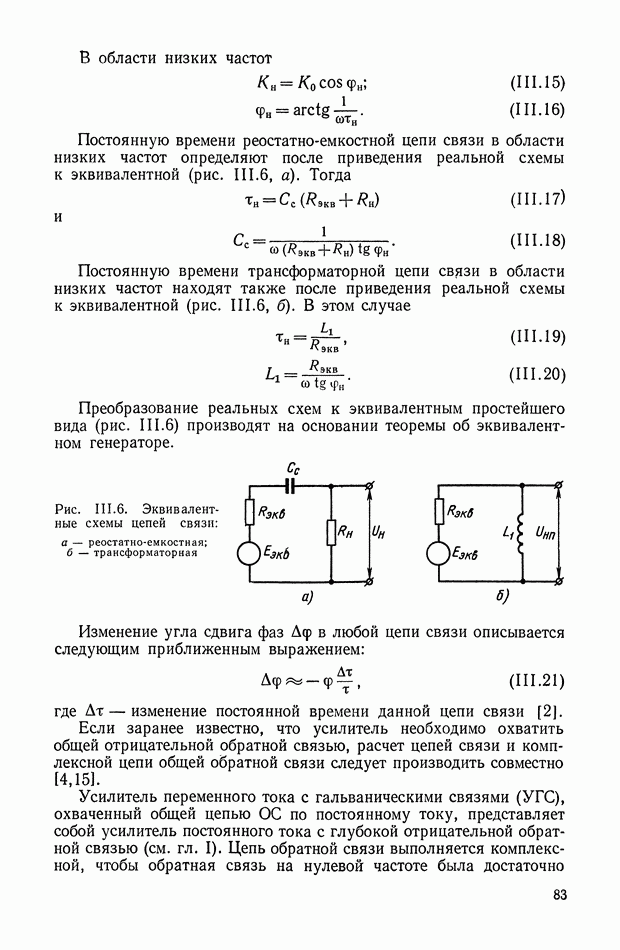
- Цепи связи.
- 2. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ СРЕДНЕГО ЗНАЧЕНИЯ ТОКА
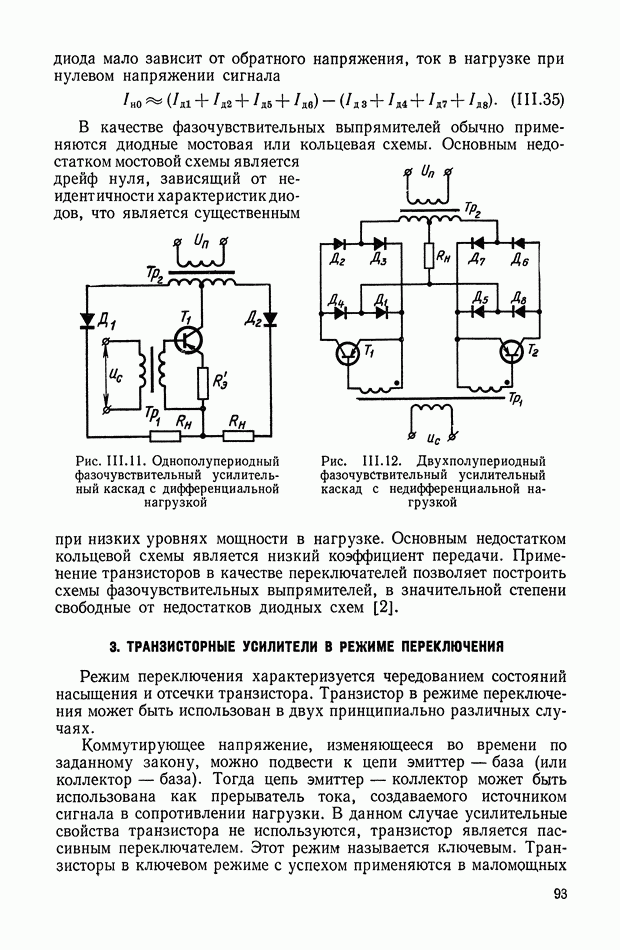
- Полупроводниковые демодуляторы.
- 3. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ В РЕЖИМЕ ПЕРЕКЛЮЧЕНИЯ
- Режимы импульсного регулирования мощности.
- Управление силовыми транзисторами.
- 4. ТРАНЗИСТОРНЫЕ УСТРОЙСТВА УПРАВЛЕНИЯ ЭЛЕКТРОДВИГАТЕЛЯМИ И ЭЛЕКТРОМАГНИТНЫМИ МЕХАНИЗМАМИ
- 5. ТИРИСТОРЫ. ХАРАКТЕРИСТИКИ, ПАРАМЕТРЫ И СВОЙСТВА
- 6. СПОСОБЫ И УСТРОЙСТВА УПРАВЛЕНИЯ ТИРИСТОРАМИ
- 7. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ (РЕГУЛИРУЕМЫЕ ВЫПРЯМИТЕЛИ)
- 8. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 9. ТИРИСТОРНЫЕ УСИЛИТЕЛИ С ПИТАНИЕМ ОТ СЕТИ ПОСТОЯННОГО ТОКА
- 10. ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 11. ОСНОВЫ РАСЧЕТА ДИЭЛЕКТРИЧЕСКИХ УСИЛИТЕЛЕЙ
- ГЛАВА IV. КВАНТОВЫЕ УСИЛИТЕЛИ И ГЕНЕРАТОРЫ
- 2. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ РАДИОДИАПАЗОНА
- Квантовые усилители радиодиапазона.
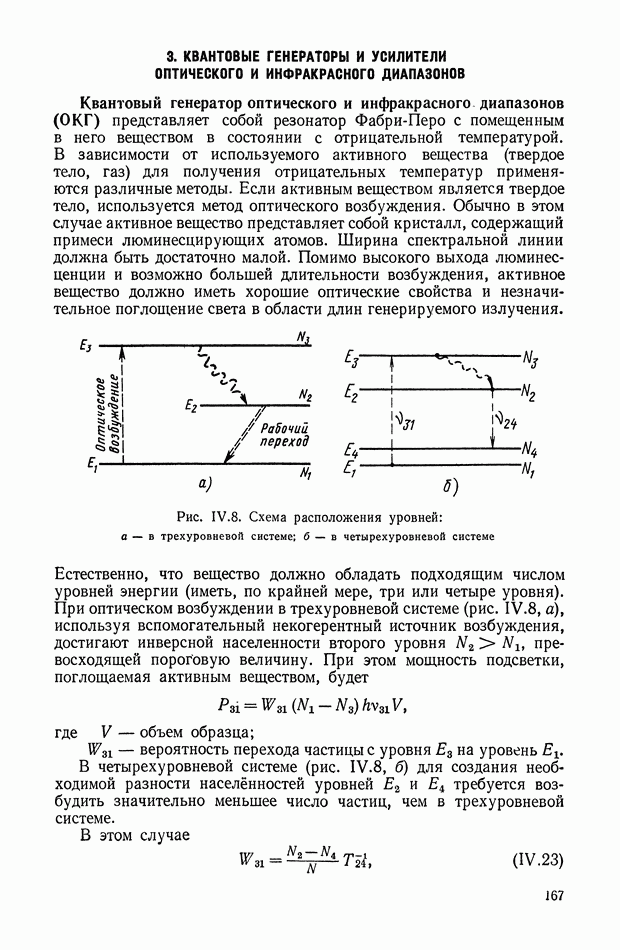
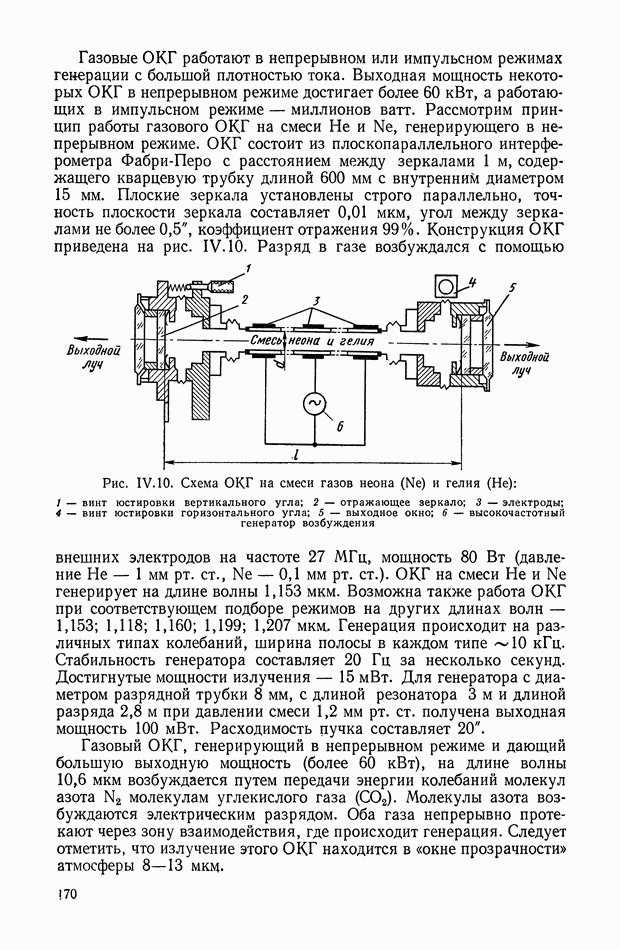
- 3. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- Оптический квантовый усилитель
- 4. ПРИМЕНЕНИЕ В САР КВАНТОВЫХ УСИЛИТЕЛЕЙ И ГЕНЕРАТОРОВ РАДИОДИАПАЗОНА, ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
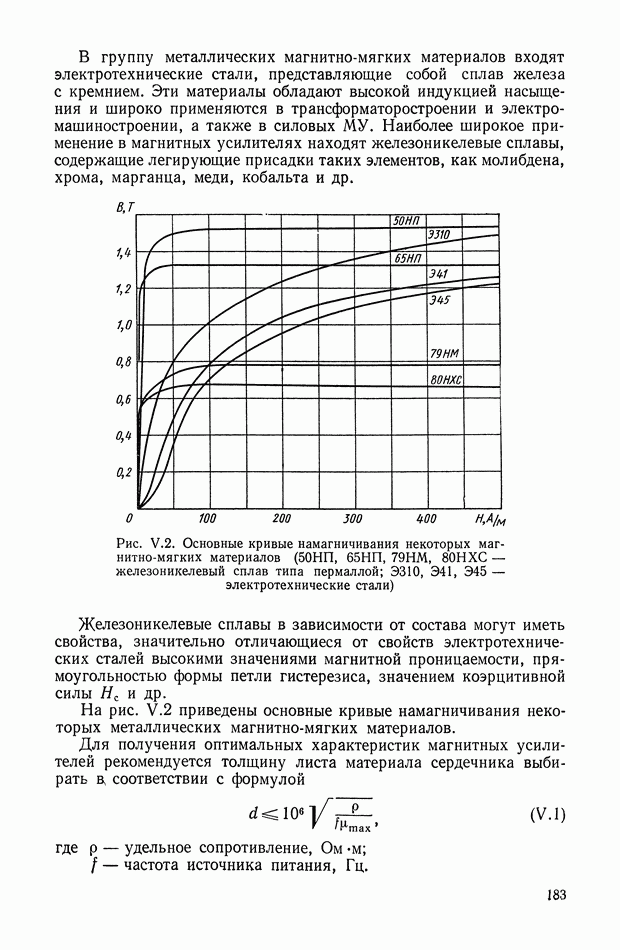
- ГЛАВА V. МАГНИТНЫЕ И МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- 2. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ МАГНИТНЫХ УСИЛИТЕЛЕЙ
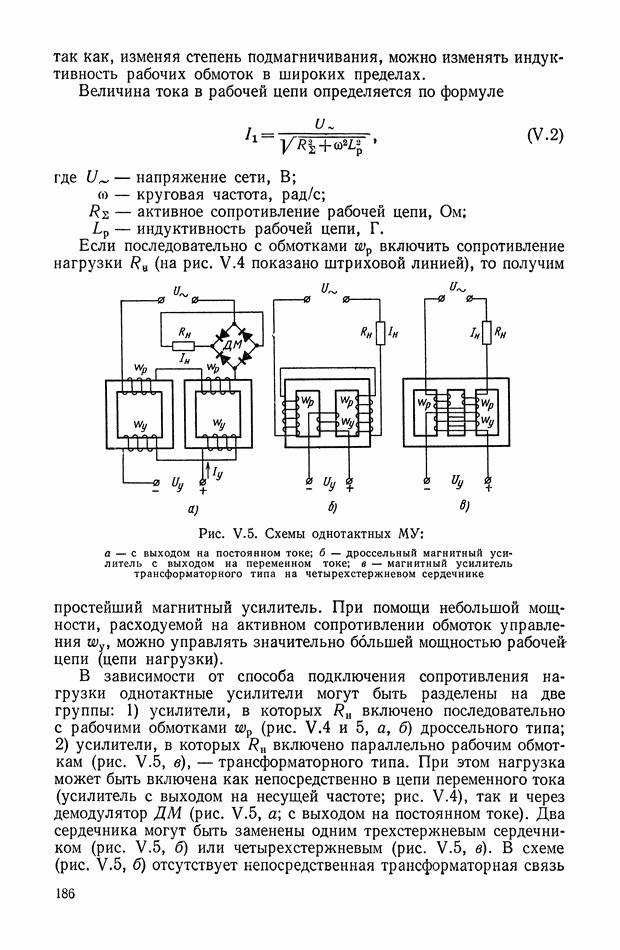
- 3. ОДНОТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ БЕЗ ОБРАТНОЙ СВЯЗИ (УПРАВЛЯЕМЫЕ ДРОССЕЛИ И ТРАНСФОРМАТОРЫ)
- 4. МАГНИТНЫЕ УСИЛИТЕЛИ С САМОНАСЫЩЕНИЕМ
- Релейный режим работы усилителей с самонасыщением.
- 5. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 6. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ
- 7. МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- ГЛАВА VI. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 2. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С НЕЗАВИСИМЫМ ВОЗБУЖДЕНИЕМ И С САМОВОЗБУЖДЕНИЕМ
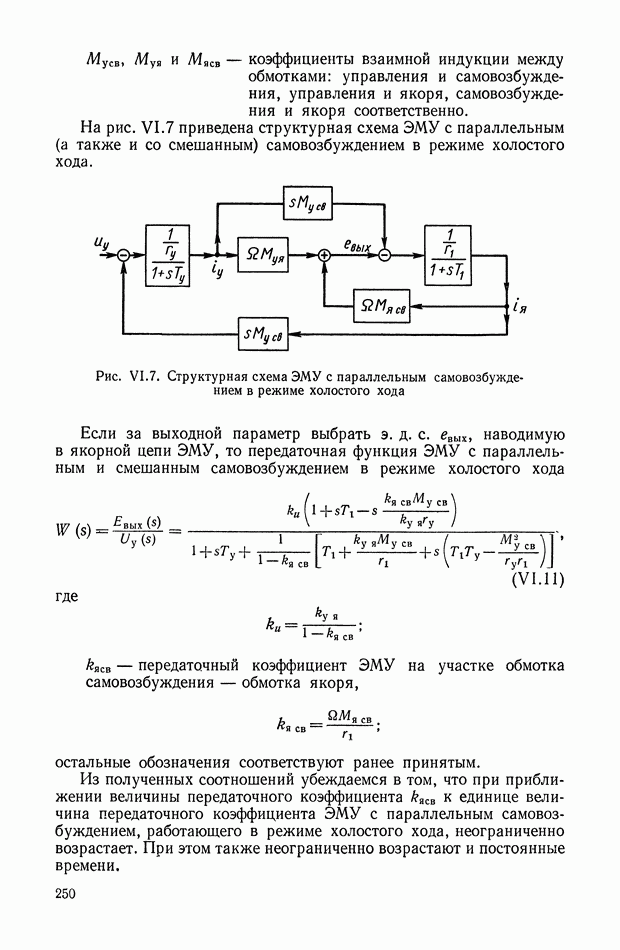
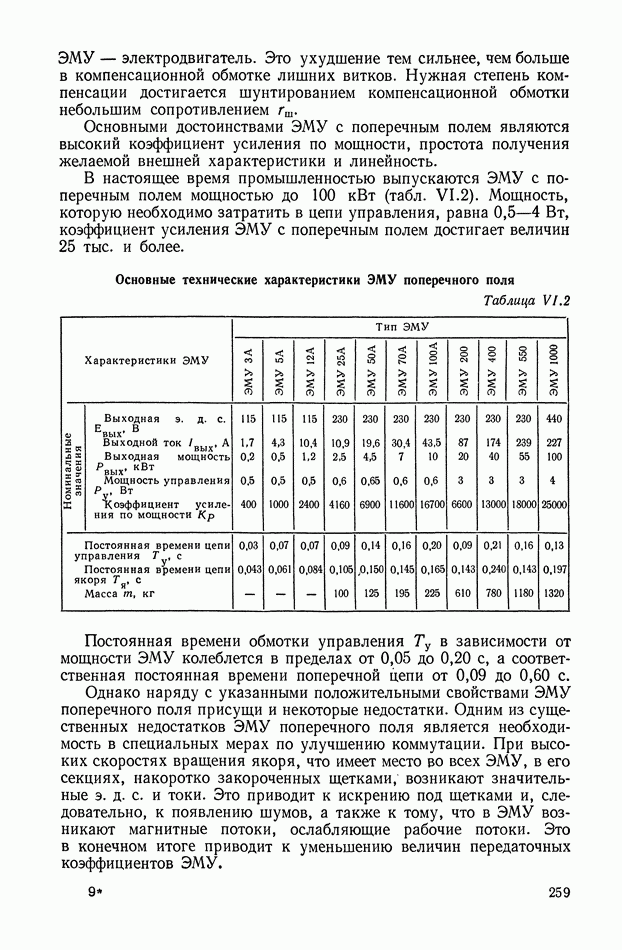
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С ПОПЕРЕЧНЫМ ПОЛЕМ
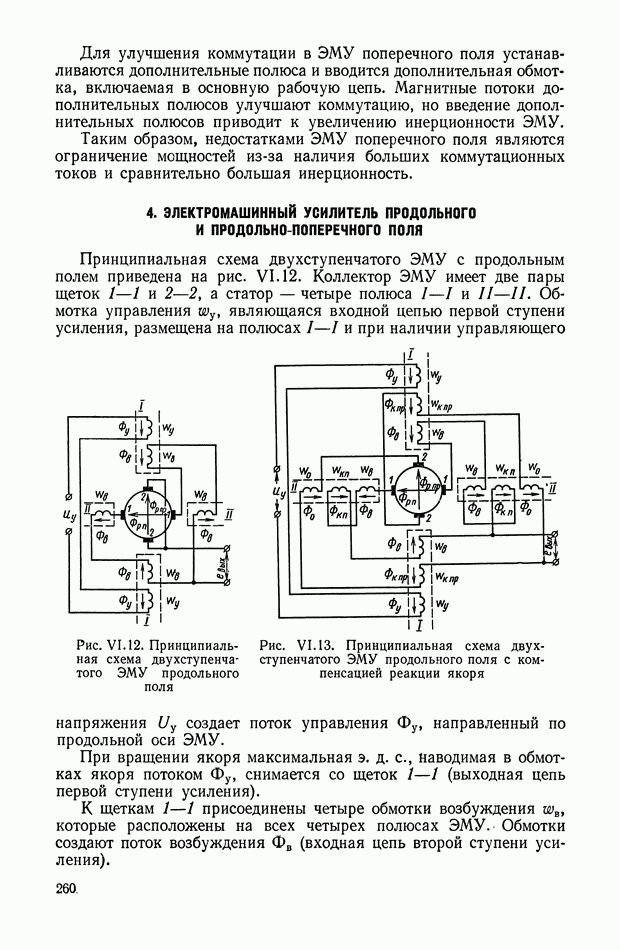
- 4. ЭЛЕКТРОМАШИННЫЙ УСИЛИТЕЛЬ ПРОДОЛЬНОГО И ПРОДОЛЬНО-ПОПЕРЕЧНОГО ПОЛЯ
- 5. ВЛИЯНИЕ НА ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭМУ ВИХРЕВЫХ И КОММУТАЦИОННЫХ ТОКОВ, ГИСТЕРЕЗИСА И СДВИГА ЩЕТОК С НЕЙТРАЛИ
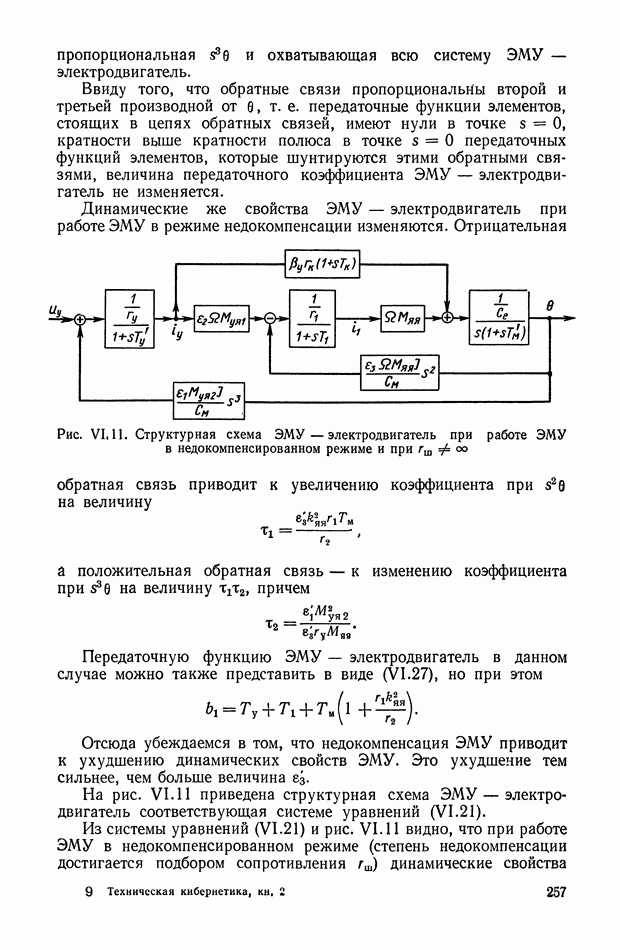
- 6. МЕТОДЫ УЛУЧШЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕКТРОМАШИННЫХ УСИЛИТЕЛЕЙ
- 7. НАГРУЗОЧНАЯ ХАРАКТЕРИСТИКА ЭЛЕКТРОМАШИННОГО УСИЛИТЕЛЯ
- ГЛАВА VII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ УСИЛИТЕЛИ
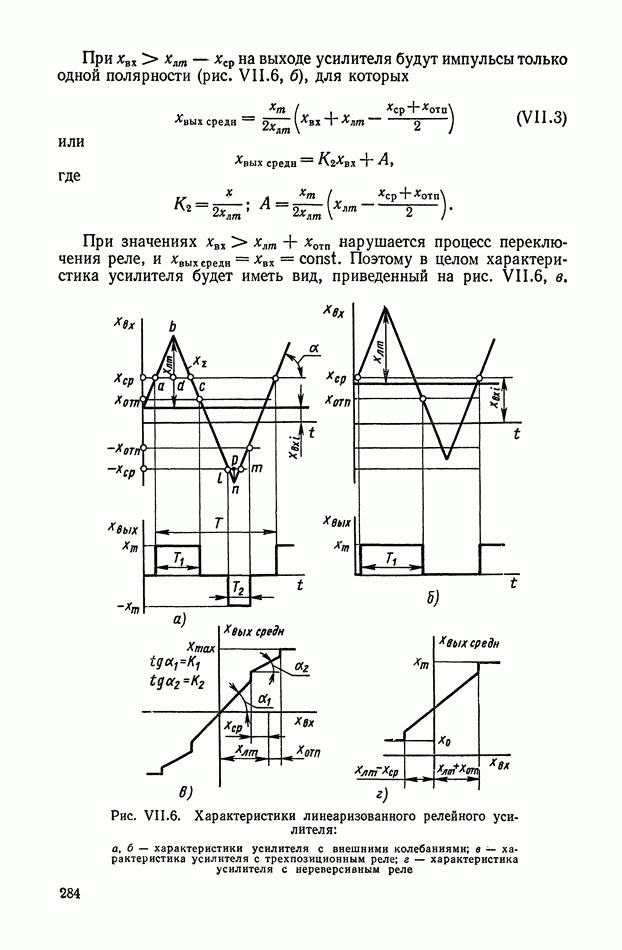
- 1. ХАРАКТЕРИСТИКИ УСИЛИТЕЛЕЙ И СПОСОБЫ ИХ ФОРМИРОВАНИЯ
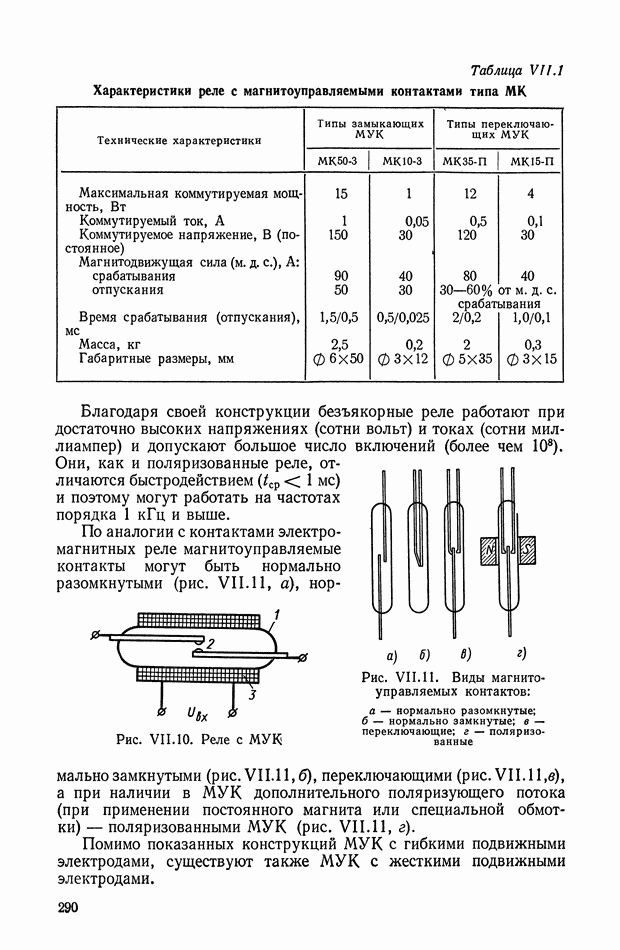
- 2. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
- 3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ЛИНЕАРИЗОВАННЫЕ УСИЛИТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ РЕЛЕ
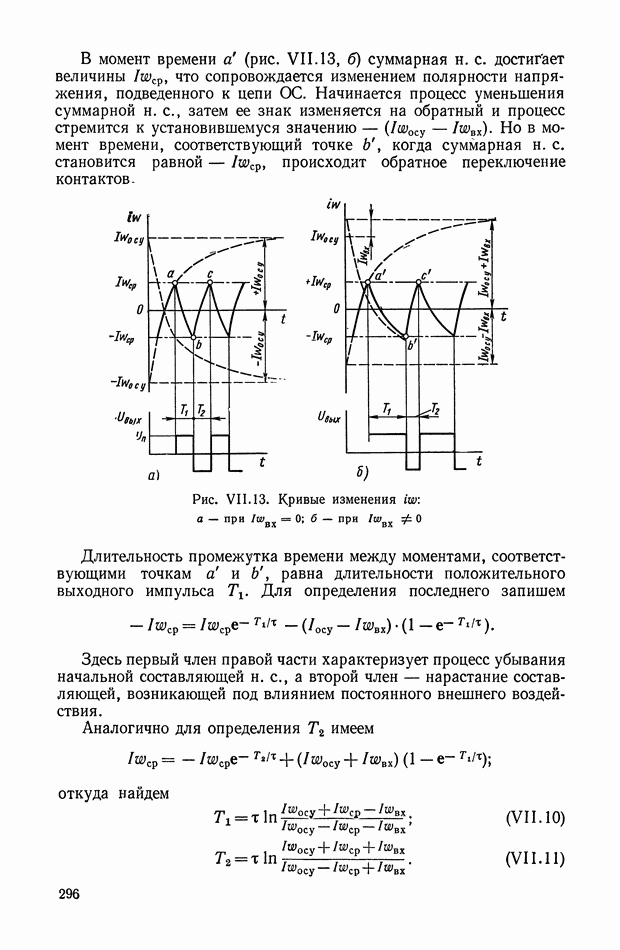
- 4. БЕСКОНТАКТНЫЕ ЛИНЕАРИЗОВАННЫЕ РЕЛЕЙНЫЕ УСИЛИТЕЛИ
- ГЛАВА VIII. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 2. ОСНОВНЫЕ ЭЛЕМЕНТЫ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ И ИХ ХАРАКТЕРИСТИКИ
- 3. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ С ЗОЛОТНИКОМ
- 4. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ СО СТРУЙНОЙ ТРУБКОЙ
- 5. СХЕМЫ И ПРИНЦИПЫ ДЕЙСТВИЯ ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 6. СТАТИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 7. ДИНАМИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
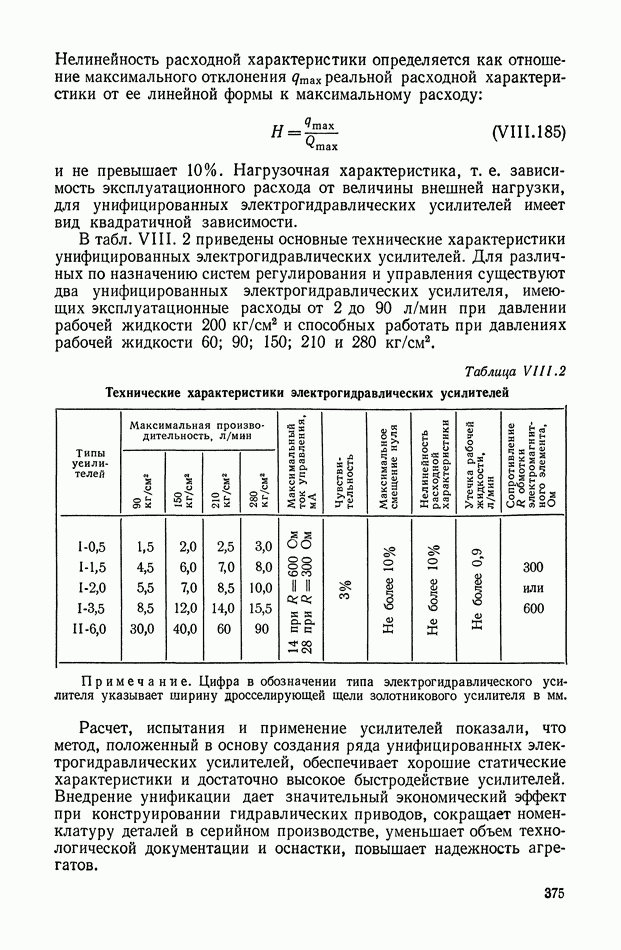
- 8. УНИФИКАЦИЯ ЭЛЕКТРОГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ ДЛЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
- ГЛАВА IX. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
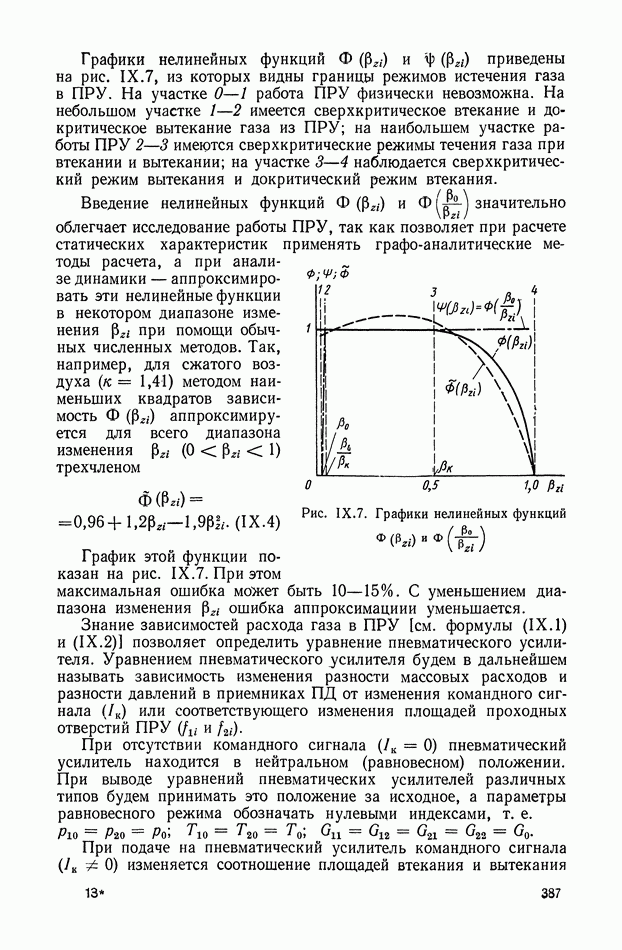
- 1. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ И ИХ КЛАССИФИКАЦИЯ
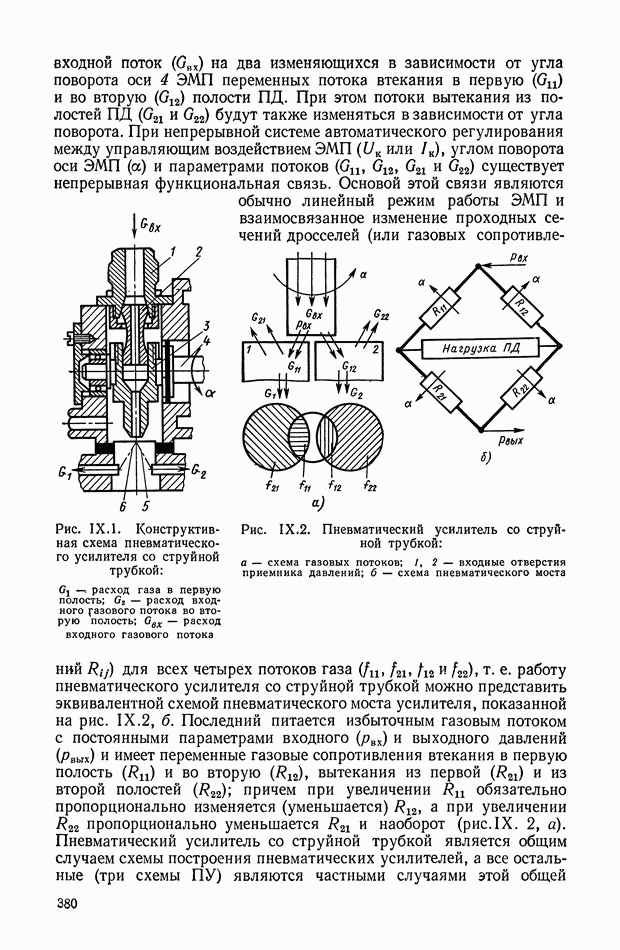
- 2. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ СО СТРУЙНОЙ ТРУБКОЙ
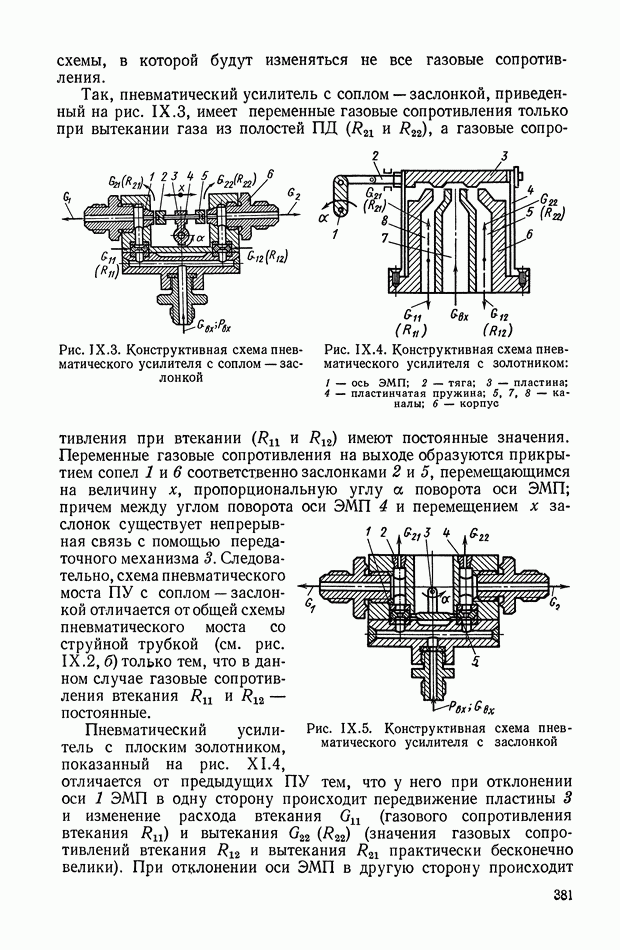
- 3. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗОЛОТНИКОМ
- 4. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С СОПЛОМ — ЗАСЛОНКОЙ
- 5. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗАСЛОНКОЙ
- 6. МНОГОКАСКАДНЫЕ ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- РАЗДЕЛ II. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ И УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ЛИНЕЙНЫХ ПАССИВНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Основные соотношения для синтеза пассивного RC-четырехполюсника.
- 3. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Активные четырехполюсники, получаемые с помощью конверторов отрицательного сопротивления.
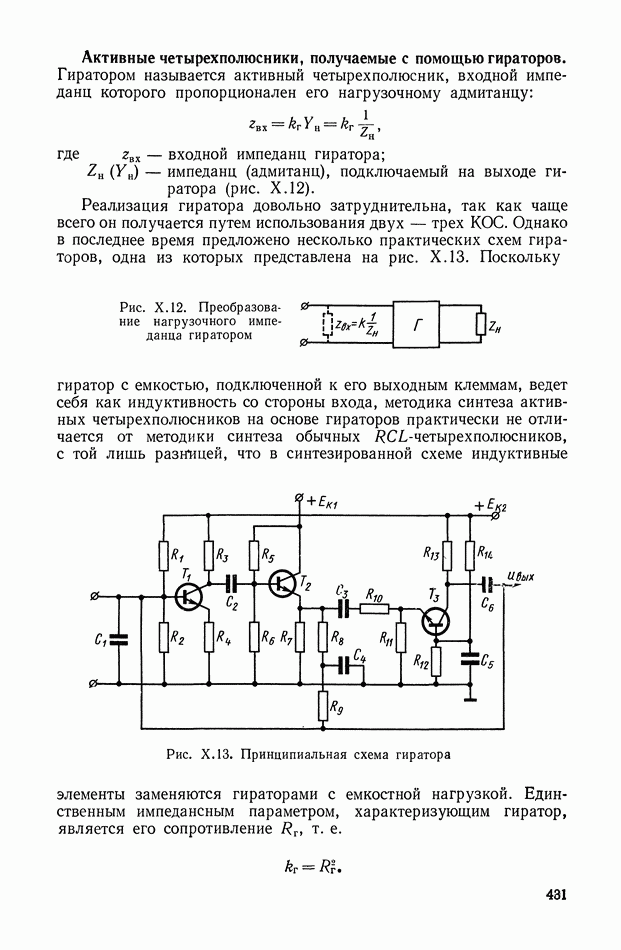
- Активные четырехполюсники, получаемые с помощью гираторов.
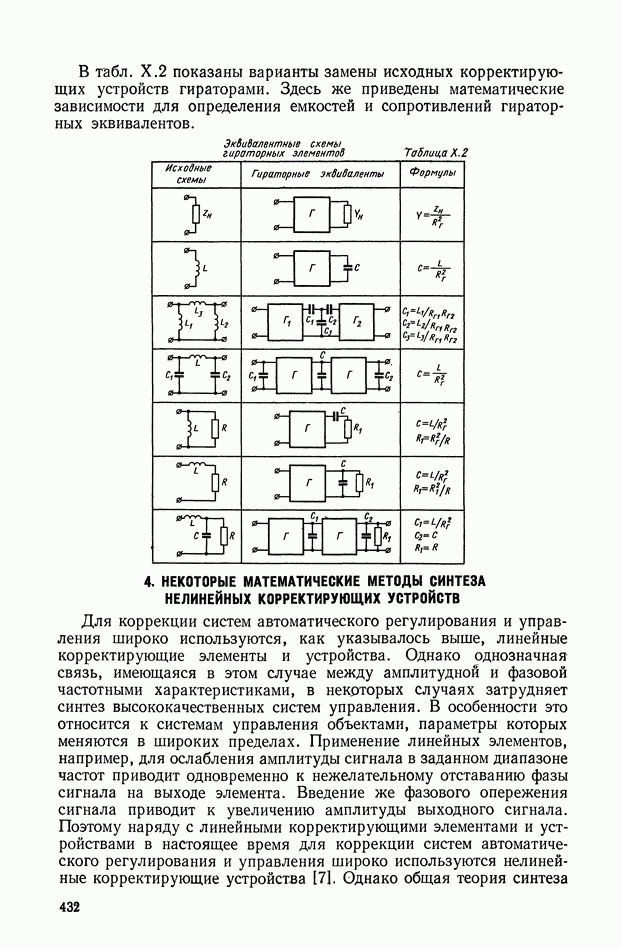
- 4. НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА НЕЛИНЕЙНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
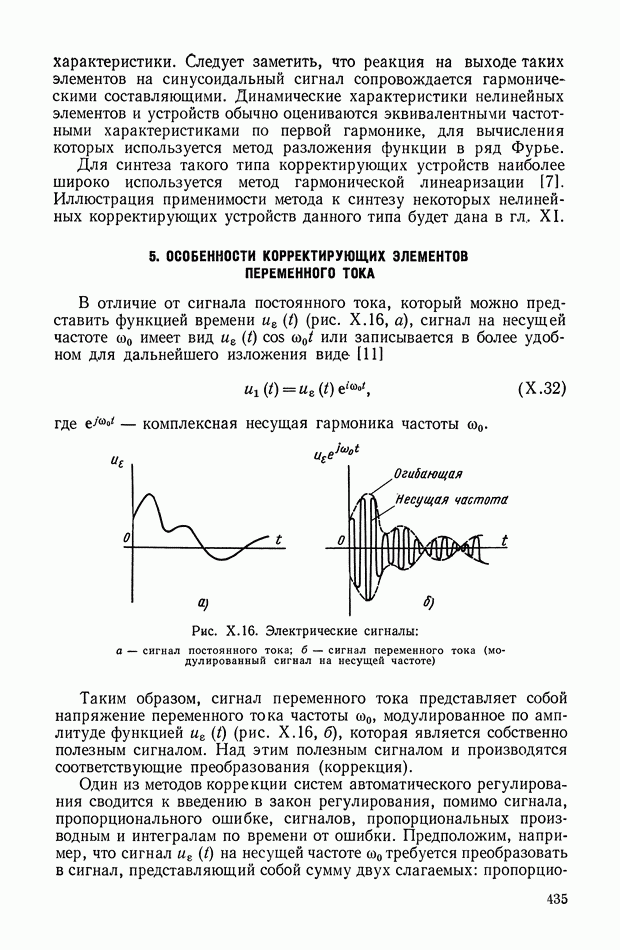
- 5. ОСОБЕННОСТИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XI. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА ПОСТОЯННОГО ТОКА
- Дифференцирующий трансформатор.
- Электрические интегрирующие элементы.
- 2. ТИПОВЫЕ ЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- 3. КОРРЕКТИРУЮЩИЕ ЧЕТЫРЕХПОЛЮСНИКИ С АКТИВНЫМИ ЭЛЕМЕНТАМИ
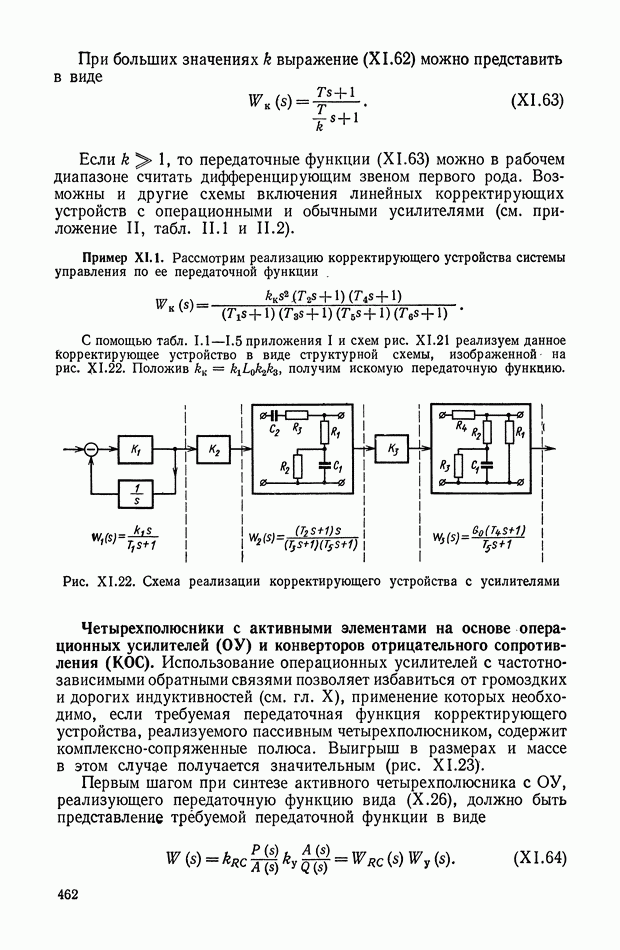
- Четырехполюсники с активными элементами на основе операционных усилителей (ОУ) и конверторов отрицательного сопротивления (КОС).
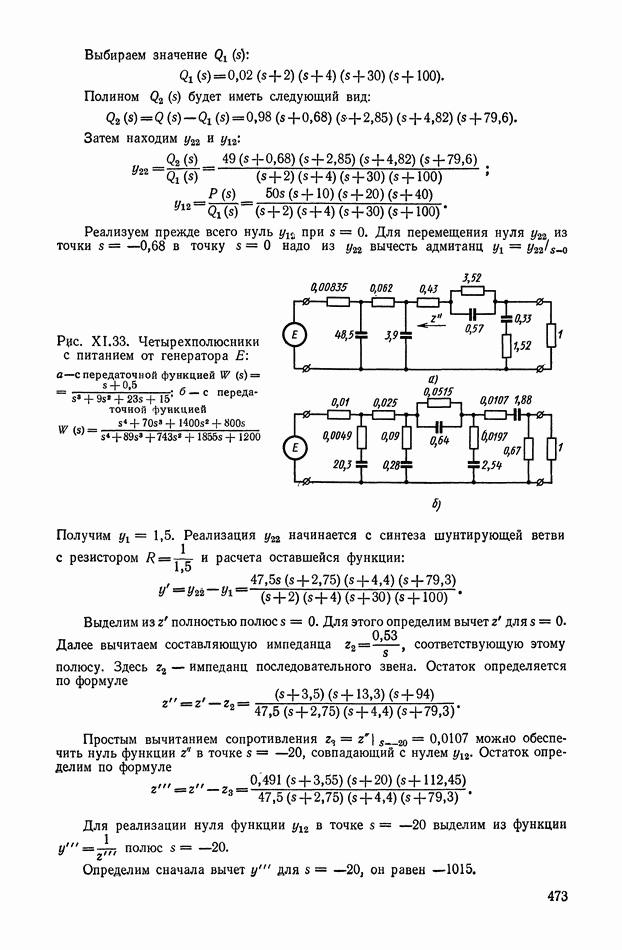
- 4. РЕАЛИЗАЦИЯ ЗАДАННОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В ВИДЕ СХЕМЫ ПАССИВНОГО ЛИНЕЙНОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА
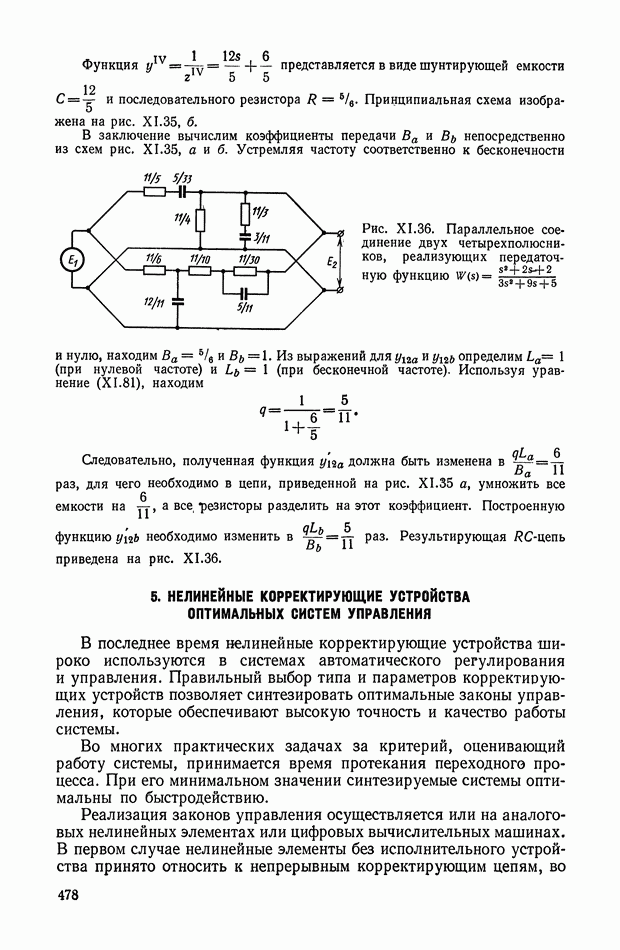
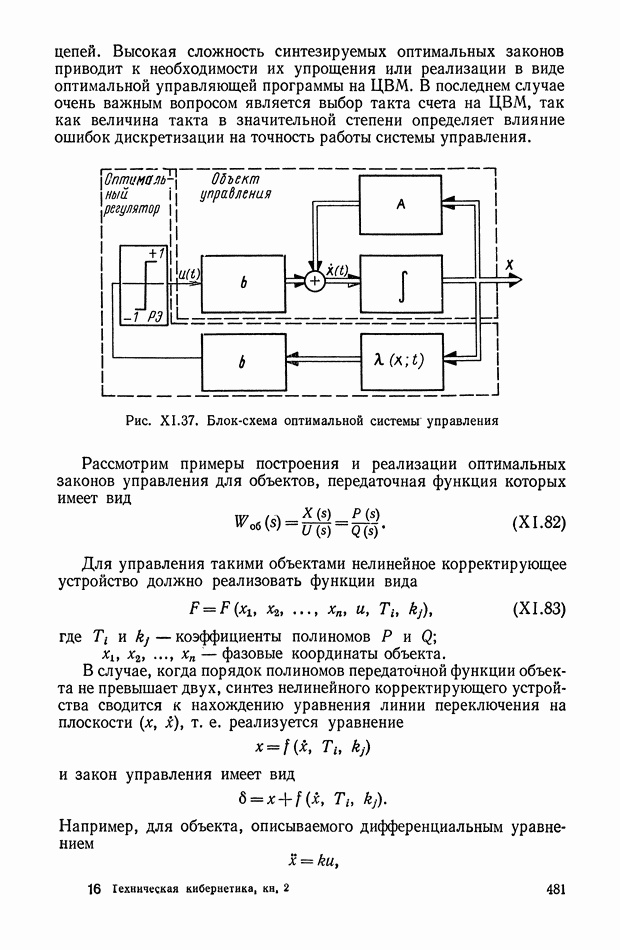
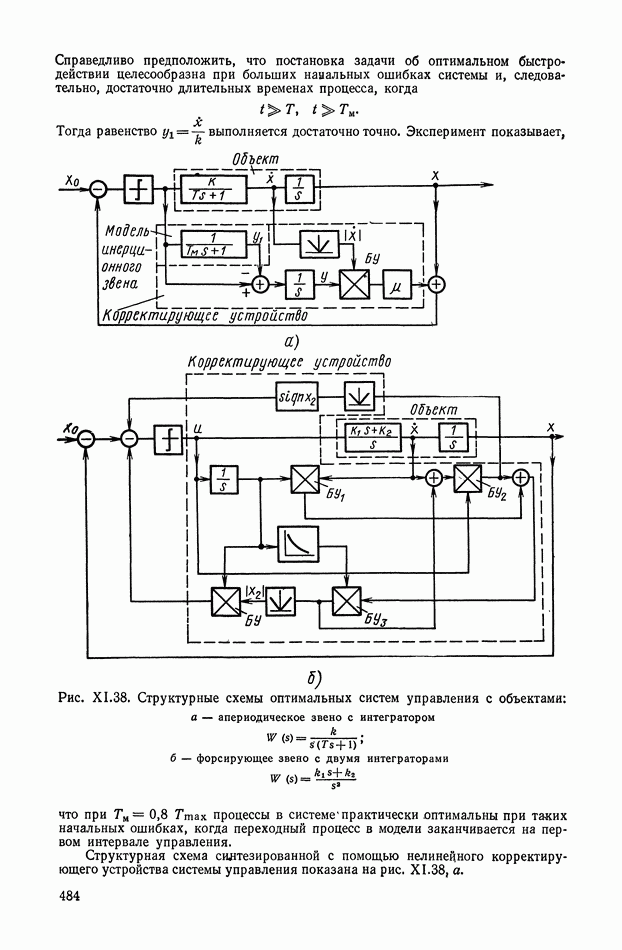
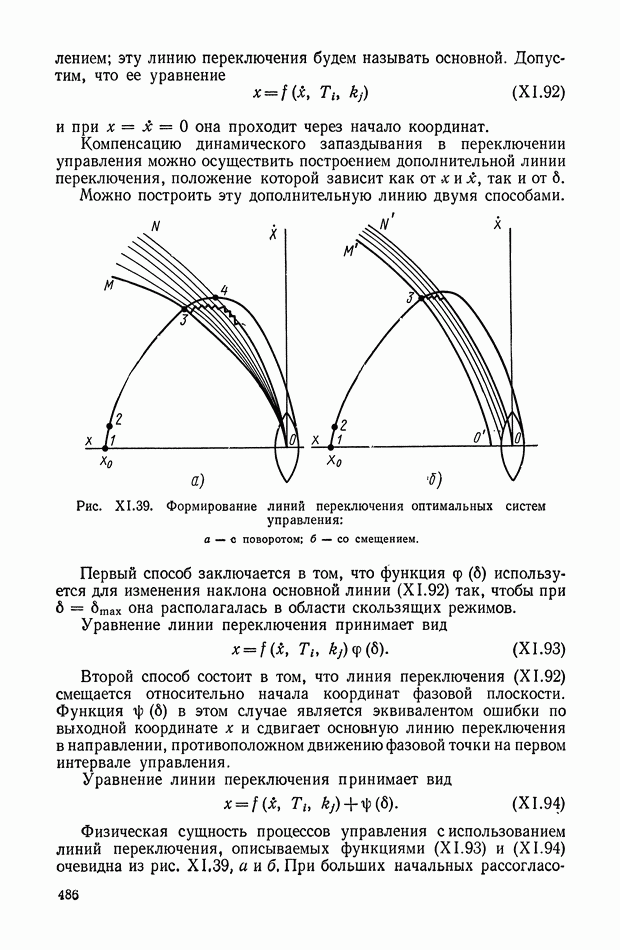
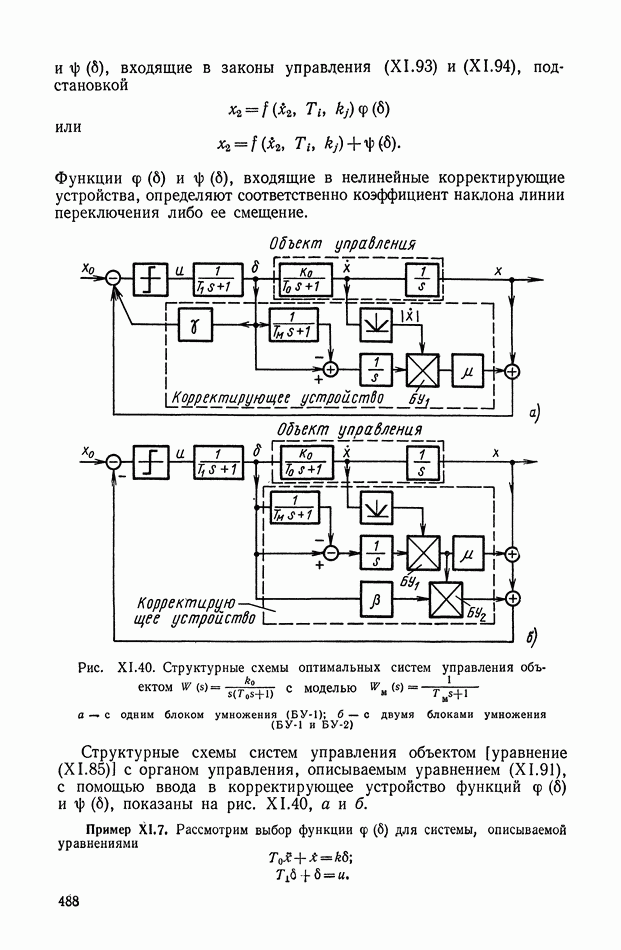
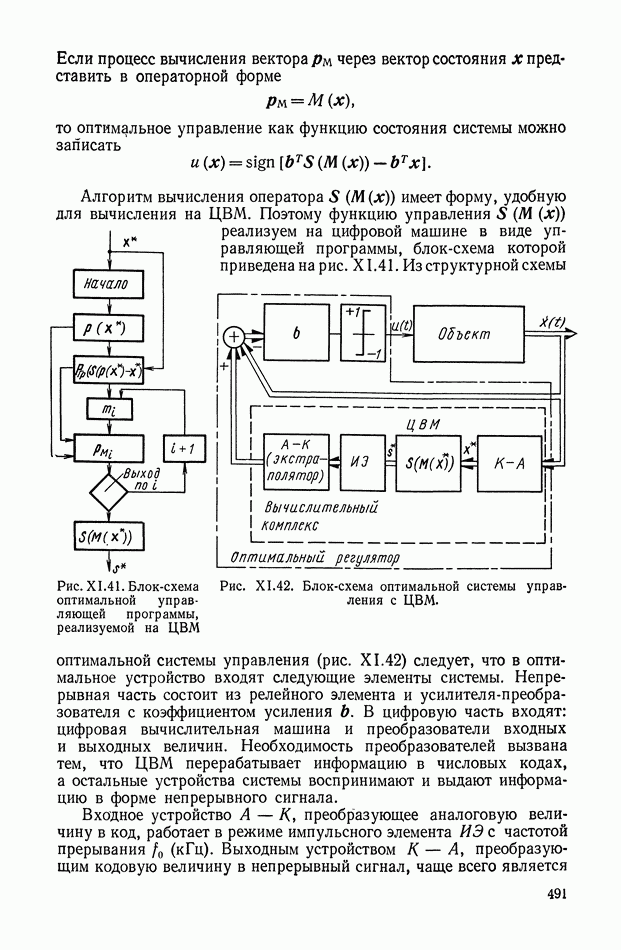
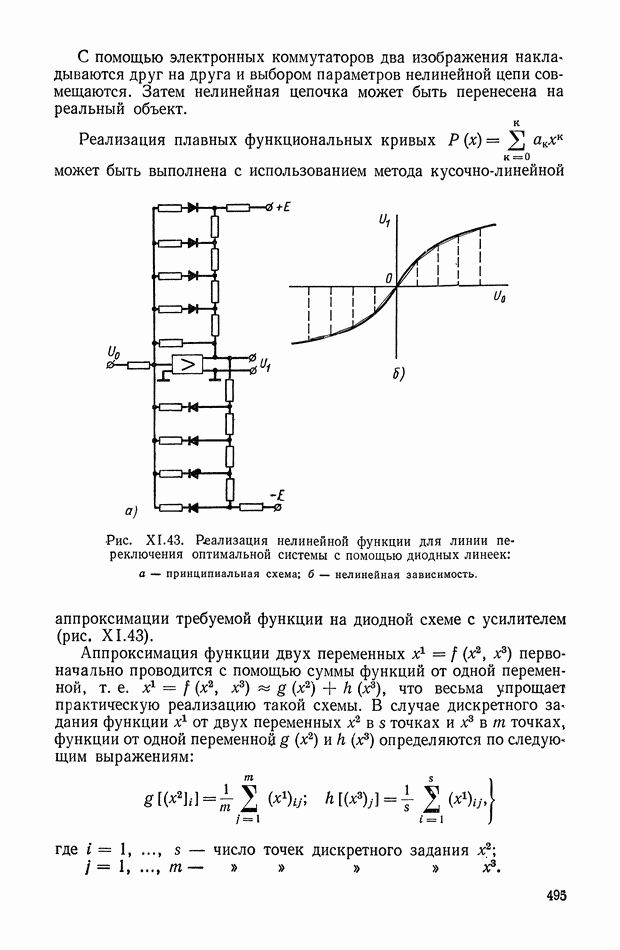
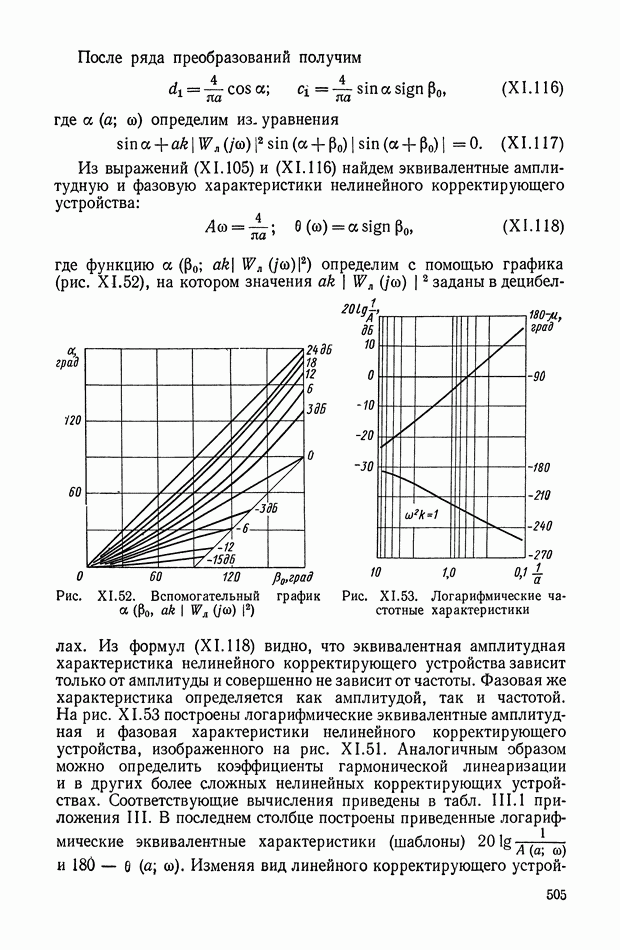
- 5. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
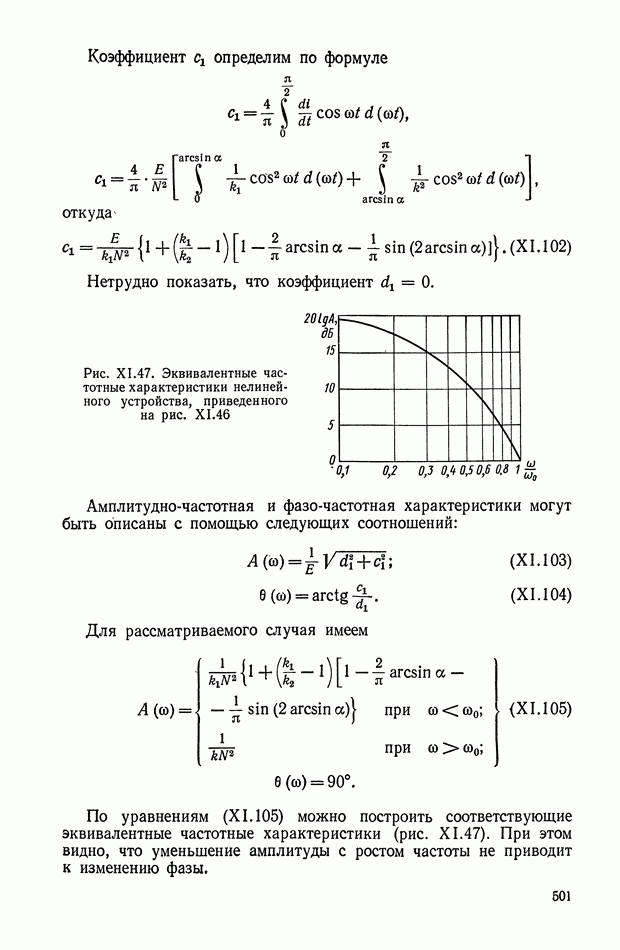
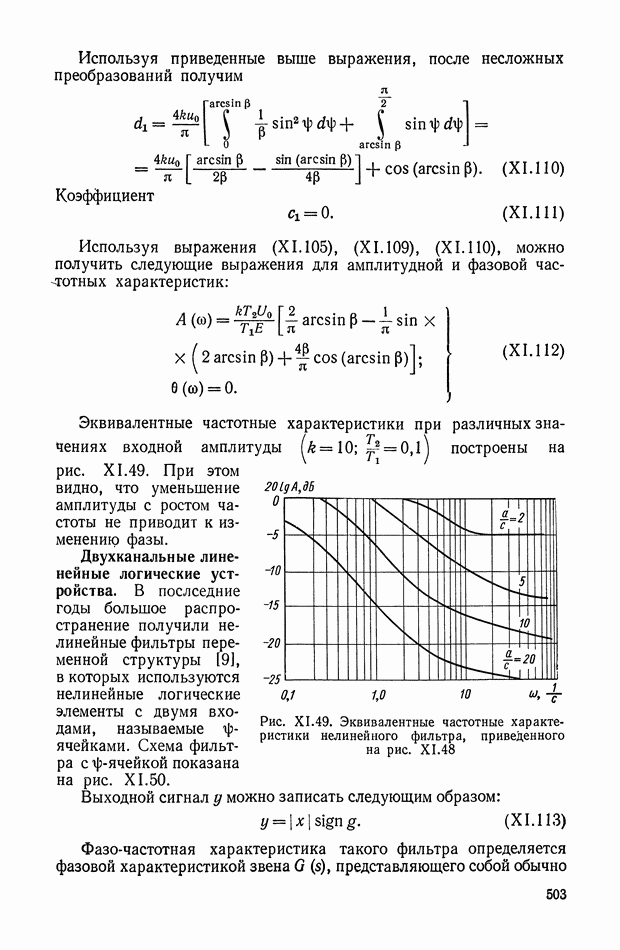
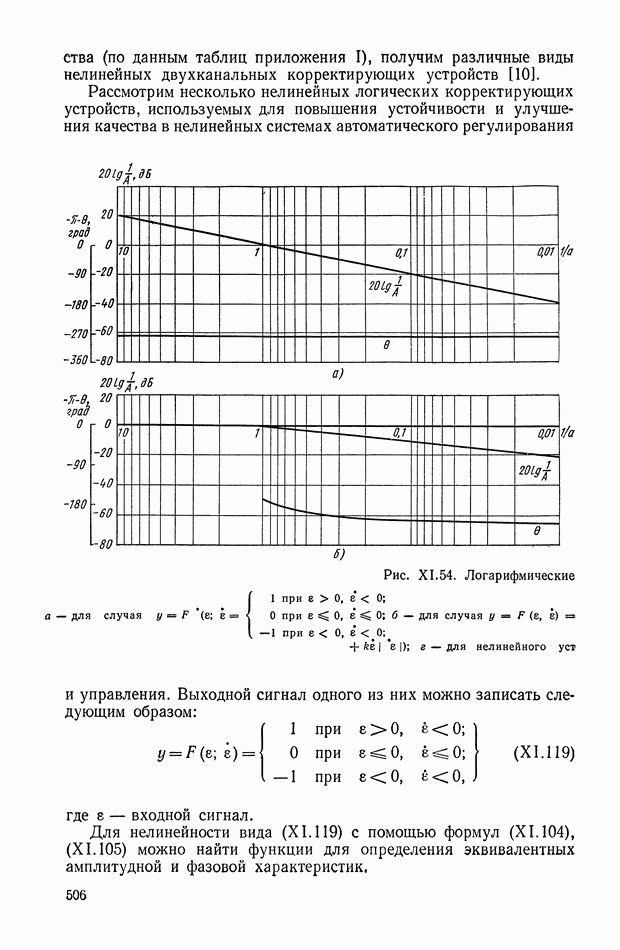
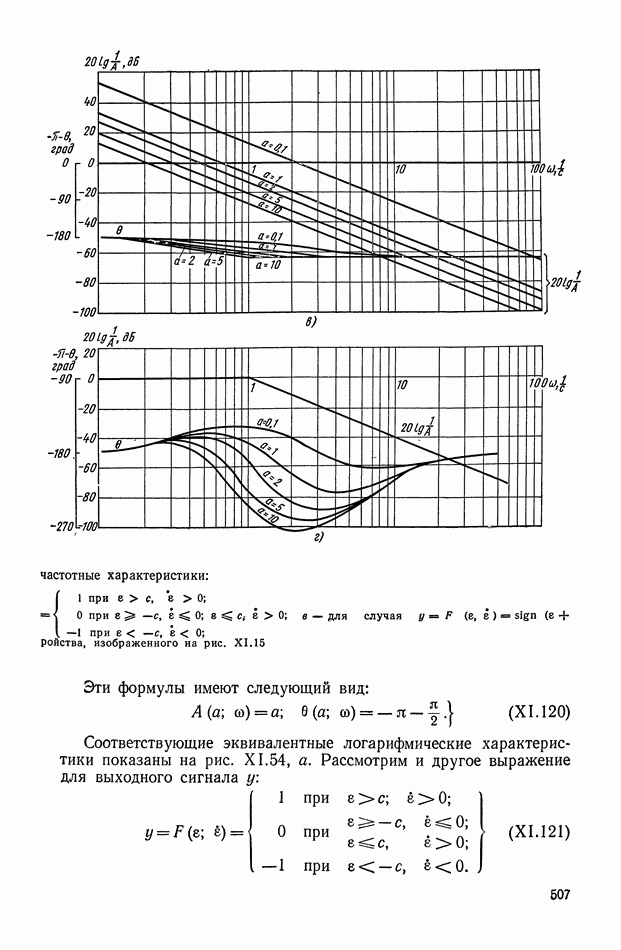
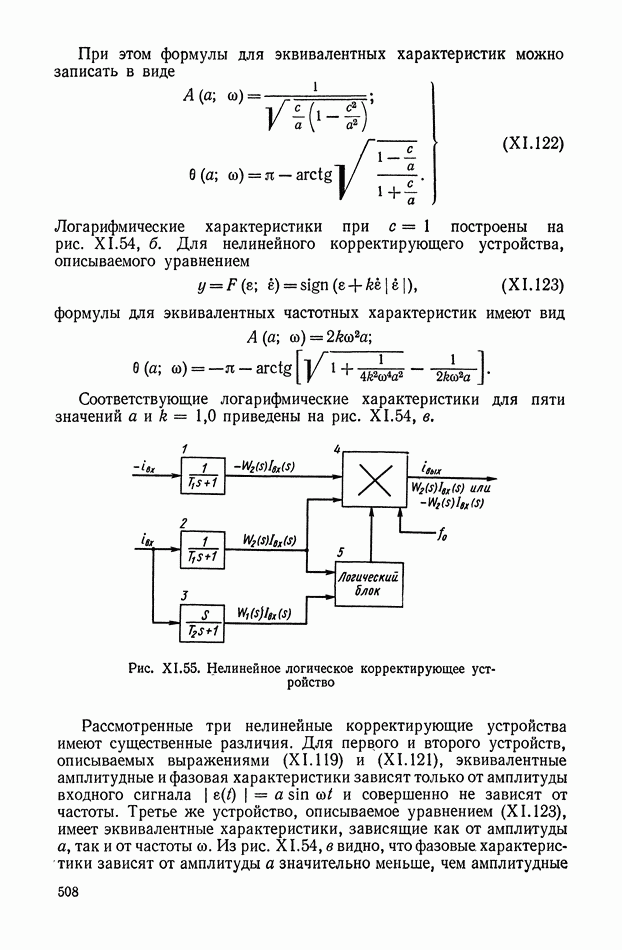
- 8. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
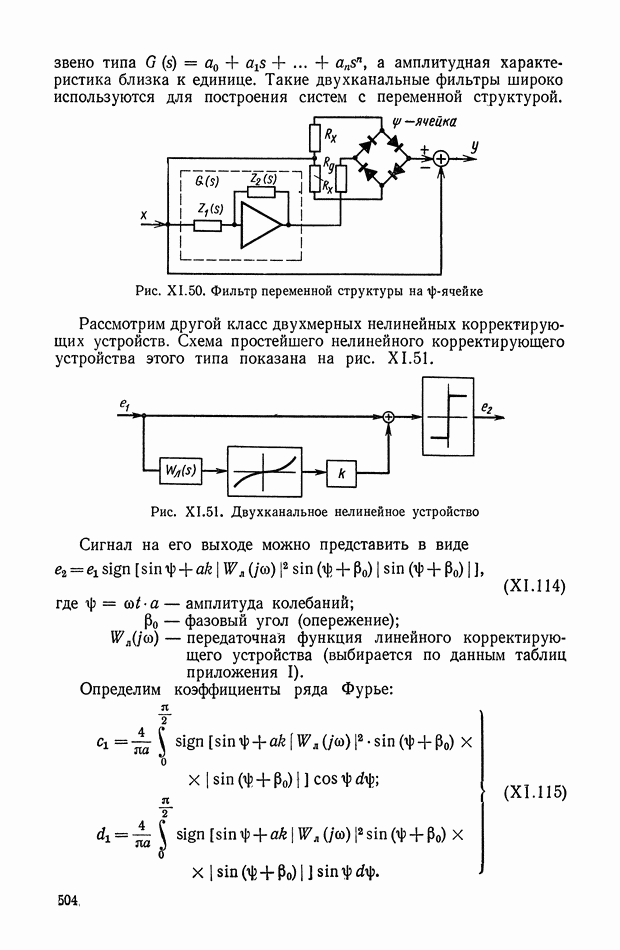
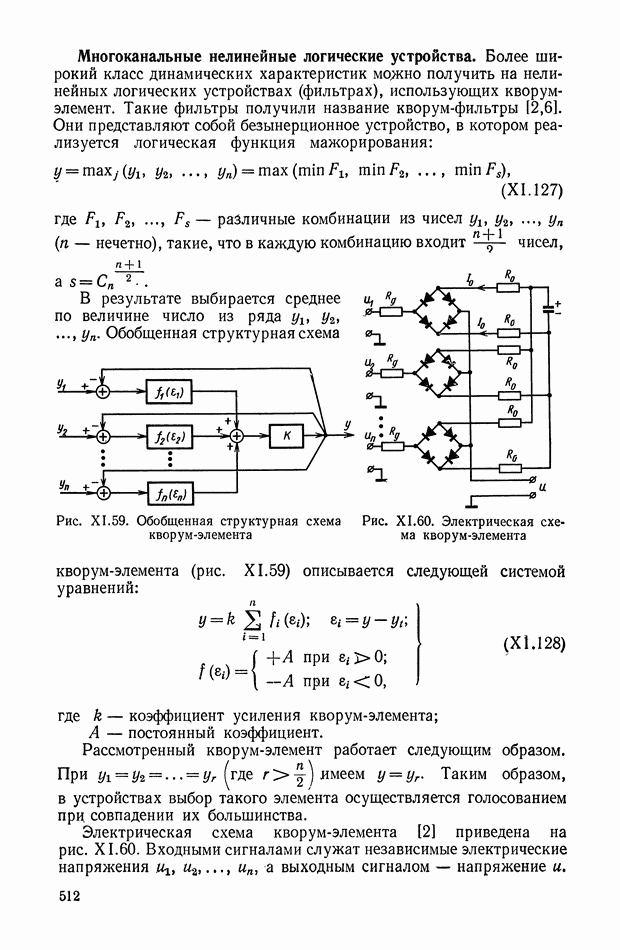
- Многоканальные нелинейные логические устройства.
- ГЛАВА XII. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- 1. КОРРЕКТИРУЮЩИЕ RLC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 2. КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 3. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 4. САМОНАСТРАИВАЮЩИЕСЯ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА
- 5. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА С ПРОМЕЖУТОЧНОЙ ДЕМОДУЛЯЦИЕЙ
- 6. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА С ПЕРЕКЛЮЧАТЕЛЯМИ
- 7. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XIII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ТАХОГЕНЕРАТОРЫ ПОСТОЯННОГО ТОКА
- Погрешности тахогенератора постоянного тока.
- 2. НЕКОТОРЫЕ СХЕМЫ ПРИМЕНЕНИЯ ТАХОГЕНЕРАТОРОВ
- 3. АСИНХРОННЫЕ ТАХОГЕНЕРАТОРЫ
- 4. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ ИЗМЕРЕНИЯ СКОРОСТИ ЭЛЕКТРОДВИГАТЕЛЕЙ
- Пассивный тахометрический мост переменного тока.
- Активные тахометрические мосты.
- ГЛАВА XIV. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ГИДРАВЛИЧЕСКИХ СИСТЕМАХ
- 3. ЭЛЕКТРИЧЕСКИЕ ОБРАТНЫЕ СВЯЗИ
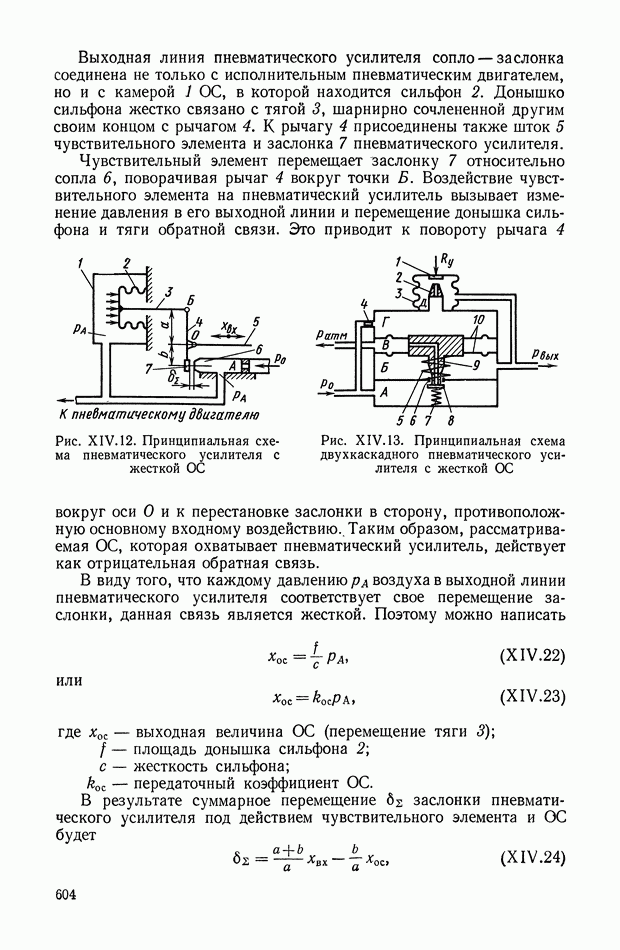
- 4. ЖЕСТКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
- 5. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ СИСТЕМАХ
- 6. СЛОЖНЫЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
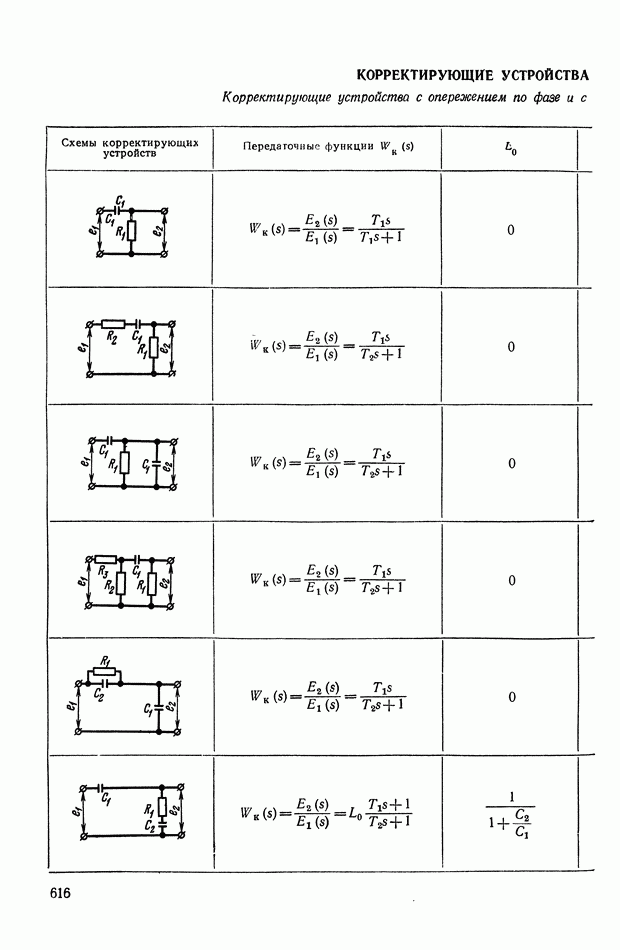
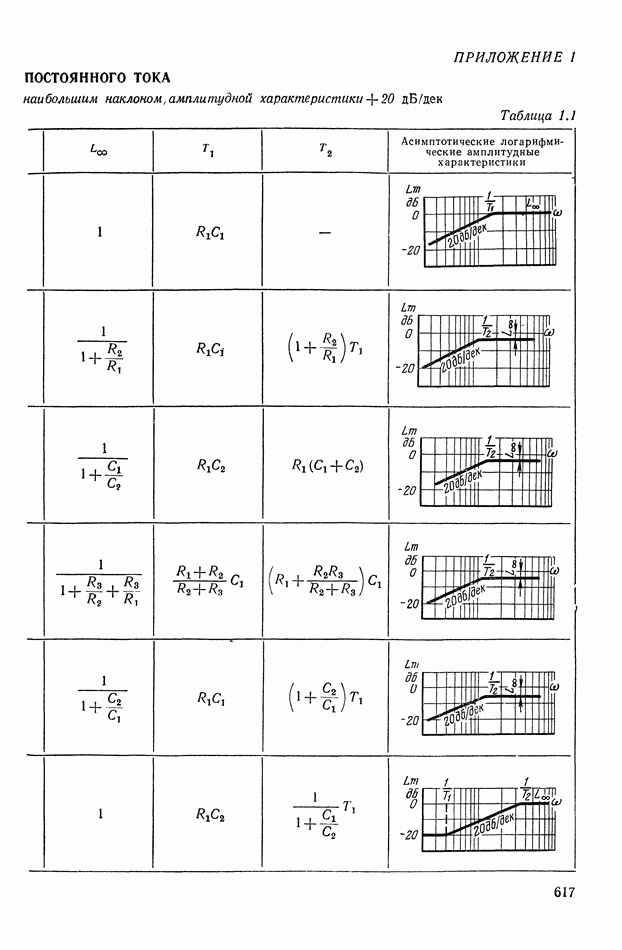
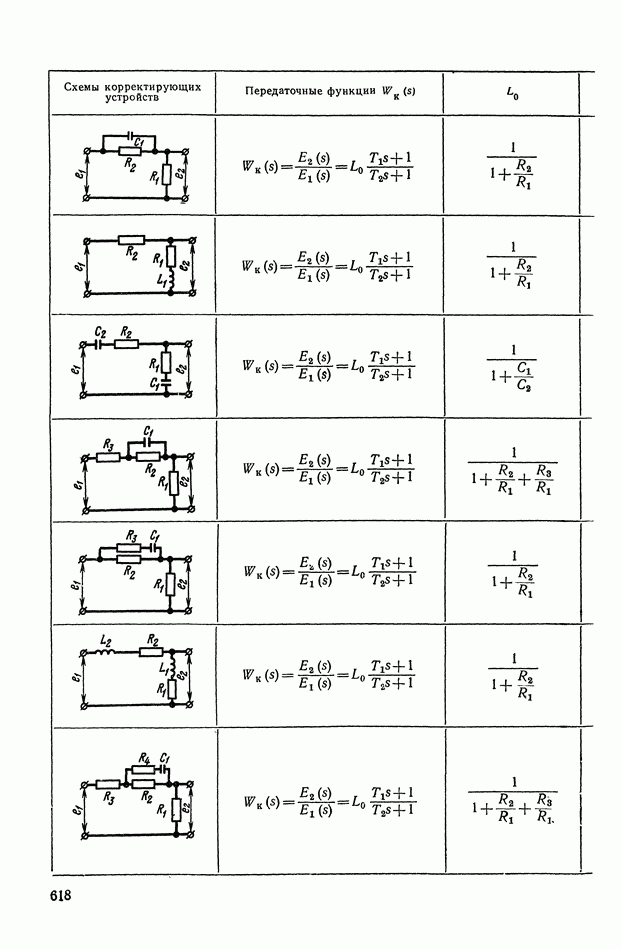
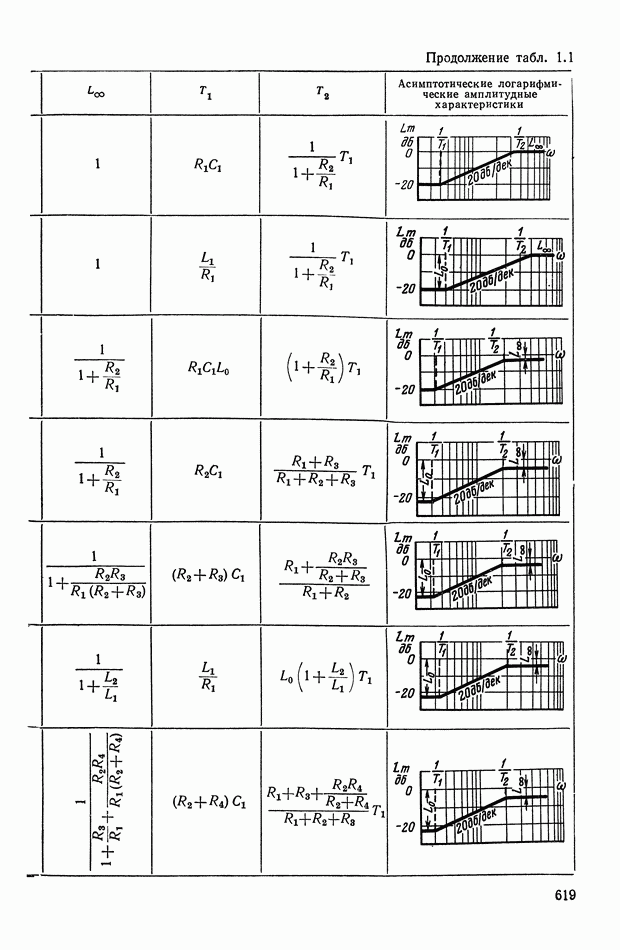
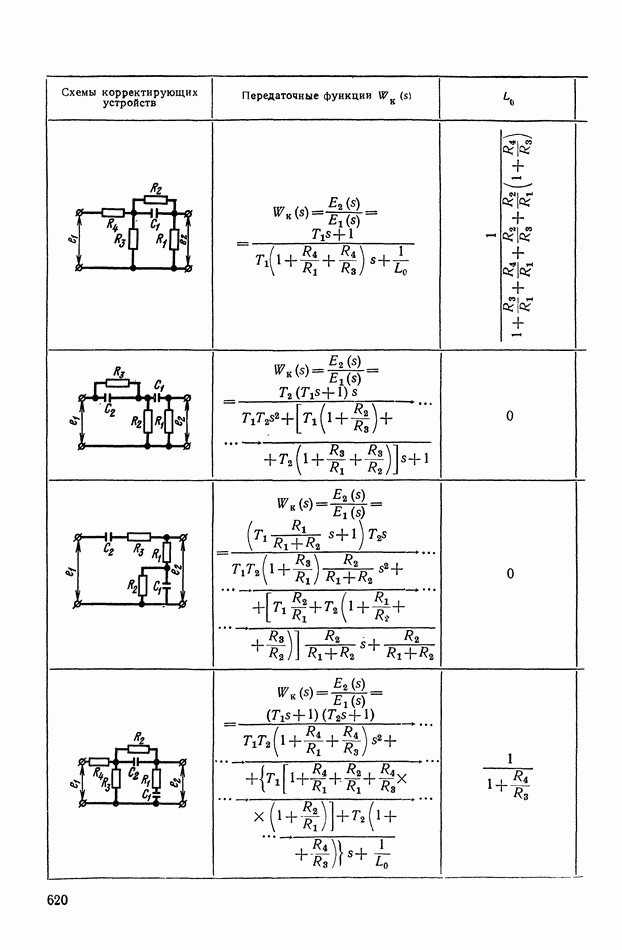
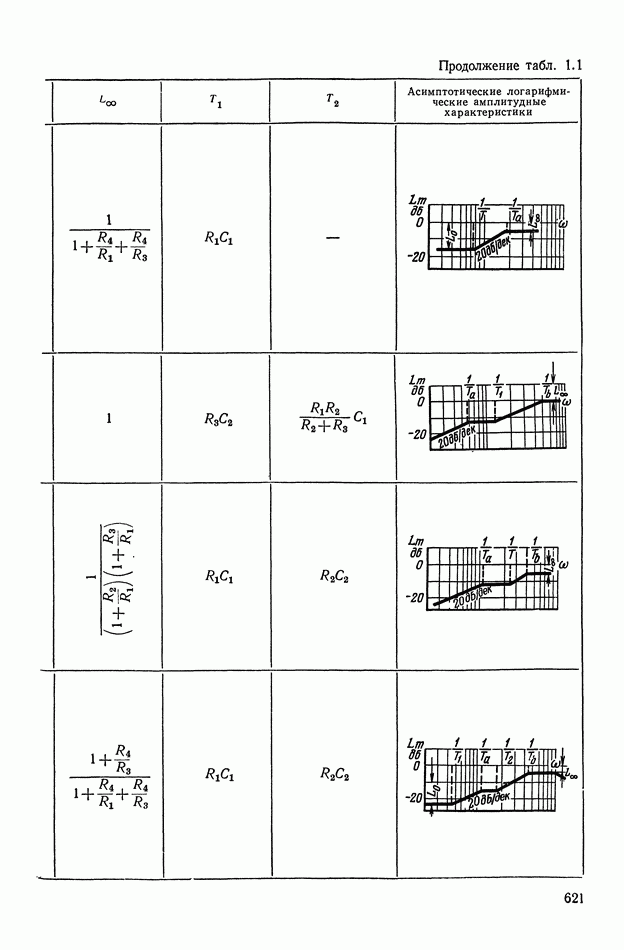
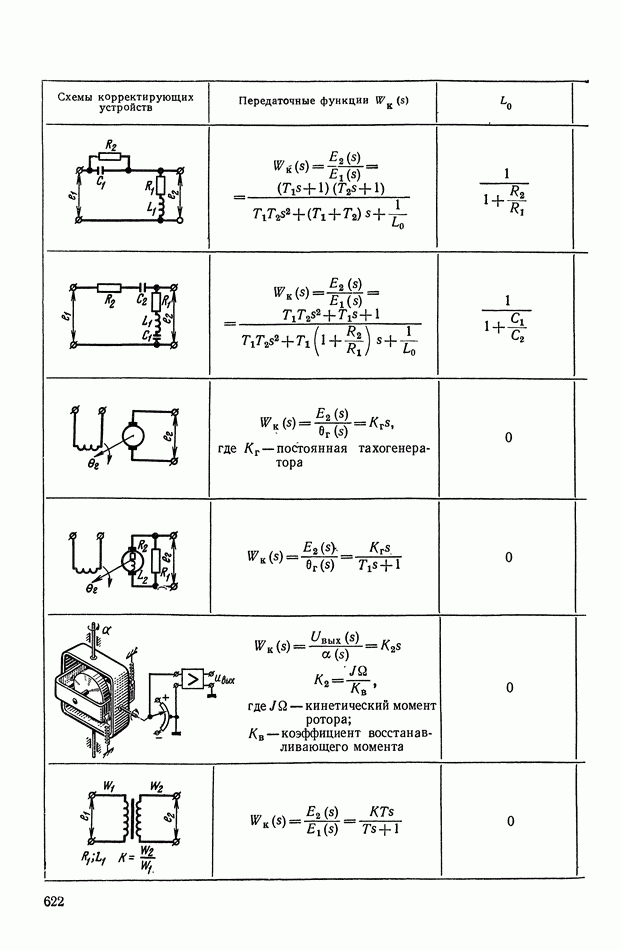
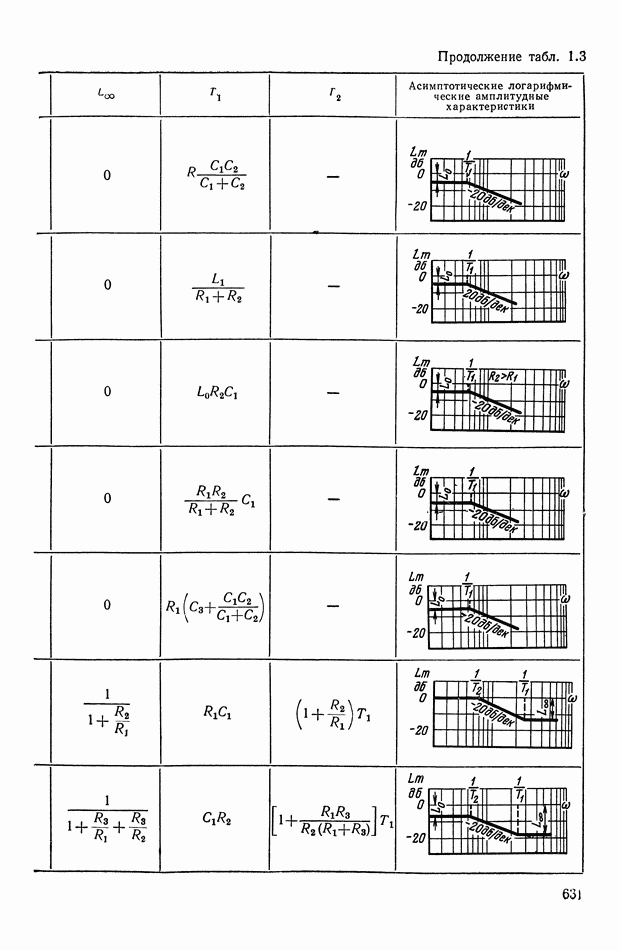
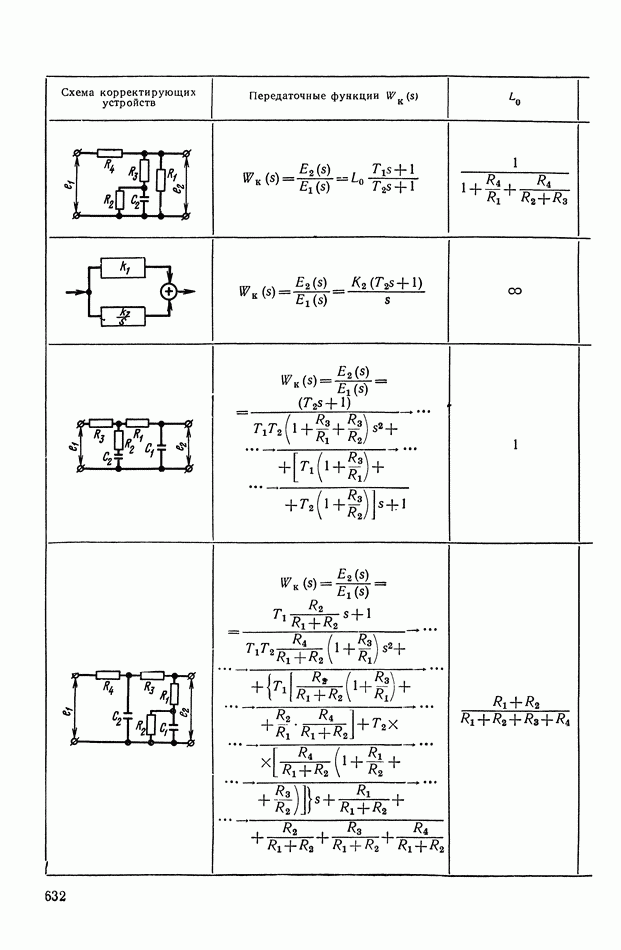
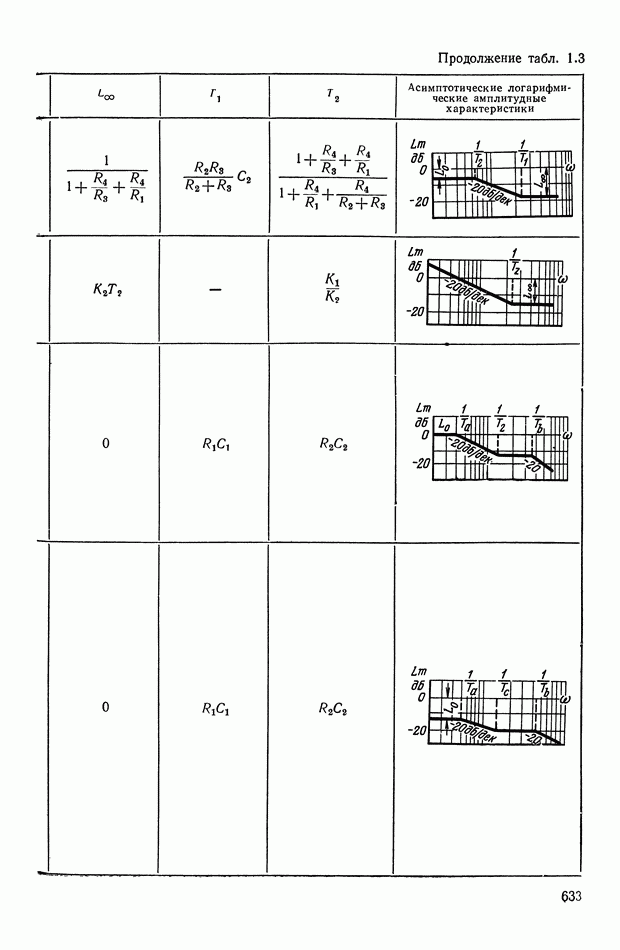
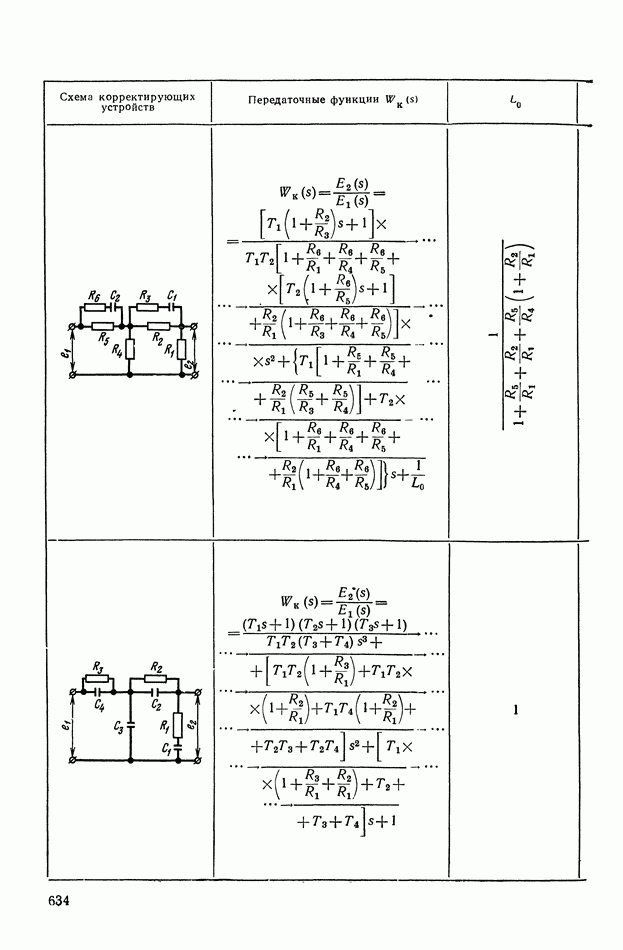
- ПРИЛОЖЕНИЕ 1. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПОСТОЯННОГО ТОКА
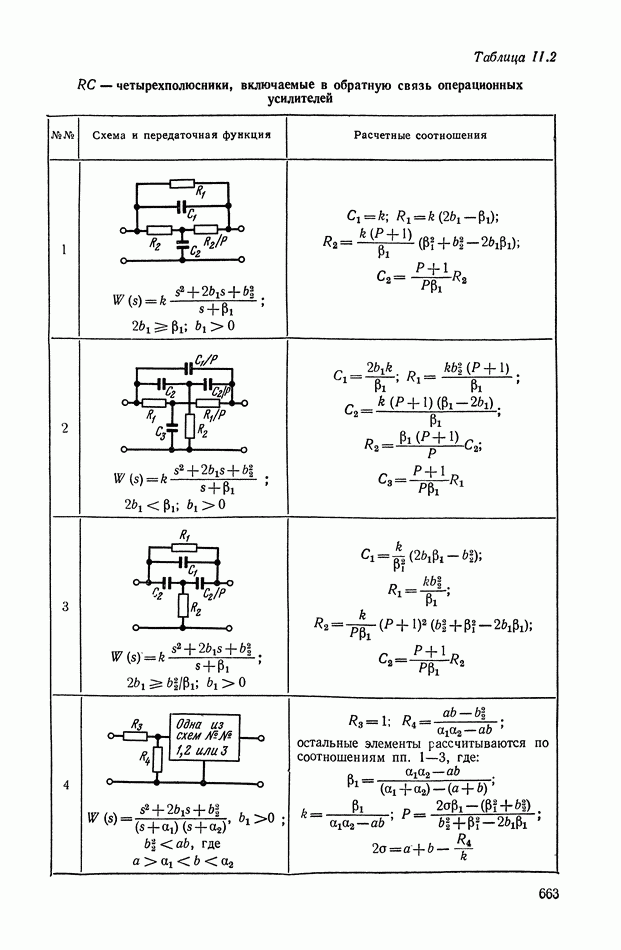
- ПРИЛОЖЕНИЕ II. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ОСНОВЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
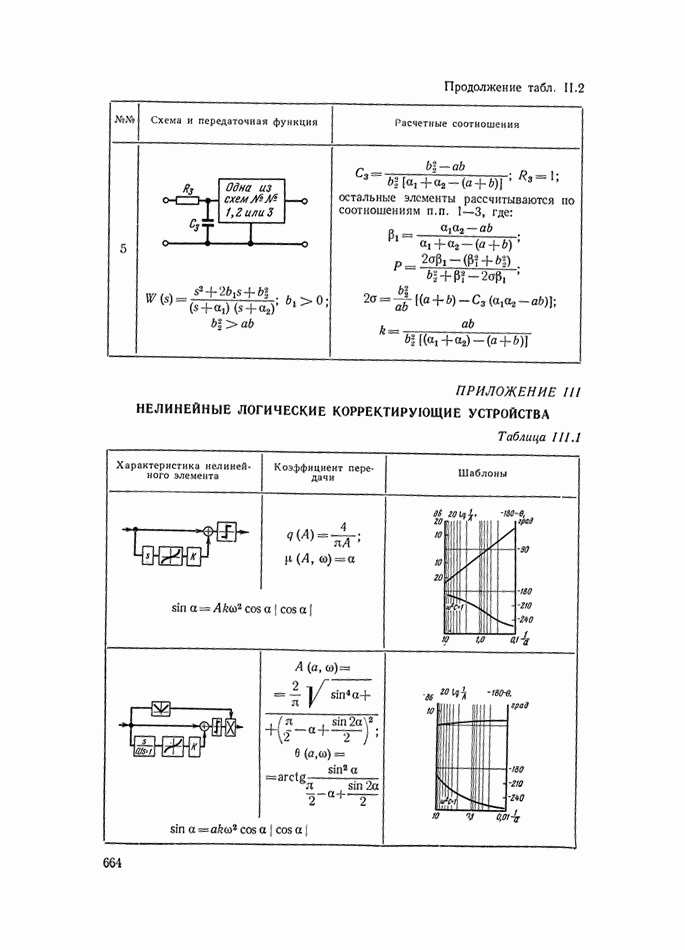
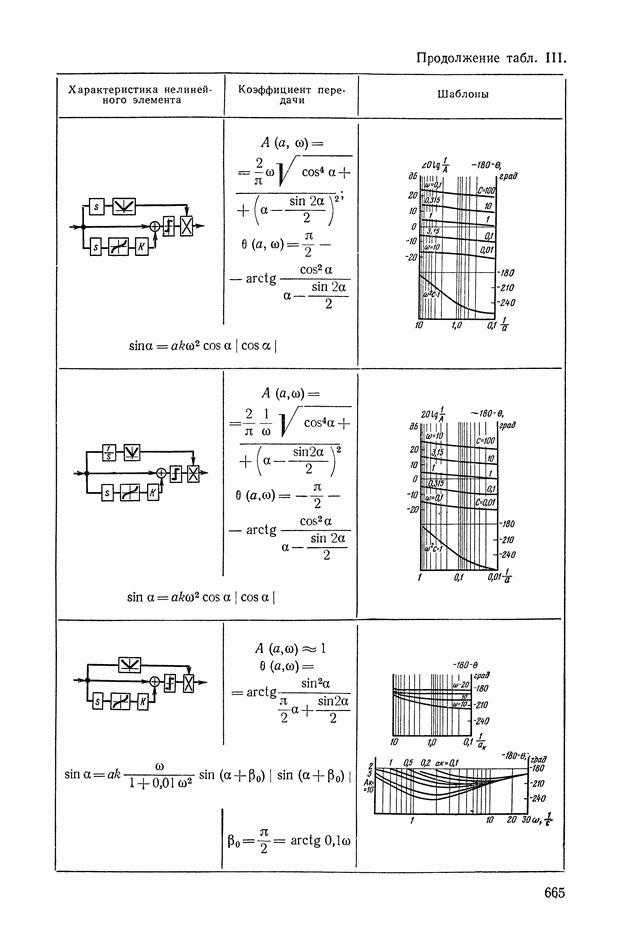
- ПРИЛОЖЕНИЕ III. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ