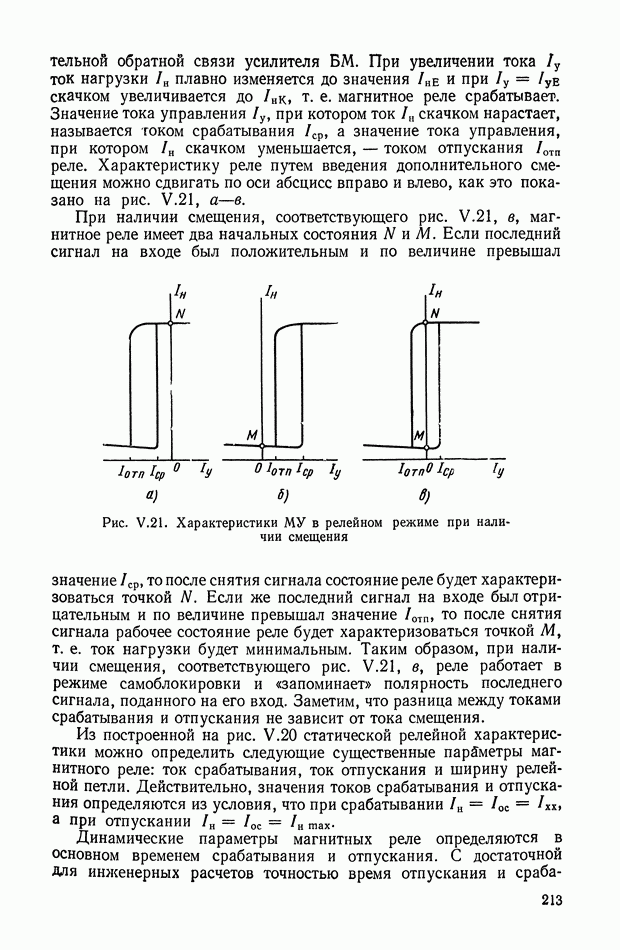
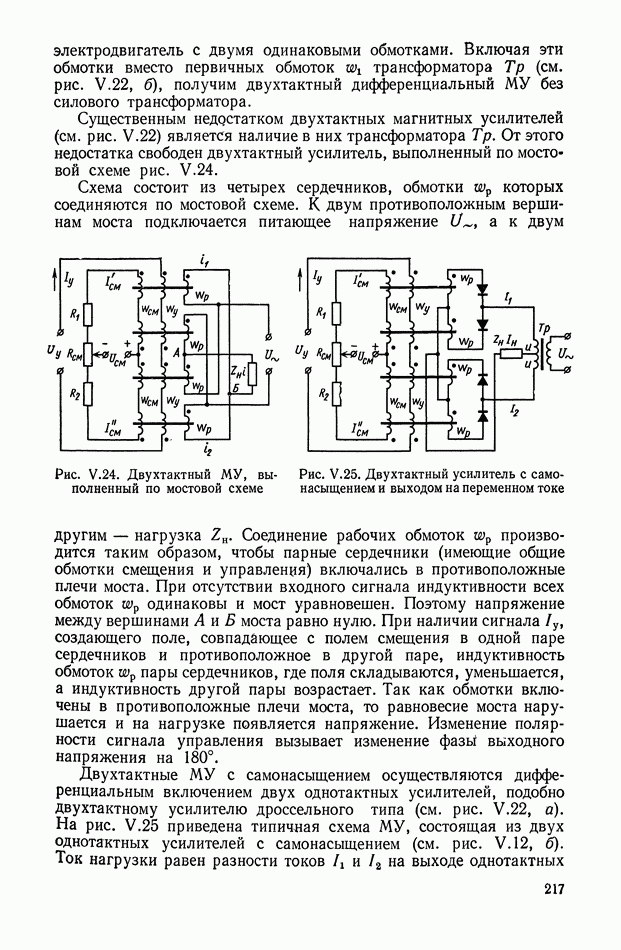
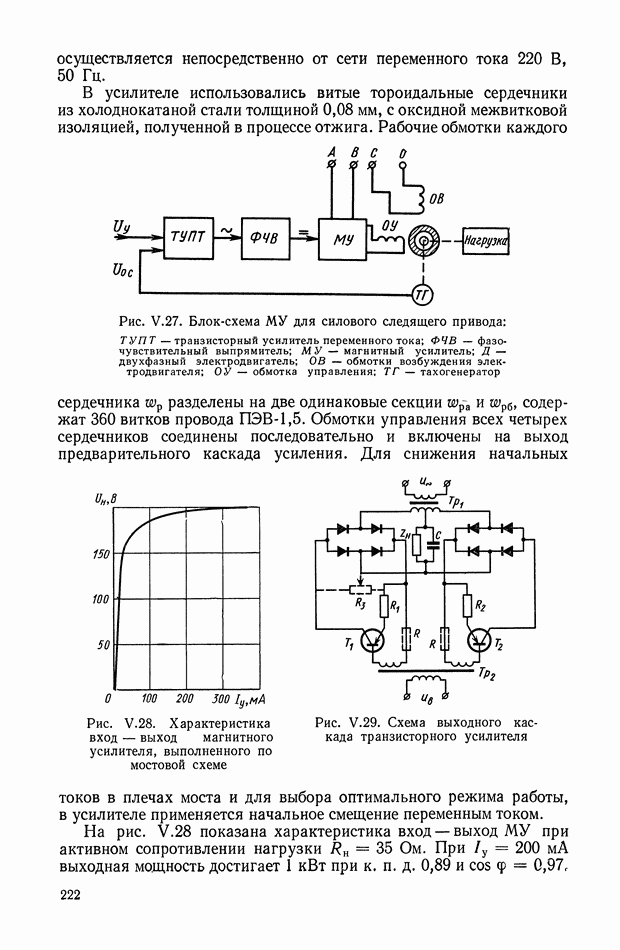
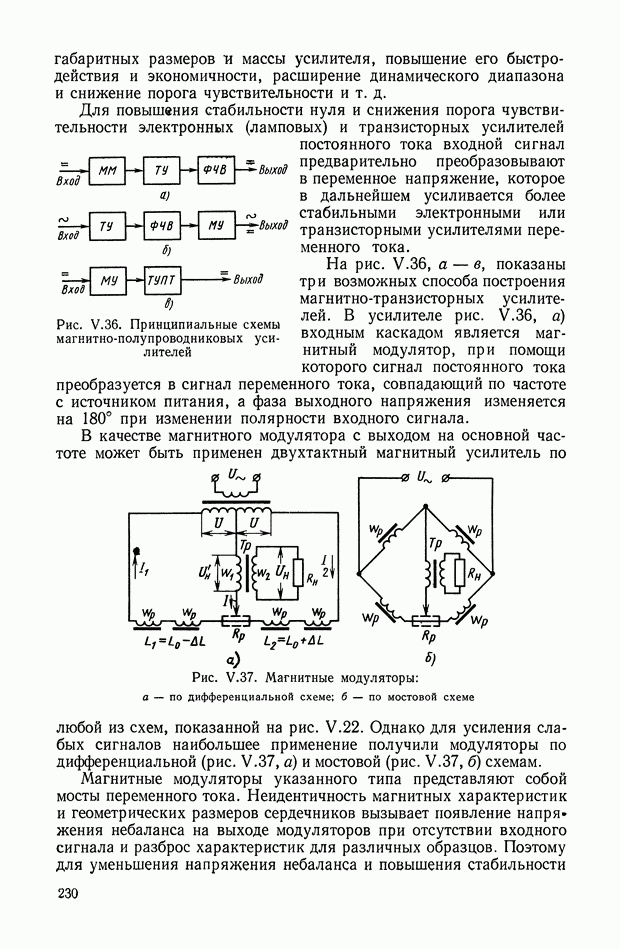
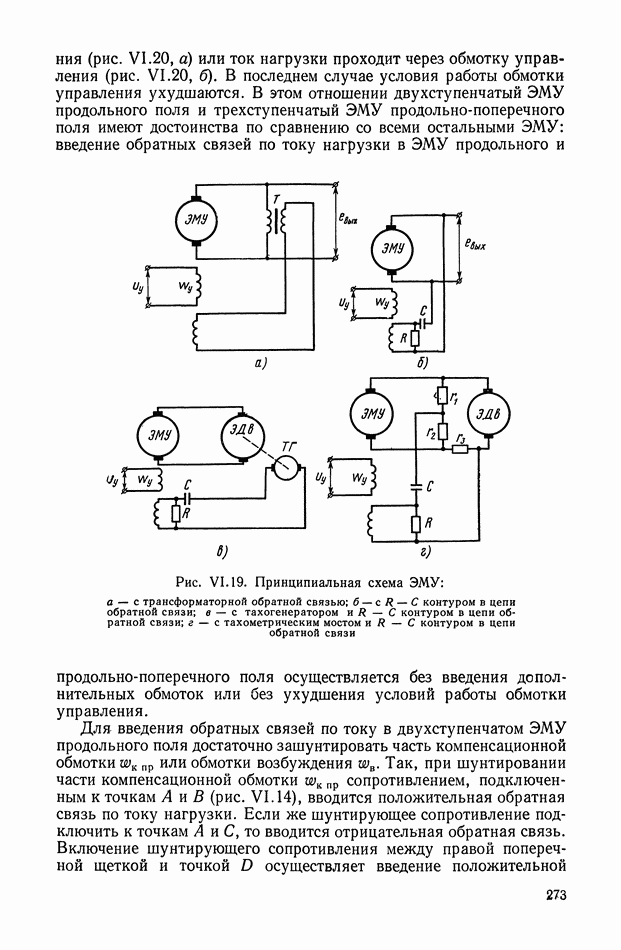
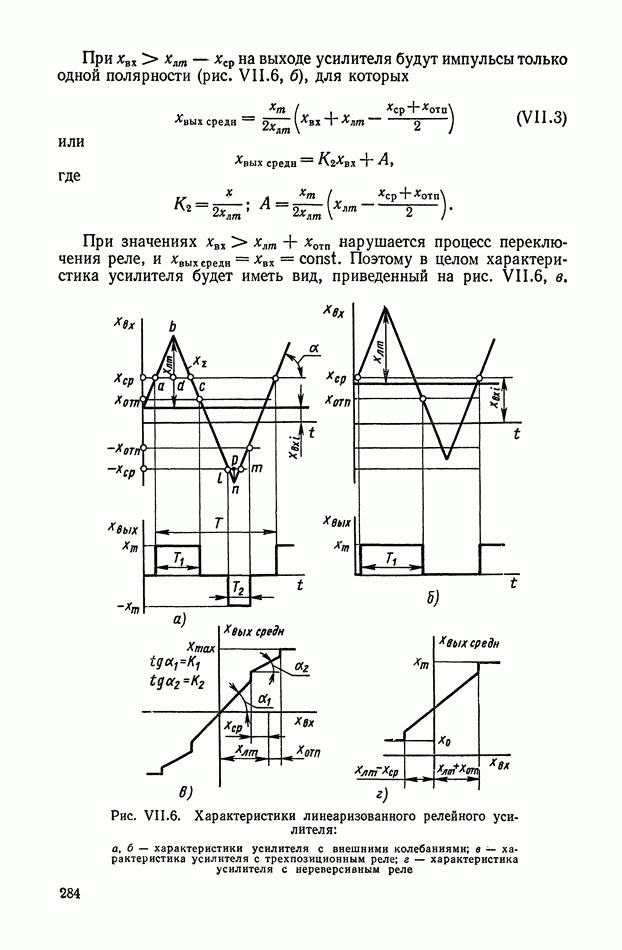
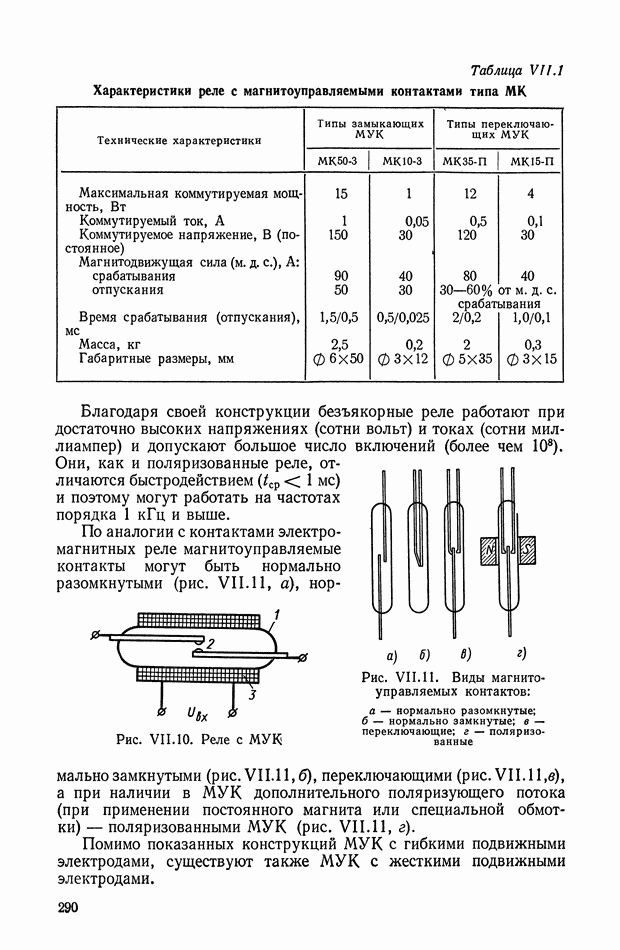
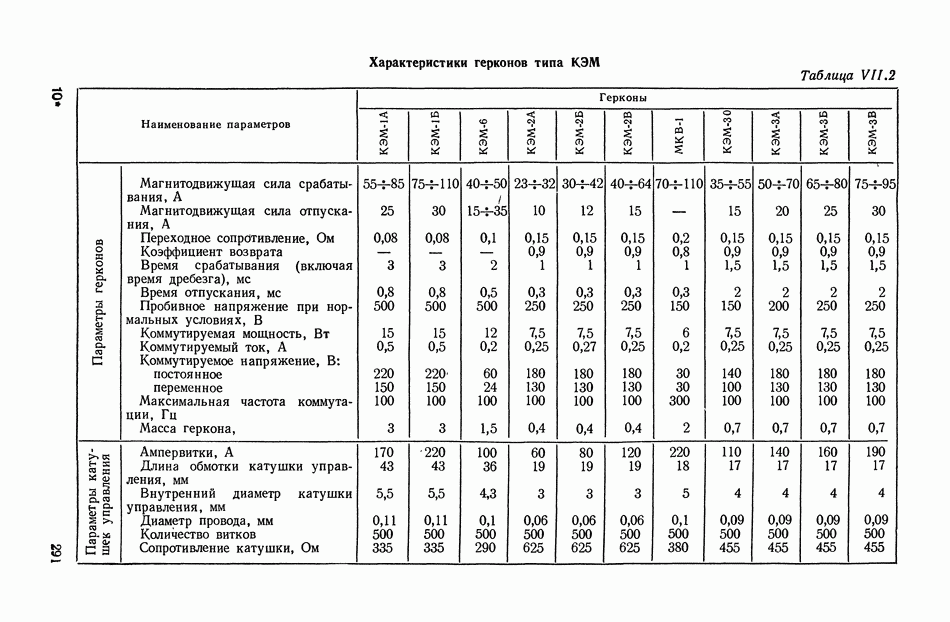
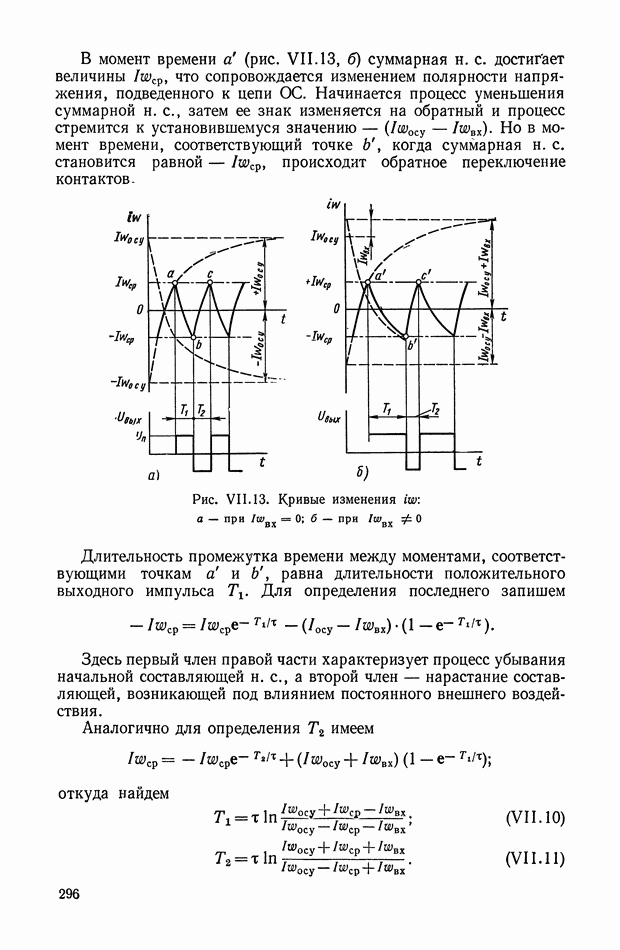
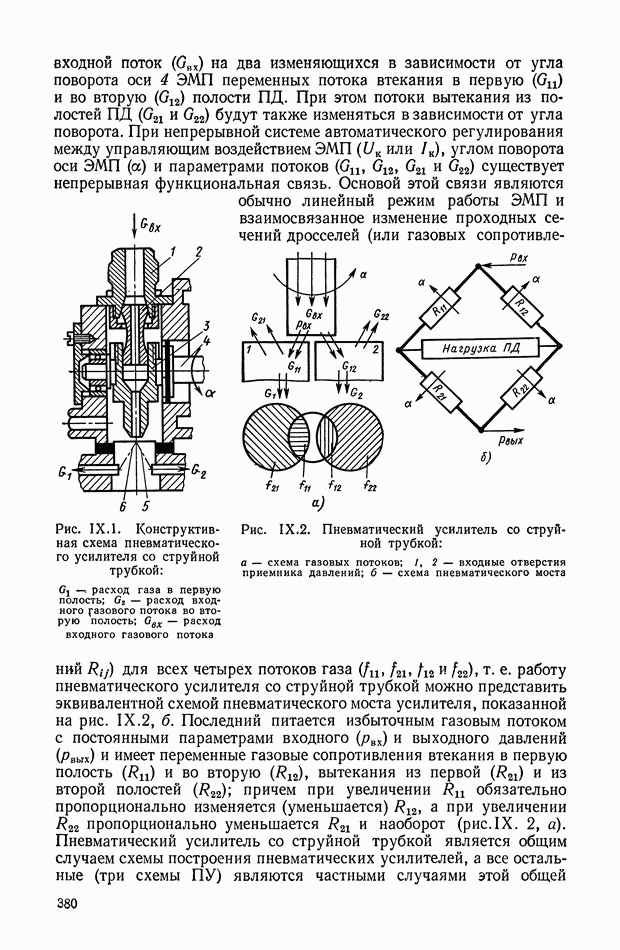
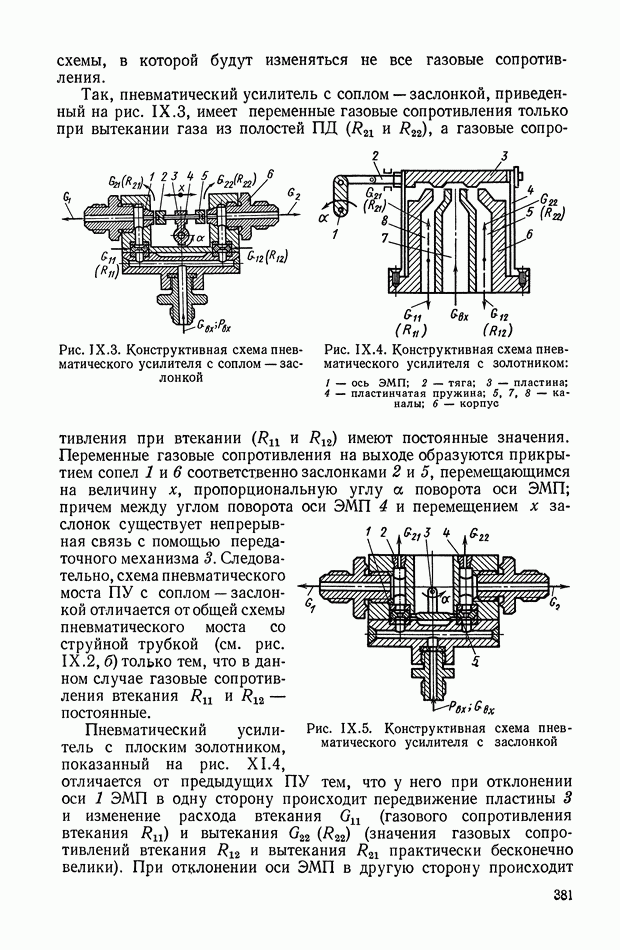
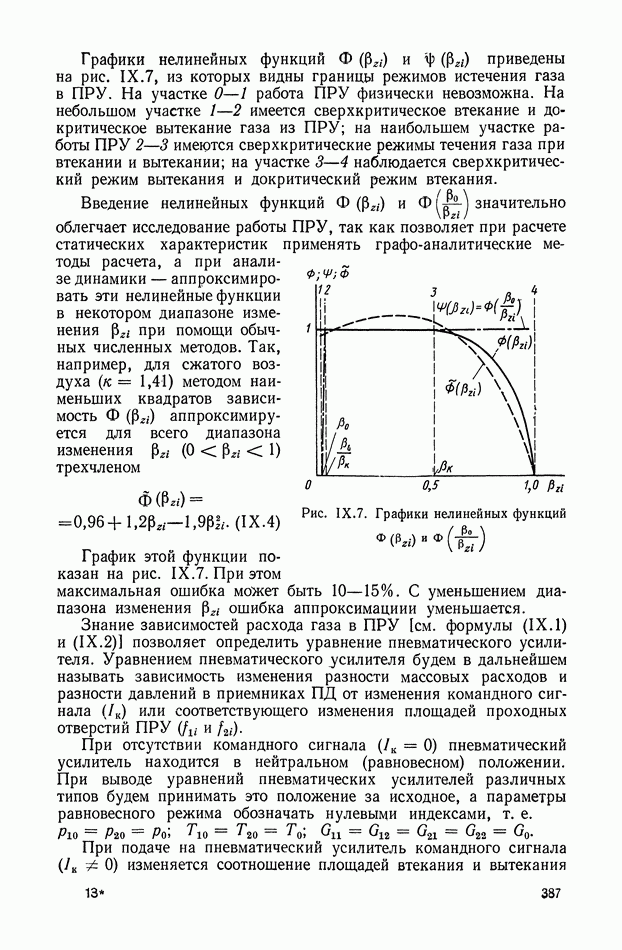
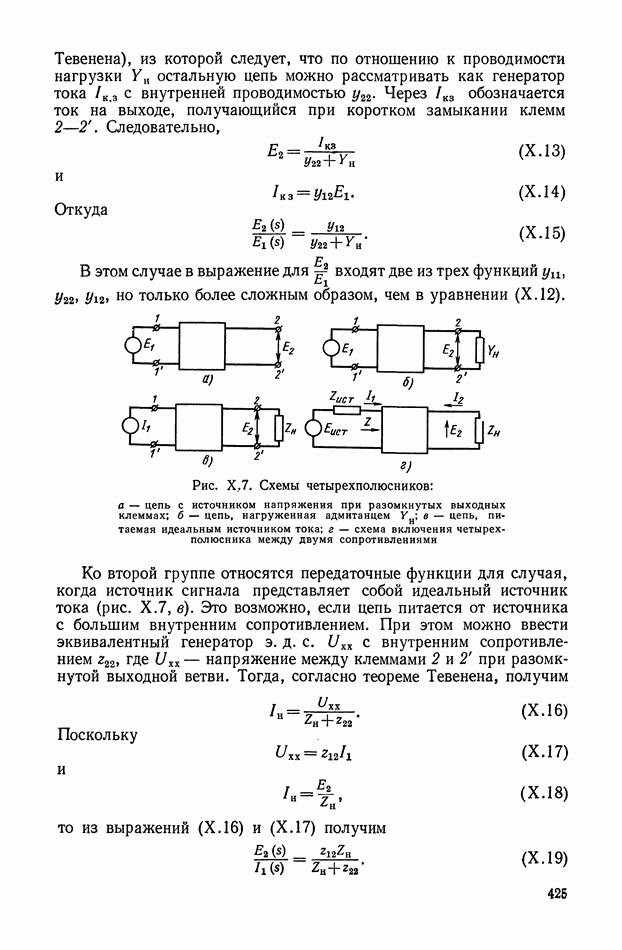
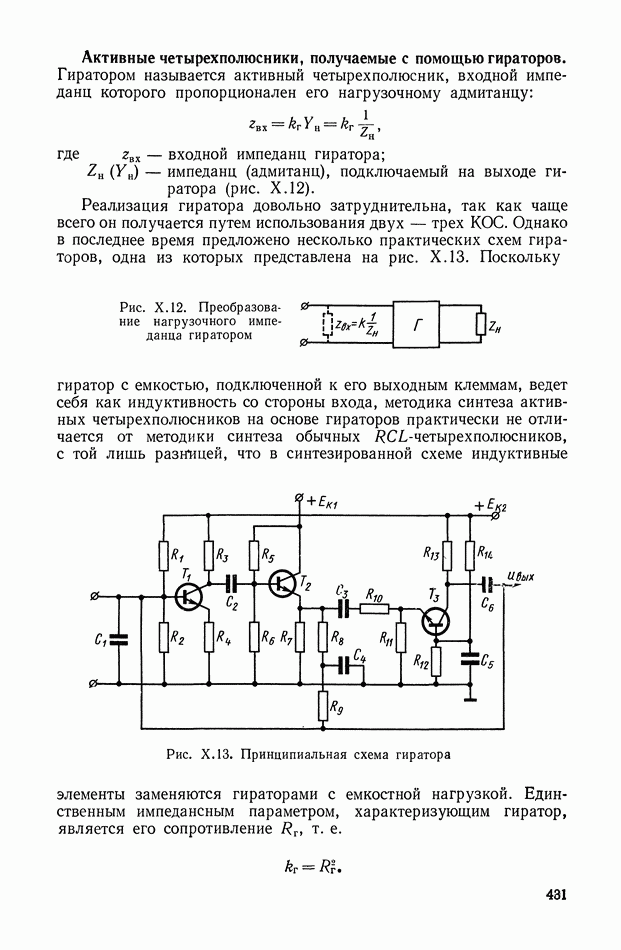
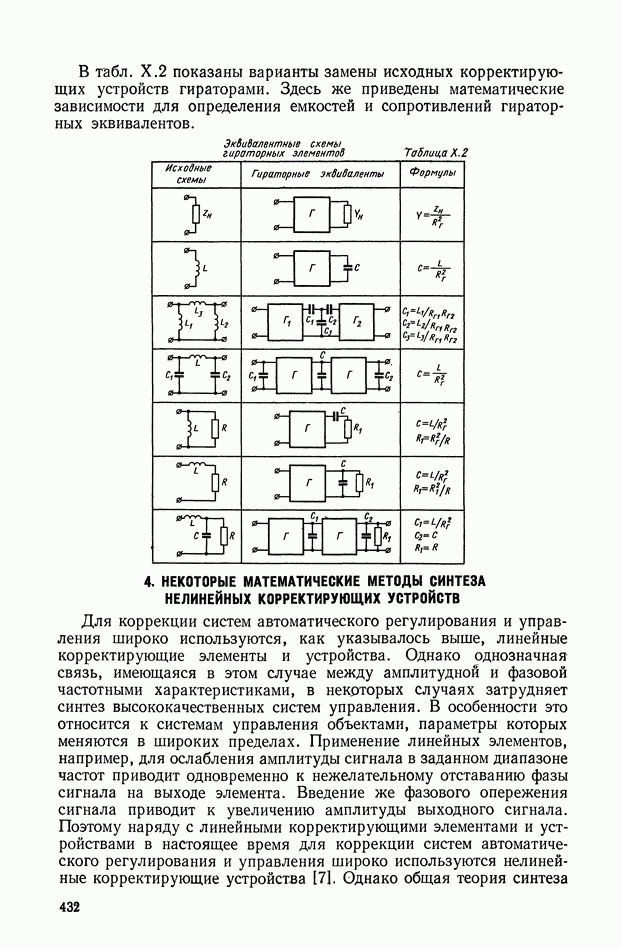
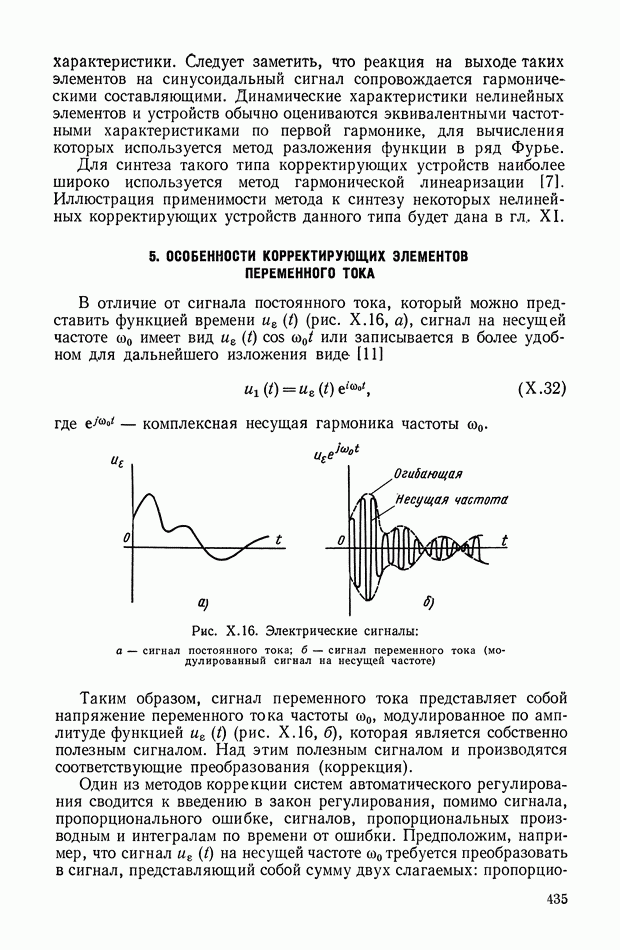
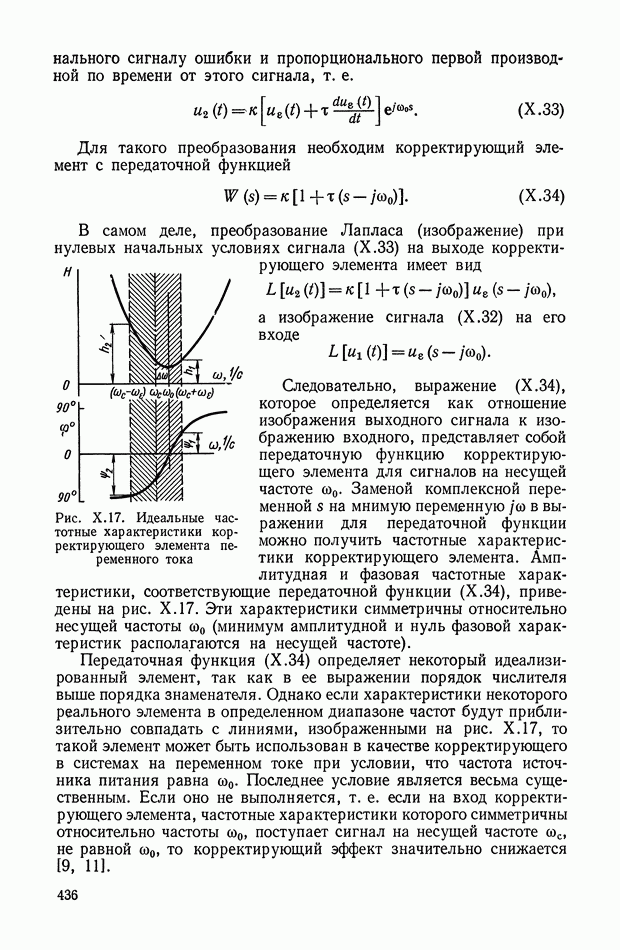
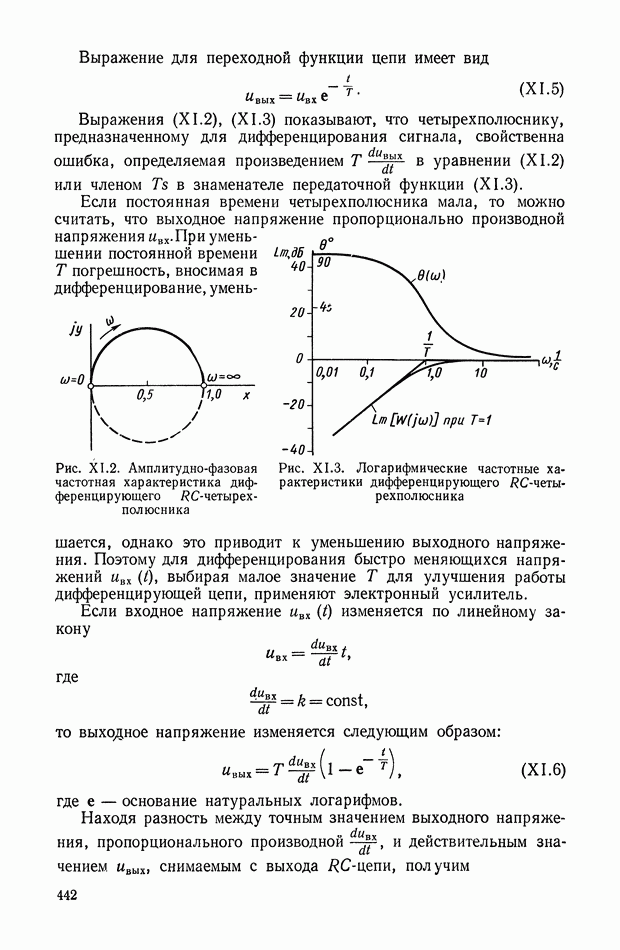
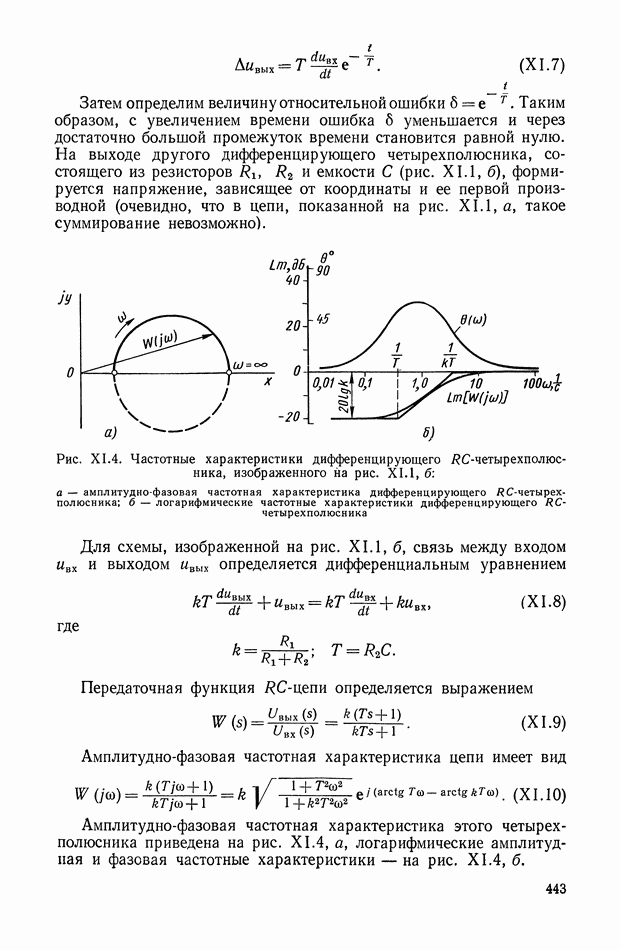
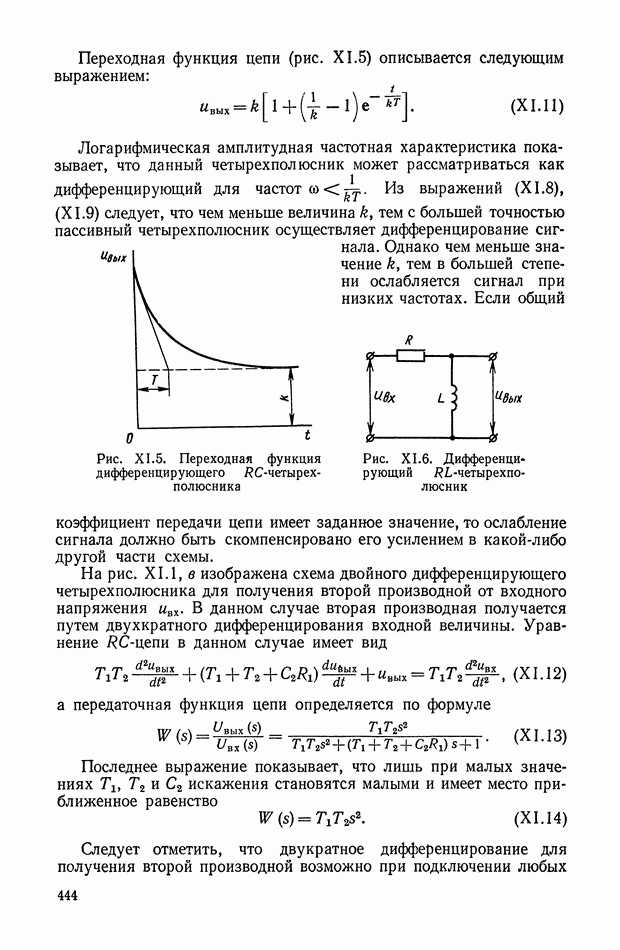
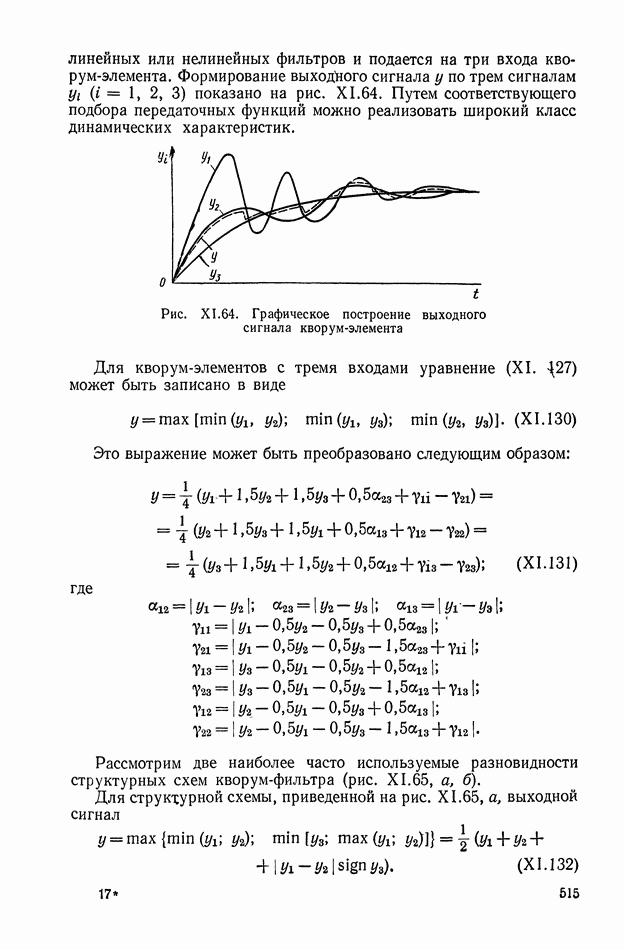
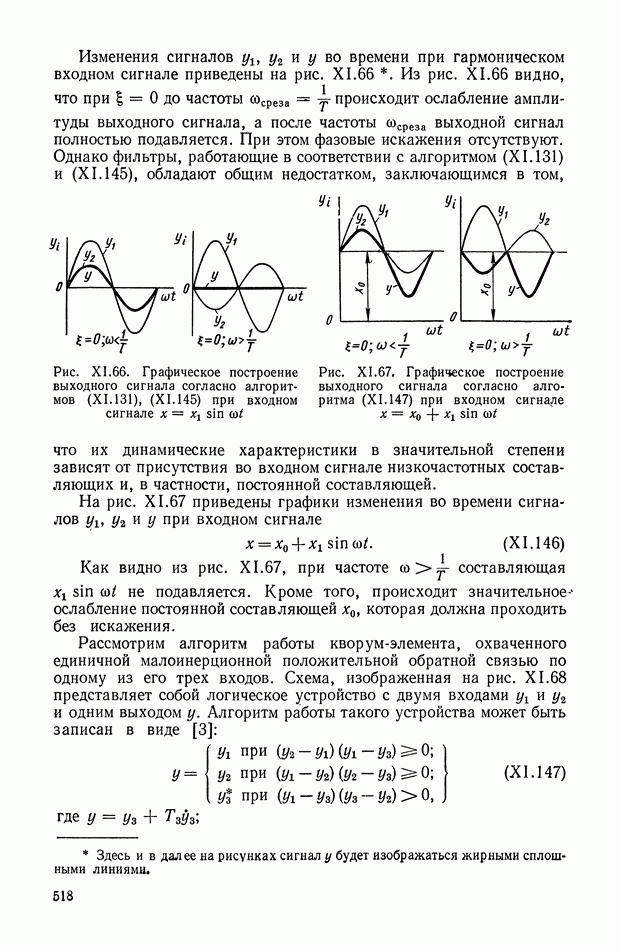
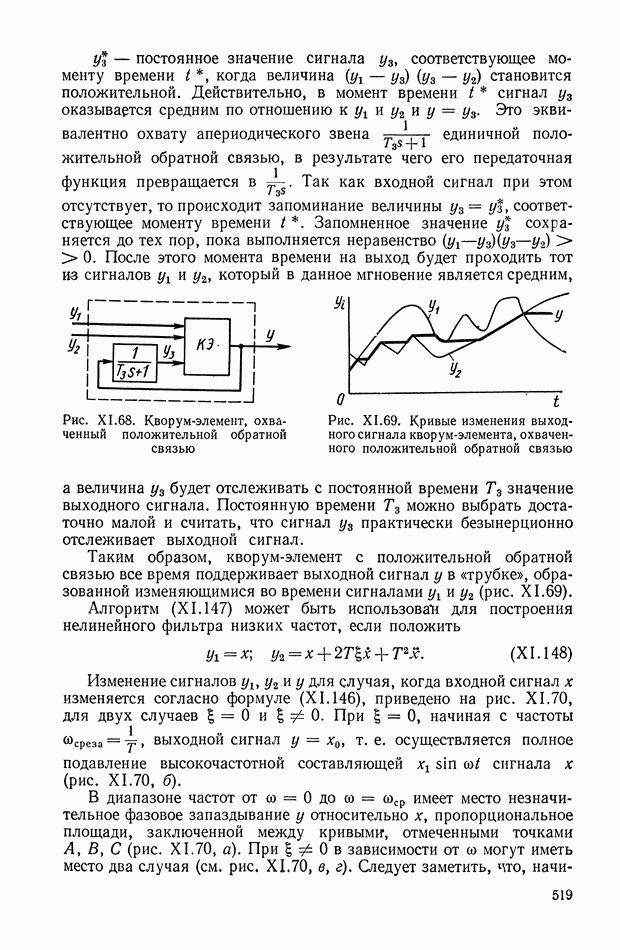
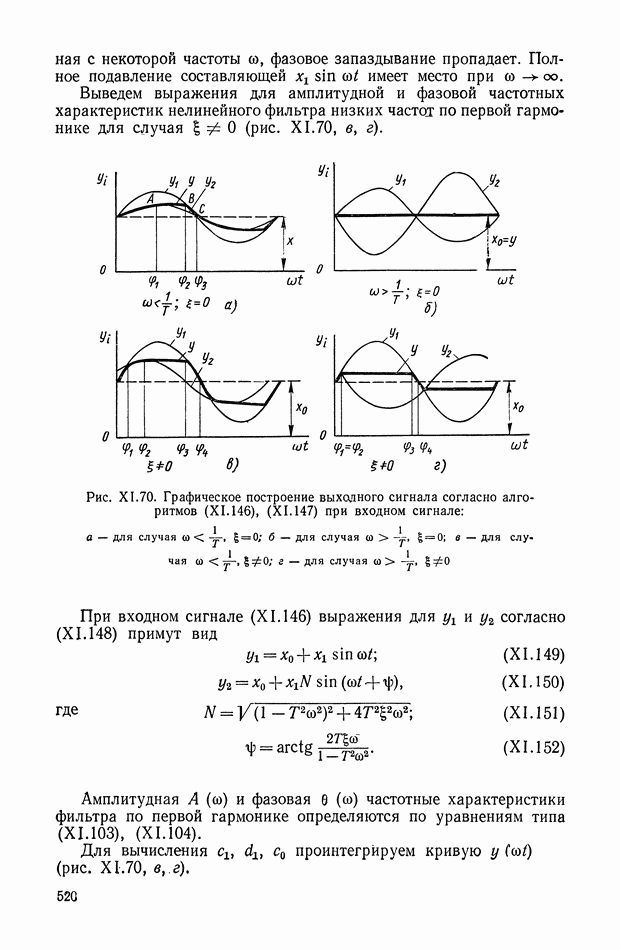
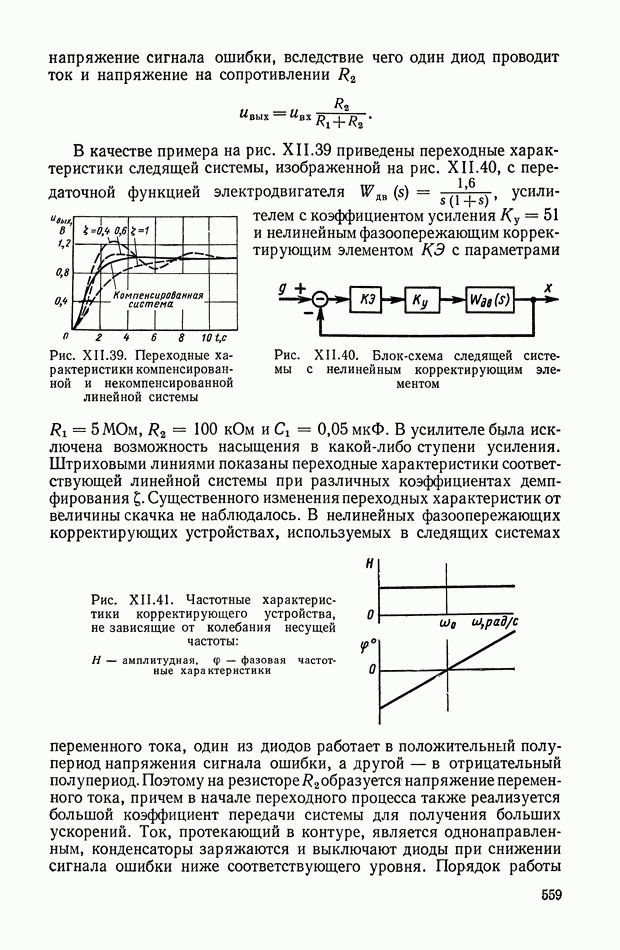
| << Предыдущий параграф | Следующий параграф >> |
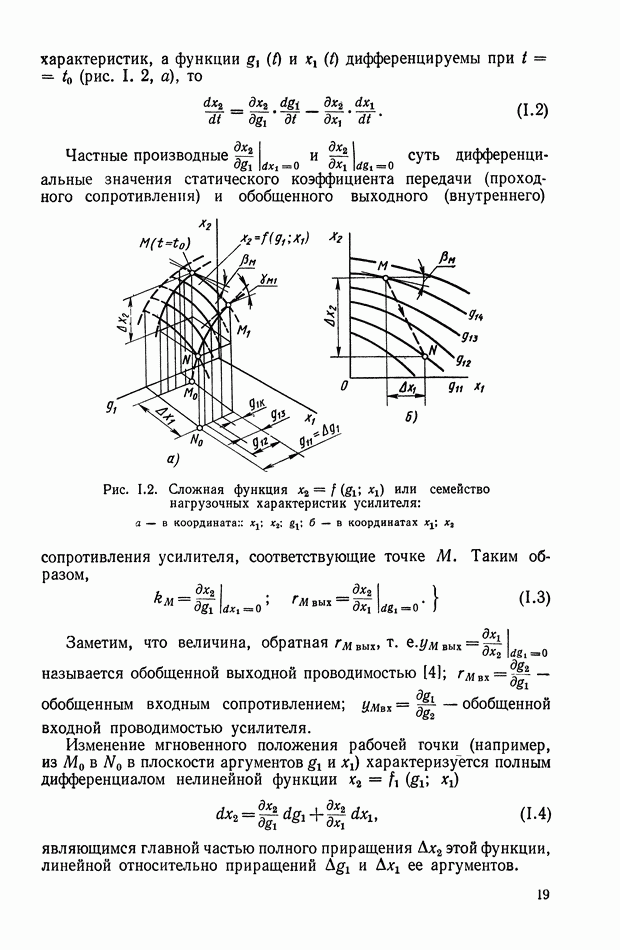
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
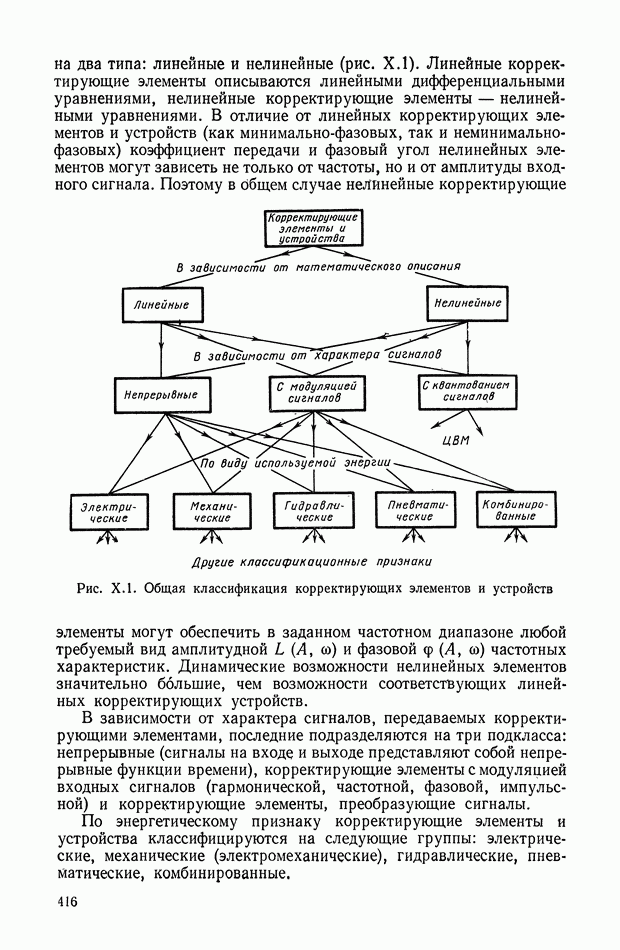
5. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
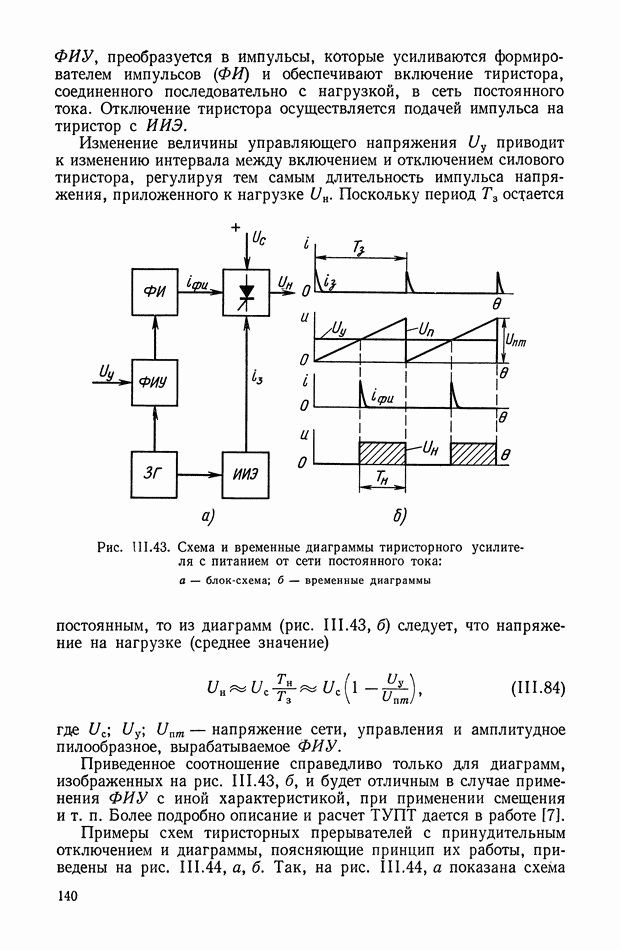
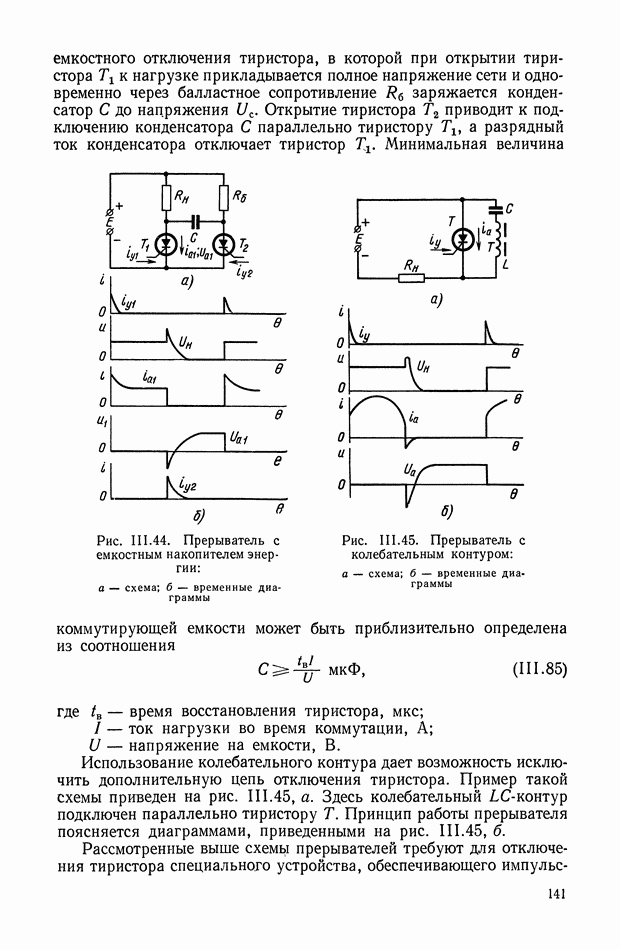
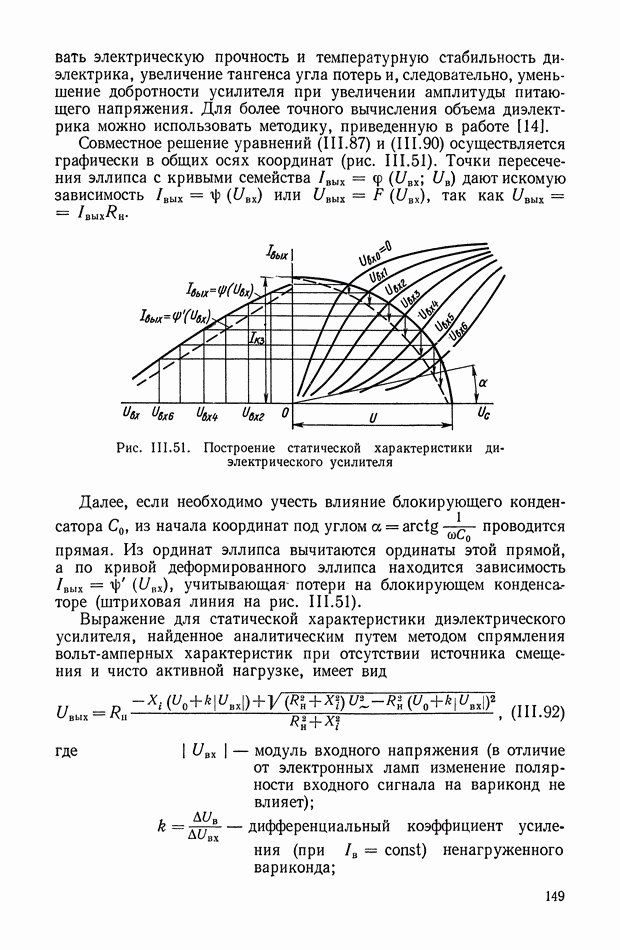
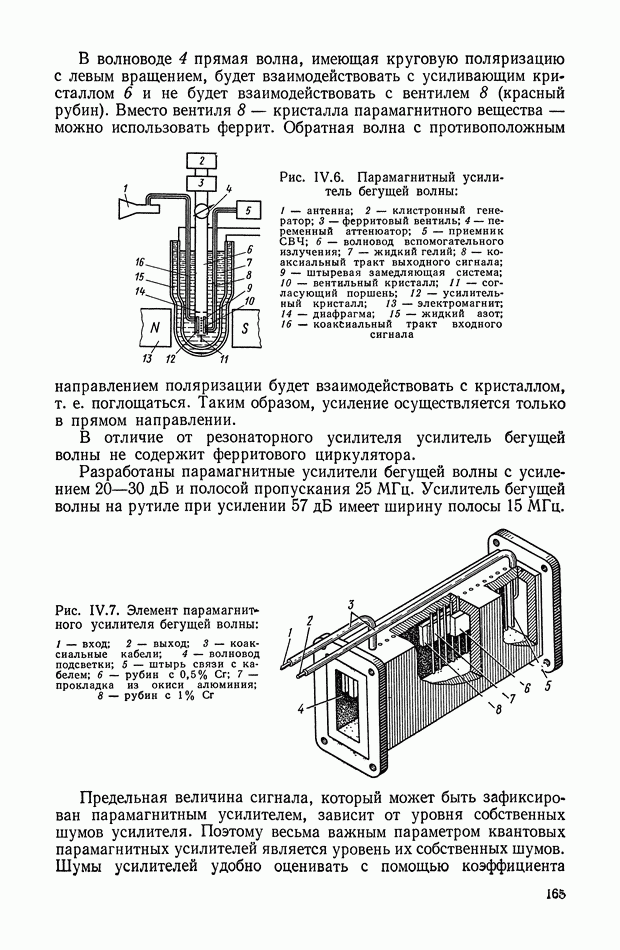
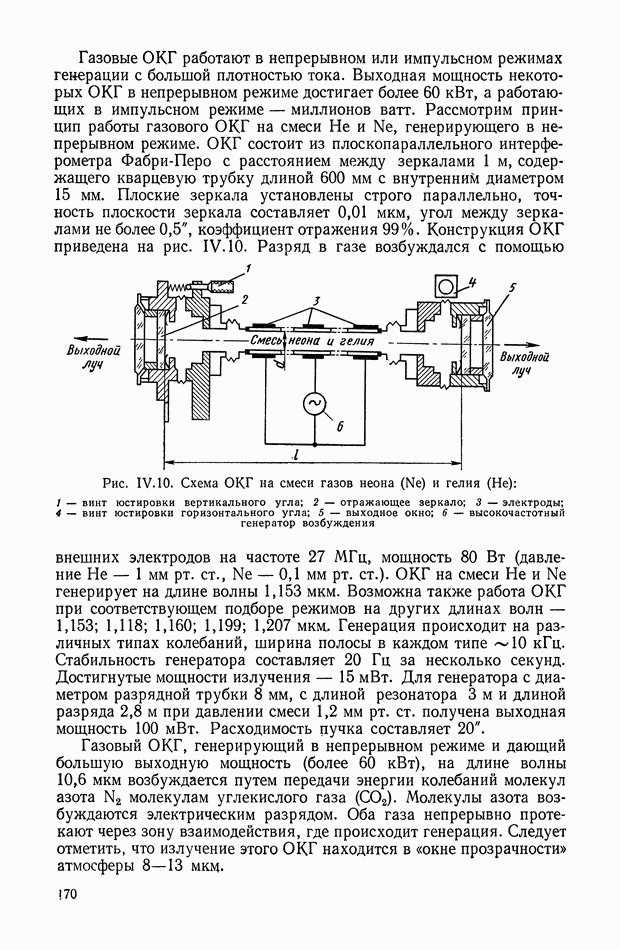
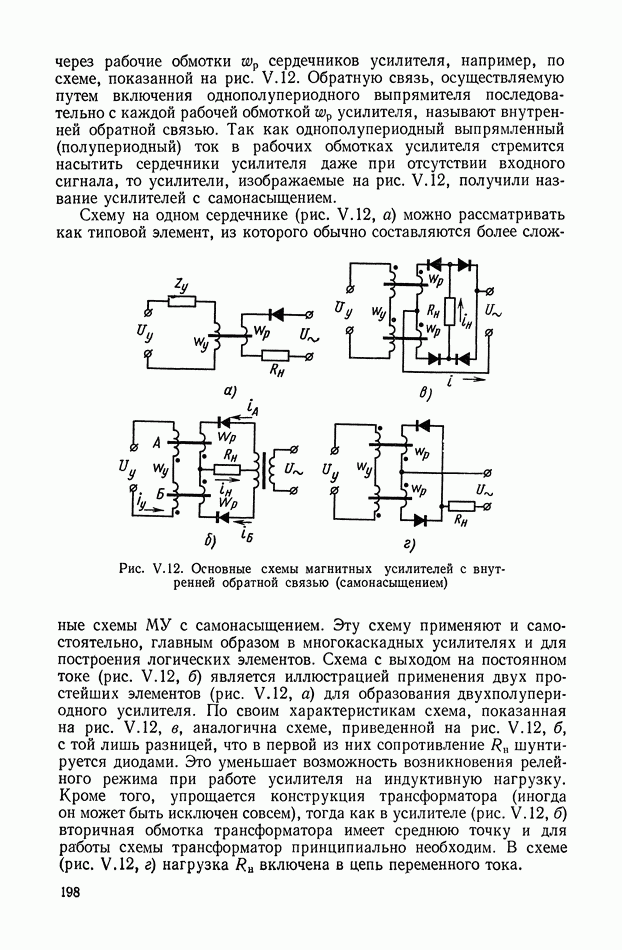
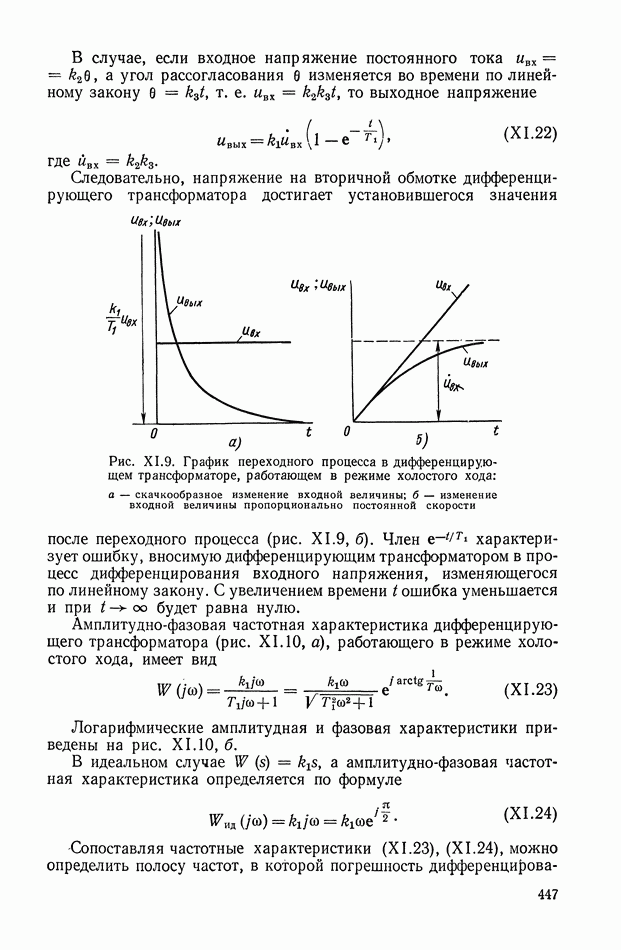
В последнее время нелинейные корректирующие устройства широко используются в системах автоматического регулирования и управления. Правильный выбор типа и параметров корректирующих устройств позволяет синтезировать оптимальные законы управления, которые обеспечивают высокую точность и качество работы системы.
Во многих практических задачах за критерий, оценивающий работу системы, принимается время протекания переходного процесса. При его минимальном значении синтезируемые системы оптимальны по быстродействию.
Реализация законов управления осуществляется или на аналоговых нелинейных элементах или цифровых вычислительных машинах. В первом случае нелинейные элементы без исполнительного устройства принято относить к непрерывным корректирующим цепям, во
втором случае — к управляющим программам (цифровые корректирующие устройства).
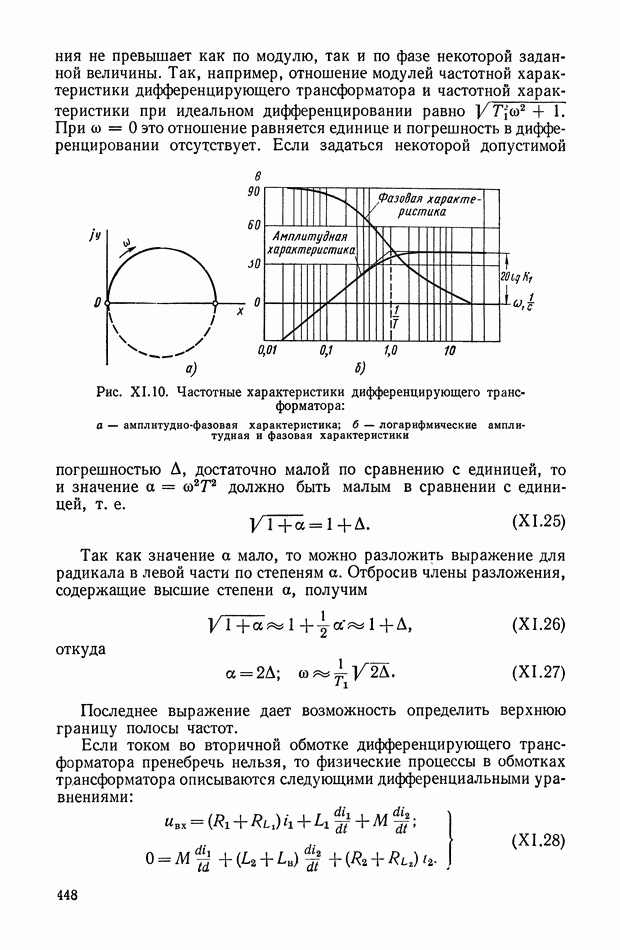
Математической основой синтеза оптимальных законов являются принцип максимума Понтрягина и метод динамического программирования Веллмана [4]. Однако при практическом применении обоих методов проектировщик сталкивается с большими математическими трудностями, усложняющими решение многих задач синтеза.
В настоящее время удается решить задачи синтеза лишь для узкого класса систем. Основными препятствиями к этому являются: порядок дифференциальных уравнений, описывающих поведение объекта управления; ограничения на фазовые координаты; виды возмущающих воздействий; наличие ряда нелинейностей в реальных системах и т. 
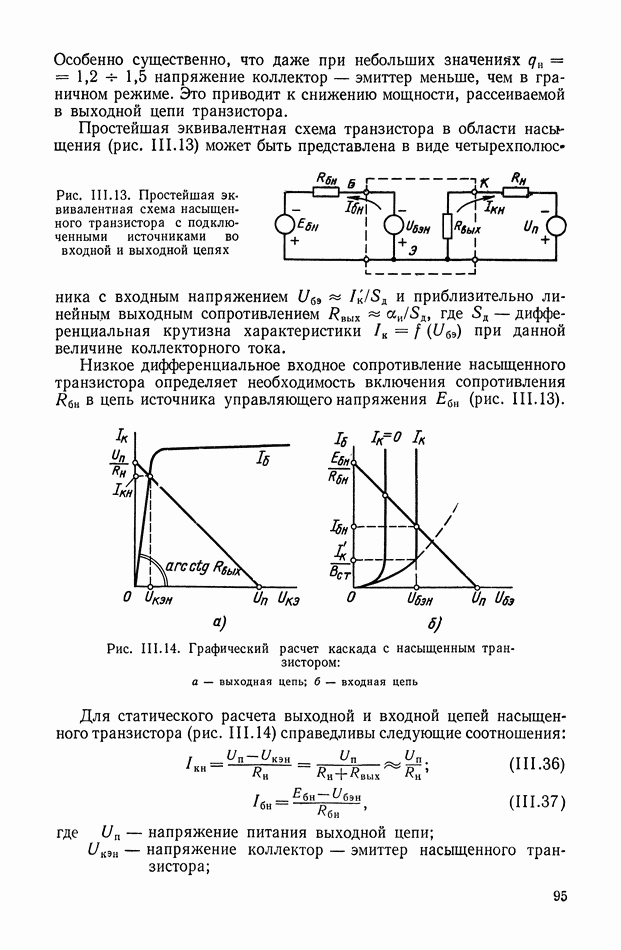
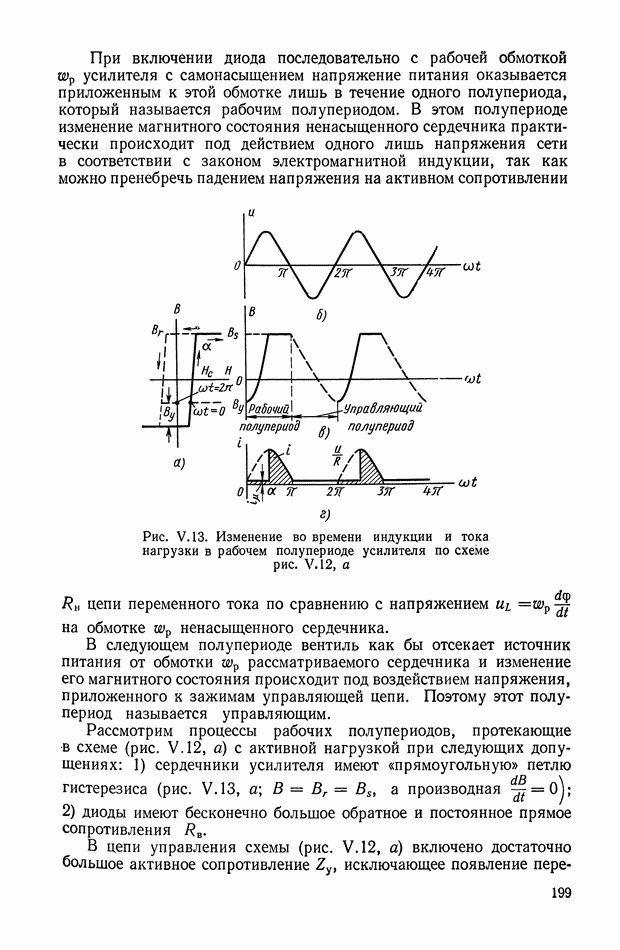
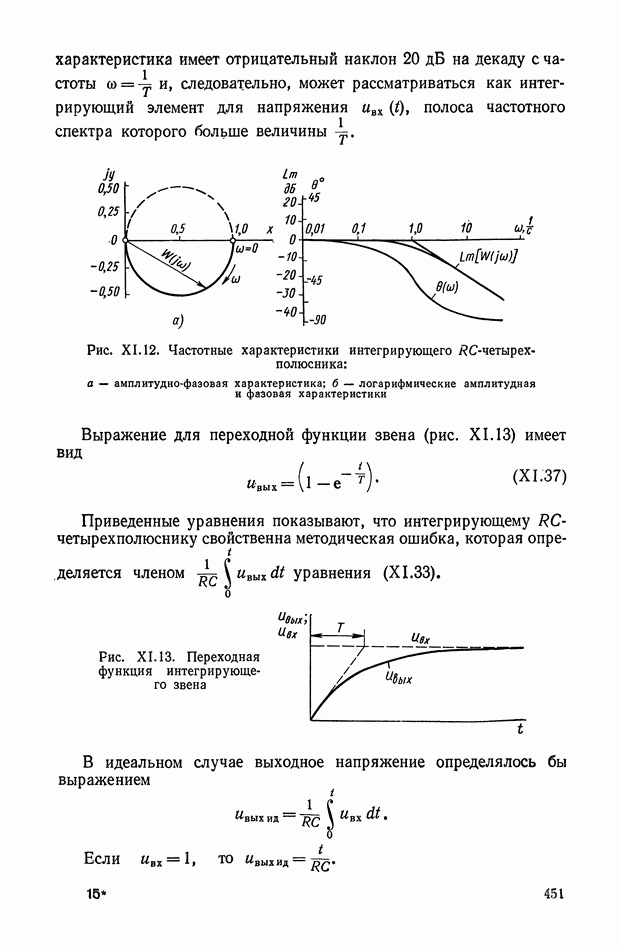
В этом параграфе рассматриваются способы получения и реализации нелинейных корректирующих устройств. Эти способы обеспечивают реализацию оптимальных по быстродействию систем регулирования и управления. Для решения этой задачи будем считать, что объект управления описывается дифференциальным урарнением в виде

Здесь  — вектор состояния; и
— вектор состояния; и  — вектор управления;
— вектор управления;  — вектор обобщенной силы, действующей в области
— вектор обобщенной силы, действующей в области

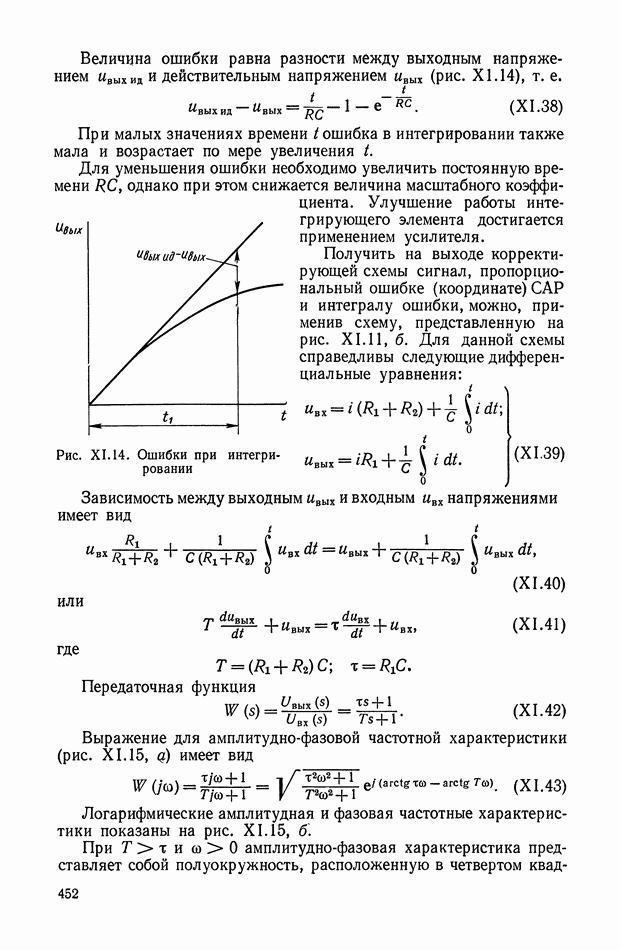
и интервала времени  Определим также функционал
Определим также функционал

оценивающий качество работы системы и граничные условия

Решение задачи управления состоит в определении таких  среди допустимых значений
среди допустимых значений  для которых функционал
для которых функционал  — принимает минимальное значение и удовлетворяются граничные условия.
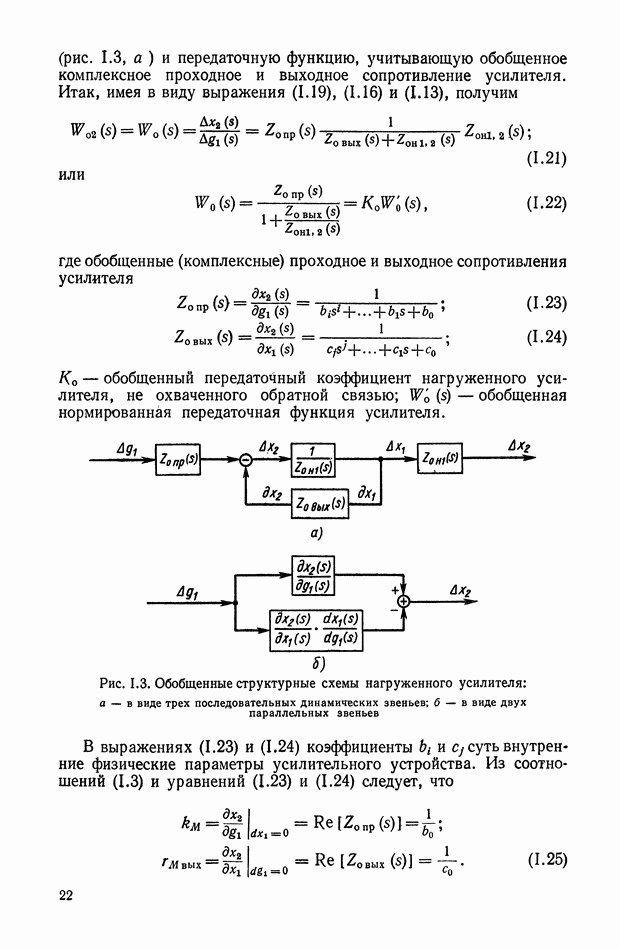
— принимает минимальное значение и удовлетворяются граничные условия.
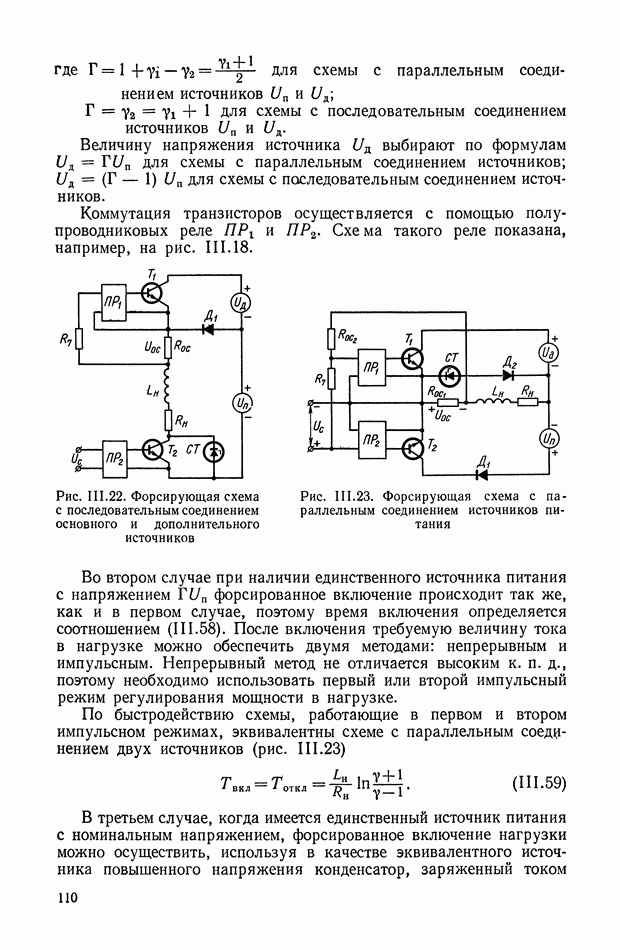
Очевидно, что наряду с решением оптимальной задачи необходимо также указать пути реализации полученных оптимальных законов управления.
Если управление определяется в виде функции вектора состояния  то принято считать, что задача синтеза решается в пространстве состояний, а устройство, формирующее оптимальное управление, представляет собой оптимальный регулятор (нелинейное корректирующее устройство).
то принято считать, что задача синтеза решается в пространстве состояний, а устройство, формирующее оптимальное управление, представляет собой оптимальный регулятор (нелинейное корректирующее устройство).
Если говорить о методах решения оптимальной задачи управления, то необходимо отметить, что наибольшее распространение получили методы, основанные на математическом аппарате принципа
максимума Понтрягина. Это объясняется тем, что принцип максимума, являющийся логическим продолжением классических вариационных методов, содержит более общие принципы проектирования оптимальных автоматических систем.
При использовании принципа максимума Понтрягина [11] экстремальные управления и траектории должны удовлетворять следующим условиям:
1) канонической системе дифференциальных уравнений

где гамильтониан системы

2) условию максимизации гамильтониана по управлению;
3) граничным условиям и условиям трансверсальности. Рассмотрим задачу синтеза оптимальных корректирующих устройств при линейном объекте

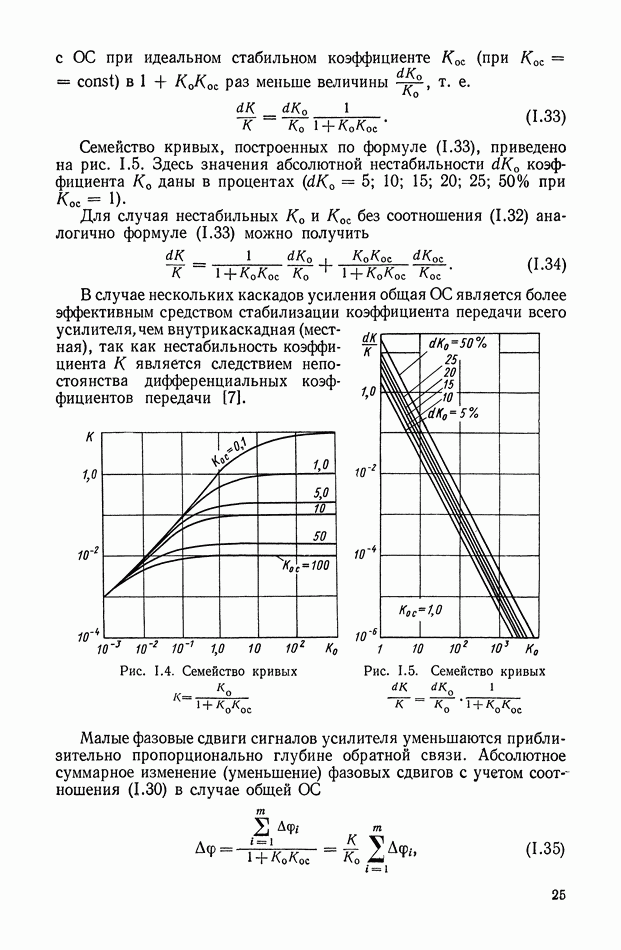
когда на управление наложены ограничения типа неравенства. В нашем случае принято, что управление является скалярной функцией, из области

При условии, что исходная задача нормальна, использование необходимых условий принципа максимума приводит к оптимальному управлению вида

а оптимальные траектории определяются, как решение следующей системы дифференциальных уравнений

при граничных условиях

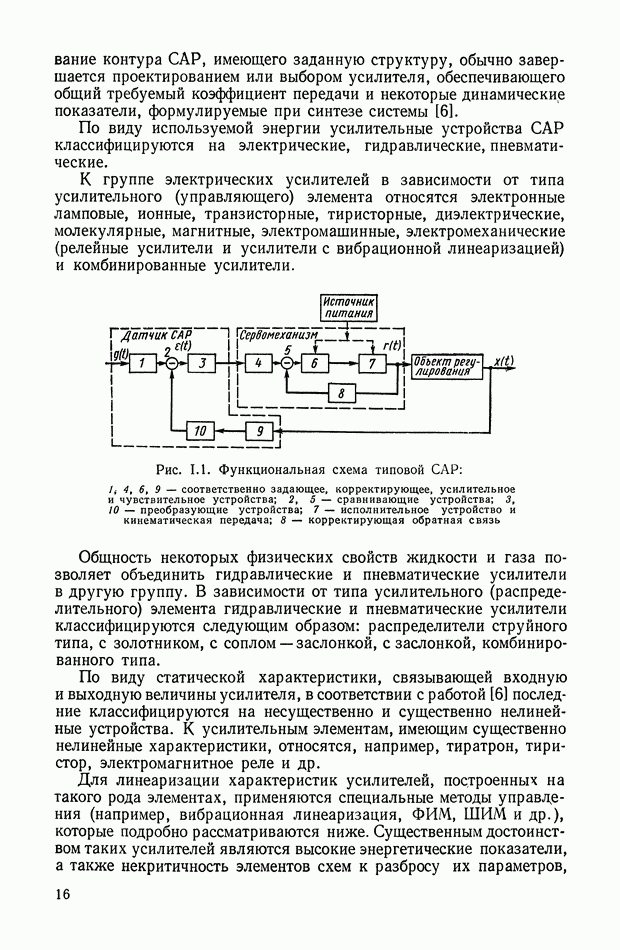
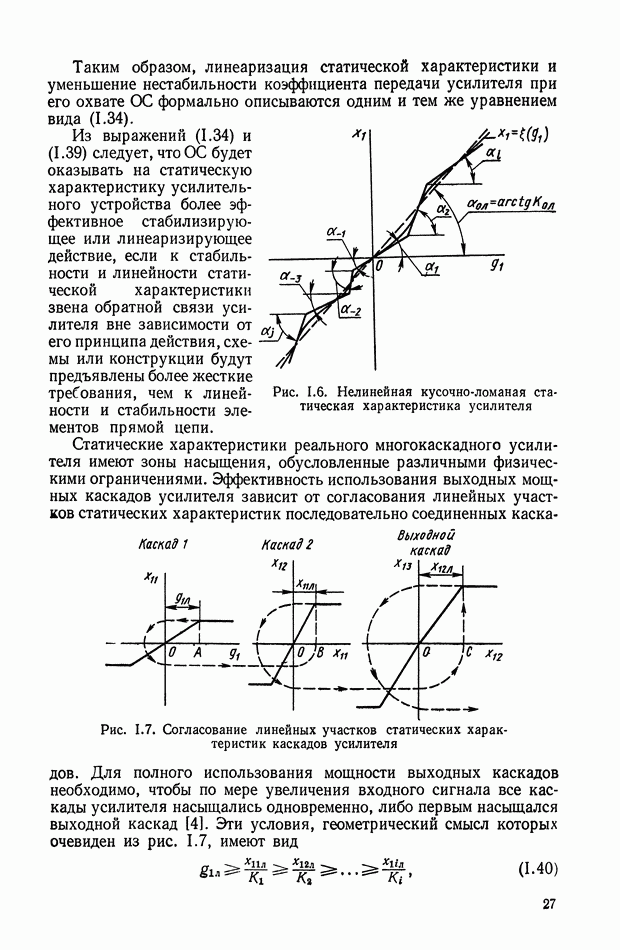
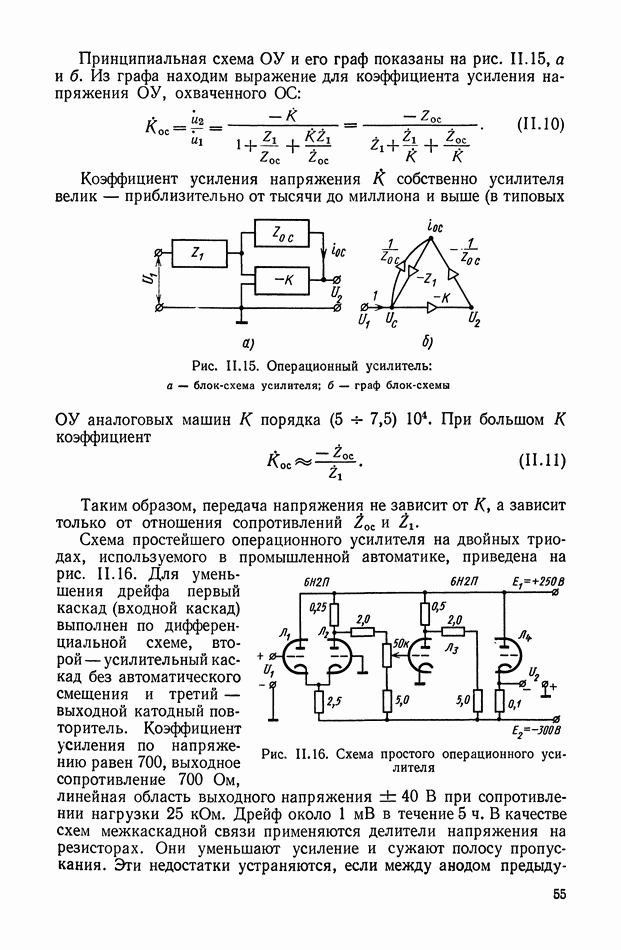
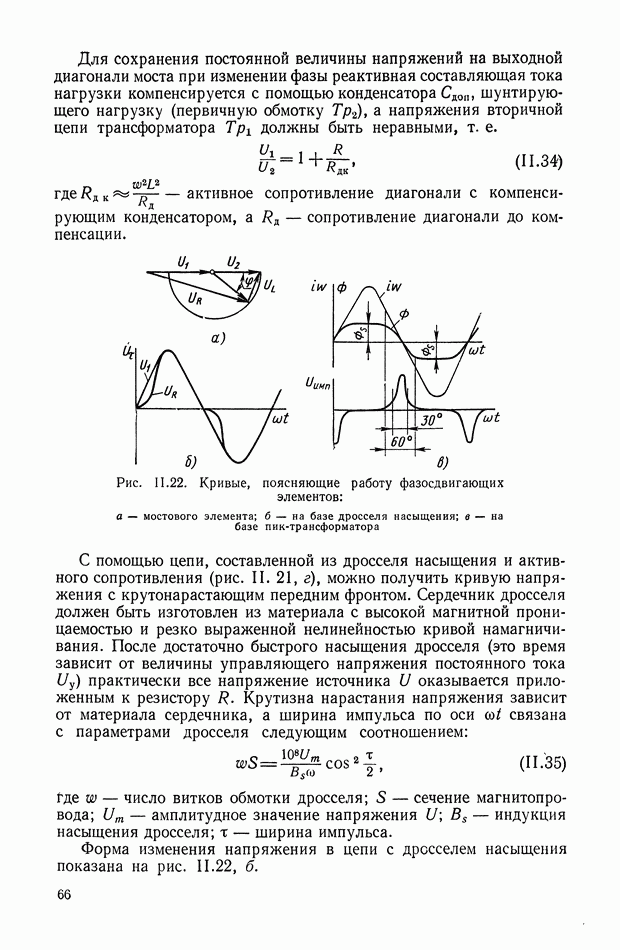
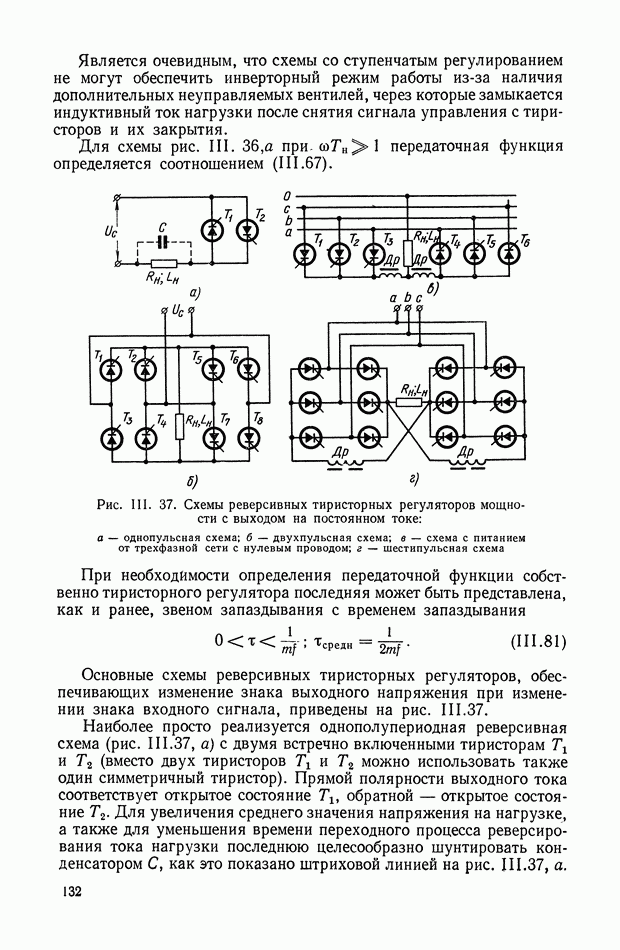
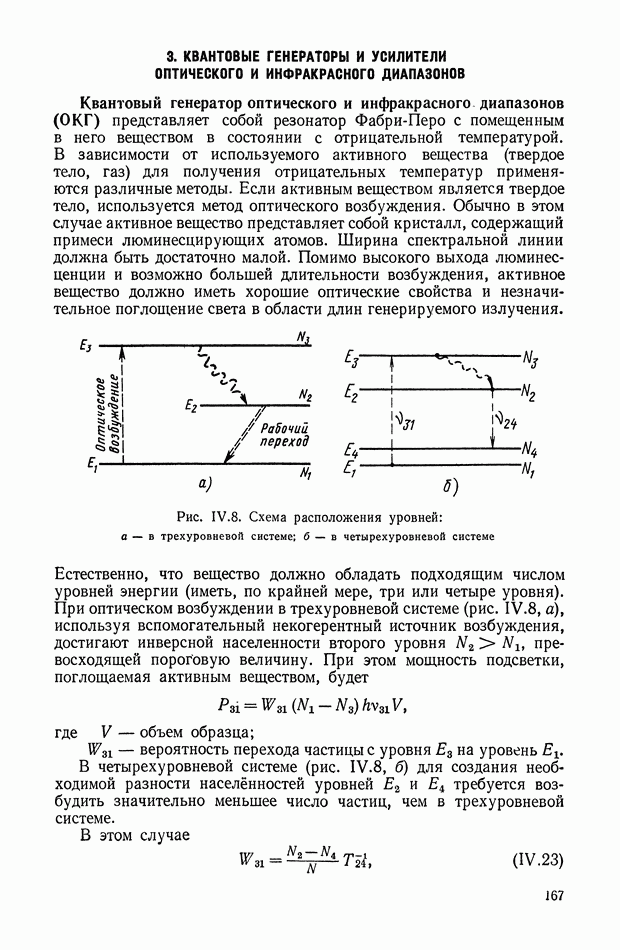
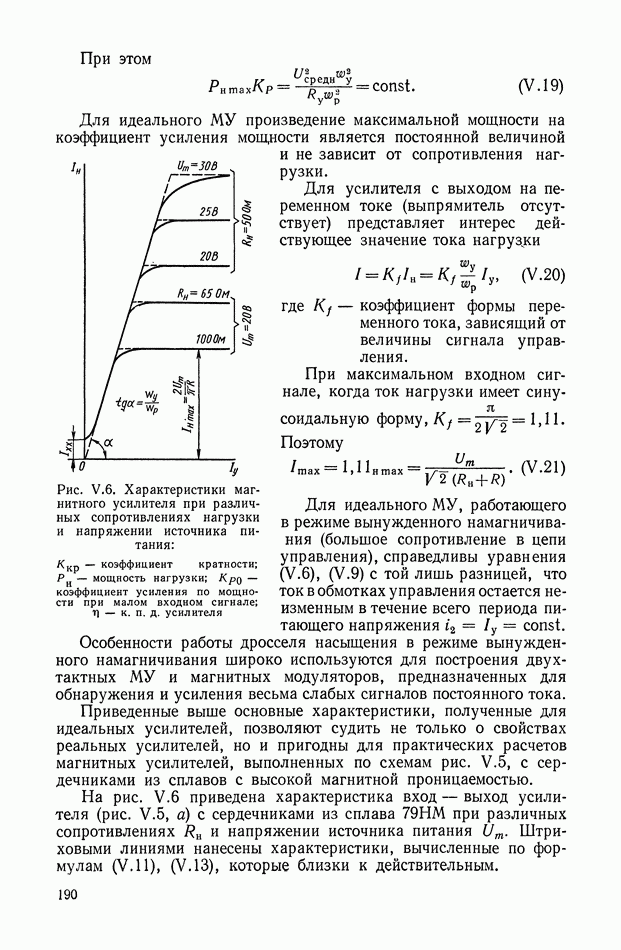
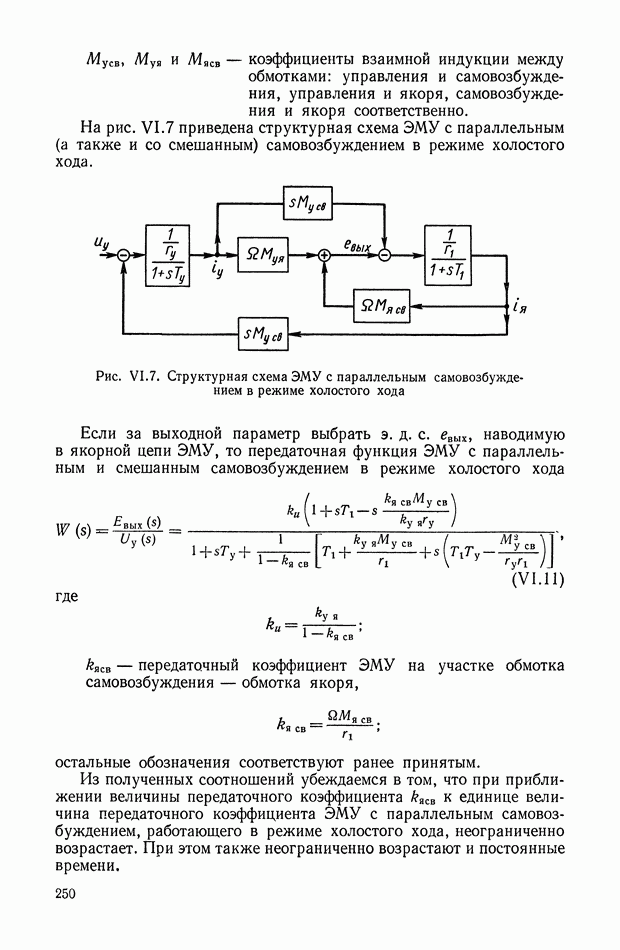
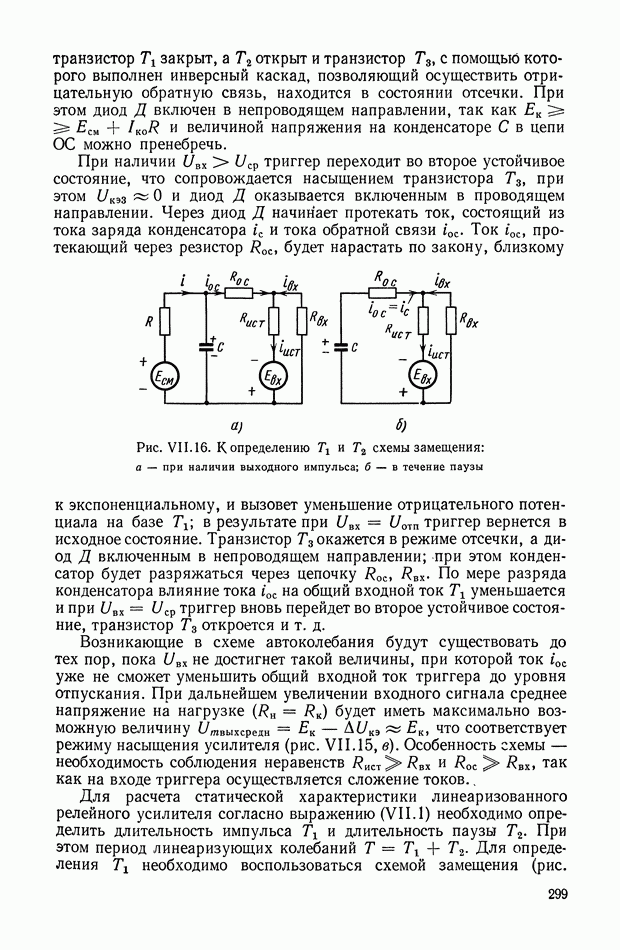
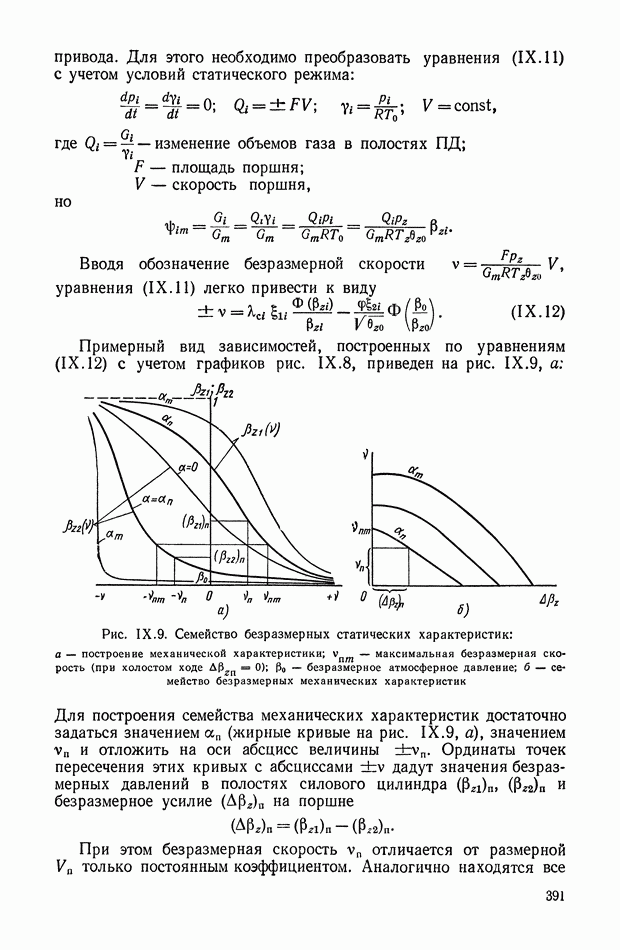
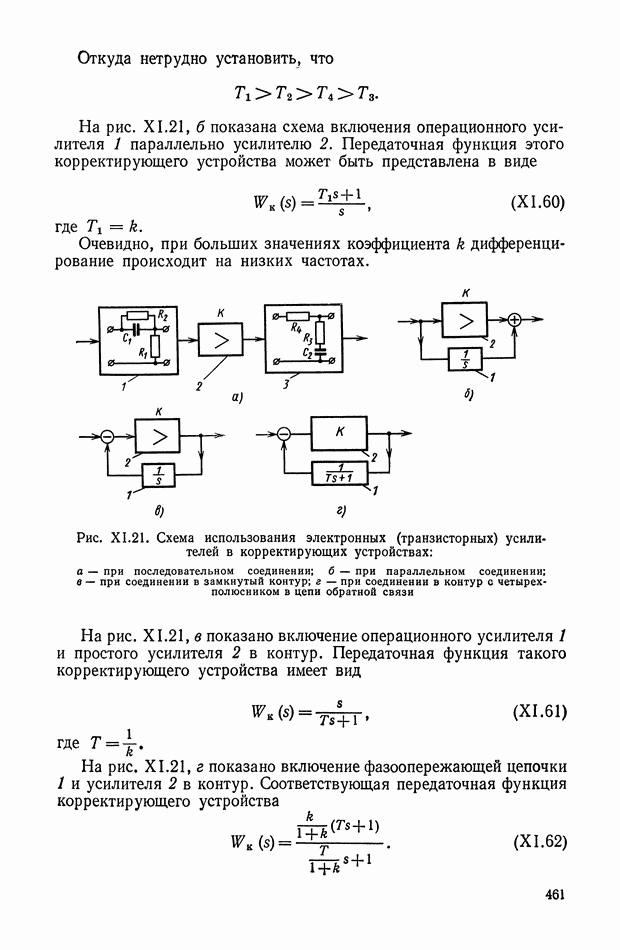
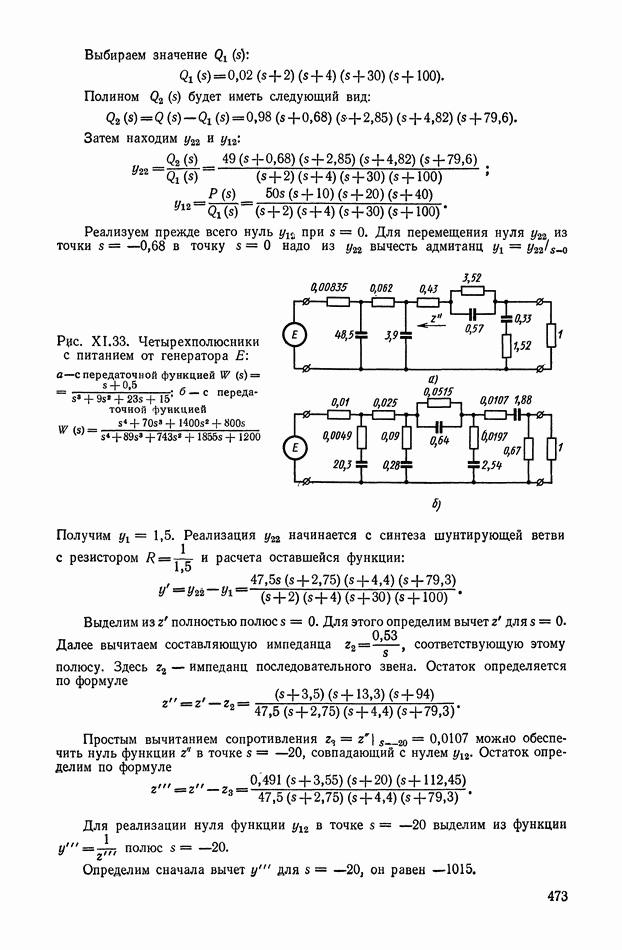
В том случае, когда систему дифференциальных уравнений удается разрешить относительно переменной  оптимальное управление становится функцией координат системы, а структурная схема оптимальной системы управления принимает вид, показанный на рис. XI.37.
оптимальное управление становится функцией координат системы, а структурная схема оптимальной системы управления принимает вид, показанный на рис. XI.37.
Как видно из структуры оптимального корректирующего устройства, его реализацию необходимо осуществлять в классе нелинейных
цепей. Высокая сложность синтезируемых оптимальных законов приводит к необходимости их упрощения или реализации в виде оптимальной управляющей программы на ЦВМ. В последнем случае очень важным вопросом является выбор такта счета на ЦВМ, так как величина такта в значительной степени определяет влияние ошибок дискретизации на точность работы системы управления.

Рис. XI.37. Блок-схема оптимальной системы управления
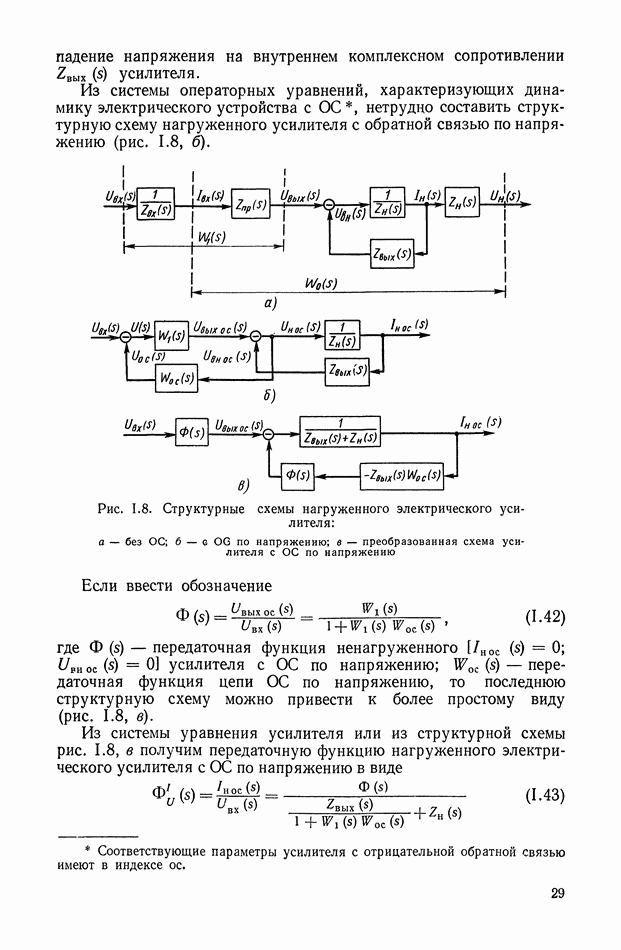
Рассмотрим примеры построения и реализации оптимальных законов управления для объектов, передаточная функция которых имеет вид

Для управления такими объектами нелинейное корректирующее устройство должно реализовать функции вида

где  — коэффициенты полиномов Р и
— коэффициенты полиномов Р и  фазовые координаты объекта.
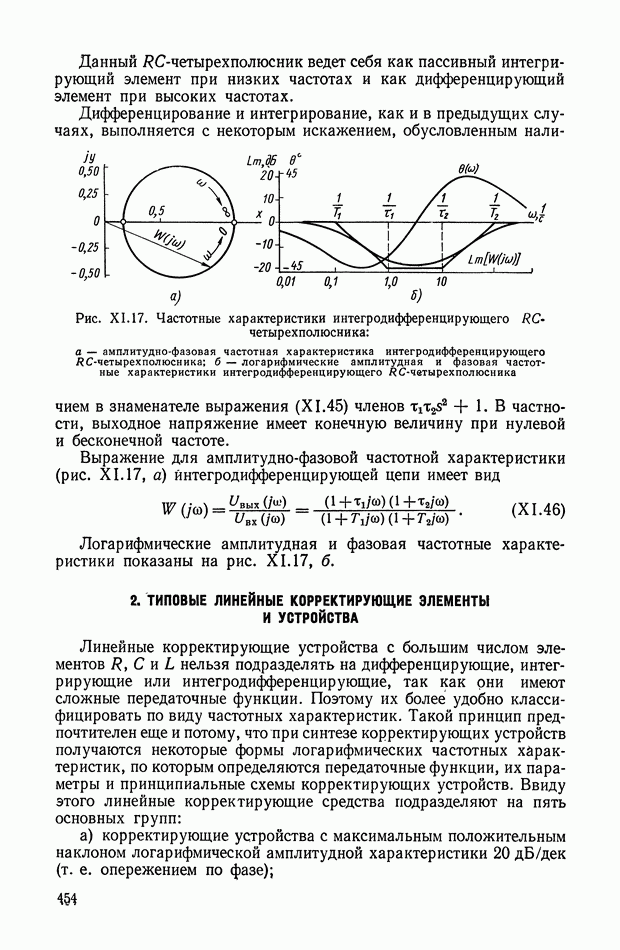
фазовые координаты объекта.
В случае, когда порядок полиномов передаточной функции объекта не превышает двух, синтез нелинейного корректирующего устройства сводится к нахождению уравнения линии переключения на плоскости  т. е. реализуется уравнение
т. е. реализуется уравнение

и закон управления имеет вид

Например, для объекта, описываемого дифференциальным уравнением

уравнение линии переключения будет

и закон управления

Корректирующее устройство должно выполнять нелинейную операцию перемножения фазовых координат и умножение на постоянный коэффициент, зависящий от параметров объекта.
Если уравнение объекта

то закон управления оптимальной по быстродействию системы будет

Нелинейное корректирующее устройство, реализующее второе слагаемое выражения (XI.84), в этом случае более сложно, так как для его реализации необходимо иметь функциональный преобразователь, воспроизводящий логарифмическую зависимость.
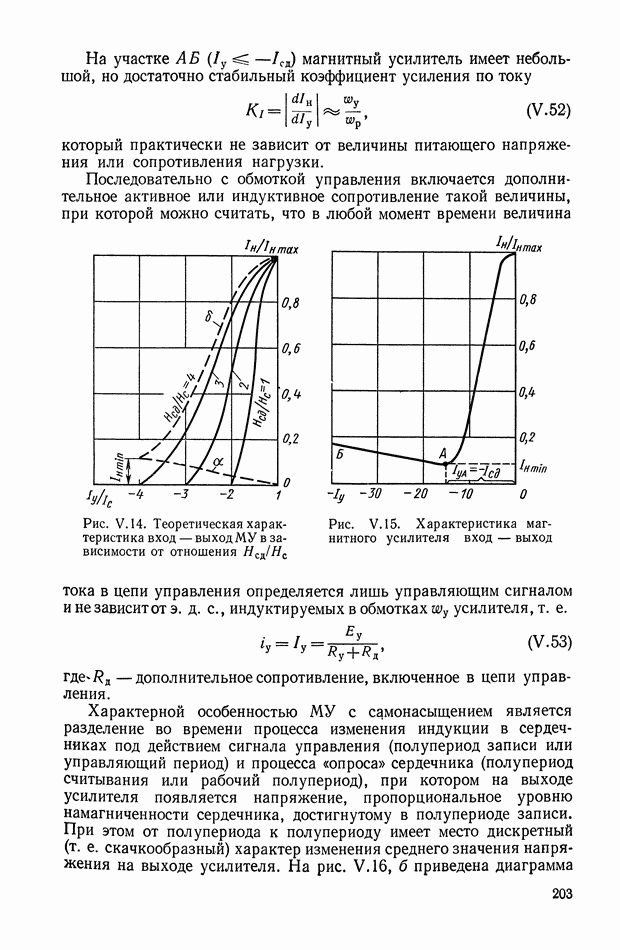
Общей чертой нелинейных корректирующих устройств систем оптимального управления является зависимость их параметров от параметров объекта управления. При изменении коэффициентов передаточной функции объекта необходимо перестраивать нелинейные зависимости. В принципе это возможно, если коэффициенты  переменны, но известны их зависимости от какого-либо внешнего параметра процесса управления. Схема управления в результате перестройки значительно усложняется.
переменны, но известны их зависимости от какого-либо внешнего параметра процесса управления. Схема управления в результате перестройки значительно усложняется.
В частном случае, когда параметры объекта изменяются, оставаясь постоянными в ходе отдельного процесса, применение нелинейных корректирующих устройств позволяет реализовать оптимальное или квазиоптимальное управление без перестройки нелинейных зависимостей. Для объектов управления не выше второго порядка такая задача решается, если исходя из основных положений теорий оптимального управления, можно построить на фазовой плоскости такую линию переключения, форма которой определяется видом уравнения объекта, а размеры — коэффициентами этого уравнения. Уравнения линии переключения представим в виде

где  — дополнительные фазовые координаты, связанные с основными через параметры уравнения объекта.
— дополнительные фазовые координаты, связанные с основными через параметры уравнения объекта.
В этом случае нелинейное корректирующее устройство должно реализовать функцию 
Покажем на конкретных примерах, как можно использовать дополнительные фазовые координаты в сочетании с нелинейными
корректирующими устройствами для синтеза оптимальных законов управления.
Пример XI.5. Пусть уравнение объекта управления

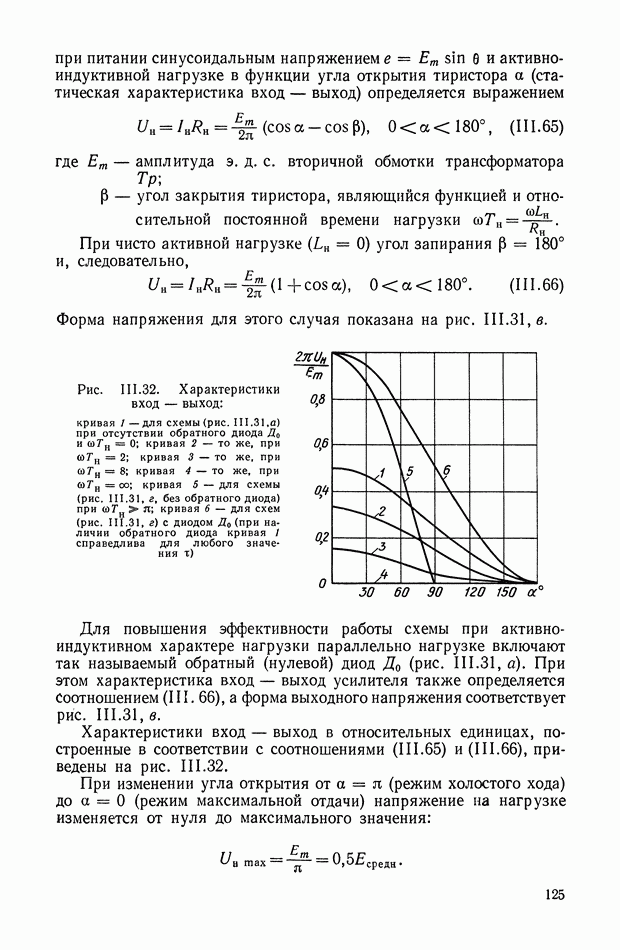
Оптимальное по быстродействию управление

Нелинейную функцию  можно достаточно точно аппроксимировать параболой
можно достаточно точно аппроксимировать параболой

которую представим в виде

где!
Координата состояния  является в рассматриваемом случае дополнительной фазовой координатой. Для ее получения используем уравнение объекта, разделив обе его части на
является в рассматриваемом случае дополнительной фазовой координатой. Для ее получения используем уравнение объекта, разделив обе его части на  т. е.
т. е.

Откуда

Величина  является второй дополнительной фазовой координатой, используемой в корректирующем устройстве. Для ее получения в схему вводится модель инерционного звена объекта с коэффициентом усиления равным I (рис.
является второй дополнительной фазовой координатой, используемой в корректирующем устройстве. Для ее получения в схему вводится модель инерционного звена объекта с коэффициентом усиления равным I (рис.  .
.
Управление  является квазиоптимальным по быстродействию при аппроксимации функции (XI.86) параболой (XI.87) при любых
является квазиоптимальным по быстродействию при аппроксимации функции (XI.86) параболой (XI.87) при любых  .
.
Реализация модели инерционного звена объекта управления в общем случае требует решения дополнительной задачи идентификации объекта, когда Т и  переменны. Если значения коэффициента Т в каждом процессе известны, то модель легко перестраивается, будучи реализованной на обычном операционном усилителе. Однако во многих случаях параметр Т известен лишь диапазоном своего изменения. Тогда можно использовать модель с постоянной времени
переменны. Если значения коэффициента Т в каждом процессе известны, то модель легко перестраивается, будучи реализованной на обычном операционном усилителе. Однако во многих случаях параметр Т известен лишь диапазоном своего изменения. Тогда можно использовать модель с постоянной времени  равной некоторому среднему значению диапазона изменения Т.
равной некоторому среднему значению диапазона изменения Т.
Уравнение изменения координаты 

На первом интервале оптимального управления координаты  изменяются по экспонентам
изменяются по экспонентам

Используя разложения в степенной ряд, получим приближенно

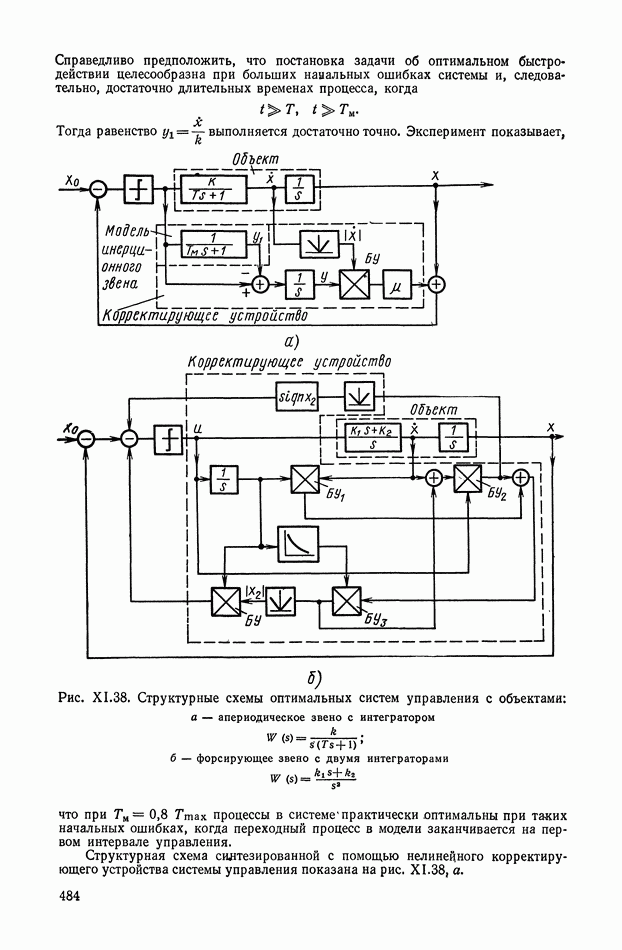
Справедливо предположить, что постановка задачи об оптимальном быстродействии целесообразна при больших нанальных ошибках системы и, следовательно, достаточно длительных временах процесса, когда что при  процессы в системепрактически оптимальны при таких начальных ошибках, когда переходный процесс в модели заканчивается на первом интервале управления.
процессы в системепрактически оптимальны при таких начальных ошибках, когда переходный процесс в модели заканчивается на первом интервале управления.

Тогда равенство  выполняется достаточно точно. Эксперимент показывает,
выполняется достаточно точно. Эксперимент показывает,
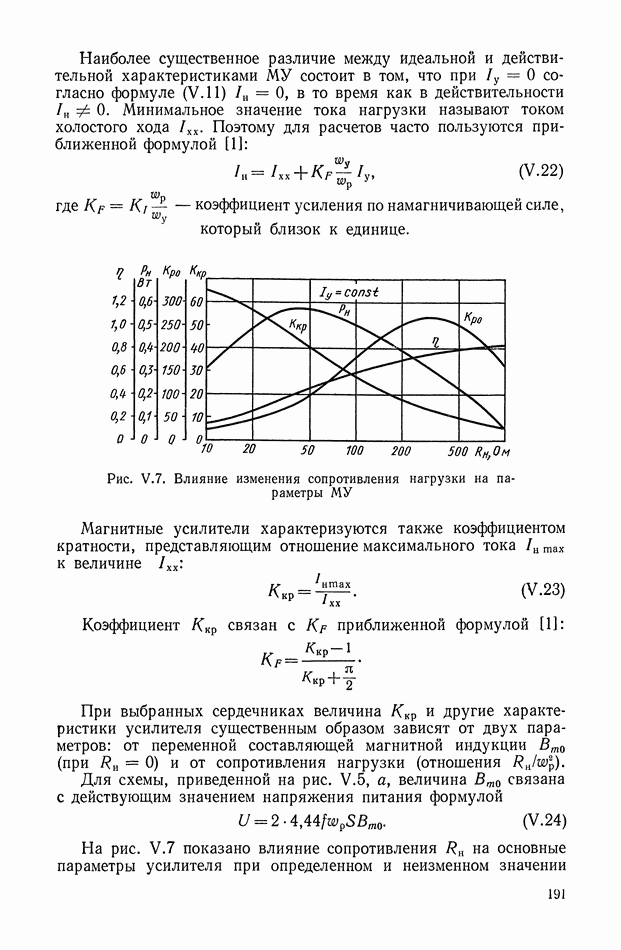
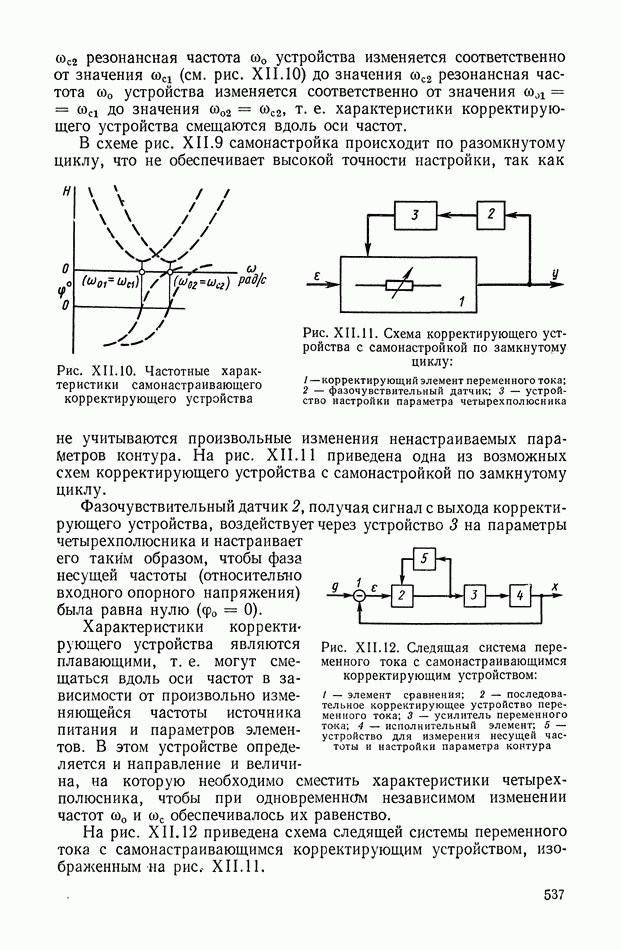
Рис. XI.38. (см. скан) Структурные схемы оптимальных систем управления с объектами: а — апериодическое звено с интегратором  б — форсирующее звено с двумя интеграторами
б — форсирующее звено с двумя интеграторами 
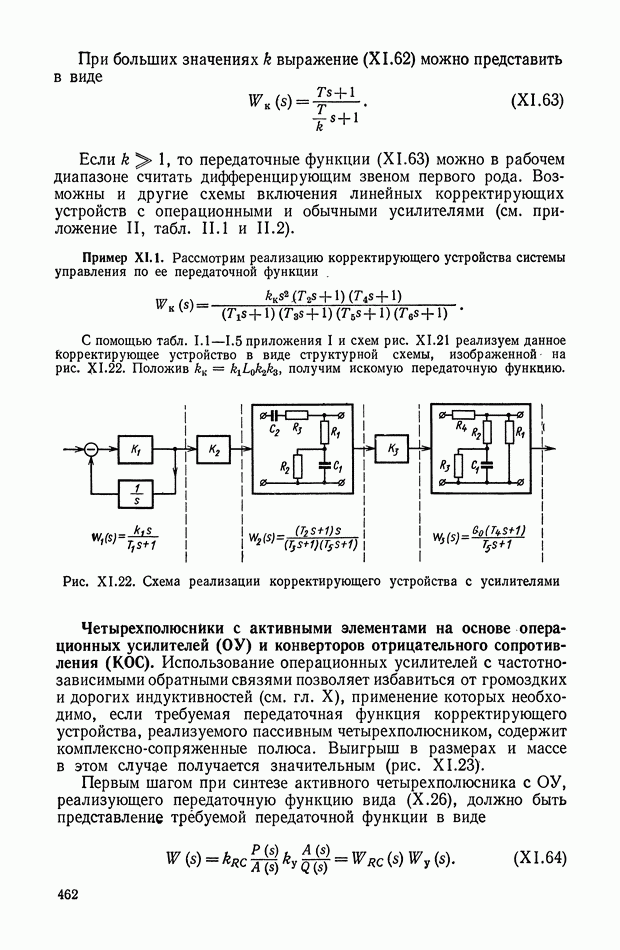
Структурная схема силтезированной с помощью нелинейного корректирующего устройства системы управления показана на рис. XI.38, а.
Пример XI.6. Пусть уравнение объекта

Его передаточная функция имеет нуль (положительный). Уравнение (XI.88) заменим эквивалентной системой

где 
Уравнение линии переключения оптимальной системы управления будет иметь вид

Корректирующее устройство должно реализовать правую часть выражения (XI.90). Для этого необходимо иметь следующие фазовые координаты:

Координата х является выходом объекта управления и, очевидно, может быть измерена. Координата  получается интегрированием управляющего воздействия.
получается интегрированием управляющего воздействия.
Чтобы получить координату  используем первое уравнение системы (XI,89), умножив обе его части на
используем первое уравнение системы (XI,89), умножив обе его части на 
Так как  то
то  тогда
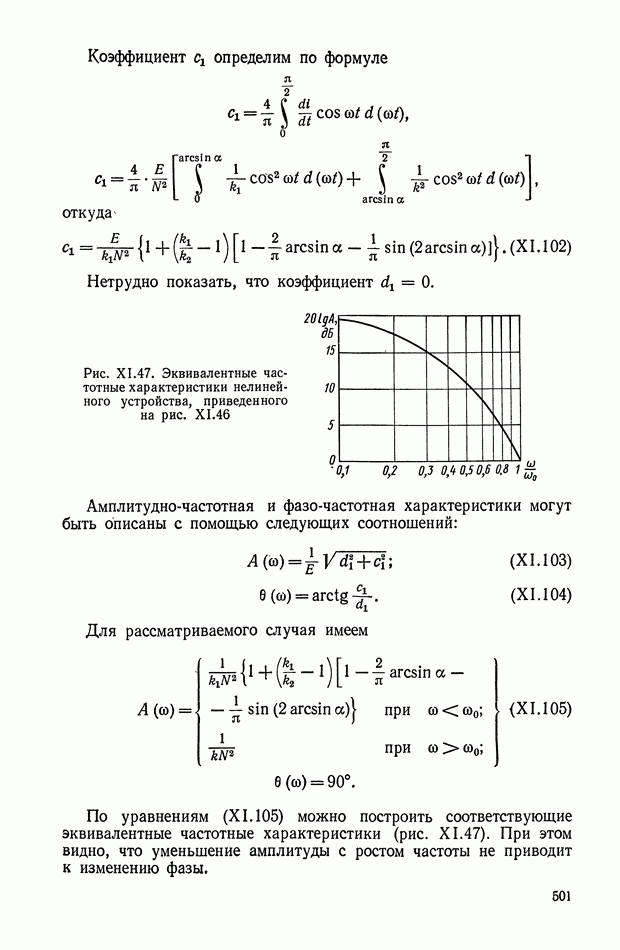
тогда

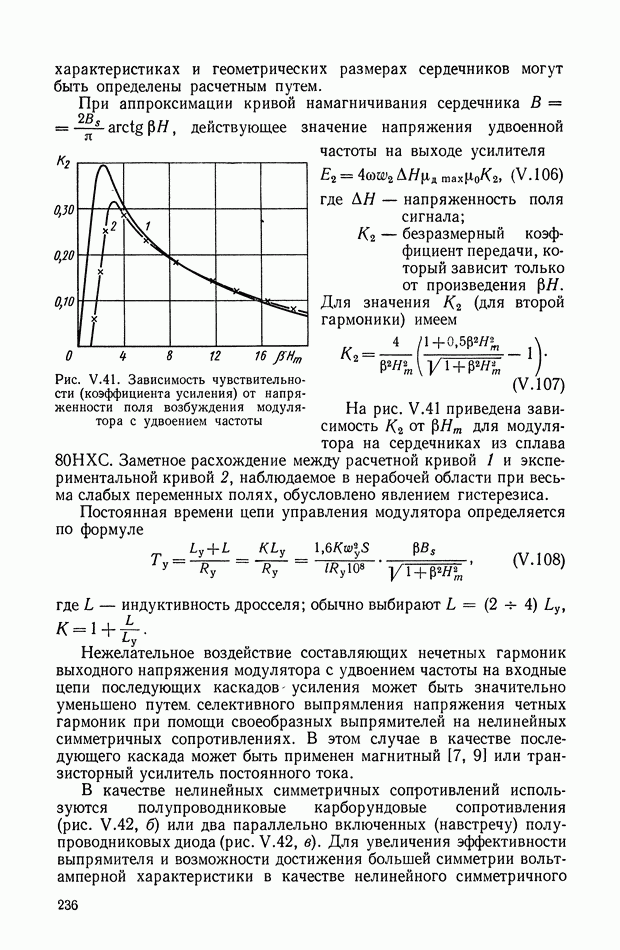
Поскольку предполагается  то величина
то величина  при введении соответствующего масштабирования эквивалентна коэффициенту
при введении соответствующего масштабирования эквивалентна коэффициенту  Тогда
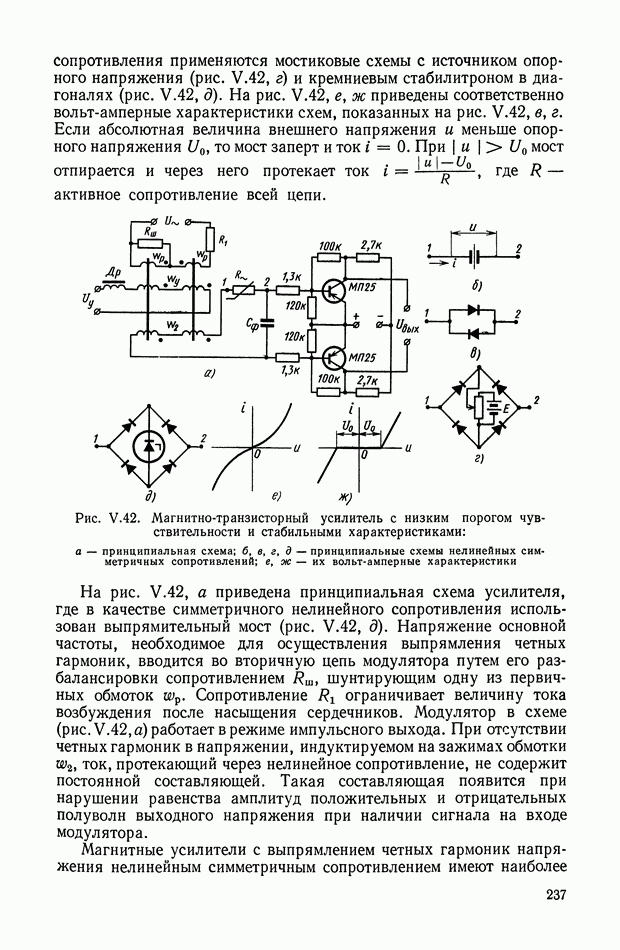
Тогда

Введя в схему нелинейный функциональный преобразователь  получим координату
получим координату 
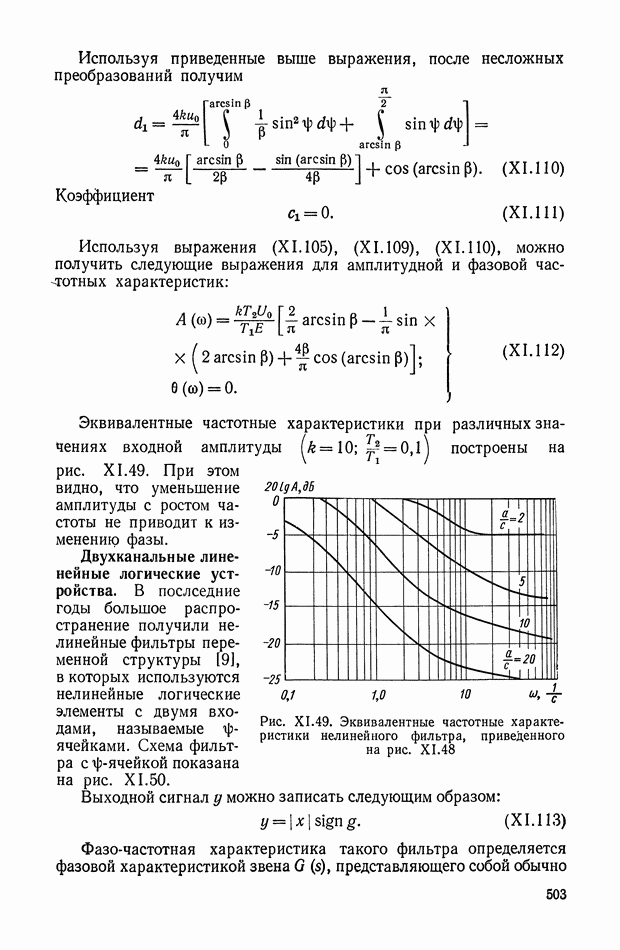
Структурная схема системы управления для этого случая приведена на рис. XI.38, б.
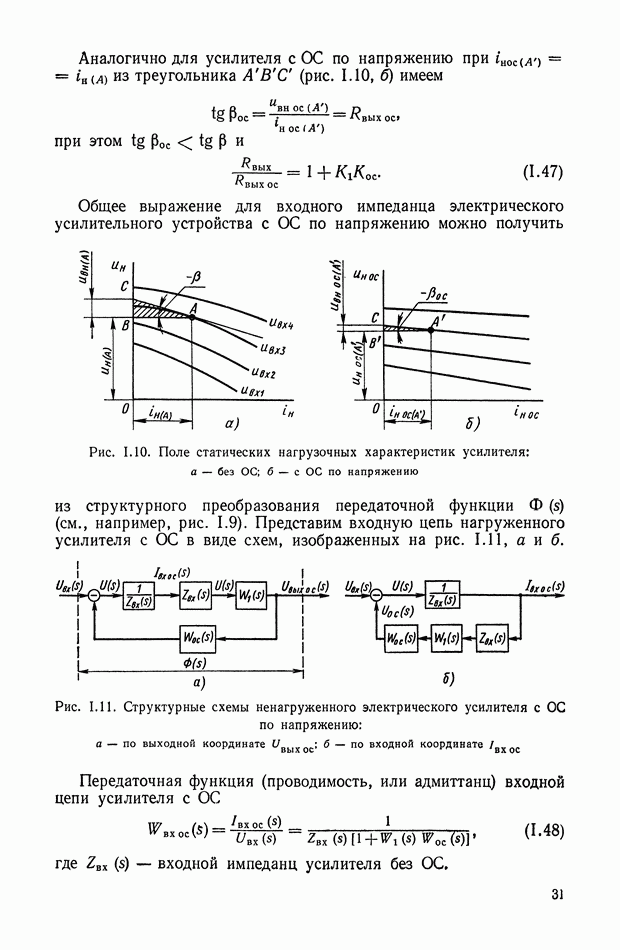
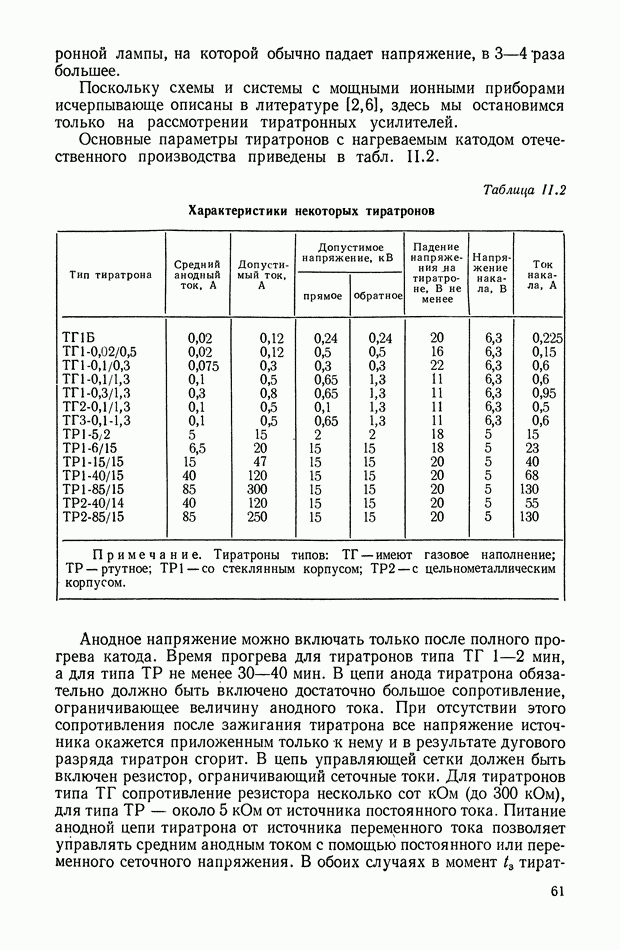
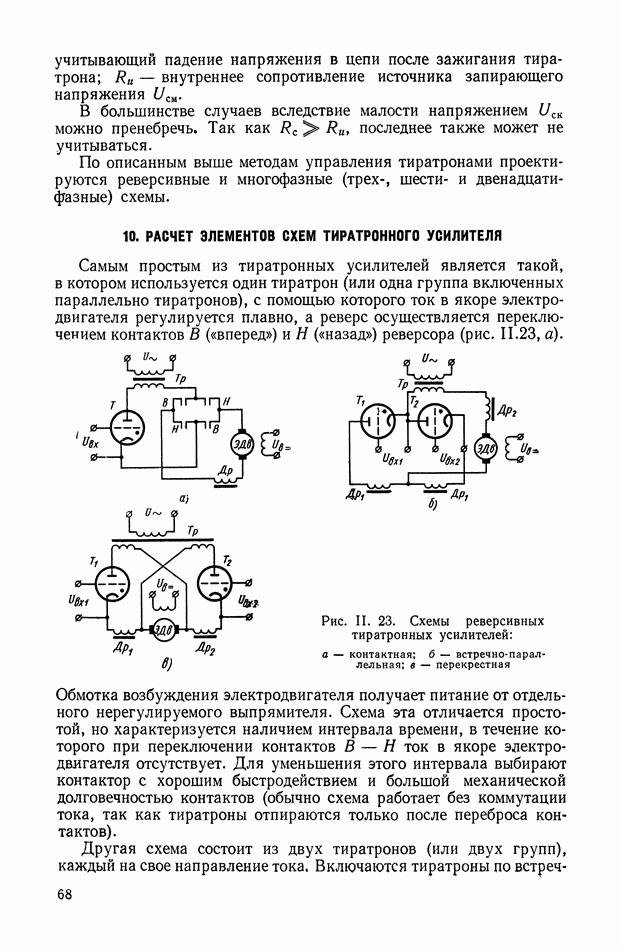
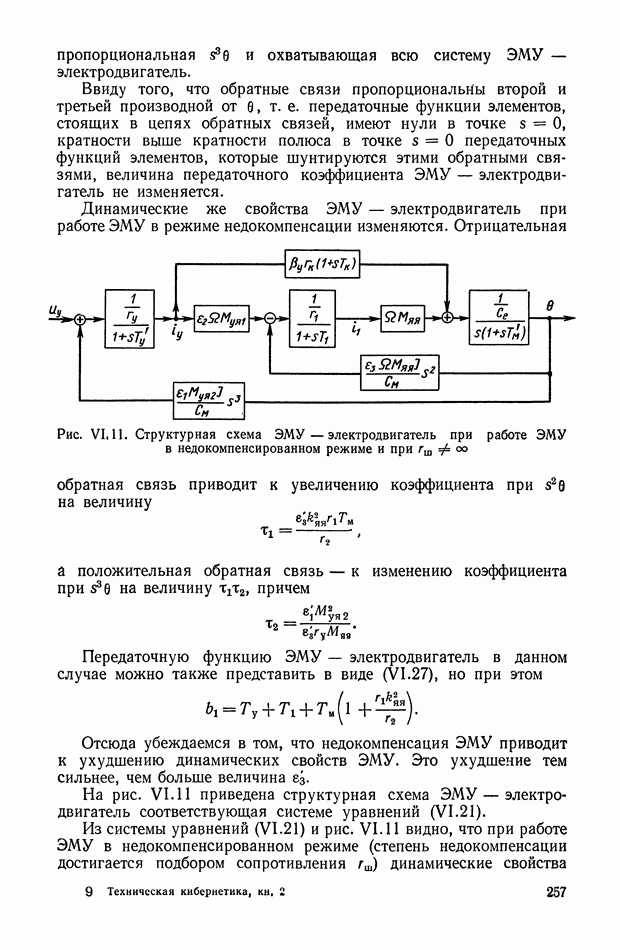
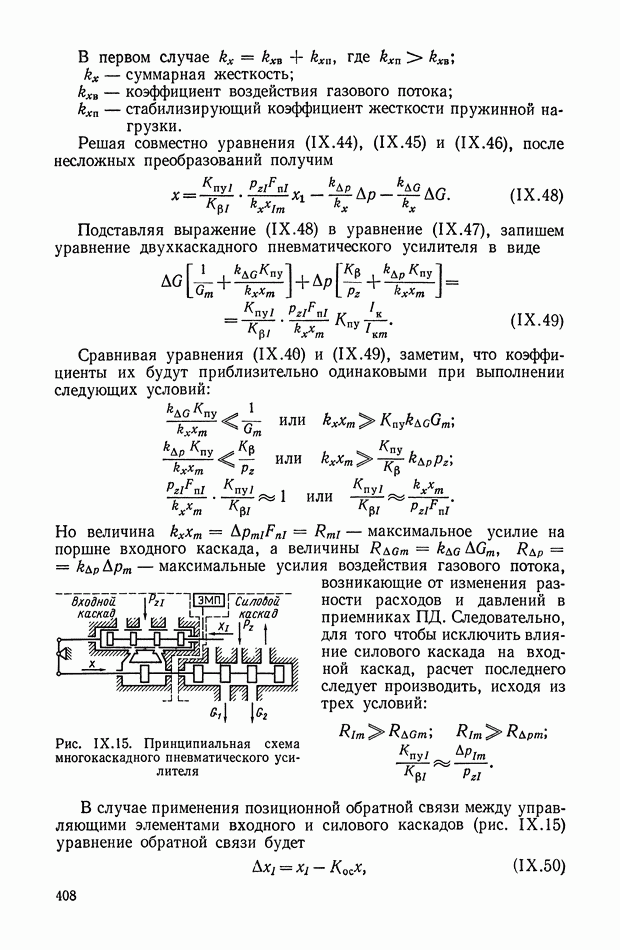
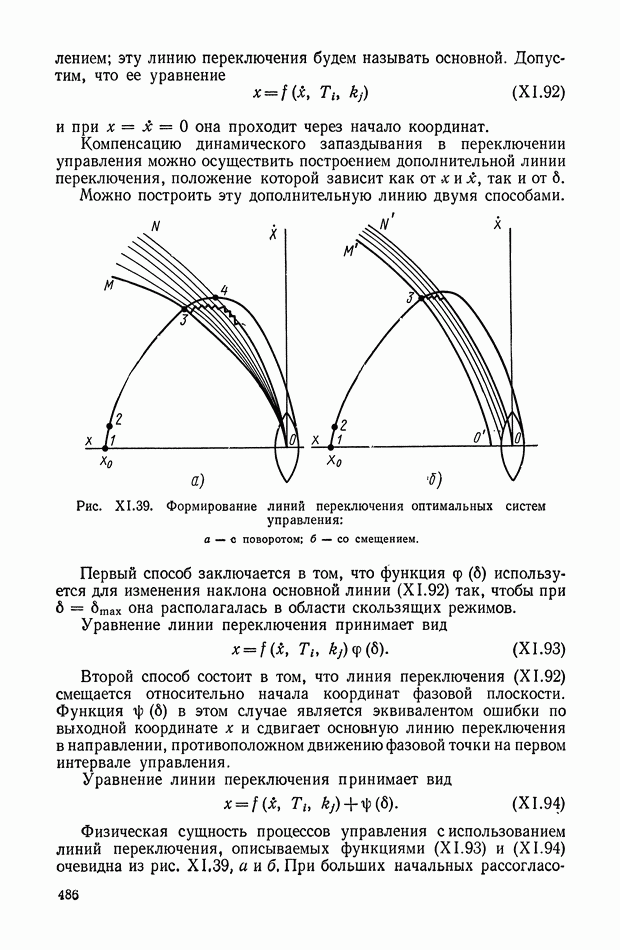
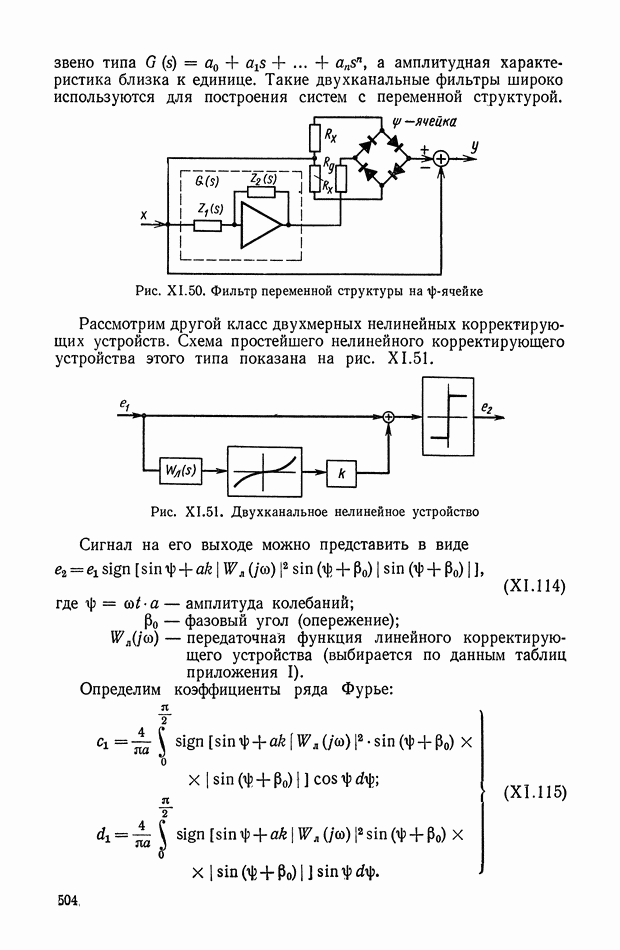
При использовании нелинейных корректирующих устройств оказывается возможным в ряде случаев синтезировать систему управления, когда она описывается дифференциальными уравнениями третьего порядка. Такой случай возникает, если необходимо учитывать инерционность исполнительных органов управления, описываемых уравнением

Целесообразно попытаться управлять такой системой (рис. XI.39), используя только две фазовые координаты  которые легко измеряются, а учет динамики управляющего воздействия
которые легко измеряются, а учет динамики управляющего воздействия  осуществить коррекцией положения линии переключения на плоскости
осуществить коррекцией положения линии переключения на плоскости 
В большинстве реальных систем объект управления более инерционен, чем органы управления  Тогда, корректируя положение линии переключения на плоскости
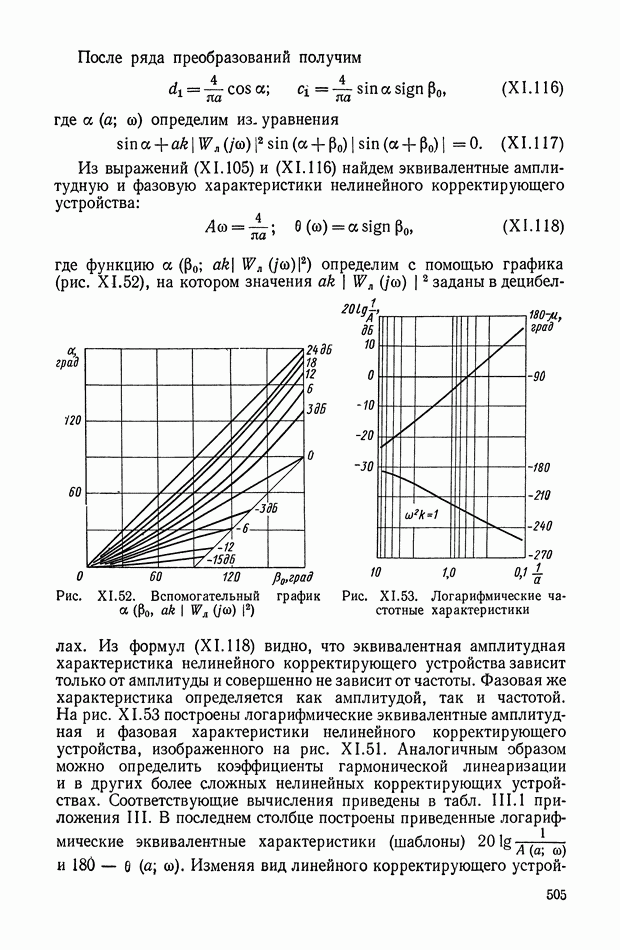
Тогда, корректируя положение линии переключения на плоскости  посредством сигналов
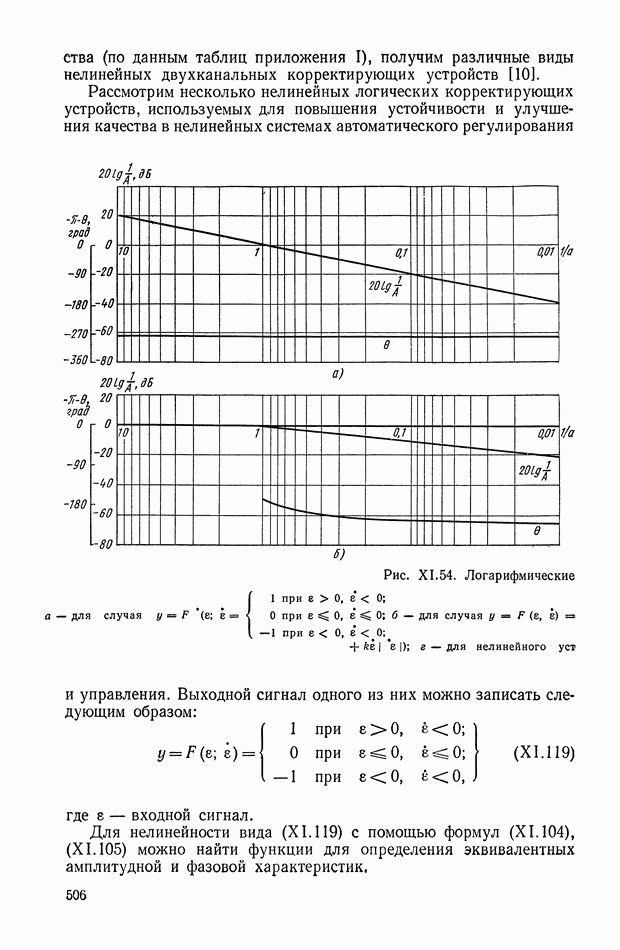
посредством сигналов  можно поместить ее в области скользящих режимов относительно линии переключения для объекта с безынерционным
можно поместить ее в области скользящих режимов относительно линии переключения для объекта с безынерционным
управлением; эту линию переключения будем называть основной. Допустим, что ее уравнение

и при  она проходит через начало координат.
она проходит через начало координат.
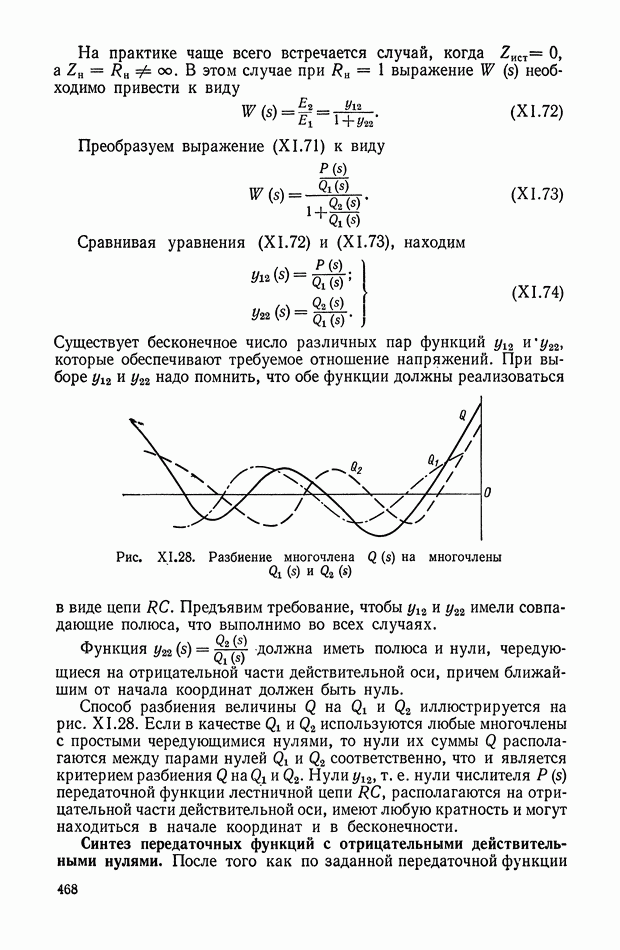
Компенсацию динамического запаздывания в переключении управления можно осуществить построением дополнительной линии переключения, положение которой зависит как от и х, так и от  Можно построить эту дополнительную линию двумя способами.
Можно построить эту дополнительную линию двумя способами.

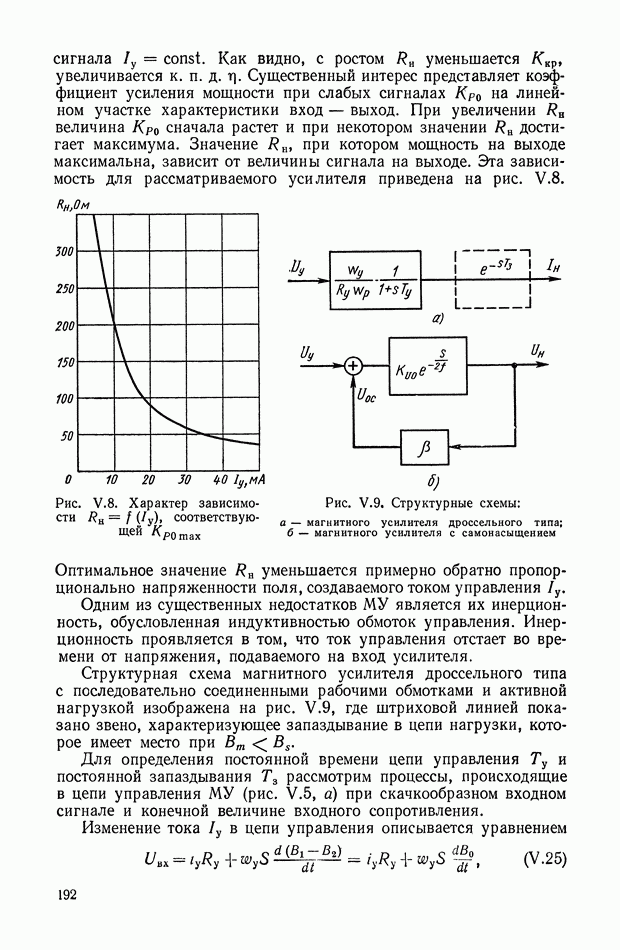
Рис. XI.39. Формирование линий переключения оптимальных систем управления: а — с поворотом; б - со смещением.
Первый способ заключается в том, что функция  используется для изменения наклона основной линии (XI.92) так, чтобы при
используется для изменения наклона основной линии (XI.92) так, чтобы при  бтах она располагалась в области скользящих режимов.
бтах она располагалась в области скользящих режимов.
Уравнение линии переключения принимает вид

Второй способ состоит в том, что линия переключения (XI.92) смещается относительно начала координат фазовой плоскости. Функция  в этом случае является эквивалентом ошибки по выходной координате х и сдвигает основную линию переключения в направлении, противоположном движению фазовой точки на первом интервале управления.
в этом случае является эквивалентом ошибки по выходной координате х и сдвигает основную линию переключения в направлении, противоположном движению фазовой точки на первом интервале управления.
Уравнение линии переключения принимает вид

Физическая сущность процессов управления с использованием линий переключения, описываемых функциями (XI.93) и (XI.94) очевидна из рис. XI.39, а  При больших начальных рассогласованиях
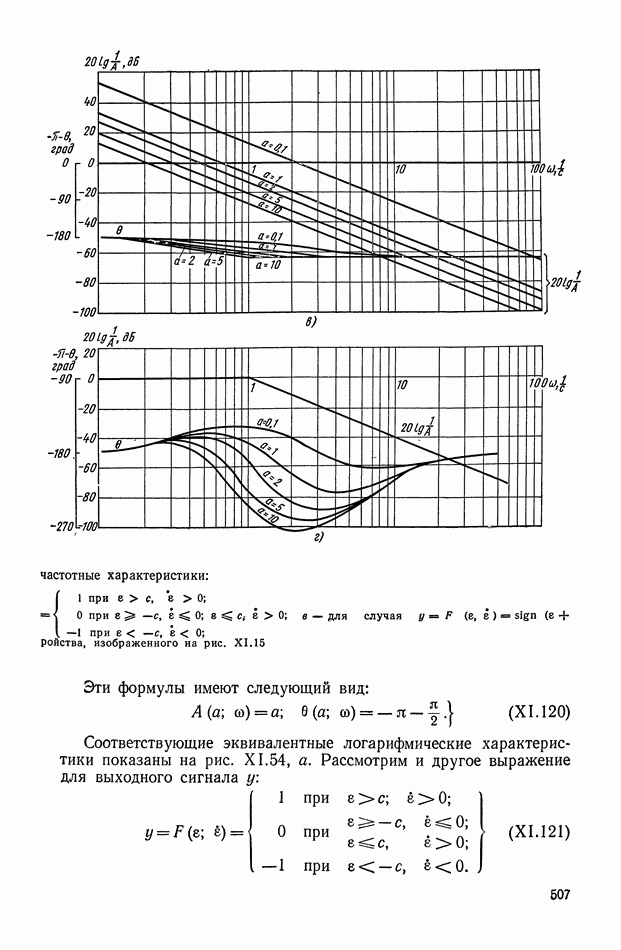
При больших начальных рассогласованиях
по координате х управляющее воздействие  достигает макси мума в точке 2 и дальнейшее движение до первой смены знака управ ления происходит по отрезку оптимальной траектории, соответствующей
достигает макси мума в точке 2 и дальнейшее движение до первой смены знака управ ления происходит по отрезку оптимальной траектории, соответствующей  . В точке 5, принадлежащей дополнительной линии переключения, происходит смена знака управления, и величина
. В точке 5, принадлежащей дополнительной линии переключения, происходит смена знака управления, и величина  начинает уменьшаться в соответствии с выражением (X 1.91). Линия переключения начинает либо вращаться [уравнение (X 1.93)], либо смещаться [уравнение (X 1.94)] навстречу изображающей точке, стремясь совместиться с основной линией переключения (XI.92). Таким образом линия переключения совершает колебания относительно взаимодействующей с ней изображающей точки. Если частота этих колебаний достаточно велика [что достигается выбором функций
начинает уменьшаться в соответствии с выражением (X 1.91). Линия переключения начинает либо вращаться [уравнение (X 1.93)], либо смещаться [уравнение (X 1.94)] навстречу изображающей точке, стремясь совместиться с основной линией переключения (XI.92). Таким образом линия переключения совершает колебания относительно взаимодействующей с ней изображающей точки. Если частота этих колебаний достаточно велика [что достигается выбором функций  или
или  то изменение управляющего воздействия после точки 3 определяется зависимостью
то изменение управляющего воздействия после точки 3 определяется зависимостью

Движение изображающей точки внутри зоны, ограниченной основной и дополнительной линиями переключения, описывается тогда уравнением [применительно к объекту вида (XI.85)]

Координаты изображающей точки  при
при  должны удовлетворять уравнению дополнительной, а при
должны удовлетворять уравнению дополнительной, а при  — основной линии переключения.
— основной линии переключения.
Решение уравнения (XI.95) при  будет
будет

где 
Постоянные  определяются из системы уравнений
определяются из системы уравнений

где  — координаты произвольной точки на основной линии переключения, представленной функцией (XI.86).
— координаты произвольной точки на основной линии переключения, представленной функцией (XI.86).
Затем найдем координаты  принадлежащие дополнительной линии переключения. Они равны
принадлежащие дополнительной линии переключения. Они равны

Если взять несколько значений координат  и найти соответствующие им значения
и найти соответствующие им значения  то можно определить функции
то можно определить функции 
и  входящие в законы управления (XI.93) и (XI.94), подстановкой
входящие в законы управления (XI.93) и (XI.94), подстановкой

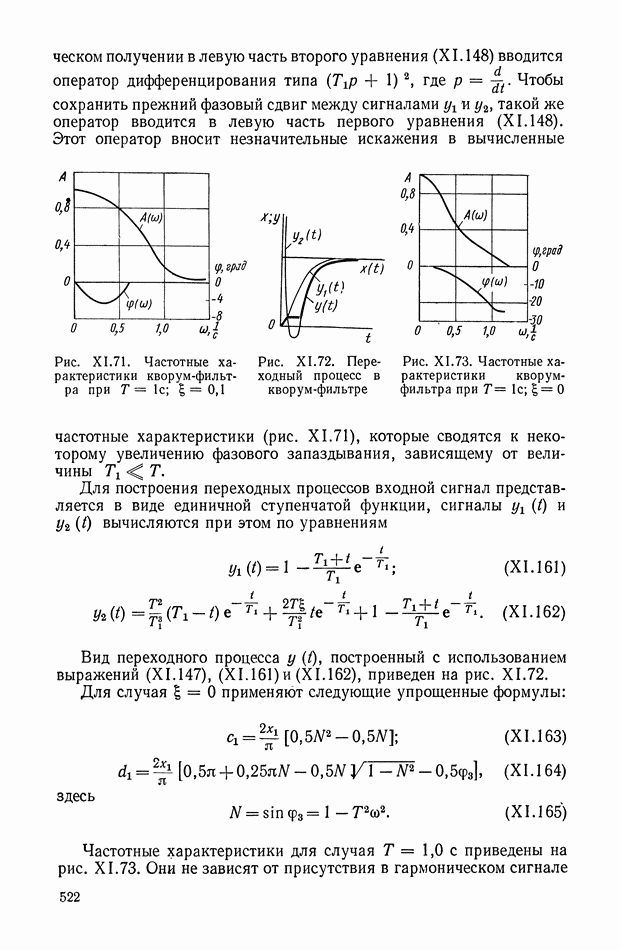
или

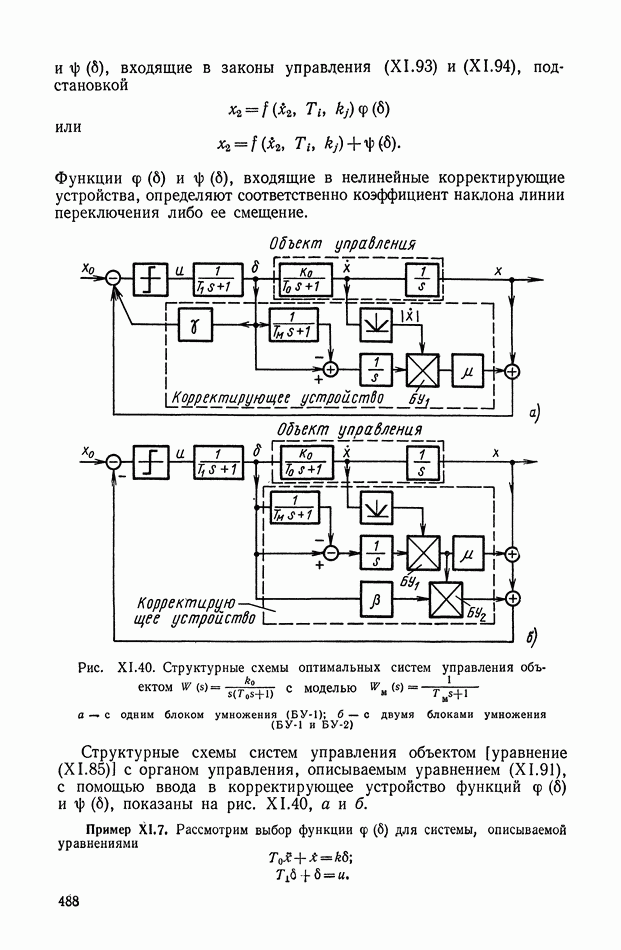
Функции  входящие в нелинейные корректирующие устройства, определяют соответственно коэффициент наклона линии переключения либо ее смещение.
входящие в нелинейные корректирующие устройства, определяют соответственно коэффициент наклона линии переключения либо ее смещение.

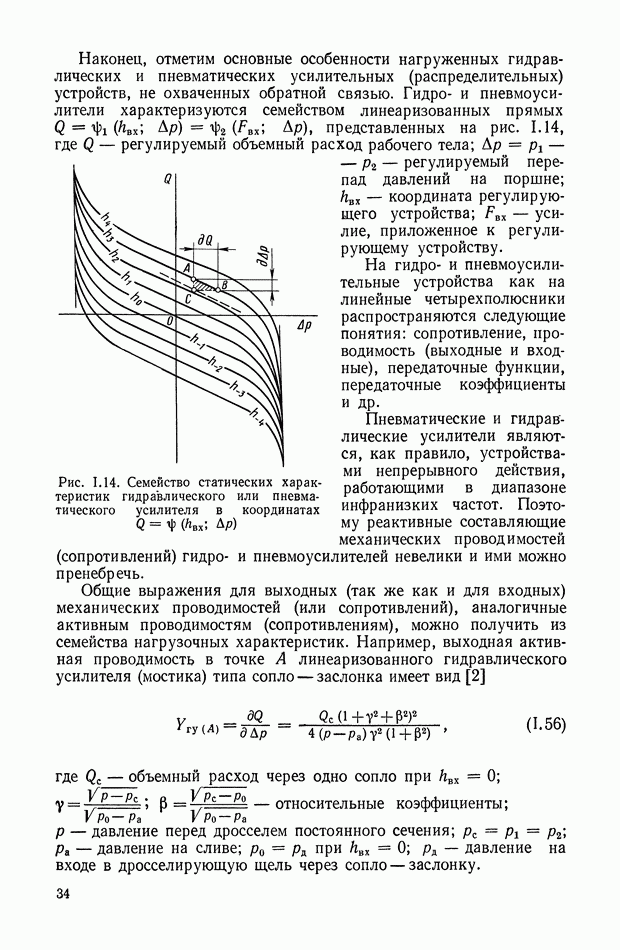
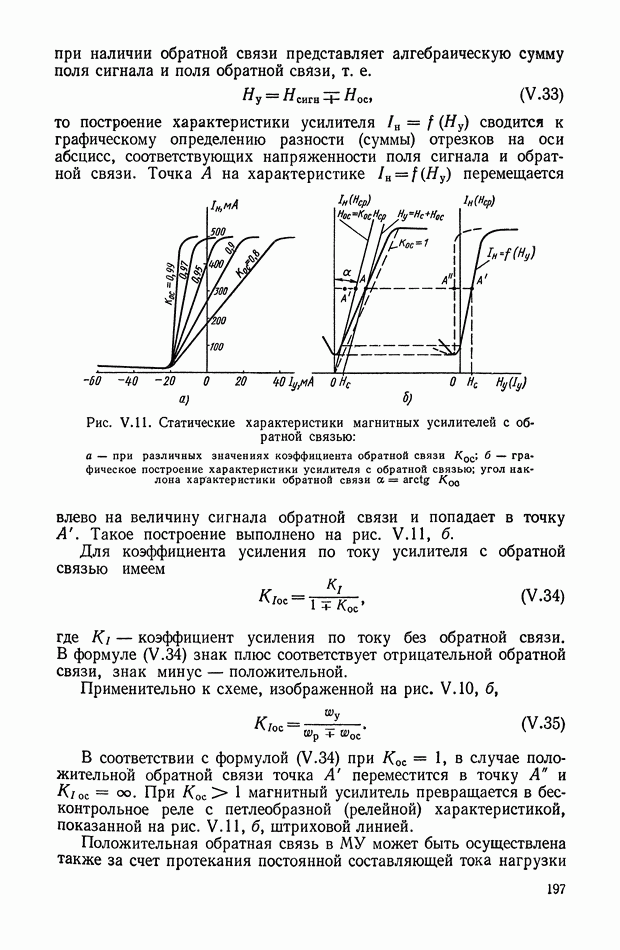
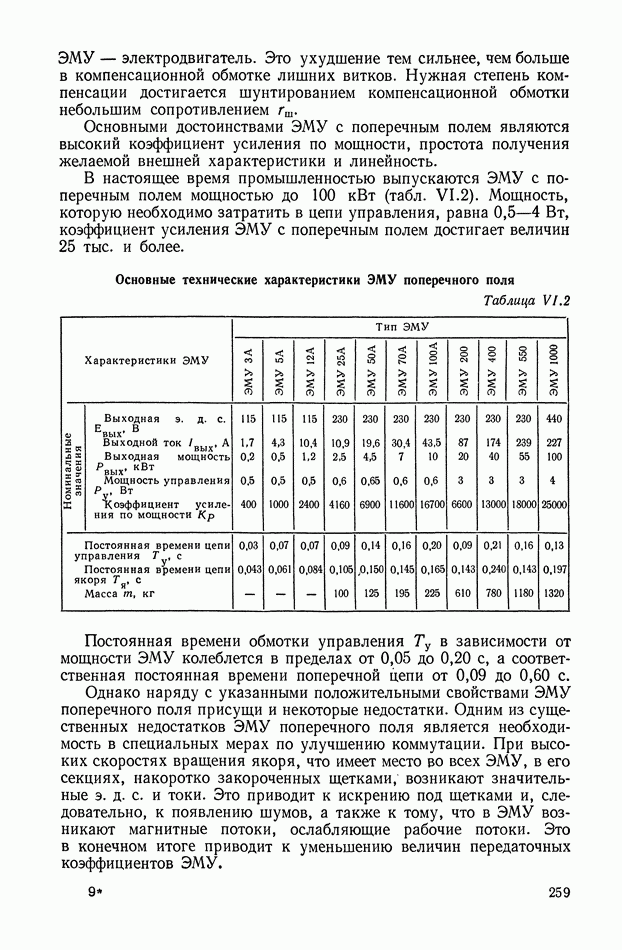
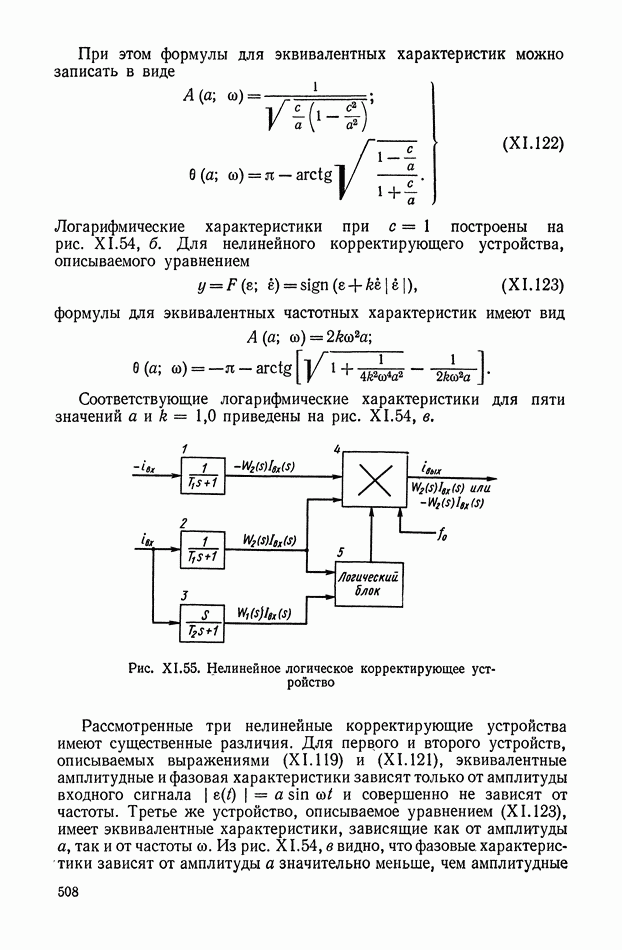
Рис. XI.40. Структурные схемы оптимальных систем управления объектом  с моделью
с моделью  а — с одним блоком умножения (БУ-1); б — с двумя блоками умножения (БУ-1 и БУ-2)
а — с одним блоком умножения (БУ-1); б — с двумя блоками умножения (БУ-1 и БУ-2)
Структурные схемы систем управления объектом [уравнение (X 1.85)] с органом управления, описываемым уравнением (X 1.91), с помощью ввода в корректирующее устройство функций  показаны на рис. XI.40, а и б.
показаны на рис. XI.40, а и б.
Пример XI.7. Рассмотрим выбор функции  для системы, описываемой уравнениями
для системы, описываемой уравнениями

Значения коэффициентов

Уравнение основной линии переключения (XI.87) имеет следующие параметры

На параболе  выберем точку с координатами
выберем точку с координатами  Постояйные
Постояйные  определим из уравнений
определим из уравнений

Откуда 
По формулам (XI.96) найдем координаты  принадлежащие дополнительной линии переключения.
принадлежащие дополнительной линии переключения.
Из уравнения (XI.83) найдем коэффициент наклона линии переключения, подставив значение координат  и значения параметров
и значения параметров  Значение
Значение  примем равным 1,5 с.
примем равным 1,5 с.
В результате нелинейная управляющая функция рассматриваемой системы будет описываться уравнениями

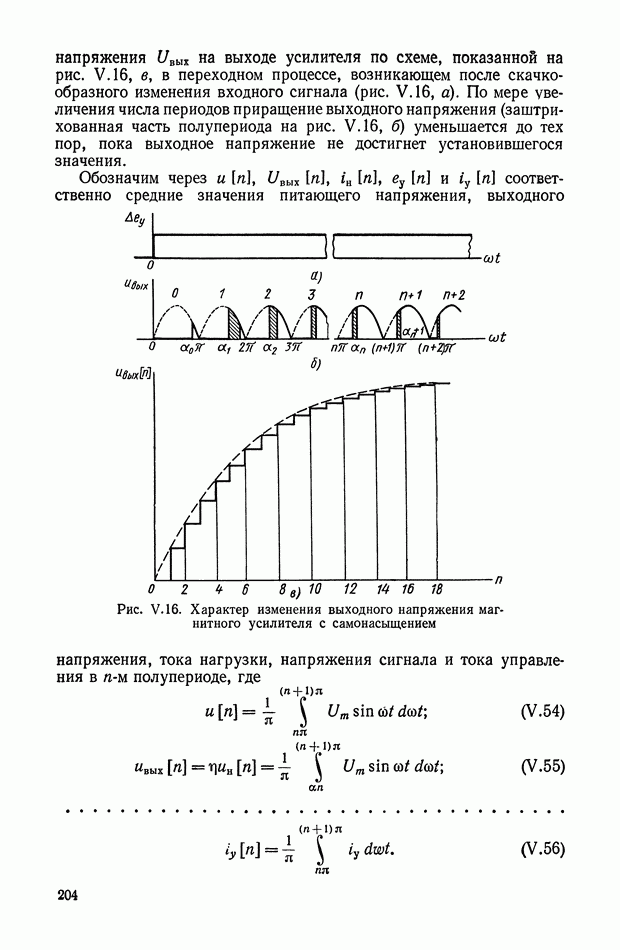
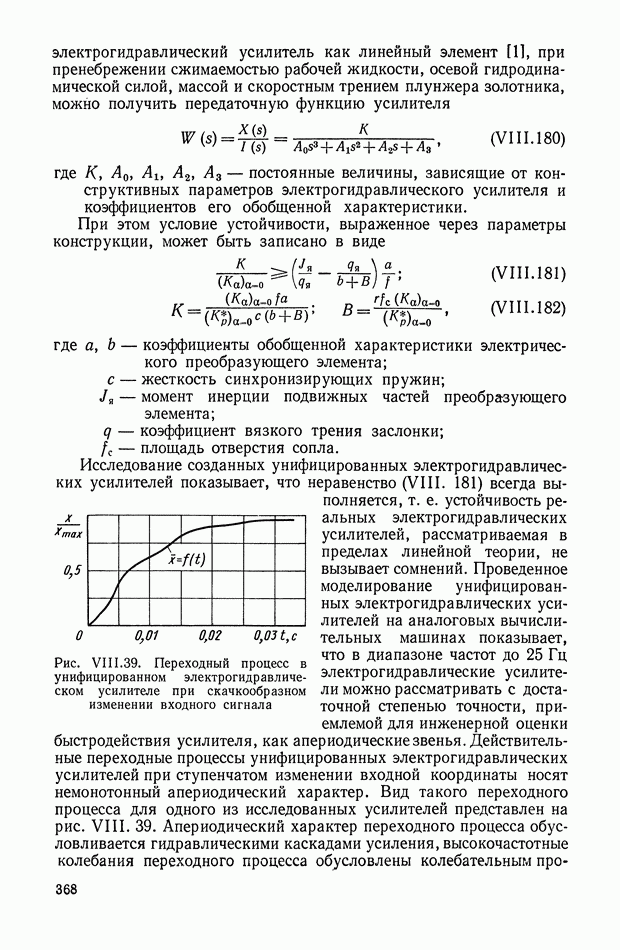
Моделирование на  показало, что переходные процессы в оптимальной системе с нелинейным корректирующим устройством (рис. 38, а) являются апериодическими. При учете динамики нелинейного исполнительного устройства, для квазиоптимальной системы (рис. 40, б) характер переходного процесса почти не изменяется. Время протекания процесса в этом случае возрастает не более чем на 5%.
показало, что переходные процессы в оптимальной системе с нелинейным корректирующим устройством (рис. 38, а) являются апериодическими. При учете динамики нелинейного исполнительного устройства, для квазиоптимальной системы (рис. 40, б) характер переходного процесса почти не изменяется. Время протекания процесса в этом случае возрастает не более чем на 5%.
В общем случае метод фазовой плоскости не позволяет синтезировать оптимальные законы управления для объектов произвольного порядка. Для решения этой задачи необходимо применять иные методы решения. Рассмотрим один из них.
Прежде всего заметим, что если  вектор начальных условий по переменной
вектор начальных условий по переменной  где
где  — оптимальное по быстродействию время управления, то значение оптимального управления в текущий момент времени равно
— оптимальное по быстродействию время управления, то значение оптимального управления в текущий момент времени равно

и, следовательно, управление как функция состояния системы определяется соотношением

Построим в пространстве  переменных
переменных  гиперплоскость
гиперплоскость

Опираясь на работу [19] и используя математический аппарат принципа максимума, можно показать, что если параметры  и
и  связаны уравнением
связаны уравнением

где

то  достигает максимума на множестве
достигает максимума на множестве  в точках которого
в точках которого

и

Из последних двух соотношений следует, что

Выясним связь между элементами  и текущим состоянием системы
и текущим состоянием системы  Обозначим через
Обозначим через  оператор проектирования вектора у на гиперплоскость
оператор проектирования вектора у на гиперплоскость  и выберем вектор
и выберем вектор  равным
равным  где
где

Тогда вектор  может быть найден из решения следующей системы операторных уравнений
может быть найден из решения следующей системы операторных уравнений

Данная система уравнений имеет единственное решение относительно неизвестных  которые могут быть определены, используя принцип сжатых отображений, по следующим рекурентным соотношениям:
которые могут быть определены, используя принцип сжатых отображений, по следующим рекурентным соотношениям:

Выражение оператора проектирования  можно найти, минимизируя норму
можно найти, минимизируя норму  при условии
при условии  где
где  — нормаль к гиперплоскости
— нормаль к гиперплоскости  Решение последней задачи приводит к следующему выражению для оператора проектирования:
Решение последней задачи приводит к следующему выражению для оператора проектирования:

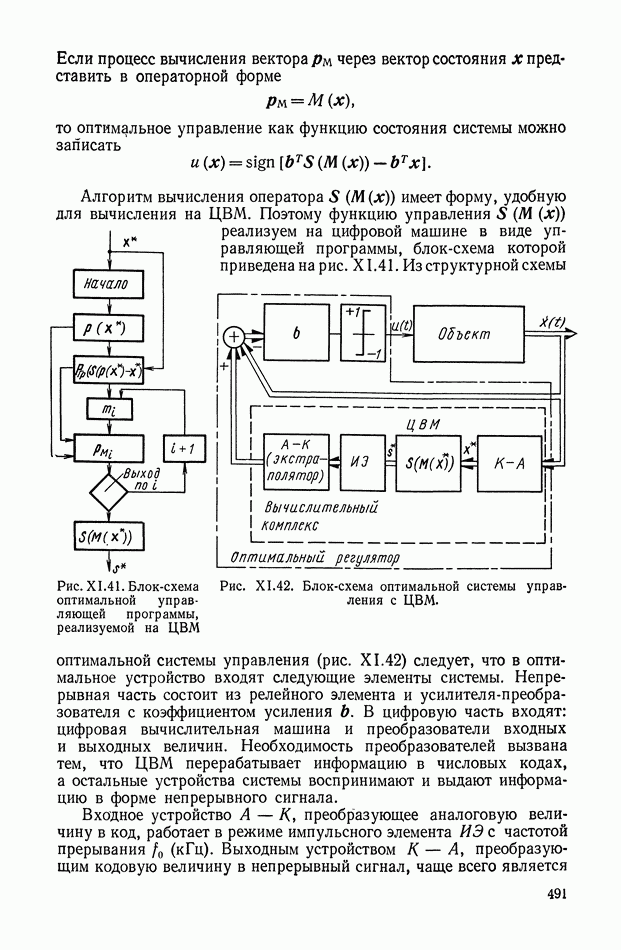
Если процесс вычисления вектора  через вектор состояния х представить в операторной форме
через вектор состояния х представить в операторной форме

то оптимальное управление как функцию состояния системы можно записать

Алгоритм вычисления оператора  имеет форму, удобную для вычисления на ЦВМ. Поэтому функцию управления
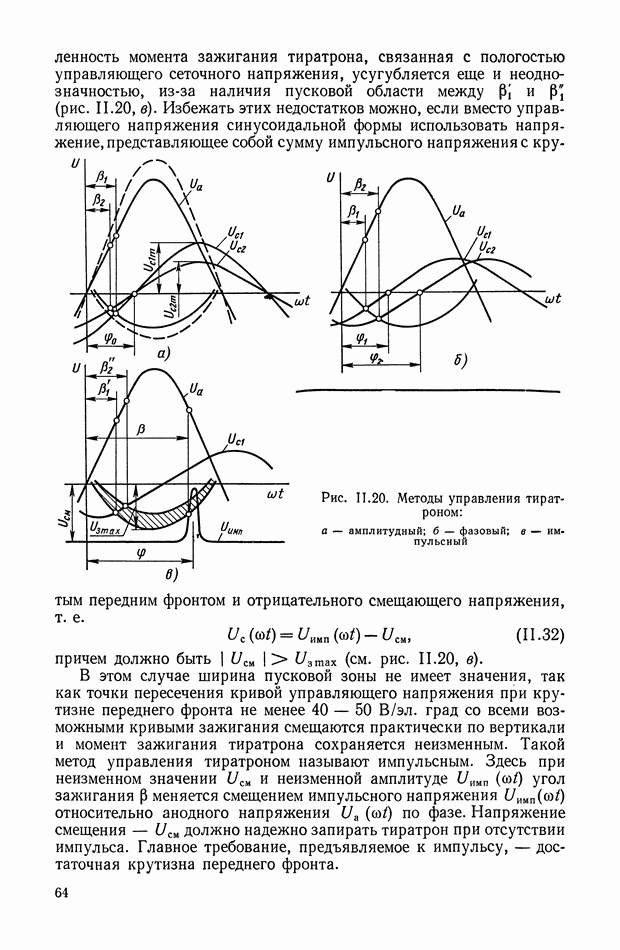
имеет форму, удобную для вычисления на ЦВМ. Поэтому функцию управления  реализуем на цифровой машине в виде управляющей программы, блок-схема которой приведена на рис. X 1.41.
реализуем на цифровой машине в виде управляющей программы, блок-схема которой приведена на рис. X 1.41.

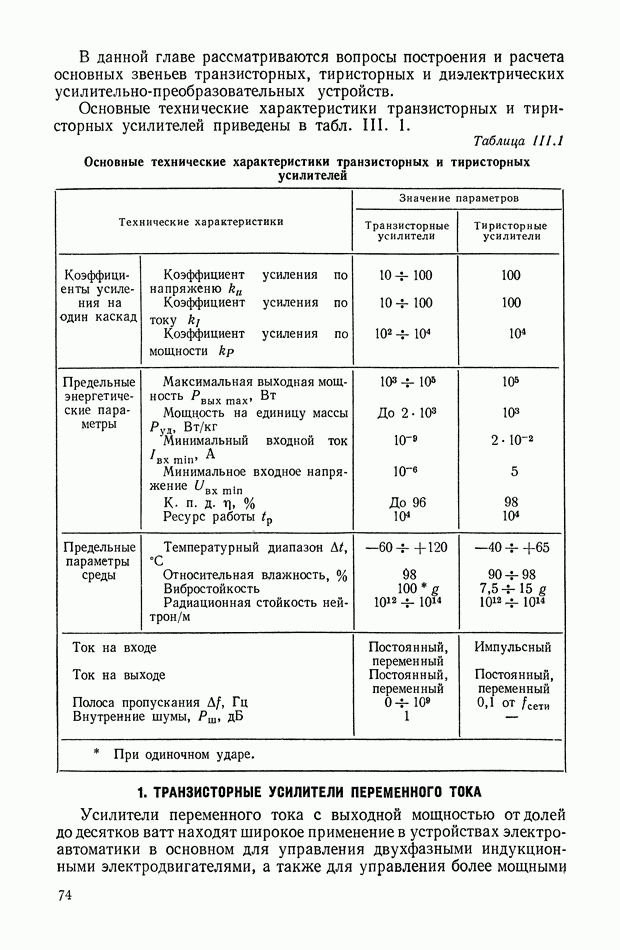
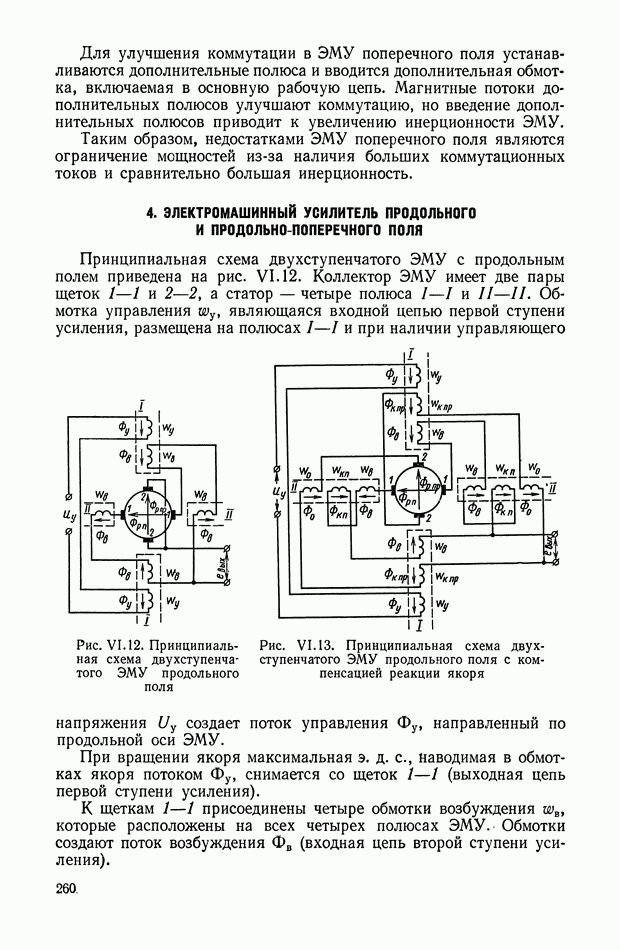
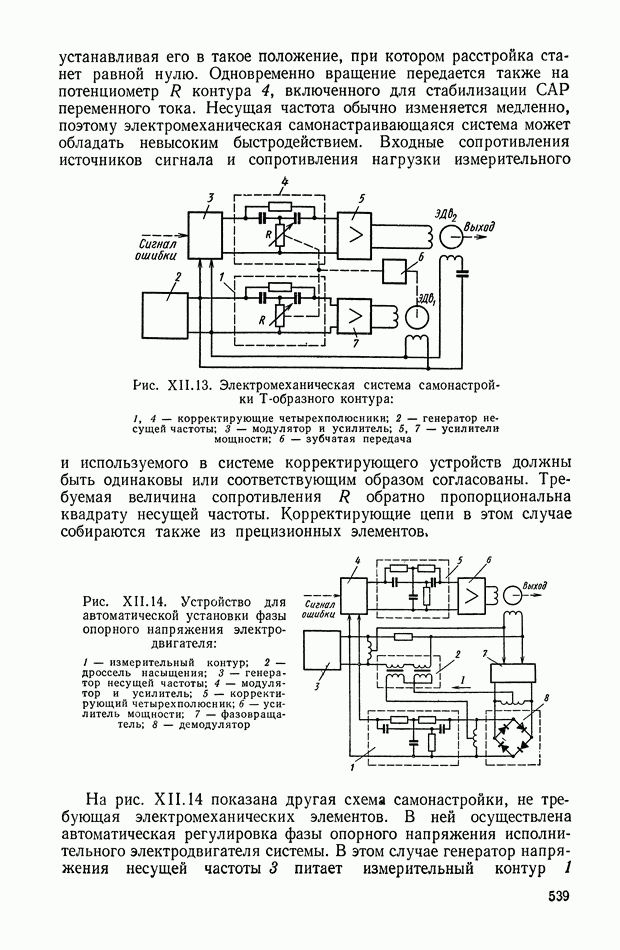
Рис. XI.41. Блок-схема оптимальной управляющей программы, реализуемой на ЦВМ

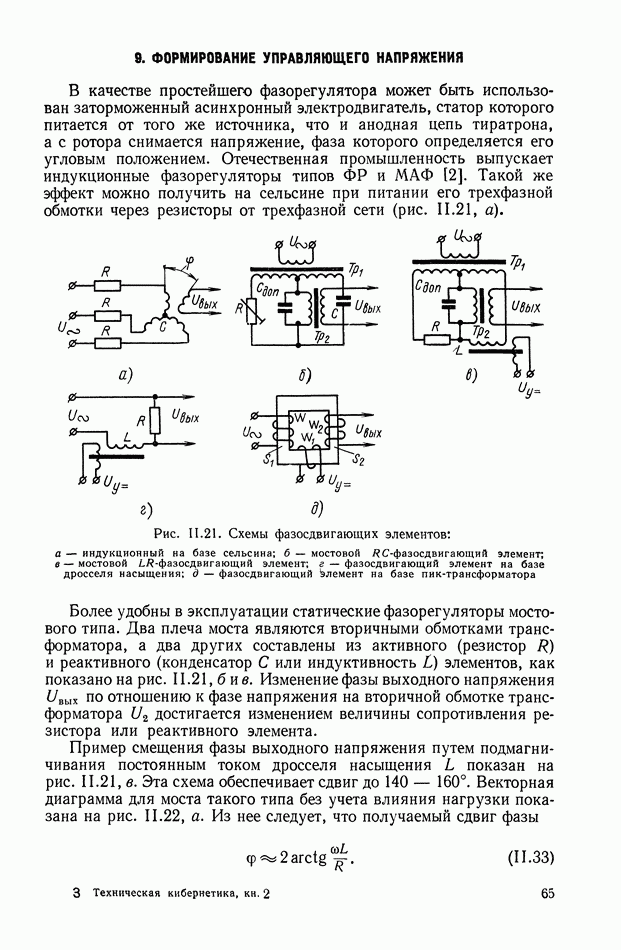
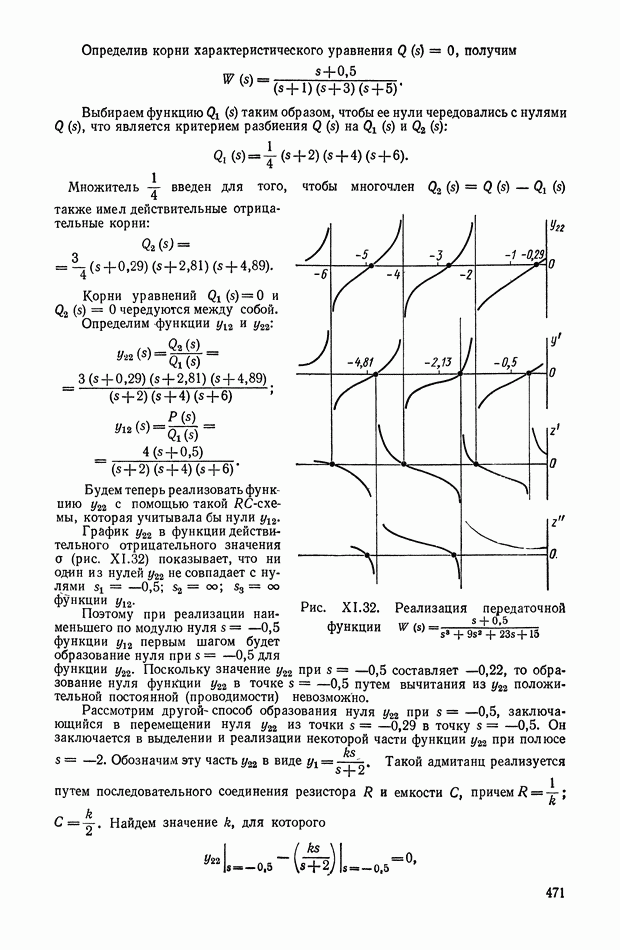
Рис. XI.42. Блок-схема оптимальной системы управления с ЦВМ.
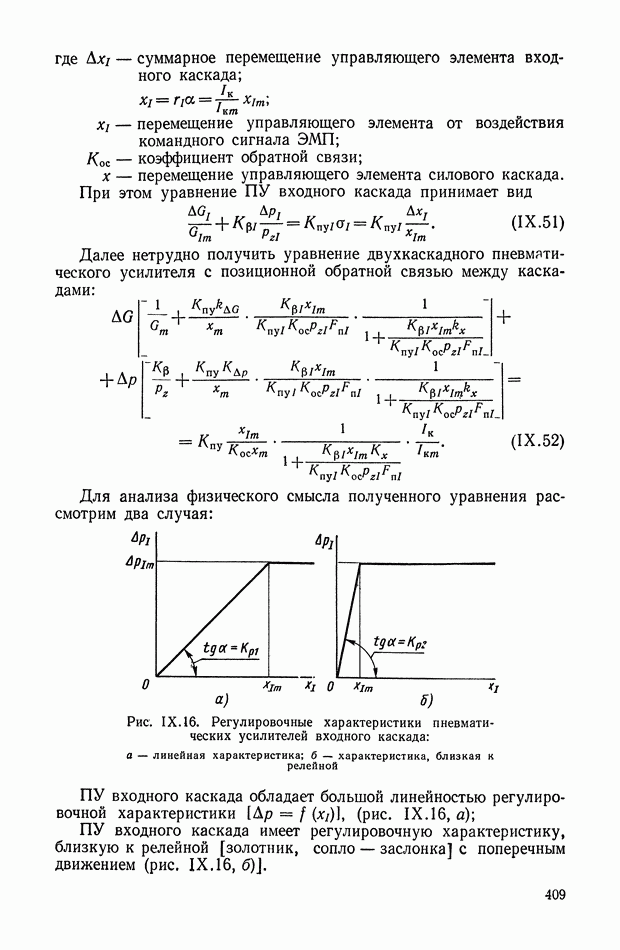
Из структурной схемы оптимальной системы управления (рис. XI.42) следует, что в оптимальное устройство входят следующие элементы системы. Непрерывная часть состоит из релейного элемента и усилителя-преобразователя с коэффициентом усиления  В цифровую часть входят: цифровая вычислительная машина и преобразователи входных и выходных величин. Необходимость преобразователей вызвана тем, что ЦВМ перерабатывает информацию в числовых кодах, а остальные устройства системы воспринимают и выдают информацию в форме непрерывного сигнала.
В цифровую часть входят: цифровая вычислительная машина и преобразователи входных и выходных величин. Необходимость преобразователей вызвана тем, что ЦВМ перерабатывает информацию в числовых кодах, а остальные устройства системы воспринимают и выдают информацию в форме непрерывного сигнала.
Входное устройство  преобразующее аналоговую величину в код, работает в режиме импульсного элемента
преобразующее аналоговую величину в код, работает в режиме импульсного элемента  с частотой прерывания
с частотой прерывания  Выходным устройством К — А, преобразующим кодовую величину в непрерывный сигнал, чаще всего является
Выходным устройством К — А, преобразующим кодовую величину в непрерывный сигнал, чаще всего является
экстраполятор нулевого порядка, передаточная функция которого имеет вид

Поскольку принцип работы ЦВМ дискретный, а исходная синтезируемая система непрерывная, то необходимо выяснить, каково влияние дискретного представления процесса управления на работу системы в целом.
Принято считать, что непрерывная система регулирования с цифровой машиной в контуре управления работает удовлетворительно, если такт работы машины  выбран из условия
выбран из условия

где  — полоса пропускания синтезируемой системы, а в межтактовые моменты времени система управления устойчива.
— полоса пропускания синтезируемой системы, а в межтактовые моменты времени система управления устойчива.
Динамика системы, представленной на рис. XI.41, в межтактовые моменты описывается следующим дифференциальным уравнением:

Данный класс систем относится к системам регулирования, в которых управление синтезировано на основе минимизации функции Ляпунова, взятой в виде нормы вектора состояния системы. Действительно, в этом случае

имеет минимум по  при
при  если
если  выбрано из условия
выбрано из условия

Следовательно, система (рис. XI. 42) устойчива, если вещественные части собственных значений матрицы А не положительны. Это говорит о возможности реализации оптимальной системы управления в виде блок-схемы, приведенной на рис. XI.42.
Рассмотрим способы реализации оптимального нелинейного корректирующего устройства с помощью аналоговых элементов.
Построение преобразователя функции многих переменных.
В результате синтеза оптимального управления некоторая синтезирующая функция определена как функция координат объекта управления. Пусть начало координат фазового пространства системы  может быть достигнуто из любых начальных точек
может быть достигнуто из любых начальных точек  и существует единственное оптимальное управление, переводящее изображающую точку в начало координат. Тогда функция оптимального управления будет однозначной функцией фазового пространства. Для рассматриваемого типа систем эти функции могут допускать разрывы лишь первого рода.
и существует единственное оптимальное управление, переводящее изображающую точку в начало координат. Тогда функция оптимального управления будет однозначной функцией фазового пространства. Для рассматриваемого типа систем эти функции могут допускать разрывы лишь первого рода.
Задача построения корректирующего элемента сводится к задаче построения такого вычислительного устройства, что если на его входы подаются значения текущих координат объекта управления, то на выходе автоматически получаются существующие значения функции и  Естественно требование, чтобы это устройство состояло из стандартных, наиболее простых элементов и обеспечивало необходимую точность вычисления.
Естественно требование, чтобы это устройство состояло из стандартных, наиболее простых элементов и обеспечивало необходимую точность вычисления.
Создание вычислительного устройства может быть получено в виде функции многих переменных, аппроксимируемых рядом функций одной переменной. Достоинство этих методов разложения заключается в том, что они обеспечивают наибыстрейшую сходимость разложения, максимальное упрощение электрической схемы и любую, практически необходимую степень разложения путем присоединения дополнительных вычислительных узлов. Для построения всей схемы в общем случае необходимы: нелинейное преобразование функции одной переменной, сложение и умножение. Такая цепочка практически безынерционна и может работать как на постоянном, так и на переменном токе прямоугольной формы. Действительно, эти операции выполняются достаточно просто и не требуют той стабилизации несущей частоты, которая необходима для реактивных корректирующих контуров, работающих на переменном токе 
Рассмотрим несколько подробнее процедуру аппроксимации функции и  Критерий приближения во всех случаях — минимум среднеквадратичной оценки
Критерий приближения во всех случаях — минимум среднеквадратичной оценки

где  — аппроксимирующая функция;
— аппроксимирующая функция;
 — число координат системы (порядок уравнения движения).
— число координат системы (порядок уравнения движения).
Для упрощения допустим, что среднее значение  . Если же
. Если же  имеет некоторое значение, то можно рассматривать функцию
имеет некоторое значение, то можно рассматривать функцию  т. е. сделанное предположение не нарушает общности рассуждений. Отметим, что уравнение и
т. е. сделанное предположение не нарушает общности рассуждений. Отметим, что уравнение и  может быть разрешено относительно
может быть разрешено относительно 
Поэтому для реализации корректирующего устройства системы  порядка необходимо аппроксимировать поверхность порядка
порядка необходимо аппроксимировать поверхность порядка  Рассматриваемые методы аппроксимации, вообще говоря, не ограничены порядком уравнения поверхности, однако при
Рассматриваемые методы аппроксимации, вообще говоря, не ограничены порядком уравнения поверхности, однако при  они представляют значительные трудности как в плане вычислений, так и аппаратурной реализации.
они представляют значительные трудности как в плане вычислений, так и аппаратурной реализации.
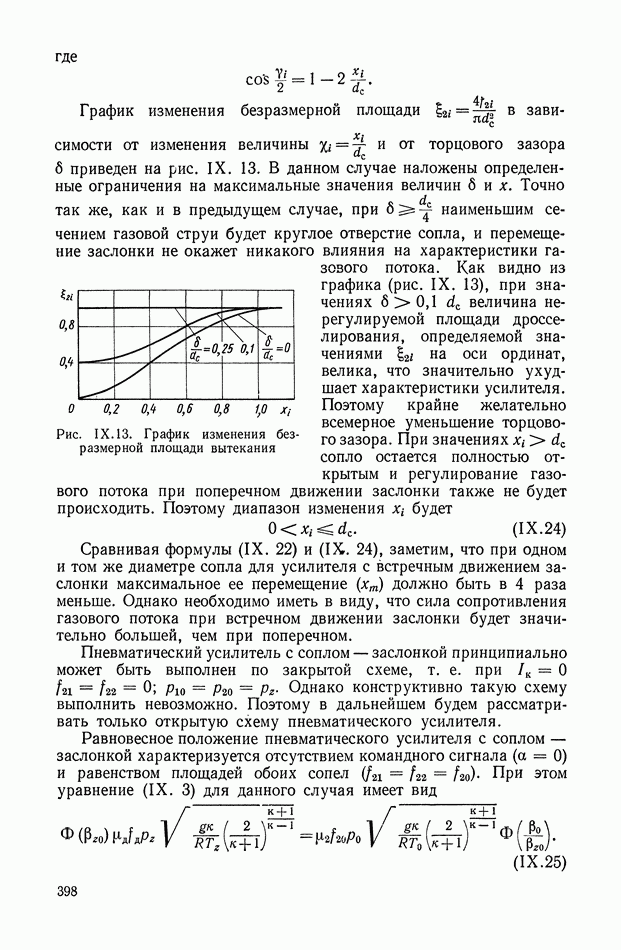
Вне зависимости от порядка уравнения движения функции  для упрощения вычислений лучше задавать не аналитически, а в виде таблиц дискретных значений х с некоторым шагом, который выбирают опытным путем с учетом вида аппроксимируемой функции (как правило, практически бывает достаточно
для упрощения вычислений лучше задавать не аналитически, а в виде таблиц дискретных значений х с некоторым шагом, который выбирают опытным путем с учетом вида аппроксимируемой функции (как правило, практически бывает достаточно  точек на каждой интегральной кривой).
точек на каждой интегральной кривой).
Аппроксимация функции одной переменной  заданной в
заданной в  дискретных точках как
дискретных точках как  осуществляется наиболее просто полиномом
осуществляется наиболее просто полиномом

Коэффициенты  находят из условия минимума суммы
находят из условия минимума суммы

Действительно, так как  при
при  то система уравнений для коэффициентов
то система уравнений для коэффициентов  будет иметь вид:
будет иметь вид:

Опыт проектирования таких систем показывает, что к может быть ограничено значениями 0, 1, 2, т. е. 
Процедура выбора оптимального нелинейного корректирующего устройства для САР второго порядка существенно упрощается, если проектировщик располагает  любого типа. В этом случае набирается разомкнутая структура объекта регулирования и выходные координаты
любого типа. В этом случае набирается разомкнутая структура объекта регулирования и выходные координаты  подаются на электронный индикатор для построения фазового портрета. Одновременно с отдельного интегратора
подаются на электронный индикатор для построения фазового портрета. Одновременно с отдельного интегратора  сигнал пилообразной формы подается на нелинейную цепочку. Величина напряжения с интегратора согласовывается с величиной напряжения реального датчика координаты
сигнал пилообразной формы подается на нелинейную цепочку. Величина напряжения с интегратора согласовывается с величиной напряжения реального датчика координаты  а развертка луча — с координатой
а развертка луча — с координатой 
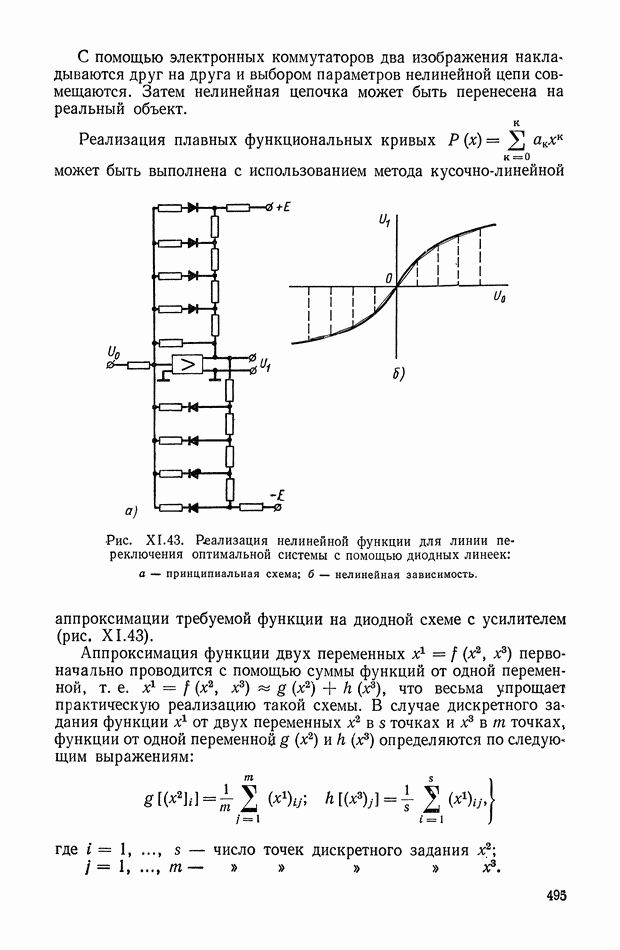
С помощью электронных коммутаторов два изображения накладываются друг на друга и выбором параметров нелинейной цепи совмещаются. Затем нелинейная цепочка может быть перенесена на реальный объект.
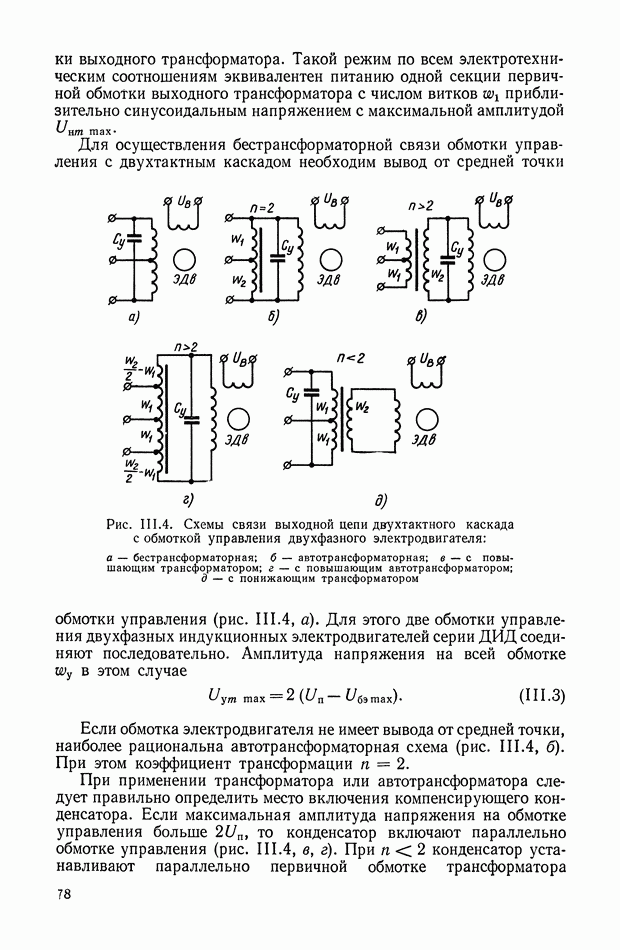
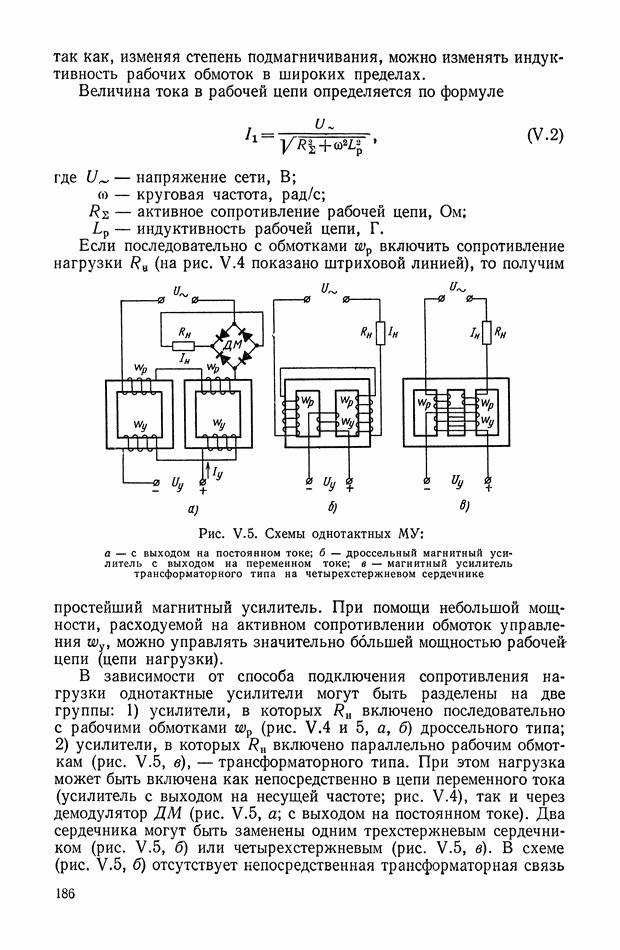
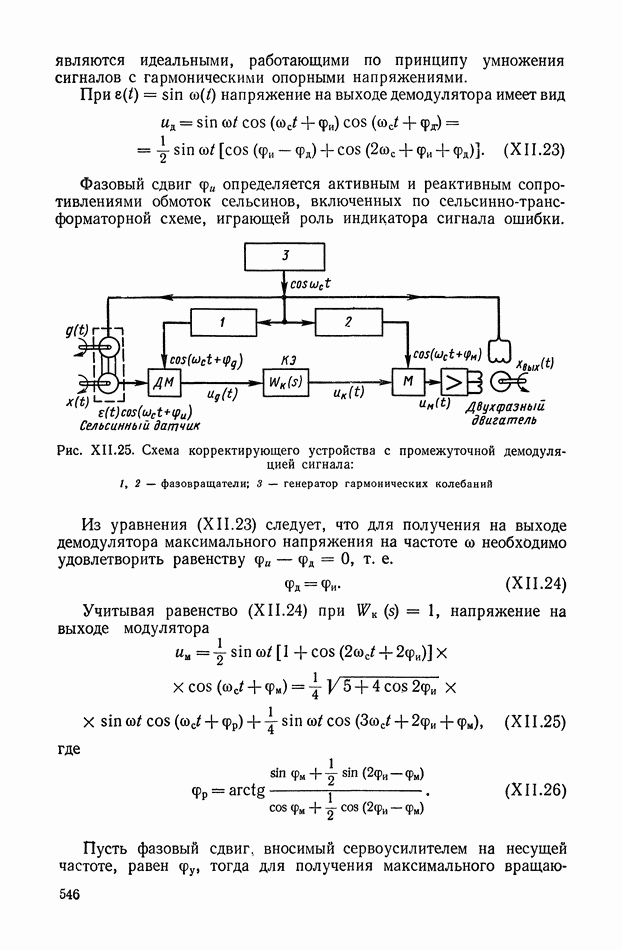
Реализация плавных функциональных кривых  может быть выполнена с использованием метода кусочно-линейной аппроксимации требуемой функции на диодной схеме с усилителем (рис. XI.43).
может быть выполнена с использованием метода кусочно-линейной аппроксимации требуемой функции на диодной схеме с усилителем (рис. XI.43).

Рис. XI.43. Реализация нелинейной функции для линии переключения оптимальной системы с помощью диодных линеек: а — принципиальная схема; б — нелинейная зависимость.
Аппроксимация функции двух переменных  первоначально проводится с помощью суммы функций от одной переменной, т. е.
первоначально проводится с помощью суммы функций от одной переменной, т. е.  что весьма упрощает практическую реализацию такой схемы. В случае дискретного задания функции
что весьма упрощает практическую реализацию такой схемы. В случае дискретного задания функции  от двух переменных
от двух переменных  в
в  точках и
точках и  точках, функции от одной переменной
точках, функции от одной переменной  определяются по следующим выражениям:
определяются по следующим выражениям:

где  — число точек дискретного задания
— число точек дискретного задания 

Зададим функцию  в виде таблицы:
в виде таблицы:

Для оценки погрешности аппроксимации оценим дисперсию

где  и максимальное отклонение
и максимальное отклонение

В случае больших ошибок аппроксимации приближающий ряд продолжается, т. е. добавляются члены, компенсирующие остаток  который можно представить как
который можно представить как

Причем  раскладываем в виде:
раскладываем в виде:

Хотя верхний предел суммы является бесконечным, но практически при  (максимум
(максимум  )
)  . Функции
. Функции  и
и  определяются из условия
определяются из условия

При этом

откуда

Приведенные уравнения решаются методом последовательных приближений. Сначала задаются значениями  или
или  и на основе этих значений методом итерации постепенно приближаются к истинным значениям функций
и на основе этих значений методом итерации постепенно приближаются к истинным значениям функций 
Составляя таблицу вторичных разностей 

вычисляют 
В случае необходимости аналогичным образом определяются  Однако следует помнить, что члены
Однако следует помнить, что члены  входят в аппроксимирующий ряд в виде произведений, т. е. в схему надо вводить множительные блоки. Аппроксимация функции трех переменных
входят в аппроксимирующий ряд в виде произведений, т. е. в схему надо вводить множительные блоки. Аппроксимация функции трех переменных  производится аналогично.
производится аналогично.
В первом приближении  можно представить как сумму функций одной переменной (в дискретном задании)
можно представить как сумму функций одной переменной (в дискретном задании)

где  — точки задания функции.
— точки задания функции.
Члены ряда  находятся из следующих выражений:
находятся из следующих выражений:

где  — переменные
— переменные  взятые при нулевых значениях по осям
взятые при нулевых значениях по осям  соответственно.
соответственно.
При недопустимо высоком остатке  ряд дополняется членами, которые в совокупности приближают остаток
ряд дополняется членами, которые в совокупности приближают остаток  к виду
к виду

определяемый аналогично вышеизложенному. Однако даже при  требуется два множительных блока, что усложняет реализацию корректирующего устройства.
требуется два множительных блока, что усложняет реализацию корректирующего устройства.
В рассматриваемых задачах корректирующее устройство, представляющее собой преобразователь функции многих переменных, может быть реализовано суммированием ряда функций от одной переменной. Наиболее просто производится реализация электрическими схемами одномерных преобразователей с распространенными функциональными зависимостями.
Зависимости кусочно-линейного типа реализуются диодными схемами, расчет которых производится на основе вольт-амперных характеристик используемого диода.
Нелинейные функции одной переменной, из которых обычно составляются схемы нелинейной коррекции, как правило, имеют вид, близкий к нечетным степенным функциям.

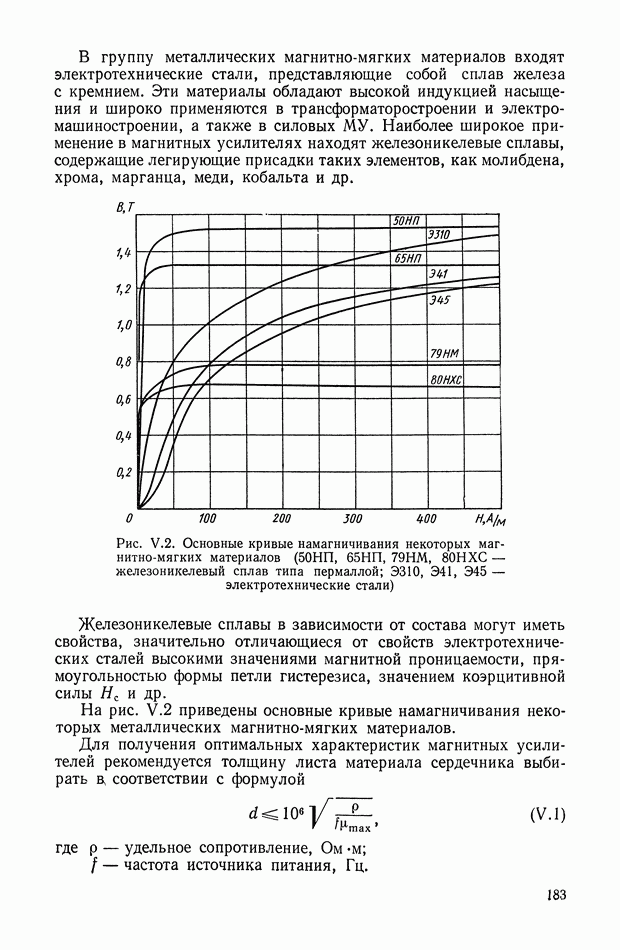
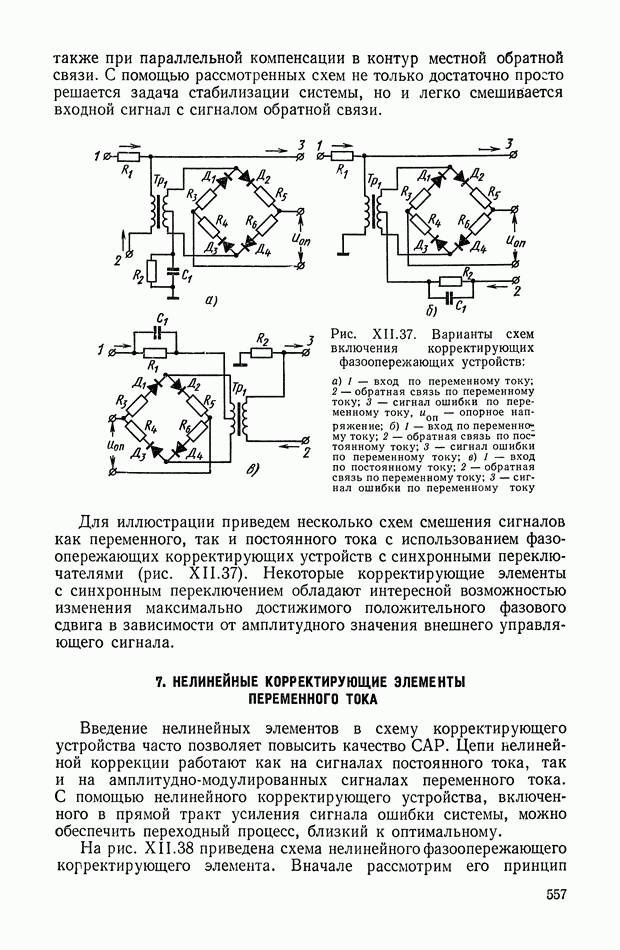
Рис. XI.44. Реализация нелинейной функции с помощью варистора и резисторов
В этих случаях их проще всего реализовывать с помощью комбинации нелинейных сопротивлений (варисторов) и линейных сопротивлений (резисторов).
Варисторы (тириты) выпускаются в настоящее время в различных модификациях, отличающихся друг от друга как электрическими параметрами, так и конструктивным оформлением. Вольт-амперные характеристики варисторов могут быть симметричны относительно начала координат и несимметричны. Характеризуются они показательными функциями типа

с различными значениями параметров.
Учитывая вид вольт-амперных характеристик варисторов и вид нелинейных функций, выбираем такие параметры схемы (рис. XI.44), которые позволят изменить характеристики варисторов необходимым образом.
Резисторы  служат для изменения характеристики варистора и выбора положения рабочей точки. Резистор с учетом сопротивления нагрузки
служат для изменения характеристики варистора и выбора положения рабочей точки. Резистор с учетом сопротивления нагрузки  устанавливает необходимый масштаб
устанавливает необходимый масштаб  для согласования с последующими цепями (например, с сумматором). При этом должно выполняться условие
для согласования с последующими цепями (например, с сумматором). При этом должно выполняться условие  Существуют и другие способы реализации нелинейных корректирующих устройств, которые рассматриваются в следующих параграфах данной главы.
Существуют и другие способы реализации нелинейных корректирующих устройств, которые рассматриваются в следующих параграфах данной главы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА САР
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ЛИНЕЙНЫХ УСИЛИТЕЛЬНЫХ УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ УСИЛИТЕЛЬНОГО УСТРОЙСТВА БЕЗ ОБРАТНОЙ СВЯЗИ
- 3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ, СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ОСОБЕННОСТИ УСИЛИТЕЛЬНОГО УСТРОЙСТВА С ОБРАТНОЙ СВЯЗЬЮ
- 4. КЛАССИФИКАЦИЯ И СВОЙСТВА УСИЛИТЕЛЬНЫХ УСТРОЙСТВ С ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 5. ВЫБОР И РАСЧЕТ УСИЛИТЕЛЬНОГО УСТРОЙСТВА
- ГЛАВА II. ЭЛЕКТРОННЫЕ ЛАМПОВЫЕ И ИОННЫЕ УСИЛИТЕЛИ
- 1. ОСНОВЫ ТОПОЛОГИЧЕСКОГО АНАЛИЗА СХЕМ ЛИНЕЙНЫХ ЭЛЕКТРОННЫХ ЛАМПОВЫХ УСИЛИТЕЛЕЙ
- 2. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПОСТОЯННОГО ТОКА
- 3. БАЛАНСНЫЕ МОСТОВЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- 4. СТАБИЛИЗАЦИЯ КОЭФФИЦИЕНТА УСИЛЕНИЯ
- 5. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- 6. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- 7. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
- 8. ОБЩИЕ СВОЙСТВА ИОННОГО (ТИРАТРОННОГО) УСИЛИТЕЛЯ МЕТОДЫ УПРАВЛЕНИЯ ТИРАТРОНОМ
- 9. ФОРМИРОВАНИЕ УПРАВЛЯЮЩЕГО НАПРЯЖЕНИЯ
- 10. РАСЧЕТ ЭЛЕМЕНТОВ СХЕМ ТИРАТРОННОГО УСИЛИТЕЛЯ
- ГЛАВА III. ПОЛУПРОВОДНИКОВЫЕ И ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
- Цепи смещения.
- Цепи связи.
- 2. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ СРЕДНЕГО ЗНАЧЕНИЯ ТОКА
- Полупроводниковые демодуляторы.
- 3. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ В РЕЖИМЕ ПЕРЕКЛЮЧЕНИЯ
- Режимы импульсного регулирования мощности.
- Управление силовыми транзисторами.
- 4. ТРАНЗИСТОРНЫЕ УСТРОЙСТВА УПРАВЛЕНИЯ ЭЛЕКТРОДВИГАТЕЛЯМИ И ЭЛЕКТРОМАГНИТНЫМИ МЕХАНИЗМАМИ
- 5. ТИРИСТОРЫ. ХАРАКТЕРИСТИКИ, ПАРАМЕТРЫ И СВОЙСТВА
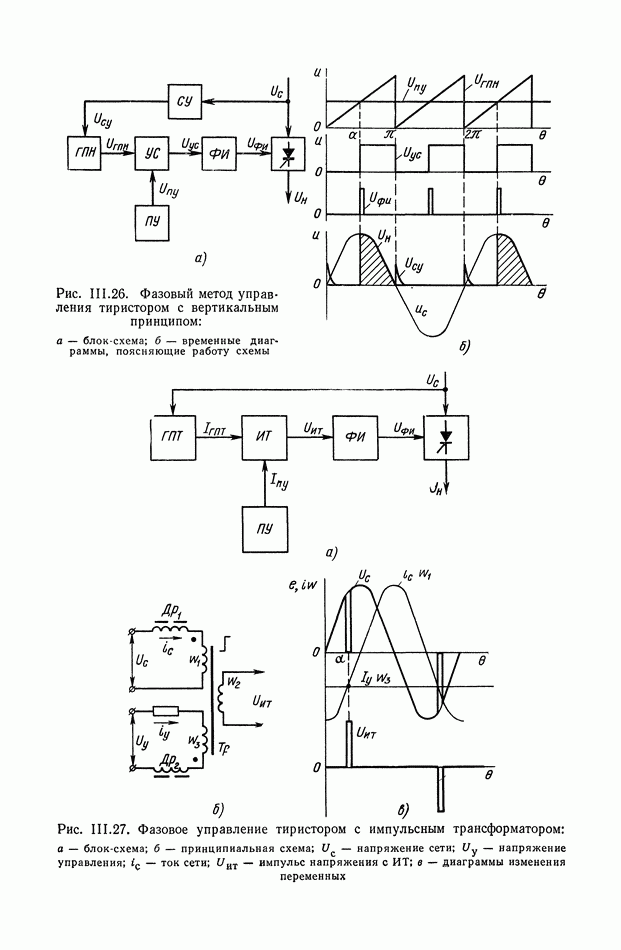
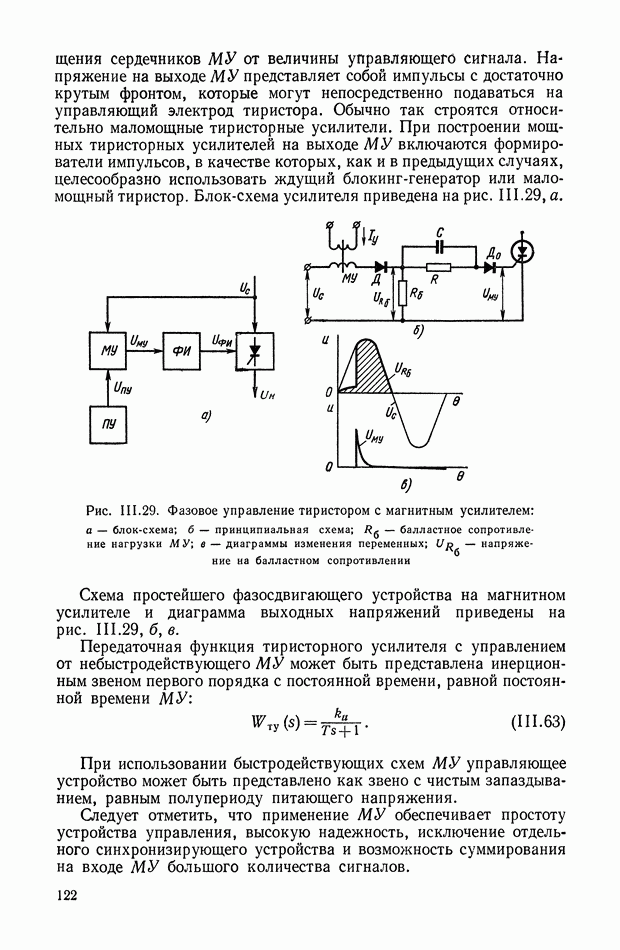
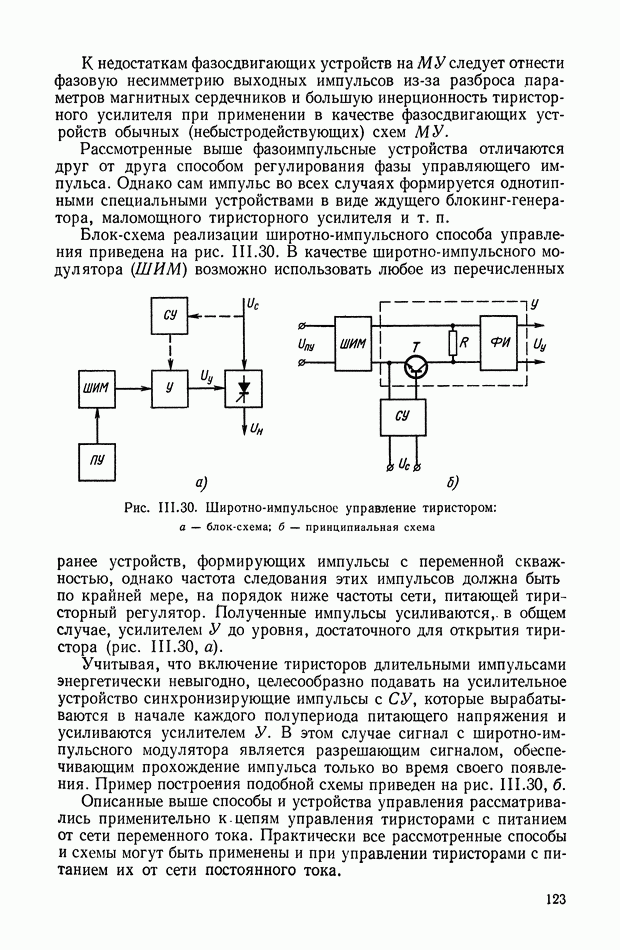
- 6. СПОСОБЫ И УСТРОЙСТВА УПРАВЛЕНИЯ ТИРИСТОРАМИ
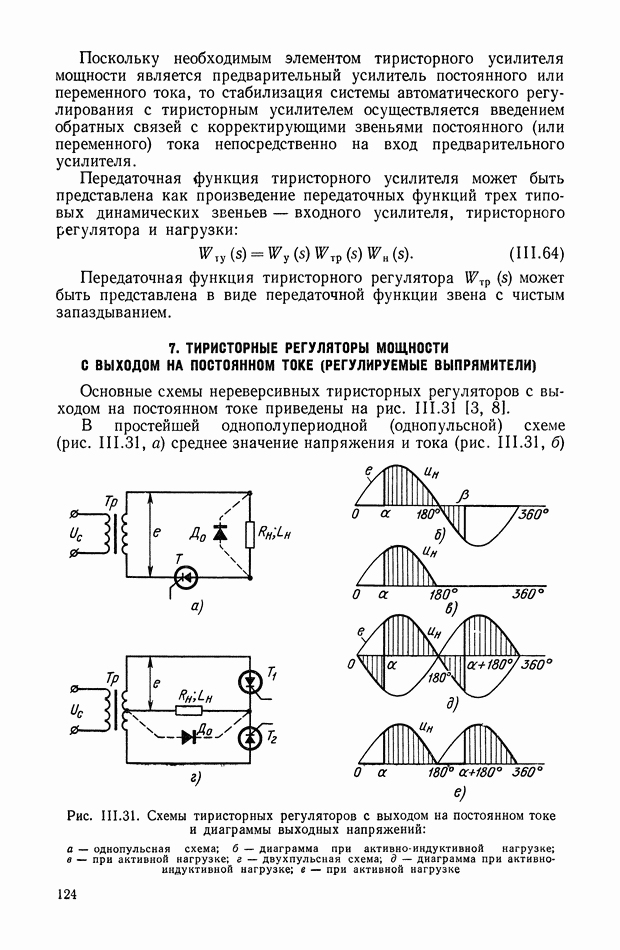
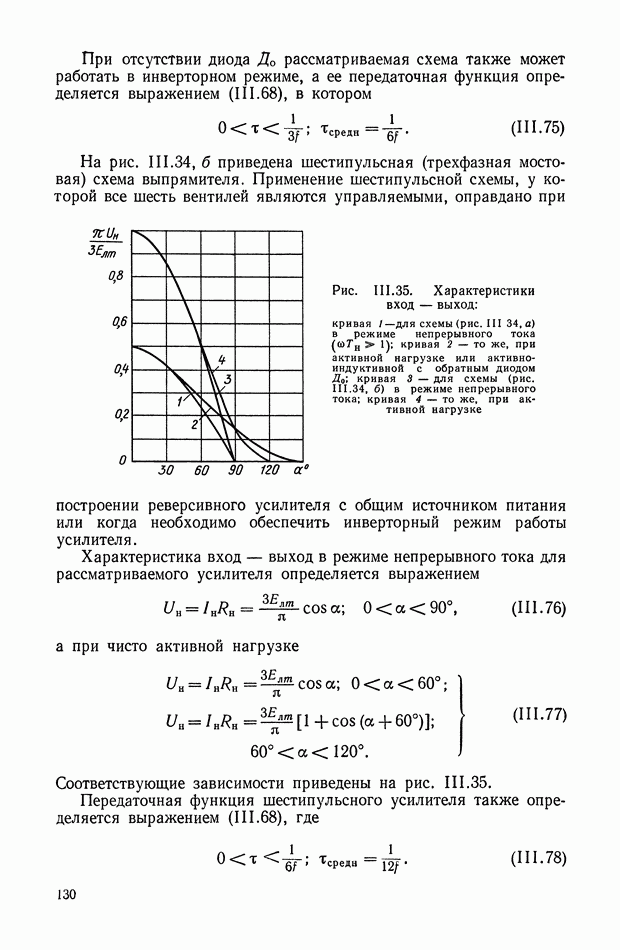
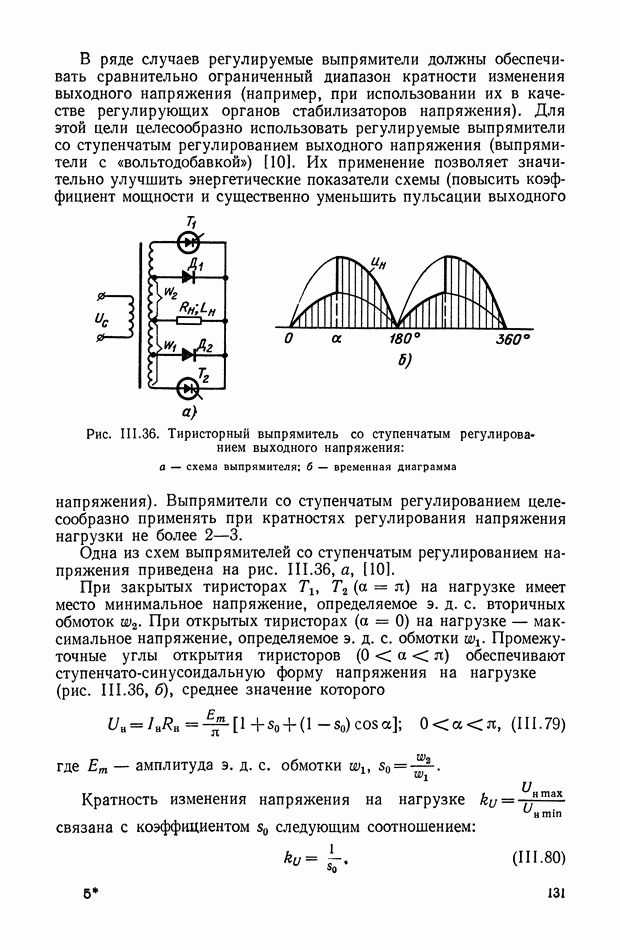
- 7. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ (РЕГУЛИРУЕМЫЕ ВЫПРЯМИТЕЛИ)
- 8. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 9. ТИРИСТОРНЫЕ УСИЛИТЕЛИ С ПИТАНИЕМ ОТ СЕТИ ПОСТОЯННОГО ТОКА
- 10. ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 11. ОСНОВЫ РАСЧЕТА ДИЭЛЕКТРИЧЕСКИХ УСИЛИТЕЛЕЙ
- ГЛАВА IV. КВАНТОВЫЕ УСИЛИТЕЛИ И ГЕНЕРАТОРЫ
- 2. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ РАДИОДИАПАЗОНА
- Квантовые усилители радиодиапазона.
- 3. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- Оптический квантовый усилитель
- 4. ПРИМЕНЕНИЕ В САР КВАНТОВЫХ УСИЛИТЕЛЕЙ И ГЕНЕРАТОРОВ РАДИОДИАПАЗОНА, ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- ГЛАВА V. МАГНИТНЫЕ И МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- 2. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ МАГНИТНЫХ УСИЛИТЕЛЕЙ
- 3. ОДНОТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ БЕЗ ОБРАТНОЙ СВЯЗИ (УПРАВЛЯЕМЫЕ ДРОССЕЛИ И ТРАНСФОРМАТОРЫ)
- 4. МАГНИТНЫЕ УСИЛИТЕЛИ С САМОНАСЫЩЕНИЕМ
- Релейный режим работы усилителей с самонасыщением.
- 5. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 6. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ
- 7. МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- ГЛАВА VI. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 2. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С НЕЗАВИСИМЫМ ВОЗБУЖДЕНИЕМ И С САМОВОЗБУЖДЕНИЕМ
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С ПОПЕРЕЧНЫМ ПОЛЕМ
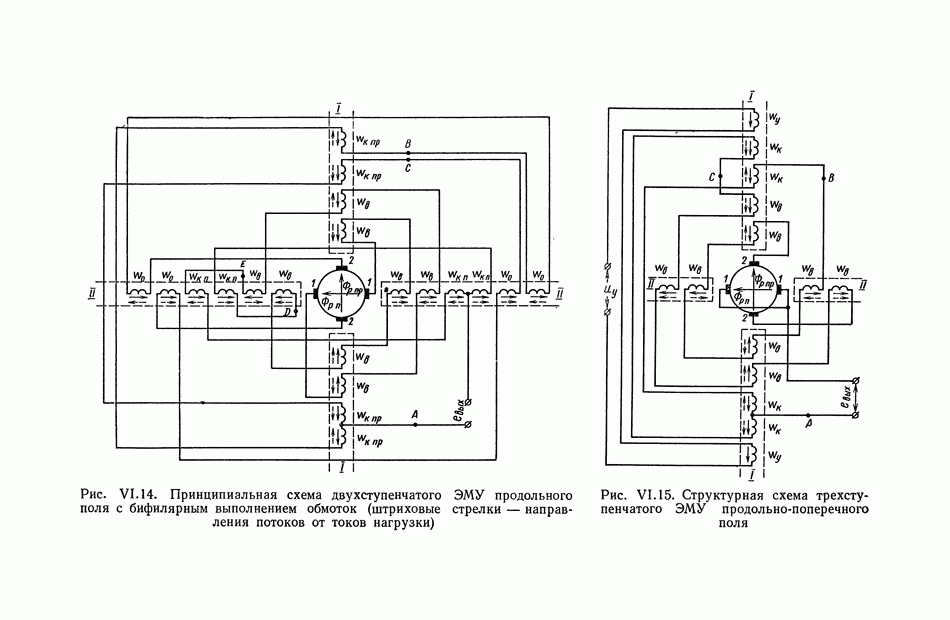
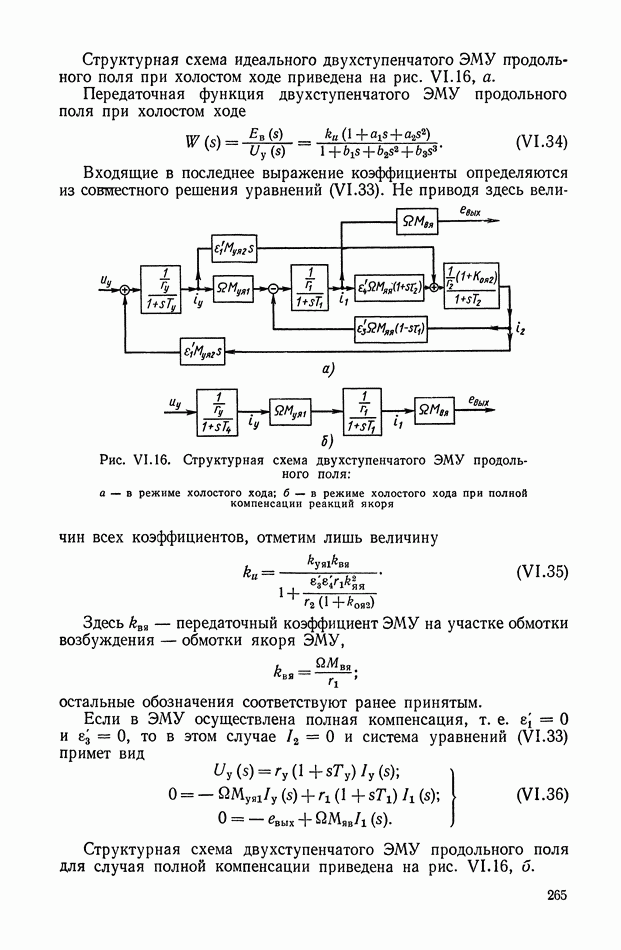
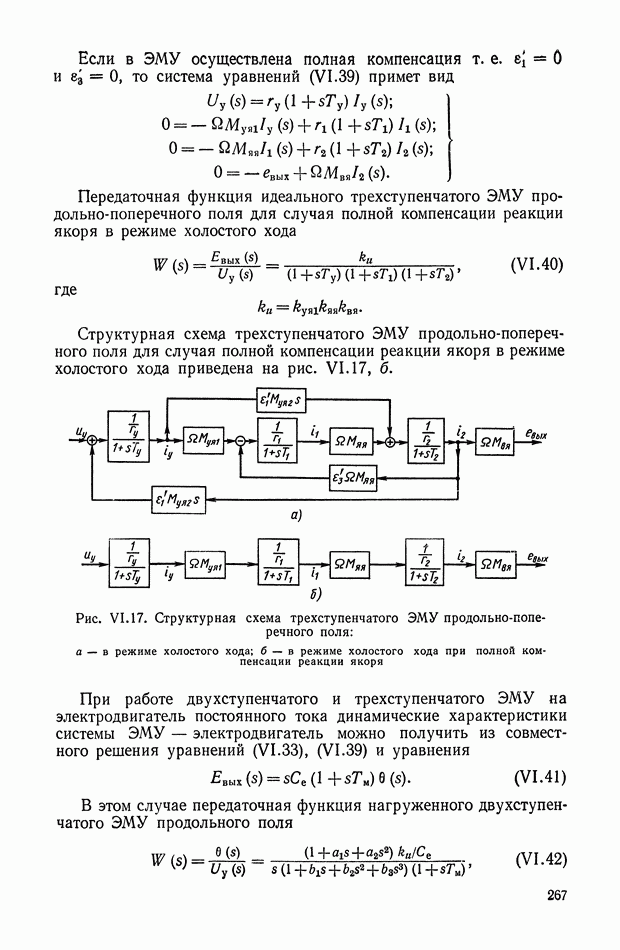
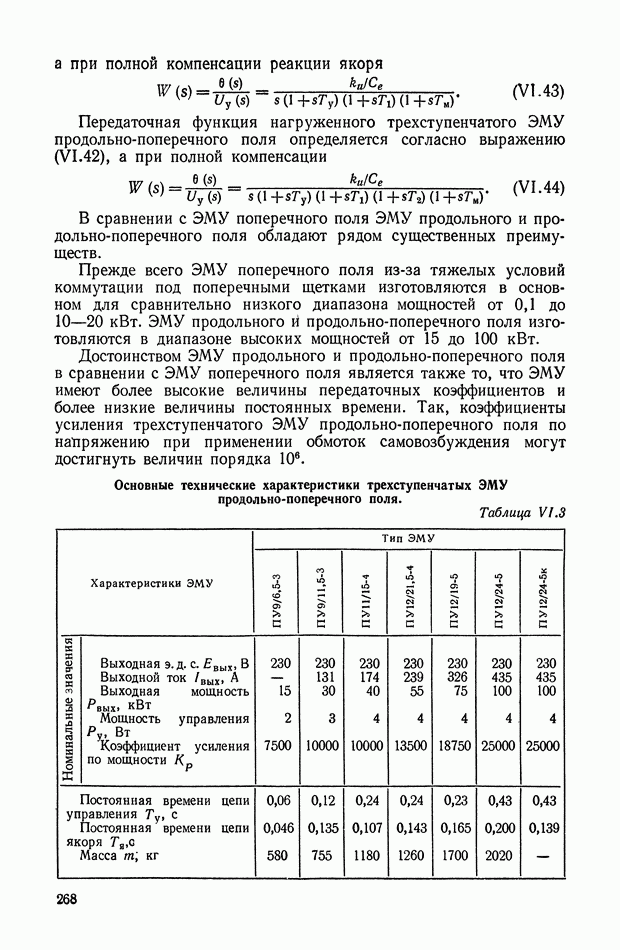
- 4. ЭЛЕКТРОМАШИННЫЙ УСИЛИТЕЛЬ ПРОДОЛЬНОГО И ПРОДОЛЬНО-ПОПЕРЕЧНОГО ПОЛЯ
- 5. ВЛИЯНИЕ НА ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭМУ ВИХРЕВЫХ И КОММУТАЦИОННЫХ ТОКОВ, ГИСТЕРЕЗИСА И СДВИГА ЩЕТОК С НЕЙТРАЛИ
- 6. МЕТОДЫ УЛУЧШЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕКТРОМАШИННЫХ УСИЛИТЕЛЕЙ
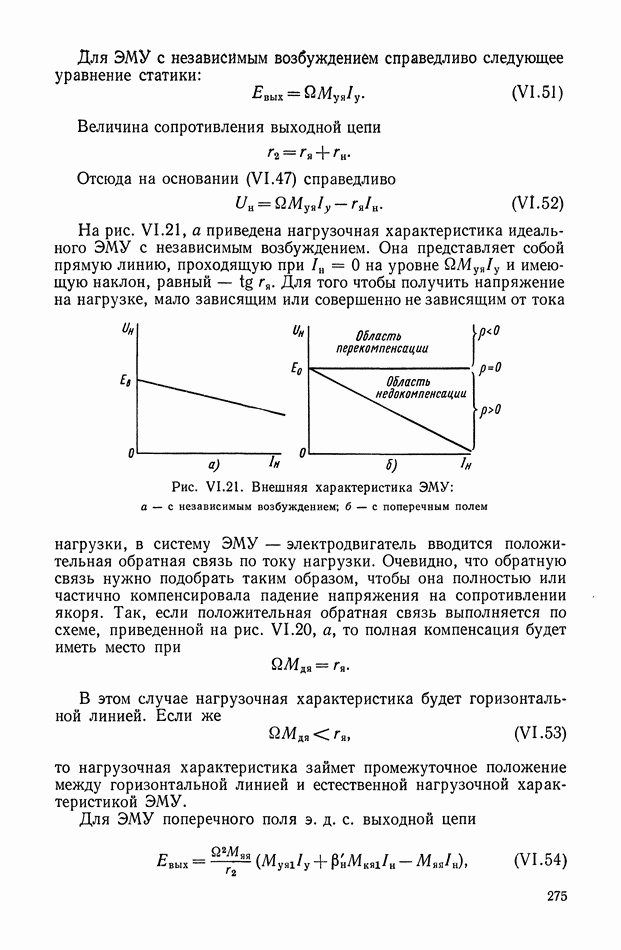
- 7. НАГРУЗОЧНАЯ ХАРАКТЕРИСТИКА ЭЛЕКТРОМАШИННОГО УСИЛИТЕЛЯ
- ГЛАВА VII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ УСИЛИТЕЛИ
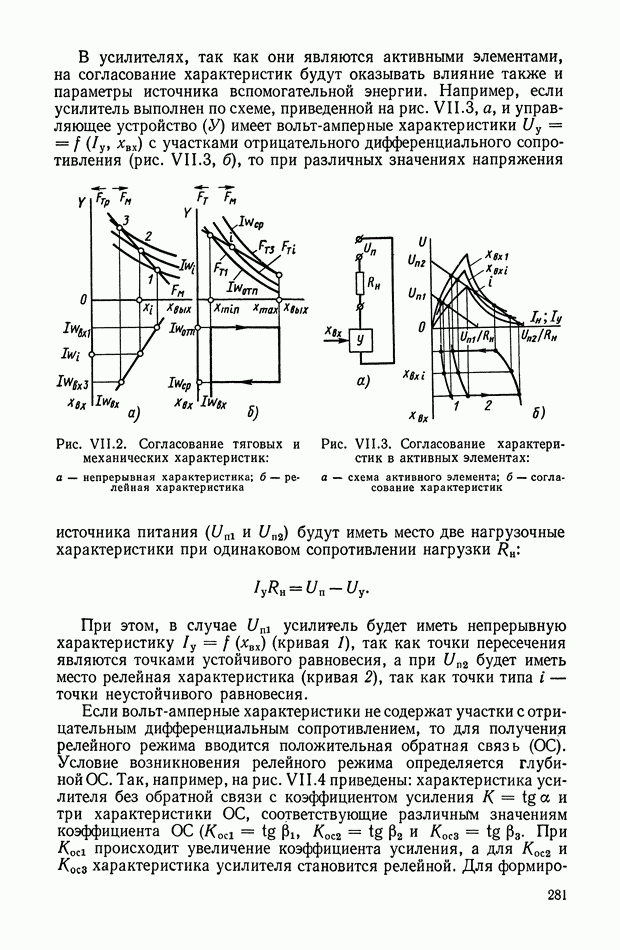
- 1. ХАРАКТЕРИСТИКИ УСИЛИТЕЛЕЙ И СПОСОБЫ ИХ ФОРМИРОВАНИЯ
- 2. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
- 3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ЛИНЕАРИЗОВАННЫЕ УСИЛИТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ РЕЛЕ
- 4. БЕСКОНТАКТНЫЕ ЛИНЕАРИЗОВАННЫЕ РЕЛЕЙНЫЕ УСИЛИТЕЛИ
- ГЛАВА VIII. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
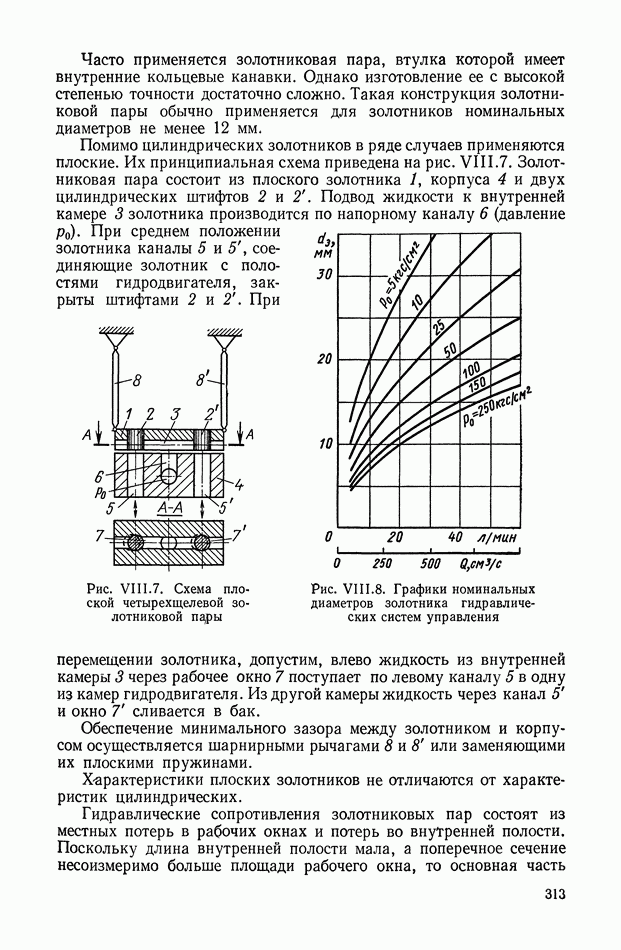
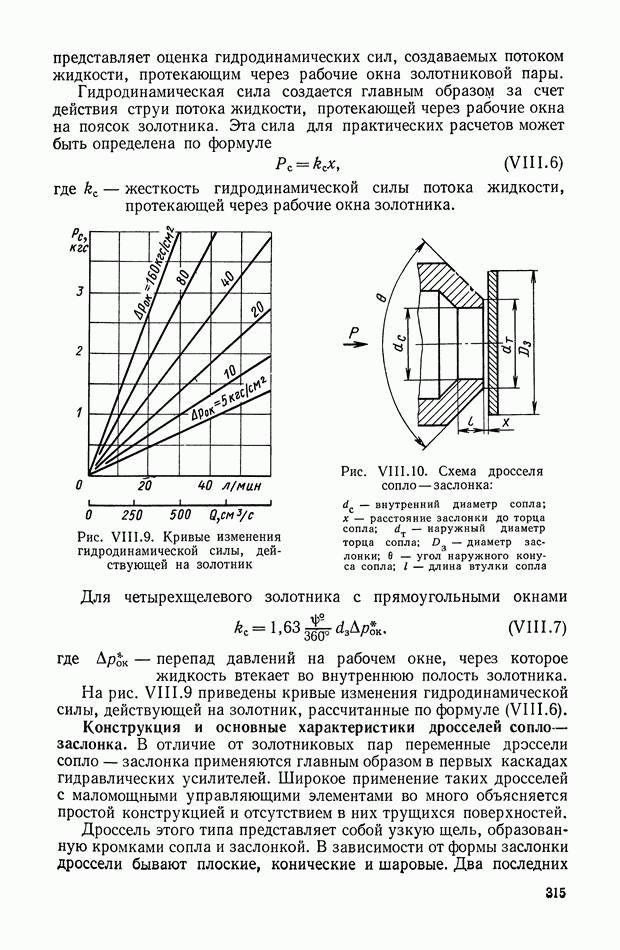
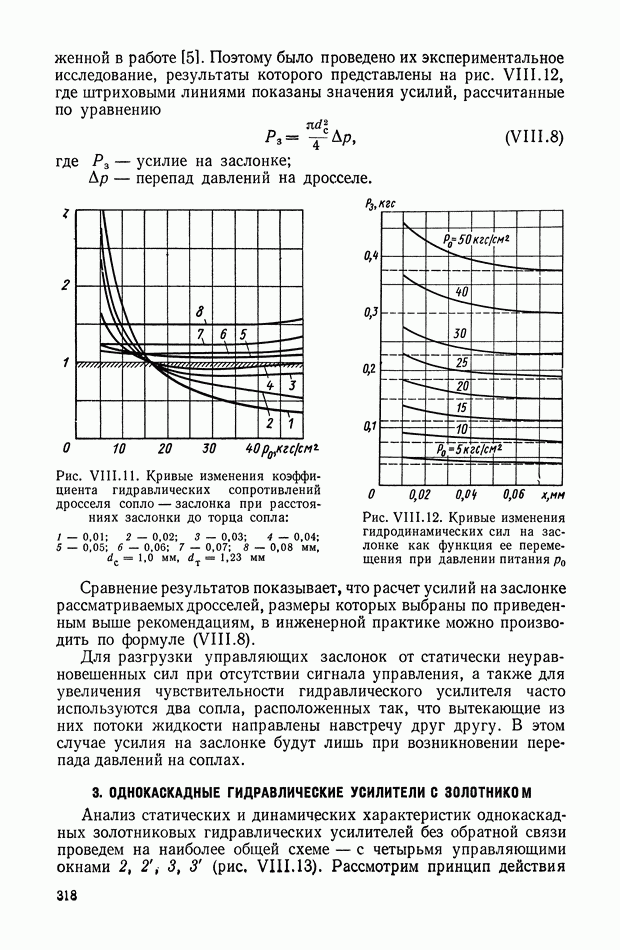
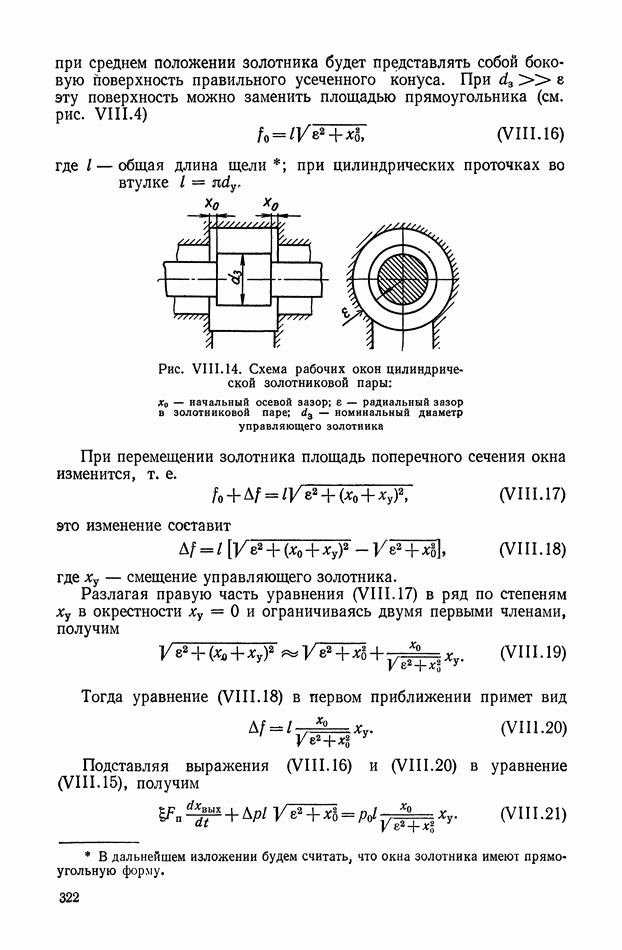
- 2. ОСНОВНЫЕ ЭЛЕМЕНТЫ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ И ИХ ХАРАКТЕРИСТИКИ
- 3. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ С ЗОЛОТНИКОМ
- 4. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ СО СТРУЙНОЙ ТРУБКОЙ
- 5. СХЕМЫ И ПРИНЦИПЫ ДЕЙСТВИЯ ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 6. СТАТИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 7. ДИНАМИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
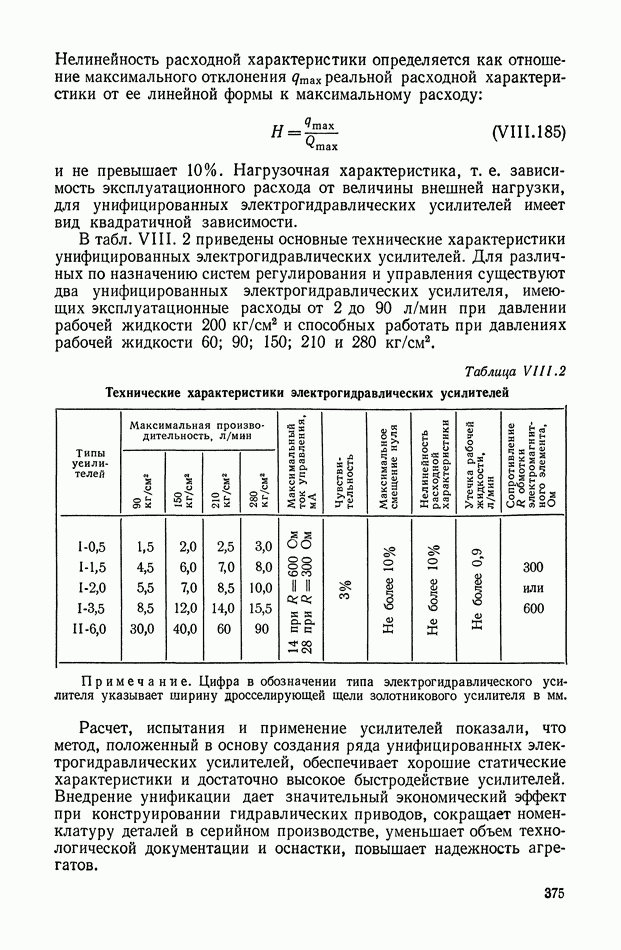
- 8. УНИФИКАЦИЯ ЭЛЕКТРОГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ ДЛЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
- ГЛАВА IX. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ И ИХ КЛАССИФИКАЦИЯ
- 2. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ СО СТРУЙНОЙ ТРУБКОЙ
- 3. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗОЛОТНИКОМ
- 4. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С СОПЛОМ — ЗАСЛОНКОЙ
- 5. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗАСЛОНКОЙ
- 6. МНОГОКАСКАДНЫЕ ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
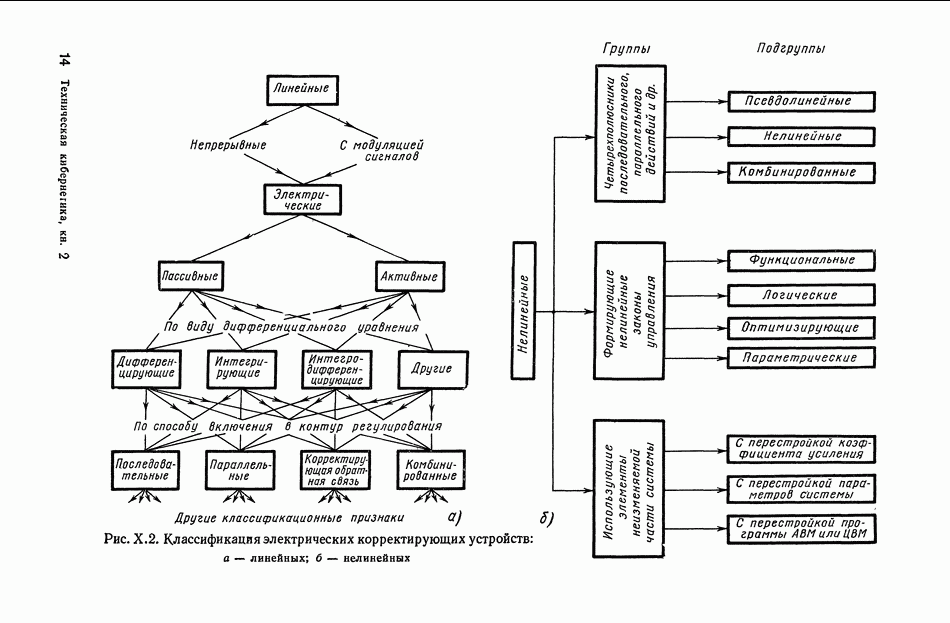
- РАЗДЕЛ II. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ И УСТРОЙСТВ
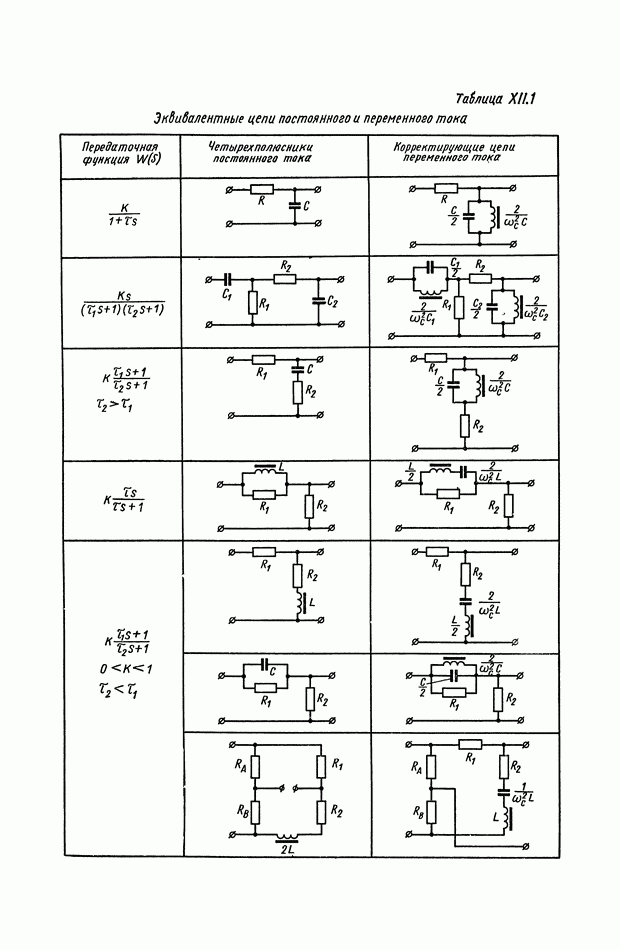
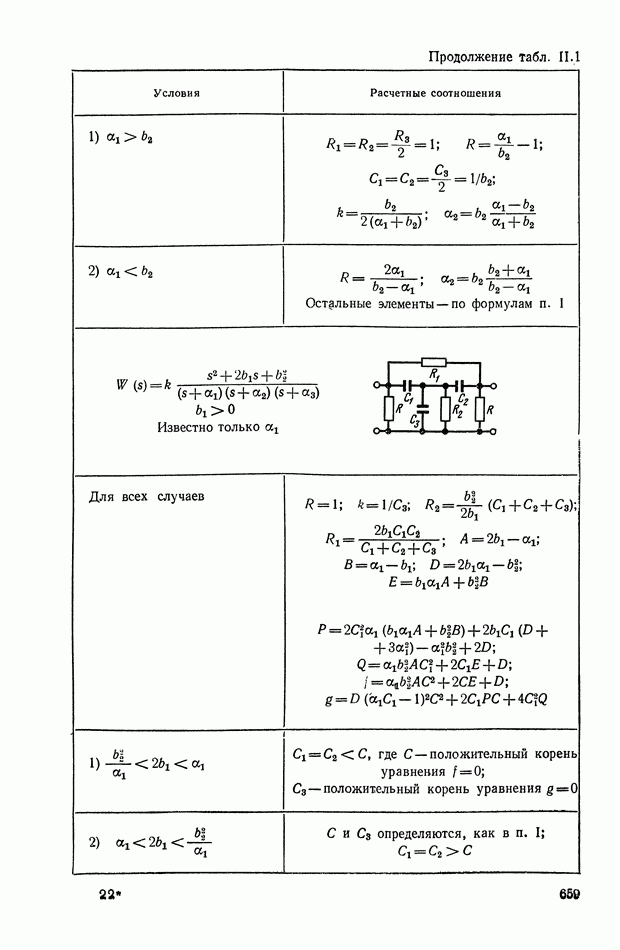
- 2. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ЛИНЕЙНЫХ ПАССИВНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Основные соотношения для синтеза пассивного RC-четырехполюсника.
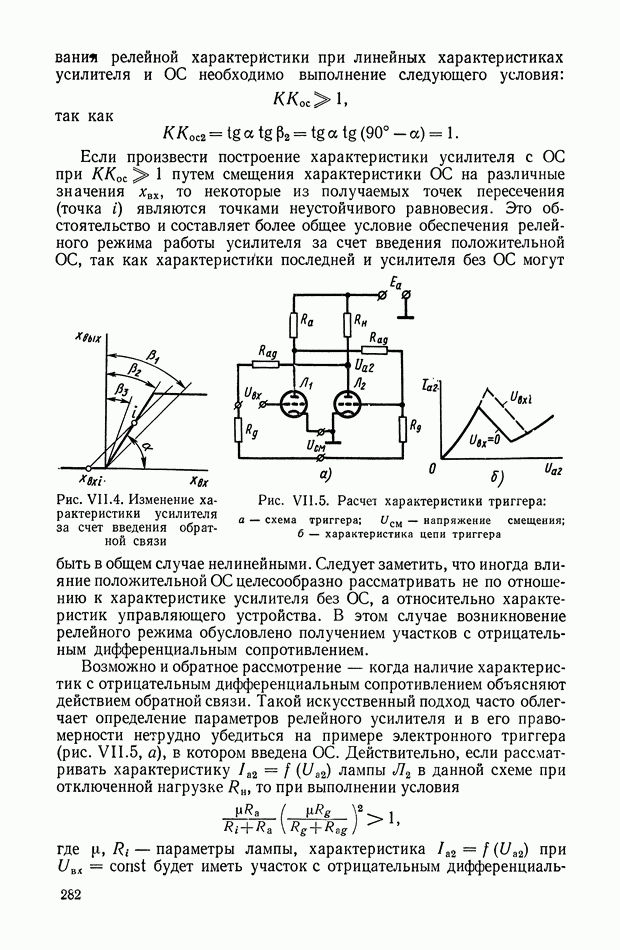
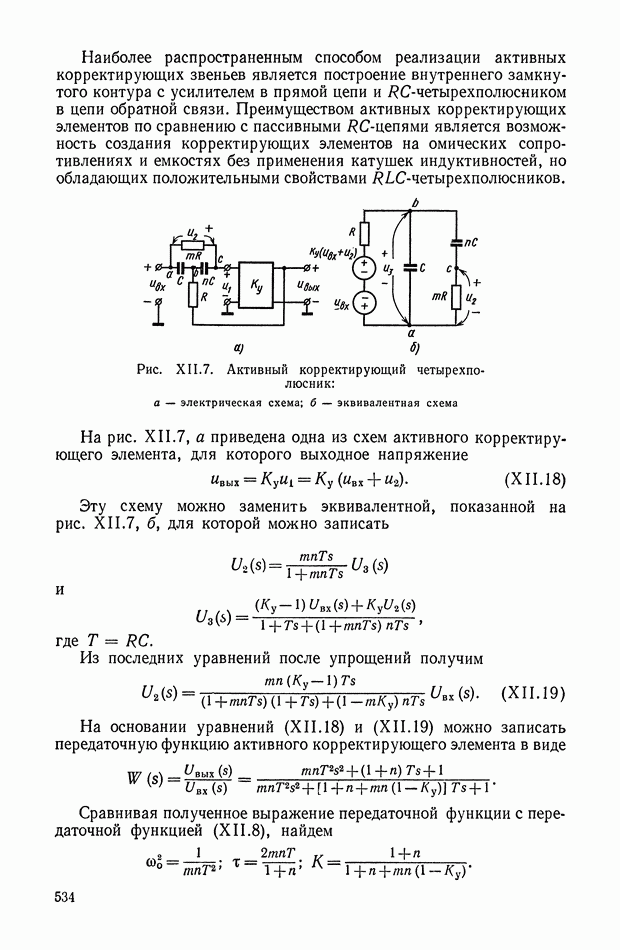
- 3. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Активные четырехполюсники, получаемые с помощью конверторов отрицательного сопротивления.
- Активные четырехполюсники, получаемые с помощью гираторов.
- 4. НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА НЕЛИНЕЙНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. ОСОБЕННОСТИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XI. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА ПОСТОЯННОГО ТОКА
- Дифференцирующий трансформатор.
- Электрические интегрирующие элементы.
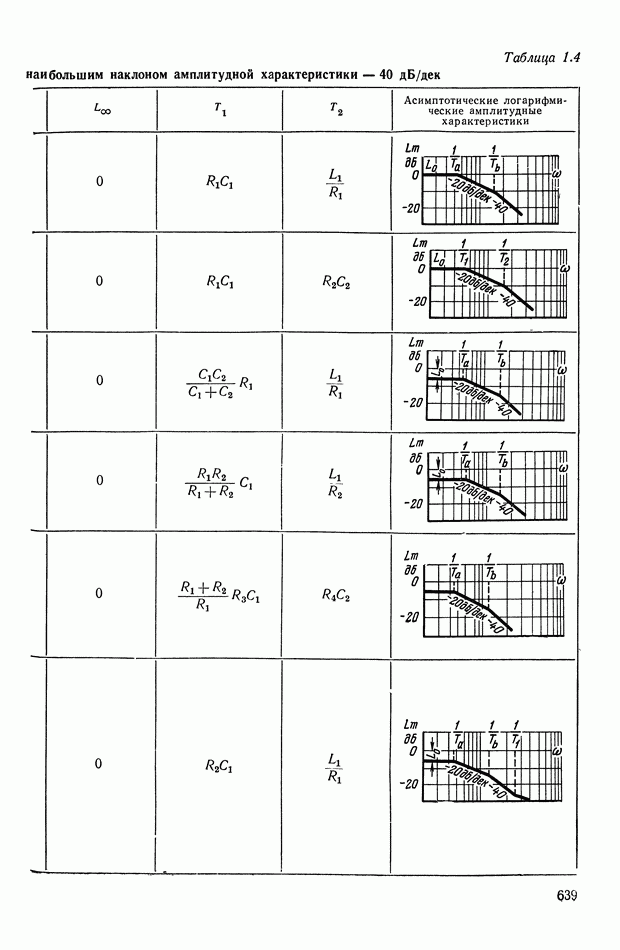
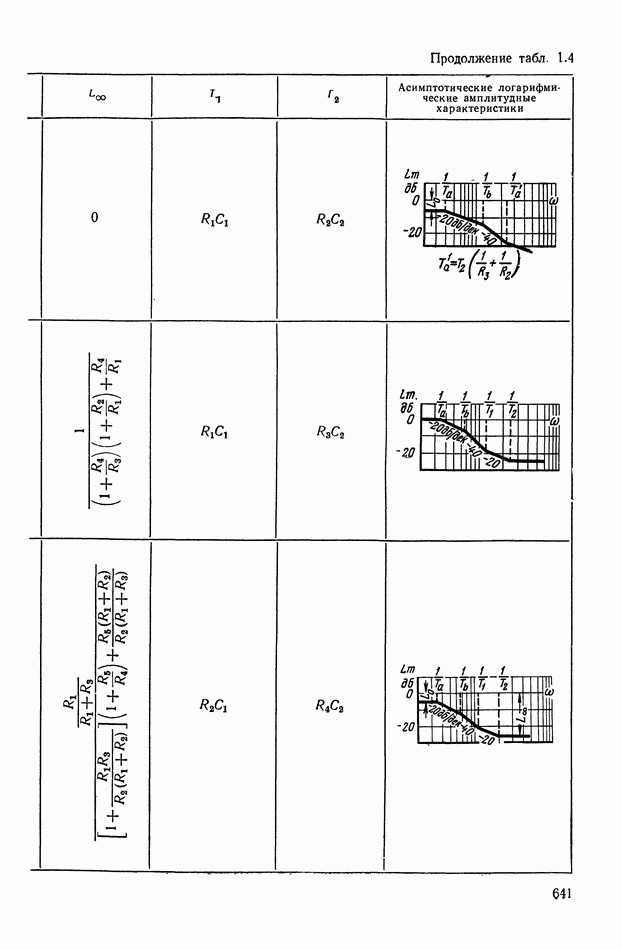
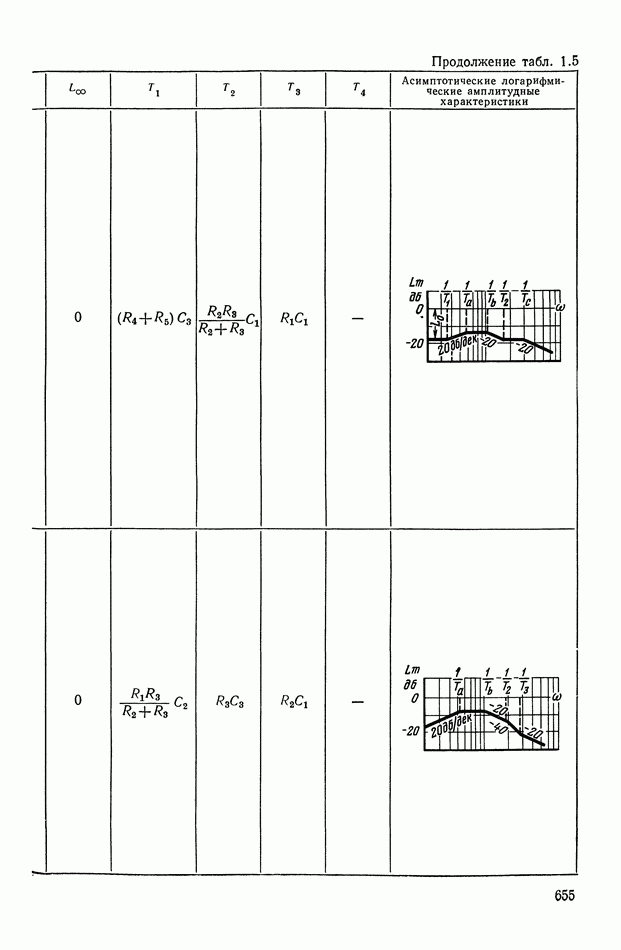
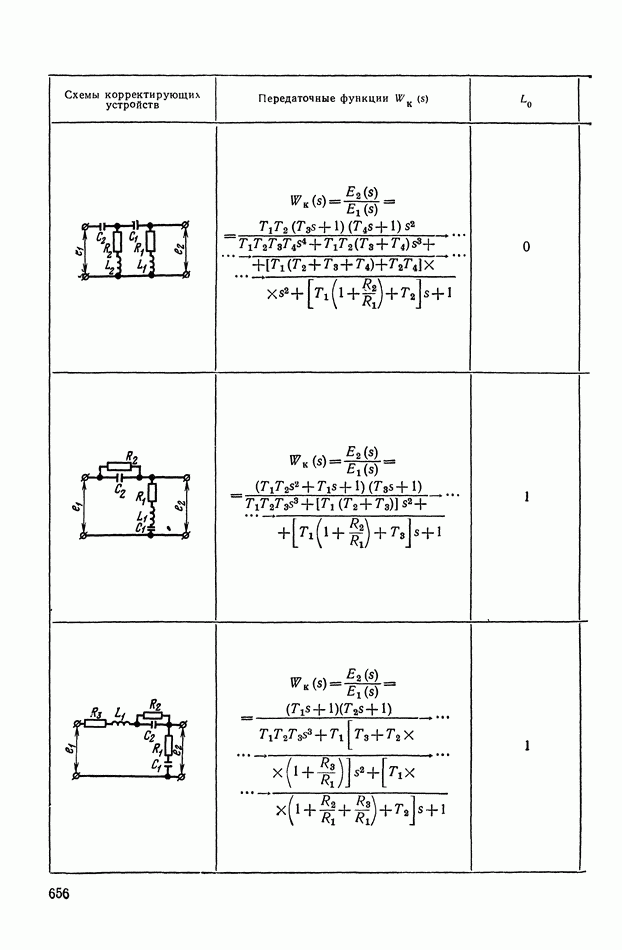
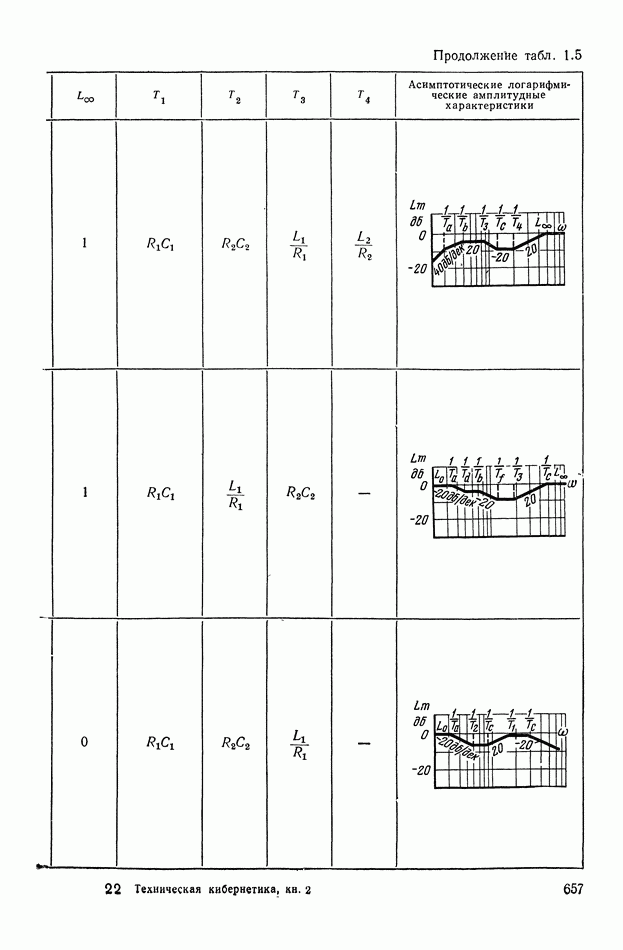
- 2. ТИПОВЫЕ ЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
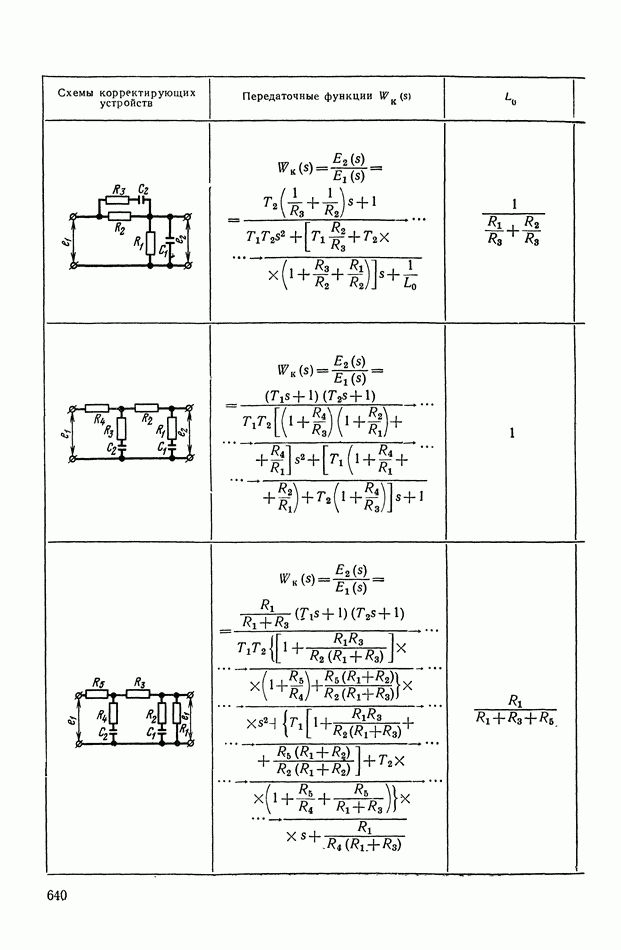
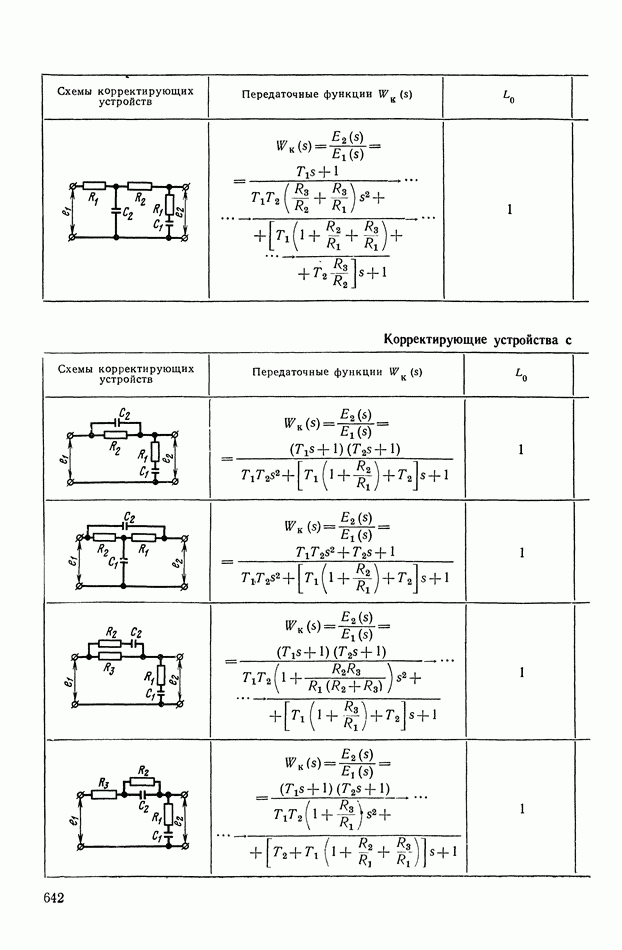
- 3. КОРРЕКТИРУЮЩИЕ ЧЕТЫРЕХПОЛЮСНИКИ С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Четырехполюсники с активными элементами на основе операционных усилителей (ОУ) и конверторов отрицательного сопротивления (КОС).
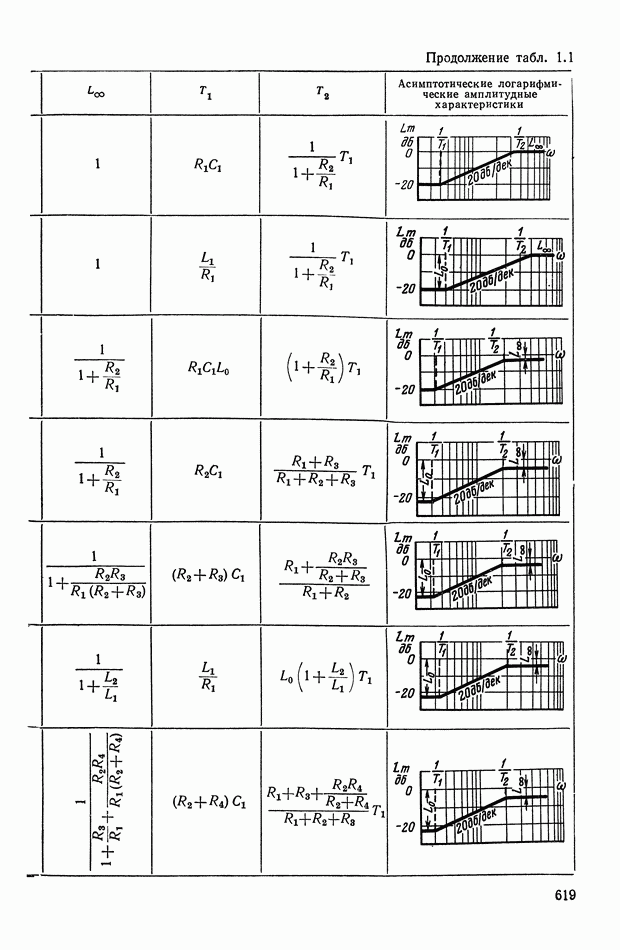
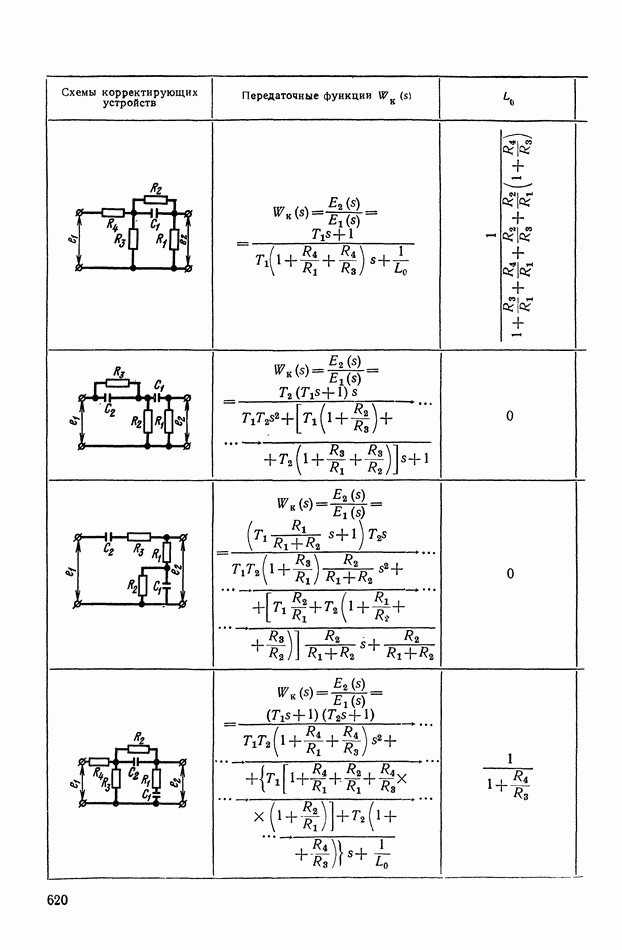
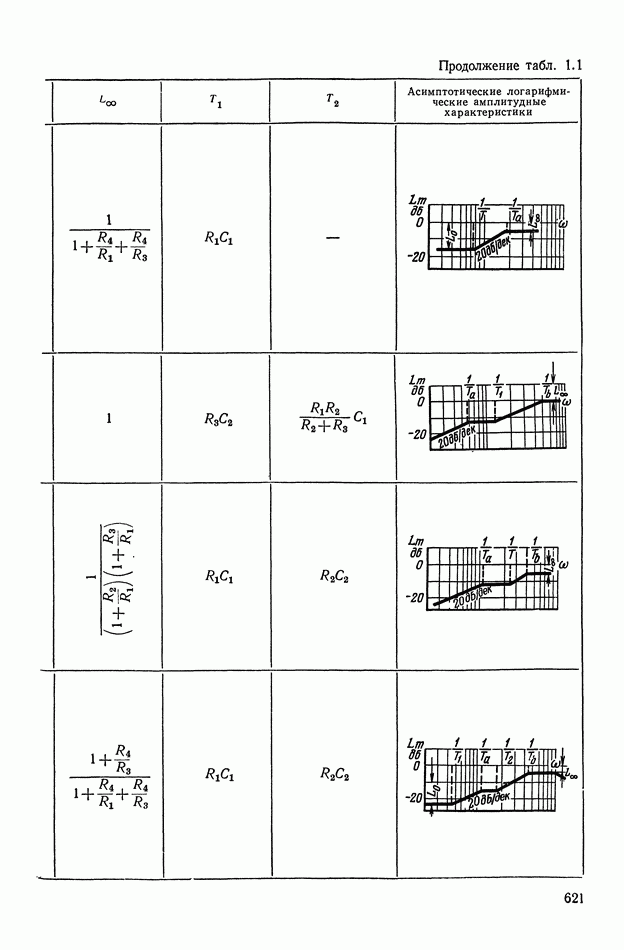
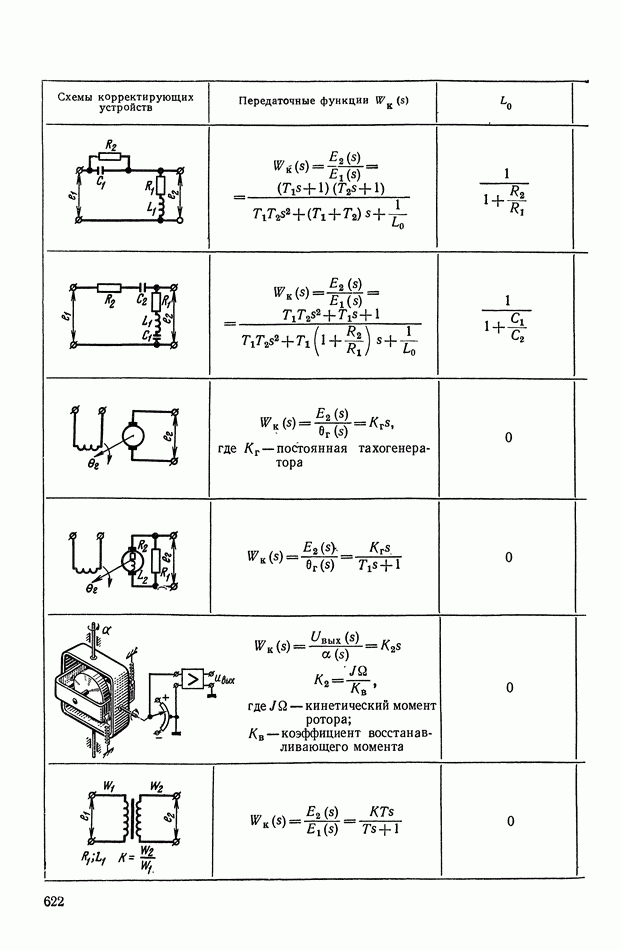
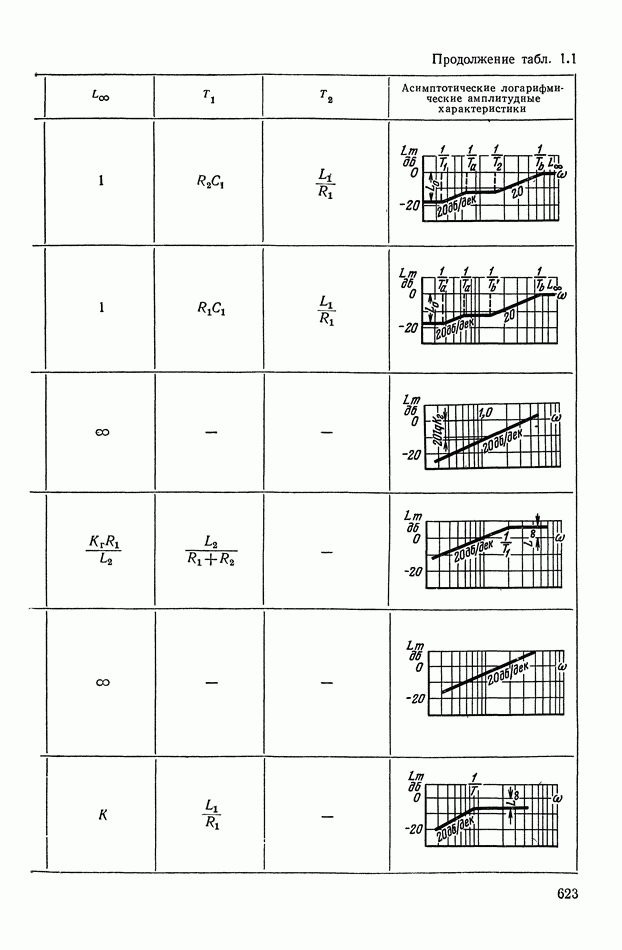
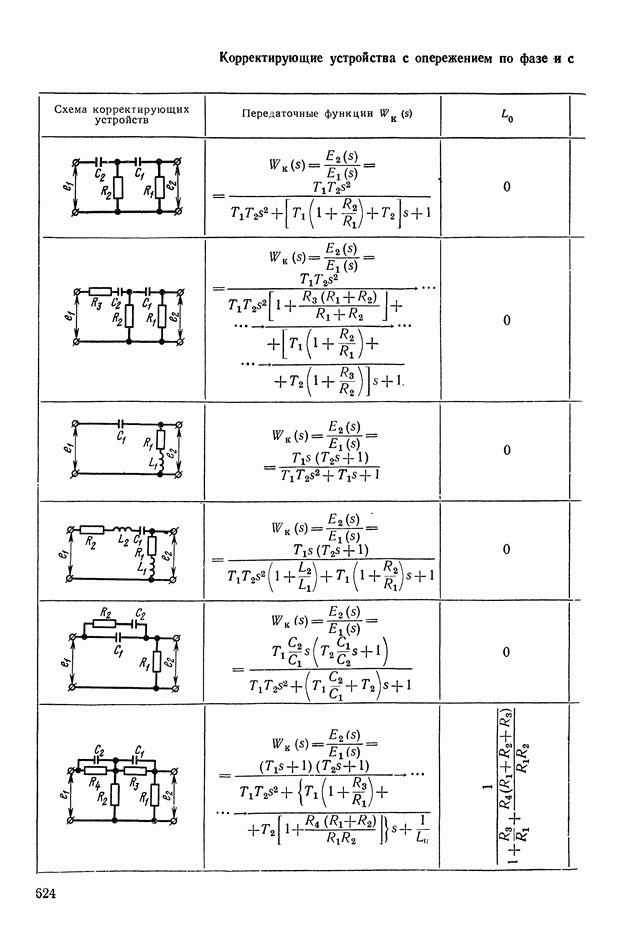
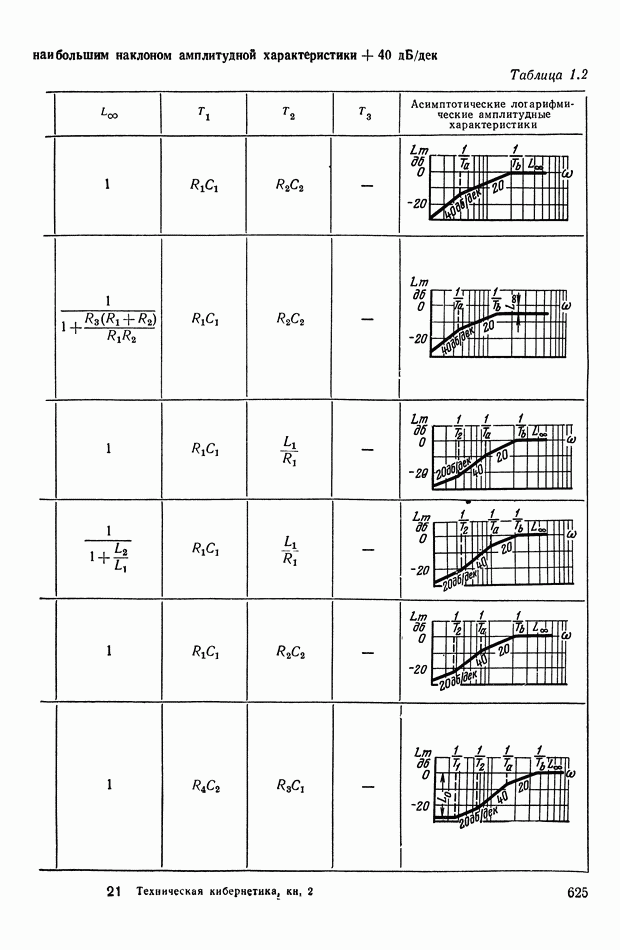
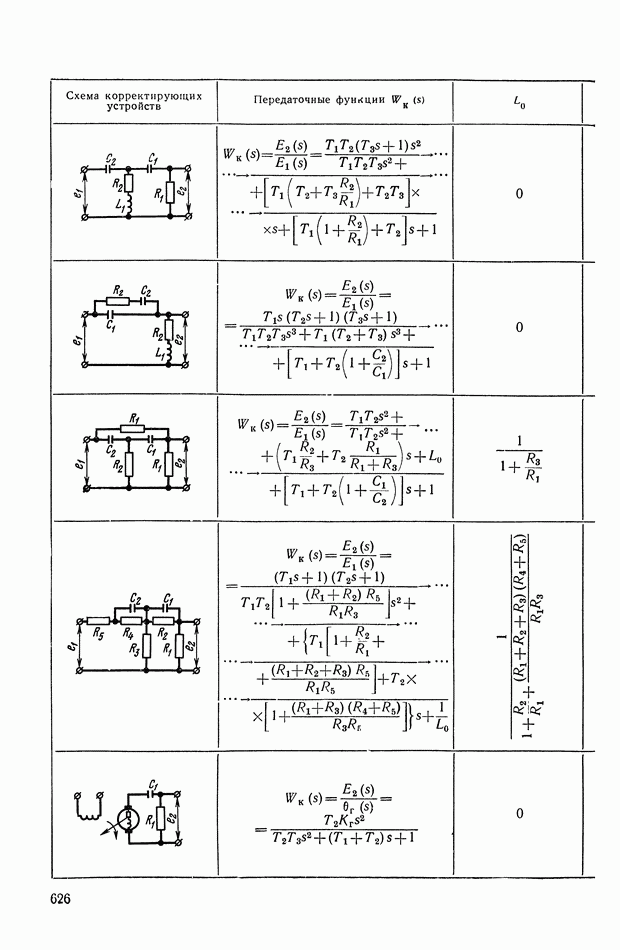
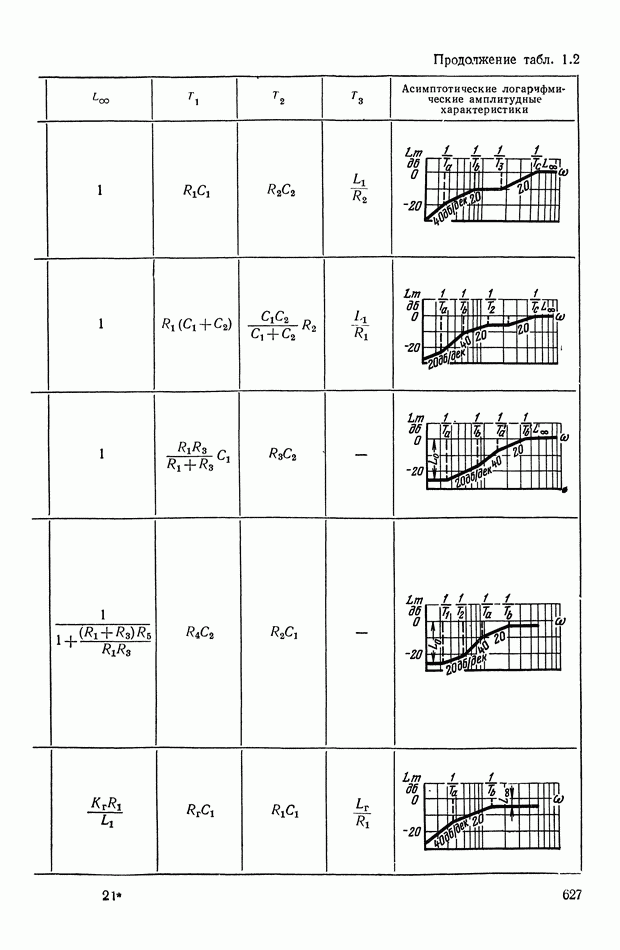
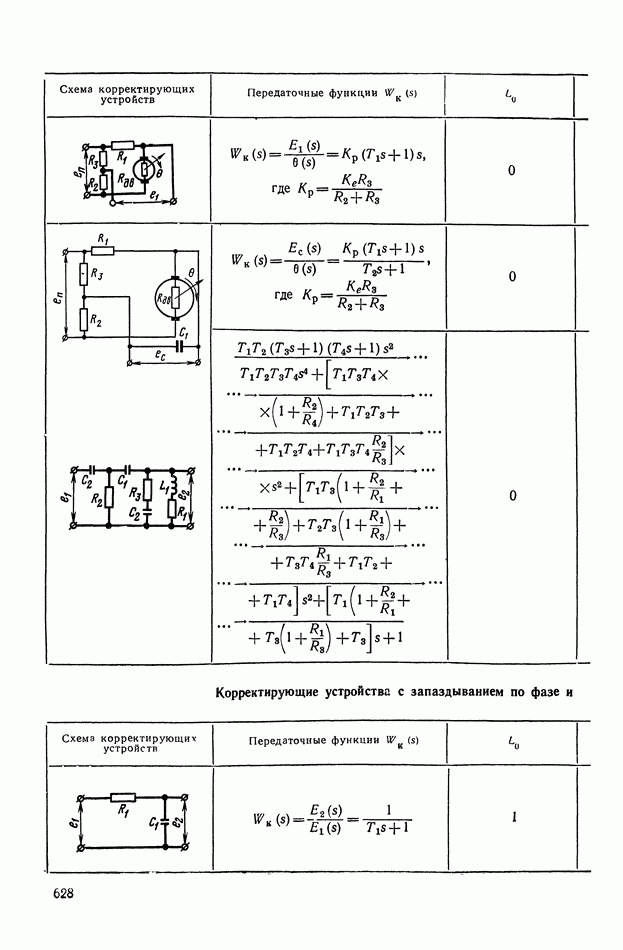
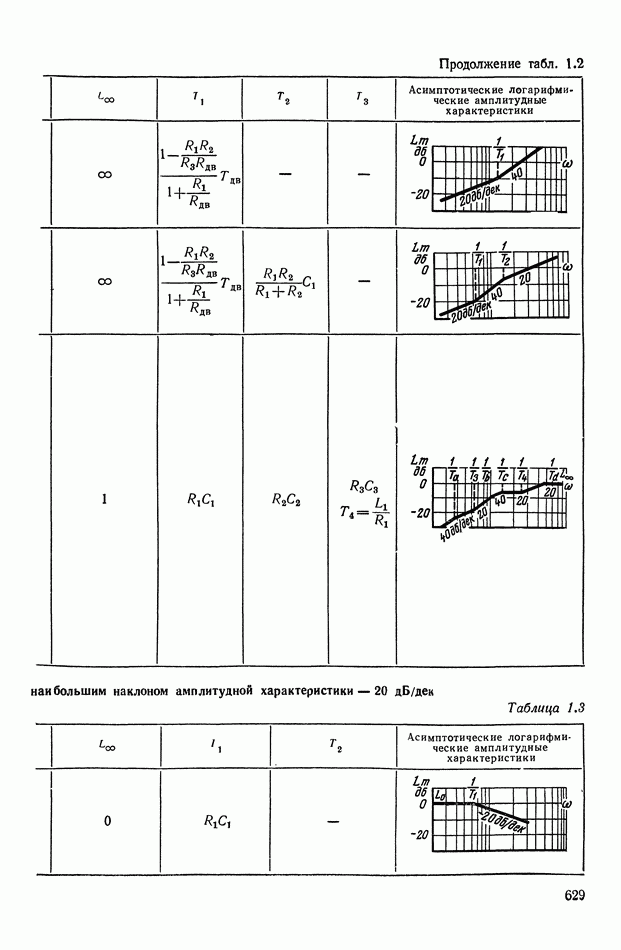
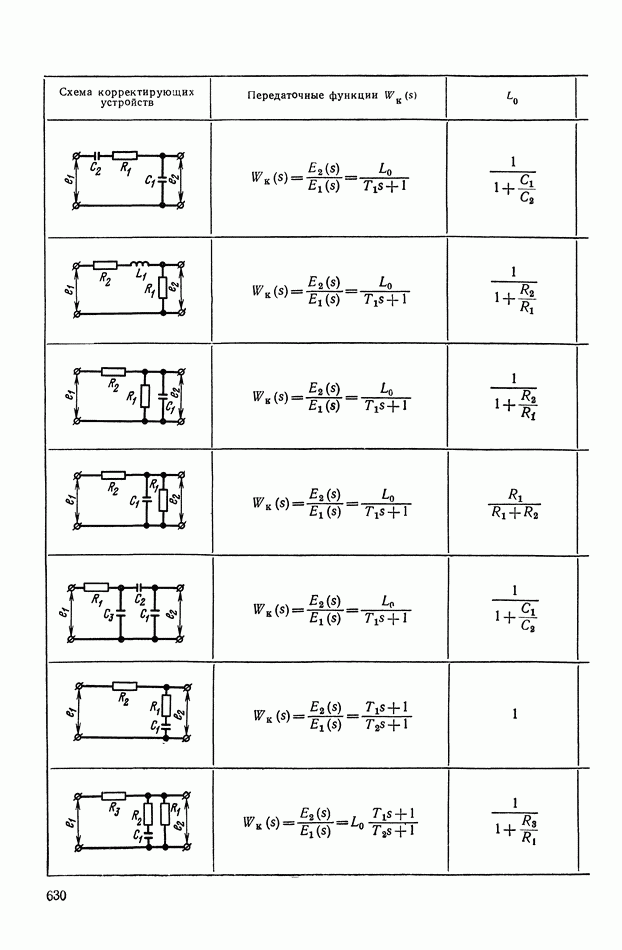
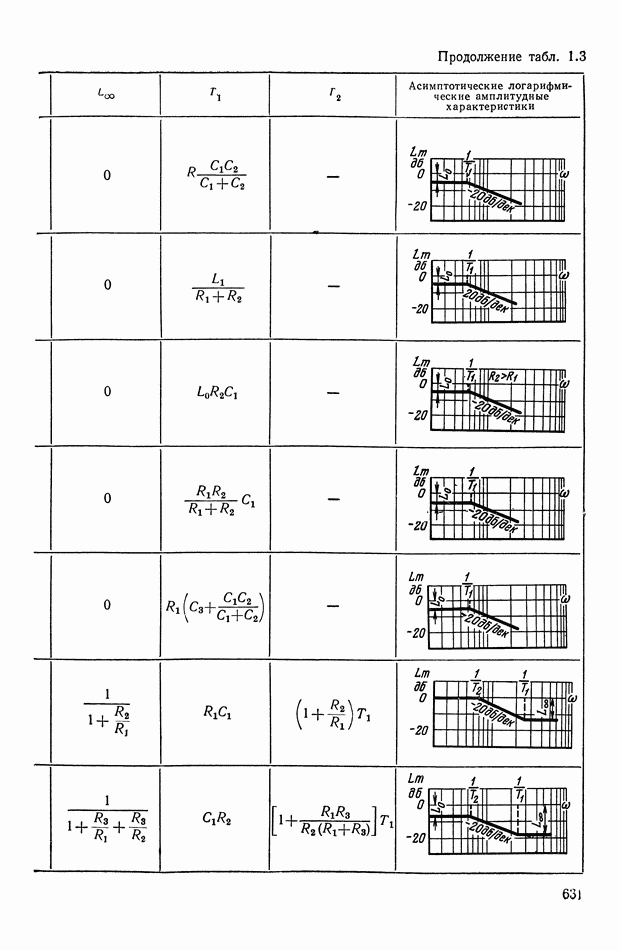
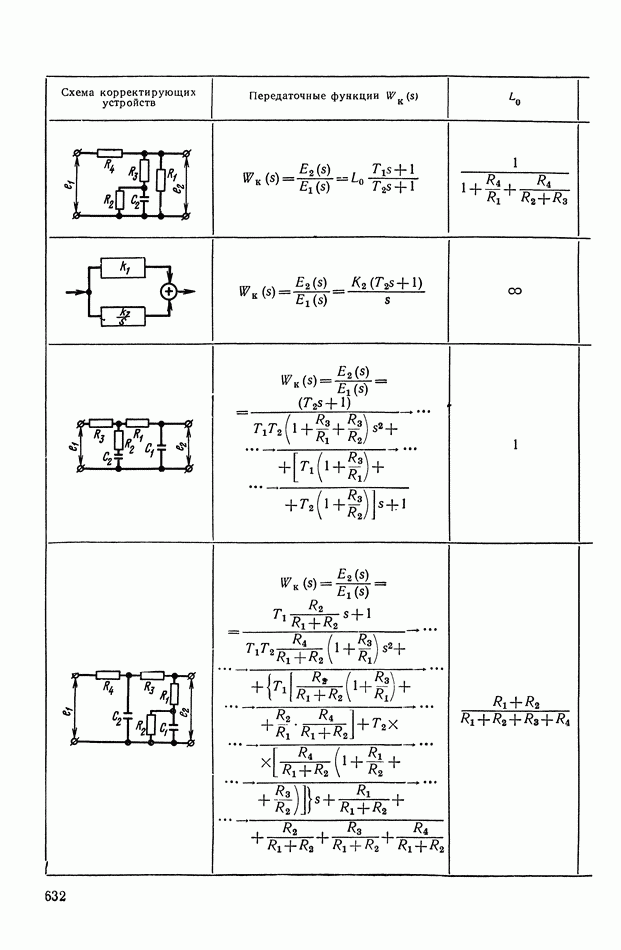
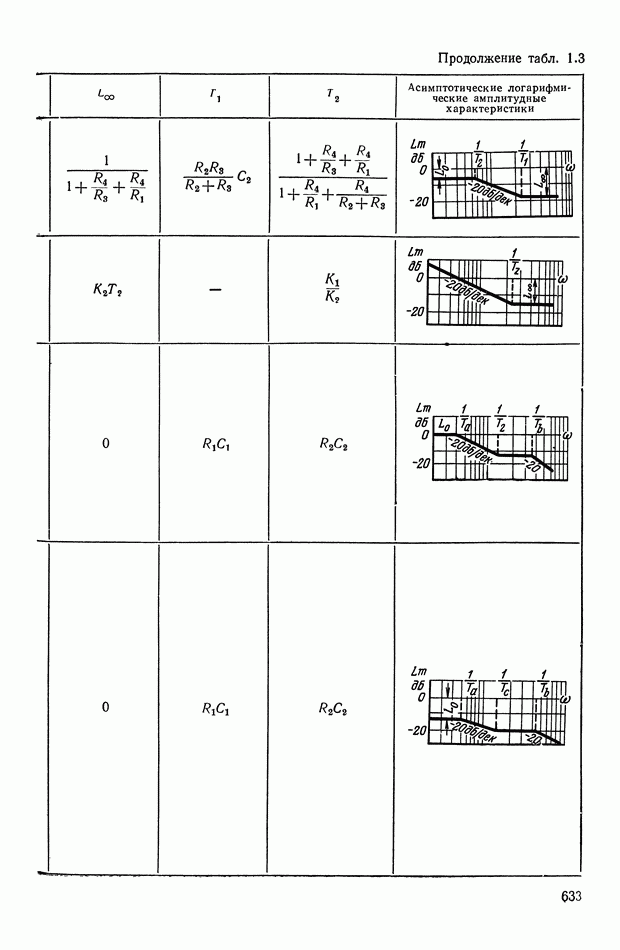
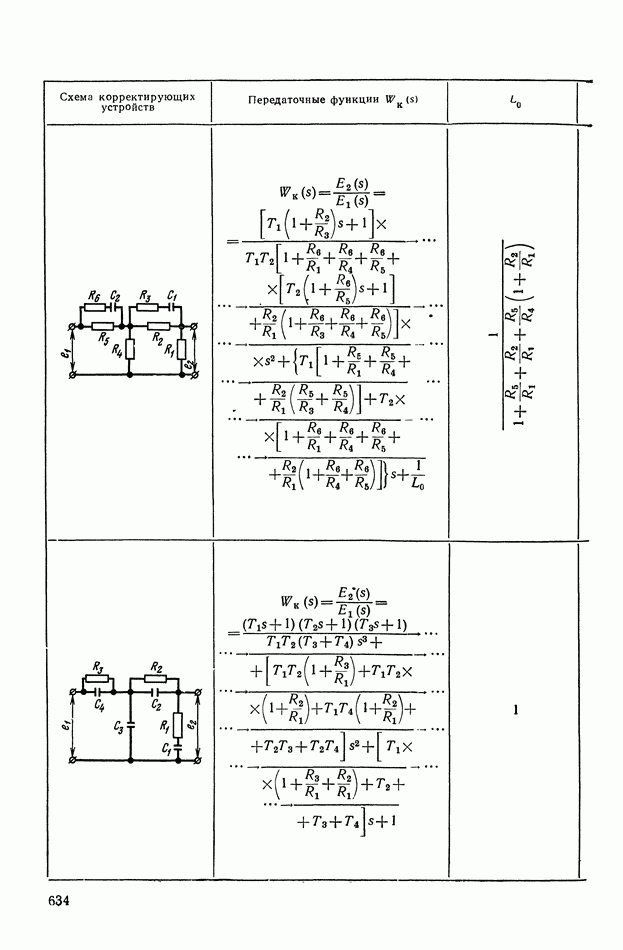
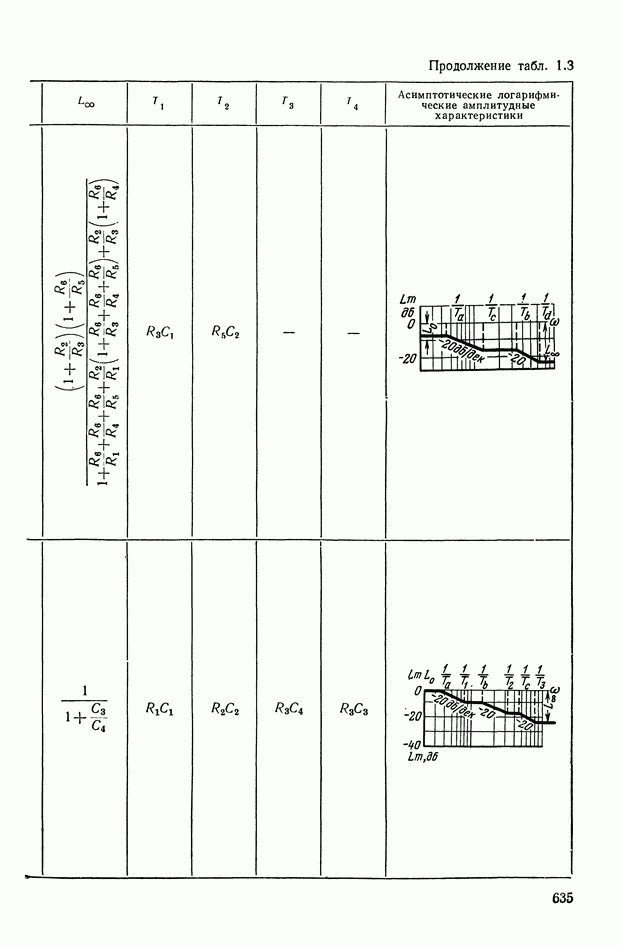
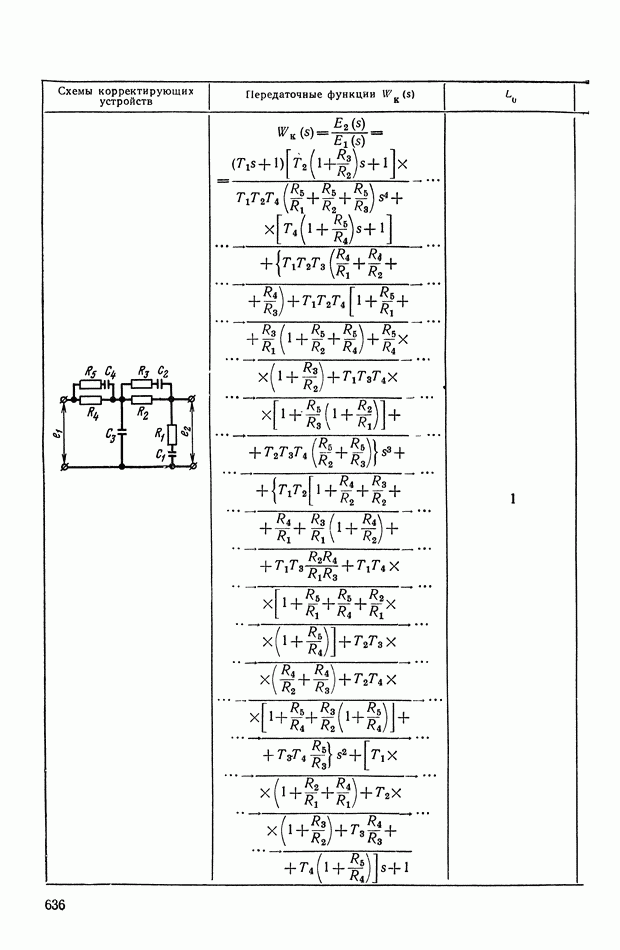
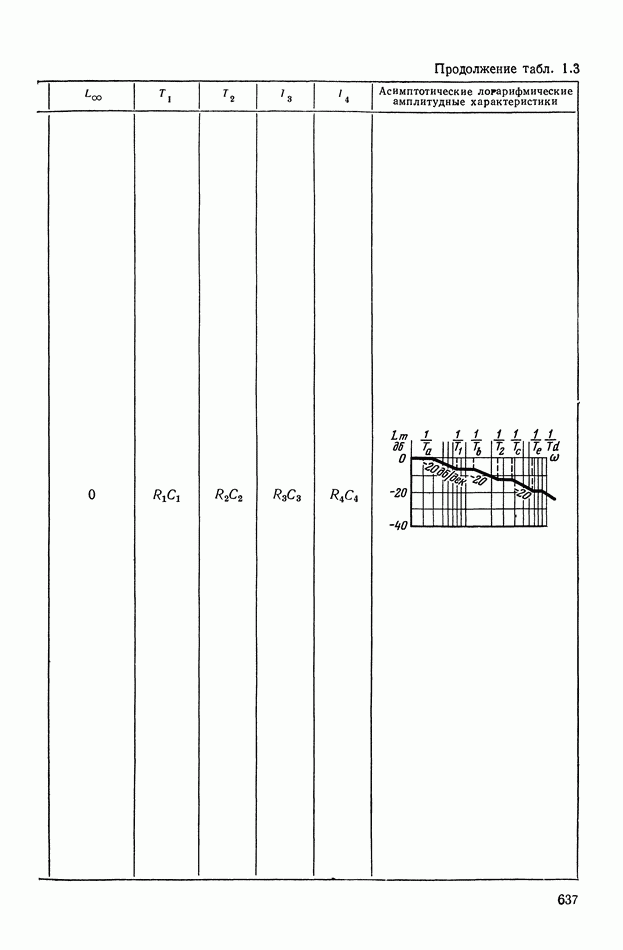
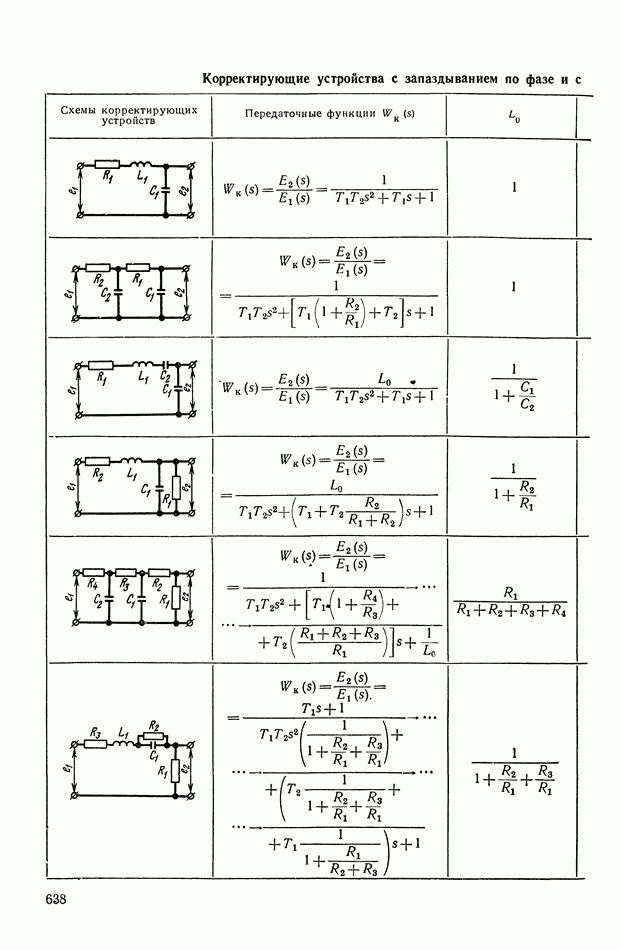
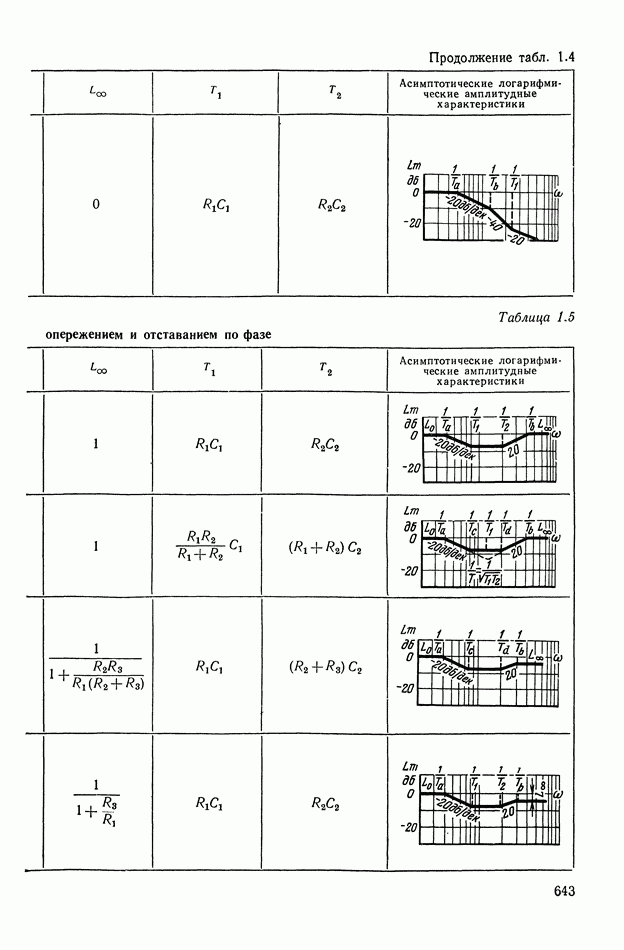
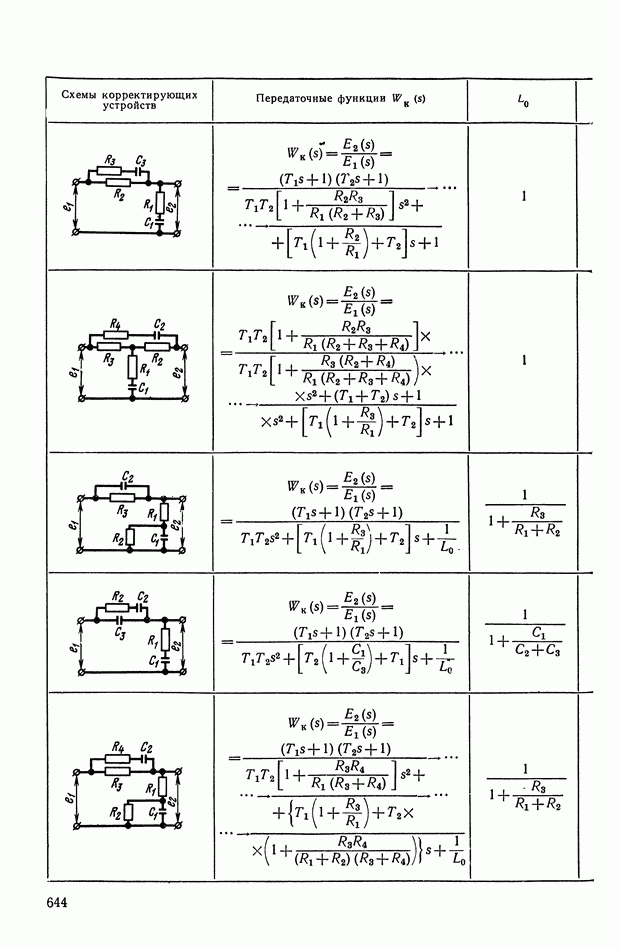
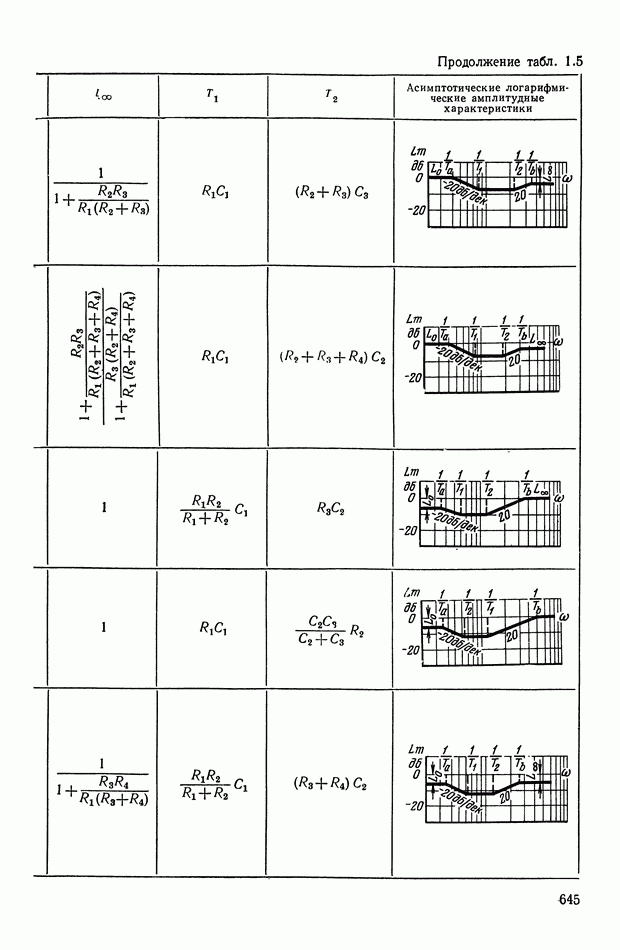
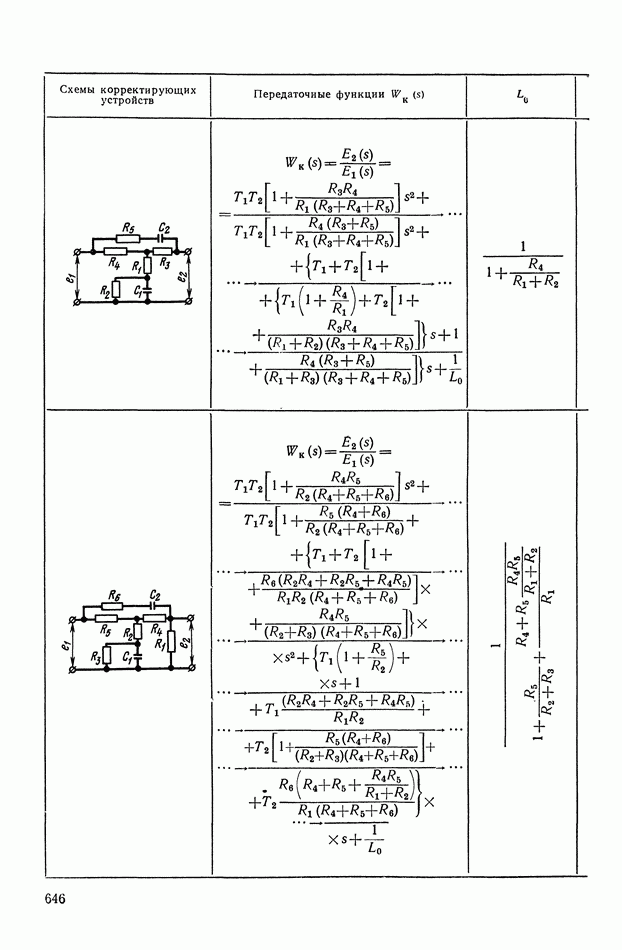
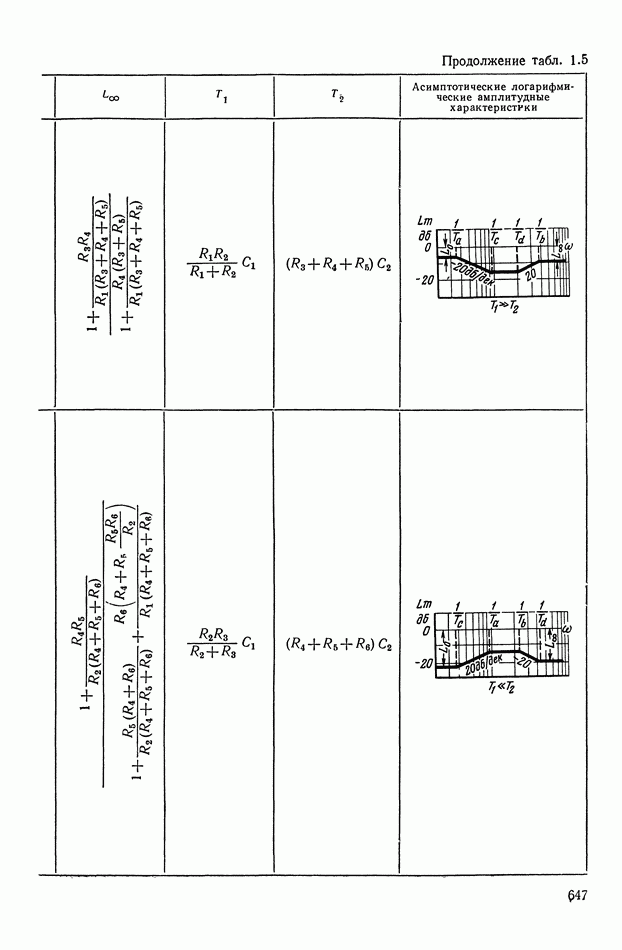
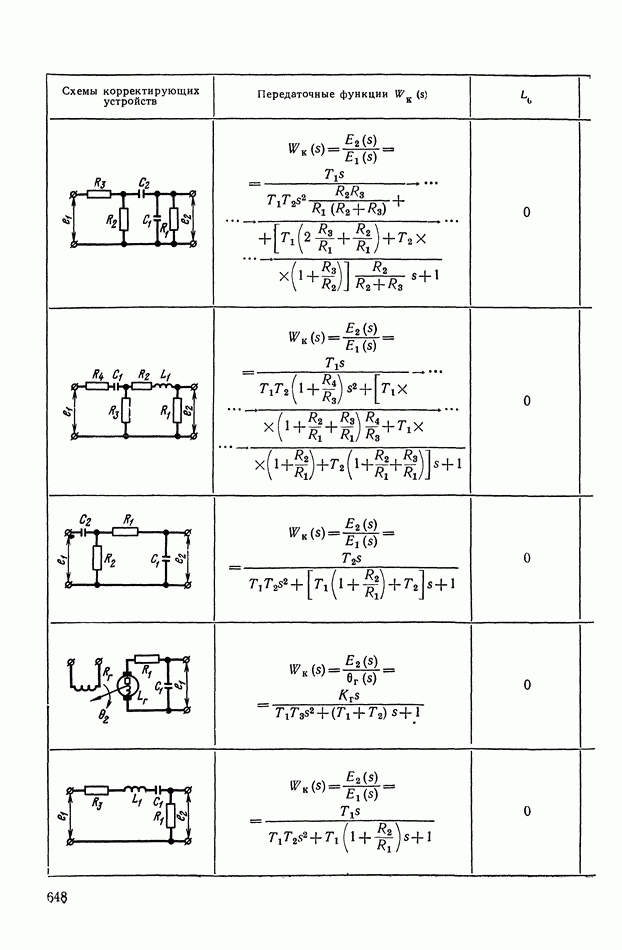
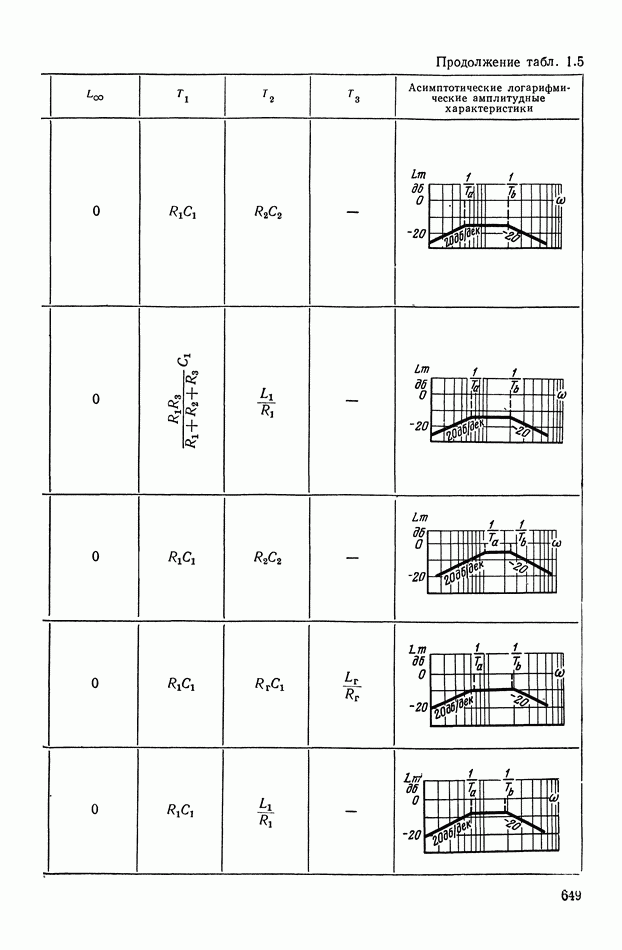
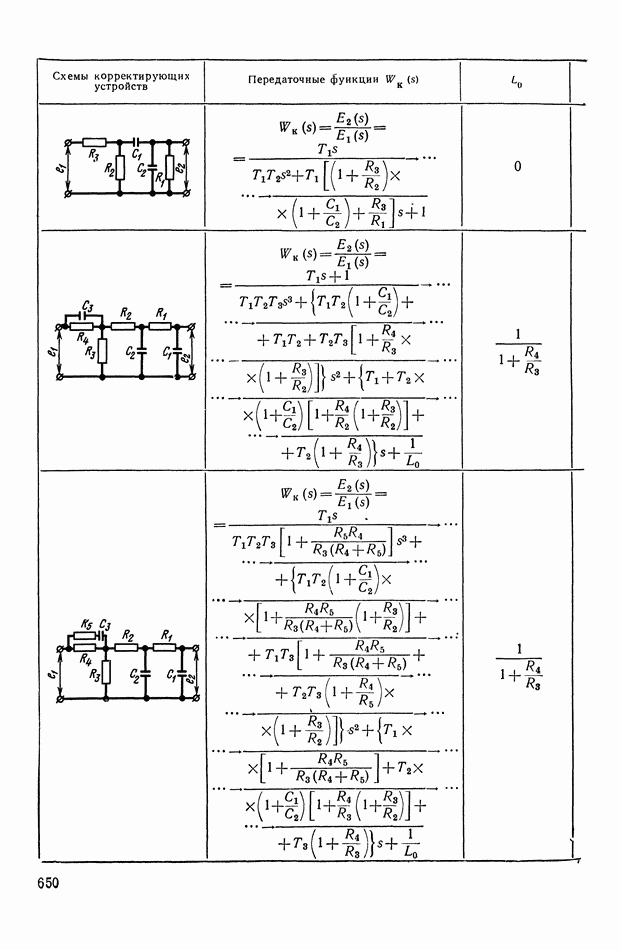
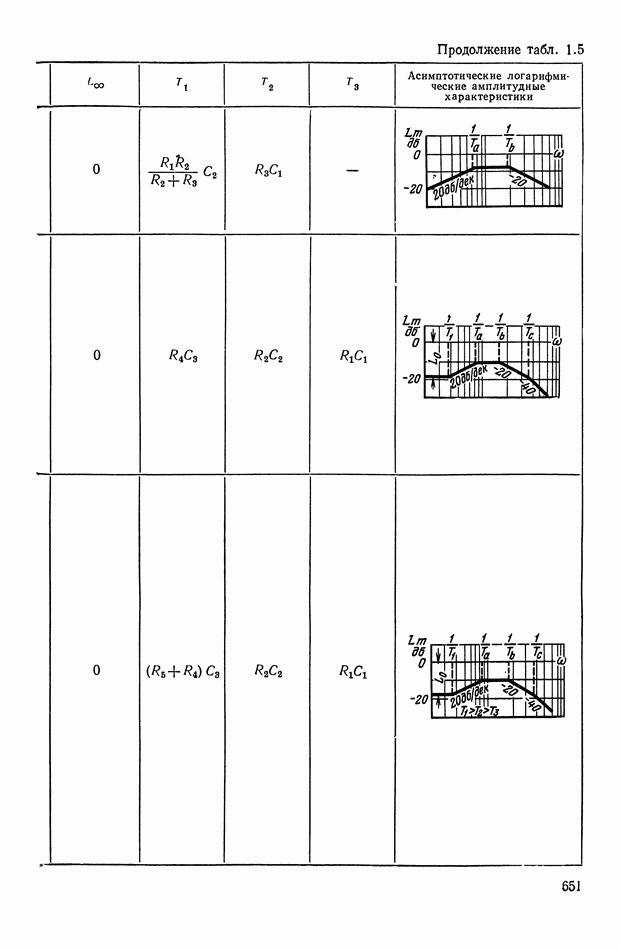
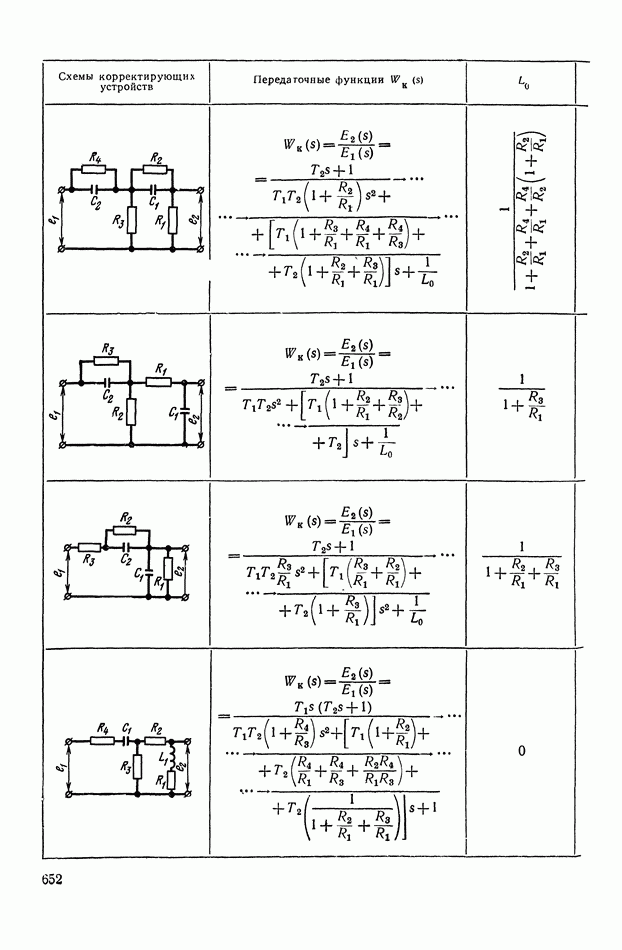
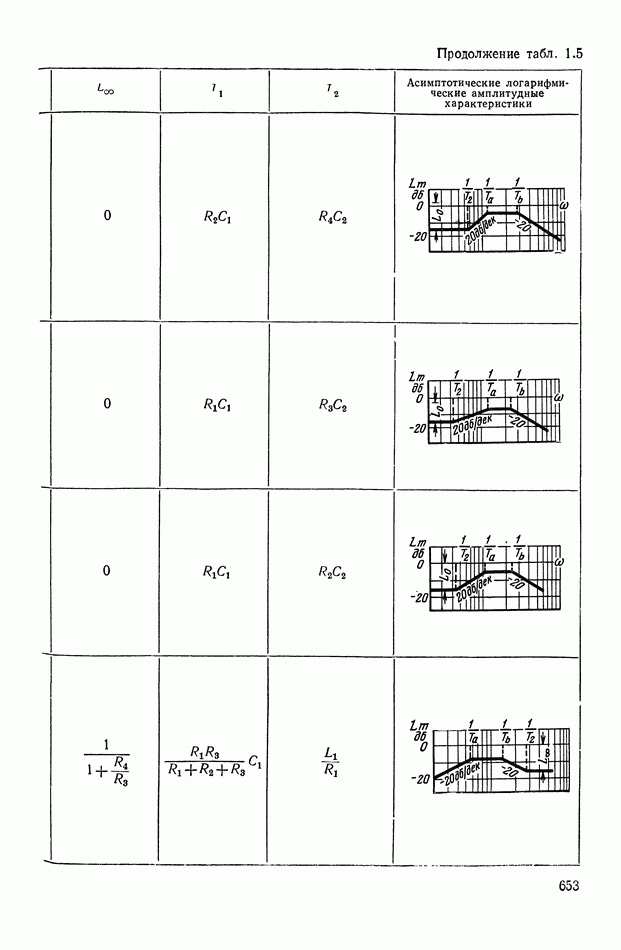
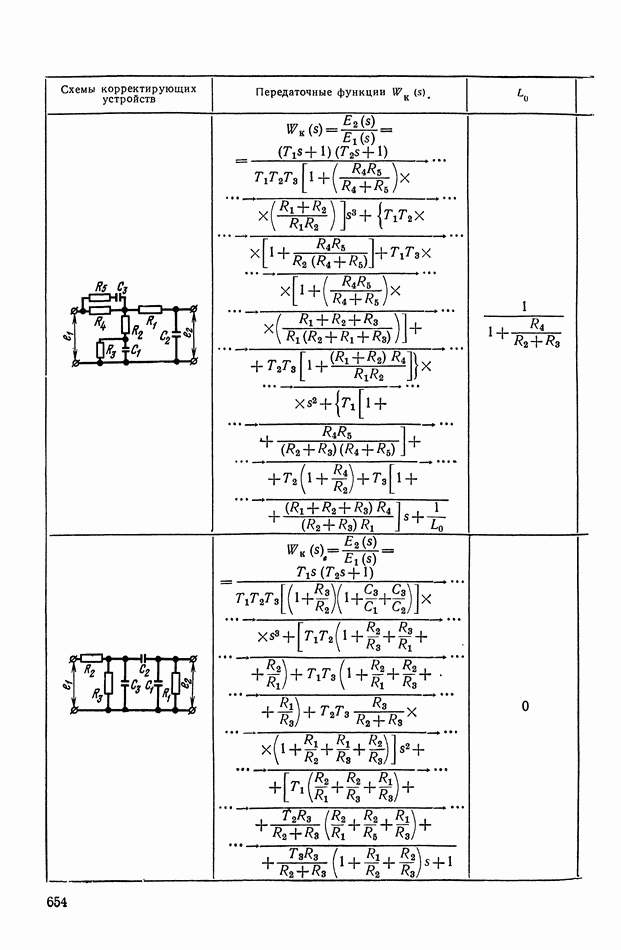
- 4. РЕАЛИЗАЦИЯ ЗАДАННОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В ВИДЕ СХЕМЫ ПАССИВНОГО ЛИНЕЙНОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА
- 5. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
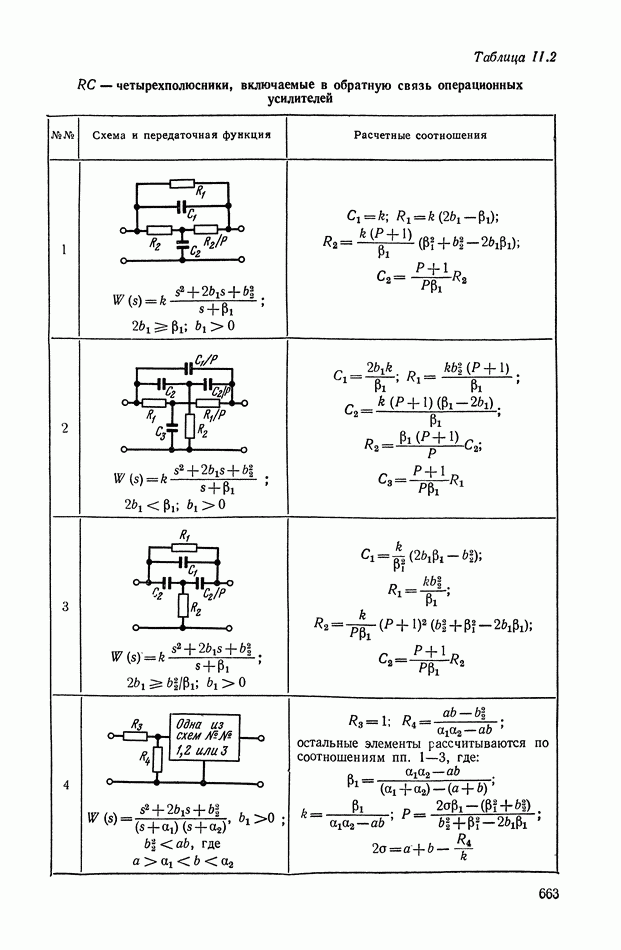
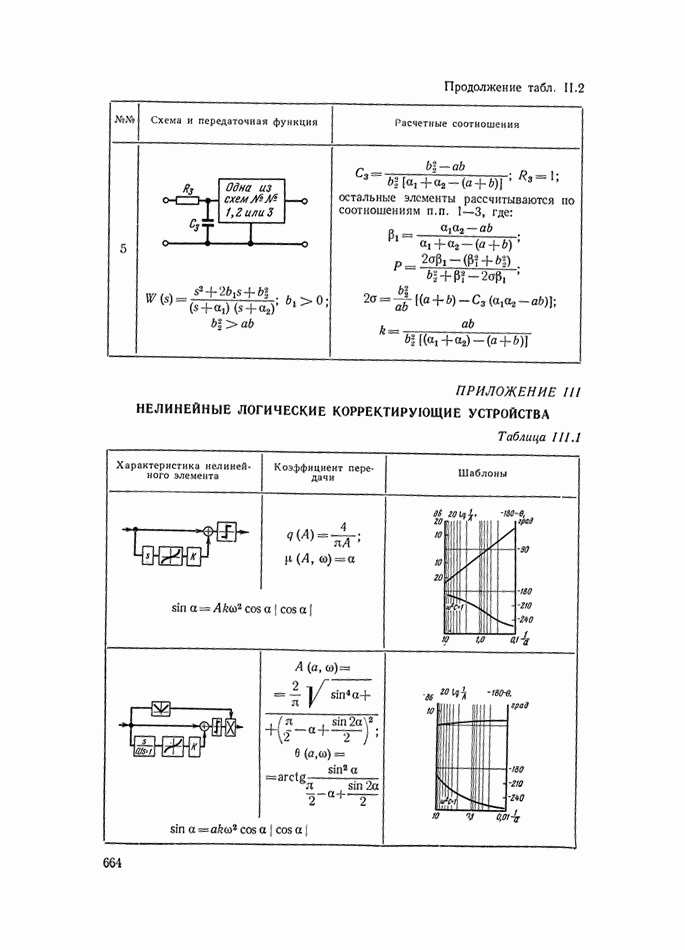
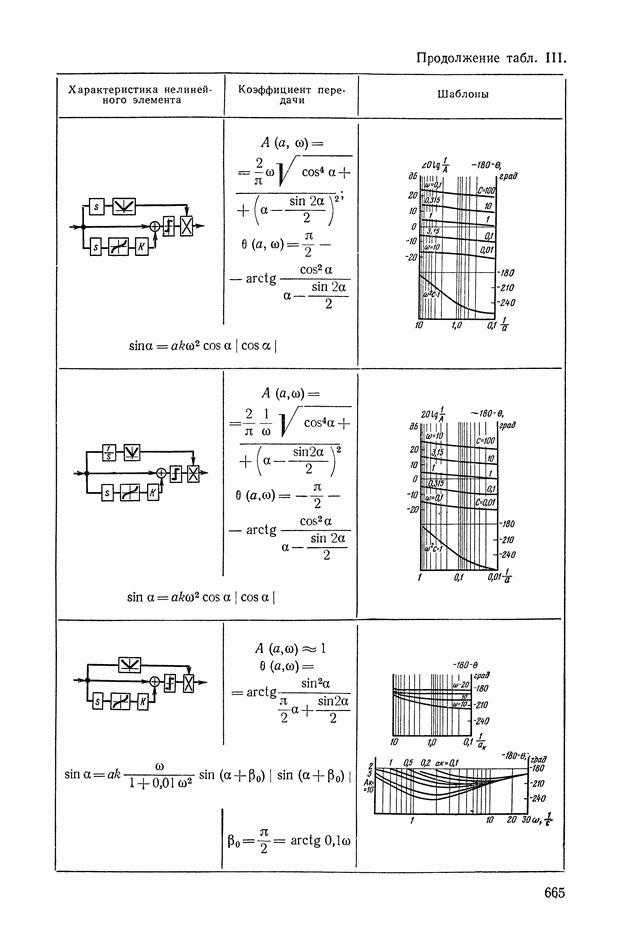
- 8. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
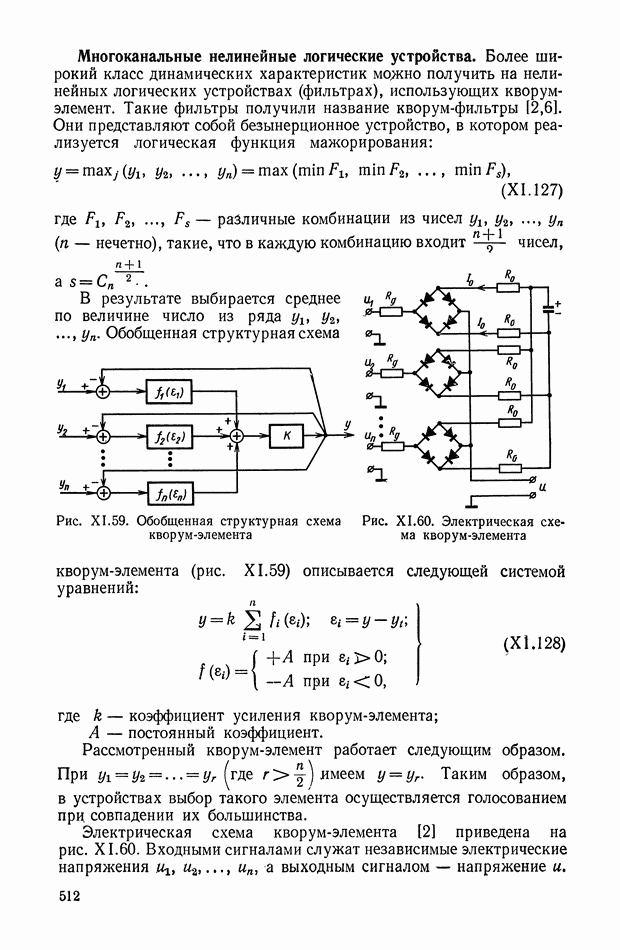
- Многоканальные нелинейные логические устройства.
- ГЛАВА XII. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- 1. КОРРЕКТИРУЮЩИЕ RLC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 2. КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
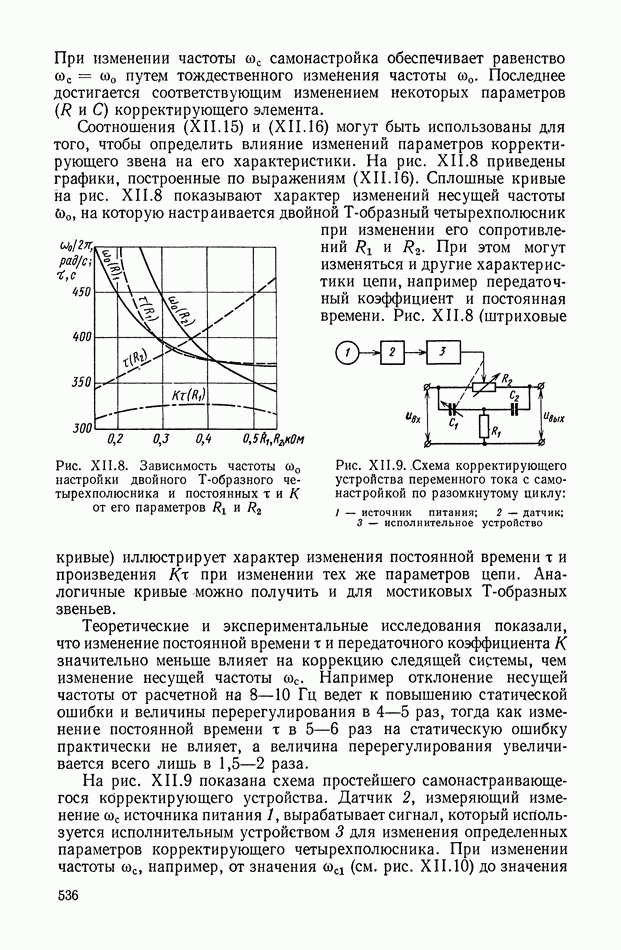
- 3. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 4. САМОНАСТРАИВАЮЩИЕСЯ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА
- 5. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА С ПРОМЕЖУТОЧНОЙ ДЕМОДУЛЯЦИЕЙ
- 6. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА С ПЕРЕКЛЮЧАТЕЛЯМИ
- 7. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XIII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ТАХОГЕНЕРАТОРЫ ПОСТОЯННОГО ТОКА
- Погрешности тахогенератора постоянного тока.
- 2. НЕКОТОРЫЕ СХЕМЫ ПРИМЕНЕНИЯ ТАХОГЕНЕРАТОРОВ
- 3. АСИНХРОННЫЕ ТАХОГЕНЕРАТОРЫ
- 4. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ ИЗМЕРЕНИЯ СКОРОСТИ ЭЛЕКТРОДВИГАТЕЛЕЙ
- Пассивный тахометрический мост переменного тока.
- Активные тахометрические мосты.
- ГЛАВА XIV. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ГИДРАВЛИЧЕСКИХ СИСТЕМАХ
- 3. ЭЛЕКТРИЧЕСКИЕ ОБРАТНЫЕ СВЯЗИ
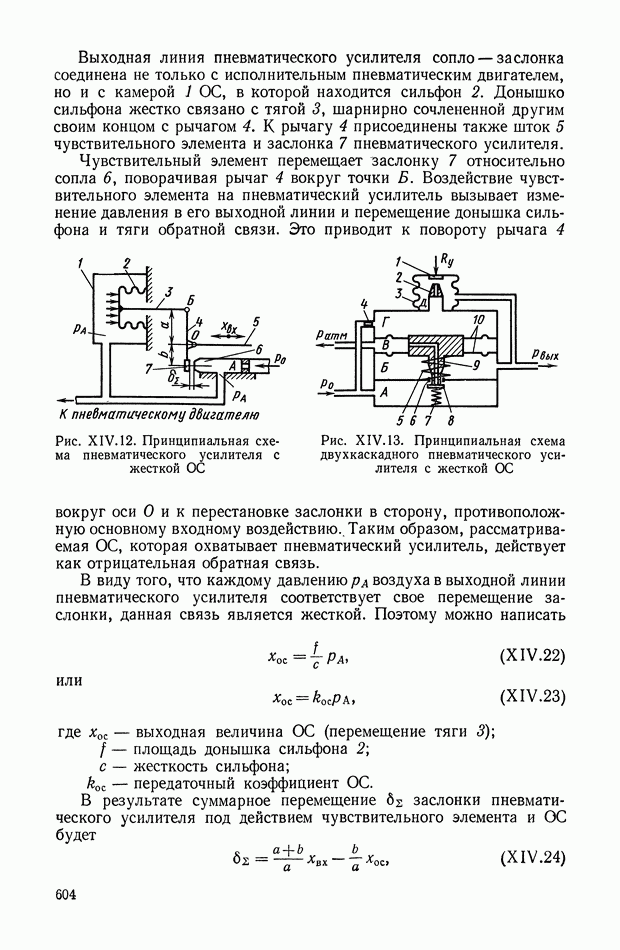
- 4. ЖЕСТКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
- 5. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ СИСТЕМАХ
- 6. СЛОЖНЫЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
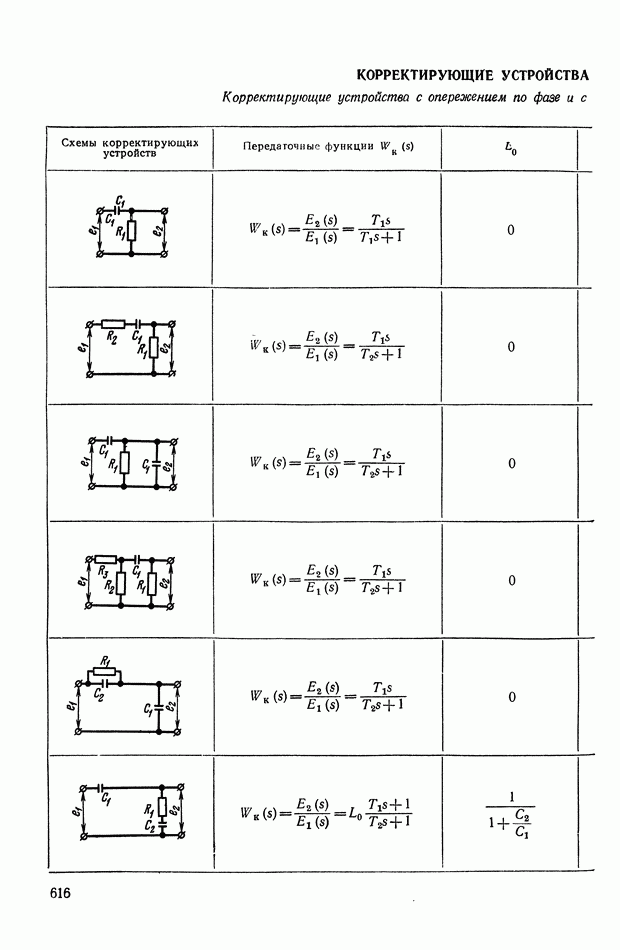
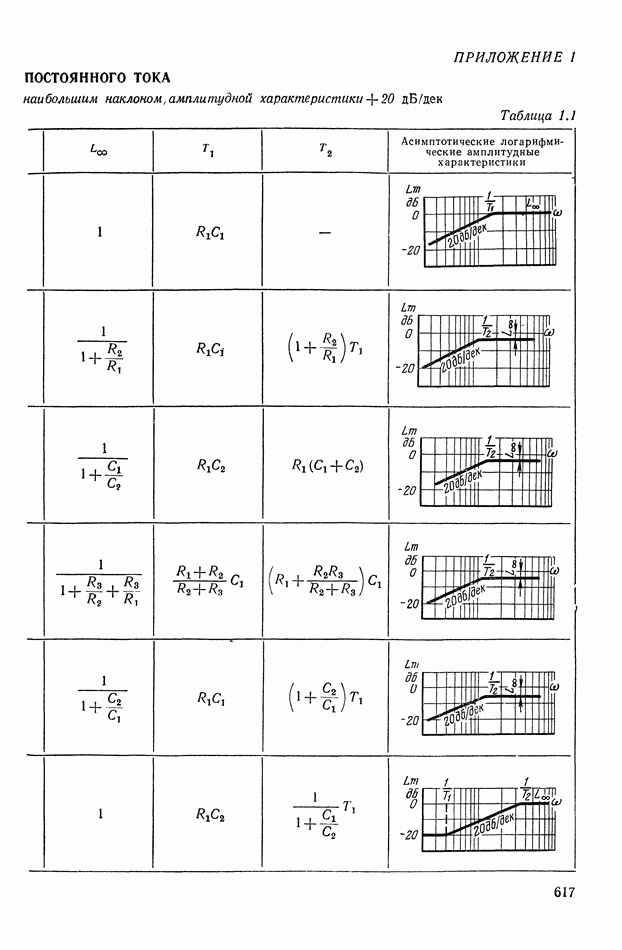
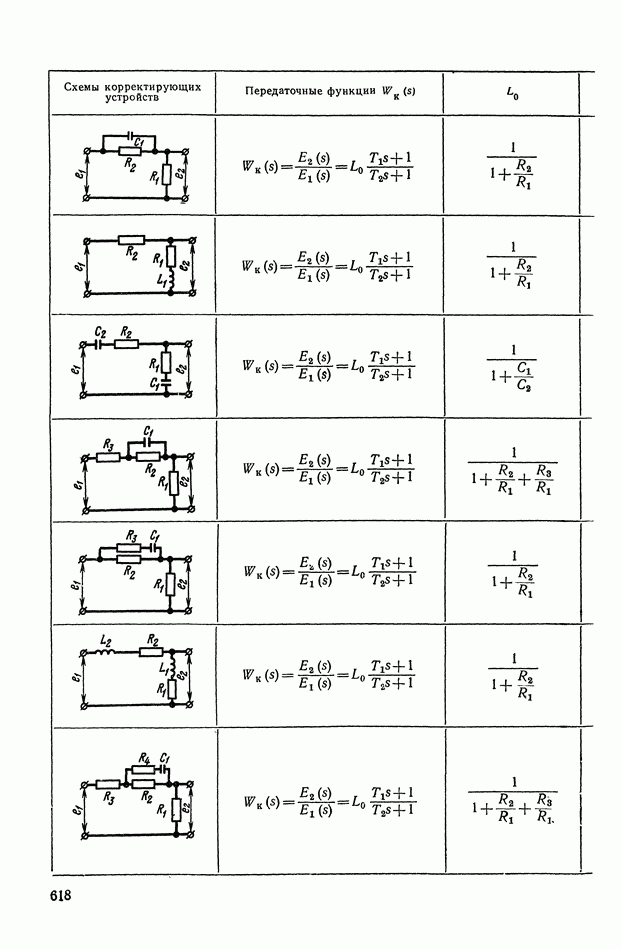
- ПРИЛОЖЕНИЕ 1. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПОСТОЯННОГО ТОКА
- ПРИЛОЖЕНИЕ II. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ОСНОВЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- ПРИЛОЖЕНИЕ III. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ