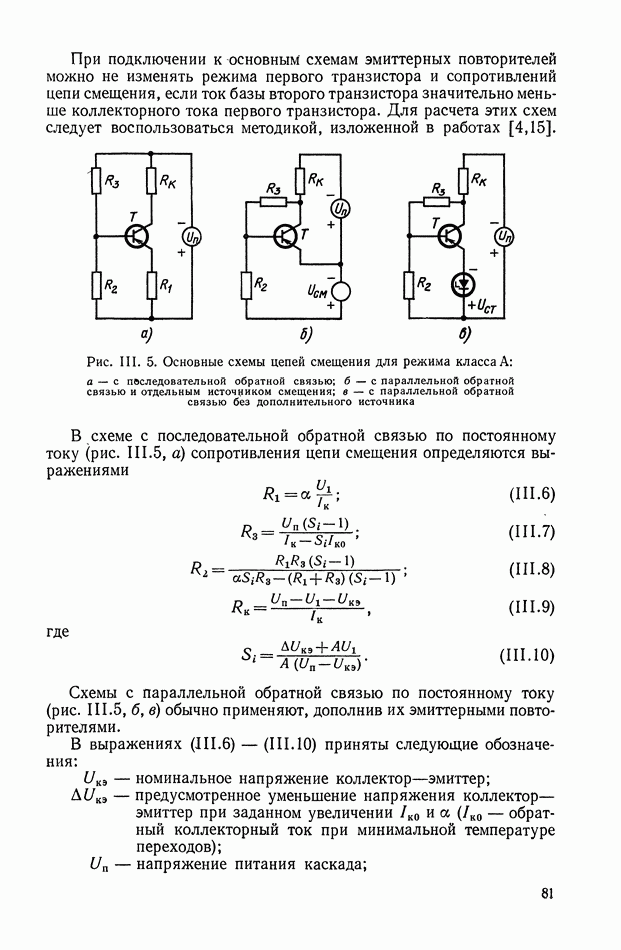
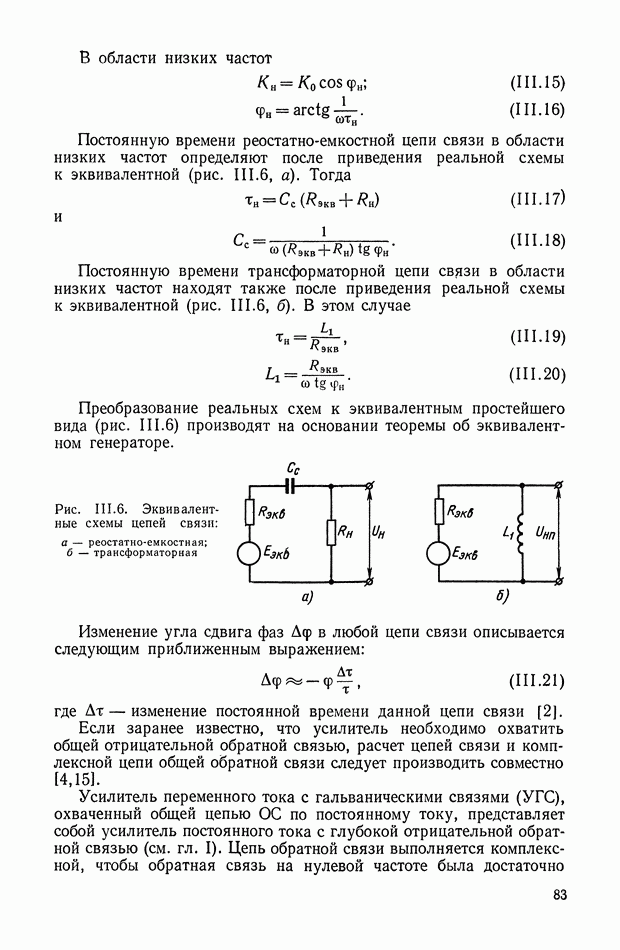
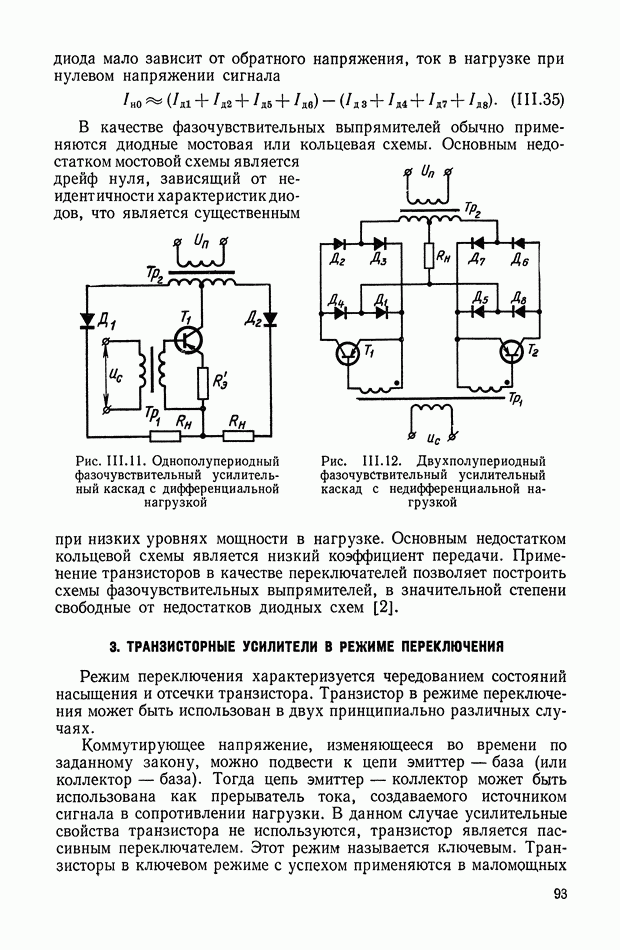
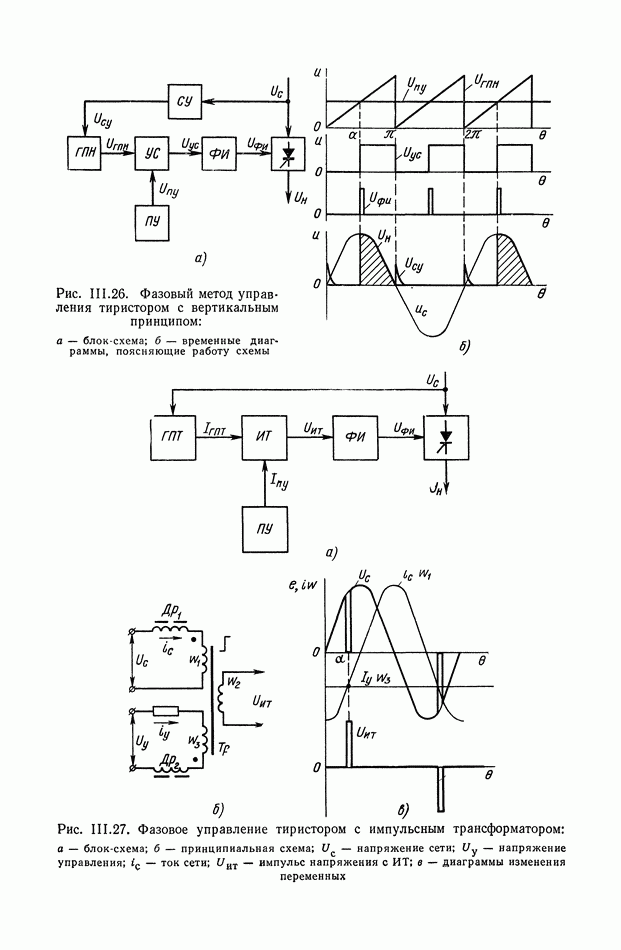
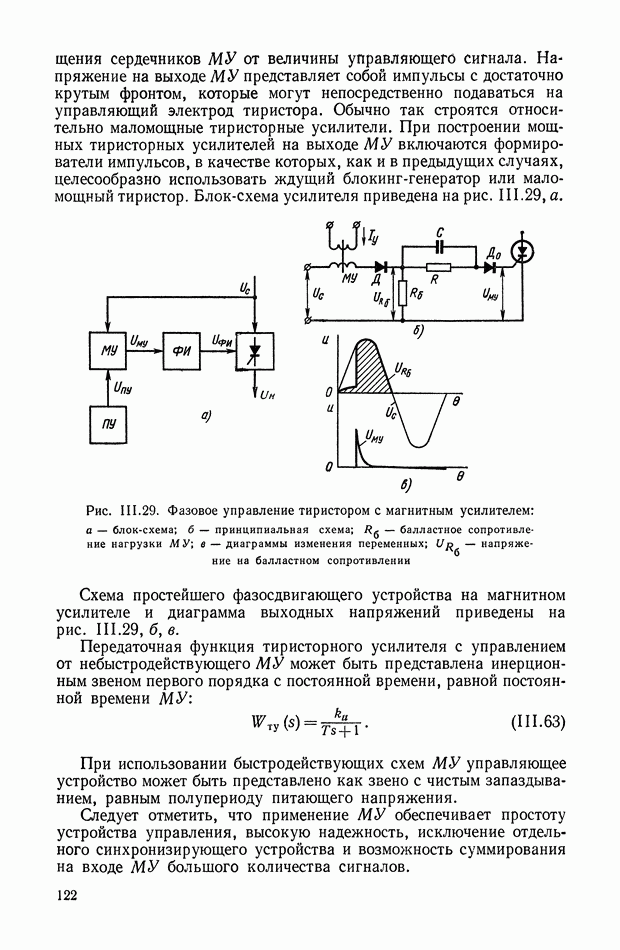
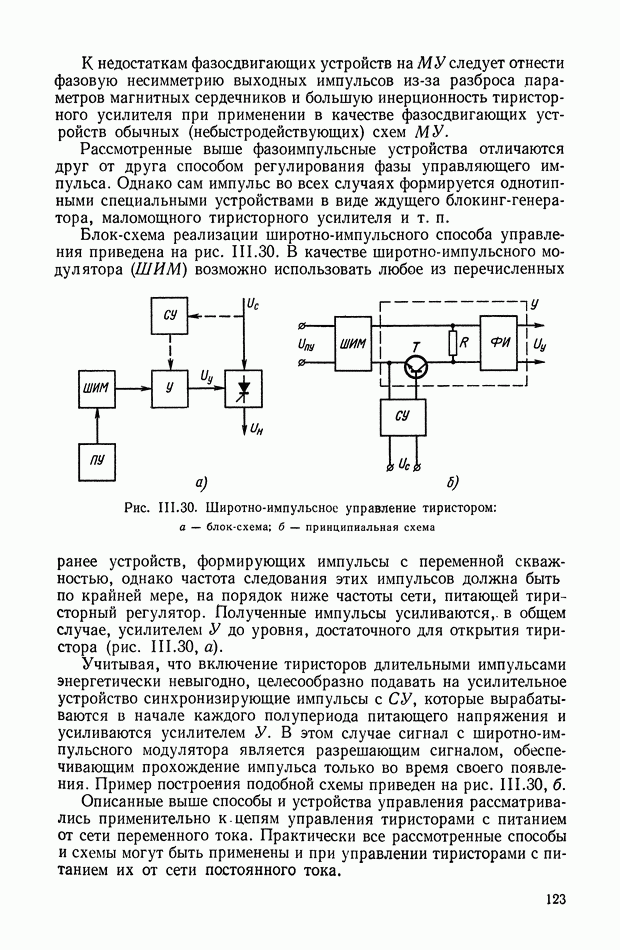
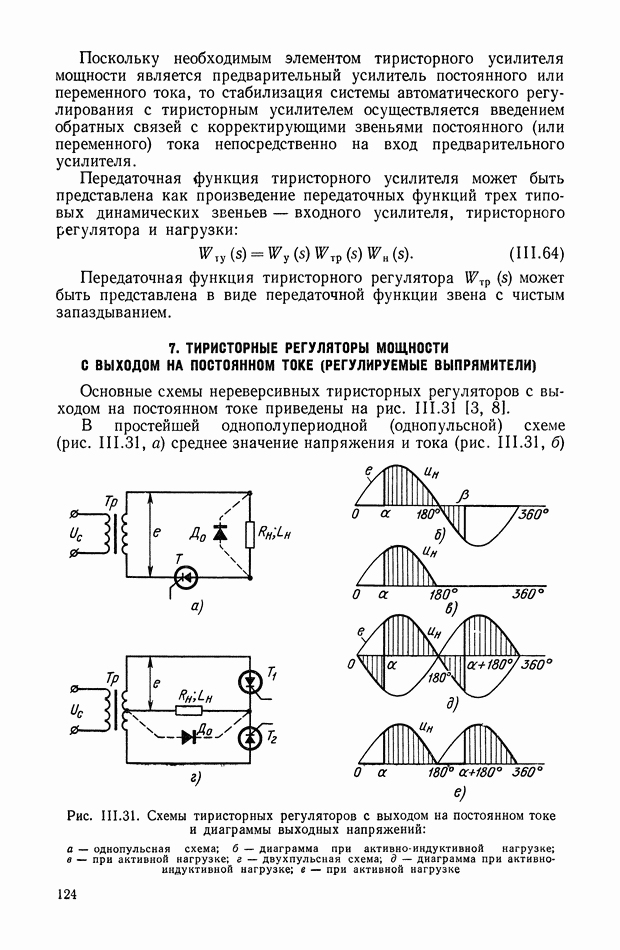
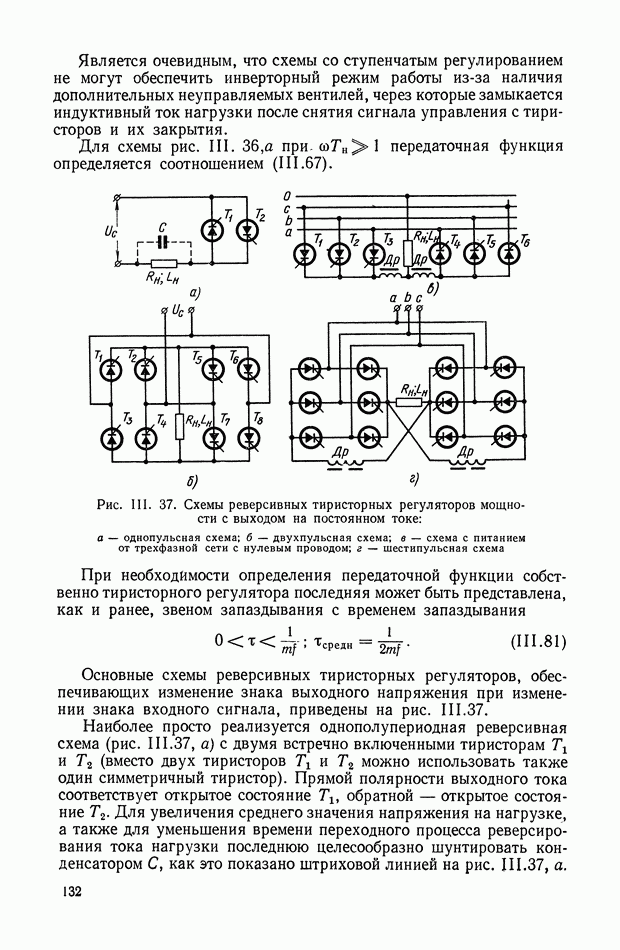
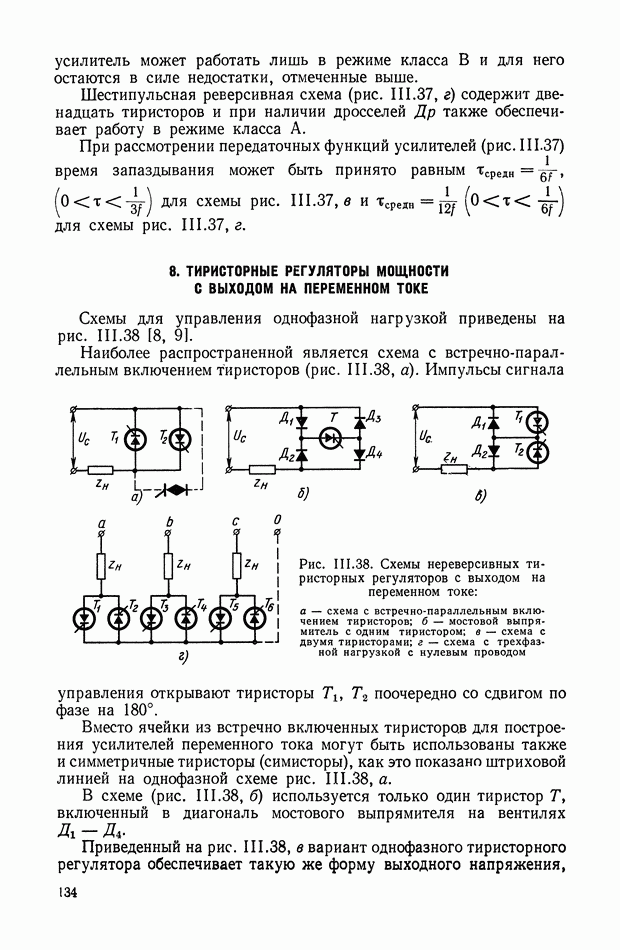
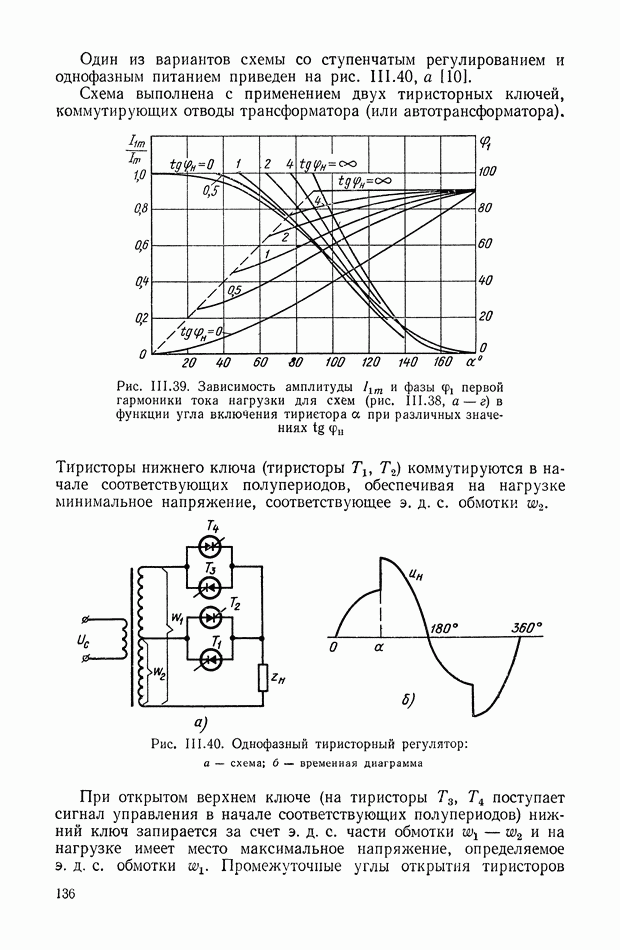
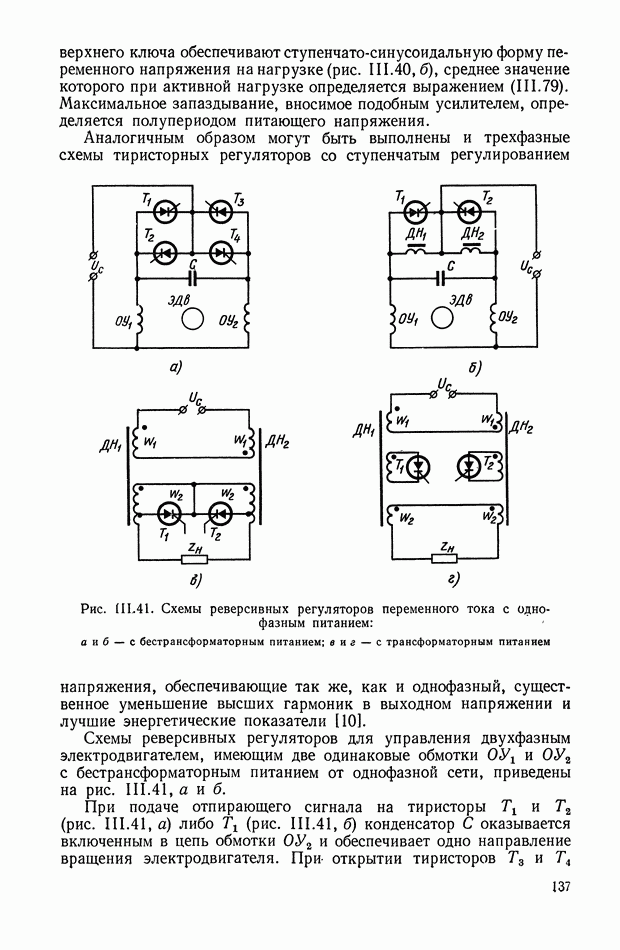
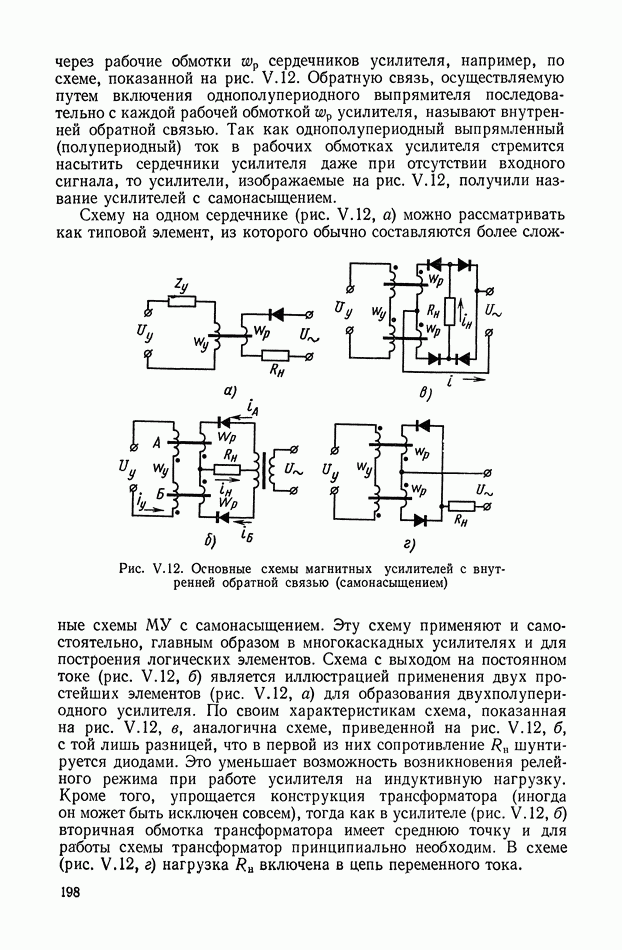
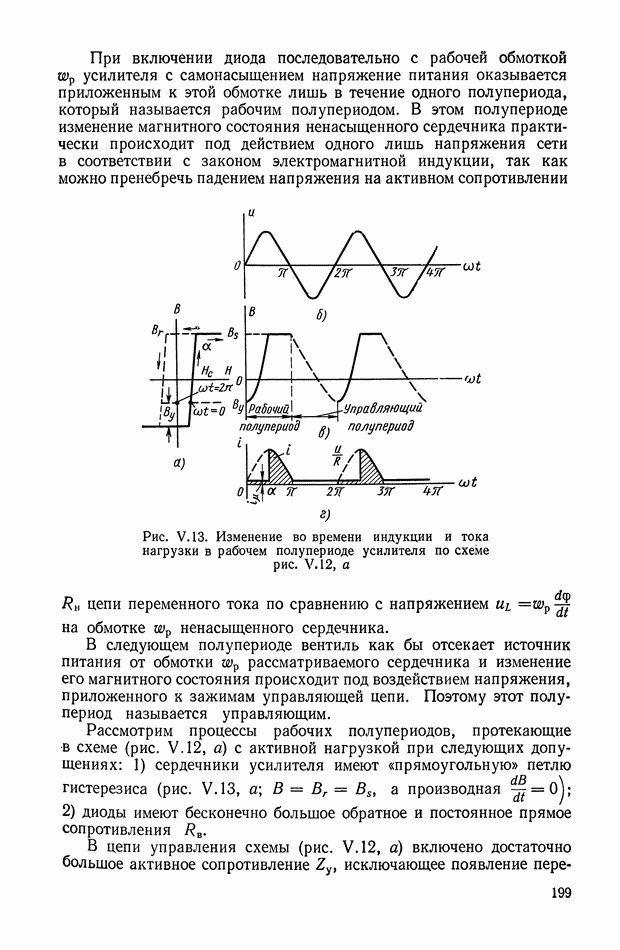
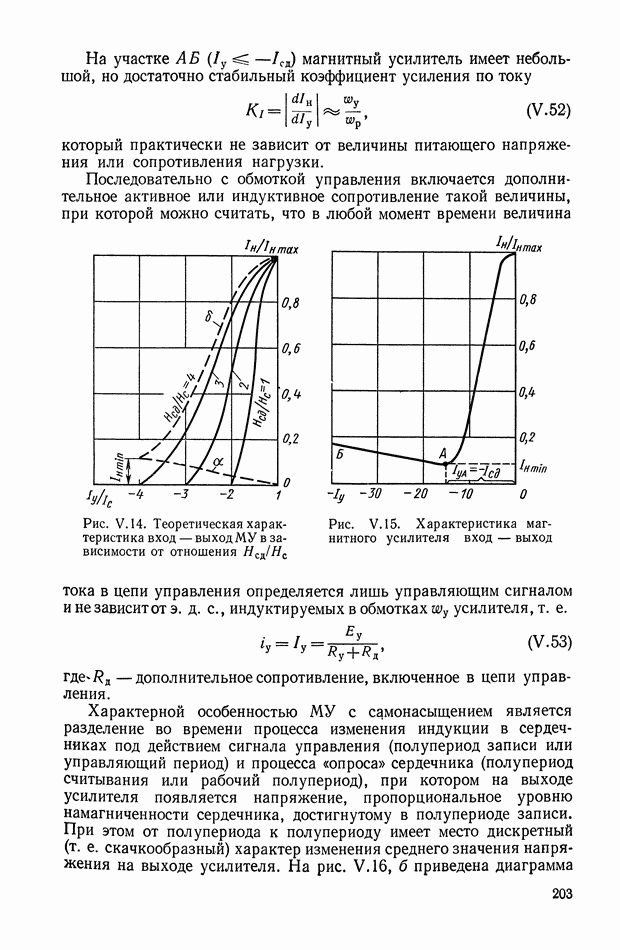
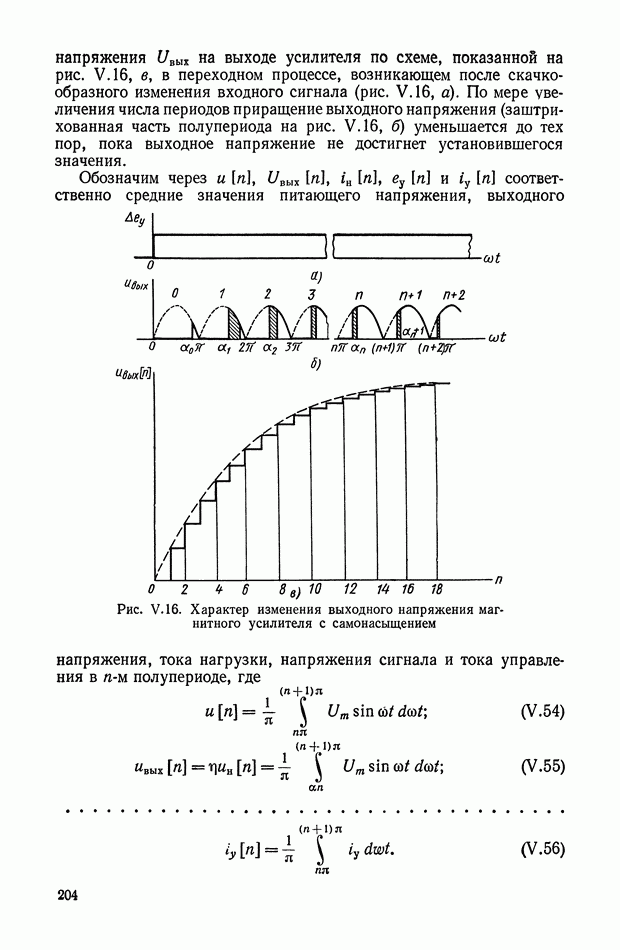
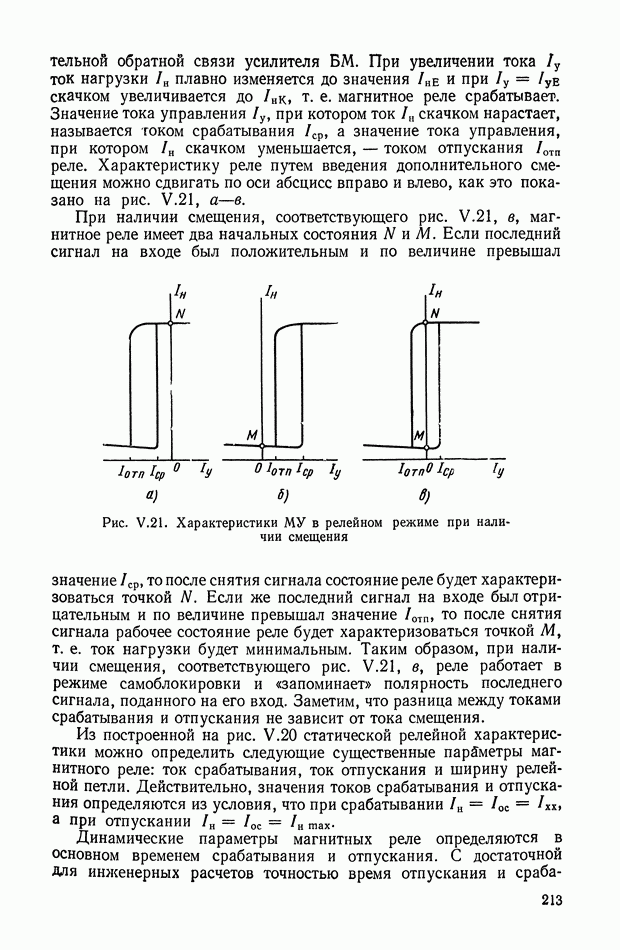
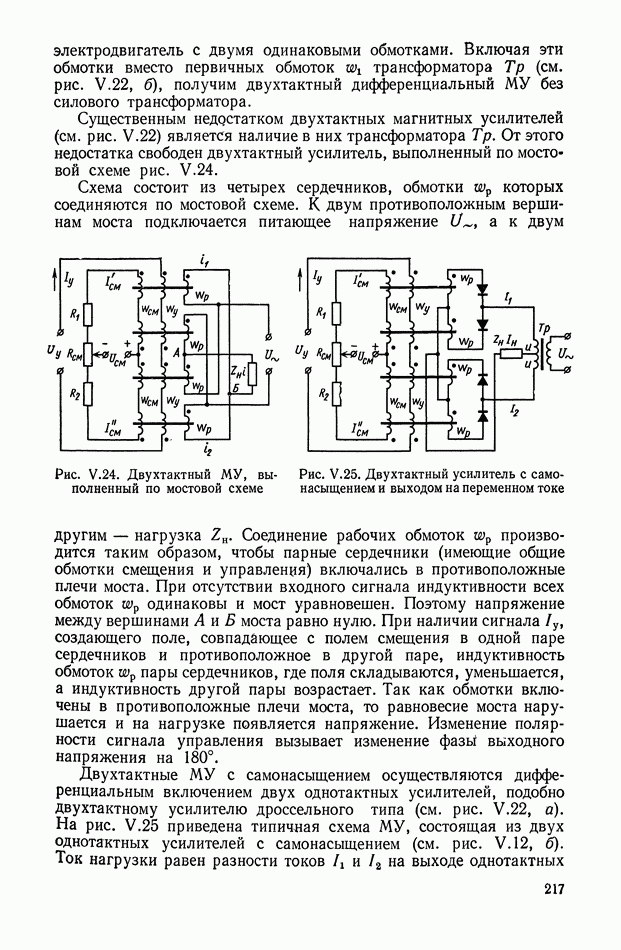
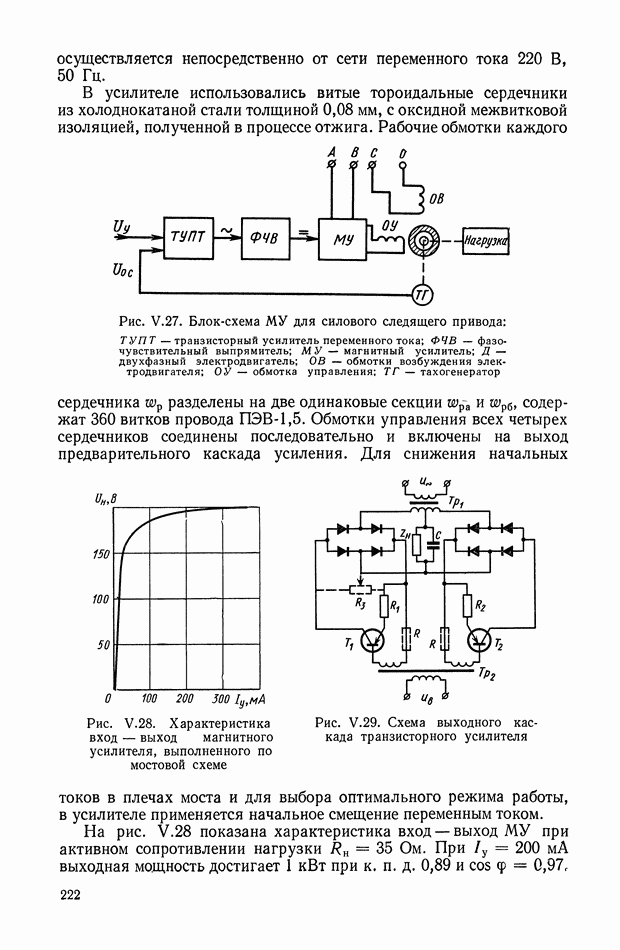
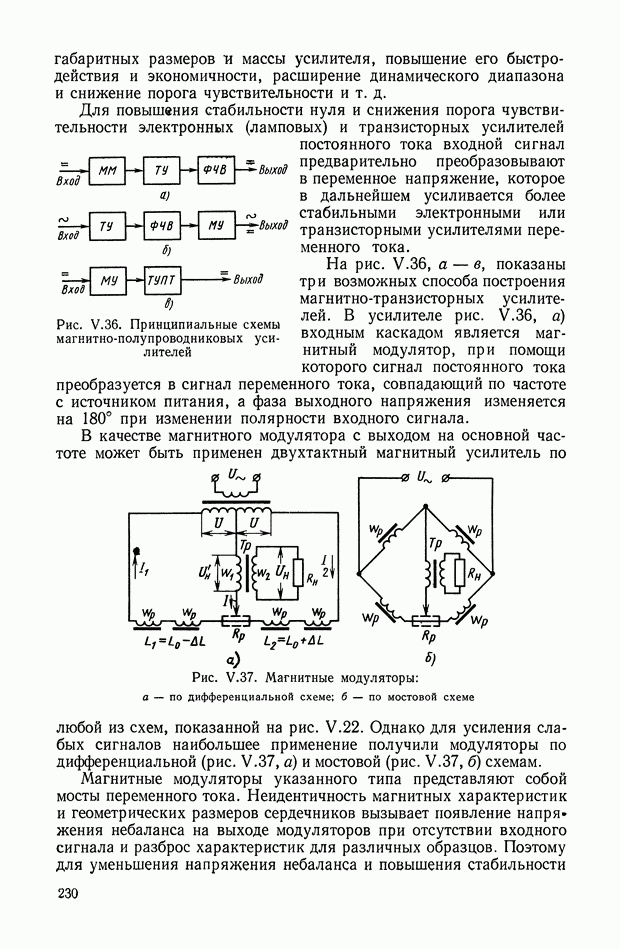
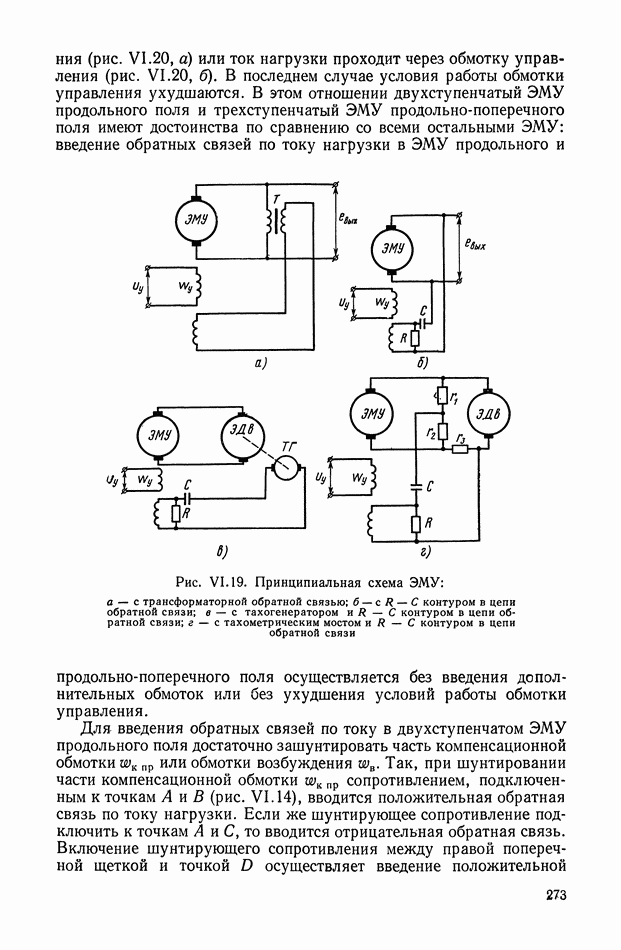
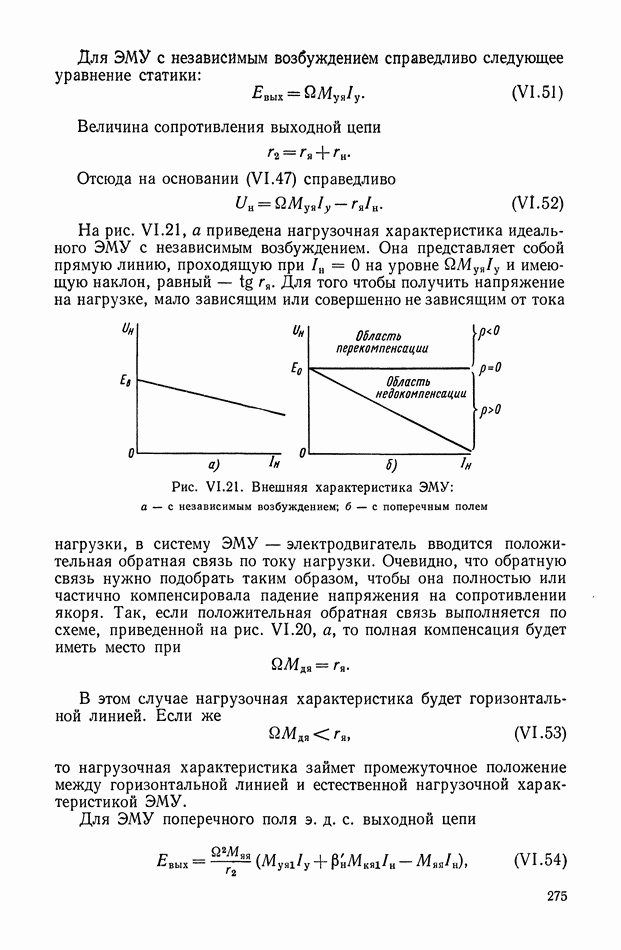
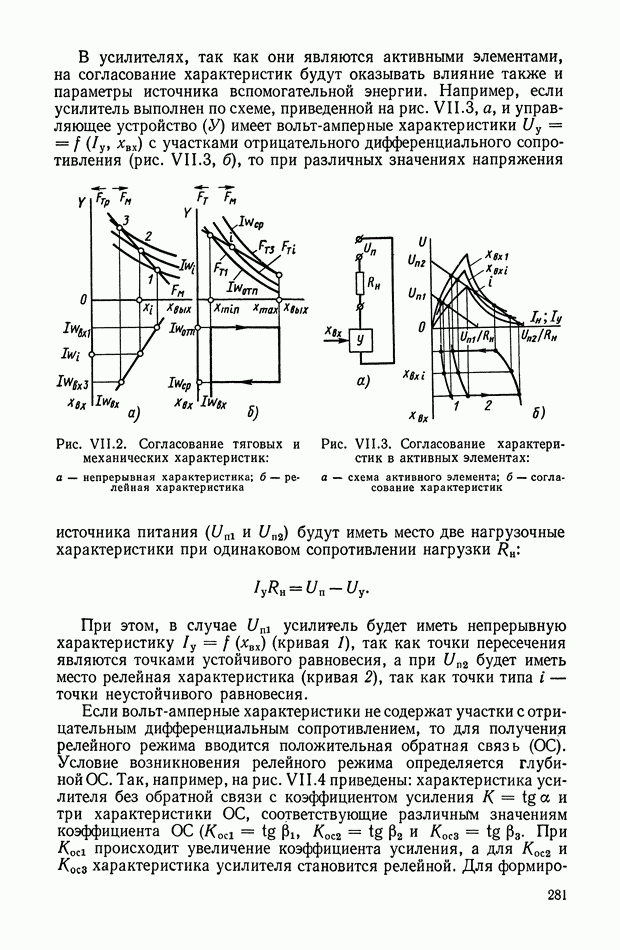
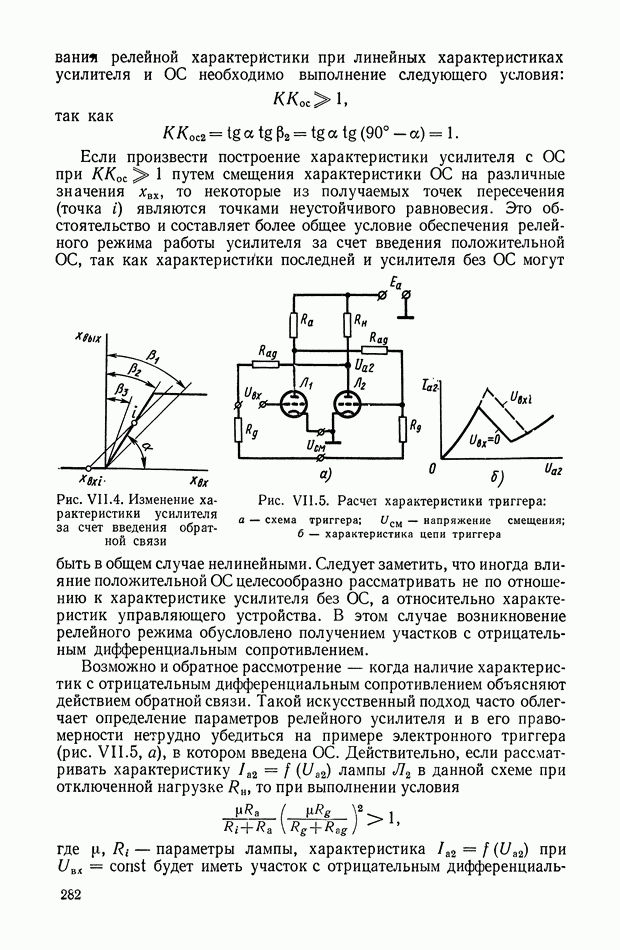
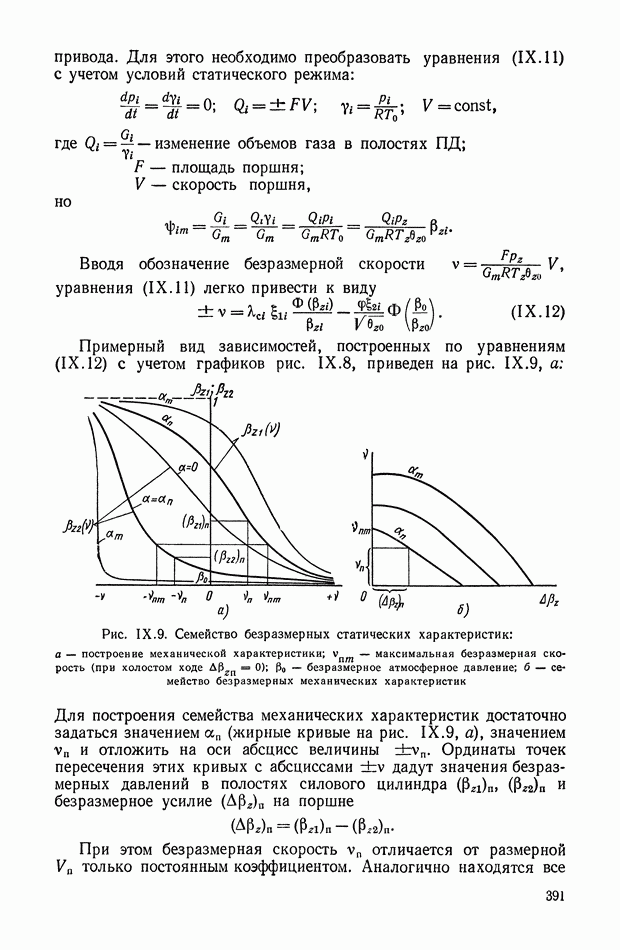
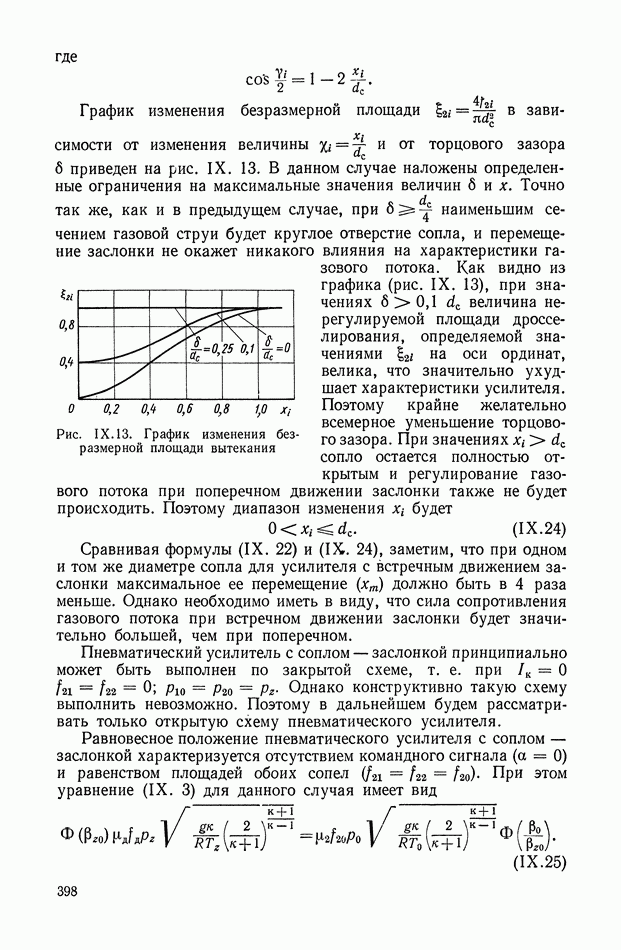
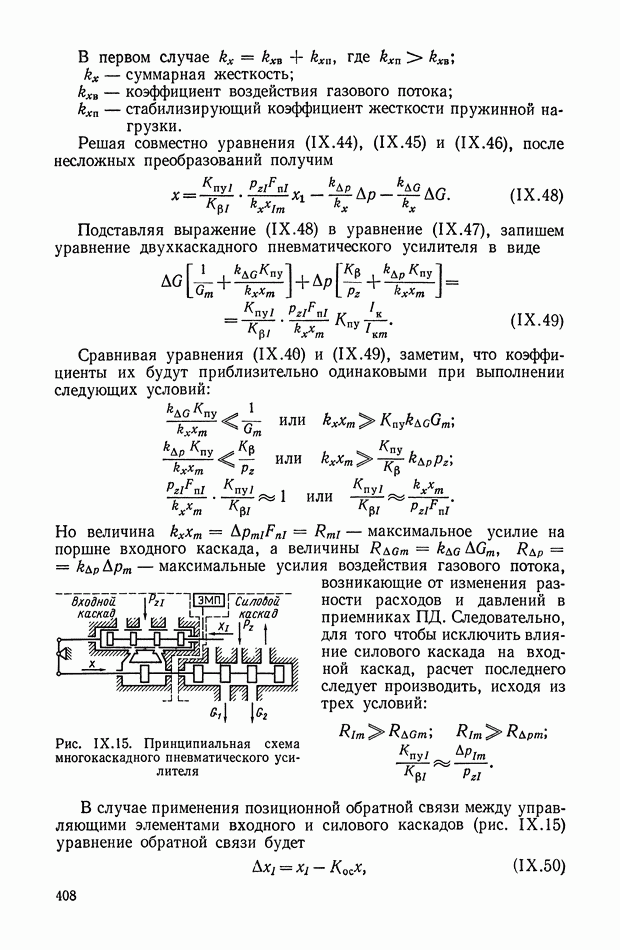
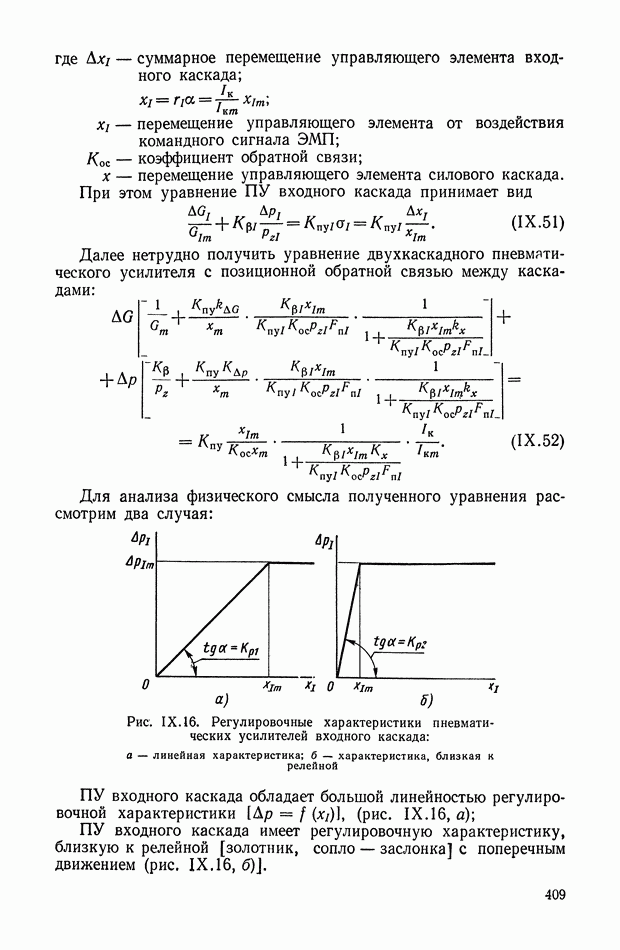
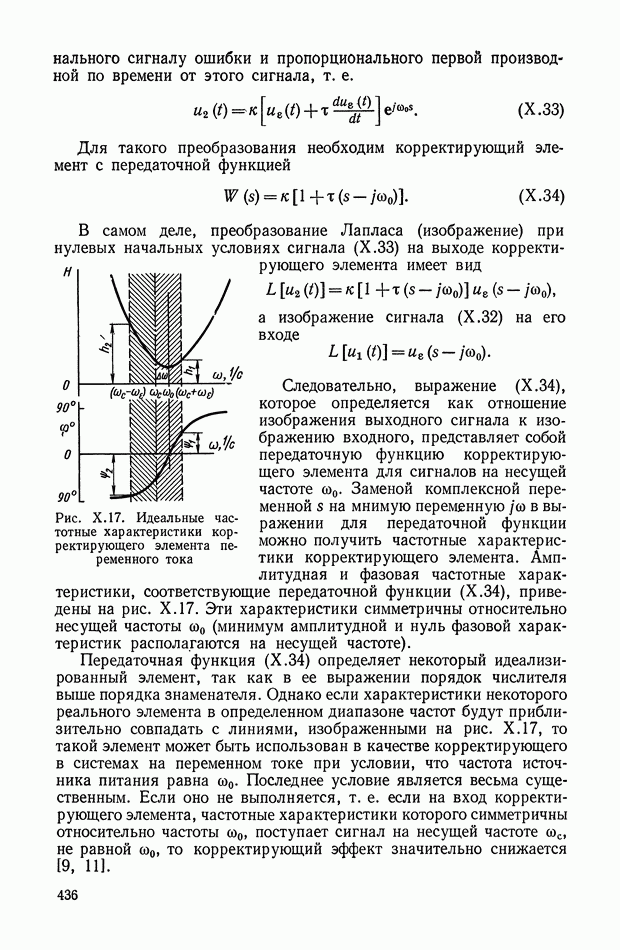
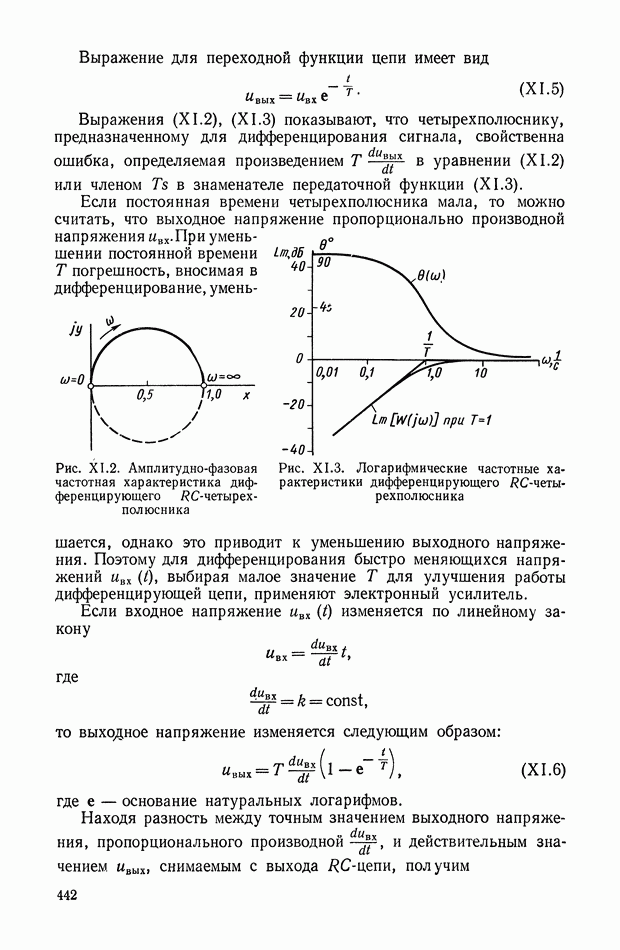
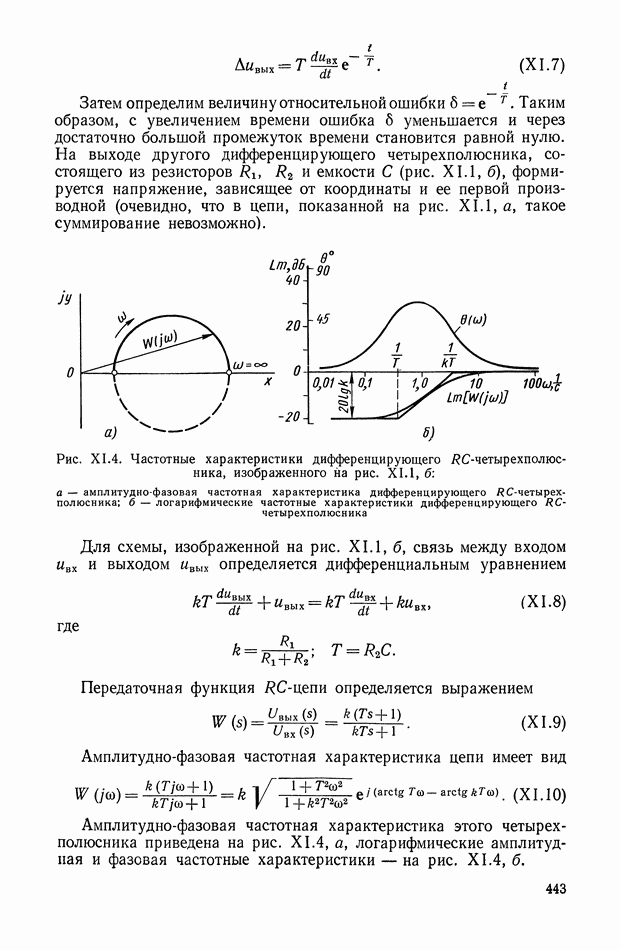
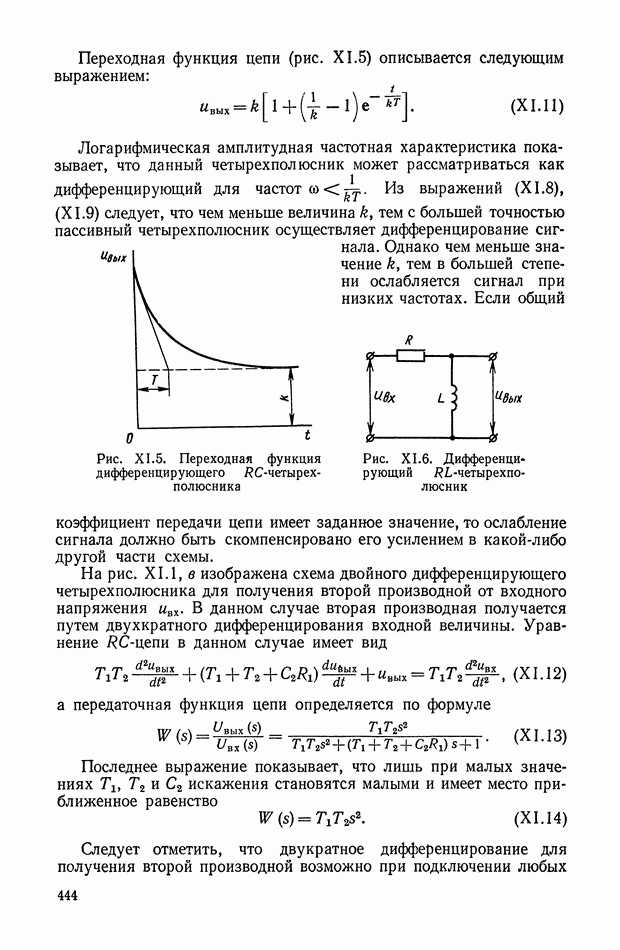
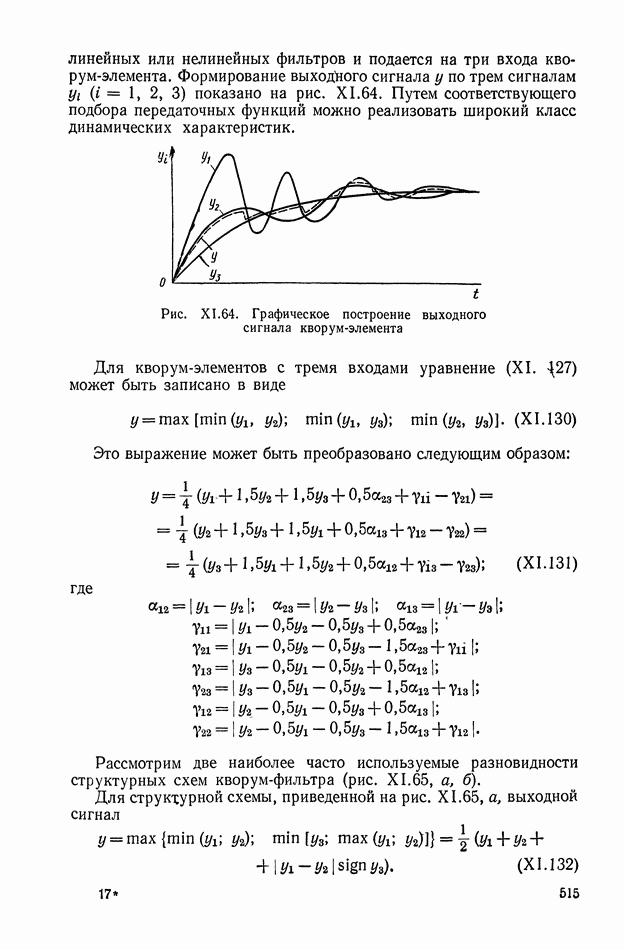
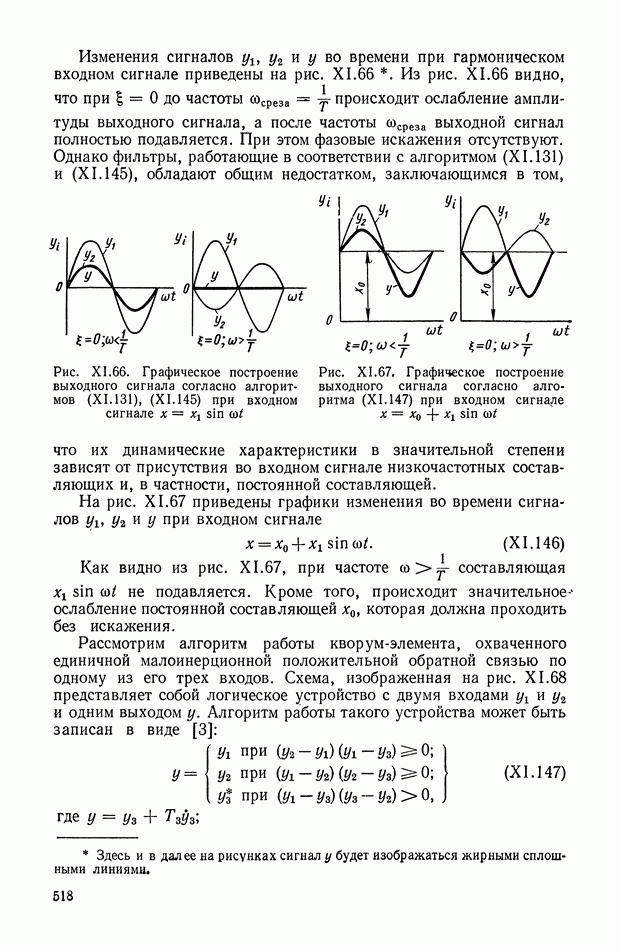
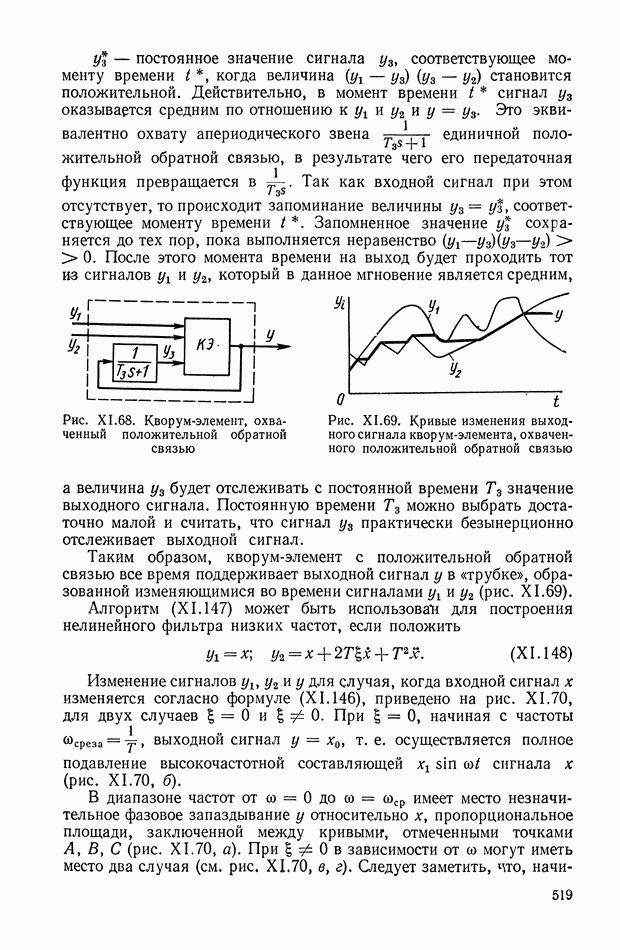
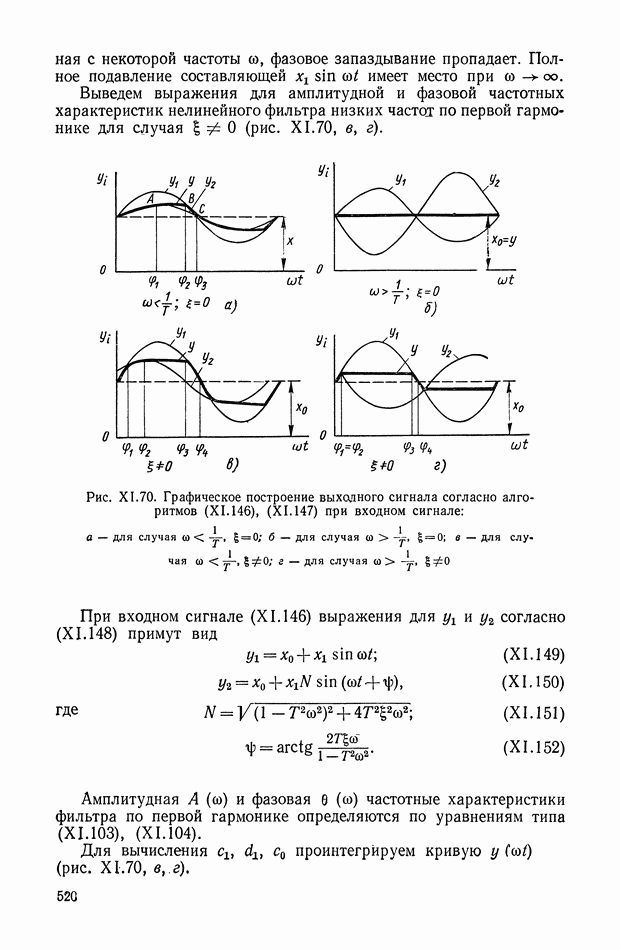
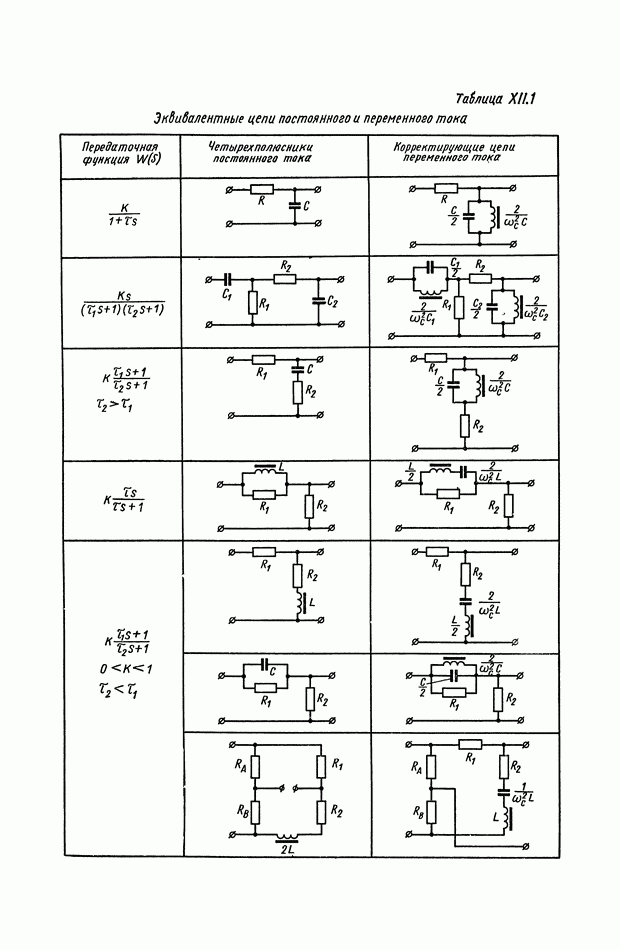
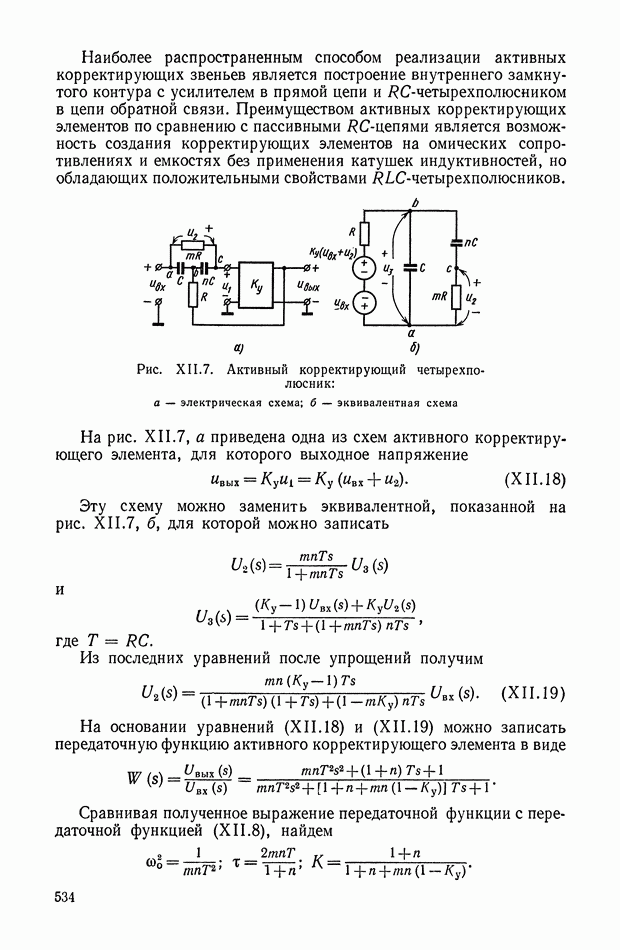
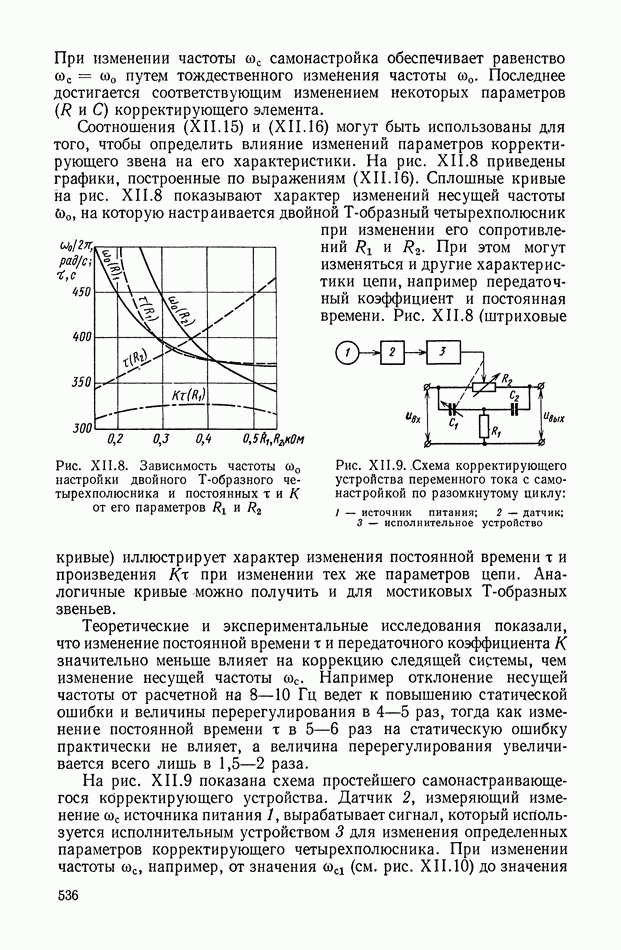
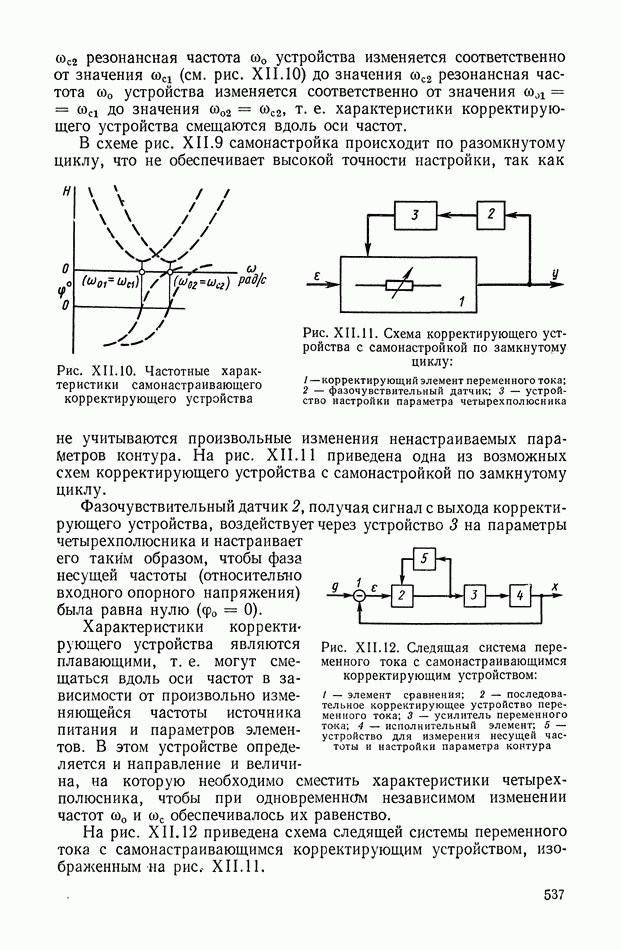
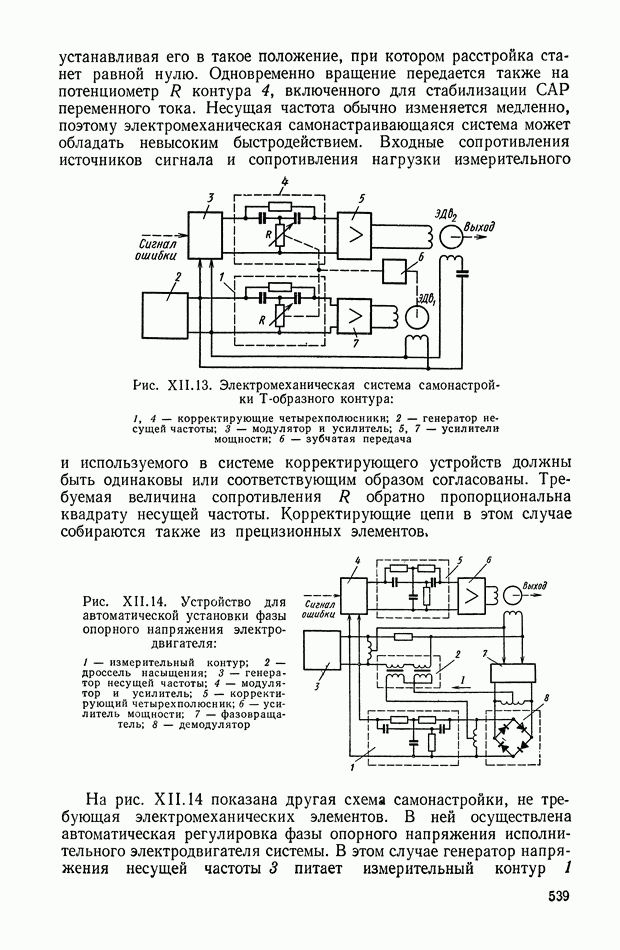
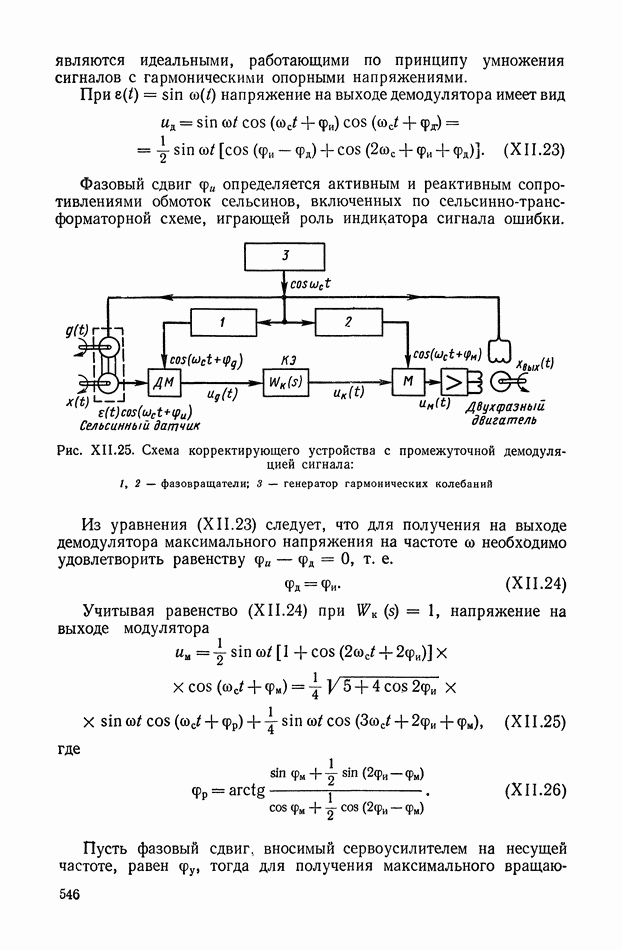
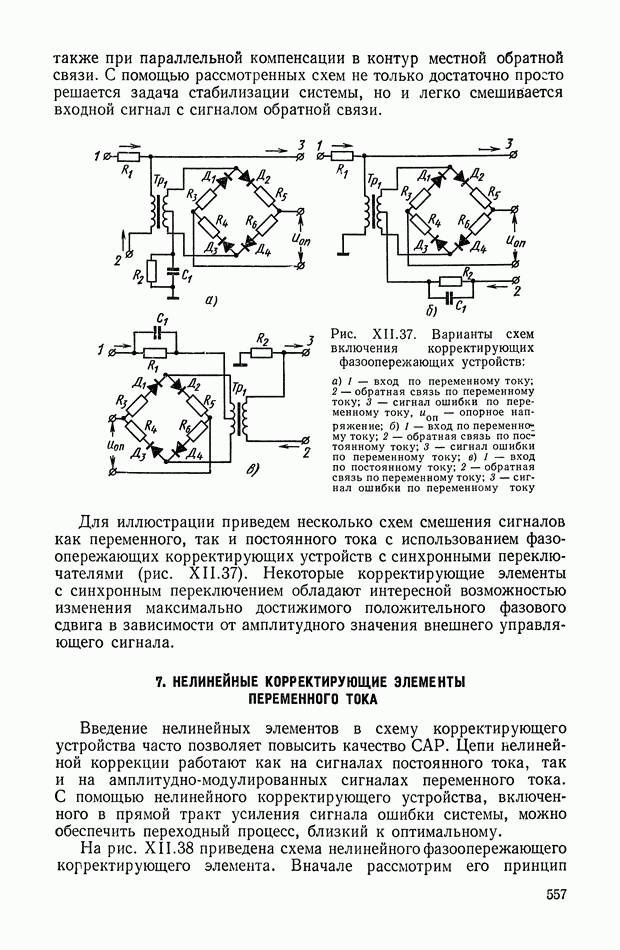
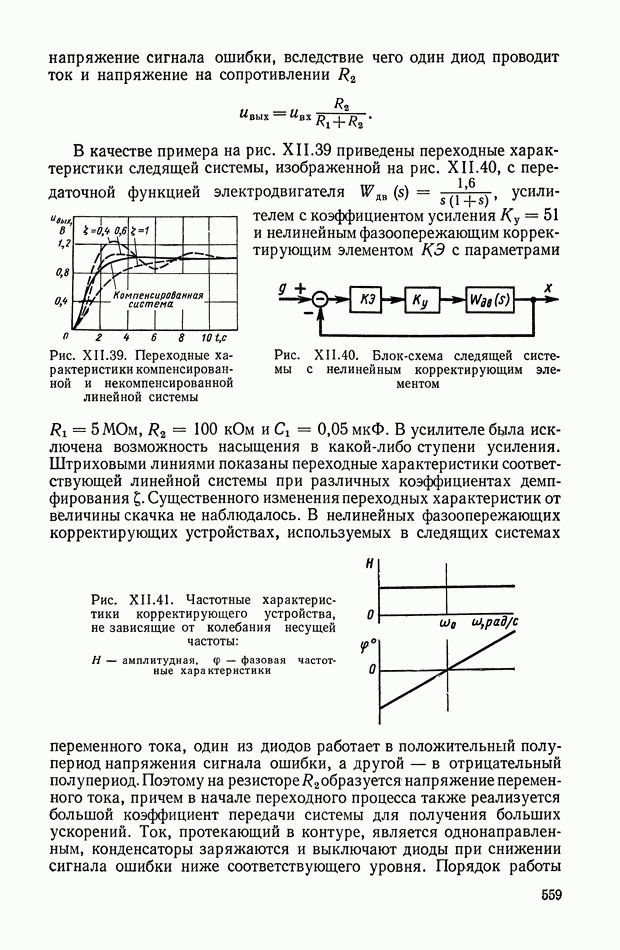
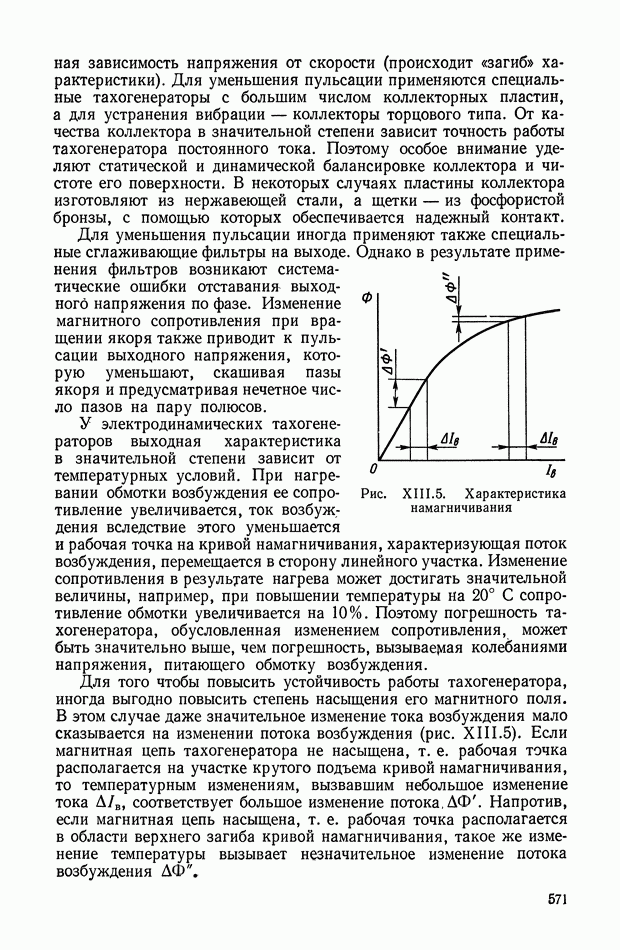
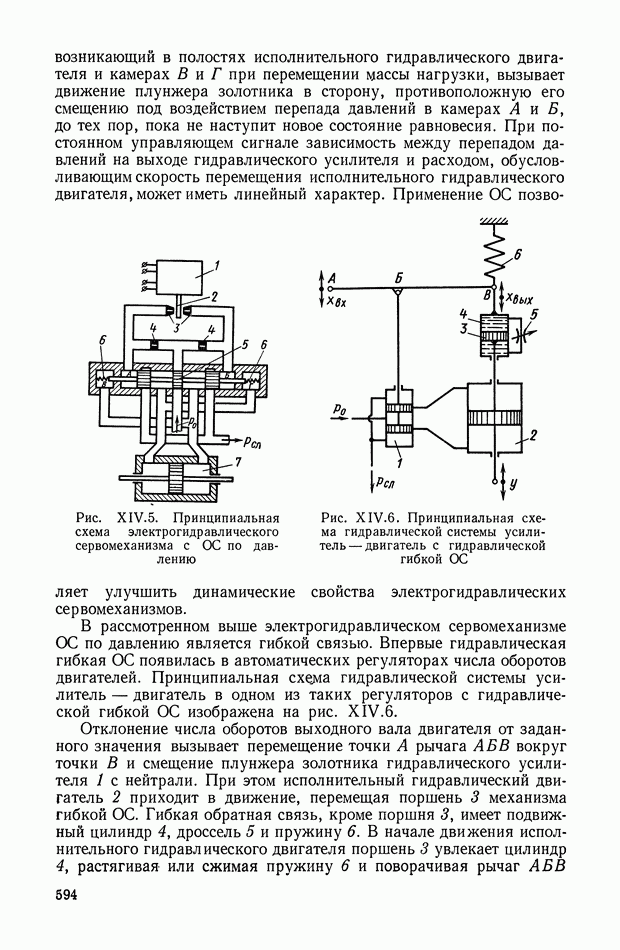
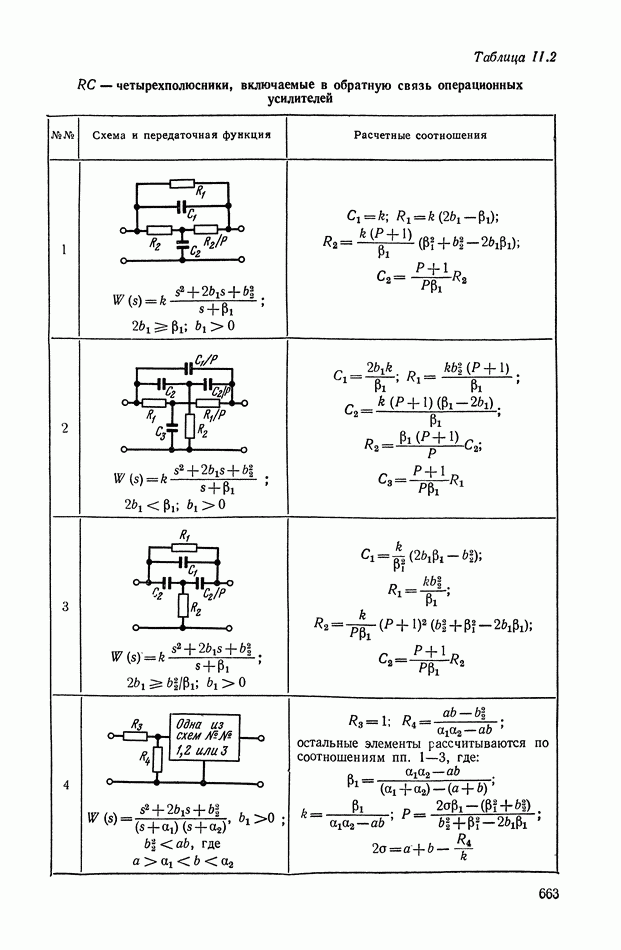
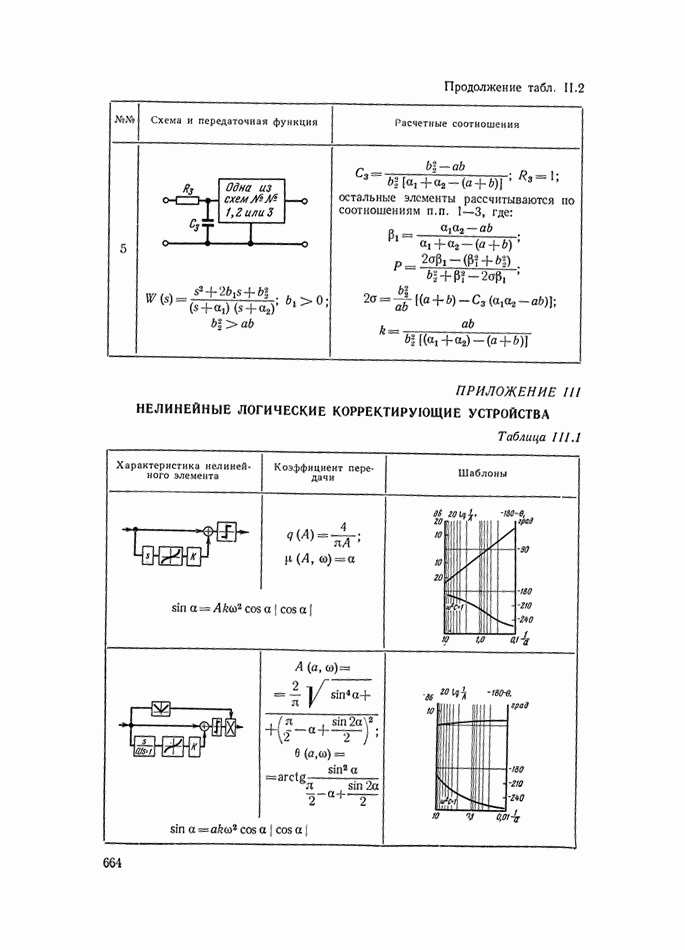
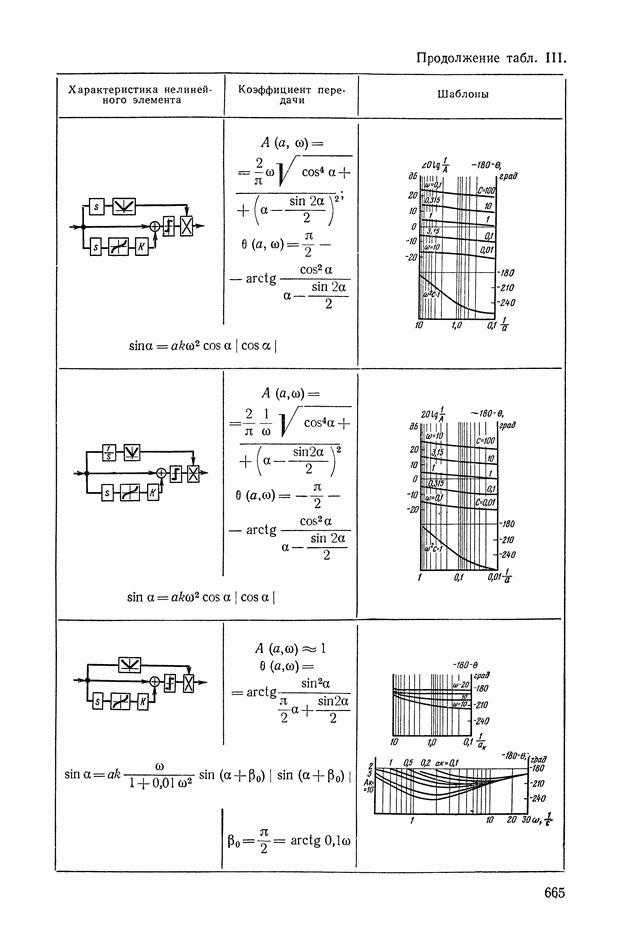
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
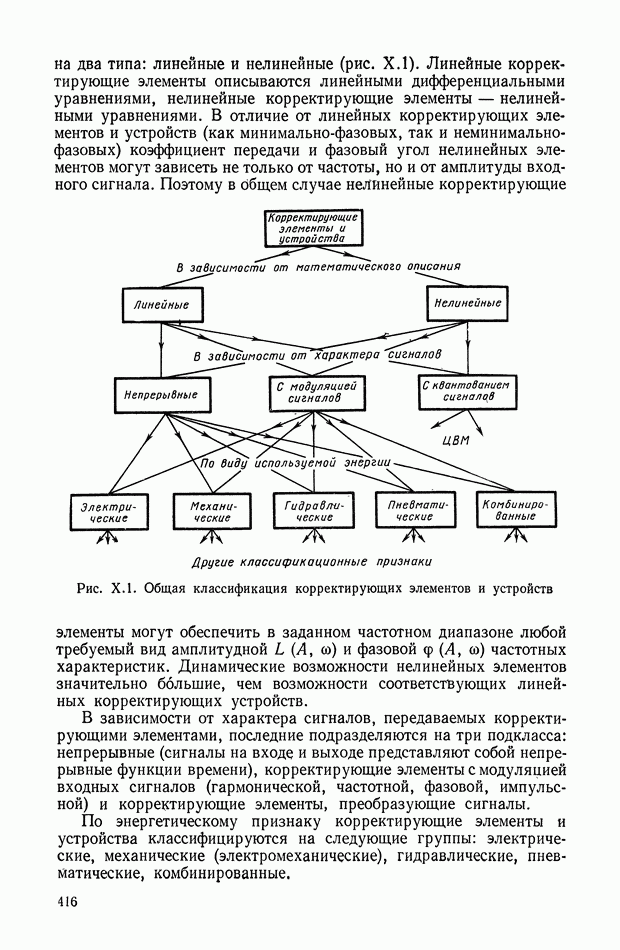
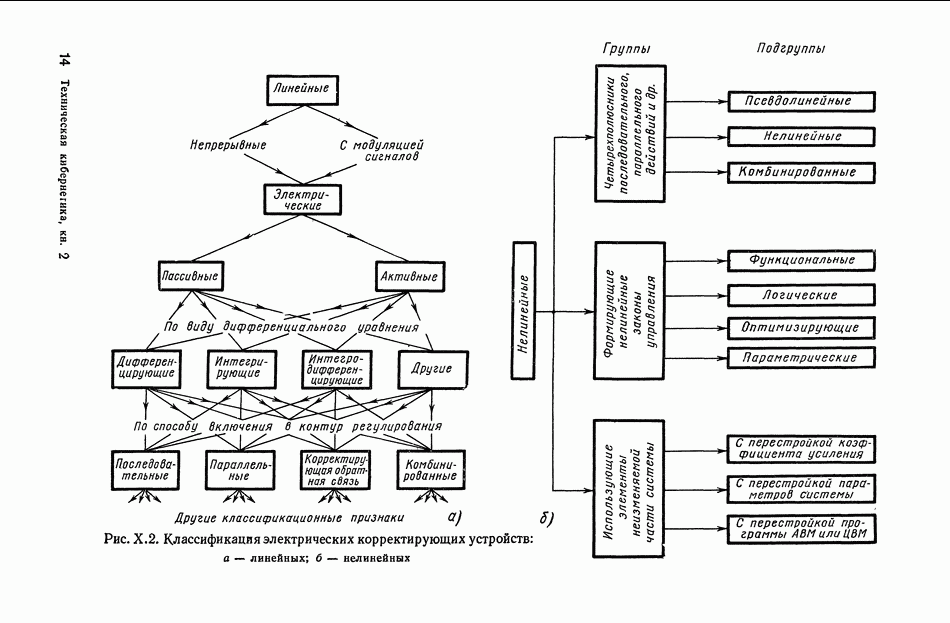
8. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
Рассмотрим несколько типов нелинейных логических корректирующих устройств.
Одноканальные нелинейные логические устройства.
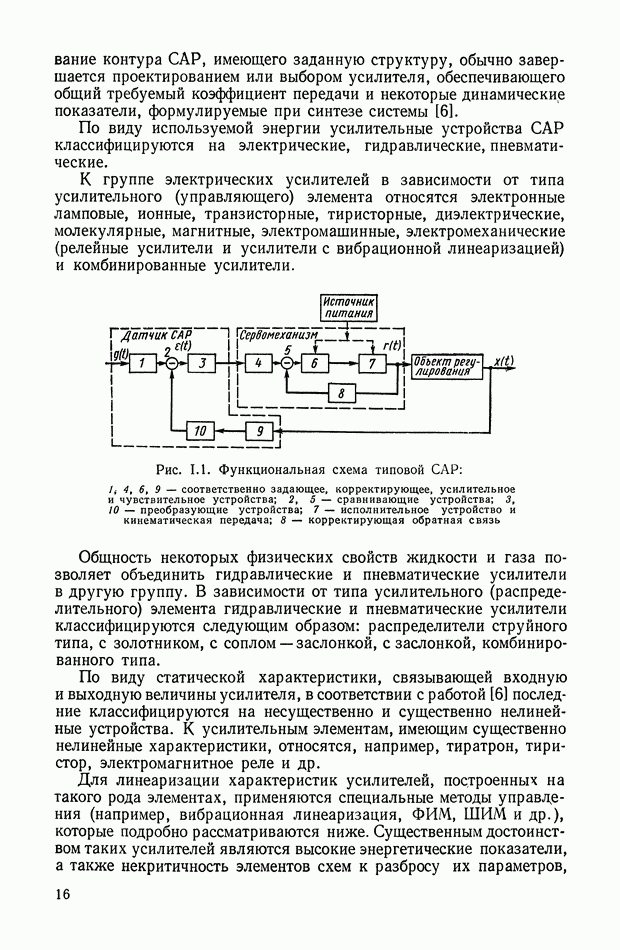
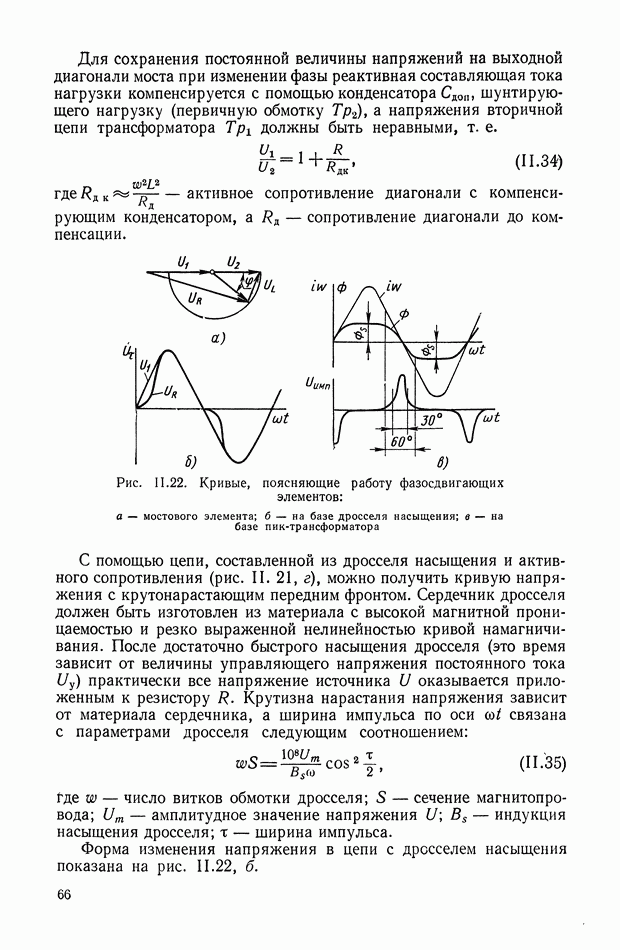
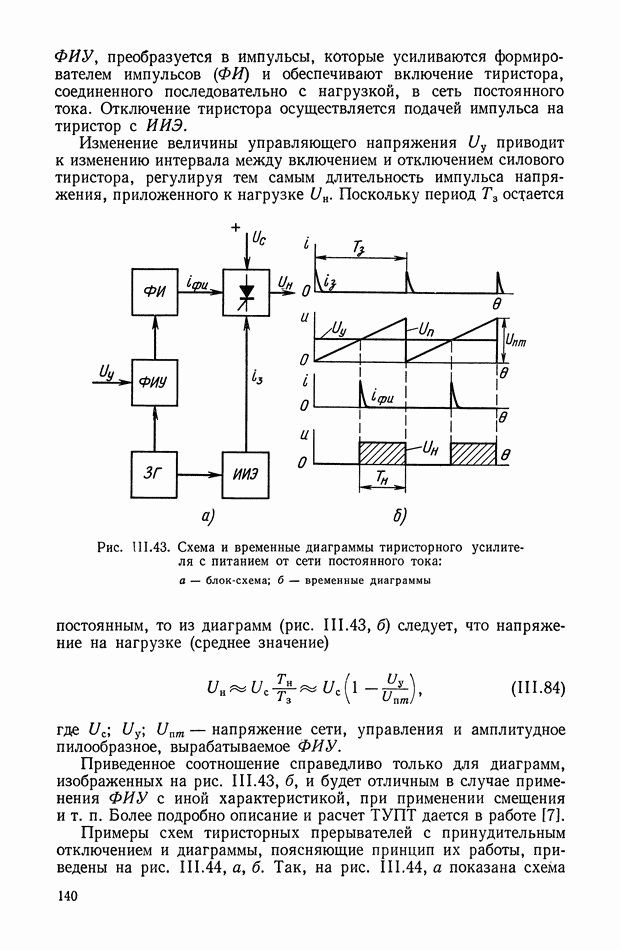
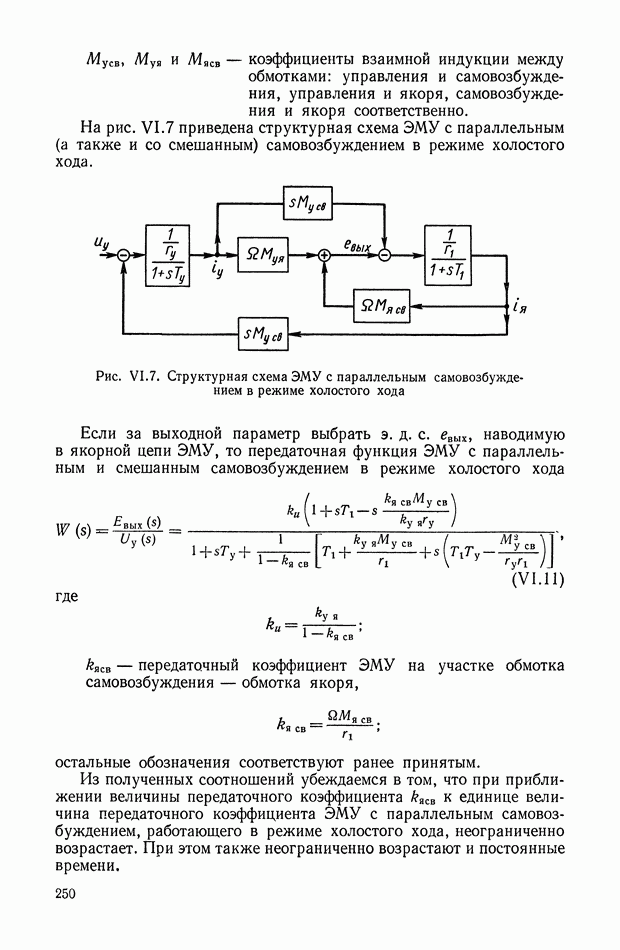
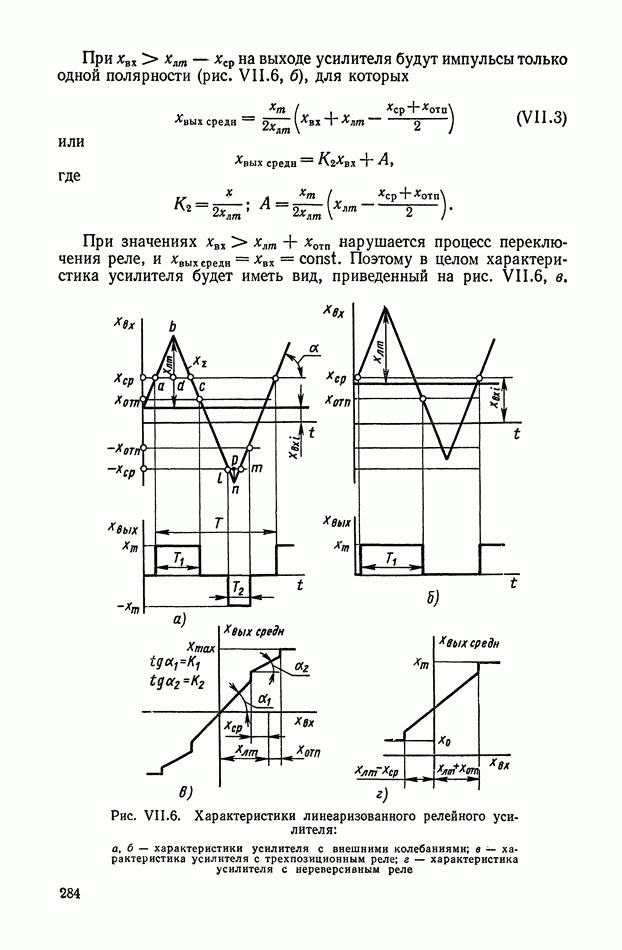
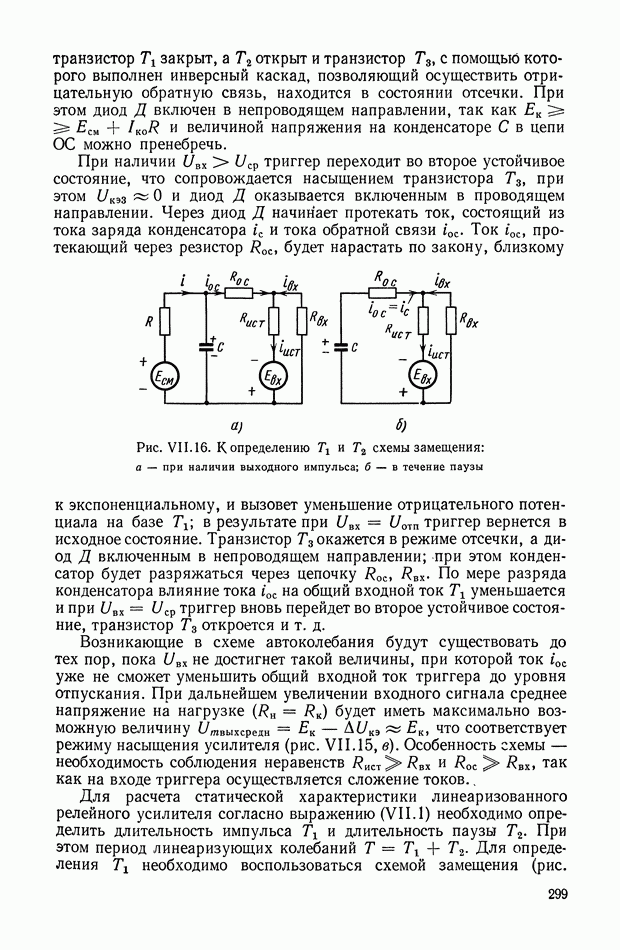
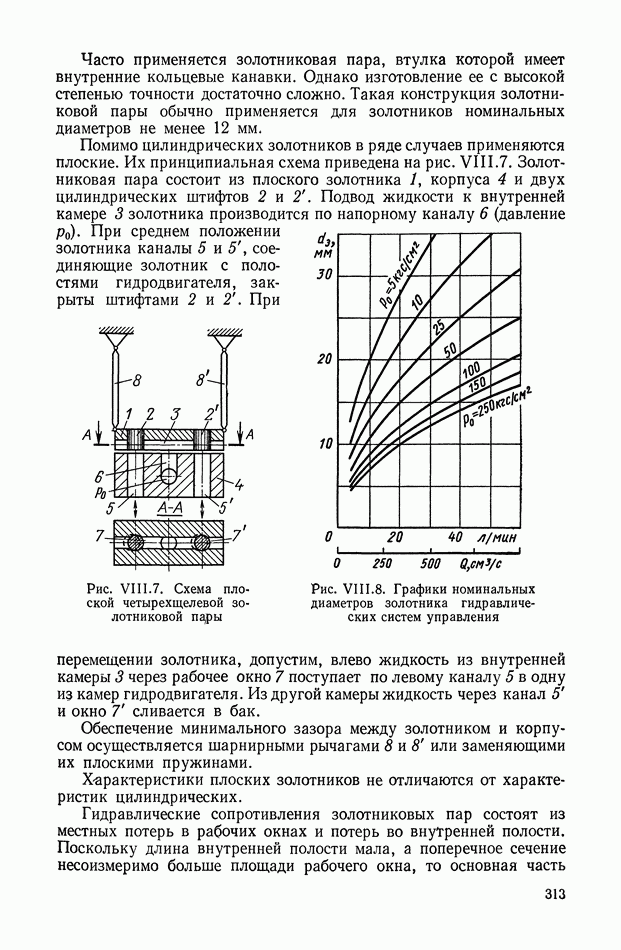
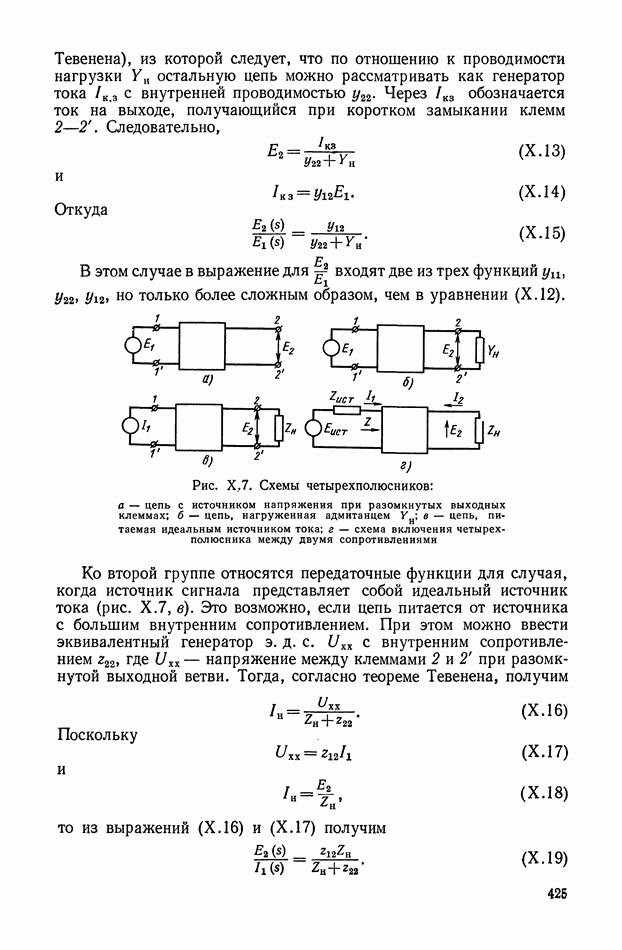
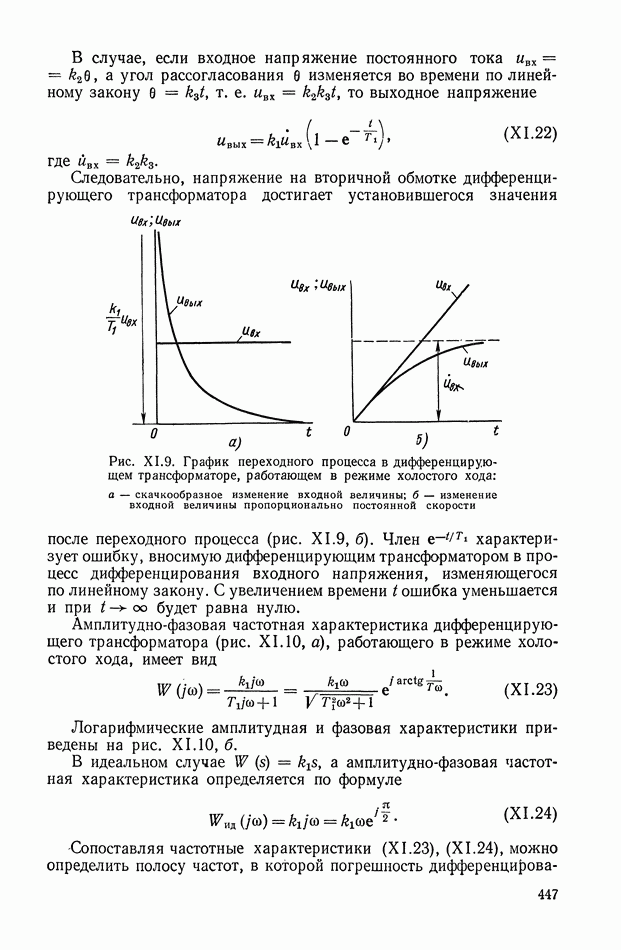
К таким устройствам прежде всего можно отнести класс нелинейных фильтров, представляющих собой последовательное соединение опережающего звена, релейного элемента и запаздывающего, звена (рис. XI.45).

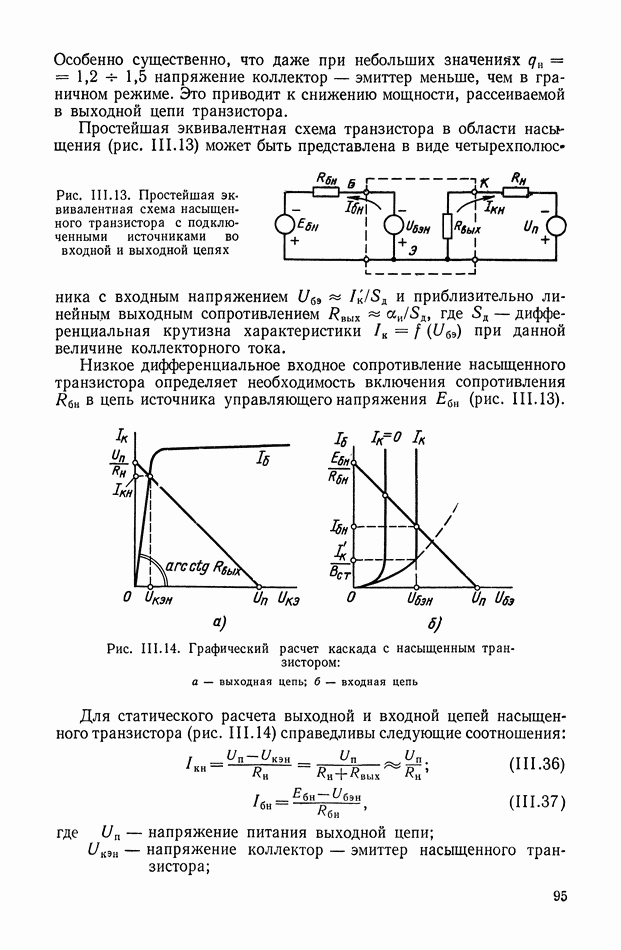
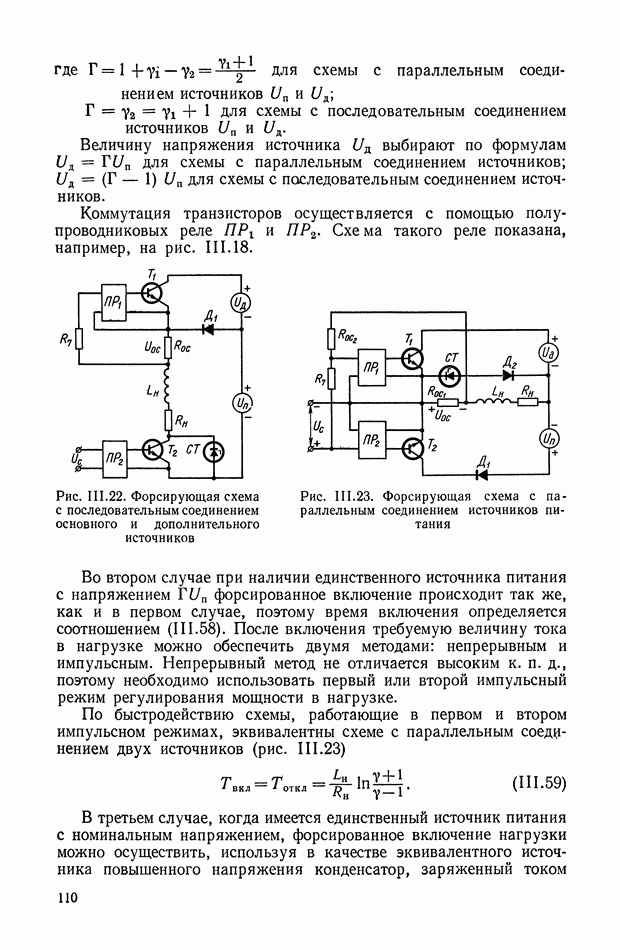
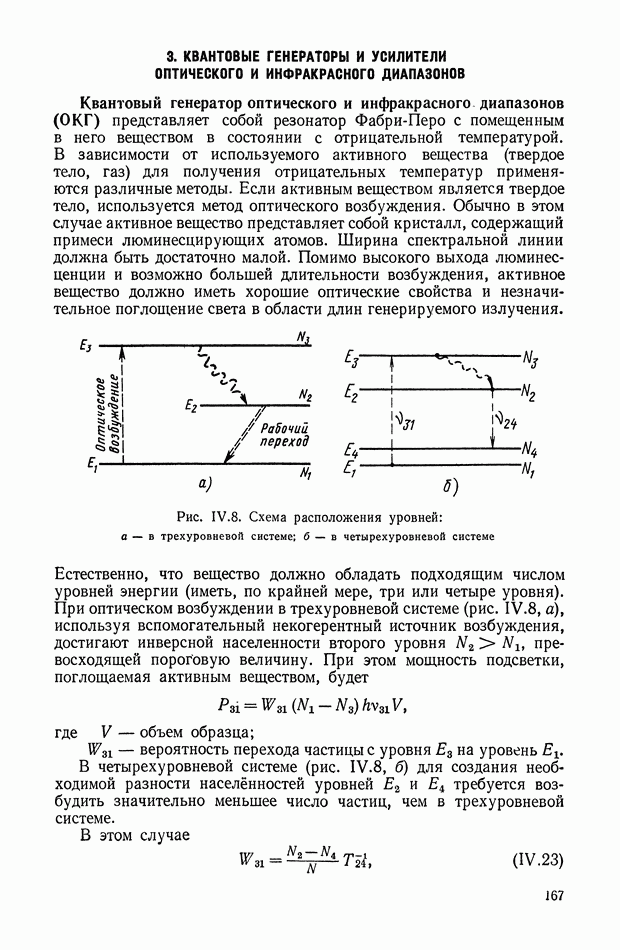
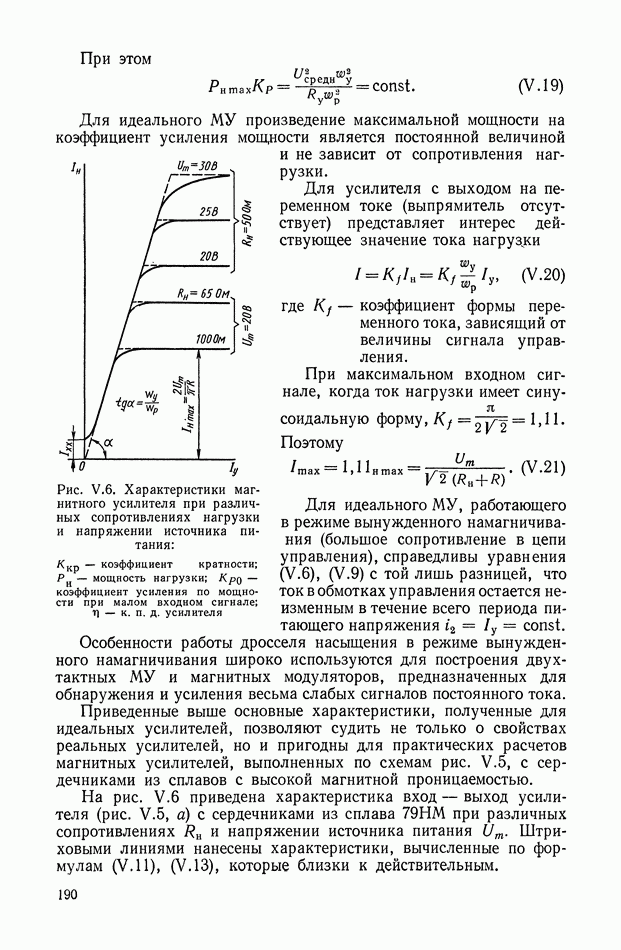
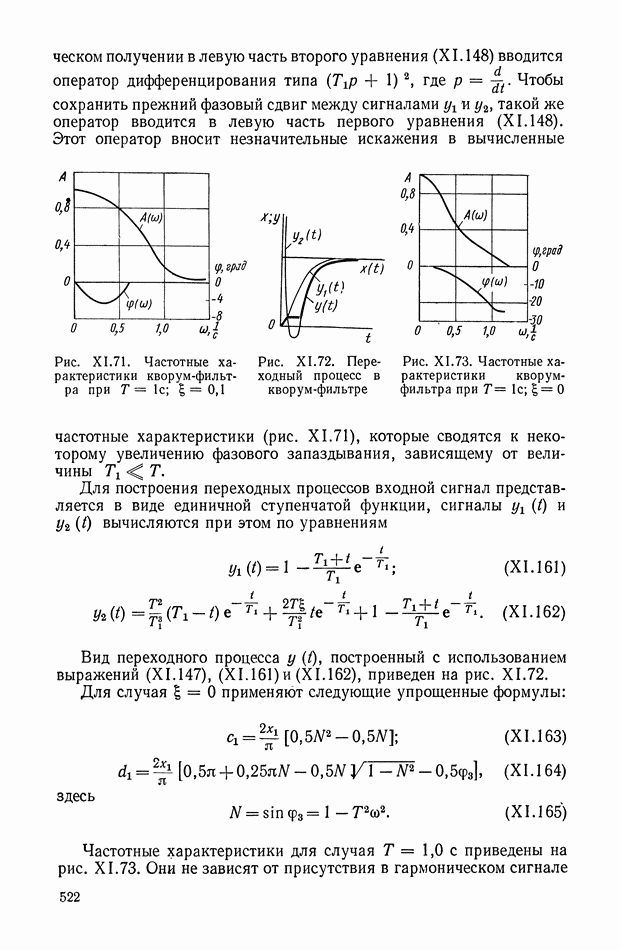
Рис. XI.45. Одноканальное нелинейное устройство с релейным элементом
Цепь имеет эквивалентную передаточную функцию, амплитудная характеристика которой при подаче синусоидального входного сигнала понижается с ростом частоты, а фазовая остается без изменения. С помощью такого устройства можно обеспечить параметрическую стабилизацию одной точки частотной характеристики замкнутой системы управления. Их используют в самонастраивающихся релейных автоколебательных системах.

Рис. XI.46. Одноканальное нелинейное устройство с индуктивностью
Основным недостатком таких систем являются автоколебания в состоянии покоя, необходимость применения опережающих фильтров до реле, зависимость амплитудной характеристики фильтра от амплитуды входного сигнала.
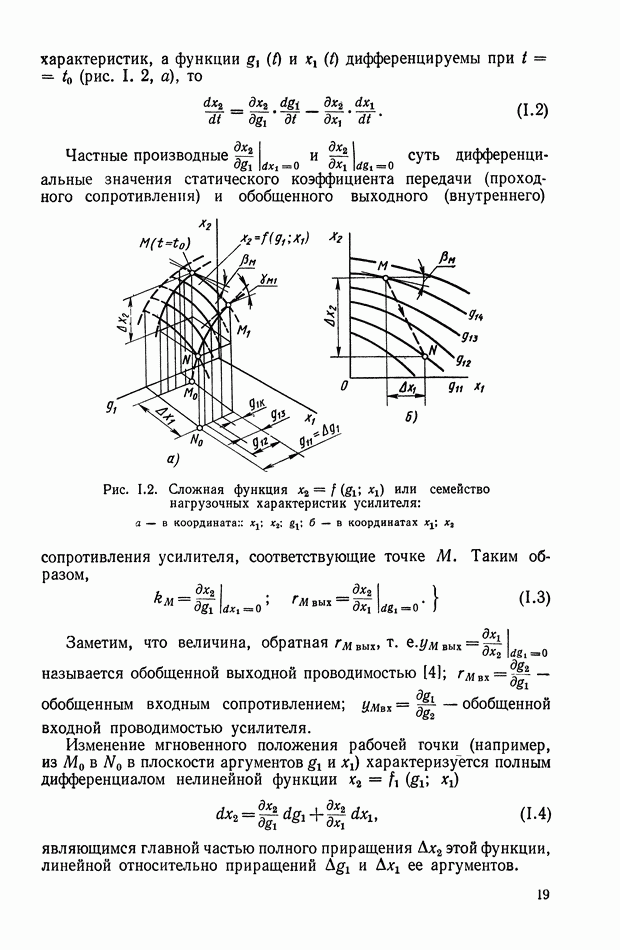
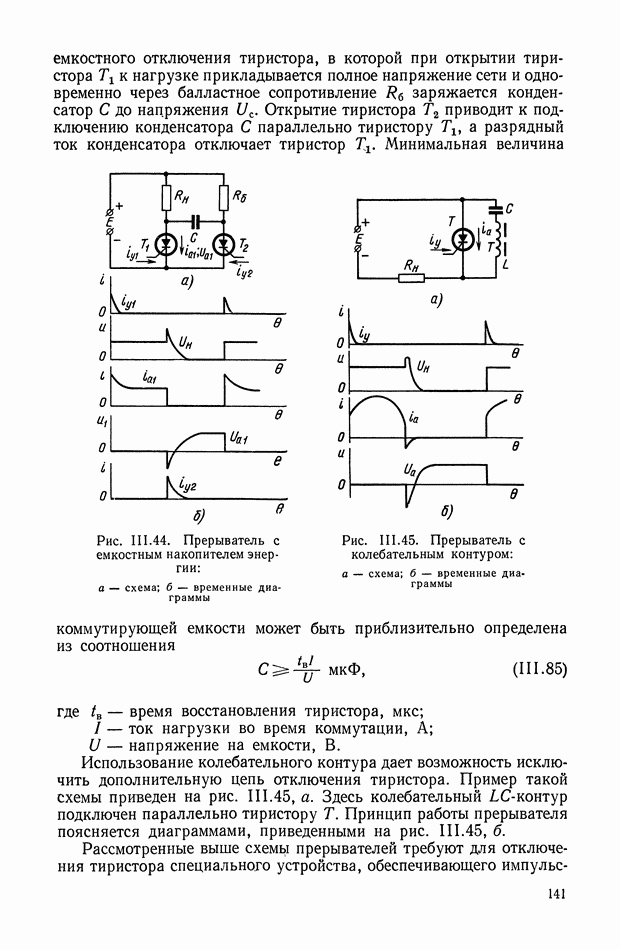
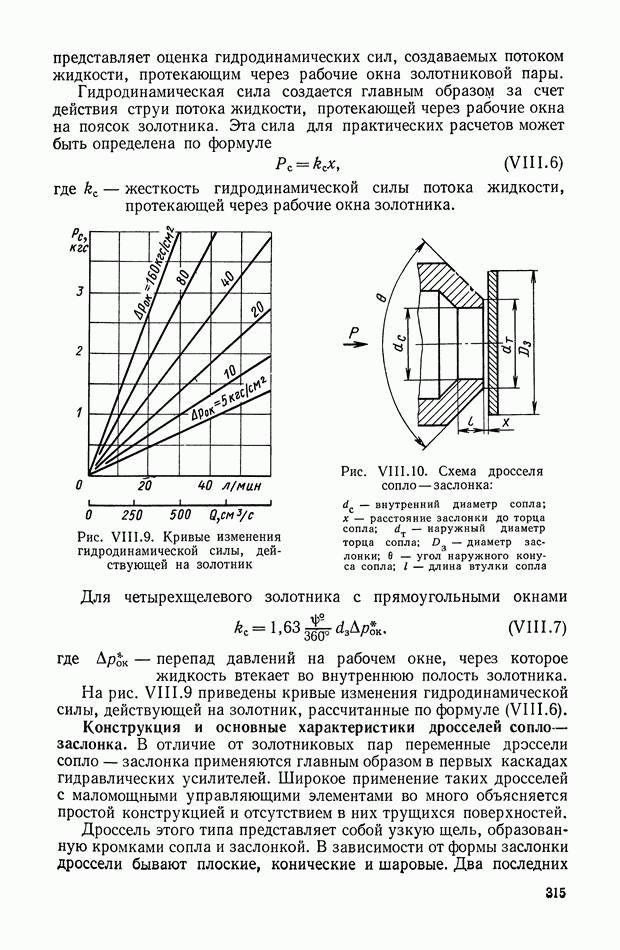
На рис. XI.46, а показано нелинейное устройство, состоящее из последовательно соединенных элементов: нелинейного 1 и линейного  нелинейный элемент представляет собой индуктивность, в которой поток изменяется по двум прямолинейным участкам (рис. XI.46, б). Линейный элемент выполнен в виде идеальной дифференцирующей цепи. Для нелинейной цепи запишем
нелинейный элемент представляет собой индуктивность, в которой поток изменяется по двум прямолинейным участкам (рис. XI.46, б). Линейный элемент выполнен в виде идеальной дифференцирующей цепи. Для нелинейной цепи запишем

или

где  — число витков; Ф — магнитный поток;
— число витков; Ф — магнитный поток;  — коэффициенты наклона магнитной характеристики.
— коэффициенты наклона магнитной характеристики.
Ток в цепи изменяется следующим образом:

Если  то можно получить
то можно получить

Дифференцируя последнее выражение, найдем

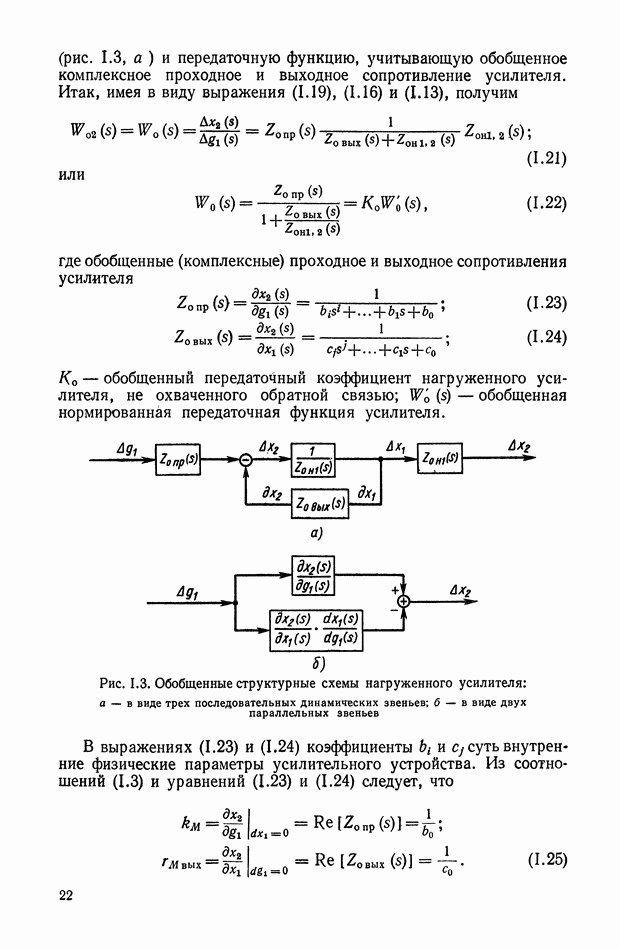
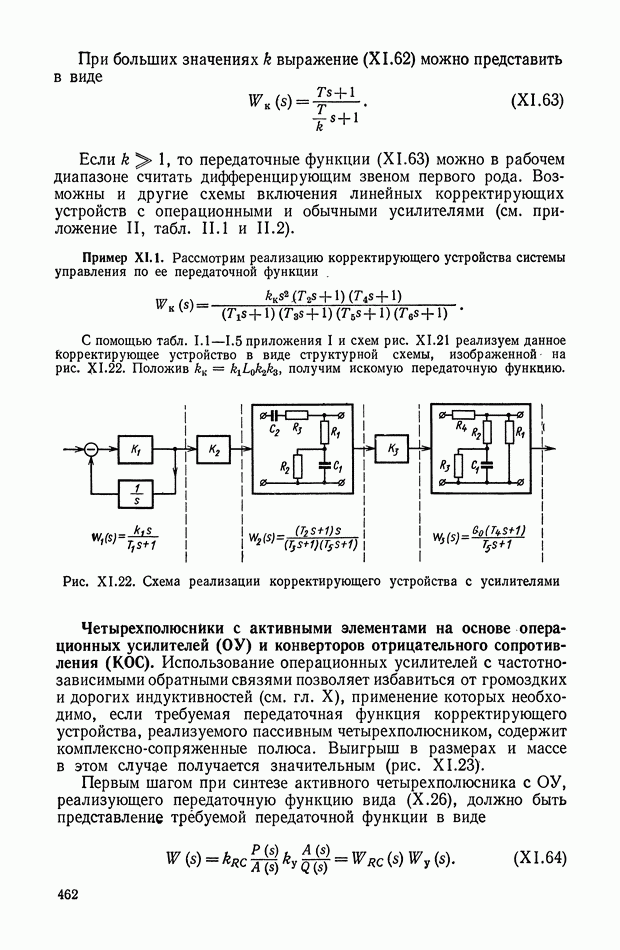
Обозначив со через  получим
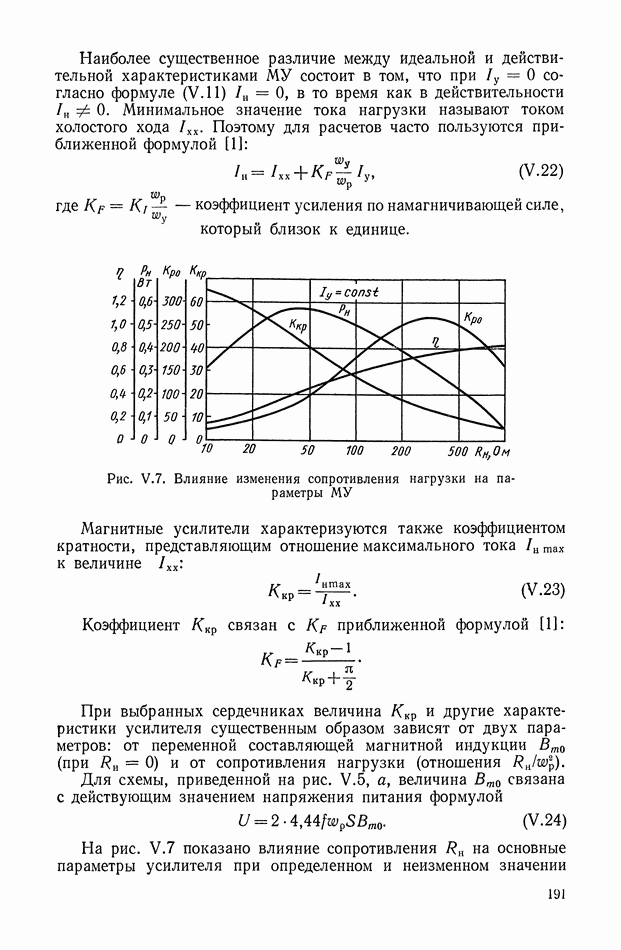
получим

и

Сигнал  может быть разложен в ряд Фурье:
может быть разложен в ряд Фурье:

здесь

Коэффициент  определим по формуле
определим по формуле

откуда

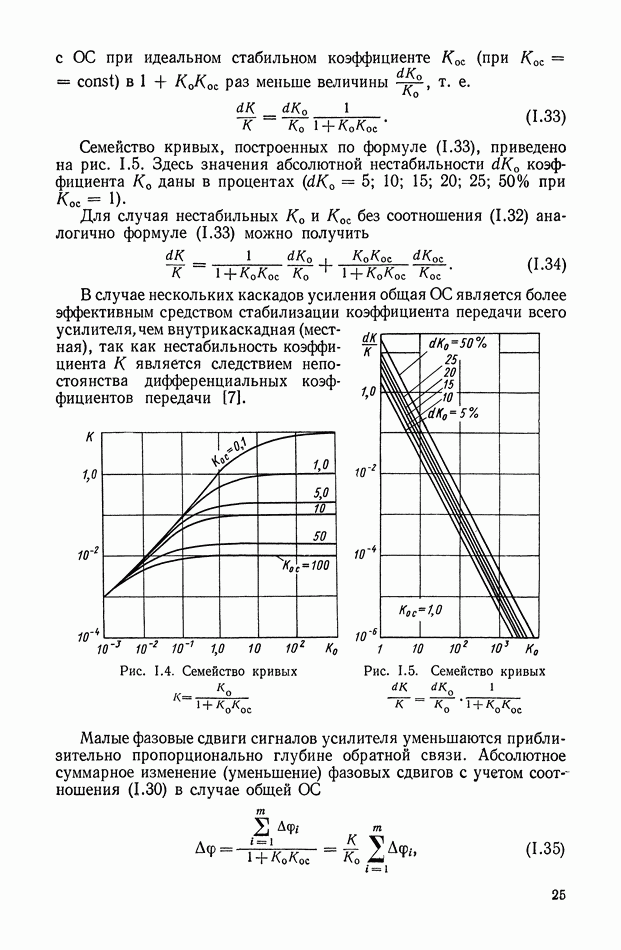
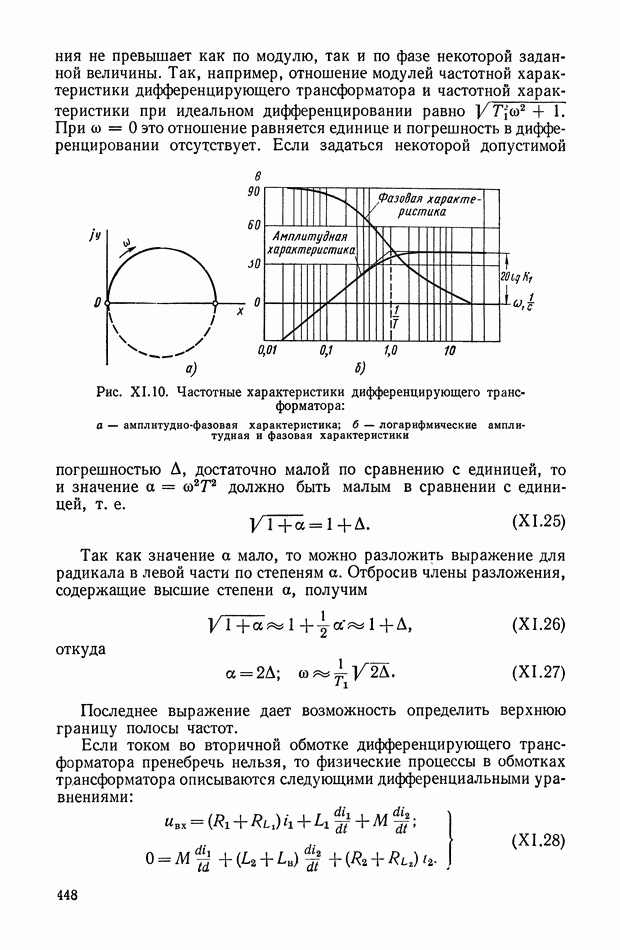
Нетрудно показать, что коэффициент 

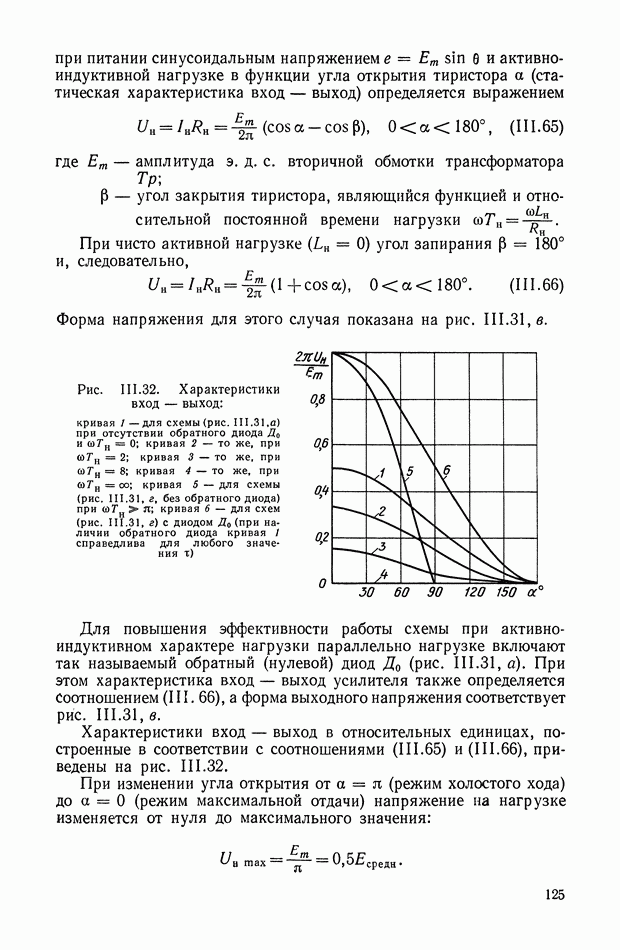
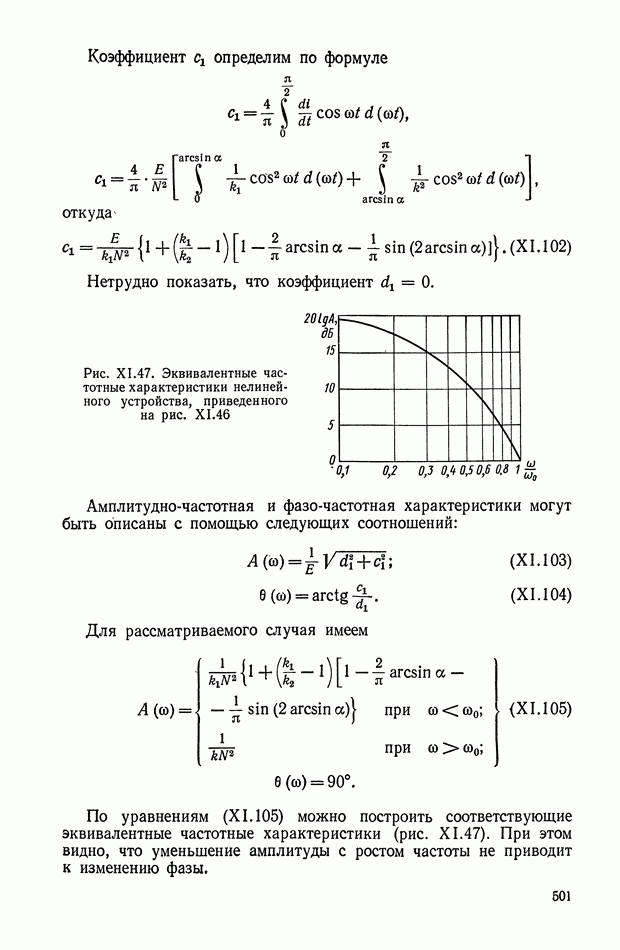
Рис. XI.47. Эквивалентные частотные характеристики нелинейного устройства, приведенного на рис. XI.46
Амплитудно-частотная и фазо-частотная характеристики могут быть описаны с помощью следующих соотношений:

Для рассматриваемого случая имеем

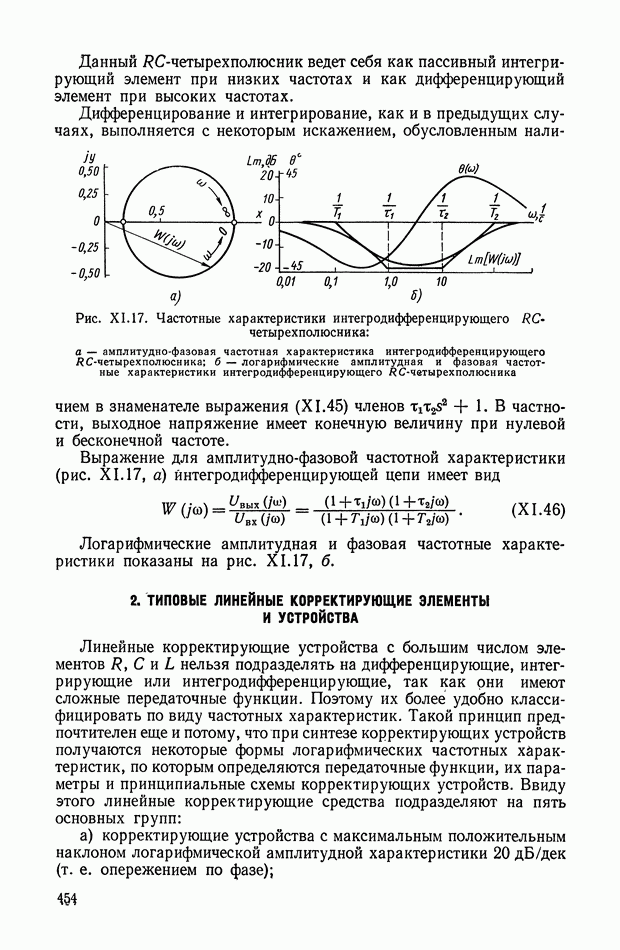
По уравнениям (XI. 105) можно построить соответствующие эквивалентные частотные характеристики (рис. XI.47). При этом видно, что уменьшение амплитуды с ростом частоты не приводит к изменению фазы.
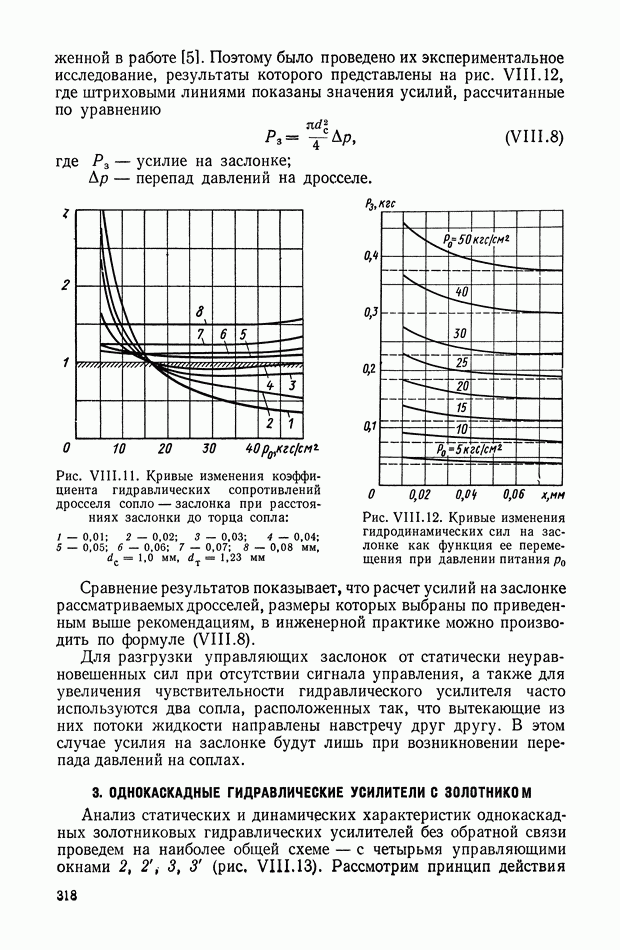
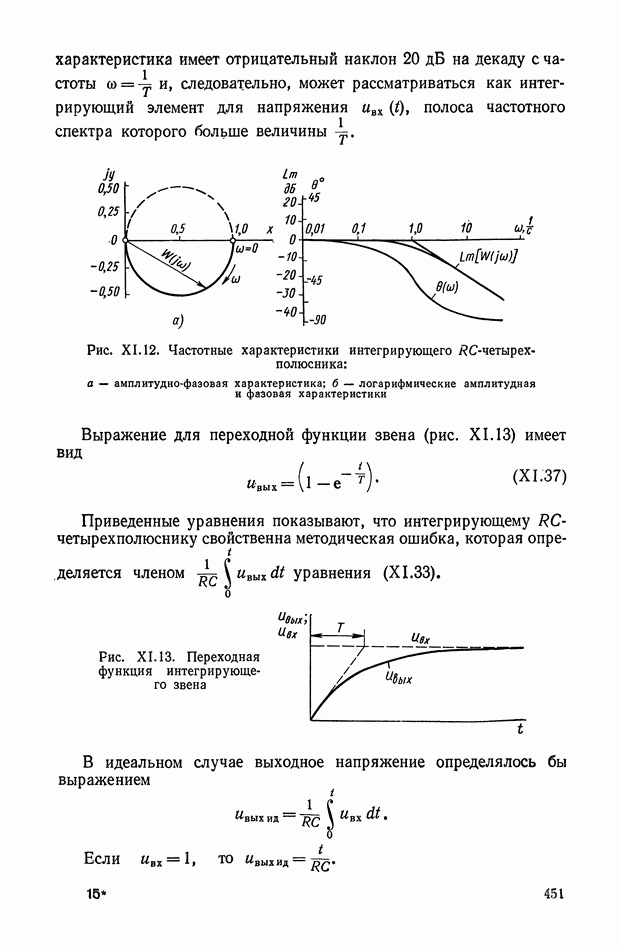
Рассмотрим теперь еще один пример корректирующего устройства с нелинейностью типа насыщения (рис. XI.48), в которое входят два линейных фильтра 1 и 3 и нелинейный элемент 2.

Рис. XI.48. Одноканальное нелинейное устройство с нелинейностью типа насыщения
Пусть на вход нелинейного корректирующего устройства поступил сигнал

тогда

где

При

для частоты  имеем
имеем  , следовательно,
, следовательно,  поэтому
поэтому

Для  имеем
имеем

тогда

где 
На выходе высокочастотного фильтра имеем

Используя приведенные выше выражения, после несложных преобразований получим

Коэффициент

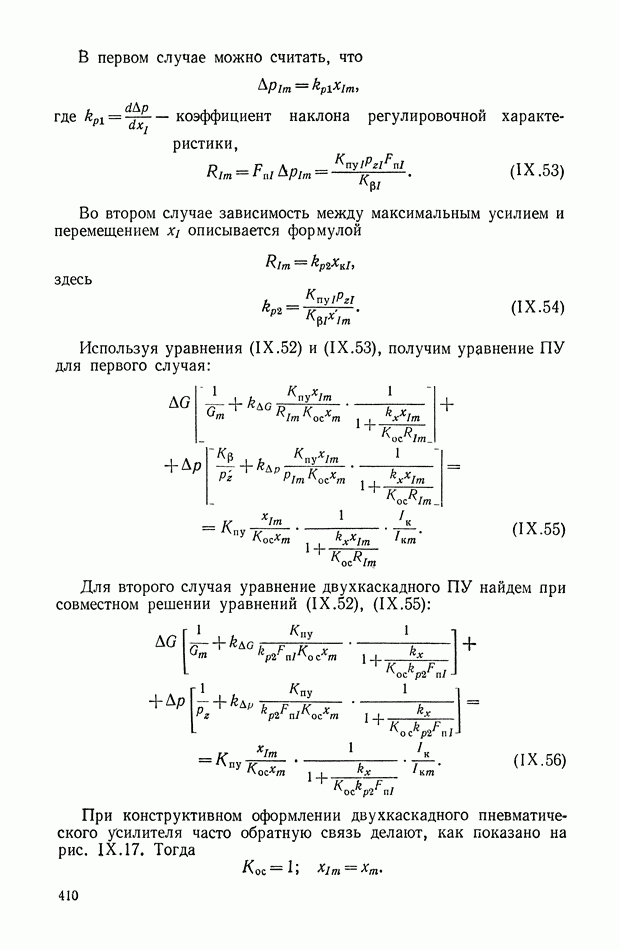
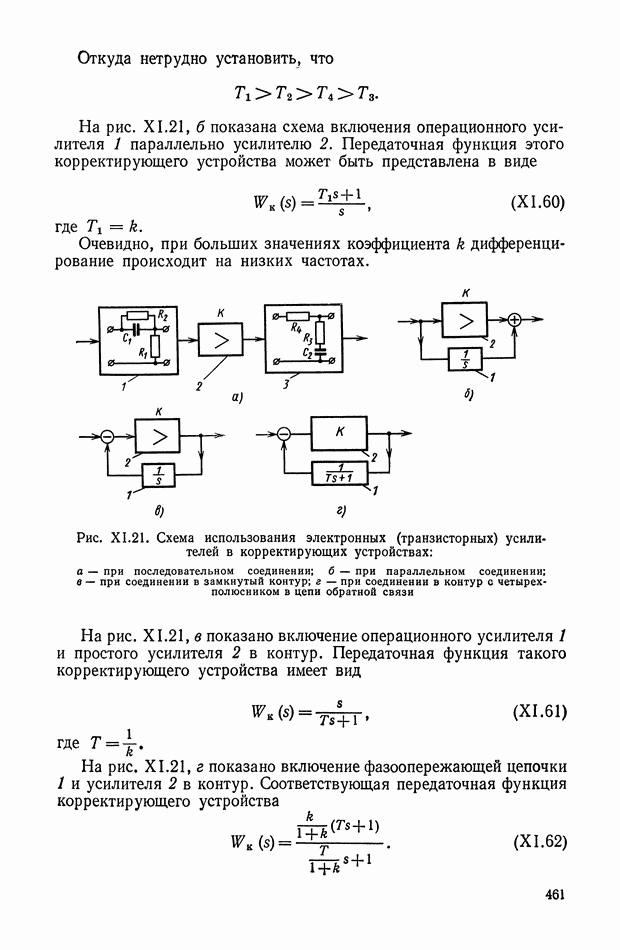
Используя выражения (XI. 105), (XI. 109), (XI. 110), можно получить следующие выражения для амплитудной и фазовой частотных характеристик:

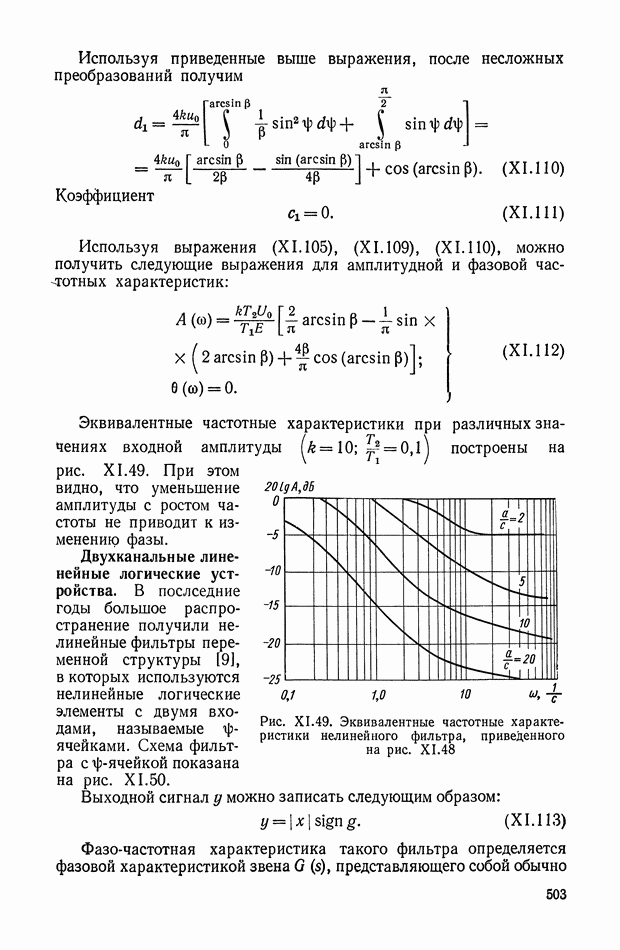
Эквивалентные частотные характеристики при различных значениях входной амплитуды  построены на рис. XI.49. При этом видно, что уменьшение амплитуды с ростом частоты не приводит к изменению фазы.
построены на рис. XI.49. При этом видно, что уменьшение амплитуды с ростом частоты не приводит к изменению фазы.

Рис. XI.49. Эквивалентные частотные характеристики нелинейного фильтра, приведенного на рис. XI.48
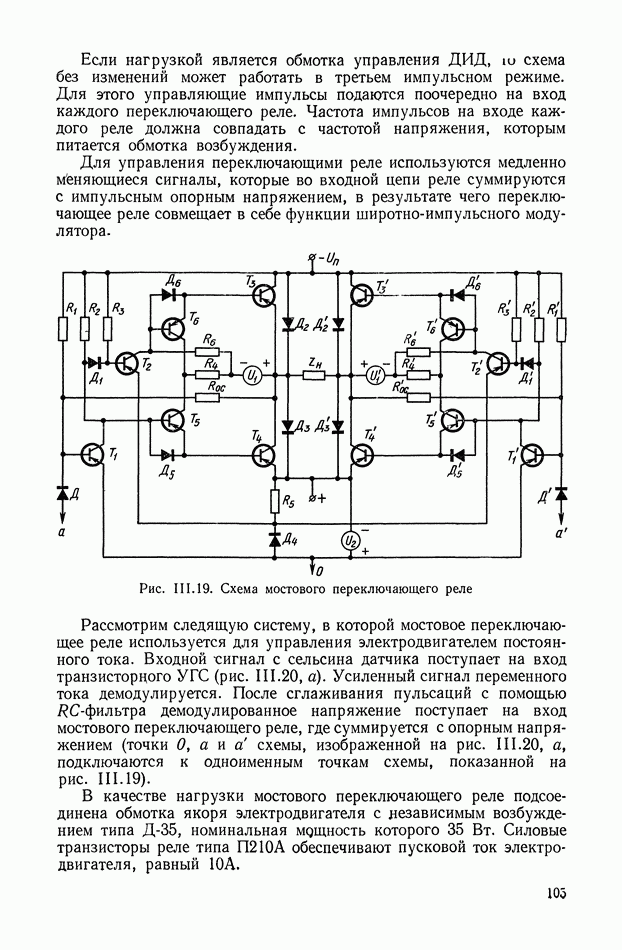
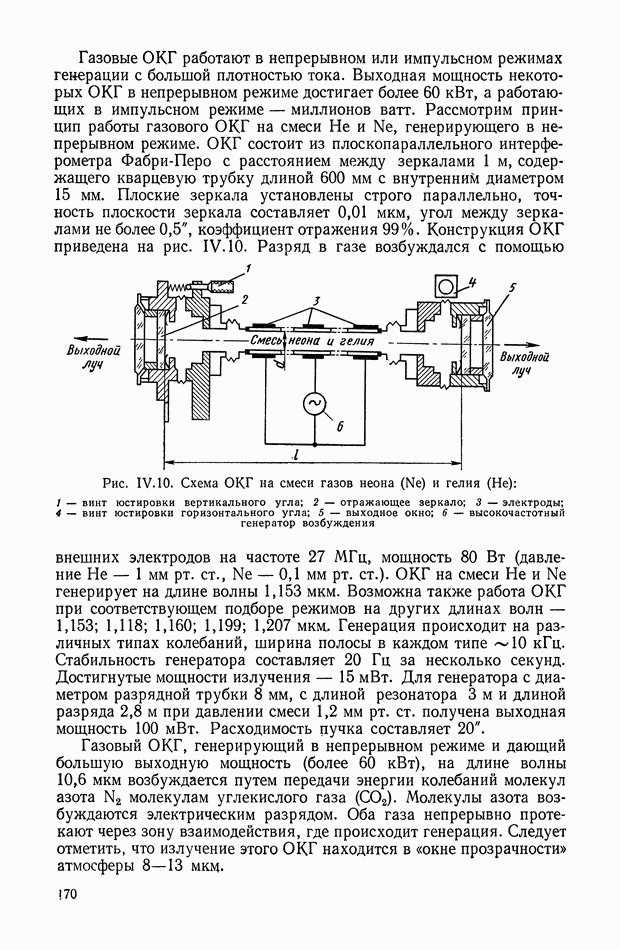
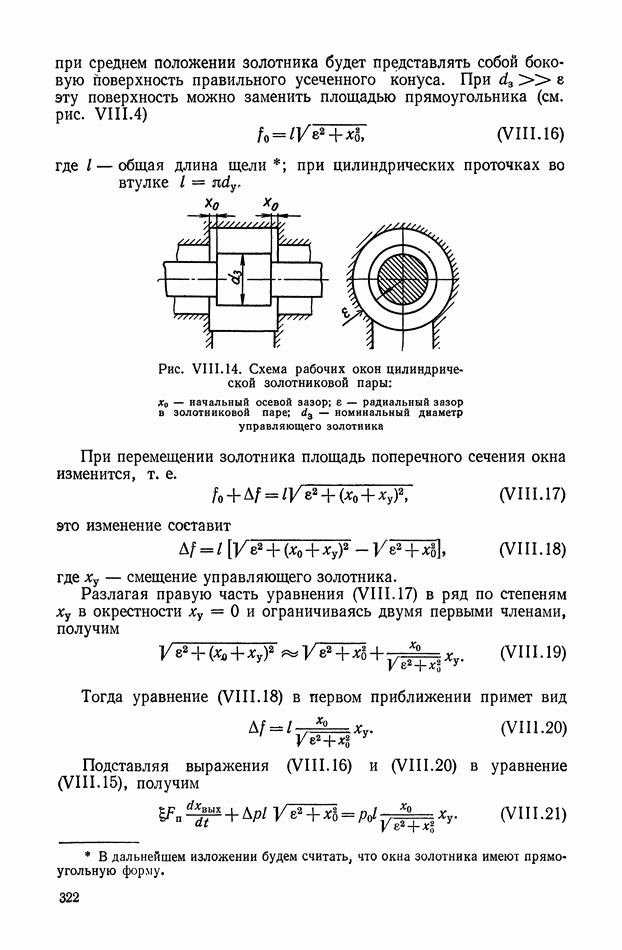
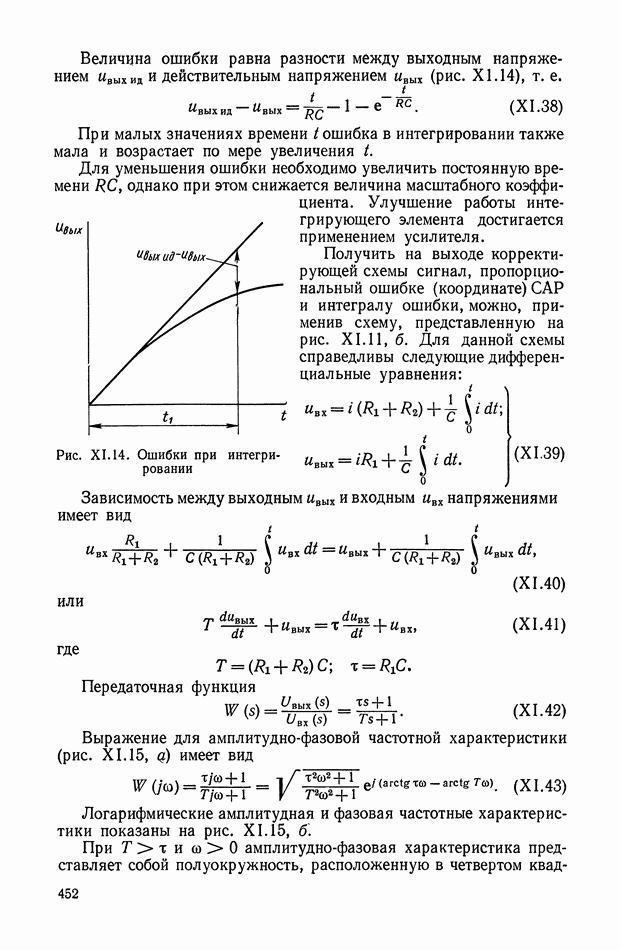
Двухканальные линенейные логические устройства. В послседние годы большое распространение получили нелинейные фильтры переменной структуры [9], в которых используются нелинейные логические элементы с двумя входами, называемые  ячейками. Схема фильтра с
ячейками. Схема фильтра с  -ячейкой показана на рис. XI.50.
-ячейкой показана на рис. XI.50.
Выходной сигнал у можно записать следующим образом:

Фазо-частотная характеристика такого фильтра определяется фазовой характеристикой звена  представляющего собой обычно
представляющего собой обычно
звено типа  а амплитудная характеристика близка к единице. Такие двухканальные фильтры широко используются для построения систем с переменной структурой.
а амплитудная характеристика близка к единице. Такие двухканальные фильтры широко используются для построения систем с переменной структурой.

Рис. XI.50. Фильтр переменной структуры на  -ячейке
-ячейке
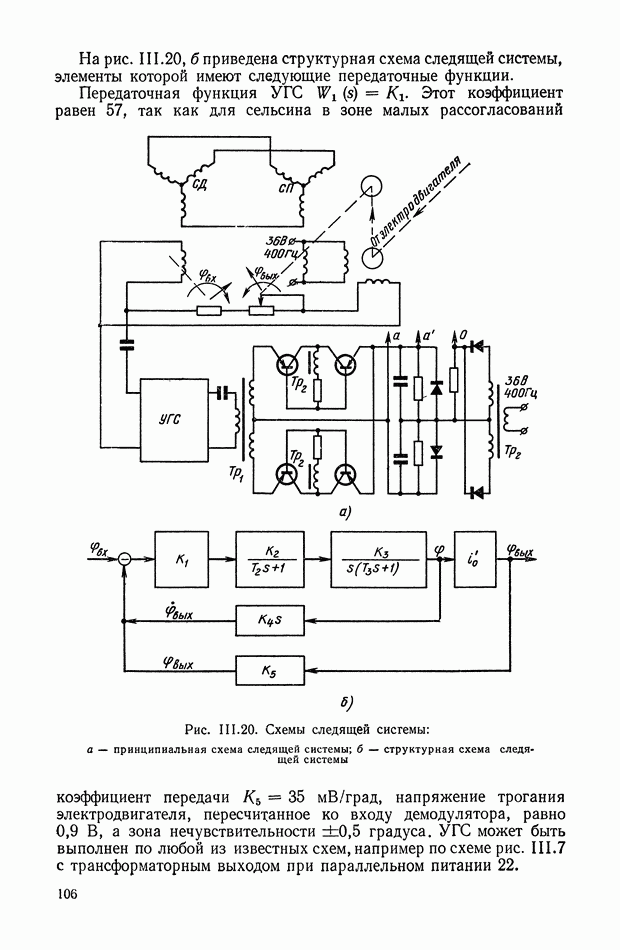
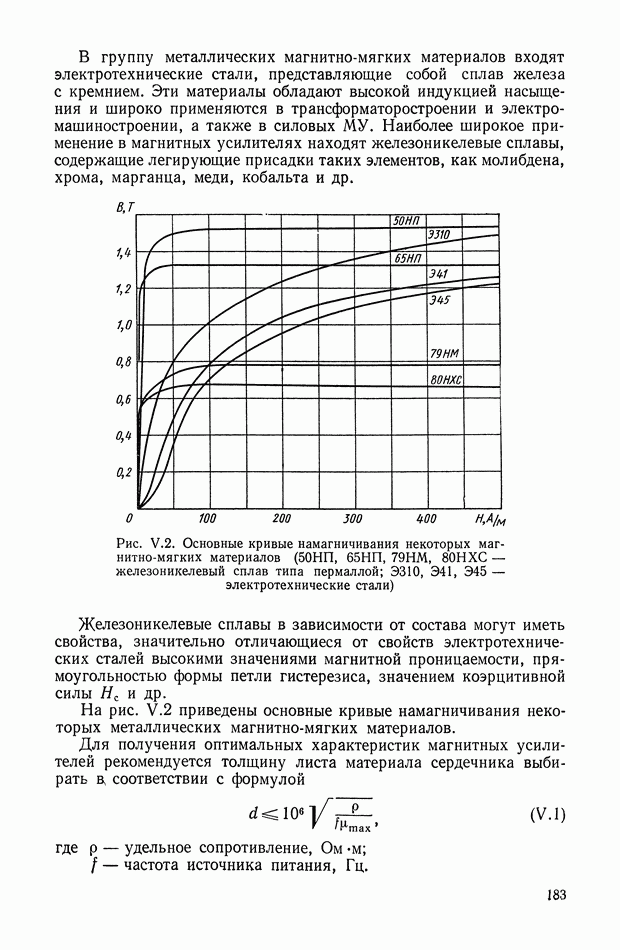
Рассмотрим другой класс двухмерных нелинейных корректирующих устройств. Схема простейшего нелинейного корректирующего устройства этого типа показана на рис. X 1.51.

Рис. XI.51. Двухканальное нелинейное устройство
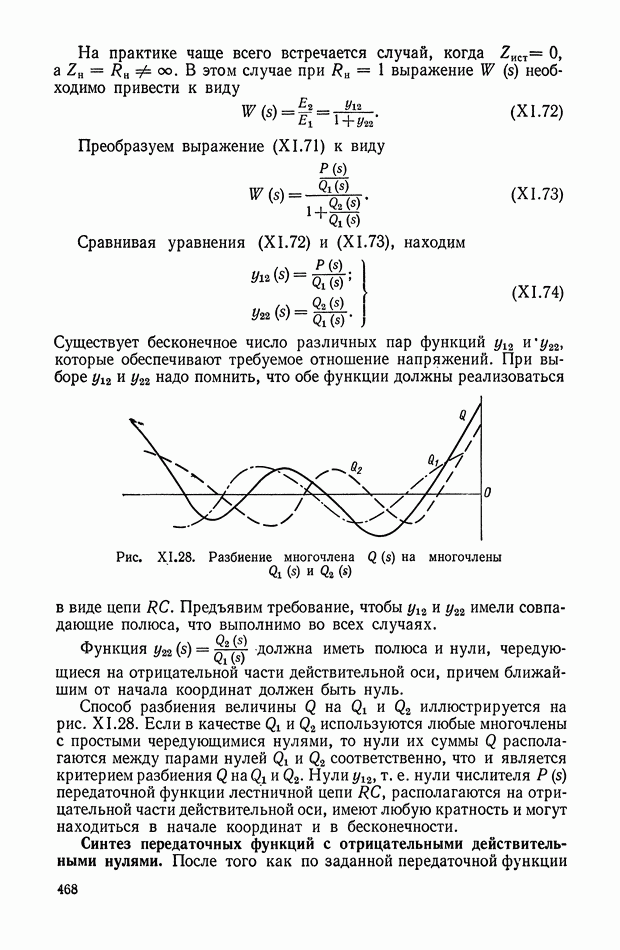
Сигнал на его выходе можно представить в виде 

где  — амплитуда колебаний;
— амплитуда колебаний;
 — фазовый угол (опережение);
— фазовый угол (опережение);
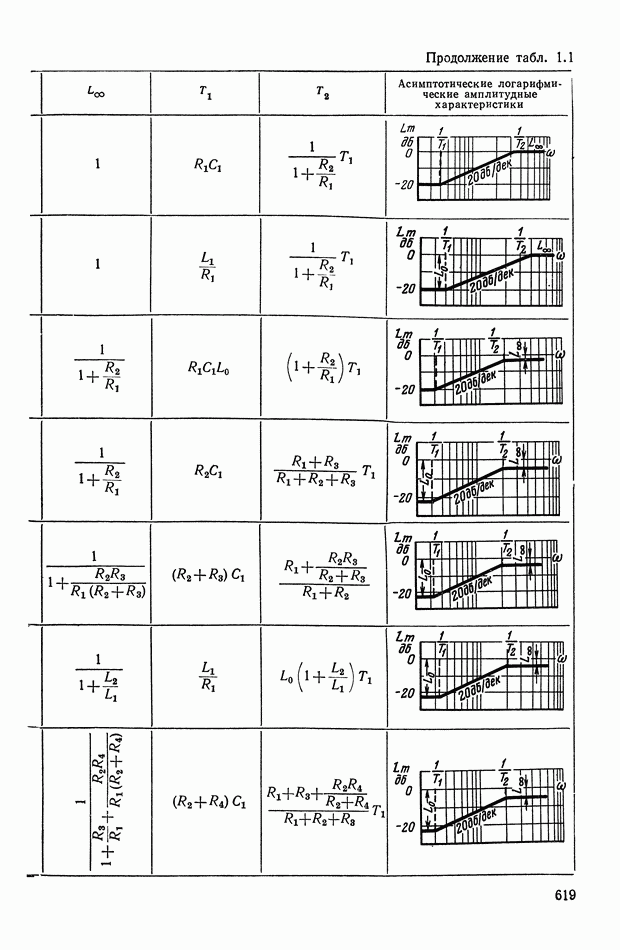
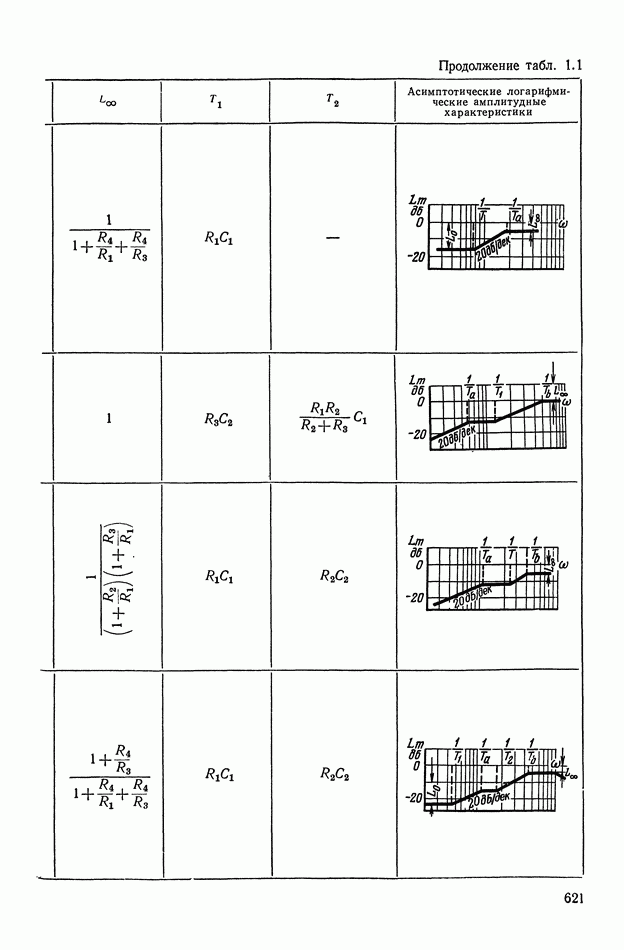
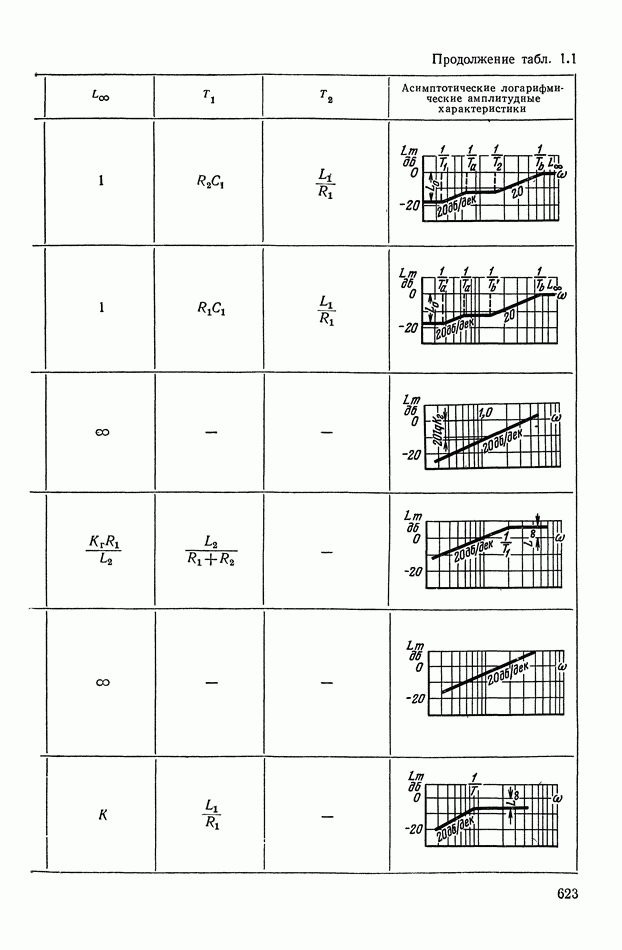
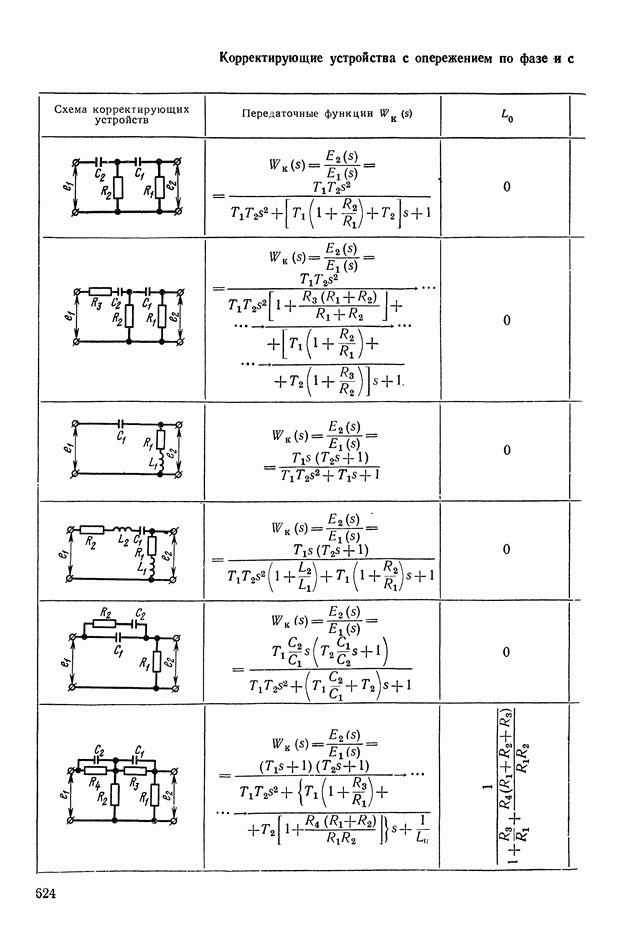
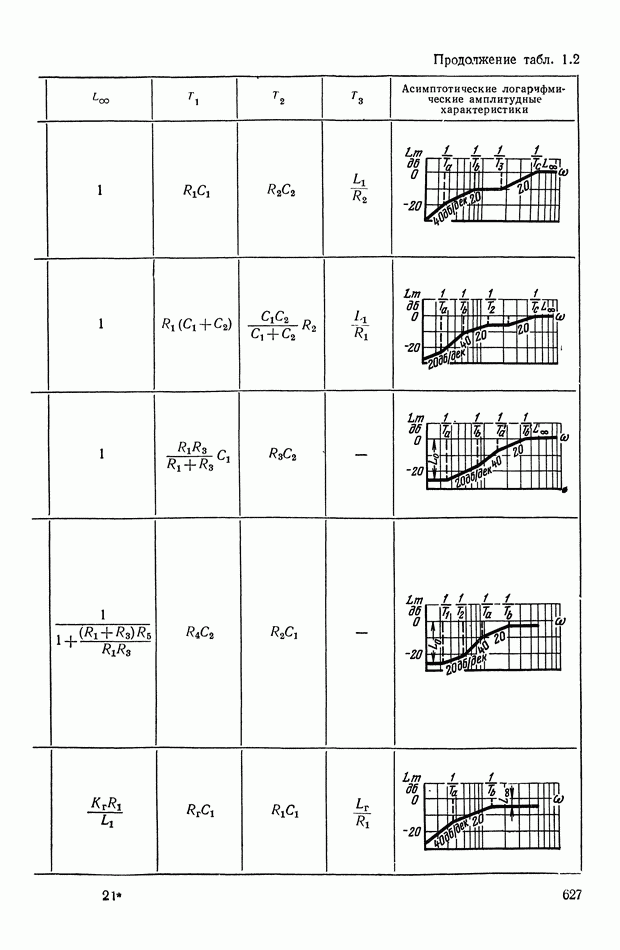
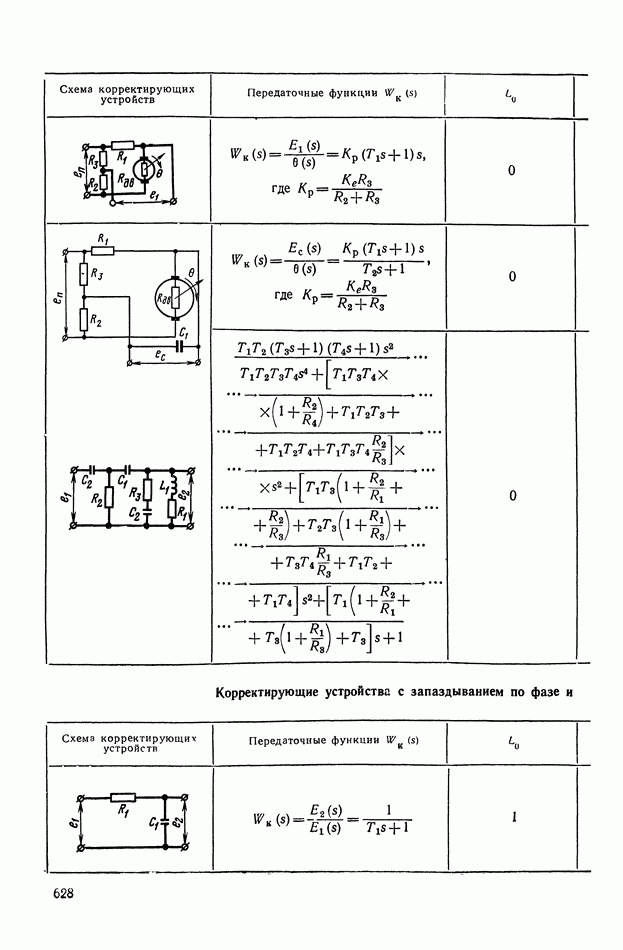
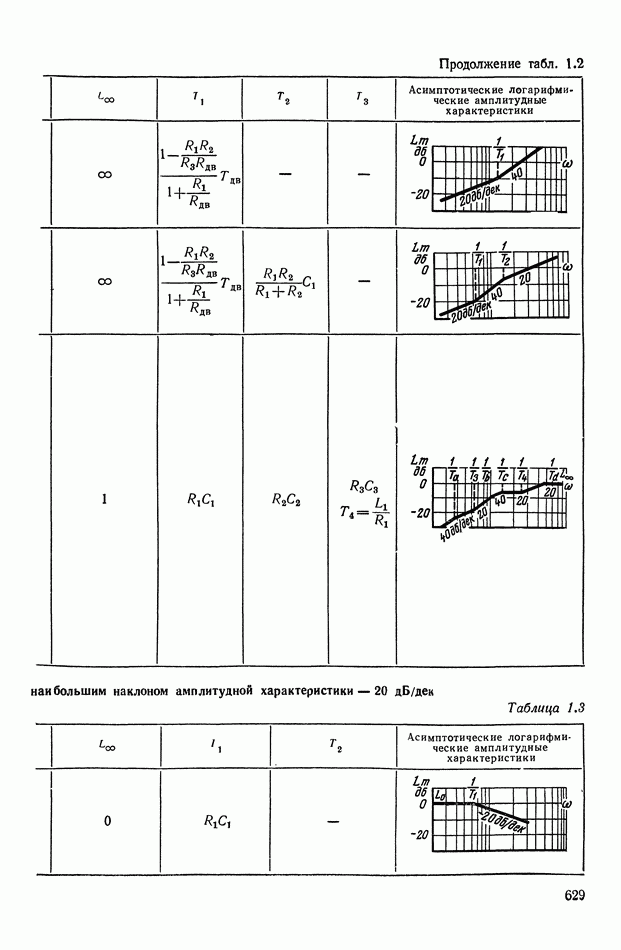
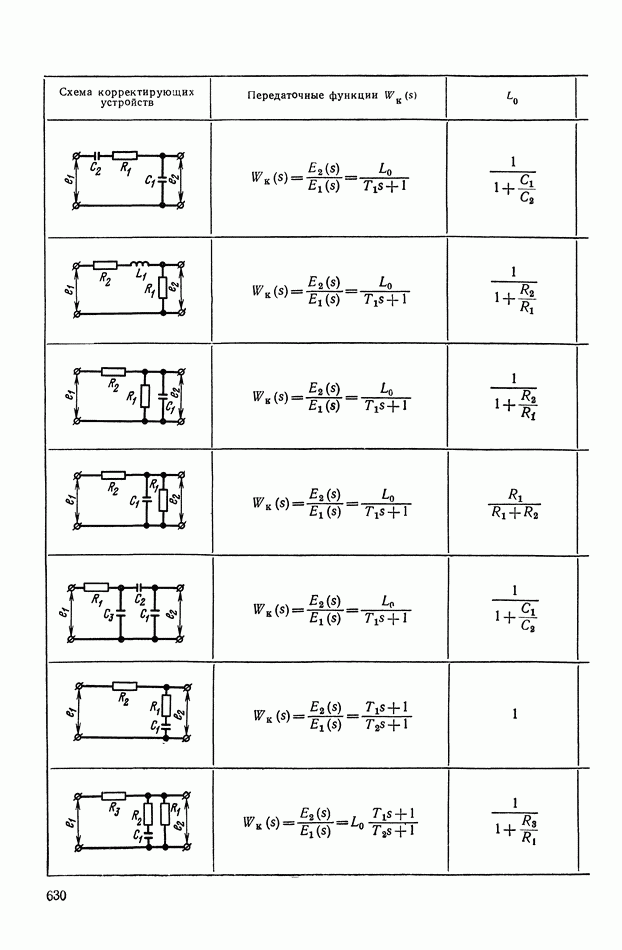
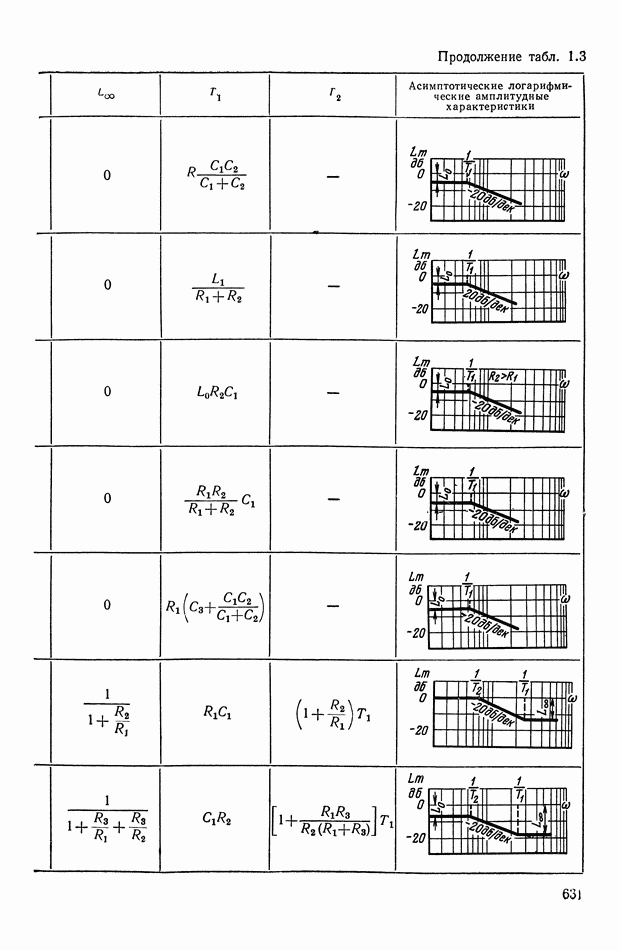
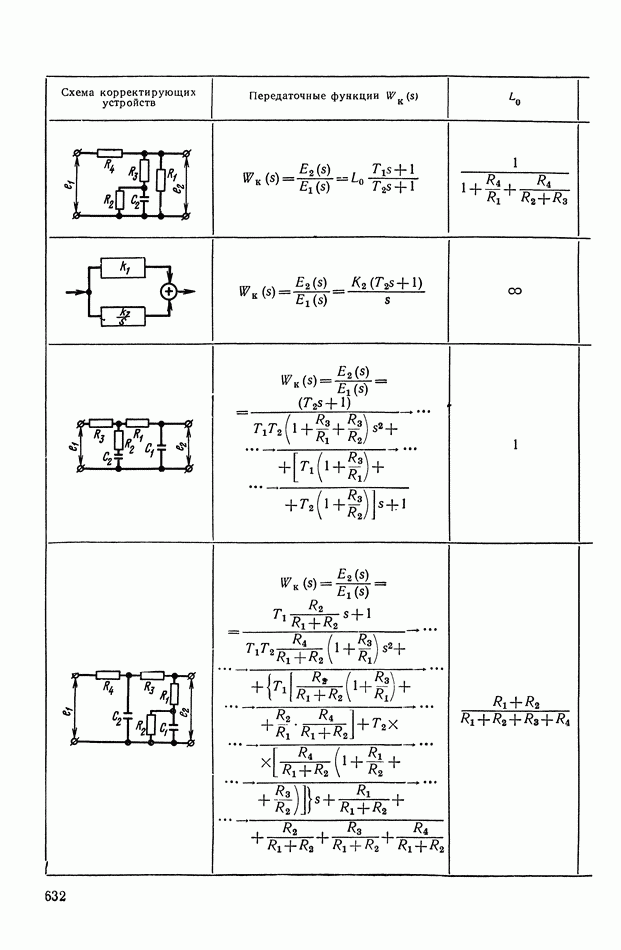
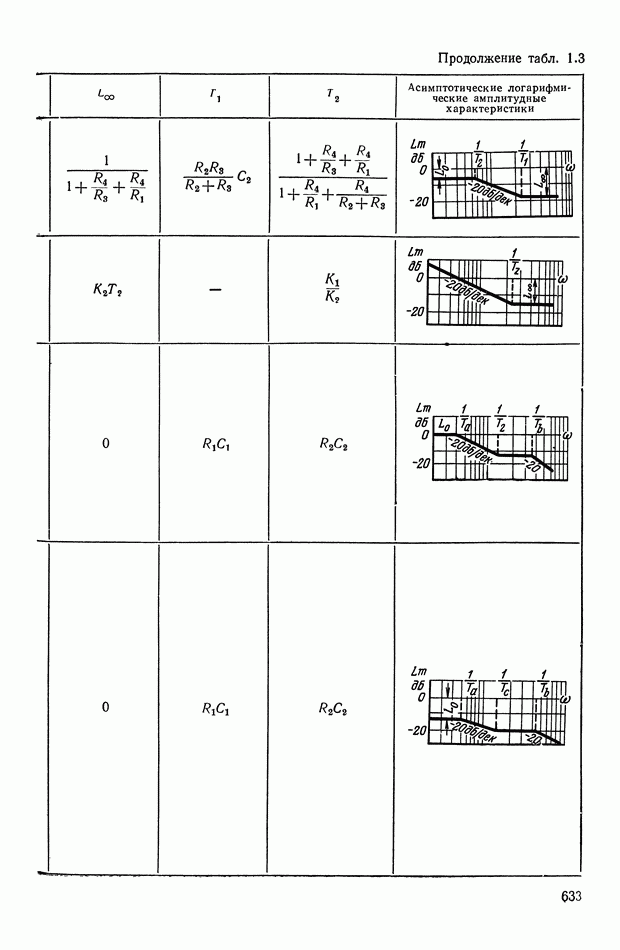
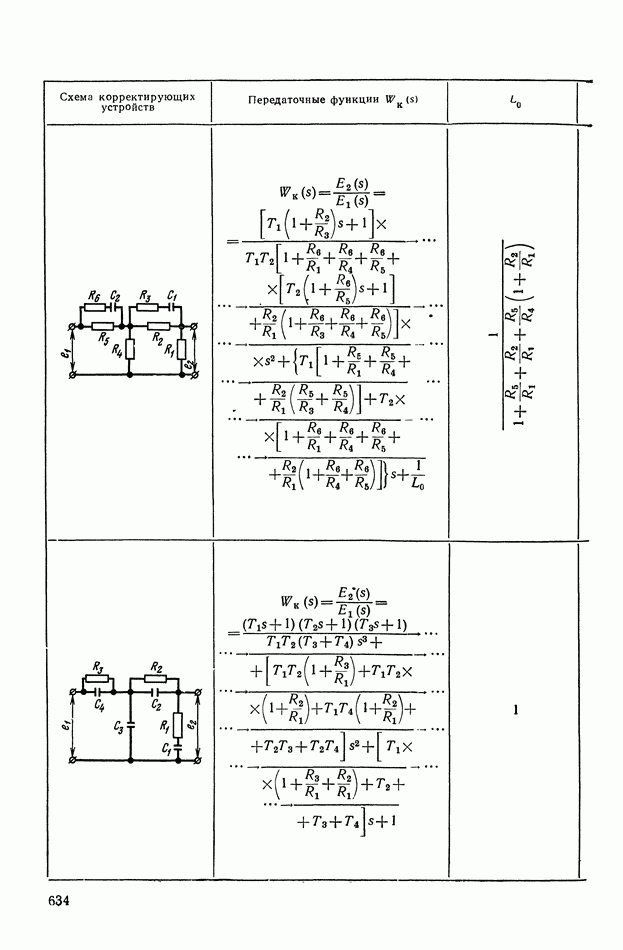
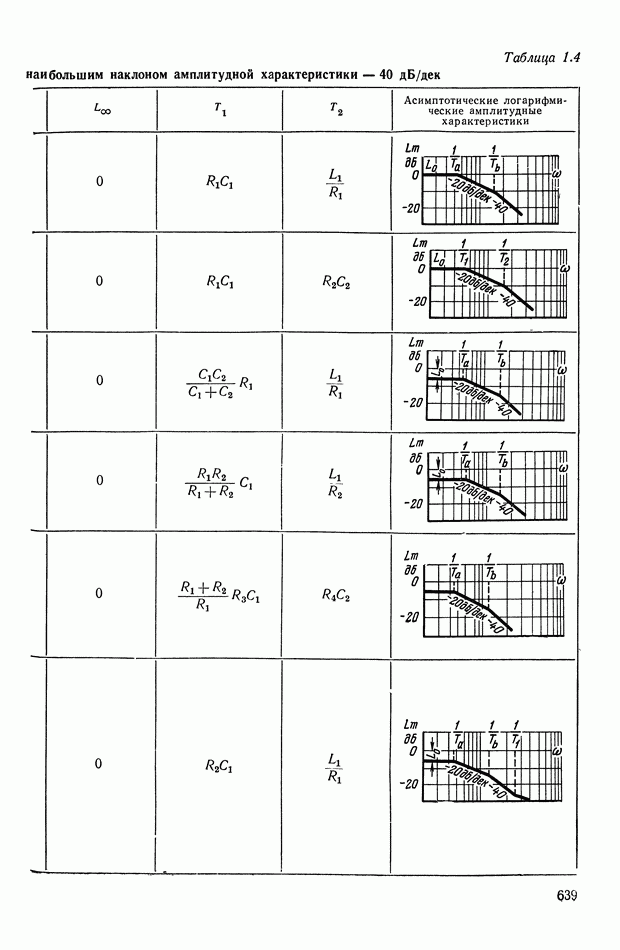
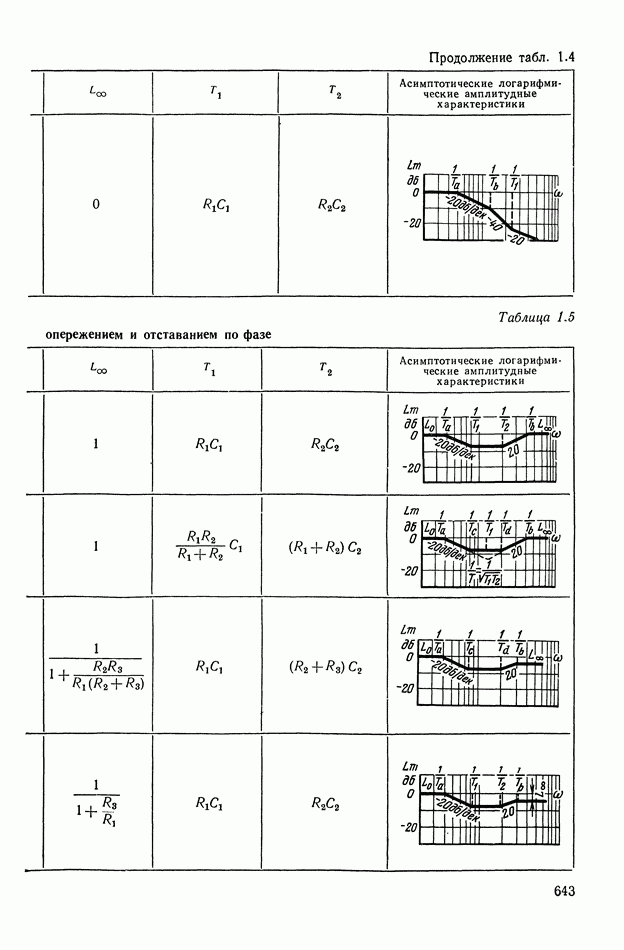
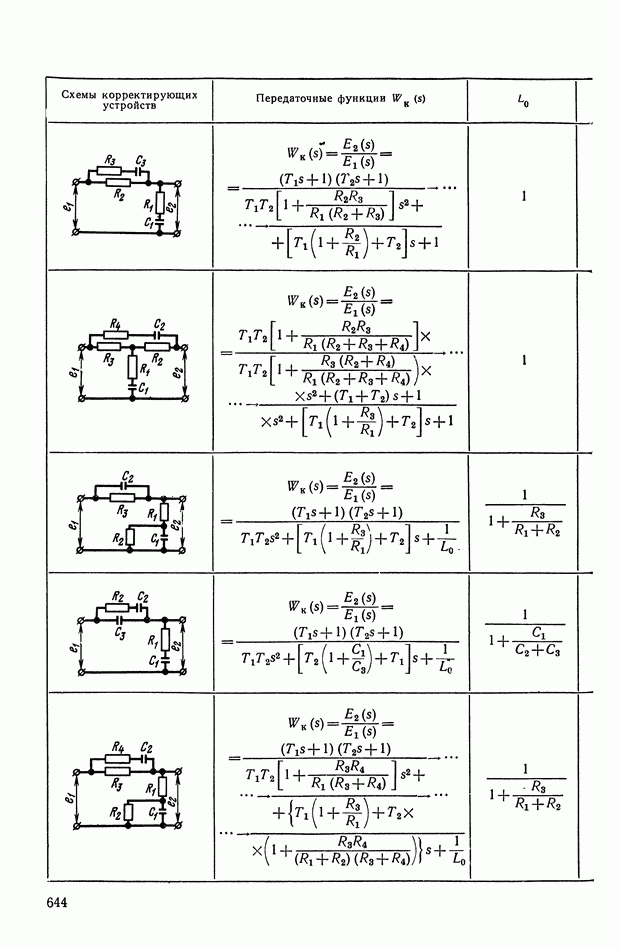
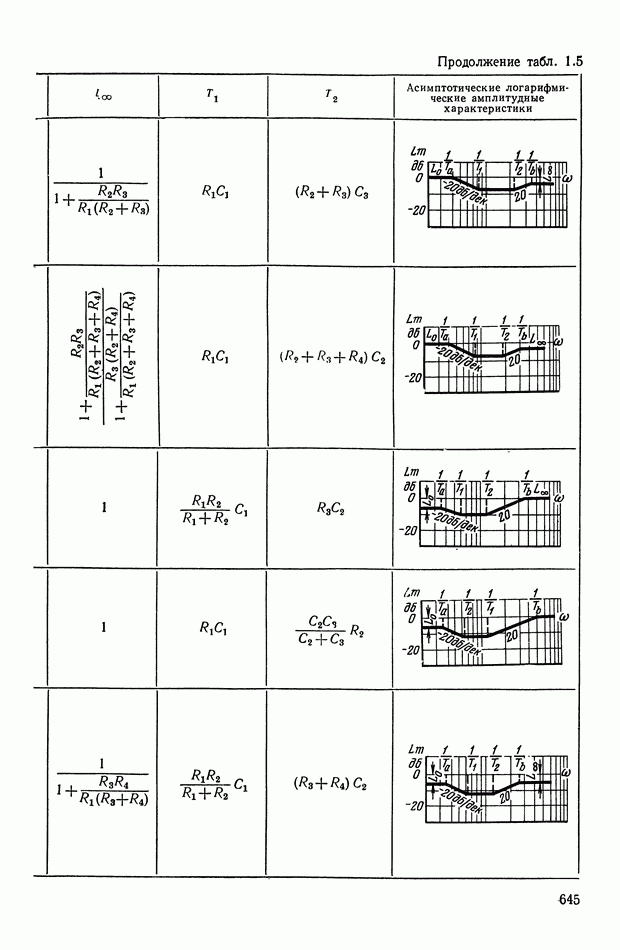
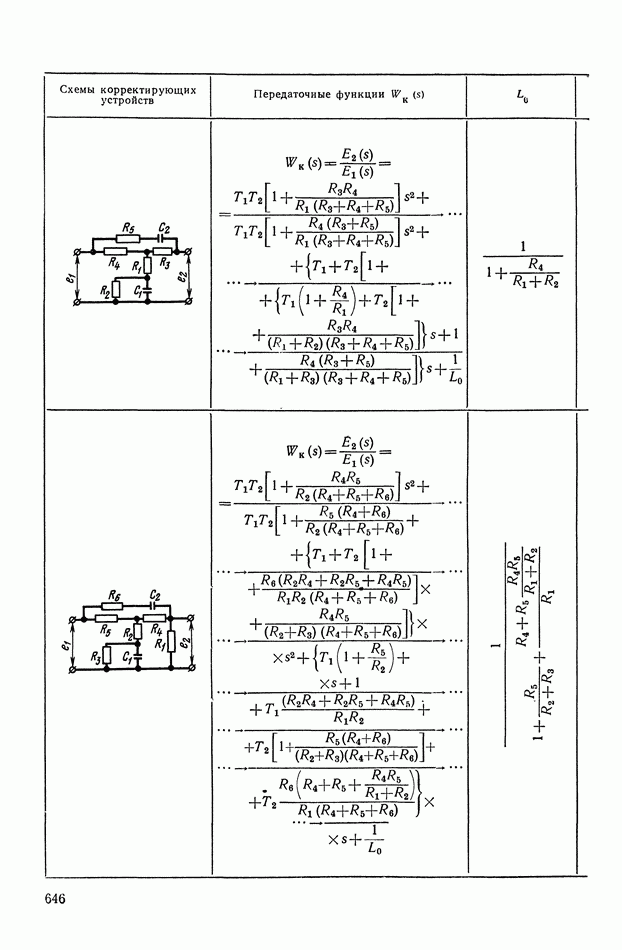
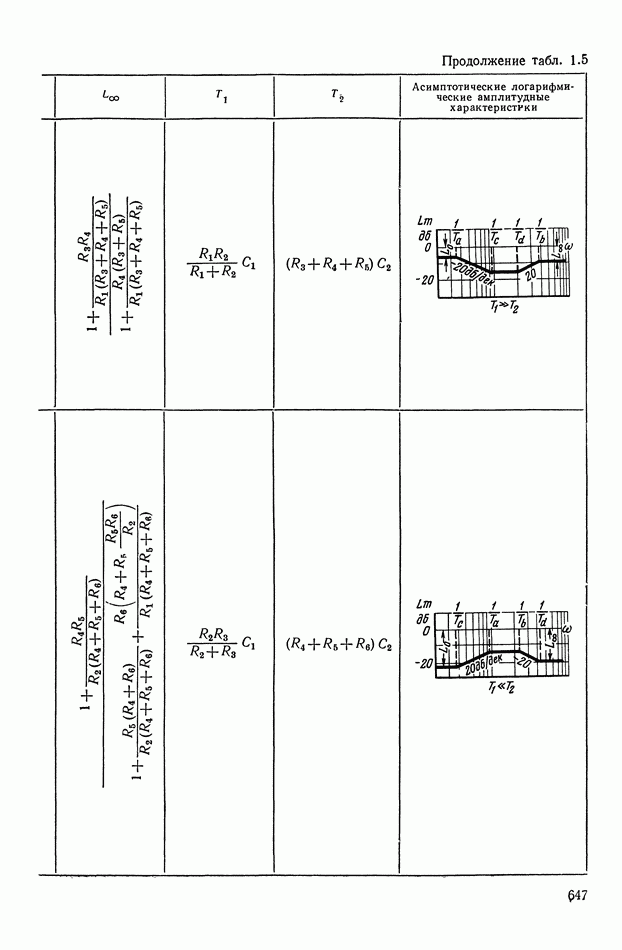
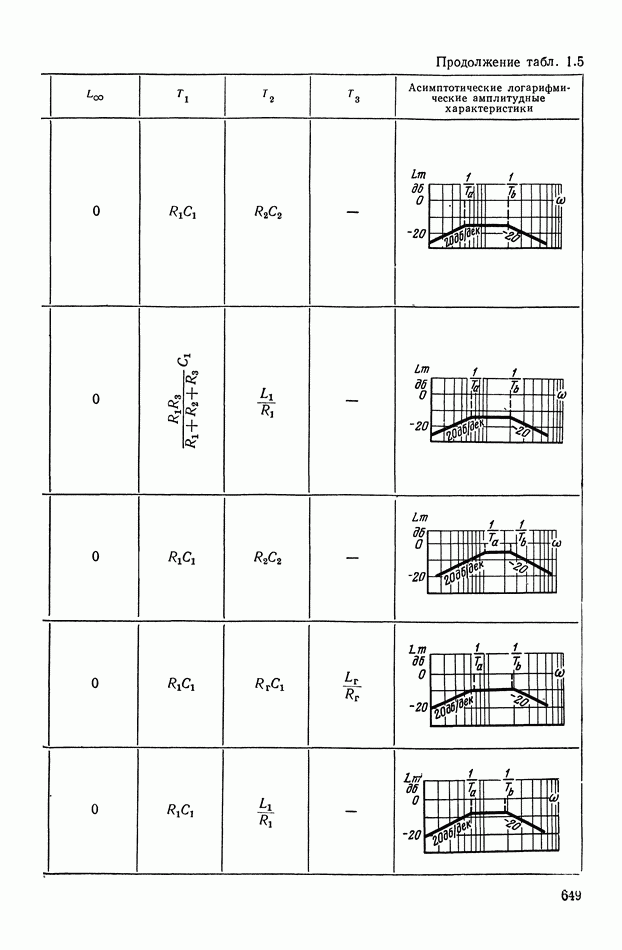
 — передаточная функция линейного корректирующего устройства (выбирается по данным таблиц приложения I).
— передаточная функция линейного корректирующего устройства (выбирается по данным таблиц приложения I).
Определим коэффициенты ряда Фурье:

После ряда преобразований получим

где  определим из уравнения
определим из уравнения

Из выражений (XI.105) и (XI.116) найдем эквивалентные амплитудную и фазовую характеристики нелинейного корректирующего устройства:

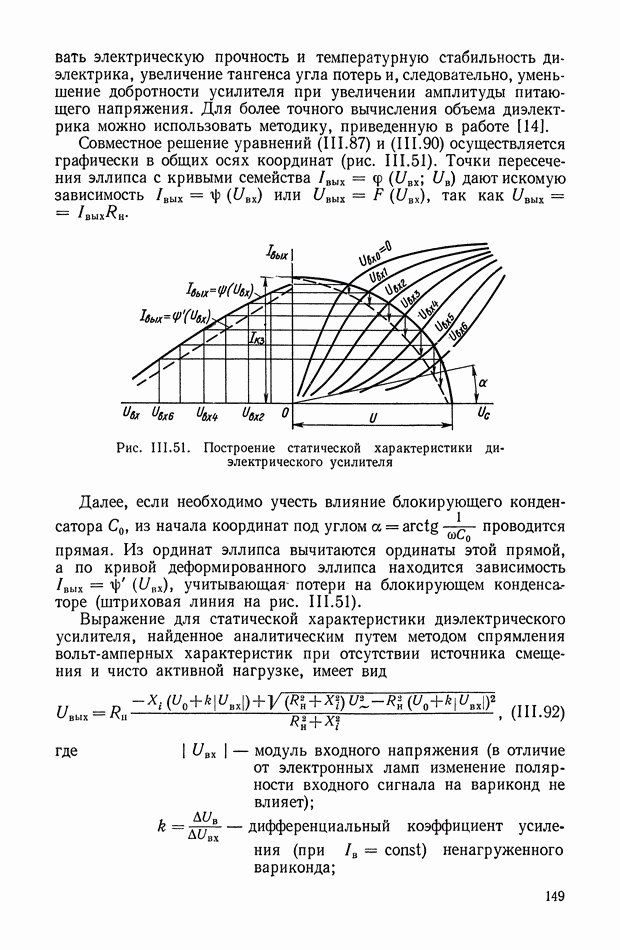
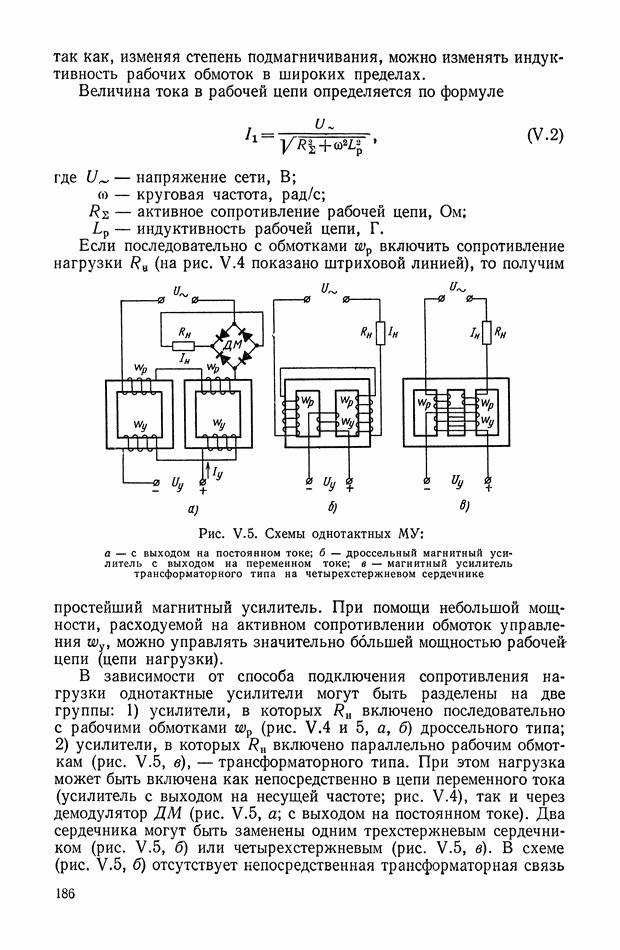
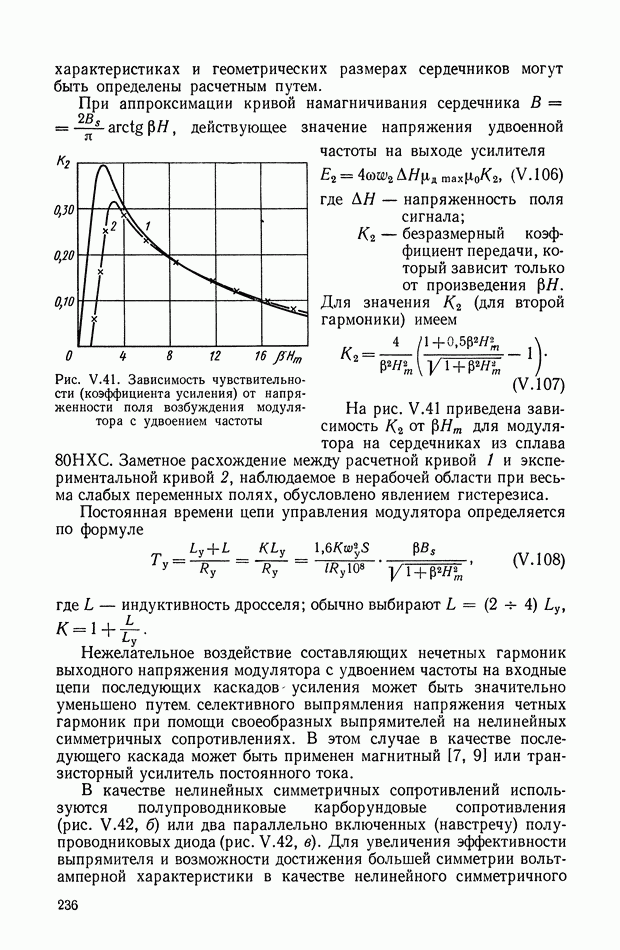
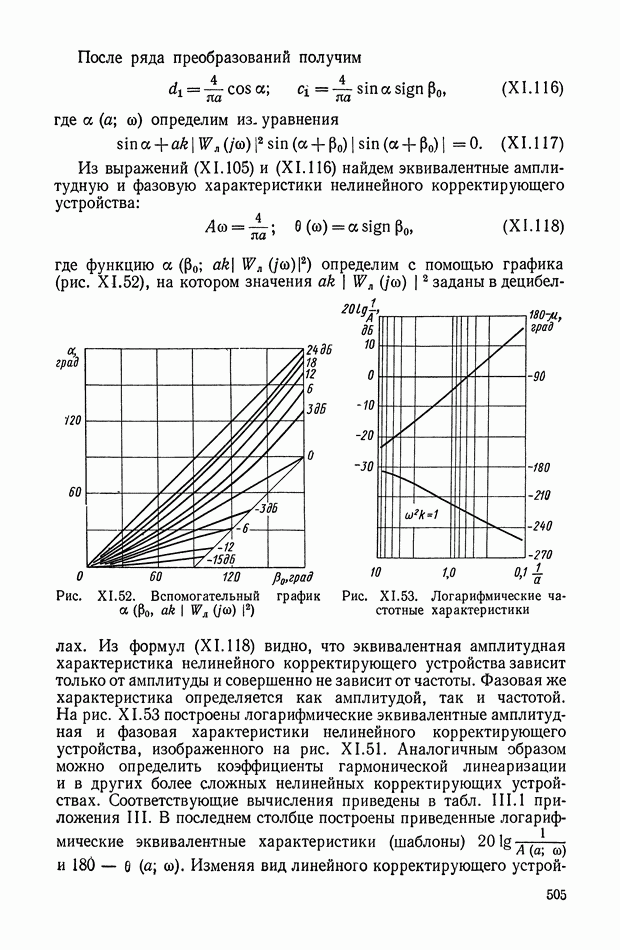
где функцию а  определим с помощью графика (рис. XI.52), на котором значения
определим с помощью графика (рис. XI.52), на котором значения  заданы в децибеллах.
заданы в децибеллах.

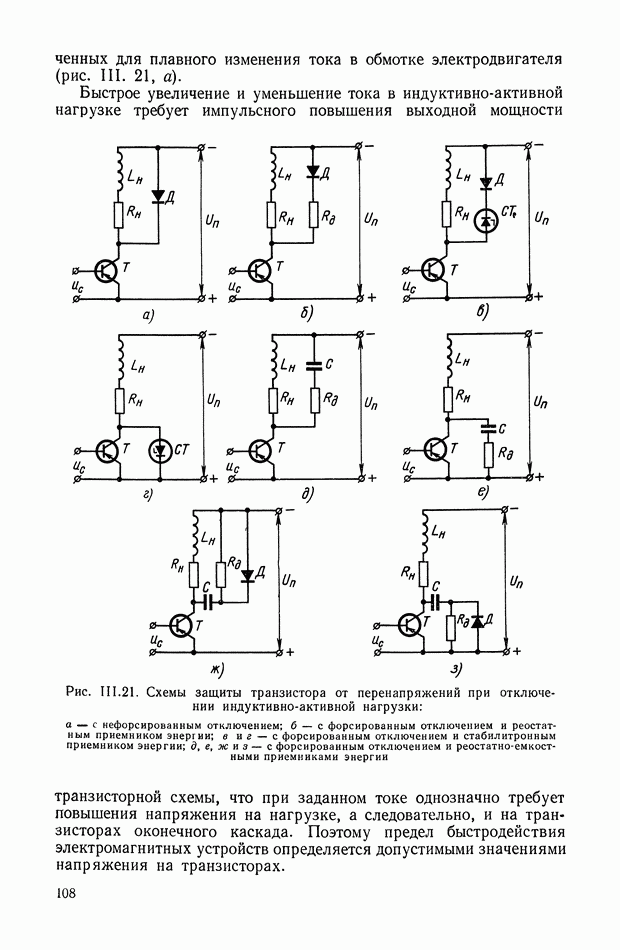
Рис. XI.52. Вспомогательный график 

Рис. XI.53. Логарифмические частотные характеристики
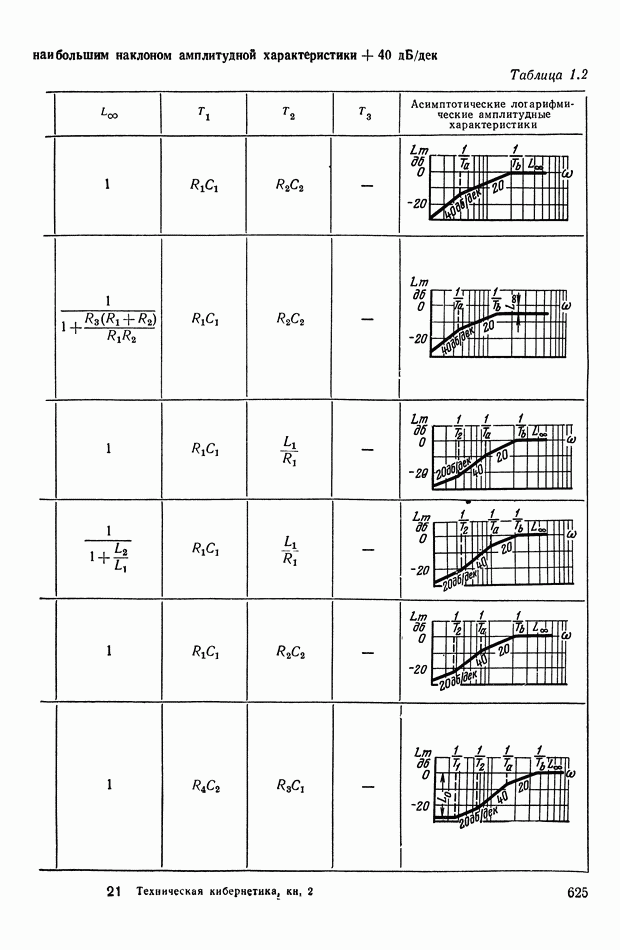
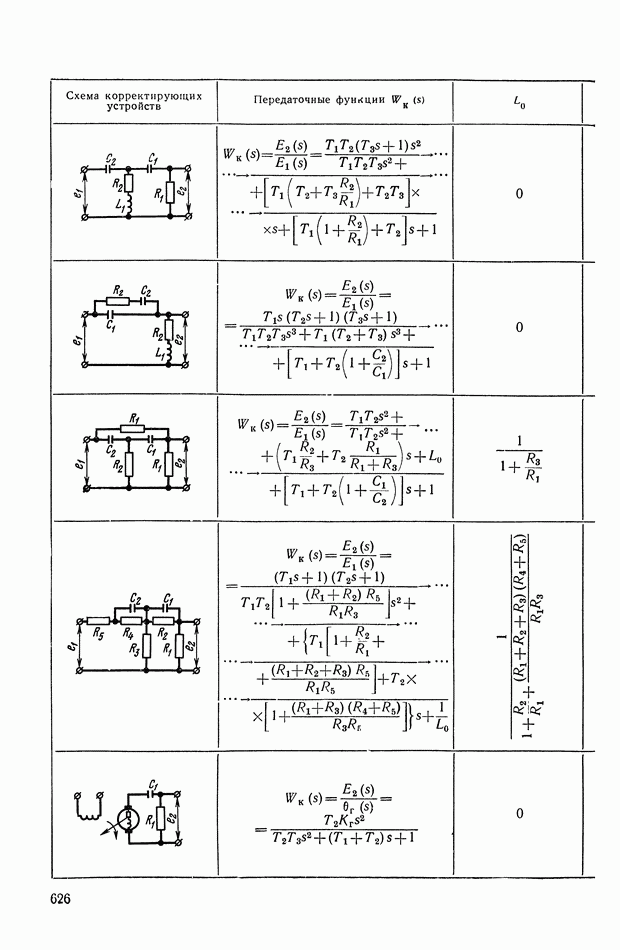
Из формул (XI. 118) видно, что эквивалентная амплитудная характеристика нелинейного корректирующего устройства зависит только от амплитуды и совершенно не зависит от частоты. Фазовая же характеристика определяется как амплитудой, так и частотой. На рис. XI.53 построены логарифмические эквивалентные амплитудная и фазовая характеристики нелинейного корректирующего устройства, изображенного на рис. X 1.51. Аналогичным образом можно определить коэффициенты гармонической линеаризации и в других более сложных нелинейных корректирующих устройствах. Соответствующие вычисления приведены в табл. III.1 приложения III. В последнем столбце построены приведенные логарифмические эквивалентные характеристики (шаблоны)  . Изменяя вид линейного корректирующего устройства
. Изменяя вид линейного корректирующего устройства
(по данным таблиц приложения I), получим различные виды нелинейных двухканальных корректирующих устройств [10].
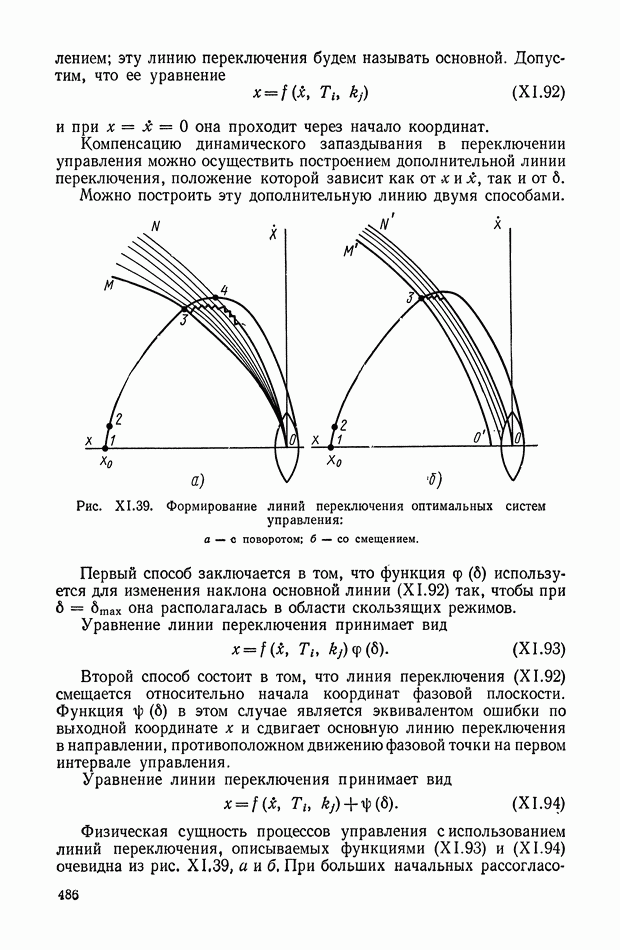
Рассмотрим несколько нелинейных логических корректирующих устройств, используемых для повышения устойчивости и улучшения качества в нелинейных системах автоматического регулирования и управления.

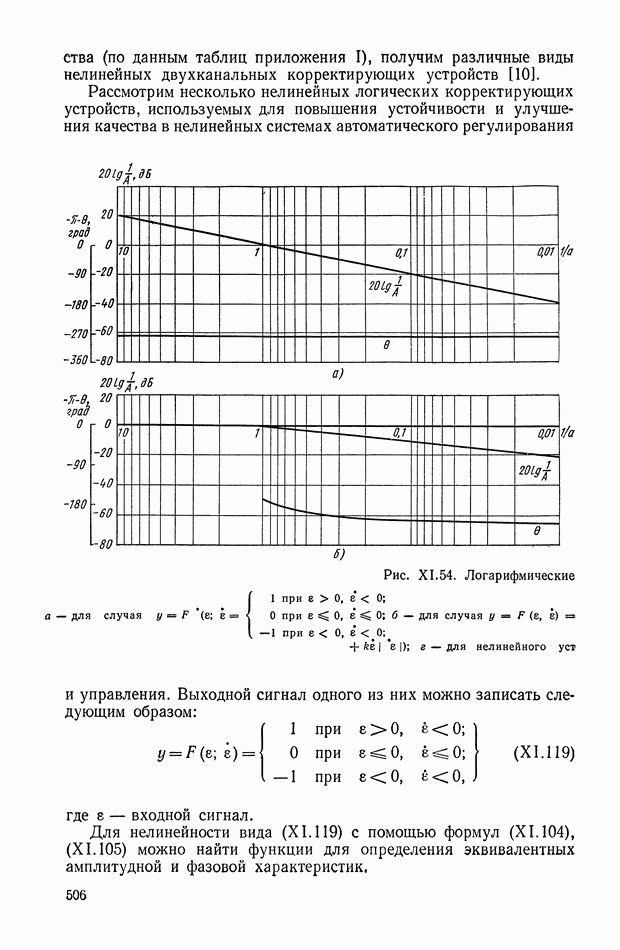
Рис. XI.54. Логарифмические 
Выходной сигнал одного из них можно записать следующим образом:

где  — входной сигнал.
— входной сигнал.
Для нелинейности вида (XI. 119) с помощью формул (XI. 104), (XI. 105) можно найти функции для определения эквивалентных амплитудной и фазовой характеристик.

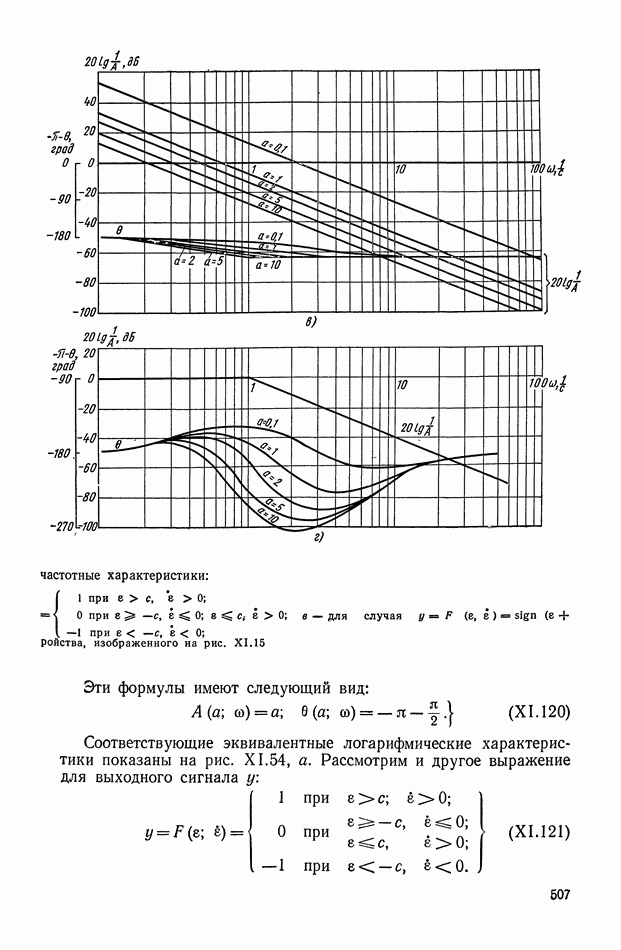
частотные характеристики: 
Эти формулы имеют следующий вид:

Соответствующие эквивалентные логарифмические характеристики показаны на рис. XI.54, а. Рассмотрим и другое выражение для выходного сигнала у:

При этом формулы для эквивалентных характеристик можно записать в виде

Логарифмические характеристики при  построены на рис. XI.54, б. Для нелинейного корректирующего устройства, описываемого уравнением
построены на рис. XI.54, б. Для нелинейного корректирующего устройства, описываемого уравнением

формулы для эквивалентных частотных характеристик имеют вид

Соответствующие логарифмические характеристики для пяти значений  приведены на рис. XI.54, в.
приведены на рис. XI.54, в.

Рис. XI.55. Нелинейное логическое корректирующее устройство
Рассмотренные три нелинейные корректирующие устройства имеют существенные различия. Для первого и второго устройств, описываемых выражениями (XI. 119) и (XI. 121), эквивалентные амплитудные и фазовая характеристики зависят только от амплитуды входного сигнала  и совершенно не зависят от частоты. Третье же устройство, описываемое уравнением (X 1.123), имеет эквивалентные характеристики, зависящие как от амплитуды а, так и от частоты
и совершенно не зависят от частоты. Третье же устройство, описываемое уравнением (X 1.123), имеет эквивалентные характеристики, зависящие как от амплитуды а, так и от частоты  Из рис. X 1.54, в видно, что фазовые характеристики зависят от амплитуды а значительно меньше, чем амплитудные
Из рис. X 1.54, в видно, что фазовые характеристики зависят от амплитуды а значительно меньше, чем амплитудные
характеристики. Поэтому в расчетах при различных а можно пользоваться одной усредненной фазовой характеристикой.
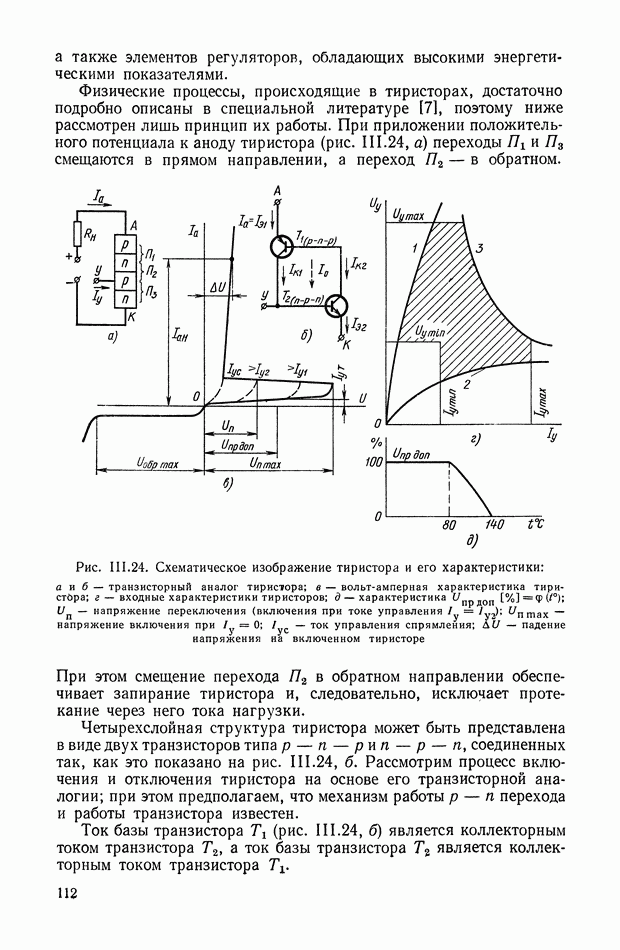
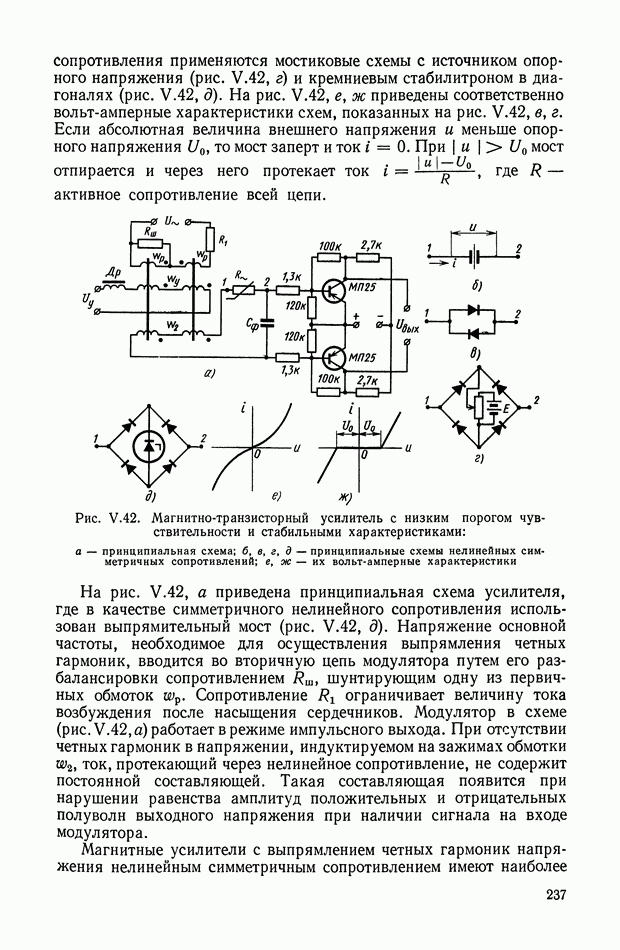
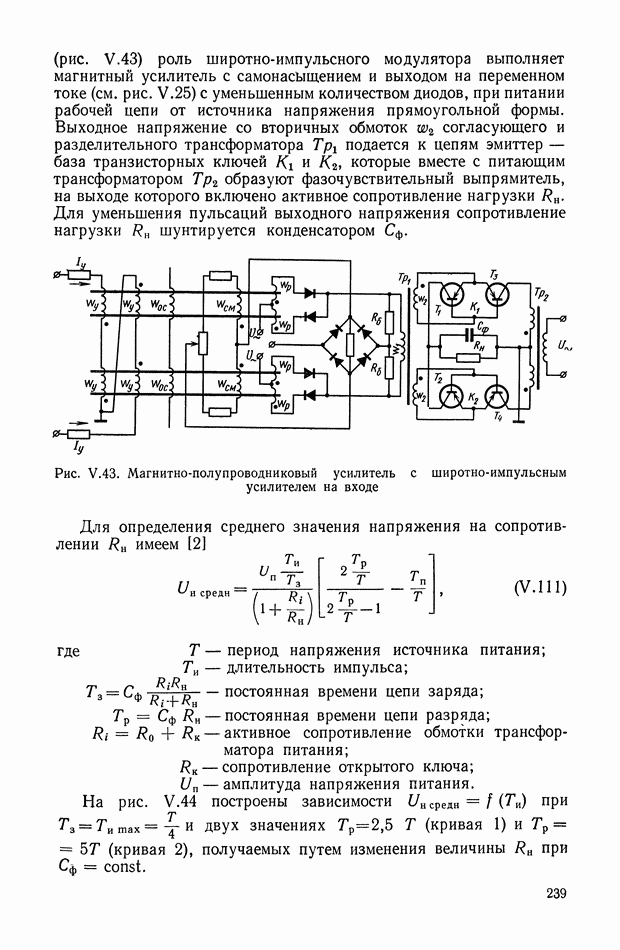
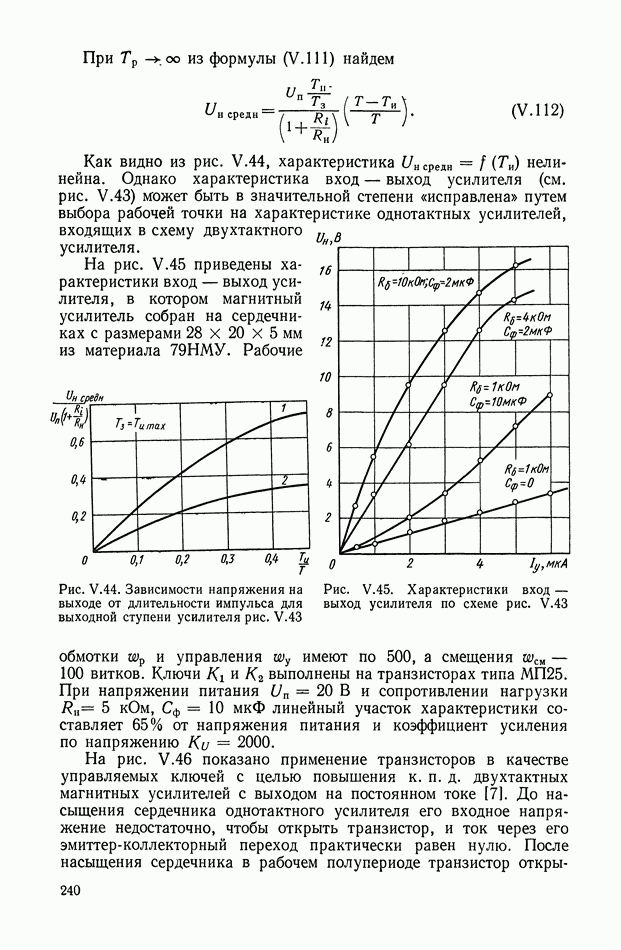
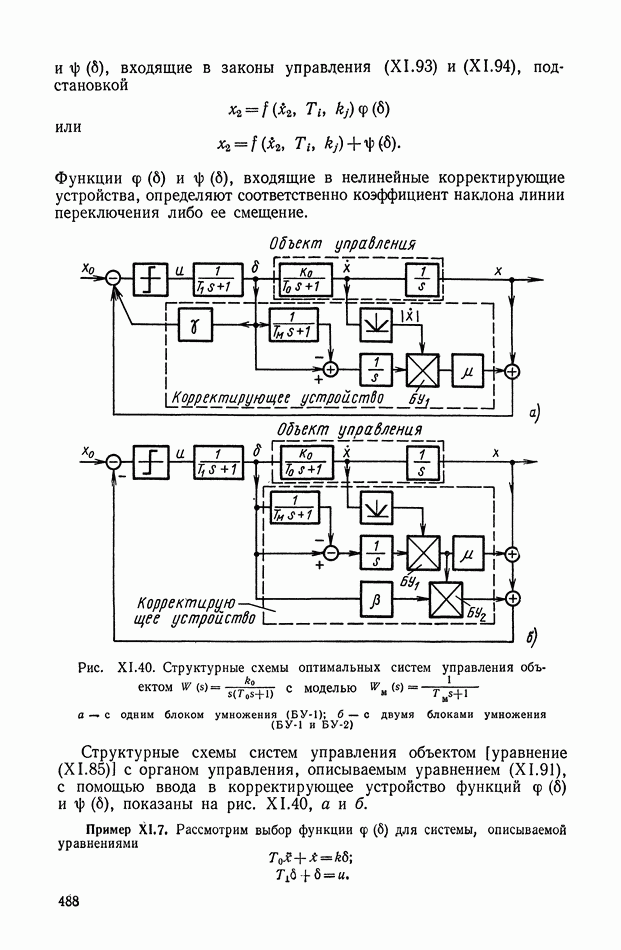
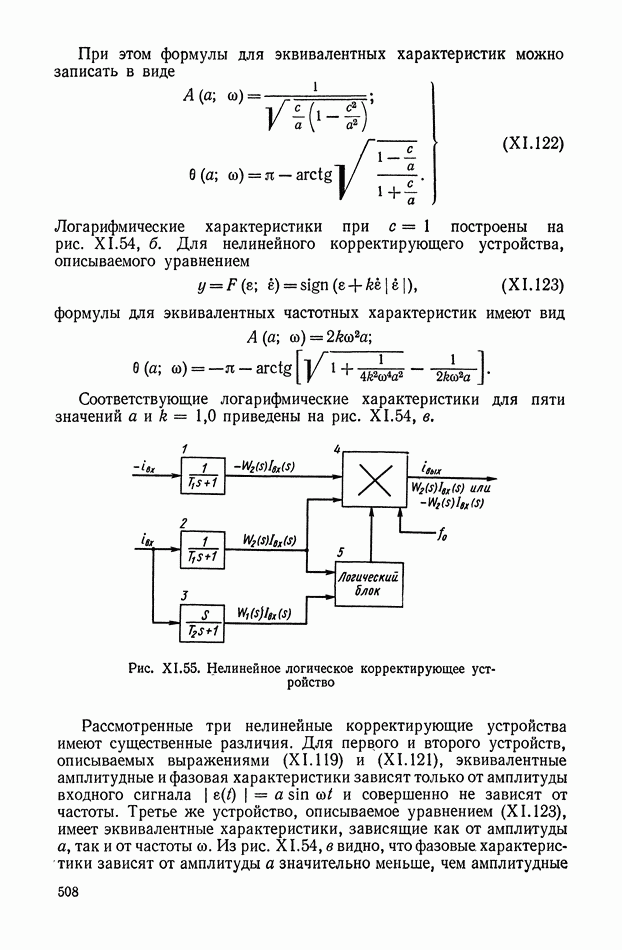
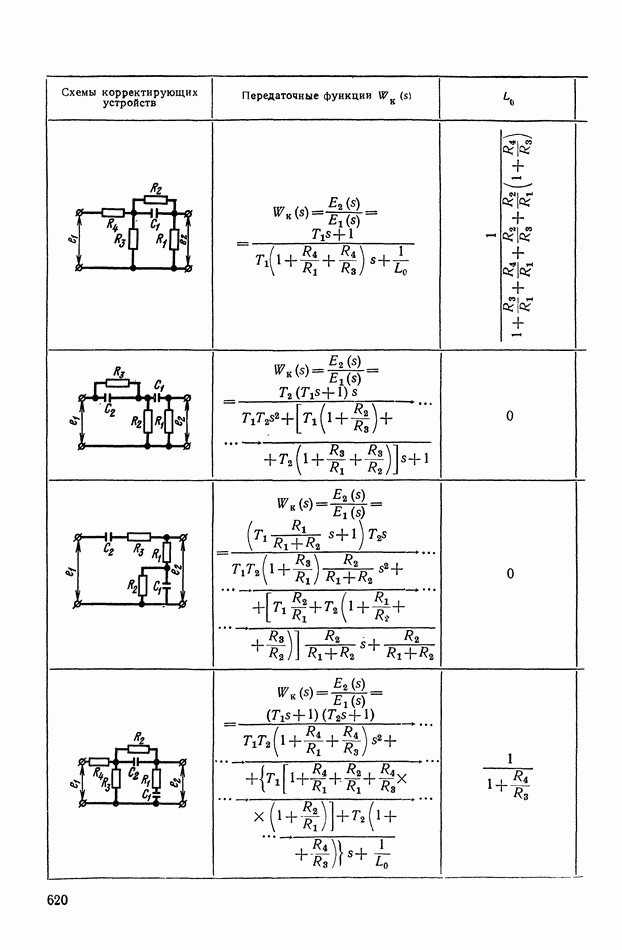
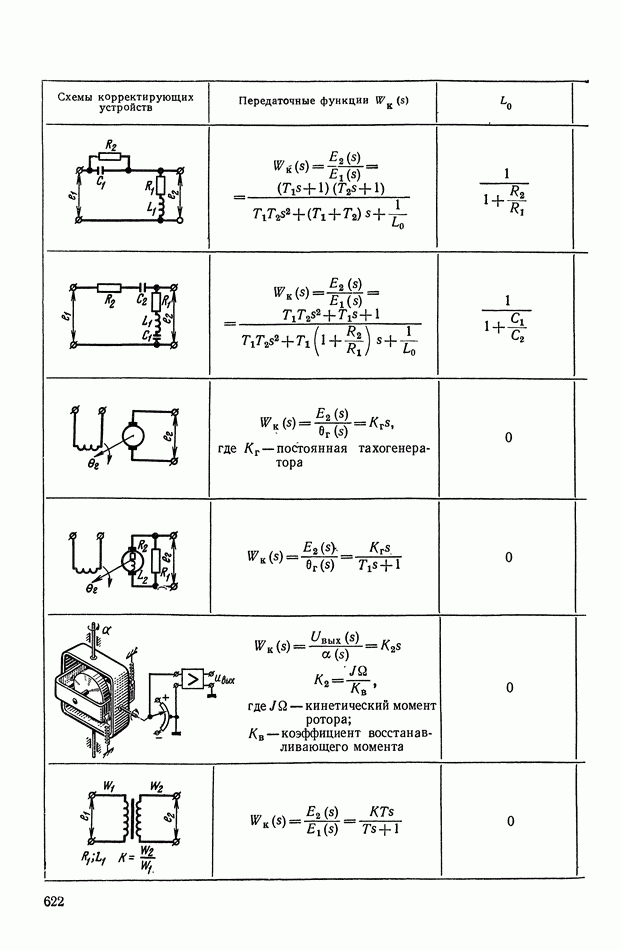
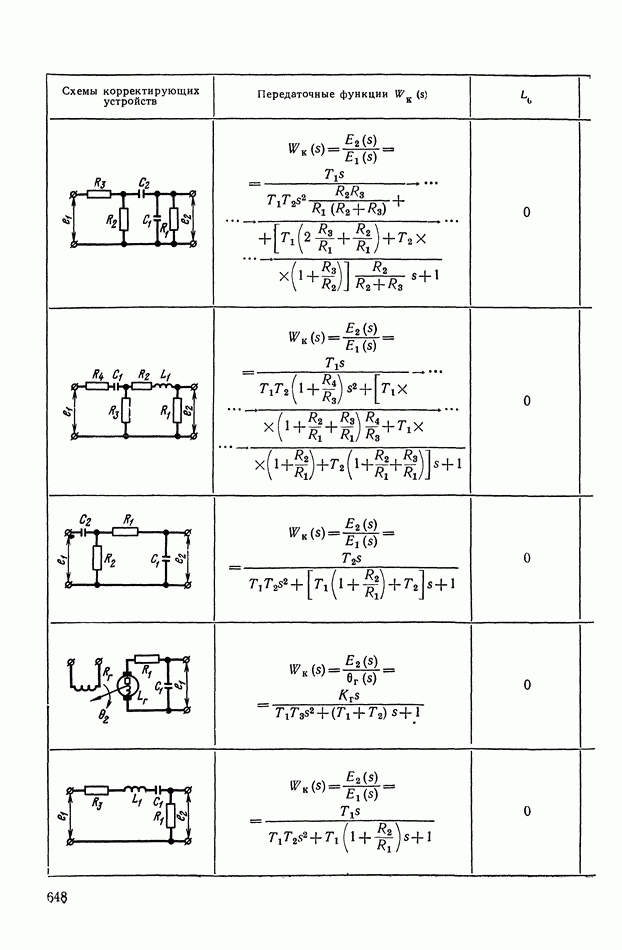
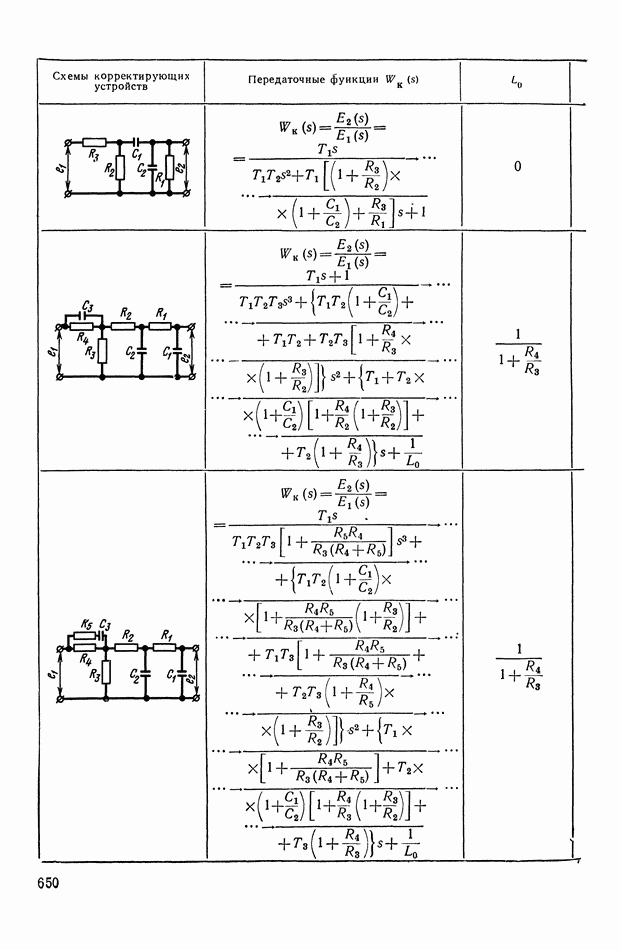
Рассмотрим более сложной нелинейное логическое корректирующее устройство (рис. XI.55), в которое входят три линейных корректирующих устройства  блок перемножения 4 и логический блок 5. Обозначим передаточные функции
блок перемножения 4 и логический блок 5. Обозначим передаточные функции  блоков
блоков

а 3-го блока

На вход схемы подаются токи с противоположными фазами:  Ток —
Ток —  проходит через линейное устройство
проходит через линейное устройство  на блок перемножения. Ток
на блок перемножения. Ток  в свою очередь, проходит через
в свою очередь, проходит через  На выходе фильтра
На выходе фильтра  образуется сигнал
образуется сигнал  а на выходе фильтра
а на выходе фильтра  — сигнал
— сигнал  Эти сигналы поступают на логический блок, в котором выполняются следующие операции:
Эти сигналы поступают на логический блок, в котором выполняются следующие операции:

Сигнал на выходе  где А и Б — логические высказывания, можно представить в виде
где А и Б — логические высказывания, можно представить в виде

Соответствующую формулам (XI. 124) и (XI. 125) логическую схему можно реализовать на элементах типа  (рис. XI.56).
(рис. XI.56).
Составим следующую таблицу состояний:


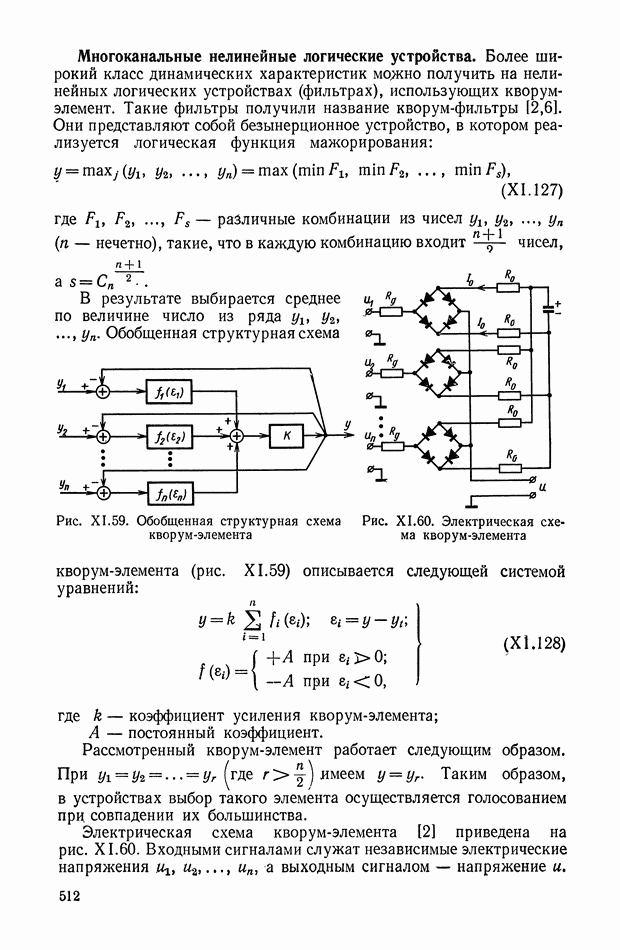
Рис. XI.56. Логическая схема
Из этой таблицы можно найти, что выходная функция

где А обозначает «не А»;
АВ обозначает «А и В».
Для полученного нелинейного логического корректирующего устройства также можно определить эквивалентные амплитудную и фазовую характеристики, которые приведены на рис. XI.54, г. При этом видно, что в зависимости от амплитуды а изменяется фазовая характеристика, а амплитудная характеристика сохраняет неизменное значение. Последним и отличается данное нелинейное корректирующее устройство (рис. XI.55) от нелинейного устройства коррекции, изображенного на рис. X 1.51, в котором изменялась амплитудная характеристика.
Возможны и другие виды нелинейных корректирующих устройств этого типа, в которых с изменением амплитуды входного сигнала значительно меняются как фазовая, так и амплитудная характеристики.

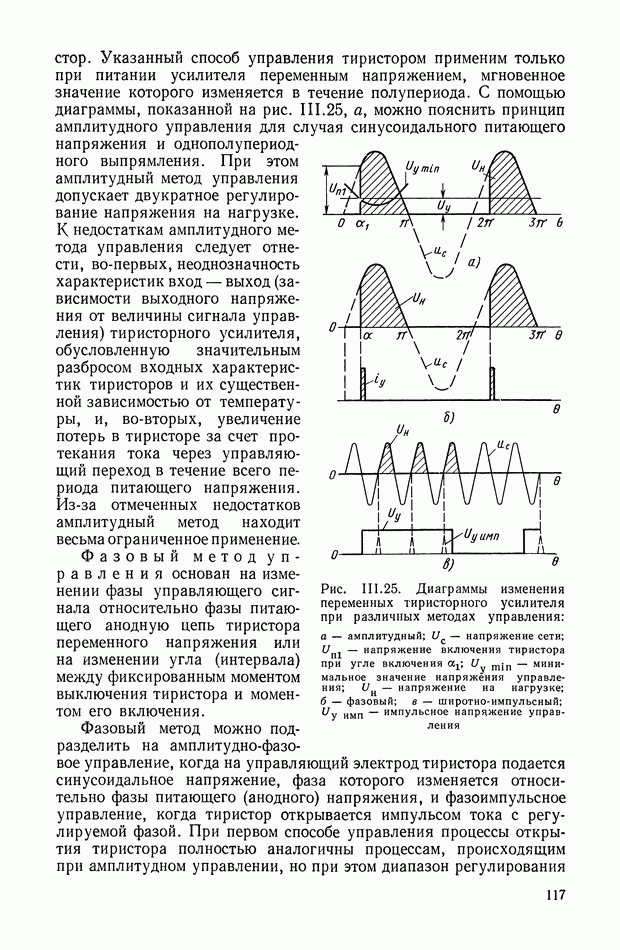
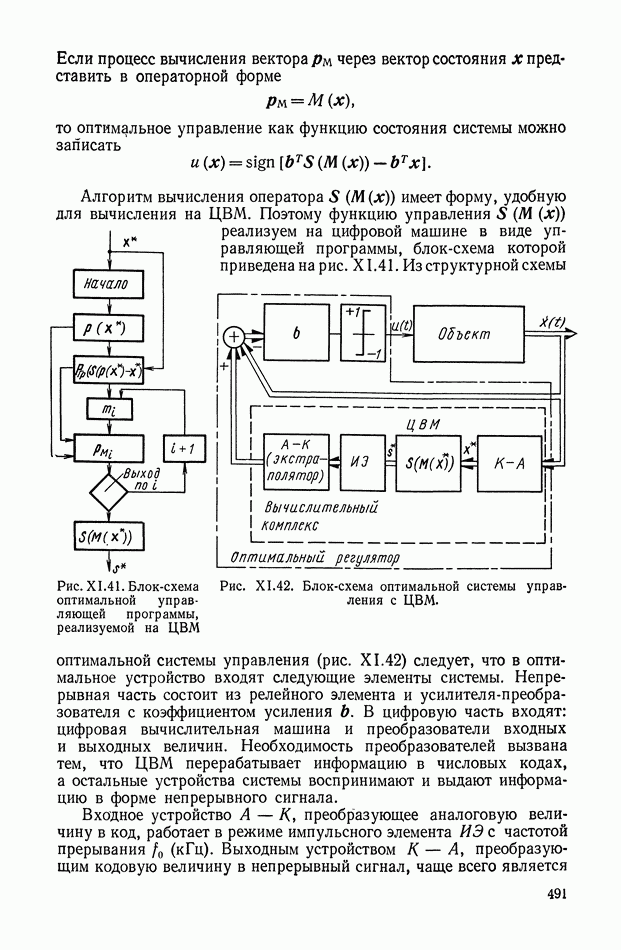
Рис. XI.57. Схема импульсного функционального преобразователя
Для реализации некоторых рассмотренных выше нелинейных корректирующих устройств необходимо множительное устройство. Одна из возможных схем, реализующих алгоритм

где у и х — электрические напряжения, символизирующие переменные параметры, приведена на рис. XI.57 [18]. В состав блока входят линейные динамические цепи  компаратор
компаратор  импульсные ключи
импульсные ключи  линия задержки
линия задержки  и заполняющий конденсатор
и заполняющий конденсатор  Работа линейных цепей синхронизируется тактирующими импульсами
Работа линейных цепей синхронизируется тактирующими импульсами  и заключается в генерировании периодических напряжений специальной формы
и заключается в генерировании периодических напряжений специальной формы  амплитудно-модулированных входными сигналами
амплитудно-модулированных входными сигналами  Тактовые импульсы поступают через
Тактовые импульсы поступают через  с выхода компаратора после определения схемой импульсного значения результата преобразования.
с выхода компаратора после определения схемой импульсного значения результата преобразования.
Узлы  и
и  образуют управляющий тракт, который вырабатывает временный интервал
образуют управляющий тракт, который вырабатывает временный интервал  зависящий от входных сигналов
зависящий от входных сигналов  а также от формы генерируемого линейной цепью
а также от формы генерируемого линейной цепью  напряжения и
напряжения и  Величина параметра
Величина параметра  отсчитывается от конца тактирующего импульса до того момента времени, когда выполняется соотношение
отсчитывается от конца тактирующего импульса до того момента времени, когда выполняется соотношение 
Последующее преобразование величины  в выходное напряжение
в выходное напряжение  осуществляется каналом, собранным на элементах
осуществляется каналом, собранным на элементах  путем фиксации мгновенного значения
путем фиксации мгновенного значения  которое представляет собой импульсную величину и зависит от входных сигналов
которое представляет собой импульсную величину и зависит от входных сигналов  и от параметров линейных цепей
и от параметров линейных цепей  и
и  Конденсатор
Конденсатор  запоминает мгновенное значение
запоминает мгновенное значение  и сохраняет его в период между импульсами, формируя выходной сигнал в виде
и сохраняет его в период между импульсами, формируя выходной сигнал в виде
непрерывного электрического напряжения. Для осуществления вычислительных операций используются переходные процессы линейных цепей  и
и  Импульсные ключи ИК блоков
Импульсные ключи ИК блоков  управляются последовательностью
управляются последовательностью  и служат для периодического подключения величин
и служат для периодического подключения величин  к контурам
к контурам  После окончания импульса
После окончания импульса  линейные цепи вырабатывают переходные процессы напряжения а
линейные цепи вырабатывают переходные процессы напряжения а  причем
причем

где  — переходные функции линейных цепей.
— переходные функции линейных цепей.
В момент равенства мгновенного значения напряжения  и управляющего сигнала х компаратор К генерирует фиксирующий импульс ФИ. Интервалу времени
и управляющего сигнала х компаратор К генерирует фиксирующий импульс ФИ. Интервалу времени  который отсчитывается от момента окончания импульса
который отсчитывается от момента окончания импульса  до момента образования импульса
до момента образования импульса  соответствуют следующие соотношения:
соответствуют следующие соотношения:

где  — функция, обратная функции
— функция, обратная функции 

Рис. XI.58. Схемы соединения линейной цепи: а — для образования  — для образования и
— для образования и 
Кратковременный импульс ФИ воздействует на ключ ИК, благодаря чему на конденсатор  поступает мгновенное значение напряжения
поступает мгновенное значение напряжения  Конденсатор запоминает потенциал
Конденсатор запоминает потенциал  и сохраняет его в период между импульсами, формируя тем самым выходное напряжение
и сохраняет его в период между импульсами, формируя тем самым выходное напряжение

или

где  функциональная зависимость, определяемая параметрами и структурой линейных цепей.
функциональная зависимость, определяемая параметрами и структурой линейных цепей.
Если напряжения и  получаются таким образом, как это показано на рис. XI.58, то имеем
получаются таким образом, как это показано на рис. XI.58, то имеем

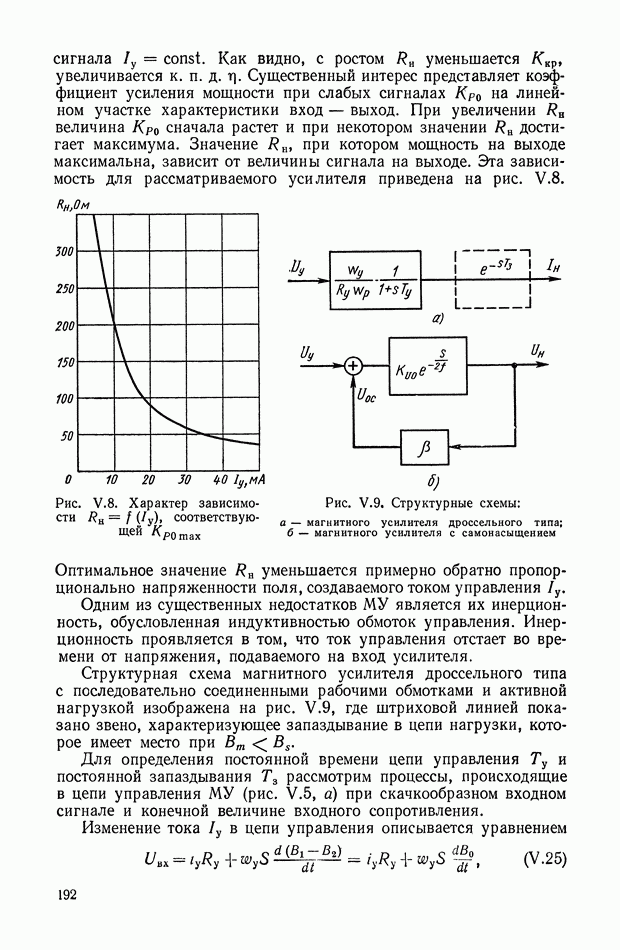
т. е. в этом случае осуществляется операция умножения. Выбирая соответствующие ячейки, можно реализовать и другие нелинейные преобразования: деления, умножения сигнала у на функцию от сигнала х и т. д.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА САР
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ЛИНЕЙНЫХ УСИЛИТЕЛЬНЫХ УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ УСИЛИТЕЛЬНОГО УСТРОЙСТВА БЕЗ ОБРАТНОЙ СВЯЗИ
- 3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ, СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ОСОБЕННОСТИ УСИЛИТЕЛЬНОГО УСТРОЙСТВА С ОБРАТНОЙ СВЯЗЬЮ
- 4. КЛАССИФИКАЦИЯ И СВОЙСТВА УСИЛИТЕЛЬНЫХ УСТРОЙСТВ С ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 5. ВЫБОР И РАСЧЕТ УСИЛИТЕЛЬНОГО УСТРОЙСТВА
- ГЛАВА II. ЭЛЕКТРОННЫЕ ЛАМПОВЫЕ И ИОННЫЕ УСИЛИТЕЛИ
- 1. ОСНОВЫ ТОПОЛОГИЧЕСКОГО АНАЛИЗА СХЕМ ЛИНЕЙНЫХ ЭЛЕКТРОННЫХ ЛАМПОВЫХ УСИЛИТЕЛЕЙ
- 2. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПОСТОЯННОГО ТОКА
- 3. БАЛАНСНЫЕ МОСТОВЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- 4. СТАБИЛИЗАЦИЯ КОЭФФИЦИЕНТА УСИЛЕНИЯ
- 5. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
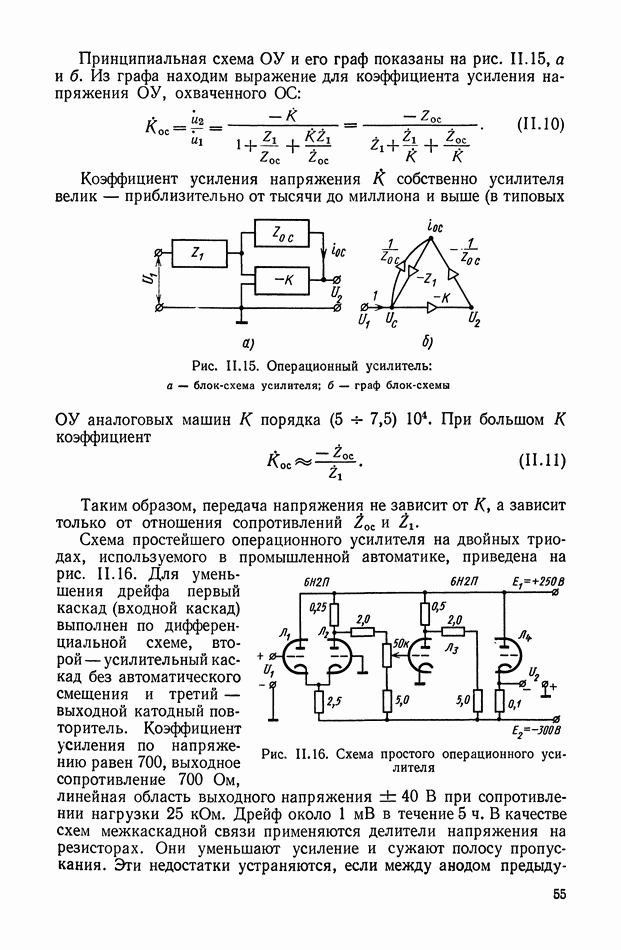
- 6. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- 7. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
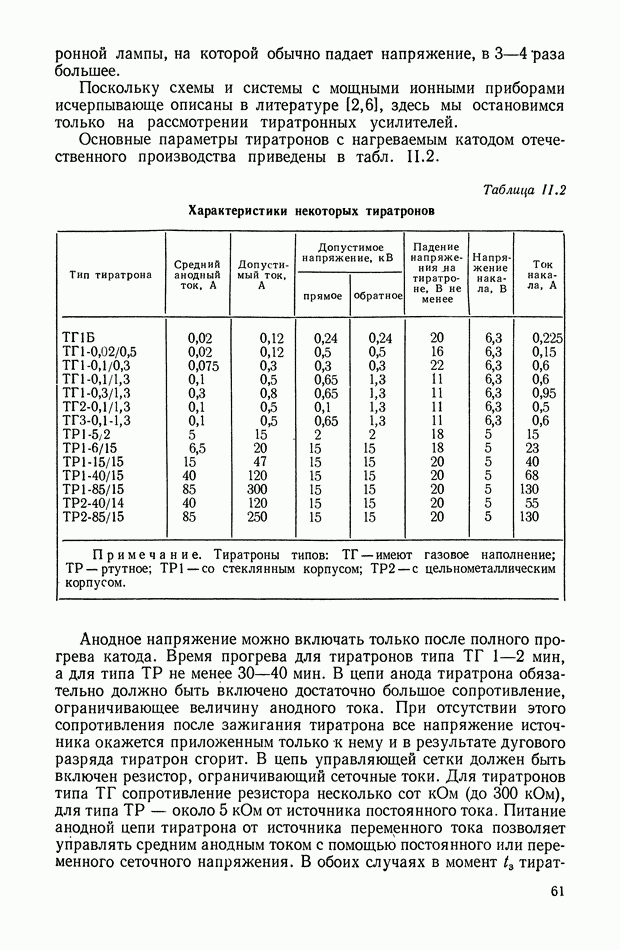
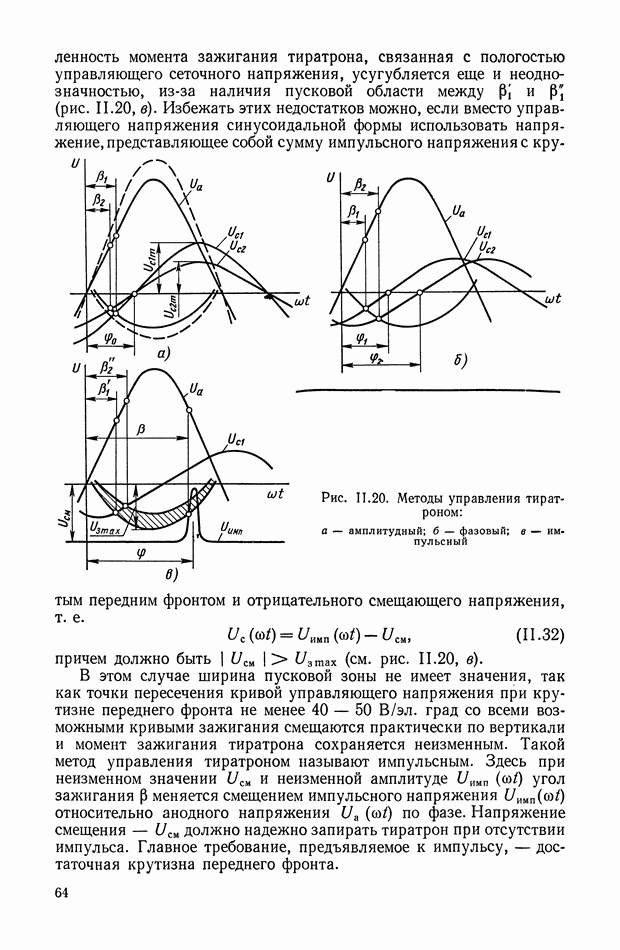
- 8. ОБЩИЕ СВОЙСТВА ИОННОГО (ТИРАТРОННОГО) УСИЛИТЕЛЯ МЕТОДЫ УПРАВЛЕНИЯ ТИРАТРОНОМ
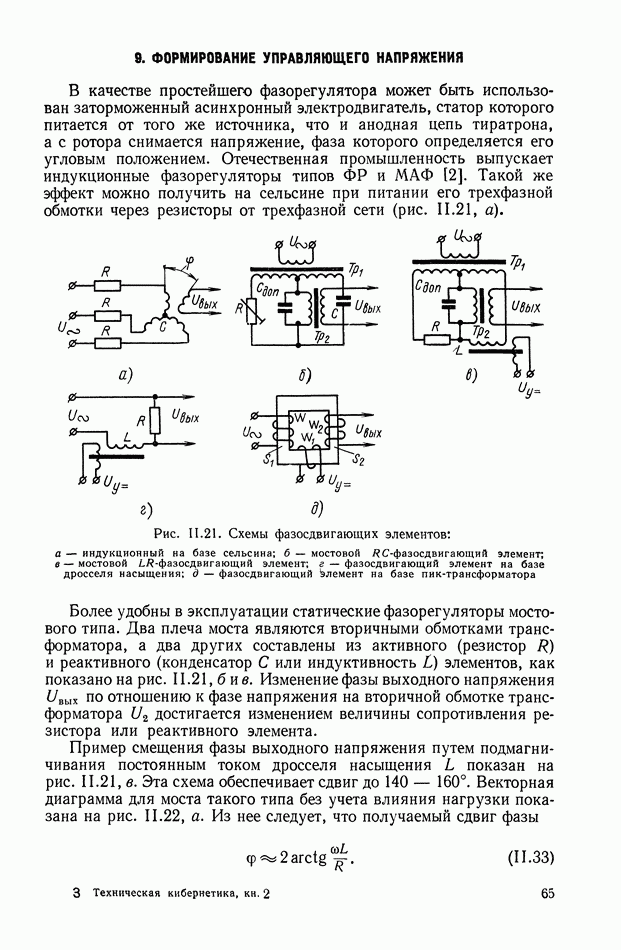
- 9. ФОРМИРОВАНИЕ УПРАВЛЯЮЩЕГО НАПРЯЖЕНИЯ
- 10. РАСЧЕТ ЭЛЕМЕНТОВ СХЕМ ТИРАТРОННОГО УСИЛИТЕЛЯ
- ГЛАВА III. ПОЛУПРОВОДНИКОВЫЕ И ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
- Цепи смещения.
- Цепи связи.
- 2. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ СРЕДНЕГО ЗНАЧЕНИЯ ТОКА
- Полупроводниковые демодуляторы.
- 3. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ В РЕЖИМЕ ПЕРЕКЛЮЧЕНИЯ
- Режимы импульсного регулирования мощности.
- Управление силовыми транзисторами.
- 4. ТРАНЗИСТОРНЫЕ УСТРОЙСТВА УПРАВЛЕНИЯ ЭЛЕКТРОДВИГАТЕЛЯМИ И ЭЛЕКТРОМАГНИТНЫМИ МЕХАНИЗМАМИ
- 5. ТИРИСТОРЫ. ХАРАКТЕРИСТИКИ, ПАРАМЕТРЫ И СВОЙСТВА
- 6. СПОСОБЫ И УСТРОЙСТВА УПРАВЛЕНИЯ ТИРИСТОРАМИ
- 7. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ (РЕГУЛИРУЕМЫЕ ВЫПРЯМИТЕЛИ)
- 8. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 9. ТИРИСТОРНЫЕ УСИЛИТЕЛИ С ПИТАНИЕМ ОТ СЕТИ ПОСТОЯННОГО ТОКА
- 10. ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 11. ОСНОВЫ РАСЧЕТА ДИЭЛЕКТРИЧЕСКИХ УСИЛИТЕЛЕЙ
- ГЛАВА IV. КВАНТОВЫЕ УСИЛИТЕЛИ И ГЕНЕРАТОРЫ
- 2. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ РАДИОДИАПАЗОНА
- Квантовые усилители радиодиапазона.
- 3. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- Оптический квантовый усилитель
- 4. ПРИМЕНЕНИЕ В САР КВАНТОВЫХ УСИЛИТЕЛЕЙ И ГЕНЕРАТОРОВ РАДИОДИАПАЗОНА, ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- ГЛАВА V. МАГНИТНЫЕ И МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- 2. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ МАГНИТНЫХ УСИЛИТЕЛЕЙ
- 3. ОДНОТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ БЕЗ ОБРАТНОЙ СВЯЗИ (УПРАВЛЯЕМЫЕ ДРОССЕЛИ И ТРАНСФОРМАТОРЫ)
- 4. МАГНИТНЫЕ УСИЛИТЕЛИ С САМОНАСЫЩЕНИЕМ
- Релейный режим работы усилителей с самонасыщением.
- 5. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 6. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ
- 7. МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- ГЛАВА VI. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 2. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С НЕЗАВИСИМЫМ ВОЗБУЖДЕНИЕМ И С САМОВОЗБУЖДЕНИЕМ
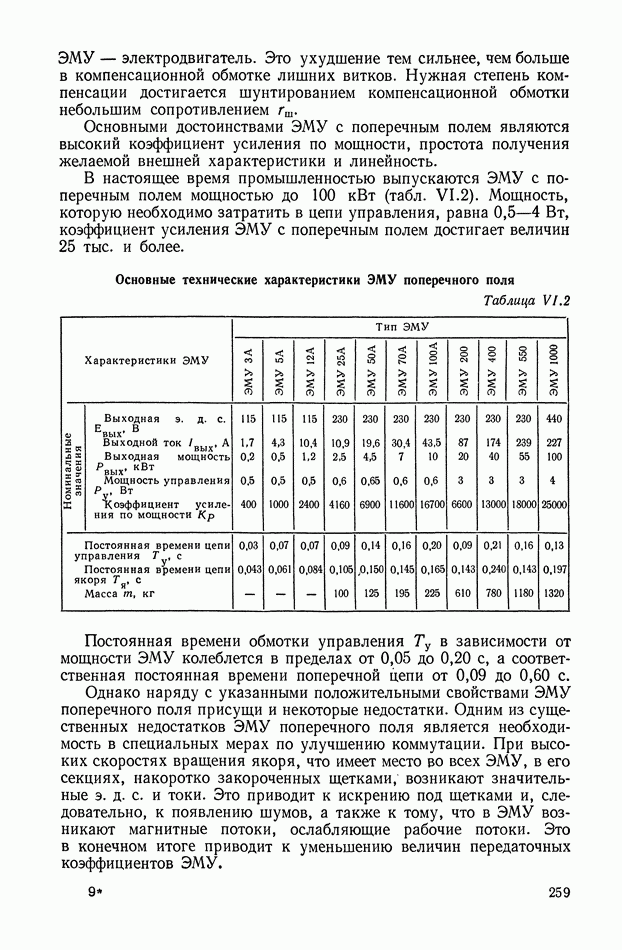
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С ПОПЕРЕЧНЫМ ПОЛЕМ
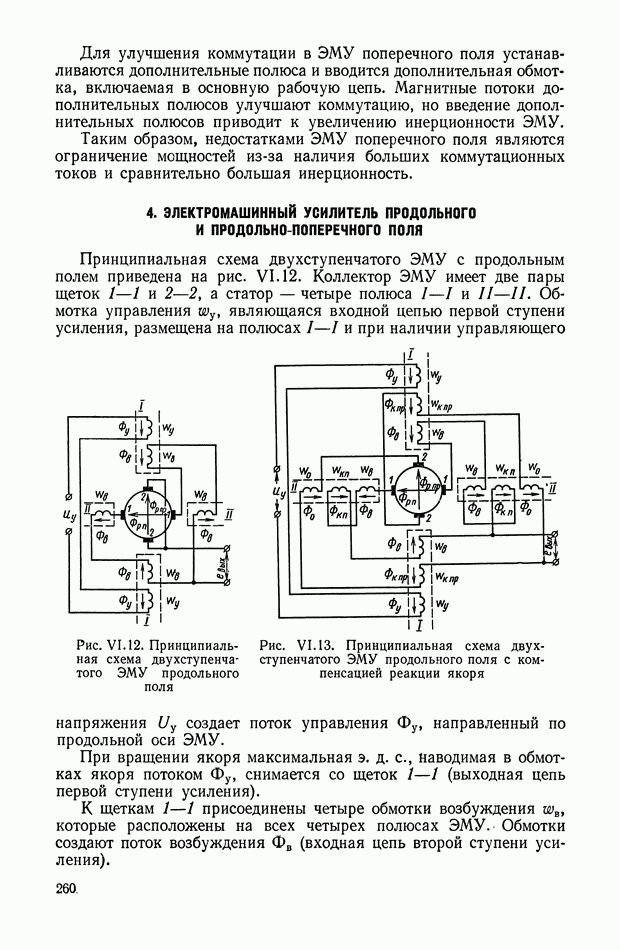
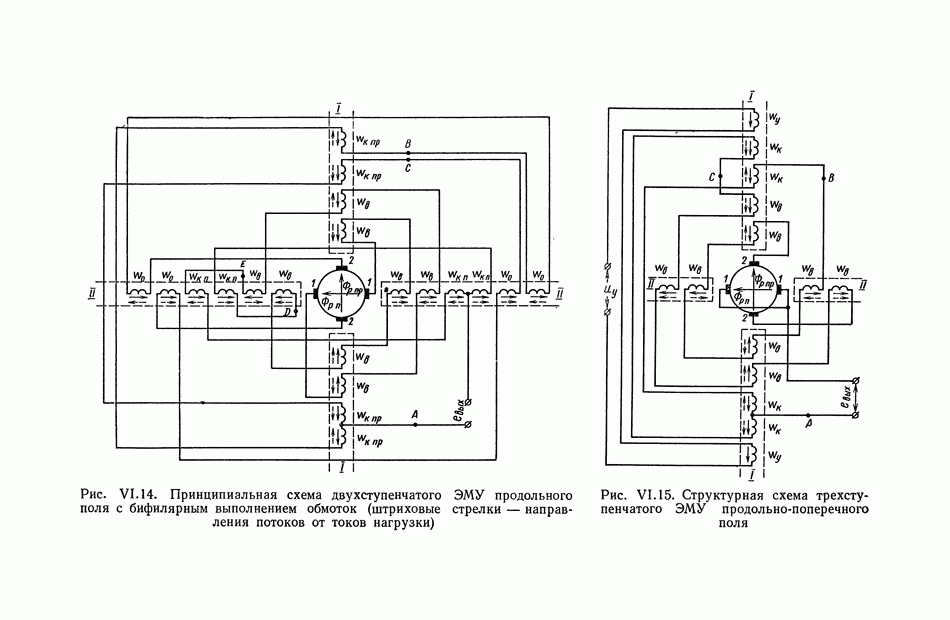
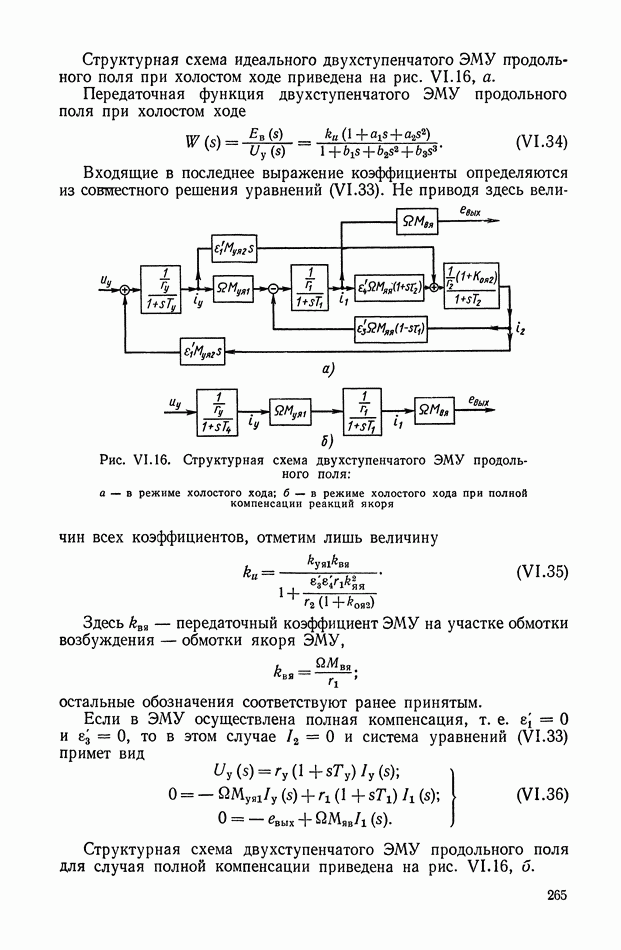
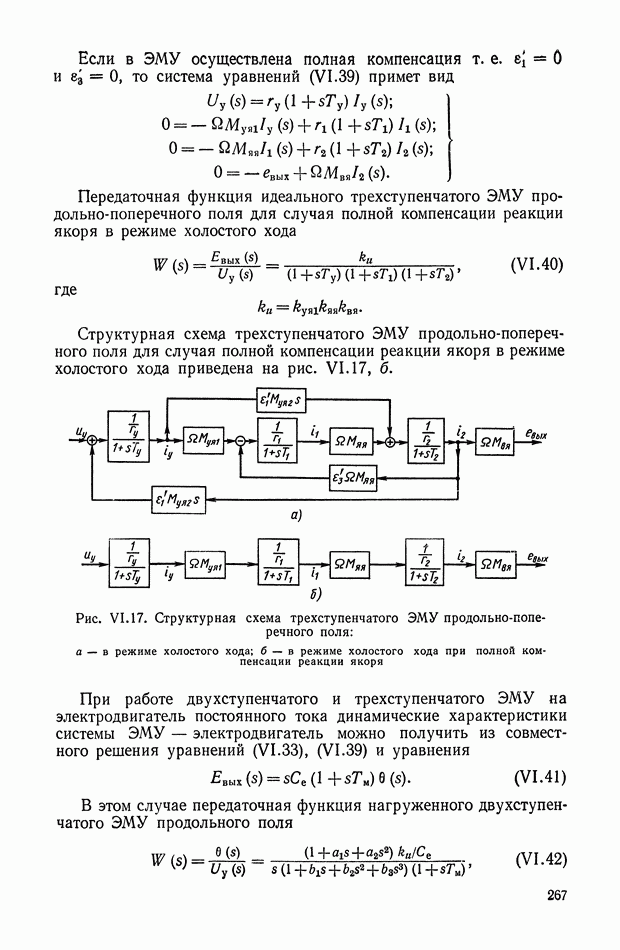
- 4. ЭЛЕКТРОМАШИННЫЙ УСИЛИТЕЛЬ ПРОДОЛЬНОГО И ПРОДОЛЬНО-ПОПЕРЕЧНОГО ПОЛЯ
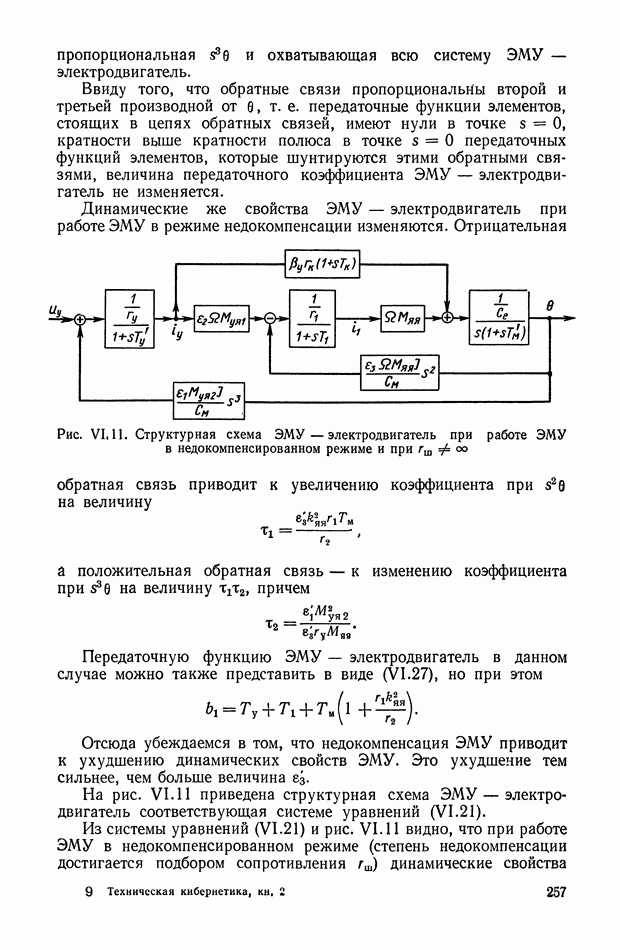
- 5. ВЛИЯНИЕ НА ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭМУ ВИХРЕВЫХ И КОММУТАЦИОННЫХ ТОКОВ, ГИСТЕРЕЗИСА И СДВИГА ЩЕТОК С НЕЙТРАЛИ
- 6. МЕТОДЫ УЛУЧШЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕКТРОМАШИННЫХ УСИЛИТЕЛЕЙ
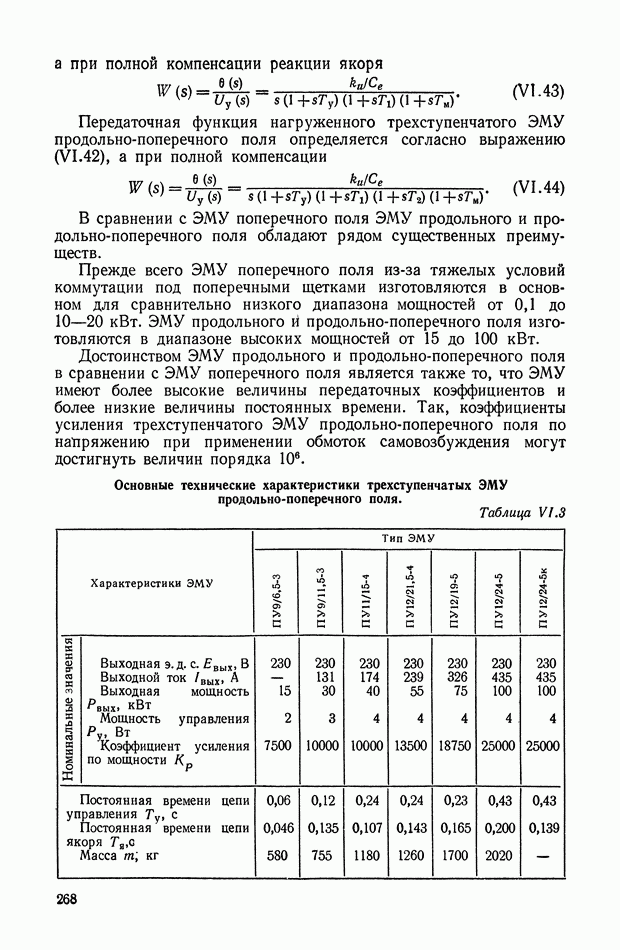
- 7. НАГРУЗОЧНАЯ ХАРАКТЕРИСТИКА ЭЛЕКТРОМАШИННОГО УСИЛИТЕЛЯ
- ГЛАВА VII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ХАРАКТЕРИСТИКИ УСИЛИТЕЛЕЙ И СПОСОБЫ ИХ ФОРМИРОВАНИЯ
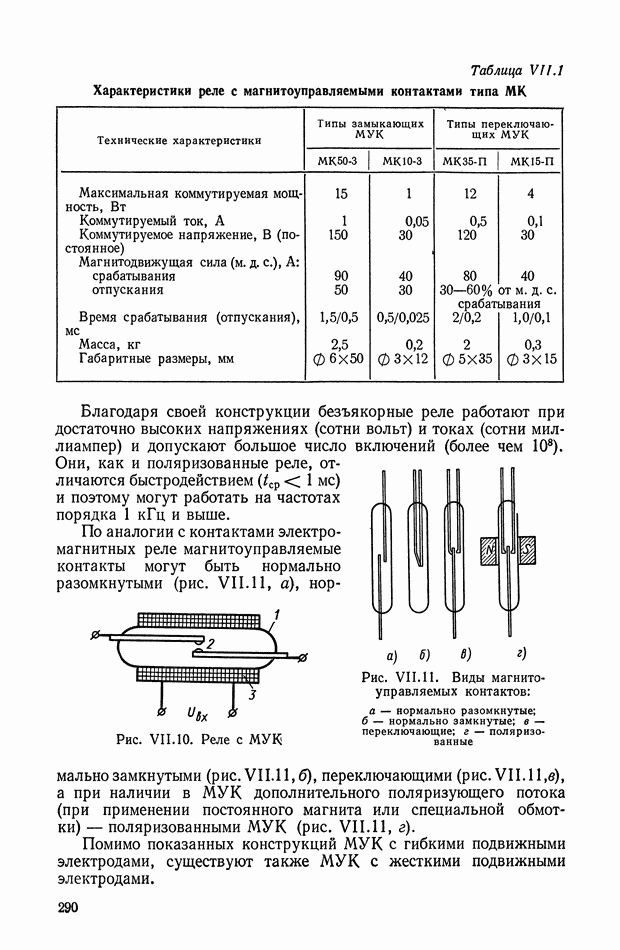
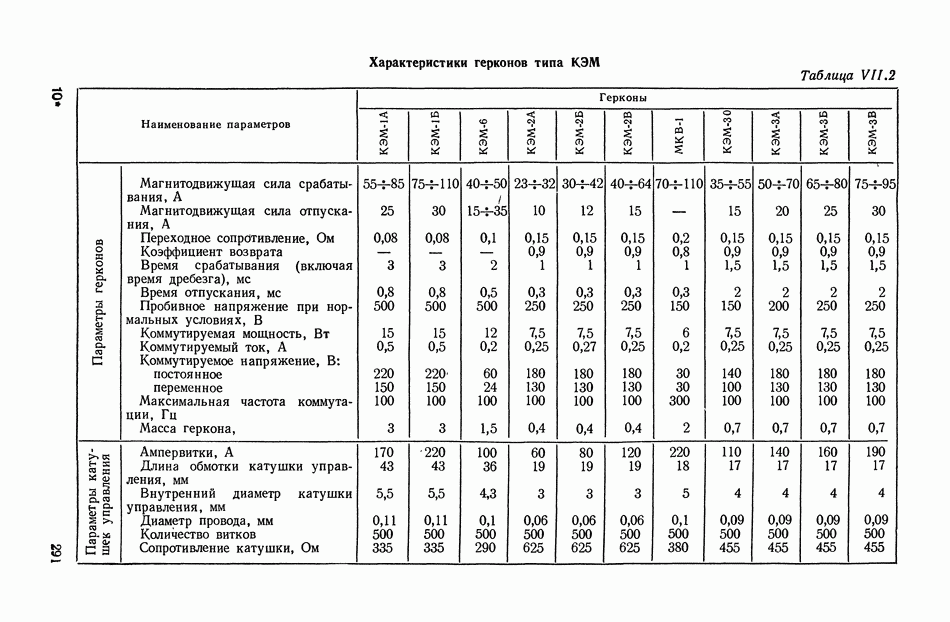
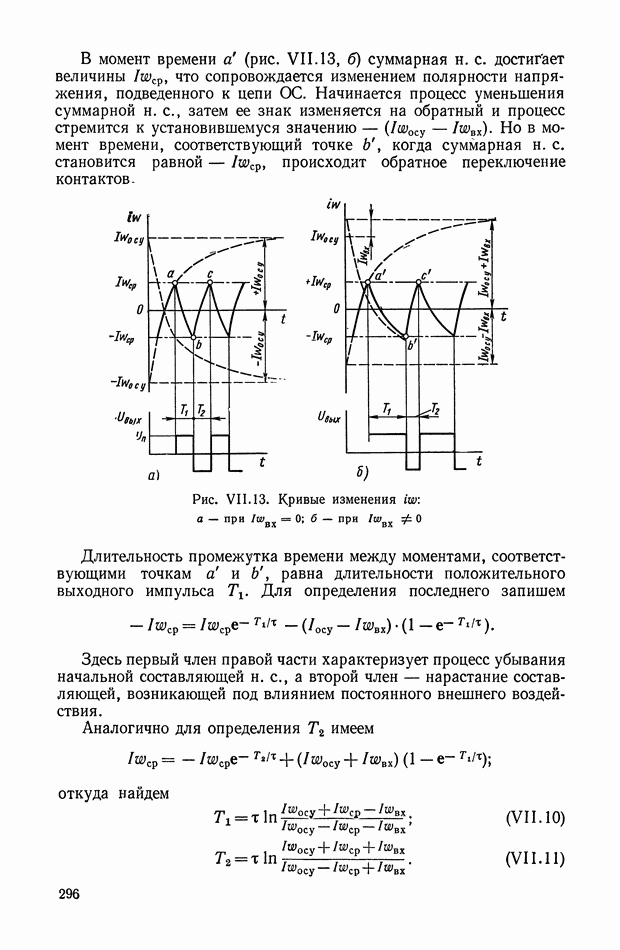
- 2. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
- 3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ЛИНЕАРИЗОВАННЫЕ УСИЛИТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ РЕЛЕ
- 4. БЕСКОНТАКТНЫЕ ЛИНЕАРИЗОВАННЫЕ РЕЛЕЙНЫЕ УСИЛИТЕЛИ
- ГЛАВА VIII. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
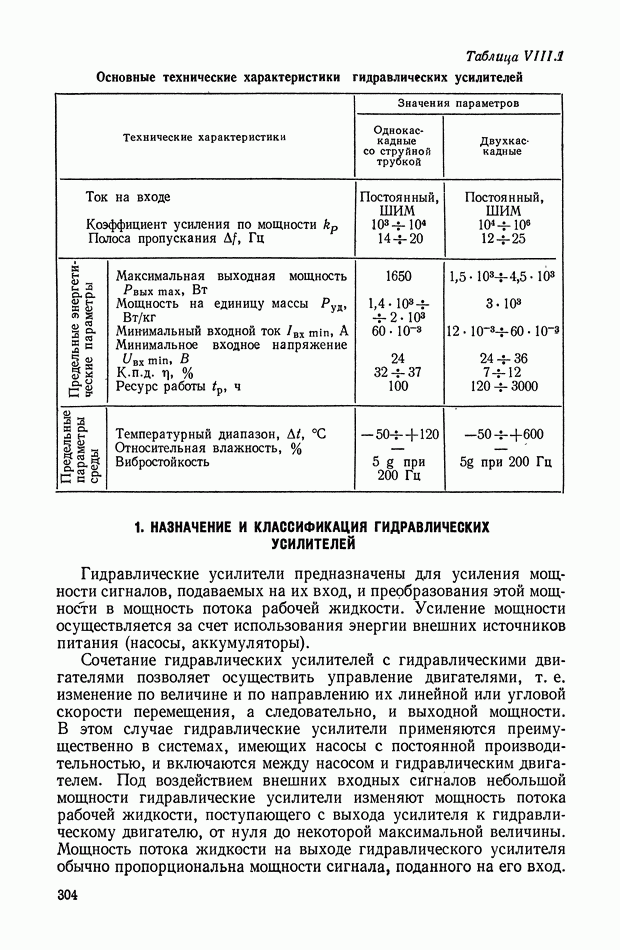
- 2. ОСНОВНЫЕ ЭЛЕМЕНТЫ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ И ИХ ХАРАКТЕРИСТИКИ
- 3. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ С ЗОЛОТНИКОМ
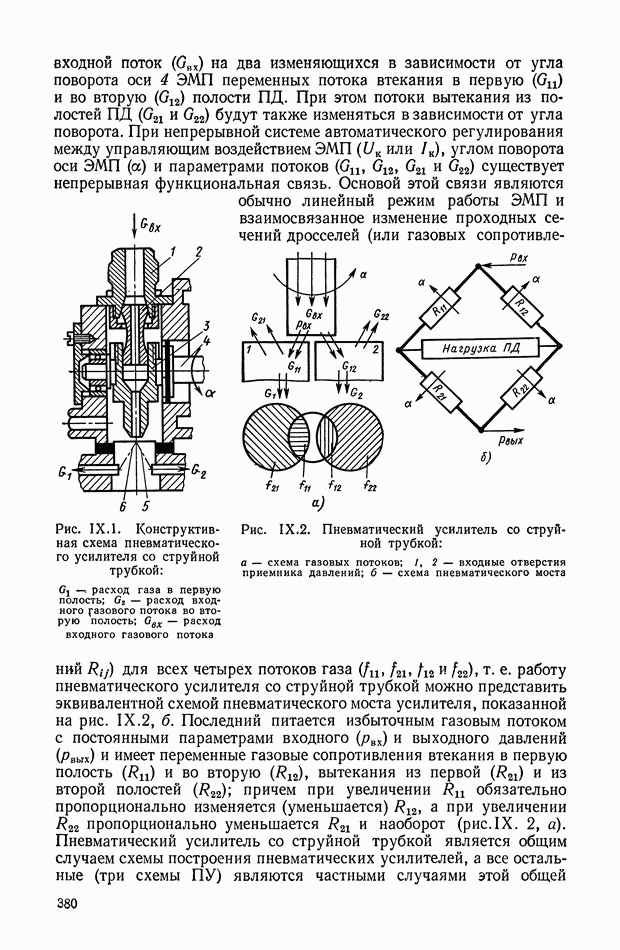
- 4. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ СО СТРУЙНОЙ ТРУБКОЙ
- 5. СХЕМЫ И ПРИНЦИПЫ ДЕЙСТВИЯ ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 6. СТАТИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 7. ДИНАМИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
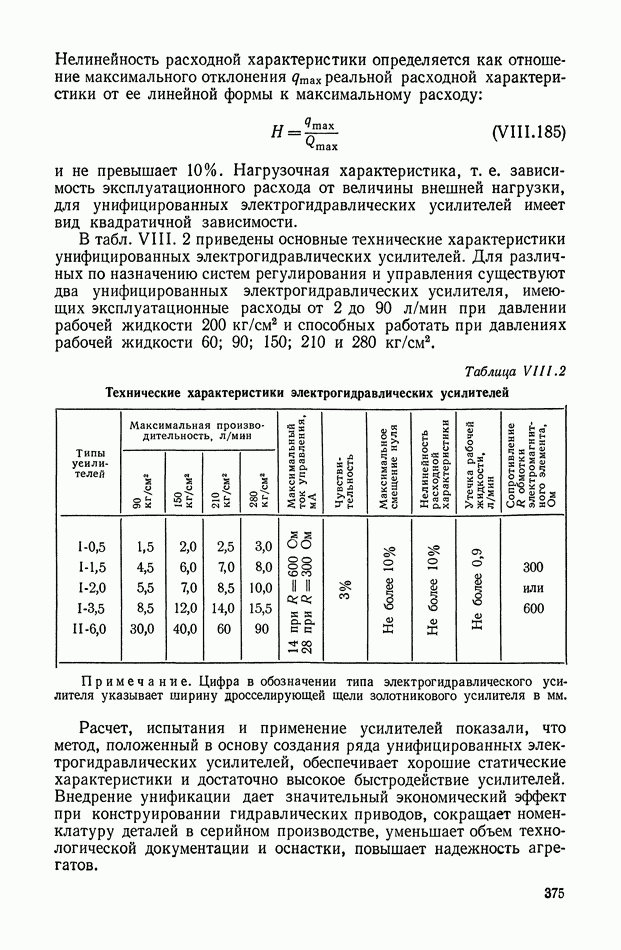
- 8. УНИФИКАЦИЯ ЭЛЕКТРОГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ ДЛЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
- ГЛАВА IX. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ И ИХ КЛАССИФИКАЦИЯ
- 2. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ СО СТРУЙНОЙ ТРУБКОЙ
- 3. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗОЛОТНИКОМ
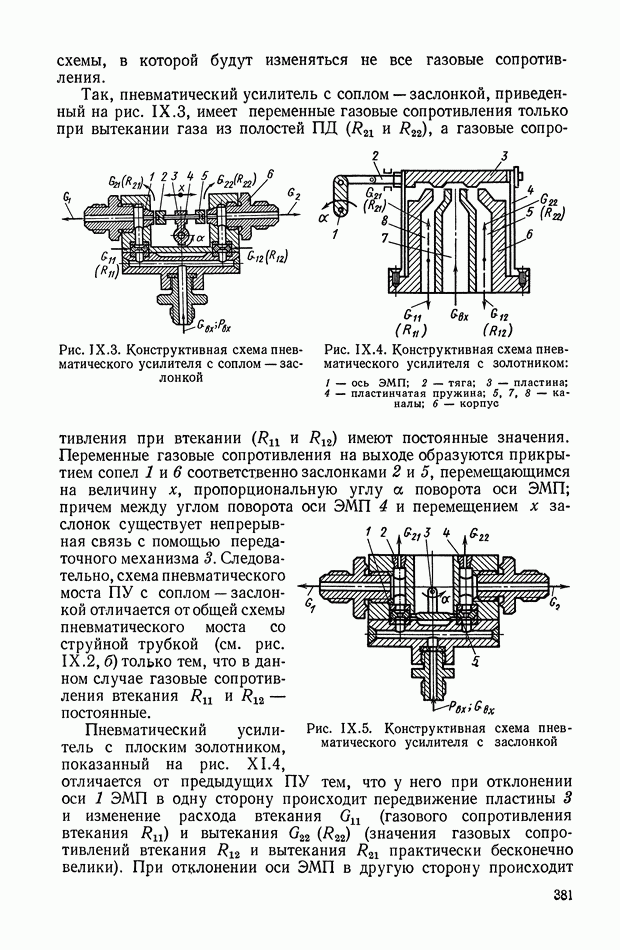
- 4. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С СОПЛОМ — ЗАСЛОНКОЙ
- 5. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗАСЛОНКОЙ
- 6. МНОГОКАСКАДНЫЕ ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- РАЗДЕЛ II. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ И УСТРОЙСТВ
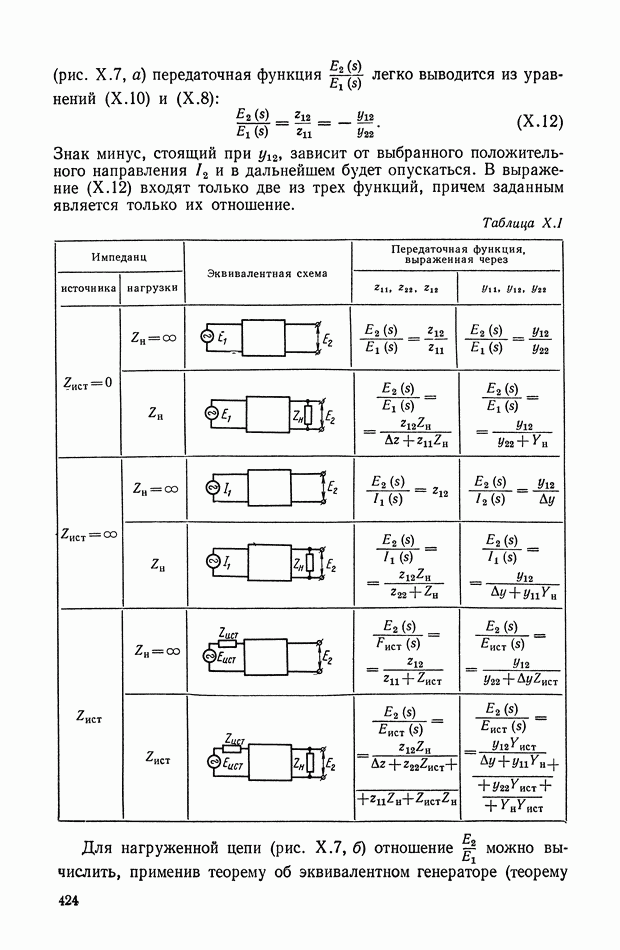
- 2. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ЛИНЕЙНЫХ ПАССИВНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Основные соотношения для синтеза пассивного RC-четырехполюсника.
- 3. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Активные четырехполюсники, получаемые с помощью конверторов отрицательного сопротивления.
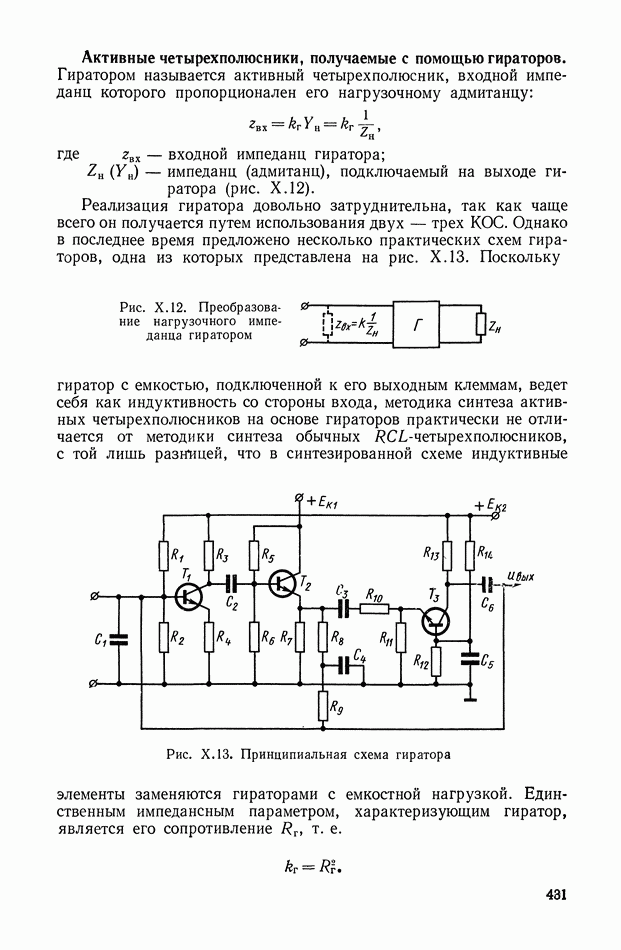
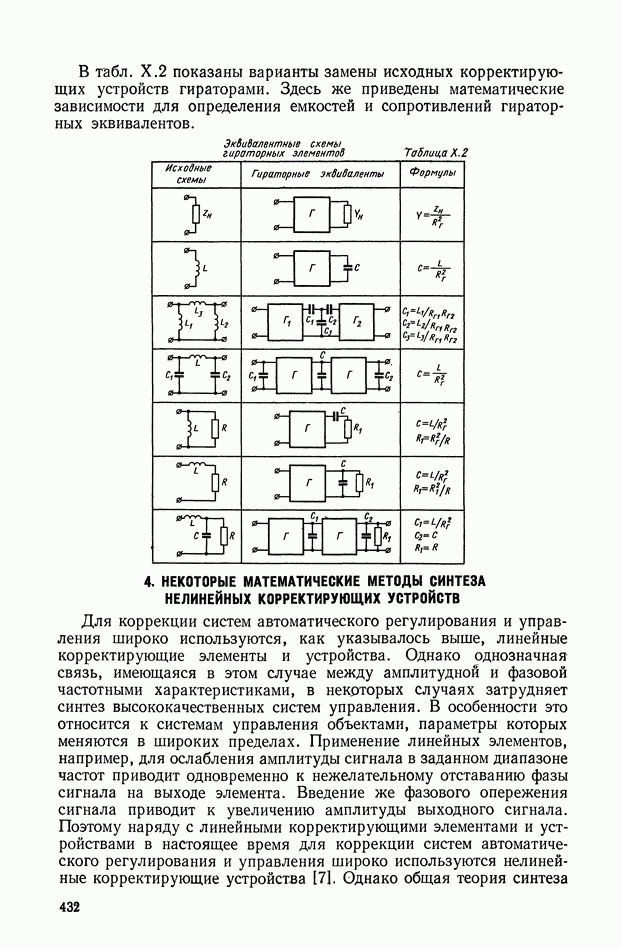
- Активные четырехполюсники, получаемые с помощью гираторов.
- 4. НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА НЕЛИНЕЙНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. ОСОБЕННОСТИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XI. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА ПОСТОЯННОГО ТОКА
- Дифференцирующий трансформатор.
- Электрические интегрирующие элементы.
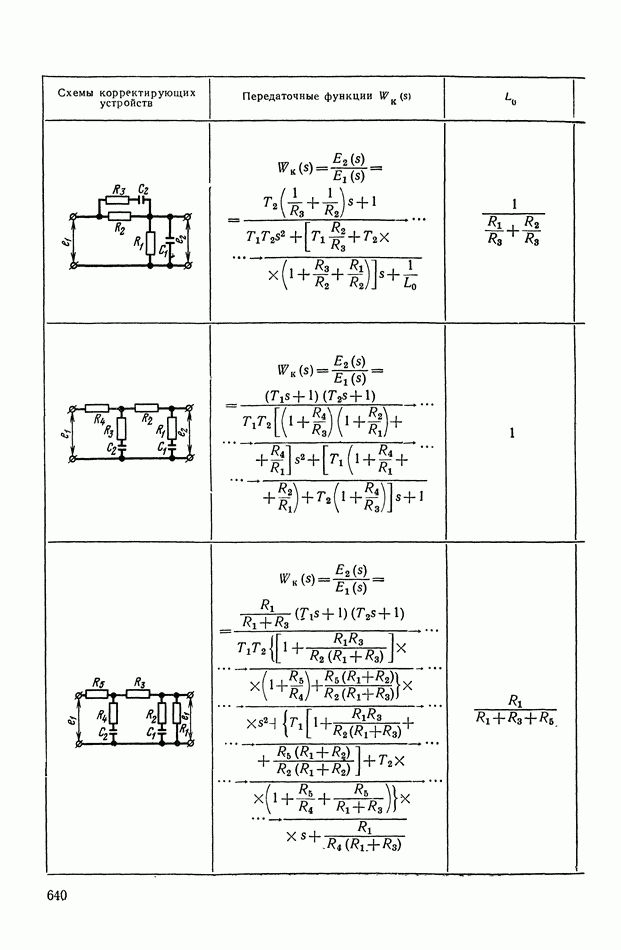
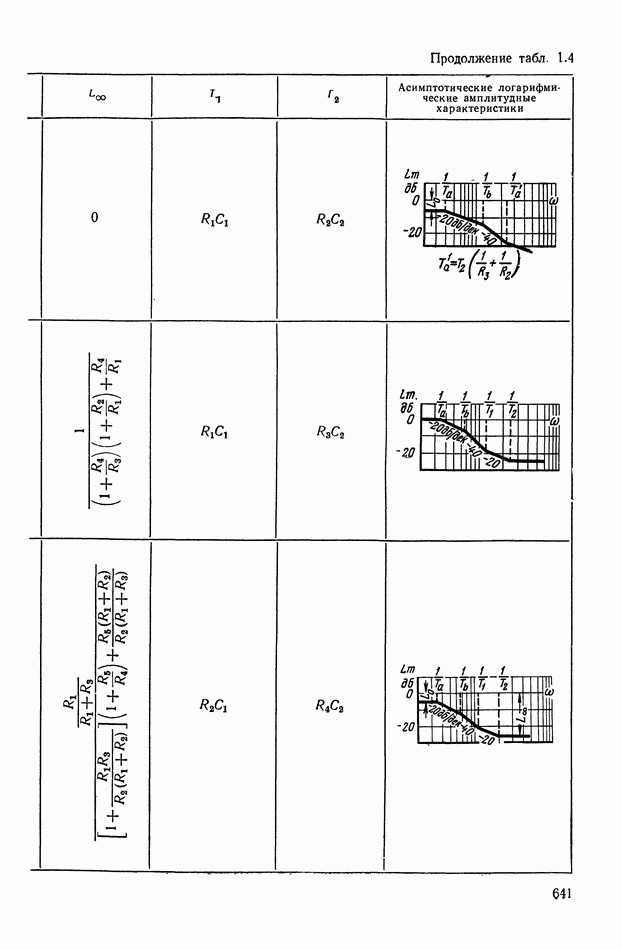
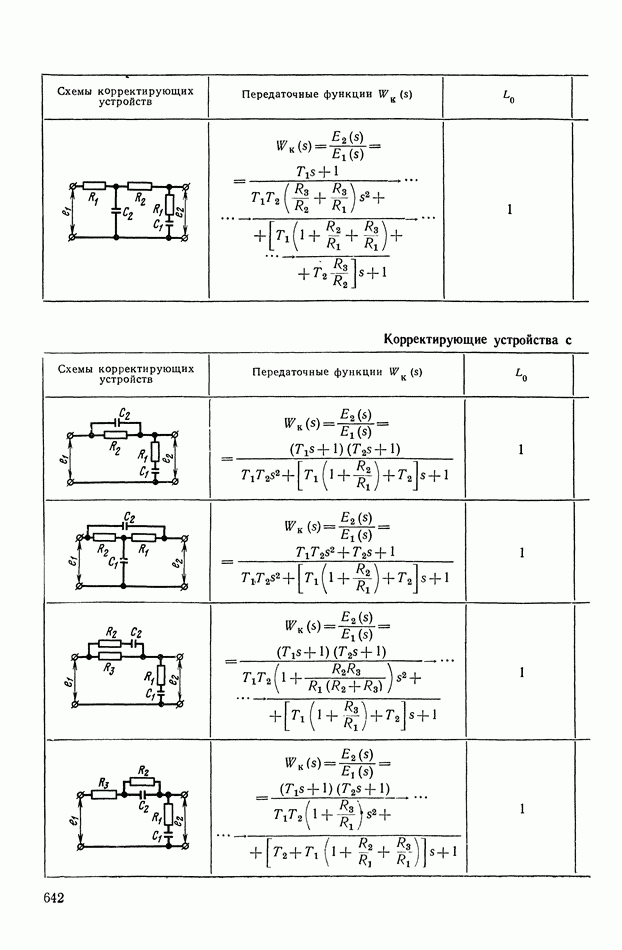
- 2. ТИПОВЫЕ ЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- 3. КОРРЕКТИРУЮЩИЕ ЧЕТЫРЕХПОЛЮСНИКИ С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Четырехполюсники с активными элементами на основе операционных усилителей (ОУ) и конверторов отрицательного сопротивления (КОС).
- 4. РЕАЛИЗАЦИЯ ЗАДАННОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В ВИДЕ СХЕМЫ ПАССИВНОГО ЛИНЕЙНОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА
- 5. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- 8. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- Многоканальные нелинейные логические устройства.
- ГЛАВА XII. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- 1. КОРРЕКТИРУЮЩИЕ RLC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 2. КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 3. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 4. САМОНАСТРАИВАЮЩИЕСЯ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА
- 5. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА С ПРОМЕЖУТОЧНОЙ ДЕМОДУЛЯЦИЕЙ
- 6. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА С ПЕРЕКЛЮЧАТЕЛЯМИ
- 7. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XIII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ТАХОГЕНЕРАТОРЫ ПОСТОЯННОГО ТОКА
- Погрешности тахогенератора постоянного тока.
- 2. НЕКОТОРЫЕ СХЕМЫ ПРИМЕНЕНИЯ ТАХОГЕНЕРАТОРОВ
- 3. АСИНХРОННЫЕ ТАХОГЕНЕРАТОРЫ
- 4. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ ИЗМЕРЕНИЯ СКОРОСТИ ЭЛЕКТРОДВИГАТЕЛЕЙ
- Пассивный тахометрический мост переменного тока.
- Активные тахометрические мосты.
- ГЛАВА XIV. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ГИДРАВЛИЧЕСКИХ СИСТЕМАХ
- 3. ЭЛЕКТРИЧЕСКИЕ ОБРАТНЫЕ СВЯЗИ
- 4. ЖЕСТКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
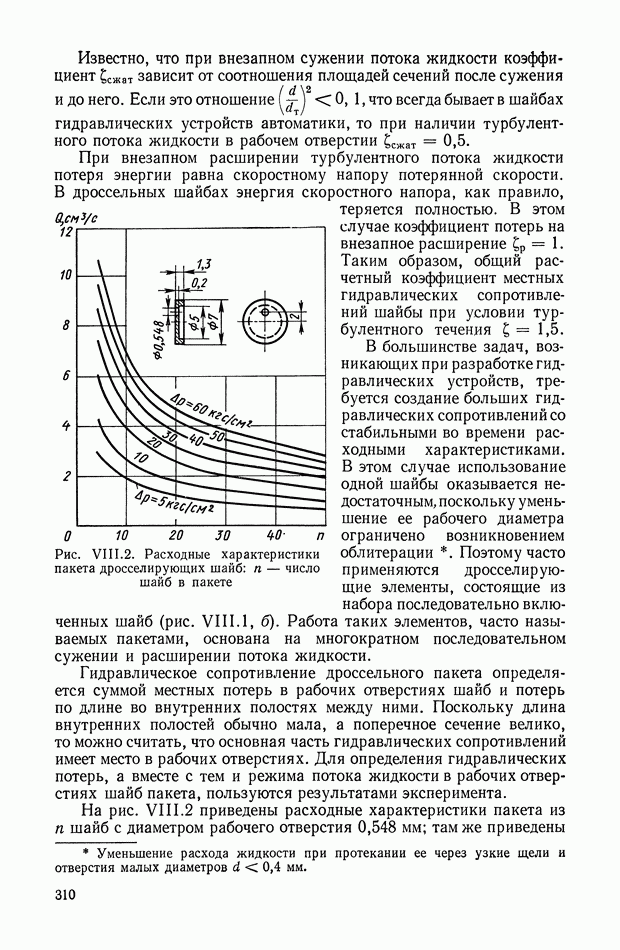
- 5. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ СИСТЕМАХ
- 6. СЛОЖНЫЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
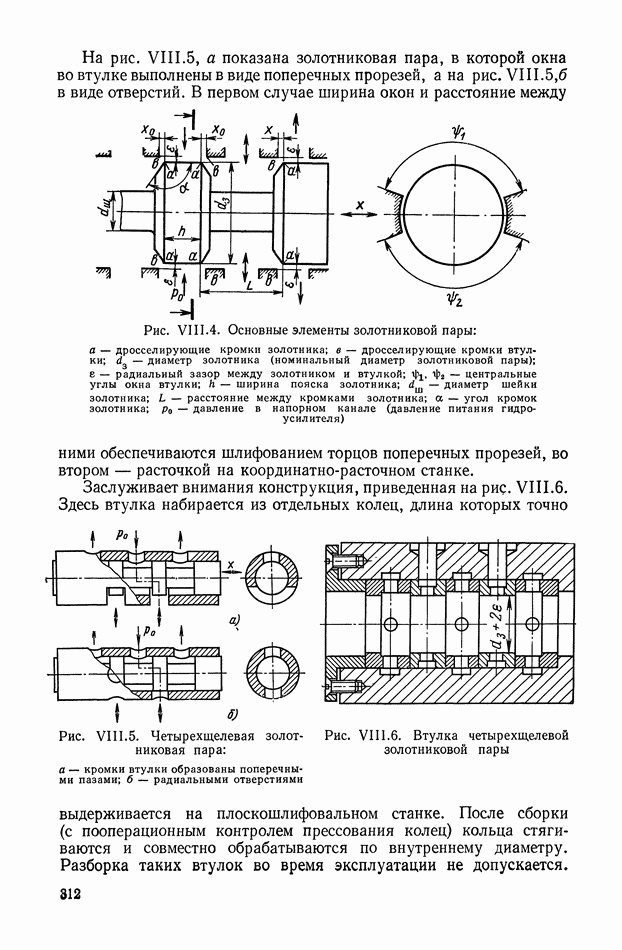
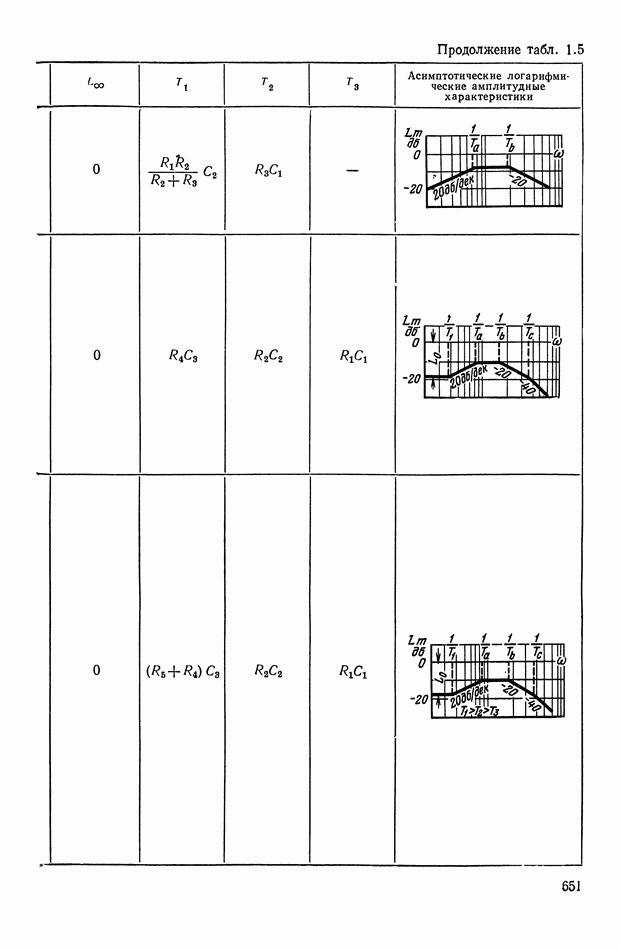
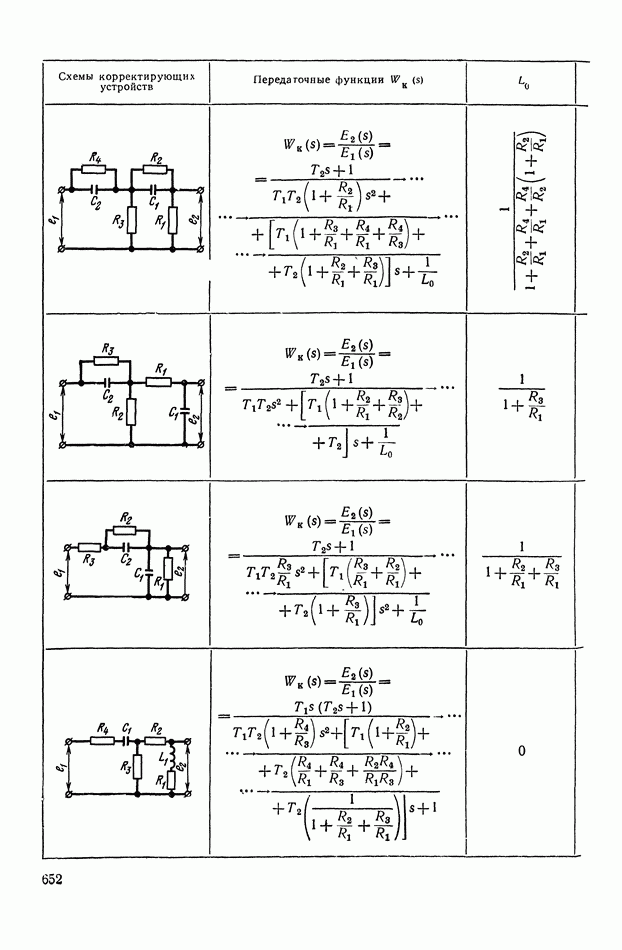
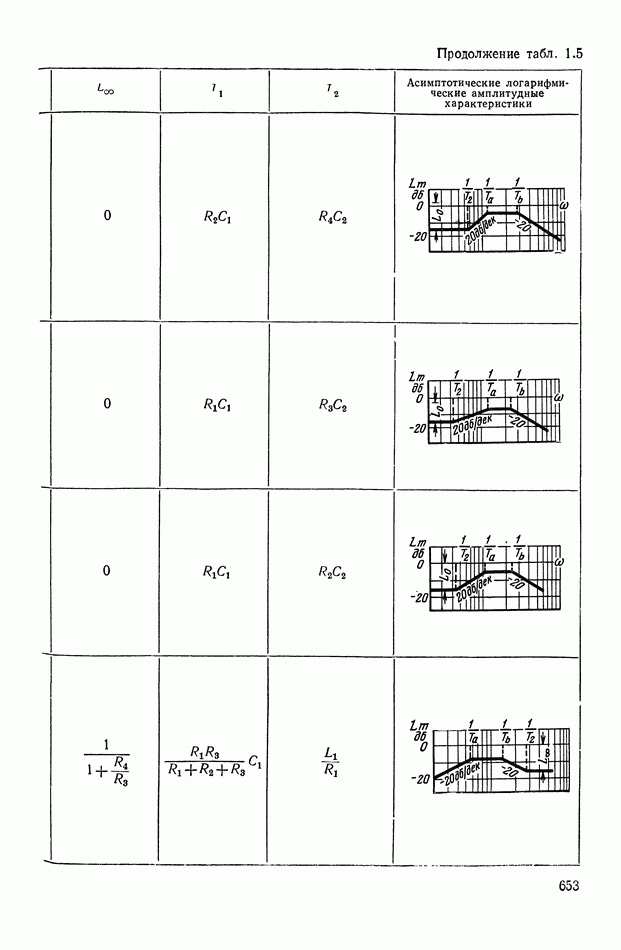
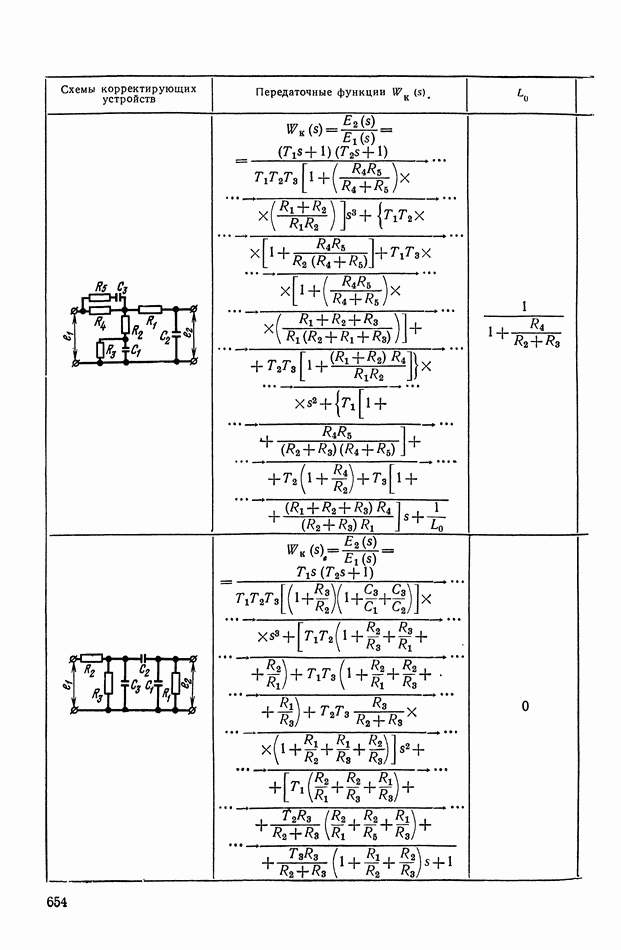
- ПРИЛОЖЕНИЕ 1. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПОСТОЯННОГО ТОКА
- ПРИЛОЖЕНИЕ II. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ОСНОВЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- ПРИЛОЖЕНИЕ III. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ