| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
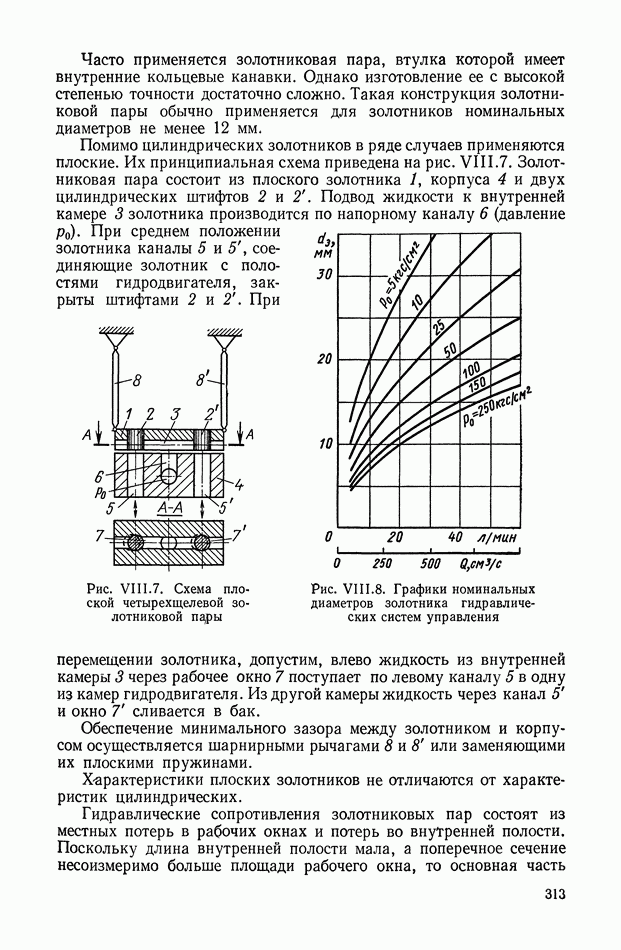
4. РЕАЛИЗАЦИЯ ЗАДАННОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В ВИДЕ СХЕМЫ ПАССИВНОГО ЛИНЕЙНОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА
Сформулируем требования, которым должны удовлетворять входные импеданцы (адмитанцы) конечной линейной пассивной цепи с сосредоточенными параметрами. Физические особенности линейных пассивных цепей с конечным числом сосредоточенных элементов
налагают на возможные аналитические выражения передаточных функций некоторые ограничения. Ниже формулируются ограничения, при выполнении которых передаточная функция физически осуществляется в виде конечной пассивной линейной цепи типа RC.
Для линейной пассивной цепи с сосредоточенными параметрами функции, представляющие собой отношение напряжений и токов, импеданц или адмитанц, можно записать в виде отношения двух полиномов относительно переменной  так как для их определения требуется решать конечное число совместных уравнений типа (X 1.72) с учетом (XI.73).
так как для их определения требуется решать конечное число совместных уравнений типа (X 1.72) с учетом (XI.73).
Входные импеданцы  должны удовлетворять следующим условиям:
должны удовлетворять следующим условиям:
все полюса и нули должны быть простыми и располагаться на отрицательной части действительной оси плоскости  (причем полюса и нули должны чередоваться);
(причем полюса и нули должны чередоваться);
ближайшим к началу координат, т. е. наименьшим по модулю, должен быть полюс, а наиболее удаленным от начала координат — нуль.
При наиболее характерном расположении нулей и полюсов функция входного импеданца, например  имеет следующий вид:
имеет следующий вид:

где величины  являются действительными положительными числами.
являются действительными положительными числами.

Рис. XI.27. Распределение полюсов и нулей для входных импеданцев С-цепи
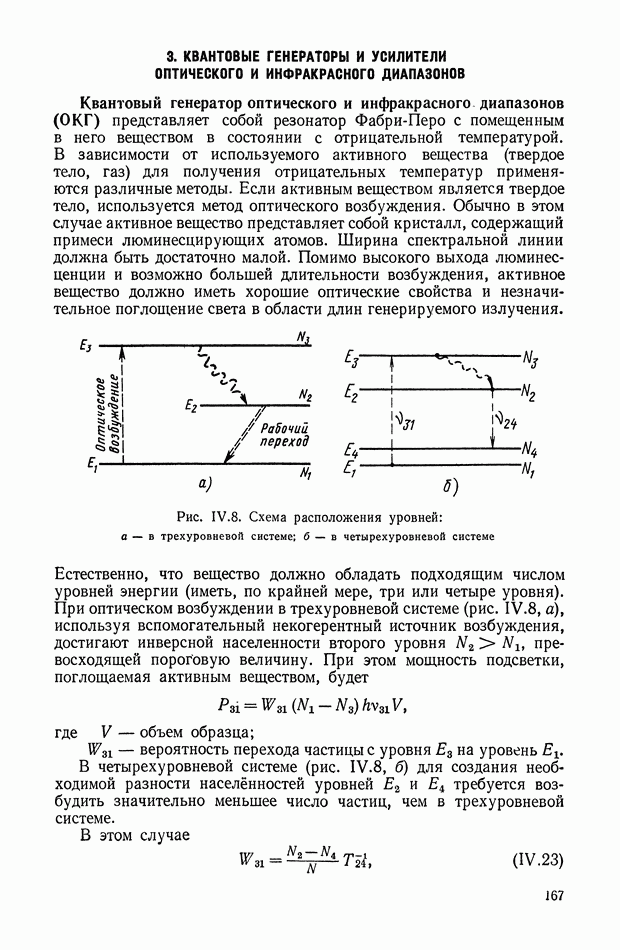
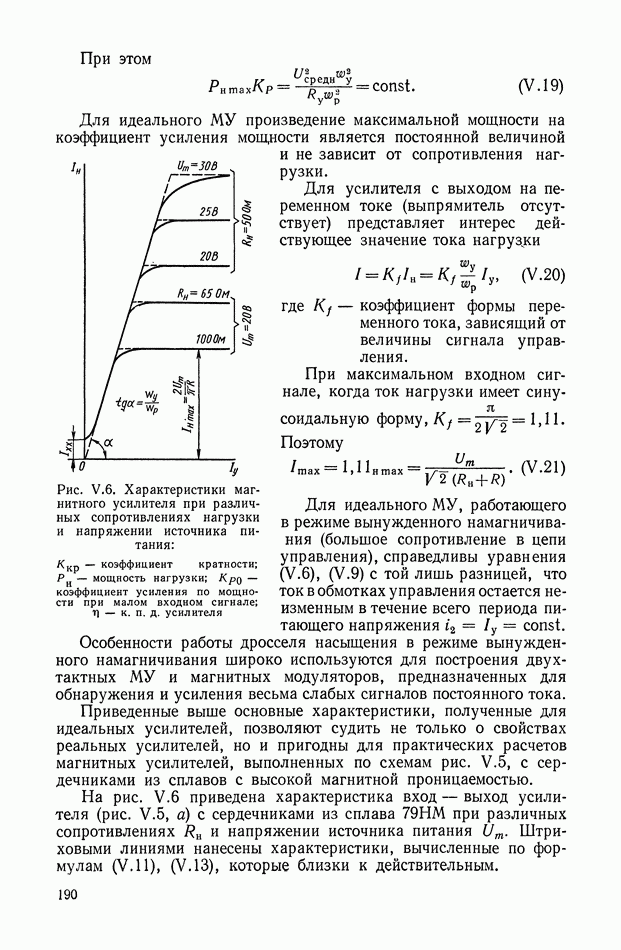
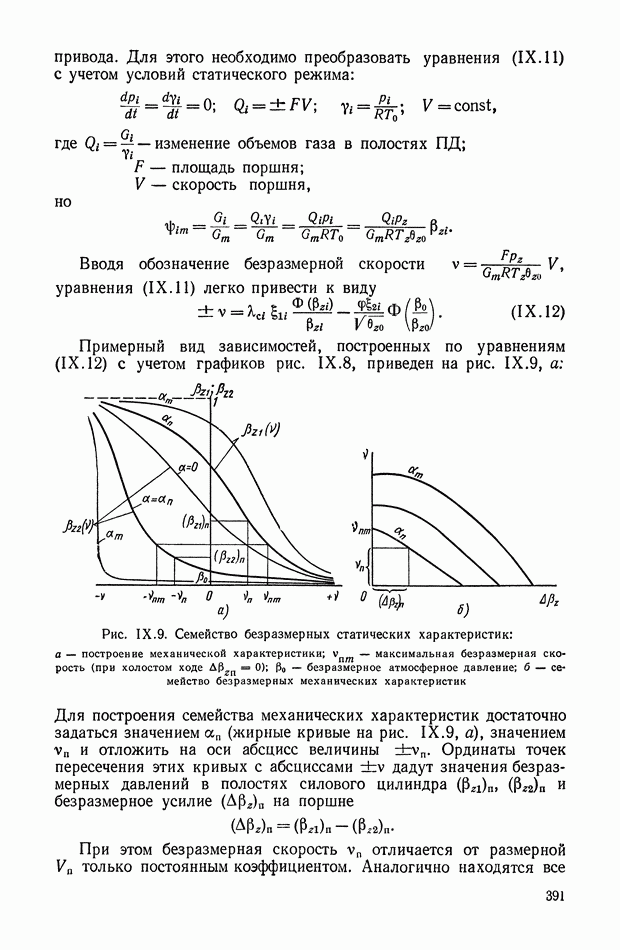
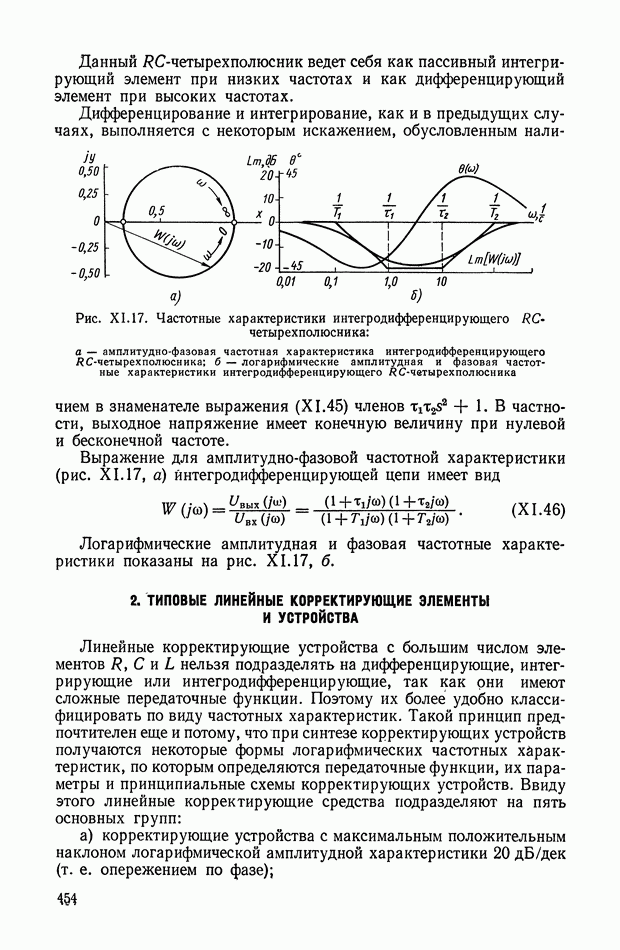
Изменение входного импеданца цепи RC вдоль вещественной оси о изображено графически на рис. XI.27. Следует указать еще на две характеристики 

б) величина отрицательна для всех значений а.
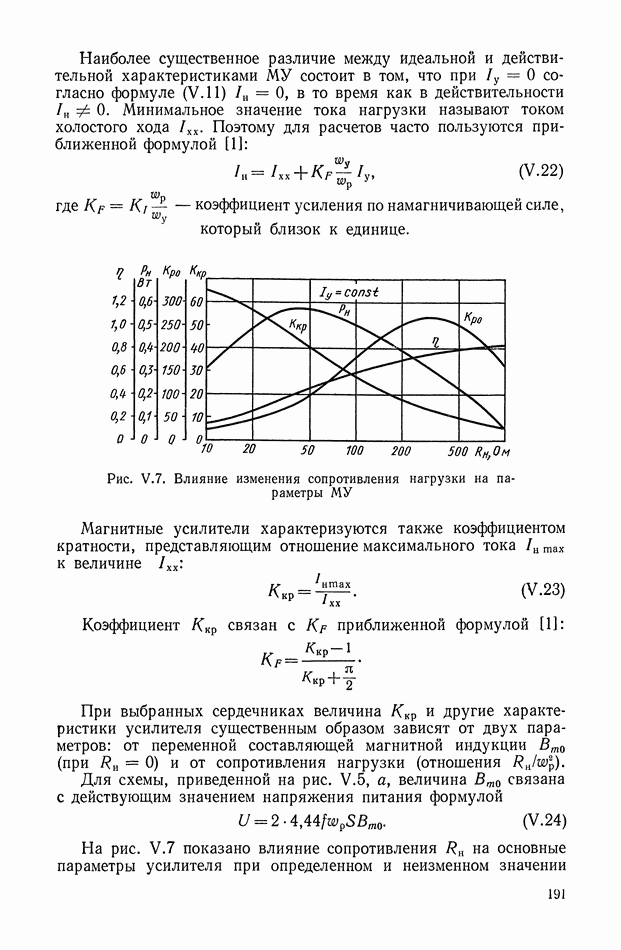
Функцию вида (XI.67) можно разложить на простые дроби:

Каждый из вычетов  так же как и постоянная
так же как и постоянная  является положительной величиной. Условия реализации функций, представляющих входные адмитанцы, отличаются тем, что в этом случае ближайшим к началу координат является нуль, а наиболее удаленным — полюс.
является положительной величиной. Условия реализации функций, представляющих входные адмитанцы, отличаются тем, что в этом случае ближайшим к началу координат является нуль, а наиболее удаленным — полюс.
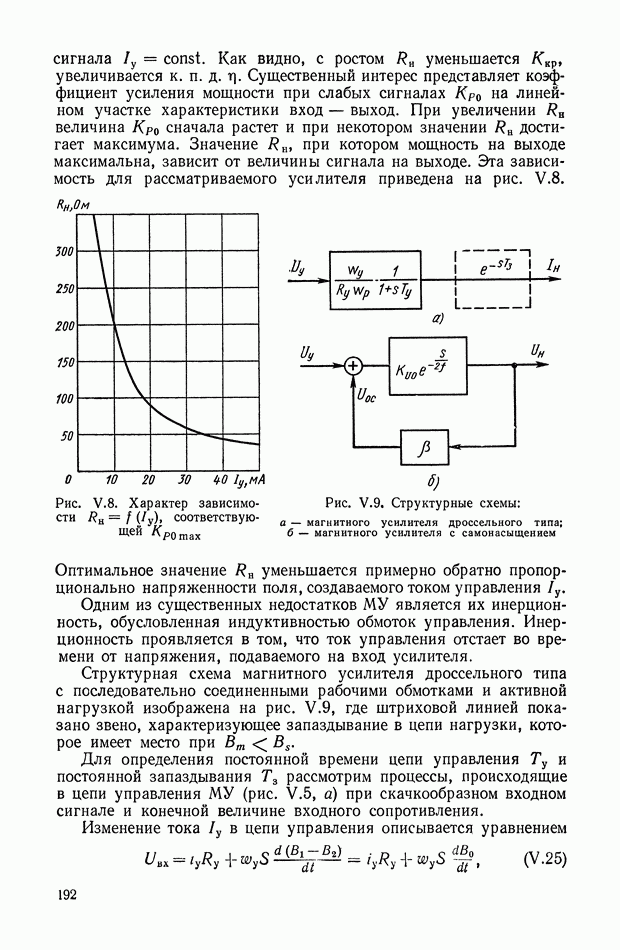
Для цеци RC величина  должна иметь простые полюса, расположенные на отрицательной части действительной оси плоскости
должна иметь простые полюса, расположенные на отрицательной части действительной оси плоскости  На нуль передаточного импеданца не накладывается каких-либо
На нуль передаточного импеданца не накладывается каких-либо
либо ограничений, и они могут располагаться в любой точке плоскости 
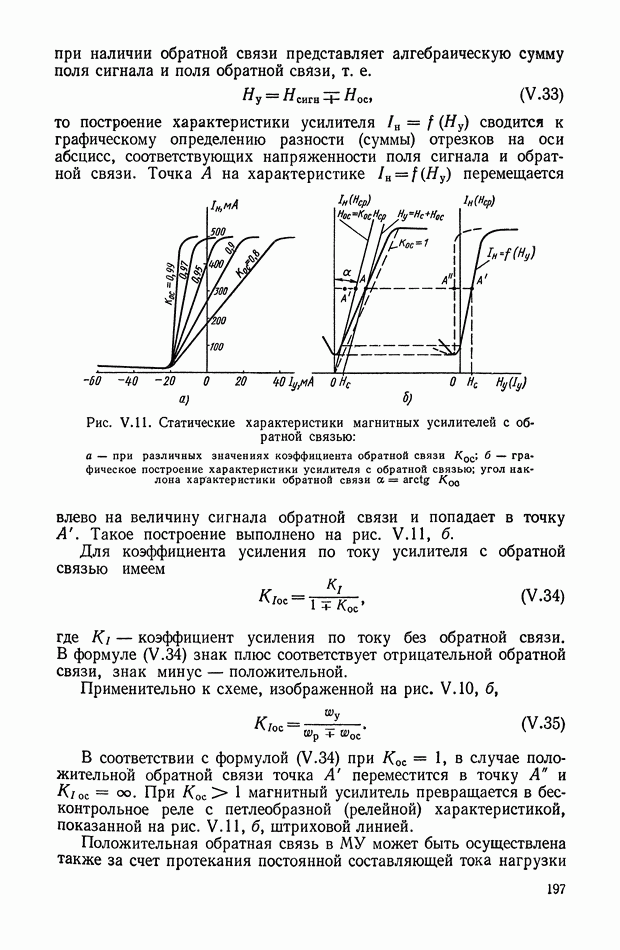
Определим требования, которым должна удовлетворять передаточная функция лестничной пассивной цепи с сосредоточенными параметрами. Из рассмотрения типовых передаточных функций четырехполюсников, приведенных в таблицах приложений I и II, следует, что они полностью определяются одной из двух групп функций  или
или  Рассмотрим случай, когда источник с нулевым внутренним сопротивлением работает на разомкнутую цепь:
Рассмотрим случай, когда источник с нулевым внутренним сопротивлением работает на разомкнутую цепь:  начале координат не может иметь полюса, так как входной импеданц
начале координат не может иметь полюса, так как входной импеданц  не может иметь нуль при нулевой частоте, Передаточные функции других типов также не могут иметь полюс при нулевой частоте.
не может иметь нуль при нулевой частоте, Передаточные функции других типов также не могут иметь полюс при нулевой частоте.
В бесконечности передаточная функция лестничного RC-четырехполюсника также не может иметь полюса, так как при высоких частотах цепь RC переходит в простую цепь, состоящую из сопротивлений, и напряжение на выходе цепи должно быть конечным.
Чтобы показать, какие ограничения накладываются на расположение нулей передаточной функции, надо разобраться в происхождении этих нулей. Так как имеется всего один путь от входных зажимов до выходных — через лестничную цепь, то нуль передачи может возникнуть только в двух случаях: либо при некоторой частоте импеданц некоторого последовательно включенного звена становится равным бесконечности, либо адмитанц параллельной ветви при некоторой частоте делается равным бесконечности.
Нули передаточной функции лестничного  -четырехполюсника должны располагаться на отрицательной части действительной оси, так как полюса импеданцев последовательных звеньев или адмитанцев параллельных ветвей находятся исключительно на этой части действительной оси; нули могут иметь любую кратность. Так, например, нуль второго порядка можёт быть получен с помощью двух последовательных звеньев, создающих нули передачи при одном и том же значении
-четырехполюсника должны располагаться на отрицательной части действительной оси, так как полюса импеданцев последовательных звеньев или адмитанцев параллельных ветвей находятся исключительно на этой части действительной оси; нули могут иметь любую кратность. Так, например, нуль второго порядка можёт быть получен с помощью двух последовательных звеньев, создающих нули передачи при одном и том же значении  с помощью двух параллельных ветвей или с помощью одного последовательного и одного параллельного звеньев.
с помощью двух параллельных ветвей или с помощью одного последовательного и одного параллельного звеньев.
Определение функций  или
или  по заданной передаточной функции. Первым шагом при синтезе передаточных функций цепей является определение функций
по заданной передаточной функции. Первым шагом при синтезе передаточных функций цепей является определение функций  или
или  по заданной передаточной функции.
по заданной передаточной функции.
Передаточную функцию можно записать в следующем виде:

Разобьем знаменатель  на сумму двух многочленов
на сумму двух многочленов 

и представим  в виде
в виде

На практике чаще всего встречается случай, когда  В этом случае при
В этом случае при  выражение
выражение  необходимо привести к виду
необходимо привести к виду

Преобразуем выражение (XI.71) к виду

Сравнивая уравнения (XI.72) и (XI.73), находим 

Существует бесконечное число различных пар функций  которые обеспечивают требуемое отношение напряжений. При выборе
которые обеспечивают требуемое отношение напряжений. При выборе  помнить, что обе функции должны реализоваться в виде цепи RC.
помнить, что обе функции должны реализоваться в виде цепи RC.

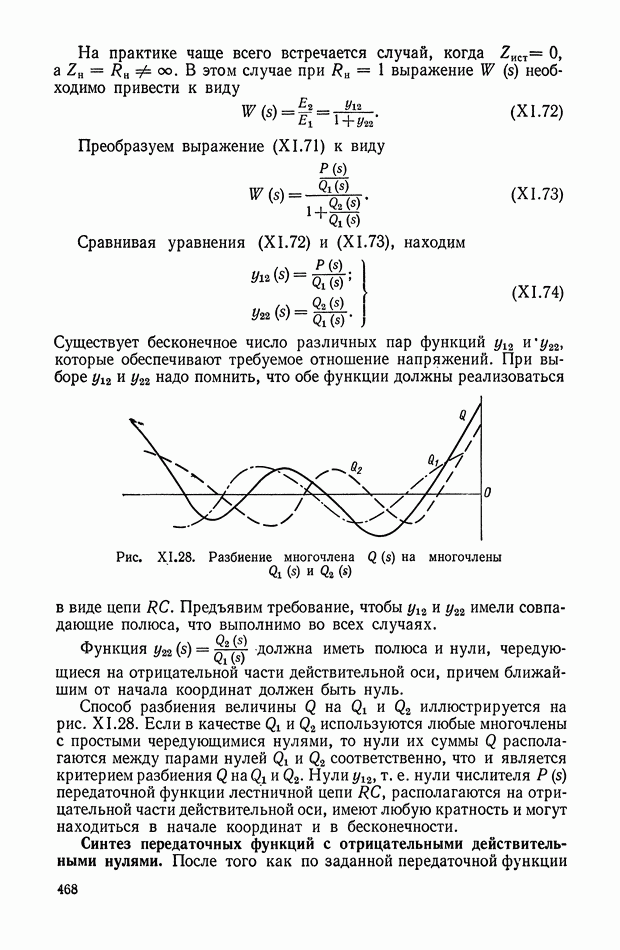
Рис. XI.28. Разбиение многочлена  на многочлены
на многочлены 
Предъявим требование, чтобы  имели совпадающие полюса, что выполнимо во всех случаях.
имели совпадающие полюса, что выполнимо во всех случаях.
Функция  должна иметь полюса и нули, чередующиеся на отрицательной части действительной оси, причем ближайшим от начала координат должен быть нуль.
должна иметь полюса и нули, чередующиеся на отрицательной части действительной оси, причем ближайшим от начала координат должен быть нуль.
Способ разбиения величины  на
на  иллюстрируется на рис. XI.28. Если в качестве
иллюстрируется на рис. XI.28. Если в качестве  используются любые многочлены с простыми чередующимися нулями, то нули их суммы
используются любые многочлены с простыми чередующимися нулями, то нули их суммы  располагаются между парами нулей
располагаются между парами нулей  соответственно, что и является критерием разбиения
соответственно, что и является критерием разбиения  на
на  Нули
Нули  т. е. нули числителя
т. е. нули числителя  передаточной функции лестничной цепи RC, располагаются на отрицательной части действительной оси, имеют любую кратность и могут находиться в начале координат и в бесконечности.
передаточной функции лестничной цепи RC, располагаются на отрицательной части действительной оси, имеют любую кратность и могут находиться в начале координат и в бесконечности.
Синтез передаточных функций с отрицательными действительными нулями. После того как по заданной передаточной функции
 найдены функции
найдены функции  остается по этим функциям синтезировать четырехполюсник в виде такой лестничной цепи, которая реализует как функцию
остается по этим функциям синтезировать четырехполюсник в виде такой лестничной цепи, которая реализует как функцию  так и
так и  Следует еще раз подчеркнуть, что в большинстве случаев передаточная функция цепи определяется двумя из следующих трех характеризующих функций:
Следует еще раз подчеркнуть, что в большинстве случаев передаточная функция цепи определяется двумя из следующих трех характеризующих функций:  или
или  Лишь в случае, когда заданы сопротивление источника сигнала
Лишь в случае, когда заданы сопротивление источника сигнала  сопротивление нагрузки
сопротивление нагрузки  , синтез требует реализации всех трех характеризующих функций. Однако этот случай можно обычно свести к одному из более простых случаев следующим образом. Рассматривая
, синтез требует реализации всех трех характеризующих функций. Однако этот случай можно обычно свести к одному из более простых случаев следующим образом. Рассматривая  или
или  как часть синтезируемой цепи и проводя синтез так же, как в одном из простейших случаев, стремимся к тому, чтобы часть требуемого сопротивления на входе цепи реализовалась за
как часть синтезируемой цепи и проводя синтез так же, как в одном из простейших случаев, стремимся к тому, чтобы часть требуемого сопротивления на входе цепи реализовалась за  а сама цепь заканчивалась с требуемым нагружением
а сама цепь заканчивалась с требуемым нагружением 
Функция  может быть реализована при помощи бесчисленного множества RC-цепей, из которых требуется выбрать такую цепь, которая одновременно реализовала бы нули функции
может быть реализована при помощи бесчисленного множества RC-цепей, из которых требуется выбрать такую цепь, которая одновременно реализовала бы нули функции  (полюсы функций
(полюсы функций  всегда совпадают). Реализовывать функцию
всегда совпадают). Реализовывать функцию  будем, начиная со стороны выходных зажимов четырехполюсника
будем, начиная со стороны выходных зажимов четырехполюсника  по направлению к входным клеммам
по направлению к входным клеммам  Если
Если  содержит нуль
содержит нуль  , являющийся одновременно нулем
, являющийся одновременно нулем  то первым этапом при синтезе
то первым этапом при синтезе  -четырехполюсника будет реализация этого нуля
-четырехполюсника будет реализация этого нуля  , следовательно, нуля
, следовательно, нуля  Рассматриваемый нуль может быть реализован с помощью последовательного звена лестничного
Рассматриваемый нуль может быть реализован с помощью последовательного звена лестничного  -четырехполюсника (рис. XI.29), имеющего импеданц
-четырехполюсника (рис. XI.29), имеющего импеданц  с полюсом
с полюсом  где
где  — вычет функции
— вычет функции  в точке
в точке  . Импеданц
. Импеданц  легко может быть реализован в виде параллельного соединения резистора
легко может быть реализован в виде параллельного соединения резистора  и конденсатора С, величины которых определяем по формулам
и конденсатора С, величины которых определяем по формулам

Оставшаяся после реализации  функция
функция  (рис. XI.29) не содержит уже нуля при
(рис. XI.29) не содержит уже нуля при  . Если же функции
. Если же функции  общего нуля не имеют, то вводя на выходе четырехполюсника параллельную ветвь с адмитанцем
общего нуля не имеют, то вводя на выходе четырехполюсника параллельную ветвь с адмитанцем  необходимо сместить несколько нули функции
необходимо сместить несколько нули функции  и образовать для нее нуль, совпадающий с одним из нулей
и образовать для нее нуль, совпадающий с одним из нулей  Адмитанц
Адмитанц  может быть равен либо положительному числу
может быть равен либо положительному числу  что соответствует включению на выходе четырехполюсника параллельного шунтирующего резистора
что соответствует включению на выходе четырехполюсника параллельного шунтирующего резистора  (рис. XI.30, а), либо адмитанца
(рис. XI.30, а), либо адмитанца  что соответствует параллельной ветви в виде последовательного соединения резистора
что соответствует параллельной ветви в виде последовательного соединения резистора  и конденсатора С (рис. XI.30, б), величины которых вычисляем по формулам
и конденсатора С (рис. XI.30, б), величины которых вычисляем по формулам

Оставшаяся после реализации адмитанца  функция
функция  представляет собой входной адмитанц четырехполюсника со стороны клемм
представляет собой входной адмитанц четырехполюсника со стороны клемм  и ее нуль совпадает с одним из нулей
и ее нуль совпадает с одним из нулей  Далее этот нуль
Далее этот нуль  реализуется так же, как это было изложено выше (рис. XI.29).
реализуется так же, как это было изложено выше (рис. XI.29).

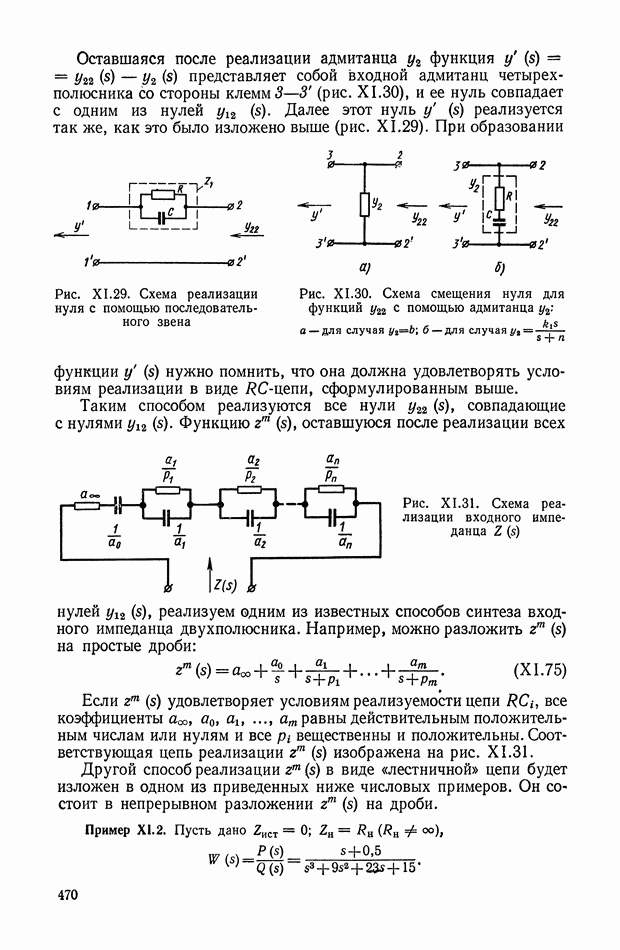
Рис. XI.29. Схема реализации нуля с помощью последовательного звена

Рис. XI.30. Схема смещения нуля для функций  с помощью адмитанца
с помощью адмитанца  а — для случая
а — для случая  ; б — для случая
; б — для случая 
При образовании функции  нужно помнить, что она должна удовлетворять условиям реализации в виде RС-цепи, сформулированным выше.
нужно помнить, что она должна удовлетворять условиям реализации в виде RС-цепи, сформулированным выше.
Таким способом реализуются все нули  совпадающие с нулями
совпадающие с нулями 

Рис. X 1.31. Схема реализации входного импеданца 
Функцию  оставшуюся после реализации всех нулей
оставшуюся после реализации всех нулей  реализуем одним из известных способов синтеза входного импеданца двухполюсника. Например, можно разложить
реализуем одним из известных способов синтеза входного импеданца двухполюсника. Например, можно разложить  на простые дроби:
на простые дроби:

Если  удовлетворяет условиям реализуемости цепи
удовлетворяет условиям реализуемости цепи  все коэффициенты
все коэффициенты  равны действительным положительным числам или нулям и все
равны действительным положительным числам или нулям и все  вещественны и положительны. Соответствующая цепь реализации
вещественны и положительны. Соответствующая цепь реализации  изображена на рис. XI.31.
изображена на рис. XI.31.
Другой способ реализации  в виде «лестничной» цепи будет изложен в одном из приведенных ниже числовых примеров. Он состоит в непрерывном разложении
в виде «лестничной» цепи будет изложен в одном из приведенных ниже числовых примеров. Он состоит в непрерывном разложении  на дроби.
на дроби.
Пример XI. 2. Пусть дано 

Определив корни характеристического уравнения  получим
получим

Выбираем функцию  таким образом, чтобы ее нули чередовались с нулями
таким образом, чтобы ее нули чередовались с нулями  что является критерием разбиения
что является критерием разбиения  на
на 

Множитель введен для того, чтобы многочлен  также имел действительные отрицательные корни:
также имел действительные отрицательные корни:

Корни уравнений  чередуются между собой.
чередуются между собой.
Определим функции 


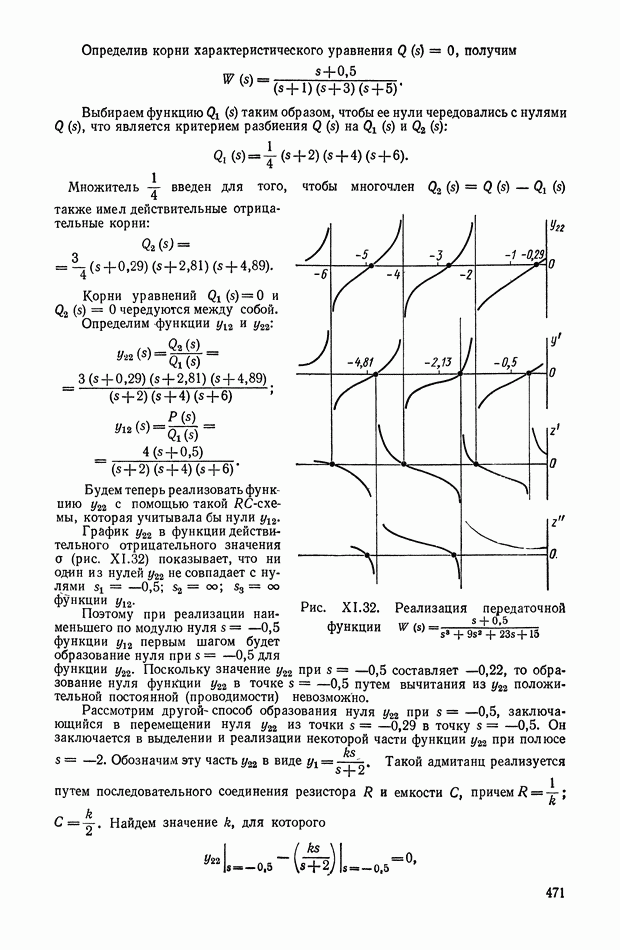
Рис. XI.32. Реализация передаточной функции 
Будем теперь реализовать функцию  с помощью такой RC-схемы, которая учитывала бы нули
с помощью такой RC-схемы, которая учитывала бы нули 
График  в функции действительного отрицательного значения а (рис. XI.32) показывает, что ни один из нулей
в функции действительного отрицательного значения а (рис. XI.32) показывает, что ни один из нулей  не совпадает с нулями
не совпадает с нулями  функции
функции 
Поэтому при реализации наименьшего по модулю нуля  функции
функции  первым шагом будет образование нуля при
первым шагом будет образование нуля при  для функции
для функции  Поскольку значение
Поскольку значение  при
при  составляет —0,22, то образование нуля функции
составляет —0,22, то образование нуля функции  в точке
в точке  путем вычитания из
путем вычитания из  положительной постоянной (проводимости) невозможно.
положительной постоянной (проводимости) невозможно.
Рассмотрим другой способ образования нуля  при
при  , заключающийся в перемещении нуля
, заключающийся в перемещении нуля  из точки
из точки  в точку
в точку  . Он заключается в выделении и реализации некоторой части функции
. Он заключается в выделении и реализации некоторой части функции  при полюсе
при полюсе  Обозначим эту часть
Обозначим эту часть  в виде
в виде  Такой адмитанц реализуется путем последовательного соединения резистора
Такой адмитанц реализуется путем последовательного соединения резистора  и емкости С, причем
и емкости С, причем 
Найдем значение  для которого
для которого

откуда имеем

Искомая часть  будет равна
будет равна

Реализация  начинается с синтеза на выходе четырехполюсника шунтирующей ветви с резистором
начинается с синтеза на выходе четырехполюсника шунтирующей ветви с резистором  и емкостью
и емкостью  Оставшаяся функция
Оставшаяся функция

содержит нуль при  (рис. XI.32). Рассмотрим далее
(рис. XI.32). Рассмотрим далее  Выделим из нее и реализуем часть, соответствующую полюсу
Выделим из нее и реализуем часть, соответствующую полюсу  тем самым будет реализован нуль функции
тем самым будет реализован нуль функции  при
при  Для этого определим вычет функции
Для этого определим вычет функции  для
для  Он оказывается равным 1,76. Затем, вычитая составляющую импеданца
Он оказывается равным 1,76. Затем, вычитая составляющую импеданца  соответствующую этому полюсу, получим остаток:
соответствующую этому полюсу, получим остаток:

График  приведенный на рис. XI.32, показывает, что функция
приведенный на рис. XI.32, показывает, что функция  удовлетворяет условиям реализации в виде цепи RC. Все конечные нули
удовлетворяет условиям реализации в виде цепи RC. Все конечные нули  реализованы.
реализованы.
Двукратный нуль  функции
функции  получается попутно при реализации оставшейся функции
получается попутно при реализации оставшейся функции  в виде «лестничной» цепи. Функция
в виде «лестничной» цепи. Функция  представляет собой дробно рациональную функцию, которую можно представить в виде непрерывной дроби путем последовательного деления: числитель
представляет собой дробно рациональную функцию, которую можно представить в виде непрерывной дроби путем последовательного деления: числитель  делим на знаменатель и представляем
делим на знаменатель и представляем  как сумму частного 0,43 и единицы, деленной на обращенный остаток. Те же действия выполняем со стоящим в знаменателе обращенным остатком и т.
как сумму частного 0,43 и единицы, деленной на обращенный остаток. Те же действия выполняем со стоящим в знаменателе обращенным остатком и т.  т. е.
т. е.

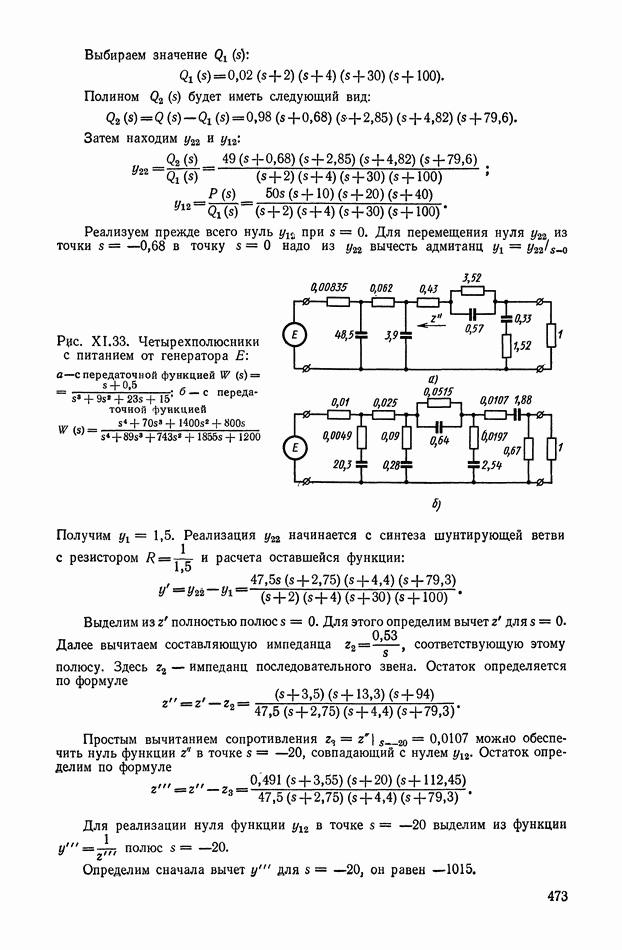
Функцию  представленную в виде непрерывной дроби, достаточно просто реализовать при помощи «лестничной» цепи (рис. XI.33). Сначала реализуется импеданц 0,43, затем адмитанц
представленную в виде непрерывной дроби, достаточно просто реализовать при помощи «лестничной» цепи (рис. XI.33). Сначала реализуется импеданц 0,43, затем адмитанц  далее импеданц 0,062 и адмитанц 48,5. Цепь заканчивается импеданцем
далее импеданц 0,062 и адмитанц 48,5. Цепь заканчивается импеданцем  Она содержит два параллельно включенных конденсатора, реализующих двукратный нуль
Она содержит два параллельно включенных конденсатора, реализующих двукратный нуль 
Замыкая синтезированный четырехполюсник на нагрузочное сопротивление в 1 Ом, получим необходимый четырехполюсник (рис. XI.33, а)
Пример XI.3. Рассмотрим более сложную передаточную функцию

После определения корней получим

Выбираем значение 

Полином  будет иметь следующий вид:
будет иметь следующий вид:

Затем находим 

Реализуем прежде всего нуль  при
при  Для перемещения нуля
Для перемещения нуля  из точки
из точки  в точку
в точку  надо из
надо из  вычесть адмитанц
вычесть адмитанц 

Рис. XI.33. Четырехполюсники с питанием от генератора  передаточной функцией
передаточной функцией  б - с передаточной Функцией
б - с передаточной Функцией 
Получим  Реализация
Реализация  начинается с синтеза шунтирующей ветви с резистором
начинается с синтеза шунтирующей ветви с резистором  и расчета оставшейся функции:
и расчета оставшейся функции:

Выделим из  полностью полюс
полностью полюс  Для этого определим вычет
Для этого определим вычет  для
для  Далее вычитаем составляющую импеданца
Далее вычитаем составляющую импеданца  соответствующую этому полюсу. Здесь
соответствующую этому полюсу. Здесь  — импеданц последовательного звена. Остаток определяется по формуле
— импеданц последовательного звена. Остаток определяется по формуле

Простым вычитанием сопротивления  можно обеспечить нуль функции
можно обеспечить нуль функции  в точке
в точке  совпадающий с нулем
совпадающий с нулем  Остаток определим по формуле
Остаток определим по формуле

Для реализации нуля функции  в точке
в точке  выделим из функции
выделим из функции  полюс
полюс 
Определим сначала вычет  для
для  он равен —1015.
он равен —1015.
Будем находить адмитанц  -реализующий нуль
-реализующий нуль  Коэффициент
Коэффициент  определим из уравнения
определим из уравнения

Реализовав  с помощью последовательно соединенного резистора
с помощью последовательно соединенного резистора  и емкости
и емкости  получим остаток
получим остаток

Можно образовать нуль в точке  выделением части полюса при
выделением части полюса при  В этом случае переместим нуль при
В этом случае переместим нуль при  в точку
в точку  Выражение для импеданца будет иметь вид
Выражение для импеданца будет иметь вид

Коэффициент  вычисляется из уравнения
вычисляется из уравнения

Реализовав  получим остаток
получим остаток

Выделим из функции  полностью полюс
полностью полюс  Вычет функции
Вычет функции  при
при  Реализуем адмитанц
Реализуем адмитанц  где
где  определим из уравнения
определим из уравнения

В результате получим

 откуда найдем остаток
откуда найдем остаток 
Последний йуль  при
при  можно образовать простым вычитанием сопротивления
можно образовать простым вычитанием сопротивления  из функции
из функции 

Остаток получится равным

Обратную величину  можно представить следующим образом:
можно представить следующим образом:

Реализуем функцию  виде параллельной ветви из резистора
виде параллельной ветви из резистора  и емкости
и емкости  Затем найдем последний резистор
Затем найдем последний резистор  Замыкая четырехполюсник, на нагрузочный резистор в 1 Ом, получим требуемый четырёхполюсник изображенный на рис. XI.33,б.
Замыкая четырехполюсник, на нагрузочный резистор в 1 Ом, получим требуемый четырёхполюсник изображенный на рис. XI.33,б.
Синтез передаточных функций с комплексными нулями.
Выше был описан метод синтеза «лестничных» RC-четырехполюсников для случая отрицательных действительных нулей. Рассмотрим передаточные функции, содержащие комплексные нули. Сохраним только требование отсутствия нулей на вещественной части действительной оси.
Первый этап синтеза состоит также в определении по заданной передаточной функции  функций
функций  Так как процесс реализации в случае отрицательных действительных нулей известен, то можно попытаться разложить
Так как процесс реализации в случае отрицательных действительных нулей известен, то можно попытаться разложить  на составляющие, нули которых находились бы на отрицательной части действительной оси. Учитывая последнее, рассмотрим параллельное соединение «лестничных»
на составляющие, нули которых находились бы на отрицательной части действительной оси. Учитывая последнее, рассмотрим параллельное соединение «лестничных»  -четырехполюсни-ков, показанное на рис. XI.34.
-четырехполюсни-ков, показанное на рис. XI.34.

Рис. XI.34. Параллельное соединение четырехполюсников
Очевидно, в случае параллельного соединения результирующая функция  равна сумме функций
равна сумме функций  отдельных четырехполюсников; то же относится и к функциям
отдельных четырехполюсников; то же относится и к функциям  Пусть
Пусть

и

Запишем  в виде суммы более простых функций:
в виде суммы более простых функций:

Числитель последнего члена содержит одну или две составляющие в зависимости от того, является  четным или нечетным. Каждую отдельную составляющую функции
четным или нечетным. Каждую отдельную составляющую функции  теперь можно реализовать вместе с заданной
теперь можно реализовать вместе с заданной  в виде «лестничного»
в виде «лестничного»  -четырехполюсника, так как нули передачи целиком лежат на отрицательной части действительной оси, включая начала координат и бесконечность.
-четырехполюсника, так как нули передачи целиком лежат на отрицательной части действительной оси, включая начала координат и бесконечность.
Таким образом, синтезируются или при четном  звеньев. Желаемые функции
звеньев. Желаемые функции  реализуются путем параллельного соединения этих звеньев.
реализуются путем параллельного соединения этих звеньев.
Представим  в виде
в виде

где  или
или  — коэффициенты передачи отдельных составляющих
— коэффициенты передачи отдельных составляющих  Предполагается, что коэффициенты передачи самих
Предполагается, что коэффициенты передачи самих  равны единице.
равны единице.
При реализации составляющих звеньев мы не имеем возможности контролировать величины коэффициентов передачи  Они, без сомнения, будут отличаться от
Они, без сомнения, будут отличаться от  Поэтому если соединить отдельные «лестничные» цепи параллельно, то результирующая
Поэтому если соединить отдельные «лестничные» цепи параллельно, то результирующая  будет отлична от исходной.
будет отлична от исходной.
Изменим полученные функции  каждой
каждой  цепи в
цепи в  раз, где
раз, где  еще не известен. Результирующая функция
еще не известен. Результирующая функция  построенная по заданной
построенная по заданной  имеет вид
имеет вид

Изменения в функциях  приведут к изменению
приведут к изменению  Результирующая функция
Результирующая функция  построенной цепи:
построенной цепи:

Для того чтобы полученная функция  была равна заданной
была равна заданной  должно выполняться условие
должно выполняться условие

Итак, для построения параллельного «лестничного»  -четырехполюсника необходимо выполнить следующие операции:
-четырехполюсника необходимо выполнить следующие операции:
записать числитель заданной функции  в виде суммы слагаемых, каждое из которых имеет нули только на отрицательной части действительной оси;
в виде суммы слагаемых, каждое из которых имеет нули только на отрицательной части действительной оси;
построить по заданной функции  составляющие «лестничные» С-цепи, каждая из которых реализует нули одной из составляющих функций
составляющие «лестничные» С-цепи, каждая из которых реализует нули одной из составляющих функций 
найти коэффициент передачи  каждой С-цепи; вычислить значение
каждой С-цепи; вычислить значение  по формуле (X 1.81);
по формуле (X 1.81);
изменить передаточный адмитанц  цепи в
цепи в 
соединить отдельные RС-цепи параллельно на входе и выходе.
Пример XI.4. Пусть задана передаточная функция вида

Определим  как
как  тогда
тогда

Функции  примут вид
примут вид

Разложим числитель  на два полинома, каждый из которых имеет нули только на отрицателъной части действенной оси
на два полинома, каждый из которых имеет нули только на отрицателъной части действенной оси

на основании которого две составляющие функции  равны соответственно:
равны соответственно:

Построим сначала RC-цепь для  Выделим полностью полюс
Выделим полностью полюс  функции
функции 

Реализовав  в виде шунтирующеи цепи из последовательно соединенных резистора
в виде шунтирующеи цепи из последовательно соединенных резистора  и емкости
и емкости  получим остаток
получим остаток

Поскольку  имеет нуль в начале координат, надо сместить в эту точку нуль у путем реализации
имеет нуль в начале координат, надо сместить в эту точку нуль у путем реализации 

Полюс  начале координат реализуется затем как последовательная емкость, а остающаяся функция — как активное сопротивление. Принципиальная схема изображена на рис. XI.35, а.
начале координат реализуется затем как последовательная емкость, а остающаяся функция — как активное сопротивление. Принципиальная схема изображена на рис. XI.35, а.

Рис. XI.35. Реализация передаточной функции  с помощью
с помощью  схем четырехполюсника
схем четырехполюсника
Теперь реализуем цепь с  При этом
При этом  содержит нуль при
содержит нуль при  который является одним из нулей
который является одним из нулей  Реализуем его в первую очередь. Для этого представим:
Реализуем его в первую очередь. Для этого представим:

Реализовав  получим остаток
получим остаток

Другой нуль  находится в бесконечности. Поэтому вычтем из
находится в бесконечности. Поэтому вычтем из  его значение при
его значение при  равное
равное  . Реализовав
. Реализовав  получим остаток
получим остаток

Функция  представляется в виде шунтирующей емкости
представляется в виде шунтирующей емкости  и последовательного резистора
и последовательного резистора  Принципиальная схема изображена на рис. XI.35, б.
Принципиальная схема изображена на рис. XI.35, б.
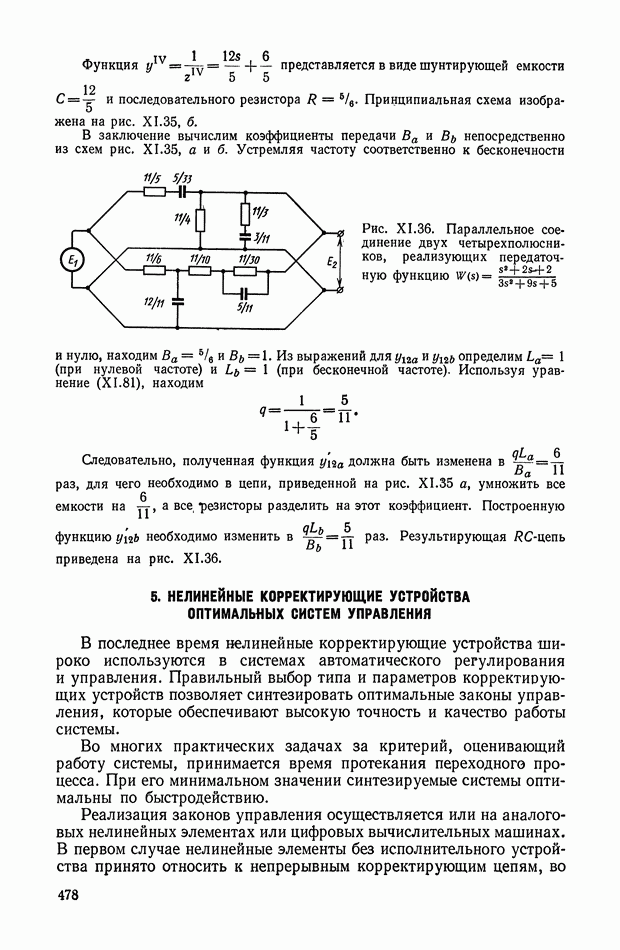
В заключение вычислим коэффициенты передачи  непосредственно из схем рис. XI.35, а и б. Устремляя частоту соответственно к бесконечности и нулю, находим
непосредственно из схем рис. XI.35, а и б. Устремляя частоту соответственно к бесконечности и нулю, находим 

Рис. XI.36. Параллельное соединение двух четырехполюсников, реализующих передаточную функцию 
Из выражений для  определим
определим  (при нулевой частоте) и
(при нулевой частоте) и  (при бесконечной частоте). Используя уравнение (XI.81), находим
(при бесконечной частоте). Используя уравнение (XI.81), находим

Следовательно, полученная функция  должна быть изменена в
должна быть изменена в  раз, для чего необходимо в цепи, приведенной на рис. XI.35 а, умножить все емкости на а все резисторы разделить на этот коэффициент. Построенную функцию
раз, для чего необходимо в цепи, приведенной на рис. XI.35 а, умножить все емкости на а все резисторы разделить на этот коэффициент. Построенную функцию  необходимо изменить в Раз Результирующая RС-цепь приведена на рис. XI.36.
необходимо изменить в Раз Результирующая RС-цепь приведена на рис. XI.36.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА САР
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ЛИНЕЙНЫХ УСИЛИТЕЛЬНЫХ УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ УСИЛИТЕЛЬНОГО УСТРОЙСТВА БЕЗ ОБРАТНОЙ СВЯЗИ
- 3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ, СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ОСОБЕННОСТИ УСИЛИТЕЛЬНОГО УСТРОЙСТВА С ОБРАТНОЙ СВЯЗЬЮ
- 4. КЛАССИФИКАЦИЯ И СВОЙСТВА УСИЛИТЕЛЬНЫХ УСТРОЙСТВ С ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 5. ВЫБОР И РАСЧЕТ УСИЛИТЕЛЬНОГО УСТРОЙСТВА
- ГЛАВА II. ЭЛЕКТРОННЫЕ ЛАМПОВЫЕ И ИОННЫЕ УСИЛИТЕЛИ
- 1. ОСНОВЫ ТОПОЛОГИЧЕСКОГО АНАЛИЗА СХЕМ ЛИНЕЙНЫХ ЭЛЕКТРОННЫХ ЛАМПОВЫХ УСИЛИТЕЛЕЙ
- 2. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПОСТОЯННОГО ТОКА
- 3. БАЛАНСНЫЕ МОСТОВЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- 4. СТАБИЛИЗАЦИЯ КОЭФФИЦИЕНТА УСИЛЕНИЯ
- 5. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- 6. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- 7. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
- 8. ОБЩИЕ СВОЙСТВА ИОННОГО (ТИРАТРОННОГО) УСИЛИТЕЛЯ МЕТОДЫ УПРАВЛЕНИЯ ТИРАТРОНОМ
- 9. ФОРМИРОВАНИЕ УПРАВЛЯЮЩЕГО НАПРЯЖЕНИЯ
- 10. РАСЧЕТ ЭЛЕМЕНТОВ СХЕМ ТИРАТРОННОГО УСИЛИТЕЛЯ
- ГЛАВА III. ПОЛУПРОВОДНИКОВЫЕ И ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
- Цепи смещения.
- Цепи связи.
- 2. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ СРЕДНЕГО ЗНАЧЕНИЯ ТОКА
- Полупроводниковые демодуляторы.
- 3. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ В РЕЖИМЕ ПЕРЕКЛЮЧЕНИЯ
- Режимы импульсного регулирования мощности.
- Управление силовыми транзисторами.
- 4. ТРАНЗИСТОРНЫЕ УСТРОЙСТВА УПРАВЛЕНИЯ ЭЛЕКТРОДВИГАТЕЛЯМИ И ЭЛЕКТРОМАГНИТНЫМИ МЕХАНИЗМАМИ
- 5. ТИРИСТОРЫ. ХАРАКТЕРИСТИКИ, ПАРАМЕТРЫ И СВОЙСТВА
- 6. СПОСОБЫ И УСТРОЙСТВА УПРАВЛЕНИЯ ТИРИСТОРАМИ
- 7. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ (РЕГУЛИРУЕМЫЕ ВЫПРЯМИТЕЛИ)
- 8. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 9. ТИРИСТОРНЫЕ УСИЛИТЕЛИ С ПИТАНИЕМ ОТ СЕТИ ПОСТОЯННОГО ТОКА
- 10. ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 11. ОСНОВЫ РАСЧЕТА ДИЭЛЕКТРИЧЕСКИХ УСИЛИТЕЛЕЙ
- ГЛАВА IV. КВАНТОВЫЕ УСИЛИТЕЛИ И ГЕНЕРАТОРЫ
- 2. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ РАДИОДИАПАЗОНА
- Квантовые усилители радиодиапазона.
- 3. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- Оптический квантовый усилитель
- 4. ПРИМЕНЕНИЕ В САР КВАНТОВЫХ УСИЛИТЕЛЕЙ И ГЕНЕРАТОРОВ РАДИОДИАПАЗОНА, ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- ГЛАВА V. МАГНИТНЫЕ И МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- 2. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ МАГНИТНЫХ УСИЛИТЕЛЕЙ
- 3. ОДНОТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ БЕЗ ОБРАТНОЙ СВЯЗИ (УПРАВЛЯЕМЫЕ ДРОССЕЛИ И ТРАНСФОРМАТОРЫ)
- 4. МАГНИТНЫЕ УСИЛИТЕЛИ С САМОНАСЫЩЕНИЕМ
- Релейный режим работы усилителей с самонасыщением.
- 5. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 6. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ
- 7. МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- ГЛАВА VI. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 2. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С НЕЗАВИСИМЫМ ВОЗБУЖДЕНИЕМ И С САМОВОЗБУЖДЕНИЕМ
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С ПОПЕРЕЧНЫМ ПОЛЕМ
- 4. ЭЛЕКТРОМАШИННЫЙ УСИЛИТЕЛЬ ПРОДОЛЬНОГО И ПРОДОЛЬНО-ПОПЕРЕЧНОГО ПОЛЯ
- 5. ВЛИЯНИЕ НА ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭМУ ВИХРЕВЫХ И КОММУТАЦИОННЫХ ТОКОВ, ГИСТЕРЕЗИСА И СДВИГА ЩЕТОК С НЕЙТРАЛИ
- 6. МЕТОДЫ УЛУЧШЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕКТРОМАШИННЫХ УСИЛИТЕЛЕЙ
- 7. НАГРУЗОЧНАЯ ХАРАКТЕРИСТИКА ЭЛЕКТРОМАШИННОГО УСИЛИТЕЛЯ
- ГЛАВА VII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ХАРАКТЕРИСТИКИ УСИЛИТЕЛЕЙ И СПОСОБЫ ИХ ФОРМИРОВАНИЯ
- 2. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
- 3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ЛИНЕАРИЗОВАННЫЕ УСИЛИТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ РЕЛЕ
- 4. БЕСКОНТАКТНЫЕ ЛИНЕАРИЗОВАННЫЕ РЕЛЕЙНЫЕ УСИЛИТЕЛИ
- ГЛАВА VIII. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 2. ОСНОВНЫЕ ЭЛЕМЕНТЫ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ И ИХ ХАРАКТЕРИСТИКИ
- 3. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ С ЗОЛОТНИКОМ
- 4. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ СО СТРУЙНОЙ ТРУБКОЙ
- 5. СХЕМЫ И ПРИНЦИПЫ ДЕЙСТВИЯ ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 6. СТАТИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 7. ДИНАМИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 8. УНИФИКАЦИЯ ЭЛЕКТРОГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ ДЛЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
- ГЛАВА IX. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ И ИХ КЛАССИФИКАЦИЯ
- 2. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ СО СТРУЙНОЙ ТРУБКОЙ
- 3. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗОЛОТНИКОМ
- 4. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С СОПЛОМ — ЗАСЛОНКОЙ
- 5. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗАСЛОНКОЙ
- 6. МНОГОКАСКАДНЫЕ ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- РАЗДЕЛ II. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ И УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ЛИНЕЙНЫХ ПАССИВНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Основные соотношения для синтеза пассивного RC-четырехполюсника.
- 3. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Активные четырехполюсники, получаемые с помощью конверторов отрицательного сопротивления.
- Активные четырехполюсники, получаемые с помощью гираторов.
- 4. НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА НЕЛИНЕЙНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. ОСОБЕННОСТИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XI. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА ПОСТОЯННОГО ТОКА
- Дифференцирующий трансформатор.
- Электрические интегрирующие элементы.
- 2. ТИПОВЫЕ ЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- 3. КОРРЕКТИРУЮЩИЕ ЧЕТЫРЕХПОЛЮСНИКИ С АКТИВНЫМИ ЭЛЕМЕНТАМИ
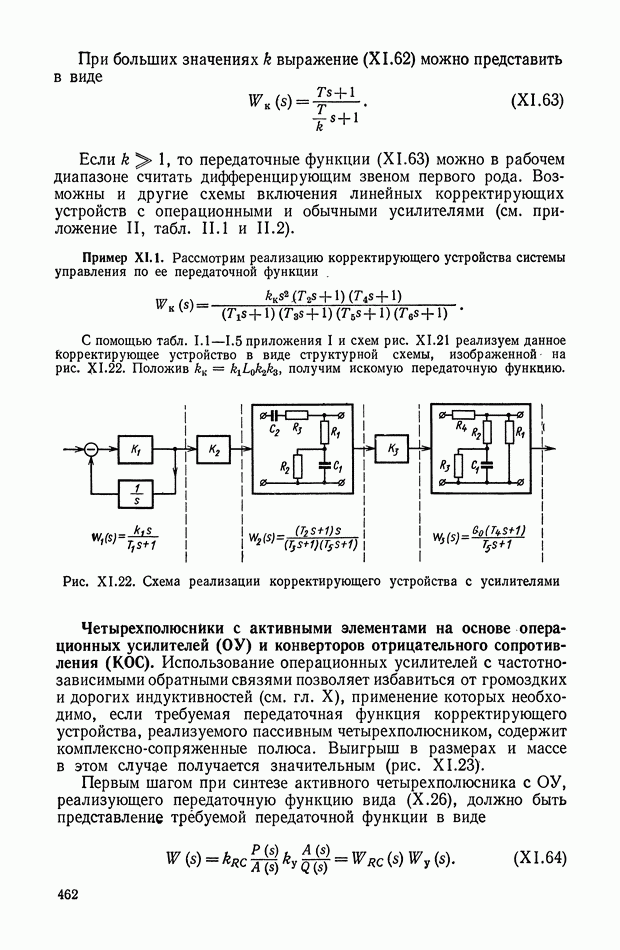
- Четырехполюсники с активными элементами на основе операционных усилителей (ОУ) и конверторов отрицательного сопротивления (КОС).
- 4. РЕАЛИЗАЦИЯ ЗАДАННОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В ВИДЕ СХЕМЫ ПАССИВНОГО ЛИНЕЙНОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА
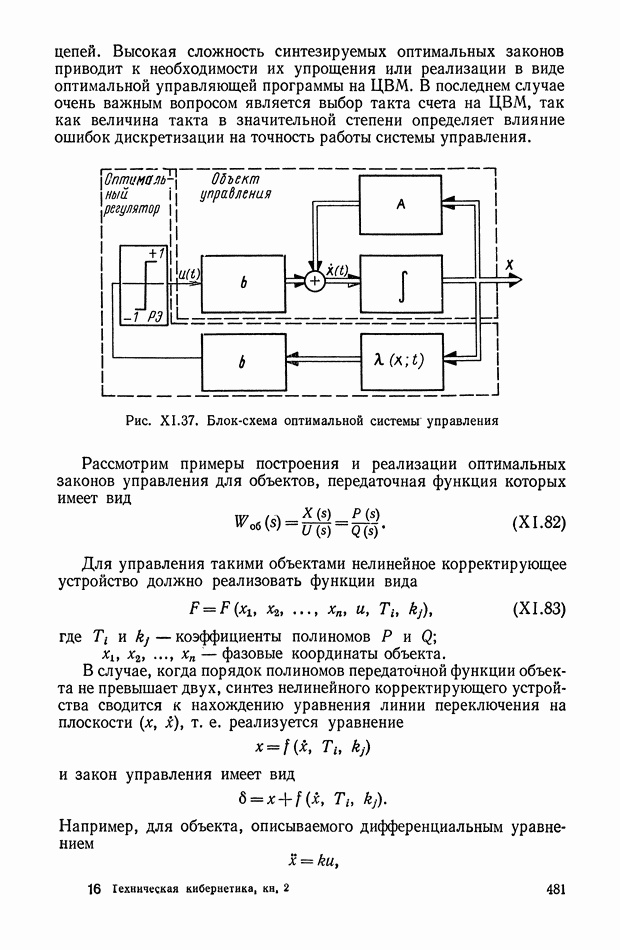
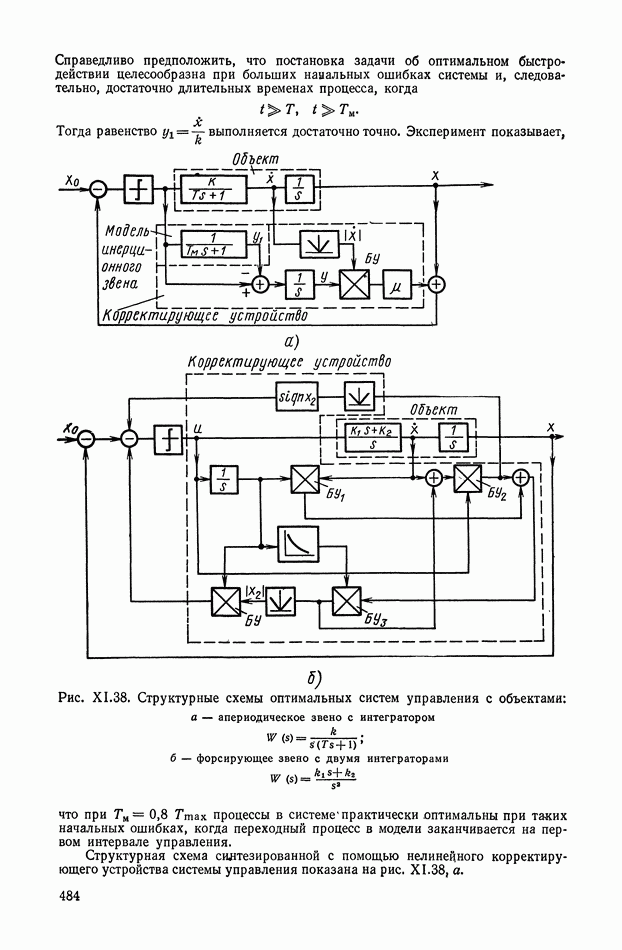
- 5. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- 8. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- Многоканальные нелинейные логические устройства.
- ГЛАВА XII. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- 1. КОРРЕКТИРУЮЩИЕ RLC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 2. КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 3. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 4. САМОНАСТРАИВАЮЩИЕСЯ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА
- 5. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА С ПРОМЕЖУТОЧНОЙ ДЕМОДУЛЯЦИЕЙ
- 6. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА С ПЕРЕКЛЮЧАТЕЛЯМИ
- 7. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XIII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ТАХОГЕНЕРАТОРЫ ПОСТОЯННОГО ТОКА
- Погрешности тахогенератора постоянного тока.
- 2. НЕКОТОРЫЕ СХЕМЫ ПРИМЕНЕНИЯ ТАХОГЕНЕРАТОРОВ
- 3. АСИНХРОННЫЕ ТАХОГЕНЕРАТОРЫ
- 4. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ ИЗМЕРЕНИЯ СКОРОСТИ ЭЛЕКТРОДВИГАТЕЛЕЙ
- Пассивный тахометрический мост переменного тока.
- Активные тахометрические мосты.
- ГЛАВА XIV. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ГИДРАВЛИЧЕСКИХ СИСТЕМАХ
- 3. ЭЛЕКТРИЧЕСКИЕ ОБРАТНЫЕ СВЯЗИ
- 4. ЖЕСТКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
- 5. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ СИСТЕМАХ
- 6. СЛОЖНЫЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
- ПРИЛОЖЕНИЕ 1. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПОСТОЯННОГО ТОКА
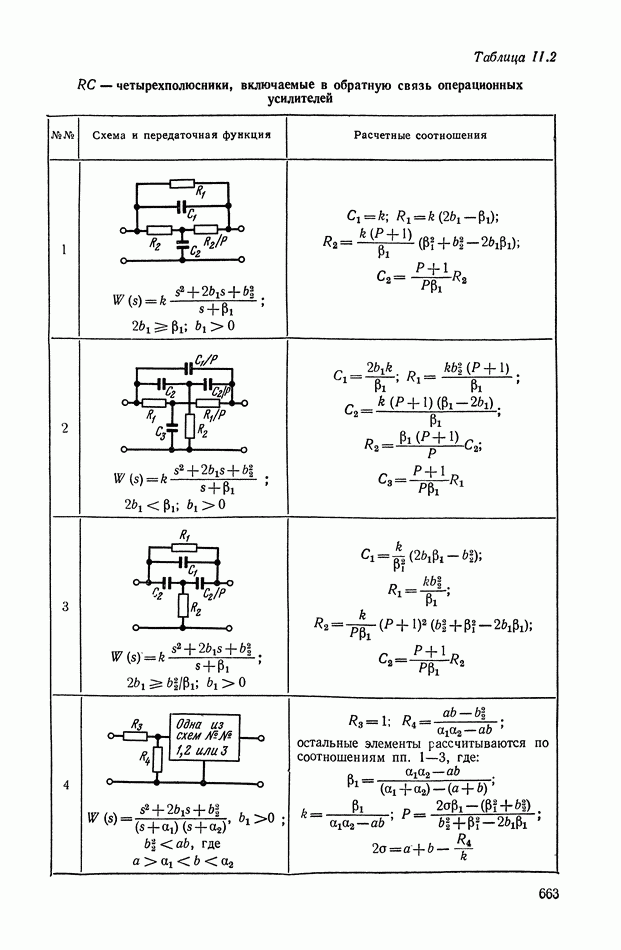
- ПРИЛОЖЕНИЕ II. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ОСНОВЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
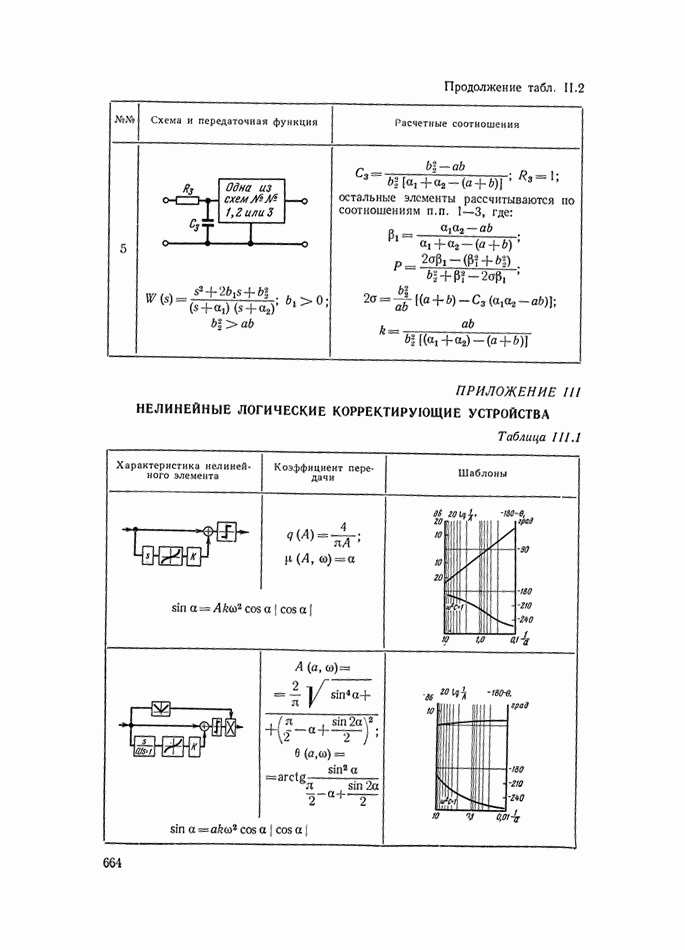
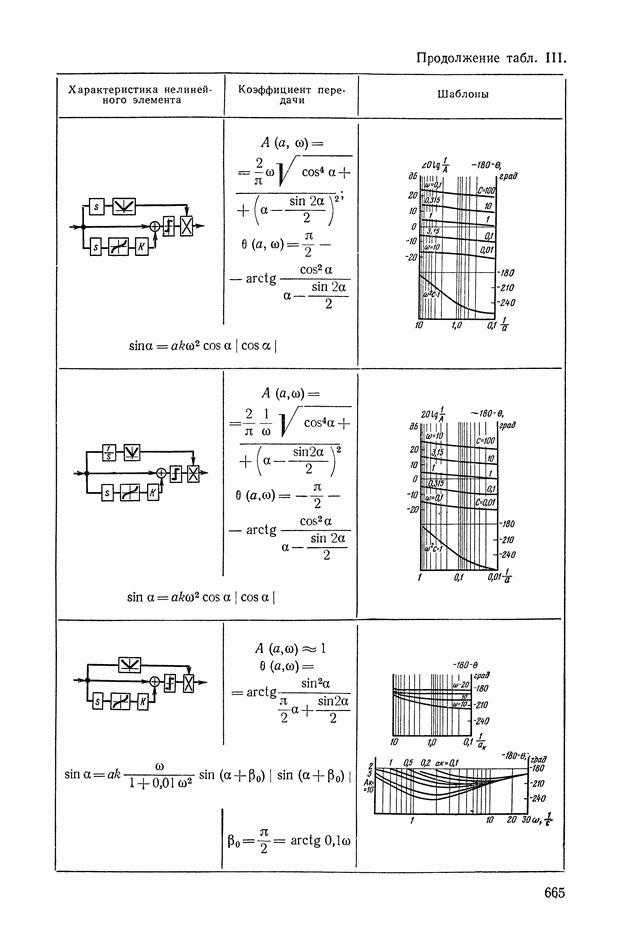
- ПРИЛОЖЕНИЕ III. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ