| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
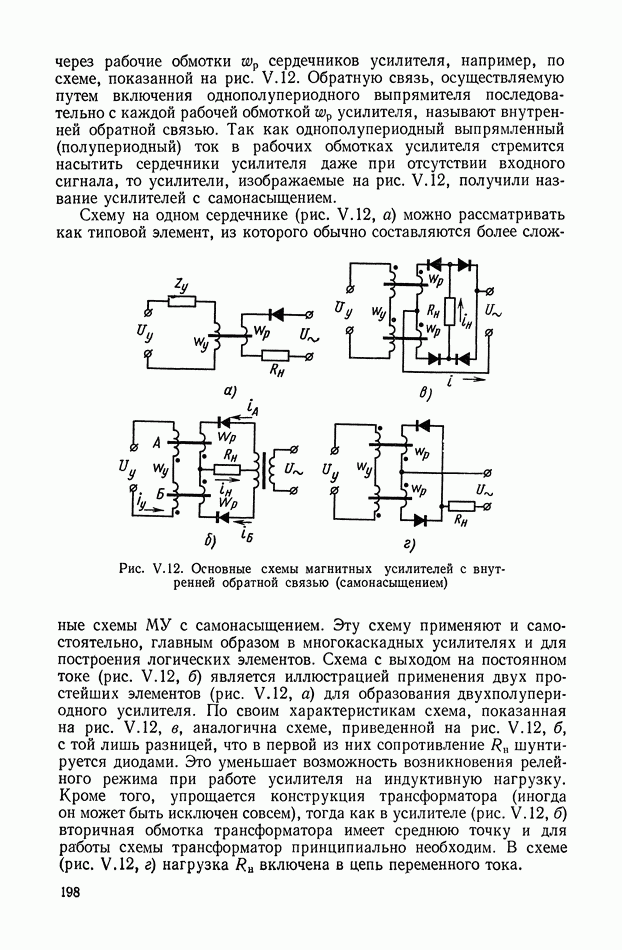
2. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ СО СТРУЙНОЙ ТРУБКОЙ
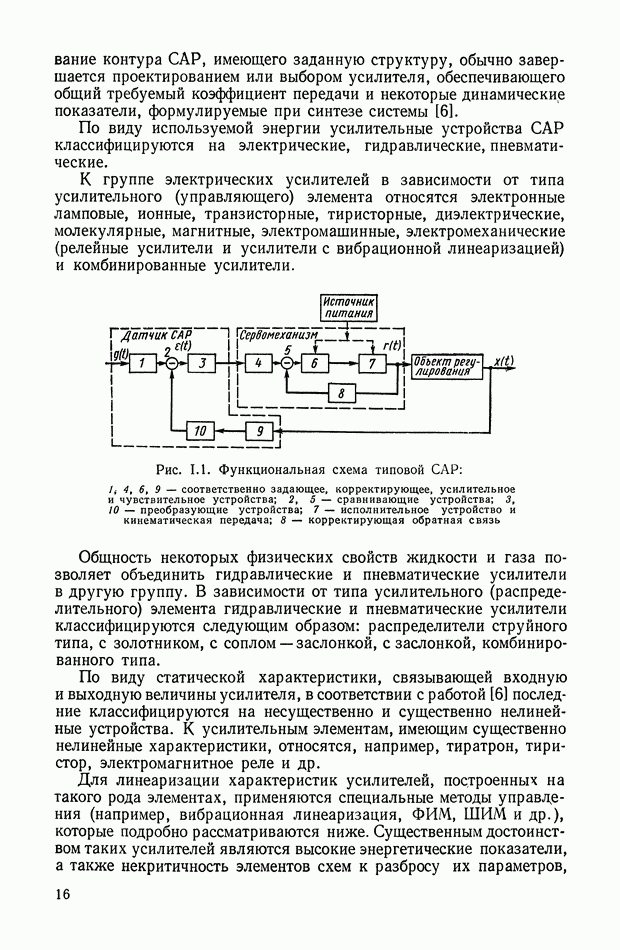
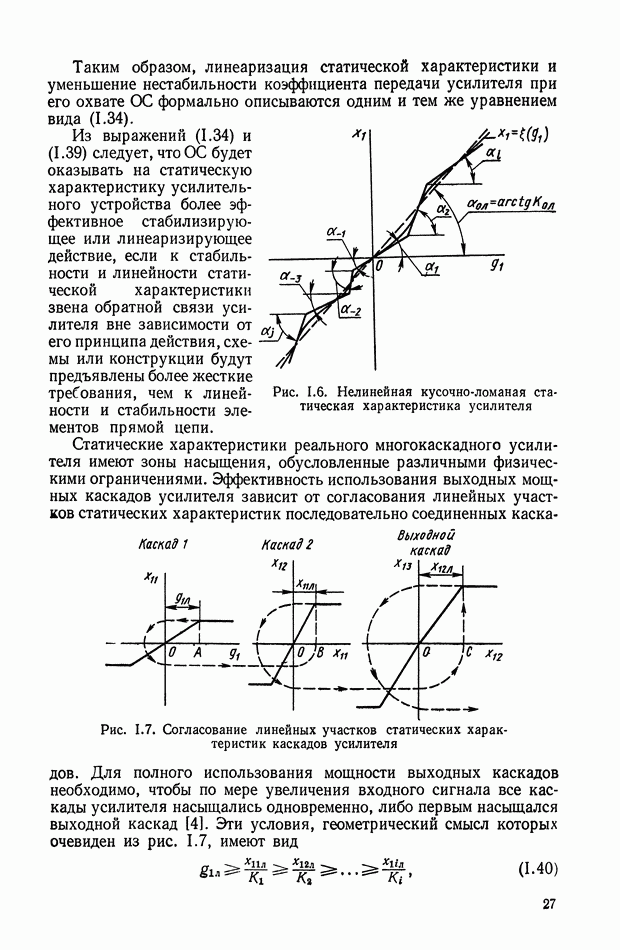
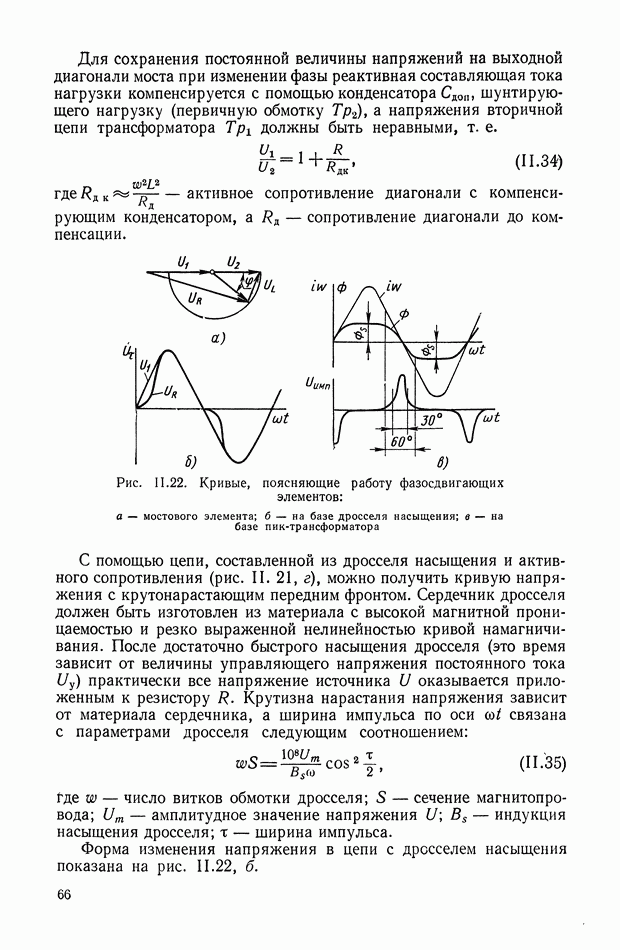
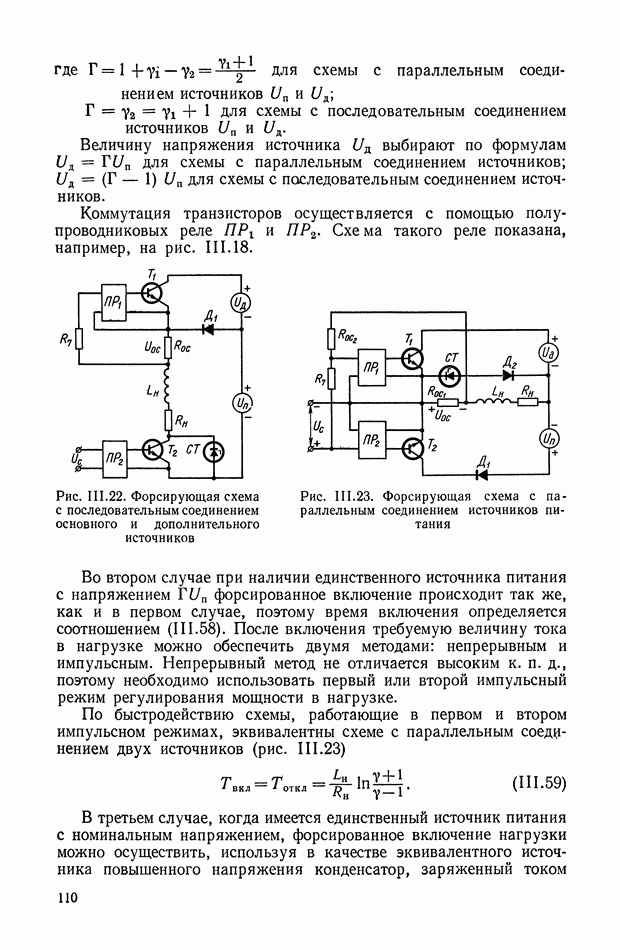
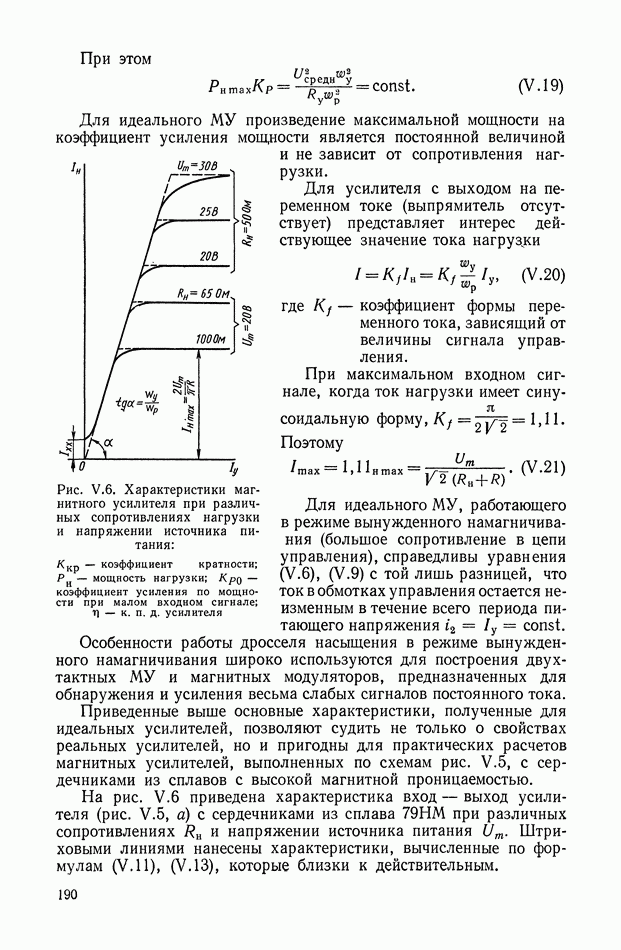
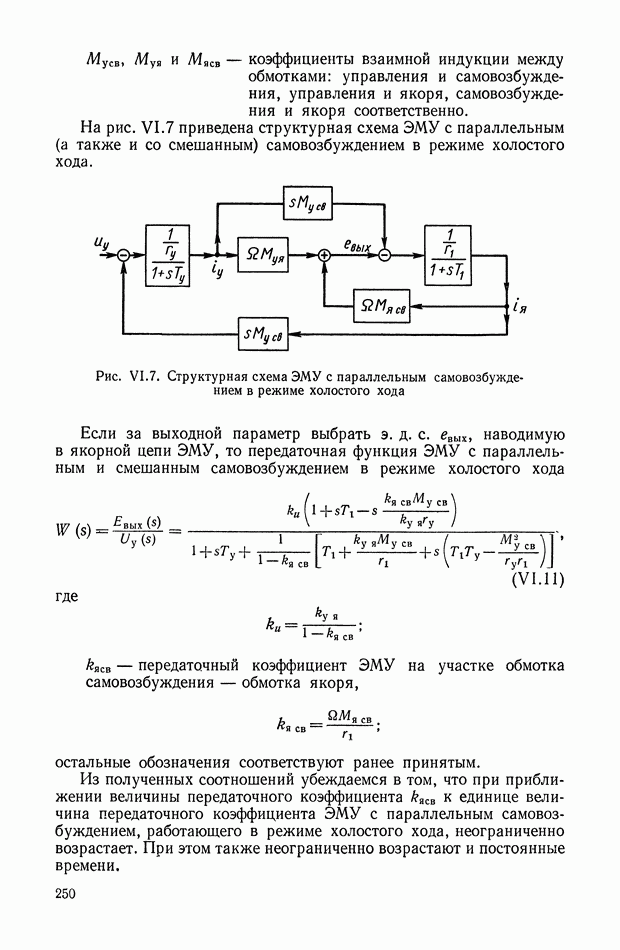
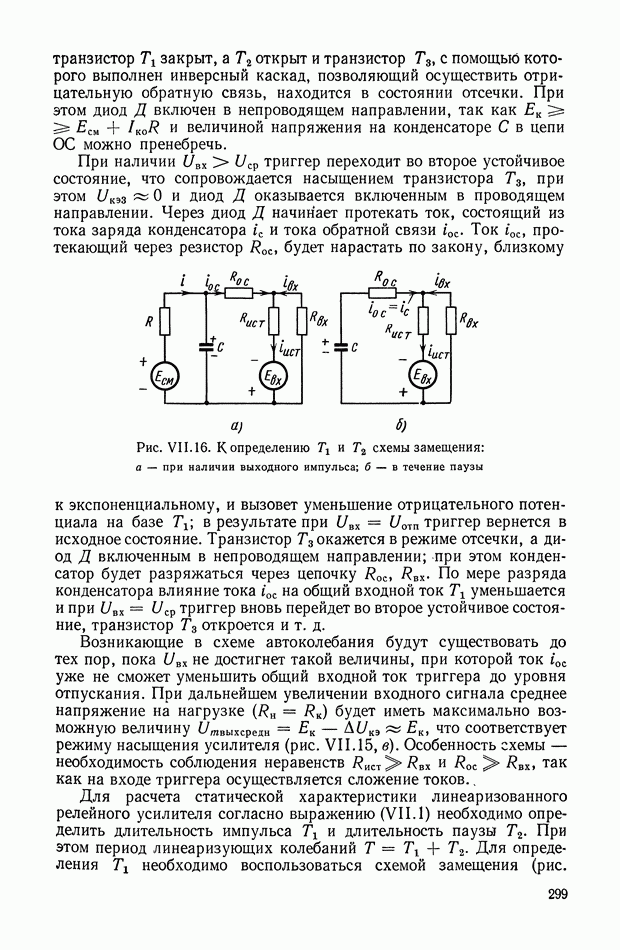
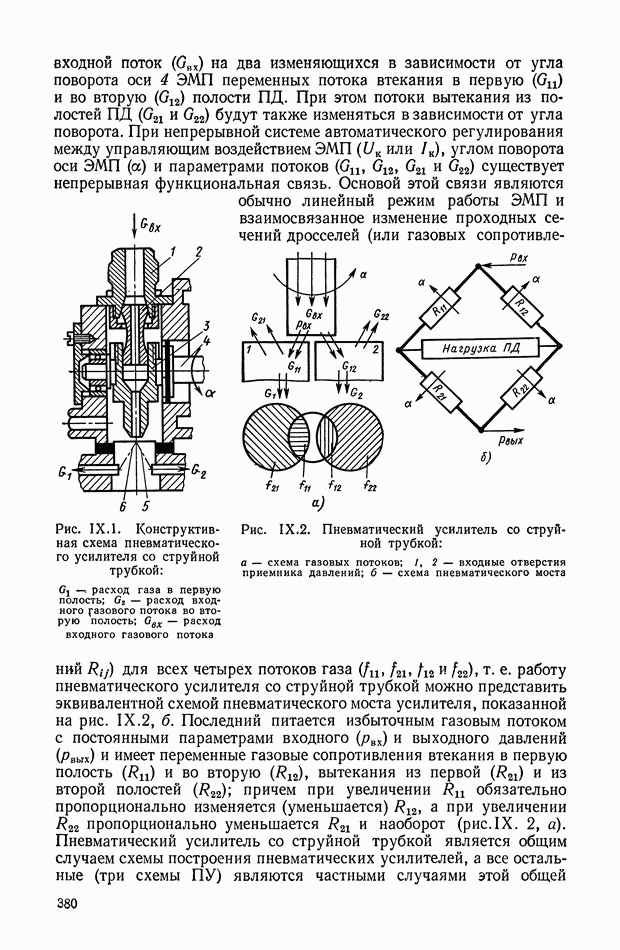
Принципиальная схема пневматического усилителя со струйной трубкой показана на рис. IX.2. Принцип работы этого усилителя заключается в перераспределении площадей втекания и вытекания  газа за счет поворота струйной трубки на угол а.
газа за счет поворота струйной трубки на угол а.
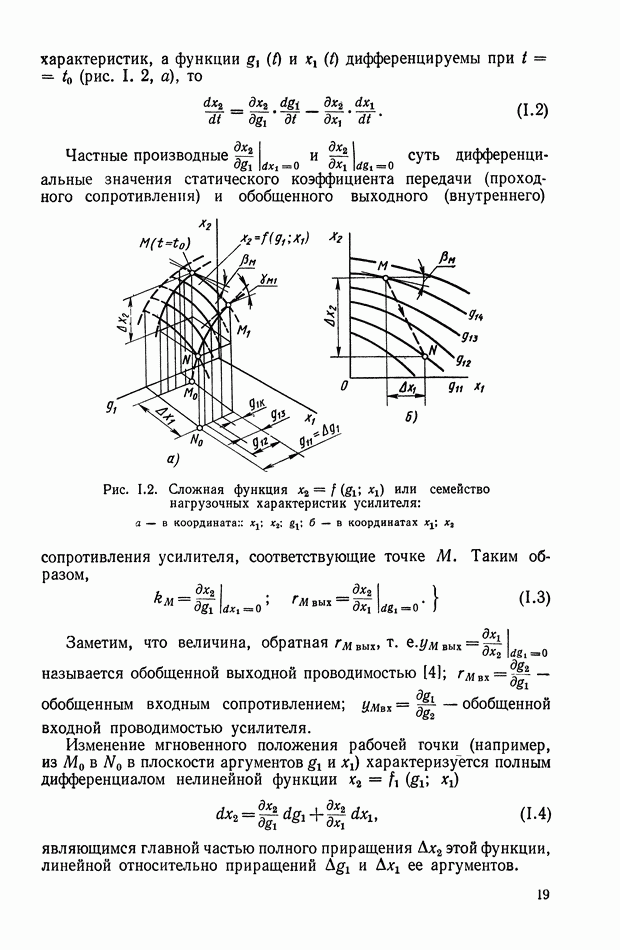
При отсутствии командного сигнала  струйная трубка находится в нейтральном положении. Параметрами этого равновесного режима являются: площади вытекания
струйная трубка находится в нейтральном положении. Параметрами этого равновесного режима являются: площади вытекания  площади втекания
площади втекания  давления
давления  и расходы газа
и расходы газа 
Для определения величины равновесного давления подставив эти параметры в выражение (IX. 3), получим

Введем обозначения

Тогда для определения  имеем уравнение
имеем уравнение

где  определяются конструкцией пневматического усилителя.
определяются конструкцией пневматического усилителя.
Для нахождения  необходимо задаться величиной
необходимо задаться величиной  т. е. равновесной температурой в приемнике ПД. Очевидно, что в зависимости от вида приемника величина 60 может значительно изменяться. Верхним пределом значения 0 является ее величина в таком приемнике, где процесс расширения газа происходит адиабатически
т. е. равновесной температурой в приемнике ПД. Очевидно, что в зависимости от вида приемника величина 60 может значительно изменяться. Верхним пределом значения 0 является ее величина в таком приемнике, где процесс расширения газа происходит адиабатически

но ввиду неизбежных теплопотерь действительное значение величины  всегда меньше величины
всегда меньше величины  Поскольку
Поскольку  оказывает значительное влияние на все характеристики пневматического привода, ее определяют путем экспериментальных продувок и прожигов. После этого находит значение параметра
оказывает значительное влияние на все характеристики пневматического привода, ее определяют путем экспериментальных продувок и прожигов. После этого находит значение параметра 
численным или графоаналитическим решением уравнения (IX.5). При этом для  режимов работы ПРУ могут быть получены аналитические выражения для определения параметра
режимов работы ПРУ могут быть получены аналитические выражения для определения параметра  т. е.
т. е.

и

При  струйная трубка смещается от равновесного положения (например, влево, см. рис. IX. 1) и
струйная трубка смещается от равновесного положения (например, влево, см. рис. IX. 1) и  Тогда расходы газа в приемнике
Тогда расходы газа в приемнике  могут быть выражены как разности расходов газа, втекающего через площадь
могут быть выражены как разности расходов газа, втекающего через площадь  и вытекающего через площадь
и вытекающего через площадь  Используя выражения (IX.3), можно записать
Используя выражения (IX.3), можно записать

Максимальный расход газа через пневматический усилитель со струйной трубкой при сверхкритическом режиме истечения

где  — площадь критического сечения струйной трубки;
— площадь критического сечения струйной трубки;
 — коэффициент расхода в критическом сечении. Преобразуя выражения (IX.8) с учетом соотношений (IX.9), (IX.6) и (IX.7), получим
— коэффициент расхода в критическом сечении. Преобразуя выражения (IX.8) с учетом соотношений (IX.9), (IX.6) и (IX.7), получим

где 
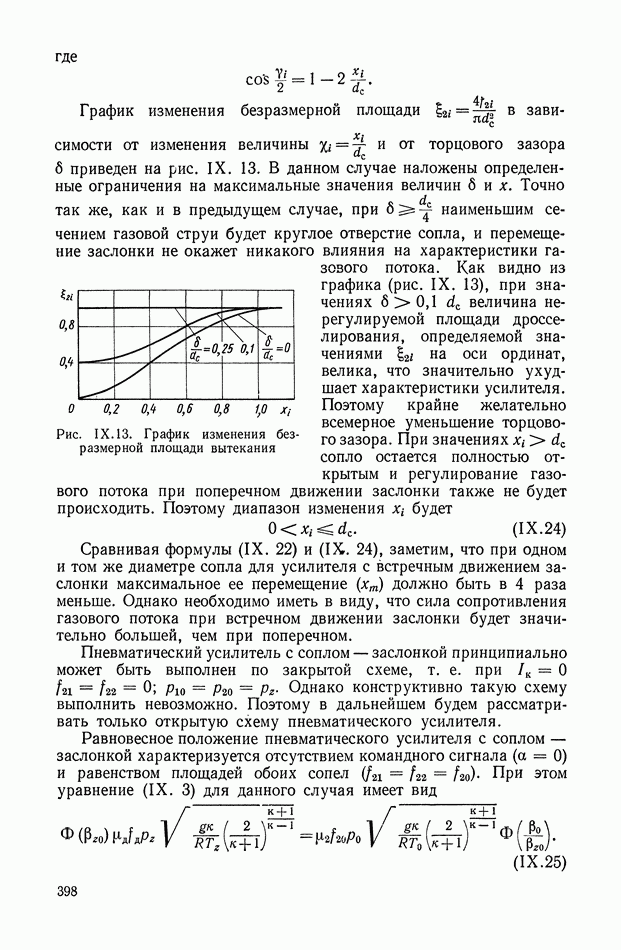
Введем безразмерный параметр  пропорциональный отношению наибольших площадей выходного и входного отверстий:
пропорциональный отношению наибольших площадей выходного и входного отверстий:

Из рис. IX.2, а видно, что максимальная площадь втекания  а максимальная площадь вытекания из любой
а максимальная площадь вытекания из любой
 приемника равна площади выхлопного окна, т. е.
приемника равна площади выхлопного окна, т. е. 
Тогда уравнение пневматического усилителя можно привести к безразмерной форме:

 — безразмерные расходы в приемнике;
— безразмерные расходы в приемнике;
 — безразмерные площади втекания;
— безразмерные площади втекания;
 — безразмерные площади вытекания;
— безразмерные площади вытекания;
 безразмерный коэффициент расхода
безразмерный коэффициент расхода 
Полученная система нелинейных уравнений (IX. 11) при принятых допущениях описывает работу пневматического усилителя со струйной трубкой во всем диапазоне изменения командного сигнала и давлений в приемниках. Эта система может быть использована при моделировании пневматического усилителя на аналоговых ЭВМ с функциональными блоками.

Рис. IX.8. Изменение безразмерных площадей втекания и вытекания:  — максимальный угол отклонения
— максимальный угол отклонения
Уравнения системы (IX.11) позволяют решить задачу о возможном поле разброса характеристик пневматического усилителя. Главной причиной разброса характеристик ПУ является технологическое несовершенство изготовления пневматического распределительного устройства, заключающееся в отклонениях размеров проходных отверстий от их номинальных размеров. В уравнениях (IX. 11) геометрия пневматического распределительного устройства определяется только видом зависимостей  (рис. IX.8). Очевидно, что с учетом технологических допусков около каждой номинальной кривой, изображенной на рис. IX. 8, появится незначительное поле разбросов, которое с учетом уравнений (IX. 11) даст поле разброса характеристик усилителя. Таким образом, по уравнениям (IX. 11) можно решать вопрос либо о технологических допусках по заданному полю разброса характеристик усилителя, либо о разбросе характеристик усилителя при заданных допусках на размеры проходных отверстий.
(рис. IX.8). Очевидно, что с учетом технологических допусков около каждой номинальной кривой, изображенной на рис. IX. 8, появится незначительное поле разбросов, которое с учетом уравнений (IX. 11) даст поле разброса характеристик усилителя. Таким образом, по уравнениям (IX. 11) можно решать вопрос либо о технологических допусках по заданному полю разброса характеристик усилителя, либо о разбросе характеристик усилителя при заданных допусках на размеры проходных отверстий.
В тех случаях, огда применяется наиболее распространенный и простой поршневой пневматический двигатель, возможно упрощение системы (IX. 11), если принять  Тогда по уравнениям (IX. 11) можно определить семейство статических (механических) характеристик однокаскадного пневматического
Тогда по уравнениям (IX. 11) можно определить семейство статических (механических) характеристик однокаскадного пневматического
привода. Для этого необходимо преобразовать уравнения  с учетом условий статического режима:
с учетом условий статического режима:

где  — изменение объемов газа в полостях ПД;
— изменение объемов газа в полостях ПД;  — площадь поршня; V — скорость поршня,
— площадь поршня; V — скорость поршня,
но

Вводя обозначение безразмерной скорости  уравнения (IX. 11) легко привести к виду
уравнения (IX. 11) легко привести к виду

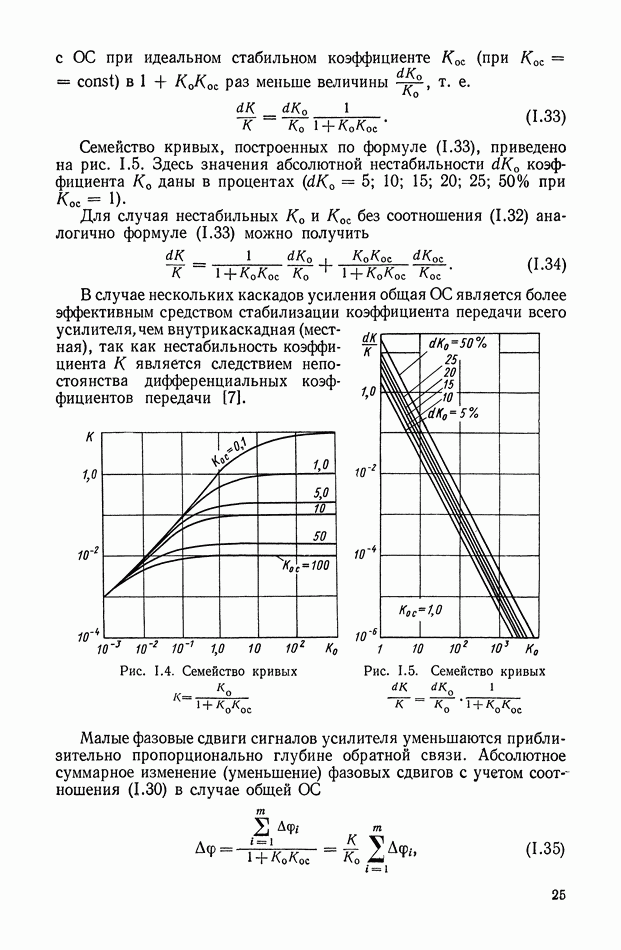
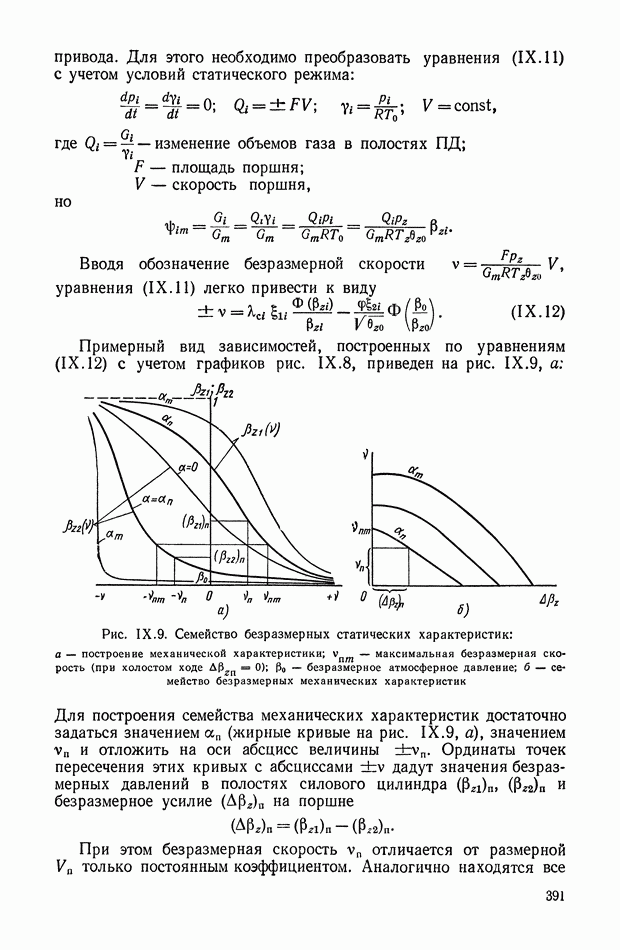
Примерный вид зависимостей, построенных по уравнениям (IX. 12) с учетом графиков рис. IX.8, приведен на рис. IX.9, а:

Рис. IX.9. Семейство безразмерных статических характеристик: а  построение механической характеристики;
построение механической характеристики;  — максимальная безразмерная скорость (при холостом ходе
— максимальная безразмерная скорость (при холостом ходе  — безразмерное атмосферное давление;
— безразмерное атмосферное давление;  — семейство безразмерных механических характеристик
— семейство безразмерных механических характеристик
Для построения семейства механических характеристик достаточно задаться значением  (жирные кривые на рис. IX.9, а), значением
(жирные кривые на рис. IX.9, а), значением  и отложить на оси абсцисс величины
и отложить на оси абсцисс величины  Ординаты точек пересечения этих кривых с абсциссами
Ординаты точек пересечения этих кривых с абсциссами  дадут значения безразмерных давлений в полостях силового цилиндра
дадут значения безразмерных давлений в полостях силового цилиндра  и безразмерное усилие
и безразмерное усилие  на поршне
на поршне

При этом безразмерная скорость  отличается от размерной
отличается от размерной  только постоянным коэффициентом. Аналогично находятся все
только постоянным коэффициентом. Аналогично находятся все
остальные точки семейства механических характеристик, показанного на рис. IX.9, б.
При расчетах газового привода часто требуется линеаризованное уравнение газового усилителя. Очевидно, что линеаризация нелинейных уравнений (IX. 11) связана с добавочными допущениями и упрощениями. Однако линеаризованные уравнения справедливы не на всем диапазоне изменения переменных величин, а только в некоторой его части. Для линеаризации системы (IX.11) примем следующие допущения:
1. Сумма давлений в полостях приемника остается постоянной

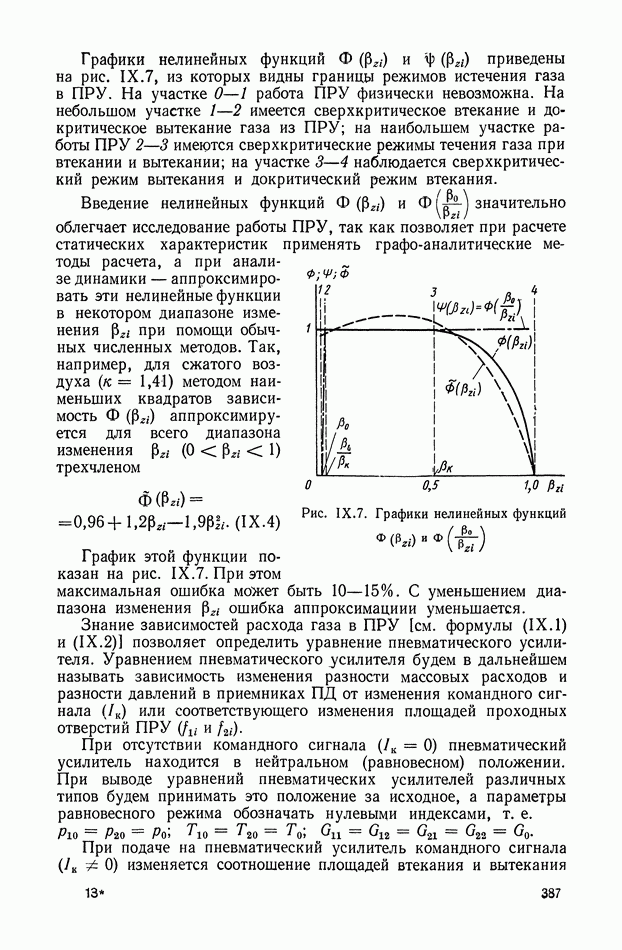
2. Нелинейные функции  рассматриваемом диапазоне изменения
рассматриваемом диапазоне изменения  можно аппроксимировать квадратными трехчленами (рис. IX.7):
можно аппроксимировать квадратными трехчленами (рис. IX.7):

3. Температуры газа в приемниках приблизительно равны, т. е.

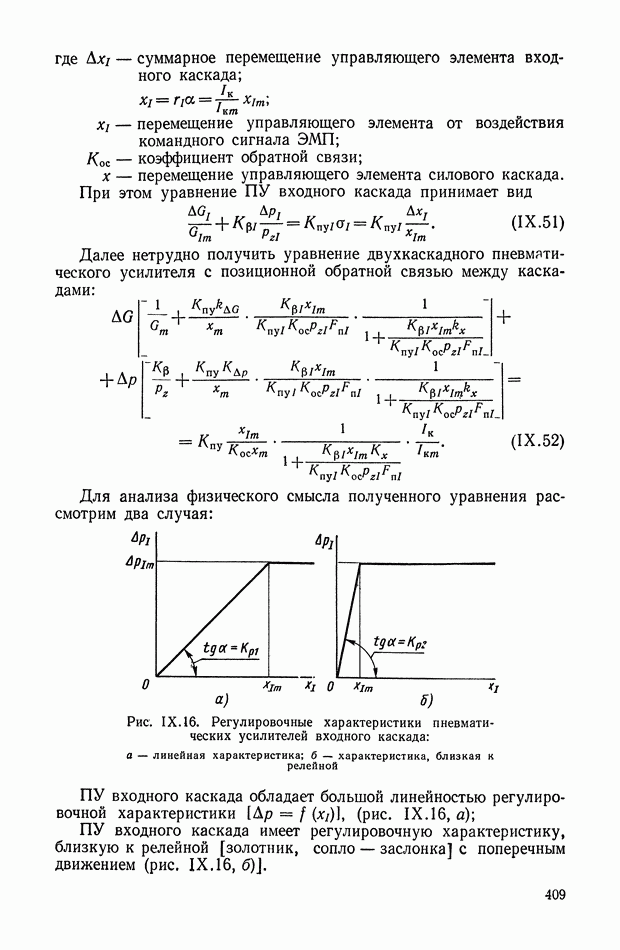
4. Изменения площадей отверстий втекания и вытекания линейно зависят от командного сигнала:

где  — коэффициенты пропорциональности.
— коэффициенты пропорциональности.
Эти допущения позволяют в инженерных расчетах получить линейную модель, параметры которой будут занижены по сравнению с действительными.
С учетом принятых допущений уравнения (IX. 11) принимают следующий вид:

примем

где

Нетрудно заметить, что  при
при 

Тогда разность уравнений (IX. 13) после преобразований можно записать в следующем виде:

где  — коэффициент обратной связи по перепаду давлений усилителя,
— коэффициент обратной связи по перепаду давлений усилителя,

 — коэффициент усиления пневматического усилителя,
— коэффициент усиления пневматического усилителя,

В конечном виде линеаризованное уравнение пневматического усилителя со струйной трубкой будет

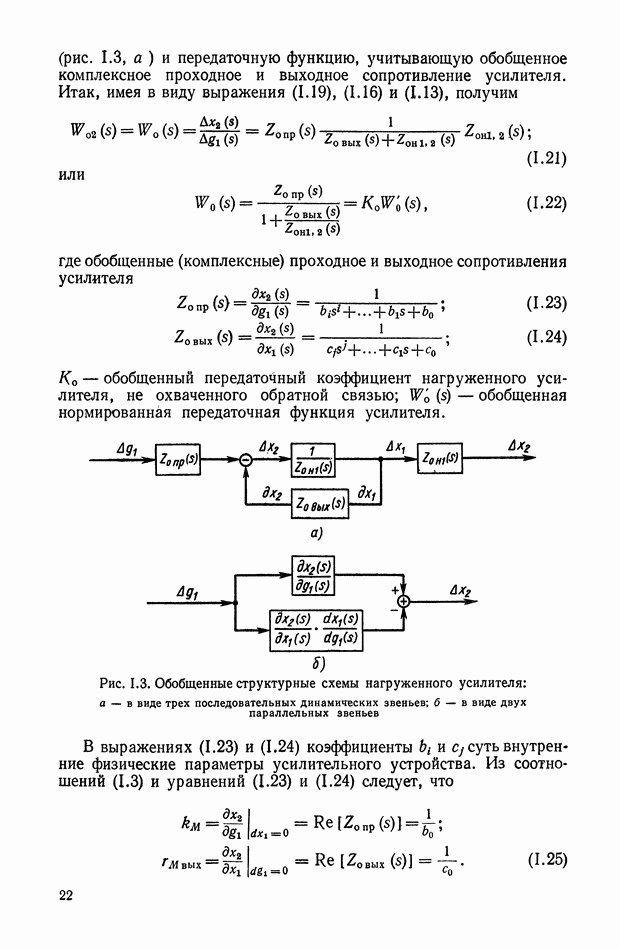
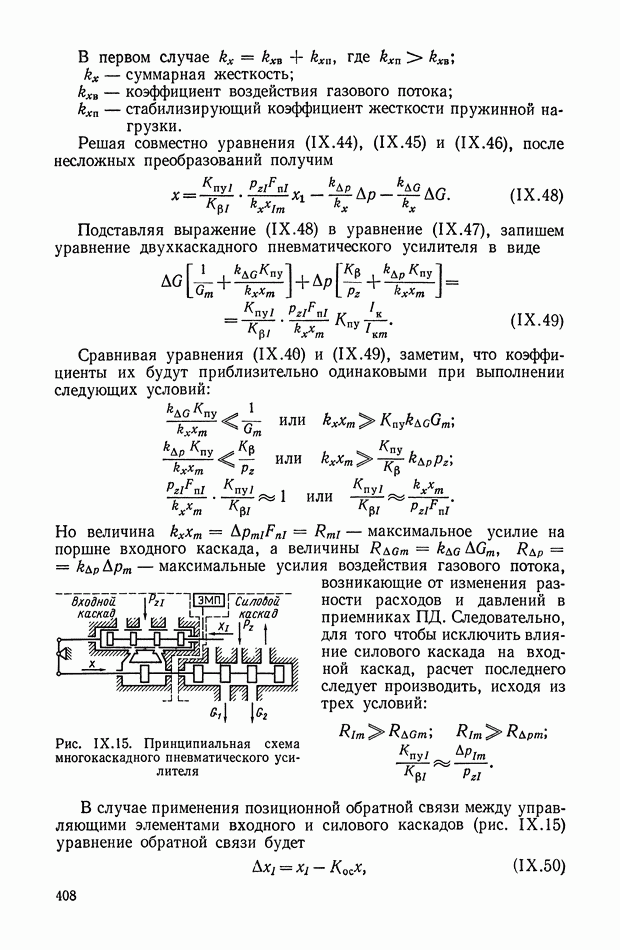
Применяя преобразования Лапласа при нулевых начальных условиях, структурную схему усилителя со струйной трубкой можно представить в виде, показанном на рис. IX. 10.

Рис. IX. 10. Структурная схема пневматического усилителя со струйной трубкбй:  — сигнал управления;
— сигнал управления;  — разность расходов в полостях приемника силового двигателя
— разность расходов в полостях приемника силового двигателя
Отрицательная связь по относительному перепаду давления  показывает зависимость функционирования пневматического усилителя от его нагрузки (пневматического двигателя), причем двигатель представлен на структурной схеме передаточной функцией
показывает зависимость функционирования пневматического усилителя от его нагрузки (пневматического двигателя), причем двигатель представлен на структурной схеме передаточной функцией 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА САР
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ЛИНЕЙНЫХ УСИЛИТЕЛЬНЫХ УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ УСИЛИТЕЛЬНОГО УСТРОЙСТВА БЕЗ ОБРАТНОЙ СВЯЗИ
- 3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ, СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ОСОБЕННОСТИ УСИЛИТЕЛЬНОГО УСТРОЙСТВА С ОБРАТНОЙ СВЯЗЬЮ
- 4. КЛАССИФИКАЦИЯ И СВОЙСТВА УСИЛИТЕЛЬНЫХ УСТРОЙСТВ С ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 5. ВЫБОР И РАСЧЕТ УСИЛИТЕЛЬНОГО УСТРОЙСТВА
- ГЛАВА II. ЭЛЕКТРОННЫЕ ЛАМПОВЫЕ И ИОННЫЕ УСИЛИТЕЛИ
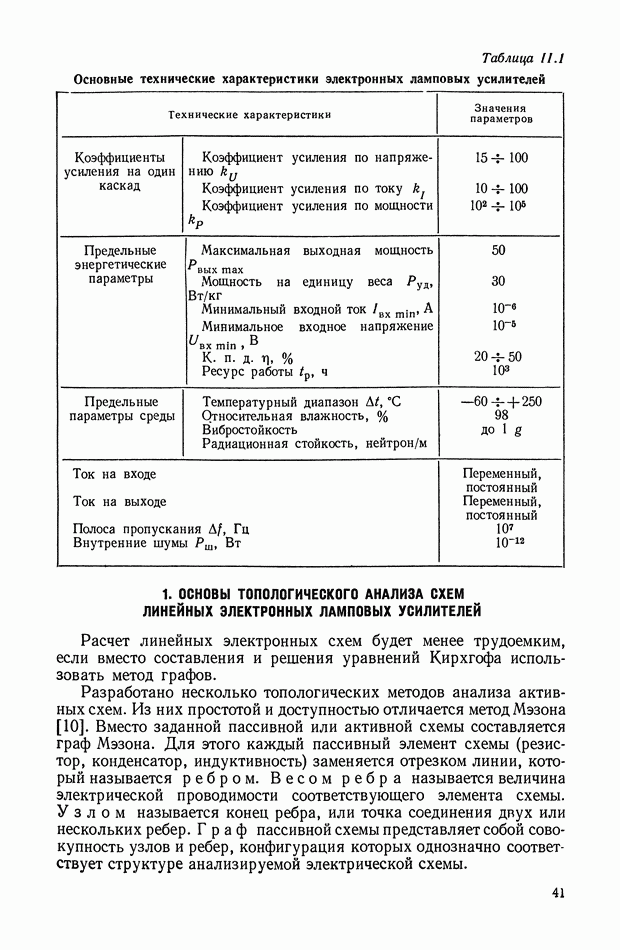
- 1. ОСНОВЫ ТОПОЛОГИЧЕСКОГО АНАЛИЗА СХЕМ ЛИНЕЙНЫХ ЭЛЕКТРОННЫХ ЛАМПОВЫХ УСИЛИТЕЛЕЙ
- 2. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПОСТОЯННОГО ТОКА
- 3. БАЛАНСНЫЕ МОСТОВЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- 4. СТАБИЛИЗАЦИЯ КОЭФФИЦИЕНТА УСИЛЕНИЯ
- 5. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
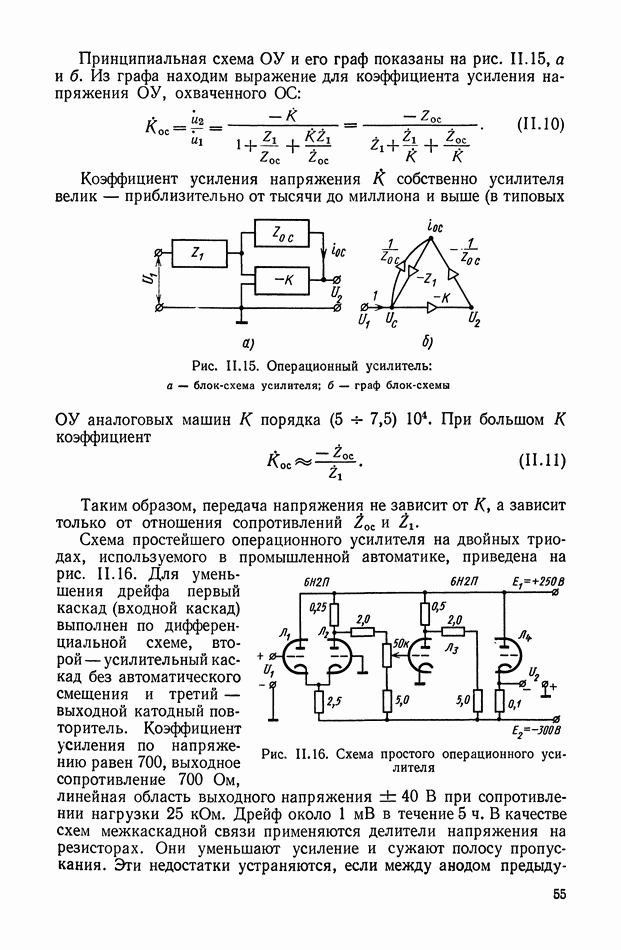
- 6. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- 7. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
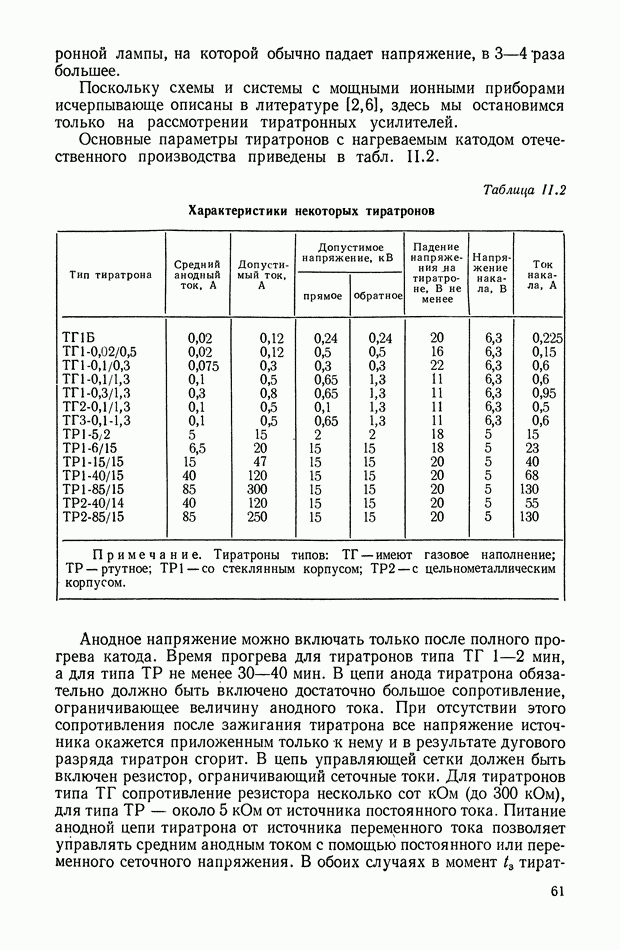
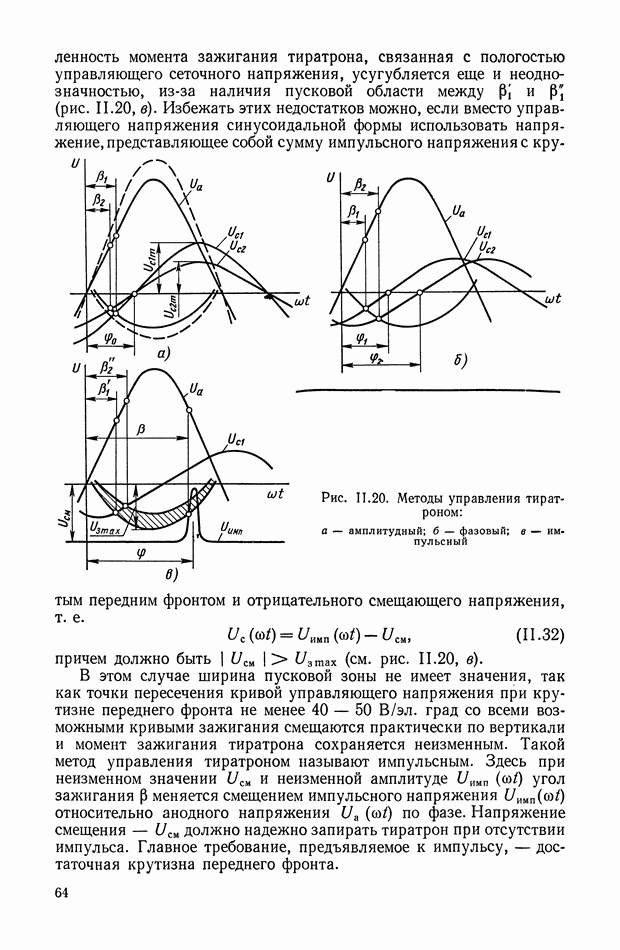
- 8. ОБЩИЕ СВОЙСТВА ИОННОГО (ТИРАТРОННОГО) УСИЛИТЕЛЯ МЕТОДЫ УПРАВЛЕНИЯ ТИРАТРОНОМ
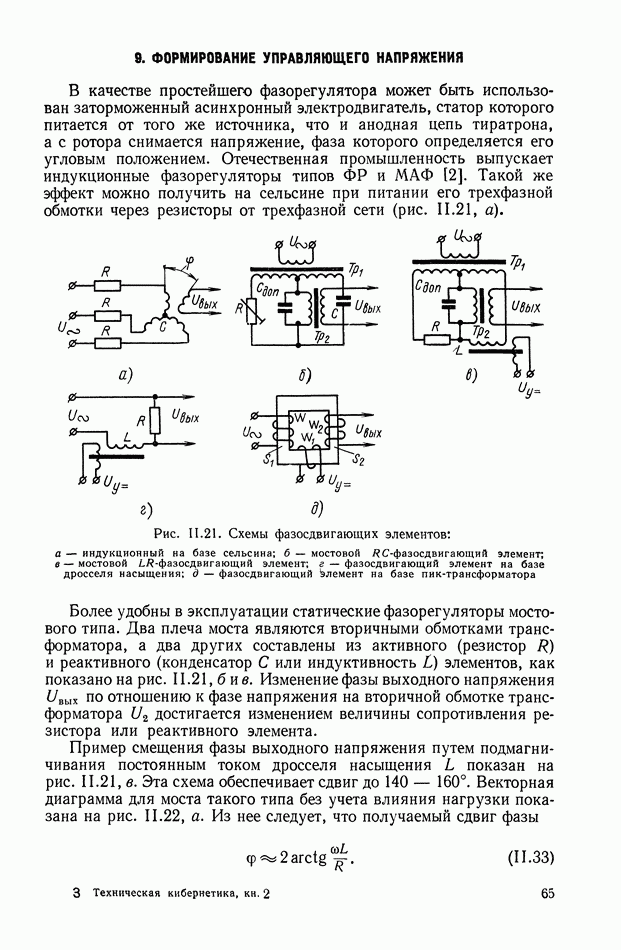
- 9. ФОРМИРОВАНИЕ УПРАВЛЯЮЩЕГО НАПРЯЖЕНИЯ
- 10. РАСЧЕТ ЭЛЕМЕНТОВ СХЕМ ТИРАТРОННОГО УСИЛИТЕЛЯ
- ГЛАВА III. ПОЛУПРОВОДНИКОВЫЕ И ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
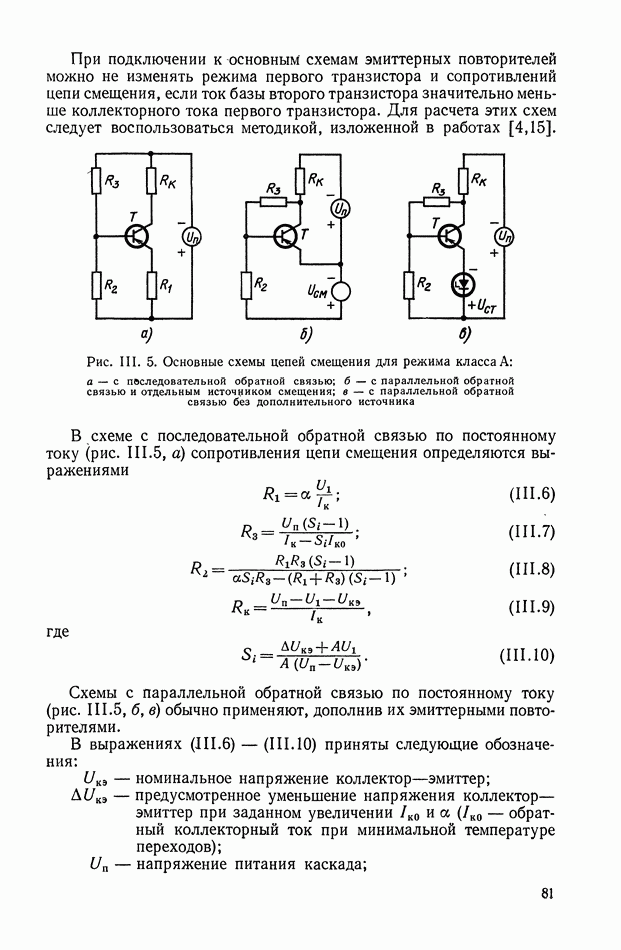
- Цепи смещения.
- Цепи связи.
- 2. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ СРЕДНЕГО ЗНАЧЕНИЯ ТОКА
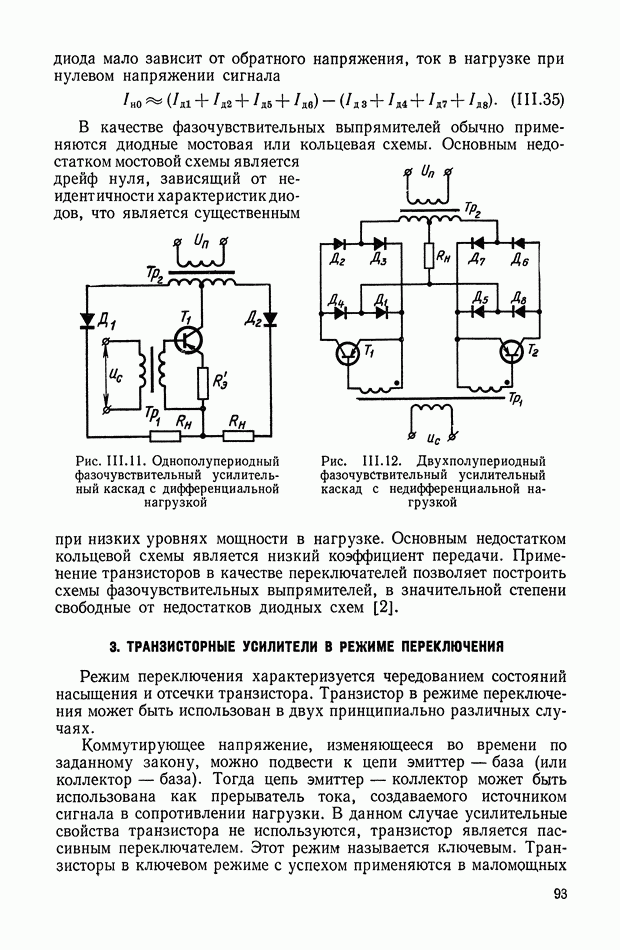
- Полупроводниковые демодуляторы.
- 3. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ В РЕЖИМЕ ПЕРЕКЛЮЧЕНИЯ
- Режимы импульсного регулирования мощности.
- Управление силовыми транзисторами.
- 4. ТРАНЗИСТОРНЫЕ УСТРОЙСТВА УПРАВЛЕНИЯ ЭЛЕКТРОДВИГАТЕЛЯМИ И ЭЛЕКТРОМАГНИТНЫМИ МЕХАНИЗМАМИ
- 5. ТИРИСТОРЫ. ХАРАКТЕРИСТИКИ, ПАРАМЕТРЫ И СВОЙСТВА
- 6. СПОСОБЫ И УСТРОЙСТВА УПРАВЛЕНИЯ ТИРИСТОРАМИ
- 7. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ (РЕГУЛИРУЕМЫЕ ВЫПРЯМИТЕЛИ)
- 8. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 9. ТИРИСТОРНЫЕ УСИЛИТЕЛИ С ПИТАНИЕМ ОТ СЕТИ ПОСТОЯННОГО ТОКА
- 10. ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 11. ОСНОВЫ РАСЧЕТА ДИЭЛЕКТРИЧЕСКИХ УСИЛИТЕЛЕЙ
- ГЛАВА IV. КВАНТОВЫЕ УСИЛИТЕЛИ И ГЕНЕРАТОРЫ
- 2. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ РАДИОДИАПАЗОНА
- Квантовые усилители радиодиапазона.
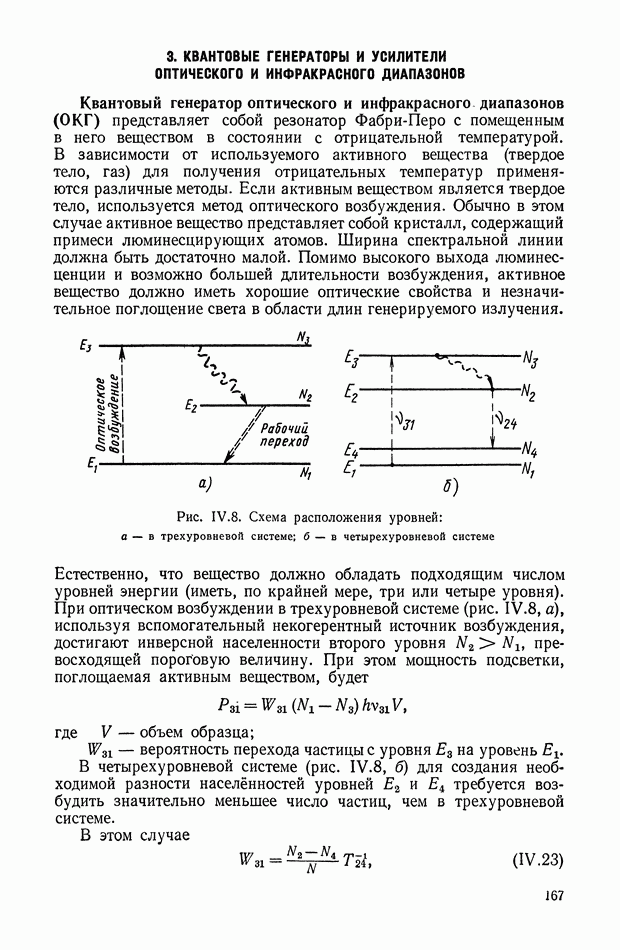
- 3. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- Оптический квантовый усилитель
- 4. ПРИМЕНЕНИЕ В САР КВАНТОВЫХ УСИЛИТЕЛЕЙ И ГЕНЕРАТОРОВ РАДИОДИАПАЗОНА, ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
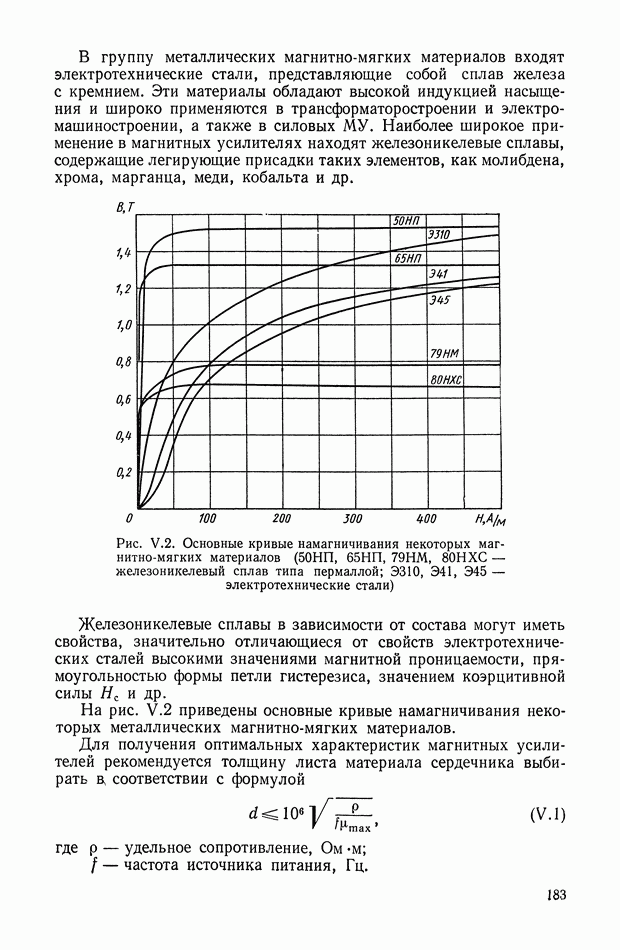
- ГЛАВА V. МАГНИТНЫЕ И МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- 2. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ МАГНИТНЫХ УСИЛИТЕЛЕЙ
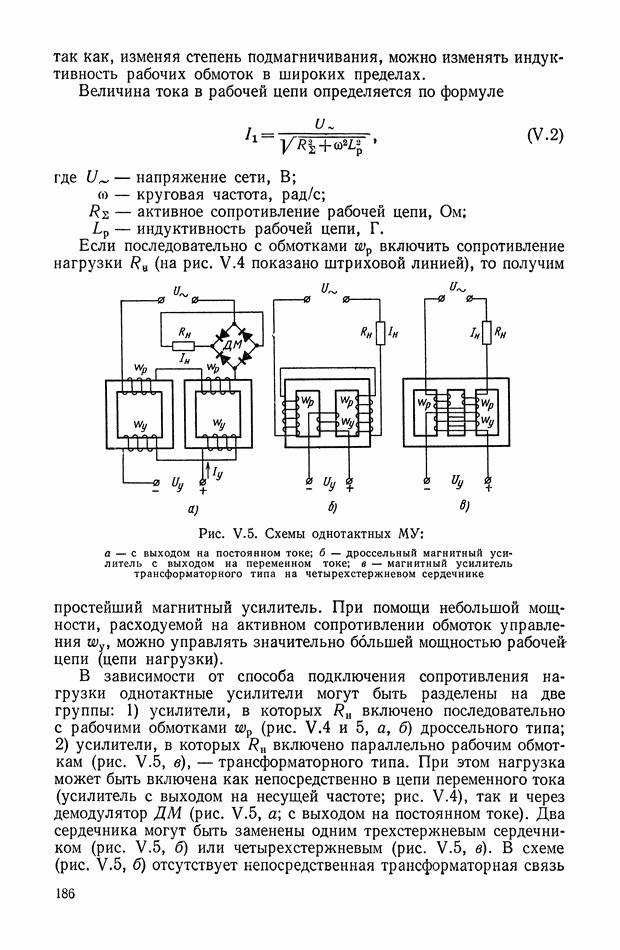
- 3. ОДНОТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ БЕЗ ОБРАТНОЙ СВЯЗИ (УПРАВЛЯЕМЫЕ ДРОССЕЛИ И ТРАНСФОРМАТОРЫ)
- 4. МАГНИТНЫЕ УСИЛИТЕЛИ С САМОНАСЫЩЕНИЕМ
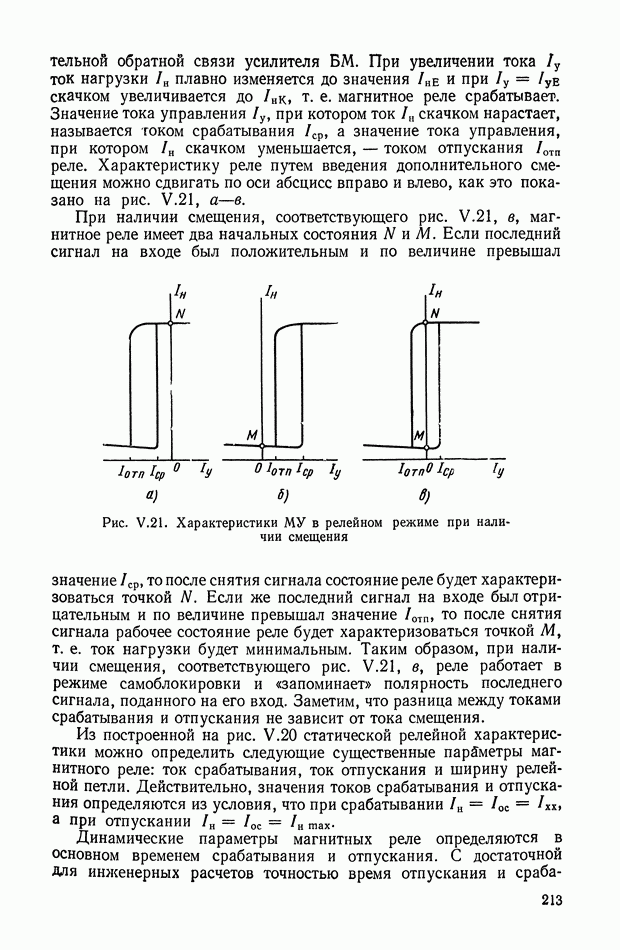
- Релейный режим работы усилителей с самонасыщением.
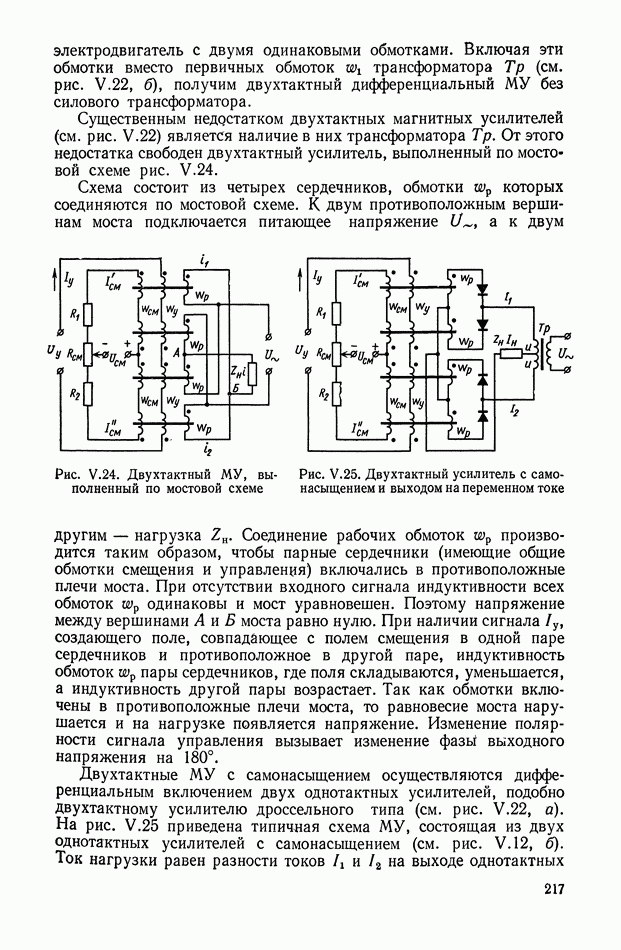
- 5. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 6. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ
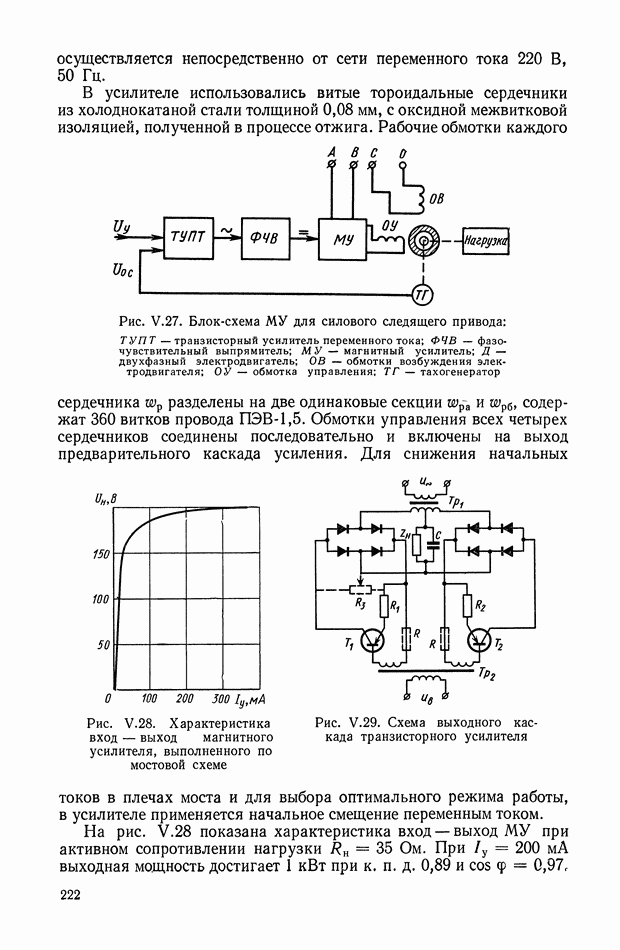
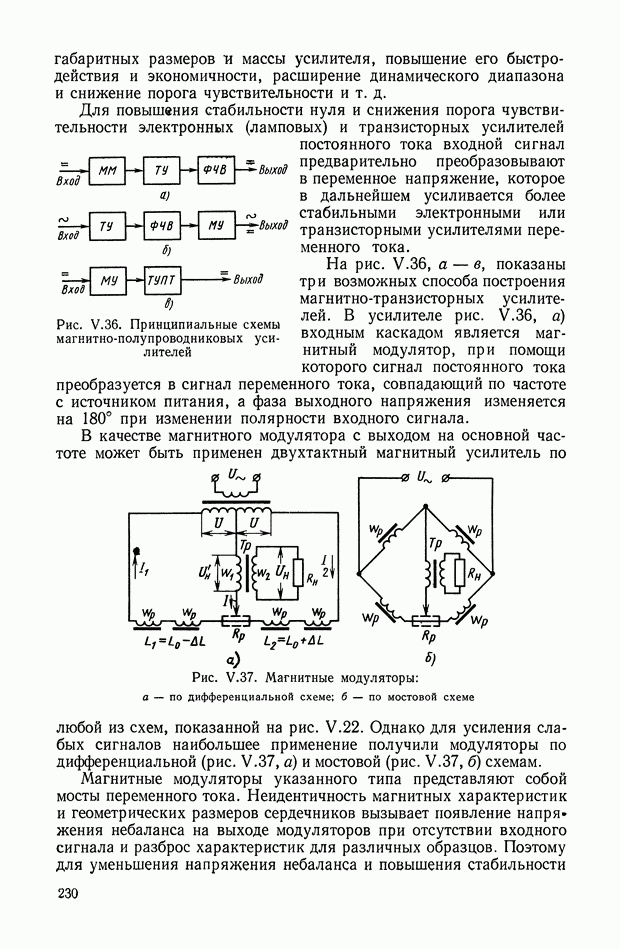
- 7. МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- ГЛАВА VI. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 2. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С НЕЗАВИСИМЫМ ВОЗБУЖДЕНИЕМ И С САМОВОЗБУЖДЕНИЕМ
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С ПОПЕРЕЧНЫМ ПОЛЕМ
- 4. ЭЛЕКТРОМАШИННЫЙ УСИЛИТЕЛЬ ПРОДОЛЬНОГО И ПРОДОЛЬНО-ПОПЕРЕЧНОГО ПОЛЯ
- 5. ВЛИЯНИЕ НА ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭМУ ВИХРЕВЫХ И КОММУТАЦИОННЫХ ТОКОВ, ГИСТЕРЕЗИСА И СДВИГА ЩЕТОК С НЕЙТРАЛИ
- 6. МЕТОДЫ УЛУЧШЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕКТРОМАШИННЫХ УСИЛИТЕЛЕЙ
- 7. НАГРУЗОЧНАЯ ХАРАКТЕРИСТИКА ЭЛЕКТРОМАШИННОГО УСИЛИТЕЛЯ
- ГЛАВА VII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ УСИЛИТЕЛИ
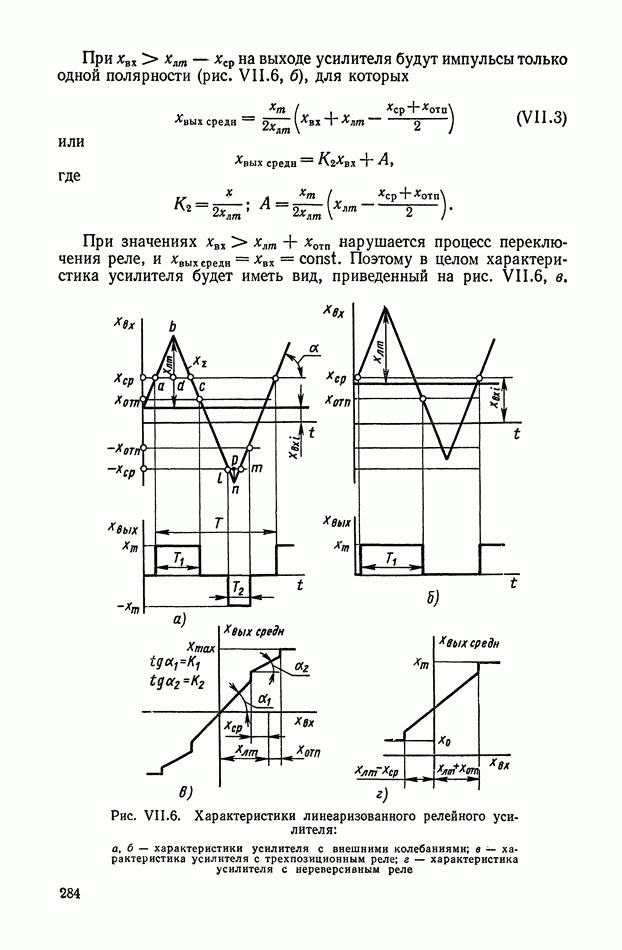
- 1. ХАРАКТЕРИСТИКИ УСИЛИТЕЛЕЙ И СПОСОБЫ ИХ ФОРМИРОВАНИЯ
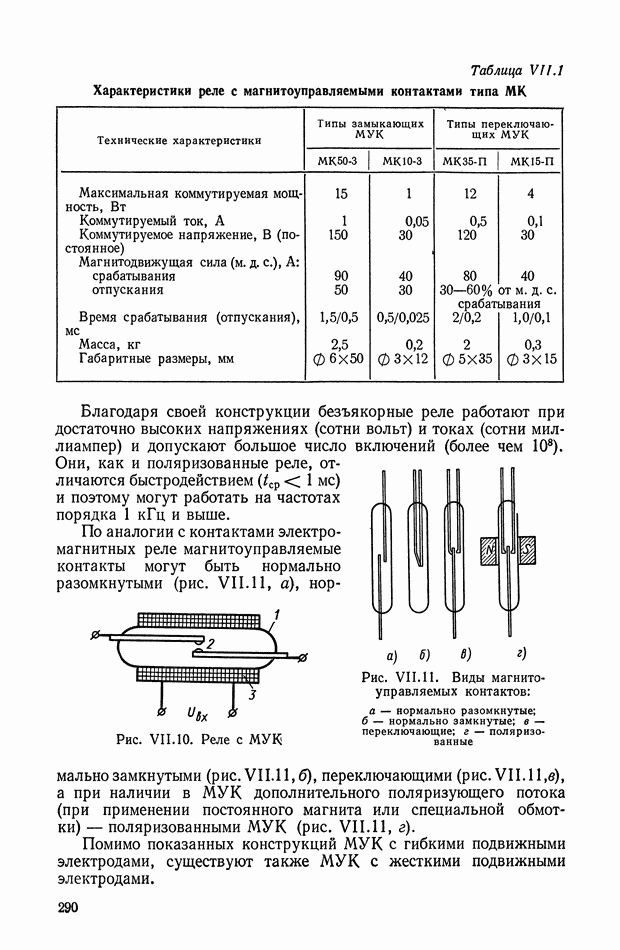
- 2. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
- 3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ЛИНЕАРИЗОВАННЫЕ УСИЛИТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ РЕЛЕ
- 4. БЕСКОНТАКТНЫЕ ЛИНЕАРИЗОВАННЫЕ РЕЛЕЙНЫЕ УСИЛИТЕЛИ
- ГЛАВА VIII. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 2. ОСНОВНЫЕ ЭЛЕМЕНТЫ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ И ИХ ХАРАКТЕРИСТИКИ
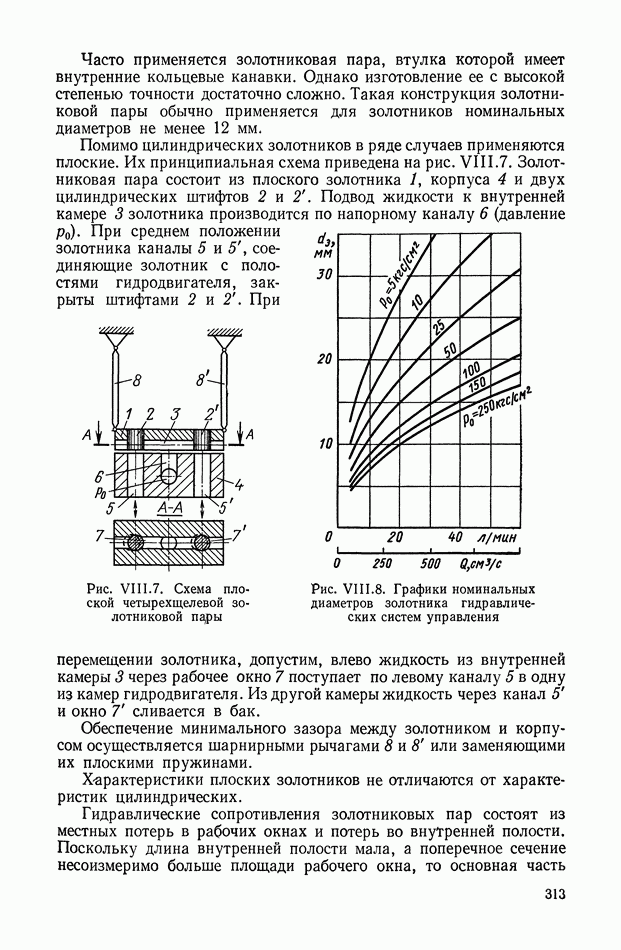
- 3. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ С ЗОЛОТНИКОМ
- 4. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ СО СТРУЙНОЙ ТРУБКОЙ
- 5. СХЕМЫ И ПРИНЦИПЫ ДЕЙСТВИЯ ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 6. СТАТИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 7. ДИНАМИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
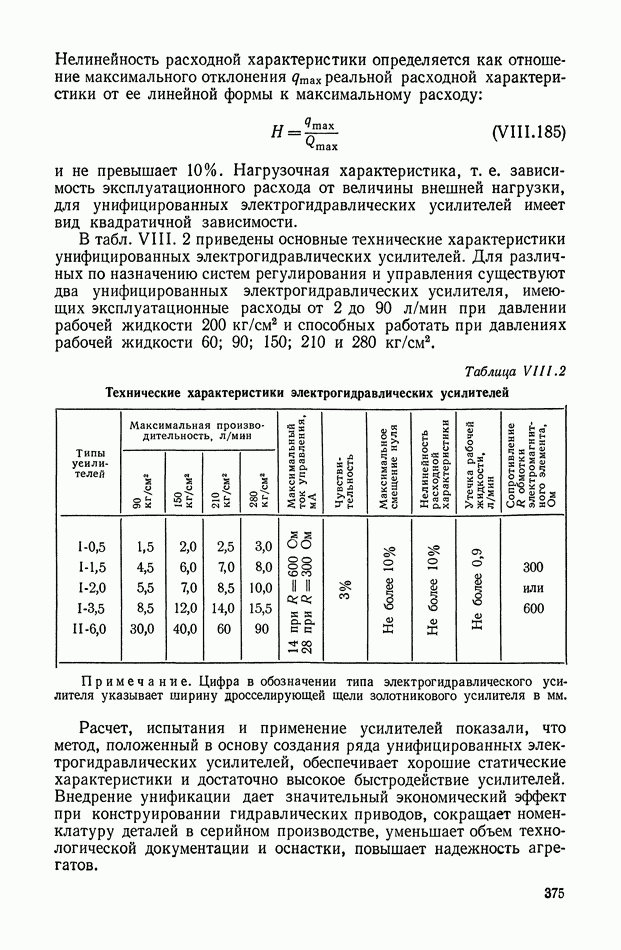
- 8. УНИФИКАЦИЯ ЭЛЕКТРОГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ ДЛЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
- ГЛАВА IX. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ И ИХ КЛАССИФИКАЦИЯ
- 2. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ СО СТРУЙНОЙ ТРУБКОЙ
- 3. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗОЛОТНИКОМ
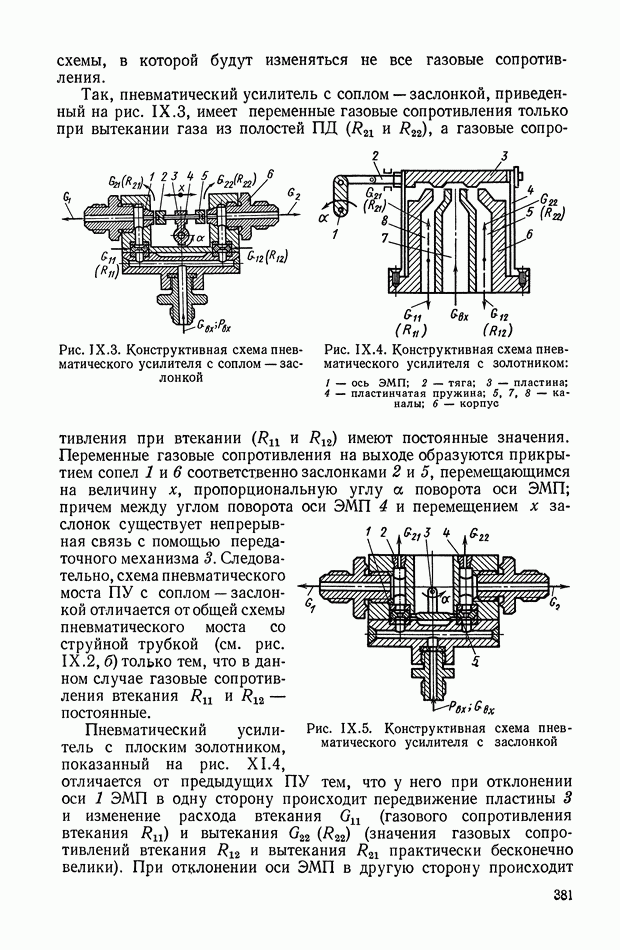
- 4. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С СОПЛОМ — ЗАСЛОНКОЙ
- 5. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗАСЛОНКОЙ
- 6. МНОГОКАСКАДНЫЕ ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- РАЗДЕЛ II. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ И УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ЛИНЕЙНЫХ ПАССИВНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Основные соотношения для синтеза пассивного RC-четырехполюсника.
- 3. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Активные четырехполюсники, получаемые с помощью конверторов отрицательного сопротивления.
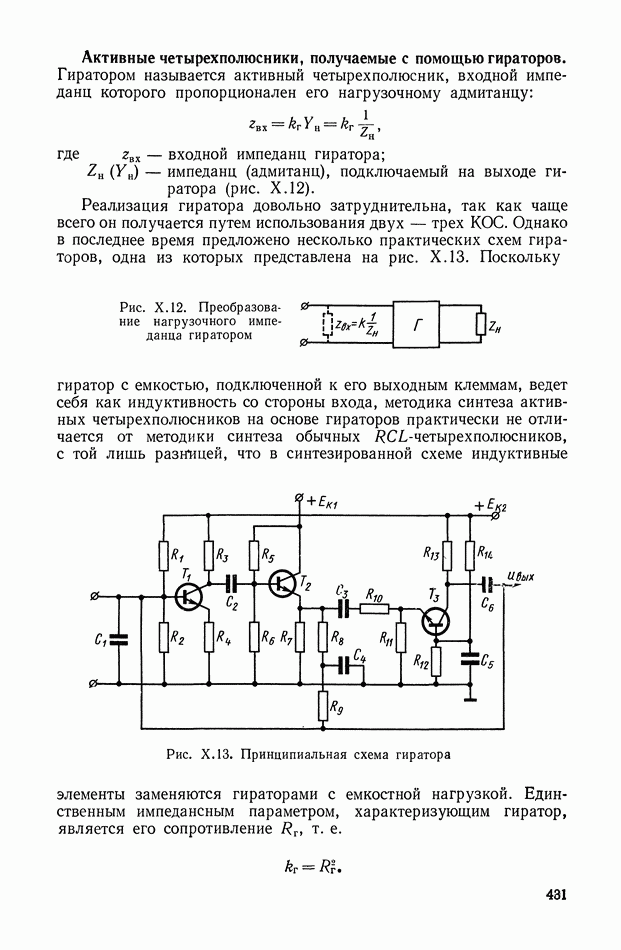
- Активные четырехполюсники, получаемые с помощью гираторов.
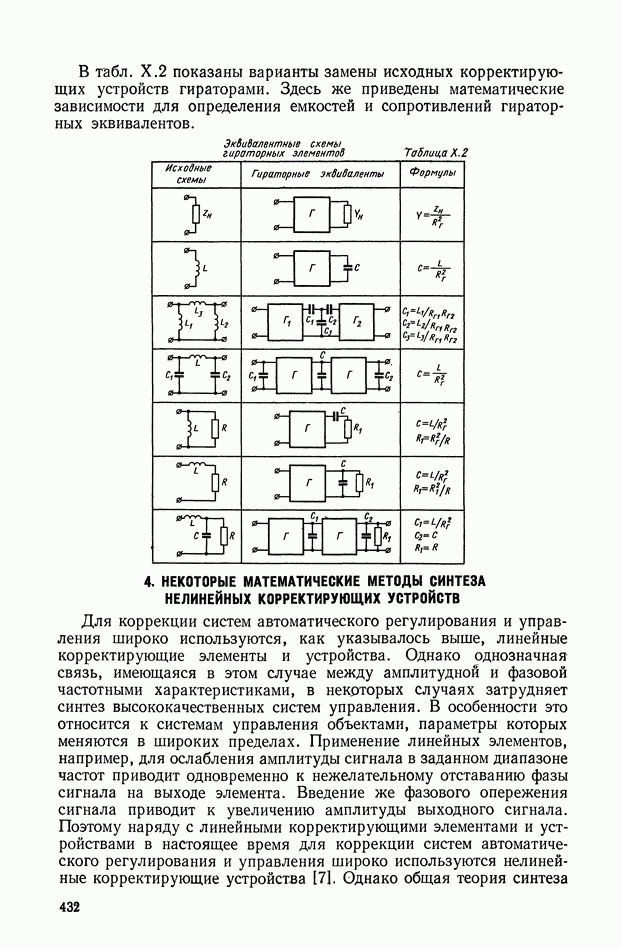
- 4. НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА НЕЛИНЕЙНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
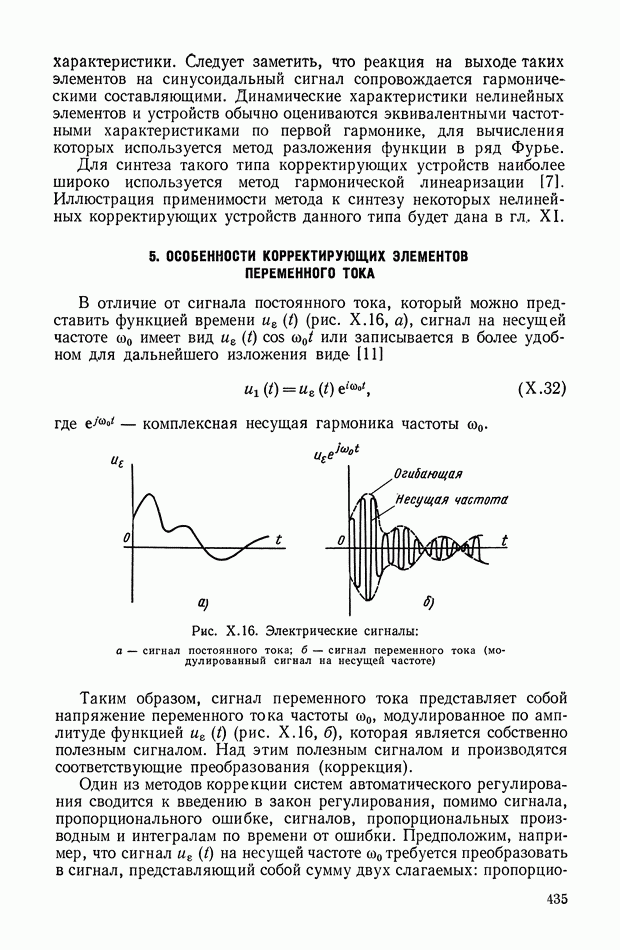
- 5. ОСОБЕННОСТИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XI. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА ПОСТОЯННОГО ТОКА
- Дифференцирующий трансформатор.
- Электрические интегрирующие элементы.
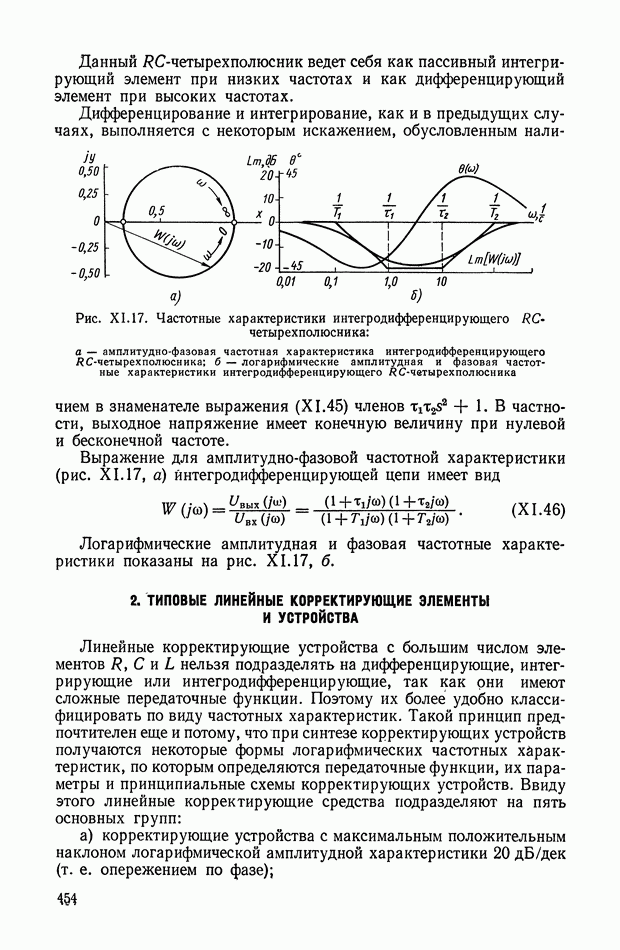
- 2. ТИПОВЫЕ ЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- 3. КОРРЕКТИРУЮЩИЕ ЧЕТЫРЕХПОЛЮСНИКИ С АКТИВНЫМИ ЭЛЕМЕНТАМИ
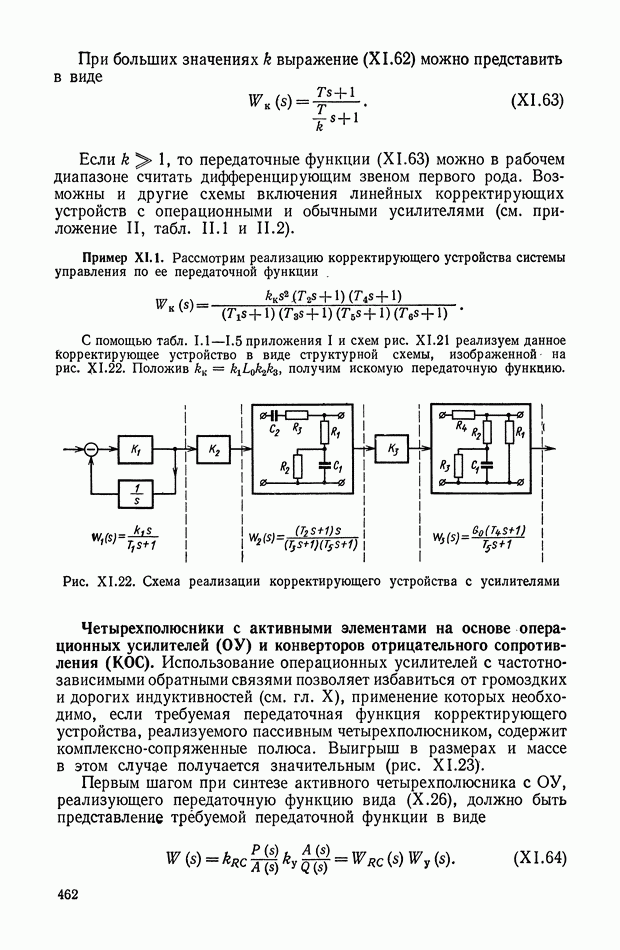
- Четырехполюсники с активными элементами на основе операционных усилителей (ОУ) и конверторов отрицательного сопротивления (КОС).
- 4. РЕАЛИЗАЦИЯ ЗАДАННОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В ВИДЕ СХЕМЫ ПАССИВНОГО ЛИНЕЙНОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА
- 5. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
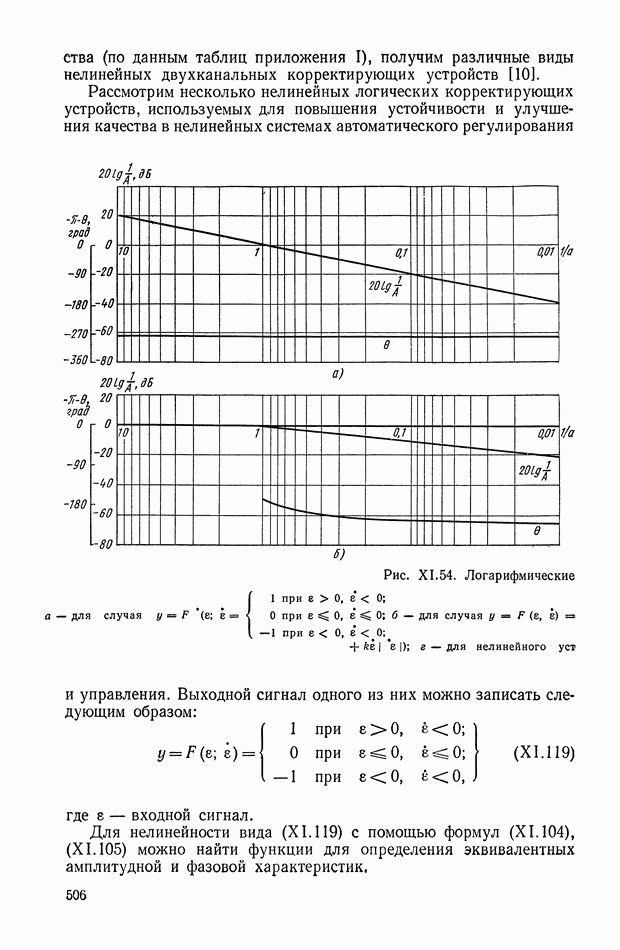
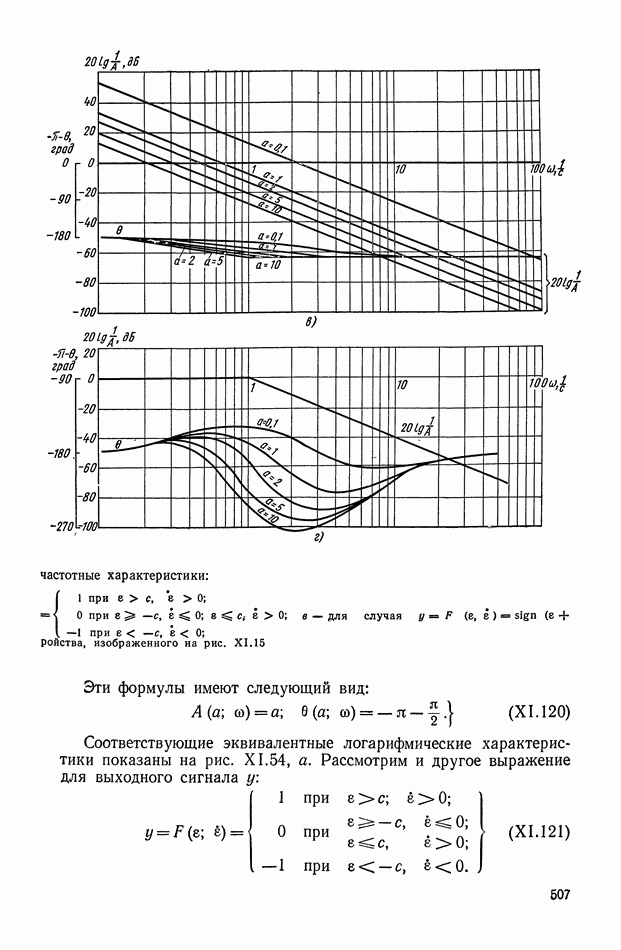
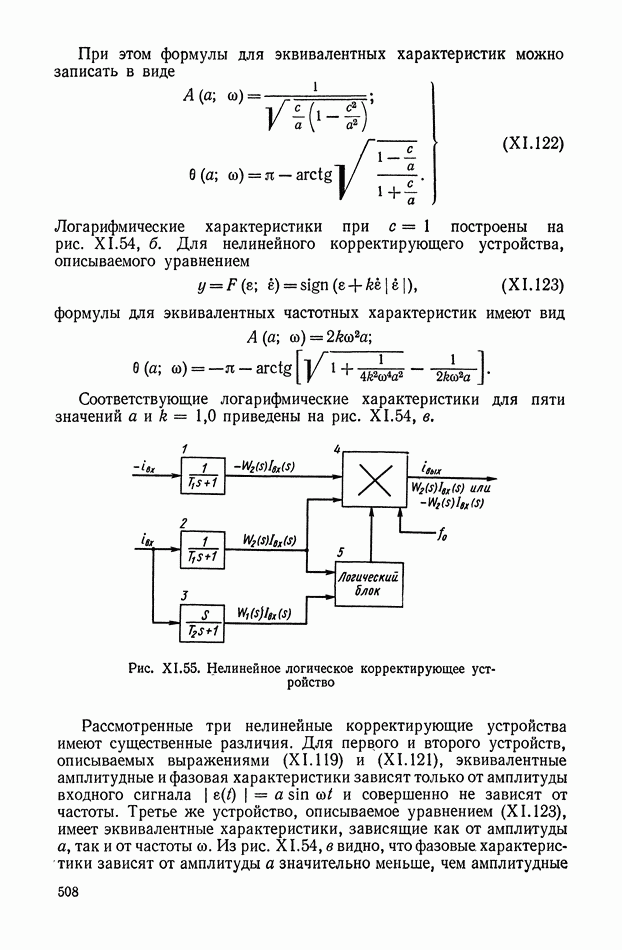
- 8. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
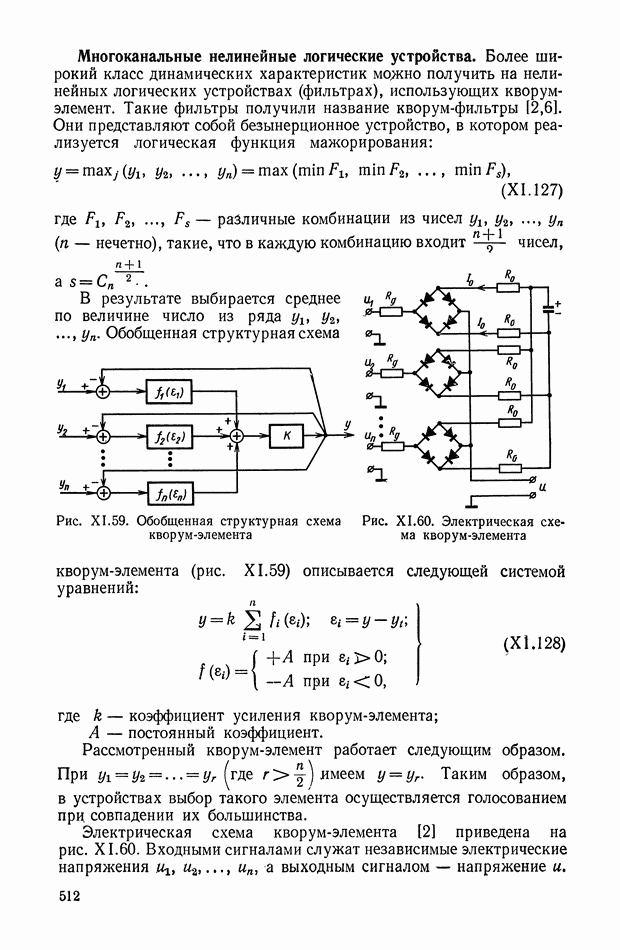
- Многоканальные нелинейные логические устройства.
- ГЛАВА XII. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- 1. КОРРЕКТИРУЮЩИЕ RLC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 2. КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 3. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 4. САМОНАСТРАИВАЮЩИЕСЯ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА
- 5. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА С ПРОМЕЖУТОЧНОЙ ДЕМОДУЛЯЦИЕЙ
- 6. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА С ПЕРЕКЛЮЧАТЕЛЯМИ
- 7. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XIII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ТАХОГЕНЕРАТОРЫ ПОСТОЯННОГО ТОКА
- Погрешности тахогенератора постоянного тока.
- 2. НЕКОТОРЫЕ СХЕМЫ ПРИМЕНЕНИЯ ТАХОГЕНЕРАТОРОВ
- 3. АСИНХРОННЫЕ ТАХОГЕНЕРАТОРЫ
- 4. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ ИЗМЕРЕНИЯ СКОРОСТИ ЭЛЕКТРОДВИГАТЕЛЕЙ
- Пассивный тахометрический мост переменного тока.
- Активные тахометрические мосты.
- ГЛАВА XIV. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ГИДРАВЛИЧЕСКИХ СИСТЕМАХ
- 3. ЭЛЕКТРИЧЕСКИЕ ОБРАТНЫЕ СВЯЗИ
- 4. ЖЕСТКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
- 5. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ СИСТЕМАХ
- 6. СЛОЖНЫЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
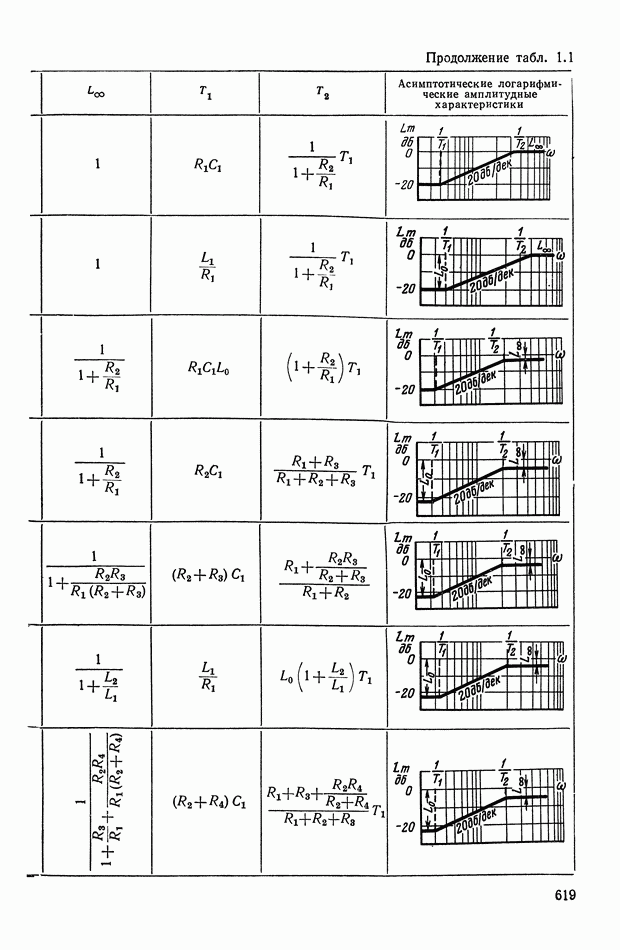
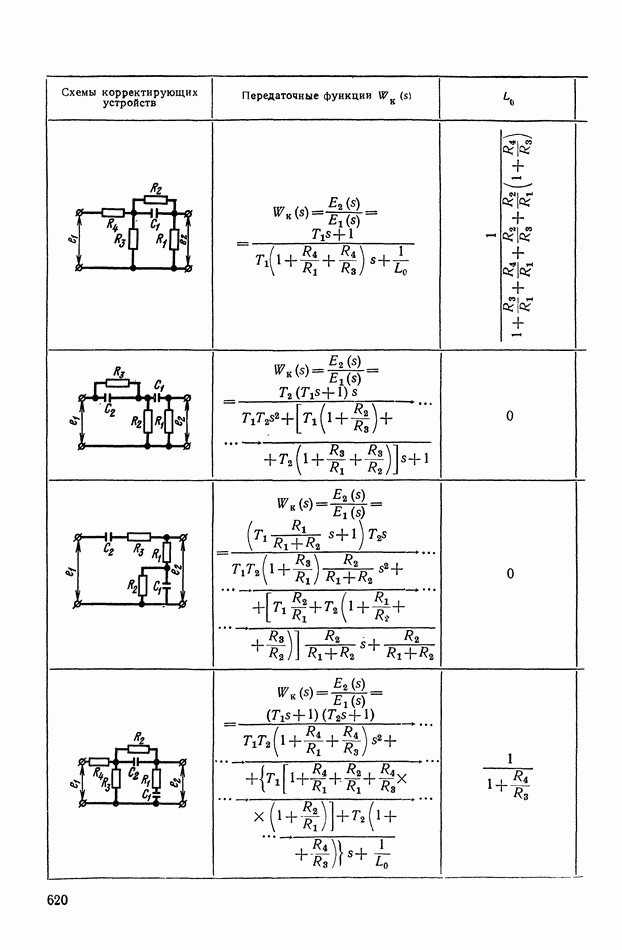
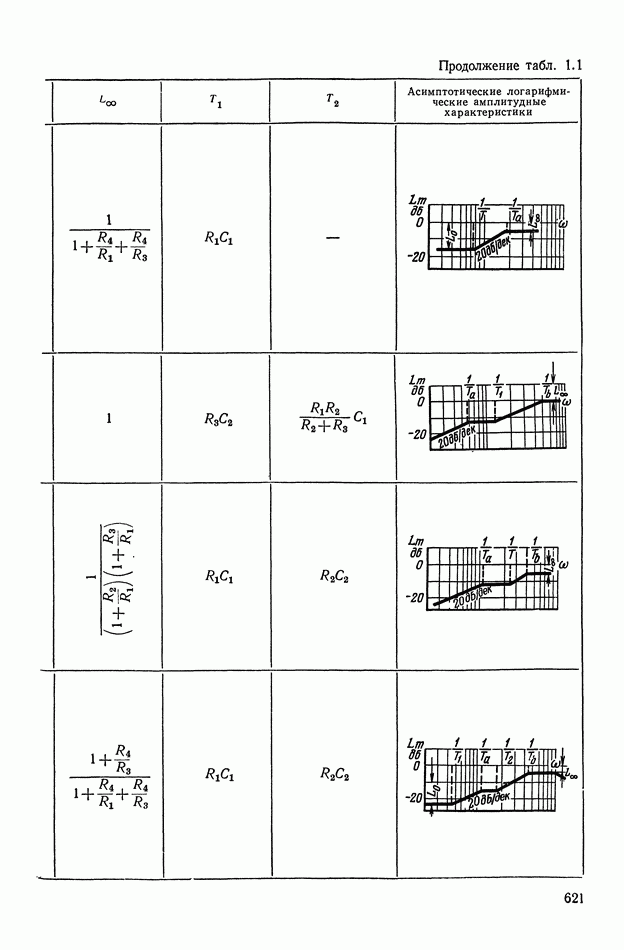
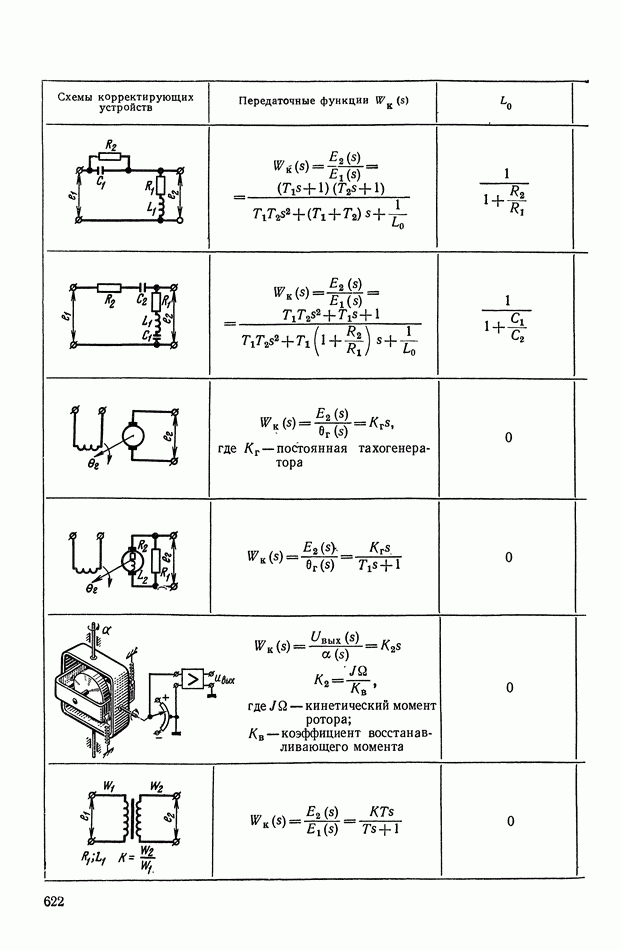
- ПРИЛОЖЕНИЕ 1. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПОСТОЯННОГО ТОКА
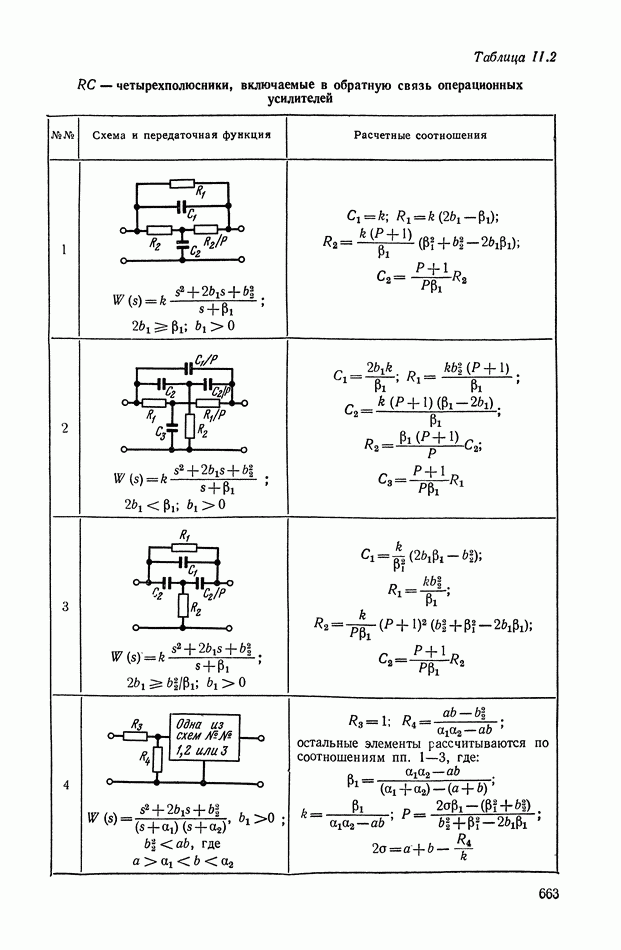
- ПРИЛОЖЕНИЕ II. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ОСНОВЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
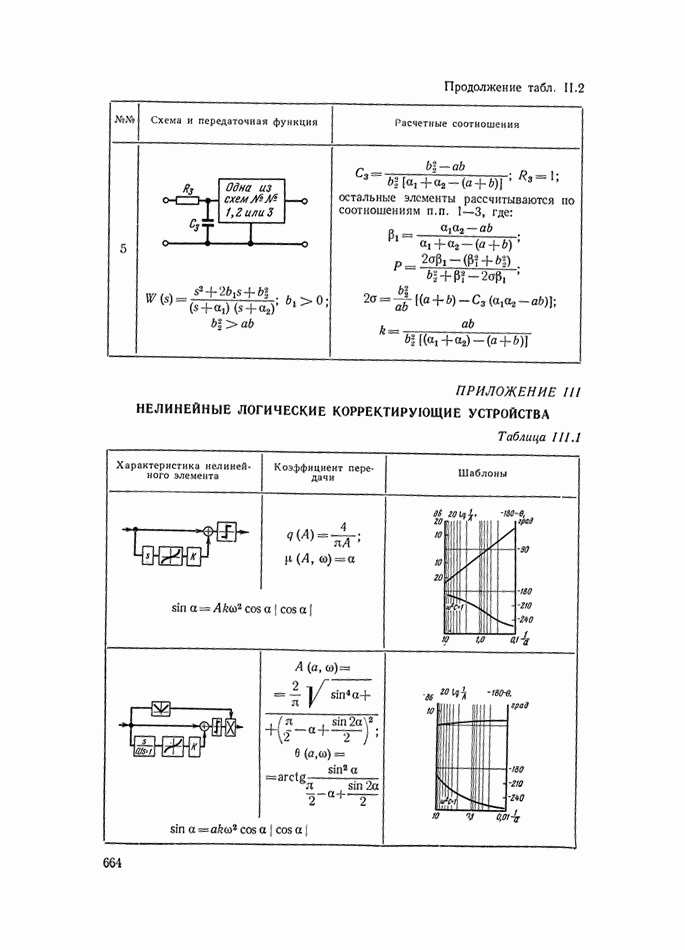
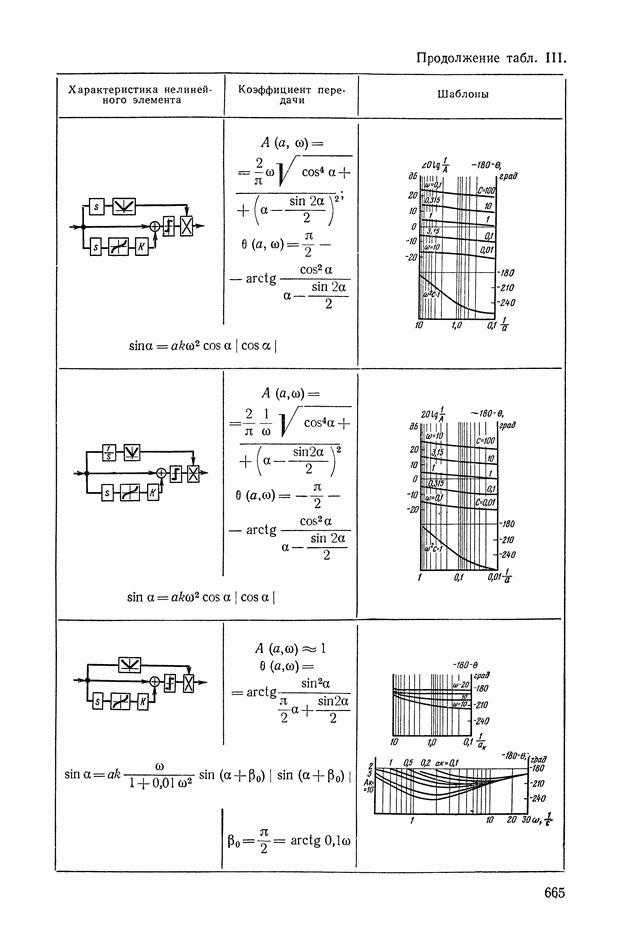
- ПРИЛОЖЕНИЕ III. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ