| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. ОСОБЕННОСТИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ ПЕРЕМЕННОГО ТОКА
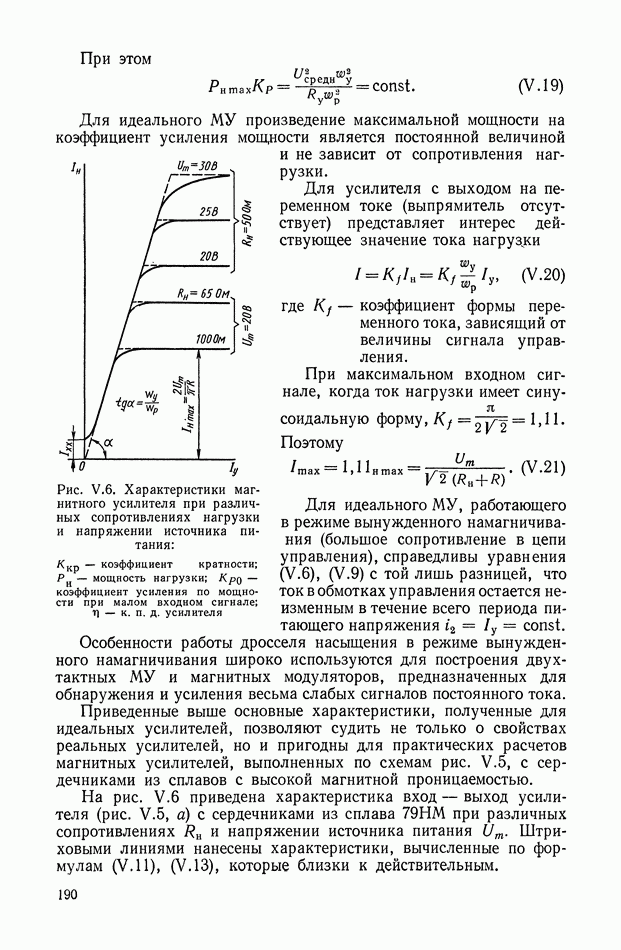
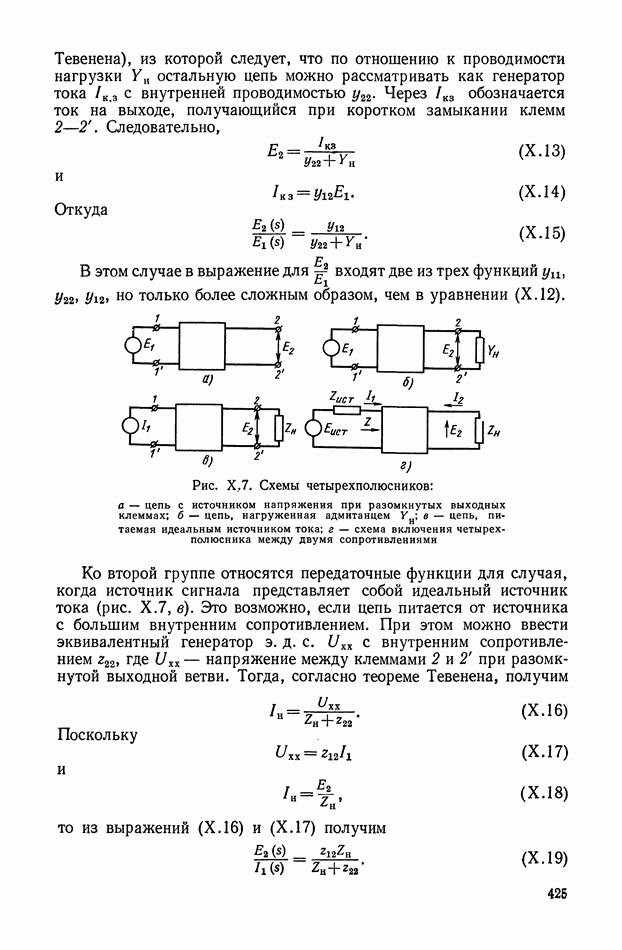
В отличие от сигнала постоянного тока, который можно представить функцией времени  (рис. Х.16, а), сигнал на несущей частоте
(рис. Х.16, а), сигнал на несущей частоте  имеет вид
имеет вид  или записывается в более удобном для дальнейшего изложения виде [11]
или записывается в более удобном для дальнейшего изложения виде [11]

где  — комплексная несущая гармоника частоты
— комплексная несущая гармоника частоты 

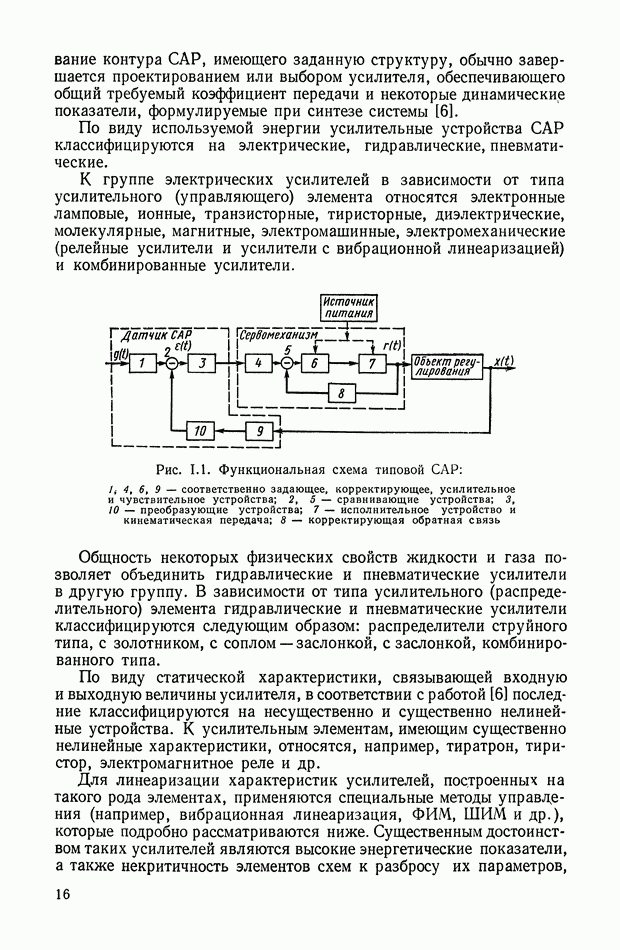
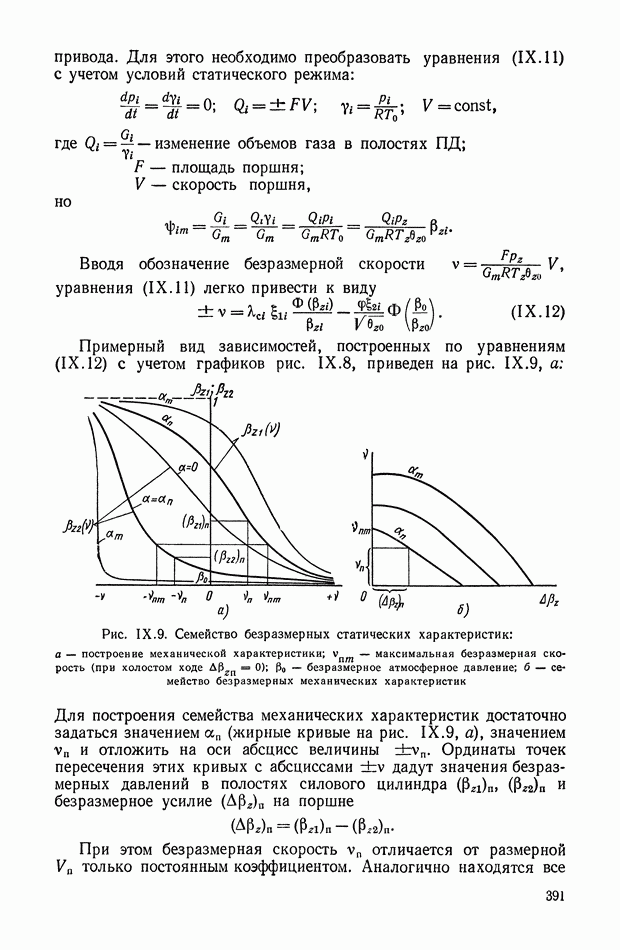
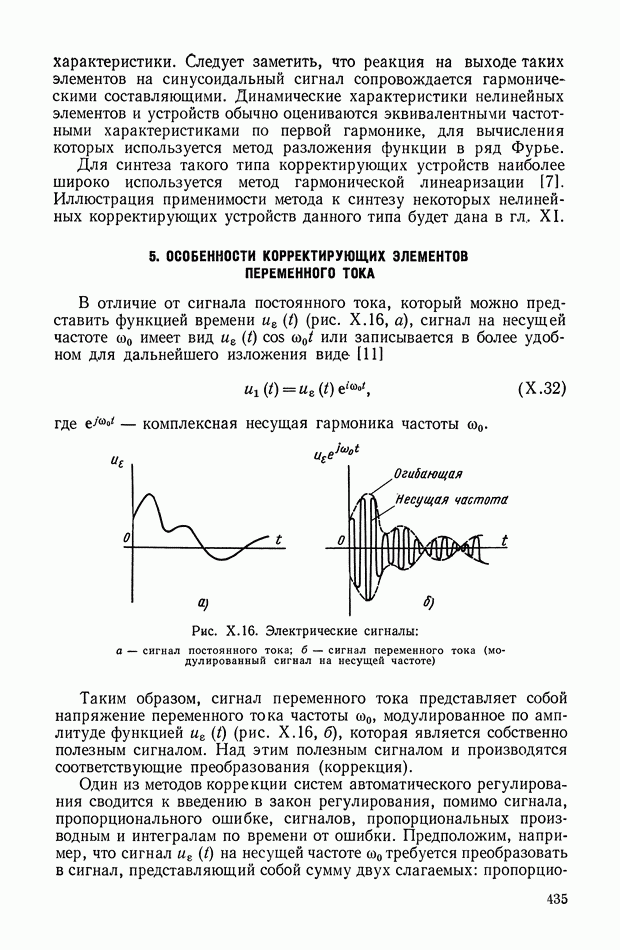
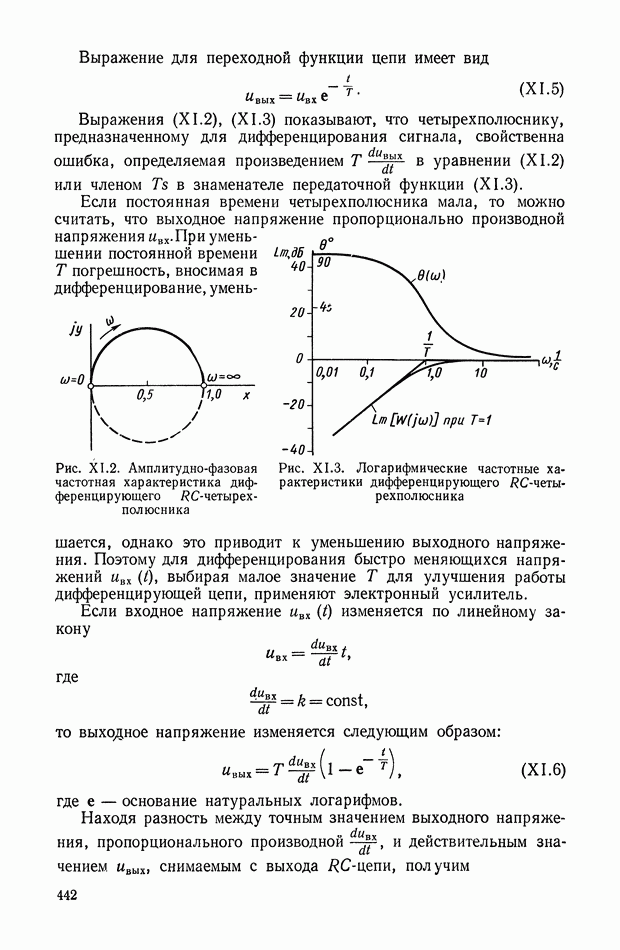
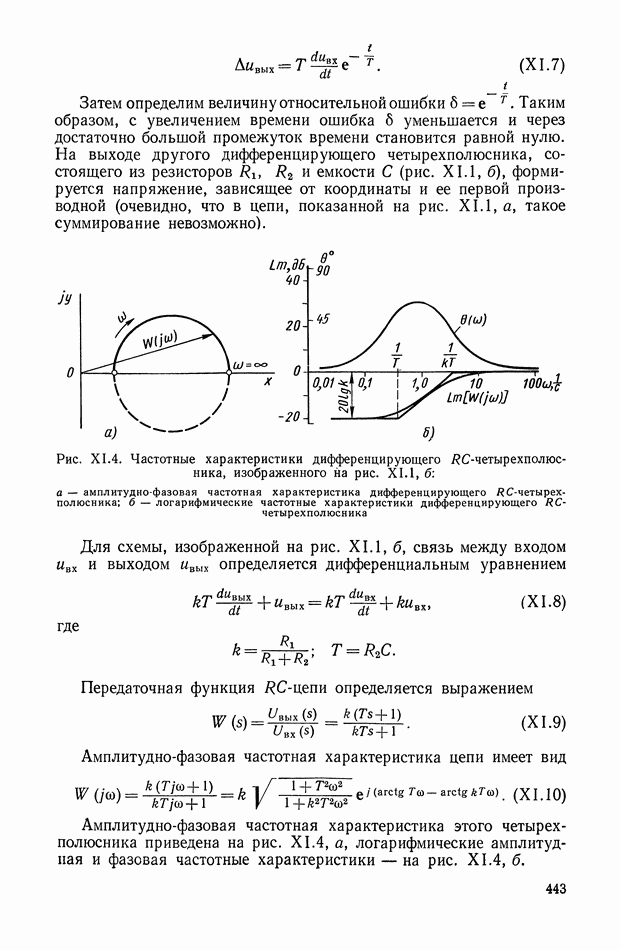
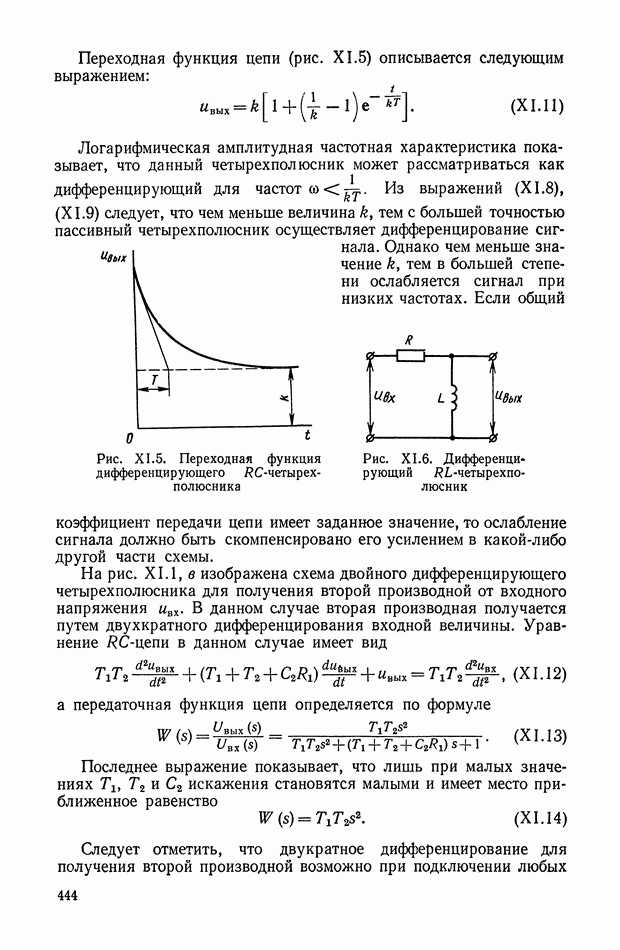
Рис. Х.16. Электрические сигналы: а — сигнал постоянного тока; б — сигнал переменного тока (модулированный сигнал на несущей частоте)
Таким образом, сигнал переменного тока представляет собой напряжение переменного тока частоты  модулированное по амплитуде функцией
модулированное по амплитуде функцией  (рис. Х.16, б), которая является собственно полезным сигналом. Над этим полезным сигналом и производятся соответствующие преобразования (коррекция).
(рис. Х.16, б), которая является собственно полезным сигналом. Над этим полезным сигналом и производятся соответствующие преобразования (коррекция).
Один из методов коррекции систем автоматического регулирования сводится к введению в закон регулирования, помимо сигнала, пропорционального ошибке, сигналов, пропорциональных производным и интегралам по времени от ошибки. Предположим, например, что сигнал  на несущей частоте
на несущей частоте  требуется преобразовать в сигнал, представляющий собой сумму двух слагаемых: пропорционального
требуется преобразовать в сигнал, представляющий собой сумму двух слагаемых: пропорционального
сигналу ошибки и пропорционального первой производной по времени от этого сигнала, т. е.

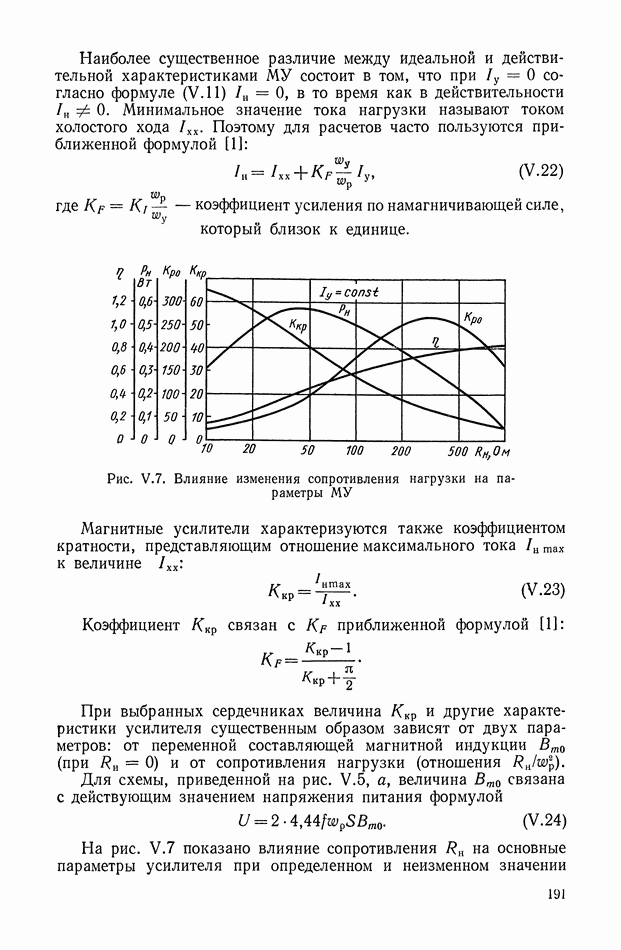
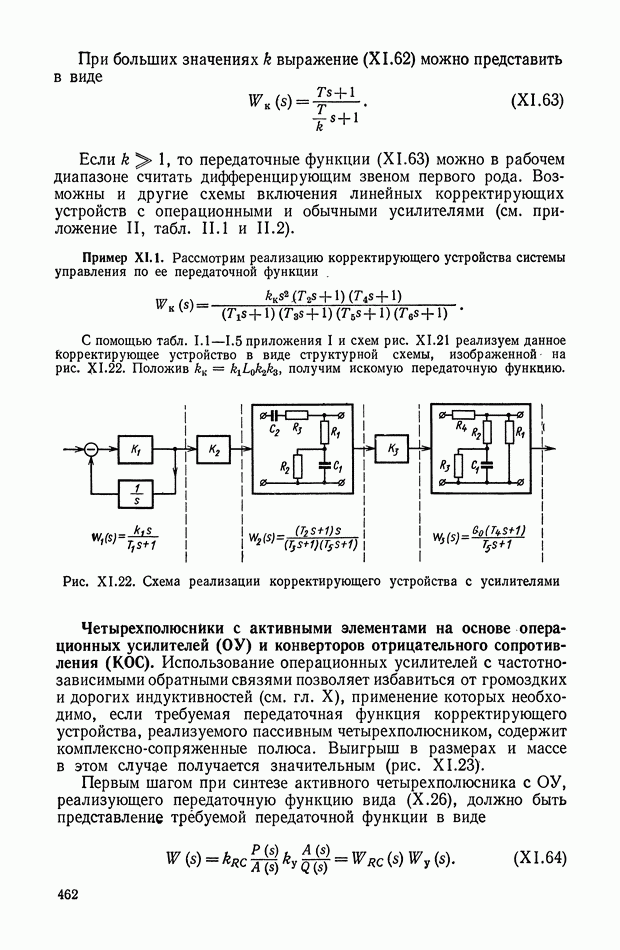
Для такого преобразования необходим корректирующий элемент с передаточной функцией

В самом деле, преобразование Лапласа (изображение) при нулевых начальных условиях сигнала (Х.ЗЗ) на выходе корректирующего элемента имеет вид

а изображение сигнала (Х.32) на его входе


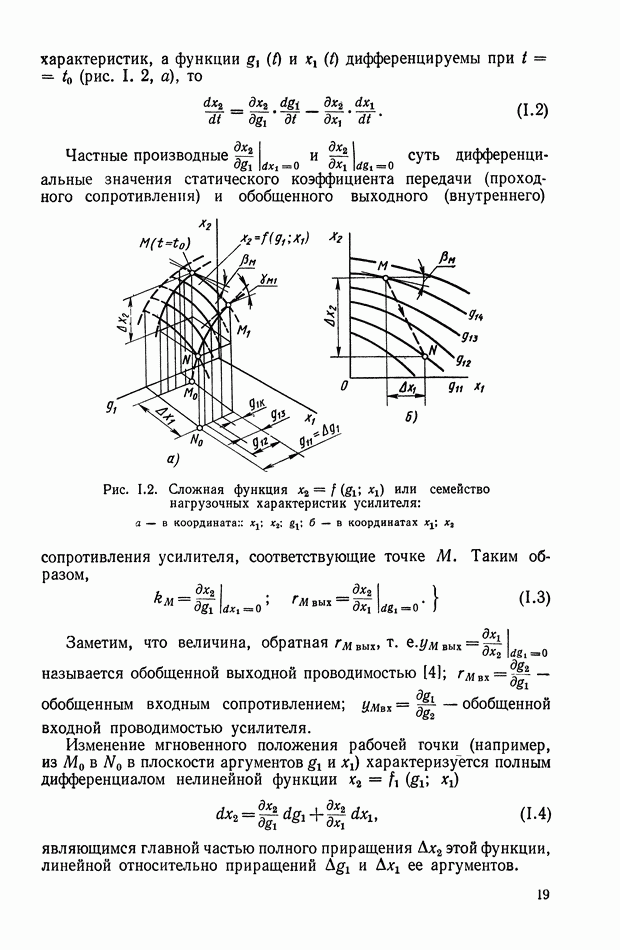
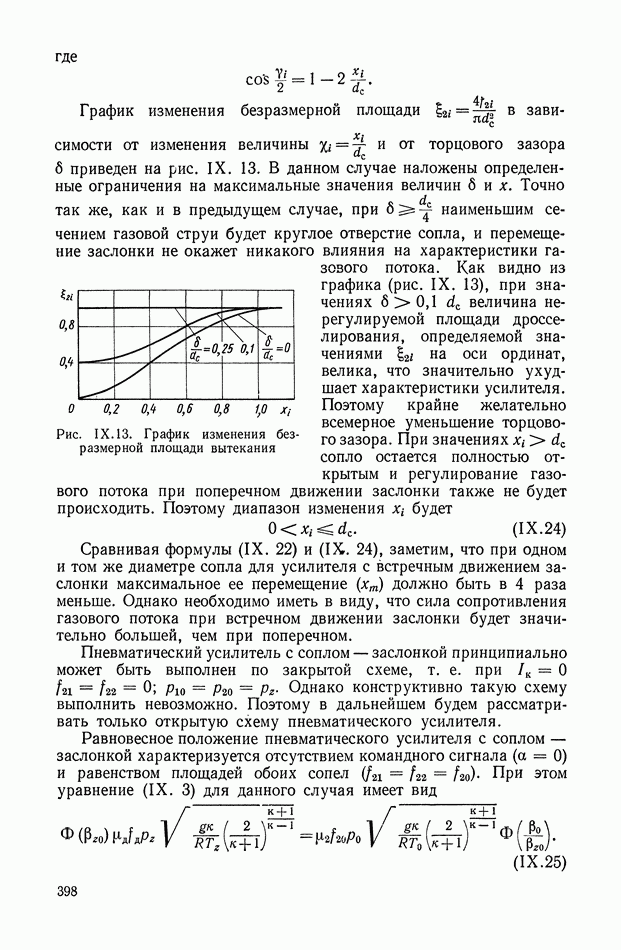
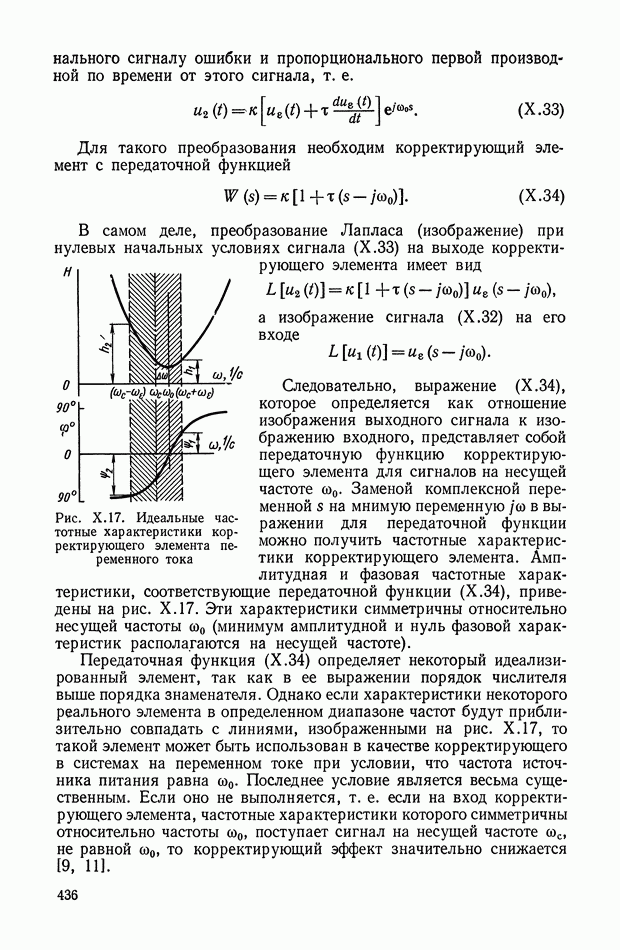
Рис. Х.17. Идеальные частотные характеристики корректирующего элемента переменного тока
Следовательно, выражение  которое определяется как отношение изображения выходного сигнала к изображению входного, представляет собой передаточную функцию корректирующего элемента для сигналов на несущей частоте
которое определяется как отношение изображения выходного сигнала к изображению входного, представляет собой передаточную функцию корректирующего элемента для сигналов на несущей частоте  Заменой комплексной переменной
Заменой комплексной переменной  на мнимую переменную
на мнимую переменную  в выражении для передаточной функции можно получить частотные характеристики корректирующего элемента. Амплитудная и фазовая частотные характеристики, соответствующие передаточной функции
в выражении для передаточной функции можно получить частотные характеристики корректирующего элемента. Амплитудная и фазовая частотные характеристики, соответствующие передаточной функции  приведены на рис. Х.17. Эти характеристики симметричны относительно несущей частоты
приведены на рис. Х.17. Эти характеристики симметричны относительно несущей частоты  (минимум амплитудной и нуль фазовой характеристик располагаются на несущей частоте).
(минимум амплитудной и нуль фазовой характеристик располагаются на несущей частоте).
Передаточная функция  определяет некоторый идеализированный элемент, так как в ее выражении порядок числителя выше порядка знаменателя. Однако если характеристики некоторого реального элемента в определенном диапазоне частот будут приблизительно совпадать с линиями, изображенными на рис.
определяет некоторый идеализированный элемент, так как в ее выражении порядок числителя выше порядка знаменателя. Однако если характеристики некоторого реального элемента в определенном диапазоне частот будут приблизительно совпадать с линиями, изображенными на рис.  то такой элемент может быть использован в качестве корректирующего в системах на переменном токе при условии, что частота источника питания равна
то такой элемент может быть использован в качестве корректирующего в системах на переменном токе при условии, что частота источника питания равна  Последнее условие является весьма существенным. Если оно не выполняется, т. е. если на вход корректирующего элемента, частотные характеристики которого симметричны относительно частоты
Последнее условие является весьма существенным. Если оно не выполняется, т. е. если на вход корректирующего элемента, частотные характеристики которого симметричны относительно частоты  поступает сигнал на несущей частоте
поступает сигнал на несущей частоте  , не равной
, не равной  то корректирующий эффект значительно снижается [9, 11].
то корректирующий эффект значительно снижается [9, 11].
Рассмотрим, например, случай, когда на вход корректирующего элемента с передаточной функцией  поступает косинусоидальный сигнал, имеющий единичную амплитуду, на несущей частоте сос:
поступает косинусоидальный сигнал, имеющий единичную амплитуду, на несущей частоте сос:

где  — частота огибающей.
— частота огибающей.
На входе такого элемента действует два косинусоидальных сигнала с частотами  Установившиеся вынужденные колебания на выходе представляют собой косинусоиды тех же частот, но отличающиеся от входных по амплитуде и фазе. Выходной сигнал
Установившиеся вынужденные колебания на выходе представляют собой косинусоиды тех же частот, но отличающиеся от входных по амплитуде и фазе. Выходной сигнал

где

После тригонометрических преобразований выражение  лримет вид
лримет вид

где

Выражение  показывает, что сигнал на выходе элемента представляет собой сумму двух составляющих, основной с амплитудой
показывает, что сигнал на выходе элемента представляет собой сумму двух составляющих, основной с амплитудой  и сдвинутой на 90° относительно основной (квадратурная составляющая) с амплитудой
и сдвинутой на 90° относительно основной (квадратурная составляющая) с амплитудой  Сдвиги фаз огибающей
Сдвиги фаз огибающей  и несущей
и несущей  одинаковые для обеих составляющих, определяются, как и величины
одинаковые для обеих составляющих, определяются, как и величины  выражениями
выражениями  Значения этих фаз и амплитуд с достаточной точностью можно определить графически по частотным характеристикам, приведенным на рис. Х.17, с использованием выражений
Значения этих фаз и амплитуд с достаточной точностью можно определить графически по частотным характеристикам, приведенным на рис. Х.17, с использованием выражений 
Теперь рассмотрим явления, происходящие в системах переменного тока при неравенстве частоты  на которую рассчитан корректирующий элемент, частоте сос источника питания системы. Исследуем случай, когда корректирующий элемент с передаточной функцией
на которую рассчитан корректирующий элемент, частоте сос источника питания системы. Исследуем случай, когда корректирующий элемент с передаточной функцией  применяется для стабилизации САР, исполнительным элементом которой является двухфазный асинхронный электродвигатель. Известно, что он нормально работает, когда постоянный
применяется для стабилизации САР, исполнительным элементом которой является двухфазный асинхронный электродвигатель. Известно, что он нормально работает, когда постоянный
фазовый сдвиг между напряжениями на его обмотках составляет около 90°. Для соблюдения этого условия в одну из обмоток включается последовательно емкость, создающая необходимое реактивное сопротивление.
Если в контуре системы регулирования имеются элементы, дополнительно изменяющие указанный фазовый сдвиг: уменьшающие или увеличивающие его по сравнению с оптимальным (90°), то момент на валу электродвигателя будет уменьшаться вплоть до нуля (при фазовых сдвигах, близких к нулю или 180°). Поэтому для нормального функционирования САР необходимо, чтобы корректирующий элемент не сдвигал фазу несущей частоты, т. е. чтобы значение  при всех условиях было постоянным, равным нулю. Кроме того, известно, что для получения наилучшего корректирующего эффекта нужно обеспечить максимальный положительный сдвиг фазы огибающей
при всех условиях было постоянным, равным нулю. Кроме того, известно, что для получения наилучшего корректирующего эффекта нужно обеспечить максимальный положительный сдвиг фазы огибающей 
Полученные соотношения  показывают, что эти условия могут быть выполнены лишь в случае, если несущая частота сигнала сос будет равна частоте
показывают, что эти условия могут быть выполнены лишь в случае, если несущая частота сигнала сос будет равна частоте  на которую рассчитан корректирующий элемент. При соблюдении равенства сос
на которую рассчитан корректирующий элемент. При соблюдении равенства сос  на выходе корректирующей цепи будет действовать только основная составляющая сигнала с амплитудой
на выходе корректирующей цепи будет действовать только основная составляющая сигнала с амплитудой  амплитуда
амплитуда  квадратурной составляющей будет равна нулю. Это благоприятно скажется на работе электродвигателя, так как квадратурная составляющая, не участвующая в образовании движущего момента, не будет его перегружать.
квадратурной составляющей будет равна нулю. Это благоприятно скажется на работе электродвигателя, так как квадратурная составляющая, не участвующая в образовании движущего момента, не будет его перегружать.
Соотношения  также показывают, что если сос
также показывают, что если сос  то не только амплитуда квадратурной составляющей
то не только амплитуда квадратурной составляющей  но и сдвиг фазы несущей
но и сдвиг фазы несущей  равен нулю. Амплитуда основной составляющей при этом
равен нулю. Амплитуда основной составляющей при этом

а сдвиг фазы огибающей  принимает максимальное значение
принимает максимальное значение  Чем больше несущая частота сос входного сигнала отличается от частоты
Чем больше несущая частота сос входного сигнала отличается от частоты  на которую рассчитан корректирующий элемент, тем больше амплитуда
на которую рассчитан корректирующий элемент, тем больше амплитуда  и сдвиг фазы
и сдвиг фазы  отличаются от нуля и тем меньше положительный сдвиг фазы
отличаются от нуля и тем меньше положительный сдвиг фазы  Если разность
Если разность  то
то  и элемент не вводит опережение по фазе, необходимое для коррекции САР. Сдвиг фазы несущей частоты
и элемент не вводит опережение по фазе, необходимое для коррекции САР. Сдвиг фазы несущей частоты  в этом случае может достигать 70°, фазовый угол между напряжениями, питающими обмотки двухфазного электродвигателя, будет значительно отличаться от оптимального (90°).
в этом случае может достигать 70°, фазовый угол между напряжениями, питающими обмотки двухфазного электродвигателя, будет значительно отличаться от оптимального (90°).
Таким образом, основное условие эффективной работы корректирующих элементов переменного тока определяется равенством

При выполнении этого равенства корректирующий элемент не будет искажать несущую гармонику  и будет выполнять надле
и будет выполнять надле
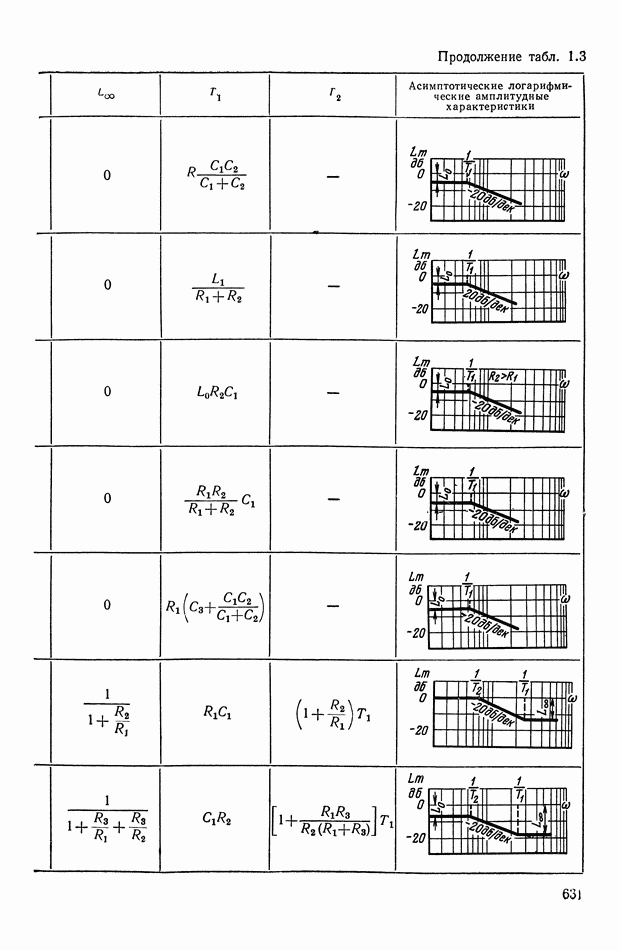
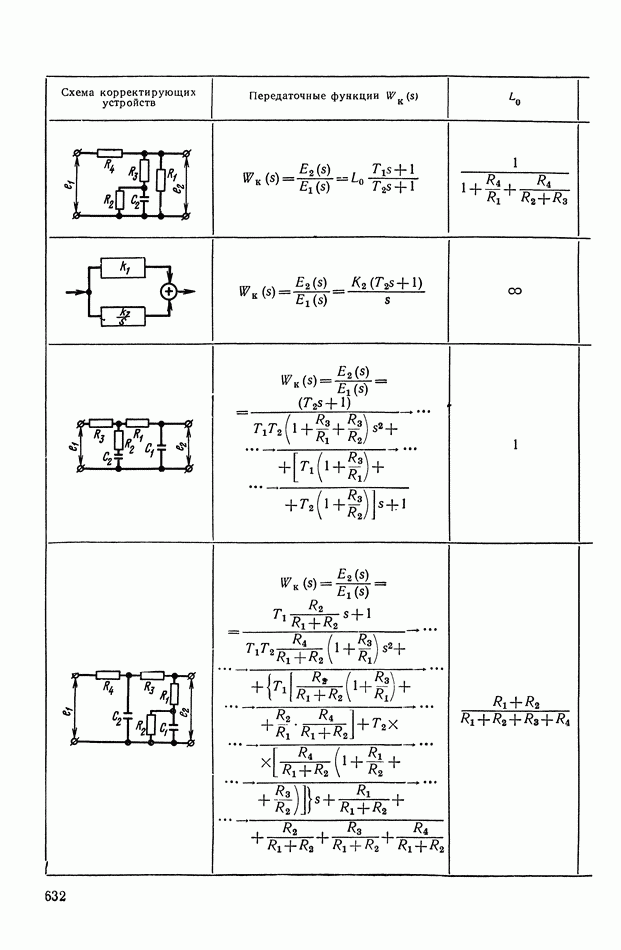
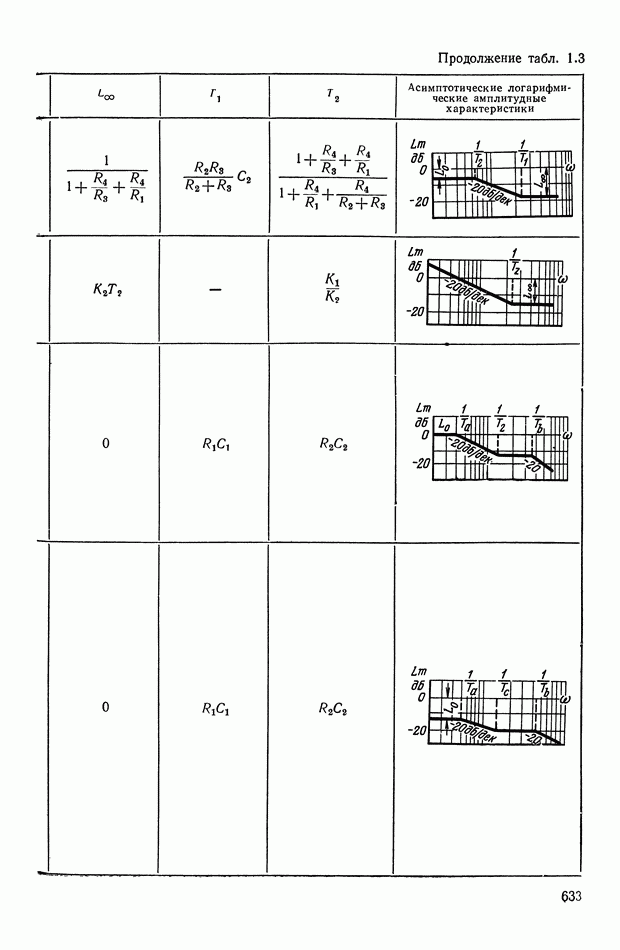
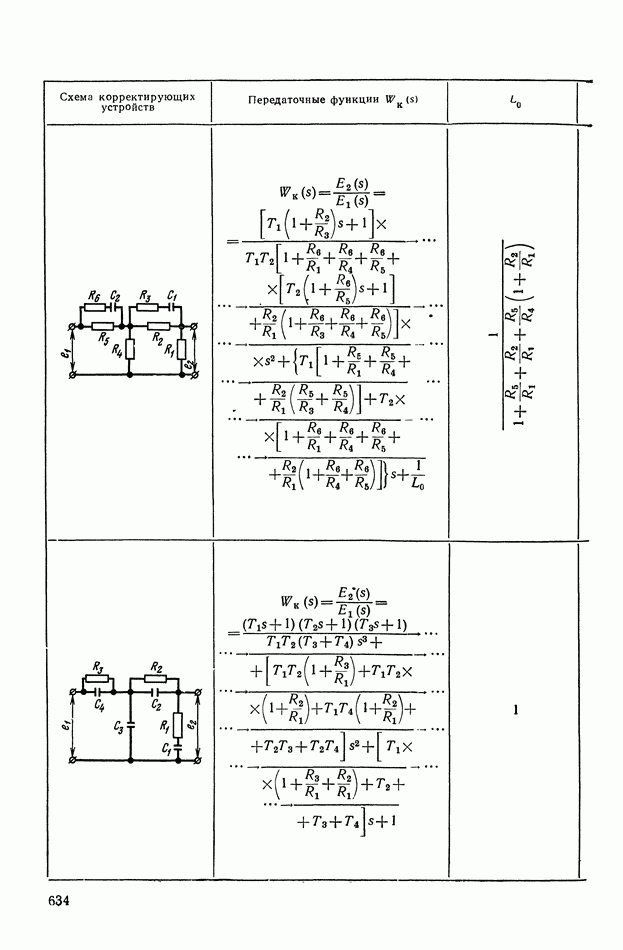
жащие преобразования огибающей — функции  в выражении (Х.32). Для подобных преобразований сигналов переменного тока используются пассивные и активные электрические RCL-четырехполюсники, корректирующие устройства с промежуточной демодуляцией сигнала, синхронно коммутируемые электрические цепи или цепи с прерывателями, электромеханические корректирующие устройства и др.
в выражении (Х.32). Для подобных преобразований сигналов переменного тока используются пассивные и активные электрические RCL-четырехполюсники, корректирующие устройства с промежуточной демодуляцией сигнала, синхронно коммутируемые электрические цепи или цепи с прерывателями, электромеханические корректирующие устройства и др.
ЛИТЕРАТУРА
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА САР
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ЛИНЕЙНЫХ УСИЛИТЕЛЬНЫХ УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ УСИЛИТЕЛЬНОГО УСТРОЙСТВА БЕЗ ОБРАТНОЙ СВЯЗИ
- 3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ, СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ОСОБЕННОСТИ УСИЛИТЕЛЬНОГО УСТРОЙСТВА С ОБРАТНОЙ СВЯЗЬЮ
- 4. КЛАССИФИКАЦИЯ И СВОЙСТВА УСИЛИТЕЛЬНЫХ УСТРОЙСТВ С ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 5. ВЫБОР И РАСЧЕТ УСИЛИТЕЛЬНОГО УСТРОЙСТВА
- ГЛАВА II. ЭЛЕКТРОННЫЕ ЛАМПОВЫЕ И ИОННЫЕ УСИЛИТЕЛИ
- 1. ОСНОВЫ ТОПОЛОГИЧЕСКОГО АНАЛИЗА СХЕМ ЛИНЕЙНЫХ ЭЛЕКТРОННЫХ ЛАМПОВЫХ УСИЛИТЕЛЕЙ
- 2. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПОСТОЯННОГО ТОКА
- 3. БАЛАНСНЫЕ МОСТОВЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- 4. СТАБИЛИЗАЦИЯ КОЭФФИЦИЕНТА УСИЛЕНИЯ
- 5. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
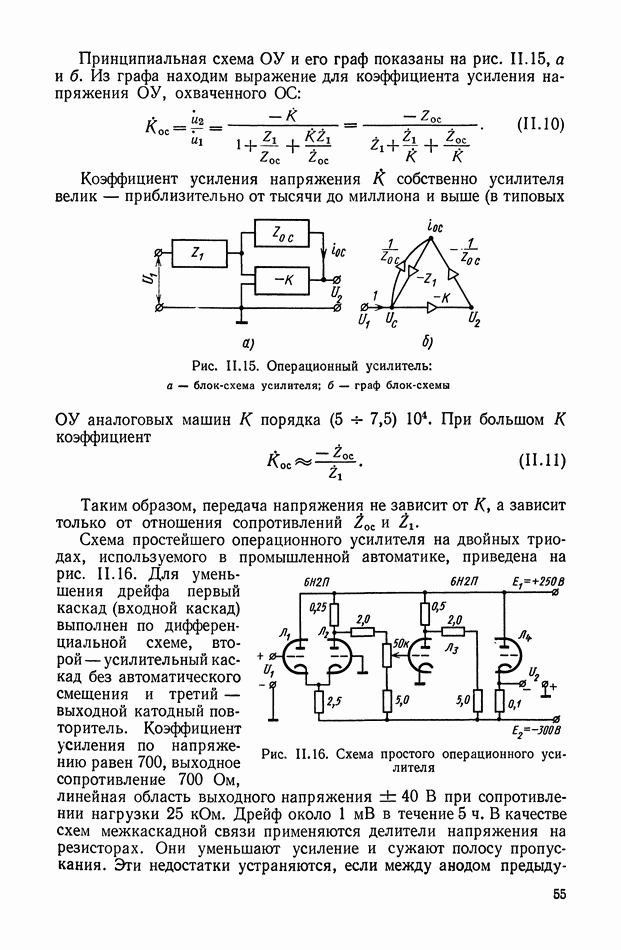
- 6. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- 7. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
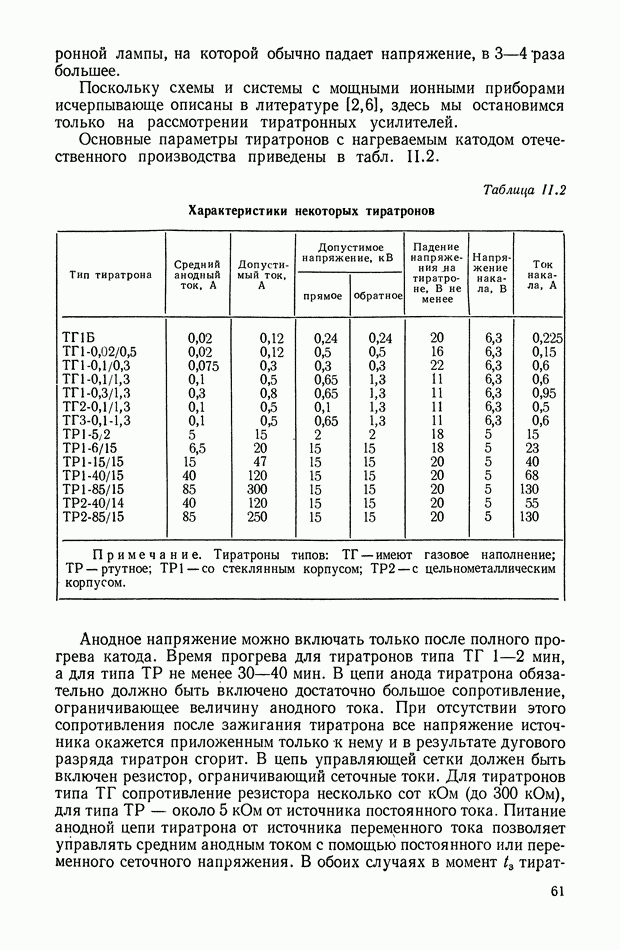
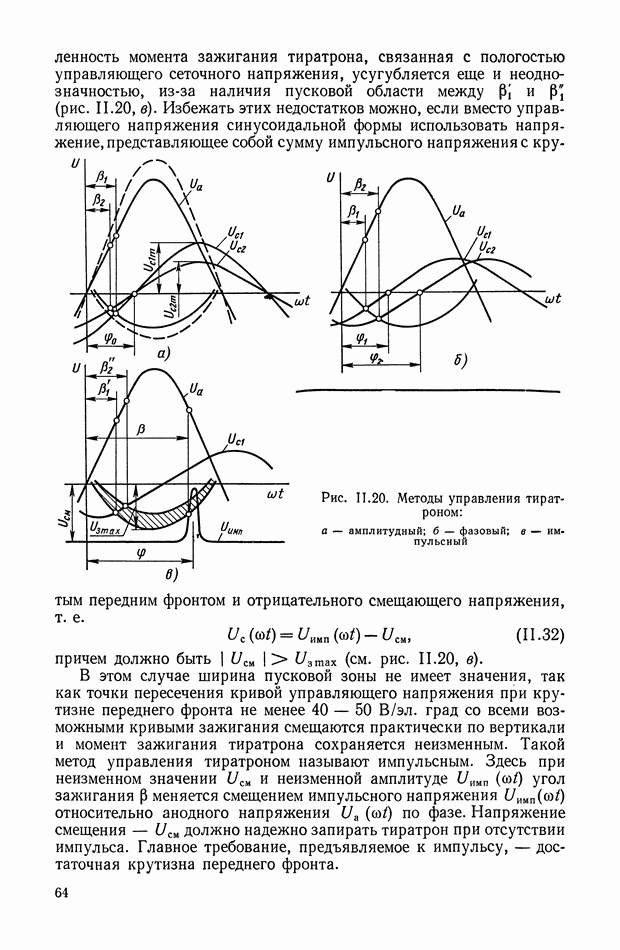
- 8. ОБЩИЕ СВОЙСТВА ИОННОГО (ТИРАТРОННОГО) УСИЛИТЕЛЯ МЕТОДЫ УПРАВЛЕНИЯ ТИРАТРОНОМ
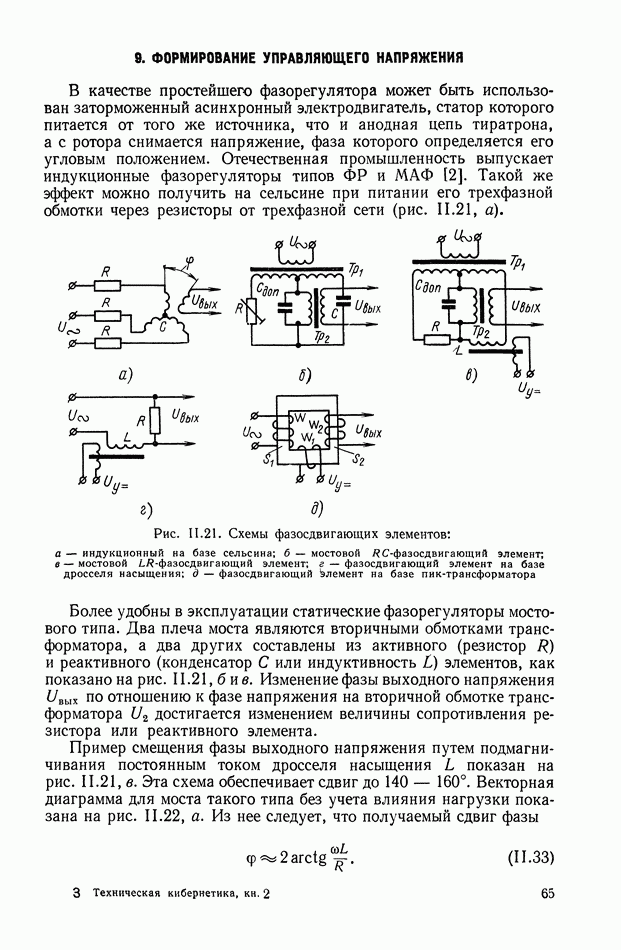
- 9. ФОРМИРОВАНИЕ УПРАВЛЯЮЩЕГО НАПРЯЖЕНИЯ
- 10. РАСЧЕТ ЭЛЕМЕНТОВ СХЕМ ТИРАТРОННОГО УСИЛИТЕЛЯ
- ГЛАВА III. ПОЛУПРОВОДНИКОВЫЕ И ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
- Цепи смещения.
- Цепи связи.
- 2. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ СРЕДНЕГО ЗНАЧЕНИЯ ТОКА
- Полупроводниковые демодуляторы.
- 3. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ В РЕЖИМЕ ПЕРЕКЛЮЧЕНИЯ
- Режимы импульсного регулирования мощности.
- Управление силовыми транзисторами.
- 4. ТРАНЗИСТОРНЫЕ УСТРОЙСТВА УПРАВЛЕНИЯ ЭЛЕКТРОДВИГАТЕЛЯМИ И ЭЛЕКТРОМАГНИТНЫМИ МЕХАНИЗМАМИ
- 5. ТИРИСТОРЫ. ХАРАКТЕРИСТИКИ, ПАРАМЕТРЫ И СВОЙСТВА
- 6. СПОСОБЫ И УСТРОЙСТВА УПРАВЛЕНИЯ ТИРИСТОРАМИ
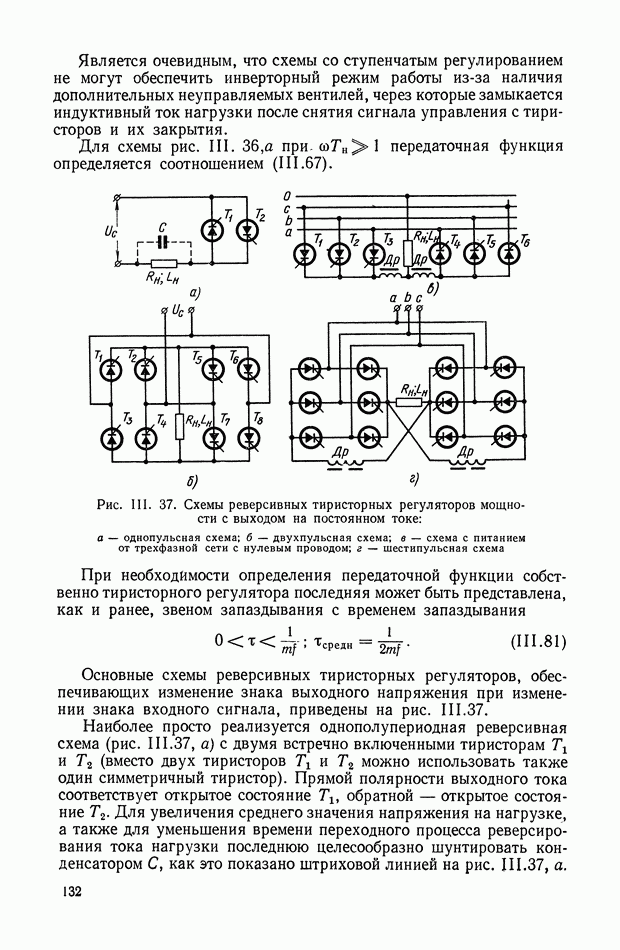
- 7. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ (РЕГУЛИРУЕМЫЕ ВЫПРЯМИТЕЛИ)
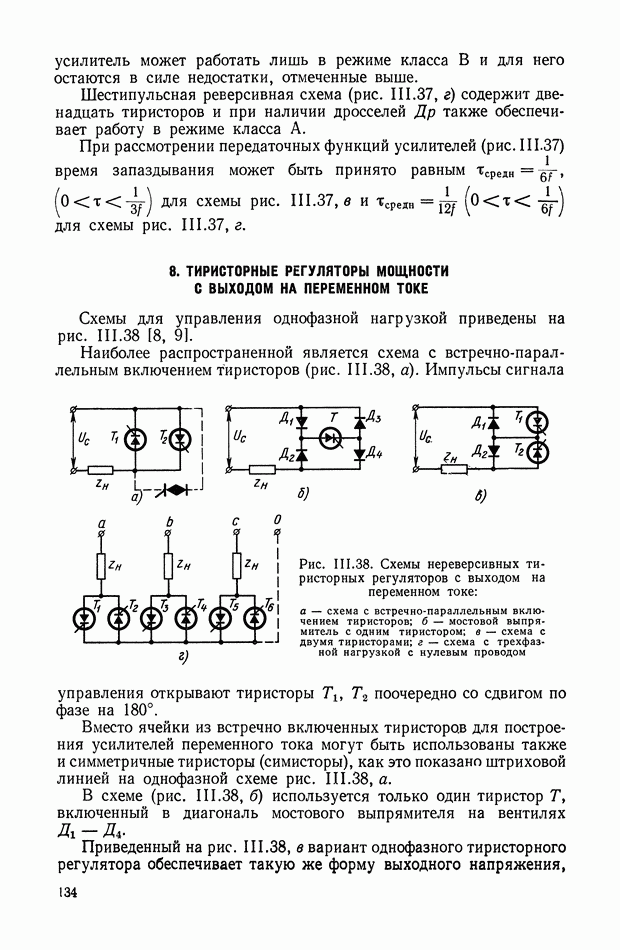
- 8. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 9. ТИРИСТОРНЫЕ УСИЛИТЕЛИ С ПИТАНИЕМ ОТ СЕТИ ПОСТОЯННОГО ТОКА
- 10. ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 11. ОСНОВЫ РАСЧЕТА ДИЭЛЕКТРИЧЕСКИХ УСИЛИТЕЛЕЙ
- ГЛАВА IV. КВАНТОВЫЕ УСИЛИТЕЛИ И ГЕНЕРАТОРЫ
- 2. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ РАДИОДИАПАЗОНА
- Квантовые усилители радиодиапазона.
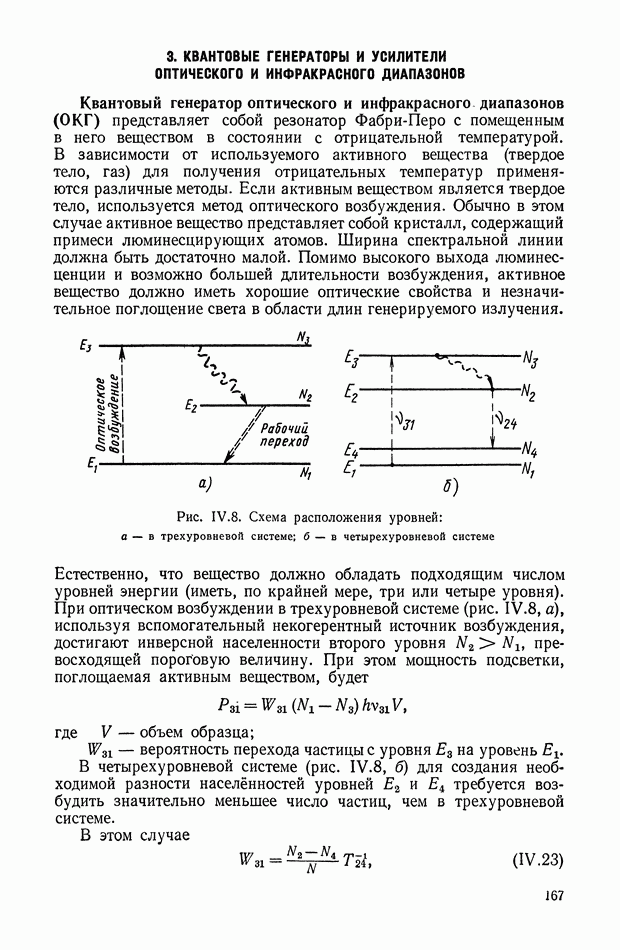
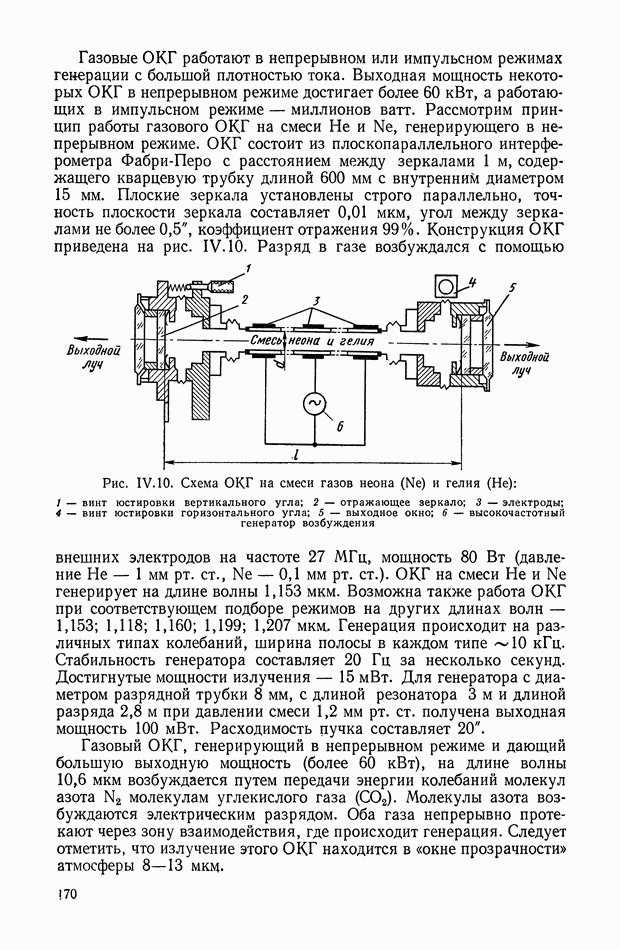
- 3. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- Оптический квантовый усилитель
- 4. ПРИМЕНЕНИЕ В САР КВАНТОВЫХ УСИЛИТЕЛЕЙ И ГЕНЕРАТОРОВ РАДИОДИАПАЗОНА, ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
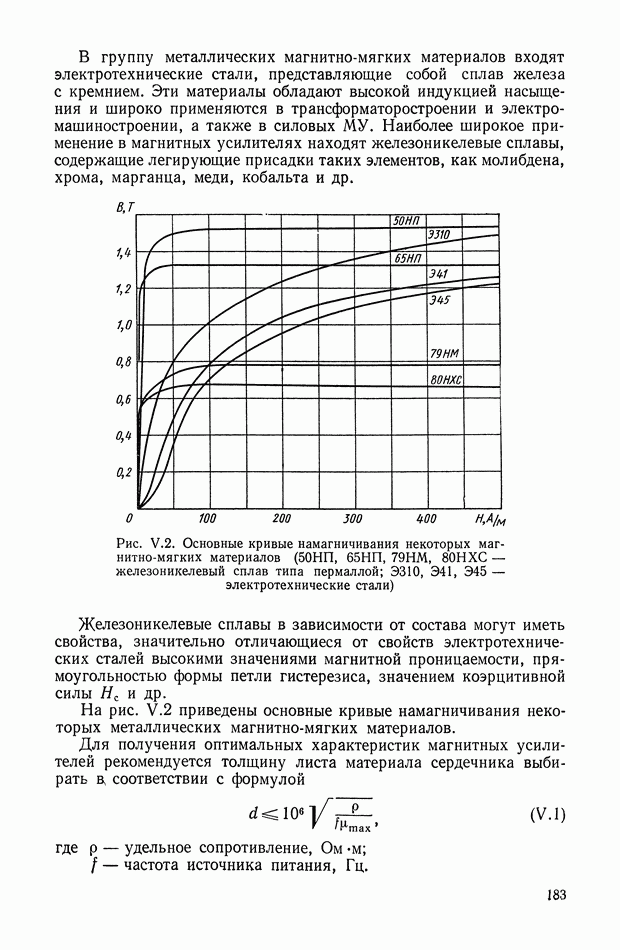
- ГЛАВА V. МАГНИТНЫЕ И МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- 2. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ МАГНИТНЫХ УСИЛИТЕЛЕЙ
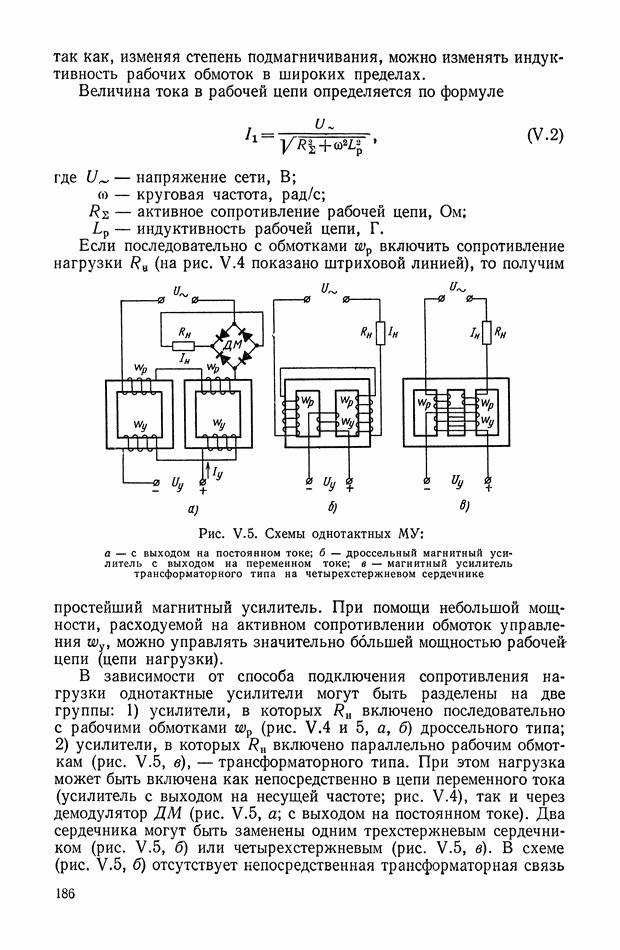
- 3. ОДНОТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ БЕЗ ОБРАТНОЙ СВЯЗИ (УПРАВЛЯЕМЫЕ ДРОССЕЛИ И ТРАНСФОРМАТОРЫ)
- 4. МАГНИТНЫЕ УСИЛИТЕЛИ С САМОНАСЫЩЕНИЕМ
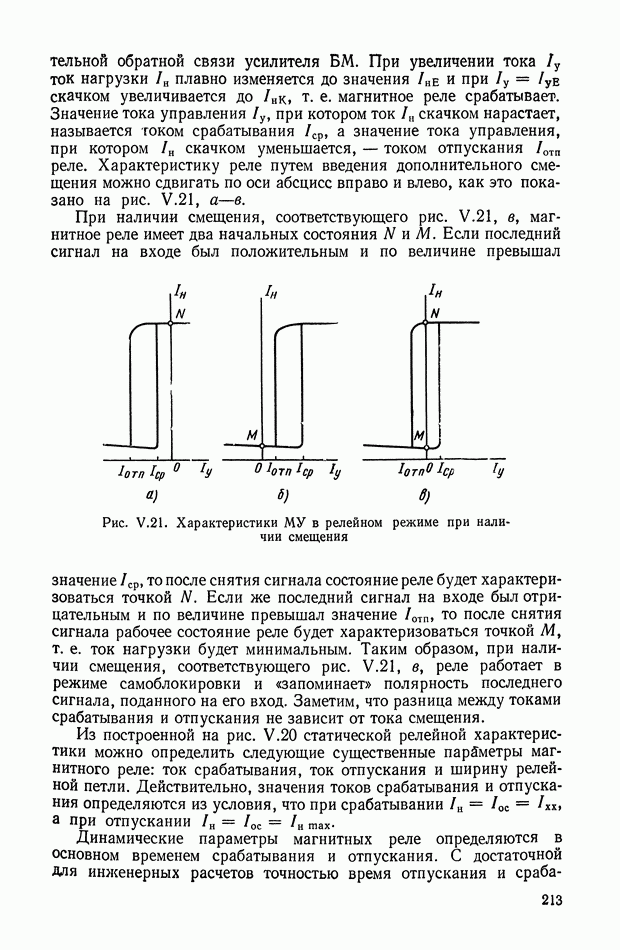
- Релейный режим работы усилителей с самонасыщением.
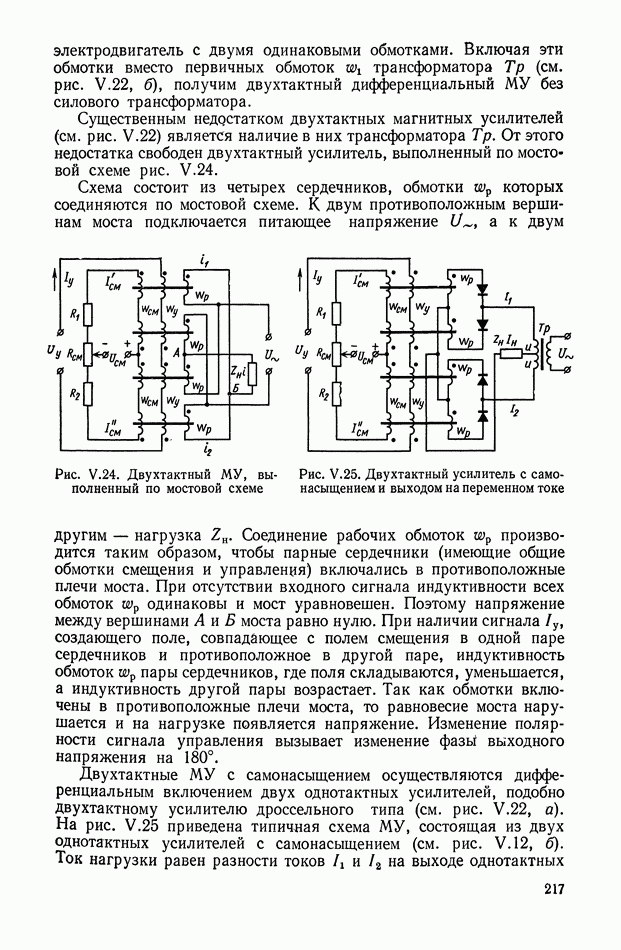
- 5. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 6. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ
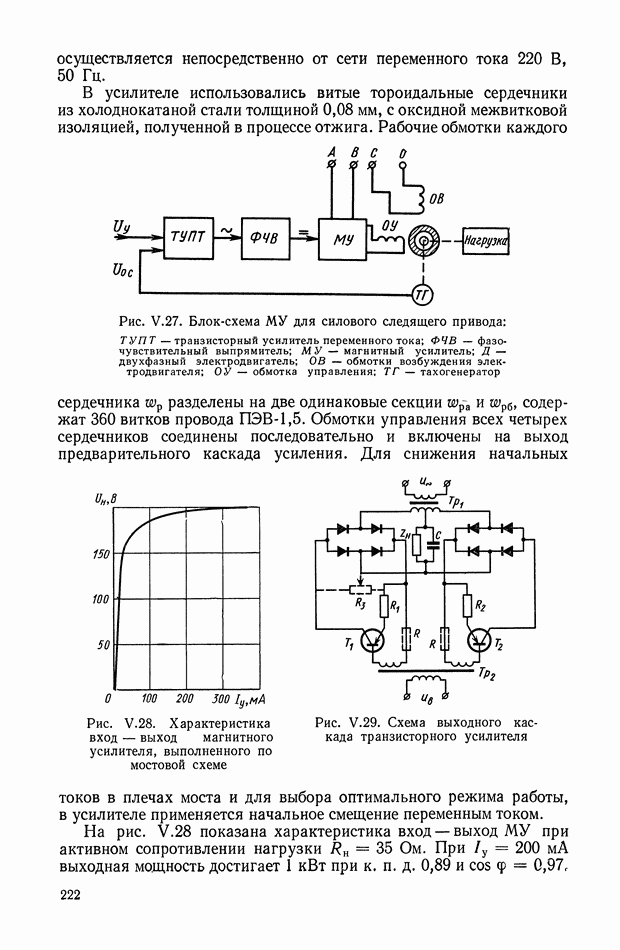
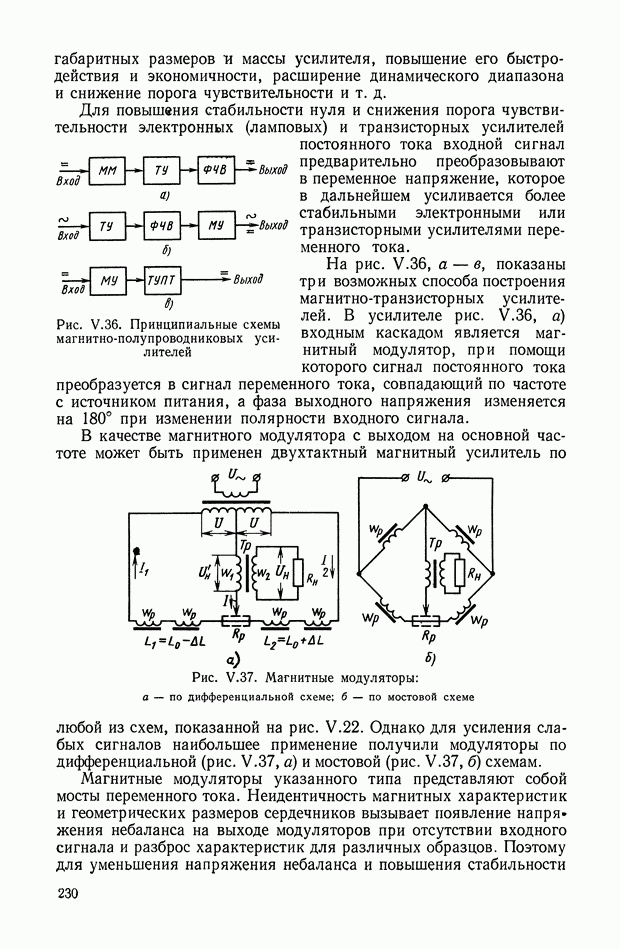
- 7. МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- ГЛАВА VI. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 2. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С НЕЗАВИСИМЫМ ВОЗБУЖДЕНИЕМ И С САМОВОЗБУЖДЕНИЕМ
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С ПОПЕРЕЧНЫМ ПОЛЕМ
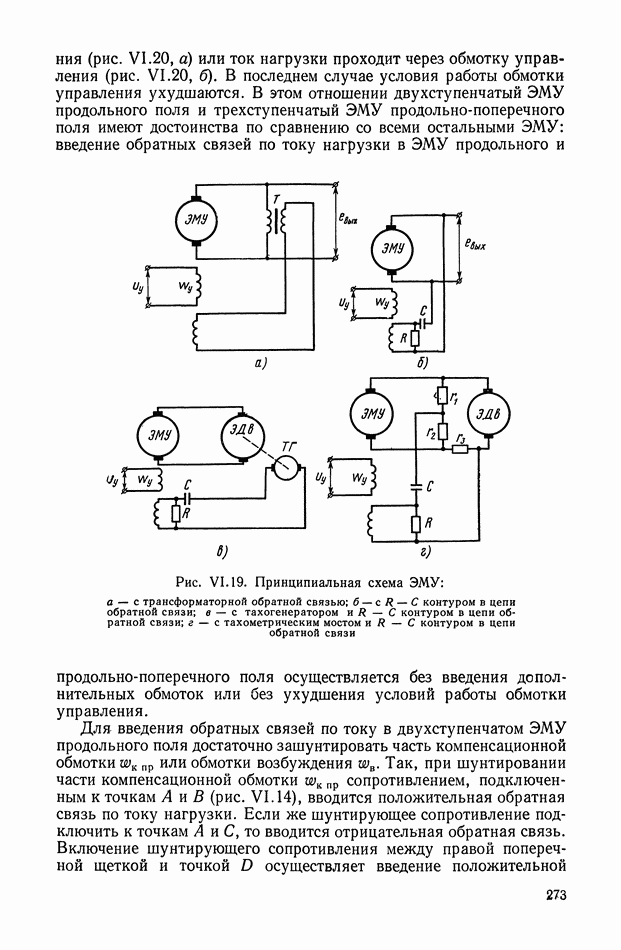
- 4. ЭЛЕКТРОМАШИННЫЙ УСИЛИТЕЛЬ ПРОДОЛЬНОГО И ПРОДОЛЬНО-ПОПЕРЕЧНОГО ПОЛЯ
- 5. ВЛИЯНИЕ НА ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭМУ ВИХРЕВЫХ И КОММУТАЦИОННЫХ ТОКОВ, ГИСТЕРЕЗИСА И СДВИГА ЩЕТОК С НЕЙТРАЛИ
- 6. МЕТОДЫ УЛУЧШЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕКТРОМАШИННЫХ УСИЛИТЕЛЕЙ
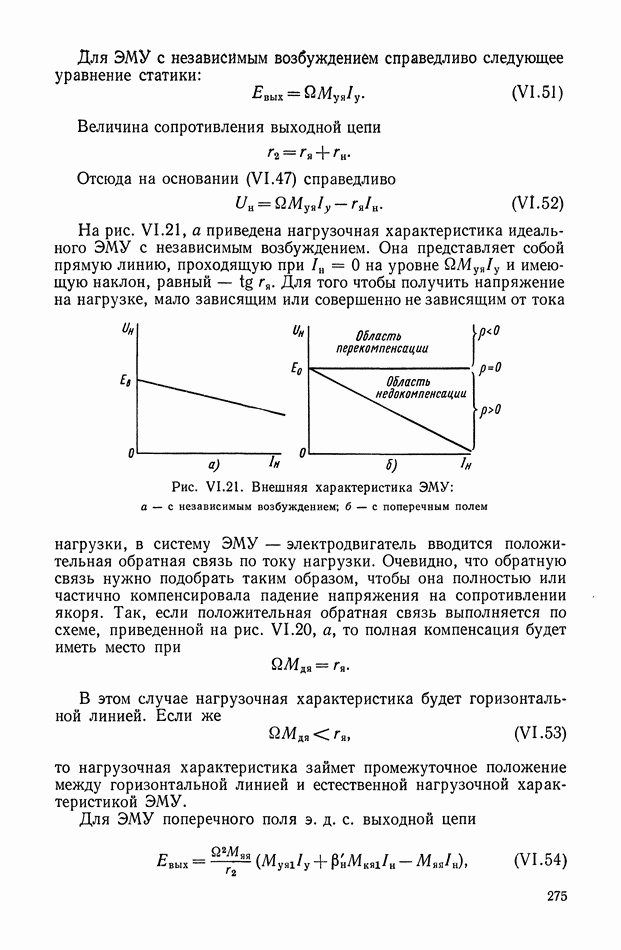
- 7. НАГРУЗОЧНАЯ ХАРАКТЕРИСТИКА ЭЛЕКТРОМАШИННОГО УСИЛИТЕЛЯ
- ГЛАВА VII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ УСИЛИТЕЛИ
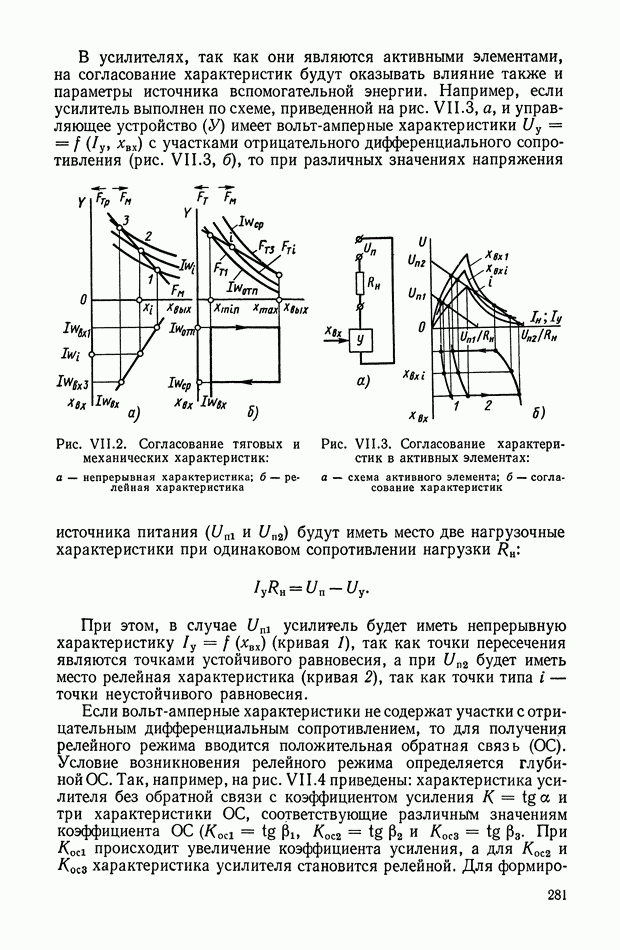
- 1. ХАРАКТЕРИСТИКИ УСИЛИТЕЛЕЙ И СПОСОБЫ ИХ ФОРМИРОВАНИЯ
- 2. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
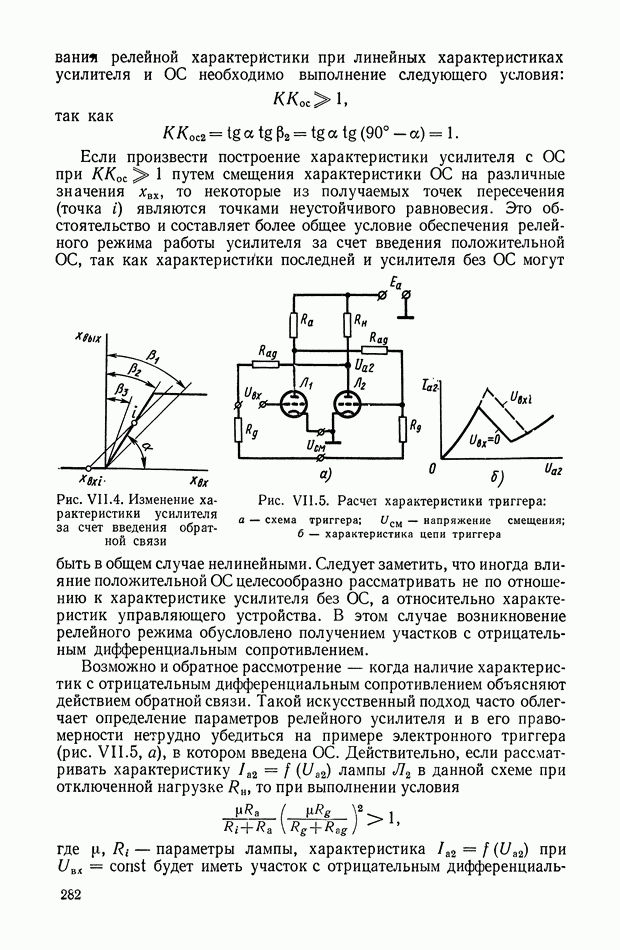
- 3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ЛИНЕАРИЗОВАННЫЕ УСИЛИТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ РЕЛЕ
- 4. БЕСКОНТАКТНЫЕ ЛИНЕАРИЗОВАННЫЕ РЕЛЕЙНЫЕ УСИЛИТЕЛИ
- ГЛАВА VIII. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 2. ОСНОВНЫЕ ЭЛЕМЕНТЫ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ И ИХ ХАРАКТЕРИСТИКИ
- 3. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ С ЗОЛОТНИКОМ
- 4. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ СО СТРУЙНОЙ ТРУБКОЙ
- 5. СХЕМЫ И ПРИНЦИПЫ ДЕЙСТВИЯ ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 6. СТАТИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 7. ДИНАМИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
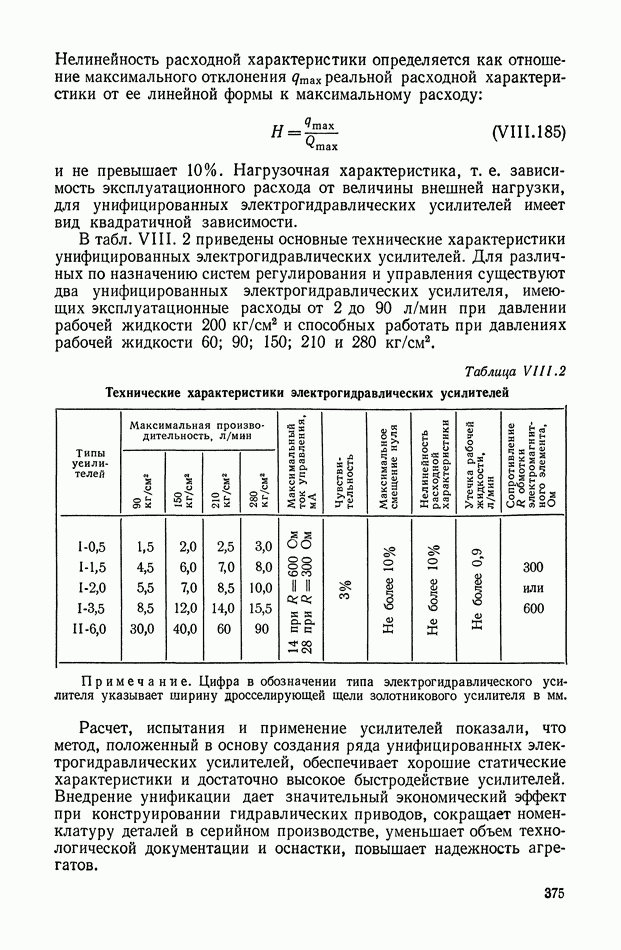
- 8. УНИФИКАЦИЯ ЭЛЕКТРОГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ ДЛЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
- ГЛАВА IX. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ И ИХ КЛАССИФИКАЦИЯ
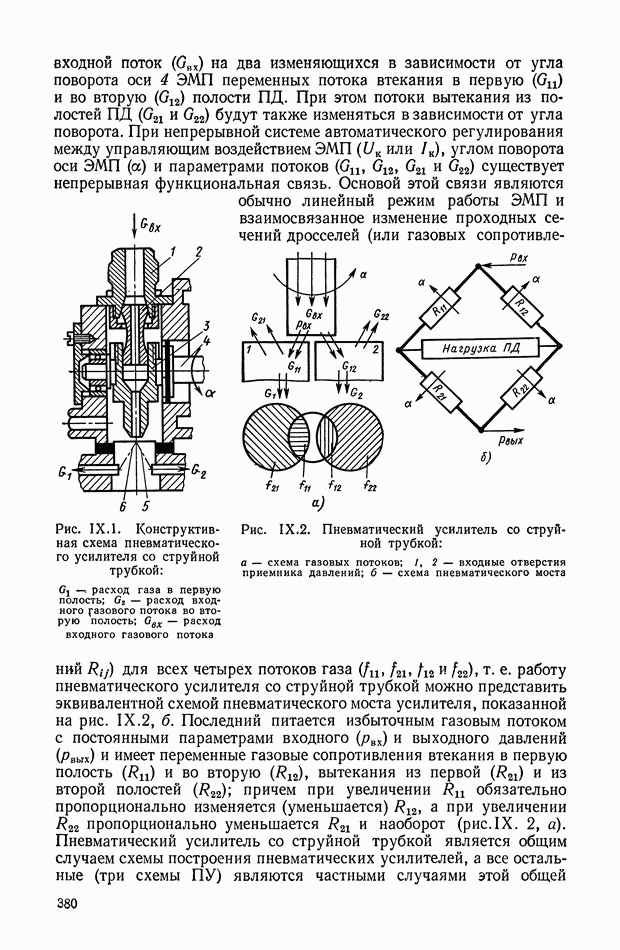
- 2. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ СО СТРУЙНОЙ ТРУБКОЙ
- 3. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗОЛОТНИКОМ
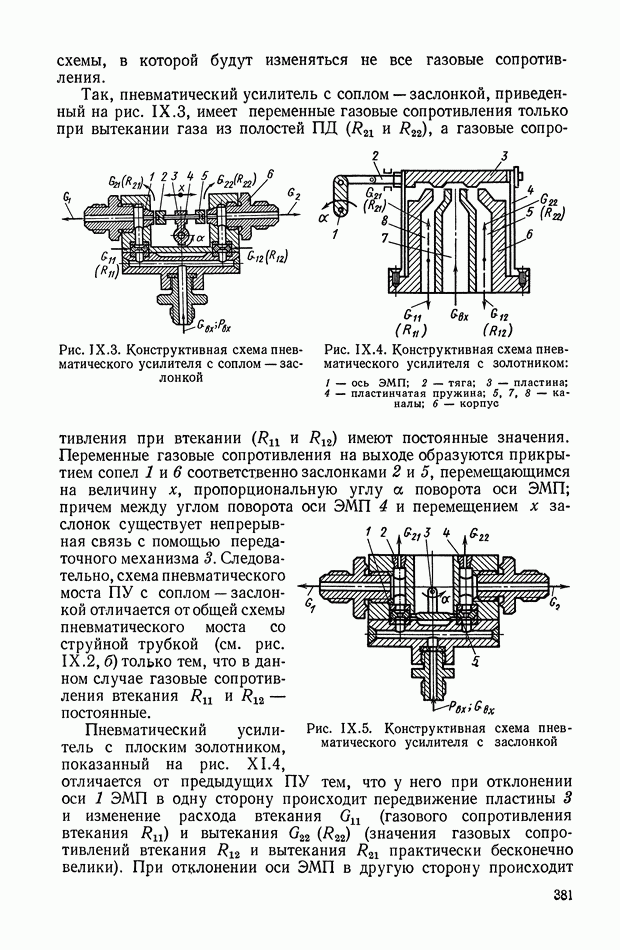
- 4. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С СОПЛОМ — ЗАСЛОНКОЙ
- 5. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗАСЛОНКОЙ
- 6. МНОГОКАСКАДНЫЕ ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- РАЗДЕЛ II. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ И УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ЛИНЕЙНЫХ ПАССИВНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Основные соотношения для синтеза пассивного RC-четырехполюсника.
- 3. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Активные четырехполюсники, получаемые с помощью конверторов отрицательного сопротивления.
- Активные четырехполюсники, получаемые с помощью гираторов.
- 4. НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА НЕЛИНЕЙНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. ОСОБЕННОСТИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XI. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА ПОСТОЯННОГО ТОКА
- Дифференцирующий трансформатор.
- Электрические интегрирующие элементы.
- 2. ТИПОВЫЕ ЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- 3. КОРРЕКТИРУЮЩИЕ ЧЕТЫРЕХПОЛЮСНИКИ С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Четырехполюсники с активными элементами на основе операционных усилителей (ОУ) и конверторов отрицательного сопротивления (КОС).
- 4. РЕАЛИЗАЦИЯ ЗАДАННОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В ВИДЕ СХЕМЫ ПАССИВНОГО ЛИНЕЙНОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА
- 5. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- 8. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- Многоканальные нелинейные логические устройства.
- ГЛАВА XII. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- 1. КОРРЕКТИРУЮЩИЕ RLC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 2. КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 3. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 4. САМОНАСТРАИВАЮЩИЕСЯ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА
- 5. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА С ПРОМЕЖУТОЧНОЙ ДЕМОДУЛЯЦИЕЙ
- 6. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА С ПЕРЕКЛЮЧАТЕЛЯМИ
- 7. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XIII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ТАХОГЕНЕРАТОРЫ ПОСТОЯННОГО ТОКА
- Погрешности тахогенератора постоянного тока.
- 2. НЕКОТОРЫЕ СХЕМЫ ПРИМЕНЕНИЯ ТАХОГЕНЕРАТОРОВ
- 3. АСИНХРОННЫЕ ТАХОГЕНЕРАТОРЫ
- 4. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ ИЗМЕРЕНИЯ СКОРОСТИ ЭЛЕКТРОДВИГАТЕЛЕЙ
- Пассивный тахометрический мост переменного тока.
- Активные тахометрические мосты.
- ГЛАВА XIV. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ГИДРАВЛИЧЕСКИХ СИСТЕМАХ
- 3. ЭЛЕКТРИЧЕСКИЕ ОБРАТНЫЕ СВЯЗИ
- 4. ЖЕСТКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
- 5. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ СИСТЕМАХ
- 6. СЛОЖНЫЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
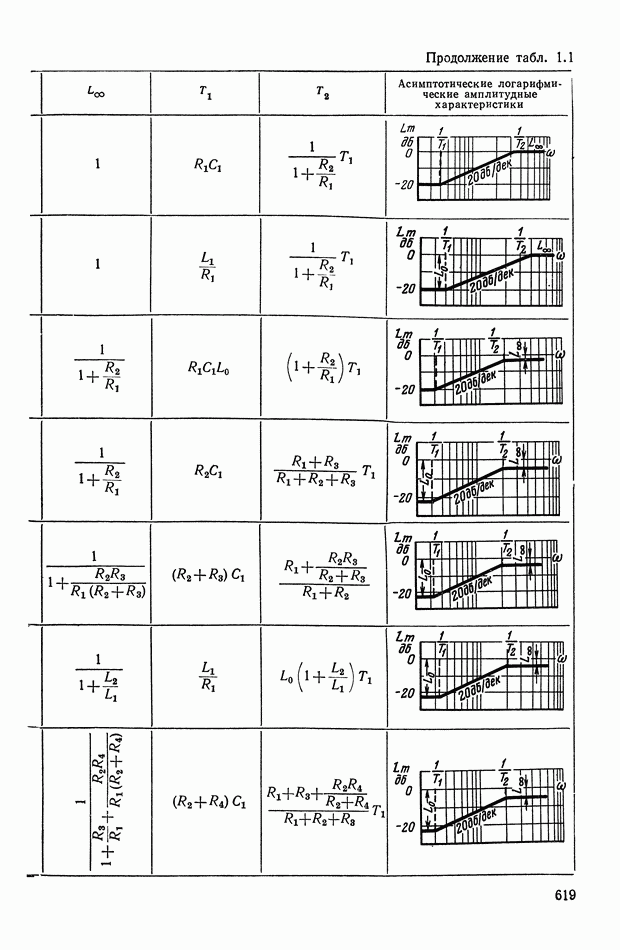
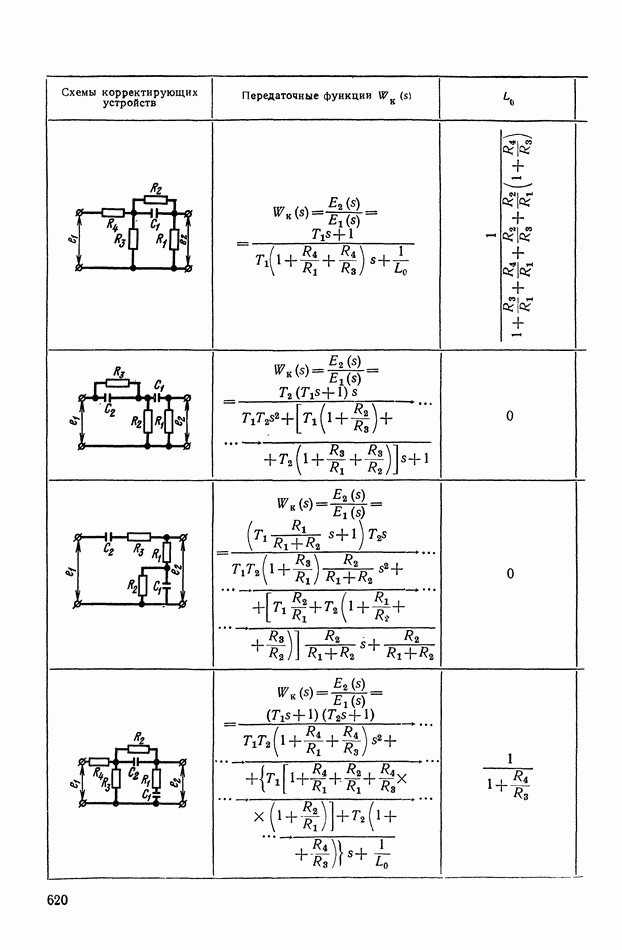
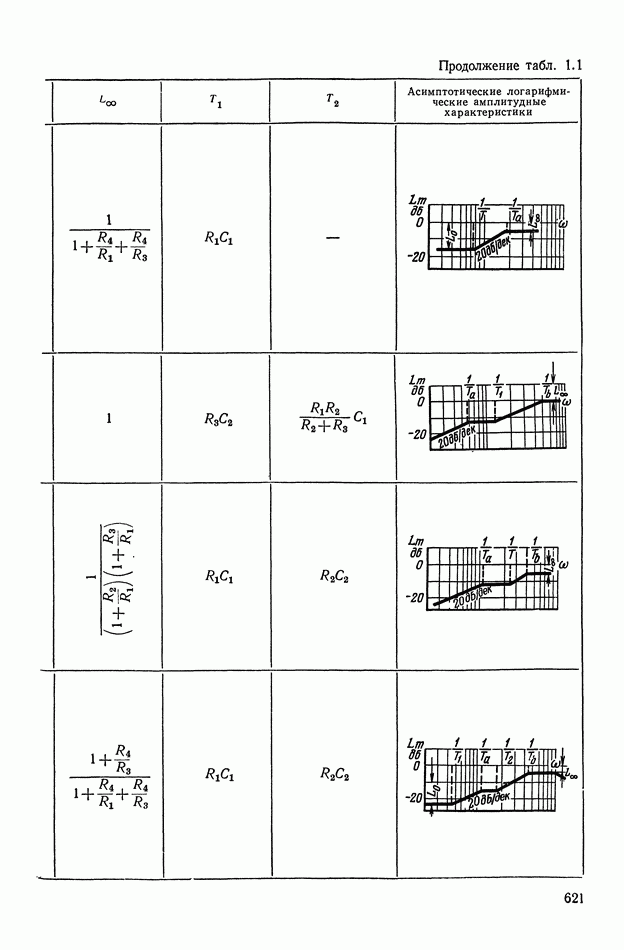
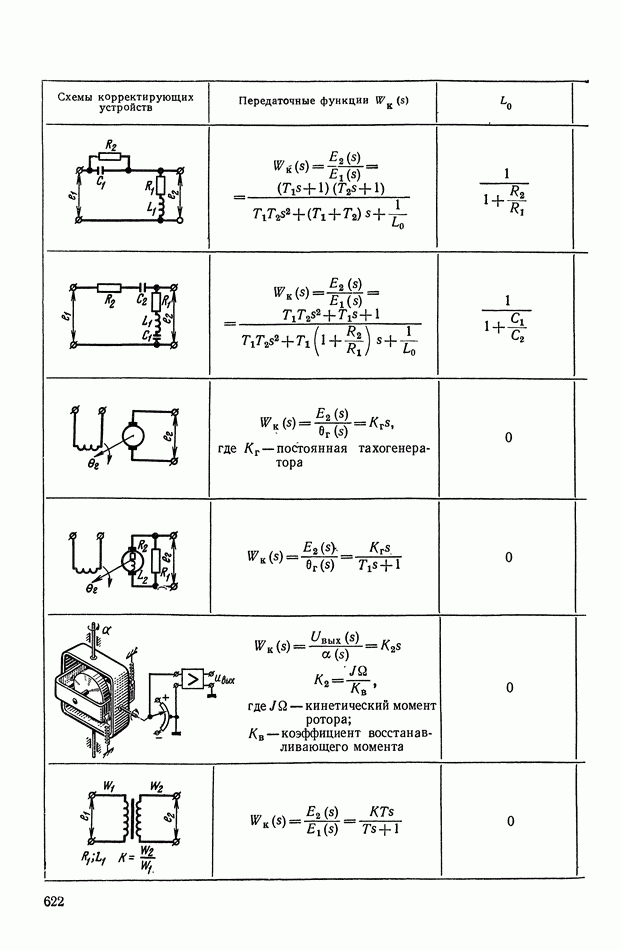
- ПРИЛОЖЕНИЕ 1. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПОСТОЯННОГО ТОКА
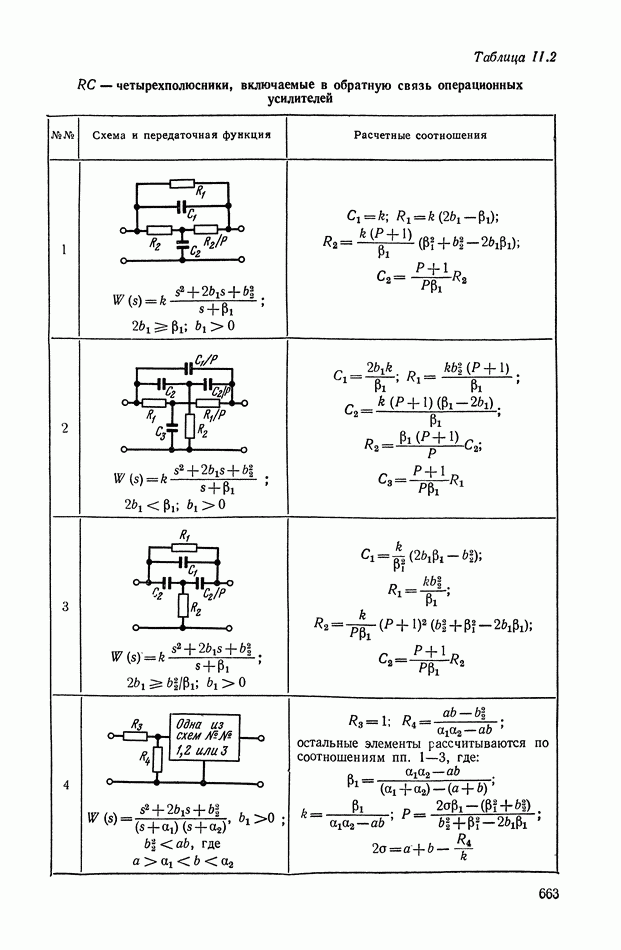
- ПРИЛОЖЕНИЕ II. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ОСНОВЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
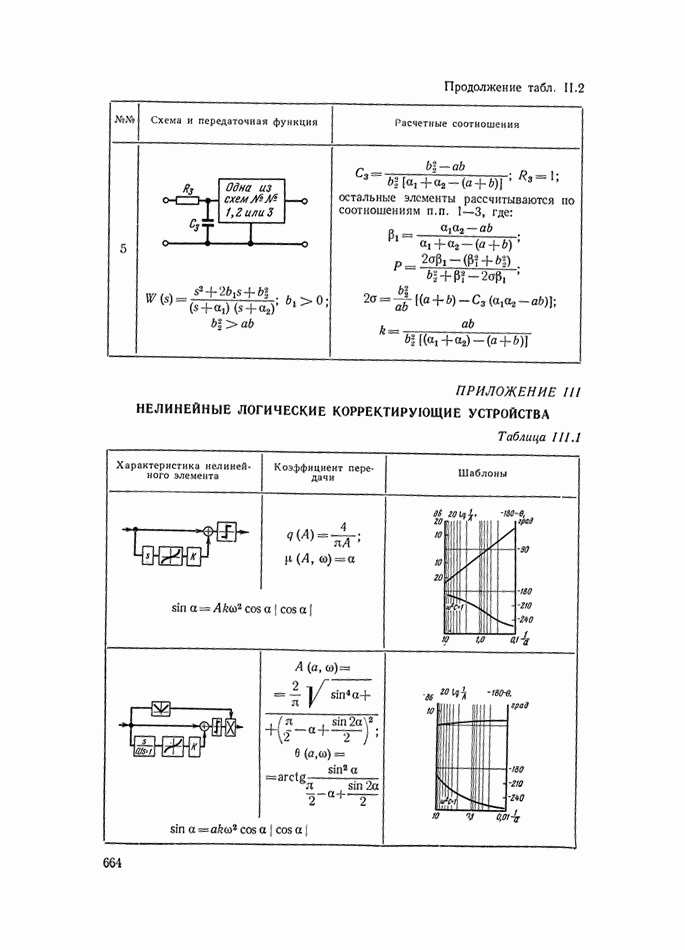
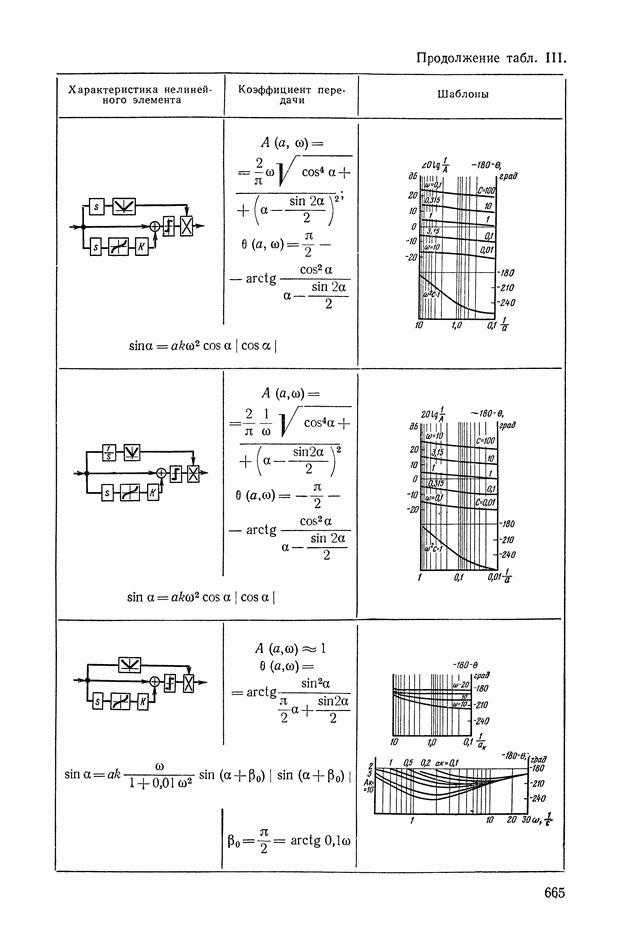
- ПРИЛОЖЕНИЕ III. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ