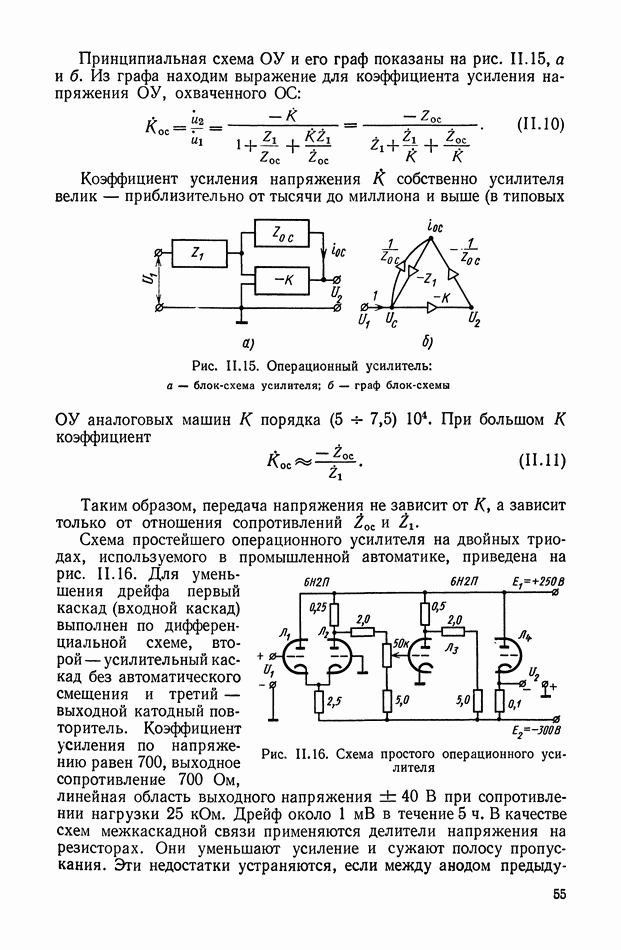
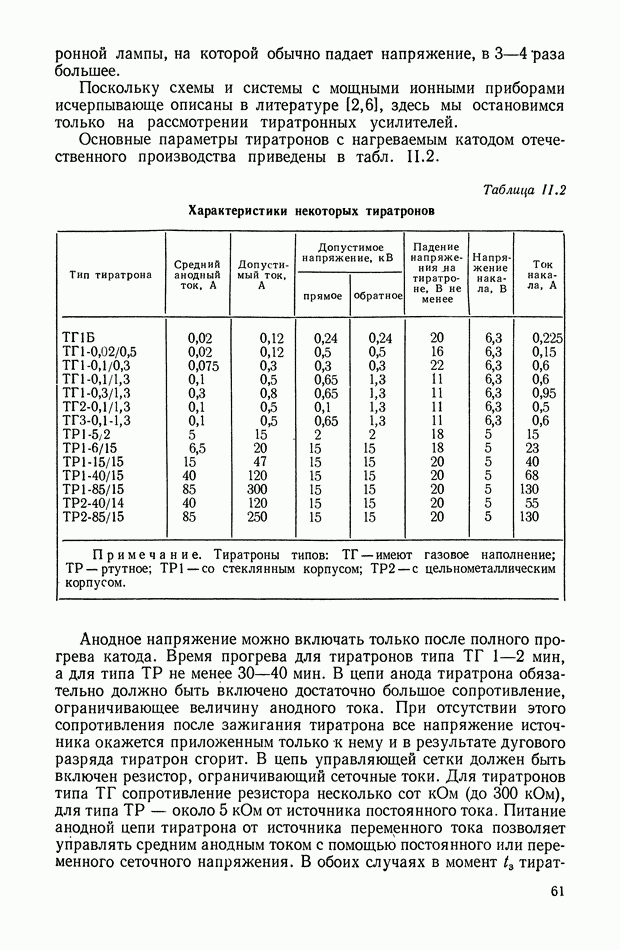
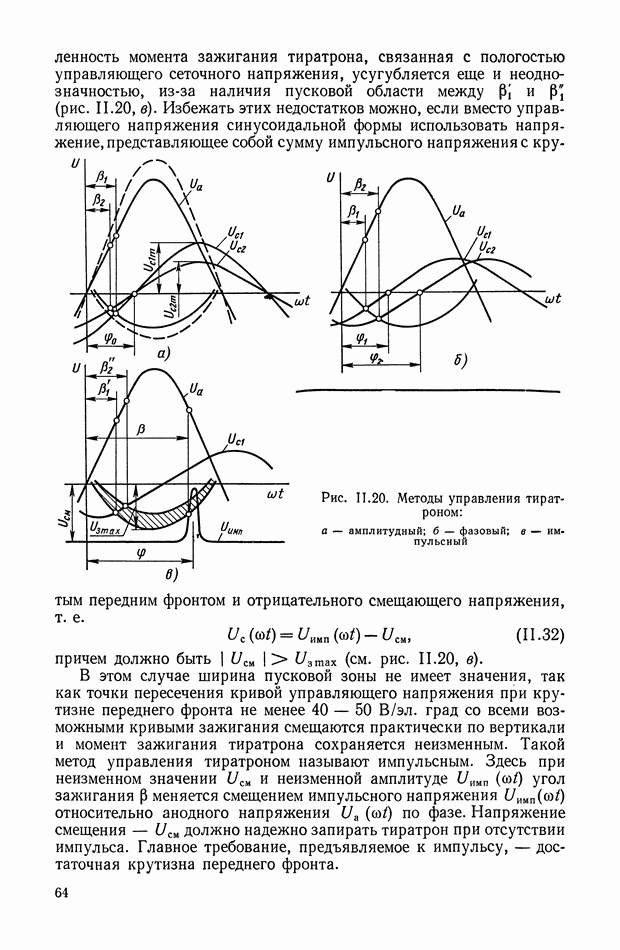
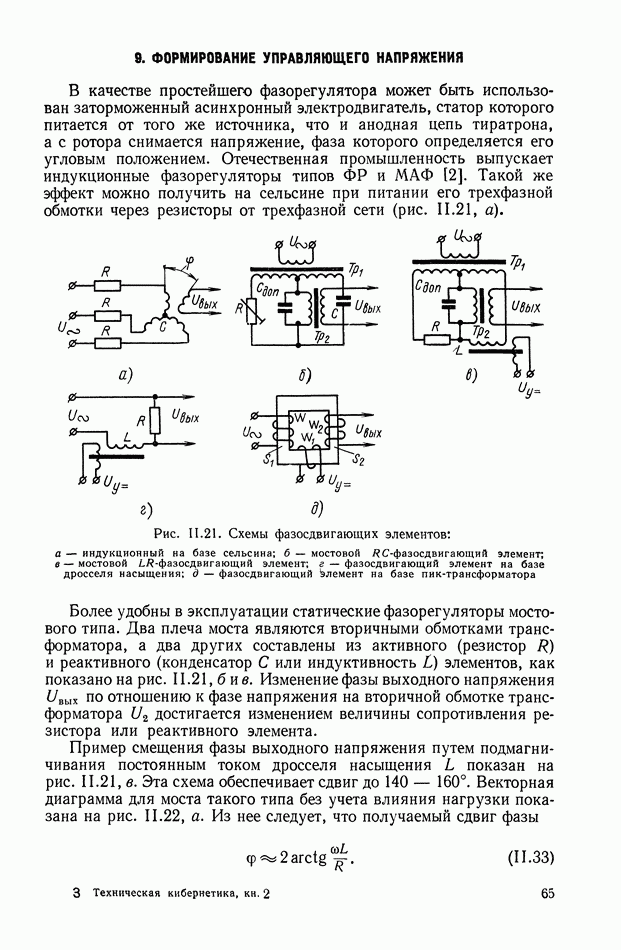
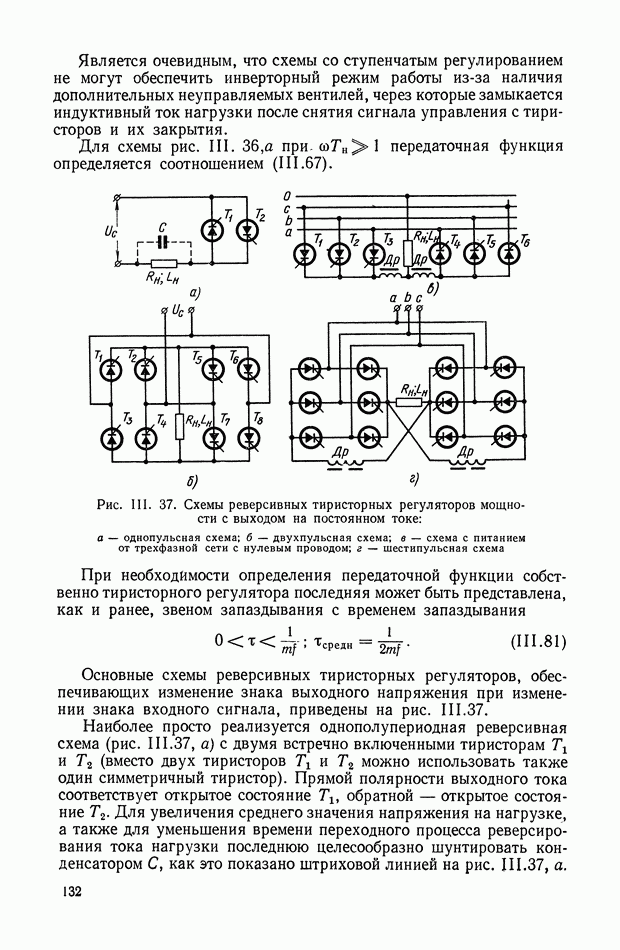
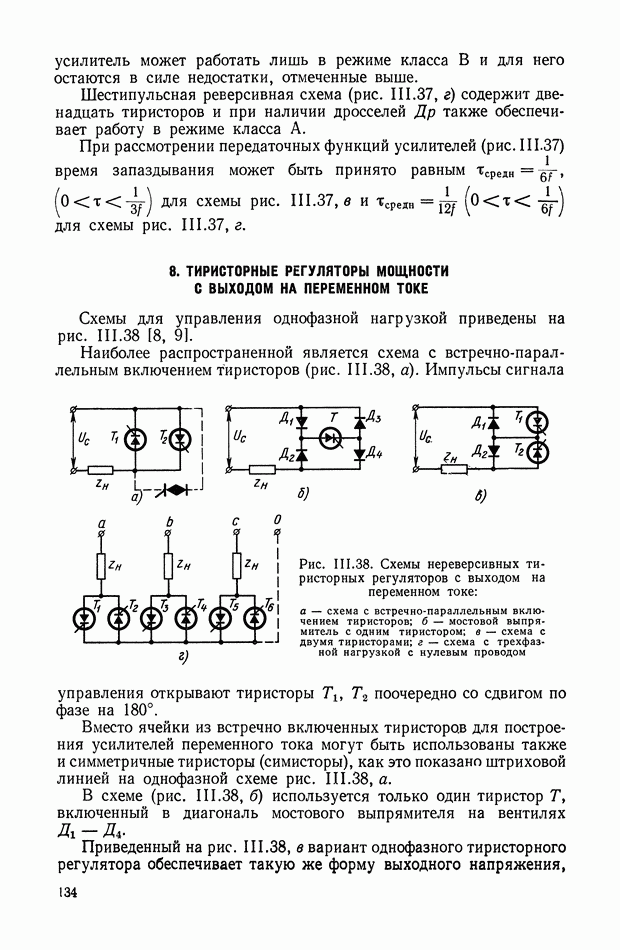
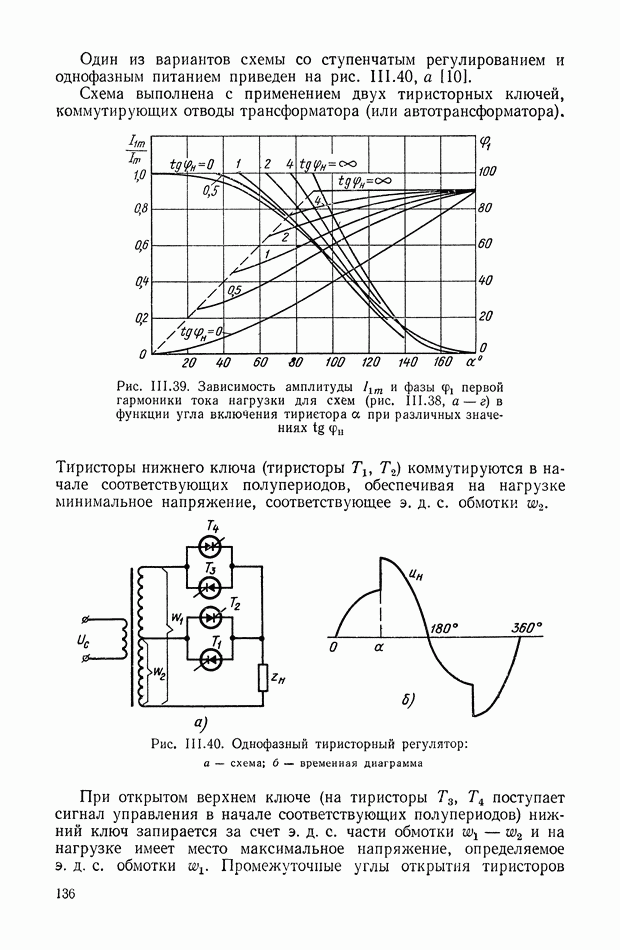
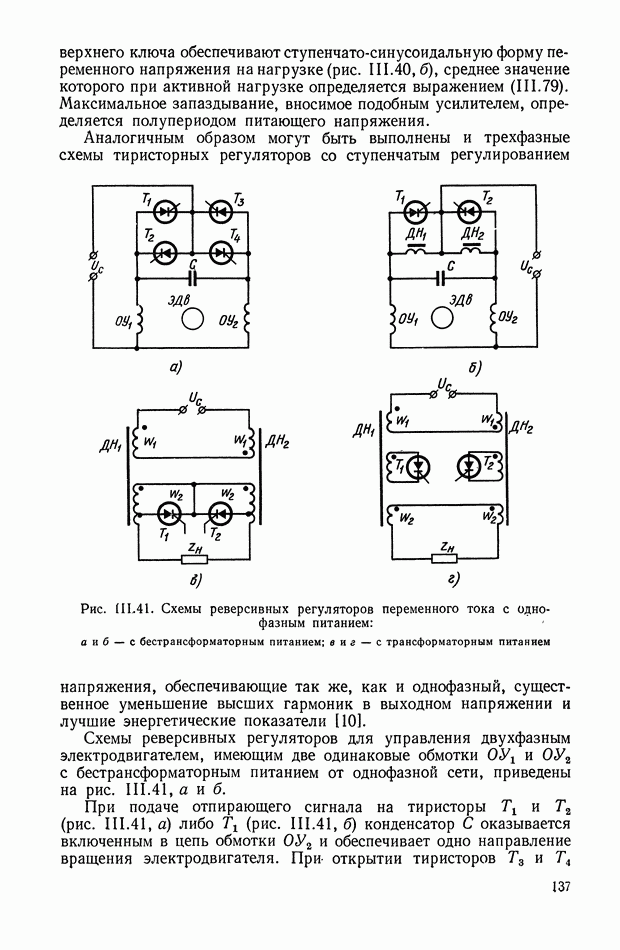
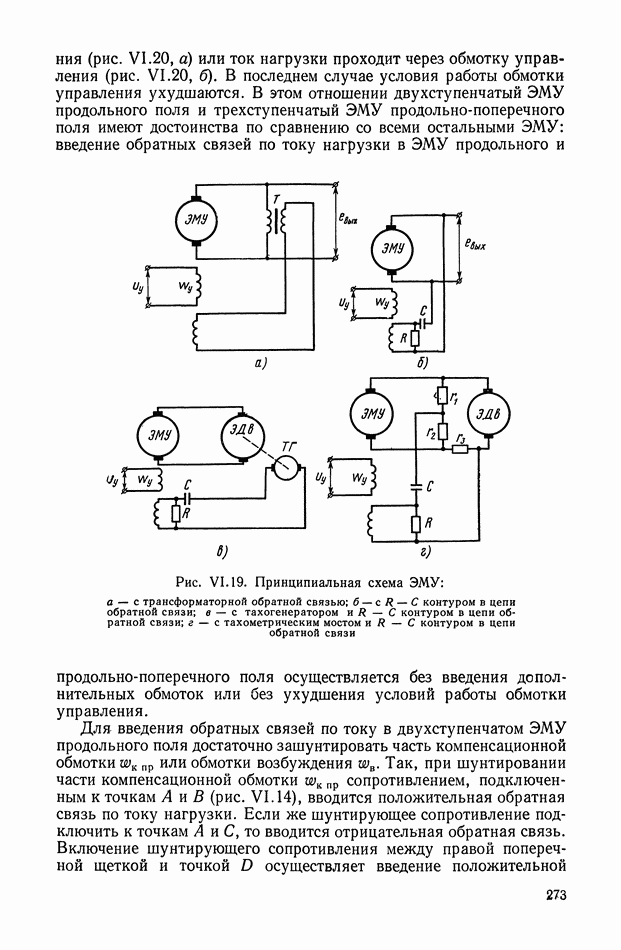
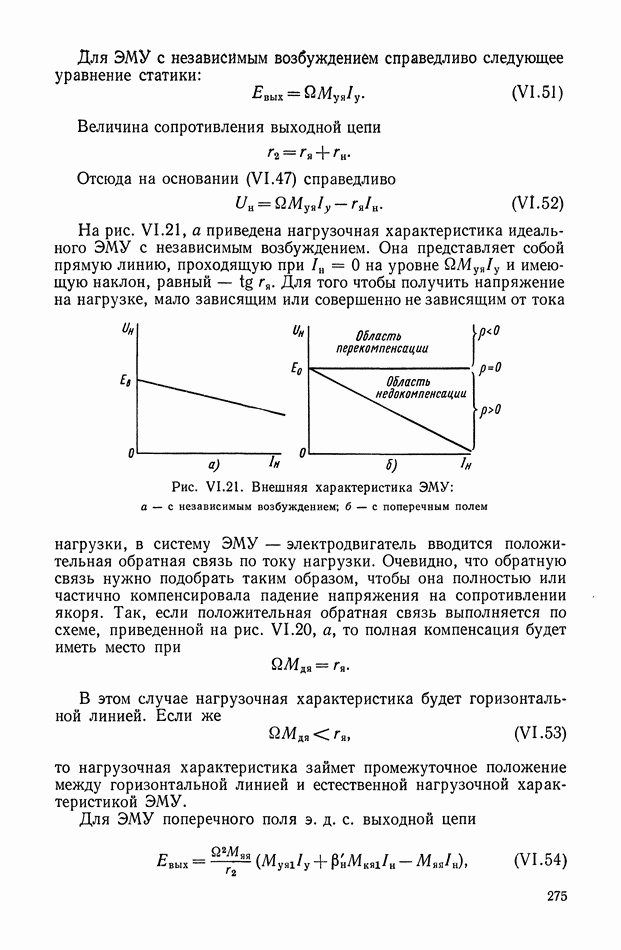
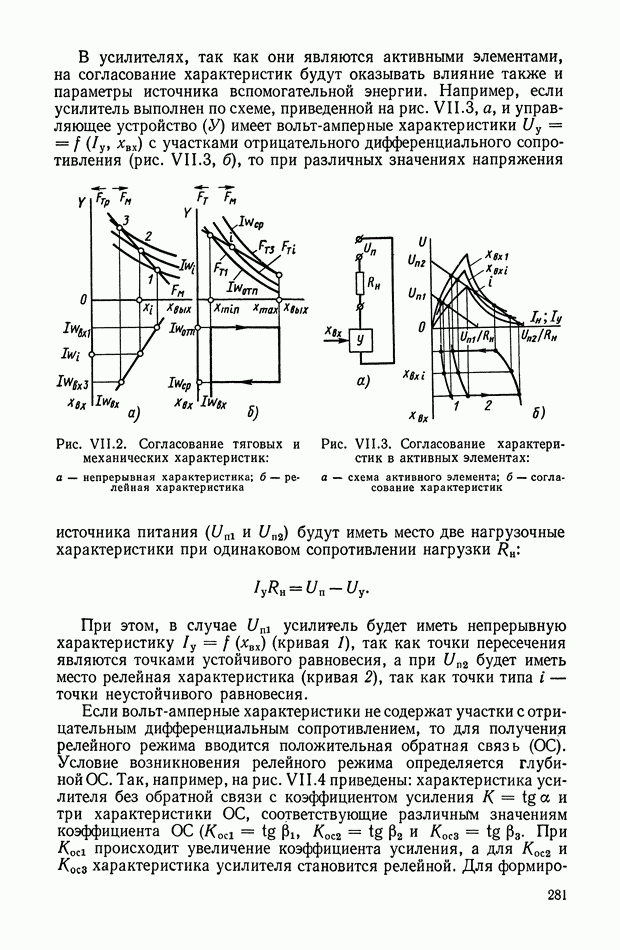
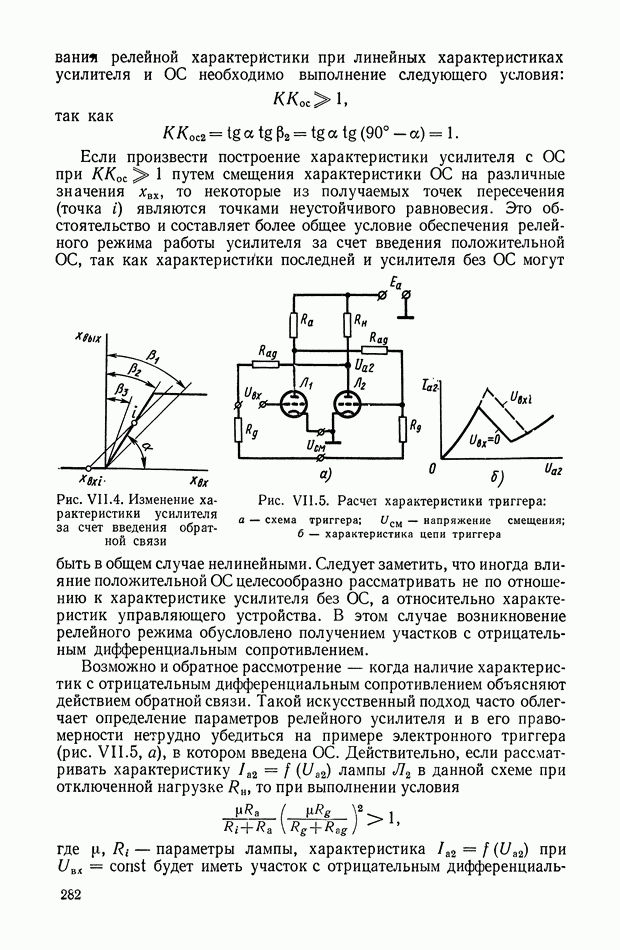
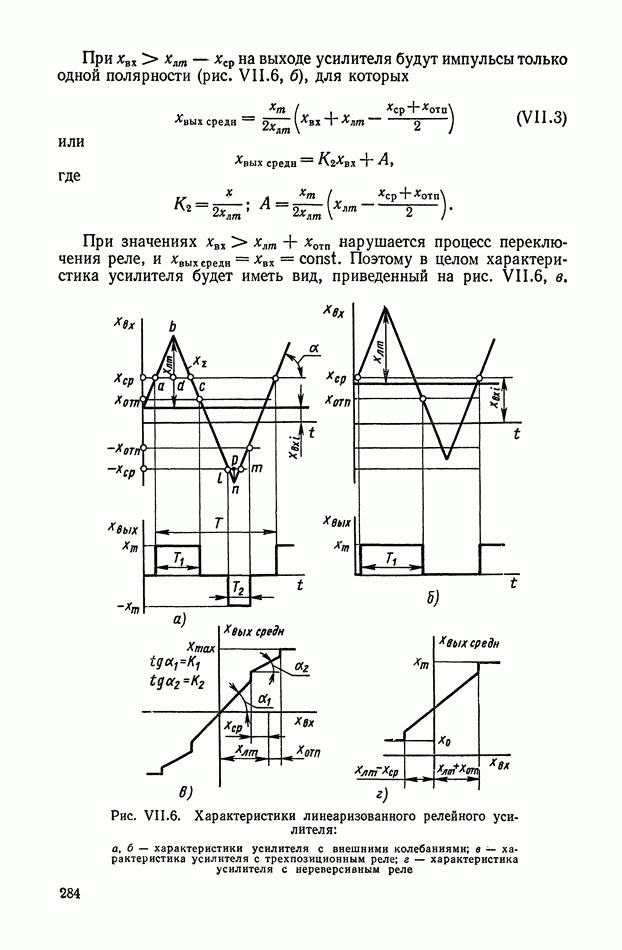
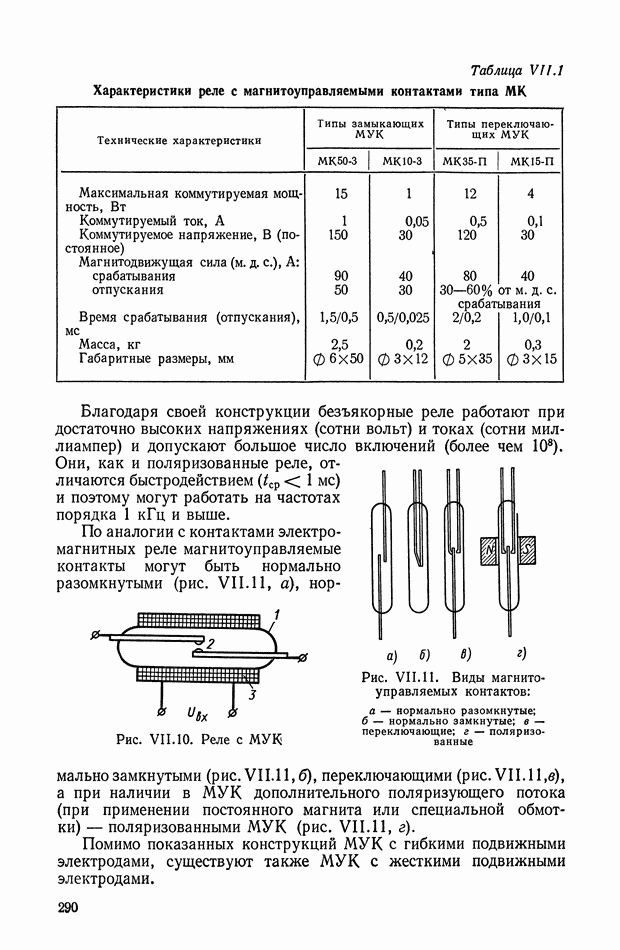
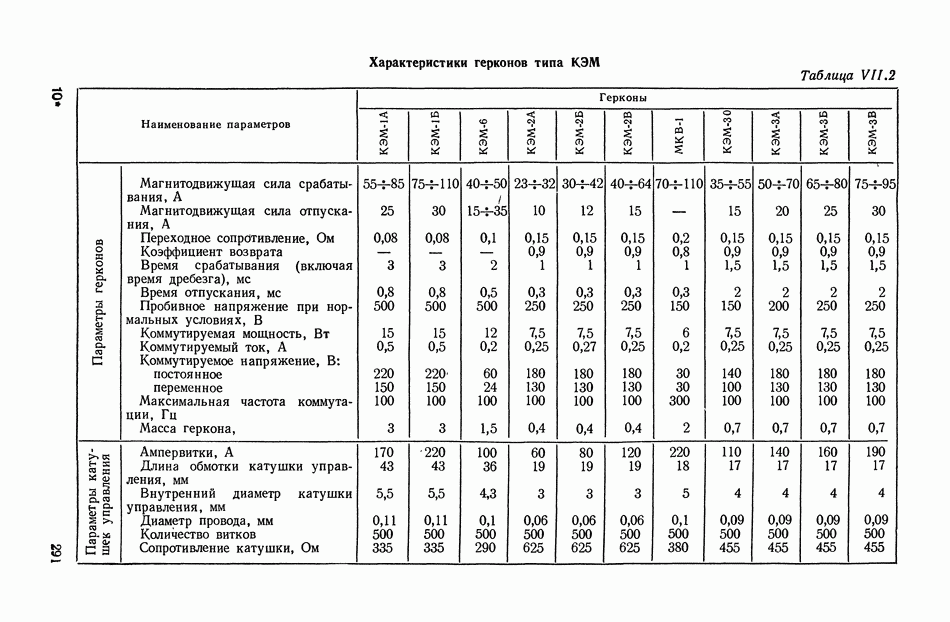
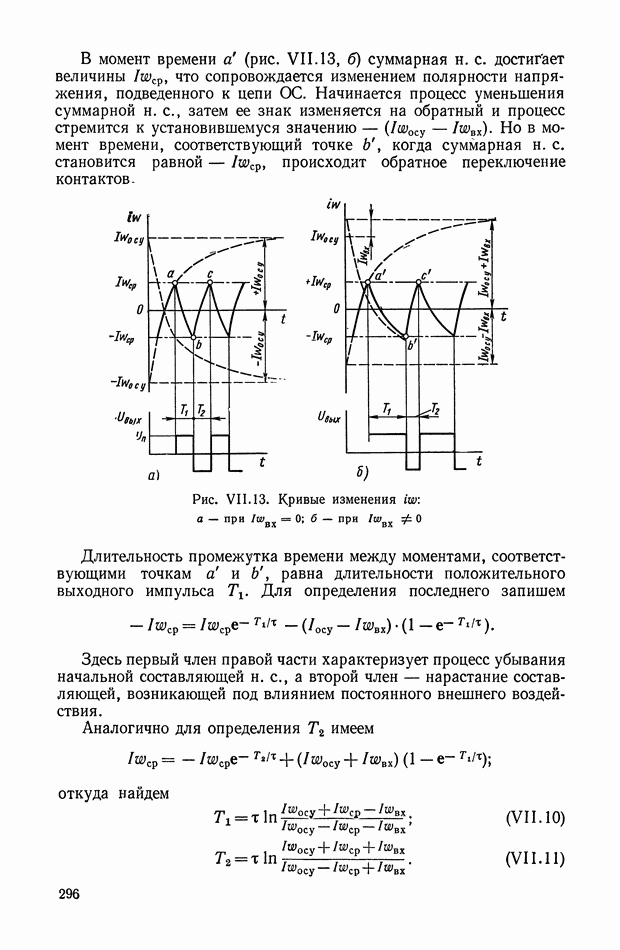
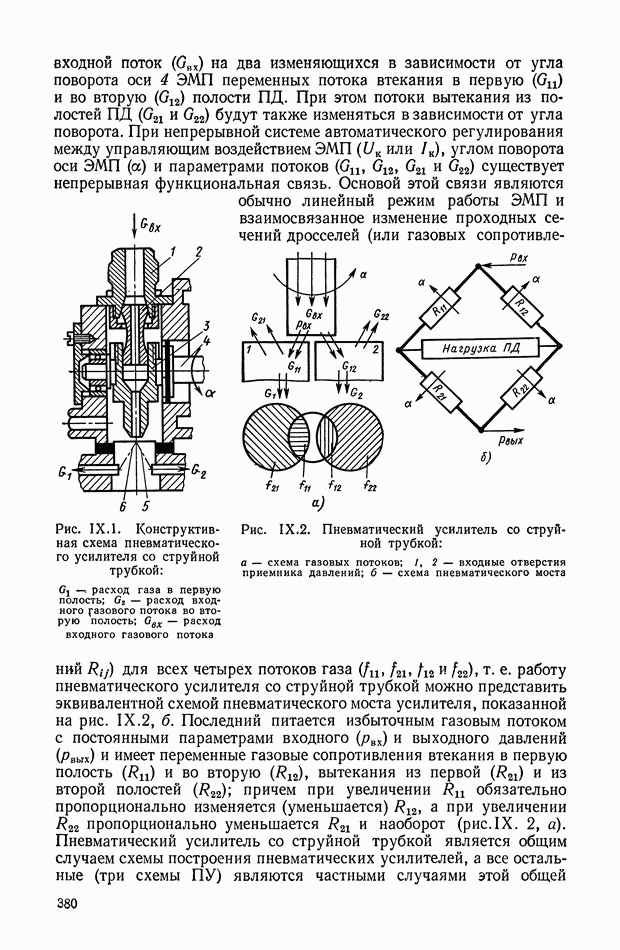
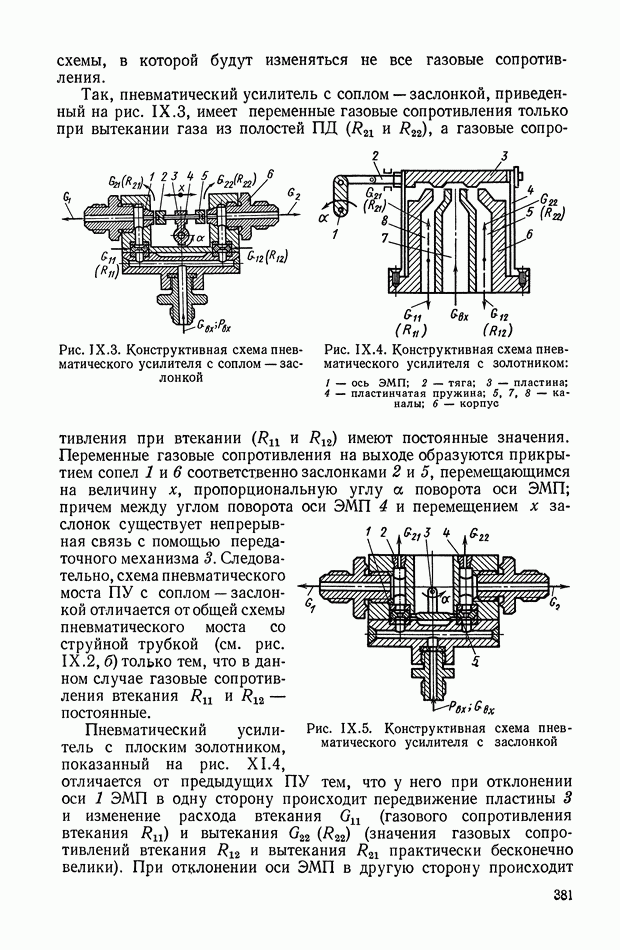
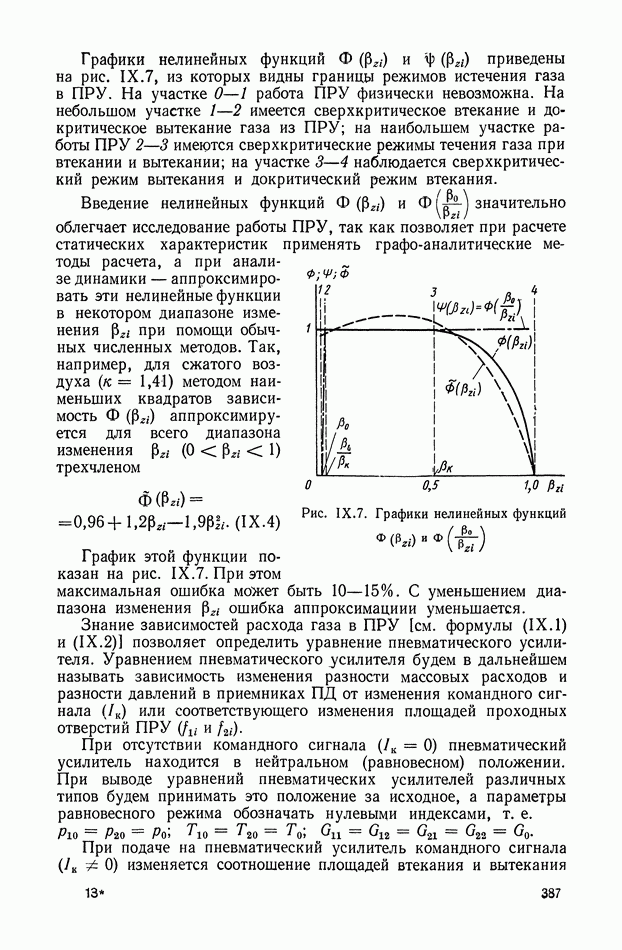
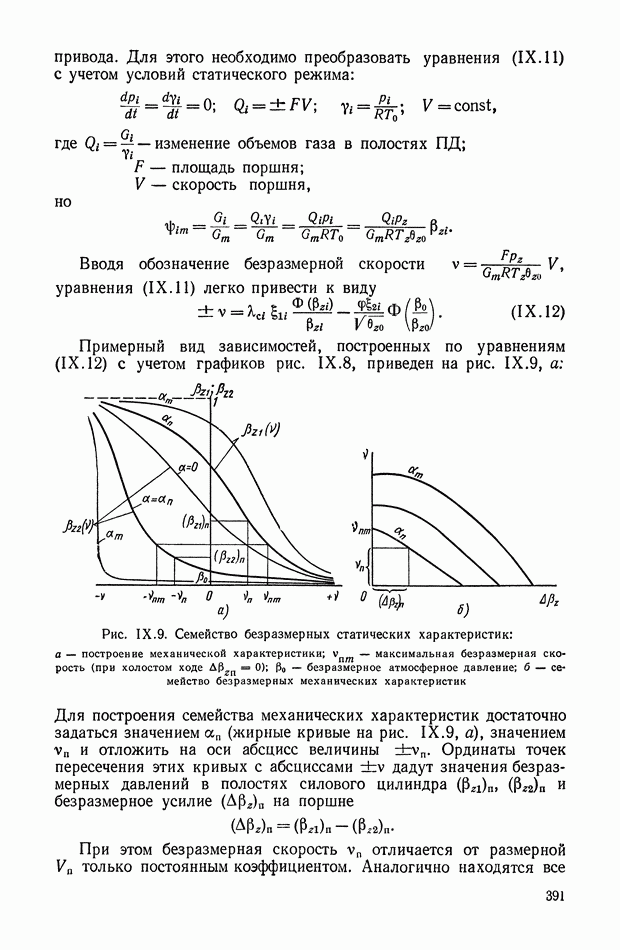
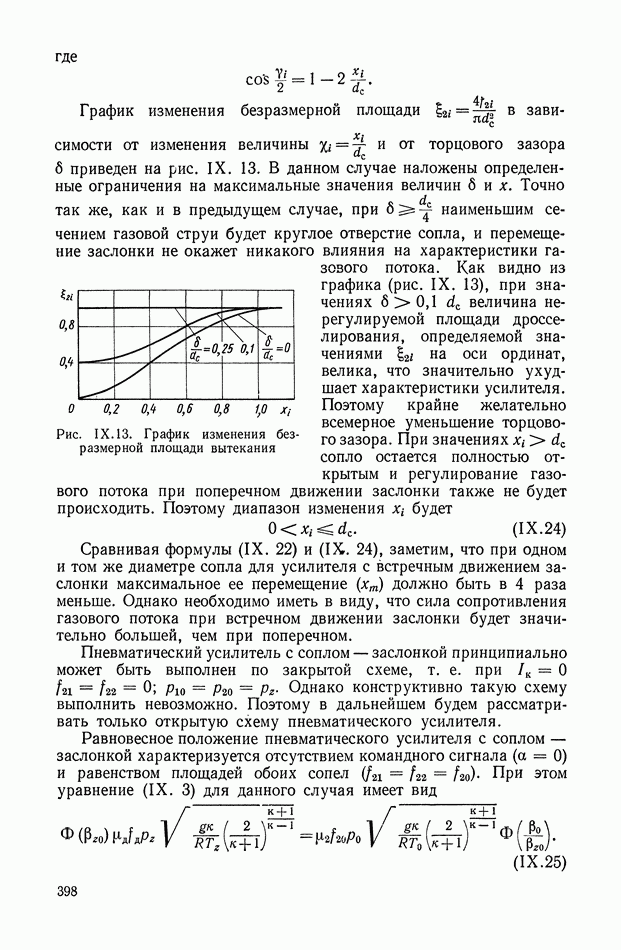
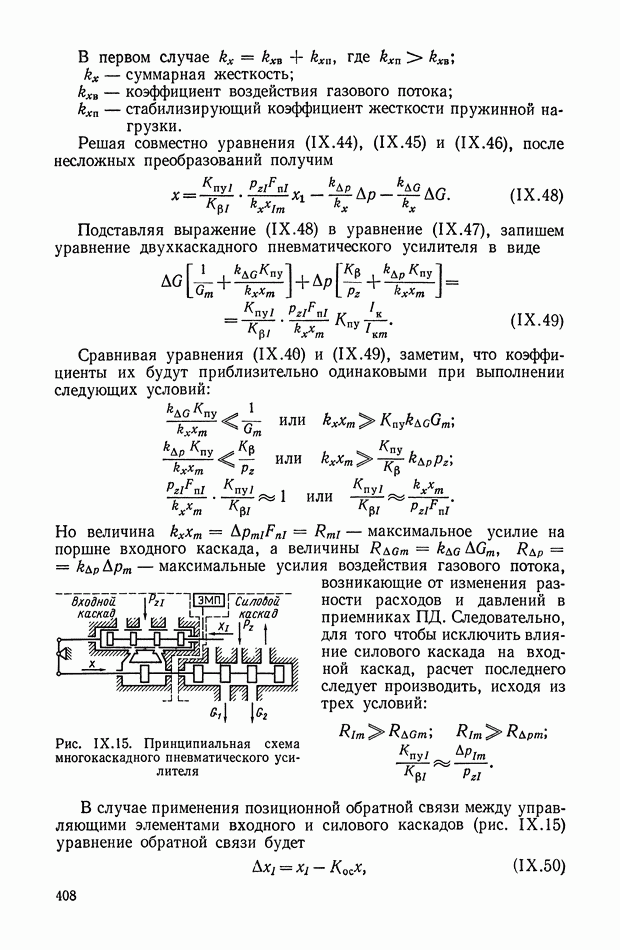
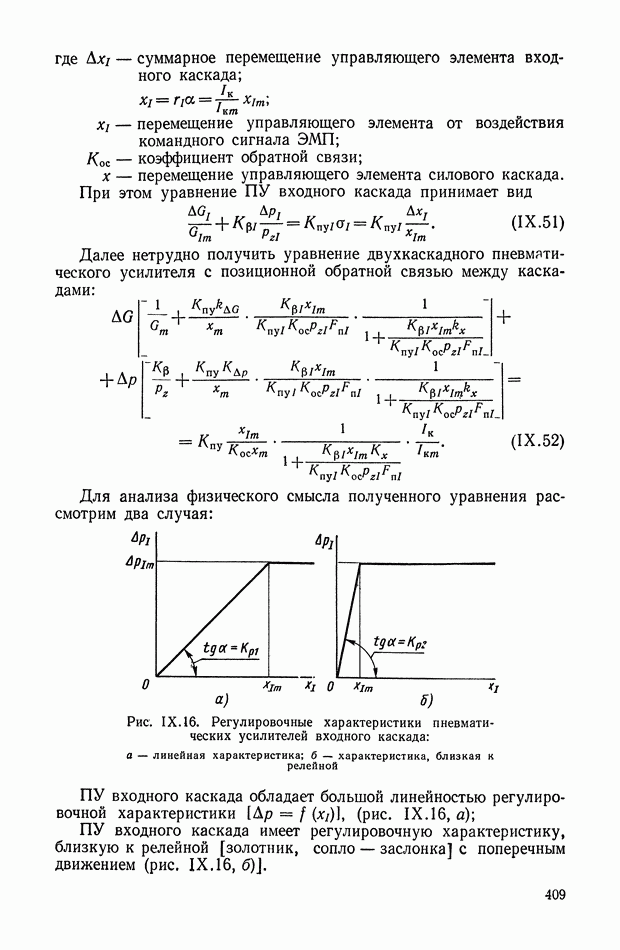
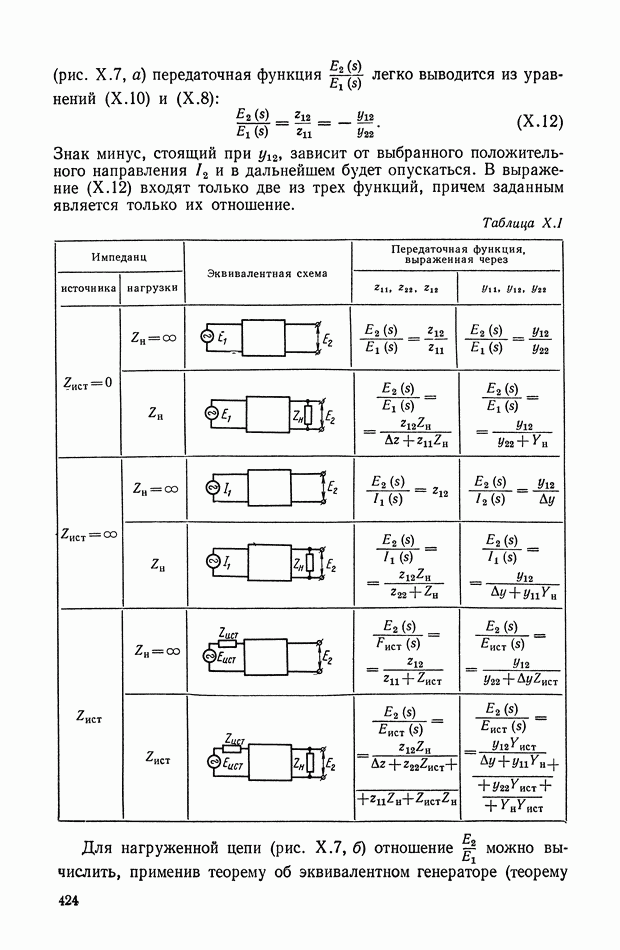
| << Предыдущий параграф | Следующий параграф >> |
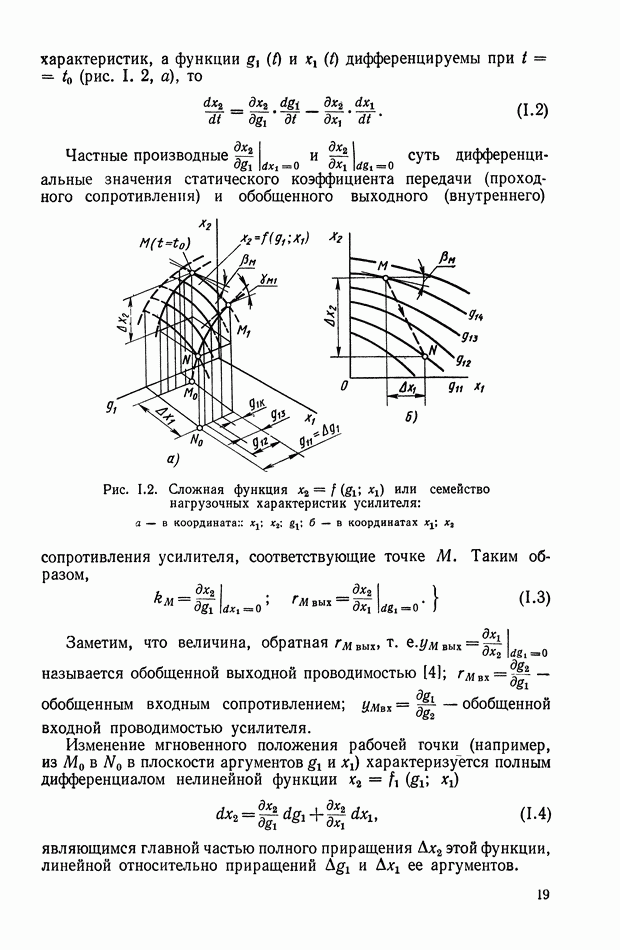
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
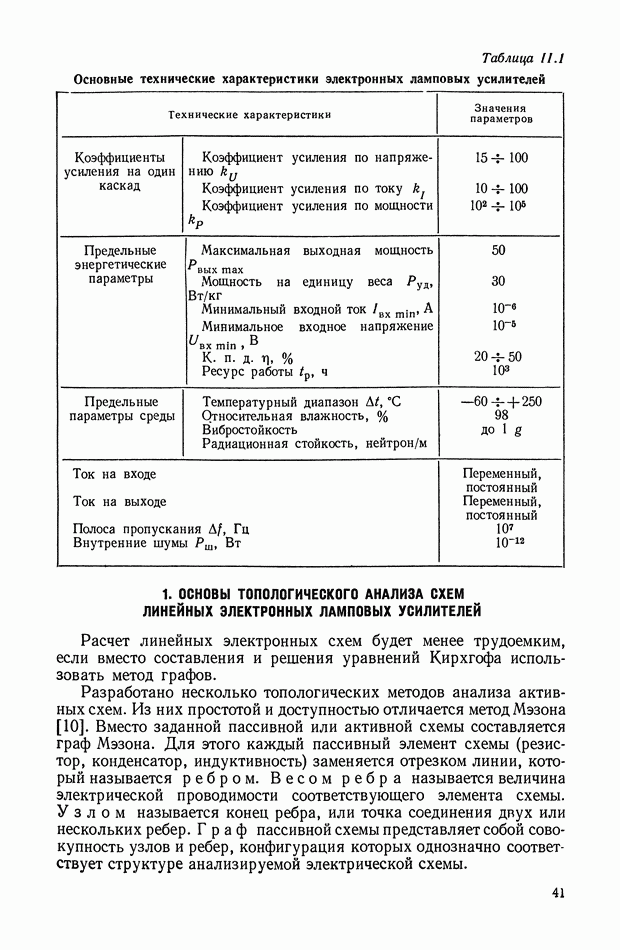
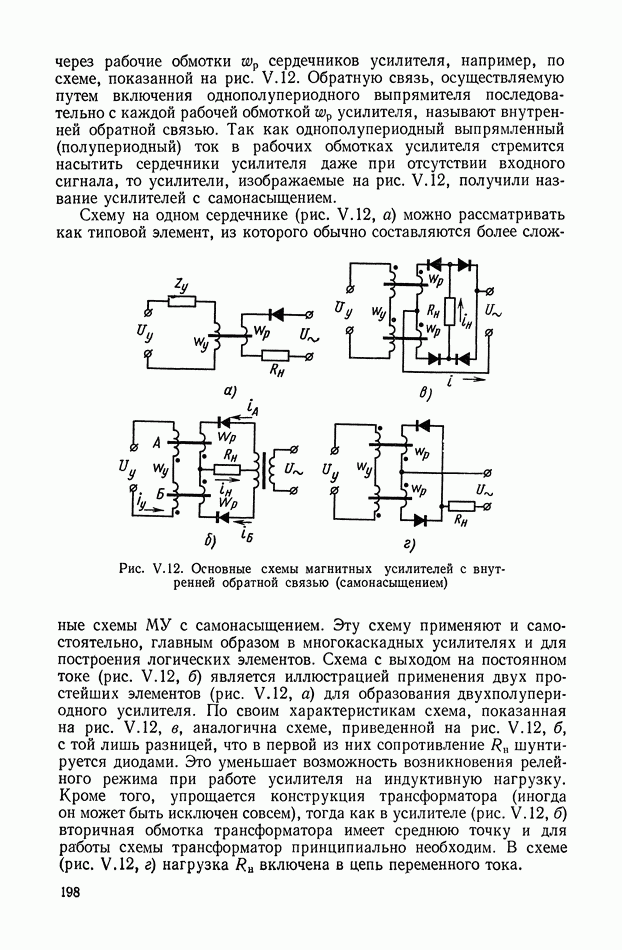
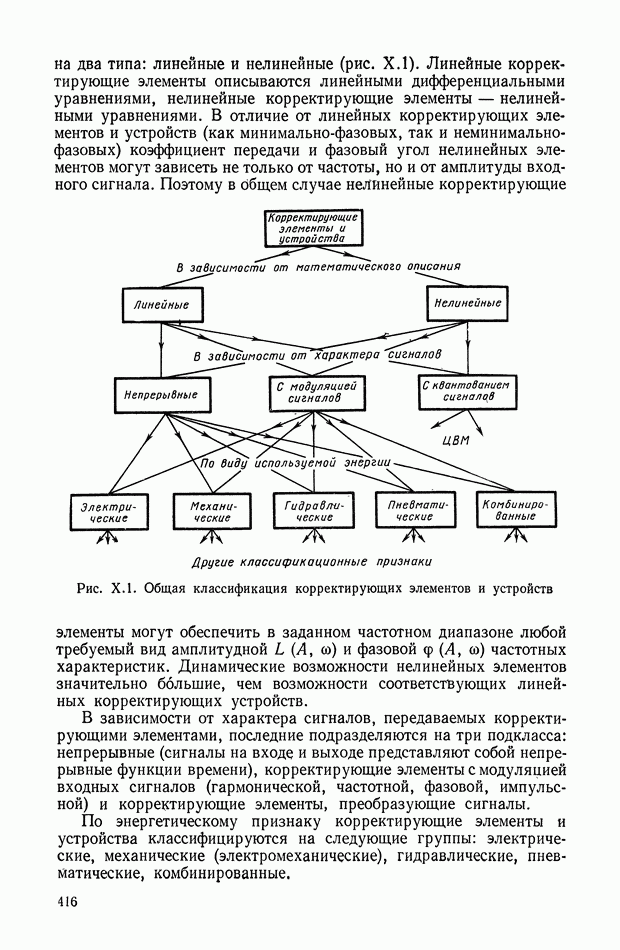
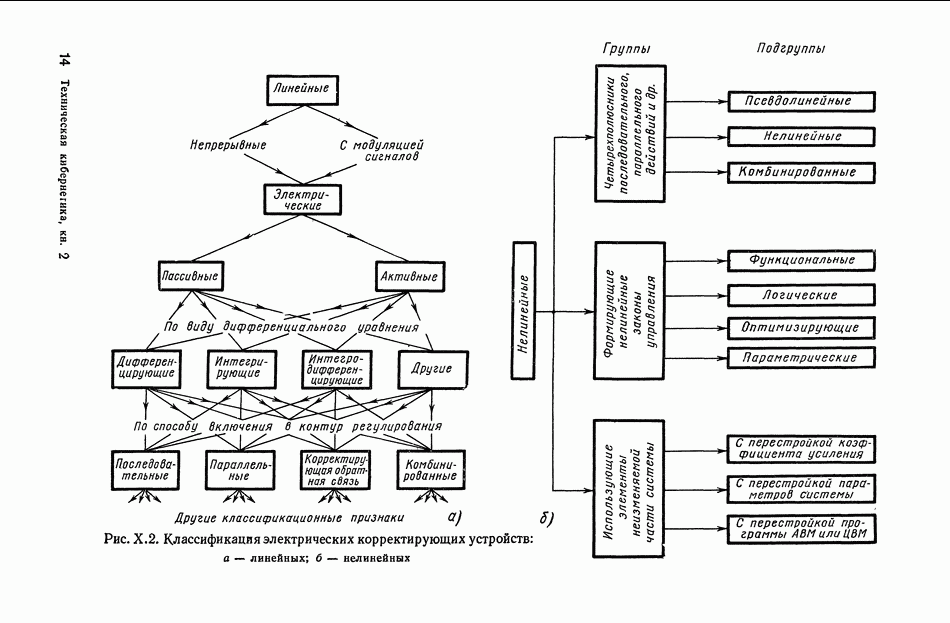
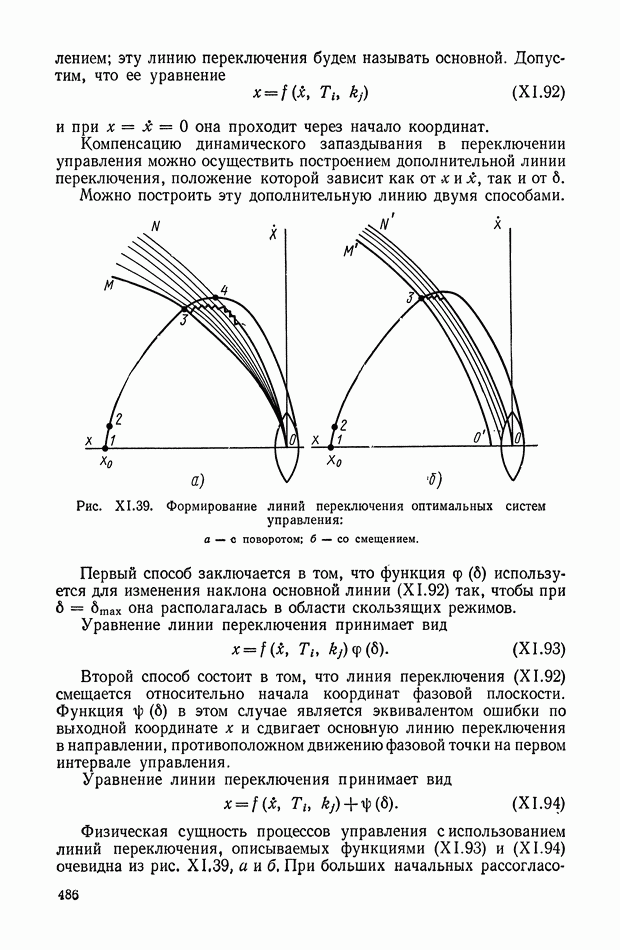
Многоканальные нелинейные логические устройства.
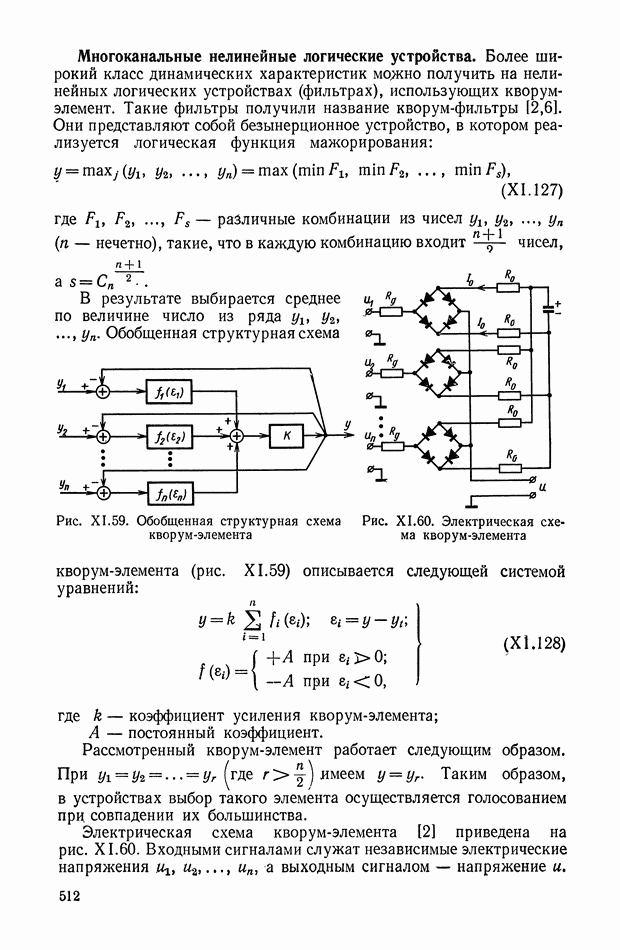
Более широкий класс динамических характеристик модою получить на нелинейных логических устройствах (фильтрах), использующих кворум-элемент. Такие фильтры получили название кворум-фильтры [2,6]. Они представляют собой безынерционное устройство, в котором реализуется логическая функция мажорирования:

где  — различные комбинации из чисел
— различные комбинации из чисел  — нечетно), такие, что в каждую комбинацию входит чисел,
— нечетно), такие, что в каждую комбинацию входит чисел, 
В результате выбирается среднее по величине число из ряда 

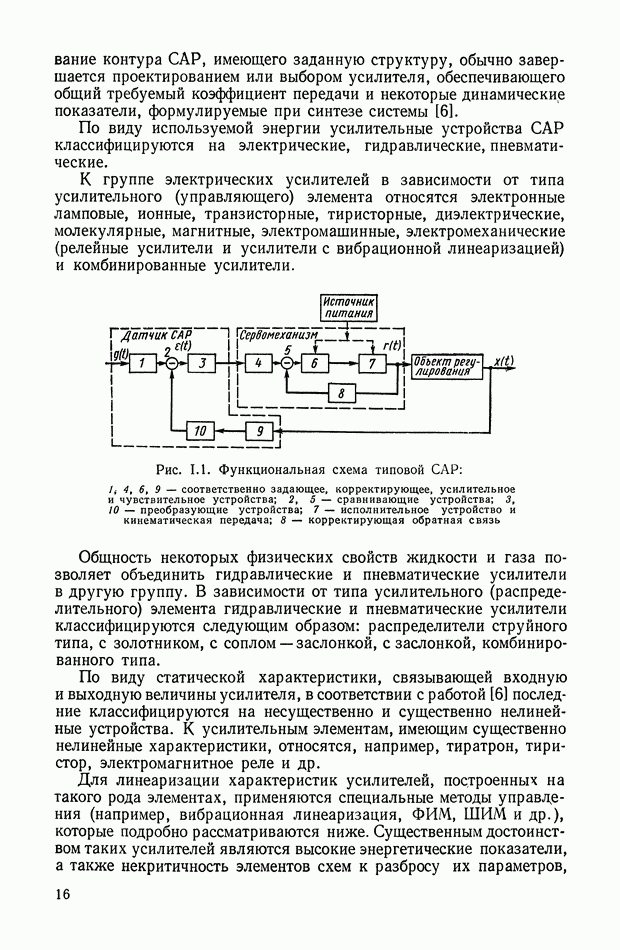
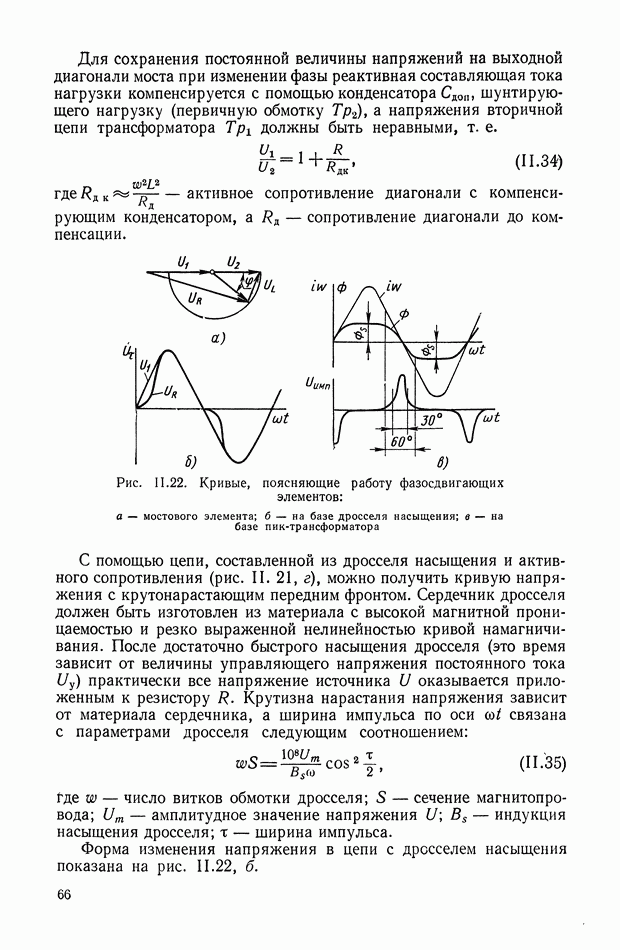
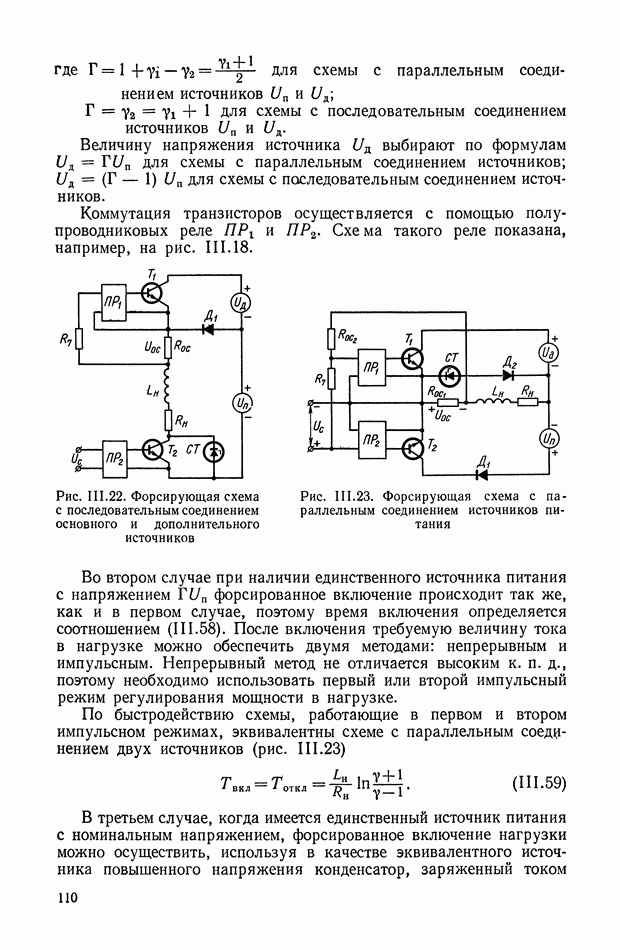
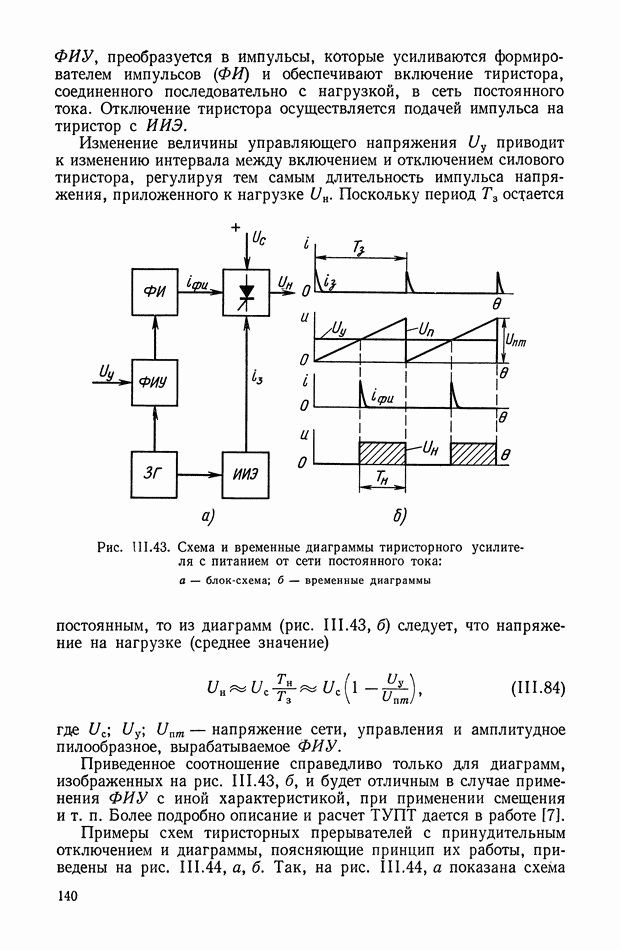
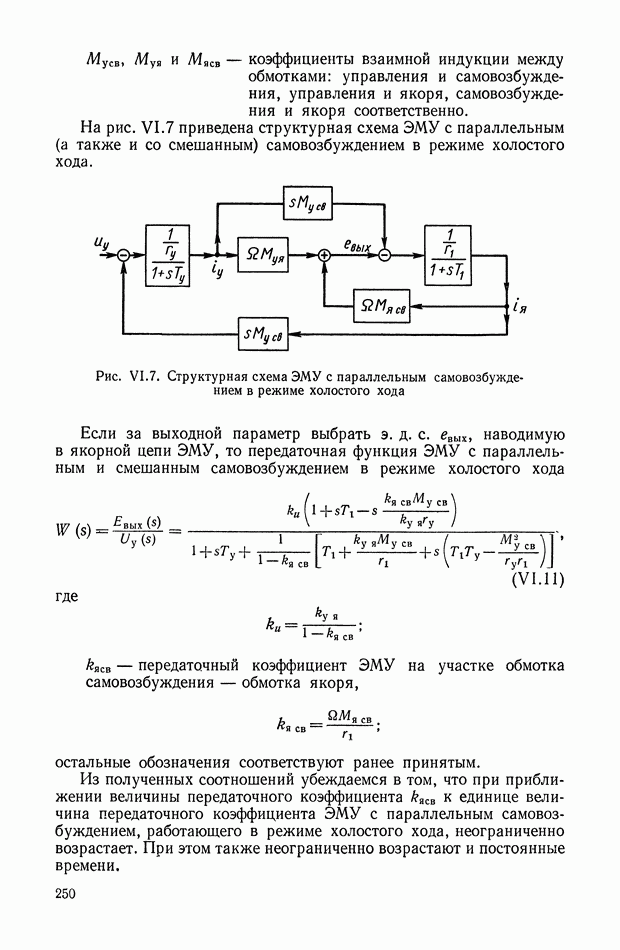
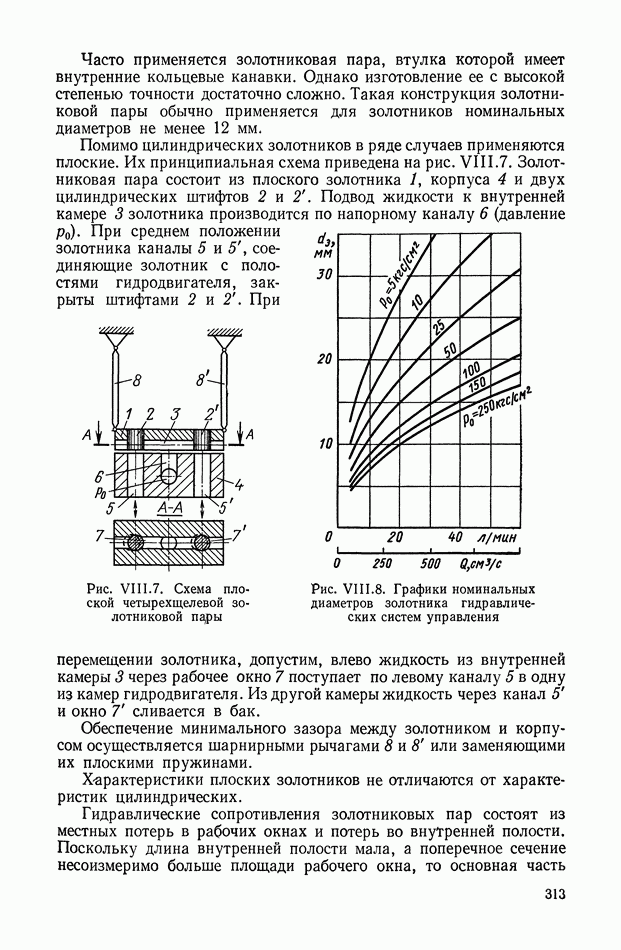
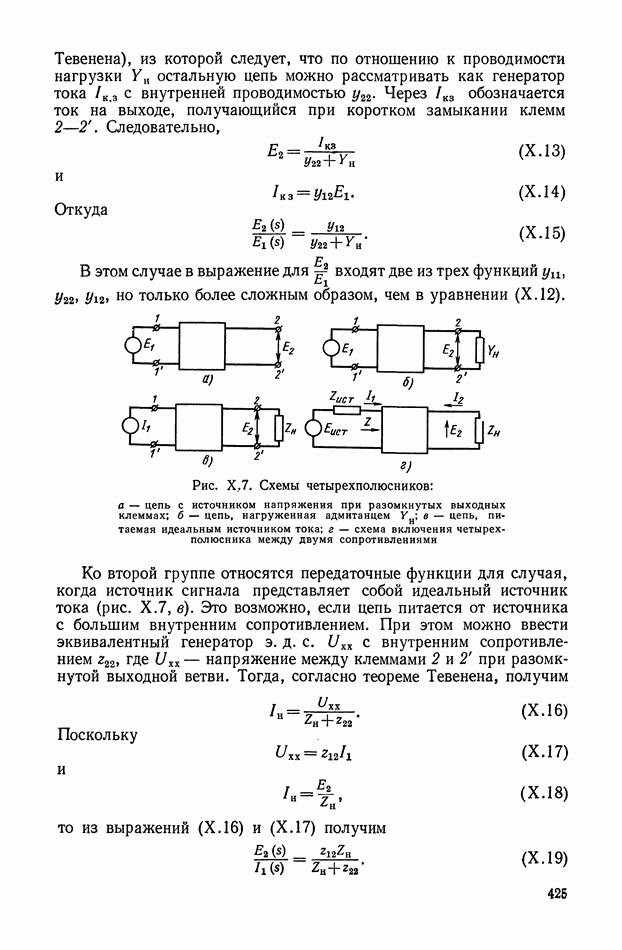
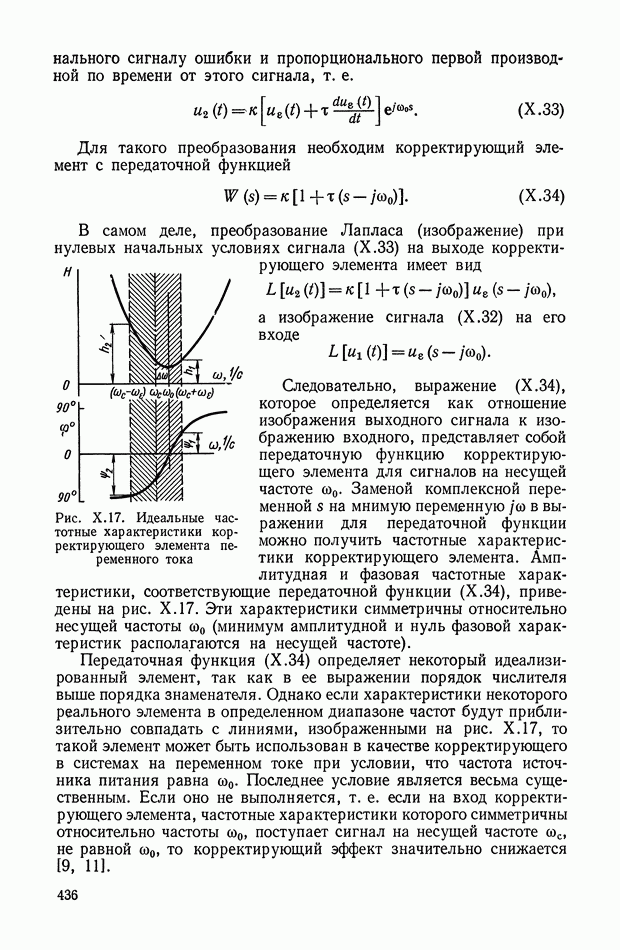
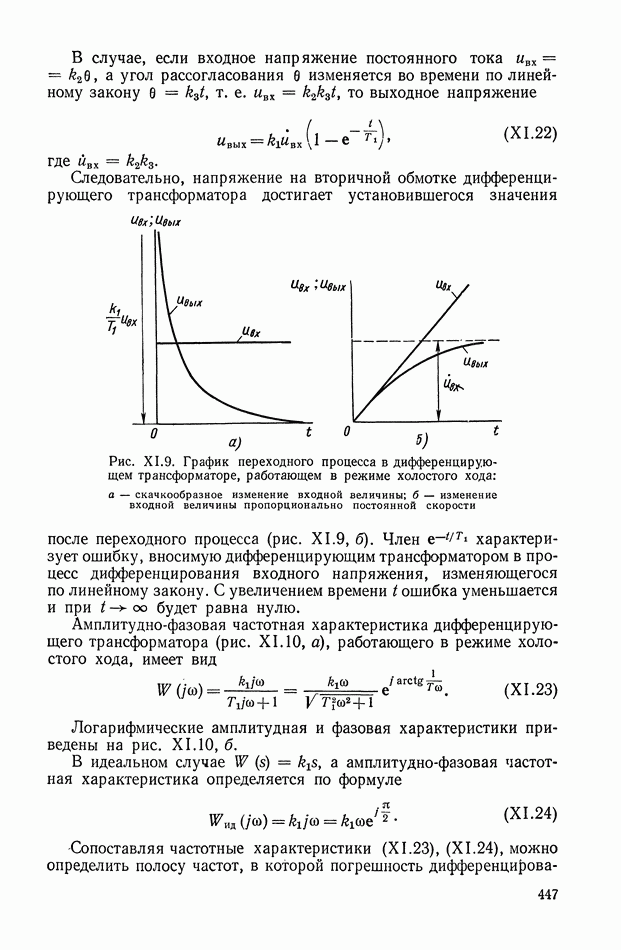
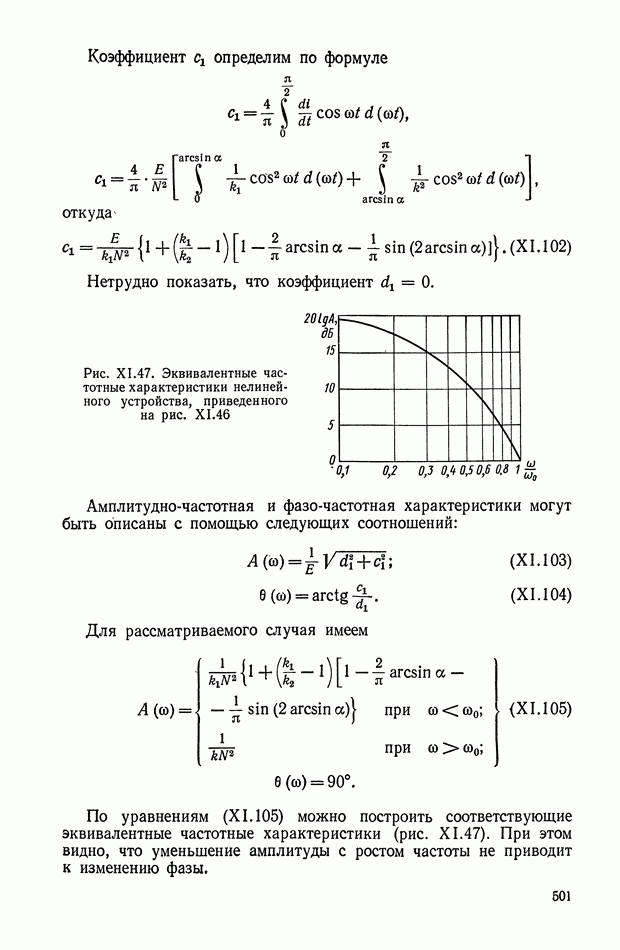
Рис. XI.59. Обобщенная структурная схема кворум-элемента

Рис. XI.60. Электрическая схема кворум-элемента
Обобщенная структурная схема кворум-элемента (рис. XI.59) описывается следующей системой уравнений:

где  — коэффициент усиления кворум-элемента;
— коэффициент усиления кворум-элемента;
 — постоянный коэффициент.
— постоянный коэффициент.
Рассмотренный кворум-элемент работает следующим образом.
При  Таким образом, в устройствах выбор такого элемента осуществляется голосованием при совпадении их большинства.
Таким образом, в устройствах выбор такого элемента осуществляется голосованием при совпадении их большинства.
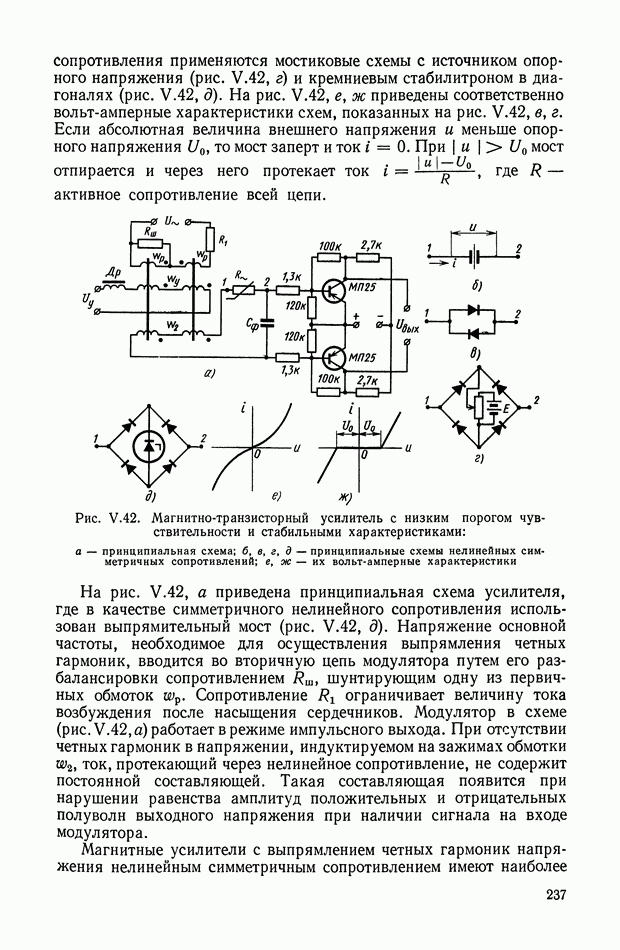
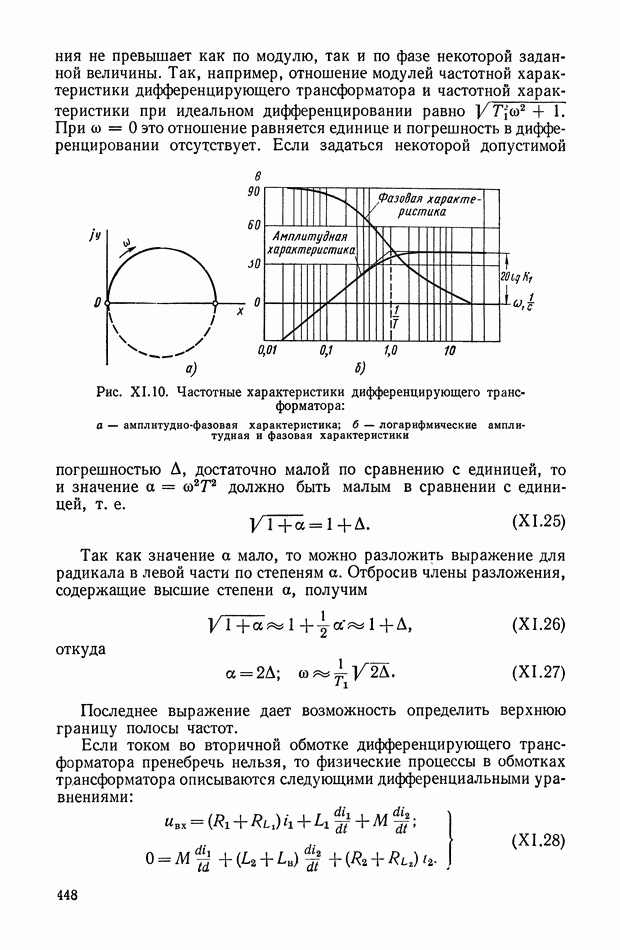
Электрическая схема кворум-элемента [2] приведена на рис. XI.60. Входными сигналами служат независимые электрические напряжения  а выходным сигналом — напряжение
а выходным сигналом — напряжение  .
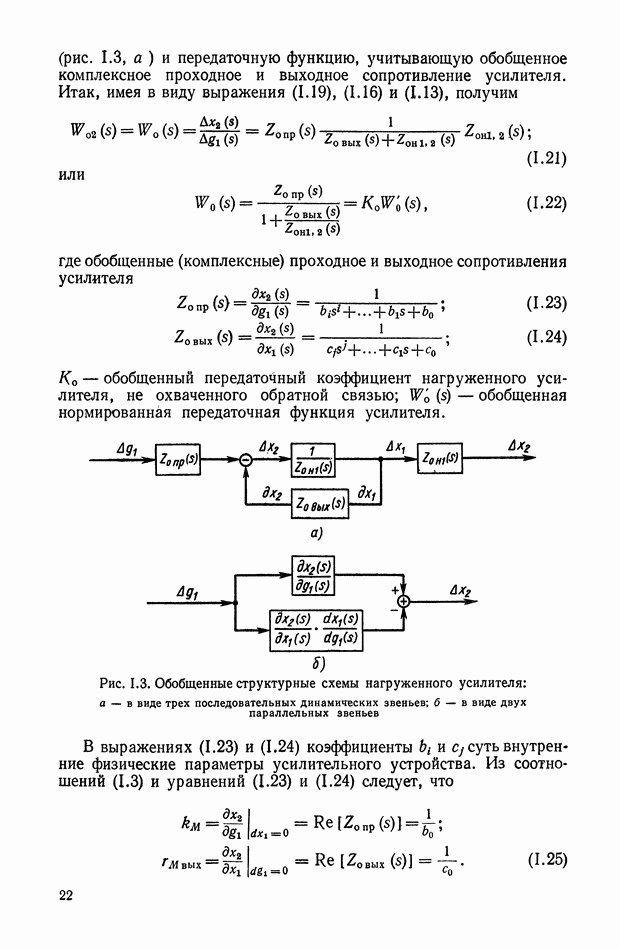
.
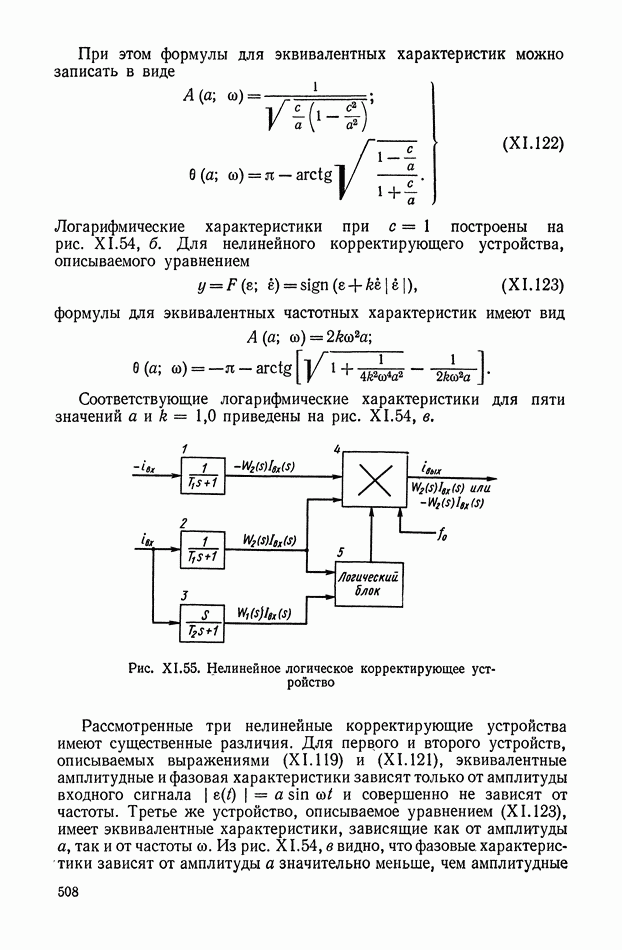
Сравнивающее звено можно рассматривать как нелинейное сопротивление с вольт-амперной характеристикой с насыщением по току. Релейный участок характеристики создается диодным мостом.
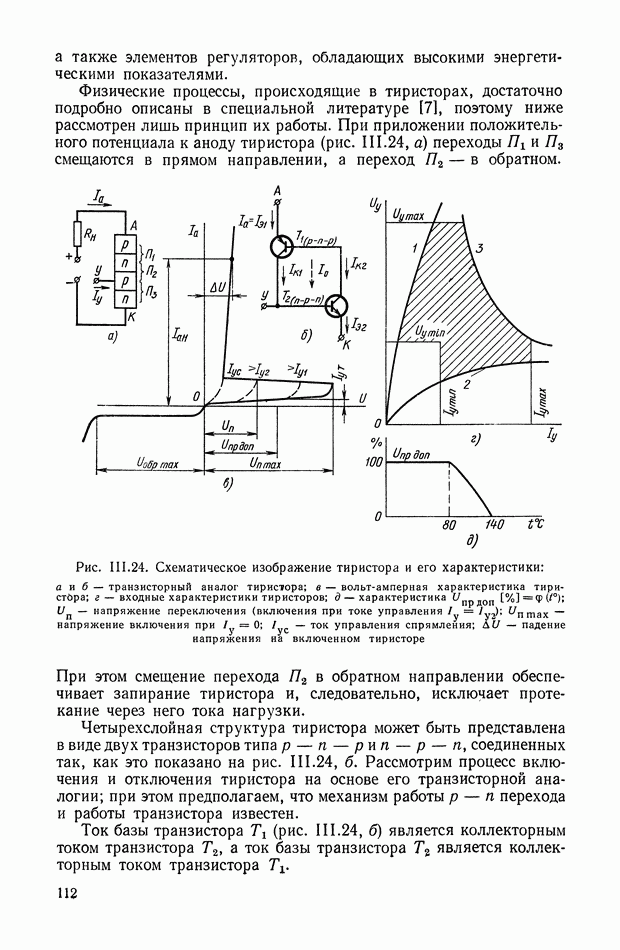
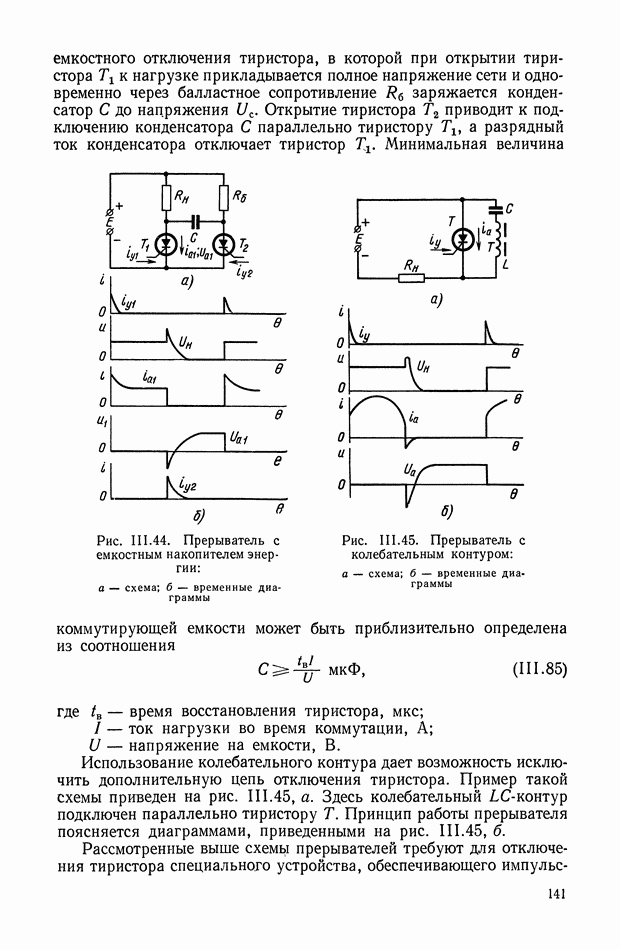
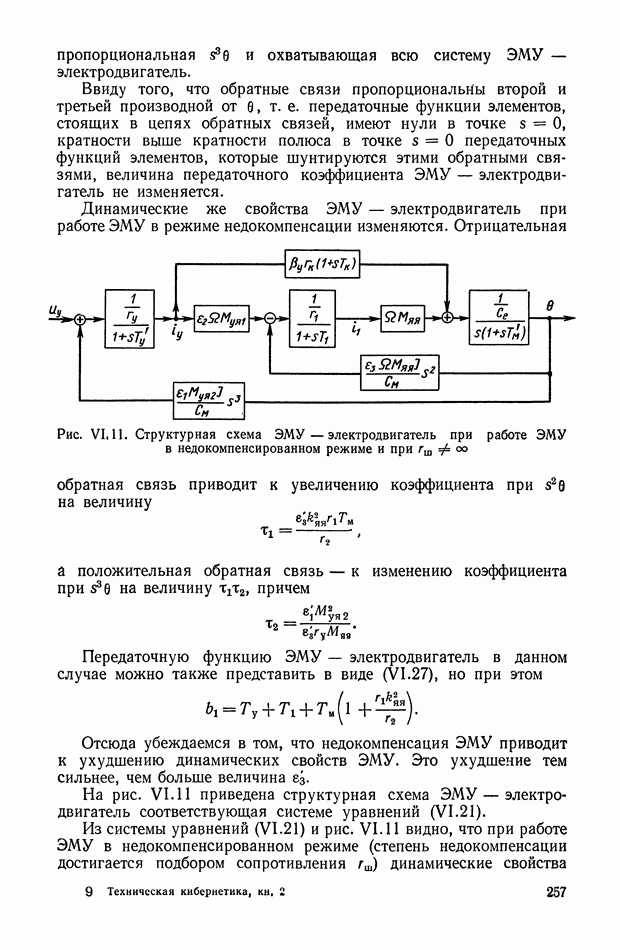
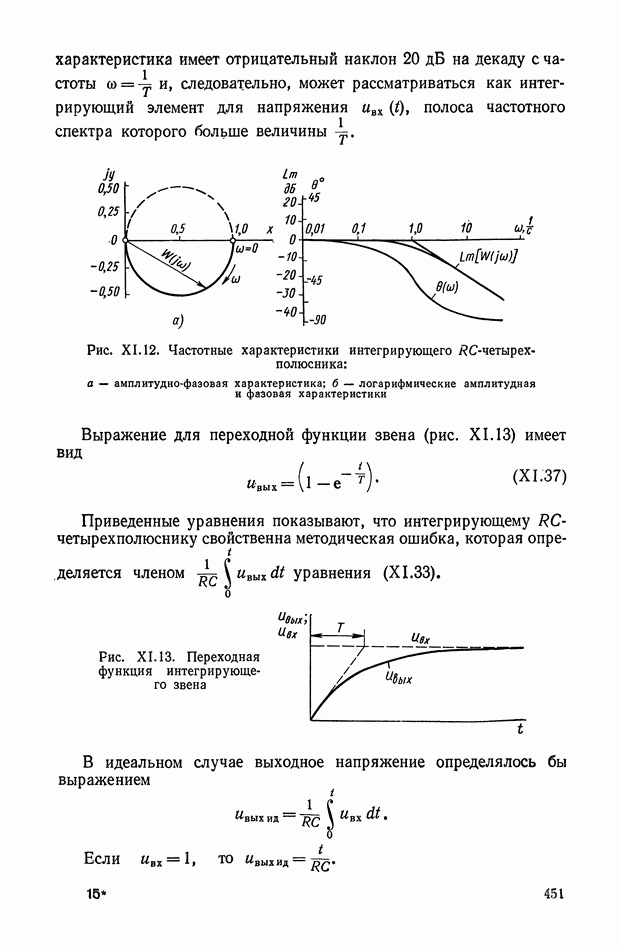
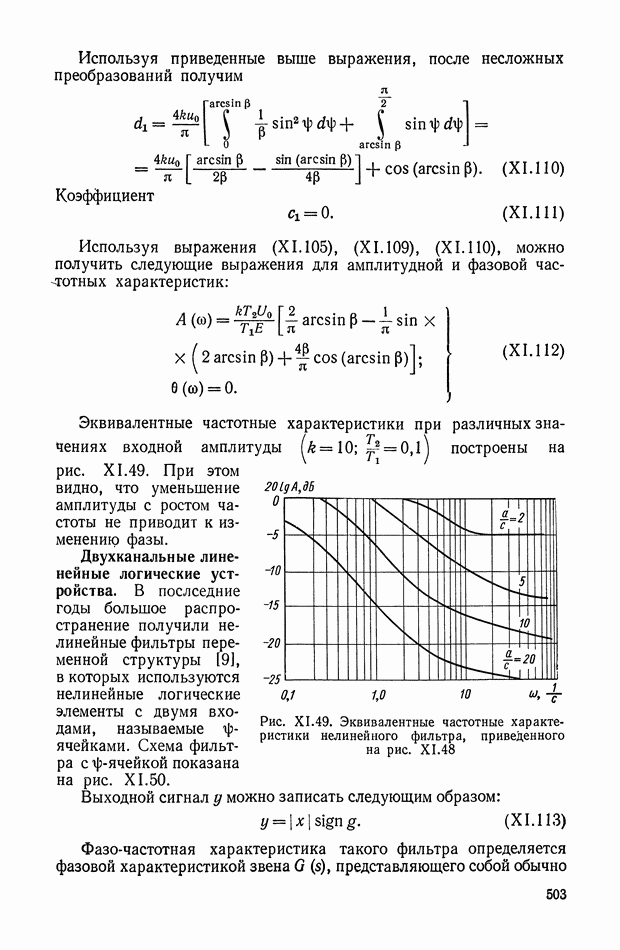
Для более детального пояснения работы кворум-элемента рассмотрим принципиальную схему устройства, приведенную на рис. X 1.61, а, на схеме показано несколько нелинейных элементов, включенных на сопротивление нагрузки  Устройство в общем случае должно осуществлять следующее: преобразование
Устройство в общем случае должно осуществлять следующее: преобразование  электрических сигналов, поступающих в виде напряжений
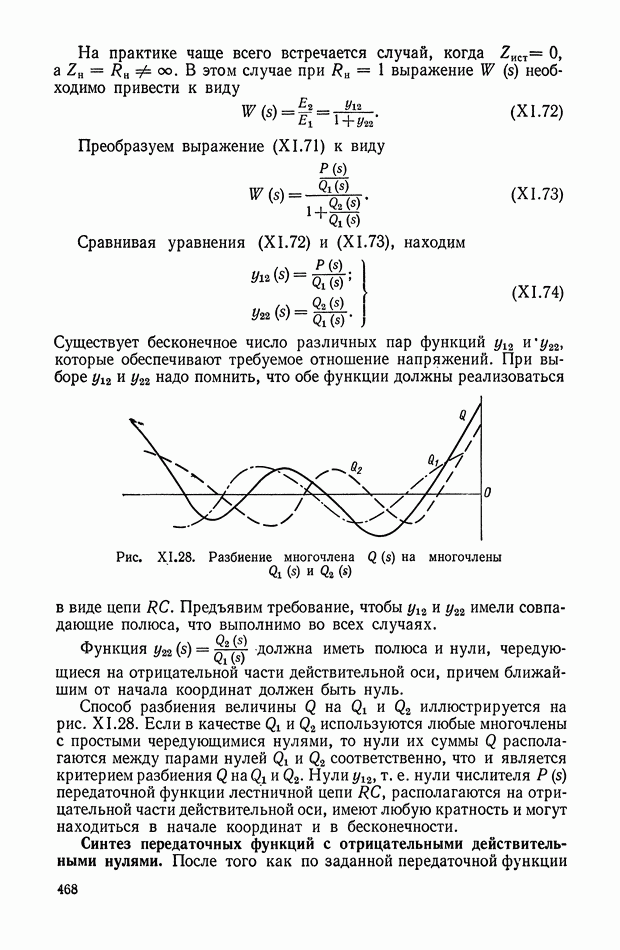
электрических сигналов, поступающих в виде напряжений  усреднение большинства сигналов, мало отличающихся по величине, и отбрасывание сигналов, существенно отличающихся от средневесового значения остальных.
усреднение большинства сигналов, мало отличающихся по величине, и отбрасывание сигналов, существенно отличающихся от средневесового значения остальных.

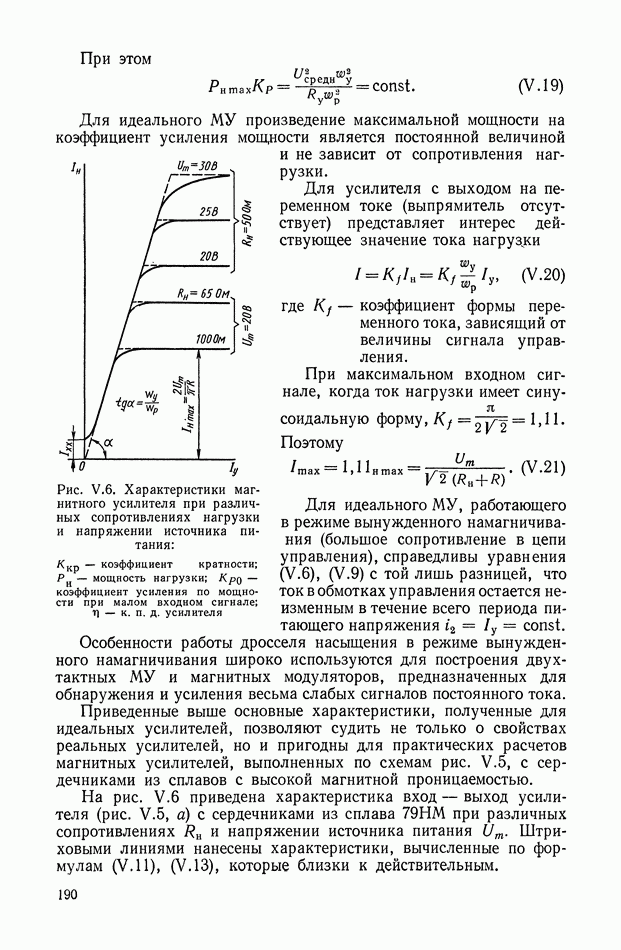
Рис. X 1.61. Принципиальная схема и характеристика кворум-элемента: а — блок-схема; б — нелинейная характеристика
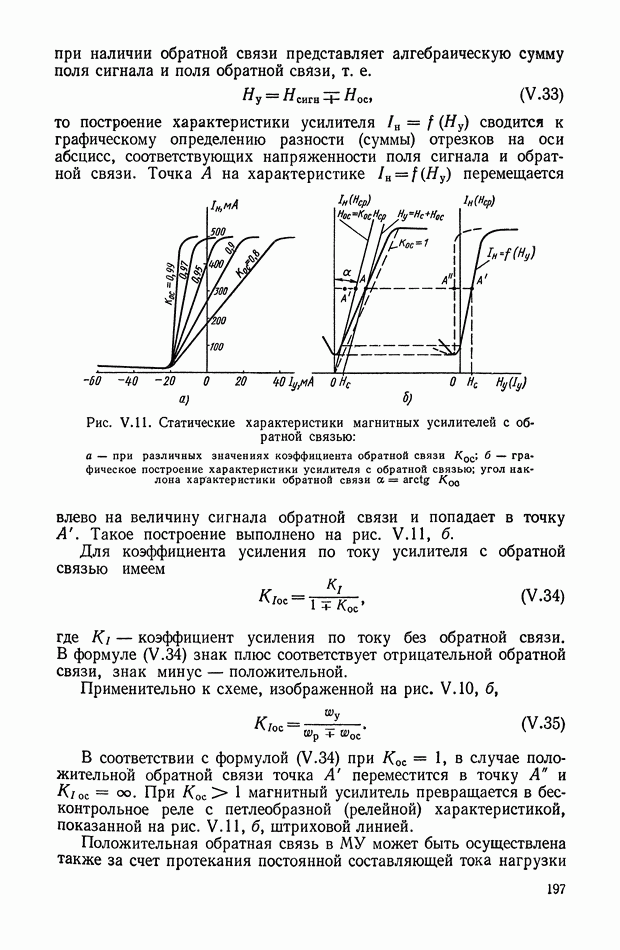
Выходной сигнал  определяется выражением
определяется выражением

где  — коэффициент преобразования;
— коэффициент преобразования;
 — пороговое значение напряжений.
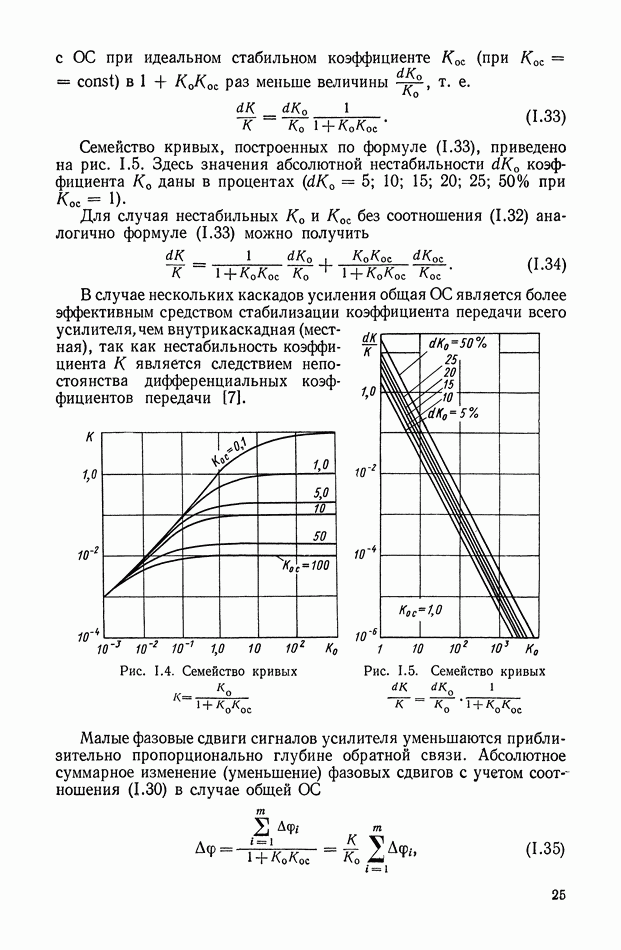
— пороговое значение напряжений.
Присвоим  сигналам, которые существенно отличаются от средневесового значения остальных, номера от
сигналам, которые существенно отличаются от средневесового значения остальных, номера от  до
до  При
При  работа устройства будет описываться уравнением типа (XI, 127).
работа устройства будет описываться уравнением типа (XI, 127).
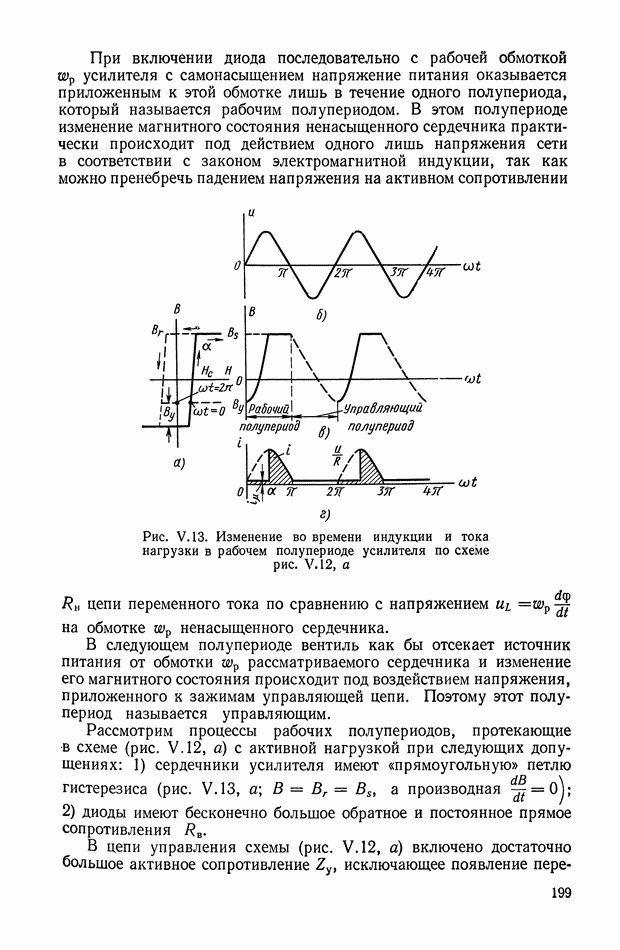
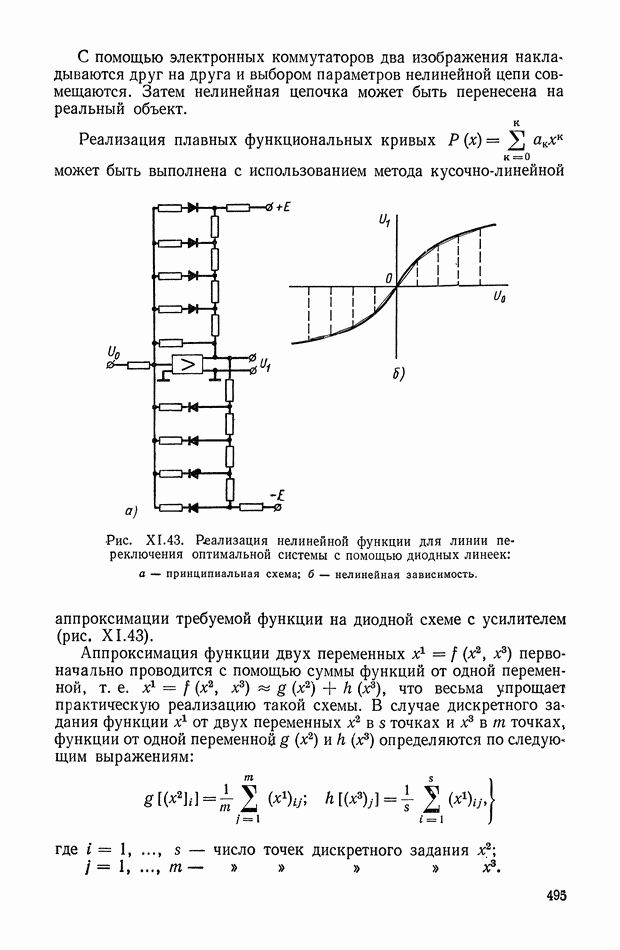
Для реализации алгоритма (XI. 129) статическая вольт-амперная характеристика нелинейного элемента должна иметь вид, показанный на рис.  Она состоит из двух участков, разграниченных током отсечки
Она состоит из двух участков, разграниченных током отсечки  и напряжением отсечки. Сопротивление первого
и напряжением отсечки. Сопротивление первого
участка равно  динамическое сопротивление второго участка
динамическое сопротивление второго участка  причем
причем  Напряжение отсечки
Напряжение отсечки 
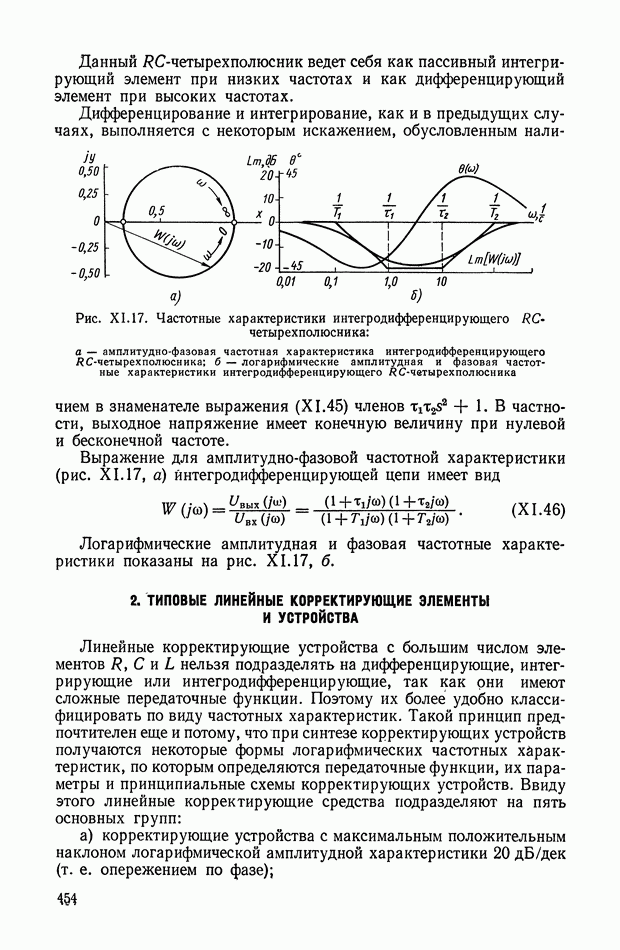
Рассмотрим принцип действия мажоритарного устройства для случая  принимая для простоты
принимая для простоты  Нелинейные элементы характеризуются параметрами
Нелинейные элементы характеризуются параметрами  Выделим три режима работы: осреднения, запирания цепи одного из сигналов и выборки промежуточного сигнала.
Выделим три режима работы: осреднения, запирания цепи одного из сигналов и выборки промежуточного сигнала.
Для случая  имеет место только режим выборки промежуточного сигнала, а для случая
имеет место только режим выборки промежуточного сигнала, а для случая  режим выборки наблюдается при значительном расхождении напряжений
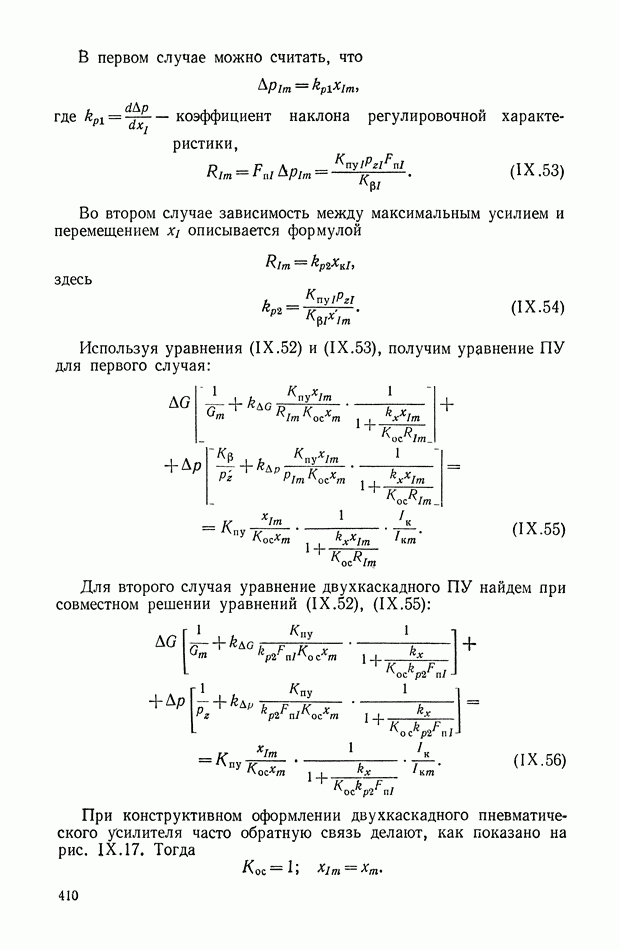
режим выборки наблюдается при значительном расхождении напряжений  так что
так что  их —
их — 

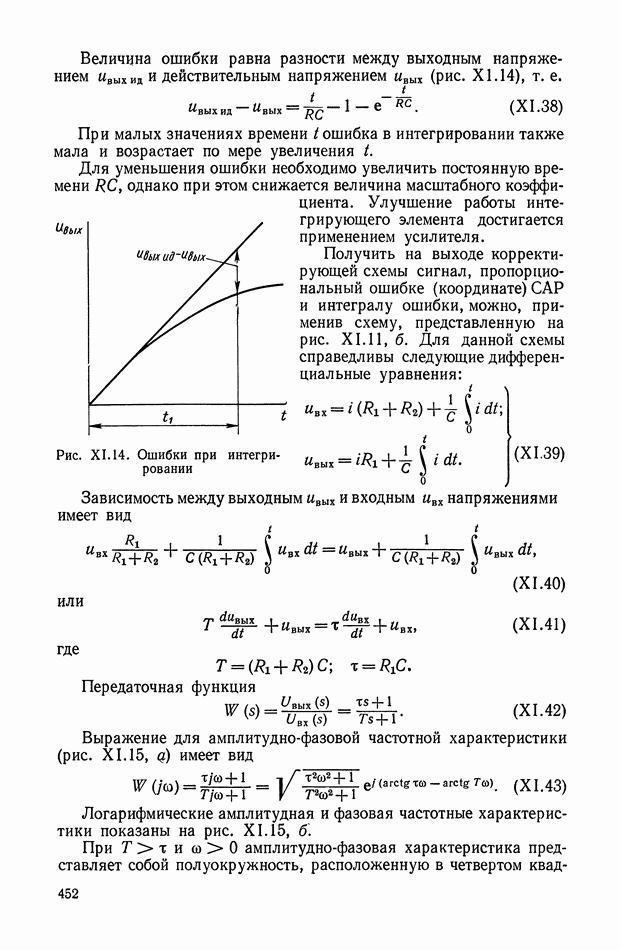
Рис. XI.62. Схема нелинейного элемента на диодах

Рис. XI.63. Структурная схема кворум-фильтра
Пусть  Уравнительный ток
Уравнительный ток  в режиме выборки замыкается по 1 и
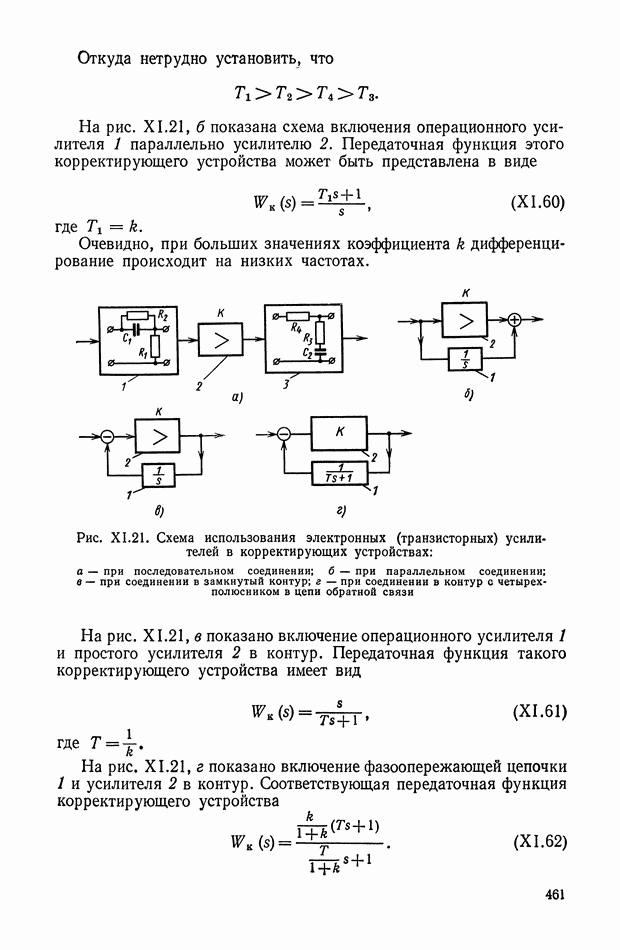
в режиме выборки замыкается по 1 и  каналам, причем
каналам, причем  канале ток отсутствует. Вследствие насыщения
канале ток отсутствует. Вследствие насыщения  и
и  каналах имеют место бесконечные динамические сопротивления. Благодаря малости сопротивления
каналах имеют место бесконечные динамические сопротивления. Благодаря малости сопротивления  канала
канала 
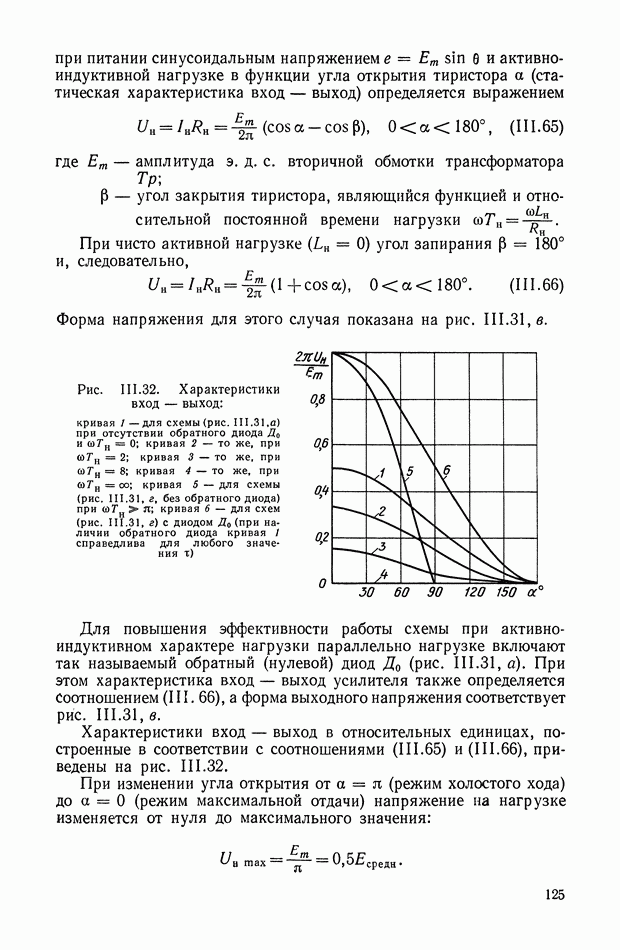
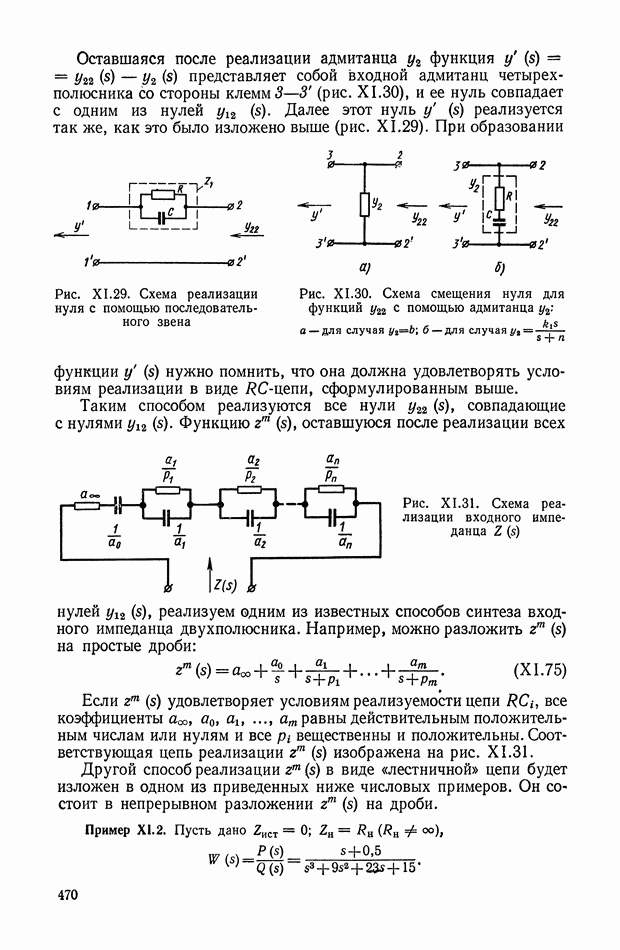
Нелинейный элемент представляет собой диодный мост (рис. XI.62), по диагонали  которого протекает ток от источника постоянного напряжения
которого протекает ток от источника постоянного напряжения  через весьма большие резисторы
через весьма большие резисторы  Данный ток создает на полупроводниковых элементах схемы падение напряжения, приложенное к диодам в прямом направлении, и снижает тем самым сопротивление диагонали АВ до величины динамического сопротивления открытого диода
Данный ток создает на полупроводниковых элементах схемы падение напряжения, приложенное к диодам в прямом направлении, и снижает тем самым сопротивление диагонали АВ до величины динамического сопротивления открытого диода  .
.
Выходной ток  приводит к появлению на элементах
приводит к появлению на элементах  компенсирующего напряжения. При величине тока
компенсирующего напряжения. При величине тока  отпирающее напряжение на диодах полностью компенсируется, мост запирается и динамическое сопротивление диагонали
отпирающее напряжение на диодах полностью компенсируется, мост запирается и динамическое сопротивление диагонали  определяется величиной сопротивлений
определяется величиной сопротивлений

Таким образом, рассмотренный диодный мост обладает характеристикой, приведенной на рис. XI.61, б.
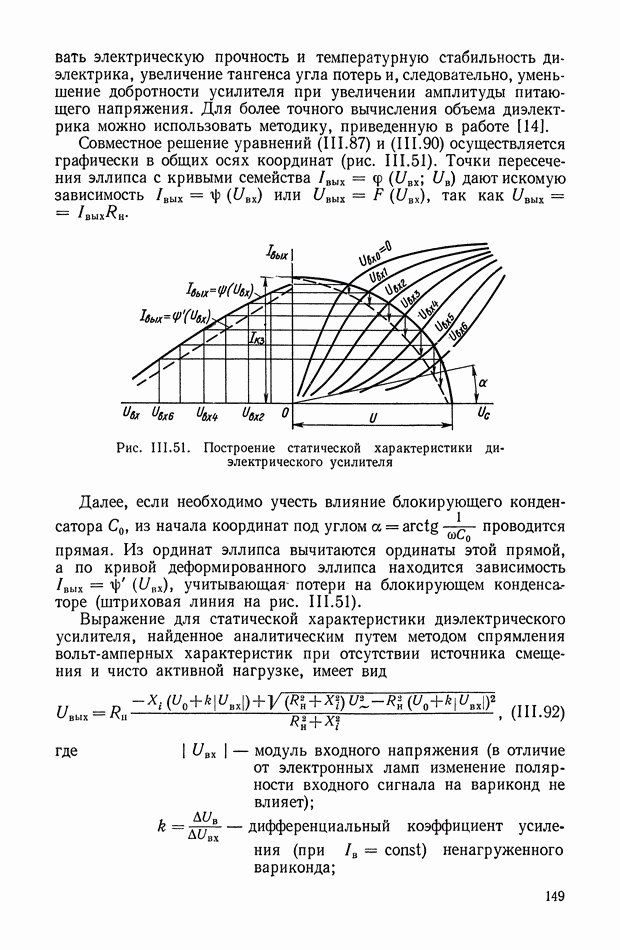
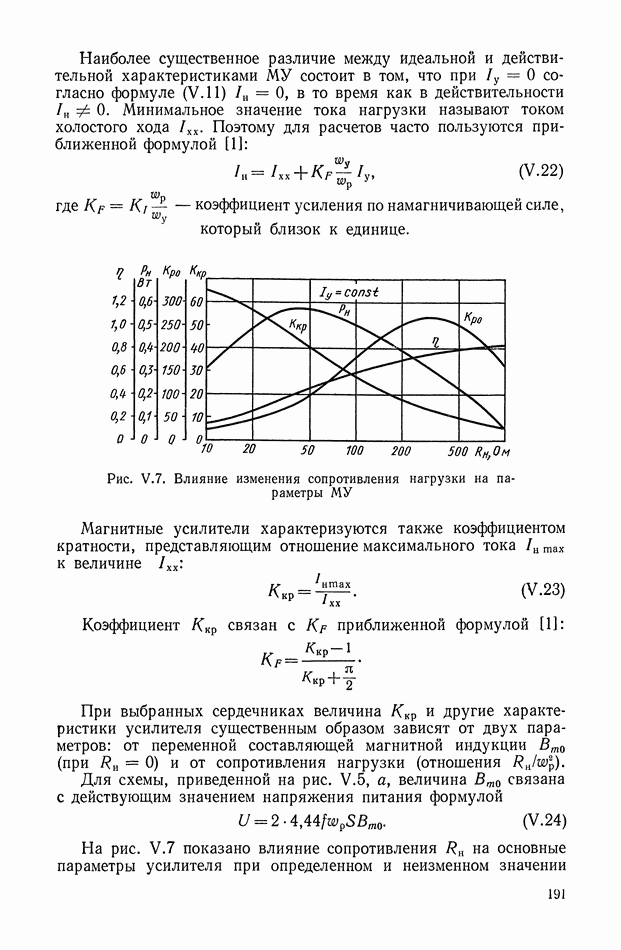
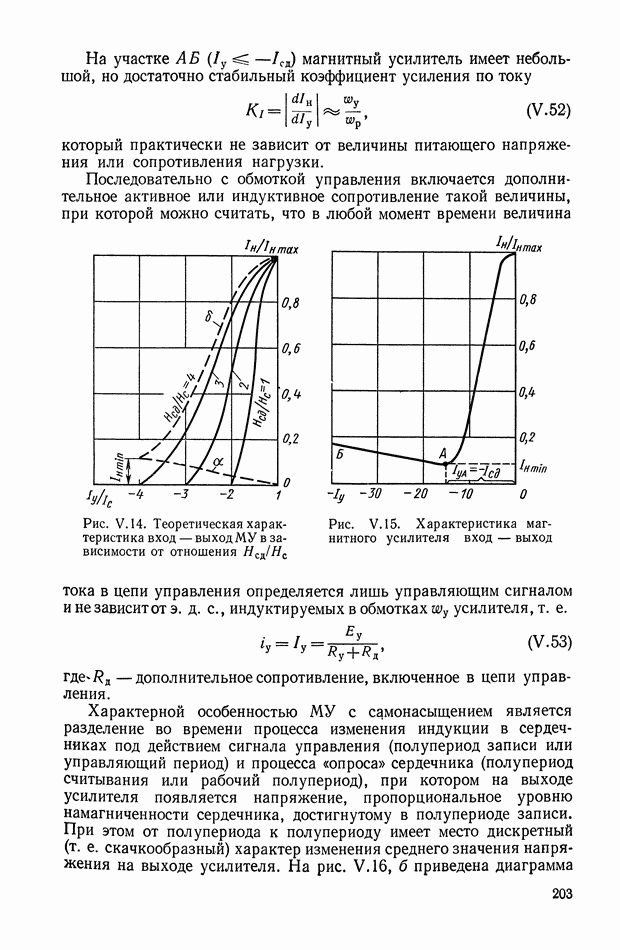
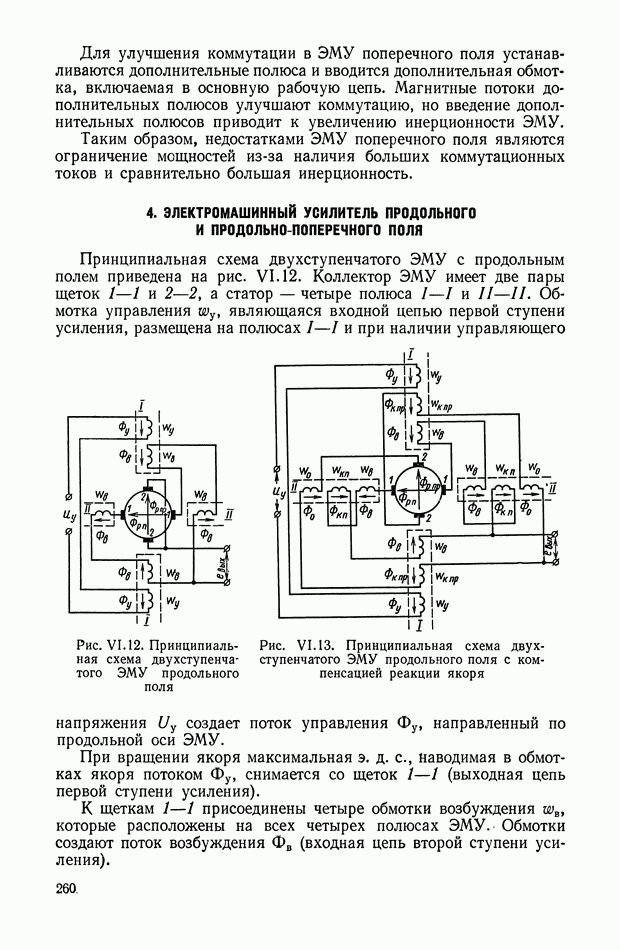
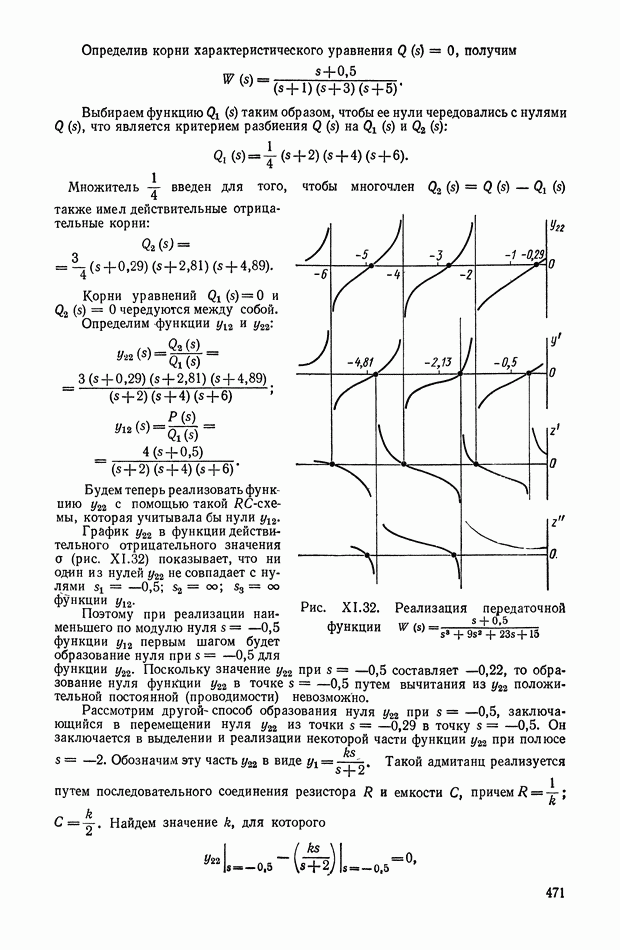
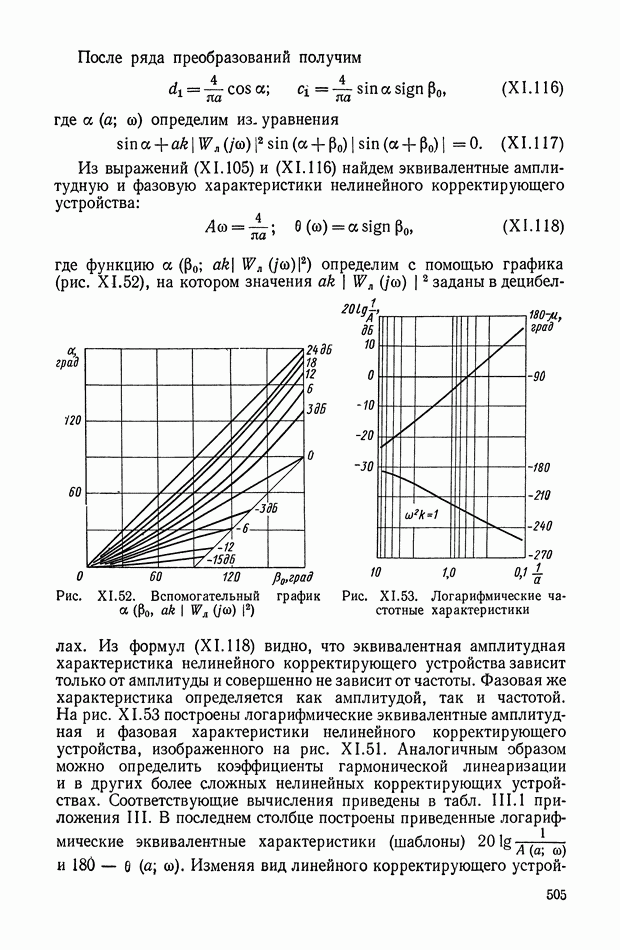
Структурная схема кворум-фильтра с тремя каналами приведена на рис. XI.63. Входной сигнал х преобразуется с помощью трех
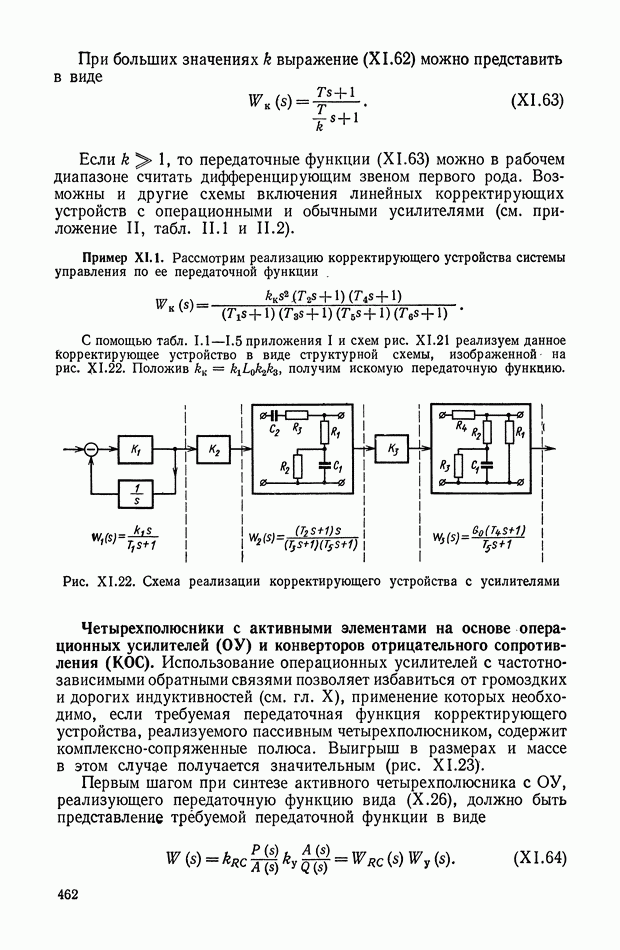
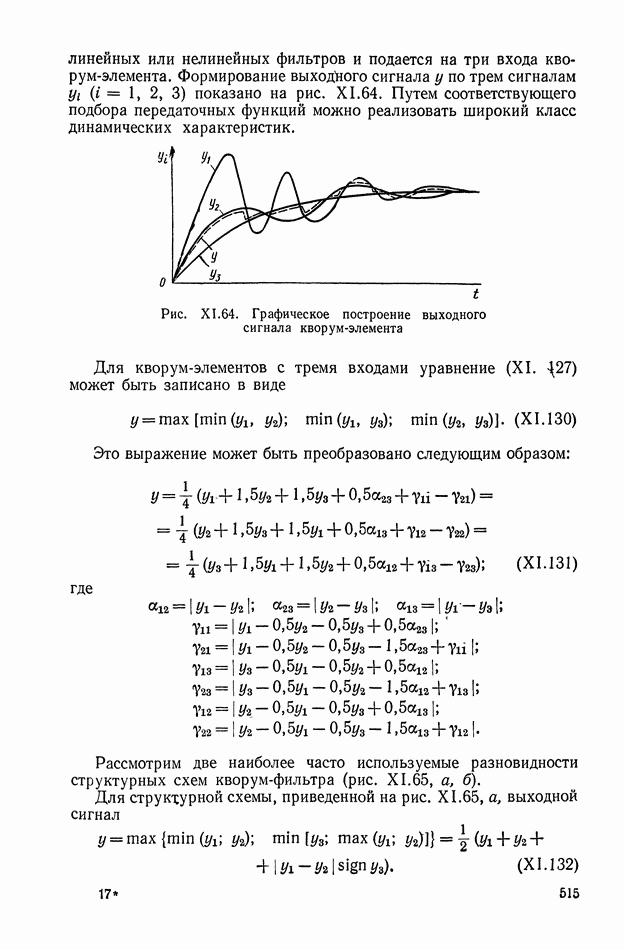
линейных или нелинейных фильтров и подается на три входа кворум-элемента. Формирование выходного сигнала у по трем сигналам  показано на рис. XI.64. Путем соответствующего подбора передаточных функций можно реализовать широкий класс динамических характеристик.
показано на рис. XI.64. Путем соответствующего подбора передаточных функций можно реализовать широкий класс динамических характеристик.

Рис. XI.64. Графическое построение выходного сигнала кворум-элемента
Для кворум-элементов с тремя входами уравнение (XI. 27) может быть записано в виде

Это выражение может быть преобразовано следующим образом:

где

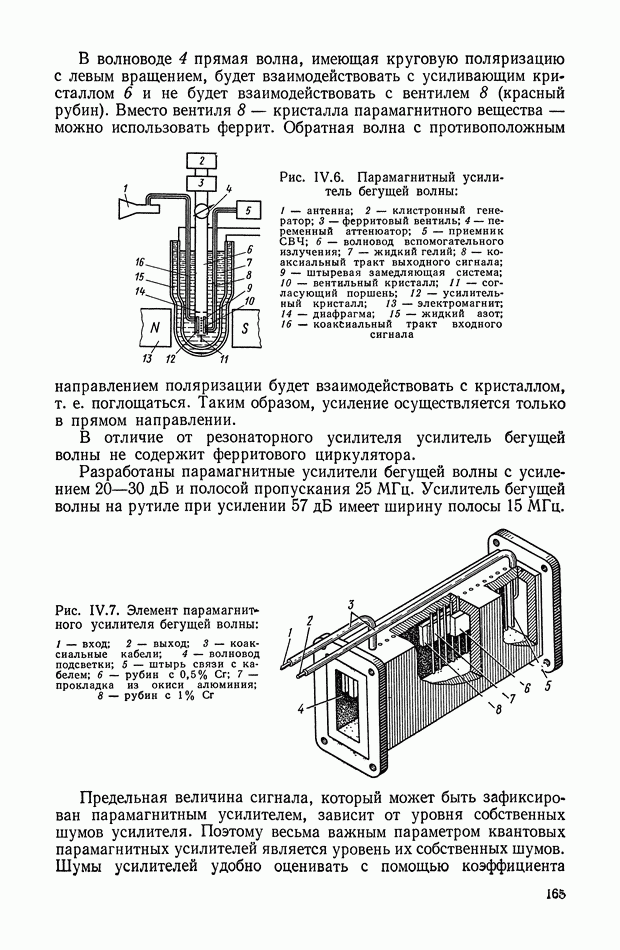
Рассмотрим две наиболее часто используемые разновидности структурных схем кворум-фильтра (рис. XI.65, а, б).
Для структурной схемы, приведенной на рис. XI.65, а, выходной сигнал

Для структурной схемы, приведенной на рис. XI.65, б, выходной сигнал

где

Для построения частотных характеристик таких фильтров можно использовать метод гармонической линеаризации. При подаче на вход кворум-фильтра сигнала  выходной сигнал у может быть разложен в ряд Фурье.
выходной сигнал у может быть разложен в ряд Фурье.

Рис. XI.65. Схемы кворум-фильтров: а — с тремя элементами и релейным блоком; б — с двумя элементами
Задача состоит в определении коэффициентов Фурье. Представим операторы линейных фильтров в виде

Примем следующие обозначения:

Тогда выражение (XI. 132) можно представить в виде

На отрезке  равенство (XI. 136) может быть записано в более удобной для вычисления коэффициентов Фурье форме:
равенство (XI. 136) может быть записано в более удобной для вычисления коэффициентов Фурье форме:

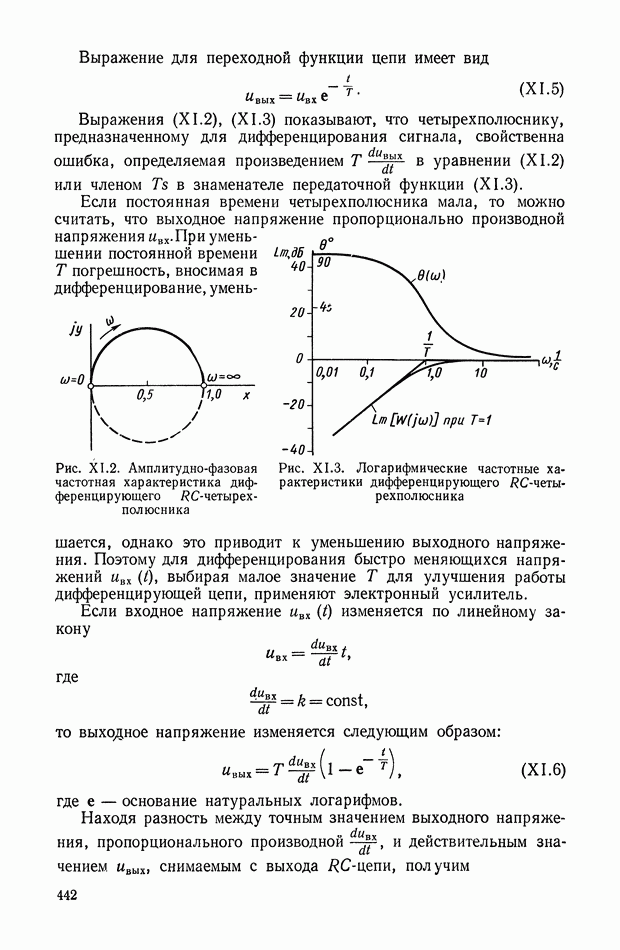
Подставив выражение для  в систему уравнений
в систему уравнений  и произведя соответствующие вычисления, получим формулы для вычисления
и произведя соответствующие вычисления, получим формулы для вычисления 

Амплитудная и фазовая частотные характеристики гармонически линеаризованного фильтра по первой гармонике определяются по формулам типа (XI.103), (XI.104). Аналогично можно вычислить коэффициенты Фурье для структурной схемы кворум-фильтра, приведенной на рис. XI.65, б:

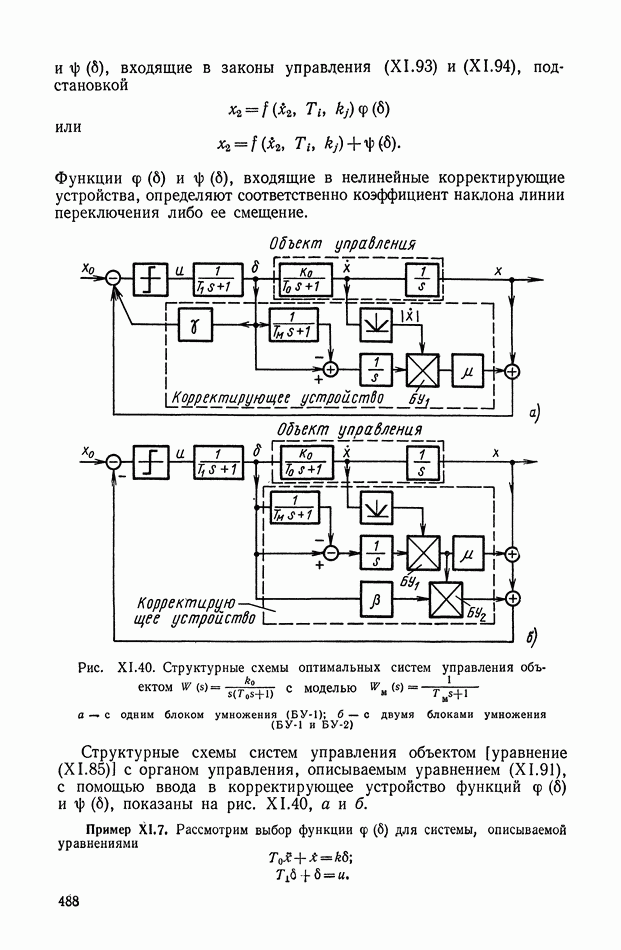
Для построения нелинейного корректирующего устройства, описываемого уравнением типа (XI. 132), в схеме на рис. XI.65, а достаточно принять

Для построения нелинейного фильтра низких частот с круто падающей амплитудно-частотной характеристикой без фазового запаздывания достаточно принять

что соответствует следующим выражениям для  :
:

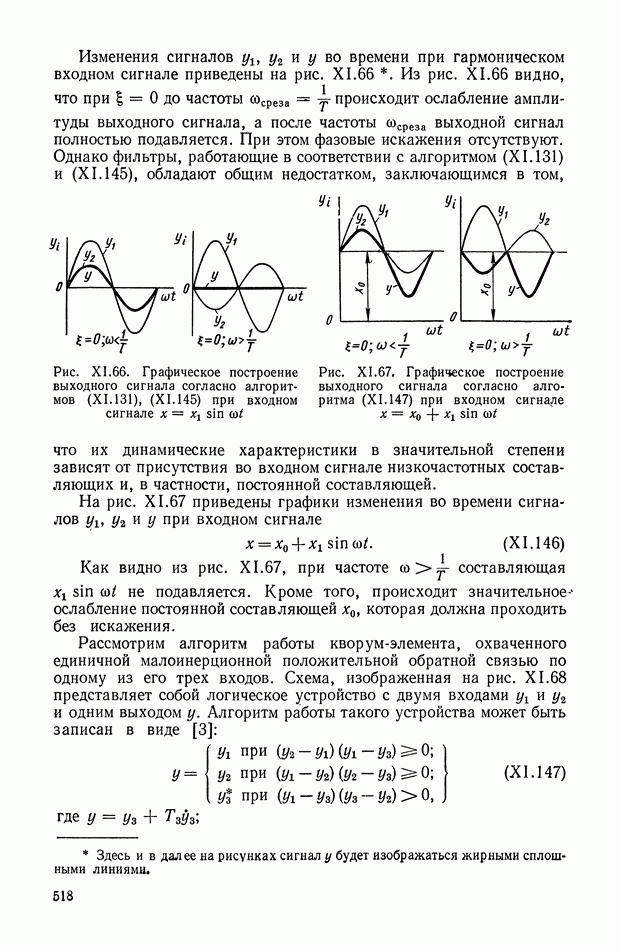
Изменения сигналов  и у во времени при гармоническом входном сигнале приведены на рис. XI.66. Из рис. XI.66 видно, что при
и у во времени при гармоническом входном сигнале приведены на рис. XI.66. Из рис. XI.66 видно, что при  до частоты
до частоты  происходит ослабление амплитуды выходного сигнала, а после частоты
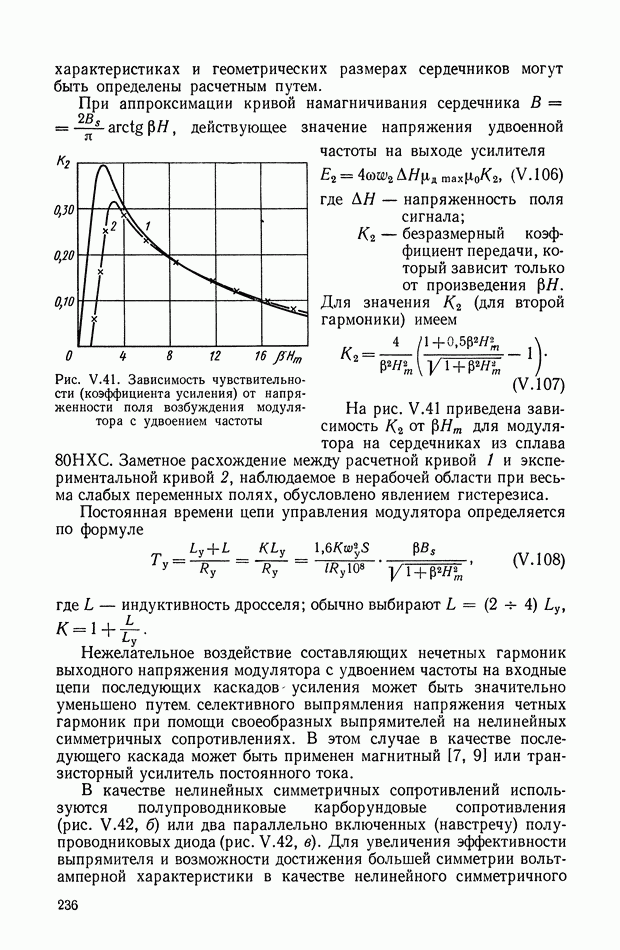
происходит ослабление амплитуды выходного сигнала, а после частоты  выходной сигнал полностью подавляется. При этом фазовые искажения отсутствуют.
выходной сигнал полностью подавляется. При этом фазовые искажения отсутствуют.

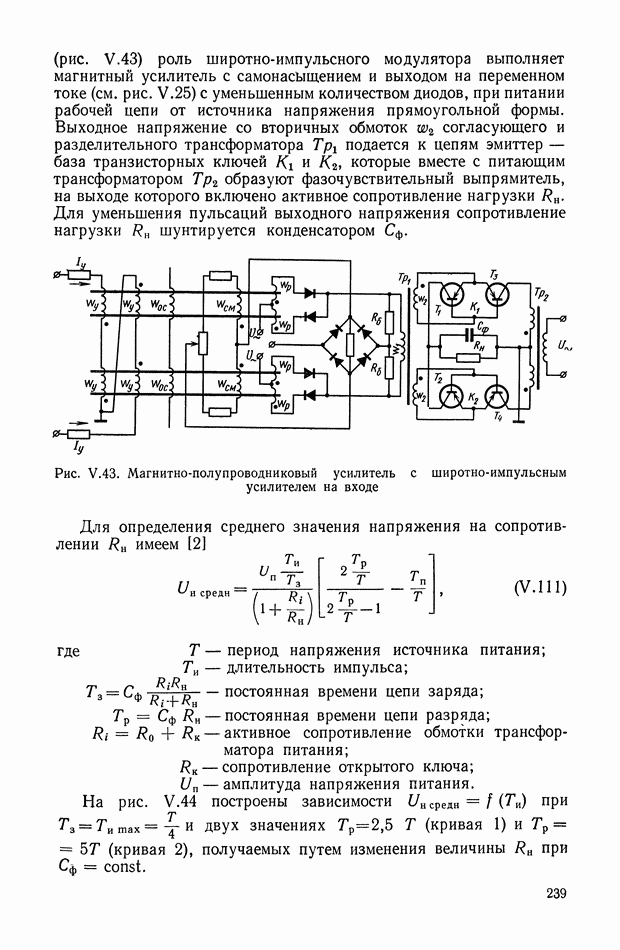
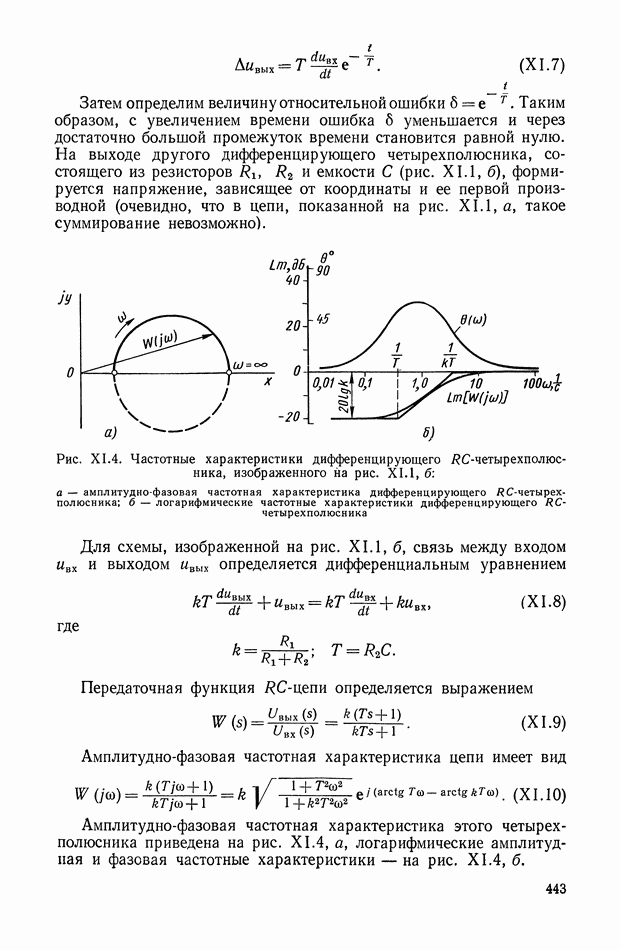
Рис. XI.66. Графическое построение выходного сигнала согласно алгоритмов (XI. 131), (XI. 145) при входном сигнале 

Рис. XI.67. Графическое построение выходного сигнала согласно алгоритма (XI. 147) при входном сигнале 
Однако фильтры, работающие в соответствии с алгоритмом (XI. 131) и (XI. 145), обладают общим недостатком, заключающимся в том, что их динамические характеристики в значительной степени зависят от присутствия во входном сигнале низкочастотных составляющих и, в частности, постоянной составляющей.
На рис. XI.67 приведены графики изменения во времени сигналов  и у при входном сигнале
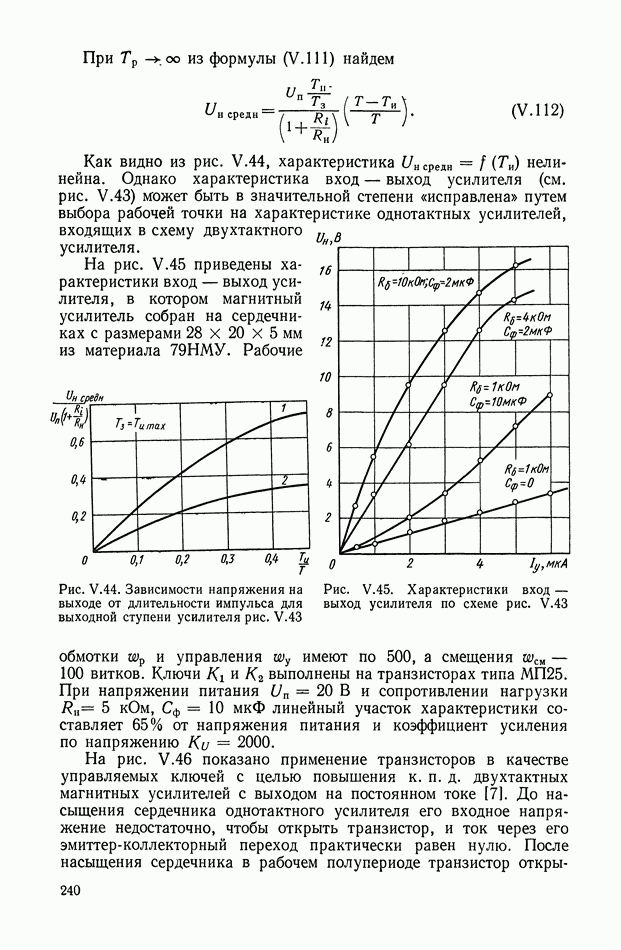
и у при входном сигнале

Как видно из рис. XI.67, при частоте  составляющая
составляющая  не подавляется. Кроме того, происходит значительное ослабление постоянной составляющей
не подавляется. Кроме того, происходит значительное ослабление постоянной составляющей  которая должна проходить без искажения.
которая должна проходить без искажения.
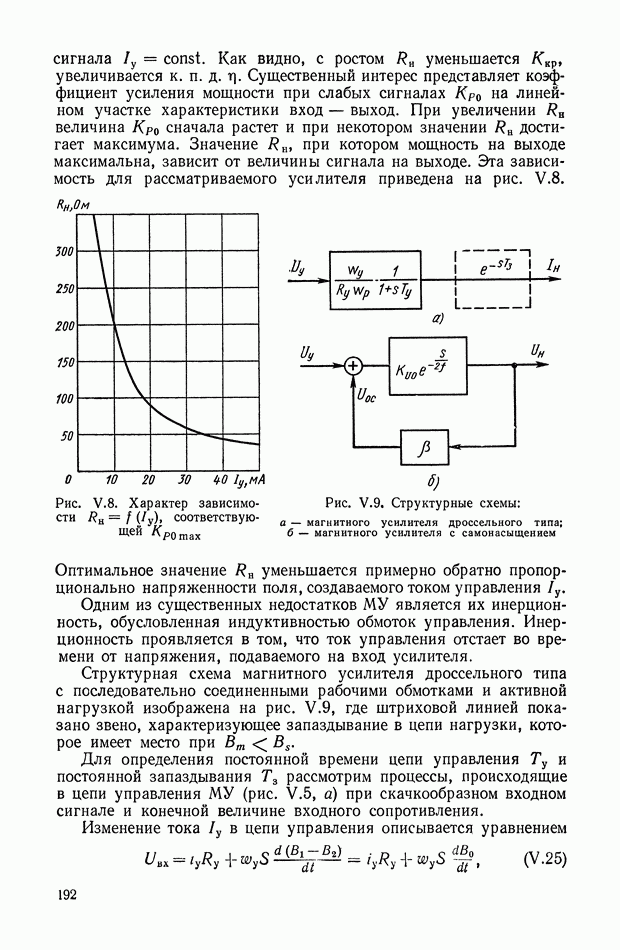
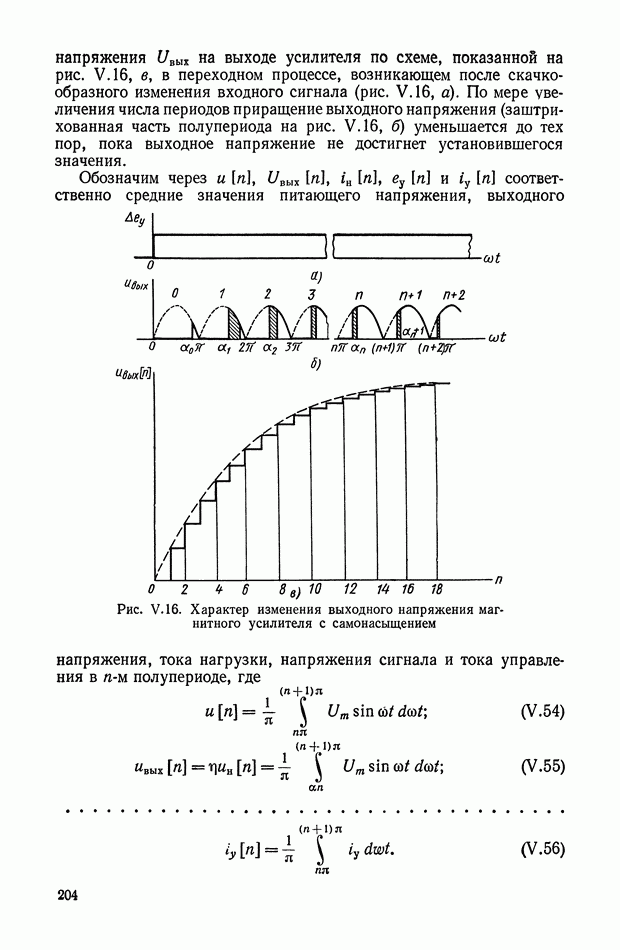
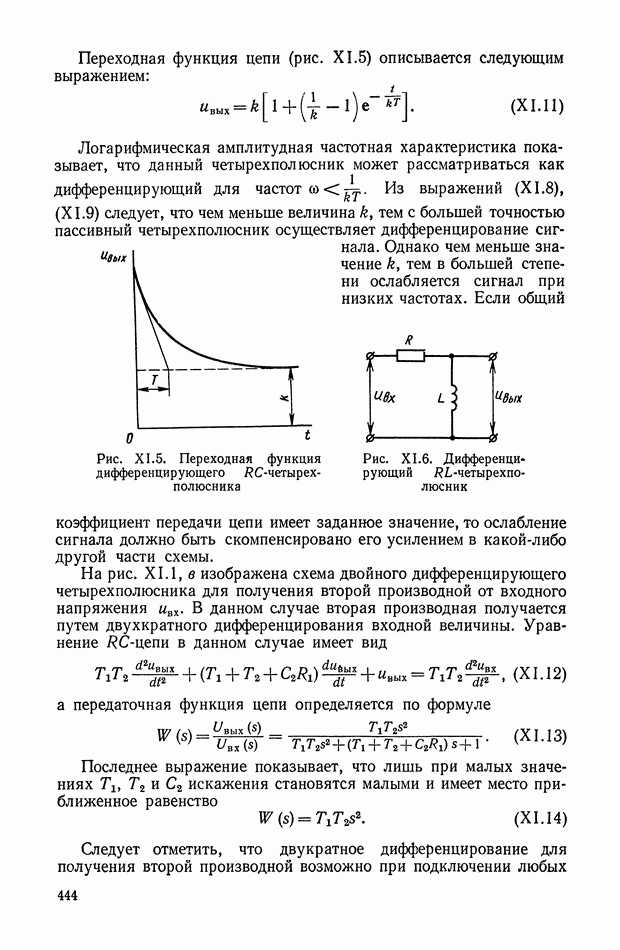
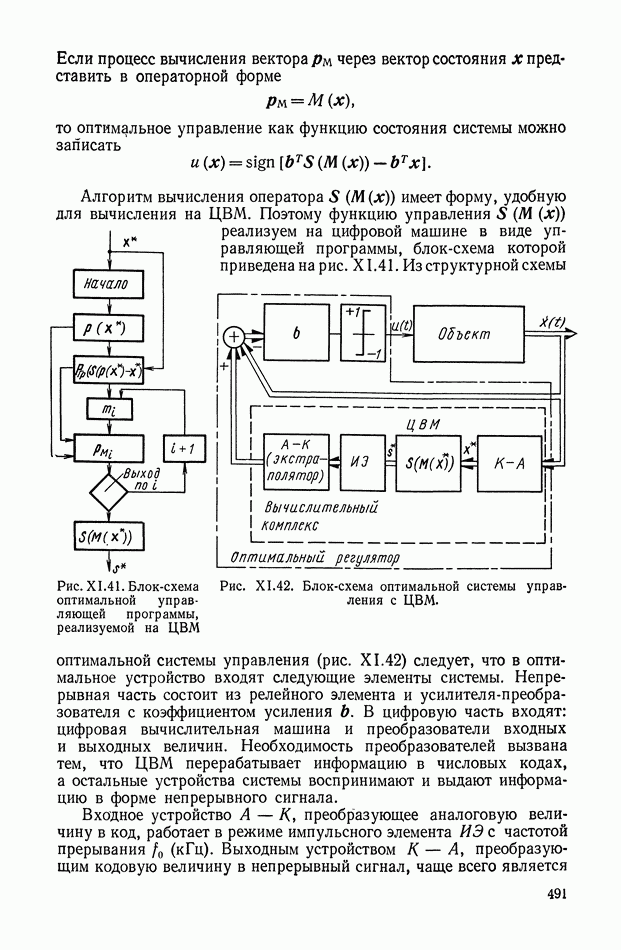
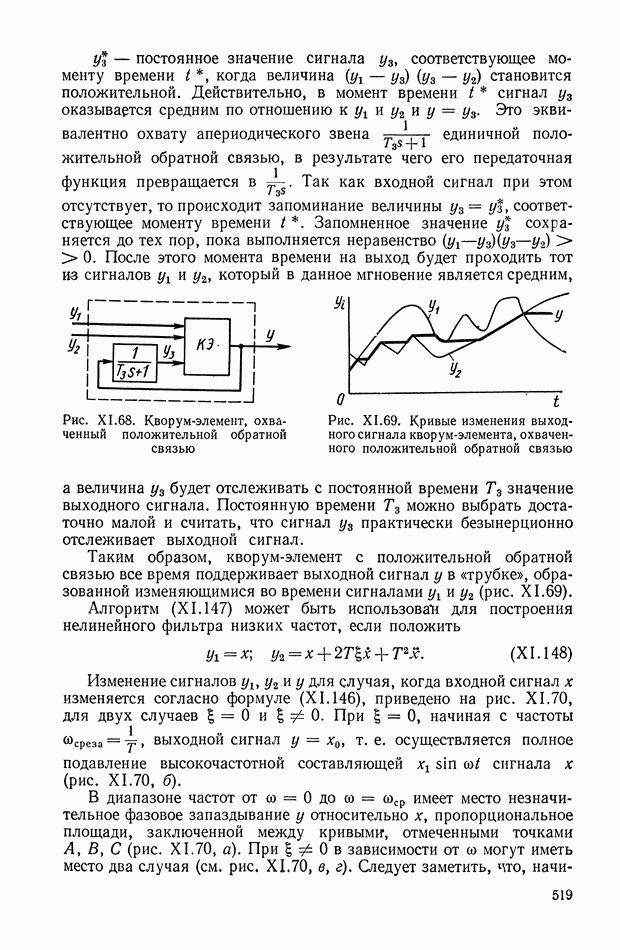
Рассмотрим алгоритм работы кворум-элемента, охваченного единичной малоинерционной положительной обратной связью по одному из его трех входов. Схема, изображенная на рис. XI.68 представляет собой логическое устройство с двумя входами  и одним выходом у. Алгоритм работы такого устройства может быть записан в виде [3]:
и одним выходом у. Алгоритм работы такого устройства может быть записан в виде [3]:

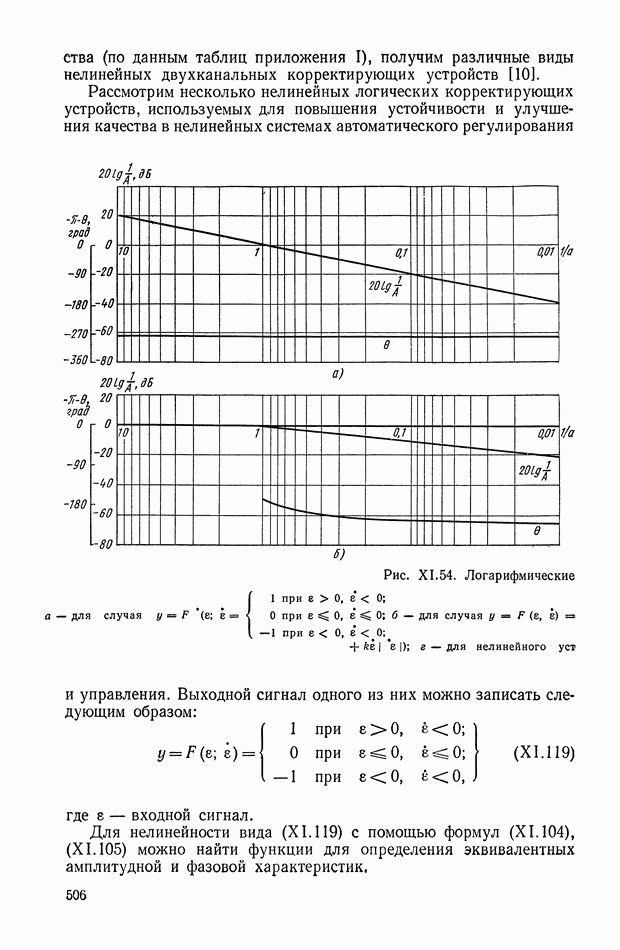
где 
 постоянное значение сигнала
постоянное значение сигнала  соответствующее моменту времени
соответствующее моменту времени  когда величина
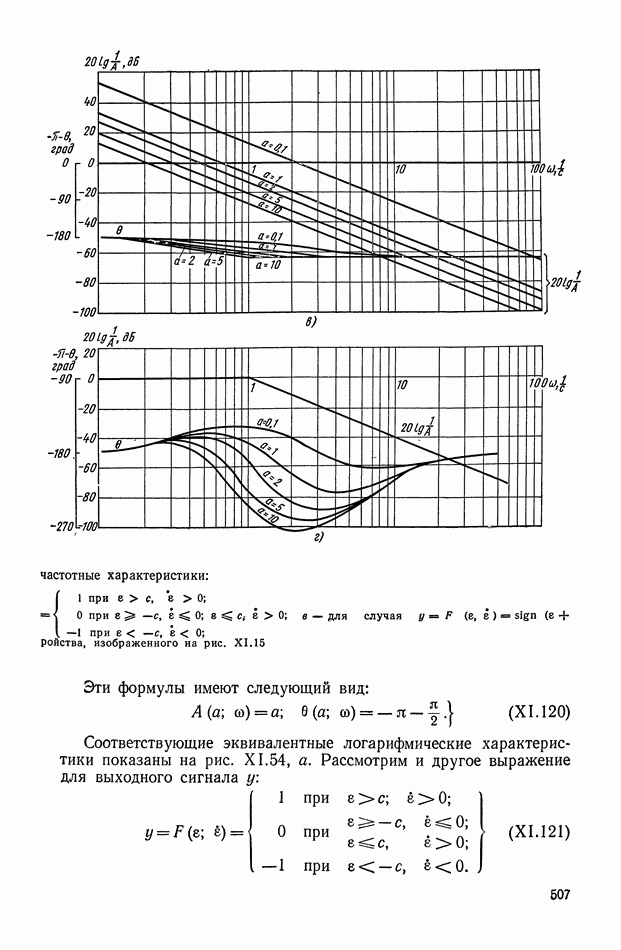
когда величина  становится положительной. Действительно, в момент времени
становится положительной. Действительно, в момент времени  сигнал
сигнал  оказывается средним по отношению к
оказывается средним по отношению к  Это эквивалентно охвату апериодического звена
Это эквивалентно охвату апериодического звена  единичной положительной обратной связью, в результате чего его передаточная функция превращается в Так как входной сигнал при этом отсутствует, то происходит запоминание величины
единичной положительной обратной связью, в результате чего его передаточная функция превращается в Так как входной сигнал при этом отсутствует, то происходит запоминание величины  соответствующее моменту времени
соответствующее моменту времени  Запомненное значение
Запомненное значение  сохраняется до тех пор, пока выполняется неравенство
сохраняется до тех пор, пока выполняется неравенство  После этого момента времени на выход будет проходить тот из сигналов
После этого момента времени на выход будет проходить тот из сигналов  который в данное мгновение является средним, а величина
который в данное мгновение является средним, а величина  будет отслеживать с постоянной времени
будет отслеживать с постоянной времени  значение выходного сигнала.
значение выходного сигнала.

Рис. XI.68. Кворум-элемент, охваченный положительной обратной связью

Рис. XI.69. Кривые изменения выходного сигнала кворум-элемента, охваченного положительной обратной связью
Постоянную времени  можно выбрать достаточно малой и считать, что сигнал
можно выбрать достаточно малой и считать, что сигнал  практически безынерционно отслеживает выходной сигнал.
практически безынерционно отслеживает выходной сигнал.
Таким образом, кворум-элемент с положительной обратной связью все время поддерживает выходной сигнал у в «трубке», образованной изменяющимися во времени сигналами  (рис. XI.69).
(рис. XI.69).
Алгоритм (XI. 147) может быть использован для построения нелинейного фильтра низких частот, если положить

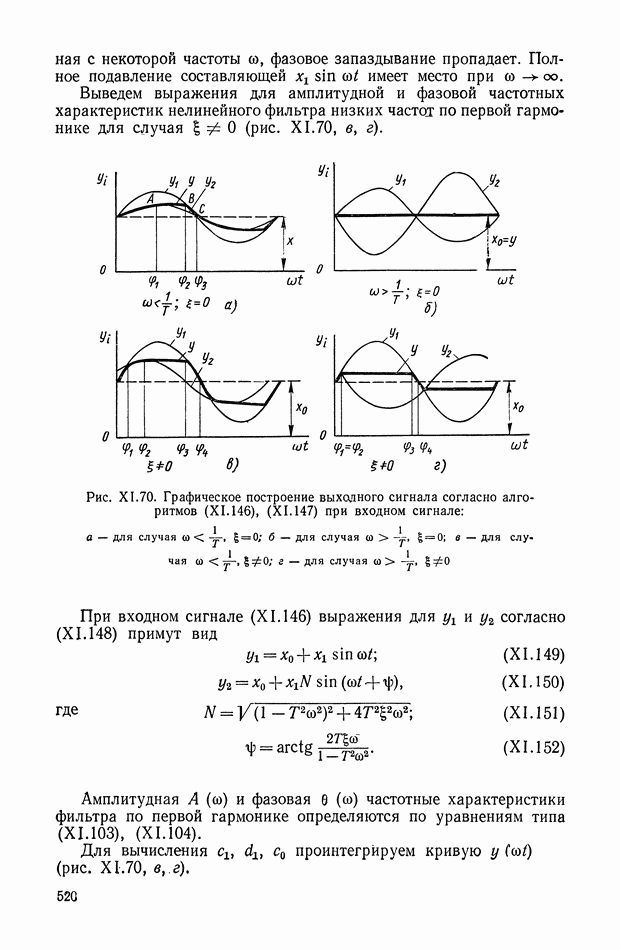
Изменение сигналов  для случая, когда входной сигнал х изменяется согласно формуле (XI. 146), приведено на рис. XI.70, для двух случаев
для случая, когда входной сигнал х изменяется согласно формуле (XI. 146), приведено на рис. XI.70, для двух случаев  . При
. При  начиная с частоты
начиная с частоты  выходной сигнал
выходной сигнал  т. е. осуществляется полное подавление высокочастотной составляющей
т. е. осуществляется полное подавление высокочастотной составляющей  сигнала х (рис. XI.70, б).
сигнала х (рис. XI.70, б).
В диапазоне частот от  до
до  соср имеет место незначительное фазовое запаздывание у относительно
соср имеет место незначительное фазовое запаздывание у относительно  пропорциональное площади, заключенной между кривыми, отмеченными точками А, В, С (рис. XI.70, а). При
пропорциональное площади, заключенной между кривыми, отмеченными точками А, В, С (рис. XI.70, а). При  в зависимости от со могут иметь место два случая (см. рис. XI.70, в, г). Следует заметить, что,
в зависимости от со могут иметь место два случая (см. рис. XI.70, в, г). Следует заметить, что,
начиная с некоторой частоты  фазовое запаздывание пропадает. Полное подавление составляющей
фазовое запаздывание пропадает. Полное подавление составляющей  имеет место при со
имеет место при со 
Выведем выражения для амплитудной и фазовой частотных характеристик нелинейного фильтра низких частот по первой гармонике для случая  (рис. XI.70, в, г).
(рис. XI.70, в, г).

Рис. XI.70. Графическое построение выходного сигнала согласно алгоритмов (XI. 146), (XI. 147) при входном сигнале: а — для случая  ; б — для случая
; б — для случая  ; в — для случая
; в — для случая  — для случая
— для случая 
При входном сигнале (XI. 146) выражения для  согласно (XI. 148) примут вид
согласно (XI. 148) примут вид

где (XI.151)

Амплитудная  и фазовая
и фазовая  частотные характеристики фильтра по первой гармонике определяются по уравнениям типа (XI.103), (XI.104).
частотные характеристики фильтра по первой гармонике определяются по уравнениям типа (XI.103), (XI.104).
Для вычисления  проинтегрируем кривую
проинтегрируем кривую  (рис. X 1.70, в, г).
(рис. X 1.70, в, г).
Поскольку кривая  симметрична, то интервал интегрирования можно взять равным от 0 до
симметрична, то интервал интегрирования можно взять равным от 0 до 

где

Аналогично определяются  и
и 

здесь

Значение угла  находится из условия
находится из условия

Угол  для случая
для случая  определяется из уравнения
определяется из уравнения

Для случая  имеем
имеем

Угол  для случая
для случая  определяется из условия
определяется из условия

При  имеем
имеем

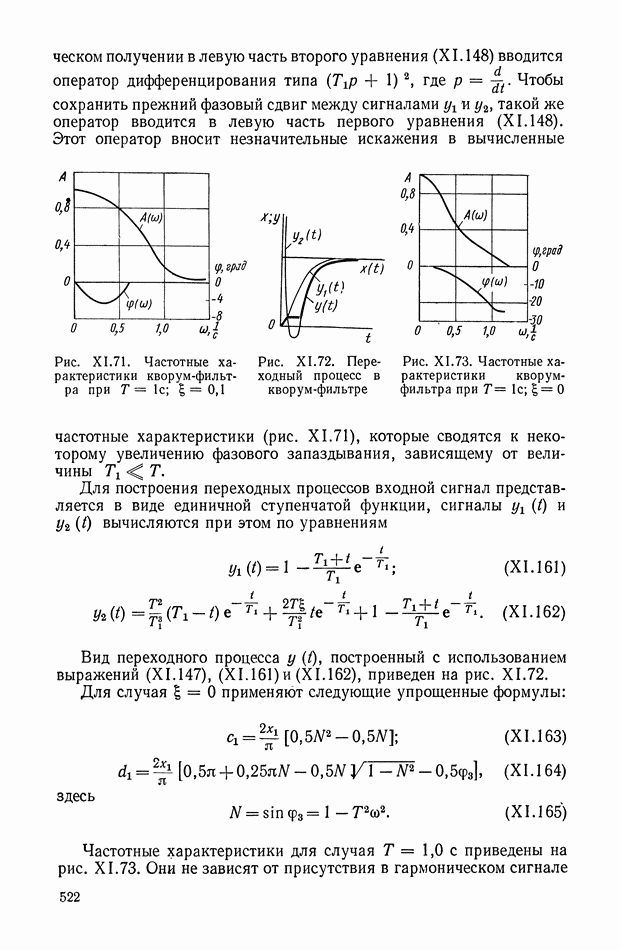
Частотные характеристики фильтра при  приведены на рис. XI.71. Следует заметить, что «чистую» вторую производную сигнала практически получить нельзя. При ее
приведены на рис. XI.71. Следует заметить, что «чистую» вторую производную сигнала практически получить нельзя. При ее
практическом получении в левую часть второго уравнения (XI. 148) вводится оператор дифференцирования типа  , где
, где  Чтобы сохранить прежний фазовый сдвиг между сигналами
Чтобы сохранить прежний фазовый сдвиг между сигналами  такой же оператор вводится в левую часть первого уравнения (XI.148).
такой же оператор вводится в левую часть первого уравнения (XI.148).

Рис. XI.71. Частотные характеристики кворум-фильтра при 

Рис. XI.72. Переходный процесс в кворум-фильтре

Рис. XI.73. Частотные характеристики кворум-фильтра при 
Этот оператор вносит незначительные искажения в вычисленные частотные характеристики (рис. XI.71), которые сводятся к некоторому увеличению фазового запаздывания, зависящему от величины 
Для построения переходных процессов входной сигнал представляется в виде единичной ступенчатой функции, сигналы  вычисляются при этом по уравнениям
вычисляются при этом по уравнениям

Вид переходного процесса  построенный с использованием выражений (XI.147), (XI.161) и (XI.162), приведен на рис. XI.72.
построенный с использованием выражений (XI.147), (XI.161) и (XI.162), приведен на рис. XI.72.
Для случая  применяют следующие упрощенные формулы:
применяют следующие упрощенные формулы:

здесь

Частотные характеристики для случая  с приведены на рис. XI.73. Они не зависят от присутствия в гармоническом сигнале
с приведены на рис. XI.73. Они не зависят от присутствия в гармоническом сигнале
постоянной составляющей. Такой нелинейный фильтр низких частот может найти применение для стабилизации системы управления, параметры которой изменяются во время работы в широких пределах.
ЛИТЕРАТУРА
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА САР
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ЛИНЕЙНЫХ УСИЛИТЕЛЬНЫХ УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ УСИЛИТЕЛЬНОГО УСТРОЙСТВА БЕЗ ОБРАТНОЙ СВЯЗИ
- 3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ, СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ОСОБЕННОСТИ УСИЛИТЕЛЬНОГО УСТРОЙСТВА С ОБРАТНОЙ СВЯЗЬЮ
- 4. КЛАССИФИКАЦИЯ И СВОЙСТВА УСИЛИТЕЛЬНЫХ УСТРОЙСТВ С ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 5. ВЫБОР И РАСЧЕТ УСИЛИТЕЛЬНОГО УСТРОЙСТВА
- ГЛАВА II. ЭЛЕКТРОННЫЕ ЛАМПОВЫЕ И ИОННЫЕ УСИЛИТЕЛИ
- 1. ОСНОВЫ ТОПОЛОГИЧЕСКОГО АНАЛИЗА СХЕМ ЛИНЕЙНЫХ ЭЛЕКТРОННЫХ ЛАМПОВЫХ УСИЛИТЕЛЕЙ
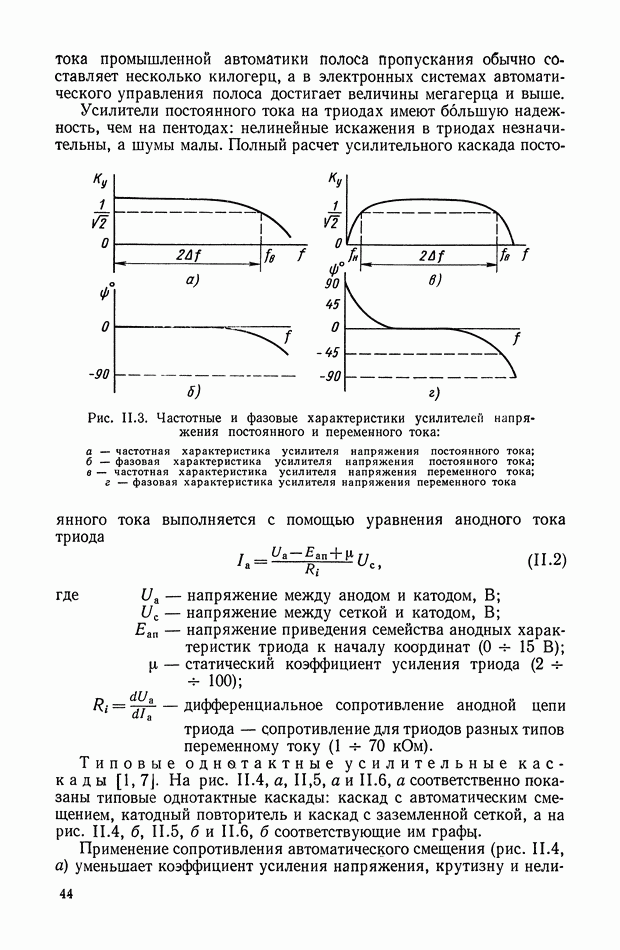
- 2. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПОСТОЯННОГО ТОКА
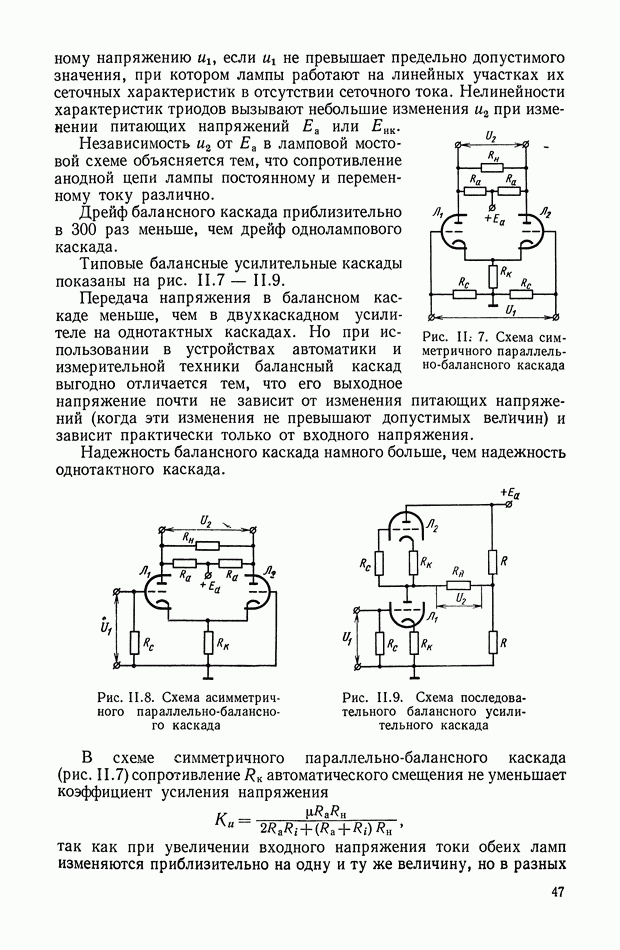
- 3. БАЛАНСНЫЕ МОСТОВЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
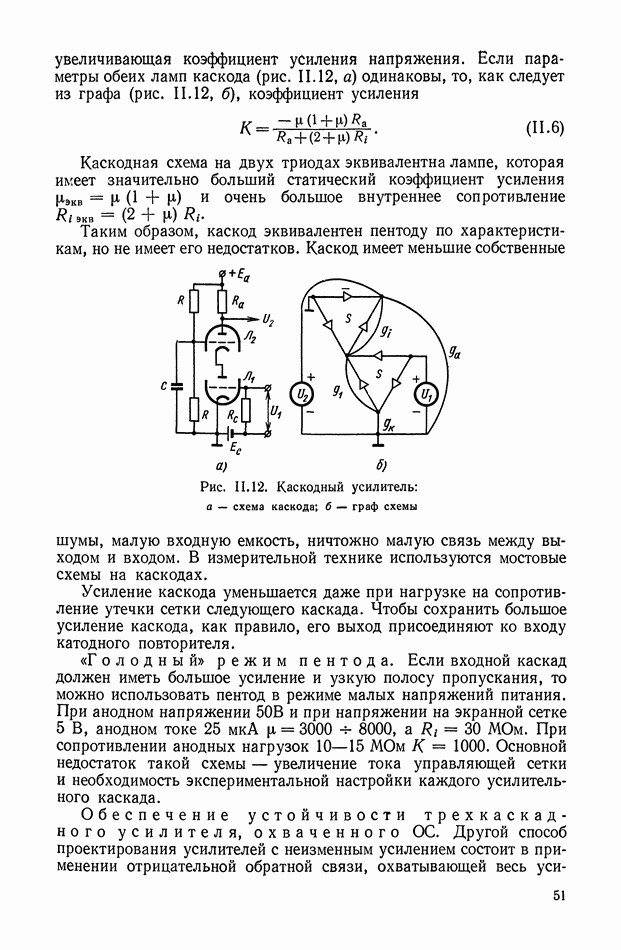
- 4. СТАБИЛИЗАЦИЯ КОЭФФИЦИЕНТА УСИЛЕНИЯ
- 5. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- 6. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- 7. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
- 8. ОБЩИЕ СВОЙСТВА ИОННОГО (ТИРАТРОННОГО) УСИЛИТЕЛЯ МЕТОДЫ УПРАВЛЕНИЯ ТИРАТРОНОМ
- 9. ФОРМИРОВАНИЕ УПРАВЛЯЮЩЕГО НАПРЯЖЕНИЯ
- 10. РАСЧЕТ ЭЛЕМЕНТОВ СХЕМ ТИРАТРОННОГО УСИЛИТЕЛЯ
- ГЛАВА III. ПОЛУПРОВОДНИКОВЫЕ И ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
- Цепи смещения.
- Цепи связи.
- 2. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ СРЕДНЕГО ЗНАЧЕНИЯ ТОКА
- Полупроводниковые демодуляторы.
- 3. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ В РЕЖИМЕ ПЕРЕКЛЮЧЕНИЯ
- Режимы импульсного регулирования мощности.
- Управление силовыми транзисторами.
- 4. ТРАНЗИСТОРНЫЕ УСТРОЙСТВА УПРАВЛЕНИЯ ЭЛЕКТРОДВИГАТЕЛЯМИ И ЭЛЕКТРОМАГНИТНЫМИ МЕХАНИЗМАМИ
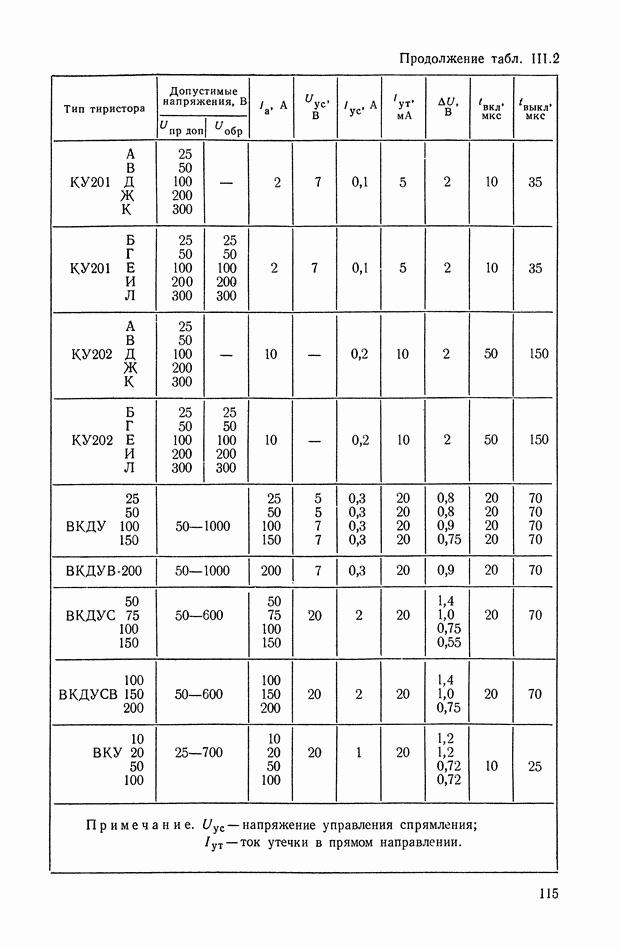
- 5. ТИРИСТОРЫ. ХАРАКТЕРИСТИКИ, ПАРАМЕТРЫ И СВОЙСТВА
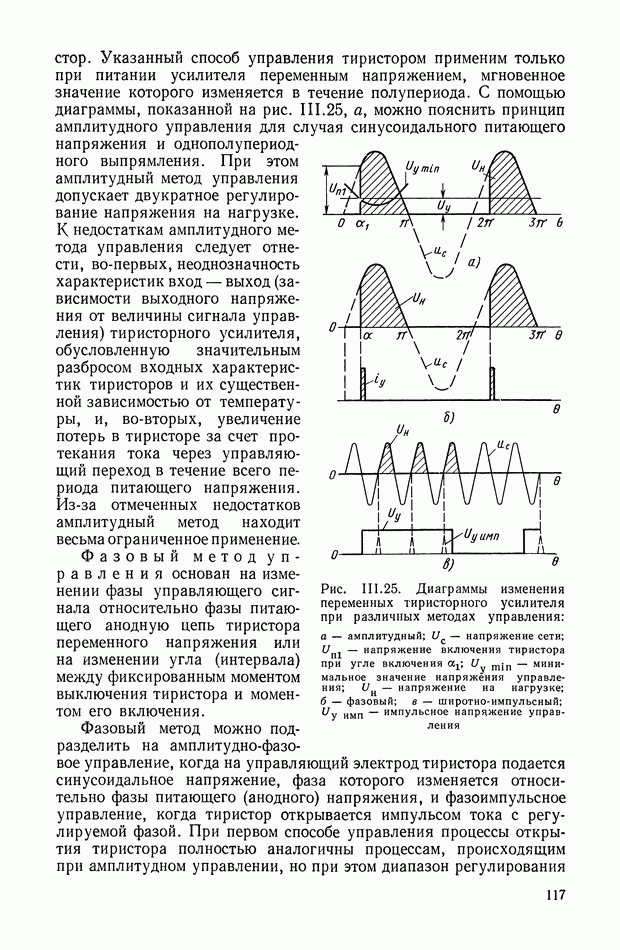
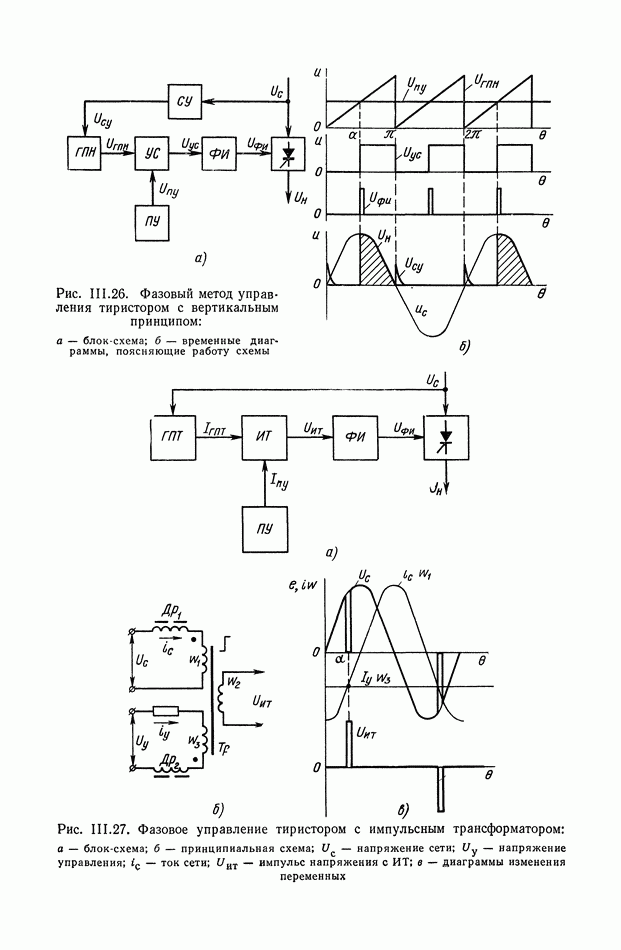
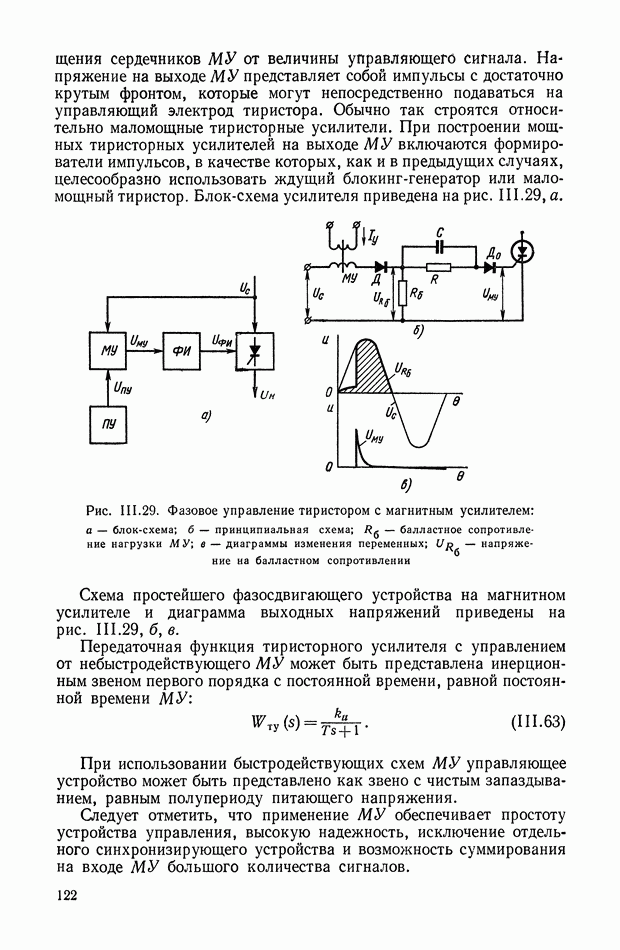
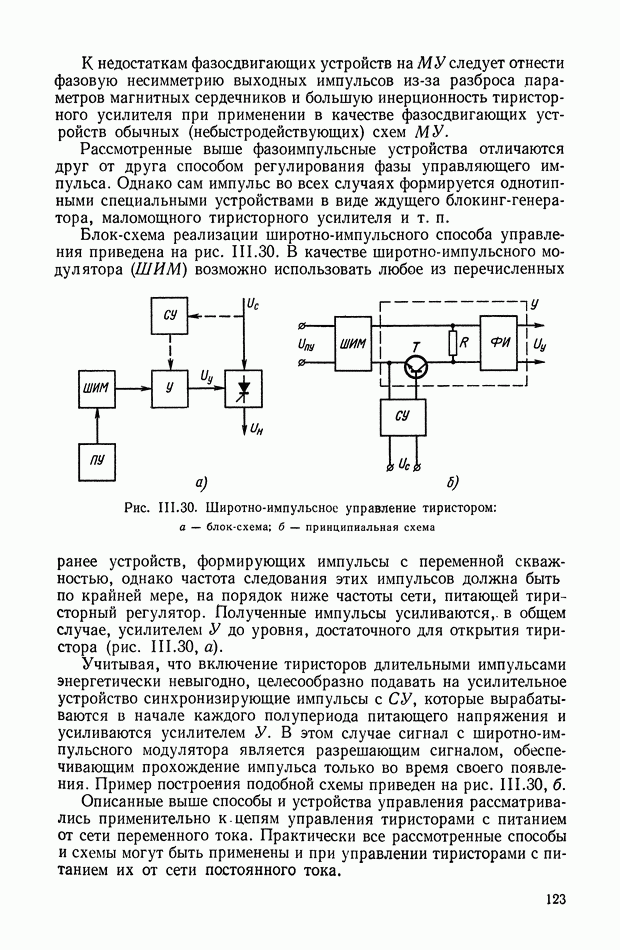
- 6. СПОСОБЫ И УСТРОЙСТВА УПРАВЛЕНИЯ ТИРИСТОРАМИ
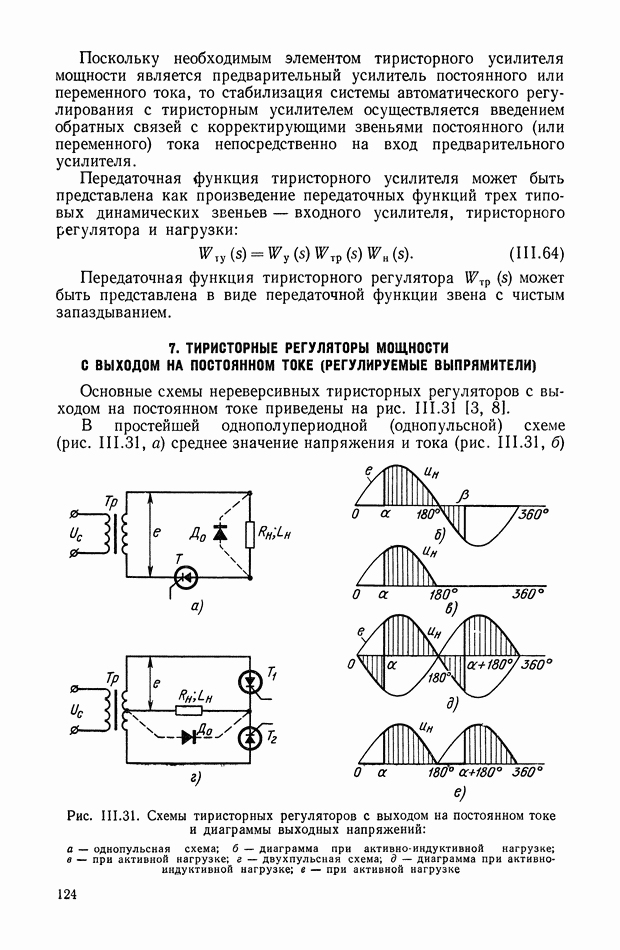
- 7. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ (РЕГУЛИРУЕМЫЕ ВЫПРЯМИТЕЛИ)
- 8. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 9. ТИРИСТОРНЫЕ УСИЛИТЕЛИ С ПИТАНИЕМ ОТ СЕТИ ПОСТОЯННОГО ТОКА
- 10. ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 11. ОСНОВЫ РАСЧЕТА ДИЭЛЕКТРИЧЕСКИХ УСИЛИТЕЛЕЙ
- ГЛАВА IV. КВАНТОВЫЕ УСИЛИТЕЛИ И ГЕНЕРАТОРЫ
- 2. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ РАДИОДИАПАЗОНА
- Квантовые усилители радиодиапазона.
- 3. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- Оптический квантовый усилитель
- 4. ПРИМЕНЕНИЕ В САР КВАНТОВЫХ УСИЛИТЕЛЕЙ И ГЕНЕРАТОРОВ РАДИОДИАПАЗОНА, ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- ГЛАВА V. МАГНИТНЫЕ И МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- 2. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ МАГНИТНЫХ УСИЛИТЕЛЕЙ
- 3. ОДНОТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ БЕЗ ОБРАТНОЙ СВЯЗИ (УПРАВЛЯЕМЫЕ ДРОССЕЛИ И ТРАНСФОРМАТОРЫ)
- 4. МАГНИТНЫЕ УСИЛИТЕЛИ С САМОНАСЫЩЕНИЕМ
- Релейный режим работы усилителей с самонасыщением.
- 5. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 6. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ
- 7. МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- ГЛАВА VI. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 2. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С НЕЗАВИСИМЫМ ВОЗБУЖДЕНИЕМ И С САМОВОЗБУЖДЕНИЕМ
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С ПОПЕРЕЧНЫМ ПОЛЕМ
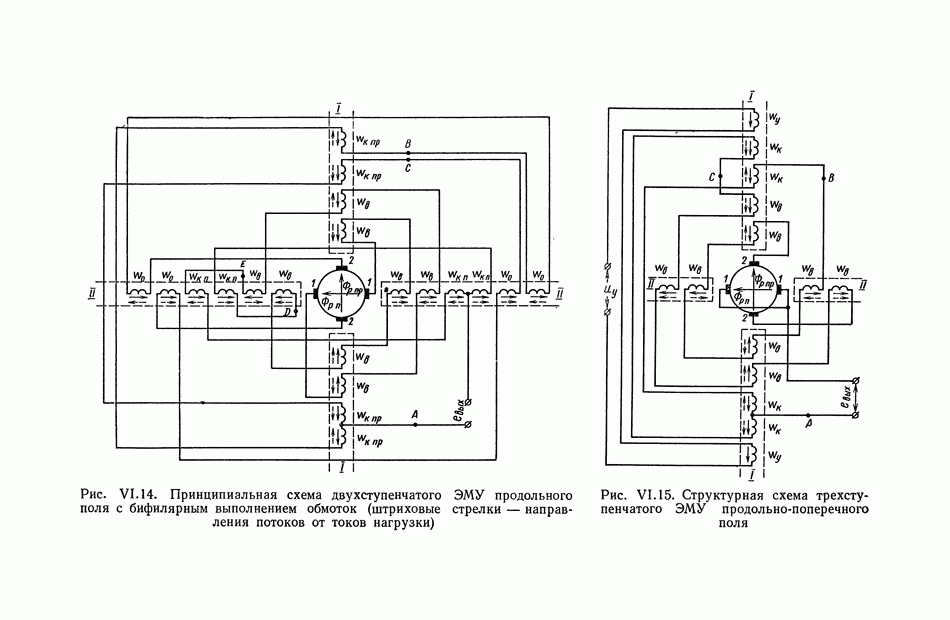
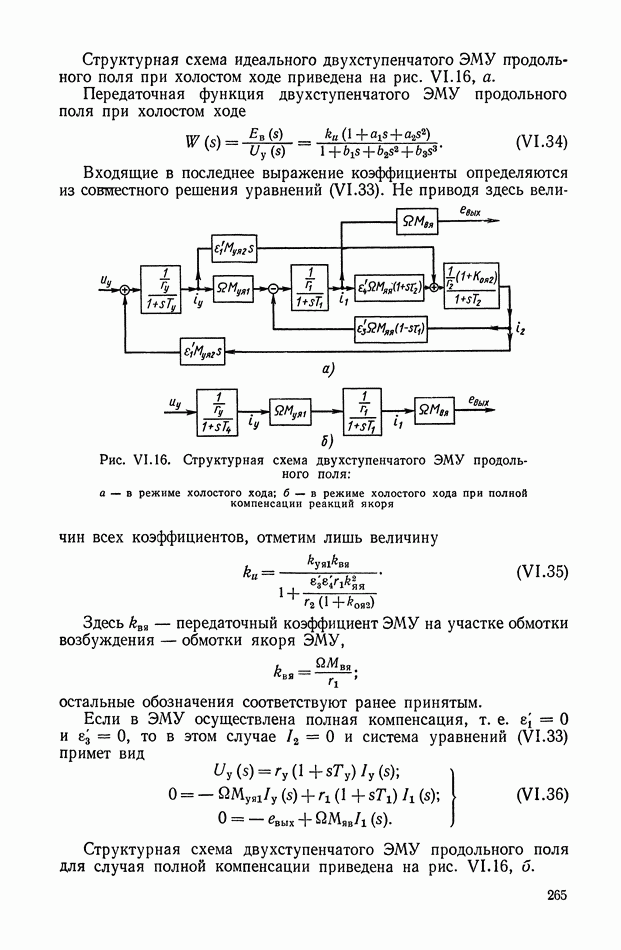
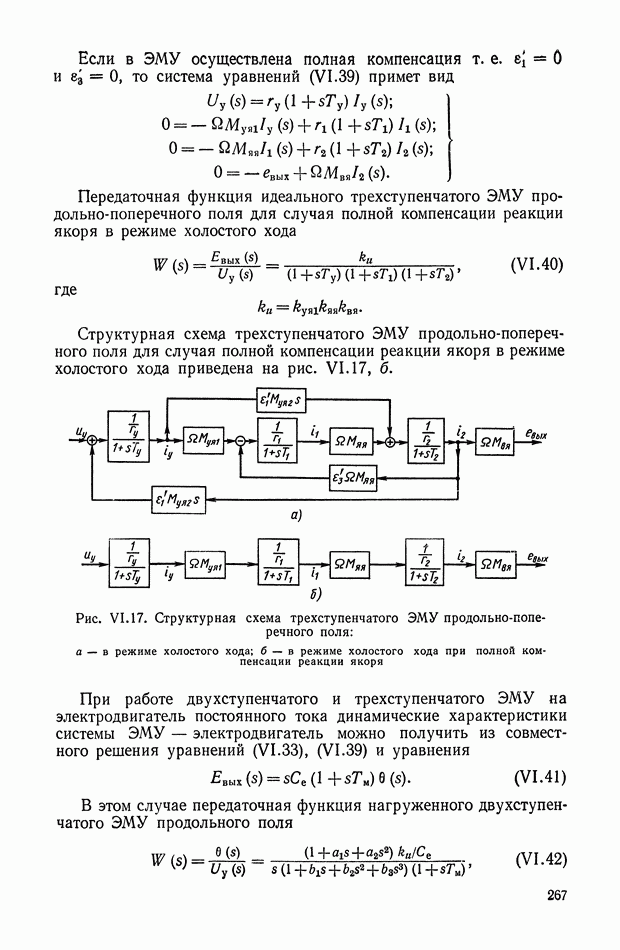
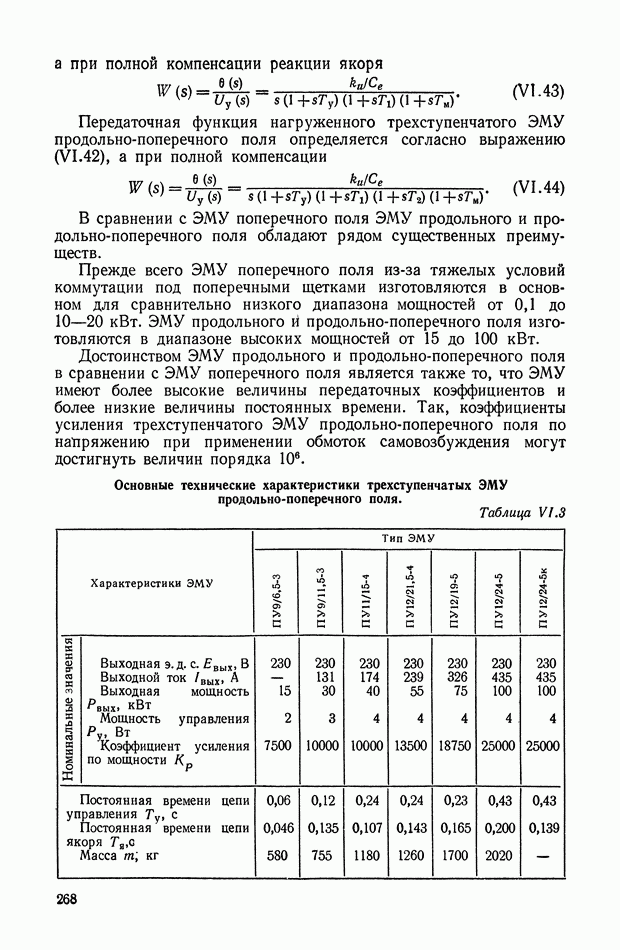
- 4. ЭЛЕКТРОМАШИННЫЙ УСИЛИТЕЛЬ ПРОДОЛЬНОГО И ПРОДОЛЬНО-ПОПЕРЕЧНОГО ПОЛЯ
- 5. ВЛИЯНИЕ НА ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭМУ ВИХРЕВЫХ И КОММУТАЦИОННЫХ ТОКОВ, ГИСТЕРЕЗИСА И СДВИГА ЩЕТОК С НЕЙТРАЛИ
- 6. МЕТОДЫ УЛУЧШЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕКТРОМАШИННЫХ УСИЛИТЕЛЕЙ
- 7. НАГРУЗОЧНАЯ ХАРАКТЕРИСТИКА ЭЛЕКТРОМАШИННОГО УСИЛИТЕЛЯ
- ГЛАВА VII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ХАРАКТЕРИСТИКИ УСИЛИТЕЛЕЙ И СПОСОБЫ ИХ ФОРМИРОВАНИЯ
- 2. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
- 3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ЛИНЕАРИЗОВАННЫЕ УСИЛИТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ РЕЛЕ
- 4. БЕСКОНТАКТНЫЕ ЛИНЕАРИЗОВАННЫЕ РЕЛЕЙНЫЕ УСИЛИТЕЛИ
- ГЛАВА VIII. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 2. ОСНОВНЫЕ ЭЛЕМЕНТЫ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ И ИХ ХАРАКТЕРИСТИКИ
- 3. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ С ЗОЛОТНИКОМ
- 4. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ СО СТРУЙНОЙ ТРУБКОЙ
- 5. СХЕМЫ И ПРИНЦИПЫ ДЕЙСТВИЯ ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 6. СТАТИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 7. ДИНАМИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
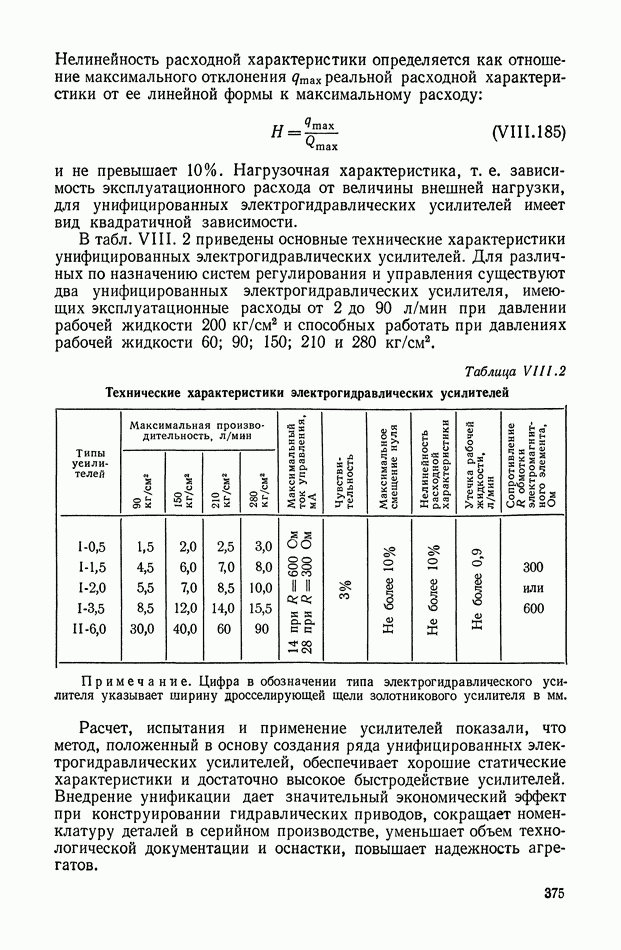
- 8. УНИФИКАЦИЯ ЭЛЕКТРОГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ ДЛЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
- ГЛАВА IX. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ И ИХ КЛАССИФИКАЦИЯ
- 2. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ СО СТРУЙНОЙ ТРУБКОЙ
- 3. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗОЛОТНИКОМ
- 4. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С СОПЛОМ — ЗАСЛОНКОЙ
- 5. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗАСЛОНКОЙ
- 6. МНОГОКАСКАДНЫЕ ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- РАЗДЕЛ II. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ И УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ЛИНЕЙНЫХ ПАССИВНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
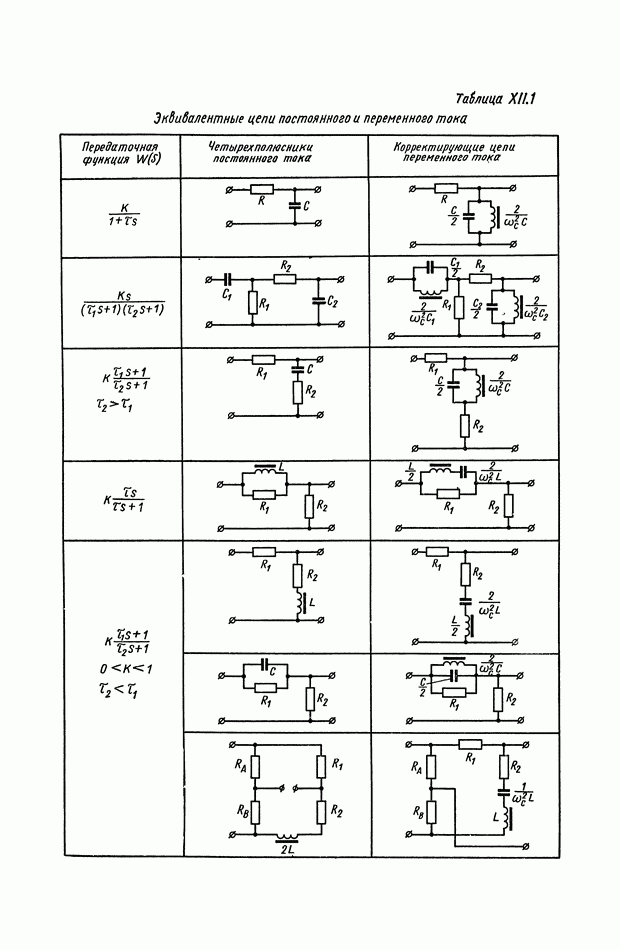
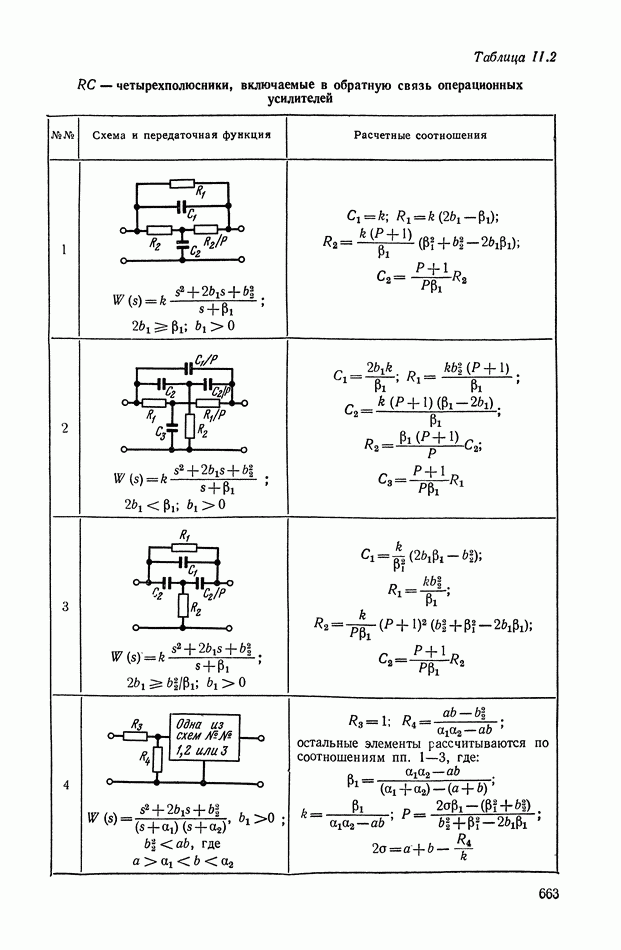
- Основные соотношения для синтеза пассивного RC-четырехполюсника.
- 3. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Активные четырехполюсники, получаемые с помощью конверторов отрицательного сопротивления.
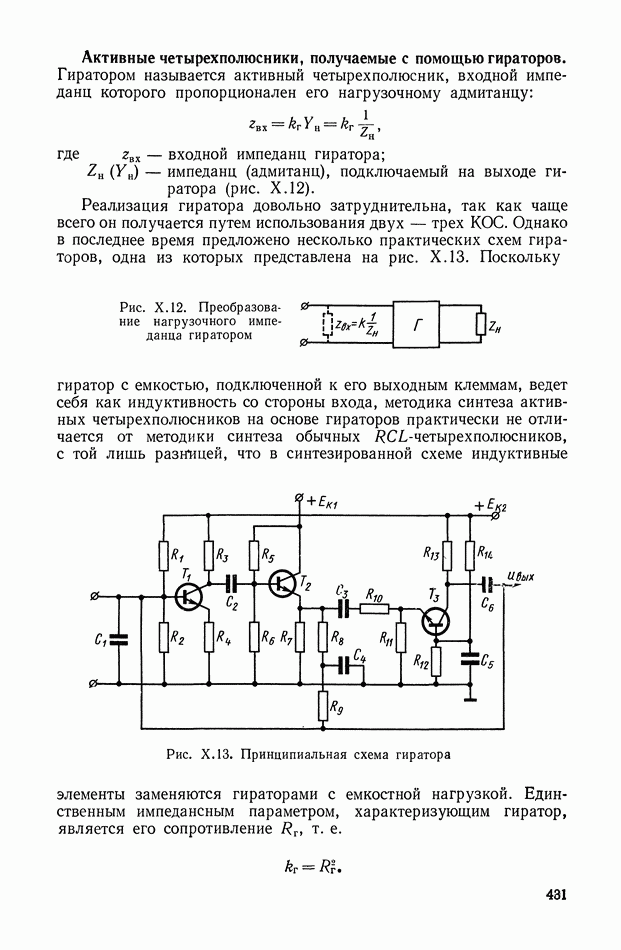
- Активные четырехполюсники, получаемые с помощью гираторов.
- 4. НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА НЕЛИНЕЙНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. ОСОБЕННОСТИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XI. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА ПОСТОЯННОГО ТОКА
- Дифференцирующий трансформатор.
- Электрические интегрирующие элементы.
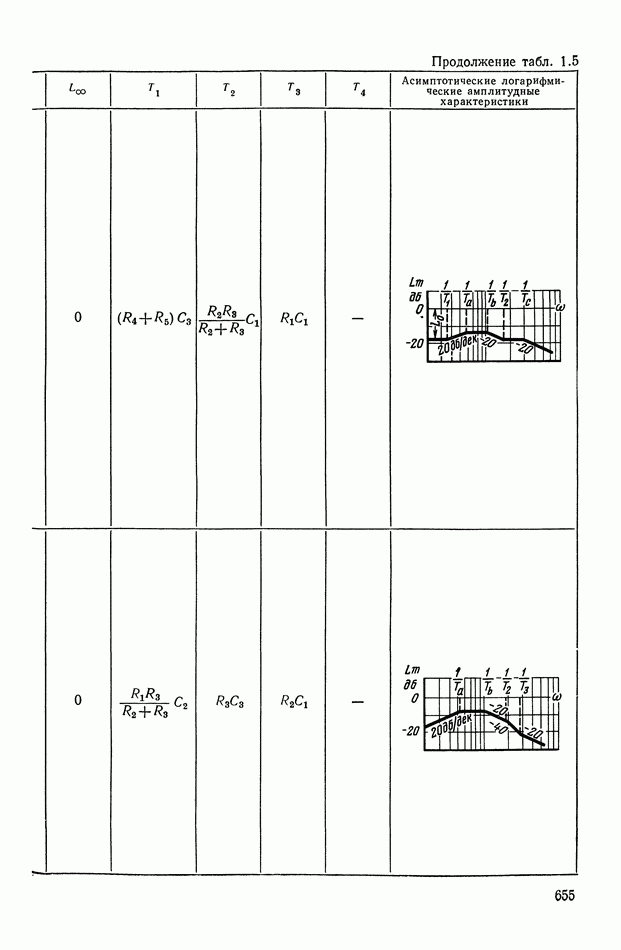
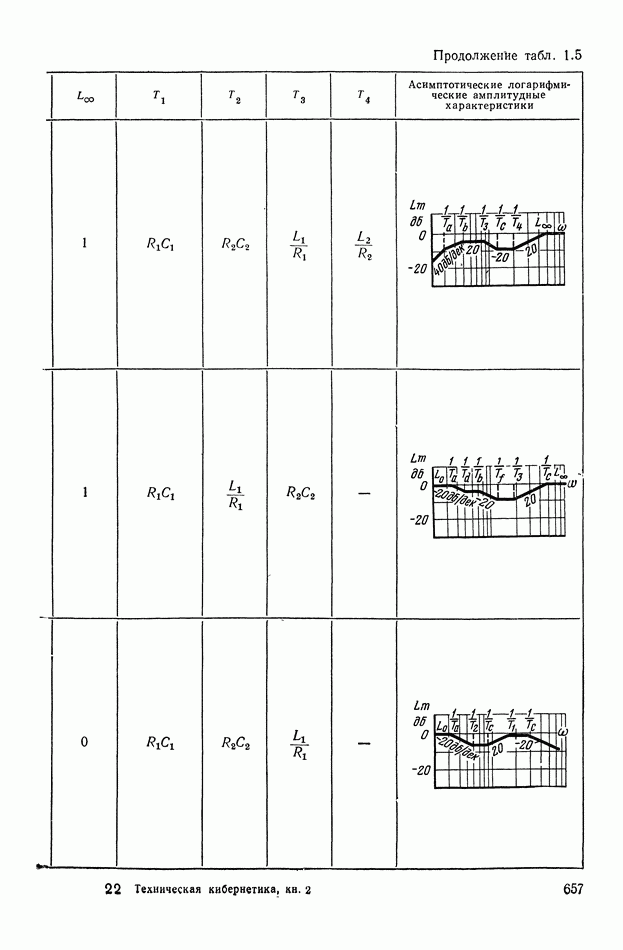
- 2. ТИПОВЫЕ ЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
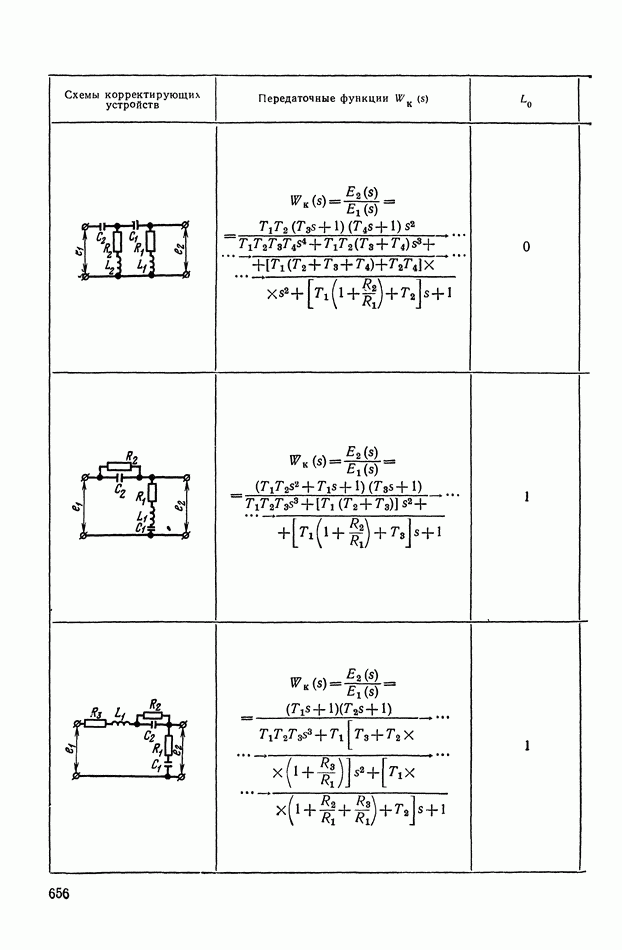
- 3. КОРРЕКТИРУЮЩИЕ ЧЕТЫРЕХПОЛЮСНИКИ С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Четырехполюсники с активными элементами на основе операционных усилителей (ОУ) и конверторов отрицательного сопротивления (КОС).
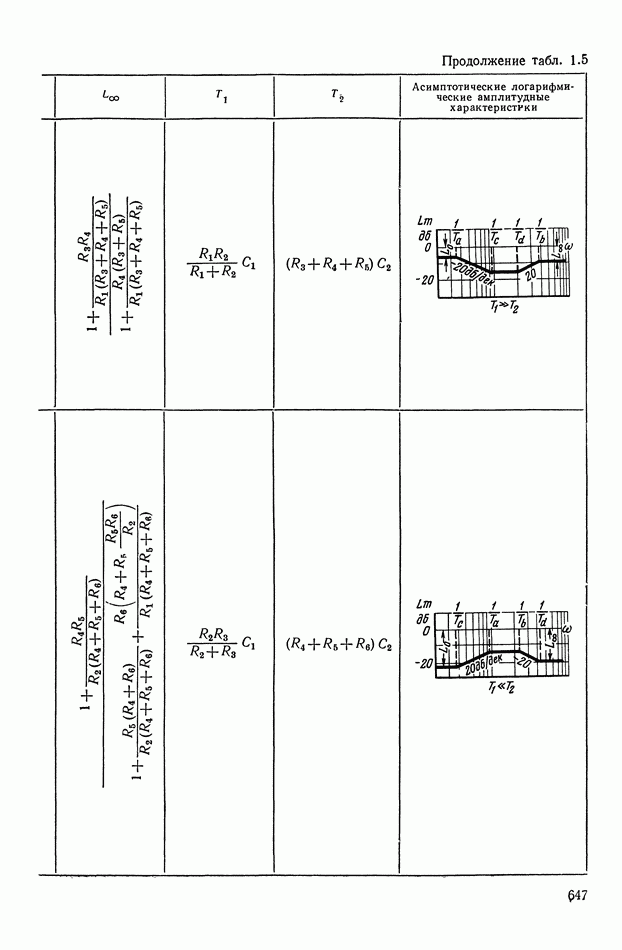
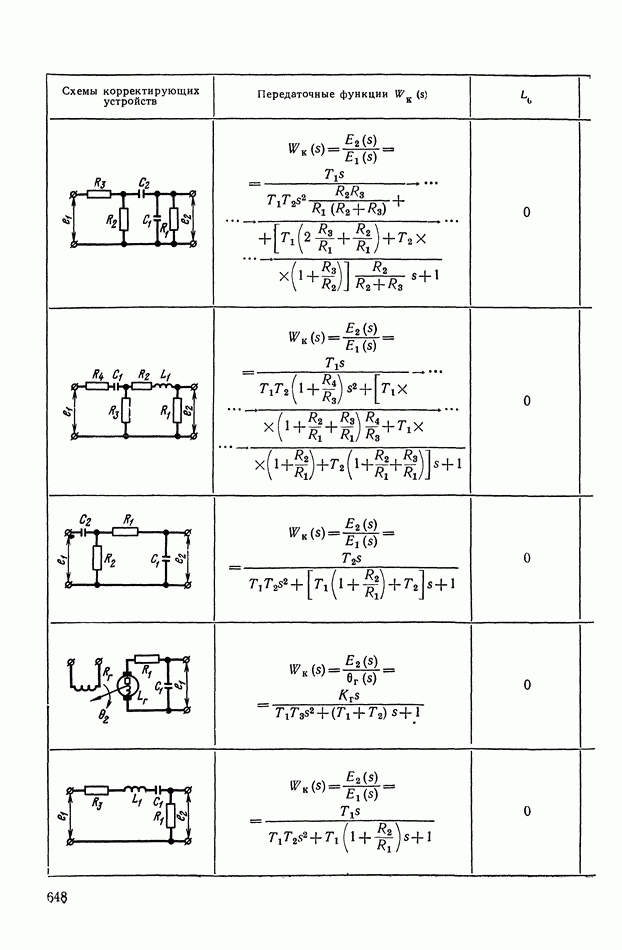
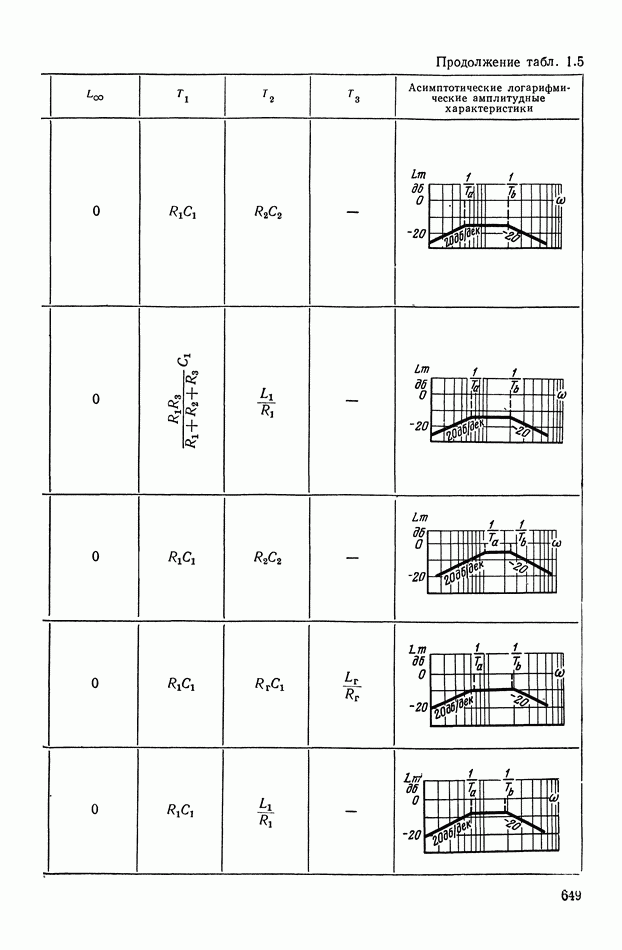
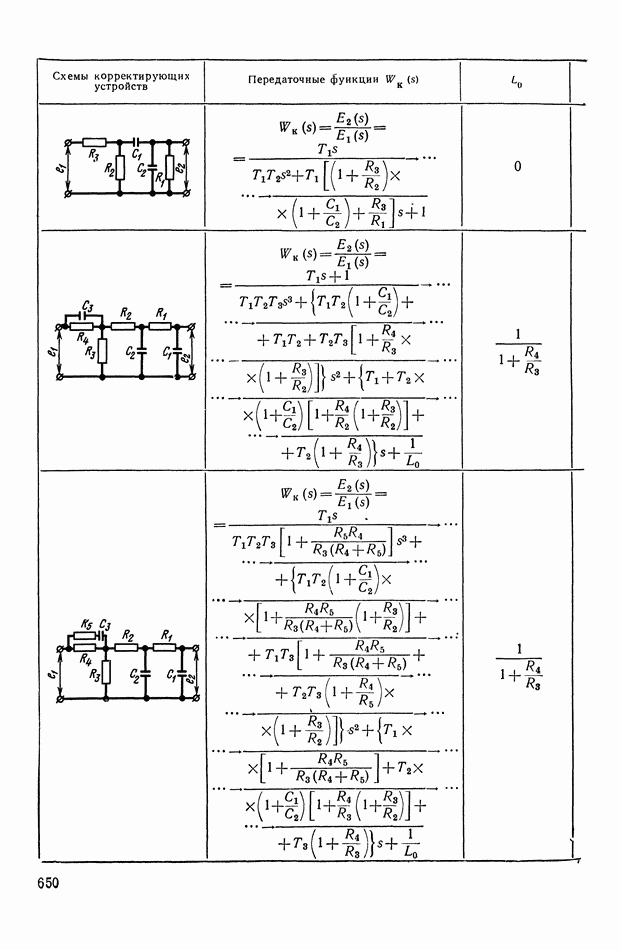
- 4. РЕАЛИЗАЦИЯ ЗАДАННОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В ВИДЕ СХЕМЫ ПАССИВНОГО ЛИНЕЙНОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА
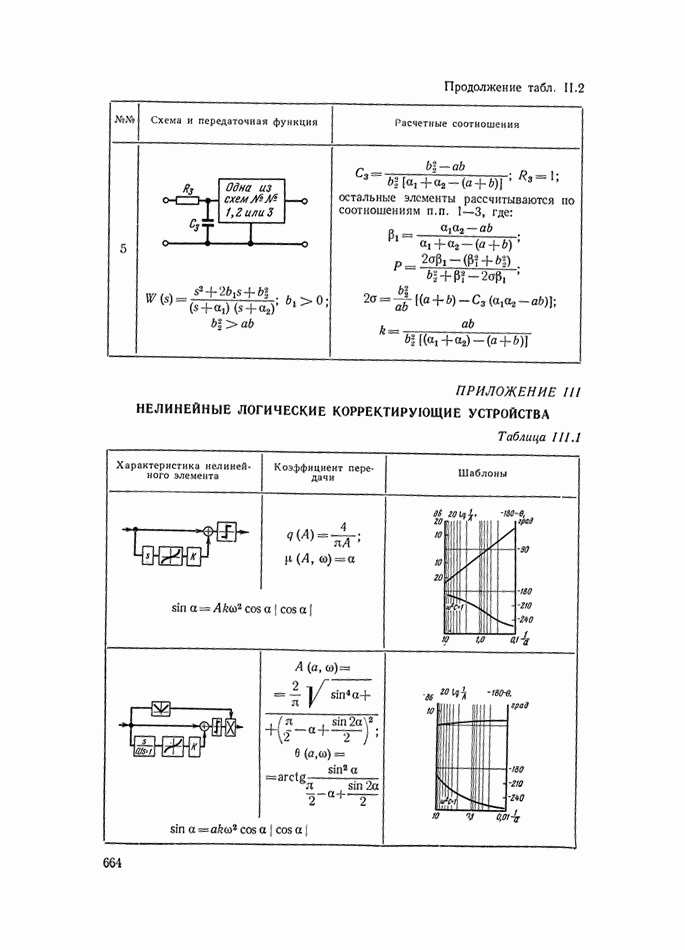
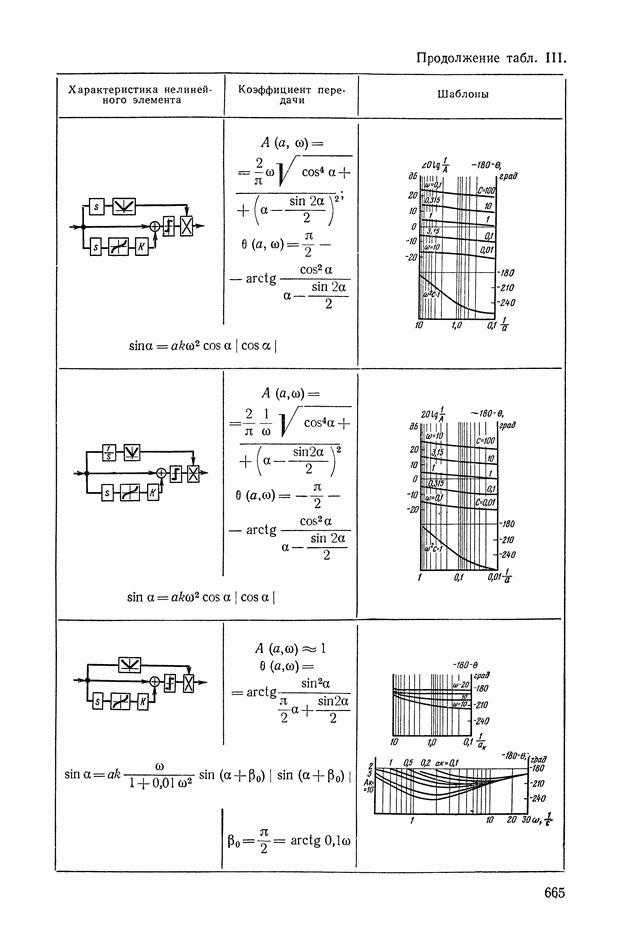
- 5. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- 8. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- Многоканальные нелинейные логические устройства.
- ГЛАВА XII. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- 1. КОРРЕКТИРУЮЩИЕ RLC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 2. КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 3. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
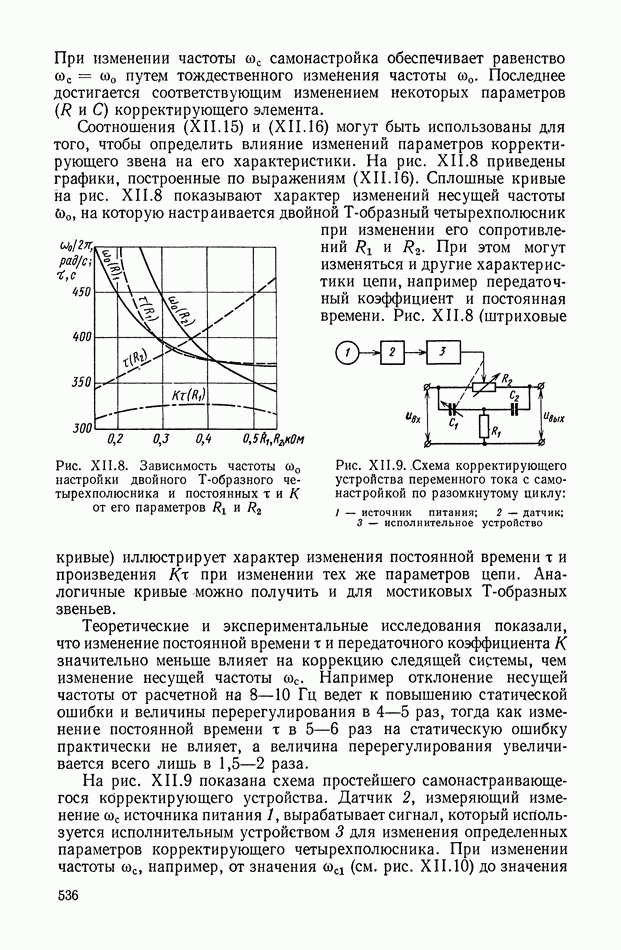
- 4. САМОНАСТРАИВАЮЩИЕСЯ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА
- 5. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА С ПРОМЕЖУТОЧНОЙ ДЕМОДУЛЯЦИЕЙ
- 6. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА С ПЕРЕКЛЮЧАТЕЛЯМИ
- 7. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XIII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ТАХОГЕНЕРАТОРЫ ПОСТОЯННОГО ТОКА
- Погрешности тахогенератора постоянного тока.
- 2. НЕКОТОРЫЕ СХЕМЫ ПРИМЕНЕНИЯ ТАХОГЕНЕРАТОРОВ
- 3. АСИНХРОННЫЕ ТАХОГЕНЕРАТОРЫ
- 4. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ ИЗМЕРЕНИЯ СКОРОСТИ ЭЛЕКТРОДВИГАТЕЛЕЙ
- Пассивный тахометрический мост переменного тока.
- Активные тахометрические мосты.
- ГЛАВА XIV. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ГИДРАВЛИЧЕСКИХ СИСТЕМАХ
- 3. ЭЛЕКТРИЧЕСКИЕ ОБРАТНЫЕ СВЯЗИ
- 4. ЖЕСТКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
- 5. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ СИСТЕМАХ
- 6. СЛОЖНЫЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
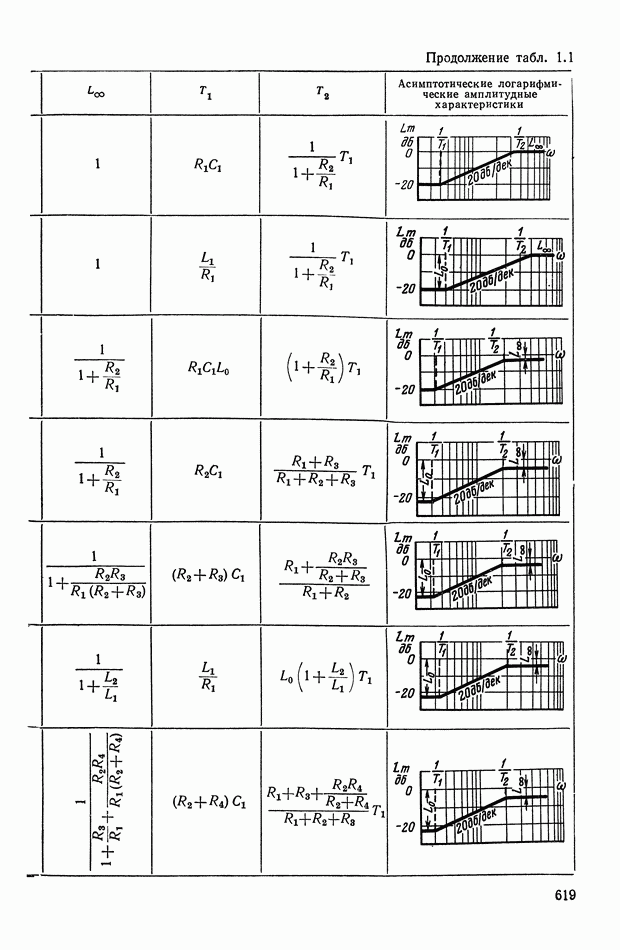
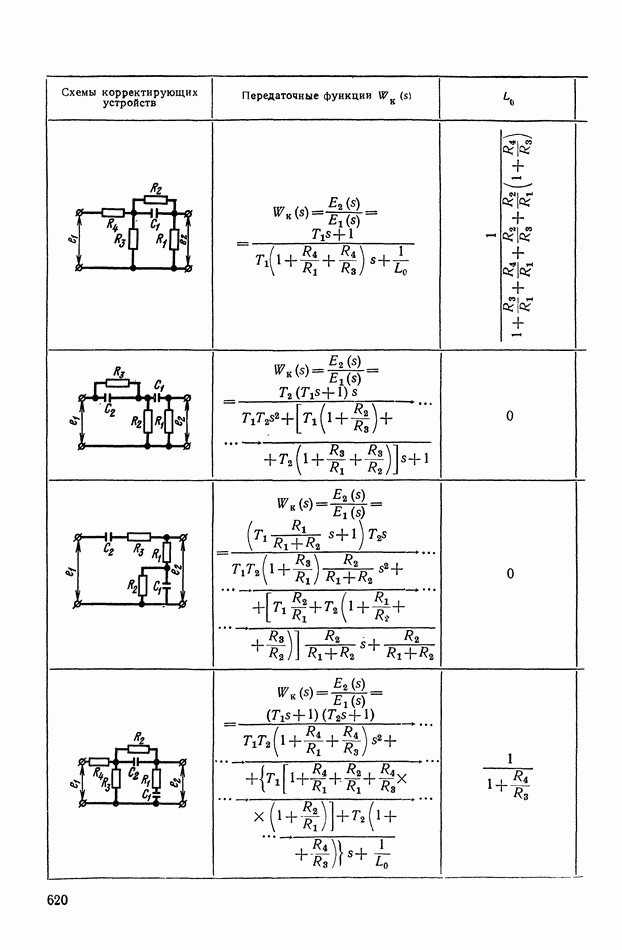
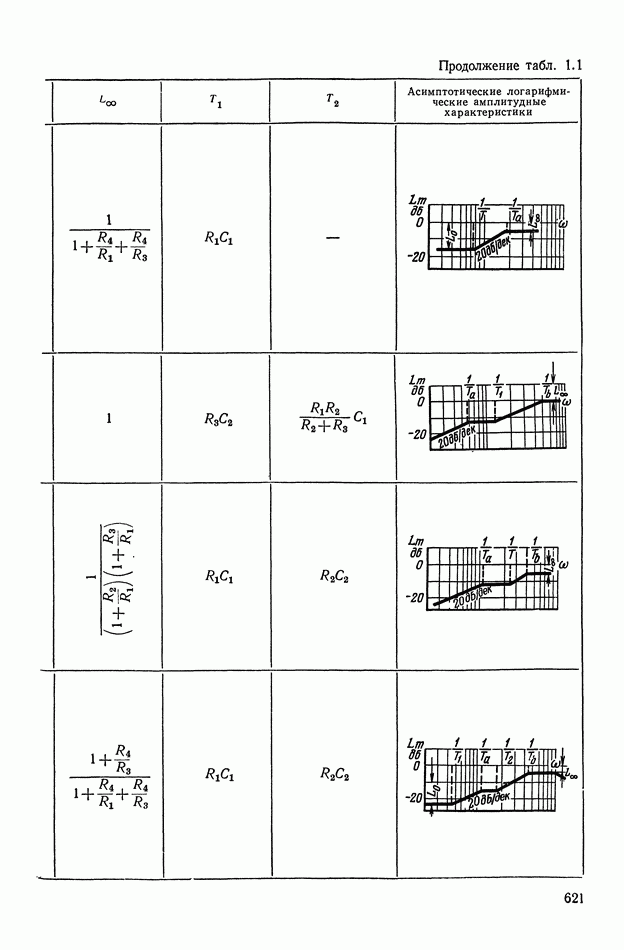
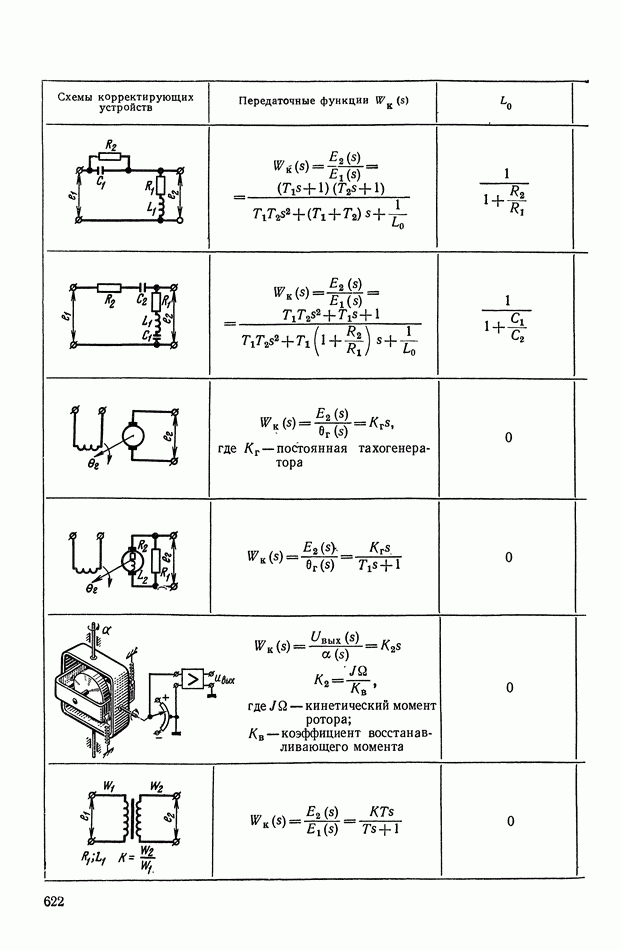
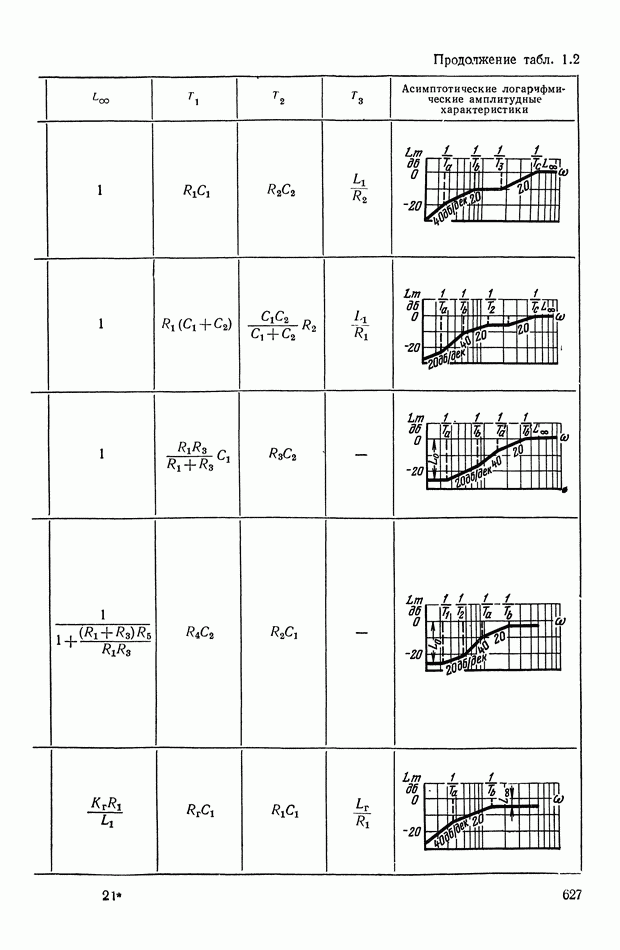
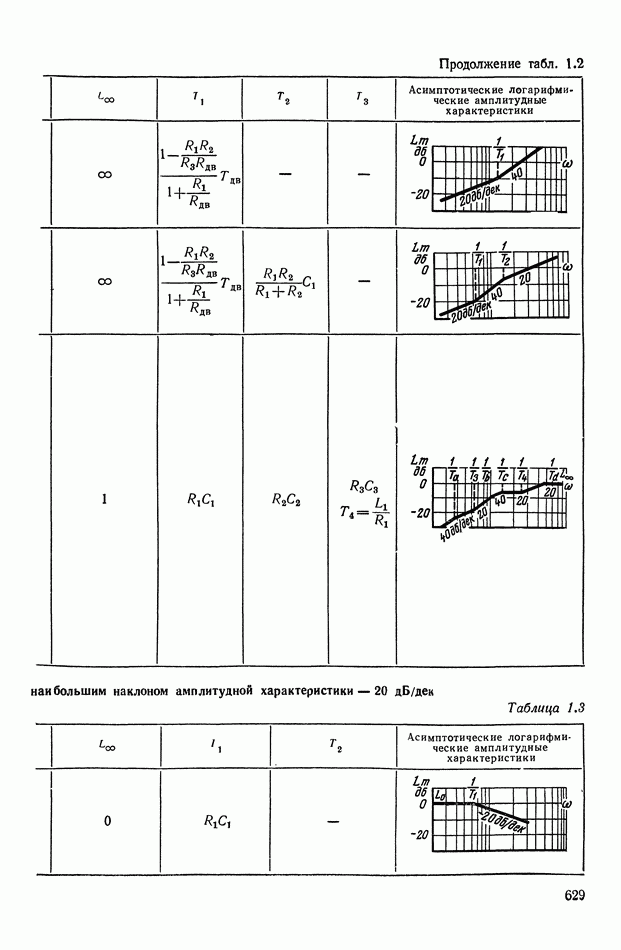
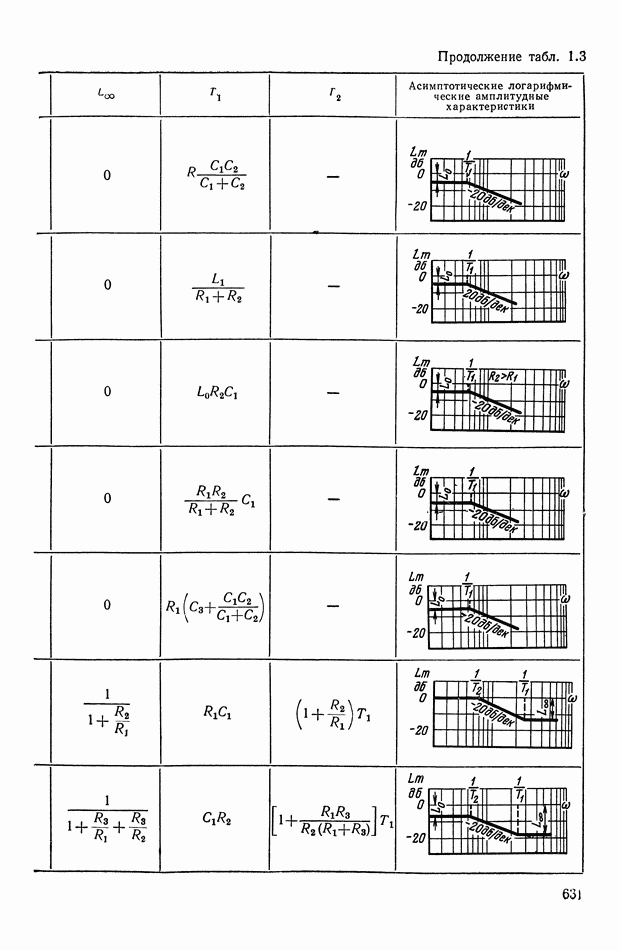
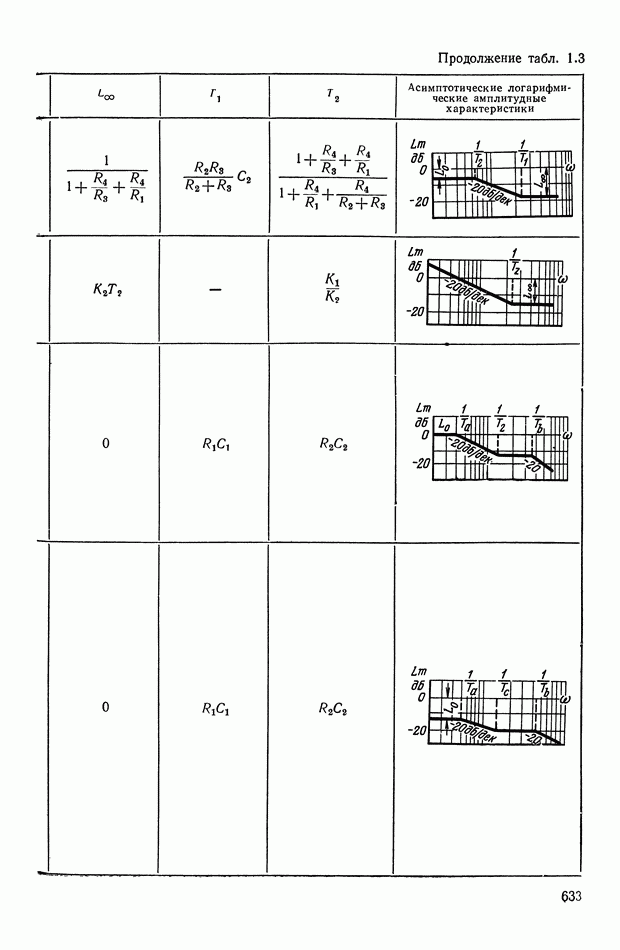
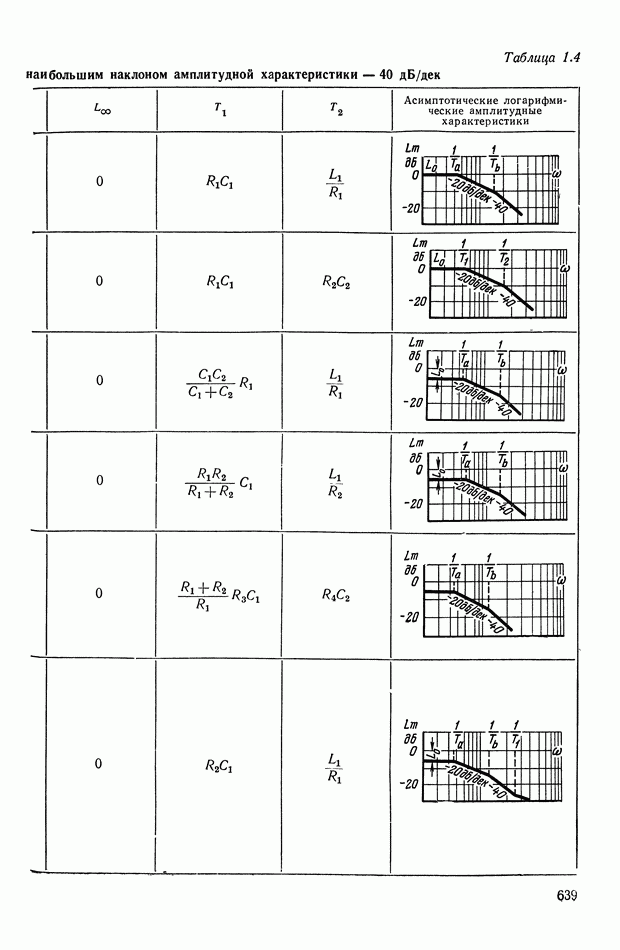
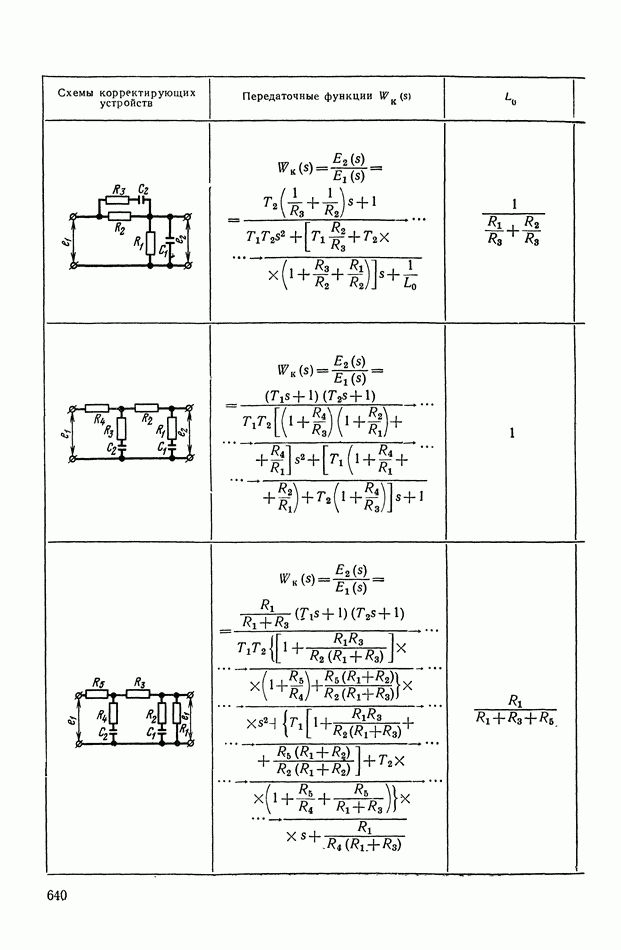
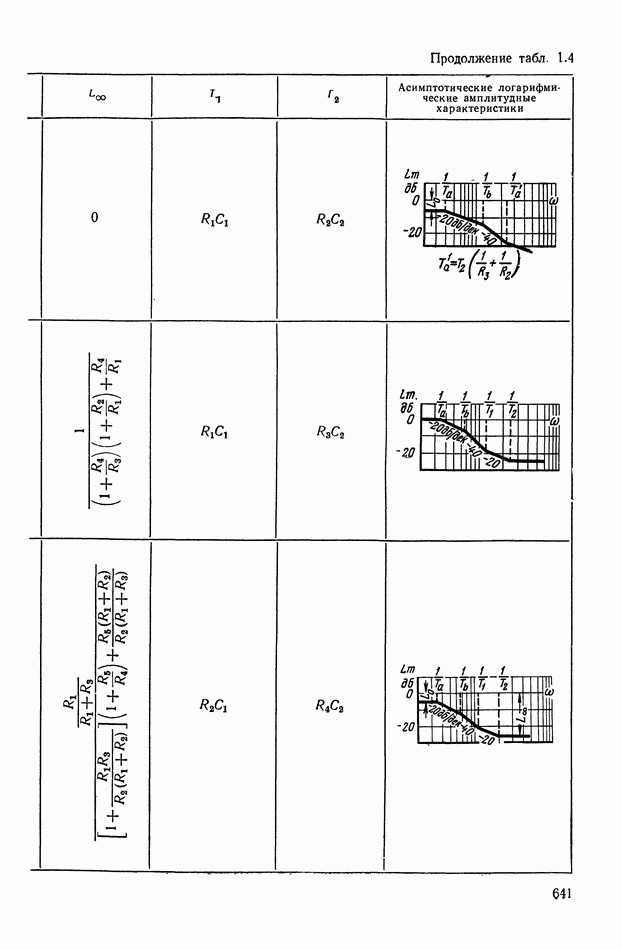
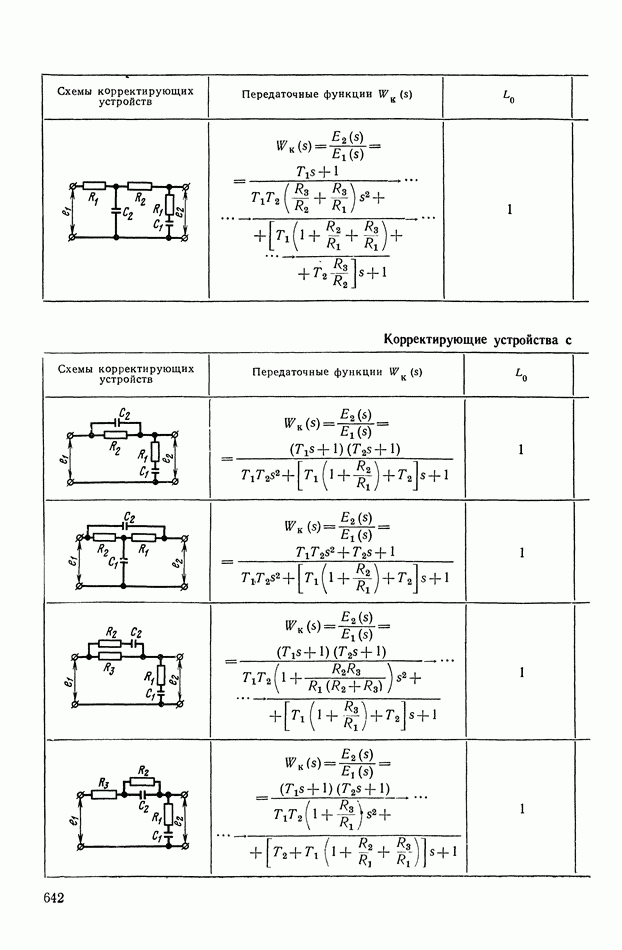
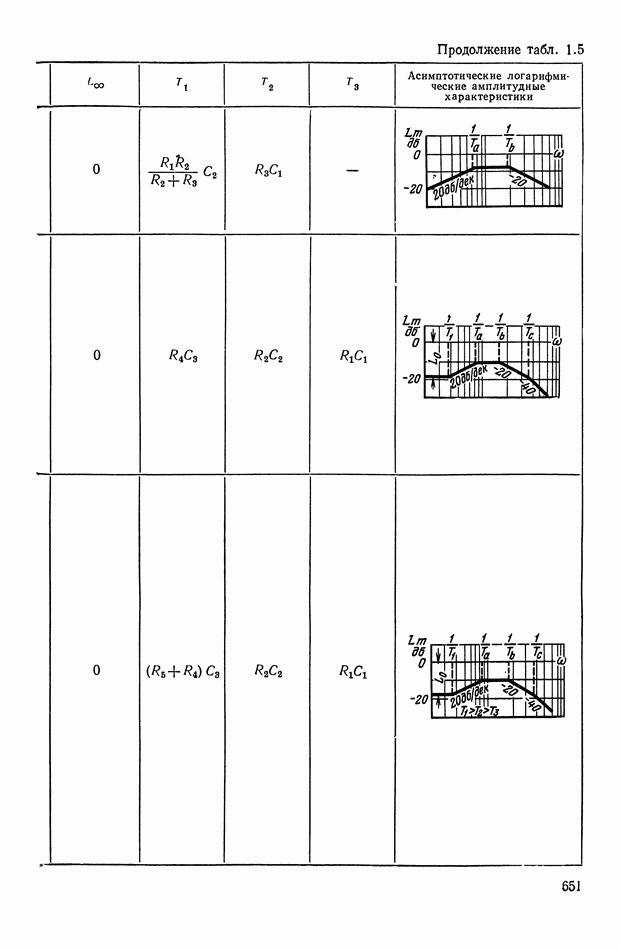
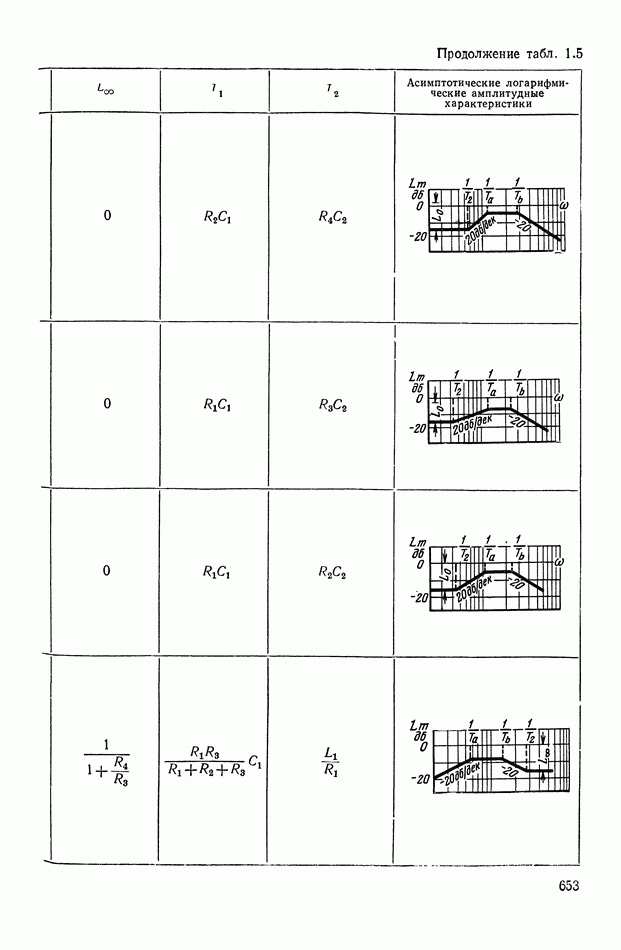
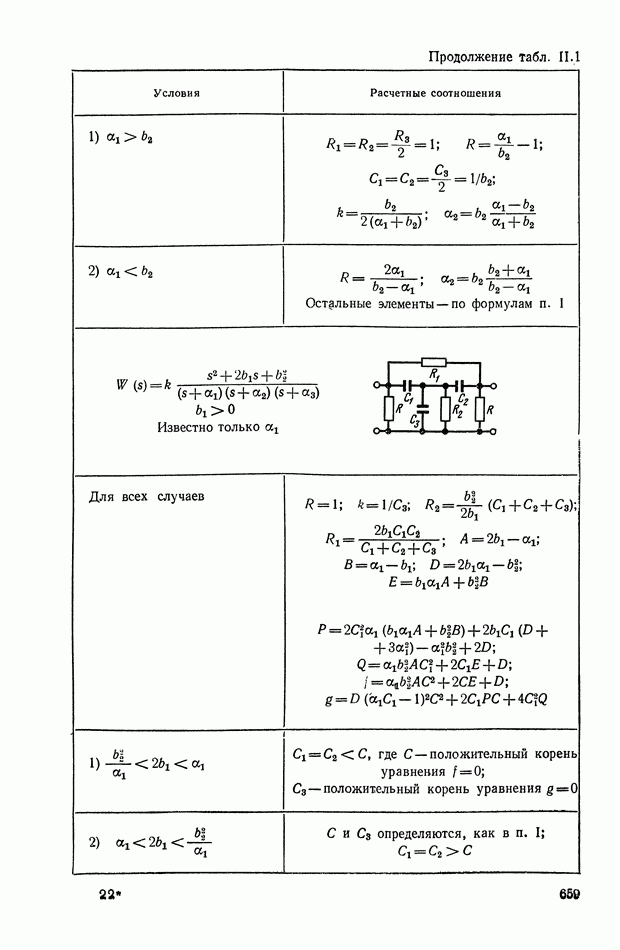
- ПРИЛОЖЕНИЕ 1. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПОСТОЯННОГО ТОКА
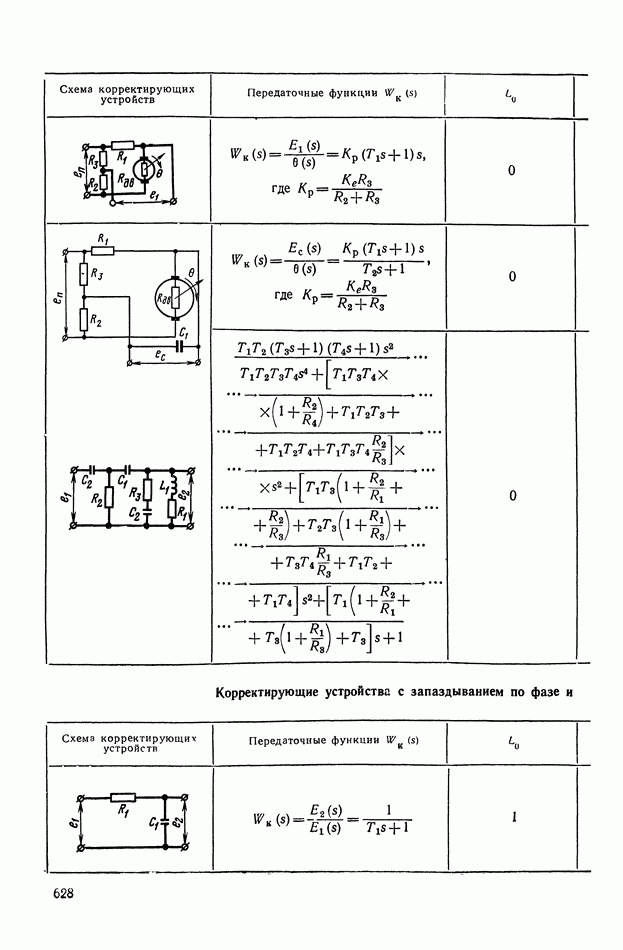
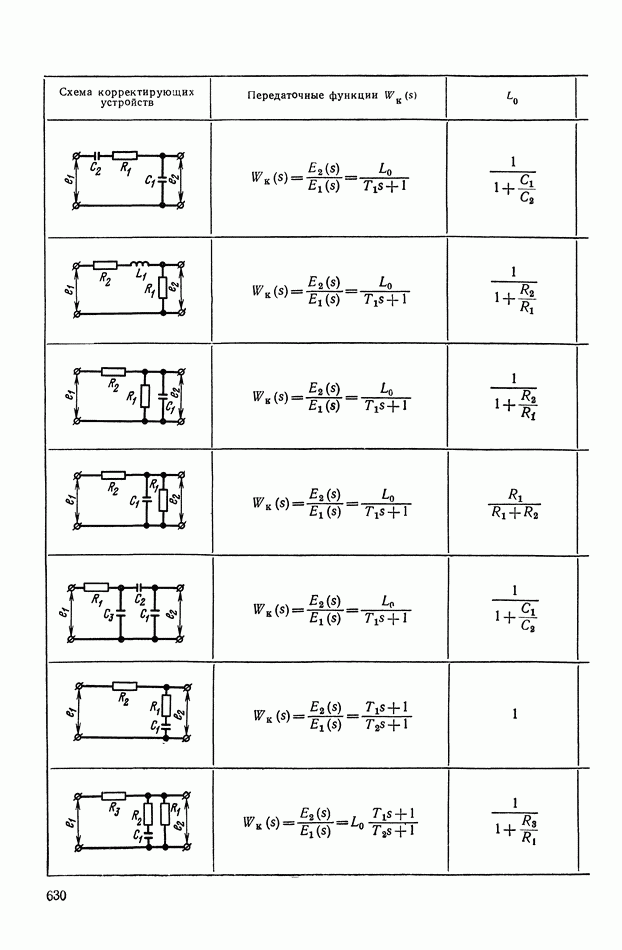
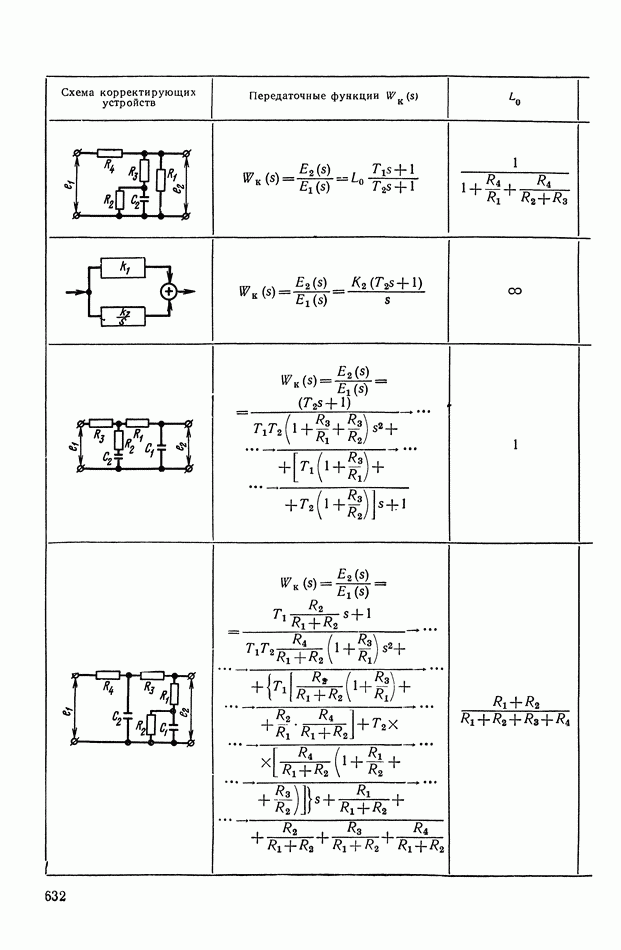
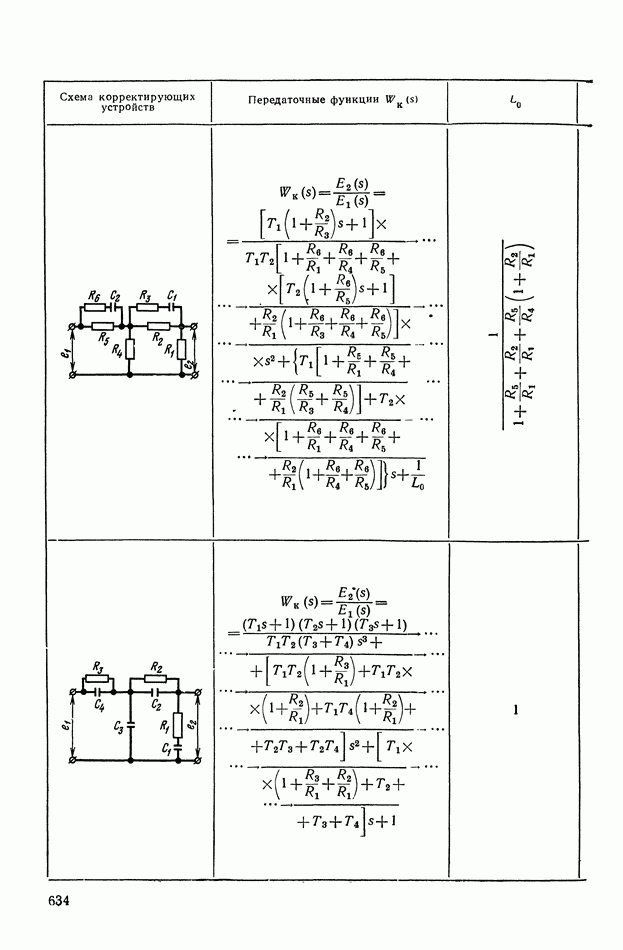
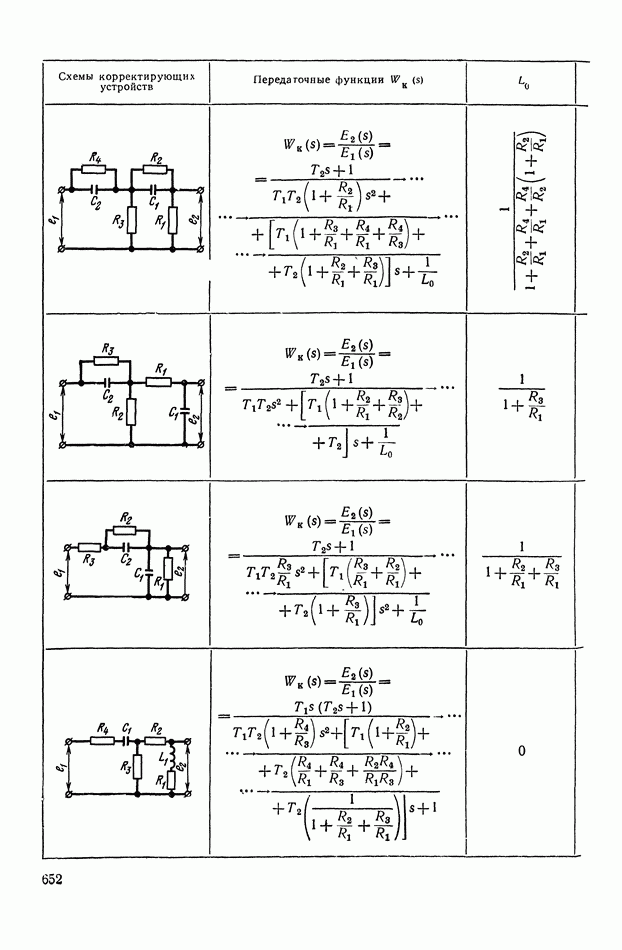
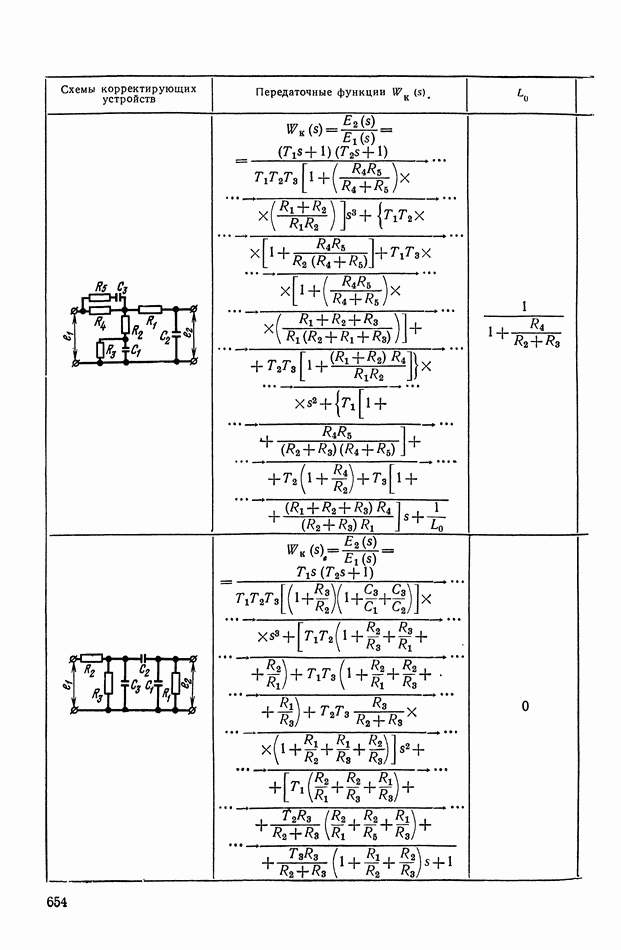
- ПРИЛОЖЕНИЕ II. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ОСНОВЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- ПРИЛОЖЕНИЕ III. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ