| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
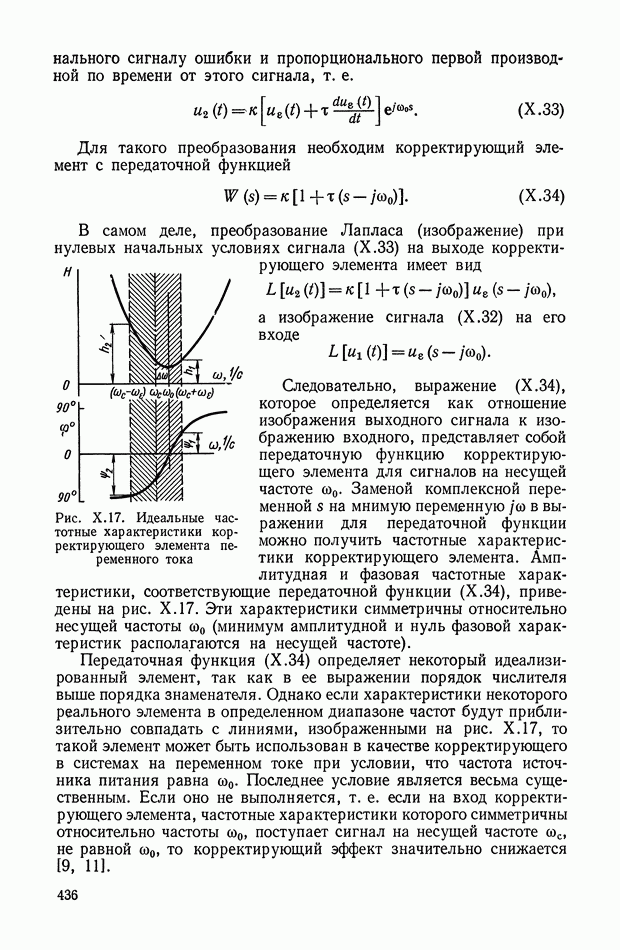
2. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ЛИНЕЙНЫХ ПАССИВНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
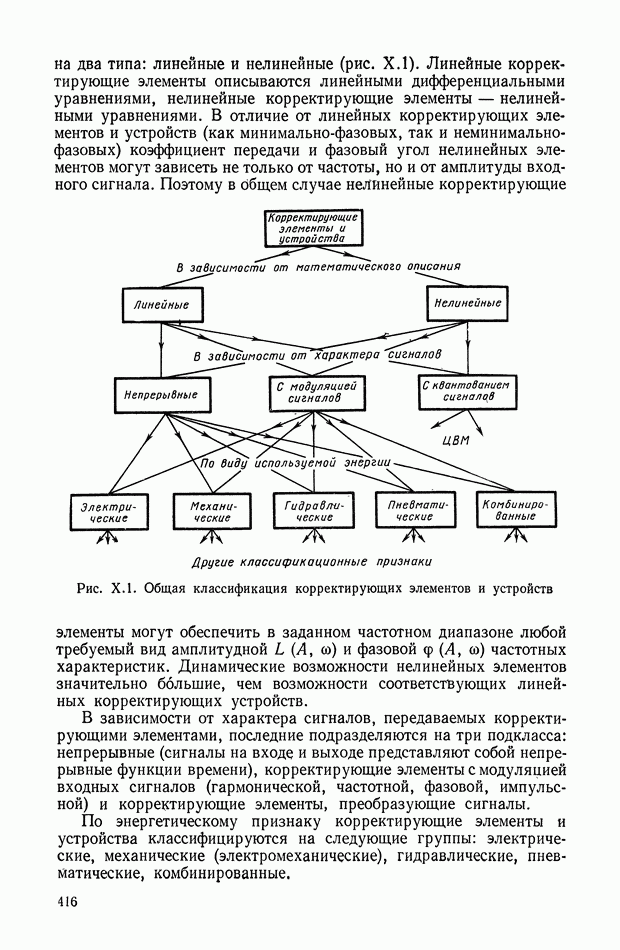
В качестве схем корректирующих устройств часто используют пассивные четырехполюсники типа RC, не имеющие индуктивностей. Это особенно важно в системах, работающих в диапазоне низких частот, для которых трудно изготовить индуктивности
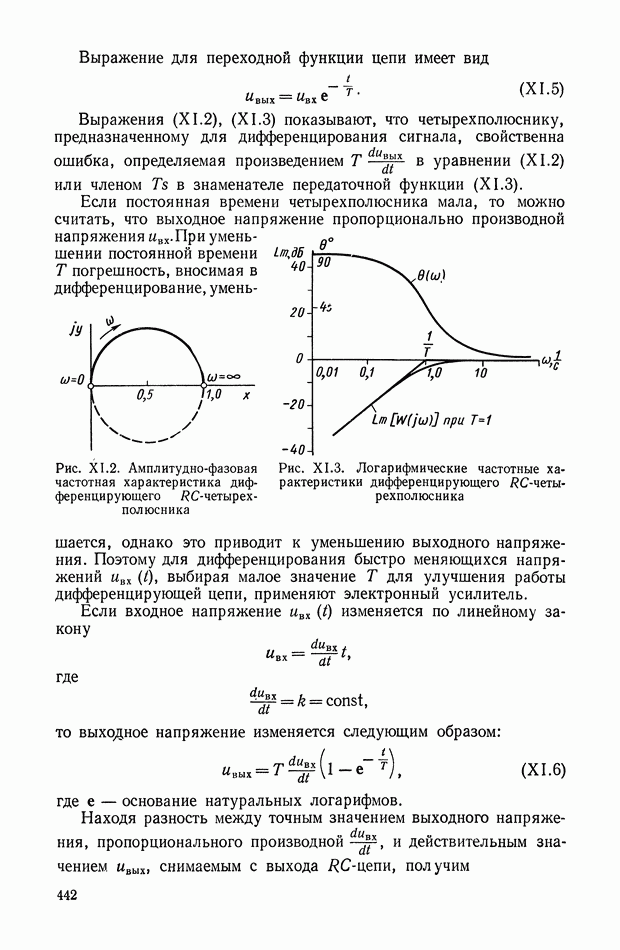
небольших размеров. Следует отметить, что несмотря на значительные ограничения, которые накладываются на реализуемую передаточную функцию при отказе от использования индуктивностей, такие четырехполюсники являются достаточно гибкими. Поэтому любая заданная амплитудно-частотная характеристика может быть аппроксимирована с любой степенью точности при использовании лишь резисторов и емкостей [4].
Широко известны типовые корректирующие цепи постоянного тока, реализующие большой класс передаточных функций. В общем же случае для реализации сложной передаточной функции в виде RC-четырехполюсника необходимо использовать некоторые вопросы теории синтеза цепей. Задача синтеза состоит в нахождении цепи, которая будет обладать заданной передаточной функцией.

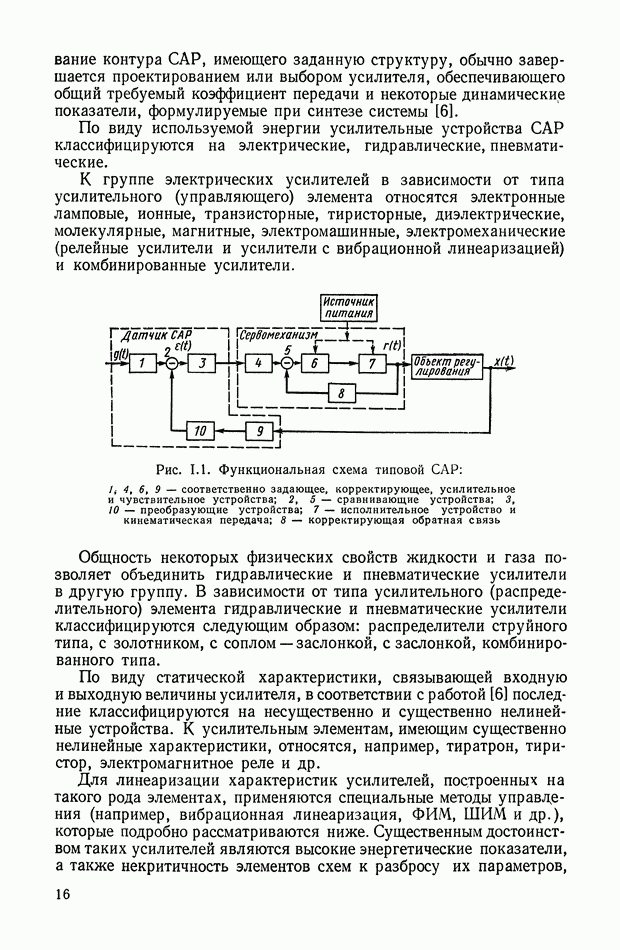
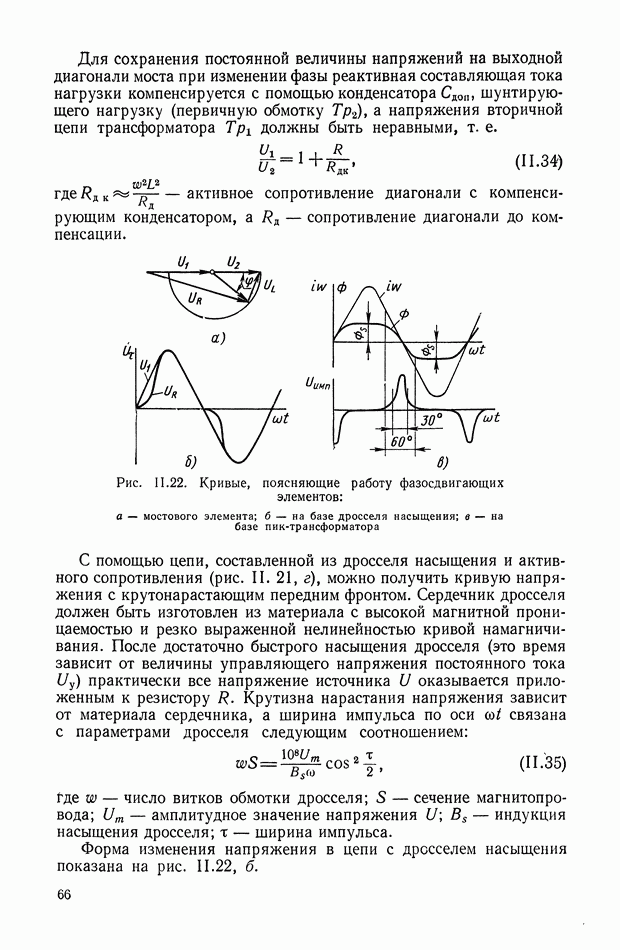
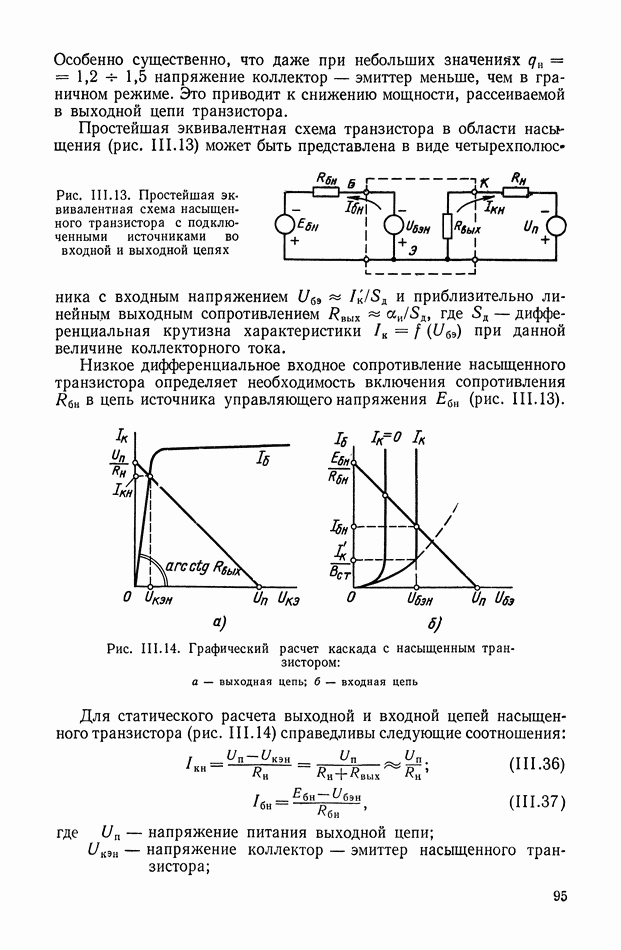
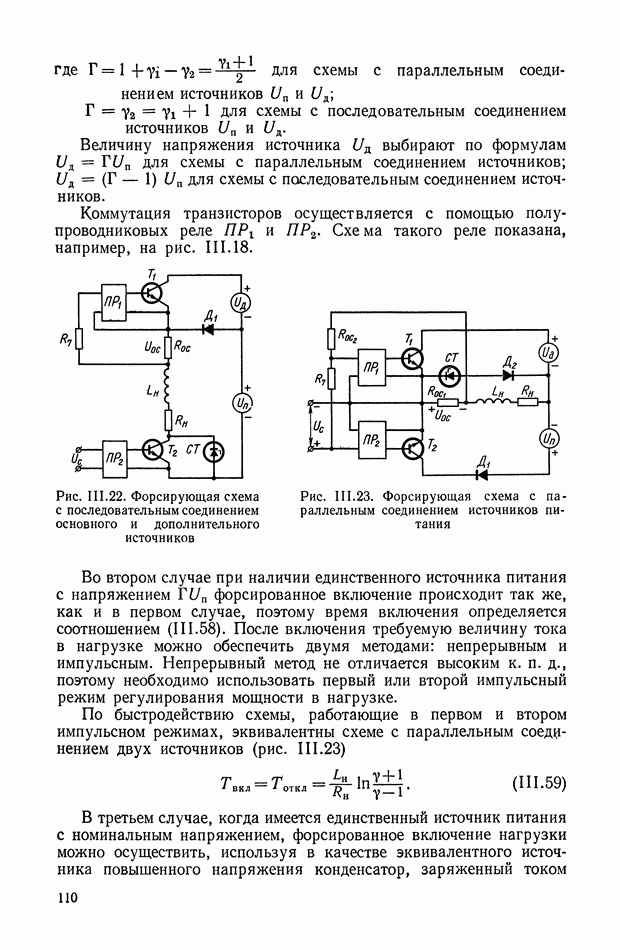
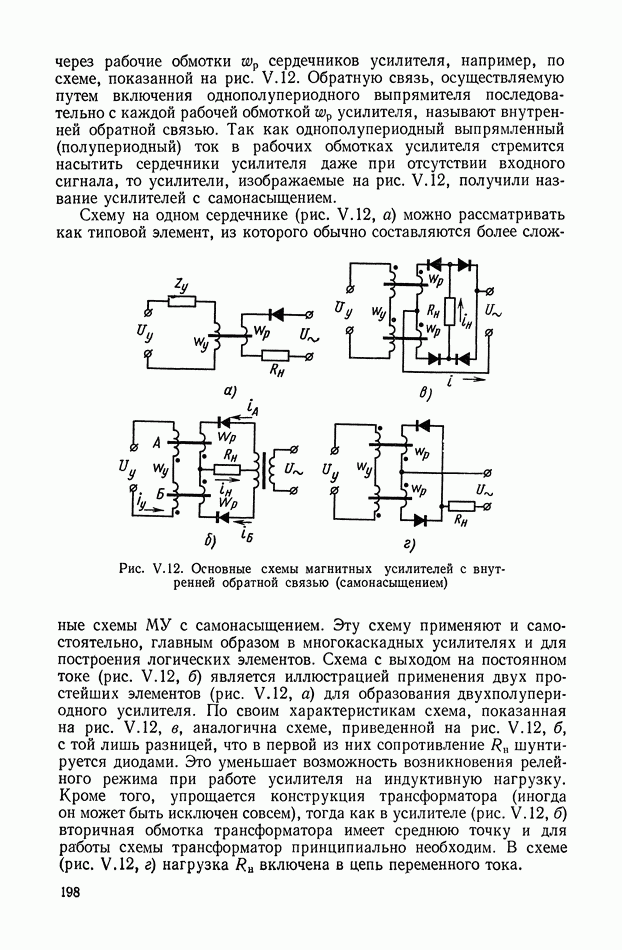
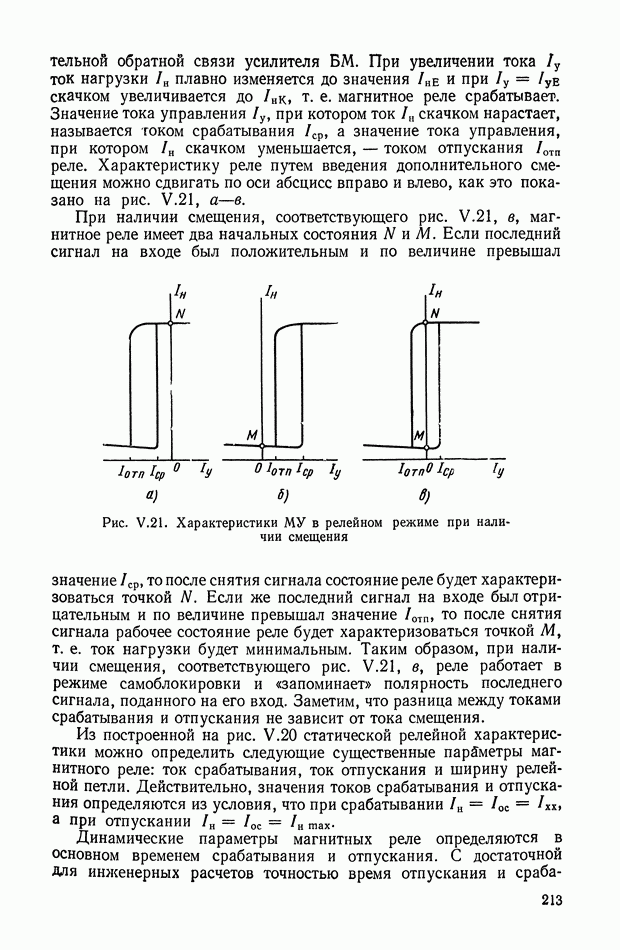
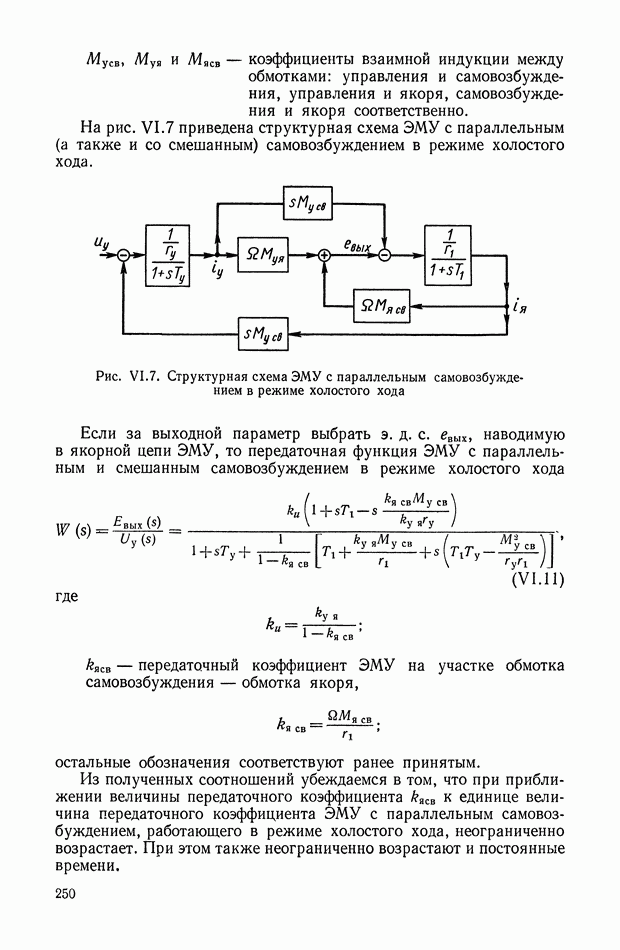
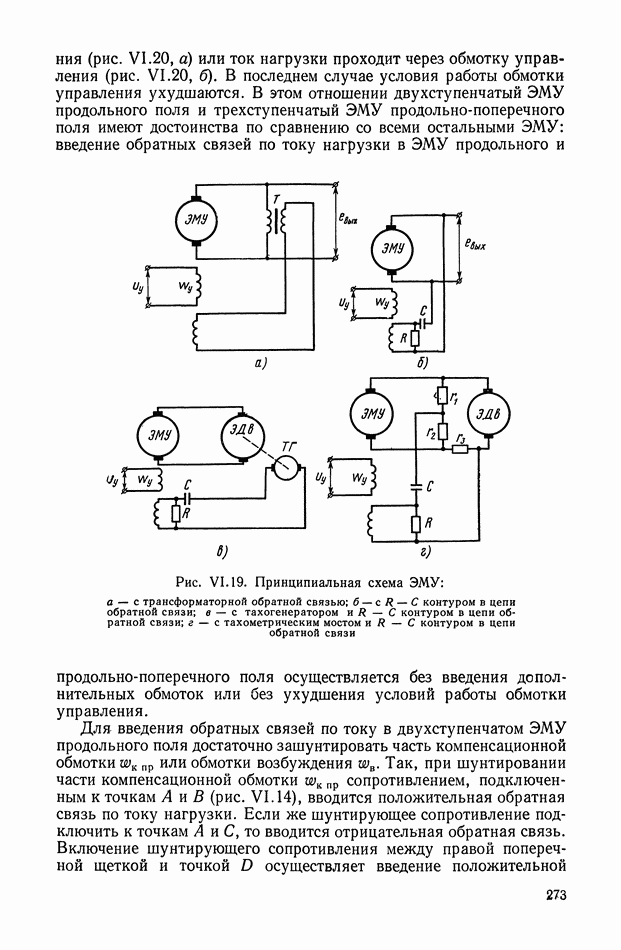
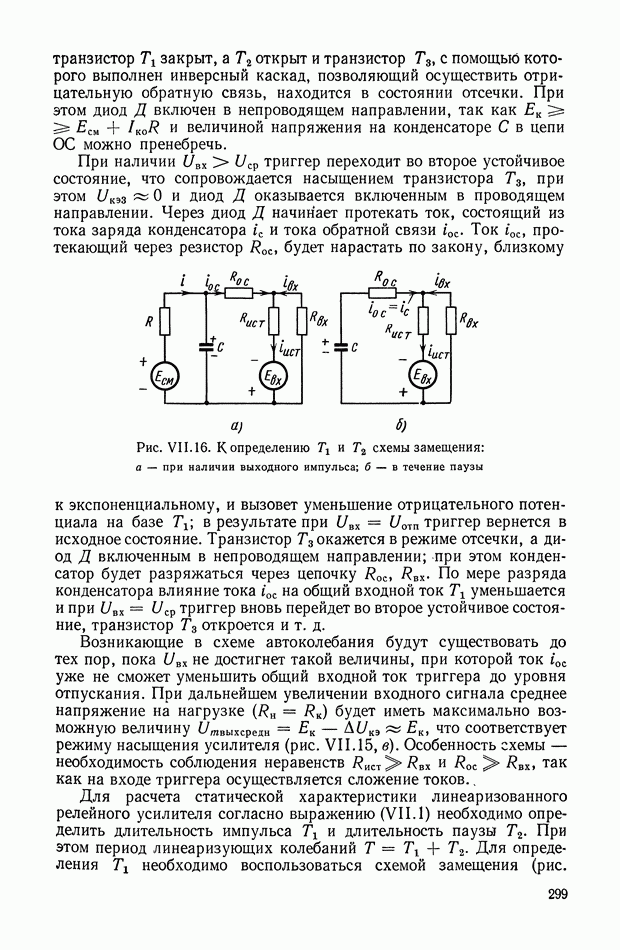
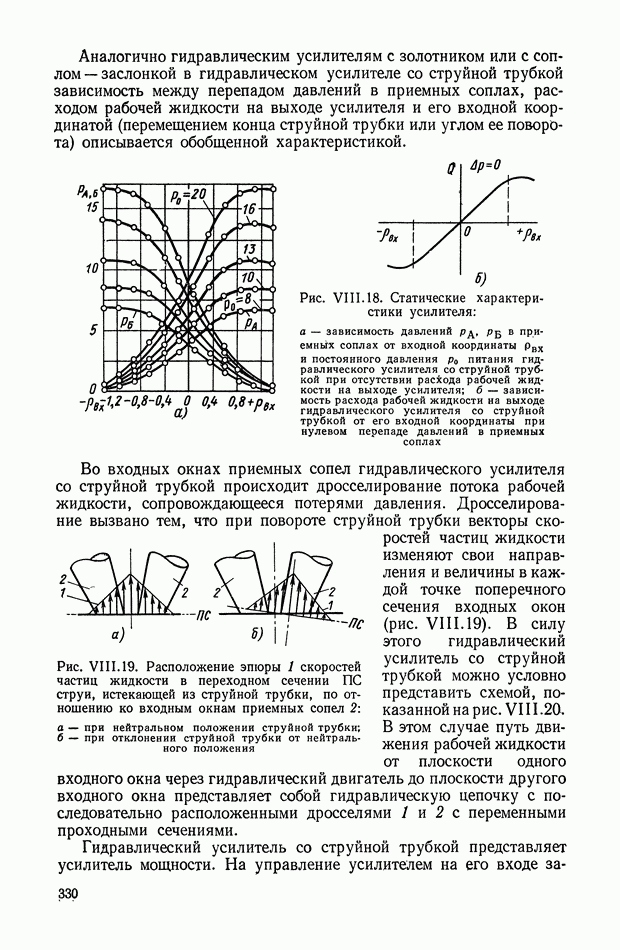
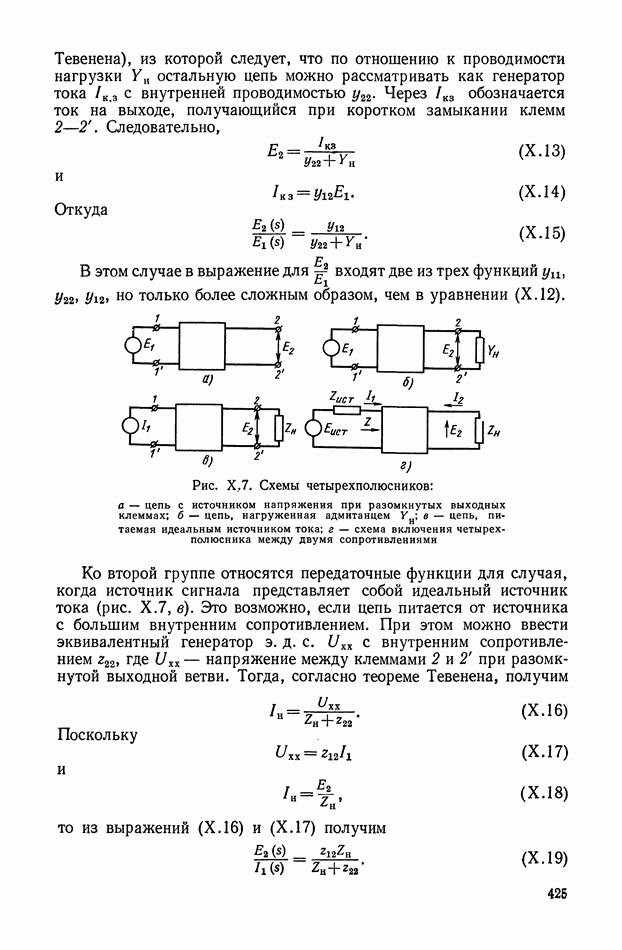
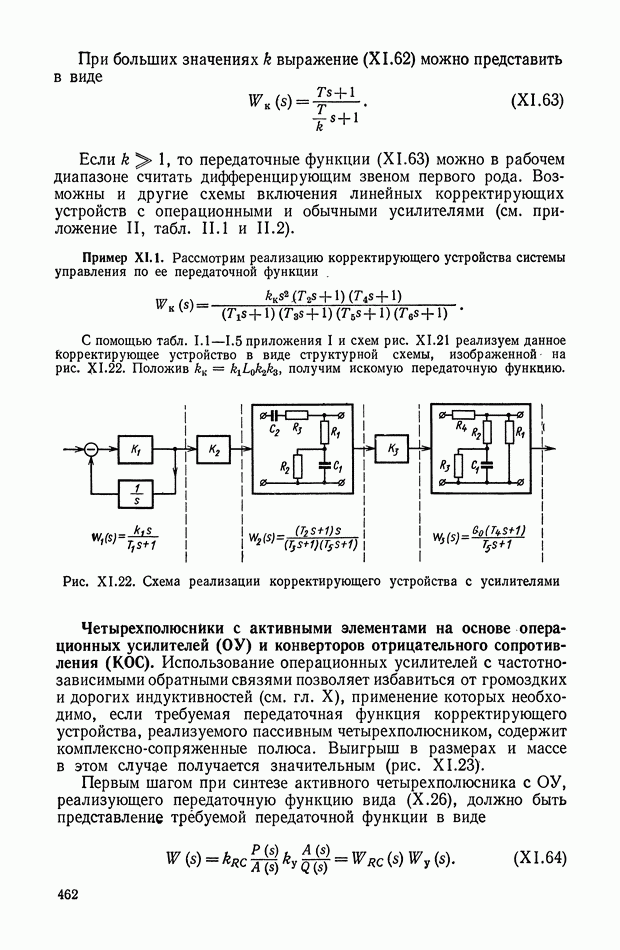
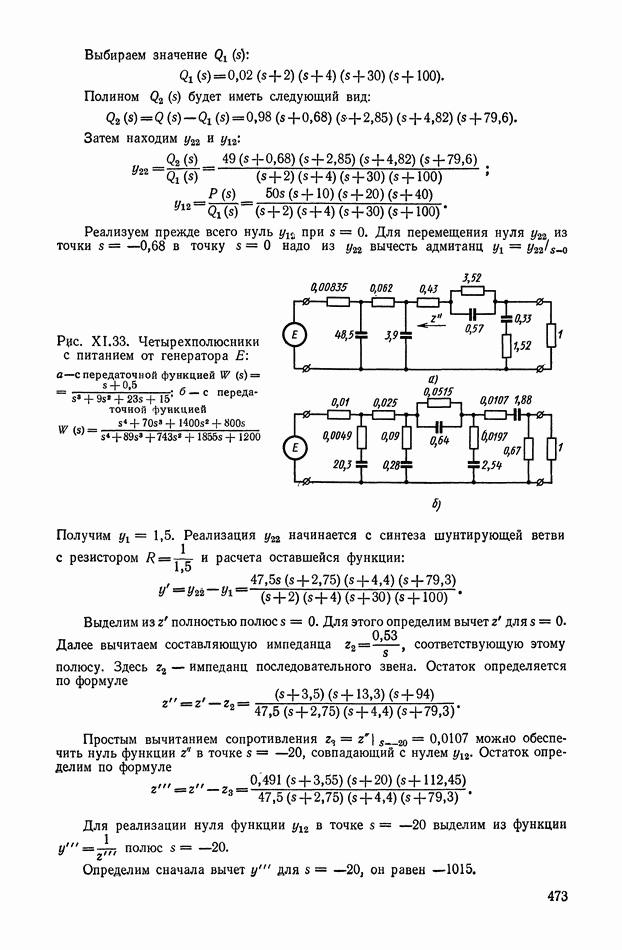
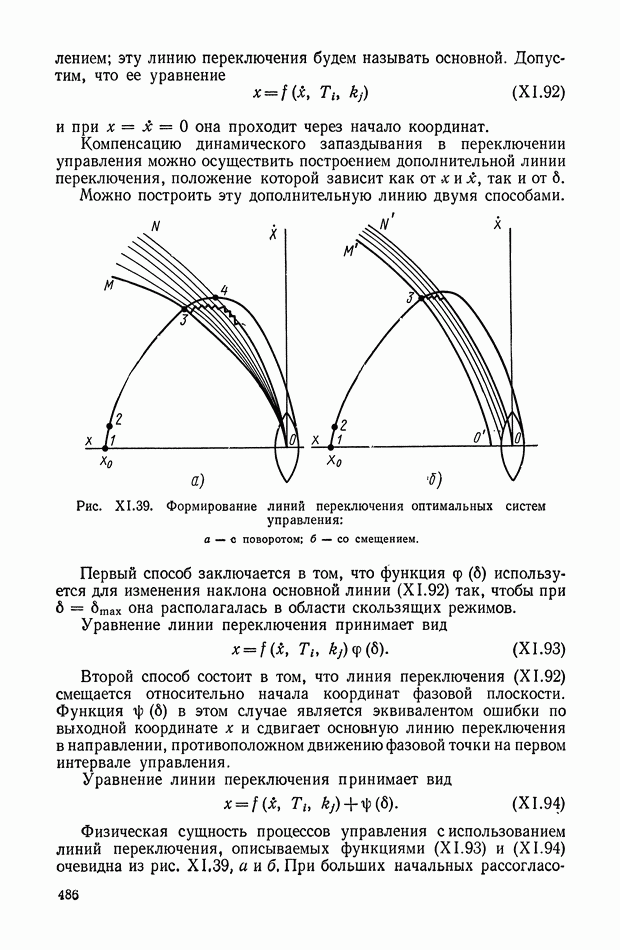
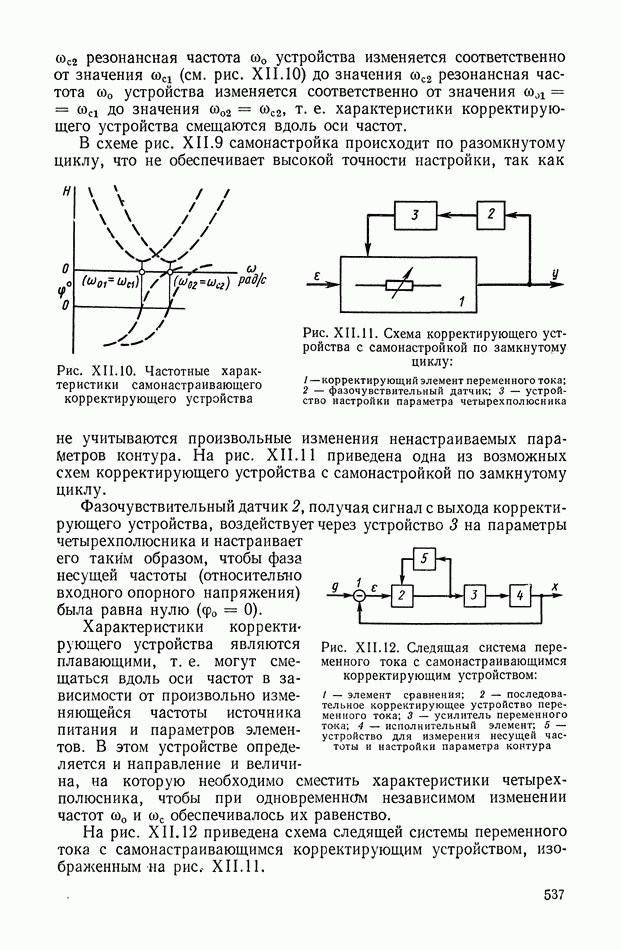
Рис. Х.3. Схемы четырехполюсников: а — «лестничный» четырехполюсник;  -образная схема, реализующая передаточную функцию
-образная схема, реализующая передаточную функцию 
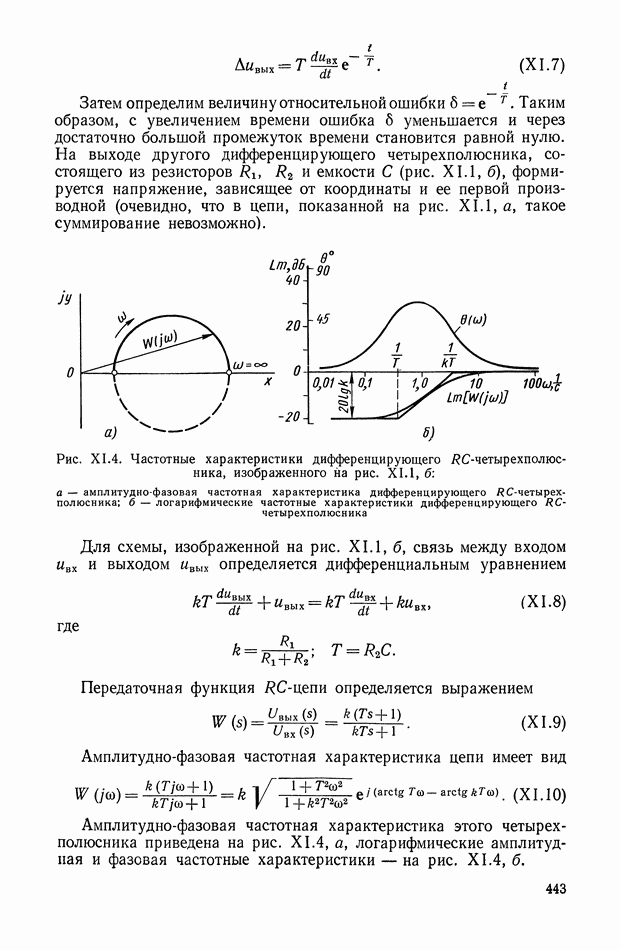
В качестве основной схемы четырехполюсника принимаем схему, показанную на рис. Х.3, а. Данная схема не сбалансирована относительно земли, что важно для практического применения. Эти RC-четырехполюсники дают возможность реализовать передаточные функции, содержащие нули и полюса, расположенные на отрицательной части действительной оси плоскости комплексной переменной  Для реализации комплексных нулей, расположенных как в левой, так и в правой полуплоскости, можно рекомендовать параллельное соединение нескольких «лестничных» четырехполюсников. Передаточные функции, содержащие нули, расположенные на положительной части действительной оси, реализуются лишь с помощью схем, сбалансированных относительно земли, например. Х-образных схем (рис. Х.3, б). Если передаточная функция содержит полюса в любой части левой полуплоскости, то для ее реализации целесообразно применять активные четырехполюсники, рассмотренные в § 3 настоящей главы.
Для реализации комплексных нулей, расположенных как в левой, так и в правой полуплоскости, можно рекомендовать параллельное соединение нескольких «лестничных» четырехполюсников. Передаточные функции, содержащие нули, расположенные на положительной части действительной оси, реализуются лишь с помощью схем, сбалансированных относительно земли, например. Х-образных схем (рис. Х.3, б). Если передаточная функция содержит полюса в любой части левой полуплоскости, то для ее реализации целесообразно применять активные четырехполюсники, рассмотренные в § 3 настоящей главы.
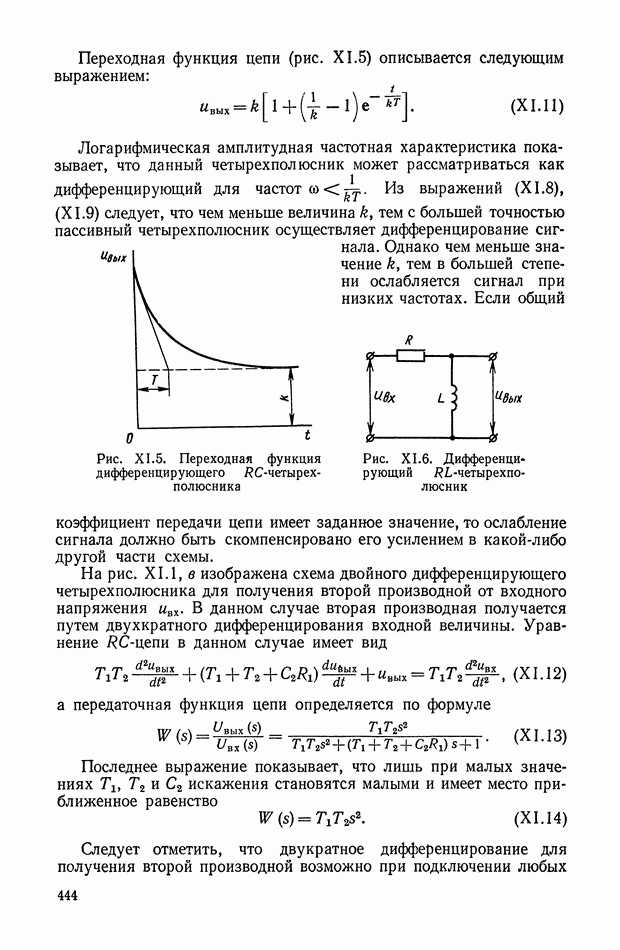
Ниже будет рассмотрен лишь метод синтеза RC-четырехполюсников, позволяющих реализовать передаточные функции с нулями, расположенными как в левой, так и правой полуплоскости, исключая положительную часть действительной оси, и с полюсами, расположенными на отрицательной части действительной оси.
Методика синтеза электрических цепей, реализующих определенные частотные характеристики, особенно важна для схем, в которых затруднено использование разделяющих усилителей. Если такие усилители могут быть применены, то требуемую передаточную функцию легко реализовать с помощью дифференцирующих, интегрирующих и интегродифференцирующих четырехполюсников.

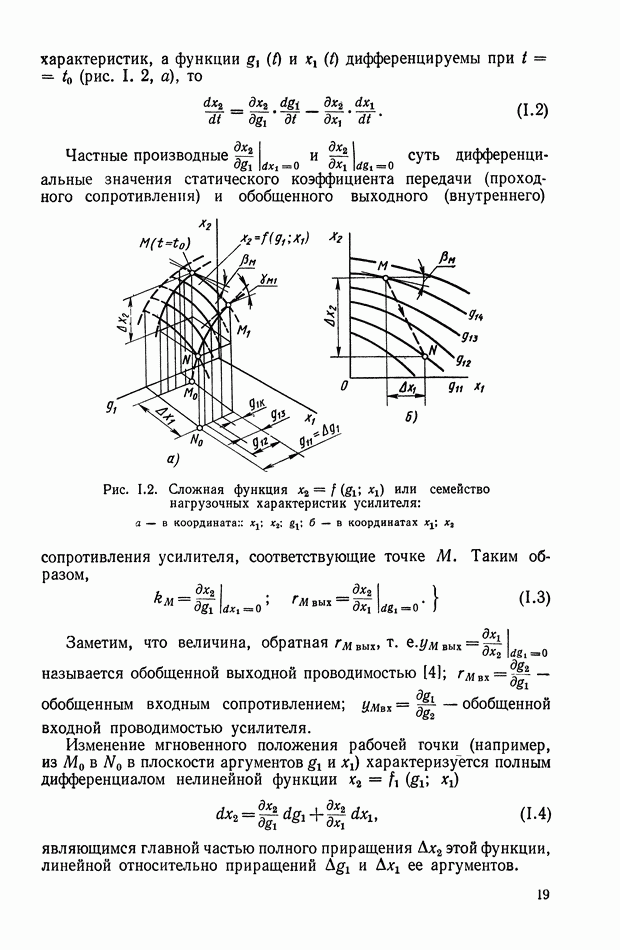
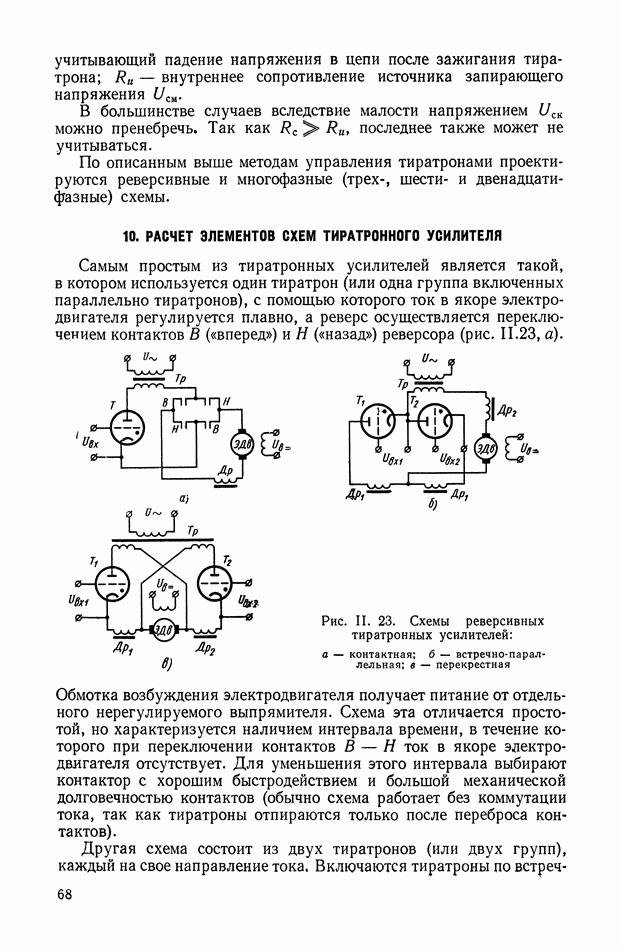
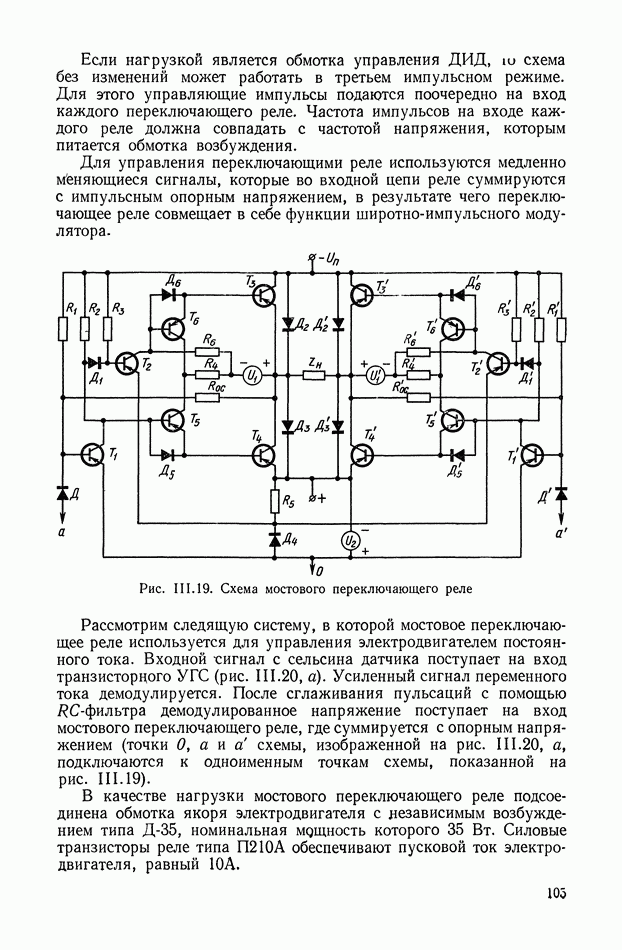
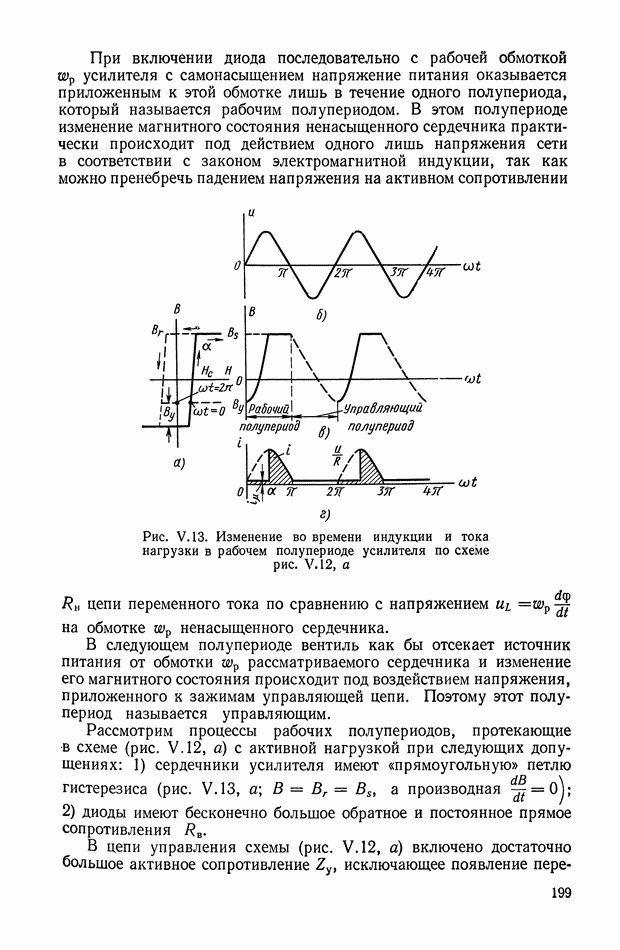
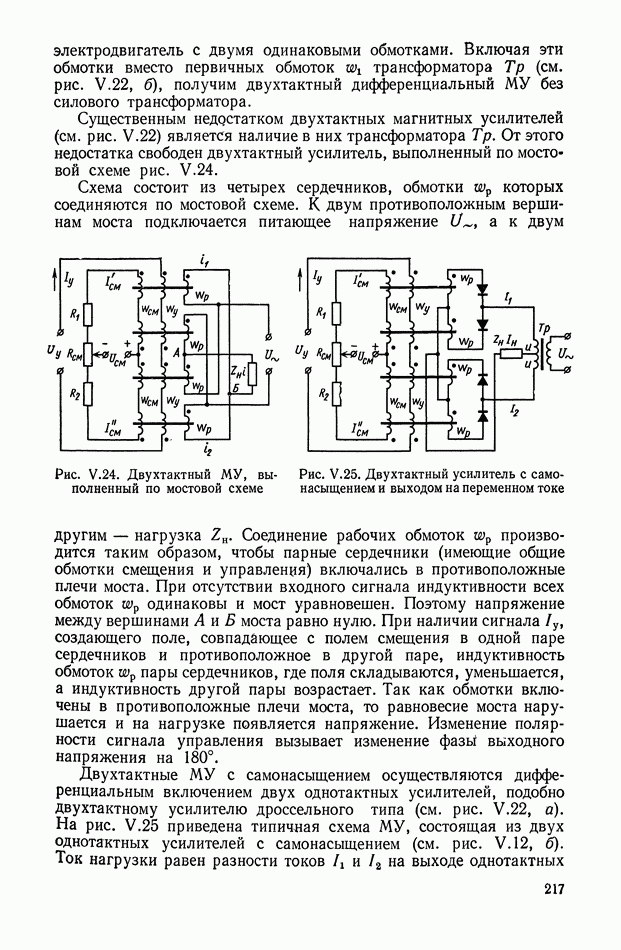
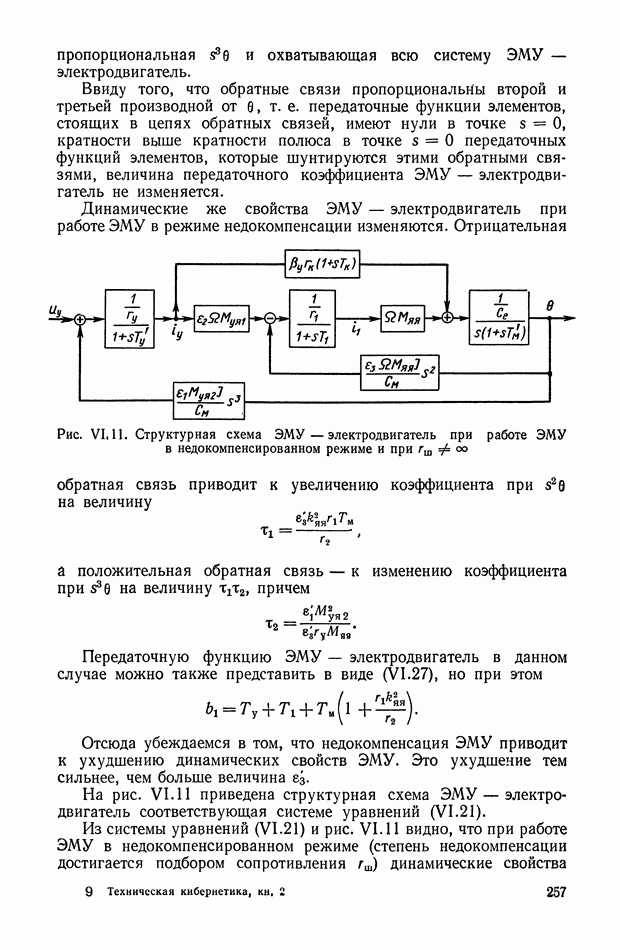
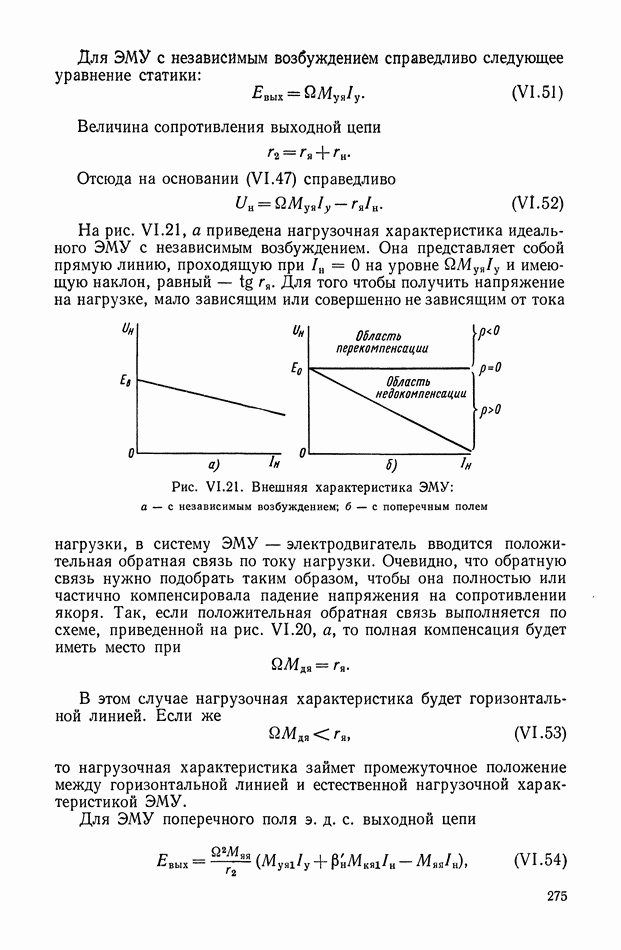
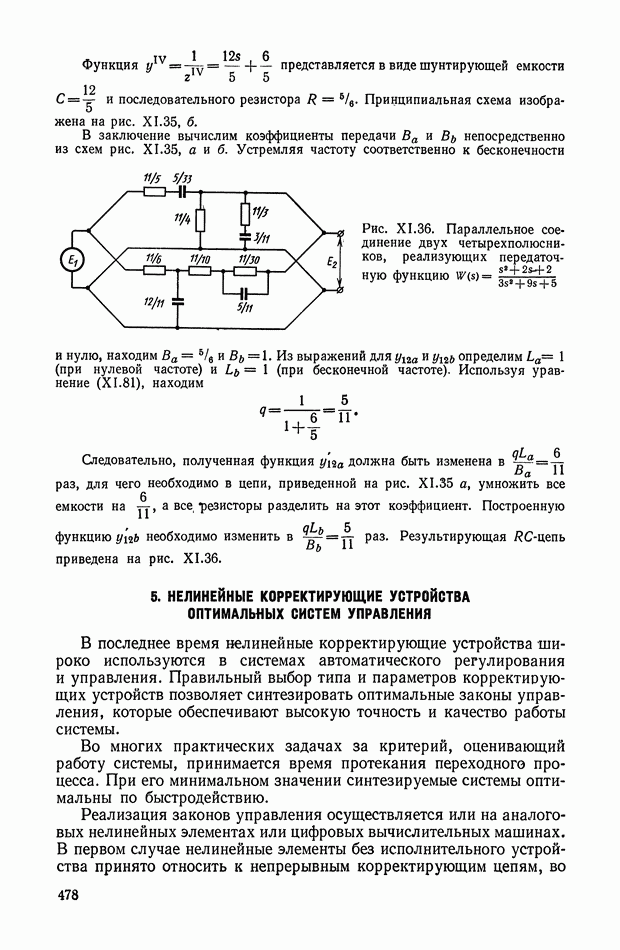
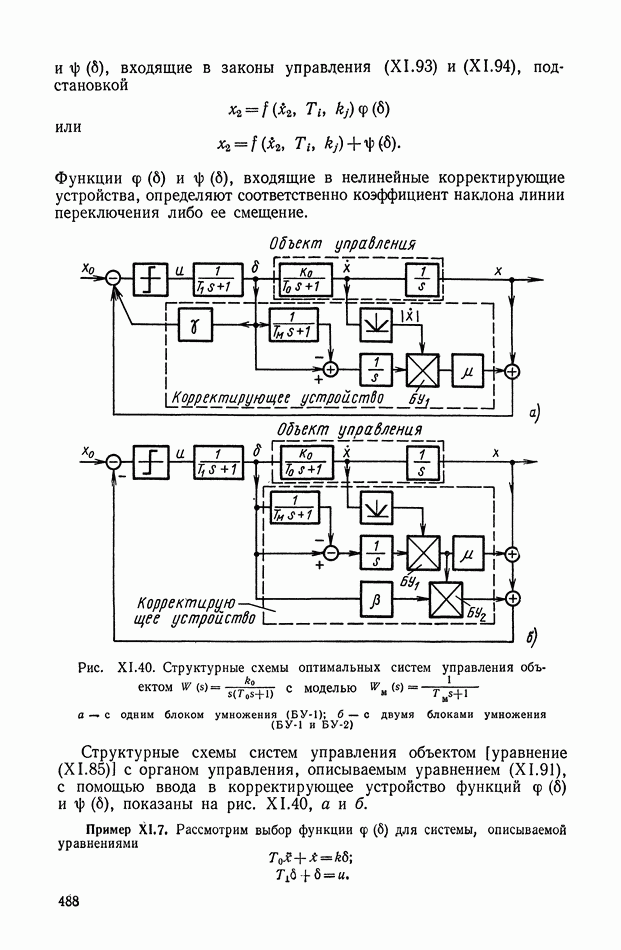
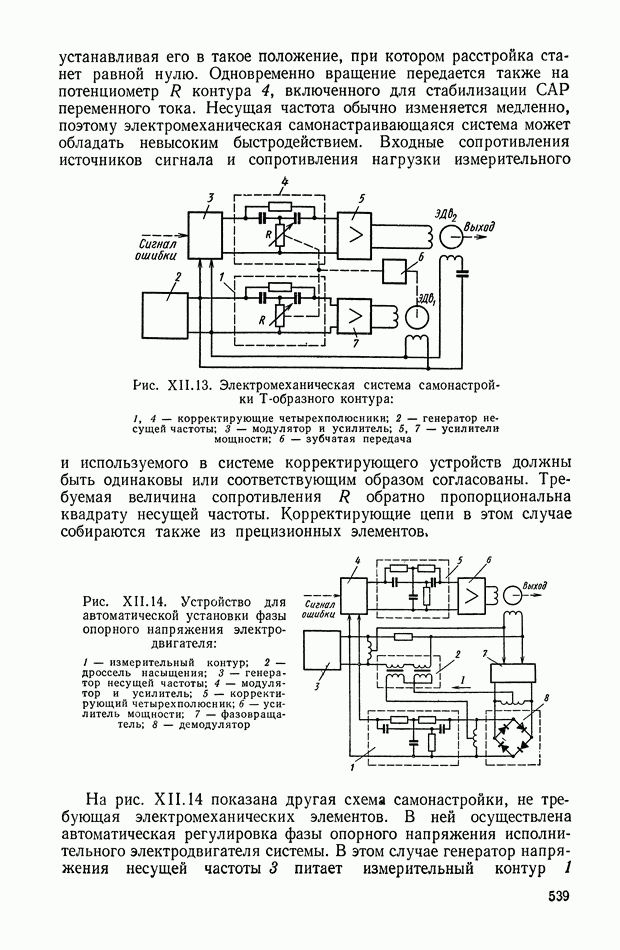
Рис. Х.4. Четырехполюсники с тремя интегрирующими звеньями: а — с разделяющими усилителями; б — без разделяющих усилителей
Для схемы, изображенной на рис. Х.4, а, общая передаточная функция равна произведению передаточных функций трех звеньев, т. е.

где

Если разделительные усилители не могут быть использованы, то передаточную функцию, определяемую выражением  реализовать сложнее. При простом последовательном соединении отдельных четырехполюсников (рис. Х.4, б) желаемой передаточной функции не получается, поскольку имеет место влияние последующего звена на предыдущее.
реализовать сложнее. При простом последовательном соединении отдельных четырехполюсников (рис. Х.4, б) желаемой передаточной функции не получается, поскольку имеет место влияние последующего звена на предыдущее.
Анализ электрических цепей.
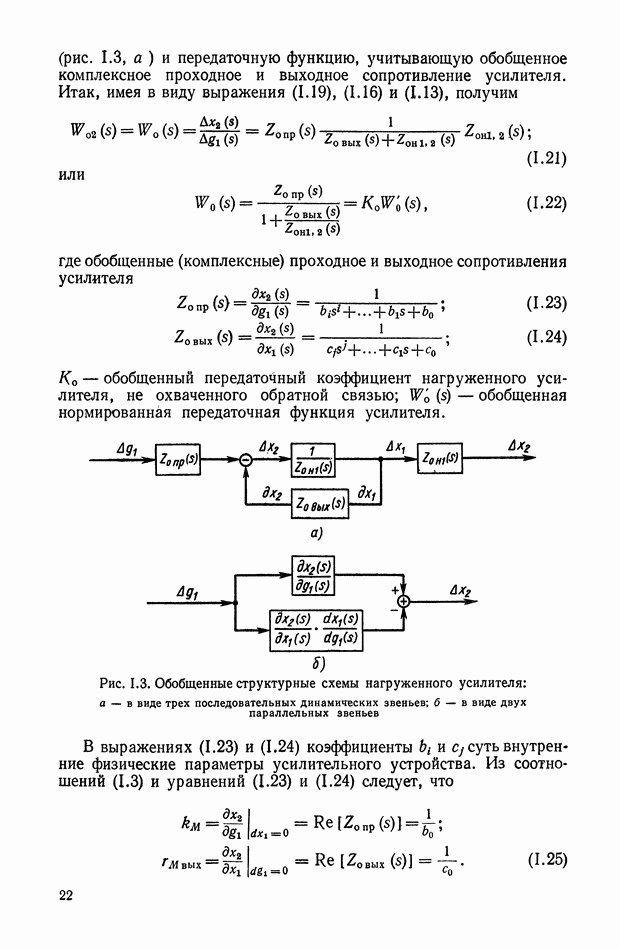
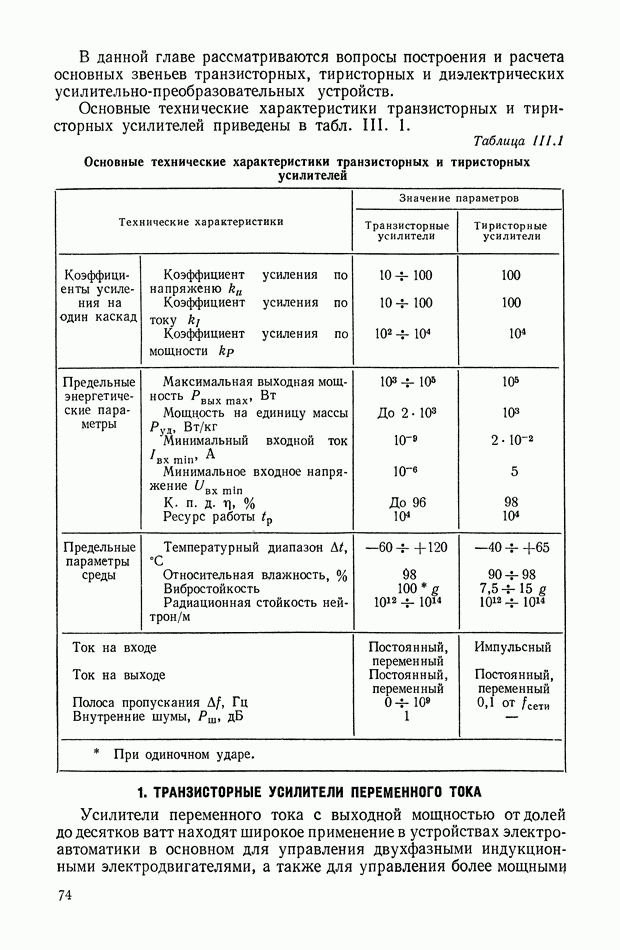
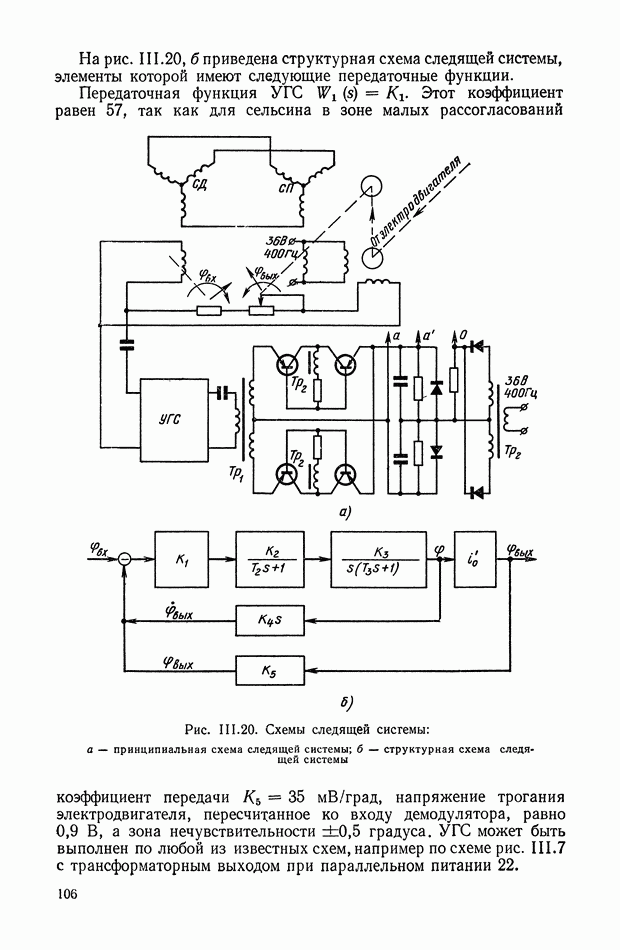
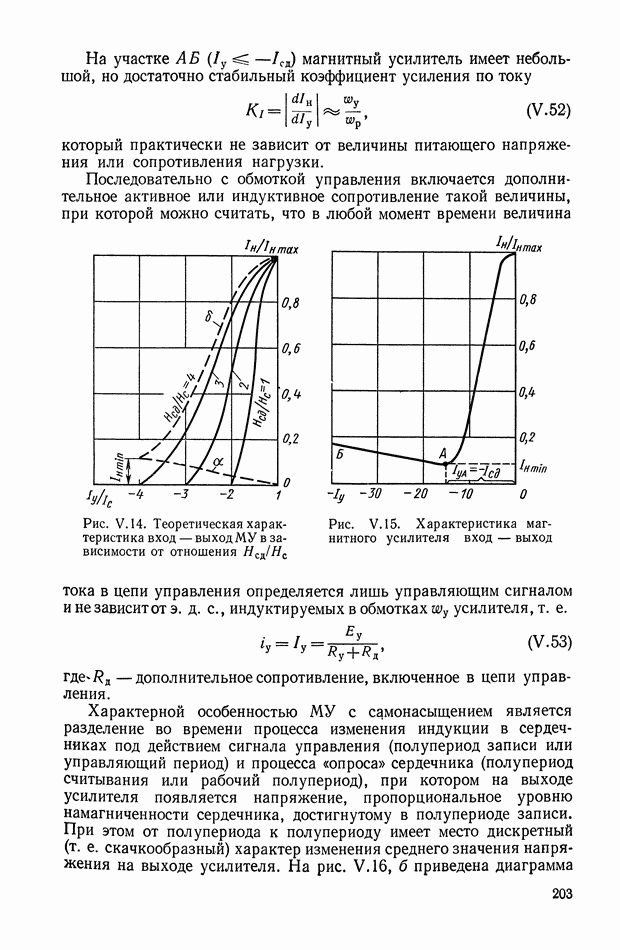
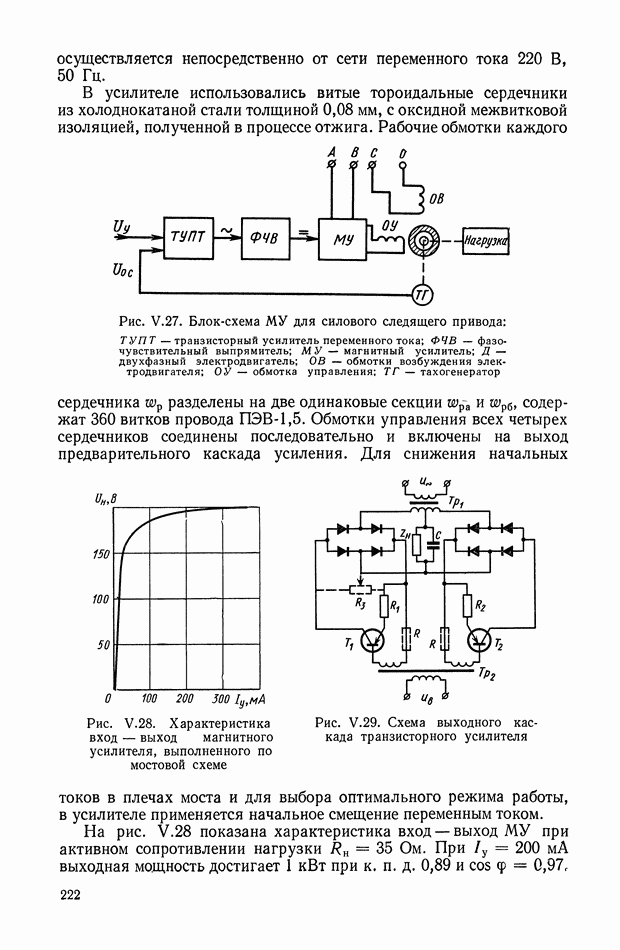
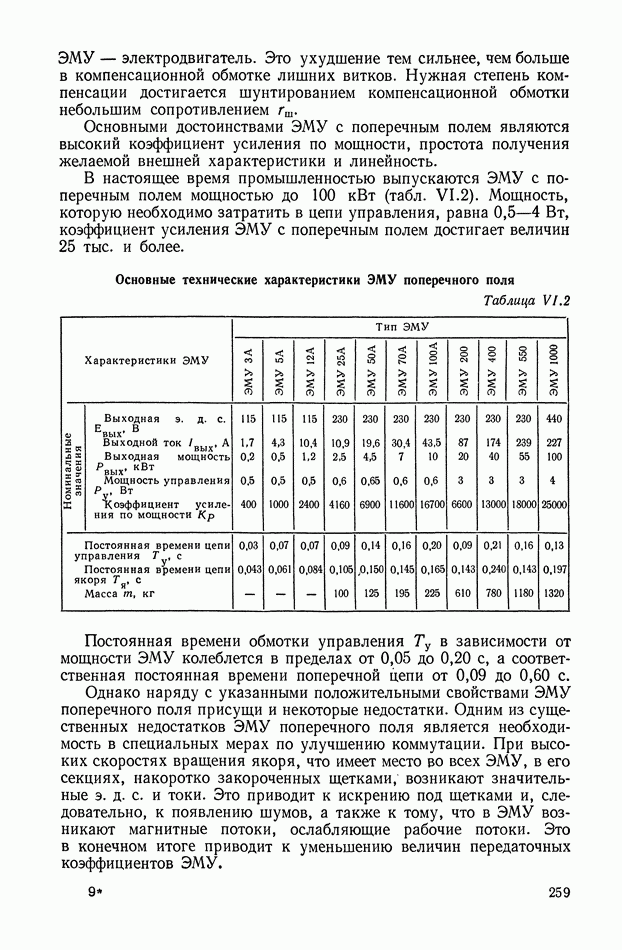
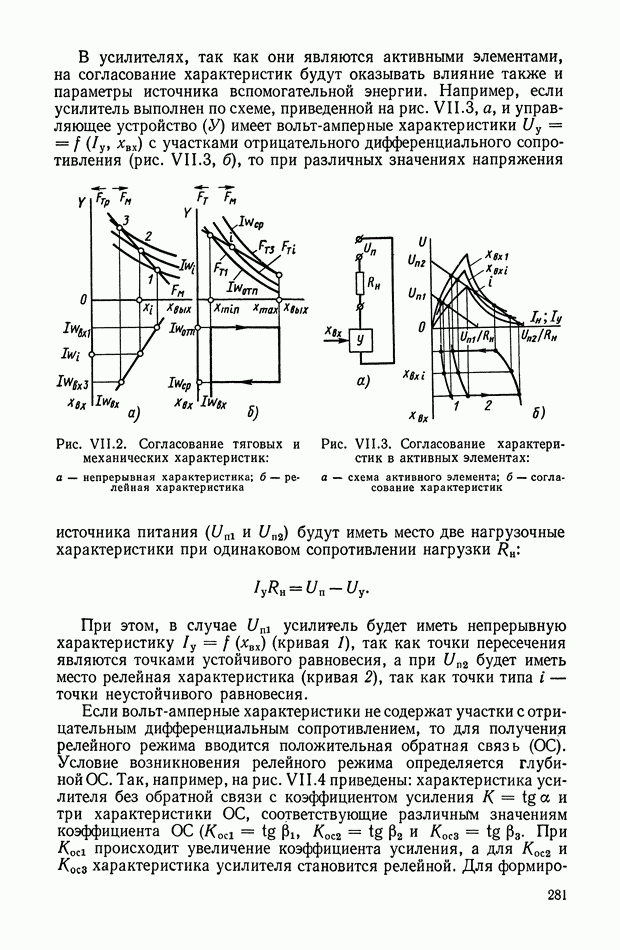
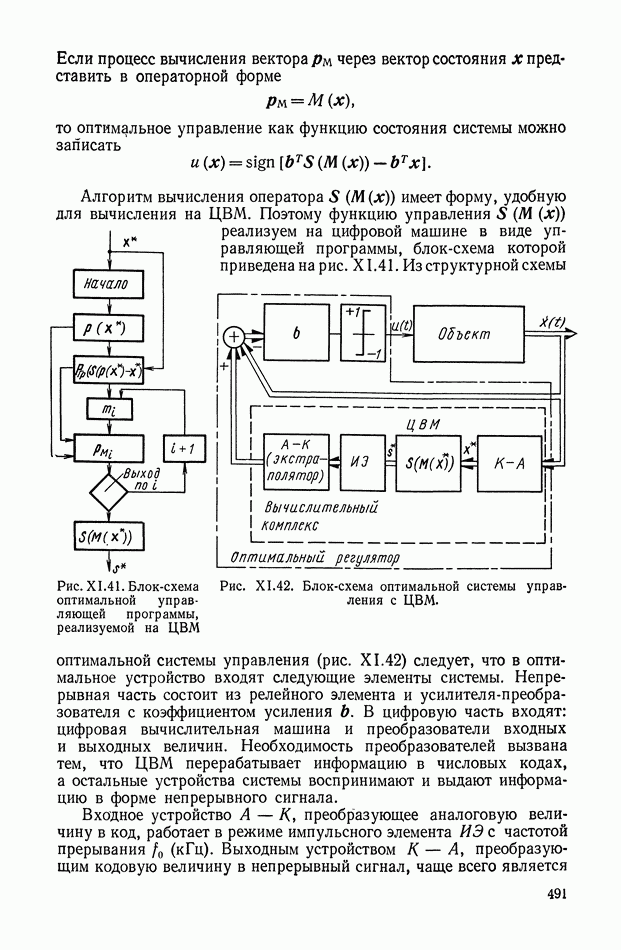
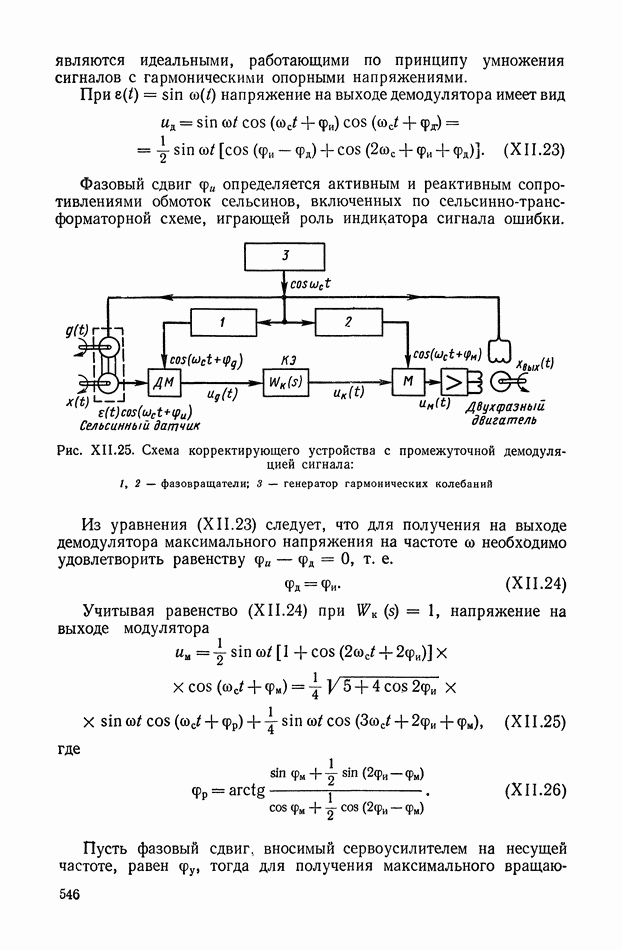
На рис. Х.5, а изображена произвольная линейная электрическая цепь с сосредоточенными параметрами, имеющая двустороннее питание. В общем случае она может быть активной, т. е. содержать источники электрической энергии. Применяя второй закон Кирхгофа, можно записать систему линейных интегрально-дифференциальных уравнений

где  общая индуктивность контуров
общая индуктивность контуров  и к, причем знак плюс относится к случаю, когда положительные направления токов
и к, причем знак плюс относится к случаю, когда положительные направления токов  в общей ветви совпадают; при
в общей ветви совпадают; при  имеем:
имеем:
 — сумма всех индуктивностей
— сумма всех индуктивностей  контура;
контура;
 — сопротивления соответственно общей ветви и
— сопротивления соответственно общей ветви и  контура;
контура;
 и
и  — величины, обратные емкостям общей ветви и
— величины, обратные емкостям общей ветви и  контура.
контура.
Систему уравнений  можно переписать в следующем виде:
можно переписать в следующем виде: 

где  — контурные токи;
— контурные токи;
 — контурные э. д. с.
— контурные э. д. с.

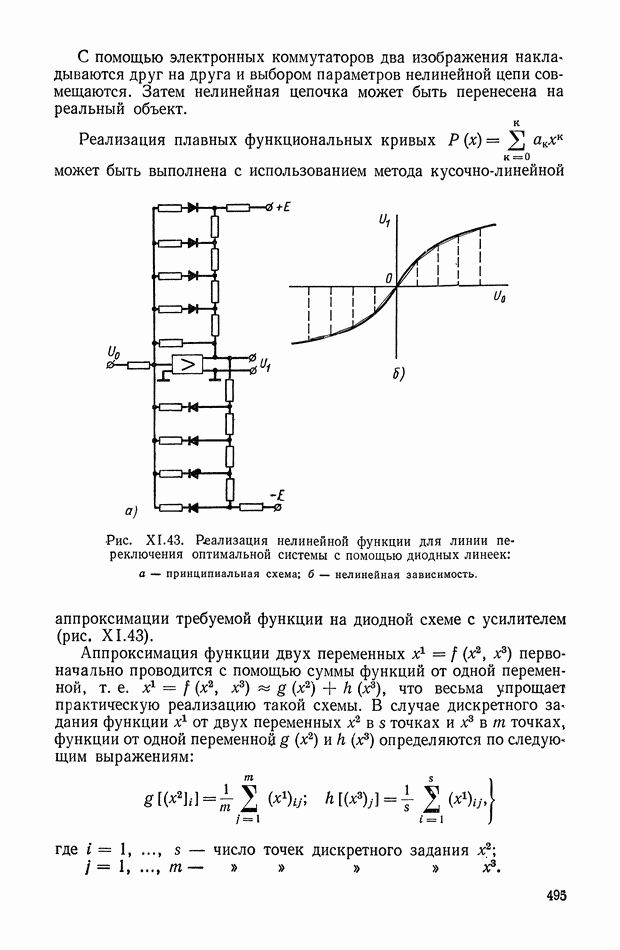
Рис. Х.5. Схемы электрических цепей: а — общая схема с двусторонним питанием; б — схема двухполюсника; в — схема четырехполюсника
Преобразование Лапласа дает возможность найти решение для любого источника напряжения. Считая начальные условия нулевыми, можно записать систему  в виде
в виде

где

Тогда изображение контурного тока находится по формуле

где  — определитель системы (Х.4);
— определитель системы (Х.4);
 — алгебраическое дополнение.
— алгебраическое дополнение.
На рис. X.5, б изображена самая простая электрическая цепь — двухполюсник. Он содержит всего одну пару клемм для соединения с внешней цепью. Двухполюсник характеризуется только одной
функцией — входным импеданцем, т. е. отношением  Это отношение можно получить из формулы
Это отношение можно получить из формулы  положив равными нулю все э. д. с., кроме
положив равными нулю все э. д. с., кроме  Таким образом,
Таким образом,

Очевидно, что  двухполюсника является рациональной функцией с вещественными коэффициентами. Это справедливо и для адмитанца двухполюсника
двухполюсника является рациональной функцией с вещественными коэффициентами. Это справедливо и для адмитанца двухполюсника  Нули и полюса
Нули и полюса  являются соответственно корнями
являются соответственно корнями  представляющими собой собственные частоты электрической цепи соответственно при замкнутых накоротко и разомкнутых зажимах. Очевидно, что нули и полюса
представляющими собой собственные частоты электрической цепи соответственно при замкнутых накоротко и разомкнутых зажимах. Очевидно, что нули и полюса  не могут находиться в правой половине комплексной плоскости, т. е. они будут либо вещественными и отрицательными, либо комплексными с отрицательной вещественной частью. Комплексные нули и полюса должны составлять сопряженные пары, чтобы обеспечить вещественность коэффициентов.
не могут находиться в правой половине комплексной плоскости, т. е. они будут либо вещественными и отрицательными, либо комплексными с отрицательной вещественной частью. Комплексные нули и полюса должны составлять сопряженные пары, чтобы обеспечить вещественность коэффициентов.
На рис. Х.5, в изображен четырехполюсник, т. е. электрическая цепь с двумя парами клемм. Свойства четырехполюсника определяются соотношениями между входными и выходными напряжениями и токами. Одно такое соотношение можно получить из уравнения  сведением к нулю всех напряжений, за исключением
сведением к нулю всех напряжений, за исключением 

где

Если решить уравнение  относительно Е, то можно записать
относительно Е, то можно записать

где

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА САР
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ЛИНЕЙНЫХ УСИЛИТЕЛЬНЫХ УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ УСИЛИТЕЛЬНОГО УСТРОЙСТВА БЕЗ ОБРАТНОЙ СВЯЗИ
- 3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ, СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ОСОБЕННОСТИ УСИЛИТЕЛЬНОГО УСТРОЙСТВА С ОБРАТНОЙ СВЯЗЬЮ
- 4. КЛАССИФИКАЦИЯ И СВОЙСТВА УСИЛИТЕЛЬНЫХ УСТРОЙСТВ С ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 5. ВЫБОР И РАСЧЕТ УСИЛИТЕЛЬНОГО УСТРОЙСТВА
- ГЛАВА II. ЭЛЕКТРОННЫЕ ЛАМПОВЫЕ И ИОННЫЕ УСИЛИТЕЛИ
- 1. ОСНОВЫ ТОПОЛОГИЧЕСКОГО АНАЛИЗА СХЕМ ЛИНЕЙНЫХ ЭЛЕКТРОННЫХ ЛАМПОВЫХ УСИЛИТЕЛЕЙ
- 2. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПОСТОЯННОГО ТОКА
- 3. БАЛАНСНЫЕ МОСТОВЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- 4. СТАБИЛИЗАЦИЯ КОЭФФИЦИЕНТА УСИЛЕНИЯ
- 5. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛЬНЫЕ КАСКАДЫ
- 6. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- 7. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
- 8. ОБЩИЕ СВОЙСТВА ИОННОГО (ТИРАТРОННОГО) УСИЛИТЕЛЯ МЕТОДЫ УПРАВЛЕНИЯ ТИРАТРОНОМ
- 9. ФОРМИРОВАНИЕ УПРАВЛЯЮЩЕГО НАПРЯЖЕНИЯ
- 10. РАСЧЕТ ЭЛЕМЕНТОВ СХЕМ ТИРАТРОННОГО УСИЛИТЕЛЯ
- ГЛАВА III. ПОЛУПРОВОДНИКОВЫЕ И ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ ПЕРЕМЕННОГО ТОКА
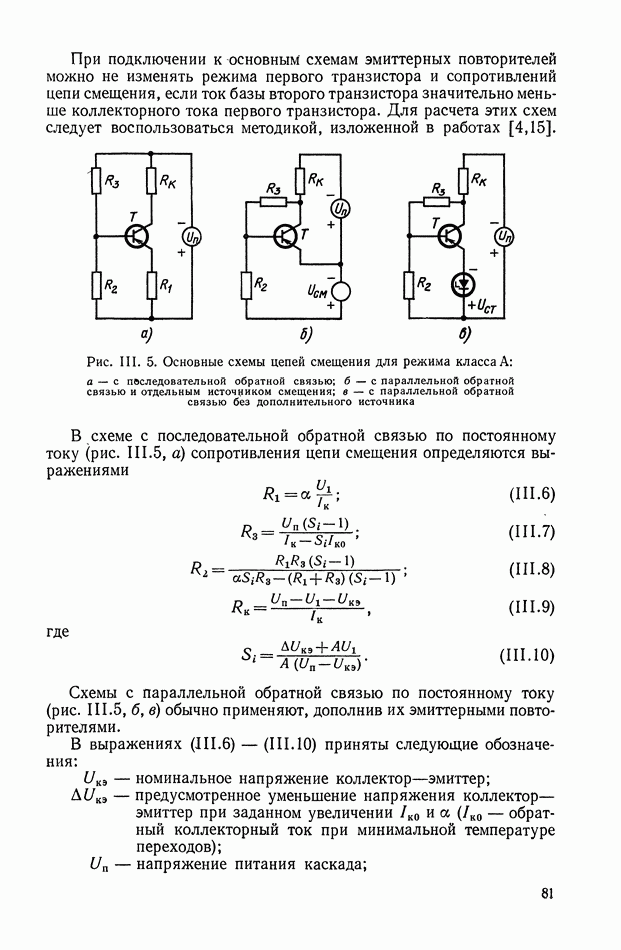
- Цепи смещения.
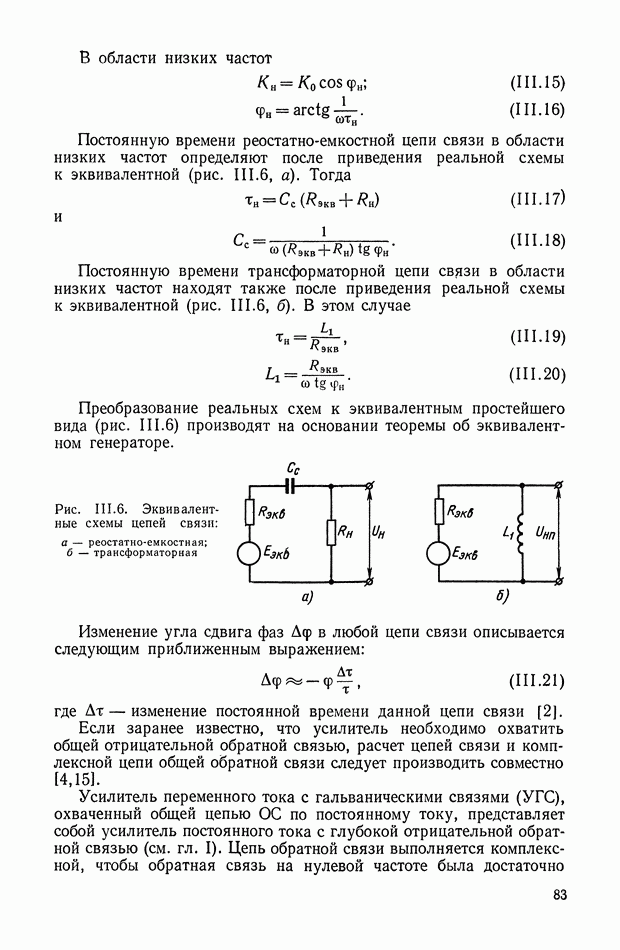
- Цепи связи.
- 2. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ СРЕДНЕГО ЗНАЧЕНИЯ ТОКА
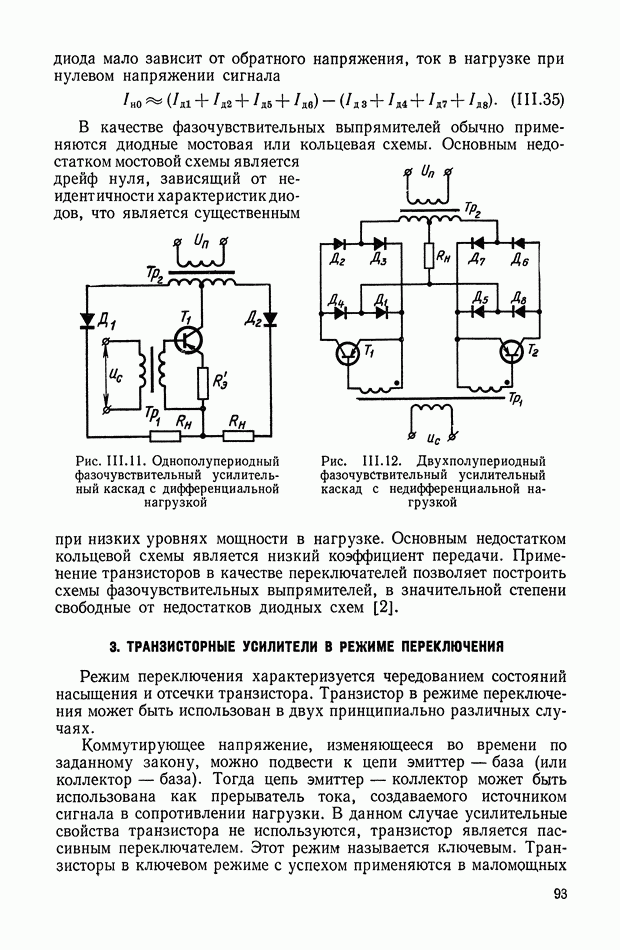
- Полупроводниковые демодуляторы.
- 3. ТРАНЗИСТОРНЫЕ УСИЛИТЕЛИ В РЕЖИМЕ ПЕРЕКЛЮЧЕНИЯ
- Режимы импульсного регулирования мощности.
- Управление силовыми транзисторами.
- 4. ТРАНЗИСТОРНЫЕ УСТРОЙСТВА УПРАВЛЕНИЯ ЭЛЕКТРОДВИГАТЕЛЯМИ И ЭЛЕКТРОМАГНИТНЫМИ МЕХАНИЗМАМИ
- 5. ТИРИСТОРЫ. ХАРАКТЕРИСТИКИ, ПАРАМЕТРЫ И СВОЙСТВА
- 6. СПОСОБЫ И УСТРОЙСТВА УПРАВЛЕНИЯ ТИРИСТОРАМИ
- 7. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ (РЕГУЛИРУЕМЫЕ ВЫПРЯМИТЕЛИ)
- 8. ТИРИСТОРНЫЕ РЕГУЛЯТОРЫ МОЩНОСТИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
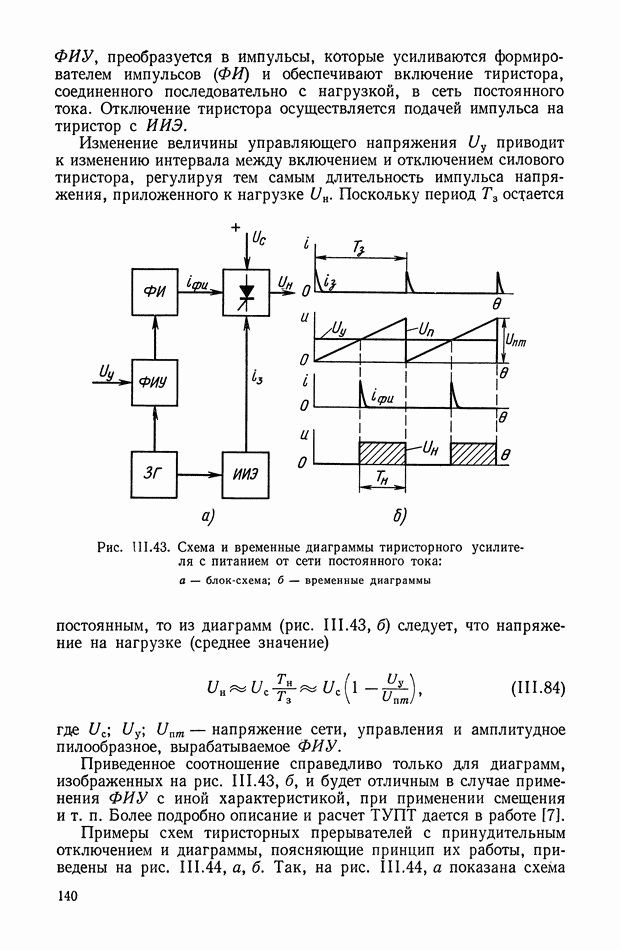
- 9. ТИРИСТОРНЫЕ УСИЛИТЕЛИ С ПИТАНИЕМ ОТ СЕТИ ПОСТОЯННОГО ТОКА
- 10. ДИЭЛЕКТРИЧЕСКИЕ УСИЛИТЕЛИ
- 11. ОСНОВЫ РАСЧЕТА ДИЭЛЕКТРИЧЕСКИХ УСИЛИТЕЛЕЙ
- ГЛАВА IV. КВАНТОВЫЕ УСИЛИТЕЛИ И ГЕНЕРАТОРЫ
- 2. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ РАДИОДИАПАЗОНА
- Квантовые усилители радиодиапазона.
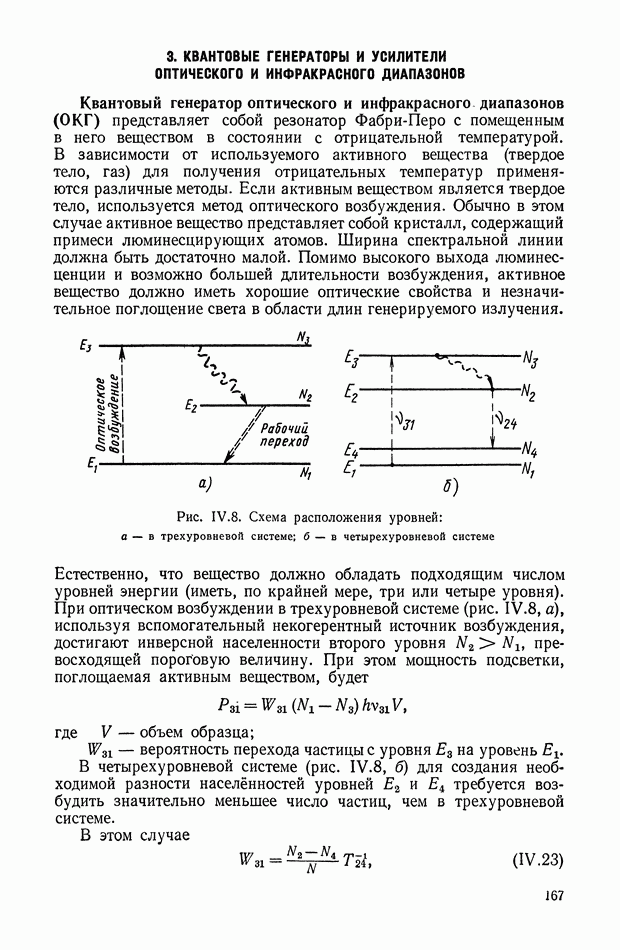
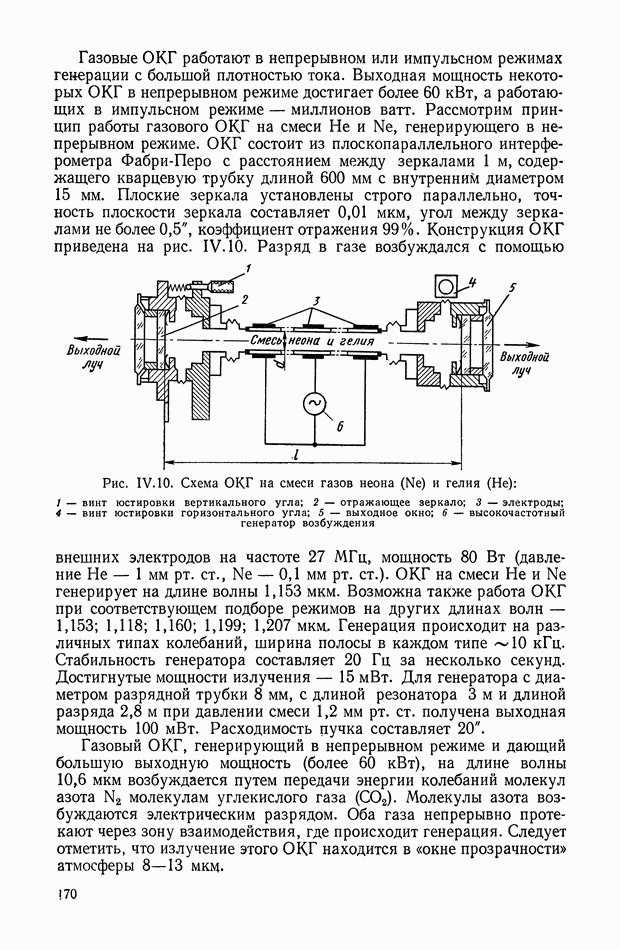
- 3. КВАНТОВЫЕ ГЕНЕРАТОРЫ И УСИЛИТЕЛИ ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
- Оптический квантовый усилитель
- 4. ПРИМЕНЕНИЕ В САР КВАНТОВЫХ УСИЛИТЕЛЕЙ И ГЕНЕРАТОРОВ РАДИОДИАПАЗОНА, ОПТИЧЕСКОГО И ИНФРАКРАСНОГО ДИАПАЗОНОВ
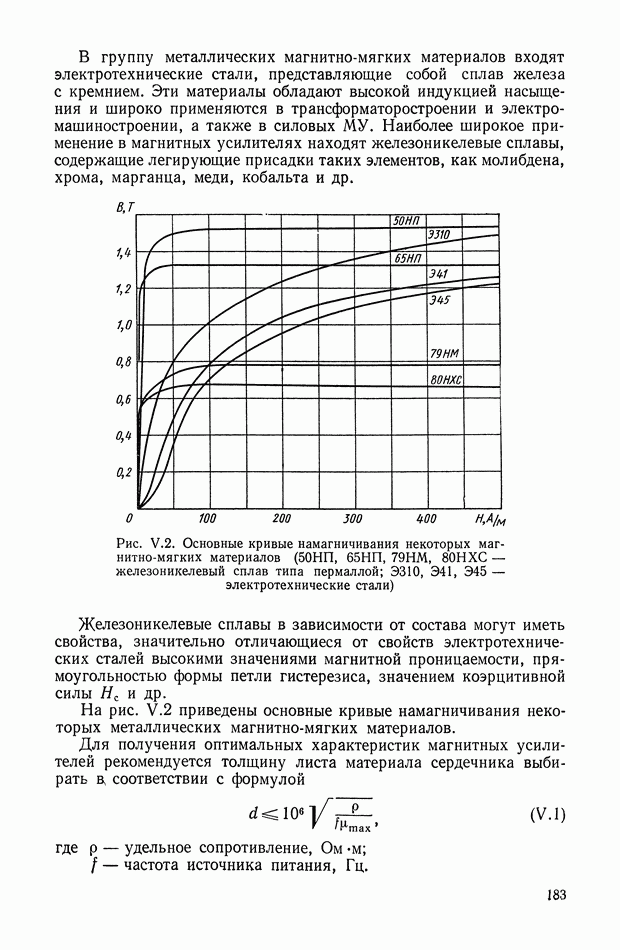
- ГЛАВА V. МАГНИТНЫЕ И МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- 2. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ МАГНИТНЫХ УСИЛИТЕЛЕЙ
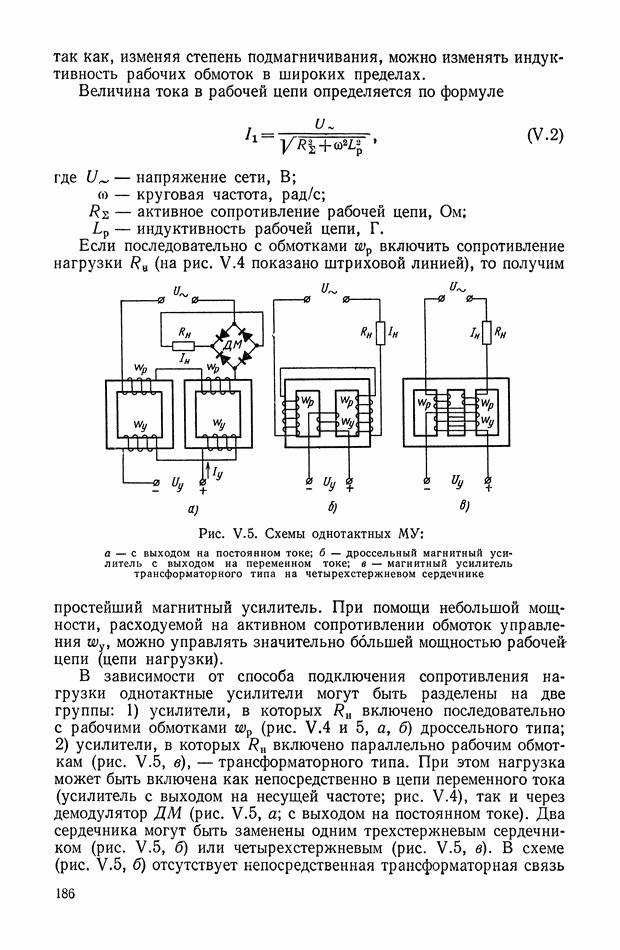
- 3. ОДНОТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ БЕЗ ОБРАТНОЙ СВЯЗИ (УПРАВЛЯЕМЫЕ ДРОССЕЛИ И ТРАНСФОРМАТОРЫ)
- 4. МАГНИТНЫЕ УСИЛИТЕЛИ С САМОНАСЫЩЕНИЕМ
- Релейный режим работы усилителей с самонасыщением.
- 5. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПЕРЕМЕННОМ ТОКЕ
- 6. ДВУХТАКТНЫЕ МАГНИТНЫЕ УСИЛИТЕЛИ С ВЫХОДОМ НА ПОСТОЯННОМ ТОКЕ
- 7. МАГНИТНО-ПОЛУПРОВОДНИКОВЫЕ УСИЛИТЕЛИ
- ГЛАВА VI. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 2. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С НЕЗАВИСИМЫМ ВОЗБУЖДЕНИЕМ И С САМОВОЗБУЖДЕНИЕМ
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ С ПОПЕРЕЧНЫМ ПОЛЕМ
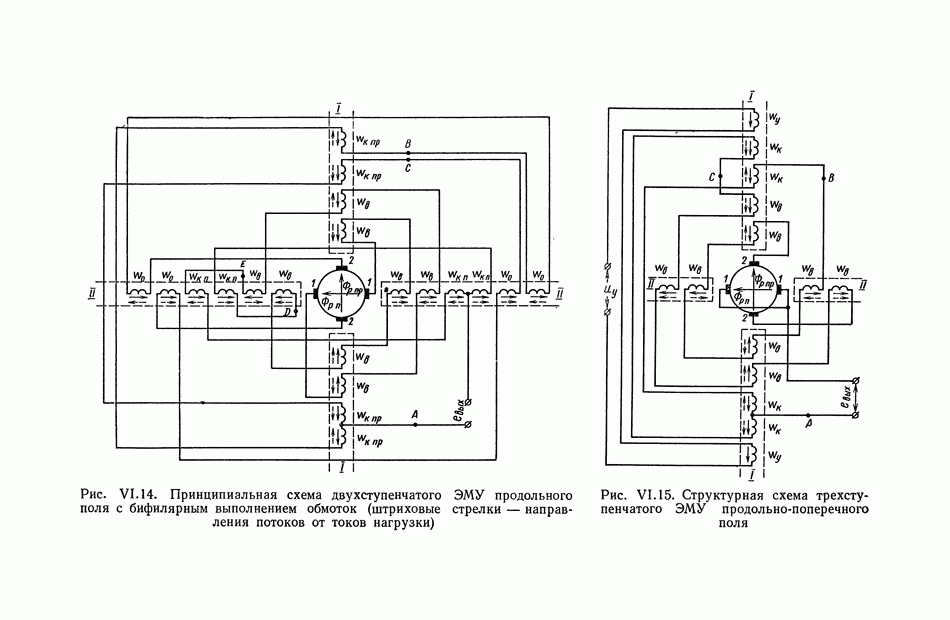
- 4. ЭЛЕКТРОМАШИННЫЙ УСИЛИТЕЛЬ ПРОДОЛЬНОГО И ПРОДОЛЬНО-ПОПЕРЕЧНОГО ПОЛЯ
- 5. ВЛИЯНИЕ НА ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭМУ ВИХРЕВЫХ И КОММУТАЦИОННЫХ ТОКОВ, ГИСТЕРЕЗИСА И СДВИГА ЩЕТОК С НЕЙТРАЛИ
- 6. МЕТОДЫ УЛУЧШЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕКТРОМАШИННЫХ УСИЛИТЕЛЕЙ
- 7. НАГРУЗОЧНАЯ ХАРАКТЕРИСТИКА ЭЛЕКТРОМАШИННОГО УСИЛИТЕЛЯ
- ГЛАВА VII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ХАРАКТЕРИСТИКИ УСИЛИТЕЛЕЙ И СПОСОБЫ ИХ ФОРМИРОВАНИЯ
- 2. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
- 3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ЛИНЕАРИЗОВАННЫЕ УСИЛИТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ РЕЛЕ
- 4. БЕСКОНТАКТНЫЕ ЛИНЕАРИЗОВАННЫЕ РЕЛЕЙНЫЕ УСИЛИТЕЛИ
- ГЛАВА VIII. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 2. ОСНОВНЫЕ ЭЛЕМЕНТЫ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ И ИХ ХАРАКТЕРИСТИКИ
- 3. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ С ЗОЛОТНИКОМ
- 4. ОДНОКАСКАДНЫЕ ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ СО СТРУЙНОЙ ТРУБКОЙ
- 5. СХЕМЫ И ПРИНЦИПЫ ДЕЙСТВИЯ ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 6. СТАТИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 7. ДИНАМИКА ДВУХКАСКАДНЫХ ГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ
- 8. УНИФИКАЦИЯ ЭЛЕКТРОГИДРАВЛИЧЕСКИХ УСИЛИТЕЛЕЙ ДЛЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
- ГЛАВА IX. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 1. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ И ИХ КЛАССИФИКАЦИЯ
- 2. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ СО СТРУЙНОЙ ТРУБКОЙ
- 3. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗОЛОТНИКОМ
- 4. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С СОПЛОМ — ЗАСЛОНКОЙ
- 5. ПНЕВМАТИЧЕСКИЙ УСИЛИТЕЛЬ С ЗАСЛОНКОЙ
- 6. МНОГОКАСКАДНЫЕ ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- РАЗДЕЛ II. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ И УСТРОЙСТВ
- 2. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ЛИНЕЙНЫХ ПАССИВНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Основные соотношения для синтеза пассивного RC-четырехполюсника.
- 3. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Активные четырехполюсники, получаемые с помощью конверторов отрицательного сопротивления.
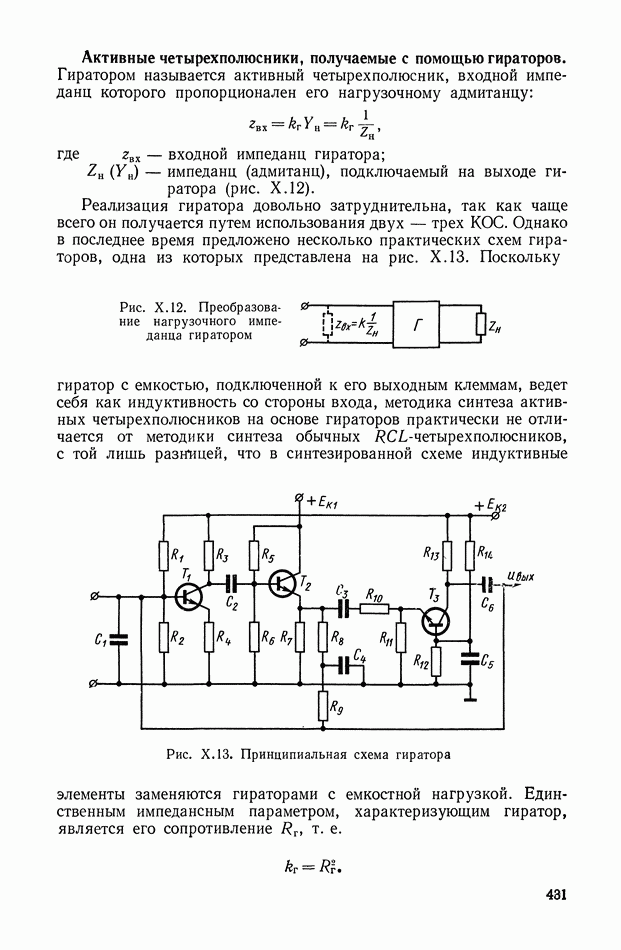
- Активные четырехполюсники, получаемые с помощью гираторов.
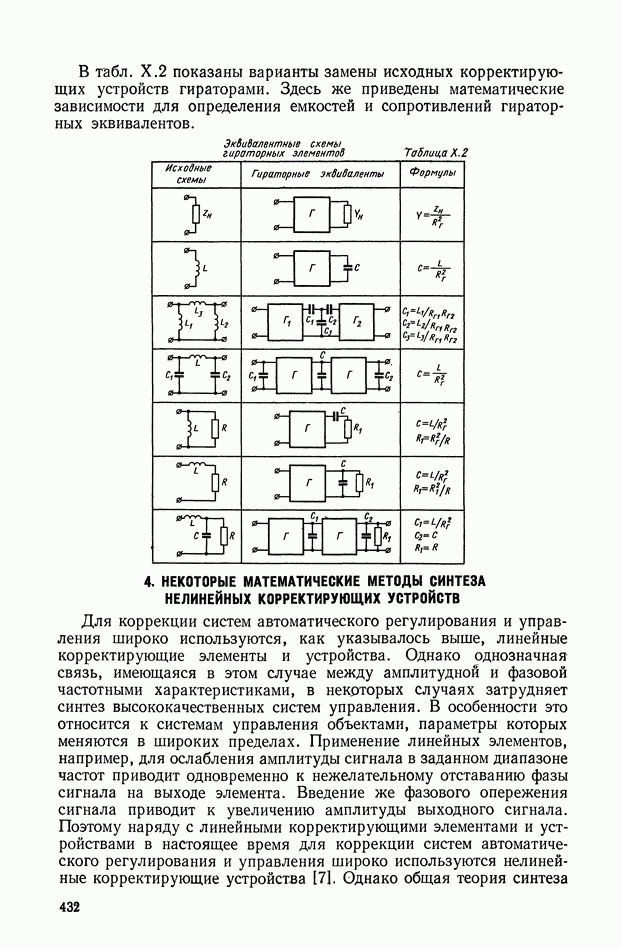
- 4. НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА НЕЛИНЕЙНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
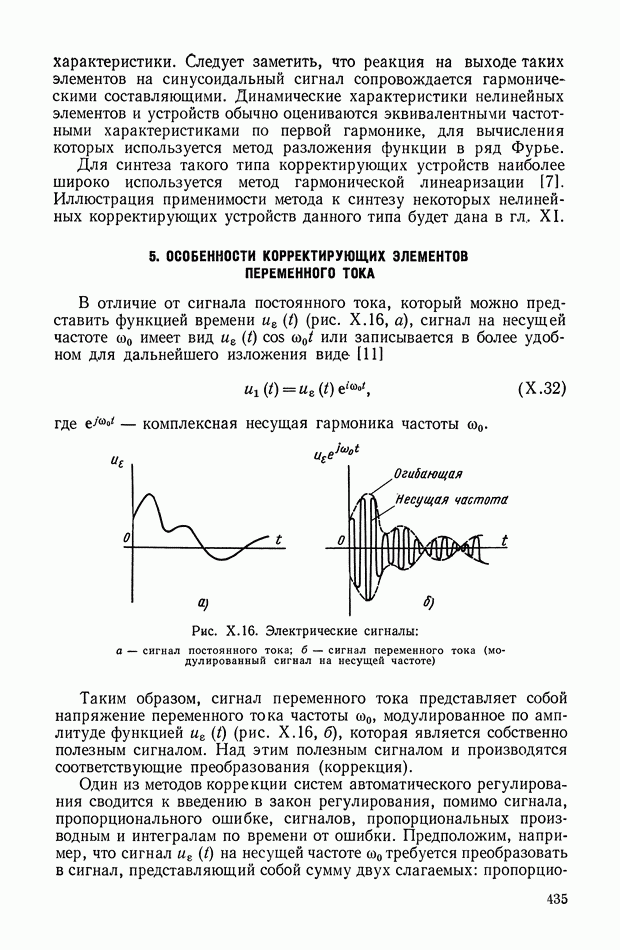
- 5. ОСОБЕННОСТИ КОРРЕКТИРУЮЩИХ ЭЛЕМЕНТОВ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XI. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА ПОСТОЯННОГО ТОКА
- Дифференцирующий трансформатор.
- Электрические интегрирующие элементы.
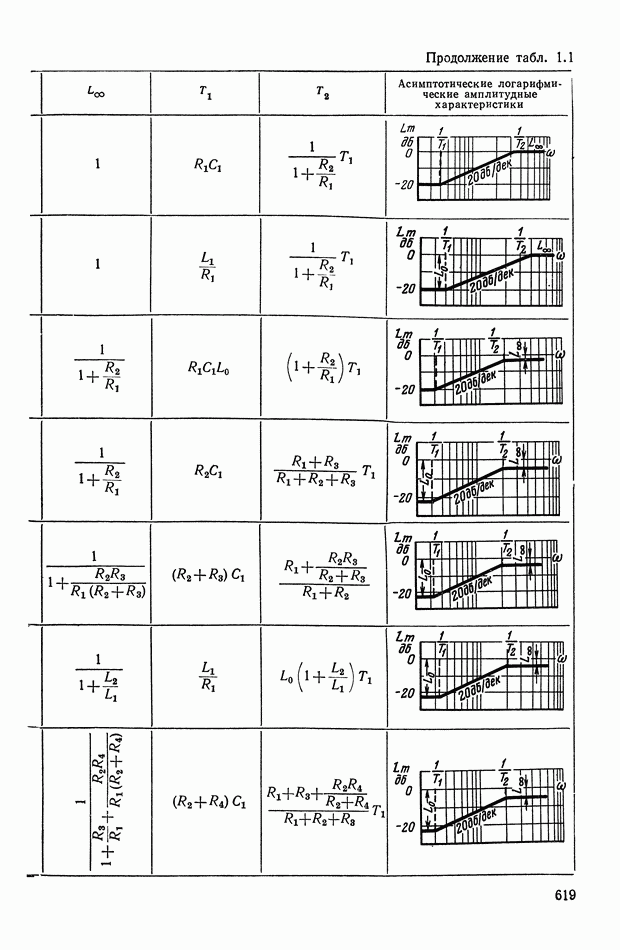
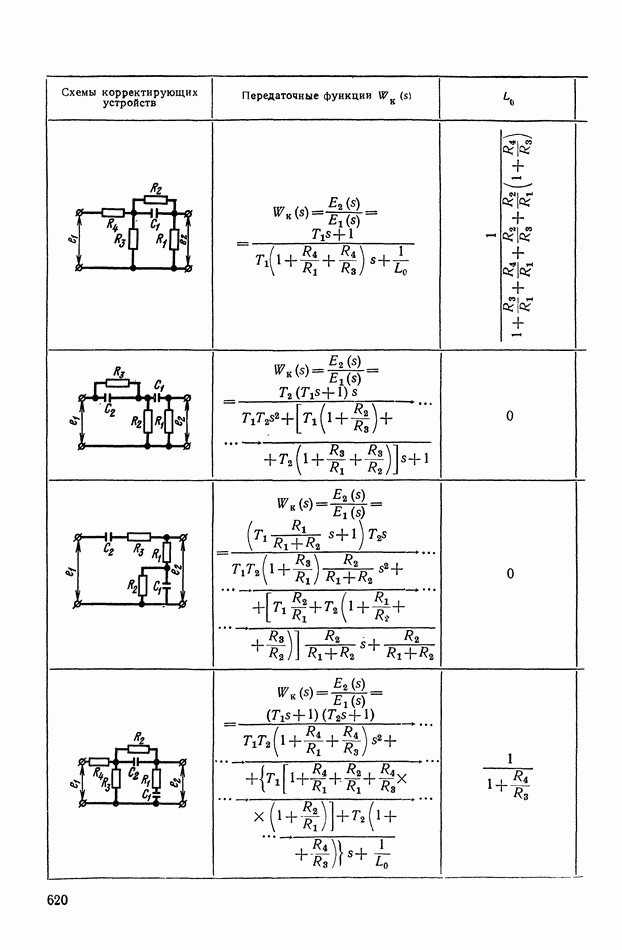
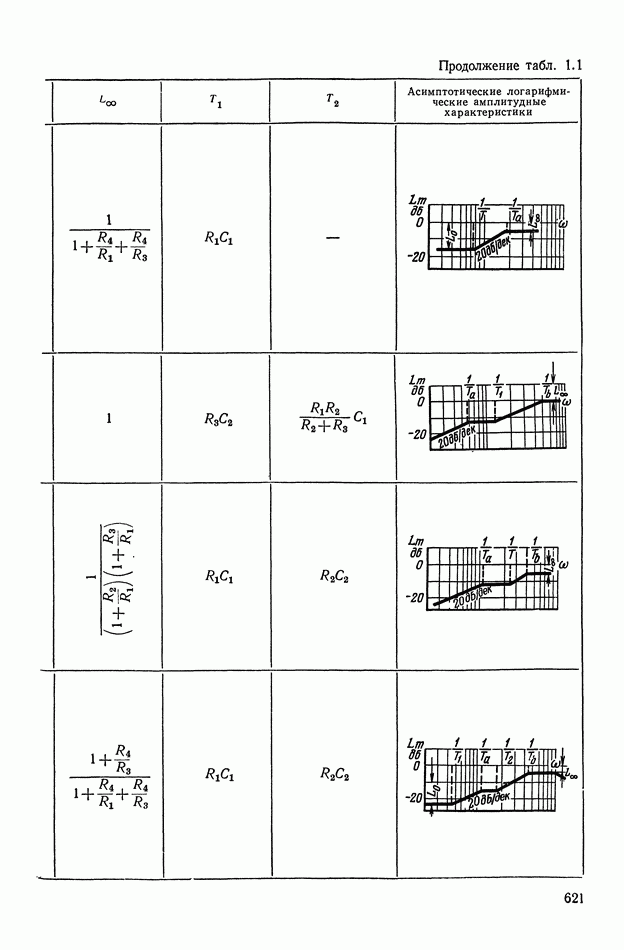
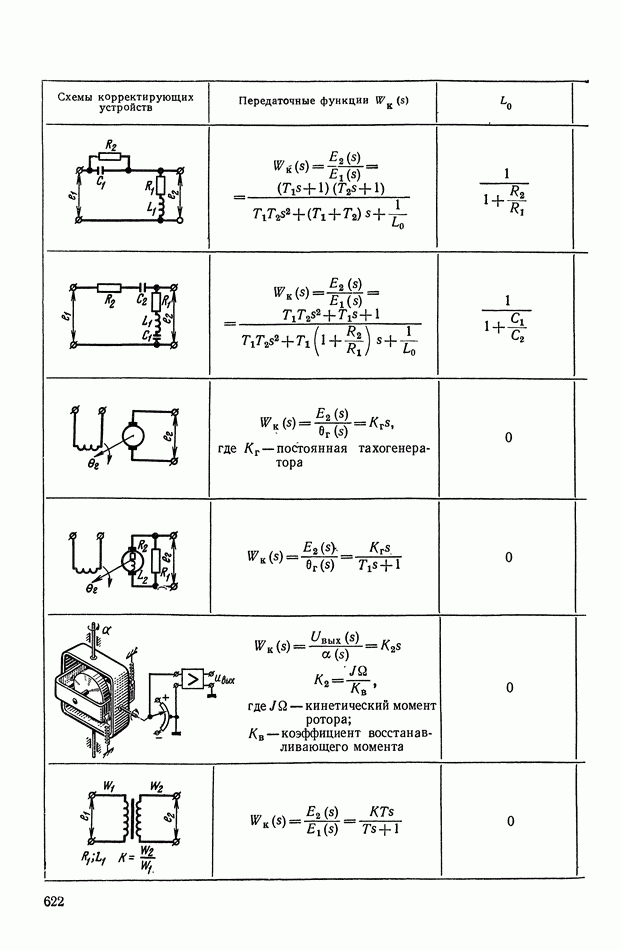
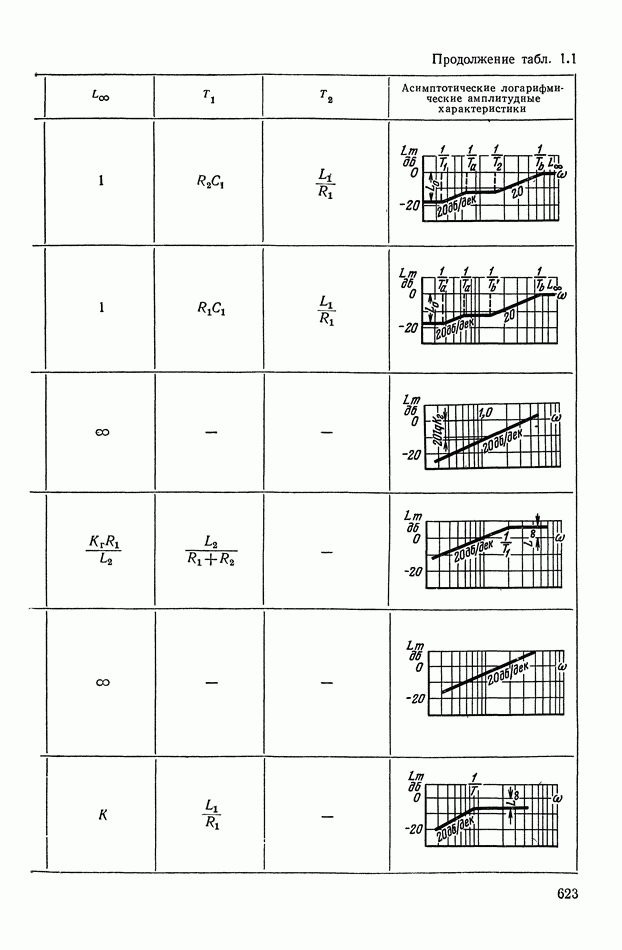
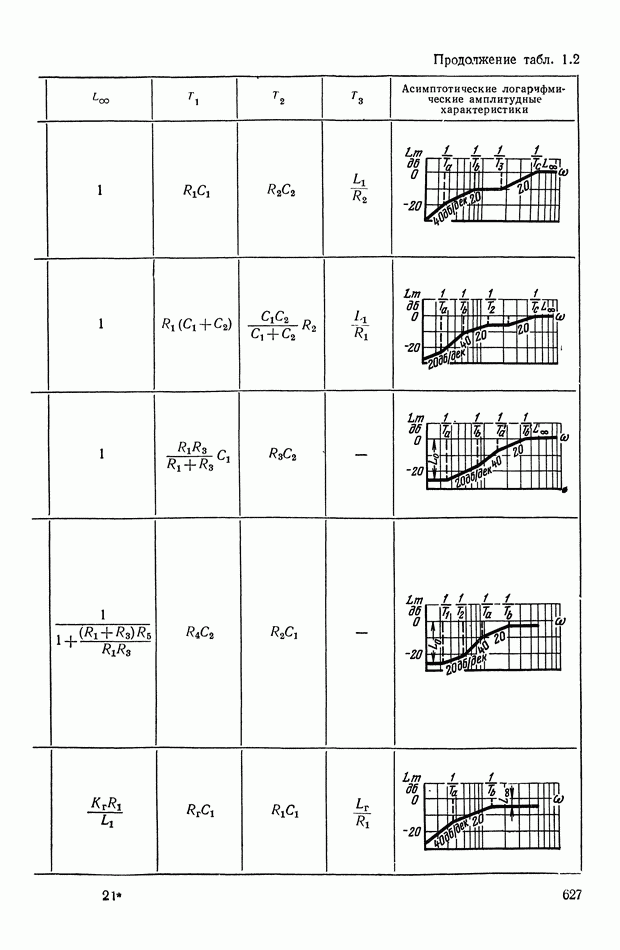
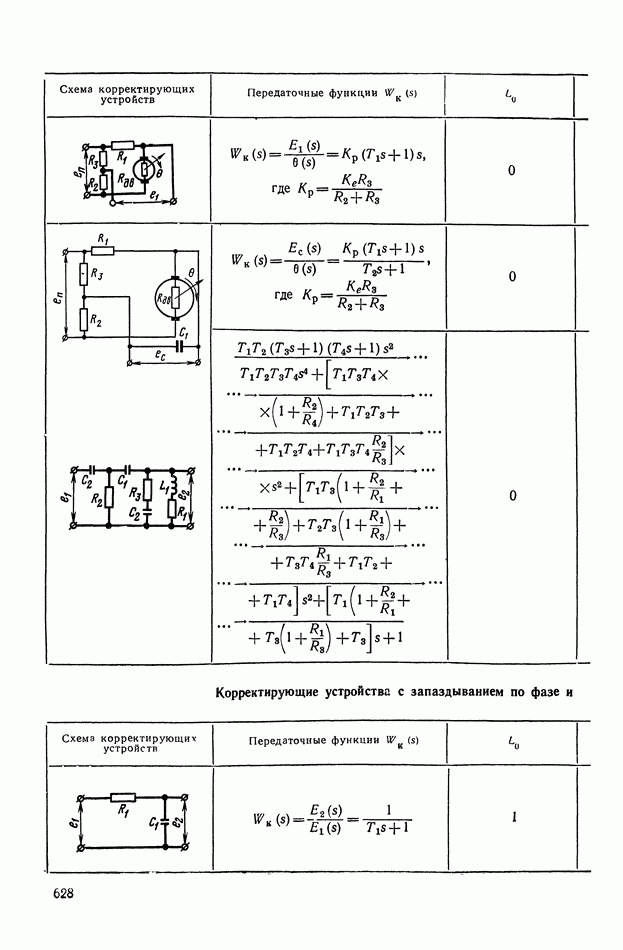
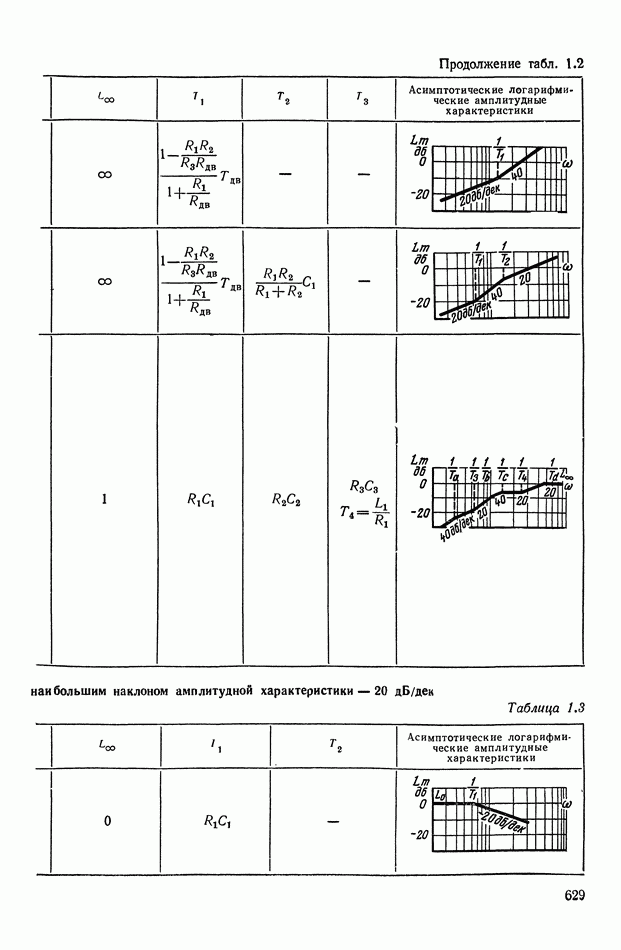
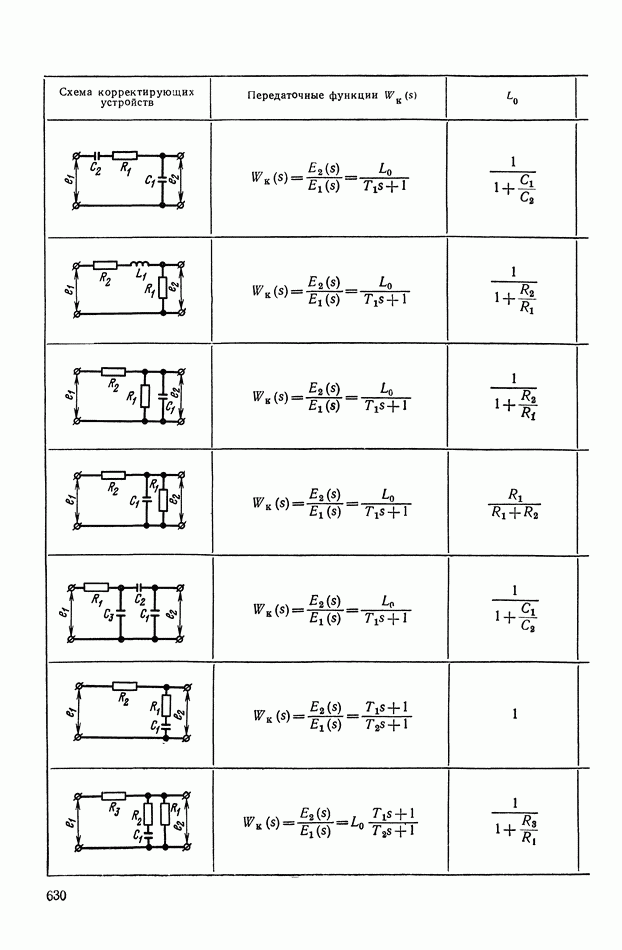
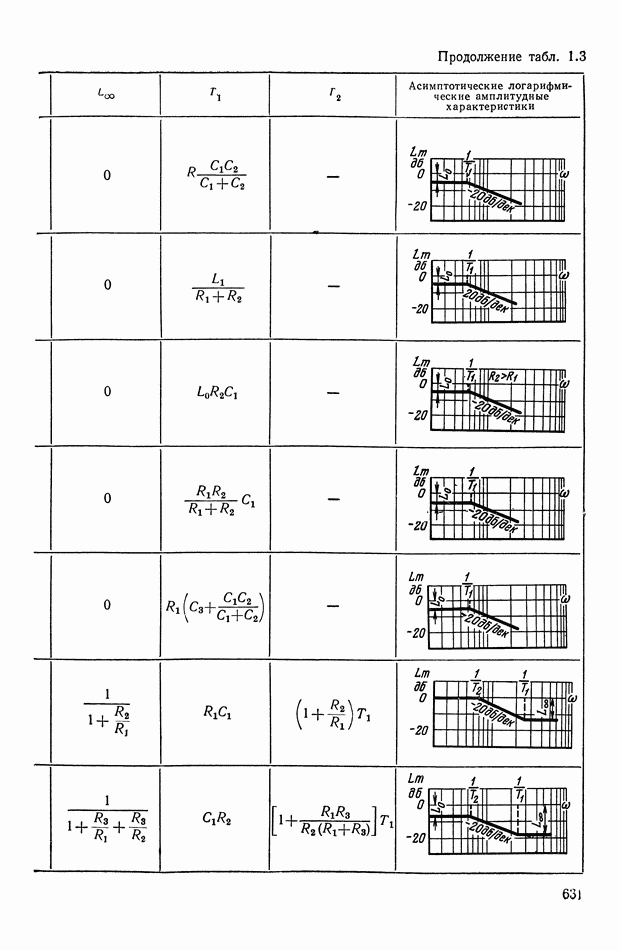
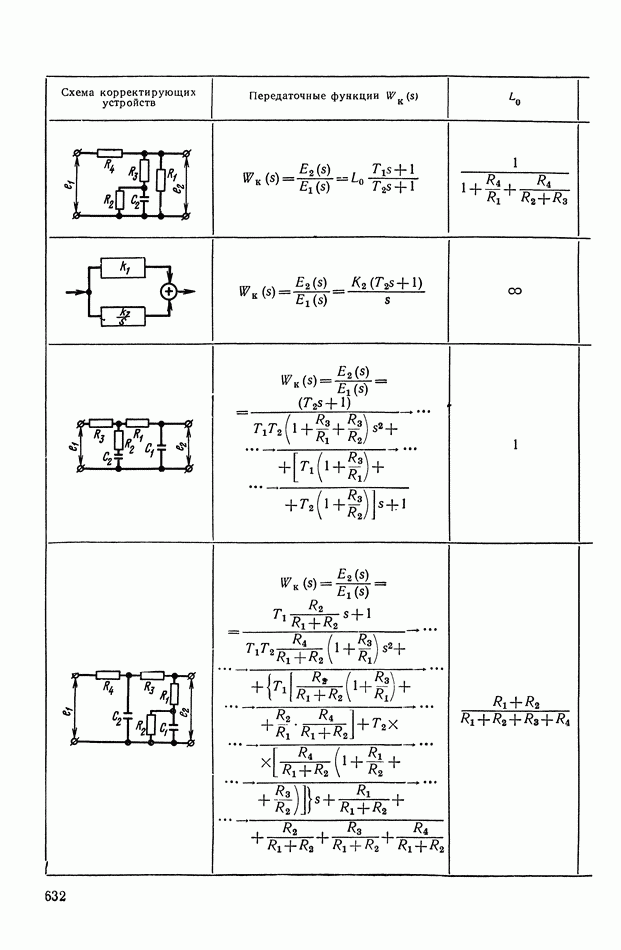
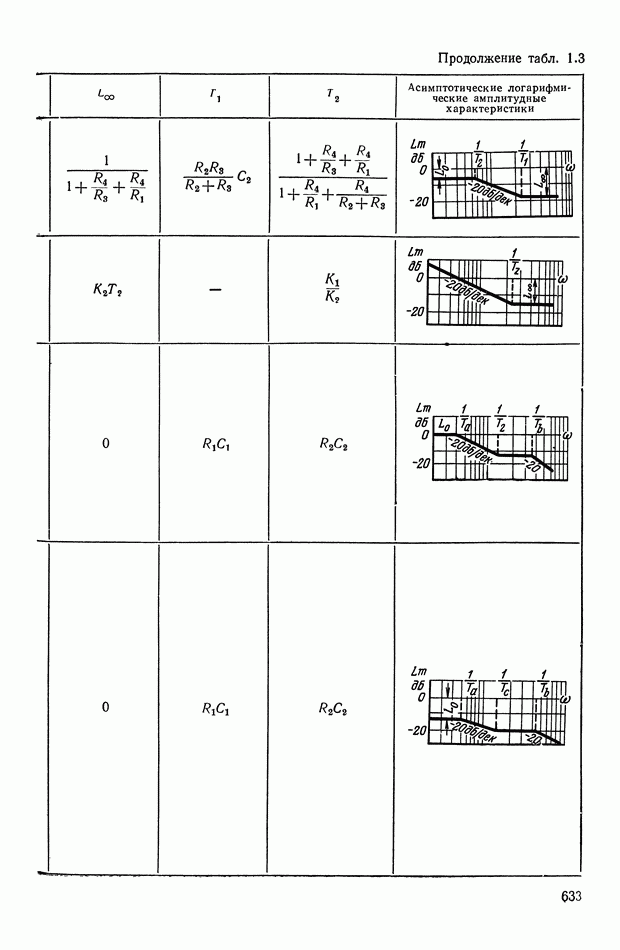
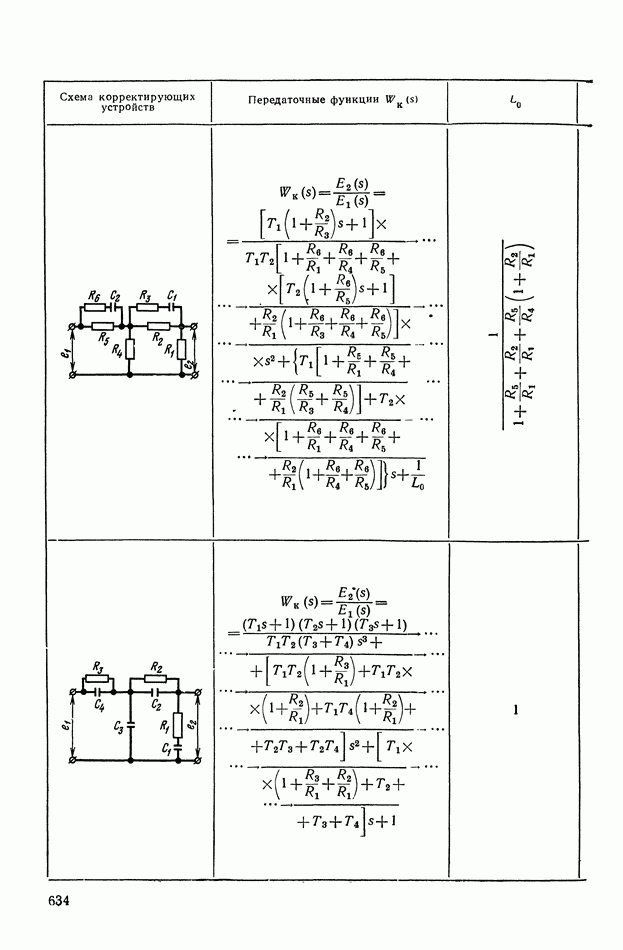
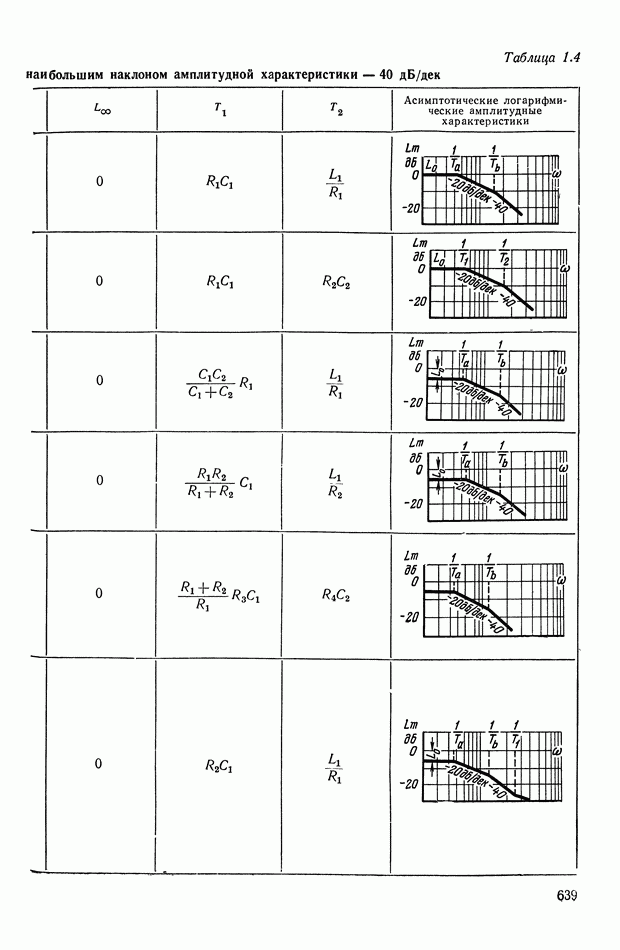
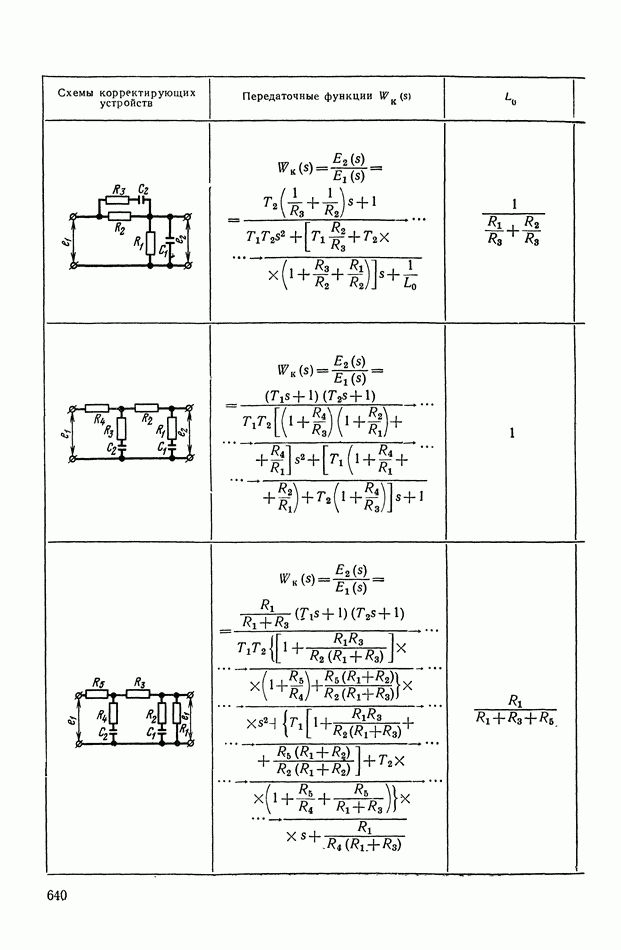
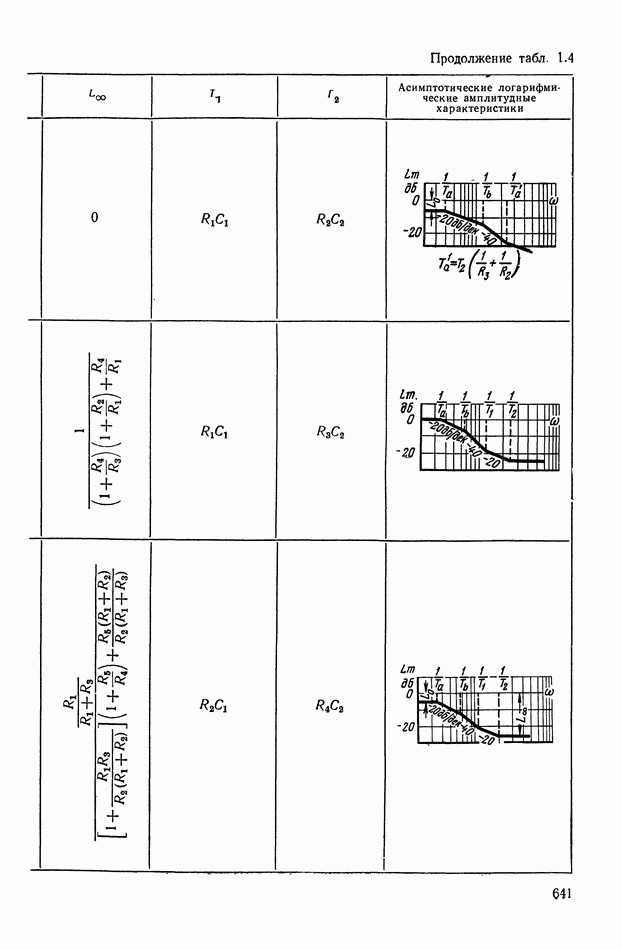
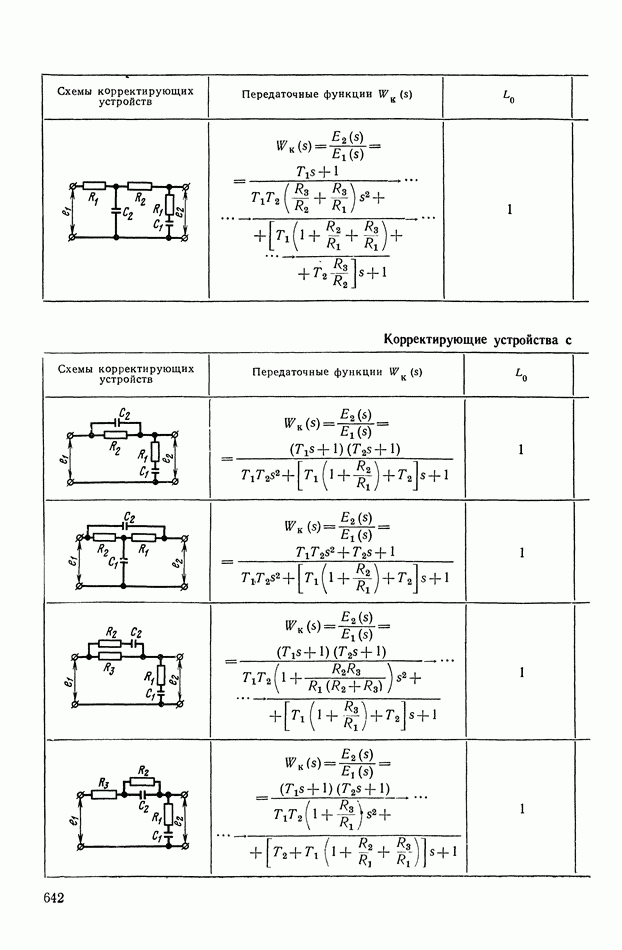
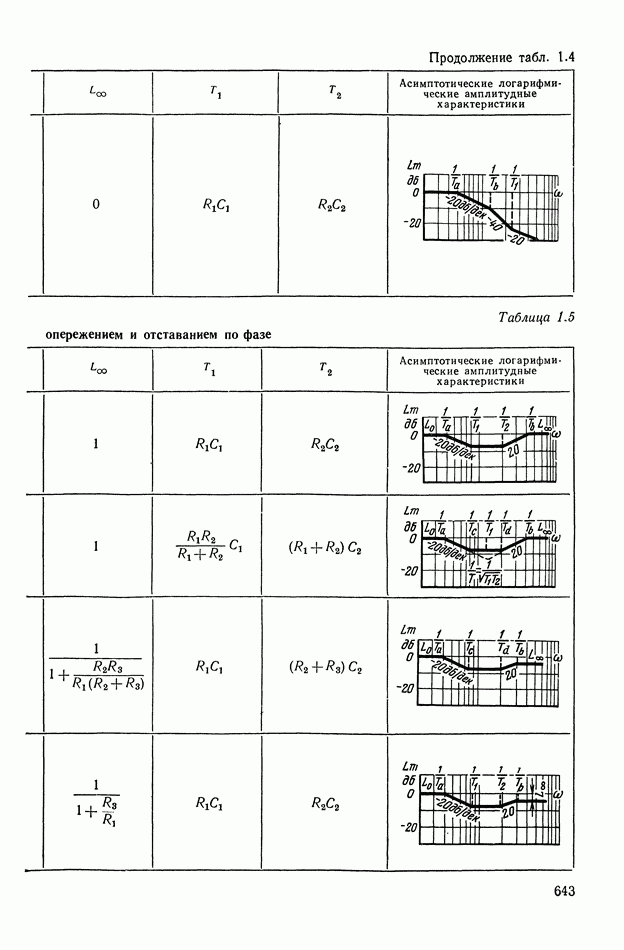
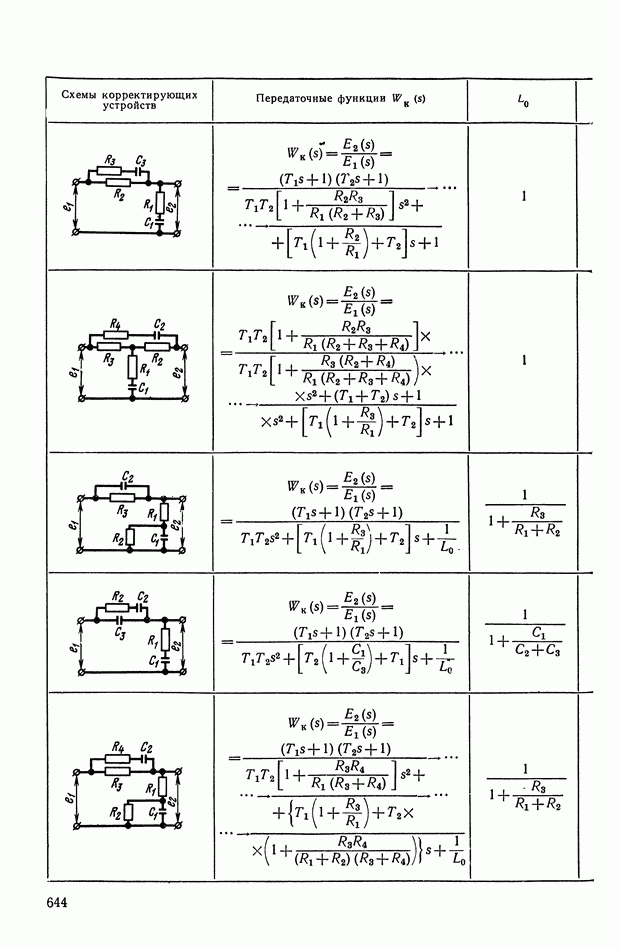
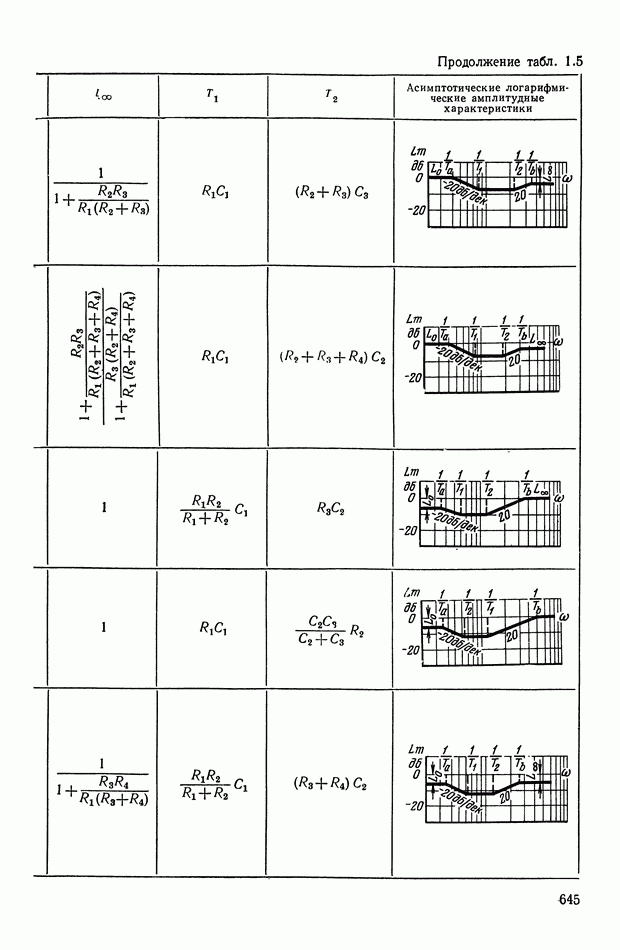
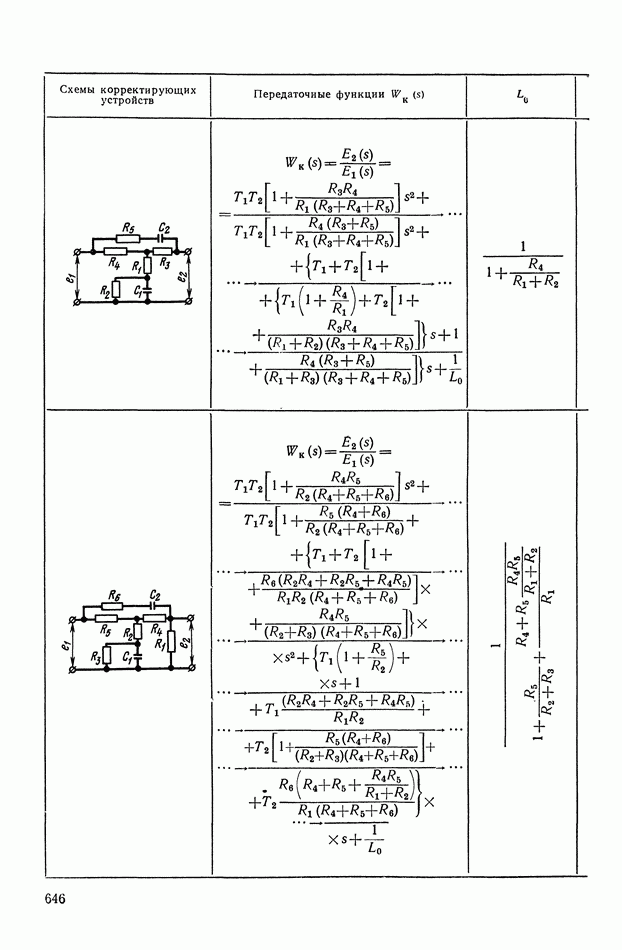
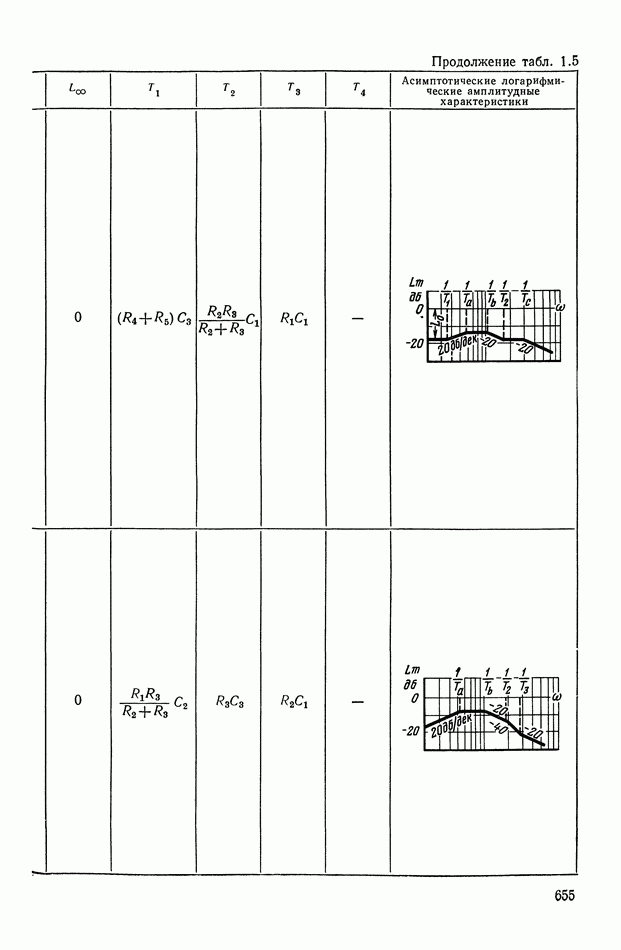
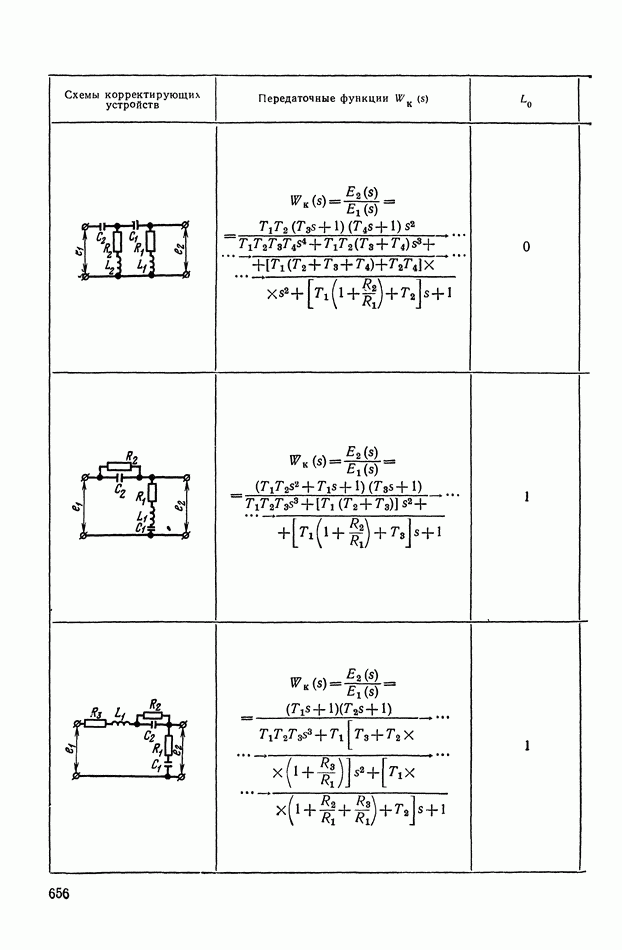
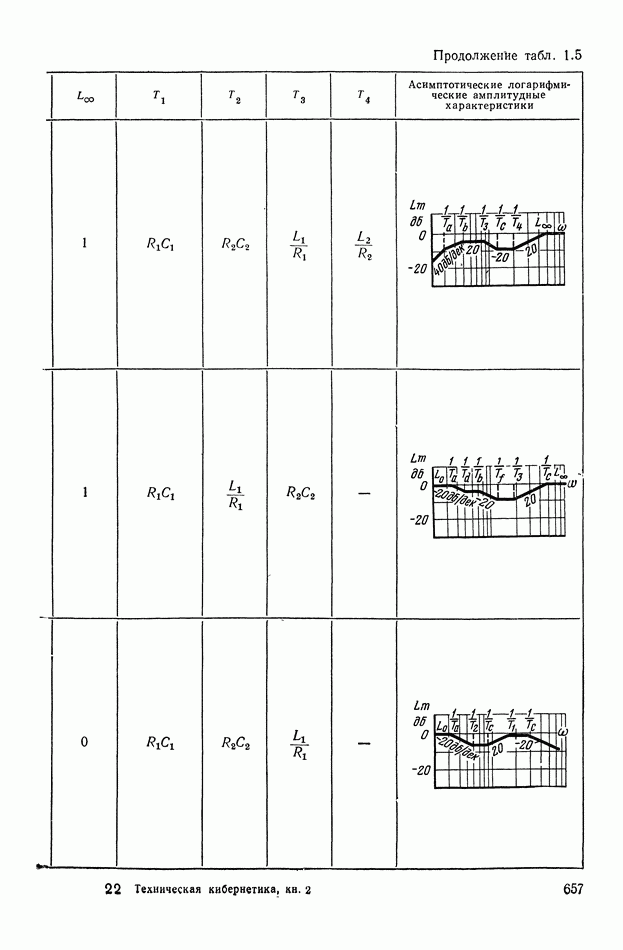
- 2. ТИПОВЫЕ ЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- 3. КОРРЕКТИРУЮЩИЕ ЧЕТЫРЕХПОЛЮСНИКИ С АКТИВНЫМИ ЭЛЕМЕНТАМИ
- Четырехполюсники с активными элементами на основе операционных усилителей (ОУ) и конверторов отрицательного сопротивления (КОС).
- 4. РЕАЛИЗАЦИЯ ЗАДАННОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В ВИДЕ СХЕМЫ ПАССИВНОГО ЛИНЕЙНОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА
- 5. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
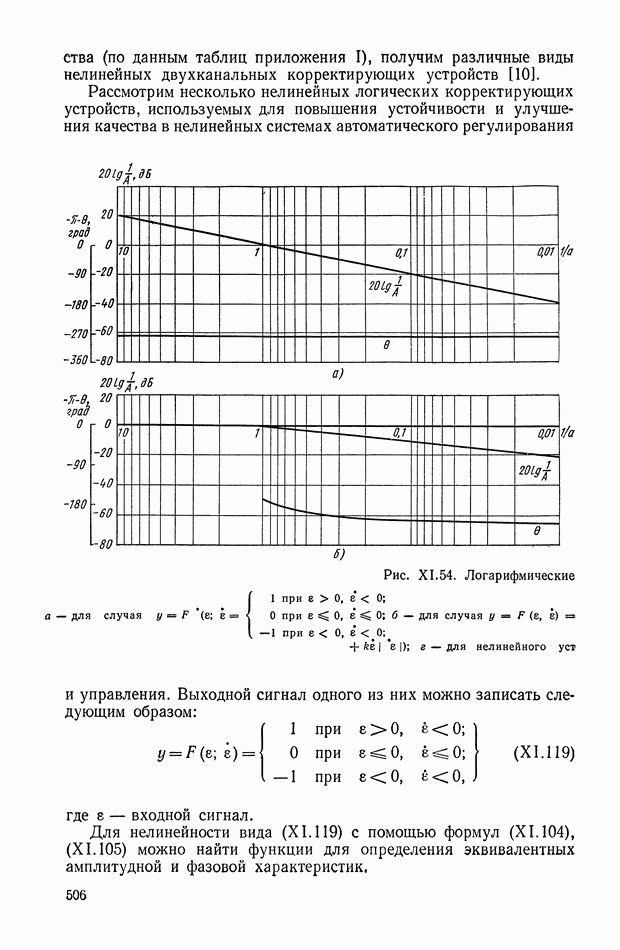
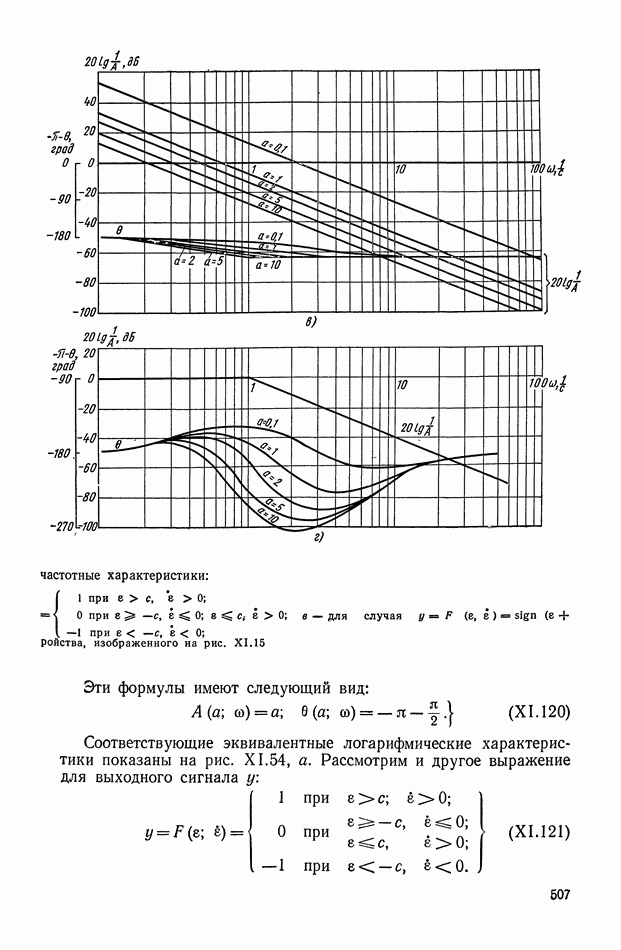
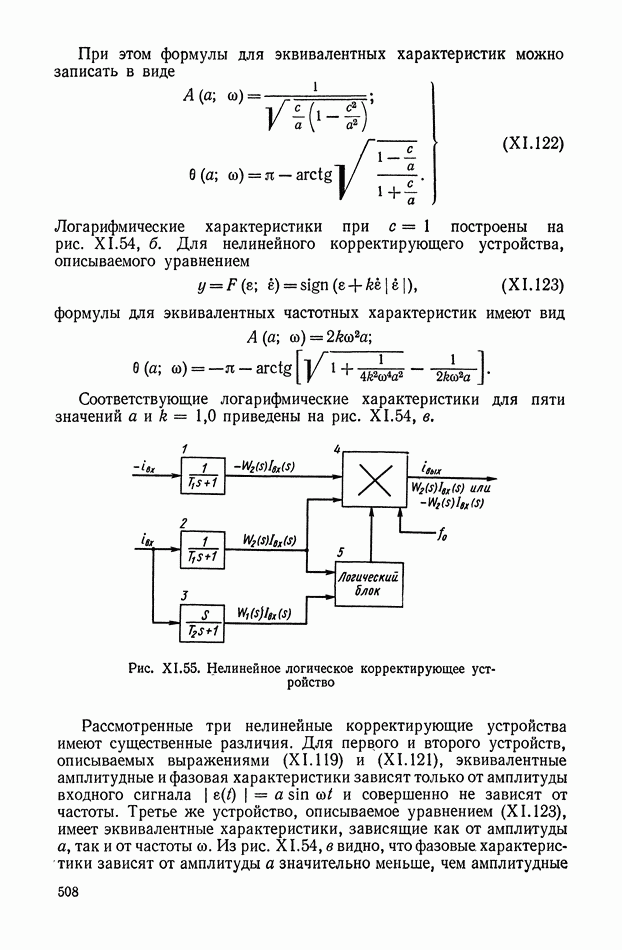
- 8. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
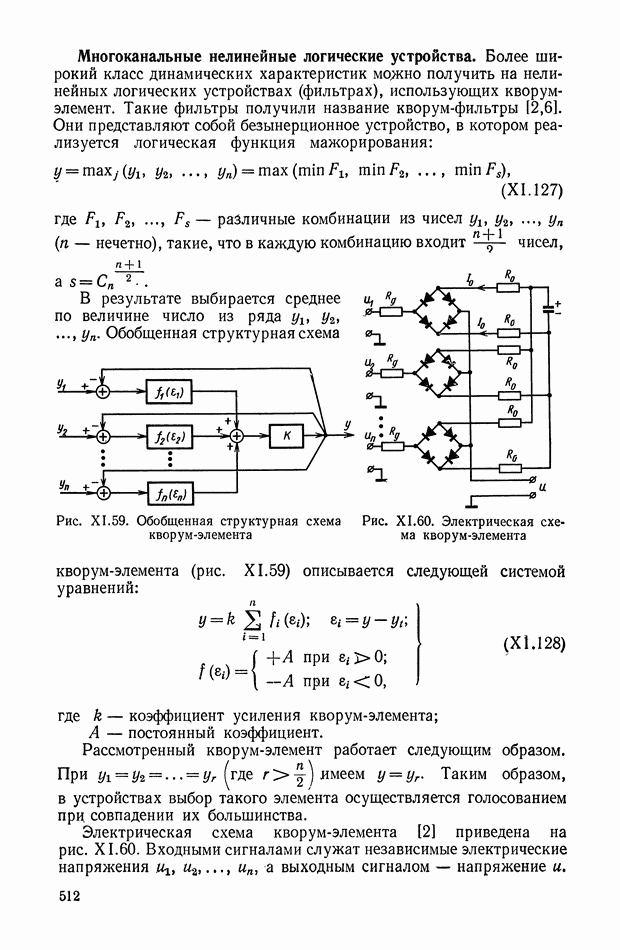
- Многоканальные нелинейные логические устройства.
- ГЛАВА XII. ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- 1. КОРРЕКТИРУЮЩИЕ RLC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 2. КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 3. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ RC-ЧЕТЫРЕХПОЛЮСНИКИ ПЕРЕМЕННОГО ТОКА
- 4. САМОНАСТРАИВАЮЩИЕСЯ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА
- 5. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПЕРЕМЕННОГО ТОКА С ПРОМЕЖУТОЧНОЙ ДЕМОДУЛЯЦИЕЙ
- 6. КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА С ПЕРЕКЛЮЧАТЕЛЯМИ
- 7. НЕЛИНЕЙНЫЕ КОРРЕКТИРУЮЩИЕ ЭЛЕМЕНТЫ ПЕРЕМЕННОГО ТОКА
- ГЛАВА XIII. ЭЛЕКТРОМЕХАНИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ТАХОГЕНЕРАТОРЫ ПОСТОЯННОГО ТОКА
- Погрешности тахогенератора постоянного тока.
- 2. НЕКОТОРЫЕ СХЕМЫ ПРИМЕНЕНИЯ ТАХОГЕНЕРАТОРОВ
- 3. АСИНХРОННЫЕ ТАХОГЕНЕРАТОРЫ
- 4. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ ИЗМЕРЕНИЯ СКОРОСТИ ЭЛЕКТРОДВИГАТЕЛЕЙ
- Пассивный тахометрический мост переменного тока.
- Активные тахометрические мосты.
- ГЛАВА XIV. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ГИДРАВЛИЧЕСКИХ СИСТЕМАХ
- 3. ЭЛЕКТРИЧЕСКИЕ ОБРАТНЫЕ СВЯЗИ
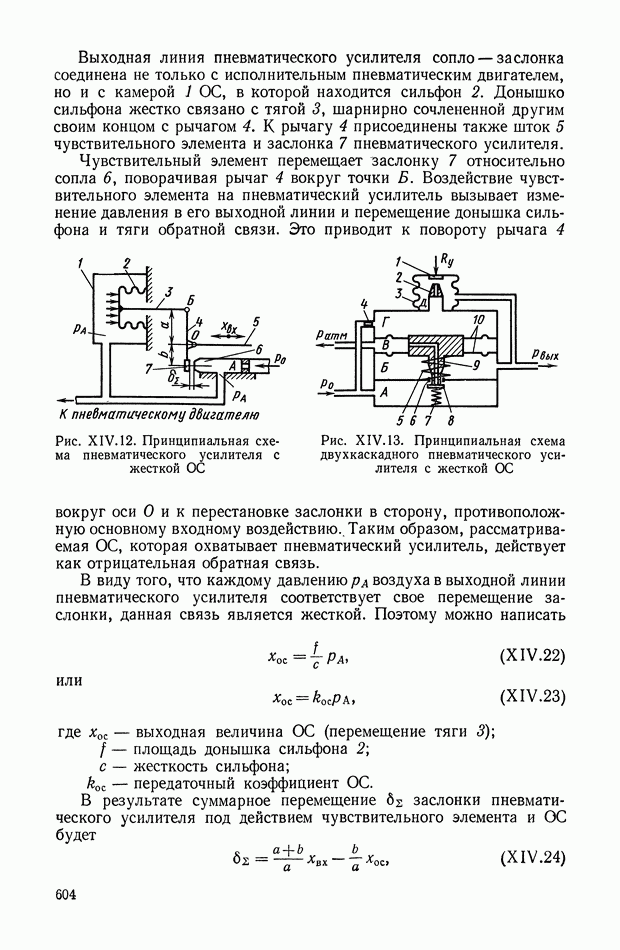
- 4. ЖЕСТКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
- 5. ГИБКИЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ СИСТЕМАХ
- 6. СЛОЖНЫЕ ОБРАТНЫЕ СВЯЗИ В ПНЕВМАТИЧЕСКИХ УСТРОЙСТВАХ
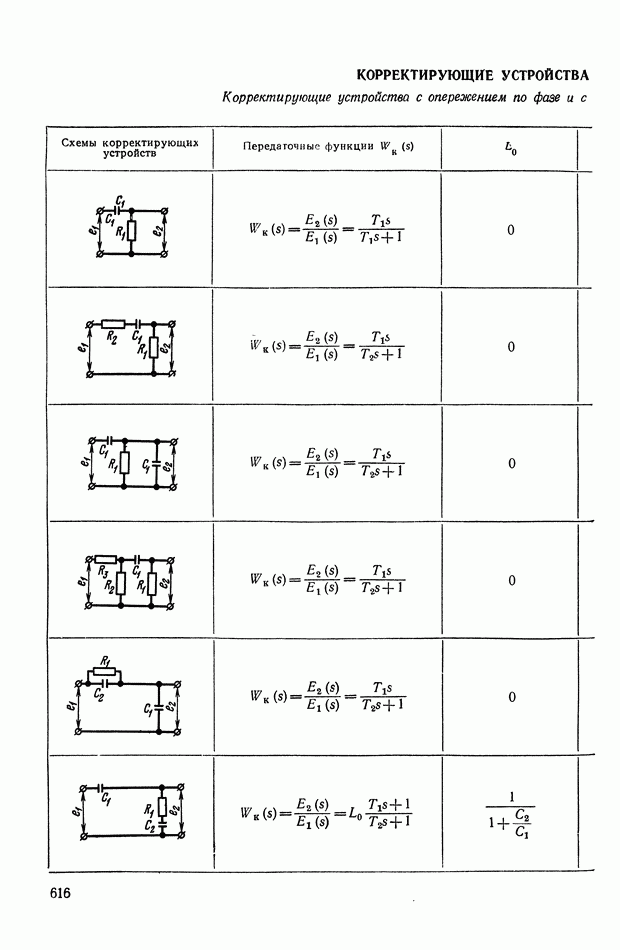
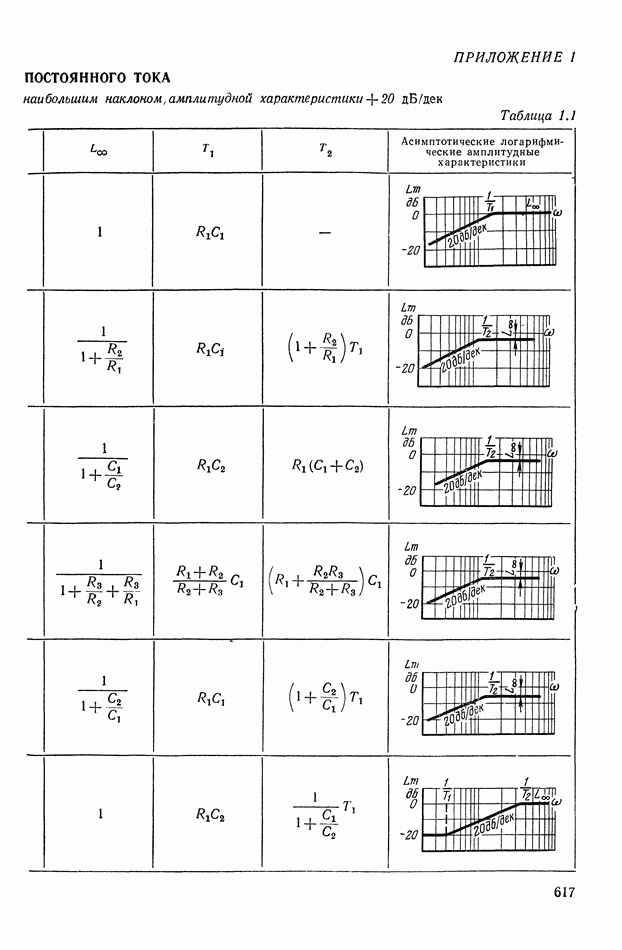
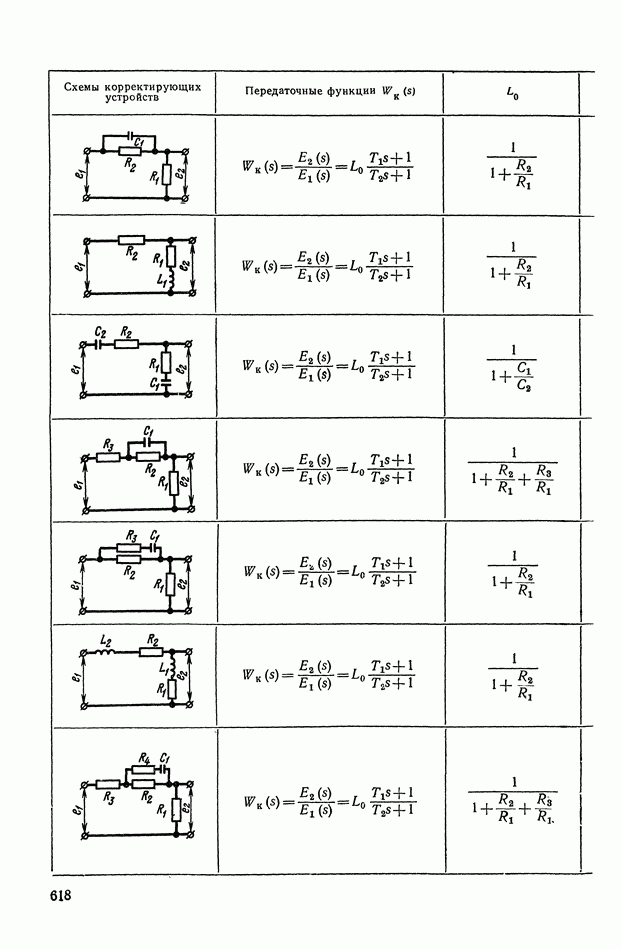
- ПРИЛОЖЕНИЕ 1. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА ПОСТОЯННОГО ТОКА
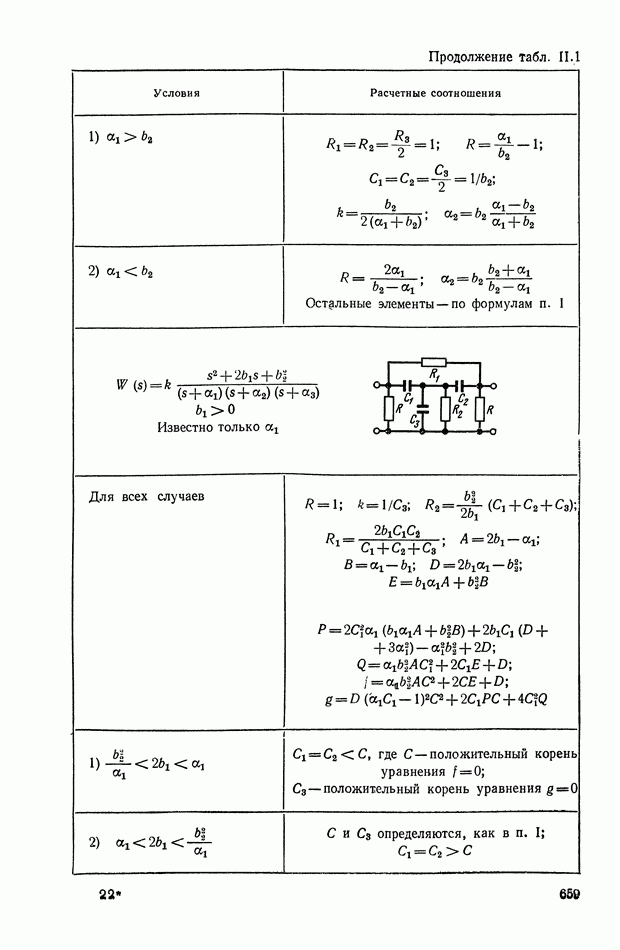
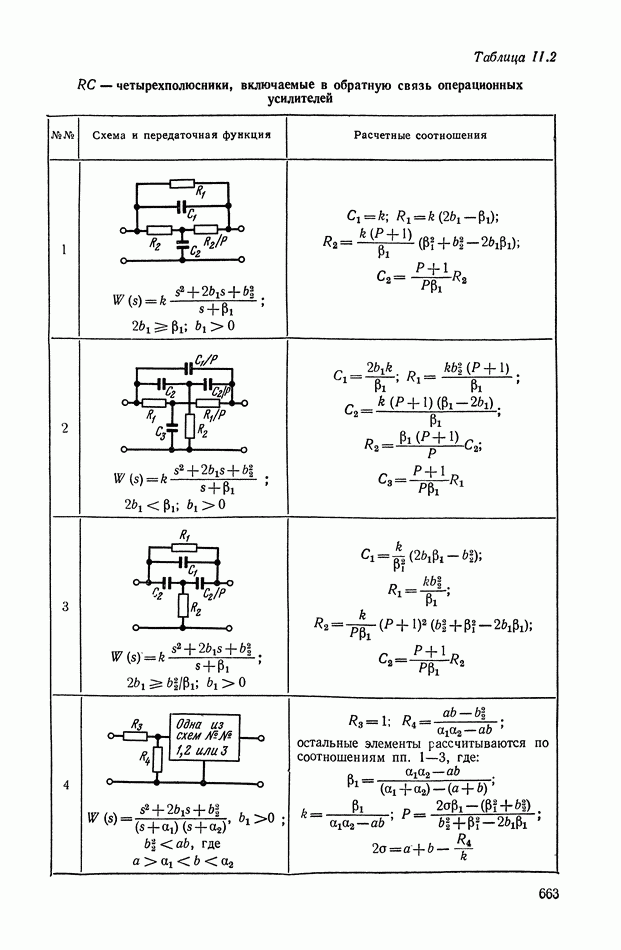
- ПРИЛОЖЕНИЕ II. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ОСНОВЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
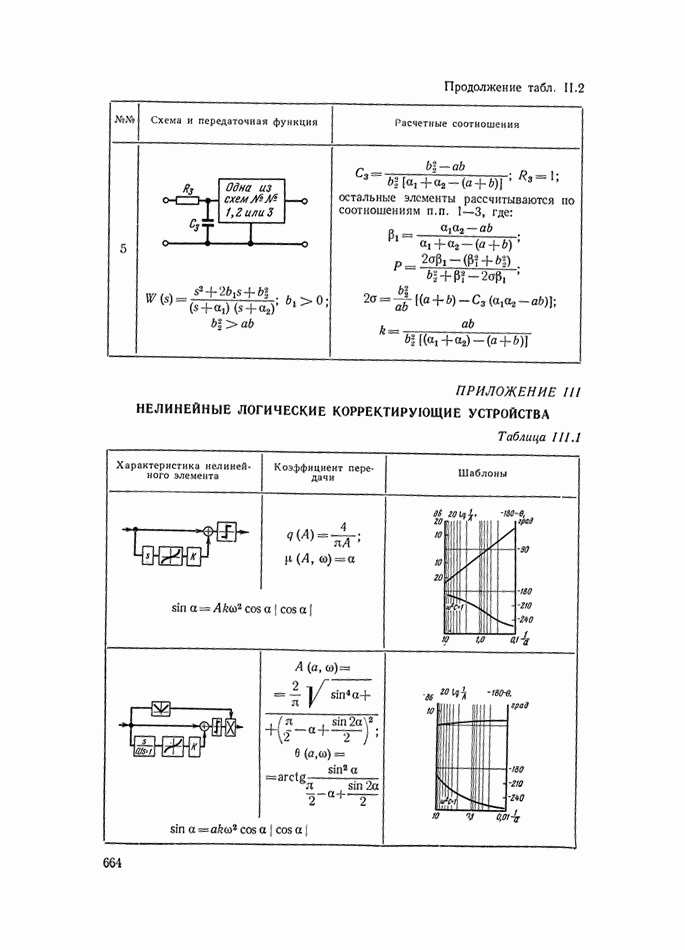
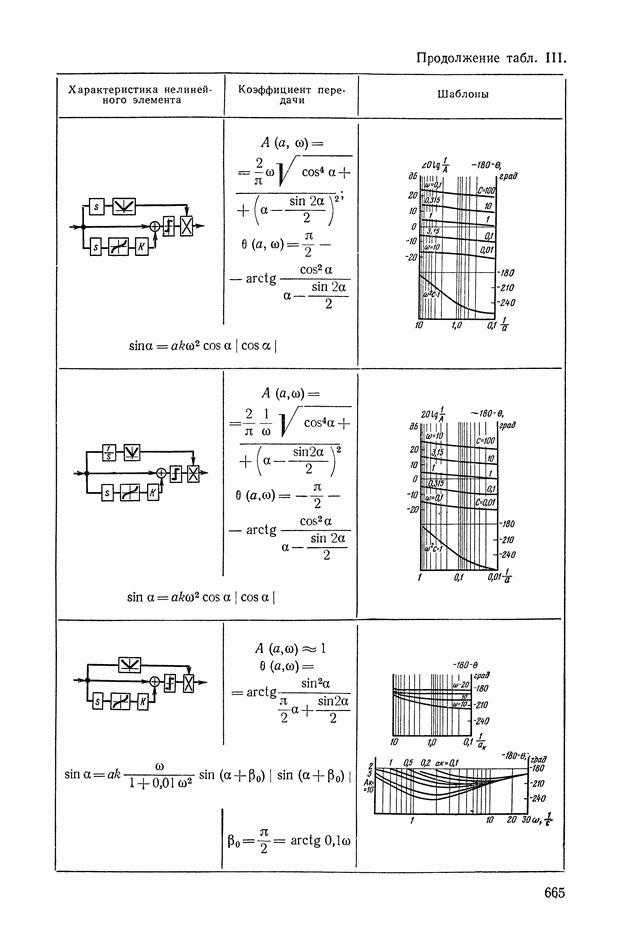
- ПРИЛОЖЕНИЕ III. НЕЛИНЕЙНЫЕ ЛОГИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ