| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
55.3. Область интегрирования.
Рассмотрим теперь ограничения на область интегрирования по  вытекающие из свойства спектральности (6). Условия, определяющие область R, могут быть записаны в общем виде, включающем физически важный случай (7):
вытекающие из свойства спектральности (6). Условия, определяющие область R, могут быть записаны в общем виде, включающем физически важный случай (7):

Эти условия определяют две пространственно-подобные и достаточно гладкие поверхности  в 4-мерном
в 4-мерном  -пространстве.
-пространстве.
Как следует из (10), связь между пространствами q и и, № осуществляется с помощью условия

Оно определяет в 4-мерном пространстве q двухполостный гиперболоид  , параметрически зависящий от переменных
, параметрически зависящий от переменных  . Будем называть этот гиперболоид допустимым, если его верхняя полость
. Будем называть этот гиперболоид допустимым, если его верхняя полость  не имеет точек, лежащих ниже
не имеет точек, лежащих ниже  , а нижняя полость
, а нижняя полость  не имеет точек, лежащих выше
не имеет точек, лежащих выше  (см. рис. 67), т. е.
(см. рис. 67), т. е.

Множество допустимых гиперболоидов соответствует множеству точек S в пятимерном  -пространстве
-пространстве 


Рис. 67. Пример допустимого гиперболоида в симметричном случае.
Ясно теперь, что если интегрирование в (10) проводится только по множеству S, то  удовлетворяет условию спектральности (6). Обратное утверждение также является справедливым, т. е. любая причинная функция
удовлетворяет условию спектральности (6). Обратное утверждение также является справедливым, т. е. любая причинная функция  , удовлетворяющая условию спектральности, представима в виде интеграла (10), причем область интегрирования содержится в S. Доказательство этого обратного утверждения основывается на единственности представления Йоста—Лемана (1957). Другое доказательство, более последовательно учитывающее сингулярный характер обобщенных функций, содержится в § 32 монографии Владимирова (1964).
, удовлетворяющая условию спектральности, представима в виде интеграла (10), причем область интегрирования содержится в S. Доказательство этого обратного утверждения основывается на единственности представления Йоста—Лемана (1957). Другое доказательство, более последовательно учитывающее сингулярный характер обобщенных функций, содержится в § 32 монографии Владимирова (1964).
Определим теперь в явном виде область S. Используя для  и явные выражения (7), получаем из (28)
и явные выражения (7), получаем из (28)

причем

и

Для симметричного случая  находим отсюда
находим отсюда

Выбирая гиперплоскость интегрирования в виде  получаем область
получаем область  интегрирования для представления Йоста — Лемана (см. рис. 67)
интегрирования для представления Йоста — Лемана (см. рис. 67)

В несимметричном случае область S оказывается несимметричной относительно замены  и выбрать поверхность интегрирования в виде
и выбрать поверхность интегрирования в виде  невозможно. В этом случае получим вместо (32) более общее ограничение, которое может быть записано в виде
невозможно. В этом случае получим вместо (32) более общее ограничение, которое может быть записано в виде

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЯ
- ВВЕДЕНИЕ
- ГЛАВА I. КЛАССИЧЕСКАЯ ТЕОРИЯ СВОБОДНЫХ ПОЛЕЙ
- 1.2. Гамильтонов и лагранжев формализмы.
- 1.3. Функция Лагранжа и принцип стационарного действия.
- 1.4. Трансформационные свойства функций поля.
- 1.5. Другие группы преобразований.
- § 2. Теорема Нётер и динамические инварианты
- 2.2. Вектор энергии-импульса.
- 2.3. Тензор момента количества движения и тензор спина.
- 2.4. Изотопический спин, заряд и вектор тока.
- § 3. Скалярное поле
- 3.2. Импульсное представление и частотные компоненты.
- 3.3. Дискретное импульсное представление.
- 3.4. Комплексное скалярное поле.
- 3.5. Поле пионов.
- § 4. Векторное поле
- 4.2. Переход к импульсному представлению.
- 4.3. Спин векторного поля.
- 4.4. Запись уравнений Клейна — Гордона в виде системы уравнений первого порядка.
- § 5. Электромагнитное поле
- 5.2. Градиентное преобразование и условие Лоренца.
- 5.3. Лагранжев формализм.
- 5.4. Поперечные, продольные и временные составляющие.
- 5.5. Спин.
- § 6. Спинорное поле. Матрицы Дирака и законы преобразования спинорных функций
- 6.2. Матрицы Дирака.
- 6.3. Уравнение Дирака.
- 6.4. Трансформационные свойства спинорного поля.
- § 7. Спинорное поле. Свойства решений и динамические инварианты
- 7.2. Разложения по спиновым состояниям и соотношения нормировки и ортогональности.
- 7.3. Лагранжев формализм и инварианты.
- 7.4. Спинорное поле с массой нуль.
- § 8. Лагранжиан системы полей
- 8.2. Локальные фазовые преобразования и калибровочные поля.
- 8.3. Поле Янга—Миллса.
- 8.4. Динамические инварианты системы полей.
- ГЛАВА II. КВАНТОВАЯ ТЕОРИЯ СВОБОДНЫХ ПОЛЕЙ
- § 9. Общие принципы квантования волновых полей
- 9.2. Представления уравнения Шредингера.
- 9.3. Трансформационные свойства амплитуды состояния и операторов поля.
- 9.4. Постулат квантования волновых полей.
- 9.5. Физический смысл положительно- и отрицательно-частотных составляющих и сопряженных функций.
- 9.6. Состояние вакуума и амплитуда состояния в фоковском представлении.
- § 10. Установление перестановочных соотношений
- 10.2. Перестановочные соотношения Ферми—Дирака и Бозе—Эйнштейна.
- 10.3. Связь спина со статистикой. Теорема Паули.
- 10.4. Нормальное произведение операторов и запись динамических переменных.
- 10.5. Перестановочные соотношения в дискретном импульсном представлении.
- § 11. Скалярное и векторное поля
- 11.2. Поле пи-мезонов.
- 11.3. Комплексное векторное поле.
- 11.4. Гамильтонов формализм и каноническое квантование.
- § 12. Электромагнитное поле
- 12.2. Индефинитная метрика.
- 12.3. Запись основных величин.
- § 13. Спинорное поле
- 13.2. Динамические переменные.
- 13.3. Зарядовое сопряжение.
- 13.4. Квантованное нейтринное поле.
- § 14. СРТ-теорема
- 14.2. P-преобразование.
- 14.3. Обращение времени.
- 14.4. СРТ-теорема.
- ГЛАВА III. СИНГУЛЯРНЫЕ ФУНКЦИИ И РЕГУЛЯРИЗАЦИЯ
- 15.2. Причинная функция Грина скалярного поля.
- 15.3. Причинные функции Грина различных полей.
- § 16. Особенности функций Грина и регуляризация
- 16.2. Явный вид и особенности функций …
- 16.3. Регуляризация Паули — Вилларса.
- 16.4. Размерная регуляризация.
- § 17. Приведение к нормальной форме
- 17.2. Теорема Вика для обычных произведений.
- 17.3. Некоторые определения.
- § 18. Коэффициентные функции
- 18.2. Некоторые свойства регуляризации Паули — Вилларса.
- § 19. Умножение операторных выражений
- 19.2. Некоторые свойства сингулярных функций.
- 19.3. Умножение операторных функций.
- ГЛАВА IV. МАТРИЦА РАССЕЯНИЯ
- § 20. Основные понятия теории взаимодействующих полей
- 20.2. Представление взаимодействия.
- 20.3. Матрица рассеяния.
- 20.4. Релятивистская ковариантность и унитарность S-матрицы.
- 20.5. Условие причинности.
- 20.6. «Классические поля» как функциональные аргументы.
- § 21. Лагранжиан взаимодействия и S-матрица
- 21.2. Условия ковариантности, унитарности и причинности для Sn.
- 21.3. Определение явного вида
- 21.4. Хронологическое произведение локальных операторов.
- 21.5. Определение функций Sn при любом n.
- 21.6. Анализ произвола в функциях Sn и наиболее общий вид S(g).
- § 22. Раскрытие хронологических произведений
- 22.2. Теорема Вика для хронологических произведений.
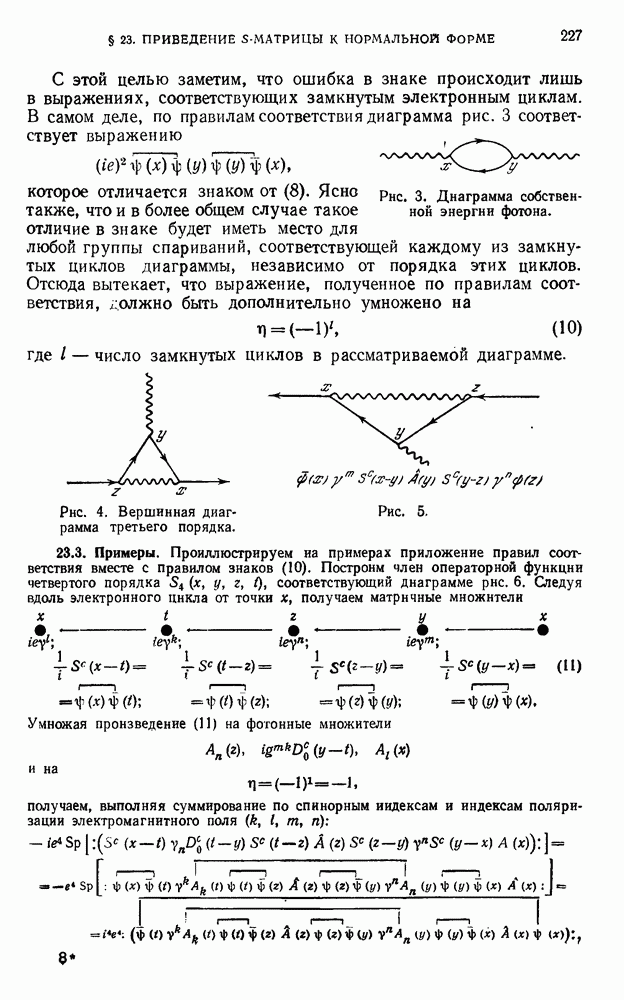
- § 23. Приведение S-матрицы к нормальной форме
- 23.2. Диаграммы Фейнмана и правила соответствия.
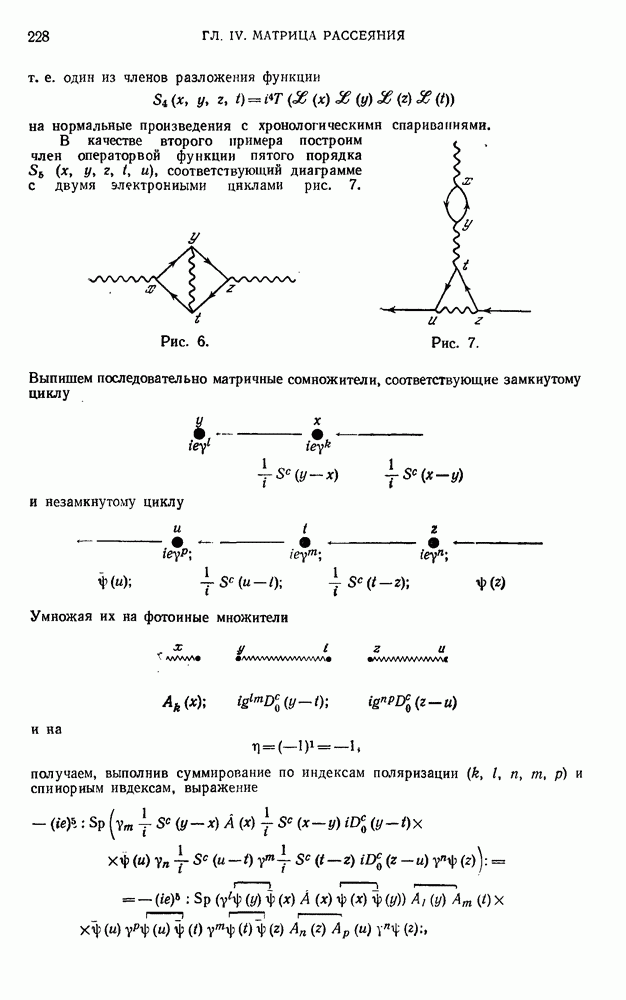
- 23.3. Примеры.
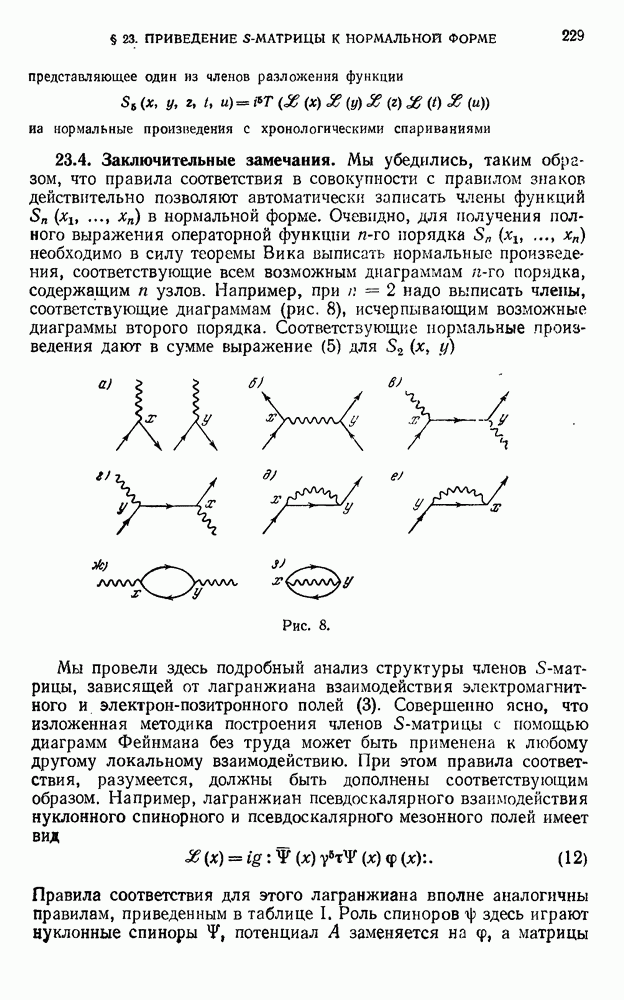
- 23.4. Заключительные замечания.
- § 24. Правила Фейнмана для вычисления матричных элементов матрицы рассеяния
- 24.2. Вычисление матричных элементов.
- 24.3. Учет свойств симметрии.
- 24.4. Рассеяние внешними полями.
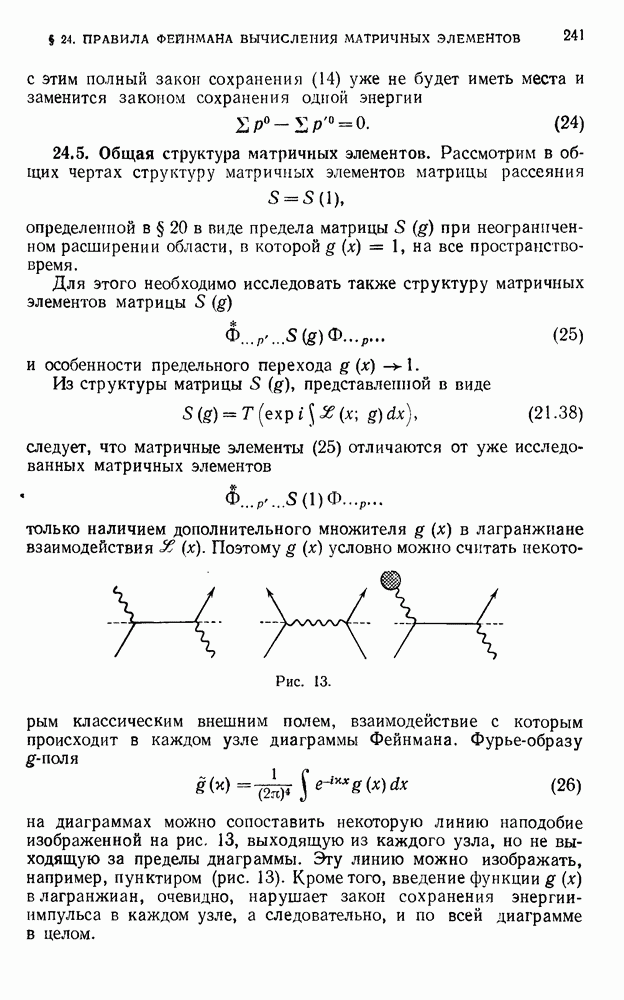
- 24.5. Общая структура матричных элементов.
- § 25. Вероятности процессов рассеяния и эффективные сечения
- 25.2. Вычисление вероятностей переходов.
- 25.3. Рассеяние двух частиц.
- 25.4. Эффективные сечения рассеяния.
- 25.5. Двухчастичный распад.
- § 26. Примеры расчета процессов второго порядка
- 26.2. Аннигиляция пары электрон — позитрон.
- 26.3. Тормозное излучение.
- ГЛАВА V. УСТРАНЕНИЕ РАСХОДИМОСТЕЙ ИЗ S-МАТРИЦЫ
- § 27. О расходимостях S-матрицы в электродинамике (второй порядок)
- 27.2. Выделение из расходящейся части.
- 27.3. Расходящаяся диаграмма с двумя внешними фотонными линиями П.
- 27.4. Выделение расходимостей из П и градиентная инвариантность.
- 27.5. Построение интегрируемой функции S2
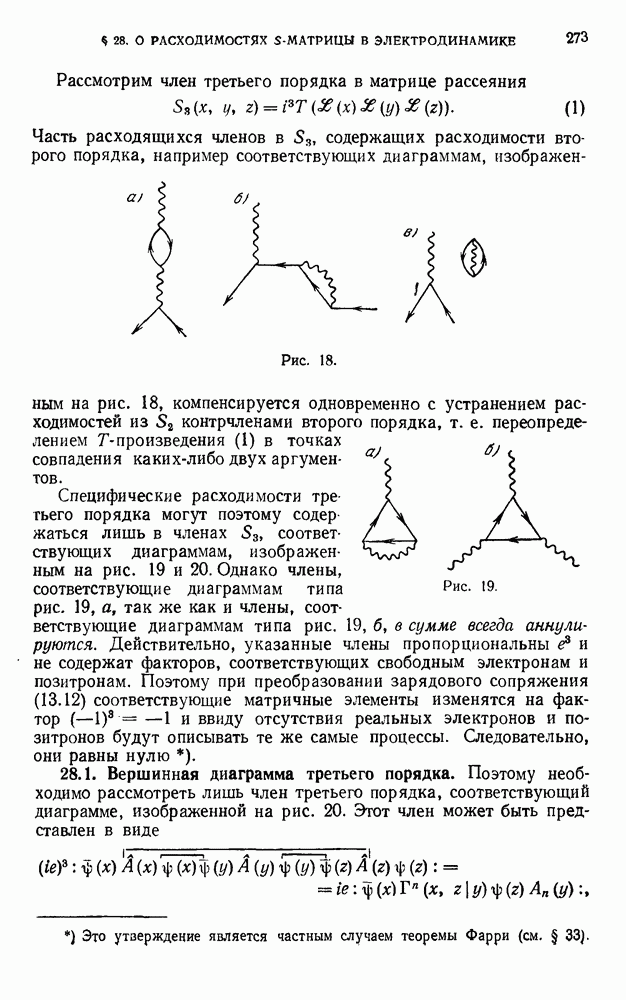
- § 28. О расходимостях S-матрицы в электродинамике (третий порядок)
- 28.2. Выделение расходимости из Г и градиентная инвариантность.
- 28.3. Тождество Уорда.
- 28.4. Получение интегрируемой функции S2.
- § 29. Общие правила устранения расходимостей из S-матрицы
- 29.2. Общий метод устранения расходимостей.
- 29.3. Графическое представление процедуры вычитания и R-операция.
- 29.4. Индекс диаграммы и степень расходимости.
- 29.5. Структура экспоненциальной квадратичной формы.
- 29.6. Выбор операции
- 29.7. Размерная перенормировка.
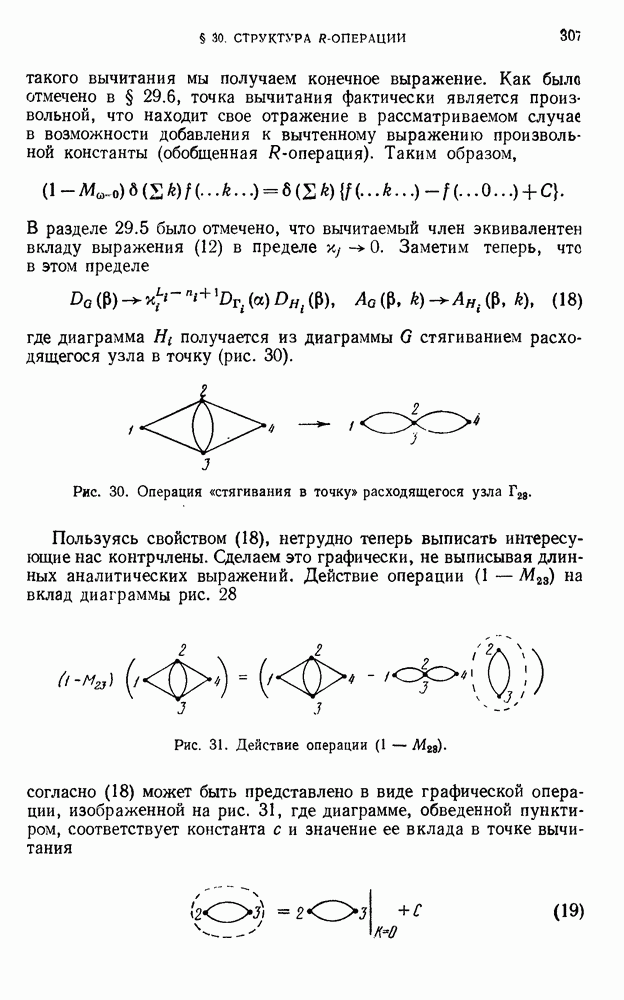
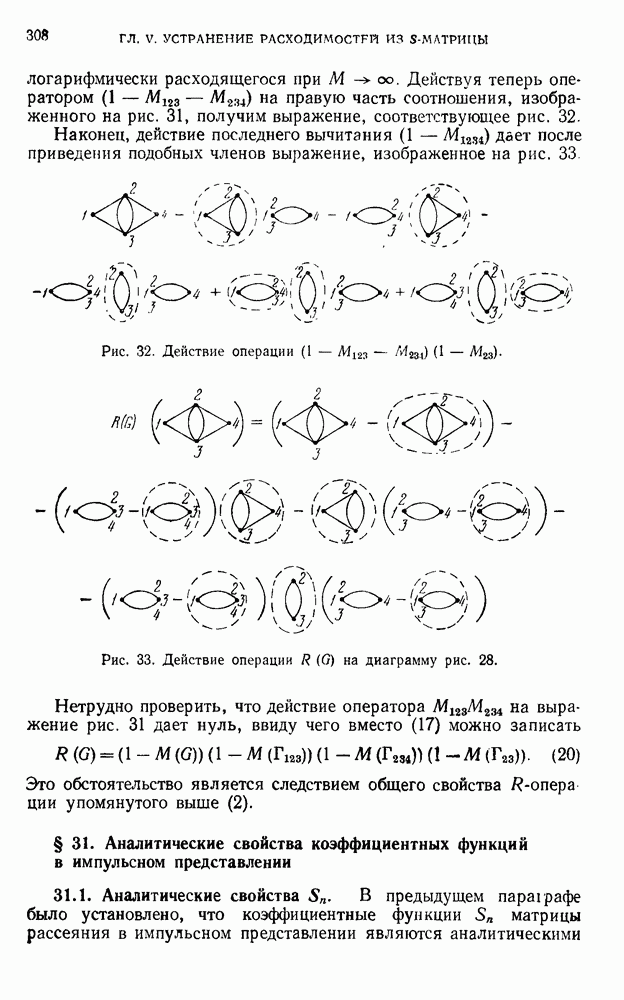
- § 30. Структура R-операции
- 30.2. Параметрическое представление.
- 30.3. Переход к пределу при е = 0.
- 30.4. Иллюстрация.
- § 31. Аналитические свойства коэффициентных функций в импульсном представлении
- 31.2. Структура функций Hn
- 31.3. Аналитические свойства функций Hn.
- § 32. Классификация ренормируемости теорий
- 32.2. Перечень взаимодействий первого рода.
- 32.3. Природа взаимодействий второго рода.
- 32.4. Фиксирование теории первого рода конечным числом констант.
- ГЛАВА VI. ПРИЛОЖЕНИЯ ОБЩЕЙ ТЕОРИИ УСТРАНЕНИЯ РАСХОДИМОСТЕЙ
- § 33. Спинорная электродинамика
- 33.2. Градиентная инвариантность матрицы рассеяния.
- 33.3. Тождества Уорда.
- 33.4. Контрчлены.
- § 34. Спинорная электродинамика.
- 34.2. Неоднозначность процесса устранения бесконечностей.
- 34.3. Полные функции Грина G, D и вершинная часть Г.
- 34.4. Радиационные поправки во внешние линии и выбор конечных постоянных.
- § 35. Спинорная электродинамика.
- 35.2. Поправки к электронной функции Грина.
- 35.3. Поправки к вершинной части.
- 35.4. Схема вычисления поправок к формуле Клейна—Нишины.
- § 36. Некоторые модели сильных взаимодействий
- 36.2. Псевдоскалярное поле с нелинейным взаимодействием.
- 36.3. Псевдоскалярная модель мезон-нуклонного взаимодействия.
- 36.4. Второй заряд, мультипликативные ренормировки и внешние линии.
- § 37. Полные функции Грина и вершинные функции
- 37.2. Источники и производящие функционалы.
- 37.3. Производящий функционал для высших функций Грина.
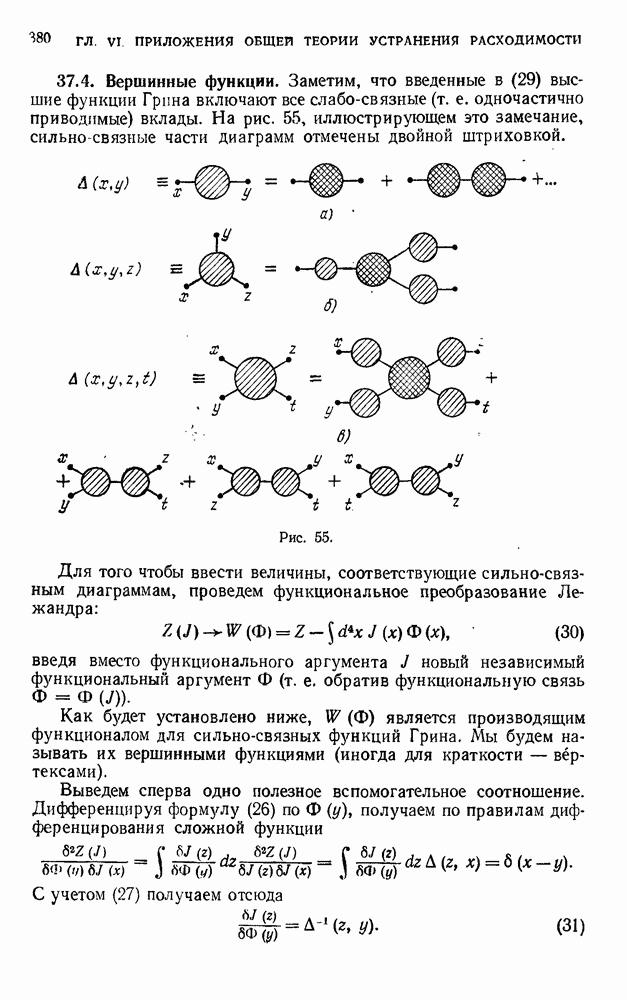
- 37.4. Вершинные функции.
- § 38. Уравнения Швингера и Дайсона
- 38.2. Редукционные формулы.
- 38.3. Уравнения Швингера.
- 38.4. Уравнения Дайсона.
- 38.5. Учет контрчленов.
- ГЛАВА VII. УРАВНЕНИЕ ШРЕДИНГЕРА И ДИНАМИЧЕСКИЕ ПЕРЕМЕННЫЕ
- § 39. Уравнение Шредингера для амплитуды состояний
- 39.2. Уравнение Шредингера в представлении взаимодействия и уравнение Томонага—Швингера.
- 39.3. Сингулярности обобщенного гамильтониана.
- 39.4. Основные свойства обобщенного гамильтониана.
- § 40. Динамические переменные системы взаимодействующих полей
- 40.2. Локальные динамические величины
- 40.3. Вектор тока.
- 40.4. Условие Лоренца.
- 40.5. Операторы волновых полей.
- § 41. Поляризация вакуума и аномальный магнитный момент электрона
- 41.2. Аномальный магнитный момент электрона.
- § 42. Уравнение Дирака с радиационными поправками
- 42.2. Обобщение уравнения Дирака.
- 42.3. Лэмбовский сдвиг уровней.
- 42.4. Заключительные замечания.
- ГЛАВА VIII. МЕТОД ФУНКЦИОНАЛЬНОГО УСРЕДНЕНИЯ
- § 43. Континуальный интеграл в квантовой теории поля
- 43.2. Вычисление …
- 43.3. Континуальные интегралы.
- 43.4. Континуальный интеграл по ферми-полям.
- § 44. Производящие функционалы и функции Грина
- 44.2. Представления для функций Грина в виде континуальных бозе-интегралов.
- § 45. Градиентные преобразования спинориой электродинамики
- 45.2. Градиентная инвариантность матрицы рассеяния.
- 45.3. Обобщенные тождества Уорда.
- 45.4. Переход к поперечной калибровке.
- 45.5. Градиентные преобразования функций Грина.
- § 46. Исследование модели Блоха — Нордсика
- 46.2. Вычисление G(х, у).
- ГЛАВА IX. РЕНОРМАЛИЗАЦИОННАЯ ГРУППА
- § 47. Группа мультипликативных ренормировок в квантовой теории поля
- 47.2. Групповой характер мультипликативных перенормировок.
- 47.3. Переход к импульсному представлению.
- 47.4. Вывод функциональных уравнений.
- 47.5. Свойства функциональных уравнений.
- § 48. Общий анализ групповых уравнений
- 48.2. Дифференциальные уравнения.
- 48.3. Общее решение уравнений.
- 48.4. Синтез ренормгруппы и теории возмущений.
- 48.5. Схемная зависимость.
- § 49. Асимптотический анализ в ультрафиолетовой области
- 49.2. Асимптотики инвариантного заряда.
- 49.3. Асимптотики функций Грина.
- 49.4. Высшие функции Грина.
- § 50. Анализ функций Грина спинорной электродинамики
- 50.2. Ультрафиолетовые асимптотики.
- 50.3. Инфракрасная асимптотика электронной функции Грина.
- 50.4. Матричные элементы и вероятности переходов.
- § 51. Модели сильных взаимодействий
- 51.2 Двухпетлевое приближение.
- 51.3. Надежность результатов. Высшие приближения.
- 51.4. Квантовая хромодинамика
- 51.5. Анализ двухзарядной модели.
- 51.6. Симметричные асимптотики высших функций Грина.
- ГЛАВА X. ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
- § 52. Основные свойства S-матрицы в локальной теории поля
- 52.2. Общие свойства матрицы рассеяния.
- 52.3. Локальные свойства.
- 52.4. Оптическая теорема.
- § 53. Спектральное представление пионной функции Грина
- 53.2. Вакуумное ожидание произведения и коммутатора двух токов.
- 53.3. Аналитические свойства …
- 53.4. Спектральное представление …
- § 54. Спектральное представление фермионной функции Грина
- 54.2. Вывод спектрального представления.
- 54.3. Близость к противоречию.
- § 55. Представление Йоста — Лемана — Дайсона
- 55.2. Общая форма представления.
- 55.3. Область интегрирования.
- 55.4. Некоторые следствия.
- § 56. Вывод дисперсионных соотношений для пион-нуклонного рассеяния
- 56.2. Переход к фиксированной системе отсчета. Трудности аналитического продолжения.
- 56.3. Схема получения дисперсионных соотношений для амплитуды рассеяния вперед.
- 56.4. Случай рассеяния при p <> 0
- § 57. Дисперсионные соотношения для пион-нуклонного рассеяния вперед
- 57.2. Изотопическая и спиновая структура.
- 57.3. Свойства симметрии по энергии.
- 57.4. Физические дисперсионные соотношения.
- 57.5. Дальнейшее развитие метода.
- ПРИЛОЖЕНИЕ 1. НЕКОТОРЫЕ СВЕДЕНИЯ ОБ ИЗОТОПИЧЕСКОМ ФОРМАЛИЗМЕ
- ПРИЛОЖЕНИЕ 2. СВОДКА СИНГУЛЯРНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ 3. СВОДКА ФОРМУЛ ДЛЯ ВЫЧИСЛЕНИЯ МАТРИЧНЫХ ЭЛЕМЕНТОВ
- ЛИТЕРАТУРА