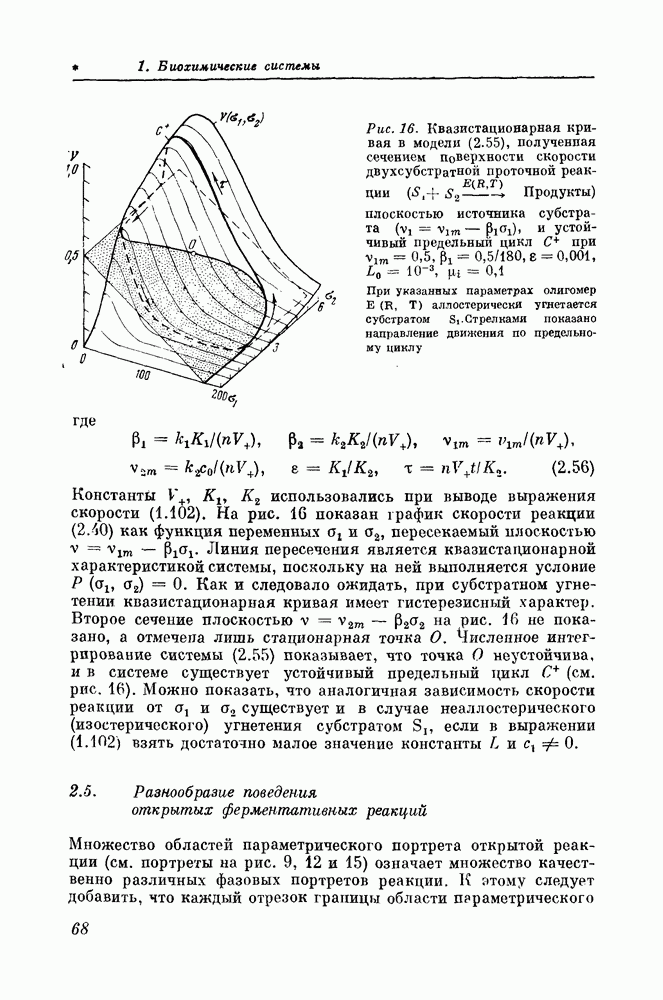
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава вторая. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОТОЧНЫХ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
2.1. Общие методы исследования системы обыкновенных дифференциальных уравнений второго порядка
Динамика ферментативных реакций, полиферментных систем, процессов мембранного транспорта и любых других биологических процессов описывается системами нелинейных дифференциальных уравнений. В тех случаях, когда пространственной протяженностью моделируемой системы можно пренебречь, ее динамика описывается системой обыкновенных дифференциальных уравнений.
Современные методы численного анализа и применение мощных электронно-вычислительных машин позволяют получить при заданных начальных условиях решение систем нелинейных дифференциальных уравнений очень высокого порядка, содержащих десятки и даже сотни независимых переменных. Однако, решая систему при различных начальных условиях, удается найти далеко не все качественно различные типы динамического поведения, поскольку всегда существует вероятность того, что при других начальных условиях поведение системы будет совершенно иным. Качественные же методы наиболее полно разработаны только для систем двух дифференциальных уравнений. Очень часто, однако, многие математические модели ферментативных реакций, полиферментных и мембранных систем удается свести именно к системам дифференциальных уравнений второго порядка. Обычно после пормализации переменных и параметров такая модель второго
порядка принимает вид:

где  — безразмерные переменные,
— безразмерные переменные,  безразмерный масштабный множитель, который иногда оказывается функцией переменных. Нормализацию, т. е. выбор единиц измерения переменных, стремятся провести таким образом, чтобы в некоторой области определения переменных
безразмерный масштабный множитель, который иногда оказывается функцией переменных. Нормализацию, т. е. выбор единиц измерения переменных, стремятся провести таким образом, чтобы в некоторой области определения переменных  представляющей наибольший интерес для моделирования, переменные и правые части имели бы одинаковые порядки величин:
представляющей наибольший интерес для моделирования, переменные и правые части имели бы одинаковые порядки величин:  После такой нормировки относительное изменение переменных определяется параметром
После такой нормировки относительное изменение переменных определяется параметром 

Подробное изложение методов качественного анализа моделей второго порядка можно найти в классических работах математической школы А. А. Андронова [65 — 67].
Чтобы не отсылать читателя слишком часто к этим работам, ниже коротко описаны те из качественных методов анализа, которые используются в последующих разделах.
Для изображения движений представляющей или фазовой точки системы (2.1) пользуются плоскостью  которая называется фазовой плоскостью. Стационарные состояния системы (2.1) определяются из условий
которая называется фазовой плоскостью. Стационарные состояния системы (2.1) определяются из условий

и являются особыми точками фазовой плоскости. Значения переменных  удовлетворяющие системе уравнений (2.3), называются стационарными. В особых точках фазовой плоскости не определен угол наклона
удовлетворяющие системе уравнений (2.3), называются стационарными. В особых точках фазовой плоскости не определен угол наклона  касательных к фазовым траекториям — траекториям, описываемым представляющей точкой с изменением времени
касательных к фазовым траекториям — траекториям, описываемым представляющей точкой с изменением времени  при различных начальных значениях переменных
при различных начальных значениях переменных  Совокупность фазовых траекторий образует фазовый портрет системы (2.1). На фазовой плоскости уравнения (2.3) определяют две линии — изоклины горизонтальных
Совокупность фазовых траекторий образует фазовый портрет системы (2.1). На фазовой плоскости уравнения (2.3) определяют две линии — изоклины горизонтальных  и вертикальных (
и вертикальных ( касательных к фазовым траекториям. Эти изоклины иначе называются главными или нуль-изоклинами.
касательных к фазовым траекториям. Эти изоклины иначе называются главными или нуль-изоклинами.
Для многих приложений большой интерес представляют так называемые релаксационные или жесткие модели второго порядка—модели вида (2.1), в которых  При
При  представляет собой медленную переменную, а у — быструю
представляет собой медленную переменную, а у — быструю
переменную, так как при движении представляющей точки вдали от нуль-изоклин скорости изменения переменных различаются в  Благодаря этому различию в модели существуют два типа движений: быстрое движение в течение времени
Благодаря этому различию в модели существуют два типа движений: быстрое движение в течение времени  в ходе которого представляющая точка движется по фазовой траектории к изоклине
в ходе которого представляющая точка движется по фазовой траектории к изоклине  и медленное движение (или медленный дрейф) представляющей точки вдоль узкой окрестности изоклины
и медленное движение (или медленный дрейф) представляющей точки вдоль узкой окрестности изоклины  Это медленное движение осуществляется по направлению к одной из устойчивых особых точек или к одному из экстремумов этой изоклины, где оно обычно теряет устойчивость и сменяется быстрым движением. При
Это медленное движение осуществляется по направлению к одной из устойчивых особых точек или к одному из экстремумов этой изоклины, где оно обычно теряет устойчивость и сменяется быстрым движением. При  все фазовые траектории вдали от изоклины
все фазовые траектории вдали от изоклины  представляют собой почти прямые линии, угол наклона которых
представляют собой почти прямые линии, угол наклона которых  В фазе медленного движения с высокой точностью выполняется условие (2.36). Значение быстрой переменной
В фазе медленного движения с высокой точностью выполняется условие (2.36). Значение быстрой переменной  удовлетворяющее условию (2.36), называют квазистационарным, фазу медленного движения — квазистационарным состоянием, а изоклину
удовлетворяющее условию (2.36), называют квазистационарным, фазу медленного движения — квазистационарным состоянием, а изоклину  квазистационарной кривой.
квазистационарной кривой.
Устойчивость и характер стационарного состояния в большинстве случаев можно определить из анализа корней характеристического уравнения системы, линеаризованной в окрестности стационарного состояния [65]. Характеристическое уравнение имеет вид

где

Частные производные в формулах для  и А являются коэффициентами линейных членов разложения правых частей системы (2.1) в ряд Тейлора в окрестности стационарной точки
и А являются коэффициентами линейных членов разложения правых частей системы (2.1) в ряд Тейлора в окрестности стационарной точки  .
.
Уравнение (2.4) имеет корни

где

При  оба корня действительны и имеют разные знаки. Такая точка неустойчива и является седлом. Случай комплексных корней (подкоренное выражение уравнения (2.5) отрицательно) соответствует точке типа фокуса, а при
оба корня действительны и имеют разные знаки. Такая точка неустойчива и является седлом. Случай комплексных корней (подкоренное выражение уравнения (2.5) отрицательно) соответствует точке типа фокуса, а при  особая точка является узлом. Как фокус, так и узел устойчивы, если
особая точка является узлом. Как фокус, так и узел устойчивы, если  и неустойчивы при
и неустойчивы при 
Если линейное приближение дает  или
или  то характер особой точки остается неопределенным в рамках линейного приближения. В том случае, когда
то характер особой точки остается неопределенным в рамках линейного приближения. В том случае, когда  точка может быть
точка может быть
центром или устойчивым (неустойчивым) сложным фокусом кратности  где
где  наименьший номер фокусной величины
наименьший номер фокусной величины  отличной от нуля [67]. Для нахождения фокусных величин необходимо использовать коэффициенты при нелинейных членах разложения правых частей системы (2.1). Значения
отличной от нуля [67]. Для нахождения фокусных величин необходимо использовать коэффициенты при нелинейных членах разложения правых частей системы (2.1). Значения  или
или  в отличие от других значений
в отличие от других значений  и А соответствуют негрубым, или сложным особым точкам и бифуркационным значениям параметров. При сколь угодно малом возмущении системы из
и А соответствуют негрубым, или сложным особым точкам и бифуркационным значениям параметров. При сколь угодно малом возмущении системы из  -кратного фокуса могут родиться не более к предельных циклов, а сложная точка с
-кратного фокуса могут родиться не более к предельных циклов, а сложная точка с  может либо распасться на несколько точек, либо исчезнуть, так как
может либо распасться на несколько точек, либо исчезнуть, так как  соответствует касанию кривых (2.2) на плоскости
соответствует касанию кривых (2.2) на плоскости  [65]. В случае одновременного равенства нулю
[65]. В случае одновременного равенства нулю  и А топологию сложной (или вырожденной) особой точки можно исследовать при помощи замены переменных, расщепляющих сложную точку на ряд простых [67].
и А топологию сложной (или вырожденной) особой точки можно исследовать при помощи замены переменных, расщепляющих сложную точку на ряд простых [67].
Для знания качественной структуры фазового портрета необходимо определить взаимное расположение конечного числа особых траекторий — особых точек, сепаратрис и предельных циклов [65—67]. Устойчивые предельные циклы соответствуют устойчивым незатухающим колебаниям, а неустойчивые предельные циклы и сепаратрисы седел играют роль «водораздела» между областями фазовой плоскости с различным поведением фазовых траекторий.
За редкими исключениями, расположение предельных циклов определяется только численным интегрированием. Однако иногда можно сделать вывод о наличии предельного цикла (устойчивого или неустойчивого), если на фазовой плоскости удается найти циклы без контакта [65—671, т. е. замкнутые кривые, которые пересекаются фазовыми траекториями в одном направлении — внутрь или наружу. Так, внутри цикла без контакта должен существовать по крайней мере один устойчивый предельный цикл, если на цикле без контакта фазовые траектории направлены внутрь, а в ограничиваемой им области нет устойчивых особых точек. Устойчивый предельный цикл существует и тогда, когда на фазовой плоскости все особые точки и бесконечность системы неустойчивы. Для некоторых систем неустойчивость бесконечности показывается весьма просто (см. разделы 2.2 и 2.3). Если же на бесконечности могут быть особые точки, то исследование этих точек проводят с использованием преобразования Пуанкаре [65, с. 366], которое отображает бесконечно удаленные точки на экватор сферы.
В зависимости от значений параметров системы (2.1) ее фазовый портрет может качественно меняться. Бифуркационные значения параметров, при которых  или
или  делят пространство параметров на ряд областей, различающихся числом и устойчивостью особых точек. Иногда помимо границ
делят пространство параметров на ряд областей, различающихся числом и устойчивостью особых точек. Иногда помимо границ  используется граница
используется граница  которая разделяет особые
которая разделяет особые
точки типа узла и фокуса. Из соображений наглядности при большом числе параметров эти границы наносятся на плоскость двух параметров, а значения остальных параметров фиксируются. Такая плоскость параметров называется параметрическим портретом. Практически построение параметрического портрета по линейному приближению сводится к построению в плоскости двух выбранных параметров системы, — скажем, параметров  границ, определяемых критическими или бифуркационными значениями параметров.
границ, определяемых критическими или бифуркационными значениями параметров.
Важнейшими границами параметрического портрета являются следующие:
линия нейтральности — граница устойчивости стационарного состояния, определяемая системой алгебраических уравнений

линия моностационарности — граница области существования однократного стационарного состояния (вне этой области существуют три стационарных состояния — одно седло и два узла или фокуса), определяемая системой

линия кратности корней характеристического уравнения — граница области существования стационарного состояния типа фокуса (вне этой границы стационарное состояние представляет собой узел), определяемая системой

Если системы (2.6), (2.7) и (2.8) не разрешаются в явном виде относительно параметров  то можно воспользоваться параметрическим заданием границ, взяв в качестве свободного параметра стационарное значение х или у.
то можно воспользоваться параметрическим заданием границ, взяв в качестве свободного параметра стационарное значение х или у.
Построенный с помощью этих границ параметрический портрет в общем случае не позволяет установить все возможные для данной модели типы фазовых портретов, так как существуют качественные изменения фазового портрета вдали от стационарных точек. Такие нелокальные изменения вызываются слиянием сепаратрис седел, слиянием или расщеплением предельных циклов, слиянием предельного цикла с петлей сепаратрис и т. д. [65—67]. Для выявления нелокальных бифуркаций обычно используются численные методы, позволяющие существенно дополнить параметрический портрет границами существования устойчивых или неустойчивых предельных циклов — границами, на которых происходят слияния различных пар сепаратрис и т. п.
Иногда при исследовании моделей специального вида оказывается выгодным использовать не фазовую плоскость, а другую систему координат. Так, например, математические модели открытых ферментативных реакций часто имеют следующую структуру:

где  скорость некоторой реакции
скорость некоторой реакции  скорости образования веществ
скорости образования веществ  а члены
а члены  учитывают расходование
учитывают расходование  в других реакциях.
в других реакциях.
При 1 модель (2.9) допускает простое графическое исследование, если использовать координаты концентрация — скорость. Нахождение квазистационарных значений  производится по точкам пересечений кривой и
производится по точкам пересечений кривой и  с прямой
с прямой  в плоскости
в плоскости  концентрация х при этом считается постоянной. Меняя значение х и определяя для каждого нового х значение скорости
концентрация х при этом считается постоянной. Меняя значение х и определяя для каждого нового х значение скорости  можно построить зависимость
можно построить зависимость  квазистационарную входную (или выходную) характеристику реакции. Точки пересечения прямой
квазистационарную входную (или выходную) характеристику реакции. Точки пересечения прямой  с квазистационарной характеристикой
с квазистационарной характеристикой  построенной в плоскости
построенной в плоскости  определяют стационарные точки модели (2.9). Такой метод позволяет очень быстро без трудоемких компьютерных расчетов определить не только возможное число стационарных точек, но и их устойчивость. Так, если единственная стационарная точка располагается на неустойчивом участке квазистационарной характеристики, то она оказывается неустойчивой. Если характеристика
определяют стационарные точки модели (2.9). Такой метод позволяет очень быстро без трудоемких компьютерных расчетов определить не только возможное число стационарных точек, но и их устойчивость. Так, если единственная стационарная точка располагается на неустойчивом участке квазистационарной характеристики, то она оказывается неустойчивой. Если характеристика  имеет гистерезис
имеет гистерезис  или
или  -образный характер), а все стационарные точки расположены на неустойчивом участке характеристики, то в модели (2.9) имеется разрывный предельный цикл. Такой графический анализ эквивалентен рассмотрению вырожденной системы
-образный характер), а все стационарные точки расположены на неустойчивом участке характеристики, то в модели (2.9) имеется разрывный предельный цикл. Такой графический анализ эквивалентен рассмотрению вырожденной системы

или эквивалентного ей уравнения

к которым редуцируется модель (2.9) с помощью предельного перехода  Справедливость замены модели (2.9) моделью (2.10) основана на теореме Тихонова 137, 381 о предельном переходе
Справедливость замены модели (2.9) моделью (2.10) основана на теореме Тихонова 137, 381 о предельном переходе
 в системах произвольного порядка (см. также работы [39—43]).
в системах произвольного порядка (см. также работы [39—43]).
Возвращаясь к общей модели (2.1), стоит заметить, что очень часто такие модели имеют  или
или  -образную нуль-изоклину
-образную нуль-изоклину  Квазистадионарные значения
Квазистадионарные значения  соответствующие ординатам точек, расположенных между двумя экстремумами этой изоклины, неустойчивы. Это приводит к тому, что любая стационарная точка модели (2.1), расположенная на неустойчивом участке изоклины
соответствующие ординатам точек, расположенных между двумя экстремумами этой изоклины, неустойчивы. Это приводит к тому, что любая стационарная точка модели (2.1), расположенная на неустойчивом участке изоклины  (на участке, где
(на участке, где  при
при  оказывается неустойчивой.
оказывается неустойчивой.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ АВТОРОВ
- ВВЕДЕНИЕ
- 1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ БИОХИМИЧЕСКИХ СИСТЕМ
- Глава первая. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НЕПРОТОЧНЫХ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
- 1.2. Ферменты — белковые катализаторы и регуляторы
- 1.3. Метод графов
- 1.4. Модели реакций, катализируемых одноцентровыми ферментами
- 1.5. Модели реакций, катализируемых олигомерными ферментами
- 1.6. Свойства реакции …
- 1.7. Свойства двухсубстратной реакции
- Глава вторая. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОТОЧНЫХ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
- 2.2. Модель открытой реакции … с субстратным угнетением
- 2.3. Модель двухсубстратной реакции с субстратным угнетением
- 2.4. Динамика открытых реакций, катализируемых олигомерными ферментами
- 2.5. Разнообразие поведения открытых ферментативных реакций
- 2.6. Эквивалентные математические и кинетические модели
- 2.7. Эффект депонирования
- Глава третья. МОДЕЛИРОВАНИЕ ПОЛИФЕРМЕНТНЫХ СИСТЕМ
- 3.1. Полиферментные системы и их модели
- 3.2. Уровни функциональной организации полиферментных систем
- 3.3. Простая модель стехиометрической структуры энергетического метаболизма
- 3.4. Два класса аллостерических регуляторных связей, контролирующих энергетический метаболизм
- 2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ВОЗБУДИМЫХ МЕМБРАН
- Глава четвертая. КАЧЕСТВЕННЫЕ МЕТОДЫ В ИССЛЕДОВАНИИ МОДЕЛЕЙ МЕМБРАН
- 4.1. Построение уравнений второго порядка для моделей Ходжкина — Хаксли и Побла
- 4.2. Фаэовые портреты систем второго порядка
- 4.3. Исследование основных режимов мембраны аксона кальмара с помощью качественных методов
- 4.4. Исследование основных режимов мембраны волокна Пуркинье сердца с помощью качественных методов
- 4.5. Математические детали асимптотического сведения уравнений Ходжкина — Хаксли к системе второго порядка Н-Н2
- Глава пятая. БИОЛОГИЧЕСКИ АКТИВНЫЕ ВЕЩЕСТВА, ИОННЫЕ ТОКИ И ЭЛЕКТРОФИЗИОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ МЕМБРАН
- 5.2. Техника анализа мембран по записям ионных токов
- 5.3. Фазовые портреты мембран сердечной, нервной и мышечной клеток
- 5.4. Анализ действия веществ на мембраны
- 5.5. Предсказание электрофизиологических эффектов с помощью качественных методов
- 5.6. Границы применимости анализа, мембран по фазовому портрету
- 5.7. Оценка на математических моделях мембран точности построения фазового портрета по записям ионных токов
- 3. ВОЗБУДИМЫЕ СРЕДЫ. ВОЛНЫ И АВТОВОЛНОВЫЕ ПРОЦЕССЫ
- 6.1. Автоволновые процессы в возбудимых средах
- 6.2. Распространение волн в однородной среде. Спиральная волна, вращающаяся вокруг отверстия, и ревербератор
- 6.3. Возникновение ревербератора в простейшей неоднородной среде
- 6.4. Ревербератор в более детальных моделях
- 6.5. Свойства ревербератора как источника волн. Размножение ревербераторов в неоднородной среде. Бремя жизни
- 6.6. Ревербератор и сердечные аритмии. Уязвимость сердечной ткани
- Глава седьмая. ЭХО — ИСТОЧНИК КОНЦЕНТРИЧЕСКИХ ВОЛН В ВОЗБУДИМЫХ СРЕДАХ
- 7.1. Эхо в простейших моделях. Источник эха и ревербератор
- 7.2. Источник эха в моделях, описываемых обыкновенными дифференциальными уравнениями
- 7.3. Эхо в непрерывных возбудимых средах
- 7.4. Эхо в модели клеток сердца. Уязвимость
- Глава восьмая. ВЗАИМОДЕЙСТВИЕ ИСТОЧНИКОВ ВОЛН. АВТОВОЛНОВЫЕ ПРОЦЕССЫ И СЕРДЕЧНЫЕ АРИТМИИ
- 8.2. Синхронизация при взаимодействии источников волн
- 8.3. Размножение ревербераторов и фибрилляция
- 8.4. Взаимодействие источников эха
- 8.5. Связь параметров возбудимых сред с характеристиками дифференциального уравнения мембраны
- 8.6. Стационарные и нестационарные режимы распространения
- 8.7. Результаты микроэлектродного исследования уязвимости
- 8.8. О параметрах, контролирующих уязвимость в математических моделях и в миокарде
- 8.9. Следствия из моделей для антиаритмических веществ
- 4. ПРОСТРАНСТВЕННАЯ ОРГАНИЗАЦИЯ БИОЛОГИЧЕСКИХ СТРУКТУР
- Глава девятая. МОДЕЛИРОВАНИЕ ОБЪЕМНЫХ КЛЕТОЧНЫХ СТРУКТУР. ВИРУСЫ, ФЕРМЕНТЫ
- 9.2. Математические основы объемной реконструкции
- 9.3. Модель трехмерной структуры отростка бактериофага
- 9.4. Голографический синтез объемного изображения поверхности клеточной мембраны
- 9.5. Моделирование структуры биологических макромолекул
- Глава десятая. АНАЛИЗ КЛЕТОЧНЫХ СТРУКТУР ПО ИХ ИЗОБРАЖЕНИЯМ. ГЛИЯ—СОСУДЫ, ХРОМОСОМЫ
- 10.1. Преобразование изображений клеток в цифровую форму
- 10.2. Определение морфометрических параметров клеток и клеточных структур
- 10.3. Исследование глиально-сосудистой системы головного мозга
- 10.4. Модель сокращения длины хромосом в митозе
- Глава одиннадцатая. ВОССТАНОВЛЕНИЕ ЛИНЕЙНОЙ СТРУКТУРЫ БИОПОЛИМЕРОВ
- 11.1. Анализ первичной последовательности нуклеиновых кислот
- 11.2. Математическая постановка проблемы
- 11.3. Восстановление слов по составу второго ранга
- 11.4. Метод подстановки при восстановлении слов
- 11.5. Оптимизация биохимического эксперимента