| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2. Модель открытой реакции ... с субстратным угнетением
Субстратное угнетение — широко распространенный тип регуляторного воздействия на активность ферментов [3, с. 72; 68; 69]. Однако трактовка физиологической роли такой регуляции долгое время встречала затруднения, за исключением, может быть, угнетения аденозинтрифосфатом фосфофруктокиназы  которое, как считают [69], способно предотвращать бесполезный синтез АТФ в гликолитической системе, когда его уровень достаточно высок. Математический анализ особенностей кинетики открытых ферментативных реакций при наличии субстратного угнетения показал возможность существования нескольких стационарных состояний с различной устойчивостью, гистерезиса и незатухающих колебаний [70—73].
которое, как считают [69], способно предотвращать бесполезный синтез АТФ в гликолитической системе, когда его уровень достаточно высок. Математический анализ особенностей кинетики открытых ферментативных реакций при наличии субстратного угнетения показал возможность существования нескольких стационарных состояний с различной устойчивостью, гистерезиса и незатухающих колебаний [70—73].
Рассмотрим односубстратную обратимую реакцию [71]

где  субстрат,
субстрат,  продукт,
продукт,  фермент, угнетаемый субстратом, и — скорость реакции,
фермент, угнетаемый субстратом, и — скорость реакции,  скорости притока соответственно
скорости притока соответственно  Примем, что
Примем, что

и что скорость реакций  описывается выражением (1.26). Тогда поведение реакции (2.12) во времени
описывается выражением (1.26). Тогда поведение реакции (2.12) во времени  можно описать системой, являющейся частным случаем системы (2.9):
можно описать системой, являющейся частным случаем системы (2.9):

Для удобства анализа приведем эту модель к безразмерному виду:

Здесь

— безразмерная скорость реакции (2.12).
Безразмерные переменные и параметры модели связаны с размерными следующим образом:

В соотношениях (2.17) использованы размерные параметры, входящие в выражение (1.26). Рассмотрим квазистационарную выходную характеристику  модели (2.15), определяемую уравнением
модели (2.15), определяемую уравнением

Из уравнений (2.16) и (2.18) следует, что

где  квазистационарные значения. Семейство квазистационарных выходных характеристик
квазистационарные значения. Семейство квазистационарных выходных характеристик  построенное по формуле (2.19), показано на рис. 6. Из этого рисунка видно, что при больших значениях
построенное по формуле (2.19), показано на рис. 6. Из этого рисунка видно, что при больших значениях  квазистационарная скорость реакции
квазистационарная скорость реакции  становится отрицательной, т. е. реакция протекает в обратном направлении:
становится отрицательной, т. е. реакция протекает в обратном направлении:  Если значение а достаточно мало, то в некотором диапазоне значений
Если значение а достаточно мало, то в некотором диапазоне значений  зависимость
зависимость  неоднозначна, что связано с наличием экстремумов у функции
неоднозначна, что связано с наличием экстремумов у функции  На рис. 6 в экстремальных точках
На рис. 6 в экстремальных точках  положительно. Покажем, что это имеет место при любых значениях параметров модели (2.15). Дифференцирование уравнения (2.18) дает
положительно. Покажем, что это имеет место при любых значениях параметров модели (2.15). Дифференцирование уравнения (2.18) дает

откуда


Рис. 6. Семейство квазистационарных выходных характеристик реакции (2.12), построенных по уравнению (2.19) при  и различных значениях а (цифры на кривых)
и различных значениях а (цифры на кривых)
Здесь и на рис. 7, 10, 11 пунктиром отмечены участки, соответствующие неустойчивым квазистационарным состояниям при 

Рис. 7. Графическое нахождение стационарных состояний реакции (2.12) Стационарные состояния  представляют собой точки пересечения гистерезисной квазистационарной выходной характеристики
представляют собой точки пересечения гистерезисной квазистационарной выходной характеристики  построенной по уравнению (2.19), с линейной характеристикой стока (источника) продукта
построенной по уравнению (2.19), с линейной характеристикой стока (источника) продукта  Параметры»
Параметры» 
В экстремальных точках должно выполняться условие  учитывая уравнение (2.21),
учитывая уравнение (2.21),

Поскольку всегда неотрицательно, то экстремумы существуют лишь при

Однако скорость, определяемая выражением (2.16), может быть отрицательной только при  что приводит к неравенству
что приводит к неравенству

которое противоречит выражению (2,23).
Из этого следует, что в случае трех стационарных состояний каждое из них имеет  (как на рис. 7).
(как на рис. 7).
Выходная характеристика имеет форму, показанную на рис. 7, только в определенной области значепий параметров. Эта область

Рис. 8. Зависимость формы выходной характеристики реакции (2.12) от параметров а — плоскость параметров  источника субстрата реакции (2.12). На плоскости построены границы (2.25) и (2.26), отделяющие области, в которых выходная характеристика реакции
источника субстрата реакции (2.12). На плоскости построены границы (2.25) и (2.26), отделяющие области, в которых выходная характеристика реакции  имеет качественно различные формы; б - качественно различные формы выходной характеристики реакции (2.12), соответствующие четырем областям, показанным на рис.
имеет качественно различные формы; б - качественно различные формы выходной характеристики реакции (2.12), соответствующие четырем областям, показанным на рис. 
ограничена с одной стороны границей

на которой экстремумы сливаются с образованием точки перегиба, а с другой стороны — границей

при пересечении которой меняется знак  в одной из экстремальных точек. Границы, определяемые уравнениями (2.25) и (2.26) в плоскости параметров
в одной из экстремальных точек. Границы, определяемые уравнениями (2.25) и (2.26) в плоскости параметров  изображены на рис. 8, а, а различные типы выходных характеристик — на рис. 8, б.
изображены на рис. 8, а, а различные типы выходных характеристик — на рис. 8, б.
Уравнение линии нейтральности модели (2.15) имеет вид

линии моностационарности —

и линии кратности —


(кликните для просмотра скана)

(кликните для просмотра скана)

Рис. 10. Предельные циклы на фазовой плоскости  модели (2.15) реакции (2.12) при различных значениях параметра
модели (2.15) реакции (2.12) при различных значениях параметра  на кривых) и
на кривых) и 
Решение уравнений  совместно с системой
совместно с системой

позволяет получить параметрическое задание всех трех линий в плоскостях  причем в качестве свободного параметра удобно взять стационарное значение
причем в качестве свободного параметра удобно взять стационарное значение  Результат построения параметрических портретов модели (2.15) показан на рис. 9. Из этих портретов видно, что реакция (2.12) может иметь одно, два (по линии
Результат построения параметрических портретов модели (2.15) показан на рис. 9. Из этих портретов видно, что реакция (2.12) может иметь одно, два (по линии  или три стационарных состояния. Как единственное стационарное состояние, так и два из трех (промежуточное — всегда седло) способны менять устойчивость и характер.
или три стационарных состояния. Как единственное стационарное состояние, так и два из трех (промежуточное — всегда седло) способны менять устойчивость и характер.
В ряде областей параметрических портретов выполняется условие существования устойчивого предельного цикла — неустойчивость всех стационарных состояний. Это условие является достаточным вследствие неустойчивости бесконечности модели (2.15) и вследствие того, что на осях и  фазовые траектории входят внутрь положительного квадранта фазовой плоскости. Неустойчивость бесконечности вытекает из отрицательности правой части уравнения
фазовые траектории входят внутрь положительного квадранта фазовой плоскости. Неустойчивость бесконечности вытекает из отрицательности правой части уравнения

при достаточно больших  [65], а направление фазовых траекторий на осях
[65], а направление фазовых траекторий на осях  можно получить, подставляя
можно получить, подставляя  соответственно в первое и второе уравнения системы (2.15). На рис. 10 показан пример устойчивого предельного цикла, окружающего единственную стационарную точку.
соответственно в первое и второе уравнения системы (2.15). На рис. 10 показан пример устойчивого предельного цикла, окружающего единственную стационарную точку.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ АВТОРОВ
- ВВЕДЕНИЕ
- 1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ БИОХИМИЧЕСКИХ СИСТЕМ
- Глава первая. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НЕПРОТОЧНЫХ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
- 1.2. Ферменты — белковые катализаторы и регуляторы
- 1.3. Метод графов
- 1.4. Модели реакций, катализируемых одноцентровыми ферментами
- 1.5. Модели реакций, катализируемых олигомерными ферментами
- 1.6. Свойства реакции …
- 1.7. Свойства двухсубстратной реакции
- Глава вторая. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОТОЧНЫХ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
- 2.2. Модель открытой реакции … с субстратным угнетением
- 2.3. Модель двухсубстратной реакции с субстратным угнетением
- 2.4. Динамика открытых реакций, катализируемых олигомерными ферментами
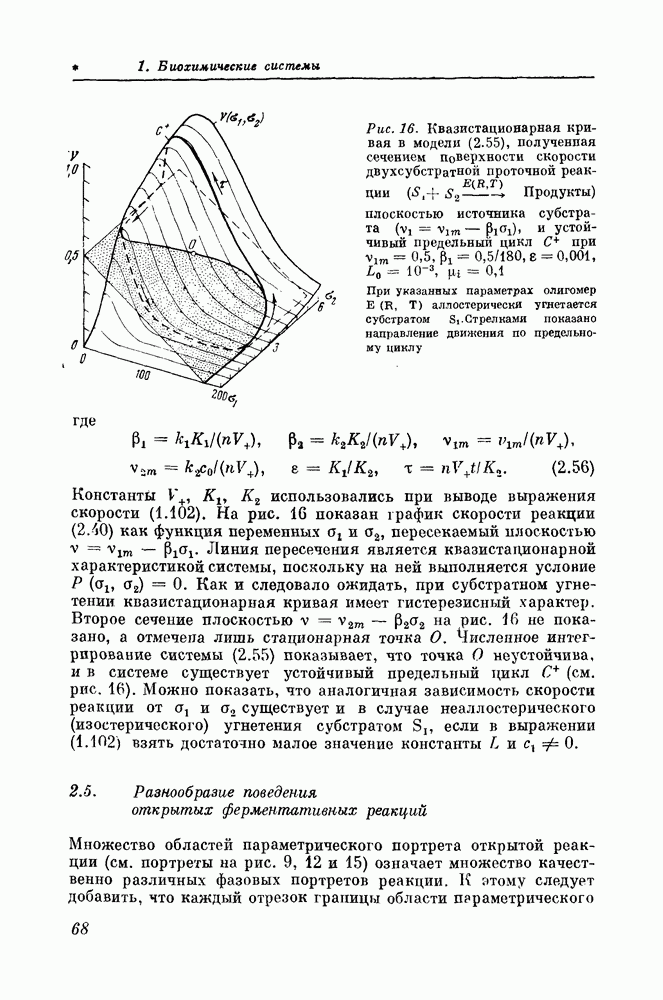
- 2.5. Разнообразие поведения открытых ферментативных реакций
- 2.6. Эквивалентные математические и кинетические модели
- 2.7. Эффект депонирования
- Глава третья. МОДЕЛИРОВАНИЕ ПОЛИФЕРМЕНТНЫХ СИСТЕМ
- 3.1. Полиферментные системы и их модели
- 3.2. Уровни функциональной организации полиферментных систем
- 3.3. Простая модель стехиометрической структуры энергетического метаболизма
- 3.4. Два класса аллостерических регуляторных связей, контролирующих энергетический метаболизм
- 2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ВОЗБУДИМЫХ МЕМБРАН
- Глава четвертая. КАЧЕСТВЕННЫЕ МЕТОДЫ В ИССЛЕДОВАНИИ МОДЕЛЕЙ МЕМБРАН
- 4.1. Построение уравнений второго порядка для моделей Ходжкина — Хаксли и Побла
- 4.2. Фаэовые портреты систем второго порядка
- 4.3. Исследование основных режимов мембраны аксона кальмара с помощью качественных методов
- 4.4. Исследование основных режимов мембраны волокна Пуркинье сердца с помощью качественных методов
- 4.5. Математические детали асимптотического сведения уравнений Ходжкина — Хаксли к системе второго порядка Н-Н2
- Глава пятая. БИОЛОГИЧЕСКИ АКТИВНЫЕ ВЕЩЕСТВА, ИОННЫЕ ТОКИ И ЭЛЕКТРОФИЗИОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ МЕМБРАН
- 5.2. Техника анализа мембран по записям ионных токов
- 5.3. Фазовые портреты мембран сердечной, нервной и мышечной клеток
- 5.4. Анализ действия веществ на мембраны
- 5.5. Предсказание электрофизиологических эффектов с помощью качественных методов
- 5.6. Границы применимости анализа, мембран по фазовому портрету
- 5.7. Оценка на математических моделях мембран точности построения фазового портрета по записям ионных токов
- 3. ВОЗБУДИМЫЕ СРЕДЫ. ВОЛНЫ И АВТОВОЛНОВЫЕ ПРОЦЕССЫ
- 6.1. Автоволновые процессы в возбудимых средах
- 6.2. Распространение волн в однородной среде. Спиральная волна, вращающаяся вокруг отверстия, и ревербератор
- 6.3. Возникновение ревербератора в простейшей неоднородной среде
- 6.4. Ревербератор в более детальных моделях
- 6.5. Свойства ревербератора как источника волн. Размножение ревербераторов в неоднородной среде. Бремя жизни
- 6.6. Ревербератор и сердечные аритмии. Уязвимость сердечной ткани
- Глава седьмая. ЭХО — ИСТОЧНИК КОНЦЕНТРИЧЕСКИХ ВОЛН В ВОЗБУДИМЫХ СРЕДАХ
- 7.1. Эхо в простейших моделях. Источник эха и ревербератор
- 7.2. Источник эха в моделях, описываемых обыкновенными дифференциальными уравнениями
- 7.3. Эхо в непрерывных возбудимых средах
- 7.4. Эхо в модели клеток сердца. Уязвимость
- Глава восьмая. ВЗАИМОДЕЙСТВИЕ ИСТОЧНИКОВ ВОЛН. АВТОВОЛНОВЫЕ ПРОЦЕССЫ И СЕРДЕЧНЫЕ АРИТМИИ
- 8.2. Синхронизация при взаимодействии источников волн
- 8.3. Размножение ревербераторов и фибрилляция
- 8.4. Взаимодействие источников эха
- 8.5. Связь параметров возбудимых сред с характеристиками дифференциального уравнения мембраны
- 8.6. Стационарные и нестационарные режимы распространения
- 8.7. Результаты микроэлектродного исследования уязвимости
- 8.8. О параметрах, контролирующих уязвимость в математических моделях и в миокарде
- 8.9. Следствия из моделей для антиаритмических веществ
- 4. ПРОСТРАНСТВЕННАЯ ОРГАНИЗАЦИЯ БИОЛОГИЧЕСКИХ СТРУКТУР
- Глава девятая. МОДЕЛИРОВАНИЕ ОБЪЕМНЫХ КЛЕТОЧНЫХ СТРУКТУР. ВИРУСЫ, ФЕРМЕНТЫ
- 9.2. Математические основы объемной реконструкции
- 9.3. Модель трехмерной структуры отростка бактериофага
- 9.4. Голографический синтез объемного изображения поверхности клеточной мембраны
- 9.5. Моделирование структуры биологических макромолекул
- Глава десятая. АНАЛИЗ КЛЕТОЧНЫХ СТРУКТУР ПО ИХ ИЗОБРАЖЕНИЯМ. ГЛИЯ—СОСУДЫ, ХРОМОСОМЫ
- 10.1. Преобразование изображений клеток в цифровую форму
- 10.2. Определение морфометрических параметров клеток и клеточных структур
- 10.3. Исследование глиально-сосудистой системы головного мозга
- 10.4. Модель сокращения длины хромосом в митозе
- Глава одиннадцатая. ВОССТАНОВЛЕНИЕ ЛИНЕЙНОЙ СТРУКТУРЫ БИОПОЛИМЕРОВ
- 11.1. Анализ первичной последовательности нуклеиновых кислот
- 11.2. Математическая постановка проблемы
- 11.3. Восстановление слов по составу второго ранга
- 11.4. Метод подстановки при восстановлении слов
- 11.5. Оптимизация биохимического эксперимента