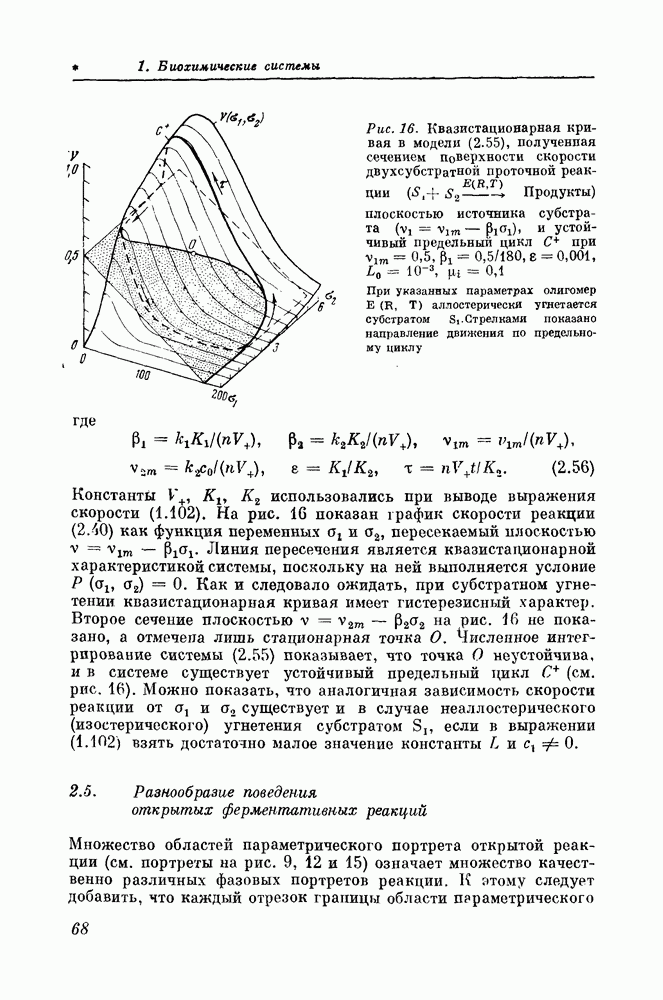
1.7. Свойства двухсубстратной реакции
Разобранные в предыдущем параграфе свойства модели реакции 
справедливы и для более сложных реакций. Рассмотрим, например, двухсубстратную реакцию
со случайным присоединением субстратов к каждому активному центру. Предполагая, что промежуточные фермент-субстратные
комплексы находятся в равновесии друг с другом [3, с. 68], и используя общее уравнение (1.65), приходим к следующей модели реакции (1.101):
Заменой переменных
и параметров
модель (1.102) при 
приводится к виду
аналогичному модели односубстратной обратимой реакции (1.87) со всеми ее свойствами: различными типами кинетических зависимостей 
или 
при различных значениях концентрации остальных субстратов, продуктной активацией, субстратным угнетением, различной чувствительностью прямой и обратной реакций к действию изо- и аллостерических метаболитов.
В зтой главе были рассмотрены математические модели, описывающие зависимости скоростей ферментативных реакций от концентраций реактантов и модификаторов в квазистационарном состоянии. При этом основное внимание было уделено очень важной для моделирования полиферментных систем теме — выводу и анализу уравнений, описывающих квазистационарные скорости сложных ферментативных реакций, т.е. реакций с большим числом реактантов, катализируемых олигомерными ферментами. Такие ферменты имеют множество идентичных или неидентичных активных центров, а их протомеры способны совершать
конформационные перестройки, изменяющие каталитическую активность фермента, а иногда и его агрегатное состояние. Выведенные уравнения для сложных реакций записаны в такой форме, которая позволяет по известным (или выводимым с помощью приведенного в этой главе метода графов) выражениям, описывающим механизм действия одиночного активного центра, легко получить уравнение квазистационарной скорости для многоцентрового фермента.
В следующей главе мы используем выведенные выше уравнения для анализа поведения ферментативных реакций в нестационарных проточных условиях — в условиях, характерных для живой клетки.
