1.4. Модели реакций, катализируемых одноцентровыми ферментами

В этом разделе мы выведем уравнения квазистационарной скорости для нескольких ферментативных реакций, катализируемых одноцентровыми ферментами. Эти уравнения мы используем позднее для вывода уравнений, описывающих скорости реакций, катализируемых олигомерными ферментами.

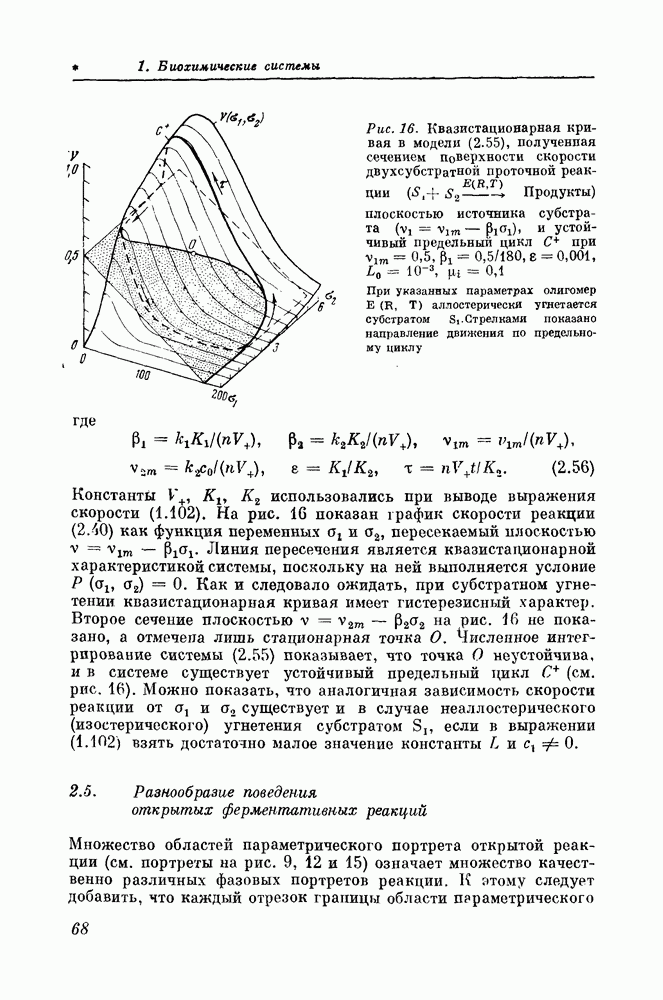
Обратимая реакция

Раскрыв определители в формуле (1.16) с помощью выражений (1.13) и (1.14), получим после несложных преобразований следующее выражение для скорости реакции (1.9), протекающей по механизму (1.10):

где

— максимальные скорости прямой и обратной реакций,

— константы Михаэлиса.

При введении безразмерных концентраций безразмерной скорости и параметрах уравнение (1.21) принимает вид

Если в графе (1.11) положить то и уравнение скорости в этом случае

описывает конкурентное угнетение [3, с. 280] продуктом или аналогом субстрата Кажущаяся константа Михаэлиса для в этом случае является функцией

Кинетические кривые описываемые уравнениями (1.22) и (1.23), представляют собой равнобочные гиперболы, либо пересекающие ось абсцисс в точке [модель (1.22)], либо выходящие из начала координат [модель (1.23)].

Обратимая моносубстратная реакция с субстратным угнетением

Рассмотрим следующий механизм субстратного угнетения:

Применение формулы (1.15) к графу (1.25) дает следующее выражение для квазистационарной скорости реакции:

где

Здесь константа субстратного угнетения.

Если ввести безразмерные переменные и параметры

то уравнение (1.26) примет вид

Зависимость скорости от концентрации первого субстрата описывает кривую с максимумом, а зависимость представляет собой гиперболу.

Обратимая двухсубстратная реакция с упорядоченным присоединением субстратов

Рассмотрим двухсубстратную обратимую реакцию

Граф такой реакции имеет вид

Согласно формуле (1.15), примененной к графу (1.31), квазистационарная скорость реакции (1.30) определяется выражением

в котором

— максимальные скорости превращений

— константы Михаэлиса для соответствующих субстратов, а -представляют собой отношения констант диссоциации фермент-субстратных комплексов к константам Михаэлиса:

Введение безразмерных концентраций

приводит уравнение (1.32) к более простой форме:

где

Рассмотрим кинетические кривые, описываемые уравнением (1.38) при

Заметим, что согласно уравнению (1.39)

Следовательно, субстрат присоединяющийся непосредственно к свободному активному центру фермента, является конкурентным ингибитором для превращения так как он не изменяет максимальной скорости реакции. Пусть В таком случае

Теперь согласно уравнению (1.41)

Таким образом, в отличие от выступает как неконкурентный ингибитор прямой реакции. С помощью подобной процедуры можно определить порядок присоединения всех субстратов реакции (1.30) к активному центру фермента. Кинетические зависимости, описываемые моделью (1.36), представляют собой гиперболы, начальный наклон и уровень насыщения которых зависят от концентраций остальных субстратов и их аналогов, способных связываться с активным центром.

Необратимая двухсубстратная реакция с субстратным угнетением

Представим двухсубстратную реакцию с субстратным угнетением графом, отражающим случайное и независимое присоединение субстратов к активному центру:

Применение уравнения (1.15) к графу (1.43) приводит к очень громоздкому выражению для Однако оно существенно упрощается, если принять, что При этом допущении скорость реакции (1.43)

В уравнении (1.44) максимальная скорость а константы диссоциации фермент-субстратных комплексов определяются выражениями

Зависимость описывается гиперболическими кривыми, а зависимость представляет собой кривую с максимумом.