| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9.5. Моделирование структуры биологических макромолекул
Исследование структуры ферментов
Разнообразие ферментов очень велико. Они представляют собой сравнительно большие белковые молекулы (молекулярный вес от  до
до  высокоспецифичные по отношению к субстрату. Это определяется структурным соответствием фермента (его активного центра) и субстрата. Механизм взаимодействия «субстрат — фермент» не может быть выяснен полностью, если не известна пространственная конфигурация молекул субстрата и фермента.
высокоспецифичные по отношению к субстрату. Это определяется структурным соответствием фермента (его активного центра) и субстрата. Механизм взаимодействия «субстрат — фермент» не может быть выяснен полностью, если не известна пространственная конфигурация молекул субстрата и фермента.
Основные структурные характеристики фермента и субстрата (размеры, вес в гидратированном состоянии и полный поверхностный заряд) можно определить в растворах физико-химическими
методами. Также можно определить число активных центров, т. е. сколько молекул субстрата могут быть связаны с одной молекулой фермента (чаще всего — от 1 до 4). По данным дисперсии оптического вращения можно рассчитать долю упорядоченных (регулярно скрученных) и неупорядоченных (скрученных нерегулярно) участков, в некоторых случаях удается получить информацию о распределении химических групп в области активного центра.
Многие белки удается получить в кристаллическом виде и с помощью рентгеноструктурного анализа воссоздать точную модель структуры молекулы с разрешением до  Однако сложности рентгеноструктурного анализа, связанные с получением информации о фазах рассеиваемого излучения, а также трудоемкость вычислений заставляют искать новые возможности в области электронной микроскопии для анализа биологических макромолекул.
Однако сложности рентгеноструктурного анализа, связанные с получением информации о фазах рассеиваемого излучения, а также трудоемкость вычислений заставляют искать новые возможности в области электронной микроскопии для анализа биологических макромолекул.
Приведем краткую характеристику фермента, используемого для иллюстрации возможностей исследования макромолекул в электронной микроскопии. Лейцинаминопептидаза (ЛАП) - фермент, гидролитически расщепляющий пептиды со свободной аминогруппой  -концевого аминокислотного остатка. Молекулярный вес ЛАП, выделенной в кристаллической форме из хрусталика быка,
-концевого аминокислотного остатка. Молекулярный вес ЛАП, выделенной в кристаллической форме из хрусталика быка,  Молекула ЛАП состоит из шести идентичных субъединиц с молекулярным весом
Молекула ЛАП состоит из шести идентичных субъединиц с молекулярным весом  [35]. Агрегация субъединиц может быть различной, исключена, по-видимому, лишь плоская гексагональная упаковка [351. Возможна агрегация субъединиц в форме тригональной призмы или октаэдра (рис. 111, а) [35, 36].
[35]. Агрегация субъединиц может быть различной, исключена, по-видимому, лишь плоская гексагональная упаковка [351. Возможна агрегация субъединиц в форме тригональной призмы или октаэдра (рис. 111, а) [35, 36].
Целью работы явилось уточнение пространственной организации кристаллических агрегатов ЛАП по электроино-микроскопическим данным с использованием моделирования на УЦВМ и оптической обработки изображений в когерентных системах [34]. Необходимо было уточнить, под каким углом две группы тримеров расположены по отношению друг к другу.
Интерпретация электронно-микроскопических изображений кристаллической лейцинаминонептидазы
На рис. 111, б показано электронно-микроскопическое изображение кристаллических агрегатов ЛАП с увеличением 300 000. С целью исключения артефактов для контрастирования использовали как катионные (уранилаксалат), так и анионные (метил-аминовольфрамат) контрастирующие вещества.
Негатив электронно-микроскопического изображения ЛАП (рис. 111, б) помещали в дифрактометр. Описание дифрактометра

(кликните для просмотра скана)
имеется в работе [2]. Дифракционный спектр участка микрофотографии приведен на рис. 111, в. Как показали замеры, дифракционные максимумы спектра располагаются на концентрических окружностях (рис. 111, г), радиусы которых представляются рядом чисел:  В соответствии с выражением (9.3) от спектра изображения можно перейти опять к плоскому изображению. При построении модельных изображений использовались статистические параметры расположения дифракционных максимумов в спектре.
В соответствии с выражением (9.3) от спектра изображения можно перейти опять к плоскому изображению. При построении модельных изображений использовались статистические параметры расположения дифракционных максимумов в спектре.
На рис. 111, д, е показаны модельные изображения с истинным характером симметрии. Распределение энергии в спектре по направлениям 0,60, 120° (рис. 111, в, г) соответствует распределению интенсивности в структуре вдоль направлений, указанных стрелками 1, 3, 2 (поворот на 90°, рис. 111, в); составляющие спектра вдоль направлений 30, 90, 150° (рис. 111, г) соответствуют распределениям интенсивности в структуре по направлениям, указанным стрелками 6, 5, 4 (рис. 111, д). Положение рефлексов на окружности радиусов и  (рис. 111, в, г) соответствует расстояниям в реальной структуре
(рис. 111, в, г) соответствует расстояниям в реальной структуре  и (рис. 111, е).
и (рис. 111, е).
Проекция каждой пары тримеров обладает симметрией третьего порядка, узлы решетки представляют собой центры симметрии шестого порядка (рис. 111, д). Элементарная ячейка  путем трансляций вдоль направлений 1, 3 формирует изображение структуры.
путем трансляций вдоль направлений 1, 3 формирует изображение структуры.
Следующий этап обработки изображения состоял в том, чтобы точно определить геометрические параметры элементарной ячейки структуры. Для этого была проведена двумерная амплитудная фильтрация электронно-микроскопического изображения [2]. Результатом фильтрации явился «очищенный» от шумов участок электронно-микроскопического снимка, на котором видно, что пара тримеров в проекции представляет собой шестиугольник с неравными сторонами (рис. 112, а). Чтобы убедиться в этом, с помощью денситометра оптическая плотность каждого участка отфильтрованного снимка была оцифрована. Затем участки одинаковой плотности были соединены линией. Одно из изображений пары тримеров, оконтуренное линией равной плотности, показано на рис. 112, б, где  стороны шестиугольника. На основе измерений величин
стороны шестиугольника. На основе измерений величин  была построена гистограмма (рис. 112, в). Из гистограммы видно, что отношение наиболее вероятных значений сторон шестиугольника составляет
была построена гистограмма (рис. 112, в). Из гистограммы видно, что отношение наиболее вероятных значений сторон шестиугольника составляет  а распределение близко к нормальному.
а распределение близко к нормальному.
Итак, после проведенных измерений (рис. 112,в), имея априорную информацию о возможной агрегации субъединиц в пространстве (рис. 111,а), можно с помощью моделирования на УЦВМ попытаться определить угловое расположение субъедшшц по отношению друг к другу.
Рис. 112. (см. скан) Определение размера сторон шестиугольника, образованного парой тримеров а — иаображение кристаллической лейцинаминопецтидазы, полученное в результате оптической фильтрации; б - контур равной оптической плотности; в — гистограмма распределения соотношения сторон
При изучении реальных биологических структур мы сталкиваемся с трудностями при их описании. Поэтому для задач моделирования исследуемая объемная система нуждается в некоторых упрощениях.
Эти упрощения должны обеспечить построение математической модели, содержащей в себе основные элементы

Рис. 113. Результат моделирования структуры кристаллической лейцина-минопептидазы на УЦВМ а — изменение соотношения сторон шестиугольника в зависимости от углового расположения пары тримеров; б - условное изображение пары тримеров на экране дисплея
оригинала и в то же время обеспечивающей возможность анализа структуры оптимальным образом.
В данном случае каждый тример на первом этапе моделирования на УЦВМ был представлен в виде трех шариков равномерной плотности. Структурная связь между тримерами в одной плоскости заменялась условием касания соседних тримеров и соответствующих тримеров в параллельной плоскости. Варьировался угол поворота а верхнего тримера относительно нижнего в пределах  Построенные таким образом модификации модели обрабатывались с помощью УЦВМ путем введения математического оператора, соответствующего формированию реального изображения структуры в электронном микроскопе [см. выражение (9.1)]. Полученные цифровые массивы распределения плотности модельного «изображения» структуры сравнивались с массивом плотности пары тримеров на электронно-микроскопической фотографии структуры, полученным на денситометре. За критерий близости выбирался минимум среднеквадратичных отклонений, вычисленный по соответствующим точкам массива реальной структуры и модельных вариантов, полученных при разных углах ориентации тримеров. Кроме математического критерия оценки проводилась визуальная оценка близости модели и объекта с помощью дисплея, а также цифровых распечаток рассматриваемых массивов, также производилось сравнение и по двумерным спектрам. Для этого с помощью быстрого преобразования Фурье на УЦВМ строились «дифракционные» картинки от разных модификаций моделей и сравнивались с дифракционными спектрами реальной структуры.
Построенные таким образом модификации модели обрабатывались с помощью УЦВМ путем введения математического оператора, соответствующего формированию реального изображения структуры в электронном микроскопе [см. выражение (9.1)]. Полученные цифровые массивы распределения плотности модельного «изображения» структуры сравнивались с массивом плотности пары тримеров на электронно-микроскопической фотографии структуры, полученным на денситометре. За критерий близости выбирался минимум среднеквадратичных отклонений, вычисленный по соответствующим точкам массива реальной структуры и модельных вариантов, полученных при разных углах ориентации тримеров. Кроме математического критерия оценки проводилась визуальная оценка близости модели и объекта с помощью дисплея, а также цифровых распечаток рассматриваемых массивов, также производилось сравнение и по двумерным спектрам. Для этого с помощью быстрого преобразования Фурье на УЦВМ строились «дифракционные» картинки от разных модификаций моделей и сравнивались с дифракционными спектрами реальной структуры.
Моделирование с использованием УЦВМ позволило в процессе работы выявлять между моделью и реальным объектом как сходство, так и расхождения, обусловленные или построением модели,
или влиянием случайных «шумов». Последовательное сглаживание таких расхождений приводило к постепенному уточнению модели. В результате было рассчитано отношение длин сторон как функция от взаимного угла поворота Пары тримеров, расположенных в двух параллельных плоскостях (рис. 113, а). Соотношению сторон  соответствовал угол
соответствовал угол  На рис. 113,б показано одно из изображений модели, рассчитанной на УЦВМ, сфотографированное с экрана дисплея.
На рис. 113,б показано одно из изображений модели, рассчитанной на УЦВМ, сфотографированное с экрана дисплея.
Таким образом, сочетание оптической обработки изображений с математическим моделированием структуры на УЦВМ помогает количественной интерпретации пространственной организации объекта. Оба метода исследования дополняют друг друга, подсказывая новые пути для более успешного моделирования.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ АВТОРОВ
- ВВЕДЕНИЕ
- 1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ БИОХИМИЧЕСКИХ СИСТЕМ
- Глава первая. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НЕПРОТОЧНЫХ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
- 1.2. Ферменты — белковые катализаторы и регуляторы
- 1.3. Метод графов
- 1.4. Модели реакций, катализируемых одноцентровыми ферментами
- 1.5. Модели реакций, катализируемых олигомерными ферментами
- 1.6. Свойства реакции …
- 1.7. Свойства двухсубстратной реакции
- Глава вторая. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОТОЧНЫХ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
- 2.2. Модель открытой реакции … с субстратным угнетением
- 2.3. Модель двухсубстратной реакции с субстратным угнетением
- 2.4. Динамика открытых реакций, катализируемых олигомерными ферментами
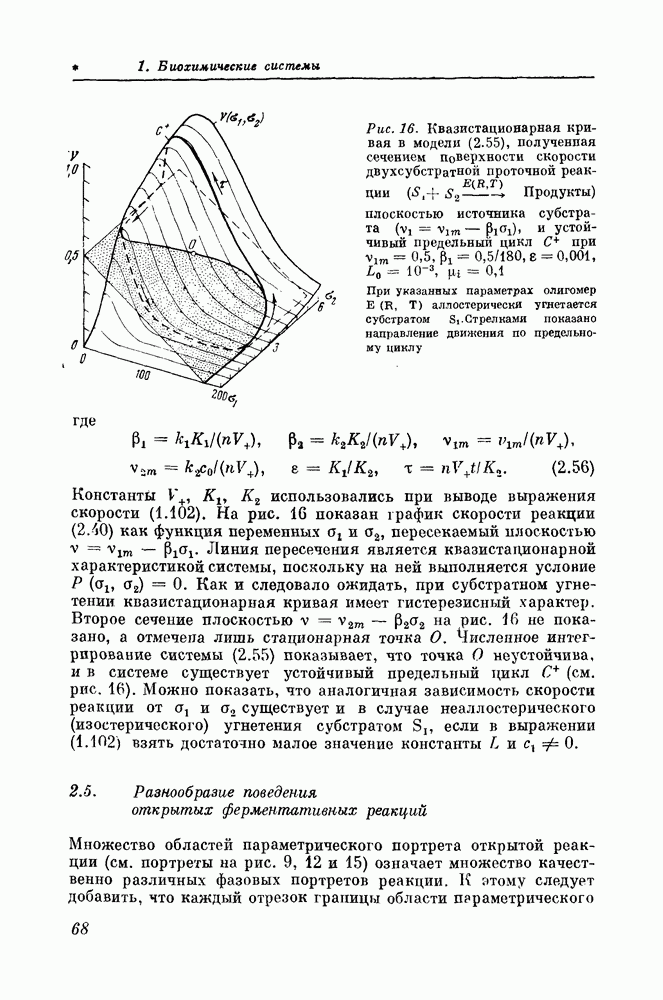
- 2.5. Разнообразие поведения открытых ферментативных реакций
- 2.6. Эквивалентные математические и кинетические модели
- 2.7. Эффект депонирования
- Глава третья. МОДЕЛИРОВАНИЕ ПОЛИФЕРМЕНТНЫХ СИСТЕМ
- 3.1. Полиферментные системы и их модели
- 3.2. Уровни функциональной организации полиферментных систем
- 3.3. Простая модель стехиометрической структуры энергетического метаболизма
- 3.4. Два класса аллостерических регуляторных связей, контролирующих энергетический метаболизм
- 2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ВОЗБУДИМЫХ МЕМБРАН
- Глава четвертая. КАЧЕСТВЕННЫЕ МЕТОДЫ В ИССЛЕДОВАНИИ МОДЕЛЕЙ МЕМБРАН
- 4.1. Построение уравнений второго порядка для моделей Ходжкина — Хаксли и Побла
- 4.2. Фаэовые портреты систем второго порядка
- 4.3. Исследование основных режимов мембраны аксона кальмара с помощью качественных методов
- 4.4. Исследование основных режимов мембраны волокна Пуркинье сердца с помощью качественных методов
- 4.5. Математические детали асимптотического сведения уравнений Ходжкина — Хаксли к системе второго порядка Н-Н2
- Глава пятая. БИОЛОГИЧЕСКИ АКТИВНЫЕ ВЕЩЕСТВА, ИОННЫЕ ТОКИ И ЭЛЕКТРОФИЗИОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ МЕМБРАН
- 5.2. Техника анализа мембран по записям ионных токов
- 5.3. Фазовые портреты мембран сердечной, нервной и мышечной клеток
- 5.4. Анализ действия веществ на мембраны
- 5.5. Предсказание электрофизиологических эффектов с помощью качественных методов
- 5.6. Границы применимости анализа, мембран по фазовому портрету
- 5.7. Оценка на математических моделях мембран точности построения фазового портрета по записям ионных токов
- 3. ВОЗБУДИМЫЕ СРЕДЫ. ВОЛНЫ И АВТОВОЛНОВЫЕ ПРОЦЕССЫ
- 6.1. Автоволновые процессы в возбудимых средах
- 6.2. Распространение волн в однородной среде. Спиральная волна, вращающаяся вокруг отверстия, и ревербератор
- 6.3. Возникновение ревербератора в простейшей неоднородной среде
- 6.4. Ревербератор в более детальных моделях
- 6.5. Свойства ревербератора как источника волн. Размножение ревербераторов в неоднородной среде. Бремя жизни
- 6.6. Ревербератор и сердечные аритмии. Уязвимость сердечной ткани
- Глава седьмая. ЭХО — ИСТОЧНИК КОНЦЕНТРИЧЕСКИХ ВОЛН В ВОЗБУДИМЫХ СРЕДАХ
- 7.1. Эхо в простейших моделях. Источник эха и ревербератор
- 7.2. Источник эха в моделях, описываемых обыкновенными дифференциальными уравнениями
- 7.3. Эхо в непрерывных возбудимых средах
- 7.4. Эхо в модели клеток сердца. Уязвимость
- Глава восьмая. ВЗАИМОДЕЙСТВИЕ ИСТОЧНИКОВ ВОЛН. АВТОВОЛНОВЫЕ ПРОЦЕССЫ И СЕРДЕЧНЫЕ АРИТМИИ
- 8.2. Синхронизация при взаимодействии источников волн
- 8.3. Размножение ревербераторов и фибрилляция
- 8.4. Взаимодействие источников эха
- 8.5. Связь параметров возбудимых сред с характеристиками дифференциального уравнения мембраны
- 8.6. Стационарные и нестационарные режимы распространения
- 8.7. Результаты микроэлектродного исследования уязвимости
- 8.8. О параметрах, контролирующих уязвимость в математических моделях и в миокарде
- 8.9. Следствия из моделей для антиаритмических веществ
- 4. ПРОСТРАНСТВЕННАЯ ОРГАНИЗАЦИЯ БИОЛОГИЧЕСКИХ СТРУКТУР
- Глава девятая. МОДЕЛИРОВАНИЕ ОБЪЕМНЫХ КЛЕТОЧНЫХ СТРУКТУР. ВИРУСЫ, ФЕРМЕНТЫ
- 9.2. Математические основы объемной реконструкции
- 9.3. Модель трехмерной структуры отростка бактериофага
- 9.4. Голографический синтез объемного изображения поверхности клеточной мембраны
- 9.5. Моделирование структуры биологических макромолекул
- Глава десятая. АНАЛИЗ КЛЕТОЧНЫХ СТРУКТУР ПО ИХ ИЗОБРАЖЕНИЯМ. ГЛИЯ—СОСУДЫ, ХРОМОСОМЫ
- 10.1. Преобразование изображений клеток в цифровую форму
- 10.2. Определение морфометрических параметров клеток и клеточных структур
- 10.3. Исследование глиально-сосудистой системы головного мозга
- 10.4. Модель сокращения длины хромосом в митозе
- Глава одиннадцатая. ВОССТАНОВЛЕНИЕ ЛИНЕЙНОЙ СТРУКТУРЫ БИОПОЛИМЕРОВ
- 11.1. Анализ первичной последовательности нуклеиновых кислот
- 11.2. Математическая постановка проблемы
- 11.3. Восстановление слов по составу второго ранга
- 11.4. Метод подстановки при восстановлении слов
- 11.5. Оптимизация биохимического эксперимента