4.5. Математические детали асимптотического сведения уравнений Ходжкина — Хаксли к системе второго порядка Н-Н2

1. В уравнениях Ходжкина — Хаксли выполнены соотношения

Эти соотношения использовались Фитц-Хью [11] для построения так называемой системы, в которой оставались быстрые переменные а медленные переменные фиксировались. Такой подход позволяет анализировать лишь быстрые движения (передний фронт но не весь

Систему второго порядка, описывающую весь мы получили для уравнений Нобла, исключив быстрые переменные (раздел 4.1). Для уравнений Ходжкина — Хаксли так удается исключить лишь переменную (здесь постоянные времени одного порядка). Соотношения (4.10) — (4.11) указывают, как можно исключить еще одну переменную: объединить описание переменных Но при этом необходимо позаботиться о решении двух вопросов. Соотношение (4.11) задает связь между установившимися значениями Что делать при произвольных начальных условиях? Соотношения (4.10), (4.11) выполняются приближенно. Можно ли быть уверенным, что при этом решения систем разойдутся мало? 2, Введем малые параметры

и рассмотрим сначала случай, когда

Покажем, что тогда в системе при начальных условиях, лежащих в области

имеется закон сохранения

Используя равенство (4.15), можно построить систему третьего порядка

Система (4.16) эквивалентна уравнениям в области (4.14).

Для доказательства существования закона сохранения (4.15) введем в систему вместо переменной переменную

и покажем, что при С учетом равенства (4.12) уравнения после замены (4.17) примут вид

Начальные условия (4.14) в новых переменных имеют вид:

Уравнение четвертое системы (4.18) при фиксированном и произвольных начальных условиях имеет решение

Выбрав любое (достаточно получим, что решение четвертого уравнения системы (4.18) удовлетворяет неравенству

Отсюда следует, что влечет и равенство (4.15) доказано.

Отметим, что ограничения (4.14) на начальные условия не сужают область применения системы для анализа экспериментальных данных, так как при отсутствии внешних воздействий мембрана довольно быстро переходит в состояние покоя. Поэтому любой эксперимент начинается из состояния покоя. А в силу условия состояние покоя лежит в области (4.14).

3. Покажем теперь, что и в случае, когда решения системы второго порядка близки к решениям исходных уравнений

Для этого докажем, что если начальное значение переменной удовлетворяет условию где задается соотношением (4.24), то при всех выполнено неравенство

В системе (4.18) при условии и последнее уравнение заменяется уравнением

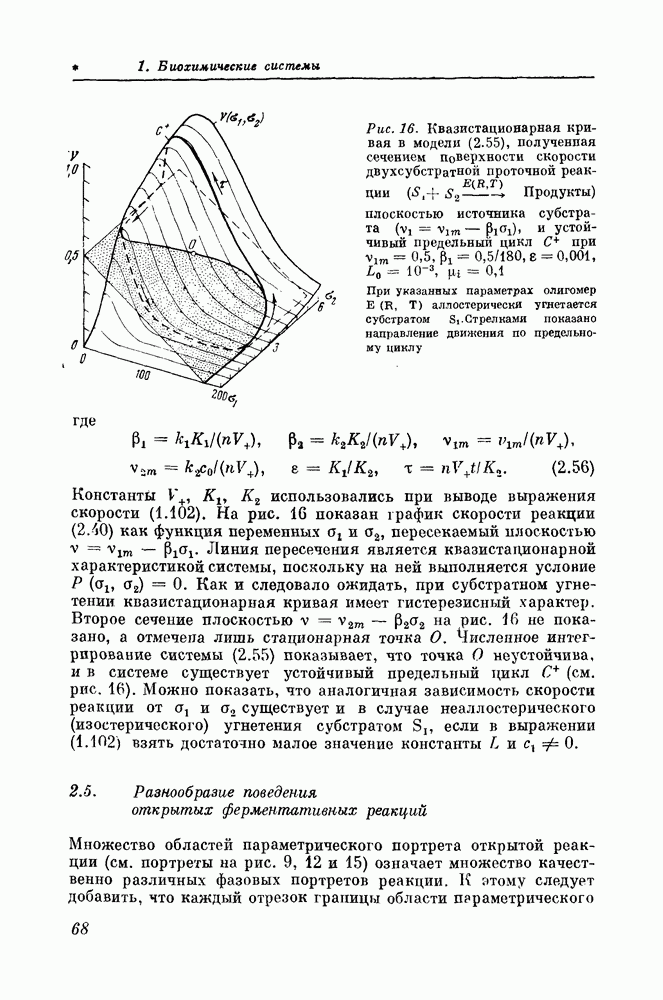
и поскольку в выполнено неравенство то

где

Рассмотрим область Как следует из уравнений (4.22) и (4.23), на границе области (т. е. при выполнено условие Но, чтобы вышла за пределы области необходимо, чтобы Отсюда сленует неравенство (4.21).

Теорема о непрерывной зависимости решений от параметра для первых трех уравнений системы (4.18) (параметр показывает, что решения систем различаются на величину — где время эксперимента.

На этом заканчивается обоснование перехода от уравнений к уравнениям поскольку переход от системы к системе обосновывается так же, как и для модели Нобла в разделе 4.1.

Таким образом, рассмотренные в этой главе примеры демонстрируют, что широкий класс электрофизиологических явлений с достаточно хорошей для эксперимента точностью может быть описан и даже предсказан на основе очень простых моделей второго порядка, полученных предельными переходами из моделей типа Ходжкина — Хаксли.