7.3. Эхо в непрерывных возбудимых средах

Эхо в волокне (уравнения с частными производными). Основная проблема, решавшаяся при моделировании эха в системе уравнений с частными производными, состояла в следующем. Возможен ли перезапуск в распределенной системе (например, в волокне) или же диффузия «размоет» разрывы в распределении состояний соседних элементов и сделает перезапуск невозможным? Это та же проблема, которая важна и для ревербератора; ее формулировка для эха имеет то преимущество, что позволяет решать одномерную задачу вместо двумерной.

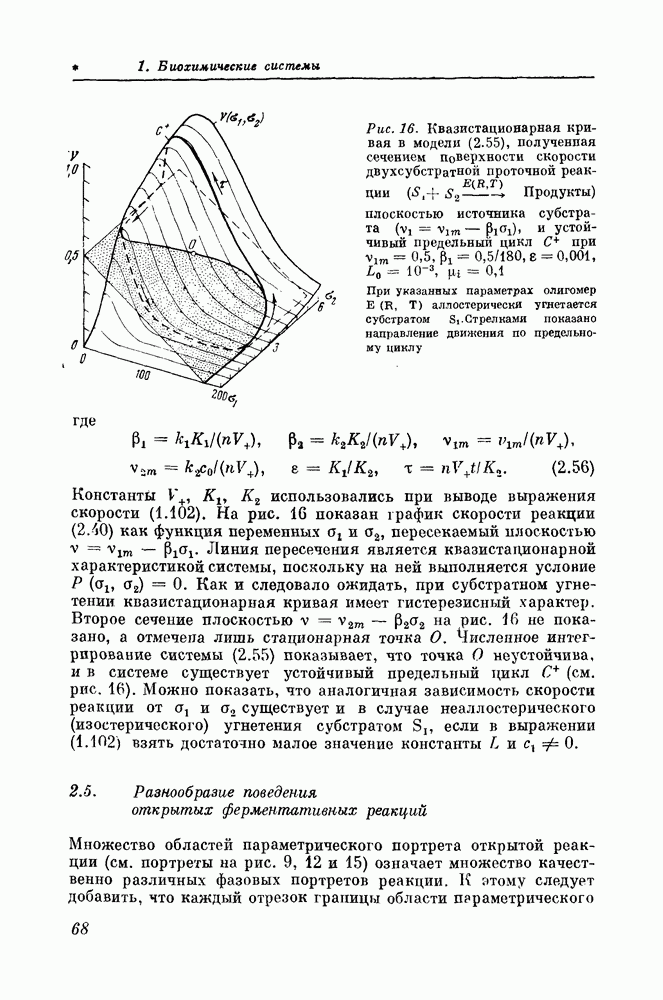
Исследовалась система, описывающая распространение возбуждения в волокне:

Граничные условия:

Здесь ток, идущий через данный элемент от соседних.

Предполагалось, что: 1. Вырожденная система

Рис. 81. Свойства одиночного возбудимого элемента волокна а — нуль-изоклины системы (7.6) при импульс, генерируемый одиночным возбудимым элементом

Рис. 82. Распространение волн в цепочке клеток в режиме эха а, б - антисимметричное; в, г - симметричное, а, в — состояние цепочки в начальный момент; состояние цепочки после того, как пробежала одна волна

абсолютно устойчива (в физиологических терминах: каждый элемент не является спонтанно активным). 2. Тривиальное решение и устойчиво (волокно, составленное из таких элементов не является спонтанно активным, т. е. нет неустойчивости, вызванной диффузией).

В такой системе для всех начальных условий, кроме некоторых специальных, решение стремится к константе и где координаты точки покоя вырожденной системы (рис. 81). Возникающие здесь при специальных начальных условиях автоколебания можно было бы назвать жесткими автоколебаниями в волокне, по аналогии с жесткими автоколебаниями в точечных системах.

Вообще говоря, если эхо в подобной системе существует, возможны два типа возбуждения волокна — антисимметричное и симметричное (рис. 82).

Антисимметричный тип эха в волокне, полученный расчетами на ЦВМ [79], приведен на рис. 83. Для получения эха в системе (7.7) функции и начальные условия выбирались так, чтобы по крайней мере для одной точки [в нашем случае точки А (с координатой за счет члена диффузии особая точка становилась неустойчивой (условие 1, раздел 7.2) и в системе обыкновенных дифференциальных уравнений период автоколебаний при внешнем токе был короче, чем удвоенная длительность импульса (условие 2, раздел 7.2).

Эхо в химической системе. Фото источников эха, полученных в химической возбудимой среде, приведены на рис. 84 [7]. Среда та же самая, в которой был получен и режим ревербератора (глава 6).

Рис. 83. Эхо в волокно (расчет на ЦВМ) а — распределение потенциалов вдоль волокна для различных моментов времени. Начальные условия отмечены индексом (вверху); правая и левая половины волокна запускают одна другую (цифры указывают время в отн. сначала правая половина возбуждается от левой затем прекращается возбуждение в левой половине волокна после чего левая половина возбуждается от правой (распределение потенциалов при почти повторяет начальные условия); возникновение новой волны (детальное изображение) в правой половине волокна

Рис. 84. Ведущий центр в химической возбудимой среде Кадры сняты с интервалом 30 с; длина волны равна [5]

Если ревербератор в такой среде получали механическим разрывом фронта волны [5] (лопаточкой или за счет резкого поворота чашки Петри, в которой происходит реакция), то для получения источника эха использовали так называемую процедуру переноса для создания начальной разности фаз. Пипеткой переносили каплю жидкости из района фронта возбуждения в область покоя, и эта область становилась периодически работающим источником волн.

Источниками концентрических волн в такой реакции могут быть кроме источника эха также и элементы объема, находящиеся в состоянии автоколебаний (например, из-за наличия микрозагрязнений [38]). Возникающий при процедуре переноса источник концентрических волн (описанный под названием ведущий центр) был идентифицирован как источник эха: при переносе капли жидкости из одной области покоя в другую или из одной области возбуждения в другую эти источники не возникали.

Оценка размера источника эха в модели уравнений с частными производными. В -модели размер источника эха оказывается нулевым в отличие от ревербератора, размер которого равен длине волны Поэтому размер источника эха необходимо оценивать на других, более детальных моделях.

Численные расчеты источника эха в волокне, описываемом дифференциальными уравнениями с частными производными [25, 39], показывают, что линейный размер источника эха оказывается порядка длины переднего фронта потенциала действия, распространяющегося в этом волокне. Всегда ли это так?

Этот вопрос был исследован в работе [40]. Рассматривалось волокно, задаваемое релаксационной системой

Используя релаксационность системы 1), с помощью качественных методов анализа удалось показать, что размер источника эха оказывается порядка длины фронта перепада в обыкновенном дифференциальном уравнении где некоторое фиксированное значение медленной переменной.