11.2. Математическая постановка проблемы

Формулировка задачи в виде восстановления слов

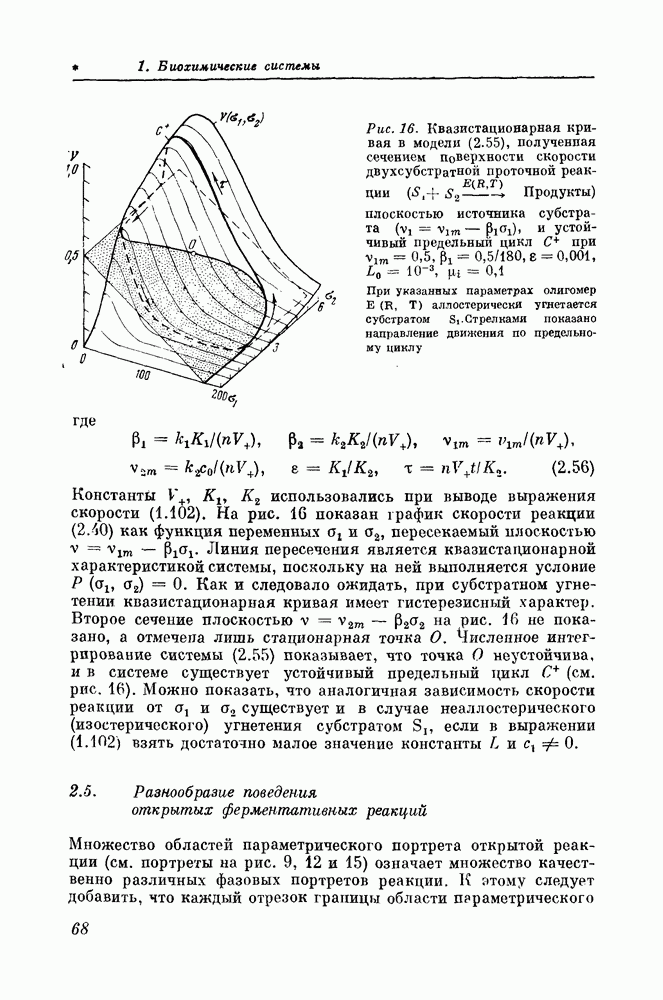
Структуру биополимера будем рассматривать как слово в некотором алфавите. Отдельным фрагментам, которые получаются гидролизом (полным или частичным), соответствуют подслова определяемого слова. Для наглядности изложения будем пользоваться геометрическим представлением слов. На рис. 121 показан фрагмент молекулы 5SPHK Е. coli в виде двух разбиений с помощью нуклеаз на подслова. Одно из разбиений соответствует гидролизу панкреатической рибонуклеазой (подслова другое— рибонуклеазой (подслова

Введем основные определения. Подслово является перекрытием подслов подслово перекрытием подслов Пусть тогда части подслов называются граничными, а подслово внутренним для подслова Например, подслово является внутренним для подслова

Задачу восстановления слова можно сформулировать следующим образом. Пусть набор произвольных подслов. Найти: а) условия существования, б) единственности и в) способ построения некоторого слова для которого подслова из набора принадлежащего образуют единую последовательность перекрывающихся подслов, а остальные подслова набора являются внутренними подсловами подслов из набора

(кликните для просмотра скана)

Обычно накладывается ограничение на искомую последовательность: она должна содержать определенное число каждой из букв.

Прежде чем дать решение этой задачи, покажем, как ее можно сформулировать на другом математическом языке.

Формулировка задачи в терминах теории графов

Для каждого подслова выберем все подслова с которыми подслово перекрывается справа, перекрытие подслов соответствует бинарному отношению на множестве такому, что в А входят пары элементов, соответствующие перекрывающимся подсловам.

Любое бинарное отношение на множестве может быть изображено в виде матрицы или в виде ориентированного графа [135, 136, 139].

Подсловам можно поставить в соответствие множество вершин графа. Если подслово, соответствующее перекрывается справа с подсловом, соответствующим то вершины соединяются направленным ребром, идущим из На ребрах указываются буквы, по которым происходит перекрытие. Проведение зтой процедуры для всех точек приводит к построению ориентированного графа, соответствующего бинарному отношению (рис. 122). Построению последовательности всех перекрывающихся подслов соответствует построение в ориентированном графе пути, проходящего в направлении ребер через все вершины по одному разу. Такой путь в графе называется гамильтоновым путем (или циклом, если путь замкнут). Впервые задача о поиске гамильтонова цикла была поставлена в 1877 г., однако до сих пор нет эффективной процедуры нахождения гамильтонова пути в произвольном графе и методов доказательства существования такого пути. У известных алгоритмов сложность вычислений (число элементарных операций) определения гамильтонова цикла растет, как экспонента числа вершин. Это связано с перебором большого числа вариантов движения по графу.

Если набор подслов таков, что для каждого подслова известны его граничные буквы, то может быть построено бинарное отношение такое, что будет представлять собой пары перекрытий (правые и левые), входящие в каждое подслово. В этом случае перекрываниям подслов можно поставить в соответствие вершины графа, а ребрам — сами подслова, выбрав направление ребра, например от левого перекрытия к правому (рис. 122, д).

Построение последовательности всех перекрывающихся подслов соответствует нахождению в таком ориентированном графе пути, проходящего через все ребра по одному разу. Такой путь

называется эйлеровым. Впервые эта задача была сформулирована в 1736 г. Для эйлерова пути известны эффективные алгоритмы и условия существования такого пути.

В терминах теории графов решение задачи восстановления слова можно интерпретировать как стремление заменить задачу Гамильтона задачей Эйлера.

Сведение задачи нахождения гамильтонова пути к задаче нахождения эйлерова пути можно рассматривать непосредственно на графе бинарных отношений подслов А [131]. Если бинарное отношение А, определяющее граф, таково, что множество его ребер (граничных букв) разбивается на непересекающиеся подмножества то каждому ребру такого графа можно поставить в соответствие вершину нового графа а каждой вершине графа ребро графа (граф назовем «сопряженным» графу Если исходная информация представляет собой набор подслов, полученных полными гидролизами, то всегда можно построить сопряженный граф и тем самым свести задачу восстановления слова к задаче Эйлера. Необходимым и достаточным условием существования гамильтонова цикла в ориентированном графе общего вида является наличие в этом графе суграфа (т. е. графа которого отсутствует часть ребер), такого, что сопряженный ему граф есть эйлеров (эйлеровым называется граф, в котором есть эйлеров цикл). В общем случае способ нахождения такого суграфа не известен.

Задача о единственности восстанавливаемого по исходной информации слова на графах интерпретируется как единственность гамильтонова или эйлерова пути и может быть решена построением всех возможных путей. В графах на рис. 122 возможны несколько путей. Способом борьбы с неоднозначностью ответа является пополнение исходной информации, например за счет увеличения числа полных или частичных гидролизов, что позволяет уменьшить число ребер на графе бинарных отношений.

Если информация задана продуктами полных гидролизов всей молекулы и полных гидролизов ее фрагментов, полученных частичным гидролизом, то для молекулы и фрагментов можно построить ориентированные графы («граф молекулы» и «графы фрагментов»). Очевидно, что множества вершин графов фрагментов будут подмножествами вершин графа молекулы, а множество ребер графов фрагментов — подмножествами ребер графа молекулы. Искомый гамильтонов путь должен проходить только через те ребра, входящие или выходящие из общих для этих графов вершин, которые являются общими для этих графов. Формально

Рис. 123. Совмещение «графа фрагментов» с «графем молекулы»

это осуществляется совмещением общих вершин графа фрагмента и графа молекулы и вычеркиванием тех из входящих в эти вершины или выходящих из них ребер, которые не являются общими для обоих графов. На рис. 123 показан «граф молекулы» (из рис. 122), построенный с учетом «графа фрагментов». Основная трудность в этой процедуре состоит в установлении общих для обоих графов вершин.

Установление тождества между вершинами различных графов, необходимое для их совмещения, называется идентификацией продуктов полных гидролизов фрагмента и всей молекулы. В общем случае идентификация не является однозначной процедурой и требует перебора вариантов, что приближает ее по сложности вычисления к задаче определения гамильтонова пути. Однако если все слова набора разные, то идентификация проводится тривиально. Идентификация может быть легко выполнена, если используемые фрагменты определенным образом упорядочены или удовлетворяют достаточно жестким условиям, например

когда у всех фрагментов один из концов общий. Использование именно таких фрагментов довольно широко практикуется биохимиками [109, 110]. Кроме того, условие связности «графа фрагмента» также ограничивает возможные способы его совмещения с «графом молекулы». Поэтому оказывается полезным использовать процедуру идентификации во многих практически встречающихся задачах восстановления первичной структуры

Рассмотрение задачи восстановления слов в терминах теории графов обеспечивает наглядность рассуждений, однако непосредственное использование графов для решения конкретных задач неудобно.

Разработано два типа алгоритмов для решения задачи восстановления слов: первоначально на основе кодирования исходной информации в виде состава второго ранга восстанавливаемого слова [128-130, 132], а затем на основе алгебраического метода подстановок [131, 133-135].