| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
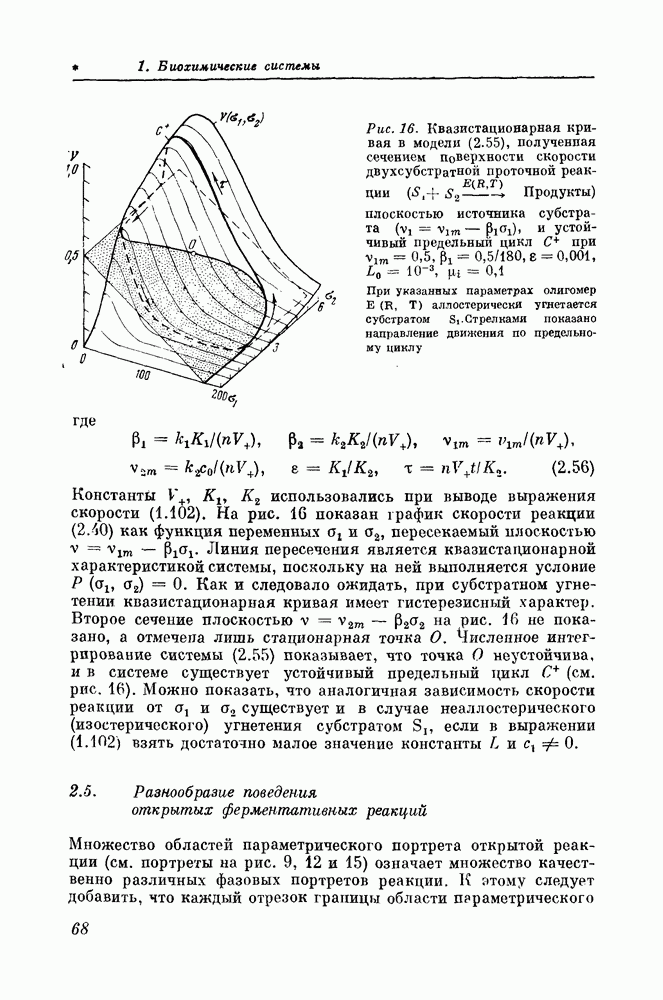
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава десятая. АНАЛИЗ КЛЕТОЧНЫХ СТРУКТУР ПО ИХ ИЗОБРАЖЕНИЯМ. ГЛИЯ—СОСУДЫ, ХРОМОСОМЫ
10.1. Преобразование изображений клеток в цифровую форму
В предыдущей главе сделан акцент на анализе пространственной организации клеточных структур в диапазоне разрешения электронного микроскопа. В этой главе остановимся на методах определения геометрических параметров изображений, полученных с помощью оптического микроскопа, на примерах исследования морфологии хромосом и некоторых срезов ткапи.
Математические методы исследования изображений представляют собой различные способы формального описания двумерных конфигураций оптической плотности с учетом дополнительной информации и целей исследования. В таком виде математическое описание клеточных структур является частным случаем задачи распознавания образов.
Для машинного исследования оптических и геометрических характеристик клеток требуется преобразовать оптическое изображение препарата  в цифровой код. Для этого необходим сканирующий оптический микроскоп.
в цифровой код. Для этого необходим сканирующий оптический микроскоп.
Трудности построения сканирующих оптических микроскопов связаны с необходимостью получения хорошего соотношения сигнал/шум при малой площади сканирующего элемента 
Требуемая величина соотношения сигнал/шум зависит от конкретной постановки задачи. Например, для подсчета числа ядер клеток соотношение сигнал/шум допускается  а для измерения геометрических параметров с ошибкой не более 2% должно быть
а для измерения геометрических параметров с ошибкой не более 2% должно быть  Кроме того, существует множество факторов, искажающих форму сигнала, несущего информацию о структуре клетки (дифракция, нестабильность источников света и светоприемников, расфокусировка и т. д.). Влияние этих факторов на точность измерений проанализировано в работах [39, 50]. В настоящее время создано несколько типов сканирующих оптических микроскопов, в которых ошибки в получении информации о структуре клеток сведены к минимуму.
Кроме того, существует множество факторов, искажающих форму сигнала, несущего информацию о структуре клетки (дифракция, нестабильность источников света и светоприемников, расфокусировка и т. д.). Влияние этих факторов на точность измерений проанализировано в работах [39, 50]. В настоящее время создано несколько типов сканирующих оптических микроскопов, в которых ошибки в получении информации о структуре клеток сведены к минимуму.
Сканирующие системы осуществляют последовательный просмотр поля изображения, выполняя фиксированные шаги вдоль направления осей х, у, и измеряют оптический сигнал после очередного шага. Таким образом, осуществляются квантование плоскости изображения и представление самого изображения в виде матрицы, связывающей значение оптического сигнала с координатами точки, где он был измерен. Процесс квантования приводит к геометрическим искажениям, которые в общем случае трудно поддаются учету [40—42, 50].
Дискретизация оптической плотности структуры объекта  по амплитуде также приводит к различного рода искажениям. Естественно, что квантование значений функции тесно связано с квантованием ее аргументов, однако указанные случаи геометрических искажений предполагали наличие черно-белого изображения, т. е.
по амплитуде также приводит к различного рода искажениям. Естественно, что квантование значений функции тесно связано с квантованием ее аргументов, однако указанные случаи геометрических искажений предполагали наличие черно-белого изображения, т. е.  при
при  принадлежащем к
принадлежащем к  при
при  за пределами А, где А — множество точек объекта. Реальные изображения биологических структур имеют полутона, которые, с одной стороны, обусловлены переменной прозрачностью самих объектов, а с другой — связаны с ограниченным пространственным разрешением приборов, формирующих изображение.
за пределами А, где А — множество точек объекта. Реальные изображения биологических структур имеют полутона, которые, с одной стороны, обусловлены переменной прозрачностью самих объектов, а с другой — связаны с ограниченным пространственным разрешением приборов, формирующих изображение.
Удобно процесс получения изображения рассматривать в частотной области. С помощью преобразования Фурье распределение интенсивности света на изображении можно представить как результат наложения пространственных синусоидальных составляющих. В таком случае устройство ввода изображения можно рассматривать как фильтр низких частот, хорошо пропускающий низкие пространственные частоты (т. е. крупные детали изображения) и ослабляющий высокие частоты (т. е. мелкие детали).
Частотная характеристика изображения описывается выражением (9.2):


(кликните для просмотра скана)
Восстановление изображения в частотной области может быть осуществлено путем коррекции аппаратной функции системы (см. раздел 9.1):

где  частотная характеристика восстановленного изображения,
частотная характеристика восстановленного изображения,  функция, корректирующая частотную характеристику устройства ввода и процесс дискретизации. Сказанное означает, что для восстановления частотной характеристики изображения необходимо соответствующим образом изменить амплитуды его частотных составляющих.
функция, корректирующая частотную характеристику устройства ввода и процесс дискретизации. Сказанное означает, что для восстановления частотной характеристики изображения необходимо соответствующим образом изменить амплитуды его частотных составляющих.
После корректирования частотной характеристики необходимо сделать переход в действительную область и определить истинное распределение интенсивностей света на изображении:

Подобный способ восстановления изображения позволяет уменьшить искажения, вызванные процессом ввода и дискретизацией. Однако он связан с большим количеством вычислений. Кроме того, иногда он малоэффективен, так как значительный подъем частотной характеристики в области высоких частот может вызвать дополнительное «зашумление» изображения. Изображение хромосом на метафазной пластинке является таким изображением, где высокочастотные пространственные гармоники имеют существенное значение. В то же время световой микроскоп, работающий в видимой области, не пропускает высокочастотные составляющие.
Основная трудность при анализе изображений состоит в определении того, что следует считать границей объектов. Поскольку существует непрерывная функция плотности  то нельзя объективно указать такого значения уровня ограничения, где плоскость 1(х, у)
то нельзя объективно указать такого значения уровня ограничения, где плоскость 1(х, у)  соответствовала бы реальной форме объекта. В качестве иллюстрации на рис. 114 представлена модель дифракции на хромосоме в предположении, что истинное изображение имело бы во всех точках, принадлежащих хромосоме, значение яркости, равное 32 условным единицам. Как видно, ни одна линия изоплотности не соответствует истинной границе хромосомы.
соответствовала бы реальной форме объекта. В качестве иллюстрации на рис. 114 представлена модель дифракции на хромосоме в предположении, что истинное изображение имело бы во всех точках, принадлежащих хромосоме, значение яркости, равное 32 условным единицам. Как видно, ни одна линия изоплотности не соответствует истинной границе хромосомы.
Естественной моделью объекта являлась бы функция  типа:
типа:


Рис. 115. Коррекция изображений а — матрица весов; б, в — изображения хромосомы до корректировки при двух уровнях ограничения; г, д - изображения той же хромосомы после корректировки при тех же уровнях ограничения
где  уровень плотности объекта,
уровень плотности объекта,  уровень плотности фона. При этом границей объекта является линия разрыва значений
уровень плотности фона. При этом границей объекта является линия разрыва значений  определяющая контур объекта
определяющая контур объекта  Преобразование плотности изображения в соответствии с указанной моделью объекта называют бинаризацией изображения (превращением полутонового изображения в черно-белое).
Преобразование плотности изображения в соответствии с указанной моделью объекта называют бинаризацией изображения (превращением полутонового изображения в черно-белое).
В настоящее время в распоряжении исследователей имеется много эвристических методов коррекции изображений, обеспечивающих подчеркивание границ объектов [45]. Применяют преобразование изображения с помощью локального оператора Лапласа [46]. В цифровой форме это выражается в виде суммирования с некоторыми весами оптических плотностей в данной и соседних с ней точках (рис. 115, а). Такое преобразование понижает до нуля уровень плотности в районе, где он был примерно постоянным.
Практически распределение весов выбирается исходя из визуального исследования результатов преобразования. Для каждого устройства ввода необходимо свое распределение весов.
На рис. 115, б, д приведены результаты обработки изображения одной хромосомы. Видно, что в результате коррекции бинарное изображение объекта становится менее критичным к выбору порога дискриминации плотности. Вместе с тем преобразование с помощью весовой матрицы требует значительно меньше вычислений (только 12 суммирований на каждую точку растра). Интересный алгоритм для выбора порога в наиболее крутом месте усредненного фронта нарастания плотности предложен в работах [48—49].
Однако, несмотря на большое количество методов для коррекции границ клеток (обычно в литературе они называются методами предобработки), истинные границы удается найти далеко не всегда. Возможно, поэтому многие исследователи рассматривают бинарное преобразование как выбор подходящего уровня ограничения, а весь дальнейший анализ стремятся выполнить так, чтобы на него как можно меньше влияли погрешности определения границ.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ АВТОРОВ
- ВВЕДЕНИЕ
- 1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ БИОХИМИЧЕСКИХ СИСТЕМ
- Глава первая. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НЕПРОТОЧНЫХ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
- 1.2. Ферменты — белковые катализаторы и регуляторы
- 1.3. Метод графов
- 1.4. Модели реакций, катализируемых одноцентровыми ферментами
- 1.5. Модели реакций, катализируемых олигомерными ферментами
- 1.6. Свойства реакции …
- 1.7. Свойства двухсубстратной реакции
- Глава вторая. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОТОЧНЫХ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
- 2.2. Модель открытой реакции … с субстратным угнетением
- 2.3. Модель двухсубстратной реакции с субстратным угнетением
- 2.4. Динамика открытых реакций, катализируемых олигомерными ферментами
- 2.5. Разнообразие поведения открытых ферментативных реакций
- 2.6. Эквивалентные математические и кинетические модели
- 2.7. Эффект депонирования
- Глава третья. МОДЕЛИРОВАНИЕ ПОЛИФЕРМЕНТНЫХ СИСТЕМ
- 3.1. Полиферментные системы и их модели
- 3.2. Уровни функциональной организации полиферментных систем
- 3.3. Простая модель стехиометрической структуры энергетического метаболизма
- 3.4. Два класса аллостерических регуляторных связей, контролирующих энергетический метаболизм
- 2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ВОЗБУДИМЫХ МЕМБРАН
- Глава четвертая. КАЧЕСТВЕННЫЕ МЕТОДЫ В ИССЛЕДОВАНИИ МОДЕЛЕЙ МЕМБРАН
- 4.1. Построение уравнений второго порядка для моделей Ходжкина — Хаксли и Побла
- 4.2. Фаэовые портреты систем второго порядка
- 4.3. Исследование основных режимов мембраны аксона кальмара с помощью качественных методов
- 4.4. Исследование основных режимов мембраны волокна Пуркинье сердца с помощью качественных методов
- 4.5. Математические детали асимптотического сведения уравнений Ходжкина — Хаксли к системе второго порядка Н-Н2
- Глава пятая. БИОЛОГИЧЕСКИ АКТИВНЫЕ ВЕЩЕСТВА, ИОННЫЕ ТОКИ И ЭЛЕКТРОФИЗИОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ МЕМБРАН
- 5.2. Техника анализа мембран по записям ионных токов
- 5.3. Фазовые портреты мембран сердечной, нервной и мышечной клеток
- 5.4. Анализ действия веществ на мембраны
- 5.5. Предсказание электрофизиологических эффектов с помощью качественных методов
- 5.6. Границы применимости анализа, мембран по фазовому портрету
- 5.7. Оценка на математических моделях мембран точности построения фазового портрета по записям ионных токов
- 3. ВОЗБУДИМЫЕ СРЕДЫ. ВОЛНЫ И АВТОВОЛНОВЫЕ ПРОЦЕССЫ
- 6.1. Автоволновые процессы в возбудимых средах
- 6.2. Распространение волн в однородной среде. Спиральная волна, вращающаяся вокруг отверстия, и ревербератор
- 6.3. Возникновение ревербератора в простейшей неоднородной среде
- 6.4. Ревербератор в более детальных моделях
- 6.5. Свойства ревербератора как источника волн. Размножение ревербераторов в неоднородной среде. Бремя жизни
- 6.6. Ревербератор и сердечные аритмии. Уязвимость сердечной ткани
- Глава седьмая. ЭХО — ИСТОЧНИК КОНЦЕНТРИЧЕСКИХ ВОЛН В ВОЗБУДИМЫХ СРЕДАХ
- 7.1. Эхо в простейших моделях. Источник эха и ревербератор
- 7.2. Источник эха в моделях, описываемых обыкновенными дифференциальными уравнениями
- 7.3. Эхо в непрерывных возбудимых средах
- 7.4. Эхо в модели клеток сердца. Уязвимость
- Глава восьмая. ВЗАИМОДЕЙСТВИЕ ИСТОЧНИКОВ ВОЛН. АВТОВОЛНОВЫЕ ПРОЦЕССЫ И СЕРДЕЧНЫЕ АРИТМИИ
- 8.2. Синхронизация при взаимодействии источников волн
- 8.3. Размножение ревербераторов и фибрилляция
- 8.4. Взаимодействие источников эха
- 8.5. Связь параметров возбудимых сред с характеристиками дифференциального уравнения мембраны
- 8.6. Стационарные и нестационарные режимы распространения
- 8.7. Результаты микроэлектродного исследования уязвимости
- 8.8. О параметрах, контролирующих уязвимость в математических моделях и в миокарде
- 8.9. Следствия из моделей для антиаритмических веществ
- 4. ПРОСТРАНСТВЕННАЯ ОРГАНИЗАЦИЯ БИОЛОГИЧЕСКИХ СТРУКТУР
- Глава девятая. МОДЕЛИРОВАНИЕ ОБЪЕМНЫХ КЛЕТОЧНЫХ СТРУКТУР. ВИРУСЫ, ФЕРМЕНТЫ
- 9.2. Математические основы объемной реконструкции
- 9.3. Модель трехмерной структуры отростка бактериофага
- 9.4. Голографический синтез объемного изображения поверхности клеточной мембраны
- 9.5. Моделирование структуры биологических макромолекул
- Глава десятая. АНАЛИЗ КЛЕТОЧНЫХ СТРУКТУР ПО ИХ ИЗОБРАЖЕНИЯМ. ГЛИЯ—СОСУДЫ, ХРОМОСОМЫ
- 10.1. Преобразование изображений клеток в цифровую форму
- 10.2. Определение морфометрических параметров клеток и клеточных структур
- 10.3. Исследование глиально-сосудистой системы головного мозга
- 10.4. Модель сокращения длины хромосом в митозе
- Глава одиннадцатая. ВОССТАНОВЛЕНИЕ ЛИНЕЙНОЙ СТРУКТУРЫ БИОПОЛИМЕРОВ
- 11.1. Анализ первичной последовательности нуклеиновых кислот
- 11.2. Математическая постановка проблемы
- 11.3. Восстановление слов по составу второго ранга
- 11.4. Метод подстановки при восстановлении слов
- 11.5. Оптимизация биохимического эксперимента