| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава пятая. БИОЛОГИЧЕСКИ АКТИВНЫЕ ВЕЩЕСТВА, ИОННЫЕ ТОКИ И ЭЛЕКТРОФИЗИОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ МЕМБРАН
Результаты, приведенные в предыдущей главе, показывают, что с помощью качественных методов удается определить основные характеристики математических моделей мембран и проанализировать их поведение при различных изменениях параметров. Поэтому естественно попытаться перенести эти методы на исследование живых мембран. Однако для этого необходимо уметь получать нуль-изоклины непосредственно в эксперименте. Рассмотрим один из подходов к решению этой задачи.
В работах [27—29] описывается метод, позволяющий строить нуль-изоклины и фазовые портреты исследуемых мембран непосредственно по записям токов при фиксации потенциала на мембране. Этот метод отличается простотой: для построения нуль-изоклин достаточно экспериментально определить две вольт-амперные характеристики (для быстрой и медленной компонент мембранного тока) вместо большого числа кривых, которые необходимы для идентификации параметров модели Ходжкина—Хаксли.
Проиллюстрируем этот метод на примерах различных возбудимых мембран (гигантского аксона кальмара, нервного волокна омара, перехвата Ранвье нервного волокна лягушки, волокна портняжной мышцы лягушки, клеток сердца). В конце главы рассмотрим применение этого метода для поиска биологически активных веществ.
5.1. Построение фазового портрета мембраны, по записям ионных токов при фиксации потенциала
Модель мембраны. Как показано в главе 4, уравнения Ходжкина-Хаксли и Нобла с хорошей точностью аппроксимируются системами уравнений второго порядка.
Для анализа реальных мембран преобразуем системы (4.2), (4.5) к виду, удобному для обработки записей ионных токов:

Здесь  мембранный потенциал,
мембранный потенциал,  проводимость для медленного тока I, определяемая как
проводимость для медленного тока I, определяемая как

 потенциал реверсии медленного тока),
потенциал реверсии медленного тока),  экспериментально определяемая вольт-амперная характеристика для установившегося быстрого ионного тока,
экспериментально определяемая вольт-амперная характеристика для установившегося быстрого ионного тока,  внешиий ток,
внешиий ток,  некоторая неизвестная функция, описывающая динамику проводимости медленного тока. Для построения нуль-изоклин знание функции
некоторая неизвестная функция, описывающая динамику проводимости медленного тока. Для построения нуль-изоклин знание функции  не потребуется; нужно будет лишь экспериментально определить зависимость установившегося значения
не потребуется; нужно будет лишь экспериментально определить зависимость установившегося значения  от
от  (при
(при 
Построение нуль-изоклин. Для построения фазового портрета исследуемой мембраны необходимо восстановить по экспериментальным данным только нуль-изоклины  системы (5.1). Удобно рассматривать их отображение на плоскость
системы (5.1). Удобно рассматривать их отображение на плоскость  с помощью уравнения (5.2), поскольку в эксперименте измеряются
с помощью уравнения (5.2), поскольку в эксперименте измеряются

Рис. 43. Построение фазового портрета мембраны по записям токов при фиксации потенциала а — вольт-амперные характеристики для пикового  и установившегося
и установившегося  токов;
токов;  построенные по ним нуль-изоклины уравнений мембраны
построенные по ним нуль-изоклины уравнений мембраны  изоклина
изоклина  изоклина
изоклина 

Рис. 44. Траектория движения изображающей точки во время потенциала действия а — в переменных  ;
;  -отображение на плоскость
-отображение на плоскость  Граница устойчивой и неустойчивой областей (например, точка С) смещена по сравнению с ее положением на плоскости
Граница устойчивой и неустойчивой областей (например, точка С) смещена по сравнению с ее положением на плоскости  непосредственно ионные токи. В результате уравнения изоклин принимают вид:
непосредственно ионные токи. В результате уравнения изоклин принимают вид:

где  вольт-амперная кривая полного установившегося тока.
вольт-амперная кривая полного установившегося тока.
Уравнение первое системы (5.3) следует непосредственно из первого уравнения системы (5.1). Уравнение второе системы (5.3) получается следующим образом. Из равенств  и (5.2) следует, что медленный ток
и (5.2) следует, что медленный ток  равен своему установившемуся значению I:
равен своему установившемуся значению I:

 находится из очевидного равенства
находится из очевидного равенства

(полный установившийся ток  равен сумме установившихся быстрого
равен сумме установившихся быстрого  и медленного I токов). Из равенств (5.5) и (5.4) следует второе уравнение системы (5.3).
и медленного I токов). Из равенств (5.5) и (5.4) следует второе уравнение системы (5.3).
Фазовый портрет мембраны строится следующим образом. Меняя фиксируемый потенциал  экспериментатор получает записи ионных токов
экспериментатор получает записи ионных токов  и по ним строит вольт-амперные характеристики для полного установившегося тока
и по ним строит вольт-амперные характеристики для полного установившегося тока  и для быстрого установившегося (пикового) тока
и для быстрого установившегося (пикового) тока  Построенные по ним с помощью уравнения (5.3) нуль-изоклины показаны на рис. 43.
Построенные по ним с помощью уравнения (5.3) нуль-изоклины показаны на рис. 43.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ АВТОРОВ
- ВВЕДЕНИЕ
- 1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ БИОХИМИЧЕСКИХ СИСТЕМ
- Глава первая. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НЕПРОТОЧНЫХ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
- 1.2. Ферменты — белковые катализаторы и регуляторы
- 1.3. Метод графов
- 1.4. Модели реакций, катализируемых одноцентровыми ферментами
- 1.5. Модели реакций, катализируемых олигомерными ферментами
- 1.6. Свойства реакции …
- 1.7. Свойства двухсубстратной реакции
- Глава вторая. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОТОЧНЫХ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
- 2.2. Модель открытой реакции … с субстратным угнетением
- 2.3. Модель двухсубстратной реакции с субстратным угнетением
- 2.4. Динамика открытых реакций, катализируемых олигомерными ферментами
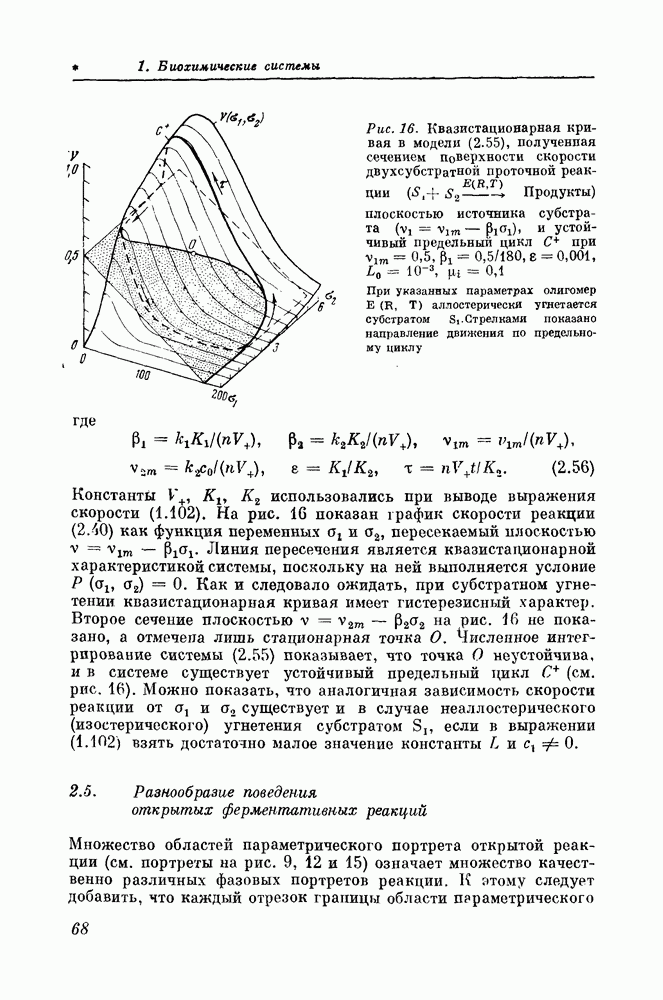
- 2.5. Разнообразие поведения открытых ферментативных реакций
- 2.6. Эквивалентные математические и кинетические модели
- 2.7. Эффект депонирования
- Глава третья. МОДЕЛИРОВАНИЕ ПОЛИФЕРМЕНТНЫХ СИСТЕМ
- 3.1. Полиферментные системы и их модели
- 3.2. Уровни функциональной организации полиферментных систем
- 3.3. Простая модель стехиометрической структуры энергетического метаболизма
- 3.4. Два класса аллостерических регуляторных связей, контролирующих энергетический метаболизм
- 2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ВОЗБУДИМЫХ МЕМБРАН
- Глава четвертая. КАЧЕСТВЕННЫЕ МЕТОДЫ В ИССЛЕДОВАНИИ МОДЕЛЕЙ МЕМБРАН
- 4.1. Построение уравнений второго порядка для моделей Ходжкина — Хаксли и Побла
- 4.2. Фаэовые портреты систем второго порядка
- 4.3. Исследование основных режимов мембраны аксона кальмара с помощью качественных методов
- 4.4. Исследование основных режимов мембраны волокна Пуркинье сердца с помощью качественных методов
- 4.5. Математические детали асимптотического сведения уравнений Ходжкина — Хаксли к системе второго порядка Н-Н2
- Глава пятая. БИОЛОГИЧЕСКИ АКТИВНЫЕ ВЕЩЕСТВА, ИОННЫЕ ТОКИ И ЭЛЕКТРОФИЗИОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ МЕМБРАН
- 5.2. Техника анализа мембран по записям ионных токов
- 5.3. Фазовые портреты мембран сердечной, нервной и мышечной клеток
- 5.4. Анализ действия веществ на мембраны
- 5.5. Предсказание электрофизиологических эффектов с помощью качественных методов
- 5.6. Границы применимости анализа, мембран по фазовому портрету
- 5.7. Оценка на математических моделях мембран точности построения фазового портрета по записям ионных токов
- 3. ВОЗБУДИМЫЕ СРЕДЫ. ВОЛНЫ И АВТОВОЛНОВЫЕ ПРОЦЕССЫ
- 6.1. Автоволновые процессы в возбудимых средах
- 6.2. Распространение волн в однородной среде. Спиральная волна, вращающаяся вокруг отверстия, и ревербератор
- 6.3. Возникновение ревербератора в простейшей неоднородной среде
- 6.4. Ревербератор в более детальных моделях
- 6.5. Свойства ревербератора как источника волн. Размножение ревербераторов в неоднородной среде. Бремя жизни
- 6.6. Ревербератор и сердечные аритмии. Уязвимость сердечной ткани
- Глава седьмая. ЭХО — ИСТОЧНИК КОНЦЕНТРИЧЕСКИХ ВОЛН В ВОЗБУДИМЫХ СРЕДАХ
- 7.1. Эхо в простейших моделях. Источник эха и ревербератор
- 7.2. Источник эха в моделях, описываемых обыкновенными дифференциальными уравнениями
- 7.3. Эхо в непрерывных возбудимых средах
- 7.4. Эхо в модели клеток сердца. Уязвимость
- Глава восьмая. ВЗАИМОДЕЙСТВИЕ ИСТОЧНИКОВ ВОЛН. АВТОВОЛНОВЫЕ ПРОЦЕССЫ И СЕРДЕЧНЫЕ АРИТМИИ
- 8.2. Синхронизация при взаимодействии источников волн
- 8.3. Размножение ревербераторов и фибрилляция
- 8.4. Взаимодействие источников эха
- 8.5. Связь параметров возбудимых сред с характеристиками дифференциального уравнения мембраны
- 8.6. Стационарные и нестационарные режимы распространения
- 8.7. Результаты микроэлектродного исследования уязвимости
- 8.8. О параметрах, контролирующих уязвимость в математических моделях и в миокарде
- 8.9. Следствия из моделей для антиаритмических веществ
- 4. ПРОСТРАНСТВЕННАЯ ОРГАНИЗАЦИЯ БИОЛОГИЧЕСКИХ СТРУКТУР
- Глава девятая. МОДЕЛИРОВАНИЕ ОБЪЕМНЫХ КЛЕТОЧНЫХ СТРУКТУР. ВИРУСЫ, ФЕРМЕНТЫ
- 9.2. Математические основы объемной реконструкции
- 9.3. Модель трехмерной структуры отростка бактериофага
- 9.4. Голографический синтез объемного изображения поверхности клеточной мембраны
- 9.5. Моделирование структуры биологических макромолекул
- Глава десятая. АНАЛИЗ КЛЕТОЧНЫХ СТРУКТУР ПО ИХ ИЗОБРАЖЕНИЯМ. ГЛИЯ—СОСУДЫ, ХРОМОСОМЫ
- 10.1. Преобразование изображений клеток в цифровую форму
- 10.2. Определение морфометрических параметров клеток и клеточных структур
- 10.3. Исследование глиально-сосудистой системы головного мозга
- 10.4. Модель сокращения длины хромосом в митозе
- Глава одиннадцатая. ВОССТАНОВЛЕНИЕ ЛИНЕЙНОЙ СТРУКТУРЫ БИОПОЛИМЕРОВ
- 11.1. Анализ первичной последовательности нуклеиновых кислот
- 11.2. Математическая постановка проблемы
- 11.3. Восстановление слов по составу второго ранга
- 11.4. Метод подстановки при восстановлении слов
- 11.5. Оптимизация биохимического эксперимента