| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
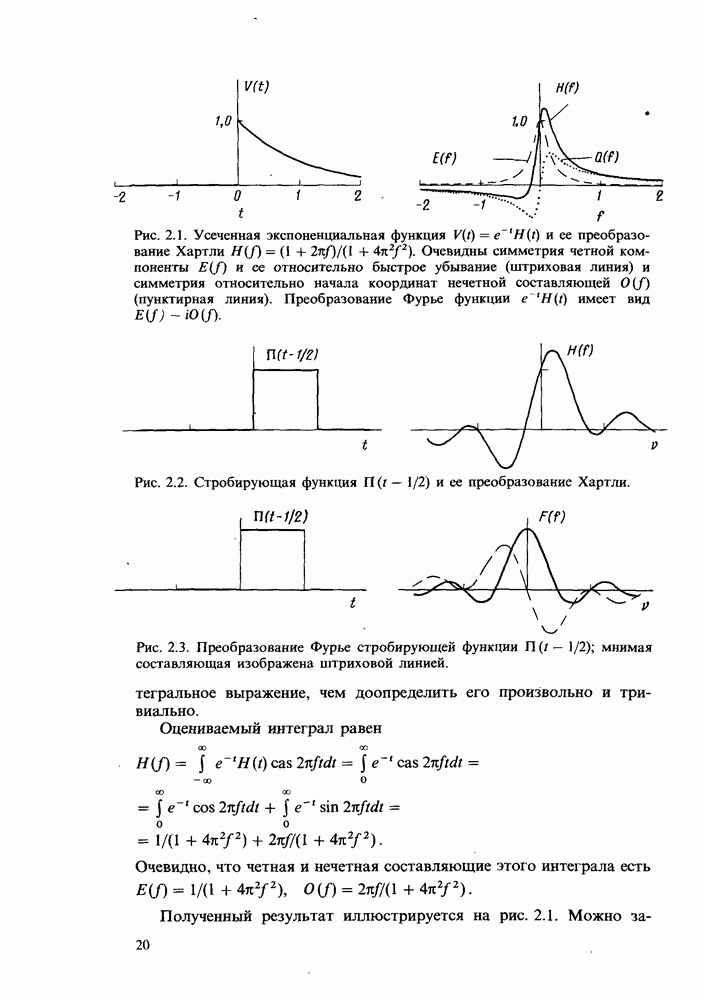
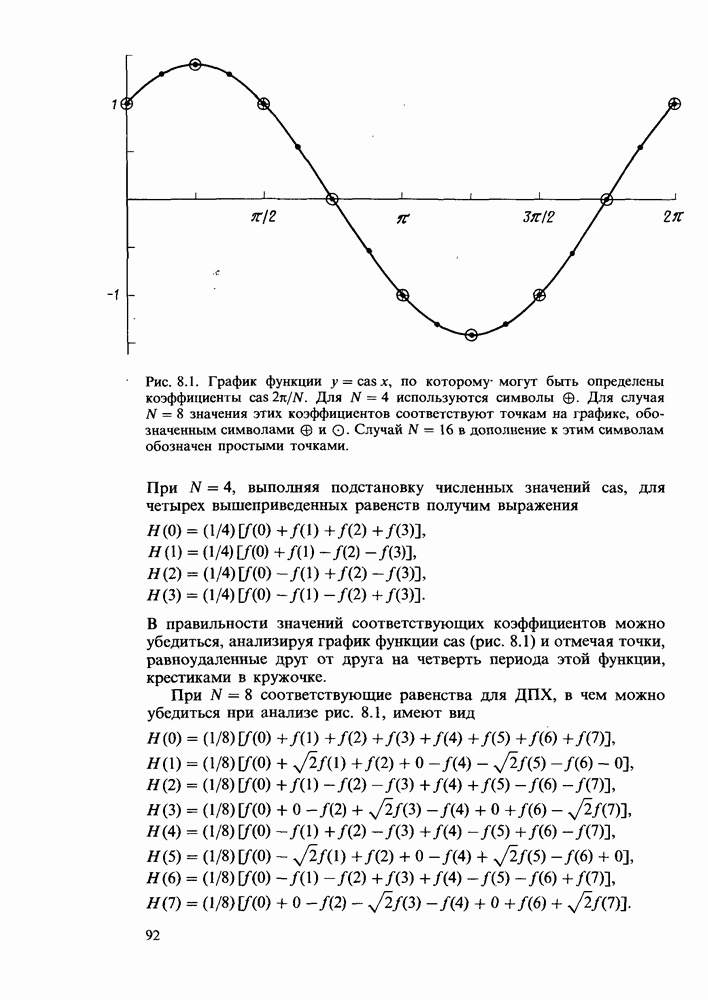
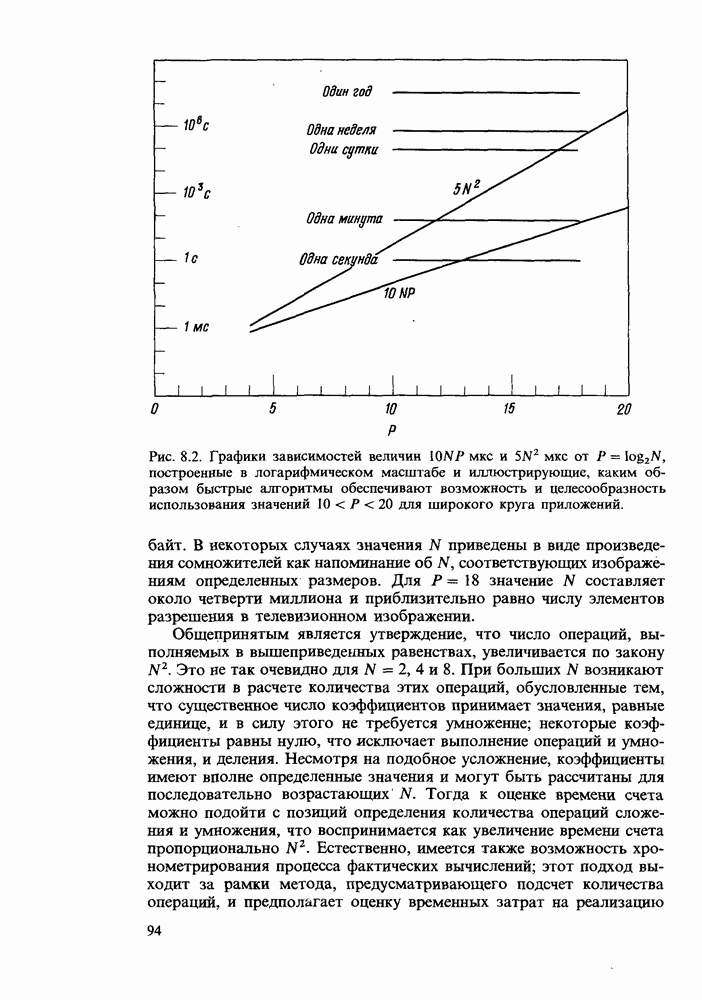
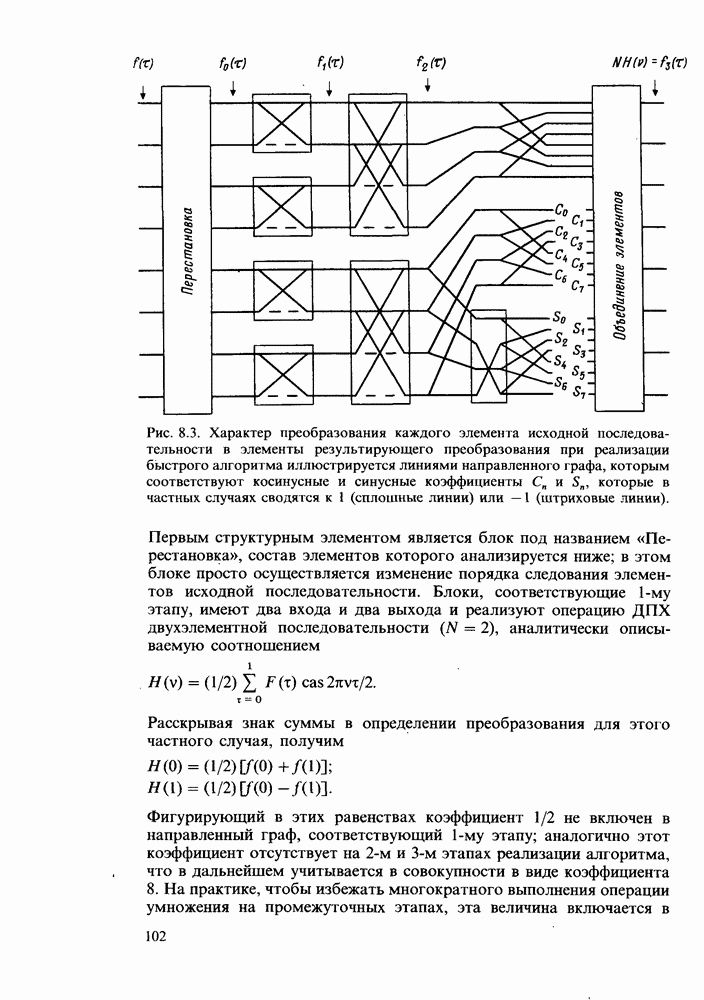
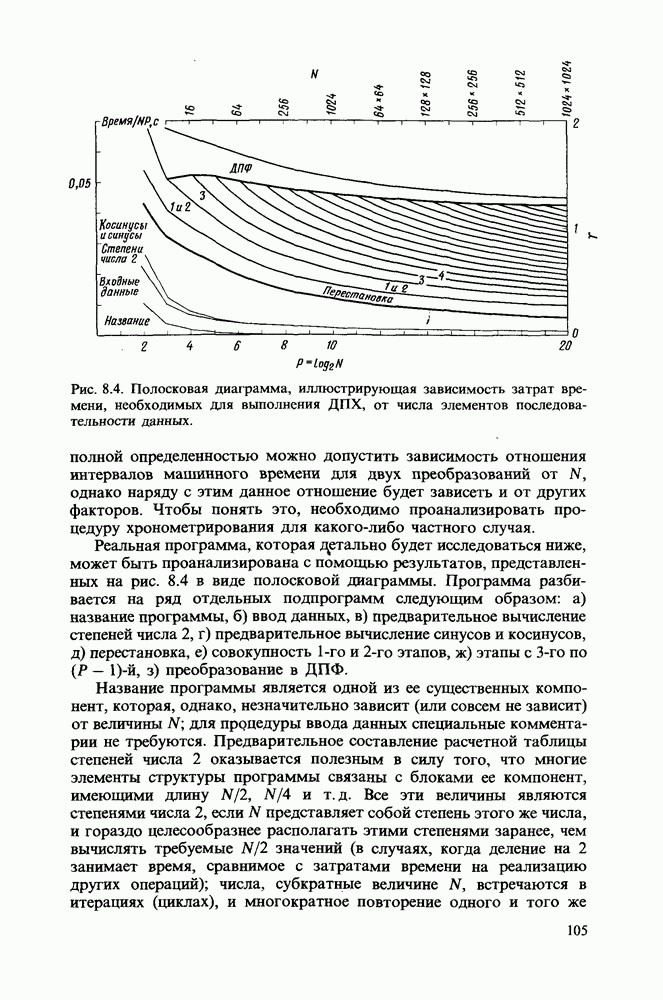
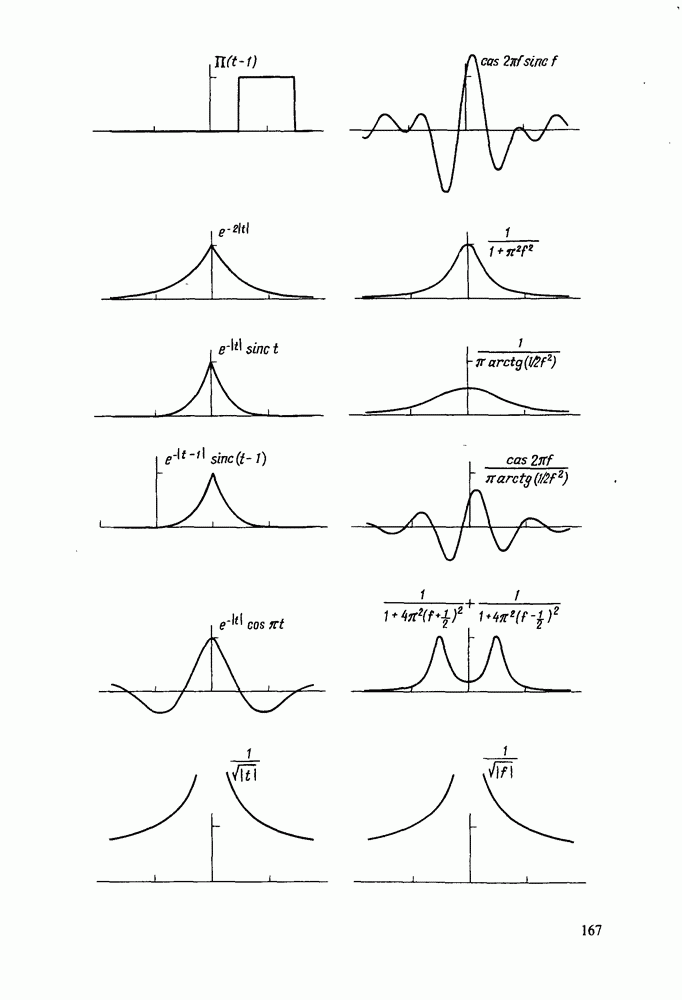
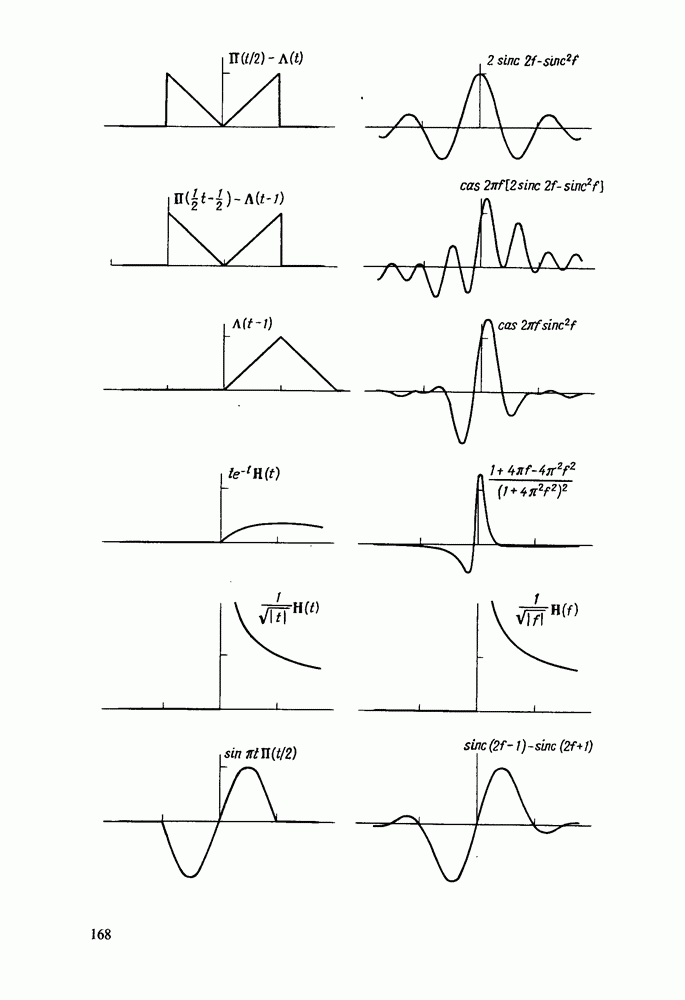
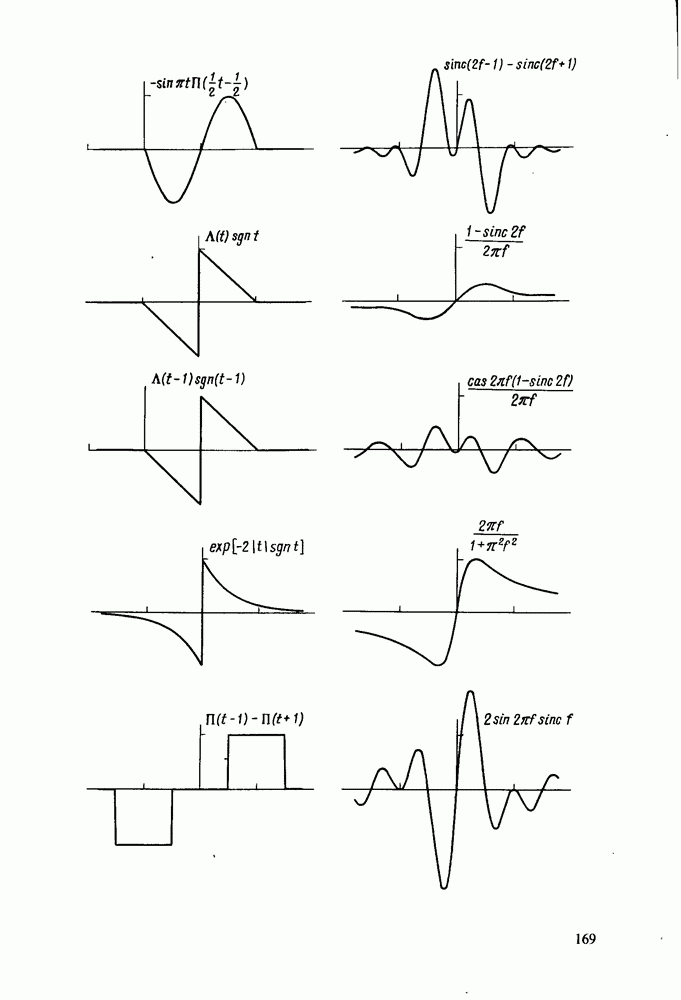
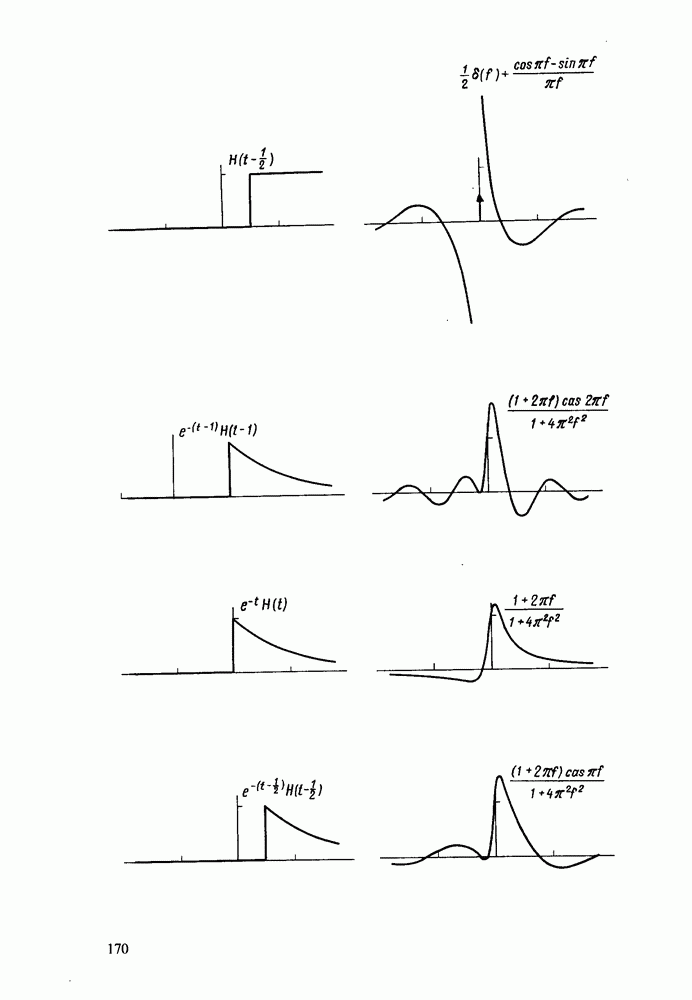
Примеры дискретных преобразований Хартли
Ниже приводится ряд примеров, иллюстрирующих свойства ДПХ. Сначала будут рассмотрены аналитические выражения, а затем проанализирован ряд последовательностей, заданных в численной форме.
Экспоненциалъно-убывающая функция. Для сравнения с примером, приведенным в гл. 2 для непрерывной функции, рассмотрим функцию

которая представляет рассмотренную выше непрерывную функцию с помощью  равноотстоящих отсчетов. Функции
равноотстоящих отсчетов. Функции  при аргументе
при аргументе  соответствующем разрыву колебания
соответствующем разрыву колебания  присваивается значение
присваивается значение  Соответствующее преобразование
Соответствующее преобразование  показанное на рис. 4.1, имеет явное сходство с отсчетами непрерывной функции, взятыми через интервалы
показанное на рис. 4.1, имеет явное сходство с отсчетами непрерывной функции, взятыми через интервалы 

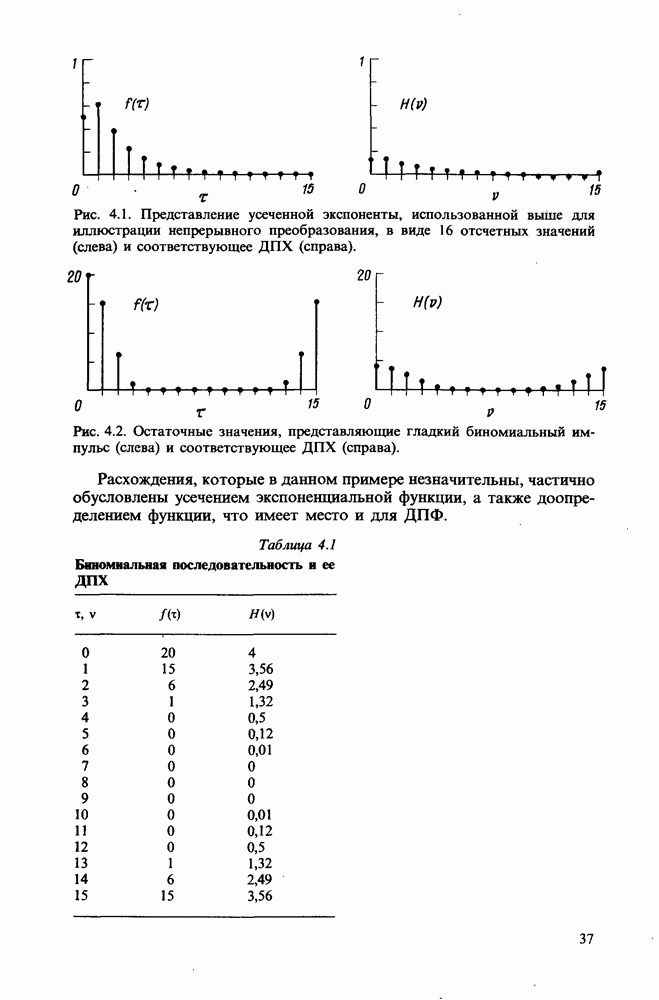
Рис. 4.1. Представление усеченной экспоненты, использованной выше для иллюстрации непрерывного преобразования, в виде 16 отсчетных значений (слева) и соответствующее ДПХ (справа).

Рис. 4.2. Остаточные значения, представляющие гладкий биномиальный импульс (слева) и соответствующее ДПХ (справа).
Расхождения, которые в данном примере незначительны, частично обусловлены усечением экспоненциальной функции, а также доопределением функции, что имеет место и для ДПФ.
Таблица 4.1. Биномиальная последовательность и ее ДПХ


Рис. 4.3. Н(v) стробирующей функции.

Рис. 4.4. Н(v) стробирующей функции, симметричной относительно 
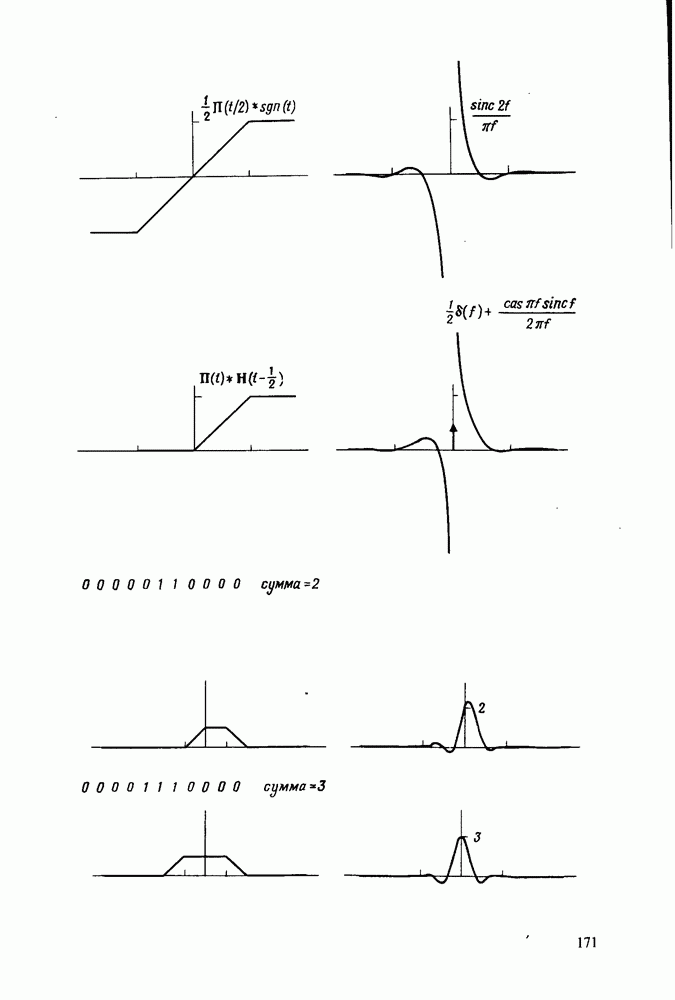
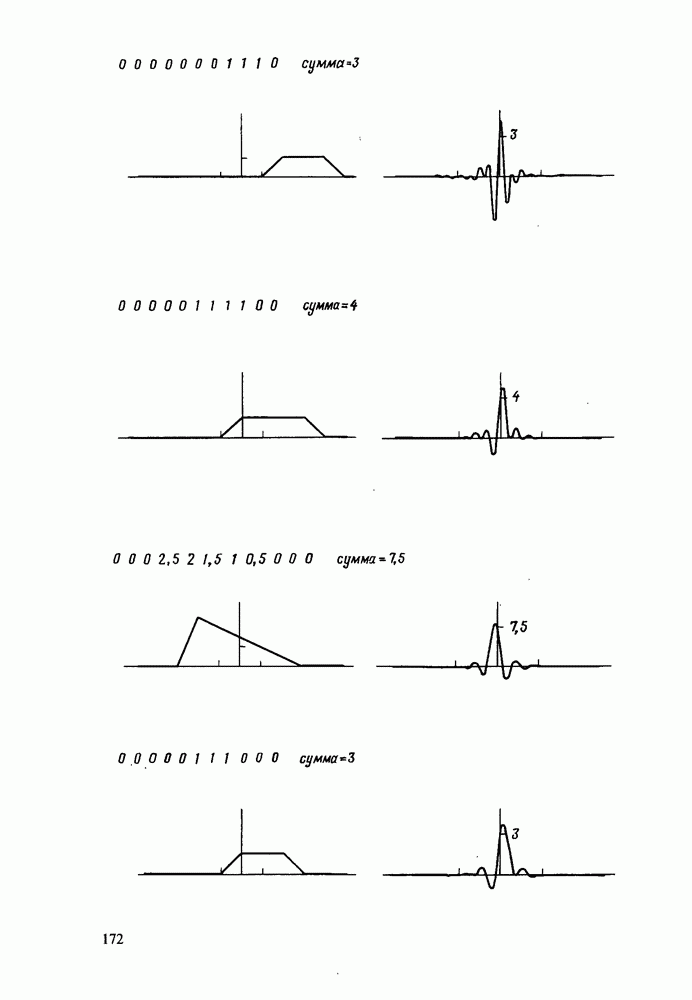
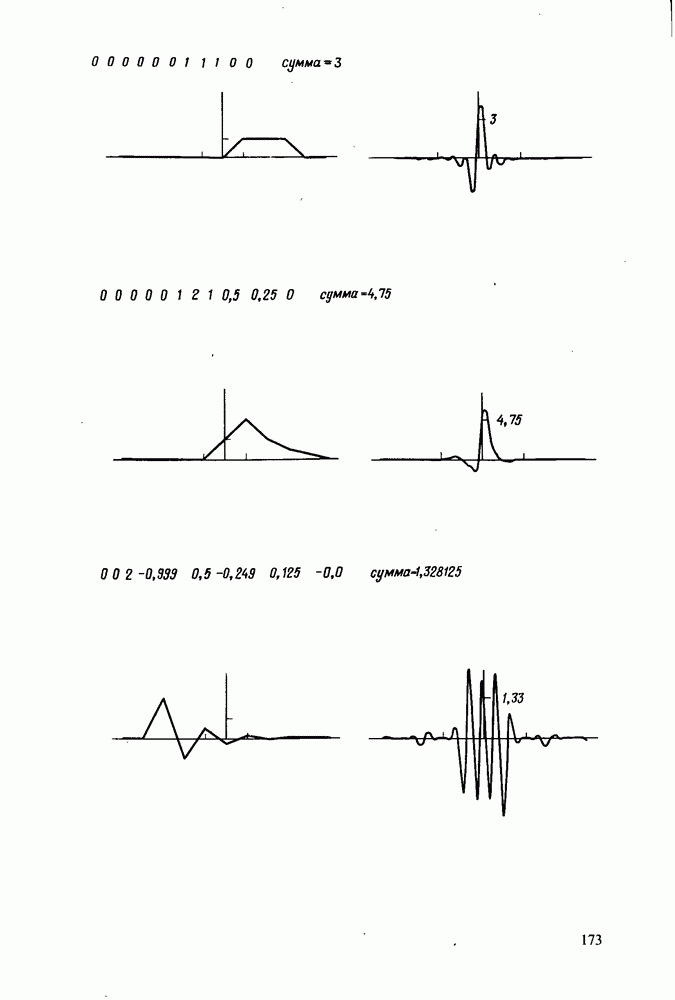
Биномиальный импульс. В качестве более наглядного примера рассмотрим биномиальную последовательность  представляющую собой отсчеты гладкого импульса. Для получения наиболее простого результата будем считать, что значение функции
представляющую собой отсчеты гладкого импульса. Для получения наиболее простого результата будем считать, что значение функции  максимально при
максимально при  Таким образом,
Таким образом,  и (см. табл. 4.1 и рис. 4.2) представляет сглаженный импульс, максимум которого имеет место при v = 0.
и (см. табл. 4.1 и рис. 4.2) представляет сглаженный импульс, максимум которого имеет место при v = 0.
Для численной проверки полезно знать, что сумма значений ДПХ вида  равна
равна  . И обратно, сумма значений
. И обратно, сумма значений  равна
равна  Таким образом, если
Таким образом, если  имеет
имеет  то
то 
Стробирующая функция. Рассмотрим оператор стробирования, обеспечивающий выборку из последовательности, состоящей из 16 элементов, второй группы в составе 4 элементов и заменяющий остальные 12 элементов нулями; эта операция эквивалентна умножению исходной последовательности на последовательности вида

Ее ДПХ  показано на рис. 4.3. Если теперь рассмотрим другой оператор стробирования вида
показано на рис. 4.3. Если теперь рассмотрим другой оператор стробирования вида

то получим его  отличающееся от
отличающееся от  и представленное на рис. 4.4. Численные результаты для обоих случаев нормированы к единице и приведены в табл. 4.2.
и представленное на рис. 4.4. Численные результаты для обоих случаев нормированы к единице и приведены в табл. 4.2.
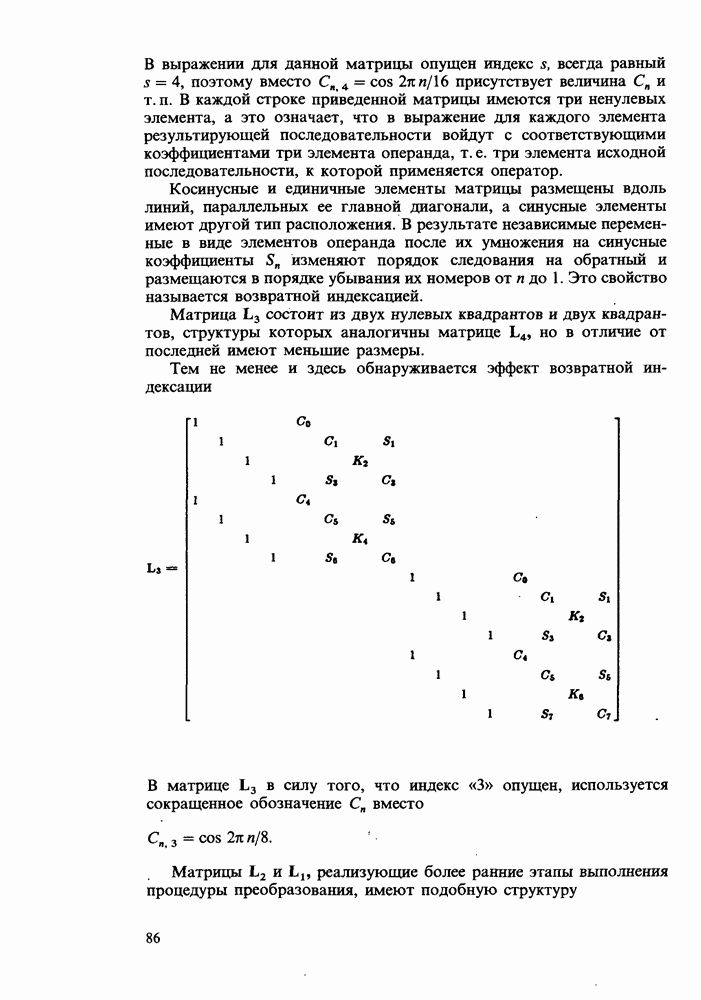
Во втором случае имеет место стробирование, симметричное
Таблица 4.2. ДПХ двух стробирующих функций

относительно  и имеющее циклическое представление. Следовательно, в преобразовании
и имеющее циклическое представление. Следовательно, в преобразовании  отсутствуют быстрые колебания, а само преобразование напоминает функцию вида
отсутствуют быстрые колебания, а само преобразование напоминает функцию вида  соответствующую центрированному прямоугольному импульсу.
соответствующую центрированному прямоугольному импульсу.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Преобразование Хартли
- Четная и нечетная составляющие
- Формулы связи
- Примеры
- Энергетический и фазовый спектры
- Глава 3. ТЕОРЕМЫ
- Свертка
- Соотношения между преобразованиями во временной и частотой областях
- Глава 4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Физический смысл величин «тау» и v
- Четная и нечетная составляющие
- Примеры дискретных преобразований Хартли
- Степени свободы
- Другие вещественные ядра
- Теоремы
- Выводы
- Глава 5. ЦИФРОВАЯ ФИЛЬТРАЦИЯ ПОСРЕДСТВОМ СВЕРТКИ
- Циклическая свертка
- Дополнение нулями
- Обращение свертки
- Теорема о свертке
- Теорема о свертке в частотной области (спектральное сглаживание)
- Числовой пример свертки
- Коэффициент
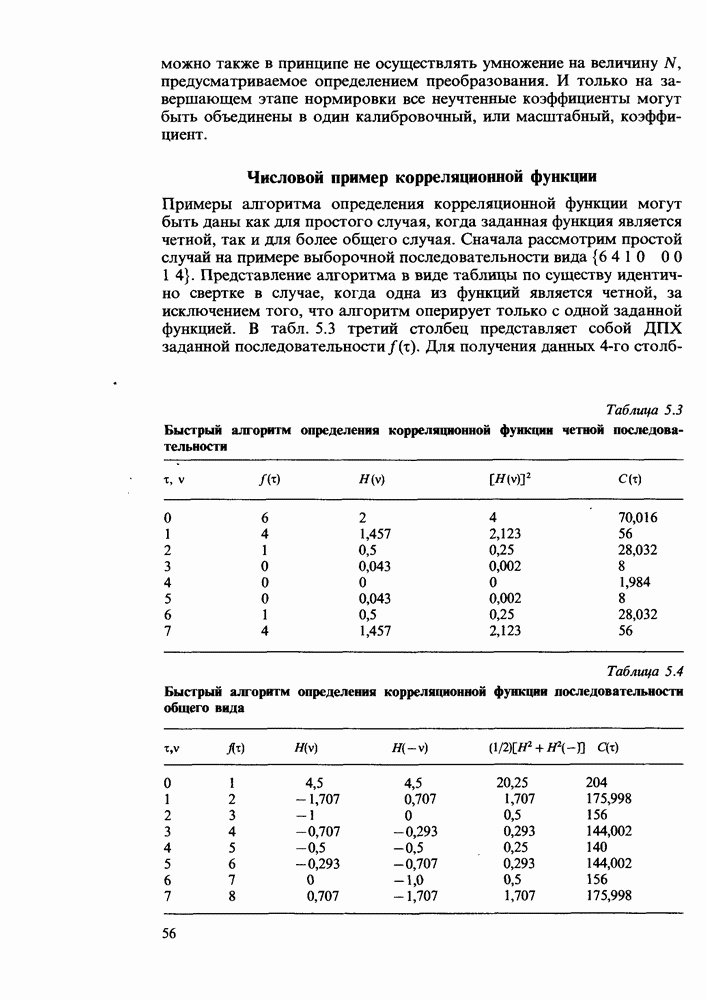
- Числовой пример корреляционной функции
- Низкочастотная фильтрация
- Подчеркивание границ
- Свертка с использованием быстрого преобразования Хартли
- Способ без использования перестановок
- Свертка как умножение матриц
- Глава 6. Двумерные преобразования
- Двумерное преобразование Хартли
- Симметрия и антисимметрия
- Примеры
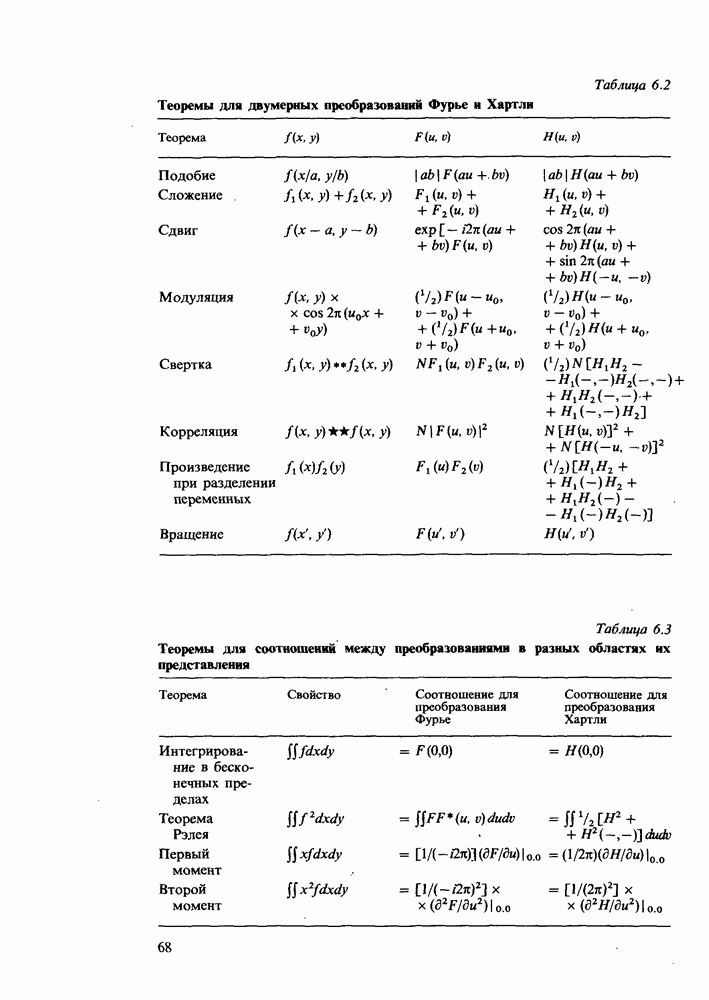
- Теоремы для двумерных преобразований
- Круговая симметрия
- Двумерная фильтрация
- Цикличность для двумерного случая
- Трехмерный случай
- Глава 7. ФАКТОРИЗАЦИЯ МАТРИЦЫ ПРЕОБРАЗОВАНИЯ
- Перестановка
- Перестановочные диаграммы
- Перестановочная матрица
- Ячеистая структура перестановочной диаграммы
- Каскадные матрицы
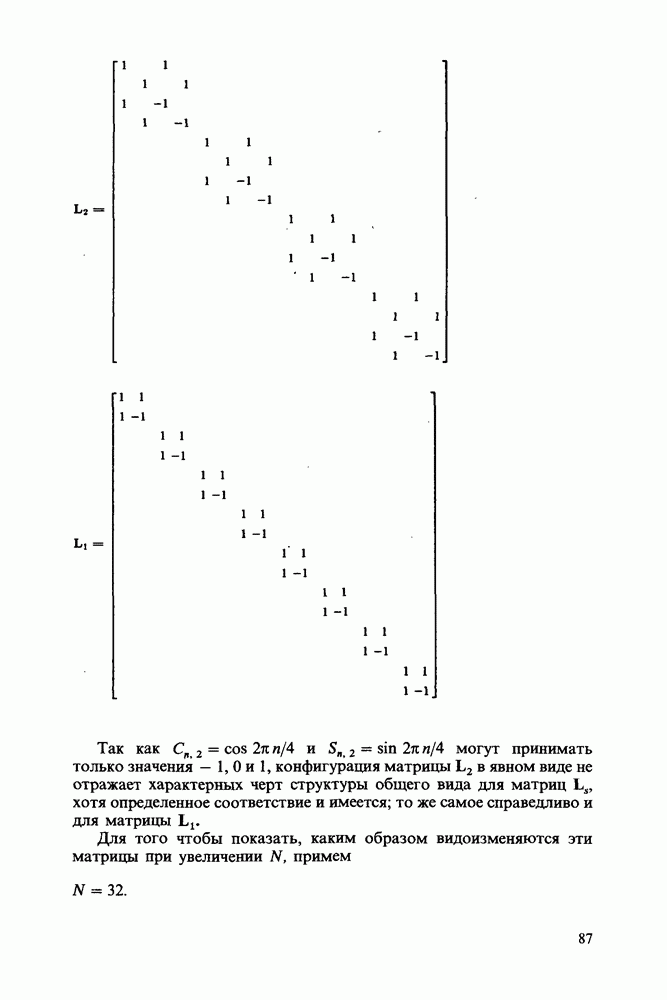
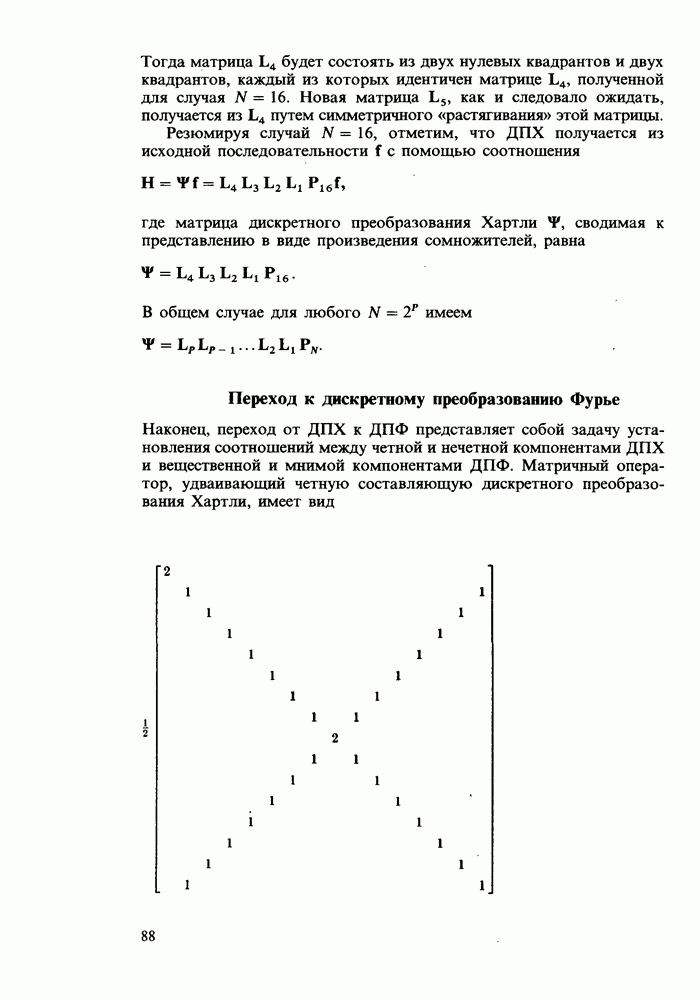
- Переход к дискретному преобразованию Фурье
- Глава 8. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ
- Свойство N log N
- Повторное разбиение последовательностей
- Преобразование с использованием разложения на подпоследовательности
- Общая формула разложения.
- Направленный сигнальный граф
- Вычисление с замещением
- Анализ временных затрат на вычисление с помощью полосковой диаграммы
- Степепи числа 2
- Тригонометрические функции
- Быстрое вычисление синусов
- Операция быстрого поворота
- Быстрая перестановка
- Преобразование для последовательностей с основанием 4 и другие модификации
- Ранее применявшиеся подходы к преобразованию вещественных данных
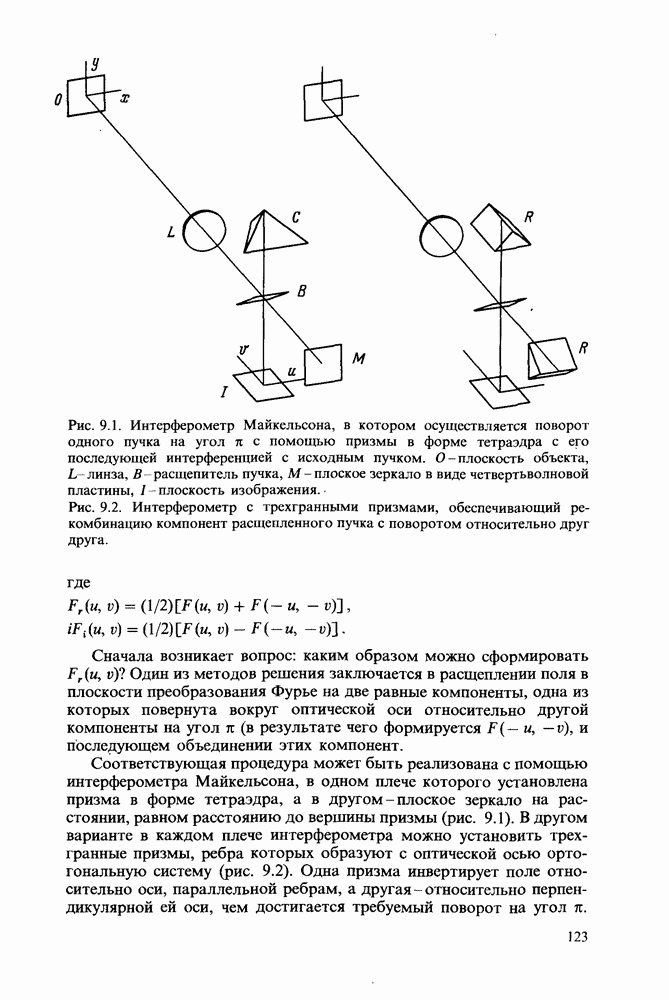
- Глава 9. ПРЕОБРАЗОВАНИЕ ХАРТЛИ В ОПТИКЕ
- Свойства симметрии
- Осуществление преобразования Хартли, использующее поляризацию
- Практическое осуществление
- Источник некогерентного излучения
- Пример
- Голография в плоскости Хартли
- Приложение 1. ПРОГРАММЫ ВЫЧИСЛЕНИЙ НА ЭВМ
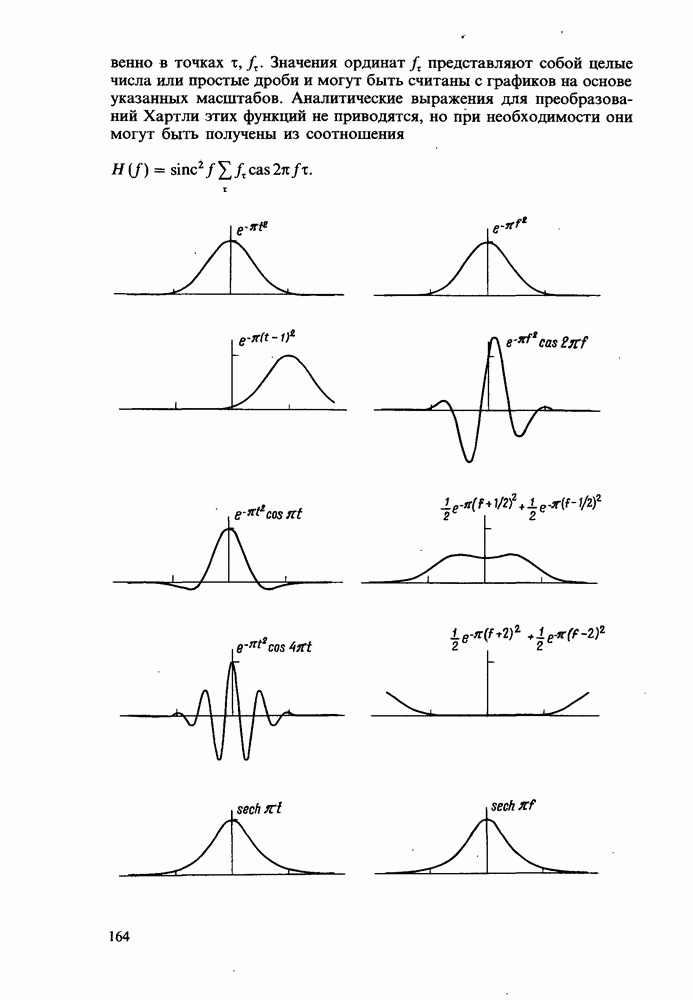
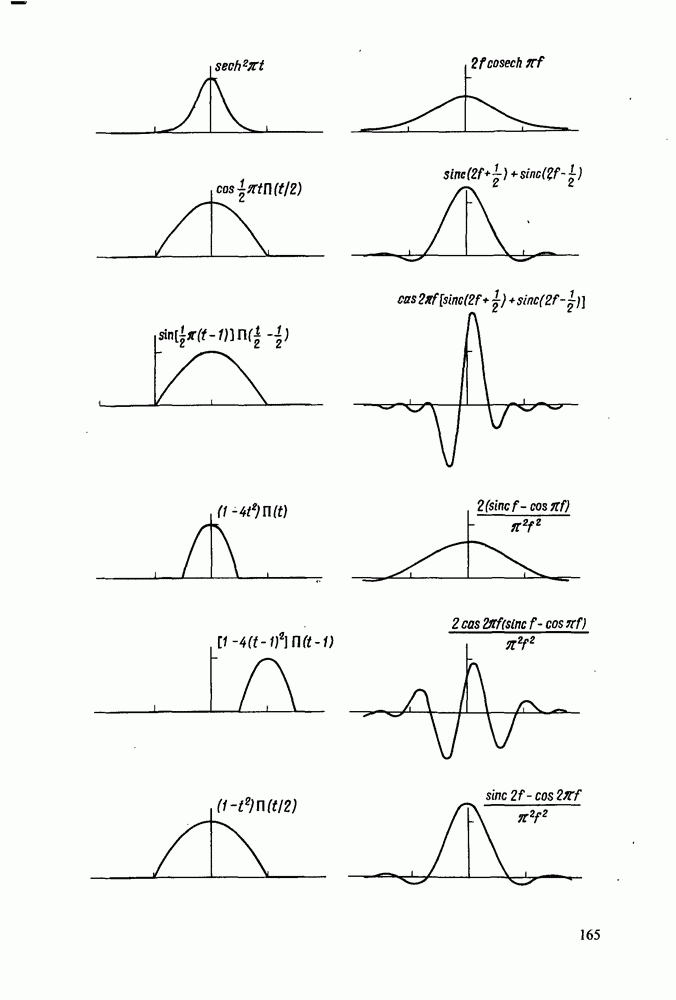
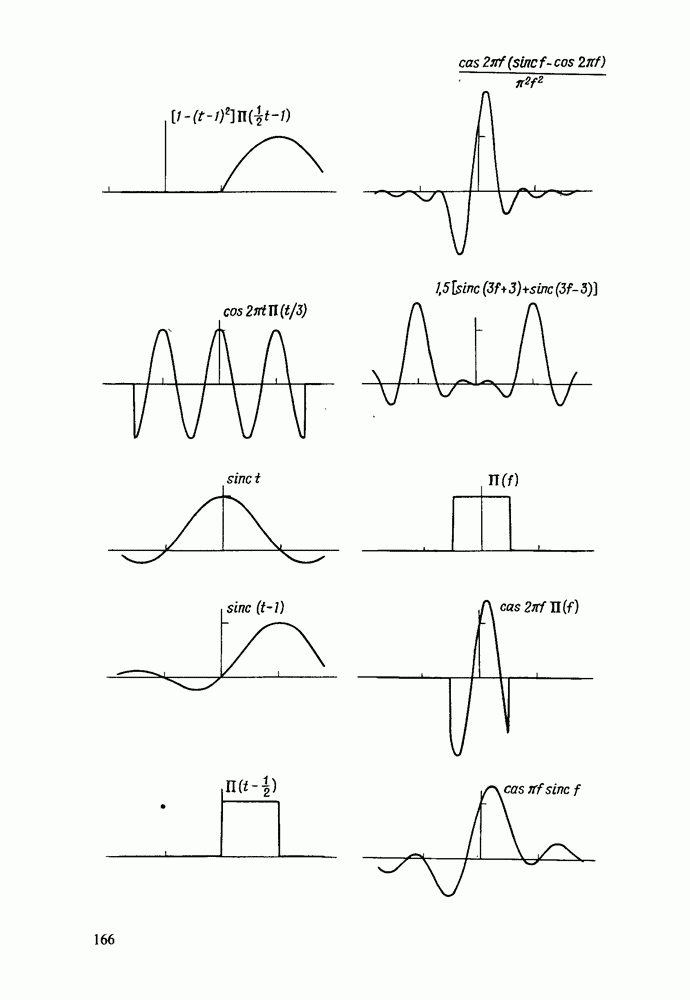
- Приложение 2. АТЛАС ПРЕОБРАЗОВАНИЙ ХАРТЛИ