| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Теоремы
Каждой теореме дискретного преобразования Фурье соответствует подобная теорема для дискретного преобразования Хартли. Для полноты представления материала в табл. 4.3 и 4.4 даются все теоремы, в том числе теоремы о свертке и корреляции, одиако рассмотрение последних будет отложено до следующей главы. На данном этапе достаточно сделать замечание, что свертка функций непрерывного аргумента, обозначаемая символом  отличается от процедуры циклической свертки дискретных последовательностей, для обозначения которой используется символ
отличается от процедуры циклической свертки дискретных последовательностей, для обозначения которой используется символ 
Можно отметить, что среднее значение последовательности  определяется величиной
определяется величиной  значение ее среднего квадрата равно
значение ее среднего квадрата равно 
Некоторые теоремы для двух различных преобразований характеризуются
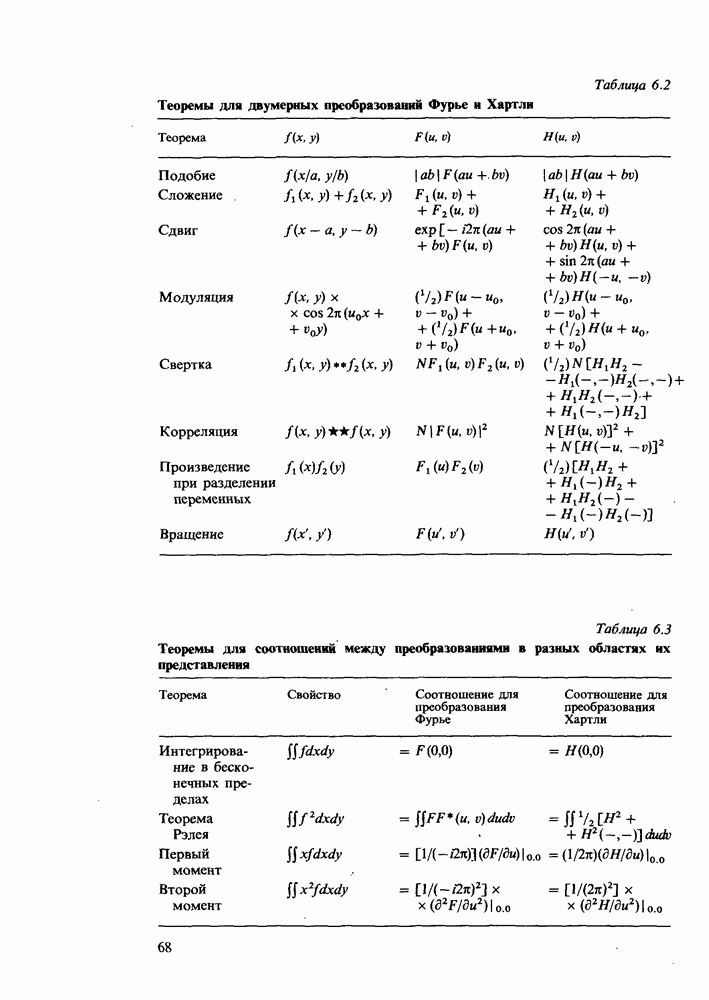
Таблща 4.3. Теоремы для операций при дискретных преобразованиях

Таблица 4.4. Теоремы для соотношений между дискретными преобразованиями

точным соответствием, как, например,

тогда как в других случаях имеют место различия.
Теорема о зеркальном изображении. Если из последовательности  сформировать ее зеркальное изображение
сформировать ее зеркальное изображение  , то в результате ведущий (нулевой) элемент сохранит неизменное положение, а остальные элементы изменят порядок следования на обратный. Таким образом, вместо элемента
, то в результате ведущий (нулевой) элемент сохранит неизменное положение, а остальные элементы изменят порядок следования на обратный. Таким образом, вместо элемента  исходной последовательности имеем член
исходной последовательности имеем член  , который интерпретируется как
, который интерпретируется как  и равен
и равен  , т. е. является последним элементом новой последовательности. Следовательно, вместо последовательности
, т. е. является последним элементом новой последовательности. Следовательно, вместо последовательности  имеем
имеем  что в области преобразования соответствует замене вида
что в области преобразования соответствует замене вида  .
.
Теорема сложения. Свойство суперпозиции, иллюстрируемое теоремой сложения, просто отражает линейность оператора ДПХ.
Теорема о сдвиге. Сначала рассмотрим пример, в котором реализуется единичный сдвиг последовательности  имеющей ДПХ вида
имеющей ДПХ вида  . В соответствии с теоремой о сдвиге для
. В соответствии с теоремой о сдвиге для  имеем последовательность
имеем последовательность  для которой ДПХ равно
для которой ДПХ равно

где 
Для выполнения данной операции сдвига мы перемещаем каждый элемент исходной последовательности на одну позицию вправо. Последний элемент в соответствии с принятым свойством цикличности перемещается на первую позицию.
ДПХ состоит из двух последовательностей, одна из которых содержит косинусные, другая - синусные коэффициенты. ДПФ также представляет собой совокупность двух последовательностей с синусными и косинусными коэффициентами, однако для ДПХ в отличие от ДПФ для синусной компоненты характерно зеркальное отображение - это свойство именуется обратной индексацией. Для доказательства теоремы о сдвиге подставим  в формулу,
в формулу,
определяющую прямое ДПХ, и получим

Теорема о свертке. В общем случае преобразование свертки  содержит четыре компоненты. Основными величинами, которые должны быть вычислены, являются прямые произведения
содержит четыре компоненты. Основными величинами, которые должны быть вычислены, являются прямые произведения  и смешанные произведения
и смешанные произведения  . С использованием этих обозначений имеем
. С использованием этих обозначений имеем

Таким образом, данная процедура включает два, а не четыре действия умножения. Теперь если  — четная функция (т. е.
— четная функция (т. е. 

Точно так же простую формулу получим в случае, когда  является нечетной функцией; при этом имеем
является нечетной функцией; при этом имеем

Вследствие коммутативности  если либо
если либо  либо
либо  являются четными функциями. Часто одна либо другая функция обладает свойствами симметрии или антисимметрии, что приводит к более простым соотношениям. Ввиду важности операции свертки мы вернемся к ней в следующей главе.
являются четными функциями. Часто одна либо другая функция обладает свойствами симметрии или антисимметрии, что приводит к более простым соотношениям. Ввиду важности операции свертки мы вернемся к ней в следующей главе.
Теорема о произведении. В теореме о произведении четыре компоненты предполагают выполнение только двух операций свертки, так как две другие просто реализуются путем зеркального отображения двух сомножителей.
Теорема о растяжении. Сходство этой теоремы с соответствующей теоремой для случая непрерывной независимой переменной относится к изменению масштаба по оси абсцисс, когда  преобразуется в
преобразуется в  Так как величина Т может быть либо больше, либо меньше единицы, операция может представлять собой либо растяжение, либо сжатие. В случае дискретной переменной изменения масштаба также имеют практическое значение, например когда последовательность регулярных измерений должна быть повторена с большей или меньшей скоростью. Функция
Так как величина Т может быть либо больше, либо меньше единицы, операция может представлять собой либо растяжение, либо сжатие. В случае дискретной переменной изменения масштаба также имеют практическое значение, например когда последовательность регулярных измерений должна быть повторена с большей или меньшей скоростью. Функция  определена для любого Тпри заданной
определена для любого Тпри заданной  но это утверждение несправедливо для при заданной функции
но это утверждение несправедливо для при заданной функции  где
где  Следовательно,
Следовательно,
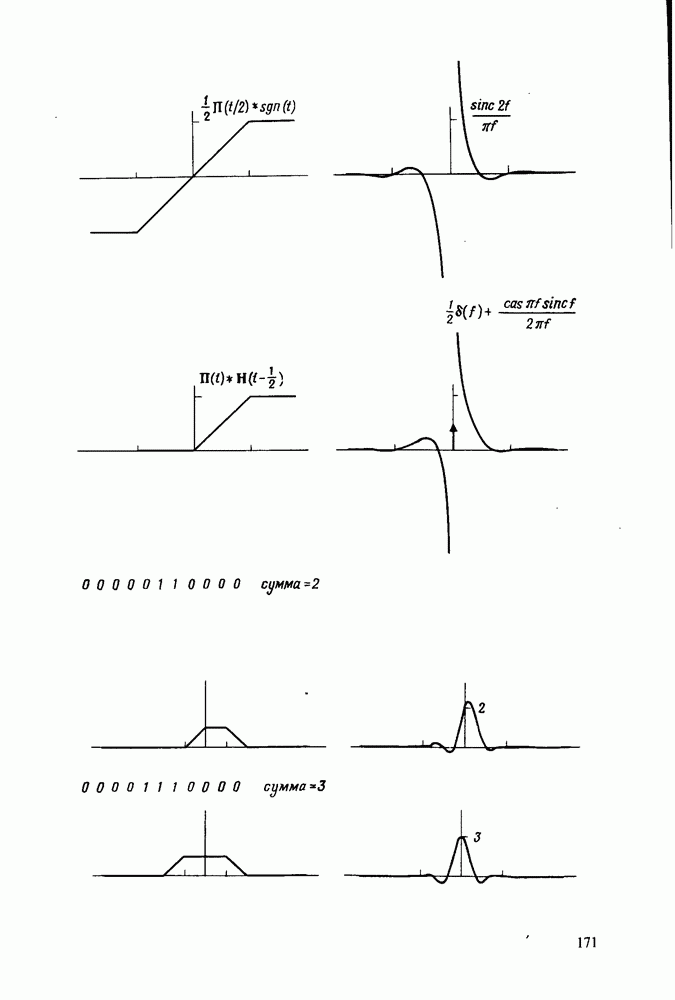
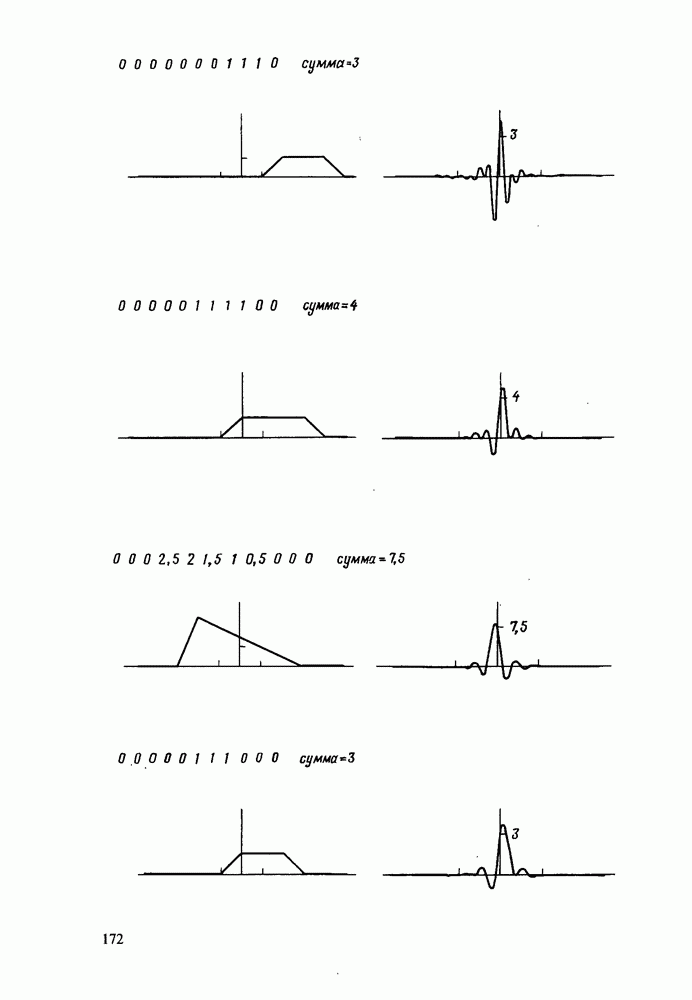
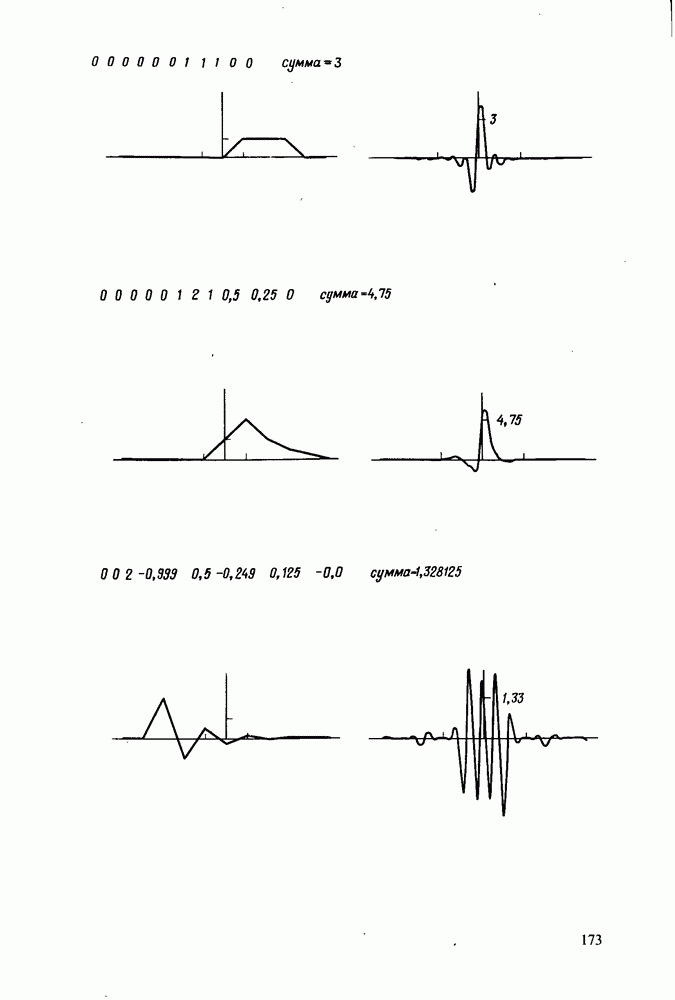
применительно к теореме подобия отсутствует строгая аналогия. Теорема о растяжении имеет отношение только к увеличению масштаба времени, что осуществляется добавлением нулей в исходную последовательность. Наиболее просто это можно проиллюстрировать на примере.
Пусть последовательность  имеет последовательность ДПХ
имеет последовательность ДПХ  . Тогда последовательности
. Тогда последовательности  соответствует последовательность ДПХ вида
соответствует последовательность ДПХ вида 
В правомерности этого результата можно убедиться, анализируя выражение для прямого ДПХ:

Убеждаемся в том, что при  имеем
имеем  При нечетном
При нечетном  сумма равна нулю, для четного
сумма равна нулю, для четного  эта сумма сводится к выражению:
эта сумма сводится к выражению:  для которого обратное преобразование Хартли имеет вид:
для которого обратное преобразование Хартли имеет вид: 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Преобразование Хартли
- Четная и нечетная составляющие
- Формулы связи
- Примеры
- Энергетический и фазовый спектры
- Глава 3. ТЕОРЕМЫ
- Свертка
- Соотношения между преобразованиями во временной и частотой областях
- Глава 4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Физический смысл величин «тау» и v
- Четная и нечетная составляющие
- Примеры дискретных преобразований Хартли
- Степени свободы
- Другие вещественные ядра
- Теоремы
- Выводы
- Глава 5. ЦИФРОВАЯ ФИЛЬТРАЦИЯ ПОСРЕДСТВОМ СВЕРТКИ
- Циклическая свертка
- Дополнение нулями
- Обращение свертки
- Теорема о свертке
- Теорема о свертке в частотной области (спектральное сглаживание)
- Числовой пример свертки
- Коэффициент
- Числовой пример корреляционной функции
- Низкочастотная фильтрация
- Подчеркивание границ
- Свертка с использованием быстрого преобразования Хартли
- Способ без использования перестановок
- Свертка как умножение матриц
- Глава 6. Двумерные преобразования
- Двумерное преобразование Хартли
- Симметрия и антисимметрия
- Примеры
- Теоремы для двумерных преобразований
- Круговая симметрия
- Двумерная фильтрация
- Цикличность для двумерного случая
- Трехмерный случай
- Глава 7. ФАКТОРИЗАЦИЯ МАТРИЦЫ ПРЕОБРАЗОВАНИЯ
- Перестановка
- Перестановочные диаграммы
- Перестановочная матрица
- Ячеистая структура перестановочной диаграммы
- Каскадные матрицы
- Переход к дискретному преобразованию Фурье
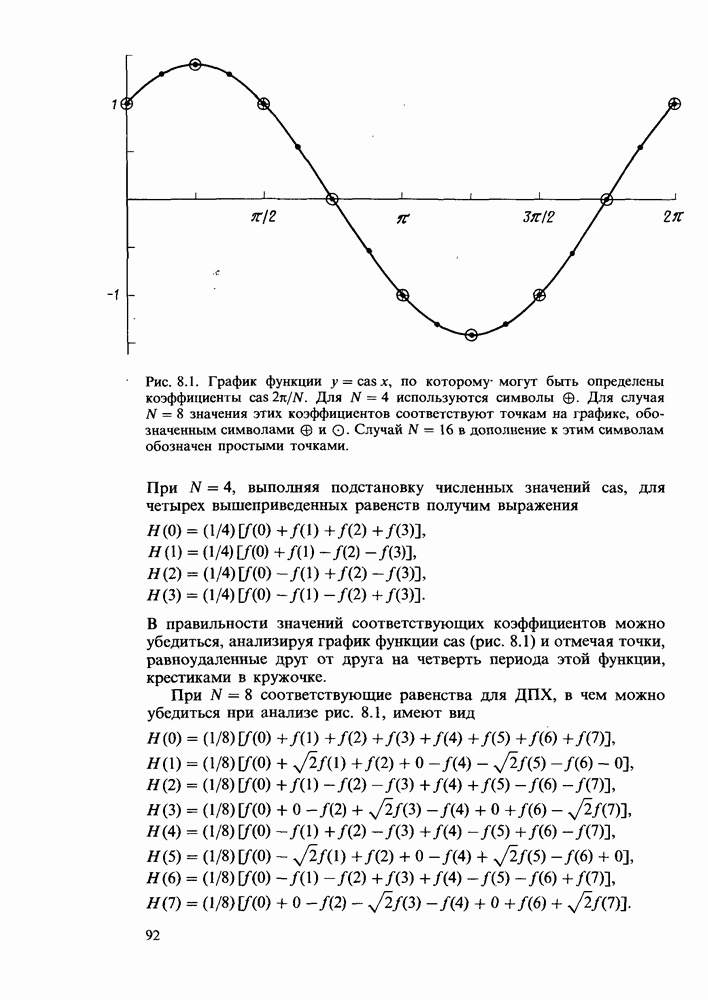
- Глава 8. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ
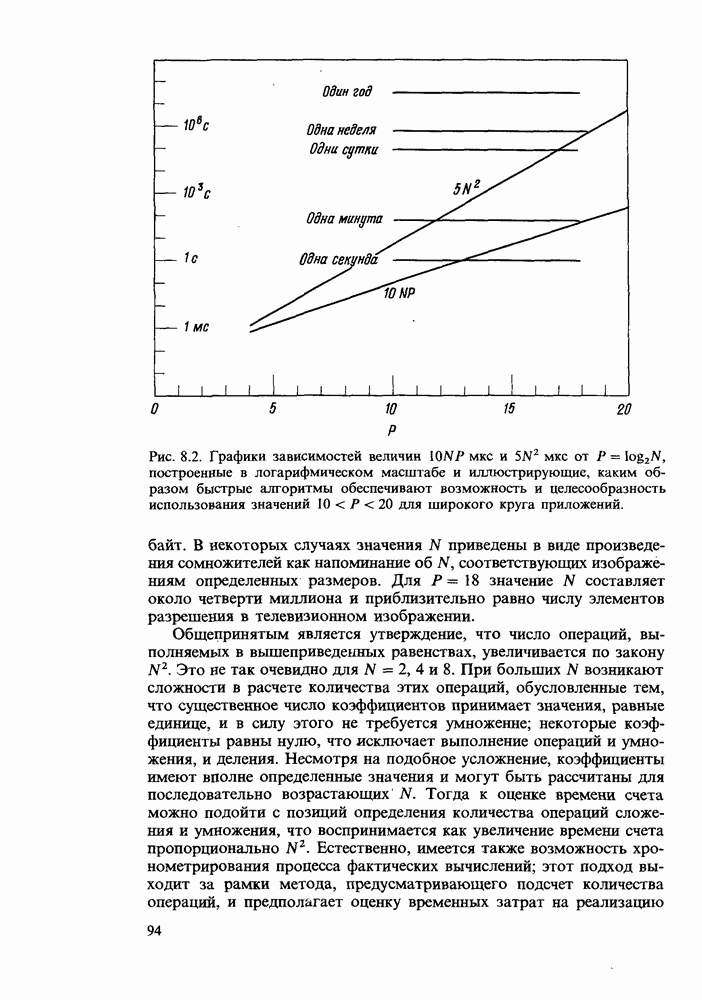
- Свойство N log N
- Повторное разбиение последовательностей
- Преобразование с использованием разложения на подпоследовательности
- Общая формула разложения.
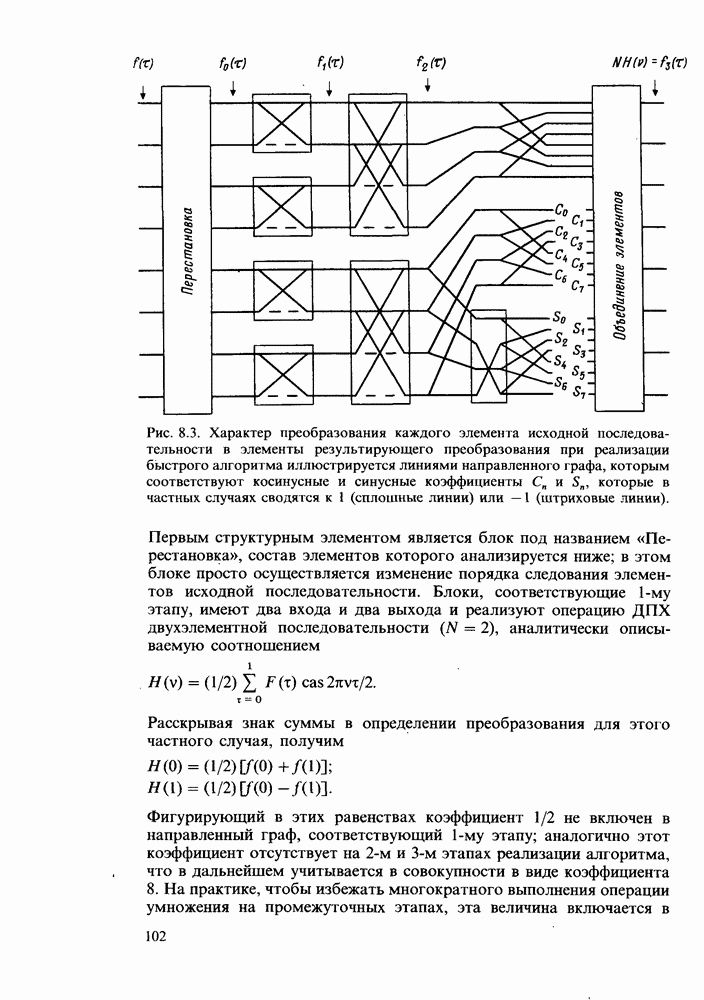
- Направленный сигнальный граф
- Вычисление с замещением
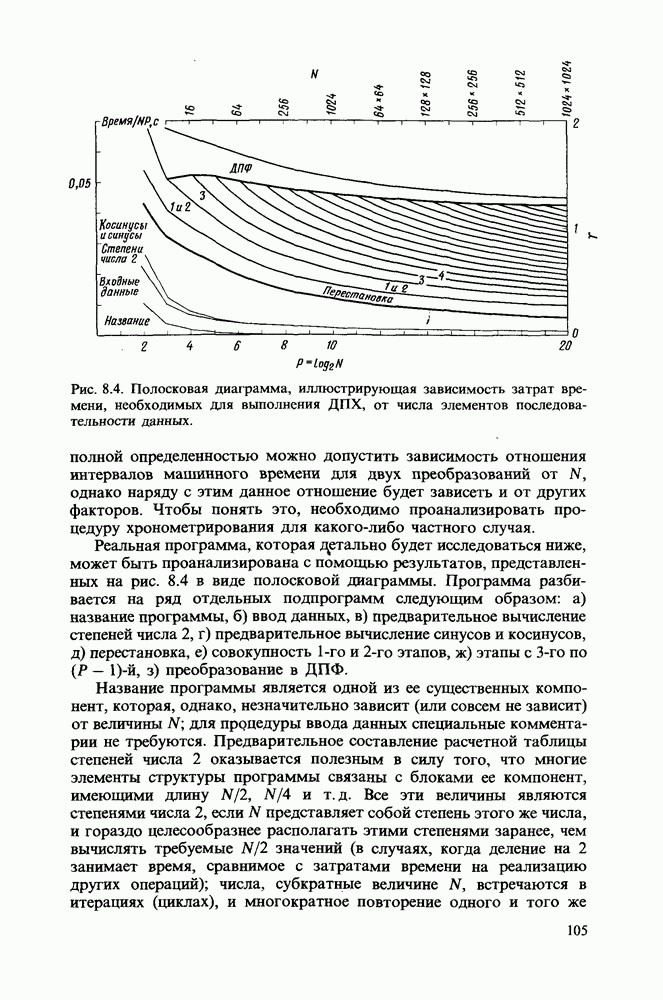
- Анализ временных затрат на вычисление с помощью полосковой диаграммы
- Степепи числа 2
- Тригонометрические функции
- Быстрое вычисление синусов
- Операция быстрого поворота
- Быстрая перестановка
- Преобразование для последовательностей с основанием 4 и другие модификации
- Ранее применявшиеся подходы к преобразованию вещественных данных
- Глава 9. ПРЕОБРАЗОВАНИЕ ХАРТЛИ В ОПТИКЕ
- Свойства симметрии
- Осуществление преобразования Хартли, использующее поляризацию
- Практическое осуществление
- Источник некогерентного излучения
- Пример
- Голография в плоскости Хартли
- Приложение 1. ПРОГРАММЫ ВЫЧИСЛЕНИЙ НА ЭВМ
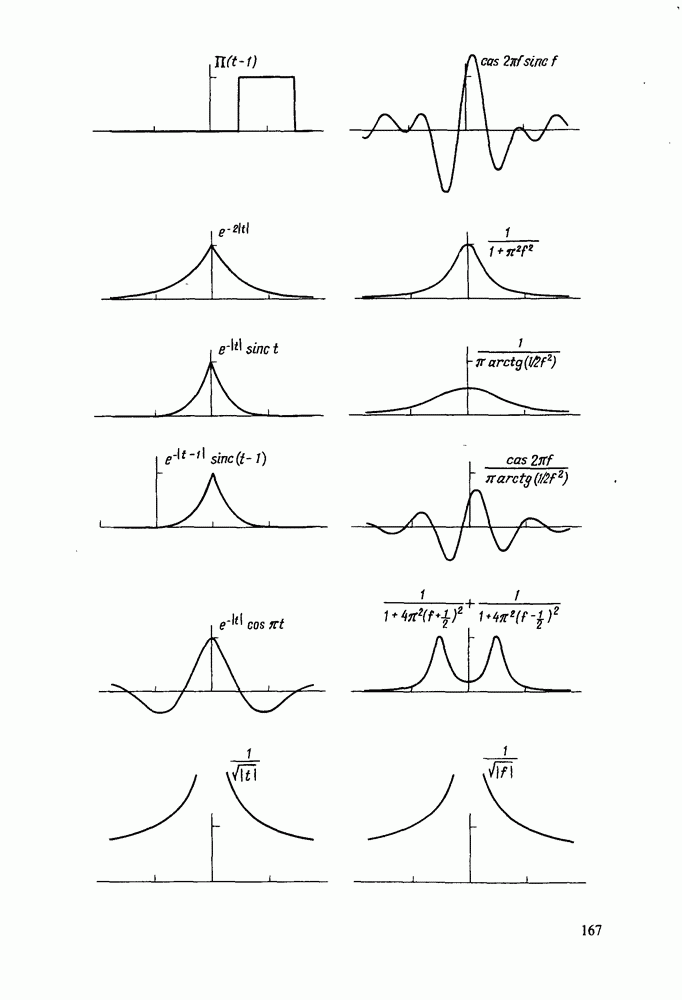
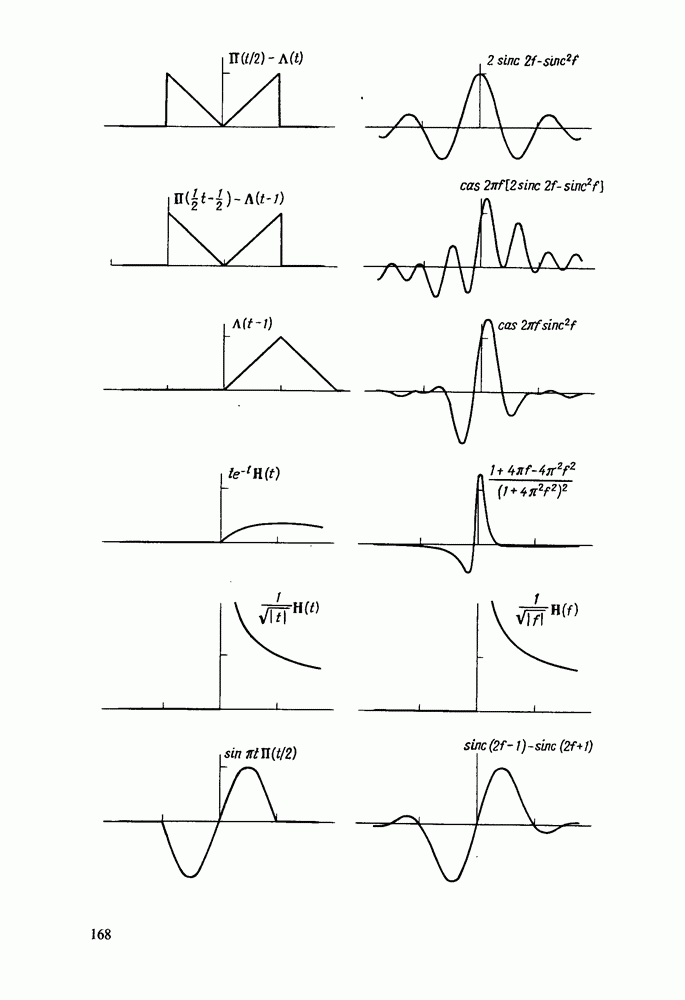
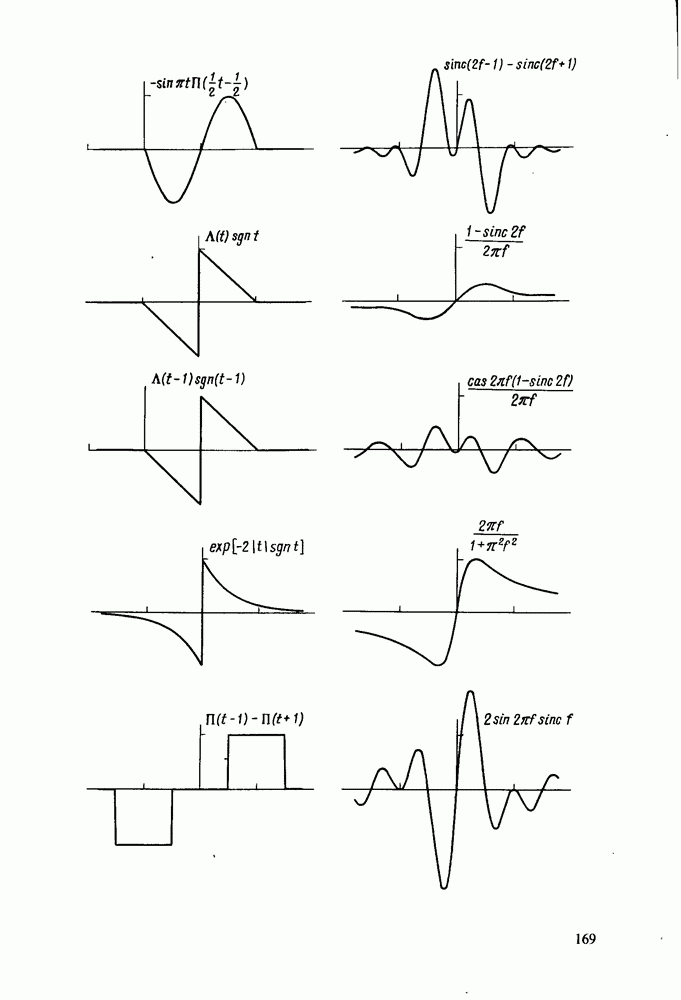
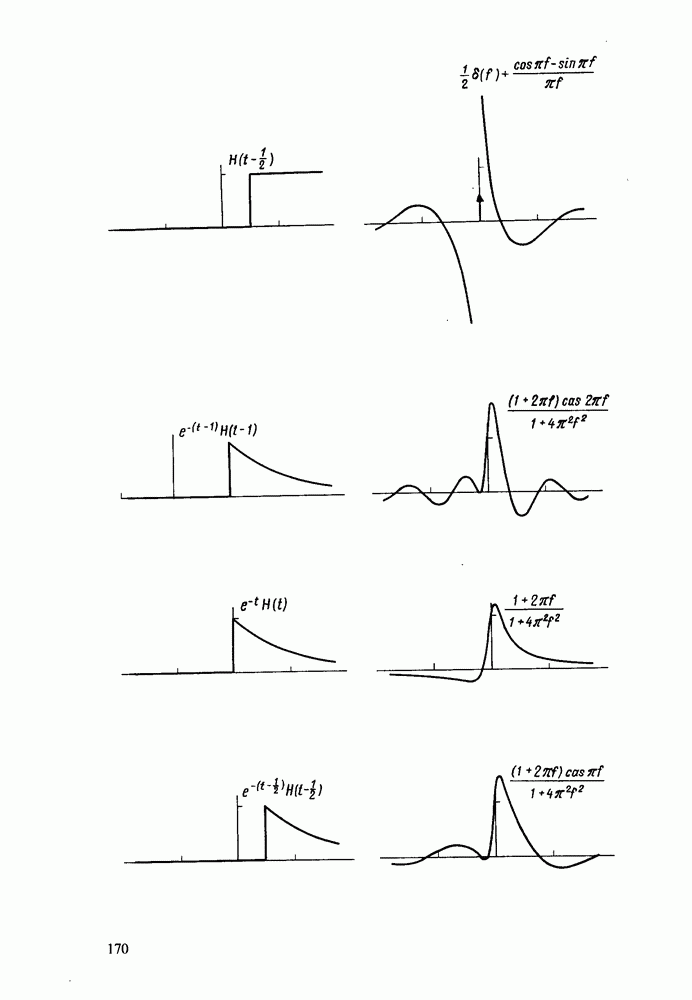
- Приложение 2. АТЛАС ПРЕОБРАЗОВАНИЙ ХАРТЛИ